آمار فضایی چیست؟دکتر سعید جوی زاده نویسنده کتاب های آمار فضایی در این پست شما را با علم آمار فضایی آشنا می کند.
مقدمه
آمار فضايي[1] مجموعهای از روش‌های اکتشافی برای توصیف و مدلسازی توزیع فضایی، الگوها، فرآیندها و روابط است. اگر چه آمار فضایی شبیه به آمار کلاسیک است، اما آمار فضايي روابط فضایی را نيز در محاسبات ادغام میکند. در آمار فضایی معمولاً انتظار میرود بین پدیدههای مجاور رابطه نسبتاً قابل توجهی وجود داشته باشد (مارتينز[2] و همکاران، 2016). از اینرو در آمار فضایی، نزدیک بودن[3] پدیدهها موضوع مهمي است. پديدههايي که نزدیکتر هستند ارتباط بیشتری با هم دارند. این شاخه از آمار میکوشد تا بین مقادیر مختلف یک متغیر، فاصله و جهتگیري آنها ارتباط برقرار کند. این ارتباط فضایی، ساختار فضایی[4] نام دارد. موقعیت مکانی، تأثیرپذیری مکانی و به کارگیری نقشه از موضوعات مهم در آمار فضایی محسوب میشود (جویزاده و همکاران، 1396). ArcGIS Desktop داراي جعبه ابزار آمار فضايي[5] است که در تمام سطوح تحت مجوز اين نرمافزار قابل دسترس است. در این جعبه ابزار، ابزارهايي براي تحلیل توزیع فضایی، الگوها، خوشهبندی و روابط موجود در مجموعه دادههای GIS گنجانده شده است. در کتاب حاضر هر کدام از ابزارهای ارائه شده در جعبه ابزار آمار فضايي مورد بحث و بررسي قرار ميگيرد.
در اين فصل موضوعات زير مورد بررسي قرار خواهد گرفت:
– مقدمه‌ای بر آمار فضایی؛
– معرفی نرمافزار ArcGIS؛
– مرور اجمالی بر قابلیتهای نرمافزاری ArcGIS؛
– مرور اجمالي جعبه ابزار آمار فضایی در ArcGIS؛
مقدمه ای بر آمار فضایی
با چند تعریف از آمار فضایی شروع ميکنيم. فرهنگ لغت GIS که در آدرس زير در دسترس است:
Http://gisgeography.com/GIS-Dictionary-Definition-glossary
آمار فضایی را رشته مطالعاتی مربوط به روش‌های آماری میداند که از روابط مکاني و فضایی (براي نمونه، فاصله، ناحیه، حجم، طول، ارتفاع، جهتگیری[1]، مرکزگرايي[2] و یا سایر ویژگیهای فضایی دادهها) در محاسبات ریاضی استفاده ميکند. بابلی[3] و گاتریل[4] (1995) طی مطالعاتی، تعاریف و اهداف علم آمار فضایی را جمع آوری نموده و این گونه بیان میکنند: «دادههای مشاهده شدنی، در برخی فرآیندهای عملیاتی در فضا قابل دسترس هستند، و روشهايي به دنبال توصیف یا توضیح رفتار خودشان و یا سایر پدیدههای فضایی دیگر که با آنها در ارتباط هستند، میباشند». آمار فضايي در انواع مختلف تحليلها از جمله تحلیل الگو[5]، تحلیل شکل[6]، مدلسازی و پیشبینی سطح[7]، رگرسیون فضایی، مقایسه آماری مجموعه دادههای فضایی، مدلسازی آماري و پیشبینی درهم کنش فضایی[8]، مورد استفاده قرار ميگيرد. اين شاخه از علم آمار، انواع آمار توصیفی، استنباطی، اکتشافي[9]، زمين آمار[10]، و آمار اقتصادی را نيز شامل ميشود (پیمپلر[11]، 2017).
آمار فضایی در رشته‌های زیست محیطی از جمله کشاورزی، زمین شناسی، علوم خاک، هیدرولوژی، محیط زیست، اقیانوس شناسی، جنگلداری، هواشناسی و … کاربرد دارد. بسیاری از رشته‌های اجتماعی و اقتصادی، از جمله اپیدمیولوژی[12]، تحلیل جرم و جنایت، املاک، برنامهریزی و مانند آن نیز از تحلیلهاي آمار فضایی استفاده ميکنند. این گونه تحلیلها میتواند عرصههای وسیعی در زمینه تحقیقاتی و پژوهشی بر روی دانشجویان، پژوهشگران، برنامهریزان و تحلیلگران بگشاید. پیشرفتهای ایجاد شده در زمینه جمعآوری و پردازش دادههای فضایی امکان کاربرد آمار فضایی را بیش از پیش گسترش داده است (جوی زاده ، 1390).
از مهمترین اهداف آمار فضایی در تحقیقات مختلف میتوان به موارد زیر اشاره کرد:
- تشخیص رفتار مکانی پنهان پدیدههای طبیعی و انسانی؛
- شناسایی الگوهای فضایی و روندهای آن؛
- تحلیل نحوه توزیع پدیدهها در محیط مکانی – فضایی؛
- تصمیمسازی و تصمیمگیری بهتر؛
- ارزیابی پدیدهها در سطح اطمینان بالاتر؛
- پیشبینی مقادیر در مناطقی که مشاهدات پدید نیامدهاند؛
- موقعیتهای فضایی را میتوان به طور مستقیم در ارزیابی آن با ویژگیهای دیگر ادغام کرد.
معرفی نرم افزار ArcGIS
در عرصه پیشرفتهای تکنولوژی، طی سالهای اخیر، تعداد قابل توجهی نرمافزار که هر کدام برخی از تحلیلهای آمار فضایی را انجام میدهند به بازار عرضه شدهاند. نرمافزار ArcGIS که توسط «موسسه تحقیقات سیستمهای محیطی»[1] تهیه و به بازار ارایه شده است از جمله نرمافزارهای سیستمهای اطلاعات جغرافیایی است که در حال حاضر بیشترین کاربر را در سطح جهان دارد.
سیستمهای اطلاعات جغرافیایی بنا بر تعریف سیستمهایی هستند که امکان سازماندهی، تولید، تکثیر، تحلیل و نمایش دادههای فضایی را فراهم آورده و امکان شناسایی روندها، روابط و الگوهای موجود بین دادهها را به دست میدهند.
از ابتدای پیدایش نرمافزارهای سیستمهای اطلاعات جغرافیایی به تدریج ابزارهای تحلیلی آن نیز تکمیل و توسعه داده شدهاند و در شکلهاي مختلف مانند تحلیلهای شبکه[2]، تحلیلهای فضايي[3]، تحلیلهای سهبعدی[4]، تحلیلهای زمينآماری[5]، و ابزارهای تحلیلی مخصوص فعالیتهای مختلف مانند امور تجاری[6]، تدارکات[7]، تخصیص منابع و مانند آنها ارائه گردیدهاند. برای مدتها عدم امکان انجام تحلیلهای آمار فضایی در نرمافزارهای رایج سیستمهای اطلاعات جغرافیایی نوعی کاستي محسوب میگردید و این باعث شده بود که نرمافزارهای ویژهای مانند SpaceStat و GeoDat برای انجام تحلیلهای آمار فضایی به وجود آیند. اگر چه این نرمافزارها کاستي هاي موجود را تا حدی پوشش میدادند ولی به دلیل آن که هیچ کدام از آنها نرمافزارهای سیستمهای اطلاعات جغرافیایی محسوب نمیشوند کاربران در نهایت مجبور بودند که دادههای خود را از نرمافزارهای سیستمهای اطلاعات جغرافیایی به این نرمافزارها منتقل کرده و تحلیلهای مورد نظر را انجام و سپس نتایج را به نرمافزار سیستمهای اطلاعات جغرافیایی منتقل کنند. از سال 2004 موسسه ESRI اقدام به افزودن مجموعه ابزارهای تحلیلی جدیدی به نرمافزار ArcGIS کرد که تحت عنوان ابزارهای آمار فضایی شناخته میشوند (عسگری، 1390).
قابلیت های نرم افزار ArcGIS
ArcGIS نرمافزاری است که امکان ایجاد یک سیستم کامل اطلاعات جغرافيايي را فراهم مینماید. این نرمافزار ابزارهای لازم برای جستجو، تحلیل دادهها و نمایش نتایج را با کیفیت مناسب در اختیار کاربران قرار میدهد. چون سیستمهای اطلاعات جغرافیایی قابلیتهای متفاوتی دارند، کاربران آنها نیز انتظارات متفاوتی از آنها دارند. برخی از قابلیتهای نرم افزار ArcGIS را میتوان به صورت زیر خلاصه نمود:
– قابلیت استفاده برای مکانیابی پروژه های مختلف؛
– قابلیت ردیابی و بررسی تغییرات مکان های جغرافیایی در طول زمان؛
– توانایی انجام محاسبات آماری مانند محاسبه مساحت و محیط پدیده های مشخص شده؛
– داشتن دقت، کارآیی، سرعت عمل زیاد و سهولت در به هنگام سازی داده ها؛
– توانایی انجام طیف وسیعی از تحلیلها؛
– قابلیت برقراری ارتباط بین اطلاعات جغرافیایی که از طریق نقشه به دست آمدهاند و اطلاعاتی که از طریق جداول به دست میآیند؛
– قابلیت جمعآوری، ذخیره، بازیابی و تحلیل اطلاعات با حجم زیاد؛
– محیط کاری و گرافیکی آسان؛
– توانایی بررسی همزمان دادههای مکانی و غیر مکانی؛
– تبدیل و انتقال دادهها به فرمتهای مختلف؛
– تهیه گزارش به اشکال مختلف؛ و
– کلینمایی، کوچکنمایی و بزرگ نمایی و حرکت در نقشه.
مرور اجمالی بر جعبه ابزار آمار فضایی در ArcGIS
ابزارهای آمار فضایی شامل مجموعهای از تکنیکها و روشها برای توصیف و مدلسازی دادههای فضایی میباشند. در برخی از موارد این ابزارها همان کارهایی را انجام میدهند که ما میتوانیم با ملاحظه نقشهها و با استفاده از چشم و ذهن خود نیز انجام دهیم ولی در مواردی که حجم دادهها زیاد است و توزیع و یا پراکندگی آنها در فضا پیچیدهتر است استفاده از آمارههای فضایی میتواند به افزایش دقت نتایج و مشاهدات کمک زیادی نماید.
جعبه ابزار آمار فضايي در تمامي سطوح تحت مجوز ArcGIS Desktop ازجمله سطح پايه[1]، استاندارد و پیشرفته، در دسترس است. اين جعبه ابزار شامل تعدادی ابزار به شرح زیر است:
– دسته ابزار سنجش توزیع جغرافیایی[2]
– دسته ابزار تجزیه و تحلیل الگو[3]
دسته ابزار سنجش توزیع جغرافیایی
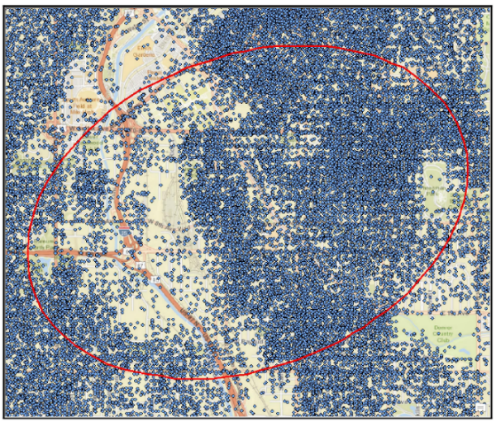
سنجش توصیفی دادههای فضایی، در ارزیابی مفاهیم بنیادین جغرافیایی مانند سطوح دسترسی و پراکندگی حائز اهمیت میباشد (جویزاده و همکاران، 1396). دسته ابزار سنجش توزيع جغرافيايي در جعبه ابزار آمار فضايي شامل مجموعه ابزارهایی است که آمار توصیفی جغرافیایی را بررسي ميکنند. از جمله اين ابزارها عبارتند از: عارضه مرکزی[1]، توزیع جهت دار[2]، ميانگين جهت دار خطی[3]، مرکز ميانگين[4]، مرکز میانه[5] و فاصله استاندارد[6]. این مجموعه ابزار روي هم رفته اکتشاف آماری پایه را انجام ميدهند. آمار توصیفی پایه، نقطه شروع و آغازين تحلیلهاي آماري ميباشد. شکل 1-1 خروجی ابزار توزیع جهتدار را در تحلیل دادههای جرم و جنایت نشان میدهد.
ابزارهای عارضه مرکزي، مرکز میانگین و مرکز میانه قابليتهاي مشابهي دارند. خروجي همه اين ابزارها يک کلاس عارضه[7] است که فقط يک عارضه دارد و بيانگر مرکزگرايي مجموعه داده جغرافیایی است. ابزار میانگین جهتدار خطی، میانگین جهت[8]، طول و مرکز جغرافیایی مجموعه خطوط را مشخص میکند. خروجی این ابزار یک کلاس عارضه حاوي یک عارضه خطی است. ابزارهاي فاصله استاندارد و توزیع جهتدار به دلیل اندازهگیری درجه تمرکز يا پراکنش عوارض حول مرکز هندسي، با يکديگر مشابه هستند؛ اما ابزار توزیع جهتدار، که با عنوان «بيضي انحراف استاندارد[9]» نيز معرفي ميشود قادر به اندازهگیری جهتگیری مجموعه دادهها نيز ميباشد.
شکل (1-1): خروجي ابزار توزيع جهت¬دار
دسته ابزار تحلیل الگوها
شناخت الگوها و کشف روندهای موجود در دادههای فضایی اهمیت زیادی در آمار فضایی دارد (توني[1]، 2016)؛ چرا که پیش از هرگونه تحلیل و تهیه نقشه بايستي این پیشداوری صورت گیرد که دادهها چگونه در فضا توزیع شدهاند و توزیع آنها در فضا از چه الگو و قاعدهای پیروی میکند (ایلان[2] و همکاران، 1971).
دسته ابزار تحلیل الگوها در جعبه ابزار آمار فضايي شامل مجموعه ابزارهایی است که به ارزیابی عارضهها یا مقادير مربوط به عوارض با الگوي فضايي خوشهاي، پراکنده یا تصادفی کمک میکند. این ابزارها یک نتیجه منحصر به فرد برای مجموعه دادههای مورد نظر ایجاد میکنند. نتیجه کار به صورت نقشه نیست بلکه همانطور که در شکل 1-2 زير ميبينيد به صورت خروجی آماري است.
شکل (1-2): خروجي دسته ابزار تحليل الگو
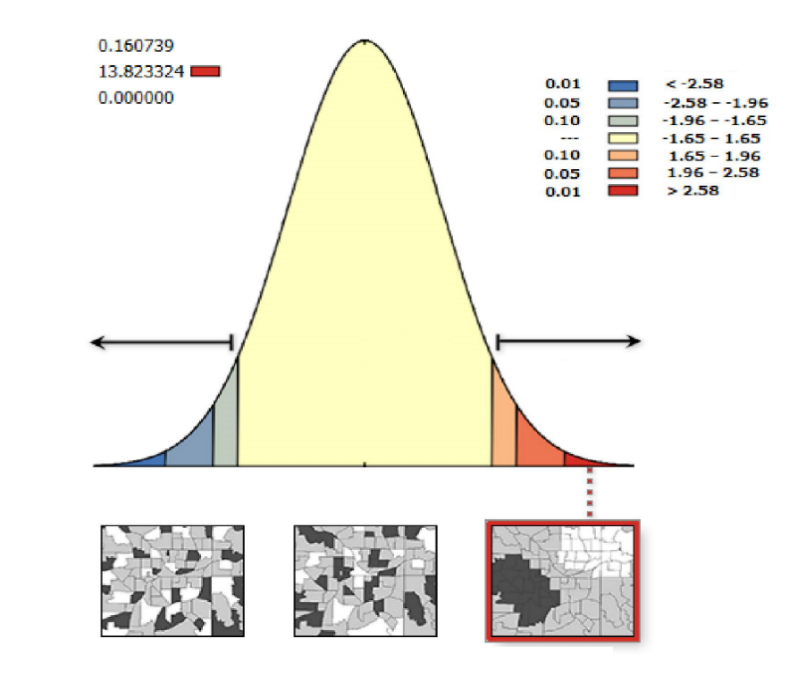
خروجي اين ابزارها چيزي است که به آمار استنباطي معروف است و مشخص ميکند احتمال اطمينان از اينکه الگوي موجود از نوع پراکنده یا خوشهای باشد چقدر است. ابزارهای موجود در دسته ابزار تحليل الگوها عباتند از:
میانگین نزدیکترین همسايگي[1]: این ابزار، شاخص نزدیکترین همسايه[2] را بر اساس میانگین فاصله هر عارضه نسبت به نزدیکترین همسايه خود محاسبه میکند. برای هر عارضه در یک مجموعه داده، فاصله تا
نزدیکترین همسايه محاسبه شده و سپس يک ميانگين فاصله محاسبه میشود. اين ميانگين فاصله با ميانگين فاصله قابل انتظار مقایسه میشود. در انجام این کار، نسبت ANN به وجود می‌آید که نسبت «مشاهده شده به قابل انتظار» ميباشد. اگر اين نسبت کمتر از 1 باشد، میتوان گفت که دادهها الگوي خوشهای دارند، در حالی که مقادیر بیشتر از 1 نشان دهنده الگوی پراکنده در دادهها ميباشد.
خودهمبستگي فضایی[3]: این ابزار با سنجش همزمان موقعيت عارضهها و مقادير اطلاعات توصيفي، خودهمبستگي فضايي را اندازهگیری ميکند. اگر عارضههاي نزدیک به هم دارای مقادیر مشابه باشند، آنها راخوشه‌ای مینامند. با این حال، اگر عارضههاي نزدیک به هم مقادیر مختلف داشته باشند، داراي الگوی پراکنده هستند. این ابزار مقدار شاخص Iموران[4] را همراه با یک نمره Z[5] و یک مقدار p[6] مشخص ميکند.
خودهمبستگي فضايي (Morans I): کارکرد این ابزار مشابه با ابزار قبلی است، اما خودهمبستگي فضايي را برای طیف وسیعی از فواصل اندازهگیری میکند و میتواند یک نمودار پراکندگي را از فواصل همراه با نمرههاي Z مربوطه ارائه کند. این ابزار مشابه با ابزار لکه داغ بهينه[7] عمل ميکند اما اغلب برای نتیجهگیری از آن استفاده نمی‌شود و معمولاً به عنوان کمکي ابزارهاي تحليل لکه داغ و تراکم نقطه[8] مورد استفاده قرار میگیرد.
خوشه بندی زیاد / کم (G عمومي گتيس-اُرد[9]): آماره عمومي گتيس و اُرد زماني به کار ميرود که وجود الگوی خوشهای در نقاط برداشت دادهها محرز است، اما پژوهشگر ميخواهد بداند که مقادیر زیاد موجب الگوی خوشهبندی شده یا مقادیرکم خوشهها را ايجاد کرده است (بوتس[10] و همکاران، 1988). این ابزار براي بررسي خوشه‌های مقادير زیاد و خوشه‌های مقادير کم به کار ميرود. به عبارت ديگر اين ابزار تراکم مقادیر زیاد یا کم را در يک محدوده مورد مطالعه اندازهگيري کرده و G عمومي مشاهده شده[11]، G عمومي قابل انتظار[12]، نمره Z، و مقدار p را مشخص ميکند و استفاده از آن زمانی که مقادیر نسبتاً یکسان توزیع شده باشند مناسب است.
تحلیل خوشه بندي فضایی چند فاصلهای (تابع K ريپليز)[13]: این ابزار تعیین میکند که عارضهها از نظر موقعيت، خوشهبندی یا پراکندگی قابل توجه نشان میدهند یا نه. اما بر خلاف ساير ابزارهای تعيين الگوي فضایی که در این بخش مورد بررسی قرار ميگيرد، اين ابزار یک مقدار را در مکان مورد نظر اندازهگيري نميکند و فقط خوشهبندي موجود در مکان عارضهها را تعیین مينمايد. اين ابزار اغلب در رشتههايي مانند مطالعات زیست محیطی، بهداشت و جرم شناسی مورد استفاده قرار ميگيرد که در آنها سعی بر اين است که تأثير يک عارضه بر عارضههاي دیگر مشخص شود.
دسته ابزار تهیه نقشه خوشه ها
اين دسته ابزار رايجترين و پرکاربردترين دسته ابزار موجود در جعبه ابزار آمار فضایی است. خروجی نمايشي این ابزارها براي تحلیل پدیده خوشهای شدن مفيد و مناسب است. مثالهاي متعددي از خوشهاي شدن در مسکن، کسب و کار، پوشش گياهي، جرمشناسي و مانند آن وجود دارد. درجه این خوشهها نیز مهم است. ابزارهاي موجود در دسته ابزار تهيه نقشه خوشه ها فقط به این سؤال پاسخ نمی‌دهند که آیا خوشه وجود دارد؟، بلکه به این سؤال هم پاسخ ميدهند که خوشهبندی کجاست؟. ابزارهای موجود در دسته ابزار تهيه نقشه خوشه ها یکی از رایج‌ترین ابزارهای موجود در جعبه ابزار آمار فضايي ميباشند و عبارتند از:
تحلیل لکه داغ[1]: یکی از رايجترين ابزارهاي موجود در جعبه ابزار آمار فضايي است و با توجه به عارضههاي وزندهي شده و با استفاده از آماره * گتيس-اُرد[2]، به صورت آماري لکههاي داغ و سرد را شناسایی میکند. از مهمترين کاربردهاي اين آماره، تشخیص لکههای داغ و سرد میباشد. اگر مقادیر بالا در فضا به گونهای قرار بگیرند که نزدیک به یکدیگر باشند باعث به وجود آمدن خوشهبندی مثبت (زياد)[3] یا لکه داغ میشوند و در صورتی که خوشهبندی فضايي به این دلیل باشد که در پدیده مورد بررسی مقادیر پایین نزدیک به یکدیگر قرار گرفتهاند به آن خوشهبندی منفي (کم)[4] یا لکه سرد میگویند. به عنوان مثال، لکههاي داغ و سرد در مورد فعالیت فروش املاک در شکل 1-3 نشان داده شده است.
شکل (1-3): خروجي ابزار تحليل لکه داغ در مورد فروش املاک در شهر دنور (ايالات متحده)
جستجوي مشابهت[1]: از این ابزار برای مشخص کردن مشابهترين يا غيرمشابهترين عارضهها با يک يا چند عارضه ورودي از نظر اطلاعات توصيفي استفاده ميشود. جستجوي ناهمگونی (عدم مشابهت)
میتواند به اندازه جستجوي مشابهت حائز اهميت باشد. به عنوان مثال، یک سازمان توسعه اجتماعي در تلاش برای جذب کسب و کار جدید ميتواند با استفاده از اين ابزار نشان دهد که شهر هدف از نظر آمار جرم و جنایت مشابه با شهرهای دیگر در حال رقابت هست و يا نیست.
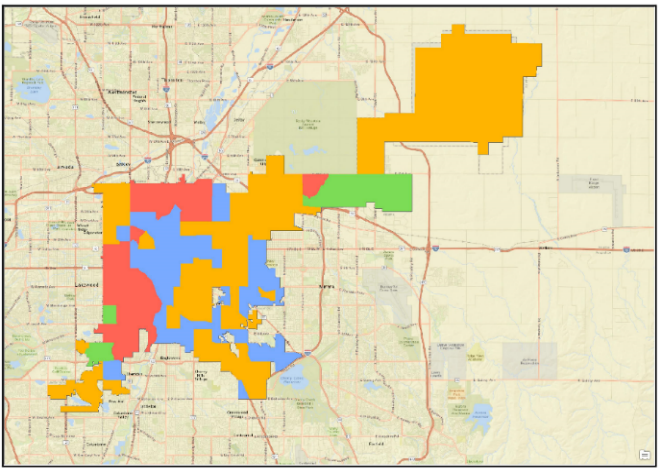
تحليـل گروه بنـدي[1]: این ابزار عوارض را بر اساس اطلاعـات توصيفي و برخي محدوديـتهاي مکاني يا زماني گروهبندی میکند. خروجی این ابزار ایجاد گروه‌های مشخص داده در جايي است که عوارض سازنده يک گروه تا جاي ممکن به هم شباهت دارند و ساير عوارض تا جاي ممکن با يکديگر ناهمگون هستند. ابزار تحليل گروهبندي قادر به تحلیل چند متغیره نيز ميباشد و خروجی آن به صورت نقشه و گزارش است. نقشه خروجی ممکن است گروه‌های مجاور یا گروه‌های غیر مجاور داشته باشد (شکل 1-4).
شکل (1-4): خروجي ابزار تحليل گروه¬بندي
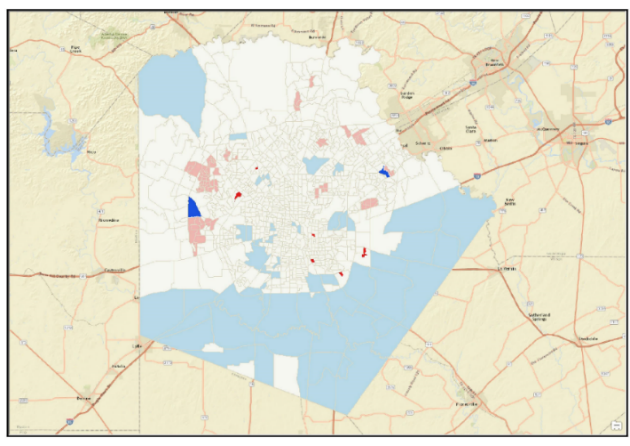
تحلیل خوشهبندي و دادههای پرت[1]: آخرين ابزار موجود در دسته ابزار تهيه نقشه خوشه ها ميباشد. این ابزار علاوه بر تحلیل لکه داغ، مقادیر پرت را نيز در دادهها شناسایی میکند. دادههاي پرت انواع مختلف تحليلها را تحت تأثير قرار ميدهند. اين ابزار با جدا کردن عارضهها و همسايگان از منطقه مورد مطالعه کار خود را آغاز ميکند. هر عارضه در مقابل تمامي عوارض دیگر بررسی میشود تا مشخص شود که آیا تفاوت قابل ملاحظهاي با ديگر عوارض دارد يا خير. به همين ترتيب، هر همسايه نيز در ارتباط با سایر همسايگان مورد بررسی قرار میگیرد تا مشخص شود که آیا از نظر آماری با سایر همسايگان تفاوت دارد یا خیر. نمونهاي از خروجي ابزار تحليل خوشه بندي و داده هاي پرت در شکل 1-5 نشان داده شده است.
شکل (1-5): خروجي ابزار تحليل خوشه¬بندي و داده¬هاي پرت
دسته ابزار مدل سازی روابط فضایی[1]
دسته ابزار مدلسازی روابط فضایی شامل تعدادی از ابزارهای تحليل رگرسيون است که به بررسي يا کميسازي ارتباط بين عوارض کمک ميکند. اين ابزارها چگونگي ارتباط فضايي عوارض موجود در يک مجموعه داده را مشخص ميکنند. ابزارهاي رگرسیون موجود در جعبه ابزار آمار فضایی، روابط بین متغیرهای عددي عوارض جغرافیایی را مدلسازي ميکنند و اجازه میدهند مقادیر نامعلوم را پيشبيني کرده و يا عوامل کلیدی مؤثر بر متغیر مدلسازي شده را بهتر درک کرد. روش‌های رگرسیون اين امکان را فراهم ميکنند که روابط مورد نظر را صحتسنجي[2] کرده و ضعف يا قوت اين روابط را اندازهگيري نمود. با استفاده از ابزار رگرسیون اکتشافی[3] ميتوان به سرعت تعداد زیادی از مدل‌های «حداقل مربعات معمولي[4]» را بررسی کرد، روابط بين متغیرها را خلاصه[5] کرده و تعیین نمود که آیا هر ترکیبی از متغیرهای توضيحي[6] (مستقل) مورد نظر ميتواند تمامي نيازهاي روش OLS را برآورده کند يا خير. سه ابزار تحلیل رگرسیون در ArcGIS وجود دارد که عبارتند از:
حداقل مربعات معمولي: ابزار رگرسیون خطی است و برای پیشبینی یا مدل کردن متغیر وابسته با توجه به روابط آن با مجموعهای از متغیرهای توضیحی (مستقل) استفاده میشود. OLS معروفترين تکنیک رگرسیون است و نقطه شروع خوبی برای تحلیل رگرسیون فضایی ميباشد. این ابزار مدل عمومي[7] متغیر یا فرآیندی را که قصد شناخت يا پیشبینی آن وجود دارد، فراهم ميکند. نتیجه آن يک معادله رگرسیون ساده است که یک رابطه مثبت یا منفی خطی را نشان میدهد. شکل 1-6 يکي از خروجیهاي اين ابزار را نشان میدهد.
شکل (1-6): يکي از خروجي¬هاي ابزار حداقل مربعات معمولي
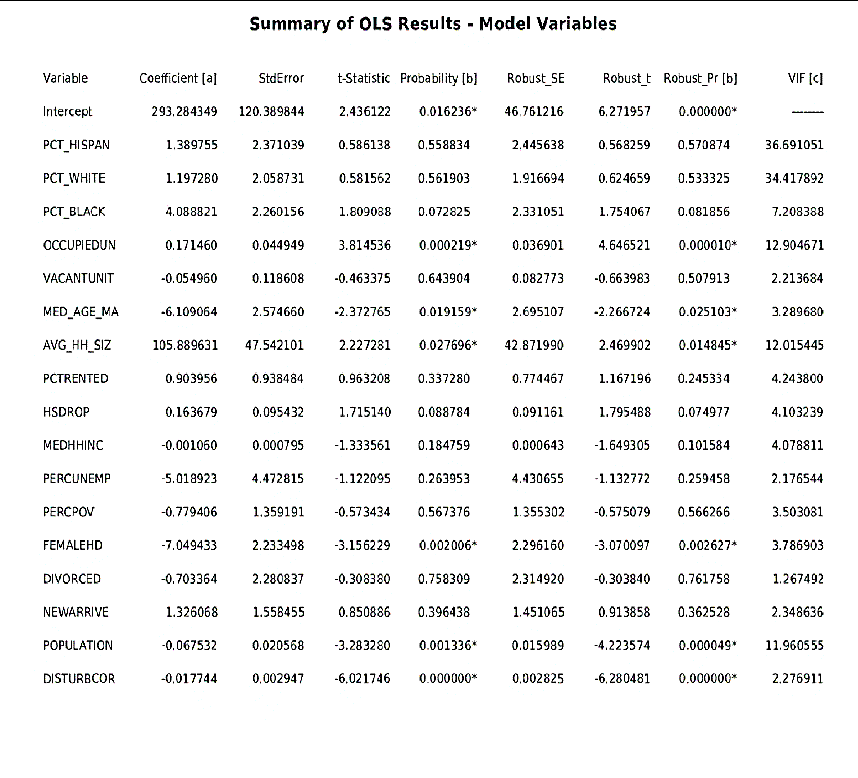
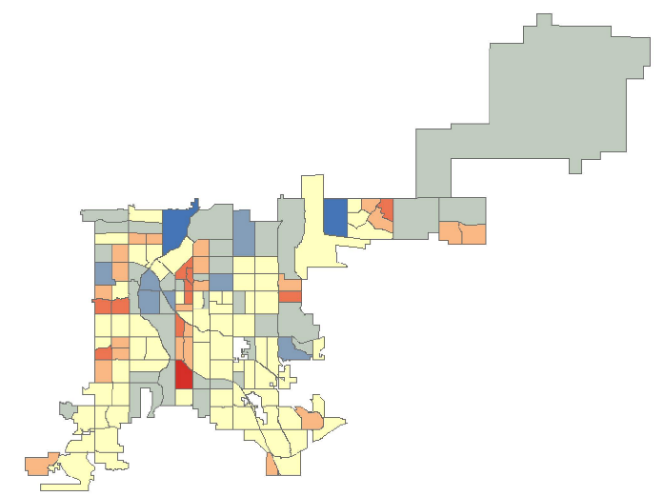
رگرسیون موزون جغرافیایی[1]: GWR یا رگرسیون موزون جغرافیایی شکل محلی[2] رگرسیون خطی برای مدلسازی روابط متغیر فضايي است. این ابزار به مجوز پیشرفته ArcGIS نياز دارد. GWR براي هر عارضه يک معادله جداگانه ایجاد میکند و وقتی کارآمد است که چند صد عارضه وجود داشته باشد. خروجي این ابزار یک جدول و يک کلاس عارضه ميباشد (شکل 1-7). جدول خروجی شامل خلاصه‌ای از عمليات اجرايي ابزار است. هنگام اجرای GWR، لازم است از همان متغیرهای توضیحی (مستقل) مدل OLS استفاده کرد.
رگرسیون اکتشافی[3]: این ابزار را میتوان برای ارزیابی ترکیبی از متغیرهای اکتشافی در مدلهاي OLS، که به بهترین صورت توضیح دهنده متغیر وابسته میباشند، استفاده کرد. رگرسيون اکتشافي يک ابزار داده کاوي[4] براي پیدا کردن متغیرهایی است که برازش مناسبي دارند و کمک ميکند تا با صرفهجويي در زمان، ترکیب مناسبي از متغیرها را پيدا کرد. نتایج این ابزار در يک پنجره گزارش پيشرفت کار و يک فایل گزارش (اختیاری) ارائه ميشود. در شکل 1-8 نمونه خروجی اين ابزار نشان داده شده است.
شکل (1-7): خروجي ابزار رگرسيون موزون جغرافيايي
شکل (1-8): نمونه خروجي ابزار رگرسيون اکتشافي (پنجره گزارش پيشرفت کار)
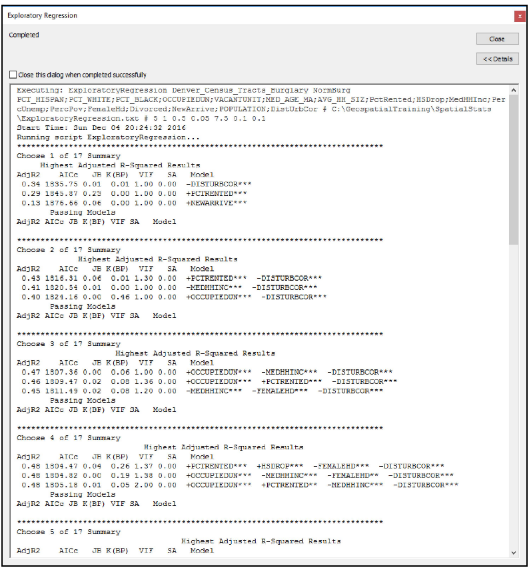
منابع مطالعاتی بیشتر
Bailey, T. C., and Gatrell, A. C., (1995), Interactive Spatial Data Analysis. Essex: Addison WesleyLongman Limited.
Cressie, N., and Kornak, J., (2002), Spatial statistics in the presence of location error with an application to remote sensing of the environment. Department of Statistics Preprint No. 701, The Ohio State University. Available by request at http://www.stat.ohio-state.edu/~sses/papers.html.
Fox, J., (2005), Getting Started with the R Commander:a Basic-Statistics Graphical User Interface to R. Journal of Statistical Software, 14: 1-42.
Gandrud, C., (2013), Reproducible Research with R and R Studio. CRC Press. 294 p.
Laffan, S.W., (2002), Using process models to improve spatial analysis. International Journal of Geographic Information Science, 16(3): 245-257.
Lowson, A. B., (2001), Statistical Method In Spatial Epidemiology. John Wiely.
Moore, M., (2001), Spatial Statistics: Methodological Aspects and Applications. Number 159 in Lecture Notes in Statistics. Springer.
Moran, P. A. P., (1948), The Interpretation of Statistical Maps. Journal of the Royal Statistical Society, series B 10, 243–51.
Paelinck, J. H. P., and Klaassen, L. H., 1979, Spatial Econometrics. Westmead, Farnborough, England: Saxon House .
Tobler, W. R., (1963), Geographic area and map projections. Geographical Review 53: 59–78.
Waller, L. A., and Gotway, C. A., (2004), Applied Spatial Statistics for Public Health Data. Wiley, Hoboken, NJ.
[1] Geographically Weighted Regression
[2] Local
[3] Exploratory Regression
[4] Data Mining
[1] Modeling Spatial Relationships Toolset
[2] Verify
[3] Exploratory Regression
[4] Ordinary Least Squares
[5] Summerize
[6] Explanatory variables
[7] Global
[1] Cluster and Outlier Analysis
[1] Grouping Analysis
[1] Similarity Search
[1] Hot Spot Analysis
[2] Getis-Ord Gi* statistics
[3] High Clustering
[4] Low Clustering
[1] Average Nearest Neighbor
[2] Nearest Neighbor Index
[3] Spatial Autocorrelation
[4] Moran’s I index
[5] Z Score
[6] p-value
[7] Optimized Hot Spot
[8] Point Density
[9] High/Low Clustering (Getis-Ord General G):
[10] Boots
[11] Observed General G
[12] Expected General G
[13] Multi-Distance Spatial Cluster Analysis (Ripleys K Function)
[1] Tonny
[2] Iilan
[1] Central Feature
[2] Directional Distribution
[3] Linear Directional Mean
[4] Mean Center
[5] Median Center
[6] Standard Distance
[7] Feature Class
[8] Mean Direction
[9] Standard Deviational Ellipse
[1] Basic
[2] Measuring Geographic Distribution
[3] Analyzing Pattern
[1] Environmental Systems Research Institute
[2] Network Analyst
[3] Spatial Analyst
[4] 3D Analyst
[5] Geostatistical
[6] Business Analyst
[7] ArcLogistic
[1] Orientation
[2] Centrality
[3] Bailey
[4] Gatrell
[5] Pattern analysis
[6] Shape Analysis
[7] Surface Prediction
[8] Spatial interaction
[9] Exploratory
[10] Geostatististics
[11] Pimpler
[12] علم مطالعه امراض مسري
[1] Spatial Statistics
[2] Martinez
[3] Proximity
[4] Spatial Structure
[5] Spatial Statistics Toolbox
بدون دیدگاه