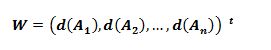روش تحلیل سلسله مراتبی فازی(FAHP)
فرايند تحليل سلسله مراتبي بر تجربه و دانش تصميم گيرنده استوار است؛ اما از آنجايي كه تصميم گيرندگان از تواناييهاي ذهني و تجربههاي خود براي انجام مقايسهها استفاده ميكنند؛ بنا به دلايلي مانند دانش و اطلاعات ناكافي، پيچيدگي مسأله، نداشتن اطمينان دربارة محيط تصميمگيري و نبود يك مقياس مناسب نميتوانند ترجيحهاي خود را در قالب اعداد محض بيان كنند؛ بنابراين AHP سنتي امكان سبك تفكر انساني را بهطور كامل ندارد براي رفع اين نارسايي ميتوان از نظرية مجموعههاي فازي استفاده كرد. منطق فازي بهعنوان منطق مدلسازي رياضي فرايندهاي غيردقيق و مبهم،عدم قطعيت دربارة دادهها و عدمدقت مرتبط با آگاهيهاي تصميمگيرنده در اختصاص دادن وزن دقيق به معيارها را در نظر ميگيرد و از اينرو بستري را براي مدلسازي در شرايط عدم اطمينان فراهم ميسازد. تحلیل سلسله مراتبی فازی دو روش شناخته شده دارد که عبارتند از روش چانگ (Chang) و روش یاگر (Yager) ،روش چانگ معروف ترین و متداول ترین روش در ایران است که در سال 1996یک محقق چینی به نام «یونگ چانگ» روش تحلیل توسعهای را ارائه کرد. در این روششناسی، اعداد فازی مثلثی همه عناصر را در ماتریس قضاوت قرار دارد. بردارهای وزن این روش، به علت سادگی محاسباتش، در اکثر تحقیقات به کار میرود.
به طور خلاصه مدل Fuzzy AHP دارای مراحل زیر است:
-رسم نمودار سلسله مراتبی
– تعریف اعداد فازی به منظور انجام مقایسههای زوجی
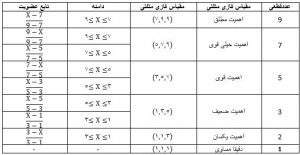
برای انجام مقایسهها نیاز به تعریف اعداد فازی و مقیاسهای فازی میباشد. در جدول زیر نمونهای از اعداد مقایسه زوجی آورده شده است.
– تشکیل ماتریس مقایسه زوجی با به کارگیری اعداد فازی
متغیرهای زبانی و فازی و مقیاسهای آن جهت اولویتبندی معیارها
محاسبه Si برای هر یک از سطرهای ماتریس مقایسه زوجی: Si که خود یک عدد فازی مثلثی است از رابطه زیر بدست میآید:
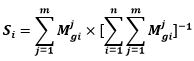
که در این رابطه i بیانگر شماره سطر و j بیان کننده شماره ستون میباشد. در فرمول فوق اعداد فازی مثلثی ماتریسهای مقایسه زوجی هستند.
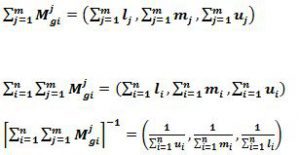
در روابط بالا li و mi و ui به ترتیب مؤلفههای اول تا سوم اعداد فازی هستند.

محاسبه درجه بزرگی Si ها نسبت به همدیگر: به طور کلی درجه بزرگی Si نسبت به Sj از معادلۀ زیر بدست میآید.

محاسبه وزن معیارها و گزینهها در ماتریسهای مقایسه زوجی:
برای محاسبه وزن نرمال نشده معیار باید میزان بزرگی یک عدد فازی مثلثی با سایر اعداد فازی مثلثی محاسبه شود و در نهایت حداقل میزان بزرگی، نشان دهندۀ وزن نرمال نشده معیار است. بدین منظور از رابطه زیر استفاده میشود.
![]()
بردار وزن نهایی از نرمال کردن بردار وزن معیارها به دست میآید.