نرخ سازگاری در فرايند تحليل سلسله مراتبي
نرخ سازگاری در فرايند تحليل سلسله مراتبي بسیار مهم و کلیدی است.در این پست قصد داریم که دراین باره صحبت و به بحث بنشینیم.
تقريباً تمامي محاسبات مربوط به فرايند تحليل سلسله مراتبي بر اساس قضاوت اوليه تصميم گيرنده كه در قالب ماتريس مقايسات زوجي ظاهر ميشود، صورت ميپذيرد و هر گونه خطا و ناسازگاري در مقايسه و تعيين اهميت بين گزينهها و شاخصها نتيجه نهايي به دست آمده از محاسبات را مخدوش ميسازد. نرخ ناسازگاري كه در ادامه با نحوه محاسبه آن آشنا خواهيم شد، وسيلهاي است كه سازگاري را مشخص ساخته و نشان ميدهد كه تا چه حد ميتوان به اولويتهاي حاصل از مقايسات اعتماد كرد. تجربه نشان داده است كه اگر نرخ ناسازگاري كمتر از 10/0 باشد سازگاري مقايسات قابل قبول بوده و در غير اينصورت مقايسهها بايد تجديد نظر شود. قدمهاي زير براي محاسبه نرخ ناسازگاري به كار گرفته ميشود:
گام 1. محاسبه بردار مجموع وزني: ماتريس مقايسات زوجي را در بردار ستوني «وزن نسبي» ضرب كنيد بردار جديدي را كه به اين طريق بدست ميآوريد، بردار مجموع وزني بناميد.
گام 2. محاسبه بردار سازگاري: عناصر بردار مجموع وزني را بر بردار اولويت نسبي تقسيم كنيد. بردار حاصل بردار سازگاري ناميده ميشود.
گام 3. بدست آوردن lmax، ميانگين عناصر برداري سازگاري lmax را به دست ميدهد.
گام 4. محاسبه شاخص سازگاري: شاخص سازگاري بصورت زير تعريف ميشود:
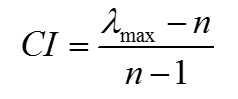
n عبارتست از تعداد گزينههاي موجود در مساله
گام 5. محاسبه نسبت سازگاري: نسبت سازگاري از تقسيم شاخص سازگاري برشاخص تصادفي بدست ميآيد.
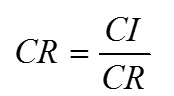
نسبت سازگاري 1/0 يا كمتر سازگاري در مقايسات را بيان ميكند(مهرگان،1383،ص173-170)
شاخص تصادفي از جدول زیر استخراج ميشود.
جدول 2 شاخص تصادفي (مهرگان،1383،ص173)
| 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | N |
| 51/1 | 45/1 | 41/1 | 32/1 | 24/1 | 12/1 | 9/0 | 58/0 | 0 | 0 | RI |
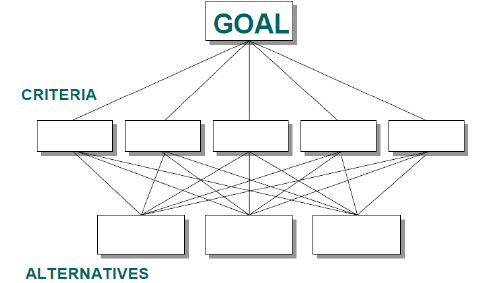
روش فرایند تحلیل سلسله مراتبی (AHP)
فرایند تحلیل سلسله مراتبی یکی از روشهای تصمیمگیری است. واژه AHP مخفف عبارت Analytical Hierarchy process به معنی فرایند تحلیل سلسله مراتبی است.انتخاب سنجهها یا criterion بخش اول واکاوی AHP است. سپس براساس سنجههای شناسایی شده نامزدها ارزیابی میشوند. واژه گزینهها یا نامزدها هم معنای واژه alternative یا candidates بوده و به جای هم بکار روند. علت سلسله مراتبی خواندن این روش آن است که ابتدا باید از اهداف و راهبردهای سازمان در راس هرم آغاز کرد و با گسترش آنها سنجهها را شناسایی کرد تا به پایین هرم برسیم.
این روش یکی از روشهای پرکاربرد برای رتبهبندی و تعیین اهمیت عوامل است که با استفاده از مقایسات زوجی گزینهها به اولویت بندی هر یک از معیارها پرداخته میشود. چنانچه گزینهها زیاد باشد تشکیل ماتریس مقایسات زوجی کار دشواری است.[۱]
هدف تکنیک فرایند تحلیل سلسله مراتبی انتخاب بهترین گزینه براساس معیارهای مختلف از طریق مقایسه زوجی است. این تکنیک برای وزن دهی به معیارها نیز استفاده می شود. چون افزایش تعداد عناصر هر خوشه مقایسه زوجی را دشوار می کند بنابراین معمولا معیارهای تصمیم گیری را به زیرمعیارهایی تقسیم میکنند.
معیار : آن چیزی است که براساس آن انتخاب می کنید مثلا در انتخاب یک مدیر برای سازمان، معیارهای تصمیم گیری تحصیلات، پیشینه، شخصیت و … است.
گزینه: آن چیزی است که از میان آن انتخاب می کنید مثلا در انتخاب یک مدیر کاندیداهای موجود همان گزینهها هستند.
مدل های زیر به عنوان مدلهای معروف در روش AHP مورد استفاده قرار می گیرند.
- هدف – معیار
- هدف – معیار – زیرمعیار
- هدف – معیار – گزینه
- هدف – معیار – زیرمعیار – گزینه
در یک مدل فرایند تحلیل سلسلهمراتبی ممکن است بخواهید فقط معیارها را تعیین وزن کنید. ممکن است زیرمعیارهایی نیز وجود داشته باشد و هدف تعیین وزن زیرمعیارها باشد. روش AHP شامل هدف، معیار و گزینه است که در ادامه با یک مثال کاربردی آموزش داده می شود.

مدل سازی فرایند تحلیل سلسله مراتبی AHP
فرض کنید قرار است برای سازمان یک مدیر انتخاب کنید. ابتدا باید معیارهائی برای انتخاب مدیر در نظر بگیرید.
در این مثال معیارهای تصمیم گیری عبارتند از: ویژگیهای شخصیتی (کاریزما)، پیشینه کاری، تحصیلات و شرایط سنی
در این مثال سه کاندیدا برای مدیریت وجود دارد: مادلین، سوف و راجر که در تصویر مشاهده میشوند.
حال دو سوال مطرح است: اول اینکه ممکن است برخی افراد از لحاظ یک معیار بر دیگری ارجحیت داشته باشند و دوم اینکه برخی معیارها ممکن است با همدیگر متناقض باشند. بحث تصمیم گیری با معیارهای چندگانه را به خاطر آورید. این همان مساله تصمیم گیری با معیارهای چندگانه (MCDM) است.
بنابراین مساله به صورت ساختار سلسلهمراتبی زیر نوشته می شود:
هدف: انتخاب مدیر برای سازمان
معیارهای انتخاب مدیر: کاریزما، پیشینه، تحصیلات و سن
گزینهها: مادلین، سوف و راجر

مقایسه زوجی عناصر و طراحی پرسشنامه خبره
برای تعیین وزن معیارها و رتبه بندی گزینه ها از مقایسه زوجی استفاده می شود. پرسشنامه مورد استفاده برای تحلیلهای سلسهمراتبی و تصمیمگیری چندمعیاره به پرسشنامه خبره موسوم است. برای تهیه پرسشنامه خبره از مقایسه زوجی عناصر استفاده میشود. برای هر سطح از سلسله مراتب یک ماتریس مقایسه زوجی تهیه میشود. برای امتیاز دهی از مقیاس نه درجه ساعتی به صورت زیر استفاده میشود. نمونه پرسشنامه AHP را مشاهده کنید.
پژوهشگران معمولا از طیف پنج نقطه زیر استفاده میکنند که سادهتر بوده و نتایج یکسانی بدست میدهد:
ترجیح یکسان کمی بهتر بهتر خیلی بهتر کاملا بهتر ۱ ۳ ۵ ۷ ۹
با استفاده از این مقیاس هیات مدیره هر یک از گزینهها را براساس هر یک از عوامل به صورت زوجی مقایسه میکنند. نتایج این مقایسه به صورت زیر است.
مقایسه زوجی و تعیین وزن معیارها
سطح دوم سلسلهمراتب را معیارهای اصلی تشکیل میدهد. نخست با مقایسه زوجی معیارهای اصلی براساس هدف، وزن هر یک از معیارهای اصلی تعیین می شود. بنابراین باید معیارها را براساس هدف دوبهدو با هم مقایسه میکنیم. برای مثال هیات مدیره تصمیمی مشابه زیر میگیرد:
پیشینه سن کاریزما تحصیلات بردار ویژه پیشینه ۱ ۷ ۳ ۴ ۰٫۵۴۷ سن ۱/۷ ۱ ۱/۵ ۱/۳ ۰٫۰۵۶ کاریزما ۱/۳ ۵ ۱ ۳ ۰٫۲۷۰ تحصیلات ۱/۴ ۳ ۱/۳ ۱ ۰٫۱۲۷
برای تعیین وزن هر معیار، میانگین هندسی عناصر هر سطر محاسبه می شود. اکزل و ساعتی (۱۹۸۳) استفاده از میانگین هندسی را بهترین روش برای ترکیب مقایسات زوجی معرفی کردهاند. وزنهای بدست آمده نرمال نیستند. منظور از وزن نرمال آن است که جمع اوزان برابر ۱ باشد. بنابراین میانگین هندسی بدست آمده در هر سطر را بر مجموع عناصر ستون میانگین هندسی تقسیم کنید. ستون جدید که حاوی وزن نرمال شده هر معیار است را بردار ویژه یا Egienvalue گویند. وزن نهائی هر ماتریس همان ستون بردار ویژه است. براساس جدول بالا معیار پیشینه از بیشترین اهمیت برخوردار است. ویژگیهای کاریزماتیک در اولویت دوم قرار دارد. تحصیلات سومین معیار با اهمیت است و سن نیز از کمترین اولویت برخوردار است.
برخی معیارها مانند سن یا قیمت یک عدد ثابت هستند. برای این منظور مقایسه زوجی نیازی به دیدگاه کارشناسی ندارد.
هر معیار ممکن است خود از یک مجموعه زیرمعیار تشکیل شده باشد. برای نمونه معیار پیشینه در مثال بالا میتواند شامل سابقه کاری در سازمان حاضر، تجربه کار در سازمانهای دیگر، تجربه مدیریتی و زیرمعیارهای دیگر باشد. در اینصورت یک سطح دیگر به مدل AHP اضافه میشود.
مقایسه زوجی گزینهها براساس معیارها
پس از تعیین وزن هر یک از معیارها در گام بعد باید گزینهها بصورت زوجی براساس هر معیار مقایسه شوند. برای مثال مقایسه زوجی گزینهها براساس پیشینه نشان داده است : مادلین در مقایسه با راجر امتیاز ۴ میگیرد و سوف در مقایسه با راجر امتیاز ۹ میگیرد. همچنین سوف در مقایسه با رمادلین امتیاز ۴ کسب میکند. بعد از اینکه مقایسه ها انجام شد دادهها را به ماتریسی مانند زیر منتقل میکنند که همان ماتریس مقایسه زوجی است.
پیشینه مادلین سوف راجر مادلین ۱ ۱/۴ ۴ سوف ۴ ۱ ۹ راجر ۱ ۱/۹ ۱
گام بعدی فرایند تحلیل سلسله مراتبی تعیین اولویت است. برای تعیین اولویت از مفهوم نرمال سازی (normalize) که در گام قبلی توضیح داده شد استفاده میشود. پس از نرمال کردن وزن هر گزینه براساس معیار مورد نظر بدست خواهد آمد. به عبارت دیگر محاسبه مقدار ویژه هر سطر با تخمین میانگین هندسی: میانگین هندسی آن سطر به جمع میانگین هندسی سطرها
پیشینه مادلین سوف راجر اولویت مادلین ۱ ۱/۴ ۴ ۰٫۲۱۷ سوف ۴ ۱ ۹ ۰٫۷۱۷ راجر ۱/۴ ۱/۹ ۱ ۰٫۰۶۶
یک تصور اشتباه این است که برای AHP باید نرم افزار Expert Choice استفاده شود. میتوانید از محیط اکسل یا نرم افزار Super Decision استفاده کنید.
به مقادیر بدست آمده حاصل از محسابات که ستون اولویت را تشکیل میدهند بردار ویژه (eigenvector) گویند. همین مقایسههای زوجی را برای سایر معیارها انجام میدهیم. به این ترتیب اولویت هر فرد را براساس هر معیار مانند فوق محاسبه میکنیم. مهم همان ستون اولویتها است. در نهایت به ماتریسی مانند زیر خواهید رسید:
پیشینه سن کاریزما تحصیلات مادلین ۰٫۲۱۷ ۰٫۲۶۵ ۰٫۷۴۳ ۰٫۱۸۸ سوف ۰٫۷۱۷ ۰٫۶۷۲ ۰٫۱۹۴ ۰٫۰۸۱ راجر ۰٫۰۶۶ ۰٫۰۶۳ ۰٫۰۶۳ ۰٫۷۳۱
محاسبه سازگاری مقایسههای زوجی
اساس محاسبات فرایند تحلیل سلسله مراتبی بر اساس قضاوت اولیه تصمیم گیرنده که در قالب ماتریس مقایسهها زوجی ظاهر میشود، صورت میپذیرد. بنابراین هرگونه خطا و ناسازگاری در مقایسه عناصر، نتیجه نهایی به دست آمده از محاسبات را تحت تاثیر قرار میدهد. مطلب آموزش محاسبه نرخ ناسازگاری مقایسهزوجی را مطالعه کنید.
محاسبه اولویتهای نهایی
اکنون به سادگی با استفاده از میانگین موزون مدیر سازمان را انتخاب میکنیم.
امتیاز هر گزینه = مجموع حاصلضرب اولویت آن گزینه براساس معیار i ضربدر اولویت آن معیار
Madlin: (0.217 x 0.547) + (0.188 x 0.127) + ( 0.703 x 0.270) + ( 0.265 x 0.056) = 0.358
به همین ترتیب سوف ۰٫۴۹۲ امتیاز کسب کرد و راجر نیز ۰٫۱۴۹ امتیاز بدست آورد. خوب مساله انتخاب مدیر به روش فرایند تحلیل سلسله مراتبی انجام گرفت و سوف با کسب بیشترین امتیاز به عنوان مدیر انتخاب گردید. البته پیرایشهای دیگری نیز وجود دارد که میتوانید در مقالات دیگر آنها را نیز فرا بگیرید. دانش را مرزی نیست و همیشه نکاتی برای افزودن هست.


