شروع با ArcGIS Urban: ایجاد اولین طرح شما

پیاده‌سازی پایتون از رگرسیون وزن‌دار جغرافیایی چند مقیاسی برای بررسی ناهمگونی و مقیاس فضایی فرآیند

چکیده

رگرسیون وزن‌دار جغرافیایی (GWR) یک تکنیک آماری فضایی است که تشخیص می‌دهد که مدل‌های رگرسیون «جهانی» سنتی ممکن است زمانی محدود شوند که فرآیندهای فضایی با بافت مکانی متفاوت باشد. GWR ناهمگونی فضایی فرآیند را با اجازه دادن به اثرات متفاوت در فضا ثبت می کند. برای انجام این کار، GWR مجموعه‌ای از مدل‌های خطی محلی را در هر تعداد مکان با استفاده از داده‌های نزدیک «قرض‌گرفته‌شده» کالیبره می‌کند. این سطحی از تخمین پارامترهای خاص مکان را برای هر رابطه در مدل ارائه می دهد که اجازه دارد از نظر مکانی متفاوت باشد، و همچنین یک پارامتر پهنای باند واحد که شهودی را در مورد مقیاس جغرافیایی فرآیندها ارائه می دهد. گسترش اخیر به این چارچوب اجازه می دهد تا هر رابطه بر اساس یک پارامتر مقیاس فضایی متمایز تغییر کند، و بنابراین به عنوان چند مقیاسی (M)GWR شناخته می شود. این مقاله mgwr را معرفی می کند، اجرای MGWR مبتنی بر پایتون که به صراحت بر تحلیل چند مقیاسی ناهمگونی فضایی تمرکز دارد. این عملکرد جدید برای استنتاج و تجزیه و تحلیل اکتشافی فرآیندهای فضایی محلی، تشخیص‌های جدید منحصر به فرد برای مدل‌های محلی چند مقیاسی، و بهبودهای چشمگیر در کارایی در روال‌های تخمین ارائه می‌کند. ما علاوه بر بررسی مفاهیم اصلی مدل‌های محلی، دو مطالعه موردی را با استفاده از mgwr ارائه می‌کنیم. ما این را در یک سبک برنامه‌نویسی باسواد ارائه می‌کنیم، و یک نمای کلی از عملکرد نرم‌افزار اولیه و نمایش‌هایی از استفاده پیشنهادی در کنار بحث مفاهیم اولیه و نمایش پیشرفت‌های انجام‌شده در mgwr ارائه می‌کنیم. این عملکرد جدید برای استنتاج و تجزیه و تحلیل اکتشافی فرآیندهای فضایی محلی، تشخیص‌های جدید منحصر به فرد برای مدل‌های محلی چند مقیاسی، و بهبودهای چشمگیر در کارایی در روال‌های تخمین ارائه می‌کند. ما علاوه بر بررسی مفاهیم اصلی مدل‌های محلی، دو مطالعه موردی را با استفاده از mgwr ارائه می‌کنیم. ما این را در یک سبک برنامه‌نویسی باسواد ارائه می‌کنیم، و یک نمای کلی از عملکرد نرم‌افزار اولیه و نمایش‌هایی از استفاده پیشنهادی در کنار بحث مفاهیم اولیه و نمایش پیشرفت‌های انجام‌شده در mgwr ارائه می‌کنیم. این عملکرد جدید برای استنتاج و تجزیه و تحلیل اکتشافی فرآیندهای فضایی محلی، تشخیص‌های جدید منحصر به فرد برای مدل‌های محلی چند مقیاسی، و بهبودهای چشمگیر در کارایی در روال‌های تخمین ارائه می‌کند. ما علاوه بر بررسی مفاهیم اصلی مدل‌های محلی، دو مطالعه موردی را با استفاده از mgwr ارائه می‌کنیم. ما این را در یک سبک برنامه‌نویسی باسواد ارائه می‌کنیم، و یک نمای کلی از عملکرد نرم‌افزار اولیه و نمایش‌هایی از استفاده پیشنهادی در کنار بحث مفاهیم اولیه و نمایش پیشرفت‌های انجام‌شده در mgwr ارائه می‌کنیم.

کلمات کلیدی: چند مقیاسی ; gwr ; آمار مکانی ; ناهمگونی ؛ مقیاس ; mgwr

1. مقدمه

رگرسیون وزن‌دار جغرافیایی (GWR) یک تکنیک آماری فضایی است که مانند رگرسیون محلی فضایی، تشخیص می‌دهد که مدل‌های رگرسیون جهانی سنتی ممکن است زمانی محدود شوند که فرآیندها بر اساس زمینه متفاوت باشند. GWR ناهمگونی فضایی فرآیند (یعنی تغییرات فرآیند بر اساس بافت فضایی) را از طریق عملیاتی‌سازی قانون اول جغرافیایی توبلر نشان می‌دهد: “همه چیز به هر چیز دیگری مرتبط است، اما چیزهای نزدیک بیشتر از چیزهای دور مرتبط هستند” [ 1 ]]. مجموعه‌ای از مدل‌های خطی محلی در هر تعداد مکان با «قرض گرفتن» داده‌های نزدیک کالیبره می‌شوند. نتیجه، سطحی از تخمین‌های پارامتر خاص مکان برای هر رابطه در مدل است که ممکن است از نظر مکانی متفاوت باشد، و همچنین یک پارامتر پهنای باند واحد که شهودی را در مورد مقیاس جغرافیایی فرآیندها ارائه می‌کند. علاوه بر این، GWR معمولاً افزایش تناسب مدل و کاهش خودهمبستگی فضایی باقیمانده را در مقایسه با رگرسیون «جهانی» سنتی ارائه می‌کند که فرض می‌کند روابط در فضا ثابت هستند [ 2 ].

گسترش اخیر به چارچوب GWR به هر رابطه در مدل اجازه می دهد تا در مقیاس فضایی منحصر به فرد متفاوت باشد و بنابراین به عنوان چند مقیاسی (M)GWR [ 3 ] شناخته می شود. MGWR در مفروضات خود نسبت به GWR بسیار محدودتر است، زیرا رابطه بین پاسخ و یک متغیر کمکی مجاز است به صورت محلی، منطقه ای متفاوت باشد، و یا اصلاً تغییر نکند. حذف این محدودیت که همه روابط در یک مقیاس فضایی متفاوت هستند، می‌تواند تناسب بیش از حد را به حداقل برساند، تعصب در تخمین پارامترها را کاهش دهد، و هم‌نشینی را کاهش دهد (یعنی همخطی به دلیل تبدیل‌های عملکردی مشابه). بنابراین، MGWR به عنوان مشخصات مدل محلی پیش‌فرض هنگام استفاده از GWR برای بررسی ناهمگنی فضایی و مقیاس فرآیند پیشنهاد شده است.

این مقاله mgwr را معرفی می‌کند (در سراسر این دست‌نوشته mgwr به پیاده‌سازی نرم‌افزار اشاره دارد، در حالی که MGWR به تکنیک به طور کلی‌تر اشاره دارد)، یک بسته نرم‌افزاری مبتنی بر پایتون برای استقرار مدل‌های GWR و MGWR. اگرچه گزینه‌های نرم‌افزاری موجود وجود دارد، اما از نظر عملکرد در دسترس، کارایی محاسباتی یا هر دو محدود هستند. به عنوان مثال، یک ابزار GWR در جعبه ابزار تحلیل فضایی در ArcGIS [ 4 ] وجود دارد و چندین گزینه در اکوسیستم R وجود دارد، مانند spgwr [ 5 ] و gwrr [ 6 ].]. با این حال، هیچ یک از این پیاده‌سازی‌ها قابلیت کالیبره کردن یک مدل MGWR و یا توانایی محاسبه ماتریس کلاه (یعنی ماتریس طرح‌ریزی) و تشخیص‌های مدل جدید مرتبط شرح داده شده در [ 7 ] را ارائه نمی‌دهند، که شامل شاخص‌های متغییر خاص مقیاس و چارچوب استنتاج است. . مدل GW مبتنی بر R [ 8 ] برخی از قابلیت‌های MGWR را ارائه می‌کند، اگرچه تمرکز در درجه اول بر روی معیارهای فاصله خاص پارامتر [ 9 ] است نه مقیاس‌های چندگانه تحلیل و همچنین فاقد برخی پیشرفت‌های محاسباتی اخیر است که از ذخیره‌سازی و دستکاری آرایه‌های عددی بزرگ جلوگیری می‌کند. کلاه در GWR/MGWR [ 10]. در نتیجه، mgwr یک بسته نرم‌افزاری کارآمد محاسباتی ارائه می‌دهد که به صراحت بر تجزیه و تحلیل چند مقیاسی فرآیندهای ناهمگن فضایی تمرکز دارد. علاوه بر این، mgwr پیاده سازی های رایگان و منبع باز مبتنی بر R (یعنی spgwr، gwrr و GWmodel) را با ارائه جایگزین مبتنی بر پایتون، افزایش دسترسی کلی ابزارهای GWR و MGWR را تحسین می کند.

ساختار باقی مانده این مقاله به شرح زیر است. ابتدا، کجا می توان کد منبع را پیدا کرد، چگونه آن را نصب کرد، و مجموعه داده های مورد استفاده در سراسر مقاله مورد بحث قرار می گیرد. سپس، برخی از مفاهیم اصلی GWR بررسی و نشان داده می‌شوند. در مرحله بعد، مفاهیم و عملکردهای جدید مورد نیاز برای استقرار افزونه MGWR و تشخیص های اخیر ارائه شده است. در نهایت، mgwr با دو پیاده سازی نرم افزار دیگر برای مقایسه کارایی محاسباتی مقایسه می شود. در طول مقاله، بهترین روش‌ها در مجموعه داده‌های تجربی پیشنهاد و نشان داده شده‌اند.

2. کد منبع و مجموعه داده ها

2.1. کد منبع و نصب

کد منبع mgwr (نمونه‌های موجود در این مقاله با استفاده از mgwr نسخه 2.0.1 ایجاد شده است) به عنوان یک ماژول از کتابخانه تحلیل فضایی پایتون (PySAL) ( https://pysal.org ) سازمان‌دهی شده است و بنابراین از یک مخزن در دسترس است. صفحه GitHub پروژه PySAL ( https://github.com/pysal/mgwr). هر ماژول PySAL با «رشته‌های اسناد» (یعنی اسناد ورودی و خروجی) برای همه توابع و نمونه‌های کد موجود (یعنی نوت‌بوک‌های Jupyter) کامل است که تکرار و گسترش مثال‌ها را به برنامه‌های جدید ساده می‌کند. به‌علاوه، «آزمایش‌های واحد» ارائه شده‌اند که به کد منبع اجازه می‌دهند به طور مداوم در حین توسعه یکپارچه شوند. این تضمین می‌کند که ویژگی‌های جدید و به‌روزرسانی‌های وابستگی ناخودآگاه ویژگی‌های موجود را از بین نبرند.

در حال حاضر mgwr دارای چهار وابستگی است: numpy، scipy، libpysal و spglm. دو وابستگی اول، numpy و scipy، در اکوسیستم محاسبات علمی پایتون ابتدایی هستند و ساختارهای داده اصلی و توابع دستکاری داده ها را ارائه می دهند. وابستگی سوم، libpysal، مرکزی برای PySAL است و مخزنی از مجموعه داده‌های نمونه را فراهم می‌کند. از آنجایی که libpysal به پانداها وابسته است، پس پانداها یک وابستگی غیرمستقیم برای mgwr است و اغلب برای خواندن و مدیریت جداول داده مفید است. وابستگی نهایی، spglm، یک چارچوب مدل خطی تعمیم‌یافته سبک وزن برای کالیبره کردن هر یک از تخمین‌های پارامتر محلی در (M)GWR از طریق حداقل مربعات وزن‌دار تکراری ارائه می‌کند. جدیدترین نسخه پایدار mgwr به همراه این وابستگی های مستقیم و غیرمستقیم،

pip نصب mgwr

برای به دست آوردن ویژگی های در حال توسعه، نصب mgwr به طور مستقیم از کد منبع نیز امکان پذیر است:

نصب پیپ https://github.com/pysal/mgwr/archive/master.zip

بسته های اضافی، یعنی matplotlib و geopandas، برای ارائه نتایج از نمایش های تجربی استفاده می شوند و همچنین می توانند از طریق pip به دست آیند. با این حال، آنها برای توابع mgwr اصلی مورد نیاز نیستند. پس از نصب تمام بسته های لازم، می توان آنها را برای استفاده در مثال های زیر وارد کرد:

>>> numpy را به عنوان np وارد کنید

>>> پانداها را به صورت PD وارد کنید

>>> libpysal را به عنوان ps وارد کنید

>>> از mgwr.gwr واردات GWR، MGWR

>>> از mgwr.sel_bw واردات Sel_BW

>>> از mgwr.utils وارد کردن compare_surfaces, truncate_colormap

>>> geopandas را به عنوان gp وارد کنید

>>> matplotlib.pyplot را به عنوان plt وارد کنید

>>> matplotlib را به صورت mpl وارد کنید

2.2. مجموعه داده ها

دو مجموعه داده در سراسر این مقاله برای نشان دادن عملکردهای مختلف (M)GWR استفاده شده است. اول، مجموعه داده شناخته شده جورجیا است که در [ 2 ] (2002) و همچنین انتشارات بعدی [ 7 ، 11 ] توضیح داده شده است. مورد دوم نمونه ای از داده های اجاره Airbnb از محله Prenzlauer Berg برلین از InsideAirbnb است که نمونه جدیدتری با حجم نمونه نسبتاً بزرگتر ارائه می دهد.

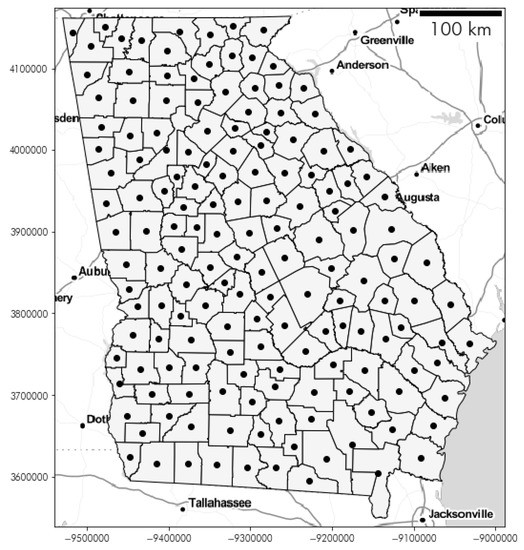
2.2.1. مجموعه داده گرجستان

مجموعه داده جورجیا از 159 شهرستان در ایالت جورجیا تشکیل شده است ( شکل 1 )، و ویژگی های اجتماعی و جمعیت شناختی را از سرشماری 1990 ایالات متحده ثبت می کند. مکان‌های شهرستان به‌عنوان مرکز انتزاع می‌شوند تا بتوان فواصل بین شهرستانی را در روال (M)GWR محاسبه کرد، اگرچه تجسم خروجی مدل با استفاده از چند ضلعی‌های شهرستان راحت است، زیرا آنها مقیاسی هستند که مشاهدات در آن جمع می‌شوند. زیرمجموعه کوچکی از متغیرهای موجود در اینجا برای مدل سازی دستاوردهای آموزشی انتخاب شده است. متغیرهای کمکی در جدول 1 توضیح داده شده است. کد پایتون برای بارگذاری و تجسم مجموعه داده جورجیا به شرح زیر است:

#بارگذاری مجموعه داده جورجیا و ایجاد نمودار شهرستان های جورجیا ( شکل 1 )

>>> گرجستان = gp.read_file(ps.examples.get_path('G_utm.shp'))

>>> fig, ax = plt.subplots(figsize = (10, 10))

>>> georgia.plot(ax=ax، **{'edgecolor': 'سیاه'، 'facecolor': 'سفید'})

>>> georgia.centroid.plot(ax = تبر، c = 'سیاه')

>>> plt.savefig('georgia_shp')

>>> plt.show()

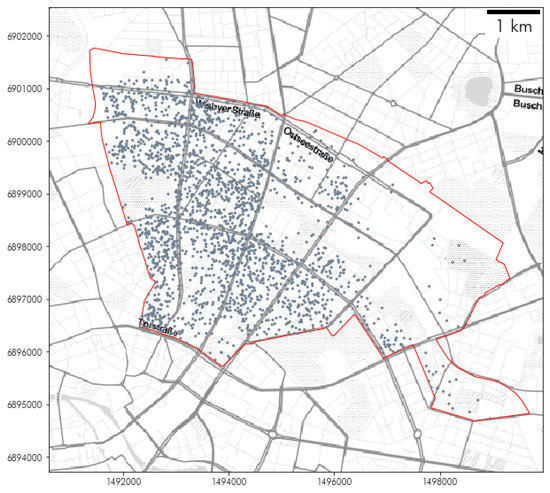
2.2.2. مجموعه داده های Airbnb برلین

مجموعه داده برلین از 2203 مشاهدات تشکیل شده است که نمونه‌های مکان‌یابی شده از املاک اجاره‌ای Airbnb ( شکل 2 ) و ویژگی‌های مرتبط با آن‌ها از سال 2017 در محله پرنزلاوئر برگ هستند. Prenzlauer Berg محله‌ای باشکوه است که به‌خاطر صحنه‌های هنری، خرید و تفریحات شبانه‌اش شناخته می‌شود و بنابراین یک مقصد گردشگری محبوب است. زیرمجموعه کوچکی از متغیرها برای مثال مدل‌سازی قیمت اجاره انتخاب شدند که در جدول 2 توضیح داده شده‌اند . توجه داشته باشید که در اینجا از لگاریتم قیمت اجاره برای اصلاح چولگی متغیر استفاده شده است. از آنجایی که داده ها تجمیع نمی شوند، تجزیه و تحلیل و تجسم نتایج در سطح نقطه انجام می شود.

#بارگذاری مجموعه داده برلین و ایجاد نمودار خواص ( شکل 2 )

>>> prenz = gp.read_file(ps.examples.get_path('prenzlauer.zip'))

>>> prenz_bound = gp.read_file(ps.examples.get_path('prenz_bound.zip'))

>>> fig, ax = plt.subplots(figsize = (10, 10))

>>> prenz_bound.plot(ax = تبر، **{'Edgecolor': 'سیاه'، 'facecolor': 'White'})

>>> prenz.plot(ax = ax, markersize = 10, **{'edgecolor': 'black',

'facecolor': 'سیاه'})

>>> plt.savefig('prenz')

>>> plt.show()

3. عملکرد GWR

GWR یک مدل رگرسیون جداگانه را در هر مکان از طریق یک طرح استقراض داده کالیبره می کند که مشاهدات از هر مکان را به عنوان نقطه رگرسیون وزن می کند. یک مدل GWR ممکن است به عنوان مشخص شود

y من = β من 0 + \sum k = 1 پ β من ک ایکس من ک + ϵ من ، i = 1 ، \dots ، n ،

(1)

جایی که $y_{i}$ متغیر وابسته در مکان i است، $β_{i 0}$ ضریب رهگیری در مکان i است، $x_{i k}$ k- امین متغیر توضیحی در مکان i است، $β_{i k}$ k- امین ضریب رگرسیون محلی برای k امین متغیر توضیحی در مکان i است، و $ϵ_{i}$ عبارت خطای تصادفی مرتبط با مکان i است. توجه داشته باشید که i معمولاً با مختصات جغرافیایی دو بعدی نمایه می شود. $(u_{i}, v_{i})$ ، نشان دهنده محل نقطه رگرسیون است. در شکل ماتریسی، برآوردگر GWR برای تخمین پارامترهای محلی در سایت i است:

β^(من) = [ایکس “ دبلیو (من) X] - 1 ایکس “ دبلیو (من) y ،

(2)

جایی که $X$ یک ماتریس n در k از متغیرهای توضیحی است، $W (i) = diag [w_{1} (i), \dots, w_{n} (i)]$ ماتریس وزن مورب n در n است که هر مشاهده را بر اساس فاصله آن از مکان i وزن می کند ، $\hat{β} (i)$ بردار k در 1 ضرایب است و $y$ بردار k در 1 مشاهدات متغیر وابسته است. ورودی های مدل، $X$ ، $y$ و مختصات جغرافیایی $(u, v)$ ، برای مجموعه داده های گرجستان و برلین به شرح زیر آماده شده اند:

# ورودی های مجموعه داده گرجستان را آماده کنید

>>> g_y = گرجستان['PctBach'].values.reshape((-1, 1))

>>> g_X = گرجستان[['PctFB', 'PctBlack', 'PctRural']].values

>>> u = گرجستان['X']

>>> v = گرجستان['Y']

>>> g_coords = لیست (zip(u, v))

# ورودی های مجموعه داده برلین را آماده کنید

#لگاریتم متغیر قیمت را برای اصلاح انحراف در نظر بگیرید

>>> b_y = np.log(prenz['price'].values.reshape((-1, 1)))

>>> b_X = prenz[['review_sco',

"اسکان دادن"،

'حمام']]. ارزش ها

>>> u = prenz['X']

>>> v = prenz['Y']

>>> b_coords = لیست (zip(u, v))

به منظور ساخت

W (i)

و محاسبه کنید

\hat{β} (i)

با استفاده از معادله ( 2 ) لازم است یک طرح وزنی فاصله انتخاب شود. این شامل ابتدا انتخاب یک تابع هسته و نوع هسته است. در مرحله بعد، پارامتر پهنای باند که شدت وزن دهی انجام شده توسط هسته را کنترل می کند باید انتخاب شود. در نهایت، پارامترهای مدل را می توان به همراه چندین تشخیص تخمین زد. این وظایف در زیر مورد بحث قرار گرفته است.

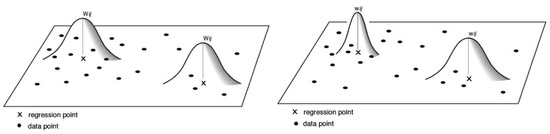
3.1. طرح فاصله وزنی

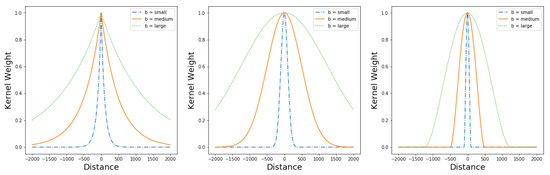
3.1.1. توابع هسته

برای محاسبه ماتریس وزن ها، یک تابع هسته برای فواصل بین مشاهدات و نقاط کالیبراسیون اعمال می شود. این هسته تاکید بیشتری بر مشاهدات نزدیکتر از مشاهدات دورتر دارد. بسته mgwr سه تابع هسته پرکاربرد را ارائه می دهد که عبارتند از توابع گاوسی، نمایی و دو مربعی همانطور که در جدول 3 نشان داده شده است. یک مشکل بالقوه با توابع هسته گاوسی و نمایی این است که همه مشاهدات بدون توجه به اینکه چقدر از محل کالیبراسیون فاصله دارند وزن غیر صفر را حفظ می کنند. این بدان معنی است که حتی مشاهدات دور نیز می توانند برای پارامترهای پهنای باند متوسط تا بزرگ تأثیرگذار باقی بمانند ( شکل 3)). در نتیجه، رفتار پیش‌فرض در mgwr استفاده از یک هسته دو مربعی است زیرا از این موضوع جلوگیری می‌کند و یک تفسیر بصری دارد: پارامتر پهنای باند فاصله یا تعداد نزدیک‌ترین همسایگان دورتر در فضا است که مشاهدات باقی‌مانده هیچ تأثیری ندارند. نمودار پایین در شکل 3 نشان می دهد که برای هسته دو مربعی، حتی پهنای باند بزرگ منجر به مشاهداتی می شود که دقیقاً صفر وزن دارند. با این وجود، هسته را می توان با تغییر پارامتر ورودی هسته در جایی که گزینه موجود است، به یک تابع گاوسی یا یک تابع نمایی تغییر داد ( جدول 3 را ببینید ).

3.1.2. انواع هسته

دو نوع تابع هسته در mgwr موجود است: ثابت و تطبیقی. اولی پارامتر پهنای باند را به گونه‌ای ثابت می‌کند که برای هر مکان کالیبراسیون، داده‌ها با شدت یکسان وزن می‌شوند، به موجب آن این شدت با اندازه‌گیری فاصله از محل کالیبراسیون مشخص می‌شود. محدودیت هسته‌های پهنای باند ثابت این است که وقتی مناطق پرجمعیت یک منطقه مورد مطالعه وجود دارد، ممکن است مشکلات کالیبراسیون وجود داشته باشد. نوع دوم هسته که به عنوان هسته پهنای باند تطبیقی شناخته می شود، از این موضوع جلوگیری می کند. تعریف نزدیکترین همسایه از پهنای باند تضمین می کند که تعداد مشاهدات یکسانی برای هر رگرسیون محلی وجود دارد زیرا فاصله ای که نزدیکترین همسایه ها را در بر می گیرد از مکانی به مکان دیگر تطبیق می یابد. تفاوت بین این دو نوع هسته در نشان داده شده است شکل 4 . هسته های ثابت (بالا) بدون توجه به توزیع داده ها یکسان هستند در حالی که هسته های تطبیقی (پایین) بسته به توزیع فضایی داده ها از نظر شکل متفاوت هستند. در نتیجه، یک هسته پهنای باند تطبیقی بهتر می‌تواند مناطق مطالعه با شکل نامنظم، توزیع‌های فضایی غیریکنواخت مشاهدات و اثرات لبه را مدیریت کند و بنابراین رفتار پیش‌فرض در mgwr است. در صورتی که یک هسته پهنای باند ثابت مورد نظر باشد، می توان آن را با تنظیم fixed = True در جایی که در دسترس است انتخاب کرد.

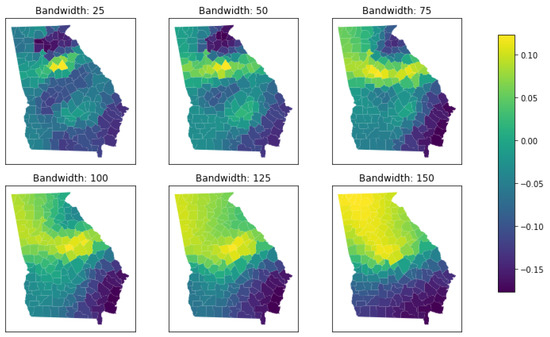
3.2. انتخاب پهنای باند

انتخاب پهنای باند یا با بهینه سازی یک معیار مناسب مدل یا با مشخصات دستی انجام می شود. انتخاب بهینه زمانی ترجیح داده می شود که هیچ راهنمای نظری برای تعیین دستی پهنای باند وجود نداشته باشد. در این مورد، کلاس Sel_BW عملکردی را برای اعمال روال‌های بهینه‌سازی مختلف و معیار برازش مدل فراهم می‌کند. ابتدا، یک نمونه از کلاس Sel_BW با ارسال ورودی های مدل، نمونه سازی می شود.

X

y

و مختصات جغرافیایی

(u, v)

. در این مورد، برای هر دو نمونه جورجیا و برلین، گزینه‌ها به مقادیر پیش‌فرض خود رها می‌شوند، که دلالت بر یک هسته دو مربعی تطبیقی نزدیک‌ترین همسایه با استفاده از مختصات پیش‌بینی‌شده (یعنی فواصل اقلیدسی) دارد. گزینه‌های موجود هسته قبلاً مورد بحث قرار گرفته‌اند و مختصات کروی مانند (طول و عرض جغرافیایی) را می‌توان با تنظیم کروی = True در نظر گرفت. علاوه بر این، یک لیست کامل از گزینه های موجود برای عملکرد Sel_BW از طریق رشته اسناد کلاس در دسترس است. سپس، متد جستجو بر روی شی Sel_BW که نمونه سازی شده بود فراخوانی می شود. روش جستجو روش بهینه سازی و معیار برازش مدل را کنترل می کند. تنظیمات پیش‌فرض استفاده از یک روال بهینه‌سازی جستجوی بخش طلایی و یک معیار اطلاعاتی اصلاح‌شده Akaike (AICc) را به عنوان معیار مناسب مدل مشخص می‌کند. یک روال بهینه‌سازی جستجوی بازه‌ای مساوی را می‌توان با تنظیم search_method = ‘interval’ و تنظیم گزینه فاصله بر روی بازه نمونه‌گیری مورد نظر انتخاب کرد. معیارهای برازش مدل موجود در نشان داده شده است جدول 4 ; با این حال یک AICc پیشنهاد می‌شود زیرا پهنای باند کوچک‌تر را جریمه می‌کند که منجر به مدل‌های پیچیده‌تر می‌شود که درجات بیشتری از آزادی را مصرف می‌کنند. زیر [ 2 ] یک AICc مخصوص GWR به شکل زیر است:

یک I سی ج = 2 n ورود به سیستم ه (آر اس اس n) + n ورود به سیستم ه (2 π) + n {n + t r ( S ) n - 2 - t r ( S )} ،

(3)

که در آن n تعداد مشاهدات است، $S$ ماتریس نفوذ یا کلاه است و $R S S$ مجموع مربعات باقی مانده است.

#نمونه هایی از انتخاب پهنای باند بهینه

#آبجایی انتخاب پهنای باند

>>> انتخابگر = Sel_BW (g_coords، g_y، g_X)

#جستجوی پیش‌فرض بخش طلایی با استفاده از معیار AICc

>>> bw = selector.search()

>>> چاپ (bw)

117.0

#جستجوی بازه ای با استفاده از معیار AICc

>>> bw = selector.search(search_method = 'interval',

فاصله = 2،

bw_min = 101،

bw_max = 150)

>>> چاپ (bw)

117

3.3. کالیبراسیون مدل

کالیبراسیون مدل ابتدا با نمونه سازی یک شی مدل GWR انجام می شود. سپس، متد فیت برای شی GWR برای برازش مدل فراخوانی می شود. یک ورودی مهم که باید برای کالیبراسیون GWR مشخص شود، پارامتر پهنای باند است که می تواند از طریق روال انتخاب پهنای باند بهینه که در بالا بحث شد انتخاب شود.

#یک مدل GWR را برای مجموعه داده جورجیا با استفاده از پهنای باند انتخاب شده محاسباتی کالیبره کنید

>>> gwr_selector = Sel_BW(g_coords، g_y، g_X)

>>> gwr_bw = gwr_selector.search()

>>> چاپ (gwr_bw)

117.0

>>> gwr_model = GWR(g_coords، g_y، g_X، gwr_bw)

>>> gwr_results = gwr_model.fit()

>>> print(gwr_results.resid_ss)

1650.85969828

پهنای باند را نیز می توان به صورت دستی انتخاب کرد، زمانی که یک پایه نظری قوی وجود دارد یا برای کشف ناهمگنی فضایی بالقوه. شکل 5 الگوهای مختلفی را نشان می دهد که برای سطح تخمین پارامتر درصد روستایی زمانی که پهنای باند از 25 تا 150 نزدیکترین همسایه تغییر می کند، ایجاد می شود.

#مدل GWR را برای مجموعه داده جورجیا کالیبره کنید

#استفاده از پهنای باند تنظیم دستی

>>> gwr_model = GWR(g_coords، g_y، g_X، 117)

>>> gwr_results = gwr_model.fit()

>>> print(gwr_results.resid_ss)

1650.85969828

#کاوش ناهمگونی فضایی با تغییر دستی پهنای باند

>>> fig, ax = plt.subplots(2, 3, figsize = (10, 6))

>>> bws = (x برای x در محدوده (25، 175، 25))

>>> vmins = []

>>> vmaxs = []

>>> برای ردیف در محدوده (2):

برای col در محدوده (3):

bw = بعدی (bws)

gwr_model = GWR (g_coords، g_y، g_X، bw)

gwr_results = gwr_model.fit()

گرجستان['rural'] = gwr_results.params[:, -1]

georgia.plot('rural', ax = ax[ ردیف, col])

ax[row,col].set_title('پهنای باند:' + str(bw))

ax[row,col].get_xaxis().set_visible(False)

ax[row,col].get_yaxis().set_visible(False)

vmins.append(گرجستان['rural'].min())

vmaxs.append(گرجستان['rural'].max())

>>> sm = plt.cm.ScalarMappable(norm=plt.Normalize(vmin=min(vmins)، vmax=max(vmaxs)))

>>> fig.tight_layout()

>>> fig.subplots_adjust(right=0.9)

>>> cax = fig.add_axes([0.92، 0.14، 0.03، 0.75])

>>> sm._A = []

>>> cbar = fig.colorbar(sm, cax=cax)

>>> cbar.ax.tick_params(labelsize=10)

>>> plt.savefig ('کاوش')

>>> plt.show()

3.4. مدل های احتمال

اگرچه مثال‌های این مقاله بر کالیبره کردن مدل‌های GWR گاوسی برای داده‌های پیوسته تمرکز دارند، همچنین می‌توان یک پواسون GWR را برای داده‌های شمارش یا یک GWR لجستیک دوجمله‌ای برای داده‌های بولی کالیبره کرد. برای انجام این کار، شی خانواده مناسب باید از بسته spglm وارد شود:

از spglm.family import Poisson، Binomial

و سپس لازم است که خانواده = Poisson() یا Family = Binomial() را هنگام نمونه سازی یک شی Sel_BW یا GWR تنظیم کنید. به طور کلی، وارد کردن یا مشخص کردن یک شی خانواده گاوسی ضروری نیست زیرا این رفتار پیش فرض در سراسر mgwr است.

3.5. تشخیص مدل

پس از تکمیل کالیبراسیون مدل GWR، چندین ابزار تشخیصی و آمار در دسترس هستند.

3.5.1. مدل مناسب

تناسب مدل را می توان با استفاده از آمارهای جهانی مانند AIC، AICc یا شبه ارزیابی کرد.

R^{2}

، که همگی به عنوان ویژگی های شیء GWRResults که از کالیبراسیون مدل موفق برگردانده می شود در دسترس هستند. همچنین می توان تناسب مدل را در هر مکان کالیبراسیون با نقشه برداری محلی ارزیابی کرد

R^{2}

آمار این معیار محلی تناسب، نشان می دهد که مدل چقدر بر داده های هموار شده، متمرکز شده در هر سایت، مطابقت دارد. شکل 6 نشان می دهد که مدل های رگرسیون فردی که مدل GWR را تشکیل می دهند دارای برازش های مدل هستند که هم بزرگتر و هم کوچکتر از مدل جهانی هستند.

R^{2}

. همچنین واضح است که تنوع در تناسب مدل از نظر فضایی با برازش مدل بالاتر در شمال نسبت به جنوب الگوبرداری شده است.

#مدل جهانی~فیت

>>> gwr_selector = Sel_BW(g_coords، g_y، g_X)

>>> gwr_bw = gwr_selector.search()

>>> چاپ (gwr_bw)

117.0

>>> gwr_model = GWR(g_coords، g_y، g_X، gwr_bw)

>>> gwr_results = gwr_model.fit()

>>> چاپ (gwr_results.aic)

848.915407053

>>> چاپ (gwr_results.aicc)

851.350292784

>>> print(gwr_results.R2)

0.678074266959

#مدل محلی مناسب

>>> گرجستان['R2'] = gwr_results.localR2

>>> georgia.plot('R2', legend = True)

>>> ax = plt.gca()

>>> ax.get_xaxis().set_visible(False)

>>> ax.get_yaxis().set_visible(False)

>>> plt.savefig('local_R2')

>>> plt.show()

3.5.2. استنتاج بر برآورد پارامترهای فردی

از آنجایی که GWR توسعه چارچوب رگرسیون سنتی است، ابزارهای استنتاجی سنتی در دسترس هستند. یک آزمون t را می توان برای هر پارامتر، j ، در هر مکان کالیبراسیون، i انجام داد، که در آن مقادیر t محلی توسط:

تی (من ، ج) = β ^ ( من ، ج ) س ه ( من ، ج ) ،

(4)

جایی که $s e_{(i, j)}$ خطای استاندارد مرتبط با $i j^{t h}$ تخمین پارامتر با این حال، ماهیت طرح وزن‌دهی فاصله به طور بالقوه می‌تواند باعث شود که نمونه‌های فرعی محلی وابسته باشند و اصلاحی برای محاسبه آزمون‌های فرضیه‌های وابسته چندگانه ایجاد شده است [ 12 ]. به جای استفاده از معمولی $α = 0.05$ ارزشی که به الف مربوط می شود $95 %$ فاصله اطمینان، جایگزین اصلاح شد $α$ از رابطه زیر بدست می آید:

α = ξ E ن پ پ ،

(5)

جایی که $E N P$ تعداد مؤثر پارامترهایی است که با گرفتن ردی از ماتریس کلاه GWR به دست می‌آید (نشان داده شده با $S$ ، p تعداد متغیرهای توضیحی است و $ξ$ میزان خطای مورد نظر نوع I در مجموعه آزمایشات است. نسبت $\frac{E N P}{p}$ ( $E N P > p$ ) معرف تعداد تست های متعدد است و اگر $p_{e} = p$ سپس $ξ = α$ و تعداد تست های انجام شده توسط GWR و یک رگرسیون جهانی معادل هستند.

روش‌های adj_alpha و filter_t برای محاسبه آلفای اصلاح‌شده و فیلتر کردن پارامترهایی که بازه‌های اطمینان آنها با صفر همپوشانی دارند (یعنی از نظر آماری ناچیز) در دسترس هستند. اعمال تصحیح معمولاً منجر به آزمون‌های فرضیه محافظه‌کارانه‌تر می‌شود که منجر به فرضیه صفر می‌شود.

\hat{β_{i}} = 0

بیشتر پذیرفته شدن این در شکل 7 نشان داده شده است، جایی که پانل سمت راستی که از تصحیح استفاده می کند، تخمین پارامترهای آماری معنی داری را نشان می دهد (یعنی آنهایی که خاکستری سایه ندارند)، تا پانل میانی که از اصلاح برای تخمین پارامترهای متولد شده خارجی مجموعه داده جورجیا استفاده نمی کند. ، رفتار پیش فرض روش filter_t این است که به طور خودکار از تصحیح تعریف شده در معادله ( 5 ) با استفاده از

ξ

= 0.05.

#تجسم آزمون های فرضیه برای اهمیت تخمین پارامترها

>>> gwr_selector = Sel_BW(g_coords، g_y، g_X)

>>> gwr_bw = gwr_selector.search()

>>> چاپ (gwr_bw)

117.0

>>> gwr_model = GWR(g_coords، g_y، g_X، gwr_bw)

>>> gwr_results = gwr_model.fit()

#رفتار پیش‌فرض با استفاده از آلفای اصلاح‌شده

>>> filter_tc = gwr_results.filter_tvals()

#بدون اصلاح با استفاده از آلفای مشترک

>>> filter_t = gwr_results.filter_tvals (آلفا = 0.05)

>>> گرجستان['fb'] = gwr_results.params[:, 1]

>>> گرجستان['fb_t'] = filter_t[:, 1]

>>> گرجستان['fb_tc'] = filter_tc[:، 1]

>>> fig, ax = plt.subplots(1, 3, figsize = (12, 3))

>>> georgia.plot('fb',

**{'edgecolor': 'مشکی'،

'آلفا': 0.65،

'linewidth': .5}،

تبر = تبر[0]،

افسانه = درست)

>>> ax[0].get_xaxis().set_visible(False)

>>> ax[0].get_yaxis().set_visible(False)

>>> ax[0].set_title('Parameter برآوردها')

>>> georgia.plot('fb',

**{'edgecolor': 'مشکی'،

'آلفا': 0.65،

'linewidth': .5}،

تبر = تبر [1]،

افسانه = درست)

>>> گرجستان[filter_t[:, 1] == 0].plot(color = 'grey',

تبر = تبر [1]،

**{'edgecolor': 'مشکی'،

'linewidth': .5})

>>> ax[1].get_xaxis().set_visible(False)

>>> ax[1].get_yaxis().set_visible(False)

>>> ax[1].set_title('Composite')

>>> georgia.plot('fb',

**{'edgecolor': 'مشکی'،

'آلفا': 0.65،

'linewidth': .5}،

تبر = تبر [2]،

افسانه = درست)

>>> گرجستان[filter_tc[:، 1] == 0].plot(color = 'خاکستری',

تبر = تبر [2]،

**{'edgecolor': 'مشکی'،

'linewidth': .5})

>>> ax[2].get_xaxis().set_visible(False)

>>> ax[2].get_yaxis().set_visible(False)

>>> ax[2].set_title('کامپوزیت با تصحیح')

plt.savefig ("تست")

plt.show()

3.5.3. استنتاج بر روی سطح تخمین پارامترها

همچنین می توان اهمیت آماری هر سطح از برآورد پارامترهای تولید شده توسط GWR از طریق روش های مونت کارلو را آزمایش کرد. آزمون تغییرپذیری فضایی مشاهدات در فضا را به هم می‌ریزد، GWR را روی داده‌های تصادفی‌سازی مجدد کالیبره می‌کند در حالی که مشخصات مدل را ثابت نگه می‌دارد، و سپس تغییرپذیری تخمین‌های پارامتر حاصل را برای هر سطح محاسبه می‌کند. این فرآیند تکرار می‌شود و تعداد دفعاتی که تغییرپذیری هر سطح از داده‌های تصادفی‌سازی‌شده بیشتر از تغییرپذیری هر سطح اصلی است، برای ساخت مقادیر p شبه برای آزمایش فرضیه استفاده می‌شود. مقدار شبه p کوچکتر از 0.05 نشان می دهد که تنوع فضایی مشاهده شده یک سطح ضریب در سطح اطمینان 95٪ (یعنی غیر تصادفی) قابل توجه است.

یکی از مسائل مربوط به آزمون تغییرپذیری فضایی این است که نیاز به کالیبره شدن GWR چندین بار دارد که از نظر محاسباتی گران است. حتی ممکن است استفاده از آزمون برای مجموعه داده های بزرگتر از نظر محاسباتی منع شود و کاربران باید در تعداد تکراری که برای آزمایش تعیین می کنند احتیاط کنند، با در نظر گرفتن اینکه تعداد پیش فرض تکرارها 1000 است. در مثال زیر، چهار مقدار p تولید شده مطابق با سطوح برآورد پارامتر برای رهگیری، متغیر متولد خارجی، متغیر آمریکایی آفریقایی تبار، و متغیر روستایی است. برای یک مدل GWR با پهنای باند 50 و تکرارهای 100، 1000 یا 2000، مقدار p برای متغیر رهگیری و روستایی بزرگتر از 0.05 است و نشان می دهد که سطوح برآورد پارامترها هیچ گونه تغییر محلی قابل توجهی را نشان نمی دهند.

#تجسم آزمون های فرضیه برای معناداری پارامتر ~ برآورد

#دستی پهنای باند را روی 50 تنظیم کنید و متناسب کنید

>>> gwr_model = GWR(g_coords، g_y، g_X، 50)

>>> gwr_results = gwr_model.fit()

100 تکرار

>>> p_vals_100 = gwr_results.spatial_variability(gwr_selector, 100)

>>> چاپ (p_vals_100)

[ 0.153 0.019 0.026 0.155]

#پیش فرض 1000 تکرار است

>>> p_vals_1000 = gwr_results.spatial_variability(gwr_selector)

>>> چاپ (p_vals_1000)

[ 0.12 0.03 0.04 0.14]

#2000 تکرار

>>> p_vals_2000 = gwr_results.spatial_variability(gwr_selector, 2000)

>>> چاپ (p_vals_2000)

[ 0.1515 0.0195 0.023 0.146 ]

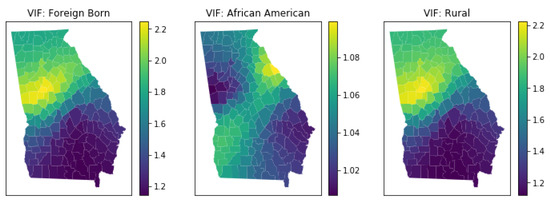
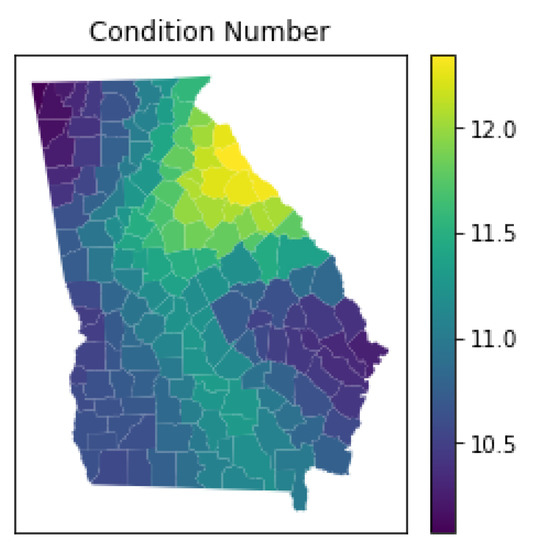
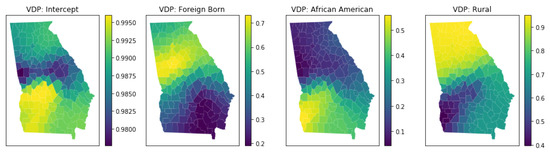
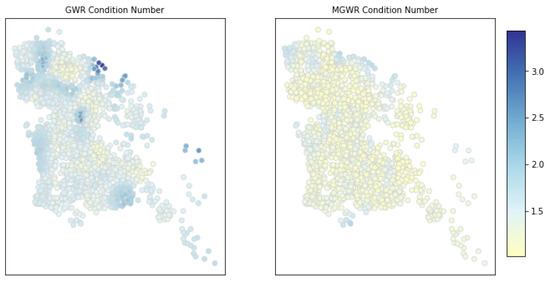
3.5.4. چند خطی محلی

اگرچه ابزارهای زیادی برای ارزیابی چند خطی بودن در بین متغیرهای توضیحی برای مدل‌های رگرسیون سنتی وجود دارد، اما برای مدل‌های محلی که داده‌ها را از مکان‌های مجاور قرض می‌گیرند، مراقبت بیشتری لازم است. در هر مدل محلی، ممکن است سطوح بالاتری از همخطی نسبت به مجموعه داده به عنوان یک کل وجود داشته باشد [ 13 ]. سطوح بالاتر همخطی با مشکلاتی مانند ناپایداری تخمینی، علائم پارامترهای نامشهود، بالا همراه است.

R^{2}

تشخیص علیرغم تعداد کمی یا عدم وجود پارامترهای مهم، و خطاهای استاندارد متورم برای تخمین پارامترها [ 14 ، 15 ]. در نتیجه، ابزارهای تشخیصی برای تشخیص سطوح چند خطی محلی، از جمله ضرایب همبستگی محلی (CC)، عوامل تورم تغییرات محلی (VIF)، شماره شرایط محلی (CN)، و نسبت‌های تجزیه تغییرات محلی (VDP) طراحی شده‌اند [ 13 ، 16 ].

هر معیار محلی دارای یک قانون کلی است که نشان می دهد ممکن است مشکلی به دلیل چند خطی بودن وجود داشته باشد: CC بالاتر از 0.8. VIF بالاتر از 10؛ CN بالاتر از 30: VDP بالاتر از 0.5 هر کدام در برخی معیارها چند خطی بودن را نشان می دهد. با این حال، این قوانین مطلق نیستند و به دست آوردن مقادیر کمتر به این معنی نیست که همخطی بودن بی ضرر است، و همچنین به دست آوردن مقادیر بزرگتر تضمین کننده هم خطی بودن واقعاً مشکل ساز نیست. علاوه بر این، CCهای محلی و VIFهای محلی عبارت رهگیری محلی را در نظر نمی گیرند، در حالی که CN محلی به جای تولید یک اندازه گیری جداگانه برای هر متغیر، یک اندازه گیری مجموع برای همه متغیرها است. شکل 8 ، شکل 9 ، شکل 10 و شکل 11 نقشه های CC های محلی، VIF های محلی، CN های محلی و VDP های محلی را به ترتیب برای مثال جورجیا با استفاده از پهنای باند بهینه سازی شده AICc نشان می دهد. VDP نشان می دهد که برخی از مناطق ممکن است در معرض اثرات هم خطی باشند. با این حال، هیچ یک از CC، VIF و یا CN نشان نمی دهد که هم خطی بودن برای هر یک از مکان های کالیبراسیون مشکل ساز است. علاوه بر این، نشان داده شده است که چند خطی بودن ذاتاً در GWR [ 17 ] از رگرسیون سنتی مشکل‌سازتر نیست و برخی از الگوهای تئوری‌شده مرتبط با چند خطی بودن ممکن است نشان‌دهنده [ 18 ] واقعیت یا به دلیل تعیین نادرست مقیاس باشند [ 19 ] .

>>> gwr_selector = Sel_BW(g_coords، g_y، g_X)

>>> gwr_bw = gwr_selector.search()

>>> چاپ (gwr_bw)

117.0

>>> gwr_model = GWR(g_coords، g_y، g_X، gwr_bw)

>>> gwr_results = gwr_model.fit()

>>> LCC، VIF، CN، VDP = gwr_results.local_collinearity()

>>> names = ['متولد خارجی در مقابل آمریکایی آفریقایی تبار',

متولدین خارجی در مقابل روستایی،

"آفریقایی آمریکایی در مقابل روستایی"]

>>> fig, ax = plt.subplots(1, 3, figsize = (12, 4))

>>> برای col در محدوده (3):

گرجستان['vif'] = LCC[:, col]

georgia.plot('vif', ax = ax[col], legend = True)

ax[col].set_title('LCC:' + names[col])

ax[col].get_xaxis().set_visible(False)

ax[col].get_yaxis().set_visible(False)

>>> names = ['متولد خارجی'، 'آفریقایی آمریکایی'، 'روستایی']

>>> fig, ax = plt.subplots(1, 3, figsize = (12, 4))

>>> برای col در محدوده (3):

گرجستان['vif'] = VIF[:، col]

georgia.plot('vif', ax = ax[col], legend = True)

ax[col].set_title('VIF:' + names[col])

ax[col].get_xaxis().set_visible(False)

ax[col].get_yaxis().set_visible(False)

>>> fig, ax = plt.subplots(1, 1, figsize = (4, 4))

>>> گرجستان['cn'] = CN

>>> georgia.plot('cn', legend = True, ax = ax)

>>> ax.set_title ('شماره شرط')

>>> ax.get_xaxis().set_visible(False)

>>> ax.get_yaxis().set_visible(False)

>>> names = ['رهگیری'، 'متولد خارجی'، 'آفریقایی آمریکایی'، 'روستایی']

>>> fig, ax = plt.subplots(1, 4, figsize = (16, 4))

>>> برای col در محدوده (4):

گرجستان['vdp'] = VDP[:، col]

georgia.plot('vdp', ax = ax[col], legend = True)

ax[col].set_title('VDP:' + names[col])

ax[col].get_xaxis().set_visible(False)

ax[col].get_yaxis().set_visible(False)

3.6. پیش‌بینی فضایی خارج از نمونه

اگرچه تمرکز اصلی mgwr بر استنتاج است، اما می توان از GWR به عنوان ابزاری برای پیش بینی فضایی خارج از نمونه به روشی مشابه روش های درونیابی استفاده کرد [ 20 ]]. به عنوان مثال، می توان ابتدا یک مدل GWR را با استفاده از داده هایی کالیبره کرد که در آن هر دو متغیر وابسته و مستقل مشاهده می شوند تا یک پهنای باند بهینه AIC به دست آید. سپس پیش‌بینی‌های خارج از نمونه با استقراض داده‌های برون‌زا در مکان‌های مشاهده نشده از سایت‌های اطراف بر اساس پهنای باند تخمین زده شده قبلی، تخمین پارامترهای سایت پیش‌بینی، و سپس محاسبه مقادیر پیش‌بینی‌شده متغیر وابسته با استفاده از متغیرهای کمکی توضیحی به‌دست می‌آیند. و برآوردها این امر در زیر با تقسیم مجموعه داده جورجیا به یک مجموعه داده کالیبراسیون برای به دست آوردن پهنای باند و انجام برخی مشاهدات برای پیش‌بینی نشان داده می‌شود.

# پیش‌بینی خارج از نمونه با استفاده از ~GWR

#تقسیم داده ها به مجموعه های کالیبراسیون و پیش بینی

>>> np.random.seed(908)

>>> نمونه = np.random.choice(range(159)، 10)

>>> mask = np.ones_like(g_y، dtype = bool).flatten()

>>> mask[samp] = نادرست

>>> cal_coords = np.array(g_coords)[mask]

>>> cal_y = g_y[ماسک]

>>> cal_X = g_X [ماسک]

>>> pred_coords = np.array(g_coords)[~mask]

>>> pred_y = g_y[~mask]

>>> pred_X = g_X[~mask]

#مدل GWR را کالیبره کنید

>>> gwr_selector = Sel_BW (cal_coords، cal_y، cal_X)

>>> gwr_bw = gwr_selector.search(bw_min = 2)

>>> چاپ (gwr_bw)

109.0

>>> مدل = GWR (cal_coords، cal_y، cal_X، gwr_bw)

>>> gwr_results = model.fit()

#پیش بینی کنید

>>> pred_results = model.predict(pred_coords، pred_X)

#همبستگی بین مقادیر شناخته شده و پیش بینی شده را بررسی کنید

>>> corr = np.corrcoef(pred_results.predictions.flatten()

pred_y.flatten())[0][1]

چاپ (تصحیح)

0.914249268428

4. قابلیت MGWR

تاکنون، تمام مفاهیم و مثال‌های مورد بحث در این مقاله فرض کرده‌اند که محدوده وام‌گیری داده (یعنی پهنای باند)، یا مقیاس فرآیند برای هر رابطه در یک مدل مشخص یکسان است. هر زمان که مقیاس‌های فضایی متمایز متعددی وجود داشته باشد که داده‌ها را تولید می‌کنند و GWR اعمال می‌شود، یک یا چند مقیاس به اشتباه مشخص می‌شوند، که می‌تواند منجر به تخمین پارامترهای مغرضانه شود. یک فرض شهودی تر این است که هر رابطه ممکن است در مقیاس متفاوتی رخ دهد. MGWR توسعه‌ای را ارائه می‌کند که به هر متغیر اجازه می‌دهد تا با قالب‌گیری مجدد GWR به‌عنوان یک مدل افزایشی تعمیم‌یافته (GAM) با پهنای باند مجزایی مرتبط شود به‌طوری‌که:

y = \sum j = 1 ک f j + ϵ ،

(6)

جایی که $f_{j}$ یک تابع هموارسازی (به عنوان مثال، طرح استقراض داده) است که به آن اعمال می شود $j^{t h}$ متغیر توضیحی که ممکن است با پارامتر پهنای باند مجزا مشخص شود [ 3 ]. در این بخش، مفاهیم و عملکرد جدید لازم برای کالیبراسیون و ارزیابی یک مدل MGWR با توجه ویژه به جزئیاتی که با عملکرد GWR قبلا معرفی شده متفاوت است، معرفی می‌شوند.

4.1. استانداردسازی متغیرها

برای مقایسه هر یک از پهنای باند به دست آمده از یک مدل MGWR، لازم است متغیرهای وابسته و مستقل به گونه ای استاندارد شوند که در مرکز صفر و بر اساس محدوده تغییرات یکسان باشند. در غیر این صورت ممکن است مقایسه عینی پهنای باند تخمین زده شده دشوار باشد زیرا ممکن است آنها معرف مقیاس و تنوع متغیرهای مستقل نیز باشند [ 3 ].

#استاندارد کردن متغیرها

مجموعه داده #گرجستان

>>> g_X = (g_X - g_X.mean(axis = 0)) / g_X.std(axis = 0)

>>> g_y = (g_y - g_y.mean(axis = 0)) / g_y.std(axis = 0)

#استاندارد کردن مجموعه داده برلین

>>> b_X = (b_X - b_X.mean(axis = 0)) / b_X.std(axis = 0)

>>> b_y = (b_y - b_y.mean(axis = 0)) / b_y.std(axis = 0)

4.2. انتخاب پهنای باند و کالیبراسیون مدل

MGWR از یک الگوریتم back-fitting برای کالیبراسیون مدل، بر اساس روش‌های برازش GAM استفاده می‌کند [ 3 ، 7 ]. این شامل کالیبراسیون متوالی یک سری از مدل‌های GWR تک متغیره بر اساس باقیمانده‌های جزئی از تکرار قبلی است تا زمانی که مدل MGWR به یک راه‌حل همگرا شود. دو تفاوت اصلی در نحوه تعیین و کالیبره شدن یک مدل MGWR در mgwr در مقایسه با GWR وجود دارد. اول، اگرچه استفاده از یک شی GWR بدون انجام انتخاب پهنای باند محاسباتی امکان پذیر است، این موضوع در مورد MGWR صادق نیست زیرا انتخاب پهنای باند و تخمین پارامتر ذاتاً به هم مرتبط هستند. در عوض، یک شی Sel_BW باید به یک شی MGWR ارسال شود تا کالیبراسیون MGWR انجام شود، که در زیر نشان داده شده است:

#نمونه کالیبراسیون MGWR (داده های برلین)

>>> mgwr_selector = Sel_BW (b_coords، b_y، b_X، multi = True)

>>> mgwr_bw = mgwr_selector.search()

>>> چاپ (mgwr_bw)

[191.0، 1279.0، 79.0، 2200.0]

>>> mgwr_results = MGWR(b_coords، b_y، b_X، mgwr_selector).fit()

یک شی Sel_BW برای به دست آوردن نتایج مدل ضروری است زیرا تخمین پارامتر همزمان با انتخاب پهنای باند اتفاق می افتد و بنابراین، بسیاری از نتایج Sel_BW برای تهیه خروجی مدل و محاسبه تشخیص مدل MGWR مورد نیاز است. تفاوت دوم بین MGWR و GWR این است که روتین MGWR باید با مقادیر شروع پارامترها برای هر متغیر مقداردهی شود. مرجع. [ 3 ] نشان می‌دهد که چگونه استفاده از تخمین‌های پارامتر محلی از یک GWR کالیبره‌شده می‌تواند کالیبراسیون MGWR را به جای شروع از صفر یا فرض پهنای باند جهانی (یعنی با استفاده از نتایج OLS) سرعت بخشد. در نتیجه، این رفتار پیش فرض در mgwr است.

4.3. تنظیم دستی پهنای باند خاص متغیر کمکی

اگرچه کالیبراسیون MGWR به استفاده از یک شی Sel_BW نیاز دارد، اما هنوز هم می توان با تنظیم حداقل و حداکثر پهنای باند روی یک مقدار با استفاده از گزینه های ورودی multi_bw_min و multi_bw_max، پارامترهای پهنای باند را به صورت دستی انتخاب کرد. تفاوت بین این گزینه ها و آرگومان های bw_min و bw_max مورد استفاده برای کالیبراسیون GWR این است که اولی باید با استفاده از یک لیست مشخص شود. اگر لیستی با یک مقدار مشخص شده باشد، این مقدار برای همه متغیرها اعمال می شود. با این حال، امکان تعیین حداقل و حداکثر مقدار پهنای باند برای هر متغیر در مدل نیز وجود دارد. هر یک از این گزینه ها در زیر نشان داده شده است:

#نمونه انتخاب دستی پهنای باند در ~MGWR

# پهنای باند یکسان را برای همه متغیرها اعمال کنید

>>> mgwr_selector = Sel_BW (b_coords، b_y، b_X، multi = True)

>>> mgwr_bw = mgwr_selector.search(multi_bw_min = [500]،

multi_bw_max = [500])

>>> چاپ (mgwr_bw)

[500.0، 500.0، 500.0، 500.0]

>>> mgwr_results = MGWR(b_coords، b_y، b_X، mgwr_selector).fit()

# پهنای باند دستی منحصر به فرد

>>> mgwr_selector = Sel_BW (b_coords، b_y، b_X، multi = True)

>>> mgwr_bw = mgwr_selector.search(multi_bw_min = [150، 500، 750، 1000]،

multi_bw_max = [150، 500، 750، 1000])

>>> چاپ (mgwr_bw)

[150.0، 500.0، 750.0، 1000.0]

>>> mgwr_results = MGWR(b_coords، b_y، b_X، mgwr_selector).fit()

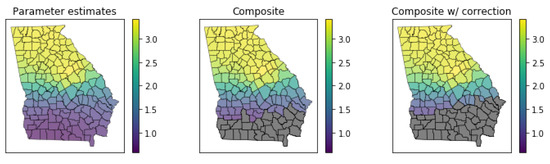
4.4. مدل مناسب

اگرچه امکان محاسبه یک

R^{2}

برای ارزیابی تناسب مدل برای MGWR، ایده آل است که از معیار برازش مدل استفاده شود که پیچیدگی مدل [ 2 ] را بهتر نشان دهد، مانند AICc معرفی شده در معادله ( 3 ). تا همین اواخر، محاسبه AICc برای MGWR ممکن نبود، زیرا الگوریتم back-fitting مورد استفاده برای کالیبراسیون یک ماتریس کلاه تولید نمی کرد (به عنوان مثال،

S

در معادله ( 3 )). پیاده‌سازی‌های نرم‌افزار قبلی که قادر به کالیبره کردن هستند (یعنی یک پارامتر خاص از تابع psdm در GWmodel)، یک مقدار AICc را گزارش می‌کنند. با این حال، این مقدار حداقل AICc است که در سراسر مجموعه اجزای GWR تک متغیره به دست می‌آید که شامل GAM مورد استفاده برای کالیبره کردن MGWR [ 21 ] است. در مقابل، mgwr الگوریتم جدیدی را پیاده‌سازی می‌کند که توسط [ 7 ] ارائه شده است که یک ماتریس کلاهی تولید می‌کند، که اجازه می‌دهد یک مقدار AICc مناسب که برای کل مدل MGWR اعمال می‌شود طبق رابطه ( 3 ) محاسبه شود. این معیار برازش مدل AICc برای MGWR را می توان در mgwr به روشی مشابه با GWR با استفاده از mgwr_results.aicc ارزیابی کرد.

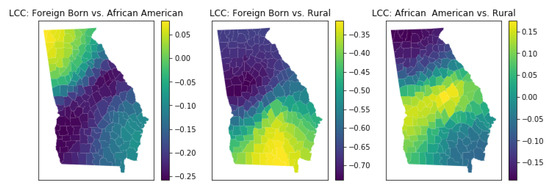
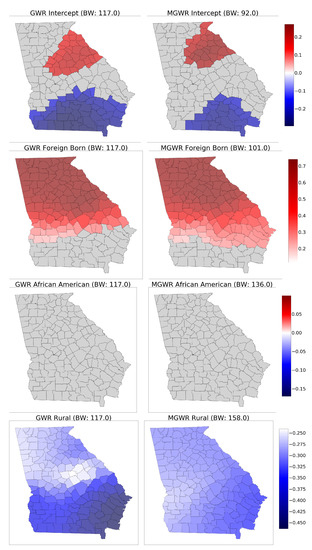
4.5. استنباط بر برآورد پارامترها

همانند GWR، لازم است چارچوب آزمایش فرضیه اصلاح شده که در بالا توضیح داده شد، اعمال شود. با این حال، در مورد MGWR، این امکان وجود دارد که چارچوب آزمون را برای فرموله کردن یک آزمون فرضیه تصحیح شده با متغیر کمکی برای هر سطح از تخمین‌های پارامتر گسترش دهیم. این روش جدید در [ 7 ] توضیح داده شده است و عملکرد لازم در حال حاضر در سایر نرم افزارهای پیاده سازی غیر از mgwr موجود نیست. در MGWR، ماتریس کلاه،

S

، که متغیر وابسته مشاهده شده را بر روی مقادیر برازش متغیر وابسته ترسیم می کند، می تواند به مشارکت های خاص متغیر وابسته تجزیه شود،

R_{j}

. با این کار، می توان اندازه گیری متمایز از تعداد موثر پارامترها (ENP) برای هر سطح پارامتر را محاسبه کرد:

E ن پ j = t r (آر j)

(7)

با استفاده از ENP های ویژه متغیرهای کمکی، معادله ( 5 ) را می توان به روز رسانی کرد:

α j = ξ متر E ن پ j ،

(8)

جایی که p حذف می شود زیرا برای هر رابطه $p = 1$ . رفتار پیش فرض در mgwr استفاده است $α_{j}$ برای محاسبه یک مقدار t بحرانی ویژه متغیر کمکی برای آزمون فرضیه. امکان بازرسی هر کدام وجود دارد $E N P_{j}$ ، $α_{j}$ و مقادیر t تنظیم شده به صورت زیر است:

#اولین مدل راه اندازی

>>> mgwr_selector = Sel_BW (b_coords، b_y، b_X، multi = True)

>>> mgwr_bw = mgwr_selector.search()

>>> mgwr_results = MGWR(b_coords، b_y، b_X، mgwr_selector).fit()

#ENP مختص به متغیر

>>> print(mgwr_results.ENP_j)

[31.89989861، 4.77588266، 73.79013919، 1.40343481]

آلفای تعدیل‌شده خاص #Covarriate در 95% CI

>>> print(mgwr_results.adj_alpha_j[:, 1])

[ 0.0015674 0.01046927 0.0006776 0.03562688]

مقدار t بحرانی تعدیل شده #متغیرهای کمکی

>>> print(mgwr_results.critical_tval())

[ 3.16585816 2.56212889 3.40333525 2.10245302]

استفاده از این مقادیر برای استنباط با روش filter_tvals امکان پذیر است. به‌طور پیش‌فرض filter_tvals آرایه‌ای از t -values را برمی‌گرداند که در آن تخمین‌های «ناچیز» هستند (در

95 %

سطح معنی داری) روی صفر تنظیم شود.

>>> mgwr_filtered_t = mgwr_results.filter_tvals()

سپس، می توان تنها ضرایب مرتبط با مقادیر t غیر صفر را تجسم کرد. علاوه بر این، توصیه می‌شود سطوح حاصل از MGWR را در مقایسه با سطوح GWR تجسم کنید تا درک کنید که چگونه سطوح تحت فرض‌های مختلف در مورد مقیاس فرآیند تغییر می‌کنند. تابع compare_surfaces به طور خاص برای تجسم مقایسه ای بین دو سطح در دسترس است و در زیر در دو مثال از استنتاج در MGWR نشان داده شده است.

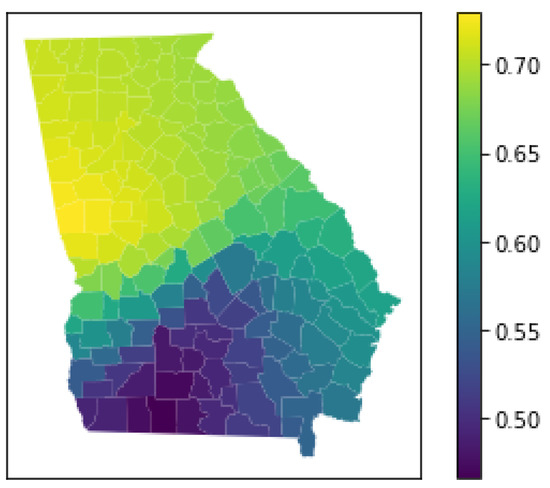
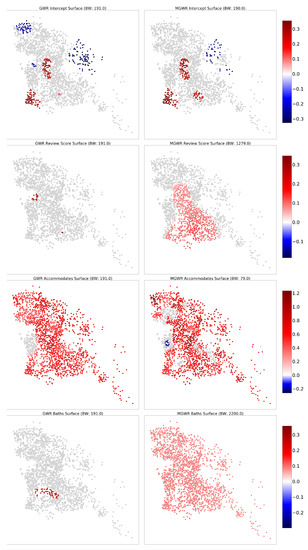
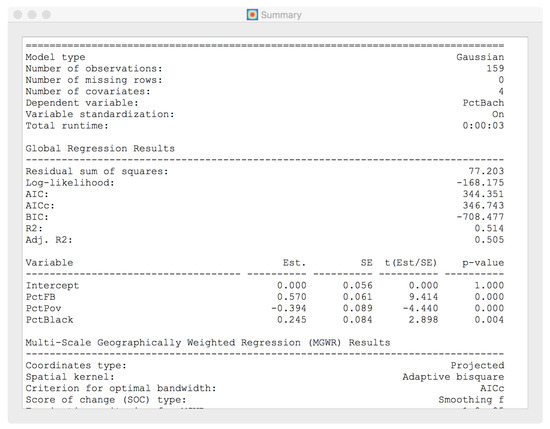
4.5.1. مجموعه داده جورجیا

کد زیر استنتاج با استفاده از MGWR را با استفاده از مجموعه داده جورجیا نشان می دهد (این مثال با جزئیات بیشتر در Yu و همکاران [ 7 ] موجود است). از آنجایی که پهنای باند GWR 117.0 نسبتاً بزرگ است و هیچ یک از پهنای باند MGWR کوچک نیستند، تنها تفاوت های جزئی بین GWR و MGWR همانطور که در شکل 12 نشان داده شده است وجود دارد.. برای رهگیری، متولدین خارجی و آمریکایی آفریقایی تبار، الگوهای روابط برای تخمین پارامترهای مهم و ناچیز همگی بسیار مشابه هستند. این به دلیل این واقعیت است که برای این سطوح، پهنای باند MGWR همه از نظر بزرگی نسبتاً مشابه هستند (یعنی +/- تقریباً 15 نزدیکترین همسایه). در مقابل، تفاوت بیشتری در الگوی ضرایب برای متغیر روستایی بین GWR و MGWR و تفاوت بزرگ‌تری بین پهنای باند (یعنی 41 نزدیکترین همسایه) وجود دارد. با این وجود، سطوح برآورد پارامترهای روستایی برای هر دو GWR و MGWR هنوز مشابه هستند و هر دو از برآوردهای آماری منفی معنی‌دار تشکیل شده‌اند. به طور کلی، این نتایج نشان می دهد که وقتی GWR و MGWR پهنای باند مشابهی را تخمین می زنند، تخمین پارامترهای مرتبط و آزمون های فرضیه نیز مشابه هستند.

#GWR را با استفاده از داده های استاندارد شده کالیبره کنید

>>> gwr_selector = Sel_BW(g_coords، g_y، g_X)

>>> gwr_bw = gwr_selector.search()

چاپ (gwr_bw)

117.0

>>> gwr_model = GWR(g_coords، g_y، g_X، gwr_bw)

>>> gwr_results = gwr_model.fit()

#نتایج GWR را برای نقشه برداری آماده کنید

#پارامترهای GWR را به GeoDataframe اضافه کنید

>>> گرجستان['gwr_intercept'] = gwr_results.params[:, 0]

>>> گرجستان['gwr_fb'] = gwr_results.params[:, 1]

>>> گرجستان['gwr_aa'] = gwr_results.params[:, 2]

>>> گرجستان['gwr_rural'] = gwr_results.params[:, 3]

#T-vals فیلتر شده بر اساس اصلاح چندگانه تست را دریافت کنید

>>> gwr_filtered_t = gwr_results.filter_tvals()

#مدل MGWR را کالیبره کنید

>>> mgwr_selector = Sel_BW (g_coords، g_y، g_X، multi = True)

>>> mgwr_bw = mgwr_selector.search(multi_bw_min = [2])

چاپ (mgwr_bw)

[92.0، 101.0، 136.0، 158.0]

>>> mgwr_results = MGWR(g_coords، g_y، g_X، mgwr_selector).fit()

#نتایج MGWR را برای نقشه برداری آماده کنید

#پارامترهای MGWR را به GeoDataframe اضافه کنید

>>> گرجستان['mgwr_intercept'] = mgwr_results.params[:, 0]

>>> گرجستان['mgwr_fb'] = mgwr_results.params[:, 1]

>>> گرجستان['mgwr_aa'] = mgwr_results.params[:, 2]

>>> گرجستان['mgwr_rural'] = mgwr_results.params[:, 3]

#T-vals فیلتر شده بر اساس اصلاح چندگانه تست را دریافت کنید

>>> mgwr_filtered_t = mgwr_results.filter_tvals()

>>> kwargs1 = {'edgecolor': 'black', 'alpha': 0.65}

>>> kwargs2 = {'edgecolor': 'black'}

>>> compare_surfaces(گرجستان، 'gwr_intercept'، 'mgwr_intercept',

gwr_filtered_t[:، 0]، gwr_bw، mgwr_filtered_t[:، 0]،

mgwr_bw[0]، 'Intercept'، kwargs1، kwargs2،

savefig = 'g1')

>>> compare_surfaces(گرجستان، 'gwr_fb'، 'mgwr_fb'، gwr_filtered_t[:، 1]،

gwr_bw، mgwr_filtered_t[:، 1]، mgwr_bw[1]،

'متولد خارجی'، kwargs1، kwargs2، savefig = 'g2')

>>> compare_surfaces(گرجستان، 'gwr_aa'، 'mgwr_aa'، gwr_filtered_t[:, 2]،

gwr_bw، mgwr_filtered_t[:، 2]، mgwr_bw[2]،

'آفریقایی آمریکایی'، kwargs1، kwargs2، savefig = 'g3')

>>> compare_surfaces(گرجستان، 'gwr_rural'، 'mgwr_rural'، gwr_filtered_t[:, 3]،

gwr_bw، mgwr_filtered_t[:، 3]، mgwr_bw[3]،

'Rural'، kwargs1، kwargs2، savefig = 'g4')

4.5.2. مجموعه داده برلین

تحلیل مشابهی در زیر موجود است که استنتاج در MGWR را با استفاده از مجموعه داده برلین نشان می دهد و در شکل 13 نشان داده شده است. همانطور که در مثال بالا در جورجیا، MGWR نشان می‌دهد که برخی از تخمین‌های پهنای باند مشابه برآوردهای GWR هستند: یک پهنای باند بسیار مشابه برای رهگیری منجر به الگوی مشابهی با دو خوشه اضافی از تخمین‌های پارامتر منفی در شمال و شرق می‌شود. و پهنای باند کمی کوچکتر برای انطباقمتغیر به پارامترهای آماری معنی‌دار کمتری منجر می‌شود، اما با الگوی مشابه و افزودن خوشه‌ای کوچک از تخمین‌های پارامتر منفی. با این حال، برخی از تفاوت‌ها در پهنای باند MGWR از پهنای باند GWR وجود دارد: پهنای باند بسیار بزرگ‌تر برای متغیر حمام و متغیر امتیاز بررسی، تخمین‌های پارامترهای مثبت آماری بسیار بیشتری را تولید می‌کنند. به طور خاص، متغیر امتیاز بررسی دارای پهنای باند است که به این معنی است که تقریباً همه همسایگان در نظر گرفته شده‌اند، که منجر به این می‌شود که همه تخمین‌های پارامتر از نظر آماری معنی‌دار و به‌طور قابل‌توجهی ثابت باشند (یعنی یک رابطه جهانی) در سراسر منطقه مورد مطالعه. این نتایج نشان می‌دهد که وقتی MGWR و GWR پهنای باند مشابهی را تخمین می‌زنند، تخمین‌ها و استنتاج‌های پارامتر مشابهی را تولید می‌کنند. با این حال، هنگامی که آنها از هم جدا می شوند، می توان نتایج بسیار متفاوتی را به دست آورد. بنابراین، استفاده از MGWR برای اطمینان از استفاده صحیح از مقیاس های وام گیری داده برای هر رابطه ضروری است.

#GWR را با استفاده از داده های استاندارد شده کالیبره کنید

>>> gwr_selector = Sel_BW(b_coords، b_y، b_X)

>>> gwr_bw = gwr_selector.search()

>>> چاپ (gwr_bw)

191.0

>>> gwr_model = GWR(b_coords، b_y، b_X، gwr_bw)

>>> gwr_results = gwr_model.fit()

#نتایج GWR را برای نقشه برداری آماده کنید

#پارامترهای GWR را به GeoDataframe اضافه کنید

>>> prenz['gwr_intercept'] = gwr_results.params[:, 0]

>>> prenz['gwr_score'] = gwr_results.params[:، 1]

>>> prenz['gwr_accom'] = gwr_results.params[:, 2]

>>> prenz['gwr_baths'] = gwr_results.params[:, 3]

#T-vals فیلتر شده بر اساس اصلاح چندگانه تست را دریافت کنید

>>> gwr_filtered_t = gwr_results.filter_tvals()

#مدل MGWR را کالیبره کنید

>>> mgwr_selector = Sel_BW (b_coords، b_y، b_X، multi = True)

>>> mgwr_bw = mgwr_selector.search(multi_bw_min = [2])

>>> چاپ (mgwr_bw)

[190.0، 1279.0، 79.0، 2200.0]

>>> mgwr_results = MGWR(b_coords، b_y، b_X، mgwr_selector).fit()

#نتایج MGWR را برای نقشه برداری آماده کنید

#پارامترهای MGWR را به GeoDataframe اضافه کنید

>>> prenz['mgwr_intercept'] = mgwr_results.params[:, 0]

>>> prenz['mgwr_score'] = mgwr_results.params[:، 1]

>>> prenz['mgwr_accom'] = mgwr_results.params[:، 2]

>>> prenz['mgwr_baths'] = mgwr_results.params[:, 3]

#T-vals فیلتر شده بر اساس اصلاح چندگانه تست را دریافت کنید

>>> mgwr_filtered_t = mgwr_results.filter_tvals()

>>> kwargs1 = {'Edgecolor': 'خاکستری روشن'، 'Markersize': 175}

>>> kwargs2 = {'facecolor': 'خاکستری روشن', 'markersize': 175}

>>> compare_surfaces(prenz، 'gwr_intercept'، 'mgwr_intercept',

gwr_filtered_t[:، 0]، gwr_bw،

mgwr_filtered_t[:، 0]، mgwr_bw[0]،

'Intercept'، kwargs1، kwargs2، savefig = 'b1')

>>> compare_surfaces(prenz، 'gwr_score'، 'mgwr_score'، gwr_filtered_t[:، 1]،

gwr_bw، mgwr_filtered_t[:، 1]، mgwr_bw[1]،

'امتیاز بررسی'، kwargs1، kwargs2، savefig = 'b2')

>>> compare_surfaces(prenz، 'gwr_accom'، 'mgwr_accom'، gwr_filtered_t[:، 2]،

gwr_bw، mgwr_filtered_t[:، 2]، mgwr_bw[2]،

'Accommodates'، kwargs1، kwargs2، savefig = 'b3')

>>> compare_surfaces(prenz، 'gwr_baths'، 'mgwr_baths'، gwr_filtered_t[:, 3]،

gwr_bw، mgwr_filtered_t[:، 3]، mgwr_bw[3]،

'Baths', kwargs1, kwargs2, savefig = 'b4')

4.6. چند خطی محلی

اجازه دادن به پهنای باند متمایز برای هر رابطه نیز می تواند پیامدهایی برای چند خطی بودن محلی داشته باشد. هنگامی که هر رابطه با یک تابع هسته و پارامتر پهنای باند مشخص می شود، به این معنی است که آنها در معرض تغییر وزن یکسانی هستند، که ممکن است همخطی بین متغیرها را تشدید کند و گاهی اوقات همخوانی نامیده می شود. با اجازه دادن به پهنای باند برای تغییر، این امکان وجود دارد که متغیرها در معرض تبدیل‌های متفاوتی قرار گیرند، که می‌تواند از القای چند خطی/همراهی جلوگیری کند. تعداد شرایط محلی به راحتی از زمینه GWR به زمینه MGWR گسترش می یابد زیرا می توان آن را مستقیماً بر روی ماتریس طراحی محاسبه کرد که در آن هر ستون یک متغیر است و می تواند تحت تبدیل وزنی فضایی مربوطه قرار گیرد. مثال زیر تفاوت بین اعداد شرایط محلی برای GWR و MGWR برای مجموعه داده برلین را نشان می دهد. که در شکل 14 آشکار است که وقتی پهنای باند مجاز به تغییر در MGWR (راست) باشد، اعداد شرایط محلی کمتر از GWR (سمت چپ) است که در آن پهنای باند مجاز به تغییر نیست. با این حال، همچنین آشکار است که برای این مثال داده شده، هیچ یک از اعداد شرط محلی نشان نمی‌دهد که چند خطی بودن موضوعی است زیرا همه آنها زیر قاعده 30 هستند. Comber et al. [ 22 ] همچنین شواهدی ارائه می‌کند که استفاده از معیارهای فاصله متفاوت، که دلالت بر پهنای باند متفاوت دارد، می‌تواند بر درجه چند خطی محلی در (M)GWR تأثیر بگذارد. با بهترین دانش نویسندگان، عملکرد ارائه شده در اینجا اولین ابزار موجود برای بررسی صریح چند خطی محلی در زمینه MGWR است.

#شماره شرط GWR/MGWR را برای نقشه برداری آماده کنید

>>> gwr_lc = gwr_results.local_collinearity()

>>> mgwr_lc = mgwr_results.local_collinearity()

>>> prenz['gwr_cn'] = gwr_lc[2]

>>> prenz['mgwr_cn'] = mgwr_lc[0]

>>> fig, axes = plt.subplots (nrows = 1, ncols = 2, figsize = (10, 5))

>>> ax0 = محور[0]

>>> ax0.set_title ('شماره وضعیت GWR'، فونت = 10)

>>> ax1 = محور[1]

>>> ax1.set_title ('شماره شرط MGWR'، فونت = 10)

>>> cmap = mpl.cm.RdYlBu

>>> vmin = np.min([prenz['gwr_cn'].min()، prenz['mgwr_cn'].min()])

>>> vmax = np.max([prenz['gwr_cn'].max()، prenz['mgwr_cn'].max()])

>>> اگر (vmin < 0) و (vmax < 0):

cmap = truncate_colormap (cmap، 0.0، 0.5)

>>> elif (vmin > 0) و (vmax > 0):

cmap = truncate_colormap(cmap, 0.5, 1.0)

>>> sm = plt.cm.ScalarMappable(cmap = cmap,

norm = plt.Normalize(vmin = vmin,

vmax = vmax))

>>> prenz.plot('gwr_cn', cmap = sm.cmap, ax = ax0,

vmin = vmin، vmax = vmax،

**{'رنگ لبه': 'خاکستری روشن'،

'آلفا': 0.95،

'linewidth': 0.75})

>>> prenz.plot('mgwr_cn', cmap = cmap, ax = ax1,

vmin = vmin، vmax = vmax،

**{'رنگ لبه': 'خاکستری روشن'،

'آلفا': 0.95،

'linewidth': 0.75})

>>> fig.tight_layout()

>>> fig.subplots_adjust (راست = 0.9)

>>> cax = fig.add_axes([0.92، 0.14، 0.03، 0.75])

>>> sm._A = []

>>> cbar = fig.colorbar(sm, cax = cax)

>>> cbar.ax.tick_params(اندازه برچسب = 10)

>>> ax0.get_xaxis().set_visible(False)

>>> ax0.get_yaxis().set_visible(False)

>>> ax1.get_xaxis().set_visible(False)

>>> ax1.get_yaxis().set_visible(False)

>>> plt.savefig('compare_collin')

>>> plt.show()

5. ویژگی های اضافی

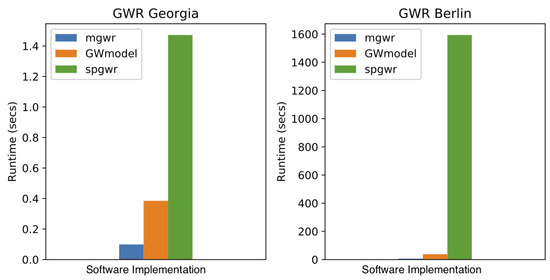
5.1. کارایی محاسباتی

از آنجایی که GWR و MGWR بر اساس مجموعه‌ای از رگرسیون‌های محلی هستند، سربار محاسباتی می‌تواند با افزایش تعداد مشاهدات و مکان‌های کالیبراسیون بزرگ شود. بنابراین، در نظر گرفتن کارایی محاسباتی مهم است و اغلب برای درک مزایای پیاده سازی نرم افزارهای مختلف برای انجام وظایف مشابه مورد توجه است. در اینجا mgwr به دلیل کارایی محاسباتی آن در مقایسه با دو اجرای فعال منبع باز دیگر برجسته شده است: GWmodel و spgwr. شکل 15زمان اجرا کالیبراسیون های GWR را از mgwr، GWmodel و spgwr برای هر دو مجموعه داده جورجیا و برلین مقایسه می کند. هر پیاده سازی برای کالیبره کردن یک مدل با استفاده از هسته فضایی تطبیقی دو مربعی و جستجوی بخش طلایی بر اساس کمینه سازی AICc با استفاده از متغیرهای مورد بحث در بالا (یعنی 3 متغیر توضیحی برای هر مدل) استفاده شد. محاسبات روی یک مک بوک پرو با پردازنده مرکزی Core i7 اینتل 2.8 گیگاهرتزی (4 هسته) و 16 گیگابایت رم 1600 مگاهرتزی DDR3 انجام شد. مشاهده می شود که برای GWR کالیبره شده بر روی مجموعه داده کوچکتر جورجیا، mgwr تقریباً 4× سریعتر از GWmodel و 15× سریعتر از spgwr است و برای مجموعه داده بزرگتر برلین، mgwr حدود 6× سریعتر از GWmodel و 262× سریعتر از spgwr است. نتایج نشان می‌دهد که mgwr نه تنها سریع‌ترین در بین این سه مجموعه داده است، بلکه مقیاس‌پذیرترین است. 10 ]، یک پیاده‌سازی ساده GWR که می‌تواند با استفاده از موازی‌سازی به میلیون‌ها مشاهدات تبدیل شود. به طور خاص، سربار محاسباتی با به حداقل رساندن محاسبه تشخیص های غیر ضروری مدل در طول روش های جستجوی انتخاب پهنای باند کاهش می یابد.

این صرفه‌جویی‌های محاسباتی به MGWR نیز تعمیم می‌یابد زیرا الگوریتم backfitting مورد استفاده برای کالیبراسیون مستلزم یک سری کالیبراسیون GWR است. شکل 16نشان می‌دهد که چگونه این بهینه‌سازی‌ها منجر به زمان اجرا سریع‌تر برای کالیبراسیون‌های MGWR برای مجموعه داده‌های جورجیا و برلین در mgwr در مقایسه با GWmodel با استفاده از مشخصات مدل و تجهیزات محاسباتی مشابه با بالا می‌شوند. علیرغم این واقعیت که GWmodel تشخیص استنتاج تخمین پارامتر MGWR را محاسبه نمی کند (نسخه 2.0-6 به عنوان جدیدترین نسخه در زمان انجام این تحقیق مورد استفاده قرار گرفت)، mgwr هنوز حدود 1.6 برابر سریعتر از GWmodel برای مجموعه داده جورجیا است. و حدود 3.2× سریعتر برای مجموعه داده برلین. هیچ مقایسه ای با spgwr انجام نمی شود زیرا از کالیبراسیون MGWR پشتیبانی نمی کند. همچنین شایان ذکر است که GWmodel از همان الگوریتم پس‌برازش پیشنهادی در [ 3 ] استفاده نمی‌کند و در عوض از یک استراتژی بهینه‌سازی موقتی که در [3] معرفی شده است استفاده می‌کند. 21 ]. این استراتژی فرض می‌کند که هر پهنای باند خاص متغیر کمکی پس از پایداری برای دو تکرار فرآیند backfitting دیگر تغییر نخواهد کرد. با این حال، استحکام این بهینه سازی هنوز به طور گسترده نشان داده نشده است و بنابراین در mgwr مشخص نشده است.

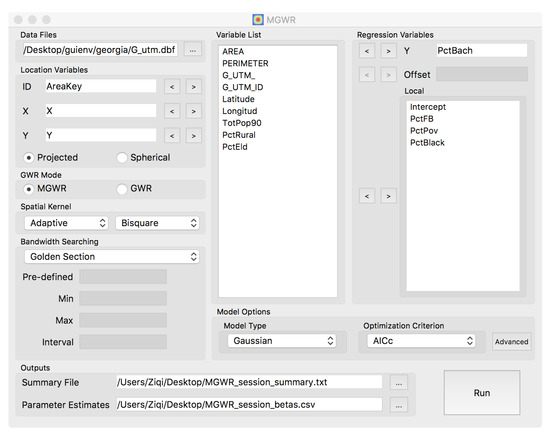
5.2. دسترسی

ویژگی منحصر به فرد mgwr این است که یک رابط کاربری گرافیکی (GUI) در بالای پایه کد منبع باز ایجاد شده است تا عملکرد را در دسترس تر کند و برای هر دو سیستم عامل ویندوز و مک پشتیبانی می شود. رابط اصلی رابط کاربری گرافیکی در شکل 17 نشان داده شده است و به GWR و MGWR اجازه می دهد تا با خواندن در جدول داده (مثلاً فایل های مقادیر جدا شده با کاما، صفحه گسترده اکسل یا فایل پایگاه داده) و با استفاده از عملکرد نقطه و کلیک کالیبره شوند. مدل مورد نظر و روال کالیبراسیون را مشخص کنید. علاوه بر این، تمام عیب های ذکر شده در اینجا نیز می توانند با استفاده از رابط کاربری گرافیکی محاسبه شوند. پس از تکمیل روال، یک فایل خلاصه از تشخیص های جهانی و محلی تولید می شود ( شکل 18، و همچنین جدولی از تخمین پارامترها، تشخیص استنتاج مربوط به آنها (یعنی خطاهای استاندارد و مقادیر t)، مقادیر پیش بینی شده، و باقیمانده ها.

6. نتیجه گیری

این مقاله mgwr را معرفی می‌کند، یک پیاده‌سازی مبتنی بر پایتون برای کالیبراسیون کارآمد انواع مدل‌های GWR و MGWR و مجموعه‌ای از تشخیص‌های جدید که بر روی گرفتن و تفسیر ناهمگنی فضایی چند مقیاسی تمرکز دارند. در ارائه این مدل‌ها، ما چند روش برتر برای تخمین و تفسیر GWR/MGWR با استفاده از بسته mgwr پیشنهاد کردیم. اینها شامل استفاده از “هسته های تطبیقی” است که عرض آنها به نمونه های توزیع شده فضایی غیریکنواخت تنظیم می شود، شامل مقیاس های تجزیه و تحلیل متعدد با استفاده از MGWR بر روی GWR، استفاده از متغیرهای استاندارد و هسته های دو مربعی برای افزایش تفسیرپذیری مقیاس فرآیند، و استفاده از یک ماتریس کلاه MGWR مناسب برای تخمین و استنتاج مدل دقیق بحث در مورد این بهترین شیوه ها مجموعه ای مفید از پیشنهادات را برای تحقیقات کاربردی ارائه می دهد.

پس از معرفی این بهترین شیوه‌ها علاوه بر نحوه اجرای آنها در نرم‌افزار mgwr، استفاده پیشنهادی را در مجموعه داده‌های جورجیا و برلین نشان دادیم. در مورد مجموعه داده جورجیا، اجازه دادن به مقیاس‌های چندگانه تجزیه و تحلیل از طریق استفاده از MGWR بر روی بیشتر سطوح تخمین پارامترهای حاصل تأثیری نمی‌گذارد زیرا پهنای باند ویژه متغیر کمکی تخمین زده شده نسبتاً مشابه پهنای باند متوسط منفرد است که از طریق استفاده از GWR. در مقابل، تجزیه و تحلیل مجموعه داده های برلین نشان می دهد که وقتی پهنای باند تخمین زده شده از طریق MGWR به شدت با پهنای باند تخمین زده شده توسط GWR متفاوت است، سپس سطوح تخمین پارامتر و آزمون های اهمیت مرتبط نیز ممکن است واگرا شوند. به طور کلی،

اگرچه mgwr سریع‌ترین پیاده‌سازی‌های GWR و MGWR را ارائه می‌کند، هنوز چندین پیشرفت در آینده وجود دارد که می‌تواند بسته را بهبود بخشد و پیشرفته‌ترین فناوری را در تحلیل فضایی چندمقیاسی ارتقا دهد. اول، آزمون‌های تشخیصی مبتنی بر شبیه‌سازی‌های مونت کارلو، مانند آزمون‌های تغییرپذیری فضایی سطوح برآورد پارامتر می‌توانند بهینه شوند. این تست‌ها بسیار محاسباتی هستند و حتی برای اندازه‌های نمونه متوسط نیز می‌توانند زمان بسیار زیادی را اجرا کنند. دوم، اقدامات چند خطی محلی اضافی را می توان به MGWR غیر از شماره شرایط محلی گسترش داد. سوم، عملکرد پیش‌بینی خارج از نمونه را می‌توان به MGWR که در حال حاضر برای GWR در دسترس است، گسترش داد. چهارم، مدل‌های احتمال برای نتایج گسسته و باینری را می‌توان با چارچوب MGWR تطبیق داد. سرانجام، 10 ]. این اضافات، تجزیه و تحلیل فضایی چند مقیاسی را برای استفاده در طیف گسترده‌تری از حوزه‌ها و حوزه‌های کاربردی قابل دسترس‌تر و قوی‌تر می‌سازد.

مشارکت های نویسنده

مفهوم سازی، تیلور ام. اوشان; روش شناسی، تیلور ام. اوشان، زیکی لی، وی کانگ، لوی جی. ولف و آ. استوارت فاثرینگهام. نرم افزار، Taylor M. Oshan، Ziqi Li، Wei Kang و Levi J. Wolf; اعتبارسنجی، تیلور ام. اوشان و لوی جی. ولف. تحلیل رسمی، Taylor M. Oshan and Ziqi Li; تحقیق، Taylor M. Oshan; منابع، Taylor M. Oshan و Levi J. Wolf; سرپرستی داده، تیلور ام. اوشان و لوی جی. ولف. نوشتن – آماده سازی پیش نویس اصلی، Taylor M. Oshan; نوشتن-بررسی و ویرایش، تیلور ام. اوشان، زیکی لی، وی کانگ، لوی جی. ولف و آ. استوارت فاثرینگهام. تجسم، Taylor M. Oshan; نظارت، A. Stewart Fotheringham; مدیریت پروژه، تیلور ام. اوشان؛ تامین مالی، A. Stewart Fotheringham، Taylor M. Oshan و Levi J. Wolf.

منابع مالی

این تحقیق با کمک مالی بنیاد ملی علوم ایالات متحده (NSF) به شماره 1758786 تامین شده است.

تضاد علاقه

نویسندگان هیچ تضاد منافع را اعلام نمی کنند.

منابع

Tobler, WR یک فیلم کامپیوتری شبیه سازی رشد شهری در منطقه دیترویت. اقتصاد Geogr. 1970 , 46 , 234. [ Google Scholar ] [ CrossRef ]
Fotheringham، AS; براندون، سی. چارلتون، ام. رگرسیون وزن‌دار جغرافیایی: تحلیل روابط متغیر فضایی . جان وایلی و پسران: هوبوکن، نیوجرسی، ایالات متحده آمریکا، 2002. [ Google Scholar ]
Fotheringham، AS; یانگ، دبلیو. کانگ، دبلیو. رگرسیون وزنی جغرافیایی چند مقیاسی. ان صبح. دانشیار Geogr. 2017 ، 107 ، 1247-1265. [ Google Scholar ]
موسسه تحقیقات سیستم های محیطی (ESRI). جعبه ابزار تحلیل فضایی ArcMap 10.3 . ESRI: Redlands، CA، USA، 2018. [ Google Scholar ]
بیوند، ر. یو، دی. ناکایا، تی. گارسیا-لوپز، MA spgwr : رگرسیون وزن‌دار جغرافیایی ، بسته R نسخه 0.6-32. 2017. [ Google Scholar ]
Wheeler، D. gwrr : متناسب با مدل‌های رگرسیون دارای وزن جغرافیایی با ابزارهای تشخیصی ، بسته R نسخه 0.2-1. 2013. [ Google Scholar ]
یو، اچ. Fotheringham، AS; لی، ز. اوشان، تی. کانگ، دبلیو. استنتاج Wolf، LJ در رگرسیون وزن‌دار جغرافیایی چند مقیاسی. Geogr. مقعدی 2019 . [ Google Scholar ] [ CrossRef ]
لو، بی. هریس، پی. چارلتون، ام. بروندسون، سی. نایاکا، تی. Gollini ، I. GWmodel : Geographically-Weighted Models ، بسته R نسخه 2.0-5. 2018. [ Google Scholar ]
لو، بی. براندون، سی. چارلتون، ام. هریس، پی. رگرسیون وزن‌دار جغرافیایی با معیارهای فاصله خاص پارامتر. بین المللی جی. جئوگر. Inf. علمی 2017 ، 31 ، 982-998. [ Google Scholar ] [ CrossRef ]
لی، ز. Fotheringham، AS; لی، دبلیو. اوشان، تی. رگرسیون وزن‌دار جغرافیایی سریع (FastGWR): یک الگوریتم مقیاس‌پذیر برای بررسی ناهمگونی فرآیند فضایی در میلیون‌ها مشاهده. بین المللی جی. جئوگر. Inf. علمی 2018 . [ Google Scholar ] [ CrossRef ]
گریفیث، DA مشارکت‌های مبتنی بر فیلتر فضایی در نقد رگرسیون وزن‌دار جغرافیایی (GWR). محیط زیست طرح. A 2008 , 40 , 2751-2769. [ Google Scholar ] [ CrossRef ]
داسیلوا، آر. Fotheringham، AS مسئله آزمایش چندگانه در رگرسیون وزن‌دار جغرافیایی: مسئله آزمایش چندگانه در GWR. Geogr. مقعدی 2015 . [ Google Scholar ] [ CrossRef ]
ویلر، دی. Tiefelsdorf، M. چند خطی و همبستگی بین ضرایب رگرسیون محلی در رگرسیون وزنی جغرافیایی. جی. جئوگر. سیستم 2005 ، 7 ، 161-187. [ Google Scholar ] [ CrossRef ]
بلزی، دی. کوه، ای. Welsch، RE Regression Diagnostics: شناسایی داده‌های تأثیرگذار و منابع هم‌خطی . Wiley: نیویورک، نیویورک، ایالات متحده آمریکا، 1980. [ Google Scholar ]
اوبرین، RM یک احتیاط در مورد قوانین سرانگشتی برای عوامل تورم واریانس. کیفیت مقدار. 2007 ، 41 ، 673-690. [ Google Scholar ] [ CrossRef ]
Wheeler، ابزارهای تشخیصی DC و یک روش اصلاحی برای هم خطی در رگرسیون وزن‌دار جغرافیایی. محیط زیست طرح. A 2007 , 39 , 2464-2481. [ Google Scholar ] [ CrossRef ]
Fotheringham، AS; اوشان، TM رگرسیون وزنی جغرافیایی و چند خطی: رد اسطوره. جی. جئوگر. سیستم 2016 ، 18 ، 303-329. [ Google Scholar ] [ CrossRef ]
اوشان، TM; Fotheringham، AS مقایسه تخمین‌های ضریب رگرسیون فضایی با استفاده از تکنیک‌های وزن‌دار جغرافیایی و مبتنی بر فیلتر فضایی: مقایسه رگرسیون متغیر فضایی. Geogr. مقعدی 2017 . [ Google Scholar ] [ CrossRef ]
موراکامی، دی. لو، بی. هریس، پی. براندون، سی. چارلتون، ام. ناکایا، تی. گریفیث، DA اهمیت مقیاس در مدل‌سازی ضریب متغیر فضایی. arXivt 2017 , arXiv:1709.08764. [ Google Scholar ] [ CrossRef ]
هریس، پی. Fotheringham، AS; کرسپو، آر. چارلتون، ام. استفاده از رگرسیون دارای وزن جغرافیایی برای پیش بینی فضایی: ارزیابی مدل ها با استفاده از مجموعه داده های شبیه سازی شده. ریاضی. Geosci. 2010 ، 42 ، 657-680. [ Google Scholar ] [ CrossRef ]
لو، بی. یانگ، دبلیو. Ge، Y. Harris, P. بهبودهایی در کالیبراسیون یک رگرسیون وزن‌دار جغرافیایی با معیارهای فاصله و پهنای باند خاص پارامتر. محاسبه کنید. محیط زیست سیستم شهری 2018 . [ Google Scholar ] [ CrossRef ]
کامبر، ا. چی، ک. کوانگ هوی، ام. نگوین، کیو. لو، بی. هوو فه، اچ. هریس، P. انتخاب متریک فاصله می‌تواند هم خطی بودن را در رگرسیون وزن‌دار جغرافیایی کاهش دهد و هم القا کند. محیط زیست طرح. ب مقعد شهری. علوم شهر 2018 . [ Google Scholar ] [ CrossRef ]

شکل 1. 159 شهرستان در ایالت جورجیا. توجه: نقشه پایه و نوار مقیاس با استفاده از کد اضافی اضافه شده است.

شکل 2. 2203 ملک اجاره ای در محله Prenzlauer Berg برلین. توجه: نقشه پایه و نوار مقیاس با استفاده از کد اضافی اضافه شده است.

شکل 3. نمونه هایی از هسته های نمایی ( بالا )، هسته های گواسی ( وسط )، و هسته های دوگانه ( پایین ) برای پارامتر پهنای باند کوچک، متوسط و بزرگ.

شکل 4. بازتولید شده از [ 2 ]. نمونه هایی از هسته های پهنای باند ثابت ( چپ ) و تطبیقی ( راست ).

شکل 5. ناهمگونی فضایی درصد سطح پارامتر روستایی برای مجموعه داده جورجیا با استفاده از پهنای باند مختلف.

شکل 6. تنوع فضایی محلی

R^{2}

آمار برازش مدل برای مجموعه داده جورجیا. تناسب مدل در شمال بالاترین و در جنوب غربی بدترین است.

شکل 7. تخمین پارامتر برای متغیر خارجی ( سمت چپ )، ترکیبی از تخمین‌های پارامتر معنی‌دار و ناچیز (خاکستری) بدون تصحیح برای آزمون‌های فرضیه‌های وابسته چندگانه ( وسط ) و با تصحیح برای آزمون‌های فرضیه وابسته چندگانه ( سمت راست ).