
رگرسیون وزندار جغرافیایی اصلاح شده
رگرسیون وزندار جغرافیایی (GWR) یک تکنیک مدلسازی است که برای مقابله با غیرایستایی فضایی طراحی شده است، به عنوان مثال، مقادیر میانگین براساس مکانها متفاوت است. به طور گسترده ای به عنوان یک ابزار تجسم برای کشف الگوهای داده های مکانی استفاده شده است. با این حال، GWR زمانی که پارامترهای میانگین دارای تغییرات قابل توجهی هستند، تمایل به تولید سطوح غیرصاف دارد، تا حدی به این دلیل که تمام تخمینهای پارامتر از یک محدوده ثابت (پهنای باند) مشاهدات مشتق شدهاند. به منظور مقابله با مشکل پهنای باند متغیر، این مقاله یک رویکرد جایگزین، یعنی رگرسیون جغرافیایی وزن دار شرطی (CGWR) را پیشنهاد می کند.
مواد و روش ها
تخمین CGWR بر اساس یک روش تکراری، مشابه مسئله بهینه سازی عددی است. شبیهسازی کامپیوتری، تحت تنظیمات واقعی، برای مقایسه عملکرد بین GWR سنتی، CGWR، و یک اصلاح خطی محلی GWR استفاده میشود. علاوه بر این، این مطالعه همچنین CGWR را برای دو مجموعه داده تجربی برای ارزیابی عملکرد مدل اعمال میکند. اولین مجموعه داده شامل وضعیت ناتوانی سالمندان تایوان به همراه برخی متغیرهای اجتماعی-اقتصادی و دیگری مجموعه داده های جنایی اوهایو است.
نتایج
تحت سناریوی همبستگی مثبت، متوجه شدیم که CGWR تناسب بهتری برای سطح پاسخ ایجاد میکند. هم شبیهسازی رایانهای و هم تحلیل تجربی از رویکرد پیشنهادی پشتیبانی میکنند زیرا به طور قابلتوجهی سوگیری و واریانس برازش دادهها را کاهش میدهد. علاوه بر این، سطح پاسخ از CGWR ویژگی های فضایی محلی را با توجه به متغیرهای مربوطه بررسی می کند.
نتیجه گیری
به عنوان یک ابزار توضیحی برای داده های مکانی، تولید سطح دقیق به منظور ارائه اولین نگاه به داده ها ضروری است. هر گونه پیامد تحریف شده احتمالاً تحلیل زیر را گمراه می کند. از آنجایی که CGWR می تواند سطح دقیق تری تولید کند، استفاده از آن برای کاوش داده هایی که حاوی متغیرهای مشکوک با ویژگی های متفاوت هستند مناسب تر است.
زمینه
داده های جمع آوری شده امروزه متنوع بوده و بسیاری از آنها دارای سوابق مکان ها، یعنی داده های مکانی هستند. رگرسیون مکانی یک ابزار محبوب برای تجزیه و تحلیل داده های مکانی است [ 2 ، 35 ] و ایستایی مرتبه اول یک فرض رایج است، به این معنی که مقادیر (میانگین) مورد انتظار در مکان های مختلف ثابت می شوند. شرایط خطای رگرسیون فضایی معمولاً مستقل نیستند و مانند تحلیل سریهای زمانی، کوواریانس آنها از برخی مدلهای فضایی مانند مدلهای خودرگرسیون همزمان (SAR) و میانگین متحرک (MA) پیروی میکند [ 12 ، 30 ، 34 ] . با این حال، ایستایی مرتبه اول در عمل یک فرض مشکوک است و مشکل واحد منطقه ای قابل اصلاح (MAUP) اغلب رخ می دهد [5 ، 13 ، 22 ]. MAUP یک نسخه فضایی از پارادوکس سیمپسون است، که در آن روندهایی که در گروههای جداگانه دادهها ظاهر میشوند با دادههای کل متفاوت است. تخمین های مغرضانه ممکن است نتیجه یکسان نبودن مقادیر پارامتر در منطقه مورد مطالعه و گنجاندن داده ها با ویژگی های مختلف باشد.
از آنجایی که مقادیر پارامتر در مکانهای مختلف یکسان نیستند، تخمین از طریق حداقل مربعات معمولی (OLS) با همه مشاهدات احتمالاً تمایز محلی را مخدوش میکند. یک راه حل ممکن این است که فقط مکان های داده با ویژگی های مشابه (به عنوان مثال، همگنی) را شامل شود. با این حال، تصمیم گیری در مورد تعداد گروه ها با ویژگی های مختلف و شناسایی مکان داده ها در هر گروه دشوار است. علاوه بر این، مقدار میانگین یک فرآیند غیر ثابت معمولاً یک تابع پله ای [ 8 ] است یا در سراسر فضا پیوسته است، و یافتن مرز دقیق مکان های مناسب دشوار است. امکان دیگر استفاده از مدل ضرایب متغیر [ 10 ] است که به شرایط ضرایب اجازه می دهد تا با توجه به مکان ها متفاوت باشند. سپس، مدل شکلی از مدلهای خطی محلی است [15 ] و می تواند برای کشف ویژگی دینامیکی داده های مکانی استفاده شود. بر اساس مفهوم مدل ضرایب متغیر، رگرسیون وزندار جغرافیایی (GWR) برای حل MAUP اصلاح میشود [ 6 ].
GWR به ضرایب رگرسیون اجازه می دهد تا در فضا متفاوت باشد، و تخمین ضرایب همه متغیرها از یک پنجره داده متحرک به دست می آید، که مشابه رگرسیون هسته برای به دست آوردن تخمین هموارسازی است. همچنین یک ابزار محبوب برای تجزیه و تحلیل داده های اکتشافی (EDA) بر روی داده های مکانی است [ 19 ، 32 ]. به طور خاص، GWR اغلب یک ابزار تجسم محبوب در سیستم اطلاعات جغرافیایی است، برای کشف الگوهای احتمالی یک منطقه مورد مطالعه و به دست آوردن اطلاعات ارزشمند برای تجزیه و تحلیل بیشتر داده ها (مانند تشخیص خوشه ها) [ 11 ، 36 ]. توجه داشته باشید که عرض (یا پهنای باند) بهینه پنجره های متحرک در یک GWR توسط اعتبارسنجی متقابل (CV) یا معیار اطلاعات Akaike (AIC) تعیین می شود [ 16 ].]. OLS را می توان به عنوان یک مورد خاص از GWR با پنجره ای با عرض نامحدود در نظر گرفت (اگرچه تمایز محلی احتمالاً با میانگین گیری همه مشاهدات از بین می رود).
بسیاری از تغییرات در GWR در انتخاب و آزمایش پهنای باند است. به عنوان مثال، استفاده از CV و AIC برای انتخاب پهنای باند، یک روش مبتنی بر داده است، شبیه به روش رگرسیون هسته، که در آن برآوردها به مقادیر پرت حساس هستند [ 16 ]. علاوه بر این، تغییرات داده ها لزوماً یکسان نیستند و یک پهنای باند ثابت احتمالاً باعث ایجاد اختلاف در برآورد پارامترها در مکان های مختلف می شود. از سوی دیگر، آزمون فرضیه پارامترها به پهنای باند نیز بستگی دارد. به عنوان مثال، لئونگ و همکاران. [ 21 ] تست های برازش خوب را پیشنهاد کرد و دریافت که درجه آزادی باقیمانده های GWR تابعی از پهنای باند است، و این انتخاب پهنای باند را تا حدودی ذهنی می کند.
تعیین پهنای باند احتمالاً تمرکز اصلاح GWR در طول سالها است. براندون و همکاران [ 7 ] یک مدل GWR مختلط با پهنای باند برداری را معرفی کرد، که به ضرایب اجازه میدهد پهنای باند متفاوتی داشته باشند (از طریق یک الگوریتم backfitting) و پهنای باند تابعی از چگالی داده باشند. شی و همکاران [ 27 ] وزن داده ها را به جای فاصله بین مشاهدات، توسط ویژگی های آنها تعیین می کند. علاوه بر این، Farber و Páez [ 16 ] دریافتند که کاهش سوگیری با اصلاح روش CV امکان پذیر است. متعاقبا، وانگ و همکاران. [ 31 ] تخمین خطی محلی یا یک تکنیک برازش چند جمله ای را برای کاهش تعصب در برآورد پارامترها معرفی کرد.
دلیل در نظر گرفتن پهنای باند متفاوت این است که GWR علاوه بر تخمین های مغرضانه، تمایل به تولید سطوح ناهموار دارد. فرض کنید سطوح واقعی خطی یا خطی هستند. همانطور که در شکل 1 نشان داده شده است ، نقاط داغ (کاذب) و نقاط سرد (کاذب) در تخمین GWR وجود دارد، و به ویژه در لبه ها و گوشه ها، جایی که مقادیر واقعی و سطوح تخمین زده شده در ردیف اول و دوم قرار دارند، مشهود هستند. ، به ترتیب. تعصب GWR برای سطوح برآمدگی (و سایر سطوح غیر خطی) بزرگتر می شود و به نظر می رسد GWR تفسیرهای گمراه کننده ارائه می دهد. بحث های مفصل برآوردهای GWR بعداً در این دست نوشته ارائه شده است.
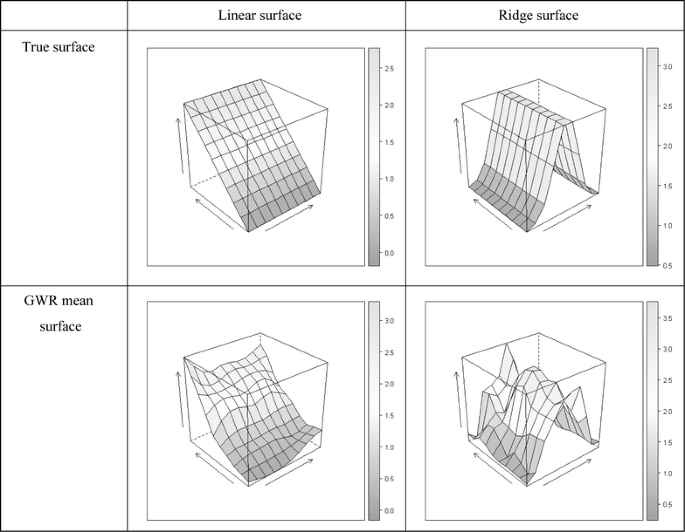
سطوح واقعی و سطح میانگین GWR. شکل سطوح واقعی و سطح پاسخ GWR تخمینی را مقایسه می کند (سطح خطی و خط الراس)
در این مطالعه، تمرکز ما نیز بر روی انتخاب پهنای باند برای هر متغیر با استفاده از همبستگی بین متغیرهای مستقل است. ایده رویکرد پیشنهادی استفاده از همبستگیها برای بهبود تخمین از طریق یک الگوریتم تکرار، مشابه روش کنترل تغییر در کاهش واریانس است [ 24 ]. تجزیه و تحلیل تجربی GWR نشان داد که اغلب همبستگی بین ضرایب GWR وجود دارد. برای مثال، بیوند و برونستاد [ 4 ] دریافتند که ضرایب در یک مطالعه موردی همبستگی بالایی دارند. ما دریافتیم که سطوح ضریب ناهموار می توانند صاف تر باشند (شکل 1 ) اگر ضرایب همبستگی مثبت داشته باشند.
برای ادامه این مقاله، ابتدا GWR و اصلاح پیشنهادی GWR، GWR شرطی (CGWR) و نتایج نظری آن را معرفی میکنیم. سپس از شبیه سازی برای ارزیابی روش پیشنهادی و مقایسه آن با GWR پایه و روش خطی محلی پیشنهاد شده توسط وانگ و همکاران استفاده می کنیم. [ 31 ]. علاوه بر شبیهسازی، روش پیشنهادی را برای دو مجموعه داده برای مطالعه تجربی نیز اعمال میکنیم. در نهایت، با بحث هایی در مورد محدودیت ها و کاربرد آتی روش پیشنهادی به پایان می رسیم.
مواد و روش ها
GWR یک متغیر وابسته y را از طریق یک تابع خطی از مجموعهای از p متغیرهای مستقل مدلسازی میکند، \(x_{1},x_{2}, \ldots,x_{p}\) یا
که در آن \(\beta_{ik}\) و \(x_{ik}\) پارامترها و مقادیر مشاهدهشده متغیر مستقل k \((k = 1, \ldots ,p)\) برای مشاهده i هستند. \(\varepsilon_{i}\) عبارت خطای مشاهده i است که معمولاً فرض میشود از یک توزیع نرمال با میانگین صفر و واریانس ثابت \(\sigma^{2}\) است (یعنی \(\varepsilon_ {i} \sim N(0,\sigma^{2} )\) ). زیرنویس i نشان دهنده مکان فضایی مشاهده i \((i = 1, \ldots ,n)\) است. به عبارت دیگر، هر مکان دارای مدل رگرسیون خاص خود در مدل GWR است. ایده پشت معادله (1 ) این است که داده های نزدیک هر مکان معمولاً دارای ویژگی های مشابه هستند. بنابراین، انتخاب یک محدوده مناسب (که در این مطالعه به عنوان “پهنای باند” نامیده می شود) برای به دست آوردن یک رگرسیون محلی خوب قابل قبول است.
مجموعه پارامتر \(\varvec{\beta}_{\varvec{i}}\) مشاهده i توسط جبر ماتریسی مشتق شده است، یا
جایی که \(\hat{\varvec{\beta }}_{\varvec{i}} = (\hat{\beta }_{i0} ,\hat{\beta }_{i1} , \ldots ,\hat {\beta }_{ip} ^{T},{\mathbf{X}} = ({\mathbf{1}},\varvec{x}_{1} , \ldots ,\varvec{x}_ {p} )^{T}،\varvec{Y} = ({\text{Y}}_{1}، \ldots،{\text{Y}}_{\text{n}})^{\ text{T}}\) و \({\mathbf{W}}_{{\mathbf{i}}}\) ماتریس وزنی (مورب) با وزن آن \(w_{ij}\) ردیف i است. و ستون j به صورت زیر تعریف می شود:
همانطور که قبلا ذکر شد، انتخاب پهنای باند به طور کلی با به حداقل رساندن امتیاز CV یا AIC کالیبره می شود. با این حال، اگر مکانهای دادهها در منطقه مورد مطالعه پراکنده باشند، هسته وزندار فاصله ممکن است به دلیل اطلاعات ناکافی مناسب نباشد. براندون و همکاران [ 8 ] روشهای مبتنی بر رتبه و k نزدیکترین همسایگی را برای مقابله با دادههای پراکنده معرفی کرد. علاوه بر GWR، یکی از اصلاحات آن توسط وانگ و همکاران را نیز در نظر می گیریم. [ 31 ]. این یک رویکرد خطی محلی، یا یک نسخه گسترش تیلور از GWR است، و انتظار می رود اگر سطح جغرافیایی خطی شکل باشد، برازش بهتری داشته باشد.
استفاده از یک پهنای باند واحد در GWR احتمالاً تخمین های رضایت بخشی ایجاد می کند اگر ویژگی های متغیرهای مستقل مشابه نباشند. به عنوان مثال، متغیرهای مستقل با تغییرات بزرگتر به پهنای باند بیشتر (و مشاهدات بیشتر) نیاز دارند. از سوی دیگر، نمونهگیری محلی (یعنی پهنای باند باریکتر) بر نمونهبرداری جهانی (یعنی پهنای باند وسیعتر) برای مناطقی با تغییرات گرادیان بزرگتر ترجیح داده میشود. این مفهوم شبیه به نمونه برداری با اهمیت به طور گسترده شناخته شده [ 25 ] است که وزن نمونه بیشتری را به منطقه اطلاعاتی اختصاص می دهد. بنابراین، اجازه دادن به پهنای باند متفاوت برای هر متغیر مستقل به نظر میرسد اصلاح مطلوبی برای GWR باشد. متأسفانه، پهنای باند متغیر را نمی توان با حداقل مربعات وزن دار یا معادله مدیریت کرد. ( 2 ). براندون و همکاران [ 7] یک الگوریتم پشتیبان برای انتخاب پهنای باند مختلف پیشنهاد کرد، اما انتخاب پهنای باند تا حدودی عینی است و معمولاً به زمان محاسبات زیادی نیاز دارد.
در این مطالعه، ما یک رویکرد (GWR مشروط؛ CGWR) را برای تعیین پهنای باند برای هر متغیر مستقل با تکرار معرفی میکنیم که از روش پهنای باند برداری براندون و همکاران الهام گرفته شده است. [ 7 ] و روش هموارسازی هسته در مدل ضریب متغیر وو و چیانگ [ 33 ]. برای روش پیشنهادی، ما ایدههای مدل اعتیادی تعمیم یافته (GAM) و تکرار Jacobi [ 17 ، 20 ، 23 ، 28 ] را برای تعیین پهنای باند مناسب تطبیق میدهیم. با استفاده از فرمت GAM، مدل GWR را می توان دوباره به صورت بیان کرد
جایی که \(f_{ik} = \beta_{ik} \times x_{ik}\) و \(\beta_{ik}\) ضریب پارامتر متغیر k در مکان i است. اگر \(f_{ik}\) وقفه باشد، \(x_{ik}\) روی 1 تنظیم میشود. سپس میتوانیم از تکرار Jacobi برای حل معادلات استفاده کنیم. ( 4 )، یک به یک، برای پارامتر \(f_{ik}\) . مجدداً، فرض میکنیم که \(\varvec{f}_{k} \{ l\}\) نشاندهنده l امین بردار تکرار \(\varvec{f}_{k}\) است و \(\varvec{ f}_{k} \{ l\}\) نشان دهنده یک بردار n × 1 متشکل از \(f_{k}\) است.. سپس، روش پیشنهادی را می توان به صورت تکراری به صورت زیر خلاصه کرد:
- مرحله 1. راه حل اولیه \(\varvec{f}_{k}\) را صفر کنید، یعنی \(\varvec{f}_{k} \{ 0\} = {\mathbf{0}} \) ، جایی که \(k = 1، \ldots ,p\) و اجازه دهید \(l = 1\) .
- مرحله 2. برای هر عنصر \(\varvec{f}_{k} \{ l\}\) ، مدل پایه GWR را تنها با یک متغیر مستقل، \(x_{k} .\) اعمال کنید. متغیر \(\varvec{y}^{*} = \varvec{y} – \sum\nolimits_{\begin{زیرآرایه}} j = 1 \\ j \ne k \end{زیرآرایه} }^{ p} {\varvec{f}_{j} \{ \varvec{l} – {\mathbf{1}}\} }\) ، یعنی ما پسرفت می کنیم \(\left( {\varvec{y} – \sum \nlimits_{\begin{زیرآرایه}{l} j = 1 \\ j \ne k \end{زیرآرایه} }^{p} {\varvec{f}_{j} \{ l – 1\} } } \ راست)\) روی متغیر \(\varvec{x}_{k}\) بدون وقفه مناسب. پهنای باند با به حداقل رساندن مجموع مربعات تایید شده متقاطع (CVSS) یا AIC به دست می آید.
- مرحله 3. مرحله 2 را تا رسیدن به معیار توقف داده شده تکرار کنید.
حداقل دو دلیل برای یافتن راه حل های پهنای باند بهینه به صورت جداگانه با استفاده از تکرار Jacobi وجود دارد. اولاً، اگرچه روشهای عددی پیچیدهتری (مانند روش شبه نیوتن) میتوانند استفاده شوند، تکرار ژاکوبی معمولاً به زمان محاسبات کمتری نیاز دارد. دوم، اگرچه الگوریتمهایی وجود دارند که سریعتر از تکرار Jacobi همگرا میشوند، اما احتمالاً تخمینهای مغرضانهای را تولید میکنند. به عنوان مثال، در فرآیند تکرار گاوس-سیدل، تخمین یک متغیر بر اساس برآوردهای همزمان سایر متغیرها به روز می شود. اگر برآورد برخی از متغیرها دارای سوگیری شدید باشد، ممکن است تخمین سایر متغیرها را آلوده کند.
ما فکر می کنیم که فرآیند تخمین پیشنهادی می تواند همگرایی CGWR را تضمین کند. به طور خاص، اگر پهنای باند در طول تکرار از پیش تعیین شده باشد، ضرایب GWR به یک ثابت برای هر مکان همگرا خواهند شد. ما باید از حالت دو ضریب برای نشان دادن همگرایی استفاده کنیم و اثبات کلی در ضمیمه A در فایل اضافی 1 آورده شده است. توجه داشته باشید که روش Brunsdon و همکاران. [ 7 ] را می توان به عنوان یک مورد خاص از روش CGWR در نظر گرفت که پهنای باند هرگز به روز نمی شود. در بخش بعدی از شبیه سازی کامپیوتری برای ارزیابی پایداری CGWR و مقایسه آن با GWR پایه و اصلاح خطی محلی آن توسط وانگ و همکاران استفاده خواهیم کرد. [ 31 ].
نتایج و بحث
داده های شبیه سازی شده
شبیه سازی کامپیوتری به دو بخش سناریوهای بدون خوشه و با خوشه تقسیم می شود. برای سناریوی دوم، یک خوشه به وقفه اضافه می شود تا میانگین مداخله شیفت را نشان دهد. سناریوی خوشه ای ارزیابی عملکرد روش های برآورد تحت تأثیر یک تغییر سیستماتیک (یا نقاط داغ) در فضا، مانند منابع آلودگی است. علاوه بر این، فرض میشود که ضرایب یکی از چهار سطح زیر را دنبال میکنند: خطی، درجه دوم، خط الراس یا دامنه، و این تنظیمات برای بررسی این است که کدام یک باعث ناهمواری در سطوح تخمین زده میشود. برای سناریوی قبلی، ما همچنین دو نوع سطح را بررسی می کنیم: تک نوع و نوع مخلوط. تفاوت بین این دو نوع سطح در این است که آیا ضرایب از یک نوع سطوح (تک نوع) یا انواع مختلف سطوح (مختلط) پیروی می کنند.
برای سادهتر شدن بحث، فرض کنید فقط دو ضریب، یعنی یک مقطع و یک متغیر مستقل در رگرسیون فضایی وجود دارد، یا
جایی که i یک عدد طبیعی است که محل مشاهده را نشان می دهد. در مرحله بعد، نسبت سیگنال به نویز را تعریف می کنیم، یعنی نسبت S/N، که در آن سیگنال تغییرات سطح ضرایب را نشان می دهد و نویز نوسانات تصادفی مشاهدات است. نسبت S/N بزرگتر با تغییرات بزرگتر در سطوح ضریب همراه است، در این صورت الگوی ضریب تشخیص آسانتر است. به طور خاص، ما فرض می کنیم که سیگنال = \(3 \times \left( {\frac{{\sum\nolimits_{i} {(\beta_{ik} – \bar{\beta }_{k})^{2 } } }}{n – 1}} \right)^{1/2}\)و نویز برابر با انحراف استاندارد عبارت خطا است. در اینجا 0.5 است. بایاس و واریانس تخمین ها را می توان با هم برای ارزیابی دقت CGWR پیشنهادی استفاده کرد. میانگین نرخ تنزیل را به صورت زیر تعریف می کنیم:
که در آن MSE به میانگین مربعات خطا یعنی مجموع واریانس و مجذور بایاس اشاره دارد. توجه داشته باشید که MSE برآورد OLS به عنوان یک معیار برای مقایسه در معادله استفاده می شود. ( 6 ) و می توان آن را برای همه مکان ها با استفاده از میانگین وزنی داده شده توسط:
همانطور که در شکل 2 نشان داده شده است، چهار نوع سطح برای ضرایب وجود دارد . سطوح 1 و 2 توابع چند جمله ای (مربوط به توابع خطی) از متغیرهای مستقل و سطوح 3 و 4 غیر خطی هستند. تنظیمات مشابهی نیز در مطالعات قبلی در مورد GWR [ 30 ] ظاهر میشود و اینها پیامدهای عملی دارند. به عنوان مثال، سطح درجه دوم (سطح 2) اغلب در موقعیتهای مربوط به قیمت مسکن رخ میدهد، که در آن قیمتها برای مکانهای نزدیک به مرکز شهر یا مرکز حملونقل بهطور قابلتوجهی بالاتر است [ 14 ، 31 ]. علاوه بر این، رابطه بین عامل محیطی و قیمت املاک می تواند در مناطق شهری متفاوت از روستاها باشد [ 9 ]]. علاوه بر این، رابطه بین بیماری و عوامل محیطی ممکن است در سطح جغرافیایی غیرخطی ظاهر شود. به عنوان مثال، میزان بروز بیماری دنگی با تراکم جمعیت بسیار مرتبط است، اما به نظر میرسد در صورت وجود سیاست مناسب برای پیشگیری از بیماری، این رابطه از بین میرود . در نتیجه سطح ضرایب می تواند غیر خطی باشد. برای هر سطح غیر ساکن، فرض می کنیم که 10 × 10 نقطه شبکه منظم (یعنی 100 مکان) وجود دارد.
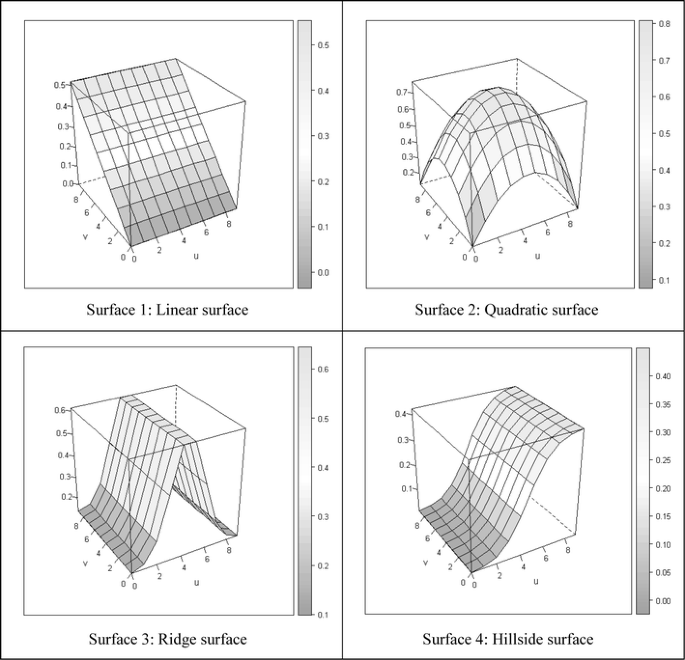
سطوح چهار ضریب. شکل، انواع سطوح مختلف را در تنظیمات شبیه سازی نشان می دهد (1 و 2 چند جمله ای هستند و 3 و 4 غیر چند جمله ای هستند)
برای یک سناریوی بدون خوشه، چندین مورد تحت نسبت های مختلف S/N آزمایش می شوند. حالت اول سطح تک نوع است که هر دو متغیر رهگیر و مستقل از یک نوع سطح پیروی می کنند. حالت دوم، یعنی سطح مخلوط، فرض می کند که رهگیری و متغیر مستقل از انواع سطوح مختلف پیروی می کنند. برای مورد دوم، ما فقط دو ترکیب را بررسی میکنیم: خطی – درجه دوم (یک سطح چند جملهای) و پشته-تپه (یک سطح غیر چند جملهای).
برای سناریوی خوشهها، دو خوشه را در یک فاصله اضافه میکنیم. خوشه ها دایره ای هستند و 18 درصد فضای منطقه مورد مطالعه را اشغال می کنند. فرض دایره ای در مطالعات جغرافیایی کاملاً معمول است، و ادبیات ثابت می کند که 10-20٪ از منطقه خوشه ای یک پدیده رایج است [ 29 ]. دو سطح از تغییرات میانگین، مانند 1σ و 2σ، نیز در مکان های خوشه اضافه شده است. تنظیمات شبیه سازی هر دو سناریو در جدول 1 آمده است. برای همه سناریوها، خطاها از توزیع نرمال با میانگین 0 و انحراف استاندارد 0.5 ترسیم می شوند. دلیل انتخاب انحراف استاندارد 0.5 ترکیب مقادیر نسبت S/N است. همه نتایج بر اساس 100 اجرای شبیه سازی است.
برای CGWR، هسته گاوسی انتخاب می شود و پهنای باند بهینه آن است که حداقل CVSS را داشته باشد. علاوه بر این، ما به محدوده معقولی از پهنای باند نیاز داریم تا از محلی سازی یا جهانی شدن تخمین به ترتیب برای پهنای باند بسیار کوچک یا بزرگ جلوگیری کنیم. حد بالایی محدوده حداکثر طول روی نقشه است و کران پایینی باید حداقل دارای پنج نقطه داده هر یک از وزن 1/5 باشد. تنظیمات قبلی همچنین در بسته ‘spgwr’ [ 3 ] (نسخه 0.5-4) R، یک نرم افزار آماری رایگان، استفاده می شود.
ابتدا نتایج شبیه سازی سناریو را بدون خوشه نشان خواهیم داد. به طور خاص، ما سه تخمین GWR را با صافی سطح متوسط، میانگین نرخ تنزیل، میانگین پهنای باند، واریانس متوسط و میانگین بایاس برآوردها مقایسه خواهیم کرد. معیار توقف برای CGWR زمانی حاصل می شود که میانگین نرخ تغییر نسبی مطلق \(\beta_{0}\) و \(\beta_{1}\) کمتر از 0.005٪ از مرحله قبل باشد. نتایج شبیه سازی در صورت اتخاذ معیارهای توقف کوچکتر مشابه هستند.
برای ساده کردن نماد، از \(\beta_{0}\) و \(\beta_{1}\) به ترتیب برای نشان دادن ضرایب فاصله و شیب متغیر مستقل x استفاده می کنیم . در مورد سطوح تک نوع و سطوح مخلوط، این دو ضریب به ترتیب کاملاً همبسته مثبت و نزدیک به غیر همبسته فرض می شوند. ما همبستگی منفی را در نظر نگرفتیم زیرا الگوریتم پیشنهادی زمانی که ضرایب همبستگی مثبت ندارند کار نمی کند. با این وجود، زمانی که ضرایب همبستگی مثبت نداشته باشند، یک اصلاح دو مرحله ای برای CGWR در نظر خواهیم گرفت.
سطوح تک نوع
ابتدا صافی سه روش مختلف GWR را با هم مقایسه می کنیم. به عنوان مثال، میانگین سطوح از 100 اجرای شبیهسازی برای سطوح درجه دوم و دامنه تپه با نسبت S/N \(\beta_{0}\) = \(\beta_{1}\) = 5 در شکلها نشان داده شده است. 3 و 4 . بدیهی است که CGWR بهترین تناسب را ایجاد می کند و سطوح متوسط تقریباً مشابه سطوح واقعی هستند همانطور که در شکل ها نشان داده شده است. 2 و 3 و 4 . GWR تمایل به تولید سطوح ناهموار دارد که برای \(\beta_{1}\) ناهموارتر هستند.سطوح اثر لبه GWR آشکار است. این ممکن است به این دلیل باشد که مشاهدات کمتری در تخمین استفاده شده است. از سوی دیگر، روش خطی محلی تمایل به تولید سطوح خطی مانند دارد و اطلاعات تحریف شده را برای سطوح غیرخطی و سطوح \(\beta_{1}\) فراهم میکند. در مقابل، CGWR تناسب قابل توجهی را حتی در سطوح پیچیده ایجاد می کند و اطلاعات ارزشمندی را برای تجزیه و تحلیل بیشتر داده ها فراهم می کند.
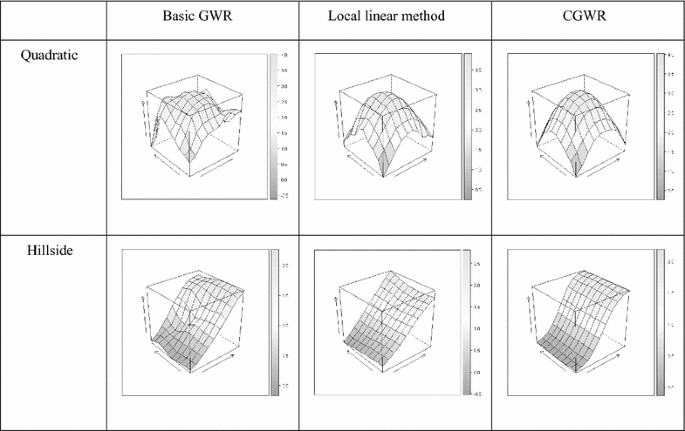
\(\beta_{ 0}\) سطح متوسط. سطح پاسخ رهگیری تخمینی حاصل از روش های مختلف (سطوح درجه دوم و دامنه تپه، نسبت S/N \(\beta_{ 0}\) = \(\beta_{1}\) = 5)
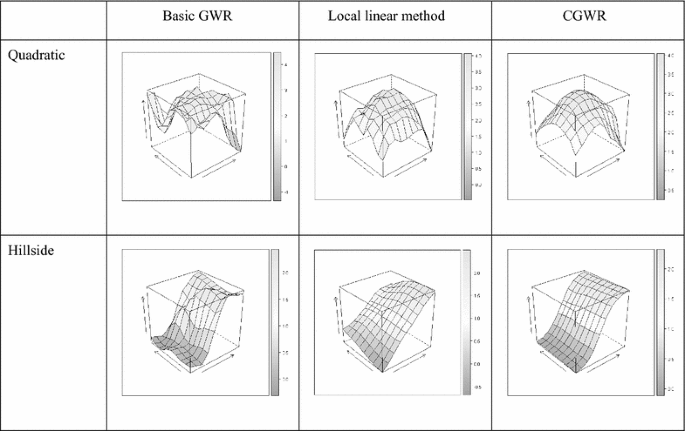
\(\beta_{ 1}\) سطح متوسط. سطح پاسخ رهگیری تخمینی حاصل از روش های مختلف (سطوح درجه دوم و دامنه تپه، نسبت S/N \(\beta_{ 0}\) = \(\beta_{1}\) = 5)
جدول 2 نتایج نرخ های تخفیف را در مواردی نشان می دهد که \(\beta_{0}\) و \(\beta_{1}\) از یک سطح خطی پیروی می کنند. می بینیم که هم روش CGWR پیشنهادی و هم روش خطی محلی پیشرفت های قابل توجهی نسبت به روش پایه GWR دارند. جالب توجه است که روش خطی محلی (با توجه به نرخ های تخفیف کمتر) بهتر از GWR است که نسبت S/N بزرگ باشد، اما GWR پایه زمانی بهتر است که S/N کوچک باشد. دلیل ممکن است این باشد که صداهای بزرگتر نوسانات بزرگتری ایجاد می کنند و بنابراین میانگین خط مماس در روش خطی محلی نادرست یا ناپایدار است. نتایج مشابهی برای سه سطح دیگر نیز یافت شده است، همانطور که در جداول 3 ، 4 و 5 مشاهده می شود.. این نشان می دهد که اگر نسبت S/N کوچک باشد، روش خطی محلی ممکن است خیلی پایدار نباشد.
CGWR و روش خطی محلی مجدداً در مورد یک سطح درجه دوم از روش GWR پایه بهتر عمل می کنند. با این حال، به نظر می رسد که CGWR بهترین است، و مزیت زمانی که S/N افزایش یابد، آشکارتر است. برای سطوح غیر خطی، CGWR به طور رضایت بخشی به کار خود ادامه می دهد، در حالی که مدل خطی محلی اینطور نیست. در واقع، مدل خطی محلی حتی ممکن است نتایج بدتری نسبت به GWR پایه داشته باشد. CGWR هنوز برای سطوح غیر خطی قابل اعتماد است و نسبت به دو روش دیگر بسیار بهتر عمل می کند.
به طور شهودی، ما انتظار داریم که اگر S/N بزرگ باشد، پهنای باند کوچک باشد زیرا مشاهدات دور میتوانند بسیار متفاوت باشند و باعث تخمینهای مغرضانه شوند. به طور کلی، هر سه روش GWR زمانی که نسبت S/N از یک به سه افزایش مییابد، افت قابل توجهی در پهنای باند دارند. علاوه بر این، پهنای باند برای یک سطح خطی باید بزرگتر از پهنای باند برای یک سطح غیر خطی تحت همان نسبت S/N باشد زیرا تغییر سطح در هر جهت کاملاً همگن است.
از نتایج پهنای باند نیز می توان برای توضیح اینکه چرا CGWR از دو روش دیگر بهتر عمل می کند استفاده کرد. ما دو سطح (خطی و دامنه تپه) را برای بحث در مورد این نتایج انتخاب خواهیم کرد. جدول 6 میانگین پهنای باند را نشان می دهد. روش خطی محلی اغلب پهنای باند بزرگتری به دست می دهد. اگر سطح واقعی نزدیک به خطی باشد، میتوانیم روی مشاهدات در پهنای باند بزرگتر تکیه کنیم و بنابراین، واریانسهای کوچکتری نسبت به سطوح غیرخطی داشته باشیم. از آنجایی که شکل دامنه تپه نزدیک به خطی است، پهنای باند در مورد دامنه تپه بسیار شبیه به حالت خطی است. آنها همچنین بسیار بزرگتر از موارد درجه دوم و برجستگی هستند. برای جزئیات بیشتر، به پیوست B در فایل اضافی 1 مراجعه کنید.
به نظر می رسد پهنای باند CGWR با قدرت سیگنال مرتبط باشد. به عنوان مثال، اگر نسبت S/N کوچک باشد، انتظار می رود که پهنای باند بزرگ باشد تا یک تخمین پایدار ارائه شود. اگر نسبت S/N \(\beta_{1}\) را ثابت کنیم ، پهنای باند \(\beta_{0}\) CGWR با نسبت S/N \(\beta_{0}\ کاهش مییابد. ) برای هر چهار سطح افزایش می یابد (پیوست B در فایل اضافی 1 ). اگر نسبت S/N \(\beta_{0}\) را ثابت کنیم، نتایج مشابهی برای پهنای باند \(\beta_{1}\) باقی خواهد ماند . نتایج شبیه سازی CGWR با انتظارات ما مطابقت دارد.
از واریانس ها و بایاس های تخمین های سه روش GWR نیز می توان برای مقایسه استفاده کرد. مجدداً از موارد سطوح خطی و برآمدگی برای بحث مفصل استفاده خواهیم کرد. علاوه بر این، از آنجا که ترکیبهای زیادی برای نسبت S/N \(\beta_{0}\) و \(\beta_{1}\) وجود دارد، ما فقط زمانی نتایج را نشان دادهایم که نسبت S/N برابر با یک و پنج باشد. . نتایج در جداول 7 و 8 نشان داده شده است. برخلاف مقایسههای قبلی، ما واریانسها و سوگیریهای تخمین OLS را نیز ارائه میکنیم. به طور کلی، نسبت S/N بزرگتر تمایل به ایجاد یک سوگیری بزرگتر دارد. علاوه بر این، تخمینهای OLS نمیتوانند روند مکانی را که بیشترین سوگیری را ایجاد میکند، ثبت کند، اما از تمام مشاهدات در تخمین (یعنی پهنای باند نامحدود) استفاده میکند و بنابراین کمترین واریانس را دارد. در مورد سه تخمین GWR، واریانس برآوردگرها به طور کلی بزرگتر از بایاس ها هستند.
نتایج سطح خطی در جدول 7 آمده است. همانطور که قبلا ذکر شد، میانگین پهنای باند روش خطی محلی، بزرگترین هستند، که احتمالاً نشان دهنده کوچکترین واریانس ها است. علاوه بر این، روش خطی محلی دارای کمترین بایاس و کمترین نرخ تنزیل برای سطوح خطی است (جدول 2 ). اگرچه CGWR نسبت به روش خطی محلی در مورد سطح خطی بایاس بزرگتری دارد، اما با توجه به واریانس و بایاس بر روش GWR اصلی غالب است. CGWR بهترین عملکرد را با سطوح برآمدگی دارد و از GWR پایه و روش خطی محلی با توجه به واریانس و بایاس بهتر عمل می کند.
سطوح از نوع مخلوط
بعد، ما همان مقایسهها را برای سه روش تخمین GWR با سطوح مخلوط تکرار میکنیم. نتایج مشابه سطوح تک نوع است و بنابراین ما فقط نتایج نرخ های تخفیف را نشان خواهیم داد. همانطور که قبلاً ذکر شد، در این سناریو دو حالت وجود دارد: خطی-مربع (یک سطح چند جمله ای) و دامنه پشته-تپه (یک سطح غیر چند جمله ای). در حالت اول، سطح زیرین برش خطی است و شیب آن درجه دوم است. در حالت دوم، تمام سطوح از نوع غیر چند جمله ای هستند و از سطح اول پیچیده تر است.
اساساً، CGWR همچنین نرخ های تخفیف کمتری نسبت به GWR پایه برای سطوح مخلوط دارد (جدول 9 ، 10 ). ما بر نتایجی تمرکز خواهیم کرد که با نتایج سطوح تک نوع متفاوت است. اگرچه برآورد خطی محلی بهتر از GWR برای سطوح خطی-مربع است، اما برای سطوح پشته-تپهای عملکرد نامطلوبی دارد. استفاده از روش برازش خطی برای تقریب سطوح غیر خطی، مانند حالت یال- دامنه تپه، کافی نیست. در مقابل (شبیه به موارد تک نوع) CGWR بر دو روش دیگر در هر دو مورد غالب است.
روش نصب دو مرحله ای
ما دریافتیم که CGWR زمانی که یک همبستگی مثبت وجود دارد به خوبی کار می کند. با این حال، در واقعیت، احتمال زیادی وجود دارد که متغیرها همبستگی مثبت نداشته باشند. برای غلبه بر این مشکل، CGWR را می توان به یک فرآیند دو مرحله ای تغییر داد. در مرحله اول متغیرها را به دو گروه تقسیم می کنیم. در هر دو گروه، متغیرها در گروه همبستگی غیرمنفی (یا مثبت) دارند. هر دو متغیر اگر از گروه های مختلف باشند، همبستگی غیرمثبت (یا منفی) دارند. یک گروه از متغیرها را انتخاب می کنیم و روش GWR پایه را برای این گروه اعمال می کنیم. در مرحله دوم، روش CGWR را با ثابت در نظر گرفتن متغیرهای گروه اول (انتخاب شده در مرحله اول) برای گروه دیگر متغیرها اعمال می کنیم.
ما از یک مثال برای نشان دادن برازش دو مرحله ای استفاده می کنیم. فرض کنید دو متغیر مستقل و یک وقفه وجود دارد. اجازه دهید ضرایب دو متغیر مستقل همبستگی منفی داشته باشند. به عبارت دیگر اجازه دهید ضرایب متغیرهای x 1 و x 2 همبستگی منفی داشته باشند و ضرایب بین x 1 و intercepts همبستگی مثبت داشته باشند. ابتدا GWR پایه را روی x 2 در مرحله اول اعمال می کنیم و سپس CGWR را روی قطع و x 1 را در مرحله دوم اعمال می کنیم. ما از یک شبیه سازی برای ارزیابی اصلاح دو مرحله ای استفاده خواهیم کرد و نتایج سطوح خطی و دامنه تپه را در شکل 5 نشان خواهیم داد.. مشابه شبیهسازی قبلی، به نظر میرسد که CGWR دو مرحلهای به خوبی کار میکند حتی زمانی که متغیرها همبستگی مثبت ندارند.
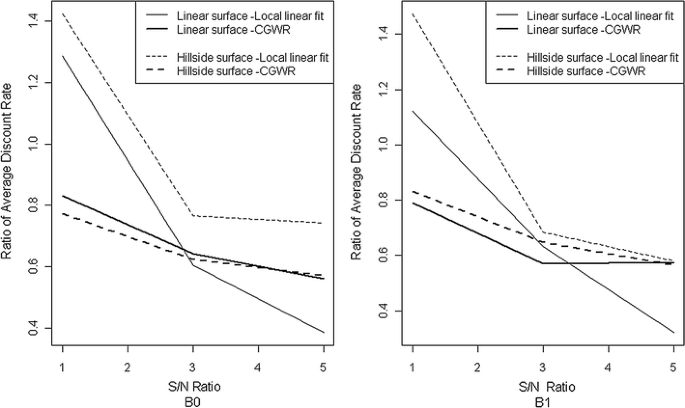
میانگین نرخهای تخفیف براساس \(x_{2}\) . میانگین نرخ تنزیل متغیرهای توضیحی اضافی در طول مطالعه شبیهسازی. خط پایه GWR است. نسبت میانگین نرخ تنزیل تحت نسبت سیگنال به نویز مختلف. پانل سمت چپ عملکرد را در \(\beta_{0}\) نشان میدهد و عملکرد را در \(\beta_{ 1}\) برای پانل سمت راست نشان میدهد.
سطوح تک نوع با خوشه
هدف از در نظر گرفتن سناریو با خوشه ها، بررسی این است که آیا سطح تخمین زده شده تحت تأثیر مداخله خوشه در \(\beta_{ 0}\) قرار می گیرد یا خیر . شکل 6 مکان خوشه و میانگین سطح جابجایی را نشان می دهد. سطوح تک نوع برای ارزیابی عملکرد تحت مداخله خوشه ای فرض می شود. میانگین همواری و میانگین نرخ تنزیل \(\beta_{ 0}\) در شکل 7 و جدول 11 آمده است.. CGWR دوباره بهترین عملکرد را دارد و دقیق ترین اطلاعات مربوط به مکان و اندازه خوشه ها را ارائه می دهد. اگرچه به نظر میرسد GWR مکانهای خوشه واقعی را نشان میدهد، اما از برازش ناهموار رنج میبرد و باعث ایجاد «خوشههای کاذب» میشود. به نظر میرسد روش خطی محلی سطح را بیش از حد صاف میکند و الگوی محلی را محو میکند، اگرچه این ممکن است خوشهای احتمالی در لبهها را نشان دهد.
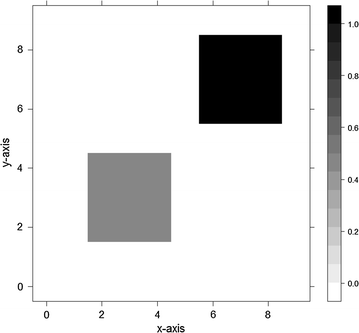
مکان خوشه و میانگین سطح جابجایی. منطقه مداخله خوشه ای را در مطالعه شبیه سازی نشان می دهد . عمق سایه در نمودار اول نشان دهنده میانگین سطح جابجایی است. منطقه شبیه سازی شده در محصول دکارتی در 0 و 1 قرار می گیرد (یعنی [0، 1] × [0،1]). دو خوشه مصنوعی (نقاط داغ) در پایین-چپ و بالا-راست قرار دارند. خوشه پایین سمت چپ ریسک نسبی کمتری دارد و خوشه بالا سمت راست ریسک نسبی بالاتری دارد

\(\beta_{ 0}\) سطح متوسط در تنظیمات خوشه. سطح پاسخ رهگیری تخمینی حاصل از روش های مختلف (سطوح درجه دوم و دامنه تپه، نسبت S/N \(\beta_{ 0}\) = \(\beta_{1}\) = 5)
از مطالعات شبیهسازی رایانهای قبلی، متوجه شدیم که روش CGWR پیشنهادی نسبت به روش پایه GWR پیشرفت قابلتوجهی دارد. اگرچه روش خطی موضعی در سطح خطی به خوبی رفتار می کند، اما اگر سطوح ضریب غیر خطی باشند، CGWR از روش خطی محلی نیز بهتر عمل می کند. در بحث بعدی، از دو مجموعه داده واقعی برای مقایسه CGWR و دو روش دیگر و ارائه شواهد بیشتر در حمایت از CGWR استفاده خواهیم کرد.
داده های تجربی
ما CGWR را به دو مجموعه داده تجربی اعمال میکنیم: اولی از سرشماری سال 2000 تایوان و دیگری دادههای جنایت اوهایو ارائه شده توسط Anselin [ 1 ]. این دو مثال طراحی شده اند تا نشان دهند که CGWR نتایج تخمین بهتری را به همراه دارد. برای دادههای تایوان، هدف ما بررسی رابطه بین نسبت ناتوانی سالمندان و عوامل اجتماعی است. جمعیت سالمندان در تایوان به سرعت در سراسر کشور در حال افزایش است، در حالی که منابع پزشکی هنوز در مناطق شهری (یا شمال تایوان) متمرکز است. هو و یو [ 18 ] مدل رگرسیون فضایی را برای دادههای ناتوانی سالمندان در سطح شهرستان به کار بردند و دریافتند که از نظر فضایی همبستگی خودکار دارند. براندون [ 7] استدلال کرد که به نظر می رسد خودهمبستگی فضایی ناشی از عدم ایستایی فضایی (یعنی قابلیت شناسایی) است. ادعای او ما را به بررسی مجدد داده ها با استفاده از مدل مبتنی بر GWR تشویق می کند.
داده های تایوان
سرشماری 2000 تایوان شامل داده های 350 شهرستان است و نسبت سالمندان معلول آنها به عنوان متغیر وابسته تنظیم شده است. از آنجایی که به نظر میرسد این متغیر دارای انحراف راست است، یک تبدیل گزارش (یعنی \(y_{i}^{*} = \log (y_{i} + 1)\) ) اعمال میشود. چهار متغیر مستقل انتخاب شده اند: تراکم جمعیت (POP)، نسبت سالمندان (ELD)، میزان مرگ و میر سالمندان (EMR)، و سطح تحصیلات (EDU). این متغیرهای مستقل در بازه [0، 1] استاندارد شده اند. قبل از اعمال GWR، ابتدا عدم ایستایی فضایی را با آزمون F پیشنهاد شده توسط Leung و همکارانش آزمایش می کنیم. [ 21 ]. آزمون F نشان می دهد که مدل از نظر فضایی با مقدار p <0.001 غیر ثابت است. این فرضیه براندون را تایید می کند [7 ] و انگیزه ای برای وصل کردن آنالیز نوع GWR ایجاد می کند.
همبستگی رهگیری و متغیر POP 0.463 است (جدول 12 ) و در یک گروه قرار می گیرند. به طور مشابه، متغیرهای ELD، EMR و EDU در گروه دیگر قرار دارند زیرا به صورت زوجی همبستگی مثبت دارند. بنابراین، ما از اصلاح دو مرحلهای استفاده میکنیم و CGWR را روی گروه متغیرهای همبسته مثبت (یعنی رهگیری و متغیر POP) اعمال میکنیم. ابتدا، ما متغیرهای ELD، EMR و EDU را پس از به دست آوردن تخمین از روش پایه GWR به عنوان ثابت در نظر می گیریم. سپس، CGWR را به وقفه و متغیر POP را به صورت \(\left( {y_{i}^{*} – \hat{\beta }_{i2}^{GWR} ELD_{i} – \hat اعمال میکنیم. {\beta }_{i3}^{GWR} HMR_{i} – \hat{\beta }_{i4}^{GWR} EDU_{i} } \right) = \hat{\beta }_{i0} ^{CGWR} + \hat{\beta }_{i1}^{CGWR} POP_{i} + r_{i}\). پس از نصب CGWR، پهنای باند کالیبره شده در بین متغیرها متفاوت است. همچنین مرزهای پایین و بالایی پهنای باند را به ترتیب 1 و 400 کیلومتر تعیین کردیم.
تفاوت قابل توجهی بین تخمین های CGWR و سایر روش ها وجود دارد (شکل 8 ). سطوح ضریب روش خطی محلی به نظر می رسد در جهت شمال-جنوب یا شرق-غرب با مرزهای خطی گسترش می یابند. به طور مشابه، سطوح GWR پایه نیز الگوهای نزولی (یا صعودی) اما با مرزهای منحنی را نشان میدهند. با این حال، رهگیری CGWR خوشهها (یا غلظت) از نرخ بالای ناتوانی را در داخل (مناطق کوهستانی) نشان میدهد. برای متغیر POP، تعداد سطوح ضرایب در بین مدلهای مختلف متفاوت است و جهت انتشار آنها یکسان نیست. GWR دارای کمترین سطح و روش خطی محلی دارای بزرگترین است. گسترش در جهت شرق به غرب برای روش خطی محلی، متفاوت از روش های دیگر است.
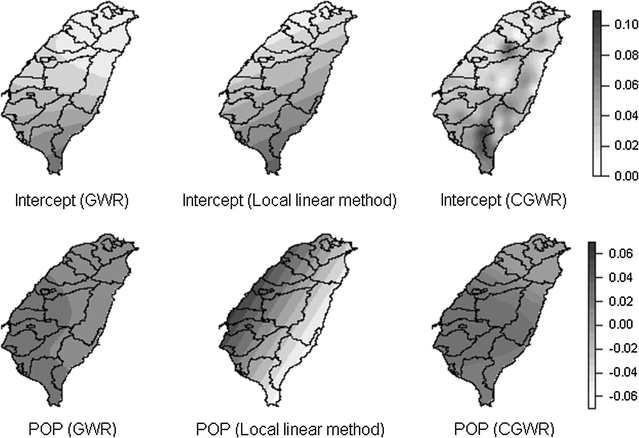
سطح رهگیری و POP متغیر برای روش های مختلف GWR. مقایسه روش های مختلف با استفاده از داده های ناتوانی تایوان
ما همچنین از مقادیر شبه مربع R و نمودارهای باقیمانده برای ارزیابی مدل استفاده می کنیم (شکل 9). شبه R مربع ضریب همبستگی لحظه ضرب پیرسون مقدار برازش و مقدار مشاهده شده است. یک مقدار بزرگ معمولا نشان دهنده تناسب بهتر است. مقدار شبه R مربع CGWR 0.894 است که بزرگترین در بین سه روش است. علاوه بر این، نمودارهای باقیمانده نیز به نفع CGWR هستند زیرا مقادیر پرت کمتری وجود دارد، و به نظر میرسد که CGWR واریانس کمتری دارد. به جز یک مشاهده (باقیمانده استاندارد شده بزرگتر از 3)، هیستوگرام باقیمانده CGWR (350 مشاهده) متقارن تر و کمتر به سمت راست متمایل به نظر می رسد نسبت به روش GWR پایه و روش خطی محلی. لازم به ذکر است که یکی از مجموعه های متغیر را می توان به عنوان ثابت انتخاب کرد. اگر رویه CGWR را برای گروه دیگر متغیرها (یعنی ELD، EMR و EDU) اعمال کنیم.
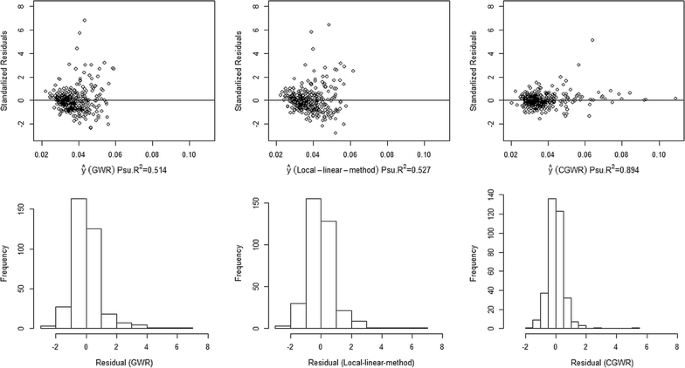
نمودارهای باقیمانده برای روش های مختلف GWR (داده های تایوان). این نمودارها تجزیه و تحلیل باقیمانده را پس از برازش با مدل های مختلف نشان می دهد. باقیمانده ها از داده های ناتوانی تایوان تولید می شوند
داده های اوهایو
دادههای اوهایو، دادههای جنایات اوهایو است (که در بسته ‘spgwr’ یافت میشود) با اطلاعات 49 محله از جمله جنایت به ازای هر ساکن، میانگین ارزش درآمد و میانگین هزینههای مسکن. در این تحقیق جرم به ازای هر ساکن را متغیر وابسته و بقیه آنها را پیش بینی کننده تعریف می کنیم. ابتدا داده ها را با مدل GWR برازش می کنیم. با معیار اعتبار سنجی متقاطع، پهنای باند بهینه 2.27 است (جدول 13 ). و با این حال، لئونگ و همکاران. آزمون F [ 21 ] نشان می دهد که هیچ یک از متغیرها غیر ثابت نیستند. بنابراین، تجزیه و تحلیل OLS اعمال می شود و یک مشاهده به عنوان دور از ذهن در نظر گرفته می شود و بر این اساس حذف می شود.
سپس، دادهها را با CGWR برازش میکنیم و نتیجه تخمین را با نتایج OLS، GWR و مدلهای خطی محلی مقایسه میکنیم. جدول 14 شبه مربع R و مقدار p آزمون نرمال بودن (آزمون کولموگروف-اسمیرنوف) را برای باقیمانده ها فهرست می کند و شکل 10 نمودار باقیمانده ها را نشان می دهد. به طور کلی، CGWR بهترین عملکرد را در تخمین دارد و نتیجه قابل اطمینان تری را ایجاد می کند. برای روش های دیگر، هیچ یک از آنها تخمین رضایت بخشی ارائه نمی دهند. به عنوان مثال، علیرغم اینکه GWR یک شبه R-square بزرگ تولید می کند، باقیمانده های آن به طور معمول توزیع نمی شوند و واریانس آن احتمالاً ثابت نیست. OLS نیز با قضاوت از اطلاعات آزمون نرمال بودن و واریانس ثابت، یک مدل عملی نیست.

نمودارهای باقی مانده از مدل های مختلف (داده های اوهایو). طرح باقیمانده متفاوت از داده های جنایی اوهایو. توجه داشته باشید که قبل از انجام تست F داده ها بر اساس مقادیر برازش شده به نصف تقسیم می شوند . قبل از انجام آزمون واریانس ثابت، داده ها با توجه به مقادیر برازش شده به نصف تقسیم می شوند. به عنوان مثال، نقطه میانی مقادیر برازش GWR حدود 29.1 است. ابتدا داده ها را به دو مجموعه (قبل از 29.1 و بعد از 29.1) تقسیم کردیم. پس از آن، آزمون F برای بررسی اینکه آیا هر دو قسمت دارای واریانس برابر هستند (یعنی \({\text{H}}0:\upsigma^{1} =\upsigma^{2}\) ) انجام می شود، که این فرض اساسی است. در تحلیل رگرسیون مقدار p کوچک نشان می دهد که فرض واریانس ثابت به احتمال زیاد درست نیست
نتیجه گیری
GWR از زمان معرفی خود به ابزاری محبوب برای تجزیه و تحلیل داده های توضیحی و تشخیص ناپایداری فضایی تبدیل شده است. GWR اطلاعات مفیدی را برای تجزیه و تحلیل داده ها فراهم می کند، به ویژه در تصمیم گیری برای متغیرهای توضیحی مهم مفید است. این تکنیک به ضرایب رگرسیون اجازه می دهد تا در فضا تغییر کنند و تخمین های خود را از پهنای باند مشاهدات با توجه به ویژگی داده بدست می آورد. با این حال، GWR تمایل به تولید سطوح ناهموار دارد (همانطور که در شکل 1 نشان داده شده است، و یک پهنای باند ثابت ممکن است مناسب نباشد زیرا متغیرهای مستقل برای همگن بودن ضروری هستند (مثلاً تغییرات آنها می تواند کاملاً متفاوت باشد). در این مطالعه، ما یک اصلاح برای GWR، یعنی CGWR پیشنهاد کردیم، که به گروه متغیرهای مستقل همبستگی مثبت اجازه میدهد تا از طریق یک فرآیند کالیبراسیون تکرار شونده، پهنای باند خاص خود را داشته باشند.
ما از داده های شبیه سازی شده کامپیوتری و تجربی برای مقایسه روش پیشنهادی با GWR و اصلاح خطی محلی آن توسط وانگ و همکاران استفاده کردیم. [ 31 ]. بر اساس نتایج شبیهسازی، متوجه شدیم که CGWR از دو روش دیگر، با توجه به بایاس و واریانس، زمانی که ضرایب رگرسیون همبستگی مثبت دارند، بهتر عمل میکند. این مزیت به ویژه در مورد سطوح غیر خطی قابل توجه است. به طور خاص، خوشه ها تأثیر کمی بر تخمین CGWR دارند. نتایج مطالعات تجربی نیز از CGWR پشتیبانی میکند و به طور کلی دارای R-square بزرگتر است و دارای نقاط پرت شدید کمتری (به عنوان مثال، قدر مطلق باقیمانده استاندارد شده بزرگتر از 2 یا 3) نسبت به GWR و روش خطی محلی است.
با این حال، روش پیشنهادی محدودیت های خود را دارد. اول، احتمالاً بحرانیترین محدودیت، تنظیم فعلی CGWR تنها در صورتی کار میکند که متغیرهای مستقل با همبستگی مثبت وجود داشته باشد. اگرچه در اینجا نشان داده نشده است، اما دریافتیم که CGWR در مورد متغیرهای مستقل با همبستگی منفی به خوبی کار نمی کند. این مانند تنوع ضد در کاهش واریانس ادغام مونت کارلو است. متغیر ضد یکی از روش های کاهش واریانس محبوب است، اما تنها زمانی کار می کند که دو متغیر همبستگی منفی داشته باشند [ 25 ]]. بنابراین، پیشنهاد می کنیم ابتدا ضرایب همبستگی بین متغیرهای مستقل را محاسبه کنید. سپس گروهی از متغیرها را تشکیل دهید که به صورت جفتی همبستگی مثبت دارند و CGWR را فقط برای این گروه از متغیرها اعمال کنید. احتمال دیگر این است که متغیرهای مستقل اغلب می توانند به دو گروه تقسیم شوند و متغیرهای درون/بین گروه ها همبستگی مثبت/منفی دارند، همانطور که در داده های سرشماری 2000 تایوان دیده می شود. ما می توانیم CGWR دو مرحله ای را برای دو گروه از متغیرها اعمال کنیم.
دوم، CGWR یک روش فشرده کامپیوتری است و زمان محاسبات آن با افزایش تعداد متغیرها به سرعت افزایش مییابد، اگرچه میتوان همگرایی ضرایب را با استفاده از روش میانگین متحرک سرعت بخشید. ثالثاً، CGWR در صورت وجود متغیرهای زیاد، تضمینی برای کارکردن ندارد و تا کنون برای مورد تا چهار متغیر مؤثر است. یک اصلاح احتمالی در مورد با متغیرهای بیشتر، جداسازی متغیرها به دو گروه و استفاده از تکرار مضاعف است. سپس، CGWR را می توان برای هر گروه از متغیرها که حلقه داخلی را تشکیل می دهند اعمال کرد و فرآیند را دوباره بین دو گروه که حلقه بیرونی را تشکیل می دهند، تکرار کرد تا زمانی که هر دو گروه متغیرها همگرا شوند. برای نشان دادن امکانپذیری این ایده، آزمایشی را با شش متغیر انجام دادیم و آنها را به دو گروه سه متغیری تقسیم کردیم.
علاوه بر پهنای باند ثابت، به نظر می رسد هنوز در مورد GWR جا برای بهبود وجود دارد. به ویژه، زمانی که نسبت S/N کوچک است، سطوح ضریب تخمینی غیرخطی خواهند بود (یعنی سطوح ناهموار)، حتی زمانی که سطوح واقعی خطی باشند. علاوه بر این، کاهش واریانس CGWR نسبت به GWR آشکارتر از کاهش سوگیری است. این نشان میدهد که برآوردهای GWR زمانی که نسبت S/N کوچک است، واریانس زیادی دارند. به عبارت دیگر، اگر واریانس تخمینهای GWR کاهش یابد، بایاس نیز میتواند بیشتر کاهش یابد و تخمینهای پایدارتری تولید کند.
Fatal error: Uncaught TypeError: ltrim(): Argument #1 ($string) must be of type string, WP_Error given in /home/gisland/public_html/wp-includes/formatting.php:4486 Stack trace: #0 /home/gisland/public_html/wp-includes/formatting.php(4486): ltrim(Object(WP_Error)) #1 /home/gisland/public_html/wp-content/themes/xtra/functions.php(3349): esc_url(Object(WP_Error)) #2 /home/gisland/public_html/wp-content/themes/xtra/single.php(19): Codevz_Core_Theme::generate_page('single') #3 /home/gisland/public_html/wp-includes/template-loader.php(106): include('/home/gisland/p...') #4 /home/gisland/public_html/wp-blog-header.php(19): require_once('/home/gisland/p...') #5 /home/gisland/public_html/index.php(17): require('/home/gisland/p...') #6 {main} thrown in /home/gisland/public_html/wp-includes/formatting.php on line 4486


