ارزیابی دقت و تحلیل مقایسه ای IDW، Spline و Kriging در درونیابی فضایی شکل زمین (توپوگرافی): یک مطالعه تجربی
کلید واژه ها
درونیابی فضایی ، IDW ، کریجینگ ، اسپلاین و مدلسازی ارتفاع
1. مقدمه
هدف درونیابی یافتن مقادیر یک تابع  برای یک
برای یک 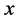 بین
بین 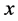 مقادیر مختلف است
مقادیر مختلف است 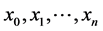 که در آن مقادیر
که در آن مقادیر 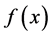 داده شده است. مقادیر داده شده
داده شده است. مقادیر داده شده
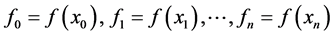 (1)
(1)
را می توان از یک تابع ریاضی یا از یک تابع تجربی مدل سازی شده از مشاهدات یا آزمایشات بدست آورد [ 1 ]. بنابراین درونیابی فضایی به منظور تخمین مقادیر یک پدیده یا تابع فضایی (دما، ارتفاع و غیره) در نقاط مشاهده نشده/تخمین زده شده، مقادیر داده شده پدیده در نقاط مشاهده شده/برآورد شده است.
درونیابی فضایی همچنان ابزار مهمی برای تخمین متغیرهای محیطی فضایی پیوسته برای تصمیمگیری مؤثر است. بسیاری از ابزارهای مدل سازی از جمله سیستم اطلاعات جغرافیایی به دانشمندان زمین و محیط زیست توانایی انجام درونیابی فضایی به طور معمول برای تولید داده های پیوسته فضایی مفید برای انواع تحلیل ها را ارائه می دهند [ 2 ]. درون یابی در سناریوهایی که وضوح، جهت یا اندازه سلول یک سطح گسسته شده با آنچه مورد نیاز است متفاوت است، بسیار مفید و ضروری است. همچنین زمانی به کار می رود که سطح پیوسته با یک مدل داده متفاوت از آنچه مورد نظر است نشان داده شود، و زمانی که پراکندگی داده ها منطقه مورد نظر را به طور کامل پوشش نمی دهد [ 3 ]] . روش های درونیابی فضایی ابزاری برای پیش بینی مقادیر یک پارامتر محیطی در مکان اندازه گیری نشده با استفاده از داده های اندازه گیری های نقطه ای در فضای نمونه می دهد [ 4 ]. در یک وضعیت ایده آل، مجموعه محدودی از ورودی ها تغییراتی را در یک پارامتر محیطی ایجاد می کنند و دقیقاً با یک قانون فیزیکی تثبیت شده مطابقت دارند. در صورت برقراری رابطه، می توان مقادیر پارامتر مورد نظر را به درستی تخمین زد. رابطه بین متغیر هدف و محیط فیزیکی را نمی توان دقیقاً به دلیل پیچیدگی آن مدل سازی کرد [ 5] . این به دلیل عدم آگاهی کافی از موارد زیر است: (الف) فهرست کامل ورودیهای مدل (ب) رابطه مورد نیاز برای تعیین خروجی از این ورودیها و (ج) اهمیت بخش تصادفی سیستم. تخمین مدل با استفاده از اندازه گیری میدانی پارامتر مورد نظر تنها راه می شود [ 6 ].
برای نمونه ای از یک متغیر هدف  ، که به صورت
، که به صورت 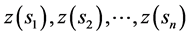 (
( 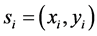 مکان موقعیت مکانی است،
مکان موقعیت مکانی است، 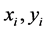 مختصات در فضای جغرافیایی هستند و
مختصات در فضای جغرافیایی هستند و 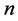 تعداد مشاهدات است)، نشان داده می شود، دامنه جغرافیایی مورد علاقه را می توان به عنوان A نشان داد. توجه تنها به نمونه هایی داده
تعداد مشاهدات است)، نشان داده می شود، دامنه جغرافیایی مورد علاقه را می توان به عنوان A نشان داد. توجه تنها به نمونه هایی داده  می شود که متوجه می شوند. یک فرآیند
می شود که متوجه می شوند. یک فرآیند 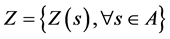 [ 6 ].
[ 6 ].
به گفته میتاس و میتاسووا [ 7 ]، انتخاب روش های درونیابی مناسب برای پدیده ها و مجموعه داده های مختلف، مشکلات زیادی را به همراه دارد. پیچیدگی میدانهای مدلسازیشده، دادههای فضایی متنوع نمونهبرداری غیربهینه، وجود ناپیوستگیهای قابلتوجه، و نویزها چالشهای رایج هستند. علاوه بر این، مجموعه دادههای بهدستآمده از منابع مختلف با دقتهای متفاوت معمولاً بسیار بزرگ 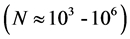 هستند. روشهای درونیابی قابل اعتماد مناسب برای کاربردهای GIS باید برخی از الزامات ضروری مانند دقت و قدرت پیشبینی، فرمولبندی ابعادی، تخمین مستقیم مشتقات، قابلیت کاربرد در مجموعه دادههای بزرگ، راندمان محاسباتی 3+ و سهولت استفاده را برآورده کنند.
هستند. روشهای درونیابی قابل اعتماد مناسب برای کاربردهای GIS باید برخی از الزامات ضروری مانند دقت و قدرت پیشبینی، فرمولبندی ابعادی، تخمین مستقیم مشتقات، قابلیت کاربرد در مجموعه دادههای بزرگ، راندمان محاسباتی 3+ و سهولت استفاده را برآورده کنند.
در حال حاضر، یافتن روشی که تمام الزامات ذکر شده در بالا را برای طیف گسترده ای از داده های جغرافیایی ارجاع داده شده برآورده کند، دشوار است. بنابراین، انتخاب صحیح مناسب ترین روش با پارامترهای مناسب برای کاربردها در اولویت قرار دارد. روش های مختلف نمایش های فضایی متفاوتی را در مجموعه داده های مختلف تولید می کنند. همچنین، دانش عمیق پدیده مورد بحث برای ارزیابی اینکه کدام یک از روش های درونیابی نتایج نزدیک به واقعیت را ایجاد می کند ضروری است. استفاده از یک روش نامناسب یا پارامترهای نامناسب می تواند منجر به مدل تحریف شده توزیع فضایی شود که منجر به تصمیمات بالقوه اشتباه بر اساس اطلاعات مکانی گمراه کننده می شود. نتایج درونیابی اشتباه زمانی بسیار حیاتی می شود که برآوردها ورودی برای شبیه سازی باشند.7 ] .
در حالی که عوامل خارجی مانند تراکم داده ها، توزیع مکانی داده های نمونه، نوع سطح، اندازه نمونه و طرح نمونه گیری و غیره [ 4 ] ممکن است بر عملکرد یک روش درونیابی تأثیر بگذارد، درک فرمول ریاضی این روش ها اطلاعاتی را در مورد مناسب بودن آنها برای مدلسازی زمین
در این مقاله سعی شده است دقت روش های درون یابی فضایی در مدل سازی شکل زمین (توپوگرافی) در رابطه با فرمول ریاضی آنها بررسی شود. مطالعه تجربی این کار از یک منطقه شامل یک شیب و یک دشت به عنوان منطقه آزمایشی سازگاری با فرم زمین استفاده میکند و بر تحلیل مقایسهای سه روش درونیابی متداول کریجینگ، اسپلاین و وزندهی با فاصله معکوس، IDW تمرکز دارد. بخش زیر پایه های نظری و ریاضی روش های مختلف درونیابی شناخته شده از جمله سه روش درونیابی مورد بحث را خلاصه می کند. بخش 3 روش های تجزیه و تحلیل دقت مورد استفاده در این مقاله را معرفی می کند در حالی که بخش 4 تجزیه و تحلیل تجربی را ارائه می دهد. بخش 5 نتایج را مورد بحث قرار می دهد و بخش 6 نتیجه گیری می کند.
2. مفهوم ریاضی و نظری IDW، Spline و Kriging
روشهای درونیابی فضایی مختلف در حوزههای مختلف برای کاربردهای مختلف توسعه یافتهاند. با توجه به [ 6 ]، بسیاری از مدل های خطی استاندارد، موارد خاصی از یک مدل پیش بینی عمومی تر هستند. قانون اول جغرافیای توبلر، همه چیز با هر چیز دیگری مرتبط است، اما چیزهای نزدیک بیشتر از چیزهای دور مرتبط هستند [ 8 ] اصل کلی بسیاری از روش های درونیابی را تشکیل می دهد. برخی از روشها فقط برای فیلدهای داده پیوسته مناسب هستند که توزیع نرمال مجموعه داده را فرض میکنند. روش های درون یابی فضایی را می توان به دو گروه عمده طبقه بندی کرد:
الف) روشهای مکانیکی / قطعی / غیر زمین آماری. از جمله روشهای دیگر، وزندهی با فاصله معکوس (IDW) و Splines.
ب) روش های خطی آماری/ تصادفی/ زمین آماری. که شامل کریجینگ در میان دیگران است [ 4 ]، [ 6 ].
2.1. وزن معکوس فاصله (IDW)
این روش فرض می کند که مقدار در یک مکان ناشناخته را می توان به عنوان میانگین وزنی مقادیر در نقاطی در یک فاصله قطع مشخص یا از تعداد معینی از نزدیکترین نقاط (معمولاً 10 تا 30) تقریب زد. وزن ها معمولاً با توان فاصله [ 9 ] نسبت معکوس دارند که در یک مکان نمونه s غیرنمونه ای به تخمینگر منتهی می شود که در رابطه (2) زیر آمده است.
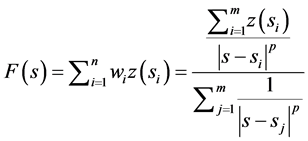 (2)
(2)
که در آن p یک پارامتر است (معمولاً 2 =) [ 7 ] . IDW روشی است که استفاده از آن آسان است و به راحتی در دسترس است. غالباً شکل محلی را که توسط داده ها نشان داده شده است تولید نمی کند و در نقاط داده، اکسترم های محلی تولید می کند [ 7 ]. برخی از تغییرات باعث ایجاد یک کلاس از سطوح و حجم های IDW ترکیبی چند متغیره شده است [ 9 ]. فرض IDW این است که نقاط اندازهگیری شده نزدیکتر به نقطه مجهول شبیهتر از نقاطی هستند که از نظر مقادیر دورتر هستند. وزن به صورت زیر داده می شود:
 (3)
(3)
که 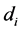 در آن فاصله بین
در آن فاصله بین 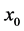 و
و  ، p پارامتر توان است، و n تعداد نقاط اندازه گیری شده مورد استفاده برای تخمین است. عامل اصلی موثر بر دقت IDW مقدار پارامتر توان [ 10 ] است. با افزایش فاصله، وزنها کاهش مییابد، بهویژه زمانی که مقدار پارامتر توان افزایش مییابد، بنابراین نمونههای نزدیک وزن سنگینتری دارند و تأثیر بیشتری بر تخمین دارند، و درونیابی فضایی حاصل محلی است [ 10 ]. انتخاب پارامتر قدرت و اندازه محله دلخواه است [ 11] . محبوب ترین انتخاب p 2 است و روش حاصل اغلب فاصله معکوس مربع یا مجذور فاصله معکوس (IDS) نامیده می شود. پارامتر توان همچنین می تواند بر اساس اندازه گیری خطا انتخاب شود (به عنوان مثال، حداقل میانگین خطای مطلق)، که منجر به IDW بهینه می شود [ 2 ]. صافی سطح تخمین زده شده مستقیماً با پارامتر توان تغییر می کند، و مشخص شد که نتایج برآورد شده زمانی که p 1 و 2 است در مقایسه با زمانی که pis 4 است کمتر رضایت بخش می شود [ 12 ]. IDW بهعنوان «میانگین متحرک» وقتی پیس صفر [ 13 ]، «درون یابی خطی» در پی 1 و «میانگین متحرک وزنی» زمانی که پی با 1 برابر نیست [ 3 ] نامیده میشود.
، p پارامتر توان است، و n تعداد نقاط اندازه گیری شده مورد استفاده برای تخمین است. عامل اصلی موثر بر دقت IDW مقدار پارامتر توان [ 10 ] است. با افزایش فاصله، وزنها کاهش مییابد، بهویژه زمانی که مقدار پارامتر توان افزایش مییابد، بنابراین نمونههای نزدیک وزن سنگینتری دارند و تأثیر بیشتری بر تخمین دارند، و درونیابی فضایی حاصل محلی است [ 10 ]. انتخاب پارامتر قدرت و اندازه محله دلخواه است [ 11] . محبوب ترین انتخاب p 2 است و روش حاصل اغلب فاصله معکوس مربع یا مجذور فاصله معکوس (IDS) نامیده می شود. پارامتر توان همچنین می تواند بر اساس اندازه گیری خطا انتخاب شود (به عنوان مثال، حداقل میانگین خطای مطلق)، که منجر به IDW بهینه می شود [ 2 ]. صافی سطح تخمین زده شده مستقیماً با پارامتر توان تغییر می کند، و مشخص شد که نتایج برآورد شده زمانی که p 1 و 2 است در مقایسه با زمانی که pis 4 است کمتر رضایت بخش می شود [ 12 ]. IDW بهعنوان «میانگین متحرک» وقتی پیس صفر [ 13 ]، «درون یابی خطی» در پی 1 و «میانگین متحرک وزنی» زمانی که پی با 1 برابر نیست [ 3 ] نامیده میشود.
2.2. اسپلاین
Splines متعلق به گروهی از interpolators به نام توابع پایه شعاعی (RBF) است. روشهای این گروه عبارتند از Spline با صفحه نازک (TPS)، Spline منظم با کشش، و Inverse Multi-Quadratic Spline [ 14 ]. این مدل ها از توابع ریاضی برای اتصال نقاط داده نمونه برداری شده استفاده می کنند. آنها سطوح مستمر ارتفاع و درجه را تولید می کنند در حالی که خمش سطح تولید شده را به حداقل محدود می کنند. مدلهای RBF به بهترین وجه در سطوح صافی که اندازه دادههای نمونه موجود برای آنها بزرگ است، استفاده میشوند، زیرا عملکرد آنها برای سطوحی با تغییرات قابلملاحظه در محدودههای کوتاه کمتر از حد مطلوب است. در IDW [ 14] . توابع Spline معادل های ریاضی نقشه نگاران خط کش انعطاف پذیر هستند که به آنها spline می گویند تا منحنی های صاف را در چندین نقطه ثابت قرار دهند. این یک چند جمله ای تکه تکه متشکل از چندین بخش است که هر یک از آنها به تعداد کمی از نقاط برازش داده می شود به گونه ای که هر یک از بخش ها در نقاطی که به آنها نقاط شکست می گویند به هم می پیوندند. این مزیت سازگاری با تنظیمات محلی را دارد، اگر در یک نقطه تغییری در مقدار داده وجود داشته باشد، و به یک درونیابی چند جمله ای ساده ترجیح داده می شود زیرا پارامترهای بیشتری را می توان تعریف کرد، از جمله میزان هموارسازی [ 3 ].] . Splines معمولاً با استفاده از چند جملهایهای مرتبه پایین (یعنی مرتبه دوم یا سوم) محدود شده برای پیوستن به بالا برازش میشوند. آنها ممکن است دو بعدی (به عنوان مثال هنگام صاف کردن یک خط کانتور) یا سه بعدی (هنگام مدل سازی یک سطح) باشند. تابع spline هموارسازی نیز وجود یک خطای اندازه گیری را در داده ها فرض می کند که باید به صورت محلی هموار شوند [ 3 ]. در میان بسیاری از نسخه ها و اصلاحات درون یابی اسپلاین، پرکاربردترین تکنیک، اسپلاین های صفحه نازک [ 15 ] و همچنین اسپلاین منظم با کشش و صاف کردن [ 7 ] است.
2.2.1. اسپلاین منظم با کشش
برای اسپلاین منظم با کشش و هموارسازی، پیشبینی توسط:
 (4)
(4)
که در آن a 1 یک ثابت است و R(v i ) تابع پایه شعاعی است که توسط:
 (5)
(5)
و
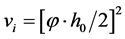 (6)
(6)
که  در آن تابع انتگرال نمایی است،
در آن تابع انتگرال نمایی است،  ثابت اویلر است،
ثابت اویلر است،  پارامتر کشش تعمیم یافته
پارامتر کشش تعمیم یافته  است و جدایی بین نقطه جدید و درونیابی است. ضرایب
است و جدایی بین نقطه جدید و درونیابی است. ضرایب  و
و  با حل سیستم به دست می آیند،
با حل سیستم به دست می آیند،
 (7)
(7)
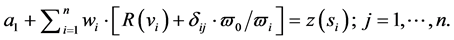 (8)
(8)
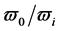 عوامل وزنی مثبت برای پارامتر هموارسازی در هر مکان کجا هستند [ 7 ]. پارامتر کشش
عوامل وزنی مثبت برای پارامتر هموارسازی در هر مکان کجا هستند [ 7 ]. پارامتر کشش  فاصله ای را تعیین می کند که نقاط داده شده بر روی سطح حاصل تأثیر می گذارد، در حالی که پارامتر هموارسازی انحراف عمودی سطح از مکان های نمونه را کنترل می کند. استفاده از ترکیب مناسب کشش و صاف کردن سطحی را ایجاد می کند که به درستی با دانش تجربی در مورد تغییرات مورد انتظار مطابقت دارد [ 7 ].
فاصله ای را تعیین می کند که نقاط داده شده بر روی سطح حاصل تأثیر می گذارد، در حالی که پارامتر هموارسازی انحراف عمودی سطح از مکان های نمونه را کنترل می کند. استفاده از ترکیب مناسب کشش و صاف کردن سطحی را ایجاد می کند که به درستی با دانش تجربی در مورد تغییرات مورد انتظار مطابقت دارد [ 7 ].
2.2.2. Spline صفحه نازک
وهبا و وندلبرگر [ 16 ] خطوط صفحه نازک (TPS) را که قبلاً خطوط صاف کننده لاپلاسی نامیده می شد، برای مدل سازی داده های اقلیمی فرموله کردند [ 4 ]. یک راه حل اساسی برای معادله دو هارمونیک، شکل دارد
 (9)
(9)
جایی که r فاصله بین نقاط نمونه و مکان های نمونه برداری نشده است [ 17 ].
رابطه زیر سطحی را با حداقل خمش تقریبی می کند
 (10)
(10)
در جایی که عبارات  قسمت خطی سطح را که یک دشت مسطح را که به بهترین وجه با تمام نقاط کنترل مطابقت دارد با استفاده از حداقل مربع ها مدل می کنند، آخرین عبارت نیروهای خمشی ناشی از m نقاط نمونه برداری شده را مدل می کند،
قسمت خطی سطح را که یک دشت مسطح را که به بهترین وجه با تمام نقاط کنترل مطابقت دارد با استفاده از حداقل مربع ها مدل می کنند، آخرین عبارت نیروهای خمشی ناشی از m نقاط نمونه برداری شده را مدل می کند،  ضرایب نقاط کنترل
ضرایب نقاط کنترل  است و جدایی نقطه نمونه برداری
است و جدایی نقطه نمونه برداری  و مکان است .
و مکان است .  . مجهولات
. مجهولات  و
و  با استفاده از رابطه ارزیابی می شوند
با استفاده از رابطه ارزیابی می شوند
 (11)
(11)
جایی که
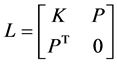 (12)
(12)
و V بردار ارتفاع نقطه است. K ماتریسی از فاصله بین نقاط نمونه برداری شده و P ماتریسی از مختصات نقاط نمونه برداری است.  با محاسبه معکوس L یا حل معادله 11 با V جایگزین شده با ماتریس ارتفاع نقاط نمونه برداری شده H با صفر به دست می آید [ 18 ]. هنگامی که مجهولات ارزیابی شدند، می توان EQ.10 را برای تعیین ارتفاع نقاط مجهول محاسبه کرد. TPS با محدود کردن تابع اعتبار سنجی متقابل تعمیم یافته، GVC، یک عامل هموارسازی را محاسبه می کند، و یک مدل نسبتاً محکم را ایجاد می کند زیرا محدود کردن GVC دقت تخمین ها را بهبود می بخشد. و کمتر به دقت خود مدل متکی است. TPS تعیین دقت مکانی را ارائه می دهد [ 7 ].
با محاسبه معکوس L یا حل معادله 11 با V جایگزین شده با ماتریس ارتفاع نقاط نمونه برداری شده H با صفر به دست می آید [ 18 ]. هنگامی که مجهولات ارزیابی شدند، می توان EQ.10 را برای تعیین ارتفاع نقاط مجهول محاسبه کرد. TPS با محدود کردن تابع اعتبار سنجی متقابل تعمیم یافته، GVC، یک عامل هموارسازی را محاسبه می کند، و یک مدل نسبتاً محکم را ایجاد می کند زیرا محدود کردن GVC دقت تخمین ها را بهبود می بخشد. و کمتر به دقت خود مدل متکی است. TPS تعیین دقت مکانی را ارائه می دهد [ 7 ].
2.2.3. اسپلاین چند درجه دوم معکوس
رابطه زیر تابع spline چند درجه دوم معکوس را نشان می دهد
 (13)
(13)
 فاصله اقلیدسی بین نقاط کنترل
فاصله اقلیدسی بین نقاط کنترل  و نقطه مجهول کجاست
و نقطه مجهول کجاست  [ 15 ] . سطح توسط تابع مدل شده است
[ 15 ] . سطح توسط تابع مدل شده است
 (14)
(14)
که در آن وزن  ها برای اطمینان از برآورد دقیق در هر نقطه داده انتخاب می شوند به طوری که
ها برای اطمینان از برآورد دقیق در هر نقطه داده انتخاب می شوند به طوری که
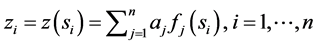 (15)
(15)
و توسط رابطه محاسبه می شود
 (16)
(16)
در جایی که z با بردار مقادیر داده های نمونه گیری شده جایگزین می شود، F یک ماتریس تابع مربعی است که توسط،
 (17)
(17)
تابع تخمین تولید شده با این وزن ها در نقاط داده نمونه برداری شده صاف و دقیق است [ 19 ].
Splines به طور گسترده ای به عنوان بسیار مناسب برای برآورد ارتفاعات متراکم نمونه برداری شده و متغیرهای آب و هوایی [ 7 ]، [ 15 ] دیده می شود. از جمله معایب آن، ناتوانی در ادغام مقادیر بیشتری از نقشه های کمکی در مدل سازی بخش قطعی تغییر و همچنین انتخاب دلخواه پارامترهای هموارسازی و کشش به طور گسترده مورد انتقاد قرار گرفته است [ 7 ]. بنابراین پیشبینیهای بهدستآمده از splines تا حد زیادی به تصمیمهایی مانند ترتیب چندجملهای مورد استفاده، تعداد نقاط شکست و غیره که توسط کاربر گرفته میشود وابسته است. Splines همچنین ممکن است برای جلوگیری از تولید مقادیر بیش از حد بالا یا پایین که در برخی از splineهای دقیق معمول است مدل سازی شوند [ 3 ]] . برخلاف روشهای IDW، مقادیر پیشبینیشده توسط RBFها به محدوده مقادیر اندازهگیری شده محدود نمیشوند، به عنوان مثال، مقادیر پیشبینیشده میتوانند بالاتر از حداکثر یا کمتر از حداقل مقدار اندازهگیریشده [ 14 ] باشند.
2.3. کریجینگ
کریجینگ، مترادف با درونیابی زمین آماری، در صنعت معدن به عنوان وسیله ای برای بهبود تخمین ذخایر سنگ معدن در اوایل دهه 1950 آغاز شد [ 6 ]. مهندس معدن DG Krige و آماردان HS Sichel آن را فرموله کردند. پس از تقریبا یک دهه، ریاضیدان فرانسوی G. Matheron فرمولها را استخراج کرد و کل زمینه زمین آمار خطی را ایجاد کرد [ 11 ]. کریجینگ بر اساس مفهومی از توابع تصادفی با سطح یا حجم فرض شده یک تحقق تابع تصادفی با کوواریانس فضایی شناخته شده است [ 7 ].
نظریه متغیر منطقه ای شده فرض می کند که تغییرات مکانی هر متغیر را می توان به صورت مجموع سه جزء زیر بیان کرد:
الف) یک جزء ساختاری با میانگین یا روند ثابت.
ب) یک متغیر منطقه ای، که جزء تصادفی اما همبسته مکانی است.
ج) یک نویز تصادفی اما از نظر مکانی نامرتبط یا جزء باقیمانده.
د) از نظر ریاضی، برای یک متغیر تصادفی z در x، عبارت است
 (18)
(18)
جایی  که یک تابع ساختاری است که مؤلفه ساختاری را مدلسازی میکند،
که یک تابع ساختاری است که مؤلفه ساختاری را مدلسازی میکند،  باقیمانده تصادفی همبسته فضایی
باقیمانده تصادفی همبسته فضایی  (متغیر منطقهای)
(متغیر منطقهای)  است و نویز تصادفی است که معمولاً با میانگین صفر و واریانس توزیع میشود
است و نویز تصادفی است که معمولاً با میانگین صفر و واریانس توزیع میشود  [ 3 ].
[ 3 ].
کریجینگ معمولی
کریجینگ معمولی (OK) نسخه استاندارد کریجینگ است که در آن پیشبینیها بر اساس مدل است.
 (19)
(19)
که در آن  تابع ثابت ثابت یا میانگین جهانی
تابع ثابت ثابت یا میانگین جهانی  است، و بخش تصادفی اما همبسته فضایی تغییرات است. پیش بینی ها به صورت انجام می شود
است، و بخش تصادفی اما همبسته فضایی تغییرات است. پیش بینی ها به صورت انجام می شود
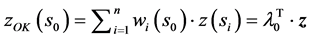 (20)
(20)
که  در آن بردار وزن های کریجینگ (
در آن بردار وزن های کریجینگ (  ) و z بردار n نمونه در مکان های اولیه است. کریجینگ، به نوعی، بهبود درون یابی فاصله معکوس است که در آن مشکل کلیدی درون یابی فاصله معکوس (تعیین میزان اهمیت داده شده به هر همسایه) به گونه ای مورد توجه قرار می گیرد که وزن های تخمین زده شده برای فضای واقعی محاسبه شود. ساختار خودهمبستگی تازگی کریجینگ در تجزیه و تحلیل داده های نقطه ای، استخراج و ترسیم تفاوت های نیمه واریانس بین مقادیر همسایه است [ 6 ].
) و z بردار n نمونه در مکان های اولیه است. کریجینگ، به نوعی، بهبود درون یابی فاصله معکوس است که در آن مشکل کلیدی درون یابی فاصله معکوس (تعیین میزان اهمیت داده شده به هر همسایه) به گونه ای مورد توجه قرار می گیرد که وزن های تخمین زده شده برای فضای واقعی محاسبه شود. ساختار خودهمبستگی تازگی کریجینگ در تجزیه و تحلیل داده های نقطه ای، استخراج و ترسیم تفاوت های نیمه واریانس بین مقادیر همسایه است [ 6 ].
با فرض ثابت بودن، می توان یک نیمه متغیر  ، برای داده ها را تخمین زد
، برای داده ها را تخمین زد  که به صورت تعریف شده است
که به صورت تعریف شده است
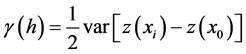 (21)
(21)
که در آن h فاصله بین نقطه  و
و  [ 21 ] است. این مربوط به کوواریانس فضایی
[ 21 ] است. این مربوط به کوواریانس فضایی  توسط،
توسط،
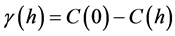 (22)
(22)
که در آن  مقدار نیمه واریوگرام در بی نهایت (آستانه) [ 7 ] است. وزنهای کریجینگ معمولی (OK) با ضرب کوواریانسها ارزیابی میشوند.
مقدار نیمه واریوگرام در بی نهایت (آستانه) [ 7 ] است. وزنهای کریجینگ معمولی (OK) با ضرب کوواریانسها ارزیابی میشوند.
 (23)
(23)
که در آن C ماتریس کوواریانس به دست آمده برای یک ماتریس نمونه nxn با یک سطر و ستون اضافی اضافه شده برای اطمینان از مجموع وزن ها برابر با یک  است و بردار کوواریانس ها در یک مکان جدید است [ 6 ]. کوواریانس در فاصله صفر
است و بردار کوواریانس ها در یک مکان جدید است [ 6 ]. کوواریانس در فاصله صفر  طبق تعریف میانگین خطای باقیمانده [ 6 ] است. واریوگرام های تجربی معمولاً دارای برخی ویژگی های مشخصه هستند که از جمله آنها می توان به موارد زیر اشاره کرد:
طبق تعریف میانگین خطای باقیمانده [ 6 ] است. واریوگرام های تجربی معمولاً دارای برخی ویژگی های مشخصه هستند که از جمله آنها می توان به موارد زیر اشاره کرد:
1) مقادیر پایین h دارای واریانس کوچک با افزایش واریانس به نسبت مستقیم با h هستند و در یک نقطه معین تراز می شوند تا آستانه را تشکیل دهند.
2) در فواصل کمتر از محدوده (فاصلهای که سطح واریانس کاهش مییابد)، نقاط نزدیکتر به هم به احتمال زیاد مقادیر مشابهی نسبت به نقاط دورتر از هم دارند، در حالی که در فواصل بزرگتر از محدوده، نقاط تأثیری بر خودشان ندارند. بنابراین، این محدوده ایده ای از بزرگی شعاع جستجو برای درونیابی وزنی از راه دور به دست می دهد.
3) نیمه واریانس زمانی که h صفر است دارای یک مقدار مثبت است که به عنوان قطعه نامیده می شود و میزان نویز خودهمبسته غیرمکانی را نشان می دهد [ 3 ].
نیمه واریانس نمایش داده شده در واریوگرام تجربی با یک تابع ریاضی بسته به شکل واریوگرام تجربی مدل می شود. زمانی که واریوگرام شکل کلاسیک داشته باشد از مدل کروی استفاده می شود و زمانی که نزدیک شدن به آستانه تدریجی باشد از مدل نمایی استفاده می شود. مدل گاوسی زمانی که قطعه کوچک است و تغییرات بسیار صاف است و از مدل خطی زمانی که آستانه وجود ندارد استفاده می شود. واریوگرام حاوی روندی که باید به طور جداگانه مدل شود، به طور فزاینده ای شیب دار با مقادیر بزرگتر h است. اگر واریانس قطعه بزرگ باشد و واریوگرام تمایلی به ناپدید شدن تدریجی با مقادیر کوچکتر h نشان ندهد، یا فاصله بین مشاهدات بزرگتر از محدوده باشد (یعنی نقاط نمونه خیلی از هم دور باشند تا بر یکدیگر تأثیر بگذارند)، در این صورت درون یابی منطقی نیست. و بهترین برآورد میانگین کلی مشاهدات است. واریوگرام پر از نویز که الگوی خاصی را نشان نمی دهد ممکن است به این معنی باشد که مشاهدات بسیار کم هستند. یک واریوگرام که در فواصل بزرگتر از محدوده برای ایجاد یک اثر حفره فرو می رود، نشان می دهد که فضای نمونه ممکن است برای منعکس کردن برخی تغییرات طول موج طولانی در داده ها بسیار کوچک باشد.3 ] . سطح درون یابی با استفاده از شرایط آماری بی طرفی و حداقل واریانس [ 7 ] ساخته شده است. سه شرط مهم برای کریجینگ معمولی عبارتند از:
(i) تابع روند ثابت است
(ii) واریوگرام در کل ناحیه مورد نظر ثابت است
(iii) متغیر هدف (تقریبا) به طور معمول توزیع شده است.
این الزامات اغلب برآورده نمی شوند و یک نقطه ضعف جدی برای کریجینگ معمولی هستند [ 6 ]. با این حال، یک مزیت عمده اشکال مختلف کریجینگ (و سایر روشهای درونیابی تصادفی) این است که تخمینهای خطاهای پیشبینی مدل را میتوان محاسبه کرد، در تحلیل گنجاند و همراه با سطح پیشبینیشده رسم کرد. چنین اطلاعات خطای ابزار مهمی در فرآیند تصمیم گیری مکانی است [ 14 ].
3. روش ارزیابی دقت
شاخصهای ارزیابی دقت که معمولاً مورد استفاده قرار میگیرند عبارتند از، میانگین خطا (ME)، میانگین خطای مطلق (MAE)، میانگین مربعات خطا (MSE) و خطای میانگین مربعات ریشه (RMSE). برای n مشاهدات، p مقدار پیش بینی شده و o مقدار مشاهده شده، این شاخص ها با استفاده از عبارات فهرست شده در زیر ارزیابی می شوند:
 (24)
(24)
 (25)
(25)
 (26)
(26)
 (27) [ 4 ]
(27) [ 4 ]
ME برای تعیین درجه سوگیری در برآوردهایی که اغلب به عنوان سوگیری [ 10 ] نامیده می شود استفاده می شود. از آنجایی که تخمینهای مثبت و منفی یکدیگر را خنثی میکنند، ME حاصل از خطای واقعی کمتر است و در استفاده از آن بهعنوان شاخص دقت، احتیاط را برمیانگیزد [ 4 ]. RMSE اندازهگیری اندازه خطا را ارائه میکند، اما نسبت به موارد پرت حساس است، زیرا وزن زیادی بر روی خطاهای بزرگ میگذارد [ 4 ]. MSE از همان اشکالات RMSE رنج می برد. در حالی که MAE نسبت به مقادیر شدید [ 20 ] حساسیت کمتری دارد و نشان میدهد که تخمین تا چه حد ممکن است در خطا باشد [ 21 ]] . استدلال میشود که MAE و RMSE معیارهای مشابهی هستند و میانگین خطا را تخمین میزنند، اما اطلاعاتی در مورد اندازه نسبی تفاوت میانگین و ماهیت تفاوتهای شامل آنها ارائه نمیدهند [ 20 ]. البته اعتبار متقاطع همراه با این اندازهگیریها برای ارزیابی عملکرد روشهای درونیابی استفاده میشود [ 4 ]. در این مقاله از ME و RMSE (موجود بر روی نرم افزار مورد استفاده) برای ارزیابی عملکرد روش های درون یابی IDW، Spline و Kriging در بخش تحلیل تجربی این مطالعه استفاده می شود. اعتبار سنجی متقاطع به عنوان آزمایش بیشتر دقت پیش بینی انجام می شود.
4. تجزیه و تحلیل تجربی
منطقه مورد مطالعه همانطور که در شکل 1 و شکل 2 توضیح داده شده است، گستره ای از زمین به وسعت حدود بیست و یک (21) هکتار است که در طول  و عرض جغرافیایی Ikot Ukapon
و عرض جغرافیایی Ikot Ukapon  در قسمت شمال شرقی ایالت Akwa Ibom نیجریه قرار دارد. این منطقه عمدتاً تپه ای است و دشتی حدود بیست (20%) از کل مساحت آن را پوشش می دهد. دادههای ارتفاع ارتومتری، بهدستآمده از دفتر نقشهبردار کل ایالتی، شامل چهارصد و شصت و دو (462) نقطه نمونهبرداری تصادفی در سراسر منطقه است که از طریق بررسی میدانی با استفاده از GPS دیفرانسیل سری Kolida K9-T جمعآوری شده است.
در قسمت شمال شرقی ایالت Akwa Ibom نیجریه قرار دارد. این منطقه عمدتاً تپه ای است و دشتی حدود بیست (20%) از کل مساحت آن را پوشش می دهد. دادههای ارتفاع ارتومتری، بهدستآمده از دفتر نقشهبردار کل ایالتی، شامل چهارصد و شصت و دو (462) نقطه نمونهبرداری تصادفی در سراسر منطقه است که از طریق بررسی میدانی با استفاده از GPS دیفرانسیل سری Kolida K9-T جمعآوری شده است.
داده های به دست آمده از نمونه های میدانی در قالب Microsoft Excel .xls بود. پایین ترین ارتفاع منطقه 27.018 متر و بالاترین ارتفاع 98.719 متر از سطح متوسط دریا است. کاوش اولیه داده ها با استفاده از ArcGIS ESRI (نسخه 9.3) نشان می دهد که داده ها به طور معمول توزیع نشده اند، همانطور که توسط پارامترهای توزیع در جدول 1 نشان داده شده است .

شکل 1 . نقشه منطقه مورد مطالعه که توزیع نقاط داده را در منطقه مورد مطالعه نشان می دهد.
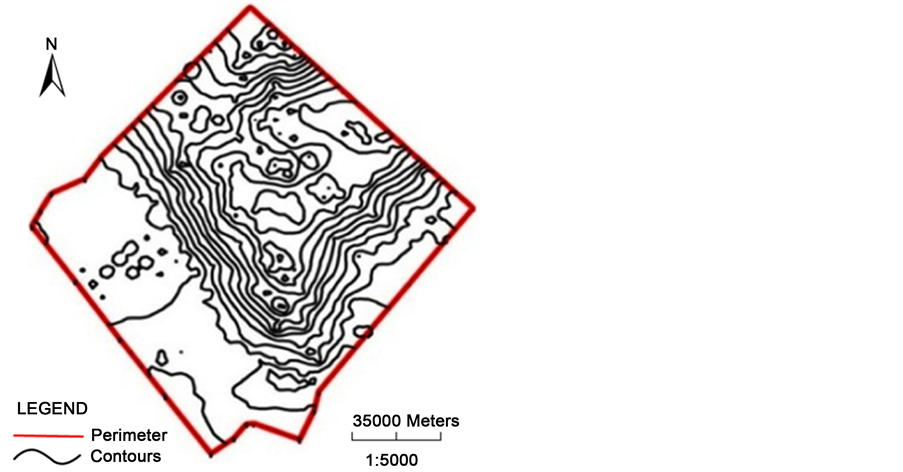
شکل 2 . نقشه کانتور منطقه مورد مطالعه.
4.1. روش IDW
سطح پر کنتور زیر که در شکل 3 نشان داده شده است، برای درون یابی IDW با توان، p از 2، ضریب هموارسازی 0.5 و اندازه همسایگی 15 برای داده های بایاس ایجاد شده است.
4.2. روش اسپلاین
درون یابی Spline منظم، که به عنوان تابع پایه شعاعی (RBF) پیاده سازی شده است، با نظم 2، نقشه پر شدن کانتور را در شکل 4 برای توان = 2، ضریب هموارسازی = 0.5 و اندازه محله = 15 نشان می دهد.
4.3. کریجینگ
کریجینگ با این فرض کار می کند که مجموعه داده نرمال شده است، بنابراین، قبل از اجرای درونیابی کریجینگ، نرمال سازی Box-Cox را روی داده ها انجام دادیم.

شکل 3 . نقشه پر کنتور IDW.

شکل 4 . نقشه پر کردن کانتور Spline منظم.
داده ها با استفاده از ابزار Geostatistical Analyst در ArcGIS به زیر مجموعه های آموزشی و آزمایشی به نسبت 80:20 تقسیم شدند و مقادیر پارامتر بهینه (تولید شده توسط ArcGIS و تعیین بهترین مقدار ممکن برای هر پارامتر) برای پیش بینی در زیر مجموعه آموزشی استفاده شد. سپس زیر مجموعه آزمون با این پارامترهای بهینه برای اعتبارسنجی استفاده شد. پارامترهای توزیع دادهها پس از نرمالسازی باکس-کاکس مطابق جدول 2 است.
نقشه های پر کانتور با استفاده از کریجینگ با مدل گاوسی و
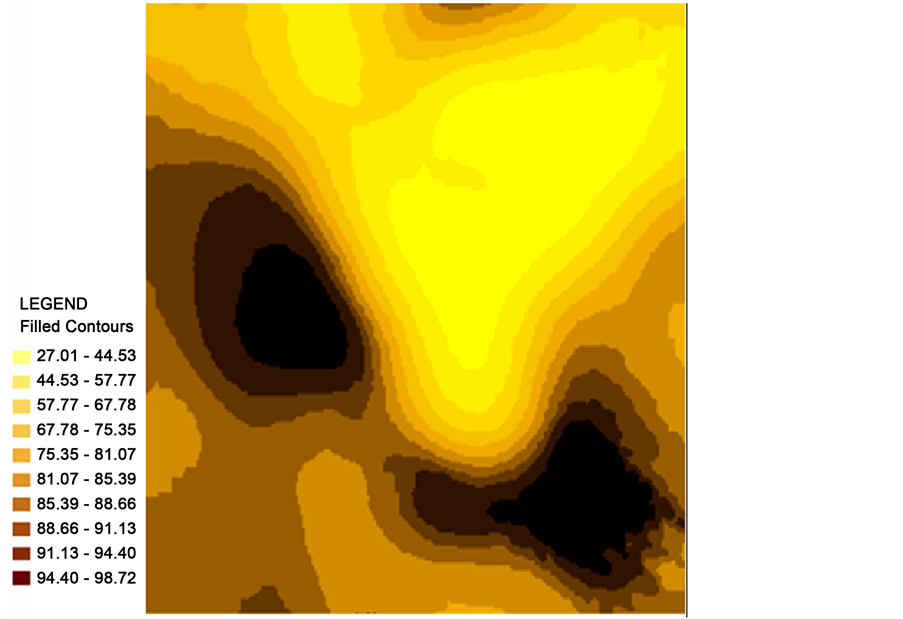
مدل کروی به ترتیب برای مقادیر محاسبه شده خودکار برای قطعه، آستانه، محدوده متوسط، اندازه تاخیر 54.401 و عدد تاخیر = 12 مانند شکل 5 (الف) و شکل 5 (ب) نشان داده شده است.
نقشه های IDW، Spline و Kriging پس از اعتبارسنجی بهینه داده ها در شکل 6(a)-(c) نشان داده شده است.
5. نتیجه و بحث
از خطاهای پیشبینی جدولبندیشده در جدول 3 و جدول 4 ، سطح سوگیری در برآورد برای Kriging کمترین و برای IDW بالاترین است، همانطور که توسط ME مربوطه نشان داده شده است. این وجود سوگیری انتظار میرود، زیرا دادههای قد تصادفی نبودند که در جدول 1 نشان داده شده است. نرمال سازی Box-Cox داده ها نیز منجر به توزیع نرمال نشد ( جدول 2 را ببینید، این بدان معنی است که داده ها بسیار مغرضانه بودند. این سناریو اغلب در عمل با آن مواجه میشویم، زیرا مجموعه میدانی دادههای ارتفاع معمولاً به جای تصادفی بودن، بر ثبت تغییرات درک شده در ارتفاع متمرکز است. با این حال، سوگیری برای دادههای تایید شده، برای کریجینگ بالاترین و برای Spline کمترین است، احتمالاً به دلیل کاهش تعداد نمونههای مورد استفاده برای اعتبارسنجی. معیار بهتری از خطا در پیشبینی، RMSE، برای Spline کمترین و برای Kriging برای پیشبینی و اعتبار نشان داده شده در جدول 3 و جدول 4 بالاترین است.. این نشاندهنده یک مدل ارتفاعی است که به آنچه روی زمین برای Splines است نزدیکتر است. با این حال، در خارج از مناطقی که داده های درون یابی به دست آمده است، Spline پیش بینی های غیر قابل اعتمادی را تولید می کند. بنابراین برای مواردی که داده های خارج از منطقه گرفته شده مورد نظر است (برون یابی) مناسب نیست. IDW مدلی تولید می کند که بهتر از کریجینگ است اما به خوبی مدل Spline نیست. پیش بینی های آن در خارج از منطقه ضبط شده نیز بهتر از کریجینگ و اسپلاین است. این بدان معنا نیست که Kriging برای مدلسازی زمین مناسب نیست یا بهتر از IDW و Spline عمل نمیکند. کریجینگ توزیع نرمال داده ها را فرض می کند و توزیع فضایی یک رویداد جغرافیایی را به عنوان تحقق تابعی که تصادفی است مدل می کند. بنابراین پیشبینیهای آن وابسته به دادههایی است که معیارهای آماری بیطرفی و حداقل واریانس را برآورده میکنند. فرمول ریاضی آن را برای داده هایی که نامناسب می کند
 (الف)
(الف) (ب)
(ب)
شکل 5 . (الف) و (ب) نقشه پر کردن کانتور کریجینگ را پس از نرمالسازی باکس کاکس که به ترتیب با مدل گاوسی و با مدل کروی ایجاد شده است، نشان میدهد.
 (الف)
(الف) (ب)
(ب) (ج)
(ج)
شکل 6 . (الف) نقشه پیش بینی با وزن معکوس فاصله (IDW). (ب) Spline; (ج) نقشه پیشبینی کریجینگ معمولی.
 Translate
Translate
Go to original page
جدول 3 . خطاهای پیش بینی برای سه روش درونیابی در پارامترهای بهینه.
ME میانگین خطای پیشبینی و RMSE ریشه میانگین مربع خطای استاندارد پیشبینی است.
ME میانگین خطای پیشبینی و RMSE ریشه میانگین مربع خطای استاندارد پیشبینی است.
به طور معمول توزیع نمی شود یا عادی سازی آن دشوار است. از سوی دیگر، Splines از یک مدل فیزیکی استفاده میکند که مطابق با تغییر در خواص کشسانی تابع تخمین تغییر میکند. با مدلسازی پدیدههای فیزیکی مانند زمین، به خوبی عمل میکند. IDW از ترکیب خطی مقادیر در مکانهای رویداد ضبطشده استفاده میکند، وزنها را با تابعی معکوس از جدایی بین مکان رویدادی که باید تخمین زده شود و نقاط گرفته شده برای تخمین مقادیر مکان ناشناخته اختصاص میدهد. اگرچه وزنها بهطور دلخواه مشخص میشوند، نرمافزار ArcGIS یک تابع مدیریت وزن بهینه را ارائه میکند که وزنی را که برای نقاط درون مجموعه دادههای گرفته شده مناسبتر است، اختصاص میدهد. پیشبینیها تحت تأثیر این تخصیص وزن هستند، اما از نظر خطا نسبت به آنچه با استفاده از کریجینگ بهدست میآیند قابل اعتمادتر هستند. پذیرفته شده است که کریجینگ با داده های کمکی مانند داده های دما بسیار خوب عمل می کند، اما داده ها باید تا حد امکان به صورت تصادفی گرفته شوند. این اغلب به دست نمی آید. دانش خوب از داده های مورد استفاده و همچنین نقاط قوت و ضعف روش های درون یابی موجود در تصمیم گیری در مورد روشی برای استفاده برای درونیابی برای یک هدف معین ضروری است.
6. نتیجه گیری
در این مطالعه، Spline مدل و نتیجه دقیقتری را برای دادههای ارتفاعی بهدستآمده مستقیماً از بررسی میدانی ارائه میکند که بهطور تصادفی همگن و نرمالسازی نشده بودند. از نتیجه درون یابی که به دست آوردیم، روش Spline در خارج از ناحیه داده نیز مجدداً تأیید می کند که پیش بینی های RBFs به محدوده مقادیر اندازه گیری شده محدود نمی شوند، به عنوان مثال، مقادیر پیش بینی شده می توانند بالاتر از حداکثر یا کمتر از حداقل مقدار اندازه گیری شده باشند. تان و خو [ 22] از آزمایش خود بر روی مدلسازی زمین با استفاده از دادههای یک نقشه دیجیتالی به این نتیجه رسیدند که IDW از نظر دقت مدل بهتری نسبت به Spline یا Kriging ارائه کرده است. این به احتمال زیاد به دلیل ابزارهایی است که داده های آزمون از آن به دست آمده اند. دادههای آزمایشی آنها از یک نقشه کانتور دیجیتالی شد و به طور همگن توزیع شد. بنابراین دانش منبع داده ها ممکن است در انتخاب روش درونیابی اهمیت داشته باشد.
منابع




 Translate
Translate

بدون دیدگاه