استخراج ناهمگونی‌های فضایی پیوسته و گسسته: مدل همجوشی مدل ضریب متغیر فضایی و مدل‌سازی پراکنده

پدیده های جغرافیایی اغلب دارای ناهمگونی فضایی هستند که ناشی از تفاوت در فرآیند تولید داده از مکانی به مکان دیگر است. دو نوع ناهمگونی فضایی وجود دارد: پیوسته و گسسته، و بحث های زیادی در مورد چگونگی تجزیه و تحلیل یک نوع ناهمگونی فضایی وجود دارد. اگرچه پدیده‌های زمین‌فضایی می‌توانند هر دو نوع ناهمگونی فضایی را داشته باشند، مطالعات قبلی به اندازه کافی درباره چگونگی در نظر گرفتن این دو نوع مختلف ناهمگونی فضایی به طور همزمان و نحوه تشخیص آنها به طور جداگانه بحث نکرده‌اند، که ممکن است منجر به تخمین‌های مغرضانه و تفسیر نادرست از پدیده‌های مکانی شود. این مطالعه با ترکیب مدل ضریب متغیر مکانی مبتنی بر فیلتر فضایی بردار ویژه (ESF-SVC)، رویکرد جدیدی را برای تحلیل داده‌های مکانی با هر دو ناهمگنی پیشنهاد می‌کند. که ناهمگنی فضایی پیوسته و تخمین کمند تعمیم یافته (GL) را فرض می کند، که ناهمگنی فضایی گسسته را فرض می کند و مدل ESF-GL-SVC را پیشنهاد می کند. عملکرد ESF-GL-SVC از طریق آزمایش‌های مبتنی بر شبیه‌سازی مونت کارلو ارزیابی شد و تأیید می‌کند که ESF-GL-SVC عملکرد بهتری در تخمین ضرایب با هر دو نوع ناهمگونی فضایی نسبت به دو مدل قبلی نشان داد. کاربرد داده‌های اجاره آپارتمان نشان داد که ESF-GL-SVC نتیجه را با کوچک‌ترین مقدار BIC خروجی می‌دهد و ضرایب تخمینی ناهمگنی فضایی پیوسته و گسسته را در مجموعه داده به تصویر می‌کشد. ضرایب معقول با استفاده از ESF-GL-SVC برآورد شد، اگرچه برخی از ضرایب توسط ESF-SVC برآورد نشدند. که ناهمگونی فضایی گسسته را فرض می کند و مدل ESF-GL-SVC را پیشنهاد می کند. عملکرد ESF-GL-SVC از طریق آزمایش‌های مبتنی بر شبیه‌سازی مونت کارلو ارزیابی شد و تأیید می‌کند که ESF-GL-SVC عملکرد بهتری در تخمین ضرایب با هر دو نوع ناهمگونی فضایی نسبت به دو مدل قبلی نشان داد. کاربرد داده‌های اجاره آپارتمان نشان داد که ESF-GL-SVC نتیجه را با کوچک‌ترین مقدار BIC خروجی می‌دهد و ضرایب تخمینی ناهمگنی فضایی پیوسته و گسسته را در مجموعه داده به تصویر می‌کشد. ضرایب معقول با استفاده از ESF-GL-SVC برآورد شد، اگرچه برخی از ضرایب توسط ESF-SVC برآورد نشدند. که ناهمگونی فضایی گسسته را فرض می کند و مدل ESF-GL-SVC را پیشنهاد می کند. عملکرد ESF-GL-SVC از طریق آزمایش‌های مبتنی بر شبیه‌سازی مونت کارلو ارزیابی شد و تأیید می‌کند که ESF-GL-SVC عملکرد بهتری در تخمین ضرایب با هر دو نوع ناهمگونی فضایی نسبت به دو مدل قبلی نشان داد. کاربرد داده‌های اجاره آپارتمان نشان داد که ESF-GL-SVC نتیجه را با کوچک‌ترین مقدار BIC خروجی می‌دهد و ضرایب تخمینی ناهمگنی فضایی پیوسته و گسسته را در مجموعه داده به تصویر می‌کشد. ضرایب معقول با استفاده از ESF-GL-SVC برآورد شد، اگرچه برخی از ضرایب توسط ESF-SVC برآورد نشدند. عملکرد ESF-GL-SVC از طریق آزمایش‌های مبتنی بر شبیه‌سازی مونت کارلو ارزیابی شد و تأیید می‌کند که ESF-GL-SVC عملکرد بهتری در تخمین ضرایب با هر دو نوع ناهمگونی فضایی نسبت به دو مدل قبلی نشان داد. کاربرد داده‌های اجاره آپارتمان نشان داد که ESF-GL-SVC نتیجه را با کوچک‌ترین مقدار BIC خروجی می‌دهد و ضرایب تخمینی ناهمگنی فضایی پیوسته و گسسته را در مجموعه داده به تصویر می‌کشد. ضرایب معقول با استفاده از ESF-GL-SVC برآورد شد، اگرچه برخی از ضرایب توسط ESF-SVC برآورد نشدند. عملکرد ESF-GL-SVC از طریق آزمایش‌های مبتنی بر شبیه‌سازی مونت کارلو ارزیابی شد و تأیید می‌کند که ESF-GL-SVC عملکرد بهتری در تخمین ضرایب با هر دو نوع ناهمگونی فضایی نسبت به دو مدل قبلی نشان داد. کاربرد داده‌های اجاره آپارتمان نشان داد که ESF-GL-SVC نتیجه را با کوچک‌ترین مقدار BIC خروجی می‌دهد و ضرایب تخمینی ناهمگنی فضایی پیوسته و گسسته را در مجموعه داده به تصویر می‌کشد. ضرایب معقول با استفاده از ESF-GL-SVC برآورد شد، اگرچه برخی از ضرایب توسط ESF-SVC برآورد نشدند. کاربرد داده‌های اجاره آپارتمان نشان داد که ESF-GL-SVC نتیجه را با کوچک‌ترین مقدار BIC خروجی می‌دهد و ضرایب تخمینی ناهمگنی فضایی پیوسته و گسسته را در مجموعه داده به تصویر می‌کشد. ضرایب معقول با استفاده از ESF-GL-SVC برآورد شد، اگرچه برخی از ضرایب توسط ESF-SVC برآورد نشدند. کاربرد داده‌های اجاره آپارتمان نشان داد که ESF-GL-SVC نتیجه را با کوچک‌ترین مقدار BIC خروجی می‌دهد و ضرایب تخمینی ناهمگنی فضایی پیوسته و گسسته را در مجموعه داده به تصویر می‌کشد. ضرایب معقول با استفاده از ESF-GL-SVC برآورد شد، اگرچه برخی از ضرایب توسط ESF-SVC برآورد نشدند.

کلید واژه ها:

ناهمگونی فضایی ; بردار ویژه مدل ضریب متغیر فضایی مبتنی بر فیلتر فضایی ; کمند عمومی

1. مقدمه

در سال‌های اخیر، به دلیل افشای فعال داده‌ها توسط سازمان‌های دولتی و شرکت‌های خصوصی، داده‌های مکانی دقیق با وضوح مکانی بالا در دسترس قرار گرفته‌اند که به ما امکان می‌دهد واقعیت فعالیت‌های اجتماعی-اقتصادی را با جزئیات بیشتر درک کنیم.

داده‌های جغرافیایی معمولاً دارای خاصیتی به نام خودهمبستگی فضایی هستند که به نام «قانون اول جغرافیا» [ 1 ] نیز شناخته می‌شود، که در آن داده‌های مکان‌های نزدیک‌تر به یکدیگر همبستگی قوی‌تری دارند. یک رویکرد برای تجزیه و تحلیل داده های مکانی با خودهمبستگی مکانی این است که فرض کنیم فرآیند تولید داده بدون توجه به مکان رایج است و مدل هایی بسازیم که نشان دهنده همبستگی خودکار مکانی متغیرهای وابسته، اختلالات و غیره باشند. مدل های رگرسیون مکانی در زمینه فضایی اقتصادسنجی (به عنوان مثال، [ 2 ])، مدل کریجینگ جهانی در زمینه آمار فضایی (به عنوان مثال، [ 3 ])، و مدل فیلتر فضایی بردار ویژه (ESF) در زمینه جغرافیای کمی [ 4 ، 5 ]] نمونه هایی از این رویکرد هستند.

رویکرد دیگر این است که وجود ناهمگونی فضایی را فرض کنیم، به این معنی که فرآیند تولید داده براساس مکان متفاوت است. این مطالعه بر روی این رویکرد متمرکز است، که می‌توان آن را به طور کلی بسته به فرضیات در مورد ساختار ناهمگونی فضایی به دو نوع تقسیم کرد [ 6 ]. یک فرض این است که تأثیر عوامل تشکیل داده به طور مداوم با توجه به مکان مکانی متفاوت است. فرض رقیب این است که تأثیر عوامل تشکیل داده به طور ناپیوسته در مرزهای فضایی خاص متفاوت است.

مدل هایی که از فرض اول استفاده می کنند، یعنی عوامل تشکیل داده ها به طور مداوم تغییر می کنند، به عنوان مدل های ضریب متغیر مکانی (SVC) شناخته می شوند و کاربردی ترین مدل رگرسیون وزنی جغرافیایی (GWR) است [ 6 ، 7 ، 8 ]. یک روش حداقل مربعات وزن‌دار، که از یک تابع واپاشی فاصله برای دادن وزن‌های بزرگ به داده‌های مکانی در مجاورت یک نقطه هدف تحلیلی استفاده می‌کند، برای به دست آوردن تخمین‌های نقطه‌ای خاص از ضرایب که به آرامی در فضا متفاوت هستند، استفاده می‌شود. مدل ضریب متغیر فضایی مبتنی بر فیلتر فضایی بردار ویژه (ESF-SVC) [ 9 ، 10 ، 11 ] بسط ESF [ 4 ، 5 ] است.]، که ساختار همبستگی فضایی را با استفاده از بردارهای ویژه ماتریس وزن فضایی نشان می دهد و ضرایبی را که به طور مداوم در فضا تغییر می کنند، تخمین می زند. ESF-SVC یک روش تجزیه و تحلیل بسیار مفید با چندین مزیت نسبت به GWR است، مانند توانایی نمایش ساختار ناهمگونی فضایی با انعطاف‌پذیری بیشتر، تخمین آسان‌تر، و کاربرد بهبود یافته برای داده‌های مقیاس بزرگ [ 11 ]. برای تحلیل های منطقه ای مختلف [ 12 ، 13 ، 14 ، 15 ] استفاده شده است.

مدل‌هایی که از فرض دوم استفاده می‌کنند، یعنی عوامل شکل‌گیری داده‌ها به‌طور گسسته در مرزهای فضایی خاص متفاوت است، برای تجزیه و تحلیل بخش‌های جغرافیایی بازار املاک و مستغلات در علوم منطقه‌ای و تشخیص خوشه‌های رویداد نقطه‌ای، مانند خوشه‌های جغرافیایی عفونی استفاده شده است. شیوع بیماری در اپیدمیولوژی و زمینه های تمرکز جنایی در جرم شناسی در تجزیه و تحلیل بخش‌های جغرافیایی بازار املاک و مستغلات، مقیاس ناهمگونی فضایی در ارزیابی‌های دارایی با مقایسه مدل‌ها با مجموعه‌های جغرافیایی مختلف، مانند نواحی مدرسه و محله‌ها، تحلیل می‌شود (به عنوان مثال، [ 16 ، 17 ]). در تشخیص خوشه های رویداد نقطه ای، آمار اسکن فضایی [ 18]، که روش های معرف توسعه یافته در زمینه اپیدمیولوژی فضایی هستند، و تجزیه و تحلیل تراکم [ 19 ، 20 ]، که روش کنترل نرخ کشف نادرست [ 21 ] را اعمال می کند، برای تعیین اینکه آیا فراوانی رویدادهای نقطه ای در یک منطقه خاص استفاده شده است. با توجه به تقسیمات منطقه ای از پیش تعیین شده با مناطق دیگر متفاوت است. از آنجایی که هر دو رویکرد تقسیم‌بندی‌های منطقه‌ای را از پیش تعریف می‌کنند، محدودیت‌هایی در تحلیل مجموعه‌ای از مناطق متعدد با ناهمگونی فضایی دارند. برای حل محدودیت های ذکر شده در بالا، کمند تعمیم یافته (GL) [ 22 ] برای تجزیه و تحلیل ناهمگنی فضایی گسسته [ 23 ، 24 ، 25 ، 26 ] استفاده شده است., 27 , 28 , 29 ]. GL گسترش کمند [ 30 ] با معرفی ₁ℓ منظم سازی به تفاوت بین ضرایب مناطق مجاور است. با استفاده از مدلی که در آن هر منطقه دارای یک ضریب است که نشان دهنده تفاوت از روند کلی است، یک سری از مناطق با همان سطح ناهمگونی فضایی را می توان با منظم کردن تفاوت بین ضرایب مناطق همجوار استخراج کرد.

رویکردهای فوق از مفروضات مختلفی در مورد ناهمگونی فضایی استفاده می کنند. اولی ناهمگونی را فرض می کند که به طور مداوم در فضا تغییر می کند، در حالی که دومی ناهمگونی را فرض می کند که به طور مجزا در مرزهای جغرافیایی خاص تغییر می کند. با این حال، اینکه کدام فرض برای نشان دادن ناهمگونی فضایی داده‌های مکانی کافی است، هنوز مشخص نیست.

با استفاده از تجزیه و تحلیل بازار املاک و مستغلات به عنوان مثال، کسانی که ترجیح می دهند در مرکز شهر زندگی کنند و کسانی که ترجیح می دهند در حومه شهر زندگی کنند، املاک املاک را متفاوت ارزیابی می کنند. اولی نزدیکی به خدمات شهری و دومی نزدیکی به محیط طبیعی و فضای وسیع را ارزش می‌دهند. ضرایب متغیرهای توضیحی نشان دهنده نزدیکی به آن خدمات بر اساس مکان متفاوت است. اگر هیچ مرز مشخصی بین مناطق شهری و حومه شهر وجود نداشته باشد، همانطور که در مناطق شهری ژاپن وجود دارد، منطقی است که فرض کنیم ضرایب به طور مداوم در فضا تغییر می کنند. بعلاوه، اگر محله های خاصی به عنوان مناطق مسکونی مرتفع شناخته شوند، ممکن است ارزش گذاری با مناطق اطراف متفاوت باشد و قیمت املاک و مستغلات در مرز آن محله ها ناپیوستگی نشان می دهد. با توجه به موارد فوق، ممکن است ناهمگونی مکانی پیوسته و گسسته در داده های قیمت املاک وجود داشته باشد. با این حال، مطالعات قبلی به اندازه کافی درباره چگونگی در نظر گرفتن این دو نوع مختلف ناهمگونی فضایی به طور همزمان و نحوه تشخیص آنها به طور جداگانه بحث نکرده اند، که ممکن است منجر به تخمین های مغرضانه و تفسیر نادرست از پدیده های مکانی شود.

این مقاله یک رویکرد جدید برای تجزیه و تحلیل داده‌های مکانی با ناهمگنی فضایی پیوسته و گسسته با ترکیب ESF-SVC و GL پیشنهاد می‌کند و عملکرد آن را برای تأیید اثربخشی آن از طریق استفاده از تجزیه و تحلیل داده‌های مکانی ارزیابی می‌کند.

ادامه این مقاله به شرح زیر سازماندهی شده است. در بخش 2 ، پس از تشریح ESF-SVC و GL، مدل همجوشی، فیلتر فضایی بردار ویژه، و مدل ضریب متغیر فضایی مبتنی بر کمند تعمیم یافته (ESF-GL-SVC) ارائه شده و با استفاده از داده های شبیه سازی ارزیابی می شوند. در بخش 3 ، مدل‌های ESF-GL-SVC، ESF-SVC، و GL را برای داده‌های اجاره مسکونی در بخش جنوب غربی منطقه شهری توکیو اعمال می‌کنیم، نتایج برآورد شده را تفسیر می‌کنیم و در مورد اثربخشی ESF-GL- بحث می‌کنیم. مدل SVC. در نهایت، بخش 4 مطالعه را به پایان می رساند.

2. ESF-GL-SVC: مدلی برای تحلیل ناهمگونی فضایی پیوسته و گسسته

ما ابتدا دو مدل قبلی را توضیح می دهیم که با ناهمگنی فضایی سروکار دارند، ESF-GL-SVC را معرفی می کنیم، که تلفیقی از این دو است، و سپس ارزیابی عملکرد را نشان می دهیم.

2.1. مدل های قبلی برای ناهمگونی فضایی

2.1.1. مدل ضریب متغیر مکانی مبتنی بر فیلتر فضایی ویژه (ESF-SVC)

مدل ESF-SVC از آزمون آماری رایج برای خودهمبستگی فضایی، موران I، برای بیان ناهمگنی فضایی ضرایب استفاده می‌کند. در اینجا ما این تحلیل را در نظر می گیریم که داده های مکانی در مکان i , y _i , بر روی ویژگی های نوع K از ویژگی های آن x _ij رگرسیون می شوند. اجازه دهید N تعداد مکان‌ها را نشان دهد، y نشان‌دهنده N با 1 بردار متغیر وابسته، X نشان‌دهنده N با K ماتریس متغیرهای توضیحی است که ستون اول آن N بر 1 بردار یک است. β a استK در 1 بردار ضریب رگرسیون y بر روی X و اولین عنصر یک قطع است.

اجازه دهید C نشان دهنده یک N با N ماتریس مجاورت فضایی بین N مکان، 1 نشان دهنده N با 1 بردار از یک ها، من یک N با N ماتریس هویت، و M نشان دهنده N با N ماتریس کانترینگ برای N با 1 بردار باشد، که M = ( I – 1 1′ / N ). سپس آمار موران I MC از متغیرهای وابسته y در N مشاهده شدمکان ها عبارتند از:

م سی (y) = ن 1 “ M 1 y “ M C M y y “ M y

(1)

اصطلاح MCM نشان دهنده ساختار خودهمبستگی y است که مجاورت فضایی با C بیان می شود .

گریفیث [ 4 ] یک ESF را پیشنهاد کرد که از بردارهای ویژه ماتریس MCM به عنوان متغیرهای توضیحی در مدل های رگرسیون خطی برای بیان همبستگی فضایی متغیرهای وابسته و حذف همبستگی از اغتشاشات استفاده می کند. بردارهای ویژه که با مقادیر ویژه بزرگ مطابقت دارند الگوهای همبستگی فضایی پیوسته جهانی را نشان می دهند و بردارهای ویژه با مقادیر ویژه کوچک و مثبت نشان دهنده الگوهای همبستگی فضایی پیوسته محلی هستند.

اجازه دهید E یک N را با ماتریس M نشان دهد، که شامل اولین بردارهای ویژه M ، که مقادیر ویژه آنها بزرگترین هستند، ماتریس MCM است و ستون i آن یک بردار ویژه i – e _i است، γ نشان دهنده یک بردار M با 1 ضریب برای ماتریس توضیحی E. مدل خطی پایه ESF به صورت زیر ارائه می شود:

y = X β + E γ + ε

(2)

جایی که $E (ε) = 0, V a r (ε) = σ^{2} I$ . فرض بر این است که اغتشاش ε همسانی دارند و هیچ همبستگی ندارند.

گریفیث [ 9 ] ESF را به یک مدل ESF-SVC برای تخمین ضرایب متغیر فضایی که نشان دهنده ناهمگونی ضرایب متغیرهای توضیحی است، گسترش داد. ضریب مکان محور برای متغیرهای توضیحی x _k و $β_{k}^{E S F}$ توسط:

β E اس اف ک = β ک 1 + E γ ک

(3)

جایی که $γ_{k} = {(γ_{k 1}, \dots, γ_{k m})}^{'}$ ضرایبی را نشان می دهد که بر اساس مکان متفاوت است و مدل ESF-SVC:

y = \sum k = 1 ک ایکس ک \circ β E اس اف ک + ε

(4)

جایی که $\circ$ نشان دهنده محصول هادامارد و $E (ε) = 0, V a r (ε) = σ^{2} I$ . فرض بر این است که خودهمبستگی مکانی متغیرهای وابسته با ناهمگنی نشان داده می شود. $β_{k}^{E S F}$ و هیچ خودهمبستگی مکانی روی اغتشاشات باقی نمانده است.

مدل ESF-SVC که از بسیاری از بردارهای ویژه استفاده می کند ممکن است باعث ایجاد مشکل اضافه برازش شود. یک راه حل این است که فقط از بردارهای ویژه استفاده کنیم که آمار موران I آنها بزرگتر از یک چهارم آمار I موران اولین بردار ویژه باشد [ 31 ]. معلوم می شود که تنها بردارهای ویژه ای هستند که با مقادیر ویژه بزرگ مطابقت دارند و ناهمگنی فضایی جهانی پیوسته را نشان می دهند برای بیان ناهمگنی فضایی ضرایب متغیر مکانی مورد استفاده قرار می گیرند، سپس ناهمگنی فضایی محلی پیوسته آنها را نمی توان در مدل در نظر گرفت.

در این مطالعه از مدل ESF-SVC استفاده می‌شود، زیرا می‌توان آن را به عنوان یک مدل رگرسیون خطی توصیف کرد و سازگاری بالایی با GL دارد، که نظم‌دهی ℓ ₁ را برای یک مدل رگرسیون خطی انجام می‌دهد.

2.1.2. کمند عمومی (GL)

کمند (حداقل عملگر انقباض و انتخاب مطلق) [ 30 ] رایج‌ترین روش مدل‌سازی پراکنده است که برای بدست آوردن تخمین‌های پراکنده ضرایب، ℓ ₁ عبارت جریمه به تابع هدف تخمین اضافه می‌کند. اغلب در انتخاب متغیر استفاده می شود. تخمین مدل رگرسیون خطی توسط کمند به صورت زیر ارائه می شود:

β ˆ = arg min β ⎡⎣ 1 2 \sum i = 1 ن (y من - \sum j = 1 ک β j ایکس من ج) 2 + λ \sum j = 1 ک | β j | ⎤⎦

(5)

که در آن λ وزنی را برای عبارت جریمه نشان می دهد.

GL [ 22 ] بسط کمندی است که ℓ ₁ جمله جریمه را به تفاوت بین ضرایب “همجوار” به اضافه ℓ ₁ جمله جریمه روی خود ضرایب اضافه می کند. می‌تواند نقاط تغییر را زمانی که برای تحلیل‌های سری زمانی و مرزها در تحلیل‌های فضایی اعمال می‌شود، تشخیص دهد. تخمین مدل رگرسیون خطی با GL به صورت زیر نشان داده می شود:

β ˆ = arg min β ⎡⎣ 1 2 \sum i = 1 ن (y من - \sum j = 1 ک β j ایکس من ج) 2 + δ λ \sum j = 1 ک | β j | + λ \sum (i, j) \in C | β من - β j | ⎤⎦

(6)

که در آن λ و δ فراپارامترهای وزن در شرایط جریمه هستند و C مجموعه ای از جفت ضرایب مجاور است.

GL برای تشخیص ناهمگنی فضایی گسسته استفاده شده است. این نه تنها برای تحلیل‌های رگرسیون خطی [ 22 ، 23 ، 24 ]، بلکه برای بسیاری از انواع تحلیل‌ها، مانند تخمین تابع کوواریانس فضایی خاص منطقه [ 25 ]، تخمین تابع کمیت مکانی و زمانی [22] اعمال می‌شود. 26 ]، و تشخیص خوشه فضایی رویدادهای نقطه ای بر اساس مدل های رگرسیون پواسون [ 27 ، 28 ، 29 ].

2.2. ESF-GL-SVC

ما یک مدل ESF-GL-SVC برای تجزیه و تحلیل ناهمگنی فضایی پیوسته و گسسته به طور همزمان با ترکیب ESF-SVC و GL پیشنهاد می کنیم.

ناهمگنی مداوم با ضرایب ESF-SVC نشان داده می شود. مدل ESF-GL-SVC از بردارهای ویژه ای استفاده می کند که آمار موران I بزرگتر از یک چهارم آمار موران I اولین بردار ویژه است [ 31 ]. ناهمگنی گسسته با ضرایب متغیرهای ساختگی α نشان داده می شود که برای همه مناطق فرعی در منطقه مورد مطالعه تنظیم شده است. اجازه دهید D نشان دهنده ماتریس متغیر ساختگی subregion باشد. اگر نقطه i در زیر منطقه r باشد ، عنصر D _ir یک و در غیر این صورت صفر است. سپس مدل ESF-GL-SVC به صورت زیر بیان می شود:

y = \sum k = 1 ک ایکس ک \circ β E اس اف ک + D α + ε ، β E اس اف ک = β ک 1 + E γ ک

(7)

تخمین مدل ESF-GL-SVC با عبارت منظم سازی GL را می توان با رابطه (8) نشان داد، که در آن C مجموعه ای از ترکیبات زیرمنطقه _های مجاور را نشان می دهد و λ ، _δ1 و δ2 فراپارامترها هستند .

(α ˆ ، β ˆ ، γ ˆ) = arg min α ، β ، γ ⎡⎣ 1 2 \sum i = 1 ن (y من - \sum j = 1 ک (β j + \sum l = 1 L ه من l γ l j) ایکس من ج - \sum m = 1 م د من_α متر) 2 + λ \sum (p, q) \in C | α پ - α q | + δ 1 λ \sum m = 1 م | α متر | + δ 2 λ \sum l = 1 L \sum j = 1 ک | γ l j | ⎤⎦

(8)

عبارت دوم، عبارت مجازات ℓ ₁ در تفاوت بین ضرایب زیرمنطقه‌های مجاور، استخراج یک سری از مناطق فرعی با همان سطح ناهمگونی گسسته فضایی را امکان‌پذیر می‌سازد. می تواند مسائل مربوط به مقیاس مربوط به تقسیم بندی از پیش تعیین شده مناطق فرعی را کاهش دهد. جمله سوم، عبارت جریمه ℓ ₁ بر روی ضرایب متغیرهای ساختگی زیرمنطقه، و جمله چهارم، ℓ ₁عبارت جریمه در ضرایب ESF-SVC، اثر القای یک راه حل پراکنده را دارد. زمانی که داده ها فقط ناهمگنی فضایی پیوسته دارند، توابع جمله سوم به یک نتیجه تخمین منتهی می شود که در آن مقادیر ضرایب ساختگی های زیرمنطقه صفر است، و زمانی که داده ها فقط ناهمگنی فضایی گسسته دارند، توابع جمله چهارم به یک نتیجه تخمین منتهی می شود که در آنجا به یک نتیجه تخمینی منجر می شود. مقادیر ضرایب ESF-SVC صفر است. منظم‌سازی ضرایب می‌تواند بروز مشکلات شناسایی پارامتر را بین ESF-SVC و ضرایب متغیر ساختگی زیرمنطقه کاهش دهد.

سه فراپارامتر باید با توجه به تناسب مدل ها انتخاب شود. معیار اطلاعات بیزی (BIC) ممکن است یک گزینه باشد. با این حال، از آنجایی که ضرایب تخمین زده شده به دلیل شرایط منظم سازی کمند، مغرضانه هستند [ 32]، انتخاب مدل استفاده شده توسط برآوردهای معادله (8) مناسب نیست. بنابراین، ابتدا با معادله (8) تخمین ضرایب را پیشنهاد کردیم، مدلی ساختیم که با نتایج تخمین زده شده مطابقت دارد با حذف ضرایب تخمین زده شده به عنوان صفر و تعیین یک ضریب زیرمنطقه ساختگی مشترک اگر زیرمنطقه های مجاور برآوردهای یکسانی داشته باشند، مدل را بدون قاعده سازی تخمین بزنیم. شرایط، و ارزیابی نتایج توسط BIC. این روش ها از تخمین های مغرضانه جلوگیری می کنند و برازش مدل به طور مناسب ارزیابی می شود. تخمین مدل ESF-GL-SVC توسط بسته ‘genlasso’ [ 33 ] در R اجرا می شود. این بسته ضرایب را با تغییر تدریجی فراپارامتر λ تحت نسبت ثابتی از وزن δ ، تخمین می زند . این مطالعه هر دو را تنظیم کردδ ₁ و δ ₂ در تخمین مدل همجوشی و δ برای تخمین GL به صورت {0.1، 1 و 10} و نتیجه تخمین را با حداقل مقدار BIC جستجو کردند. ارزیابی مبتنی بر BIC همچنین ممکن است در کاهش احتمال مشکلات شناسایی پارامتر با انتخاب مدل‌هایی با ضرایب غیر صفر کمتر مفید باشد.

2.3. ارزیابی عملکرد توسط آزمایش های شبیه سازی

ما عملکرد ESF-GL-SVC اعمال شده بر روی داده های شبیه سازی شده را با ناهمگنی فضایی پیوسته و گسسته ارزیابی کردیم. تنظیمات برای تولید داده های شبیه سازی در زیر مشخص شده است.

یک مربع با طول ضلع 1 را به عنوان منطقه مطالعه قرار دادیم و تعداد نقاط از پیش تعیین شده را در آن ایجاد کردیم. مختصات نقاط با توزیع یکنواخت بین 0 و 1 تولید می شود. داده های شبیه سازی شده از:

y = 1 \circ β E اس اف 1 + x \circ β E اس اف 2 + D α + ε ، β E اس اف ک = β ک 1 + E γ ک ، ε \sim N (0, σ 2 ε من)

(9)

که در آن x بردار متغیرهای توضیحی است که عناصر آن از توزیع یکنواخت بین 0 و 1 تولید می شوند.

برای تولید مقادیر داده با ناهمگنی فضایی پیوسته در هر نقطه، یک ماتریس مجاورت فضایی C توسط هسته گاوسی که عرض آن 0.2 است، بردارهای ویژه ماتریس MCM را با محاسبه تقریبی با [ 34 ] به دست آوردیم، بردارهای ویژه انتخاب شد که بردارهای ویژه بزرگتر بودند. بیش از یک چهارم از بزرگترین مقادیر ویژه مطابق [ 31 ]، و داده های شبیه سازی را در هر نقطه با تنظیم ضرایب β s و γ s ایجاد کرد. برای شبیه‌سازی ضرایب متغیر فضایی با ساختارهای مختلف ناهمگونی فضایی برای هر آزمایش، یک بردار ویژه به‌طور تصادفی برای هر متغیر توضیحی انتخاب شد. ضریب γاز بردارهای ویژه منتخب یک و سایر ضرایب روی صفر قرار گرفتند. ضرایب غیر مکانی متغیر، β1 و β2 ، به _{یک تنظیم}_شدند .

برای تولید مقدار داده با ناهمگنی فضایی گسسته، منطقه مورد مطالعه را به زیرمنطقه های 10 در 10 مربع با طول ضلع 0.1 تقسیم کردیم و یک متغیر ساختگی به هر زیر منطقه اختصاص دادیم. فرض کنید α بردار متغیرهای ساختگی زیرمنطقه و D نشانگر ماتریسی برای تخصیص متغیرهای ساختگی زیرمنطقه به هر نقطه باشد. ضرایب متغیرهای ساختگی چهار زیرمنطقه در مرکز منطقه مورد مطالعه در ردیف های پنجم و ششم و ستون های پنجم و ششم یک و ضرایب دیگر صفر شد.

سپس مقدار شبیه‌سازی‌شده در هر نقطه با اضافه کردن اغتشاشات مستقل و به طور یکسان بر اساس توزیع نرمال ایجاد شد.

جدول 1 تنظیمات تولید داده های شبیه سازی را برای سه آزمایش زیر خلاصه می کند. دو آزمایش اول عملکرد ESF-GL-SVC را با تغییر مقدار داده ها و اندازه واریانس اختلالات ارزیابی می کنند. آخرین آزمایش عملکرد ESF-GL-SVC را با عملکرد ESF-SVC و GL مقایسه می کند. داده های شبیه سازی 1000 بار برای همه آزمایش ها تولید می شوند. کدهای آزمایش های شبیه سازی در مواد تکمیلی موجود است.

2.3.1. تأثیر مقدار داده بر عملکرد ESF-GL-SVC

پنج تنظیمات مختلف برای تعداد کل امتیازها برای بررسی تأثیر بر تخمین مدل تنظیم شد. هنگام تولید داده هایی که میانگین تعداد نقاط آن در هر زیر منطقه به دو، پنج و ده تنظیم شده بود، تعداد نقاط هر زیر منطقه یکسان و موقعیت نقاط به طور تصادفی در هر زیر منطقه تنظیم شد. هنگام تولید داده ها توسط تنظیمات دیگر، نقاط به طور تصادفی در کل منطقه توزیع شده و سپس تعداد نقاط در هر زیر منطقه یکسان نبود.

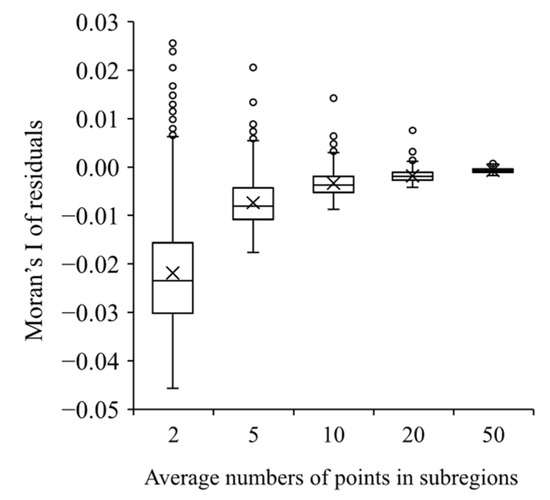
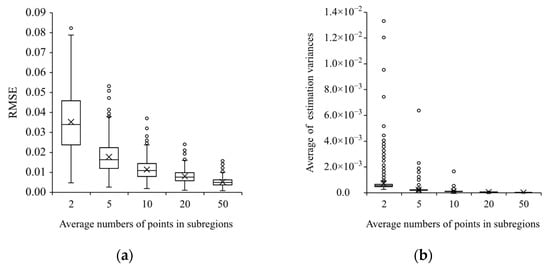
شکل 1 رابطه بین مقدار داده ها و آمار موران I باقیمانده ها را نشان می دهد و شکل 2 و شکل 3 ریشه میانگین مربعات خطا (RMSE) بین ضرایب شبیه سازی شده و تخمین زده شده و میانگین واریانس های تخمینی ضرایب رهگیری را نشان می دهد.

β_{1}^{E S F}

و متغیر توضیحی

β_{2}^{E S F}

، به ترتیب.

دقت تخمین با افزایش تعداد نقاط افزایش می یابد. هنگامی که تعداد نقاط در هر زیر منطقه دو و پنج باشد، RMSE بین ضرایب شبیه سازی شده و تخمین زده شده و واریانس های تخمینی بسیار زیاد است. با این حال، زمانی که تعداد نقاط در هر زیر منطقه از 10 فراتر رفت، تأیید شد که دقت تخمین بالا بوده و همبستگی فضایی در باقیمانده‌ها حذف شد. این آزمایش نشان می‌دهد که نتایج برآورد شده زمانی تثبیت می‌شوند که تعداد نقاط در هر زیر منطقه بزرگتر از 10 باشد.

2.3.2. تأثیر بزرگی واریانس اختلالات بر عملکرد ESF-GL-SVC

پنج تنظیمات مختلف برای انحراف استاندارد اختلالات برای تعیین تأثیر آنها بر تخمین مدل مورد آزمایش قرار گرفت. شکل 4 و شکل 5 RMSE بین ضرایب شبیه سازی شده و تخمین زده شده و واریانس های تخمینی ضرایب قطع را نشان می دهد.

β_{1}^{E S F}

و متغیرهای توضیحی

β_{2}^{E S F}

، به ترتیب.

هنگامی که انحراف استاندارد اختلالات روی 0.8 و 1.2 تنظیم شد، ضرایب متغیر مکانی به درستی برآورد نشدند. RMSE بین ضرایب شبیه سازی شده و تخمینی و واریانس تخمینی ضرایب در این تنظیمات زیاد بود. با توجه به اینکه مقادیر

1 \circ β_{1}^{E S F} + x \circ β_{2}^{E S F} + D α

مقادیر شبیه‌سازی‌شده قبل از افزودن اغتشاش‌ها، دارای انحراف استاندارد 710/0 در میانگین شبیه‌سازی‌ها بودند، تأیید می‌شود که اگر انحراف معیار اغتشاش‌ها از تأثیر متغیرهای توضیح‌داده شده بیشتر باشد، ناهمگونی فضایی ضرایب قابل تعیین نیست.

2.3.3. مقایسه با مدل های قبلی

ما ضرایب مدل‌های ESF-GL-SVC، ESF-SVC و GL را تخمین زدیم و عملکرد آن‌ها را با BIC محاسبه‌شده توسط مدل بدون شرایط منظم‌سازی، آمار موران I از باقیمانده‌ها و RMSE بین ضرایب شبیه‌سازی شده و تخمینی هر مکان ارزیابی کردیم. . نمودار توزیع فضایی ضرایب برآورد شده نیز برای ارزیابی در نظر گرفته شد.

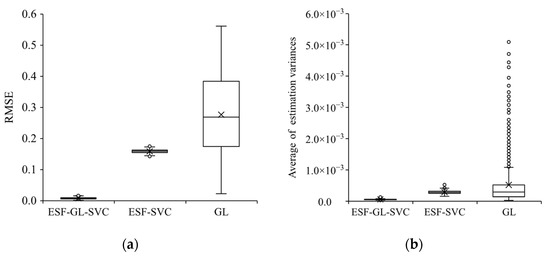
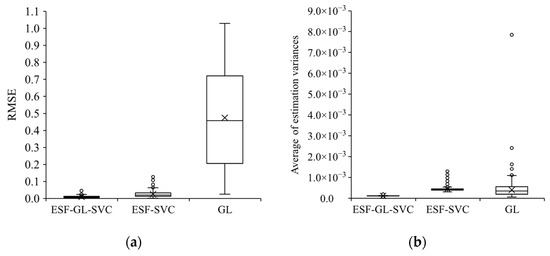
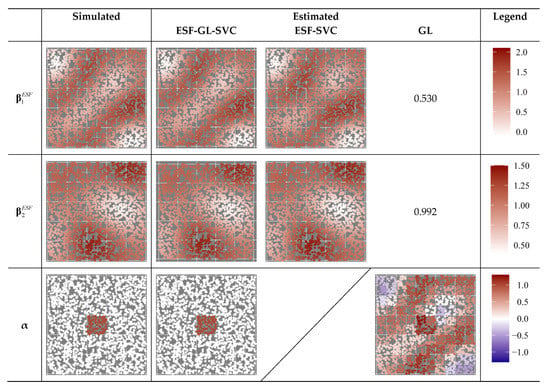
توزیع آمار BIC و موران I از باقیمانده ها برای داده ها با ناهمگنی فضایی پیوسته و گسسته در شکل 6 ، توزیع RMSE ها بین ضرایب شبیه سازی شده و تخمین زده شده و میانگین واریانس تخمینی ضرایب نشان داده شده است و در شکل 7 و شکل 8 نشان داده شده است. به ترتیب، و توزیع فضایی ضرایب شبیه سازی شده و برآورد شده توسط سه مدل در یک شبیه سازی در شکل 9 نشان داده شده است.

توزیع BIC ها و آمار موران I از باقیمانده ها نشان می دهد که ESF-GL-SVC نتایج را با کوچکترین BIC خروجی می دهد و همبستگی مکانی را از باقی مانده ها حذف می کند. تفاوت بین برآوردگرها توسط ESF-GL-SVC و ضرایب شبیه‌سازی شده بسیار کوچک است، که نشان‌دهنده ناهمگنی پیوسته با تخمین ضرایب متغیر مکانی و ناهمگنی گسسته توسط تخمین‌های ضرایب ساختگی زیرمنطقه است. از سوی دیگر، مدل‌های ESF-SVC و GL نتوانستند همبستگی مکانی را از باقی‌مانده‌ها حذف کنند و برآوردگرها با ضرایب شبیه‌سازی شده با واریانس‌های زیاد متفاوت بودند.

شکل 9نشان می‌دهد که ESF-SVC ناهمگنی گسسته را با ضرایب متغیر فضایی پیوسته نشان می‌دهد و GL نشان‌دهنده ناهمگنی پیوسته توسط ضرایب مبتنی بر زیرمنطقه گسسته است. حتی اگر ضرایب متغیرهای ساختگی زیرمنطقه مدل پیشنهادی به طور بالقوه می تواند برای نشان دادن ناهمگنی فضایی پیوسته استفاده شود، تنها ناهمگنی گسسته در این تخمین توسط آنها استخراج می شود. این ممکن است نشان دهد که تنظیم برای ضرایب متغیرهای ساختگی زیرمنطقه و انتخاب مدل بر اساس BIC در اجتناب از مشکلات شناسایی پارامتر بین ناهمگنی فضایی پیوسته و گسسته موثر است. اگر ناهمگونی فضایی پیوسته و گسسته وجود داشته باشد، آنها در استخراج ساختار ناهمگونی فضایی شکست خواهند خورد.

آزمایش‌ها تأیید کردند که مدل ESF-GL-SVC عملکرد بهتری نسبت به سایر داده‌ها با ناهمگنی فضایی پیوسته و گسسته نشان داد.

3. درخواست برای داده های اجاره آپارتمان

3.1. داده ها و مدل ها

ما مدل‌های ESF-GL-SVC، ESF-SVC، و GL را برای داده‌های اجاره آپارتمان در بخش‌های Shibuya، Setagaya، و Meguro در بخش جنوب غربی منطقه شهری توکیو در سال ۲۰۱۷ اعمال کردیم. داده‌ها توسط «At Home» جمع‌آوری شد. Co., Ltd.’; این شرکت اطلاعات قیمت املاک و مستغلات را منتشر می کند.

کانکس های بلندمرتبه که تعداد طبقات آنها بیش از 15 طبقه است، مستثنی شدند، زیرا اجاره آنها ساختار قیمت گذاری متفاوتی با قیمت گذاری سایر آپارتمان ها دارد. اگر داده‌های اجاره از یک ساختمان بیشتر داده‌ها را برای آن محله تشکیل دهد، ممکن است در برآورد ضرایب مشکل ایجاد کند زیرا متغییرهای توضیحی دارای مقادیر یکسان یا مشابه هستند. بنابراین، برای جلوگیری از چنین مسائلی، از هر طبقه از هر ساختمان فقط یک آپارتمان به طور تصادفی انتخاب شد. در نتیجه تعداد کل رکوردها 13748 بود.

متغیر وابسته لگاریتم اجاره بهای هر متر مربع به ین ژاپن (JPY) و متغیرهای توضیحی لگاریتم «سطح طبقه»، «سن ساختمان»، «اندازه ملک»، «زمان پیاده‌روی تا نزدیک‌ترین ایستگاه قطار» هستند. از این پس، «زمان تا سرویس قطار»)، و «میانگین زمان سفر با قطار به پنج ایستگاه اصلی واقع در مناطق تجاری مرکزی (CBD)» (از این پس، «زمان به CBD»). از آنجایی که املاکی وجود دارند که سن ساختمان آنها صفر است، زمانی که لگاریتم سن ساختمان را محاسبه کردیم یک را اضافه کردیم. ایستگاه های اصلی انتخاب شده شینجوکو، ایکبوکورو، شیبویا، توکیو و شیناگاوا بودند که بیشترین تعداد مسافران را در منطقه متروپولیتن توکیو ارائه می کنند. ما زمان سفر را شامل نیمی از مسیر قطار به پنج ایستگاه اصلی هنگام خروج از ایستگاه در ظهر روز هفته در سرویس برنامه ریزی مسیر حمل و نقل عمومی یاهو بررسی کردیم! ترانزیت و محاسبه میانگین وزنی با تعداد مسافران در ایستگاه های اصلی.جدول 2 آمار توصیفی متغیرهای وابسته و توضیحی را خلاصه می کند. از آنجایی که مقیاس متغیرهای توضیحی بر شرایط منظم سازی در برآورد هر ضریب تأثیر می گذارد، متغیرهای توضیحی با میانگین صفر و واریانس واحد استاندارد شدند.

برای نشان دادن ناهمگنی پیوسته با ضرایب متغیر مکانی در مدل‌های ESF-GL-SVC و ESF-SVC، عناصر ماتریس مجاورت فضایی C با وارد کردن فواصل بین ویژگی‌ها در تابع هسته گاوسی با باند در فواصل 500 متری از 1 کیلومتر تنظیم شدند. تا 5 کیلومتر برای هر تنظیم باند، بردارهای ویژه MCMکه مقادیر ویژه آنها بزرگتر از یک چهارم بزرگترین مقدار ویژه است، به عنوان متغیرهای توضیحی در دو مدل انتخاب شدند. در این برنامه، باند 4.5 کیلومتری را برای ESF-GL-SVC و 2 کیلومتری را برای ESF-SVC انتخاب کردیم که کوچکترین BIC را برای هر مدل تولید می کند. در برآورد GL، ضرایب مبتنی بر بخش برای متغیرهای توضیحی برای نشان دادن ناهمگونی ارزش گذاری در مقیاس جهانی برآورد شد.

برای نشان دادن ناهمگونی فضایی گسسته توسط آدمک‌های زیرمنطقه‌ای در مدل‌های ESF-GL-SVC و GL، منطقه مورد مطالعه به 445 محله (چو و cho-me در ژاپنی) تقسیم شد و حداقل یک ملک مستغلات در 431 محله وجود داشت. برای هر محله به جز محله مرجع، Hachimanyama 3 cho-me ، یک ساختگی منطقه فرعی تنظیم شد . محله مرجع انتخاب شده محله ای است که ریشه میانگین مربعات باقیمانده توسط ESF-SVC حداقل است. مجاورت ضرایب آدمک‌های زیرمنطقه زمانی تنظیم می‌شود که چند ضلعی‌های همسایگی مرزهای مشترک داشته باشند.

این تجزیه و تحلیل از همان فرآیند جستجوی بهترین تنظیمات فراپارامتر برای هر مدل به عنوان آزمایش‌های شبیه‌سازی استفاده کرد. δ1 و δ2 در مدل ESF-GL-SVC و δ در GL روی { 0.1، _{1 ،}₁₀ } تنظیم شده‌اند، و تخمین با تغییر λ با استفاده از بسته R از ‘genlasso’ انجام شد. نتایج با منظم‌سازی ℓ ₁ فقط برای انتخاب متغیرهایی که تخمین‌گر آنها غیر صفر هستند استفاده شد. سپس، BIC ها از طریق تخمین OLS مدل ها با متغیرهای انتخاب شده محاسبه شدند. کد و داده های نمونه برای تجزیه و تحلیل در مواد تکمیلی موجود است.

3.2. نتایج تخمین

جدول 3 نتایج برآورد شده از سه مدل را خلاصه می کند. اول، هر سه مدل به طور موثر خود همبستگی فضایی متغیرهای وابسته را در نظر می گیرند، زیرا آمار موران I از باقیمانده ها نشان می دهد که باقیمانده ها خودهمبستگی مکانی ندارند. دوم، تایید می شود که مدل ESF-GL-SVC بهترین عملکرد را نشان می دهد زیرا ضرایب تعیین حداکثر و BIC حداقل است.

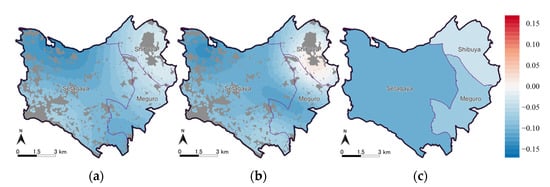
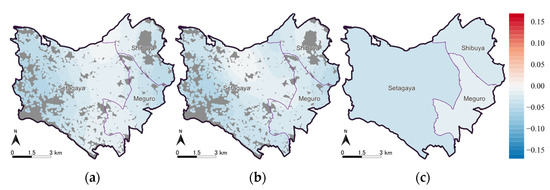
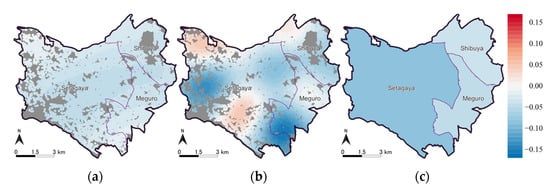
رهگیری ها و ضرایب تخمینی متغیرهای توضیحی توسط مدل های ESF-GL-SVC و ESF-SVC به ترتیب در جدول 4 و جدول 5 و ضرایب بر اساس بخش برآورد شده توسط GL در جدول 6 خلاصه شده است. توزیع فضایی برش ها در شکل 10 نشان داده شده است ، توزیع فضایی ضرایب زیرمنطقه توسط مدل ESF-GL-SVC و GL در شکل 11 نشان داده شده است ، و توزیع فضایی ضرایب متغیرهای توضیحی در شکل 12 ، شکل نشان داده شده است. 13 ، شکل 14 ، شکل 15 و شکل 16 .

3.3. بحث از طریق مقایسه نتایج توسط سه مدل

3.3.1. رهگیری ها و ضرایب آدمک های زیرمنطقه

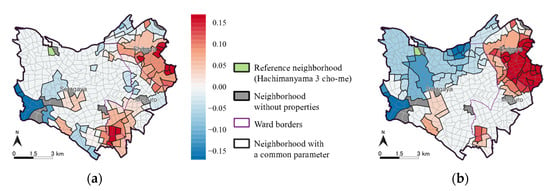
اول، ما بر روی رهگیری های مدل های ESF-GL-SVC و ESF-SVC ( شکل 10 ) و آدمک های زیرمنطقه با استفاده از مدل ESF-GL-SVC ( شکل 11 a) تمرکز کردیم. مجموع نتایج تخمین زده شده رهگیری ها و آدمک های فرعی توسط مدل ESF-GL-SVC و نتایج تخمینی رهگیری ها با مدل ESF-SVC در قسمت شرقی منطقه مورد مطالعه که به CBD نزدیک تر است، مقادیر بالاتری دارند که نشان می دهد که اجاره در منطقه گران است. با این حال، حداکثر فاصله نشان داده شده در جدول 4 کوچکتر از جدول 5 است، زیرا ناهمگونی فضایی گسسته با ضرایب آدمک های زیرمنطقه توسط مدل ESF-GL-SVC نشان داده می شود.

جنوب بخش Meguro یک منطقه مسکونی با کلاس بالا است. مدل ESF-GL-SVC ناهمگنی فضایی گسسته را که توسط ضرایب زیرمنطقه مثبت نشان داده شده است و مدل ESF-SVC ناهمگنی فضایی پیوسته را با مقادیر بزرگ‌تر رهگیری فضایی متفاوت استخراج می‌کند. در بخش بعدی در مورد اینکه کدام شناسایی ناهمگونی فضایی با نتایج تخمین ضرایب متغیرهای توضیحی مناسب است، توضیح خواهیم داد.

دوم، ما برآوردهای GL را با دو مدل دیگر مقایسه کردیم. رهگیری برآورد شده توسط GL نزدیک به میانگین ضرایب توسط مدل‌های ESF-GL-SVC و ESF-SVC است. تعداد مناطق فرعی با ضرایب غیر صفر توسط GL بزرگتر از مدل ESF-GL-SVC است. مدل GL ناهمگونی فضایی اجاره را با ناهمگونی مبتنی بر زیرمنطقه نشان می دهد ( شکل 11 ب). نتیجه GL نشان‌دهنده الگوهای فضایی مشابه با مدل‌های ESF-GL-SVC و ESF-SVC است. با این حال، مدل GL دارای BIC بالاتر و ضریب تعیین کمتری نسبت به مدل ESF-GL-SVC است. به نظر می رسد که ناهمگونی فضایی گسسته تنها برای نمایش ناهمگونی فضایی رانت مناسب نیست.

3.3.2. ضرایب متغیرهای توضیحی

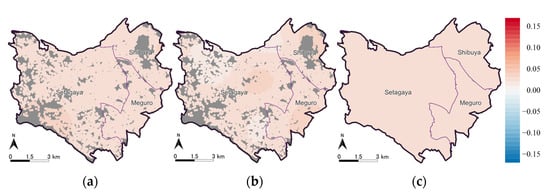
اول، تأیید می شود که هر سه مدل می توانند تشخیص دهند که آیا ضرایب متغیرهای توضیحی ناهمگنی فضایی دارند یا خیر. الگوهای فضایی برآوردها نشان می‌دهد که ضرایب “سطح طبقه” و “سن ساختمان” ناهمگنی ضعیفی دارند، اما ضرایب “اندازه ملک”، “زمان برای آموزش خدمات” و “زمان تا CBD” ناهمگنی قوی دارند.

دوم، تخمین‌های مدل‌های ESF-GL-SVC و ESF-SVC مشابه هستند، به جز ضرایب «زمان تا CBD». تخمین‌های مربوط به “اندازه ملک” و “زمان برای آموزش خدمات” برای مدل‌های ESF-GL-SVC و ESF-SVC تقریباً یکسان است و تخمین‌ها برای GL نیز الگوهای فضایی مشابهی را نشان می‌دهند، اگرچه وضوح فضایی بخش ضرایب مبتنی بر بسیار پایین است.

اگر ضرایب همسایگی برای همه متغیرهای توضیحی در مدل GL تنظیم شده باشد، ممکن است ناهمگونی فضایی ضرایب را با دقت بیشتری نشان دهیم. با این حال، از آنجایی که ترتیب محاسبه GL به صورت O ( mn ² + Tm ² ) تخمین زده می شود، که m تعداد محدودیت ها، n تعداد متغیرهای توضیحی است، و T تعداد تکرار است و باید بزرگتر یا مساوی باشد. به m [ 22 ]، امکان برآورد مدل وضوح بالا با m و n بزرگکم است. بنابراین، مدل ESF-GL-SVC نسبت به مدل GL در استفاده از مدل ضرایب متغیر فضایی برای بیان ناهمگنی فضایی پیوسته مزایایی دارد.

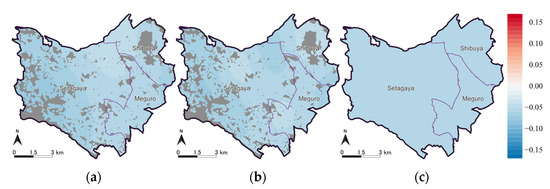
سوم، ضرایب “زمان تا CBD” مزیت مدل ESF-GL-SVC را نسبت به ESF-SVC نشان می دهد. طبیعی است که ضرایب “زمان تا CBD” منفی است، اما تخمین‌های ESF-SVC دارای مقادیر مثبت و منفی هستند، به‌ویژه که مقادیر مثبت بزرگی را در گوشه شمال غربی و جنوب غربی منطقه مورد مطالعه نشان می‌دهند. از سوی دیگر، برآوردهای مدل ESF-GL-SVC همه با استفاده از تنظیمات بردار ویژه منفی هستند.

این نشان می دهد که ESF-SVC بیش از حد به مجموعه داده ها تناسب دارد. این ناشی از استفاده از یک باند کوتاهتر برای ماتریس مجاورت فضایی C و بردارهای ویژه بیشتر است که الگوهای ناهمگونی فضایی محلی را در مدل ESF-SVC نشان می دهد. دلیل اضافه برازش احتمالاً به این دلیل است که «زمان به CBD» دارای همبستگی مکانی قوی در مقیاس جهانی است، اگرچه سایر متغیرهای توضیحی اینطور نیستند. با ضرب ضرایب و متغیرهای توضیحی که هر دو دارای خود همبستگی مکانی هستند، می توان همبستگی مکانی متغیرهای وابسته را بیان کرد. اجاره ها در جنوب بخش Meguro دارای ناهمگونی مکانی قوی و گسسته هستند که توسط ضرایب تخمینی آدمک های زیرمنطقه نشان داده شده در شکل 11 نشان داده شده است.. مدل ESF-SVC سعی کرد ناهمگنی محلی را با رهگیری ( شکل 10 ب) و ضریب “زمان تا CBD” ( شکل 16 ب) بیان کند. در نتیجه، ضرایب “زمان تا CBD” در منطقه اطراف بسیار متغیر بود و تفسیر آن دشوار بود. اگر تنها باند طولانی‌تر برای ماتریس مجاورت فضایی C تنظیم شده باشد، این تعریف اشتباه توسط ESF-SVC قابل اجتناب است . با این حال، زمانی که باند طولانی‌تر تنظیم شد، بردارهای ویژه تنها الگوهای فضایی جهانی را نشان می‌دهند و مدل ESF-SVC قدرت توضیحی ناهمگونی محلی را از دست می‌دهد.

3.4. خلاصه کاربرد تحلیل داده های اجاره آپارتمان

کاربرد داده های اجاره آپارتمان نشان می دهد که مدل ESF-GL-SVC از دو مدل قبلی بهتر عمل می کند. مزایایی در استخراج ناهمگنی فضایی پیوسته و گسسته دارد که داده‌های اجاره آپارتمان دارند.

مدل ESF-GL-SVC قادر به تخمین ضرایب متغیر مکانی بود که قابل تفسیر هستند، اگرچه مدل ESF-SVC چنین نبود. تجزیه و تحلیل توسط مدل ESF-GL-SVC ساختار ناهمگونی فضایی اثر متغیرهای توضیحی را روشن می کند. ضرایب اندازه دارایی بیشترین ناهمگنی فضایی را دارند. اندازه بر اجاره هر متر مربع در نزدیکی CBD تأثیر نمی گذارد اما در مناطق حومه شهر کاهش می یابد. همچنین وجود ناهمگونی فضایی گسسته توسط ضرایب همسایگی را به تصویر می‌کشد.

4. بحث

این مطالعه تجزیه و تحلیلی را برای استخراج ناهمگنی فضایی پیوسته و گسسته توسط ESF-GL-SVC با ترکیب ESF-SVC و GL پیشنهاد کرد. از طریق تجزیه و تحلیل داده های شبیه سازی شده و داده های اجاره آپارتمان، تأیید می شود که مدل ESF-GL-SVC می تواند ناهمگنی فضایی پیوسته و گسسته مجموعه داده را جدا کند. می توان از برازش بیش از حد مجموعه داده ها جلوگیری کرد و تخمین های قابل تفسیر را به دست آورد.

سه راه برای بهبود مدل ESF-GL-SVC وجود دارد. اولین پیشرفت کاهش اثر ناشی از برآوردهای مغرضانه از کمند است. اشاره شد که برآوردگر کمند به سمت صفر سوگیری دارد و دارای خاصیت اوراکل نیست، که شامل ثبات در انتخاب متغیر و نرمال مجانبی [ 32 ] است. جریمه مقعر حداقل (MCP) برای کاهش تعصب [ 35 ] پیشنهاد شد و به MCP ذوب شده [ 36 ] گسترش یافت، که می تواند بایاس GL را کاهش دهد. ما تقسیم‌بندی بازار جغرافیایی اجاره آپارتمان [ 37 ] و استخراج تغییرات مکانی-زمانی در قیمت‌های بازار املاک را تجزیه و تحلیل کردیم [ 38 ]] توسط fused-MCP و تایید کرد که fused-MCP تخمین بهتری نسبت به GL دارد. با این حال، یک مسئله پیچیدگی محاسباتی وجود دارد. ساخت یک مدل همجوشی ESF-SVC و fused-MCP با تخمین کارآمد یک توسعه موثر است. بهبود دوم کاهش مشکل اضافه برازش ESF-SVC است. موراکامی و همکاران [ 10 ] یک مدل اثرات تصادفی ESF-SVC (RE-ESF-SVC) بر اساس مشخصات اثرات تصادفی ESF [ 34 ] و موراکامی و همکاران پیشنهاد کردند. [ 39] تایید کرد که RE-ESF-SVC یکی از مدل هایی است که می تواند ساختار ضرایب متغیر مکانی را به طور دقیق تخمین بزند و از نظر محاسباتی کارآمدترین است. استفاده از RE-ESF-SVC تخمین ضرایب متغیر مکانی را بهبود می بخشد. با این حال، از آنجایی که برآورد RE-ESF به روش حداکثر احتمال محدود نیاز دارد، معرفی منظم سازی با ℓ ₁توابع هنجار یا MCP ممکن است چالش برانگیز باشند. سومین پیشرفت، افزایش توانایی روش برای تجزیه و تحلیل ناهمگونی فضایی در مقیاس های مختلف است. روش پیشنهادی برای تجزیه و تحلیل پدیده‌های متشکل از ناهمگنی فضایی کلی و پیوسته و ناهمگنی فضایی محلی و گسسته ساختار یافته است. ممکن است ناهمگونی فضایی محلی و مداوم، مانند تأثیر یک پارک کوچک بر محیط محله، و ناهمگونی فضایی جهانی و گسسته، مانند تأثیر مرزهای منطقه ای در مناطق شهری به هم پیوسته، وجود داشته باشد. RE-ESF-SVC و GWR چند مقیاسی [ 40 ] به‌عنوان روش‌هایی برای در نظر گرفتن مقیاس‌های مختلف در تحلیل ناهمگنی فضایی پیوسته، و کمند گروهی [ 41 ] و کمند گروهی با ساختار درختی [ 42 ] پیشنهاد شده‌اند.انتظار می رود مقیاس های متعدد ناهمگونی فضایی گسسته را در نظر بگیرند. در نظر گرفتن ناهمگنی چند مقیاسی برای ناهمگنی فضایی پیوسته و گسسته، جهت توسعه مهمی برای این تحقیق است.

منابع

Tobler, W. یک فیلم کامپیوتری شبیه سازی رشد شهری در منطقه دیترویت. اقتصاد Geogr. 1970 ، 46 ، 234-240. [ Google Scholar ] [ CrossRef ]
Anselin, L. اقتصاد سنجی فضایی: روش ها و مدل ها . Kluwer Academic Publishers: Dordrecht, The Netherlands, 1988. [ Google Scholar ]
Cressie، NAC Statistics for Spatial Data ; Wiley: نیویورک، نیویورک، ایالات متحده آمریکا، 1991. [ Google Scholar ]
گریفیث، DA خودهمبستگی فضایی و توابع ویژه ماتریس وزن های جغرافیایی همراه با داده های جغرافیایی مرجع. می توان. Geogr. 1996 ، 40 ، 351-367. [ Google Scholar ] [ CrossRef ]
گریفیث، DA خودهمبستگی فضایی و فیلتر فضایی ; Springer: برلین/هایدلبرگ، آلمان، 2003. [ Google Scholar ]
Fotheringham، AS; Sachdeva، M. در مورد اهمیت تفکر محلی برای آمار و جامعه. تف کردن آمار 2022 ، در دست چاپ . [ Google Scholar ] [ CrossRef ]
براندون، سی. فاثرینگهام، اس. چارلتون، ام. رگرسیون وزن‌دار جغرافیایی: روشی برای کاوش غیرایستایی فضایی. Geogr. مقعدی 1996 ، 28 ، 281-298. [ Google Scholar ] [ CrossRef ]
Fotheringham، AS; براندون، سی. چارلتون، ام. رگرسیون وزن‌دار جغرافیایی: تحلیل روابط متغیر فضایی . Wiley: West Sussex، UK، 2002. [ Google Scholar ]
گریفیث، DA مشارکت‌های مبتنی بر فیلتر فضایی در نقد رگرسیون وزن‌دار جغرافیایی (GWR). محیط زیست طرح. یک اقتصاد. Space 2008 , 40 , 2751–2769. [ Google Scholar ] [ CrossRef ]
موراکامی، دی. یوشیدا، تی. سیا، ح. گریفیث، دی. یاماگاتا، ی. رویکرد اثرات مختلط مبتنی بر ضریب موران برای بررسی روابط متغیر فضایی. تف کردن آمار 2017 ، 19 ، 68-89. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
موراکامی، دی. گریفیث، DA مدل‌سازی ضریب متغیر فضایی برای مجموعه داده‌های بزرگ: حذف N از رگرسیون‌های فضایی. تف کردن آمار 2019 ، 30 ، 39–64. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
تان، اچ. چن، ی. ویلسون، جی پی؛ ژانگ، جی. کائو، جی. چو، تی. یک مدل ضریب متغیر مکانی مبتنی بر فیلتر فضایی بردار ویژه برای PM2. 5 تخمین غلظت: مطالعه موردی در منطقه دلتای رودخانه یانگ تسه چین. اتمس. محیط زیست 2020 , 223 , 117205. [ Google Scholar ] [ CrossRef ]
موراکامی، دی. کاجیتا، م. Kajita، S. انتخاب مدل مقیاس پذیر برای مدل سازی ترکیبی افزودنی فضایی: کاربرد در تجزیه و تحلیل جرم. ISPRS Int. J. Geo-Inf. 2020 ، 9 ، 577. [ Google Scholar ] [ CrossRef ]
پنگ، ز. Inoue, R. مشخص کردن ناهمگونی فضایی چند مقیاسی در بازار مسکن اجاره: مورد منطقه شهری توکیو. In Proceedings of the GIScience 2021 Short Paper Proceedings, Poznań, Poland, 29 سپتامبر 2021. [ Google Scholar ] [ CrossRef ]
پنگ، ز. Inoue, R. شناسایی مقیاس های چندگانه ناهمگونی فضایی در قیمت مسکن بر اساس رویکردهای فیلتر فضایی بردار ویژه. ISPRS Int. J. Geo-Inf. 2022 ، 11 ، 283. [ Google Scholar ] [ CrossRef ]
گودمن، ای سی؛ تقسیم بندی بازار مسکن تیبودو، TG. جی. هاوس. اقتصاد 1998 ، 7 ، 121-143. [ Google Scholar ] [ CrossRef ]
گودمن، ای سی؛ تیبودو، تقسیم‌بندی بازار مسکن TG و دقت پیش‌بینی لذت‌گرا. جی. هاوس. اقتصاد 2003 ، 12 ، 181-201. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
کولدورف، ام. Nagarwalla، N. خوشه های بیماری فضایی: تشخیص و استنتاج. آمار پزشکی 1995 ، 15 ، 707-715. [ Google Scholar ] [ CrossRef ] [ PubMed ]
کاسترو، ام سی; سینگر، BH کنترل نرخ کشف نادرست: یک برنامه کاربردی جدید برای محاسبه تست های متعدد و وابسته در آمار محلی تداعی فضایی. Geogr. مقعدی 2006 ، 38 ، 180-208. [ Google Scholar ] [ CrossRef ]
براندون، سی. چارلتون، ام. ارزیابی اثربخشی آزمون فرضیه‌های چندگانه برای تشخیص ناهنجاری جغرافیایی. محیط زیست طرح. B طرح. دس 2011 ، 38 ، 216-230. [ Google Scholar ] [ CrossRef ]
بنیامینی، ی. Hochberg, Y. کنترل نرخ کشف نادرست: یک رویکرد عملی و قدرتمند برای آزمایش چندگانه. JR Stat. Soc. سر. B 1995 ، 57 ، 289-300. [ Google Scholar ] [ CrossRef ]
طبشیرانی، ر.ج. Taylor, J. مسیر حل کمند تعمیم یافته. ان آمار 2011 ، 39 ، 1335-1371. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
اینو، آر. ایشیاما، آر. سوگیورا، الف. شناسایی تقسیم بندی جغرافیایی بازار آپارتمان های اجاره ای در منطقه شهری توکیو. در مجموعه مقالات دهمین کنفرانس بین المللی علوم اطلاعات جغرافیایی 2018، ملبورن، استرالیا، 30 اوت 2018. [ Google Scholar ] [ CrossRef ]
اینو، آر. ایشیاما، آر. سوگیورا، الف. شناسایی تقسیم بندی جغرافیایی بازار مسکن اجاره ای در منطقه شهری توکیو توسط کمند ذوب شده تعمیم یافته. J. Jpn. Soc. مدنی مهندس سر. D3 (Infrastruct. Plan. Manag.) 2020 ، 76 ، 251-263. (به ژاپنی) [ Google Scholar ] [ CrossRef ]
پارکر، RJ; رایش، بی‌جی؛ Eidsvik, J. یک رویکرد کمند ذوب شده برای تخمین کوواریانس فضایی غیر ساکن. جی. آگریک. Biol. محیط زیست آمار 2016 ، 21 ، 569-587. [ Google Scholar ] [ CrossRef ]
سان، ی. وانگ، اچ جی. Fuentes, M. کمند تطبیقی ذوب شده برای تخمین تابع کمیت مکانی و زمانی. فن سنجی 2016 ، 58 ، 127-137. [ Google Scholar ] [ CrossRef ]
وانگ، اچ. Rodríguez، A. شناسایی خوشه‌های سرطان کودکان در فلوریدا با استفاده از مدل‌های log-linear و مجازات‌های کمند تعمیم‌یافته. آمار سیاست عمومی 2014 ، 1 ، 86-96. [ Google Scholar ] [ CrossRef ] [ PubMed ]
چوی، اچ. آهنگ، ای. هوانگ، اس اس؛ Lee, W. یک الگوریتم کمند تعمیم یافته اصلاح شده برای تشخیص خوشه های فضایی محلی برای داده های شمارش. ASTA Adv. آمار مقعدی 2018 ، 102 ، 537-563. [ Google Scholar ] [ CrossRef ]
ماسودا، ر. Inoue، R. تشخیص خوشه رویداد نقطه ای از طریق کمند ذوب شده تعمیم یافته بیزی. ISPRS Int. J. Geo-Inf. 2022 ، 11 ، 187. [ Google Scholar ] [ CrossRef ]
تبشیرانی، آر. انقباض و انتخاب رگرسیون از طریق کمند. JR Stat. Soc. سر. B (Stat. Methodol.) 1996 ، 58 ، 267-288. [ Google Scholar ] [ CrossRef ]
گریفیث، دی. Chun, Y. خودهمبستگی فضایی و فیلتر فضایی بردار ویژه. در کتابچه راهنمای علوم منطقه ای ; Fischer, M., Nijkamp, P., Eds. Springer: برلین/هایدلبرگ، آلمان، 2014; ص 1477-1507. [ Google Scholar ] [ CrossRef ]
فن، جی. Li, R. انتخاب متغیر از طریق احتمال جریمه شده غیر مقعر و خواص اوراکل آن. مربا. آمار دانشیار 2001 ، 95 ، 1348-1360. [ Google Scholar ] [ CrossRef ]
آرنولد، سل؛ تیبشیرانی، الگوریتم مسیر RJ برای مسائل کمند تعمیم یافته. 2020. در دسترس آنلاین: https://cran.r-project.org/web/packages/genlasso/genlasso.pdf (در 20 مارس 2022 قابل دسترسی است).
موراکامی، دی. گریفیث، DA مشخصات اثرات تصادفی در فیلتر فضایی بردار ویژه: یک مطالعه شبیه سازی. جی. جئوگر. سیستم 2015 ، 17 ، 311-331. [ Google Scholar ] [ CrossRef ]
Zhang, CH انتخاب متغیر تقریباً بی‌طرفانه تحت جریمه مقعر کمینه. ان آمار 2010 ، 38 ، 894-942. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
جینگ، بی. یانگ، جی. یو، ایکس. Zhang, C. Fused-MCP با کاربرد برای پردازش سیگنال. جی. کامپیوتر. نمودار. آمار 2018 ، 27 ، 872-886. [ Google Scholar ] [ CrossRef ]
اینو، آر. ایشیاما، آر. Sugiura، A. شناسایی تفاوت های محلی با fused-MCP: مطالعه موردی بازار اجاره آپارتمان در تشخیص تقسیم بندی جغرافیایی. Jpn. J. Stat. اطلاعات علمی 2020 ، 3 ، 183-214. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
دن، ک. Inoue, R. استخراج منطقه و دوره نفوذ خدمات ریلی جدید در بازار املاک و مستغلات با استفاده از fused-MCP. In Proceedings of the GeoComputation 2019، Queenstown، نیوزیلند، 19 سپتامبر 2019. [ Google Scholar ] [ CrossRef ]
موراکامی، دی. لو، بی. هریس، پی. براندون، سی. چارلتون، ام. ناکایا، تی. گریفیث، DA اهمیت مقیاس در مدل‌سازی ضرایب متغیر فضایی. ان صبح. دانشیار Geogr. 2019 ، 109 ، 50-70. [ Google Scholar ] [ CrossRef ]
Fotheringham، AS; یانگ، دبلیو. کانگ، دبلیو. رگرسیون وزنی جغرافیایی چند مقیاسی. ان صبح. دانشیار Geogr. 2017 ، 107 ، 1247-1265. [ Google Scholar ] [ CrossRef ]
یوان، م. Lin, Y. انتخاب مدل و تخمین در رگرسیون با متغیرهای گروه بندی شده. JR Stat. Soc. سر. B (Stat. Methodol.) 2006 ، 68 ، 49-67. [ Google Scholar ] [ CrossRef ]
ژائو، پی. روشا، جی. Yu, B. خانواده جریمه های مطلق ترکیبی برای انتخاب متغیر گروهی و سلسله مراتبی. ان آمار 2009 ، 37 ، 3468-3497. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]

شکل 1. میانگین تعداد نقاط در زیرمنطقه ها و آمار موران I از باقیمانده ها.