در کاربردهای مختلف بلاک چین، نحوه فهرست‌بندی داده‌های مکانی-زمانی کارآمدتر به موضوعی پیوسته تبدیل شده است. پرس و جو داده های مکانی-زمانی موجود در بلاک چین با افزودن فضای ذخیره خارجی اضافی یا شاخص مکانی-زمانی ثابت در بلوک، بدون در نظر گرفتن توزیع خود پرس و جوی مکانی-زمانی و عملکرد اثباتی همراه با پرس و جو، محقق می شود. ما یک روش شاخص بلاک چین مکانی-زمانی تطبیقی ​​به نام Verkle AR*-tree پیشنهاد می‌کنیم که تأیید زمان و مکان را در بلاک چین بدون ذخیره‌سازی اضافی اضافه می‌کند و شاخص مکانی-زمانی را با امضای رمزگذاری‌شده محقق می‌کند. Verkle AR*-tree همچنین یک الگوریتم تطبیقی ​​را ارائه می دهد که ساختار درختی را با توجه به پرس و جوی تاریخی تنظیم می کند تا ساختار شاخص بهینه شده را تولید کند.

کلید واژه ها:

بلاک چین ؛ شاخص مکانی – زمانی ; Verkle AR*-tree ; پرس و جو تطبیقی

1. مقدمه

بلاک چین یک فناوری دفتر کل توزیع شده است که به سرعت در حال پیشرفت است [ 1 ] که از تراکنش های مالی غیرمتمرکز اولیه به برنامه های کاربردی در دنیای واقعی گسترش یافته است [ 2 ]] از جمله تجارت کالا، خدمات زنجیره تامین، خدمات تخصیص منابع، حمل و نقل کالا، اینترنت اشیا، و غیره. بلاک چین نه تنها به تکمیل تأیید امنیت تراکنش غیرمتمرکز نیاز دارد، بلکه به طور موثر ذخیره سازی داده های توزیع شده را برای دستیابی به عملکرد بهینه پرس و جو داده ایجاد می کند. به عنوان مثال، در تراکنش‌های تجاری، بلاک چین مسئول اطمینان از صحت معاملات شرکت A در محیط غیرمتمرکز است، اکنون باید اطمینان حاصل کند که «تراکنش‌های شرکت A در بندر شانگهای در تاریخ 3 ژانویه 2022 درست است». و بازیابی “تمام معاملات انجام شده توسط شرکت A در بندر شانگهای در ژانویه” را تسهیل می کند.
پیشرفت‌های زیادی در تحقیقات بلاک چین ادغام شده با داده‌های مکانی-زمانی صورت گرفته است. زنجیره های جانبی [ 3 ] بر روی بلاک چین تحت سلطه بیت کوین [ 4 ] ارائه می شوند، که در آن اطلاعات زمانی در زنجیره اصلی و اطلاعات مکانی در زنجیره جانبی ذخیره می شود، و قفل متقابل اطلاعات فضا-زمان از طریق SPV تحقق می یابد. (Simplified Payment Verification Proof) میخ دو طرفه [ 5 ]. در اتریوم [ 6 ، 7 ]، اترنت db تجزیه کننده را از ذخیره سازی بلوکی به یک پایگاه داده رابطه ای می شناسد و فناوری پرس و جوی مکانی-زمانی سنتی را برای بلاک چین قابل اجرا می کند. در بلاک چین مبتنی بر Block-DAG (گراف غیر چرخشی مستقیم BlockChain) [ 8]، یک درخت امضا شده رمزنگاری شده [ 9 ] معرفی شده است، که در آن یک درخت Merkle KD پیاده سازی شده است، و سر بلاک چین دارای یک شاخص فضایی با اطلاعات تجاری است.
در حال حاضر، مشکلات فناوری بلاک چین مکانی-زمانی بر افزایش عملکرد پرس و جوهای داده های مکانی-زمانی بدون افزایش هزینه قابلیت های کلیدی استقلال، قابلیت شنیدن و تغییرناپذیری آن متمرکز است. بنابراین، تا آنجا که ممکن است باید از تبدیل ساختارهای داده در مقیاس بزرگ یا معرفی پایگاه های داده خارجی در بلاک چین خودداری شود. علاوه بر این، کارایی شاخص مکانی-زمانی در بلاک چین همیشه با توزیع مکانی پرس و جوی مکانی-زمانی مرتبط است، در حالی که شاخص مکانی-زمانی سنتی توسط خود داده های مکانی-زمانی تعیین می شود و توزیع آماری را نادیده می گیرد. پرس و جوی مکانی-زمانی، که باعث می شود شاخص مکانی-زمانی سازگاری نداشته باشد. برای رسیدگی به این وضعیت، Verkle AR*-Tree را پیشنهاد می کنیم،10 ]، و پیکربندی مجدد نمایه تطبیقی ​​را برای توزیع پرس و جوی مکانی-زمانی انجام می دهد. بر اساس Verkle AR*-Tree، ما به ذخیره سازی سه نوع اطلاعات مکانی-زمانی در بلاکچین، شامل تراکنش با زمان و مکان، اطلاعات حساب با آخرین مکان و مسیر مکانی-زمانی حساب پی برده ایم. ما پرس و جوی منطقه مکانی-زمانی را از طریق نمایه سازی تطبیقی ​​تسریع می کنیم و کارایی اثبات داده ها را از طریق تعهد برداری Verkle بهبود می بخشیم. نتایج تجربی نشان می‌دهد که روش ما می‌تواند به طور موثر داده‌های مکانی-زمانی را در بلاک چین جاسازی کند و کارایی پرس و جو بهتر از بلاک چین شاخص مکانی-زمانی استاتیک موجود است.
بقیه این مقاله به شرح زیر سازماندهی شده است: تحقیقات مرتبط در بخش 2 خلاصه شده است و جزئیات مربوط به ساخت درخت Verkle AR* در بخش 3 آمده است. ارزیابی در بخش 4 ارائه شده است . بخش 5 بحث است و بخش 6 این کار را به پایان می رساند.

2. کارهای مرتبط

2.1. شاخص مکانی- زمانی

شاخص های مکانی-زمانی یک منطقه مکانی-زمانی معین را به صورت سلسله مراتبی تقسیم می کنند و اشیاء مکانی-زمانی را در یک گره تقسیم شده قرار می دهند. با توجه به روش‌های مختلف سازمان‌دهی شی فضایی، روش‌های شاخص فضایی به طور کلی به نقشه‌برداری شی، مرزبندی شی، برش و لایه‌های چندگانه تقسیم می‌شوند [ 11 ]. ما به سادگی شاخص‌های مکانی-زمانی را به دو دسته تقسیم می‌کنیم: منظم‌سازی و نامنظم‌سازی، اولی هیچ نواحی همپوشانی مکانی-زمانی از گره‌ها در همان لایه ندارد و پارتیشن همیشه از طریق یک منطقه فرعی مانند درخت چهار درخت [ 12 ]، KD اجرا می‌شود. درخت [ 13 ] و درخت BD [ 14 ]، و دومی مانند درخت BSP[ 15 ]، MLS3 [ 16 ]، درخت R [17 ، 18 ، 19 ]. R-tree در واقع یک خانواده شاخص مکانی-زمانی است. درخت R به عنوان یک درخت متعادل که از داده های فضایی با ابعاد بالا پشتیبانی می کند، به طور گسترده ای در مدیریت داده های مکانی-زمانی استفاده می شود. R-tree یک ساختار داده شاخص مکانی-زمانی پویا است. درج، حذف و پرس و جو گره ها می تواند موازی باشد. اشیاء فضایی در گره های برگ با حداقل مستطیل های مرزی ذخیره می شوند و مناطق فضایی نشان داده شده توسط هر گره می توانند همپوشانی داشته باشند. گاهی اوقات همپوشانی بیش از حد بر عملکرد پرس و جوی داده تأثیر می گذارد، بنابراین انواعی مانند درخت R+[ 18 ]، درخت سلول [ 20 ]] اجازه دهید یک شی به چندین گره برگ تعلق داشته باشد تا از عقب نشینی بیش از حد در جستجوی گره های درختی جلوگیری شود. یکی دیگر از پیشرفت ها، بهینه سازی استفاده از فضای گره و تعادل درخت R است. برای مثال، هیلبرت R-tree [ 21 ] از منحنی فراکتال هیلبرت برای مرتب کردن داده‌های k بعدی در یک بعد استفاده می‌کند. R*-Tree [ 19 ] معتقد است که همپوشانی نواحی فضای گره را می توان با درج اجباری گره و کاهش تعداد تقسیم گره بهبود بخشید.
پس از 40 سال تحقیق، شاخص مکانی-زمانی تعداد زیادی الگوریتم و ساختار داده را توسعه داده است. به عنوان یک زمینه بالغ، علاقه اخیر بر کاربرد صنایع مختلف متمرکز شده است. با این حال، تقریباً همه الگوریتم‌ها به جای توزیع پرس و جوها، فقط بر اشیاء مکانی-زمانی متکی هستند. همانطور که در شکل 1 نشان داده شده است، (A) نتیجه تقسیم پنج شی فضایی دو بعدی (a، b، c، d، e) در الگوریتم درخت R است، که در آن (a، c، d) متعلق به گره فرزند A، و ( b، e) متعلق به گره فرزند B است. (B) نتیجه تقسیم الگوریتم R*-tree را نشان می دهد، که از آن می توان دریافت که R*-tree دارای ناحیه همپوشانی گره کوچک تری است، اما همپوشانی گره کوچکتر به معنای بالاتر نیست. عملکرد پرس و جو همانطور که در (C) نشان داده شده است، برای پنجره پرس و جو مکرر W، هم R-tree و هم R*-tree باید به دو گره دسترسی داشته باشند، اگرچه فقط شی b به نتیجه پرس و جو تبدیل می شود. شاخص مکانی-زمانی هنوز نیاز به گسترش دارد تا سازگاری پرس و جو داشته باشد.

2.2. بلاک چین

2.2.1. معماری بلاک چین

بلاک چین یک فناوری دفتر کل غیرمتمرکز و غیرقابل اعتماد است که تراکنش های قابل اعتمادی را فراهم می کند. امنیت، تمرکززدایی و مقیاس پذیری را نمی توان با هم ترکیب کرد [ 22 ]. در تعادل این سه، فناوری بلاک چین دستخوش سه نسل تکامل شده است.
اولین نسل از معماری بلاک چین 1.0 که توسط بیت کوین ارائه می شود، یک زنجیره منفرد متشکل از بلوک ها است که در آن هر بلوک شامل یک سر و بدنه ای از اطلاعات چندین تراکنش است. ساختارهای داده کلیدی در بلوک در شکل 2 نشان داده شده است. هدر بلوک حاوی اطلاعات نسخه بلوک، گره ریشه درخت Merkle، مقدار هش و مهر زمانی بلوک والد و غیره است. بدنه بلوک سوابق تراکنش رمزگذاری شده و مقدار هش اطلاعات رمزگذاری شده را ذخیره می کند، اما جزئیات را ذخیره نمی کند. اطلاعات حساب. در معماری بلاک چین 2.0 که توسط اتریوم ارائه شده است، Merkle Tree به Merkle Patricia Tree (MPT) ارتقا یافته است [ 23]. MPT از مدیریت تجارت و ذخیره سازی حساب پشتیبانی می کند. این مزیت‌های درختان مرکل و درختان پاتریشیا را ترکیب می‌کند، جایی که درختان پاتریشیا شاخصی برای درخت‌های پیشوندی هستند و می‌توانند سریع‌تر پرس و جو و به‌روزرسانی کنند و منابع محاسباتی کمتری هزینه کنند. یک پروتکل مقیاس پذیر Block-DAG به نام Phantom در [ 24 ] پیشنهاد شده است که معماری اصلی بلاک چین 3.0 است. Block-DAG می‌تواند کارایی تراکنش‌های زنجیره بلوکی را تا حد زیادی بهبود بخشد، زیرا به هر بلوک اجازه می‌دهد بیش از یک بلوک والد برای پشتیبانی از پردازش موازی داشته باشد.
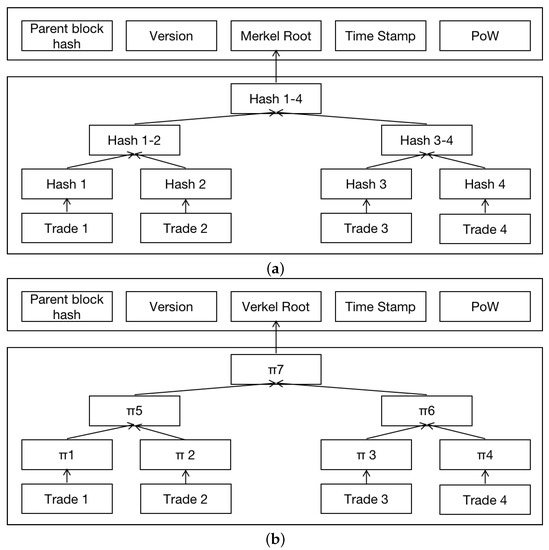
2.2.2. درختان مرکل و درختان ورکل
درخت مرکل [ 25] یک درخت متعادل باینری بر اساس مقدار هش است که می تواند یک چارچوب امضای دیجیتال کارآمد باشد و اطمینان حاصل کند که داده های هر بلوک در شبکه های توزیع شده خراب نمی شوند. امنیت طرح امضای دیجیتال مبتنی بر درخت Merkle تنها به امنیت تابع هش بستگی دارد و نیازی به مفروضات نظری زیادی ندارد، که امضای دیجیتالی مبتنی بر درخت Merkle را ایمن‌تر و کاربردی‌تر می‌کند. در درخت Merkle، مقدار هش هر تراکنش در گره برگ ذخیره می شود. هش ترکیبی دو گره برگ مجاور به عنوان مقدار هش جدید از پایین به بالا در نظر گرفته می شود، ریشه Merkle حاصل باید در هدر بلوک ذخیره شود. مشتری می تواند به سرعت بررسی کند که آیا گره به درخت Merkle تعلق دارد یا خیر از طریق مقدار گره، مقدار ریشه Merkle و مسیر مربوطه،
همچنین در اثبات صحت داده ها در بلاک چین پیشرفت هایی صورت گرفته است. در [ 10 ] درختان Verkle را پیشنهاد می کند، جایگزینی با پهنای باند موثرتر برای درختان مرکل. در مورد دوم، گره والد هش فرزندان خود است، در حالی که در اولی، گره والد تعهد برداری فرزندان خود است. همانطور که در شکل 2 نشان داده شده است ، اثبات Merkle برای تجارت 2 نیاز به ارائه هش (هش 2، هش 1، هش 3-4) همه گره های خواهر و برادر دارد، که با افزایش عمق درخت و k-args افزایش می یابد، در حالی که Verkle اثبات فقط نیاز به ارائه اثبات در مسیر از گره برگ به گره ریشه دارد ( π2�2، π5�5، π7�7).
2.2.3. شاخص فضایی-زمانی در بلاک چین
در ارتقای مستمر معماری بلاک چین، بسیاری از فن‌آوری‌هایی که داده‌های مکانی-زمانی را در بلاک چین ادغام می‌کنند، پیشنهاد شده‌اند [ 3 ، 7 ، 26 ، 27 ، 28 ، 29 ]. در کار خود، ما بر فناوری بلاک چین مکانی-زمانی تمرکز می کنیم که قابلیت های اعتبارسنجی داده های مکانی-زمانی را یکپارچه می کند، که به ساختار اثبات داده تراکنش همراه با نمایه سازی مکانی-زمانی نیاز دارد. یکی از جنبه های مهم بلاک چین مکانی-زمانی، تأیید صحت داده های مکانی-زمانی است. روش‌های شاخص مکانی-زمانی قابل تأیید شناخته شده شامل Merkle KD-Tree [ 9 ، 30 ] و Merkle R-Tree [ 31 ] است.]، اما ادغام فناوری تأیید و بازیابی شاخص فضایی با قابلیت جستجوی تطبیقی ​​در آخرین درخت Verkle هنوز وجود ندارد.
Merkle KD-tree [ 9 ] در block-DAG ارائه شده است که یکپارچگی را از طریق تاریخچه امضا شده رمزنگاری شده حفظ می کند و پرس و جوهای زمانی- مکانی کارآمد را بدون ذخیره محلی اضافی حفظ می کند. در Merkle KD-tree، یک KD-tree برای نمایه سازی اشیاء نقطه سه بعدی در block-DAG ادغام می شود، اثبات Merkle به گره های KD-Tree اضافه می شود، خلاصه آن در هدر بلوک قرار می گیرد و برچسب زمانی تراکنش به طور مستقل در هدر بلوک ذخیره می شود. آزمایش‌ها نشان می‌دهند که Merkle KD-Tree عملکرد بهتری در پرس‌و‌جوهای مکانی-زمانی مختلف، مانند پرس‌وجوهای محدوده، کوئری‌های KNN و غیره دارد. اشکال درخت Merkle KD این است که فقط برای اشیاء نقطه‌ای اعمال می‌شود، و اطلاعات زمانی نیاز به جدا از اطلاعات مکانی نمایه شده است.
Merkle R-Tree [ 31 ] فناوری دیگری است که نمایه سازی مکانی-زمانی را در زنجیره بلوکی پیاده سازی می کند، جایی که هر گره داخلی با هضم Merkle بر روی MBR ها و هضم فرزندانش مرتبط است. نقص اصلی آن این است که داده‌های تراکنش در بلوک ذخیره می‌شوند، در حالی که شاخص فضایی-زمانی R-tree و اثبات Merkle در یک پایگاه داده برون‌سپاری پیاده‌سازی می‌شوند که در واقع تضمین امنیتی بلاک چین را کاهش می‌دهد.

3. Verkle AR*-Tree در بلاک چین فضایی-زمانی

3.1. مقدماتی

ما در این بخش تعاریف مفاهیم مرتبط را ارائه می کنیم.
تعریف 1 (MBR): حداقل مستطیل مرزی (MBR) اجسام فضایی دو بعدی نامنظم تاپل <چپ، راست، بالا، پایین> است.
تعریف 2 (TMBR): حداقل مستطیل کراندار با مُهر زمانی (TMBR) اجسام مکانی-زمانی تاپلی <چپ، راست، بالا، پایین، شروع، پایان> است.
تعریف 3 (TWST): تراکنش با اطلاعات مکانی-زمانی (TWST) به صورت چندگانه <geoId, TMBR, account, event> است. یک تراکنش به عنوان جریانی با امضای رمزنگاری ذخیره می شود.
تعریف 4 (AWLP): حساب با اطلاعات آخرین موقعیت (AWLP) یک <accountId, lastposition, timestamp, data> با یک کلید هش است که توسط نام حساب ایجاد می شود.
تعریف 5 (Block): بلوک شامل یک هدر بلوک و یک بدنه بلوک متشکل از سوابق تراکنش مربوطه است. سوابق تراکنش ها با استفاده از طرح اثبات عضویت مانند درخت مرکل، درخت ورکل و غیره در یک ساختار درختی مونتاژ می شوند. در کار ما از درخت ورکل استفاده می کنیم. سربرگ بلوک چندگانه است <blockID, parenthash, statetrieRoot, trantrieRoot, trajetrieRoot, TMBR, timestamp, nonce> که در آن پرنت هش بلوک والد است، statetrieRoot خلاصه ای از trie حساب است، trantrieRoot خلاصه ای از trie تراکنش، is a trajectorytrie است. خلاصه مسیر حساب در یک بازه زمانی معین، مهر زمانی نشان دهنده زمان ایجاد بلوک است، و nonce یک هش 64 بیتی است که مقدار کافی محاسبه را ثابت می کند.
تعریف 6 (مدل هزینه): مدل هزینه به میانگین احتمال بازدید از هر گره هنگام ارائه محدوده پرس و جو اشاره دارد که همچنین تابعی از عمق درخت و توزیع فضایی گره ها در تمام سطوح است.
تعریف 7 (پرس و جو): ما سه نوع پرس و جو را در نظر می گیریم: (1) پرس و جو منطقه ای تراکنش ها. با توجه به پنجره TMBR، ما تمام اطلاعات تراکنش را که با TMBR فضایی-زمانی تقاطع یافته اند با اثبات Verkle مربوط به آن پرس و جو می کنیم. (2) آخرین اطلاعات مکان حساب. با توجه به کلید هش یک حساب، داده های حساب و آخرین اطلاعات مکان آن را پیدا کنید. (3) مسیرهای حساب. با توجه به پنجره پرس و جو TMBR و کلید هش یک حساب، مسیرهای حساب را در TMBR پرس و جو کنید.

3.2. Verkle AR*-Tree

سه نوع داده در بدنه بلوک ذخیره می شود. اطلاعات حساب شامل نام حساب با آخرین موقعیت حساب و داده های مربوطه است که به طور مکرر تغییر می کند، در حالی که تراکنش پس از ایجاد بلوک تغییر نمی کند. مسیرهای حسابی که فقط یک دوره ثابت در بلوک را برای جلوگیری از سرریز بلوک حفظ می کنند، باید مرتباً جستجو و حذف شوند. ما از روش های نمایه سازی متفاوتی برای این سه نوع داده استفاده می کنیم. برای اطلاعات حساب، از Verkle Patricia Trie (VPT)، برای تراکنش ها و مسیرها، از Verkle AR*-Tree استفاده می کنیم.

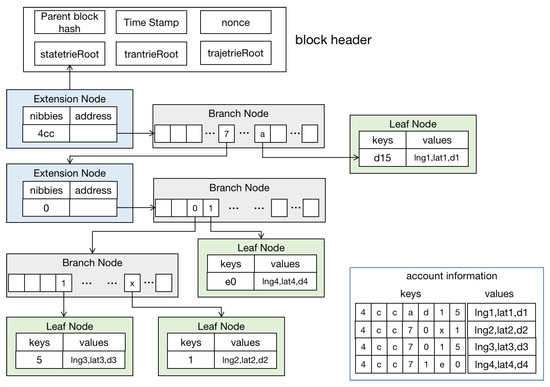
3.2.1. فهرست حساب با آخرین مکان

اطلاعات حساب در Verkle Patricia trie (VPT) با داده های مکان ذخیره می شود و ساختار ذخیره سازی در شکل 3 نشان داده شده است . هر حساب شامل کلید و مقدار هش شده است. درخت VPT سه نوع گره دارد. گره برگ داده های حساب و تعهد Verkle را ذخیره می کند. گره پسوند شامل یک کلید و یک آدرس است که به گره شاخه اشاره می کند. گره شاخه شامل حداکثر 256 آدرس و یک تعهد Verkle است که به ترتیب به گره فرزند یا گره برگ بعدی بعدی اشاره می کند.
با توجه به کلید هش یک حساب، مانند “4ccad15″، به گره پسوند (4cc) از گره ریشه دسترسی پیدا کنید، سپس نود و هفتمین مورد (کد ‘a’) گره شاخه را پیدا کنید و در نهایت به گره برگ دسترسی پیدا کنید. d15)، مقدار رمزگذاری شده گره برگ و مقادیر تعهد برداری تمام گره های موجود در مسیر را با هم دریافت کنید.
با توجه به اطلاعات به روز شده حساب، الگوریتم به روز رسانی VPT (الگوریتم 1) به شرح زیر است.
الگوریتم 1 به روز رسانی الگوریتم VPT.
  ورودی:
vpt: سعی کنید Verkle patricia
گره: گره فعلی در VPT
acc (کلیدها، مقادیر): اطلاعات حساب که باید به روز شود
خروجی:
vpt: VPT به روز شده
  1:   اگر گره صفر باشد پس
  2:   گره ← createLeafNode ( acc )
  3:   vpt.root ← گره
  4:   دیگری
  5:   اگر node.type LeftNode باشد، پس
  6:     p ← maxLengthPrefix ( acc.keys ، node.keys )
  7:     newe ، newb ← createExtensionNode ( p )، createBranchNode ()
  8:     newb.children [ node.keys [ len ( p )]] ← node
  9:     newb.children [ acc.keys ( len ( p ))] ← createLeftNode ( acc )
10:     newb.parent ، newe.parent ← newe ، node.parent
11:   other if node.type ExtensionNode است پس
12:     p ← maxLengthPrefix ( acc.keys ، node.nibbs )
13:     اگر p == node.nibbs پس
14: acc.keys = acc.keys[len(p):]
15: به روز رسانی (vpt، node.next، acc)
16:     else if node.nibbs.startWith(p) سپس
17:       newe ، newb ← createExtensionNode ( p )، createBranchNode ()
18:       newb.children [ node.nibbs [ len ( p )]] getsnode
19:       newb.children [ acc.keys ( len ( p ))] ← createLeftNode ( acc )
20:       newb.parent ، newe.parent ← newe ، node.parent
21:     دیگری
22:       newb ← createBranchNode ()
23:       newb.parent ← node.parent
24:       newb.children [ acc.keys [0]] ← createLeftNode ( acc )
25:       newb.children [ node.nibbs [0]] ← node
26:       node.nibbs ← node.nibbs [1:]
27:     پایان اگر
28:   else اگر node.type BranchNode است، پس
29:     اگر node.children[acc.keys[0]] صفر باشد، پس
30:       node.children [ acc.keys [0]] ← createLeftNode ( acc )
31:     دیگری
32:       acc.keys ← acc.keys [1:]
33: به‌روزرسانی (vpt,node.children[acc.keys[0]],acc)
34:     پایان اگر
35:   پایان اگر
36:   پایان اگر
این الگوریتم اطلاعات حساب را به عنوان گره برگ در درخت وارد می کند. الگوریتم چهار حالت را متمایز می کند. اگر گره فعلی خود یک گره برگ باشد، به ترتیب یک گره پسوند جدید E و گره شاخه B ایجاد می شود و E به عنوان گره والد B گرفته می شود و گره برگ اصلی و گره برگ جدید زیر B قرار می گیرند. گره فعلی یک گره پسوند است، طولانی‌ترین پیشوند عمومی p کلید حساب و نوک‌های گره افزونه را دریافت کنید. سه امکان در مورد p وجود دارد: p برابر است با نوک گره گسترش، سپس گره فرزند گره گسترش به عنوان گره فعلی تنظیم می شود و الگوریتم به صورت بازگشتی فراخوانی می شود. اگر p تنها بخشی از نوک های گره پسوند باشد، یک گره پسوند جدید و گره شاخه به عنوان گره والد گره پسوند اصلی ایجاد می شود. اگر p صفر باشد، یک گره شاخه جدید ایجاد می شود و اطلاعات حساب در زیر گره شاخه قرار می گیرد. اگر گره فعلی یک گره شاخه باشد، الگوریتم تعیین می کند که آیا آیتم فرعی در گره شاخه مربوط به کلیدهای حساب خالی است یا خیر. در این صورت، اطلاعات حساب مستقیماً در زیرمجموعه قرار می گیرد، در غیر این صورت، آیتم فرعی به عنوان گره فعلی گرفته شده و به صورت بازگشتی اجرا می شود.
3.2.2. فهرست اطلاعات معاملات
برای اطلاعات تراکنش، Verkle AR*-tree اتخاذ شده است و ساختار ذخیره سازی در شکل 4 نشان داده شده است . درخت Verkle AR* از گره های برگ و گره های میانی تشکیل شده است. هر گره برگ حاوی اطلاعات تراکنش هش شده، TMBR، تعداد مرجع و تعهد برداری است. گره میانی از اتحاد TMBR، تعداد مرجع و تعهد برداری همه فرزندانش تشکیل شده است.
ایجاد Verkle AR*-tree با ایجاد بلوک انجام می شود. هر تراکنش طبق الگوریتم [ 32 ] درج می شود. تنها تغییر این است که هر گره باید تعهد برداری را محاسبه کند.
بلاک چین پرس و جوی تراکنش بسیار متداول است، بنابراین کارایی پرس و جو برای برنامه های بلاک چین بسیار مهم است. R*-tree توزیع خود پرس و جو را در نظر نمی گیرد. این بخش بیشتر Verkle AR*-tree را برای افزایش توانایی تطبیقی ​​معرفی می‌کند. ما ابتدا مدل هزینه پرس و جو R*-tree را پیشنهاد می کنیم و سپس بهبود تطبیقی ​​را بر اساس مدل هزینه ارائه می دهیم.

با توجه به پنجره پرس و جو W (wx,wy) و شی فضایی O (rx,ry)، که در آن wx,wy و rx,ry به ترتیب مقادیر نرمال شده عرض و ارتفاع W و O هستند، سپس احتمال تقاطع پنجره پرس و جو با شیء این است:

پr = ( r x + w x ) ∗ ( r y+ w y) / 4��=(��+��)∗(��+��)/4

با توجه به R*-tree کامل با گره‌های M، اگر توزیع پرس و جو یکنواخت باشد، [ 33 ] میانگین تعداد گره‌های قابل دسترسی را به صورت زیر نشان می‌دهد:

پn =∑i = 1م( رایکسمن+ w x ) ( ryمن+ w y) / 4��=∑�=1�(���+��)(���+��)/4
معادله ( 2 ) فرض می کند که داده ها و پرس و جو هر دو یکنواخت هستند، که با وضعیت واقعی ناسازگار است. علاوه بر این، یک فرآیند پرس و جو لایه به لایه در امتداد گره های درختی انجام می شود، بنابراین میانگین تعداد گره های بازدید شده توسط یک پنجره پرس و جو معین صرفاً مجموع احتمال دسترسی هر گره نیست. مجموع حاصل ضرب احتمال تقاطع هر گره با پنجره پرس و جو و تعداد تقاطع گره های فرزند گره است.

فرض کنید یک درخت R* کامل وجود دارد که توسط N شی فضایی ساخته شده است، تعداد گره ها در لایه i برابر است.متر( من)�(�)، 1 ≤ I≤ اچ1≤�≤�، که در آن H ارتفاع درخت و M حداکثر تعداد گره های فرزند گره است. با توجه به یک پنجره پرس و جو W(wx,wy)، احتمال تقاطع بین مستطیل فضایی آرمن ج( r x ، r y)���(��,��)از هر گره R-tree و W به عنوان نشان داده می شود پآرمن ج����، i تعداد لایه و j تعداد گره لایه i است. سپس میانگین تعداد دسترسی به گره لایه k برابر است با:

nک=∑i = 1متر( ک )( صآرk i×∑j = ( i − 1 ) m + 1من _پآرk + 1 ، j)��=∑�=1�(�)(����×∑�=(�−1)�+1�����+1,�)

میانگین تعداد گره‌هایی که در درخت R به آن‌ها دسترسی دارند، مجموع گره‌های دسترسی به هر لایه است (گره ریشه همیشه قابل دسترسی است).

پn= 1 +∑k = 1اچ(∑i = 1متر( ک )( صآرk i∑j = ( i − 1 ) M+ 1من مپآر( k + 1 ) j) )= 1 +∑k = 1اچ(∑i = 1متر( ک )(14( رایکسk i+ w x ) ( ryk i+ w y)∑j = ( i − 1 ) M+ 1من م( رایکس( k + 1 ) j+ w x ) ( rک( k + 1 ) j+ w y) /4))پ�=1+∑ک=1اچ(∑من=1متر(ک)(پآرکمن∑�=(من-1)م+1منمپآر(ک+1)�))=1+∑ک=1اچ(∑من=1متر(ک)(14(�ایکسکمن+�ایکس)(��کمن+��)∑�=(من-1)م+1منم(�ایکس(ک+1)�+�ایکس)(�ک(ک+1)�+��)/4))
معادله ( 4 ) نشان می دهد که کارایی پرس و جو درخت R* ارتباط نزدیکی با توزیع گره های فرعی دارد. هر چه تعداد دفعاتی که پنجره پرس و جو گره های فرزند یک گره را قطع کند، عملیات بک ردیابی کمتری مورد نیاز است. بنابراین، ایده بهبودیافته این است که به صورت پویا فرکانس پنجره پرس و جو را ثبت کنیم و توزیع گره درخت R* را با توجه به این فرکانس ها تنظیم کنیم تا گره های فرزند با پرس و جوهای مکرر تا آنجا که ممکن است در زیر همان گره والد ادغام شوند. این می تواند کارایی پرس و جو R*-tree را بهبود بخشد.
فرکانس پرس و جو هر گره و شی فضایی را ثبت می کنیم. بهینه سازی تطبیقی ​​درخت Verkle AR* شامل دو جنبه است: بازسازی درخت Verkle AR* در حین ایجاد بلوک و بهبود الگوریتم تقسیم. الگوریتم بازسازی (الگوریتم 2) به شرح زیر است.
الگوریتم 2 ایجاد مجدد.
  ورودی:
درخت: R*-tree
خروجی:
درخت: درخت R* بازسازی شده
  1:   ورودی‌ها ← tree.allentries ()
  2:   گره ها ← گوشواره ها ( ورودی ها )
  3:   در حالی که True do
  4:   نتایج ← rearragenodes ( گره ها )
  5:   والدین ← [ createNode ( فرزندان = r ) برای نتایج ]
  6:   اگر parent.length ≤ context.maxchildrennum سپس
  7:     tree.root ← createNode ( فرزندان = والدین )
  8: بازگشت
  9:   پایان اگر
10:   نتایج ، گره‌ها ← []، والدین
10:   پایان در حالی که
الگوریتم از تمام گره های برگ شروع می شود و لایه به لایه بازسازی می کند، یعنی تمام گره های هر لایه به گونه ای گروه بندی می شوند که تعداد گره های هر گروه از آستانه بیشتر نباشد. در عین حال، سطح همپوشانی بین گروه ها کمتر از آستانه است و واریانس بین گروهی فرکانس دسترسی بزرگترین است. الگوریتم گروه بندی هر لایه به صورت زیر پیاده سازی شده است (الگوریتم 3).
الگوریتم 3 Rearragenodes.
  ورودی:
درخت: R*-tree
گره ها: تمام گره های یک لایه
خروجی:
گروه ها: گروه های گره
  1:   برای گره ∈ گره ها انجام می دهند
  2:   برای d = 0 به node.dimension انجام دهید
  3:     برای j = 0 تا 1 انجام دهید
  4:       g 1, g 2 ← split ( گره ها , d , node , j )
  5: plans.add(g1,g2)
  6:     پایان برای
  7:   پایان برای
  8:   پایان برای
  9:   طرح‌ها ← مرتب‌شده ( طرح‌ها ، ‘ cov ‘، معکوس شده )
10:   maxcov ← برنامه‌ها [0]. cov
11:   برنامه ها ← طرح ها [ cov == maxcov ]
12:   طرح‌ها ← مرتب‌شده ( طرح ، « همپوشانی »)
13: برنامه های بازگشت[0]
الگوریتم فوق سعی می کند تمام گره ها را به دو گروه در مرز هر بعد برای هر MBR تقسیم کند. سطح همپوشانی چنین گروه هایی و واریانس بین گروهی فرکانس دسترسی به ترتیب محاسبه می شود. همه گروه ها باید بر اساس واریانس بین گروهی به ترتیب نزولی مرتب شوند و اولین k (در پنج حداکثر واریانس بین گروهی) رزرو شود. سپس بر اساس حداقل سطح همپوشانی مرتب شده و اولین مورد به عنوان طرح گروه بندی بهینه در نظر گرفته می شود. این فرآیند تا زمانی تکرار می شود که تعداد گره ها در هر گروه کمتر از آستانه باشد. این الگوریتم با الگوریتم درج مجدد R*-tree متفاوت است که در آن درخت را از پایین به بالا از تمام برگ ها بازسازی می کنیم.
الگوریتم تقسیم مشابه الگوریتم بازسازی بالا است. همه اشیاء مکانی-زمانی بر اساس لبه های تمام ابعاد همه اشیاء تقسیم می شوند. به این ترتیب، 2 × N× D2×ن×دیطرح های تقسیم را می توان به دست آورد. N تعداد اشیا و D بعد اجسام مکانی – زمانی است. فرکانس دسترسی، واریانس بین گروهی، مساحت و ناحیه همپوشانی هر طرح تقسیم به ترتیب محاسبه می شود. الگوریتم ابتدا یکی با واریانس بین گروهی زیاد فرکانس دسترسی را انتخاب می کند (تفاوت بین حداکثر واریانس بین گروهی بیش از 5 نیست)، سپس یکی را با مساحت کل کوچک (در 20 درصد از حداقل کل) انتخاب می کند. منطقه)، و در نهایت طرح تقسیم با کوچکترین ناحیه همپوشانی را انتخاب می کند. الگوریتم تقسیم بهبود یافته به شرح زیر است (الگوریتم 4).
الگوریتم 4 تقسیم.
  ورودی:
ورودی ها: ورودی هایی که باید تقسیم شوند
خروجی:
گره ها: مجموعه گره های تقسیم شده
  1:   برای ورود ∈ ورودی انجام دهید
  2:   برای d = 0 به enter.dimension انجام دهید
  3:     برای j = 0 تا 1 انجام دهید
  4:       g 1, g 2 ← تقسیم ( ورودی ها , d , ورودی , j )
  5: plans.add(g1,g2)
  6:     پایان برای
  7:   پایان برای
  8:   پایان برای
  9:   طرح‌ها ← مرتب‌شده ( طرح‌ها ، ‘ cov ‘، معکوس شده )
10:   maxcov ← برنامه‌ها [0]. cov
11:   برنامه ها ← طرح ها [ cov == maxcov ]
12:   طرح‌ها ← مرتب شده ( طرح‌ها ، ‘ minarea ‘)
13:   minarea ← پلان [0]. حوزه
14:   plans ← plans.trim ( minarea , 0.)
15:   پلان‌ها مرتب‌شده ( طرح‌ها ، ‘ همپوشانی ‘ )
16:   Optima ← plans [0]
17:   بازگشت اپتیما
مثالی برای نمایش الگوریتم آورده شده است. همانطور که در شکل 5 نشان داده شده است ، یک گره دارای چهار گره فرزند است و الگوریتم به دنبال تقسیم بهینه این گره است. فرض کنید که فرکانس پرس و جو از چهار گره فرعی a = 0، b = 4، c = 1، d = 3 است. در مجموع 16 طرح تقسیم ممکن وجود دارد. اگر با توجه به حداقل مساحت کل یا حداقل سطح همپوشانی (R*-tree)، C و D باید به عنوان یک گروه انتخاب شوند، در حالی که با توجه به فرکانس دسترسی، B و D باید به عنوان یک گروه انتخاب شوند.
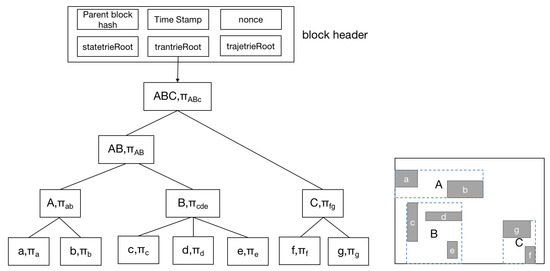
3.2.3. شاخص مسیر
از شاخص مسیر برای پرس و جوهایی مانند “پیدا کردن مسیر همه کاربران در بندر شانگهای در سال جاری” استفاده می شود. ما هنوز از Verkle R*-tree (VR) استفاده می کنیم که در آن TMBR چهار بعدی است و یک بعد حساب به TMBR اضافه می شود. مقدار هر حساب در این بعد فاصله همینگ از کلید حساب (16 بیت) تا “aa…aa” (16 بیت) است. شکل 6 یک مثال دو بعدی ساده شده را نشان می دهد که در آن مسیر دو کاربر به صورت دایره و مستطیل نشان داده شده است. الگوریتم درج همانند الگوریتم 2 است و تابع حذف دوره ای اضافه می شود.

4. آزمایش کنید

4.1. راه اندازی آزمایشی

در [ 9 ]، یک الگوریتم پرس و جو درخت KD و یک الگوریتم فضای اسکن در بلاک چین مکانی-زمانی پیشنهاد شده است. ما از این الگوریتم برای آزمایش های مقایسه ای استفاده می کنیم. ما از همان مجموعه داده پوکمن ( https://github.com/ILDAR9/spatiotemporal_blockdag ، قابل دسترسی در 1 ژوئیه 2022) استفاده می کنیم که 18732 رکورد را ارائه می دهد که هر کدام شامل طول جغرافیایی، عرض جغرافیایی، زمان و نوع پوکمن است. داده های مکانی و مهر زمانی به (0-1) نرمال می شوند. ما با سه ویژگی الگوریتم خود سروکار داریم:
  • اینکه آیا عملکرد پرس و جوی مکانی-زمانی Verkle AR*-tree پیشنهاد شده در کار ما بهتر از معیار در [ 9 ] است که گزارش می دهد عملکرد پرس و جو مکانی-زمانی تا حد زیادی تحت تأثیر اندازه بلوک قرار می گیرد، بنابراین از اندازه های مختلف بلوک استفاده می کنیم. عملکرد پرس و جو را مقایسه کنید
  • مقایسه عملکرد بین AR*-tree و R*-tree تطبیقی ​​در بلاک چین.
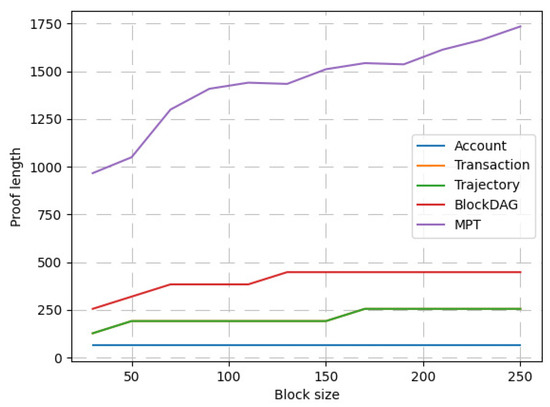
  • طول تعهد بردار ارائه شده توسط درخت Verkle به عمق درخت مربوط است، اما مستقل از عرض درخت است. بنابراین باید از نظر عملکرد بهتر از درخت مرکل باشد. با این حال، تفاوت در اثبات عملکرد درختان Verkle AR* در اندازه‌های مختلف مشخص نیست، که نیاز به مقایسه بیشتر در آزمایش‌ها دارد.
همه آزمایش‌ها به زبان Python3.7 کدگذاری شده‌اند و روی دستگاهی با پردازنده Intel(R) Xeon(R) Gold با فرکانس ۲.۶ گیگاهرتز و ۸ گیگابایت رم انجام شده‌اند. همه کدها و داده ها را می توان از https://github.com/bio-neuroevolution/VRstarTree دانلود کرد (در 17 ژوئیه 2022 قابل دسترسی است).

4.2. نتیجه

4.2.1. عملکرد جستجوی فضایی-زمانی Verkle AR*-Tree

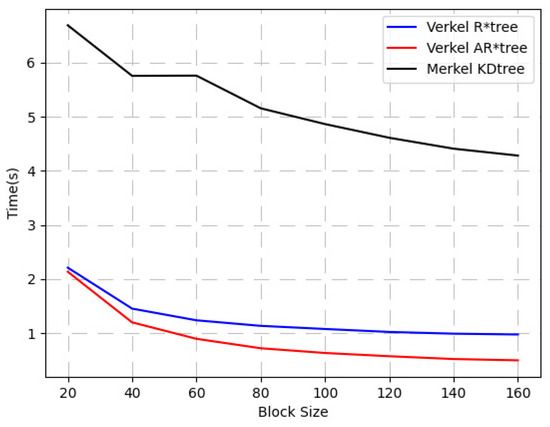
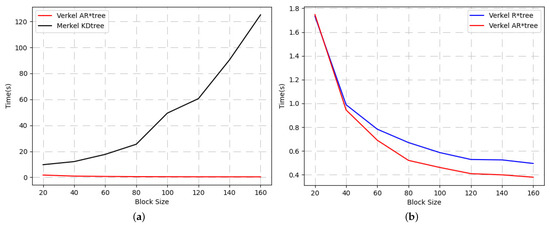
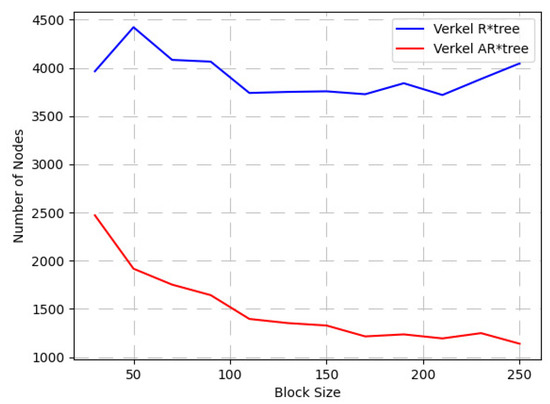
ما حداکثر عرض درخت Verkle AR* را روی 8 قرار دادیم. ما از مراکز منطقه پرس و جو از مدل گاوسی مختلط زیر در یک منطقه عادی متشکل از عرض جغرافیایی، طول جغرافیایی و مهر زمانی نمونه برداری کردیم. عرض هر مکعب پرس و جو بر روی یک توزیع گاوسی با مرکز 0.05 و واریانس 0.1 نمونه برداری می شود.

p ( x ) =18× ∑ N(تومن، من) ( x )پ(ایکس)=18×∑ن(تومن،من)(ایکس)

جایی که تومنتومنهشت نقطه انتهایی مکعب است که با <0.33،0.33،0.33> و <0.66،0.66،0.66> احاطه شده اند. اندازه بلوک را از 20 تا 160 با فاصله 20 تنظیم می کنیم. برای هر اندازه بلوک، به طور تصادفی از 200 مکعب پرس و جو نمونه برداری می کنیم و پرس و جوها را روی Verkle R*-tree (عدم تطبیق)، Verkle AR*-tree (تطبیقی ​​شامل) اجرا می کنیم. و Merkle KD tree [ 9 ] به ترتیب. آزمایش پنج بار اجرا شد و میانگین تمام آزمایش‌ها به عنوان نتیجه در نظر گرفته شد، همانطور که در شکل 7 نشان داده شده است.

هر دو درخت تطبیقی ​​Verkle AR* و Verkle R*-tree عملکرد بهتری نسبت به Merkle KD-tree دارند که با نتایج تجربی در [ 34 ] مطابقت دارد. با توجه به اینکه خود KD-tree فقط برای داده های نقطه ای مناسب است، در حالی که R*-tree از داده های نقطه ای و منطقه ای پشتیبانی می کند. ما KD-tree را برای پشتیبانی از داده های منطقه ای تغییر می دهیم: وقتی داده های منطقه ای از خط تقسیم درخت KD عبور می کنند، داده ها را به هر دو زیر درخت چپ و راست اختصاص می دهیم. ما به طور تصادفی 20٪ از مجموعه داده های پوکمن را انتخاب می کنیم و این نقاط را با ایجاد عرض هندسی از طریق سه توزیع گاوسی (N (0.001,0.5)، N (0.01،0.5)، N (0.05،0.5)) به مکعب تغییر می دهیم. احتمالات 0.5، 0.3 و 0.2. پس از انجام همان آزمایش فوق، نتایج در شکل 8 نشان داده شده است.
در شکل 8 الف، عملکرد درخت KD با افزایش اندازه بلوک بسیار کاهش می یابد. برای داده‌های مکعبی، زیردرخت‌های چپ و راست گره Merkle KD-tree دارای تعداد زیادی مکعب همپوشانی هستند که در نتیجه با افزایش داده‌ها، عمق درخت بیشتر می‌شود. در شکل 8 ب، درخت Verkle AR*-درخت بهتر از Verkle R*-tree عمل می کند، که نشان می دهد الگوریتم Verkle AR*-tree برای داده های مکعب نیز قابل استفاده است. علاوه بر این، افزایش اندازه بلوک داده‌های مکعب بیشتری را به ارمغان می‌آورد و در نتیجه بایاس توزیع پرس و جو بیشتر می‌شود، بنابراین Verkle AR*-tree می‌تواند عملکرد را سریع‌تر از Verkle R*-tree افزایش دهد که اندازه بلوک افزایش می‌یابد، که شبیه به پرس و جو نقطه‌ای است. مشخصات در شکل 7 .
4.2.2. تجزیه و تحلیل عملکرد تطبیقی
درخت Verkle AR* با قابلیت تطبیق داده‌های قابل دسترسی را با فرکانس مشابه و از نظر فضایی در مجاورت همان گره والد تا حد امکان قرار می‌دهد تا با کاهش تعداد گره‌های پس‌گرد، عملکرد پرس و جو را بهبود بخشد. شکل 9 تعداد دسترسی های گره دو الگوریتم را در اندازه های مختلف بلوک در آزمایش قبلی نشان می دهد. مشاهده می شود که بهبود عملکرد پرس و جوی درخت Verkle AR* از کاهش تعداد گره های دسترسی حاصل می شود.
با این حال، عملکرد تطبیقی ​​Verkle AR*-tree تا حد زیادی تحت تاثیر توزیع پرس و جو و حداکثر اندازه فرزندان گره است. ما هفت روش نمونه برداری برای پنجره پرس و جو طراحی می کنیم.
  • نمونه گیری مرکزی مرکز تمام پنجره های پرس و جو در مرکز کل منطقه فضا-زمان ثابت است. عرض هر بعد از پنجره پرس و جو با نمونه برداری از توزیع گاوسی N(0.3,0.05) بدست می آید. استثنا این است که عرض بعد زمانی پنجره پرس و جو (بعد سوم) روی 0.5 ثابت شده است تا بلاک های بیشتری به طور موثر پرس و جو شوند.
  • نمونه گیری گاوسی توزیع پرس و جو یک تابع گاوسی است (تعداد نقاط مرکزی 9 است و عرض پنجره پرس و جو از توزیع نرمال با مقدار مرکزی 0.1 و واریانس 0.05 پیروی می کند).
  • نمونه گیری دیریکله هم موقعیت مرکزی و هم عرض پنجره پرس و جو از توزیع دیریکله با آلفا = 3 و k = 4 پیروی می کنند.
  • نمونه گیری نمایی: نقطه مرکز پرس و جو از توزیع نمایی چند متغیره با مقیاس = 2 پیروی می کند و عرض پنجره پرس و جو از توزیع نرمال با مقدار مرکزی 0.1 و واریانس 0.05 پیروی می کند.
  • نمونه گیری Weibull: موقعیت مرکز پرس و جو از توزیع Weibull با شکل = 5 پیروی می کند و عرض پنجره query از توزیع نرمال با مقدار مرکزی 0.1 و واریانس 0.05 پیروی می کند.
  • نمونه گیری یکنواخت نمونه گیری یکنواخت مرکز پرس و جو را با توزیع یکنواخت در کل منطقه مکانی-زمانی ایجاد می کند و عرض هر بعد از پنجره پرس و جو 0.05 است.
  • نمونه گیری شبکه ای تعداد کل پرس‌و‌جوها را برطرف می‌کنیم و سپس کل فضا را با توجه به تعداد کوئری‌ها به شبکه‌هایی تقسیم می‌کنیم. هر شبکه فقط مربوط به یک پنجره پرس و جو است. این یک نمونه گیری یکنواخت مطلق است، که در آن نمونه گیری یکنواخت نمونه برداری با توزیع احتمال است.
در روش های 2-3، مکان نمونه گیری پرس و جو قبلی مستقل از پرس و جوی بعدی است، در حالی که در روش های 4-5، پرس و جو قبلی بر مکان پرس و جو بعدی تأثیر می گذارد. روش 1 را می توان یک مورد خاص از پرس و جوهای گاوسی در نظر گرفت، در حالی که روش 7 را می توان یک مورد خاص از پرس و جوهای توزیع شده یکنواخت در نظر گرفت.

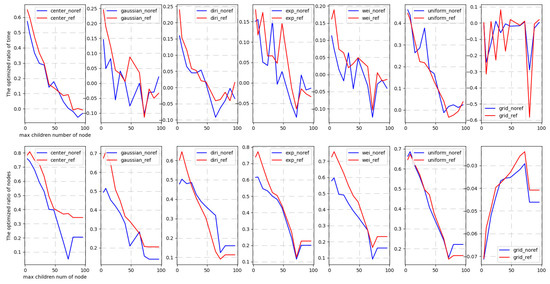
برای هر یک از روش های نمونه گیری فوق، الگوریتم بازسازی تطبیقی ​​را دو بار اجرا می کنیم. اولی (به نام غیر ref) از فرکانس پرس و جوی تاریخی استفاده نمی کند، اما دومی (به نام ref) از فرکانس پرس و جو استفاده می کند. برای اولی، خطوط 10-11 در الگوریتم realragenodes اجرا نمی شوند. برای هر نمونه برداری، 6000 پنجره پرس و جو دریافت می کنیم تا کل زمان پرس و جو و تعداد گره های قابل دسترسی را ثبت کنیم. ما به ترتیب نسبت بهینه شده زمان دسترسی و تعداد گره های دسترسی را محاسبه می کنیم. نسبت بهینه سازی با فرمول زیر تعریف می شود، که در آن ORT نسبت بهینه سازی شده زمان است، TBR زمان پرس و جو قبل از بازسازی، TAR زمان پرس و جو پس از بازسازی، و ORN نسبت بهینه شده گره ها، NBR تعداد گره هایی است که قبل از بازسازی به آن دسترسی پیدا کرده اند. بازسازی، NAR تعداد گره هایی است که پس از بازسازی به آنها دسترسی پیدا می کنند.

O R TO R N=( تیB R – TA R )تیبی آر=( نB R – NA R )نبی آر�آرتی=(تیبآر-تیآآر)تیبآر�آرن=(نبآر-نآآر)نبآر

هدف از آزمایش بررسی بهبود عملکرد نسبی الگوریتم بازسازی بر اساس فرکانس توزیع پرس و جو است. شماره گره معماری را برای [4,8,16,24,32,40,48,64,72,80,88,96] تنظیم می کنیم و آزمایشات فوق را انجام می دهیم. نتایج تجربی در شکل 10 نشان داده شده است.

برای نمونه‌گیری مرکزی و نمونه‌برداری گاوسی، بازسازی مبتنی بر فرکانس پرس و جو تاریخ همیشه بهتر از نمونه‌گیری استفاده نشده است. برای نمونه گیری یکنواخت و نمونه گیری شبکه ای، نتایج اجرای چندگانه نشان می دهد که تفاوت بین این دو نامشخص می شود.
برای چهار نمونه توزیع پرس و جو رایج (توزیع گاوسی، توزیع دیریکله، توزیع نمایی چند متغیره و توزیع Weibull)، الگوریتم‌های تطبیقی ​​به بهبود عملکرد در همه آنها کمک می‌کنند. درجه بهبود عملکرد چهار الگوریتم ( ای آرتیr e f– O Rتیn o r e f�آرتی�ه�-�آرتی���ه�) به ترتیب 0.041، 0.022، 0.017 و 0.039 است که در این میان الگوریتم تطبیقی ​​با توزیع گاوسی بهترین عملکرد را دارد.
با توجه به نتایج تجربی بالا، دامنه کاربردی الگوریتم تطبیقی ​​Verkle AR*-tree محدود است. در کاربردهای واقعی، لازم است که رکوردهای پرس و جوی تاریخی را برای یک دوره زمانی معین جمع آوری کنیم، و سپس تصمیم بگیریم که آیا الگوریتم تطبیقی ​​را بر اساس نتایج برازش توزیع این رکوردهای پرس و جو اعمال کنیم یا خیر.
4.2.3. تحلیل عملکرد تعهد برداری
در درخت مرکل، شواهد یک مقدار مجموعه کاملی از تمام گره‌های خواهر و برادر است، در حالی که در درخت Verkle، شواهد فقط باید در طول مسیر درخت ارائه شوند، که طول اطلاعات اثبات همراه پرس و جو را کاهش می‌دهد. در آزمایش، ما به طور تصادفی 10 بار پرس و جو می کنیم و فرض می کنیم که حداقل طول اثبات مورد نیاز برای داده های معتبر در هر گره برگ 64 بایت است. همانطور که در شکل 11 نشان داده شده است، به ترتیب هزینه درخت MPT و درخت Verkle و اثبات درخت KD-tree و Verkle AR*-درخت را مقایسه می کنیم . سازه های Verkle همیشه دارای سربار اثبات کمتری نسبت به سازه های Merkle برای اندازه های مختلف درخت هستند.
اطلاعات حساب در Verkle Patricia trie (VPT) با داده های مکان ذخیره می شود و عمق درخت فقط به کلید حساب مربوط می شود نه به مکان. در آزمایش، جستجوی اطلاعات حساب کوتاه‌ترین طول اثبات برداری را به‌دست آورد که ارتباط چندانی با اندازه بلوک ندارد. شاخص Verkle AR*-tree هم برای تراکنش ها و هم برای مسیرها استفاده می شود. حجم داده هر دو یکسان است و طول داده هر گره به طور یکنواخت روی 64 بایت تنظیم شده است که در نتیجه طول های اثبات آنها در اندازه های مختلف بلوک همپوشانی دارند. با افزایش اندازه بلوک، طول اثبات آنها نیز افزایش می یابد، اما آنها از MPT و Merkle KD-tree کوچکتر هستند.

5. بحث

در آزمایش اول، پرس و جوهایی را بدون سربار اثبات متعهد انجام دادیم. در این مورد، تراکنش‌ها در هر بلاک چین به شکل R*-tree سازماندهی می‌شوند و اندازه درخت به اندازه یک بلوک محدود می‌شود. اشیاء فضایی ذخیره شده در زنجیره بلوکی سه بعدی، طول جغرافیایی، عرض جغرافیایی و بعد زمانی هستند و به 0-1 نرمال می شوند. ما به هزینه ساخت بلوک اهمیت نمی دهیم، بلکه به عملکرد جستجوی منطقه مکانی-زمانی بلادرنگ در بلوک اهمیت می دهیم. اگرچه R*-tree برای نمایه سازی داده های ذخیره سازی دیسک در مقیاس بزرگ مناسب تر گزارش شده است، اما می توانیم ببینیم که R*-tree حافظه تحت محدودیت ظرفیت بلوک نیز عملکرد بهتری دارد. چه برای اشیاء نقطه ای و چه برای اشیاء مکعبی، عملکرد پرس و جو بهتر از درخت مرکل KD موجود است.
در آزمایش دوم، عملکرد پرس و جو R*-tree تطبیقی ​​پیشنهادی و R*-tree موجود را مقایسه می کنیم. نتایج تجربی نشان می‌دهد که بهبود عملکرد درخت R*-تطبیقی ​​عمدتاً به دلیل کاهش تعداد گره‌های بازدید شده است که تحت تأثیر توزیع پرس و جو تاریخی و حداکثر ظرفیت گره فرزند درخت قرار می‌گیرد، بنابراین چنین نیست. همیشه موثر علاوه بر این، الگوریتم تطبیقی ​​نیاز به بازسازی کل درخت از پایین به بالا به طور منظم دارد. در آزمایش ما، سربار قفل شدن بلوک در طول بازسازی نادیده گرفته می شود.
در آزمایش سوم، تعهد برداری را به بلاک چین اضافه کردیم. شی پرس و جو و اطلاعات اثبات مربوطه در هر پرس و جو به دست می آید که می تواند به مشتری در تأیید صحت داده ها کمک کند. تأیید از سه فرآیند جداگانه تشکیل شده است. اولین مورد، فرآیند تولید تعهد برداری Verkle است که در طول ایجاد بلوک اتفاق می‌افتد و زمانی که هر شی مکانی-زمانی درج می‌شود، ایجاد می‌شود. دوم بازگرداندن اطلاعات تعهد همراه با نتایج پرس و جو است. سومین فرآیند احراز هویت است که بر روی مشتری انجام می شود. در بین سه فرآیند، فرآیند دوم بیشترین تأثیر را بر عملکرد دارد و طول اطلاعات اثبات عملکرد فرآیند را تعیین می‌کند. در اثبات مرکل، طول اثبات مربوط به اندازه کل درخت است.
ما سه نوع ذخیره‌سازی داده را در بلاک چین پیاده‌سازی کرده‌ایم که شامل حساب‌هایی با آخرین مکان، اطلاعات تراکنش و مسیرهای هر حساب می‌شود. اولی از Verkle Patricia Tree و دو دومی Verkle R*-tree استفاده می کند. ما این سه درخت را با درخت مرکل پاتریشیا (MPT) و درخت مرکل KD در Block-DAG [ 9 ] مقایسه می کنیم. در آزمایش، 10 پرس و جو تصادفی روی هر درخت انجام می دهیم و طول اثبات را محاسبه می کنیم. نتایج نشان می دهد که اثبات مبتنی بر ورکل بهتر از اثبات مرکل در ساختارهای درختی مختلف است.

6. نتیجه گیری و کار آینده

در این مقاله، ما فناوری ذخیره‌سازی و جستجوی داده‌های مکانی-زمانی در بلاک چین را بدون افزودن فضای ذخیره‌سازی اضافی مطالعه می‌کنیم. ما یک Verkle AR*-tree را پیشنهاد می کنیم که در آن اثبات های برداری درختان Verkle با R*-tree ادغام می شوند. در مقایسه با روش مرکل KD-tree موجود، ما شاخص فضایی را از نقطه به مکعب گسترش می‌دهیم و عملکرد پرس و جوی مکانی-زمانی را بهبود می‌بخشیم. ما توانایی تطبیقی ​​مبتنی بر توزیع پرس و جو را به R*-tree اضافه می کنیم و عملکرد پرس و جو از R*-tree موجود فراتر می رود حتی زمانی که توزیع پرس و جو یکنواخت نیست. ما از تعهد برداری درخت Verkle برای ارائه اثبات برای پرس و جوهای فضایی-زمانی استفاده می کنیم و کارایی اثبات آن نیز از درخت Merkle بالاتر است. بر اساس فناوری فوق، ما سه شاخص داده مکانی به بلاک چین اضافه کردیم.
در آینده، مایلیم نسخه موازی Verkle AR*-tree را بیشتر پیاده سازی کنیم و سعی کنیم آن را در برنامه ها اعمال کنیم.

منابع

  1. خو، ام. چن، ایکس. Kou, G. بررسی سیستماتیک بلاک چین. مالی نوآوری. 2019 ، 5 ، 27. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
  2. کازینو، اف. داساکلیس، TK; پاتساکیس، سی. بررسی ادبیات سیستماتیک برنامه های کاربردی مبتنی بر بلاک چین: وضعیت فعلی، طبقه بندی و مسائل باز. Telemat. به اطلاع رساندن. 2019 ، 36 ، 55–81. [ Google Scholar ] [ CrossRef ]
  3. ورلی، سی. Skjellum، A. معاوضه ها و چالش های بلاک چین برای کاربردهای فعلی و در حال ظهور: تعمیم، تکه تکه شدن، زنجیره های جانبی و مقیاس پذیری. در مجموعه مقالات کنفرانس بین المللی IEEE 2018 در مورد اینترنت اشیا (iThings) و محاسبات سبز و ارتباطات IEEE (GreenCom) و IEEE Cyber, Physical and Social Computing (CPSCom) و IEEE Smart Data (SmartData)، هالیفاکس، NS، کانادا، 30 جولای–3 اوت 2018; صص 1582-1587. [ Google Scholar ] [ CrossRef ]
  4. Nakamoto، S. Bitcoin: یک سیستم نقدی الکترونیکی همتا به همتا. در دسترس آنلاین: https://bitcoin.org/bitcoin.pdf (در 22 مه 2022 قابل دسترسی است).
  5. برگشت، A.; کورالو، ام. دشجر، ل. فریدنباخ، م. ماکسول، جی. میلر، آ. پولسترا، ا. تیمون، جی. Wuille, P. فعال کردن نوآوری های بلاک چین با زنجیره های جانبی متصل. در دسترس آنلاین: https://blockstream.com/sidechains.pdf (در 22 مه 2022 قابل دسترسی است).
  6. ووجیچیچ، دی. یاگودیچ، دی. Ranđić، S. فناوری بلاک چین، بیت کوین و اتریوم: مروری کوتاه. در مجموعه مقالات 2018 هفدهمین سمپوزیوم بین المللی Infoteh-Jahorina (INFOTEH)، سارایوو شرقی، بوسنی و هرزگوین، 21–23 مارس 2018؛ صص 1-6. [ Google Scholar ] [ CrossRef ]
  7. هلمر، اس. روگیا، م. ال یوینی، ن. Pahl, C. EthernityDB – ادغام عملکرد پایگاه داده در یک بلاک چین. در مجموعه مقالات کنفرانس اروپایی پیشرفت در پایگاه های داده و سیستم های اطلاعاتی، بوداپست، مجارستان، 2 تا 5 سپتامبر 2018؛ Springer: برلین/هایدلبرگ، آلمان، 2018; صص 37-44. [ Google Scholar ] [ CrossRef ]
  8. سومپلینسکی، ی. ویبورسکی، اس. Zohar, A. PHANTOM GHOSTDAG: A Scalable Generalization of Nakamoto Consensus: 2 سپتامبر 2021. در مجموعه مقالات سومین کنفرانس ACM در مورد پیشرفت در فناوری های مالی، آرلینگتون، VA، ایالات متحده آمریکا، 26-28 سپتامبر 2021. صص 57-70. [ Google Scholar ]
  9. نورگلیف، آی. مزمل، م. Qu, Q. فعال کردن بلاک چین برای پردازش پرس و جوی مکانی-زمانی کارآمد. در مجموعه مقالات کنفرانس بین المللی مهندسی سیستم های اطلاعات وب، ملبورن، VIC، استرالیا، 20 تا 24 اکتبر 2018؛ Springer: برلین/هایدلبرگ، آلمان، 2018; صص 36-51. [ Google Scholar ]
  10. درختان Kuszmaul، J. Verkle. در دسترس آنلاین: https://math.mit.edu/research/highschool/primes/materials/2018/Kuszmaul.pdf (در 22 مه 2022 قابل دسترسی است).
  11. Ahn، HK; مامولیس، ن. وانگ، اچ. بررسی روش‌های دسترسی چند بعدی. در دسترس آنلاین: https://dspace.library.uu.nl/bitstream/handle/1874/2491/2001-14.pdf (در تاریخ 22 مه 2022 قابل دسترسی است).
  12. سامت، اچ. چهار درخت و ساختارهای داده سلسله مراتبی مرتبط. کامپیوتر ACM. Surv. 1984 ، 16 ، 187-260. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  13. اوی، بی. مکدونل، ک. Sacks-davis, R. فضایی kd-tree: مکانیزم نمایه سازی برای پایگاه های داده فضایی. در مجموعه مقالات کنفرانس بین المللی نرم افزار کامپیوتر و برنامه های کاربردی IEEE، توکیو، ژاپن، 5 تا 6 اکتبر 1987. ص 433-438. [ Google Scholar ]
  14. اوهساوا، ی. Sakauchi, M. The BD-Tree – ساختار داده‌های N بعدی با ویژگی‌های دینامیکی بسیار کارآمد. در مجموعه مقالات نهمین کنگره جهانی کامپیوتر IFIP، پاریس، فرانسه، 19 تا 23 سپتامبر 1983. صص 539-544. [ Google Scholar ]
  15. تائو، ز. چنگ، سی. پان، ز. Shi, J. تولید و کاربردهای درخت BSP با وضوح چندگانه. جی. سافتو. 2001 ، 12 ، 117-125. [ Google Scholar ]
  16. لی، سی. وو، زی. وو، پی. Zhao, Z. یک روش ساخت تطبیقی ​​از شاخص مکانی-زمانی سلسله مراتبی برای داده های برداری تحت شبکه های همتا به همتا. ISPRS Int. J. Geo-Inf. 2019 ، 8 ، 512. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
  17. بکمن، ن. کریگل، اچ پی؛ اشنایدر، آر. Seeger, B. R*-tree: یک روش دسترسی کارآمد و قوی برای نقاط و مستطیل ها. ACM SIGMOD 1990 ، 19 ، 322-331. [ Google Scholar ] [ CrossRef ]
  18. شوماک، م. Gurský, P. R ++ -Tree: یک روش دسترسی فضایی کارآمد برای داده‌های نقطه‌ای بسیار زائد. در روندهای جدید در پایگاه های داده و سیستم های اطلاعاتی ; Springer: برلین/هایدلبرگ، آلمان، 2014; صص 37-44. [ Google Scholar ]
  19. شکر، س. شیونگ، اچ. Zhou، X. (ویرایش) R-Tree. در دایره المعارف GIS ; Springer: برلین/هایدلبرگ، آلمان، 2017; پ. 1805. [ Google Scholar ] [ CrossRef ]
  20. Gunther, O. طراحی درخت سلولی: ساختار شاخص شی گرا برای پایگاه های داده هندسی. در مجموعه مقالات پنجمین کنفرانس بین المللی مهندسی داده، لس آنجلس، کالیفرنیا، ایالات متحده آمریکا، 6-10 فوریه 1989; صص 598-605. [ Google Scholar ] [ CrossRef ]
  21. کامل، من. Faloutsos، C. Hilbert R-Tree: An Improved R-Tree با استفاده از فراکتال ها. در مجموعه مقالات بیستمین کنفرانس بین المللی پایگاه های داده بسیار بزرگ (VLDB ’94)، سانتیاگو دی شیلی، شیلی، 12 تا 15 سپتامبر 1994. صص 500–509. [ Google Scholar ]
  22. الطراونه، ع. هرشبرگ، تی. مدوری، اس. کنده، ف. Skjellum، A. Buterin’s Scalability Trilemma از طریق یک طبقه بندی مبتنی بر تغییر حالت برای الگوریتم های اجماع مشترک مشاهده شده است. در مجموعه مقالات دهمین کارگاه و کنفرانس سالانه محاسبات و ارتباطات (CCWC) 2020، لاس وگاس، NV، ایالات متحده، 6 تا 8 ژانویه 2020؛ صص 727-736. [ Google Scholar ] [ CrossRef ]
  23. Wan, L. یک روش بهینه سازی پرس و جو در تراکنش الکترونیکی بلاک چین بر اساس حساب گروهی. در مجموعه مقالات کنفرانس بین المللی تجزیه و تحلیل داده های بزرگ برای سیستم های سایبری-فیزیکی، شانگهای، چین، 28-29 دسامبر 2021؛ Springer: برلین/هایدلبرگ، آلمان، 2021؛ صص 1358–1364. [ Google Scholar ] [ CrossRef ]
  24. سومپلینسکی، ی. Zohar, A. PHANTOM: A Scalable BlockDAG Protocol. در مجموعه مقالات سومین کنفرانس ACM در مورد پیشرفت‌ها در فناوری‌های مالی، آرلینگتون، VA، ایالات متحده آمریکا، 26 تا 28 سپتامبر 2021. [ Google Scholar ]
  25. Szydlo، M. Merkle Tree Traversal in Log Space and Time. در کنفرانس بین المللی تئوری و کاربرد تکنیک های رمزنگاری ; Springer: برلین/هایدلبرگ، آلمان، 2004; صص 541-554. [ Google Scholar ]
  26. کامل بولوس، MN; ویلسون، جی تی; Clauson، KA Geospatial blockchain: وعده ها، چالش ها و سناریوها در سلامت و مراقبت های بهداشتی. بین المللی J. Health Geogr. 2018 ، 17 ، 25. [ Google Scholar ]
  27. لیو، اچ. تای، دبلیو. وانگ، ی. وانگ، اس. چارچوب تجارت داده های فضایی مبتنی بر بلاک چین. پیش چاپ. 2021. در دسترس آنلاین: https://www.researchgate.net/publication/348709925_A_Blockchain-Based_Spatial_Data_Trading_Framework (در 22 مه 2022 قابل دسترسی است).
  28. سان، ی. ژانگ، ال. فنگ، جی. یانگ، بی. کائو، بی. عمران، ام. تجزیه و تحلیل عملکرد برای سیستم‌های اینترنت اشیاء بی‌سیم مبتنی بر بلاک چین مبتنی بر مدل تمپو-مکانی. در مجموعه مقالات کنفرانس بین المللی 2019 در زمینه محاسبات توزیع شده مبتنی بر سایبری و کشف دانش (CyberC)، گویلین، چین، 17 تا 19 اکتبر 2019؛ صص 348-353. [ Google Scholar ] [ CrossRef ]
  29. دمنکوف، م. دمنکوا، ای. Shishmanova, S. کاربرد فناوری بلاک چین برای ذخیره سازی اطلاعات روی اشیاء فضایی. وستن فناوری دولتی آستاراخان دانشگاه سر. مدیریت محاسبه کنید. علمی به اطلاع رساندن. 2019 ، 1 ، 61–72. [ Google Scholar ] [ CrossRef ]
  30. Qu، Q. نورگلیف، آی. مزمل، م. جنسن، CS; Fan, J. در مورد پردازش پرس و جو بلاک چین مکانی-زمانی. ژنرال آینده. محاسبه کنید. سیستم 2019 ، 98 ، 208-218. [ Google Scholar ] [ CrossRef ]
  31. موراتیدیس، ک. ساچاریدیس، دی. Pang، HH طرح هضم جزئی تحقق یافته: یک روش تأیید کارآمد برای پایگاه های داده برون سپاری شده. VLDB J. 2009 ، 18 ، 363-381. [ Google Scholar ] [ CrossRef ]
  32. کریگل، اچ پی؛ کونات، پ. Renz، M. R*-Tree. در دایره المعارف GIS ; Shekhar, S., Xiong, H., Eds. Springer: برلین/هایدلبرگ، آلمان، 2008; ص 987-992. [ Google Scholar ] [ CrossRef ]
  33. Pagel، BU; شش، HW; توبن، اچ. Widmayer, P. Towards an Analysis of Range Query Performance in Spatial Data Structures. در مجموعه مقالات دوازدهمین سمپوزیوم ACM SIGACT-SIGMOD-SIGART در اصول سیستم های پایگاه داده، واشنگتن، دی سی، ایالات متحده آمریکا، 25-28 مه 1993. صص 214-221. [ Google Scholar ] [ CrossRef ]
  34. گرین، دی. پیاده سازی و تجزیه و تحلیل عملکرد روش های دسترسی به داده های مکانی. در مجموعه مقالات پنجمین کنفرانس بین المللی مهندسی داده، لس آنجلس، کالیفرنیا، ایالات متحده آمریکا، 6-10 فوریه 1989; ص 606-615. [ Google Scholar ] [ CrossRef ]
Ijgi 11 00409 g001 550
شکل 1. R-tree و R*-tree. ( الف ) درخت R. ( ب ) R*-tree. ( ج ) R*-tree با پنجره پرس و جو.
Ijgi 11 00409 g002 550
شکل 2. درخت مرکل و درخت ورکل. ( الف ) درخت مرکل. ب ) درخت ورکل.
Ijgi 11 00409 g003 550
شکل 3. Verkle Patricia Trie.
Ijgi 11 00409 g004 550
شکل 4. اطلاعات تراکنش ذخیره شده در Verkle AR*-tree.
Ijgi 11 00409 g005 550
شکل 5. شماتیک الگوریتم تقسیم.
Ijgi 11 00409 g006 550
شکل 6. مسیرهای ذخیره شده در Verkle R*-tree.
Ijgi 11 00409 g007 550
شکل 7. عملکرد پرس و جو در اندازه های مختلف بلوک برای اشیاء نقطه ای.
Ijgi 11 00409 g008 550
شکل 8. عملکرد پرس و جو در اندازه های مختلف بلوک برای اشیاء مکعبی. ( الف ) Merkle KD-tree و Verkle AR*-tree. ( ب ) Verkle R*-tree و Verkle AR*-tree.
Ijgi 11 00409 g009 550
شکل 9. تعداد دسترسی های گره دو الگوریتم تحت اندازه بلوک های مختلف.
Ijgi 11 00409 g010 550
شکل 10. عملکرد پرس و جو از دو الگوریتم تحت توزیع پرس و جو متفاوت.
Ijgi 11 00409 g011 550
شکل 11. تحلیل عملکرد تعهد برداری.

مقالات داخلی و بین المللی

مطالب مرتبط ...

4 نظرات

دیدگاهتان را بنویسید