همه گیری COVID-19 منجر به مرگ و میر و اختلالات اقتصادی بسیاری در سراسر جهان شده است. مطالعات متعددی اثر عوامل خطر سلامت مربوطه را در مکان‌های مختلف مورد بررسی قرار داده‌اند، اما مشکل ناهمگونی فضایی به اندازه کافی مورد توجه قرار نگرفته است. هدف از این مقاله بررسی چگونگی ارتباط عوامل خطر سلامت انتخاب شده با میزان عفونت همه گیر در ابعاد مختلف مطالعه و نشان دادن ویژگی های متفاوت مکانی عوامل خطر سلامت خاص بود. یک مدل ضریب متغیر فضایی مبتنی بر فیلتر فضایی بردار ویژه (ESF-SVC) برای کشف اینکه چگونه تأثیر عوامل خطر سلامت انتخاب شده در فضا و زمان متفاوت است، توسعه داده شد. ESF-SVC در مقایسه با حداقل مربعات معمولی (OLS) قادر بود مشکلات بیش از حد برازش را به خوبی کنترل کند.2و اعتبار متقاطع پایین تر RMSE. تأثیر عوامل خطر بهداشتی با تغییر وسعت مطالعه متفاوت بود: در استان هوبی، تنها تراکم جمعیت و سرعت باد تأثیر قابل‌توجهی از نظر فضایی ثابت را نشان دادند. در حالی که در سرزمین اصلی چین، سایر عوامل از جمله امتیاز مهاجرت، تراکم ساختمان، دما و ارتفاع از نظر مکانی تأثیر متفاوتی را نشان دادند. تأثیر نمره مهاجرت در شهرهای اطراف ووهان کمتر از شهرهای دورتر بود، در حالی که ارتفاع نقش قوی‌تری در کاهش نرخ آلودگی در شهرهای مرتفع نشان داد. دما با گذشت زمان با ضرایب مثبت و منفی به ترتیب در 2.42 درجه سانتیگراد و 8.17 درجه سانتیگراد همبستگی مخلوطی را نشان داد. این مطالعه می‌تواند با در نظر گرفتن مشکل خودهمبستگی و ناهمگونی فضایی که در مدل‌سازی COVID-19 وجود دارد، مسیری امکان‌پذیر برای بهبود تناسب مدل ارائه دهد. ضرایب ESF-SVC بازده همچنین می‌تواند روشی بصری برای کشف تأثیرات مختلف عوامل تأثیرگذار در سراسر فضا در مناطق مطالعه بزرگ ارائه دهد. امید است که این یافته ها آگاهی عمومی و دولتی را در مورد خطرات بالقوه سلامتی بهبود بخشد و در نتیجه بر استراتژی های کنترل همه گیر تاثیر بگذارد.

کلید واژه ها:

COVID-19 ؛ ناهمگونی فضایی ; بردار ویژه فیلتر فضایی ; ضرایب متغیر مکانی

1. مقدمه

همه‌گیری COVID-19 که در ابتدا در ووهان چین در دسامبر 2019 گزارش شد، فوق‌العاده عفونی است و تأثیر زیادی بر جهان گذاشته است [ 1 ]. سازمان بهداشت جهانی (WHO) COVID-19 را در 11 مارس 2020 به عنوان یک بیماری همه گیر جهانی معرفی کرد [ 2 ]. این ویروس به سرعت در سراسر جهان گسترش یافته و تقریباً در همه کشورها موارد تأیید شده مشاهده شده است. تا نوامبر 2021، تعداد موارد تجمعی در جهان بیش از 256 میلیون و مرگ و میر بالای 5.1 میلیون نفر بود و این تعداد همچنان در حال افزایش است [ 3 ].
با توجه به این پیشینه، محققان تعداد زیادی و متنوعی از مطالعات (به عنوان مثال، تحقیقات بالینی، مدل سازی آماری و تجزیه و تحلیل رفتار) را انجام داده اند. بسیاری بر تحلیل روند و پیش‌بینی سری‌های زمانی تمرکز کرده‌اند [ 4 ، 5 ، 6 ، 7 ، 8 ]، که می‌تواند به طور موثری نقطه شیوع و نقطه عطف همه‌گیری COVID-19 را تخمین بزند و همچنین به ارزیابی اثربخشی اقدامات کمک کند. و اینکه آیا استراتژی ها باید تقویت شوند [ 9 ، 10 ، 11 ]. با این حال، این مطالعات عمدتاً تأثیر عوامل خطر خارجی را در نظر نگرفته‌اند که در تحلیل اپیدمی نیز مهم هستند [ 12 ].].
محققان رابطه بین عوامل اجتماعی-اقتصادی و همچنین عوامل زیرساختی و گسترش ویروس COVID-19 را بررسی کرده‌اند [ 13 ، 14 ، 15 ، 16 ، 17 ]. برخی دریافته‌اند که کووید-19 تأثیر مهم‌تری بر مناطق فقیر داشته است [ 18 ، 19 ] در حالی که برخی دریافته‌اند که تأثیر درآمد در مناطق مورد مطالعه خاص قابل‌توجه نبوده است [ 20 ، 21 ]. عواملی مانند تراکم جمعیت، تحرک جمعیت و دسترسی به بیمارستان ها نیز در رابطه با گسترش COVID-19 در بسیاری از مطالعات در نظر گرفته شده است [ 22 ، 23 ، 24 ]., 25 , 26 ]. علاوه بر این، تعدادی از محققین ارتباط بین عوامل محیطی و انتقال COVID-19، به ویژه تأثیر کیفیت هوا، باد، رطوبت و همچنین دما بر موارد COVID-19 را تخمین زده اند [ 27 ، 28 ، 29 ، 30 ، 31 ، 32 . ، 33 ]. با این حال، در این مطالعات، روابط فضایی بین شهرها یا کشورها دست کم گرفته شد. از آنجایی که شیوع بیماری‌های عفونی اغلب از نظر مکانی همبستگی خودکار دارد، مدل‌های آماری غیرمکانی سنتی چندان مناسب نیستند زیرا داده‌ها معیار استقلال را نقض می‌کنند [ 12 ، 34 ،35 ، 36 ].
برای حل مشکل خودهمبستگی فضایی، بسیاری از مدل‌های فضایی مانند مدل‌های خطای مکانی (SEM) و مدل‌های مدل‌های تاخیر مکانی (SLM) در تجزیه و تحلیل COVID-19 استفاده شده‌اند [ 20 ، 37 ، 38 ، 39 ]. مطالعات بالا خودهمبستگی فضایی را از دیدگاه جهانی در نظر گرفتند. با این حال، یک مشکل این است که داده های اپیدمی مکانی اغلب ناهمگنی فضایی بالایی را نشان می دهند [ 34 ، 40 ]. مدل‌های جهانی برای بررسی تأثیر عوامل خطر که ممکن است در فضا متفاوت باشد چندان مفید نیستند. برخی از محققان از مدل GWR و تغییرات آن استفاده کرده اند [ 41 ، 42] برای در نظر گرفتن ویژگی‌های متفاوت فضایی که در عوامل خطرات بهداشتی COVID-19 نهفته است [ 43 ، 44 ، 45 ، 46 ، 47 ، 48 ]. با این حال، اغلب بایاس چند خطی در ضرایب وجود داشت، بدون اینکه به مشکل انتخاب پهنای باند مناسب در مدل‌سازی GWR اشاره کنیم [ 49 ]. گریفیث [ 50 ] یک روش ضرایب متغیر فضایی مبتنی بر فیلتر فضایی بردار ویژه (ESF-SVC) را برای کنترل ناهمگنی فضایی توسعه داد. یکی از مزایای این روش این است که ماتریس وزن های فضایی را به بردارهای ویژه ای که حاوی اطلاعات الگوهای فضایی مختلف است تجزیه می کند. موراکامی و همکاران [ 51 ، 52] یک رویکرد مدلسازی ESF-SVC را با در نظر گرفتن اثرات تصادفی توسعه داد و دریافت که روش ESF-SVC از نظر دقت مدل بهتر از رویکرد GWR است. مزیت دیگر روش ESF-SVC این است که می تواند تشخیص دهد که آیا ضرایب متغیرهای مستقل باید از نظر مکانی متغیر یا ثابت باشند از طریق معیارهای کمینه سازی اطلاعات بیزی (BIC). خروجی مدل ESF-SVC شامل ضرایب برآورد شده (از نظر مکانی متغیر یا ثابت) و همچنین اهمیت آماری آنها است که می تواند به شناسایی ویژگی های متغیر مکانی کمک کند [ 53 ]. با این حال، این روش در مطالعه COVID-19 استفاده نشده است.
شکاف اصلی تحقیقاتی در مطالعات COVID-19 ذکر شده این است که بسیاری نمی توانند ناهمگونی فضایی را به روشی موثر مدل کنند. بنابراین، یک مدل ESF-SVC ساخته شد تا تأثیر فضایی متفاوت برخی از عوامل اجتماعی و محیطی بر گسترش COVID-19 را نشان دهد. این رابطه فضایی را به بردارهای ویژه سپرده و آنها را با عوامل خطر سلامت انتخاب شده ترکیب کرد و بنابراین قادر به تشخیص اینکه آیا ضرایب عوامل خطر سلامت از نظر مکانی متغیر هستند یا ثابت بودند. اهداف اصلی این مقاله عبارت بودند از: (1) بررسی اینکه چگونه عوامل خطر سلامت انتخاب شده با میزان عفونت COVID-19 در ابعاد مختلف مطالعه مرتبط هستند. (2) برای کشف اینکه آیا تأثیر عوامل خطر سلامت انتخاب شده در مکان و زمان متفاوت است و چگونه آنها متفاوت هستند. با در نظر گرفتن در دسترس بودن داده ها و عقلانیت، 10 عامل، از جمله عوامل اجتماعی و زیست محیطی، به عنوان عوامل خطر اولیه سلامت با توجه به بررسی ادبیات ذکر شده در بالا استفاده شد. عوامل اجتماعی شامل تراکم جمعیت، مهاجرت انسان، ظرفیت بیمارستان، تولید ناخالص داخلی و تراکم ساختمان، در حالی که عوامل محیطی شامل بارش، سرعت باد، دما، ارتفاع متوسط ​​و فشار هوا بود. نتایج مدل ESF-SVC با مدل‌های OLS، ESF و GWR مقایسه شد و نتایج نشان داد که ESF-SVC پیشنهادی یک روش امیدوارکننده در زمینه مدل‌سازی خطر سلامت COVID-19 و کشف ویژگی‌های متغیر فضایی بود. .

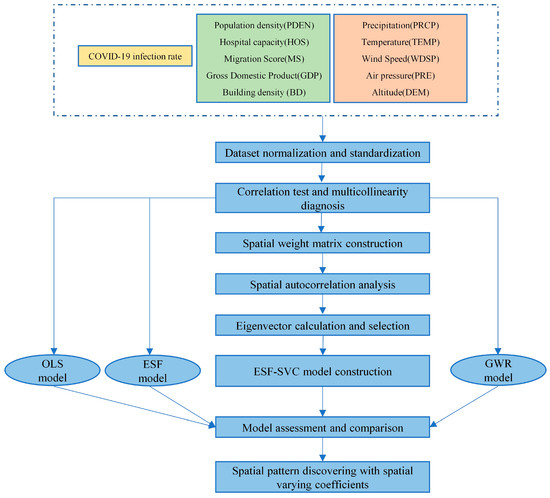
2. مواد و روشها

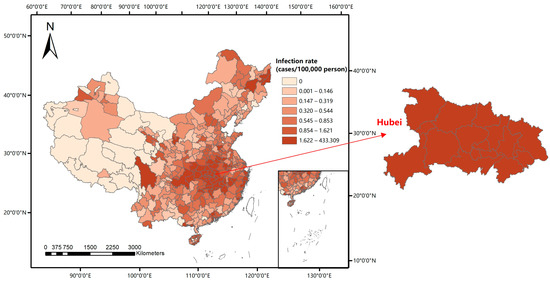
2.1. منطقه مطالعه

چین که در امتداد طول جغرافیایی 73 درجه و 33 دقیقه شرقی تا 135 درجه و 05 دقیقه شرقی، عرض جغرافیایی 3 درجه و 51 دقیقه شمالی تا 53 درجه و 33 دقیقه شمالی قرار دارد، کشوری بزرگ با بیش از 1.4 میلیارد شهروند است. استان هوبی که در محدوده طول جغرافیایی 108 درجه 21 دقیقه شرقی تا 116 درجه و 01 دقیقه شرقی، عرض جغرافیایی 29 درجه و 01 دقیقه شمالی تا 33 درجه و 16 دقیقه شمالی قرار دارد و بیش از 59.17 میلیون نفر ساکن دارد، نرخ بالایی از ابتلا به کووید-19 داشته است. در مقایسه با سایر استان های چین در مراحل اولیه همه گیری. برای بررسی اینکه آیا ویژگی عوامل تأثیرگذار با تغییرات وسعت مطالعه متفاوت است یا خیر، استان هوبی و سرزمین اصلی چین هر دو به عنوان مناطق مورد مطالعه در نظر گرفته شدند. آزمایش‌ها در وضوح فضایی سطح شهر انجام شد ( شکل 1). با توجه به کیفیت و در دسترس بودن داده ها، 17 و 362 شهر به ترتیب به عنوان واحدهای مطالعه در استان هوبی و سرزمین اصلی چین (به استثنای هنگ کنگ، ماکائو، تایوان، ژوشان و سانشا) انتخاب شدند.

2.2. منابع داده و پیش پردازش

موارد تایید شده روزانه کووید-19 از ژانویه تا آوریل 2020 جمع آوری شد. عوامل موثر طبیعی شامل دمای متوسط ​​(TEMP)، بارندگی (PRCP)، سرعت باد (WDSP)، فشار هوا (PRE) و همچنین ارتفاع (DEM) بود. داده های اجتماعی و اقتصادی شامل تولید ناخالص داخلی (GDP) و داده های تراکم جمعیت (PDEN) بود. امتیاز مهاجرت (MS) با استفاده از داده‌های مهاجرت روزانه محاسبه شد. داده‌های زیرساخت، از جمله مختصات بیمارستان‌ها و ساختمان‌های دیگر، با رابط برنامه‌نویسی نقشه بایدو (Baidu map API)، یک سرویس نقشه وب که داده‌های مکان، برنامه‌ریزی مسیر و سایر محصولات را به منظور محاسبه ظرفیت بیمارستان فراهم می‌کند، به‌دست آمد. HOS) و تراکم ساختمان (BD). منابع داده مربوطه در جدول 1 فهرست شده است.

برای بررسی رابطه بین نرخ عفونت COVID-19 و عوامل خطر سلامت، میانگین هفتگی نرخ عفونت COVID-19 (که با IFR مشخص می شود) به عنوان متغیر وابسته در نظر گرفته شد. از آنجایی که توزیع داده‌های میزان آلودگی COVID-19 منحرف شد، از روش تبدیل Box-Cox [ 61 ] استفاده شد تا داده‌ها تقریباً به طور معمول توزیع شوند و بنابراین بتوانند با فرض داده‌های پایه برای مدل‌های رگرسیونی مطابقت داشته باشند [ 62 ]. فرمول در رابطه (1) نشان داده شده است:

منافR i =⎧⎩⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪(17∑7k = 1c o n fمن هستم _ _دکp o p)p o w– 1p o w, ( p o w ≠ 0 )  l n (17∑k = 17c o n fمن هستم _ _دکp o p) ، ( p o w = 0 )   ����={(17∑�=17�������������)���−1���,  (���≠0)��(17∑�=17�������������),  (���=0) 

جایی که منافR i����میانگین تغییر یافته نرخ عفونت COVID-19 در هفته i است، c o n fمن هستم _ _دک����������تعداد موارد تایید شده در k روز هفته i است، pow پارامتر تبدیل Box-Cox مربوطه است که با روش تخمین حداکثر درستنمایی تخمین زده می شود، که نه تنها وضعیت تبدیل توان را در نظر می گیرد، بلکه تبدیل مربع را نیز در نظر می گیرد. p o w���= 0.5)، تبدیل گزارش ( p o w���= 0) و تبدیل متقابل ( p o w���= -1). در این مطالعه، p o w���= -0.3 در استان هوبی و p o w���= 0.11 در سرزمین اصلی چین. p o p���تعداد ساکنان هر شهر بود. هیستوگرام های قبل و بعد از تبدیل داده ها در مواد تکمیلی (S1) گنجانده شده است. تراکم جمعیت (PDEN) با جمعیت / منطقه (km2) محاسبه شد .

از آنجایی که دوره نهفتگی موارد کووید-19 به طور کلی از 0 تا 14 روز متغیر است، برای در نظر گرفتن اثرات تاخیر زمانی، متغیرهای هواشناسی در دو هفته قبل (هفته i -2 و هفته i -1) در مدل سازی میانگین میانگین گیری شدند. نرخ عفونت COVID-19 در هفته i [ 63 ، 64 ]. داده های هواشناسی 376 ایستگاه را با رکورد روزانه پوشش داد. برای شهرهایی که ایستگاه‌هایی در داخل خود دارند، میانگین دمای TEMP، PRCP و WDSP هر دو هفته یکبار محاسبه شد. برای شهرهایی که ایستگاه‌های درون خود نداشتند، لازم بود ایستگاه‌های نزدیک را در محدوده 50 کیلومتری بافر تطبیق داده و از روش وزن‌دهی معکوس فاصله برای بدست آوردن میانگین اطلاعات آب و هوا استفاده کنند.
داده‌های مهاجرت به‌دست‌آمده از نقشه Baidu Qianxi از 1 ژانویه 2020 تا 1 فوریه 2020 شامل دو بخش بود: مقیاس مهاجرت و نسبت مهاجرت. بردار مقیاس مهاجرت M1 (1× m ) نشان دهنده تعداد کل افرادی است که از ووهان به مکان های دیگر در m ( m = 32) روز نقل مکان کرده اند، در حالی که نسبت مهاجرت روزانه (M2) m × n ( m = 32 ) است. ، n = 17 در استان هوبی؛ m = 32، n = 362 در سرزمین اصلی چین) بردار که درصد روزانه مهاجران ووهان را نشان می دهد که به n شهر دیگر در عرض متر نقل مکان کرده اند.روزها. بردار نمره مهاجرت MS (1 × n ) با استفاده از M1 × M2 محاسبه شد.

داده‌های زیرساخت، از جمله مکان و نوع بیمارستان‌ها و همچنین ساختمان‌های دیگر، با API نقشه بایدو به‌دست آمدند. ساختمان‌های دیگری مانند مراکز خرید، هتل‌ها، رستوران‌ها و جاذبه‌های گردشگری نیز در تجمع جمعیت و گسترش بیماری همه‌گیر نقش داشتند، بنابراین تعداد این نوع ساختمان‌ها در هر کیلومتر مربع در هر شهر محاسبه و به عنوان یک عامل خطر انتخاب شد. ، و به عنوان تراکم ساختمان (BD) نشان داده شد. ظرفیت بیمارستان (HOS) با مجموع وزنی بیمارستان ها در سطوح مختلف در یک شهر محاسبه شد، همانطور که در رابطه (2) نشان داده شده است:

اچای اس= 0.5 ∗ h o s 3 A + 0.25 ∗ h o s 3 + 0.15 ∗ h o s 2 + 0.1 ∗ h o s 1���=0.5∗ℎ��3�+0.25∗ℎ��3+0.15∗ℎ��2+0.1∗ℎ��1

جایی که ساعت 3 A _ _ℎ��3�تعداد بیمارستان های سطح سوم A است، ساعت 3 _ _ℎ��3تعداد سایر بیمارستان های عالی است. از آنجایی که بیمارستان های درجه سوم، به ویژه بیمارستان های 3A، دارای مهم ترین منابع پزشکی در چین هستند، وزن نسبتاً بالاتری دارند [ 65 ]. ساعت 2 _ _ℎ��2تعداد بیمارستان های ثانویه و ساعت 1 _ _ℎ��1تعداد بیمارستان های دیگر است.

همه 10 عامل خطر ذکر شده در بالا نرمال شده بودند تا بین 0 تا 1 برای مقایسه بهتر قرار گیرند و روش عادی سازی در رابطه (3) نشان داده شده است.

ایکسn o r m a l i ze d= ( X- _ایکسm i n) / (ایکسm a x–ایکسm i n)ایکس���مترآلمن�هد=(ایکس-ایکسمترمن�)/(ایکسمترآایکس-ایکسمترمن�)

جایی که ایکسn o r m a l i ze d����مترآلمن�هدعامل تأثیرگذار نرمال شده است و ایکسm a xایکسمترآایکسو ایکسm i nایکسمترمن�حداکثر و حداقل مقادیر فاکتور هستند ایکسایکس.

سپس قبل از مدل‌سازی از آزمون‌های همبستگی پیرسون و تشخیص چند خطی با استفاده از ضریب تورم واریانس (VIF) استفاده شد. اگر مقدار VIF کوچکتر از 10 بود، چند خطی بودن در متغیرها جدی نبود، در غیر این صورت متغیرها با استفاده از روش رگرسیون گام به گام حذف شدند [ 66 ].

2.3. مواد و روش ها

از آنجایی که موارد تایید شده در اکثر شهرهای داخل سرزمین اصلی چین از 10 مارس تا 1 ژوئن افزایش چندانی نداشت (297 شهر صفر مورد تایید شده جدید داشتند، 57 شهر موارد تایید شده جدید کمتر از 10 در طول 3 ماه داشتند)، این تحقیق بر روی دوره مطالعه از 22 ژانویه 2020 تا 10 مارس 2020. این آزمایش طی 7 هفته در دو محدوده مطالعه (استان هوبی و سرزمین اصلی چین) انجام شد. نقشه‌های ضرایب متغیر فضایی برای کشف الگوی فضایی و تعیین اینکه چگونه اثرات عوامل خطر سلامت در شهرها متفاوت است استفاده شد. این روش شامل پنج وظیفه اصلی بود: (1) ساخت ماتریس وزن‌های فضایی. (2) استخراج بردار ویژه. (3) انتخاب متغیر و ساخت مدل ESF-SVC. (4) ارزیابی و مقایسه مدل. و (5) کشف الگوی فضایی.

2.3.1. ساخت ماتریس وزن های فضایی

ماتریس وزن های فضایی دبلیودبلیودر این مطالعه یک ماتریس مجاورت نزدیکترین همسایگان K است، که یک ماتریس مبتنی بر فاصله است و می تواند با مشکل واحدهای “انزوا” مقابله کند [ 67 ، 68 ]. برای هر واحد مطالعه i ، ابتدا فاصله بین مرکز واحد i و n -1 واحد دیگر را محاسبه کنید.دمن 1،دمن 2…دمن – 1، دمن + 1, … ,  دn��1,��2…��−1, ��+1, …, ��) و آنها را بر اساس فاصله رتبه بندی کنید. سپس k نزدیکترین واحدها را به i بیابید و آنها را در مقابل واحدهای دیگر همسایه نشان دهید. وقتی شهرهای i و j همسایه هستند، دبلیومن ج���مقادیر غیر صفر می گیرد (یک، برای یک ماتریس باینری)، در غیر این صورت صفر [ 69 ].

سپس ماتریس وزن های فضایی دبلیودبلیوکه در بالا ذکر شد در یک ماتریس وزن فضایی C به شرح زیر در رابطه (4) متمرکز می شود:

C = ( I –11تیn) دبلیو( من –11تیn)C=(I−11T�)�(I-11تی�)

جایی که n نشان دهنده واحدهای چند ضلعی شهر در این مطالعه است، n = 17 در مطالعه استان هوبی، n = 362 در مطالعه سرزمین اصلی چین، منمنیک ماتریس هویت n بعد و 1 بردار n در 1 یک ها است.

2.3.2. استخراج بردار ویژه

ماتریس وزن فضایی متمرکز C به بردارهای ویژه و مقادیر ویژه مانند معادله (5) تجزیه شد:

C = E∧EتیC = E∧Eتیسی=�∧�تیسی=�∧�تی

جایی که E = ( E1�1، E2�2، E3�3,…, En��) مجموعه ای از بردارهای ویژه است، ∧∧یک ماتریس مورب n × n از مقادیر ویژه است ( λ1�1، λ2�2، λ3�3,…, λn��) که مقدار MC بردارهای ویژه مربوطه را تعریف می کند، λ1�1بزرگترین مقدار ویژه است و λn��کوچکترین مقدار ویژه است.

برای گرفتن همبستگی مثبت فضایی، زیر مجموعه بردارهای ویژه سیسیابتدا با استفاده از معیار انتخاب شد λمنλ1> 0.25�من�1>0.25برای مدل زیر یک روش انتخاب متغیر گام به گام در استخراج بردار ویژه بیشتر برای جلوگیری از چند خطی استفاده شد. تعداد بردارهای ویژه نامزد انتخاب شده 3 در استان هوبی و 85 در سرزمین اصلی چین بود.
2.3.3. انتخاب متغیر و ساخت مدل ESF-SVC

یک مدل SVC مبتنی بر ESF توسعه یافته را می توان به صورت زیر نشان داد:

Yˆ≈⎛⎝⎜β01 +∑k = 1ک0Eکβ0 ، k⎞⎠⎟+∑p = 1پ⎛⎝⎜βپ1 +∑k = 1کپEکβp ، k⎞⎠⎟⋅ایکسپ+ ε�^≈(�01+∑ک=1ک0�ک�0،ک)+∑پ=1پ(�پ1+∑ک=1کپ�ک�پ،ک)·ایکسپ+�

جایی که ایکسپایکسپهست یک n × 1�×1بردار از پ�-امین عامل خطر سلامت، کپ��تعداد بردارهای ویژه در مجموعه بردار ویژه انتخاب شده است که با عامل خطر سلامت ترکیب شده است پ�، Eک��هست ک�بردار ویژه در مجموعه بردار ویژه که با عامل خطر سلامت ترکیب شده است پ�، β0،βپ،β0 ، k،βp ، k�0,��,�0,�,��,�ضرایب رگرسیونی هستند که با استفاده از روش حداکثر درستنمایی محدود برآورد شده اند، ε�نشان دهنده اختلال تصادفی و ” ⋅ ““·”عملگر محصول از نظر عنصر را نشان می دهد. Eکβp ، k�ک�پ،کضرایب فضایی متغیر عامل خطر سلامت را به دست می دهد پپ.

برای مدل سازی موارد COVID-19، معادله (6) را می توان به صورت زیر بیان کرد:

منافR =βR – Eاساف0+βR – Eاساف1پD Eنوع گره ناشناخته: فونتنوع گره ناشناخته: فونتنوع گره ناشناخته: فونتنوع گره ناشناخته: فونتنوع گره ناشناخته: فونتنوع گره ناشناخته: فونتنوع گره ناشناخته: فونتنوع گره ناشناخته: فونتنوع گره ناشناخته: فونتنوع گره ناشناخته: فونتنوع گره ناشناخته: فونتنوع گره ناشناخته: فونتنوع گره ناشناخته: فونتنوع گره ناشناخته: فونتنوع گره ناشناخته: فونتنوع گره ناشناخته: فونتنوع گره ناشناخته: فونتنوع گره ناشناخته: فونتنوع گره ناشناخته: فونتنوع گره ناشناخته: فونتنوع گره ناشناخته: فونتنوع گره ناشناخته: فونتنوع گره ناشناخته: فونتنوع گره ناشناخته: فونتR – Eاساف4اچای اس+βR – Eاساف5B D +βR – Eاساف6تیEمپ+βR – Eاساف7پآر سیپ+βR – Eاساف8پR E+βR – Eاساف9دبلیودی اسپ+βR – Eاساف10D Eم+ εمنافآر=�0آر-�اساف+�1آر-�اسافپ��نوع گره ناشناخته: فونتنوع گره ناشناخته: فونتنوع گره ناشناخته: فونتنوع گره ناشناخته: فونتنوع گره ناشناخته: فونتنوع گره ناشناخته: فونتنوع گره ناشناخته: فونتنوع گره ناشناخته: فونتنوع گره ناشناخته: فونتنوع گره ناشناخته: فونتنوع گره ناشناخته: فونتنوع گره ناشناخته: فونتنوع گره ناشناخته: فونتنوع گره ناشناخته: فونتنوع گره ناشناخته: فونتنوع گره ناشناخته: فونتنوع گره ناشناخته: فونتنوع گره ناشناخته: فونتنوع گره ناشناخته: فونتنوع گره ناشناخته: فونتنوع گره ناشناخته: فونتنوع گره ناشناخته: فونتنوع گره ناشناخته: فونتنوع گره ناشناخته: فونت4آر-�اسافاچ�اس+�5آر-�اسافب�+�6آر-�اسافتی�مپ+�7آر-�اسافپآرسیپ+�8آر-�اسافپآر�+�9آر-�اسافدبلیو�اسپ+�10آر-�اساف��م+�

جایی که

βR – Eاسافک=βk 0+∑k = 1کEγک�کآر-�اساف=�ک0+∑ک=1ک��ک
ضرایب βR – Eاسافک�کآر-�اسافدر رابطه (7) شامل دو بخش است: بخش اول، βk 0�ک0، نشان دهنده اثر ثابت مکانی عوامل خطر سلامت بر میزان آلودگی COVID-19 است و بخش دوم، Eγک��ک، نشان دهنده تأثیر فضایی بر عوامل خطر سلامت و تأثیر محلی آنها بر میزان آلودگی COVID-19 است.
2.3.4. ارزیابی و مقایسه مدل
چهار مدل با توابع پیوند گاوسی -OLS، GWR، ESF و ESF-SVC- ساخته و با فرمول‌های مربوط به سه مدل دیگر مقایسه شدند (این‌ها در مواد تکمیلی پیوست شده‌اند (به S2-S4 مراجعه کنید ). معیارهای مقایسه در زیر مشخص شد.
در ابتدا، R2 تعدیل شده ، AIC و میانگین مربعات خطای ریشه شده (RMSE) به عنوان معیار عملکرد برای ارزیابی قابلیت اطمینان مدل انتخاب شدند. R2 و RMSE تنظیم شده دو معیار معمولی هستند که برای ارزیابی تناسب مدل با توجه به مقدار مطلق و نسبت استفاده می‌شوند. معیار اطلاعات Akaike (AIC) معیاری است که برای ارزیابی پیچیدگی مدل استفاده می شود. گنجاندن مشترک این معیارهای ارزیابی به این معنی است که برازش مدل می تواند به روشی جامع تر ارزیابی شود. محاسبه مربوطه را می توان در مواد تکمیلی (S5) یافت.
سپس از روش اعتبارسنجی متقاطع برای آزمایش بیشتر ثبات مدل و دقت برازش استفاده شد. مدل هایی با عملکرد اعتبار سنجی متقاطع بهتر را می توان به عنوان دارای مشکلات بیش از حد برازش کمتر در نظر گرفت [ 70 ، 71 ]. به جای اعتبار سنجی متقاطع 10 برابری، یک روش اعتبار سنجی متقاطع ترک یک خروجی وقت گیرتر اما بی طرفانه تر (LOOCV) برای کاهش مشکل همبستگی خودکار فضایی که ممکن است در مجموعه داده آزمون وجود داشته باشد استفاده شد [ 72 ، 73 ]]. یعنی فقط یک شهر با متغیرهای مربوطه به عنوان نمونه اعتبار سنجی عمل می کند و سایر شهرها به عنوان مجموعه آموزشی عمل می کنند. این فرآیند تا زمانی تکرار شد که هر شهر به عنوان نمونه اعتبار سنجی گرفته شد و میانگین RMSE به عنوان معیار ارزیابی در نظر گرفته شد.

در نهایت، مقدار Moran’s I، شاخصی که برای تشخیص خودهمبستگی فضایی استفاده می‌شود [ 74 ]، همچنین به عنوان یک معیار عملکرد برای آزمایش اینکه آیا خودهمبستگی فضایی در باقیمانده‌ها با موفقیت فیلتر شده است، در نظر گرفته شد. محاسبه مقدار I موران در رابطه (8) نشان داده شده است.

من موران =n∑i = ni = 1∑j = nj = 1سیمن ج(Yمن–Y¯¯¯) (Yj–Y¯¯¯)∑i = ni = 1∑j = nj = 1سیمنج∑من= nمن= 1(Yمن–Y¯¯¯)من موران=�∑من=1من=�∑�=1�=�سیمن�(�من-�¯)(��-�¯)∑من=1من=�∑�=1�=�سیمن�∑من=1من=�(�من-�¯)

که n = 17 در وسعت استان هوبی و n = 362 در وسعت سرزمین اصلی چین. سیمن جسیمن�ورودی در ماتریس وزن فضایی مرکزی C است که وزن رابطه فضایی بین واحدهای i و j را نشان می دهد. Y متغیر پاسخ است و در این مطالعه نشان دهنده باقیمانده مدل است. Y¯¯¯�¯مقدار میانگین Y است. مقدار I موران از 1- تا 1 متغیر است، و اگر مقدار I موران بالا و معنی دار باشد، نشان می دهد که باقیمانده ها از نظر مکانی همبستگی خودکار دارند، که فرضیه استقلال در رگرسیون خطی را نقض می کند.

به طور کلی، هرچه R 2 تنظیم شده بالاتر باشد ، RMSE، AIC و RMSE LOOCV کمتر باشد، Moran’s I برای باقیمانده‌ها کوچکتر و کمتر است و عملکرد مدل بهتر است.
2.3.5. کشف الگوی فضایی
خروجی مدل ESF-SVC شامل ضرایب (از نظر مکانی متغیر یا ثابت) و همچنین اهمیت آماری آنها بود، که نشان می‌دهد عوامل خطر چگونه و تا چه اندازه بر میزان آلودگی COVID-19 تأثیر می‌گذارند و چگونه آنها در فضا تغییر می‌کنند. برای تجسم بهتر، ضرایب عوامل خطر مربوطه در طول 7 هفته ترسیم شد. از روش چندک برای درجه بندی افسانه استفاده شد و هر عامل خطر همان ابعاد نقشه برداری را داشت. شهرهایی که ضریب اهمیت آنها کمتر از 1/0 بود با نقاط پراکنده برچسب‌گذاری شدند. در مجموع 28 (چهار ضریب × 7 هفته) نقشه ضریب نمایش داده شد. با مقایسه ضرایب عوامل خطر مختلف در سراسر فضا در 7 هفته، می‌توان بررسی کرد که چگونه تأثیرات بر میزان عفونت COVID-19 در شهرهای مختلف در طول زمان متفاوت است.شکل 2 .

3. نتایج

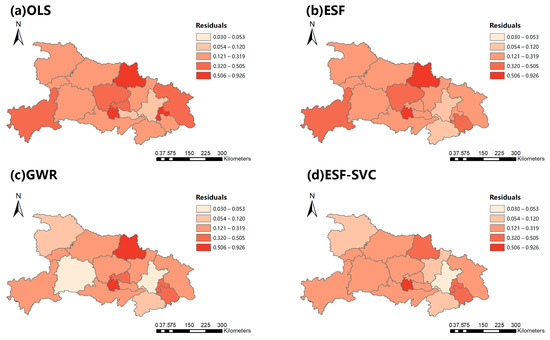
3.1. استان هوبی

3.1.1. تجزیه و تحلیل همبستگی و تشخیص چند خطی

جدول 2ضرایب همبستگی پیرسون را بین عوامل خطر سلامت و میزان عفونت COVID-19 در استان هوبی نشان می دهد. در 3 هفته اول، از 22 ژانویه تا 11 فوریه، همه 10 عامل خطر ارتباط معنی داری با نرخ ابتلا به COVID-19 در 0.1 نشان ندادند. از هفته 4 تا هفته 7، PDEN، MS، BD و WDSP شروع به نشان دادن همبستگی مثبت معنی‌دار کردند، در حالی که PRE و DEM همبستگی منفی معنی‌داری را در 0.01 یا 0.05 نشان دادند. PRCP از هفته سوم تا چهارم فقط آزمون معناداری 0.05 را گذراند. سایر عوامل خطر شامل HOS، GDP، PRCP و TEMP آزمون معنی داری را قبول نکردند. ضرایب همبستگی پیرسون که آزمون معنی‌دار را پشت سر گذاشتند بیشتر بالای 0.7 یا زیر 0.55- بودند. برای آزمایش اینکه آیا چند خطی بودن بین متغیرهای همبسته قابل توجهی وجود دارد، آزمون VIF انجام شد.جدول 3 . از آنجایی که برخی از مقادیر VIF بزرگتر از 10 بودند، با MS و BD بزرگتر از 100، مشکل چند خطی وجود داشت. بنابراین، یک روش رگرسیون گام به گام برای انتخاب متغیر برای جلوگیری از چند خطی استفاده شد. در نهایت، تنها PDEN و WDSP حفظ شدند و سایر متغیرها غربال شدند.
3.1.2. مقایسه عملکرد مدل
نتایج مدل های مختلف در جدول 4 نشان داده شده است. از نظر برازش مدل، مدل ESF-SVC با میانگین R 2 تعدیل شده 0.770، 16.31، 5.48 درصد و 18.83 درصد بهترین عملکرد را داشت که بالاتر از GWR (0.662)، ESF (0.730) و مدل های OLS (0.648). R 2 تنظیم هفتگی ESF-SVCهمچنین از هفته های یک تا پنج بالاترین میزان بود، اما کمی کوچکتر از مدل ESF در هفته های شش و هفت بود. از نظر خطاهای مدل، مدل ESF-SVC با میانگین RMSE 0.310 در مقایسه با 0.327، 0.374 و 0.445 مدل های GWR، ESF و OLS بهترین عملکرد را داشت. اما AIC مدل ESF-SVC بزرگتر از مدل‌های دیگر بود که به دلیل ضرایب متغیر مکانی و افزایش پیچیدگی مدل بود.
نتایج LOOCV در جدول 5 نشان داده شده است. میانگین LOOCV RMSE برای مدل های ESF-SVC، ESF، GWR و OLS به ترتیب 0.607، 0.675، 0.801 و 0.882 بود. بنابراین، از نظر استحکام اعتبارسنجی متقاطع، مدل ESF-SVC بهترین عملکرد را داشت. مدل ESF نیز بهتر از مدل GWR عمل کرد.
مقادیر Moran’s I برای باقیمانده های مدل در جدول 6 نمایش داده شده است. باقیمانده‌های OLS به‌طور قابل‌توجهی در طول سه هفته اول از نظر مکانی همبستگی خودکار داشتند، اما در هفته‌های پایانی همبستگی فضایی معنی‌داری را نشان ندادند. باقیمانده‌های GWR فقط خودهمبستگی فضایی معنی‌داری را در هفته دوم نشان دادند. هیچ یک از باقیمانده‌های مدل‌های ESF و ESF-SVC از نظر فضایی همبستگی خودکار نداشتند، که نشان می‌دهد بهتر می‌توانند تأثیر همبستگی مکانی را فیلتر کنند.
برای تجزیه و تحلیل شهودی تناسب مدل، مطلق میانگین باقیمانده مدل در شکل 3 نشان داده شده است. افسانه نقشه بر اساس چندک از باقیمانده های هر چهار مدل درجه بندی شد. هر چه رنگ روشن تر باشد، میانگین خطای مدل کوچکتر است. میانگین باقیمانده‌ها برای مدل‌های ESF-SVC و GWR تقریباً در همان سطح باقی ماندند، با تنها چهار و پنج واحد در عمیق‌ترین دو رنگ. هر دو مدل ESF-SVC و مدل GWR بهتر از مدل های OLS و ESF عمل کردند.
3.1.3. ضرایب مدل ESF-SVC
ضرایب مدل ESF-SVC ساخته شده در جدول 7 نشان داده شده است. همه 10 متغیر مستقل عادی شدند به طوری که مقادیر پارامترهای ضریب نشان دهنده چگونگی تأثیر عوامل خطر بر نرخ عفونت COVID-19 در استان هوبی است.
در طول سه هفته اول، هیچ یک از 10 عامل خطر آزمون همبستگی پیرسون و آزمون معنی داری 0.1 را قبول نکردند، اما آنها در برش های مکانی متفاوت تولید شده توسط بردارهای ویژه، که نشان دهنده الگوهای خودهمبستگی فضایی هستند، ثبت شدند. بنابراین، هیچ ضرایب ESF-SVC برای عوامل خطر سلامت به دست آمد. PDEN و WDSP آزمون اهمیت مدلسازی را از هفته چهارم تا هفتم گذراندند. WDSP با میانگین ضریب 1.172 از هفته چهارم به بعد نقش مهم تری در رشد نرخ آلودگی به COVID-19 در استان هوبی ایفا کرد. هیچ نقشه ضرایب متغیر مکانی تولید نشد زیرا ضرایب عامل خطر سلامت ثابت بود.

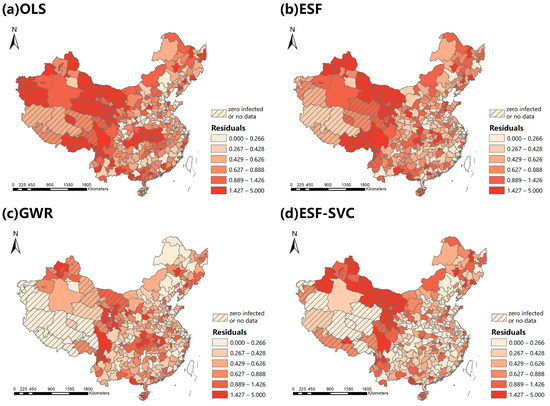
3.2. سرزمین اصلی چین

3.2.1. تجزیه و تحلیل همبستگی و تشخیص چند خطی

جدول 8 متغیرهای کمکی را نشان می دهد که با میانگین هفتگی نرخ آلودگی به کووید-19 همبستگی داشتند. در سرزمین اصلی چین، همه عوامل خطر (PRCP و WDSP) به جز دو عامل خطر، آزمون معناداری 0.05 را در 7 هفته گذراندند. PRCP فقط از هفته سوم تا هفته ششم آزمون معنی داری را پشت سر گذاشت و ضرایب مثبت بود. WDSP فقط در هفته اول آزمون قابل توجهی را پشت سر گذاشت. به طور کلی، بین PDEN، HOS، MS، GDP، BD، TEMP و IFR همبستگی مثبت و معنادار وجود داشت، در حالی که PRE و DEM با IFR همبستگی منفی داشتند. جدول 9 VIF عوامل خطر را نشان می دهد. همه مقادیر VIF کمتر از 10 بودند، که به این معنی است که چند خطی در بین این عوامل ضعیف بود و می‌توان آن را برای مدل‌سازی اضافه کرد.
3.2.2. مقایسه عملکرد مدل
جدول 10 نتایج را برای چهار مدل در سرزمین اصلی چین نشان می دهد. از نظر تناسب مدل، مدل ESF-SVC با میانگین R 2 تعدیل شده 0.624 بهترین عملکرد را داشت که به ترتیب 10.25، 19.54 و 105.94 درصد بیشتر از مدل های GWR، ESF و OLS بود. از نظر AIC، نتایج تولید شده با مدل ESF-SVC همیشه بهتر از سایر مدل‌ها نبودند، زیرا ضرایب متغیر فضایی پیچیدگی مدل را افزایش می‌دهند. در هفته های پنجم و ششم، RMSE مدل ESF-SVC کوچکتر از سه مدل دیگر بود. با این حال، در هفته‌های دیگر، RMSE مدل GWR کمترین میزان را داشت.
اگرچه میانگین RMSEهای مدل ESF-SVC همیشه در سرزمین اصلی چین کوچکترین نبود، اما نتیجه اعتبارسنجی متقاطع مدل ESF-SVC از سه مدل دیگر بهتر بود، با میانگین RMSE LOOCV 3.067، بسیار کمتر از GWR (5.732). ، مدل های ESF (3.422) و OLS (5.805) ( جدول 11 ). LOOCV RMSE های هفتگی ESF-SVC نیز کوچکترین بودند. از این رو، مدل ESF-SVC بار دیگر از نظر LOOCV از سایر مدل ها بهتر عمل کرد.
مقادیر Moran’s I برای باقیمانده های مدل در جدول 12 نمایش داده شده است. همه باقیمانده‌های مدل OLS به طور قابل‌توجهی از نظر فضایی همبستگی خودکار داشتند، و برخی از مدل‌های ESF (هفته اول) و GWR (هفته پنجم و ششم) همبستگی فضایی قابل‌توجهی را نشان دادند. هیچ یک از مقادیر I موران برای باقیمانده‌های مدل ESF-SVC آزمون معنی‌داری را رد نکرد و نشان می‌دهد که مدل ESF-SVC می‌تواند تأثیر خودهمبستگی فضایی را بهتر فیلتر کند.
شکل 4 مطلق میانگین باقیمانده در سرزمین اصلی چین را نشان می دهد. نواحی با آلودگی صفر به منظور تجسم اینکه کدام مدل در نواحی آلوده صفر تناسب بهتری دارد و کدام مدل در نواحی آلوده تناسب بهتری دارد، با اسلش پوشانده شدند. افسانه نقشه بر اساس چندک درجه بندی شد. مدل OLS بدترین عملکرد را داشت ( شکل 4 a) و خطاهای مدل سازی بزرگی را در استان هوبی و در غرب چین نشان داد. مدل ESF بهتر عمل کرد اما خطاهای مدلسازی بزرگی را در غرب چین ایجاد کرد ( شکل 4 ب). میانگین خطاهای مدل‌سازی برای مدل‌های GWR و ESF-SVC در کل سرزمین اصلی چین مشابه بود. با این حال، مدل ESF-SVC ( شکل 4د) خطاهای نسبتاً بزرگی را در شمال غربی (به ویژه شهرهایی با عفونت های گزارش شده اندک) ایجاد کرد در حالی که مدل GWR ( شکل 4 ج) خطاهای مدل سازی نسبتاً بزرگی را در مرکز چین ایجاد کرد، جایی که شهرهایی با نرخ آلودگی نسبتاً بالاتر قرار دارند.
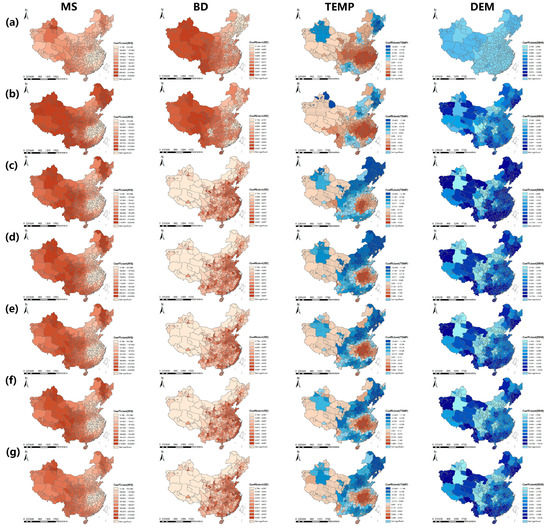
3.2.3. ضرایب مدل ESF-SVC
ضرایب مدل ESF-SVC ساخته شده در جدول 13 نشان داده شده است. MS با میزان آلودگی COVID-19 با میانگین ضریب متغیر مکانی 171.81 همبستگی مثبت داشت. میانگین هفتگی ضریب MS در ابتدا افزایش یافت و به اوج خود یعنی 188.48 در هفته دوم رسید، سپس به 170.41 کاهش یافت و پس از هفته 5 حدود 171 کاهش یافت. BD همچنین با نرخ عفونت COVID-19 ارتباط مثبت و معنی داری داشت، با عبور از همه شهرها. آزمون معنی دار بعد از هفته سوم با میانگین ضریب متغیر فضایی 4.69. DEM با نرخ آلودگی COVID-19 با میانگین ضریب متغیر مکانی -4.02 همبستگی منفی داشت. اگرچه میانگین کل ضریب متغیر مکانی TEMP 0.60- بود، اما تأثیر آن بر میزان آلودگی COVID-19 پیچیده تر بود زیرا ضرایب شامل ترکیبی از مقادیر مثبت و منفی بود: میانگین هفتگی ضریب TEMP ابتدا در هفته های اول و دوم مثبت بود اما از هفته سوم به بعد منفی شد. PDEN و PRE فقط آزمون معنی دار مدل را در هفته اول گذراندند و هر دو ضرایب آنها ثابت بودند.
شکل 5 نقشه ضریب متغیر فضایی چهار عامل خطر انتخابی (MS، BD، TEMP و DEM) را در طول هفت هفته نشان می دهد. شکل 5 MS (a-g) نشان می دهد که ام اس در شهرهای مرکزی و غربی-شمالی بیشتر از سایر نقاط سرزمین اصلی چین در ابتلا به COVID-19 نقش داشته است. میانگین ضرایب MS در استان‌هایی که دارای ووهان هستند یا در نزدیکی آن قرار دارند از 77.75 تا 132.17 با میانگین 106.16 متغیر است. در حالی که میانگین ضرایب ام اس در استان های دور از ووهان از 204.11 تا 227.34 با میانگین 214.02 متغیر بود که 101.06 درصد بیشتر از استان های حاوی یا نزدیک ووهان بود. شهرهایی که ضرایب MS غیر قابل توجهی دارند بیشتر در نزدیکی مرز چین رخ می دهند. BD همچنین با میزان عفونت COVID-19 همبستگی مثبت داشت ( شکل 5BD (a-g)) و ضرایب در کل منطقه مورد مطالعه معنی دار و در شهرهای جنوب چین نسبتاً بزرگتر از سایر مناطق پس از هفته دوم بودند. با این حال، تغییرات ضرایب BD بین شهرها کم بود و میانگین مقدار آن از 4.41 تا 4.91 متغیر بود. ضرایب دما ( شکل 5 TEMP (a-g)) در دو هفته اول با مقدار متوسط ​​0.555 بیشتر مثبت بود. با این حال، تعداد شهرهای دارای ضرایب منفی به ویژه در جنوب شرقی و شمال شرقی چین با گذشت زمان افزایش یافت. ضرایب DEM ( شکل 5DEM (a-g)) عمدتاً منفی بودند و شهرهایی که آزمون معنی‌داری را پشت سر گذاشتند و ضرایب مدل بالایی داشتند پس از هفته سوم، بیشتر در استان‌های یونان، گوانگشی، گوئیژو، سیچوان، نیمنگ، سین‌کیانگ، لیائونینگ و گانسو با میانگین ارتفاع رخ داده‌اند. 1299.7 متر.

4. بحث

4.1. بهبود دقت مدل

با توجه به نتایج ارزیابی مدل، مدل ESF-SVC بهتر از سه مدل دیگر در مدل‌سازی نرخ آلودگی COVID-19 عمل کرد.
در استان هوبی، میانگین R2 تنظیم شده مدل ESF-SVC به ترتیب 16.31، 5.48 و 18.83 درصد بیشتر از مدل های GWR، ESF و OLS بود. هنگامی که منطقه مورد مطالعه به سرزمین اصلی چین گسترش یافت، میانگین R2 تنظیم شده مدل ESF-SVC به ترتیب 10.25٪، 19.54٪ و 105.94٪ بیشتر از مدل های GWR، ESF و OLS بود.
میانگین مقدار RMSE مدل ESF-SVC بسیار کوچکتر از مدل های ESF و OLS بود. اگرچه RMSE آن کمی بزرگتر از GWR در سرزمین اصلی چین بود، نتایج LOOCV برای مدل ESF-SVC کوچکترین بود. این نشان می‌دهد که مدل ESF-SVC می‌تواند ارتباط بین نرخ عفونت COVID-19 و عوامل خطر سلامت را در مناطق مختلف تخمین بزند و مشکلات بیش از حد برازش را که مدل GWR را آزار می‌داد، به خوبی کنترل کرد و در نتیجه مدل قوی‌تری ارائه کرد [ 49 ] , 51 , 75 ].
میانگین نقشه‌های باقیمانده نشان داد که مدل ESF-SVC خطاهای مدل‌سازی نسبتاً بزرگی را در شمال غربی چین ایجاد می‌کند، در حالی که مدل GWR خطاهای بزرگی را در مرکز چین ایجاد می‌کند. به طور خاص، مدل ESF-SVC از سه مدل دیگر بهتر عمل کرد، زمانی که فقط مناطق آلوده مدل‌سازی شدند. هیچ یک از MC های تولید شده با باقیمانده های مدل ESF-SVC قابل توجه نبودند، که نشان می دهد مدل ESF-SVC بهتر می تواند تأثیر همبستگی خودکار فضایی را در مناطق بزرگ فیلتر کند.

4.2. تأثیر عوامل خطر سلامت

مقادیر متغیر فضایی ضرایب مدل ESF-SVC منعکس کننده چگونگی تأثیر عوامل خطر مربوطه بر نرخ عفونت COVID-19 است. اگر یک عامل خطر در طول مدل‌سازی تست معنی‌داری را پشت سر بگذارد، ضریب مطلق بزرگ‌تر و سهم آن در میزان آلودگی COVID-19 بیشتر است.
در استان هوبی، هر 10 عامل خطر ارتباط معنی داری با میزان عفونت کووید-19 در سه هفته اول نشان ندادند. این ممکن است به این دلیل باشد که روش تشخیص اسید نوکلئیک بالغ نبوده و منابع تشخیص در ابتدا در مناطق پرخطر کافی نبود، به طوری که بسیاری از بیماران در برخی مکان‌ها (به عنوان مثال، استان هوبی) خیلی سریع تشخیص داده نمی‌شوند. کمیسیون مراقبت های بهداشتی چین روش بهبود یافته ای را برای شناسایی موارد تایید شده در 12 فوریه اعلام کرد، زمانی که هفته چهارم این مطالعه آغاز شد. در هفته‌های بعد، PDEN و WDSP آزمون معنی‌داری نهایی را پشت سر گذاشتند و برای مدل‌سازی انتخاب شدند. WDSP، با میانگین ضریب بزرگتر از PDEN، کمک بیشتری به افزایش نرخ عفونت پس از 12 فوریه داشت. نتایج مشابهی نیز توسط Shahin [32 ]. این ممکن است به این دلیل باشد که ویروس می تواند در شرایط سرعت باد کم یا متوسط ​​راحت تر پخش شود [ 76 ، 77 ]. با این حال، با گسترش منطقه مورد مطالعه به سرزمین اصلی چین، WDSP تأثیر قابل‌توجهی بر افزایش COVID-19 نشان نداد، که نشان می‌دهد تأثیر سرعت باد در مناطق کوچک اما پرخطر بیشتر است. مطالعات قبلی همچنین هیچ ارتباط معنی‌داری را بین سرعت باد و میزان آلودگی COVID-19 مشاهده نکردند، زمانی که وسعت مطالعه در سطح کشور بود [ 78 ، 79 ].
در سرزمین اصلی چین، هشت عامل از ده عامل خطر ارتباط معنی‌داری با میزان آلودگی به کووید-19 نشان دادند، و شش مورد آزمون اهمیت مدل (PDEN، MS، BD، TEMP، PRES و DEM) را گذراندند و برای توسعه مدل‌های نهایی انتخاب شدند. ام اس بیشترین تأثیر را در افزایش نرخ ابتلا به کووید-19 داشت. مشخص شد که مهاجرت به خارج از ووهان در شهرهای نزدیک ووهان نسبت به شهرهای دورتر کمتر کمک کننده و کمتر قابل توجه است. این ممکن است به این دلیل باشد که تعامل شدیدی بین ووهان و شهرهای مجاور وجود داشت، چه با ماشین شخصی یا سایر روش‌های سفر که در پلت فرم بایدو کیانشی ثبت نشده بود. هنگام سفر به شهرهای دورتر، مردم به احتمال زیاد وسایل حمل و نقل عمومی را انتخاب می کنند، بنابراین امتیاز مهاجرت مربوطه بیشتر با نرخ آلودگی مرتبط است. تأثیر ام اس بر میزان عفونت کووید-19 در هفته دوم (حدود 29 ژانویه 2020) به اوج خود رسید و سپس کاهش یافت. این ممکن است با سیاست قرنطینه شهری اعلام شده در 23 ژانویه 2020، حدود سه هفته پس از اولین مورد گزارش شده COVID-19 در ووهان توضیح داده شود. این سیاست تا 8 آوریل 2020 از خروج یا ورود افراد به ووهان با هر وسیله حمل‌ونقلی جلوگیری می‌کرد و تا قبل از آن هیچ مورد تایید شده افزایشی برای مدت 21 روز وجود نداشت. حمل و نقل عمومی، مشاغل و مکان های تفریحی در ووهان برای اطمینان از قرنطینه خانگی سخت بسته شد. پس از اعلام سیاست قرنطینه شهری، سایر شهرها، به ویژه شهرهای اطراف ووهان، سطوح واکنش اضطراری خود را تنظیم کردند و به مردم پیشنهاد کردند تا حد امکان در خانه بمانند و تجمعات و رویدادها را لغو کنند که تا حد زیادی شیوع ویروس را تضعیف کرد.28 ، 33 ، 80 ، 81 ، 82]. تراکم ساختمان (BD) بعد از هفته سوم (حدود 5 فوریه 2020) تأثیر نسبتاً بیشتری بر شهرهای جنوب چین داشت، اما تغییرات ضرایب بین شهرها کم بود. این نشان می‌دهد که خوشه‌بندی مکان‌های تفریحی گسترش COVID-19 را تسریع کرد، اما اگر فاصله‌گذاری اجتماعی قوی بود، اندازه تأثیر آن و تفاوت‌های بین شهرها کاهش یافت. از نظر دما، ضرایب در دو هفته اول بیشتر مثبت بوده و میانگین دمای آن 2.42 درجه سانتیگراد بوده است. با گذشت زمان، شهرهای بیشتری، به ویژه شهرهای شمال شرقی و جنوب غربی چین (به عنوان مثال، شهرهایی در استان های گوانگدونگ، گوانگشی، یوننان و فوجیان) دارای ضرایب منفی بودند که آزمون قابل توجهی را با میانگین دمای 8.17 درجه سانتیگراد پشت سر گذاشتند. یافته ها حاکی از آن است که وقتی دما به یک نقطه معین رسید، افزایش دما ممکن است منجر به کاهش نرخ ابتلا به COVID-19 شود. نتایج مشابهی در مورد تأثیر دما نیز در برخی از مطالعات خاص کشور و در سراسر جهان یافت شد.26 ، 83 ، 84 ]. در مورد ارتفاع (DEM)، شهرهایی که آزمون معنی‌داری را گذرانده‌اند و ضرایب مدل بالایی داشتند، عمدتاً در مناطق فلات یافت می‌شوند، که نشان می‌دهد مناطق با ارتفاع بالا ممکن است ظرفیت کمتری برای بقای ویروس داشته باشند. مطالعه دیگری همچنین نشان داد که افرادی که در مناطق مرتفع زندگی می کنند ممکن است تحمل بهتری نسبت به هیپوکسی داشته باشند و ممکن است در برابر ویروس COVID-19 مقاومت بیشتری داشته باشند [ 85 ]]. برخلاف گستره استان هوبی، تراکم جمعیت تنها در هفته اول تأثیر ضعیفی بر میزان آلودگی به کووید-19 نشان داد و ضرایب آن ثابت بود، که نشان می‌دهد در ابعاد وسیع مطالعه، تراکم جمعیت نمی‌تواند افزایش آلودگی کووید-19 را توضیح دهد. در مقایسه با جریان خروجی مهاجرت و خوشه‌بندی ساختمان‌ها، نرخ بسیار خوبی دارد [ 21 ]. همچنین، فاصله گذاری اجتماعی و محدودیت های سفر به کاهش تأثیر تراکم جمعیت بر گسترش COVID-19 کمک کرد [ 86 ].

4.3. محدودیت ها

اگرچه مدل ESF-SVC ساخته شده در مدل‌سازی ناهمگونی فضایی با برازش و استحکام مدل بهبود یافته در زمینه مطالعه COVID-19 به خوبی عمل کرد، این مطالعه هنوز محدودیت‌های متعددی دارد. اول، برخی از عوامل خطر مانند ساختار سن، سطح تحصیلات، سیاست دولت و پاسخ جامعه استفاده نشد. دوم، اگرچه اثر تأخیر زمانی با استفاده از میانگین متغیرها در هفته‌های قبل در نظر گرفته شد، اما سایر ویژگی‌های زمانی که ممکن است بر میزان آلودگی COVID-19 تأثیر بگذارد، مانند اثرات تأخیر زمانی در سطح روزهای فردی نیز باید در نظر گرفته شود. 63 ، 64]. سوم، تأثیر عوامل خطر سلامت ممکن است در مناطق مختلف، مقیاس‌های مطالعاتی مختلف و دوره‌های مختلف موج COVID-19 متفاوت باشد. امتیاز مهاجرت در این مطالعه فقط شامل خروجی از ووهان تا 23 ژانویه 2020 (روز پس از قرنطینه) بود، اما خروج جمعیت از منابع عفونت ثانویه را در نظر نگرفت [ 87 ]. علاوه بر این، از آنجایی که اتصال مهاجرت یکی از عوامل کلیدی در گسترش COVID-19 بود، توپولوژی مرسوم یا ماتریس وزن فضایی مبتنی بر فاصله در مدل‌سازی فضایی ممکن است کافی نباشد. بنابراین، یک ماتریس شبکه اتصال مهاجرت بین واحدهای مطالعه باید در نظر گرفته شود.

5. نتیجه گیری ها

در این مقاله، یک روش ESF-SVC برای بررسی اینکه چگونه عوامل خطر سلامت بر میزان عفونت COVID-19 به طور متفاوت در مکان و زمان تأثیر می‌گذارند، توسعه داده شد. می‌تواند به طور همزمان تأثیر همبستگی و ناهمگنی فضایی را در نظر بگیرد و می‌تواند مشکلات چندخطی و بیش از حد برازش را که مدل GWR را با میانگین R2 تنظیم‌شده بالاتر، بهتر کنترل کند . همچنین، RMSEهای اعتبار متقابل مدل ESF-SVC نیز تا حد زیادی کمتر از سه مدل دیگر بود، که نشان می‌دهد می‌تواند ارتباط بین میزان آلودگی COVID-19 و عوامل خطر سلامت را در مناطق مختلف تخمین بزند و در نتیجه مدل قوی‌تری ارائه دهد.
ضرایب متغیر فضایی ESF-SVC در دوره های مختلف می تواند الگوهای مکانی و زمانی عوامل تأثیرگذار را کشف کند. مشخص شد که با تغییر دامنه مطالعه و دوره مطالعه، تأثیر عوامل خطر سلامت متفاوت است. در استان هوبی، WDSP بیشتر از سایر عوامل خطر بهداشتی پس از 12 فوریه در افزایش نرخ عفونت نقش داشته است. هنگامی که این مطالعه به سرزمین اصلی چین گسترش یافت، امتیاز مهاجرت بیشترین سهم را در میزان آلودگی کووید-19 داشت، به دنبال آن تراکم ساختمان، ارتفاع و دما، و همه آنها ویژگی‌های متفاوت فضایی قابل توجهی را نشان دادند. امتیاز مهاجرت در شهرهای نزدیک ووهان کمتر از شهرهای دورتر بود، در حالی که شهرهایی با ضرایب تراکم ساختمانی بیشتر عمدتاً در جنوب چین یافت شدند. DEM به کاهش نرخ آلودگی COVID-19 کمک کرد و با گذشت زمان تأثیر آن در شهرهای مرتفع بیشتر شد. تاثیر دما در ابتدا با نرخ آلودگی به کووید-19 همبستگی مثبت داشت، اما پس از 11 فوریه، نشان داد که افزایش TEMP تأثیر ضعیف اما قابل توجهی بر کاهش نرخ آلودگی COVID-19 در شهرهای جنوب شرقی و شمال غربی دارد. .
این یافته‌ها در مورد تأثیر عوامل خطر سلامت تا حدی با مطالعات قبلی در مورد COVID-19 و سایر بیماری‌های عفونی تنفسی مطابقت دارد، که می‌تواند به افزایش آگاهی عمومی و دولتی در مورد خطرات بالقوه سلامتی کمک کند و بنابراین بر استراتژی‌های کنترل COVID-19 تأثیر بگذارد. به عنوان مثال، WDSP تأثیر قابل توجهی در استان هوبی نشان داد. بنابراین، پوشیدن ماسک در این منطقه پرخطر هنگام بیرون رفتن، پاسخ ترجیحی خواهد بود، که توسط سایر مطالعات مرتبط در مناطق مختلف مطالعه نیز توصیه شده است. در همین حال، پس از حدود 29 ژانویه، نفوذ MS و BD در سرزمین اصلی چین کاهش یافت، که نشان می‌دهد سیاست‌های قرنطینه و فاصله‌گذاری اجتماعی موثر بوده و می‌توان آن را به مناطق دیگر ارجاع داد.
از آنجایی که روش پیشنهادی محدود به مجموعه داده‌ها نبود، می‌تواند مرجعی برای سایر مطالعات اپیدمیولوژی فضایی باشد. در آینده، ما قصد داریم متغیرهای زمانی اضافه کنیم و مدل ESF-SVC را به یک مدل ضریب متغیر مکانی-زمانی مبتنی بر ESF گسترش دهیم، در نتیجه روابط مکانی-زمانی بین COVID-19 و عوامل خطر سلامت (به عنوان مثال، اثر تاخیر زمانی عوامل و تأثیر منابع ثانویه عفونت). یک ماتریس وزن اتصال مهاجرت پویا برای بهبود مدل اضافه خواهد شد. ما همچنین چگونگی گسترش منطقه مورد مطالعه را به کل جهان و کشف الگوهای مکانی-زمانی شیوع COVID-19 در کشورها و قاره‌های مختلف در نظر خواهیم گرفت.

منابع

  1. او، جی. چن، جی. جیانگ، ی. جین، آر. شورتریج، ا. آگوستی، س. او، م. وو، جی. دوارته، سی ام. کریستاکوس، جی. مدل سازی مقایسه ای عفونت و کنترل الگوهای انتقال COVID-19 در چین، کره جنوبی، ایتالیا و ایران. علمی کل محیط. 2020 , 747 , 141447. [ Google Scholar ] [ CrossRef ] [ PubMed ]
  2. کوسینوتا، دی. Vanelli، M. WHO COVID-19 را یک بیماری همه گیر اعلام کرد. Acta Biomed. 2020 ، 91 ، 157-160. [ Google Scholar ] [ CrossRef ]
  3. سازمان بهداشت جهانی (WHO). به‌روزرسانی عملیاتی هفتگی در مورد COVID-19. به‌روزرسانی‌های وضعیت اضطراری ، 23 نوامبر 2021؛ 1-10. [ Google Scholar ]
  4. چادسوتی، س. مودچانگ، سی. مدل‌سازی اثربخشی استراتژی‌های مداخله برای کنترل شیوع کووید-19 و برآورد تقاضای مراقبت‌های بهداشتی در آلمان. عمل بهداشت عمومی 2021 ، 2 ، 100121. [ Google Scholar ] [ CrossRef ]
  5. فانلی، دی. Piazza, F. تجزیه و تحلیل و پیش‌بینی شیوع COVID-19 در چین، ایتالیا و فرانسه. Chaos Solitons Fractals 2020 , 134 , 109761. [ Google Scholar ] [ CrossRef ]
  6. رینر، آر. باربر، ر. کالینز، جی. ژنگ، پی. آدولف، سی. آلبرایت، جی. آنتونی، سی. آراوکین، ا. باخمایر، اس. بنگ جنسن، بی. و همکاران مدل سازی سناریوهای COVID-19 برای ایالات متحده. نات. پزشکی 2021 ، 27 ، 94-105. [ Google Scholar ] [ CrossRef ]
  7. آرون کومار، KE; کالاگا، دی وی؛ سای کومار، سی ام. چیلکور، جی. کواجی، م. برنزا، TM پویایی موارد تجمعی COVID-19 (تأیید شده، بهبودیافته و مرگ‌ومیرها) را برای 16 کشور برتر با استفاده از مدل‌های یادگیری ماشین آماری پیش‌بینی می‌کند: میانگین متحرک یکپارچه رگرسیون خودکار (ARIMA) و میانگین متحرک یکپارچه خودکار پس‌رونده فصلی. Appl. محاسبات نرم. 2021 , 103 , 107161. [ Google Scholar ] [ CrossRef ]
  8. هو، بی. نینگ، پی. کیو، جی. تائو، وی. Devlin، AT; چن، اچ. وانگ، جی. لین، اچ. مدل‌سازی گسترش کامل فضایی و زمانی اپیدمی COVID-19 در سرزمین اصلی چین. بین المللی ج. عفونی کردن. دیس 2021 ، 110 ، 247-257. [ Google Scholar ] [ CrossRef ]
  9. بن خدر، ن. کلسی، ال. Alsaif, H. یک مدل SEIR چند مرحله‌ای برای پیش‌بینی پتانسیل موج جدید COVID-19 در KSA پس از برداشتن همه محدودیت‌های سفر. الکس. مهندس J. 2021 , 60 , 3965-3974. [ Google Scholar ] [ CrossRef ]
  10. گلریوز، دی. پیش بینی شیوع کووید-19 در ترکیه؛ مقایسه مدل‌های باکس-جنکینز، هموارسازی نمایی براون و حافظه کوتاه‌مدت فرآیند Saf. محیط زیست Prot. 2021 ، 149 ، 927-935. [ Google Scholar ] [ CrossRef ] [ PubMed ]
  11. Desai، PS News Sentiment Informed Series Time-series Analysing AI (SITALA) برای مهار گسترش COVID-19 در هیوستون. سیستم خبره Appl. 2021 ، 180 ، 115104. [ Google Scholar ] [ CrossRef ]
  12. جیا، پی. لیکرولد، جی. وو، جی. استین، ا. ریشه، ای. سابل، سی. ورمولن، آر. ریمیس، جی. چن، ایکس. براونسون، آر. و همکاران 10 اولویت تحقیقاتی در اپیدمیولوژی دوره حیات فضایی. محیط زیست چشم انداز سلامتی 2019 , 127 , 74501. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  13. هاوکینز، RB; چارلز، ای جی; Mehaffey، JH وضعیت اجتماعی-اقتصادی و موارد مرتبط با COVID-19 و تلفات. بهداشت عمومی 2020 ، 189 ، 129-134. [ Google Scholar ] [ CrossRef ]
  14. مارتینز، LD; دا سیلوا، آی. باتیستا، وی وی. دفاطما آندراده، م. د فریتاس، ED; Martins، JA چگونه متغیرهای اجتماعی-اقتصادی و جوی بر شیوع COVID-19 و آنفولانزا در مناطق گرمسیری و نیمه گرمسیری برزیل تأثیر می گذارد. محیط زیست Res. 2020 ، 191 ، 110184. [ Google Scholar ] [ CrossRef ] [ PubMed ]
  15. ممکن است.؛ ژائو، ی. لیو، جی. او، X. وانگ، بی. فو، اس. یان، جی. نیو، جی. ژو، جی. لو، بی. اثرات تغییرات دما و رطوبت بر مرگ کووید-19 در ووهان، چین. علمی کل محیط. 2020 , 724 , 138226. [ Google Scholar ] [ CrossRef ] [ PubMed ]
  16. راویندرا، ک. گویال، ا. مور، اس. آیا گرده های موجود در هوا بر شیوع COVID-19 تأثیر می گذارد؟ حفظ کنید. جامعه شهرها 2021 ، 70 ، 102887. [ Google Scholar ] [ CrossRef ] [ PubMed ]
  17. دامیالیس، ا. ژیل، اس. سوفیف، م. سوفیوا، وی. کولک، اف. بایر، دی. پلازا، نماینده مجلس؛ لیر-ویرتز، وی. کاشوبا، اس. Ziska، LH; و همکاران همانطور که از 31 کشور در سراسر جهان مشهود است، غلظت بالاتر گرده هوا با افزایش نرخ عفونت SARS-CoV-2 مرتبط است. Proc. Natl. آکادمی علمی USA 2021 , 118 , e2019034118. [ Google Scholar ] [ CrossRef ] [ PubMed ]
  18. مسنر، دبلیو. زمینه نهادی و فرهنگی تنوع فراملی در شیوع کووید-19. medRxiv 2020 . [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  19. رحمان، م. اسلام، م. شیمانتو، MH; فردوس، ج. رحمان، AA-NS; ساگور، PS; Chowdhury, T. تجزیه و تحلیل جهانی در مورد تأثیر دما، عوامل اجتماعی-اقتصادی و محیطی بر گسترش و میزان مرگ و میر بیماری همه گیر COVID-19. محیط زیست توسعه دهنده حفظ کنید. 2021 ، 23 ، 9352-9366. [ Google Scholar ] [ CrossRef ]
  20. اندرسن، ال.ام. هاردن، اس آر. Sugg، MM; رانکل، جی دی. Lundquist، TE تجزیه و تحلیل عوامل مکانی انتقال محلی COVID-19 در ایالات متحده. علمی کل محیط. 2021 ، 754 ، 142396. [ Google Scholar ] [ CrossRef ] [ PubMed ]
  21. Kwok، CYT؛ وونگ، ام اس؛ چان، KL; کوان، ام.-پی. نیکول، جی. لیو، CH; وانگ، JYH؛ وای، AKC؛ چان، LWC; خو، ی. و همکاران تجزیه و تحلیل فضایی تأثیر هندسه شهری و ویژگی های اجتماعی و جمعیت شناختی بر COVID-19، مطالعه ای در هنگ کنگ. علمی کل محیط. 2021 ، 764 ، 144455. [ Google Scholar ] [ CrossRef ]
  22. سیرکچی، آی. Murat Yüceşahin، M. کرونا و مهاجرت: تجزیه و تحلیل تحرک انسان و گسترش COVID-19. مهاجرت Lett. 2020 ، 17 ، 379-398. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  23. لی، جی. یوان، پی. هفرنان، جی. ژنگ، تی. اوگدن، ن. ساندر، بی. لی، جی. لی، کیو. بلیر، جی. کنگ، جی دی. و همکاران بیمارستان‌های سرپناه Fangcang در طول اپیدمی COVID-19، ووهان، چین. گاو نر ارگان بهداشت جهانی. 2020 ، 98 ، 830. [ Google Scholar ] [ CrossRef ]
  24. راکلوف، جی. Sjödin, H. تراکم بالای جمعیت باعث گسترش COVID-19 می شود. J. Travel Med. 2020 ، 27 ، taaa038. [ Google Scholar ] [ CrossRef ]
  25. لو، ام. کوین، اس. تان، بی. کای، م. یو، ی. Xiong، Q. تحرک جمعیت و خطر انتقال COVID-19 در ووهان، چین. ISPRS Int. J. Geo-Inf. 2021 ، 10 ، 395. [ Google Scholar ] [ CrossRef ]
  26. وو، ایکس. یین، جی. لی، سی. شیانگ، اچ. Lv، M. Guo, Z. محیط طبیعی و انسانی به طور تعاملی الگوی گسترش COVID-19 را هدایت می کند: یک مطالعه مدل سازی در سطح شهر در چین. علمی کل محیط. 2020 , 756 , 143343. [ Google Scholar ] [ CrossRef ]
  27. لیم، YK; Kweon، OJ; کیم، منابع انسانی؛ کیم، T.-H. لی، ام.-ک. تأثیر متغیرهای محیطی بر گسترش COVID-19 در جمهوری کره. علمی Rep. 2021 , 11 , 5977. [ Google Scholar ] [ CrossRef ]
  28. بشیر، م.ف. MA، B. شهزاد، ال. مروری کوتاه بر تأثیرات اجتماعی-اقتصادی و زیست محیطی COVID-19. کیفیت هوا اتمس. سلامت 2020 ، 13 ، 1403-1409. [ Google Scholar ] [ CrossRef ]
  29. چی، اچ. شیائو، اس. شی، ر. بخش، نماینده مجلس؛ چن، ی. تو، دبلیو. سو، کیو. وانگ، دبلیو. وانگ، ایکس. Zhang, Z. انتقال COVID-19 در سرزمین اصلی چین با دما و رطوبت مرتبط است: تجزیه و تحلیل سری زمانی. علمی کل محیط. 2020 , 728 , 138778. [ Google Scholar ] [ CrossRef ]
  30. زو، ی. زی، جی. هوانگ، اف. Cao, L. ارتباط بین قرار گرفتن کوتاه مدت در معرض آلودگی هوا و عفونت COVID-19: شواهدی از چین. علمی کل محیط. 2020 , 727 , 138704. [ Google Scholar ] [ CrossRef ]
  31. گوپتا، اس. Raghuwanshi، GS; چاندا، الف. تأثیر آب و هوا بر گسترش COVID-19 در ایالات متحده: یک مدل پیش‌بینی برای هند در سال 2020. علمی. کل محیط. 2020 , 728 , 138860. [ Google Scholar ] [ CrossRef ]
  32. شاهین، ام. تاثیر آب و هوا بر همه گیری کووید-19 در ترکیه. علمی کل محیط. 2020 , 728 , 138810. [ Google Scholar ] [ CrossRef ] [ PubMed ]
  33. وانگ، کیو. دونگ، دبلیو. یانگ، ک. رن، ز. هوانگ، دی. ژانگ، پی. وانگ، جی. تحلیل زمانی و مکانی انتقال COVID-19 در چین و عوامل مؤثر بر آن. بین المللی ج. عفونی کردن. دیس 2021 ، 105 ، 675-685. [ Google Scholar ] [ CrossRef ] [ PubMed ]
  34. الیوت، پی. وارتنبرگ، دی. اپیدمیولوژی فضایی: رویکردهای فعلی و چالش های آینده. محیط زیست چشم انداز سلامتی 2004 ، 112 ، 998-1006. [ Google Scholar ] [ CrossRef ]
  35. جیا، پی. دونگ، دبلیو. یانگ، اس. ژان، ز. تو، ال. لای، S. اپیدمیولوژی و تحقیقات بیماری های عفونی دوره حیات فضایی. روند پارازیتول. 2020 ، 36 ، 235-238. [ Google Scholar ] [ CrossRef ] [ PubMed ][ نسخه سبز ]
  36. Tobler, WR یک فیلم کامپیوتری شبیه سازی رشد شهری در منطقه دیترویت. اقتصاد Geogr. 1970 , 46 , 234. [ Google Scholar ] [ CrossRef ]
  37. Huang, Z. الگوهای تکامل مکانی-زمانی همه‌گیری COVID-19 با استفاده از تجمع فضا-زمان و آمار فضایی: چشم‌انداز جهانی. ISPRS Int. J. Geo-Inf. 2021 ، 10 ، 519. [ Google Scholar ] [ CrossRef ]
  38. صنیگراهی، س. پیلا، اف. باسو، بی. باسو، ا. Mölter, A. بررسی ارتباط بین ترکیب اجتماعی-جمعیتی و تلفات ناشی از COVID-19 در منطقه اروپا با استفاده از رویکرد رگرسیون فضایی. حفظ کنید. جامعه شهرها 2020 , 62 , 102418. [ Google Scholar ] [ CrossRef ]
  39. یو، اچ. لی، جی. بردین، اس. گو، اچ. فن، سی. دینامیک فضایی-زمانی انتشار COVID-19 در چین: تحلیل مدل خودرگرسیون فضایی پویا. ISPRS Int. J. Geo-Inf. 2021 ، 10 ، 510. [ Google Scholar ] [ CrossRef ]
  40. بیل، ال. آبلان، جی. هاجسون، اس. Jarup, L. مسائل روش شناختی و رویکردهای اپیدمیولوژی فضایی. محیط زیست چشم انداز سلامتی 2008 ، 116 ، 1105-1110. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  41. Fotheringham، AS; یانگ، دبلیو. کانگ، دبلیو. رگرسیون جغرافیایی وزن دار چند مقیاسی (MGWR). ان صبح. دانشیار Geogr. 2017 ، 107 ، 1247-1265. [ Google Scholar ] [ CrossRef ]
  42. براندون، سی. Fotheringham، AS; چارلتون، ME رگرسیون وزن‌دار جغرافیایی: روشی برای بررسی ناپایداری فضایی. Geogr. مقعدی 1996 ، 28 ، 281-298. [ Google Scholar ] [ CrossRef ]
  43. هان، ی. یانگ، ال. جیا، ک. لی، جی. فنگ، اس. چن، دبلیو. ژائو، دبلیو. Pereira, P. ویژگی های توزیع فضایی همه گیری COVID-19 در پکن و رابطه آن با عوامل محیطی. علمی کل محیط. 2021 ، 761 ، 144257. [ Google Scholar ] [ CrossRef ]
  44. مولالو، ع. واحدی، ب. Rivera، مدل‌سازی فضایی مبتنی بر KM GIS نرخ بروز COVID-19 در قاره ایالات متحده. علمی کل محیط. 2020 , 728 , 138884. [ Google Scholar ] [ CrossRef ]
  45. Karaye, IM; Horney، JA تأثیر آسیب پذیری اجتماعی بر COVID-19 در ایالات متحده: تحلیلی از روابط متفاوت فضایی. صبح. J. قبلی پزشکی 2020 ، 59 ، 317-325. [ Google Scholar ] [ CrossRef ]
  46. اسنایدر، BF; پارکز، V. تنوع فضایی در آسیب پذیری اجتماعی-اکولوژیکی در برابر کووید-19 در ایالات متحده مجاور. Health Place 2020 , 66 , 102471. [ Google Scholar ] [ CrossRef ] [ PubMed ]
  47. منصور، س. الکندی، ع. السعید، ع. السعید، ع. اتکینسون، P. عوامل اجتماعی جمعیت‌شناختی نرخ‌های بروز COVID-19 در عمان: مدل‌سازی مکانی با استفاده از رگرسیون وزن‌دار جغرافیایی چند مقیاسی (MGWR). حفظ کنید. جامعه شهرها 2021 ، 65 ، 102627. [ Google Scholar ] [ CrossRef ] [ PubMed ]
  48. مایتی، ع. ژانگ، کیو. صنیگراهی، س. پرامانیک، س. چاکرابورتی، اس. سردا، ا. Pilla, F. بررسی اثرات مکانی-زمانی عوامل محرک بر بروز COVID-19 در ایالات متحده مجاور. حفظ کنید. جامعه شهرها 2021 ، 68 ، 102784. [ Google Scholar ] [ CrossRef ]
  49. ویلر، دی. Tiefelsdorf، M. چند خطی و همبستگی بین ضرایب رگرسیون محلی در رگرسیون وزنی جغرافیایی. جی. جئوگر. سیستم 2005 ، 7 ، 161-187. [ Google Scholar ] [ CrossRef ]
  50. گریفیث، DA مشارکت‌های مبتنی بر فیلتر فضایی در نقد رگرسیون وزن‌دار جغرافیایی (GWR). محیط زیست طرح. A 2008 , 40 , 2751-2769. [ Google Scholar ] [ CrossRef ]
  51. موراکامی، دی. یوشیدا، تی. سیا، ح. گریفیث، دی. یاماگاتا، ی. رویکرد اثرات مختلط مبتنی بر ضریب موران برای بررسی روابط متغیر فضایی. تف کردن آمار 2017 ، 19 ، 68-89. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  52. تان، اچ. چن، ی. ویلسون، جی پی؛ ژانگ، جی. کائو، جی. چو، تی. یک مدل ضریب متغیر مکانی مبتنی بر فیلتر فضایی بردار ویژه برای تخمین غلظت PM2.5: مطالعه موردی در منطقه دلتای رودخانه یانگ تسه چین. اتمس. محیط زیست 2020 , 223 , 117205. [ Google Scholar ] [ CrossRef ]
  53. موراکامی، دی. مدل‌سازی رگرسیون فضایی با استفاده از بسته spmoran: نمونه‌های داده قیمت مسکن بوستون. arXiv 2017 , arXiv:1703.04467. [ Google Scholar ]
  54. داده های همه گیر COVID-19 در چین. در دسترس آنلاین: https://www.nhc.gov.cn/xcs/yqtb/list_gzbd.shtml (در 21 ژوئن 2020 قابل دسترسی است).
  55. اسمیت، ا. لات، ن. Vose, R. پایگاه داده سطحی یکپارچه: توسعه ها و مشارکت های اخیر. گاو نر صبح. هواشناسی Soc. 2011 ، 92 ، 704-708. [ Google Scholar ] [ CrossRef ]
  56. پایگاه داده سطحی یکپارچه در دسترس آنلاین: https://www.ncei.noaa.gov/products/land-based-station/integrated-surface-database (در 16 ژوئن 2020 قابل دسترسی است).
  57. رویتر، HI; نلسون، ا. Jarvis, A. ارزیابی روشهای درونیابی پر کردن فضای خالی برای داده های SRTM. بین المللی جی. جئوگر. Inf. علمی 2007 ، 21 ، 983-1008. [ Google Scholar ] [ CrossRef ]
  58. جارویس، ا. رویتر، HI; نلسون، AE; گوارا، E. Hole-Filled Seamless SRTM Data V4، مرکز بین المللی کشاورزی گرمسیری (CIAT). 2008. در دسترس آنلاین: https://srtm.csi.cgiar.org (دسترسی در 20 ژوئن 2020).
  59. کتاب سال آماری 2018. در دسترس آنلاین: https://data.cnki.net/Yearbook (در 21 ژوئن 2020 قابل دسترسی است).
  60. پلت فرم Baidu Qianxi. در دسترس آنلاین: https://qianxi.baidu.com/ (در 21 ژوئن 2020 قابل دسترسی است).
  61. جعبه، GEP؛ Cox, DR An Analysis of Transformations. JR Stat. Soc. سر. B 1964 , 26 , 211-243. [ Google Scholar ] [ CrossRef ]
  62. گریفیث، DA خودهمبستگی فضایی و توابع ویژه ماتریس وزن‌های جغرافیایی همراه با داده‌های مرجع جغرافیایی. می توان. Geogr./Le Géogr. می توان. 1996 ، 40 ، 351-367. [ Google Scholar ] [ CrossRef ]
  63. رانکل، جی دی. Sugg، MM; لیپر، RD; رائو، ی. متیوز، جی ال. Rennie, JJ اثرات کوتاه‌مدت رطوبت و دمای خاص بر ابتلا به COVID-19 در شهرهای منتخب ایالات متحده. علمی کل محیط. 2020 , 740 , 140093. [ Google Scholar ] [ CrossRef ]
  64. ممکن است.؛ چنگ، بی. شن، جی. وانگ، اچ. فنگ، اف. ژانگ، ی. جیائو، اچ. ارتباط بین عوامل محیطی و COVID-19 در شانگهای، چین. محیط زیست علمی آلودگی Res. 2021 ، 28 ، 45087-45095. [ Google Scholar ] [ CrossRef ]
  65. چن، ی. وانگ، بی. لیو، ایکس. لی، X. نقشه برداری از نابرابری های فضایی در خدمات مراقبت های بهداشتی شهری با استفاده از داده های مسیر تاکسی. ترانس. GIS 2018 ، 22 ، 602-615. [ Google Scholar ] [ CrossRef ]
  66. کازلا، جی. فاینبرگ، اس. Olkin, I. Springer Texts in Statistics ; Springer International Publishing: New Yorker, NY, USA, 2006; جلد 102، ISBN 9780387781884. [ Google Scholar ]
  67. گرکمن، ال.ام. Ahlgren، N. پیشنهادهای عملی برای تعیین ماتریس وزن k-نزدیکترین همسایه. تف کردن اقتصاد مقعدی 2014 ، 9 ، 260-283. [ Google Scholar ] [ CrossRef ]
  68. Lesage, JP; فیشر، MM رگرسیون رشد فضایی: مشخصات مدل، برآورد و تفسیر. تف کردن اقتصاد مقعدی 2008 ، 3 ، 275-304. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  69. راجرسون، ص. روشهای آماری برای جغرافیا . انتشارات SAGE: Thousand Oaks، CA، USA، 2001. [ Google Scholar ]
  70. پیکارد، RR; کوک، اعتبارسنجی متقابل RD مدل های رگرسیون. مربا. آمار دانشیار 1984 ، 79 ، 575-583. [ Google Scholar ] [ CrossRef ]
  71. قوجوق، ب. Crowley, M. Theory Behind Overfitting, Cross Validation, Regularization, Bagging, and Boosting: Tutorial. arXiv 2019 ، arXiv:1905.12787. [ Google Scholar ]
  72. رفائیل زاده، پ. تانگ، ال. لیو، اچ. اعتبارسنجی متقاطع BT. در دایره المعارف سیستم های پایگاه داده ; Liu, L., Özsu, MT, Eds. Springer: Boston, MA, USA, 2009; صص 532-538. شابک 978-0-387-39940-9. [ Google Scholar ]
  73. برنینگ، الف. اعتبار متقابل فضایی و راه‌اندازی برای ارزیابی قوانین پیش‌بینی در سنجش از راه دور: بسته R sperrorest. در مجموعه مقالات سمپوزیوم بین المللی زمین شناسی و سنجش از دور IEEE 2012، مونیخ، آلمان، 22 تا 27 ژوئیه 2012. صص 5372–5375. [ Google Scholar ]
  74. گریفیث، DA ضریب موران برای داده های غیر عادی. J. Stat. طرح. استنتاج 2010 ، 140 ، 2980-2990. [ Google Scholar ] [ CrossRef ]
  75. هلبیچ، ام. گریفیث، DA مدل‌های ضریب متغیر فضایی در املاک و مستغلات: فیلتر فضایی بردار ویژه و رویکردهای جایگزین. محاسبه کنید. محیط زیست سیستم شهری 2016 ، 57 ، 1-11. [ Google Scholar ] [ CrossRef ]
  76. کوشکون، اچ. یلدیریم، ن. Gündüz، S. گسترش ویروس COVID-19 از طریق تراکم جمعیت و باد در شهرهای ترکیه. علمی کل محیط. 2021 ، 751 ، 141663. [ Google Scholar ] [ CrossRef ]
  77. Coccia، M. چگونه سرعت باد کم و سطوح بالای آلودگی هوا از گسترش COVID-19 حمایت می کنند؟ اتمس. آلودگی Res. 2021 ، 12 ، 437-445. [ Google Scholar ] [ CrossRef ]
  78. عبدالعال، MAM; التوخی، AEE; نبهان، م. AlDurgam، MM تأثیر شاخص های آب و هوا بر همه گیری COVID-19 در عربستان سعودی. محیط زیست علمی آلودگی Res. 2021 . [ Google Scholar ] [ CrossRef ]
  79. صبا، هوش مصنوعی؛ الشیخ، AH پیش بینی شیوع شیوع COVID-19 در مصر با استفاده از شبکه های عصبی مصنوعی اتورگرسیو غیرخطی. فرآیند Saf. محیط زیست Prot. 2020 ، 141 ، 1-8. [ Google Scholar ] [ CrossRef ] [ PubMed ]
  80. شی، دبلیو. تانگ، سی. ژانگ، ا. وانگ، بی. شی، ز. یائو، ی. Jia, P. یک مدل تخمین تراکم هسته وزنی توسعه یافته خطر شروع کووید-19 را پیش‌بینی می‌کند و تغییرات مکانی-زمانی اثرات قرنطینه را در چین شناسایی می‌کند. اشتراک. Biol. 2021 ، 4 ، 126. [ Google Scholar ] [ CrossRef ]
  81. لاو، اچ. خسروی پور، و. کوکباخ، پی. Mikolajczyk، A. شوبرت، جی. بانیا، ج. خسروی پور، تی. تاثیر مثبت قرنطینه در ووهان بر مهار شیوع کووید-19 در چین. J. Travel Med. 2020 ، 27 ، taaa037. [ Google Scholar ] [ CrossRef ] [ PubMed ][ نسخه سبز ]
  82. سان، ز. ژانگ، اچ. یانگ، ی. وان، اچ. Wang, Y. تأثیر عوامل جغرافیایی و تراکم جمعیت بر شیوع COVID-19 تحت سیاست‌های قرنطینه چین. علمی کل محیط. 2020 , 746 , 141347. [ Google Scholar ] [ CrossRef ] [ PubMed ]
  83. گوا، سی. پسر.؛ لین، سی. لی، HB؛ زنگ، ی. ژانگ، ی. حسین، ام اس; چان، JWM; یونگ، DW; کواک، ک. و همکاران عوامل هواشناسی و بروز COVID-19 در 190 کشور: یک مطالعه مشاهده ای. علمی کل محیط. 2021 ، 757 ، 143783. [ Google Scholar ] [ CrossRef ]
  84. اوجی، م. تسوزوکی، اس. Ohmagari, N. اثر دما بر عفونت COVID-19. بین المللی ج. عفونی کردن. دیس 2020 ، 95 ، 301-303. [ Google Scholar ] [ CrossRef ] [ PubMed ]
  85. ژو، ک. یانگ، اس. Jia, P. به سمت مدیریت دقیق بیماران قلبی عروقی مبتلا به COVID-19 برای کاهش مرگ و میر. Prog. قلب و عروق. دیس 2020 ، 63 ، 529-530. [ Google Scholar ] [ CrossRef ]
  86. یین، اچ. سان، تی. یائو، ال. جیائو، ی. ما، ال. لین، ال. Graff, JC; آلیا، ال. Postlethwaite، A.; گو، دبلیو. و همکاران ارتباط بین تراکم جمعیت و میزان آلودگی نشان دهنده اهمیت فاصله گذاری اجتماعی و محدودیت سفر در کاهش همه گیری COVID-19 است. محیط زیست علمی آلودگی Res. 2021 ، 28 ، 40424-40430. [ Google Scholar ] [ CrossRef ]
  87. لی، تی. وانگ، جی. هوانگ، جی. یانگ، دبلیو. Chen, Z. بررسی تأثیرات پویای COVID-19 بر سفرهای بین شهری در چین. J. Transp. Geogr. 2021 ، 95 ، 103153. [ Google Scholar ] [ CrossRef ]
Ijgi 11 00067 g001 550
شکل 1. دو منطقه مورد مطالعه (سرزمین اصلی چین و استان هوبی).
Ijgi 11 00067 g002 550
شکل 2. نمودار جریان روش تحقیق و روش های آزمایشی.
Ijgi 11 00067 g003 550
شکل 3. نقشه های باقیمانده برای مدل برازش شده در استان هوبی.
Ijgi 11 00067 g004 550
شکل 4. نقشه های باقیمانده برای مدل نصب شده در سرزمین اصلی چین.
Ijgi 11 00067 g005 550
شکل 5. ESF-SVC نقشه های ضریب متغیر مکانی عوامل خطر سلامت در سرزمین اصلی چین، هر ستون یک عامل خطر (MS، BD، TEMP، DEM) و هر خط ( a – g ) یک هفته را نشان می دهد.

مقالات داخلی و بین المللی

مطالب مرتبط ...

بدون دیدگاه

دیدگاهتان را بنویسید