الگوریتم ساده‌سازی خط برداری بر اساس الگوریتم داگلاس-پوکر، زنجیره‌های یکنواخت و دوگانگی

خلاصه

هنگام استفاده از الگوریتم سنتی داگلاس-پیکر (D-P) برای ساده کردن اشیاء خطی، تولید نتایج حاوی خطاهای خودتقاطع آسان است، بنابراین بر کاربرد الگوریتم D-P تأثیر می گذارد. برای حل مشکل خود تقاطع، یک الگوریتم ساده سازی خط برداری جدید بر اساس الگوریتم D-P، زنجیره های یکنواخت و دوگانگی، در این مقاله پیشنهاد شده است. ابتدا از الگوریتم سنتی D-P برای ساده سازی خطوط اصلی استفاده می شود و سپس خطوط ساده شده به چندین زنجیره یکنواخت تقسیم می شوند. دوم، دوگانگی برای جستجوی موثر موقعیت‌های تقاطع زنجیره‌های یکنواخت استفاده می‌شود و زنجیره‌های یکنواخت متقاطع پردازش می‌شوند، بنابراین مشکلات خود تقاطع حل می‌شوند. دو گروه از داده های تجربی بر اساس مجموعه داده های بزرگ انتخاب می شوند.

کلید واژه ها:

ساده سازی خط ؛ الگوریتم داگلاس-پوکر ؛ زنجیره یکنواخت ; دوگانگی

1. معرفی

با توسعه فناوری سنجش از دور، فناوری حسگر و وب 2.0، مقادیر زیادی از داده های برداری فضایی به دست آمده چالش های بزرگی را در ذخیره سازی، پردازش و انتقال داده ها ایجاد می کند. برای افزایش قابلیت پردازش داده‌های برداری فضایی عظیم، الگوریتم‌های ساده‌سازی داده‌های برداری جدید با کارایی و استحکام بالا به فوریت مورد نیاز است.

روش‌های کلاسیک زیادی برای ساده‌سازی داده‌های برداری استفاده می‌شوند، از جمله الگوریتم داگلاس-پیکر (الگوریتم D-P) [ 1 ]، الگوریتم رامر [ 2 ]، و الگوریتم‌های دیگر [ 3 ، 4 ، 5 ، 6 ، 7 ، 8 ، 9 . ]. الگوریتم D-P [ 1 ] و الگوریتم رامر [ 2 ] از یک تلورانس فاصله معین برای تعیین اینکه کدام رئوس روی یک خط باید حذف یا حفظ شود، استفاده می‌کنند. Lang [ 3 ] از تلورانس فاصله عمودی برای فیلتر کردن داده ها استفاده کرد، اما این روش بسیار وقت گیر بود [ 1 ]]. مک مستر بر اساس مجموعه ای متوالی از پنج رویه [4 ] یک مدل مفهومی برای پردازش داده های دیجیتال خطی ارائه کرد. این روش به کار گرفته شده از تحمل فاصله عمودی پیشنهاد شده توسط Lang [ 4 ] برای ساده کردن خطوط استفاده کرد و از تکنیک های هموارسازی برای تولید قابل قبول ترین نتایج از نظر زیبایی شناختی استفاده کرد. بر اساس انتخاب حداقل و حداکثر محلی، الگوریتمی برای فشرده سازی داده های کانتور دیجیتال توسط لی [ 5 ] توسعه داده شده است. الگوریتم جدید کارآمدتر از الگوریتم D-P بود، اما نتیجه مانند الگوریتم D-P باقی ماند. Visvalingam و Whyatt [ 6 ] از “منطقه موثر” برای ساده کردن ویژگی های خط استفاده کردند و تأثیر خطاهای گرد کردن را بر نسخه ای از الگوریتم Ramer-Douglas-Peucker مورد بحث قرار دادند.1 , 2 ] برای ساده سازی خط. برای نشان دادن چگونگی ساخت الگوریتم های سیستم های اطلاعات جغرافیایی (GIS) قوی، دقیق و قابل تکرار، Ratschek و همکاران. [ 7 ] یک نسخه قوی از الگوریتم RD-P پیشنهاد کرد. وانگ و مولر [ 8 ] بر اساس شناخت اشکال خطوط و فیلتر کردن آنها در برابر قوانین نقشه برداری، یک الگوریتم Bend Simplify را پیشنهاد کردند. الگوریتم ساده سازی خمشی تلاش می کند تا ساده سازی خط دستی را با استفاده از قوانین نقشه برداری شبیه سازی کند، و معمولاً برای ساده سازی ویژگی های طبیعی مانند دریاچه ها و کانال های جریان استفاده می شود [ 10 ]. بر اساس الگوریتم Li-Openshaw [ 11 ]، الگوریتم D-P، و روش ساده سازی متعامد، Samsonov و Yakimova [ 12 ]] یک روش و مدل تعمیم برای ساده سازی هندسی مجموعه داده های خط ناهمگن پیشنهاد کرد.

نتایج ساده‌سازی خط پردازش شده توسط الگوریتم‌های فوق شامل مجموعه‌ای از رئوس چند خطی اصلی بدون نقاط “اشتاینر” بود. محققان دیگر از “نقاط اشتاینر” [ 13 ] برای ساده کردن ویژگی های خطی استفاده کرده اند [ 14 ، 15 ]. مفهوم نقاط اشتاینر از رشته هندسه محاسباتی سرچشمه می گیرد و به عنوان نقطه یا مجموعه ای از نقاط معرفی می شود که هنگام حل یک مسئله بهینه سازی هندسی برای بهبود راه حل های مبتنی بر مجموعه اصلی نقاط معرفی می شوند [ 13,16 ] . بر اساس الگوریتم سنتی D-P [ 1 ]، کراملی [ 14] از “نقاط اشتاینر” برای ساده کردن یک خط استفاده کرد. نتایج تجربی نشان داد که روش پیشنهادی از نظر محاسباتی سریعتر از الگوریتم سنتی D-P [ 1 ] است. بر اساس روش ارائه شده توسط لی و اوپنشاو [ 11 ]، Raposo [ 15 ] یک الگوریتم ساده سازی خطوط نقشه برداری با مقیاس خاص را با استفاده از یک تسلیح شش ضلعی به جای شبکه مربع ارائه کرد. الگوریتم کوانتیزاسیون شش ضلعی از نمونه‌گیری و تئوری تفکیک نقشه و همچنین مفهوم خوشه‌بندی راس از گرافیک رایانه‌ای استفاده می‌کند تا روشی ساده و مؤثر به دست دهد.

نتایج تجربی که در الگوریتم‌های ساده‌سازی خط بالا مورد بررسی قرار گرفته‌اند نشان می‌دهد که نتایج خوبی برای هر روش به دست آمده است و با موفقیت در زمینه‌های مربوطه اعمال شده است. این باید به دلیل تمام مزایای مربوط به الگوریتم D-P باشد – این الگوریتم در حفظ شکل خط بسیار موثر است، در فشرده سازی منحنی برداری در حضور مقادیر آستانه منحصر به فرد است و مهمتر از همه، در موقعیت بالاتر دقیق است. ، که در نتیجه اغلب برای ساده کردن خطوط استفاده می شود [ 16 ، 17 ]. با این حال، الگوریتم D-P ناقص است زیرا ممکن است یک انحراف ناحیه بزرگ ایجاد شود [ 18 ]]. علاوه بر این، این روش تنها به خود منحنی ها می پردازد تا روابط توپولوژیکی منحنی ها، بنابراین منجر به مشکلات خود تقاطع [ 19 ] می شود. بنابراین، بسیاری از محققان الگوریتم D-P را برای حل این مشکلات خود تقاطع بهبود داده اند. یک طرح نمایش سلسله مراتبی برای منحنی های مسطح توسط هو و کیم [ 20 ] ارائه شد که از تقریب طبیعی و محلی سازی کارآمد استفاده می کرد. این در حذف خود تقاطع ها در تمام تقریب های ممکن برای یک منحنی با استفاده از تکنیک پیوند متقابل موثر بود و زمان محاسبه را به طور قابل توجهی کاهش داد. مانتلر و اسنوئینک [ 21] الگوریتم جدیدی را معرفی کرد. آنها مفهوم مجموعه ایمن را تعریف کردند، که قطعاتی از ویژگی های خطی هستند که می توانند بدون معرفی تقاطع ها یا تغییرات توپولوژی ساده شوند. این الگوریتم همچنین می تواند به شناسایی مجموعه ای از مجموعه ایمن با استفاده از نمودار نقاط Voronoi کمک کند، اما برای تولید نمودار Voronoi لازم است، کارایی الگوریتم محدود است. برای حل مسائل خود تقاطع، Avelar و Müller [ 22] یک الگوریتم برای محاسبه روابط توپولوژیکی هنگام فشرده سازی ویژگی های چند خطی پیشنهاد کرد. در این الگوریتم از عملیات هندسی ساده استفاده شده و مرحله به مرحله آزمایش می شود تا بررسی شود که آیا روابط توپولوژیکی پس از فشرده سازی تغییر کرده است یا خیر. اگر روابط توپولوژیکی تغییر نکند، الگوریتم خاتمه می یابد. در غیر این صورت، روابط توپولوژیکی حفظ خواهد شد. وو و مارکز [ 23 ] یک الگوریتم ستاره شکل (الگوریتم ST) را برای ساده کردن منحنی ها پیشنهاد کردند. منحنی های اصلی ابتدا اسکن می شوند و سپس به مناطق “ستاره” تقسیم می شوند. در نهایت، الگوریتم D-P برای فشرده سازی مناطق “ستاره” اعمال می شود. الگوریتم ستاره ای شکل مشکلات خودتقاطع را حل می کند، اما بدترین حالت را دارد. O(nمتر)پیچیدگی زمانی، جایی که nتعداد رئوس ورودی و متربسته به تعداد مناطق ستاره‌دار، مصرف زمان و کارایی این روش نسبتاً زیاد است.

بسیاری از الگوریتم‌های بهبود یافته D-P در بالا، مشکلات خود تقاطع را برای ساده‌سازی اشیاء خطی حل کردند. با این حال، الگوریتم های مورد استفاده دارای معایب کارایی پایین و مراحل پیچیده هستند. برای حل مشکلات خود تقاطع هنگام استفاده از الگوریتم D-P برای ساده کردن اشیاء خطی و بهبود کارایی الگوریتم، یک الگوریتم ساده سازی خط برداری جدید که ترکیبی از الگوریتم D-P، زنجیره های یکنواخت و دوگانگی است در این مقاله پیشنهاد شده است. . چهار مرحله اصلی وجود دارد: اول، الگوریتم D-P برای پردازش خطوط اصلی استفاده می شود. دوم، روش زنجیره یکنواخت برای تقسیم خطوط ساده شده به زنجیره های یکنواخت استفاده می شود اگر خطوط ساده شده دارای مشکلات خودتقاطع باشند. سوم، دوگانگی برای تعیین سریع و دقیق موقعیت خودتقاطع خطوط ساده شده استفاده می شود. مشکلات خود تقاطع را پردازش کنید و نتیجه نهایی را بدست آورید. در نهایت، نتایج تجربی در این بخش ارائه می‌شود و نتایج آزمایش‌ها نشان می‌دهد که روش پیشنهادی ما عملکرد مؤثرتر و بالاتری را نشان می‌دهد.

ادامه این مقاله به شرح زیر سازماندهی شده است. تئوری های اساسی، روش ها و مراحل الگوریتم جدید در بخش 2 معرفی شده اند . نتایج تجربی و تجزیه و تحلیل در بخش 3 گزارش شده است. نتیجه گیری در بخش 4 ترسیم شده است.

2. روش شناسی

در این بخش ابتدا تئوری های اساسی الگوریتم D-P، زنجیره های یکنواخت و روش دوگانگی را معرفی می کنیم. سپس، مراحل اساسی الگوریتم بهبود یافته با جزئیات بیشتر معرفی می‌شوند. نمودار جریان روش تحقیق پیشنهادی در شکل 1 نشان داده شده است .

2.1. نظریه پایه الگوریتم داگلاس-پوکر (D-P).

الگوریتم D-P یک الگوریتم کلاسیک است که برای فشرده سازی منحنی استفاده می شود. این الگوریتم برای ساده سازی چند خطوط با حذف رئوس غیر مشخصه و حفظ رئوس ویژگی استفاده می شود. تئوری اساسی و مراحل محاسباتی الگوریتم D-P به شرح زیر است [ 1 ، 24 ]:

مرحله 1: برای یک منحنی L، که تشکیل شده است نرئوس مختصات، رئوس مختصات مجموعه Vبه صورت نوشته شده است V={v1،v2،…،vمن،…،vن}،(من=1،2،…،ن). ابتدا راس اول را وصل کنید v1و آخرین راس vن، برای به دست آوردن یک خط مستقیم جدید Lv1vن. دوم، کمترین فاصله را بین رئوس باقی مانده محاسبه کنید {v2،…،vن-1}و خط مستقیم جدید Lv1vنو کوتاه ترین مجموعه های مسافت را بدست آورید D={D2،…Dک،…،Dن-1}( Dککوتاه ترین فاصله بین راس است vکو خط مستقیم جدید Lv1vن)

مرحله 2: انتخاب حداکثر فاصله ( Dحداکثر) با کمترین فاصله D، Dحداکثر=Dک( Dککوتاه ترین فاصله بین راس است vکو خط مستقیم جدید Lv1vن). با توجه به فاصله εبه عنوان آستانه فاصله، اگر Dحداکثر<ε، سپس رئوس باقی مانده {v2،…،vن-1}از مجموعه رئوس V={v1،v2،…،vن}منحنی داده شده حذف می شوند Lدر یک خط مستقیم فشرده می شود Lv1vنو الگوریتم D-P به پایان رسید. اگر Dحداکثر≥ε، سپس رئوس تنظیم می شوند V={v1،v2،…،vن}به دو زیر مجموعه تقسیم می شود Vتیو Vس، به این معنا که، V=Vتی+Vس( Vتی={v1،v2،…،vک}، Vس={vک،vک+1،…،vن})

مرحله 3: برای زیر مجموعه ها Vتیو Vس، مرحله 1 و 2 را به ترتیب تکرار کنید. اگر همه کوتاهترین مسافتهای محاسبه شده کمتر از آستانه فاصله دادن باشند ( ε، سپس الگوریتم D-P را پایان دهید.

2.2. زنجیره های یکنواخت و دوگانگی

تئوری زنجیره یکنواخت عمدتاً از هندسه محاسباتی مشتق شده است [ 12 ، 25 ]. برای منحنی L ، زنجیره یکنواخت به صورت زیر تعریف می شود:

زنجیره یکنواخت: برای یک منحنی L، که تشکیل شده است مرئوس مختصات، رئوس مختصات مجموعه Vبه صورت بیان می شود V={v1،v2،…،vمن،…،vم}،(من=1،2،…،م); ایکسمنهست ایکسمختصات محور راس vمن، و yمنهست Yمختصات محور راس vمن. در جهت ایکسمحور، برای مجموعه رئوس مختصات ایکس={ایکس1،ایکس2،…،ایکسمن،…،ایکسم}،(من=1،2،…،م)، اگر ایکسمن≤ایکسمن+1 (من=1،2،…،م)یا ایکسمن>ایکسمن+1 (من=1،2،…،م)، منحنی Lزنجیره افزایشی (یا کاهشی) یکنواخت محور X نامیده می شود. به طور مشابه، در جهت Yمحور، برای مجموعه رئوس مختصات Y={y1،y2،…،yمن،…،yم}،(من=1،2،…،م) (من=1،2،…،م)، اگر yمن≤yمن+1 (من=1،2،…،م)یا yمن>yمن+1 (من=1،2،…،م)، منحنی Lزنجیره افزایشی (یا کاهشی) یکنواخت محور Y نامیده می شود.

دوگانگی: دوگانگی یکی از متداول ترین الگوریتم های جستجو برای دنباله های ترتیبی است و کارایی جستجوی بالایی دارد [ 12 ، 13 ]. با توجه به عنصر هدف تیو دنباله دستور داده شده ک={ک1،ک2،…،کمن،…،کU}،(من=1،2،…،U)، ( تی∈ک)، برای جستجوی عنصر هدف تیاز جانب ک، نظریه اصلی دوگانگی به شرح زیر است:

مرحله 1 : برای عنصر هدف تی، مقایسه کنید تیبا عنصر میانی کU2از دنباله ک. اگر تی≠کU2، سپس کبه دو بخش تقسیم خواهد شد: ک1و ک2، ک=ک1∪ک2، ک1={ک1،ک2،…،کمن،…،کU2} (من=1،2،…،U)، ک2={کU2،کU2+1،…،کj،…،کU} (j=U2،U2+1،…،U).

مرحله 2 : برای عنصر هدف تی، اگر تی≥کU2، سپس مرحله 1 را در قسمت اجرا کنید ک2تا عنصر هدف تیاز سفارش یافته یافت می شود ک2; اگر تی<کU2، سپس مرحله 1 را در قسمت اجرا کنید ک1تا عنصر هدف تیاز سفارش یافته یافت می شود ک1.

در ساختار داده های مکانی برداری، به خوبی شناخته شده است که یک منحنی ساده از تعدادی پاره خط تشکیل شده است. برای یک منحنی L، وجود دارد نرئوس مختصات: پ={پ1،پ2،…،پمن،…،پن}،(من=1،2،…،ن)، و منحنی Lاز چند پاره خط تشکیل شده است مانند: L=L1،2″+L2،3″+…+Lمن،j”+…+Lن-1،ن”( نتعداد رئوس مختصات است). شکل 2 آن منحنی را نشان می دهد Lاز 26 راس مختصات تشکیل شده است ( 0،1،2،…،25). در سیستم مختصات مستطیلی صفحه گاوس-کروگر، محور افقی، محور Y و محور عمودی، محور X بود. در امتداد محور Y، Lرا می توان به دو زنجیره یکنواخت تقسیم کرد Lمن”( من=0،1،2،…،13) و L”jمن( j=13،14،…،25). برای L”من، در طول Y- محور، رأس پ0کوچکترین و رأس است پ13بزرگترین است، و L”منیک زنجیره افزایشی یکنواخت است. برای L”j، در طول Y- محور، رأس پ13بزرگترین و رأس است پ25کوچکترین است و L”jیک زنجیره کاهشی یکنواخت است. هنگام استفاده از الگوریتم D-P برای پردازش منحنی L، لازم به ذکر است که اگر نتیجه نهایی دارای مشکلات خودتقاطع باشد، ناشی از زنجیره های یکنواخت مربوطه بوده است. L”منو L”j.

2.3. الگوریتم ساده سازی خط برداری جدید بر اساس الگوریتم D-P، زنجیره های یکنواخت و دوگانگی

این مقاله از زنجیره های یکنواخت و دوگانگی برای حل مسئله خود تقاطع در ساده سازی خط فضایی هنگام پردازش توسط الگوریتم D-P استفاده کرد. در روش پیشنهادی ما، ابتدا از الگوریتم D-P برای ساده‌سازی چند خط اصلی استفاده می‌کنیم م، و چند خط ساده شده را بدست آورید تی; در مرحله دوم، ما مشکلات خود تقاطع را بررسی می کنیم تی. اگر تیمشکلات خودتقاطع ندارد، سپس به این روش پیشنهادی پایان می دهیم، در غیر این صورت، از فناوری زنجیره یکنواخت برای تقسیم سریع استفاده می کنیم. تیبه چندین زنجیره یکنواخت متوالی. ثالثاً، از روش دوگانگی، MER (مستطیل محصور با حداقل مساحت، که به مستطیلی با کوچکترین مساحتی که چندخط را محصور می کند اشاره دارد) و روش محاسبه هندسی برای پردازش زنجیره های یکنواخت متوالی، به منظور تعیین سریع موقعیت های خود استفاده می شود. -مسائل تقاطع زنجیره های یکنواخت متوالی و حل مسائل خود تقاطع، برای به دست آوردن نتایج نهایی.

این استراتژی روش پیشنهادی نه تنها ویژگی های منحنی یک چند خط را در نظر می گیرد، بلکه زمان مصرف روش پیشنهادی را نیز بهبود می بخشد. مراحل اصلی روش پیشنهادی در زیر توضیح داده شده است.

مرحله 1 : از الگوریتم D-P برای پردازش یک منحنی استفاده کنید م(خطاهای خود تقاطع وجود ندارد م) و یک منحنی جدید بدست آورید تی.

مرحله 2 : مشکلات خود تقاطع را بررسی کنید تی; اگر خطاهای خود تقاطع وجود دارد، مرحله 3 را انجام دهید. در غیر این صورت، تینتیجه نهایی ساده سازی خط است.

مرحله 3 : برای تی، پس از مرحله 2 پردازش، در صورت وجود خطاهای خود تقاطع، با توجه به دنباله رئوس مختصات، از فناوری زنجیره یکنواخت (همانطور که در بخش 2.2 توضیح داده شد ) برای تقسیم استفاده کنید.تیبه چندین زنجیره یکنواخت متوالی تی1″، تی2″,…, تیمن”,…, تیj”,…, تیn” (من،j∈[1،n]).

مرحله 4: برای زنجیره های یکنواخت تیمن”و تیj”، که به ترتیب رئوس را شامل و هماهنگ می کنند n≥متر، سپس از دوگانگی برای تقسیم سریع استفاده کنید تیمن”به دو زنجیره یکنواخت: L”1،تیو L”تی،n( تی=n2، چه زمانی nیکنواخت بود یا تی=n2+1، چه زمانی nعجیب بود، nیک عدد صحیح است و n>1) L”1،تیو L”تی،nهمچنین دو زنجیره یکنواخت هستند. به طور مشابه، اگر n<متر، سپس تقسیم کنید تیj”به دو زنجیره یکنواخت اس”1،تیو استی،متر”( تی=متر2، چه زمانی متریکنواخت بود یا تی=متر2+1، چه زمانی مترعجیب بود، متریک عدد صحیح است و متر>1) اس”1،تیو استی،متر”همچنین دو زنجیره یکنواخت هستند.

مرحله 5: اگر n≥متر، MER را محاسبه کنید L”1،تی، L”تی،nو تی”j، به ترتیب، به عنوان آرL1،تی، آرLتی،nو آرتیj. به طور مشابه، اگر n<متر، MER را محاسبه کنید اس”1،تی، استی،متر”و تی”من، به ترتیب، به عنوان آراس1،تی، آراستی،nو آرتیمن.

مرحله 6: برای آرL1،تی، آرLتی،nو آرتیj، اگر آرL1،تی∩آرتیj= آرLتی،n∩آرتیj= ϕ، سپس یک عدم تقاطع بین وجود دارد تیمن”و تیj”; اگر آرL1،تی∩آرتیj ≠ϕ، و آرLتی،n∩آرتیj=ϕ، ممکن است یک مشکل تقاطع بین زنجیره یکنواخت وجود داشته باشد L”1،تیو تیj”، و یک عدم تقاطع بین وجود دارد L”تی،nو تیj”; اگر آرL1،تی∩آرتیj= ϕ، و آرLتی،n∩آرتیj ≠ϕ، ممکن است یک مشکل تقاطع بین زنجیره یکنواخت وجود داشته باشد L”تی،nو تیj”، و یک عدم تقاطع بین وجود دارد L”1،تیو تیj”; اگر آرL1،تی∩آرتیj ≠ϕ، و آرLتی،n∩آرتیj ≠ϕ، ممکن است یک مشکل تقاطع بین زنجیره یکنواخت وجود داشته باشد L”1،تیو تیj”، و ممکن است یک مشکل تقاطع بین زنجیره یکنواخت وجود داشته باشد L”تی،nو تیj”. با استفاده از همین روش، می توانیم محاسبه کنیم که آیا مشکلات تقاطع بین آنها وجود دارد یا خیر آراس1،تی، آراستی،n، و آرتیمن.

مرحله 7: تمام زنجیره های یکنواخت متوالی را پردازش کنید تی1″، تی2″,…, تیمن”,…, تیj”,…, تیn” (من،j∈[1،n])با استفاده از مرحله 4، مرحله 5 و مرحله 6، تا زمانی که تمام مشکلات تقاطع زنجیره های یکنواخت پیدا شود.

مرحله 8: پس از پردازش مرحله 1 تا مرحله 7، تمام مشکلات تقاطع زنجیره های یکنواخت پیدا می شود. در این مرحله، مثالی می زنیم تا نشان دهیم روش پیشنهادی چگونه با این مشکلات تقاطع برخورد می کند.

برای یک منحنی تیکه توسط الگوریتم D-P همانطور که در شکل 3 نشان داده شده است پردازش می شود ، تیشامل 25 راس مختصات است. با استفاده از مرحله 2 و مرحله 3 می توانیم سه زنجیره یکنواخت بدست آوریم تی1″، تی2″و تی3″(همانطور که در شکل 3 ب نشان داده شده است). تی1″شامل شش راس مختصات ( پ1،…،پ6) و پ1و پ6رئوس انتهایی هستند تی1″; تی2″شامل نه راس مختصات ( پ6،…،پ14) و پ6و پ14رئوس انتهایی هستند تی2″; تی3″شامل 12 راس مختصات ( پ14،…،پ25) و پ14و پ25رئوس انتهایی هستند تی3″. پس از استفاده از مرحله 4، مرحله 5، مرحله 6 و مرحله 7، یک مشکل تقاطع بین وجود دارد تی1″و تی3″، و مشکل تقاطع دیگری بین آن وجود دارد تی2″و تی3″.

با استفاده از شکل 3 c به عنوان مثال، پس از پردازش توسط مرحله 6، با فرض وجود یک مشکل تقاطع بین تی1″و تی3″، برای به دست آوردن پاره خط تقاطع ک5،6و ک17،18با روش محاسبه هندسی [ 12 , 25 ] و رئوس مختصات را بدست آورید. پ5، پ6، و پ17، پ18. اگر رئوس مختصاتی وجود داشته باشد (vپ،vپ+1،…vمن،…،vq،من∈[پ،q])( پ،qدو عدد صحیح هستند) بین پ17و پ18که به منحنی اصلی تعلق دارند م، سپس کوتاهترین فاصله بین رئوس را محاسبه کنید (vپ،vپ+1،…vمن،…،vq،من∈[پ،q])و بخش خط ک17،18و حداکثر مقدار ( Dحداکثر) از کوتاه ترین فاصله و نقطه هماهنگ مربوطه پمن.

اتصال پ17پمن، و پمنپ18و دو زنجیره یکنواخت جدید بدست آورید تی17من”و تیمن18″. محاسبه کنید که آیا مشکلات تقاطعی بین دو زنجیره یکنواخت جدید وجود دارد یا خیر تی17من”، تیمن18″و زنجیره یکنواخت تی1″. اگر مشکلی در تقاطع وجود ندارد، این الگوریتم را نتیجه گیری کنید. زنجیره یکنواخت تی3″به دو زنجیره یکنواخت جدید تقسیم خواهد شد تی17من”و تیمن18″. اگر خطاهای تقاطع دیگری وجود دارد، مرحله 8 و مرحله 9 را دوباره اجرا کنید تا زمانی که خطای تقاطع بین آنها وجود نداشته باشد. تی1″و تی3″.

به طور مشابه، اگر رئوس مختصاتی بین آنها وجود داشته باشد پ5و پ6که به منحنی اصلی تعلق دارند م، مراحل 8 و 9 را مجدداً اجرا کنید تا زمانی که خطای تقاطع بین آن وجود نداشته باشد تی1″و تی3″.

مراحل 4 تا 8 را تا زمانی که خطای تقاطعی بین تمام زنجیره های یکنواخت وجود نداشته باشد اجرا کنید و سپس نتیجه نهایی را به دست آورید. تی”. شکل 3 d نتیجه نهایی را نشان می دهد، کمنو کjدو راس مختصات از منحنی اصلی هستند م.

مرحله 9 : پس از پردازش در مرحله 1 تا مرحله 8، تمام مسائل تقاطع پردازش شده است، سپس روش پیشنهادی را پایان می دهیم و نتایج نهایی را به دست می آوریم.

3. آزمایش ها و تجزیه و تحلیل

ما دو گروه از داده های تجربی را برای تأیید اعتبار الگوریتم پیشنهادی انتخاب می کنیم. اولین گروه از داده ها خط جاده استان جیانگشی در چین است. طول کل آن تقریباً 1.56 × 10 ⁵^{کیلومتر} است و حجم داده تقریباً 92000 بایت است که شامل تقریباً 5.13 × 106 رئوس است. گروه دوم داده ها، خط کاربری اراضی شهرستان دینگنان در استان جیانگشی در چین است. طول کل آن تقریباً 1.41 × 10 ⁴^{کیلومتر} است و حجم داده تقریباً 26000 بایت است که شامل تقریباً 1.24 × 106 رئوس است.

3.1. ارزیابی

در این مطالعه، ما تعدادی روش مختلف را برای ساده‌سازی دو گروه داده و مقایسه عملکرد روش پیشنهادی اتخاذ کردیم. این به دلیل الگوریتم ST [ 23]، که همچنین بر اساس الگوریتم D-P است که می تواند مشکلات خودتقاطع را حل کند، در این مقاله، عملکرد روش پیشنهادی را با الگوریتم ST و الگوریتم D-P مقایسه کردیم. مقیاس آزمایشی داده ها 1:10000 است و نتایج در نسبت های هدف رئوس اصلی به ترتیب 60 و 70 درصد است. در نتیجه، دو گروه از داده ها به صورت حجم زیاد نمایش داده می شوند. بنابراین نشان دادن جزئیات بیشتر مورد، در همان محیط آزمایشی دشوار است. علاوه بر این، به جای آن، شش مسئله خود-تقاطع را از دو گروه داده انتخاب کردیم. نتایج ساده شده از شش مسئله خود تقاطع در شکل 4 نشان داده شده است.

همانطور که در شکل 4 نشان داده شده است ، نتایج ساده شده از هر گروه از داده ها، الگوریتم D-P مشکلات خود تقاطع را ایجاد می کند، اما روش پیشنهادی می تواند مشکلات خودتقاطع و همچنین الگوریتم ST را پردازش کند. برای مقایسه عملکرد روش های مختلف، چهار معیار شامل زمان مصرف، میانگین جابجایی برداری [ 3 ، 26 ]، فاصله هاسدورف (HD) [ 27 ] و اندازه گیری استاندارد شده جابجایی (SMD) [ 28 ] انتخاب شده است.

زمان مصرف نشان می دهد که الگوریتم چقدر زمان می برد.

میانگین جابجایی بردار به عنوان میانگین جابجایی بردار بین رئوس اصلی و نسخه ساده شده همان رئوس محاسبه می شود.

فاصله Hausdorff (HD) بین دو جسم هندسی بزرگترین حداقل فاصله بین نقاط یک جسم به جسم دیگر است [ 27 ].

اندازه گیری استاندارد جابجایی (SMD) توسط Joao [ 28 ] تعریف شده است و فرمول محاسبه به صورت زیر نشان داده شده است:

اسمD(%)=(1-(دبلیو-O)/دبلیو)×100

(1)

دبلیوفاصله از رئوس مختصات است که حداکثر جابجایی بین چند خط اصلی و چند خط ساده شده تا خط مستقیم را دارد. این با اتصال اولین و آخرین گره پلی لاین و Oجابجایی واقعی رئوس مختصات بین چند خط اصلی و چند خط ساده شده است.

3.2. نتایج

معیارهای ارزیابی ساده سازی داده های پردازش شده با روش به شرح زیر نشان داده شده است: آمار حاصل با استفاده از دو گروه از مجموعه داده های تجربی محاسبه می شود.

(1) مصرف زمان: نتایج مصرف زمان سه روش ساده سازی خط در شکل 5 نشان داده شده است و زمان مصرف بر حسب میلی ثانیه (ms) اندازه گیری شده است.

(2) جابجایی میانگین بردار : نتایج جابجایی میانگین بردار از سه روش ساده سازی خط در شکل 6 نشان داده شده است. میانگین جابجایی بردار بر حسب متر (m) اندازه گیری می شود.

(3) فاصله Hausdorff (HD) : نتایج فاصله Hausdorff (HD) از سه روش ساده سازی خط در شکل 7 نشان داده شده است. HD بر حسب متر (متر) اندازه گیری می شود.

(4) اندازه گیری استاندارد شده جابجایی (SMD) : نتایج اندازه گیری استاندارد شده جابجایی (SMD) از سه روش ساده سازی خط در شکل 8 نشان داده شده است.

3.3. تحلیل و بررسی

از شکل 5 تا شکل 8 موارد زیر را مشاهده می کنیم:

(1) روش پیشنهادی می تواند به طور موثر برای ساده سازی خط برداری استفاده شود. ما از دو گروه داده برای تأیید روش پیشنهادی استفاده کردیم. از نتایج تجربی می توان نشان داد که روش پیشنهادی نه تنها می تواند مشکل خودتقاطع ناشی از الگوریتم D-P را حل کند، بلکه از راندمان اجرایی بالایی نیز برخوردار است. شکل 4 شش نتیجه ساده سازی دو گروه داده را با استفاده از سه روش نشان می دهد. در شش مسئله خودتقاطع همانطور که در شکل 4 نشان داده شده است ، چند خطوط شش ناحیه منحنی های پیچیده با تعدادی خمش سلسله مراتبی را نشان می دهند. همانطور که در شکل 4 نشان داده شده است، الگوریتم D-P مشکلات خود تقاطع را ایجاد می کند، اما روش پیشنهادی و الگوریتم ST از این مشکلات جلوگیری می کند. این به این دلیل است که الگوریتم ST نیز بر اساس الگوریتم D-P است. در نتیجه، این سه روش نتایج تجربی مشابهی را در برخی موارد شناسایی کردند.

(2) الگوریتم D-P مشخص شد O(nمتر)زمان مورد بدتر و O(nورود به سیستمn)زمان مورد انتظار، جایی که nتعداد رئوس ورودی و مترتعداد قطعات چند خطی ساده شده بود [ 23 ]. الگوریتم ST عمدتاً از سه مرحله تشکیل شده بود. بدترین حالت O(nمتر)پیچیدگی زمانی، جایی که nتعداد رئوس ورودی و متربستگی به تعداد مناطق ستاره ای شکل دارد [ 23 ]. روش پیشنهادی در این مقاله شامل دو مرحله کلیدی است: اول، ما ابتدا از الگوریتم D-P برای ساده‌سازی منحنی‌های اصلی استفاده کردیم و مشکلات خود تقاطع را بررسی کردیم. سپس از روش‌های زنجیره یکنواخت و دوگانگی برای پرداختن به مقادیر خود تقاطع استفاده کردیم. در مرحله اول، الگوریتم ما زمان اجرای مشابهی با الگوریتم D-P داشت. در مرحله دوم، الگوریتم ما در انجام شد O(مترورود به سیستممتر)زمان، در حالی که مترتعداد قطعات خود تقاطع چند خط ساده شده بود.

نتایج مصرف زمان سه روش برای پردازش دو گروه داده در نشان داده شده است شکل 5 نشان داده شده است. برای گروه اول داده ها، نتایج مصرف زمان الگوریتم D-P، روش پیشنهادی و الگوریتم ST به ترتیب 5523375 میلی ثانیه، 6954155 میلی ثانیه و 10283326 میلی ثانیه است. برای گروه دوم داده ها، نتایج مصرف زمان الگوریتم D-P، روش پیشنهادی و الگوریتم ST به ترتیب 75325 میلی ثانیه، 93256 میلی ثانیه و 310201 میلی ثانیه است. از نتایج تجربی هر گروه از داده ها می توان دریافت که زمان مصرف روش پیشنهادی کمی بیشتر از الگوریتم D-P با روش پیشنهادی است و پس از پردازش الگوریتم D-P، از زنجیره های یکنواخت استفاده می کنیم. و دوگانگی برای اصلاح مشکلات خود تقاطع. بدیهی است که زمان مصرف روش پیشنهادی بسیار کمتر از الگوریتم ST است.

(3) ما از جابجایی میانگین بردار برای اندازه گیری دقت مکان استفاده می کنیم. همانطور که در شکل 6 نشان داده شده است ، گروه اول داده ها، میانگین نتایج جابجایی بردار الگوریتم D-P، روش پیشنهادی و الگوریتم ST به ترتیب 79/6 متر، 57/6 متر و 83/7 متر می باشد. داده های گروه دوم نشان داد که میانگین نتایج جابجایی برداری الگوریتم D-P، روش پیشنهادی و الگوریتم ST به ترتیب 92/4 متر، 63/4 متر و 81/5 متر است. برای هر گروه از داده ها، میانگین جابجایی برداری روش پیشنهادی مشابه الگوریتم D-P است اما بسیار کمتر از الگوریتم ST است.

(4) شکل 7 فاصله Hausdorff سه روش برای پردازش دو گروه داده را نشان می دهد. برای گروه اول داده ها، فواصل هاسدورف الگوریتم D-P، روش پیشنهادی و الگوریتم ST به ترتیب 25/6 متر، 08/6 متر و 85/6 متر است. گروه دوم داده ها نشان داد که فواصل هاسدورف الگوریتم D-P، روش پیشنهادی و الگوریتم ST به ترتیب 75/4 متر، 68/4 متر و 23/5 متر است. برای هر گروه از داده ها، فاصله Hausdorff روش پیشنهادی مشابه الگوریتم D-P و الگوریتم ST است.

(5) ما همچنین از یک اندازه گیری استاندارد جابجایی (SMD) برای اندازه گیری دقت مکان استفاده کردیم. همانطور که در شکل 8 نشان داده شده است ، داده های گروه اول، SMD های الگوریتم D-P، روش پیشنهادی و الگوریتم ST به ترتیب 46/3، 58/3 و 25/4 درصد است، داده های گروه دوم نشان داد که SMD ها از الگوریتم D-P، روش پیشنهادی و الگوریتم ST به ترتیب 1.83٪، 1.79٪ و 2.81٪ هستند. برای هر گروه از داده ها، میانگین جابجایی برداری روش پیشنهادی مشابه الگوریتم D-P است اما بسیار کمتر از الگوریتم ST است.

4. نتیجه گیری

ساده سازی خطوط برداری به طور گسترده در گرافیک کامپیوتری، GIS و غیره استفاده می شود. الگوریتم D-P یکی از پرکاربردترین روش‌ها برای ساده‌سازی خطوط برداری است. هنگامی که متخصصان از الگوریتم D-P برای پرداختن به منحنی های پیچیده استفاده می کنند، متوجه می شویم که تولید مشکلات خودتقاطع آسان است. برای گسترش بیشتر کاربرد الگوریتم D-P، در این مقاله یک الگوریتم ساده سازی خط جدید که الگوریتم D-P، زنجیره های یکنواخت و دوگانگی را ترکیب می کند، پیشنهاد شده است. در پایان، دو آزمایش برای مقایسه نتایج روش پیشنهادی ما با الگوریتم D-P و الگوریتم ST طراحی شده‌اند. از تجزیه و تحلیل نتیجه، واضح است که الگوریتم پیشنهادی چندین مزیت دارد: (1) در مقایسه با الگوریتم D-P، الگوریتم پیشنهادی کارایی اجرای یکسانی دارد اما بدون مشکلات خودتقاطع. (2) در مقایسه با الگوریتم ST، روش پیشنهادی توانایی یکسانی برای حل مسائل خود تقاطع دارد اما کارایی اجرای بهتری دارد. در عین حال، الگوریتم پیشنهادی دارای کاستی هایی است که باید بیشتر مورد مطالعه قرار گیرد: (1) روش پیشنهادی بر حذف مشکلات خود تقاطع متمرکز است، با این حال، مشکلات حفظ منطقه پس از ساده سازی چند خط در نظر گرفته نمی شود. (2) شبیه به الگوریتم D-P، این روش پیشنهادی ویژگی‌های خمشی منحنی‌ها را در نظر نمی‌گیرد. در خاتمه، این دو کاستی موضوعی محور تحقیقات آینده ما خواهد بود. (1) روش پیشنهادی بر حذف مشکلات خود تقاطع متمرکز است، با این حال، مشکلات حفظ منطقه پس از ساده‌سازی چند خط در نظر گرفته نمی‌شود. (2) شبیه به الگوریتم D-P، این روش پیشنهادی ویژگی‌های خمشی منحنی‌ها را در نظر نمی‌گیرد. در خاتمه، این دو کاستی موضوعی محور تحقیقات آینده ما خواهد بود. (1) روش پیشنهادی بر حذف مشکلات خود تقاطع متمرکز است، با این حال، مشکلات حفظ منطقه پس از ساده‌سازی چند خط در نظر گرفته نمی‌شود. (2) شبیه به الگوریتم D-P، این روش پیشنهادی ویژگی‌های خمشی منحنی‌ها را در نظر نمی‌گیرد. در خاتمه، این دو کاستی موضوعی محور تحقیقات آینده ما خواهد بود.

منابع

داگلاس، دی اچ. الگوریتم های Peucker، TK برای کاهش تعداد نقاط مورد نیاز برای نمایش یک خط دیجیتالی یا کاریکاتور آن. می توان. کارتوگر. 1973 ، 10 ، 112-122. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
رامر، U. یک روش تکراری برای تقریب چند ضلعی منحنی های صفحه. محاسبه کنید. نمودار. فرآیند تصویر 1972 ، 1 ، 244-256. [ Google Scholar ] [ CrossRef ]
Lang, T. قوانین برای طراحان روبات. Geogr. Mag. 1969 ، 42 ، 50-51. [ Google Scholar ]
McMaster, RB ادغام الگوریتم های ساده سازی و هموارسازی در تعمیم خط. می توان. کارتوگر. 1989 ، 26 ، 101-121. [ Google Scholar ] [ CrossRef ]
Li، ZL الگوریتمی برای فشرده سازی داده های کانتور دیجیتال. کارتوگر. J. 1988 , 25 , 143-146. [ Google Scholar ] [ CrossRef ]
Visvalingam، M. وایات، جی. تعمیم خط با حذف مکرر کوچکترین ناحیه. گزارش فنی، مقاله بحث 10، گروه تحقیقاتی سیستم های اطلاعات نقشه برداری (CISRG) ; دانشگاه هال: هال، انگلستان، 1992. [ Google Scholar ]
راتچک، اچ. رکنه، جی. Leriger, M. استحکام در اجرای الگوریتم GIS با کاربرد به ساده سازی خط. بین المللی جی. جئوگر. Inf. علمی 2001 ، 15 ، 707-720. [ Google Scholar ] [ CrossRef ]
وانگ، ZS; مولر، جی.-سی. تعمیم خط بر اساس تجزیه و تحلیل ویژگی های شکل. کارتوگر. Geogr. Inf. سیستم 1998 ، 25 ، 3-15. [ Google Scholar ] [ CrossRef ]
ژائو، ز. Saalfeld، A. الگوریتم های ساده سازی چند خط آستین-زمان خطی. در مجموعه مقالات AutoCarto 13، سیاتل، WA، ایالات متحده آمریکا، 7-10 آوریل 1997; منتشر شده توسط کنگره آمریکا در نقشه برداری و نقشه برداری و انجمن آمریکایی فتوگرامتری و سنجش از دور، مریلند. صص 214–223، ISBN -1-57083-043-6. [ Google Scholar ]
گری، RH; ویلسون، AD; Archuleta، CM; تامپسون، FE; Vrabel, J. تولید مجموعه داده‌های هیدروگرافی ملی با مقیاس 1:1000000 برای ایالات متحده: انتخاب ویژگی، ساده‌سازی و اصلاح . گزارش تحقیقات علمی سازمان زمین شناسی ایالات متحده 2009-5202. تجدید نظر شده در می 2010; سازمان زمین شناسی ایالات متحده: Reston، VA، ایالات متحده آمریکا، 2010; 22p. [ CrossRef ]
Li، ZL; Openshaw, S. الگوریتم‌های تعمیم خودکار خط بر اساس یک اصل طبیعی تعمیم عینی. بین المللی جی. جئوگر. Inf. علمی 1992 ، 6 ، 373-389. [ Google Scholar ] [ CrossRef ]
سامسونوف تیموفی، ای. Yakimova، OP شکل ساده سازی تطبیقی هندسی مجموعه داده های خط ناهمگن. بین المللی جی. جئوگر. Inf. علمی 2017 ، 31 ، 1485-1520. [ Google Scholar ] [ CrossRef ]
دی برگ، ام. ون کرولد، ام. اورمارس، ام. اورمارس، ام. Schwarzkopf, O. Computational Geometry: Algorithms and Applications , 2nd ed.; Springer: برلین، آلمان، 2000. [ Google Scholar ]
کراملی، ساده سازی خط محور اصلی RG. محاسبه کنید. Geosci. 1992 ، 18 ، 1003-1011. [ Google Scholar ] [ CrossRef ]
Raposo، P. ساده‌سازی خط خودکار ویژه مقیاس با خوشه‌بندی راس روی یک تسلیح شش ضلعی. کارتوگر. Geogr. Inf. سیستم 2013 ، 40 ، 427-443. [ Google Scholar ] [ CrossRef ]
Kronenfeld، BJ; استانیسلاوسکی، LV; باتنفیلد، BP; تایلر، ب. ساده‌سازی چند خطوط با فروپاشی قطعه: به حداقل رساندن جابجایی ناحیه با حفظ مساحت. بین المللی جی. کارتوگر. 2020 ، 6 ، 22-46. [ Google Scholar ] [ CrossRef ]
شی، WZ; Cheung، CK ارزیابی عملکرد الگوریتم های ساده سازی خط برای تعمیم برداری. کارتوگر. J. 2006 ، 43 ، 27-44. [ Google Scholar ] [ CrossRef ]
Mi، XJ; شنگ، جنرال موتورز; ژانگ، جی. بای، HX; Hou, W. الگوریتم جدیدی از فشرده سازی تاریخ برداری بر اساس تحمل خطای ناحیه در GIS. علمی Geogr. گناه 2012 ، 32 ، 1236-1240. [ Google Scholar ]
Saalfeld، A. ساده سازی خط سازگار از نظر توپولوژیکی با الگوریتم داگلاس-پوکر. کارتوگر. Geogr. Inf. علمی 1999 ، 26 ، 7-18. [ Google Scholar ] [ CrossRef ]
هو، PS; Kim, MH یک طرح سلسله مراتبی برای نمایش منحنی ها بدون خود تقاطع. در مجموعه مقالات کنفرانس انجمن کامپیوتری IEEE 2001 (CVPR 2001)، Kauai، HI، ایالات متحده آمریکا، 8 تا 14 دسامبر 2001. [ Google Scholar ] [ CrossRef ]
منتلر، ا. Snoeyink، J. مجموعه ایمن برای ساده سازی خطوط. در دهمین کارگاه پاییز سالانه هندسه محاسباتی . دانشگاه استونی بروک: نیویورک، نیویورک، ایالات متحده آمریکا، 2000; در دسترس آنلاین: https://citeseerx.ist.psu.edu/viewdoc/summary?doi.10.1.1.32.402 (در 29 مارس 2020 قابل دسترسی است).
آولار، اس. مولر، ام. ایجاد نقشه های شماتیک توپولوژیکی صحیح. در مجموعه مقالات نهمین سمپوزیوم بین المللی مدیریت داده های مکانی ; گزارش فنی؛ مؤسسه فدرال فناوری سوئیس زوریخ: زوریخ، سوئیس، 2000; ص 4-28. [ Google Scholar ] [ CrossRef ]
وو، ST; مارکز، MRG الگوریتم داگلاس-پوکر بدون خود تقاطع. در مجموعه مقالات شانزدهمین سموزیوم برزیل در زمینه گرافیک کامپیوتری و پردازش تصویر (SIBGRAPI)، سائو کارلوس، برزیل، 12 تا 15 اکتبر 2003. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
Ebisch, K. یادداشت کوتاه: اصلاحی برای تعمیم خط داگلاس-پوکر. محاسبه کنید. Geosci. 2002 ، 28 ، 995-997. [ Google Scholar ] [ CrossRef ]
Yan، HW; وانگ، MX؛ هندسه محاسباتی وانگ، ZH : الگوریتم پردازش داده های فضایی . انتشارات علمی: پکن، چین، 2012. [ Google Scholar ]
وایت، ارزیابی ER الگوریتم های تعمیم خط با استفاده از نقاط مشخصه. کارتوگر. Geogr. Inf. علمی 1985 ، 12 ، 17-28. [ Google Scholar ] [ CrossRef ]
Hangouët، JF محاسبه فاصله هاسدورف بین چند خطوط بردار مسطح. در Auto-Carto XII: مجموعه مقالات سمپوزیوم بین المللی کارتوگرافی به کمک کامپیوتر، شارلوت، کارولینای شمالی ؛ کنگره آمریکا در نقشه برداری و نقشه برداری و انجمن آمریکایی فتوگرامتری و سنجش از دور: Gaithersburg، MD، ایالات متحده آمریکا، 1995; جلد 4، ص 1-10. شابک -1-57083-019-3. [ Google Scholar ]
Joao، EM Gauses و عواقب تعمیم نقشه ; تیلور و فرانسیس: لندن، بریتانیا، 1998. [ Google Scholar ]

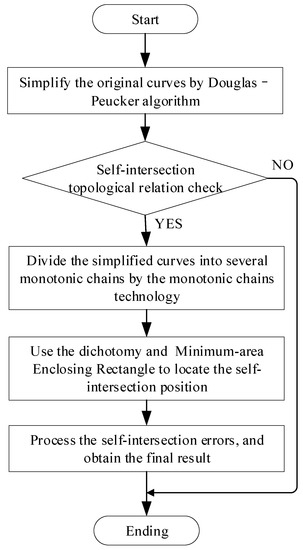
شکل 1. نمودار جریان روش پیشنهادی.

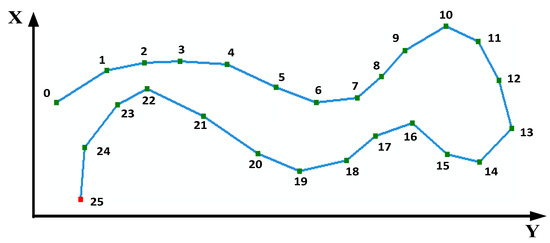
شکل 2. نمودار شماتیک زنجیره یکنواخت.

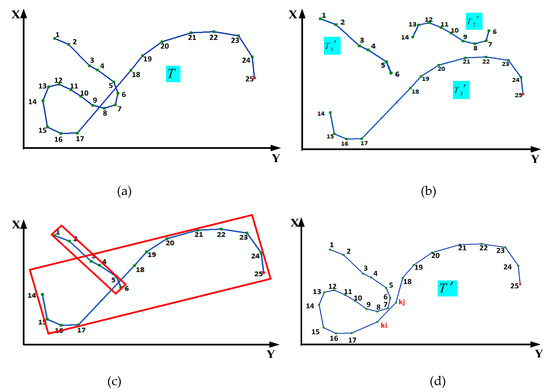
شکل 3. ( الف ) منحنی تیکه توسط الگوریتم D-P پردازش شده است. ( ب ) سه زنجیره یکنواخت تی1″، تی2″و تی3″پردازش شده توسط فناوری زنجیره یکنواخت؛ ( ج ) مستطیل محصور با حداقل مساحت (MER) از تی1″و تی3″; ( د ) نتیجه نهایی تی”.

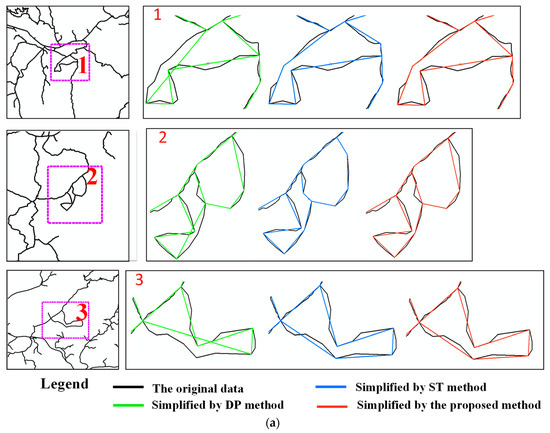
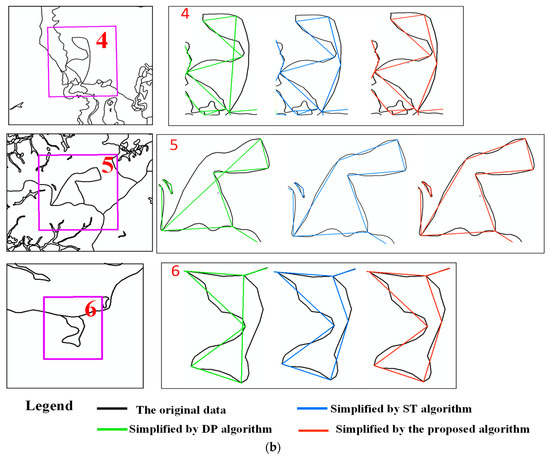
شکل 4. شش نتیجه ساده شده از سه روش کاربردی از دو گروه داده. ( الف ) سه مشکل خودتقاطع شناسایی شده از گروه اول داده ها. ( ب ) سه مشکل خودتقاطع شناسایی شده از گروه دوم داده ها. یادداشت ها: الگوریتم DP الگوریتم داگلاس-پیکر است که توسط داگلاس و پیکر [ 1 ] پیشنهاد شده است. الگوریتم ST یک الگوریتم ستاره شکل است که توسط وو و مارکز [ 23 ] پیشنهاد شده است.

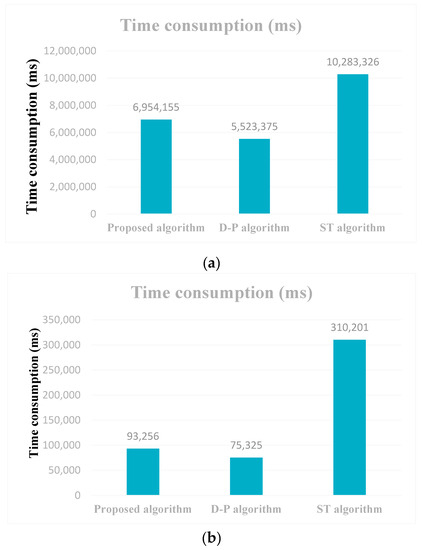
شکل 5. نتایج زمان مصرف. ( الف ) زمان مصرف داده های گروه اول؛ ( ب ) مصرف زمان گروه دوم از داده ها.

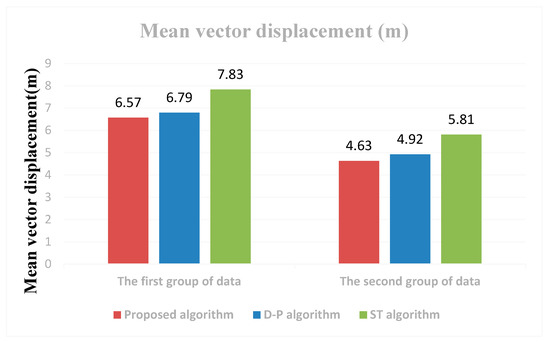
شکل 6. نتایج جابجایی بردار میانگین (m).

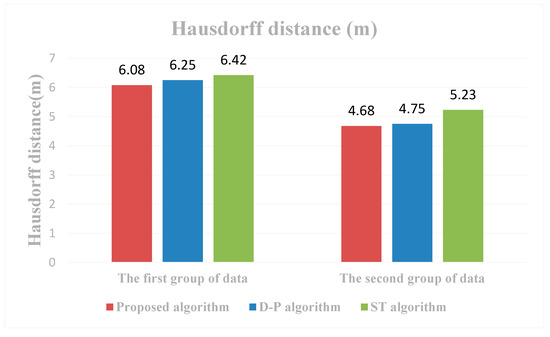
شکل 7. نتایج فاصله هاسدورف (m).

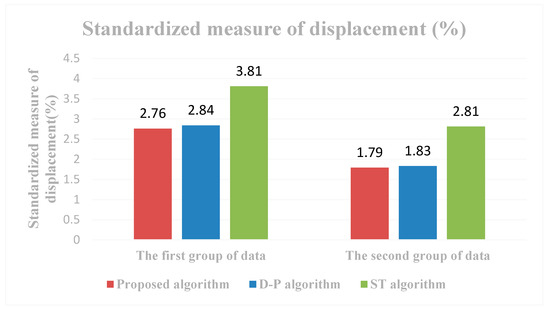
شکل 8. معیار استاندارد شده نتایج جابجایی (%).

مقالات داخلی و بین المللی

بدون دیدگاه

دیدگاهتان را بنویسید لغو پاسخ

برای نوشتن دیدگاه باید وارد بشوید.

مشاورین هوش پیروزی

خلاصه

کلید واژه ها:

1. معرفی

2. روش شناسی