الگوریتم نمایه سازی چهار درخت شبکه برای یک سیستم شبکه جهانی گسسته شش ضلعی

خلاصه

سیستم‌های شبکه جهانی گسسته شش ضلعی مدل‌های داده ترجیحی هستند که از ترکیب اطلاعات مکانی چندمنبعی پشتیبانی می‌کنند. تحقیقات مرتبط نگرانی های گسترده ای را در جامعه دانشگاهی برانگیخته است و الگوریتم های نمایه سازی سلسله مراتبی یکی از محورهای اصلی تحقیقات هستند. در این مقاله، ما یک الگوریتم برای نمایه سازی سلول یک منطقه فضایی حلقه ای بر اساس ساختار چهار درختی شبکه شش ضلعی (HLQT) و ویژگی های نمایه سازی پیشنهاد می کنیم. ابتدا یک الگوریتم نمایه سازی تک رزولوشن طراحی می کنیم که در آن نمایه سازی از درخت چهارگانه اولیه شروع می شود و با استفاده از عملیات کدگذاری حلقه را با حلقه گسترش می دهد و ساختار چهار درختی برای تسریع این فرآیند اعمال می شود. دوم، الگوریتم نمایه سازی سلسله مراتبی بر اساس نمایه سازی تک رزولوشن پیاده سازی می شود و یک مدل سلسله مراتبی هرمی ایجاد می شود. سرانجام، ما آزمایش های مقایسه ای را با الگوریتم های موجود انجام می دهیم. نتایج آزمایش‌ها نشان می‌دهد که بازده نمایه‌سازی تک سطحی الگوریتم پیشنهادی تقریباً دو برابر روش سنتی و بازده نمایه‌سازی سلسله مراتبی تقریباً 67 برابر روش سنتی است. این یافته ها امکان سنجی و برتری الگوریتم پیشنهادی در این مقاله را تأیید می کند.

کلید واژه ها:

سیستم شبکه جهانی گسسته ؛ شش ضلعی ; مشبک ; نمایه سازی چهار درخت

1. معرفی

در سال های اخیر، کاربرد داده های مکانی به طور فزاینده ای گسترده شده است. مقیاس، شکل، طرح ریزی و داده های مرجع این داده ها بسیار متنوع است، که تجمیع، پردازش و استخراج مجموعه داده ها را بسیار دشوار می کند [ 1 ]. تقاضایی برای ایجاد یک مدل تداعی داده جدید شناسایی شده است که از مکان‌های مکانی به‌عنوان کلید اصلی برای رمزگذاری و ادغام/فوتینگ اطلاعات مبتنی بر مکان چند منبعی استفاده می‌کند [ 2 ]. مدل سنتی سیستم اطلاعات جغرافیایی (GIS)، که در آن کارشناسان GIS داده ها را پردازش و یکپارچه می کنند، در مواجهه با جریان روزافزون داده ها ناپایدار است [ 1 ].

یک سیستم شبکه جهانی گسسته (DGGS) از یک روش خاص برای گسسته کردن زمین به طور یکنواخت استفاده می کند تا یک ساختار سلسله مراتبی شبکه یکپارچه و چند وضوحی را با استفاده از کدهای سلولی به جای مختصات جغرافیایی سنتی برای انجام عملیات داده تشکیل دهد [ 1 ، 2 ، 3 ، 4 ]. یک DGGS شبیه صفحه گسترده ای از سلول ها در سطح زمین است [ 2 ]. این رویکرد تجزیه و تحلیل به موقع داده ها، پردازش و استفاده مجدد را ترویج می کند و اطلاعات مناسب را برای استخراج چند منبع جغرافیایی حفظ می کند. علاوه بر این، این روش می‌تواند به سرعت و بدون در نظر گرفتن منابع داده‌های جغرافیایی جدید و شبکه‌های حسگر جدید با حجم بالا یا متفاوت، بدون در نظر گرفتن مقیاس، مبدا، وضوح، فرمت قدیمی، داده‌ها یا طرح‌ریزی، جذب کند.1 ، 2 ].

سیستم شبکه چهار ضلعی مسطح ارتباط مستقیمی با ساختار داده‌های چهار درختی دارد و الگوریتم نمایه‌سازی مبتنی بر مربعات مستقیماً قابل اجرا است [ 5 ]. با این حال، در یک سطح کروی، یک DGGS چهار ضلعی به شدت در عرض های جغرافیایی بالا تغییر شکل می دهد و سلول های شبکه در قطب شمال و جنوب به مثلث هایی تبدیل می شوند که باید متفاوت از سلول های دیگر رفتار شوند. علاوه بر این، چهارضلعی ها مجاورت یکنواختی را نشان نمی دهند، که پیچیدگی تحلیل فضایی را افزایش می دهد [ 6 ]. گورسکی و همکاران یک چارچوب شبکه جهانی گسسته چهار ضلعی به نام HEALPix (پیکسل‌بندی هم عرض مساوی سلسله مراتبی یک کره) برای گسسته‌سازی کارآمد و تجزیه و تحلیل/ترکیب سریع توابع تعریف‌شده بر روی یک کره ایجاد کرد [ 6 ]، 7 ]. GeoFusion کره زمین را به شش ناحیه تقسیم می‌کند، که چهار منطقه توسط شبکه‌های مستطیلی بین 45 درجه شمالی و جنوبی و دو منطقه توسط شبکه‌های مثلثی در عرض‌های جغرافیایی بالا پوشیده شده‌اند [ 8 ]. سیستم SEE-Grid استرالیا (Solid Earth and Environment Grid) بر اساس مکعب هایی با استفاده از شبکه های چهار ضلعی ساخته شده است و عمدتاً برای نظارت بر محیط زیست استفاده می شود [ 9 ]. برناردین و همکاران یک سیستم شبکه چهار ضلعی به نام Crusta ساخت که از یک سه ضلعی لوزی شکل 30 وجهی شروع شد تا از داده ها و تصاویر توپوگرافی با وضوح بالا پشتیبانی کند [ 10 ]. لامبرز و همکاران نقشه مکعب بیضی سیستم شبکه چهار ضلعی (ECM) را ایجاد کرد که از اصلاح یک به چهار در وجه مکعبی استفاده می کند که یک زمین بیضی شکل را در بر می گیرد [ 11]. چنگ و همکاران شبکه تقسیم مختصات جغرافیایی را با کدگذاری عدد صحیح یک بعدی بر روی 2nطرح کدگذاری شبکه درختی (GeoSOT)، که عمدتاً برای سازماندهی و مدیریت داده های سنجش از دور استفاده می شود [ 12 ].

شبکه های مثلثی می توانند با مدل چهار درختی ارتباط برقرار کنند و راندمان رندر بالایی برای تجسم داشته باشند. با این حال، رابطه مجاورت واحد به طور قابل توجهی در موقعیت‌های مختلف تغییر می‌کند، که به جستجوی همسایه پیچیده و الگوریتم‌های تحلیل فضایی نیاز دارد. داتون مدل مش مثلثی چهارگوش (QTM) را بر اساس ساختار هشت وجهی منظم پیشنهاد کرد و یک روش نمایه سازی سلسله مراتبی طراحی کرد [ 13 ]. سیستم ساختار داده های مکانی سلسله مراتبی Goodchild (HSDS) نیز با استفاده از یک ساختار هشت وجهی با اصلاح مثلثی یک به چهار تخمین های جهانی را ارائه می دهد [ 14 ]. بارتولدی و گلدزمن یک مکانیسم نمایه سازی جهانی متوالی بر اساس سلسله مراتب مثلث کروی ایجاد کردند [ 15 ]]. ژائو شبکه چهار درختی منحط (DQG) را پیشنهاد کرد و طرح کدگذاری مربوطه و الگوریتم جستجوی همسایه را طراحی کرد [ 16 ].

سازه های شش ضلعی به دلیل مزایایی که دارند مورد توجه زیادی قرار گرفته اند. در میان سه نوع چند ضلعی منتظم که صفحه را کاشی می کنند (مثلث، چهارگوش و شش ضلعی)، شش ضلعی ها فشرده ترین هستند [ 3 ] و بیشترین وضوح زاویه ای را ارائه می دهند [ 17 ]. بر خلاف شبکه های مربع و مثلث، شبکه های شش ضلعی مجاورت یکنواخت دارند، به این معنی که هر سلول شش ضلعی دارای شش همسایه است و همه همسایه ها با شش ضلعی یک لبه مشترک دارند و مراکزی دقیقاً به همان اندازه از مرکز آن فاصله دارند [ 3 ]. وینس سیستم شبکه جهانی گسسته شش ضلعی هشت وجهی 3 دیافراگم را ایجاد کرد، که برای آن از نمایه سازی مبتنی بر مختصات بر اساس مختصات باریسنتریک برای نمایه سازی سلول ها استفاده می شود [ 18 ]]. بن و همکاران مدل را برای توسعه سیستم نمایه سازی سیستم شبکه جهانی گسسته شش ضلعی 4 دیافراگم هشت وجهی [ 19 ] بهبود داد. پترسون، وینس و همکاران طرح نمایه سازی سلسله مراتبی PYXIS را برای شش ضلعی 3 دیافراگم مساوی اسنایدر (ISEA3H) طراحی کرد، یک الگوریتم تبدیل فوریه را پیاده سازی کرد و نرم افزار یکپارچه سازی داده های مکانی را برای پردازش و تجزیه و تحلیل بلادرنگ مجموعه داده های چند منبعی توسعه داد [ 20 ، 21 ، 22 ]. سحر یک رویکرد مبتنی بر سلسله مراتب مشابه را با استفاده از نمایه سازی هرمی مبتنی بر مختصات بر اساس سیستم های مختصات شش ضلعی پیشنهاد کرد [ 23 ]. با این حال، طرح هرمی تنها برای یک تفکیک پذیری واحد توسعه داده شد [ 1]. سحر مفهوم یک سیستم شبکه شش ضلعی با دیافراگم مختلط را پیشنهاد کرد که چندین دیافراگم را ترکیب می کند. او طرح نمایه سازی مکان مرکزی (CPI) [ 24 ] را طراحی کرد و الگوریتم پایه را در DGGRID [ 25 ، 26 ] پیاده سازی کرد. تانگ و همکاران ساختار متوازن چهار ضلعی شش ضلعی (HQBS) [ 27 ] را پیشنهاد کرد و روابط سلسله مراتبی را بین سطوح مختلف شبکه های شش ضلعی بر روی مثلث ایکو وجهی ایجاد کرد. با این حال، زمانی که نرمال‌سازی کد با شکست مواجه می‌شود، عملیات اغلب به عقب برمی‌گردند که منجر به کارایی پایین می‌شود [ 28 ]. مهدوی امیری و همکاران. یک طرح نمایه سازی و تجسم سلسله مراتبی برای انواع شبکه های شش ضلعی بر اساس یک سیستم مختصات ویژه بر روی سطح الماس طراحی کرد [ 29 ]]. مهدوی امیری [ 30 ] برای بهره‌گیری از مزایای انواع شبکه‌ها، یک روش تبدیل بین شبکه‌های شش ضلعی، چهار ضلعی و مثلثی را برای ذخیره و رندر بهتر پیشنهاد کرد. شش ضلعی ها همخوانی نشان نمی دهند، و بنابراین غیرممکن است که دقیقاً یک شش ضلعی را به شش ضلعی های کوچکتر تجزیه کنیم [ 3 ]. بنابراین، اعمال الگوریتم‌های نمایه‌سازی سلسله‌مراتبی چند رزولوشن کارآمد و ساختارهای داده‌ای چهار درختی روی یک DGGS شش ضلعی به طور مستقیم دشوار است. برای پرداختن به این موضوع، وانگ و همکاران. طرح رمزگذاری ساختار چهار درختی شبکه شش ضلعی (HLQT) را بر اساس تئوری اعداد ریشه پیچیده [ 31 ] ایجاد کرد.]. یک ساختار داده چهار درختی برای نمایش سلسله مراتبی و عملیات اساسی با شبکه های شش ضلعی استفاده شد، اما تحقیقاتی در مورد نمایه سازی سلسله مراتبی هنوز انجام نشده است.

به طور خلاصه، مطالعات اخیر در مورد مدل سازی شبکه و نمایه سازی کد برای DGGS ها پیشرفت زیادی داشته است. DGGS های چهار ضلعی و مثلثی همبستگی مستقیمی با ساختار داده های چهار درختی دارند. الگوریتم‌های نمایه‌سازی کارآمد موجود را می‌توان مستقیماً تغییر داد، اما این نوع DGGSها ویژگی‌های مجاورت یکنواخت ندارند و تغییر شکل سلول در عرض‌های جغرافیایی بالا شدید است. بنابراین، چنین روش هایی برای سازماندهی و پردازش داده های مکانی جهانی مناسب نیستند. شبکه های شش ضلعی دارای خواص مجاورت یکنواخت ایده آل و مزیت پوشش یکنواخت کل جهان هستند. با این حال، آنها ویژگی های خود شباهت را ندارند. بنابراین، اکثر نتایج را نمی توان به ساختار داده های چهار درختی تعمیم داد. با هدف رفع خلأهای پژوهشی فعلی، این مقاله یک الگوریتم نمایه سازی بر اساس HLQT طراحی می کند که نمایه سازی را با استفاده از عملیات کد و ویژگی های ساختاری درخت چهارگانه تسریع می کند. کارایی و قابلیت اطمینان طرح با آزمایش‌های مقایسه تایید می‌شود.

2. طرح رمزگذاری HLQT

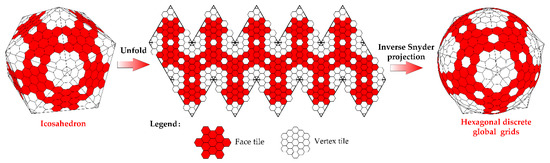
وانگ و همکاران یک طرح رمزگذاری مسطح HLQT [ 31 ] ایجاد کرد. وینس و همکاران [ 32 ] و بن و همکاران. [ 28 ] دیافراگم 3 DGGS را به دو بخش (کاشی راس و کاشی چهره) با توجه به مرز ایکوسادرون تقسیم کرد و به کدگذاری شبکه شش ضلعی با دیافراگم جهانی 3 دست یافت. با توجه به این مفهوم، یک طرح رمزگذاری HLQT ایکو وجهی نیز می تواند ایجاد شود [ 33 ]، و یک طرح ریزی چند وجهی اسنایدر برای نگاشت سطح ایکو وجهی به کره استفاده می شود [ 34 ]. ساختار کاشی در شکل 1 نشان داده شده است .

در شکل 1 ، ساختار کاشی صورت روی وجه مثلث ایکوس وجهی یکسان است و کاشی رأس بر اساس کاشی وجهی، یک برداشت جزئی و انبساط است. ما مرکز سلول را به عنوان نقطه شبکه تعریف می کنیم تا سلول را به طور معادل جایگزین کنیم و اجازه دهیم ℙn(n≥1)نقاط شبکه سطح را نشان می دهد n. ما نقاط شبکه سطح اول را همانطور که در شکل 2 الف نشان داده شده است، تعریف می کنیم. هر نقطه شبکه چهار نقطه شبکه فرزند ایجاد می کند و ℙn(n>2)به نوبه خود تولید می شوند. همانطور که در شکل 2 ب نشان داده شده است، ℙ2با ایجاد چهار نقطه شبکه فرزند از ℙ1به طور مستقل، و بنابراین ساختار سلسله مراتبی یک درخت چهارگانه را تشکیل می دهد.

همانطور که در شکل 2 الف نشان داده شده است، در صفحه مختلط، اجازه می دهیم ω=12+32من(جایی که منیک واحد خیالی است) و ℙ1با پنج مجموعه زیر نمایش داده می شود ( L”j(1≤j≤5)):

L”1={0،ωه|1≤ه≤6};
L”2={2ωه|1≤ه≤6};
L”3={ωه+ω(ه+1)%6|1≤ه≤6};
L”4={2α|α∈L3″}; و
L”5={2ωه1+ωه2||ه1-ه2|=1،1≤ه1،ه2≤6یا ه1=1،ه2=6یا ه1=6،ه2=1}،ه،ه1،ه2∈ز.

علاوه بر این، ما اجازه می دهیم ω”=-12+32من، L={0،ω”،ω”2،ω”3}. پس از یک اثبات دقیق، مجموعه نقاط شبکه سیستم شبکه شش ضلعی 4 دیافراگم را می توان به صورت منحصر به فرد به صورت زیر نشان داد:

{ℙn=ℙ1+∑j=2n12jLℙ1=12L”

(1)

در فرمول (1) L”=L”1∪L”2∪L”3∪L”4∪L”5. فرمول (1) نشان می دهد که سیستم شبکه شش ضلعی دیافراگم 4 اساساً یک سیستم شمارش است که در آن شبکه ها اعدادی هستند با شکل خاصی در میدان مختلط و دقیقاً مشابه اعداد باینری و اعشاری در فیلد اعداد واقعی هستند. سیستم شمارش دارای مقدار باینری دو است و مجموعه ارقام هستند L”و L. برای ایکس∈ℙn، فرم خاص در فرمول (2) نشان داده شده است.

ایکس=12ل1+14ل2+⋯+12nلn (ل1∈L”،ل2،⋯،لn∈L)

(2)

مشابه یک عدد اعشاری، با حذف توان توان، فرمول (2) را می توان همانطور که در فرمول (3) نشان داده شده است بیان کرد.

ایکس≡.ل1ل2⋯لn (ل1∈L”،ل2،⋯،لn∈L)

(3)

جایگزین می کنیم ل1در فرمول (3) طبق قوانین زیر:

(1): برای ل1∈L”1، اجازه دهید ل1→ه(1≤ه≤6);
(2): برای ل1∈L”2، اجازه دهید ل1→100ه(1≤ه≤6);
(3): برای ل1∈L”3، ل1→10((ه+1)%6)(1≤ه≤6);
(4): برای ل1∈L”4، ل1→100ل”1(ل”1ارقام کد پس از جایگزینی هستند α) و
(5): برای ل1∈L”5، ل1→100ه1+ه2.
(6): به طور مشابه، ما جایگزین می کنیم لj(2≤j≤n)با لj=ωه→ه(1≤ه≤3).
(7): مجموعه دیجیتال L”با مجموعه رقم کد شده جایگزین می شود E”={ 0،1،2،3،4،5،6،10،20،30، 40،50،60،100،200،300،400،500،600،106،601،201،102،302،203،403،304،504،405،605، 506،1000،2000،3000،4000،5000،6000}، و مجموعه دیجیتال Lبا مجموعه رقم کد شده جایگزین می شود E={0،1،2،3}. شناسه منحصر به فرد برای ایکسدر فرمول (4) نشان داده شده است.

ایکس=ه1ه2⋯هn (ه1∈E”،هj∈E(2≤j≤n))

(4)

با توجه به اصل جمع بردار ریشه پیچیده، جدول اضافه کد تعریف می شود. نمونه ای از یک عملگر اضافه کدگذاری در شکل 3 نشان داده شده است .

3. الگوریتم نمایه سازی

روش اصلی نمایه سازی فضایی این است که کل فضا را به مناطق جستجوی مختلف تقسیم کرده و موجودیت های فضایی را در این مناطق به ترتیب خاصی پیدا کنید. کاشی‌های صورت و کاشی‌های راس در HLQT کره زمین را به مناطق جستجوی مختلف تقسیم می‌کنند و از رویکرد پردازش جداگانه برای نمایه‌سازی استفاده می‌شود. تمرکز این مقاله یک الگوریتم نمایه سازی تک سطحی و سلسله مراتبی مبتنی بر کاشی است. با توجه به معادل بودن طرح‌های کدگذاری بین کاشی‌ها، چنین الگوریتم نمایه‌سازی برای طیف وسیعی از مناطق، از جمله کل کره زمین قابل اجرا است [ 28 ].

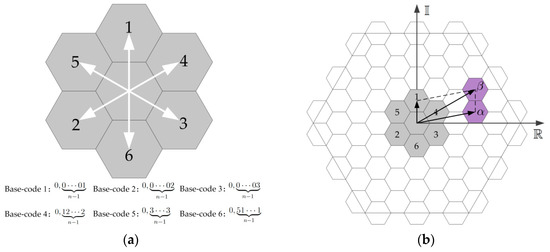
عملیات اضافه نمایه سازی از عملیات ممیز شناور جلوگیری می کند و کارایی سلول های جستجو را بهبود می بخشد. بر اساس این روش، این مقاله یک ساختار افزودن کد متشکل از کد سلول مرکزی یک کاشی و شش کد سلول اطراف (که از این پس به عنوان کدهای پایه، شماره‌های 1-6 نامیده می‌شود) طراحی می‌کند. این کدها به ساختار سلسله مراتبی مربوط می شوند. ساختار اضافه کد سطح n در شکل 4 الف نشان داده شده است. طبق طرح عملیات کدگذاری HLQT، سلول های مجاور هر سلول در یک کاشی را می توان با جمع محاسبه کرد. همانطور که در شکل 4 ب، سلول مجاور نشان داده شده استβاز αدر یک کاشی را می توان با اضافه کردن کد پایه 1 به دست آورد α، و کدهای سلول های اطراف را می توان به طور مشابه با جمع محاسبه کرد.

3.1. الگوریتم نمایه سازی تک رزولوشن

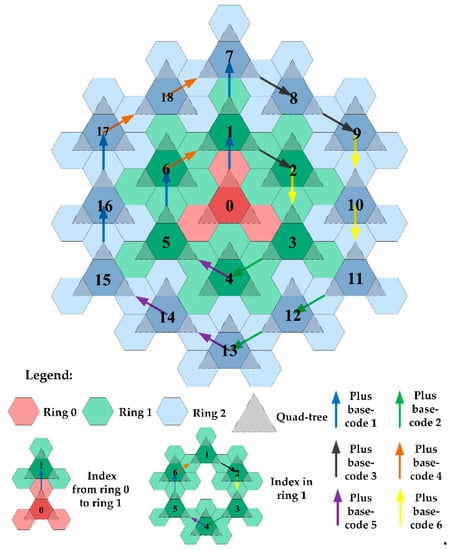
ما یک الگوریتم نمایه سازی طراحی می کنیم که از یک درخت چهارگانه آغاز می شود و حلقه به حلقه به بیرون رشد می کند. عملیات افزودن کد بین درخت های چهارگانه مجاور استفاده می شود و فقط آخرین رقم سلول های درخت باید تغییر کند که به طور قابل توجهی کارایی نمایه سازی را بهبود می بخشد. ساختار شاخص در شکل 5 نشان داده شده است .

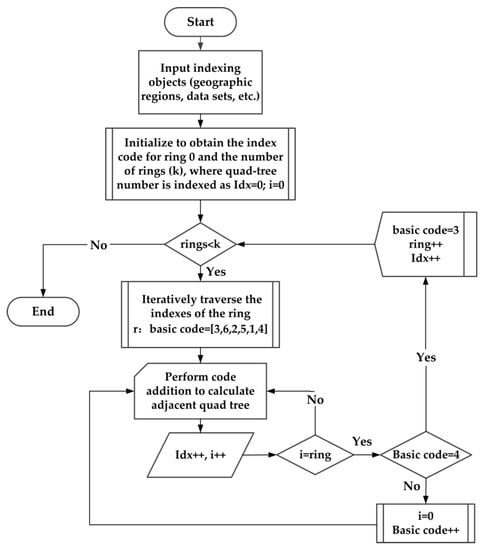
همانطور که در شکل 5 نشان داده شده است ، الگوریتم نمایه سازی به طور کامل از ساختار چهار درختی HLQT استفاده می کند. حلقه 0 چهار درخت نمایه سازی اولیه است و سلول ها طبق یک الگوریتم خاص حلقه به حلقه جستجو می شوند. به جز حلقه 0، حلقه rاز (6✕ r) چهار درخت. فرآیند نمایه سازی به دو بخش تقسیم می شود: نمایه سازی بین حلقه ها و نمایه سازی در یک حلقه. الگوریتم نمایه سازی خاص چهار مرحله را به شرح زیر انجام می دهد:

(1): اشیاء (مناطق جغرافیایی، مجموعه داده ها و غیره) را که باید نمایه شوند را وارد کنید. سپس داده ها را مقداردهی اولیه کنید تا شاخص های حلقه 0 و تعداد حلقه ها را بدست آورید که به صورت نشان داده شده است. ک.
(2): حلقه بعدی را نمایه کنید. اولین درخت چهارگانه حلقه بعدی با افزودن کد پایه 1 به درخت چهارگانه حلقه قبلی به دست می آید. در شکل 5 ، نمایه سازی درخت چهارگانه اولیه به درخت اول و نمایه سازی درخت چهارگانه اول به درخت هفتم نمونه هایی از نمایه سازی بین حلقه ها هستند.
(3): از شاخص های حلقه عبور کنید r. هر حلقه باید جابجایی های چهار درختی را در شش جهت مختلف تکمیل کند که مربوط به شش کد اصلی ساختار جمع کد است. به عنوان مثال، برای حلقه اول، انتقال هستند 1→2،2→3،3→4،4→5،5→6،6→1. توجه داشته باشید که برای حلقه r، عملیات جمع در هر جهت انجام می شود rبار. همانطور که در شکل 4 نشان داده شده است ، در حلقه 1، نمایه سازی درخت چهارگانه اول به درخت دوم نیاز به یک اضافه دارد و برای حلقه 2، نمایه سازی چهار درخت هفتم به درخت نهم نیاز به دو اضافه دارد.
(4): مرحله (3) را در حالی که تعداد حلقه ها < ک.

با در نظر گرفتن پکن، چین، به عنوان مثال، سطح سیستم شبکه 13 است. کدهای سلولی طبق الگوریتم نمایه سازی فوق به دست می آیند. نتایج نمایه سازی را در چهار لحظه مختلف ثبت می کنیم و آنها را به شبکه هایی تبدیل می کنیم که در شکل 6 نشان داده شده است. کل فرآیند الگوریتم در شکل 7 نشان داده شده است .

3.2. الگوریتم نمایه سازی سلسله مراتبی

الگوریتم نمایه سازی منطقه فضای حلقه ای در بالا پیاده سازی شده است، اما این رویکرد تنها برای یک تفکیک پذیری واحد است و هیچ ارتباطی بین سطوح شبکه وجود ندارد. در عملیات با وضوح چندگانه، مانند بزرگنمایی داده ها، تبدیل بین شبکه های درشت و ریز در زمان واقعی ضروری است و یک الگوریتم نمایه سازی سلسله مراتبی کارآمد نقش مهمی در این فرآیند ایفا می کند. این مقاله سطوح مختلف نمایه سازی را بر اساس نمایه سازی منطقه حلقه ای تک سطحی پیاده سازی می کند. الگوریتم خاص مراحل زیر را به کار می گیرد:

(1): یک شی (مجموعه داده یا تقسیم اداری) را وارد کنید و آن را طبق الگوریتم نمایه سازی تک سطحی ( شکل 7 ) در وضوح اولیه شبکه فهرست کنید.
(2): هنگام انجام یک عملیات بزرگنمایی برای شی، هر سلول در وضوح اولیه یک درخت چهارگانه ایجاد می کند که شامل چهار سلول فرزند است. سپس، سلول به یک سطح بالاتر نمایه می شود، همانطور که در شکل 8 ب نشان داده شده است.
(3): با مرحله (2) ادامه دهید تا شبکه های بالاترین سطح همه ایندکس شوند.
(4): هنگامی که عملیات بزرگنمایی برای یک شی انجام می شود، هر چهار درخت از شبکه با وضوح بالا به سلول والد سطح قبلی منحط می شود و این روند تکراری تا زمانی ادامه می یابد که درشت ترین شبکه ها فهرست شوند.

الگوریتم نمایه سازی سلسله مراتبی اساساً یک الگوریتم چهار درختی است که فقط شامل جمع و حذف آخرین رقم رمزگذاری شده است و نیازی به عملیات جمع کردن کامل کد نیست. تنها زمانی که شاخص در وضوح اولیه تعیین می شود، به یک الگوریتم نمایه سازی تک سطحی نیاز است.

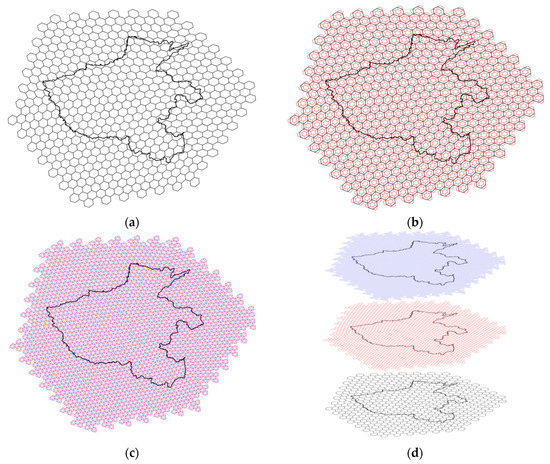
نمایه سازی سطوح 10 تا 11 و 12 با مثالی از استان هنان، چین انجام می شود، همانطور که در شکل 8 b,c نشان داده شده است. یک مدل شاخص هرمی بین سطوح برای نمایه سازی شبکه ای از درشت به ریز و از ریز به درشت شکل می گیرد، همانطور که در شکل 8 d نشان داده شده است.

4. آزمایش ها و تجزیه و تحلیل

4.1. نمایه سازی داده ها با دامنه وسیع

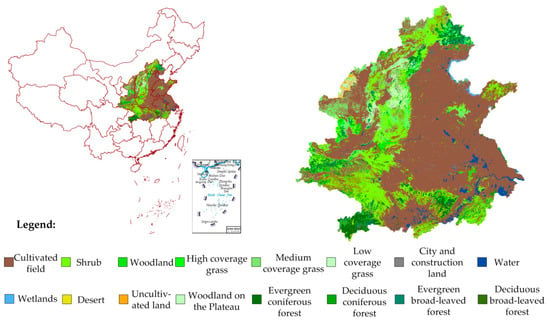
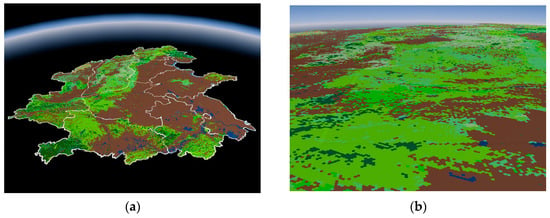
داده های تجربی مورد استفاده در این مقاله شامل داده های شبکه پوشش گیاهی چین است که از مرکز داده های علوم منابع و محیط زیست آکادمی علوم چین در سال 2000 به دست آمده است. داده ها در طرح مخروطی مساحت آلبرس هستند و اندازه هر شبکه 1 است. x 1 کیلومتر ما ده استان و شهر در چین (استان های هبی، پکن، تیانجین، شاندونگ، جیانگ سو، آنهویی، هوبی، شانشی، شانشی و هنان) را برای آزمایش انتخاب کردیم. همانطور که در شکل 9 نشان داده شده است، 1204186 نقطه نمونه برداری وجود دارد .

ما یک آزمایش مقایسه ای را برای تأیید کارایی الگوریتم نمایه سازی پیشنهادی طراحی می کنیم. نشان داده شده است [ 31 ] که کارایی عملیات افزودن کد HLQT بیشتر از HQBS و PYXIS است. بنابراین، الگوریتم نمایه سازی ارائه شده در این مقاله کارآمدتر از HQBS و PYXIS است زیرا ما از ساختار کدگذاری درخت چهار برای تسریع عملیات شاخص استفاده می کنیم. بنابراین، ما در اینجا مقایسه کارایی انجام نمی دهیم.

مهدوی امیری و همکاران. [ 29 ] یک طرح نمایه سازی سلسله مراتبی به نام “نقشه های اتصال” برای شبکه های شش ضلعی طراحی کرد. این طرح دو وجه مثلثی ایکوسادرون ها را به عنوان الماس ترکیب کرد و از الماس ها به عنوان شی اصلی برای پالایش دیافراگم 3، 4 یا 7 استفاده کرد. کار در این مقاله از ساختار کاشی روی ایکوس وجهی به عنوان شیء اصلی اصلاح استفاده می کند ( شکل 1) طرح پالایش هر کاشی یکسان است و دیافراگم پالایش 4 است. نقشه‌های اتصال پیشرفت‌های قابل‌توجهی در نمایه‌سازی سلول‌های همسایگی و سلسله مراتبی داشتند و ساختار الماس تجسم را تسهیل می‌کرد. عملیات جستجوی همسایگی به سادگی با افزودن بردارهای همسایگی به شاخص یک شش ضلعی انجام شد و جستجوی سلسله مراتبی سلول با ضرب R یا R (اسکالر) در شاخص یک سلول مشخص (که در آن R نشان دهنده یک چرخش، مقیاس بندی یا ماتریس ترجمه است) انجام شد. . در طرح نمایه سازی پیشنهادی، سلول های مجاور را می توان به سرعت با افزودن کد، همانطور که در شکل 4 نشان داده شده است، به دست آورد . جستجوی سلسله مراتبی سلول تنها نیاز به افزایش یا کاهش یک رقمی در انتهای کد دارد.

سحر از یک (من،j)طرحی برای نمایه های سلول های شبکه شش ضلعی در پروژه منبع باز DGGRID [ 25 ، 26 ]. جستجوی مجاور مزیت بر اساس کدهای ردیف و ستون است و این مقایسه می تواند اثربخشی طرح نمایه سازی پیشنهادی را منعکس کند. سحر مثلث های ایکو وجهی را در 10 چهارگوش ترکیب کرد تا هر چهارگوش را جداگانه پردازش کند. طرح نمایه سازی حداقل منطقه جغرافیایی چهار ضلعی برون سپاری شده را در هر چهار ضلعی ایجاد می کند (مثال در شکل 10 استان هنان، چین است)، همانطور که در شکل 10 نشان داده شده است.

مراحل اساسی در الگوریتم نمایه سازی DGGRID را می توان به صورت زیر خلاصه کرد.

(1) داده ها را از طول و عرض جغرافیایی به کد تبدیل کنید q،(من،j)(جایی که qعدد چهار ضلعی است) و منتهیات آن را محاسبه کنید منو jبدست آوردن (منمترمنn،منمترآایکس)و (jمترمنn،jمترآایکس)مختصات پایین سمت چپ حداقل چهارضلعی برون سپاری شده به صورت نشان داده می شود orمنgمنn(منمترمنn،jمترمنn)، و مختصات بالا سمت راست به صورت نشان داده می شود توپپهrrمنgnتی(منمترآایکس،jمترآایکس)برای محدوده داده داده شده

(2) داده ها را از طول و عرض جغرافیایی به (من،j)دوباره، و محور مختصات را ترجمه کنید تا محدوده شاخص را باریک کنید و حداقل چهارضلعی برون سپاری شده را به دست آورید، همانطور که در شکل 10 نشان داده شده است. فرمول (5) برای به دست آوردن کد جدید است:

{من=من-orمنgمنn.منجی=j-orمنgمنn.j

(5)

(3) کوچکترین کواد برون سپاری شده را فهرست کنید و آن را به کدهای واقعی در سیستم مختصات اصلی تبدیل کنید.

برای اطمینان از مقایسه های منصفانه و عینی، پارامترهای موقعیت یابی ایکو وجهی [ 3 ] V0(15.381درجهن،149.75درجهE)،α=-86.669درجهبرای اطمینان از عدم عبور شبکه ها از سطح انتخاب می شوند. زمان نمایه سازی در قطعنامه های مربوطه ثبت می شود. محاسبات ده بار تکرار می شوند و سپس میانگین می شوند و تعداد سلول های نمایه سازی در هر سطح محاسبه می شود. در نهایت، کارایی به عنوان تعداد سلول های نمایه شده در هر میلی ثانیه تعیین می شود. نتایج در جدول 1 و جدول 2 نشان داده شده است و منحنی های مقایسه بازده در شکل 11 و شکل 12 نشان داده شده است. هر برنامه برای نسخه منتشر شده کامپایل شده بود و روی یک دسکتاپ کار می کرد (CPU شش هسته ای Core i7-8700@3.20 گیگاهرتز، رم 8G WDC WDS480G2G0A-00JH30 480G SSD؛ Windows 7 X64 Ultimate SP1؛ نرم افزار توسعه: Microsoft Visual C2+d 5).

نتایج آزمایش مقایسه نشان می دهد که کارایی الگوریتم پیشنهادی بیشتر از الگوریتم DGGRID است. میانگین بازده نمایه سازی تک سطحی تقریباً دو برابر الگوریتم DGGRID است و میانگین بازده نمایه سازی سلسله مراتبی تقریباً 67 برابر بیشتر است. دلایل این نتایج به شرح زیر است:

(1): روش رمزگذاری DGGRID استفاده می کند (من،j)اعداد و مزیت اصلی آن جستجوی مجاورت است [ 4 ]. با این حال، در مورد نمایه سازی سلولی برای مناطق، از آنجایی که کدها باید به ترتیب فهرست شوند، یک چهارضلعی کوچک برون سپاری، همانطور که در شکل 10 نشان داده شده است ، باید تعیین شود تا محدوده نمایه سازی را برای کاهش مصرف حافظه، که نیازمند محاسبات تبدیل های متعدد است، محدود کند. در کاهش راندمان
(2): الگوریتم پیشنهادی نیازی به انجام نمایه سازی متوالی ندارد و فقط باید مختصات مرکزی و محدوده شاخص شی را “دانست”. بنابراین، عملیات کد و ساختار کدگذاری درخت چهارگانه، روند نمایه سازی را تسریع می کند. همانطور که در شکل 11 نشان داده شده است، با افزایش سطح، فرکانس افزودن کد افزایش می‌یابد و طول رقم کد طولانی‌تر می‌شود و در نتیجه کارایی کاهش می‌یابد، همانطور که در شکل 11 نشان داده شده است.
(3): یکی از ویژگی های اصلی الگوریتم نمایه سازی سلسله مراتبی در این مقاله، ایجاد روابط چهار درختی بین سطوح است. هنگام نمایه سازی از طریق رویکرد پیشنهادی، فقط باید یک رقم را در انتهای کد اضافه یا کم کنیم، در حالی که روش DGGRID از اطلاعات سلسله مراتبی [ 25 ] استفاده نمی کند و حداقل محدوده چهار ضلعی سطح بعدی باید محاسبه شود. علاوه بر این، همانطور که در جدول 2 نشان داده شده است، تعداد سلول های نمایه سازی زیاد است . بنابراین، همانطور که در شکل 12 الف نشان داده شده است، الگوریتم پیشنهادی برتر است ، اما با افزایش سطح، طول کد HLQT افزایش می‌یابد و در نتیجه هزینه پردازش رقم کد بالاتر می‌رود. در نتیجه، همانطور که در شکل 12 نشان داده شده است، نسبت کارایی کاهش می یابدب
(4): برای پردازش داده در مقیاس بزرگ، از جمله جهانی، در کاربردهای عملی، پردازش سطح جزئیات (LOD) اغلب اتخاذ می شود [ 35 ]. محدوده مناطق با وضوح بالا نزدیک به دیدگاه کوچک است و در نتیجه تعداد کمی سلول ایجاد می شود. وضوح دور از دیدگاه پایین است، و الگوریتم پیشنهادی بازده نمایه سازی بالاتری در زمانی که وضوح شبکه پایین است، دارد. بنابراین، الگوریتم در این مقاله در کاربردهای عملی سودمند است.

نتایج نمایه سازی در شکل 13 نشان داده شده است. هنگامی که سطح شبکه روی 13 تنظیم می شود [ 25 ]، وضوح معادل با داده های اصلی است ( شکل 9 ).

4.2. نمایه سازی داده ها با دامنه کوچک

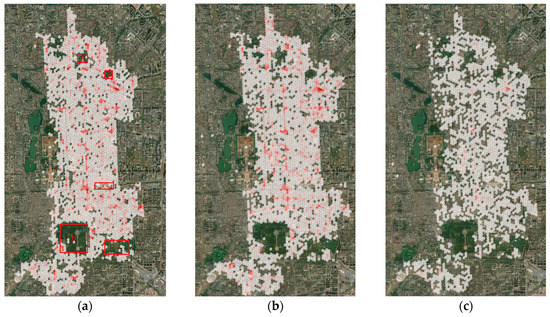
به طور مشابه، الگوریتم نمایه سازی ما را می توان برای نمایه سازی داده های محدوده کوچک، مانند داده های اشتراک دوچرخه در شهرها، به کار برد. اگرچه دامنه داده های به اشتراک گذاری دوچرخه کوچک است، داده ها به طور مداوم به روز می شوند و در نتیجه حجم زیادی از داده ها به وجود می آید. بنابراین، تجزیه و تحلیل به موقع و موثر داده ها از اهمیت ویژه ای برخوردار است. در این آزمایش، داده‌های اشتراک‌گذاری دوچرخه از ناحیه Dongcheng در پکن توسط آزمایشگاه مهندسی Beijing از ناوبری Beidou و فناوری LBS [ 36 ] ارائه شد.]. دوره‌های مختلف یک روز کاری را برای آزمایش‌ها انتخاب می‌کنیم و سطح شبکه روی 17 تنظیم می‌شود. سپس مختصات طول و عرض جغرافیایی داده‌ها را به کد تبدیل می‌کنیم و تعداد دوچرخه‌ها در هر سلول شمارش می‌شود. در نهایت، با توجه به تعداد دوچرخه‌های موجود، عمق رنگ‌های متفاوتی به سلول‌ها اختصاص می‌یابد (هرچه تعداد دوچرخه‌ها بیشتر باشد، رنگ تیره‌تر است). ما کدها را با استفاده از الگوریتم نمایه سازی تک رزولوشن خود نمایه می کنیم ( شکل 5 ) و داده های شش ضلعی را بر روی نقشه وب ارائه می کنیم. نتایج آزمایش ها در شکل 14 نشان داده شده است.

تجزیه و تحلیل زیر را می توان از آزمایش های فوق بدست آورد:

(1): تعداد دوچرخه ها در ساعات شلوغی ( شکل 14 الف، ب) به طور قابل توجهی بیشتر از عصرها ( شکل 14 ج) است، زیرا مردم برای رفت و آمد به محل کار خود نیاز به استفاده از دوچرخه دارند، اما دوچرخه معمولاً در شب لازم نیست.
(2): توزیع دوچرخه در دوره های زمانی مختلف اساساً یکسان است. بنابراین، شرکت ها باید دوچرخه ها را در مناطقی با رنگ های تیره اضافه کنند، همانطور که در شکل 14 نشان داده شده است.
(3): پارک کردن در مناطق A تا E ( شکل 14 a) ممنوع است. در نتیجه دوچرخه های کمی در این مناطق وجود دارد. اگر دوچرخه در این مناطق وجود دارد، شرکت باید سریعا آنها را پیدا و حذف کند.

در حالی که در نمایه سازی و تجزیه و تحلیل چنین داده های پویا و متغیری استفاده می شود، شش ضلعی ها انتخاب مطلوبی هستند. شش ضلعی ها می توانند خطای کوانتیزاسیون ایجاد شده هنگام حرکت دوچرخه ها در شهر را به حداقل برسانند. از آنجایی که لبه یا طول تماس در هر طرف یکسان است، مرکز هر همسایه به یک اندازه فاصله دارد. یافتن همسایگان با استفاده از یک شبکه شش ضلعی ساده تر است. الگوریتم نمایه سازی شش ضلعی ما جستجوی همسایگی را با عملیات اضافه کد و ساختار کمربندی چهار درختی تسریع می بخشد، که برای نمایه سازی داده های پویا و تجزیه و تحلیل بصری مفید است. علاوه بر این، الگوریتم ما یک منطقه حلقه‌دار شبیه به یک دایره را فهرست‌بندی می‌کند که به ما امکان می‌دهد شعاع‌ها را به راحتی تقریب کنیم و برای جستجوی دوچرخه‌های اطراف مفید است.

5. نتیجه گیری و مسیرهای تحقیقاتی آتی

در این مقاله، ما یک الگوریتم نمایه سازی منطقه حلقه ای بر اساس HLQT با استفاده از عملیات اضافه کد و ساختار چهار درختی برای تسریع نمایه سازی سلسله مراتبی طراحی می کنیم. آزمایش‌های مقایسه امکان‌سنجی و کارایی الگوریتم پیشنهادی را تأیید می‌کنند، با الگوریتم پیشنهادی نه تنها کارایی روش نمایه‌سازی تک رزولوشن را بهبود می‌بخشد، بلکه کارایی نمایه‌سازی را در بین سطوح چند وضوحی نیز بهبود می‌بخشد.

با استفاده از شبکه‌های شش ضلعی برای سازماندهی و مدیریت داده‌های فضایی متعدد، الگوریتم نمایه‌سازی پیشنهادی در این مقاله می‌تواند داده‌های چند وضوحی را با یک منطقه حلقه مشخص به سرعت و با دقت فهرست‌بندی کند. ما دو سناریو کاربردی بالقوه ارائه می دهیم: (الف) در یک تجزیه و تحلیل فضایی GIS، ممکن است داده های واقع در n را جستجو کنیم.کیلومتر در اطراف یک موقعیت خاص، مانند در مورد مشتریانی که به دنبال هتل در فاصله سه کیلومتری هستند یا کاربران تاکسی در حال جستجوی تاکسی در فاصله پنج کیلومتری هستند. از آنجایی که مزیت اصلی الگوریتم ارائه شده در این مقاله، نمایه سازی سلسله مراتبی است، می توانیم ابتدا ناحیه حلقه شده را با وضوح پایین تری ایندکس کنیم و سپس برای تعیین موقعیت هدف، نمایه سازی سلسله مراتبی را از درشت به ریز انجام دهیم. (ب) در تجزیه و تحلیل بصری داده‌های فضایی با وضوح چندگانه، الگوریتم ارائه‌شده در این مقاله می‌تواند داده‌ها را در سطوح چندگانه از طریق نمایه‌سازی سلسله مراتبی کارآمد خود نمایش دهد.

با این حال، الگوریتم پیشنهادی فقط وضعیت یک کاشی را در نظر می‌گیرد. هنگامی که محدوده شی بزرگ است، سلول های سطحی باید جداگانه پردازش شوند. این موضوع محور تحقیقات آینده ما خواهد بود.

منابع

مهدوی امیری، ع. آلدرسون، تی. سماواتی، ف. بررسی زمین دیجیتال. محاسبه کنید. نمودار. 2015 ، 53 ، 95-117. [ Google Scholar ] [ CrossRef ]
پترسون، PR سیستم های شبکه جهانی گسسته. بین المللی دایره Geogr. مردم محیط زمین. تکنولوژی 2016 ، 1-10. [ Google Scholar ] [ CrossRef ]
سحر، ک. سفید، دی. سیستم های شبکه جهانی گسسته Kimerling، AJ Geodesic. کارتوگر. Geogr. Inf. علمی 2003 ، 30 ، 121-134. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
مهدوی امیری، ع. سماواتی، ف. پترسون، P. طبقه بندی و تبدیل برای روش های نمایه سازی سیستم های شبکه جهانی گسسته. ISPRS Int. J. Geo-Inf 2015 ، 4 ، 320-336. [ Google Scholar ] [ CrossRef ]
Samet, H. مبانی ساختارهای داده چند بعدی و متریک ; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 2005. [ Google Scholar ]
گورسکی، KM; هیوون، ای. باندی، ای جی; Wandelt، BD; هانسن، FK; راینکه، ام. Bartelmann, M. HEALPix: چارچوبی برای گسسته سازی با وضوح بالا و تجزیه و تحلیل سریع داده های توزیع شده در کره. اخترفیزیک. J. 2005 , 622 , 759. [ Google Scholar ] [ CrossRef ]
هیوون، ای. گورسکی، KM; Reinecke، M. HEALPix-تجزیه و تحلیل داده ها، شبیه سازی و تجسم در کره. در دسترس آنلاین: https://sourceforge.net/projects/healpix/ (دسترسی در 10 اکتبر 2019).
GeoFusion. کتابچه راهنمای برنامه نویس GeoMatrix Toolkit. در دسترس آنلاین: https://www.geofusion.com/ (در 12 اکتبر 2019 قابل دسترسی است).
SEEGrid. صفحه اصلی SCENZGrid SEEGrid. در دسترس آنلاین: https://www.seegrid.csiro.au/wiki/SCENZGrid/WebHome (در 12 اکتبر 2019 قابل دسترسی است).
برناردین، تی. کاوگیل، ای. کریلوس، او. بولز، سی. طلا، پ. هامان، بی. Kellogg, L. Crusta: یک کره مجازی جدید برای تجسم در زمان واقعی توپوگرافی دیجیتال زیر متری در مقیاس سیاره ای. محاسبه کنید. Geosci. 2011 ، 37 ، 75-85. [ Google Scholar ] [ CrossRef ]
لمبرز، ام. Kolb، A. نقشه‌های مکعب بیضی برای ارائه دقیق داده‌های زمین در مقیاس سیاره‌ای. Cg.informatik.uni 2012 . [ Google Scholar ] [ CrossRef ]
چنگ، سی. شبکه زیربخش جهانی بر اساس تقسیم نقشه توسعه یافته و کدگذاری آدرس آن. Acta Geod. کارتوگر. گناه 2010 ، 39 ، 295-302. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
داتون، جی. یک سیستم مختصات سلسله مراتبی برای ژئوپردازش و کارتوگرافی . Springer: برلین، آلمان، 1999. [ Google Scholar ]
Goodchild، MF; Shiren, Y. ساختار داده های مکانی سلسله مراتبی برای سیستم های اطلاعات جغرافیایی جهانی (89-5). Ncgia Nat. مرکز Geogr. Inf. مقعدی 1989 ، 54 ، 31-44. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
بارتولدی، جی جی; گلدزمن، پی. نمایه سازی مستمر زیربخش های سلسله مراتبی جهان. بین المللی جی. جئوگر. Inf. علمی 2001 ، 15 ، 489-522. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
ژائو، ایکس. کوی، ام. LI، A.; ژانگ، ام. الگوریتم جستجوی مجاور شبکه چهاردرخت منحط در وجه کروی. Geomat. Inf. علمی دانشگاه ووهان 2009 ، 34 ، 479-482. [ Google Scholar ] [ CrossRef ]
Golay، MJE تبدیل الگوی موازی شش ضلعی. IEEE Trans. محاسبه کنید. 1969 ، 100 ، 733-740. [ Google Scholar ] [ CrossRef ]
وینس، الف. نمایه سازی شبکه جهانی گسسته شش ضلعی دیافراگم 3. J. Vis. اشتراک. تصویر نشان می دهد. 2006 ، 17 ، 1227-1237. [ Google Scholar ] [ CrossRef ]
بن، جی. تانگ، ایکس سی; ژو، CH; ژانگ، الگوریتم ساخت و ساز KX سیستم های شبکه شش ضلعی مبتنی بر هشت وجهی. J. Geo-Inf. علمی 2015 ، 6 ، 54-61. [ Google Scholar ] [ CrossRef ]
PYXIS Innovation Inc. چگونه PYXIS کار می کند. در دسترس آنلاین: https://www.pyxisinnovation.com/pyxwiki/index.php?title (در 12 اکتبر 2019 قابل دسترسی است).
پیترسون، P. مرتب سازی داده های فضایی با همپوشانی چند رزولوشن، با بسته بندی یکنواخت و یکنواخت. ثبت اختراع ایالات متحده شماره 0,8018,458, 13 سپتامبر 2011. [ Google Scholar ]
وینس، ا. تبدیل ژنگ، حساب XX و تبدیل فوریه برای مدل زمین دیجیتال با وضوح چندگانه PYXIS. بین المللی جی دیجیت. زمین 2009 ، 2 ، 59-79. [ Google Scholar ] [ CrossRef ]
Sahr, K. کدگذاری مکان بر روی شبکه‌های جهانی گسسته با دیافراگم 3 شش ضلعی. محاسبه کنید. محیط زیست سیستم شهری 2008 ، 32 ، 174-187. [ Google Scholar ] [ CrossRef ]
سحر، ک. نمایه سازی مکان مرکزی: سیستم های نمایه سازی خطی سلسله مراتبی برای سیستم های شبکه جهانی گسسته شش ضلعی با دیافراگم مختلط. Cartographica 2019 ، 54 ، 16-29. [ Google Scholar ] [ CrossRef ]
Sahr, K. DGGRID نسخه 6.4: مستندات کاربر برای نرم افزار تولید شبکه جهانی گسسته. در دسترس آنلاین: https://webpages.sou.edu/~sahrk/docs/dggridManualV64.pdf (در 12 اکتبر 2019 قابل دسترسی است).
Sahr, K. DGGRID کاربران. در دسترس آنلاین: https://www.discreteglobalgrids.org/dggrid-users/ (در 12 اکتبر 2019 قابل دسترسی است).
تانگ، ایکس سی; بن، جی. وانگ، ی. ژانگ، YS؛ پی، تی. کدگذاری کارآمد و طرح عملیات فضایی برای سیستم شبکه جهانی گسسته شش ضلعی دیافراگم 4. بین المللی جی. جئوگر. Inf. علمی 2013 ، 27 ، 898-921. [ Google Scholar ] [ CrossRef ]
بن، جی. Li، YL; ژو، CH; وانگ، آر. طرح رمزگذاری جبری Du، LY برای سیستم شبکه جهانی گسسته شش ضلعی دیافراگم 3. علمی علوم زمین چین 2018 ، 61 ، 215-227. [ Google Scholar ] [ CrossRef ]
مهدوی امیری، ع. هریسون، ای. Samavati، F. نقشه های اتصال شش ضلعی برای زمین دیجیتال. بین المللی جی دیجیت. زمین 2014 ، 8 ، 750-769. [ Google Scholar ] [ CrossRef ]
مهدوی امیری، ع. هریسون، ای. سماواتی، ف. تبدیل شبکه سلسله مراتبی. محاسبه کنید. به دس کمک کرد. 2016 ، 79 ، 12-26. [ Google Scholar ] [ CrossRef ]
وانگ، آر. بن، جی. Du، LY; ژو، جی بی. Li, ZX رمزگذاری و عملکرد سیستم شبکه شش گوشه با دیافراگم مسطح. Acta Geotech. کارتوگر. گناه 2018 ، 47 ، 1018–1025. [ Google Scholar ] [ CrossRef ]
وینس، الف. نمایه سازی یک شبکه جهانی گسسته. در موضوعات ویژه در محاسبات و تحقیقات فناوری اطلاعات و ارتباطات، پیشرفت در مدل سازی سیستم ها و کاربردهای فناوری اطلاعات و ارتباطات ؛ Fountain Publishers: Kampala, Uganda, 2006; جلد 2، ص 3-17. [ Google Scholar ]
وانگ، آر. بن، جی. Du، LY; ژو، جی بی. Li, ZX طرح عملیات کد برای سیستم شبکه شش ضلعی 4 دیافراگم ایکو وجهی. Geomat. Inf. علمی دانشگاه ووهان 2019 . [ Google Scholar ] [ CrossRef ]
اسنایدر، جی پی پیش‌بینی نقشه با مساحت مساوی برای گلوب‌های چندوجهی. Cartographica 1992 ، 29 ، 10-21. [ Google Scholar ] [ CrossRef ]
ساسنر، جی. داکسباخر، سی. Greiner، G. LOD شش ضلعی برای رندر تعاملی زمین. در مجموعه مقالات مدلسازی و تجسم چشم انداز، ارلانگن، آلمان، 16-18 نوامبر 2005. صص 666-675. [ Google Scholar ]
داده‌های اشتراک‌گذاری دوچرخه از آزمایشگاه مهندسی پکن از فناوری ناوبری و LBS Beidou. در دسترس آنلاین: https://www.chinalbs.org/engineer.html (در 15 ژانویه 2020 قابل دسترسی است).

شکل 1. ساختار کاشی ایکوس وجهی و کروی ساختار چهاردرختی شبکه ای شش ضلعی (HLQT) طرح رمزگذاری.

شکل 2. سطح اول نقاط شبکه برای کاشی های صورت و ساختار سلسله مراتبی چهاردرخت: ( الف ) توزیع نقاط شبکه سطح اول در صفحه کاشی پیچیده و ( ب ) ساختار سلسله مراتبی چهار درختی ℙ1و ℙ2.

شکل 3. مثالی از یک عملگر اضافه کدگذاری.

شکل 4. ساختار اضافه کد و محاسبه کد سلول همسایه: ( الف ) ساختار اضافه کد (با n نشان دهنده سطح) و ( ب ) محاسبه کد سلول همسایه.

شکل 5. شماتیک الگوریتم نمایه سازی کد تک سطحی.

شکل 6. نتایج نمایه سازی کد در زمان های مختلف در پکن (t4 > t3 > t2 > t1): ( الف ) نتیجه نمایه سازی در زمان t1. ( ب ) نتیجه نمایه سازی در زمان t2، ( ج ) نتیجه نمایه سازی در زمان t3، و ( د ) نتیجه نمایه سازی در زمان t4.

شکل 7. نمودار فرآیند یک الگوریتم نمایه سازی کد تک سطحی.

شکل 8. الگوریتم نمایه سازی سلسله مراتبی و مدل هرم: ( الف ) نتیجه نمایه سازی شبکه های سطح 10 (رزولیشن اولیه). ( ب ) نمایه سازی از سطوح شبکه 10 تا 11. ( ج ) نمایه سازی از سطوح 11 تا 12. و ( د ) مدل هرمی الگوریتم شاخص سلسله مراتبی.

شکل 9. طبقه بندی پوشش گیاهی در برخی استان ها و شهرهای چین.

شکل 10. نمودار شماتیک الگوریتم نمایه سازی DGGRID.

شکل 11. نمودارهای خط مقایسه کارایی برای نمایه سازی تک سطحی: ( الف ) قدر مطلق و ( ب ) نسبت.

شکل 12. نمودار خط مقایسه کارایی برای نمایه سازی سلسله مراتبی: ( الف ) قدر مطلق و ( ب ) نسبت.

شکل 13. نتایج تجسم برای الگوریتم نمایه سازی پیشنهادی در این مقاله: ( الف ) دیدگاه کلی و ( ب ) دیدگاه محلی.

شکل 14. نتایج تجسم داده‌های اشتراک‌گذاری دوچرخه از ناحیه دونگ‌چنگ در پکن با استفاده از الگوریتم نمایه‌سازی پیشنهادی در این مقاله: ( الف ) از ساعت 8:00 تا 9:00، جایی که مناطق از A تا E پارک دیتان، سفارت روسیه است. به ترتیب ایستگاه راه آهن پکن، پارک معبد بهشت و پارک لانگتان. ( ب ) از ساعت 17:00 تا 18:00؛ و ( ج ) از ساعت 20:00 تا 21:00.

مقالات داخلی و بین المللی

بدون دیدگاه

دیدگاهتان را بنویسید لغو پاسخ

برای نوشتن دیدگاه باید وارد بشوید.

مشاورین هوش پیروزی

خلاصه

کلید واژه ها:

1. معرفی

2. طرح رمزگذاری HLQT

3. الگوریتم نمایه سازی