انتخاب مدل مقیاس پذیر برای مدل سازی ترکیبی افزودنی فضایی: کاربرد در تجزیه و تحلیل جرم

خلاصه

رشد سریع مجموعه داده‌های باز فضایی منجر به تقاضای زیادی برای رویکردهای رگرسیونی شده است که اثرات مکانی و غیر مکانی را در داده‌های بزرگ تطبیق می‌دهند. انتخاب مدل رگرسیون به ویژه برای برآورد پایدار مدل های رگرسیون انعطاف پذیر مهم است. با این حال، روش های مرسوم می توانند برای نمونه های بزرگ کند باشند. از این رو، ما یک رویکرد انتخاب مدل سریع و عملی برای مدل‌های رگرسیون فضایی ایجاد می‌کنیم، با تمرکز بر انتخاب انواع ضرایب که شامل ضرایب ثابت، متغیر مکانی و غیرمکانی متغیر است. یک رویکرد پیش پردازش، که از طریق کاهش ابعاد، ماتریس های داده را با محصولات داخلی کوچک جایگزین می کند، سرعت محاسبات انتخاب مدل را به طور چشمگیری تسریع می کند. آزمایش‌های عددی نشان می‌دهند که رویکرد ما یک مدل را با دقت و از نظر محاسباتی کارآمد انتخاب می‌کند. برجسته کردن اهمیت انتخاب مدل در زمینه رگرسیون فضایی. سپس، رویکرد حاضر به داده‌های باز برای بررسی عوامل محلی مؤثر بر جرم در ژاپن اعمال می‌شود.
دوره-آموزش-حرفه-ای-gis
نتایج نشان می‌دهد که رویکرد ما نه تنها برای انتخاب عوامل مؤثر بر خطر جرم، بلکه برای پیش‌بینی رویدادهای جرم مفید است. این انتخاب مدل مقیاس‌پذیر برای تعیین مناسب مدل‌های رگرسیون فضایی انعطاف‌پذیر و در مقیاس بزرگ در عصر داده‌های بزرگ کلید خواهد بود. رویکرد انتخاب مدل توسعه‌یافته در spmoran بسته R پیاده‌سازی شد. نتایج نشان می‌دهد که رویکرد ما نه تنها برای انتخاب عوامل مؤثر بر خطر جرم، بلکه برای پیش‌بینی رویدادهای جرم مفید است. این انتخاب مدل مقیاس‌پذیر برای تعیین مناسب مدل‌های رگرسیون فضایی انعطاف‌پذیر و در مقیاس بزرگ در عصر داده‌های بزرگ کلید خواهد بود. رویکرد انتخاب مدل توسعه‌یافته در spmoran بسته R پیاده‌سازی شد. نتایج نشان می‌دهد که رویکرد ما نه تنها برای انتخاب عوامل مؤثر بر خطر جرم، بلکه برای پیش‌بینی رویدادهای جرم مفید است. این انتخاب مدل مقیاس‌پذیر برای تعیین مناسب مدل‌های رگرسیون فضایی انعطاف‌پذیر و در مقیاس بزرگ در عصر داده‌های بزرگ کلید خواهد بود. رویکرد انتخاب مدل توسعه‌یافته در spmoran بسته R پیاده‌سازی شد.

کلید واژه ها:

انتخاب مدل ؛ رگرسیون فضایی ; جرم و جنایت ؛ محاسبه سریع ؛ مدل‌سازی ضریب متغیر مکانی

1. معرفی

مدل‌سازی رگرسیون به طور گسترده‌ای برای بررسی عوامل پدیده‌های جغرافیایی مانند شیوع طاعون، توزیع گونه‌ها، تراکم اقتصادی و میزان جرم و جنایت استفاده می‌شود. به عنوان مثال، [ 1 ، 2 ، 3 ] از مدل های رگرسیون برای مطالعه تأثیر ثروت محله، نژاد، نرخ بیکاری، و امکانات، مانند فروشگاه ها و ایستگاه های مشروب، و سایر متغیرهای کمکی بر ریسک جرم استفاده می کند. امروزه تعداد فزاینده ای از مجموعه داده های باز آمار جرم و جنایت در دسترس است [ 4 ]. به عنوان مثال، دولت متروپولیتن توکیو ( https://www.bouhan.metro.tokyo.lg.jp/opendata/index.html، آمار جرم و جنایت (2014–اکنون)، طبقه بندی شده بر اساس نوع جرم و مناطق کوچک شهرداری را در دسترس عموم قرار داده است. علاوه بر این، بسیاری از آمار جرم و جنایت دارای تفکیک‌های جغرافیایی خوبی در سطح ناحیه یا سایر مقیاس‌های جریمه فضایی هستند و هزاران تا ده‌ها هزار ورودی داده را در هر دوره زمانی ثبت می‌کنند. برای چنین داده های مکانی-زمانی بزرگ، یک رویکرد رگرسیون محاسباتی کارآمد بسیار مهم است.
در تحلیل کاربردی فضایی، تخمین و شناسایی اثرات خطی و اثرات فضایی به متغیرهای عینی به طور فعال مورد مطالعه قرار می‌گیرد. به عنوان مثال، مدل های اقتصادسنجی فضایی برای تخمین اثرات خطی در حضور وابستگی فضایی استفاده می شود [ 5 ]. مدل‌های فرآیند گاوسی برای تطبیق طیف گسترده‌ای از اثرات فضایی در زمین‌آمار گسترش یافته‌اند [ 6 ]. رگرسیون وزنی جغرافیایی (GWR) [ 7 ] برای تخمین ضرایب متغیر مکانی (SVCs) روی متغیرهای کمکی [ 8 ] استفاده می شود. در میان اثرات فضایی، ما به‌ویژه بر مدل‌سازی SVC تمرکز می‌کنیم که امکان تخمین عوامل تعیین‌کننده محلی جرایم را فراهم می‌کند [ 2 ، 9 ، 102 ]. برای مثال،  دریافت که ثروت باعث کاهش جرم و جنایت در منطقه حومه پورتلند، اورگان می شود، در حالی که باعث افزایش جرم و جنایت در مرکز شهر می شود. درک چنین تفاوت های محلی در وقوع جرم هنگام در نظر گرفتن اقدامات امنیتی در برابر جرایم مهم است.
جدای از اثرات فضایی، تأثیر متغیرهای کمکی نیز می‌تواند بسته به زمان، کمیت یا سایر متغیرها یا رویدادها به صورت غیر مکانی متفاوت باشد [ 11 ]. متأسفانه وقتی تمام اثرات ممکن در مدل گنجانده شود، پارامترسازی بیش از حد اتفاق می افتد و مدل ناپایدار می شود. برای متعادل کردن دقت و پیچیدگی مدل، انتخاب مدل بسیار مهم است. به عنوان مثال، در تجزیه و تحلیل جرم، لازم است که به طور مناسب عوامل کلیدی پشت جرایم مشخص شوند.
روش‌های انتخاب مدل زیادی برای مدل‌های SVC [ 12 ، 13 ، 14 ] و سایر مدل‌های افزودنی وجود دارد که اثرات فضایی و/یا غیر فضایی را در خود جای می‌دهند [ 15 ، 16 ]. انتخاب مدل معمولاً از طریق تکرارهای به‌روزرسانی مدل از طریق گنجاندن/حذف اثرات (مثلاً SVC) تا زمان همگرایی انجام می‌شود. با این حال، در مورد نمونه‌های بزرگ، انتخاب مدل SVC با برازش تکراری از نظر محاسباتی نیاز دارد. به عنوان مثال، GWR مخلوط/نیمه پارامتریک [ 12 ، 17 ]، که ضرایب ثابت یا SVC را انتخاب می کند، به پیچیدگی زمانی محاسباتی O ( N2 ) در هر تکرار نیاز دارد [ 18]]، که در آن N حجم نمونه و O ( ·) نشان دهنده ترتیب است. اگرچه رویکردهای سریعی برای انتخاب افکت‌های فضایی و/یا غیرمکانی وجود دارد، اما هنوز هم مراحل برازش مدل را با پیچیدگی محاسباتی O( N ) تکرار می‌کنند.
با توجه به این پیشینه، این مطالعه یک رویکرد محاسباتی کارآمد را برای انتخاب اثرات فضایی و/یا غیرمکانی تحت چارچوب مدل‌سازی ترکیبی افزودنی فضایی توسعه می‌دهد [ 19 ، 20 ]. از یک درمان پیش شرطی برای کاهش هزینه محاسباتی تخمین پارامتر استفاده می کند، اما برای انتخاب مدل/اثرات اعمال نمی شود. با گسترش ایده [ 19 ، 20 ]، ما یک رویکرد مقیاس پذیر برای انتخاب هر دو اثر فضایی/غیر فضایی ایجاد می کنیم. این روش پیچیدگی زمانی محاسباتی مراحل برازش تکراری را به طور قابل توجهی کاهش می دهد به طوری که هزینه مستقل از اندازه نمونه N است .
ادامه این مقاله به شرح زیر سازماندهی شده است. بخش 2 مدل ما را معرفی می کند. بخش 3 روش های انتخاب مدل ما را توسعه می دهد و بخش 4 عملکرد آن را از طریق آزمایش های شبیه سازی مونت کارلو بررسی می کند. بخش 5 رویکرد توسعه یافته را برای مدل سازی و پیش بینی جرم اعمال می کند و بخش 6 بحث ما را به پایان می رساند.

2. مدل ترکیبی افزودنی فضایی

2.1. مدل

ما مدل ترکیبی افزودنی فضایی زیر را در نظر می گیریم:

y=∑پ=1پایکسپدرجهfپ+ε،                    ε~ن(0،σ2من)

جایی که درجهاپراتور محصول از نظر عنصر است، yبردار متغیرهای پاسخ است ( ن×1)، N حجم نمونه است، ایکسپبردار متغیر کمکی p است ، εبردار اختلالات با واریانس است σ2، 0 بردار صفر است و I یک ماتریس هویت است. fپبردار ضرایبی است که تأثیر متغیر کمکی p را توصیف می کند .

مشخصات زیادی برای fپ. اساسی ترین مشخصات ثابت است fپ=بپ1، جایی که بپیک ضریب است و 1بردار یک ها است که در مدل های رگرسیون خطی رایج فرض می شود.

یکی از ایده های کلیدی مورد استفاده در این مطالعه، مشخص کردن است fپSVC ها به عنوان مثال، [ 21 ] مشخصات زیر را اتخاذ کرد:

fپ=بپ1پ+τپ(س)σE(س)Λαپتوپ(س)،             توپ(س)~ن(0پ،σ2منپ)

E(س)هست یک (ن×Lپ)ماتریس از Lپبردارهای ویژه مربوط به مقادیر ویژه مثبت که بردارهای ویژه موران (ME) نامیده می شوند. آنها از یک ماتریس مجاورت فضایی با مرکز دوگانه استخراج می شوند [ 22 ]. Λهست یک Lپ×Lپماتریس مورب که عناصر آن مقادیر ویژه مثبت هستند. توپ(س)هست یک (Lپ×1)بردار متغیرهای تصادفی که قبل از تثبیت تخمین SVC به عنوان گاوسی عمل می کند. این αپو τپ(س)پارامترها مقیاس و خطای استاندارد فرآیند فضایی را تعیین می کنند. یک مزیت مشخصه رویکرد ME این است که SVC حاصل ( fپ) از طریق ضریب موران قابل تفسیر است که یک آمار مورب وابستگی مکانی است و مقدار آن در صورت وجود وابستگی فضایی مثبت (منفی) می تواند مثبت (منفی) باشد. به طور خاص، هنگام در نظر گرفتن تمام ME هایی که دارای مقادیر ویژه مثبت هستند، τپ(س)σE(س)Λαپتوپیک الگوی نقشه وابسته مثبت را توصیف می کند. به عبارت دیگر، معادله (2) یک فرآیند فضایی وابسته مثبت را ارائه می‌کند، که در بسیاری از موارد دنیای واقعی [ 23 ] به طور کارآمد غالب است. مقدار ضریب موران افزایش می یابد αپرشد می کند.

این fپتابع را می توان بر حسب یک ضریب متغیر غیر مکانی (NVC) نیز تعیین کرد. این مشخصات تأثیر متفاوت را با توجه به متغیر کمکی نشان می دهد ایکسپبه شرح زیر است:

fپ=بپ1پ+τپ(n)σEپ(n)توپ(n)،             توپ(n)~ن(0پ،σ2منپ)

جایی که Eپ(n)هست یک ن×Lپماتریس از Lپ،و تابع پایه تولید شده از ایکسپ. τپ(n)واریانس اثرات غیر فضایی را نشان می دهد.

مشخصات زیر که ضرایب متغیر مکانی و غیر مکانی (S&NVC) را در همه متغیرهای کمکی فرض می کند نیز امکان پذیر است:

fپ=بپ1پ+τپ(س)σE(س)Λαپتوپ(س)+τپ(n)σEپ(n)توپ(n)،     توپ(س)~ن(0پ،σ2منپ)،   توپ(n)~ن(0پ،σ2منپ)
مرجع. [ 24 ] نشان داد که مدل S&NVC در برابر همبستگی های جعلی قوی است، در حالی که مدل های ساده SVC تمایل به داشتن همبستگی های جعلی دارند [ 25 ]. در نهایت، شکل 1 ضرایبی را که در این مطالعه در نظر خواهیم گرفت را نشان می دهد.

به طور خلاصه، fپ، ثابت با یک ضریب ثابت داده می شود ( بپ)، در حالی که SVC، NVC و S&NVC با مجموع (ترکیبات خطی) اثرات ثابت و تصادفی مشخص می شوند. با جایگزینی این مقادیر، معادله مدل (1) به صورت زیر فرموله می شود:

y=ایکسب+E˜(Θ)U+ε،          U~ن(0، σ2من)،           ε~ن(0،σ2من)

ایکس=[ایکس1،…،ایکسپ]، ب=[ب1،…،بپ]”، U=[تو1،…،توپ]”، و Θ∈{θ1،…،θپ}،جایی که ” ” نشان دهنده جابجایی ماتریس است. E˜(Θ)=[ایکس1درجهE1V1(θ1)،…،ایکسپدرجهEپVپ(θپ)]، جایی که ” آدرجهب” یک عملگر است که یک بردار ستون را ضرب می کند آاز نظر عنصر با هر ستون از ب. ماتریس ها Eپ، Vپ(θپ)، و پارامتر θپدر جدول 1 تعریف شده اند . معادله (5) نشان می دهد که مدل ما به عنوان یک مدل خطی با اثرات مختلط [ 26 ] با اثرات ثابت فرموله شده است.ایکسب، اثرات تصادفی، E˜(Θ)U،و ε.

اگرچه این مطالعه بر چهار ویژگی تمرکز دارد، اما موارد دیگر fپتوابع برای نشان دادن اثرات خطی، اثرات غیر خطی، اثرات گروهی و سایر اثرات، همانطور که در [ 11 ] بیان شد، پیشنهاد شده است. با توجه به انعطاف پذیری آن، مدل ترکیبی افزودنی در حال حاضر در بسیاری از مطالعات کاربردی استفاده می شود [ 27 ، 28 ].

2.2. برآورد کردن

در میان الگوریتم‌های تخمین برای مدل‌های ترکیبی افزودنی فضایی، ما بر تخمین حداکثر احتمال محدود سریع (REML) [ 19 ] تمرکز می‌کنیم که هم برای اندازه نمونه N و هم برای تعداد اثرات P مقیاس‌پذیر است . گلوگاه محاسباتی در اینجا یک ارزیابی تکراری از احتمال ورود به سیستم محدود است لogلمنکآر(Θ)از معادله (1) (یا معادله (5)) برای تخمین عددی پارامترهای واریانس Θ∈{θ1،⋯θپ}( به پیوست A مراجعه کنید ). برای کاهش هزینه، [ 19 ] یک تخمین متوالی از {θ1،⋯θپ}پارامترها با اعمال رابطه (6) تا همگرایی.

θ^پ= ارگحداکثرθپ  لogلمنکآر(θپ|Θ-پ)

در حالی که حداکثر کردن مستقیم معادله (6) هنوز هم بار محاسباتی یکسانی دارد، [ 19 ] روش زیر را برای REML سریع توسعه داد:

(من)
جایگزینی ماتریس های داده {  y،ایکس،E1،…،Eپ} که ابعاد آن به N وابسته است ، با محصولات درونی آنها که ابعاد آن مستقل از N است.
(II)
با استفاده از محصولات داخلی، محاسبات زیر را به ترتیب تکرار کنید پ∈{1،…،پ}:
(II-1)
تخمین زدن θ^پبا به حداکثر رساندن لogلمنک(θپ|Θ^-پ)با Θ-پ∈{θ1،⋯θپ-1،θپ+1،⋯θپ}.
(II-2)
اگر مقدار احتمال همگرا شد به (III) بروید. در غیر این صورت، به (II-1) بازگردید.
(III)
خروجی مدل نهایی
در این الگوریتم، قبل از مرحله ارزیابی احتمال تکراری، ماتریس های داده با محصولات درونی خود جایگزین می شوند. پس از همه، پیچیدگی محاسباتی ارزیابی احتمال تکراری برای پیدا کردن θ^پدر مرحله (II-1) به کاهش می یابد O(Lپ3)[ 19 ]. به عبارت دیگر، پس از مرحله پیش شرطی سازی (I)، پیچیدگی محاسباتی REML سریع هم برای اندازه نمونه N و هم برای تعداد اثرات P بسیار مقیاس پذیر است . با توجه به این ویژگی، معادله مدل ترکیبی افزودنی فضایی (1) را می توان به طور موثر حتی زمانی که N و P بسیار بزرگ هستند تخمین زد.

3. انتخاب مدل

3.1. معرفی

همانطور که در بخش 2 توضیح داده شد ، ضرایب در معادله (1) می تواند ثابت، SVC، NVC، یا S&NVC باشد. پیچیدگی مدل به طور قابل توجهی به انتخاب نوع ضریب بستگی دارد. به عنوان مثال، اگر همه ضرایب ثابت فرض شوند، رابطه (1) فقط دارای ضرایب P است. از سوی دیگر، در مورد مدل مبتنی بر SVC، تعداد پارامترهای ضریب برابر است با ∑پ=1پLپ،از آنجایی که مدل استفاده می کند Lپ-بعد بردارهای ویژه موران برای نمایش ضریب P آن . پارامترهای بیش از حد می تواند منجر به بیش از حد برازش و برآورد بیش از حد اهمیت آماری شود، در حالی که پارامترهای بسیار کم می تواند باعث عدم تناسب شود. این مسئله را می توان با انتخاب یک مدل بهینه که تعادل مناسبی از اندازه پارامترها و مجموعه داده ها با توجه به دقت مدل فراهم می کند، برطرف کرد.
در انتخاب تعداد زیادی مدل کاندید یک مشکل وجود دارد. 4 مشخصات مدل P برای معادله (1) وجود دارد . برای مثال، اگر P = 9، که بعداً فرض خواهیم کرد، 4 9 = 262144 مدل وجود دارد. با این حال، در عمل، یافتن یا تقریبی بهترین مدل در عرض چند ثانیه یا چند دقیقه مطلوب است. از این رو، این مطالعه یک رویکرد انتخاب مدل کارآمد محاسباتی را توسعه می‌دهد. ما سعی می کنیم مدل را با به حداقل رساندن تابع هزینه جستجو کنیم، که می تواند با معیار اطلاعات آکایک (AIC) یا معیار اطلاعات بیزی (BIC) تعریف شود.
توجه به این نکته مهم است که ثابت، SVC، NVC و S&NVC اثر ثابت یکسانی دارند ( بپ1، در حالی که اثرات تصادفی آنها با یکدیگر متفاوت است. به عبارت دیگر، ما افکت های تصادفی را انتخاب می کنیم. در چنین حالتی، AIC و BIC مبتنی بر REML برای انتخاب مدل مدل‌های ترکیبی افزودنی خطی در دسترس هستند [ 29 ]. در حالی که مشخصات AIC/BIC حاشیه ای و مشروط وجود دارد، ما به دلایل زیر بر BIC حاشیه ای تمرکز می کنیم:
  • این رایج ترین مشخصات برای مدل های اثرات مختلط خطی [ 30 ]، از جمله مدل های ترکیبی افزودنی فضایی است.
  • عملکرد ضعیف انتخاب مدل مشروط مبتنی بر AIC/BIC هنگام در نظر گرفتن دو یا چند اثر تصادفی گزارش شد (نگاه کنید به [ 31 ، 32 ])، در حالی که [ 33 ] نشان داد که AIC/BIC شرطی هنگام مقایسه مدل‌های با یا بدون یک اثر تصادفی بهتر عمل می‌کند.
  • اگرچه مشخصات حاشیه ای از یک سوگیری نظری رنج می برد، [ 32 ] نشان داد که تأثیر سوگیری بر نتیجه انتخاب مدل بسیار کم است.
بر اساس یک تحلیل اولیه، ما تصمیم گرفتیم از BIC حاشیه ای مبتنی بر REML استفاده کنیم که توسط -2لogلمنکآر(Θ)-2سورود به سیستم(ن)، که در آن Q تعداد ضرایب ثابت ( P ) و پارامترهای واریانس در استΘدر تجزیه و تحلیل جرم در بخش 4 .

3.2. مراحل انتخاب مدل

این بخش روش‌های عملی جدیدی را برای انتخاب مدل پیشنهاد می‌کند. اولی یک انتخاب مدل را در تخمین متوالی REML گنجانده است (به بخش 2.2 مراجعه کنید ). برای کاهش شانس به دام افتادن به بهینه محلی، رویکرد دوم بر شبیه سازی مونت کارلو (MC) تکیه دارد که تخمین متوالی REML را تکرار می کند. ما اولی را روش انتخاب ساده می نامیم که بر سادگی و عملی بودن تأکید دارد و دومی را روش انتخاب MC می نامیم ( پیوست B را ببینید ). بخش 3.2.1 و بخش 3.2.2 این روش ها را توضیح می دهند.

3.2.1. روش انتخاب ساده

روش انتخاب ساده شامل مراحل انتخاب مدل در تخمین متوالی REML است. روال این روش به شرح زیر است:
(آ)
جایگزینی ماتریس های داده {  y،ایکس،E1،…،Eپ} با محصولات داخلی همانطور که در مرحله (II) در بخش 2.2 پردازش شده است .
(ب)
محاسبه زیر را به ترتیب برای هر کدام انجام دهید پ∈{1،…،پ}:
(b-1)
SVC p -ام را با حداکثر کردن تخمین بزنیدلogلمنک(θپ(س)|Θ^-پ(س))با توجه به θپ(س)، که زیر مجموعه ای از θپمشخص کردن SVC، و Θ^-پ(س)مجموعه ای از پارامترهای واریانس را نشان می دهد θ^پاز جانب Θ^.
(b-2)
اگر مقدار تابع هزینه را بهبود می بخشد، SVC را انتخاب کنید (به عنوان مثال، BIC). در غیر این صورت، آن را با یک ثابت جایگزین کنید.
(b-3)
p -th NVC را با حداکثر کردن تخمین بزنیدلogلمنک(θپ(n)|Θ^-پ(n))با توجه به θپ(n)، که زیر مجموعه ای از θپمشخص کردن NVC، و Θ^-پ(س)مجموعه ای از پارامترهای واریانس را نشان می دهد θ^پ(n)از جانب Θ^.
(b-4)
NVC در صورتی انتخاب می شود که مقدار تابع هزینه را بهبود بخشد (به عنوان مثال، BIC). در غیر این صورت، با یک ثابت جایگزین می شود.
(ج)
اگر تابع هزینه همگرا شد به (d) بروید. در غیر این صورت به (ب) برگردید.
(د)
خروجی مدل نهایی
در حالی که رویکردهای انتخاب مشابهی وجود دارد [ 34 ]، روش ما متمایز است زیرا پیچیدگی محاسباتی آن برای انتخاب مدل مستقل از اندازه نمونه است، به دلیل مرحله (الف) که تمام ماتریس های داده را در محصولات درونی آنها ارائه می کند. با توجه به کاهش شدید ابعاد، این روش ساده برای نمونه های بسیار بزرگ مناسب است. به طور خاص، پیچیدگی محاسباتی بخش تکراری در روش انتخاب مدل برابر است O(Lپ3)، که برای ارزیابی مقدار احتمال log در مرحله (b–1) و (b–3) مورد نیاز است. از آنجا که پیچیدگی محاسباتی بسیار کوچک و مستقل از اندازه نمونه N است ، روش انتخاب مدل ما حتی برای نمونه های بزرگ بسیار سریع است.
یک مشکل تعداد زیادی از ترکیب های توالی از پیش تعیین شده است پ∈{1،…،پ}. به عنوان مثال، اگر P = 9، وجود دارد پ!=362،880دنباله ها برخی از آنها ممکن است منجر به نتیجه انتخاب مدل ضعیف شوند (یعنی بهینه محلی). حداقل، بر خلاف برآورد حداکثر احتمال یا اعتبار متقابل، REML تمایل دارد که بهینه محلی نداشته باشد [ 35 ، 36 ]. بخش 4 بررسی می کند که آیا این رویکرد ساده مدل واقعی را از طریق آزمایشات مونت کارلو به طور دقیق تقریب یا انتخاب می کند.
3.2.2. روش انتخاب مونت کارلو (MC).
برای کاهش خطر افتادن در بهینه محلی، توالی‌ها را به‌طور تصادفی نمونه‌برداری می‌کنیم پ∈{1،…،پ}و تخمین مبتنی بر REML را با توجه به دنباله تکرار کنید. به طور خاص، ما رویکرد انتخاب مدل زیر را پیشنهاد می‌کنیم:
(آ)
جایگزینی ماتریس های داده {  y،ایکس،E1،…،Eپ} با محصولات داخلی.
(ب)
با استفاده از حاصلضرب های داخلی، محاسبه زیر را G بار تکرار کنید:
(B-1)
به صورت تصادفی از دنباله g- ام نمونه برداری کنید{1g،…،پg}بدون تعویض
(B-2)
محاسبه زیر را به ترتیب برای هر کدام انجام دهید پg∈{1g،…،پg}:
(B–2a)
را برآورد کنید پg-ام SVC با به حداکثر رساندن لogلمنک(θپg(س)|Θ^-پg(س))، کجا { θپg(س)،Θ^-پg(س)}به طور مشابه تعریف می شوند {θپ(س)،Θ^-پ(س)}.
(B-2b)
اگر مقدار تابع هزینه را بهبود می بخشد، SVC را انتخاب کنید (به عنوان مثال، BIC). در غیر این صورت، آن را با یک ثابت جایگزین کنید.
(B-2c)
را برآورد کنید پg-ام NVC با به حداکثر رساندن لogلمنک(θپg(n)|Θ^-پg(n))، کجا { θپg(n)،Θ^-پg(n)}به طور مشابه تعریف می شوند {θپ(n)،Θ^-پ(n)}.
(B–2d)
NVC در صورتی انتخاب می شود که مقدار تابع هزینه را بهبود بخشد (به عنوان مثال، BIC). در غیر این صورت، با یک ثابت جایگزین می شود.
(B-3)
اگر تابع هزینه همگرا شد به (B-4) بروید. در غیر این صورت به (B-2) برگردید.
(B-4)
مقدار تابع هزینه مدل انتخاب شده را محاسبه کنید.
(C)
خروجی بهترین مدل در مدل های انتخابی G از نظر تابع کمترین هزینه.
همانند روش انتخاب ساده، هزینه محاسباتی برای مرحله تکراری (B) مستقل از حجم نمونه است. علاوه بر این، مرحله تکراری به راحتی موازی می شود. بنابراین، این یک روش محاسباتی کارآمد انتخاب مدل است. مرحله (B) یک شبیه سازی MC را برای به حاشیه راندن G و به دست آوردن توزیع ارزش هزینه انجام می دهد. ما این رویکرد را رویکرد انتخاب MC می نامیم.
دوره-آموزش-حرفه-ای-gis

4. آزمایش های عددی

4.1. جزئیات محاسباتی

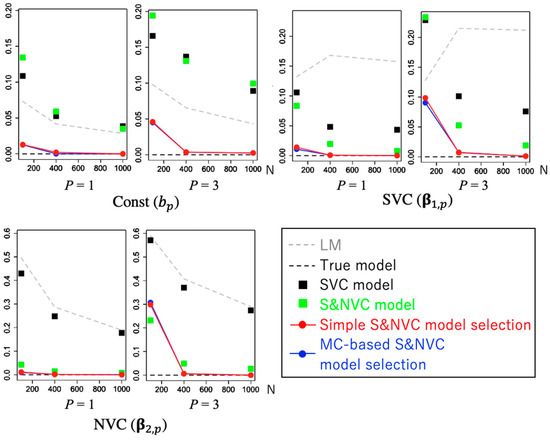
در اینجا، بررسی می کنیم که آیا این روش انتخاب ساده به طور دقیق به مدل واقعی تقریب می زند، یعنی مدلی که همه انواع ضرایب (به عنوان مثال، ثابت، SVC، NVC، یا S&NVC) به درستی تعریف شده اند، یا اینکه برای دستیابی به روش انتخاب MC نیاز است. انتخاب دقیق مدل از طریق آزمایش های مقایسه ای مونت کارلو ما با / بدون مدل انتخاب اثرات با برازش این مدل‌ها با داده‌های مصنوعی تولید شده از آن مقایسه می‌کنیم

y=β0+∑پ=1پایکسپبپ+∑پ=1پایکس1،پβ1،پ+∑پ=1پایکس2،پβ2،پ+ε،          ε~ن(0،من)
β0=1+سی˜تو0،                         تو0~ن(0،من)،
β1،پ=1+سی˜تو1،پ،            تو1،پ~ن(0،τ1،پ2من)،
β2،پ=1+E2،پتو2،پ،       تو2،پ~ن(0،τ2،پ2من)،

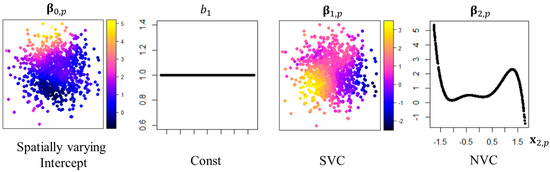
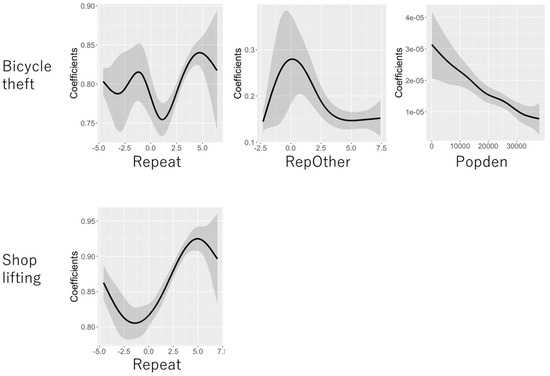
جایی که متغیرهای کمکی {ایکس1،…،ایکس1}،{ایکس1،پ،…،ایکس1،پ}،{ایکس2،پ،…،ایکس2،پ}از توزیع های نرمال استاندارد مستقل تولید می شوند. ماتریکس سی˜از استانداردسازی ردیف ماتریس اتصال فضایی ساخته شده است سی، که عنصر ( i , j ) -امین آن برابر است انقضا(-دمن،j)، جایی که دمن،jفاصله اقلیدسی بین سایت های نمونه i و j است . سایت های نمونه از دو توزیع نرمال استاندارد مستقل تولید شدند. SVC ها β0و β1،پتوسط فرآیندهای میانگین متحرک فضایی تعریف می شوند. β2،پیک NVC است که با توجه به آن متفاوت است ایکس2،پ، که در آن E2،پماتریسی از 10 تابع پایه چند جمله ای است که از آن تولید می شود ایکس2،پ. شکل 2 ضرایب به دست آمده از این فرآیندهای تولید را نشان می دهد.

هدف اصلی مقایسه دقت تخمین ضریب و کارایی محاسباتی انتخاب‌های مدل S&NVC ساده و مبتنی بر MC با گزینه‌های جایگزین است. برای انتخاب مدل MC، ما 30 تکرار را در نظر گرفتیم. این مدل ها 200 بار در حالی که متفاوت بودند نصب شدند پ∈{1، 2، 3}و حجم نمونه ن∈{50، 200، 1000}.

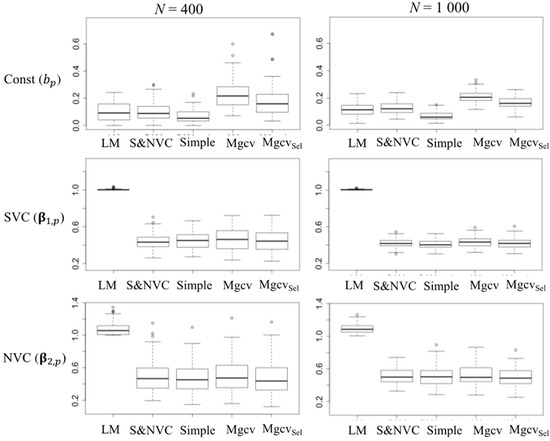
دقت تخمین ضریب با استفاده از ریشه میانگین مربعات خطا (RMSE) ارزیابی می شود که به صورت تعریف می شود.

آرماسE(βمن،پ)=1200ن∑منتیهr=1200∑من=1ن(β^من،پ(منتیهr)-βمن،پ)2

جایی که iter نشان دهنده عدد تکرار است، βمن،پعنصر i- امین استβپ، و β^من،پ(منتیهr)تخمین داده شده در تکرار تکراری است . سوگیری برآوردها با استفاده از ارزیابی می شود

بمنآس(βمن،پ)=1200ن∑منتیهr=1200∑من=1ن(β^من،پ(منتیهr)-βمن،پ)
تحت این تنظیمات، بخش 4.2 بررسی می کند که آیا رویکردهای ما به طور دقیق بهترین مدل را انتخاب می کنند، در حالی که بخش 4.3 رویکردهای ما را با رویکردهای دیگر مقایسه می کند.

4.2. عملکرد انتخاب مدل

در این آزمایش شش مدل زیر را با هم مقایسه می کنیم. به عنوان مدل های پایه، مدل رگرسیون خطی (LM) و SVCs در سراسر ضرایب (مدل SVC) استفاده می شود. به‌عنوان پایه دیگر، از مدلی استفاده می‌کنیم که انواع ضرایب واقعی را فرض می‌کند (یعنی ضریب ثابت در ایکسپSVC روشن است ایکس1،پو NVC روشن است ایکس2،پ(الگوی واقعی)). توجه داشته باشید که مدل واقعی مقادیر ضرایب را ناشناخته فرض می‌کند (یعنی فقط انواع ضرایب شناخته شده هستند)، و مقادیر از نمونه‌ها مانند مدل‌های دیگر برآورد می‌شوند. تخمین ها دارای خطای تخمینی خواهند بود. ما یک مدل کامل می سازیم که S&NVC را در سراسر ضرایب فرض می کند (مدل S&NVC). علاوه بر این، ما رویکردهای انتخاب مدل S&NVC ساده و مبتنی بر MC را آماده می‌کنیم که ضرایب خود را از بین ثابت، SVC، NVC و S&NVC به ترتیب با استفاده از رویکرد ساده و رویکرد مونت کارلو انتخاب می‌کنند.
شکل 3 RMSE ضرایب برآورد شده را خلاصه می کند. همانطور که انتظار می رود، LM به دلیل نادیده گرفتن تغییرات مکانی و غیر مکانی در ضرایب رگرسیون، خطاهای تخمین بالاتری دارد. اگرچه مدل SVC در آمار فضایی محبوب است، اما RMSE برای NVCها به طور قابل توجهی بالا است. علاوه بر این، احتمالاً به دلیل خطا، دقت تخمین ضرایب ثابت توسط مدل SVC بدتر از مدل LM است. این نتایج نشان می دهد که مدل های مبتنی بر SVC در حضور ضرایب ثابت یا غیر مکانی ناپایدار می شوند.
با توجه به مدل S&NVC بدون انتخاب مدل، SVCها و NVCهای برآورد شده به اندازه مدل واقعی دقیق هستند. با این حال، مقادیر RMSE آن برای ثابت ها، احتمالاً به دلیل پارامترسازی بیش از حد، بالاترین مقدار را در بین مدل ها دارند. از سوی دیگر، RMSE های انتخاب مدل S&NVC ساده و مبتنی بر MC به مدل واقعی در تمام ضرایب نزدیک است. این نتایج اهمیت انتخاب اثر را در مدل‌سازی رگرسیون فضایی نشان می‌دهد.
شکل 4 سوگیری خطاهای استاندارد ضریب را ترسیم می کند که برای ارزیابی اهمیت آماری استفاده می شود. سوگیری رو به پایین خطاهای استاندارد باعث برآورد بیش از حد اهمیت آماری می شود، در حالی که عکس این امر برای سوگیری رو به بالا صادق است. در اینجا، خطاهای استاندارد برآورد شده از مدل واقعی به عنوان مقادیر واقعی در نظر گرفته می شوند. خطاهای استاندارد ضرایب ثابت برآورد شده از مدل های LM، SVC و S&NVC به سمت پایین سوگیری دارند. برای SVC، آنهایی که از LM تخمین زده می شوند به سمت بالا سوگیری دارند در حالی که مدل های SVC و SNVC به سمت پایین بایاس می شوند. برای NVC، خطاهای استاندارد برآورد شده از مدل های LM و SVC به سمت بالا سوگیری دارند. RMSE خطاهای استاندارد به دست آمده توسط مدل های LM، SVC و S&NVC نیز بالا است همانطور که در نشان داده شده است.همانطور که در شکل 5. بر اساس نتایج، مدل‌های بدون انتخاب اثر (مدل‌های LM، SVC، و S&NVC) از تخمین بیش‌ازحد یا دست‌کم‌گرفتن اهمیت آماری رنج می‌برند.
برعکس، خطاهای استاندارد تخمین زده شده از رویکردهای انتخاب مدل ساده و مبتنی بر MC تقریباً با خطاهای مدل واقعی یکسان است، به جز موردی با P = 3 و N = 100، که شدیدترین مورد است، با تخمین 10 اثر. از 100 نمونه رویکردهای انتخاب اثرات ما برای بهبود دقت تخمین هم برای ضرایب و هم برای خطاهای استاندارد آنها مفید است. با کمال تعجب، همچنین مشخص شد که نتایج حاصل از رویکرد انتخاب مدل ساده تقریباً مشابه رویکرد مبتنی بر MC است، علی‌رغم این واقعیت که رویکرد ساده به دنباله‌ای از پیش تعیین‌شده متکی است. پ∈{1،…،پ}برای انتخاب مدل، در حالی که روش مبتنی بر MC به طور ضمنی آن را بهینه می کند. این به پایداری REML نسبت داده می شود (به بخش 3.2.1 مراجعه کنید ).

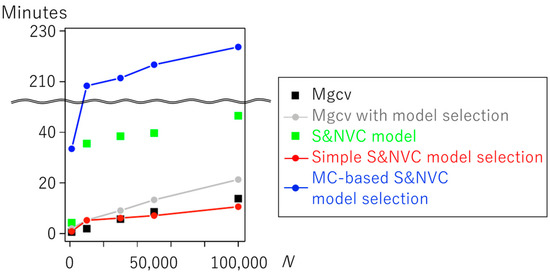
4.3. مقایسه معیار روشهای انتخاب مدل

در اینجا، ما رویکرد انتخاب مدل خود را با یکی دیگر از روش‌های رایج انتخاب مدل مقایسه می‌کنیم. از بین رویکردهای موجود، ما رویکرد پیاده‌سازی شده در بسته mgcv در R ( https://cran.r-project.org/web/packages/mgcv/index.html ) را به دلایل زیر انتخاب کردیم: (i) mgcv یکی از محبوب ترین بسته ها برای مدل سازی مخلوط افزودنی. (2) روش انتخاب اثرات در mgcv از نظر محاسباتی بسیار مقیاس پذیر است [ 37 ]، و یک معیار معقول برای آزمایش دقت و کارایی محاسباتی رویکرد ما است.
مدل‌های زیر مقایسه می‌شوند: LM، مدل S&NVC، انتخاب مدل ساده S&NVC، مدل دیگر S&NVC برآورد شده از mgcv (Mgcv) و انتخاب مدل Mgcv بر اساس دو جریمه [37 ] . رویکرد دو پنالتی روش انتخاب مدل پیش فرض در بسته mgcv است. به طور کلی، رویکرد پنالتی مضاعف، پارامترهای جریمه را برای انتخاب اثرات علاوه بر پارامترهای جریمه معمول در مدل‌های افزایشی که صاف بودن هر اثر را تعیین می‌کند، اعمال می‌کند. [ 37 ] دقت برتر این رویکرد را نسبت به جایگزین ها نشان داد. برای محاسبات سریعتر، ما Mgcv و Mgcv را با انتخاب مدل دو پنالتی با استفاده از تابع bam در بسته mgcv، با استفاده از REML سریع تخمین زدیم [ 38] تخمین زدیم.]. همانطور که در بخش قبل، معادلات (7) – (10) را به عنوان مدل واقعی در نظر گرفتیم و هر مدل به طور تکراری 200 بار برازش شد.
شکل 6 RMSE ها را برای ضرایب تخمینی در زمانی که P = 3 و خلاصه می کندن∈{400،1000}. برای SVC و NVC، مقادیر RMSE به‌دست‌آمده از همه مدل‌ها به جز LM کاملاً مشابه هستند. با توجه به اثر ثابت، انتخاب ساده مدل S&NVC ما کمترین خطای برآورد را به همراه دارد. بنابراین، رویکرد ما یک جایگزین امیدوارکننده برای Mgcv با/بدون انتخاب مدل دو پنالتی است که اکنون به طور گسترده استفاده می‌شود.
در نهایت، شکل 7 زمان محاسباتی را در موارد 10 = P و مقایسه می کندن∈{1000،10،000، 30،000،50،000، 100،000}. در اینجا، برآوردها در هر مورد پنج بار انجام شد و زمان‌های محاسباتی حاصل میانگین‌گیری شد. Mgcv با انتخاب مدل بر اساس دو جریمه کمی کندتر از Mgcv است زیرا اولی پارامترهای جریمه اثرات انتخاب را نیز تخمین می زند. همانطور که در بخش 1 توضیح داده شد ، چنین زمان محاسباتی اضافی برای انتخاب مدل/اثر مسلم است. از سوی دیگر، روش ساده انتخاب مدل S&NVC نسبت به مدل ساده S&NVC زمان محاسباتی بسیار کوتاه‌تری دارد، زیرا اولی فقط اثرات انتخابی را هنگام ارزیابی احتمال در هر تکرار بررسی می‌کند، در حالی که دومی شامل تمام اثرات هنگام ارزیابی احتمال می‌شود. علاوه بر این، با توجه به روش پیش شرطی، افزایش زمان محاسباتی با توجه به Nبا توجه به جایگزین های مبتنی بر Mgcv سرکوب می شود. در مقابل، همانطور که در شکل 7 نشان داده شده است، انتخاب مدل S&NVC مبتنی بر MC کندتر از گزینه های جایگزین است . بر اساس دقت تخمین و کارایی محاسباتی، ما انتخاب مدل ساده S&NVC را به عنوان انتخاب پیش‌فرض توصیه می‌کنیم.
از نظر تئوری، انتخاب مدل ساده S&NVC به دلایل زیر سریعترین است: شبیه سازی مونت کارلو برخلاف رویکرد مبتنی بر MC مورد نیاز نیست. این نیاز به تعداد کمتری از پارامترهای جریمه نسبت به Mgcv با استفاده از پارامترهای کیفی K برای انتخاب صافی دارد در حالی که از سایر پارامترهای K برای انتخاب مدل استفاده می کند. نتایج در اینجا کارایی محاسباتی رویکرد انتخاب ساده ما را به صورت تجربی تایید می‌کند.
به طور خلاصه، نتایج تجزیه و تحلیل نشان می دهد که رویکرد ما اثرات را به طور دقیق و محاسباتی کارآمد انتخاب می کند، حتی در مقایسه با رویکردهای پیشرفته.

5. کاربرد در مدل سازی جرم

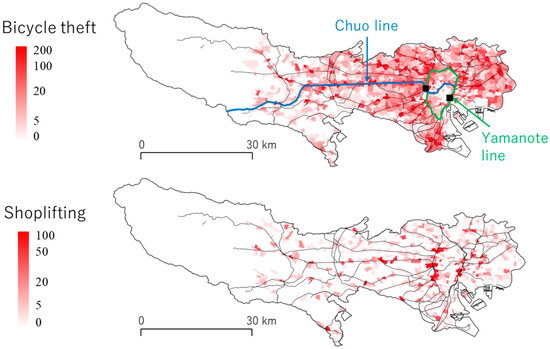
5.1. طرح کلی

این بخش یک رویکرد ساده را برای پایگاه داده شبکه Dai-Tokyo Bouhan ( https://www.bouhan.metro.tokyo.lg.jp/ ) اعمال می کند که توسط دفتر ارتقای ایمنی شهروندان، دولت شهری توکیو ( https:// www.tomin-anzen.metro.tokyo.lg.jp/english/ ). این پایگاه داده آمار جرم و جنایت را بر اساس نوع جرم و 1529 منطقه کوچک شهری در توکیو، ژاپن طبقه بندی می کند. زون های ناحیه به صورت همگن در هر ناحیه مشخص شده اند. نواحی در مناطق شهری بسیار کوچک هستند در حالی که برخی از مناطق در مناطق کوهستانی غربی بزرگ هستند. حداقل مساحت معادل 0.003 کیلومتر مربع ، ربع اول 0.301 کیلومتر مربع ، میانه 0.657 کیلومتر مربع ، ربع سوم 1.102 کیلومتر مربع است.و حداکثر 68.714 کیلومتر است. مربع .
این مطالعه بر دزدی دوچرخه و دزدی از مغازه متمرکز است، دو جنایت غیرقابل سرقت که در بین سال‌های 2017 و 2018 گزارش شده‌اند. حجم نمونه 12232 نفر بود. شکل 8 تراکم جرم و جنایت را بر اساس مناطق کوچک شهری (تعداد وقوع در کیلومتر 2 ) ترسیم می کند (سه ماهه اول 2017). ناحیه شرقی در راه آهن حلقه ای (خط Yamanote) ناحیه مرکزی است و سایر راه آهن ها در تمام جهات از راه آهن حلقه امتداد دارند، همانطور که در شکل نشان داده شده است. خط Chuo یکی از این خطوط است.

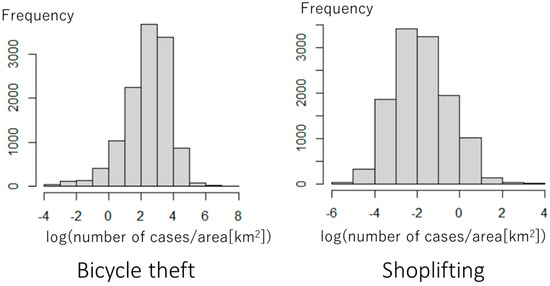
ما تعداد ثبت‌شده سرقت دوچرخه و موارد دزدی از مغازه را در هر منطقه بر اساس منطقه به‌ترتیب مدل می‌کنیم. بر اساس شکل 9 ، که هیستوگرام تراکم جرم را نشان می دهد، توزیع داده ها تقریباً گوسی است. یک مدل خطی (گاوسی) در مورد ما قابل قبول خواهد بود. این مطالعه از مدل خطی زیر استفاده می کند:

yمن،تیج=βمن،0+βمن،1yمن،تی-1ج+βمن،2Yمن،تی-1-ج+∑ک=36βمن،کایکسمن،ک+gد(من)(س)+gq(من)(تی)+εمن،          εمن~ن(0،σ2)

جایی که yمن،تیجتعداد ج -مین جرم در هر منطقه در ناحیه یکم در سه ماهه t (مقیاس ورود) است.

سپس متغیرهای توضیحی را در نظر می گیریم. بر اساس تئوری فعالیت معمول [ 39]، سه مورد زیر محرک جرایم هستند: (1) مجرم بالقوه، (2) هدف مناسب، و (3) عدم وجود قیم. در حالی که سطح پیشگیری از جرم توضیح دهنده (iii) تقریباً در سراسر توکیو برابر است، (i) و (ii) بسته به منطقه به طور قابل توجهی تغییر می کند. در مورد سرقت دوچرخه، تراکم جمعیت در شب (Popden) را به عنوان یک متغیر توضیحی تقریبی (i) تعداد مهاجمان بالقوه در نظر می گیریم. از آنجایی که دوچرخه ها به طور گسترده برای خرید در منطقه مورد مطالعه استفاده می شوند، ما Popden و تعداد خرده فروشان (Retail) را به عنوان متغیرهای توضیحی در نظر می گیریم که (ii) تعداد اهداف یا دوچرخه ها را توصیف می کنند. در مورد دزدی از فروشگاه، تراکم جمعیت در روز (Dpopden) را به عنوان متغیری در نظر می گیریم که (i) تعداد مهاجمان را توضیح می دهد، در حالی که Retail را به عنوان متغیر توضیحی دیگری در نظر می گیریم که (ii) تعداد اهداف را توضیح می دهد.
در جغرافیای جرم، قربانی شدن نزدیک به تکرار [ 40 ]، تبیین تمایل به تکرار جرایم در منطقه مشابه، به عنوان یک پدیده رایج شناخته می شود. چنین تمایل تکراری به دلیل ناهمگونی منطقه‌ای، مانند ویژگی‌های ساکن (فرضیه ناهمگونی خطر) یا جرایم تکراری توسط همان گروهی که در مورد حوزه جرم اطلاعات دارند (فرضیه وابستگی رویداد) رخ می‌دهد (به [41] مراجعه کنید ) . برای در نظر گرفتن چنین تکرارهای محلی، تراکم جرم را در سه ماهه قبل لحاظ می کنیم yمن،تی-1جبه عنوان یک متغیر توضیحی و این متغیر را تکرار کنید. از آنجایی که چنین تمایلات تکراری می تواند در انواع جرایم رخ دهد، تراکم ثبت شده جرایم غیر دزدی را نیز لحاظ می کنیم. Yمن،تی-1-ج(RepOther) جدا از جنایت ج در سه ماهه قبل. برای مدل سرقت دوچرخه، Yمن،تی-1-جبر اساس گزارش (تعداد جرایم غیر دزدی به جز دزدی دوچرخه/منطقه (کیلومتر 2 ))، در حالی که Yمن،تی-1-جبرای مدل دزدی مغازه نیز به طور مشابه تعریف شده است.
علاوه بر این، متغیرهای توضیحی زیر را نیز شامل می‌شویم {ایکسمن،3،ایکسمن،4،ایکسمن،5،ایکسمن،6}توصیف عوامل محیطی محلی: نسبت خارجی ها در میان ساکنان (Fpopden). نسبت بیکاری (UnEmp)؛ نسبت ساکنان فارغ التحصیل از دانشگاه (Univ). این سه متغیرهای نیابتی نژاد، محرومیت اقتصادی و تحصیلات هستند. تأثیر قوی از چنین عوامل محیطی محلی در مطالعات مربوط به مدل‌سازی زمین در معرض خطر نشان داده شده است (RTM؛ [ 42 ]). این داده ها از آمار سرشماری ملی توسط مناطق شهری کوچک در سال 2015 جمع آوری شده است.
همانطور که در بخش قبل، ما یک رهگیری از نظر مکانی متفاوت را فرض می کنیم βمن،0برای حذف وابستگی فضایی باقیمانده و انتخاب نوع ضریب { βمن،1،…،βمن،6} در میان {constant, SVC, NVC, S&NVC} با استفاده از یک رویکرد ساده. علاوه بر این، برای به دست آوردن ناهمگونی بین مناطق و دوره های زمانی فردی، ما در نظر می گیریم gد(من)(س)~ن(0،τ(س)2)و gq(من)(تی)~ن(0،τ(تی)2)، به ترتیب، در کجا τ(س)2و τ(تی)2پارامترهای واریانس هستند. این عبارات نشان دهنده اثرات گروهی ناحیه هستند د(من)و ربع q(من)که در آن نمونه i- ام مشاهده می شود. آنها به ترتیب ضرایب ثابت بر اساس ناحیه و چهارم هستند (به عنوان مثال، gد(من)(س)در ولسوالی‌هایی که تعداد جرایم بیشتر است، ارزش‌های مثبت بیشتری به خود می‌گیرد). شمول یا حذف از {gد(من)(س)،gq(من)(تی)}همچنین به طور خودکار با رویکرد ساده انتخاب می شود.

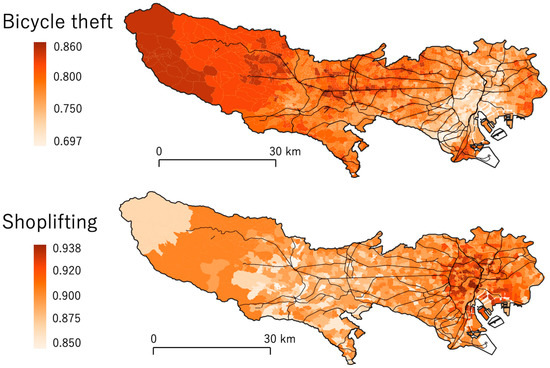
5.2. نتایج تخمین ضریب

مقدار مربع R تنظیم شده (شرطی) برای مدل سرقت دوچرخه 0.914 و برای مدل سرقت از مغازه 0.928 است. صحت این مدل ها تایید شد. برآورد این مدل ها به ترتیب 67.3 ثانیه و 52.0 ثانیه طول کشید که کارایی محاسباتی رویکرد ما را تأیید می کند.
جدول 2 و جدول 3 ضرایب برآورد شده و اهمیت آماری آنها را خلاصه می کند. برای سرقت دوچرخه، متغیرهای Repeat، RepOther، و Popden از نظر آماری مثبت در سطح 1٪ در سراسر مناطق معنی دار هستند. نتایج نشان می‌دهد که تمایل شدید به قربانی شدن تقریباً تکراری نه تنها در همان نوع جرم، بلکه در بین انواع جرم نیز وجود دارد. با توجه به اینکه تراکم جمعیت بالاتر به معنی تعداد بیشتری از مجرمان و اهداف بالقوه است (نگاه کنید به بخش 5.1 مراجعه کنید.)، علامت مثبت پاپدن به طور شهودی معقول است. نوع ضریب انتخاب شده برای Repeat S&NVC بود، در حالی که برای RepOther و Popden NVC بود. اگرچه NVCها به ندرت در مدلسازی فضایی در نظر گرفته شده اند، این نتایج نشان دهنده اهمیت در نظر گرفتن NVCها است. Fpopden، UnEmp و Univ که ضرایب آنها ثابت تخمین زده می شود، از نظر آماری ناچیز هستند ( جدول 3 ). از جمله اثرات گروهی gq(من)(تی)انتخاب شد. به طور خلاصه، قربانی شدن تقریباً تکراری، جمعیت و فصل عوامل تعیین کننده غالب هستند، در حالی که تعداد افراد خارجی، وضعیت اقتصادی و تحصیلات اینگونه نیستند. بعداً ضرایب تخمینی را با جزئیات بیشتری بررسی خواهیم کرد.
برای دزدی از مغازه، Repeat و RepOther دوباره دارای اهمیت مثبت هستند، که نشان می دهد نه تنها دزدی از مغازه، بلکه سایر جرایم غیر دزدی در یک چهارم، دزدی از مغازه را در سه ماهه بعدی افزایش می دهد. Dpopden نیز مثبت معنادار است. این نشان می دهد که دزدی از مغازه در مناطق مرکزی که مردم در طول روز تمرکز می کنند افزایش یافته است. اثرات خرده فروشی، Fpopden، UnEnp، Univ و دو گروه ناچیز هستند. برای متغیرهای معنی دار، نوع ضرایب انتخاب شده به شرح زیر است: S&NVC برای Repeat; NVC برای RepOther و Dpopden؛ برای بقیه ثابت است در مجموع، تمایل به تکرار و جمعیت در طول روز به عنوان عوامل تعیین کننده مهمی برای دزدی از مغازه نشان داده شده است.
شکل 10 S&NVC تخمینی را در تکرار ترسیم می کند. ضرایب سرقت دوچرخه در ناحیه مرکزی و جنوب غربی مرکز کاهش می یابد. این مناطق مناطق مرفه نشین هستند. پیش بینی می شود سرقت دوچرخه در این مناطق کمتر تکرار شود. برعکس، در ناحیه میانی، ضرایب در امتداد خط چوئو که یک راه آهن اصلی است افزایش می‌یابد ( شکل 8).) خط. تمایل تکراری به ویژه در نزدیکی ایستگاه های اصلی در خط قوی است. از آنجایی که مسیرهای مترو و اتوبوس در منطقه مرفه پراکنده شده اند (اگرچه در شکل نشان داده نشده است)، کاربران دوچرخه در این منطقه نسبتاً محدود هستند. علاوه بر این، اکثر ساکنان این منطقه توانایی خرید دوچرخه را دارند. این ویژگی ها ممکن است تعداد مجرمان بالقوه دزدی دوچرخه را کاهش دهد. در مقابل، در منطقه میانی، مسیرهای راه آهن و اتوبوس نسبتاً محدود است و بسیاری از مردم از دوچرخه برای خرید یا رفتن به ایستگاه‌های راه‌آهن استفاده می‌کنند. دوچرخه در این منطقه واقعا مورد نیاز است. علاوه بر این، سطح درآمد در این منطقه نسبت به منطقه مرفه پایین است. این ویژگی ها ممکن است مجرمان بالقوه را افزایش دهند.
در مورد دزدی از مغازه، ضرایب Repeat در ناحیه مرکزی که خط Yamanote در آن اجرا می شود افزایش می یابد ( شکل 8 را ببینید ). این منطقه شامل مناطق تجاری مرکزی در نزدیکی ایستگاه شینجوکو و ایستگاه توکیو است. محصولات متنوعی در این مناطق به فروش می رسد. علاوه بر این، فروشگاه های لوکس در این مناطق متمرکز شده اند. چنین ویژگی هایی ممکن است مجرمان بالقوه را جذب کرده و قربانی شدن تقریباً تکراری را افزایش دهند.
شکل 11 NVC های تخمینی را نشان می دهد. هم برای دزدی دوچرخه و هم برای دزدی از مغازه، NVC روی Repeat که در S&NVC است، اگر Repeat زیاد باشد، مقدار بالایی می گیرد (دو پانل سمت چپ شکل 11 را ببینید ) . این بدان معنی است که اگر در سه ماهه قبل جرایم زیادی وجود داشته باشد، تمایل تکراری قوی می شود. در مقابل، یک RepOther کوچکتر ضرایب بالاتری دارد. این بدان معنی است که تعداد سرقت دوچرخه و دزدی از مغازه با سایر جرایم در مناطق کم خطر (یعنی مقادیر کم RepOther) مرتبط است. برای سرقت دوچرخه، Popden و Dpopden بالاتر ضرایب کمتری دارند. این بدان معناست که با افزایش جمعیت، سرقت دوچرخه افزایش می یابد، اما با افزایش جمعیت، میزان افزایش آن کاهش می یابد.
در نهایت، جدول 4 اثرات برآورد شده گروهی بر سرقت دوچرخه را به تفکیک سه ماهه خلاصه می کند. نتایج مربوط به دزدی از فروشگاه نشان داده نمی شود زیرا هر دو اثر گروه انتخاب نشده اند. یکی از یافته های جالب این است که موارد سرقت دوچرخه در سه ماهه اول (ژانویه تا مارس) کاهش می یابد، در حالی که در سه ماهه دوم (آوریل تا ژوئن) افزایش می یابد. این نشان می دهد که موارد سرقت دوچرخه در سه ماهه دوم (آوریل تا ژوئن) احتمالاً به دلیل افزایش آب و هوای گرم کاربران دوچرخه و/یا تغییر در شیوه زندگی و فعالیت های معمول در فصل بهار افزایش می یابد (به [43] مراجعه کنید ) .
در حالی که مدل‌های رگرسیون فضایی برای مدل‌سازی جرم استفاده شده‌اند، نتایج آنها به شدت به مفروضات مدل بستگی دارد. به عنوان مثال، مطالعات با استفاده از GWR همیشه برآوردهای ضرایب را مورد بحث قرار می دهند که به طور هموار در فضای جغرافیایی تغییر می کنند در حالی که مطالعات اقتصادسنجی فضایی تخمین ضرایب ثابت را در حضور وابستگی مکانی مورد بحث قرار می دهند. در مقابل، نتایج ما، که انواع ضرایب را انتخاب کردند، کمتر به چنین فرضیات مدل‌سازی وابسته هستند. نتایج ما قابل اعتمادتر است. علاوه بر این، نتایج ما تأثیر قوی NVCها را نشان می‌دهد که در آمار فضایی به جای SVCها نادیده گرفته شده‌اند، خطر استفاده از مدل رگرسیون فضایی بدون انتخاب مدل را نشان می‌دهد. رویکرد انتخاب مدل ما برای افزایش قابلیت اطمینان تحلیل رگرسیون فضایی مفید خواهد بود.
دوره-آموزش-حرفه-ای-gis

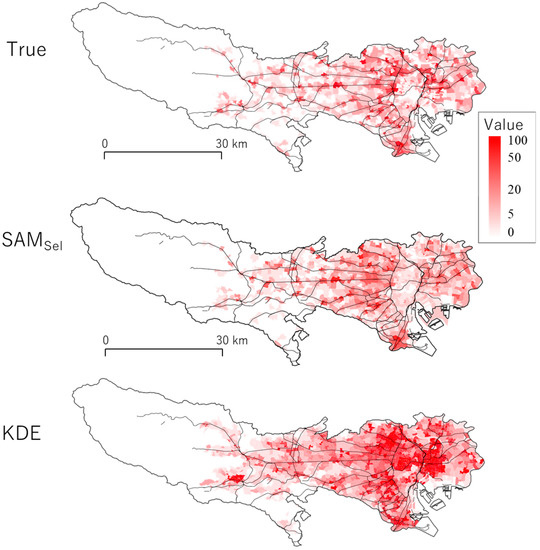
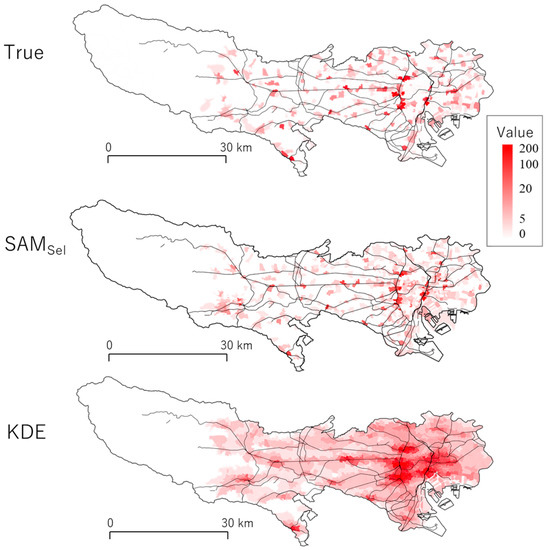
5.3. کاربرد در پیش بینی جرم

پیش‌بینی جرم برای آینده نزدیک برای پیشگیری از جرایم مهم است. در اینجا، ما مدل خود (SNM Sel ) را برای پیش‌بینی تعداد موارد سرقت دوچرخه و دزدی از مغازه در مناطق کوچک شهرداری در سه ماهه اول سال 2019 با استفاده از مدل آموزش دیده با داده‌های بین سال‌های 2017 و 2018 اعمال می‌کنیم. دقت با تخمین چگالی هسته (KDE)، که یک روش رایج پیش‌بینی جرم در این زمینه است [ 44 ]. بسته ks ( https://cran.r-project.org/web/packages/ks/index.html ) در R برای تخمین و پیش‌بینی مدل KDE استفاده شد. انتخابگر پلاگین [ 45 ] برای بهینه سازی پهنای باند هسته استفاده می شود.
شکل 12 و شکل 13 به ترتیب تعداد پیش بینی شده و واقعی موارد سرقت دوچرخه و دزدی از مغازه را در هر منطقه مقایسه می کنند. برای هر دو مورد، نتایج KDE بیش از حد هموار می شوند. مقادیر RMSE به ترتیب 5.77 و 6.93 است. در مقابل، با توجه به گنجاندن اثرات فضایی و غیر فضایی، رویکرد ما به طور مناسب نقاط داغ محلی را تشخیص می‌دهد. الگوی نقشه حاصل کاملاً شبیه به اعداد مشاهده شده است. RMSE ها 3.53 برای سرقت دوچرخه و 1.62 برای دزدی از مغازه هستند که به طور قابل توجهی کمتر از KDE هستند. این نشان می دهد که رویکرد ما برای پیشگیری از جرم، مانند طراحی مسیرهای گشت زنی کارآمد، مفید است.
به طور خلاصه، ما سودمندی رویکرد خود را با در نظر گرفتن مدل‌سازی جرم به عنوان مثال نشان داده‌ایم. در حالی که ما نویز داده‌ها را با معرفی یک اصطلاح نویز در نظر گرفتیم، نمی‌توانیم سوگیری داده‌های بالقوه مربوط به ثبت/گزارش‌دهی کم، سؤالات نظرسنجی برای بررسی‌های جنایی، که تغییر جزئی آنها می‌تواند به طور چشمگیری پاسخ‌ها را تغییر دهد و دلایل دیگر را در نظر بگیریم (به عنوان مثال، [46] را ببینید . 47 ]). در نظر گرفتن سوگیری در داده های جرم، گام بعدی مهم برای مدل سازی جرایم قابل اعتمادتر خواهد بود. علاوه بر این، ما تکرار را در سطح منطقه در نظر گرفتیم. با این حال، بر اساس مطالعات در مورد تکرار قربانی شدن [ 48 ، 49]، چنین تکراری در مقیاس فضایی دقیق تر، مانند ویژگی های فردی، بخش های خیابان، و شبکه های 250 متری برجسته تر است. این یکی دیگر از وظایف مهم آینده است که به جای داده‌های سطح ناحیه، داده‌های جرم فضایی تفکیک‌شده بیشتری را در نظر بگیریم. با توجه به اینکه PredPol ( https://www.predpol.com/ ) و بسیاری از سیستم‌های پیش‌بینی جرم دیگر در مقیاس فضایی دقیق‌تری مانند شبکه‌های 250 متری عمل می‌کنند، گسترش مدل جرم ما برای پیش‌بینی دقیق‌تر فضایی نیز یک کار باقی‌مانده خواهد بود. به سمت اجرای اجتماعی

6. نکات پایانی

این مطالعه یک مدل یا رویکرد انتخاب نوع ضریب را برای مدل‌های ترکیبی افزودنی فضایی توسعه می‌دهد. آزمایش‌های شبیه‌سازی نشان می‌دهد که رویکرد ساده حاضر مدل واقعی را با دقت انتخاب می‌کند. علاوه بر این، حتی اگر انتخاب مدل معمولا زمان محاسباتی را افزایش می دهد، انتخاب مدل ما به طور چشمگیری آن را کاهش می دهد. این ویژگی برای تخمین یک مدل پیچیده که شامل بسیاری از اثرات کاندید از نمونه های بزرگ است، ارزشمند خواهد بود. تجزیه و تحلیل جنایی نشان می دهد که رویکرد ما نتایج معقولی را ارائه می دهد. رویکرد ما اثرات پنهان متعددی را در پشت پدیده‌های جغرافیایی برجسته و کمیت می‌کند. این ویژگی های برجسته برای طیف گسترده ای از تحلیل ها مانند تجزیه و تحلیل جرم، مطالعات زیست محیطی و مطالعات زیست محیطی مفید خواهد بود.
با این حال، مسائل زیادی وجود دارد که باید مورد توجه قرار گیرد. اول، ما باید تغییرات مکانی-زمانی را در ضرایب رگرسیون یا باقیمانده ها بگنجانیم. ضرایب متغیر مکانی و زمانی (STVC) توسط [ 50 ، 51 ، 52 مورد مطالعه قرار گرفته است.] و دیگران مورد مطالعه قرار گرفته است. با این حال، بحث در مورد انتخاب SVC، STVC یا سایر ضرایب هنوز در آمار فضایی محدود است. فرآیند مکانی-زمانی، که شامل فرآیندهای تعامل مکانی-مکانی، ناب-زمانی و مکانی-زمانی است، بسیار پیچیده تر از تغییرات فضایی صرف است. انتخاب به خوبی دستکاری شده از انواع SVC، STVC یا سایر انواع ضریب در بهبود دقت و پایداری مدل‌سازی مکانی-زمانی بسیار مهم خواهد بود. در نظر گرفتن رفتار زمانی پویا در آن مهم است [ 53 ، 54 ]. دوم، در نظر گرفتن تعداد بیشتری از ضرایب، مانند بیش از 100، مهم است . ]، در تخمین SVC، NVC، یا مفید خواهند بود. سایر ضرایب متغیر در حالی که از برازش بیش از حد جلوگیری می شود. سوم، ما باید رویکرد خود را برای مدل‌سازی داده‌های غیر گاوسی گسترش دهیم و در عین حال کارایی محاسباتی را حفظ کنیم. به عنوان مثال، بسط برای پواسون یا رگرسیون دو جمله ای منفی یک کار مهم در آینده برای مدل سازی تعداد جرم به جای تراکم جرم خواهد بود (به عنوان مثال، [ 1 ] را ببینید)، در حالی که رگرسیون با توزیع اریب برای مدل‌سازی حداکثر دما یا سایر داده‌های مربوط به شدید مفید خواهد بود. مقادیر (به عنوان مثال، [ 57]).
روش انتخاب مدل توسعه‌یافته در یک بسته R بسته spmoran ( https://cran.r-project.org/web/packages/spmoran/index.html ) پیاده‌سازی شد.

پیوست A. تابع Log-Likelihood محدود مدل ترکیبی افزودنی فضایی

REML سریع احتمال نهایی را به حداکثر می رساند لogلمنکآر(Θ)تعریف شده با ادغام { ب،U}از احتمال کامل، که به صورت فرموله شده است

لogلمنکآر(Θ)=-12لog|ایکس”ایکسایکس”E˜(Θ)E˜”(Θ)ایکسE˜”(Θ)E˜(Θ)+من| -ن-ک2(1+لog(2πد(Θ)ن-ک))

جایی که E˜(Θ)=[ایکس1درجهE1V1(θ1)،…،ایکسپدرجهEپVپ(θپ)]. در ترم دوم معادله (6)، د(Θ)=ε^”ε^+∑پ=1پتو^”پتو^پواریانس نویز و واریانس اثرات تصادفی را متعادل می کند

ε^=y-ایکسب^-E˜(Θ)U^
[ب^U^]=[ایکس”ایکسایکس”E˜(Θ)E˜”(Θ)ایکسE˜”(Θ)E˜(Θ)+من]-1[ایکس”yE˜”(Θ)y]
مدل ترکیبی افزودنی به آسانی با: (i) تخمین زده می شود Θ^با به حداکثر رساندن لogلمنکآر(Θ)، و (ii) برآورد ضرایب ثابت و تصادفی [ب^”، U^”]”با جایگزین کردن Θ^به معادله (11). یکی از مشکلات عمده، هزینه محاسباتی برآورد است Θ^در مرحله (i) زیرا هزینه با توجه به تعداد پارامترهای موجود به صورت تصاعدی افزایش می یابد Θ^. زمان محاسباتی می تواند به طرز ناامیدکننده ای طولانی باشد، حتی برای 10 پارامتر واریانس. متأسفانه، برای جذب انعطاف‌پذیر تأثیر بسیاری از متغیرهای کمکی، معمولاً به 10 پارامتر واریانس یا بیشتر نیاز است.

ضمیمه B. جزئیات رویکردهای انتخاب مدل

این پیوست جزئیات محاسباتی روش انتخاب مدل ساده را توضیح می دهد. سپس جزئیات روش MC توضیح داده شده است.
در مرحله (الف) روش ساده (به بخش 3.2.1 مراجعه کنید )، ماتریس های داده ها {y،ایکس،E1،…، Eپ}با محصولات داخلی زیر جایگزین می شوند: م0،0=ایکس”ایکس، م0،پ=ایکس”(ایکسپدرجهEپ)، مپ،پ˜=(ایکسپدرجهEپ)”(ایکسپ˜درجهEپ)، متر0=ایکس”y، مترپ=(ایکسپدرجهEپ)”y، و مترy،y=y”y، جایی که ” آدرجهب” بردار ستون را ضرب می کند آبا هر ستون ماتریس B از نظر عنصر.

احتمال ورود محدود حداکثر شده در مرحله (ب) (به بخش 3.2.1 مراجعه کنید) با جایگزین کردن این محصولات داخلی در معادله (A1) [ 19 ] بازنویسی می شود :

لogلمنکآر(Θ)=-12لn|پ| -ن-ک2(1+لn(2π∥ε^∥2+∑پ=1پ∥تو^∥پ2ن-پ))،

جایی که

پ=[م0،0م0،1V1(θ1)V1(θ1)م1،0V1(θ1)م1،1V1(θ1)+من⋯م0،پVپ(θپ)⋯V1(θ1)م1،پVپ(θپ)⋮⋮Vپ(θپ)مپ،0Vپ(θپ)مپ،1V1(θ1)⋱⋮⋯Vپ(θپ)مپ،پVپ(θپ)+من]،
∥ε^∥2=مترy،y-2[ب^”،تو^”1،⋯تو^”پ][متر0V1(θ1)متر1⋮Vپ(θپ)مترپ]+[ب^”،تو^”1،⋯تو^”پ]پ0[ب^تو^1⋮تو^پ]،
[ب^تو^1⋮تو^پ]=پ-1[متر0V1(θ1)متر1⋮Vپ(θپ)مترپ].
معادلات (A4)-(A7) هیچ ماتریسی را که اندازه آن به N بستگی دارد، شامل نمی شود . بنابراین، در مرحله (ب)، احتمال با هزینه محاسباتی مستقل از اندازه نمونه ارزیابی می شود.

تکرار P- امین مرحله (ب) را به عنوان مثال در نظر بگیرید . در مرحله (b-1) از تکرار P- امین، لogلمنکآر(θپ(س)|Θ^-پ(س))با توجه به به حداکثر می رسد θپ(س). حداکثر سازی شامل ارزیابی تکراری است |پ| و پ-1که پیچیدگی محاسباتی آن برابر است O((∑پ=1پLپ)3)، که در هنگام در نظر گرفتن بسیاری از اثرات می تواند کند باشد، همانطور که در مورد ما وجود دارد. برای کاهش هزینه، معادله (A7)، از جمله پ-1، به شرح زیر گسترش می یابد:

[ب^تو^1⋮تو^پ]=[V˜-پ-100Vپ(θپ(س))-1]س-1[متر-پمترپ]    -[V˜-پ-1س-پ،پ∗Vپ(θپ(س))-1سپ،پ∗](Vپ(θپ(س))2+سپ،پ∗)-1[سپ،-پ∗متر-پ+سپ،پ∗مترپ]،

جایی که  V˜-پ=[من⬚⬚V1⬚⬚⬚⬚⬚⬚⬚⬚⋱⬚⬚Vپ-1]، جایی که Vپ=Vپ(θ^پ). Θ^-پ(س)∈{θ^1،…،θ^پ-1،θ^پ(n)} که در این مرحله رفع شده است برای سادگی حذف شده است. س=[م˜-پ،-پ+V˜-پ-2م˜-پ،پم˜پ،-پمپ،پ]، جایی که  م˜-پ،-پ=[م0،0م0،1م1،0م1،1+V1-2⋯م0،پ-1⋯م1،پ-1⋮⋮مپ-1،0مپ-1،1⋱⋮⋯مپ-1،پ-1+Vپ-1-2]و م˜-پ،پ=[مپ،0مپ،1⋯مپ،پ-1]”، و [س-پ،-پ*س-پ،پ*سپ،-پ*سپ،پ*]=س-1.

از سوی دیگر، | P | که یکی دیگر از بخش های خسته کننده است، عبارت زیر را دارد:

|پ|=|V˜-پ|2|Vپ(θپ(س))|2|م˜-پ،-پ+V˜-پ-2||Vپ(θپ(س))-2+مپ،پ-م˜پ،-پ(م˜-پ،-پ+V˜-پ-2)-1م˜-پ،پ|.
برای به حداکثر رساندن احتمال عددی، معادلات (A8) و (A9) باید به طور مکرر در حالی که متغیر هستند ارزیابی شوند. θپ(س). خوشبختانه، بسیاری از عناصر در معادله (A8) حتی زمانی که تغییر نمی کنند θپ(س)تغییر کرده است. در نتیجه اگر عناصری که مستقل از θپ(س)به صورت پیشینی ارزیابی می شوند، پیچیدگی محاسباتی برای ارزیابی تکراری معادله (A8) فقط O است ( Lپ3) که برای ارزیابی لازم است (V(θپ(س))2+سپ،پ*)-1. به همین ترتیب، پیچیدگی ارزیابی تکراری معادله (A9) در حالی که متفاوت است θپ(س)فقط O است ( Lپ3). بنابراین، مرحله تخمین مدل (b-1) برای اندازه نمونه N و تعداد اثرات P بسیار خوب مقیاس می شود . همین امر برای مرحله تخمین NVC (b-3) نیز صادق است.

در مرحله انتخاب مدل (b-2)، باید تابع هزینه (به عنوان مثال، BIC) مدل را با P – th SVC که در مرحله (b-1) تخمین زده شده است، با مدل بدون P مقایسه کنیم. -ام SVC. برای این کار، ما همچنین باید احتمال مدل اخیر را با استفاده از معادله (A4) ارزیابی کنیم. احتمال را می توان با جایگزینی معادلات (A8) و (A9) با معادلات (A10) و (A11) ارزیابی کرد.

[ب^تو^1⋮تو^پ-1]= V˜-پ-1(م˜-پ،-پ+V˜-پ-2)-1متر-پ
|پ|=|V˜-پ|2|م˜-پ،-پ+V˜-پ-2|
تمام عناصر موجود در معادله (A11) قبلاً در مرحله (b-1) معادله (A6) ارزیابی شده اند. بنابراین، معادله (A11) بدون هیچ گونه هزینه محاسباتی اضافی مورد ارزیابی قرار گرفت. با اينكه (م˜-پ،-پ+V˜-پ-2)-1باید علاوه بر محاسبه معادله (A10)، پیچیدگی محاسباتی است O((∑پ=1پ-1Lپ)3)، که هنوز مستقل از حجم نمونه است. علاوه بر این، ارزیابی تکراری در این بخش مورد نیاز نیست زیرا هزینه محاسبه در مرحله (b-2) بی اهمیت است. همین امر برای مرحله انتخاب مدل دیگر (b-4) صدق می کند.
به طور خلاصه، هر دو مرحله تخمین و انتخاب مدل به صورت محاسباتی کارآمد انجام شد.

منابع

  1. تجزیه و تحلیل رگرسیون مبتنی بر Osgood، DW Poisson از میزان جرم کل. جی. کوانت. Criminol. 2000 ، 16 ، 21-43. [ Google Scholar ] [ CrossRef ]
  2. کیهیل، م. مولیگان، جی. استفاده از رگرسیون وزن‌دار جغرافیایی برای کشف الگوهای جرم محلی. Soc. علمی محاسبه کنید. Rev. 2007 , 25 , 174-193. [ Google Scholar ] [ CrossRef ]
  3. برناسکو، دبلیو. بلوک، R. Robbery در شیکاگو: تجزیه و تحلیل سطح بلوک از تأثیر عوامل جنایت، مجذوبان جرم، و نقاط لنگر مجرم. J. Res. جنایت دلینق. 2011 ، 48 ، 33-57. [ Google Scholar ] [ CrossRef ]
  4. مگوایر، ام. McVie, S. داده های جرم و آمار جنایی: بازتاب انتقادی. در کتاب راهنمای جرم شناسی آکسفورد ؛ Maruna, S., McAra, L., Eds. انتشارات دانشگاه آکسفورد: آکسفورد، انگلستان، 2017; صص 163-189. [ Google Scholar ]
  5. LeSage، JP; Pace, RK مقدمه ای بر اقتصاد سنجی فضایی ; CRC Press: Boca Raton، FL، USA، 2009. [ Google Scholar ]
  6. کرسی، ن. Wikle، آمار CK برای داده های مکانی-زمانی ; جان وایلی و پسران: هوبوکن، نیوجرسی، ایالات متحده آمریکا، 2011. [ Google Scholar ]
  7. براندون، سی. فاثرینگهام، اس. چارلتون، ام. رگرسیون وزنی جغرافیایی. JR Stat. Soc. سر. D (آمار) 1998 ، 47 ، 431-443. [ Google Scholar ] [ CrossRef ]
  8. Fotheringham، AS; براندون، سی. چارلتون، ام. رگرسیون وزن‌دار جغرافیایی: تجزیه و تحلیل روابط متغیر فضایی . جان وایلی و پسران: وست ساسکس، انگلستان، 2002. [ Google Scholar ]
  9. لی، اس. کانگ، دی. کیم، ام. عوامل تعیین کننده وقوع جرم در کره: یک رویکرد GWR مخلوط. در مجموعه مقالات کنفرانس جهانی انجمن اقتصاد سنجی فضایی، بارسلون، اسپانیا، 8 تا 10 ژوئیه 2009. صص 8-10. [ Google Scholar ]
  10. آرنیو، AN; باومر، جمعیت شناسی EP، سلب حق اقامه دعوی، و جرم: ارزیابی ناهمگونی فضایی در مدل های معاصر نرخ جرم محله. Demogr. Res. 2012 ، 26 ، 449-486. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  11. املاوف، ن. آدلر، دی. کنیب، تی. لانگ، اس. Zeileis، A. مدل‌های رگرسیون افزودنی ساختاریافته: رابط R برای BayesX. J. Stat. نرم افزار 2015 ، 21 ، 63. [ Google Scholar ]
  12. ناکایا، تی. فاثرینگهام، اس. چارلتون، ام. Brunsdon، C. مدلسازی خطی تعمیم یافته با وزن جغرافیایی نیمه پارامتریک در GWR 4.0. در مجموعه مقالات دهمین کنفرانس بین المللی محاسبات جغرافیایی، سیدنی، استرالیا، 30 نوامبر تا 2 دسامبر 2009. [ Google Scholar ]
  13. ویلر، DC جریمه ضریب همزمان و انتخاب مدل در رگرسیون وزن‌دار جغرافیایی: کمند وزن‌دار جغرافیایی. محیط زیست طرح. A 2009 , 41 , 722-742. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  14. کامبر، ا. براندون، سی. چارلتون، ام. دونگ، جی. هریس، آر. لو، بی. لو، ی. موراکامی، دی. ناکایا، تی. وانگ، ی. و همکاران نقشه مسیر GWR: راهنمای کاربرد آگاهانه رگرسیون وزن‌دار جغرافیایی. arXiv 2020 ، arXiv:2004.06070. [ Google Scholar ]
  15. هوانگ، جی. هوروویتز، جی ال. Wei, F. انتخاب متغیر در مدل‌های افزودنی ناپارامتریک. ان آمار 2010 ، 38 ، 2282. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
  16. آماتو، U. آنتونیادیس، ا. De Feis، I. انتخاب مدل افزودنی. آمار Methods Appl. 2016 ، 25 ، 519-654. [ Google Scholar ] [ CrossRef ]
  17. Mei، CL; او، SY; نیش، KT یادداشتی در مورد مدل رگرسیون ترکیبی وزن‌دار جغرافیایی. J. Reg. علمی 2004 ، 44 ، 143-157. [ Google Scholar ] [ CrossRef ]
  18. لی، ز. Fotheringham، AS; لی، دبلیو. Oshan, T. Fast Geographically Weighted Regression (FastGWR): یک الگوریتم مقیاس پذیر برای بررسی ناهمگونی فرآیند فضایی در میلیون ها مشاهده. بین المللی جی. جئوگر. Inf. علمی 2019 ، 33 ، 155-175. [ Google Scholar ] [ CrossRef ]
  19. موراکامی، دی. گریفیث، DA مدل‌سازی ضریب متغیر فضایی برای مجموعه داده‌های بزرگ: حذف N از رگرسیون‌های فضایی. تف کردن آمار 2019 ، 30 ، 39–64. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  20. موراکامی، دی. گریفیث، DA یک مدل‌سازی ترکیبی افزودنی فضایی بدون حافظه برای داده‌های فضایی بزرگ. Jpn. J. Stat. اطلاعات علمی 2020 ، 3 ، 215-241. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  21. موراکامی، دی. یوشیدا، تی. سیا، ح. گریفیث، دی. یاماگاتا، ی. رویکرد اثرات مختلط مبتنی بر ضریب موران برای بررسی روابط متغیر فضایی. تف کردن آمار 2017 ، 19 ، 68-89. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  22. گریفیث، DA خودهمبستگی فضایی و فیلتر فضایی: به دست آوردن درک از طریق تئوری و تجسم علمی . Springer Science & Business Media: برلین، آلمان، 2003. [ Google Scholar ]
  23. تیفلسدورف، ام. گریفیث، DA فیلتر نیمه پارامتریک همبستگی فضایی: رویکرد بردار ویژه. محیط زیست طرح. A 2007 , 39 , 1193-1221. [ Google Scholar ] [ CrossRef ]
  24. موراکامی، دی. گریفیث، DA متوازن کردن تغییرات فضایی و غیر فضایی در مدل‌سازی ضرایب متغیر: درمانی برای همبستگی جعلی. arXiv 2020 ، arXiv:2005.09981. [ Google Scholar ]
  25. ویلر، دی. Tiefelsdorf، M. چند خطی و همبستگی بین ضرایب رگرسیون محلی در رگرسیون وزنی جغرافیایی. جی. جئوگر. سیستم 2005 ، 7 ، 161-187. [ Google Scholar ] [ CrossRef ]
  26. بیتس، دی. ماچلر، ام. بولکر، بی. واکر، اس. برازش مدل‌های خطی با جلوه‌های مختلط با استفاده از lme4. arXiv 2014 ، arXiv:1406.5823. [ Google Scholar ]
  27. زمستان، بی. Wieling، M. چگونگی تجزیه و تحلیل تغییر زبانی با استفاده از مدل های ترکیبی: تجزیه و تحلیل منحنی رشد و مدل سازی افزایشی تعمیم یافته. جی. لانگ. تکامل. 2016 ، 1 ، 7-18. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  28. بااین، ح. واسیشت، س. کلیگل، آر. بیتس، دی. غار سایه ها: پرداختن به عامل انسانی با مدل های ترکیبی افزودنی تعمیم یافته. جی. مم. لنگ 2017 ، 94 ، 206-234. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  29. Gurka, MJ انتخاب بهترین مدل خطی مختلط تحت REML. صبح. آمار 2006 ، 60 ، 19-26. [ Google Scholar ] [ CrossRef ]
  30. مولر، اس. Scealy، JL; انتخاب مدل ولز، AH در مدل های مختلط خطی. آمار علمی 2013 ، 28 ، 135-167. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  31. دیمووا، RB; مارکاتو، م. روش‌های اطلاعاتی طلال، AH برای انتخاب مدل در مدل‌های اثرات مختلط خطی با کاربرد در داده‌های HCV. محاسبه کنید. آمار داده آنال. 2011 ، 55 ، 2677-2697. [ Google Scholar ] [ CrossRef ]
  32. Sakamoto، W. Bias معیارهای اطلاعات حاشیه ای Akaike را بر اساس روش مونت کارلو برای مدل های خطی اثرات مختلط کاهش داد. Scand. J. Stat. 2019 ، 46 ، 87-115. [ Google Scholar ] [ CrossRef ]
  33. گریون، اس. Kneib, T. در مورد رفتار AIC حاشیه ای و شرطی در مدل های خطی مختلط. Biometrika 2010 ، 97 ، 773-789. [ Google Scholar ] [ CrossRef ]
  34. بلیتز، سی. Lang, S. انتخاب همزمان متغیرها و پارامترهای هموارسازی در مدل های رگرسیون افزودنی ساختاریافته. محاسبه کنید. آمار داده آنال. 2008 ، 53 ، 61-81. [ Google Scholar ] [ CrossRef ]
  35. ریس، PT; Todd Ogden, R. انتخاب پارامتر هموارسازی برای کلاسی از مدل های خطی نیمه پارامتریک. JR Stat. Soc. سر. B (Stat. Methodol.) 2009 ، 71 ، 505-523. [ Google Scholar ] [ CrossRef ]
  36. Wood, SN برآورد حداکثر احتمال محدود شده با ثبات سریع و احتمال حاشیه ای مدل های خطی تعمیم یافته نیمه پارامتری. JR Stat. Soc. سر. B (Stat. Methodol.) 2011 ، 73 ، 3-36. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  37. مارا، جی. Wood, SN انتخاب متغیر عملی برای مدل های افزودنی تعمیم یافته. محاسبه کنید. آمار داده آنال. 2011 ، 55 ، 2372-2387. [ Google Scholar ] [ CrossRef ]
  38. چوب، SN; لی، ز. شادیک، جی. آگوستین، NH مدل‌های افزودنی تعمیم‌یافته برای گیگاداده: مدل‌سازی داده‌های روزانه شبکه دود سیاه بریتانیا. مربا. آمار دانشیار 2017 ، 112 ، 1199-1210. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  39. Felson, M. Crime and Everyday Life: Insights and Implications for Society (The Pine Forge Press Library Science Social Science) ; Pine Forge: Berks، PA، USA، 1994. [ Google Scholar ]
  40. فارل، جی. جلوگیری از تکرار قربانی شدن. عدالت جنایی 1995 ، 19 ، 469-534. [ Google Scholar ] [ CrossRef ]
  41. جانسون، SD تکرار قربانی سرقت: داستانی از دو نظریه. J. Exp. Criminol. 2008 ، 4 ، 215-240. [ Google Scholar ] [ CrossRef ]
  42. Caplan، JM; کندی، LW; میلر، جی. مدل‌سازی زمین ریسک: نظریه جرم‌شناسی و روش‌های GIS برای پیش‌بینی جرم. عدالت Q. 2011 ، 28 ، 360-381. [ Google Scholar ] [ CrossRef ]
  43. رانسون، ام. جنایت، آب و هوا و تغییرات آب و هوایی. جی. محیط زیست. اقتصاد مدیریت 2014 ، 67 ، 274-302. [ Google Scholar ] [ CrossRef ]
  44. هارادا، ی. شیمادا، تی. بررسی تأثیر دقت کدگذاری جغرافیایی آدرس بر تراکم تخمینی مکان‌های جرم. محاسبه کنید. Geosci. 2006 ، 32 ، 1096-1107. [ Google Scholar ] [ CrossRef ]
  45. عصا، نماینده مجلس؛ Jones، MC Multivariate پلاگین انتخاب پهنای باند. محاسبه کنید. آمار 1994 ، 9 ، 97-116. [ Google Scholar ]
  46. یو، او. ژانگ، ال. ثبت کم جرم توسط پلیس در چین: مطالعه موردی. پلیس بین المللی J. 1999 , 22 , 252-264. [ Google Scholar ] [ CrossRef ]
  47. تباروک، ع. هیتون، پی. هلند، E. معیار رذیلت و گناه: مروری بر کاربردها، محدودیت‌ها و پیامدهای داده‌های جرم. هندب اقتصاد جنایت 2010 ، 3 ، 53-81. [ Google Scholar ]
  48. فارل، جی. فیلیپس، سی. Pease, K. مانند خوردن آب نبات – چرا قربانی تکرار اتفاق می افتد. برادر J. Criminol. 1995 ، 35 ، 384-399. [ Google Scholar ] [ CrossRef ]
  49. فارل، جی. Pease, K. Repeat Victimization ; مطبوعات عدالت کیفری: نیویورک، نیویورک، ایالات متحده آمریکا، 2001. [ Google Scholar ]
  50. گلفاند، AE; کیم، اچ جی. سیرمنز، سی اف. Banerjee, S. مدلسازی فضایی با فرآیندهای ضریب متغیر مکانی. مربا. آمار دانشیار 2003 ، 98 ، 387-396. [ Google Scholar ] [ CrossRef ]
  51. هوانگ، بی. وو، بی. Barry, M. رگرسیون وزن‌دار جغرافیایی و زمانی برای مدل‌سازی تغییرات مکانی-زمانی قیمت مسکن. بین المللی جی. جئوگر. Inf. علمی 2010 ، 24 ، 383-401. [ Google Scholar ] [ CrossRef ]
  52. Fotheringham، AS; کرسپو، آر. یائو، جی. رگرسیون وزنی جغرافیایی و زمانی (GTWR). Geogr. مقعدی 2015 ، 47 ، 431-452. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  53. Mohler, G. مدل‌سازی و برآورد خوشه‌بندی چند منبعی در داده‌های جرم و امنیت. ان Appl. آمار 2013 ، 7 ، 1525-1539. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  54. کاجیتا، م. کاجیتا، اس. پیش‌بینی جرم با روش تابع گرین مبتنی بر داده. بین المللی J. پیش بینی. 2020 ، 36 ، 480-488. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  55. هستی، تی. طبشیرانی، ر. Wainwright, M. Statistical Learning with Sparity: The Lasso and Generalizations ; CRC Press: نیویورک، نیویورک، ایالات متحده آمریکا، 2015. [ Google Scholar ]
  56. فن، جی. Li, R. انتخاب متغیر از طریق احتمال جریمه شده غیر مقعر و خواص اوراکل آن. مربا. آمار دانشیار 2001 ، 96 ، 1348-1360. [ Google Scholar ] [ CrossRef ]
  57. کولی، دی. تحلیل ارزش افراطی و مطالعه تغییرات آب و هوا. صعود چانگ. 2009 ، 97 ، 77. [ Google Scholar ] [ CrossRef ]
Ijgi 09 00577 g001 550
شکل 1. نمونه هایی از ضرایب که در نظر خواهیم گرفت. S&NVC (ضریب متغیر مکانی و غیر مکانی) مجموع SVC (ضریب متغیر مکانی) و NVC (ضریب متغیر غیرمکانی) است. همانطور که در اینجا نشان داده شده است، SVC و NVC به ترتیب با توابع غیر خطی در یک فضای جغرافیایی و یک فضای ویژگی تعریف می شوند.
Ijgi 09 00577 g002 550
شکل 2. ضرایب به دست آمده از فرآیندهای مولد فرضی ما. این الگوها در هر تکرار تغییر می کنند.
Ijgi 09 00577 g003 550
شکل 3. ریشه میانگین مربعات خطا (RMSEs) برآورد ضرایب. N نشان دهنده حجم نمونه است. P = 1 به معنای مدلی با ضریب ثابت، SVC و NVC در فرآیند تولید داده است (معادلات (7)-(10)) در حالی که P = 3 به معنای سه ضریب ثابت، سه SVC و سه NVC در فرآیند است. .
Ijgi 09 00577 g004 550
شکل 4. تعصب برآورد خطای استاندارد.
Ijgi 09 00577 g005 550
شکل 5. RMSE برآورد خطای استاندارد.
Ijgi 09 00577 g006 550
شکل 6. نمودار جعبه ای RMSE ها برای تخمین ضرایب (LM: مدل خطی؛ S&NVC: مدل S&NVC؛ ساده: انتخاب مدل ساده S&NVC؛ Mgcv: Mgcv بدون انتخاب مدل؛ Mgcv sel: Mgcv با انتخاب مدل بر اساس جریمه مضاعف ) .
Ijgi 09 00577 g007 550
شکل 7. زمان محاسبه. برای نام مدل ها به شکل 4 مراجعه کنید . ما از یک مک پرو (3.5 گیگاهرتز، پردازنده 6 هسته ای Intel Xeon E5 با حافظه 64 گیگابایتی) استفاده کردیم. R (نسخه 4.0.0؛ https://cran.r-project.org/ ) برای تخمین مدل استفاده شد.
Ijgi 09 00577 g008 550
شکل 8. تراکم جنایت بر اساس مناطق کوچک شهری (تعداد حوادث/km2 ) (سه ماهه اول 2017). خطوط راه آهن را به جز مترو نشان می دهند. مربع های سیاه در پانل بالایی ایستگاه شینجوکو (شمال غربی) و ایستگاه توکیو (جنوب شرقی) هستند که ایستگاه های راه آهن اصلی هستند.
Ijgi 09 00577 g009 550
شکل 9. هیستوگرام تراکم جرم ثبت شده در هر منطقه در هر سه ماهه.
Ijgi 09 00577 g010 550
شکل 10. تخمین S&NVC در تکرار.
Ijgi 09 00577 g011 550
شکل 11. NVCهای تخمینی. خطوط یکپارچه نشان دهنده برآورد ضرایب و مناطق خاکستری نشان دهنده 95% فواصل اطمینان هستند. برای Repeat، NVC از S&NVC استخراج می شود.
Ijgi 09 00577 g012 550
شکل 12. تعداد موارد سرقت دوچرخه در سه ماهه اول 2019 (با برچسب True) و نتایج پیش بینی شده.
Ijgi 09 00577 g013 550
شکل 13. تعداد موارد سرقت از فروشگاه در سه ماهه اول 2019 (با برچسب True) و نتایج پیش بینی شده.

مقالات داخلی و بین المللی

مطالب مرتبط ...

بدون دیدگاه

دیدگاهتان را بنویسید