بازسازی تصاویر ماهواره ای چند زمانی با تقسیم بندی متغیر و تجزیه و تحلیل رادیومتری

تصاویر دیجیتال و به‌ویژه تصاویر ماهواره‌ای که توسط حسگرهای مختلف به دست می‌آیند، ممکن است به دلایل زیادی نقص داشته باشند. از سال 2013، ماموریت Landsat 7 تحت تأثیر یک مسئله شناخته شده مربوط به عملکرد نادرست Scan Line Corrector که نوارهای بسیار مشخصی از داده های گم شده در باندهای تصویری تولید می کند، قرار گرفته است. در زمینه برنامه کاربردی بازسازی تصویر گسترده و بین رشته ای، آثار زیادی در چند دهه اخیر برای مقابله با مشکل پر کردن شکاف لندست 7 ارائه شده است. این کار سهم دیگری را در این زمینه ارائه می‌کند که یک روش اصلی مبتنی بر یک مدل تقسیم‌بندی تصویر متغیر همراه با آنالیز رادیومتری برای بازسازی تصاویر آسیب‌دیده به‌دست‌آمده در یک سناریوی چند زمانی، معمولی در سنجش از دور ماهواره‌ای، ارائه می‌کند. ایده اصلی این است که از برخی ویژگی‌های خاص مدل متغیر مامفورد-شاه برای تقسیم‌بندی تصویر به منظور سهولت تشخیص مناطق همگن استفاده شود که سپس برای تشکیل مجموعه‌ای از داده‌های منسجم لازم برای بازسازی رادیومتری مناطق آسیب‌دیده استفاده می‌شود. دو رویکرد بازسازی ارائه شده و به داده های SLC-off Landsat 7 اعمال می شود. یک رویکرد مبتنی بر تبدیل تطبیق هیستوگرام شناخته شده است، رویکرد دیگر بر اساس تجزیه ویژه ماتریس کوواریانس باندها و بر اساس نمونه‌برداری از توزیع‌های گاوسی است. عملکرد این روش با استفاده از تصاویر آسیب‌دیده مصنوعی برای آزمایش خود اعتبارسنجی ارزیابی می‌شود. هر دو رویکرد بازسازی پیشنهادی به نتایج قابل توجهی منجر شده بود.

کلید واژه ها:

تقسیم بندی تصویر بازسازی تصویر ; مدل متغیر ; تطبیق هیستوگرام ؛ تصاویر ماهواره ای ; نرم افزار رایگان و متن باز

1. مقدمه

تصویربرداری دیجیتال به طور فزاینده ای رایج می شود و اکنون در زمینه های مختلف از بینایی کامپیوتری گرفته تا تصویربرداری پزشکی و سنجش از راه دور مورد استفاده قرار می گیرد. به دلایل مختلف، خواه فنی یا طبیعی، تصاویر ممکن است اغلب حاوی اعوجاج های رادیومتری یا کمبود جزئی اطلاعات باشند. نیاز به بازیابی اطلاعات از دست رفته یا تحریف شده منجر به توسعه مهم الگوریتم های بازیابی و بازسازی تصویر شد.

این کار یک رویکرد جدید برای بازسازی تصویر مبتنی بر جفت یک مدل متغیر تقسیم‌بندی تصویر و تحلیل رادیومتری تصاویر ماهواره‌ای چند زمانی ارائه می‌کند. بازسازی تصاویر ماهواره ای برای بهبود عملکرد پردازش تصویر بیشتر مانند طبقه بندی، عدم اختلاط طیفی و تشخیص اشیا بسیار مهم است.

در میان بسیاری از مأموریت‌های ماهواره‌ای گذشته و فعال برای اهداف رصد زمین (EO)، مأموریت لندست 7 یک مسئله خاص از دست دادن داده‌ها را ارائه می‌دهد که علاقه زیادی را در زمینه بازسازی تصویر به خود جلب کرده و هنوز هم به خود جلب می‌کند. ماموریت Landsat 7 که از سال 1999 در برنامه ESE (Earth Science Enterprise) ناسا عملیاتی شده است، از حسگر Enhanced Thematic Mapper Plus (ETM+) بهره برداری می کند. سنسورهای +ETM باندهای طیفی قرمز، سبز و آبی (RGB)، مادون قرمز نزدیک (NIR)، مادون قرمز موج کوتاه (SWIR)، مادون قرمز میانی (MIR) و مادون قرمز حرارتی (TIR) را با 8 بیت پوشش می دهند. وضوح رادیومتری (انتقالی) و وضوح فضایی 30، 60 و 15 متر به ترتیب برای باندهای RGB/NIR/SWIR/MIR، TIR و پانکروماتیک. نوارهای تصویری با یک چرخه تکرار 16 روزه به دست می آیند. این ماموریت علمی تا اواسط سال 2021 ادامه خواهد داشت (https://www.usgs.gov/news/successful-maneuver-spells-beginning-end-landsat-7 ).

در 31 مه 2003، Scan Line Corrector (SLC)، ابزار روی بردی که جهت خط اسکن را به منظور جبران حرکت ماهواره به جلو در حین اسکن مدیریت می کند، با خرابی دائمی مواجه شد. از آن تاریخ، صحنه های Landsat 7 SLC-off نامیده می شوند. بدون SLC، خط دید ابزار نمی تواند چرخش صحیح U را در انتهای خط اسکن انجام دهد و در عوض یک الگوی زیگزاگ را ردیابی کند. این باعث می شود که صحنه ها تا حدی دوبار اسکن شوند و بخشی دیگر اصلاً اسکن نشوند. از دست دادن داده به دلیل خرابی SLC بر بخش در 22 کیلومتری مرکزی صحنه گرفته شده تأثیر نمی گذارد، اما در عوض، نوارهای از دست دادن داده متقاطع ایجاد می کند که از مرکز تصویر به لبه های آن متورم می شود. تصاویر SLC-off حدود 22 درصد از داده ها را ندارند و حداکثر عرض فاصله داده ها حدود 15 پیکسل است. مربوط به حدود 450 متر از دست دادن اطلاعات در لبه ها. نوارهای SLC-off در صحنه های مختلف دقیقاً در یک موقعیت قرار نمی گیرند و همچنین در یک صحنه می توانند توسط یک پیکسل بین باندهای مختلف به درستی تراز شوند، که علت واضح بودن پیکسل های قرمز تیره، زرد و سبز است. لبه های باندهای SLC-off.

تحقیقات در مورد بازیابی تصاویر ماهواره‌ای به ویژه پس از شکست Landsat 7 Scan Line Corrector تقویت شد، رویدادی که باعث تخریب حیاتی و دائمی در یکی از مهم‌ترین ماموریت‌های سنجش از راه دور شد. حتی اگر لندست 8 در 11 فوریه 2013 راه اندازی شد، سلف آن هنوز کار می کند و یک دوره ده ساله از تصاویر آسیب دیده باید بازیابی شود.

در واقع، تعداد زیادی الگوریتم بازسازی مختلف ارائه شد که هر کدام ویژگی‌های خاص خود را دارند که شباهت‌ها و تفاوت‌های بین آنها را برجسته می‌کند [ 1 ، 2 ، 3 ، 4 ، 5 ، 6 ، 7 ، 8 ، 9 ، 10 ] .

به طور کلی، الگوریتم های بازسازی تصویر را می توان به دو دسته اصلی تقسیم کرد:

بازسازی تک تصویری;
بازسازی چند تصویری

الگوریتم‌های بازسازی تک تصویری عمدتاً در زمینه‌های تصویربرداری پزشکی و بینایی کامپیوتری استفاده می‌شوند، در حالی که الگوریتم‌های بازسازی چند تصویری برای کاربردهای چند زمانی یا چند منبع در ماهواره‌ها برای زمینه پردازش تصویر مناسب‌تر هستند. در صفحات بعدی به یک تصویر آسیب دیده یا خراب تصویر هدف و تصویری که از آن هر نوع اطلاعاتی برای بازسازی مناطق آسیب دیده یک تصویر هدف گرفته شده باشد، تصویر پایه نامیده می شود.

رویکردها به مسئله بازسازی چند تصویری را می توان به صورت زیر طبقه بندی کرد:

رویکرد ترکیبی: پر کردن شکاف های داده در تصویر هدف به طور مستقیم با مقادیر سایر تصاویر پایه، که گاهی اوقات با استفاده از یک تبدیل خطی بر اساس مقادیر میانگین جهانی تصاویر پایه و هدف تغییر مقیاس داده می شود.
رویکرد نزدیک‌ترین همسایه: استفاده از مقادیر پیکسل‌های نزدیک به پیکسلی که باید رنگ‌آمیزی شود، به‌منظور بدست آوردن آماری از یک مخزن داده مرجع که مقادیر بازسازی‌شده از آن محاسبه می‌شوند.
رویکرد زمین آمار: استفاده از کریجینگ برای در نظر گرفتن صریح همبستگی فضایی برای پیش‌بینی مقادیر بازسازی‌شده و خطاهای تخمین.
رویکرد تقسیم‌بندی: شناسایی خوشه‌هایی از پیکسل‌های همگن به‌طور خودکار برای ایجاد مخزن‌های داده مرجع که از آنها آمار برای محاسبه مقادیری که باید بازسازی شوند استخراج می‌شود.

راه حل اصلی ارائه شده در این کار فقط از اطلاعات هندسی و رادیومتری به دست آمده از تصاویر هدف و پایه به دست آمده در یک سناریوی چند زمانی بهره می برد و به سایر اطلاعات جانبی مانند نقشه های پوشش زمین متکی نیست. روش پیشنهادی امکان بازسازی ویژگی‌های هندسی پیچیده را حتی زمانی که به طور کامل آسیب دیده باشد را می‌دهد، با این فرضیه منطقی که در فاصله زمانی بین دوره‌های اکتساب تصاویر هدف و پایه، چنین ویژگی‌هایی دستخوش تغییرات قابل‌توجهی نشدند. این روش از یک مدل متغیر تقسیم بندی تصویری که توسط مامفورد و شاه پیشنهاد شده است بهره برداری می کند [ 11] که شناسایی نواحی همدوس را در یک تصویر قطعه‌بندی شده و به دنبال آن تجزیه و تحلیل رادیومتری مناطق منسجم مرتبط شناسایی شده بر روی تصاویر هدف و پایه آسان می‌کند. به طور شهودی، مزیت اصلی مدل تنوع مامفورد-شاه این است که تصویر تحت یک فرآیند هموارسازی قرار می‌گیرد که به ناپیوستگی‌های تصویر احترام می‌گذارد. به همین دلیل، از یک سو، تغییرپذیری رادیومتری نواحی تقسیم‌بندی شده به دلیل کاهش نویز مرتبط با فرآیند هموارسازی کاهش می‌یابد، و از سوی دیگر، کیفیت هندسی نواحی قطعه‌بندی‌شده توسط فرآیند هموارسازی یکسان به خطر نمی‌افتد. اقدام به طور خودکار در مرزهای منطقه سرکوب می شود. در نتیجه، مناطق تقسیم‌بندی شده با کیفیت بالا منجر به شناسایی بهتر مناطق منسجم شد. دو رویکرد مختلف برای آنالیزهای رادیومتریک برای بازسازی در نظر گرفته شده است: رویکرد اول مبتنی بر تبدیل تطبیق هیستوگرام (HM) و روش دوم مبتنی بر تجزیه ویژه (ED) ماتریس کوواریانس مجموعه‌ای از باندهای تصویری و نمونه‌برداری است. توزیع های گاوسی کل این روش با استفاده از نرم افزار رایگان و متن باز و با استفاده از برنامه های اصلی اجرا شد. بخش‌بندی و تشخیص نواحی منسجم با استفاده از GRASS GIS انجام شد، در حالی که تحلیل‌ها و بازسازی‌های رادیومتری با استفاده از کد پایتون و رابط برنامه‌نویسی کاربردی PyGRASS (API) پیاده‌سازی شدند. رویکرد اول مبتنی بر تبدیل تطبیق هیستوگرام (HM) و روش دوم بر اساس تجزیه ویژه (ED) ماتریس کوواریانس مجموعه‌ای از باندهای تصویری و نمونه‌برداری از توزیع‌های گاوسی است. کل این روش با استفاده از نرم افزار رایگان و متن باز و با استفاده از برنامه های اصلی اجرا شد. بخش‌بندی و تشخیص نواحی منسجم با استفاده از GRASS GIS انجام شد، در حالی که تحلیل‌ها و بازسازی‌های رادیومتری با استفاده از کد پایتون و رابط برنامه‌نویسی کاربردی PyGRASS (API) پیاده‌سازی شدند. رویکرد اول مبتنی بر تبدیل تطبیق هیستوگرام (HM) و روش دوم بر اساس تجزیه ویژه (ED) ماتریس کوواریانس مجموعه‌ای از باندهای تصویری و نمونه‌برداری از توزیع‌های گاوسی است. کل این روش با استفاده از نرم افزار رایگان و متن باز و با استفاده از برنامه های اصلی اجرا شد. بخش‌بندی و تشخیص نواحی منسجم با استفاده از GRASS GIS انجام شد، در حالی که تحلیل‌ها و بازسازی‌های رادیومتری با استفاده از کد پایتون و رابط برنامه‌نویسی کاربردی PyGRASS (API) پیاده‌سازی شدند.12 ]. روش پیشنهادی برای اهداف خود اعتبارسنجی برای تصاویر آسیب‌دیده مصنوعی اعمال شد. باندهای WorldView-3 و Landsat 7 پردازش شدند، با استفاده از مقادیر مختلف پارامترهای مدل متغیر، کیفیت باندهای بازسازی شده از نظر آماری با استفاده از تصاویر اصلی بدون آسیب به عنوان اطلاعات مرجع ارزیابی شد. نتایج برای شماره‌های دیجیتال 8 بیتی لندست 7 (DN) نشان می‌دهد که خطا در اطراف است

10^{- 2}

با انحراف معیار چند واحد شدت (واریانس خطا در محدوده

(10^{0}, 10^{1}

) و

R^{2}

ضریب تعیین بسیار نزدیک به 1، به جداول 2 و 4 مراجعه کنید. برنامه های کاربردی برای لندست 7 آسیب دیده واقعی کیفیت بازسازی های به دست آمده با استفاده از روش را تایید می کند، به شکل های 19 و 20 مراجعه کنید.

محتوای دست‌نوشته به شرح زیر است: برخی از الگوریتم‌های موجود برای بازسازی تصاویر ماهواره‌ای در بخش 2 معرفی شده‌اند . ارائه مختصری از مدل تغییرات مامفورد-شاه برای تقسیم‌بندی تصویر و جنبه‌های تحلیلی آن در بخش 3 ارائه شده است . روش پیشنهادی در بخش 4 به تفصیل آمده است . نتایج کاربرد این روش برای داده های WorldView-3 و Landsat 7 در بخش 5 ارائه شده و در بخش 6 به همراه مشکلات و دیدگاه های باز مورد بحث قرار گرفته است.

2. مروری بر الگوریتم های استاندارد انتخاب شده

2.1. روش های تطبیق هیستوگرام

تطبیق هیستوگرام شامل تبدیل مقادیر یک مجموعه داده با تراز کردن تابع توزیع تجمعی تجربی (ECDF) مجموعه داده با ECDF یک مجموعه داده دیگر است. به طور گسترده ای در زمینه های مختلف پردازش تصویر استفاده می شود. اسکاراموزا و همکاران [ 13] اولین الگوریتمی را برای مقابله با مشکل لندست 7 SLC-off پیشنهاد کرد. این الگوریتم بعداً به عنوان یک روش فاز 1 توسط USGS به منظور تولید محصولات پر از شکاف Landsat 7 SLC در نظر گرفته شد. الگوریتم شامل نقشه برداری است که کدام پیکسل ها در یک تصویر SLC-off معتبر هستند و باید پر شوند و یک ماسک شکاف برای هر باند ایجاد می کند. یک رابطه خطی بین یک صحنه پایه و صحنه هدف شناسایی شده و برای تبدیل هیستوگرام هدف استفاده می شود. شناسایی پارامتر مدل از نظر محاسباتی گران است و بنابراین با روش به اصطلاح گشتاورها برای تخمین مقادیر بهره و بایاس بر اساس میانگین و انحراف استاندارد دو مجموعه داده جایگزین می‌شود. این روش اخیر، پس از اعمال بر روی کل تصاویر، به عنوان تطبیق هیستوگرام خطی جهانی (GLHM) شناخته می شود. این روش در صحنه های همگن به خوبی عمل می کند، در صحنه های مناظر ناهمگون مؤثر نیست و در صحنه های با برف یا ابر بی فایده است. به این دلایل، GLHM با یک مدل تطبیق هیستوگرام خطی محلی (LLHM) جایگزین شد که در آن بهره و بایاس فقط از آن مقادیر در یک پنجره متحرک محاسبه می‌شوند. این الگوریتم به طور کلی خوب عمل می کند و به تلاش محاسباتی بسیار کمی نیاز دارد، اما مقداری نوار یا سایه در اطراف لبه های تیز یا تغییرات ناگهانی پوشش زمین ایجاد می کند. الگوریتم فاز 1 توسط USGS بیشتر بهبود یافته و به روز شد [ اما در اطراف لبه های تیز یا تغییرات ناگهانی پوشش زمین مقداری نوار یا سایه ایجاد می کند. الگوریتم فاز 1 توسط USGS بیشتر بهبود یافته و به روز شد [ اما در اطراف لبه های تیز یا تغییرات ناگهانی پوشش زمین مقداری نوار یا سایه ایجاد می کند. الگوریتم فاز 1 توسط USGS بیشتر بهبود یافته و به روز شد [14 ] و از این رو رسماً به عنوان روش فاز 2 پذیرفته شد. این بهبود امکان استفاده از مجموعه‌ای از صحنه‌های پایه را به جای یک صحنه فراهم می‌کند. پس از تعریف یک ترتیب ترجیحی در تصاویر پایه موجود، الگوریتم LLHM به کوچکترین پنجره حاوی حداقل تعداد پیکسل های معتبر در داده های پایه و هدف اعمال می شود. پیشرفت‌های دیگری نیز به منظور تصحیح سودها و نقاط دورافتاده غیرمنطقی و کاهش اثر ابرها و برف انجام شده است. نتایج الگوریتم فاز 2 به ترتیب تصاویر پایه حساس است و همه این پیشرفت‌ها در هر صورت منجر به نتایج ضعیف در صحنه‌هایی می‌شوند که با درخشش خورشید، برف، ابرها یا ناهمگونی زیاد مشخص می‌شوند، و به ویژه در صحنه‌هایی که از تعداد زیادی کوچک تشکیل شده‌اند. امکانات. آقامحمدنیا و عابدینی [ 15] یک الگوریتم بهبود یافته را با هدف افزایش نتایج الگوریتم‌های انتخاب همسایه متحرک با جفت کردن آنها با یک طرح انتخاب مورفولوژی پیشنهاد کرد. در مرحله اول، از روش LLHM برای پوشاندن نوارهای SLC-off استفاده می شود، سپس یک عملگر مورفولوژیکی برای استخراج پیکسل های بیرونی نوارهای SLC-off مورد سوء استفاده قرار می گیرد. سپس برای هر پیکسل، یک خط بخیه با استفاده از الگوریتمی ایجاد می‌شود که شبیه‌ترین پیکسل‌ها را از نظر پرتوسنجی از گروه‌های پیکسل‌های مجاور پر شده یا غیرپر شده جستجو می‌کند. خطوط بخیه را می توان با تکرار این روش با استفاده از پیکسل های تازه یافت شده به عنوان نقاط مرکزی گسترش داد. سپس پیکسل های مرزی با استفاده از میانگین وزنی محلی به روز می شوند. کل روش را می توان با در نظر گرفتن مقادیر به روز شده به عنوان پر نشده، و سپس به روز رسانی پیکسل های داخلی خطوط بخیه تکرار کرد.

2.2. روش درونیابی پیکسل مشابه همسایگی

روش درونیابی پیکسلی مشابه همسایگی (NSPI)، پیشنهاد شده توسط چن و همکاران. [ 7]، بر این فرض استوار است که پیکسل‌های یک پوشش زمین، در یک همسایگی مشخص از پیکسلی که قرار است بازیابی شود، ویژگی‌های طیفی و الگوهای زمانی مشابهی را ارائه می‌دهند. فرض اصلی NSPI این است که هیچ تغییر قابل توجهی در مقیاس بزرگ پوشش زمین بین به دست آوردن یک پایگاه و یک تصویر هدف اعمال نمی شود. ابتدا، خارج از شکاف، پیکسل‌های رایج در هر دو تصویر پایه و هدف انتخاب می‌شوند، سپس جستجو برای پیکسل‌های همسایه مشابه بر روی تصویر پایه با یک روش جستجوی مبتنی بر پنجره متحرک تطبیقی انجام می‌شود. پس از ارزیابی یک اندازه معین از شباهت طیفی پیکسل های همسایه در پنجره متحرک، مقدار پیکسل هدف در همه باندها تخمین زده می شود، با استفاده از میانگین وزنی بر اساس اندازه گیری شباهت و بر اساس فاصله اقلیدسی هر پیکسل معتبر از پیکسل هدف سپس از دو روش مختلف برای تخمین مقدار یک پیکسل هدف استفاده می شود. روش اول بر اساس میانگین وزنی پیکسل‌های همسایه از نظر پرتوسنجی مشابه است، در حالی که روش دوم تلاش می‌کند تا تغییرات زمانی پیکسل‌های هدف را در نظر بگیرد و از وزن‌های محاسبه‌شده برای تخمین تغییر مقادیر پیکسلی که بین دو دوره اکتساب رخ داده است، استفاده کند. دقت دو روش به ناهمگنی نواحی مشاهده شده بستگی دارد: روش اول باید برای تصاویر با همگنی نسبی و تغییر زمانی آهسته استفاده شود، روش دوم برای تصاویر با مناطق ناهمگن مناسب تر است. ترکیبی از این دو روش نیز امکان پذیر است و با هدف یافتن سازشی بین همگنی فضایی همزمان و تکامل دیاکرونیک است. روش NSPI به طور کلی بهتر از LLHM عمل می کند،

2.3. روش زمین آماری

ژانگ و همکاران [ 16] پیشنهاد استفاده از یک تکنیک زمین آماری برای بهره برداری از همبستگی فضایی برای بازسازی مقادیر از دست رفته در یک تصویر آسیب دیده است. مدل‌های کریجینگ زمین‌آماری الگوریتم‌های درون‌یابی هستند که تخمین‌های بی‌طرفانه با حداقل واریانس خطا ارائه می‌کنند. همبستگی فضایی با استفاده از مدل‌های خاص برازش به اصطلاح نیمه متغیرهای تجربی توصیف می‌شود. روش حداقل مربعات در تخمین پارامترهای مدل اتخاذ شده برای پیش بینی مقدار متغیر مدل شده در یک مکان خاص دخالت دارد. در الگوریتم‌های پر کردن شکاف تصاویر ماهواره‌ای، تکنیک‌های زمین‌آمار مختلفی را می‌توان در نظر گرفت، به‌ویژه، زمانی که تصویر پایه در دسترس نباشد، می‌توان از مدل‌های تک متغیری استفاده کرد.17]). به طور کلی، تکنیک های کریجینگ برای درون یابی مقادیر متغیر در مکان های دلخواه استفاده می شود. در مورد خاص از دست دادن داده های SLC-off، شکاف ها دارای یک الگوی عجیب و غریب هستند و این تضمین می کند که پارامترهای مدل فقط یک بار برای هر الگوی تخمین زده شوند، به طوری که زمان محاسبات به شدت کاهش می یابد. علاوه بر این، یک تبدیل نمره عادی معمولا برای کاهش اثرات منفی چولگی قوی در مجموعه داده اعمال می شود. در مقایسه با مدل LLHM، نتایج رویکردهای مبتنی بر کریجینگ تقریباً در همه جا به جز در مرزهای بین پوشش‌های مختلف زمین، خطوط و مصنوعات بصری را کاهش می‌دهند. به طور کلی، مدل‌های کریجینگ داده‌ها را با تنوع فضایی کمتری نسبت به داده‌های مشاهده‌شده پیش‌بینی می‌کنند، بنابراین، هنگام تجزیه و تحلیل نوارهای بازسازی‌شده، تجانس قوی تری را می توان مشاهده کرد و بازسازی مناطق و مرزهای مختلف پوشش زمین به راحتی قابل دستیابی نیست. علاوه بر این، مدل‌های کریجینگ معمولاً در یک باند به استثنای امکان در نظر گرفتن کوواریانس باند احتمالاً مرتبط اعمال می‌شوند.

3. مدل متغیر مامفورد-شاه برای تقسیم بندی تصویر

مامفورد و شاه (1989) برای حل مشکل تقسیم بندی در علوم کامپیوتر با یافتن یک تجزیه پیشنهاد کردند.

R = R_{1} \cup R_{2} \cup \dots \cup R_{n}

از یک داده ورودی g داده شده در یک دامنه دو بعدی

Ω

با استفاده از به حداقل رساندن یک تابع بسته به یک تقریب صاف قطعه عاقلانه u از g . تابع تقریبی به آرامی در هر یک متفاوت است

R_{i}

، و مجاز است که روی یک مجموعه یک بعدی قابل اندازه گیری K از منحنی ها ناپیوسته باشد، به عنوان مثال، مرزهای عناصر R ، اما نه فقط آنها.

تقسیم بندی MS با به حداقل رساندن عملکردهای زیر به دست می آید:

ام اس (u ، K) : = 🔻 Ω | u - g | 2 د x + λ 🔻 Ω ∖ K | \nabla u | 2 د x + α H (ک \cap Ω),

(1)

جایی که: $u \in C^{1} (Ω ∖ K)$ و $H$ اندازه گیری هاسدورف 1 بعدی است.

پارامترها

λ

α

به عنوان سهم متعادل کننده وزن سه عبارت تابعی مامفورد-شاه عمل کنید. نقش های این سه عبارت عبارتند از:

تا جایی که ممکن است به g نزدیک شود .

تا جایی که ممکن است شما را در همه جا صاف نگه دارید به جز بالای K.

برای کوتاه نگه داشتن طول مجموعه ناپیوستگی u تا حد امکان،

جایی که آخرین اقدام برای اجتناب از راه حل های بی اهمیت بیش از حد بخش بندی شده لازم است.

معادله تابعی مامفورد-شاه ( 1 ) یک مثال کلاسیک از مسائل ناپیوستگی آزاد را نشان می‌دهد که توسط دی جورجی [ 18 ] معرفی شد و امروزه به طور گسترده در پردازش سیگنال یک‌بعدی و در حوزه‌های سه‌بعدی مانند مواردی که درگیر هستند، استفاده می‌شود. تجزیه و تحلیل شکستگی

علیرغم ساختار واضح آن، نتایج تحلیلی برای تابع مامفورد-شاه ( 1 ) بسیار دشوار است زیرا هر دو انرژی سطح و خط درگیر هستند و پشتیبانی انرژی خط به مجموعه ای ناشناخته بستگی دارد.

پس از [ 19 ]، آمبروسیو و همکاران. [ 20 ] و Modica و Mortola [ 21 ] یک تابع آرام معادل پیشنهاد کردند که از نظر محاسباتی قابل حل و ساده‌تر است. به طور خلاصه، کلاس متفاوتی از توابع تقریبی در نظر گرفته می شود تا تابع جدید دیگر به مجموعه مجهول k وابسته نباشد . علاوه بر این، یک تابع دو بعدی کمکی s معرفی شده است که انتگرال آن به طول مجموعه ناپیوسته یک بعدی همگرا می شود. $S_{u}$ تابع تقریبی به این ترتیب، تابع جدید فقط به تابع تقریبی u بستگی دارد و فقط انرژی های سطحی را شامل می شود:

اف ϵ (u s) : =_🔻 Ω | u - g | 2 + λ س 2 | \nabla u | 2 + α [ϵ | \nabla s | 2 + 1 4 ϵ (s - 1) 2] د x_

(2)

جایی که u به فضای توابع ویژه تنوع محدود تعلق دارد $S B V (Ω)$ [ 20 ]، $ϵ$ پارامتر همگرایی است، $s : Ω \to [0, 1]$ تابع نشانگر مجموعه ناپیوستگی را تقریبی می کند $S_{u}$ ، و برابر با 0 در روشن است $S_{u}$ و 1 در جای دیگر.

از منظر عملی،

λ

را می توان به عنوان یک پارامتر مقیاس کنترل کننده صافی محلول مشاهده کرد. هر چه ارزش آن بزرگتر باشد

λ

، تابع تقریبی بیشتر به یک جواب ثابت قطعه ای نزدیک است. پارامتر

α

در عوض می توان آن را به عنوان یک پارامتر حساسیت نویز دید که بر فرآیند تشخیص ناپیوستگی تأثیر می گذارد. برای

α

مقادیر نزدیک به 0، تعداد زیادی از مناطق کوچک تقسیم شده، و از این رو بسیاری از ناپیوستگی، یافت می شود.

اطلاعات بیشتر در مورد جنبه های تحلیلی و عددی عملکرد مامفورد-شاه و اجرای آن را می توان در [ 22 ] یافت.

4. تقسیم بندی متغیر و تجزیه و تحلیل رادیومتری برای بازسازی تصاویر چند زمانی

روش پیشنهادی شامل مجموعه ای از مراحل است که باید به ترتیب متوالی اعمال شوند:

تقسیم بندی متغیر باندهای تصویری پایه و هدف.
ترکیب باندهای قطعه بندی شده اعداد صحیح.
شناسایی و برچسب گذاری اجزای متصل (کلوپ) مقادیر ترکیبی؛
محاسبه محصول متقاطع برچسب های پایه و توده هدف.
بازسازی رادیومتریک

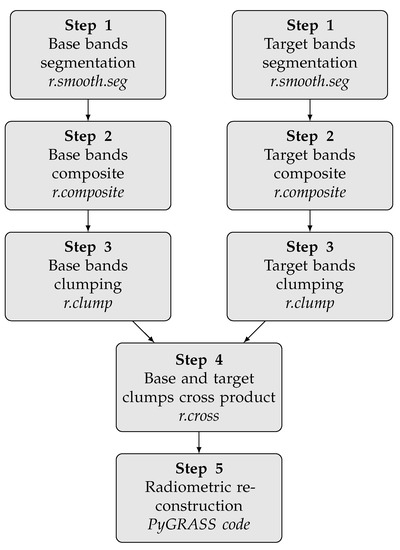
یک نمودار جریان از روش پیشنهادی در شکل 1 نشان داده شده است . هر مرحله از این به بعد مفصل است.

مرحله 1: تقسیم بندی متغیر مامفورد-شاه برای باندهای تصویری پایه و هدف در دست اعمال می شود. در این کار، پردازش بر روی اعداد دیجیتال انجام شد. یک ماسک منحصر به فرد از نوارهای SLC-off برای پردازش باندهای هدف استفاده می شود. مقادیر پارامترهای مدل $α$ و $λ$ پس از چند آزمایش بر اساس یک پایه تجربی انتخاب می شوند. هنگام کار با Landsat 7 و DN ها، می توان با آن شروع کرد $α = 500$ و $λ = 8$ . مقادیر پارامتر یکسان در باندهای پردازش هر صحنه منفرد، چه پایه و چه هدف، استفاده شد. مقادیر پارامترهای متفاوت بین صحنه‌ها، به عنوان مثال، دوره‌های اکتساب، به راحتی انتخاب می‌شوند تا تفاوت‌های رادیومتری بین دوره‌ها را در نظر بگیرند. برای بررسی اینکه آیا مقادیر پارامترهای مختلف نتایج بین دوره ای منسجمی را ارائه می دهند، به عنوان مثال، مناطق تقسیم شده با ابعاد و شکل قابل مقایسه، باندهای پایه و هدف تقسیم شده را می توان به صورت بصری یا خودکار مقایسه کرد. در این مرحله، انتخاب مقادیر بسیار متفاوت پارامتر ممکن است به تفاوت‌های رادیومتریک بسیار بالا بین باندهای پایه و هدف بستگی داشته باشد که نیاز به جستجوی تصاویر پایه بهتر برای سهولت بازسازی رادیومتری مناطق هدف آسیب‌دیده را نشان می‌دهد. تقسیم بندی متغیر مامفورد-شاه یک تقریب صاف با ارزش واقعی را به دست می دهد. مقادیر بخش‌بندی شده برای بازیابی سازگاری اعداد صحیح با ورودی DN گرد می‌شوند. گرد کردن تغییرات جزئی با توجه به واریانس‌های DN معمولی در تصاویر ماهواره‌ای و بسیار کمتر از میزان کاهش نویز که در مناطق تقسیم‌بندی شده رخ می‌دهد، ایجاد می‌کند.
مرحله 2: ترکیب باندهای قطعه بندی شده اعداد صحیح یک راه آسان برای طبقه بندی خروجی های مرحله قبل است. در عمل، در مجموع از 32 سطح شدت در هر باند در ترکیب بندی استفاده می شود، در نتیجه زمانی که ترکیب سه باند انجام می شود، یک تصویر 15 بیتی با 32768 مقدار ممکن ایجاد می شود.
مرحله 3: پرداختن به تصاویر تشکیل‌شده اعداد صحیح، شناسایی و برچسب‌گذاری اجزای متصل را بسیار ساده می‌کند. در غیر این صورت، اگر مقادیر واقعی پردازش می‌شدند، یک تجمع فازی مبتنی بر آستانه یا یک الگوریتم طبقه‌بندی پیچیده‌تر برای شناسایی و برچسب‌گذاری مناطق تقسیم‌بندی شده به روشی مناسب ضروری است.
مرحله 4: محصول متقاطع برچسب‌های دسته‌ای پایه و هدف، همه ترکیب‌های ممکن از برچسب‌های کلوپ بین صحنه را تولید می‌کند. هر ترکیب یافت شده با مقادیر برچسب‌های دسته‌بندی پایه و هدف مرتبط است و امکان بازگشت به مقادیر تقسیم‌بندی اعداد صحیح اصلی را فراهم می‌کند.

خروجی این مرحله به عنوان یک لایه اطلاعات پایه برای مرحله بازسازی عمل می کند. ماسک نواری SLC-off اجازه می دهد تا مناطقی را که باید بازسازی شوند از مناطقی که تجزیه و تحلیل رادیومتری از آنها انجام می شود، جدا کرد.

برای هر توده ای که در داخل مناطقی که باید بازسازی شوند، مجموعه داده های بازسازی از تمام پیکسل های متعلق به هر توده پایه غیر خراب که سطح شدت یکسانی در نقشه ترکیبی پایه دارند، ساخته می شود.

با توجه به مقدار سطح شدت در نقشه مرکب پایه، می توان به مقادیر تقسیم بندی اعداد صحیح اصلی بازگشت تا به عنوان مجموعه داده برای بازسازی رادیومتری استفاده شود.

اگر هیچ سطح شدت یکسانی یافت نشود، پایگاه داده بازسازی شامل تمام توده‌هایی با سطح شدت تا حد امکان نزدیک به سطح شدت ورودی است. اندازه‌گیری فاصله، فاصله اقلیدسی در فضای باند تقسیم‌بندی شده اعداد صحیح و یک معیار مجاورت مبتنی بر آستانه است که برای ساخت پایگاه‌داده بازسازی اتخاذ شده است.
مرحله 5: دو معیار مختلف برای بازسازی نهایی رادیومتری در نظر گرفته شد.

اولین رویکرد مبتنی بر تبدیل HM است. ECDF تصاویر پایه و هدف فقط با در نظر گرفتن مناطق غیر خراب محاسبه می شوند و پارامترهای تبدیل HM برآورد می شوند. برای هر پیکسلی که باید بازسازی شود، مقدار آن در تصویر پایه $x_{b}$ خوانده می شود و مقدار فرکانس تجمعی آن $F_{b} (x_{b})$ ارزیابی می شود. مقدار بازسازی شده در تصویر هدف ${\hat{x}}_{t}$ کسی است که برابری را حفظ می کند $F_{t} ({\hat{x}}_{t}) = F_{b} (x_{b})$ .

رویکرد دوم مبتنی بر نمونه‌گیری توزیع ED و گاوسی است. برای مناطق همگن پایه، ماتریس کوواریانس باند محاسبه می شود. مجموعه داده‌ها بر اساس ED تغییر شکل می‌دهند تا نمونه‌گیری آماری از توزیع‌های گاوسی نامرتبط با میانگین و واریانس شناخته شده امکان‌پذیر باشد. نمونه برداری یک بار برای هر پیکسلی که باید بازسازی شود ترسیم می شود. برای مجموعه‌های نواحی خراب پایه با تعداد کل زیر 30 واحد، نمونه‌برداری ED و Gaussian انجام نمی‌شود و مقادیر بازسازی‌شده روی مقدار میانگین مجموعه مناطق غیرفاسد پایه تنظیم می‌شوند.

این روش با توجه به پردازش DN ها توسعه داده شد. انجام بازسازی رادیومتری DNها اجازه می دهد تا با مشاهدات خام آشکارسازهای ماهواره ای قبل از انجام سایر پردازش های استاندارد مقابله کنیم. علاوه بر این، پرداختن به مقادیر صحیح امکان استفاده مؤثر از ابزارهای ساده، مانند ترکیب باند و تجزیه و تحلیل اجزای متصل، را برای تشکیل مناطق همگن منسجم برای استفاده در رویکردهای بازسازی رادیومتری مبتنی بر آماری که در سطح تصویر هدف اجرا می‌شوند، باز می‌کند. در واقع، هنگامی که رویکرد HM درگیر است، تطبیق هیستوگرام ها بر اساس متناظر توده های پایه و هدف است، و همچنین، زمانی که رویکرد ED درگیر است، تجزیه و تحلیل آماری برای بازسازی در واقع در سطح هدف انجام می شود. خوب. با این اوصاف، این روش را می توان به راحتی برای پردازش مقادیر فیزیکی Top Of Atmosphere (TOA) و Bottom Of Atmosphere (BOA) که از مقادیر DN مشتق شده اند، تطبیق داد. در این موارد، به دلیل ماهیت شناور مقادیر بازتاب/تابش، باید از یک روش طبقه‌بندی پیچیده‌تر برای تولید توده‌ها استفاده شود. هنگامی که توده ها در دسترس هستند، مراحل زیر از روش تحت تأثیر کاهش DN ها به مقادیر فیزیکی باقی می مانند، همانطور که برای تقسیم بندی تغییرات اولیه آنها وجود دارد.

5. نتایج

5.1. برنامه های کاربردی برای خود اعتبارسنجی

برخی از برنامه‌ها برای تأیید اجرای رویه و ارزیابی عملکرد رویه در غیاب تغییرات رادیومتری در یک سناریوی خود اعتبارسنجی انجام شد. برای آن، در هر یک از برنامه های زیر، تصاویر پایه به طور مصنوعی برای تولید تصاویر هدف مصنوعی خراب شدند. بسیاری از آزمایش‌های خود اعتبارسنجی، با ترکیب باندهای مختلف، انجام شد (

α

λ

) پارامترها و با استفاده از هر دو روش بازسازی مبتنی بر ED و HM. در بخش‌های بعدی، نتایج دو آزمون خود اعتباری توضیح داده شده است. درخواست برای یک مورد واقعی بعداً در بخش اختصاصی ارائه می شود.

5.1.1. تست خودتأیید بر روی یک گروه منفرد Worldview-3

این روش روی یک باند WorldView-3 (Panchromatic، وضوح رادیومتری 11 بیتی، وضوح فضایی 40 سانتی متر، 5870 × 3660 پیکسل) اعمال شد. این آزمایش برای نشان دادن عملکرد در بازسازی ساختارهای پیچیده فضایی تصور شد.

باند: پانکروماتیک (P) – پارامترهای قطعه بندی $α$ = 4000، $λ$ = 20

شکل 2 تصویر پایه را نشان می دهد و تصویر هدف تخریب شده مصنوعی در شکل 3 نشان داده شده است . نتایج حاصل از تقسیم بندی متغیر با بازسازی های رادیومتری مبتنی بر HM و ED به ترتیب در شکل 4 و شکل 5 نشان داده شده است. در جدول 1 ، آمار خطای بازسازی های HM و ED گزارش شده است. برای هر رویکرد بازسازی، میانگین، واریانس و ضریب تعیین

R^{2}

تفاوت بین مقادیر اصلی و بازسازی شده داده شده است. نمودارهای پراکندگی تفاوت ها در شکل 6 a,b نشان داده شده است.

شکل 7 بخشی از صحنه WorldView-3 و تقریب تغییرات مربوط به آن u را به ترتیب در ردیف اول و دوم نشان می دهد. در ردیف سوم، تابع ناپیوستگی s همراه با توده های پایه رسم می شود.

در ستون های سمت چپ شکل 8 و شکل 9 ، دو جزئیات از صحنه WorldView-3 نشان داده شده است و نتایج بازسازی های HM و SVM به ترتیب در مرکز و در ستون های سمت راست ترسیم شده است.

همانطور که در شکل 8 و شکل 9 مشاهده می شود ، کیفیت بازسازی اساساً به دلیل افزایش اطلاعات هندسی و رادیومتری تولید شده توسط تقسیم بندی مامفورد-شاه و تشخیص زیر مناطق منسجم مورد استفاده در تحلیل رادیومتری بسیار بالا است.

5.1.2. تست های خود اعتبارسنجی روی مجموعه ای از باندهای Landsat 7

این رویه در صحنه Landsat 7 LE71920282000332NSG00 اعمال شد که نقص SLC-off را نشان نمی‌دهد (داده‌ها در اواسط سال 2000، قبل از شکست SLC به دست آمدند). صحنه‌ای که به‌عنوان تصویر پایه عمل می‌کرد، با اعمال شکاف‌های SLC-off مانند برای تولید تصاویر هدف، به‌طور مصنوعی آسیب دید. داده‌های اصلی و بازسازی‌شده برای چند زیرمجموعه سه باندی به منظور ارزیابی عملکرد روش ارائه می‌شوند. در مرحله تقسیم بندی، حدود ده آزمایش با مقادیر مختلف پارامترها (

α

λ

). در هر آزمایشی که بعداً گزارش می شود، مقادیر یکسان پارامترها (

α

λ

) برای تقسیم بندی باندهای پایه و هدف استفاده شد. پارامترهای انتخاب شده آنهایی هستند که به بهترین نتایج در آزمون ها منجر شده اند. برای مقایسه، هر آزمون با آمار نتایج به‌دست‌آمده با استفاده از جفت‌های مختلف مقادیر پارامتر تکمیل می‌شود. برای این آزمایش ها، تصاویر بازسازی شده از نظر کیفی بسیار شبیه به آنچه در این بخش گزارش شده بود، بود.

مجموعه باند: قرمز، سبز، آبی (RGB) – پارامترهای تقسیم بندی $α$ = 500، $λ$ = 8

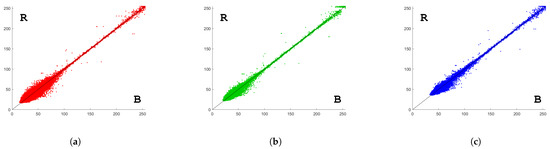
شکل 10 بازسازی های پایه، هدف، HM و ED را نشان می دهد. در شکل، رنگ ها تنها پس از پردازش و فقط برای تسهیل تفسیر بصری به طور مصنوعی تغییر داده شدند. سطح روشنایی پیکسل در فضای RGB به صورت دستی با استفاده از برنامه دستکاری تصویر گنو (GIMP) اصلاح شد. در جدول 2 ، آمار خطای بازسازی های HM و ED گزارش شده است. برای هر رویکرد بازسازی، میانگین، واریانس و ضریب تعیین

R^{2}

تفاوت بین مقادیر اصلی و بازسازی شده داده شده است. نمودارهای پراکندگی تفاوت ها در شکل 11 و شکل 12 نشان داده شده است. برای مقایسه، آمار خطای بازسازی های HM و ED با مقادیر مختلف پارامترهای تقسیم بندی به دست آمد.

(α, λ) = (1200, 8)

و منجر به نتایج بدتر در جدول 3 گزارش شده است.

مجموعه باند: مادون قرمز نزدیک، قرمز، سبز (NRG) – پارامترهای تقسیم بندی $α$ = 500، $λ$ = 8

شکل 13 بازسازی پایه، هدف و HM را نشان می دهد. در جدول 4 ، آمار خطای بازسازی های HM و ED گزارش شده است. برای هر رویکرد بازسازی، میانگین، واریانس و ضریب تعیین

R^{2}

تفاوت بین مقادیر اصلی و بازسازی شده داده شده است. نمودارهای پراکندگی تفاوت ها در شکل 14 و شکل 15 نشان داده شده است. برای مقایسه، آمار خطای بازسازی های HM و ED با مقادیر مختلف پارامترهای تقسیم بندی به دست آمد.

(α, λ) = (1600, 12)

و منجر به نتایج بدتر در جدول 5 گزارش شده است.

5.2. کاربردهای مورد واقعی

این رویه برای صحنه هدف Landsat 7 LE71920282014306NSG100 که تحت تأثیر اختلالات SLC-off قرار گرفته است و با در نظر گرفتن صحنه بدون اختلال Landsat 7 LE71920282002257EDC00 به عنوان تصویر پایه، اعمال شد، به شکل 16 مراجعه کنید .

تقسیم بندی متغیر برای باندهای پایه و هدف، پارامترهای مامفورد-شاه اعمال شد.

α

λ

) تنظیم شدند

(500, 8)

برای باندهای پایه و به

(100, 4)

برای باندهای هدف، مرحله 1 در شکل 1 .

شکل 17 مولفه های متصل برچسب شده (کلوپ) مجموعه های سه باند RGB پایه و هدف، مرحله 3 در شکل 1 را نشان می دهد.

در شکل 18 ، طرح پشت رویکردهای بازسازی رادیومتری نشان داده شده است: تصویر پایه (B) در سمت چپ در شکل 18 a نشان داده شده است، تصویر هدف (T) در سمت راست است. در شکل 18 ب، مرزهای منطقه، که پس از شناسایی اجزای متصل ساخته شده اند، روی تصاویر پایه و هدف قرار گرفته اند و یک منطقه برای بازسازی به رنگ سبز ترسیم شده است. در شکل 18 ج، نواحی منسجم مربوط به ناحیه ای که باید بازسازی شود به رنگ سبز روشن در تصویر پایه رسم شده است. در شکل 18 د، نواحی منسجم مربوط به ناحیه ای که باید بازسازی شود به رنگ آبی روشن در تصویر هدف رسم شده است.

شکل 19 هدف و تصاویر RGB بازسازی شده HM را نشان می دهد، یک منطقه بزرگنمایی شده در شکل 20 نشان داده شده است . در شکل، رنگ ها تنها پس از پردازش و فقط برای تسهیل مقایسه بصری به طور مصنوعی تغییر داده شدند. منحنی روشنایی پیکسل در فضای RGB به صورت دستی با استفاده از برنامه دستکاری تصویر گنو (GIMP) اصلاح شد.

6. بحث

تقسیم بندی تصویر متغیر در بازیابی تصویر موثر است: عمل صاف کردن، با کاهش سطح نویز داده های ورودی، و ویژگی حفظ ناپیوستگی، شناسایی مناطق همگن را آسان می کند و از این رو تشکیل مجموعه های منطقه منسجم برای استفاده در تجزیه و تحلیل رادیومتری را آسان می کند. که بازسازی بر آن استوار است. شناسایی مجموعه‌های ناحیه منسجم با استفاده از ترکیب باند، کلوخه‌سازی و محصولات متقاطع سطوح شدت تصاویر پایه و هدف انجام می‌شود. این ویژگی‌ها با هم، امکان بازسازی صحنه‌های پیچیده هندسی را نیز فراهم می‌کنند ( شکل 5 را ببینید.). در تقسیم بندی متغیر، برای وضوح فضایی معین، استفاده از مقادیر پارامتر بالا منجر به نتایج بهتر در هنگام پردازش صحنه های کم تکه تکه می شود، در عوض مقادیر کمتر برای صحنه های پیچیده تر، مانند مناطق کوهستانی و شهری توصیه می شود. برای هدایت انتخاب مقادیر پارامتر مناسب، می‌توان پیشنهاد کرد که برخی از آزمایش‌ها را بر روی یک بخش آسیب‌دیده از صحنه اجرا کرده و نتایج را بر اساس سناریویی مانند خود اعتبارسنجی ارزیابی کرد.

دو کاربرد مختلف پیشنهاد شده است که هر دو اهداف خود را با نتایج معتبر همانطور که در جدول 2 و جدول 4 گزارش شده است برآورده می کنند.در جایی که میانگین خطاهای کوچک اساساً به دلیل گرد کردن عدد صحیح لازم برای رعایت نوع داده DN ها است. بازسازی صرفاً با انتخاب داده‌ها از پیکسل‌های همسایه انجام نمی‌شود، بلکه با تکیه بر رویه‌ای انجام می‌شود که مناطق مختلف منسجم را بر اساس رادیومتریک به هم پیوند می‌دهد. برنامه ها عملکرد بهتری از رویکرد بازسازی مبتنی بر HM در مقایسه با ED نشان دادند. هنگامی که فقط یک باند پردازش می شود و زمانی که داده های با وضوح مکانی بالا در نظر گرفته می شوند، تفاوت ها افزایش می یابد. این اساساً به دلیل قابلیت رویکرد HM برای بازتولید الگوهای رادیومتری بین منطقه‌ای، انتخاب نمونه‌گیری توزیع گاوسی، و به دلیل حساسیت پایین تبدیل HM به ECDF‌های غیر گاوسی است. در این چارچوب، استفاده از تبدیل قدرت را می توان در نظر گرفت [ 23 ، 24]. تبدیل قدرت خانواده ای از توابع است که برای ایجاد یک تبدیل یکنواخت داده ها با استفاده از توابع قدرت اعمال می شود. این یک تکنیک تبدیل داده مفید است که واریانس را تثبیت می کند و نمونه هایی با توزیع نرمال تری تولید می کند.

از نقطه نظر عملی، روش پیشنهادی می تواند در چارچوب پردازش تصویر ماهواره ای مفصل تر شامل الگوریتم های ابر، سایه ابر و تشخیص برف [ 25 ، 26 ] گنجانده شود. نتایج اولیه همچنین تأثیر مثبت قوی تقسیم‌بندی متغیر را به عنوان یک مرحله پیش‌فرایند در برنامه‌های نگاشت pansharpening و وضوح فوق‌العاده نشان داد.

از نقطه نظر تحلیلی، یک توسعه احتمالی به اتخاذ یک مدل متغیر پیشرفته و پیچیده‌تر برای تقسیم‌بندی تصویر مربوط می‌شود. در مدل مامفورد-شاه، وجود هنجار گرادیان (اصطلاح هموارسازی) تنها راه‌حل‌های تکه‌ای تقریباً ثابت را مجاز می‌سازد. در تصاویر ماهواره‌ای، مناطقی با شیب تند رادیومتری رایج هستند و تقریب مامفورد-شاه ممکن است مصنوعات پلکان مانندی را در چنین مناطقی نشان دهد. اوون [ 27 ] یک مدل متغیر مرتبه دوم را برای غلبه بر محدودیت های مدل مامفورد-شاه پیشنهاد کرد. راه حل های تولید شده توسط مدل بلیک-زیسرمن اساساً تقریب های تقریباً خطی داده ها هستند [ 22 ، 28 ، 29 ، 30 ، 31، 32 ].

منابع

اوبرت، جی. کورنپرابست، ص. مسائل ریاضی در پردازش تصویر . Springer: New York, NY, USA, 2006. [ Google Scholar ] [ CrossRef ][ Green Version ]
ژانگ، Q. یوان، Q. زنگ، سی. لی، ایکس. Wei, Y. بازسازی داده های گمشده در تصویر سنجش از دور با یک شبکه عصبی کانولوشنال عمیق فضایی-زمانی- طیفی. IEEE Trans. Geosci. Remote Sens. 2018 , 56 , 4274–4288. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
ژو، جی. لی، ک. Hao, B. بازیابی تصاویر سنجش از دور بر اساس منظم‌سازی تغییرات کلی با مرتبه بالا محدود شده غیر محدب. J. Appl. Remote Sens. 2019 ، 13 ، 1–17. [ Google Scholar ] [ CrossRef ]
شن، اچ. لی، ایکس. چنگ، کیو. زنگ، سی. یانگ، جی. لی، اچ. Zhang, L. اطلاعات گمشده بازسازی داده های سنجش از دور: بررسی فنی. IEEE Geosci. سنسور از راه دور Mag. 2015 ، 3 ، 61-85. [ Google Scholar ] [ CrossRef ]
علی، ل. Kasetkasem، T. خان، دبلیو. چانویمالوانگ، تی. ناکاهارا، اچ. ارزیابی عملکرد الگوریتم‌های مختلف نقاشی داخلی برای تصاویر سنجش از دور. در مجموعه مقالات سومین کنفرانس آسیایی فناوری دفاعی 2017 (ACDT)، پوکت، تایلند، 18 تا 20 ژانویه 2017؛ ص 43-48. [ Google Scholar ] [ CrossRef ]
دونگ، جی. یین، آر. سان، ایکس. لی، کیو. یانگ، ی. Qin, X. Inpainting تصاویر SST سنجش از راه دور با شبکه دشمنان مولد عمیق. IEEE Geosci. سنسور از راه دور Lett. 2019 ، 16 ، 173-177. [ Google Scholar ] [ CrossRef ]
چن، جی. زو، ایکس. Vogelmann، JE; گائو، اف. Jin, S. یک روش ساده و موثر برای پر کردن شکاف در تصاویر Landsat ETM+ SLC-off. سنسور از راه دور محیط. 2011 ، 115 ، 1053-1064. [ Google Scholar ] [ CrossRef ]
بروکس، ای. وین، آر. Thomas, V. استفاده از رگرسیون پنجره برای پر کردن شکاف Landsat ETM+ Post SLC-Off Data. Remote Sens. 2018 , 10 , 1502. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
قریشی، م. دریچه، م. بغدادی، ع. امین، ع. بررسی انتقادی معیارهای ارزیابی کیفیت نقاشی با کیفیت تصویر پیشرفته. J. Vis. اشتراک. تصویر نشان می دهد. 2017 ، 49 ، 177-191. [ Google Scholar ] [ CrossRef ]
Asare, YM; Forkuo، EK; فورکور، جی. Thiel, M. ارزیابی روش‌های پر کردن شکاف برای تصویر Landsat 7 ETM+ SLC-off برای طبقه‌بندی LULC در یک چشم‌انداز ناهمگن از غرب آفریقا. بین المللی J. Remote Sens. 2020 , 41 , 2544–2564. [ Google Scholar ] [ CrossRef ]
مامفورد، دی. شاه، جی. تقریب های بهینه توسط توابع صاف تکه ای و مسائل متغیر مرتبط. اشتراک. Pure Appl. ریاضی. 1989 ، 42 ، 577-685. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
زامبلی، پ. گبرت، اس. Ciolli، M. Pygrass: یک رابط برنامه نویسی کاربردی پایتون شی گرا (API) برای سیستم پشتیبانی تجزیه و تحلیل منابع جغرافیایی (GRASS) سیستم اطلاعات جغرافیایی (GIS). ISPRS Int. J. Geo-Inf. 2013 ، 2 ، 201-219. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
اسکاراموزا، پ. میسییویک، ای. Gyanesh, C. SLC Gap-Filled Products—Phase One Methodology. در دسترس آنلاین: https://www.usgs.gov/media/files/landsat-7-slc-gap-filled-products-phase-one-methodology (در 1 دسامبر 2020 قابل دسترسی است).
USGS. محصولات پر شده با شکاف SLC – روش‌شناسی فاز دوم. در دسترس آنلاین: https://www.usgs.gov/media/files/landsat-7-slc-gap-filled-products-phase-two-methodology (در 1 دسامبر 2020 قابل دسترسی است).
آقامحمدنیا، م. عابدینی، ع. یک روش مورفولوژی – دوخت برای بهبود تصاویر لندست SLC-off با راه راه. Geod. ژئودین. 2014 ، 5 ، 27-33. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
ژانگ، سی. لی، دبلیو. تراویس، دی. پر کردن شکاف های تصویر ماهواره ای SLC-off Landsat ETM+ با استفاده از رویکرد زمین آماری. بین المللی J. Remote Sens. 2007 ، 28 ، 5103-5122. [ Google Scholar ] [ CrossRef ]
Gaohong، Y. مک کیب، ام.اف. ماریتوز، جی. پر کردن شکاف تصاویر Landsat 7 با استفاده از روش نمونه گیری مستقیم. Remote Sens. 2016 ، 9 ، 12. [ Google Scholar ]
De Giorgi, E. مسائل ناپیوستگی آزاد در حساب تغییرات. در مرزهای ریاضیات محض و کاربردی، مجموعه مقالاتی که به JL Lions به مناسبت شصتمین سالگرد تولد او تقدیم شده است . Dautray, R., Ed. هلند شمالی: آمستردام، هلند، 1991; صص 55-62. [ Google Scholar ]
دی جورجی، ای. کریرو، ام. Leaci، A. قضیه وجود برای یک مسئله حداقل با مجموعه ناپیوستگی آزاد. قوس. جیره. مکانیک. مقعدی 1989 ، 108 ، 195-218. [ Google Scholar ] [ CrossRef ]
آمبروسیو، ال. فوسکو، ن. Pallara، D. توابع تغییرات محدود و مسائل ناپیوستگی آزاد . انتشارات دانشگاه آکسفورد: آکسفورد، انگلستان، 2000. [ Google Scholar ]
مودیکا، ال. مورتولا، S. Un esempio di Gamma-convergenza. بول. dell’Unione Matatematica ایتالیا. 1977 ، B-14 ، 285-299. [ Google Scholar ]
Vitti، A. مدل متغیر مامفورد-شاه برای تقسیم‌بندی تصویر: مروری بر نظریه، اجرا و استفاده. ISPRS J. Photogramm. Remote Sens. 2012 ، 69 ، 50-64. [ Google Scholar ] [ CrossRef ]
بله، آی کی; جانسون، RA خانواده جدیدی از تبدیل قدرت برای بهبود عادی یا تقارن. Biometrika 2000 ، 87 ، 954-959. [ Google Scholar ] [ CrossRef ]
جعبه، GEP؛ Cox, DR An Analysis of Transformations. JR Stat. Soc. سر. B (Methodol.) 1964 ، 26 ، 211-243. [ Google Scholar ] [ CrossRef ]
Baetens، L. دژاردین، سی. اعتبار سنجی ماسک های ابری Copernicus Sentinel-2 از پردازنده های MAJA، Sen2Cor، و FMask با استفاده از ماسک های ابر مرجع تولید شده با یک روش یادگیری فعال نظارت شده، Hagolle، O. Remote Sens. 2019 , 11 , 433. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
زو، ز. Woodcock، CE ابر خودکار، سایه ابر و تشخیص برف در داده های چندزمانی Landsat: الگوریتمی که به طور خاص برای نظارت بر تغییر پوشش زمین طراحی شده است. سنسور از راه دور محیط. 2014 ، 152 ، 217-234. [ Google Scholar ] [ CrossRef ]
Owen, T. Visual Reconstruction توسط اندرو بلیک و اندرو زیسرمن، انتشارات MIT، ماساچوست، ایالات متحده آمریکا، 1987، 1987 (£ 22.50). Robotica 1988 , 6 , 166. [ Google Scholar ] [ CrossRef ]
کریرو، ام. لیسی، ا. Tomarelli، F. ناپیوستگی گرادیان آزاد و نقاشی درون تصویر. جی. ریاضی. علمی 2012 ، 181 ، 805-819. [ Google Scholar ] [ CrossRef ]
برقی، ع. کانیتزارو، ال. Vitti، A. تکنیک‌های پیشرفته برای تشخیص ناپیوستگی در سری‌های زمانی مختصات GNSS. مطالعه موردی ایتالیایی در سمپوزیوم های انجمن بین المللی ژئودزی ; Springer: برلین، آلمان، 2012; جلد 136، ص 627–634. [ Google Scholar ] [ CrossRef ]
Vitti، A. Sigseg: ابزاری برای تشخیص ناپیوستگی های موقعیت و سرعت در سری های زمانی ژئودتیک. راه حل GPS. 2012 ، 16 ، 405-410. [ Google Scholar ] [ CrossRef ]
زانتی، م. Vitti، A. مدل بلیک-زیسرمن برای تقسیم‌بندی مدل‌های سطح دیجیتال. ISPRS Ann. فتوگرام حسگر از راه دور اسپات. Inf. علمی 2013 ، II-5/W2 ، 355-360. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
بنچولینی، بی. روجیرو، وی. ویتی، ا. زانتی، ام. شناسایی هواپیماهای سقفی از طریق یک مدل تغییرات مرتبه دوم. ISPRS J. Photogramm. Remote Sens. 2018 , 138 , 101–120. [ Google Scholar ] [ CrossRef ]

شکل 1. فلوچارت روش پیشنهادی برای بازسازی تصویر.

شکل 2. تصویر پایه.

شکل 3. تصویر هدف.

شکل 4. بازسازی HM.

شکل 5. بازسازی ED.

شکل 6. آزمایش خود اعتبارسنجی پانکروماتیک – بازسازی های رادیومتری. B = مقادیر شدت پایه، R = مقادیر شدت بازسازی شده. ( الف ) نمودار پراکندگی مقادیر پانکروماتیک – بازسازی مبتنی بر HM. ( ب ) نمودار پراکندگی مقادیر پانکروماتیک-بازسازی مبتنی بر ED.

شکل 7. تصویر WorldView-3 و نقشه های میانی. ( الف ) نوار پانکروماتیک؛ ( ب ) تقریب تغییرات u از باند پانکروماتیک WorldView-3 شکل 7 a; ( ج ) تابع ناپیوستگی s با توده هایی از تقریب تغییرات تصویر پایه شکل 7 a.

شکل 8. باند پانکروماتیک و بازسازی های رادیومتری – جزئیات 1. ( الف ) باند پانکروماتیک WorldView-3; ( ب ) بازسازی HM; ( ج ) بازسازی ED.

شکل 9. باند پانکروماتیک و بازسازی های رادیومتری – جزئیات 2. ( الف ) باند پانکروماتیک WorldView-3; ( ب ) بازسازی HM; ( ج ) بازسازی ED.

شکل 10. بازسازی های پایه، هدف، HM و ED مجموعه باند RGB صحنه لندست 7 LE71920282000332NSG00 . ( الف ) تصویر پایه؛ ( ب ) تصویر هدف؛ ( ج ) بازسازی HM; ( د ) بازسازی ED.

شکل 11. آزمون خود اعتبارسنجی RGB – بازسازی مبتنی بر HM. B = مقادیر شدت پایه، R = مقادیر شدت بازسازی شده. ( الف ) نمودار پراکندگی مقادیر قرمز؛ ( ب ) نمودار پراکندگی مقادیر سبز. ( ج ) نمودار پراکندگی مقادیر آبی.

شکل 12. آزمون خود اعتبارسنجی RGB-بازسازی مبتنی بر ED. B = مقادیر شدت پایه، R = مقادیر شدت بازسازی شده. ( الف ) نمودار پراکندگی مقادیر قرمز؛ ( ب ) نمودار پراکندگی مقادیر سبز. ( ج ) نمودار پراکندگی مقادیر آبی.

شکل 13. بازسازی پایه، هدف، HM مجموعه باند NRG صحنه لندست 7 LE71920282000332NSG00 . ( الف ) تصویر پایه؛ ( ب ) تصویر هدف؛ ( ج ) بازسازی HM.

شکل 14. تست خود اعتبارسنجی NRG – بازسازی مبتنی بر HM. B = مقادیر شدت پایه، R = مقادیر شدت بازسازی شده. ( الف ) نمودار پراکندگی مقادیر مادون قرمز نزدیک. ( ب ) نمودار پراکندگی مقادیر قرمز. ( ج ) نمودار پراکندگی مقادیر سبز.

شکل 15. تست خود اعتبارسنجی NRG – بازسازی مبتنی بر ED. B = مقادیر شدت پایه، R = مقادیر شدت بازسازی شده. ( الف ) نمودار پراکندگی مقادیر نزدیک به مادون قرمز. ( ب ) نمودار پراکندگی مقادیر قرمز. ( ج ) نمودار پراکندگی مقادیر سبز.

شکل 16. تصاویر پایه و هدف از صحنه های LE71920282002257EDC00 و LE71920282014306NSG100 Landsat 7. ( الف ) تصویر پایه؛ ( ب ) تصویر هدف.

شکل 17. نقشه های توده ای برای تصاویر پایه و هدف شکل 16 . ( الف ) توده های پایه؛ ( ب ) توده های هدف.

شکل 18. طرحی برای ساخت مجموعه داده های رادیومتری برای بازسازی. ( الف ) تصاویر پایه و هدف؛ ( ب ) تصاویر پایه و هدف با مرزهای ناحیه قرمز و یک منطقه به رنگ سبز. ( ج ) تصاویر پایه و هدف با مرزهای ناحیه قرمز و یک منطقه به رنگ سبز و با مناطق منسجم پایه به رنگ سبز روشن. ( د ) تصاویر پایه و هدف با مرزهای ناحیه قرمز و یک منطقه به رنگ سبز، مناطق همدوس پایه به رنگ سبز روشن و با مناطق منسجم هدف به رنگ آبی روشن.

شکل 19. بازسازی هدف و HM، به شکل 16 مراجعه کنید . ( الف ) تصویر هدف؛ ( ب ) بازسازی HM.

شکل 20. بازسازی هدف و HM (بخشی از)، به شکل 16 مراجعه کنید . ( الف ) تصویر هدف؛ ( ب ) بازسازی HM.

مقالات داخلی و بین المللی

بدون دیدگاه

دیدگاهتان را بنویسید لغو پاسخ

برای نوشتن دیدگاه باید وارد بشوید.

مشاورین هوش پیروزی

کلید واژه ها:

1. مقدمه