1. مقدمه
شکل یک ویژگی اساسی برای بیان اشیاء فضایی و انتقال پدیده های فضایی است. نمایش شکل و رمزگذاری همیشه یکی از مشکلات اساسی در زمینههای علوم زمین و علوم کامپیوتر بوده است و نقش مهمی در بسیاری از کاربردها از جمله شناخت فضایی [ 1 ، 2 ، 3 ]، تعمیم نقشه [ 4 ، 5 ، 6 ] ایفا میکند. ]، تشخیص الگوی فضایی [ 7 ، 8 ]، و تطبیق شکل و بازیابی [ 9 ، 10 ، 11]. از منظر شناختی، شکل را می توان به عنوان نوعی ویژگی ساختاری بصری درک کرد که توسط خود یک شی یا پدیده درک می شود [ 12 ]. با این حال، تعریف رسمی ویژگی های ساختاری بسیار دشوار است، و آنها به طور جامع در تعاملات و ترکیب بسیاری از اجزا، مانند محیط های داخلی، مرزی و خارجی منعکس می شوند.
در دهه های اخیر، روش های متعددی برای نمایش شکل پیشنهاد شده است [ 13 ، 14 ]. این روشها را میتوان به طور تقریبی به سه دسته تقسیم کرد: روشهای منطقهمحور، ساختارمحور و روشهای مرزی. روش های مبتنی بر منطقه عمدتاً از طریق عملیات واحدهای منطقه ای (مثلاً پیکسل) به دست می آیند. این عملیات می تواند بر اساس یک چارچوب مورفولوژیکی ریاضی [ 15 ]، یا آمار توزیع چگالی [ 16 ] یا تبدیل های دو بعدی مبتنی بر منطقه (به عنوان مثال، توصیفگرهای فوریه) [ 17 ] باشد. پرکاربردترین روش مبتنی بر ساختار، روش اسکلت است [ 18]، که از محور مرکزی برای نشان دادن مورفولوژی و توپولوژی کلی شکل استفاده می کند. روشهای مبتنی بر مرز عبارت است از استخراج ویژگیهای توصیفی برای نمایش یک شکل با استفاده از مرز آن. این ویژگی ها شامل توصیفگر زمینه شکل (SC) محاسبه شده توسط توزیع نقاط مرزی [ 9 ]، تابع چرخش (TF) تعریف شده توسط تغییرات زاویه در امتداد مرز [ 19 ]، و تقعر تحدب چند مقیاسی (MCC) [ 20 ] و نمایش مساحت مثلث (TAR) [ 21] توصیفگرها با ویژگیهای مقعر-محدب محلی یا جهانی اندازهگیری میشوند. این روشها با معیارهای هندسی و آماری، با مزایای شهودی بودن و ثبات محاسباتی، که کاربرد گسترده آنها را در اندازهگیریهای شباهت شکل و بازیابی شکل ترویج میکنند، غالب هستند. با این حال، این روشها فاقد مکانیسمهای شناختی هستند و با تواناییهای شناختی انسان برابری نمیکنند. با توجه به اینکه اشکال بسیار پیچیده و از نظر شناختی مرتبط هستند، تمرکز فقط بر روی طراحی الگوریتمهای هندسی و نه بر بهبود خصوصیات عمیق، برای بازنمایی و شناخت شکل مفید نیست.
در سال های اخیر، یادگیری عمیق عمیقاً بر توسعه چندین رشته تأثیر گذاشته است [ 22 ]. از طریق ماژول های چند لایه ساده اما غیرخطی، یادگیری عمیق قابلیت نمایش قدرتمندی برای ویژگی های بصری محلی دارد. این مزایا همچنین کاربرد موفقیت آمیز یادگیری عمیق را برای بسیاری از وظایف تحلیل نقشه برداری، از جمله تشخیص الگو [ 7 ، 23 ]، تعمیم نقشه [ 24 ، 25 ] و درون یابی فضایی [ 26 ] ممکن کرده است.]. استفاده از یادگیری عمیق برای ساخت یک روش رمزگذاری شکل یک رویکرد مثبت و امیدوارکننده است که به طور موثر روش های سنتی را تکمیل می کند. علاوه بر این، یادگیری عمیق به طور تجربی ثابت شده است که یک تعصب شکل را نشان می دهد. یعنی یک شی ترجیحاً از نظر شکل به جای رنگ یا بافت متمایز می شود [ 27 ]. برخی از محققان سعی کرده اند روش های یادگیری عمیق را برای استخراج ویژگی های نهفته برای توصیف اشکال معرفی کنند. به عنوان مثال، یان و همکاران. [ 3 ] یک مدل رمزگذار خودکار گراف (GAE) برای رمزگذاری شکل به عنوان یک بردار ویژگی یک بعدی پیشنهاد کرد، لیو و همکاران. [ 28 ] یک شبکه کانولوشنال نقطه عمیق با استفاده از عملگر TriangleConv که به خوبی طراحی شده بود برای تشخیص و طبقه بندی اشکال ساختمان ساخت و Hu و همکارانش. [ 29] یک روش تشخیص شکل ردپای ساختمان را بر اساس یک شبکه ارتباطی با چند نمونه برچسبگذاری شده پیشنهاد کرد.
با این حال، استفاده از یادگیری عمیق برای شکل دادن به بازنمایی و رمزگذاری هنوز در مراحل ابتدایی خود است و بسیاری از مسائل کلیدی حل نشده باقی مانده اند [ 30 ، 31 ]]. به عنوان مثال، روشهای مختلفی برای مدلسازی یک شکل و بهعنوان ورودی برای مدلهای یادگیری وجود دارد، از جمله روشهای مبتنی بر شطرنجی، مبتنی بر توالی و مبتنی بر نمودار. روشهای مختلف مدلسازی اساساً متفاوت هستند و باید با استفاده از روشهای محاسبه ویژگیهای مختلف و معماریهای یادگیری پردازش شوند. در این راستا، این مطالعه یک ارزیابی مقایسه ای از روش های مختلف یادگیری عمیق برای نمایش شکل و رمزگذاری اشیاء جغرافیایی انجام داد. به طور خاص، ما ابتدا یک چارچوب رمزگذاری شکل را بر اساس معماری رمزگذار-رمزگشای عمیق پیشنهاد کردیم. سپس، برای روشهای مدلسازی مبتنی بر شطرنجی، مبتنی بر توالی، و مبتنی بر نمودار یک شکل، ما سه رمزگذار-رمزگر مختلف طراحی کردیم و یادگیری خود نظارتی را برای به دست آوردن رمزگذاری یکبعدی برای هر شکل انجام دادیم. سرانجام،
ادامه این مقاله به شرح زیر سازماندهی شده است. بخش 2 چارچوب رمزگذاری شکل را بر اساس یادگیری عمیق شرح می دهد و سه رمزگذار-رمزگشای عمیق را می سازد. بخش 3 نتایج تجربی رمزگذاری شکل را ارائه می دهد و آنها را از طریق بازرسی بصری و ارزیابی کمی تجزیه و تحلیل می کند. بخش 4 مقاله را به پایان می رساند.
2. روش شناسی
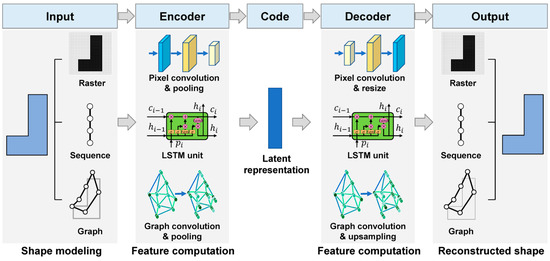
رمزگذار-رمزگشا نوعی شبکه عصبی بدون نظارت است که برای یادگیری رمزگذاری کارآمد داده های بدون برچسب استفاده می شود [ 22 ]. این شامل پنج جزء اصلی است: ورودی، رمزگذار، کد، رمزگشا و خروجی. رمزگذار برای رمزگذاری ورودی ها به کد استفاده می شود و رمزگشا ورودی را از روی کد بازسازی می کند. هدف از یادگیری این است که خروجی را تا حد ممکن شبیه به ورودی کند.
محاسبات ویژگی های مورد استفاده در رمزگذار و رمزگشا برای روش های مختلف مدل سازی شکل متفاوت است. در این تحقیق، روشهای مبتنی بر شطرنجی، توالی و مبتنی بر نمودار برای مدلسازی اشکال دو بعدی در نظر گرفته شد. به همین ترتیب، سه رمزگذار-رمزگشا عمیق برای استخراج ویژگی های رمزگذاری پنهان برای نمایش اشکال، همانطور که در شکل 1 نشان داده شده است، ساخته شد . بخشهای زیر جزئیات سه رمزگذار-رمزگشا را شرح میدهند.
2.1. مدل کدگذاری شکل مبتنی بر پیکسل
روش شطرنجی معمولاً برای کار با دادههای مبتنی بر برداری فضایی استفاده میشود، زیرا سازماندهی منظم بهتر با بسیاری از الگوریتمها یا مدلها [ 31 ]، مانند شبکههای عصبی کانولوشنال عمیق سازگار است. مزیت دیگر این رویکرد این است که ویژگی های منطقه ای اشکال در نظر گرفته می شود.
برای به دست آوردن یک تصویر مبتنی بر شطرنجی برای یک شکل، تفاوت بین مقادیر حداکثر و حداقل در محورهای افقی و عمودی محاسبه شد و مقدار بزرگتر به عنوان طول لبه در نظر گرفته شد تا مربعی با مرکز شکل در نظر گرفته شود. مرکز. این مربع به طور مناسب به سمت بیرون منبسط شد (مثلاً 10٪) تا از یکپارچگی شکل اطمینان حاصل شود. سپس یک شبکه مناسب برای شطرنجی کردن مربع ایجاد شد. اندازه سلول های شبکه مستقیماً بر وضوح نمایش محتوای داده تأثیر می گذارد. اگر اندازه سلول خیلی بزرگ باشد، یک پدیده موزاییک جدی رخ می دهد که ارائه جزئیات طرح کلی را دشوار می کند. اگر اندازه سلول خیلی کوچک باشد، راندمان آموزشی مدل تحت تأثیر قرار می گیرد. با در نظر گرفتن وضوح تصاویر و پیچیدگی مدل به طور جامع، اندازه شبکه در این مطالعه 28 × 28 پیکسل تعیین شد. در نهایت، سلول شبکه باینریزه می شود. یعنی وقتی یک سلول در شکلی با بیش از نیمی از مساحت قرار می گیرد، سلول روی سیاه قرار می گیرد. در غیر این صورت سفید است.
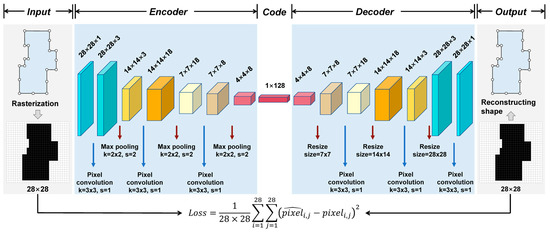
پس از تبدیل شکل به یک تصویر مبتنی بر شطرنجی، رمزگذار-رمزگر کلاسیک مبتنی بر توپولوژی شبکه مانند میتواند برای استخراج نمایش نهفته شکل استفاده شود. شکل 2 معماری رمزگذار-رمزگذار مبتنی بر پیکسل (PixelNet) را نشان می دهد که در این مطالعه برای رمزگذاری شکل استفاده شده است.
رمزگذار در PixelNet تصویر ورودی 28 × 28 را به عنوان یک بردار 128 بعدی کدگذاری کرد. این شامل سه لایه کانولوشن با اندازه هسته 3 × 3 و اعداد هسته به ترتیب 3، 18 و 8 بود. پس از هر لایه کانولوشن، یک لایه max-pooling با اندازه پنجره k = 2 × 2 و طول گام s = 2 متصل شد. رمزگشا همچنین شامل سه لایه کانولوشن با 8، 18 و 3 هسته بود. نمونه برداری، برعکس اندازه ادغام شده، تصویر را به اندازه اصلی خود بازگرداند. در نهایت، یک لایه کانولوشن با ویژگی یک اضافه شد تا اطمینان حاصل شود که بعد ویژگی خروجی با ورودی مطابقت دارد.
2.2. مدل رمزگذاری شکل مبتنی بر توالی
مرز یک شکل یک دنباله طبیعی است که شامل یک سری نقاط به هم پیوسته است. بنابراین، ساخت یک چارچوب نمایش و تحلیل شکل بر اساس توالی مرزی یک استراتژی امیدوارکننده است.
از آنجا که فاصله بین دو گره مجاور در یک مرز شکل یکسان نیست، واحد پردازش ثابت نیست. برای پرداختن به این موضوع، مرز به مجموعهای از واحدهای خطی متوالی با طولهای مساوی تقسیم شد که لیکسل نامیده میشوند [ 32 ] و نقاط میانی لیکسلها به عنوان گرههای دنباله در نظر گرفته شدند. برای هر گره دنباله ای، تفاوت های افقی و عمودی بین دو انتهای لیکسل مرتبط به عنوان دو ویژگی برای توصیف آن استفاده شد. در نهایت، یک بردار، PN×2={p1,p2,…,pN}، حاوی Nگرههای دنبالهای با ویژگیهای دو بعدی، به عنوان ورودی برای مدل رمزگذاری شکل ساخته شدند. با اشاره به تنظیمات پارامتر استفاده شده در ادبیات [ 3 ]، Nروی 64 تنظیم شد.
برای پردازش توالی ساخته شده، از یک شبکه عصبی برای ساخت یک رمزگذار-رمزگر استفاده شد. از آنجایی که شبکه عصبی کلاسیک ترتیب گره ها را به ترتیب در نظر نمی گیرد، شبکه Seq2seq (SeqNet) [ 33 ]، که از حافظه کوتاه مدت بلند مدت (LSTM) [ 34 ] به عنوان رمزگذار و رمزگشا استفاده می کند، استفاده شد. معماری در شکل 3 نشان داده شده است .
رمزگذار یک شبکه LSTM بود که دنباله را دریافت کرد PN×2به عنوان ورودی تعداد نورون ها در لایه پنهان روی تنظیم شد zsize=128، یعنی بعد رمزگذاری شکل ورودی. تابع Tanh برای فعال کردن نورون ها استفاده شد تا اطمینان حاصل شود که هر مقدار بردار خروجی از 1- تا 1 متغیر است. محاسبه هر مرحله زمانی در حلقه به شرح زیر است:
جایی که hiو ciبه ترتیب مقادیر خروجی و حالت واحد LSTM را نشان می دهد. piنشان دهنده ویژگی های ورودی، و fe(⋅)نشان دهنده محاسبه هر مرحله زمانی در رمزگذار است. خروجی آخرین مرحله زمانی رمزگذاری شکل است، به عنوان مثال، z=hT، جایی که Tتعداد مراحل زمانی را نشان می دهد.
رمزگشا شامل یک شبکه LSTM و یک لایه کاملاً متصل بود. ترکیبی از رمزگذاری شکل متوسط و ویژگی ها را دریافت کرد piبه عنوان ورودی، یعنی ورودی یک بود N×(zsize+2)ماتریس تعداد نورون های لایه پنهان روی تنظیم شد zsizeبرای حفظ همان بعد مقدار حالت در رمزگذار. تابع Tanh نیز به عنوان یک تابع فعال سازی مورد استفاده قرار گرفت. خروجی LSTM یک لایه کاملاً متصل خطی اضافه کرد که بعد خروجی دنباله را به بعد ورودی محدود کرد تا توالی اصلی را بازسازی کند. فرآیند محاسبات به شرح زیر است:
جایی که Hiو Ciمقادیر خروجی و حالت واحد LSTM را نشان می دهد، [pi;z]نشان دهنده ورودی رمزگشا است که توسط رمزگذاری شکل و ویژگی تشکیل شده است، fd(⋅)محاسبه هر مرحله زمانی در رمزگشا را نشان می دهد، Wiو biوزن ها و بایاس های لایه کاملا متصل هستند و pˆiویژگی بازسازی شده توسط مدل است.
هدف یادگیری به حداقل رساندن ورودی ها بود، PN×2={p1,p2,…pN}و خروجی ها P^N×2={pˆ1,pˆ2,…,pˆN}و این تفاوت با استفاده از میانگین مربعات خطا محاسبه شد:
رمزگشا از طریق رویکرد “معلم اجباری” آموزش داده شد تا همگرایی مدل را سرعت بخشد، به عنوان مثال، هر ورودی رمزگشا از خروجی مرحله زمانی قبلی استفاده نمی کند بلکه مستقیماً از مقدار موقعیت مربوطه در آموزش استفاده می کند. داده ها.
2.3. رمزگذار خودکار شکل مبتنی بر نمودار
در مقایسه با دنباله، نمودار بهتر می تواند رابطه بین گره های غیر مجاور را بیان کند. یک گراف به صورت ریاضی نشان داده می شود G=(V,E,A)، جایی که V={v1,…,vN}و Eمجموعه ای از Nگره ها و لبه های متصل کننده آنها به ترتیب و Aهست یک N×Nماتریس مجاورت که وزن لبه ها را ثبت می کند. ماتریس لاپلاس Lاز Aبه عنوان محاسبه می شود L=IN−D−1/2AD−1/2، جایی که INهست Nماتریس هویت سفارش و D=diag(d1,⋯,dN)ماتریس درجه است که از درجه تشکیل شده است di=∑jAi,jاز گره i. بردارهای ویژه از Lبا نشان داده می شوند {xTl}N−1l=0، و مقادیر ویژه مربوطه هستند {λTl}N−1l=0. راضی می کنند L=XΛXT، جایی که Xماتریسی است که توسط {xTl}N−1l=0، و Λیک ماتریس مورب از است {λTl}N−1l=0.
همانطور که یک دنباله ساخته شد، نقاط میانی لیکسل ها به عنوان گره های گراف در نظر گرفته شد و تفاوت های افقی و عمودی بین دو انتها به عنوان ویژگی گره های گراف استفاده شد. برای محاسبه وزن لبه، یک مثلث Delaunay (DT) با استفاده از تمام گره ها ساخته شد. اگر یک لبه DT بین دو گره وجود داشته باشد، وزن لبه متصل کننده آنها به عنوان متقابل طول لبه DT تعیین می شود. در غیر این صورت، 0 بود. در نهایت، گره گراف ماتریس ویژگی ها، fN×2و ماتریس مجاورت، آ، برای خدمت به عنوان ورودی مدل به دست آمدند. نهمچنین روی 64 تنظیم شد تا اطمینان حاصل شود که تعداد گره و ویژگیها با روش SeqNet برای مقایسه بهتر مطابقت دارند.
یک رمزگذار رمزگذار مبتنی بر گراف (GraphNet) برای پردازش گراف ساخته شده ساخته شد. معماری کلی در شکل 4 نشان داده شده است . رمزگذار شامل یک لایه کانولوشن گراف با 32 نقشه ویژگی (یعنی تعداد هسته) بود و ترتیب چند جمله ای هر هسته روی 3 تنظیم شد. همچنین شامل دو لایه ادغام گراف بود. پس از ادغام، تعداد گره ها و ابعاد ویژگی به ترتیب 32 و 24 و 16 و 8 تعیین شد. خروجی آخرین لایه در رمزگذار به یک بردار ویژگی 128 بعدی، یعنی رمزگذاری شکل، گسترش یافت. به همین ترتیب، دو لایه upsampling گراف و یک لایه کانولوشن گراف در رمزگشا وجود داشت تا اندازه گراف را به همان اندازه ورودی بازگرداند.
لایه کانولوشن توسط یک عملیات پیچیدگی گراف سریع و محلی، که بر اساس تبدیل فوریه گراف [ 35 ] تعریف شد، پیاده سازی شد. این jویژگی های خروجی ( ل+1) -مین لایه fj[ل+1]توسط قانون انتشار رو به جلو لایه به لایه محاسبه می شود:
جایی که σ(·)یک تابع فعال سازی غیر خطی را نشان می دهد. fمن(ل)هست مننمودار از للایه؛ تیک(ایکس)مرتبه K چبیشف چند جمله ای است که به صورت بازگشتی توسط محاسبه می شود تیک(ایکس)=2ایکستیک–1(ایکس)–تیک–2(ایکس)، با تی0(ایکس)=1و تی1(ایکس)=ایکس; λمترآایکسبزرگترین مقدار ویژه است L; θمن،jکو بj(ل)قابل آموزش هستند افمنn×افoتوتی×کضرایب و 1×افoتوتیبردار سوگیری در للایه به ترتیب و افمنnو افoتوتیتعداد نمودارهای هستند لو (ل+1)لایه ها به ترتیب
لایه کانولوشن گراف از ماتریس لاپلاسی برای ترسیم ویژگی های گره استفاده می کند fn×افمنnبه fn×افoتوتی. این فرآیند ویژگی های گره گراف را به روز می کند، اما اندازه گراف (یعنی تعداد گره های گراف) را تغییر نمی دهد. در این راستا، از روش DIFFPOOL [ 36 ] برای اجرای عملیات جمعآوری و نمونهبرداری نمودار استفاده شد که به تغییر اندازه نمودار و استخراج ویژگیهای سلسله مراتبی کمک میکند. این لایه یک ماتریس انتساب قابل تفکیک را می آموزد اس∈ℝn×متربرای نقشه برداری nگره ها به مترگره ها برای به دست آوردن ویژگی های گره با دانه بندی های مختلف. از طریق دو پیچیدگی نمودار پیاده سازی می شود: زn×q(ل)=سیonvهمتربهد(آn×n(ل)، fn×q(ل))و اسn×متر(ل)=سیonvپooل(آn×n(ل)، fn×q(ل))، جایی که سیonvهمتربهدویژگی های نود جدید را تولید می کند و سیonvپooلماتریس انتساب را تولید می کند. ویژگی های ماتریس مجاورت و گره گراف در (ل+1)لایه به صورت زیر محاسبه می شود:
این فرآیند تعداد و ویژگی های گره های گراف را تغییر می دهد. اگر مترکمتر است از n، به این معنی است که تعداد گره ها کاهش می یابد، که می تواند به عنوان یک عملیات ادغام درک شود. برعکس، تعداد گره ها افزایش می یابد، یعنی عملیات upsapling.
GraphNet به روشی بدون نظارت آموزش داده شد تا تفاوت بین ورودی و خروجی را به حداقل برساند. با توجه به دشواری بهینهسازی ماتریسهای تخصیص در لایه ادغام، دو محدودیت به تابع ضرر [ 36 ] اضافه شد: به حداقل رساندن اختلاف ماتریسهای مجاور. آبرای هر لایه و به حداقل رساندن آنتروپی ماتریس های تخصیص اسردیف به ردیف اولی پایداری لبهها را در ماتریسهای مجاور تضمین میکند و دومی تضمین میکند که انتساب برای هر گره نزدیک به یک بردار یک داغ است تا رابطه با لایه بعدی را به وضوح توصیف کند. تابع ضرر نهایی به صورت زیر تعریف می شود:
جایی که Lتعداد تمام لایه ها (یعنی شش در این مطالعه)، و “·“افو اچ(·)به ترتیب هنجار فروبنیوس و تابع آنتروپی را نشان می دهند.
3. نتایج تجربی و تجزیه و تحلیل
سه رمزگذار-رمزگشای عمیق با استفاده از پایتون در TensorFlow پیادهسازی شدند و آزمایشها روی دو مجموعه داده با محیطی از پردازنده مرکزی Intel(R) Core (TM) i9-9920X و NVIDIA GeForce RTX 2080Ti برای آزمایش عملکرد آنها برای رمزگذاری شکل انجام شد. بخشهای زیر مجموعه دادههای تجربی، نتایج و تحلیلها را تشریح میکنند و بحثی را ارائه میکنند.
3.1. مجموعه داده های تجربی
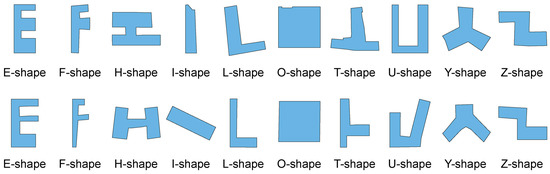
یک مجموعه داده شکل ساختمان باز در آزمایش ها استفاده شد [ 3 ]. به عنوان یک ویژگی جغرافیایی مصنوعی معمولی، ساختمان ها اغلب در نقشه ها به صورت اشکال دو بعدی، با ویژگی های بصری آشکار مانند چرخش های راست زاویه و تقارن نشان داده می شوند. در این مجموعه داده، 10 دسته از ساختمان ها با توجه به اشکال حروف انگلیسی، همانطور که در شکل 5 نشان داده شده است، متمایز شدند . هر دسته شامل 501 ساختمان با مجموع 5010 شکل بود.
از آنجایی که PixelNet، SeqNet و GraphNet همگی مدلهای بدون نظارت هستند، مجموعه دادههای ساختمان به مجموعههای آموزشی و آزمایشی تقسیم نشدند. تمام ساختمان ها برای آموزش این سه مدل مورد استفاده قرار گرفتند تا در نهایت یک بردار یک بعدی برای هر ساختمان رمزگذاری شود. اندازه دسته آموزشی روی 50 تنظیم شد و هر مدل برای 50 دور با استفاده از بهینه ساز Adam [ 37 ] با نرخ یادگیری 0.01 آموزش داده شد.
3.2. نتایج تجربی و تجزیه و تحلیل
3.2.1. ارزیابی کمی
از چهار معیار بازیابی شکل برای ارزیابی اثربخشی رمزگذاری شکل به صورت کمی استفاده شد: نزدیکترین همسایه (NN)، ردیف اول (FT)، ردیف دوم (ST)، و سود تجمعی تنزیل شده (DCG). همه معیارها از 0 تا 1 متغیر هستند و مقدار بالاتر نشان دهنده عملکرد بهتر است. برای اطلاعات بیشتر در مورد تعاریف و محاسبات این معیارها، به کار Shilane و همکاران مراجعه کنید. [ 38 ].
برای محاسبه FT، ST و DCG، یک شکل بهطور تصادفی از هر دسته بهعنوان شی بازیابی انتخاب شد و بقیه شکلهایی بودند که باید بازیابی شوند. علاوه بر این، ما همچنین میانگین زمان هزینه محاسبه شباهتهای بین هر شی بازیابی و اشکال دیگر را برای ارزیابی کارایی بازیابی مدلها محاسبه کردیم. برای مقایسه، یک مدل یادگیری عمیق مبتنی بر نمودار موجود (GAE) پیشنهاد شده توسط یان و همکاران. [ 3 ] و دو روش سنتی، یعنی، توصیفگر شکل فوریه (FD) [ 9 ] و نمایش تابع مماس (TF) [ 19 ]] نیز اجرا شد. تفاوتهای بین روشهای GAE و GraphNet در این است که GAE از یک دنباله برای نشان دادن مرزهای شکل استفاده میکند، در حالی که GraphNet از یک نمودار برای مدلسازی اشکال استفاده میکند و یک عملیات ادغام را در شبکه یکپارچه میکند. علاوه بر این، ویژگی های ورودی آنها متفاوت است. جدول 1 نتایج ارزیابی بازیابی شکل در مجموعه داده های ساختمان را فهرست می کند.
چندین مشاهدات از طریق مقایسه انجام شد. ابتدا، GraphNet از PixelNet و SeqNet برای هر چهار معیار در کار بازیابی شکل ساختمان بهتر عمل کرد. GraphNet نه تنها اتصالات گرههای غیر مجاور را از طریق یک لبه DT در مرحله ساخت گراف در نظر گرفت، بلکه نزدیکی فضایی بین گرهها را با استفاده از کانولوشن گراف نیز در نظر گرفت. این ملاحظات ممکن است برای گرفتن ویژگی های زمینه ای مفید باشد. دوم، عملکرد کلی PixelNet چیزی بین مدلهای GraphNet و SeqNet بود. این نتیجه ثابت می کند که هر دو روش مبتنی بر شطرنجی و مبتنی بر بردار برای رمزگذاری شکل امکان پذیر هستند. روش مبتنی بر شطرنجی ساده و شهودی است، در حالی که روش مبتنی بر برداری دارای مزایای افزونگی کم، دقت بالا و فشرده بودن اطلاعات است. برای روش های بردار، روش گراف قادر به استخراج روابط توپولوژیکی بین گره های غیر مجاور نسبت به روش توالی است. به همین دلیل، اگرچه روشهای GraphNet و SeqNet دارای ویژگیهای ورودی یکسانی هستند، GraphNet قابلیتهای کدگذاری شکل بهتری را نسبت به SeqNet برای مجموعه داده ساختمان نشان داده است.
علاوه بر این، در مقایسه با روشهای سنتی FD و TF، چهار روش یادگیری عمیق (روشهای GraphNet، PixelNet، SeqNet و GAE) بهتر عمل کردند. این نتیجه اثربخشی فناوری های یادگیری عمیق را در استخراج ویژگی های ضمنی اشکال و به دست آوردن رمزگذاری های ارزشمند اثبات می کند. علاوه بر این، با مقایسه زمان هزینه، مشخص شد که یادگیری عمیق تا حد زیادی کارایی بازیابی شکل را بهبود می بخشد. این به این دلیل است که معیارهای تشابه شکل به دست آمده با استفاده از روش های FD و TF به شدت با نقطه شروع مرزهای محصور مرتبط است. برای بازیابی مطمئن تر، شباهت بین دو شکل به طور مکرر با عبور از تمام گره ها در مرزها به عنوان نقطه شروع محاسبه شد. این فرآیند هزینه محاسباتی قابل توجهی را به همراه دارد. متقابلا،
3.2.2. تجزیه و تحلیل تجسم
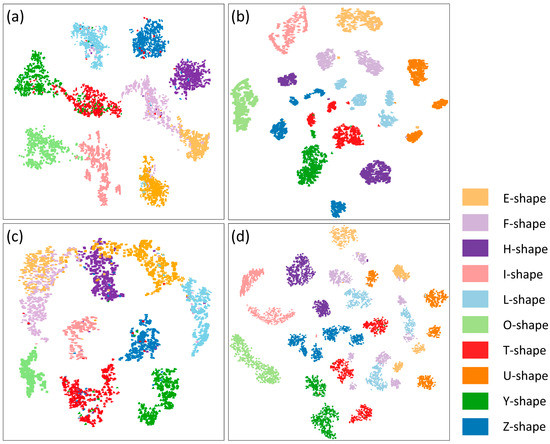
برای نشان دادن عملکرد رمزگذاری شکل به صورت شهودی تر، از الگوریتم t-SNE [ 39 ] برای کاهش بعد رمزگذاری های شکل به دو و تجسم آنها در یک فضای مسطح استفاده شد، همانطور که در شکل 6 نشان داده شده است. در شرایط ایده آل، دو شکل از یک دسته به هم شباهت بیشتری دارند، موقعیت آنها در فضا نزدیکتر است و موقعیت اشکال با دسته های مختلف از هم دورتر است. در نهایت، تمام رمزگذاریهای شکل ساختمان، خوشههای مستقلی را تشکیل میدهند.
از نتایج، رمزگذاری شکل تولید شده توسط چهار روش یک پدیده تجمع خاصی را نشان داد. یک مقایسه دقیق نشان میدهد که رمزگذاریهای شکل تولید شده توسط روشهای GraphNet و PixelNet تجمع قویتری دارند، در حالی که خوشههای تشکیلشده توسط همان اشکال در نتایج SeqNet و GAE جدایی آشکاری را نشان میدهند. تجزیه و تحلیل نشان داد که این پدیده ممکن است ناشی از جهت شکل و نقطه شروع باشد. اگرچه ویژگیهای استخراجشده در روشهای SeqNet و GAE اسکالر هستند، ویژگیهای گره دنبالههای ورودی با انتخاب نقاط شروع بسیار متفاوت است. این منجر به تفاوت قابل توجهی در رمزگذاری شکل می شود. در مقابل، جداسازی اشکال با همان دسته در نتایج روشهای GraphNet و PixelNet تا حد زیادی کاهش یافت. این به این دلیل رخ داد که هر شکل با استفاده از یک شبکه شطرنجی یکپارچه بدون توجه به انتخاب نقطه شروع در روش PixelNet نمایش داده شد. در روش GraphNet، این مشکل به طور موثر با در نظر گرفتن روابط توپولوژیکی بین گره ها کاهش یافت. این جداسازی ها منجر به خطاهای غیر قابل چشم پوشی در اندازه گیری شباهت شکل شد، که ممکن است توضیح دهد که چرا معیارهای ارزیابی روش های SeqNet و GAE برای کار بازیابی شکل کمی کمتر از روش GraphNet است.
علاوه بر این، مشاهده شد که برای برخی از رمزگذاریهای شکل در نتایج GraphNet و PixelNet همپوشانی وجود دارد. به خصوص، در نتیجه PixelNet، رمزگذاری های E-shaped و F-shaped همپوشانی آشکاری دارند. این پدیده ممکن است به این دلیل رخ دهد که برخی از اشکال شباهت بصری خاصی دارند، برای مثال، شکل E و F هر دو مستطیل مانند و دندانه دار بودند. این همپوشانی همچنین منجر به خطاهایی در معیار تشابه شکل شد. بنابراین، معیارهای ارزیابی روش PixelNet برای کار بازیابی شکل از معیارهای روش GraphNet پایینتر بود. از این دو مشاهدات، روشهای SeqNet و GAE قادر به گروهبندی اشکال با نقطه شروع و جهتگیری یکسان در یک دسته هستند. با این حال، برای دو شکل با جهت های مختلف، این دو روش ممکن است شباهت آنها را به اشتباه اندازه گیری کنند.
3.2.3. اندازه گیری شباهت بین جفت های شکل
برای توضیح بهتر نتایج فوق، جدول 2 شباهتهای شکلی را بین برخی از جفتهای شکل معمولی که با استفاده از روشهای مختلف به دست آمدهاند فهرست میکند. شباهت بین دو شکل با استفاده از فاصله اقلیدسی بین رمزگذاری آنها محاسبه شد. هر چه مقدار آن کوچکتر باشد، این دو شکل بیشتر شبیه هستند.
برای اولین جفت شکل، جهتگیریها، نقاط شروع و اشکال کلی نسبتاً نزدیک بودند و هر سه روش میتوانستند شباهتهای آنها را به دقت توصیف کنند. جهت گیری ها و نقاط شروع جفت شکل دوم مشابه بود، اما اشکال متفاوت بود و شباهت های محاسبه شده با سه روش کم بود. نتایج نشان میدهد که سه روش میتوانند ویژگیهای شکل را در شرایط ایدهآل، یعنی با جهتگیریها و نقاط شروع ثابت، به خوبی تشخیص دهند. جفت شکل سوم نقاط شروع و شکلهای یکسانی دارد، اما جهتگیریها متفاوت است، SeqNet عملکرد خوبی داشت، GraphNet نسبتاً خوب بود، و PixelNet بدترین عملکرد را داشت. این نتیجه نشان می دهد که جهت گیری عملکرد PixelNet را به طور قابل مشاهده تحت تاثیر قرار داده است. همچنین گراف نت را تا حدی اما در محدوده قابل قبولی تحت تاثیر قرار داد. نتایج جفتهای شکل چهارم و پنجم نشان داد که روش SeqNet همیشه زمانی که نقاط شروع متفاوت بودند، ضعیف عمل میکند، حتی زمانی که جهتگیریها یکسان بود. این بدان معنی است که این روش ها هنوز هم به ترتیب نقاط بسیار حساس هستند، حتی اگر ویژگی های استخراج شده بدون اسکالر باشند. این مشکل در GraphNet به میزان قابل توجهی کاهش یافت. این نتایج تجزیه و تحلیل مقایسه ای دقیق با نتایج کمی قبلی سازگار است. حتی اگر ویژگی های استخراج شده بدون اسکالر هستند. این مشکل در GraphNet به میزان قابل توجهی کاهش یافت. این نتایج تجزیه و تحلیل مقایسه ای دقیق با نتایج کمی قبلی سازگار است. حتی اگر ویژگی های استخراج شده بدون اسکالر هستند. این مشکل در GraphNet به میزان قابل توجهی کاهش یافت. این نتایج تجزیه و تحلیل مقایسه ای دقیق با نتایج کمی قبلی سازگار است.
3.3. بحث در مورد بعد کدگذاری
متغیر بعد رمزگذاری برای روش رمزگذار – رمزگشا حیاتی است. بنابراین، یک آزمایش تکمیلی برای بررسی اثرات این پارامتر بر عملکرد سه روش انجام شد. برای دستیابی به تغییر در ابعاد، PixelNet و GraphNet تعداد هستههای کانولوشن را در آخرین لایه کانولوشن و SeqNet تعداد نورونهای لایه پنهان را تنظیم کردند. جدول 3 معیارهای ارزیابی عملکرد رمزگذاری روش های مختلف را با تغییر بعد کدگذاری از 32 تا 512 فهرست می کند.
در تئوری، زمانی که بعد رمزگذاری بالاتر باشد، توانایی نمایش ویژگی قوی تر است. با این حال، نتایج تجربی با این یافته تناقض داشت. مقایسه نشان داد که عملکرد هر سه روش ابتدا بهبود یافت اما سپس با افزایش بعد رمزگذاری تثبیت یا حتی کاهش یافت. GraphNet بهترین عملکرد را زمانی داشت که بعد رمزگذاری 128 بود. برای روشهای PixelNet و SeqNet، مناسبترین بعد رمزگذاری 256 بود. این نتیجه را میتوان به عدم وجود پراکندگی در آموزش برای محدود کردن بردار پایه نسبت داد، که منجر به کاهش عملکرد به دلیل بیش از حد کامل بودن در ابعاد رمزگذاری بالاتر.
3.4. آزمایش با مجموعه داده پیچیده تر
از آنجایی که اشکال ساختمان مورد استفاده در این مطالعه نسبتاً ساده بودند، ما روشهای مختلف رمزگذاری شکل را بر روی یک مجموعه داده پیچیدهتر، مجموعه داده MPEG-7 [ 40 ] آزمایش کردیم تا عملکرد را تأیید و مقایسه کنیم. این پایگاه داده با طیف گسترده ای از دسته بندی ها مشخص می شود. این شامل 70 دسته شکل است که حیوانات، گیاهان و لوازم را پوشش می دهد. هر دسته شامل 20 شکل، در مجموع 1400 شکل است. شکل 7 نمونه هایی از مجموعه داده را نشان می دهد.
برای چهار مدل یادگیری عمیق، تمام اشکال موجود در مجموعه داده MPEG-7 برای آموزش آنها استفاده شد و هر شکل به عنوان یک بردار کدگذاری شد. برای هر دسته، یک شکل به طور تصادفی برای بازیابی اشکال دیگر انتخاب شد. چهار معیار کمی و زمان هزینه کار بازیابی با استفاده از روش های مختلف در جدول 4 آمده است.. مقایسه نشان میدهد که GraphNet همچنان در هر چهار معیار کمی در مقایسه با روشهای PixelNet و SeqNet بهتر عمل میکند، و نتایج کلی با نتایج مربوط به مجموعه داده ساختمان سازگار است، که نشان میدهد GraphNet همچنین دارای مزایای خاصی برای اندازهگیریهای شباهت و بازیابی است. از اشکال پیچیده چهار معیار روش GAE هنوز کمتر از روش Graph بود، اما شکاف کمتر شده بود. تجزیه و تحلیل دقیق نشان داد که دلیل این نتیجه ممکن است این باشد که GAE معماری شبکه سادهتری داشت و ویژگیهای ورودی بیشتری دریافت میکرد، و بنابراین در مجموعه داده MPEG-7 با دستهبندیهای پیچیده و اشکال کمتر، پایدارتر عمل کرد. همچنین مشاهده شد که معیارهای FT و ST در آزمایشات با مجموعه داده MPEG-7، به ویژه برای روشهای FD و TF بهبود یافته است.
علاوه بر این، زمان هزینه کار بازیابی برای چهار روش یادگیری عمیق به دلیل اشیاء بازیابی کمتر در مجموعه داده کوتاه شد. با این حال، روشهای FD و TF به زمان بیشتری نیاز داشتند زیرا اشکال پیچیدهتر و تعداد گرهها بیشتر بود. این نتیجه بیشتر مزایای روش های یادگیری عمیق را از نظر کارایی بازیابی نشان می دهد.
4. نتیجه گیری
نمایش شکل و رمزگذاری یک مشکل اساسی در نقشه کشی و علوم زمین است. با توجه به سه روش اصلی مدلسازی شکل، سه روش رمزگذاری شکل مختلف مبتنی بر یادگیری عمیق PixelNet، SeqNet و GraphNet در این مطالعه ساخته شد. PixelNet بر اساس مدلسازی مبتنی بر شطرنجی، SeqNet بر اساس مدلسازی مبتنی بر توالی، و GraphNet بر اساس مدلسازی مبتنی بر برداری با استفاده از ساختار نمودار ساخته شده است. تجزیه و تحلیل تجربی با استفاده از دو مجموعه داده نتایج زیر را به دست آورد: (1) روشهای رمزگذار-رمزگشا مبتنی بر یادگیری عمیق میتوانند به طور موثر ویژگیهای شکل را محاسبه کنند و رمزگذاریهای معناداری را برای پشتیبانی از اندازهگیری شکل و کار بازیابی به دست آورند. (2) روشهای یادگیری عمیق مزایایی را نسبت به روشهای سنتی FD و TF در مجموعه داده ساختمان نشان میدهند. معیارهای FT و ST روش های FD و TF به طور قابل توجهی در مجموعه داده MPEG-7 بهبود یافته است. (3) GraphNet به دلیل استفاده از گراف برای مدلسازی روابط توپولوژیکی بین گرهها و عملیات تلفیقی و ادغام گراف کارآمد برای پردازش ویژگیهای گره، بهتر از SeqNet و PixelNet عمل کرد.
تحقیقات بیشتر از جنبه های زیر انجام می شود: (1) مسئله رمزگذاری شکل مسطح باید به یک مسئله رمزگذاری شکل سه بعدی (3 بعدی) و عملکرد رمزگذار-رمز برای رمزگذاری اشیاء سه بعدی، از جمله ساختمان های سه بعدی و سه بعدی گسترش یابد. امتیاز، باید ارزیابی شود. (2) برای استخراج ویژگی گرههای شکل، ویژگیهای اضافی مستحق مطالعه هستند تا مورفولوژی و ارتباطات توپولوژیکی بین گرههای شکل، مانند توصیفکنندههای بافت شکل، به دست آید. (3) از نظر معماری یادگیری، برخی از تکنیکهای یادگیری در حال ظهور، مانند مکانیسمهای توجه و یادگیری تقویتی، میتوانند برای افزایش قابلیت بازنمایی در نظر گرفته شوند.








بدون دیدگاه