برنامه ریزی کاربری منطقه ای کارآمد عملی با استفاده از بهینه سازی الگوریتم ژنتیک چندهدفه و سیستم اطلاعات جغرافیایی

چکیده

برنامه‌ریزی کارآمد منطقه‌ای کاربری زمین به برنامه‌ریزان نیاز دارد تا بین کاربری‌های رقیب، سیاست‌های منطقه‌ای، سازگاری‌های فضایی و اولویت‌ها در حوزه‌های اجتماعی، اقتصادی و زیست‌محیطی تعادل برقرار کنند. بهینه‌سازی الگوریتم ژنتیک برنامه‌ریزی پیچیده‌ای را پیش برده است، اما چالش‌ها در توسعه جایگزین‌های عملی برای مقداردهی اولیه تصادفی، جهش‌های ژنتیکی و ایجاد تعادل عملی در اهداف رقیب باقی مانده است. برای برآوردن این نیازهای عملی، ما یک مدل بهینه‌سازی فضایی چندهدفه با شدت استفاده از زمین (LIr-MSO) با مقدار اولیه‌سازی اندازه پچ واقعی‌تر، جهش جدید، استراتژی‌های نخبه، و اهداف متعادل‌شده از طریق اسمی‌سازی و وزن‌دهی ایجاد کردیم. ما مدل را برای داپنگ، چین آزمایش کردیم که در آن آزمایش‌ها تناسب اندام جامع (براساس هزینه تبدیل، تولید ناخالص داخلی (GDP) را مقایسه کردند. ارزش خدمات اکوسیستم، فشردگی و درجه تضاد) با سه آزمایش کنتراست، که در آن تغییرات به طور جداگانه در مقداردهی اولیه و جهش ایجاد شد. مدل جامع در مقایسه با آزمایش‌های کنتراست، تناسب بهتری ارائه کرد. تکرارها به سرعت به سمت بهینه شدن نزدیک شدند، اما همگرایی نهایی شامل جهش های والد-فرزند بسیار کندتر بود. مبادله بین هزینه تبدیل و فشردگی قوی‌ترین بود، و درجه تضاد تا حدی به عنوان ویژگی نوظهور اتصال اجتماعی فضایی که در الگوریتم ما تعبیه شده بود، بهبود یافت. مشاهدات تکرار سریع تا نزدیک به بهینه بودن با مدل ما می‌تواند شبیه‌سازی تعاملی را تسهیل کند، که با مدل‌های فعلی امکان‌پذیر نیست، که شامل برنامه‌ریزان کاربری زمین و مدیران منطقه‌ای می‌شود. که در آن تغییرات به طور جداگانه در مقداردهی اولیه و جهش ایجاد شد. مدل جامع در مقایسه با آزمایش‌های کنتراست، تناسب بهتری ارائه کرد. تکرارها به سرعت به سمت بهینه شدن نزدیک شدند، اما همگرایی نهایی شامل جهش های والد-فرزند بسیار کندتر بود. مبادله بین هزینه تبدیل و فشردگی قوی‌ترین بود، و درجه تضاد تا حدی به عنوان ویژگی نوظهور اتصال اجتماعی فضایی که در الگوریتم ما تعبیه شده بود، بهبود یافت. مشاهدات تکرار سریع تا نزدیک به بهینه بودن با مدل ما می‌تواند شبیه‌سازی تعاملی را تسهیل کند، که با مدل‌های فعلی امکان‌پذیر نیست، که شامل برنامه‌ریزان کاربری زمین و مدیران منطقه‌ای می‌شود. که در آن تغییرات به طور جداگانه در مقداردهی اولیه و جهش ایجاد شد. مدل جامع در مقایسه با آزمایش‌های کنتراست، تناسب بهتری ارائه کرد. تکرارها به سرعت به سمت بهینه شدن نزدیک شدند، اما همگرایی نهایی شامل جهش های والد-فرزند بسیار کندتر بود. مبادله بین هزینه تبدیل و فشردگی قوی‌ترین بود، و درجه تضاد تا حدی به عنوان ویژگی نوظهور اتصال اجتماعی فضایی که در الگوریتم ما تعبیه شده بود، بهبود یافت. مشاهدات تکرار سریع تا نزدیک به بهینه بودن با مدل ما می‌تواند شبیه‌سازی تعاملی را تسهیل کند، که با مدل‌های فعلی امکان‌پذیر نیست، که شامل برنامه‌ریزان کاربری زمین و مدیران منطقه‌ای می‌شود. تکرارها به سرعت به سمت بهینه شدن نزدیک شدند، اما همگرایی نهایی شامل جهش های والد-فرزند بسیار کندتر بود. مبادله بین هزینه تبدیل و فشردگی قوی‌ترین بود، و درجه تضاد تا حدی به عنوان ویژگی نوظهور اتصال اجتماعی فضایی که در الگوریتم ما تعبیه شده بود، بهبود یافت. مشاهدات تکرار سریع تا نزدیک به بهینه بودن با مدل ما می‌تواند شبیه‌سازی تعاملی را تسهیل کند، که با مدل‌های فعلی امکان‌پذیر نیست، که شامل برنامه‌ریزان کاربری زمین و مدیران منطقه‌ای می‌شود. تکرارها به سرعت به سمت بهینه شدن نزدیک شدند، اما همگرایی نهایی شامل جهش های والد-فرزند بسیار کندتر بود. مبادله بین هزینه تبدیل و فشردگی قوی‌ترین بود، و درجه تضاد تا حدی به عنوان ویژگی نوظهور اتصال اجتماعی فضایی که در الگوریتم ما تعبیه شده بود، بهبود یافت. مشاهدات تکرار سریع تا نزدیک به بهینه بودن با مدل ما می‌تواند شبیه‌سازی تعاملی را تسهیل کند، که با مدل‌های فعلی امکان‌پذیر نیست، که شامل برنامه‌ریزان کاربری زمین و مدیران منطقه‌ای می‌شود.

کلمات کلیدی: بهینه سازی کاربری زمین الگوریتم ژنتیک ; فشردگی فضایی

1. مقدمه

رشد جمعیت جهانی و گسترش نامتوازن سریع شهری در قرن بیست و یکم [ 1 ] باعث بسیاری از مسائل اجتماعی – زیست محیطی مانند تخریب جنگل ها، فرسایش خاک، کاهش تنوع زیستی و تغییرات غیرقابل برگشت در برخی از کاربری ها شده است [ 2 ]. علاوه بر این، فشارهای ناشی از رشد جمعیت، تقاضای کاربری زمین برای حمل و نقل، صنایع، ساختمان‌های تجاری و مسکن را افزایش داده است که منجر به تضاد بین کاربری‌های مختلف زمین در مناطق محدود جغرافیایی می‌شود [ 3 ]. برنامه ریزی شهری موثر شامل تخصیص و حل و فصل مناسب کاربری های متضاد زمین است که همچنین باید تقاضا و عرضه منابع زمین منطقه ای را متعادل کند [ 4 ]]. بنابراین، بهینه‌سازی سیستماتیک کاربری زمین شامل ایجاد توازن بین مبادلات تخصیص بین اهداف پیچیده کاربری زمین است که باید با محدودیت‌ها و آرزوهای توسعه منطقه‌ای همسو باشد. ترجیحاً، برنامه‌ریزان را نیز شامل می‌شود که با مدل‌ها تعامل دارند تا تأثیرات عدم قطعیت‌ها و فرمول‌های جایگزین را بررسی کنند. بنابراین، هدف ما از این مطالعه، جزئیات بهبود در روش برنامه‌ریزی کاربری زمین با یک نمایش کاربردی واقعی است که بسیار بهتر از مطالعات قبلی حل شده است.

مدل‌های بهینه‌سازی کاربری زمین مبتنی بر الگوریتم ژنتیک کنونی (GA) عموماً بر متعادل کردن اهداف رقابتی و تغییرات در حال تحول در الگوهای جایگزین بالقوه قابل دوام برای افزایش قابلیت اطمینان بهینه‌سازی متمرکز هستند [ 5 ، 6 ، 7 ]. با این حال، چالش‌های اجرایی عملی در تولید بهینه‌سازی‌های کاربری نهایی که الزامات محدودیت‌ها و اولویت‌های سیاست‌های منطقه‌ای را برآورده می‌کنند، باقی می‌ماند. اول، مقداردهی اولیه سلول‌ها با کاربری تصادفی زمین منجر به تکه‌های بسیار پراکنده، الگوهای کاربری نامناسب و ناکارآمدی محاسباتی در تکرارهای سخت به سمت یک راه‌حل بالقوه زودرس و غیربهینه می‌شود [ 8 ], 9 , 10 , 11 ]. دوم، برخی از اپراتورهای داخلی در GA (به عنوان مثال، متقاطع و جهش) به طور اساسی بر سازگاری کاربری های جایگزین و کارایی مدل تأثیر می گذارند [ 5 ، 12 ، 13 ، 14 ]. بنابراین، ملاحظات بیشتری در مورد منطقی بودن تبدیل کاربری زمین مورد نیاز برای حل و فصل الگوها مورد نیاز است. ثالثا، تعادل بین کاربری های متضاد زمین مستلزم مقیاس بندی و وزن دهی دقیق است تا از مقایسه نامتعادل اهداف رقیب با پروفایل های ارزشی متفاوت جلوگیری شود [ 14 ، 15 ]., 16 , 17 , 18 ]—به عنوان مثال، تفاوت های اقتصادی بین زمین های مسکونی با ارزش بسیار بالا و جنگل های با ارزش نسبتا کم.

بهینه‌سازی کاربری زمین اساساً در مورد دستیابی به مصالحه در همزیستی کاربری زمین است، یک روش زنده، که در یک مفهوم توافق‌شده بهترین تعادل را در آرزوهای جامعه منطقه‌ای برای جامعه، بوم‌شناسی و اقتصاد برقرار می‌کند [ 8 ]. با این حال، تفاوت بین محلات منجر به ترکیبات مختلفی از اهداف متضاد می شود. بنابراین، معاوضه مورد نیاز است، زیرا برآوردن کامل نیازهای همه اهداف در همه جا غیرممکن است. در حال حاضر، اهداف برنامه ریزان عمدتاً به سه دسته رقیب تقسیم می شوند: منافع اقتصادی، منافع محیطی و منافع اجتماعی [ 7 ]. سود اقتصادی عمدتاً با خروجی واحد یا هزینه تبدیل هر کاربری اندازه گیری می شود [ 19 , 20 ]]، به ترتیب با تخصیص تولید ناخالص داخلی (GDP) یا هزینه تبدیل. در مدل های کاربری زمین، عوامل اقتصادی را می توان برای حداکثر ظرفیت مسکن، حداکثر برابری اجتماعی و حداقل مالیات ارزیابی کرد [ 18 ، 21 ، 22 ، 23 ]. در میان عوامل مختلف اکولوژیکی، ارزش خدمات اکوسیستم (ESV)، یعنی ارزش خدمات اکوسیستم و سرمایه طبیعی تخمین زده شده توسط قوانین اقتصادی، به دلیل اهمیت علمی واضح و سهولت محاسبه آن به طور گسترده مورد استفاده قرار می گیرد [ 24 ، 25 ، 26 ].]. علاوه بر این، بهره وری اولیه خالص (NPP)، فرسایش خاک، و کنترل آلودگی را می توان در صورت لزوم برای مطابقت با سیاست های حفاظت از محیط زیست انتخاب کرد [ 27 ، 28 ]. برای اندازه‌گیری منافع اجتماعی، سازگاری یا ناسازگاری کاربری زمین اغلب مورد استفاده قرار می‌گیرد [ 29 ، 30 ، 31 ]، در حالی که فشرده‌بودن و درجه تعارض (بین محل‌های کاربری همسایه) نیز برای اهداف اجتماعی استفاده می‌شود [ 3 ، 32 ، 33 ].

الگوریتم‌های بهینه‌سازی کاربری فعلی به طور کلی سه نوع هستند: بهینه‌سازی خطی، اتوماتای سلولی (CA)، و الگوریتم هوشمند [ 33 ]. بهینه‌سازی خطی، مساحت بهینه فضایی هر کاربری زمین را تخمین می‌زند و نمی‌تواند با ترتیبات فضایی مقابله کند [ 9 ، 34 ]. CA از قوانین تبدیل همسایه فضایی برای گام‌های زمانی در تغییر الگوی کاربری زمین استفاده می‌کند، اما نمی‌توان از آن برای کشف روابط بین عوامل اقتصادی، اکولوژیکی و سایر عوامل استفاده کرد [ 35 ]]. الگوریتم هوشمند کاستی های دو الگوریتم بالا را با حل مسائل سخت چند جمله ای غیر قطعی (NP) غلبه می کند، که طبق تعریف، مسائل تصمیم گیری هستند که به صورت قطعی و گام به گام در زمان حل نمی شوند، اما راه حل های آنها توسط غیر قطعی به دست آمده است. روش‌ها (ماشین تورینگ غیر قطعی)، به راحتی از ارزش تناسب آن قابل بررسی هستند. اگرچه الگوریتم های هوشمند ممکن است در برخی موارد به راه حل های بهینه همگرا نشوند، به دلیل پیچیدگی مسئله، راه حل های نزدیک به بهینه نیز معنادار هستند [ 10 ]. از این رو، این رویکرد اتخاذ شده برای این مطالعه است.

الگوریتم های هوشمند از نوعی دانش تخصصی در تصمیم گیری استفاده می کنند [ 36 ، 37 ] و شامل الگوریتم بازپخت شبیه سازی شده (SA) [ 19 ]، روش بهینه سازی کلونی مورچه ها (ACO) [ 38 ]، بهینه سازی ازدحام ذرات (PSO) [ 39 ]، و GA [ 40 ]. اگرچه SA می تواند از تله های بهینه سازی محلی جلوگیری کند، Aerts و همکاران. (2005) نشان داد که GA برای زمان حل و فشردگی بهتر از SA عمل می کند [ 41]. PSO ترکیبی نیاز به تنظیم نسبت ثابت کاربری زمین به عنوان یک محدودیت قبل از تخصیص فضا دارد، در حالی که این مورد در GA [ 42 ] مورد نیاز نیست. ماهیت ACO اصلاح احتمال انتقال سلول ها از طریق حلقه های بازخورد مثبت است [ 43 ]. با این حال، به دلیل ماهیت متضاد اهداف، مشخص نیست که کدام هدف باید به عنوان بازخورد در طول فرآیند تکاملی مورد استفاده قرار گیرد. این ملاحظات کلی ما را بر آن داشت تا با توجه به قابلیت جستجوی جهانی و استحکام آن، GA را برای مطالعه خود انتخاب کنیم.

بهینه‌سازی جهانی با الگوریتم‌های GA به‌طور مکرر (غیر قطعی) تکامل راه‌حل‌ها را با انتخاب طبیعی ژن‌های با کیفیت بالاتر («تناسب») بهبود می‌بخشد، یعنی راه‌حل‌های فرزندی که به طور مکرر از راه‌حل‌های والد توسط عملیات متوالی انتخاب، متقاطع و جهش [ 3 ، 25 ، 44 ]. تکرار در اینجا به معنای تکرار الگوریتمی غیر قطعی (نه لزوماً مرحله‌ای زمانی) است که در آن می‌توان بررسی کرد که آیا «تناسب» راه‌حل تکرار شده در حال بهبود است یا خیر.

قابلیت اطمینان راه‌حل در اجتناب از تله‌های بهینه نزدیک به بهینه یا محلی، می‌تواند توسط اپراتورهای داخلی بهبود یافته یا با ترکیب با سایر الگوریتم‌ها افزایش یابد. به عنوان مثال، برای افزایش دقت مدل، کائو و همکاران. (2012) یک عملگر جهش سه مرحله ای را بر اساس تنوع مبتنی بر پچ، مبتنی بر مرز و حذف راه حل ها برای ارضای محدودیت ها طراحی کرد [ 10 ]. ما و همکاران (2018) از احتمال تطبیقی و استراتژی نخبه برای جلوگیری از تله‌های بهینه‌سازی محلی استفاده کرد [ 32 ]. هوانگ و همکاران (2014) GA و CA را برای به دست آوردن راه حل بهینه پارتو برای شهرهای در حال گسترش پویا ترکیب کردند [ 18]. اگرچه آن روش‌ها می‌توانند قابلیت اطمینان مدل را بهبود بخشند، ما پیشنهاد می‌کنیم که بهینه‌سازی‌های مناسب‌تر برای اجرای عملی را می‌توان در صورتی به دست آورد که محدودیت اندازه حداقل پچ، یک نیاز رایج برنامه‌ریزی کاربری زمین، در مقداردهی اولیه پیاده‌سازی شود. به عنوان مثال، برخی از بهبودهای اولیه مانند ایجاد راه حل های والد با احتمال تبدیل سلولی [ 25 ] انجام شده است.]. بحث اساسی با بهبودهای اولیه این است که الگوهای اولیه استفاده از زمین به راه‌حل بهینه (نسبت به تخصیص تصادفی) نزدیک‌تر است و بنابراین باید کارایی جستجو و توزیع نهایی کاربری زمین را بهبود بخشد. در مقابل، بذرهای اولیه تصادفی، کاربری‌های زمینی بسیار تکه تکه را تشکیل می‌دهند، که باعث ایجاد مشکلاتی در دستیابی به تجمعات فضایی قابل دوام در تکه‌های رشد جدید می‌شود. علاوه بر این، در متقاطع یا جهش، تغییرات سلولی بیشتر به تعداد سلول های مجاور از همان نوع بستگی دارد، در حالی که عوامل دیگر (مثلاً مزایای اجتماعی و فضایی) به ندرت برای بهبود کارایی در نظر گرفته می شوند.

در حل مشکلات فوق، و در تعقیب یک الگوی کاربری فشرده با سلول‌های کمتر ایزوله و افزایش توانایی تجمع، مدلی به نام «بهینه‌سازی فضایی چندهدفه با شدت استفاده از زمین» (LIr-MSO) ایجاد کردیم که بهبود می‌بخشد. راهبردهای اولیه، جهش و نخبگان در چند هدف. ما دو هدف اقتصادی، یک هدف اکولوژیکی و دو هدف اجتماعی را انتخاب کردیم، در حالی که سیاست‌ها و استانداردهای برنامه‌ریزی دولتی در محدودیت‌های خاص مستتر هستند. مطالعه ما سه مشارکت متمایز ارائه می‌کند: اولی تنظیم استراتژی اولیه برای بهبود قابلیت اطمینان بهینه‌سازی نهایی با محدود کردن حداقل اندازه‌های پچ برای کاربری‌های مختلف زمین است. دوم بهبود استراتژی جهش و نخبگان برای کارآمدتر کردن آن است. در نهایت، در برنامه،

2. مواد و روش ها

2.1. حوزه مطالعه و منبع داده

جامعه داپنگ، واقع در شرق شهر شنژن، به عنوان منطقه مطالعه نمایشی مورد استفاده قرار گرفت. از نظر طول، حدود 14.2 کیلومتر از شمال به جنوب و 18.8 کیلومتر از شرق به غرب است و مساحت کل آن حدود 88.3 کیلومتر مربع ^است . بیش از 45000 نفر در این منطقه زندگی و کار می کنند (تا سال 2018). برای تسهیل محاسبات بهینه سازی، کل منطقه به 1878 × 1418 = 2,663,004 سلول شطرنجی می شود که اندازه هر سلول 10×10 متر است ( شکل 1 ). این تعداد سلول نسبت به مدل‌های گذشته افزایش قابل توجهی دارد و نشان‌دهنده پیشرفت ما به سمت مدل‌های واقعی‌تر از شبیه‌سازی‌های گذشته است. به عنوان مثال، 16779 سلول توسط Cao، Huang، Wang و Lin استفاده شد [ 10] و 1600 سلول در مدل اولیه توسط Stewart، Janssen و Herwijnen [ 32 ] استفاده شد.

به هر سلول یک نوع کاربری منحصر به فرد از طبقات زیر داده می شود (مخفف حروف بزرگ): زمین مسکونی (R)، زمین تجاری (C)، زمین صنعتی (I)، زمین زراعی (Ar)، زمین آبزی پروری (Aq)، زمین جنگلی (F)، زمین دیگر (O)، ساحل (B)، زمین عمومی (P) و آب (W).

داده های اجتماعی و اقتصادی از سیزدهمین برنامه پنج ساله جدید داپنگ و سالنامه آماری 2017 ناحیه داپنگ [ 45 ] استخراج شده است. انواع کاربری زمین (زمین ساختمانی، زمین جنگلی، زمین زراعی، زمین پرورش آبزیان، ساحل و آب) به صورت بصری تفسیر و سپس از تصاویر سنجش از دور دیجیتالی شدند (GF-1، 2017) [ 46 ]، و در نهایت، زمین ساخت و ساز بیشتر شد. با کالیبراسیون با نقاط مورد علاقه از نقشه بایدو [ 47 ] به زمین های تجاری، زمین های صنعتی، زمین های عمومی و زمین های مسکونی تقسیم می شود . سپس داده‌های کاربری زمین به گستره و وضوح فضایی فرمول‌بندی‌شده شطرنجی شدند. داده های مدل دیجیتال ارتفاع (DEM) از SRTM (ماموریت توپوگرافی رادار شاتل) [ 48 ] بریده شدند و به شبکه شطرنجی استفاده از زمین درون یابی شدند.

2.2. مدل برای بهینه سازی کاربری زمین: LIr-MSO

همانطور که بحث شد، عوامل/ارزش‌های تاثیر تناسب برای الگوهای مبادله و تعیین یکی (مناسب‌ترین) که به طور بهینه محدودیت‌ها و الزامات اهداف کاربری زمین را برآورده می‌کند، ضروری هستند. این عوامل عبارتند از بهره وری اقتصادی، حفاظت از محیط زیست، تخصیص فضایی و سیاست های توسعه منطقه ای. با توجه به ویژگی‌های ذاتی چنین عواملی، عوامل اقتصادی، اکولوژیکی و فضایی اغلب به‌عنوان اهدافی در نظر گرفته می‌شوند که باید بهینه شوند، و عوامل اجتماعی به طور ضمنی با محدودیت‌ها و کنار هم قرار دادن مجاز کاربری متناوب زمین در اعمال سیاست‌های دولتی و استانداردهای اجتماعی مرتبط نشان داده می‌شوند.

شکل 2روند گردش کار LIr-MSO را نشان می دهد که شامل مقداردهی اولیه، محاسبه تناسب، تکامل ژنتیکی، و سپس بازخورد به محاسبه تناسب اندام از استراتژی نخبگان است تا زمانی که الگوی استفاده از زمین بهینه شود یا به حداکثر تکرار برسد. اول، الگوهای اولیه با تنظیم حداقل اندازه وصله برای انواع مختلف کاربری زمین به دست می آیند. دوم، تناسب الگو برای اهداف و محدودیت‌های سفارشی‌سازی شده و نامی محاسبه می‌شود. سوم، رولت برای انتخاب نامزدها بر اساس تناسب اندام اتخاذ می شود. سپس، اگر با احتمال متقاطع آنها اجازه داده شود، هر دو الگو از نامزدها برای متقاطع انتخاب می شوند تا یک الگوی جدید ایجاد شود. در مرحله بعد، این الگو با استفاده از یک عملگر جهش فضایی دو مرحله‌ای، مبتنی بر بلوک و نقطه‌ای بهینه‌سازی می‌شود. و با مقایسه تناسب بین الگو و والدینش، برای تعیین اینکه آیا باید به مرحله بعدی برویم یا به حلقه بعدی، قضاوت می شود. در نهایت، استراتژی نخبگان تعیین می کند که آیا تناسب الگوی بهینه در این نسل بهتر از نسل قبلی است یا خیر، و راه حل نهایی پس از تکرارهای سفارشی به دست می آید.

2.2.1. اهداف

از آنجایی که تغییر کاربری زمین به ترتیب شامل تنظیمات ایستا و دینامیکی برای ارزش ذاتی و تبدیلی است، یک شاخص واحد نمی تواند به طور جامع منافع اقتصادی را نشان دهد. بنابراین، ما هر دو هزینه تبدیل (پویا) و تولید ناخالص داخلی (ایستا) را برای نشان دادن منافع اقتصادی انتخاب می کنیم. برای منافع محیطی، ESV به دلیل کاربرد گسترده آن انتخاب شده است. علاوه بر این، هم میزان فشردگی و هم درجه تعارض برای ارزیابی سود اجتماعی به دلیل مزایای آنها در اندازه‌گیری سازگاری اجتماعی کاربری زمین اتخاذ می‌شوند.

هدف 1: به حداقل رساندن هزینه تبدیل

هزینه تبدیل هزینه توسعه مجدد نوع کاربری زمین یک سلول به کاربری زمین دیگر است [ 49 ]. با توجه به ادبیات و دانش تخصصی، یک ماتریس از ضرایب انتقال برای نشان دادن هزینه تبدیل در واحد سطح بین تمام تبدیل‌های ممکن کاربری زمین استفاده می‌شود [ 20 ، 28 ، 50 ]. مجموع حاصلضرب ضریب انتقال و مساحت تغییر یافته نشان دهنده کل هزینه تبدیل برای یک الگوی کاربری زمین موجود است. ضریب انتقال از 0 تا 1 متغیر است. فرمول هدف 1 (

O 1)

به شرح زیر است:

حداقل O 1 = \sum ک s = 1 \sum ک t = 1 ب s t T A s t .

(1)

B _st نشان دهنده ضریب انتقال از نوع کاربری موجود s به نوع t است . TA _st نشان‌دهنده منطقه انتقال از نوع کاربری s به نوع t است . $K$ تعداد انواع کاربری زمین است.

هدف 2: حداکثر سازی تولید ناخالص داخلی

تولید ناخالص داخلی با توجه به سطح توسعه اقتصادی منطقه ای متفاوت است و ارزش واقعی آن شامل اجزای منطقه ای، اجتماعی و زیست محیطی است که در بین کاربری های مختلف زمین تقسیم شده است. در این مقاله ارزش واحد تولید ناخالص داخلی برای هر کاربری با استفاده از آمار مساحت کاربری و تولید ناخالص داخلی محاسبه شده است. کل تولید ناخالص داخلی برای یک الگوی کاربری معین با جمع کردن حاصلضرب ارزش واحد تولید ناخالص داخلی و مساحت کاربری مربوطه به دست آمد. فرمول هدف 2 (

O 2)

به شرح زیر است:

حداکثر O 2 = \sum ک k = 1 U ک آ ک .

(2)

U _k مقدار واحد تولید ناخالص داخلی برای نوع کاربری زمین k است . A _k مساحت کل تغییر کاربری زمین نوع k است . $K$ تعداد انواع کاربری زمین است.

هدف 3: به حداکثر رساندن ESV

ESV به طور کلی به عنوان ارزش خدمات ارائه شده توسط اکوسیستم ها و فرآیندهای اکولوژیکی مورد استفاده توسط انسان تفسیر می شود [ 51 ]. منافع زیست محیطی برای هدف 3 (

O 3)

به شرح زیر تخمین زده می شود (کوستانزا و همکاران، 1997) [ 26 ]:

حداکثر O 3 = \sum ک k = 1 آ ک V ک .

(3)

V _k نشان دهنده ESV نوع کاربری زمین k در واحد سطح است. A _k کل مساحت تغییر یافته کاربری زمین نوع k را نشان می دهد . $K$ تعداد انواع کاربری زمین است.

هدف 4: به حداکثر رساندن فشردگی

یک الگوی معقول معمولاً هر سلول کاربری زمین را در همراهی منسجم با کاربری های مشابه و مکمل برای دستیابی به اهداف استفاده اجتماعی ترتیب می دهد. متراکم بودن کاربری زمین به عنوان یک عامل کلیدی در نظر گرفته می شود که راحتی زندگی و بهره وری استفاده از زمین را افزایش می دهد. روش‌های اندازه‌گیری فشردگی شامل خوشه‌بندی مبتنی بر مجاورت، فشردگی مبتنی بر ناحیه محیطی، و تجمع بلوکی [ 10 ، 19 ، 29 است.]. پس از بررسی این رویکردها، ما فشردگی مبتنی بر ناحیه محیطی را به دلیل سادگی در کاربرد آن انتخاب کردیم. در این روش، فشردگی با محیط تقسیم بر جذر مساحت تعریف می شود. مقادیر بالاتر نشان‌دهنده تجمع فشرده کمتر از همان نوع کاربری زمین و بالعکس برای مقادیر کمتر است. فرمول هدف 4 (

O 4)

به شرح زیر است:

حداقل O 4 = \sum ک k = 1 \sum اچ ک h = 1 پ h k آ h k \sqrt اچ ک .

(4)

P _hk محیط h- امین پچ در نوع کاربری زمین k است . _hk مساحت h- امین پچ در نوع کاربری زمین k است . H _k تعداد تکه‌های کاربری زمین k است. $K$ تعداد انواع کاربری زمین است.

هدف 5: به حداقل رساندن درجه تعارض

برای بهبود مناسب بودن محیط زندگی، ناسازگاری بین انواع کاربری های مختلف زمین باید به حداقل برسد. ناسازگاری اغلب ناشی از درگیری های ناشی از سر و صدای شهری، آلودگی، تراکم کاربری زمین و عوامل دیگر است. بنابراین، اندازه گیری کمی تعارض ضروری است. ما از درجه نامناسب بودن بین دو نوع کاربری مجاور به عنوان معیار درجه تضاد (که در مقیاس 0 تا 8 اندازه‌گیری می‌شود) استفاده می‌کنیم، که برای اطمینان از هماهنگی بین کاربری‌ها باید کم باشد. فرمول هدف

O 5

با استفاده از هشت همسایه (j)، در اطراف هر سلول مرکزی (i)، همانطور که در زیر نشان داده شده است ( شکل 3 ) محاسبه می شود.

سپس فرمول هدف 5 ( O5 ) به صورت زیر محاسبه می شود:

حداقل O 5 = \sum ن i = 1 \sum 8 j = 1 \sum ک k = 1 \sum ک l = 1 ایکس من ک ایکس j l سی k l .

(5)

X _ik یک متغیر باینری است. X _ik = 1 هنگامی که سلول i به نوع کاربری زمین تبدیل می شود _، در غیر این صورت X ik = 0. C _kl درجه تضاد بین دو سلول مجاور با کاربری زمین نوع k و l در منطقه تغییر یافته است. $K$ تعداد انواع کاربری زمین است.

2.2.2. محدودیت ها

محدودیت‌های خاصی که با سیاست‌های برنامه‌ریزی فعلی و استانداردهای کاربری زمین همخوانی دارند به شرح زیر است:

1. یک نوع کاربری منحصر به فرد به هر سلول اختصاص داده شده است تا انسجام خود را حفظ کند و از درگیری جلوگیری کند. این به طور ضمنی در الگوریتم جهش اصلاح شده است.

2. محدوده بالا و پایین هر کاربری برای مطابقت با معیارهای برنامه‌ریزی و سیاست‌های دولت محدود می‌شود و در نتیجه پراکندگی زیاد را به حداقل می‌رساند.

3. تغییر کاربری زمین در خط قرمز اکولوژیکی که توسط دولت محلی مشخص شده است، برای بهبود زندگی پایدار حذف می شود.

4. زمین با شیب های تندتر از 25 درجه فقط می تواند به عنوان زمین جنگلی برای جلوگیری از اثرات زیست محیطی مانند فرسایش استفاده شود.

2.2.3. رویه های مدل LIr-MSO

برای بهبود کارایی مدل، برخی پیشرفت‌ها در این روش انجام شده است که شامل شش مرحله است: مقداردهی اولیه، محاسبه تناسب، انتخاب، متقاطع، جهش و استراتژی نخبگان. مسئله بهینه سازی فضایی چند هدفه را می توان به صورت زیر تعریف کرد:

حداکثر \sum O i, i \in [1, 5]

(6)

که در آن حداقل اهداف ( i = 1 تا 5) پس از عادی سازی به حداکثر اهداف تبدیل می شوند.

مرحله 1: مقداردهی اولیه

در طول مقداردهی اولیه، تکه‌هایی در ناحیه قابل تغییر به‌طور تصادفی ایجاد می‌شوند تا راه‌حل‌های N برای تشکیل یک جمعیت اولیه به دست آید. هر جایگزین کاربری زمین به عنوان مشابه کروموزوم در نظر گرفته می‌شود که در آن ژن‌ها با سلول‌های شبکه‌ای مطابقت دارند، که مقدار آن نشان‌دهنده نوع خاصی از کاربری زمین است. بنابراین، تعامل ژنتیکی بین کروموزوم‌های مختلف می‌تواند منجر به الگوهای مختلف کاربری زمین و نتایج بهینه‌سازی شود. مقداردهی اولیه که معمولاً مورد استفاده قرار می گیرد، سلول های تغییر یافته را در یک الگوی تصادفی متشکل از بسیاری از سلول های جدا شده توزیع می کند. این تقسیم‌بندی بر کارایی الگوریتم تأثیر می‌گذارد، زیرا آزمایش‌های انباشتگی زیادی در کل منطقه ضروری است، که منجر به تکرارهای زیادی می‌شود که پیشرفت به سوی راه‌حل نهایی را کند می‌کند [ 21 ].].

همانطور که توسط Maitland [ 52 ] در نظریه ساختار شهری حداقل پیشنهاد شده است، بسامد گره هایی که با اشکال شهری آشکار نمایش داده می شوند (به عنوان مثال، چهارراه) ساختار اتمی اساسی یک شهر را تشکیل می دهد. Maitland [ 52 ] پیشنهاد کرد که 200 متر (4 هکتار در منطقه برای یک بلوک 200 × 200 متر) می تواند به عنوان ساختار واحد حداقل یک شهر برای هدایت توسعه و ساخت و ساز بزرگتر استفاده شود. بنابراین، برای به دست آوردن یک الگوی کاربری معرف و عملی، گسترش کاربری زمین باید با یک واحد حداقل کاربری زمین به عنوان یک بلوک ساختمانی اتمی (با اندازه‌های اتم/بلوک مختلف برای کاربری‌های مختلف) برای ژنتیک بزرگ‌تر آغاز شود. سازه های کاربری زمین

با هدایت نظریه مقیاس بلوک حداقلی Maitland [ 52 ] و استانداردهای برنامه ریزی شهری در چین، حداقل مساحت زمین مسکونی 2 هکتار (شامل 200 سلول، هر 100 متر مربع)، و برای زمین های تجاری، زمین های صنعتی، تعیین ^شده است. و زمین عمومی، حداقل مساحت به ترتیب 0.5 هکتار (50 سلول) است. همانطور که در آزمایش‌های زیر نشان داده شد، چنین شروعی به جلوگیری از تکه تکه شدن و پدیده تکه‌های بزرگ که تکه‌های کوچک را در عملگرهای زیر می‌پوشانند (به عنوان مثال، متقاطع و جهش) کمک می‌کند که به موجب آن برخی از تکه‌های تولید شده اولیه ممکن است در راه‌حل نهایی ادغام شوند، و همچنین برخی از آنها جدا شوند. سلول هایی با اندازه غیرعملی ممکن است هنوز وجود داشته باشند.

ما الگوهای اولیه را بسته به احتمال تبدیل هر کاربری زمین ایجاد کردیم، فرمول به شرح زیر است:

سی آر ک = \sum ک t = 1 سی پ t k آ t k .

(7)

CP _tk احتمال تبدیل از نوع کاربری زمین t به کاربری زمین نوع k است . a _tk کل مساحت تغییر یافته از نوع کاربری زمین به نوع k است .

K

تعداد انواع کاربری زمین است.

مرحله 2: محاسبه تناسب اندام

در حال حاضر دو روش به طور گسترده مورد استفاده قرار گرفته است: یکی روش مبتنی بر پارتو و دیگری روش وزنی. اولی مجموعه راه حل های بهینه را بدون به خطر انداختن اهداف مختلف حل می کند. از این رو اولویت نسبی اهداف تعیین کننده بهینه بودن نیست. دومی وزن‌های نسبی را تعیین می‌کند، که به صورت اکتشافی تعیین می‌شوند، که هر هدف را اولویت‌بندی می‌کند، به طوری که مجموع وزنی اهداف نشان‌دهنده یک معیار تناسب واحد است که می‌تواند به عنوان شاخص بهینه بودن استفاده شود. ما مورد دوم را برای محاسبه تناسب اندام اتخاذ کردیم، زیرا به برنامه ریزان و مدیران اجازه می دهد اولویت های خود را از طریق انتخاب وزنه های مناسب تنظیم کنند. برای محاسبه تفاوت‌های بزرگی اهداف، هر کدام را در محدوده‌ای از 0 تا 1 نرمال‌سازی کردیم. با توجه به ویژگی‌های ذاتی اهداف، سه استراتژی عادی‌سازی را اتخاذ کردیم:

ز (V) = V - V m i n V m a x - V m i n .

(8)

اهداف 1 (هزینه تبدیل) و 5 (درجه تضاد) باید به حداقل برسد بنابراین نامگذاری آنها به شرح زیر است:

ز (V) = V حداکثر - V V m a x - V m i n .

(9)

V تناسب هدف خام است.

V_{\max}, V_{\min}

حداکثر و حداقل تناسب مربوطه برای آن هدف هستند.

برای هدف 4 (فشردگی)، فرمول نرمال سازی اجازه می دهد تا فشردگی دارای حداقل مقدار ثابت باشد (برای یک بلوک مربع = 4 * R/

\sqrt{R^{2}}

= 4، که در آن R طول بلوک است):

ن (X) = ایکس m i n ایکس .

(10)

X تناسب هدف خام است. $X_{\min}$ حداقل تناسب اندام اسمی 4 برای یک مربع است.

سپس تناسب وزنی به صورت زیر بدست می آید:

f i t (x) = w 1 Z (O 1) + w 2 ز (O 2) + w 3 ز (O 3) + w 5 Z (O 4) + w 4 ن (O 5)

(11)

که در آن fit ( x ) نشان دهنده تناسب کروموزوم x ام است. w _i نشان دهنده وزن هدف i است. مجموع اوزان 1 است.

مرحله 3: انتخاب

ما در عملیات انتخاب از رولت استفاده می کنیم تا احتمال انتخاب هر کروموزوم با تناسب آن نسبت مستقیم داشته باشد. هر چه تناسب کروموزوم بیشتر باشد، احتمال انتخاب آن در نسل بعدی بیشتر است. فرمول احتمال سلول i (سلول های 1 تا N) به شرح زیر است:

پ (x من) = f i t (x من) / (\sum ن i = 1 f i t (x من)) .

(12)

الگوریتم زیر جزئیات انتخاب رولت x _i را شرح می دهد :

R = رند ()

(13)

s = {10 R < P (x من) R > P (x من) .

(14)

R یک عدد تصادفی بین 0 و 1 است. اگر امتیاز ( های ) انتخاب برابر با 1 باشد، x _i برای شرکت در مرحله بعدی پذیرفته می شود. در غیر این صورت، برای تعیین s وارد انتخاب بعدی می شود . که در آن احتمال دیگر این است که انتخاب نشود ( s = 0).

مرحله 4: متقاطع

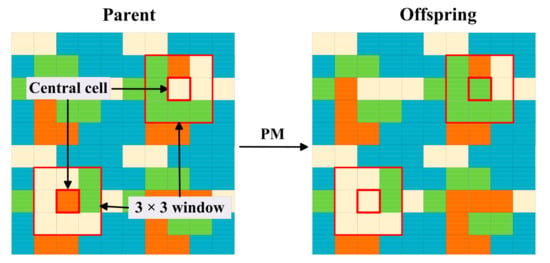
هدف متقاطع کاهش پراکندگی الگوهای کاربری زمین است [ 25 ]. روش متقاطع [ 7 ، 33 ] به شرح زیر است: پس از محاسبه احتمالات متقاطع والدین، والد 1 (والد اصلی) به همراه والد 2 (والدین فرعی) انتخاب می شود. بخشی از سلول های والدین به طور تصادفی بر اساس احتمالات متقاطع آنها (که به عنوان فراوانی وقوع تعیین می شود) انتخاب می شوند. به عنوان مثال، در شکل 4 ، فرض کنید دو سلول، یکی از والد 1 و دیگری از والدین 2، انواع کاربری متفاوتی دارند ( a و bبه ترتیب) در همان موقعیت؛ یک پنجره 3*3 در اطراف سلول انتخاب شده برای شمارش جداگانه تعداد سلول های والد 1 که متعلق به a و b هستند استفاده می شود. سلول انتخاب شده در والد 1 ( a ) با b جایگزین می شود اگر تعداد جدید سلول های b پس از جایگزینی بیشتر از a باشد.

مرحله 5: جهش

جهش با ایجاد تغییراتی در ژن‌های کروموزوم، تنوع محلول را افزایش می‌دهد. برای جلوگیری از تله‌های بهینه محلی و ارتقای فشردگی کاربری زمین، از عملگر جهش فضایی دو مرحله‌ای استفاده می‌کنیم:

(1) جهش مبتنی بر بلوک (BM) فشردگی را به شرح زیر ترویج می کند: پس از سفارشی کردن احتمال BM و انتخاب یک والد، بخشی از سلول های والد به طور تصادفی با توجه به احتمال BM انتخاب می شود. سپس، یک پنجره 3*3 در اطراف سلول انتخاب شده برای شمارش تعداد سلول های هر نوع کاربری استفاده می شود. در مرحله بعد، هزینه تبدیل از یک نوع کاربری به نوع دیگر با توجه به ضریب انتقال محاسبه می شود. در نهایت سلول‌های داخل پنجره با نوعی جایگزین می‌شوند که کمترین هزینه تبدیل را داشته باشد.

(2) جهش مبتنی بر نقطه (PM) پس از BM برای کاهش پراکندگی جغرافیایی انجام می شود ( شکل 5 ). روش اصلی به شرح زیر است: پس از سفارشی سازی احتمال PM و انتخاب والد، بخشی از سلول های والد به طور تصادفی با توجه به احتمال PM انتخاب می شود. فرض کنید نوع کاربری سلول انتخاب شده a است ، یک پنجره 3*3 در اطراف سلول انتخاب شده برای تغییر سلول استفاده می شود اگر تعداد سلول ها از انواع دیگر کمتر باشد. به عنوان مثال، اگر نوع b بیشتر باشد، سلول انتخاب شده با b جایگزین می شود. یک راه جایگزین برای فکر کردن به این جهش، فیلتر میانی است که در آن سلول مرکزی با اغلب موارد درون پنجره جایگزین می‌شود. از این طریق، عملیات جهش به عنوان یک فیلتر صاف کننده فضایی عمل می کند.

مرحله 6: استراتژی نخبگان

استراتژی نخبگان، یا “بقای شایسته ترین ها” اغلب برای ارتقای همگرایی با حفظ شایسته ترین افراد در هر نسل اتخاذ می شود [ 52 ]. با این حال، تکرار در استراتژی نخبگان می تواند به آرامی به سمت تناسب اندام کمتر از حد مطلوب در میان یک مجموعه نوجوان (پیش بالغ) از والدین همگرا شود. به منظور اجتناب از این تله محلی و ترویج همگرایی جهانی به سمت بلوغ و بهینه، یک حالت جایگزین اتخاذ شده است ( شکل 6 ). در این حالت، بهترین الگو به عنوان یک منبع اضافی برای استفاده زمانی که تناسب نسل فعلی کمتر از نسل قبلی باشد، حفظ می‌شود. فرض کنید A ( n ) جمعیت والد است، A ( n + 1) یک جمعیت جدید تولید شده است و n تعداد تکرار است. در حالت جایگزینی، ما سه مورد را مورد بحث قرار می دهیم: بهترین تناسب اندام در A ( n ) بالاتر از A ( n + 1)، بهترین تناسب اندام در A ( n ) برابر با A ( n + 1) و بهترین تناسب اندام است. در A ( n ) کمتر از A است( n + 1). متقاطع تنها در صورتی پذیرفته می شود که حداکثر تناسب در A ( n + 1) از A ( n ) بیشتر نباشد، بنابراین اطمینان حاصل می شود که تناسب اندام افزایش می یابد.

مرحله 7: الگوریتم را خاتمه دهید

ما اطمینان حاصل می کنیم که تعداد کروموزوم های تولید شده با تعداد اولیه در کل فرآیند مطابقت دارد. الگوریتم تا زمانی که تکرارهای N -time (500 در مطالعه موردی) به پایان برسد یا برازش به همگرایی برسد (برازش در بسیاری از تکرارها تغییر نمی کند) به نتیجه مطلوب دست نخواهد یافت.

3. نتایج

3.1. کمیت و محدودیت های هدف

پارامترهای اساسی برای اهداف از چندین مقاله، گزارش های منتشر شده و دانش تخصصی تعیین شده است که در جداول زیر آورده شده است.

جدول 1 : ضرایب انتقال بین دو نوع کاربری از مطالعات منتشر شده [ 20 ، 28 ، 50 ] گردآوری شده و در جدول 1 ارائه شده است که در آن ردیف ها کاربری اراضی منتقل شده، در حالی که ستون ها کاربری زمین منبع هستند. بدنه های آبی، سواحل، و زمین های آبزی پروری مناطق غیرقابل تغییر هستند. بنابراین، ضرایب انتقال آنها 0 است.

در جدول 2 ، واحد تولید ناخالص داخلی کاربری های مختلف زمین بر اساس تفسیر سنجش از دور و آمارهای اقتصادی منطقه ای تعیین شد. جدول 2 همچنین ESV را برای هر کاربری که از کاربری فعلی زمین در چین تعیین شده است، فهرست می کند [ 51 ]. تولید ناخالص داخلی زمین مسکونی به عنوان حداکثر برای نامگذاری استفاده می شود، در حالی که برای ESV، ارزش جنگل استفاده می شود زیرا آب قابل تغییر نیست، علیرغم اینکه ESV آن بالاتر است.

در جدول 3 ، درجه تضاد برای هر دو کاربری از ادبیات حاضر و دانش تخصصی خلاصه شده است [ 28 ، 30 ]. علاوه بر این، محدودیت های مساحت برای هر کاربری در جدول 4 نشان داده شده است.

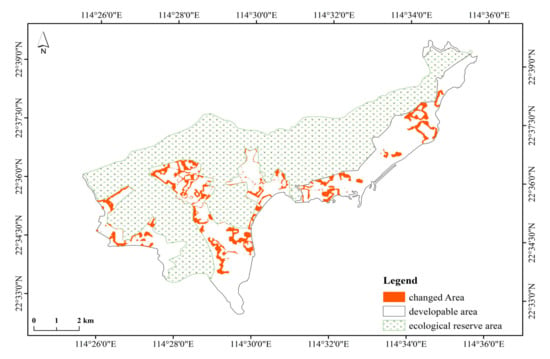
منطقه غیرقابل تغییر در شکل 7 الف نشان داده شده است، شامل روستاهای حفاظت شده (به عنوان مثال، شهر باستانی داپنگ) و مناطق حفاظت شده زیست محیطی. شکل 7 ب یک نقشه شیب-محدودیت را نشان می دهد که زمین های ساخت و ساز بالقوه را که شیب کمتر از 25 درجه است، مشخص می کند.

3.2. اجرا و ارزیابی

هر هدف به طور منحصر به فرد بر مزایای مربوطه تأثیر می گذارد و تعیین اینکه کدام هدف مهم ترین است دشوار است. در عمل، دانش تخصصی از معاوضه‌های وزن‌دهی ضروری است، که احتمالاً در ارتباط با آزمایش سناریو است. از آنجایی که این هدف اصلی این مطالعه نیست، برای اهداف نمایشی فرض می کنیم که توسعه منطقه ای متعادل است به طوری که هر هدف دارای وزن برابر باشد. بنابراین، وزن آنها همه 0.2 تنظیم شده است [ 8 ، 24 ، 36 ]. علاوه بر این، احتمال جهش متقاطع، جهش مبتنی بر BM و جهش مبتنی بر PM به ترتیب 0.06، 0.05 و 0.3 است که از مطالعات گذشته تعیین شده است [ 18 ، 25 ، 31 ]. در مجموع 100 کروموزوم در ابتدا تنظیم می شود و حداکثر 500 تکرار (به دست آمده از آزمایش اولیه) انجام می شود.

^{یکی از دشواری‌های نام‌گذاری مربوط به ارزش‌گذاری‌های تولید ناخالص داخلی است که بیش از هفت} مرتبه بزرگی (≈107 ) بین بالاترین ارزش و کمترین مقدار (به ترتیب 30467 برای مسکونی تا 0.001 برای جنگل) متفاوت است. در آزمایش‌های اولیه، اسمی‌سازی معادله (8) را آزمایش کردیم و متوجه شدیم که ارزش تناسب تولید ناخالص داخلی اسمی الگوی بهینه در مقایسه با فشردگی بیش از 0.9، خیلی بیشتر از 0.08 نیست، که منجر به ایفای نقش بسیار ناچیزی GDP می‌شود. در سهم کلی تناسب اندام با چنین اختلاف زیادی در مقادیر تولید ناخالص داخلی، ما برای بالا بردن ارزش اسمی تولید ناخالص داخلی (به بیش از 0.8) به گرفتن log ₁₀ از صورت و مخرج معادله (8) متوسل شدیم.

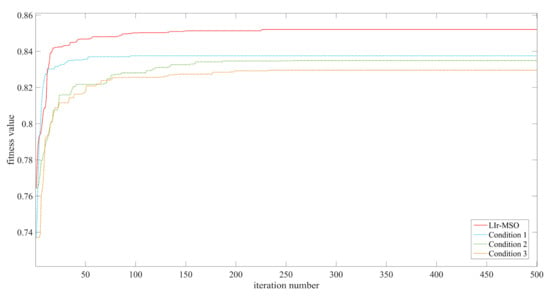
قبل از دستیابی به راه حل نهایی، مقدار مجموع اهدافی که به تناسب اندام کمک می کنند افزایش می یابد تا زمانی که برازش به یک همگرایی برسد (یا به حداکثر تکرار تعیین شده برسد). تغییر تناسب با تکرارها ( شکل 8) مرحله اولیه افزایش سریع تناسب اندام را تا حدود 21 تکرار نشان می دهد و سپس یک مرحله بسیار کندتر از افزایش تدریجی تناسب اندام را نشان می دهد، از جمله مراحل تقریباً ایستا که در آن تناسب اندام از طریق تکرارهای متوالی نسبتاً پایدار می ماند. دوره‌های کوتاه‌تر این فازهای ساکن در فاز سریع نیز قابل‌توجه است، بنابراین یک جنبه منحصر به فرد از فاز تغییر کند نیست. دلیل فاز استاتیک این است که در این مدل، اگر مقدار در نسل والد بیشتر از نسل باشد، الگوی بهینه در نسل والد حفظ می‌شود. منحنی پس از 226 تکرار پایدار به نظر می رسد – بیش از 10 برابر تعداد تکرارهای مورد نیاز برای اولین مرحله سریع.

حداکثر تناسب اندام پس از 226 تکرار حدود 0.8520 است، در حالی که تناسب اندام در پایان فاز سریع پس از افزایش از 0.7645 در 21 تکرار، 0.8422 است. بنابراین، تغییر تناسب اندام در فاز سریع، نسبت به محدوده شروع تا پایان، حدود هشت برابر بیشتر از فاز آهسته است. علاوه بر این، نرخ تغییر (تغییر نسبی در هر تکرار) در طول فاز سریع حدود 77 برابر بیشتر است، که نشان‌دهنده آن است که مدل LIr-MSO در دستیابی به تناسب اندام تقریباً بهینه در مدت زمان نسبتاً کوتاه بسیار کارآمد است. از تکرارها در مقایسه با تکرارهای بسیار طولانی‌تر گزارش‌شده در مطالعات دیگر (مانند کائو، هوانگ، وانگ و لین [ 10 ]) برای مدل‌های بسیار کوچک‌تر.

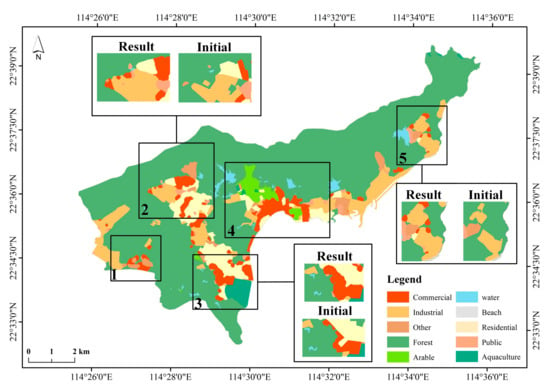
پنج منطقه نماینده برای توصیف تفاوت بین الگوهای اولیه و بهینه انتخاب شده اند ( شکل 9 ). در مقایسه با الگوی اولیه ( جدول 5 ، شکل 9 و شکل 10بهترین راه حل، زمین های تجاری، صنعتی، عمومی و مسکونی بیشتر است، در حالی که زمین های جنگلی، زراعی و دیگر زمین ها کاهش می یابد. دلایل اصلی این تغییر نیازهای توسعه ای اقتصاد است. این نشان می دهد که هنوز پتانسیل برای توسعه بیشتر در منطقه مورد مطالعه در عین حفاظت از محیط زیست محیطی وجود دارد. در الگوی بهینه، زمین های مسکونی 7.81 درصد افزایش یافت، عمدتاً در مناطق 2 و 3. افزایش مناطق مسکونی در نزدیکی لکه های موجود، تراکم را افزایش داد. زمین های تجاری 107.07% افزایش یافته است، برخی از تکه ها در منطقه 2 ادغام شدند، و برخی از تکه های تازه ایجاد شده در منطقه 1 و منطقه 5 ظاهر می شوند. برخی افزایش زمین های تجاری در امتداد ساحل نشان دهنده افزایش استفاده موثر از منابع ساحلی برای تولید ناخالص داخلی منطقه است. بیشتر زمین های جنگلی کاهش یافته برای توسعه بیشتر به تجاری تبدیل شد. زمین صنعتی و مسکونی علاوه بر این، در هر دو الگوی اولیه و بهینه، زمین‌های صنعتی واقع در سواحل غربی و شرقی همواره توسط زمین‌های جنگلی احاطه شده‌اند که می‌تواند تأثیر آلودگی صنعتی بر سکونتگاه‌های انسانی را به طور موثر کاهش دهد. علاوه بر این، کاربری اراضی صنعتی 24.39 درصد به طور عمده در منطقه 2 و منطقه 5 افزایش یافته است و چندین تکه تجاری و مسکونی تکمیلی در منطقه صنعتی ظاهر می شود که می تواند فضای زندگی کارگران را برای بهبود کیفیت زندگی آنها فراهم کند.

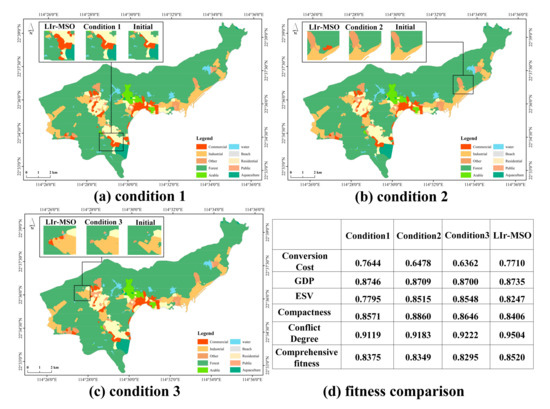
به منظور نشان دادن قابلیت اطمینان مدل، سه آزمایش کنتراست انجام شد: (1) بدون تجدید نظر اولیه، یعنی تکه‌های تولید شده بدون محدودیت منطقه (شرط 1). (2) بدون تجدید نظر جهش (شرط 2)، یعنی تمام هشت همسایه در اطراف سلول مرکزی به نوع کاربری زمین سلول مرکزی تبدیل شده اند. (3) بدون بازنگری اولیه و جهش (شرط 3).

در شرایط 1 ( شکل 11 الف)، اگرچه مدل کامل تناسب اندام را 1.74% افزایش داده است، اگر هیچ محدودیتی در منطقه اتخاذ نشود، کاربری زمین عمدتاً از طریق گسترش وصله، انقباض و ادغام تغییر خواهد کرد. بنابراین، وصله های جدید ایجاد نخواهد شد. علاوه بر این، این منجر به تکه‌های گسترش‌یافته با ظاهر گردتر می‌شود که به احتمال زیاد به دلیل هدف فشردگی است، همانطور که در الگوی بهینه جامع نیز مشهود است. در حالی که از منظر فشردگی بهینه است، در عمل، گرد کردن مرزهای مستقیم مرتبط با حمل و نقل ممکن است در شرایط خاص غیر قابل قبول باشد.

الگوی شرط 2 ( شکل 11 ب) نشان می دهد که اپراتور جهش پیشنهادی، تکه های جدا شده را بهتر کنترل می کند زیرا در این شبیه سازی، قطعاتی وجود دارد و شبیه سازی تناسب اندام جامع 2.05٪ بهتر است.

در شرایط 3 ( شکل 11 ج)، تناسب مدل کامل با بیشترین حاشیه 2.71 درصد بهتر است. این الگو بسیار شبیه به الگوی شرط 1 است، اما کاربری زمین در شرایط 3 کمتر تغییر کرده است و روند گسترش کمتر از شرایط 1 است – که نشان می دهد این الگو احتمالاً در معرض استفاده ناکارآمد از زمین است، همانطور که از کمترین امتیاز برای هزینه تبدیل برای این شبیه سازی.

نتایج آزمایش نشان می‌دهد که مدل ما به تصمیم‌گیرندگان و مدیران، کاربری‌های فضایی دلپذیر، کارآمد و کمتر متضاد در یک محیط توسعه منطقه‌ای را ارائه می‌دهد، و اینکه اصلاح جهش پیشنهادی به طور قابل‌توجهی تناسب اندام کلی را افزایش می‌دهد در حالی که به حداقل الزامات اندازه پچ نیز پایبند است. علاوه بر این، نزدیک به بهینه بودن نسبتاً سریع حاصل می شود.

4. بحث

در دهه‌های گذشته، پیشرفت قابل‌توجهی در بهینه‌سازی چند هدفه با استفاده از الگوریتم‌های ژنتیک برای بهینه‌سازی کاربری زمین صورت گرفته است. با این حال، اکثر مطالعات الگوهای اولیه تصادفی غیرعملی را بدون محدودیت حداقل اندازه وصله ایجاد کردند، که منجر به استفاده از محاسبات قابل‌توجه به سمت توسعه آهسته وصله‌های بزرگ که وصله‌های کوچک را در بر می‌گرفتند. علاوه بر این، عوامل اجتماعی و فضایی تنها در اهداف به جای الگوریتم اجرا شده در نظر گرفته شد، که منجر به تفاوت بین راه حل بهینه و برنامه ریزی واقعی کاربری زمین شد. علاوه بر این، تله های بهینه محلی ممکن است به دلیل فرآیند داخلی ناکافی در GA ظاهر شوند که باعث همگرایی زودرس به راه حل های غیر بهینه می شود.

برای حل این مشکلات، مدل LIr-MSO را توسعه دادیم که راه‌اندازی اولیه پچ‌ها، جهش و استراتژی نخبگان را بهبود می‌بخشد. ابتدا، محدودیت‌های اندازه وصله برای کاربری‌های مختلف زمین در مقداردهی اولیه برای به دست آوردن تجمع‌های فضایی عملی اعمال شد. دوم، تخصیص فضایی با روابط اجتماعی ضمنی از طریق یک عملگر جهش دو مرحله‌ای برای محدود کردن تکه تکه شدن و تبدیل سلولی تقویت شد. در نهایت، نارسی از طریق استراتژی نخبگان اصلاح شده به حداقل رسید.

جامعه Dapeng به عنوان منطقه مورد مطالعه برای نشان دادن توانایی مدل برای ارائه پشتیبانی قابل اعتماد برای برنامه ریزی کاربری زمین و توسعه پایدار مورد استفاده قرار گرفت. مدل از هزینه تبدیل، تولید ناخالص داخلی، ESV، فشردگی و درجه تضاد به عنوان اهداف استفاده کرد. با توجه به مقیاس حداقل بلوک و استانداردهای مربوطه برنامه‌ریزی شهری در چین، حداقل مساحت تولیدی زمین مسکونی، تجاری، صنعتی و عمومی را به ترتیب 2، 0.5، 0.5 و 0.5 هکتار تعیین کردیم. یک عملگر جهش دو مرحله‌ای استفاده شد که شامل جهش مبتنی بر بلوک و جهش مبتنی بر نقطه بود: جهش مبتنی بر بلوک از ضرایب انتقال برای تعیین تغییر نوع کاربری زمین با کمترین هزینه تبدیل برای سلول‌ها در یک پنجره 3×3 استفاده کرد. ، در حالی که جهش مبتنی بر نقطه با ارزیابی اینکه آیا نوع کاربری زمین سلول مرکزی کمترین تعداد را در یک پنجره 3*3 دارد یا خیر، سلول های جدا شده را از بین برد. علاوه بر این، استراتژی نخبگان با تقسیم حالت جایگزینی به سه شرط بهبود یافت.

از آنجایی که الگوی بهینه استفاده از زمین یک مبادله برای همه اهداف است، ما دریافتیم که جامعه داپنگ هنوز پتانسیل زیادی برای توسعه دارد. در الگوی بهینه، اراضی مسکونی، تجاری و صنعتی به ترتیب 81/7 درصد، 07/107 درصد و 39/24 درصد افزایش یافت. زمین مسکونی فضای جدیدی در اطراف منطقه اصلی ایجاد کرد. اراضی تجاری از طریق خوشه بندی و ادغام بیش از دو برابر شد. زمین های قابل کشت تقریباً بدون تغییر باقی ماند. و برخی از زمین های تجاری و مسکونی در پاسخ به ضرایب انتقال کاربری جایگزین مطلوب در اطراف زمین های صنعتی ظاهر شدند.

برای نشان دادن اولویت مدل، آزمایش‌هایی بدون عملگرهای بهبودیافته با سه آزمایش انجام شد: بدون مقداردهی اولیه یا جهش یا بدون هر دو. برازش جامع مدل LIr-MSO به ترتیب 1.74٪، 2.05٪ و 2.71٪ بیشتر از هر شرایط بود. آزمایش‌های بدون جهش بهبودیافته، استفاده از زمین ناکارآمد با هزینه تبدیل بهینه کمتر داشتند. این مقایسه نشان می‌دهد که LIr-MSO می‌تواند تحت اهداف و محدودیت‌های مفروض، به الگوی استفاده از زمین واقعی‌تر دست یابد. با این حال، پیامدهای برنامه‌ریزی کاربری اراضی هدف تراکم مستقل از اندازه وصله و در گرد کردن تکه‌ها (به دلیل گرد کردن و کاهش فشردگی) نیاز به بررسی بیشتر دارد، به‌ویژه در شرایطی که شبکه‌های حمل‌ونقل موجود را نمی‌توان دوباره توسعه داد.

در نهایت، مسیر تناسب اندام یک فاز اولیه سریع و نزدیک به بهینه و پیشرفت جهش والد-فرزند بسیار کندتر به الگوی بهینه را نشان داد. با توجه به اینکه شبیه‌سازی واقعی میلیون‌ها شمارش شطرنجی ساعت‌ها یا روزها طول می‌کشد تا در یک لپ‌تاپ معمولی همگرا شود، این مشاهدات می‌تواند در شبیه‌سازی‌های سریع واقع‌گرایانه استفاده شود که تنها به راه‌حل‌های تقریباً بهینه برای ارزیابی تعاملی تأثیرات نام‌گذاری‌های جایگزین و وزن‌دهی اهداف می‌پردازند. . این مزیت غیرمنتظره مدل ما امکان شبیه‌سازی‌های تعاملی شامل برنامه‌ریزان و مدیرانی را که اکنون می‌توانند حساسیت عدم قطعیت‌های برنامه‌ریزی را قبل از اجرای یک شبیه‌سازی همگرا نهایی ارزیابی کنند، باز می‌کند.

5. نتیجه گیری ها

الگوریتم ژنتیک چندهدفه پیشنهادی ما مدل LIr-MSO به برنامه ریزان کاربری زمین با بهینه سازی کاربری واقعی تر، کارآمدتر و مناسب تر از طریق الگوهای بسیار دقیق تر، محدودیت های حداقل اندازه وصله اولیه، مقیاس بندی متعادل تر و جایگزین های ژنتیکی جدید در استراتژی جهش و نخبگان بهبودهای تولید سلول منجر به افزایش سریع تناسب تا نزدیک به بهینه می‌شود و به نظر می‌رسد الگوهای تناسب نهایی با توجه به اندازه‌های وصله کاربری‌های مختلف زمین و قرارگیری آنها نسبت به یکدیگر عملی هستند. مرحله تناسب اندام سریع می تواند شبیه سازی های واقعی سریع را تسهیل کند که به برنامه ریزان اجازه می دهد تا با عدم قطعیت ها و مدل های جایگزین آزمایش کنند.

قابلیت اطمینان مدل در یک برنامه کاربردی در جامعه Dapeng، شنژن آزمایش شد که نشان داد برازش مدل 2.71٪ بیشتر از آن بدون بهبود در مقداردهی اولیه و جهش بود. با این حال، درصد افزایش تناسب از الگوی اولیه تا نهایی، افزایش قابل توجهی در برخی از کاربری‌های زمین را منعکس نمی‌کند – به عنوان مثال، در کاربری تجاری زمین، که بیش از دو برابر شد.

با این حال، بهبود مدل بهینه سازی هنوز برای کاربردهای عملی مورد نیاز است. ابتدا با توجه به پیچیدگی توسعه شهری، باید اهداف موثرتری در نظر گرفته شود. به عنوان مثال، مجموعه اهداف باید شامل افزایش فشار جمعیت، ترافیک، دسترسی، زیست پذیری و کنترل آلودگی باشد. تعادل این اهداف در تعیین کاربری نهایی نیز به آزمایش بیشتر با برنامه ریزان برای تعیین مجموعه ای از وزن های نسبی مناسب نیاز دارد، که اکنون با استفاده از راه حل های نزدیک به بهینه از نظر محاسباتی قابل قبول به نظر می رسد. راه حل های سریع تقریباً بهینه همچنین به تصمیم گیرندگان اجازه می دهد تا در برنامه ریزی کاربری زمین مشارکت نزدیک داشته باشند. بدین ترتیب، ممکن است بتوان مدل‌هایی را با هم ترکیب کرد که می‌توانند فرآیند تصمیم‌گیری را از عوامل مختلف شبیه‌سازی کنند – مانند سیستم‌های چند عاملی – به‌ویژه آن‌هایی که در برنامه‌ریزی حمل‌ونقل با توجه به مبادلات بالقوه بین فشردگی و تغییرات در شبکه‌های حمل‌ونقل نقش دارند. علاوه بر این، سناریوهای برنامه ریزی در قالب سیاست ها و برنامه های توسعه منطقه ای جایگزین باید برای رفع نیازهای مختلف در برنامه ریزی کاربردی کاربری زمین طراحی شود. به عنوان مثال، با مفهوم اول محیط زیست، بهینه سازی فضایی مبتنی بر امنیت اکولوژیکی را می توان آزمایش کرد.

مشارکت های نویسنده

همه نویسندگان در ساخت این دستنوشته مشارکت داشتند: Tingting Pan و Yu Zhang این تحقیق را تصور کردند و تمام داده ها را جمع آوری کردند. Fenzhen Su، Tingting Pan و Yu Zhang آزمایش را طراحی کردند و نسخه خطی را تهیه کردند. وینسنت لین، هان شیائو و فی چنگ در مورد زبان کمک کردند و نسخه خطی را بررسی کردند. همه نویسندگان نسخه منتشر شده نسخه خطی را خوانده و با آن موافقت کرده اند.

منابع مالی

این تحقیق توسط بنیاد ملی علوم طبیعی چین با شماره کمک مالی 41890854 تامین شده است.

بیانیه هیئت بررسی نهادی

قابل اجرا نیست.

بیانیه رضایت آگاهانه

قابل اجرا نیست.

بیانیه در دسترس بودن داده ها

برای دسترسی به داده ها لطفا با نویسندگان تماس بگیرید.

تضاد علاقه

نویسندگان هیچ تضاد منافع را اعلام نمی کنند.

منابع

سویی، دی.زی. Zeng، H. مدل‌سازی پویایی ساختار چشم‌انداز در مناطق نوظهور دساکوتا در آسیا: مطالعه موردی در شنژن. Landsc. طرح شهری. 2001 ، 53 ، 37-52. [ Google Scholar ] [ CrossRef ]
دنگ، JS; که، دبلیو. یانگ، اچ. Qi، JG پویایی فضایی-زمانی و تکامل تغییر کاربری زمین و الگوی منظر در پاسخ به شهرنشینی سریع. Landsc. طرح شهری. 2009 ، 92 ، 187-198. [ Google Scholar ] [ CrossRef ]
یائو، جی. موری، AT; وانگ، جی. Zhang, X. ارزیابی و توسعه برنامه های کاربری پایدار شهری از طریق بهینه سازی فضایی. ترانس. GIS 2019 ، 23 ، 705-725. [ Google Scholar ] [ CrossRef ]
بای، ایکس. تحقق رویای شهری چین. طبیعت 2014 ، 509 ، 158-160. [ Google Scholar ] [ CrossRef ] [ PubMed ]
پورتا، جی. پاراپار، ج. دوالو، آر. ریورا، FF; سانته، آی. Crecente, R. الگوریتم ژنتیک با کارایی بالا برای برنامه ریزی کاربری اراضی. محاسبه کنید. محیط زیست سیستم شهری 2013 ، 37 ، 45-58. [ Google Scholar ] [ CrossRef ]
صاحبقرانی، ع. بهینه سازی کاربری اراضی چندهدفه از طریق الگوریتم ازدحام ذرات موازی: مطالعه موردی منطقه بابلدشت اصفهان، ایران. J. Urban. محیط زیست مهندس 2016 ، 10 ، 42-49. [ Google Scholar ]
شواب، ج. دب، ک. گودمن، ای. لاتنباخ، اس. ون استرین، ام جی; Grêt-Regamey، A. بهبود عملکرد الگوریتم های ژنتیک برای مشکلات تخصیص کاربری زمین. بین المللی J. GIS 2018 ، 32 ، 907-930. [ Google Scholar ] [ CrossRef ]
کائو، ک. لیو، ام. وانگ، اس. لیو، ام. هوانگ، ب. بهینه سازی کاربری زمین چندهدفه فضایی به سمت زیست پذیری بر اساس الگوریتم ژنتیک مبتنی بر مرز: مطالعه موردی در سنگاپور. ISPRS Int. J. Geo-Inf. 2020 ، 9 ، 40. [ Google Scholar ] [ CrossRef ]
لیو، ی. تانگ، دبلیو. او، جی. لیو، ی. آی، تی. لیو، دی. یک مدل بهینه‌سازی فضایی کاربری زمین بر اساس بهینه‌سازی ژنتیکی و نظریه بازی. محاسبه کنید. محیط زیست سیستم شهری 2015 ، 49 ، 1-14. [ Google Scholar ] [ CrossRef ]
کائو، ک. هوانگ، بی. وانگ، اس. Lin, H. بهینه سازی کاربری پایدار زمین با استفاده از الگوریتم ژنتیک سریع مبتنی بر مرز. محاسبه کنید. محیط زیست سیستم شهری 2012 ، 36 ، 257-269. [ Google Scholar ] [ CrossRef ]
هوانگ، Q. Song, W. یک مدل تخصیص بهینه فضایی کاربری زمین که یک سیستم چند عاملی را با الگوریتم جهش قورباغه به هم ریخته جفت می کند. محاسبه کنید. محیط زیست سیستم شهری 2019 ، 77 ، 101360. [ Google Scholar ] [ CrossRef ]
داتا، دی. دب، ک. Fonseca، CM; لوبو، FG; Condado، PA; Seixas، J. الگوریتم تکاملی چند هدفه برای مشکل مدیریت کاربری زمین. گل میخ. محاسبه کنید. هوشمند 2007 ، 3 ، 1-24. [ Google Scholar ]
کاراکوستاس، اس. Economou، D. الگوریتم بهینه سازی چند هدفه پیشرفته برای منابع انرژی تجدیدپذیر: توسعه فضایی بهینه مزارع بادی. بین المللی J. GIS 2014 ، 28 ، 83-103. [ Google Scholar ] [ CrossRef ]
شایگان، م. علیمحمدی، ع. منصوریان، ع. گوارا، ZS; کلامی، رویکرد بهینه‌سازی چندهدفه فضایی SM برای تخصیص کاربری اراضی با استفاده از NSGA-II. Sel. بالا. Appl. Obs زمین. Remote Sens. 2014 , 7 , 906–916. [ Google Scholar ] [ CrossRef ]
آهنگ، م. Chen, DM یک NSGA-II با دانش بهبود یافته برای تخصیص زمین چند هدفه (MOLA). ژئو اسپات. Inf. علمی 2018 ، 21 ، 273-287. [ Google Scholar ] [ CrossRef ]
چندرامولی، م. هوانگ، بی. Xue, L. بهینه سازی تغییر فضایی: ادغام GA با تجسم برای تولید سناریوهای سه بعدی. فتوگرام مهندس Remote Sens. 2009 , 75 , 1015–1022. [ Google Scholar ] [ CrossRef ]
شیائو، ن. بنت، دی. آرمسترانگ، MP استفاده از الگوریتم های تکاملی برای ایجاد جایگزین برای مشکلات جستجوی سایت چندهدفه. محیط زیست طرح. A 2002 , 34 , 639-656. [ Google Scholar ] [ CrossRef ]
بو، اچ. Zhang، W. برنامه ریزی کاربری پایدار زمین برای منطقه دریاچه مرکز شهر در چین مرکزی: رویکرد بهینه سازی چند هدفه با کمک مدل سازی رشد شهری. طرح شهری. توسعه دهنده 2014 ، 140 ، 04014002. [ Google Scholar ]
Aerts، JC; Heuvelink، GB استفاده از بازپخت شبیه سازی شده برای تخصیص منابع. بین المللی J. GIS 2002 ، 16 ، 571-587. [ Google Scholar ] [ CrossRef ]
کائو، ک. باتی، م. هوانگ، بی. لیو، ی. یو، ال. چن، جی. بهینه‌سازی کاربری زمین چند هدفه فضایی: برنامه‌های افزودنی به الگوریتم ژنتیک مرتب‌سازی غیرمسلط-II. بین المللی J. GIS 2011 ، 25 ، 1949-1969. [ Google Scholar ] [ CrossRef ]
لی، ی. گوا، اچ. لی، اچ. خو، جی. وانگ، ز. کنگ، سی. مدل برنامه ریزی زمین ترانزیت محور با در نظر گرفتن پایداری حمل و نقل ریلی انبوه. ج. طرح شهری. توسعه دهنده 2010 ، 136 ، 243-248. [ Google Scholar ] [ CrossRef ]
لیو، ایکس. سون، ال. شیا، ال. خو، X. وانگ، اس. یک مدل شبیه‌سازی کاربری زمین در آینده (FLUS) برای شبیه‌سازی سناریوهای کاربری چندگانه با جفت کردن اثرات انسانی و طبیعی. Landsc. طرح شهری. 2017 ، 168 ، 94-116. [ Google Scholar ] [ CrossRef ]
بالینگ، RJ; تابر، JT; براون، MR; روز، ک. برنامه ریزی شهری چندهدفه با استفاده از الگوریتم ژنتیک. ج. طرح شهری. توسعه دهنده 1999 ، 125 ، 86-99. [ Google Scholar ] [ CrossRef ]
استوارت، تی جی; Janssen, R. الگوریتم برنامه ریزی کاربری زمین مبتنی بر GIS چندهدفه. محاسبه کنید. محیط زیست سیستم شهری 2014 ، 46 ، 25-34. [ Google Scholar ] [ CrossRef ]
لی، ایکس. Parrott, L. یک الگوریتم ژنتیک بهبود یافته برای بهینه سازی فضایی تخصیص کاربری زمین چند هدفه و چند سایت. محاسبه کنید. محیط زیست سیستم شهری 2016 ، 59 ، 184-194. [ Google Scholar ] [ CrossRef ]
کوستانزا، آر. d’Arge، R. دی گروت، آر. فاربر، اس. گراسو، ام. هانون، بی. لیمبورگ، ک. نعیم، س. اونیل، آر وی. پارولو، جی. ارزش خدمات اکوسیستم و سرمایه طبیعی جهان. طبیعت 1997 ، 387 ، 253-260. [ Google Scholar ] [ CrossRef ]
کائو، ک. ژانگ، دبلیو. وانگ، تی. بهینه‌سازی چندهدفه کاربری فضایی-زمانی: مطالعه موردی در چین مرکزی. ترانس. GIS 2019 ، 23 ، 726-744. [ Google Scholar ] [ CrossRef ]
ژانگ، دبلیو. Huang، B. ارزیابی فرسایش خاک در یک شهر به سرعت در حال شهرنشینی (شنژن، چین) و اجرای بهینه‌سازی کاربری زمین فضایی. محیط زیست علمی آلودگی Res. 2015 ، 22 ، 4475-4490. [ Google Scholar ] [ CrossRef ] [ PubMed ]
فنگ، سی. Lin, J. استفاده از الگوریتم ژنتیک برای تولید نقشه های طرح جایگزین برای برنامه ریزی شهری. محاسبه کنید. محیط زیست Urban Syst 1999 ، 23 ، 91-108. [ Google Scholar ] [ CrossRef ]
لیگمان-زیلینسکا، آ. کلیسا، آر. Jankowski، P. بهینه سازی فضایی به عنوان یک تکنیک مولد برای تخصیص کاربری چند هدفه پایدار. بین المللی J. GIS 2008 ، 22 ، 601-622. [ Google Scholar ] [ CrossRef ]
ما، X. چن، ایکس. لی، ایکس. دینگ، سی. Wang, Y. برنامه ریزی پایدار در سطح ایستگاه: یک مدل طراحی یکپارچه حمل و نقل و کاربری زمین برای توسعه حمل و نقل محور. J. Clean Prod. 2018 ، 170 ، 1052-1063. [ Google Scholar ] [ CrossRef ]
استوارت، تی جی; یانسن، آر. Herwijnen، Mv یک رویکرد الگوریتم ژنتیک برای برنامه‌ریزی کاربری چندهدفه زمین. محاسبه کنید. اپراتور Res. 2004 ، 31 ، 2293-2313. [ Google Scholar ] [ CrossRef ]
یانسن، آر. ون هروینن، م. استوارت، تی جی; پشتیبانی تصمیم چندهدفه Aerts، JC برای برنامه ریزی کاربری زمین. محیط زیست طرح شهری. ب: طرح دس. 2008 ، 35 ، 740-756. [ Google Scholar ] [ CrossRef ]
آرتور، جی ال. Nalle، DJ Clarification در مورد استفاده از برنامه نویسی خطی و GIS برای مدل سازی کاربری زمین. بین المللی J. GIS 1997 ، 11 ، 397-402. [ Google Scholar ] [ CrossRef ]
سانته ریویرا، آی. بولون-ماگان، ام. Crecente-Maseda، R.; الگوریتم Miranda-Barrós، D. بر اساس بازپخت شبیه سازی شده برای تخصیص کاربری زمین. محاسبه کنید. Geosci. 2008 ، 34 ، 259-268. [ Google Scholar ] [ CrossRef ]
لی، ایکس. بله، AGO ادغام الگوریتم های ژنتیک و GIS برای جستجوی مکان بهینه. بین المللی J. GIS 2005 ، 19 ، 581-601. [ Google Scholar ] [ CrossRef ]
بروکس، CJ یک الگوریتم ژنتیک برای طراحی تنظیمات بهینه پچ در GIS. بین المللی J. GIS 2001 ، 15 ، 539-559. [ Google Scholar ] [ CrossRef ]
هوانگ، بی. لیو، ن. Chandramouli، M. A GIS از الگوریتم مورچه برای مسئله پوشش ویژگی خطی با محدودیت های فاصله پشتیبانی می کند. تصمیم می گیرد. سیستم پشتیبانی 2006 ، 42 ، 1063-1075. [ Google Scholar ] [ CrossRef ]
معصومی، ز. مسگری، ام اس; همراه، م. تخصیص کاربری های شهری با الگوریتم بهینه سازی ازدحام ذرات چند هدفه. بین المللی J. GIS 2013 ، 27 ، 542-566. [ Google Scholar ] [ CrossRef ]
دی یونگ، ک. یادگیری با الگوریتم های ژنتیک: یک مرور کلی. ماخ فرا گرفتن. 1988 ، 3 ، 121-138. [ Google Scholar ] [ CrossRef ]
آرتس، جی. ون هروینن، م. یانسن، آر. استوارت، تی. ارزیابی تکنیک‌های طراحی فضایی برای حل مشکلات تخصیص کاربری زمین. جی. محیط زیست. برنامه مدیریت. 2005 ، 48 ، 121-142. [ Google Scholar ] [ CrossRef ]
لیو، ایکس. او، جی. لی، ایکس. Ai، B. ترکیب دینامیک سیستم و بهینه سازی ازدحام ذرات ترکیبی برای تخصیص کاربری زمین. Ecol. مدل. 2013 ، 257 ، 11-24. [ Google Scholar ] [ CrossRef ]
لیو، ایکس. لی، ایکس. شی، ایکس. هوانگ، ک. لیو، ی. روش بهینه‌سازی کلنی مورچه‌ها چند نوع (MACO) برای تخصیص بهینه استفاده از زمین در مناطق بزرگ. بین المللی J. GIS 2012 ، 26 ، 1325-1343. [ Google Scholar ] [ CrossRef ]
هالند، سازگاری JH در سیستم‌های طبیعی و مصنوعی: تحلیل مقدماتی با کاربردهای زیست‌شناسی، کنترل و هوش مصنوعی . انتشارات MIT: کمبریج، MA، ایالات متحده آمریکا، 1992. [ Google Scholar ]
داپنگ دولت آنلاین. در دسترس آنلاین: https://www.dpxq.gov.cn/ (در 1 ژوئن 2019 قابل دسترسی است).
مرکز خدمات داده های ماهواره ای اقیانوس چین. در دسترس به صورت آنلاین: https://osdds.nsoas.org.cn (در 23 آوریل 2019 قابل دسترسی است).
نقشه بایدو. در دسترس آنلاین: https://map.baidu.com/ (در 1 ژوئن 2019 قابل دسترسی است).
ماموریت توپوگرافی رادار شاتل. در دسترس آنلاین: https://srtm.csi.cgiar.org/SELECTION/inputCoord.asp (در 21 آوریل 2019 قابل دسترسی است).
گلدبرگ، الگوریتم‌های ژنتیک DE در جستجو، بهینه‌سازی و یادگیری ماشینی ؛ انتشارات Addison-Wesley Longman: Boston, MA, USA, 1989; جلد 36. [ Google Scholar ]
ژانگ، اچ. زنگ، ی. Bian, L. شبیه سازی تخصیص بهینه سازی فضایی چند هدفه کاربری زمین بر اساس ادغام سیستم چند عاملی و الگوریتم ژنتیک. بین المللی جی. محیط زیست. Res. 2010 ، 4 ، 765-776. [ Google Scholar ]
Xie، GD; ژن، ال. چون-شیا، لو. شیائو، ی. چن، سی. روش ارزیابی مبتنی بر دانش متخصص خدمات اکوسیستمی در چین. جی. نات. منبع. 2008 ، 23 ، 911-919. [ Google Scholar ]
Maitland، B. به سوی یک نظریه حداقلی ساختار شهری. Gosling D Maitland B Concepts Urban Des. 1984 ، 153-155. [ Google Scholar ]

شکل 1. نقشه کاربری اراضی جامعه داپنگ در سال 2017 (نقشه سمت راست)، واقع در منطقه خلیج بزرگ (نقشه سمت چپ پایین) چین (نقشه بالا سمت چپ). برای اهداف مدل‌سازی، نقشه کاربری زمین به سلول‌های 1878 × 1418 تقسیم شده است که اندازه هر سلول 10 × 10 متر است. کدهای رنگی انواع مختلف کاربری زمین را همانطور که در افسانه ذکر شده است نشان می دهد.

شکل 2. روش گردش کار مدل بهینه سازی فضایی چندهدفه با شدت کاربری محدود (LIr-MSO) برای استخراج مکرر مناسب ترین الگوی کاربری بهینه از یک الگوی اولیه.

شکل 3. تصویر آرایش ماتریس 3 × 3 که در آن درجه تضاد در اطراف یک سلول (i = 1 تا N، که N تعداد کل سلول ها است) با توجه به هر یک از همسایگان آن محاسبه می شود (j = 1 تا 8). ).

شکل 4. تصویر شماتیکی از روش متقاطع از دو والدین قابل دوام (Parent1 و Parent2) با دو کاربری متفاوت (به ترتیب a و b) در سلول های مرکزی. متقاطع برای تشکیل یک Offspring با جایگزینی سلول مرکزی در Parent1 انجام می شود، اگر نوع سلول مرکزی جدید بیشتر از نوع قدیمی باشد.

شکل 5. روش جهش مبتنی بر نقطه (PM) که در آن سلول مرکزی در یک پنجره 3 × 3 در والد با بیشترین نوع جایگزین می شود.

شکل 6. حالت جایگزینی در استراتژی نخبگان برای نسل فعلی و آینده ( به ترتیب A ( n ) و A ( n + 1)) برای سه مورد مقایسه تناسب نسبی اعمال می شود.

شکل 7. محدودیت ها در جامعه داپنگ در رابطه با ( الف ) زمین قابل تغییر و غیرقابل تغییر، و ( ب ) مناطق توسعه مجاز که در آن شیب زمین از 25 درجه تجاوز نمی کند.

شکل 8. تغییر در امتیاز تناسب اندام مدل جامع با تعداد تکرارها که یک تغییر نسبتاً سریع را تا حدود 21 تکرار نشان می دهد و به دنبال آن یک انتقال به سمت مرحله افزایش بسیار آهسته تر، با دوره های تناسب استاتیک مشخص می شود. دوره های کوتاه تر از تغییرات نسبتا ایستا نیز در فاز سریع قابل توجه است. شرایط مختلف به آزمایش های کنتراست توصیف شده در متن اصلی اشاره دارد: (1) بدون تجدید نظر اولیه. (2) بدون تجدید نظر جهش. (3) بدون مقداردهی اولیه و جهش. LIr-MSO به مدل جامعی اشاره دارد که هم شامل مقداردهی اولیه و هم تجدید نظر جهش است.

شکل 9. الگوی بهینه نهایی استفاده از زمین که کاربری های مختلف زمین را نشان می دهد (رنگی مطابق با افسانه) با مثال بزرگنمایی شده در مقایسه. تغییرات کاربری اراضی در مناطق شماره گذاری شده از 1 تا 5 در متن اصلی ذکر شده است.

شکل 10. الگوی مناطق تغییر کاربری اراضی (بدون توجه به نوع) در منطقه قابل توسعه بین الگوی کاربری اصلی و بهینه. هیچ منطقه تغییر یافته ای در منطقه ذخیره اکولوژیکی رخ نمی دهد.

شکل 11. مقایسه، از جمله درج‌های بزرگنمایی شده، الگوهای کاربری نهایی زمین در سه آزمایش کنتراست ( a – c ): 1. بدون بازبینی اولیه. 2. بدون تجدید نظر جهش. 3. بدون مقداردهی اولیه و تجدید نظر جهش. در ( d )، مقادیر نرمال شده برای هر آزمایش/شرط فهرست شده و با راه حل بهینه به دست آمده با مدل LIr-MSO مقایسه می شود.

مقالات داخلی و بین المللی

1 نظر

دیدگاهتان را بنویسید لغو پاسخ

برای نوشتن دیدگاه باید وارد بشوید.

مشاورین هوش پیروزی

برنامه ریزی کاربری منطقه ای کارآمد عملی با استفاده از بهینه سازی الگوریتم ژنتیک چندهدفه و سیستم اطلاعات جغرافیایی

برنامه ریزی کاربری منطقه ای کارآمد عملی با استفاده از بهینه سازی الگوریتم ژنتیک چندهدفه و سیستم اطلاعات جغرافیایی

چکیده

1. مقدمه