خلاصه
شبکه‌های عصبی گراف (GNN) در زمان‌های اخیر به دلیل عملکردشان در وظایف استنتاج برای داده‌های بدون ساختار مورد تحسین قرار گرفته‌اند. به طور معمول، GNN ها با بهره برداری از اطلاعات ساختاری محلی در نمودارها و نادیده گرفتن ساختار جهانی آنها عمل می کنند. این تحت تأثیر مفروضات توزیع طبقاتی همجنسگرا و بی طرفانه است. در نتیجه، این می تواند عملکرد مدل را در نمودارهای دنیای واقعی پر سر و صدا مانند نمودارهای فضایی که در آن این مفروضات ممکن است به اندازه کافی رعایت نشوند، مختل کند. در این مقاله به بررسی مشکل یادگیری نمودار بر روی نمودارهای فضایی می پردازیم. به ویژه، ما بر روش‌های یادگیری انتقالی برای موارد نامتعادل تمرکز می‌کنیم. با توجه به ماهیت این نمودارها، ما فرض می کنیم که در نظر گرفتن ساختار کلی نمودار هنگام جمع آوری اطلاعات محلی، به ویژه با توجه به تعمیم پذیری، سودمند خواهد بود. بنابراین، ما یک رویکرد جدید برای آموزش GNN برای این نوع نمودارها پیشنهاد می کنیم. ما این را از طریق یک تکنیک نمونه‌گیری به دست می‌آوریم: نمونه‌برداری آگاه از ساختار (SAS)، که از اهرمفاصله های درون کلاسی و جهانی-ژئودزیکی بین گره ها. ما مشکل را به عنوان یک طبقه بندی گره برای شبکه های خیابانی با واریانس بالا بین اندازه کلاس ها مدل می کنیم. ما رویکرد خود را با استفاده از نمودارهای بزرگ دنیای واقعی در مقابل روش‌های پیشرفته ارزیابی می‌کنیم. در اکثر موارد، رویکرد ما تا میانگین امتیاز F1 20% از روش‌های سنتی بهتر عمل می‌کند.
کلید واژه ها:
GeoAI ; گراف شبکه های عصبی ; شبکه های فضایی
چکیده گرافیکی
1. معرفی
یادگیری بر روی داده های بدون ساختار یک مشکل مهم و جالب است [ 1 ] که به بسیاری از وظایف با ماهیت فضایی مانند برنامه ریزی مسیر، پیش بینی تقاضای خودرو، درک گسترش بیماری (اپیدمیولوژی)، غنی سازی معنایی شبکه های فضایی، و روباتیک مستقل مربوط می شود [2] . , 3 , 4 , 5 , 6 , 7 , 8 ]. این وظایف را می توان با استفاده از نمودارها مدلسازی کرد. رویکردهای یادگیری عصبی سنتی مانند شبکه‌های عصبی کانولوشن (CNN) و شبکه‌های عصبی مکرر (RNN) با موفقیت برای حل مشکلات بینایی و ترجمه ماشینی چالش‌برانگیز در میان بسیاری دیگر استفاده شده‌اند [ 9 ،10 ]. با این حال، آنها برای شبکه های منظم یا ساختارهای اقلیدسی طراحی شده اند. از این رو، یک انگیزه کلیدی برای شبکه های عصبی گراف (GNN) نیاز به مدل هایی است که بتوانند ساختارهای نامنظم مانند نمودارها را یاد بگیرند. در این راستا، GNN ها می توانند محدودیت های رابطه همسایگی (بایاس استقرایی رابطه ای) بین موجودیت های گراف مانند گره ها یا یال ها را در طول یادگیری رمزگذاری کنند [ 1 ]. به طور کلی، GNN ها با بهره برداری از اطلاعات نمودار محلی کار می کنند، که یا از طریق ارسال پیام یا جمع آوری اطلاعات از همسایگان با استفاده از تعبیه [ 11 ، 12 ] به دست می آید. محلیاینجا به همسایگی یک گره گراف اشاره دارد. به عنوان مثال، در یک شبکه خیابانی که در آن بخش های خیابان گره هستند، محلی بودن یک بخش خیابان مجموعه خیابان هایی است که به آن خیابان ارتباط دارند. در این مقاله، ما محل را به همسایه های تک هاپ، یعنی اتصال مستقیم محدود می کنیم. بهره برداری از اطلاعات گراف محلی معمولاً به بهای نادیده گرفتن ساختار نمودار جهانی اجرا می شود. مسلماً، این رویکرد تا حد زیادی تحت تأثیر مفروضات ساختاری در مورد نمودارها مانند توزیع های کلاسی همجنسگرا و بی طرفانه است [ 11 ، 12]]. در نتیجه، این دو محدودیت ممکن ایجاد می کند. اولاً، ظرفیت مدل می تواند تحت تأثیر بی توجهی به ساختار نمودار جهانی باشد. ثانیاً، GNNها نمی‌توانند به خوبی بر روی نمودارهای دنیای واقعی پر سر و صدا مانند نمودارهای فضایی که این مفروضات ممکن است به اندازه کافی وجود نداشته باشند، تعمیم دهند.
در این مقاله شبکه های خیابانی را شبکه های فضایی در نظر می گیریم. به طور کلی، نمودارها بدون ساختار در نظر گرفته می شوند به این معنا که ویژگی های توپولوژیکی مانند درجه گره نامحدود هستند. با این حال، این لزوماً برای شبکه‌های خیابانی صدق نمی‌کند، زیرا فقط می‌تواند تعداد معینی از خیابان‌ها در مجاورت یک خیابان وجود داشته باشد. علاوه بر این، شبکه های خیابانی تراکم کمتری نسبت به شبکه های سنتی دارند. به عنوان مثال، میانگین درجه شبکه های خیابانی در لس آنجلس، رم و ونکوور به ترتیب 4.47، 4.13 و 4.98 است. در مقایسه، یک شبکه استنادی، یک شبکه اجتماعی و نمودارهای تعامل پروتئین-پروتئین (PPI) به ترتیب دارای درجه متوسط 9.15، 492 و 28.8 هستند [ 13 ]. علاوه بر این، شبکه‌های خیابانی هوموفیلی فرار را نشان می‌دهند [ 14]. این پدیده را می توان از طریق مفهوم چند مرکزیت فضایی بهتر درک کرد [ 15 ، 16 ]. با استفاده از توزیع انواع خیابان ها در سراسر یک شهر به عنوان مثال، چند مرکزیت فضایی نشان می دهد که شبکه خیابان های یک شهر لزوماً طبقات خیابانی را در زیرساختارها جمع نمی کند، در نتیجه با تعریف کلی هموفیلی در تضاد است. در همین راستا، شبکه های خیابانی عدم تعادل طبقاتی بالایی را نشان می دهند، با تفاوت بین دو طبقه به اندازه سه مرتبه بزرگی [ 7 ]
GNNها می‌توانند مستعد برازش بیش از حد باشند و وقتی روی نمودارهای دنیای واقعی اعمال می‌شوند غیرقابل پیش‌بینی هستند [ 17 ، 18 ]. این محدودیت زمانی تشدید می‌شود که تضاد قبلاً مورد بحث بین مفروضات اجرایی GNN و ویژگی‌های شبکه‌های خیابانی را در نظر بگیریم، به ویژه در پرتو واریانس بسیار بالا بین توزیع‌های طبقاتی که در بسیاری از شبکه‌های فضایی وجود دارد [7 ] . بنابراین، در این مقاله، GNN ها را برای طبقه بندی گره ها در شبکه های خیابانی مطالعه می کنیم. به طور خاص، ما به دنبال بررسی رابطه بین دو ویژگی مرتبط شبکه‌های فضایی با GNN هستیم. این ویژگی ها یک ساختار نمودار جهانی و توزیع های کلاسی بایاس هستند. در نتیجه سؤالات زیر را طرح می کنیم:
-
GNN های وانیلی چقدر در نمودارهای فضایی نامتعادل تعمیم می دهند؟
-
آیا می توان عملکرد GNN ها را با رمزگذاری دانش در مورد ساختار جهانی شبکه های فضایی بهبود بخشید؟
-
آیا می توان ظرفیت تعمیم GNN ها را برای نمودارهای فضایی نامتعادل در زمانی که ساختار جهانی به حساب می آید، بهبود بخشید؟
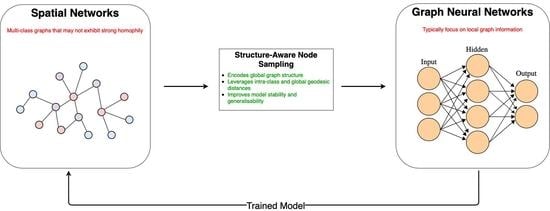
این سوالات در بخش 7 مطرح شده است . ما مشکل خود را به عنوان یک طبقه بندی گره چند کلاسه برای نمودارهایی که به شدت نامتعادل هستند طراحی می کنیم. به طور خاص، ما بر مسئله تحقیق باز غنی‌سازی معناشناسی شبکه‌های فضایی تمرکز می‌کنیم [ 7 ، 8 ]. در این راستا، ما یک رویکرد نمونه‌گیری جدید را پیشنهاد می‌کنیم: نمونه‌برداری آگاه از ساختار (SAS)، که ساختار نمودار سراسری را در مدل با اعمال نفوذ درون‌کلاسی و جهانی -ژئودزیک کدگذاری می‌کند.فاصله بین گره ها ما یک چارچوب عصبی را با استفاده از این تکنیک نمونه‌گیری برای آموزش مدلی برای نمودارهای فضایی ایجاد می‌کنیم. ما پیشنهاد خود را با روش‌های پیشرفته در نمودارهای فضایی بزرگ در دنیای واقعی ارزیابی می‌کنیم. نتایج ما بهبود واضحی را در اکثر موارد نشان می‌دهد، با 20% بهبود امتیاز F1 به طور متوسط نسبت به روش‌های سنتی. رویکرد ما در شکل 1 خلاصه شده است .
ما مشارکت های خود را به اختصار خلاصه می کنیم:
-
ما نشان می‌دهیم که GNNهای وانیلی به اندازه کافی برای نمودارهای فضایی نامتعادل تعمیم نمی‌یابند.
-
ما یک تکنیک نمونه‌گیری جدید (SAS) برای آموزش GNN برای شبکه‌های فضایی پیشنهاد می‌کنیم که ظرفیت مدل را به طور قابل‌توجهی بهبود می‌بخشد.
-
ما نشان می‌دهیم که رمزگذاری ساختار گراف (از طریق تکنیک نمونه‌برداری ما) برای آموزش GNNها، تعمیم‌پذیری مدل‌ها را با میانگین امتیاز F1 20٪ حتی با عدم تعادل کلاس بهبود می‌بخشد.
ادامه این مقاله به صورت زیر سازماندهی شده است: در بخش 2 ، موضوعات و رویکردهای مرتبط را شرح می دهیم. مقدمات تعریف شده و مشکل در بخش 3 فرموله شده است . ما رویکرد خود را در بخش 4 و روش شناسی تجربی را در بخش 5 شرح می دهیم . ما نتایج خود را در بخش 6 ارائه و مورد بحث قرار می دهیم . ما نتایج خود را در بخش 7 خلاصه می کنیم .
2. کارهای مرتبط
کار ما در این مقاله دو حوزه تحقیقاتی گسترده را در بر می گیرد: شبکه های عصبی نمودار (GNN) و غنی سازی معنایی شبکه های فضایی. رویکردهای GNN را می‌توان با ماهیت مشکلاتی که حل می‌کنند، مانند طبقه‌بندی گره، پیش‌بینی پیوند یا طبقه‌بندی گراف توصیف کرد. دامنه ما در این مقاله محدود به طبقه بندی گره است و کارهای مربوطه را بررسی می کنیم.
2.1. رویکردهای یادگیری نمودار
هدف رویکردهای عصبی برای گراف ها یادگیری نمایشی برای یک گره با استفاده از یک مکان تعریف شده است . این فرض هم از موفقیت رویکردهای عصبی سنتی و هم از نیاز به گسترش آنها به حوزه های بدون ساختار مانند نمودارها الهام گرفته شده است [ 1 ]. به طور کلی، GNN ها را می توان به دو دسته تقسیم کرد: رویکردهای طیفی و فضایی . GNN های طیفی از ایده کانولوشن ها [ 9 ] در حوزه فویر از طریق عملیات روی ماتریس لاپلاسی گراف [ 11 ، 19 ، 20 ، 21 ] استفاده می کنند. این عملیات از نظر محاسباتی گران هستند و مسائل عملی را با مقیاس پذیری [ 11]. از سوی دیگر، رویکردهای فضایی نمایش‌ها را با استفاده از تجمیع ویژگی‌های همسایگی محاسبه می‌کنند [ 12 ، 13 ]. روش‌های مبتنی بر توجه گونه‌ای از GNNها هستند که اهمیت اطلاعات جمع‌آوری‌شده از همسایگان یک گره را از طریق محاسبه یک مقدار توجه رتبه‌بندی می‌کنند [ 12 ]. آنها روش‌های پیشرفته‌تری را انجام داده‌اند و در نمودارهای پر سر و صدا دنیای واقعی استحکام نشان داده‌اند [ 12 ، 22 ]. ما در این مقاله از یک رویکرد GNN فضایی مبتنی بر توجه استفاده می کنیم که در بخش 4 توضیح داده شده است .
ادبیات GNN برای شبکه های فضایی هنوز در حال توسعه است و در حال حاضر آثار مرتبط بسیار کمی وجود دارد. در [ 14 ]، نویسندگان شبکه ای را پیشنهاد می کنند که با تعبیه ویژگی های بین لبه و لبه شبکه های فضایی یاد می گیرد. آنها این را برای کارهایی مانند پیش بینی سرعت رانندگی و طبقه بندی محدودیت سرعت اعمال می کنند. با این حال، آنها شبکه فضایی را هدایت شده می دانند در حالی که ما جهت دهی شبکه را در ویژگی های آن جاسازی می کنیم. علاوه بر این، ما از مجموعه ای غنی تر از ویژگی ها برای هر گره استفاده می کنیم. کار انجام شده در [ 23] یک GNN مبتنی بر طیفی برای پیش‌بینی ترافیک پیشنهاد می‌کند. شبکه آنها از وابستگی مکانی-زمانی بین موجودیت ها در طول آموزش استفاده می کند. اجرای آنها بر جنبه های زمانی این شبکه ها متمرکز است و به طور مستقیم با محدوده ما در این مقاله قابل مقایسه نیست. تا جایی که ما می دانیم، مقاله ما اولین مقاله ای است که تلاش می کند تا استحکام GNN ها را در شبکه های فضایی نسبت داده شده برای طبقه بندی گره ها، به ویژه با در نظر گرفتن ماهیت مغرضانه و چند کلاسه آنها، بهبود بخشد.
2.2. غنی سازی معنایی شبکه های فضایی
استفاده از یادگیری ماشینی برای غنی سازی معناشناسی نمودارهای فضایی جدید نیست. تمرکز قابل توجه این تلاش پژوهشی بر استنباط داده های نقشه بوده است. ما تعریف معناشناسی را از [ 6 ] به عنوان جزئیات توصیفی در مورد اشیاء فضایی، به عنوان مثال، کلاس خیابان ها (بزرگراه و خیابان های فرعی) و استفاده از ساختمان ها (ساختمان های مسکونی و تجاری) اقتباس می کنیم. در [ 5 ]، آنها سعی می کنند معنای خیابان ها را در OpenStreetMap با استفاده از هندسه آنها پیش بینی کنند. در [ 24 ]، آنها مدل های تقسیم بندی ضعیف و نیمه نظارت شده را برای ساختن نقشه ها پیشنهاد کردند. در [ 6 ]، آنها مدل های قابل انتقال را برای غنی سازی معناشناسی نقشه پیشنهاد می کنند در حالی که [ 7] از استفاده از اطلاعات زمینه ای برای پیش بینی معنایی خیابان ها در OpenStreetMap استفاده می کند. با این حال، یک ویژگی متحد کننده این رویکردها بی توجهی آنها به وابستگی رابطه ای بین موجودیت ها است [ 1 ، 5 ، 6 ، 25 ، 26 ، 27 ، 28 ]. GNN ها فرصتی برای پر کردن این شکاف هستند. ما کارهای اخیر انجام شده در [ 8] که در آن نویسندگان یک روش ترکیبی متشکل از CNN و GNN را برای پیش‌بینی معنایی داده‌های نقشه نشان می‌دهند. با این وجود، دامنه آنها فقط به دو کلاس خیابانی محدود می شود. این مسئله مشکل کلاس‌های بایاس را در نمودارهای فضایی چند کلاسه نادیده می‌گیرد، که بیشتر معرف سناریوهای دنیای واقعی است. کار ما با در نظر گرفتن نه کلاس خیابانی به این موضوع می‌پردازد و راه‌حلی برای آموزش GNNها برای غنی‌سازی معناشناسی شبکه‌های فضایی زمانی که اندازه کلاس‌ها بسیار مغرضانه است، پیشنهاد می‌کند.
3. مقدمات
3.1. نمادها
ما نمادهای استفاده شده در این مقاله را در جدول 1 با تعاریف آنها خلاصه می کنیم.
3.2. فرمول مسأله
اجازه دهید جی=(V،E)نشان دهنده یک نمودار فضایی همگن، بدون وزن، بدون جهت، متصل، چند کلاسه از اندازه ن=|V|با گره ها υمن∈Vو لبه ها (υمن،υj)∈E. ویژگی های گره ها در جیبا نشان داده می شود اچ={ساعت→1،⋯،ساعت→ن}∈آرن×r، که دارای یک r-نمایش برداری واقعی بعدی صفات ∀υ∈V. برچسب های کلاس از Vاز رابطه زیر بدست می آید Y={y1،⋯،yج}∈آرج، که در آن c تعداد برچسب های کلاس موجود در آن است جی. ما در این مقاله نه کلاس را در نظر می گیریم. هدف ما ایجاد یک تابع است اف(·)که یک نمودار داده می شود جیو زیر مجموعه ای از Vبا ویژگی های نقشه برداری شده آن از اچ، یادگیری نگاشت بین Vو Y.
3.3. شبکه های عصبی نموداری
شبکه عصبی گراف (GNN) یک شبکه عصبی است که مستقیماً از ساختار گراف یاد می‌گیرد. این پارادایم با استفاده از اطلاعات محلی در همسایگی یک گره [ 9 ] به این مهم دست می یابد. این اطلاعات محلی با استفاده از ارسال پیام یا تجمیع همسایگی نشان داده می شود [ 11 ، 12 ، 29 ]. شکل کلی یک GNN یک شبکه عصبی است که یک نمودار می گیرد جی=(V،E)به عنوان ورودی و مجموعه ای از ویژگی ها با ارزش واقعی اچ={ساعت→1،⋯،ساعت→ن}∈آرن×r. در این مثال، ما فرض می کنیم اچبه گره های نگاشت می شود جیاما بسته به مورد می تواند به لبه ها نیز نگاشت شود. این ویژگی ها توسط شبکه عصبی برای ایجاد نمایشی برای گره ها استفاده می شود که اطلاعات را در همسایگی محلی یک گره به کار می گیرد. نمن. پیاده سازی ما تجمیع همسایگی ویژگی ها را برای گره انجام می دهد υمن. سپس، GNN مقادیر توجه را برای اطلاعات جمع‌آوری شده از همسایگان محاسبه می‌کند. به این ترتیب، می‌تواند کمیت کند که بر کدام ویژگی‌های همسایه تأکید شود یا نه. یک تابع فعال سازی برای ترکیب این مقادیر و ویژگی های آنها اعمال می شود و به لایه بعدی در شبکه منتقل می شود. از این رو، نمایش هر گره تابعی از همسایگی آن است. لایه نهایی GNN ها شامل یک تابع فعال سازی است که بر روی نمایش های ارسال شده از لایه قبلی برای محاسبه احتمالات کلاس عمل می کند. در این مقاله از تابع فعال سازی softmax [ 30 ] استفاده می کنیم که برای مشکل طبقه بندی چند کلاسه ما مناسب است.
4. مدل پیشنهادی
در این مقاله روشی به نام SAS-GAT: Structure-Aware Sampling- Graph Attention Networks پیشنهاد می کنیم. ما از این شبکه برای آموزش مدلی برای طبقه‌بندی گره‌ها در شبکه‌های خیابانی استفاده می‌کنیم، که در آن گره‌ها بخش‌های خیابان را نشان می‌دهند و مدل تابعی را برای پیش‌بینی کلاس آنها می‌آموزد. ما اجزای معماری پیشنهادی را شرح می دهیم.
4.1. نمونه برداری آگاه از ساختار (SAS)
اولین جزء معماری ما یک فرآیند نمونه برداری است که برای بهبود قدرت تعمیم شبکه طراحی شده است. ما پیشنهاد می‌کنیم که با نمونه‌برداری از مهم‌ترین گره‌ها برای آموزش، دانش مربوط به ساختار نمودار در شبکه عصبی خود را رمزگذاری کنیم. با توجه به ماهیت چند کلاسه نمودارها در محدوده ما، ما با استفاده از فواصل درون کلاسی و جهانی-ژئودزیکی گره ها در نمودار به این موضوع می پردازیم. ما در اینجا به کلاس به عنوان برچسب مشخصه ای اشاره می کنیم که توسط یک گره در یک گراف وجود دارد. در این مقاله، برچسب ها انواع خیابانی هستند. ثابت شده است که تأثیر یا اهمیت یک گره را می توان از موقعیت آن در نمودارها استنباط کرد. 31]. به طور مشابه، معیارهای مختلف شبکه را می توان برای تعیین کمیت اهمیت محلی یا جهانی یک گره استفاده کرد. بنابراین، اهمیت یک گره در یک گراف فضایی چند کلاسه را به صورت زیر بیان می کنیم:
من(υ)=12∑(سی،ب).
اینجا، من(υ)نشان دهنده اهمیت گره است υ، سینشان دهنده فواصل درون کلاسی و بنشان دهنده فواصل جهانی-ژئودزیکی است . ایده کلیدی در پشت معادله ( 1 ) نمونه برداری از گره هایی است که نه تنها در کلاس خود تأثیرگذار هستند، بلکه در ساختار کلی نمودارها نیز مهم هستند. پس از آن نتیجه می شود که ما معیارهای مرکزیت نزدیکی و بین بودن را با مدل تطبیق می دهیم سیو ببه ترتیب [ 32 ]. ما شکل کلی مرکزیت نزدیک را همانطور که در معادله ( 2 ) تعریف شده است گسترش می دهیم تا توزیع های کلاس را در نظر بگیریم. از این رو، مرکزیت نزدیکی یک گره υمن∗، که در آن ∗ کلاس داده شده توسط:
سی(υمن∗)=ن∗∑υj∗∈V∗د(υمن∗،υj∗)
جایی که د(·)فاصله بین دو گره، N است ، Vهمانطور که در بخش 3.1 تعریف شده است . در این مقاله، ما را در نظر می گیریم V∗از هر کلاس، بزرگترین مجموعه گره های متصل آن کلاس باشد. مرکزیت بین بودن بدین صورت تعریف می شود:
ب(υمن)=∑متر،n∈Vγ(متر،n|υمن)γ(متر،n)
γ(متر،n)تعداد است متر،n-کوتاه ترین مسیرها در V، و γ(متر،n|υمن)نسبت کوتاهترین مسیرهایی است که می گذرد υمن. با توجه به پیچیدگی این اندازه گیری، به ویژه برای نمودارهای بزرگ، ما تکنیک تقریب شرح داده شده در [ 33 ] را تطبیق می دهیم. در این مقاله، ما این را تنها با استفاده از ۲۵ درصد گره‌های گراف پیاده‌سازی می‌کنیم. ما یک توصیف بصری بصری از هر دو اندازه گیری را ارائه می کنیم زیرا به ساختارهای گراف چند کلاسه مربوط می شود در شکل 2 . در نهایت، مقادیر معادلات ( 2 ) و ( 3 ) را قبل از محاسبه معادله ( 1 ) نرمال می کنیم.
ما اجرای محاسباتی معادله ( 1 ) را در الگوریتم 1 توصیف می کنیم. این الگوریتم به عنوان ورودی ساختار نمودار را می گیرد. جی، مجموعه گره های آموزشی Vتی، برچسب های کلاس برای گره ها Yو مجموعه مقادیر آستانه برای هر کلاس ک، سی(·)و ب(·)همانطور که در معادلات ( 2 ) و ( 3 ) تعریف شده است. B و C با تنظیم مقادیر آنها در محدوده (0، 1) نرمال می شوند. این الگوریتم مجموعه ای از گره های k بالا را بر اساس آستانه های از پیش تعیین شده برمی گرداند ( ک) برای هر کلاس.
| الگوریتم 1: نمونه گره ها با استفاده از SAS |
 |
4.2. جمع آوری اطلاعات محله در سطح گره با توجه
پس از نمونه برداری از مهم ترین گره ها از طریق SAS، به بهره برداری از اطلاعات گره های محلی می پردازیم. در این راستا، ما بر اساس رویکرد توجه گره برای نمودارها (GAT: Graph Attention Networks) شرح داده شده در [ 12 ] برای توسعه شبکه خود ایجاد می کنیم. این رویکرد امکان محاسبه شباهت های بین گره ها را با استفاده از ویژگی های آنها فراهم می کند. با این حال، این رویکرد در مورد ساختار نمودار جهانی ساده لوحانه است که می تواند برای ظرفیت مدل مضر باشد. بنابراین، در معماری عصبی خود، آن را با رمزگذاری اطلاعات نمودار جهانی همانطور که در بخش 4.1 توضیح داده شده است، گسترش می دهیم . اکنون، ما استفاده از ویژگی های سطح گره را برای پیاده سازی مکانیزم توجه توضیح می دهیم.
با توجه به مجموعه ای از ویژگی های گره اچ={ساعت→1،⋯،ساعت→ن}از یک شبکه گراف جی، جایی که ساعت→من∈آرrو r تعداد ویژگی های گره ها است υ∈V، تنظیم کردیم اچبه ویژگی هایی که با گره های برگردانده شده توسط الگوریتم 1 مطابقت دارند. این را می توان به عنوان زیر مجموعه ای از همه ویژگی های گره در نظر گرفت. ما یک مکانیسم توجه a را ابتدا با انجام یک تبدیل خطی اجرا می کنیمدبلیوساعت→مندر مورد ویژگی های یک گره ساعت→من. اگر yمن=دبلیوساعت→من، سپس می توانیم مقدار توجه را برای هر دو جفت گره محاسبه کنیم υمن،υjکه دارای یک لبه به صورت زیر هستند:
همنj=آ(yمن،yj).
مقادیر توجه بین هر جفت گره با استفاده از تابع softmax عادی می شود، بنابراین:
αمنj=سافت مکسj(همنj)=انقضاLeakyReLUآ→تیyمن”yj∑ک∈نمنانقضاLeakyReLUآ→تیyمن”yک.
اینجا، آ→بردار وزن است، ·تیtranspose است، ‖ عملگر الحاق است، و نمنهمسایگی یک گره است υمن. برای هدف این مقاله، ما فقط همسایگان مستقیم یک گره را در نظر می گیریم، یعنی یک هاپ. سپس، مقادیر توجه نرمال شده به عنوان یک ترکیب خطی از ویژگی‌های گره که نشان می‌دهند، از طریق یک تابع غیرخطی به لایه بعدی داده می‌شوند. σ(ما در این مقاله از نرم افزار مکس استفاده می کنیم) به این صورت:
ساعت→من”=σ∑j∈نمنαمنj·yj.
علاوه بر این، معادله ( 6 ) را می توان با استفاده از مکانیسم های توجه مستقل متعدد به شرح زیر گسترش داد:
ساعت→من”=”ک=1کσ∑j∈نمنαمنjک·yjک.
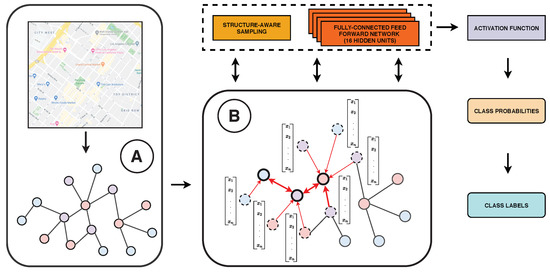
در اینجا، K تعداد مکانیسم های توجه مستقل را نشان می دهد، ‖ نشان دهنده عملیات الحاق است. αمنjکنشان دهنده مقادیر توجه نرمال شده است که توسط کمکانیسم توجه، و yjکماتریس وزن مربوطه است. ما K را روی هشت مکانیسم توجه در شبکه خود تنظیم کردیم. این مقدار K پایدارترین نتایج را در تحقیقات اولیه ما ایجاد کرد. با این وجود، ما نتایجی را برای سایر مکانیسم‌های توجه در بخش 6 نشان می‌دهیم . با استفاده از مکانیسم توجه چندگانه، ما تحولات هر مکانیزم را در لایه نهایی به هم متصل نمی کنیم. بلکه میانگین آنها را قبل از اعمال تابع softmax غیر خطی محاسبه می کنیم ( σمانند [ 12 ]. برای توضیح چارچوب عصبی ما به شکل 3 مراجعه کنید .
5. آزمایشات
ما آزمایش‌هایی را انجام می‌دهیم و مدل پیشنهادی را در برابر روش‌های پیشرفته ارزیابی می‌کنیم. این بخش شرحی از طرح آزمایشی به کار گرفته شده در این مقاله است.
5.1. توضیحات داده ها
داده های مورد استفاده در آزمایش های ما از OpenStreetMap (OSM) جمع آوری شد. ما از شبکه های خیابانی سه شهر – لس آنجلس، رم، و ونکوور که از طریق OSMNx API جمع آوری شده اند استفاده می کنیم [ 34 ]. این شهرها سه کشور و دو قاره را در بر می گیرند که نشان دهنده مجموعه متنوعی از الگوهای خیابانی است که اساس انتخاب آنها را تشکیل می دهد [ 6 ، 7 ، 35 ، 36 ]. شبکه‌های اصلی خیابان‌ها را با استفاده از نمایش لبه‌ای رمزگذاری می‌کردند که هر یال نشان‌دهنده یک خیابان بود. ما این نمایش را با استفاده از الگوریتم نمودار خطی [ 37 ] به معادل گره-گره آن تبدیل می کنیم. در اصل، این به این معنی است ن=|V|=|E|. کجا، N و |V|تعداد گره ها در نمایش گره-گره تبدیل شده است و |E|تعداد لبه های شبکه اصلی است. هر شبکه خیابانی یک نمودار توپولوژیکی است که در آن گره ها نشان دهنده موجودیت های خیابان و لبه های بین گره ها نشان دهنده تقاطع بین خیابان ها هستند. توجه داشته باشید که نمایش نمودار هر شبکه یک مولتی گراف بدون جهت است. اطلاعات مربوط به جهت دهی هر خیابان، یعنی یک طرفه بودن یا نبودن آن با استفاده از ویژگی های گره در نمودار کدگذاری می شود. ما گره ها را با آرایه ای غنی از اطلاعات زمینه ای با استفاده از رویکرد بافر چندگانه ثابت توضیح داده شده در [ 7 ] نسبت می دهیم. ما این رویکرد را در زیر در بخش 5.2 توضیح می دهیم. ما نه برچسب جاده را در نظر می گیریم: مسکونی، ثانویه، اولیه، تنه، پیوند اولیه، سوم، طبقه بندی نشده، پیوند بزرگراه و بزرگراه. لازم به ذکر است که تمامی نمودارها به هم متصل بودند.
ما توزیع کلاس نمودارها را در شکل 4 نشان می دهیم . در اینجا، می‌توانیم تنوع بالا بین کلاس‌ها را در هر گراف ببینیم. به یاد داشته باشید که این انگیزه اصلی پیشنهاد ما است. در جدول 2 ، آمار خلاصه ای از مجموعه داده ها را ارائه می کنیم. همانطور که در بخش 1 ذکر شد ، می بینیم که میانگین درجه ≤ 5 است. علاوه بر این، شایان ذکر است که چگالی این نمودارها بسیار کم است. مقادیر چگالی بین 1-بالا (بسیار متصل، خوشه ای) و 0-کم (بسیار گسترده) متغیر است.
5.2. نسبت دادن گره های گراف
ما گره های نمودار را با استفاده از اطلاعات توصیفی در مورد خیابان با استفاده از رویکرد بافر چندگانه ثابت توضیح داده شده در [ 7 ] نسبت می دهیم. تعداد اشیاء از پیش تعیین شده را در بافرهای متعددی که روی هر خیابان گذاشته شده اند جمع آوری می کنیم. بافرها چند ضلعی با گوشه های گرد هستند که شکل خیابان ها را به خود می گیرند. بافرها چند ضلعی با سوراخ هستند، به استثنای چند ضلعی اول. برای آزمایش‌های خود، شعاع چندضلعی‌ها را از 10 متر تا 1000 متر تنظیم کردیم. مجموعه ای از اشیاء در نظر گرفته شده در بافرها در جدول 3 نشان داده شده است. در OSM، اطلاعات توصیفی در مورد اشیا با استفاده از انواع برچسب گروه بندی می شوند. هر نوع برچسب می تواند چندین مقدار تگ را در خود جای دهد. ما پنج نوع تگ و 34 مقدار تگ را در نظر می گیریم. علاوه بر این، اطلاعات توصیفی در مورد خیابان‌های جمع‌آوری‌شده از OSM مانند طول خیابان‌ها و یک مقدار بولی که نشان می‌دهد گره یک خیابان یک طرفه است یا خیر را شامل می‌شود. تعداد کل صفات برای هر نمودار در جدول 2 آورده شده است . اختلاف ثبت شده برای لس آنجلس به دلیل در دسترس نبودن برخی از مقادیر برچسب جمع آوری شده برای شهرهای دیگر است.
5.3. الگوی استراتژی آموزشی
ما شبکه عصبی خود را که در بخش 4 توضیح داده شده است با استفاده از الگوریتم 2 برای 100 دوره آموزش می دهیم. معماری ما یک شبکه پیشخور 2 لایه با یک لایه پنهان است که از لایه توجهی که در [ 12 ] توضیح داده شده است اقتباس شده است. خروجی لایه پنهان با استفاده از واحد خطی نمایی (ELU) فعال می‌شود، فعال‌سازی softmax برای تولید احتمالات کلاس به لایه نهایی اعمال می‌شود [ 30 ]. ما نرخ یادگیری را تعیین می کنیم، λ=1×10-3شایان ذکر است که این مقدار در آزمایشات اولیه ما بهترین نتایج را به همراه داشت. تابع ضرر ما تلفات آنتروپی متقابل است و با استفاده از قانون بهینه‌سازی Adam [ 38 ] در PyTorch [ 39 ] به حداقل می‌رسد. برای اهداف آزمایشی، شبکه را با استفاده از تعداد سرهای توجه زیر آموزش دادیم {2،3،4،6،8،10}.
گره های مورد استفاده برای آموزش با استفاده از الگوریتم 1 انتخاب می شوند. گره های اعتبار سنجی و آزمون قبل از زمان قطار تنظیم می شوند. در آزمایش‌های خود، تعداد گره‌های اعتبارسنجی و آزمایش را برای هر شهر برای همه مدل‌ها برابر تعیین کردیم. بنابراین، علی‌رغم تفاوت در تعداد اندازه‌های کلاس، این یکنواختی به بینشی عینی در عملکرد هر مدل اجازه می‌دهد. ما اندازه گره های اعتبار سنجی و آزمایش را به عنوان تابعی از کمترین کلاس در هر مجموعه داده از پیش تعیین می کنیم. ما توقف زودهنگام را در طول آموزش مدل با ذخیره بهترین مدل اعمال می کنیم که بعداً برای ارزیابی استفاده می شود. توجه داشته باشید که بهترین مدل با استفاده از گره های اعتبارسنجی ارزیابی می شود. مدل در هر دوره با استفاده از مجموعه ای از گره های اعتبار سنجی تعریف شده توسط ماسک تایید می شود Vv=ρ(جی). ماسک مجموعه ای از مقادیر بولی است که گره هایی را که باید انتخاب شوند، توصیف می کند. ارزیابی مدل با استفاده از گره های آزمایشی در بخش 6 ارائه شده است .
| الگوریتم 2: آموزش مدل. |
 |
علاوه بر این، ما مدل ها را به دو صورت متوازن و متناسب آموزش می دهیم . برای اولی، ما اطمینان می‌دهیم که گره‌های قطار متعادل هستند، نمونه‌برداری شده تا کمترین کلاس است. برای دومی، نمونه ای از گره های قطار را برای هر کلاس به نسبت اندازه آن در نمودار انتخاب می کنیم. این رویکرد آموزشی دو طرفه طراحی شده است تا هم یک مورد ایده آل (متعادل) و هم مورد کلاس مغرضانه (متناسب) را نشان دهد. از الگوریتم 2، τبه طور جداگانه برای هر دو رویکرد آموزشی بر اساس اندازه کلاس یا مورد متعادل تعریف شده است، در حالی که ρبرای همه آزمایش ها یکسان باقی می ماند. ما نتایج این آزمایش‌ها را در بخش 6 ارائه می‌کنیم . شبکه های عصبی با استفاده از PyTorch [ 39 ] پیاده سازی می شوند.
5.4. روش های پایه
علاوه بر ارزیابی پیشنهاد ما در برابر GAT [ 12 ]، ما پیشنهاد خود را با دو روش پیشرفته مقایسه می کنیم: GCN [ 11 ] و GraphSAGE [ 13 ]. هر دو روش در این مقاله با آموزش 100 دوره اجرا شده است. ما مدل های آموزش دیده را در مجموعه اعتبارسنجی ارزیابی می کنیم و بهترین عملکرد را ذخیره می کنیم. فراپارامترهای ذکر شده در اینجا پس از ارزیابی عملکرد اولیه انتخاب شدند. از دست دادن آنتروپی متقاطع با استفاده از قانون بهینه‌سازی آدام به حداقل می‌رسد.
5.4.1. Graph Convolutional Network (GCN)
ما شبکه کانولوشن گراف پیشنهاد شده در [ 11 ] را پیاده سازی می کنیم. شبکه ما یک شبکه فید فوروارد 2 لایه با 16 ویژگی پنهان است. ما استفاده می کنیم آرELUتابع فعال سازی برای لایه پنهان در طول آموزش، ما از L2منظم سازی با λ=0.0001. لایه نهایی با استفاده از تابع softmax فعال می شود.
5.4.2. GraphSAGE
ما شبکه پیشنهادی در [ 13 ] را به عنوان یک شبکه پیشخور سه لایه با 16 ویژگی پنهان راه اندازی کردیم. تابع فعال سازی برای لایه های پنهان است آرELUو softmax برای لایه خروجی. طرح تجمیع محله استفاده شده میانگین است. ما نرخ یادگیری را تعیین می کنیم λ=0.001.
5.5. پیچیدگی الگوریتمی
هزینه محاسباتی استفاده از سرهای توجه چندگانه ( K ) در چارچوب عصبی ما، حافظه و زمان مورد نیاز را با ضریب K افزایش می‌دهد . علاوه بر این، محاسبه معادله ( 1 ) نیازمند پیمایش گره‌ها در نمودار حداقل یک بار است. به ویژه، این می تواند در هنگام محاسبه بسیار گران باشد ب، نیاز دارد Θ(V3)زمان با استفاده از یک رویکرد ساده لوحانه در اجرای خود، ما تقریب می کنیم ببا استفاده از رویکرد شرح داده شده در [ 33 ] با یک نمونه 25٪ از گره های نمودار. این امر زمان مورد نیاز را کاهش می دهد O(V·E)، جایی که Vو Eتعداد گره ها و یال ها را به ترتیب در نمودار نشان دهید. با این وجود، زمانی که منابع محاسباتی محدود هستند، این هنوز می‌تواند چالشی ایجاد کند و ما این را به عنوان محدودیت احتمالی پیشنهاد خود می‌دانیم.
6. نتایج
6.1. ارزیابی مدل های آموزش دیده
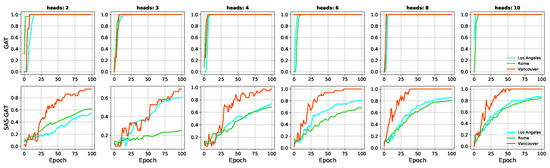
در شکل 5 و شکل 6 ، دقت مدل را در زمان قطار ارائه می کنیم. برای اختصار، ما فقط دقت های به دست آمده از مدل هایی را نشان می دهیم که با استفاده از مجموعه متعادلی از گره های قطار آموزش دیده اند. ما مدل‌هایی را که ساده‌لوحانه با استفاده از رویکرد شرح‌داده‌شده در [ 12 ] آموزش داده شده‌اند را با رویکرد خود مقایسه می‌کنیم (SAS-GAT). در شکل 5 ، می‌توانیم پیشرفت ثابت مدل را در حین همگرایی مشاهده کنیم. این یک تضاد آشکار با نتایج عملکرد مدل GAT است که به سرعت به اوج خود می رسد. این مشاهدات نشان‌دهنده اضافه‌برازش مدل، نقص شناخته‌شده شبکه‌های عصبی نمودار [ 17 ] است.
ما مدل های آموزش دیده را با ارزیابی آنها با استفاده از میانگین نمره F1 میکرو و کلان مقایسه می کنیم. فرمول کلی امتیاز F1 در معادله ( 8 ) آورده شده است. به طور خاص، ما مدل های آموزش دیده را با مجموعه متعادل گره های آموزشی (به بخش 5.3 مراجعه کنید ) با استفاده از امتیاز F1 میکرو مقایسه می کنیم. در حالی که، برای مدل‌هایی که با استفاده از گره‌های آموزشی متناسب با اندازه کلاس آنها ساخته شده‌اند، از امتیاز F1 ماکرو استفاده می‌کنیم، زیرا این معیار اندازه کلاس‌ها را جریمه می‌کند:
اف1-نمره=2∗(پrهجمنسمنon∗rهجآلل)(پrهجمنسمنon+rهجآلل).
ما نتایج را در جدول 4 ارائه می کنیم . در این جداول می بینیم که نتایج با توجه به تعداد هدهای استفاده شده برای آموزش مدل نشان داده شده است. مقادیر موجود در این جداول میانگین هایی است که پس از 10 بار تکرار گرفته شده و انحراف معیار آنها در کنار آن ارائه شده است. می بینیم که تقریباً در همه موارد، انحراف معیار ناچیز است که نشان می دهد نتایج مدل های ما تصادفی نیستند.
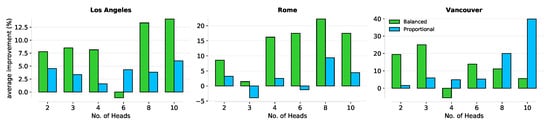
ما عملکرد چارچوب عصبی خود را با استفاده از روش نمونه‌گیری پیشنهادی در شکل 7 برجسته می‌کنیم . مقادیر ترسیم شده در این شکل میانگین درصد بهبود (نمره F1) ثبت شده از چارچوب عصبی ما است. ما موارد را برای تعداد سرهای مختلف نشان می دهیم. مشاهده می شود که بهبود کلی ناشی از استفاده بیشتر از سرهای توجه تحت تأثیر رویکرد ما قرار نمی گیرد. به طور کلی، می‌توانیم ببینیم که پیشنهاد ما در مقایسه با روش سنتی، منجر به یک مدل تعمیم‌پذیرتر می‌شود.
6.2. ارزیابی تعمیم پذیری GNN ها
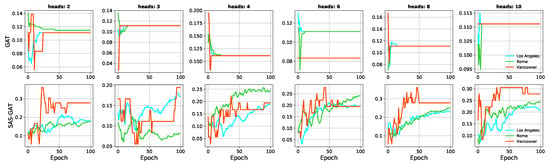
از شکل 5 می توان مشاهده کرد که دقت تمرین GNN وانیلی به سرعت در 20 دوره اول در همه موارد به اوج می رسد. این رفتار معمولاً نشان دهنده این است که یک مدل بیش از حد برازش می کند. برازش بیش از حد مدل و هموارسازی بیش از حد به عنوان محدودیت های GNN ها [ 17 ] شناسایی شده است. این زمانی تایید می شود که شکل 6 را در نظر بگیریم که دقت اعتبارسنجی مدل ها را نشان می دهد. در اینجا، می‌توانیم ببینیم که نمونه‌گیری ما، مدل را قادر می‌سازد تا در هر دوره بهتر شود و تعمیم یابد. شایان ذکر است که مجموعه یکسانی از گره‌های اعتبارسنجی برای هر مجموعه داده برای همه مدل‌ها استفاده می‌شود.
ظرفیت تعمیم را در دو بعد مورد ارزیابی قرار می دهیم: حالت متعادل و حالت نامتعادل. ما نتایج را در جدول 4 ارائه می کنیم . در اولی، گره های آموزشی متعادل هستند در حالی که در دومی، نسبتی از اندازه های کلاس استفاده می شود. ما از دو نوع (ریز و کلان) امتیاز F1 برای نشان دادن این موارد استفاده می کنیم. به وضوح و همانطور که انتظار می رود، حالت متعادل تعمیم بهتری برای همه مجموعه داده ها ایجاد می کند. با این حال، می‌توانیم ببینیم که در هر دو مورد، چارچوب عصبی ما بهتر تعمیم می‌یابد. در حالت نامتعادل، جایی که واریانس بین اندازه‌های کلاس می‌تواند مدل را به بیش از حد برازش در کلاس اکثریت سوق دهد، می‌بینیم که رویکرد نمونه‌گیری ما قادر به کاهش این مشکل و تولید نتایج برتر است.
6.3. مقایسه خطوط پایه
ما روش نمونه‌گیری خود را بر اساس دو خط پایه دیگر ارزیابی می‌کنیم: یک شبکه کانولوشن گراف همانطور که در [ 11 ] پیشنهاد شده است و GraphSAGE [ 13 ]. برای هر دو روش، ما تکنیک نمونه گیری خود را به کار می بریم. آموزش مدل بر روی همان گره های گراف استفاده شده برای روش های دیگر انجام می شود. ما خلاصه ای از نتایج را در جدول 5 ارائه می کنیم. نتایج ارائه شده میانگین نمرات F1 میکرو و کلان است. متریک امتیاز F1 میکرو برای مدل‌هایی که با استفاده از مجموعه متوازن گره‌ها آموزش دیده‌اند، استفاده می‌شود، در حالی که متریک امتیاز F1 کلان برای حالت متناسب استفاده می‌شود. می بینیم که استفاده از روش نمونه گیری ما (SAS) در برخی موارد منجر به نتایج بهتر می شود. علاوه بر این، از ستون‌های کلان مشاهده می‌شود که تکنیک نمونه‌گیری ما به طور کلی عملکرد را زمانی بهبود می‌بخشد که اندازه کلاس‌ها بایاس باشد. با این وجود، عملکرد این مدل ها به اندازه مدل توجه چشمگیر نیست (در جدول 4 مشاهده می شود ). این مشاهدات نشان می دهد که مدل های توجه ممکن است برای نمودارهای پر سر و صدا دنیای واقعی مناسب تر باشند [ 12 ، 22 ].
7. نتیجه گیری
در این مقاله، ما یک رویکرد جدید برای نمونه‌گیری گره‌ها در هنگام آموزش شبکه‌های عصبی گراف برای نمودارهای فضایی پیشنهاد کردیم. انگیزه این کار نیاز به بهبود تعمیم پذیری GNN ها برای نمودارهای پر سر و صدا در دنیای واقعی است. متعاقباً، این رویکرد دستیابی به این هدف را با رمزگذاری ساختار نمودار جهانی در فرآیند توسعه مدل پیشنهاد می‌کند. با استفاده از ساختار نمودار با استفاده از درون کلاسی و جهانی-ژئودزیکی اجرا شد.فاصله ها. این مشکل به عنوان یک طبقه بندی گره با یکی برای نمودارهای نویزدار، مغرضانه و چند کلاسه فرموله شد. این رویکرد بر روی سه مجموعه داده بزرگ در دنیای واقعی که دارای واریانس بالایی بین اندازه‌های کلاس هستند، ارزیابی شد. ارزیابی‌های ما نشان داد که رویکرد نمونه‌گیری ما می‌تواند مشکل بیش از حد برازش و هموار شدن بیش از حد مشاهده شده در GNNها را کاهش دهد. علاوه بر این، ما تشخیص دادیم که تکنیک ما به یک مدل قابل تعمیم تر منجر می شود. در نتیجه به سوالات مطرح شده در بخش 1 پرداختیم: (1) GNNهای وانیلی در نمودارهای فضایی به خوبی تعمیم نمی‌یابند، حداقل در مقایسه با رویکردی که از ساختار جهانی استفاده می‌کند. (2) وقتی ساختار جهانی در نظر گرفته شود، عملکرد مدل‌های GNN می‌تواند به طور قابل توجهی بهبود یابد. (3) ظرفیت تعمیم مدل های GNN را می توان با در نظر گرفتن ساختار نمودار جهانی بهبود بخشید.
اهمیت نتایج ما با توجه به علاقه اخیر به روش‌های عصبی گراف در میان محققان قدردانی می‌شود. محدودیت روش‌های سنتی یادگیری ماشینی این است که آنها استقلال بین موجودیت‌ها را فرض می‌کنند. این باعث می شود آنها در موقعیت هایی که موجودیت ها یک رابطه مشترک دارند (یعنی وابستگی نشان می دهند) نامناسب باشند. شبکه‌های عصبی نمودار (GNN) با حفظ وابستگی رابطه‌ای بین موجودات در طول یادگیری، این شکاف را پر می‌کنند. با این حال، تمرکز GNN ها بر همسایگی محلی با بی توجهی به ساختار جهانی می تواند استحکام مدل را برای نمودارهای فضایی مختل کند. ما بر این باوریم که کار ما در این مقاله الهام‌بخش تحقیقات گسترده‌تری برای بهبود GNN برای وظایف فضایی خواهد بود. در این مقاله، اهمیت ساختار جهانی برای یادگیری در نمودارهای فضایی را نشان دادیم. برای کارهای آینده،
منابع
- Battaglia، PW; همریک، جی بی. باپست، وی. سانچز-گونزالس، آ. زامبالدی، وی. مالینوفسکی، م. تاچتی، آ. راپوسو، دی. سانتورو، آ. فاکنر، آر. و همکاران سوگیری های استقرایی رابطه ای، یادگیری عمیق و شبکه های نموداری. arXiv 2018 , arXiv:1806.01261. [ Google Scholar ]
- لی، جی. کای، دی. او، X. نمایش نمودار در سطح یادگیری برای کشف دارو. arXiv 2017 , arXiv:1709.03741. [ Google Scholar ]
- تولستایا، ای. گاما، اف. پائولوس، جی. پاپاس، جی. کومار، وی. Ribeiro، A. یادگیری کنترل‌کننده‌های غیرمتمرکز برای ازدحام ربات‌ها با شبکه‌های عصبی گراف. arXiv 2019 ، arXiv:1903.10527. [ Google Scholar ]
- لیو، ز. چن، سی. یانگ، ایکس. ژو، جی. لی، ایکس. Song, L. گراف ناهمگن شبکه های عصبی برای شناسایی حساب های مخرب. در مجموعه مقالات بیست و هفتمین کنفرانس بین المللی ACM در مدیریت اطلاعات و دانش، تورین، ایتالیا، 22 تا 26 اکتبر 2018؛ ص 2077–2085. [ Google Scholar ]
- کورکوران، پ. جیلانی، م. مونی، پی. برتولتو، ام. استنتاج معناشناسی از هندسه: مورد شبکه های خیابانی. در مجموعه مقالات بیست و سومین کنفرانس بین المللی SIGSPATIAL در مورد پیشرفت در سیستم های اطلاعات جغرافیایی، Bellevue، WA، ایالات متحده، 3-6 نوامبر 2015. پ. 42. [ Google Scholar ]
- ایدیانوزی، سی. مک آردل، جی. پارادایم یادگیری انتقالی برای شبکه های فضایی. در مجموعه مقالات سی و چهارمین سمپوزیوم ACM/SIGAPP در محاسبات کاربردی، لیماسول، قبرس، 8 تا 12 آوریل 2019؛ صص 659-666. [ Google Scholar ]
- ایدیانوزی، سی. برتولتو، ام. مکاردل، جی. کاوش یادگیری بودجه برای استنتاج معنایی داده محور از طریق توابع شهری. دسترسی IEEE 2020 ، 8 ، 32258–32269. [ Google Scholar ] [ CrossRef ]
- او هست.؛ باستانی، ف. جگوانی، س. پارک، ای. آببر، س. علیزاده، م. بالاکریشنان، اچ. چاولا، س. مدن، اس. صادقی، MA RoadTagger: استنتاج ویژگی های جاده ای قوی با شبکه های عصبی نمودار. در مجموعه مقالات سی و چهارمین کنفرانس AAAI در مورد هوش مصنوعی، AAAI 2020، نیویورک، نیویورک، ایالات متحده آمریکا، 7 تا 12 فوریه 2020؛ صفحات 10965-10972. [ Google Scholar ]
- LeCun، Y.; Bengio، Y. شبکه‌های Convolutional برای تصاویر، گفتار و سری‌های زمانی. هندب نظریه مغز شبکه عصبی. 1995 ، 3361 ، 1995. [ Google Scholar ]
- کارپاتی، ا. جانسون، جی. Fei-Fei, L. تجسم و درک شبکه های تکراری. arXiv 2015 , arXiv:1506.02078. [ Google Scholar ]
- Kipf، TN; Welling, M. طبقه بندی نیمه نظارت شده با شبکه های کانولوشن گراف. arXiv 2016 , arXiv:1609.02907. [ Google Scholar ]
- ولیچکوویچ، پ. کوکورول، جی. کازانووا، آ. رومرو، آ. لیو، پی. Bengio، Y. گراف شبکه های توجه. arXiv 2017 , arXiv:1710.10903. [ Google Scholar ]
- همیلتون، دبلیو. یینگ، ز. Leskovec, J. یادگیری نمایش استقرایی در نمودارهای بزرگ. در مجموعه مقالات پیشرفت‌ها در سیستم‌های پردازش اطلاعات عصبی 30: کنفرانس سالانه سیستم‌های پردازش اطلاعات عصبی 2017، لانگ بیچ، کالیفرنیا، ایالات متحده آمریکا، 4 تا 9 دسامبر 2017. صص 1024–1034. [ Google Scholar ]
- جپسن، تی اس؛ جنسن، CS; Nielsen، TD Graph شبکه های کانولوشنال برای شبکه های جاده ای. در مجموعه مقالات بیست و هفتمین کنفرانس بین‌المللی ACM SIGSPATIAL در مورد پیشرفت‌ها در سیستم‌های اطلاعات جغرافیایی، شیکاگو، IL، ایالات متحده آمریکا، 5 تا 8 نوامبر 2019؛ صص 460-463. [ Google Scholar ]
- راث، سی. کانگ، اس ام. باتی، م. Barthélemy, M. ساختار جنبش های شهری: فعالیت چند مرکزی و جریان های سلسله مراتبی درهم تنیده. PLoS ONE 2011 ، 6 ، e15923. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
- Barthélemy، M. شبکه های فضایی. فیزیک Rep. 2011 , 499 , 1-101. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
- لی، کیو. هان، ز. بینش Wu، XM Deeper در مورد شبکه های کانولوشن گراف برای یادگیری نیمه نظارت شده. در مجموعه مقالات سی و دومین کنفرانس AAAI در مورد هوش مصنوعی، ریورساید، NO، ایالات متحده آمریکا، 2 تا 7 فوریه 2018. [ Google Scholar ]
- رانگ، ی. هوانگ، دبلیو. خو، تی. Huang, J. Dropedge: به سمت شبکه های پیچیده گراف عمیق در طبقه بندی گره. arXiv 2019 ، arXiv:1907.10903. [ Google Scholar ]
- برونا، جی. زارمبا، دبلیو. اسلم، آ. LeCun، Y. شبکه های طیفی و شبکه های متصل به صورت محلی روی نمودارها. arXiv 2013 , arXiv:1312.6203. [ Google Scholar ]
- Duvenaud، DK; مکلارین، دی. Iparraguirre، J. بومبارل، آر. هیرزل، تی. آسپورو-گوزیک، ع. آدامز، RP شبکه های کانولوشن بر روی نمودارها برای یادگیری اثر انگشت مولکولی. در مجموعه مقالات پیشرفت‌ها در سیستم‌های پردازش اطلاعات عصبی 28: کنفرانس سالانه سیستم‌های پردازش اطلاعات عصبی 2015، مونترال، QC، کانادا، 7 تا 12 دسامبر 2015. صص 2224–2232. [ Google Scholar ]
- دیفرارد، ام. برسون، ایکس. Vandergheynst، P. شبکه‌های عصبی کانولوشنال روی نمودارها با فیلتر کردن طیفی سریع محلی. در مجموعه مقالات پیشرفت‌ها در سیستم‌های پردازش اطلاعات عصبی 29: کنفرانس سالانه سیستم‌های پردازش اطلاعات عصبی 2016، بارسلون، اسپانیا، 5 تا 10 دسامبر 2016. صص 3844–3852. [ Google Scholar ]
- ژو، جی. کوی، جی. ژانگ، ز. یانگ، سی. لیو، ز. وانگ، ال. لی، سی. Sun، M. گراف شبکه های عصبی: بررسی روش ها و کاربردها. arXiv 2018 , arXiv:1812.08434. [ Google Scholar ]
- دیائو، ز. وانگ، ایکس. ژانگ، دی. لیو، ی. زی، ک. او، S. نمودار پویا فضایی-زمانی شبکه های عصبی کانولوشن برای پیش بینی ترافیک. در مجموعه مقالات سی و سومین کنفرانس AAAI در مورد هوش مصنوعی، هونولولو، HI، ایالات متحده آمریکا، 27 ژانویه تا 1 فوریه 2019؛ جلد 33، ص 890–897. [ Google Scholar ]
- بونافیلیا، دی. گیل، جی. باسو، س. یانگ، دی. ساختن نقشه‌های با وضوح بالا برای کمک‌های بشردوستانه و توسعه با یادگیری ضعیف و نیمه نظارت. در مجموعه مقالات کنفرانس IEEE در کارگاه های آموزشی بینایی رایانه و تشخیص الگو، لانگ بیچ، کالیفرنیا، ایالات متحده آمریکا، 16 تا 17 ژوئن 2019؛ صفحات 1-9. [ Google Scholar ]
- بلژیک، م. تاملینوویچ، آی. لامپولتشامر، تی. بلاشکه، تی. Höfle, B. طبقه‌بندی مبتنی بر هستی‌شناسی انواع ساختمان‌های شناسایی شده از داده‌های اسکن لیزری هوابرد. Remote Sens. 2014 , 6 , 1347–1366. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
- سیاه، خود همبستگی شبکه WR در شبکه حمل و نقل و سیستم های جریان. Geogr. مقعدی 1992 ، 24 ، 207-222. [ Google Scholar ] [ CrossRef ]
- چن، جی. لای، سی. منگ، ایکس. خو، جی. Hu, H. خوشه بندی اشیاء متحرک در شبکه های فضایی. در کنفرانس بین المللی سیستم های پایگاه داده برای کاربردهای پیشرفته ; Springer: برلین/هایدلبرگ، آلمان، 2007; صص 611-623. [ Google Scholar ]
- کائول، م. یانگ، بی. Jensen, CS ساخت شبکه های فضایی سه بعدی دقیق برای فعال کردن نسل بعدی سیستم های حمل و نقل هوشمند. در مجموعه مقالات چهاردهمین کنفرانس بین المللی IEEE در سال 2013 در مدیریت داده های تلفن همراه، میلان، ایتالیا، 3 تا 6 ژوئن 2013. جلد 1، ص 137–146. [ Google Scholar ]
- گیلمر، جی. Schoenholz، SS; رایلی، پی اف. وینیالز، او. ارسال پیام عصبی دال، جنرال الکتریک برای شیمی کوانتومی. در مجموعه مقالات سی و چهارمین کنفرانس بین المللی یادگیری ماشین، ICML 2017، سیدنی، NSW، استرالیا، 6 تا 11 اوت 2017. صص 1263-1272. [ Google Scholar ]
- دان، RA; کمپبل، NA در مورد جفت شدن توابع جریمه فعال سازی سافت مکس و آنتروپی متقابل و استخراج تابع فعال سازی سافت مکس. در مجموعه مقالات هشتمین کنفرانس استرالیا در مورد شبکه های عصبی 1997; منبع: ملبورن، استرالیا، 1997; جلد 181، ص. 185. [ Google Scholar ]
- اولدهام، اس. فولچر، بی. پارکز، ال. آرناتکوویچیوت، ا. سو، سی. فورنیتو، الف. سازگاری و تفاوت بین معیارهای مرکزیت در میان طبقات مجزا از شبکه‌ها. PLoS ONE 2019 , 14 . [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
- شفاف سازی مفهومی فریمن، LC مرکزیت در شبکه های اجتماعی. Soc. شبکه 1978 ، 1 ، 215-239. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
- برندز، یو. Pich, C. تخمین مرکزیت در شبکه های بزرگ. بین المللی جی. بیفورک. آشوب 2007 ، 17 ، 2303-2318. [ Google Scholar ] [ CrossRef ]
- بوئینگ، G. OSMnx: روش‌های جدید برای دستیابی، ساخت، تجزیه و تحلیل و تجسم شبکه‌های خیابانی پیچیده. محاسبه کنید. محیط زیست سیستم شهری 2017 ، 65 ، 126-139. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
- شکر، س. ایوانز، ام آر. کانگ، جی.ام. Mohan, P. شناسایی الگوها در اطلاعات فضایی: بررسی روشها. وایلی اینتردیسیپ. Rev. Data Min. بدانید. کشف کنید. 2011 ، 1 ، 193-214. [ Google Scholar ] [ CrossRef ]
- Alexander, C. A City is Not a Tree ; Sustasis Press/Off The Common Books: White Salmon، WA، ایالات متحده آمریکا، 2017. [ Google Scholar ]
- همینگر، آر. Beineke، L. نمودارهای خط و نمودارهای خط، موضوعات منتخب در نظریه گراف . Lowell, WB, Wilson, RJ, Eds. The Academic Press: کمبریج، MA، ایالات متحده آمریکا، 1978. [ Google Scholar ]
- Kingma، DP; Ba, J. Adam: روشی برای بهینه سازی تصادفی. arXiv 2014 ، arXiv:1412.6980. [ Google Scholar ]
- پاسسکه، آ. گراس، اس. ماسا، اف. لرر، ا. بردبری، جی. چانان، جی. کیلین، تی. لین، ز. گیملشاین، ن. آنتیگا، ال. و همکاران PyTorch: یک سبک ضروری، کتابخانه یادگیری عمیق با کارایی بالا. در مجموعه مقالات پیشرفت‌ها در سیستم‌های پردازش اطلاعات عصبی 32: کنفرانس سالانه سیستم‌های پردازش اطلاعات عصبی 2019، NeurIPS 2019، ونکوور، BC، کانادا، 8 تا 14 دسامبر 2019. [Google Scholar ]
شکل 1. شرح روش پیشنهادی ما برای مورد یادگیری انتقالی. ما نمونه برداری گره را با استفاده از ساختار کلی نمودار انجام می دهیم. ورودی شبکه عصبی گراف (GNN) یک گراف ورودی تا حدی برچسب گذاری شده است. ساختار گراف جهانی و ویژگی های گره برای آموزش شبکه ما استفاده می شود. نمودار خروجی کاملاً برچسب گذاری شده است، جایی که رنگ های گره نشان دهنده عضویت در کلاس است.
شکل 2. تصویری از تأثیر گره در نمودارهای چند کلاسه. رنگ ها عضویت یک کلاس گره را نشان می دهند. ( 1 ) گره سبز دارای مرکزیت نزدیکی بالایی در میان گروه گره ها خواهد بود. در این مورد، فرض می کنیم همه آنها متعلق به یک کلاس هستند. ( 2 ) گره سبز دارای مرکزیت بین دو کلاستر است. در اینجا، گره سبز می تواند به هر یک از خوشه های گره تعلق داشته باشد.
شکل 3. شرح روش ما. ( الف ) گره های شبکه خیابانی با استفاده از اطلاعات زمینه ای آنها نسبت داده می شوند. ( ب ) روش نمونه‌گیری پیشنهادی برای انتخاب گره‌ها بر اساس موقعیت آنها در نمودار استفاده می‌شود. گره های دارای خطوط پررنگ، نمونه برداری شده و گره های دارای خطوط نقطه چین همسایه آنها هستند. وزن خطوط قرمز نشان دهنده قدرت توجه داده شده به اطلاعات از یک گره است.
شکل 4. توزیع برچسب خیابان ها در شهرهای مختلف. ما شاهد واریانس بالایی بین طبقات مختلف خیابان هستیم. محور y نسبت هر کلاس خیابان است که بر روی آن ترسیم شده است لogمقیاس
شکل 5. نمودارهایی که دقت آموزش مدل را در هر دوره در زمان قطار نشان می دهد. هر ستون نشان دهنده تعداد سرهای توجه مورد استفاده برای آموزش مدل ها است. ردیف ها دقت GAT و روش ما را نگه می دارند.
شکل 6. نمودارهایی که دقت اعتبارسنجی مدل را در هر دوره برای مجموعه اعتبار سنجی نشان می دهد. هر ستون نشان دهنده تعداد سرهای توجه مورد استفاده برای آموزش مدل ها است. ردیف ها دقت GAT و روش ما را نگه می دارند.
شکل 7. نمودارهایی که میانگین درصد بهبود را نشان می دهند. هر نمودار نشان دهنده نتایج تجربی از هر شهر است و خطوط نشان می دهد که آیا گره های آموزشی متعادل بودند یا نسبتی از اندازه کلاس اصلی. با استفاده از روش نمونه گیری ما شاهد بهبودی تا 20 درصد هستیم.
بدون دیدگاه