بهینه ترین تخمین جزر و مد نجومی با استفاده از تخمینگر حداکثر احتمال با هیبریداسیون مدل های اقیانوسی چندگانه

خلاصه

توسعه یک پایین‌ترین جزر و مد نجومی دقیق (LAT) به شکل پیوسته برای بسیاری از کاربردهای دریایی ضروری است، زیرا می‌توان از آن برای توسعه داده‌های کنترل عمودی پیوسته دقیق برای برنامه‌های بررسی هیدروگرافی و تولید نمودارهای ناوبری الکترونیکی پویا دقیق برای ناوبری ایمن دریایی توسط دریانوردان استفاده کرد. . LAT را می توان در یک (سطح) پیوسته با استفاده از یک مدل سطح تخمینی LAT از مدل اقیانوس هیدرودینامیکی همراه با مقادیر نقطه LAT گسسته ساحلی که از مجموعه داده های اندازه گیری جزر و مد به دست می آید توسعه داد تا مدل سطح LAT اصلاح شده را ارائه دهد. در این مقاله، یک مدل سطح دقیق LAT برای مطالعه موردی دریای سرخ با استفاده از برآوردگر حداکثر احتمال (MLE) با هیبریداسیون مدل‌های اقیانوسی هیدرودینامیکی متعدد، یعنی مدل‌های WebTide، FES2014، DTU10 و EOT11a توسعه داده شد. مشخص شد که مدل LAT ترکیبی بهینه توسعه‌یافته با استفاده از MLE با هیبریداسیون مدل‌های هیدرودینامیکی اقیانوسی متعدد از 0.1 متر تا 1.63 متر، مرتبط با حدود 2.4 سانتی‌متر عدم قطعیت در سطح اطمینان 95 درصد در منطقه مورد مطالعه دریای سرخ است. برای تأیید صحت مدل توسعه‌یافته، مقایسه بین مدل LAT ترکیبی بهینه ایجاد شده از هیبریداسیون مدل‌های اقیانوسی هیدرودینامیکی چندگانه با استفاده از روش MLE با مدل‌های LAT منفرد برآورد شده از مدل‌های اقیانوسی WebTide، FES2014، DTU10 یا EOT11a انجام شد. عدم قطعیت های مرتبط در سطح اطمینان 95 درصد برآورد شده است. مشخص شد که دقت مدل LAT هیبریدی بهینه نسبت به مدل‌های LAT منفرد تخمین زده‌شده از مدل‌های اقیانوس منفرد با بهبودی حدود 50 درصد به طور متوسط، بر اساس عدم قطعیت‌های برآورد شده، برتر است.

کلید واژه ها:

دریای سرخ ؛ LAT ; اقیانوس ; MLE ; مدل هیبریدی

1. معرفی

داده‌های عمق سنجی به نمودار ملی کاهش می‌یابد که عمدتاً پایین‌ترین جزر و مد نجومی (LAT) را در یک زمان خاص نشان می‌دهد. بنابراین، نیاز به توسعه یک نمودار نمودار به شکل پیوسته ضروری است تا بتوان آن را از/به داده پیوسته دیگری مانند میانگین سطح دریا (MSL) تبدیل کرد. با استفاده روزافزون از موقعیت یابی عمودی دقیق سیستم ماهواره ای ناوبری جهانی (GNSS) در کاربردهای دریایی، خطاهای وارد شده به نمودارها با استفاده کنونی از داده های سنتی نقاط گسسته از گیج های جزر و مد می تواند به بخش مهمی از کل خطای عمودی تبدیل شود. بنابراین، یک سطح مرجع پیوسته برای مبدأ کنترل عمودی بهتر توسط مبدل‌ها و مبدل‌های پیوسته ارائه می‌شود [ 1]. توسعه یک LAT دقیق به صورت پیوسته برای بسیاری از کاربردهای دریایی ضروری است، جایی که می توان از آن برای توسعه یک داده کنترل عمودی پیوسته دقیق برای کاربردهای بررسی هیدروگرافی و تولید نمودارهای ناوبری الکترونیکی دینامیکی دقیق برای ناوبری ایمن دریایی توسط دریانوردان استفاده کرد [ 2 ].

مبنا نمودار پیوسته یک سطح مرجع دوبعدی نسبت به یک مبدأ مرجع عمودی پیوسته مانند مدل بیضی LAT تا WGS-84 است. سازمان‌های هیدروگرافیک متعددی در سرتاسر جهان متوجه شده‌اند که داده‌های عمودی هیدروگرافیک، مانند داده‌های نمودار، اکنون نیاز به درمان مداوم دارند. این داده‌های نمودار پیوسته، به‌ویژه در اداره ملی اقیانوسی و جوی (NOAA’s VDatum datum [ 3 ])، دفتر هیدروگرافی بریتانیا (مقصد VORF UKHO [ 4 ])، Service Hydrographique et Oceanographique de la Marine (SHOM’s datum datum [4]) وجود دارد. [ 5 ])، سرویس هیدروگرافی استرالیا (AusCoastVDT AHS [ 6 ])، سرویس هیدروگرافی کانادا (مقصد CCVD CHS [7 ، 8 ، 9 ، 10 ]، و داده مرجع عمودی هلند و بلژیک (NEVREF [ 11 ]). اخیراً، داده نمودار پیوسته عربستان سعودی (مدل بیضی LAT تا WGS-84) در خلیج عربی با استفاده از مدل اقیانوس هیدرودینامیکی WebTide ایجاد شده است و عدم قطعیت کلی بین 11 سانتی متر تا 16 سانتی متر است [ 2 ]. با این حال، همه این داده‌های نمودار پیوسته ملی با استفاده از مدل اقیانوس هیدرودینامیکی منفرد توسعه داده شدند.

یک مدل هیدرودینامیکی پیوسته برای ایجاد یک نمودار ادامه دارد که در آن مدل دندانه‌داری مدل LAT به MSL می‌تواند تخمین زده شود. مدل‌های هیدرودینامیکی منطقه‌ای برای دریای سرخ توسعه یافتند و یک توافق معقول بین مقادیر جزر و مدی برآورد شده از مدل و مقادیر جزر و مدی برآورد شده از مشاهدات جزر و مد یافت شد [ 12 ، 13 ، 14 ]. با این حال، مدل‌های جزر و مدی منطقه‌ای دریای سرخ با تعداد محدودی مشاهدات اندازه‌گیری جزر و مد توسعه یافتند و این مدل نمی‌تواند برای تخمین مدل LAT به MSL قابل اعتماد در منطقه دریای سرخ مورد استفاده قرار گیرد. بنابراین، مدل LAT به MSL در این مقاله با استفاده از مدل‌های اقیانوسی هیدرودینامیکی به خوبی تثبیت شده، یعنی مدل WebTide [ 15 ] توسعه داده شد.]، مدل اقیانوسی راه حل المان محدود 2014 (FES2014) [ 16 ]، مدل اقیانوسی دانشگاه فنی دانمارک 10 (DTU10) [ 17 ]، و مدل اقیانوسی تجربی جزر و مد اقیانوس 11a (EOT11a) [ 18 ]. اجزای جزر و مدی این چهار مدل اقیانوس به صورت عمومی و رایگان برای دسترسی از طریق وب سایت های آنها در دسترس است.

سهم LAT در عدم قطعیت مدل جداسازی MSL در عدم قطعیت کلی داده نمودار پیوسته ملی هنگام استفاده از مدل اقیانوس هیدرودینامیکی منفرد تقریباً نیمی از عدم قطعیت کلی به طور متوسط است [ 2 ].]. در نتیجه، هر گونه بهبود قابل توجهی در مدل LAT به MSL، دقت کلی نمودار پیوسته ملی را بهبود می بخشد. این مقاله توسعه یک مدل LAT دقیق را با استفاده از روش برآوردگر حداکثر احتمال (MLE) با هیبریداسیون مدل‌های اقیانوسی هیدرودینامیکی متعدد برای منطقه مورد مطالعه دریای سرخ بررسی کرد. مدل LAT با استفاده از MLE با استفاده از ترکیبی از چهار مدل اقیانوس هیدرودینامیکی توسعه داده شد: مدل WebTide، مدل اقیانوسی FES2014، اقیانوس DTU10 و مدل اقیانوس EOT11a. هدف توسعه یک مدل سطح بهینه LAT در دریای سرخ به عنوان مطالعه موردی بود. این مدل سطح بهینه LAT با استفاده از روش MLE با هیبریداسیون مدل‌های اقیانوسی هیدرودینامیکی چندگانه برای ارائه یک مدل سطح پیوسته ترکیبی LAT به MSL (که در این مقاله به سادگی مدل LAT نامیده می‌شود) توسعه داده شد.

2. تخمین حداکثر احتمال

روش MLE یک روش دقیق در نظر گرفته می‌شود که می‌تواند با چندین مدل به کار گرفته شود تا یک تخمین مقادیر مدل ترکیبی و عدم قطعیت‌های مرتبط را ارائه دهد. فرض کنید که N تعداد مدل اقیانوس هیدرودینامیکی برای تخمین مقادیر اولیه مدل LAT استفاده شده است ( $X_{1}^{o}$ به $X_{N}^{o}$ ) از نقاط شبکه مدل کل منطقه مورد مطالعه. مقادیر LAT اولیه تخمین زده شده با مقادیر LAT برآورد شده از داده‌های جزر و مد در ایستگاه‌های ساحلی هم‌محل مقایسه می‌شوند تا مقادیر مدل LAT تصحیح شده ارائه شود. ${\hat{X}}_{1}$ به ${\hat{X}}_{N}$ ) از نقاط شبکه مدل برای کل منطقه مورد مطالعه و ماتریس های کوواریانس مرتبط و ( $S_{{\hat{X}}_{1} {\hat{X}}_{1}}$ به $S_{{\hat{X}}_{N} {\hat{X}}_{N}}$ ) با استفاده از روش درونیابی با فاصله معکوس (IDW) [ 8 ]. سپس مقادیر مدل LAT بهینه ترکیبی ( ${\hat{X}}_{h}$ ) و ماتریس کوواریانس مرتبط ( $S_{{\hat{X}}_{h} {\hat{X}}_{h}}$ ) را می توان با استفاده از روش MLE تخمین زد. روش MLE بر اساس حداکثر کردن تابع درستنمایی زیر ایجاد شده است که تابع چگالی احتمال مشترک را با استفاده از ضرب توابع چگالی احتمال چندگانه نشان می‌دهد [ 19 ، 20 ، 21 ]:

L (X) = \prod i = 1 ن پ (ایکس من)

(1)

پ (ایکس من) = (2 π) - د / 2 ∣∣ اس ایکس^من ایکس^من ∣∣ - 1/2__exp (- 1 2 (ایکس من - ایکس^من) تی اس ایکس^من ایکس^من - 1 (ایکس من - ایکس^من))

(2)

جایی که $L (X)$ تابع احتمال حالت هیبریداسیون است، N تعداد مدل ها و $P (X_{i})$ تابع چگالی احتمال چند متغیره برای یک مدل منفرد با مقدار متغیر d با توزیع نرمال چند متغیره است. $M V N ({\hat{X}}_{i}, S_{{\hat{X}}_{i} {\hat{X}}_{i}})$ [ 20 ].

هدف تخمین پارامتر مدل بهینه ترکیبی ( ${\hat{X}}_{h}$ ) که تابع درستنمایی را به حداکثر می‌رسانند و بالاترین برآورد احتمال را برای پارامتر مدل بهینه ترکیبی با استفاده از یک راه‌حل دقیق (تخمین بهینه) تضمین می‌کنند. برای ساده سازی تخمین، لگاریتمی طبیعی برای تابع درستنمایی انجام شده و تابع log-lihood $l (X)$ را می توان به عنوان جمع توابع چگالی احتمال چند متغیره به صورت زیر ساده کرد [ 19 ، 20 ، 21 ]:

ل (X) = ln ⎛⎝⎜ \prod i = 1 ن پ (ایکس من) ⎞⎠⎟ .

(3)

به خوبی شناخته شده است که لگاریتمی طبیعی متغیرهای ضرب شده معادل مجموع متغیر است. در نتیجه، معادله (3) را می توان به صورت زیر بیان کرد:

ل (X) = \sum i = 1 ن ln (P (ایکس من))

(4)

ل (X) = \sum i = 1 ن ln ((2 π) - د 2 ∣∣ اس ایکس^من ایکس^من ∣∣ - 1 2) + \sum i = 1 ن ln (exp (- 1 2 (ایکس من - ایکس^من) تی اس ایکس^من ایکس^من - 1 (ایکس من - ایکس^من))

(5)

ل (X) = \sum i = 1 ن ln ((2 π) - د 2 ∣∣ اس ایکس^من ایکس^من ∣∣ - 1 2) + \sum i = 1 ن (- 1 2 (ایکس من - ایکس^من) تی اس ایکس^من ایکس^من - 1 (ایکس من - ایکس^من)) ln (انقضا)

(6)

ل (X) = \sum i = 1 ن ln ((2 π) - د 2 ∣∣ اس ایکس^من ایکس^من ∣∣ - 1 2) + \sum i = 1 ن (- 1 2 (ایکس من - ایکس^من) تی اس ایکس^من ایکس^من - 1 (ایکس من - ایکس^من)) .

(7)

جایی که به خوبی شناخته شده است $\ln (\exp)$ = 1. برای تخمین پارامتر مدل بهینه ترکیبی ( ${\hat{X}}_{h}$ )، انتظار اولین مشتق جزئی تابع log-likelihood، با مقدار پارامتر معادل ${\hat{X}}_{h}$ ، به صورت زیر برابر با صفر خواهد بود [ 19 , 20 , 21 ]:

E (\partial ( l ( X ) ) \partial X) ایکس = ایکس^ساعت = 0

(8)

E ⎛⎝⎜⎜⎜⎜ \partial ( \sum ن i = 1 ln ( ( 2 π ) - د 2 ∣∣ اس ایکس ^ من ایکس ^ من ∣∣ - 1 2 ) + \sum ن i = 1 ( - 1 2 ( ایکس من - ایکس ^ من ) تی اس ایکس ^ من ایکس ^ من - 1 ( ایکس من - ایکس ^ من ) )) ) \partial X ⎞⎠⎟⎟⎟⎟ ایکس = ایکس^ساعت = 0

(9)

ساده سازی معادله (9)، بر اساس جبر ماتریسی و عملیات، تخمین پارامتر مدل بهینه ترکیبی را ارائه می دهد. ${\hat{X}}_{h}$ ) همانطور که در معادله زیر نشان داده شده است:

ایکس^ساعت = (\sum ن i = 1 اس ایکس^من ایکس^من - 1) - 1 \cdot \sum ن i = 1 اس ایکس^من ایکس^من - 1 ایکس^من .

(10)

ماتریس کوواریانس ( $S_{{\hat{X}}_{h} {\hat{X}}_{h}}$ ) پارامتر مدل ترکیبی معادل منفی انتظار ماتریس هسین معکوس است که نشان دهنده دومین مشتق جزئی تابع log-relihood با مقدار پارامتر معادل است. ${\hat{X}}_{h}$ و می توان به صورت زیر بیان کرد [ 19 ، 20 ، 21 ]:

اس ایکس^ساعت ایکس^ساعت = ⎛⎝ - E (\partial 2 ( ل ( X ) ) \partial ایکس 2) ∣∣∣∣ ایکس = ایکس^ساعت ⎞⎠ - 1 .

(11)

ساده سازی معادله (11)، بر اساس جبر ماتریسی و عملیات، تخمین تابع کوواریانس را ارائه می دهد. $S_{{\hat{X}}_{h} {\hat{X}}_{h}}$ ) همانطور که در معادله زیر به دست می آید:

اس ایکس^ساعت ایکس^ساعت = ⎛⎝⎜ \sum i = 1 ن اس ایکس^من ایکس^من - 1 ⎞⎠⎟ - 1 .

(12)

از معادلات (11) و (12) برای تخمین پارامتر مدل LAT بهینه استفاده می شود.

{\hat{X}}_{h}

) و ماتریس کوواریانس مرتبط (

S_{{\hat{X}}_{h} {\hat{X}}_{h}}

) به ترتیب با استفاده از روش MLE با چند مدل اقیانوسی هیدرودینامیکی. جذر عناصر قطری ماتریس کوواریانس (

S_{{\hat{X}}_{h} {\hat{X}}_{h}}

) خطاهای استاندارد را ارائه دهید (

\sqrt{s_{{\hat{x}}_{h j}}}, j = 1 : d where d is the number of grid nodes

) از مقادیر مدل LAT بهینه توسعه یافته، که نشان دهنده عدم قطعیت مدل توسعه یافته است. برای آزمایش اینکه آیا پارامتر مدل LAT برآورد شده (

{\hat{X}}_{h}

) از نظر آماری در سطح اطمینان خاص معنادار است (

c l

)، مقادیر آزمون برای هر گره شبکه ای از مدل اقیانوس (

{\hat{x}}_{h j} / \sqrt{s_{{\hat{x}}_{h j}}}

، j = 1: d ، جایی که

{\hat{x}}_{h j}

عناصر پارامتر مدل LAT هستند

{\hat{X}}_{h}

) باید از حد بحرانی آماری تجاوز کند (

z_{α / 2}

) از جدول توزیع نرمال استاندارد در سطح معنی داری از

(α = 1 - c l)

. برای جزئیات بیشتر در مورد روش MLE، [ 19 ، 20 ، 21 ] را ببینید. در این مقاله، از چهار مدل اقیانوسی (مدل‌های WebTide، FES2014، DTU10 و EOT011a) برای تخمین پارامتر مدل LAT بهینه استفاده شد.

{\hat{X}}_{h}

) و ماتریس کوواریانس مرتبط (

S_{{\hat{X}}_{h} {\hat{X}}_{h}}

) با استفاده از روش MLE.

3. روش شناسی

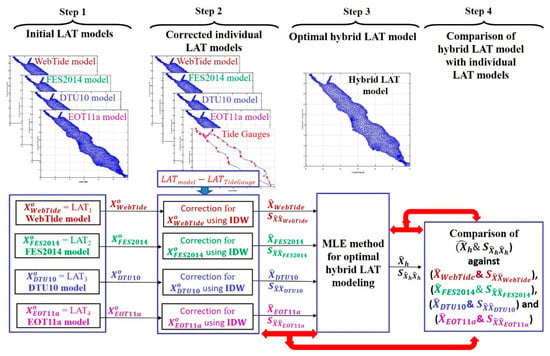
این تحقیق در چهار مرحله اصلی انجام شد. اجرای این چهار مرحله همانطور که در شکل 1 نشان داده شده است از طریق: 1) برآورد مقادیر اولیه LAT (

X_{W e b T i d e}^{o}, X_{F E S 2014}^{o}, X_{D T U 10}^{o}, and X_{E O T 11 a}^{o}

) برای کل گره های شبکه مطالعه موردی دریای سرخ با استفاده از اجزای هارمونیک WebTide، FES2014، DTU10، و EOT11a مدل های هیدرودینامیکی، به ترتیب. 2) برآورد مقادیر تک تک اصلاح شده LAT (

{\hat{X}}_{W e b T i d e}

{\hat{X}}_{F E S 2014}

{\hat{X}}_{D T U 10}

، و

{\hat{X}}_{E O T 11 a}

) همراه با کوواریانس مدل های آنها (

S_{{\hat{\hat{X} X}}_{W e b T i d e}}

S_{\hat{X} {\hat{X}}_{F E S 2014}}

S_{\hat{X} {\hat{X}}_{D T u 10}}

، و

S_{{\hat{\hat{X} X}}_{E O T 11 a}}

برای کل گره‌های شبکه مطالعه موردی دریای سرخ با درون یابی تفاوت‌های بین مقادیر LAT اولیه برآورد شده از چهار مدل و مقادیر LAT برآورد شده از اندازه‌گیری‌های جزر و مد در ایستگاه‌های ساحلی هم‌محل با استفاده از روش IDW و اضافه کردن این تفاوت‌های درون‌یابی ( سطح تصحیح کننده) به مقادیر اولیه LAT تخمین زده شده از چهار مدل. 3) برآورد مقادیر مدل LAT ترکیبی بهینه (

{\hat{X}}_{h}

) همراه با ماتریس کوواریانس (

S_{{\hat{X}}_{h} {\hat{X}}_{h}}

) برای کل گره های شبکه مطالعه موردی دریای سرخ با استفاده از روش MLE با هیبریداسیون مدل هیدرودینامیکی اقیانوس چندگانه. و 4) مقایسه بین مدل LAT ترکیبی بهینه با مدل‌های LAT منفرد اصلاح‌شده برآورد شده از مدل‌های اقیانوسی WebTide، FES2014، DTU10، یا EOT11a بر اساس عدم قطعیت‌های مرتبط. در نهایت، پارامتر مدل LAT برآورد شده (

{\hat{X}}_{h}

(

{\hat{x}}_{h j} / \sqrt{s_{{\hat{x}}_{h j}}}

j = 1: d که در آن d تعداد گره های شبکه است) در برابر حد بحرانی آماری (

Z_{0.025}

) از جدول توزیع نرمال استاندارد استخراج شده است. تمامی مراحل پردازش با استفاده از نرم افزار MATLAB [ 22 ] اجرا شد.

4. نتایج و بحث

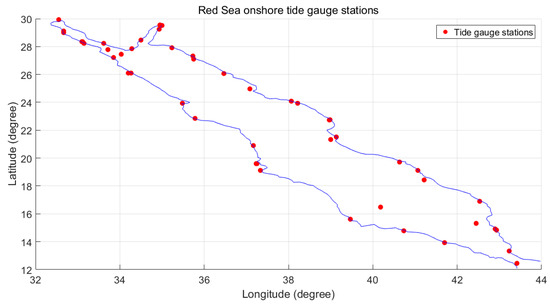
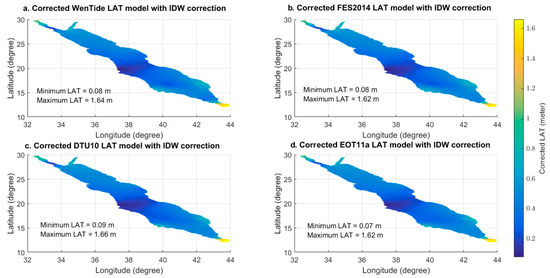
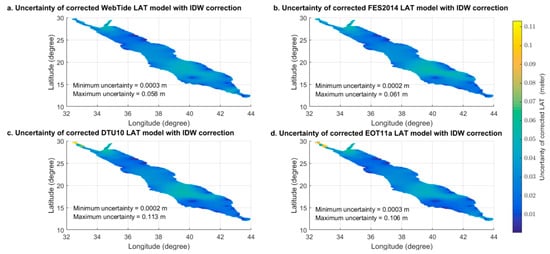
ابتدا مقادیر LAT اولیه در هر گره شبکه مدل اقیانوس با استفاده از چهار مدل اقیانوس هیدرودینامیکی (WebTide، FES2014، DTU10 و EOT011a) برآورد شد. شکل 2 تخمین مقادیر اولیه LAT را به ترتیب بر اساس چهار مدل WebTide، FES2014، DTU10 و EOT011a نشان می دهد. سپس، تفاوت بین مقادیر LAT برآورد شده از چهار مدل و مقادیر LAT تخمین زده شده از ایستگاه های جزر و مد که در 52 ایستگاه ساحلی قرار دارند، در شکل 3 نشان داده شده است.میز 1مقادیر همبستگی و ریشه میانگین مربع (RMS) را هنگامی که مقادیر LAT از چهار مدل با مقادیر LAT برآورد شده از ایستگاه های جزر و مد مقایسه شد، نشان می دهد. ضریب همبستگی بین مقادیر LAT برآورد شده از مدل‌های WebTide، FES2014، DTU10، و EOT011a در مقایسه با مقادیر LAT برآورد شده از جزر و مد 52 ایستگاه، به ترتیب 0.86، 0.84، 0.74 و 0.67 بود. خطاهای RMS برآورد شده از مدل‌های WebTide، FES2014، DTU10 و EOT011a در مقایسه با مقادیر LAT برآورد شده از اندازه‌گیری جزر و مد 52 ایستگاه، به ترتیب 0.13 متر، 0.14 متر، 0.17 متر و 0.19 متر بود.شکل 4 و شکل 5 مقادیر اصلاح شده LAT و توزیع هیستوگرام مقادیر LAT برآورد شده در هر گره شبکه ای از مدل اقیانوسی را به ترتیب با استفاده از چهار مدل اقیانوس هیدرودینامیکی (WebTide، FES2014، DTU10، و EOT011a) نشان می دهد. شکل 4 تقریباً یک الگوی مشابه را نشان می دهد که در آن بالاترین مقادیر LAT در مناطق شمالی و جنوبی دریای سرخ قرار دارد، با این حال، کمترین مقادیر LAT در ناحیه میانی دریای سرخ قرار دارد. شکل 5 نشان می دهد که بیشتر مقادیر LAT اصلاح شده به طور معمول توزیع شده اند. عدم قطعیت مقادیر LAT اصلاح شده در شکل 6 نشان داده شده استکه در آن حداکثر عدم قطعیت از 6 سانتی‌متر تا 11 سانتی‌متر با بهترین سناریوهای مدل‌های WebTide و FES2014 با تقریباً 6 سانتی‌متر عدم قطعیت و بدترین سناریوها از مدل‌های DTU10 و EOT11a با تقریباً 11 سانتی‌متر عدم قطعیت متغیر است. ارقام الگوهای مشابهی را نشان می‌دهند که در آن حداکثر عدم قطعیت به احتمال زیاد در مناطق فراساحلی و در مناطق بدون محدودیت (بدون اندازه‌گیری جزر و مد) رخ داده است.

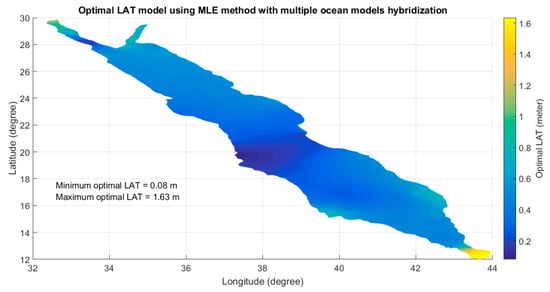
برای بهبود دقت، مدل LAT بهینه همراه با ماتریس کوواریانس مرتبط در هر گره شبکه مدل اقیانوس با استفاده از روش MLE (معادلات (11) و (12) در بخش 2 ) با WebTide، FES2014، DTU10، و برآورد شد. هیبریداسیون EOT011a برای ارائه مدل LAT ترکیبی/بهینه. شکل 7 و شکل 8 مقادیر بهینه مدل LAT و عدم قطعیت های مرتبط برآورد شده در هر گره شبکه مدل اقیانوس را نشان می دهد. می توان مشاهده کرد که مقادیر مدل LAT ترکیبی بهینه از 0.1 متر تا 1.63 متر متغیر بود و با حداکثر عدم قطعیت تقریباً 3 سانتی متر همراه بود که مدل LAT با ترکیب چهار مدل با استفاده از روش MLE در مطالعه موردی دریای سرخ توسعه یافت. حوزه. شکل 8نشان می‌دهد که حداکثر عدم قطعیت به احتمال زیاد در مناطق فراساحلی رخ داده است که در آن این مناطق هیچ محدودیتی ندارند (بدون اندازه‌گیری جزر و مد)، با این حال، مناطق خشکی با محدودیت‌های جزر و مد سنج با عدم قطعیت‌های تقریباً صفر همراه بودند.

شایان ذکر است که پارامتر مدل LAT تخمین زده شده با مقایسه مقادیر آزمون برای هر گره شبکه مدل اقیانوس آزمایش شد که آیا از نظر آماری در سطح اطمینان 95٪ معنی‌دار است یا خیر.

{\hat{x}}_{S j} / \sqrt{s_{{\hat{x}}_{S j}}}

، j = 1: m که در آن m تعداد گره های شبکه است) در برابر حد بحرانی آماری (

Z_{0.025} = 1.96

) از جدول توزیع نرمال استاندارد استخراج شده است. مشخص شد که مقادیر مدل LAT بهینه برآورد شده برای هر گره شبکه مدل اقیانوسی با استفاده از روش MLE با هیبریداسیون مدل‌های اقیانوسی هیدرودینامیکی متعدد از نظر آماری در سطح اطمینان 95 درصد معنی‌دار بود.

برای تأیید صحت مدل توسعه‌یافته، مقایسه بین مدل LAT ترکیبی بهینه ایجاد شده از هیبریداسیون مدل هیدرودینامیکی اقیانوس چندگانه با استفاده از روش MLE و مدل‌های LAT منفرد برآورد شده از مدل‌های اقیانوس هیدرودینامیک فردی با استفاده از WebTide، FES2014، DTU10 یا EOT11a انجام شد. مدل‌های اقیانوس بر اساس عدم قطعیت‌های مرتبط شکل 8 توزیع عدم قطعیت های تجمعی برآورد شده از عدم قطعیت های مرتبط با مدل LAT ترکیبی بهینه و توزیع عدم قطعیت تجمعی برآورد شده از عدم قطعیت های مرتبط با مدل های LAT منفرد را نشان می دهد. توزیع عدم قطعیت های تجمعی در شکل 9برای تخمین عدم قطعیت‌ها در سطح اطمینان 95% برای مدل ترکیبی LAT بهینه و مدل‌های LAT منفرد استفاده شد. جدول 2 حداکثر عدم قطعیت ها و عدم قطعیت های تخمین زده شده در سطح اطمینان 95% را از مدل بهینه ترکیبی LAT و مدل های تک تک LAT نشان می دهد. از جدول 2 می توان دریافت که مدل LAT هیبریدی بهینه توسعه یافته مرتبط با حدود 2.4 سانتی متر عدم قطعیت در سطح اطمینان 95 درصد نسبت به مدل های LAT فردی مرتبط با حدود 5 سانتی متر عدم قطعیت به طور متوسط در سطح اطمینان 95 درصد برتر است. به طور متوسط حدود 50 درصد بهبود یافته است. علاوه بر این، شکل 10تفاوت بین مقادیر LAT اصلاح شده برآورد شده از چهار مدل اقیانوسی (WebTide، FES2014، DTU10، و EOT11a) و مقادیر LAT بهینه برآورد شده از مدل ترکیبی توسعه‌یافته را نشان می‌دهد. نشان داده شده است که تفاوت بین مقادیر LAT اصلاح شده از چهار مدل و مقادیر LAT بهینه مدل ترکیبی از -21 سانتی متر تا +13 سانتی متر با خطای RMS 5 سانتی متر در سطح اطمینان 95٪ متغیر است. لازم به ذکر است که خطای RMS با عدم قطعیت های تخمینی مدل های اقیانوس منفرد نشان داده شده در جدول 2 مطابقت دارد .

بنابراین، با چند سانتی‌متر سطح عدم قطعیت‌های مرتبط با مدل LAT بهینه توسعه‌یافته در این مقاله بر اساس روش MLE با هیبریداسیون مدل‌های اقیانوسی هیدرودینامیکی چندگانه، می‌توان عدم قطعیت‌های کلی داده نمودار عمودی پیوسته را به میزان قابل‌توجهی کاهش داد و تمام الزامات سفارش‌های نقشه برداری هیدروگرافی را برآورده کرد. ارائه شده توسط سازمان بین المللی هیدروگرافی (IHO). علاوه بر این، مدل LAT بهینه توسعه‌یافته می‌تواند بسیاری از الزامات کاربردهای دریایی را که به چند سانتی‌متر برای سطح دقت نیاز دارند، برآورده کند.

5. نتیجه گیری و پیشنهاد

در این مقاله، مدل LAT بهینه با استفاده از روش MLE با هیبریداسیون مدل هیدرودینامیکی اقیانوس چندگانه که چهار مدل اقیانوس هیدرودینامیکی (مدل‌های WebTide، FES2014، DTU10 و EOT11a) را ترکیب می‌کند، توسعه داده شد و مقادیر LAT مرتبط با عدم قطعیت را در هر گره شبکه ارائه کرد. مدل اقیانوس در منطقه مطالعه دریای سرخ مشخص شد که مدل ترکیبی LAT بهینه را می توان با حداکثر عدم قطعیت 3 سانتی متر و حدود 2.4 سانتی متر عدم قطعیت برآورد شده در سطح اطمینان 95 درصد در منطقه مورد مطالعه دریای سرخ به دست آورد. برای تأیید صحت مدل توسعه‌یافته، مقایسه بین مدل LAT ترکیبی بهینه ایجاد شده از هیبریداسیون مدل هیدرودینامیکی اقیانوس چندگانه با استفاده از روش MLE با مدل LAT منفرد برآورد شده از مدل‌های اقیانوس منفرد با استفاده از WebTide، FES2014، DTU10 انجام شد. یا مدل های اقیانوس EOT11a بر اساس عدم قطعیت های مرتبط. مشخص شد که مدل LAT بهینه ترکیبی برآورد شده از مدل‌های اقیانوسی چندگانه نسبت به مدل‌های LAT منفرد برآورد شده از مدل‌های اقیانوس منفرد با حدود 50 درصد بهبود در میانگین بر اساس عدم قطعیت‌های برآورد شده در سطح اطمینان 95 درصد، برتر است. اهمیت توسعه یک مدل LAT بهینه با دقت بالا در این است که می‌تواند توسط هیدروگراف‌ها برای ایجاد یک کنترل عمودی دقیق برای برنامه‌های بررسی هیدروگرافی استفاده شود و همچنین می‌تواند توسط دریانوردان برای تولید نمودارهای ناوبری الکترونیکی دینامیکی دقیق در Red مورد استفاده قرار گیرد. منطقه دریا.

منابع

داد، دی. Mills-Usa, J. مدل‌های جداسازی بررسی‌های بیضی ارجاع‌شده ; هفته کاری FIG: رم، ایتالیا، 2012. [ Google Scholar ]
الدیاستی، م. الحربی، س. پاگیاتاکیس، س. توسعه داده نمودار پیوسته عربستان: مطالعه موردی خلیج عربی. Geomat. نات. خطر خطرات 2019 ، 10 ، 1738-1749. [ Google Scholar ] [ CrossRef ]
گش، دی. ویلسون، آر. توسعه یک مدل ارتفاعی توپوگرافی/حمام سنجی بدون درز چند منبعی خلیج تامپا. فن آوری مارس. Soc. J. 2001 ، 35 ، 58-64. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
ایلیف، جی سی. زیبارت، MK; ترنر، جی اف. تالبوت، ای جی؛ Lesnoff، AP دقت سطوح داده عمودی در مناطق ساحلی و فراساحلی. Surv. Rev. 2013 , 45 , 254-262. [ Google Scholar ] [ CrossRef ]
Pineau-Guillou، L.; Dorst, L. ایجاد سطوح مرجع عمودی در دریا با استفاده از ارتفاع سنجی و GPS. بین المللی دانشیار علامت ژئودزی 2012 ، 138 ، 229-235. [ Google Scholar ] [ CrossRef ]
کیزر، JH; Quadros، ND; Collier، PA در حال توسعه روشی برای ایجاد یک داده عمودی مشترک قبل از ادغام داده‌های ارتفاع زمین با داده‌های عمق بستر نزدیک به ساحل . وزارت تغییرات آب و هوا و بهره وری انرژی، دولت مشترک المنافع استرالیا: کانبرا، استرالیا، 2013. [ Google Scholar ]
رابین، سی. نودز، اس. مکالی، پی. گودین، آ. بوم، BDL; بارتلت، جی. سطوح جداسازی عمودی هیدروگرافیک (HyVSEPs) برای آبهای جزر و مدی کانادا. Mar. Geodesy 2016 ، 39 ، 195-222. [ Google Scholar ] [ CrossRef ]
رابین، سی. گودین، ا. مکالی، پی. دی لانگ، بی. لیفایور، دی. هرون، تی. سینوت، دی. بالانتاین، ا. مالتیس، ال. Veronneau, M. Canadian Hydrographic Continuous Vertical Datum: Methodology and Accuracy. در مجموعه مقالات کنفرانس CHC 2012، آبشار نیاگارا، ON، کانادا، 15 تا 17 مه 2012. [ Google Scholar ]
De Lange، B. مدل های جداسازی مبنا عمودی برای ساحل بریتیش کلمبیا. در مجموعه مقالات کنفرانس CHC 2012، آبشار نیاگارا، ON، کانادا، 15 تا 17 مه 2012. [ Google Scholar ]
لیفایور، دی. داد، دی. گودین، آ. هرون، تی. مک آلی، پی. Sinnott، D. پروژه آب‌های کانادا با داده عمودی پیوسته (آغاز، چشم‌انداز، روش‌ها و پیشرفت). در مجموعه مقالات کنفرانس CHC 2010، کبک، QC، کانادا، 24 تا 27 فوریه 2010. [ Google Scholar ]
Slobbe، CD; سومیهر، ج. فردریکسه، تی. ورلان، ام. کلیس، آر. زجل، ف. فراهانی، ح. بروکمن، آر. رویکرد فیلتر کالمن برای تحقق پایین ترین سطح جزر و مد نجومی. Mar. Geodesy 2017 ، 41 ، 44-67. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
Shamji، VR Tidal Dynamics در امتداد ساحل شرقی دریای سرخ. OALib 2019 ، 6 ، 1-9. [ Google Scholar ] [ CrossRef ]
گوو، دی. کارتادیکاریا، آر. ژان، پی. زی، جی. لی، ام. Hoteit، I. شبیه سازی جزر و مد باروکلینیک در دریای سرخ: مقایسه با مشاهدات و ویژگی های اساسی. جی. ژئوفیس. Res. اقیانوس‌ها 2018 ، 123 ، 9389–9404. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
غربی، س. البرکاتی، ع. الصافانی، م. پی پی، اس. الرادادی، تی. شبیه سازی هیدرودینامیک جزر و مدی در دریای سرخ با استفاده از مدل COHERENS. Reg. گل میخ. مارس Sci. 2018 ، 22 ، 49-60. [ Google Scholar ] [ CrossRef ]
BIO، موسسه اقیانوس شناسی بدفورد. مدل پیش‌بینی جزر و مد WebTide (V0.7.1) . در دسترس آنلاین: https://www.bio.gc.ca/science/research-recherche/ocean/webtide/index-en.php (در 8 مه 2020 قابل دسترسی است).
لیارد، اف. کارر، ال. Cancet، M. گیلات، آ. لموئین، جی.-ام. اطلس جزر و مدی FES2014، ارزیابی دقت برای ارتفاع سنجی ماهواره ای و سایر کاربردهای ژئوفیزیکی. جی. ژئوفیس. Res. 2016 , 18 . [ Google Scholar ]
چنگ، ی. مدلسازی تجربی جزر و مد اقیانوس اندرسن، OB Multimission برای آبهای کم عمق و دریاهای قطبی. جی. ژئوفیس. Res. فیزیک فضایی 2011 , 116 . [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
مایر-گور، تی. ساوچنکو، آر. بوش، دبلیو. داراس، من. فلچتنر، اف. Dahle، C. جزر و مد اقیانوس از ارتفاع سنجی ماهواره ای و GRACE. جی. جئودین. 2012 ، 59 ، 28-38. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
Eliason، SR برآورد حداکثر احتمال: منطق و تمرین . Sage Publications, Inc.: Thousand Oaks, CA, USA, 1993. [ Google Scholar ]
جانسون، RA; Wichern، DW Applied Multivariate Statistical Analysis ; پرنتیس هال: هوبوکن، نیوجرسی، ایالات متحده آمریکا، 2002. [ Google Scholar ]
Mtw; مدل های رگرسیون طولانی، JS برای متغیرهای وابسته طبقه بندی شده و محدود. مربا. آمار دانشیار 1997 ، 92 ، 1655. [ Google Scholar ] [ CrossRef ]
متلب. MATLAB 2018a: شروع کار با MATLAB . The MathWorks, Inc.: Natick, MA, USA, 2018. [ Google Scholar ]

شکل 1. تخمین مدل بهینه کمترین جزر و مد نجومی (LAT) با استفاده از روش برآوردگر حداکثر احتمال (MLE) با هیبریداسیون مدل اقیانوسی هیدروگرافیک چندگانه.

شکل 2. LAT اولیه با استفاده از WebTide ( a )، راه حل المان محدود 2014 (FES2014) ( b )، دانشگاه فنی دانمارک 10 (DTU10) ( c )، و مدل های اقیانوس تجربی تجربی 11a (EOT11a) ( d ).

شکل 3. مکان ایستگاه های جزر و مد خشکی.

شکل 4. مدل های WebTide تصحیح شده ( a )، FES2014 ( b )، DTU10 ( c )، و EOT11a ( d ) LAT با اصلاح وزن معکوس فاصله (IDW).

شکل 5. توزیع هیستوگرام و چگالی نرمال برازش شده برای WebTide ( a )، FES2014 ( b )، DTU10 ( c )، و EOT11a ( d ) LAT با تصحیح IDW.

شکل 6. عدم قطعیت مدل های WebTide اصلاح شده ( a )، FES2014 ( b )، DTU10 ( c )، و EOT11a ( d ) LAT با تصحیح IDW.

شکل 7. LAT هیبرید بهینه با استفاده از روش MLE با هیبریداسیون مدل هیدرودینامیکی اقیانوسی چندگانه.

شکل 8. عدم قطعیت LAT هیبرید بهینه با استفاده از روش MLE با هیبریداسیون مدل هیدرودینامیکی اقیانوسی چندگانه.

شکل 9. توزیع عدم قطعیت های تجمعی برآورد شده از عدم قطعیت های مرتبط با مدل ترکیبی بهینه LAT و مدل های تک تک LAT.

شکل 10. تفاوت بین مدل اصلاح شده LAT WebTide ( a )، مدل اصلاح شده FES2014 ( b )، مدل اصلاح شده LAT DTU10 ( c )، و مدل اصلاح شده LAT EOT11a ( d )، و مدل LAT ترکیبی بهینه.

مقالات داخلی و بین المللی

بدون دیدگاه

دیدگاهتان را بنویسید لغو پاسخ

برای نوشتن دیدگاه باید وارد بشوید.

مشاورین هوش پیروزی

خلاصه

کلید واژه ها:

1. معرفی

2. تخمین حداکثر احتمال

3. روش شناسی

4. نتایج و بحث

5. نتیجه گیری و پیشنهاد

منابع

قبلیرتبه بندی دارایی ها با توجه به قرار گرفتن آنها در معرض خطر زمین لغزش: یک پیشنهاد GIS

بعدیادغام تصمیمات برنامه ریزی کاربری زمین و انرژی های تجدیدپذیر: راهنمای نقشه برداری فنی برای دولت محلی

مطالب مرتبط ...

آموزش مقاله نویسی در رشته ادبیات فارسی

تأثیر همسایگی درونیابی DEM بر عوامل زمین

رگرسیون وزنی جغرافیایی تطبیقی غیر منفی برای تخمین تراکم جمعیت بر اساس نور شب

بدون دیدگاه

دیدگاهتان را بنویسید لغو پاسخ

درباره سرزمین فناوری مکانی GISLAND

دسترسی سریع

اطلاعات

خبرنامه

خبرنامه

درباره سرزمین فناوری مکانی GISLAND

دسترسی سریع

اطلاعات

دسترسی سریع

مشاورین هوش پیروزی

بهینه ترین تخمین جزر و مد نجومی با استفاده از تخمینگر حداکثر احتمال با هیبریداسیون مدل های اقیانوسی چندگانه

خلاصه

کلید واژه ها:

1. معرفی

2. تخمین حداکثر احتمال

3. روش شناسی

4. نتایج و بحث

5. نتیجه گیری و پیشنهاد

منابع

قبلیرتبه بندی دارایی ها با توجه به قرار گرفتن آنها در معرض خطر زمین لغزش: یک پیشنهاد GIS

بعدیادغام تصمیمات برنامه ریزی کاربری زمین و انرژی های تجدیدپذیر: راهنمای نقشه برداری فنی برای دولت محلی

مطالب مرتبط ...

آموزش مقاله نویسی در رشته ادبیات فارسی

تأثیر همسایگی درونیابی DEM بر عوامل زمین

رگرسیون وزنی جغرافیایی تطبیقی ​​غیر منفی برای تخمین تراکم جمعیت بر اساس نور شب

بدون دیدگاه

دیدگاهتان را بنویسید لغو پاسخ

درباره سرزمین فناوری مکانی GISLAND

دسترسی سریع

اطلاعات

خبرنامه

خبرنامه

درباره سرزمین فناوری مکانی GISLAND

دسترسی سریع

اطلاعات

دسترسی سریع

رگرسیون وزنی جغرافیایی تطبیقی غیر منفی برای تخمین تراکم جمعیت بر اساس نور شب