بهینه سازی بسط توابع پیچیده برای پیش بینی های گاوس-کروگر

در مقایسه با بسط های پیچیده و طولانی سری طرح ریزی گاوس-کروگر و عبارات اعداد واقعی، ما نمایش تابع پیچیده پیش بینی های گاوس-کروگر را بهبود می بخشیم و آنها را به “فرم زاویه چندگانه”، “فرم نمایی” و “فرم زاویه دوتایی” بازنویسی می کنیم. ضرایب در سری توان بر اساس خروج از مرکز اول گسترش یافته است هو سومین مسطح کردن nبه ترتیب، و تفاوت برش زمانی که به ترتیب‌های مختلف گسترش می‌یابد برای به دست آوردن فرمول‌های عملی ساده شده برای هر فرم با فرض برآورده کردن الزامات دقت ژئودزی مورد تجزیه و تحلیل قرار گرفت. از طریق تجزیه و تحلیل عددی، کارایی محاسباتی راه حل های رو به جلو و معکوس طرح گاوس-کروگر تجزیه و تحلیل می شود که برتری “فرم زاویه دوتایی” را نشان می دهد. از طریق اقدامات فوق، عبارات راه حل های رو به جلو و معکوس طرح گاوس-کروگر به دست می آیند، که الزامات دقت را با بازده محاسباتی بالاتر و شکل مختصرتر برآورده می کنند.

کلید واژه ها:

پیش بینی نقشه ; تابع پیچیده ؛ تجزیه و تحلیل تفاوت برش ; سیستم جبر کامپیوتری

1. مقدمه

ناوبری از نقشه ها جدایی ناپذیر است. بدون نقشه های با دقت بالا به عنوان حامل اطلاعات، یک سیستم ناوبری تنها یک سیستم موقعیت یابی است [ 1 ، 2 ، 3 ]. به طور خاص، روند توسعه الکترونیکی و هوشمند نقشه ها و نمودارها همچنین الزامات بالاتری را در مورد کارایی و دقت فرمول های حل معکوس و جلویی پیش بینی ها مطرح می کند [ 4 ، 5 ، 6 ، 7 ]. طرح ریزی گاوس-کروگر یکی از مهم ترین پیش بینی های منسجم است و به طور گسترده در ژئودزی، نقشه برداری، نقشه برداری مهندسی و سایر زمینه ها استفاده می شود [ 8 ]]. دارای مزایای منحصر به فردی در نقشه انتقال زمین به دریا و ساخت نقشه در مقیاس بزرگ است. در حال حاضر از این طرح به عنوان مبنای ریاضی نقشه های توپوگرافی جهان و بسیاری از کشورها استفاده می شود. [ 9 ].

نظریه فرافکنی گاوس کروگر مدتهاست که توسط محققان مورد مطالعه قرار گرفته و پیشرفت جدیدی در تحقیقات مدرن داشته است. ابی و همکاران کاربرد طرح ریزی مورب مرکاتور در بررسی های مهندسی مدرن را مورد بحث قرار داد و برتری آن را از طریق محاسبات نشان داد [ 10 ]. سرجیو پیش‌بینی‌های مستقیم و عرضی از نوع Mercator را برای نگاشت هم‌نوع سطح به صفحه با ارتفاع ثابت به دست آورد، و دقت فرمول با تجزیه و تحلیل عددی [ 11 ] تجزیه و تحلیل شد.]. با این حال، به دلیل محدودیت شرایط تاریخی، بسیاری از فرآیندهای تحلیل ریاضی در آن زمان به صورت دستی تکمیل می شد و نظم و دقت فرمول های بسط نمی توانست خیلی زیاد باشد. گاهی اوقات، اشتباهات کوچکی وجود داشت که یافتن آنها آسان نبود، به ویژه از آنجایی که راه حل معکوس اغلب به عنوان یک شکل تکراری ارائه می شد که برای تجزیه و تحلیل ریاضی مناسب نبود [ 12 ]. بنابراین لازم است از تحلیل جبری کامپیوتری پیشرفته برای انجام اصلاحات و نوآوری های لازم استفاده شود.

به دلیل ارتباط بین تئوری توابع پیچیده و پیش‌بینی‌های هم‌شکل، معمولاً نشان دادن مختصات با اعداد مختلط هنگام کار با نگاشت‌های هم‌شکل مفید است [ 13 ، 14 ]. تئوری نمایش توابع پیچیده از پیش‌بینی‌های نقشه به اندازه تحلیل پیچیده قدیمی است. بسیاری از علما در این زمینه آثار بسیار معناداری ساخته اند. Bowring نمایش تابع پیچیده طرح گاوس-کروگر [ 15 ] را مورد بحث قرار داد. کلوتز به طرح ریزی گاوس-کروگر یک راه حل تابع پیچیده برای پهنای باند دلخواه بر اساس یک فرمول بازگشتی مؤثر داد [ 16 ]]. شوهر برنامه فوترن را از راه حل های جلو و عقب طرح گاوس- کروگر ارائه کرد که با توابع پیچیده مطابق فرمول در [ 16 ] بیان شده بود و آنها را محاسبه کرد [ 17 ]. با کمک یک سیستم جبر کامپیوتری، فرمول های حل رو به جلو و معکوس بیان تابع پیچیده طرح ریزی گاوس-کروگر توسط راه حل های تکراری محاسبه می شود و نسبت مقیاس و زاویه همگرایی نصف النهار عبارت تابع مختلط به دست می آید [ 18 ، 19 ، 20]. همه اینها برتری استفاده از توابع پیچیده برای حل مسئله ریاضی طرح ریزی گاوس-کروگر را نشان می دهد. گو جیاچون فرآیند غیر تکراری راه حل های رو به جلو و معکوس طرح ریزی گاوس-کروگر را بر اساس فرمول لی دریافت و فرآیند اساسی طرح ریزی گاوس-کروگر را آشکار کرد [ 21 , 22]. کارنی دو الگوریتم را برای طرح ریزی عرضی مرکاتور توصیف کرد که یکی از آنها بر اساس فرمول دقیق تر تامپسون و لی است و به دقت 9 نانومتر در کل بیضی دست می یابد و الگوریتم دیگر روش بسط سری است. از آنجا که طرح گاوس- کروگر را نمی توان بر حسب توابع ابتدایی بیان کرد، نگاشت معمولاً با استفاده از یک سری کوتاه محاسبه می شود. کارنی تحقیقات کروگر را بیشتر کرد و سری اصلی را به آن گسترش داد n30که منجر به الگوریتم جدید مرکاتور عرضی با دقت چند نانومتر در محدوده معین شد [ 23 ، 24 ]. با این حال، اگرچه بسط مرتبه بالا به دقت بسیار بالایی دست می یابد، اما بسط سری را نسبتاً طولانی و پیچیده می کند، که انتشار فرمول را دشوار می کند و راندمان محاسباتی پایین است.

در این مقاله، بیان توابع پیچیده طرح ریزی گاوس- کروگر با استفاده از بسط سری مورد مطالعه قرار گرفته است. عبارات نمادین راه حل های رو به جلو و معکوس بدون تکرار مشتق شده اند. ما راه‌حل‌های رو به جلو و معکوس سنتی پیش‌بینی گاوس کروگر بیضی‌ها را بهبود و اصلاح می‌کنیم و آن‌ها را در عبارات تابع پیچیده بیان‌شده در «شکل زاویه‌ای چندگانه»، «شکل نمایی» و «فرم زاویه دوتایی» بازنویسی می‌کنیم. بر اساس اولین خروج از مرکز هو سومین مسطح کردن nضرایب موجود در فرمول ها به ترتیب در سری های توانی بسط می یابند و اختلاف برش ضرایب گسترش یافته به مرتبه های مختلف برای به دست آوردن فرمول های عملی ساده شده هر فرم با فرض برآوردن الزامات دقت ژئودزی تجزیه و تحلیل می شود. از طریق تجزیه و تحلیل عددی، کارایی محاسباتی راه حل های رو به جلو و معکوس طرح گاوس- کروگر تجزیه و تحلیل می شود و الگوریتم حل جلو و معکوس طرح گاوس- کروگر با بالاترین بازده محاسباتی به دست می آید.

2. بیان تابع پیچیده پروجکشن گاوس-کروگر

با توجه به ادبیات [ 25 ، 26 ]، در صفحه طرح ریزی گاوس-کروگر، x یک مختصات است که مختصات شمالی است. و y نمایانگر آبسیسا، یعنی مختصات شرقی است. علاوه بر این، لنشان دهنده اختلاف طول جغرافیایی است، بنشان دهنده عرض جغرافیایی است، ایکس(ب)=آ(1-ه2)🔻0بدب(1-ه2گناه2ب)3/2، ن=آ1-ه2گناه2ب، تی=برنزهب، و η2=ه”2cos2ب. در راه حل معکوس، عرض جغرافیایی نقطه پایه بfباید به صورت تکراری حل شود سپس، بیان اعداد واقعی طرح ریزی سنتی گاوس کروگر به صورت زیر است:

{ایکس=ایکس+نتیcos2بل2ρ2[0.5+124(5-تی2+9η2+4η4)cos2بل2ρ2+1720(61-58تی2+تی4)cos4بل4ρ4]y=نcosبلρ[1+16(1-تی2+η2)cos2بل2ρ2+1120(5-18تی2+تی4+14η2-58تی2η2)cos4بل4ρ4]{ب=بf-ρتیf2مfy(yنf)[1-112(5+3تیf2+ηf2-9ηf2تیf2)(yنf)2+1360مfنf5(61+90تیf2+45تیf4)(yنf)4]ل=ρcosبf(yنf)[1-16(1+2تیf2+ηf2)(yنf)2+1120(5+28تیf2+24تیf4+6η52+8ηf4تیf2)(yنf)4]

(1)

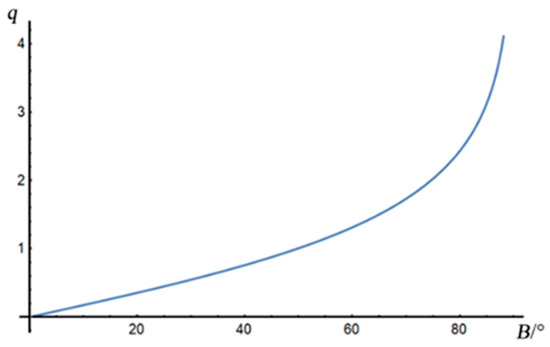
در محاسبات عملی، معادله (1) اغلب به صورت سری توان اختلاف طول جغرافیایی بیان می شود ل. به منظور کاهش تغییر شکل در جهت شرق به غرب، اغلب لازم است که آن را به مناطق 3 درجه یا 6 درجه تقسیم کنیم. نقشه پهنه بندی را می توان با استفاده از رابطه ریاضی معادله (1)، همانطور که در شکل 1 نشان داده شده است، ترسیم کرد .

اگرچه پهنه بندی قابلیت استفاده از طرح گاوس-کروگر را در جهت شرق-غرب افزایش می دهد، همچنین عدم تداوم ایجاد می کند، به خصوص در نقشه های قطبی، که تکه تکه هستند و نمی توان آنها را اعمال کرد. با توجه به رابطه طبیعی بین توابع پیچیده و نگاشت هم‌شکل، برخی از محققان این روش ریاضی را در سال‌های اخیر در مطالعه طرح‌ریزی هم‌شکل معرفی کرده‌اند. Bian Shaofeng راه حل های رو به جلو و معکوس طول قوس نصف النهار را از میدان اعداد واقعی به میدان اعداد مختلط از طریق روش های تکراری ریاضی گسترش داد و فرمول تابع متغیر مختلط طرح گاوس-کروگر [ 15 ، 27 ] را ارائه داد:

{q=آرکتان(گناهب)-ه⋅آرکتان(هگناهب)w=q+من ل=آرکتان(گناهب)-ه⋅آرکتان(هگناهب)+من لφ=آرکسین[tanh(w)]z=ایکس+منy=آ(آ0φ+آ2گناه2φ+آ4گناه4φ+آ6گناه6φ+آ8گناه8φ+آ10گناه10φ)

(2)

در فرمول (2) w=q+منلعبارتی است برای عرض ایزومتریک در زمینه توابع پیچیده، که در آن qعرض ایزومتریک است که بیانگر عرض جغرافیایی است ب، لاختلاف طول جغرافیایی است و آمنضریب ثابتی است که با خروج از مرکز اول بیان می شود ه. بسط طرح ریزی گاوس- کروگر که با تابع مختلط نشان داده شده است، شکل سری توانی اولین گریز از مرکز است. هاز بیضی که دارای مزایای همگرایی سریع و عدم نیاز به تقسیم است.

با این حال، برای منطقه قطبی، زمانی که عرض جغرافیایی بنزدیک به 90 درجه، عرض جغرافیایی ایزومتریک qبه بی نهایت نزدیک می شود، که باعث ایجاد مشکل برای راه حل های رو به جلو و معکوس طرح گاوس- کروگر در ناحیه قطبی می شود. به منظور حل این مشکل، هم عرض جغرافیایی منسجم θ=π2-φمعرفی شده است، جایی که φعرض جغرافیایی منسجم است، φ=2آرکتان1+گناهب1-گناهب(1-هگناهب1+هگناهب)ه-π2، سپس عرض جغرافیایی منسجم را می توان به صورت زیر بیان کرد:

θ=π-2آرکتان1+گناهب1-گناهب(1-هگناهب1+هگناهب)ه=2(π2-آرکتان(انقضا(q)))=2آرکتان(انقضا(-q))=2آرکتان1-گناهب1+گناهب(1+هگناهب1-هگناهب)ه

(3)

منحنی تغییر عرض جغرافیایی ایزومتریک qو عرض جغرافیایی منسجم θبا عرض جغرافیایی بدر شکل 2 و شکل 3 نشان داده شده است .

با توجه به معادله (3) و شکل 3 ، زمانی که 0درجه≤ب≤90درجه، θهمیشه در دسترس است. با تعویض θدر معادله (2)، بیان جواب رو به جلو تابع پیچیده طرح ریزی گاوس-کروگر را می توان به دست آورد:

{q=آرکتان(گناهب)-ه⋅آرکتان(هگناهب)w=q+من ل=آرکتان(گناهب)-ه⋅آرکتان(هگناهب)+من لθ=2آرکتان[انقضا(-w)]z=ایکس+منy=آ(α0θ-α2گناه2θ+α4گناه4θ-α6گناه6θ+α8گناه8θ-α10گناه10θ)

(4)

با توجه به ادبیات [ 26 ]، رابطه بین مسطح شدن سوم nو اولین خروج از مرکز هاز بیضی است:

n=آ-بآ+ب=1-1-ه21+1-ه2

(5)

با کمک سیستم جبر کامپیوتری؛ ضرایب در رابطه (4) بر حسب بسط می‌یابد هتا ه10و از نظر nتا n5که در جدول 1 نشان داده شده است :

می توان دریافت که وقتی ضرایب در فرمول (4) در یک سری توانی بر اساس مسطح سوم گسترش می یابند. n، فرم مرتب تر و فشرده تر و ضرایب ساده تر است که تا حدودی فرمول را ساده می کند و کارایی محاسبات را بهبود می بخشد. هم عرض جغرافیایی θو توابع پیچیده معرفی شده اند تا بتوان معادله (4) را در ناحیه قطبی نیز اعمال کرد.

با توجه به ادبیات [ 24 ، 25 ]، فرمول حل معکوس طرح گاوس-کروگر را می توان از رابطه (4) به دست آورد:

{ω=zآα0=ایکس+منyآα0θ=-ω+ب2گناه2ω+ب4گناه4ω+ب6گناه6ω+ب8گناه8ω+ب10گناه10ω

(6)

به همین ترتیب، ضرایب در رابطه (6) بر حسب بسط می‌یابد هتا ه10و از نظر nتا n5که در جدول 2 نشان داده شده است :

پس از به دست آوردن هم عرض جغرافیایی پیچیده θ، با توجه به تعریف آن θ=2آرکتان(انقضا(-q+منل))می توان معادله (7) زیر را بدست آورد:

برنزهθ2=انقضا(-q+منل)=انقضا(-q)cosل-منانقضا(-q)گناهل⇒θ=2آرکتان|برنزهθ2|⇒φ=π2-θ

(7)

پس از عرض جغرافیایی منسجم φاز معادله (7)، عرض جغرافیایی محاسبه می شود بمی توان با توجه به [ 28 ] به دست آورد:

ب=φ+متر2گناه2φ+متر4گناه4φ+متر6گناه6φ+متر8گناه8φ+متر10گناه10φ

(8)

در رابطه (8)، ضرایب در جدول 3 نشان داده شده است :

به طور خلاصه، معادلات (4) و (6) مسائل راه حل های رو به جلو و معکوس طرح گاوس-کروگر را حل می کند و از منطقه بندی اجتناب می کند. در مقایسه با ضرایب فوق می توان نتیجه گرفت که وقتی سومین مسطح nاولین خروج از مرکز را جایگزین می کند ه، ضرایب هر عبارت از نظر مقدار کوچکتر و از نظر شکل فشرده تر است که کارایی تبدیل مختصات را تا حدی بهبود می بخشد.

3. اصلاح فرم بیان تابع پیچیده پروجکشن گاوس-کروگر

کار کارتوگرافی عملی نه تنها شامل تبدیل مختصات نقاط، بلکه همچنین نقشه برداری از خطوط و سطوح است. فرآیند پیش‌بینی نقشه شامل تعداد زیادی محاسبات است که الزامات بالاتری را برای بازده محاسبه روابط ریاضی طرح‌ریزی پیش‌بینی می‌کند. با توجه به این موضوع، برای راحتی توضیح، معادلات (4) و (6) به ترتیب به عنوان “شکل زاویه چندگانه” عبارت تابع پیچیده طرح ریزی گاوس-کروگر تعریف می شوند. در این بخش تغییراتی در آنها ایجاد می شود تا فرم مناسب تری برای محاسبه کامپیوتری به دست آید.

3.1. فرم 1: “فرم نمایی قدرت”

بر اساس رابطه (4)، فرمول حل جلو تابع پیچیده طرح ریزی گاوس-کروگر “شکل نمایی توان” به صورت زیر مشتق می شود:

z=ایکس+منy=آج0θ+آcosθ(ج1گناهθ+ج3گناه3θ+ج5گناه5θ+ج7گناه7θ+ج9گناه9θ)

(9)

طبق رابطه (4)، ضرایب موجود در رابطه (9) عبارتند از:

{ج0=آ0ج1=-2آ2+4آ4-6آ6+8آ8-10آ10ج3=-8آ4+32آ6-80آ8+160آ10ج5=-32آ6+192آ8-672آ10ج7=-128آ8+1024آ10ج9=-512آ10

(10)

به همین ترتیب، ضرایب در رابطه (9) بر حسب بسط می‌یابد هتا ه10و از نظر nتا n5که در جدول 4 نشان داده شده است

پس از محاسبه z، سایر فرآیندهای محاسباتی با معادله (4) مطابقت دارد و در اینجا توضیح داده نخواهد شد.

بر اساس رابطه (6)، فرمول حل معکوس تابع پیچیده طرح ریزی گاوس- کروگر “شکل نمایی توان” به صورت زیر بدست می آید:

θ=-ω+(j1گناهω+j3گناه3ω+j5گناه5ω+j7گناه7ω+j9گناه9ω)cosω

(11)

طبق رابطه (6) ضرایب موجود در رابطه (11) عبارتند از:

{j1=2ب2+4ب4+6ب6+8ب8+10ب10j3=-8ب4-32ب6-80ب8+160ب10j5=32ب6+192ب8+672ب10j7=-128ب8-1024ب10j9=512ب10

(12)

به همین ترتیب، ضرایب در رابطه (11) بر حسب بسط می‌یابد هتا ه10و از نظر nتا n5که در جدول 5 نشان داده شده است :

پس از محاسبه θ، سایر فرآیندهای محاسباتی با معادله (6) مطابقت دارند و در اینجا توضیح داده نمی شوند.

3.2. فرم 2: “فرم زاویه دوتایی”

بر اساس معادله (4)، فرمول حل جلو تابع پیچیده طرح ریزی گاوس-کروگر که با “فرم زاویه دوتایی” نشان داده شده است به صورت زیر مشتق می شود:

z=ایکس+منy=آک0θ+آگناه2θ(ک1+(ک2+(ک3+(ک4+ک5cos2θ)cos2θ)cos2θ)cos2θ)

(13)

مطابق رابطه (4)، ضرایب موجود در رابطه (13) عبارتند از:

{ک0=آ0ک1=-آ2+آ6-آ10ک2=2آ4-4آ8ک3=-4آ6+12آ10ک4=8آ8ک5=-16آ10

(14)

به همین ترتیب، ضرایب در رابطه (13) بر حسب بسط می‌یابد هتا ه10و از نظر nتا n5که در جدول 6 نشان داده شده است :

بر اساس رابطه (6)، فرمول حل معکوس تابع متغیر پیچیده طرح ریزی گاوس- کروگر که با “فرم زاویه دوتایی” نشان داده شده است به صورت زیر مشتق می شود:

θ=-ω+گناه2ω(ل1+(ل2+(ل3+(ل4+ل5cos2ω)cos2ω)cos2ω)cos2ω)

(15)

طبق رابطه (6) ضرایب موجود در رابطه (15) عبارتند از:

{ل1=ب2-ب6+ب10ل2=2ب4-4ب8ل3=4ب6-12ب10ل4=8ب8ل5=16ب10

(16)

به همین ترتیب، ضرایب در رابطه (15) بر حسب بسط می‌یابد هتا ه10و از نظر nتا n5که در جدول 7 نشان داده شده است :

به طور خلاصه، بر اساس تئوری توابع مختلط، سه نوع عبارات تابع پیچیده از طرح ریزی گاوس-کروگر توسط سیستم جبری رایانه ای مشتق شده اند. این عبارات کاملاً معادل هستند و همگی عباراتی نمادین هستند که برای هر بیضی مرجع مناسب هستند.

4. تجزیه و تحلیل تفاوت برش

با توجه به اصل بسط سری، هر چه ترتیب بسط بزرگتر باشد، دقت مربوطه بیشتر است و بیان مربوطه طولانی تر است. بسط های مشتق شده از معادلات (4)، (6)، (9)، (11)، (13) و (15) عبارات نمادین قابل استفاده برای بیضی زمین با هر پارامتری هستند. در این مقاله، سیستم مختصات ژئودزی ملی CGCS2000 به عنوان نمونه ای برای انجام تحلیل عددی بر روی سه شکل از عبارت تابع پیچیده طرح ریزی گاوس-کروگر و تجزیه و تحلیل تفاوت برش آنها در صورت گسترش به ترتیب های مختلف، در نظر گرفته شده است. پارامترهای بیضی CGCS2000: محور اصلی: آ=6378137 متر; صاف بودن: f=1/298.257222101; اولین خروج از مرکز: ه=0.0818191910428152[ 29 ].

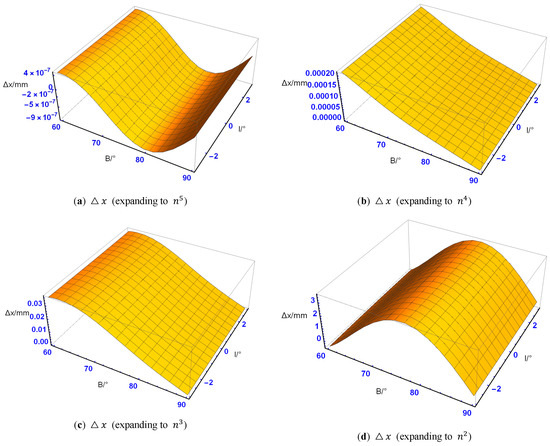
ایده اصلی تجزیه و تحلیل به شرح زیر است: یک باند طرح ریزی گاوس-کروگر را انتخاب کنید پ={(ب،ل):|ل|≤3∘،60∘≤ب≤90∘}، مختصات طرح ریزی را محاسبه کنید (ایکس0،y0)از طریق فرمول اعداد واقعی سنتی ارائه شده در [ 15 ، 27 ]، مقدار مختصات را محاسبه کنید (ایکسمن،yمن)از طریق فرمول گسترش راه حل رو به جلو فرمول (4) از “شکل زاویه چندگانه”، و محاسبه تفاوت، به ترتیب، برای به دست آوردن تفاوت محاسباتی راه حل طرح ریزی رو به جلو. توزیع تفاوت در شکل 4 و شکل 5 نشان داده شده است نشان داده شده است :

به طور مشابه، انتخاب باند طرح ریزی گاوس-کروگر پ={(ب،ل):|ل|≤3∘،60∘≤ب≤90∘}، توزیع اختلاف انبساط محلول رو به جلو به صورت زوایای متعدد بر اساس انبساط سومین مسطح n در شکل 6 و شکل 7 نشان داده شده است. نشان داده شده است :

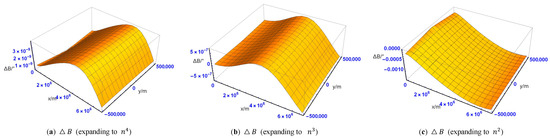
به طور مشابه، انتخاب یک باند طرح ریزی گاوس-کروگر س={(ایکس،y):0 کیلومتر≤ایکس≤6600 کیلومتر، |y|≤500 کیلومتر}، مختصات بیضی (ب0،ل0)با فرمول حل معکوس داده شده در [ 26 ] و سپس مختصات محاسبه می شود(بمن،لمن)با فرمول انبساط معکوس حل معکوس (6) به شکل “زاویه چندگانه” و اختلاف محاسبه محاسبه می شود. (Δب، Δل)حل معکوس به ترتیب با محاسبه اختلاف بدست می آید. توزیع تفاوت در شکل 8 و شکل 9 نشان داده شده است نشان داده شده است :

به طور مشابه، بر اساس انبساط سومین مسطح n ، توزیع تفاوت انبساط محلول معکوس “شکل زاویه چندگانه” در شکل 10 و شکل 11 نشان داده شده است. نشان داده شده است :

همانطور که از شکل 4 ، شکل 5 ، شکل 6 ، شکل 7 ، شکل 8 ، شکل 9 ، شکل 10 و شکل 11 مشاهده می شود، زمانی که عبارات تابع مختلط رو به جلو و معکوس طرح ریزی گاوس- کروگر به همان ترتیب بر اساس بسط می شوند. در خارج از مرکز بیضی هو سومین مسطح کردن n ، تفاوت های محاسباتی تفاوت چندانی با هم ندارند که می توان آن را با دقت برابر در نظر گرفت. هنگامی که بیان راه حل جلو به گسترش می یابد ه10و n5، تفاوت محاسبه مختصات (Δایکس، Δy)از مرتبه هستند 10-7میلی متر هنگامی که عبارت حل معکوس به گسترش می یابد ه10و n5، ترتیب تفاوت محاسبه مختصات (Δایکس، Δy)است 10-9″. تفاوت برش راه حل رو به جلو و معکوس می تواند الزامات ژئودزی را به خوبی برآورده کند، اما فرمول های بسط سری توان مربوطه نیز کمی طولانی و پیچیده هستند. با توجه به [ 26 ]، دقت محاسبه انبساط به ترتیب بسط مرتبط است. وقتی عبارات به ه6و n3، ترتیب بزرگی تفاوت محاسباتی (Δایکس، Δy)از راه حل رو به جلو است 10-2میلی متر و ترتیب بزرگی تفاوت محاسباتی (Δب، Δل)از راه حل معکوس است 10-4″، که هر دو الزامات دقت را برآورده می کنند. علاوه بر این، عبارات مختصرتر و کاربردی تر هستند.

به طور مشابه، برای عبارت راه حل رو به جلو (9) در “شکل نمایی توان”، با تجزیه و تحلیل تفاوت های کوتاهی عبارت گسترش یافته به عبارت های مختلف، می توان نتیجه گرفت که وقتی عبارت به بسط می شود ج5، ترتیب بزرگی تفاوت محاسباتی (Δایکس، Δy)از راه حل رو به جلو است 10-3میلی متر توزیع از (Δایکس، Δy)در شکل 12 و شکل 13 نشان داده شده است :

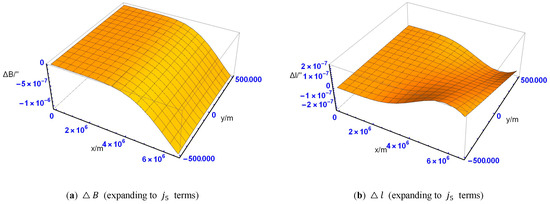
برای عبارت حل معکوس (11) به شکل «نمای توان»، با تجزیه و تحلیل اختلاف برش انبساط به عبارات مختلف، می توان نتیجه گرفت که ترتیب بزرگی تفاوت محاسباتی جواب معکوس زمانی که عبارت بسط می شود. به j5شرایط است 10-6″. روند تغییرات تفاوت محاسبه طول و عرض جغرافیایی (Δب، Δل)در شکل 14 و 15 نشان داده شده است :

برای عبارت حل جلویی (13) به صورت «فرم زاویه دوتایی»، با تجزیه و تحلیل اختلاف برش عبارت بسط داده شده به عبارات مختلف، می توان نتیجه گرفت که ترتیب بزرگی تفاوت محاسباتی جواب جلو برابر است. 10-2میلی متر وقتی که عبارت به ک3شرایط، و روند تغییرات تفاوت محاسبه مختصات (Δایکس، Δy)در شکل 16 و 17 نشان داده شده است :

برای عبارت حل معکوس (15) به شکل “شکل زاویه دوتایی”، با تجزیه و تحلیل اختلاف برش انبساط به عبارات مختلف، می توان نتیجه گرفت که ترتیب بزرگی تفاوت محاسباتی جواب معکوس زمانی که عبارت بسط می شود. به ل3شرایط است 10-7″”و روند تغییرات تفاوت محاسبه طول و عرض جغرافیایی (Δب، Δل)در شکل 18 و شکل 19 نشان داده شده است نشان داده شده است :

به طور خلاصه، با فرض برآوردن الزامات دقت ژئودزی، عبارات ساده شده توابع پیچیده سه شکل طرح ریزی گاوس-کروگر به شرح زیر است:

عبارت در “شکل زاویه چندگانه”:

z=ایکس+منy≈آ(α0θ-α2گناه2θ+α4گناه4θ-α6گناه6θ)

(17)

θ≈-ω+ب2گناه2ω+ب4گناه4ω+ب6گناه6ω

(18)

عبارت در “شکل نمایی”:

z=ایکس+منy≈آج0θ+آcosθ(ج1گناهθ+ج3گناه3θ+ج5گناه5θ)

(19)

θ≈-ω+(j1گناهω+j3گناه3ω+j5گناه5ω)cosω

(20)

عبارت در “شکل زاویه دوتایی”:

z=ایکس+منy≈آک0θ+آگناه2θ(ک1+(ک2+ک3cos2θ)cos2θ)

(21)

θ≈-ω+گناه2ω(ل1+(ل2+ل3cos2ω)cos2ω)

(22)

5. تحلیل موردی و تحلیل کارایی محاسبه

از طریق اشتقاق بالا، سه شکل از عبارات ساده شده (17-22) برای توابع پیچیده طرح ریزی گاوس-کروگر به دست می آید که الزامات دقت را برآورده می کند. به منظور بررسی کارایی آنها، ثابت بیضی CGCS2000 برای تجزیه و تحلیل مثال انتخاب شده است. منطقه را بگیرید 0∘≤ب≤90∘،-3∘≤ل≤3∘ (0 کیلومتر≤ایکس≤6000 کیلومتر،-500 کیلومتر≤y≤500 کیلومتر)که شامل قطب ها است، که در آن تعداد نقاط را می توان با وضوح جهات جغرافیایی و طول جغرافیایی تعیین کرد. رزولوشن را بگیرید 1″×1″ (2 کیلومتر×2 کیلومتر)به عنوان مثال، از جمله 5401×217(3001 ×501) امتیاز.

با در نظر گرفتن منطقه فوق به عنوان مثال، کارایی محاسباتی تمام فرمول های موجود در مقاله مورد تجزیه و تحلیل قرار می گیرد. از طریق فرمول سنتی اعداد حقیقی (فرمول (1))، جواب رو به جلو می گیرد تیfو جواب معکوس می گیرد تیمن.

از طریق فرمول “شکل زاویه چندگانه”، هنگام گسترش به آ10شرایط، طول می کشد تی1fبرای راه حل رو به جلو (فرمول (4))؛ و هنگام گسترش به ب10شرایط، طول می کشد تی1منبرای حل معکوس (فرمول (6)). هنگام گسترش به آ6، طول می کشد تی1fبرای راه حل رو به جلو (فرمول (17))؛ و زمانی که به ب6، طول می کشد تی1منبرای حل معکوس (فرمول (18)).

از طریق فرمول “شکل نمایی”، هنگام گسترش آن به ج9شرایط، طول می کشد تی2fبرای راه حل رو به جلو (فرمول (9))؛ و هنگام گسترش به j9شرایط، طول می کشد تی2منبرای حل معکوس (فرمول (11)). هنگام گسترش به ج5، طول می کشد تی2fبرای راه حل رو به جلو (فرمول (19))؛ و هنگام گسترش به j5، طول می کشد تی2منبرای حل معکوس (فرمول (20)).

از طریق فرمول “فرم زاویه دوتایی”، هنگام گسترش آن به ک5شرایط، طول می کشد تی3fبرای راه حل رو به جلو (فرمول (13))؛ و هنگام گسترش به ل5شرایط، طول می کشد تی3منبرای حل معکوس (فرمول (15)). هنگام گسترش به ک3، طول می کشد تی3fبرای راه حل رو به جلو (فرمول (21))؛ و زمانی که به ل3، طول می کشد تی3منبرای حل معکوس (فرمول (22)).

الگوریتم مشتق شده بر روی یک پردازنده 2.90 گیگاهرتزی اینتل توسط نرم افزار Matlab2017a کامپایل و اجرا می شود. نتایج محاسبات در جدول 8 نشان داده شده است :

طبق جدول 8 ، به دلیل عملیات ادغام و تکرار درگیر، بازده محاسبه هنگام استفاده از فرمول واقعی سنتی بسیار پایین است. هنگامی که توابع پیچیده معرفی می شوند و بسط سری اتخاذ می شود، فرمول های راه حل رو به جلو و معکوس جدید فقط شامل جمع و ضرب توابع مثلثاتی است که کارایی محاسباتی را تا حد زیادی بهبود می بخشد. با مقایسه تی1f، تی2f، و تی3fمی توان دریافت که راندمان محاسباتی فرم «زاویه مضاعف» بالاترین است که به شکل «زاویه چندگانه» نزدیک است، در حالی که بازده محاسبه شکل «نمایی» کمترین است. با مقایسه تی1f، تی2f، و تی3f، می توان دریافت که بازده محاسبه سه شکل فرمول حل معکوس نیز قانون مشابهی دارد. با مقایسه تی1fو تی1f، می توان دریافت که عبارت های مرتبه پایین تر برای راه حل های رو به جلو و معکوس کارآمدتر هستند. در نتیجه، پس از تجزیه و تحلیل دقیق، تجزیه و تحلیل اختلاف برش، و تجزیه و تحلیل بازده محاسبه، بیان تابع پیچیده طرح ریزی گاوس-کروگر در “فرم زاویه دوتایی” نه تنها الزامات ژئودزی را برآورده می کند، بلکه کارایی محاسبات را نیز به خوبی بهبود می بخشد. ک3مقررات؛ به خصوص در مورد وضوح بالاتر و نقاط بیشتر، برتری فرمول بهبود یافته برجسته تر است و بهتر می تواند الزامات نمودارهای الکترونیکی مدرن را برای وضوح نقشه بالاتر و تبدیل طرح ریزی کارآمدتر برآورده کند.

6. خلاصه

در این مقاله، رابطه نگاشت ریاضی بین مختصات بیضی و مختصات صفحه نقشه بر اساس تئوری توابع مختلط حل شده است. با کمک سیستم جبری کامپیوتری Mathematica، عبارات توابع پیچیده بهبود یافته طرح ریزی گاوس-کروگر به سه شکل مشتق شده است. فرمول های مشتق شده عبارت های نمادین هستند و برای هر بیضی مرجع قابل استفاده هستند. علاوه بر این، هر فرمول در یک سری قدرت بر اساس گسترش یافته است هو n، به ترتیب. با در نظر گرفتن بیضی مرجع CGCS2000 به عنوان مثال، تجزیه و تحلیل عددی انجام می شود. با تجزیه و تحلیل تفاوت برش زمانی که عبارت به مرتبه های مختلف بسط می یابد، فرمول انبساط ساده تری که نیاز دقت ژئودتیکی را برآورده می کند، به دست می آید که کارایی محاسبه را تا حد معینی بهبود می بخشد و استفاده و گسترش فرمول را آسان تر می کند. علاوه بر این، گرفتن 5401×217(3001 ×501) به عنوان مثال، با مقایسه زمان لازم برای محاسبه جواب مختصات رو به جلو و معکوس با فرمول های مختلف، تأیید می شود که بیان تابع پیچیده طرح گاوس-کروگر “فرم زاویه دوتایی” کمترین زمان است. -مصرف و بالاترین بازده محاسباتی. به طور خلاصه، این مقاله از مبنای ریاضی تئوری طرح ریزی نقشه شروع می شود، بسط های پیچیده و طولانی مرتبه بالاتر کنار گذاشته می شوند و ما با بهبود فرمول تبدیل مختصات بر اساس اطمینان از دقت طرح ریزی، کارایی تبدیل طرح ریزی را بهبود می بخشیم. دگرگونی.

منابع

گرافرند، ای. شما، آر. Syffus, R. Map Projections ; Springer: Berlin/Heidelberg, Germany, 2014. [ Google Scholar ]
لاپاین، ام. Usery, EL Map Projection Definition ; Springer: برلین/هایدلبرگ، آلمان، 2017; فصل 9; صص 213-228. [ Google Scholar ] [ CrossRef ]
اسکوپلیتی، ا. Tsoulos، L. انتخاب یک پروجکشن مناسب برای ناوبری در قطب شمال. مار. جئود. 2013 ، 36 ، 234-259. [ Google Scholar ] [ CrossRef ]
بوگایفسکی، ال. Snyder, J. Map Projections: A Reference Manual . تیلور و فرانسیس: لندن، بریتانیا، 1995. [ Google Scholar ]
دنگ، ایکس. تانگ، ز. هوآ، ایکس. Shu, Y. Gauss-Krüger Projection Forward and Reverse Calculation of After Elipsoid Transformation. جی. جئود. ژئودین. 2010 ، 30 ، 49-52. [ Google Scholar ]
Bildirici، IO تبدیل معکوس عددی برای پیش بینی نقشه. محاسبه کنید. Geosci. 2003 ، 29 ، 1003-1011. [ Google Scholar ] [ CrossRef ]
گوا، ی. چن، اچ. Zhang، X. تحقق الگوریتم تبدیل دقیق بین مختصات UTM Google Earth و مختصات ژئودتیک. Surv. نقشه جئول معدن کار. منبع. 2012 ، 28 ، 10-13. [ Google Scholar ]
Zhuang، P. Gauss-Krüger Projection Calculation. Surv. نقشه جئول معدن کار. منبع. 1998 ، 24-27. [ Google Scholar ]
دیکین، RE; هانتر، MN; کارنی، سی. طرح گاوس-کروگر. 2010. در دسترس آنلاین: https://www.academia.edu/354352/The_Gauss_Krueger_Projection (در 4 نوامبر 2022 قابل دسترسی است).
ابی، دی. وولهاوس، ال. Featherstone، W. The Oblique Mercator برای مهندسی و بررسی. Surv. Rev. 2022 , 1-12. [ Google Scholar ] [ CrossRef ]
بازلگا، اس. دو پیش بینی منسجم برای نقشه برداری سطح با ارتفاع ثابت تا صفحه. J. Surv. مهندس 2021 , 147 , 06020004. [ Google Scholar ] [ CrossRef ]
بیان، اس. لی، اچ. لی، زی. پیشرفت تحقیق در تجزیه و تحلیل ریاضی طرح ریزی نقشه توسط جبر رایانه ای. Acta Geod. کارتوگر. گناه 2017 ، 46 ، 1557-1569. [ Google Scholar ]
Clenshaw, CW یادداشتی در مورد جمع بندی سریال Chebyshev. ریاضی. محاسبه کنید. 1955 ، 9 ، 118-120. [ Google Scholar ] [ CrossRef ]
Ablowitz، MJ; Fokas, AS Complex Variables: کاربردهای نظریه توابع مختلط ; انتشارات دانشگاه کمبریج: کمبریج، انگلستان، 2003. [ Google Scholar ]
Bowring، B. The Transverse Mercator Projection-A Solution by اعداد مختلط. Surv. Rev. 1978 , 30 , 325-342. [ Google Scholar ] [ CrossRef ]
Klotz، J. Eine Analy Tische Lösung der Gauss-Krueger-Abbildung. Z. Für Vermess. 1993 ، 118 ، 106-115. [ Google Scholar ]
Schuhr, P. Transformationen zwischen ellipsoidischen geographischen Konformen Gauss-Krueger bzw UTM-Koordinaten. انجمن 1995 ، 5 ، 259-264. [ Google Scholar ]
بیان، اس. Zhang, C. نمایش تابع پیچیده از طرح ریزی گاوس. J. Inst. Surv. نقشه 2001 ، 18 ، 157-159. [ Google Scholar ]
لی، اچ. بیان، اس. بیان طرح ریزی گاوس توسط اعداد مختلط. Acta Geod. کارتوگر. گناه 2008 ، 37 ، 5-9. [ Google Scholar ]
لیو، کیو. بیان، اس. Li, Z. فرمول های بسته پروجکشن گاوس با تغییر شکل آن در کره. جی. ناو. دانشگاه مهندس 2015 ، 27 ، 45-49. (به زبان چینی) [ Google Scholar ]
گوا، جی. شن، دبلیو. نینگ، جی. توسعه روش دقیق لی برای طرح ریزی گاوس-کروگر. جی. جئود. 2020 ، 94 ، 1-16. [ Google Scholar ] [ CrossRef ]
لی، ال. پیش بینی های منسجم بر اساس توابع بیضوی ژاکوبین. بین المللی جی. جئوگر. Inf. Geovisualization 1976 ، 13 ، 67-101. [ Google Scholar ] [ CrossRef ]
Karney, C. Mercator عرضی با دقت چند نانومتر. جی. جئود. 2011 ، 85 ، 475-485. [ Google Scholar ] [ CrossRef ]
Bermejo-Solera، M. Otero, J. فرمول های ساده و بسیار دقیق برای محاسبه مختصات Mercator عرضی از طول جغرافیایی و عرض ایزومتریک. جی. جئود. 2009 ، 83 ، 1-12. [ Google Scholar ] [ CrossRef ]
یانگ، کیو. اسنایدر، جی. Tobler, W. Map Projection Transformation: Principles and Applications ; CRC Press: Boca Raton، FL، USA، 2020. [ Google Scholar ]
Xiong، J. ژئودزی بیضی ; انتشارات ارتش آزادیبخش خلق چین: پکن، چین، 1988. [ Google Scholar ]
بیان، اس. ژانگ، سی. طرح گاوس – راه حلی با اعداد مختلط. J. Pla Inst. Surv. نقشه 2001 ، 18 ، 157-159. [ Google Scholar ]
لی، ایکس. لی، اچ. لیو، جی. بیان، اس. جیائو، سی. بسط های ساده شده عرض های جغرافیایی مشترک با عرض جغرافیایی و عرض جغرافیایی به عنوان متغیر. Appl. علمی 2022 ، 12 ، 7818. [ Google Scholar ] [ CrossRef ]
پنگ، ایکس. گائو، جی. Wang, J. تحقیق در مورد تبدیل مختصات بین WGS84 و CGCS2000. جی. جئود. ژئودین. 2015 ، 35 ، 219-221. [ Google Scholar ]