خلاصه

یک روش جدید برای انتخاب مقیاس‌های بهینه هنگام نقشه‌برداری ویژگی‌های توپوگرافی یا هیدروگرافی معرفی شده است. این روش از پارتیشن اندازه رتبه ای از توزیع های دم سنگین برای تشخیص گره های تغییرپذیری مقیاس مجدد در سلسله مراتب زیربنایی مجموعه داده استفاده می کند. این گره ها که به شکستگی سر/دم معروفند، می توانند برای نشان دادن مقیاس های بهینه استفاده شوند. سپس، الگوریتم تقسیم‌بندی ارزیابی شبکه فراکتال (FNEA) با سطوح توپوگرافی یا هیدروگرافی برای تولید اشیا با مقیاس بهینه اعمال می‌شود. یک تبدیل توپولوژیکی اجازه می دهد تا دو فرآیند (پارتیشن و تقسیم بندی) را به هم پیوند دهیم، در حالی که بعد فراکتالی فرآیند مقیاس بندی مجدد به عنوان یک متریک بهینه استفاده می شود. روش جدید با دو حوضه بزرگ رودخانه در یونان، یعنی حوضه رودخانه پینیوس و آچلوس آزمایش شده است. با استفاده از مدل رقومی ارتفاع به عنوان تنها مجموعه داده ورودی. این روش در شناسایی مجموعه‌ای از مقیاس‌های بهینه برای نقشه‌برداری ارتفاع، شیب و تجمع جریان موفق بود. انحراف از شرایط ایده آل برای اجرای شکستن سر/دم مورد بحث قرار گرفته است. پیاده‌سازی این روش به یک برنامه تحلیل مبتنی بر شی و تعداد کمی توابع جغرافیایی رایج در اکثر برنامه‌های GIS نیاز دارد. روش جدید به آشکار کردن فرآیندهای زیست محیطی زیربنایی در زمینه های مختلف علوم زمین کمک می کند و بنابراین به تصمیم گیری مدیریت زمین و تعمیم نقشه ها کمک می کند. پیاده‌سازی این روش به یک برنامه تحلیل مبتنی بر شی و تعداد کمی توابع جغرافیایی رایج در اکثر برنامه‌های GIS نیاز دارد. روش جدید به آشکار کردن فرآیندهای زیست محیطی زیربنایی در زمینه های مختلف علوم زمین کمک می کند و بنابراین به تصمیم گیری مدیریت زمین و تعمیم نقشه ها کمک می کند. پیاده‌سازی این روش به یک برنامه تحلیل مبتنی بر شی و تعداد کمی توابع جغرافیایی رایج در اکثر برنامه‌های GIS نیاز دارد. روش جدید به آشکار کردن فرآیندهای زیست محیطی زیربنایی در زمینه های مختلف علوم زمین کمک می کند و بنابراین به تصمیم گیری مدیریت زمین و تعمیم نقشه ها کمک می کند.

کلید واژه ها:

شکستگی سر/دم ؛ بعد فراکتال FNEA ; پینیوس ; آخلوس

1. معرفی

بیشتر ویژگی ها یا فرآیندهای منظر، طبیعی یا انسانی (به عنوان مثال، یک جنگل، یک شبکه راه آهن، یک منطقه شهری، یک سیل، یا فرسایش)، وابسته به مقیاس هستند [1 ] . وابستگی مقیاس به این دلیل است که هر ویژگی یا فرآیند دارای مقیاس عملکردی خاص خود است، به عنوان مثال، یک بازه زمانی خاص که در آن یکپارچه می‌شود یا برای ارائه پیام هموار می‌شود. مقیاس عملکردی، به نوبه خود، مقیاس نگاشت مناسب را تعیین می کند، به عنوان مثال، واحد فضایی و زمانی مورد نیاز برای تجسم این ویژگی ها برای نقشه خوان ها.
مناظر از سطوحی به هم پیوسته تشکیل شده‌اند که در مقیاس‌های زمانی و مکانی مجزا عمل می‌کنند و به‌عنوان گره‌هایی از یک سلسله مراتب ذاتی تعامل دارند. برای تفسیر تعاملات احتمالی بین این سطوح، لازم است آنها را به بخش های اساسی خود تجزیه کنیم [ 2 ].
وابستگی مقیاس و ضرورت رویکرد سلسله مراتبی چندمقیاسی به عنوان یک موضوع مهم در تحقیقات هیدرولوژیکی از دیرباز مطرح شده است. انتخاب یک مقیاس مناسب هنگام نقشه برداری ویژگی های توپوگرافی یا هیدروگرافی یکی از پیچیده ترین مشکلات، به ویژه در پروژه های کاربری و مدیریت زمین بوده است [ 3 ].
نگرانی اصلی در مورد مقیاس این است که چگونه ممکن است بر جمع آوری داده های مکانی و نتایج تجزیه و تحلیل با توجه به دقت و قابلیت اطمینان تأثیر بگذارد [ 1 ]. مشکل مقیاس نیز توسط ژانگ و همکاران بیان شده است. (2018) [ 4 ] از طریق این سوال: چند مقیاس لازم است (یادداشت نویسندگان: برای توصیف یک ویژگی یا فرآیند خاص) و “فاصله” بین این مقیاس ها چقدر است؟ مقیاس هایی که با این پرسش مضاعف مطابقت دارند (یعنی “چند” و “در چه فاصله ای”) را می توان “بهینه” نامید.
به طور معمول، مقیاس های “بهینه” در وظایف نقشه برداری توپوگرافی و هیدروگرافی با شهود یا تجربه انتخاب می شوند. به عنوان مثال، کاریداس و پاناگوس (2016) [ 5 ] یک مقیاس درشت و ظریف از کاربرد را در چارچوب نقشه برداری بازده رسوب در قبرس، از نظر کالیبراسیون مدل فرسایش، ترکیب کردند. اگر تعیین مقیاس های بهینه قبل از مطالعه یک مشکل محیطی یا مدیریت زمین امکان پذیر بود، می توان ویژگی ها یا فرآیندهای مناسب را به شیوه ای سریع، صحیح، موثر و قوی مدل سازی کرد. به عنوان یک پارادایم، معرفی مقیاس عملکردی توسط جیانگ (2013) [ 6] در مشکل نقشه‌برداری شهر منجر به مفهوم‌سازی «شهرهای طبیعی» به‌عنوان یک فرآیند از پایین به بالا و مبتنی بر داده‌ها شده است، به طوری که همه شهرهای نقشه‌برداری شده در کشورهای مختلف قابل مقایسه هستند [7 ] .
برای سال‌های متمادی، مقیاس در مجموعه داده‌های شطرنجی ویژگی‌های توپوگرافی یا هیدروگرافی تنها با اندازه سلول مرتبط بود [ 8 ]. با این حال، سلول ها به طور پیش فرض یک شکل مستطیلی دارند، و بنابراین، تغییر اندازه سلول به عنوان یک فرآیند تغییر مقیاس محدودیت جدی در گرفتن شکل طبیعی و توزیع فضایی ویژگی های مورد نظر دارد. جایگزین تغییر اندازه سلول، تبدیل سلول‌ها به اشیا با استفاده از تکنیک‌های تقسیم‌بندی تصویر، روش مناسب‌تری برای مطالعه چشم‌انداز در مقیاس‌های چندگانه نشان داده شده است (به شرطی که وضوح فضایی مجموعه داده اصلی به اندازه کافی بالا باشد تا ویژگی‌ها یا فرآیندهای مورد مطالعه را به تصویر بکشد) [ 9 ].
در این راستا، تحقیقات زیادی در طول زمان در چارچوب تجزیه و تحلیل تصویر مبتنی بر شی جغرافیایی (GEOBIA) انجام شده است. انتخاب مقیاس‌های بهینه با تکنیک‌های آزمون و خطا، تا کنون، رایج‌ترین عمل بوده است، اگرچه به صرف زمان و کار [ 10 ]. در شناخته شده ترین تلاش تاکنون، Drǎguţ و همکاران. (2010) [ 11] ‘ESP’ (تخمین پارامتر مقیاس)، یک نرم افزار تعبیه شده در برنامه Definiens (پرکاربردترین نرم افزار OBIA) را توسعه داد. ESP امکان تخمین سریع پارامترهای مقیاس را در «تقسیم بندی چند رزولوشن» (یک اصطلاح معادل برای تقسیم بندی چند مقیاسی)، چه برای تصاویر و چه برای لایه های موضوعی، فراهم می کند. ESP داده های تعریف شده توسط کاربر را پس از درج شش پارامتر مختلف توسط کاربر (شامل طرح های سلسله مراتبی در صورت وجود) به طور خودکار بخش بندی می کند و سپس واریانس محلی را به عنوان انحراف استاندارد در اشیاء ایجاد شده برای هر سطح تقسیم بندی محاسبه می کند. نتایج در یک محیط گرافیکی کاربر پسند نشان داده شده است.
تلاش های کمتر عمومی دیگری نیز صورت گرفته است. Romstad و Etzelmüller (2012) [ 12 ] روشی را برای تقسیم بندی ژئومورفیک معرفی کردند که اجسام را بر اساس مقادیر میانگین انحنای آنها ایجاد می کند. می توان گفت که این رویکرد بدون در نظر گرفتن تغییرات توپوگرافی احتمالی در هر شی ایجاد شده، سادگی هندسی را تضمین می کند. اخیراً نیوتن و همکاران. (2019) [ 13] سه روش تقسیم بندی (بخش بندی مورفولوژیکی روی لبه ها، تجزیه و تحلیل پایداری کانتور و خطوط فعال) را برای شناسایی ویژگی و عملکرد در تعیین مرز ویژگی مقایسه کرد. نتایج نشان می‌دهد که هیچ روش تقسیم‌بندی به طور مداوم برای همه موارد آزمایش برتر نیست، اما رویکرد مقایسه برای کشف و بهینه‌سازی جایگزین‌های تقسیم‌بندی برای سناریوهای مشخصه‌بندی مبتنی بر ویژگی مفید بود.
با این حال، هیچ یک از روش‌های توسعه‌یافته تاکنون به یک رویکرد تقسیم‌بندی کاملاً خودکار از پایین به بالا و داده‌محور دست پیدا نکرده‌اند. ESP ممکن است فرآیند تقسیم‌بندی را در یک چارچوب کلی چند مقیاسی تسهیل کرده باشد، اما واقعاً بر رویکرد آزمون و خطا غلبه نکرده است. سایر روش ها یا فاقد کلیت هستند یا در یک چارچوب تک مقیاسی محدود می شوند. برای نقد روش‌های از پیش موجود در تقسیم‌بندی و تحلیل تصویر، به Karydas (2020) [ 14 ] مراجعه کنید.
به گفته لام و همکاران. (2002) [ 15 ]، “ابزاری مناسب برای تشخیص تغییرات از طریق مقیاس‌ها در سلسله‌مراتب فرآیند منظر پیچیده” تحلیل فراکتال است. جیانگ و برانت (2016) [ 1 ] استدلال می کنند که طبیعت فراکتال ذاتی در همه پدیده های جغرافیایی است و علاوه بر این، منبع اصلی وابستگی به مقیاس آنها است. بیشتر ویژگی‌های توپوگرافی، مانند شیب و جنبه، یا ویژگی‌های هیدرولوژیکی، مانند شبکه نهرها و حوزه‌های آبخیز، همگی ماهیت فراکتالی را نشان می‌دهند.

ویژگی اساسی ویژگی های فراکتال این است که طول، مساحت یا حجم تابعی از مقیاس اندازه گیری است [ 16 ]. فراکتال ها عمدتاً به دلیل دشواری در تجزیه و تحلیل فرم ها و فرآیندهای فضایی توسط بعد توپولوژیکی (عدد صحیح) هندسه اقلیدسی معرفی شدند. ذاتی ترین پارامتر در هندسه فراکتال بعد فراکتال است که به عنوان نسبت تغییرات لگاریتمی در جزئیات تعریف می شود. n) به تغییر لگاریتمی در مقیاس ( س) از ویژگی های جغرافیایی [ 17 ]:

D=ورود به سیستم(nν+1nν)ورود به سیستم(سν+1سν)
از معادله (1) به دست می آید که بعد فراکتال ممکن است مقادیر اعشاری را بگیرد، به عنوان مثال 1.26 یا 2.65.
مقیاس در هندسه فراکتال در درجه اول به روشی تعریف می شود که در آن یک سری از مقیاس ها در یک سلسله مراتب مقیاس به یکدیگر مرتبط هستند. برای مثال، خط ساحلی مجموعه‌ای از خم‌های تعریف‌شده بازگشتی است که سلسله‌مراتب مقیاس‌بندی خم‌های بسیار کوچک‌تر از خم‌های بزرگ را تشکیل می‌دهد. تجزیه و تحلیل فراکتال نباید تنها به عنوان یک روش در نظر گرفته شود، بلکه عمدتاً به عنوان یک الگوی جدید شامل الگوی مقیاس بندی جهانی در تمام مقیاس ها از کوچکترین به بزرگ ترین [ 1 ] است.
در این راستا، جیانگ و یین (2014) [ 18 ] ‘ht-index’ را به عنوان معیاری از پیچیدگی در ساختار سلسله مراتبی مجموعه داده معرفی کردند، که بعد فراکتالی به تنهایی نمی تواند به طور موثر بیان کند. نویسندگان با موفقیت با یک تصویر در مقیاس خاکستری، یک مدل ارتفاعی دیجیتال و شبکه های جاده ای شهرهای بسیار متفاوت آزمایش کردند. اخیراً، Karydas (2020) [ 14] از شکاف های سر/دم برای توسعه روشی جدید برای انتخاب مقیاس های بهینه برای تقسیم بندی چند مقیاسی تصاویر ماهواره ای به عنوان ابزاری برای تسهیل رویکرد از پایین به بالا در طبقه بندی تصاویر مبتنی بر شی استفاده کرد. این روش از بعد فراکتال به عنوان معیاری از تغییرپذیری مقیاس در خروجی های تقسیم بندی استفاده می کند. یک تبدیل توپولوژیکی اجازه می دهد تا پارتیشن را با فرآیند تقسیم بندی پیوند دهیم.
هدف اصلی این تحقیق توسعه یک روش جدید، سریع، آسان، عینی و قوی برای انتخاب مقیاس‌های بهینه هنگام نقشه‌برداری ویژگی‌های توپوگرافی یا هیدروگرافی بود. طبق گفته Meentemeyer (1989) [ 19 ]، مقیاس‌های بهینه آن‌هایی هستند که تأثیرگذارترین متغیرهای ویژگی‌های نقشه‌برداری شده با تغییر مقیاس ثابت باقی می‌مانند. سان و همکاران (2006) [ 16 ] استدلال می کنند که عدم تغییر در مقیاس مجدد را می توان با استفاده از بعد فراکتال نشان داد. بنابراین، فرضیه اصلی این تحقیق این بود که انتخاب مقیاس‌های بهینه هنگام نگاشت ویژگی‌های توپوگرافی یا هیدروگرافی را می‌توان با استفاده از بعد فراکتالی به عنوان معیار قضاوتی هدایت کرد که در صورت ثابت ماندن در مقیاس مجدد، انتظار می‌رود مقیاس‌های بهینه را نشان دهد. روش جدید روش کاریداس (2020) را گسترش می دهد [14 ]، از تجزیه و تحلیل تصویر مبتنی بر شی تا تقسیم بندی چند مقیاسی مدل های ارتفاعی دیجیتال (DEM) و مشتقات آنها.

2. روش شناسی

روش جدید بهینه بودن مقیاس را در ساختار مجموعه داده های توپوگرافی یا هیدروگرافی تشخیص می دهد و سپس با ترکیب سه تکنیک متمایز، الگوهای مقیاس بندی شده بهینه را در زمینه فضایی تعریف می کند:
  • تقسیم‌بندی داده‌های توپوگرافی یا هیدروگرافی با قانون اندازه رتبه (همچنین به عنوان شکستگی سر/دم شناخته می‌شود)، بنابراین ساختار داده سلسله مراتبی را تعیین می‌کند [ 20 ].
  • تقسیم بندی سطوح توپوگرافی یا هیدروگرافی با استفاده از ارزیابی تکامل شبکه فراکتال (FNEA)، بنابراین سلول های موضوعی را به اشیاء معنی دار تبدیل می کند [ 21 ].
  • پیوند دو فرآیند فوق از طریق یک تبدیل توپولوژیکی، که نتایج پارتیشن بندی را به داده های توپوگرافی یا هیدروگرافی قطعه بندی شده نشان می دهد [ 14 ].
پارتیشن با قانون اندازه رتبه فرآیندی است که از طریق آن یک مجموعه داده به صورت بازگشتی به دو زیر مجموعه تقسیم می شود: یکی شامل تمام مقادیر بالای میانگین به نام “گروه سر” و دیگری حاوی تمام مقادیر زیر میانگین به نام “” گروه دم’ [ 22 ]. پارتیشن بندی اجازه می دهد تا ساختار سلسله مراتبی ذاتی توسط خود داده ها تعیین شود. امکان پارتیشن بندی یک مجموعه داده با قانون اندازه رتبه با توزیع های سنگین مرتبط است، به عنوان مثال، مجموعه داده هایی که در آن مقادیر بسیار کوچک تری نسبت به مقادیر بزرگ یافت می شود [ 6 ، 23 ]. انواع توزیع های دم سنگین شامل توزیع های توان-قانونی، نمایی یا لگ نرمال است.
تقسیم بندی یک روش مقیاس مجدد مناسب برای یک مجموعه داده شطرنجی است، زیرا ناهمگونی محلی ویژگی مورد علاقه به حداقل می رسد، بنابراین مقیاس هایی را نشان می دهد که در آنها اشیاء معنی دار (یعنی سطوح مشخص شده به طور طبیعی) قابل تشخیص هستند. یکی از رایج‌ترین الگوریتم‌های تقسیم‌بندی، ارزیابی تکامل خالص فراکتال (FNEA) است که به «تقسیم‌بندی چندتحلیلی» نیز معروف است. با FNEA، اشیاء با به حداقل رساندن ناهمگونی درونی مقادیر سلولی از طریق یک روش رشد گام به گام ناحیه ایجاد می شوند تا زمانی که یک آستانه تعریف شده توسط کاربر (به نام “عامل مقیاس”) برسد [21 ] . ضریب مقیاس بر اندازه و شکل شی مورد نظر، با توجه به معیارهای طیفی و/یا دو شکل [ 24] تأثیر می گذارد.]. معیار طیفی اعمال شده با مجموعه داده های تصویری به عنوان انحراف استاندارد مقادیر طیفی موجود در یک شی کاندید تعریف می شود [ 25 ]. اما در این تحقیق به‌جای مقادیر طیفی، از معیار موسوم به «معیار طیفی» برای اندازه‌گیری انحراف معیار مقادیر موضوعی مربوطه (مثلاً ارتفاع، شیب، جنبه و غیره) استفاده می‌شود.

FNEA ثابت کرده است که یکی از موفق ترین الگوریتم های تقسیم بندی تصویر در چارچوب GEOBIA [ 10 ] است. Bobick و Bolles (1992) [ 26 ] استدلال می کنند که اطلاعات ذخیره شده در یک لایه پردازش شده با FNEA به عنوان فراکتال در نظر گرفته می شود، از نظر داشتن درجه یکسانی از عدم نظم در همه مقیاس ها یا (برعکس) خود شباهت در هر مقیاس. یافته‌های تحقیقات قبلی نشان می‌دهد که وقتی FNEA با تصاویر ماهواره‌ای به کار می‌رود، یک معادله قانون قدرت از ضریب مقیاس در مقابل میانگین اندازه جسم مشتق می‌شود [ 14 ، 27 ، 28 ]:

f=آ سfب

جایی که f : ضریب مقیاس; s f : میانگین اندازه شی (در مقیاس f (در m2 ) ؛ a، b : ثابت ها ( a در m -2 و b بدون بعد). نیومن (2005) [ 29 ] استدلال می کند که «رفتار قانون قدرت ممکن است شناسایی شود. به‌علاوه، وودوک (1997) [ 30 ] بیان می‌کند که اشیاء فراکتالی، به‌طور پیش‌فرض، از توزیع‌های آماری قانون قدرت مقیاس‌گذاری پیروی می‌کنند.

با پیروی از پارادایم کاریداس (2020) [ 14 ] برای تصاویر ماهواره ای، یک معادله قانون قدرت بین ضریب مقیاس و میانگین اندازه جسم برای هر یک از ویژگی های توپوگرافی یا هیدروگرافی مورد علاقه را می توان برای یک منطقه مورد مطالعه، با استفاده از یک سری داده استخراج کرد. تقسیم بندی – برای مثال، دوازده توان اول 2، به عنوان مثال، {1، 2، 4، 8، …، 2048}. آزمایش با تصاویر نشان می دهد که چنین سری برای نشان دادن یک تابع کاملا دقیق کافی است (با ضریب تعیین بالا، R2 > 0.9).

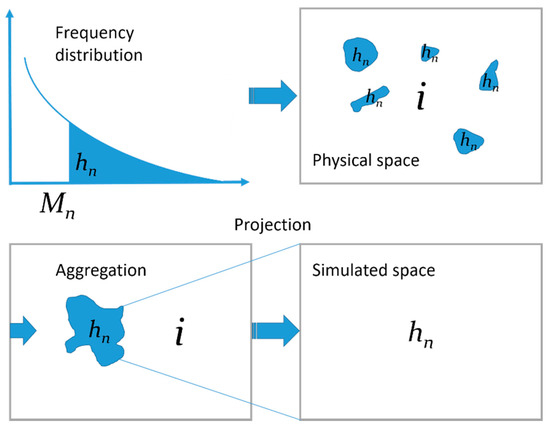
یک تبدیل توپولوژیکی برای انتقال مقیاس‌های بهینه شناسایی‌شده در توزیع فرکانس با شکستگی‌های سر/دم به فضای فیزیکی معرفی شد. این دگرگونی با این واقعیت توجیه می شود که سطح مربوط به یک گروه سر (تولید شده با قانون رتبه بندی) که در واقع به قطعات کوچکتر در کل سطح مورد مطالعه پراکنده شده است، اگر این قطعات کوچک به هم پیوسته باشند، می تواند یک شی واحد را تشکیل دهد. (نوعی تجمع مجازی)؛ این شی منفرد اندازه بهینه را خواهد داشت، مشروط بر اینکه نتیجه یک تقسیم بندی مقیاس بهینه باشد. هافمن و همکاران (1998) [ 31 ] استدلال می کنند که انتظار می رود اطلاعات بهینه برای پردازش و تجزیه و تحلیل بیشتر توسط بهترین نتایج تقسیم بندی ارائه شود. با توجه به کاریداس (2020) [ 14]، اندازه ای که یک شی پس از تبدیل فوق باید داشته باشد را می توان «اندازه متوسط ​​شیء شبیه سازی شده» (SMOS) نامید، و تعداد اشیاء مربوط به SMOS را می توان «شماره شی شبیه سازی شده» (SON) نامید. عملا، SMOS برای هر سطح پارتیشن با تقسیم کل وسعت منطقه مورد مطالعه بر وسعت گروه سر (مرتبط با آن سطح پارتیشن) محاسبه می شود، در حالی که SON برابر است با نسبت وسعت گروه سر نسبت به SMOS:

سn=منساعتn
نn=ساعتnسn

که در آن، s n : اندازه متوسط ​​شیء شبیه سازی شده (SMOS) در پارتیشن n-ام (بدون بعد). i : وسعت کل منطقه مورد مطالعه (m2 ) ؛ h n : وسعت گروه سر در پارتیشن n ام (m2 ) ؛ نn: شماره شی شبیه سازی شده (SON). این تبدیل اجازه می دهد تا خروجی های فضایی فرآیند پارتیشن بندی (پس از میانگین های بازگشتی) به وسعت کل منطقه مورد مطالعه (جایی که تقسیم بندی اعمال می شود) نمایش داده شود. به عبارت دیگر، فضای فیزیکی به یک فضای شبیه سازی شده پیش بینی شده است و این نوع طرح ریزی را می توان به عنوان یک ابزار نگاشت، انتقال بهینه مقیاس از ساختار سلسله مراتبی (جهانی) به الگوهای فضایی (محلی) در نظر گرفت (شکل 1 ) .

در نهایت، SMOS های محاسبه شده حاصل از تبدیل توپولوژیک در معادله (2) درج می شوند تا فاکتورهای مقیاس بهینه برای تقسیم بندی بدست آید. برای تأیید اینکه مقیاس‌های محاسبه‌شده بهینه هستند، ابعاد فراکتالی تمام مقادیر فاکتور مقیاس متوالی محاسبه می‌شود و باید ثابت شود.
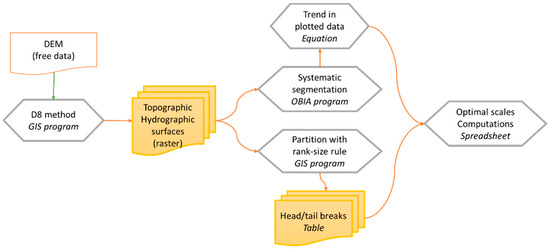
کل روش محاسباتی روش جدید را می توان در سه مرحله مجزا انجام داد (همچنین به شکل 2 مراجعه کنید ):
  • تقسیم بندی سیستماتیک سطح مورد نظر و استخراج یک خط روند (مرتبط با معادله (2)) با استفاده از الگوریتم ارزیابی تکامل خالص فراکتال (FNEA) (معمولاً در یک برنامه OBIA تعبیه شده است).
  • پیاده‌سازی پارتیشن با قانون اندازه رتبه و محاسبه شکست‌های سر/دم در یک صفحه گسترده مشترک. توابع ساده جغرافیایی جاسازی شده در یک برنامه سیستم اطلاعات جغرافیایی (GIS) را می توان برای محاسبه میانگین پارتیشن های متوالی استفاده کرد.
  • محاسبه فاکتورهای مقیاس بهینه با استفاده از معادله روند بر روی شکستگی های سر/دم که از پارتیشن حاصل می شود. اندازه متوسط ​​شیء شبیه سازی شده (SMOS) به عنوان یک خروجی میانی محاسبه می شود. یک صفحه گسترده مشترک برای انجام این محاسبات ساده کافی است.
همانطور که مشخص شد، فرآیند پارتیشن با قانون اندازه رتبه از میانگین استفاده می کند، در حالی که فرآیند تقسیم بندی از انحراف استاندارد استفاده می کند. مقادیر کل مجموعه داده تحت پارتیشن بندی از یک توزیع دم سنگین پیروی می کنند، در حالی که مقادیر موجود در هر شی حاصل از تقسیم بندی از یک توزیع نرمال پیروی می کنند. با توجه به زمینه فضایی دو فرآیند، شکستن سر/دم به طور پیش‌فرض یک فرآیند غیرمکانی است که در مقیاس جهانی اعمال می‌شود، در حالی که تقسیم‌بندی یک فرآیند جغرافیایی است که در مقیاس محلی اعمال می‌شود. در اینجاست که تبدیل توپولوژیکی معرفی‌شده دو رویه را به منظور انتقال نتایج پارتیشن از نمودار فرکانس به خروجی‌های تقسیم‌بندی، پیوند می‌دهد، بنابراین یک ساختار سلسله مراتبی را به یک ساختار فضایی تبدیل می‌کند ( جدول 1 ).

3. آزمایش

3.1. منطقه مطالعه و آماده سازی داده ها

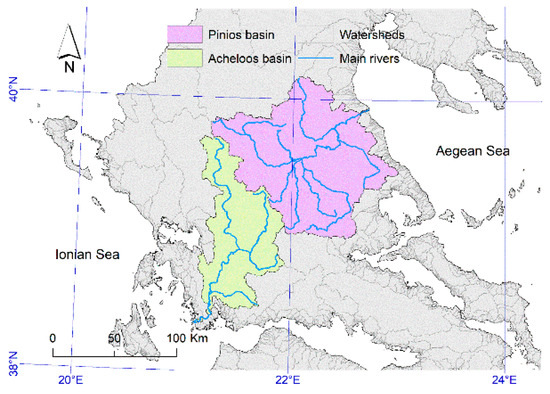
دو حوضه بزرگ رودخانه در یونان، یعنی حوضه رودخانه پینیوس و حوضه رودخانه آچلوس، که به ترتیب در بخش مرکزی-شرق و مرکز-غرب یونان قرار دارند، برای آزمایش با روش جدید انتخاب شدند. حوضه رودخانه پینیوس دارای سطح پیش بینی شده در حدود 10701 کیلومتر مربع با محیطی در حدود 888 کیلومتر است و به دریای اژه (ساحل شرقی سرزمین اصلی یونان) می ریزد. این منطقه عمدتاً دشتی است که توسط محصولات کشاورزی پوشیده شده است. حوضه رودخانه آچلوس دارای سطح پیش بینی شده در حدود 5686 کیلومتر مربع با محیطی در حدود 823 کیلومتر است و به دریای ایونی (سواحل غربی سرزمین اصلی یونان) می ریزد. این منطقه عمدتاً توسط کوه های جنگلی پوشیده شده است ( شکل 3 ).
یک محصول ASTER GDEM V2 (Advanced Spaceborne Thermal Emission and Reflection Radiometer Global Digital Elevation Model, نسخه 2) به عنوان تنها مجموعه داده ورودی (به صورت رایگان از: https://earthdata.nasa.gov/ دانلود شده ) استفاده شد. مدل های رقومی ارتفاع (DEM) به طور گسترده برای نقشه برداری و تحلیل حوضه های رودخانه استفاده می شود [ 8 ، 32 ].
محصول ASTER GDEM با تصاویر جفت استریو به دست آمده با ابزار ASTER روی ماهواره Terra (EOS AM-1) تولید شد و در اکتبر 2011 توسط وزارت اقتصاد، تجارت و صنعت (METI) ژاپن و ملی منتشر شد. سازمان هوانوردی و فضایی (ناسا) ایالات متحده آمریکا. محصولات ASTER GDEM در قالب GeoTIFF در اندازه پیکسل 30 متر و کاشی های 1 × 1 درجه ارائه شده است.
با این حال، باید توجه داشت که مقادیر اصلی در ASTER GDEM از طریق ابزارهای نوری، یعنی آنهایی که اندازه‌گیری‌های بازتاب را ثبت می‌کنند، تخمین زده می‌شوند و بنابراین در مقایسه با محصولات LIDAR (تشخیص نور و محدوده، یا تصویربرداری لیزری، تشخیص، و محدوده) دقت کمتری دارند. . LIDAR از داده‌های سنجش از راه دور لیزری در شبکه‌های نقطه‌ای منظم استفاده می‌کند و می‌تواند برای ایجاد نمایش‌های سطح سه بعدی نیز استفاده شود [ 33 ، 34 ].
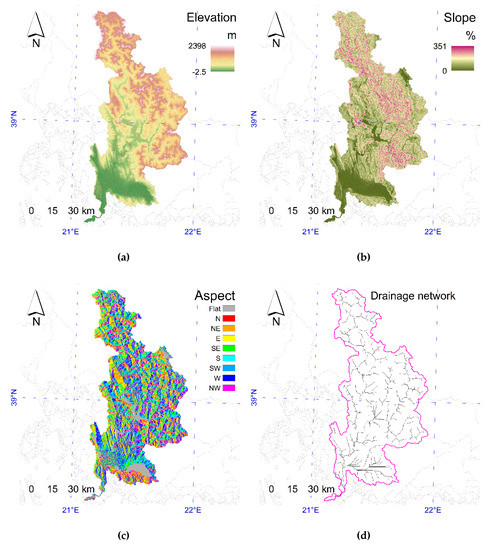
این آزمایش بر روی چهار ویژگی توپوگرافی یا هیدروگرافی مشترک، یعنی ارتفاع، شیب، جنبه، و تجمع جریان متمرکز شد. کاشی های مورد نیاز محصولات اصلی ASTER GDEM موزاییک شده و به خطوط کلی دو حوضه رودخانه مورد مطالعه بریده شدند. مقادیر ارتفاع یکسان با مقادیر سلولی اصلی مربوطه DEM ها (بر حسب متر ارتفاع) گرفته شد، در حالی که شیب، جنبه و تجمع جریان از مقادیر DEM در پنجره های 3×3 با استفاده از Spatial Analyst در برنامه ArcGIS محاسبه شد. الگوریتم D8 برای تخمین انباشت جریان استفاده شد [ 32 ، 35 ]). آریزا-ویلاورده و همکاران. (2015) [ 36] استدلال می کنند که الگوریتم D8 یک روش معقول است که شرایط جریان همگرا غالب است و نشان داده است که بین الگوهای جریان مختلف سازگار است.
شبکه‌های جریان و حوضه در دو حوضه رودخانه با آستانه‌گذاری لایه‌های تجمع جریان (رستر) (فرآیندی به نام «آستانه تجمع جریان» یا FAT) نقشه‌برداری شدند [37 ]]. لایه های خروجی می توانند به تعداد آستانه های مختلف انتخاب شده باشند و معمولاً در قالب برداری تبدیل و ذخیره می شوند (به ترتیب چند خطوط و چند ضلعی برای نهرها و حوضه). در اینجا، FAT = 10000 برای استخراج شبکه رودخانه در هر دو حوضه رودخانه تنها برای اهداف ژئوویژوالی استفاده شد. انتخاب هر آستانه چربی برای نمایشگر بر تجزیه و تحلیل (نه فرآیندهای پارتیشن و نه تقسیم بندی)، که در کل سلول های تجمع جریان اعمال می شود، تأثیر نمی گذارد. حوضه رودخانه پینیوس دارای میانگین ارتفاع 421.5 متر، حداکثر مقدار 2810 متر و ضریب تغییرات 86.5٪ بود. میانگین شیب حوضه 16.7٪، با ضریب تغییرات 102٪ است. میانگین ابعاد حوضه 167.5 با ضریب تغییرات 63.2 درصد است. جنبه کمی به سمت شرق، در مقایسه با میانگین مورد انتظار 180◦، به این معنی است که رشته کوه های واقع در سمت غرب در ترسیم حوضه ها غالب هستند. شاخص شکل حوضه 2.147 محاسبه شد. شاخص شکل یک متریک از پیچیدگی هندسی یک جسم است و به عنوان نسبت محیط به چهار برابر جذر مساحت جسم تعریف می شود. مقادیر بالاتر مربوط به پیچیدگی بالاتر است. مستطیل کمترین پیچیدگی (یا منظم ترین) شکل است، با مقدار شاخص شکل 1 [ مقادیر بالاتر مربوط به پیچیدگی بالاتر است. مستطیل کمترین پیچیدگی (یا منظم ترین) شکل است، با مقدار شاخص شکل 1 [ مقادیر بالاتر مربوط به پیچیدگی بالاتر است. مستطیل کمترین پیچیدگی (یا منظم ترین) شکل است، با مقدار شاخص شکل 1 [25 ] ( شکل 4 ).
حوضه رودخانه آچلوس دارای میانگین ارتفاع 811.8 متر، حداکثر مقدار 2398 متر و ضریب تغییرات 63.2٪ درصد است. میانگین شیب حوضه 34.8٪، با ضریب تغییرات 69.5٪ است. میانگین ابعاد حوضه 168.9 با ضریب تغییرات 62.5٪ است. جهت اندکی به سمت شرق در مقایسه با میانگین پیش بینی شده 180◦ نیز به این معنی است که کوه های سمت غرب در ترسیم حوضه ها غالب هستند. شاخص شکل حوضه به 2.729 محاسبه شد ( شکل 5 ). برخی از اطلاعات توصیفی و معیارهای دو حوضه رودخانه مورد مطالعه در جدول 2 خلاصه شده است .

3.2. پیش شرط ها و روش پیاده سازی

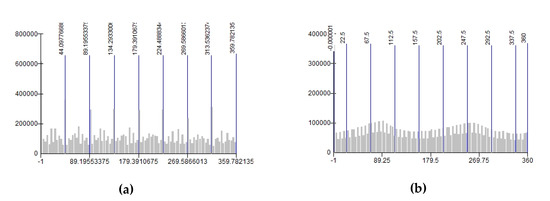
روش جدید تنها با لایه‌های انباشتگی ارتفاع، شیب و جریان، به استثنای لایه‌های جنبه اعمال شد. دلیل آن این است که مقادیر جنبه تقریباً به طور مداوم (یا فقط با تمایزات جزئی) در سراسر طیف وسیعی از مقادیر ممکن (یعنی 0-360 درجه) توزیع می‌شوند، بنابراین توزیع فرکانس تقریباً مستقیم و افقی را نشان می‌دهند. بنابراین، جنبه شرط اساسی برای اعمال قاعده اندازه رتبه، یعنی اینکه داده ها باید از توزیع دم سنگین پیروی کنند، برآورده نمی شود. انتظار می‌رود که این محدودیت برای یک کوه نیز وجود داشته باشد و تنها در صورت وجود یک شیب کوچک می‌توان پارتیشن را اجرا کرد ( شکل 6 ).
برای هر یک از لایه های انباشتگی ارتفاع، شیب و جریان، یک سری دوازده بخش بندی با الگوریتم FNEA با استفاده از برنامه eCognition Developer انجام شد. ضریب مقیاس رسم در مقابل میانگین اندازه شی مجاز برای استخراج یک معادله پیش بینی است، که در آن محاسبه عوامل مقیاس بهینه (متغیر وابسته، y) با وارد کردن SMOS (به عنوان متغیر مستقل، x) است. نتایج تقسیم بندی رسم شده و معادلات پیش بینی (به صورت عددی و به صورت خطوط روند) برای شش لایه در شکل 7 نشان داده شده است .
سپس پارتیشن بندی متوالی تمامی لایه ها بر اساس قانون رتبه بندی اجرا شد. گستره‌های حاصل از شکستگی‌های سر/دم پارتیشن ثبت شد و SMOS و SON به ترتیب با توجه به معادلات (3) و (4) محاسبه شدند. سه پیش نیاز آشکار برای تعیین فاکتورهای مقیاس بهینه در نظر گرفته شد: (الف) SMOS باید بزرگتر از اندازه سلول باشد (در اینجا، 900 متر مربع)، (ب) SON باید مساوی یا بزرگتر از 1 باشد ، و ج) فاکتورهای مقیاس محاسبه شده باید بزرگتر از صفر باشد.

3.3. نتایج

خروجی های اجرای روش جدید برای هر یک از خواص مورد مطالعه (ارتفاع، شیب و تجمع جریان) برای حوضه های رودخانه مورد مطالعه (پینیوس و آچلوس) در جدول 3، جدول 4، جدول 5 ، جدول 6 ، جدول 7 ارائه شده است . جدول 8 .

بعد فراکتالی جفت‌های پارتیشن متوالی برای همه ویژگی‌های مورد علاقه با استفاده از معادله مندلبروت (ماندلبروت 1982) [ 17 ] که توسط Karydas 2020 [ 14 ] با این روش اقتباس شده است، به دست آمد:

Dn=ورود به سیستم(سnسn-1)ورود به سیستم(fnfn-1)

جایی که s n : اندازه متوسط ​​شیء شبیه سازی شده در پارتیشن n-امین (بدون بعد)؛ f n : ضریب مقیاس در پارتیشن n- امین (بدون بعد). خروجی های معادله (3) برای هر یک از ویژگی های مورد مطالعه ثابت است ( جدول 3 ، جدول 4 ، جدول 5 ، جدول 6 ، جدول 7 و جدول 8) از 1.1587 برای تجمع جریان آچلوس تا 1.9146 برای شیب آچلوس متغیر است. به طور کلی، دو حوضه رودخانه مقادیر ابعاد فراکتال مشابهی را برای ارتفاع (1.5461 در مقابل 1.5537) و تجمع جریان (1.1935 در مقابل 1.1587) نشان دادند، در حالی که آنها فقط برای تجمع جریان (1.3784 در مقابل 1.914) تفاوت اساسی داشتند.

3.4. بحث

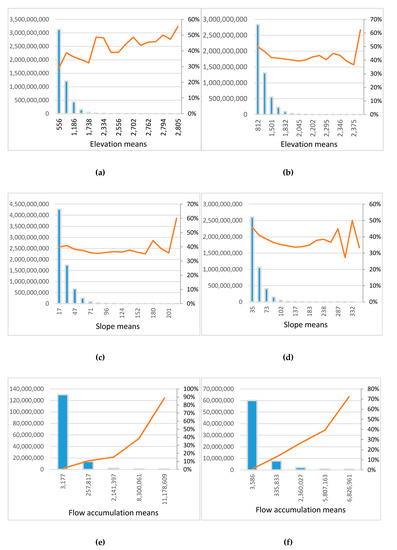
فاکتورهای مقیاس بهینه محاسبه‌شده برای تقسیم‌بندی‌های ارتفاعی یا شیب و همچنین میانگین اندازه جسم مربوطه برای واحدهای شکل زمین بسیار کوچک هستند. به طور مشخص، حتی برای بالاترین ضریب مقیاس محاسبه شده برای ارتفاع در حوضه رودخانه پینیوس (یعنی 16.9)، میانگین اندازه جسم مربوطه تنها حدود 16 هکتار است ( شکل 8)). به طور مشابه، برای شیب Pinios، بالاترین ضریب مقیاس محاسبه شده (یعنی 8.4) منجر به اندازه متوسط ​​شی 7 هکتار شد. در مقابل آن، فاکتورهای مقیاس بهینه محاسبه‌شده برای انباشت جریان بسیار بزرگ‌تر از عوامل محاسبه‌شده برای ارتفاع و شیب برای هر دو حوضه رودخانه هستند. این را می توان به این واقعیت نسبت داد که لایه های انباشت جریان “خالی” از مقادیر بالا یا به طور معکوس پر از مقادیر 0 تا حد زیادی هستند. به عبارت دیگر، مقادیر بالا از الگوهای خطی پیروی می کنند و اجسام همگن بزرگ با مقادیر کم را ترک می کنند تا سطح را در هر جای دیگری پر کنند. در نتیجه این الگوی فضایی خاص، میانگین اندازه جسم برای تجمع جریان بسیار بزرگتر از دو نوع ویژگی دیگر بود، و در نتیجه، ضریب مقیاس به طور مشابه بزرگ بود.
تعداد کل ردیف ها در جداول محاسباتی ( جدول 3 ، جدول 4 ، جدول 5 ، جدول 6 ، جدول 7 و جدول 8 ) مربوط به متریک فراکتالی دیگری است که به نام ht-index معرفی شده توسط جیانگ و یین (2014) [ 18] .]. Ht-index یک عدد صحیح است که تعداد سطوح سلسله مراتبی یک مجموعه داده را نشان می دهد و به این ترتیب، معیاری از پیچیدگی ساختار سلسله مراتبی آن است. در کار خود، نویسندگان شاخص ht ارتفاع در ایالات متحده آمریکا را با استفاده از وضوح DEM 1800 متری 16 برآورد کردند. مقادیر شاخص ht مشابه (14 یا 15) در مطالعه فعلی برای ارتفاع و شیب نیز محاسبه شد. تفاوت بین دو وضوح (30 در مقابل 1800 متر) نباید به عنوان مانعی برای مقایسه در نظر گرفته شود، زیرا مقیاس جغرافیایی بین دو مطالعه موردی نیز بسیار متفاوت است. مقادیر به طور قابل توجهی پایین تر برای تجمع جریان در مطالعه فعلی (چهار در هر دو مورد) پیدا شد. با این حال، هیچ مطالعه مشابه دیگری برای انجام مقایسه در دسترس نیست.جدول 9 ).
در برخی موارد (به عنوان مثال، در نقشه برداری شیب پینیوس)، واگرایی های قابل توجهی بین بعد فراکتالی به دست آمده از معادله مندلبرو (1982) [ 17 ] (رجوع کنید به معادله (3)) و آن چیزی که از «شیب» استنتاج شده است، تشخیص داده شد. خط روند، همانطور که توسط نمودارهای سری تقسیم بندی تعریف شده است (به شکل 4 مراجعه کنید ). این انحراف مورد انتظار بود و می‌توان آن را به ضریب تعیین کمتر (در مقایسه با سایر ویژگی‌ها) نسبت داد ( R2) معادلات به دست آمده از نمودارها. در همه موارد، مقادیر ابعاد فراکتال محاسبه‌شده با معادله (3) دقیق‌ترین مقادیر هستند زیرا از داده‌های بهینه به دست می‌آیند، در حالی که خطوط روند تنها با برخی تقسیم‌بندی‌های سیستماتیک اما نه لزوما بهینه مطابقت دارند. انحرافات مشابهی توسط کاریداس (2020) [ 14 ] در اجرای اولیه روش با انواع تصاویر ماهواره ای مشاهده شد .
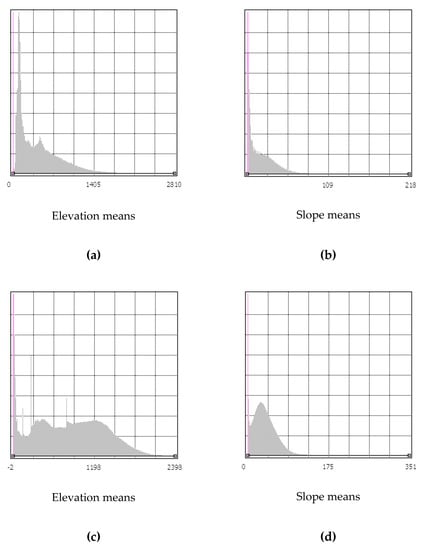
با این حال، اجرای روش جدید با DEM و مشتقات آن، مشکلات بیشتری را نسبت به تصاویر نشان داد. همانطور که از نمودارهای توزیع ارتفاع و شیب آچلوس می توان فهمید، توزیع فرکانسی آنها از شکل دم سنگین ایده آل پیروی نمی کند. به طور خاص، توزیع ارتفاعی آچلوس دو قله و دره اضافی را نشان می‌دهد، در حالی که توزیع شیب آچلوس از توزیع نرمال انحرافی به سمت چپ تقلید می‌کند. در مقابل، ارتفاع پینیوس تنها یک قله اضافی کوچک را نشان می‌دهد، در حالی که هر دو توزیع شیب به اشکال دم سنگین نزدیک‌تر از هر چیز دیگری هستند ( شکل 9 ). بنابراین، تنها توزیع انباشت جریان هر دو حوضه رودخانه از شکل ایده آل دم سنگین بود.
مشکل دیگر این بود که قانون اندازه رتبه در هر دو حوضه رودخانه منجر به فراز و نشیب های زیادی برای رسیدن به آستانه نهایی شد، در حالی که برخی از گروه های سر در اوایل فرآیند تقسیم بندی نزدیک به 50٪ شناسایی شدند (شکل 10 ) . در چنین مواردی، قابل بحث است که آیا می توان از پارتیشن بندی استفاده کرد یا بهتر از آن اجتناب کرد. توجه داشته باشید که برای مدل‌های ارتفاعی دیجیتال، آستانه پایانی معمولاً کمتر یا مساوی 40٪ تنظیم می‌شود (جیانگ 2015) [ 19 ].

با این وجود، صرف نظر از ناهنجاری های فوق، نتایج فعلی به وضوح نشان می دهد که روش جدید در همه موارد موفق بوده است. علاوه بر این، رسم تقسیم بندی در مقابل داده های پارتیشن بندی هر یک از ویژگی های مورد مطالعه نشان می دهد که عوامل مقیاس بهینه را می توان مستقیماً از مقادیر میانگین به دست آمده از پارتیشن ها محاسبه کرد. به طور مشخص، دو حوضه رودخانه مورد مطالعه معادلات زیر را برای ارتفاع به دست آوردند (همچنین به شکل 11 مراجعه کنید ):

برای پینیوس: f=4·10-13ه0.0111مn(آر2=0.9023)
برای آخلوس: f=2·10-18ه0.0184مn(آر2=0.8046)

جایی که f : ضریب مقیاس; مn: میانگین در پارتیشن n. اگر معادلات (4) و (5) به یک واحد برای هر حوضه رودخانه تعمیم داده شود، عوامل مقیاس بهینه برای هر ویژگی را می توان مستقیماً از مقادیر میانگین متوالی فرآیند تقسیم به تنهایی محاسبه کرد و بنابراین، فرآیند تقسیم بندی را می توان نادیده گرفت. . با توجه به اینکه ضریب مقیاس معادل انحراف معیار در اشیاء نامزد است، معادلات (4) و (5)، در واقع، دو آمار اصلی را در هر مجموعه داده به هم مرتبط می‌کنند. علاوه بر این، همبستگی بالایی بین سری های دیگر داده های مورد استفاده در این مطالعه نیز شناسایی شده است (به عنوان مثال، وسعت سر با عوامل مقیاس محاسبه شده). این را می توان به این واقعیت نسبت داد که گروه های سر با میانگین های متوالی مجموعه داده مطابقت دارند، در حالی که اشیاء قطعه بندی شده در مقیاس های مختلف با انحرافات استاندارد متوالی اشیاء ایجاد شده مطابقت دارند.

4. نتیجه گیری

در این تحقیق، یک روش جدید برای بهینه‌سازی مقیاس هنگام نقشه‌برداری از ارتفاع، شیب یا تجمع جریان توسعه داده شد و با دو بزرگ‌ترین حوضه رودخانه در یونان آزمایش شد. Aspect شرایط اساسی برای اعمال قاعده اندازه رتبه را ندارد و بنابراین روش جدید را نمی توان با لایه های جنبه اعمال کرد.
روش جدید از شکسته‌های سر/دم برای نشان دادن مقیاس‌های بهینه در ساختار داده سلسله مراتبی و یک تبدیل توپولوژیکی برای نمایش نتایج به بافت فضایی استفاده می‌کند. بعد فراکتال برای تأیید بهینه بودن داده‌های مکانی استفاده می‌شود. این روش کار کاریداس (2020) [ 14 ] را برای تقسیم‌بندی چند مقیاسی داده‌های تصویر، به مجموعه داده‌های شطرنجی توپوگرافی و هیدروگرافیک گسترش می‌دهد.
آزمایش برخی از انحرافات را از شرایط ایده آل در مورد توزیع های دم سنگین و پارتیشن بندی نشان داد. با این حال، صرف نظر از امکان برآورده نشدن شرایط ایده آل، این روش برای شناسایی مجموعه ای از مقیاس های بهینه در همه موارد موفق بود. بنابراین، فرضیه اصلی تحقیق مبنی بر اینکه انتخاب مقیاس‌های بهینه در نقشه‌برداری توپوگرافی و هیدروگرافی می‌تواند با بعد فراکتالی به عنوان معیار بهینه‌سازی مقیاس هدایت شود، در تمامی شرایط تأیید شد.
مقیاس های بهینه شناخته شده قبل از حل مشکلات زیست محیطی و وظایف مدیریت زمین، فرآیندهای زیربنایی (یا حتی پنهان) را آشکار می کند، بنابراین از تصمیم گیری حمایت می کند. علاوه بر این، روش جدید ممکن است مقیاس‌های نگاشت مناسب را برای تعمیم شی در چارچوب تحلیل توپوگرافی و زمین تعریف کند، جایی که نسبت مناسبی از تنوع بین چگالی‌ها و بافت‌ها باید حفظ شود. به عنوان مثال، فرآیند انتخاب در مقیاس شی را می توان با یک فرآیند فیلتر برای نقشه برداری وب تقریباً زمان واقعی برابر دانست.
اجرای روش جدید مستلزم یک برنامه تجزیه و تحلیل مبتنی بر شی (برای انجام وظایف تقسیم بندی)، یک برنامه GIS (برای تهیه لایه های مورد نیاز و محاسبه آمار فضایی) و یک صفحه گسترده (برای انجام محاسبات خروجی های جزئی و نهایی) است. ).
با توجه به حوضه های رودخانه مورد مطالعه، نشان داده شد که حوضه رودخانه پینیوس از نظر ارتفاع ناهمگن تر و از نظر شیب کمتر از حوضه آچلوس است، در حالی که از نظر جنبه ناهمگن بودند. هر دو حوضه رودخانه به طور مشابه پیچیده هستند، زیرا آنها مقادیر مشابهی از ht-index داشتند. بعد فراکتال برای شیب بین دو حوضه متفاوت بود، در حالی که برای ارتفاع و تجمع جریان مشابه بود.
به طور خلاصه، ثابت شد که روش جدید سریع (زمان کوتاه برای انجام)، آسان (فرایندهای ساده)، عینی (کاملا عددی) و قوی است (نتایج حتی با پیش‌شرط‌های غیر ایده‌آل به دست آمدند). این روش را می توان با استفاده مستقیم از مقادیر میانگین پارتیشن برای محاسبه عوامل مقیاس بهینه ساده تر کرد، مشروط بر اینکه آزمایش های بیشتری با حوضه های رودخانه های متنوع به سمت تعمیم انجام شود. در چنین حالتی، پارتیشن تنها فرآیند مورد نیاز برای انجام خواهد بود، به طوری که رسم داده ها معادلات غیر خطی لازم را به همراه خواهد داشت. در شکل کلی خود، این روش می تواند به شناسایی بهترین مجموعه داده ها برای استخراج ویژگی های یک اندازه خاص کمک کند.
در نهایت، با هدف روشن شدن و مشخص کردن بیشتر پیش‌شرط‌های مورد نیاز، باید به ویژگی‌های توزیع‌های دم سنگین اشاره کرد. تحقیقات آینده همچنین باید این روش را به نوع داده های برداری ویژگی های هیدروگرافی، به عنوان مثال، به شبکه های جریان و حوضه ها گسترش دهد.

منابع

  1. جیانگ، بی. برانت، SA یک دیدگاه فراکتالی در مقیاس در جغرافیا. ISPRS Int. J. Geo-Inf. 2016 ، 5 ، 95. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
  2. هی، GJ; بلاشکه، تی. مارسئو، دی جی؛ بوچارد، A. مقایسه سه روش تصویر-شیء برای تحلیل چند مقیاسی ساختار منظر. ISPRS J. Photogramm. Remote Sens. 2003 , 57 , 327-345. [ Google Scholar ] [ CrossRef ]
  3. کلمش، وی. مفهوم سازی و مقیاس در هیدرولوژی. جی هیدرول. 1983 ، 65 ، 1-23. [ Google Scholar ]
  4. ژانگ، ایکس. دو، اس. مینگ، دی. انتخاب مقیاس تقسیم بندی در تجزیه و تحلیل تصویر مبتنی بر شی جغرافیایی. در سنجش از دور با وضوح فضایی بالا: داده ها، تجزیه و تحلیل، و برنامه های کاربردی . He, Y., Weng, Q., Eds. Taylor & Francis Group LLC: Abingdon، UK; CRC Press: بوکا راتون، فلوریدا، ایالات متحده آمریکا، 2018؛ ص 201-228. [ Google Scholar ]
  5. کاریداس، سی جی; پاناگوس، ص. مدلسازی تلفات ماهانه خاک و بازده رسوب در قبرس. بین المللی جی دیجیت. زمین 2016 ، 9 ، 766-787. [ Google Scholar ] [ CrossRef ]
  6. Jiang, B. Head/tail breaks: یک طرح طبقه بندی جدید برای داده ها با توزیع دم سنگین. پروفسور Geogr. 2013 ، 65 ، 482-494. [ Google Scholar ] [ CrossRef ]
  7. جیانگ، بی. ساختار زنده تا زمین و تا آسمان: کریستوفر الکساندر. علوم شهری 2019 ، 3 ، 96. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
  8. وو، اس. لی، جی. Huang, GH مطالعه ای بر روی ویژگی های توپوگرافی اولیه مشتق از DEM برای کاربردهای هیدرولوژیکی: حساسیت به تفکیک داده های ارتفاعی. Appl. Geogr. 2008 ، 28 ، 210-223. [ Google Scholar ] [ CrossRef ]
  9. Blaschke, T. تجزیه و تحلیل تصویر مبتنی بر شی برای سنجش از راه دور. ISPRS J. Photogramm. Remote Sens. 2010 , 65 , 2-16. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  10. ویتارانا، سی. Civco، DL بهینه‌سازی مقیاس تقسیم‌بندی چند وضوحی با استفاده از روش‌های تجربی: بررسی حساسیت اندازه‌گیری اختلاف نظارت شده فاصله اقلیدسی 2 (ED2). ISPRS J. Photogramm. Remote Sens. 2014 ، 87 ، 108-121. [ Google Scholar ] [ CrossRef ]
  11. Drǎguţ، L. تاید، دی. Levick, S. ESP: ابزاری برای تخمین پارامتر مقیاس برای تقسیم‌بندی تصویر با وضوح چندگانه داده‌های سنجش از راه دور. بین المللی جی. جئوگر. Inf. علمی 2010 ، 24 ، 859-871. [ Google Scholar ] [ CrossRef ]
  12. رامستاد، بی. اتزلمولر، ب. حوضه های آبخیز متوسط ​​انحنا: یک روش ساده برای تقسیم بندی یک مدل ارتفاعی دیجیتال به واحدهای زمین. ژئومورفولوژی 2012 ، 139-140 ، 293-302. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  13. نیوتن، ال. سنین، ن. اسمیت، بی. Chatzivagiannis، E. لیچ، R. مقایسه و اعتبار روش‌های تقسیم‌بندی توپوگرافی سطحی برای توصیف مبتنی بر ویژگی سطوح همجوشی بستر پودر فلزی. موج سواری. توپوگر. مترو Prop. 2019 , 7 , 045020. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
  14. کاریداس، CG بهینه‌سازی تقسیم‌بندی چند مقیاسی تصاویر ماهواره‌ای با استفاده از هندسه فراکتال. بین المللی J. Remote Sens. 2020 , 41 , 2905–2933. [ Google Scholar ] [ CrossRef ]
  15. لام، NS-N. کیو، HL; Quattrochi، DA; امرسون، CW ارزیابی روش های فراکتال برای توصیف پیچیدگی تصویر. کارتوگر. Geogr. Inf. علمی 2002 ، 29 ، 25-35. [ Google Scholar ] [ CrossRef ]
  16. سان، دبلیو. خو، جی. گونگ، پی. لیانگ، اس. تجزیه و تحلیل فراکتالی تصاویر سنجش از راه دور: بررسی روش ها و کاربردها. بین المللی J. Remote Sens. 2006 ، 27 ، 4963-4990. [ Google Scholar ]
  17. مندلبروت، بی. هندسه فراکتالی طبیعت . WH Freeman and Co.: New York, NY, USA, 1982. [ Google Scholar ]
  18. جیانگ، بی. Yin, J. Ht-Index برای تعیین کمیت ساختار فراکتال یا مقیاس بندی ویژگی های جغرافیایی. ان دانشیار صبح. Geogr. 2014 ، 104 ، 2014. [ Google Scholar ] [ CrossRef ]
  19. Meentemeyer, V. دیدگاه های جغرافیایی فضا، زمان و مقیاس. Landsc. Ecol. 1989 ، 3 ، 163-173. [ Google Scholar ] [ CrossRef ]
  20. جیانگ، ب. تجزیه و تحلیل جغرافیایی نیاز به روش متفاوتی از تفکر دارد: مشکل ناهمگونی فضایی. روندها فضایی. مقعدی مدل جئوژورنال 2018 ، 19 ، 23–40. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  21. بنز، UC؛ هافمن، پی. ویلهاک، جی. لینگنفلدر، آی. Heynen، M. تجزیه و تحلیل فازی با وضوح چندگانه، شی گرا داده های سنجش از دور برای اطلاعات آماده GIS. ISPRS J. Photogramm. Remote Sens. 2004 ، 58 ، 239-258. [ Google Scholar ] [ CrossRef ]
  22. Zipf، GK Human Behavior and the Principle of Last Effort ; Addison-Wesley: Boston, MA, USA, 1949. [ Google Scholar ]
  23. Chen, Y. رابطه ریاضی بین قانون Zipf و قانون مقیاس بندی سلسله مراتبی. فیزیک یک آمار مکانیک. Appl. 2012 ، 391 ، 3285-3299. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  24. کیم، ام. مدن، م. وارنر، تی. تخمین اندازه شیء تصویر بهینه برای تقسیم‌بندی توده‌های جنگلی با تصاویر چندطیفی IKONOS. در تجزیه و تحلیل تصویر مبتنی بر شی – مفاهیم فضایی برای کاربردهای سنجش از راه دور مبتنی بر دانش . Blaschke, T., Lang, S., Hay, GJ, Eds. Springer: برلین، آلمان، 2008; صص 291-307. [ Google Scholar ]
  25. بااتز، ام. بنز، یو. دهقانی، س. هاین، م. Holtje، A. هافمن، پی. لینگنفلدر، آی. میملر، ام. سولباخ، م. وبر، ام. و همکاران راهنمای کاربر ECognition ؛ Definiens Imaging GmbH، دیجیتال: مونیخ، آلمان، 2002. [ Google Scholar ]
  26. بابیک، ا. بولس، آر. پارادایم فضای بازنمایی توصیفات شیء در حال تکامل همزمان. IEEE Trans. الگوی مقعدی ماخ هوشمند 1992 ، 14 ، 146-156. [ Google Scholar ] [ CrossRef ]
  27. کاریداس، سی. تومپولیدو، م. کالایتزیدیس، سی. Gitas، I. بخش بندی یک تصویر WorldView2 برای شناسایی ویژگی در محیط های بسیار ناهمگن. در مجموعه مقالات پنجمین کنفرانس GEOBIA، تسالونیکی، یونان، 21-24 مه 2014. صص 717-720. [ Google Scholar ]
  28. ماناکوس، آی. تکنیتو، ای. پترو، ز. کاریداس، سی. توماسلی، وی. ورونیکو، جی. Mountrakis، G. تولید پایگاه دانش چندوجهی از تصاویر ماهواره ای با وضوح بسیار بالا برای نقشه برداری زیستگاه. یورو J. Remote Sens. 2016 ، 49 ، 1033-1060. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  29. نیومن، قوانین قدرت MEJ، توزیع پارتو و قانون Zipf. تحقیر کردن فیزیک 2005 ، 46 ، 323-351. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  30. Vuduc, R. تقسیم بندی تصویر با استفاده از ابعاد فراکتال . GEOL634، گزارش; دانشگاه کرنل: ایتاکا، نیویورک، ایالات متحده آمریکا، 1997. [ Google Scholar ]
  31. هافمن، پی. بلاشکه، تی. استروبل، جی. کمی سازی استحکام مجموعه قوانین فازی در تجزیه و تحلیل تصویر مبتنی بر شی. بین المللی J. Remote Sens. 2011 ، 32 ، 7359-7381. [ Google Scholar ] [ CrossRef ]
  32. ژانگ، اچ. Huang, G. ساخت شبکه های کانال برای مناطق مسطح در مدل های دیجیتال ارتفاع. هیدرول. روند. 2009 ، 23 ، 2879-2887. [ Google Scholar ] [ CrossRef ]
  33. شان، جی. Toth, CK Topographic Laser Ranging and Scanning: Principles and Processing , 2nd ed.; CRC Press: Boca Raton، FL، USA، 2018. [ Google Scholar ]
  34. جنسون، SK; Domingue، JO استخراج ساختار توپوگرافی از داده های ارتفاعی دیجیتال برای تجزیه و تحلیل سیستم اطلاعات جغرافیایی. فتوگرام مهندس Remote Sens. 1988 , 54 , 1593-1600. [ Google Scholar ]
  35. بارو، PA; مک دانل، RA اصول سیستم های اطلاعات جغرافیایی ; انتشارات دانشگاه آکسفورد: نیویورک، نیویورک، ایالات متحده آمریکا، 1998; 190p. [ Google Scholar ]
  36. Ariza-Villaverde, AB; Jiménez-Hornero، FJ; Gutiérrez de Ravé، E. تأثیر وضوح DEM بر استخراج شبکه زهکشی: تجزیه و تحلیل چندفراکتال. ژئومورفولوژی 2015 ، 241 ، 243-254. [ Google Scholar ] [ CrossRef ]
  37. O’Callaghan، JF; Mark, DM استخراج شبکه های زهکشی از داده های رقومی ارتفاعات، Computer Vision. نمودار. فرآیند تصویر 1984 ، 28 ، 328-344. [ Google Scholar ]
Ijgi 09 00631 g001 550
شکل 1. تصویری از تبدیل توپولوژیکی معرفی شده روش جدید: از پارتیشن n-ام بعد از میانگین ( Mn ) و ایجاد گروه های سر ( hn ) ، تا تجمع (مجازی) آنها در فضای فیزیکی و طرح ریزی آنها . به فضای شبیه سازی شده
Ijgi 09 00631 g002 550
شکل 2. مروری بر رویه محاسباتی روش جدید.
Ijgi 09 00631 g003 550
شکل 3. مناطق مورد مطالعه حوضه های رودخانه پینیوس و آچلوس در یونان و شبکه اصلی رودخانه آنها (منبع: توصیف و مدل سازی حوضه، CCM – پایگاه داده رودخانه و حوضه برای اروپا).
Ijgi 09 00631 g004 550
شکل 4. نقشه های توپوگرافی و هیدروگرافی حوضه رودخانه پینیوس: ( الف ) ارتفاع. ( ب ) شیب؛ ( ج ) جنبه؛ ( د ) شبکه زهکشی (به دست آمده با آستانه تجمع جریان (FAT) = 10000).
Ijgi 09 00631 g005 550
شکل 5. نقشه های توپوگرافی و هیدروگرافی حوضه رودخانه آچلوس: ( الف ) ارتفاع. ( ب ) شیب؛ ( ج ) جنبه؛ ( د ) شبکه زهکشی (به دست آمده با FAT = 10000).
Ijgi 09 00631 g006 550
شکل 6. نمودارهای توزیع فراوانی مقادیر جنبه برای دو حوضه رودخانه مورد مطالعه: ( الف ) پینیوس و ( ب ) آچلوس.
Ijgi 09 00631 g007 550
شکل 7. نمودارهای Log-log ضریب مقیاس در مقابل میانگین اندازه جسم و معادلات پیش بینی استخراج شده برای: ( الف ) ارتفاع پینیوس. ( ب ) ارتفاع آچلوس. ( ج ) شیب پینیوس; ( د ) شیب آچلوس; ( ه ) تجمع جریان پینیوس. ( f ) تجمع جریان آشلوس.
Ijgi 09 00631 g008 550
شکل 8. چکیده ای از نتایج تقسیم بندی مورد ارتفاع پینیوس. خطوط کانتور 100 متری و مقادیر ارتفاعی که با شکستگی‌های سر/دم طبقه‌بندی شده‌اند برای مقایسه روی هم گذاشته شده‌اند.
Ijgi 09 00631 g009 550
شکل 9. توزیع داده های توپوگرافی مطالعه: ( الف ) توزیع ارتفاعی پینیوس (یک قله اضافی کوچک). ( ب ) توزیع شیب پینیوس. ( ج ) توزیع ارتفاعی آشلوس (دو قله اضافی). ( د ) توزیع شیب آشلوس (توزیع نرمال اریب).
Ijgi 09 00631 g010 550
شکل 10. وسعت گروه سر (که با ستون ها مشخص می شود؛ در متر مربع ) و درصد (که با خطوط مشخص می شود) در مقابل میانگین پارتیشن برای: ( الف ) ارتفاع پینیوس. ( ب ) ارتفاع آچلوس. ( ج ) شیب پینیوس; ( د ) شیب آچلوس; ( ه ) تجمع جریان پینیوس. ( f ) تجمع جریان آشلوس.
Ijgi 09 00631 g011 550
شکل 11. نمودارهای log-log نشانگر ضریب مقیاس بهینه در مقابل میانگین ارتفاع برای دو حوضه رودخانه مورد مطالعه. ( الف ) پینیوس و ( ب ) آچلوس.

مقالات داخلی و بین المللی

مطالب مرتبط ...

بدون دیدگاه

دیدگاهتان را بنویسید