1. معرفی
سیستم های اشتراک دوچرخه (BSS) یک جزء مهم در سیستم حمل و نقل شهری امروزی است [ 1 ، 2 ]. به عنوان یک روش حمل و نقل پایدارتر، اشتراک دوچرخه پتانسیل کاهش استفاده از خودرو، حل مشکل اول/آخرین مایل و کمک به خرده فروشی محلی را دارد [ 3 ، 4 ، 5 ]. تاریخچه اشتراک دوچرخه را می توان به دهه 1960 زمانی که این مفهوم برای اولین بار در آمستردام، هلند معرفی شد، ردیابی کرد [ 6 ]. در طول دهههای گذشته، سیستمهای اشتراک دوچرخه در طول نسلهای مختلف تکامل یافتهاند. نسلهای اولیه ثبت نام قبلی نداشتند و شکست خوردند، زیرا بسیاری از دوچرخهها خراب شدند یا به استفاده خصوصی تبدیل شدند [ 6 ، 7]]. از سال 95 ثبت نام قبلی الزامی است. یک مشتری ثبت نام شده می تواند یک دوچرخه را در تعدادی از ایستگاه های دوچرخه ثابت کرایه و بازگرداند. این سیستم ها همچنین به عنوان سیستم های اشتراک گذاری دوچرخه مبتنی بر ایستگاه (SBBSS) شناخته می شوند [ 8] و با موفقیت در چندین شهر در سراسر جهان مستقر شده اند. با بهره گیری از فناوری های پیشرفته اخیر مانند تلفن های هوشمند، GPS و سیستم های پرداخت یکپارچه، جدیدترین نسل اشتراک دوچرخه شامل نداشتن ایستگاه دوچرخه ثابت است. بدون ایستگاههای اتصال، سیستمهای اشتراکگذاری دوچرخه بدون ایستگاه (SFBSS) به کاربران این امکان را میدهند که از یک برنامه تلفن هوشمند برای پیدا کردن دوچرخه در نزدیکی آن استفاده کنند و پس از استفاده آن را در هر مکان مناسب پارک کنند. به دلیل انعطاف پذیری و راحتی بالا، SFBSS ها در چند سال گذشته محبوبیت قابل توجهی به دست آورده اند و به طور گسترده در بسیاری از کشورها از جمله چین، بریتانیا، سنگاپور، ایالات متحده و هلند مورد استفاده قرار گرفته اند [9 ]]. تخمین زده شد که در سال 2018، 16 تا 18 میلیون دوچرخه بدون ایستگاه در سراسر جهان در حال استفاده بودند، در مقایسه با 3.7 میلیون دوچرخه ایستگاهی [ 10 ].
وضعیت متعادل به وضعیتی اشاره دارد که عرضه دوچرخه با تقاضای دوچرخه مطابقت دارد. هر دو سیستم اشتراک دوچرخه بدون ایستگاه و مبتنی بر ایستگاه اغلب از نوسانات مکانی و زمانی تقاضا رنج می برند که منجر به مشکل عدم تعادل می شود. بدون تلاش های به موقع تعادل مجدد، مشکل عدم تعادل ممکن است عملکرد سیستم را به طور قابل ملاحظه ای کاهش دهد. برای یک SBBSS، مشکل عدم تعادل ممکن است منجر به صفر بودن موجودی در برخی از ایستگاه ها و عدم وجود فضایی برای پارک در برخی دیگر شود. در نتیجه، اجاره و بازگشت ممکن است تنها در تعداد محدودی از ایستگاهها امکانپذیر باشد، و بسیاری از مناطق/تقاضا را بدون خدمات یا کمخدمت باقی بگذارند [ 11]]. برای یک SFBSS، مشکل عدم تعادل جدی تر است. در حالی که خواسته های برآورده نشده باقی مانده است، هیچ محدودیتی در جایی که کاربر می تواند دوچرخه را بردارد یا پارک کند ممکن است منجر به تجمع دوچرخه ها و مسدود کردن پیاده روهای شهر شود.
مطالعات زیادی برای ارزیابی وضعیت عدم تعادل یک SBBSS و طراحی استراتژی تعادل مجدد مرتبط انجام شده است [ 12 ، 13 ، 14 ، 15 ، 16 ]. در حالی که ارزیابی عدم تعادل در یک SBBSS نسبتاً ساده است [ 17 ، 18 ]، به دلیل عدم وجود ایستگاه های ثابت در یک SFBSS، هیچ مقیاس فضایی یا مناطق جغرافیایی مشخصی برای ارزیابی موجودی دوچرخه، ارزیابی وضعیت عدم تعادل، و انجام عملیات وجود ندارد. تجزیه و تحلیل مجدد تعادل بعدی مطالعات موجود مقیاس های تجزیه و تحلیل مختلفی از جمله مناطق تجزیه و تحلیل ترافیک و شبکه های منظم با اندازه های مختلف را بررسی کرده اند [ 19 ، 20 ، 21، 22 ]. انتخاب این مقیاس های تحلیلی نسبتاً دلخواه بوده است. هیچ بحثی در مورد مقیاس مناسب مورد نیاز برای ارزیابی و رسیدگی به موضوع عدم تعادل در SFBSS وجود ندارد. از یک طرف، وضعیت متعادل ارزیابی شده با استفاده از مناطق بزرگ (به عنوان مثال، شبکه های 10 × 10 کیلومتر) ممکن است حاوی چندین سایت کمبود/اضافی دوچرخه محلی باشد که می تواند به طور قابل توجهی عملکرد سیستم را به خطر بیندازد. از سوی دیگر، تجزیه و تحلیل انجام شده با استفاده از مناطق کوچک (به عنوان مثال، شبکه های 10 × 10 متر) ممکن است تا حد زیادی به بار محاسباتی اضافه کند. بنابراین، مقیاس تحلیل، مدلسازی/تحلیل و الزامات محاسباتی مرتبط هستند و انتخاب مقیاس تحلیل مناسب برای ارزیابی عدم تعادل یک SFBSS و تجزیه و تحلیل مجدد تعادل زیر ضروری است.
2. بررسی ادبیات
اخیراً تعدادی از مطالعات سیستم های اشتراک دوچرخه را با تمرکز بر دو حوزه مورد بررسی قرار داده اند [ 23 ، 24 ، 25 ، 26 ]. حوزه اول به شناسایی عوامل مؤثر بر تقاضای اشتراک دوچرخه مربوط می شود و این عوامل شامل وضعیت اجتماعی-اقتصادی، محیط ساخته شده، زیرساخت های ترافیکی، کیفیت هوا و آب و هوا است [ 27 ، 28 ، 29 ]. حوزه دوم بر مسئله عدم تعادل سیستم اشتراک دوچرخه و استراتژی های تعادل مجدد مرتبط تمرکز دارد. در این مطالعه، ما عمدتاً به دومی علاقه مندیم.
برای حل مشکل عدم تعادل در یک سیستم اشتراک دوچرخه، استراتژی های مختلف تعادل مجدد توسعه داده شده است. جدول 1 خلاصه ای از ادبیات اخیر در مورد این استراتژی های تعادل مجدد را ارائه می دهد. به طور خاص، روشهای مبتنی بر کاربر و مبتنی بر اپراتور دو نوع اصلی استراتژیهای تعادل مجدد هستند [ 8 ، 12 ، 30 ]. در استراتژی تعادل مجدد مبتنی بر کاربر، مشوق هایی به شکل کوپن جایزه یا تخفیف اغلب برای تشویق کاربران به انتقال دوچرخه ها از مناطق مازاد به مناطق کمبود استفاده می شود. به عنوان مثال، در سال 2008، سیستم اشتراک دوچرخه Vélib’ در پاریس یک استراتژی قیمت گذاری تخفیفی [ 31 ] راه اندازی کرد تا کاربران را تشویق کند که دوچرخه ها را به ایستگاه های سربالایی بازگردانند. یک استراتژی قیمت گذاری توسط Chemla و همکاران توسعه داده شد. [32 ] برای تشویق کاربران به بازگرداندن دوچرخهها به ایستگاههای نزدیک به کمترین بار، و یک استراتژی تشویقی قیمت آنلاین پویا توسط Pfrommer و همکاران پیشنهاد شد. [ 33 ] برای ایجاد انگیزه در کاربران برای انتخاب مکانهای جایگزین برای برداشتن یا بازگرداندن دوچرخهها. با این حال، بسته به مشارکت کاربران، تعادل مجدد مبتنی بر کاربر ممکن است برای دستیابی به تعادل مجدد سطح سیستم کافی نباشد [ 30 ]. از این رو، استراتژی های تعادل مجدد مبتنی بر کاربر اغلب به عنوان مکمل استراتژی های مبتنی بر اپراتور استفاده می شود. این دو نوع استراتژی را می توان برای کمک به کاهش هزینه های تعادل مجدد ترکیب کرد [ 33 ]. در حال حاضر، اکثر سیستمهای اشتراکگذاری دوچرخه موجود (به عنوان مثال، Mobike و Ofo در چین) از استراتژیهای تعادل مجدد مبتنی بر اپراتور استفاده میکنند [ 8 ].
چند مطالعه بر توسعه روشهای تعادل مجدد مبتنی بر اپراتور کارآمد متمرکز شدهاند. در یک عملیات تعادل مجدد مبتنی بر اپراتور، ناوگانی از وسایل نقلیه اغلب برای جابجایی دوچرخه ها از سایتی به سایت دیگر ارسال می شوند. از جمله، روشهای بهینهسازی فضایی [ 42 ] به طور گسترده برای تعیین تعداد وسایل نقلیه جابجایی و مسیرهای مرتبط برای انجام عملیات تعادل مجدد استفاده شده است [ 8 ، 34 ، 38 ، 39 ]. تمام مطالعات موجود در جدول 1 بر اساس روش های بهینه سازی هستند به جز Ji et al. [ 41 ]. این مسائل اغلب با استفاده از برنامه نویسی عدد صحیح مختلط (MIP) فرموله شده اند [ 34 ، 38]. برخی از این مطالعات GIS را در مدلهای مکانیابی کلاسیک، از جمله مسئله p -median و مشکلات مکان پوشش، برای دستیابی به طراحی متعادلسازی مجدد بهینه، ادغام کردند [ 8 ، 18 ]. طیف وسیعی از اهداف/اهداف در طراحی تعادل مجدد دوچرخه مورد بررسی قرار گرفته است. این اهداف شامل به حداقل رساندن هزینهها، متغیر از هزینههای سفر تا هزینههای متعادل مجدد کلی (شامل هزینههای سفر، کامیون، بارگیری و تخلیه)، و به حداکثر رساندن تعادل سطح سیستم ارزیابی شده با استفاده از معیارهای مختلف (مانند حداقل انحراف مطلق از تعداد هدف دوچرخه) است. (همچنین به جدول 1 مراجعه کنید ). در حالی که برخی از مطالعات بر یک هدف واحد تمرکز داشتند [ 35 ، 43]، چند مطالعه چندین هدف را به طور همزمان در نظر گرفتند [ 44 ، 45 ].
همانطور که در جدول 1 نشان داده شده است، مدل های موجود تعادل مجدد دوچرخه عمدتاً مبتنی بر ایستگاه هستند و برای رسیدگی به مسئله عدم تعادل یک SBBSS ساخته شده اند. در یک SBBSS، ایستگاه ها واحدهای تحلیلی هستند که برای انجام ارزیابی عدم تعادل و تجزیه و تحلیل مجدد تعادل بعدی استفاده می شوند. در یک SFBSS، اگر یک منطقه را به مجموعه ای از مناطق فرعی تقسیم کنیم و هر زیر منطقه را به عنوان یک “ایستگاه” در نظر بگیریم، می توانیم یک مدل تعادل مجدد مبتنی بر ایستگاه را برای حل مشکل عدم تعادل در یک SFBSS اعمال کنیم. در واقع، مناطق تحلیل ترافیک [ 20 ] و شبکه های منظم [ 19 ، 21 ، 41] قبلاً برای انجام ارزیابی عدم تعادل برای SFBSS ها استفاده شده است. اگرچه مناطق تجزیه و تحلیل ترافیک (TAZs) به طور گسترده در برنامه ریزی حمل و نقل استفاده می شوند، اما عمدتاً بر اساس ترافیک موتوری مشخص می شوند و به طور کلی برای دریافت تغییرات عرضه و تقاضای دوچرخه با توجه به فاصله کوتاهی که کاربران دوچرخه معمولاً مایل به پیاده روی برای دسترسی هستند، بسیار خشن هستند. دوچرخه ها در مورد رویکردهای مبتنی بر شبکه، انتخاب اندازه شبکه یا دلخواه یا نامشخص بوده است [ 19 ، 21 ، 41]]. تا آنجا که ما می دانیم، هیچ مطالعه ای در مورد تأثیر مقیاس تحلیل بر ارزیابی عدم تعادل و طراحی تعادل مجدد مرتبط در یک SFBSS وجود نداشته است. مقیاس میتواند در یک مطالعه SFBSS حیاتی باشد: یک وضعیت متعادل در مقیاس بزرگ ممکن است شامل چندین محل کمبود/مازاد دوچرخه محلی باشد، و در نتیجه، استراتژی تعادل مجدد طراحیشده بر اساس مقیاس بزرگ ممکن است مشکل عدم تعادل را به طور کامل حل نکند. در مقابل، تجزیه و تحلیل انجام شده با استفاده از مقیاس های ظریف ممکن است با چالش های محاسباتی مواجه شود و مقیاسی که خیلی خوب است (مانند 1 متر) ممکن است ضروری یا حتی معنی دار نباشد.
جدول 1 همچنین تعداد واحدهای تجزیه و تحلیل (به عنوان مثال، زیرمناطق/شبکهها در یک SFBSS یا ایستگاهها در یک SBBSS) را که در مطالعات فعلی تعادل مجدد دوچرخه استفاده میشوند، خلاصه میکند، از 28 تا 1185. از آنجایی که یک مشکل تعادل مجدد میتواند از نظر محاسباتی غیرقابل حل باشد وقتی که یک مشکل بزرگ وجود دارد. تعداد واحدهای تحلیل درگیر هستند، بسیاری از مطالعات بر روی شهرها/مناطق کوچک متمرکز شدهاند یا از مقیاس درشت استفاده میکنند [ 19 ، 21 ]. به عنوان مثال، مدل ارائه شده توسط Chemla و همکاران. [ 32 ] به دلیل اندازه بزرگ مشکل قادر به شبیه سازی فرآیند تعادل مجدد مبتنی بر کاربر برای بیش از 250 ایستگاه نبود. تمرکز بر مناطق کوچک یا استفاده از واحدهای تجزیه و تحلیل در مقیاس درشت ممکن است بینش محدودی را در مورد استراتژی های موازنه مجدد موثر برای یک منطقه شهری بزرگ ارائه دهد.
بنابراین، شناسایی مقیاس تحلیل مناسب و طراحی استراتژیهای متعادلسازی مجدد دوچرخه کارآمد و مؤثر برای SFBSS در شهرهای بزرگ مورد نیاز است. در این مطالعه، هدف ما این است که با تمرکز بر دو سؤال مهم، شکاف های تحقیقاتی را پر کنیم: (1) چگونه مقیاس بر ارزیابی عدم تعادل یک SFBSS و طراحی تعادل مجدد مرتبط تأثیر می گذارد، و (2) چگونه با چالش های محاسباتی برای اندازه های بزرگ مقابله کنیم. مشکلات تعادل مجدد ما یک مدل بهینهسازی فضایی را برای بهینهسازی استراتژیک تلاشهای تعادل مجدد دوچرخه ایجاد میکنیم. ما همچنین یک روش تجزیه منطقه را برای حل مسائل با اندازه بزرگ که بر اساس مقیاسهای تحلیل خوب ساخته شدهاند، پیشنهاد میکنیم. ما رویکرد را برای مطالعه SFBSS در مرکز شهر پکن اعمال می کنیم. بر اساس مطالعه تجربی،
3. روش شناسی
3.1. حوزه و داده های مطالعه
منطقه مورد مطالعه ما از شش ناحیه در مرکز پکن تشکیل شده است: دانگ چنگ، شیچنگ، چائویانگ، هایدیان، فنگتای و شیجینگشان. پکن، پایتخت چین، در میان معدود شهرهایی است که برای اولین بار در سال 2015 SFBSS را پذیرفت. طبق گزارش کمیسیون حمل و نقل شهرداری پکن، در نیمه دوم سال 2018، میانگین استفاده روزانه از دوچرخه مشترک در پکن 1.3 میلیون نفر بود که اکثریت آنها خوشه ای بودند. در منطقه مطالعه ما ما از مجموعه داده استفاده از دوچرخه در سطح سفر در این مطالعه استفاده می کنیم. مجموعه دادهها از Mobike، یک شرکت بزرگ اشتراکگذاری دوچرخه بدون ایستگاه در چین بهدست آمد. مجموعه داده شامل اطلاعات مربوط به شناسه سفارش، شناسه دوچرخه، شناسه کاربر، زمان شروع، مکان شروع و مکان پایان است. ما از داده های سفر با دوچرخه در روز چهارشنبه، 10 مه 2017 به عنوان یک روز معمولی هفته برای نشان دادن روش خود استفاده می کنیم.
3.2. مقیاس های جایگزین و پیش پردازش داده ها
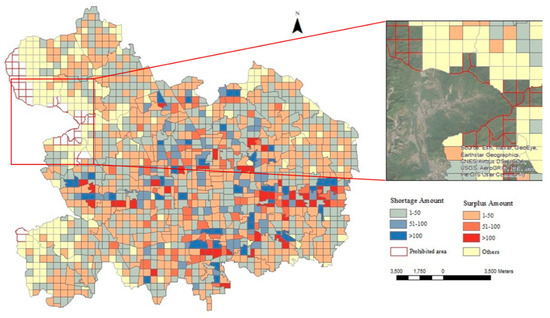
کل منطقه مورد مطالعه به شبکه های منظم تقسیم شده است. هر شبکه به عنوان یک “ایستگاه” دوچرخه در نظر گرفته می شود، جایی که وانت و رها کردن دوچرخه برای ارزیابی وضعیت عدم تعادل خلاصه می شود. در این مطالعه، ما هفت مقیاس جایگزین (2 کیلومتر، 1.5 کیلومتر، 1 کیلومتر، 800 متر، 400 متر، 200 متر، 100 متر) را بررسی می کنیم. به طور خاص، مقیاس 100 متر در جی و همکاران استفاده شد. [ 41 ] برای طراحی یک استراتژی تعادل مجدد مبتنی بر کاربر برای SFBSS. 400 متر مسافت قابل پیاده روی است که به طور گسترده پذیرفته شده است [ 46 ]. طبق نظرسنجی یانگ و دیز روکس، 800 متر میانگین فاصله سفرهای پیاده روی است [ 47 ]. 1 کیلومتر مربع میانگین مساحت واحدهای مورد مطالعه (مناطق تحلیل ترافیک) بود که Xu et al. [ 20] برای ارزیابی وضعیت عدم تعادل یک SFBSS استفاده می شود. 2 کیلومتر حداکثر مسافتی است که افراد مایل به پیاده روی هستند بر اساس دستورالعمل برنامه ریزی عمومی در ایالات متحده و بریتانیا [ 48 ]. علاوه بر این، 200 متر و 1.5 کیلومتر در مجموعه به عنوان مقیاس های میانی برای بررسی ضربه های مقیاس گنجانده شده است. شکل 1نمونهای از تقسیمبندی منطقه مورد مطالعه به شبکههای 1×1 کیلومتری با حفظ مرز Jiedao را نشان میدهد. جیدائو حداقل واحد سرشماری در چین است و عمدتاً بر اساس موانع طبیعی یا سازههای دستساز، از جمله رودخانهها، راهآهنها و خیابانها/بزرگراههای اصلی تقسیمبندی شده است. بنابراین، مرزهای Jiedao ممکن است تأثیری بر استفاده از دوچرخه داشته باشد. علاوه بر این، با حفظ مرزهای Jiedao، می توان به راحتی شبکه ها را با داده های سرشماری پیوند داد. در این مطالعه، ما همچنین مناطقی را که در آن دوچرخه مشترک مجاز نیست، از جمله مناطق کوهستانی، مناطق حفاظت شده طبیعی و پارک ها شناسایی و حذف کردیم. در هر شبکه، پیکاپ ها و برگشت های دوچرخه را بر اساس مکان شروع و پایان دوچرخه در یک روز شمارش می کنیم. سپس، کمبود/مازاد دوچرخه با مقایسه مقدار پیکاپ و بازگشت محاسبه میشود: منطقه کمبود / مازاد دوچرخه منطقه ای است که وانت دوچرخه بیشتر / کمتر از برگشت دوچرخه است. در این مطالعه، ما همچنین یک کران پایینی کمبود/مازاد و کران بالایی را معرفی میکنیم تا به یک SFBSS اجازه دهد تا کمی از وضعیت تعادل کامل منحرف شود.
3.3. مدل جریان تعادل مجدد Bike-Share
در این مطالعه، ما یک مدل جریان تعادل مجدد دوچرخه-سهم را برای بهینهسازی استراتژیک تلاشهای تعادل مجدد دوچرخه معرفی میکنیم. هنگام پرداختن به مشکل عدم تعادل، هدف این مدل شناسایی مکانیابی بهینه دوچرخه با حداقل فاصله تغییر موقعیت کلی دوچرخه است. در این مدل، ما خود را به یک استراتژی تعادل مجدد خاص، مبتنی بر کاربر یا مبتنی بر اپراتور محدود نمیکنیم. بنابراین، هدف این مدل نه طراحی مسیر بهینه برای وسایل نقلیه برای توزیع مجدد دوچرخهها و نه توسعه یک استراتژی قیمتگذاری برای تشویق کاربران به مشارکت در تلاشهای متعادلسازی مجدد است. این تجزیه و تحلیل استراتژیک به طراحی استراتژی های تعادل مجدد خاص مورد نیاز برای حل مشکل عدم تعادل در SFBSS کمک می کند.
در مدل، ما یک کران پایین L و یک کران بالا U را روی نسبت تعادل مجدد قرار می دهیم تا به یک SFBSS اجازه دهیم کمی از وضعیت تعادل کامل منحرف شود. برای منطقه ای با مقدار معینی کمبود/مازاد دوچرخه، تعادل مجدد کامل شامل حمل و نقل به داخل/خروج دوچرخه هایی است که همان مقدار کمبود/مازاد دوچرخه را دارند. در این مدل، L و U حداقل و حداکثر درصد دوچرخههای نامتعادل را مشخص میکنند که باید برای رسیدن به وضعیت تعادل حمل و نقل شوند. اگر L = 0.9 و U را تنظیم کنیم= 1.1، برای منطقه ای با عدم تعادل اضافی 100، تعداد دوچرخه هایی که باید در طول فرآیند تعادل مجدد حمل شوند باید بیشتر یا مساوی 90 باشد، اما نمی تواند از 110 تجاوز کند. برای یک عملیات متعادل سازی کامل، می توان L و U 1 باشد. نماد زیر را در نظر بگیرید ( جدول 2 ):
مدل جریان تعادل مجدد سهم دوچرخه به صورت زیر فرموله شده است:
در تابع هدف (1)، هدف ما به حداقل رساندن مسافت کلی دوچرخه های تغییر موقعیت است. محدودیتهای (2) و (3) تضمین میکنند که برای همه مناطق دارای مازاد دوچرخه، خروجی خالص تعادل مجدد بیشتر از حد پایین است اما از حد بالایی تجاوز نمیکند. محدودیت های (4) و (5) مشخص می کند که برای تمام مناطق با کمبود دوچرخه، جریان خالص مجدد تعادل بیشتر از حد پایین است اما از حد بالایی تجاوز نمی کند. محدودیتها (6) تضمین میکنند که برای مناطقی که دوچرخههای اشتراکی را ممنوع میکنند، جریان متعادلسازی مجدد وجود ندارد. محدودیتهای (7) یک محدودیت عدد صحیح مثبت را بر میزان دوچرخههایی که قرار است تغییر مکان دهند، تحمیل میکنند. در مطالعه تجربی خود، ما از متریک فاصله مستقیم برای ارزیابی مسافت کلی سفر استفاده می کنیم:
جایی که، [ خطای پردازش ریاضی ]آمنمختصات x مرکز ناحیه i است ، [ خطای پردازش ریاضی ]بمنمختصات y مرکز ناحیه i است . در بسیاری از مناطق شهری، جاده ها و تقاطع های با تراکم بالا، مسافت سفر را نزدیک به فاصله مستقیم می کنند [ 49 ]. علاوه بر این، جادهها در بسیاری از بخشهای مرکز شهر پکن الگوی شبکهای را نشان میدهند، که باعث میشود فاصله مستطیلی به یک معیار معقول برای اندازهگیری فاصله سفر تبدیل شود [ 50 ].
3.4. رویکرد تجزیه منطقه
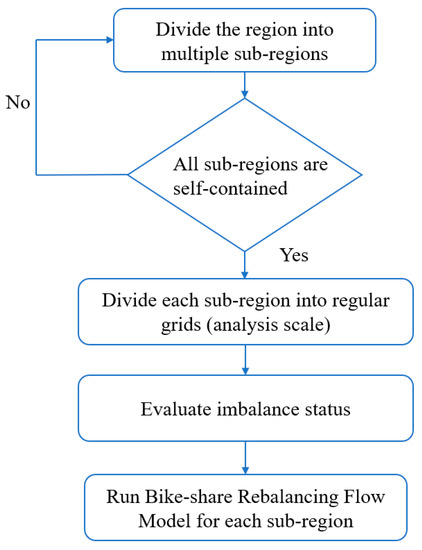
همانطور که قبلاً بحث شد، مدلهای متعادلسازی مجدد که با استفاده از مقیاسهای ظریف ساخته شدهاند، معمولاً برای حل چالشبرانگیز هستند. در نظر بگیرید که مردم اغلب از دوچرخه های مشترک برای طی مسافت کوتاه استفاده می کنند. به عنوان مثال، سفرهای مشترک دوچرخه در چین به طور متوسط 1.5 کیلومتر است ( https://global.chinadaily.com.cn/ ). برای یک منطقه بزرگ، ممکن است چندین منطقه فرعی وجود داشته باشد که در آن سفرهای مشترک دوچرخه عمدتاً در یک منطقه فرعی منفرد انجام می شود. با توجه به این، ما یک اکتشافی را با تجزیه یک منطقه بزرگ به چندین منطقه فرعی خود شامل برای کاهش اندازه مشکل ایجاد می کنیم. شکل 2گردش کار اکتشافی را نشان می دهد. اول، کل منطقه به چندین منطقه فرعی در مقیاس نسبتاً درشت تقسیم می شود. سپس وضعیت عدم تعادل برای هر زیر منطقه ارزیابی می شود. اگر منطقه فرعی معیار تعادل را داشته باشد، منطقه فرعی به عنوان یک منطقه فرعی خودکفا در نظر گرفته می شود. اگر یک منطقه فرعی وجود داشته باشد که مستقل نباشد، یک تقسیم منطقه جایگزین مورد نیاز است تا زمانی که همه زیرمنطقه های حاصل به خودی خود محدود شوند. سپس، هر زیر منطقه بیشتر به شبکههای دقیقتر (یعنی مقیاس تحلیل) تقسیم میشود و بر اساس مقیاس دقیقتر، وضعیت عدم تعادل ارزیابی میشود. در نهایت، مدل جریان تعادل مجدد دوچرخه به اشتراک گذاری برای به دست آوردن راه حل بهینه برای هر زیر منطقه پیاده سازی شده است.
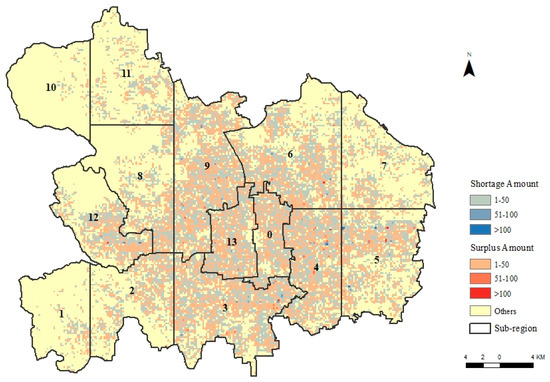
در مطالعه موردی ما، آزمایشهای محاسباتی بر روی یک ایستگاه کاری انجام میشود که توسط یک CPU Intel Core i7 با رم 16 گیگابایتی که یک سیستم عامل 64 بیتی را اجرا میکند، تغذیه میشود. نمونه های مسئله با مقیاس های تحلیل 800 متر و درشت تر به طور مستقیم با استفاده از نرم افزار بهینه سازی تجاری CPLEX حل می شوند. مسائل مربوط به مقیاس های ظریف تر آنقدر بزرگ هستند که به طور مستقیم با استفاده از CPLEX قابل حل نیستند. برای این مشکلات، اکتشافی تجزیه منطقه اعمال می شود. در اکتشافی، کل منطقه مورد مطالعه با استفاده از شبکههای 10 × 10 کیلومتری به 14 منطقه فرعی تقسیم میشود، در حالی که مرزهای منطقه حفظ میشود ( شکل 3 را ببینید ). این مناطق فرعی به طور متوسط 98 کیلومتر مربع مساحت دارند. برای بررسی اینکه آیا این مناطق فرعی مستقل هستند یا خیر، نسبت کمبود/مقدار مازاد به مصرف روزانه دوچرخه را محاسبه میکنیم. اگر قدر مطلق نسبت کمتر از 10 درصد باشد، منطقه فرعی مستقل در نظر گرفته می شود. سپس، هر زیر منطقه خود شامل بیشتر بر اساس مقیاس تجزیه و تحلیل (به عنوان مثال، 100، 200، و 400 متر) تقسیم می شود. شکل 3 مناطق فرعی خودکفا را نشان می دهد که در مطالعه موردی به همراه ارزیابی مازاد/کمبود انجام شده در مقیاس 200 متری به دست آمده است.
4. نتایج
4.1. ارزیابی عدم تعادل در مقیاس ها
جدول 3 خلاصه ای از تجزیه و تحلیل عدم تعادل دوچرخه در مرکز شهر پکن را ارائه می دهد. علاوه بر هفت مقیاسی که قبلاً مورد بحث قرار گرفت، ما دو مقیاس درشت 10 کیلومتری و 5 کیلومتری را برای ارزیابی عدم تعادل در مقیاسهای بسیار بزرگ قرار میدهیم. با کاهش اندازه شبکه از 10 کیلومتر به 100 متر، تعداد شبکه ها به طور قابل توجهی افزایش می یابد. ستون های “حداکثر مازاد” و “حداکثر کمبود” به ترتیب حداکثر مازاد و کمبود دوچرخه را در هر مقیاس ثبت می کنند. جدول 3نشان می دهد که در حالی که حداکثر مازاد و کمبود به نظر می رسد در سراسر مقیاس نسبتاً ثابت است، عدم تعادل کل به طور قابل توجهی افزایش می یابد زمانی که از شبکه های ریز استفاده می شود. به عنوان مثال، هنگامی که مقیاس از 5 کیلومتر به 200 متر تغییر می کند، حداکثر مازاد و کمبود مشابه باقی می ماند، اما عدم تعادل کل بیش از 17 برابر افزایش می یابد. این نشان می دهد که ارزیابی عدم تعادل در مقیاس بزرگ ممکن است بسیاری از سایت های نامتعادل محلی را رد کند. ستون “شبکه های نامتعادل” مقدار کل شبکه هایی را که مازاد/کمبود آنها بیش از 10٪ استفاده روزانه است را گزارش می دهد. ستون “درصد شبکه های نامتعادل” درصد شبکه های نامتعادل را با استفاده از آستانه عدم تعادل 10 درصد محاسبه می کند. به طور کلی، درصد شبکه های نامتعادل ابتدا افزایش می یابد، در مقیاس 800 متر به حداکثر می رسد و سپس با استفاده از مقیاس های ریزتر کاهش می یابد. این همچنین نشان می دهد که تجزیه و تحلیل در مقیاس درشت ممکن است بسیاری از سایت های عدم تعادل محلی را نادیده بگیرد. هنگامی که مقیاس بسیار درشت است (10 کیلومتر در این مطالعه موردی)، کل سیستم متعادل است. توجه داریم که در مقیاس بسیار خوب، اگرچه سایتهای محلی نامتعادلتری شناسایی شدهاند، بسیاری از شبکهها سایتهایی هستند که موجودی/استفاده از دوچرخه ندارند. به عنوان مثال، دادههای ما نشان میدهد که وقتی تجزیه و تحلیل در مقیاس 100 متر انجام میشود، 106719 شبکه (حدود 75٪) بدون استفاده از دوچرخه وجود دارد.
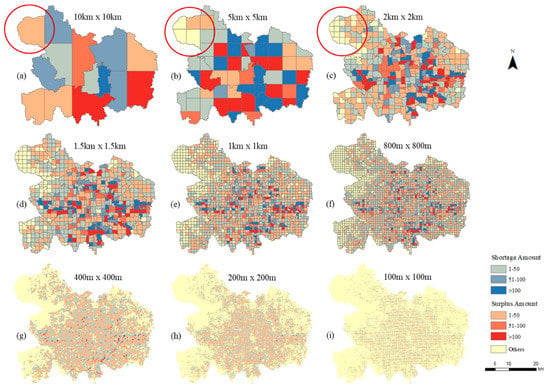
شکل 4 نشان می دهد که مناطق نامتعادل شناسایی شده در یک مقیاس ممکن است با استفاده از مقیاس جایگزین تغییر کنند. به عنوان مثال، در مقیاس 10 کیلومتری، شبکه شمال غربی (که در شکل 4 الف دایره شده است) دارای دوچرخه اضافی است. در مقیاس 5 کیلومتری، مازاد دوچرخه در گوشه شمال شرقی منطقه متمرکز شده است. اگر به کاهش مقیاس به 2 کیلومتر ادامه دهیم، شروع به یافتن کمبود و مازاد دوچرخه محلی در مکان هایی می کنیم که در مقیاس 5 کیلومتری متعادل در نظر گرفته می شوند. هنگامی که مقیاس تحلیل را بیشتر کاهش می دهیم، الگوی مشابهی مشاهده می شود. به طور کلی، هنگامی که از شبکه های درشت برای انجام ارزیابی عدم تعادل استفاده می شود، مازاد و کمبود محلی تمایل به خنثی شدن دارد که منجر به وضعیت نامتوازن کلی می شود.
4.2. تعادل مجدد نتایج در مقیاس های مختلف
جدول 4 خلاصه ای از نتایج تعادل مجدد را در مقیاس های مختلف ارائه می دهد. برای نسبت تعادل مجدد، کران پایینی L = 0.9 و کران بالایی U = 1.1 را تعیین می کنیم. هنگام حل مشکل تعادل مجدد، مقیاس های 5 کیلومتر و 10 کیلومتر را حذف می کنیم، زیرا این دو مقیاس بسیار درشت هستند. جدول 4نشان میدهد که وقتی از مقیاسهای ظریفتر استفاده میشود، اگرچه تعداد دوچرخههای تغییر مکانیافته افزایش مییابد، فاصله سفر در هر دوچرخه با میانگین کلی نزدیک به مقیاس مورد استفاده در تجزیه و تحلیل کاهش مییابد. به عنوان مثال، در مقیاس 2 کیلومتری، دوچرخه های تغییر موقعیت باید کمی بیشتر از 2 کیلومتر را در مقایسه با میانگین مسافت 100 متری دوچرخه در مقیاس 100 متری طی کنند. ستون “هدف” کل مسافتی را که دوچرخه های تغییر موقعیت یافته باید طی فرآیند تعادل مجدد طی کنند را گزارش می دهد. هنگامی که مقیاس از 2 کیلومتر به 1 کیلومتر کاهش می یابد، کل مسافت سفر افزایش می یابد. این به این دلیل است که میزان افزایش تعداد دوچرخههای جابجا شده کمی بیشتر از میزان کاهش میانگین مسافت طی شده با دوچرخه است. هنگامی که مقیاس از 1 کیلومتر به 100 متر کاهش می یابد، اگرچه دوچرخه های بیشتری باید تغییر مکان دهند، فاصله کلی سفر کاهش می یابد. این به این دلیل است که میانگین مسافت سفر با دوچرخه به میزان قابل توجهی در مقیاس های خوب کاهش می یابد. به عنوان مثال، هنگامی که مقیاس از 1 کیلومتر به 100 متر کاهش می یابد، تعداد دوچرخه های تغییر مکان حدود 4 برابر افزایش می یابد، در حالی که میانگین مسافت طی شده با دوچرخه 13 برابر کاهش می یابد. ستون «جفتهای OD» تعداد جفتهای شبکه مبدا-مقصد درگیر در فرآیند تغییر موقعیت دوچرخه را گزارش میکند.جدول 4 نشان می دهد که مقدار کل جفت های OD با استفاده از مقیاس های تحلیل ظریف افزایش می یابد. با توجه به اینکه مقدار کلی شبکه های نامتعادل با مقیاس های ریزتر افزایش می یابد، منطقی است (همچنین به جدول 3 مراجعه کنید ). ستون «متوسط دوچرخههایی که به ازای هر جفت OD تغییر موقعیت میدهند» میانگین تعداد دوچرخههایی را که بین یک جفت شبکه OD تغییر مکان دادهاند، خلاصه میکند. نتایج نشان می دهد که با مقیاس های ریزتر کاهش می یابد. در مقیاس 100 متر، به طور متوسط تنها حدود سه دوچرخه با جریان تغییر موقعیت مرتبط هستند.
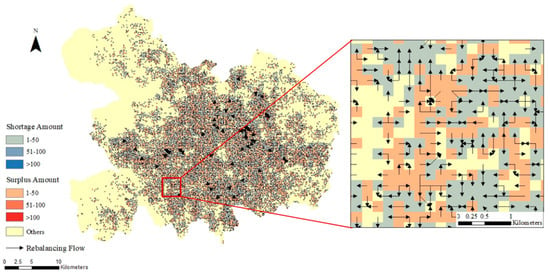
شکل 5 جریان های متعادل کننده مجدد را در مقیاس 200 متر ترسیم می کند. همانطور که در شکل 5نشان می دهد، بیشتر جریان های تعادل مجدد در میان شبکه های همسایه رخ می دهد. شبکههای با عدم تعادل مازاد معمولاً منشأ جریانهای متعادلسازی مجدد هستند و شبکههایی با عدم تعادل کمبود احتمالاً مقصد جریانهای متعادلسازی مجدد هستند. همچنین متوجه میشویم که جریانهای ورودی/خروجی در برخی از شبکهها وجود دارد که از قبل معیار تعادل را برآورده میکنند. چنین جریان هایی اغلب برای کمک به شبکه های همسایه برای دستیابی به وضعیت تعادل استفاده می شود. برخی از شبکه ها هدف “انتقال” را انجام می دهند. این شبکهها بهجای توزیع مستقیم دوچرخهها از شبکهی مازاد دوچرخه به شبکهی کمبود دوچرخه، دوچرخهها را از مناطق مازاد دوچرخه دریافت میکنند و برخی از آنها را به یک/چند نواحی کمبود دوچرخه توزیع میکنند. از آنجایی که در مطالعه تجربی از فاصله مستقیم استفاده می شود، “انتقال” فاصله کلی تغییر مکان را افزایش نمی دهد، اما منجر به کاهش میانگین مسافت سفر دوچرخه می شود.
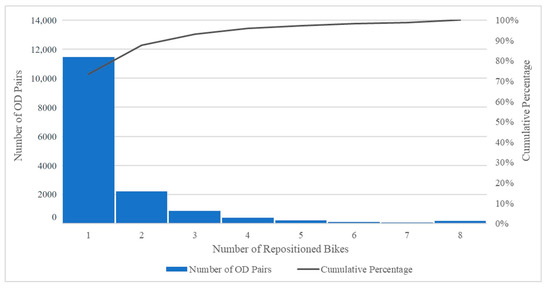
شکل 6 توزیع فرکانس فواصل جابجایی دوچرخه را هنگامی که مقیاس 200 متر در تحلیل استفاده می شود نشان می دهد. طبق این شکل، حدود 71 درصد از دوچرخه های تغییر موقعیت از 200 تا 300 متر و 99 درصد از دوچرخه های تغییر موقعیت کمتر از 500 متر حرکت می کنند. شکل 7 توزیع فرکانس مقدار دوچرخه های تغییر موقعیت مرتبط با هر جریان متعادل کننده را نشان می دهد. مطابق شکل 775 درصد از جریان های متعادل کننده شامل یک تا پنج دوچرخه است و 99 درصد جریان ها شامل کمتر از 35 دوچرخه است. الگوی مشابهی را میتوان در مقیاسهای دیگر نیز یافت: (1) تعادل مجدد سفر بر روی شبکههای همسایه متمرکز میشود. (2) میانگین مسافت سفر دوچرخه های تغییر موقعیت مشابه با مقیاس تجزیه و تحلیل است. (3) تعداد دوچرخه های جابجا شده در هر جریان متعادل کننده کم است.
جدول 5زمان مورد نیاز برای حل تمام موارد مشکل را نشان می دهد. نمونه های مسئله با مقیاس 800 متر یا درشت تر به طور بهینه با استفاده از CPLEX حل می شوند. برای این مشکلات، زمان حل کلی با استفاده از مقیاس های ریزتر افزایش می یابد. به عنوان مثال، زمانی که مقیاس از 2 کیلومتر به 800 متر کاهش می یابد، زمان مورد نیاز برای حل مدل تعادل مجدد از 14 ثانیه به بیش از 3 دقیقه افزایش می یابد. نمونه های مسئله با مقیاس 400 متر یا ریزتر با استفاده از اکتشافی تجزیه منطقه حل می شوند. به طور کلی، زمان حل مسئله نیز با استفاده از مقیاس های ظریف تر افزایش می یابد. به عنوان مثال، زمانی که مقیاس از 400 متر به 100 متر کاهش می یابد، زمان محاسبه کلی از 13 دقیقه به بیش از 2 ساعت افزایش می یابد. برای ارزیابی کیفیت یک راه حل به دست آمده با استفاده از اکتشافی تجزیه منطقه، ما همچنین اکتشافی تجزیه منطقه را برای حل نمونه مسئله با مقیاس تحلیل 800 متر اعمال می کنیم. راه حل ارائه شده توسط اکتشافی تجزیه منطقه حدود 4٪ بدتر از راه حل بهینه است.
5. بحث
مقیاس در ارزیابی عدم تعادل و طراحی مجدد تعادل یک SFBSS حیاتی است. تجزیه و تحلیل انجام شده بر اساس مقیاس های بزرگ (مثلاً 1 کیلومتر یا درشت تر) تصویری منطقه ای از وضعیت عدم تعادل ارائه می دهد و از نظر محاسباتی کارآمد است. از نقطه نظر تعادل مجدد مبتنی بر اپراتور، یک تجزیه و تحلیل در مقیاس بزرگ به یک برنامه ریزی تعادل مجدد استراتژیک کمک می کند. یک استراتژی تعادل مجدد بر اساس تجزیه و تحلیل در مقیاس بزرگ معمولاً شامل تغییر مکان دوچرخه های کمتر و در نتیجه اندازه ناوگان کوچکتر و هزینه های کمتر مرتبط با بارگیری و تخلیه دوچرخه است. با این حال، با توجه به اینکه تجزیه و تحلیل در مقیاس بزرگ ممکن است بسیاری از سایتهای عدم تعادل محلی را از دست بدهد، ممکن است اثربخشی عملیات متعادلسازی مجدد مبتنی بر تجزیه و تحلیل در مقیاس بزرگ به خطر بیفتد. علاوه بر این، تجزیه و تحلیل در مقیاس بزرگ ممکن است برای طراحی یک رویکرد تعادل مجدد مبتنی بر کاربر کمتر مفید باشد.
تجزیه و تحلیل با استفاده از مقیاس های کوچک (مثلاً 100، 200 متر) تعداد زیادی از دوچرخه ها را که نیاز به تغییر مکان دارند شناسایی می کند. برای یک رویکرد تعادل مجدد مبتنی بر اپراتور، جابجایی تعداد زیادی از دوچرخه ها مستلزم هزینه های بالایی برای بارگیری و تخلیه دوچرخه است. با این حال، با توجه به اینکه مکانهای عدم تعادل را میتوان با دقت بیشتری شناسایی کرد که از مقیاسهای آنالیز ظریف استفاده میشود، یک استراتژی متعادلسازی مجدد مبتنی بر اپراتور که بر اساس مقیاسهای ریز طراحی شده است، مؤثرتر از استفاده از مقیاس درشت خواهد بود. تجزیه و تحلیل در مقیاس کوچک همچنین بینش های ارزشمندی را در مورد طراحی استراتژی های متعادل سازی مجدد مبتنی بر کاربر موثر ارائه می دهد. نتایج تجربی ما نشان می دهد که بسیاری از مازاد و کمبود دوچرخه محلی را می توان با جابجایی دوچرخه ها بین مناطق همسایه برطرف کرد. مثلا، در مقیاس 200 متر، اکثر سفرهای تعادل مجدد شامل جابجایی دوچرخه کمتر از 300 متر است. در این مورد، مشوق ها ممکن است برای کاربران موثر باشد تا به تعادل مجدد سیستم کمک کنند.
بر اساس مطالعه تجربی، ما 800 متر را به عنوان مقیاس مناسب برای طراحی استراتژیهای تعادل مجدد مبتنی بر اپراتور توصیه میکنیم. در مقیاس 800 متر، درصد دوچرخه های نامتعادل به حداکثر می رسد. این نشان میدهد که در این مقیاس، بسیاری از سایتهای عدم تعادل محلی بدون معرفی بسیاری از مناطق غیر مرتبط شناسایی شدهاند. علاوه بر این، در مقیاس 800 متر، اندازه مسئله تعادل معقول است و حل مشکل تعادل مجدد کارآمد است، که امکان طراحی استراتژی های تعادل مجدد پویا در زمان واقعی را ممکن می سازد. علاوه بر این، حتی اگر سایتهای کمبود/مازاد محلی در یک شبکه 800 متری وجود داشته باشد، با توجه به اینکه 800 متر فاصله متوسط سفرهای پیادهروی است [47]، برای بسیاری از کاربران قابل قبول است که از یک سایت کمبود محلی به یک سایت مازاد محلی پیاده روی کنند. دوچرخه بردار
در مورد استراتژیهای تعادل مجدد مبتنی بر کاربر، ما مقیاسهای ظریف مانند 100 و 200 متر را به عنوان واحد تحلیل توصیه میکنیم. در مقیاس 100 متر، مطالعه تجربی نشان میدهد که تعادل مجدد زیادی را میتوان در فاصله بسیار کوتاهی (به طور متوسط 100 متر) به دست آورد. در این صورت مصرف کنندگان نیازی به پیاده روی ندارند و انگیزه بالایی برای مشارکت در فرآیند تعادل خواهند داشت. مطالعه ما همچنین نشان می دهد که به طور متوسط فقط چند دوچرخه باید بین یک جفت OD توزیع شود، بنابراین در بیشتر موارد، تعداد کمی از کاربران برای کمک به حرکت دوچرخه ها بین دو سایت خاص مورد نیاز هستند. در مقیاس خوب، بسیاری از سایتها میتوانند بهعنوان «ایستگاههای انتقال» عمل کنند، که به کاربران اجازه میدهد در یک یا چند بخش از سفرهای متعادل کننده شرکت کنند.
به طور کلی، مشکلات تعادل مجدد در اندازه بزرگ، چالشهایی را برای حل مشکل ایجاد میکنند. در این مطالعه، ما اکتشافی تجزیه منطقه را برای حل نمونههای مسئله با اندازه بزرگ معرفی میکنیم. مطالعه تجربی نشان می دهد که اکتشافی می تواند برای حل مسائلی استفاده شود که توسط نرم افزار بهینه سازی تجاری موجود قابل رسیدگی نیستند. ما توجه می کنیم که کیفیت راه حل اکتشافی به شدت به تعیین مناطق فرعی “خود شامل” بستگی دارد. در مطالعه تجربی، ما از یک رویکرد تصادفی برای ترسیم این مناطق فرعی استفاده میکنیم و راهحلهای تولید شده توسط اکتشافی کمی بدتر از راهحل بهینه هستند. مطالعه آینده میتواند بر توسعه استراتژیهایی برای شناسایی مناطق فرعی مستقل و مقیاس مرتبط برای بهبود کیفیت راهحل تمرکز کند.
باید اذعان داشت که این مطالعه دارای محدودیت هایی است. ابتدا، مشابه بسیاری از روشهای موجود، در یک SFBSS، یک منطقه را به تعدادی زیرمنطقه تقسیم میکنیم و هر زیر ناحیه را بهعنوان یک «ایستگاه» در نظر میگیریم که همه دوچرخهها در داخل همان منطقه فرعی در مرکز زیرمنطقه جمع شدهاند. -حوزه. چنین رویکردی ممکن است زمانی مشکل ساز باشد که واحدهای تجزیه و تحلیل / زیرمنطقه ها بزرگ باشند، زیرا دوچرخه های داخل یک منطقه فرعی به احتمال زیاد دور از مرکز یک منطقه فرعی هستند. دوم، در مدل تعادل مجدد، ما به یک SFBSS اجازه می دهیم تا با معرفی یک کران بالانس و کران پایین، کمی از وضعیت تعادل کامل منحرف شود. در مطالعه تجربی، ما یک کران پایین 0.9 و یک کران بالایی 1.1 را بررسی می کنیم.
6. نتیجه گیری
SFBSS به طور گسترده در بسیاری از شهرهای جهان مورد استفاده قرار گرفته است. با این حال، اجازه دادن به کاربران برای برداشتن یا رها کردن دوچرخه در چندین سایت در یک SFBSS باعث ایجاد مشکل عدم تعادل دوچرخه در یک SFBSS می شود. مسئله عدم تعادل نه تنها باعث سرکوب تقاضای بالقوه در مناطق کم عرضه می شود، بلکه باعث ایجاد آشفتگی دوچرخه در مناطق با عرضه مازاد می شود. بدون ایستگاه دوچرخه ثابت، مطالعات قبلی واحدهای تجزیه و تحلیل دلخواه را برای تجزیه و تحلیل یک SFBSS اتخاذ کرده اند. این مطالعه تاثیرات مقیاس را بر ارزیابی عدم تعادل یک SFBSS و طراحی استراتژی تعادل مجدد مرتبط بررسی میکند. یک مدل بهینهسازی فضایی برای اجرای مجدد تعادل استراتژیک همراه با یک اکتشافی برای حل مسائل با اندازه بزرگ توسعه داده شده است. مطالعه تجربی در مرکز شهر پکن نشان میدهد که نتایج ارزیابی عدم تعادل میتواند به میزان قابل توجهی با مقیاس متفاوت باشد. ارزیابی عدم تعادل در مقیاس بزرگ نه تنها بسیاری از سایتهای عدم تعادل محلی را از دست نمیدهد، بلکه در شناسایی دقیق مکان عدم تعادل نیز ناکام میماند. در مورد تلاشهای متعادلسازی مجدد، جابهجایی دوچرخه در مناطق همسایه انجام میشود. توصیه هایی در مورد انتخاب مقیاس برای دو استراتژی اصلی تعادل مجدد ارائه شده است. نتایج تحقیقات بینش های مهمی را در مورد برنامه ریزی حمل و نقل پایدار دوچرخه ارائه می دهد. همچنین میتوان بینشهایی از این مطالعه بهدست آورد تا به حل مشکل عدم تعادل در سایر سیستمهای تحرک مشترک، از جمله سیستمهای اشتراکگذاری خودرو و اشتراک اسکوتر کمک کند. توصیه هایی در مورد انتخاب مقیاس برای دو استراتژی اصلی تعادل مجدد ارائه شده است. نتایج تحقیقات بینش های مهمی را در مورد برنامه ریزی حمل و نقل پایدار دوچرخه ارائه می دهد. همچنین میتوان بینشهایی از این مطالعه بهدست آورد تا به حل مشکل عدم تعادل در سایر سیستمهای تحرک مشترک، از جمله سیستمهای اشتراکگذاری خودرو و اشتراک اسکوتر کمک کند. توصیه هایی در مورد انتخاب مقیاس برای دو استراتژی اصلی تعادل مجدد ارائه شده است. نتایج تحقیقات بینش های مهمی را در مورد برنامه ریزی حمل و نقل پایدار دوچرخه ارائه می دهد. همچنین میتوان بینشهایی از این مطالعه بهدست آورد تا به حل مشکل عدم تعادل در سایر سیستمهای تحرک مشترک، از جمله سیستمهای اشتراکگذاری خودرو و اشتراک اسکوتر کمک کند.






بدون دیدگاه