1. معرفی
اکثر تحقیقات انجام شده در مورد اتوماسیون تعمیم نقشه تاکنون به نقشه های توپوگرافی، با تمرکز بر تعمیم جاده ها، مرزها، شبکه های رودخانه و ساختمان ها اختصاص یافته است. یعنی با تمرکز بر اجسام خطی یا اجسام با مساحت کوچک. تعمیم انواع نقشه های موضوعی، از جمله نقشه های طبقه بندی شده (مثلا نقشه های زمین شناسی، خاک یا کاربری زمین)، کمتر مورد توجه قرار گرفته است، شاید از آنجایی که نقشه های طبقه بندی شامل چند ضلعی هایی با اشکال و اندازه های بالقوه دلخواه هستند و آنها را پیچیده تر از اشکال معمولی می کند. به عنوان مثال، برای ساختمان های روی نقشه توپوگرافی. با این وجود، نقشههای طبقهبندی، با نقشههای زمینشناسی بهعنوان نماینده برجسته، یک نوع نقشه مکرر هستند و به روشهای خاصی برای تعمیم خودکار نیاز دارند. به عنوان مثال، در نقشه های توپوگرافی، ساختمانها معمولاً شکلی منظم دارند و اغلب بهصورت منظم چیده میشوند (مثلاً در ترازهای خطی)، در حالی که در نقشههای طبقهبندی، ویژگیهای چندضلعی میتوانند شکل دلخواه داشته باشند که در ترتیبات فضایی دلخواه رخ میدهند. صرفاً استفاده مجدد از رویکرد و فرآیندهای تعمیم نقشه توپوگرافی برای نقشه برداری طبقه ای راه حل مناسبی ارائه نمی دهد.1 ، 2 ]، زیرا الزامات برای تعمیم نقشه های طبقه بندی شده و بنابراین زمین شناسی با موارد مورد استفاده برای نقشه برداری توپوگرافی، همانطور که در بخش 2 شرح داده شده است، متفاوت است.
در طول دو دهه گذشته، تکنیکهای مبتنی بر محدودیت به عنوان پارادایم پیشرو برای مدلسازی و خودکارسازی فرآیند تعمیم نقشه [ 3 ، 4 ، 5 ، 6 ] و ارزیابی نتایج تعمیم [ 7 ] تکامل یافتهاند. با این حال، در حالی که استفاده از پارادایم مبتنی بر محدودیت در نقشه برداری توپوگرافی گسترده است، روش های تعمیم برای نقشه های طبقه بندی و زمین شناسی به ندرت این رویکرد را اتخاذ کرده اند ( برای یک استثنا به [ 8 ] مراجعه کنید). این تا حدودی ناامیدکننده است، زیرا پیچیدگی نقشههای طبقهبندی میتواند رویکردی را برای اجازه مدلسازی و نظارت متمایز و انطباقی بر شرایط حاکم بر فرآیند تعمیم نقشه، مورد استفاده قرار دهد.
هدف این مقاله ارائه روشی با استفاده از محدودیت ها، به طور خاص به اصطلاح محدودیت های اندازه، به عنوان مبنایی برای تعمیم نقشه های زمین شناسی است. محدودیتهای اندازه با حداقل مساحت و روابط فاصله در یک یا جفت ویژگی نقشه سروکار دارند. آنها همچنین محدودیت های متریک یا گرافیکی [ 4 ] نامیده می شوند و محدودیت های طبیعی ادراک انسان را در ابعاد حداقلی و قابل اندازه گیری بیان می کنند [ 8 ]]. رویکرد پیشنهادی ابتدا فهرستی از محدودیتهای اندازه، مقادیر هدف و معیارهای آنها را مشخص میکند. همچنین درمان منطقی محدودیت ها را در اولویت قرار می دهد، که به نوبه خود دنباله ای از عملگرها و الگوریتم های تعمیم را دیکته می کند که در صورت نقض یک محدودیت مورد استفاده قرار گیرند. محرک اصلی برای روش پیشنهادی محدودیت “حداقل مساحت” (MA) است که بر سایر محدودیتها تأثیر میگذارد و با ویژگیهای توصیفی ویژگیهای چند ضلعی که در حال تعمیم هستند همراه است. در یک گردش کار تطبیقی، MA و محدودیتهای مربوطه بهطور متوالی آزمایش میشوند و در صورت نقض، عملگرهای تعمیم مناسب، از جمله حذف شی (یعنی انتخاب)، بزرگنمایی، تجمع و جابجایی را راهاندازی میکنند.
استفاده از رویکرد مبتنی بر محدودیت در تعمیم نقشه عمدتاً به پارادایم مبتنی بر عامل مرتبط است [ 3 ، 5 ، 6 ، 8 ، 9]. با این حال، از آنجایی که ساخت موتور عامل به هیچ وجه کار بی اهمیتی نیست، پذیرش رویکرد مبتنی بر عامل و همراه با آن رویکرد مبتنی بر محدودیت، در عمل محدود شده است. از این رو، سهم اصلی این تحقیق نشان دادن استفاده از محدودیتها، با تمرکز بر محدودیتهای اندازه، برای تعمیم خودکار نقشههای زمینشناسی است، زیرا این رویکرد تاکنون بهطور صریح برای تعمیم خودکار نقشههای زمینشناسی اعمال نشده است. علاوه بر این، ما از یک رویکرد مبتنی بر گردش کار متشکل از دنباله ای از چندین عملگر تعمیم استفاده می کنیم، زیرا این پتانسیل بهتری برای پذیرش در عمل دارد. اگرچه با در نظر گرفتن نقشه های زمین شناسی طراحی شده است، اما این رویکرد برای سایر نقشه های طبقه بندی شده نیز قابل اجرا است: نقشه هایی که کاملاً با ویژگی های چند ضلعی پوشیده شده اند (به عنوان مثال، به اصطلاح تقسیمات چند ضلعی) مانند نقشه های خاک، نقشه های پوشش گیاهی یا نقشه های کاربری و پوشش زمین. در آزمایشها، ما نشان میدهیم که روش پیشنهادی، علیرغم سادگی نسبیاش، قادر به تعمیم مناسبتر نقشههای زمینشناسی، با کنترل محلی بهتر بر عملیات تعمیمسازی است که در مقایسه با نتایج ایجاد شده توسط راهحلهای پیشرفته که به کار میروند. از رویکرد مبتنی بر محدودیت استفاده نکنید. در نهایت، ما می دانیم که با تمرکز بر محدودیت های اندازه، روش شناسی ما دارای محدودیت هایی است که در ادامه به آن اشاره می کنیم. با کنترل محلی بهتر بر عملیات تعمیم که در مقایسه با نتایج ایجاد شده توسط راه حل های پیشرفته که از رویکرد مبتنی بر محدودیت استفاده نمی کنند، اعمال می شود. در نهایت، ما می دانیم که با تمرکز بر محدودیت های اندازه، روش شناسی ما دارای محدودیت هایی است که در ادامه به آن اشاره می کنیم. با کنترل محلی بهتر بر عملیات تعمیم که در مقایسه با نتایج ایجاد شده توسط راه حل های پیشرفته که از رویکرد مبتنی بر محدودیت استفاده نمی کنند، اعمال می شود. در نهایت، ما می دانیم که با تمرکز بر محدودیت های اندازه، روش شناسی ما دارای محدودیت هایی است که در ادامه به آن اشاره می کنیم.بخش 6 ، ارائه سرنخ برای تحقیقات بیشتر.
در بخش 2 ، ویژگی های نقشه های زمین شناسی مورد بحث قرار می گیرد. بخش 3 مروری بر کار مرتبط در تعمیم نقشه های زمین شناسی ارائه می دهد. بخش 4 هسته مقاله را نشان می دهد و عناصر روش شناسی مبتنی بر محدودیت اندازه را یک به یک معرفی می کند. بخش 5 نتایج یک سری آزمایش را ارائه می کند، ابتدا برای نشان دادن اثر عملگرهای تعمیم فردی، و سپس برای پارامترهای مختلف گردش کار ترکیبی. در نهایت، بخش 6 بحثی در مورد نتایج تجربی ارائه می دهد، در حالی که بخش 7 مقاله را با نتیجه گیری و یک چشم انداز پایان می دهد.
2. نقشه های زمین شناسی: هدف و ویژگی ها
نقشههای زمینشناسی از پیچیدهترین نقشههای موضوعی هستند که اشکال و ساختارهای متنوعی دارند. این امر فرآیند تعمیم را نیازمندتر می کند، و بنابراین قبل از فرآیند تعمیم، تجزیه و تحلیل عمیق این ساختارها مورد نیاز است [ 2 ، 10 ]. ایجاد نقشه های زمین شناسی نه تنها به تخصص نقشه برداری بلکه به دانش عمومی زمین شناسی نیاز دارد. بنابراین، برای مثال، دانش در مورد شکلگیری و ساختار انواع سنگهایی که در یک منطقه مورد مطالعه اتفاق میافتند، زمانی که نوبت به شناسایی اهمیت نسبی ویژگیهای نقشه میرسد، حیاتی خواهد بود. با این حال، اهمیت برخی از ویژگی های نقشه ممکن است بسته به هدف و نوع نقشه زمین شناسی که قرار است ساخته شود، متفاوت باشد.
سنگهای بستر به زمینشناسان در به تصویر کشیدن تاریخ طبیعی یک منطقه مورد مطالعه و شناسایی صخرههای مرتبط کمک میکنند. آنها همچنین دارای منابع معدنی ضروری مانند زغال سنگ، نفت و اورانیوم هستند که در کانون توجه صنعت معدن قرار دارند. بنابراین، یک نقشه برای اهداف معدن، سنگهای بستر باستانی را که ممکن است مواد معدنی خاصی را حمل کنند، برجسته میکند، در حالی که سنگهای رسوبی را نادیده میگیرد، زیرا آنها جدیدتر هستند [ 11 ]. ژئوفیزیکدانان به نوبه خود تأکید بیشتری بر ویژگی های ذاتی ویژگی هایی مانند تخلخل و نفوذپذیری در سنگ و رسوبات دارند [ 12 ].
هدف یک نقشه زمین شناسی “به تصویر کشیدن تفسیری برهمکنش های مکانی و زمانی بین سنگ ها، مواد زمین و شکل های زمین در سطح زمین” است [ 13 ]. مواد زمین شناسی سنگ های آذرین، دگرگونی و رسوبی و رسوبات سطحی هستند که چشم انداز اطراف ما را تشکیل می دهند. اکثر نقشه های زمین شناسی از رنگ ها و برچسب ها برای نشان دادن مناطقی از مواد مختلف زمین شناسی استفاده می کنند که واحدهای زمین شناسی نامیده می شوند. ساختارهای زمین شناسی، گسست ها و بسترهایی در ساختارهای زمین شناسی هستند که در نتیجه نیروهای آهسته اما قوی که جهان را تشکیل می دهند، به وجود می آیند [ 14 ].]. «نقشه های زمین شناسی موقعیت این سازه ها را با انواع خطوط مختلف نشان می دهد. از آنجایی که زمین پیچیده است، هیچ دو نقشه ای مواد و ساختارهای یکسانی را نشان نمی دهد، بنابراین معنای رنگ ها، برچسب ها و خطوط در هر نقشه توضیح داده شده است.» [ 15 ].
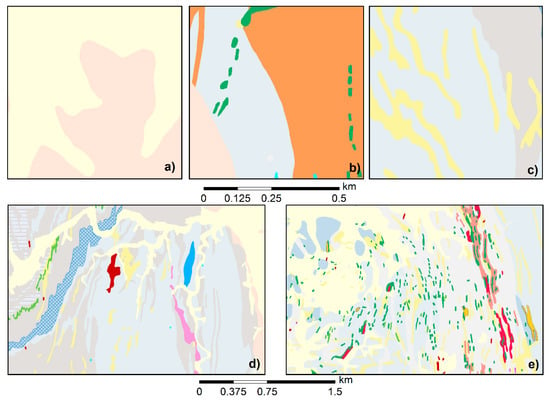
نقشههای زمینشناسی شامل الگوهای متنوعی است که توسط پارچهای از چندضلعیها، بهعلاوه اجرام خطی اضافی (مثلاً خطوط گسل) و اشیاء نقطهای (مثلاً چاهها) تشکیل شدهاند که در اینجا جای نگرانی نیست. چند ضلعی ها را می توان با ویژگی های فضایی، ساختاری و معنایی برای ارزیابی شباهت ها یا تفاوت ها و در نتیجه استنتاج الگوهای فضایی مربوط به ساختار ادراکی یا آرایش ویژگی های چندضلعی بر روی نقشه توصیف کرد [ 16 ]. شکل 1 نمونه گزیده ای از نقشه های زمین شناسی را نشان می دهد که با افزایش پیچیدگی هندسی و گرافیکی مرتب شده اند. در عصاره نقشه ساده شکل 1الف، تعداد کمی از واحدهای زمین شناسی با اشکال نسبتاً ساده درگیر هستند که صرفاً با استفاده از عملگرهای سادهسازی قابل تعمیم است. سطح بعدی پیچیدگی شامل چند ضلعی های کوچک از واحدهای زمین شناسی یکسان یا مشابه است ( شکل 1 ب)، که ممکن است با حذف یا به طور متناوب واحدها یا زیر واحدها در یک گروه واحد تعمیم داده شوند. سطح دیگر شامل مجموعه ای از چند ضلعی های کشیده از همان واحد است که در واحدهای دیگر تعبیه شده اند و احتمالاً از یکدیگر عبور می کنند ( شکل 1).ج)، جایی که یک نقشهنگار ممکن است ادغام واحدهای همسایه را در حالی که سعی میکند آرایش کلی آنها را حفظ کند (یعنی با استفاده از به اصطلاح عملگر تایپسازی) توصیه کند. شکل پیچیده دیگری که در نقشه های زمین شناسی یافت می شود، اشکال درخت مانند و دندریتی است که در مراحل بعدی دوره چهارم توسط رودخانه ها و نهرهای حامل رسوبات و سایر کانی ها ایجاد شده اند. این نوع همچنین موقعیت یک سیستم رودخانه را مشخص می کند ( شکل 1 د). در این مورد، یک راه حل ممکن جایگزینی چندین شاخه با تعداد کمتری از شاخه های درخت ساده شده است. شکل 1e نشان می دهد که انواع مختلفی از واحدهای متشکل از چند ضلعی های کوچک و بزرگ/طول و باریک و ساختارهای درخت مانند نیز ممکن است در کنار هم وجود داشته باشند و فرآیند تعمیم را حتی چالش برانگیزتر کند. تعمیم چنین پارچه های پیچیده ای مستلزم اتخاذ تصمیمات تعمیم چندگانه، مرتبط (و احتمالاً متناقض) است.
چند مثال در شکل 1 نشان می دهد که لایه چند ضلعی نقشه های زمین شناسی دارای تنوع بسیار بیشتری در طبقه بندی، اندازه، شکل، سینوسیته مرزی و روابط توپولوژیکی (به ویژه مهار) چند ضلعی های مربوطه است که معمولاً در نقشه های توپوگرافی مشاهده می شود. . آرایش فضایی چند ضلعی ها در نقشه های زمین شناسی می تواند اشکال مختلفی داشته باشد، همانطور که در شکل 1 قابل توجه است ، اگرچه حتی در نقشه پیچیده شکل 1e ما می توانیم ترازها و خوشه های چندضلعی ها را درک کنیم. کلاسهای ویژگی کلیدی در نقشههای توپوگرافی عمدتاً انسانزا هستند و از این رو تمایل به شکلهای منظمتر و درجه تغییرپذیری کمتری دارند و اغلب در ترازهای منظم قرار میگیرند (مثلاً شبکههای خیابانی شبکهای یا ترازهای مستقیم ساختمانها). کلاسهای ویژگی «طبیعی»، مانند پوشش زمین، در نقشههای توپوگرافی معمولاً به چند دسته محدود میشوند (مثلاً جنگلها، آبها، مناطق ساختهشده) و در اولویت دوم قرار دارند. از این رو، ما استدلال می کنیم که در حالی که عملگرهای یکسان (حذف، ساده سازی، تجمع، جابجایی نوع و غیره) در هر دو حوزه معتبر هستند، الگوریتم های تعمیم متفاوت، یا حداقل ترکیب های متفاوتی از الگوریتم ها، باید برای انطباق با ویژگی های خاص استفاده شوند. نقشه های زمین شناسی یا به طور کلی نقشه های طبقه بندی شده.
بخش بعدی مروری بر روش های مختلف تعمیم ارائه می کند که به صراحت برای پرداختن به ویژگی های نقشه های زمین شناسی ذکر شده در بالا پیشنهاد شده اند.
3. کارهای مرتبط
اولین تلاش قابل توجه برای تعمیم ویژه نقشه های زمین شناسی توسط نویسندگان [ 17 ] انجام شد که سعی کردند تعمیم یک نقشه زمین شناسی در مقیاس 1:250000 را از نقشه منبع مقیاس 1:50000 (محصول سازمان زمین شناسی بریتانیا) به طور خودکار انجام دهند. BGS))، با استفاده از مدل مفهومی که قبلا در [ 18 ] پیشنهاد شده بود. در حالی که نتایج بهدستآمده دلگرمکننده بود، BGS به این نتیجه رسید که این استراتژی همچنان نیازمند مداخله توسط اپراتور انسانی است، که آن را کمتر انعطافپذیر و ذهنیتر میکند. با این حال، نکته مهم این است که این کار اولیه اهمیت پایه گذاری فرآیند تعمیم را بر درک ساختارها و الگوهای اساسی ذاتی نقشه منبع برجسته می کند، وظیفه ای که البته مختص نقشه های زمین شناسی نیست.18 ، 19 ].
نویسندگان [ 20 ] یک مدل گردش کار مفهومی را ارائه کردند که به تعمیم نیمه خودکار نقشه های موضوعی با سه مرحله اصلی اختصاص داشت: تحلیل ساختاری، تعمیم و تجسم. تجزیه و تحلیل ساختاری (یا “تشخیص ساختار” طبق [ 18 ]) بسیار مهم تلقی شد، زیرا هنگامی که تمام ساختارهای مربوطه موجود در یک نقشه شناخته می شوند، این اطلاعات می تواند از تصمیم “زمان و نحوه تعمیم” حمایت کند [ 21 ]. مرحله دوم مدل مفهومی آنها شامل مدلسازی محدودیت در یک سیستم چند عاملی با هدف ایجاد یک گردش کار عینی و انعطافپذیر بود.
با الهام از مدل مفهومی فوق الذکر [ 20 ]، نویسنده [ 22 ] یک گردش کار تعمیم را بر اساس ابزارهای ArcGIS توسعه داد. یک نقشه زمین شناسی نمونه در مقیاس 1:24000 به سه مقیاس هدف یعنی 1:50000، 1:100000 و 1:250000 تعمیم داده شد. نتایج مطالعه با نقشههای زمینشناسی مربوط به سازمان زمینشناسی ایالات متحده (USGS) مقایسه شد و به خلاصه کردن نقاط قوت و محدودیتهای ابزارهای موجود برای تعمیم در آن زمان در ArcGIS کمک کرد.
آزمایش دیگری در مورد اثربخشی ArcGIS توسط Smirnoff و همکاران انجام شد. [ 23 ]، جایی که یک رویکرد اتوماتای سلولی (CA) به طور خاص برای تعمیم نقشه های زمین شناسی با استفاده از ابزار ArcGIS به عنوان پایه توسعه داده شد. هنگام مقایسه نتایج آنها با نتایج یک فرآیند با استفاده از ابزارهای تعمیم که مستقیماً در ArcGIS موجود است، به این نتیجه رسیدند که مدل خودکار مبتنی بر سلول یا سلولی دارای مزایای اساسی برای تعمیم خودکار نقشههای زمینشناسی است. در تحقیقات جدیدتر [ 24]، جعبه ابزار ArcGIS به نام “GeoScaler” بر روی نقشه های سطحی و سنگ بستر آزمایش شد. نتایج مورد ارزیابی قرار گرفت و کافی یافت شد. همچنین، با حفظ مقداری مداخله انسان در فرآیند، نتایج قابل تکراری به دست آمد. بسیار مهم است، از آنجایی که جعبه ابزار GeoScaler به صورت رایگان در دسترس قرار گرفت، این روش می تواند در عمل نقشه برداری زمین شناسی مورد استفاده قرار گیرد و بنابراین وضعیت ابزارهای تعمیم برای تعمیم نقشه های زمین شناسی را تعریف کرده است، که امروزه نیز وجود دارد. با این حال، این رویکرد ویژگیهای فردی و محلی ویژگیهای زمینشناسی مانند اندازه، شکل، و جهت چندضلعیها یا فاصله بین آنها را که برای انتقال الگوهای حیاتی نقشه منبع به نقشههای مشتقشده حیاتی است، در نظر نمیگیرد. نقشه علاوه بر این، از آنجایی که بیشتر داده های نقشه زمین شناسی در قالب برداری وجود دارد،
از این رو، یک رویکرد مبتنی بر برداری که از ترکیبی از عملگرهای تعمیم استفاده می کند که می تواند بسته به موقعیت محلی به صورت تطبیقی اعمال شود، مناسب تر به نظر می رسد. در این راستا، نویسندگان [ 25 ] الگوریتمهایی را برای چندین عملگر تعمیم چند ضلعی، از جمله حذف، بزرگشدن، تجمع و جابجایی، بر اساس اصل توپ غلتان، مطابق با مثلثسازی دلون و رویکردهای اسکلت پیشنهاد کردند. نویسندگان [ 8 ، 26 ] فهرستی از محدودیتها و یک فرآیند مبتنی بر عامل را برای تعمیم نقشههای چندضلعی پیشنهاد کردند، و کارهای قبلی نویسندگان [ 4 ، 5 ، 9 ] را گسترش دادند.
احتمالاً جامعترین کار در رابطه با مدلسازی محدودیتها برای نقشههای زمینشناسی توسط ادواردز و مکنز [ 27 ] ارائه شد که مجموعهای غنی از محدودیتها را ایجاد و نشان دادند و راههایی را برای نمایش این محدودیتها به زبان رسمی ارائه کردند. در حالی که از نظر مفهومی جذاب بود، مجموعه محدودیتهای پیشنهادی متأسفانه به الگوریتمهای تعمیم خاصی مرتبط نبود و اجرا نشد. این مطالعه همچنین پیچیدگی گستردهای را که در تلاش برای مدلسازی جامع محدودیتهای حاکم بر نقشههای زمینشناسی و قرار دادن آنها در فرآیندی مبتنی بر رایانه وجود دارد، نشان داد.
مولر و وانگ [ 28 ] یک روش خودکار برای تعمیم پچ منطقه پیشنهاد کردند که شامل حذف، بزرگکردن/انقباض، ادغام و جابجایی عملگرها بود. آنها به مشکلی مشابه با آنچه در این مقاله پرداخته شده است، پرداختند و همچنین از مجموعه ای مشابه از عملگرها استفاده کردند. با این حال، رویکرد آنها همه چند ضلعی ها را از نظر معنایی یکسان در نظر گرفت. در مقابل، نقشههای زمینشناسی به راحتی از بیش از 20 نوع سنگ تشکیل شدهاند که نیازمند در نظر گرفتن همزمان ویژگیهای هندسی و همچنین ویژگیهای چندضلعیها هستند. رویکرد آنها همچنین انعطافپذیری کمی برای اصلاح پارامترهای کنترلی باقی میگذارد، زیرا فاقد قابلیت آزمایش راهحلهای مختلف برای یک تضاد معین است.
همانطور که در بخش 1 بحث شد ، بهترین راه برای تشخیص تضادهای کارتوگرافی و رسمی کردن و کنترل الگوریتمهای تعمیم برای حل چنین موقعیتهایی، استفاده از محدودیتها است، همانطور که در تعمیم نقشه توپوگرافی نشان داده شده است. در این مقاله، ما به دنبال نشان دادن کاربرد پارادایم مبتنی بر محدودیت در مورد نقشههای زمینشناسی هستیم. همانطور که در بخش 2 و مطالعه دیگری نشان داده شد [ 27 ]، پیچیدگی تقریبا بی نهایتی در هنگام تلاش برای حل تعمیم نقشه های زمین شناسی به طور جامع وجود دارد. بنابراین، ما بر روی یک مشکل تعمیم خاص تمرکز میکنیم: چند ضلعیهای کوچک و آزاد (تکههای ناحیه در اصطلاح [ 28 ])، که یک مورد مکرر را در نقشههای زمینشناسی نشان میدهند ( شکل 1).b,d,e) و انواع دیگر نقشه های طبقه بندی شده مانند نقشه های خاک. از آنجایی که چنین چند ضلعیهای کوچک مستعد مشکلات خوانایی در کاهش مقیاس هستند، اما اغلب واحدهای زمینشناسی با ارزش اقتصادی برتر را نشان میدهند ( بخش 4.4.2 )، ما بر محدودیتهای اندازه تمرکز میکنیم، که ساده هستند اما اجازه میدهند بسیاری از مشکلات مرتبط با چند ضلعیهای کوچک حل شوند. خطاب. مجموعه محدودی از محدودیتهای نسبتاً ساده، ردیابی اثرات استفاده از رویکرد مبتنی بر محدودیت در تعمیم نقشه چند ضلعی را کاهش میدهد.
4. روش شناسی
4.1. گردش کار کلی
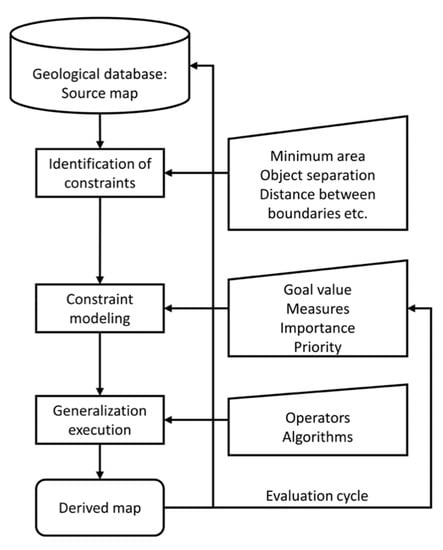
یک نمای کلی از روش پیشنهادی در شکل 2 نشان داده شده است . گردش کار کلی از یک نقشه با مقیاس بزرگ و با جزئیات ذخیره شده در یک پایگاه داده زمین شناسی (در مقیاس های 1:10000 تا 1:25000) شروع می شود تا نقشه های تعمیم یافته در مقیاس های متوسط (1:50000 تا 1:100000) به دست آید و سپس دوباره آنها را ذخیره کند. در پایگاه داده گردش کار تعمیم واقعی شامل سه مرحله اصلی است: شناسایی محدودیتها، مدلسازی محدودیتها و اجرای تعمیم. در حالی که این بخش از گردش کار شباهت هایی با مدل ارائه شده در [ 29 ] دارد، تمرکز در اینجا صرفاً بر نمایش توالی مراحل اصلی است. در مرحله اولیه ( بخش 4.2)، محدودیت های نقشه برداری مربوطه حاکم بر نقشه های زمین شناسی، در مورد ما محدودیت های اندازه مربوط به تعمیم لکه های منطقه کوچک، شناسایی می شوند. این مرحله توسط مرحله مدلسازی محدودیت دنبال میشود ( بخش 4.3 )، که هدف آن رسمیسازی محدودیتهای مذکور برای تعمیم نقشههای زمینشناسی است. مرحله سوم و اصلی، فرآیند تعمیم واقعی است ( بخش 4.4) که محدودیتهای مدلسازیشده قبلی را میگیرد و از آنها برای سازماندهی کاربرد عملگرهای تعمیم مختلف – حذف، بزرگسازی، تجمع، جابجایی – استفاده میکند که میتوانند برای رفع نقض محدودیتهای احتمالی استفاده شوند. در نهایت، نقشه به دست آمده بر اساس مقادیر هدف هر یک از محدودیت های نماینده ارزیابی می شود. اگر نقشه توسط مقادیر هدف تعیینشده رضایتبخش تلقی شود، کنترل به مرحله مدلسازی محدودیت برای کشف گزینههای جایگزین، بهینهسازی اهمیت و مقادیر اولویت محدودیتها برمیگردد. هنگامی که نقشه به دست آمده رضایت بخش در نظر گرفته شد، در پایگاه داده ذخیره می شود.
4.2. شناسایی محدودیت ها
همانطور که ما بر تعمیم وصله های منطقه کوچک در نقشه های طبقه بندی تمرکز می کنیم، مجموعه محدودیت های مربوطه به محدودیت های اندازه محدود می شود. محدودیتهای اندازه نقطه شروع فرآیند تعمیم را تشکیل میدهند، زیرا با حداقل مساحت و روابط فاصله در ویژگیهای نقشه منفرد یا جفت ویژگیهای نقشه سروکار دارند. بنابراین، در حالی که ممکن است آنها سادهتر از محدودیتهای مربوط به گروههای چند ضلعی (که پیکربندیهای الگوی فضایی را بیان میکنند) سادهتر در نظر گرفته شوند، اما از آنجایی که پایه و اساس همه محدودیتهای دیگر را تشکیل میدهند، اهمیت حیاتی دارند. محرک اصلی این محدودیت ها ناخوانا بودن اشیاء نقشه به دلیل کاهش مقیاس است، زمانی که به محدودیت های ادراک بصری انسان رسیده و چند ضلعی ها خیلی کوچک می شوند که قابل مشاهده نیستند، یا خیلی نزدیک هستند. باعث ادغام بصری می شود. بنابراین، دو محدودیت هسته محدودیتهای اندازه را تشکیل میدهند: «حداقل مساحت» (MA) و «جداسازی شی» (OS). بر اساس مطالعه ادبیات مربوط [8 ، 30 ، 31 ]، ما پنج محدودیت اندازه زیر را برای تعمیم نقشه های زمین شناسی شناسایی کردیم:
-
حداقل مساحت
-
جداسازی اشیا
-
فاصله بین مرزها
-
رئوس متوالی
-
دانه بندی طرح کلی
4.3. مدلسازی محدودیت
هنگامی که محدودیت ها شناسایی شدند، باید بیشتر تعریف شوند. با پیروی از رویکرد پیشنهادی در [ 8 ]، که از پارادایم مبتنی بر عامل پیروی می کند، یک تعریف کامل محدودیت شامل خود محدودیت، یک یا چند مقدار هدف (حداقل بعد قابل دستیابی در نقشه هدف)، یک یا چند معیار است که می تواند برآورده شدن محدودیت، طرح های ممکن (یعنی عملگرهای تعمیم در صورت نقض محدودیت) و اهمیت یا اولویت عملگرهای تعمیم را تعیین کنید.
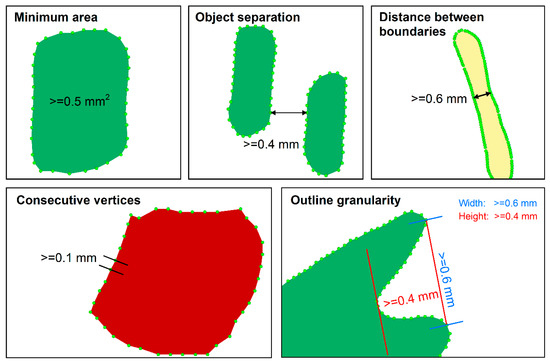
جدول 1 پنج محدودیت اندازه، علتی که ممکن است منجر به نقض آنها شود، مقادیر هدف، معیارها، عملگرهای احتمالی تعمیم و تأثیری که توسط تعمیم ایجاد خواهد شد، خلاصه می شود. شکل 3 محدودیت های اندازه را به صورت بصری نشان می دهد.
4.4. اجرای تعمیم
4.4.1. گردش کار تعمیم
محدودیت حداقل مساحت برای تعمیم نقشه های چند ضلعی اساسی است، زیرا هر نوع نقشه طبقه بندی به اندازه ویژگی های چند ضلعی مرتبط است. از این رو، به عنوان محرک اولیه و نقطه تصمیم گیری برای فرآیند تعمیم عمل می کند، که پس از یک فرآیند معمولی تعمیم نقشه در کارتوگرافی سنتی [ 32 ] مدل شده است. گردش کار در شکل 4در دو شاخه اصلی نمایش داده می شود، اما اساساً متوالی است. اول، شاخه سمت راست با چند ضلعی های بسیار کوچک سروکار دارد. اگر متعلق به یک واحد زمین شناسی ضروری نباشد، حذف می شوند. در غیر این صورت، آنها با استفاده از الگوریتم بزرگنمایی متفاوت بسته به شکل آنها بزرگ می شوند. پس از پرداختن به عملگرهای حذف و بزرگنمایی، گردش کار برمی گردد تا بررسی کند که آیا اکنون هر چند ضلعی به اندازه کافی بزرگ است یا خیر. اگر پاسخ مثبت است، شاخه سمت چپ فعال می شود که با چند ضلعی های بزرگتر از حد حداقل مساحت سروکار دارد. در اینجا، محدودیت اندازه بعدی آزمایش می شود. هنگامی که حداقل فاصله جداسازی اشیاء از همسایگانش برآورده نمی شود، اگر چند ضلعی های مربوطه از یک دسته باشند، جمع می شوند یا جابه جا می شوند تا محدودیت جداسازی شی را برآورده کنند. در غیر این صورت، چند ضلعی می تواند به نقشه یا پایگاه داده هدف خروجی شود. این کار نهایی همچنین شامل عملیات سادهسازی و هموارسازی خط بیشتر برای مراقبت از محدودیتهای “رئوس متوالی” و “گرانوله بودن طرح کلی” است.
در ادامه این بخش، عملگرها و الگوریتم های تعمیم مختلف را یک به یک معرفی می کنیم. توجه داشته باشید که ما فرض میکنیم که هرگونه عملیات طبقهبندی مجدد که زیرمجموعهها را در دستههای مافوق ادغام میکند، قبل از گردش کار ما انجام میشود.
4.4.2. حذف
عملگر حذف چند ضلعی های کوچک را در چند ضلعی های پس زمینه حل می کند. پس از اینکه یک چند ضلعی در دو تست شکست بخورد فعال می شود: محدودیت MA را برآورده نمی کند و به اندازه کافی مهم نیست که با این وجود حفظ شود. با این حال، این دو آزمون به صورت نامحدود روی چند ضلعی ها اعمال نمی شوند. با این حال، ابتدا یک مقدار هدف کلی تعیین میشود و تعداد چند ضلعیهایی که باید حذف شوند ( n elim ) از نقشه منبع (یا برعکس برای نقشه هدف انتخاب میشوند) مشخص میشود. سه روش انتخاب مختلف ابداع شدهاند، که همگی در محدودیت MA و اهمیت چندضلعیها با توجه به دسته آنها (یعنی واحد زمینشناسی در مورد ما) فاکتور میگیرند.
اولین روش انتخاب، “قانون رادیکال” [ 33 ]، به عنوان خط پایه استفاده می شود، زیرا اغلب به عنوان مرجع در تعمیم نقشه استفاده می شود. در نتیجه، تعداد چند ضلعی هایی که باید حذف شوند ( n elim ) با استفاده از قانون رادیکال تعیین می شود. مثال مفصلی از نحوه تعیین n elim در بخش 5.2 آورده شده است. Once n elimایجاد شده است، چند ضلعی هایی که باید حذف شوند باید شناسایی شوند. چند ضلعی هایی که زیر آستانه MA قرار می گیرند به ترتیب صعودی با توجه به مجموع مساحت نرمال شده آنها و مقدار اهمیت زمین شناسی نرمال شده آنها مرتب می شوند. اهمیت یک چند ضلعی تابعی از واحد زمین شناسی آن است که سن زمین شناسی را منعکس می کند. واحدهای قدیمی تر، مانند “آمفیبولیت” و “پگماتیت”، ذخایر معدنی بیشتری دارند و بنابراین ارزش اقتصادی بیشتری نسبت به سنگ های تازه تولید شده دارند [ 11 ]. بنابراین، انواع سنگهای جوانتر، مانند “کواترنری”، نسبت به لایههای باستانی “ژوراسیک” بحرانیتر در نظر گرفته میشوند. پس از اینکه ترتیب مرتب سازی ایجاد شد، n elim کوچکترین و کم اهمیت ترین چند ضلعی حذف می شوند.
در روش انتخاب دوم، که “انتخاب ناحیه از دست دادن-منفعت” نامیده می شود، چند ضلعی ها ابتدا بر اساس طبقه بندی به ترتیب صعودی مساحت خود مرتب می شوند و سپس حذف چند ضلعی بر اساس دسته (یعنی بر اساس واحد زمین شناسی) نیز انجام می شود. در هر دسته، به همان اندازه چند ضلعی کوچک حذف می شود که برای متعادل کردن افزایش مساحت چند ضلعی های کوچک هم کلاس باقیمانده توسط عملگر بزرگنمایی (بخش بعدی) مورد نیاز است. بنابراین، مساحت کل چند ضلعی های حذف شده در هر دسته همیشه با مساحت بدست آمده توسط عملگر بزرگنمایی متعادل می شود. برای این منظور، این عملگر انتخاب برای هر چند ضلعی، بهره مساحتی را که در صورت حفظ و بزرگ شدن چند ضلعی اضافه می شود، از قبل محاسبه می کند.
رویکرد سوم که “انتخاب بر حسب دسته” نامیده می شود، قانون رادیکال را به طور جداگانه برای هر دسته، همانطور که در نام آن مشخص است، اعمال می کند. به عنوان مثال، اگر نقشه ای دارای 5 دسته باشد و طبق قانون رادیکال 30 درصد چند ضلعی ها حذف شوند، در هر دسته 30 درصد از کوچکترین چند ضلعی ها حذف می شوند. توجه داشته باشید که این روش از دست دادن و افزایش مساحت چند ضلعی ها را در نظر نمی گیرد، با این حال بهتر از قانون رادیکال خالص، حذف چند ضلعی ها از هر دسته را متعادل می کند و دسته هایی که فقط از چند ضلعی های کوچک تشکیل شده اند را از ناپدید شدن محافظت می کند.
4.4.3. بزرگ شدن
پس از حذف چند ضلعیهای کوچک و بیاهمیت در مرحله حذف، چند ضلعیهایی باقی میمانند که کوچکتر از حد MA هستند، اما به دلیل اهمیت آنها برای حفظ پرچمگذاری شدهاند. بنابراین، گام بعدی بزرگنمایی آنها تا رسیدن به حد MA است و خوانایی کافی توسط چشم انسان تضمین میشود. دو الگوریتم برای انجام بزرگنمایی، بافر کردن و مقیاسبندی ابداع شدهاند. شکل 5 اثر این دو الگوریتم را نشان می دهد: بزرگ شدن با بافر کردن، اشکال چند ضلعی گرد ایجاد می کند در حالی که مقیاس گذاری، ناحیه چند ضلعی را بزرگ می کند و شکل چند ضلعی اولیه را حفظ می کند.
بافر چند ضلعی یک عملیات متداول در GIS است و انجام آن ساده است. با این حال، تمایل آن به ایجاد اشکال گرد ممکن است منجر به از بین رفتن شکل اصلی چند ضلعی شود، عمدتاً اگر چند ضلعی های بسیار کوچک درگیر باشند و/یا فاصله بافر قابل توجه باشد. از این رو، توصیه میکنیم از بزرگنمایی بافر زمانی استفاده کنید که فقط افزایش کوچکتری لازم است، و زمانی که چند ضلعیها شکل کشیدهتری دارند، جایی که اعوجاج شکل کمتر قابل توجه است.
الگوریتم مقیاسبندی میتواند چند ضلعیهای گرد را مدیریت کند و چندضلعیهای کوچک را بدون اعوجاج شکل گسترش دهد. این الگوریتم روی هر رأس حلقه می زند و فاصله آن را تا نقطه مرجع محاسبه می کند که به طور پیش فرض مرکز چند ضلعی است. سپس چند ضلعی مقیاس شده با گسترش یک خط از نقطه مرجع در سراسر هر رأس اولیه در طول مقیاس شده تولید می شود و نقطه پایانی به راس مقیاس شده تبدیل می شود. یکی از معایب الگوریتم مقیاس بندی پایه این است که وقتی از مرکز چند ضلعی به عنوان نقطه مرجع استفاده می شود، ممکن است خطاهای توپولوژیکی برای چند ضلعی های غیر محدب ایجاد شود ( شکل 5 ج)، که نیاز به جابجایی برای بازیابی توپولوژی دارد. چند ضلعی بزرگ شده در شکل 5c به دلیل فرآیند پوسته پوسته شدن از موقعیت اصلی خود به سمت راست و پایین منتقل می شود.
انتخاب بین دو الگوریتم بزرگنمایی برای هر چند ضلعی با تجزیه و تحلیل شکل آنها با استفاده از شاخص شکل «ضریب همسانسنجی» ( IPQ ) [ 34 ]، که بهعنوان معیار فشردگی در [ 35 ] استفاده میشود، هدایت میشود:
که در آن A مساحت و P محیط چند ضلعی را نشان می دهد. IPQ مقادیر را در بازه (0،1) می گیرد، جایی که مقادیر نزدیک به 0 شکل های کشیده را نشان می دهد، در حالی که مقدار 1 نشان دهنده یک دایره است. ما از آستانه 0.5 در آزمایشهای خود برای تمایز بین اشکال دراز (برای بافر کردن) و شکلهای گرد (برای پوستهگذاری) استفاده کردیم، زیرا این آستانه نقطه میانی بین دو حد را نشان میدهد.
پهنای بافر Kb که باید به چند ضلعی اضافه شود ، به عنوان تابعی از ناحیه هدف A’ محاسبه می شود که باید در مقیاس هدف (مثلاً 625 متر مربع در 1:50000)، منطقه فعلی A و جریان به دست آید. محیط P
عامل پوسته پوسته شدن کسکه به الگوریتم اجازه می دهد چند ضلعی را به ناحیه هدف A’ بزرگ کند (مثلاً 625 متر مربع در 1:50000) برابر است با جذر از ناحیه هدف A’ در ناحیه فعلی A.
4.4.4. تجمع
پس از اجرای عملگر بزرگنمایی، همه چند ضلعیهای باقیمانده باید به اندازه کافی برای مقیاس هدف بزرگ باشند و بنابراین به اندازه کافی قابل خواندن باشند. با این حال، بزرگکردن ممکن است منجر به تضاد دیگری شود: نقض محدودیت جداسازی شی، که به ترتیب با عملگر تجمع و جابجایی در این کار بررسی میشود. هر دو با نقض جداسازی اشیا ایجاد میشوند، اما تجمع این مشکل را با ادغام چند ضلعیهایی که خیلی نزدیک اما مشابه هستند حل میکند، در حالی که جابجایی چند ضلعیهای غیرمشابه را حرکت میدهد تا زمانی که حداقل فاصله تفکیک پذیری دوباره برآورده شود. تضاد بین ویژگی ها با محاسبه فاصله بین هر دو چند ضلعی، جایی که چند ضلعی ها به یکدیگر نزدیک هستند، شناسایی می شود.
شباهت چند ضلعی ها ممکن است با استفاده از چندین ویژگی، مانند شکل، اندازه، جهت و دسته چند ضلعی های درگیر تعیین شود [ 10 ]، اما در این مقاله، ما فقط از شباهت معنایی، یعنی همان دسته، برای نشان دادن دو استفاده می کنیم. چند ضلعی ها مشابه هستند. شباهت معنایی اهمیت فوقالعادهای دارد: تنها چند ضلعیهایی از دستههای یکسان (یا احتمالاً از زیرمجموعههای مشترک، در صورت وجود) منطقی است.
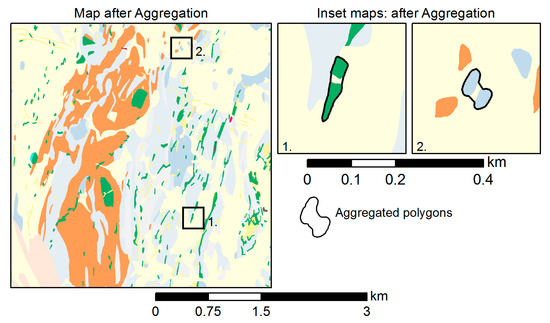
الگوریتمهای مختلفی برای تجمیع و نوعبندی ساختمانها پیشنهاد شدهاند [ 36 ، 37 ]، اما برای اهداف ما، بیشتر به الگوریتمی علاقهمند بودیم که فضاهای خالی بین چند ضلعیهایی را که بسیار نزدیک به نظر میرسند، شبیه به الگوریتم در پر کند. [ 25 ]. تجمع با ایجاد یک بدنه مقعر از رئوس طرح چندضلعی ها انجام می شود تا با استفاده از الگوریتم [ 38 ] تجمیع شوند.]. نقشه های داخلی شکل 12 نتایج نمونه این روش را برجسته می کند. الگوریتم با انتخاب اولین راس به عنوان راس با کوچکترین مقدار Y شروع می شود. در مرحله بعد، k نزدیکترین نقطه به راس فعلی به عنوان کاندیدای انتخاب راس بعدی برای چند ضلعی خروجی انتخاب می شوند. راس بعدی بر اساس بزرگترین چرخش سمت راست از محور افقی تعیین می شود. این دو مرحله تا زمانی که کاندیدای منتخب اولین راس باشد تکرار می شود. در نهایت، رئوس متوالی یافت شده توسط پاره های خط به هم متصل می شوند تا چندضلعی مقعر حاصل را تشکیل دهند. تنظیم پارامتر k امکان کنترل درجه تقعر چندضلعی انباشته شده را فراهم می کند.
4.4.5. جابه جایی
دو دلیل وجود دارد که چرا اپراتور جابجایی ممکن است فعال شود. اول، به عنوان یک پیامد مستقیم کاهش مقیاس، تمایز بصری بین اشیاء نقشه سختتر و در برخی مراحل غیرممکن میشود (اثری که اغلب ازدحام نامیده میشود؛ [ 18 ]). دوم، در نتیجه بزرگ شدن چند ضلعی، محدودیت جداسازی شی ممکن است نقض شود، زیرا چند ضلعی های بزرگ شده به فضای بیشتری نیاز دارند و ممکن است شروع به ادغام یا حتی همپوشانی کنند. در هر دو مورد، اشیاء نقشه باید یا جمع شوند یا به حداقل محدوده تفکیک پذیری جابجا شوند. در مواردی که چند ضلعیها بهطور متراکم خوشهبندی میشوند، ممکن است عملگرهای جایگزین مانند typification (که ترکیبی از حذف، تجمع و جابجایی است) ترجیح داده شوند.
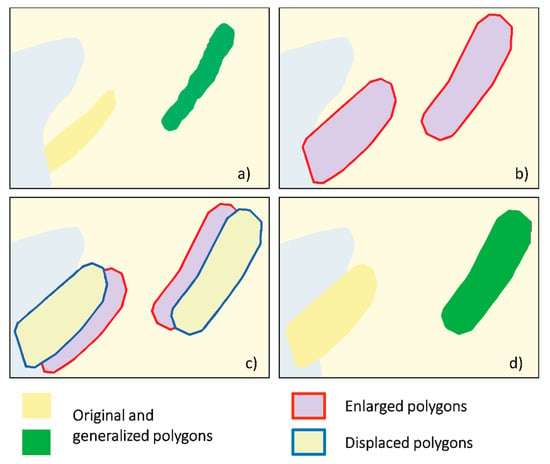
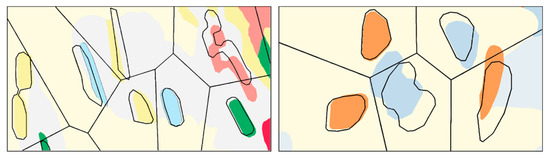
شکل 6 اثر عملگر جابجایی را نشان میدهد که توسط نقض محدودیت جداسازی جسم به دنبال بزرگ شدن چند ضلعی ایجاد میشود. پس از شناسایی تخلف، چند ضلعی ها به حداقل فاصله قابل تفکیک از یکدیگر منتقل می شوند.
ما دو الگوریتم برای پیادهسازی عملگر جابجایی ابداع کردیم: یک الگوریتم جابجایی زوجی ساده که زمانی که فقط دو چند ضلعی در تضاد هستند استفاده میشود و یک الگوریتم مبتنی بر Voronoi برای مواردی که چند ضلعیها را شامل میشود. با این حال، توجه داشته باشید که در صورت تمایل میتوان آنها را با الگوریتمهای پیچیدهتر دیگری جایگزین کرد که ویژگیهای جابجایی متفاوتی دارند [ 39 ، 40 ].
الگوریتم جابجایی زوجی از [ 41 ] الهام گرفته شده است و یک جفت چند ضلعی را در نظر می گیرد که خیلی نزدیک به هم هستند و قابل تشخیص نیستند و بنابراین باید به فاصله جداسازی شیء عقب رانده شوند. الگوریتم نزدیکترین نقاط بین دو چند ضلعی را پیدا می کند، بردارهای حرکت را برای هر چند ضلعی محاسبه می کند و چند ضلعی ها را از یکدیگر جابه جا می کند ( شکل 7 ). اندازه چند ضلعی ها درجه جابجایی هر چند ضلعی را کنترل می کند: هر چه چند ضلعی ها کوچکتر باشند، بیشتر حرکت می کنند، در حالی که چند ضلعی های بزرگتر حرکت کمتری دارند. در مثال شکل 7 ، چند ضلعی با مساحت 8666 متر مربع تنها 5 متر حرکت می کند، در حالی که چند ضلعی با مساحت 2471 متر مربع18 متر از موقعیت اولیه خود جابجا شده است.
اگر چند ضلعی در تضاد باشند، الگوریتم جابجایی زوجی نمی تواند تضمین کند که حداقل محدودیت تفکیک پذیری در همه جا برآورده شده است، زیرا نمی تواند در برابر اثرات ضربه ای احتمالی محافظت کند، به عنوان مثال، یک چند ضلعی به چند ضلعی دیگر و همسایه دیگر فشار داده می شود. نیز باید جابجا شوند. بنابراین، مناطق تضاد شامل سه یا چند چند ضلعی با رویکرد جابجایی مبتنی بر Voronoi با الهام از الگوریتمهایی که از سلولهای Voronoi یا Voronoi مانند برای کنترل جابجایی استفاده میکنند، به دست میآیند [ 42 ، 43 ].
روش مبتنی بر Voronoi به سه مرحله تقسیم می شود. ابتدا، چند ضلعی هایی شناسایی می شوند که محدودیت تفکیک شی را نقض می کنند ( شکل 8 a). در مرحله دوم، چند ضلعی ها به نقاط مرکز خود جمع می شوند که به عنوان نقاط اولیه برای نمودار ورونوی عمل می کنند ( شکل 8 ب). از نیمسازهای عمود بر چند ضلعی های ورونوی (یعنی لبه های مثلث دلونی)، بردارهای جابجایی برای هر جفت چند ضلعی مشخص می شوند. در نهایت، چند ضلعی ها به حداقل فاصله جدایی رانده می شوند در حالی که چند ضلعی ها مجبور می شوند در چند ضلعی Voronoi خود باقی بمانند ( شکل 8 ج).
شکل 9 دو نمونه از کاربرد الگوریتم جابجایی مبتنی بر Voronoi را با هر دو موقعیت چندضلعی اصلی و جابجا شده نشان میدهد.
تکمیل عملگر جابجایی همچنین پایان فرآیند ارائه شده در شکل 4 را نشان می دهد. این فرآیند در ابتدا توسط محدودیت حداقل منطقه آغاز شد و در نهایت اطمینان حاصل شد که این محدودیت و همچنین محدودیت جداسازی شیء برآورده شده است. تنها چیزی که اکنون باقی مانده است، کارهای نهایی با ساده سازی و هموارسازی خطوط چند ضلعی است تا اطمینان حاصل شود که محدودیت های “راس های متوالی” و “گرانوله بودن طرح کلی” نیز برآورده شده اند (مرحله “چند ضلعی های خروجی” در شکل 4 ). با این حال، این مرحله از الگوریتم های استاندارد با تنظیمات پارامتر محافظه کارانه استفاده می کند و بنابراین نیازی به توضیح جزئیات در اینجا نیست.
4.5. پیاده سازی
گردش کار پیشنهادی از GeoPandas 0.6.0 استفاده می کند، یک پروژه منبع باز که داده های مکانی را در زبان برنامه نویسی پایتون مدیریت می کند. روشهای ژئوپانداس مانند حل کردن، بافر کردن، شناسایی مرکز، بدنه محدب، چرخش، مقیاسبندی و ترجمه برای حذف، بزرگنمایی، جمعآوری و جابجایی چند ضلعیها استفاده میشوند. علاوه بر این، بسته ArcPy از Esri، Inc، برای پیاده سازی قابلیت های جعبه ابزار ArcGIS مانند محاسبه مساحت یا یافتن اشیاء نزدیک و نزدیک استفاده می شود. تجسم نقشه با استفاده از Esri ArcGIS 10.6 و Matplotlib، یک کتابخانه رسم برای زبان برنامه نویسی پایتون انجام می شود.
5. آزمایش ها و نتایج
5.1. داده ها
دادههای مورد استفاده برای آزمایشهای ما از «بلوک Euriowie (شامل بخشی از نهر کمپلز)» گرفته شده است. نقشه زمینشناسی در مقیاس 1:25000 منتشر شده در سال 2000 توسط سازمان زمینشناسی نیو ساوت ولز (NSW)، دپارتمان منابع معدنی، استرالیا. ( https://www.resourcesandgeoscience.nsw.gov.au ). بخشی از این نقشه در شکل 10 ، سمت چپ نشان داده شده است. “بلوک Euriowie” بخشی از بلوک زمین شناسی بزرگتر به نام “Broken Hill Block” است که در نزدیکی شهر معدنی Broken Hill، NSW قرار دارد. این شامل منابع معدنی قابل توجهی، به ویژه ذخایر فراوان و غنی سرب-نقره-روی (Pb-Ag-Zn) است. زمین شناسی بلوک تپه شکسته بسیار پیچیده است و از نظر تاریخی همیشه فعالیت های اکتشافی گسترده ای در این منطقه وجود داشته است [ 44 ,45 ]، که زمینه را برای انتخاب این نقشه خاص به ما داد. علاوه بر این، نقشه به طور آشکار برای اهداف عمومی و تحقیقاتی در دسترس است و بنابراین تکرارپذیری نتایج را ارتقا میدهد.
هدف این نقشه ارائه توزیع گسترده ای از انواع سنگ ها، به ویژه سنگ هایی با اهمیت کانی سازی یا چینه شناسی است. داده ها دارای کیفیت متوسط تا بالا، قابلیت اطمینان و سازگاری داخلی هستند. دقتی دارد که برای نقشه ای در مقیاس 1:25000 مناسب است.
نقشه زمین شناسی شامل 215 زیرمجموعه انواع یا واحدهای سنگی است که به نوبه خود بخشی از 24 دسته بالاتر هستند. کانی های کوچک مانند گروه های “هورنبلند” و “فلدسپات” تقریباً 60 درصد وزن سنگ های زمینی را تشکیل می دهند. این گروه های معدنی بیشتر مربوط به سنگ های آذرین توده ای (که به آنها نفوذی نیز می گویند) مانند پگماتیت ها (به رنگ زرد در شکل 10 نشان داده شده است )، که در اعماق سطح زمین تشکیل می شوند و از انجماد ماگما ایجاد می شوند [ 46 ]. آنها همچنین در بسیاری از انواع سنگ های دگرگونی مانند آمفیبولیت (در شکل 10 به رنگ سبز نشان داده شده است) وجود دارند.). به دنبال فرسایش، آنها در سطح زمین قرار می گیرند، اغلب به صورت تکه های کوچک، که به صورت چندضلعی های کوچک در نقشه های زمین شناسی نشان داده می شوند. از آنجایی که واحدهای آمفیبولیت و پگماتیت دارای ذخایر معدنی بیشتری هستند و در نتیجه ارزش اقتصادی بالاتری دارند، در فرآیند کاهش مقیاس مدت بیشتری حفظ خواهند شد. از آنجایی که آنها اغلب چند ضلعی های کوچک را تشکیل می دهند، این انواع سنگ کاندیدهای خوبی برای مقابله با محدودیت های حداقل اندازه هستند، که تمرکز این مقاله است.
5.2. حذف
در دنباله آزمایشهای گزارششده در بخش 5.2 ، بخش 5.3 ، بخش 5.4 و بخش 5.5 ، از مقادیر هدف برای محدودیت MA 0.5×0.5 میلیمتر و برای محدودیت جداسازی شی از مقدار 0.4 میلیمتر ارائهشده در [ 30 ] استفاده میکنیم. کل پایگاه داده نقشه Euriowie از n s = 1877 چند ضلعی در مقیاس منبع 1:25000 تشکیل شده است. با مقیاس هدف 1:50000، تعداد چند ضلعی n MA که زیر حد MA قرار می گیرند 1135 است، با توجه به حداقل مساحت 0.5 × 0.5 میلی متر بر روی نقشه یا 625 متر مربع در زمین. ( جدول 1). این بدان معنی است که تقریباً 60٪ از همه چند ضلعی ها کوچکتر از آنچه ممکن است به عنوان حد خوانایی تعریف شود، هستند. با استفاده از استراتژی “انتخاب قانون رادیکال” برای عملگر حذف ( بخش 4.4.2 )، تعداد چند ضلعی هایی که باید حفظ شوند، n t را می توان به صورت زیر محاسبه کرد (که در آن N s مخرج مقیاس منبع و N t است. مخرج مقیاس هدف):
یعنی طبق قانون رادیکال [ 33 ]، n t = 1327 چند ضلعی باید حفظ شود، یا برعکس، n elim = n s – n t = 550 چند ضلعی باید حذف شود. در نهایت، تعداد چند ضلعیهایی که زیر محدودیت MA قرار میگیرند که باید نگه داشته شوند، n keep میتوان به صورت n keep = n MA – n elim = 585 به دست آورد.
بنابراین، با استراتژی انتخاب Radical Law، n elim = 550 چند ضلعی با مساحت زیر آستانه MA باید از نقشه حذف شوند، در حالی که n keep = 585 چند ضلعی نیز کوچکتر از آستانه MA هستند، اما به اندازه کافی مهم تلقی می شوند که ثابت باشند. روی نقشه نگهداری می شود و بنابراین به عملگرهای تعمیم بعدی مانند بزرگنمایی ارسال می شود.
برای تعیین اینکه کدام چند ضلعی ها حذف می شوند، ارزش اهمیت آنها بر اساس مساحت آنها و همچنین موقعیت آنها در “سلسله مراتب زمین شناسی” تعیین می شود ( جدول 2 ). مقادیر مساحتی که در بین n چند ضلعی MA کوچکتر از حد MA رخ می دهد از 7 متر مربع تا 625 متر مربع است . سلسله مراتب زمین شناسی از ترتیب واحدهای زمین شناسی با توجه به سن آنها پیروی می کند: هر چه سنگ ها قدیمی تر باشند، اهمیت بیشتری دارند، زیرا احتمالاً محتوای معدنی بیشتری دارند. به طور کلی، در بلوک Euriowie، 15 واحد زمینشناسی را میتوان یافت که به ترتیب برای قدیمیترین واحد و 1 برای جوانترین واحد، مقدار 15 تخصیص داده میشود ( جدول 2).). برای هر چند ضلعی، مساحت آن و مقدار اهمیت آن، به ترتیب، نرمال شده و جمع می شوند تا مقدار اهمیت یکپارچه برای هر چند ضلعی به دست آید. پس از مرتبسازی به ترتیب صعودی، n elim (550) کماهمیتترین چند ضلعیها با استفاده از الگوریتم geopandas.dissolve() GeoPandas 0.6.1 حذف میشوند، که چند ضلعیهای انتخابشده را در چند ضلعیهای همسایه، که با آنها بزرگترین مرز مشترک دارند، حل میکند.
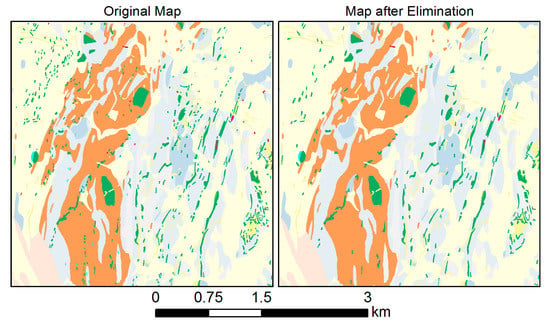
شکل 10 ، سمت راست، گزیده ای از نقشه Euriowie را پس از عملیات حذف با استفاده از رویکرد انتخاب قانون رادیکال در مقایسه با نقشه اصلی، در سمت چپ نشان می دهد. نمونه هایی با استفاده از دو استراتژی انتخاب دیگر عملگر حذف در بخش 5.6.1 ارائه خواهد شد .
5.3. بزرگ شدن
آن دسته از چند ضلعی هایی که کوچکتر از آستانه MA هستند اما به اندازه کافی مهم هستند تا در نقشه هدف نگهداری شوند ( n keep = 585) باید بزرگ شوند تا زمانی که به حداقل منطقه برسند ( بخش 4.4.3 ). بسته به شاخص شکل IPQ چند ضلعی ها، از دو الگوریتم جداگانه بافر و مقیاس بندی برای بزرگنمایی استفاده می شود.
به طور کلی، 234 چند ضلعی (تقریباً 40٪) از 585 چند ضلعی دارای مقادیر IPQ کمتر از 0.5 بودند که نشان دهنده اشکال نسبتاً کشیده بودند و بنابراین با بافر بزرگ شدند. بر این اساس، 351 چند ضلعی (حدود 60٪) دارای مقادیر IPQ بالاتر از 0.5 بودند که نشان دهنده اشکال نسبتاً گرد بود و بنابراین با مقیاس بندی بزرگ شدند. نتیجه مرحله بزرگ شدن در شکل 11 نشان داده شده است .
5.4. تجمع
به عنوان عملیات بعدی، تجمع چند ضلعی های یک دسته (یعنی واحد زمین شناسی یکسان) را که در فاصله جداسازی جسم (OS) قرار می گیرند با اعمال الگوریتم بدنه مقعر ترکیب می کند ( بخش 4.4.4 ). ما از OS = 0.4 میلیمتر ( جدول 1 ) مربوط به 20 متر روی زمین در مقیاس 1:50000 و k = 3 در الگوریتم بدنه مقعر برای تولید نتیجه نشان داده شده در شکل 12 استفاده کردیم . به طور کلی، از n نگه داشتن = 585 چند ضلعی، 78 چند ضلعی جمع شدند و 507 مورد باقی ماند.
5.5. جابه جایی
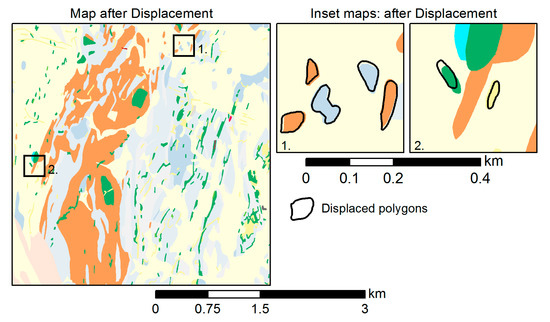
به عنوان آخرین مرحله، عملگر جابجایی برای جابجایی چند ضلعی هایی که خیلی نزدیک به هم هستند (یعنی محدودیت سیستم عامل را برآورده نمی کنند) از موقعیت اصلی خود به حداقل فاصله قابل تفکیک اجرا می کند. گزیده ای از نتیجه این عملیات و در نتیجه حاصلضرب تعمیم نهایی، در شکل 13 در مقایسه با نقشه منبع نشان داده شده است. به طور کلی، 35 چند ضلعی جابجا شدند، 24 با استفاده از الگوریتم جابجایی زوجی و 11 با استفاده از رویکرد مبتنی بر Voronoi.
5.6. حساسیت به تنظیمات پارامتر
عملگرها و الگوریتمهای متدولوژی پیشنهادی توسط پارامترهای مختلفی کنترل میشوند که همگی بسته به هدف و دامنه کاربرد نقشه مورد نظر میتوانند مقادیر متفاوتی داشته باشند. حتی برای محدودیتهای اندازه مختلف، اگرچه مقادیر هدف را در جدول 1 تعریف کردیم ، هیچ مقدار متعارف یا “درست” وجود ندارد. از این رو، در سه مورد آزمایشی، ما حساسیت نتایج تعمیم را در تغییرات پارامترهای کنترل نشان میدهیم. توجه داشته باشید که در تمام موارد آزمایشی، هیچ گونه ساده سازی و هموارسازی اعمال نشده است. این عملگرها معمولاً با استفاده از تنظیمات پارامتر محافظه کارانه اعمال می شوند و بنابراین تأثیر کمی بر نتیجه نهایی دارند ( بخش 4.4.1 ).
5.6.1. مورد آزمایشی 1
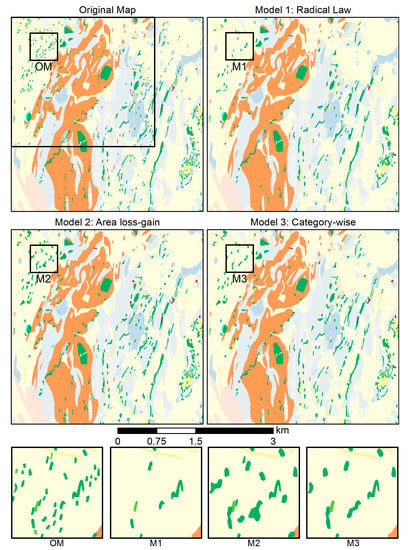
در اولین مورد آزمایشی، تأثیر استفاده از سه روش مختلف انتخاب برای عملگر حذف بر روی 1877 چند ضلعی موجود در نقشه منبع در مقیاس 1:25000 همانطور که در شکل 14 نشان داده شده است ، در انتقال به مقیاس هدف 1 آزمایش شد: 50000. این آزمایش از همان مقادیر هدف برای محدودیت MA و OS مانند بخش 5.2 ، بخش 5.3 ، بخش 5.4 و بخش 5.5 استفاده کرد. در “انتخاب قانون رادیکال”، 29.29٪ یا 563 از چند ضلعی های منبع حذف شدند ( جدول 3 ). در “انتخاب زیان – سود منطقه”، تنها 139 حذف شدند. در نهایت، “انتخاب بر حسب دسته” منجر به حذف 417 چند ضلعی شد. شکل 14امکان مقایسه بصری روش های انتخاب با یکدیگر و نقشه اصلی را فراهم می کند. این شکل همچنین شامل چهار نقشه داخلی برای مقایسه نزدیک نتایج است.
5.6.2. مورد آزمایشی 2
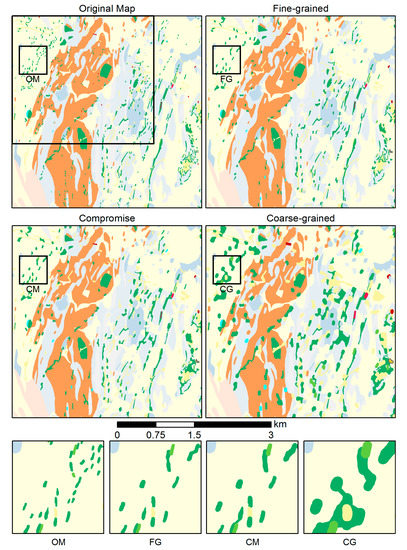
در آزمون دوم، ما سه مجموعه متفاوت از آستانهها را برای محدودیتهای اندازه، به نامهای «ریز دانه» (FG)، «سازش» (CM)، و «درشت دانه» (CG) مقایسه کردیم ( جدول 4 ). اولین مجموعه آستانه از [ 30 ] الهام گرفته شد. در حالی که مقادیر هدف ریز دانه آنها برای چند ضلعی های منظم در نقشه های توپوگرافی تعریف شده بود، نویسندگان خاطرنشان کردند که مقادیر بزرگتر باید برای چند ضلعی های رنگی و نامنظم، مانند موارد معمول نقشه های طبقه بندی شده، استفاده شود. مجموعه محدودیت دانه درشت در انتهای دیگر مقیاس دانه بندی قرار گرفت و از [ 31 ] به دست آمد، منبعی که به نمادسازی نقشه های زمین شناسی اختصاص داده شده است و حداقل اندازه چند ضلعی های رنگی را حدود 2 میلی متر مربع تعریف می کند .. مجموعه محدودیت Compromise سعی میکند بین مجموعههای دانهریز و درشتدانه تعادل برقرار کند. مقایسه بصری نتایج تعمیم تولید شده با استفاده از سه مجموعه محدودیت در شکل 15 آورده شده است. شکل همچنین مقایسه ای نزدیک از سه رویکرد و نقشه اصلی را ارائه می دهد.
5.6.3. مورد آزمایشی 3
به عنوان آزمایش نهایی، ما از مجموعه مقادیر هدف سازش و روش انتخاب بر حسب دسته، که هر دو بهترین عملکرد را در آزمونهای فوق نشان دادند، برای تولید یک سری نقشه در مقیاسهای 1:50000، 1:100000 استفاده کردیم. و 1:200000، تعمیم یافته از نقشه اصلی 1:25000. علاقه این آزمون در کاوش در محدوده مقیاسی بود که روش پیشنهادی می تواند به طور مفیدی اعمال شود. مقایسه بصری سری تعمیم حاصل با نقشه اصلی در شکل 16 ارائه شده است . جدول 5 تکامل تعداد چند ضلعی ها و مساحت ترکیبی آنها را از چهار واحد زمین شناسی منتخب موجود در شکل 16 نشان می دهد.: آمفیبولیت، پگماتیت، پروتروزوییک پسین و واحد خاک – ماسه – شن – رسی. آمفیبولیت (چند ضلعی های سبز) و پگماتیت (چند ضلعی های زرد) انتخاب شدند زیرا آنها دو دسته را نشان می دهند که هر دو عمدتاً به صورت چند ضلعی های کوچک و مکرر رخ می دهند و به دلیل سن آنها از اهمیت بالایی برخوردار هستند. از طرف دیگر، واحدهای پروتروزوییک پسین (نارنجی-قهوه ای) و خاک-شن-شن-شن-رس (زرد روشن) به ترتیب جوان و در جوان ترین سن هستند و منطقه مورد مطالعه را به تعداد چندضلعی های کم اما بزرگ پر می کنند.
5.6.4. مقایسه با رویکرد اتوماتای سلولی
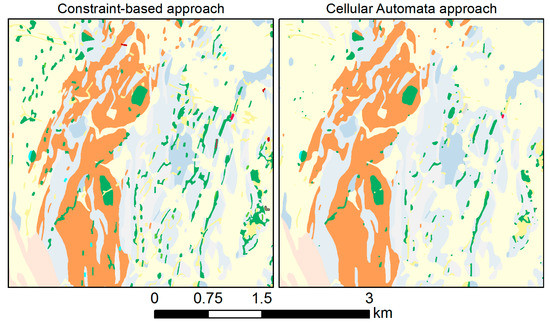
در این بخش، نتایجی را که میتوان با روش پیشنهادی به دست آورد، با نتایج یک رویکرد مبتنی بر اتوماتای سلولی (CA) [ 23 ، 24 ]، همانطور که در جعبه ابزار GeoScaler [ 47 ] پیادهسازی شد، مقایسه میکنیم. همانطور که در بخش 2 ذکر شد ، این رویکرد احتمالاً می تواند به عنوان وضعیت هنر تعمیم نقشه های زمین شناسی موجود در عمل در نظر گرفته شود، به همین دلیل است که ما از آن به عنوان یک معیار برای مقایسه استفاده کردیم. نتیجه رویکرد مبتنی بر محدودیت ما با استفاده از مقادیر هدف CM و روش انتخاب بر حسب دسته ایجاد شد ( شکل 17 ، سمت چپ). این نتیجه معادل نقشه نشان داده شده در شکل 15 است(پایین سمت چپ). از آنجایی که GeoScaler در مقایسه با متدولوژی ما (که روی چند ضلعیهای مجزا کار میکند) مبتنی بر رویکردی کاملاً متفاوت (بر اساس شطرنجی، با استفاده از CA) است، تطبیق دقیق تنظیمات پارامتر برای این دو روش دشوار است. GeoScaler همچنین انواع مختلفی از ابزارهای پس پردازش را برای بهبود بیشتر نتیجه اولیه الگوریتم CA ارائه می دهد. برای اینکه بتوانیم نتایج دو روش را در یک زمین بازی برابر مقایسه کنیم، تصمیم گرفتیم از گزینه های پس پردازش GeoScaler استفاده نکنیم و تنظیمات پارامتر را به مواردی محدود کنیم که مطابقت بین دو روش را پیدا می کنند (یعنی پارامترهایی که مربوط به محدودیت های اندازه). GeoScaler [ 47] ابتدا از کاربر مقیاس منبع و هدف (در این مورد 1:25000 و 1:50000) را می خواهد که سپس به طور خودکار ضریب کاهش مقیاس و پارامترهای مربوط به اندازه را تنظیم می کند. علاوه بر این، ما نقشه چند ضلعی را با استفاده از اندازه سلول 1 متر، بالاترین حد ممکن، شطرنجی کردیم تا کیفیت نقشه را تا حد امکان بالا نگه داریم. سپس CA بر روی نقشه شطرنجی شده با همسایگی مور با شعاع 3 و 2 تکرار نسل نهایی CA اجرا شد. پس از پردازش CA، نقشه شطرنجی دوباره به یک نقشه برداری تبدیل شد و نتیجه نشان داده شده در شکل 17 (راست) را به دست آورد.
6. بحث
این مقاله یک روش برای تعمیم نقشه های زمین شناسی با استفاده از یک رویکرد مبتنی بر محدودیت ارائه می کند. هدف اصلی این مقاله نشان دادن سودمندی رویکرد مبتنی بر محدودیت در تعمیم نقشه در زمانی که برای نقشههای زمینشناسی اعمال میشود، نه حل تعمیم نقشههای زمینشناسی به طور جامع بود (کلاسهای ویژگی بیشتر در [ 23 ، 24 ] مورد بررسی قرار گرفتهاند.]). این در شرایطی انجام شد که رویکرد مبتنی بر محدودیت تاکنون به طور صریح برای تعمیم خودکار نقشههای زمینشناسی اعمال نشده است. از این رو، روش پیشنهادی بر روی یک مسئله فرعی از تعمیم نقشه های زمین شناسی، هر چند با این وجود، یک مسئله مهم متمرکز شد. به طور خاص، بر روی محدودیتهای اندازه به عنوان نیروی محرکه اصلی حفظ خوانایی نقشه از طریق تعمیم نقشه تمرکز کرد. علاوه بر این، ما بر روی مورد چند ضلعی های کوچک و آزاد (یا تکه های منطقه؛ [ 28 ]) تمرکز کردیم، زیرا آنها یک مورد مکرر را نه تنها در نقشه های زمین شناسی، بلکه انواع دیگر نقشه های طبقه بندی مانند نقشه های خاک یا نقشه های پوشش زمین را نشان می دهند. .
بر اساس آزمایشهای گزارششده در بخش 5 ، میتوانیم چندین مشاهدات کلی انجام دهیم:
-
روش پیشنهادی مشکلات اصلی خوانایی مرتبط با چند ضلعی های کوچک را به صورت گام به گام حل می کند. نقشه به دست آمده قابل خواندن تر است و ویژگی های نقشه پس از تعمیم قابل تشخیص باقی می مانند ( شکل 13 ).
-
اگرچه مقادیر هدف محدودیتهای اندازه به طور کلی تعریف میشوند، هر چند ضلعی بهجای یک فرآیند جهانی مانند اتوماتای سلولی، بهطور جداگانه با ویژگیهای خاص خود در نظر گرفته میشود. از این رو، با در نظر گرفتن معنایی چند ضلعی های منفرد، چند ضلعی های مهم را می توان با بزرگنمایی محافظت کرد. با در نظر گرفتن ویژگی های شکل، ویژگی های شکل چند ضلعی های جداگانه تا حد زیادی حفظ می شود.
-
این رویکرد، با استناد به آزمایش اینکه آیا مقادیر هدف محدودیتها برآورده شدهاند، امکان ارزیابی خود را فراهم میکند و میتواند تضمین کند که محدودیتهای خوانایی رعایت شدهاند – اما نه بیشتر از آن. باز هم، این با رویکردهای جهانی مانند اتوماتای سلولی [ 23 ، 24 ] متفاوت است.
-
پارامترهای کمی برای کنترل روش تعمیم مورد نیاز است. این فرآیند در ابتدا توسط محدودیت MA آغاز می شود و بیشتر توسط محدودیت های اندازه اضافی (مهمتر از همه، محدودیت سیستم عامل) کمک می کند. هنگامی که مقادیر هدف محدودیتهای اندازه و پارامترهای اضافی خاص الگوریتم تنظیم شد، روش به طور خودکار و بدون دخالت بیشتر انسان عمل میکند.
-
مقادیر هدف محدودیت ها، اول از همه، تابعی از خوانایی نقشه در مقیاس هدف هستند، و از این رو اجازه می دهند تا با انتقال مقیاس مورد نظر سازگار شوند. علاوه بر این، مقادیر هدف همچنین امکان کنترل دانه بندی کلی نقشه خروجی را فراهم می کند ( جدول 4 و شکل 15 )، بسته به هدف نقشه.
-
علیرغم تعداد نسبتاً کم محدودیتها و پارامترهای کنترلی، این روش مدولار است و چندین عملگر تعمیم دارد، بنابراین به انعطافپذیری قابلتوجهی دست مییابد.
از آنجایی که روش پیشنهادی مبتنی بر مفهوم معتبر جهانی محدودیتهای مربوط به خوانایی نقشه است، این پتانسیل وجود دارد که همین رویکرد را برای تعمیم سایر نقشههای طبقهبندی، مانند نقشههای پوشش گیاهی یا خاک، اعمال کند. علاوه بر این، از آنجایی که گردش کار ماژولار است، هر یک از الگوریتم های مورد استفاده در روش شناسی ما می تواند با الگوریتم دیگری جایگزین شود که شاید برای ویژگی های مسئله تعمیم داده شده مناسب تر باشد. بنابراین، برای مثال، الگوریتمهای تجمع یا جابجایی مورد استفاده در این مقاله میتوانند در صورت تمایل با الگوریتمهای پیچیدهتر جایگزین شوند.
با استفاده از یک رویکرد گردش کار، ما نشان دادیم که چگونه روش پیشنهادی میتواند با استفاده از کتابخانههای یک GIS همه منظوره، با دستیابی به رفتاری مشابه با یک سیستم مبتنی بر عامل، اما با تلاش پیادهسازی کمتر و تلاش کمتر برای تنظیم پارامتر، پیادهسازی شود.
با مقایسه شکل 10 ، شکل 11 ، شکل 12 و شکل 13 ، که نتایج عملگرهای تعمیم فردی را ارائه می دهند، آشکار می شود که حذف و تجمیع گسترده ترین اثرات را دارند. حذف ممکن است هر دو الگوی آرایش فضایی چند ضلعی ها و همچنین توازن نسبت های مساحت دسته های مختلف ظاهر شده بر روی نقشه را حفظ کند یا از بین ببرد. در زیر، الگوریتمهای حذف موجود را به طور جداگانه از طریق تست مورد 1 مورد بحث قرار میدهیم. تجمیع عملگر دیگری است که میتواند منجر به تغییر قابلتوجه در تصویر نقشه شود، اما در این مورد با افزایش ناحیه و تغییر شکل چندضلعیهای مربوطه. همانطور که در شکل 12نشان میدهد، الگوریتم تجمیع که در گردش کار ما پیادهسازی شده است، گاهی اوقات میتواند منجر به تغییرات نامطلوب در شکل و ناحیه شود، و بهتر است با یک الگوریتم نوعبندی [ 36 ، 37 ] جایگزین شود، که با این حال نیازمند تشخیص قبلی الگوهای گروهی است که قابل تایپسازی هستند [ 10 ]. ].
حذف اولین و همچنین ریشه ای ترین مرحله روش است، زیرا برخی از چند ضلعی ها به طور دائم از نقشه هدف حذف می شوند. حذف انتخابی چند ضلعیهای جزیرهای کوچک که توسط مقادیر اهمیت پشتیبانی میشوند، جای خود را به حفظ چند ضلعیهایی میدهد که نسبت به سایرین مهم هستند، بنابراین اهمیت زمینشناسی یا ارزش اقتصادی را منعکس میکند. با این حال، در فرآیند حذف، اتصال بین چند ضلعی های همسایه در نظر گرفته نمی شود، که ممکن است منجر به حذف یا انحلال کنترل نشده الگوهای گروه خاصی (به عنوان مثال، خوشه ها، ترازها) چند ضلعی ها شود. نمونه هایی از این اثر را می توان با مقایسه شکل 10 ، سمت چپ (نقشه اصلی)، و شکل 10 ، سمت راست (نقشه پس از حذف) مشاهده کرد.
برای پرداختن به این موضوع، ما آزمون موردی 1 را بر روی سه روش انتخاب اجرا کردیم ( بخش 5.6.1 ): انتخاب قانون رادیکال، انتخاب منطقه از دست دادن-بهره، و انتخاب بر حسب دسته. مطابق شکل 14 و جدول 3برای انتقال مقیاس به 1:50000 نشان میدهد، انتخاب از دست دادن-افزایش مساحت تعداد و ساختار چندضلعیها را به بهترین نحو حفظ میکند. در مقابل، انتخاب قانون رادیکال بیشترین تأثیر مخرب را بر روی گروه های چند ضلعی داشت. با این حال، هنگامی که انتقال مقیاس بزرگتر است، به عنوان مثال، با مقیاس هدف 1:100000 یا 200000، چند ضلعی های بیشتری باید حذف شوند تا افزایش مساحت ناشی از بزرگ شدن متعادل شود. بنابراین، به نظر می رسد انتخاب بر حسب دسته، رویکرد بهتری برای عملیات حذف در کاهش مقیاس بزرگتر باشد، زیرا حذف چند ضلعی ها را به طور مساوی در هر دسته توزیع می کند. به طور کلی، انتخاب قانون رادیکال برای استفاده در تعمیم نقشه طبقهای توصیه نمیشود مگر اینکه نقشههای تعمیمیافتهتر (“بیش از حد تعمیم”) مورد نظر باشد. یکی از الزامات اساسی تعمیم نقشه طبقهای، حفظ مناطق تا حد امکان در بین محدودههای مقیاس است که میتوان با استفاده از روش انتخاب تعادل منطقه از دست دادن-به دست آورد. با این حال، بر اساس آزمون مورد 1، روش انتخاب بر حسب دسته در نهایت مناسبتر به نظر میرسد زیرا حذف چند ضلعیها را در بین دستهها یکسان میکند و همچنین سازش خوبی را نشان میدهد. با این وجود، صرف نظر از اینکه کدام یک از سه روش انتخاب مورد استفاده قرار می گیرد، هیچ کدام نمی تواند در برابر تخریب ناخواسته الگوهای گروهی، به ویژه نه در کاهش مقیاس بزرگ، محافظت کند. بنابراین، مرحله تعمیم واقعی باید با مرحله ای اختصاص داده شود که به شناخت الگوهای جمعی اساسی موجود در نقشه منبع اختصاص دارد. با این حال، بر اساس آزمون مورد 1، روش انتخاب بر حسب دسته در نهایت مناسبتر به نظر میرسد زیرا حذف چند ضلعیها را در بین دستهها یکسان میکند و همچنین سازش خوبی را نشان میدهد. با این وجود، صرف نظر از اینکه کدام یک از سه روش انتخاب مورد استفاده قرار می گیرد، هیچ کدام نمی تواند در برابر تخریب ناخواسته الگوهای گروهی، به ویژه نه در کاهش مقیاس بزرگ، محافظت کند. بنابراین، مرحله تعمیم واقعی باید با مرحله ای اختصاص داده شود که به شناخت الگوهای جمعی اساسی موجود در نقشه منبع اختصاص دارد. با این حال، بر اساس آزمون مورد 1، روش انتخاب بر حسب دسته در نهایت مناسبتر به نظر میرسد زیرا حذف چند ضلعیها را در بین دستهها یکسان میکند و همچنین سازش خوبی را نشان میدهد. با این وجود، صرف نظر از اینکه کدام یک از سه روش انتخاب مورد استفاده قرار می گیرد، هیچ کدام نمی تواند در برابر تخریب ناخواسته الگوهای گروهی، به ویژه نه در کاهش مقیاس بزرگ، محافظت کند. بنابراین، مرحله تعمیم واقعی باید با مرحله ای اختصاص داده شود که به شناخت الگوهای جمعی اساسی موجود در نقشه منبع اختصاص دارد. هیچیک نمیتوانند در برابر تخریب غیرعمدی الگوهای گروهی، بهویژه در کاهشهای مقیاس بزرگتر، محافظت کنند. بنابراین، مرحله تعمیم واقعی باید با مرحله ای اختصاص داده شود که به شناخت الگوهای جمعی اساسی موجود در نقشه منبع اختصاص دارد. هیچیک نمیتوانند در برابر تخریب غیرعمدی الگوهای گروهی، بهویژه در کاهشهای مقیاس بزرگتر، محافظت کنند. بنابراین، مرحله تعمیم واقعی باید با مرحله ای اختصاص داده شود که به شناخت الگوهای جمعی اساسی موجود در نقشه منبع اختصاص دارد.16 ، 18 ]، که ما را به ایجاد فرآیندی برای تشخیص الگوهای گروه چندضلعی [ 10 ] هدایت کرد.
در مورد آزمون 2، مستند شده در شکل 15 و جدول 4 ، ما سه مجموعه مختلف از مقادیر هدف را مقایسه کردیم تا تأثیر آنها بر دانه بندی نقشه حاصل را بررسی کنیم. ریزدانه ترین از این سه مجموعه (FG) در اصل برای نقشه برداری توپوگرافی توسعه داده شد [ 30 ]. همانطور که شکل 15 نشان می دهد، با این حال، برای تعمیم نقشه های زمین شناسی که معمولاً با چند ضلعی های رنگی و نامنظم پر شده اند که اغلب کنتراست بصری کمتری دارند (به ویژه در مورد چند ضلعی های پگماتیت زرد) به مرزهای خود می رسد. برای چنین نقشه هایی، مقادیر هدف مجموعه FG بیش از حد دقیق به نظر می رسد. بنابراین، در [ 31] استفاده از مقادیر هدف به طور قابل توجهی بالاتر برای نقشه های زمین شناسی پیشنهاد شد، که یک نتیجه نسبتاً درشت دانه با چند ضلعی های بیشتری که بزرگ و جمع می شوند ایجاد می کند. همانطور که شکل 15 نشان می دهد، این مجموعه مقادیر هدف دانه درشت (CG) ممکن است منجر به تعمیم بیش از حد و از دست دادن بیش از حد جزئیات شود، به ویژه هنگامی که تمرکز روی چند ضلعی های کوچک است، همانطور که در این مقاله وجود دارد. این با میانگین مساحت چند ضلعی و تعداد چند ضلعی ها تأیید می شود ( جدول 4) که به طور قابل توجهی با دو مجموعه دیگر از مقادیر هدف متفاوت هستند. مجموعه مقادیر هدف مصالحه (CM) اجازه می دهد تا تصویر متفاوت تری حفظ شود، در حالی که اطمینان از خوانایی حفظ می شود. توجه داشته باشید که در این مجموعه، مقادیر نزدیکتر به مقادیر مجموعه FG نسبت به مجموعه CG انتخاب شدهاند، با این هدف که تا حد امکان جزئیات را حفظ کنند، بنابراین امکان کاهش مقیاس بیشتر را نیز فراهم میکنند. این نیز با نتایج گزارش شده در جدول 4 برای میانگین مساحت چند ضلعی و تعداد چند ضلعی ها، که بسیار شبیه به نتایج بدست آمده با مجموعه FG هستند، منعکس شده است.
در مورد آزمایشی 3، ما از مقادیر هدف سازش و استراتژی انتخاب دسته بندی برای تولید یک سری نقشه های تعمیم یافته استفاده کردیم که در شکل 16 در مقیاس های هدف مربوطه نشان داده شده است. در حالی که نقشه حاصل در 1:50000 به طور کلی قانع کننده به نظر می رسد، نقشه در 1:100000 شروع به نشان دادن نشانه هایی از عدم تعادل بصری می کند. در مقیاس 1:200000، نقشه به طور کامل خراب می شود. برداشت بصری توسط جدول 5 پشتیبانی می شود، که نشان می دهد مساحت نسبی هر کلاس بعد از 1:100000 به شدت نامتعادل می شود. در نقشه اصلی، مقوله های آمفیبولیت و پگماتیت از نظر تعداد چند ضلعی ها بیشترین فراوانی را دارند که به این دلیل است که بیشتر به صورت چند ضلعی کوچک ظاهر می شوند. از این رو، آنها به دلیل اندازه کلی کوچک خود کاندید حذف هستند و تعداد آنها در انتقال از 1:100000 و 1:200000 به طور قابل توجهی کاهش می یابد ( جدول 5).). با این حال، از آنجایی که تعداد آنها بسیار زیاد است، این دو مقوله نیز بیشترین تأثیر را از بزرگ شدن و به ویژه از تجمیع می گیرند. از این رو، منطقه به دست آمده در فرآیند تعمیم نامتناسب است. باز هم، این اثر نشان می دهد که نتایج فراتر از مقیاس 1:100000 دیگر خوشایند نیستند. یک بار دیگر، این به ضرورت رویکردی مبتنی بر شناخت ساختارهای گروه محلی استوار است که سپس میتواند اپراتورهای تعمیم متنی بهبود یافته را آگاه کند [ 10 ].
شکل 17 روش شناسی مبتنی بر محدودیت پیشنهادی و رویکرد CA GeoScaler را مقایسه می کند [ 23 ، 24]، و هر دو روش در واقع نتایج قابل مقایسه ای به دست آوردند که خوانایی آن بهبود یافته بود. با این حال، رویکرد CA، از آنجایی که مبتنی بر یک عملگر پنجره متحرک است که از یک اصل، اساساً مبتنی بر اکثریت در کل نقشه استفاده میکند، تمایل به اتساع چند ضلعیهای بزرگتر دارد در حالی که چند ضلعیهای کوچک را فرسایش میدهد. از این رو، چند ضلعی های کوچک بیشتری نسبت به نتیجه روش پیشنهادی ناپدید شدند و برخی از چند ضلعی ها به سختی قابل مشاهده شدند. GeoScaler شامل عملیات پس از پردازش، مانند بزرگ کردن چند ضلعی های بسیار کوچک است که می تواند برای اطمینان از خوانایی همه چند ضلعی ها اعمال شود. با این حال، حتی آن عملیات پس پردازش نیز آن چند ضلعی های کوچک را که حذف شده اند، باز نمی گرداند. بنابراین، به طور کلی روش مبتنی بر محدودیت پیشنهادی به نظر می رسد که از رویکرد مبتنی بر CA در مورد نگهداری کافی از چند ضلعی های کوچک بهتر عمل کند.
ما قبلاً به عدم شناسایی صریح گروه چند ضلعی در عملگر حذف به عنوان اولین نقص روش پیشنهادی اشاره کردیم. در اینجا، ضعف دوم را می بینیم: از آنجایی که روش روی چند ضلعی های کوچک تمرکز می کند و با بزرگ کردن آنها، از چند ضلعی های کوچک واحدهای مهم زمین شناسی حمایت می کند، زمانی که ضریب کاهش مقیاس بزرگ است، آن چند ضلعی های کوچک به طور نامتناسبی رشد می کنند. یک بار دیگر، این به ضرورت درمان گروه های چند ضلعی به جای چند ضلعی های منفرد اشاره می کند. در حالی که روش این مقاله شامل عملگرهای تعمیم متنی (تجمع، جابجایی) است، “زمینه” صرفاً به عنوان محله فوری و مرتبه اول تعریف شده توسط محدودیت سیستم عامل درک می شود. اگر چند ضلعی ها با فاصله کمی بیشتر از حد سیستم عامل از هم جدا شوند، هیچ پیوندی شناسایی نمی شود. به همین ترتیب، هیچ امکانی برای تشخیص همسایگان مرتبه بالاتر و از این رو تشکیل گروه های بزرگتر و پیوسته از چند ضلعی ها وجود ندارد. از این رو، برای درمان کامل چند ضلعیهای کوچکی که تمرکز این مقاله را تشکیل میدهند، به روشهای تشخیص الگوی گروهی و همچنین عملگرهای تعمیم متنی که میتوانند از چنین الگوهای گروهی استفاده کنند، نیاز است. در کارهای مرتبط [10 ]، بنابراین روشی پیشنهاد میکنیم که نزدیکی و همچنین شباهتهای هندسی (شکل، اندازه و جهتگیری ویژگیهای نقشه) را در نظر میگیرد و شباهتها را برای یافتن، اصلاح و تشکیل گروههایی نسبت میدهد که میتوانند متعاقباً برای اطلاعرسانی به عملگرهای تعمیم متنی استفاده شوند، مانند به عنوان تجمیع و گونهبندی، برای غلبه بر محدودیتهای پایدار در رویکردهای تعمیم، مانند مواردی که در این مقاله نشان داده شده است.
7. نتیجه گیری
با در نظر گرفتن مثالی از محدودیتهای اندازه (حداقل مساحت، جداسازی شی، و غیره)، این مقاله نشان داد که چگونه تعمیم نقشه مبتنی بر محدودیت را میتوان برای چند ضلعیهای جزیرهای کوچک، که عمدتاً توسط محدودیتهای اندازه تحت سلطه هستند، تحقق بخشید. محدودیت های اندازه نسبتاً ساده اما بسیار اساسی هستند. همه چیز دیگر به آنها بستگی دارد. بنابراین، با شروع با اساسی ترین محدودیت – محدودیت حداقل منطقه – ما توانستیم نشان دهیم که چگونه می توان یک رویکرد مبتنی بر محدودیت ایجاد کرد و عملگرهای تعمیم متفاوت را بسته به تجزیه و تحلیل محلی موقعیت فردی یافت شده آغاز کرد. از منظر عملی، ما توانستیم نشان دهیم که چگونه چنین رویکردی را می توان با استفاده از کتابخانه های یک GIS همه منظوره پیاده سازی کرد.
همانطور که آزمایشهای ما نیز نشان داد، رویکردی که صرفاً بر محدودیتهای اندازه و تجزیه و تحلیل و عملیات محلی تمرکز میکند، برای کاهش مقیاس بزرگتر کافی نیست. بنابراین، تحقیقات آینده باید شناسایی گروههایی از چند ضلعیها را که توسط مجاورت و شباهت (در ویژگی، اندازه، شکل، جهتگیری و غیره) تعریف شدهاند، و همچنین عملگرهای تعمیم متنی برای تجمیع و نوعبندی که میتوانند از آن گروهها استفاده کنند، بررسی کنند. الگوها











بدون دیدگاه