خلاصه
توسعه پویا ساختارهای فضایی مستلزم جستجوی روش های جدید تحلیل فضایی است. هدف این مقاله توسعه یک نظریه جدید در مدلسازی فضا سازههای شبکه با توجه به شش مسیر تجمیع مقدار: اختلاف مقدار حداقل و حداکثر، کاهش مقدار حداقل و حداکثر، و افزایش مقدار حداقل و حداکثر میباشد. نویسندگان نشان میدهند که چگونه ارزشهای ارائهکننده (توصیف) پدیدهها یا حالتهای مختلف در فضای شهری را میتوان به عنوان ساختارهای شبکه طراحی کرد. توسعه پویا ساختارهای فضایی مستلزم جستجوی روش های جدید تحلیل فضایی است. این مطالعه این شبکه ها را از نظر ماهیت آنها تجزیه و تحلیل می کند: تصادفی یا بدون مقیاس. نتایج نشان میدهد که مسیرهای اختلاف مقادیر حداقل و حداکثر یک مرحله از تجمع آن مقادیر را نشان میدهند. آنها بسیاری از ساختارهای شبکه کوچک را با ماهیت تصادفی تولید می کنند. چهار مسیر بعدی تجمیع ارزش منجر به ظهور چندین سطح از تجمع ارزش و ایجاد ساختارهای شبکه سلسله مراتبی بدون مقیاس می شود. مدلهای توسعهیافته بر اساس تئوری توصیفشده، کیفیت مناطق شهری را در نسخههای مختلف ارائه میکنند. تئوری شش مسیر ترکیب ارزش شامل ابزارها و روش های جدید اندازه گیری است که می تواند کیفیت زندگی را تحت تاثیر قرار دهد و هزینه های طراحی های بد یا تخریب فضا را به حداقل برساند. آنها ابزار مناسبی برای توسعه پایدار مناطق شهری هستند. مدلهای توسعهیافته بر اساس تئوری توصیفشده، کیفیت مناطق شهری را در نسخههای مختلف ارائه میکنند. تئوری شش مسیر ترکیب ارزش شامل ابزارها و روش های جدید اندازه گیری است که می تواند کیفیت زندگی را تحت تاثیر قرار دهد و هزینه های طراحی های بد یا تخریب فضا را به حداقل برساند. آنها ابزار مناسبی برای توسعه پایدار مناطق شهری هستند. مدلهای توسعهیافته بر اساس تئوری توصیفشده، کیفیت مناطق شهری را در نسخههای مختلف ارائه میکنند. تئوری شش مسیر ترکیب ارزش شامل ابزارها و روش های جدید اندازه گیری است که می تواند کیفیت زندگی را تحت تاثیر قرار دهد و هزینه های طراحی های بد یا تخریب فضا را به حداقل برساند. آنها ابزار مناسبی برای توسعه پایدار مناطق شهری هستند.
کلید واژه ها:
مدل شبکه ; تحلیل فضایی ; شبکه بدون مقیاس ; تجمیع ارزش
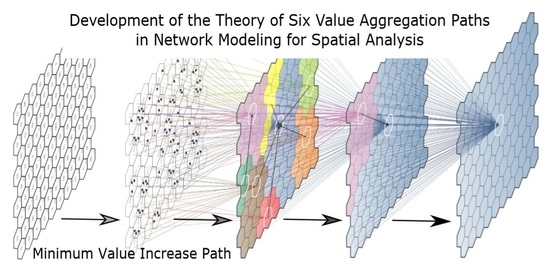
چکیده گرافیکی
1. معرفی
مدیریت فضایی نیازمند جستجوی ابزارهای جدید برای تجزیه و تحلیل تحلیل داده های مکانی برای بهینه سازی عملیات مربوط به برنامه ریزی فضایی در راستای توسعه پایدار است. بسیاری از دانشمندان سوالات زیر را مطرح کرده اند: یک فضا چگونه سازماندهی می شود؟ از چه چیزی تشکیل شده است؟ كوچك ترين قطعات آن مورد تحليل نظري و عملي چيست؟ چگونه این قطعات کل بزرگتری را تشکیل می دهند؟ [ 1 ، 2 ، 3 ]. اینها سوالاتی در مورد روابط بین عناصر فردی یک فضا هستند. این روابط شبکه ای از پیوندها را تشکیل می دهند که منجر به سازماندهی کلی فضا مبتنی بر شبکه می شود. این توسط بسیاری از نویسندگان اثبات و توصیف شده است [ 4 ، 5 ، 6 ، 7, «شبکههای جهان کوچک»8 ، 9 ، 10 ، 11 ، 12 ]. در طول تحقیقات بر روی ساختارهای شبکه در طول سالیان متمادی، الگوریتم های متعددی از جمله الگوریتم های بلمن-فورد [ 13 ]، جانسون [ 14 ]، کروسکال [ 15 ] و دایکسترا [ 16 ] توسعه یافتند. بسیاری از ساختارهای شبکه نیز توصیف شدند، از جمله نمودارهای تصادفی کلاسیک توسط Erdos و Renyi [ 17 ، 18 ]، نمودارهای تصادفی تعادلی با توزیع درجه معین [ 19 ، 20 ، 21 ، 22 ، 23،24 .و شبکه هایی که تحت مکانیسم پیوند ترجیحی در حال رشد هستند [ 25 ]. بر این اساس، برای اینکه یک شبکه وجود داشته باشد و کار کند باید از دو عنصر تشکیل شده باشد: گره ها و اتصالات بین آنها [ 26 ، 27 ، 28 ]. این ارتباطات ممکن است فیزیکی یا ناشی از روابط دیگر باشد. ظهور شبکه هایی که اشیاء فضایی را به هم پیوند می دهند، نتیجه قوانین رشد شبکه و اتصال گره های بعدی است. با توجه به تئوری شبکه های بدون مقیاس، قوانینی برای اتصال ترجیحی گره ها وجود دارد [ 6 ، 27 ، 29]. این ترجیح ممکن است ناشی از اعمال قانون طبیعت یا تصمیمات اتخاذ شده توسط انسان باشد. بنابراین، ترجیحات می توانند طبیعی (خود به خودی) باشند، برای مثال، آنهایی که یک شبکه هیدرولوژیکی [ 30 ] یا پدیده های طبیعی [ 31 ] ایجاد می کنند، یک پدیده انسانی ناشی از تصمیمات اتخاذ شده توسط انسان، مانند شبکه ای از اتصالات نقطه منظره [ 32 ]. ]، یک شبکه اتصال حمل و نقل [ 33 ، 34 ]، یک شبکه همکاری بین شهرها [ 12 ]، یا شبکه های روابط اجتماعی [ 35 ، 36 ].
برای شبکه های بدون مقیاس [ 26 ، 29]، اولویت انتخاب اتصالات در یک سلسله مراتب خاص در این واقعیت نهفته است که هنگامی که یک گره جدید ظاهر می شود، تمایل دارد به گره های موجود با تعداد زیادی از اتصالات متصل شود. این منجر به گره هایی با تعداد اتصالات فزاینده در مقایسه با گره های مجاور آنها با تعداد اتصالات کمتر می شود. شبکه های بدون مقیاس با توزیع قانون توان مشخص و از شبکه های تصادفی متمایز می شوند. در ساختارهای شبکه تصادفی، این یک توزیع نرمال است. علاوه بر این، آنچه که مشخصه ساختارهای شبکه بدون مقیاس است، وجود مراکز (هاب) است، به عنوان مثال، گره هایی که تعداد اتصالات بسیار بیشتری نسبت به بسیاری از گره ها در کل ساختار شبکه دارند. در شبکه های تصادفی، هیچ مرکزی رخ نمی دهد [ 26 ، 37،38 ]. مقایسه این دو نوع شبکه (تصادفی و بدون مقیاس) به صورت کلی در جدول 1 ارائه شده است.
از دیدگاه تحلیل فضایی، بسیار مهم است که شبکههای بدون مقیاس با مقاومت در برابر حملات تصادفی مشخص شوند. حمله تصادفی به گره(ها) که منجر به ناکارآمدی آن می شود، مانند شبکه های تصادفی تاثیر مخربی بر شبکه ندارد. به لطف ساختار ناهمگن، همیشه اتصالاتی باقی مانده است که کل شبکه را در حالت فعالیت حفظ می کند. در عین حال، آنها نسبت به حذف عمدی مراکز از ساختار شبکه بسیار حساس هستند. این شبکه ها نسبت به حملات سازماندهی شده عمدی به نقاط خاص (یعنی مراکز شبکه) بسیار حساس هستند. حمله عمدی به مراکز متعدد ممکن است منجر به از هم پاشیدگی کامل شبکه و ناکارآمدی ساختار شود.
بنابراین منطقی به نظر می رسد که شناسایی شبکه ای از اتصالات فضایی و شناخت شخصیت آنها (تصادفی یا بدون مقیاس)، با توجه به دانش ارائه شده در بالا، برای مدیریت صحیح فضا و فضا بسیار مهم است. اجزای آن
نویسندگان این مطالعه رویکردی از مدلسازی فضایی در ساختارهای شبکه با توجه به شش مسیر ترکیب ارزش برای اهداف مدیریت فضایی و بررسی ماهیت آن پیشنهاد میکنند. با توجه به تئوری شش مسیر ارائه شده در این مقاله، نشان دادن نقش ساختارهای شبکه در تحلیلهای فضایی و نشان دادن مکانیسمها و رویههای خاصی که چنین شبکههایی را تولید میکنند از این منظر حائز اهمیت است. نظریه توسعه یافته حاصل چندین سال تحقیق تجربی است. به این ترتیب، ارزشهایی که پدیدهها و ساختارهای مختلف مناطق شهری را نشان میدهند، میتوان مدلسازی و تحلیل کرد، از جمله حرکات پوسته زمین، ارزشهایی که سطح امنیت و کیفیت منظر در شهر را نشان میدهند [ 12 ، 32 ،40 ., 41 , 42 ]. این عملیات مدل سازی ساختار فضایی با هدف امکان برنامه ریزی فعال، توسعه و مدیریت ساختارهای شبکه در حالی که آنها را در یک سطح پایدار حفظ می کند، انجام می شود. به نظر می رسد این نظریه به دلیل رویکرد گسترده ای که در مدل سازی داده ها و مطالعه و سنجش کیفیت فضای شهری دارد، ابزار خوبی برای رویکرد یکپارچه به توسعه شهری پایدار باشد. بر اساس ایده توسعه پایدار، آرزوی برآوردن نیازهای انسانی و همچنین بهبود شرایط زندگی مردم نمی تواند منجر به تخریب و برهم زدن وضعیت تعادل در طبیعت شود.]. به منظور حصول اطمینان از مدیریت بهینه فضایی، مطابق با اصول توسعه پایدار، این فضا باید به خوبی مورد تحلیل قرار گیرد. توانایی مدلسازی فضا و پدیدههایی که درون آن بهعنوان یک شبکه رخ میدهند، تحلیل ساختار آنها، تعیین ماهیت آنها و استفاده از ویژگیهای مشخصکننده آن را ممکن میسازد. این ابزارهای تحقیقاتی جدید به ما امکان می دهند تا برای استفاده بهینه از فضا (مدیریت) و همچنین حفاظت از آن نتیجه گیری کنیم، به خصوص زمانی که شبکه دارای ویژگی بدون مقیاس باشد.
هدف این مقاله، خلاصه و نظامبندی تحقیقات انجامشده تا به امروز و تعریف نظریه شش مسیر تجمیع ارزش در حوزه تحلیلهای فضایی است. به منظور دستیابی به هدف اصلی، این مطالعه بر توسعه الگوریتمهای نوآورانه مدلهای شبکه سازههایی که در فضا به دلیل تمایز فضایی رخ میدهند، تمرکز دارد. نویسندگان همچنین تلاش کردند تا ویژگی این ساختارهای فضایی (تصادفی یا بدون مقیاس) را توصیف کنند و در نهایت، امکانات استفاده از ویژگیهای این مدلهای شبکه را نشان دهند.
2. توسعه نظریه شش مسیر تجمیع ارزش
فضا را می توان به عنوان یک ساختار شبکه مدل کرد. به نظر می رسد آنچه عناصر فضا را برای برقراری ارتباط (یعنی تشکیل یک ساختار شبکه) تعیین می کند، تمایز آن است. حتی حداقل تفاوت ها منجر به امکان تعیین حدود قطعات خاصی از یک فضا می شود.
مطابق با موارد فوق، نویسندگان فرض کردند که مبنای سازماندهی شبکه ای فضا، تمایز آن است که شش نوع تعامل یا اتصال ایجاد می کند. در مسیر این اتصالات، یک ناحیه همسایه کوچکتر می تواند مناطق بزرگتری را تشکیل دهد.
بنابراین، ترکیب مقادیر (داده های مکانی) که یک فضا را نشان می دهد ممکن است طبق مسیرهای زیر رخ دهد:
- –
-
حداقل تفاوت مقدار ( بخش 2.1.1 )،
- –
-
حداکثر اختلاف مقدار ( بخش 2.1.2 )،
- –
-
حداقل کاهش مقدار ( بخش 2.1.3 )،
- –
-
حداکثر کاهش مقدار ( بخش 2.1.4 )،
- –
-
حداقل افزایش مقدار ( بخش 2.1.5 )،
- –
-
حداکثر افزایش مقدار ( بخش 2.1.6 ).
همانطور که در بالا ذکر شد، هدف از این مطالعه ایجاد مبانی نظری برای تئوری شش مسیر تجمع ارزش که منجر به تجمع فضا میشود، بود. اصطلاح تراکم فضایی فرآیند ظهور مناطق بزرگتر را با استفاده از اتصالات فضایی اشیاء انتخاب شده با توجه به مقادیر یا روابط (ترجیحات) اتخاذ شده (یا ناشی از قوانین طبیعی) توصیف می کند [ 43 ، 44 ، 45 ]. در ادامه در این مقاله، نویسندگان قوانین تشکیل شبکه را با توجه به شش مسیر ترکیب مقادیر در حالی که فرآیند تجمع فضا را منعکس میکنند، به تفصیل شرح میدهند.
2.1. تعیین امکانات ترکیب ارزش های معرف یک فضا و پدیده های رخ داده در آنها
تجزیه و تحلیل احتمالات برای تمایز فضا نشان می دهد که امکان تشخیص شش مسیر تشکیل اتصال وجود دارد – فعل و انفعالات فضایی که می توان از آنها به عنوان مسیرهای تراکم فضایی نام برد.
نویسندگان بیان کردند که ویژگیهای یک فضا، که با مقادیر معین آن مشخص میشود، منجر به تمایز آن میشود. این ویژگی ها می توانند طبیعت و همچنین انسان زا باشند که از تصمیمات برنامه ریزی انسان ها ناشی می شود. اینها ویژگی ها، ویژگی ها یا ویژگی های یک فضا هستند که مبنایی برای سازماندهی فضا به ساختارهای بزرگتر (یعنی مناطق) فراهم می کنند. نمونه ای از داده های مکانی برای تشکیل یک شبکه می تواند مقدار اختصاص داده شده به یک گره شبکه (نماینده یک نقطه یا یک منطقه) باشد، که ممکن است نشان دهنده اندازه جمعیت، ارتفاع یک منطقه از سطح دریا، ارزش زیبایی شناختی منظر باشد. یا وضعیت امنیتی آن که با روش های جداگانه مشخص می شود.
شبکه ها از عناصر تشکیل شده اند و روابطی که آنها را به هم پیوند می دهد شبیه به سیستم ها است. این روابط دقیقاً اثر متقابل ویژگی های فضایی است که به دلیل روابطی که آنها را به هم پیوند می دهد، منجر به پیدایش مناطق همگن می شود.
به منظور توسعه مدلهای شبکه، شبکهای از زمینههای اساسی ارزیابی ساخته شد که در آن هر میدان دارای یک مقدار آزمایشی بود که یک پدیده را نشان میداد. تعریفی از میدان پایه توسط هاپفر، سایمرمن و نواک [ 46 ] و همچنین باجروفسکی و همکاران توضیح داده شد. [ 47 ]. Sanetra و Cieślak [ 48 ] و Lechnio [ 49 ] نیز به طور گسترده در مورد نظریه میدان های پایه نوشتند. به منظور تجزیه و تحلیل، میدان های پایه شش ضلعی ( شکل 1 ) مورد استفاده در مدل سازی نقشه برداری و ارائه نقشه برداری داده های مکانی (نقشه هگزبین) استفاده شد [ 50 ].
تمایز فضا و مقادیر نشاندهنده آن و دادههای مکانی، ترجیحات خاصی را برای ظهور اتصالات فضایی ایجاد میکند و در نتیجه رشد شبکه را به همراه دارد. در هر یک از مسیرهای ارائه شده در زیر، مناطق جدیدی به دلیل ایجاد ارتباط بین هر میدان و میدانی که دارای مرز مشترک (یک همسایه) است، در صورت افزایش یا کاهش یک رابطه خاص از تفاوت ارزش، پدیدار میشوند. نویسندگان فرض کردند که هر میدان فقط می تواند با یک میدان همسایه ارتباط برقرار کند. موضوع پیچیدگی اتصالات چندگانه در یک مطالعه جداگانه گسترش خواهد یافت. هنگامی که مقادیری که پدیده ای را نشان می دهند که در یک فضا یا منطقه خاص رخ می دهد مطابق با قوانینی که شرح داده می شود ترکیب شوند، مناطق (مناطق) جدیدی پدیدار می شوند. اینها به نوبه خود در مراحل بعدی توسعه مدل شبکه، جستجو برای اتصالات جدید با توجه به قوانین مشابه. به این ترتیب، سطوح بعدی از تجمع مقادیر نشان دهنده پدیده های خاصی است که در فضا رخ می دهد.
2.1.1. مسیر تفاوت حداقل مقدار
شبکهها ( شکل 1 ) در نتیجه اتصال گرهها (فیلدها) منفرد با یافتن رابطه حداقل تفاوت مقدار پدید آمدند.
مرحله آشکارسازی رابطه اختلاف حداقل مقدار نشان داد که تمام فیلدهایی که به عنوان گرههای شبکه در حال ظهور نامیده میشوند یک اتصال برقرار کردند ( شکل 1 a). این امر آشکار شدن مرحله 1 تجمع را که در آن 26 منطقه جدید پدیدار شد ( شکل 1 ب) را قادر ساخت. مشخصات تعداد اتصالات در سازه شکل گرفته به این روش در جدول زیر ارائه شده است ( جدول 2 ).
هیچ مرحله دیگری از تجمع رخ نمی دهد زیرا هیچ زمینه (گره) پیشرو در مناطق ظاهر نشد. فیلدهای پیشرو (گرهها) آنهایی هستند که با تمام فیلدهای دیگر تشکیلدهنده این ناحیه ارتباط دارند، گویی از طریق وقوع تمایز ارزش، آنها را به سمت خود جذب میکنند. بنابراین در ساختار تشکیل شده 26 ساختار شبکه با پیچیدگی کم قابل تشخیص است.
2.1.2. مسیر تفاوت حداکثر مقدار
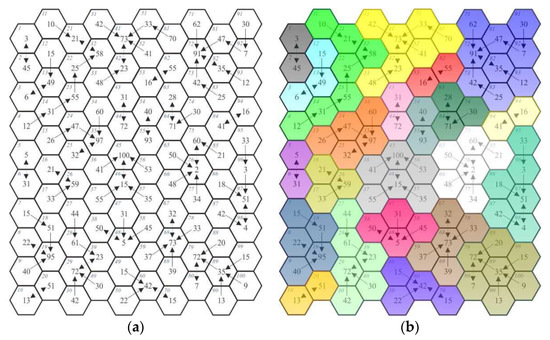
با ترکیب مقادیر بر اساس قانون اختلاف مقدار حداکثر، مرحله آشکار کردن روابط نیز نشان داد که همه فیلدها (گره ها) یک اتصال پیدا کردند ( شکل 2 a). این مدل، مشابه مدل قبلی، یک سطح از تجمع مقادیر را ارائه می دهد ( شکل 2 ب).
در مرحله اول تجمیع ارزش، 23 منطقه جدید پدیدار شد. ویژگی های ساختار شبکه های تشکیل شده با توجه به مسیر اختلاف مقدار حداکثر در جدول 3 ارائه شده است.
آنچه مشخصه مسیرهای حداقل و حداکثر اختلاف است، امکان ظهور اتصالات دو طرفه است. چنین وضعیتی را می توان هم در مدل شبکه ( شکل 1 ) که با توجه به مسیر اختلاف حداقل (مثلاً برای فیلدهای دارای شماره 2 و 13) شکل گرفته است و هم در مدل شبکه ( شکل 2) مشاهده کرد.) با توجه به مسیر حداکثر اختلاف (فیلدهای دارای شماره 5 و 6) تشکیل شده است. با ترکیب مقادیر به این روش، مناطق بزرگتری به دست می آیند که در آن رابطه تفاوت ارزش در هر دو جهت می تواند در اتصالات مختلف یک شبکه رخ دهد. این منجر به عدم وجود یک گره پیشرو برای ایجاد اتصالات بیشتر می شود. این به نوبه خود منجر به تعداد سطوح تجمع کمتر از سایر مسیرها (توضیح داده شده در بالا) و ظهور سایر ساختارهای شبکه می شود.
2.1.3. مسیر کاهش حداقل مقدار
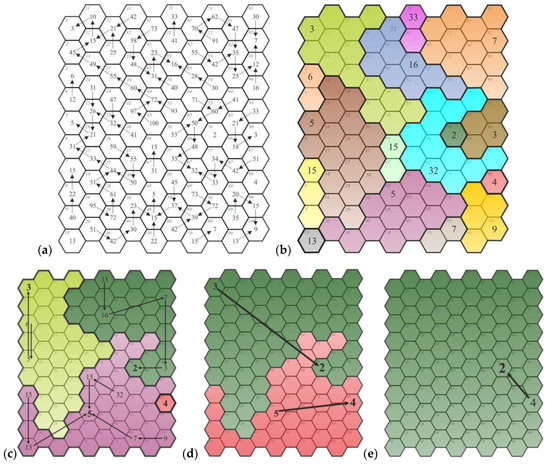
اتصالات در این شبکه بر اساس همان اصولی که قبلا توضیح داده شد (یعنی به میدان همسایه اما بر اساس اصل کاهش مقدار حداقل) ایجاد شدند. مرحله آشکارسازی روابط نشان داد که برای 84 فیلد (گره؛ شکل 3 الف)، مقدار به حداقل کاهش می یابد و بنابراین اتصالات را تشکیل می دهد. بنابراین، طبق این مسیر، مرحله 1 تجمیع، ظهور 16 منطقه جدید را امکان پذیر کرد ( شکل 3 ب). در مرحله بعدی توسعه مدل، مناطق جدید (و مرزهای آنها) به عنوان گره های جدید در شبکه در نظر گرفته شدند که با مقدار گره پیشرو نشان داده شدند (تعریف در بخش 2.1.1) .، پ. 5). مقادیر به این ترتیب ترکیب شدند تا زمانی که امکانات برای اتصال به پایان رسید (یعنی تا زمانی که مقادیر را نتوان متمایز کرد).
مسیر کاهش مقدار حداقل چهار مرحله تجمع ارزش را نشان داد. ویژگی های مدل شبکه در جدول 4 ارائه شده است.
لازم به ذکر است که مرحله نهایی (یعنی مرحله چهارم تجمیع) منجر به پیدایش یک منطقه شامل 100 میدان شد. گره ای که ارتباطی با تمام گره های دیگر ایجاد می کند پدید آمد (گره شماره 76).
با چنین مفروضاتی و داده های آزمایشی، یک مدل شبکه با ساختار شبکه مدولار و سلسله مراتب اتصال حفظ شده توسعه داده شد. در این شبکه از آنجایی که اتصالات تشکیل شده دارای جهت گیری هستند، می توان نتیجه گرفت که فقط به یک صورت وجود دارند. این به دلیل این واقعیت است که اصل کاهش مقدار حداقل برعکس عمل نمی کند (به عنوان مثال، شکل 3 a). به عنوان مثال، فیلد شماره 2 به فیلد شماره 12 متصل می شود، اما فیلد شماره 12 به فیلد شماره 2 متصل نمی شود. بنابراین، در تفسیر مدل، می توان گره هایی را که در مراحل تجمیع خاص هیچ ارتباطی ندارند و گره ای که 99 اتصال دارد.
این منعکس کننده وضعیتی است که در آن جهت اتصالات “کانال سازی” (تجمع) پدیده مورد مطالعه را به گره های درجه بالاتر (پیشرو) ایجاد می کند تا زمانی که امکانات اتصال به پایان برسد. فیلدهای شبکه (گره ها) که ارتباط با آنها برقرار می شود، به رتبه بالاتری در ساختار شبکه می رسند و به گره های پیشرو تبدیل می شوند که می توانند به درجه یک گره – مرکز یک شبکه خاص، دست یابند.
2.1.4. مسیر کاهش حداکثر مقدار
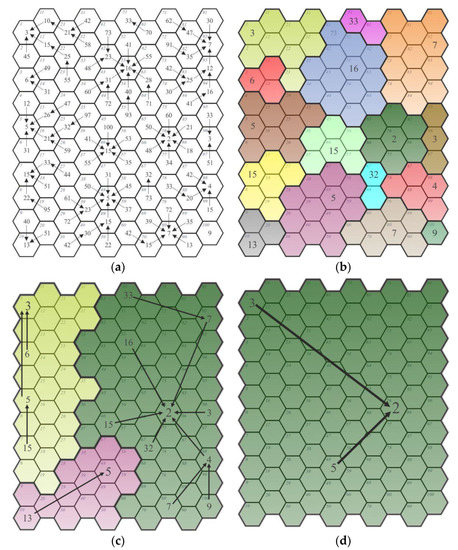
در رابطه با این مدل، هر فیلد یک اتصال را با توجه به مسیر کاهش حداکثر مقدار جستجو می کند. در این مورد، مشابه بخش 2.1.3 ، یک مدل شبکه سلسله مراتبی با عناصر ساختار مدولار نیز به دست آمد. مدل شبکه شامل سه مرحله تجمیع است ( شکل 4 ).
مرحله آشکارسازی روابط نشان داد که برای 84 فیلد (گره؛ شکل 4 الف)، مقدار حداکثر کاهش می یابد و بنابراین اتصالات را تشکیل می دهد. در مرحله اول تجمیع، 16 منطقه جدید ظاهر شد، مشابه مسیر کاهش مقدار حداقل ( شکل 3 ب). با این حال، ساختار اتصالات متفاوت است زیرا اصل اتصال متفاوت بود. ویژگی های شبکه توسعه یافته در جدول 5 ارائه شده است.
در مرحله سوم تجمیع، سه منطقه جدید پدیدار شد. این بدان معناست که سه گره پیشرو در ساختار شبکه پدید آمدند: یک گره با 14 اتصال، دیگری با 26 اتصال و آخرین گره با 57 اتصال. سطح چهارم تمام فیلدها را در یک منطقه جمع کرد. یک گره جذب (تولید کننده) 99 اتصال پدید آمد (گره شماره 76).
2.1.5. مسیر افزایش حداقل ارزش
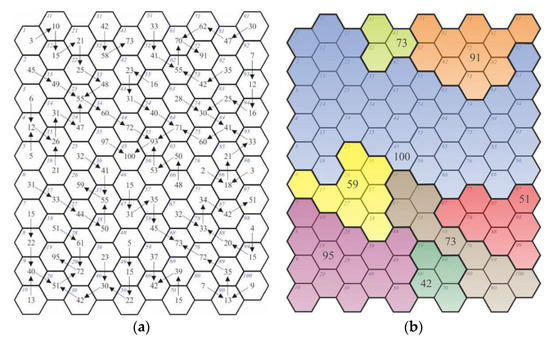
این مسیر شامل توسعه مدلی از یک شبکه و مناطق جدید در نتیجه تولید اتصال هر میدان، به نوبه خود، با یک میدان همسایه انتخابی، با توجه به مسیر افزایش مقدار حداقل است. مناطقی که به دلیل آشکار شدن روابط به وجود آمدند، بر اساس همان اصول به دنبال ارتباطات جدید هستند. مثال ارائه شده در زیر ظهور یک شبکه را در سه مرحله تجمیع نشان می دهد ( شکل 5 ).
در مرحله آشکارسازی روابط، 92 فیلد (گره) با توجه به مسیر افزایش مقدار حداقل یک اتصال پیدا کردند ( شکل 5 الف). در مرحله اول تجمیع، هشت منطقه جدید پدید آمدند ( شکل 5 ب). با این حال، ساختار اتصالات متفاوت است زیرا اصل اتصال متفاوت بود. ویژگی های شبکه توسعه یافته در جدول 6 نشان داده شده است.
مرحله نهایی (یعنی سومین) تجمیع منجر به ظهور یک منطقه متشکل از 100 میدان شد. یک گره ایجاد 99 اتصال پدید آمد (گره شماره 45).
2.1.6. مسیر افزایش حداکثر ارزش
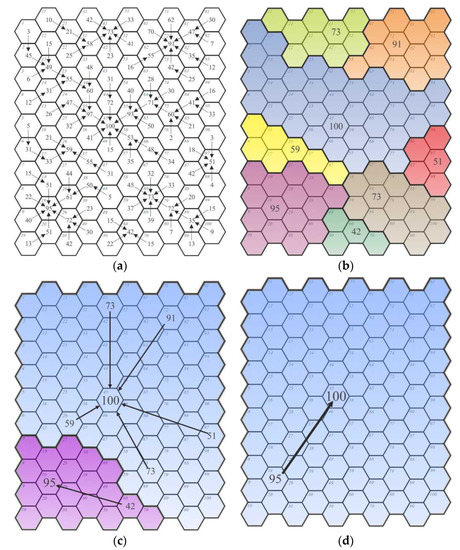
در این مسیر به دلیل ایجاد ارتباط بین هر میدان و میدان همسایه در نتیجه افزایش مقدار، مناطق جدیدی پدید آمدند. نمودار تولید شبکه ها و به تبع آن مناطق جدید با توجه به مسیر افزایش حداکثر در شکل 6 ارائه شده است .
شبکه فوق در چهار مرحله توسعه داده شد ( شکل 6 ). اولین مرحله از آشکارسازی رابطه افزایش مقدار حداکثر ( شکل 6 a) شناسایی 92 فیلد را که به یک اتصال دست یافتند، فعال کرد. به لطف این اتصالات، هشت ناحیه جدید در مرحله اول تجمیع ارزش ( شکل 6 ب)، دو ناحیه در مرحله دوم، و مرحله سوم تجمع منجر به اتصال 99 گره به یک گره (فیلد/گره شماره 45) شد. ). ویژگی های شبکه تشکیل شده به همراه تعداد گره ها و اتصالات در جدول 7 ارائه شده است.
ساختار شبکه در حال ظهور در این راه و ظهور اتصالات جدید (و در نتیجه، مناطق) را نیز می توان در یک مدل آرام نشان داد. به عنوان مثال، شکل 7 سطوح خاصی از ظهور شبکه را با توجه به مسیر افزایش مقدار حداکثر نشان می دهد.
2.2. مدل های شبکه – تصادفی یا بدون مقیاس؟
پس از تجزیه و تحلیل فرآیند پیدایش ساختار شبکه با توجه به شش مسیر پیشنهادی، می توان نتیجه گرفت که کل ساختار شبکه های منفرد، بسته به ویژگی مقادیر نشان دهنده فیلدها و خود مسیر، در تعدادی از مراحل تجمع ظاهر می شود. مراحل تجمیع آنقدر زیاد است که می توان امکانات اتصالات را طبق مسیرهای از پیش تعیین شده و در راستای اصول اتخاذ شده (ارتباط با میدان همسایه) به پایان رساند. به عبارت دیگر، گره هایی که با کمیت های خاص نشان داده می شوند، تا زمانی که یک قانون خاص عمل می کند، ترکیب می شوند.
برای مسیرهای حداکثر و حداقل تفاوت، امکان ترکیب همه گره ها در یک شبکه واحد از قبل پس از مرحله 1 تجمع به پایان رسیده است. این به دلیل این واقعیت است که در این سطح (مرحله 1 تجمع)، گره های پیشرو در مناطق جداگانه برای اتصالات بعدی ظاهر نمی شوند. مناطق جدیدی تشکیل می شوند که در قالب مدل با ساختارهای شبکه کوچکتر نشان داده می شوند. برای مسیر حداقل اختلاف، اینها 26 ساختار شبکه هستند ( بخش 2.1.1 ، شکل 1 ب). در این ساختارها حداکثر تعداد اتصالات با یک گره به هفت می رسد. از سوی دیگر، در مورد مسیر حداکثر اختلاف، در مرحله اول تجمیع، 23 ساختار شبکه که مناطق جدیدی را تشکیل میدادند، پدیدار شدند ( بخش 2.1.2 .شکل 2ب). در این مورد، حداکثر تعداد اتصالات با یک گره به هشت رسید. بنابراین می توان نتیجه گرفت که در این مرحله این ساختارها دارای ماهیت شبکه های تصادفی هستند که با توزیع های عادی نشان داده می شوند که در آن هیچ گره (یعنی مراکز) مشخصه ساختارهای بدون مقیاس قابل تشخیص نیست. بنابراین، این قوانین بدون تغییر مفروضات در مراحل بعدی کاربرد بیشتری ندارند. این موضوعی است که باید در بررسی های بعدی به آن پرداخته شود. همچنین نشان می دهد که این دو مسیر (قوانین تفاوت) با چهار مسیر بعدی متفاوت هستند زیرا قوانین دیگری را در سطوح تجمع بالاتر ایجاد می کنند.
وضعیت متفاوتی را می توان پس از انجام تجزیه و تحلیل چهار ساختار شبکه دیگر که بر اساس قوانین پیشنهادی کاهش و افزایش ارزش توسعه داده اند مشاهده کرد. شکل ارائه شده در زیر توزیع گره ها و اتصالات در ساختار شبکه های توسعه یافته بر اساس شش مسیر پیشنهادی را نشان می دهد ( شکل 8 ).
توزیع های فوق ماهیت بدون مقیاس شبکه های توسعه یافته را نشان می دهد. گره هایی در حال ظهور هستند که تعداد بسیار زیادی از اتصالات نسبت به اکثریت دارند. در چنین ساختاری، این گره ها به نام مراکز هستند که بیشترین اهمیت را دارند. حذف آنها (تخریب یا آسیب) منجر به ناکارآمدی در عملکرد کل ساختار شبکه می شود.
سازه های توسعه یافته با توجه به مسیرهای کاهش مقدار حداقل و حداکثر دارای ویژگی های ساختاری بدون مقیاس هستند. این امر با وقوع گره هایی (به عنوان مثال، مراکز یا هاب) با تعداد اتصالات بسیار بیشتر از میانگین نشان داده می شود ( شکل 8 a,b). هر چه یک گره یا یک مرکز اتصالات بیشتری داشته باشد، وزن آن در عملکرد کل سازه بیشتر می شود.
علاوه بر این، با تجزیه و تحلیل دو توزیع بعدی گره ها و اتصالات ( شکل 8 c,d)، باید نتیجه گرفت که یک ساختار بدون مقیاس در آنها پدیدار می شود. این توسط گره های بیرونی (یعنی مراکز این شبکه ها) منعکس می شود.
علاوه بر این، گره هایی ظاهر می شوند که وزن کمتری نسبت به گره های پیشرو دارند (یعنی گره هایی با تعداد متوسط اتصالات در مقایسه با اکثریت). این گره ها عنصری هستند که ممکن است مستعد رتبه بندی مراکز باشند. هر چه مراکز بیشتری در ساختار شبکه وجود داشته باشد، مقاومت آن در برابر حملات عمدی (ناکارکردی) بیشتر می شود. بنابراین، گرههای میانی اجزای مناسبی هستند که ممکن است در نتیجه عملیات خاص، با افزودن اتصالات به آنها، رتبه آنها به مراکز ارتقا یابد. یک مثال خوب یک شبکه اتصال هوایی (یک سیستم حمل و نقل) است که در آن به دلیل ظهور اتصالات جدید در گره های میانی و به دلیل بالا رفتن رتبه آنها تا یک مرکز، کل ساختار شبکه در برابر تخریب مقاومت بیشتری دارد. شرط افزایش مقاومت، حفاظت آگاهانه از مراکز در این شبکه ها است. هم مراکز و هم گره های میانی اجزای کمیاب در کل ساختار شبکه هستند.
یک مشاهدات بسیار مهم این است که در چهار مورد از شش مسیر پیشنهادی، شبکههایی پدید میآیند که ماهیت آنها شبیه به شبکههای بدون مقیاس است. همه مسیرهای تحلیل شده یکی از شرایط اساسی برای ظهور شبکه های بدون مقیاس (یعنی انتخاب ترجیحی اتصالات) را برآورده می کنند. در شبکههای بدون مقیاس، یک گره ضعیفتر به دنبال گره قویتری میگردد که اتصال به آن در ساختار شبکه موجود برایش سودمند باشد. فرض بر این بود که در ساختارهای تحلیل شده، این گره ها مطابق با قوانین شش گانه به یکدیگر متصل شوند.
3. خلاصه
نویسندگان نظریه فوق فرض کردند که یک تحلیل اطلاعات جغرافیایی از فضا برای اهداف مختلف ممکن است با استفاده از مدلسازی شبکه توسط شش مسیر ترکیب ارزش انجام شود:
- –
-
حداقل تفاوت مقدار ( بخش 2.1.1 )،
- –
-
حداکثر اختلاف مقدار ( بخش 2.1.2 )،
- –
-
حداقل کاهش مقدار ( بخش 2.1.3 )،
- –
-
حداکثر کاهش مقدار ( بخش 2.1.4 )،
- –
-
حداقل افزایش مقدار ( بخش 2.1.5 )،
- –
-
حداکثر افزایش مقدار ( بخش 2.1.6 ).
مقادیری که ترکیب می شوند ممکن است داده های مختلفی را نشان دهند. آنها ممکن است به یک نقطه و همچنین به یک زمینه اساسی خاص که شامل یک منطقه خاص و دارای یک مرجع فضایی خاص است اختصاص داده شوند. بنابراین، مرحله آماده سازی داده ها برای مدل سازی شبکه بر اساس تئوری شش مسیر شامل موارد زیر است:
-
مرحله 1. تعیین هدف تجزیه و تحلیل اطلاعات جغرافیایی و منطقه مورد تجزیه و تحلیل.
-
مرحله 2. روی هم قرار دادن شبکه ای از زمینه های اساسی ارزیابی (به عنوان مثال، شش ضلعی).
-
مرحله 3. تعیین ارزش هایی که حوزه های اساسی ارزیابی را نشان می دهند.
-
مرحله 4. مدل سازی شبکه بر اساس تئوری مسیرهای ترکیبی شش مقدار، یا فقط بر اساس مسیرهایی که ما آن را مناسب می دانیم (مثلاً مسیر کاهش حداقل مقدار).
-
مرحله 5. تفسیر مدل های شبکه توسعه یافته (تصادفی یا بدون مقیاس) و پاسخ به سوال در مورد دستیابی به هدف.
در مدل های شبکه به دست آمده از این طریق، گره ها، گره های پیشرو و مراکز متمایز می شوند. مهمترین آنها مراکز یک شبکه خاص هستند، زیرا اینها نقاط بحرانی هستند که برای عملکرد کل ساختار بسیار مهم هستند. اینها بیشترین اتصالات را در مقایسه با کل مجموعه دارند. حذف مراکز یا حتی برخی از آنها ممکن است منجر به اختلالات جدی در عملکرد یک عملکرد خاص شود.
گره های پیشرو نقاطی از شبکه هستند که مستعد نقش مراکز هستند. این گره ها می توانند از طریق توسعه طبیعی و همچنین تغییرات در فضا و در نتیجه در ساختار شبکه به مراکز تبدیل شوند. آنها همچنین می توانند از طریق عملیات آگاهانه مربوط به تغییر در ارزش در یک زمینه اساسی به مراکز تبدیل شوند. این عملیات را می توان با ایجاد تغییرات درون فضا (یعنی افزایش ارزش زیبایی شناختی منظر از طریق بازسازی ساختمان، چیدمان فضای سبز و غیره) یا ارزشی که احساس امنیت فرد را نشان می دهد (مثلاً کاربرد پیشگیری از جرم از طریق محیط زیست) بیان کرد. طرح). در ساختارهای شبکه ای که به این روش توسعه یافته اند، اتصالاتی که با جهت گیری خود نشان می دهند که چگونه روابط بین گره ها شکل می گیرد نیز مهم هستند.
این نظریه نیز مانند هر نظریه دارای محدودیت هایی است. یکی این فرضیه است که مناطق جدید به دلیل ایجاد ارتباط بین هر میدان و میدانی که دارای یک مرز مشترک (یک همسایه) است، پدیدار می شود. هر فیلد می تواند تنها یک اتصال ایجاد کند، اما شرایطی وجود دارد که فیلدهای همسایه دارای مقدار یکسانی هستند. با این فرض ما باید یکی از آنها را انتخاب کنیم. وضعیتی که در آن بیش از یک ارتباط ایجاد خواهد شد به قیام مناطق “مشترک” منجر می شود. یک گره یا فیلد به بیش از یک ناحیه تعلق دارد. پیچیدگی این نوع مدل را می توان در چارچوب تئوری مجموعه های فازی در نظر گرفت. این موضوع در مرحله تحقیق و تحلیل است.
تئوری شش مسیر تجمع ارزش در مدلسازی شبکه برای تحلیل فضایی فرض میکند که شش مسیر اتصال ارزش وجود دارد. اما ممکن است در کنار تحقیق و توسعه این نظریه، مقایسه با سایر نظریه ها و مدل سازی عملی، احتمالات (مسیر) جدیدی از ارتباطات نیز کشف شود.
نمونه ای از برنامه کاربردی
یک نمونه از کاربرد قوانین توصیف شده ترکیب مقادیر با توجه به حداقل و حداکثر افزایش ارزش ممکن است مدلسازی مسیرهای تفریحی باشد به طوری که ارزش زیبایی شناختی منظر تا نقاط دارای بالاترین مقادیر (یعنی مراکز) افزایش یابد. این مقدار ممکن است به صورت حداقلی افزایش یابد، که منجر به حرکت آهستهتر شخصی در حال پیادهروی و استفاده از مسیر میشود، یا حداکثر در جایی که مسیر توسعهیافته بر اساس این شبکه، شخص را مستقیماً به سمت «میانبر» به سمت جذابترین مسیر هدایت میکند. نقطه در داخل منطقه در این مورد، گرههای میانی، نقاطی هستند که ارزشهای زیباییشناختی منظره را بالا، اما نه بالاترین، دارند. اگر نیاز به تقویت ساختار شبکه وجود داشته باشد، ممکن است رتبه این گره های میانی افزایش یابد. به عنوان یک نتیجه از عملیات با هدف بهبود چشم انداز، به مراکز (یعنی، آنها می توانند از ماهیت بدون مقیاس خود محروم شوند). شبکه ای با یک مرکز متفاوت از شبکه ای با چهار مرکز عمل می کند. هر چه مراکز در ساختار شبکه بیشتر باشد، در برابر آسیب و ناکارآمدی مقاومت بیشتری دارد.
در مورد مدلسازی مسیرهای تفریحی نیز منطقی است که مسیر کاهش حداقل ارزش زیبایی شناختی منظر را اعمال کنیم. نویسندگان نمونه ای را در پنج مرحله ارائه می کنند:
مرحله 1. تعیین هدف تحلیل ژئواطلاعات جغرافیایی و منطقه مورد تجزیه و تحلیل: در این مورد، هدف از تجزیه و تحلیل ژئواطلاعات جغرافیایی به دست آوردن اطلاعات فضایی در مورد چگونگی کاهش ارزش زیبایی شناختی منظر در منطقه مورد مطالعه، چرایی این کار و چگونگی کاهش است. آیا می توان این را اصلاح کرد و نشان داد که چگونه مسیرهای تفریحی را برنامه ریزی نکنیم. منطقه مورد تجزیه و تحلیل در یک منطقه شهری (بخشی از شهر اولشتین در شمال شرقی لهستان) با مساحت تقریباً واقع شده است. 120 هکتار ( شکل 9 ).
مرحله 2. روی هم قرار دادن شبکه میدان های اساسی ارزیابی: یک مدل نقشه برداری ارائه شده با استفاده از نقشه هگزبین، زمینه های اساسی ارزیابی را به شکل شش ضلعی (به اندازه هر کدام 1.5 هکتار) نشان می دهد ( شکل 10 ).
مرحله 3. تعیین مقادیری که نمایانگر حوزه های اصلی ارزیابی منفرد است: هر شش ضلعی ارائه شده در شکل 9 دارای تعداد خاص خود و یک ارزش زیبایی شناختی تخمینی از چشم انداز است (تعداد ارائه شده در بخش مرکزی هر میدان، در مقیاسی از 5 تا 100). مقادیر با استفاده از روش Wejchert [ 47 ] و پر کردن برگه ارزیابی منظر شهری برآورد شد.
مرحله 4. مدل سازی شبکه با استفاده از مسیر کاهش مقدار حداقل ( شکل 10 ، شکل 11 ، شکل 12 و شکل 13 ).
مرحله 5. تفسیر مدل های شبکه توسعه یافته، و پاسخ به سوال در مورد دستیابی به هدف.
مدل شبکه توسعه یافته بر اساس قانون حداقل کاهش ارزش، در این مورد، ارزش زیباییشناختی یک منظره، وضعیتی را نشان میدهد که ارزش زیباییشناختی منظر در رابطه با زمینههای مجاور به حداقل میرسد ( شکل 10 ، شکل 11 ، شکل 12). و شکل 13). این امکان تجزیه و تحلیل بسیار دقیق و توضیح حتی این تفاوت های جزئی در ارزش زیبایی شناختی منظر را فراهم می کند. علاوه بر این، زمینه هایی که کمترین جذابیت محلی را دارند (یعنی گره های پیشرو) نیز تعیین خواهند شد. با مشاهده آنها می توان به آنچه ارزش زیبایی شناختی منظر را بسیار پایین می کند توجه کرد و اقدامات اصلاحی را برنامه ریزی کرد. در این حالت، تقویت گره های پیشرو مهم نخواهد بود، بلکه تضعیف آنها با افزایش ارزش در یک زمینه خاص مهم خواهد بود. سطوح تجمع بعدی مسیرهای کاهش ارزش جدید و گره های جدید ( شکل 12 و شکل 13 ) و در نهایت مرکز ( شکل 13) را نشان می دهد.ب). در این مورد خاص، مرکز منطقه ای با کمترین ارزش زیبایی شناختی منظر خواهد بود. عملیات بیشتر با استفاده از مدل شبکه توسعهیافته و ویژگیهای شبکه بدون مقیاس باید منجر به افزایش ارزش زیباییشناسی منظر در زمینهها (یعنی در گرههای پیشرو) و مرکز شود. این امر ساختار شبکه را تغییر میدهد و با تشکیل گرهها و مراکز جدید منجر به تغییر در اتصالات میشود. عملیات مربوط به افزایش ارزش زیبایی شناسی منظر و مدل سازی شبکه باید تا حصول وضعیت رضایت بخش فضا در زمینه برنامه ریزی مسیرهای تفریحی ادامه یابد.
یک مدل کاهش حداکثر وضعیتی را ارائه می دهد که این مقدار حداکثر کاهش می یابد. بنابراین، اتصالات درون شبکه را با یک مکان مکانی خاص نشان می دهد که به دلایل مختلف، ارزش زیبایی شناسی چشم انداز به شدت کاهش می یابد. بنابراین، منطقی است که مدلها را مطابق با مسیرهای خاص به صورت جداگانه توسعه دهیم و آنها را بر روی یکدیگر قرار دهیم تا بتوانیم تحلیلهای فضایی بعدی و به دست آوردن اطلاعات جغرافیایی انجام دهیم. آنها را می توان برای تجزیه و تحلیل میزان تغییرات در ارزش زیبایی شناختی منظر و دلایل کاهش استفاده کرد. آنها همچنین می توانند برای عملیات با هدف افزایش این مقدار استفاده شوند.
به منظور مدیریت بهینه ارزش زیبایی شناختی منظر و در نتیجه افزایش راحتی زندگی ساکنان شهر، استفاده از هر شش مسیر ترکیب ارزش منطقی به نظر می رسد. مسیرهای اختلاف حداقل و حداکثر نشان می دهد که در آن مقدار چشم انداز بسیار کم تغییر می کند و در کجا تغییر قابل توجهی در رابطه با همسایگی رخ می دهد. بخشی از اطلاعاتی که توسط این دو مسیر آشکار می شود نیز در چهار مسیر باقی مانده مربوط به کاهش و افزایش ارزش نشان داده شده است. تفاوت این است که مسیرهای مختلف ممکن است هم افزایش و هم کاهش در مقدار را نشان دهند. چنین مدلی میزان تغییرات در مقادیر منظر را نشان میدهد و ابزار خوبی برای پشتیبانی از برنامهریزی و پیشبینی حالتهای فضایی است که امکان استفاده بهینهتر از فضا را فراهم میکند و از تصمیمگیریهای اشتباه اجتناب میکند.
4. نتیجه گیری
فعل و انفعالات فضایی که ساختار شبکه ای فضا را ایجاد می کند، به عنوان یک نوع ترجیحی، ممکن است منجر به ظهور شبکه های بدون مقیاس فضایی شود. با مدلسازی فضا به این روش و تحلیل مدل، میتوان تکامل ساختار شبکه را در یک محدوده مشخص کنترل کرد. این عملیات شامل تشکیل گرهها و اتصالات جدید و استفاده از ویژگیهای شبکه بسته به ویژگی آنها (تصادفی یا بدون مقیاس) و ساختار آنها (مثلاً مدولار یا سلسله مراتبی) است.
در مورد شبکه های بدون مقیاس، برقراری ارتباط بین اشیاء به تعبیری بدون محدودیت مکانی صورت می گیرد. یک شیء جدا شده از نظر فضایی (بدون “مرز” مشترک) ممکن است با شی دیگری ارتباط برقرار کند. به عنوان مثال می توان به شبکه های اتصال هوایی، شبکه های اینترنتی یا شبکه های همکاری اجتماعی اشاره کرد.
با توجه به ظهور شبکههای فضایی که مناطق فشرده را تشکیل میدهند، این اتصالات باید در ارتباط با همسایگان بلافصل در مسیر تراکم ایجاد شوند. انتخاب ترجیحی مانند شبکههای بدون مقیاس اعمال میشود و طبق قوانین شش مسیر تجمع ارزش که در این مقاله توصیف و تعریف شده است انجام میشود و در عین حال به سمت اشیاء (مناطق) همسایه است.
دو قانون اول تجمیع اختلاف حداقل و حداکثر تنها یک سطح تجمع ایجاد می کند و منجر به ظهور یک شبکه سلسله مراتبی با ویژگی های شبکه مدولار نمی شود. این قوانین مقادیر خاصی را مدل می کنند تا آنها را به شبکه های کوچکی با ماهیت تصادفی تبدیل کنند که در آنها هیچ مرکزی قابل تشخیص نیست. این مدلها را میتوان برای انجام تحلیلهای اولیه استفاده کرد و نشان داد که در آن مقادیر نشاندهنده وضعیت فضا بسیار کم تغییر میکنند، و در کجا تغییر قابل توجهی در رابطه با همسایگی رخ میدهد. برخلاف قوانین مربوط به کاهش یا افزایش ارزش، قاعده تفاوت ارزش، صرف نظر از حداقل یا حداکثر بودن، همیشه اعمال می شود.
چهار قانون تجمع بعدی در مدلسازی ساختارهای شبکه فضایی برنامهریزی مرتبط با افزایش و کاهش مقادیر مدلسازی شده، توسعه مدلهای شبکهای را که ماهیت آنها شبیه به شبکههای بدون مقیاس است، امکانپذیر کرد. این نشان دهنده توزیع قدرت-قانون گره ها و اتصالات و امکان شناسایی مراکز در ساختار این شبکه ها است.
روشهای پیشنهادی برای مدلسازی دادههای مکانی که در بالا توضیح داده شد، تصویربرداری نه تنها تصویری پایدار از وضعیت فضا، بلکه تغییرات در حالتهای این فضا را نیز امکانپذیر میسازد. به این ترتیب می توان توزیع مقادیر موضوعات جالب مربوط به وضعیت و مدیریت فضا (مثلاً ارزش زیبایی شناختی منظر، ارزش املاک، سطح نویز، سطح ایمنی و فضا) را به صورت نقشه برداری (مدل سازی) به تصویر کشید. سطح سرمایه گذاری). ارزش افزوده مدلسازی با توجه به شش مسیر پیشنهادی، نشاندهنده روابط بین دادههای مدلسازیشده است، که اطلاعات جغرافیایی اضافی را فراهم میکند و نتیجهگیری اضافی را امکانپذیر میسازد. علاوه بر این، نه تنها به سؤال «کجا؟» پاسخ می دهد. بلکه “چرا؟” و “با آن چه باید کرد؟” چنین مدل سازی همچنین اجازه می دهد تا از ویژگی های شبکه بدون مقیاس برای شناسایی مراکز درون شبکه (یعنی مهم ترین گره ها) برای عملکرد کل ساختار استفاده شود.
مطالعات بعدی شامل اعمال شش قانون توصیف شده مسیرهای تجمع برای مدلسازی دادههای جغرافیایی و توسعه مدلهای پیچیده خواهد بود. سپس سودمندی کاربرد مدل های ترکیبی بر اساس اطلاعات جغرافیایی که ارائه می کنند ارزیابی می شود.
مدل های توسعه یافته بر اساس تئوری شرح داده شده در بالا، کیفیت مناطق شهری را در نسخه های مختلف آن نشان می دهد. تئوری شش مسیر ترکیب ارزش شامل ابزارها و روشهای جدید اندازهگیری است که میتواند بر کیفیت زندگی تأثیر بگذارد و هزینههای طراحی بد یا تخریب فضایی را به حداقل برساند. آنها همچنین ابزار مناسبی برای توسعه پایدار مناطق شهری هستند.
منابع
- Christaller , W. Central Places در جنوب آلمان Prentice-Hall: Upper Saddle River، نیوجرسی، ایالات متحده آمریکا، 1966. [ Google Scholar ]
- Domański, R. Teoretyczne Podstawy Geografii Ekonomicznej ; Państwowe Wydawnictwo Ekonomiczne: ورشو، لهستان، 1987. [ Google Scholar ]
- آلمندینگر، پی. هاتون، جی. برنامه ریزی فضایی، تفویض اختیار و فضاهای برنامه ریزی جدید. محیط زیست طرح. سیاست دولت C 2010 ، 28 ، 803-818. [ Google Scholar ] [ CrossRef ]
- اویلر، L. Leonhard Euler و پل های Königsberg. علمی صبح. 1953 ، 189 ، 66-70. [ Google Scholar ] [ CrossRef ]
- استاینهاوس، اچ. Łukaszewicz، J. O wyznaczaniu środka miedzi sieci telefonicznej. Appl. ریاضی. 1953 ، 1 ، 299-307. [ Google Scholar ] [ CrossRef ]
- Barabási، AL مرتبط: علم جدید شبکه ها ; گروه کتاب های پرسئوس: نیویورک، نیویورک، ایالات متحده آمریکا، 2003. [ Google Scholar ]
- اسید، اس. د کامپوس، LM جستوجوی ساختارهای شبکه بیزی در فضای گرافهای غیر چرخهای محدود جهتدار. جی آرتیف. هوشمند Res. 2003 ، 18 ، 445-490. [ Google Scholar ] [ CrossRef ]
- نیومن، م. برعباسی، ال. Watts, DJ ساختار و دینامیک شبکه ها ; انتشارات دانشگاه پرینستون: پرینستون، نیوجرسی، ایالات متحده آمریکا، 2011. [ Google Scholar ]
- کیلوکوویچ، ک. Kokosiński، Z. Algorytm hybrydowy dla probabilistycznego problemu komiwojażera. Czas فنی خودکار 2012 ، 109 ، 115-126. [ Google Scholar ]
- Kowalczyk، A. مدل نمادین ارزش زیبایی شناختی منظر. یورو تف کردن Res. سیاست 2012 ، 19 ، 121-128. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
- باجروفسکی، تی. Kowalczyk، AM Metody Geoinformacyjnych Analiz Jawnoźródłowych w Zwalczaniu Terroryzmu ; Wydawnictwo Uniwersytetu Warmińsko-Mazurskiego: Olsztyn، لهستان، 2013. [ Google Scholar ]
- بیلوزور، ا. Kowalczyk، AM; Bajerowski, T. نظریه شبکه های بدون مقیاس به عنوان ابزاری جدید در تحقیق ساختار و بهینه سازی برنامه ریزی فضایی. ج. طرح شهری. توسعه دهنده 2018 , 144 , 04018005. [ Google Scholar ] [ CrossRef ]
- گلدبرگ، ای وی. Radzik، T. بهبود اکتشافی الگوریتم بلمن-فورد. Appl. ریاضی. Lett. 1993 ، 6 ، 3-6. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
- اپلگیت، دی. بیکسبی، آر. چواتال، وی. Cook, W. پیاده سازی الگوریتم Dantzig-Fulkerson-Johnson برای مشکلات بزرگ فروشنده دوره گرد. ریاضی. برنامه. 2003 ، 97 ، 91-153. [ Google Scholar ] [ CrossRef ]
- گوتوسکی، PB; سانیه، ام اس; سیلوا، الگوریتم F. Kruskal برای بهینه سازی درخت پرس و جو. در مجموعه مقالات یازدهمین سمپوزیوم بین المللی مهندسی و کاربردهای پایگاه داده (IDEAS 2007)، Banff، AB، کانادا، 6-8 سپتامبر 2007. صص 296-302. [ Google Scholar ]
- Zhan، FB سه الگوریتم کوتاهترین مسیر در شبکههای واقعی جاده: ساختارها و رویههای داده. جی. جئوگر. Inf. تصمیم می گیرد. مقعدی 1997 ، 1 ، 69-82. [ Google Scholar ]
- Erdös، P. Rényi, A. در نمودارهای تصادفی. انتشار ریاضی. 1959 ، 6 ، 290-297. [ Google Scholar ]
- Erdös، P. Rényi, A. در مورد تکامل نمودارهای تصادفی. انتشار ریاضی. Inst. آویزان شد. آکادمی علمی 1960 ، 5 ، 17-60. [ Google Scholar ]
- Békéssy، A. شمارش مجانبی ماتریس های منظم. گل میخ. علمی ریاضی. آویزان شد. 1972 ، 7 ، 343-353. [ Google Scholar ]
- بندر، EA؛ Canfield، ER تعداد مجانبی از نمودارهای برچسب دار با توالی درجه داده شده. جی. شانه. نظریه A 1978 ، 24 ، 296. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
- بولوباس، ب. اثبات احتمالی یک فرمول مجانبی برای تعداد نمودارهای منظم برچسبگذاری شده. یورو جی. شانه. 1980 ، 1 ، 311-316. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
- بولوباس، بی. نظریه گراف مدرن . Springer Science & Business Media: برلین/هایدلبرگ، آلمان، 2013. جلد 184. [ Google Scholar ]
- Wormald، NC اتصال مجانبی نمودارهای منظم برچسب دار. جی. شانه. نظریه B 1981 ، 31 ، 156-167. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
- واتس، دی جی؛ استروگاتز، SH دینامیک جمعی شبکههای «جهان کوچک». Nature 1998 , 393 , 440. [ Google Scholar ] [ CrossRef ]
- Barabási, AL; آلبرت، آر. ظهور مقیاس بندی در شبکه های تصادفی. Science 1999 , 286 , 509-512. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
- Barabási, AL; راواس، ای. Vicsek، T. شبکه های بدون مقیاس قطعی. فیزیک یک آمار مکانیک. Appl. 2001 ، 299 ، 559-564. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
- Dorogovtsev، SN; مندز، JF تکامل شبکه ها: از شبکه های بیولوژیکی تا اینترنت و WWW . OUP: آکسفورد، بریتانیا، 2013. [ Google Scholar ]
- Kowlaczyk، A. تجزیه و تحلیل ساختارهای فضایی شبکه به عنوان عناصر مهم توسعه فضای پایدار. در مجموعه مقالات دهمین کنفرانس بین المللی “مهندسی محیط زیست” 2017، ویلنیوس، لیتوانی، 27-28 آوریل 2017. [ Google Scholar ]
- کاستا، LDF؛ رودریگز، FA; تراویسو، جی. ویلا بواس، روابط عمومی خصوصیات شبکه های پیچیده: بررسی اندازه گیری ها. Adv. فیزیک 2007 ، 56 ، 167-242. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
- رنسن، اچ. Knoop، JM یک شبکه جهانی مسیریابی رودخانه برای استفاده در مدلسازی هیدرولوژیکی. جی هیدرول. 2000 ، 230 ، 230-243. [ Google Scholar ] [ CrossRef ]
- آبه، اس. سوزوکی، N. شبکه بدون مقیاس زلزله. EPL Europhys. Lett. 2004 ، 65 ، 581. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
- Kowalczyk، AM استفاده از نظریه شبکه های بدون مقیاس در مدل سازی شبکه های ارزش زیبایی شناختی منظر در مناطق شهری. Geod. وستن 2015 ، 59 ، 135-152. [ Google Scholar ] [ CrossRef ]
- وانگ، WX; وانگ، BH; یین، سی. Xie، YB; Zhou، T. دینامیک ترافیک بر اساس پروتکل مسیریابی محلی در یک شبکه بدون مقیاس. فیزیک Rev. E 2006 , 73 , 026111. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
- Kocur-Bera، K. نظریه شبکه بدون مقیاس در مطالعه ساختار شبکه راه در لهستان. Promet-Traffic Transp. 2014 ، 26 ، 235-242. [ Google Scholar ] [ CrossRef ]
- Schvaneveldt، RW; Durso، FT; Dearholt، ساختارهای شبکه DW در داده های مجاورت. در روانشناسی یادگیری و انگیزش ; مطبوعات دانشگاهی: کمبریج، MA، ایالات متحده آمریکا، 1989; جلد 24، ص 249–284. [ Google Scholar ]
- Laireiter، A. باومن، U. ساختارهای شبکه و توابع پشتیبانی: تحلیل های نظری و تجربی . Hemisphere Publishing Corp.: London, UK, 1992. [ Google Scholar ]
- Barabási, AL; Bonabeau, E. شبکه های بدون مقیاس. علمی صبح. 2003 ، 288 ، 60-69. [ Google Scholar ] [ CrossRef ]
- Vazquez, A. نتایج دقیق برای مدل باراباسی پویایی انسان. فیزیک کشیش لِت 2005 ، 95 ، 248701. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
- Bednarczyk، M. کوالچیک، ک. Kowalczyk، AM شناسایی نقاط شبه گره بر اساس داده های کمپین های تسطیح دقیق و GNSS. Acta Geodyn. ژئومتر. 2018 ، 15 ، 5-16. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
- Kowalczyk، AM تحلیل و ایجاد مدل های شبکه ارزش زیبایی شناختی منظر به عنوان عناصر مهم توسعه شهری پایدار. در مهندسی محیط زیست. مجموعه مقالات کنفرانس بین المللی مهندسی محیط زیست. ICEE _ دانشگاه فنی ویلنیوس گدیمیناس، گروه اقتصاد ساخت و ساز و دارایی: ویلنیوس، لیتوانی، 2014; جلد 9، ص. 1. [ Google Scholar ]
- کوالچیک، آ. Kowalczyk، K. نظریه شبکه در فرآیند ایجاد و تجزیه و تحلیل از حرکات پوسته عمودی. در مجموعه مقالات چهاردهمین کنفرانس جغرافیایی انفورماتیک، ژئوانفورماتیک و سنجش از دور، آلبنا، بلغارستان، 17 تا 26 ژوئن 2014. صص 545-552. [ Google Scholar ]
- باجروفسکی، تی. Kowalczyk، AM; Ogrodniczak، M. ساختارهای شبکه در توسعه نقشه های مداخله خدمات یکنواخت. SGEM Surv. جئول حداقل Ecol. مدیریت 2017 ، 17 ، 619-624. [ Google Scholar ]
- پاپاجئورگیو، GJ Agglomeration. Reg. علمی اقتصاد شهری 1979 ، 9 ، 41-59. [ Google Scholar ] [ CrossRef ]
- چوانگلین، FANG پیشرفت تحقیق و تعریف کلی در مورد استانداردهای شناسایی فضای تراکم شهری. در انجمن برنامه ریزی شهری ; دانشگاه تونگجی: شانگهای، چین، 2009; جلد 4، صص 1-6. [ Google Scholar ]
- یوهانسون، بی. Quigley، JM Aglomeration و شبکه ها در اقتصاد فضایی. پاپ Reg. علمی 2004 ، 83 ، 165-176. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
- هاپفر، ا. سایمرمن، آر. Nowak، A. Ocena i Waloryzacja Gruntów Wiejskich ; Państwowe Wydaw. Rolnicze i Leśne: ورشو، لهستان، 1982. [ Google Scholar ]
- باجروفسکی، تی. بیلوزور، ا. Cieślak، I. سنترا، ا. Szczepańska، A. Ocena i Wycena Krajobrazu ; Wyd. Educaterra: Olsztyn، لهستان، 2007. [ Google Scholar ]
- سنترا، ا. Cieślak, I. Kartograficzne Aspekty Oceny i Waloryzacji Przestrzeni ; Wydaw. Uniwersytetu Warmińsko-Mazurskiego: Olsztyn، لهستان، 2004. [ Google Scholar ]
- Lechnio, J. Jednostki krajobrazowe jako pola podstawowe oceny zagrożenia środowiska przyrodniczego depozycja substancji zakwaszajacych. Problemy Ekologii Krajobrazu 2004 , 12 . [ Google Scholar ]
- دروازه تحقیق. 2019. در دسترس آنلاین: https://www.researchgate.net/figure/Hex-bin-map-of-the-formulated-Change-Index-for-the-long-term-scenario-Each-hexagon_fig5_331863624 (دسترسی در 11 فوریه 2020).

شکل 1. مراحل ظهور شبکه با توجه به مسیر اختلاف مقدار حداقل: ( الف ) مرحله آشکار شدن رابطه حداقل اختلاف، و ( ب ) مرحله اول تجمیع ارزش و ظهور مناطق جدید. منبع: تحلیل خود
شکل 2. مراحل ظهور شبکه با توجه به مسیر اختلاف مقدار حداکثر: ( الف ) مرحله آشکار کردن رابطه حداکثر اختلاف. ب ) مرحله اول تجمیع ارزش و ظهور مناطق جدید. منبع: تحلیل خود
شکل 3. مراحل ظهور شبکه با توجه به مسیر کاهش مقدار حداقل: ( الف ) مرحله آشکار شدن رابطه کاهش حداقل مقدار. ( ب ) مرحله اول تجمیع ارزش. ج ) مرحله دوم تجمیع ارزش. ( د ) مرحله سوم تجمیع ارزش. ( ه ) مرحله چهارم تجمیع ارزش.
شکل 4. مراحل ظهور شبکه با توجه به مسیر کاهش حداکثر مقدار: ( الف ) مرحله آشکار شدن رابطه کاهش حداکثر مقدار. ( ب ) مرحله اول تجمیع ارزش. ج ) مرحله دوم تجمیع ارزش. ( د ) مرحله سوم تجمیع ارزش. منبع: تحلیل خود

شکل 5. مراحل ظهور شبکه با توجه به مسیر افزایش مقدار حداقل: ( الف ) مرحله آشکار شدن رابطه افزایش حداقل مقدار. ( ب ) مرحله اول تجمیع ارزش. ج ) مرحله دوم تجمیع ارزش. ( د ) مرحله سوم تجمیع ارزش. منبع: تحلیل خود
شکل 6. سطوح ظهور شبکه ها و مناطق فضایی جدید با توجه به مسیر افزایش مقدار حداکثر: ( الف ) مرحله آشکار شدن رابطه افزایش مقدار حداقل. ( ب ) مرحله اول تجمیع ارزش. ج ) مرحله دوم تجمیع ارزش. ( د ) مرحله سوم تجمیع ارزش. منبع: تحلیل خود
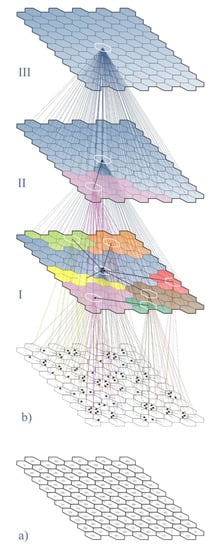
شکل 7. سطوح ظهور شبکه با توجه به مسیر حداکثر افزایش در شاخص تعامل فضایی (سطوح تجمع): ( الف ) زمینه های اساسی با مقادیر اختصاص داده شده که منعکس کننده یک پدیده مورد مطالعه است. ب ) مرحله آشکار شدن روابط. در این مورد، حداکثر مقدار افزایش می یابد. ( I ) مرحله اول تجمیع ارزش با توجه به مسیر افزایش مقدار حداکثر. ( II ) مرحله دوم تجمیع ارزش با توجه به مسیر افزایش مقدار حداکثر. ( III ) مرحله سوم تجمیع ارزش با توجه به مسیر افزایش مقدار حداکثر. منبع: تحلیل خود
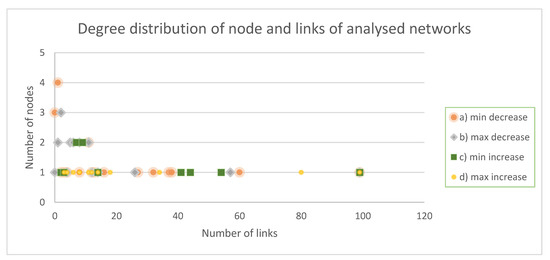
شکل 8. توزیع گره ها و پیوندها در ساختارهای شبکه توسعه یافته. کلید: مدل های شبکه بر اساس مسیرهای ( الف ) کاهش مقدار حداقل توسعه یافته است. ( ب ) حداکثر کاهش مقدار. ج ) حداقل افزایش ارزش؛ ( د ) حداکثر افزایش مقدار. منبع: تحلیل خود
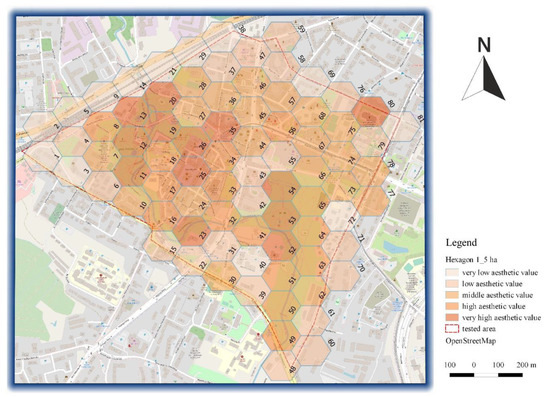
شکل 9. منطقه تجزیه و تحلیل. نقشه هگزبین ارزش زیبایی شناختی مورد نیاز برای مدل سازی شبکه. منبع: تحلیل خود در QGis و بر اساس داده های نقشه خیابان باز.
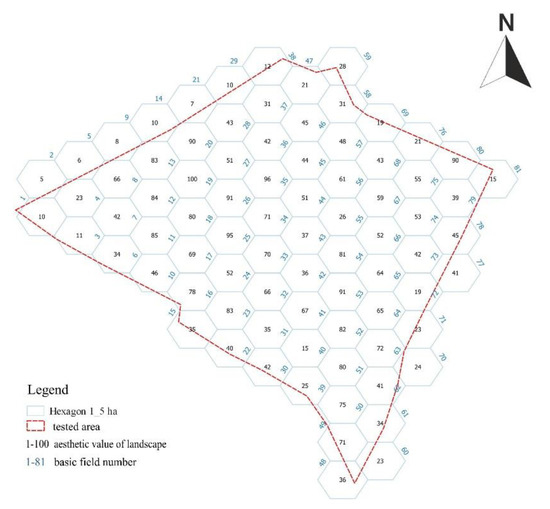
شکل 10. مرحله آشکار شدن روابط حداقل ارزش زیبایی شناختی چشم انداز کاهش می یابد. منبع: تحلیل خود
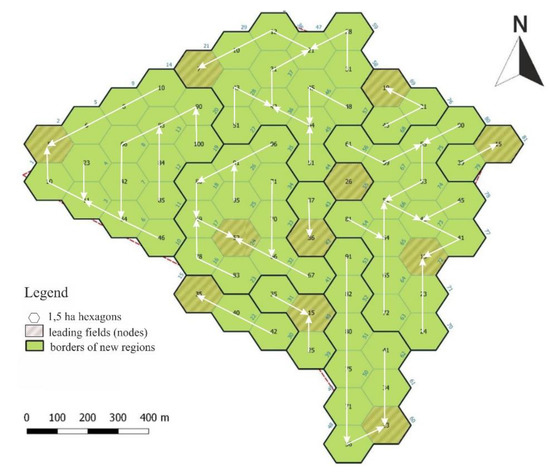
شکل 11. مرحله اول تجمیع ارزش زیبایی شناسی منظر با توجه به مسیر کاهش ارزش حداقل. کلید: فلش های سفید نشان می دهد که چگونه ارزش زیبایی شناختی منظره به حداقل کاهش می یابد.
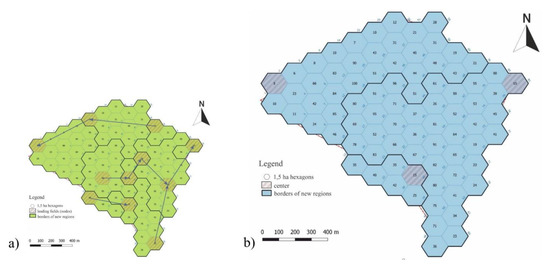
شکل 12. مرحله دوم تجمیع ارزش زیبایی شناختی منظر با توجه به مسیر کاهش ارزش حداقل. ( الف ) ترکیب مقادیر بر اساس اصل کاهش مقدار حداقل. ( ب ) مناطق جدید.
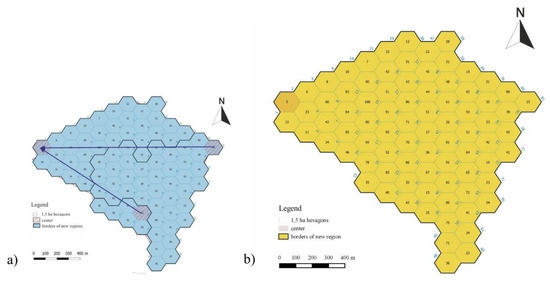
شکل 13. مرحله سوم تجمیع ارزش زیبایی شناختی منظر با توجه به مسیر کاهش حداقل ارزش. ( الف ) ترکیب مقادیر بر اساس اصل کاهش مقدار حداقل. ( ب ) مناطق جدید.





بدون دیدگاه