تکنیک های جدید زمین فضایی مبتنی بر MLR-RF: مقایسه ای با OK

روش‌های تخمین زمین‌آماری متکی به واریوگرام‌های تجربی هستند که عمدتاً نامنظم هستند و منجر به برازش مدل ذهنی و فرض توزیع نرمال در طول شبیه‌سازی‌های شرطی می‌شوند. در مقابل، الگوریتم‌های یادگیری ماشین (MLA) (1) عاری از چنین محدودیت‌هایی هستند، (2) می‌توانند اطلاعات را از منابع متعدد ترکیب کنند و بنابراین با افزایش علاقه به تخمین منابع و اتوماسیون بلادرنگ ظاهر می‌شوند. با این حال، MLA ها باید برای یادگیری قوی پدیده ها، دقت بهتر و کارایی محاسباتی مورد بررسی قرار گیرند. این مقاله MLA ها، به عنوان مثال، رگرسیون خطی چندگانه (MLR) و جنگل تصادفی (RF)، با کریجینگ معمولی (OK) مقایسه می کند. این تکنیک‌ها در مجموعه داده‌های Walkerlake در دسترس عموم اعمال شد، در حالی که مجموعه داده جامع Walker Lake تأیید شد. نتایج MLR معنی دار بود (p <10 × ^10-5 )، با ضرایب همبستگی 0.81 (R-square = 0.65) در مقایسه با 0.79 (R-square = 0.62) از روش های RF و OK. علاوه بر این، MLR خودکار شد (عاری از یک مرحله میانی از مدل‌سازی واریوگرام مانند OK)، تخمین‌های بی‌طرفانه تولید کرد، نمونه‌های کلیدی را شناسایی کرد که مناطق مختلف را نشان می‌داد، و کارایی محاسباتی بالاتری داشت.

کلید واژه ها:

کریجینگ معمولی (OK) ; جنگل تصادفی (RF) ; الگوریتم های یادگیری ماشین (MLA) ; زمین آمار ; تخمین فضایی ; SHAP ; یادگیری ماشینی قابل تفسیر

1. مقدمه

برآورد صفات توزیع شده در فضا یکی از چالش برانگیزترین مشکلات در معدن [ 1 ] (درجات ژئوشیمیایی)، نفت [ 2 ] (تخلخل، نفوذپذیری)، محیطی [ 3 ] (گازهای خطرناک، مواد)، کشاورزی [ 4 ] (خاک) است . ژئوشیمی، بازده)، ژئوفیزیک [ 5 ] (سیگنال های مقاومت)، و سایر زمینه های مهندسی [ 6 ، 7 ]. تکنیک‌های زمین‌آماری نیاز به مدل‌سازی تغییرپذیری فضایی دارند، به عنوان مثال، مدل واریوگرام ذهنی متناسب با واریوگرام‌های تجربی اغلب نامنظم [ 8 ]. تکنیک های زمین آماری فرضیات ثابت بودن و داده های نرمال شده را قبل از شبیه سازی مشروط فرض می کنند [ 2 ,9 ، 10 ، 11 ]. داده ها برای تخمین فضایی در حوزه علوم زمین عمدتاً از طریق روش های حفاری کمیاب و پرهزینه به دست می آیند [ 12 ، 13 ، 14 ، 15 ]. بنابراین، MLA های قوی باید بررسی شوند. تصمیم گیری در زمان واقعی، به ویژه تقاضا برای اتوماسیون در صنایع مختلف، نیازمند مدل های تخمین فضایی کارآمد و زمان بر است [ 16 ، 17 ]. بدون نظارت [ 8 , 18 , 19 ] و تحت نظارت [ 8 , 20 , 21 , 22 , 23 , 24 ., 25 , 26 , 27 , 28 , 29 , 30 , 31 , 32 , 33 , 34 , 35 , 36 , 37 , 38 , 39 , 40 , 41 , 42 , 4 , 4 , 4 , 4 , 4 , 4 _ _ , 50 , 51 , 52 , 53 ,54 ، 55 ] الگوریتم های یادگیری ماشین (MLAs) به عنوان جایگزین یا به عنوان ترکیبی با مدل های زمین آماری، به عنوان مثال، OK-Artificial Neural Network (ANN) [ 46 ] استفاده شده است. ماشین بردار پشتیبانی (SVM) و کریجینگ [ 55 ]; ANN-Median Indicator Kriging (MIK) [ 56 ] برای درونیابی فضایی در علوم محیطی [ 44 ، 57 ، 58 ]، پیش بینی آب و هوا [ 20 ، 59 ، 60 ]، اکولوژی [ 51 ، 61 ، 62 ]، جغرافیا [ 32 ] ، جغرافیا [ 32 ] , پیش بینی زمین لغزش [ 63 ,64 ، 65 ]، نقشه برداری ژئوشیمیایی [ 36 ، 43 ، 46 ، 48 ]، ژئوفیزیکی [ 66 ]، درونیابی درجه معدنی [ 8 ، 21 ، 45 ، 47 ، 55 ، 67 ، 68 ، [ 69 ] شبکه عصبی و انواع آنها. 29 , 34 , 53 , 54 , 70 , 71 , 72 , 73] به طور گسترده در حوزه های متعدد استفاده شده است. آنها عملکرد نسبتاً بهتری دارند اما به دلیل کمبود نمونه های آموزشی در کاربردهای فضایی، به خوبی تعمیم نمی یابند [ 74 ]. به خوبی ثابت شده است که نمونه های همسایه بر درجه درون یابی در یک موقعیت/زمان معین تأثیر می گذارند. بنابراین، افزودن نمونه‌های مرتبط، عملکرد مدل‌ها را بهبود می‌بخشد [ 75 ، 76 ]. چندین الگوریتم تخمین فضایی مبتنی بر RF نیز در ادبیات ارائه شده است [ 38 ، 49 ، 52 ، 77]. این تحقیق MLA هایی را بررسی می کند که می توانند همه نمونه ها را ترکیب کنند و الگوها را در سطح جهانی با راندمان محاسباتی بالا ثبت کنند. برای بررسی بیشتر MLAها، به عنوان مثال، چگونه و از کدام مناطق الگوهای امیدوارکننده یاد گرفته می‌شوند، از الگوریتم SHapley Additive Explanations (SHAP) [ 78 ، 79 ] استفاده شد. در عصر امروزی اتوماسیون و بهینه‌سازی/مدل‌سازی بی‌درنگ [ 16 ، 17 ]، نیاز به کشف تکنیک‌های جدید تخمین فضایی مبتنی بر هوش مصنوعی (AI) وجود دارد که می‌تواند داده‌ها را از منابع متعدد با دقت، توضیح‌پذیری و کارایی محاسباتی بهتر ترکیب کند. . بخش بعدی مروری بر ادبیات، پس‌زمینه‌ای از MLR، RF، و SHAP، و پس از آن یک مطالعه موردی، نتایج، بحث و نتیجه‌گیری ارائه می‌کند.

2. بررسی ادبیات

تکنیک‌های تخمین فضایی سنتی مانند چند ضلعی، فاصله معکوس و توان فاصله معکوس روش‌های هندسی هستند که با تکنیک‌های احتمالاتی مانند OK [ 80 ] جایگزین شده‌اند. بیشتر تکنیک های تخمین خطی ترکیبی خطی وزنی از مقادیر نمونه اطراف (مثلاً درصد عیار فلز در یک کانسار) هستند. کریجینگ به طور کلی یک مورد خاص از مدل رگرسیون خطی است [ 81 ]. وزن های به دست آمده با استفاده از روش کریجینگ بر ساختار فضایی واریوگرام متکی است، که نشان دهنده همبستگی خودکار فضایی مقادیر اندازه گیری شده از نمونه های توزیع شده تصادفی است [ 11 ]]. Simple Kriging (SK) فرض می کند که میانگین مشخص و ثابت است. OK فرض می کند که میانگین در همسایگی محلی ناشناخته و ثابت است. Universal Kriging (UK) تغییرات خطی میانگین را در حوزه فضایی به طور همزمان فرض می‌کند در حالی که متغیرهای فضایی را مدل‌سازی می‌کند [ 11 ]. انگلستان ممکن است باعث بی ثباتی شود زیرا مختصات به طور همزمان در نظر گرفته می شوند. بنابراین، محققان مدل‌سازی روند و اجزای باقی‌مانده را به طور جداگانه توصیه می‌کنند [ 31 ، 82 ]. تخمین کریجینگ نیز برای خوشه بندی در نمونه ها حساب می کند. و واریانس تخمین را گزارش می‌کند که برای مدل‌سازی عدم قطعیت از طریق شبیه‌سازی‌های شرطی علاوه بر تغییرپذیری در مقیاس کوتاه [ 83 ] استفاده می‌شود.

MLR به طور گسترده برای تخمین فضایی به اشکال مختلف استفاده شده است. به عنوان مثال، یک روش MLR متغیرهای محیطی را در مقیاس درشت‌تر و سپس در مقیاس محلی دقیق‌تر تخمین زد [ 84 ]. چندین نوع دیگر شامل رگرسیون مبتنی بر خوشه بندی [ 85 ] است. خودرگرسیون رگرسیون خطی محلی مشتق از مقادیر قبلا شناخته شده [ 86 ]. و رگرسیون غیرخطی با ماتریس وزن فضایی [ 87 ]. یک راه حل رگرسیون خطی که مسئله را با تحلیل ویژه [ 88 ] و تحلیل عاملی [ 82 ] کاهش می دهد.] نیز گزارش شده است. الگوریتم‌های مختلف با هم مقایسه می‌شوند، زیرا ترکیب‌ها مدل‌های روند و باقیمانده را به طور جداگانه نشان می‌دهند. میانگین نمره از بهترین این ترکیب ها برای گزارش برآوردهای نهایی استفاده می شود [ 31 ].

برای جلوگیری از مدل‌سازی واریوگرام متناوب، دستی و ذهنی، الگوریتم ژنتیک منطق فازی ترکیبی مبتنی بر شبکه عصبی [ 89 ]، الگوریتم ژنتیک [ 34 ] و بهینه‌سازی پارامتر مبتنی بر کلونی زنبور [ 70 ] برای تخمین فضایی استفاده شده است. گزارش شده است که الگوریتم RF عملکرد بهتری نسبت به مدل رگرسیون خطی فضایی [ 38 ، 81 ] حتی با نمونه های بسیار کمی دارد، به عنوان مثال، برای پیش بینی کانی سازی مس با استفاده از 8 ویژگی زمین شناسی و دو عنصر کمیاب [ 35 ]. RF به عنوان یک روش منعطف برای ترکیب، ترکیب و گسترش متغیرها از انواع مختلف ثابت شده است که منجر به نقشه‌برداری اطلاعاتی از خطای پیش‌بینی می‌شود [ 37 ]]. اخیراً، درون‌یابی فضایی RF از مشاهدات در نزدیک‌ترین مکان‌ها و فواصل آن‌ها از محل پیش‌بینی استفاده می‌کند [ 36 ، 77 ]. فواصل همسایگی جهت دار، به عنوان مثال، شیب بالا و پایین از نقاط مشاهده، می تواند استفاده شود. با این حال، شدت محاسباتی به طور تصاعدی با افزایش متغیرها رشد می کند [ 51 ]. بنابراین، تجزیه و تحلیل مؤلفه اصلی (PCA) به متریک فاصله از مختصات نمونه برای کاهش ابعاد فضایی برای به دست آوردن یک مدل RF-PCA که عملکرد پیش‌بینی بالاتری را در اعتبارسنجی در مقایسه با روش‌های دیگر نشان می‌دهد، اعمال شد [ 90 ].

تکنیک‌های تخمین فضایی مبتنی بر یادگیری ماشینی (ML) مناسب‌تر باید توسعه یابد که دقیق باشد و بتواند ویژگی‌های متعددی را در خود جای دهد. با این حال، بدون پیچیدگی محاسباتی. ترکیبات دیگری از اصطلاحات در یک مدل MLR ممکن است مورد بررسی قرار گیرد، که نشان دهنده تعاملاتی است که فرآیند مورد بررسی را توصیف می کند. بسته به دامنه، ویژگی های مختلفی می تواند تولید شود. به عنوان مثال، فاصله ها و درجه های نمونه های همسایه می تواند در حوزه فضایی حیاتی باشد.

3. مواد و روشها

3.1. رگرسیون خطی چندگانه (MLR)

MLR [ 47 ، 91 ، 92 ] یک تکنیک شناخته شده است که پارامترهای p + 1 را تخمین می زند. $β_{0}, β_{1}, β_{2} \dots β_{p}$ تعریف یک رابطه خطی بین ویژگی/های ورودی ( $x_{i 1}, x_{i 2} \dots x_{i p})$ و ویژگی خروجی $(y_{i})$ برای n نمونه داده شده $i = 1, 2, \dots n .$

y من ˆ = β 0 + β 1 ایکس من 1 + β 2 ایکس من 2 + \dots + β پ ایکس من ص + ε

(1)

مدل با فرضیات معتبر است که ویژگی های ورودی مستقل هستند (همبستگی بالایی ندارند)، خطا $e_{i} = \hat{y_{i}} - y_{i}$ باید ثابت (همسانی)، مستقل و به طور معمول توزیع شود. عبارت $ε$ را می توان به عنوان نویز نامرتبط نادیده گرفت، در حالی که سایر پارامترها به صورت زیر تعیین می شوند:

β = (ایکس تی ایکس) - 1 ایکس تی Y

(2)

جایی که X است $(n \times p + 1)$ ماتریسی با ستونی از وحدت و Y نشان دهنده $(1 \times p + 1)$ بردار ستون خروجی با پارامتر intercept $β_{0}$ در انتهای ستون تعداد بیشتری از ویژگی‌ها به یادگیری روابط غیرخطی کمک می‌کند و MLR را قادر می‌سازد تا مسائل پیچیده را با تنوع بالا درک کند [ 47 ، 48 ، 49 ]. یک مدل خودرگرسیون فضایی خطی در معادله (3) در زیر شامل چهار عبارت به عنوان مدل های خودرگرسیون فضایی با عبارت خطای خودرگرسیون فضایی (SAR-SAR) است [ 93 ]. اصطلاحات شامل (1) متغیرهای وابسته وزنی در یک منطقه با مقادیر همسایه مرتبط، و به دنبال آن دو عبارت رگرسیون، یعنی (2) متغیر با تاخیر مکانی متغیر وابسته، (3) متغیرهای دارای تاخیر مکانی برخی یا همه متغیرهای برون زا هستند. و (4) دو عبارت آخر نشان دهنده مدل فضایی برای اختلالات تصادفی [ 93 ] است.

y = λ W y + X β 1 + دبلیو ایکس β 2 + ρ W u + ε | λ | و | ρ | < 1

(3)

این وابستگی ها منجر به تخمین پارامترها با روش حداقل مربعات معمولی (OLS) [ 93 ] شد که تعاملات بین متغیرهای وابسته، متغیرهای کمکی مستقل و عبارات خطا را بیان می کند [ 94 ].

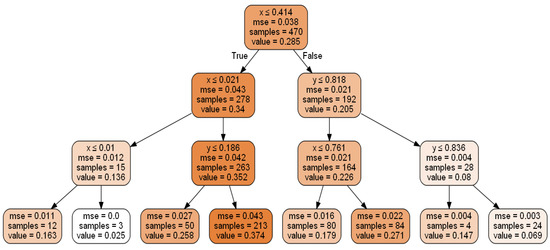
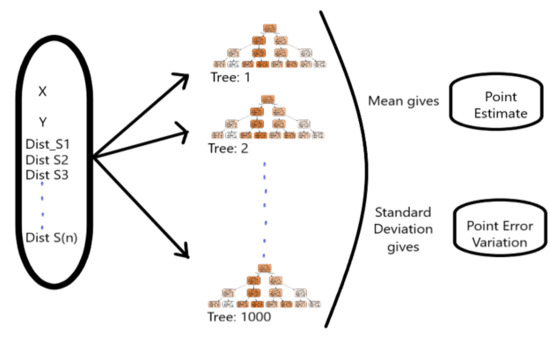
3.2. الگوریتم جنگل تصادفی

جنگل تصادفی یک MLA است که توسط Breiman [ 95 ] توسعه یافته است که از مجموعه ای از درختان تصمیم تشکیل شده است که در آن هر درخت تصمیم نشان دهنده آرایش متغیرهای آموخته شده از مجموعه داده است. برای کشف الگوهای داده از زمینه های مختلف برای حل مسائل رگرسیون [ 47 ، 48 ، 49 ] استفاده می شود. در یک درخت تصمیم، یک درخت وارونه در یک سلسله مراتب با انتخاب بهترین ویژگی ها از زیر مجموعه های مجموعه داده نمونه به صورت متوالی ساخته می شود ( شکل 1 را ببینید ). روش مجموعه بودن جنگل تصادفی از کیسه‌بندی برای ترکیب درخت‌های تصمیم چندگانه با کاهش بیش‌برازش و بهبود صحت اعتبارسنجی تصمیم درخت فردی استفاده می‌کند [ 95 ].

شکل 1 درخت تصمیم را برای پیش بینی متغیر-V (به عنوان مثال، غلظت شیمیایی خروجی بر حسب ppm) با استفاده از داده های نمونه بر اساس موقعیت های مکانی (x و y) نشان می دهد. برخی از معیارهای مورد استفاده برای توقف این فرآیند ساخت درخت عبارتند از: حداکثر عمق (عمق درخت)، حداقل نمونه‌های_برگ (حداقل نمونه‌ها در گره‌های برگ)، و آستانه یک متریک عملکرد (میانگین مطلق خطا (MAE) / میانگین مربعات خطا (MSE) ) [ 47 ، 48 ، 49 ]. درخت را می توان برای تخمین مقادیر در یک نقطه ناشناخته با پرسیدن سوالات در گره ها استفاده کرد. به عنوان مثال، یک پرس و جو به گره ریشه درخت از طریق گره های میانی و در نهایت به گره برگ، که خروجی، یعنی مقدار/کلاس پیش بینی شده را نشان می دهد، هدایت می شود.

هر کادر در شکل 1 بالا، تقسیمی از داده های نمونه را با استفاده از:

-row1: بهترین ویژگی ورودی انتخاب شده و مقادیر قطع آن در آن زیر مجموعه
-row2: میانگین مربعات خطا برای آن زیر مجموعه
-row3: تعداد نمونه ها در آن زیر مجموعه
-row4: V (خروجی به عنوان مثال، غلظت شیمیایی) در آن زیر مجموعه (مقادیر بین 0-1 نرمال می شوند، که برای درخت تصمیم ضروری نیست).

شدت رنگ، بزرگی ارزش مورد علاقه را نشان می دهد.

بهترین تقسیم (مقدار برش) برای بهترین متغیر ورودی (مختصات فضایی در فضای دکارتی) همگن ترین زیرگروه ها [ 96 ] را از نظر خروجی ها تولید می کند (مناطق کم، متوسط یا با درجه بالا در این مورد). یک الگوریتم مناسب مانند طبقه بندی و درخت رگرسیون (CART) به طور مکرر نقاط برش بالقوه را جستجو می کند و داده ها را در هر تقسیم ممکن برای انتخاب بهترین تقسیم تقسیم می کند [ 97 ]. درخت تصمیم که در شکل 1 نشان داده شده استدارای عمق 4 سطح گره ریشه در سطح 1 قرار می گیرد. سطوح 2 و 3 دارای گره های میانی هستند و گره های برگ تنها با مقادیر خروجی در سطح 4 تنظیم می شوند. در سطح 1، بهترین ویژگی انتخاب شده x است و دو زیر مجموعه برای سطح 2 بر اساس مقادیر کلاس x ایجاد شد. در سطح 2، بهترین ویژگی های انتخاب شده برای هر دو زیر مجموعه به ترتیب x و y بودند. بر اساس اهمیت x و y در هر دو زیر مجموعه در سطح 2، تقسیم بیشتر به چهار زیر مجموعه برای سطح 3 انجام شد. در سطح 3، x بهترین ویژگی برای دو زیر مجموعه بود، در حالی که y به عنوان بهترین ویژگی برای دو زیر مجموعه دیگر انتخاب شد. . بر اساس مقادیر زیر مجموعه‌های مربوطه، مجموعه داده به هشت زیر مجموعه برای گره‌های برگ/سطح 4 تقسیم شد.

همانطور که در شکل 1 مشاهده می شود ، “x” و “y” هر دو ویژگی های فضایی حیاتی برای پیش بینی خروجی “V” با منطقه بندی داده های دریاچه واکر در فضای دکارتی هستند. این توانایی برای یافتن اهمیت ویژگی زمانی که ویژگی ها به دلیل در دسترس بودن اطلاعات کمکی در مورد فرآیند به طور قابل توجهی افزایش می یابد، نقش مهمی ایفا می کند. درخت تصمیم ویژگی های اساسی را شناسایی می کند و بصری است زیرا نتایج را در مجموعه ای از قوانین if-then از گره های بالا به پایین توضیح می دهد. با این حال، نسبت به سایر تکنیک‌های رگرسیون از دقت اعتبار پایین‌تر و شانس بیشتری برای تطبیق بیشتر رنج می‌برد [ 47 ، 48 ، 49 ].

یک درخت منفرد یک نتیجه پایدار برای مجموعه داده نمونه جدید ایجاد نمی کند. بنابراین، چندین درخت از یک زیرمجموعه جداگانه از داده های تصادفی که با جایگزینی از یک مجموعه داده معین ترسیم شده اند، تولید می شوند [ 47 ، 48 ، 49 ]. Random Forest با برازش چندین درخت از طریق نمونه‌برداری مجدد تصادفی از مجموعه داده نمونه با/بدون جایگزینی، بر مشکل صحت درخت تصمیم غلبه می‌کند. برای تولید نتایج تعمیم‌یافته، RF از کیسه‌بندی برای ترکیب درختان متعدد استفاده می‌کند، به عنوان مثال، در جایی که مقدار پیش‌بینی‌شده نهایی میانگین (در صورت رگرسیون) یا احتمال وقوع (در صورت طبقه‌بندی) خروجی‌های همه درختان است [ 47 ، 48 ، 49]. درخت تصمیم نیز به عنوان یادگیرنده پایه در روش‌های گروهی مانند جنگل تصادفی برای بهبود فراپارامترها و دقت اعتبارسنجی استفاده می‌شود. ابرپارامترهای درخت تصمیم مختلف مانند Min_samples_leaf (حداقل نمونه های مورد نیاز در یک گره برگ)، Min_samples_split (حداقل نمونه های استفاده شده برای تقسیم مجموعه داده)، Max_features (حداکثر ویژگی های مجاز برای ساخت درخت)، و Max_depth (حداکثر سطح درخت تصمیم گیری) عمق) برای کاهش بیش از حد برازش تنظیم شده اند.

3.3. تعمیم مدل و تنظیم فراپارامتر

اکثر مدل‌های رگرسیون MLA از «سوگیری/زیاد برازش» یا «واریانس/بیش برازش» رنج می‌برند. بنابراین، وظیفه اصلی یافتن تعادل بین آن ها با جستجوی فراپارامترهای خاص الگوریتم است. فراپارامترها پارامترهای مرتبط با هر مدل رگرسیونی هستند که نمی توان از داده های نمونه یاد گرفت و باید قبل از فرآیند برازش تنظیم شوند [ 47 ، 48 ، 49 ]. فراپارامترهای بهینه با ارائه مجموعه‌ای از داده‌های نمونه اعتبارسنجی به دست می‌آیند که در آموزش با استفاده از تنظیم «اعتبار متقابل» یا «نگه‌دار» شرکت نکرده‌اند [ 47 ، 48 ، 49 ، 98 ]]. پس از تقسیم داده های نمونه، در صورت توقف یا اعتبارسنجی متقابل، جستجوی فراپارامترها معمولاً در یک “شبکه” با استفاده از جستجوی فاکتوریل کامل انجام می شود.

یک مدل رگرسیون برای همه ترکیبات محدوده هایپرپارامتر ساخته شده است تا بهترین ترکیب را با استفاده از یک استراتژی اعتبارسنجی مناسب پیدا کند. اعتبار سنجی یک استراتژی نگهدارنده زمانی است که 20 درصد از داده های نمونه برای اعتبارسنجی پارامترها، و اعتبار 10 برابری، به عنوان مثال، زمانی که ده زیر مجموعه داده برای تأیید پارامترهای تنظیم شده استفاده می شود [ 47 ، 48 ، 49 ، 98 ] . به عنوان مثال، در استراتژی اعتبارسنجی متقابل 10 برابری، داده ها به ده زیر مجموعه تقسیم می شوند، در حالی که آموزش بر روی 9 زیر مجموعه و آزمایش بر روی زیر مجموعه دهم انجام می شود. این فرآیند ده بار تکرار می شود و هر زیر مجموعه ای که برای آزمایش استفاده می شود متفاوت است [ 47 ، 48 ، 49 ، 98]. از سوی دیگر، در استراتژی نگه‌داری، داده‌های نمونه به طور تصادفی به دو بخش 80:20 تقسیم می‌شوند، یعنی 80 درصد داده‌های نمونه برای آموزش و 20 درصد برای اهداف تأیید در طول تنظیم فراپارامترها استفاده می‌شود. برای هر دو MLR و RF، استراتژی اعتبارسنجی متقاطع ده برابری برای یافتن مقادیر تنظیم بهینه استفاده شد. برخی از نویسندگان همچنین از ترکیبی از راهبردهای نگهدارنده و اعتبار متقابل استفاده کرده اند [ 23 ، 99 ، 100 ، 101 ، 102 ، 103 ]. با این حال، هزینه محاسباتی جستجوی شبکه به طور تصاعدی با عمق فضای جستجوی فراپارامترها، به ویژه با یک استراتژی اعتبارسنجی متقابل، افزایش می‌یابد.

3.4. سنجش عملکرد

همه مدل‌های رگرسیون رابطه ورودی به خروجی را با به حداقل رساندن یک متریک خطا (یعنی عدم تشابه بین خروجی مدل و خروجی واقعی) مانند «میانگین مربعات خطا (MSE)» یا «میانگین مطلق خطا (MAE)» بیان می‌کنند [ 47 ، 48 ، 49 ]. MSE و خطای میانگین مربعات ریشه “RMSE” قابل تمایز هستند، در حالی که MSE بیشتر از RMSE و MAE مستعد ابتلا به موارد پرت است [ 104 ]. مقدار R-squared مکمل نسبت واریانس خطا = است $\sum {(\hat{y} - y)}^{2}$ به واریانس توضیح داده شده $\sum {(y - \bar{y})}^{2}$ داده شده به صورت:

آر 2 = 1 - \sum ( y ˆ - y ) 2 \sum ( y - y ¯ ) 2

(4)

با این حال، به جای استفاده از یک معیار عملکرد واحد، مانند ضریب همبستگی یا مقدار R-squared، محققان پیشنهاد می کنند از یک “مقدار مهارت” برای ترکیب مهم ترین معیار عملکرد به عنوان یک آمار خلاصه استفاده شود [ 24 ، 25 ، 105 ]. این اصطلاح چندین معیار عملکرد مهم مانند “R_squared”، “میانگین مطلق خطا (AME)”، “میانگین مطلق خطا (MAE)” و “ریشه میانگین مربعات خطا (RMSE)” را ترکیب می کند [ 25 ]. ارزش مهارت را می توان به صورت زیر ارائه کرد:

ارزش مهارت = [AME + MAE + RMSE + 100 * (1 - R_مربع)]

(5)

بهترین روش روشی با کمترین ارزش مهارت است.

3.5. الگوریتم بهینه سازی بیزی (BOA)

منظم سازی برای یافتن بهترین تناسب بین واریانس کم، به عنوان مثال، زیر برازش، و واریانس بالا (یعنی اضافه برازش) اعمال می شود. بهترین مقادیر Hyperparameter با استفاده از یک استراتژی اعتبار سنجی متقابل Grid یا Bayesian [ 47 ، 48 ، 49 ] جستجو می شود. BOA [ 40 , 106 , 107 , 108 ] یک روش کارآمد برای یافتن فراپارامترها با استفاده از قضیه بیز است. بر اساس قضیه بیز، احتمال شرطی یک رویداد عبارت است از:

P(A|B) = P(B|A) ∗ P(A)/P(B)

(6)

اصطلاح P(B) برای عادی سازی استفاده می شود که در مورد بهینه سازی مورد نیاز نیست. بنابراین، پس از حذف P(B)، احتمال خلفی P(A|B) ضربی از احتمال P(B|A) و P(A) قبلی است. نمونه های فراپارامتر احتمالی ( $x_{1}, x_{2}, x_{3} \dots x_{n}$ ) و هزینه ارزیابی شده آنها از تابع هدف $f (x_{1}), f (x_{2}), f (x_{3}) \dots f (x_{n})$ داده D را تشکیل می دهد و برای محاسبه پیشین استفاده می شود. تابع احتمال P(D|f) با جمع آوری داده های بیشتر تغییر می کند، به عنوان مثال، $(x_{n + 1}, f (x_{n + 1}))$ . احتمال پسین که تابع هدف جایگزین P(f|D) نیز نامیده می‌شود، دانش/تقریبی تابع هدف را نشان می‌دهد و برای ارزیابی هزینه نمونه‌های کاندید مختلف با استفاده از رابطه (7) زیر استفاده خواهد شد.

P(f|D) = P(D|f) ∗ P(f)

(7)

احتمال پسین صرفاً حاصل ضرب احتمال و شرایط قبلی است. عبارت ‘f’ نشان دهنده تابع هدف است که باید حداکثر شود. D داده های متشکل از نمونه ها را نشان می دهد (مقادیر فراپارامترهای مختلف $x_{1}, x_{2}, x_{3} \dots x_{n}$ )، ارزیابی/دیده شده تا کنون) و هزینه های مرتبط با آنها $f (x_{1}), f (x_{2}), f (x_{3}) \dots f (x_{n})$ . پس از برازش تابع P(f|D) توسط یک تکنیک مدل‌سازی پیش‌بینی‌کننده مانند RF یا فرآیند گاوسی، تابع جانشین برای آزمایش نمونه‌های کاندید مختلف استفاده می‌شود. مجموعه جدیدی از مقادیر فراپارامتر از مدل با استفاده از احتمال بهبود (PI) ارائه شده در معادله (8) نمونه برداری شده است. اگر PI قابل توجه باشد، ابرپارامترها برای تعیین مقدار تابع هدف دقیق آنها با استفاده از اعتبارسنجی متقاطع 10 برابری استفاده می‌شوند و داده‌ها برای بازسازی تابع با استفاده از معادله (7) به روز می‌شوند.

PI = cdf((mu-best_mu)/stdev)

(8)

که در آن cdf() = تابع توزیع تجمعی نرمال، mu = میانگین تابع جایگزین (P(f|D)) برای یک نمونه معین x، stdev = انحراف استاندارد تابع جایگزین برای یک نمونه معین x، و best_mu = میانگین تابع جانشین برای بهترین مجموعه فراپارامترهای یافت شده تاکنون.

جزئیات گام به گام الگوریتم BOA در زیر توضیح داده شده است: راه اندازی: تولید داده ها

D_{0}

مجموعه ای از مقادیر فراپارامتر (

x_{1}, x_{2}, x_{3} \dots x_{n}

) و مقادیر تابع هدف مرتبط

f (x_{1}), f (x_{2}), f (x_{3}) \dots f (x_{n})

یعنی مقادیر R-square بر اساس اعتبارسنجی متقاطع 10 برابری از الگوریتم RF/MLR).

برای t = 1…N تکرار

1.: تابع هدف (مقدار R-square) را با استفاده از رابطه (7) مدل کنید (P(f|D _t−1 ).
2.: best_mu را پیدا کنید یعنی میانگین بهترین مقادیر از مدل (P(f|D _t−1 ))
3.: مجموعه جدیدی از بهترین نامزدها را پیدا کنید $x_{n + 1} \dots$ (مقادیر فراپارامتر) از طریق PI
4.: تابع/های هدف واقعی را محاسبه کنید $f (x_{n + 1}) \dots$ توسط الگوریتم RF/MLR، یعنی مقدار R-square بر اساس اعتبارسنجی متقاطع 10 برابری.
5.: به روز رسانی داده ها به عنوان $D_{t}$ ، یعنی $x_{1}, x_{2}, x_{3} \dots x_{n + 1}, \dots$ و مقادیر تابع هدف مرتبط $f (x_{1}), f (x_{2}), f (x_{3}) \dots f (x_{n + 1}),$ … و به مرحله 1 بروید
6.: اگر PI ناچیز است یا به N تکرار رسیده است، توقف کنید و بهترین پارامترها را گزارش کنید.

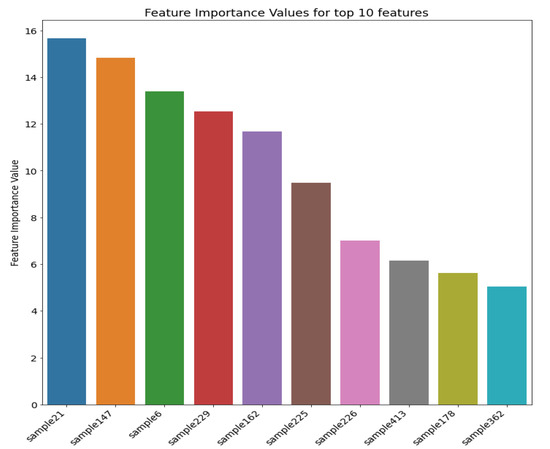
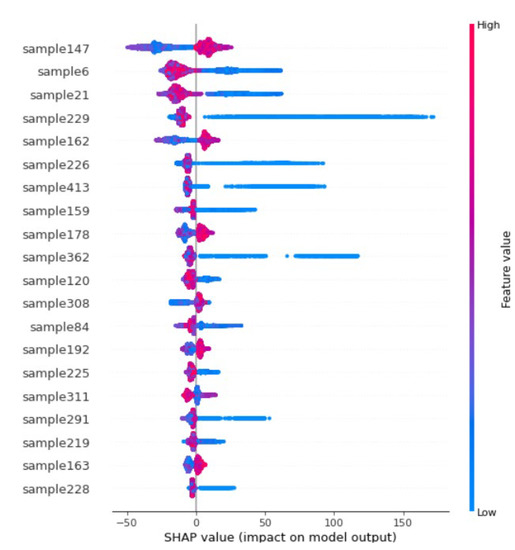
3.6. توضیحات افزودنی SHapley (SHAP)

MLA ها به عنوان مدل های جعبه سیاه عمل می کنند. بنابراین، اخیراً علاقه‌ای در میان جامعه هوش مصنوعی (AI) برای تفسیر مدل‌ها با استفاده از الگوریتم‌های هوش مصنوعی قابل توضیح [ 78 ، 80 ] ایجاد شده است. چنین تفاسیری امکان درک بهتر مکانیسم‌های درونی را فراهم می‌آورد که منجر به اطمینان بیشتر در کاربرد و استفاده از آنها می‌شود [ 109 ]. الگوریتم SHAP [ 110 ] به طور گسترده در حوزه های مختلف برای تفسیر MLA ها [ 28 ، 98 ] برای تعیین اهمیت و تأثیر ویژگی های ورودی بر مقادیر خروجی استفاده می شود.

الگوریتم SHAP از تئوری بازی های تعاونی سرچشمه گرفته است، جایی که بازیکنان مختلف برای افزایش پرداخت نهایی همکاری می کنند. در تنظیمات یادگیری ماشین، کار پیش‌بینی با استفاده از یک نمونه مجموعه داده را می‌توان یک بازی در نظر گرفت که در آن ویژگی‌های مختلف (یعنی بازیکنان) برای انجام یک بازی (یعنی پیش‌بینی مقدار خروجی) همکاری می‌کنند. در شکل اصلی، الگوریتم SHAP اهمیت نسبی بازیکنان مختلف را با گرفتن جایگشت های هر بازیکن به ترتیب و مشاهده افزایش پرداختی که هر بازیکن انجام می دهد، محاسبه می کند. به طور مشابه، مقادیر Shapley هر ویژگی را می‌توان با در نظر گرفتن تمام جایگشت‌های آن‌ها به صورت سری (برای هر نمونه) محاسبه کرد تا تفاوت میانگین مقدار پیش‌بینی و مقدار پیش‌بینی برای آن نمونه خاص را کمی‌سازی کند. به عبارت دیگر، مقدار Shapley هر ویژگی مربوط به سهم ویژگی در دور کردن پیش‌بینی نمونه از میانگین است. اهمیت جهانی هر ویژگی با در نظر گرفتن میانگین مقادیر مطلق Shapley مربوطه در سراسر مجموعه داده گزارش می شود. هر چه مقدار Shapley بیشتر باشد، سهم ویژگی بیشتر است، که نشان می‌دهد این ویژگی برای کار پیش‌بینی آن نمونه، حیاتی‌تر است. بزرگی اهمیت ویژگی مقادیر Shapley اهمیت را گزارش می‌کند، در حالی که نمودار خلاصه مقادیر Shapley نشان‌دهنده تأثیر بر خروجی است. مقدار مثبت به معنای همبستگی مثبت بین مقدار ویژگی و ویژگی پیش بینی شده از میانگین و بالعکس است. اهمیت جهانی هر ویژگی با در نظر گرفتن میانگین مقادیر مطلق Shapley مربوطه در سراسر مجموعه داده گزارش می شود. هر چه مقدار Shapley بیشتر باشد، سهم ویژگی بیشتر است، که نشان می‌دهد این ویژگی برای کار پیش‌بینی آن نمونه، حیاتی‌تر است. بزرگی اهمیت ویژگی مقادیر Shapley اهمیت را گزارش می‌کند، در حالی که نمودار خلاصه مقادیر Shapley نشان‌دهنده تأثیر بر خروجی است. مقدار مثبت به معنای همبستگی مثبت بین مقدار ویژگی و ویژگی پیش بینی شده از میانگین و بالعکس است. اهمیت جهانی هر ویژگی با در نظر گرفتن میانگین مقادیر مطلق Shapley مربوطه در سراسر مجموعه داده گزارش می شود. هر چه مقدار Shapley بیشتر باشد، سهم ویژگی بیشتر است، که نشان می‌دهد این ویژگی برای کار پیش‌بینی آن نمونه، حیاتی‌تر است. بزرگی اهمیت ویژگی مقادیر Shapley اهمیت را گزارش می‌کند، در حالی که نمودار خلاصه مقادیر Shapley نشان‌دهنده تأثیر بر خروجی است. مقدار مثبت به معنای همبستگی مثبت بین مقدار ویژگی و ویژگی پیش بینی شده از میانگین و بالعکس است. در حالی که نمودار خلاصه مقادیر Shapley نشان دهنده تأثیر بر خروجی است. مقدار مثبت به معنای همبستگی مثبت بین مقدار ویژگی و ویژگی پیش بینی شده از میانگین و بالعکس است. در حالی که نمودار خلاصه مقادیر Shapley نشان دهنده تأثیر بر خروجی است. مقدار مثبت به معنای همبستگی مثبت بین مقدار ویژگی و ویژگی پیش بینی شده از میانگین و بالعکس است.

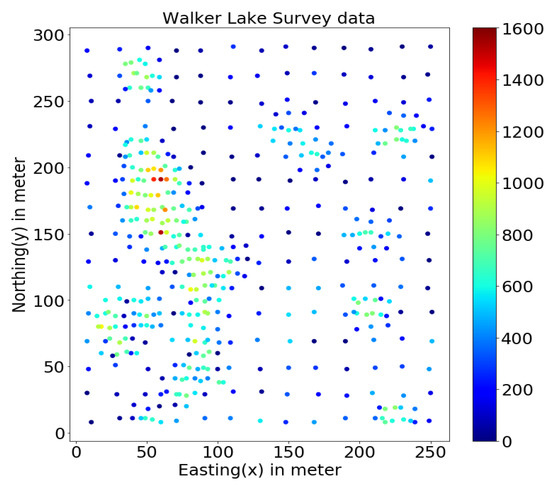
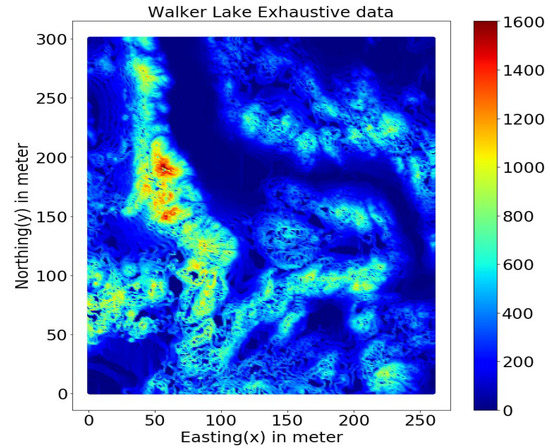
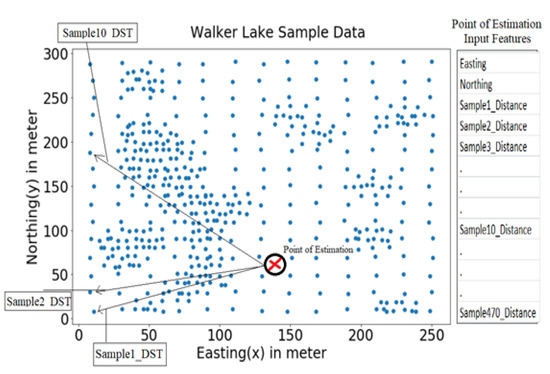
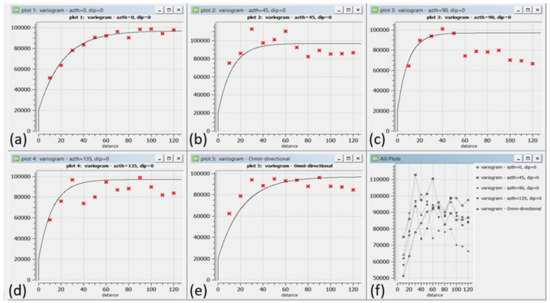
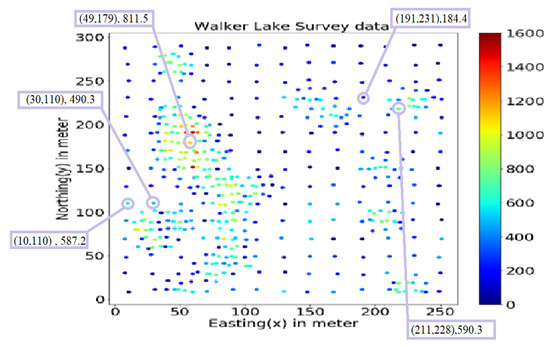
3.7. مجموعه داده دریاچه واکر

این مطالعه از مجموعه داده معروف دریاچه Walker [ 11 ] از نوادا، غرب ایالات متحده استفاده می کند. مجموعه داده Walker Lake از دو مجموعه تشکیل شده است. داده‌های بررسی دریاچه واکر، دارای 470 نمونه، و داده‌های نمونه‌برداری جامع @ 1 × 1 متر با 78000 نمونه برای متغیر “V”، همانطور که در شکل 2 و شکل 3 (شبکه مستطیلی 260 متر × 300 متر) نشان داده شده است. بررسی دریاچه واکر و داده های جامع برای اهداف آموزشی و اعتبار سنجی استفاده شد. آمار خلاصه برای داده های نظرسنجی و جامع در جدول 1 نشان داده شده است.

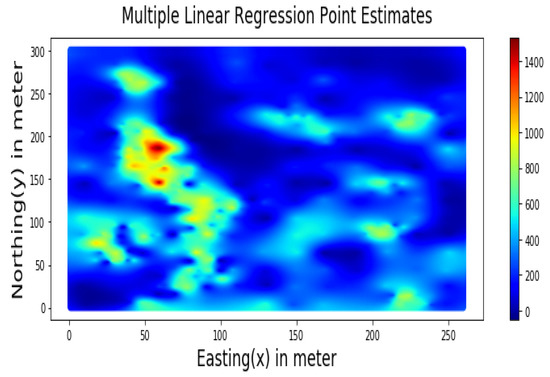
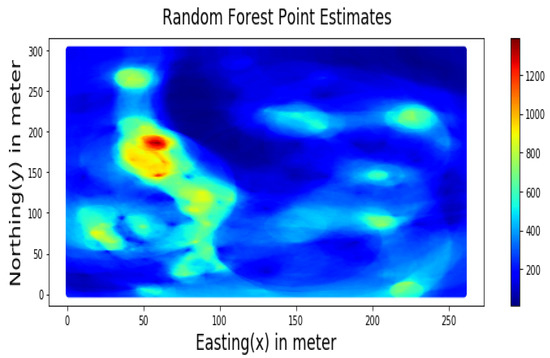
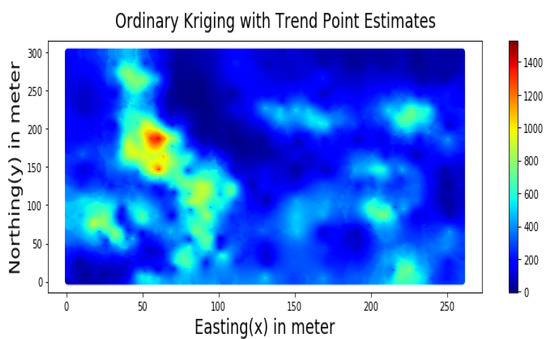
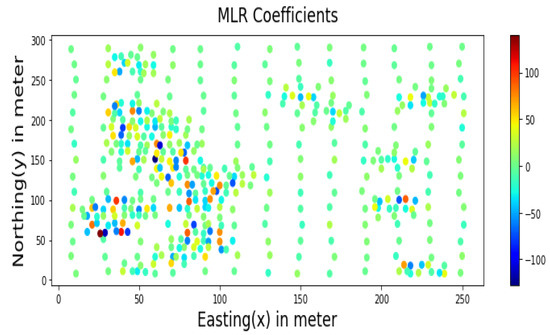
4. کاربرد MLR و RF برای تخمین فضایی

پس از حذف روند، OK برای مدل‌سازی اجزای باقی‌مانده که روند برای گزارش تخمین‌های OK نهایی به آنها اضافه شد، اعمال شد. از 470 نمونه برای ساخت واریوگرام های همه جهته و جهت دار باقیمانده ها در 0، 45، 90 و 135 آزیموت + تحمل 22.5 درجه استفاده شد. برآوردهای OK از باقیمانده ها برای تخمین 78000 امتیاز با استفاده از نرم افزار SGeMS [ 11 ] تعیین شد.

در مورد MLA (مدل های MLR و RF)؛ اولین مرحله تولید n + N ویژگی ورودی برای تخمین هر نقطه از داده های نمونه بود، یعنی 472، برای n = 2 (مختصات شرقی و شمالی) و N = 470 (فاصله های 470 نمونه از این نقطه). ). در نتیجه، هر دو MLR و RF ( شکل 4 ) از n + N ویژگی ورودی به عنوان فاصله N تمام نمونه های موجود از نقطه تخمین و n بعد مختصات فضایی نقطه تخمین استفاده کردند، همانطور که در شکل 5 نشان داده شده است. تمام تحلیل‌ها، مدل‌سازی و کارهای تجسم با استفاده از numPy، pandas، scikit-learn، skopt، shap انجام شد. و کتابخانه های matplotlib پایتون [ 111]. علاوه بر این، BOA و جستجوی شبکه انتخاب هایپرپارامتر را برای MLR و RF با استفاده از اعتبارسنجی متقاطع 10 برابری انجام دادند.

فراپارامترهای بهینه با استفاده از جستجوی Grid و یک BOA، یعنی یک روش جستجوی آگاهانه که توابع جعبه سیاه را با استفاده از اطلاعات تکرارهای قبلی در حداقل زمان بهینه می‌کند، جستجو شدند. جستجوی شبکه‌ای به‌عنوان یک جستجوی فاکتوریل کامل برای مقایسه با در نظر گرفتن تمام ترکیبات بین مقادیر شدید ابرپارامترهای مختلف ارائه‌شده در جدول 2 و جدول 3 انجام شد.به ترتیب برای RF و MLR. عملکرد (مقادیر مربع R) با استفاده از اعتبارسنجی متقاطع ده برابری برای هر ترکیب در طول جستجوی شبکه ذخیره شد. کلاس «BayesSearchCV» در بسته «skopt» پایتون نیز برای اعمال بهینه‌سازی بیزی ابرپارامترها استفاده شد. فراپارامترهای مختلف جنگل تصادفی، مانند حداقل تعداد نمونه های مجاز در برگ (Min_samples_leaf)، حداکثر عمق مجاز درخت (Max_depth)، حداکثر تعداد ویژگی های مورد استفاده (Max_features)، حداقل تعداد نمونه برای برای تقسیم کردن (Min_samps_split) استفاده شود و انتخاب یک نوع متریک فاصله مانند ‘اقلیدسی’، ‘اقلیدسی مربعی’، ‘مینکوفسکی’، ‘مهلانوبیس’، ‘کسینوس’، ‘منهتن’ و ‘چبیشف’ تنظیم شد. بهترین نتایج را بدست آورید معمولاً بیش از 128 درخت عملکرد را به طور قابل توجهی بهبود نمی بخشد.112 ]; با این حال، پارامتر تعداد درختان نیز به عنوان یک فراپارامتر انتخاب می شود. Min_samples_leaf، Max_depth، Max_features و Min_samples_split با افزایش 5% جستجو شد. در حالی که تعداد درختان با افزایش 100 برای محدوده های نشان داده شده در جدول 2 جستجو شد.

پارامتر منظم سازی MLR از 0 تا 1 با افزایش 0.05 همراه با ترکیبات مختلف فواصل نشان داده شده در جدول 3 جستجو شد.

پارامترهایی که بهترین مقدار ضریب همبستگی را گزارش می کنند به عنوان پارامترهای بهینه مورد استفاده برای آموزش مدل ها (MLR و RF) با استفاده از کل مجموعه نمونه 470 انتخاب شدند. در نهایت، روش های تخمین باید درون یابی دقیق در مکان های نمونه شناخته شده باشد. بنابراین، نقاطی که دقیقاً در موقعیت‌های نمونه قرار گرفته‌اند، یعنی فاصله 0، به همان درجه‌ها اختصاص داده می‌شوند تا درون یابی دقیق را وادار کنند.

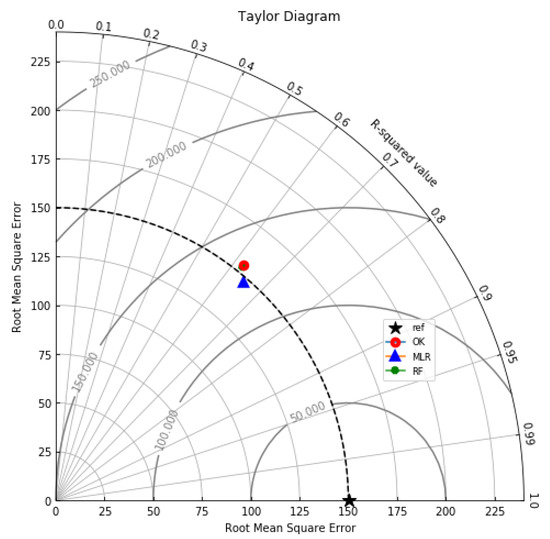
5. نتایج

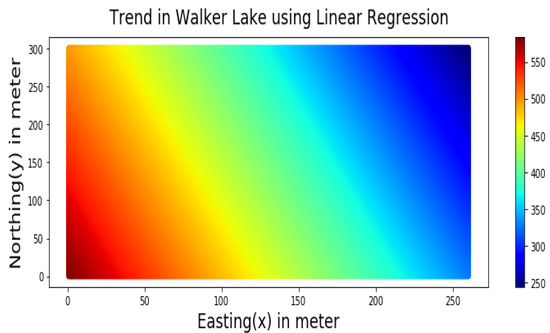
مؤلفه روند، همانطور که در شکل 6 نشان داده شده است ، با استفاده از معادله رگرسیون خطی زیر (9) با استفاده از مختصات دکارتی Easting (X) و Northing (Y) مدل شده است:

روند = 584.503 - (0.981 * X) - (0.285 * Y)

(9)

پس از حذف روند، از OK برای مدلسازی اجزای باقیمانده استفاده شد. 470 نمونه برای ساخت واریوگرام های همه جهته و جهت دار با 0، 45، 90 و 135 آزیموت + تلورانس 22.5، همانطور که در شکل 7 نشان داده شده است، استفاده شد . وزن های OK برای تخمین 78000 امتیاز با استفاده از نرم افزار SGeMS تعیین شد [ 11 ]. واریوگرام های جهت دار با مقادیر آستانه، ناگت و محدوده به ترتیب 77000، 20000 و (min = 6، med = 28.8، max = 64.8) مدل شدند، همانطور که در شکل 7 نشان داده شده است.

پس از یافتن بهترین پارامتر تنظیم برای MLR با استفاده از Grid (طول مدت دو دقیقه) و BOA (در عرض یک دقیقه)، نتایج تولید و با داده های حقیقت زمینی (کامل) حاوی 78000 نمونه مقایسه شد. برای RF، یافتن فراپارامترهای بهینه با استفاده از جستجوی Grid حدود 10 ساعت در یک پردازنده هسته ای i-7 @ 2.8 گیگاهرتز طول کشید. در حالی که بهینه‌سازی بیزی فراپارامترهای RF تنها 100 تکرار طول کشید تا در 20 دقیقه همگرا شوند، و همان مقادیر بهینه ابرپارامترها را در مورد جستجوی شبکه گزارش می‌دهد. پارامترهای بهینه مدل های RF و MLR با استفاده از جستجوی بیزی و شبکه در جدول 4 و جدول 5 گزارش شده است.

همانطور که توسط ادبیات پیشنهاد شده است، کاهش Min_samples_leaf، Min_samples_split، و افزایش Max_features، مقادیر Max_depth واریانس RF را افزایش داده و ما را قادر می سازد تا روابط پیچیده را توضیح دهیم [ 47 ، 48 ، 49 ]. مقادیر فراپارامتر بهینه یافت شده حس شهودی دارند، زیرا وظیفه گرفتن الگوهای فضایی، در این مورد، پیچیده است [ 49 ]. MLR همان رفتار را با مقدار منظم سازی 0 نشان می دهد.

آمار خلاصه برای MLR، RF، تخمین نقطه OK، و مجموعه داده های جامع در جدول 6 و نمودار تیلور در شکل 8 نشان داده شده است. نتایج به‌دست‌آمده از تکنیک‌های MLR، RF و OK با داده‌های جامع برای اعتبارسنجی، همانطور که در جدول 7 نشان داده شده است، مقایسه شد . این جداول نشان می دهد که MLR ساده از نظر RMSE، مقدار مربع R و مقادیر مهارت مربوطه به ترتیب 294.03، 319.39 و 328.64 بهتر از RF و OK عمل می کند. تخمین نقطه MLR، RF و OK در شکل 9 ، شکل 10 و شکل 11 نشان داده شده است.

جدول 7 نشان می دهد که توزیع تخمین نقطه MLR نسبت به تخمین نقطه OK به مجموعه داده واقعی (جامع) نزدیکتر است. تخمین‌های نقطه MLR بی‌طرفانه بودند، همانطور که از مقادیر میانگین MLR که به مقدار جامعی که در جدول 7 ارائه شده است، نزدیک‌تر است. پارامترهای ” n ” مرتبط با مختصات فضایی روند خطی را به طور همزمان مدل می کنند. علاوه بر این، فاصله نمونه ها از کل منطقه به عنوان ویژگی توسط “MLR” استفاده می شود. در مقابل، OK استفاده از نمونه‌های همسایه را در ناحیه ثابت، یعنی محدوده واریوگرام محدود می‌کند. بنابراین، MLR به خود اجازه می‌دهد تا الگوهای غیرخطی را از نمونه‌های دورتر و نزدیک‌تر یاد بگیرد.

شکل 12 10 ویژگی مهم (یعنی فواصل نمونه در این مورد) و معیارهای اهمیت مربوطه آنها را پس از اعمال الگوریتم SHAP در مدل RF نشان می دهد. فواصل مکان‌های فضایی پنج ویژگی اصلی را نشان می‌دهند (یعنی پنج نمونه تأثیرگذار برای هر نقطه که باید تخمین زده شود) نشان داده شده در شکل 13 ، که در داخل یا در مرزهای مناطق مهم مورد علاقه قرار دارند (به عنوان مثال، کم، متوسط، مناطق با کانی‌زایی بالا). بنابراین، شناسایی این مناطق مورد علاقه بسیار مهم است زیرا این اطلاعات نقش مهمی در تخمین نقطه‌ای مکانی ایفا می‌کند. علاوه بر این، نشان می دهد که فواصل این نمونه ها از یک نقطه تخمین معین در کل دامنه بیشترین اهمیت را در طول برآورد دارند.

به طور مشابه، نمونه‌های داخل زون‌های اصلی کانی‌سازی دارای ضرایب MLR بالاتری هستند، همانطور که در شکل 14 نشان داده شده است. بنابراین، برای مشکلات تخمینی که شامل تعداد قابل توجهی از نمونه‌ها می‌شود، تنها مراکز خوشه‌ای شناسایی‌شده توسط الگوریتم SHAP می‌توانند به‌جای همه فواصل نمونه به‌عنوان ویژگی‌های اضافی استفاده شوند.

می توان آن را از مقادیر نمودار خلاصه SHAP نشان داد (در محور افقی شکل 15) از بیست نمونه تأثیرگذار در برابر فاصله (قرمز = بزرگتر و آبی = فاصله کمتر) هر بار که در تخمین 78000 امتیاز شرکت می کنند. فرض کنید نمونه درجه/ارزش بالاتر به نقطه‌ای که تخمین زده می‌شود نزدیک‌تر باشد (فاصله کوچک‌تر با آبی نشان داده شده است). در آن صورت، دارای یک مقدار SHAP مثبت است (احتمالاً تخمین های بالاتری را گزارش می کند). برعکس، اگر یک نمونه درجه/مقدار بالاتر از نقطه تخمین زده شده دور باشد (فاصله بیشتر با رنگ قرمز نشان داده شده است)، در آن صورت، احتمالاً مقدار SHAP منفی را گزارش می‌کند، یعنی برآوردهای پایین‌تری. مقادیر برای هر فاصله نمونه به طور تصادفی افزایش و کاهش یافت تا اثر بر تخمین نقطه خروجی تعیین شود. به طور شهودی، تخمین های نقطه ای باید با افزایش فاصله از نمونه های درجه بالا کاهش یابد. این نشان می دهد که افزایش فاصله از این نمونه ها منجر به مقادیر تخمین کمتر می شود و فاصله های نزدیکتر از این نقطه مقادیر بالاتری را گزارش می کند. برعکس، مقادیر منفی SHAP نمونه های درجه بالا در فواصل بیشتر (قرمز)، به عنوان مثال، نمونه 6 و نمونه 21، نشان می دهد که نمرات پایین تر در نقطه تخمین در فاصله بیشتری از این درجه های بالا گزارش می شود.

6. بحث

الگوریتم‌های رگرسیون خطی و RF با استفاده از فواصل نمونه و مختصات فضایی برای تخمین ارزش مورد نظر در فضا اعمال شده‌اند. این تخمین‌ها نسبت به تکنیک‌های تخمین خطی قبلی بهبود یافته‌اند، زیرا ویژگی‌های فاصله نمونه‌ها تغییرات همبستگی بین عبارت‌های وابسته، مستقل و خطا را یاد می‌گیرند. الگوریتم‌ها کارایی محاسباتی بیشتری را نسبت به سایر تکنیک‌ها بدون از دست دادن اطلاعات از طریق کاهش ویژگی‌های قبلاً تمرین شده گزارش کردند، به عنوان مثال، برنامه PCA برای کاهش ویژگی‌ها [ 90]. مدل MLR سریع، بی‌طرفانه بود، نسبتاً دارای تنوع در مقیاس کوتاه بود و می‌تواند منابع داده‌ای متعددی را که می‌توانند در سیستم‌های استخراج بلادرنگ برای انجام تخمین منابع به شیوه‌ای خودکار مورد استفاده قرار گیرند، ترکیب کند. فواصل نمونه تغییرپذیری فضایی را به عنوان ویژگی‌های اضافی نشان می‌دهد که حتی یک مدل رگرسیون خطی ساده بهتر از یک مدل RF غیرخطی پیچیده عمل می‌کند. از بین پارامترهای n + N ( n = مختصات نمونه و N = تعداد نمونه)، پارامترهای ” n ” مولفه روند را مدل می کنند و پارامتر “N” تغییرپذیری در دامنه را نشان می دهد. نتایج با نتایج پیشنهاد شده توسط محققان [ 25 , 32 , 43 , 45 , 49 مطابقت دارد.]، یعنی افزودن اطلاعات کمکی (ناهمسانگردی های منطقه ای، کانی شناسی و سیگنال های ژئوفیزیکی) نتایج را بهبود می بخشد. این تحقیق بیشتر تخمین را با استفاده از حداکثر اطلاعات با بازده محاسباتی بالاتر، به ویژه با استفاده از MLR انجام می دهد. این تکنیک را می‌توان به موارد دیگر تعمیم داد و داده‌هایی از منابع دیگر را برای تقویت الگوهای آموخته‌شده ترکیب کرد. این الگوریتم اهمیت استفاده از اطلاعات سراسری (یعنی همه نمونه ها) را برای ترجمه یک مسئله بسیار غیرخطی به یک مسئله خطی نشان می دهد. این شاخص‌های جهانی و نقشه‌های موضوعی نشان می‌دهند که MLR بی‌طرف‌ترین نتایج را تولید کرده و تنوع مقیاس کوتاه را در طول تخمین گنجانده است. تجزیه و تحلیل مقادیر ضریب MLR و تحلیل حساسیت الگوریتم RF توسط الگوریتم SHAP نشان می دهد که مناطق کلیدی مورد علاقه (به عنوان مثال، بالا، زون‌های کم کانی‌زایی متوسط) نیز در طول برآورد قابل شناسایی بودند. مقادیر ضرایب MLR با روش گرادیان نزول، یک گزینه پیش‌فرض در کتابخانه‌های پایتون که ناپایدار نبودند، به دست آمد. زمان تنظیم فراپارامتر به طور قابل توجهی توسط BOA در مقایسه با جستجوی شبکه در مورد الگوریتم RF (20 دقیقه در مقایسه با 10 ساعت) در مقایسه با MLR (یک دقیقه از دو دقیقه) کاهش یافت. بنابراین، MLR نسبت به الگوریتم‌های OK و RF پیشرفت قابل‌توجه‌تری دارد و نتایج بهتری را تولید می‌کند (R-square 0.652 در مقایسه با 0.62 برای RF و OK) با راندمان محاسباتی بسیار بالا. زمان تنظیم فراپارامتر به طور قابل توجهی توسط BOA در مقایسه با جستجوی شبکه در مورد الگوریتم RF (20 دقیقه در مقایسه با 10 ساعت) در مقایسه با MLR (یک دقیقه از دو دقیقه) کاهش یافت. بنابراین، MLR نسبت به الگوریتم‌های OK و RF پیشرفت قابل‌توجه‌تری دارد و نتایج بهتری را تولید می‌کند (R-square 0.652 در مقایسه با 0.62 برای RF و OK) با راندمان محاسباتی بسیار بالا. زمان تنظیم فراپارامتر به طور قابل توجهی توسط BOA در مقایسه با جستجوی شبکه در مورد الگوریتم RF (20 دقیقه در مقایسه با 10 ساعت) در مقایسه با MLR (یک دقیقه از دو دقیقه) کاهش یافت. بنابراین، MLR نسبت به الگوریتم‌های OK و RF پیشرفت قابل‌توجه‌تری دارد و نتایج بهتری را تولید می‌کند (R-square 0.652 در مقایسه با 0.62 برای RF و OK) با راندمان محاسباتی بسیار بالا.

علاوه بر این، بر خلاف برآوردهای قبلی مبتنی بر روش‌های بدون نظارت [ 18 ، 19 ] که مناطق مختلف را ابتدا برای تخمین مقادیر درجه شناسایی می‌کند، الگوریتم SHAP مناطق بحرانی را در مرحله پس از یادگیری شناسایی کرد. این می تواند مفید باشد در صورتی که بتوان از فواصل بیشتر نمونه های حیاتی به جای تمام فواصل نمونه در شرایط استثنایی که شامل نمونه های بزرگ برای صرفه جویی در هزینه محاسباتی است، استفاده کرد. این تکنیک را می توان با استفاده از یک مطالعه موردی سه بعدی، به ویژه برای صنایع معدنی، برای ارزیابی پیچیدگی محاسباتی، کیفیت و عدم قطعیت مرتبط با تخمین ها بررسی کرد. واریانس تخمین‌ها از MLR بالاتر از روش‌های دیگر بود، که تنوع در مقیاس کوتاه را به حساب می‌آورد. با این حال، گزارش عدم قطعیت برآوردها [36 ، 113 ] برای تجزیه و تحلیل حساسیت و ریسک که می تواند در فاز بعدی برای مقایسه نتایج با شبیه سازی های مشروط مورد بررسی قرار گیرد، حیاتی است.

7. نتیجه گیری

این مقاله رگرسیون خطی چندگانه (MLR)، جنگل تصادفی (RF) و کریجینگ معمولی (OK) را با استفاده از نمونه و مجموعه داده جامع Walkerlake مقایسه می‌کند. مختصات نقطه تخمین و فواصل نمونه‌های همسایه به‌عنوان ویژگی ورودی در طول تخمین استفاده شد. میانگین کلی تخمین‌های نقطه‌ای از روش ساده MLR بی‌طرفانه بود، همانطور که از میانگین‌های مربوط به MLR، RF، OK، و مجموعه داده‌های جامع به‌عنوان 271.2، 288.2، 295.42، و 277.98 مشهود است. جدای از دقت نسبتاً بالاتر، واریانس گزارش شده 47276.1 از برآوردهای نقطه MLR به واریانس 62423.2 از داده های جامع نزدیکتر از 38476.42 از OK بود، که نشان می دهد MLR تغییرپذیری در مقیاس کوتاه را به حساب می آورد. علاوه بر این، تخمین‌ها از MLR ساده، پارامترهای جهانی داده‌های جامع را تأیید کرد. که ممکن است به دلیل استفاده از کل مجموعه نمونه به عنوان ورودی، در حین تخمین نقطه باشد، در حالی که کریجینگ اطلاعات همسایه را به ناحیه ایستایی، یعنی محدوده واریوگرام محدود می کند. روش پیشنهادی از نظر محاسباتی کارآمد است و مدل پیش‌بینی را در عرض یک ثانیه برای تخمین 78000 نقطه حل می‌کند و خودکار، یعنی بدون تعامل دستی است. الگوریتم‌های MLR و RF نشان دادند که روش پیشنهادی می‌تواند به عنوان ابزار سریع تخمین استفاده شود زیرا (1) این الگوریتم‌ها از مناطق کلیدی مهم در طول تخمین نقطه‌ای استفاده می‌کنند. (2) در مواردی که تعداد نقاط نمونه زیاد است، فقط بحرانی‌ترین فواصل نمونه‌ها را می‌توان به‌جای همه فواصل نمونه به عنوان ویژگی استفاده کرد. در حالی که کریجینگ اطلاعات همسایه را به ناحیه ایستایی، یعنی محدوده واریوگرام محدود می کند. روش پیشنهادی از نظر محاسباتی کارآمد است و مدل پیش‌بینی را در عرض یک ثانیه برای تخمین 78000 نقطه حل می‌کند و خودکار، یعنی بدون تعامل دستی است. الگوریتم‌های MLR و RF نشان دادند که روش پیشنهادی می‌تواند به عنوان ابزار سریع تخمین استفاده شود زیرا (1) این الگوریتم‌ها از مناطق کلیدی مهم در طول تخمین نقطه‌ای استفاده می‌کنند. (2) در مواردی که تعداد نقاط نمونه زیاد است، فقط بحرانی‌ترین فواصل نمونه‌ها را می‌توان به‌جای همه فواصل نمونه به عنوان ویژگی استفاده کرد. در حالی که کریجینگ اطلاعات همسایه را به ناحیه ایستایی، یعنی محدوده واریوگرام محدود می کند. روش پیشنهادی از نظر محاسباتی کارآمد است و مدل پیش‌بینی را در عرض یک ثانیه برای تخمین 78000 نقطه حل می‌کند و خودکار، یعنی بدون تعامل دستی است. الگوریتم‌های MLR و RF نشان دادند که روش پیشنهادی می‌تواند به عنوان ابزار سریع تخمین استفاده شود زیرا (1) این الگوریتم‌ها از مناطق کلیدی مهم در طول تخمین نقطه‌ای استفاده می‌کنند. (2) در مواردی که تعداد نقاط نمونه زیاد است، فقط بحرانی‌ترین فواصل نمونه‌ها را می‌توان به‌جای همه فواصل نمونه به عنوان ویژگی استفاده کرد. الگوریتم‌های MLR و RF نشان دادند که روش پیشنهادی می‌تواند به عنوان ابزار سریع تخمین استفاده شود زیرا (1) این الگوریتم‌ها از مناطق کلیدی مهم در طول تخمین نقطه‌ای استفاده می‌کنند. (2) در مواردی که تعداد نقاط نمونه زیاد است، فقط بحرانی‌ترین فواصل نمونه‌ها را می‌توان به‌جای همه فواصل نمونه به عنوان ویژگی استفاده کرد. الگوریتم‌های MLR و RF نشان دادند که روش پیشنهادی می‌تواند به عنوان ابزار سریع تخمین استفاده شود زیرا (1) این الگوریتم‌ها از مناطق کلیدی مهم در طول تخمین نقطه‌ای استفاده می‌کنند. (2) در مواردی که تعداد نقاط نمونه زیاد است، فقط بحرانی‌ترین فواصل نمونه‌ها را می‌توان به‌جای همه فواصل نمونه به عنوان ویژگی استفاده کرد.

منابع

روسی، من؛ Deutsch, CV برآورد منابع معدنی ; Springer: Dordrecht، هلند، 2014; ISBN 9781402057175. [ Google Scholar ]
Pyrcz، MJ; Deutsch, C. Geostatistical Reservoir Modeling , 2nd ed.; انتشارات دانشگاه آکسفورد: نیویورک، نیویورک، ایالات متحده آمریکا، 2002; شابک 0-19-513806-6. [ Google Scholar ]
مونستیز، پ. آلارد، دی. Froidevaux, R. geoENV III-Geostatistics for Environmental Applications. مجموعه مقالات سومین کنفرانس اروپایی زمین آمار برای کاربردهای زیست محیطی که در آوینیون، فرانسه، 22 تا 24 نوامبر برگزار شد . Springer: Dordrecht، هلند، 2000; شابک 978-0-7923-7107-6. [ Google Scholar ]
الیور، کارشناسی ارشد برنامه های زمین آماری برای کشاورزی دقیق . Springer: New York, NY, USA, 2010; شابک 978-90-481-9132-1. [ Google Scholar ]
آزودو، ال. Soares, A. Methods Geostatistical Methods for Reservoir Geophysics ; Springer: Cham, Switzerland, 2017; شابک 978-3-319-53200-4. [ Google Scholar ]
Leuangthong، O. خان، ک.د. Deutsch, CV مسائل حل شده در زمین آمار ; وایلی: هوبوکن، نیوجرسی، ایالات متحده آمریکا، 2008; شابک 978-0-470-17792-1. [ Google Scholar ]
Sarma, D. زمین آمار با کاربرد در علوم زمین ; Springer: Dordrecht، هلند، 2006; شابک 978-1-4020-9379-1. [ Google Scholar ]
تخمین درجه فام، TD با استفاده از الگوریتم‌های مجموعه فازی. ریاضی. جئول 1997 ، 29 ، 291-305. [ Google Scholar ] [ CrossRef ]
Matheron، G. اصول زمین آمار. اقتصاد جئول 1962 ، 58 ، 1246-1266. [ Google Scholar ] [ CrossRef ]
کوون، اچ. یی، اس. Choi, S. بررسی عددی برای رفتار نامنظم مدل جایگزین کریجینگ. جی. مکانیک. علمی تکنولوژی 2014 ، 28 ، 3697-3707. [ Google Scholar ] [ CrossRef ]
ایزاکس، EH; Srivastava, RM Applied Geostatistics , 1st ed.; انتشارات دانشگاه آکسفورد: نیویورک، نیویورک، ایالات متحده آمریکا، 1989; ISBN 978-0- 19-605013-4. [ Google Scholar ]
عابدی، م. علی ترابی، س. نوروزی، غلامرضا; حمزه، م. Elyasi، GR PROMETHEE II: یک روش دانش محور برای اکتشاف مس. محاسبه کنید. Geosci. 2012 ، 46 ، 255-263. [ Google Scholar ] [ CrossRef ]
دوتاوت، آر. مارکوت، دی. یک رویکرد نیمه حریصانه جدید برای افزایش برنامه ریزی حفاری. نات منبع. Res. 2020 ، 29 ، 3599–3612. [ Google Scholar ] [ CrossRef ]
فاتحی، م. اسدی، ح. حسین مرشدی، ع. طراحی سه بعدی گمانه های مکمل بهینه با تحلیل تلفیقی داده های اکتشافی مختلف با استفاده از رویکرد MADM ترتیبی. نات منبع. Res. 2020 ، 29 ، 1041-1061. [ Google Scholar ] [ CrossRef ]
کومرال، م. اوزر، کامپیوتر و علوم زمین برنامه ریزی کمپین حفاری اضافی با استفاده از الگوریتم ژنتیک دو فضایی: یک رویکرد نظری بازی. محاسبه کنید. Geosci. 2013 ، 52 ، 117-125. [ Google Scholar ] [ CrossRef ]
بندورف، جی. حرکت به سمت مدیریت زمان واقعی ذخایر معدنی – یک چارچوب حلقه بسته زمین آماری و بهینه سازی معدن. در برنامه ریزی معدن و انتخاب تجهیزات. ; Drebenstedt, C., Singhal, R., Eds. انتشارات بین المللی Springer: چم، سوئیس، 2014; صفحات 989-999. شابک 978-3-319-02678-7. [ Google Scholar ]
باکستون، ام. Benndorf, J. استفاده از داده های مشتق شده حسگر در بهینه سازی در امتداد زنجیره ارزش معدن. در مجموعه مقالات پانزدهمین کنگره بین المللی ISM، آخن، آلمان، 16 تا 20 سپتامبر 2013. صص 324-336. [ Google Scholar ]
محمد، ک. تغییرپذیری و عدم قطعیت در مقیاس کوتاه مدل سازی شیشه، HJ در حین تخمین منابع معدنی با استفاده از تکنیک تخمین فازی جدید. ژئواستند. نتایج جغرافیایی تحلیلی 2011 ، 35 ، 369-385. [ Google Scholar ] [ CrossRef ]
توتمز، بی. Tercan، AE; کیماک، یو. اپلهانس، تی. موانگومو، ای. هاردی، DR; کنف، A.; ناوس، تی. توتمز، بی. Tercan، AE; و همکاران مدلسازی فازی برای تخمین ذخیره بر اساس تغییرپذیری فضایی. ریاضی. جئول 2007 ، 39 ، 87-111. [ Google Scholar ] [ CrossRef ]
اپلهانس، تی. موانگومو، ای. هاردی، DR; کنف، A.; Nauss, T. ارزیابی رویکردهای یادگیری ماشین برای درونیابی دمای ماهانه هوا در کوه کلیمانجارو، تانزانیا. تف کردن آمار 2015 ، 14 ، 91-113. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
کاپاپریدیس، IK; دنبی، ب. مدلسازی شبکه عصبی تنوع فضایی درجه سنگ معدن. In Perspectives in Neural Computing، مجموعه مقالات ICANN، Skovde، سوئد، 2-4 سپتامبر 1998 . Niklasson, L., Bodén, M., Ziemke, T., Eds. Springer: لندن، انگلستان، 1998; ص 209-214. [ Google Scholar ]
Dean, S. Journal of Natural Gas Science and Engineering Reservoir شبیه سازی و مدل سازی بر اساس داده ها و هوش مصنوعی. جی. نات. علوم گاز مهندس 2011 ، 3 ، 697-705. [ Google Scholar ] [ CrossRef ]
دوو، جی. یونس، AP; تین بوی، دی. مرغدی، ع. ساهانا، م. زو، ز. چن، CW; خسروی، ک. یانگ، ی. Pham، BT ارزیابی الگوریتم‌های جنگل تصادفی پیشرفته و درخت تصمیم برای مدل‌سازی حساسیت زمین لغزش ناشی از بارندگی در جزیره آتشفشانی ایزو-اوشیما، ژاپن. علمی کل محیط. 2019 ، 662 ، 332-346. [ Google Scholar ] [ CrossRef ]
دوتا، اس. عملکرد پیش‌بینی الگوریتم‌های یادگیری ماشین برای تخمین ذخایر معدنی در داده‌های پراکنده و غیردقیق. Ph.D. پایان نامه، دانشگاه آلاسکا فیربنکس، فیربنکس، AK، ایالات متحده آمریکا، 2006. [ Google Scholar ]
دوتا، اس. باندوپادیای، س. گنگولی، ر. Misra, D. الگوریتم های یادگیری ماشین و کاربرد آنها در تخمین ذخایر معدنی داده های پراکنده و غیر دقیق. جی. اینتل. فرا گرفتن. سیستم Appl. 2010 ، 2 ، 86-96. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
گیلاردی، ن. Bengio، S. مقایسه چهار الگوریتم یادگیری ماشین برای تجزیه و تحلیل داده های مکانی. در نقشه برداری رادیواکتیویته در محیط – مقایسه درونیابی فضایی 1997 ; Dubois, G., Malczewski, J., DeCort, M., Eds. دفتر انتشارات رسمی جوامع اروپایی: لوکزامبورگ، 2003; ص 222-237. [ Google Scholar ]
Gonçalves، Í.G. کومیرا، اس. Guadagnin، F. کامپیوترها و علوم زمین یک رویکرد یادگیری ماشینی به روش میدان بالقوه برای مدل‌سازی ضمنی ساختارهای زمین‌شناسی. محاسبه کنید. Geosci. 2017 ، 103 ، 173-182. [ Google Scholar ] [ CrossRef ]
گوموس، ک. Sen, A. مقایسه روش‌های درونیابی فضایی و شبکه‌های عصبی چند لایه برای توزیع‌های نقطه‌ای مختلف در یک مدل ارتفاعی دیجیتال. Geod. وستن 2013 ، 57 ، 523-543. [ Google Scholar ] [ CrossRef ]
کویکه، ک. ماتسودا، اس. سوزوکی، تی. Ohmi، M. برآورد مبتنی بر شبکه عصبی محتویات فلزی اصلی در منطقه هوکوروکو، شمال ژاپن، برای کاوش ذخایر نوع Kuroko. نات منبع. Res. 2002 ، 11 ، 135-156. [ Google Scholar ] [ CrossRef ]
لئونه، اس. روتیل، اس. محدود، سی. لئون، اس. یکپارچه سازی شبکه های عصبی مصنوعی و زمین آمار برای مدل سازی بلوک های زمین شناسی سه بعدی بهینه در تخمین ذخایر معدنی – مطالعه موردی. بین المللی J. Min. علمی تکنولوژی 2015 ، 26 ، 581-585. [ Google Scholar ]
لی، جی. هیپ، AD; پاتر، ا. دانیل، جی جی استفاده از روش های یادگیری ماشین برای درونیابی فضایی متغیرهای محیطی. محیط زیست مدل. نرم افزار 2011 ، 26 ، 1647-1659. [ Google Scholar ] [ CrossRef ]
مروین، دی. کراملی، آر جی. شبکه‌های عصبی مصنوعی Civco، DL به عنوان روشی برای درونیابی فضایی برای مدل‌های ارتفاعی دیجیتال. کارتوگر. Geogr. Inf. علمی 2002 ، 29 ، 99-110. [ Google Scholar ] [ CrossRef ]
ریگل، جی پی. جارویس، CH; استوارت، N. شبکه های عصبی مصنوعی به عنوان ابزاری برای درونیابی فضایی. بین المللی جی. جئوگر. Inf. علمی 2001 ، 15 ، 323-343. [ Google Scholar ] [ CrossRef ]
یداو، ع. Satyannarayana، P. بهینه سازی الگوریتم ژنتیک چندهدفه شبکه عصبی مصنوعی برای تخمین میزان رسوب معلق در حوضه رودخانه ماهانادی، هند. بین المللی J. رودخانه Manag حوضه. 2020 ، 18 ، 207-215. [ Google Scholar ] [ CrossRef ]
Carranza، EJM; Laborte، AG مدل‌سازی پیش‌بینی جنگل تصادفی چشم‌انداز معدنی با مقادیر گمشده در آبرا (فیلیپین). محاسبه کنید. Geosci. 2015 ، 74 ، 60-70. [ Google Scholar ] [ CrossRef ]
ورونزی، اف. Schillaci، C. مقایسه بین مدل‌های زمین‌آماری و یادگیری ماشینی به عنوان پیش‌بینی‌کننده کربن آلی خاک سطحی با تمرکز بر تخمین عدم قطعیت محلی. Ecol. اندیک. 2019 ، 101 ، 1032-1044. [ Google Scholar ] [ CrossRef ]
هنگل، تی. نوسبام، م. رایت، MN; Heuvelink، GBM؛ Gräler، B. جنگل تصادفی به عنوان یک چارچوب عمومی برای مدل سازی پیش بینی متغیرهای مکانی و مکانی-زمانی. PeerJ 2018 , 2018 , e5518. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
Baez-Villanueva، OM; زامبرانو-بیگیارینی، م. بک، او؛ مک نامارا، آی. ریب، ال. ناودیت، ا. بیرکل، سی. وربیست، ک. Giraldo-Osorio، JD; Xuan Thinh، N. RF-MEP: یک روش جدید جنگل تصادفی برای ادغام محصولات بارش شبکه ای و اندازه گیری های زمینی. سنسور از راه دور محیط. 2020 , 239 , 111606. [ Google Scholar ] [ CrossRef ]
فیورنتینی، ن. معبودی، م. لوسا، م. گرک، ام. ارزیابی انعطاف‌پذیری زیرساخت‌ها در برابر رویدادهای برون‌زا با استفاده از تخمین‌های حرکت سطحی مبتنی بر ps-insar و تکنیک‌های رگرسیون یادگیری ماشین. ISPRS Ann. فتوگرام حسگر از راه دور اسپات. Inf. علمی 2020 ، 5 ، 19-26. [ Google Scholar ] [ CrossRef ]
فیورنتینی، ن. معبودی، م. لندری، پ. لوسا، م. Gerke، M. پیش‌بینی حرکت سطحی و نقشه‌برداری برای مدیریت زیرساخت‌های جاده‌ای با اندازه‌گیری‌های PS-InSAR و الگوریتم‌های یادگیری ماشین. Remote Sens. 2020 , 12 , 3976. [ Google Scholar ] [ CrossRef ]
زی، ز. چن، جی. منگ، ایکس. ژانگ، ی. کیائو، ال. Tan, L. مطالعه تطبیقی نقشه‌برداری حساسیت زمین لغزش با استفاده از وزن شواهد، رگرسیون لجستیک و ماشین بردار پشتیبان و ارزیابی شده توسط نظارت SBAS-InSAR: بخش Zhouqu به Wudu در حوضه رودخانه Bailong، چین. محیط زیست علوم زمین 2017 ، 76 ، 313. [ Google Scholar ] [ CrossRef ]
لسنیاک، ا. Porzycka، S. محاسبات زمین آماری در تجزیه و تحلیل داده های psinsar. در علوم محاسباتی-ICCS 2009 ; Allen, G., Nabrzyski, J., Seidel, E., van Albada, GD, Dongarra, J., Sloot, PMA, Eds. یادداشت های سخنرانی در علوم کامپیوتر; Springer: برلین/هایدلبرگ، آلمان، 2009; جلد 5544. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
لیو، دبلیو. دو، پ. Wang, D. Ensemble Learning برای درونیابی فضایی محتوای پتاسیم خاک بر اساس اطلاعات محیطی. PLoS ONE 2015 ، 10 ، e0124383. [ Google Scholar ] [ CrossRef ]
لیو، اس. ژانگ، ی. ما، پ. لو، بی. Su, H. یک روش جدید درون یابی فضایی بر اساس شبکه عصبی RBF یکپارچه. Procedia Environ. علمی 2011 ، 10 ، 568-575. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
کرکوود، سی. غار، م. بیمیش، دی. گربی، اس. فریرا، A. رویکرد یادگیری ماشین برای نقشه برداری ژئوشیمیایی. جی. ژئوشیم. کاوش کنید. 2016 ، 167 ، 49-61. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
دای، اف. ژو، Q. Lv، Z. وانگ، ایکس. لیو، جی. پیش‌بینی فضایی محتوای ماده آلی خاک با ادغام شبکه عصبی مصنوعی و کریجینگ معمولی در فلات تبت. Ecol. اندیک. 2014 ، 45 ، 184-194. [ Google Scholar ] [ CrossRef ]
هستی، تی. طبشیرانی، ر. Friedman, J. The Elements of Statistical Learning Data Mining, Inference, and Prediction , 2nd ed.; سری در آمار; Springer: New York, NY, USA, 2009; شابک 978-0-387-84857-0. [ Google Scholar ]
Bishop، CM Pattern Recognition and Machine Learning ; Springer: نیویورک، نیویورک، ایالات متحده آمریکا، 2006; جلد 2، ISBN 9780387310732. [ Google Scholar ]
راسل، اس جی. Norvig, P. Artificial Intelligence A Modern Approach 4th Edition , 3rd ed.; پرنتیس هال: هوبوکن، نیوجرسی، ایالات متحده آمریکا، 2003; ISBN 9780136042594. [ Google Scholar ]
Anees، MT; عبدالله، ک. نواوی، MNM; آب رحمان، NNN; Piah, AR, Mt. سیاکیر، MI; علی خان، م.م. Abdul, AK برآورد فضایی میانگین بارش روزانه با استفاده از رگرسیون خطی چندگانه با استفاده از متغیرهای توپوگرافی و سرعت باد در اقلیم گرمسیری. جی. محیط زیست. مهندس Landsc. مدیریت 2018 ، 26 ، 299-316. [ Google Scholar ] [ CrossRef ]
Baltensperger، AP; کفال، TC; اشمید، ام اس; Humphries، GRW; کوور، ال. Huettmann، F. مشاهدات فصلی و پیش‌بینی‌های مدل فضایی مبتنی بر یادگیری ماشینی برای کلاغ معمولی (Corvus corax) در محیط شهری، زیر قطب شمال فیربنکس، آلاسکا. قطبی بیول. 2013 ، 36 ، 1587-1599. [ Google Scholar ] [ CrossRef ]
بل، ال. آلارد، دی. لوران، جی.ام. چدادی، ر. بار-هن، A. الگوریتم سبد خرید برای داده های مکانی: کاربرد در داده های زیست محیطی و اکولوژیکی. محاسبه کنید. آمار داده آنال. 2009 ، 53 ، 3082-3093. [ Google Scholar ] [ CrossRef ]
چاترجی، اس. باندوپادیای، س. Machuca، D. پیش‌بینی عیار سنگ معدن با استفاده از الگوریتم ژنتیک و خوشه‌بندی مبتنی بر مدل شبکه عصبی مجموعه‌ای. ریاضی. Geosci. 2010 ، 42 ، 309-326. [ Google Scholar ] [ CrossRef ]
چاترجی، اس. باتاچرجی، ا. Samanta، B. برآورد عیار سنگ معدن یک کانسار سنگ آهک در هند با استفاده از شبکه عددی مصنوعی. Appl. GIS 2006 ، 2 ، 1-20. [ Google Scholar ] [ CrossRef ]
یوکو، سی. یونگگو، ی. Wangwen، W. پیش‌بینی ضخامت درز زغال سنگ بر اساس ماشین‌های بردار پشتیبان حداقل مربعات و روش کریجینگ. الکترون. جی.ژئوتک. مهندس 2015 ، 20 ، 167-176. [ Google Scholar ]
بادل، م. انگورانی، س. شریعت پناهی، م. کاربرد کریجینگ نشانگر میانه و شبکه عصبی در مدلسازی جمعیت مختلط در یک کانسار سنگ آهن. محاسبه کنید. Geosci. 2011 ، 37 ، 530-540. [ Google Scholar ] [ CrossRef ]
کانفسکی، م. پوزدنوخوف، ا. Timonin، V. یادگیری ماشینی برای متغیرهای محیطی فضایی . انتشارات EPFL: لوزان، سوئیس، 2018؛ ISBN 9781783980284. [ Google Scholar ]
Rigol-Sanchez، JP درونیابی فضایی سطوح تابش طبیعی با اطلاعات قبلی با استفاده از شبکه‌های عصبی مصنوعی پس انتشار. Appl. GIS 2005 ، 1 ، 1-15. [ Google Scholar ] [ CrossRef ]
گوپتا، ا. کمبل، تی. Machiwal، D. مقایسه تکنیک‌های کریجینگ معمولی و بیزی در به تصویر کشیدن تغییرپذیری بارندگی در مناطق خشک و نیمه‌خشک شمال غرب هند. محیط زیست علوم زمین 2017 ، 76 ، 512. [ Google Scholar ] [ CrossRef ]
بارگاوی، ز.ک. Chebbi, A. مقایسه دو روش درونیابی کریجینگ بکار رفته در بارندگی مکانی-زمانی. جی هیدرول. 2009 ، 365 ، 56-73. [ Google Scholar ] [ CrossRef ]
نادبی، ا. لدرو، ای. برنینگ، الف. نقشه‌برداری پیش‌بینی‌کننده غنای گونه‌های ماهی صخره، تنوع و زیست توده در زنگبار با استفاده از تصویربرداری IKONOS و تکنیک‌های یادگیری ماشینی. سنسور از راه دور محیط. 2010 ، 114 ، 1230-1241. [ Google Scholar ] [ CrossRef ]
بنیتو، ام. بلاژک، آر. نتلر، ام. روت، اس. اولرو، اچ اس. Furlanello، C. پیش بینی تناسب زیستگاه با مدل های یادگیری ماشین: منطقه بالقوه Pinus sylvestris L. در شبه جزیره ایبری. Ecol. مدل 2006 ، 7 ، 383-393. [ Google Scholar ] [ CrossRef ]
هونگ، اچ. پرادان، بی. Bui، DT; خو، سی. یوسف، ع.م. چن، دبلیو. مقایسه چهار تابع هسته مورد استفاده در ماشین‌های بردار پشتیبان برای نقشه‌برداری حساسیت زمین لغزش: مطالعه موردی در منطقه سوئیچوان (چین). Geomat. نات خطر خطرات 2017 ، 8 ، 544-569. [ Google Scholar ] [ CrossRef ]
عربامری، ع. پرادان، بی. نقشه‌برداری پهنه‌بندی فرسایش خندقی رضایی با استفاده از رگرسیون وزن‌دار جغرافیایی یکپارچه با ضریب قطعیت و مدل‌های جنگل تصادفی در GIS. جی. محیط زیست. مدیریت 2019 ، 232 ، 928–942. [ Google Scholar ] [ CrossRef ]
نوری، ع.م. پرادان، بی. ارزیابی تناسب سایت سد QM Ajaj در رودخانه زاب بزرگ در شمال عراق با استفاده از داده های سنجش از دور و GIS. جی هیدرول. 2019 ، 574 ، 964–979. [ Google Scholar ] [ CrossRef ]
صبا، ک. کاربرد الگوریتم های یادگیری ماشین در اکتشاف هیدروکربن و مشخصه سازی مخزن. پایان نامه دکتری، دانشگاه آریزونا، توسان، AZ، ایالات متحده آمریکا، 2018. [ Google Scholar ]
سامانتا، بی. باندوپادیای، س. گانگولی، ر. ارزیابی مقایسه ای الگوریتم های یادگیری شبکه عصبی برای تخمین عیار سنگ معدن. ریاضی. جئول 2006 ، 38 ، 175-197. [ Google Scholar ] [ CrossRef ]
سامانتا، بی. Bandopadhyay, S. ساخت یک شبکه تابع پایه شعاعی با استفاده از یک الگوریتم تکاملی برای تخمین عیار در یک کانسار طلای پلاسر. محاسبه کنید. Geosci. 2009 ، 35 ، 1592-1602. [ Google Scholar ] [ CrossRef ]
Tutmez, B. روش شناسی فازی عدم قطعیت گرا برای تخمین درجه. محاسبه کنید. Geosci. 2007 ، 33 ، 280-288. [ Google Scholar ] [ CrossRef ]
جعفرسته، ب. فتحیان پور، ن. الگوریتم کلونی زنبور مصنوعی اغتشاش همزمان ترکیبی و الگوریتم پس انتشار برای آموزش شبکه عصبی پایه شعاعی خطی محلی بر روی تخمین عیار سنگ معدن. محاسبات عصبی 2017 ، 235 ، 217-227 . [ Google Scholar ] [ CrossRef ]
گوسوامی، ا. Mishra, MK; پاترا، دی. بررسی معماری شبکه عصبی رگرسیون عمومی برای تخمین عیار یک کانسار سنگ آهن هند. عرب جی. ژئوشی. 2017 ، 10 ، 80. [ Google Scholar ] [ CrossRef ]
کویکه، ک. ماتسودا، اس. Gu, B. ارزیابی دقت درونیابی کریجینگ عصبی با کاربرد در تجزیه و تحلیل توزیع دما. ریاضی. جئول 2001 ، 33 ، 421-448. [ Google Scholar ] [ CrossRef ]
Matías، JM; واموند، ا. تابودا، ج. گونزالس-مانتیگا، W. مقایسه کریجینگ و شبکه های عصبی با کاربرد در بهره برداری از یک معدن تخته سنگ. ریاضی. جئول 2004 ، 36 ، 463-486. [ Google Scholar ] [ CrossRef ]
Raghuvanshi، N. فهرستی جامع از تکنیک های اثبات شده برای رسیدگی به کمبود داده در سفر هوش مصنوعی شما. در دسترس آنلاین: https://towardsdatascience.com/a-comprehensive-list-of-proven-techniques-to-address-data-scarcity-in-your-ai-journey-1643ee380f21 (در 12 مه 2022 قابل دسترسی است).
چاترجی، اس. Bandopadhyay, S. Goodnews Bay تخمین منبع پلاتین با استفاده از حداقل مربعات پشتیبان رگرسیون برداری با انتخاب ابعاد فضای ورودی و فراپارامترها. نات منبع. Res. 2011 ، 20 ، 117-129. [ Google Scholar ] [ CrossRef ]
پراسومفان، اس. Mase، S. ایجاد نقشه پیش‌بینی برای داده‌های زمین‌آماری براساس یک شبکه عصبی تطبیقی با استفاده از نزدیک‌ترین همسایه‌ها. بین المللی جی. ماخ. فرا گرفتن. محاسبه کنید. 2013 ، 3 ، 98-102. [ Google Scholar ] [ CrossRef ]
سکولیچ، آ. کلیبردا، م. Heuvelink، GBM؛ نیکولیچ، م. باجات، ب. درونیابی فضایی تصادفی جنگل. Remote Sens. 2020 , 12 , 1687. [ Google Scholar ] [ CrossRef ]
زو، جی. پتروسیان، او. هوش مصنوعی قابل توضیح: استفاده از ارزش شیپلی برای توضیح سیستم‌های مبتنی بر ML تشخیص ناهنجاری پیچیده. جلو. آرتیف. هوشمند Appl. 2020 ، 332 ، 152-164. [ Google Scholar ] [ CrossRef ]
رودریگز-پرز، آر. بایورث، جی. تفسیر مدل‌های یادگیری ماشین با استفاده از مقادیر شیپلی: کاربرد برای پیش‌بینی‌های فعالیت چند هدفه و توان ترکیبی. جی. کامپیوتر. کمک کرد. مول. دس 2020 ، 34 ، 1013-1026. [ Google Scholar ] [ CrossRef ]
کرسی، N. پیش بینی فضایی و کریجینگ معمولی. ریاضی. جئول 1988 ، 20 ، 405-421. [ Google Scholar ] [ CrossRef ]
فاکس، EW; Ver Hoef، JM; اولسن، AR مقایسه رگرسیون فضایی با جنگل های تصادفی برای مجموعه داده های محیطی بزرگ. PLoS ONE 2020 , 15 , e0229509. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
هنگل، تی. Heuvelink، GBM؛ Stein، A. چارچوبی عمومی برای پیش‌بینی فضایی متغیرهای خاک بر اساس رگرسیون-کریجینگ. ژئودرما 2004 ، 120 ، 75-93. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
ژورنل، ا. Huijbregts, C. زمین آمار معدن ; انتشارات آکادمیک: لندن، بریتانیا، 1978. [ Google Scholar ]
شی، ی. لاو، AK; نگ، ای. هو، اچ. بلال، م. یک رویکرد رگرسیونی کاربری زمین در مقیاس چندگانه برای برآورد تغییرپذیری فضایی درون شهری غلظت PM 2.5 با یکپارچه سازی مجموعه داده های چند منبعی. بین المللی جی. محیط زیست. Res. بهداشت عمومی 2022 ، 19 ، 321. [ Google Scholar ] [ CrossRef ]
واتسون، استنتاج قوی همبستگی فضایی MW در مدل‌های رگرسیون خطی و تابلویی. در دسترس آنلاین: https://www.princeton.edu/~umueller/SHAR.pdf (در 20 ژانویه 2022 قابل دسترسی است).
هالین، ام. لو، ز. Tran، LT رگرسیون فضایی خطی محلی. ان آمار 2004 ، 32 ، 2469-2500. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
اوکونلولا، OA؛ آلوبید، م. Olubusoye، OE; آینده، ک. لوکمان، اف. Szűcs، I. رگرسیون فضایی و گفتمان زمین آمار با کاربرد تجربی برای داده های بارش در نیجریه. علمی Rep. 2021 , 11 , 16848. [ Google Scholar ] [ CrossRef ]
گریث، DA یک راه حل رگرسیون خطی برای مسئله خودهمبستگی فضایی. جی. جئوگر. سیستم 2000 ، 2 ، 141-156. [ Google Scholar ] [ CrossRef ]
طهماسبی، پ. هزارخانی، ع. شبکه های عصبی ترکیبی – منطق فازی – الگوریتم ژنتیک برای تخمین درجه. محاسبه کنید. Geosci. 2012 ، 42 ، 18-27. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
آن، اس. ریو، دی. لی، اس. یک رویکرد مبتنی بر یادگیری ماشین برای تخمین فضایی با استفاده از ویژگی‌های فضایی اطلاعات مختصات. ISPRS Int. J. Geo-Inf. 2020 ، 9 ، 587. [ Google Scholar ] [ CrossRef ]
بیل، سی ام. لنون، جی جی؛ Yearsley، JM; بروور، ام جی. Elston, DA تجزیه و تحلیل رگرسیون داده های مکانی. Ecol. Lett. 2010 ، 13 ، 246-264. [ Google Scholar ] [ CrossRef ]
مدلهای رگرسیون خطی فضایی آربیا، جی. در یک آغازگر برای اقتصاد سنجی فضایی با کاربرد در R ; پالگریو مک میلان: لندن، بریتانیا، 2014; صص 51-98. شابک 978-0-230-36038-9. [ Google Scholar ]
ساپوترو، DRS؛ محسنین، RY; ویدیانینگسیه، پ. سولیستیانینگسیه. خودرگرسیون فضایی با مدل خطای خودرگرسیون فضایی و برآورد پارامتر آن با روش حداقل مربع فضایی تعمیم یافته دو مرحله ای. J. Phys. Conf. سر. 2019 , 1217 , 012104. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
Cheung، TKY; Cheung، KC مدل وابستگی فضایی با تفاوت ویژگی. J. پیش بینی. 2020 ، 39 ، 615-627. [ Google Scholar ] [ CrossRef ]
بریمن، L. جنگل های تصادفی. ماخ فرا گرفتن. 2001 ، 45 ، 5-32. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
هیز، تی. اوسامی، س. یاکوبوچی، آر. McArdle، JJ استفاده از درختان طبقه بندی و رگرسیون (CART) و جنگل های تصادفی برای تجزیه و تحلیل ساییدگی: نتایج از دو شبیه سازی. روانی پیری 2015 ، 30 ، 911-929. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
شمرات، FMJM; رنجان، ر. حسیب، ک.م. یداو، ع. صدیق، ارزیابی عملکرد AH در میان الگوریتم‌های درخت تصمیم‌گیری ID3، C4.5 و CART، الگوریتم‌های درخت تصمیم CART. در مجموعه مقالات کنفرانس بین المللی محاسبات فراگیر و شبکه های اجتماعی [ICPCSN 2021]، سالم، تامیل نادو، هند، 19 تا 20 مارس 2021؛ پ. 15. [ Google Scholar ]
یداو، س. Shukla، S. تجزیه و تحلیل k-Fold Cross-Validation بر روی Hold-Out Validation در مجموعه داده های عظیم برای طبقه بندی کیفیت. در مجموعه مقالات ششمین کنفرانس بین المللی محاسبات پیشرفته، IACC 2016، Bhimavaram، هند، 27-28 فوریه 2016. صص 78-83. [ Google Scholar ]
Bui، DT; شهابی، ح. امیدوار، ای. شیرزادی، ع. گیرتسما، م. کلگ، جی جی. خسروی، ک. پرادان، بی. فام، بی تی؛ چاپی، ک. و همکاران پیش بینی زمین لغزش کم عمق با استفاده از یک الگوریتم جدید یادگیری ماشین عملکردی ترکیبی. Remote Sens. 2019 , 11 , 931. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
پرادان، ب. مطالعه تطبیقی بر روی توانایی پیش‌بینی درخت تصمیم، ماشین بردار پشتیبان و مدل‌های عصبی فازی در نقشه‌برداری حساسیت زمین لغزش با استفاده از GIS. محاسبه کنید. Geosci. 2013 ، 51 ، 350-365. [ Google Scholar ] [ CrossRef ]
خسروی، ک. شهابی، ح. فام، بی تی؛ آداموفسکی، جی. شیرزادی، ع. پرادان، بی. دوو، جی. Ly، HB; گروف، جی. هو، اچ ال. و همکاران ارزیابی مقایسه‌ای مدل‌سازی حساسیت سیل با استفاده از روش‌های تحلیل تصمیم‌گیری چند معیاره و یادگیری ماشینی. جی هیدرول. 2019 ، 573 ، 311-323. [ Google Scholar ] [ CrossRef ]
مریانوویچ، م. کوواچویچ، م. باجات، بی. Voženílek، V. ارزیابی حساسیت زمین لغزش با استفاده از الگوریتم یادگیری ماشین SVM. مهندس جئول 2011 ، 123 ، 225-234. [ Google Scholar ] [ CrossRef ]
تهرانی، ام اس; پرادان، بی. نقشه‌برداری حساسیت به سیل جبور، MN با استفاده از یک مجموعه جدید وزن‌های شواهد و مدل‌های ماشین بردار پشتیبان در GIS. جی هیدرول. 2014 ، 512 ، 332-343. [ Google Scholar ] [ CrossRef ]
باجاج، الف. معیارهای عملکرد در یادگیری ماشین [راهنمای کامل]. در دسترس آنلاین: https://neptune.ai/blog/performance-metrics-in-machine-learning-complete-guide (در 1 مه 2022 قابل دسترسی است).
سینکلر، ای جی. Blackwell, GH Applied Mineral Inventory Estimation , 1st ed.; انتشارات دانشگاه کمبریج: کمبریج، انگلستان، 2002; ISBN 0511031459. [ Google Scholar ]
وو، جی. چن، XY; ژانگ، اچ. Xiong، LD; لی، اچ. بهینه سازی فراپارامتر دنگ، SH برای مدل های یادگیری ماشین بر اساس بهینه سازی بیزی. جی. الکترون. علمی تکنولوژی 2019 ، 17 ، 26–40. [ Google Scholar ] [ CrossRef ]
اسنوک، جی. لاروچل، اچ. آدامز، RP بهینه سازی عملی بیزی الگوریتم های یادگیری ماشین. در مجموعه مقالات NIPS’12: مجموعه مقالات بیست و پنجمین کنفرانس بین المللی سیستم های پردازش اطلاعات عصبی، دریاچه تاهو، NV، ایالات متحده آمریکا، 3-6 دسامبر 2012. صفحات 2951-2959. [ Google Scholar ]
مارتین، پی. دیوید، EG; اریک، سی.-پی. BOA: الگوریتم بهینه سازی بیزی. در مجموعه مقالات اولین کنفرانس سالانه محاسبات ژنتیکی و تکاملی – جلد 1، اورلاندو، فلوریدا، ایالات متحده آمریکا، 13 تا 17 ژوئیه 1999. Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 1999; صص 525-532. [ Google Scholar ]
خان، AU; سلمان، س. محمد، ک. حبیب، م. مدل‌سازی قابلیت انفجار گرد و غبار زغال سنگ زغال سنگ خیبر پختونخوا با استفاده از الگوریتم جنگل تصادفی. Energies 2022 , 15 , 3169. [ Google Scholar ] [ CrossRef ]
Shapely، LS یک ارزش برای بازی های n-Person. در کمک به نظریه بازی ها (AM-28)، جلد دوم. در سالنامه مطالعات ریاضی ; Kuhn, HWA, Tucker, AW, Eds. انتشارات دانشگاه پرینستون: پرینستون، نیوجرسی، ایالات متحده آمریکا، 1953; صص 307-317. [ Google Scholar ]
Py با فهرست بسته Python بسته های پایتون را پیدا، نصب و منتشر کنید. در دسترس آنلاین: https://pypi.org/ (دسترسی در 22 دسامبر 2021).
اوشیرو، TM; پرز، ص. Baranauskas، JA چند درخت در یک جنگل تصادفی؟ BT – یادگیری ماشین و داده کاوی در تشخیص الگو. در یادداشت های سخنرانی در علوم کامپیوتر، مجموعه مقالات یادگیری ماشین و داده کاوی در تشخیص الگو، MLDM 2012 ؛ پرنر، پی، اد. Springer: برلین/هایدلبرگ، آلمان، 2012; جلد 7376، صص 154–168. [ Google Scholar ]
مری، ن. مارکوت، دی. کمی کردن منابع معدنی و عدم قطعیت آنها با استفاده از دو روش یادگیری ماشینی موجود. ریاضی. Geosci. 2022 ، 54 ، 363-387. [ Google Scholar ] [ CrossRef ]

شکل 1. درخت تصمیم با عمق 4.

شکل 2. داده های بررسی دریاچه واکر.

شکل 3. داده های جامع دریاچه واکر.

شکل 4. مدل جنگل تصادفی.

شکل 5. ویژگی های ورودی برای تخمین نقطه.

شکل 6. روند متغیر V مجموعه داده Walker Lake که با معادله (9) نشان داده شده است.

شکل 7. مدل های واریوگرام تجربی و مدل سازی شده برای داده های Walkerlake. از بالا چپ به پایین راست در ( a ) 0، ( b ) 45، ( c ) 90 و ( d ) 135 درجه آزیموت شامل ( e ) یک همه جهته و ( f ) واریوگرام در همه جهات.

شکل 8. نمودار تیلور خلاصه‌ای از R-squared و RMSE مدل‌های OK، MLR و RF.

شکل 9. تخمین چند نقطه رگرسیون خطی برای مجموعه داده Walkerlake.

شکل 10. برآورد نقطه ای مبتنی بر RF برای مجموعه داده Walkerlake.

شکل 11. تخمین فضایی مجموعه داده Walkerlake توسط کریجینگ معمولی.

شکل 12. 10 ویژگی برتر (نمونه) که تأثیر مثبتی بر فرآیند تخمین فضایی در مجموعه داده Walkerlake دارند.

شکل 13. موقعیت مکانی 5 ویژگی برتر تأثیر مثبتی بر تخمین در مجموعه داده Walkerlake دارد.

شکل 14. ضرایب MLR برای پیش بینی با استفاده از مجموعه داده Walkerlake.

شکل 15. نمودار خلاصه تاثیر/تاثیر نمونه ها بر برآورد.

مقالات داخلی و بین المللی

بدون دیدگاه

دیدگاهتان را بنویسید لغو پاسخ

برای نوشتن دیدگاه باید وارد بشوید.

مشاورین هوش پیروزی

کلید واژه ها:

1. مقدمه

2. بررسی ادبیات