ابرهای نقطه داخلی با استفاده از ویژگی‌های خط دوبعدی

ثبت دو به دو درشت ابرهای نقطه داخلی با استفاده از ویژگی‌های خط دوبعدی

چکیده

ثبت نام برای LiDAR زمینی (تشخیص نور و محدوده) ابرهای نقطه اسکن ضروری است. ثبت ابرهای نقطه داخلی به دلیل انسداد و خود شباهت سازه های داخلی چالش برانگیز است. این مقاله یک روش ثبت نام درشت 4 درجه آزادی (4DOF) را پیشنهاد می‌کند که به طور کامل از دانش تراز بودن تجهیزات یا جبران شیب توسط یک سنسور شیب در جمع‌آوری داده‌ها بهره می‌برد. این روش مشکل ثبت 4DOF را به دو بخش تجزیه می‌کند: (1) تراز افقی با استفاده از تصاویر ارتو پروجکت شده و (2) تراز عمودی. تصاویر ارتو پروجکت شده با استفاده از نقاط بین کف و سقف تولید می شوند.

و تراز افقی با تطبیق تصاویر ارتو پروژکتور شده منبع و هدف با استفاده از ویژگی های خط دوبعدی شناسایی شده از آنها به دست می آید. تراز عمودی با معادل سازی ارتفاع کف و سقف در نقطه مبدا و هدف حاصل می شود. دو مجموعه داده، یکی با پنج ایستگاه و دیگری با 20 ایستگاه، برای ارزیابی عملکرد روش پیشنهادی استفاده شد. نتایج تجربی نشان داد که روش پیشنهادی به ترتیب در یک صحنه ساده و یک صحنه چالش برانگیز به ترتیب 80% و 63% نرخ ثبت موفقیت آمیز (SRRs) را به دست آورد. SRR در صحنه ساده فقط کمتر از روش مجموعه چهار نقطه‌ای متجانس (K4PCS) است. SRR در صحنه چالش برانگیز بهتر از هر پنج روش مقایسه است. اگرچه روش پیشنهادی هنوز دارای محدودیت‌هایی است،

کلید واژه ها:

ابرهای نقطه داخلی ; ثبت نام ؛ 4DOF ; تطبیق خط

1. مقدمه

دسترسی آسان به ابرهای نقطه متراکم با کیفیت بالا به این معنی است که اسکن LiDAR (تشخیص نور و محدوده) به طور گسترده در مناطقی مانند نقشه برداری [ 1 ]، موجودی جنگلداری [ 2 ] و پایش خطر [ 3 ] در طول گذشته استفاده شده است. دو دهه. در سال‌های اخیر، ابرهای نقطه‌ای داخلی برای کاربردها در تجسم تعاملی [ 4 ]، ساخت‌وساز ساخته شده [ 5 ، 6 ]، ناوبری داخلی [ 7 ]، و بازسازی مدل ساختمان [ 8 ، 9 ] مطلوب‌تر شده‌اند. روش های مقرون به صرفه، راحت و کارآمد برای تولید ابرهای نقطه داخلی با کیفیت بالا مورد انتظار است.

روش ها و تجهیزات مختلفی را می توان برای به دست آوردن ابرهای نقطه داخلی استفاده کرد. اسکن لیزری سنتی زمینی (TLS) احتمالاً اساسی ترین روشی است که برای به دست آوردن ابرهای نقطه داخلی استفاده می شود. TLS می تواند ابرهای نقطه ای با دقت بالا را به دست آورد، اما باید ایستگاه به ایستگاه اسکن شود تا نمای کامل صحنه داخلی را پوشش دهد. سیستم‌های نقشه‌برداری داخلی سیار، مانند NavVis [ 10 ]، می‌توانند ابرهای نقطه‌ای متراکم داخلی را در حالت متحرک به دست آورند، که راحت و کارآمد است، اما دقت ابرهای نقطه تولید شده کمتر از TLS است. حسگرهای RGB-depth (RGB-D) مانند Intel RealSense [ 11 ] و Microsoft Kinect [ 12 ] به دلیل هزینه کم و قابل حمل بودن، بیشتر و بیشتر در جمع آوری داده های داخلی استفاده می شوند.

ثبت نام برای روش‌های جذب ابر نقاط داخلی مبتنی بر TLS و RGB-D ضروری است. ثبت، ابرهای نقطه اسکن شده از ایستگاه های مختلف را به یک سیستم مختصات یکپارچه تبدیل می کند تا کل صحنه را به طور کامل پوشش دهد. بسته به تعداد ایستگاه ابرهای نقطه ورودی، ثبت را می توان به ثبت دو به دو و ثبت چند نمای طبقه بندی کرد. ثبت دو به دو اساس و پایه ثبت چند نمایه است. علاوه بر این، یک استراتژی درشت به ریز معمولاً برای بهبود کارایی ثبت نام زوجی استفاده می شود. مرحله درشت پارامترهای ثبت اولیه را به سرعت پیدا می کند و به عنوان ورودی ثبت خوب عمل می کند. مرحله ثبت نام دقیق پارامترهای ثبت بهینه را به دست می آورد. الگوریتم تکراری نزدیکترین نقطه (ICP) [ 13] و انواع آن [ 14 ، 15 ] و الگوریتم تبدیل توزیع نرمال (NDT) [ 16 ] و انواع آن [ 17 ، 18 ] از معروف ترین و پرکاربردترین الگوریتم های ثبت خوب هستند.

این مقاله بر روی ثبت دو به دو درشت ابرهای نقطه تمرکز دارد که نقش مهمی در پردازش ابر نقطه ایفا می کند. روش‌های مختلفی برای انجام ثبت نام‌های قوی، کارآمد و با دقت بالا ایجاد شده‌اند. این روش ها عمدتاً به دو دسته تقسیم می شوند: (1) روش های ثبت مبتنی بر ویژگی و (2) روش های ثبت احتمالی.

در میان روش های ثبت نام مبتنی بر ویژگی، ویژگی های دست ساز پرکاربردترین و متداول ترین ویژگی ها هستند. در این روش ثبت، ابتدا ویژگی‌های هندسی (مانند نقاط، منحنی‌ها، صفحات و سطوح) از ابرهای نقطه‌ای استخراج می‌شوند و سپس مطابقت‌ها از این ویژگی‌های هندسی شناسایی می‌شوند. در نهایت، تبدیل صلب بین ابرهای نقطه ای بر اساس ویژگی های هندسی مربوطه شناسایی شده تخمین زده می شود. تصاویر چرخشی [ 19 ] و تصاویر گاوسی توسعه یافته (EGI) [ 20 ] از جمله ویژگی های نقطه کلاسیکی هستند که برای ثبت ابرهای نقطه استفاده می شوند. برای توصیف بهتر هندسه محلی، Rusu و همکاران. [ 21] ویژگی های 16 بعدی (16D) را به نام هیستوگرام ویژگی های پایدار (PFHs) پیشنهاد کرد و آنها را برای ثبت ابرهای نقطه اعمال کرد. محاسبه ویژگی های PFH زمان بر است. روسو و همکاران [ 22 ] ویژگی PFH را بهبود بخشید و هیستوگرام ویژگی نقطه سریع (FPFHs) را پیشنهاد کرد. برای اینکه از نظر زمانی کارآمدتر باشد، دونگ و همکاران. [ 23 ] یک توصیفگر باینری به نام زمینه شکل باینری (BSC) برای تشخیص شی و ثبت ابر نقطه پیشنهاد کرد. ثابت شد که توصیفگر BSC از قابلیت توصیفی بالا، استحکام قوی و کارایی بالا هم در زمان و هم در حافظه برخوردار است.

ویژگی های نقطه ای مانند Spin images، EGI، PFH، FPFH و BSC از نظر تئوری برای هر نوع ابر نقطه ای مناسب هستند. با این حال، عملکرد در برخی موارد کاهش می یابد. در چنین مواردی، ویژگی‌های هندسی سطح بالا، مانند خطوط، صفحات و ویژگی‌های معنایی، برای بهبود عملکرد ثبت ابرهای نقطه‌ای استفاده می‌شوند. یانگ و زانگ [ 24 ] خطوط تاج را از ابرهای نقطه TLS استخراج کردند و یک مدل تغییر شکل به عنوان معیار تشابه برای مطابقت با خطوط تاج استخراج شده استفاده شد. تکه های مسطح برای ثبت داده های اسکن لیزری سه بعدی در [ 25 ] استخراج و مطابقت داده شدند . ساقه درختان استخراج و مطابقت داده شد تا ابرهای نقطه ای به دست آمده در جنگلداری در [ 26]. ویژگی‌های هندسی سطح بالا مانند خطوط تاج، تکه‌های مسطح و ساقه‌های درخت معمولاً فقط برای ابرهای نقطه‌ای که در صحنه‌های خاص اسکن می‌شوند مناسب هستند.

طراحی دست سازهای موثر و مستحکم دشوار است. در سال های اخیر، روش یادگیری عمیق برای یادگیری ویژگی های توصیفی سطح بالا از مقادیر زیاد داده های آموزشی به طور مستقیم و خودکار استفاده شده است. زنگ و همکاران [ 27 ] یک شبکه مبتنی بر پچ حجمی برای یادگیری مکاتبات برای ثبت داده های RGB-D پیشنهاد کرد. به طور مشابه، ژانگ و همکاران. [ 28 ] پیشنهاد کرد که ویژگی‌های عمیق سه‌بعدی را از تکه‌های حجمی برای ثبت ابرهای نقطه اسکن لیزری سیار که در مراحل مختلف به دست آمده‌اند، یاد بگیرند. در مقابل یادگیری ویژگی‌ها از تکه‌های حجمی، آلبا و همکاران. [ 29 ] همسایگی نقاط کلیدی را با وصله های RGB-D 2 بعدی و ویژگی های آموخته شده با استفاده از شبکه عصبی کانولوشنال 2 بعدی استاندارد پیش بینی کرد. بر اساس PointNet [30 ]، دنگ و همکاران. [ 31 ] شبکه ویژگی جفت نقطه (PPFNet) را برای یادگیری توصیفگرهای ویژگی محلی سه بعدی آگاهانه جهانی به طور مستقیم از نقاط نامرتب پیشنهاد کرد. به طور مشابه، Aoki و همکاران. [ 32 ] PointNet را به عنوان یک تابع “تصویربرداری” قابل یادگیری در نظر گرفت و بنابراین از الگوریتم Lucas-Kanade برای دستیابی به تراز ابرهای نقطه استفاده کرد.

علاوه بر ویژگی‌های دست‌ساز و ویژگی‌های یادگیری عمیق، مجموعه چهار نقطه‌ای متجانس (4PCS) یکی دیگر از ویژگی‌های ویژه‌ای است که برای ثبت ابرهای نقطه‌ای پیشنهاد شده است. روش های ثبت بر اساس 4PCS ابتدا پایه های چهار نقطه ای همسطح را از نقاط مبدا و مقصد استخراج می کنند. نسبت‌های ثابت وابسته با استفاده از نقاط پایه برای یافتن تناظرهای نامزد بین پایه‌های گسترده در نقاط مبدا و مقصد تعریف می‌شوند. دگرگونی‌های کاندید بر اساس متناظر 4PCS نامزد تخمین زده می‌شوند و تبدیلی که نقاط مبدا را برای داشتن بیشترین نقاط نزدیک به نقاط هدف تبدیل می‌کند به عنوان تبدیل بهینه و نهایی انتخاب می‌شود. الگوریتم 4PCS برای مجموعه‌های داده با همپوشانی‌های کوچک به خوبی کار می‌کند و در برابر نویز و موارد پرت انعطاف‌پذیر است، اما برای مجموعه‌های داده در مقیاس بزرگ زمان‌بر است. برای بهبود بازده زمانی آن، برخی از انواع بر اساس الگوریتم اصلی 4PCS توسعه یافته اند. ملادو و همکاران [33 ] الگوریتم اصلی 4PCS را با معرفی یک سازمان داده نمایه سازی هوشمند برای کاهش پیچیدگی زمانی درجه دوم به پیچیدگی زمانی خطی بهبود بخشید. الگوریتم بهبود یافته SUPER 4PCS نام دارد. 4PCS مبتنی بر Keypoint (K4PCS)، پیشنهاد شده توسط Theiler و همکاران. [ 34 ]، کارایی زمانی را با استخراج نقاط کلیدی از ابرهای نقطه و سپس تغذیه نقاط کلیدی به الگوریتم 4PCS، به جای استفاده از تمام نقاط در نقاط مبدا و مقصد، بهبود می بخشد. مشابه K4PCS، Ge [ 35 ] پیشنهاد کرد که ابتدا نقاط کلیدی معنایی استخراج شود و سپس نقاط کلیدی معنایی استخراج شده به الگوریتم 4PCS تغذیه شود.

روش‌های ثبت مبتنی بر ویژگی، ثبت ابر نقطه‌ای را با تطبیق تطابق ویژگی‌ها در ابرهای نقطه مبدا و مقصد انجام می‌دهند. در همین حال، مدل روش ثبت احتمالاتی از توزیع ابرهای نقطه ای به عنوان تابع چگالی استفاده می کند و ثبت را با استفاده از رویکرد مبتنی بر همبستگی یا با استفاده از چارچوب بهینه سازی مبتنی بر حداکثرسازی انتظار انجام می دهد [ 36 ]. Tsin و Kanade [ 37 ] پیشنهاد کردند که از یک تابع همبستگی هسته برای اندازه گیری میل ترکیبی بین ابرهای نقطه و ثبت ابرهای نقطه با یافتن حداکثر همبستگی هسته با استفاده از برآوردگر M استفاده شود. ژیان و وموری [ 38] یک چارچوب یکپارچه برای ثبت ابر نقطه صلب و غیر صلب پیشنهاد کرد که از مدل‌های مخلوط گاوسی برای نمایش ابرهای نقطه و ثبت ابرهای نقطه ورودی با به حداقل رساندن اندازه‌گیری اختلاف آماری بین دو مخلوط گاوسی استفاده می‌کند. مایروننکو و سونگ [ 39 ] الگوریتم رانش نقطه منسجم (CPD) را پیشنهاد کردند، که مرکزهای مدل مخلوط گاوسی ابر نقطه مبدا را با ابر نقطه هدف با به حداکثر رساندن احتمال به نحوی که مرکزهای GMM را مجبور می‌کند به طور منسجم حرکت کنند، منطبق می‌کند. گروه برای حفظ ساختار توپولوژیکی مجموعه های نقطه.

اگرچه ثبت ابر نقطه درشت برای مدت طولانی به طور گسترده مورد مطالعه قرار گرفته است، اما به دلیل پیچیدگی صحنه، توزیع پراکنده، انسداد و نویز ابرهای نقطه ای، به ویژه برای ابرهای نقطه داخلی، همچنان چالش برانگیز است. در مقایسه با صحنه‌های بیرونی، صحنه‌های داخلی ویژگی‌های خاص خود را دارند: (1) بسیاری از ساختارهای خود شباهت وجود دارند و (2) آنها دارای ویژگی‌های هندسی بسیار ساختارمندتری هستند. ثبت ابرهای نقطه صحنه داخلی می تواند عملکرد بهتری داشته باشد اگر ویژگی های خود به طور کامل در نظر گرفته شود. بوئنو و همکاران [ 6 ] پیشنهاد استخراج نقاط کلیدی از ابرهای نقطه داخلی و سپس تغذیه نقاط کلیدی به یک الگوریتم 4PCS برای دستیابی به ثبت ابرهای نقطه داخلی را ارائه کرد. این روش مشابه الگوریتم K4PCS است [ 34] برای صحنه های خارج از منزل، و ویژگی های ابرهای نقطه داخلی در نظر گرفته نمی شود. تسای و هوانگ [ 40 ] یک سیستم بازسازی سه بعدی داخلی را با استفاده از پان شیب و یک حسگر RGB-D طراحی کردند. الگوریتمی برای ثبت خودکار داده های به دست آمده در یک ایستگاه ثابت ایجاد شد اما ثبت جهانی ایستگاه های مختلف ارائه نشد. محمود و همکاران [ 5 ] خطوط را از یک مقطع افقی استخراج کرد و با استفاده از تطابقات ویژگی خط، مدل ساخته شده را به یک مدل طبق برنامه ریزی ثبت کرد. این روش برای ثبت ابر نقطه بخشی از ساختمان (مانند اتاق) به مدل اطلاعات کامل ساختمان (BIM) مناسب است اما برای ثبت ابر نقطه ایستگاه به ایستگاه مناسب نیست. سانچز و همکاران [ 41] الگوریتم ثبت نام مبتنی بر ویژگی صحنه ساخت یافته (SSFR) را پیشنهاد کرد که از تصاویر گاوسی برای یافتن صفحات مربوطه برای ثبت ابرهای نقطه داخلی که دارای صفحات هستند استفاده می کند. الگوریتم SSFR برای صحنه های پیچیده داخلی مناسب نیست زیرا عدد صفحه آن ثابت است. پاوان و همکاران [ 42 ] یک روش مبتنی بر مکاتبات هواپیما به هواپیما برای ثبت ابر نقاط ساختمان داخلی و خارجی پیشنهاد کرد. صفحات ابتدا با استفاده از الگوریتم اجماع نمونه تصادفی (RANSAC) تقسیم می شوند و سپس صفحات با استفاده از اعداد مختلط مطابقت داده می شوند. در نهایت، تبدیل با استفاده از مکاتبات صفحه تخمین زده می شود. این روش به دلیل مرحله تقسیم بندی RANSAC زمان بر است.

تبدیل صلب بین ابرهای نقطه‌ای دارای شش درجه آزادی (DOF) است اگر هیچ محدودیتی نداشته باشد و با سه تبدیل و سه زاویه چرخش بیان شود. برای اسکنرهای پیشرفته، تمایل تجهیزات در اکتساب داده را می توان با حسگر شیب داخلی جبران کرد و بنابراین چرخش بین ابرهای نقطه ای اسکن شده از ایستگاه های مختلف فقط به آزیموت محدود می شود. بر اساس این فرض، Cai و همکاران. [ 43 ] یک الگوریتم شاخه و کران سریع (BnB) بر اساس مکاتبات سه بعدی نقطه کلیدی برای جستجوی چرخش 1 بعدی پیشنهاد کرد و بنابراین به ثبت 4 درجه آزادی (4DOF) محاسباتی کارآمد دست یافت. در کار قبلی ما [ 44]، یک الگوریتم ثبت دو مرحله ای 4DOF برای صحنه های بیرونی پیشنهاد شده است. در گام اول، ترجمه افقی و زاویه آزیموت با ثبت تصاویر مشخصه مبتنی بر نقطه کلیدی برآورد شده است. در مرحله دوم، ترجمه عمودی با اختلاف ارتفاع مناطق همپوشانی پس از تراز افقی آنها تخمین زده می شود. Ge و Hu [ 45 ] یک الگوریتم ثبت سه مرحله ای 4DOF برای ابرهای نقطه صحنه شهری پیشنهاد کردند. در مرحله اول، تبدیل دوبعدی با استفاده از خطوط اولیه تطبیق برآورد شد. در مرحله دوم، افست عمودی با بهینه سازی حداقل مربعات جبران شد. در نهایت، تبدیل کامل توسط الگوریتم حداقل مربعات با استفاده از تکه‌های نمونه‌برداری یکنواخت اصلاح شد.

این مقاله یک الگوریتم ثبت درشت 4DOF را برای ابرهای نقطه داخلی پیشنهاد می‌کند. مشابه کار قبلی ما [ 44]، ثبت 4DOF به دو مرحله تقسیم می شود. مرحله اول به ثبت دو بعدی در صفحه افقی می رسد. مرحله دوم، ابرهای نقطه ای را در صفحه عمودی پس از تراز افقی تراز می کند. متفاوت از کار قبلی ما، این مقاله روش جدیدی را برای تولید تصاویر ارتو پروژکتوری برای ابرهای نقطه داخلی پیشنهاد می‌کند و با تطبیق ویژگی‌های خط دوبعدی در تصاویر ارتو پروجکت‌شده به‌جای استفاده از روش ثبت مبتنی بر نقطه کلید، به تراز افقی دست می‌یابد. علاوه بر این، این مقاله با معادل سازی ارتفاعات کف و سقف در ابر نقطه مبدا و ابر نقطه هدف به جای معادل سازی ارتفاعات مناطق همپوشانی، به تراز عمودی دست می یابد.

ساختار باقی مانده این مقاله به شرح زیر است. در بخش 2 ، مجموعه داده‌های ابر نقطه داخلی مورد استفاده معرفی می‌شوند و روش ثبت پیشنهادی به تفصیل شرح داده می‌شود. در بخش 3 ، نتایج ارائه شده است. در بخش 4 ، به طور خلاصه روش پیشنهادی و نتایج را مورد بحث قرار می‌دهیم. در نهایت، نتیجه گیری در بخش 5 آورده شده است.

2. مواد و روشها

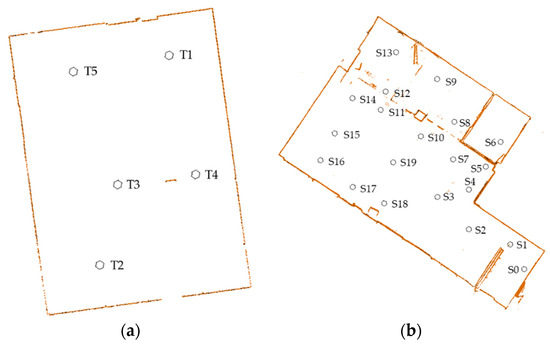
2.1. مجموعه داده های Cloud Point Indoor

دو مجموعه داده برای اعتبارسنجی روش پیشنهادی استفاده شد. اولین مورد، ارائه شده توسط ETH زوریخ ( https://ethz.ch/content/dam/ethz/special-interest/baug/igp/photogrammetry-remote-sensing-dam/documents/sourcecode-and-datasets/PascalTheiler/office .zip ) و به اختصار SR نامیده می شود، شامل پنج اسکن از یک دفتر داخلی است ( شکل 1 a). هر پنج اسکن با یکدیگر همپوشانی دارند، و بنابراین در مجموع 10 جفت تطبیق را می توان انجام داد ( جدول 1 ). تبدیل حقیقت زمینی بین جفت ها توسط ETH زوریخ ارائه شده است. مورد دوم که توسط Wuhan RGSpace Technology Co.ب). ابرهای نقطه توسط یک اسکنر خود ادغام شده با استفاده از سه Azure Kinect DK ( https://azure.microsoft.com/en-us/services/kinect-dk/ ) گرفته شدند. Azure Kinect DK در حالت WFOV (میدان دید گسترده) 2×2 binned در اکتساب داده ها کار می کرد و بنابراین محدوده اسکن کمتر از 2.9 متر بود. اسکنر با استفاده از سنسورهای شیب با دقت 0.1 درجه تراز شد و حول z چرخید.محور با فاصله زاویه ثابت از پیش کالیبره شده (30 درجه) در اکتساب داده. روابط نسبی بین سنسورهای Azure Kinect DK نیز به دقت کالیبره شد و بنابراین تمام داده‌های اسکن شده در یک ایستگاه می‌توانند به یک سیستم مختصات یکپارچه تبدیل شوند. در مجموع 19 جفت تطبیق انجام شد تا اطمینان حاصل شود که تمام 20 اسکن می توانند در نقاط اولین ایستگاه اسکن ثبت شوند. تبدیل حقیقت زمینی بین جفت ها توسط شرکت فناوری RGSpace ووهان با مسئولیت محدود ارائه شد. جفت های مورد استفاده برای انجام آزمایش ها و سایر جزئیات را می توان در جدول 1 یافت .

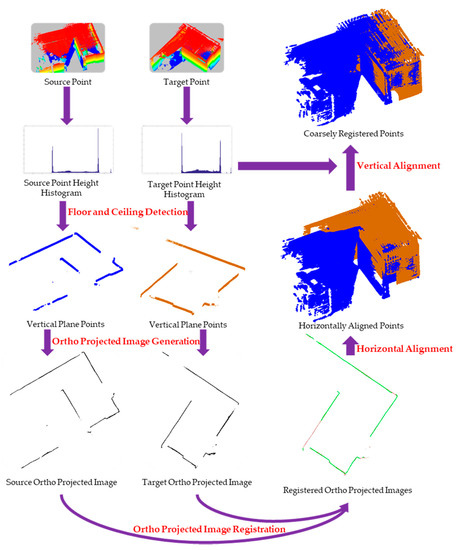
2.2. روش ثبت نام

روش ثبت ابر نقطه داخلی پیشنهادی فرض می‌کند که تجهیزات تراز شده است یا شیب توسط سنسورهای شیب در جمع‌آوری داده جبران می‌شود. کل فرآیند ثبت با سه مرحله به دست می‌آید: (1) تولید تصویر به صورت عمودی، (2) ثبت تصویر با استفاده از ویژگی‌های خط دو بعدی و (3) ثبت ابر نقطه‌ای. نمای کلی روش ثبت نام پیشنهادی در شکل 2 نشان داده شده است .

2.2.1. چارچوب ثبت نام

تبدیل صلب بین ابرهای نقطه مبدا و ابرهای نقطه هدف بدون هیچ محدودیتی را می توان به صورت زیر نوشت:

[ایکستیyتیzتی]=[تیایکستیyتیz]+آر(α)آر(β)آر(θ)[ایکسسyسzس]،

(1)

جایی که [ایکسسyسzس]تینقطه مبدا و [ایکستیyتیzتی]تینقطه هدف است [تیایکستیyتیz]تیبردار ترجمه بین نقاط مبدا و نقاط هدف است. α، β،θزوایای چرخش بین نقاط مبدا و نقاط هدف هستند. اگر تجهیزات تراز شده باشد یا شیب با یک سنسور شیب در جمع آوری داده ها جبران شود، سپس αو βبرابر با صفر هستند. در چنین شرایطی می توان معادله (1) را به صورت زیر نوشت:

[ایکستیyتیzتی]=[تیایکستیyتیz]+آر(θ)[ایکسسyسzس]،

(2)

یا

[ایکستیyتیzتی]=[تیایکستیyتیz]+[cosθ-گناهθ0گناهθcosθ0001][ایکسسyسzس].

(3)

معادله (3) را می توان به صورت زیر قالب بندی کرد:

[ایکستیyتیzتی]=[00تیz+zس-1]+[cosθ-گناهθتیایکسگناهθcosθتیy001][ایکسسyس1]،

(4)

یا

[ایکستیyتیzتی]=[00تیz+zس-1]+[آرتیایکسy01][ایکسسyس1].

(5)

از معادله (5)، می توان نتیجه گرفت که ثبت 4DOF را می توان به دو مرحله تجزیه کرد: (1) مرحله اول بردار ترجمه افقی و زاویه چرخش را در اطراف تخمین می زند. zمحور (در زیر به عنوان زاویه آزیموت نامگذاری شده است)، که مربوط به [آر،تیایکسy]; (2) مرحله دوم ترجمه عمودی را تخمین می زند، تیz.

تخمین بردار ترجمه افقی و زاویه آزیموت معادل ثبت تصاویر ارتو نقاط مبدا و نقاط هدف است. این مقاله از نقاط صفحه عمودی مانند دیوارها و درها برای تولید تصاویر ارتو پروژکتوری ابر نقطه ای برای دستیابی به تخمین بردار ترجمه افقی و زاویه آزیموت استفاده می کند. پس از تراز افقی، ترجمه عمودی با استفاده از اختلاف ارتفاع کف و سقف در نقطه مبدا و هدف برآورد می شود.

2.2.2. تولید تصویر Ortho-Projected

نقاط صفحه عمودی مانند دیوارها و درها برای تولید تصاویر ارتو پروجکت شده استفاده می شوند. برای بدست آوردن نقاط صفحه عمودی، ابتدا نقاط زمین و نقاط سقف از ابرهای خام نقطه داخلی حذف می شوند. بدیهی است که زمین و سقف بیشترین نقاط را در هیستوگرام ارتفاع دارند، همانطور که در شکل 3 نشان داده شده است ، بنابراین می توانیم با استفاده از هیستوگرام ارتفاع، ارتفاع زمین و سقف را پیدا کنیم و نقاط را با استفاده از آن حذف کنیم. zمقادیر کوچکتر از ارتفاع زمین و نقاط با zمقادیر بالاتر از ارتفاع سقف

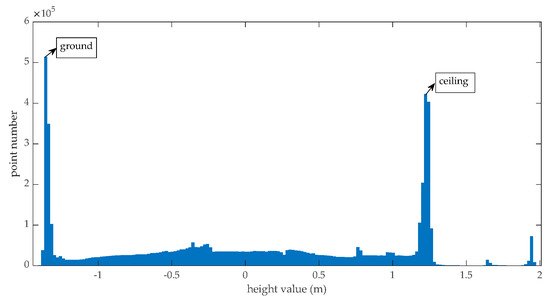
از آنجایی که تجهیزات در بالای کف نصب شده اند و مبدا مختصات سنسور روی تجهیزات است، مقادیر z نقاط کف قطعا کوچکتر از صفر و مقادیر z نقاط سقف قطعا بزرگتر از صفر هستند. ارتفاع نقاط کف را می توان با قرار دادن زیر قسمت صفر هیستوگرام ارتفاع با استفاده از توزیع مقادیر شدید یافت. بر این اساس، ارتفاع نقاط سقف را می توان با برازش بالای قسمت صفر هیستوگرام ارتفاع با استفاده از توزیع مقادیر شدید یافت. تابع چگالی احتمال استفاده شده در این مقاله به صورت معادله (6) تعریف شده است. در معادله (6) μمحل حداکثر مقدار و سیک پارامتر مقیاس است.

y=1سه-(ایکس-μ)/سه-ه-(ایکس-μ)/س.

(6)

بعد از ارتفاعات کف (به عنوان ساعتf) و سقف (به عنوان نشان داده شده است ساعتج) یافت می شوند، برای حذف اجسام متحرک فقط نقاطی با مقادیر z بین آنها وجود دارد ساعتf+دساعتfو ساعتج-دساعتجبرای تولید تصاویر ortho-projected استفاده می شود. در این صفحه، دساعتf=35(ساعتج-ساعتf)و دساعتج=15(ساعتج-ساعتf)برای جلوگیری از حرکت اجسام روی زمین و آویزان کردن اجسام روی سقف استفاده می شود.

قبل از ثبت نام، نقاط مبدا و هدف همگی در سیستم مختصات متعلق به اسکنر هستند. برای تولید تصاویر ارتو پروجکشن شده از ابر نقطه ایستگاه (نقاط منبع یا نقاط هدف)، حداقل ایکسو yمقادیر (به عنوان ایکسمترمنn و yمترمنn) از آن نقطه ابر ایستگاه یافت می شود. برای یک امتیاز (ایکس،y،z)شماره سطر و شماره ستون آن در تصویر عمودی با معادلات (7) و (8) به دست می آید. Lرزولوشن شبکه ای تصاویر ارتو پروجکت شده است. از نظر تئوری، هر چه کوچکتر باشد L، دقت تطبیق بهتر است اما پیچیدگی محاسبات بالاتر است. برای سازش بین دقت و پیچیدگی محاسباتی، Lدر این مقاله به صورت تجربی روی 0.01 متر تنظیم شده است. اگر یک پیکسل در یک تصویر ارتو پروجکت شده حاوی حداقل یک نقطه باشد، مقدار پیکسل آن 255 تنظیم می شود. در غیر این صورت، مقدار پیکسل روی 0 تنظیم می شود. به این ترتیب، می توانیم یک تصویر عمودی باینری برای منبع به دست آوریم. نقاط و نقاط هدف

ردیف=INT(y-yمترمنnL)،

(7)

سرهنگ=INT(ایکس-ایکسمترمنnL).

(8)

2.2.3. ثبت تصاویر ارتو پروجکت شده

تصاویر ارتو پروجکت شده تصاویر باینری هستند و ویژگی های خطی بیشترین ویژگی هایی هستند که در تصاویر ارتو پروجکت شده مشاهده می شوند. این مقاله از یک الگوریتم مبتنی بر خط برای ثبت تصاویر ارتو پروجکت شده استفاده می کند. خطوط در تصاویر ارتو پروژکتیو خطوط تک پیکسلی نیستند. برای تشخیص بهتر خطوط، تصاویر ارتو پروژکتیو ابتدا توسط الگوریتم نازک شدن Zhang-Suen نازک می شوند [ 46 ]. سپس، الگوریتم تبدیل احتمالی پیشرونده هاف [ 47 ] برای تشخیص خطوط استفاده می شود. در نهایت، تصاویر ارتو پروجکت شده با استفاده از خطوط 2 بعدی شناسایی شده ثبت می شوند. قسمت زیر از این بخش جزئیات ثبت منبع و هدف تصاویر ارتو پروجکت شده با استفاده از خطوط شناسایی شده است.

نقاط (ایکس،y)و (ایکس،Y)در مبدأ می‌توان تصاویر ارتو پروجکت‌شده و تصاویر هدف را در مختصات دکارتی در مختصات همگن نوشت. [ایکس y 1]تیو [ایکس Y 1]تی، به ترتیب، در کجا تینشان دهنده جابجایی است. رابطه بین نقطه تصویر ارتو پروجکت شده منبع [ایکس y 1]تی و نقطه تصویر ارتو پروجکت شده را هدف قرار دهید [ایکس Y 1]تیرا می توان به صورت زیر نوشت:

[ایکسY1]=[cosθ-گناهθتیایکسگناهθcosθتیy001][ایکسy1]،

(9)

یا

پ=آرپ.

(10)

اگر آایکس+بy+1=0یک خط در تصویر ارتو پروژکتوری منبع در مختصات دکارتی است، همان خط در مختصات همگن را می توان به صورت زیر نوشت:

[آب1][ایکسy1]=0،

(11)

یا

لتیپ=0،

(12)

جایی که لتی=[آب1]پارامتر یک خط در یک تصویر ارتو پروجکت شده منبع است. به طور مشابه، خط آایکس+بy+1=0در یک تصویر عمودی هدف در مختصات دکارتی می توان به صورت زیر نوشت:

[آب1][ایکسY1]=0،

(13)

یا

Lتیپ=0،

(14)

جایی که Lتی=[آب1]پارامتر یک خط در یک تصویر ortho-projected هدف است. ضرب دو طرف معادله (10) در سمت چپ Lتی، ما بدست می آوریم:

Lتیپ=Lتیآرپ.

(15)

از رابطه (14) می دانیم که سمت چپ معادله (15) 0 است. بنابراین، سمت راست معادله (15) 0 است، به این معنی:

Lتیآرپ=0.

(16)

با ترکیب معادلات (12) و (16) می توان نتیجه گرفت که:

Lتیآر=λلتی،

(17)

جایی که λیک پارامتر مقیاس است.

معادله (17) رابطه بین پارامترهای خط در تصاویر ارتو پروجکت شده مبدا و هدف و تبدیل بین این دو تصویر ارتو پروجکت شده را ایجاد می کند. معادله (17) را می توان به صورت تفصیلی به صورت زیر نوشت:

آcosθ+بگناهθ=λآ،

(18)

-آگناهθ+بcosθ=λب،

(19)

آتیایکس+بتیy+1=λ.

(20)

با جایگزینی معادله (20) به معادلات (18) و (19)، دو معادله (معادلات (21) و (22)) مربوط به پارامترهای ثبت نامعلوم بدست می آوریم. (θ،تیایکس،تیy)به پارامترهای خطوط متناظر در تصاویر ارتو پروجکت شده منبع و هدف.

آcosθ+بگناهθ-آآتیایکس-آبتیy-آ=0،

(21)

-آگناهθ+بcosθ-بآتیایکس-ببتیy-ب=0.

(22)

در معادلات (21) و (22) آو بپارامترهای یک خط در یک منبع تصویر ارتو پروجکت شده هستند، در حالی که آو بپارامترهای خط متناظر در یک تصویر ortho-projected هدف هستند. آ، ب، آ،و باز نتیجه یک الگوریتم تبدیل احتمالی پیشرونده هاف به دست می آیند. بنابراین، تنها سه پارامتر ناشناخته وجود دارد (θ،تیایکس،تیy)، که باید آن را در معادلات (21) و (22) حل کنیم. اگر دو خط متناظر غیر موازی در تصاویر ارتو پروجکت شده مبدا و هدف بدست آوریم، چهار معادله برای حل سه پارامتر ثبت نامعلوم داریم و بنابراین پارامترهای ثبت نام مجهول را می توان با الگوریتم حداقل مربعات پس از خطی سازی یا غیرخطی تخمین زد. الگوریتم بهینه سازی خطی، مانند الگوریتم لونبرگ-مارکوارت (LM).

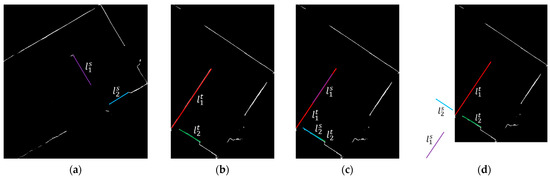
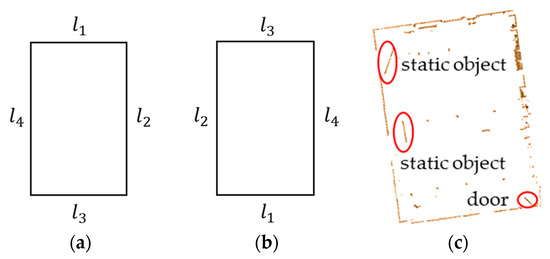
نکته ای که باید به آن توجه شود این است که اگر فقط از یک جفت خط استفاده شود، دو راه حل برای معادلات (21) و (22) وجود دارد. همانطور که در شکل 4 نشان داده شده است ، یک جفت خط در یک تصویر مبدا ارتو پروجکت شده ( ل1سو ل2سدر شکل 4 الف) را می توان با خطوط متناظر آن در تصویر ارتو پروجکت شده هدف مطابقت داد ( ل1تیو ل2تیدر شکل 4 ب) از طریق محلول 1 ( شکل 4 ج) و 2 ( شکل 4 د). ترجمه ها تیایکسو تیyاز دو راه حل یکسان است. زاویه چرخش محلول 1 (به صورت θ1) و راه حل 2 (با علامت گذاری شده است θ2) را می توان با رابطه (23) مرتبط کرد. اگر یک جواب به دست آوریم، می توانیم با استفاده از رابطه (23) راه حل دیگری به دست آوریم. سپس، این دو راه حل با استفاده از:

θ1=θ2+π،

(23)

مانند الگوریتم RANSAC، این مقاله یک جفت خط را از منبع و هدف تصاویر ارتو پروژکتیو به صورت تکراری انتخاب می‌کند و سپس پارامترهای ثبت نامعلوم با استفاده از الگوریتم حداقل مربعات مطابق معادلات (21) و (22) برآورد می‌شوند. در نهایت، پارامترهای ثبت تخمین زده شده توسط یک تابع کیفیت تطبیق خاص ارزیابی می شوند س(اس،تی)، جایی که اسنشان دهنده منبع تصویر ortho-projected و تیتصویر ortho-projected هدف را نشان می دهد. س(اس،تی)بر اساس فاصله بین پیکسل های تبدیل شده در تصویر ارتو پروجکت شده مبدا و نزدیکترین همسایه آن در تصویر عمودی هدف قرار می گیرد. در مرحله ارزیابی، پیکسل‌های موجود در تصویر مبدا ارتو پروجکت شده با استفاده از پارامترهای ثبت تخمینی به تصویر ارتو پروجکت‌شده هدف تبدیل می‌شوند. برای هر پیکسل پس از تبدیل، نزدیکترین پیکسل آن در تصویر هدف قرار داده شده پیدا می شود و کیفیت تطبیق آن به صورت زیر تعریف می شود:

س(سمن،تیj)={D(سمن،تیj) اگر D(سمن،تیj)<د،د اگر D(سمن،تیj)>د.

(24)

س(اس،تی)=∑سمن∈اسس(سمن،تیj).

(25)

در معادلات (24) و (25)، سمنپیکسل منبع تبدیل شده است و تیjنزدیکترین همسایه آن در تصویر ارتو پروژکتیو هدف است. D(سمن،تیj)فاصله اقلیدسی بین است سمنو تیj. در این مقاله آستانه دروی 5 پیکسل تنظیم شده است.

اگر مترخطوط در منبع تصویر ارتو پروجکت شده شناسایی می شوند و nخطوط در تصویر هدف اورتو پروژکتور شناسایی می شوند، در مجموع وجود دارد آمتر2جفت خطوط در منبع تصویر ortho-projected و مجموع آn2جفت خطوط در تصویر هدف اورتو پروجکت شده. هر جفت خط در تصویر مبدا ارتو پروجکت شده باید با هر جفت خط در تصویر ارتو پروجکت شده هدف آزمایش شود. اگر مترو nبزرگ هستند، فرآیند تخمین زمان بر است. خوشبختانه، ارزش های مترو nمعمولا در شرایط ما بین 4 تا 10 هستند. برای کاهش فضای جستجو، از زاویه بین دو خط برای محدود کردن جستجو استفاده می شود. اول، اگر دو خط نزدیک به موازی باشند، این جفت خط رها می شود. سپس، اگر زاویه بین دو خط از تصویر ارتو پروجکشن شده منبع به وضوح با زاویه تصویر ارتو پروجکت شده هدف متفاوت باشد، از تخمین و ارزیابی صرفنظر می شود.

2.2.4. ثبت نام در ابر نقطه

پس از به دست آوردن پارامترهای تراز افقی تیایکس، تیy،و θ، یک نقطه منبع [ایکسسyسzس]تیابتدا توسط:

[ایکس”y”z”]=[cosθ-گناهθتیایکسگناهθcosθتیy001][ایکسسyس1].

(26)

سپس، افست عمودی بین نقاط منبع تراز افقی و نقاط هدف با ارتفاع کف نقاط منبع به دست می‌آید. ساعتfسارتفاع سقف نقاط مبدا ( ساعتجسارتفاع کف نقاط هدف ( ساعتfتیو ارتفاع سقف نقاط هدف ( ساعتجتی) توسط:

تیz=0.5×[(ساعتfتی-ساعتfس)+(ساعتجتی-ساعتجس)].

(27)

در نهایت امتیاز ثبت شده [ایکستیyتیzتی]تیبه دست می آید:

[ایکستیyتیzتی]=[00تیz+zس-1]+[ایکس”y”z”].

(28)

3. نتایج

3.1. توضیحات متریک ارزیابی

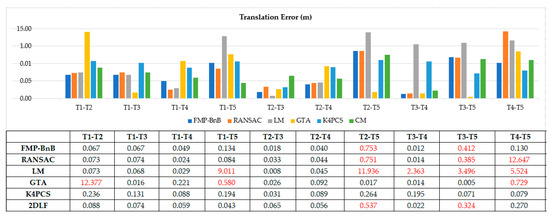
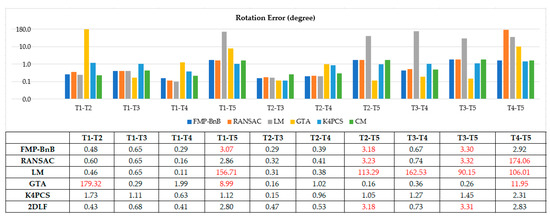
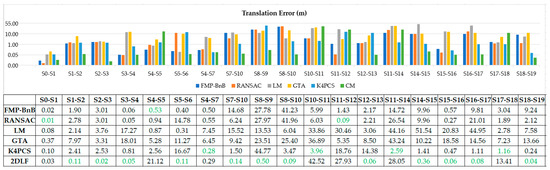
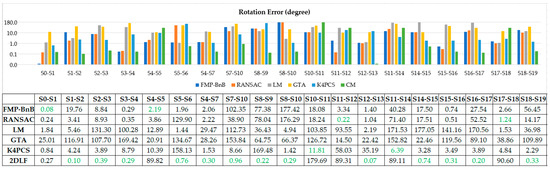
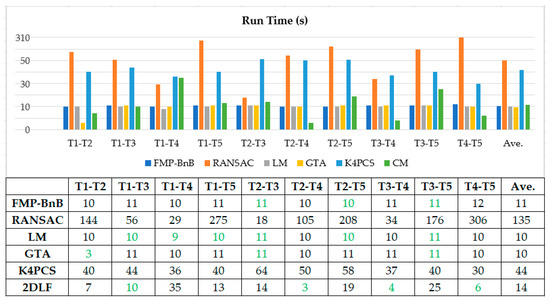
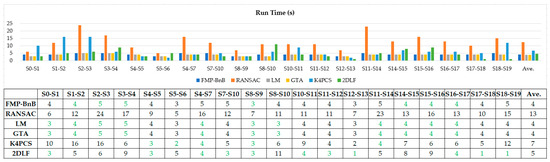
مانند بسیاری از کارهای قبلی [ 43 ، 45 ، 48 ]، خطای چرخش هآر، خطای ترجمه هتی، نرخ ثبت موفقیت آمیز (SRR) و زمان اجرا برای ارزیابی الگوریتم پیشنهادی استفاده می شود. خطای چرخش هآرو خطای ترجمه هتیبه این صورت تعریف می شوند:

هآر=آرکوسtr(آر¯-آر)-12،

(29)

هتی=”تی¯-تی”

(30)

جایی که آر¯و تی¯نشان دهنده حقیقت پایه چرخش و ترجمه، آرو تینشان دهنده چرخش و ترجمه تخمین زده شده توسط الگوریتم ثبت است، tr(.)نشان دهنده رد ماتریس و هآرزاویه چرخش در نمایش محور – زاویه است.

با توجه به خطای چرخش هآرو خطای ترجمه هتی، اگر هآرکوچکتر از σآرو هتیکوچکتر از σتی، ثبت این جفت ابر نقطه موفق تلقی می شود. در این صفحه، σآرروی 3 درجه تنظیم شده است و σتیروی 0.3 متر تنظیم شده است. نرخ بین جفت ثبت نام موفق و جفت کل به عنوان نرخ ثبت نام موفق تعریف می شود.

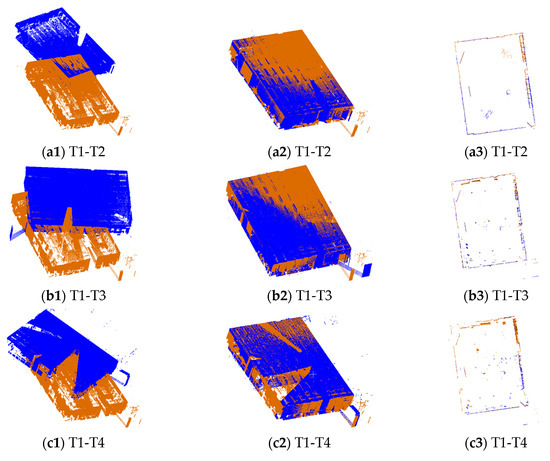
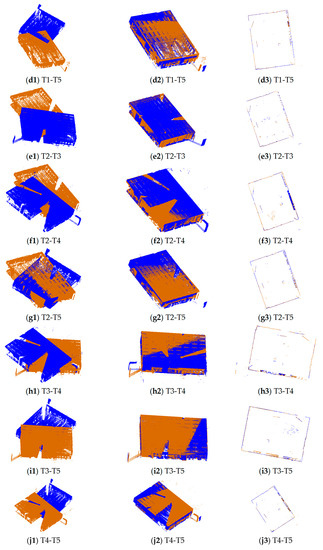
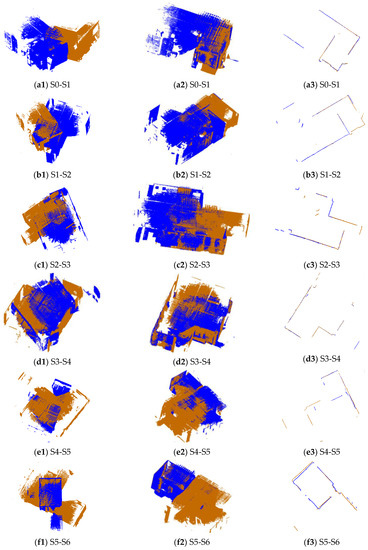
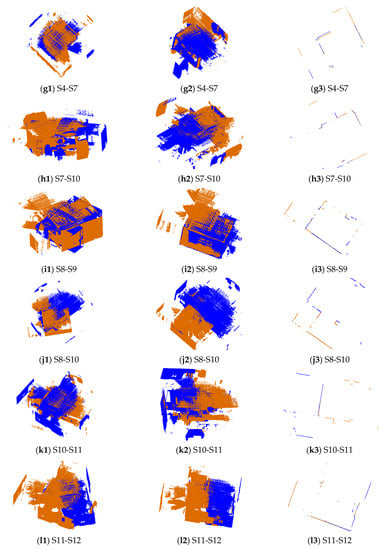
3.2. ارزیابی های کیفی

جفت ابرهای نقطه ای شرح داده شده در بخش 2.1 با استفاده از روش پیشنهادی مبتنی بر ویژگی خط دو بعدی (به نام 2DLF در زیر) ثبت شدند. نتایج ثبت مجموعه داده SR و CB در شکل 5 و شکل 6 نشان داده شده است. نقطه مبدا و مقصد قبل از ثبت نام، بعد از ثبت نام و نمای قسمت افقی ابرهای نقطه ثبت شده به ترتیب در ستون اول، ستون دوم و ستون سوم نشان داده شده است. نقاط مبدا به رنگ آبی و نقاط هدف قهوه ای رنگ می شوند. از ستون دوم و سوم شکل 5 قابل مشاهده استکه همه 10 جفت نقطه از مجموعه داده SR به خوبی ثبت شده اند. در نمای بخش افقی هیچ گونه ناهماهنگی آشکاری وجود ندارد. صحنه مجموعه داده CB بسیار پیچیده تر است. به دلیل پیچیدگی صحنه و شباهت ساختارهای داخلی، قضاوت از شکل 6 که آیا یک جفت ابر نقطه با موفقیت ثبت شده است یا خیر، دشوار است. با شناسایی دقیق، از شکل 6 مشاهده می کنیم که ابرهای نقطه بین S0 و S1، S1 و S2، S2 و S3، S3 و S4، S7 و S10، S8 و S9، S8 و S10، S12 و S13، S14 و S15. ، S15 و S16، S16 و S17 و S18 و S19 به خوبی ثبت شده اند. جفت‌های بین S5 و S6 و S4 و S7 با موفقیت ثبت شدند، اما ناهماهنگی‌های آشکاری در نتایج مشاهده می‌شود.

3.3. ارزیابی های کمی

نتایج ثبت 10 جفت ابر نقطه از مجموعه داده SR و 19 جفت ابر نقطه از مجموعه داده CB با استفاده از معیارهای شرح داده شده در بخش 3.1 به صورت کمی ارزیابی شدند . به منظور مقایسه روش پیشنهادی با سایر روش‌های پیشرفته، دو مجموعه داده نیز با روش هرس سریع منطبق بر شاخه و کران (FMP-BnB) [ 43 ]، روش 4DOF RANSAC [ 49 ] ثبت شدند. ]، نسخه 4DOF روش بلند کردن (LM) [ 50 ]، روش رویکرد نظریه بازی (GTA) [ 51 ]، و روش 4PCS (K4PCS) مبتنی بر نقطه کلید [ 34 ]. تمام نتایج با استفاده از معیارهای شرح داده شده در بخش 3.1 ارزیابی شدند .

شکل 7 و شکل 8خطای ترجمه و خطای چرخش 10 جفت ابر نقطه از مجموعه داده SR را نشان می دهد. روش FMP-BnB با موفقیت هفت جفت ابر نقطه (T1-T2، T1-T3، T1-T4، T2-T3، T2-T4، T3-T4، T4-T5) را ثبت کرد و SRR 70٪ بود. روش RANSAC با موفقیت هفت جفت ابر نقطه (T1-T2، T1-T3، T1-T4، T1-T5، T2-T3، T2-T4، T3-T4) را ثبت کرد و SRR 70٪ بود. روش LM با موفقیت پنج جفت ابر نقطه (T1-T2، T1-T3، T1-T4، T2-T3، T2-T4) را ثبت کرد و SRR 50٪ بود. روش GTA با موفقیت هفت جفت ابر نقطه (T1-T3، T1-T4، T2-T3، T2-T4، T2-T5، T3-T4، T3-T5) را ثبت کرد و SRR 70٪ بود. روش K4PCS با موفقیت تمام 10 جفت ابر نقطه را ثبت کرد و SRR 100٪ بود. روش پیشنهادی 2DLF با موفقیت هشت جفت ابر نقطه (T1-T2، T1-T3، T1-T4، T1-T5، T2-T3، T2-T4، T3-T4، را ثبت کرد. T4-T5)، و SRR 80٪ بود. در مجموعه داده SR، عملکرد روش 2DLF پیشنهادی بهتر از روش FMP-BnB، روش RANSAC، روش LM و روش GTA بود.

شکل 9 و شکل 10خطای ترجمه و خطای چرخش 19 جفت ابر نقطه در مجموعه داده CB را نشان می دهد. روش پیشنهادی 2DLF بهترین خطای ترجمه را در 12 (S1-S2، S2-S3، S3-S4، S5-S6، S7-S10، S8-S9، S8-S10، S12-S13، S14-S15، S15- به دست آورد. S16, S16-S17, S18-S19) از 19 جفت ابر نقطه. علاوه بر این، روش 2DLF پیشنهادی بهترین خطای چرخش را در 13 (S1-S2، S2-S3، S3-S4، S5-S6، S4-S7، S7-S10، S8-S9، S8-S10، S12-S13 به دست آورد. , S14-S15, S15-S16, S16-S17, S18-S19) از 19 جفت ابر نقطه. روش پیشنهادی 2DLF نسبت به پنج روش دیگر بهترین جفت‌های خطا را هم از نظر خطای ترجمه و هم از نظر چرخش به دست آورد. روش FMP-BnB با موفقیت دو جفت ابر نقطه (S0-S1، S3-S4) را ثبت کرد و SRR 10٪ بود. روش RANSAC با موفقیت چهار جفت ابر نقطه (S0-S1، S3-S4، S11-S12، را ثبت کرد. S15-S16) و SRR 21٪ بود. روش LM تنها یک جفت ابر نقطه را با موفقیت ثبت کرد و SRR 5٪ بود. روش GTA نتوانست هیچ یک از 19 جفت ابر نقطه را ثبت کند. روش K4PCS S0-S1، S4-S7 و S18-S19 را با موفقیت ثبت کرد. SRR 16٪ بود. روش پیشنهادی 12 جفت ابر نقطه (S0-S1، S1-S2، S2-S3، S3-S4، S5-S6، S4-S7، S7-S10، S8-S10، S12-S13، S15-S16 را با موفقیت ثبت کرد. ، S16-S17، S18-S19) و SRR 63٪ بود. روش پیشنهادی 2DLF بهترین SRR را در CB داده به دست آورد. روش پیشنهادی 12 جفت ابر نقطه (S0-S1، S1-S2، S2-S3، S3-S4، S5-S6، S4-S7، S7-S10، S8-S10، S12-S13، S15-S16 را با موفقیت ثبت کرد. ، S16-S17، S18-S19) و SRR 63٪ بود. روش پیشنهادی 2DLF بهترین SRR را در CB داده به دست آورد. روش پیشنهادی 12 جفت ابر نقطه (S0-S1، S1-S2، S2-S3، S3-S4، S5-S6، S4-S7، S7-S10، S8-S10، S12-S13، S15-S16 را با موفقیت ثبت کرد. ، S16-S17، S18-S19) و SRR 63٪ بود. روش پیشنهادی 2DLF بهترین SRR را در CB داده به دست آورد.

همه الگوریتم‌ها با استفاده از C++ پیاده‌سازی شدند و روی دسکتاپ با پردازنده Intel ^Core ™ i7-9700K و حافظه 64 گیگابایتی اجرا شدند. زمان ثبت هر جفت ابر نقطه ثبت شد. شکل 11 و شکل 12 زمان مورد نیاز برای ثبت جفت ابرهای نقطه در مجموعه داده SR و CB را با استفاده از روش پیشنهادی 2DLF و روش های مقایسه نشان می دهد. از شکل 11 می توان دریافت که روش 2DLF پیشنهادی کارآمدترین روش در چهار جفت ابر نقطه بود، در حالی که روش FMP-BnB، روش RANSAC، روش LM، روش GTA و روش K4PCS بودند. کارآمدترین روش در 3، 0، 6، 3، و 0 جفت ابر نقطه در مجموعه داده SR. از شکل 12 قابل مشاهده استکه روش FMP-BnB، روش RANSAC، روش LM، روش GTA، روش K4PCS و روش 2DLF بازده ترین روش در 7، 0، 11، 11، 5 و 11 جفت نقطه بودند. ابرها در مجموعه داده CB. به دلیل تعداد نقاط کمتر در هر ایستگاه، زمان کمتری برای ثبت جفت ابرهای نقطه در CB نسبت به SR صرف شد. می توان نتیجه گرفت که روش 2DLF پیشنهادی کمی بیشتر از روش FMP-BnB، روش LM و روش GTA طول کشید، اما بدیهی است که نسبت به روش RANSAC و روش K4PCS از نظر زمانی کارآمدتر بود.

4. بحث

4.1. دقت و کارایی زمان

روش پیشنهادی به دقت قابل مقایسه با روش FMP-BnB و روش K4PCS و دقت بهتری در مقایسه با روش RANSAC، روش LM و روش GTA در مجموعه داده SR دست یافت. نرخ ثبت موفقیت آمیز فقط کمتر از روش K4PCS و بهتر از روش RANSAC و روش LM در مجموعه داده SR است. در مجموعه داده CB، روش پیشنهادی با موفقیت حداکثر تعداد جفت ابرهای نقطه‌ای را ثبت کرد و دقت آن بهتر از روش‌های مقایسه است.

هر دو در مجموعه داده SR و CB، بازده زمانی روش پیشنهادی با روش FMP-BnB، روش LM و روش GTA قابل مقایسه است و نسبت به روش RANSAC و روش K4PCS از نظر زمانی کارآمدتر است. هزینه زمانی روش پیشنهادی عمدتاً توسط دو عامل تعیین می‌شود: (1) تعداد جفت‌های خط برای تطبیق و (2) بازده زمانی نتیجه مطابقت خط در الگوریتم ارزیابی. برای کاهش تعداد جفت خط، زاویه بین دو خط قبل از مطابقت بررسی می شود. اگر زاویه بین دو خط از آستانه کوچکتر باشد، جفت خط مستقیماً رها می شود. در صورتی که زوایای بین دو خط در تصویر ارتو پروجکت شده مبدا و تصویر ارتو پروجکت شده هدف تفاوت قابل توجهی داشته باشند، از تطابق صرفنظر می شود. یافتن نزدیکترین نقطه تصویر ارتو پروجکت شده منبع تبدیل شده در تصویر ارتو پروجکت شده هدف زمان بر است. برای اینکه الگوریتم ارزیابی نتیجه تطابق خط از نظر زمانی کارآمدتر باشد، می‌توان یک فیلتر شبکه‌ای را روی تصویر ارتو پروژکتوری منبع و تصویر ارتو پروژکتوری هدف اعمال کرد تا عدد نقطه را کاهش دهد.

4.2. محدودیت ها

هنگامی که ابرهای نقطه‌ای که باید ثبت شوند در یک اتاق بسته اسکن می‌شوند، تصویر متعامد تولید شده ممکن است مربع یا مستطیل باشد. در چنین شرایطی، تطبیق بین تصویر ارتو پروجکت شده منبع و تصویر ارتو پروجکت شده هدف ممکن است منجر به یک نتیجه تطبیق اشتباه شود. همانطور که در شکل 13 a,b نشان داده شده است، روش پیشنهادی نمی تواند این دو موقعیت را تشخیص دهد و ممکن است منجر به یک نتیجه تطبیق اشتباه شود. خوشبختانه، صحنه های داخلی اغلب دارای درها و اشیاء ساکن هستند (همانطور که در شکل 13 ج نشان داده شده است)، و این درها و اشیاء ساکن می توانند به ما در جلوگیری از چنین ابهامی کمک کنند. ثبت موفقیت آمیز مجموعه داده SR ثابت کرد که روش پیشنهادی می تواند با موفقیت با چنین شرایطی مقابله کند.

برای جفت‌های نقطه‌ای که یکی در داخل اتاق و دیگری در خارج از اتاق اسکن شده است (به عنوان مثال، S11 و S12 در مجموعه داده‌های CB)، ثبت ممکن است به دلیل دشواری یافتن خطوط متناظر کافی در منبع و هدف تصاویر ارتو پروژکت‌شده با شکست مواجه شود. علاوه بر این، برخی از جفت‌های ابر نقطه‌ای که در اتاق‌های بزرگ اسکن شده‌اند، ممکن است به دلیل فاصله اسکن محدود تجهیزات مورد استفاده، تنها یک خط متناظر داشته باشند، همانطور که در شکل 14 a,b نشان داده شده است. جفت های ناموفق S4-S5، S8-S9، S10-S11، S11-S14، S14-S15 و S17-S18 متعلق به این کیس هستند.

5. نتیجه گیری ها

این مقاله یک روش ثبت 4DOF را برای ثبت درشت ابرهای نقطه داخلی دوتایی پیشنهاد می‌کند که از دانش تراز بودن تجهیزات یا جبران شیب توسط یک سنسور شیب داخلی بهره می‌برد. ثبت 4DOF به تراز افقی و تراز عمودی تجزیه شد. هم ترازی افقی با تطبیق ابر نقطه تولید شده توسط تصاویر ارتو پروجکت شده به دست آمد. این مقاله یک روش جدید تولید تصویر ارتو پروژکتوری را با استفاده از نقاط بین کف و سقف و یک روش تطبیق تصویر ارتو جدید پیشنهاد می‌کند که از ویژگی‌های خط دوبعدی شناسایی‌شده از تصاویر ارتو پروجکت‌شده منبع و هدف استفاده می‌کند. علاوه بر این، این مقاله برای دستیابی به تراز عمودی با استفاده از اختلاف ارتفاع کف و سقف بین نقاط مبدا و نقاط هدف پیشنهاد می‌کند. دو مجموعه داده، یکی با پنج ایستگاه و دیگری با 20 ایستگاه، برای ارزیابی عملکرد روش پیشنهادی استفاده شد. نتایج تجربی نشان می‌دهد که روش پیشنهادی به نرخ ثبت موفقیت‌آمیز 80 درصدی در یک صحنه ساده دست یافته است که بهتر از روش FMP-BnB (70٪)، روش RANSAC (70٪)، روش LM (50٪)، و روش GTA (70%). روش پیشنهادی نسبت به روش FMP-BnB (10٪)، روش RANSAC (21٪)، روش LM (5٪)، روش GTA (0٪) در صحنه های چالش برانگیز به نرخ ثبت موفقیت آمیز بهتری (63٪) در صحنه های چالش برانگیز دست یافت. و روش K4PCS (16%). روش پیشنهادی نسبت به روش RANSAC و روش K4PCS از نظر زمانی کارآمدتر بود. حتی اگر روش پیشنهادی هنوز محدودیت‌هایی در ثبت ابر نقطه داخلی دارد، اما جایگزینی برای حل مشکل ثبت ابر نقطه داخلی فراهم می‌کند.

در این مقاله، تصاویر ارتو پروجکت شده تنها با استفاده از نقاط صفحه عمودی تولید شدند. به دلیل انسداد و محدوده اسکن محدود، ممکن است نتواند خطوط کافی را در منبع پیدا کند و تصاویر ارتو پروجکت شده را هدف قرار دهد و در نتیجه ابرهای نقطه را ثبت نکند. در آینده، تمام نقاط مبدأ و هدف ممکن است برای تولید تصاویر ارتو پروجکت شده برای بهبود استحکام روش مورد سوء استفاده قرار گیرند.

منابع

ایمان ذوالانواری، س.م. Laefer، روش برش DF برای نمای منحنی و استخراج پنجره از ابرهای نقطه ای. ISPRS J. Photogramm. 2016 ، 119 ، 334-346. [ Google Scholar ] [ CrossRef ]
لیانگ، ایکس. کانکاره، وی. Hyyppä، J.; وانگ، ی. کوکو، ا. هاگرن، اچ. یو، ایکس. کارتینن، اچ. جااکولا، ا. گوان، اف. و همکاران اسکن لیزری زمینی در فهرست جنگل ها ISPRS J. Photogramm. 2016 . [ Google Scholar ] [ CrossRef ]
لاگ، دی. برودو، ن. Leroux, J. مقایسه دقیق سه بعدی توپوگرافی پیچیده با اسکنر لیزری زمینی: کاربرد در دره Rangitikei (NZ). ISPRS J. Photogramm. 2013 ، 82 ، 10-26. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
محمود، ب. Han, S. ثبت سه بعدی ابرهای نقطه داخلی برای واقعیت افزوده . انجمن مهندسی عمران آمریکا: Reston، VA، ایالات متحده آمریکا، 2019؛ صص 1-8. [ Google Scholar ]
محمود، ب. هان، اس. لی، دی. ثبت و بومی سازی ابرهای نقطه سه بعدی صحنه های داخلی با استفاده از ویژگی های هندسی برای واقعیت افزوده مبتنی بر BIM. Remote Sens. 2020 , 12 , 2302. [ Google Scholar ] [ CrossRef ]
بوئنو، ام. گونزالس-خورخه، اچ. مارتینز-سانچز، جی. Lorenzo, H. ثبت نام درشت ابر نقطه خودکار با استفاده از توصیفگرهای هندسی نقطه کلیدی برای صحنه های داخلی. خودکار. ساخت و ساز 2017 ، 81 ، 134-148. [ Google Scholar ] [ CrossRef ]
لی، اف. زلاتانوا، اس. کوپمن، ام. بای، ایکس. Diakité، A. برنامه ریزی مسیر جهانی برای یک پهپاد داخلی. خودکار. ساخت و ساز 2018 ، 95 ، 275-283. [ Google Scholar ] [ CrossRef ]
اوچمن، اس. ووک، آر. وسل، آر. Klein, R. بازسازی خودکار مدل های ساختمانی پارامتریک از ابرهای نقطه داخلی. محاسبه کنید. نمودار 2016 ، 54 ، 94-103. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
شی، دبلیو. احمد، دبلیو. لی، ن. فن، دبلیو. شیانگ، اچ. وانگ، ام. مدل‌سازی هندسی معنایی ابر نقطه‌ای داخلی بدون ساختار. ISPRS Int. J. Geo-Inf. 2019 ، 8 ، 9. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
ناویس. قدرت ساختمان های دیجیتال را آزاد کنید. در دسترس آنلاین: https://www.navvis.com/ (در 17 سپتامبر 2020 قابل دسترسی است).
معرفی دوربین Intel RealSense LiDAR L515. در دسترس آنلاین: https://www.intel.com/content/www/us/en/architecture-and-technology/realsense-overview.html (در 17 سپتامبر 2020 قابل دسترسی است).
کینکت برای ویندوز. در دسترس آنلاین: https://developer.microsoft.com/en-us/windows/kinect/ (در 17 سپتامبر 2020 قابل دسترسی است).
بسل، پی جی؛ McKay, ND روشی برای ثبت اشکال سه بعدی. IEEE Trans. الگوی مقعدی 1992 ، 14 ، 239-256. [ Google Scholar ] [ CrossRef ]
روسینکیویچ، اس. لووی، ام. انواع کارآمد الگوریتم ICP. در مجموعه مقالات سومین کنفرانس بین المللی در مورد تصویربرداری و مدل سازی دیجیتال سه بعدی، شهر کبک، QC، کانادا، 28 مه تا 1 ژوئن 2001. صص 145-152. [ Google Scholar ]
هان، جی. یین، پی. سلام.؛ Gu، F. ICP پیشرفته برای ثبت مدل های محیطی سه بعدی در مقیاس بزرگ: یک مطالعه تجربی. Sensors 2016 , 16 , 228. [ Google Scholar ] [ CrossRef ]
بیبر، پ. Stra Ss Er, W. تبدیل توزیع های نرمال: رویکردی جدید برای تطبیق اسکن لیزری. در مجموعه مقالات کنفرانس بین المللی IEEE/RSJ 2003 در مورد ربات ها و سیستم های هوشمند (IROS 2003) (شماره گربه 03CH37453)، لاس وگاس، NV، ایالات متحده، 27-31 اکتبر 2003. صص 2743-2748. [ Google Scholar ]
تاکوچی، ای. Tsubouchi، T. تطبیق اسکن سه بعدی با استفاده از تبدیل توزیع های نرمال سه بعدی بهبودیافته برای نقشه برداری رباتیک متحرک. در مجموعه مقالات کنفرانس بین المللی IEEE/RSJ 2006 در مورد ربات ها و سیستم های هوشمند، پکن، چین، 9 تا 15 اکتبر 2006. صص 3068–3073. [ Google Scholar ]
Magnusson، M. تبدیل توزیع های عادی سه بعدی: یک نمایش کارآمد برای ثبت، تجزیه و تحلیل سطح، و تشخیص حلقه. Ph.D. پایان نامه، دانشگاه Örebro، Örebro، سوئد، 2009. [ Google Scholar ]
جانسون، AE; هبرت، ام. استفاده از تصاویر چرخشی برای تشخیص کارآمد شی در صحنه‌های سه بعدی درهم. IEEE Trans. الگوی مقعدی 1999 ، 21 ، 433-449. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
ماکادیا، ع. پترسون، ا. Daniilidis، K. ثبت تمام خودکار ابرهای نقطه سه بعدی. در مجموعه مقالات کنفرانس IEEE Computer Society در سال 2006 در مورد دید رایانه و تشخیص الگو (CVPR’06)، نیویورک، نیویورک، ایالات متحده آمریکا، 17 تا 22 ژوئن 2006. ص 1297–1304. [ Google Scholar ]
Rusu، RB; بلودو، ن. مارتون، ZC; Beetz، M. تراز کردن نماهای ابر نقطه با استفاده از هیستوگرام ویژگی های پایدار. در مجموعه مقالات کنفرانس بین المللی IEEE/RSJ در مورد ربات ها و سیستم های هوشمند، نیس، فرانسه، 22 تا 26 سپتامبر 2008. صص 3384-3391. [ Google Scholar ]
Rusu، RB; بلودو، ن. Beetz، M. هیستوگرام های ویژگی نقطه سریع (FPFH) برای ثبت سه بعدی. در مجموعه مقالات کنفرانس بین المللی IEEE در مورد رباتیک و اتوماسیون، کوبه، ژاپن، 12-17 مه 2009. صص 3212–3217. [ Google Scholar ]
دونگ، ز. یانگ، بی. لیو، ی. لیانگ، اف. لی، بی. Zang, Y. زمینه شکل باینری جدید برای توصیف سطح محلی سه بعدی. ISPRS J. Photogramm. 2017 ، 130 ، 431-452. [ Google Scholar ] [ CrossRef ]
یانگ، بی. Zang, Y. ثبت خودکار ابرهای نقطه اسکن لیزری زمینی متراکم با استفاده از منحنی ها. ISPRS J. Photogramm. 2014 ، 95 ، 109-121. [ Google Scholar ] [ CrossRef ]
دلد، سی. Brenner, C. ثبت داده های اسکن لیزری زمینی با استفاده از تکه های مسطح و داده های تصویر. بین المللی قوس. فتوگرام حسگر از راه دور اسپات. Inf. Sci.-ISPRS Arch. 2006 ، 36 ، 78-83. [ Google Scholar ]
کلبه، دی. ون آرت، جی. رومانچیک، پی. ون لیوون، م. Cawse-Nicholson، K. ثبت جفت داده‌های اسکنر لیزری زمینی جنگلی با معیارهای اطمینان جاسازی شده بدون نشانگر. IEEE Trans. Geosci. Remote 2016 , 54 , 4314–4330. [ Google Scholar ] [ CrossRef ]
زنگ، ا. آهنگ ها.؛ نیسنر، ام. فیشر، ام. شیائو، جی. Funkhouser, T. 3dmatch: یادگیری توصیفگرهای هندسی محلی از بازسازی‌های rgb-d. در مجموعه مقالات کنفرانس IEEE در مورد دید کامپیوتری و تشخیص الگو (CVPR)، Hulunono، HI، ایالات متحده آمریکا، 21-26 ژوئیه 2017؛ صفحات 1802-1811. [ Google Scholar ]
ژانگ، ز. سان، ال. ژونگ، آر. چن، دی. خو، ز. وانگ، سی. کوین، سی. سان، اچ. Li, R. ساخت ویژگی عمیق سه بعدی برای ثبت نقاط ابری اسکن لیزری موبایل. IEEE Geosci. سنسور از راه دور Lett. 2019 ، 16 ، 1904-1908. [ Google Scholar ] [ CrossRef ]
پوژول-میرو، ا. Casas, JR; رویز-هیدالگو، جی. تطبیق مکاتبات در ابرهای نقطه سه بعدی سازماندهی نشده با استفاده از شبکه های عصبی کانولوشن. کامپیوتر بینایی تصویر 2019 ، 83 ، 51-60. [ Google Scholar ] [ CrossRef ]
Qi، CR; سو، اچ. مو، ک. Guibas، LJ PointNet: یادگیری عمیق در مجموعه های نقطه برای طبقه بندی و تقسیم بندی سه بعدی. arXiv 2017 ، arXiv:1612.00593v2. [ Google Scholar ]
دنگ، اچ. بردال، تی. Ilic، S. PPFNet: ویژگی های محلی آگاه از زمینه جهانی برای تطبیق نقاط سه بعدی قوی. در مجموعه مقالات کنفرانس IEEE/CVF 2018 در مورد دید رایانه و تشخیص الگو، سالت لیک سیتی، UT، ایالات متحده آمریکا، 18 تا 23 ژوئن 2018؛ صص 195-205. [ Google Scholar ]
آئوکی، ی. گوفورث، اچ. Srivatsan، RA; Lucey, S. PointNetLK: ثبت ابر نقطه ای قوی و کارآمد با استفاده از PointNet. در مجموعه مقالات کنفرانس IEEE/CVF در مورد بینایی کامپیوتری و تشخیص الگو (CVPR)، لانگ بیچ، کالیفرنیا، ایالات متحده آمریکا، 16 تا 20 ژوئن 2019؛ صص 7163–7172. [ Google Scholar ]
ملادو، ن. آیگر، دی. Mitra, NJ SUPER 4PCS سریع ثبت جهانی نقطه ابری از طریق نمایه سازی هوشمند. محاسبه کنید. نمودار انجمن 2014 ، 33 ، 205-215. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
Theiler، PW; Wegner، JD; شیندلر، کی. مجموعه‌های متجانس 4 نقطه‌ای مبتنی بر نقطه کلید – ثبت خودکار اسکن‌های لیزری بدون نشانگر. ISPRS J. Photogramm. 2014 ، 96 ، 149-163. [ Google Scholar ] [ CrossRef ]
Ge, X. ثبت خودکار بدون نشانگر ابرهای نقطه با مجموعه‌های 4 نقطه‌ای متجانس مبتنی بر نقطه کلید معنایی. ISPRS J. Photogramm. 2017 ، 130 ، 344-357. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
Järemo Lawin، F. دانلجان، م. شهباز خان، ف. فورسن، پ. Felsberg, M. ثبت مجموعه نقطه تطبیقی چگالی. در مجموعه مقالات کنفرانس IEEE در مورد بینایی کامپیوتری و تشخیص الگو (CVPR)، سالت لیک سیتی، UT، ایالات متحده آمریکا، 18 تا 22 ژوئن 2018؛ صص 3829–3837. [ Google Scholar ]
تسین، ی. کاناد، تی. یک رویکرد مبتنی بر همبستگی برای ثبت مجموعه نقطه قوی . Springer: برلین/هایدلبرگ، آلمان، 2004; صص 558-569. [ Google Scholar ]
ژیان، بی. ثبت مجموعه نقطه قوی Vemuri، BC با استفاده از مدل های مخلوط گاوسی. IEEE Trans. الگوی مقعدی 2010 ، 33 ، 1633-1645. [ Google Scholar ] [ CrossRef ] [ PubMed ]
مایروننکو، آ. آهنگ، X. ثبت مجموعه نقطه: رانش نقطه منسجم. IEEE Trans. الگوی مقعدی 2010 ، 32 ، 2262-2275. [ Google Scholar ] [ CrossRef ] [ PubMed ][ نسخه سبز ]
تسای، سی. هوانگ، سی. چی-یی، تی. Chih-Hung، H. الگوریتم ثبت ابر نقطه صحنه داخلی بر اساس کالیبراسیون دوربین RGB-D. Sensors 2017 ، 17 ، 1874. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
سانچز، جی. دنیس، اف. چچین، پ. دوپون، اف. Trassoudaine, L. ثبت جهانی ابرهای نقطه سه بعدی LiDAR بر اساس ویژگی‌های صحنه: کاربرد در محیط‌های ساختاریافته. Remote Sens. 2017 , 9 , 1014. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
Pavan، NL; دوس سانتوس، DR; Khoshelham, K. ثبت جهانی ابرهای نقطه ای اسکنر لیزری زمینی با استفاده از مکاتبات هواپیما به هواپیما. Remote Sens. 2020 , 12 , 1127. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
کای، ز. چین، تی. بوستوس، AP; شیندلر، ک. ثبت بهینه عملی جفت‌های اسکن LiDAR زمینی. ISPRS J. Photogramm. 2019 ، 147 ، 118-131. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
لیو، اچ. ژانگ، ایکس. خو، ی. Chen, X. ثبت درشت کارآمد ابرهای نقطه ای TLS دوتایی با استفاده از تصاویر ویژگی پیش بینی شده ارتو. ISPRS Int. J. Geo-Inf. 2020 ، 9 ، 255. [ Google Scholar ] [ CrossRef ]
Ge، X. هو، اچ. ثبت افزایشی مبتنی بر شی ابرهای نقطه زمینی در یک محیط شهری. ISPRS J. Photogramm. 2020 ، 161 ، 218-232. [ Google Scholar ] [ CrossRef ]
ژانگ، تی. Suen, CY یک الگوریتم موازی سریع برای نازک کردن الگوهای دیجیتال. اشتراک. ACM 1984 ، 27 ، 236-239. [ Google Scholar ] [ CrossRef ]
ماتاسیکس، جی. کیتلری، تبدیل Hough احتمالی پیشرونده CGJ. در مجموعه مقالات کنفرانس بینایی ماشین بریتانیا، ساوتهمپتون، انگلستان، 14 تا 17 سپتامبر 1998. صفحات 26.1-26.10. [ Google Scholar ]
دونگ، ز. لیانگ، اف. یانگ، بی. خو، ی. زنگ، ی. لی، جی. وانگ، ی. دای، دبلیو. فن، اچ. Hyyppä، J.; و همکاران ثبت ابرهای نقطه اسکنر لیزری زمینی در مقیاس بزرگ: بررسی و معیار ISPRS J. Photogramm. 2020 ، 163 ، 327-342. [ Google Scholar ] [ CrossRef ]
فیشلر، MA; بولس، اجماع نمونه تصادفی RC: الگویی برای تطبیق مدل با کاربردهای آنالیز تصویر و کارتوگرافی خودکار. اشتراک. ACM 1981 ، 24 ، 381-395. [ Google Scholar ] [ CrossRef ]
ژو، Q. پارک، جی. کلتون، V. ثبت جهانی سریع ؛ Springer: برلین/هایدلبرگ، آلمان، 2016; صص 766-782. [ Google Scholar ]
آلبارلی، آ. رودولا، ای. Torsello, A. یک رویکرد نظری بازی برای ثبت سطح خوب بدون تخمین حرکت اولیه. در مجموعه مقالات کنفرانس IEEE Computer Society در سال 2010 در مورد دید رایانه و تشخیص الگو، سانفرانسیسکو، کالیفرنیا، ایالات متحده آمریکا، 13 تا 18 ژوئن 2010. صص 430-437. [ Google Scholar ]

شکل 1. محل اسکن مجموعه داده های تجربی. ( الف ) مکان های مجموعه داده SR را اسکن کنید. ( ب ) مکان‌های CB مجموعه داده را اسکن کنید.

شکل 2. مروری بر روش ثبت ابر نقطه داخلی پیشنهادی 4 درجه آزادی (4DOF).

شکل 3. هیستوگرام ارتفاع یک ابر نقطه داخلی ایستگاه.

شکل 4. دو راه حل برای تطبیق خط جفت. ( الف ) دو خط در تصویر منطبق بر مبدأ، ( ب ) دو خط متناظر در تصویر هدف، ( ج ) راه حل تطبیقی 1، ( د ) راه حل تطبیقی 2.

شکل 5. نتایج ثبت 10 جفت ابر نقطه در مجموعه داده SR. ستون اول ابرهای نقطه قبل از ثبت، ستون دوم ابرهای نقطه پس از ثبت با استفاده از روش پیشنهادی و ستون سوم نمای برش افقی ابرهای نقطه پس از ثبت است. نقاط قهوه ای نقاط هدف و نقاط آبی نقاط مبدا هستند.

شکل 6. نتایج ثبت 19 جفت ابر نقطه در مجموعه داده CB. ستون اول ابرهای نقطه قبل از ثبت، ستون دوم ابرهای نقطه پس از ثبت با استفاده از روش پیشنهادی و ستون سوم نمای برش افقی ابرهای نقطه پس از ثبت است. نقاط قهوه ای نقاط هدف و نقاط آبی نقاط مبدا هستند.

شکل 7. خطای ترجمه جفت ها از مجموعه داده SR (جفت های ناموفق قرمز رنگ می شوند).

شکل 8. خطای چرخش جفت های ابر نقطه از مجموعه داده SR (جفت های شکست خورده قرمز رنگ می شوند).

شکل 9. خطای ترجمه جفت های ابر نقطه از مجموعه داده CB (بهترین نتیجه هر جفت سبز رنگ می شود).

شکل 10. خطای چرخش جفت های ابر نقطه از مجموعه داده CB (بهترین نتیجه هر جفت به رنگ سبز است).

شکل 11. زمان اجرا برای ثبت جفت های ابر نقطه از مجموعه داده SR (کارآمدترین روش برای هر جفت به رنگ سبز است).

شکل 12. زمان اجرا برای ثبت جفت های ابر نقطه از مجموعه داده CB (کارآمدترین روش برای هر جفت به رنگ سبز است).

شکل 13. موقعیت های ابهام در تطبیق تصویر ارتو پروجکت شده مبتنی بر خط. ( الف ) تصویر ارتو طرح ریزی شده از یک اتاق مستطیل؛ ( ب ) وضعیت ابهام ( الف )؛ ( ج ) درها و اشیاء ساکن در اتاق.

شکل 14. موردی که در آن تصاویر ارتو پروژکتور شده منبع و هدف به دلیل فاصله اسکن محدود تنها یک خط متناظر دارند. ( الف ) تصویر ارتو پروژکتوری تولید شده از S17 در CB را هدف قرار دهید. ( ب ) منبع تصویر ارتو پروژکتیو تولید شده از S18 در CB. خطوط داخل دایره قرمز دیوارهای متناظر هستند.

مقالات داخلی و بین المللی

بدون دیدگاه

دیدگاهتان را بنویسید لغو پاسخ

برای نوشتن دیدگاه باید وارد بشوید.

مشاورین هوش پیروزی

ثبت دو به دو درشت ابرهای نقطه داخلی با استفاده از ویژگی‌های خط دوبعدی

ثبت دو به دو درشت ابرهای نقطه داخلی با استفاده از ویژگی‌های خط دوبعدی

چکیده

کلید واژه ها:

1. مقدمه