خوشه بندی فضایی وابسته به مقیاس های فضایی است. با استفاده گسترده از نقشه های وب، یک روش خوشه بندی سریع برای عناصر فضایی چند مقیاسی به یک نیاز جدید تبدیل شده است. بنابراین، برای خوشه‌بندی و نمایش سریع عناصر در مقیاس‌های فضایی مختلف، روشی به نام خوشه‌بندی سریع نقاط انبوه چند مقیاسی بر اساس درخت پوشا با تراکم سلسله مراتبی پیشنهاد می‌کنیم. این مطالعه به اصل اولیه خوشه‌بندی با جستجوی سریع و یافتن الگوریتم تجمع قله‌های چگالی اشاره می‌کند و مفهوم یک درخت پوشا مبتنی بر چگالی سلسله مراتبی را معرفی می‌کند، ترکیب مقیاس فضایی با پیوندهای درختی عناصر برای پیشنهاد استراتژی هرس مربوطه، و در نهایت به خوشه بندی سریع چند مقیاسی عناصر پی می برد. آزمایش اول کارایی زمانی روش را در به دست آوردن نتایج خوشه‌بندی با تنظیم مقیاس فاصله پارامترها ثابت کرد. نتایج خوشه بندی دقیق نیز به دست آمد. آزمایش دوم امکان سنجی روش را در عنصر نقطه تجمع نشان داد و اثر بصری آن را نشان داد. این توضیح بیشتری برای کاربرد ساختارهای پیوند درختی ارائه می دهد.

کلید واژه ها:

خوشه بندی چند مقیاسی ; خوشه بندی نقطه ; الگوریتم CFSFDP سلسله مراتب تراکم ; ساختار درختی

1. مقدمه

الگوریتم‌های خوشه‌بندی فضایی سعی می‌کنند عناصر فضایی را به دسته‌ها یا خوشه‌ها بر اساس شباهت بین مکان‌ها و ویژگی‌های فضایی آنها طبقه‌بندی کنند. تجزیه و تحلیل خوشه ای به طور گسترده ای در برنامه ریزی شهری، سنتز نقشه برداری، تجزیه و تحلیل لرزه ای و پردازش تصویر استفاده شده است [ 1 ]]. در زمینه تجسم آنلاین داده های عظیم، خوشه بندی فضایی به روشی موثر برای بهبود سرعت نمایش و بهینه سازی جلوه های بصری تبدیل شده است. نمایش حجم عظیمی از داده ها برای رندرینگ بصری نقشه های وب یک چالش بوده است. خوشه‌بندی می‌تواند به‌طور موثر مرکز کلاس‌ها را با چگالی بالا به‌دست آورد تا اطلاعات مکان هر کلاس به‌طور دقیق روی نقشه نمایش داده شود و در نتیجه فشار بارگذاری داده‌ها کاهش یابد. مقیاس های فضایی مختلف نتایج خوشه بندی متفاوتی را ارائه می دهند [ 2 ]. برای دستیابی به نتایج ثابت با ادراک بصری خوب، استراتژی های خوشه بندی متفاوتی در مقیاس های مختلف مورد نیاز است.
با توسعه سریع نقشه های وب، نمایش چند مقیاسی نقشه ها منجر به مطالعات زیادی در مورد سنتز نقشه برداری شده است که شامل پردازش سریع تجمع عناصر نقطه فضایی است [ 3 ]. برخی از مطالعات فعلی شبکه‌های چند مقیاسی ایجاد کرده‌اند و نقاط عظیمی را در شبکه جمع‌آوری کرده‌اند تا خوشه‌بندی کامل شود [ 4 ]. با این حال، دقت خوشه بندی توسط دانه بندی شبکه محدود شده است [ 5 ]. هرچه شبکه های بیشتر باشد، دقت بالاتر اما سرعت پایین تر است. برای دستیابی به سرعت محاسباتی بالا، دقت خوشه بندی اغلب کاهش می یابد. K-means [ 6 ]، خوشه بندی فضایی مبتنی بر چگالی برنامه های کاربردی با نویز (DBSCAN) [ 7]، و دیگر الگوریتم های کلاسیک می توانند به طور موثری به خوشه بندی عناصر نقطه ای با دقت بالا دست یابند. با این حال، در مواجهه با حجم انبوه داده، زمان پردازش داده ها بسیار بیشتر از زمان پاسخ سریع صفحه مورد نیاز کاربر است. بنابراین، الگوریتم‌های کلاسیک خوشه‌بندی الزامات خوشه‌بندی سریع در مقیاس‌های چندگانه را برآورده نمی‌کنند.
بهبود سرعت خوشه‌بندی و افزایش دقت خوشه‌بندی از الزامات مهم برای خوشه‌بندی چند مقیاسی نقشه‌های وب است. آزمایش‌ها با استفاده از الگوریتم‌های مختلف خوشه‌بندی کلاسیک، به‌جز روش شبکه-خوشه‌بندی انجام شد. مشخص شد که الگوریتم Clustering by Fast Search and Find of Density Peaks (CFSFDP) [ 8 ] می تواند به سرعت خوشه بندی سریع و دقت بالا پس از محاسبه مقادیر چگالی دست یابد. در مواجهه با داده های انبوه، این روش یک ساختار درختی بین عناصر ایجاد می کند که با اتصال عناصر کم تراکم و چگالی بالا مشخص می شود. بنابراین، خوشه های بین عناصر را می توان به سرعت و با دقت تعریف کرد [ 9]. در حال حاضر بسیاری از محققان این روش را دارای ویژگی های خوشه بندی سلسله مراتبی می دانند و بر اساس این ساختار درختی، درک و تعاریف خود را ارائه کرده اند [ 10 ]. برای مثال، Lv و همکاران. [ 11 ] از «درخت پوشای حداقلی» به عنوان نامی برای ساختار رابطه بین مرکز خوشه‌بندی و سایر عناصر استفاده می‌کند. خو و همکاران [ 12] از تعریف “درخت پیشرو” برای ترسیم چگالی سلسله مراتبی عناصر فضایی استفاده می کند. بنابراین، این مقاله از درخت پوشای تراکم سلسله مراتبی برای توصیف این نوع ساختار استفاده کرد. از آنجایی که روش‌های خوشه‌بندی سلسله مراتبی (مانند Single-link و Complete-link) به طور کلی می‌توانند خوشه‌بندی چند مقیاسی را مدیریت کنند، الگوریتم CFSFDP با ساختار سلسله مراتبی نیز توانایی انجام این کار را دارد. با این حال، روش‌های خوشه‌بندی چند مقیاسی کنونی چندین مشکل دارند. اولاً، الگوریتم‌های خوشه‌بندی کلاسیک را نمی‌توان با سناریوهای نقشه وب خوشه‌بندی چند مقیاسی که نیاز به مدیریت سریع دارند، تطبیق داد. دوم، روش‌های خوشه‌بندی نقطه‌ای برای نقشه‌های وب نمی‌توانند تجمع دقیقی از مجموعه‌های مورفولوژیکی پیچیده عناصر را به دست آورند. علاوه بر این، CFSFDP بر اساس ساختارهای درختی سلسله مراتبی به ندرت برای خوشه بندی چند مقیاسی مورد مطالعه قرار گرفته است.
بنابراین، این مقاله یک خوشه بندی سریع نقاط انبوه چند مقیاسی را بر اساس درخت پوشا با تراکم سلسله مراتبی (MSCHT) برای دستیابی به خوشه بندی سریع چند مقیاسی برای تجسم آنلاین داده های عظیم پیشنهاد می کند. ابتدا، بر اساس الگوریتم CFSFDP، نقش تراکم در تولید ساختارهای درختی برای درک بهتر مکانیسم روش مورد تجزیه و تحلیل قرار گرفت. دوم، یک ساختار پیوند درختی منطقی از روابط از عناصر کم چگالی به عناصر با چگالی بالا استخراج می‌شود تا فرآیند ادغام عناصر را توصیف کند. در نهایت، در حالی که نیازهای خوشه‌بندی مجموعه‌های عناصر مورفولوژیکی پیچیده را برآورده می‌کند، یک ساختار درختی پوشا با چگالی سلسله مراتبی برای دستیابی به خوشه‌بندی زمان واقعی چند مقیاسی و ارائه داده‌های نقطه‌ای عظیم ساخته شد.
بقیه این مقاله به شرح زیر سازماندهی شده است: بخش 2 روش های خوشه بندی کلاسیک، روش های خوشه بندی شبکه سلسله مراتبی، و روش های خوشه بندی نقشه وب برای مقیاس های چند فضایی را بررسی می کند. علاوه بر این، این مقاله ساختار درختی فراگیر تراکم سلسله مراتبی را از الگوریتم CFSFDP بررسی می‌کند. الگوریتم MSCHT پیشنهادی به تفصیل در بخش 3 توضیح داده شده است . آزمایشات روی پایگاه های داده واقعی در بخش 4 ارائه شده است. در نهایت، نتیجه گیری می شود و کارهای آینده در بخش 5 مورد بحث قرار می گیرد .

2. آثار مرتبط

2.1. روش های خوشه بندی چند مقیاسی

اثرات مقیاس در تحقیقات خوشه‌بندی مورد توجه گسترده‌ای قرار گرفته است و مقیاس‌ها به عنوان مقیاس داده، مقیاس تحلیلی، مقیاس بصری، مقیاس فضایی و غیره تعریف می‌شوند .]. از این میان، مقیاس فضایی محور کار ما است. مقیاس فضایی معمولاً به معیار اندازه فضایی مورد استفاده برای انجام تحقیقات اشاره دارد. این شاخص تغییر در گستره فضایی است. تمرکز مطالعه حاضر عمدتاً بر روی خوشه‌بندی فضایی در مقیاس نقشه یکپارچه و بصری بود که نتایج خوشه‌بندی متفاوتی در مقیاس‌های فضایی مختلف به‌دست آمد. به عبارت دیگر، این برای دستیابی به یک نتیجه خوشه‌بندی معقول در هر مقیاس فضایی بود، زمانی که چشم انسان بتواند به طور موثر جدایی خوشه‌ها را تشخیص دهد. خوشه‌بندی در مقیاس‌های فضایی چندگانه می‌تواند به طور موثر ویژگی‌های توزیع جهانی عناصر جغرافیایی را استخراج کند و ویژگی‌های خوشه‌بندی عنصری مناطق محلی را بیشتر بررسی کند. به خصوص،

2.1.1. روش های کلاسیک خوشه بندی بر اساس پارامترهای اصلاح شده

الگوریتم های کلاسیک خوشه بندی موجود را می توان به عنوان پارتیشنی، سلسله مراتبی، مبتنی بر چگالی، مبتنی بر نمودار، مبتنی بر مدل و مبتنی بر شبکه طبقه بندی کرد [ 14 ]. الگوریتم خوشه بندی کلاسیک مبتنی بر پارامترهای اصلاح شده عمدتاً به روش به دست آوردن نتایج خوشه بندی چند مقیاسی با تغییر کامل پارامترهای خود برای برآوردن نیازهای خوشه بندی سناریوهای مختلف خوشه بندی در مقیاس فضایی اشاره دارد. برای چنین روش‌هایی، هر فرآیند خوشه‌بندی در مقیاس‌های فضایی مختلف مستقل از سایرین است و نتایج خوشه‌بندی مستقل از یکدیگر هستند [ 15 ]. برای مثال، الگوریتم کلاسیک خوشه‌بندی، K-means، می‌تواند با افزایش یا کاهش مقدار k، خوشه‌ها را از کل به ظریف کشف کند [ 6 ]]. هنگامی که مقدار k کوچکتر است، هر کلاستر دارای دامنه عملکرد خوشه بندی بیشتری است و بالعکس [ 16 ]. در مثالی دیگر، DBSCAN می‌تواند شعاع جستجو ε (eps) و حداقل تعداد نقاط مورد نیاز برای تشکیل یک ناحیه متراکم (minpts) را برای تناسب با مقیاس‌های فضایی مختلف تغییر دهد [ 7 ]. زمانی که وسعت فضایی صحنه کوچک است، مقدار eps نسبتاً کوچک مورد نیاز است، و زمانی که گستره فضایی صحنه زیاد است، مقدار eps نسبتاً بزرگ مورد نیاز است [ 17 ]. الگوریتم‌های خوشه‌بندی بهبودیافته برای الگوریتم‌های فوق نیز وجود دارد، مانند Fuzzy C-Means (FCM) [ 18 ] و نقاط ترتیب برای شناسایی ساختار خوشه‌بندی (OPTICS) [ 19 ]]، اما بیشتر آنها از رویکرد پارامتر تنظیم مجدد برای مقابله با مشکلات چند مقیاسی بدون کمک شبکه ها استفاده می کنند [ 13 ]. اگرچه تجمع یا تقسیم نتایج خوشه‌بندی شناخته شده در مقیاس‌های چندگانه وجود دارد، قوانین عملیات پیچیده‌تر و سخت‌تر عمل می‌کنند.
2.1.2. روش های خوشه بندی چند مقیاسی بر اساس شبکه سلسله مراتبی
الگوریتم‌های خوشه‌بندی مبتنی بر شبکه سلسله مراتبی ویژگی‌های خاص خود را در مدیریت مقیاس‌های چندگانه دارند. استفاده از شبکه‌ها با وضوح‌های مختلف کلید دستیابی به نتایج خوشه‌بندی چند مقیاسی است. یک مثال معمولی روش خوشه بندی شبکه اطلاعات آماری (STING) است [ 5 ]. استراتژی چند وضوحی مبتنی بر شبکه، منطقه فضایی را به سلول های لحظه ای تقسیم می کند. برای سطوح مختلف وضوح، معمولاً چندین سطح از سلول های مستطیلی وجود دارد که یک سلسله مراتب را تشکیل می دهند. هر سلول شبکه در سطح بالاتر به سلول های شبکه چندگانه در سطح پایین تقسیم شد. آمار برای هر ویژگی سلول شبکه (به عنوان مثال، مقادیر میانگین، حداکثر و حداقل) از قبل محاسبه و ذخیره می شود [ 20]. این روش تجمیع داده‌ها را موثر می‌سازد. گریدینگ به یک روش کمکی مهم یا مرحله پیشین در سایر روش های خوشه بندی چند مقیاسی بهبود یافته تبدیل شده است. با این حال، کیفیت خوشه بندی شبکه به دانه بندی پایین ترین سطح ساختار شبکه بستگی دارد. اگر اندازه شبکه نسبتاً خوب باشد، هزینه پردازش به طور قابل توجهی افزایش خواهد یافت [ 21 ]. اگر اندازه لایه زیرین ساختار شبکه خیلی درشت باشد، کیفیت تجزیه و تحلیل خوشه بندی کاهش می یابد. این مشکل همچنین در Wave Cluster [ 22 ]، Clustering in Quest (CLIQUE) [ 23 ]، Clustering مبتنی بر آنتروپی (ENCLUS) [ 24 ] و روش های دیگر منعکس شده است.
2.1.3. روش خوشه بندی نقشه وب سریع
الگوریتم خوشه‌بندی نقطه‌ای نقشه وب یک روش خوشه‌بندی سریع را دنبال می‌کند که با نمایش جلویی صفحه وب سازگار می‌شود و مشکل نمایش عناصر نقطه‌ای در نقشه را به طور جداگانه حل می‌کند [ 25 ]. الگوریتم‌های خوشه‌بندی که معمولاً مورد استفاده قرار می‌گیرند، روش‌های خوشه‌بندی نقطه‌ای مبتنی بر شبکه، مبتنی بر فاصله یا شبکه و فاصله محور هستند [ 26 ]]. الگوریتم های کلاسیک خوشه بندی به دلیل کارایی عملیاتی آنها در نظر گرفته نشدند. در حال حاضر، تمام نقشه‌های وب اصلی، APIهای خوشه‌بندی نقطه‌ای را برای نمایش نتایج خوشه‌بندی نقطه‌ای مربوطه در مقیاس‌های نمایش متفاوت ارائه می‌کنند. روش های خوشه بندی مورد استفاده توسط فروشندگان اصلی نقشه وب اساساً از نظر رویکرد مشابه هستند. از آنجایی که هیچ نام ثابتی برای این روش وجود ندارد، این مقاله از «خوشه‌بندی نقشه وب» برای یکسان کردن نام استفاده می‌کند. برای تطبیق رندر جلویی، بر خلاف الگوریتم خوشه بندی شبکه ای که در بالا توضیح داده شد، نقشه وب از روش ساده تری برای خوشه بندی نقطه با شبکه استفاده می کند. فقط از آمار مجموع عناصر درون شبکه بر اساس موقعیت شبکه جاری استفاده می کند و پیچیدگی زمانی از O(n) تجاوز نمی کند. روش مبتنی بر فاصله عناصر را با فواصل کمتر بین نقاط ترکیب می کند. در دنباله بارگذاری نقاط، هنگامی که نقطه بعدی دارای نقاط قبلی دیگر در فاصله جستجو باشد، به کلاس نزدیکترین نقطه قبلی تعلق دارد. در غیر این صورت مستقل از کلاس [27 ]. با این حال، محاسبه فاصله بین نقاط زمان زیادی می برد، بنابراین این روش به ندرت در نقشه های وب استفاده می شود. الگوریتم خوشه بندی نقطه ای که بر اساس ترکیبی از شبکه و فاصله است، در حال حاضر روش اصلی خوشه بندی نقشه وب است. این روش کمی کندتر از روش مبتنی بر شبکه است، اما فقط باید یک بار برای هر نقطه اصلی محاسبه شود. هر عنصر تنها با عناصری که با شبکه همپوشانی دارند ترکیب می شود. نقاط خوشه بندی اطلاعات مکان عناصر نقطه اصلی را با دقت بیشتری منعکس می کنند. داده‌های روش خوشه‌بندی نقشه وب به عناصر نقطه‌ای محدود شد. معیار ارزیابی مناسبی برای دقت تجمع ندارد و قادر به انجام خوشه‌بندی چند مقیاسی مجموعه‌های نقطه‌ای با توزیع‌های نامنظم [ 28 ] نیست.

2.2. CFSFDP و ساختار درختی پوشا با تراکم سلسله مراتبی

اساس الگوریتم خوشه‌بندی CFSFDP این فرض است که مراکز خوشه‌ای توسط همسایه‌هایی با چگالی محلی کمتر احاطه شده‌اند و از هر نقطه با چگالی محلی بالاتر در فاصله نسبتاً زیادی قرار دارند. دو کمیت مهم برای توصیف هر نقطه داده وجود دارد: چگالی محلی و فاصله از نزدیکترین نقطه با چگالی بالا.
بسیاری از مطالعات روش‌های محاسبه چگالی محلی را برای دستیابی به اثرات خوشه‌بندی بهتر بهبود داده‌اند. برای مثال، شمارش تعداد نقاط در یک شعاع مشخص (Radius Density، RD) روش محاسبه چگالی است که در مقاله اصلی CFSFDP استفاده شده است. از آنجایی که همان مقادیر چگالی برای عناصر مجاور منجر به نتایج محاسباتی ضعیف برای روش شعاع می شود، رودریگز و لایو [ 8 ] از تابع گاوسی برای بهبود روش محاسبه چگالی استفاده کردند. زی و همکاران [ 29 ] از روش فازی K-Nearest Neighbor (KNN) برای بهبود روش محاسبه چگالی و حل خوشه‌بندی نادرست توزیع نامتعادل نقاط استفاده کرد. محمود و همکاران [ 30] از روش تخمین تراکم کرنل (KDE) به عنوان مبنایی برای محاسبات چگالی محلی برای بهبود اثرات خوشه‌بندی استفاده کرد. لیو و همکاران [ 31 ] نزدیکترین همسایه مشترک (SNN) را برای مجموعه داده های ساده و همچنین مجموعه داده های پیچیده از مقیاس های چندگانه، سیم پیچی متقاطع، تراکم های مختلف یا ابعاد بالا اعمال کرد. به طور خلاصه، تمام روش های فوق را می توان برای محاسبه مقادیر چگالی برای صحنه های خاص استفاده کرد.
در روش CFSFDP، هر نقطه دارای یک مقدار فاصله است که با محاسبه حداقل فاصله بین این نقطه و هر نقطه دیگری با چگالی بالاتر اندازه گیری می شود. مقدار فاصله نقطه ای با بیشترین چگالی محلی، حداکثر مقدار فاصله هر نقطه دیگر است. مقادیر چگالی و فاصله تمام نقاط در یک نمودار تصمیم گیری دو بعدی با چگالی به عنوان مختصات افقی و فاصله به عنوان مختصات عمودی تولید شد. برای شناسایی مراکز خوشه‌بندی، بسیاری از محققین نقاطی را با چگالی و فاصله بیشتر نسبت به سایر نقاط استخراج کردند [ 8 ، 29 ، 30 ، 31 .]. مرکزهای خوشه برجسته هستند و می توان آنها را در نمودار تصمیم مشخص کرد. بنابراین استخراج مراکز خوشه‌بندی آسان است. بسیاری از محققان بر انتخاب تعداد صحیح مراکز خوشه ای تمرکز کرده اند. خو و همکاران [ 12 ] مراکز خوشه بندی را با استفاده از روش برازش خطی به دست آوردند. این داده ها را به فواصل با تغییرات گرادیان بزرگ تقسیم می کند. ژو و همکاران [ 32 ] خوشه‌ای را با استفاده از مجموعه‌ای از اشیاء اصلی به جای یک شی واحد نمایش داد و بقیه اشیاء را بر اساس اطلاعات توزیع آنها طبقه‌بندی کرد. لی و همکاران [ 33] تعداد مناسبی از مراکز خوشه بندی را با انتخاب نقاطی با مقادیر چگالی و فاصله زیاد و ادغام نقاط نزدیک به یکدیگر به دست آورد. این یک الگوریتم خوشه‌بندی خودکار برای تعیین چگالی مراکز خوشه‌بندی است.
یک ساختار درختی سلسله مراتبی یک نتیجه میانی مهم از الگوریتم چگالی CFSFDP است. پس از یافتن مراکز خوشه، هر نقطه باقیمانده به همان خوشه به عنوان نزدیکترین همسایه با چگالی بالاتر نسبت داده می شود. رودریگز و لایو [ 8 ] پیشنهاد کردند که انتساب خوشه باید در یک مرحله انجام شود. از این رو، بسیاری از محققین برای به دست آوردن نتایج خوشه‌بندی، مشکل تخصیص تمام نقاط باقیمانده به جز مراکز خوشه‌بندی را بررسی کرده‌اند.
ساختار درختی پوششی با تراکم سلسله مراتبی محصول اضافی CFSFDP است. این شبکه ای از روابط بین عناصر است که با حفظ بردار هنگام محاسبه فاصله در هر نقطه به دست می آید. به عبارت دیگر، هر نقطه دارای نزدیکترین نقطه منحصر به فرد با چگالی بیشتر از نقطه است. مجموعه داده نقطه باید یک نقطه حداکثر چگالی منحصر به فرد داشته باشد (نقاط با مقدار چگالی یکسان را می توان با توجه به ترتیب ذخیره سازی متمایز کرد) به طوری که همه نقاط به بالاترین نقطه چگالی همگرا شوند. از آنجایی که ساختار اتصال بین عناصر، مشابه یک درخت، متقاطع نیست، CFSFDP دارای یک ویژگی سلسله مراتبی است.

3. روش شناسی

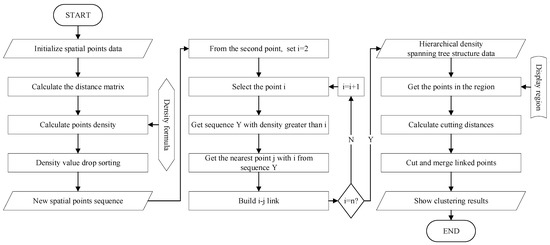
در این بخش، ما الگوریتم MSCHT را برای خوشه‌بندی چند مقیاسی نقاط عظیم پیشنهاد می‌کنیم. ابتدا نقاط توزیع سلسله مراتبی توابع چگالی مختلف را تحلیل می کند. دوم، روش تقسیم سلسله مراتبی چگالی را معرفی می کند و بر این اساس روابط درخت-ساختار را از هر نقطه ایجاد می کند. در نهایت نتایج خوشه بندی از طریق هرس درختان به دست آمد. جریان الگوریتم خاص در شکل 1 نشان داده شده است . جزئیات الگوریتم در الگوریتم 1 نشان داده شده است.

الگوریتم 1 MSCHT.
ورودی: مجموعه داده ایکس ، تراکم محاسبه روش دن ، نمایش دادن منطقه بOایکس(لon،لآتی،اچ،دبلیو), نرخ برش a
Output: نتیجه سیلتو= {C 1 , C 2 , …, C m } (که m تعداد خوشه ها است)
1. مجموعه داده را مقداردهی کنیدایکس1;
2. درخت KD بسازید ( ایکس1)
3. دیn×n={دمنj}n×n; // ساخت ماتریس فاصله دیn×n;
4. ρ=دیهn(دیn×n); // روش محاسبه چگالی Den , مانند آردی، کدیE، کنن، اسنن
5. ایکس2=Dropsortbydensity( ایکس1، ρ)
6. تی1={}; //ساخت درخت پوشا با چگالی سلسله مراتبی تهی
7. برای من=2; من<=n; من=من+1 انجام
8.  Yمن={j،ρj>ρمن};
9.  δمن=مترمنnj∈Yمن(دمنj);
10.  استوپهrپoمنnتیمن=j (دمنj=δمن); // ساخت لینک ij
11.  تی1.اضافه کردن( (من،j): دمنj)
12. پایان
13. تی2=دیroپسorتیبyدمنستیآnجه(تی1، دمنj); // درخت فراگیر تراکم سلسله مراتبی
14. تی3= تقاطع ( تی2، بOایکس) // پیوندها را در منطقه نمایش دریافت کنید بOایکس
15. دج=حداکثر(اچ،دبلیو)×آ;
16. متر=0;
17. برای هر پیوند در تی3 انجام
18.  اگر دمنj> دج سپس
19.    متر=متر+1;
20.   i ∈ C m ;
21.   سیلتو.add(C m );
22.  else سپس
23. C t .contain( j)( تی<=متر)
24.    من∈C t ;
25.  پایان
26. پایان
27. اگر متر==0 سپس
28. ج 1 ={ من،من∈تی3};
29.   سیلتو={C 1 };
30. پایان
31. بازگشت سیلتو;

3.1. محاسبه چگالی

در یک خوشه، ما فرض می کنیم که نقاط در ناحیه مرکزی مهمتر از نقاط در ناحیه لبه هستند، زیرا نقاط در ناحیه مرکزی به وضوح به این خوشه تعلق دارند. بنابراین، نقاط متعلق به یک خوشه به دلیل موقعیت‌های متفاوتشان، از نظر ارزش متفاوت هستند. نقطه با بالاترین مقدار به عنوان مرکز خوشه در نظر گرفته شد. از آنجایی که مراکز خوشه معمولاً توسط نقاطی احاطه شده اند که به یک خوشه تعلق دارند، ممکن است از نظر چگالی قطبی شدن هسته را نشان دهند. کدیE) کنن( اسنن) و سایر شاخص های اهمیت متریک و ممکن است حداکثر مقدار چگالی در خوشه باشد. محاسبات چگالی معقول می تواند به همگرایی عناصر نقطه ای به سمت مرکز خوشه کمک کند. پس از تعیین کمیت اهمیت عناصر، عناصر با ارزش بالا در مرکز کلاس به وضوح کمتر از عناصر پیرامونی هستند و تفاوت چگالی آشکاری بین عناصر وجود دارد. این تفاوت چگالی یکی از اصول اساسی CFSFDP است. چگالی ( دیهn) در هر نقطه به صورت زیر محاسبه می شود:

دن∈{آردی، کدیE، کنن، اسنن،……}

به عنوان مثال، آردیبا معادلات (2) و (3) به دست می آید:

ρمن=∑jnχ(دمنj)
χ(ایکس)={1، ایکس≤هپس0، ایکس>هپس
آردیبا استفاده از رابطه (3) محاسبه می شود. χ(ایکس)وقتی نقاط دیگر در شعاع قرار دارند برابر با 1 است هپسو 0 در غیر این صورت. χ(ایکس)برای هر کدام تعریف شده است دنو فرمول دقیق آن متفاوت است. مثلا، کدیEاز تابع گاوسی برای وزن کردن فاصله استفاده می کند هپس. کننفاصله را جمع آوری و محاسبه می کند هپسبه نزدیکترین k نقطه (‘k’ تعداد نزدیکترین همسایگان را نشان می دهد که با K-به معنی ‘k’ متفاوت است).
شکل 2 نمودار پراکندگی پنج خوشه را نشان می دهد. رنگ و اندازه عمدتا بر اساس مقدار چگالی هر نقطه بیان شد. به طور کلی، تعداد نقاط با مقادیر کم چگالی بیشتر از نقاط با مقادیر چگالی بالا است. درخت سلسله مراتب چگالی را می توان به طور منطقی تنها زمانی ایجاد کرد که هسته خوشه بندی درون کلاسی به طور دقیق به عنوان دارای مقدار چگالی بالا شناسایی شود.

3.2. درخت پوشا با تراکم سلسله مراتبی

با استفاده از فرمول (4) کمترین فاصله را از هر عنصر محاسبه کردیم منبه اشاره jبا چگالی بالاتر به عنوان معیار.

δمن={دقیقهj:ρj>ρمن(دمنj)، ρمن≠حداکثر(ρ)حداکثرj(دمنj)، ρمن=مترآایکس(ρ)
δمنبا محاسبه حداقل فاصله بین نقطه اندازه گیری می شود  منو هر نقطه دیگری با تراکم بالاتر. فاصله δمنبین نقطه منو نقطه ای با بیشترین چگالی حداکثر(ρ)با حداکثر طول به تصویب رسید دمنjاز تمام نقاط  j.
هنگامی که هر نقطه یک اتصال اشاره ایجاد می شود مننقطه را حفظ می کند  jبه عنوان نقطه برتر آن همانطور که در شکل 3 نشان داده شده است، وقتی همه نقاط دارای یک اتصال اشاره گر منحصر به فرد هستند، یک ساختار درخت مانند آشکار وجود دارد (این ساختار اندازه گیری بهتری از رابطه بین عناصر است). به عنوان مثال، چگالی نقطه A بزرگتر از نقطه B است و در مجموعه تمام نقاط بزرگتر از نقطه B، نقطه A نزدیکترین است. بنابراین، B متعلق به A است و یک گره فرزند A است. به طور مشابه، C و D گره های فرزند A هستند. در این تکرار، EFG و سایر نقاط متعلق به B هستند، و هر نقطه دارای یک تراکم سطح بالایی با ارزش بالا منحصر به فرد است. نقطه، تشکیل یک ساختار درخت N-ary مبتنی بر چگالی. فاصله بین A و B بیشتر از فاصله بین B و E است. در عین حال، این مطالعه نشان داد که به طور کلی، فاصله بین نقاط مرکز خوشه بالقوه بسیار بیشتر از فاصله بین نقاط دیگر است. شکل 3b یک درخت فراگیر تراکم سلسله مراتبی را بر اساس نشان می دهد آردی تراکم
با استفاده از ساختار درختی، نه تنها می‌توانیم پیوند بین عناصر را بدست آوریم، بلکه می‌توانیم رابطه بین طبقاتی نتایج خوشه‌بندی را نیز بدست آوریم.

3.3. استراتژی برش

استراتژی برش یک گام کلیدی در دستیابی به خوشه بندی چند مقیاسی است. ترکیب “گستره نمایش نقشه” با “درخت فراگیر تراکم سلسله مراتبی” در حال حاضر مسئله اصلی است. بر اساس روابط عنصر درخت مانند ایجاد شده، اثر خوشه‌بندی مورد انتظار را می‌توان با هرس شاخه‌ها بر اساس قوانین ریاضی خاص به دست آورد. بنابراین، هرس منطقی برای نتایج خوشه بندی بسیار مهم است. با ترسیم طرح‌های هرس سایر الگوریتم‌های خوشه‌بندی با ساختار درختی، طرح‌های هرس خوشه‌بندی زیر را می‌توان خلاصه کرد.

ما حداقل درخت پوشا (MST) و خوشه‌بندی فضایی مبتنی بر چگالی سلسله مراتبی برنامه‌ها با نویز (HDBSCAN) را به عنوان مرجع در نظر می‌گیریم، که همچنین بر فاصله بین نقاط تکیه می‌کنند تا بر جدایی بین کلاس‌ها حکم کنند. از آنجایی که MSCHT ساختار پیوند درختی نیز دارد، پیوندها زمانی قطع می شوند که فاصله از یک آستانه خاص بیشتر باشد. از آنجایی که راهبردهای هرس MST و HDBSCAN از نظر چند مقیاسی بسیار دست و پا گیر هستند، رویکرد ساده تری در این مطالعه مورد نیاز است. آستانه فاصله دجبه صورت زیر محاسبه می شود:

دج=حداکثر(اچ،دبلیو)×آ

جایی که اچارتفاع نقشه است و دبلیوعرض نقشه است. هر دو H و W متغیرهایی هستند که با وسعت نمایش نقشه در مقیاس های فضایی مختلف متفاوت هستند. آیک پارامتر ثابت برای تمام مقیاس های فضایی است و با توجه به خوشه بندی جلوه های بصری تعیین می شود و با مثال زیر مشخص می شود.

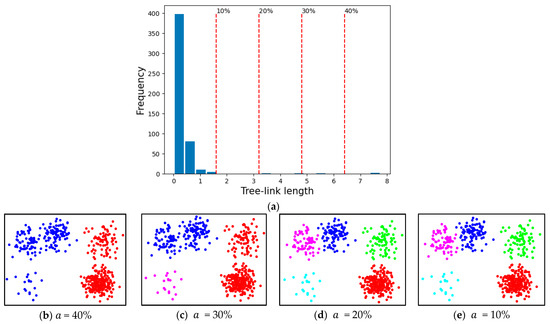
مطابق شکل 3 ، تعداد پیوندهای درختی برای فواصل طولانی کمتر و برای فواصل کوتاه بیشتر است. فراوانی وقوع هر طول پیوند درختی در داده های شکل 3 شمارش شد و در شکل 4 نشان داده شده است . با محدوده نمایش ثابت، آارزش اثر خوشه بندی را تعیین می کند. با تنظیم آدر محدوده 0 تا 50 درصد، متوجه شدیم که خوشه بندی بهترین بود آبین 10-20٪، در شکل 4 b-e. این پدیده در سایر مقیاس های نمایش نیز منعکس شده است. بنابراین، برای ارضای جلوه بصری هر مقیاس نمایش، توصیه می شود از 10-20٪ به عنوان آ-ارزش. تنظیمات آ-value برای کاربر مناسب است تا تفاوت‌های بین دسته‌های منطقه را تشخیص دهد.
چه زمانی آ تعمیر شد، دجبه عنوان جعبه محدوده نمایش تغییر می کند ( اچ،دبلیو) مقیاس بندی شده است و بر نتایج خوشه بندی تأثیر می گذارد. زمانی که یک نقطه دارای طول پیوند بزرگتر از دجدر وسعت نقشه، این عنصر واحد کلاس خود را تشکیل می دهد.

4. آزمایش ها و ارزیابی ها

4.1. مجموعه داده ها

4.1.1. مجموعه داده های مصنوعی

مجموعه داده های مصنوعی از روش بهبود تراکم CFSFDP مربوط [ 8 ، 28 ، 29 ، 30 ] و دیگر ادبیات خوشه بندی [ 34 ، 35 ، 36 ، 37 ، 38 ] برای تأیید اثر خوشه بندی الگوریتم پیشنهادی استفاده شد. جزئیات در جدول 1 نشان داده شده است.
4.1.2. مجموعه داده های واقعی
در این آزمایش از دو مجموعه داده استفاده شد: مجموعه داده اول شامل نقاط ساختمانی در پکن و مجموعه داده دوم شامل مکان های خطر زمین لغزش در شهرستان پینگوو، سیچوان بود. مجموعه داده قبلی دارای حجم و محدوده داده بزرگی است. برای آزمایش عملکرد MSCHT از نظر سرعت خوشه‌بندی و تأیید شناسایی مناطق پر تراکم محلی استفاده شد. دومی حجم و محدوده داده کمتری دارد و برای نشان دادن کاربرد خاص ساختار درختی فراگیر تراکم سلسله مراتبی برای به دست آوردن نتایج خوشه‌بندی در مقیاس‌های نمایشی مختلف استفاده می‌شود. شرح داده های خاص در جدول 2 و توزیع داده ها در شکل 5 به تفصیل آمده است .

4.2. آزمایش‌هایی روی داده‌های مصنوعی

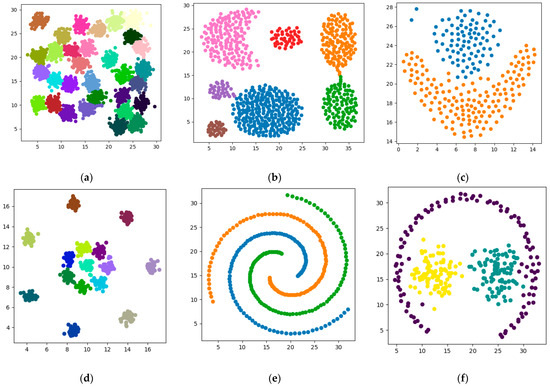
برای آزمایش اولیه اثر خوشه‌بندی MSCHT، از داده‌های مصنوعی برای اعتبارسنجی در یک مقیاس استفاده شد. به طور خاص، با اتخاذ استراتژی‌های چگالی مختلف برای ویژگی‌های توزیع فضایی داده‌های مختلف، نتایج عالی می‌توان به دست آورد. این در شکل 6 نشان داده شده است . به طور خلاصه، در این مطالعه، ما داده‌ها را با سناریوهای داده مصنوعی، مانند چگالی ناهمگن یا اتصال ضعیف، با استفاده از استراتژی‌های چگالی مختلف تطبیق دادیم. این باعث می‌شود که روش در این مقاله برای سناریوهای توزیع داده‌های بیشتر توسعه‌پذیرتر و سازگارتر باشد.

4.3. مقایسه سرعت با الگوریتم های خوشه بندی کلاسیک

برای مقایسه سرعت و دقت تفاوت بین الگوریتم خوشه بندی کلاسیک و الگوریتم خوشه بندی نقشه وب، الگوریتم های K-means و DBSCAN به عنوان نمایندگان الگوریتم کلاسیک انتخاب شدند. روش‌های خوشه‌بندی نقطه‌ای برای Leaflet، Google map و Amap به عنوان نمایندگان الگوریتم‌های خوشه‌بندی نقشه وب انتخاب شدند. از نظر ارزیابی دقت، از آنجایی که داده‌های ساختمان اصلی فاقد ویژگی دسته‌بندی هستند، طبقه‌بندی بر اساس تقسیم‌بندی‌های اداری نمی‌تواند به طور موثری انتساب دسته را متمایز کند. بنابراین، 36 کلاس شناخته شده با نمونه گیری انتخاب جعبه تنها در مناطق با تراکم ساختمانی بالا، مانند مناطق مرکزی پکن، منطقه Fengtai، و منطقه Beiyuan، به عنوان نمونه های خوشه ای دستی برای ارزیابی دقت به دست آمد.
بر اساس مشاهدات اولیه داده های نقطه ساختمان در پکن، مشخص شد که تقریباً 1000 نقطه ساختمانی در شعاع جستجوی 1000 متری در کوچکترین مناطق ساختمانی با تراکم بالا وجود دارد. فاصله بین مناطق متراکم نقاط تقریباً 5000 متر است. به طور همزمان، پکن دارای 16 منطقه شهرداری است و فرض بر این است که هر منطقه دارای حدود دو خوشه است. پارامترهای خوشه بندی اولیه برای هر روش در جدول 3 فهرست شده است. از آنجایی که وضعیت توزیع نقاط ساختمانی در پکن مشابه شکل 5 a یا شکل 5 b است. آردیبه عنوان روش محاسبه چگالی استفاده می شود. برای اینکه DBSCAN، MSCHT مناطق با چگالی بالا را به دقت شناسایی کند، مقدار eps به عنوان حداکثر شعاع دایره مماس درونی کوچکترین منطقه نمونه با چگالی بالا اختصاص داده می شود. هر دو MSCHT و DBSCAN از شعاع جستجو eps = 1000 متر برای محاسبه چگالی استفاده می کنند. MSCHT از dc = 5000 به عنوان آستانه فاصله برای کوتاه کردن روابط بین طبقاتی استفاده می کند. DBSCAN فرض می کند که تقریباً بیش از 500 نقطه در شعاع نقطه مرکزی وجود دارد. K-means فرض می کند که پکن 30 خوشه دارد. همانطور که سطح 8 نمای کامل پکن را نشان می دهد، خوشه بندی نقشه وب به طور جمعی از سطح 8 کاشی ها به عنوان حالت اولیه استفاده می کند. در طول فرآیند خوشه بندی اولیه، الگوریتم MSCHT به زمان اجرای طولانی تری نسبت به روش های دیگر (47 m 34 s) در مقایسه با 1 m 3 s برای K-means و 40 m 35 s برای DBSCAN نیاز داشت. پردازش K-means سریعتر بود زیرا نیازی به محاسبه چگالی نبود. از آنجایی که الگوریتم MSCHT به محاسبه اتصالات درختی نیاز دارد، کل زمان مورد نیاز برای محاسبه کمتر از روش محاسبه DBSCAN است. به طور خاص، با توجه به ساخت یک شاخص فضایی از نقاط، پیچیدگی کلی الگوریتم به O (nlogn) کاهش می یابد. Leaflet، Google و Gaudet همگی از محاسبه آمار داده های شبکه ای استفاده می کنند، بنابراین سرعت به ترتیب 1 m 2 s، 49 s و 40 s است (بدون احتساب زمان بارگذاری و رندر داده های front-end). در نتایج اولیه، الگوریتم MSCHT به زمان بیشتری نسبت به روش‌های دیگر نیاز داشت. کل زمان مورد نیاز برای محاسبه کمتر از روش محاسبه DBSCAN است. به طور خاص، با توجه به ساخت یک شاخص فضایی از نقاط، پیچیدگی کلی الگوریتم به O (nlogn) کاهش می یابد. Leaflet، Google و Gaudet همگی از محاسبه آمار داده های شبکه ای استفاده می کنند، بنابراین سرعت به ترتیب 1 m 2 s، 49 s و 40 s است (بدون احتساب زمان بارگذاری و رندر داده های front-end). در نتایج اولیه، الگوریتم MSCHT به زمان بیشتری نسبت به روش‌های دیگر نیاز داشت. کل زمان مورد نیاز برای محاسبه کمتر از روش محاسبه DBSCAN است. به طور خاص، با توجه به ساخت یک شاخص فضایی از نقاط، پیچیدگی کلی الگوریتم به O (nlogn) کاهش می یابد. Leaflet، Google و Gaudet همگی از محاسبه آمار داده های شبکه ای استفاده می کنند، بنابراین سرعت به ترتیب 1 m 2 s، 49 s و 40 s است (بدون احتساب زمان بارگذاری و رندر داده های front-end). در نتایج اولیه، الگوریتم MSCHT به زمان بیشتری نسبت به روش‌های دیگر نیاز داشت. به ترتیب (به استثنای زمان بارگذاری و رندر داده های جلویی). در نتایج اولیه، الگوریتم MSCHT به زمان بیشتری نسبت به روش‌های دیگر نیاز داشت. به ترتیب (به استثنای زمان بارگذاری و رندر داده های جلویی). در نتایج اولیه، الگوریتم MSCHT به زمان بیشتری نسبت به روش‌های دیگر نیاز داشت.
با این حال، به طور کلی، نتایج خوشه بندی در مقیاس های مختلف متفاوت است. برای مشاهده نتایج از دیگر منظرهای فضایی، لازم بود پارامترهای خوشه بندی قبلی با تنظیم مقیاس نمایش تنظیم شود. الگوریتم‌های DBSCAN و K-means به ارث بردن نتایج خوشه‌بندی قبلی در انتقال اول دشوار است. یعنی استفاده مجدد از برخی از نتایج مرحله دشوار است. بنابراین، تمام فرآیندهای الگوریتم‌های DBSCAN و K-means باید پس از تنظیم پارامتر دوباره محاسبه شوند. در مقابل، الگوریتم MSCHT محاسبه چگالی نقاط و اتصال ساختار درختی را در طول فرآیند خوشه‌بندی اولیه تکمیل می‌کند. این امر باعث می‌شود که محاسبه چگالی در فرآیند تنظیم بعدی غیر ضروری باشد و در نتیجه سرعت پردازش الگوریتم خوشه‌بندی افزایش می‌یابد. دجمقادیر مورد نیاز است و پیچیدگی الگوریتم فقط O(n) است. به طور مشابه، نقشه وب بر اساس یک شبکه چند مقیاسی از اتصالات درختی است و نتایج مربوطه با توجه به ویژگی‌های بزرگنمایی مختلف به دست می‌آید. بنابراین، الگوریتم MSCHT (0.023 ثانیه) بسیار سریعتر از DBSCAN (45 m 34 s) و K-means (1 m 22 s) بود. این از نظر سرعت به دست آوردن هسته های خوشه بندی با روش های خوشه بندی وب قابل مقایسه است. این کمی سریعتر است زیرا عملیات هرس MSCHT در پس زمینه انجام می شود. به ویژه، هر چه ارزش آن بیشتر باشد دجهر چه تعداد هرس کمتر و تعداد طبقات کمتر باشد، در نتیجه عملیات سریعتر و بالعکس عمل کندتر است.
برای بررسی بهتر اثر خوشه‌بندی هر روش، دقت خوشه‌بندی نمونه‌های با چگالی بالا را در سه مقیاس مختلف، یعنی مقیاس بزرگ، متوسط ​​و مقیاس کوچک ارزیابی کردیم. پس از چندین بار تنظیم پارامترها و مقیاس ها، بهترین نتایج خوشه بندی برای هر روش به دست آمد. از این میان، MSCHT در نمونه آزمایشی بر اساس تراکم بالاتر شناخته شده مناطق شهر، عملکرد بهتری دارد. جدول 4دقت خوشه بندی هر الگوریتم را در مقیاس های مختلف نشان می دهد. نتایج نشان می‌دهد که شاخص‌های ارزیابی، یعنی شاخص رند تعدیل‌شده (ARI)، اطلاعات متقابل عادی (NMI) و اطلاعات متقابل تنظیم‌شده (AMI) MSCHT نسبت به سایر روش‌ها در هر مقیاسی بالاتر بود. از آنجایی که نتایج روش های خوشه بندی مبتنی بر وب مشابه است، از نتایج خوشه بندی Leaflet به عنوان مقایسه اصلی استفاده می شود.
به طور خلاصه، الگوریتم MSCHT دارای مزایای سرعت محاسباتی در خوشه بندی چند مقیاسی با کمک درختان دارای چگالی سلسله مراتبی است. این به طور موثر خوشه بندی مناطق تجمع با چگالی بالا نقاط اصلی را شناسایی می کند. اشکال اصلی این است که فرآیند محاسباتی درخت سلسله مراتبی چگالی زمان‌بر است. برای دستیابی به یک اثر خوشه‌بندی نقشه وب جلویی با کیفیت خوب، توصیه می‌شود ساختار درختی عناصر نقطه‌ای را در رویه back-end محاسبه کنید.

4.4. جلوه های کاربردی خاص خوشه بندی چند مقیاسی

4.4.1. نتایج خوشه بندی چند مقیاسی برای نقاط ساختمانی پکن

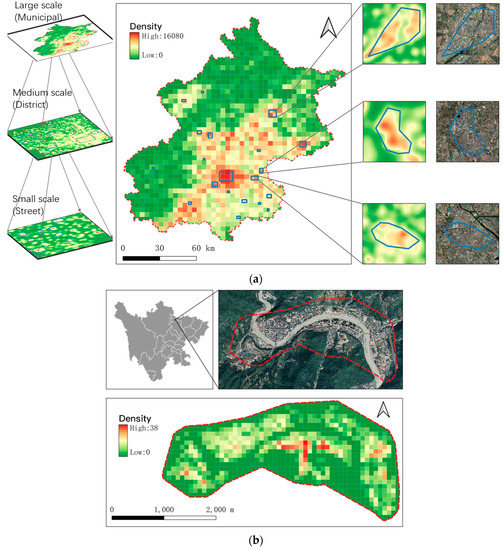
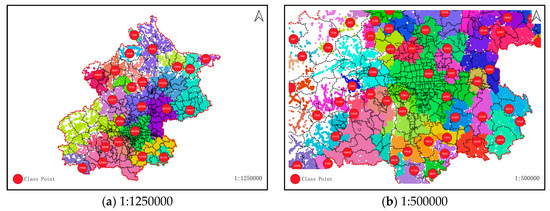
شکل 7 توزیع نتایج خوشه بندی چند مقیاسی را برای تمام داده های نقطه ساختمان در پکن نشان می دهد. اطلاعات گوشه جنوب شرقی پکن با مقیاس بندی مرحله به مرحله برای به دست آوردن نتایج خوشه بندی مربوطه به دست می آید. از آنجایی که نمایش الگوی توزیع خوشه‌بندی همه نقاط با تجمیع آنها دشوار است، ارائه اضافی از انتساب خوشه‌بندی همه نقاط ساخته می‌شود. جایی که فاصله برش دجدر هر مقیاس برابر با 16٪ از عرض فعلی است، نتایج در هر سطح به نوبه خود به دست می آید.
شکل 7 a اولین سطح نقشه را با مقیاس 1:1250000 نشان می دهد. پیوندهای درختی را به طول بیش از 20 کیلومتر قطع کردیم و 23 خوشه به دست آوردیم. منطقه مرکزی پکن دارای بیشترین نقاط خوشه ای است. نقاط ساختمان در مناطق دیگر به طور متوالی به سمت مناطق محلی با مقادیر تراکم بالا همگرا می شوند که تجمع نقطه ای در مقیاس بزرگ را به دست می آورد. از شکل 7 الف، می توان دید که مرز بین کلاس ها یک منحنی نامنظم است که نشان می دهد این روش می تواند خوشه های نقطه ای نامنظم را شناسایی کند.
شکل 7 ب سطح دوم نقشه را با مقیاس 1:500000 نشان می دهد. پیوندهای درختی به طول بیش از 8 کیلومتر قطع و 116 خوشه به دست آمد. نتایج خوشه بندی در شکل 7 ب اصلاحات اولین نتیجه خوشه بندی در مقایسه با شکل 7 الف است. شکل 7 c,d مربوط به نتایج خوشه‌بندی در مقیاس‌های 1؛ 250000 و 1:125000 است که به‌طور پیوسته کلاسترهای کلاس را در سطح قبلی تقسیم می‌کند. اثر تجمع چند مقیاسی به دست می آید.
از نظر جلوه بصری، MSCHT می تواند به طور موثری به تجمع عناصر نقطه ای چند مقیاسی دست یابد. برخلاف الگوریتم های خوشه بندی نقشه وب، هیچ پارتیشن یا محدودیتی در مرزهای شبکه وجود ندارد. بنابراین، مناطق ساختمانی محدود شده توسط درختان دارای تراکم را می توان برای مجموعه نقاط ساختمانی با توزیع نامنظم، مانند شهرها و خیابان ها، بهتر شناسایی کرد. بنابراین، ARI\NMI\AMI MSCHT بالاتر از خوشه‌بندی نقشه وب بود.
4.4.2. نتایج درخت پوشا با تراکم سلسله مراتبی
به دلیل حجم زیاد داده های پکن، نمی تواند ساختار درخت چگالی سلسله مراتبی را بهتر نشان دهد. بنابراین، آزمایش دوم تعداد کمتری از مکان‌های خطر زمین لغزش را در شهرستان پینگ‌وو، سیچوان انتخاب کرد تا ساختار چند مقیاسی را نشان دهد. قوانین زیربنای روش خوشه بندی MSCHT را می توان به صورت بصری با افزودن اتصالات خط درختی و تصاویر نقشه حرارتی نشان داد. در این حالت فاصله برش برای این نقشه 10 درصد مخرج مقیاس نقشه بود.
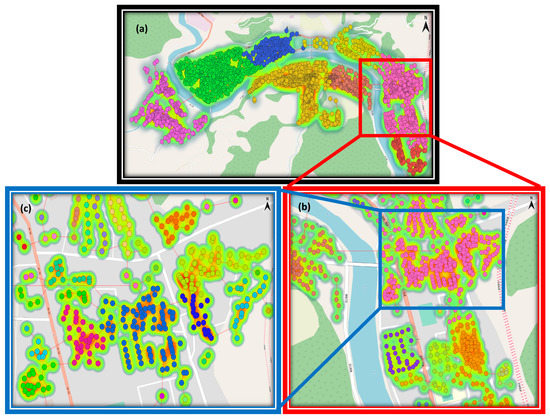
شکل 8 نتایج خوشه بندی چند مقیاسی نقاط خطر زمین لغزش در شهرستان پینگ وو را نشان می دهد. محدوده جعبه سیاه اولین سطح است. این شکل هشت خوشه را نشان می دهد، و هر نقطه به سمت یک مقدار بالای چگالی محلی متمرکز شده است. خوشه صورتی در شکل 8 a به عنوان نقاط داخلی در شکل 8 b مجدداً طبقه بندی شده است. نقاط در نیمه بالایی به عنوان یک کل باقی می مانند زیرا فاصله پیوند هنوز به نیاز قطع نرسیده است، در حالی که نقاط در نقاط نیمه پایین متمایز هستند. بنابراین، نقاط نیمه بالایی با کادر آبی نشان داده می شوند و ساختار درخت بیشتر به خوشه های میکروسکوپی تقسیم می شود. در این حالت، هر خوشه توسط یک منطقه با تراکم محلی بالا پوشیده شده است که حالت ایده آلی از تجمع است.
به طور خاص، هنگامی که بلایای بزرگ در مقیاس بزرگ مانند زمین لغزش و زلزله رخ می دهد، MSCHT می تواند به سرعت خوشه بندی چند مقیاسی را بر اساس توزیع مکان های فاجعه انجام دهد و مراکز امداد رسانی چند سطحی را مستقر کند. به عنوان مثال، زمانی که تعداد عناصر در یک کلاس از تعداد معینی بیشتر باشد، سایت های کوچکی در خوشه های آنها ایجاد می شوند. هنگامی که مقیاس افزایش یافت، سایت های بزرگ برای خوشه های بزرگ راه اندازی شد. این می تواند کمبود ظرفیت امدادی سایت های کوچک را جبران کند. به طور همزمان، می تواند مناطق با تراکم بالا را شناسایی کرده و تسکین معقول تری ارائه دهد.
علاوه بر این، تأثیر درختان پوشا با تراکم سلسله مراتبی را می توان به طور مستقیم در نقشه حرارتی درک کرد. شکل 8 نشان می دهد که درختان در فواصل کوتاه تری نسبت به خوشه های هم کلاس و در فواصل طولانی تری بین طبقات به هم متصل می شوند. نتایج به‌دست‌آمده با برش پیوندهای درختی بلند با تجسم فضایی نقشه حرارتی مطابقت دارد.

5. نتیجه گیری و کار آینده

این مقاله یک روش خوشه‌بندی چند مقیاسی بهبود یافته را بر اساس محدوده نمایش نقشه با ترسیم ساختار درختی فراگیر تراکم سلسله مراتبی الگوریتم CFSFDP پیشنهاد می‌کند. خوشه های کلاس مربوطه را بر اساس پیوندهای درخت کوتاه حفظ شده با قطع اتصالات درختی بیش از حد طولانی در سطوح مختلف نمایش به دست می آورد. آزمایش‌ها نشان می‌دهند که: (1) به دلیل ایجاد درخت‌های فراگیر تراکم سلسله مراتبی، پیچیدگی زمانی الگوریتم را به O(n) کاهش می‌دهد. این امر عملیات خوشه بندی را سرعت می بخشد و الزامات نقشه های وب را برای به دست آوردن نتایج خوشه بندی چند مقیاسی در زمان واقعی برآورده می کند. (2) توسط شبکه محدود نمی شود و می تواند به طور موثر مناطق نامنظم را در فضای جغرافیایی شناسایی کند که موجودیت ها متراکم تر هستند و دقت تجمع بالاتر است.
در آینده، باید بحث عمیقی در مورد تأثیر محاسبات تراکم بر تولید ساختارهای درختی و کاوش بهترین روش برای محاسبه تراکم در جایی که عناصر به وضوح متمایز هستند، وجود داشته باشد. علاوه بر این، الگوهای اتصال درختی به غیر از فاصله خطی باید بررسی شود و نظریه گراف برای ساخت ساختارهای درختی قوی‌تر معرفی شود. در همین حال، تحقیقات بیشتری بر روی GPU و تکنیک‌های محاسبات چگالی توزیع‌شده برای رسیدگی به مشکل زمان بیش از حد MSCHT در طول خوشه‌بندی اولیه مورد نیاز است [ 39 ]]. ارائه بصری این خوشه بندی در سمت نقشه وب برای گسترش کاربردهای آن باید مورد بررسی قرار گیرد تا به یادگیری در مورد پردازش پیچیده داده ها در مقیاس های فضایی چندگانه ادامه داده و ابزارهای اساسی برای چنین تحقیقاتی فراهم شود.

منابع

  1. نگوین، تی تی. کریشناکوماری، پ. Calvert، SC; Vu، HL؛ ون لینت، اچ. استخراج ویژگی و تجزیه و تحلیل خوشه‌بندی ازدحام بزرگراه. ترانسپ Res. قسمت C Emerg. تکنولوژی 2019 ، 100 ، 238-258. [ Google Scholar ] [ CrossRef ]
  2. لیو، کیو. لی، ز. دنگ، م. تانگ، جی. Mei, X. مدل‌سازی اثر مقیاس بر خوشه‌بندی نقاط مکانی. محاسبه کنید. محیط زیست سیستم شهری 2015 ، 52 ، 81-92. [ Google Scholar ] [ CrossRef ]
  3. Fürhoff, L. بازنگری در استفاده و تجربه خوشه بندی در نقشه برداری وب. در کنفرانس بین المللی تعامل انسان و کامپیوتر ; Springer: برلین/هایدلبرگ، آلمان، 2020. [ Google Scholar ] [ CrossRef ]
  4. وو، بی. Wilamowski، BM یک روش خوشه‌بندی مبتنی بر چگالی سریع و شبکه برای داده‌ها با اشکال و نویز دلخواه. IEEE Trans. Ind. Informatics 2016 , 13 , 1620-1628. [ Google Scholar ] [ CrossRef ]
  5. وانگ، دبلیو. یانگ، جی. Muntz, R. STING: رویکرد شبکه اطلاعات آماری برای داده کاوی مکانی. Vldb 1997 ، 97 ، 186-195. [ Google Scholar ]
  6. هارتیگان، جی. وانگ، الگوریتم MA AS 136: یک الگوریتم خوشه‌بندی k-means. JR Stat. Soc. 1979 ، 28 ، 100-108. [ Google Scholar ] [ CrossRef ]
  7. استر، ام. کریگل، اچ پی؛ ساندر، جی. Xu, X. یک الگوریتم مبتنی بر چگالی برای کشف خوشه ها در پایگاه داده های فضایی بزرگ با نویز. kdd 1996 ، 96 ، 226-231. [ Google Scholar ]
  8. رودریگز، آ. Laio، A. خوشه‌بندی با جستجوی سریع و یافتن قله‌های چگالی. Science 2014 ، 344 ، 1492-1496. [ Google Scholar ] [ CrossRef ]
  9. گوان، جی. لی، اس. او، X. ژو، جی. چن، جی. خوشه‌بندی سلسله مراتبی سریع پیک‌های چگالی محلی از طریق روش انتقال درجه ارتباط. محاسبات عصبی 2021 ، 455 ، 401-418 . [ Google Scholar ] [ CrossRef ]
  10. لانگ، ز. گائو، ی. منگ، اچ. یائو، ی. Li، T. خوشه بندی بر اساس پیک های چگالی محلی و برش نمودار. Inf. علمی 2022 ، 600 ، 263-286. [ Google Scholar ] [ CrossRef ]
  11. Lv، X.; ممکن است.؛ او، X. هوانگ، اچ. Yang, J. CciMST: یک الگوریتم خوشه بندی بر اساس حداقل درخت پوشا و مراکز خوشه. ریاضی. مشکل مهندس 2018 ، 2018 ، 8451796. [ Google Scholar ] [ CrossRef ]
  12. گی، ز. پنگ، دی. وو، اچ. طولانی، X. MSGC: خوشه‌بندی شبکه‌ای چند مقیاسی با ادغام دانه‌بندی تحلیلی و شناخت بصری برای تشخیص الگوهای فضایی سلسله مراتبی. آینده. ژنر. محاسبه کنید. سیستم 2020 ، 112 ، 1038-1056. [ Google Scholar ] [ CrossRef ]
  13. مادولاتا، تی اس مروری بر روش های خوشه بندی. IOSR J. Eng. 2012 ، 2 ، 719-725. [ Google Scholar ] [ CrossRef ]
  14. Carr، JK; Fontanella، SA; Tribby، CP شناسایی جغرافیای آبجو آمریکایی: تجزیه و تحلیل هسته-خوشه ای چند مقیاسی کارخانه های آبجوسازی ایالات متحده. پروفسور Geogr. 2018 ، 71 ، 185-196. [ Google Scholar ] [ CrossRef ]
  15. داس، ا. Waslander، SL ثبت نام اسکن با k-مقیاس چندگانه به معنی تبدیل توزیع های نرمال است. در مجموعه مقالات کنفرانس بین‌المللی IEEE/RSJ 2012 درباره ربات‌ها و سیستم‌های هوشمند، Vilamoura-Algarve، پرتغال، 7 تا 12 اکتبر 2012. [ Google Scholar ]
  16. چن، آر. ژائو، اس. لیانگ، ام. یک رویکرد خوشه‌بندی سریع چند مقیاسی بر اساس DBSCAN. سیم. اشتراک. اوباش محاسبه کنید. 2021 ، 2021 ، 1-11. [ Google Scholar ] [ CrossRef ]
  17. نایاک، ج. نایک، بی. بهرا، الگوریتم خوشه‌بندی HS فازی C-Means (FCM): مروری بر یک دهه از 2000 تا 2014. در هوش محاسباتی در داده کاوی . Springer: دهلی، هند، 2015; جلد 2، ص 133-149. [ Google Scholar ]
  18. آنکرست، م. برونیگ، MM; کریگل، اچ پی؛ Sander, J. OPTICS: نقاط ترتیب برای شناسایی ساختار خوشه بندی. ACM Sigmod Rec. 1999 ، 28 ، 49-60. [ Google Scholar ] [ CrossRef ]
  19. Rani, P. بررسی روشهای خوشه بندی مبتنی بر شبکه STING و CLIQUE. بین المللی J. Adv. Res. محاسبه کنید. علمی 2017 ، 8 ، 1510-1512. [ Google Scholar ]
  20. مرتق، ف. Contreras، P. الگوریتم‌های خوشه‌بندی سلسله مراتبی: یک نمای کلی. حداقل داده سیم بدانید. کشف کنید. 2011 ، 2 ، 86-97. [ Google Scholar ] [ CrossRef ]
  21. شیخ الاسلامی، غ. چاترجی، اس. Zhang، A. WaveCluster: یک رویکرد خوشه‌بندی مبتنی بر موجک برای داده‌های مکانی در پایگاه‌های داده بسیار بزرگ. VLDB J. 2000 ، 8 ، 289-304. [ Google Scholar ] [ CrossRef ]
  22. سانتیسری، ک. Damodaram, A. CLIQUE: خوشه بندی بر اساس تراکم در داده های استفاده از وب: آزمایش ها و نتایج آزمایش. در مجموعه مقالات سومین کنفرانس بین المللی 2011 در زمینه فناوری رایانه الکترونیک، کانیاکوماری، هند، 8 تا 10 آوریل 2011. [ Google Scholar ]
  23. چنگ، سی.-اچ. فو، AW; Zhang، Y. خوشه‌بندی زیرفضای مبتنی بر آنتروپی برای استخراج داده‌های عددی. در مجموعه مقالات پنجمین کنفرانس بین المللی ACM SIGKDD در مورد کشف دانش و داده کاوی، لانگ بیچ، کالیفرنیا، ایالات متحده آمریکا، 15 تا 18 اوت 1999. [ Google Scholar ]
  24. چنگ، ال. کانر، تی. سیرن، جی. Aanensen، DM; Corander, J. خوشه بندی سلسله مراتبی و صریح فضایی توالی های DNA با نرم افزار BAPS. مول. Biol. تکامل. 2013 ، 30 ، 1224-1228. [ Google Scholar ] [ CrossRef ] [ PubMed ]
  25. حبیبولایویچ، جی.کی. چن، ایکس. Shin, H. مکانیزم فیلترینگ و خوشه بندی کارآمد برای نقشه های گوگل. J. Adv. مدیریت علمی 2013 ، 1 ، 107-111. [ Google Scholar ] [ CrossRef ]
  26. برسنف، آ. سمنوف، آ. Panidi، E. شبکه های شش ضلعی اعمال شده برای خوشه بندی مکان ها در نقشه های وب. بین المللی قوس. فتوگرام حسگر از راه دور اسپات. Inf. علمی 2022 ، 43 ، 435-440. [ Google Scholar ] [ CrossRef ]
  27. نتک، آر. بروس، جی. Tomecka، O. تست عملکرد در خوشه بندی نشانگر و تکنیک های تجسم نقشه حرارتی: مطالعه مقایسه ای در کتابخانه های نقشه برداری جاوا اسکریپت. ISPRS Int. J. Geo-Inf. 2019 ، 8 ، 348. [ Google Scholar ] [ CrossRef ]
  28. زی، جی. گائو، اچ. زی، دبلیو. لیو، ایکس. Grant, PW خوشه‌بندی قوی با تشخیص پیک‌های چگالی و اختصاص نقاط بر اساس K-نزدیک‌ترین همسایگان با وزن فازی. Inf. علمی 2016 ، 354 ، 19-40. [ Google Scholar ] [ CrossRef ]
  29. محمود، ر. ژانگ، جی. بی، آر. داوود، اچ. احمد، H. خوشه‌بندی با جستجوی سریع و یافتن پیک‌های چگالی از طریق انتشار گرما. محاسبات عصبی 2016 ، 208 ، 210-217. [ Google Scholar ] [ CrossRef ]
  30. لیو، آر. وانگ، اچ. Yu, X. خوشه‌بندی مبتنی بر نزدیکترین همسایه با جستجوی سریع و یافتن قله‌های چگالی. Inf. علمی 2018 ، 450 ، 200-226. [ Google Scholar ] [ CrossRef ]
  31. خو، جی. وانگ، جی. Deng, W. DenPEHC: خوشه بندی سلسله مراتبی کارآمد مبتنی بر اوج چگالی. Inf. علمی 2016 ، 373 ، 200-218. [ Google Scholar ] [ CrossRef ]
  32. ژو، ز. سی، جی. سان، اچ. کو، ک. Hou, W. یک الگوریتم خوشه بندی قوی بر اساس شناسایی نقاط هسته و تخمین چگالی هسته KNN. سیستم خبره Appl. 2022 ، 195 ، 116573. [ Google Scholar ] [ CrossRef ]
  33. تائو، ال. هونگوی، جی. Shuzhi, S. خوشه بندی پیک های چگالی با تعیین خودکار مراکز خوشه. ج. جلو. محاسبه کنید. علمی تکنولوژی 2016 ، 10 ، 1614-1622. [ Google Scholar ]
  34. پنگ، دی. گی، ز. وانگ، دی. ممکن است.؛ هوانگ، ز. ژو، ی. Wu, H. خوشه‌بندی با اندازه‌گیری مرکزیت جهت محلی برای داده‌های با چگالی ناهمگن و اتصال ضعیف. نات اشتراک. 2022 ، 13 ، 5455. [ Google Scholar ] [ CrossRef ]
  35. وینمن، سی جی; ریندرز ام جی، تی. Backer, E. الگوریتم خوشه واریانس حداکثر. IEEE Trans. الگوی مقعدی ماخ هوشمند 2002 ، 24 ، 1273-1280. [ Google Scholar ] [ CrossRef ]
  36. گیونیس، ا. مانیلا، اچ. تساپاراس، ص. تجمع خوشه ای. Acm Trans. بدانید. کشف کنید. داده 2007 ، 1 ، 4-es. [ Google Scholar ] [ CrossRef ]
  37. فو، ال. Medico، E. FLAME، یک روش خوشه‌بندی فازی جدید برای تجزیه و تحلیل داده‌های ریزآرایه DNA. BMC Bioinform. 2007 ، 8 ، 3. [ Google Scholar ] [ CrossRef ] [ PubMed ]
  38. چانگ، اچ. یونگ، دی.-ای. خوشه بندی طیفی مبتنی بر مسیر قوی. تشخیص الگو 2008 ، 41 ، 191-203. [ Google Scholar ] [ CrossRef ]
  39. ژانگ، جی. زو، تبر; Huang، Q. یک رویکرد برآورد چگالی هسته تطبیقی ​​با شتاب GPU برای تجزیه و تحلیل الگوی نقطه ای کارآمد در داده های بزرگ فضایی. بین المللی جی. جئوگر. Inf. علمی 2017 ، 31 ، 2068–2097. [ Google Scholar ] [ CrossRef ]
Ijgi 12 00024 g001 550
شکل 1. نمودار جریان الگوریتم MSCHT.
Ijgi 12 00024 g002 550
شکل 2. ارزیابی توزیع چگالی.
Ijgi 12 00024 g003 550
شکل 3. نمودار شماتیک ساختار درختی. ( الف ) نمودار ساختار درختی. ( ب ) نقشه توزیع ویژگی درختی.
Ijgi 12 00024 g004 550
شکل 4. توزیع فرکانس طول پیوند درخت و نتیجه برش. ( الف ) نمودار توزیع فرکانس طول پیوند درخت (فاصله کلاس 0.4 است)، خط چین قرمز مقدار است. آبرای دج; ( ب – ث ) نتایج خوشه‌بندی به‌دست‌آمده برای مختلف آارزش های.
Ijgi 12 00024 g005 550
شکل 5. توزیع داده های تجربی. ( الف ) توزیع نقاط ساختمانی در پکن. ( ب ) توزیع نقاط خطر زمین لغزش در شهرستان پینگوو، سیچوان.
Ijgi 12 00024 g006 550
شکل 6. نتایج خوشه بندی داده های مصنوعی تحت استراتژی های چگالی مختلف. ( الف ) مجموعه داده D31، دن=کدیE. ( ب ) مجموعه داده های جمع آوری، دن=کنن. ( ج ) مجموعه داده شعله، دن=کدیE. ( د ) مجموعه داده R15، دن=آردی. ( e ) Path-based1: مجموعه داده مارپیچی، دن=کنن. ( f ) مجموعه داده مبتنی بر مسیر2، دن=اسنن.
Ijgi 12 00024 g007a 550 Ijgi 12 00024 g007b 550
شکل 7. نتایج خوشه بندی چند مقیاسی نقطه ساختمان پکن. ( الف – د ) نتایج خوشه بندی در مقیاس های مختلف.
Ijgi 12 00024 g008 550
شکل 8. نتایج خوشه بندی چند مقیاسی نقاط خطر زمین لغزش در شهرستان پینگ وو. ( الف – ج ) نتایج خوشه‌بندی و ساختار درختی در مقیاس‌های مختلف.

مقالات داخلی و بین المللی

مطالب مرتبط ...

بدون دیدگاه

دیدگاهتان را بنویسید