خلاصه

یافتن خوشه‌هایی از رویدادها یک کار مهم در بسیاری از تحلیل‌های فضایی است. هر دو روش تاییدی و اکتشافی برای انجام این کار وجود دارد. تکنیک‌های آماری سنتی به‌عنوان تأییدی یا مشاهده‌ای در نظر گرفته می‌شوند، زیرا محققان یک فرضیه پیشینی را تأیید می‌کنند. این روش‌ها اغلب زمانی که برای انواع جدیدتر داده‌ها مانند داده‌های شی متحرک و داده‌های بزرگ اعمال می‌شوند، شکست می‌خورند. داده های شی متحرک حداقل سه بخش را شامل می شود: مکان، زمان و ویژگی ها. این مقاله یک رویکرد خوشه‌بندی فضا-زمان بهبود یافته را پیشنهاد می‌کند که بر خوشه‌بندی سلسله مراتبی تجمعی برای شناسایی گروه‌بندی‌ها در داده‌های حرکتی متکی است. این رویکرد، به عنوان مثال، خوشه‌بندی سلسله مراتبی فضا-زمان، اطلاعات مکان، زمان و ویژگی‌ها را برای شناسایی گروه‌ها در یک ساختار تودرتو که منعکس کننده تفسیر سلسله مراتبی مقیاس است، در بر می‌گیرد. شبیه‌سازی‌ها برای درک اثرات پارامترهای مختلف و مقایسه با روش‌های خوشه‌بندی موجود استفاده می‌شوند. این رویکرد به طور موفقیت آمیزی در رویکردهای سنتی با اجازه دادن به انعطاف پذیری برای درک هر دو مؤلفه مکانی و زمانی هنگام اعمال بر داده ها بهبود می یابد. این روش برای داده‌های ردیابی حیوانات برای شناسایی خوشه‌ها یا نقاط داغ فعالیت در محدوده خانه حیوان اعمال می‌شود.

کلید واژه ها:

فضایی و زمانی خوشه بندی ; مسیرها

1. معرفی

یافتن خوشه‌هایی از رویدادها یک کار مهم در بسیاری از تحلیل‌های فضایی است. هر دو روش تاییدی و اکتشافی برای انجام این کار وجود دارد [ 1 ]. تکنیک‌های آماری سنتی به‌عنوان تأییدی یا مشاهده‌ای در نظر گرفته می‌شوند، زیرا محققان یک فرضیه پیشینی را تأیید می‌کنند. روش‌های خوشه‌بندی تأییدی تلاش می‌کنند تا حضور خوشه‌بندی شبکه‌ها یا داده‌های نقطه‌ای را شناسایی کنند یا مکان این خوشه‌ها را بیابند. در مقابل، روش‌های اکتشافی برای شناسایی گروه‌هایی از داده‌ها در فضای n بعدی با استفاده از متریک شباهت یا عدم تشابه بر الگوریتم‌های یادگیری ماشینی بدون نظارت تکیه می‌کنند [ 2 ].]. روش‌های اکتشافی که خوشه‌های داده‌های مکانی-زمانی را شناسایی می‌کنند، در حوزه کشف دانش جغرافیایی (GKD) قرار می‌گیرند، جایی که هدف «کشف الگوها، روندها و روابط جدید و غیرمنتظره» در داده‌ها است ([ 3 ]، ص 149).
در هر دو حالت اکتشافی یا تأییدی، بسیاری از روش‌های موجود برای شناسایی خوشه‌ها، فضا-مکان یا فضاهای ویژگی را در نظر نمی‌گیرند، و اغلب در معرض به اصطلاح اثرات لبه‌ای هستند که به مرز منطقه مورد مطالعه گره خورده‌اند [ 4 ]. برای در نظر گرفتن این اثرات، رویدادهای نزدیک به لبه نسبت به رویدادهای دورتر از لبه های منطقه مورد مطالعه وزن بیشتری دارند. این بدان معناست که هیچ ملاحظه صریحی در مورد اینکه چگونه خوشه بندی بر اساس مقیاس متفاوت است وجود ندارد. علاوه بر این، روش‌های تأیید سنتی اغلب زمانی که برای انواع جدیدتر داده‌ها مانند داده‌های شی متحرک و داده‌های بزرگ اعمال می‌شوند، شکست می‌خورند. منیس و گوو [ 5] سه دلیل برای شکست این روش‌های سنتی با داده‌های جدید را فهرست می‌کند: دیدگاه محدود یا مدل رابطه‌ای (مثلاً رگرسیون خطی)، آنها برای پردازش مقدار زیادی اطلاعات طراحی نشده‌اند، و برای انواع داده‌های جدید [در حال ظهور] طراحی نشده‌اند. (مانند مسیر حرکت اجسام…)» ([ 5 ]، ص 403).
داده های شی متحرک حداقل سه بخش را شامل می شود: مکان، زمان و ویژگی ها. این ویژگی ها ممکن است شامل اطلاعاتی در مورد نحوه حرکت عامل (به عنوان مثال، سرعت، حالت، یا جهت)، ویژگی های عامل (به عنوان مثال، سن، جنس، یا درآمد)، یا عوامل محیطی / زمینه ای (مانند کاربری زمین، دما، آب و هوا). حرکت جسم ممکن است به صورت دنباله ای از نقاط (مانند یک مسیر) یا رویدادهای متمایز نشان دهنده مکان های شناخته شده عامل [ 6 ] نشان داده شود. اگرچه، در حالت اول، تداوم از طریق درونیابی بین مکان های شناخته شده ایجاد می شود. ایده توالی دلالت بر وابستگی بین مشاهداتی دارد که در زمان پس از یکدیگر رخ می دهند. عدم قطعیت بین مکان ها ممکن است به عنوان یک منشور فضا-زمان نشان داده شود 78 ،8 ، 9 ].
اگر اشیاء عوامل انسانی باشند، حرکت آنها اغلب به شبکه های حمل و نقل موجود گره خورده است و ممکن است رویدادهای محدود شبکه [ 10 ] باشد، یعنی رویدادهایی که در یک فضای یک بعدی رخ می دهند. نشان داده شده است که روش‌های خوشه‌بندی تأییدی، خوشه‌بندی را برای رویدادهای نقطه‌ای با محدودیت خطی بیش از حد برآورد می‌کنند [ 11 ، 12 ، 13 ، 14 ]. این به این دلیل است که استفاده از فاصله اقلیدسی فاصله بین نقاط را دست کم می گیرد. بنابراین، یک متریک فاصله شبکه ترجیح داده می شود [ 14 ].
این مقاله یک رویکرد جدید خوشه‌بندی فضا-زمان را پیشنهاد می‌کند که بر خوشه‌بندی سلسله مراتبی تجمعی برای شناسایی گروه‌بندی‌ها در داده‌های حرکتی متکی است. رویکرد، خوشه‌بندی سلسله مراتبی فضا-زمان، اطلاعات مکان، زمان و ویژگی‌ها را برای شناسایی گروه‌ها در یک ساختار تودرتو که منعکس کننده تفسیر سلسله مراتبی مقیاس است، در بر می‌گیرد. 15 ].]. این سه مولفه با استفاده از ترکیب خطی وزنی برای ایجاد یک متریک فاصله اصلاح شده ترکیب می شوند. هر یک از مولفه ها از طریق یک ضریب مقیاس محدود می شوند. این روش برای مطالعه مشاهدات رویدادهای نقطه گسسته ای که ممکن است در داخل و خارج از یک شبکه رخ دهد، توسعه یافته است. هدف از این رویکرد جدید، به حساب آوردن ماهیت چرخه ای زمان، در حالی که شامل فاصله فیزیکی، و پتانسیل مشاهده خوشه ها در مقیاس های زمانی و مکانی متعدد است. که در رویکردهای موجود به خوبی در نظر گرفته نشده اند. تاکید بر نقاطی است که مشاهدات مکرر را برای یک دوره معین نشان می‌دهند، مانند چرخه 24 ساعته یک روز. شبیه‌سازی‌ها برای درک اثرات پارامترهای مختلف و مقایسه با روش‌های خوشه‌بندی موجود استفاده می‌شوند. سرانجام،
مقاله بصورت زیر مرتب شده است. بخش بعدی الگوریتم‌های خوشه‌بندی موجود و محدودیت‌های آنها برای داده‌های مکانی-زمانی را مورد بحث قرار می‌دهد. تاکید ویژه ای بر خوشه بندی سلسله مراتبی داده شده است زیرا این امر برای بقیه مقاله اساسی است. بخش 2 متریک فاصله را برای الگوریتم خوشه بندی سلسله مراتبی ارائه می کند و هر یک از مؤلفه ها را به طور جداگانه مورد بحث قرار می دهد. بخش 3 شبیه سازی های مورد استفاده برای تخمین پارامترهای مختلف در متریک فاصله را مورد بحث قرار می دهد و خوشه بندی سلسله مراتبی فضا-زمان را با گزینه های بالقوه مقایسه می کند. در نهایت، رویکرد جدید برای داده‌های ردیابی حیوانات اعمال می‌شود و نتایج مورد بحث قرار می‌گیرند.

1.1. زمینه

داده کاوی مکانی، یا به طور کلی GKD، زیرشاخه ای از داده کاوی و یادگیری ماشینی است که بر اکتشاف داده های مکانی و مکانی-زمانی تمرکز دارد – به طور خاص، حجم عظیمی از داده های با وضوح خوب که از خدمات مبتنی بر مکان، داده های زمان واقعی به دست می آید، اطلاعات جغرافیایی داوطلبانه (VGI)، یا سنجش از دور [ 1 ، 16 ، 17 ، 18 ]. کشف دانش جغرافیایی بر توسعه روش‌هایی برای مدیریت این داده‌های تخصصی با هدف استخراج دانش متمرکز است. حوزه‌های وسیع عبارتند از: تقسیم‌بندی یا خوشه‌بندی، طبقه‌بندی، استخراج قوانین تداعی فضایی، انحرافات، روندها و تجسم‌های زمین [ 3 ، 5 ].
اغلب، داده‌های GKD نامرتب خواهند بود و اولین قدم برای استخراج دانش، فیلتر کردن یا پاک کردن آن خواهد بود. مکان ممکن است از طریق GPS دستگاه تلفن همراه یا مکان مبتنی بر شبکه سلولی مستعد خطاهای اندازه گیری باشد [ 18 ، 19 ]. مراحل مختلف برای فیلتر کردن یا تمیز کردن آن ممکن است تبدیل یا تجمیع مکان‌ها به یک مکان قابل توجه باشد، یا همانطور که اشبروک و استارنر [ 20 ] آن را بیان می‌کنند، مکانی که «یک کاربر وقت خود را در آن سپری می‌کند» ([ 20 ]، ص 278). ). فاصله زمانی یک مکان قابل توجه نباید بیش از چند روز باشد بلکه چند دقیقه باشد. آندرینکو و همکاران [ 21] از ایده توقف برای تعریف یک مکان مهم استفاده کنید: «مکانی که برای یک فرد مهم است را می توان از تعداد و مدت توقف ها تشخیص داد» ([ 20 ]، ص 10). توقف مکانی است که یک نماینده برای مدت معینی در آن می ماند. این “با یک شکاف زمانی بین رکوردهای موقعیت متوالی آشکار می شود” ([ 21 ]، ص 10).

1.2. تکنیک های رایج خوشه بندی

خوشه‌بندی «فرایند گروه‌بندی مجموعه‌های بزرگ داده بر اساس شباهت آنهاست» ([ 22 ]، ص 208). دو مشخصه تعیین‌کننده هر تحلیل خوشه‌بندی، تعیین معیار شباهت (یا عدم تشابه) و الگوریتم مورد استفاده برای شناسایی خوشه‌ها است. چندین معیار تشابه وجود دارد که فاصله بین مشاهدات را محاسبه می کند، اما فاصله اقلیدسی رایج ترین آنهاست [ 23 ]. روش‌های اکتشافی خوشه‌بندی فضایی داده‌های نقطه‌ای به چهار دسته تقسیم می‌شوند: روش‌های تقسیم‌بندی، روش‌های سلسله مراتبی (انباشتگی یا تقسیم‌بندی)، روش‌های مبتنی بر چگالی و روش‌های مبتنی بر شبکه [ 22 ].]. مهم است که وظیفه مفهومی خوشه بندی را از الگوریتم ها و معیارهای شباهت مورد استفاده برای دستیابی به آن کار جدا کنیم [ 23 ]. الگوریتم‌های زیادی برای دستیابی به خوشه‌بندی سلسله مراتبی استفاده می‌شوند که ممکن است از روش‌های مشابه یا متفاوتی برای اندازه‌گیری شباهت استفاده کنند. روش های مختلف خوشه بندی و الگوریتم های رایج در جدول 1 خلاصه شده است.
یک محدودیت با چندین الگوریتم خوشه بندی فهرست شده در جدول 1 که برای داده های مکانی اعمال می شود این است که آنها لزوماً مرزهای منطقه یا محدودیت های فضایی را در نظر نمی گیرند [ 24 ]. این بدان معنی است که خوشه های تولید شده از داده های مکانی ممکن است نزدیک یا به هم پیوسته نباشند. Guo [ 24 ] منطقه‌بندی را به‌عنوان «شکل ویژه‌ای از خوشه‌بندی که به دنبال گروه‌بندی اقلام داده‌ها… به خوشه‌های به‌هم پیوسته فضایی… در حالی که یک تابع هدف را بهینه می‌کند (مثلاً یک معیار همگنی بر اساس شباهت‌های چند متغیره در مناطق)» تعریف می‌کند. 24 ]).]، پ. 329). این زمانی پیچیده تر می شود که دو جزء وجود داشته باشد که باید در خوشه با مرزهای مختلف ادغام شوند: یک مرز فیزیکی/مکانی و یک مرز زمانی. تفاوت زمانی و مرز زمانی بین دو رویداد به برنامه بستگی دارد. خوشه‌بندی که هم فضا و هم زمان را در بر می‌گیرد به طور سنتی از معیاری استفاده می‌کند که هم شباهت مکانی و هم زمانی را مشخص می‌کند [ 25 ].
رویکردهای پیشنهادی مختلفی برای ترکیب اطلاعات زمانی وجود دارد. Birant و Kut [ 22 ] در بسط فضا-زمان خود از خوشه‌بندی فضایی مبتنی بر چگالی برنامه با الگوریتم نویز (ST-DBSCAN)، از فیلتری برای اندازه‌گیری فاصله بین همسایگان استفاده می‌کنند که بسته به مقیاس زمانی متوالی رخ داده باشند. سال، روز، ساعت و غیره). آنها همچنین اطلاعات مکانی و “غیر مکانی” را به دو محاسبه فاصله جداگانه جدا می کنند تا محله هایی را که گروه بندی ها را ایجاد می کنند تعریف کنند [ 22 ]. وانگ و همکاران [ 26 ] همچنین از جستجوی همسایگی برای انطباق الگوریتم DBSCAN (که ST-DBSCAN نیز نامیده می شود) و همچنین رویکرد ST-GRID استفاده کنید. آگراوال و همکاران [ 27] رویکرد مشابهی را در گسترش فضا-زمان خود از الگوریتم OPTICS (ST-OPTICS) اتخاذ می کنند.
در برخی موارد، فاصله مکانی توسط مولفه زمانی وزن می شود [ 25 ، 28 ]. در موارد دیگر، فضا و زمان با یکدیگر ترکیب می شوند تا یک فاصله زمانی- مکانی را تشکیل دهند. روش Andrienko و Andrienko [ 29 ] “به طور متناسب t [زمان] را به یک فاصله فضایی معادل تبدیل می کند” و سپس از فاصله اقلیدسی برای ترکیب این دو استفاده می کند ([ 29 ]، ص 19). اولیویرا و همکاران [ 30 ] رویکرد خوشه‌بندی مبتنی بر چگالی مشترک نزدیکترین همسایه (SNN) را برای ترکیب اطلاعات فضا-زمان و غیر مکانی با استفاده از ترکیب وزنی از سه مؤلفه (SNN-4D+) تطبیق داد [ 31]. روش‌های دیگری توسعه یافته‌اند که به‌طور خاص به‌جای رویدادهای گسسته، خوشه‌بندی مسیر را مورد هدف قرار می‌دهند (به‌عنوان مثال الگوریتم خوشه‌بندی مسیر [ 32 ] لی و همکاران (TRAJCLUS) را ببینید)، یا برای اندازه‌گیری شباهت مسیرها [ 33 ].
مشترک هر یک از این روش ها که در بالا مورد بحث قرار گرفت این است که چگونه این الگوریتم ها به زمان نزدیک می شوند. به طور معمول، به عنوان یک تابع خطی و افزایشی در نظر گرفته می شود، به طوری که می توان تفاوت بین دو رویداد زمانی را محاسبه کرد. البته روش های مختلفی برای مشاهده زمان وجود دارد، مانند چرخه ای یا به عنوان زمان روز. غالباً به نظر می رسد که گنجاندن زمان در این روش ها یک فکر بعدی باشد. فاصله زمانی باید سازگار باشد. آن‌ها همچنین با داده‌هایی که دارای محدودیت شبکه هستند مقابله نمی‌کنند و از فاصله اقلیدسی برای محاسبه خود استفاده می‌کنند، اگرچه فاصله منهتن می‌تواند جایگزین شود. فاصله اقلیدسی فاصله خط مستقیم کلاسیک است (هنگامی که کلاغ پرواز می کند)، و منهتن تلاش می کند تا فواصل درون یک شبکه را تنظیم کند.
آگراوال و همکاران [ 27 ] همچنین چندین الزام برای خوشه بندی داده های فضا-زمان فراهم می کند. روش ها باید قادر به شناسایی گروه هایی با اشکال دلخواه یا نامنظم باشند. آنها باید قادر به مدیریت داده های با ابعاد بالا و مقیاس پذیر (از نظر قدرت محاسباتی) باشند. جای تعجب نیست که آنها باید “توانایی برخورد با ویژگی های مکانی، غیر مکانی و زمانی” را داشته باشند. که همچنین دلالت بر این دارد که آنها باید بتوانند هر یک از این اجزا را در صورت نیاز اضافه و حذف کنند ([ 27 ]، ص 389). به عنوان گوو [ 24] همچنین پیشنهاد می کند، آنها باید بتوانند خوشه های تودرتو و مجاور را مستقل از ترتیبی که در الگوریتم وارد می شوند، مدیریت کنند. در نهایت، برای مفید بودن، نتایج باید قابل تفسیر باشند. علاوه بر این موارد، این تحقیق همچنین نشان می‌دهد که گنجاندن مفهوم مقیاس در تجزیه و تحلیل، به ویژه برای خوشه‌بندی تودرتو، مهم است. این را می توان با رویکرد خوشه بندی سلسله مراتبی انجام داد.

1.3. خوشه بندی سلسله مراتبی

خوشه‌بندی سلسله مراتبی به تکنیک‌های انبوهی و تقسیمی تقسیم می‌شود، بسته به این که رویکرد باید از پایین شروع شود و مشاهدات فردی که هر کدام به عنوان یک خوشه در نظر گرفته می‌شوند و سپس انباشته می‌شوند، یا بالا با همه مشاهدات به عنوان یک خوشه در نظر گرفته شده و سپس تقسیم می‌شوند. در رویکرد تجمعی، حداقل چهار روش برای ادغام خوشه ها وجود دارد: پیوند تک پیوندی، پیوند کامل، پیوند گروهی متوسط ​​و پیوند مرکزی. تک پیوند فاصله بین گروه ها را به عنوان فاصله بین نزدیکترین اعضای خوشه تعریف می کند. روش های پیوند کامل از دورترین فاصله بین اعضای خوشه ها استفاده می کنند. پیوند گروهی متوسط ​​میانگین فواصل بین اعضای خوشه ها را می گیرد، یا ممکن است از میانگین وزنی استفاده شود (روش وارد نمونه ای از این است).2 ]. رویکرد میانگین که به عنوان روش گروه زوج وزنی با میانگین حسابی (UPGMA) نیز شناخته می‌شود، هنگام استفاده از یک متریک فاصله سفارشی که در زیر تعریف می‌شود، مناسب است [ 34 ]. این روش میانگین (وزنی) فواصل بین اعضای خوشه ها را همانطور که در رابطه (1) نشان داده شده است، می گیرد. در این معادله کو Lدو خوشه متفاوت هستند، در حالی که جمن،جjاعضای خوشه هستند و D(·)مقداری تابع فاصله است.

DکL=1نکنL∑من∈سیک∑j∈سیLD(جمن،جj)

2. رویکرد پیشنهادی

2.1. خوشه بندی سلسله مراتبی فضا-زمان با ویژگی ها

خوشه‌بندی سلسله مراتبی فضا-زمان از ترکیب وزنی خطی خاصی از فاصله مکانی، فاصله زمانی و فواصل ویژگی استفاده می‌کند که در زیر با عمق بیشتری مورد بحث قرار گرفته‌اند. این محاسبات فاصله توسط الگوریتم خوشه بندی سلسله مراتبی سنتی برای شناسایی خوشه ها استفاده می شود. رویکرد خوشه‌بندی سلسله مراتبی فضا-زمان پیشنهادی که در اینجا ارائه شده است، الزامات اساسی تعیین شده توسط Agrawal و همکاران را برآورده می‌کند. [ 27 ]. یک رویکرد منعطف اتخاذ شده است که به مفاهیم مختلف فاصله مکانی و فاصله زمانی اجازه می دهد تا به راحتی در یک متریک فاصله واحد گنجانده شوند. فقط با تغییر متریک فاصله ( D(·)) به جای توسعه یک الگوریتم جدید، این روش به راحتی می تواند به الگوریتم های موجود مانند آنهایی که در جدول 1 فهرست شده اند، «وصل» شود ، اگرچه خوشه بندی سلسله مراتبی برای این مقاله انتخاب شده است. این الگوریتم موجود انتخاب شده است تا استفاده از آن در نرم افزارهای موجود راحت تر باشد. انتخاب یک سلسله مراتب انبوهی به دو دلیل انتخاب می شود: هیچ نیازی برای از پیش انتخاب کردن تعداد خوشه ها وجود ندارد، و به راحتی مفهوم مقیاس سلسله مراتبی و توانایی مشاهده خوشه ها (و خوشه های تودرتو) را در سطوح مختلف به ارمغان می آورد. متریک فاصله جدید که برای خوشه‌بندی سلسله مراتبی استفاده می‌شود، ترکیبی خطی وزن‌دار از فواصل مکانی و زمانی، و ویژگی‌ها یا متغیرهای غیر مکانی زمانی است. در حالی که از نظر مفهومی مشابه رویکرد اتخاذ شده توسط اولیویرا، سانتوس و مورا پیرس است [30 ]، تغییرات متعددی در وزن دهی، مقیاس بندی و مدیریت اجزای مکانی و زمانی وجود دارد.

با توجه به دو خوشه (یا مشاهدات)، جمنو جj، شباهت آنها با ترکیب مکان آنها در زمان و مکان و هر متغیر خارجی اندازه گیری می شود، همانطور که در E2 نشان داده شده است. هر جزء با یک محاسبه فاصله متفاوت انجام می شود، سپس قبل از جمع کردن، نرمال و وزن می شود. تابع فاصله، Dمتر(·)، فاصله بین دو مکان نشان داده شده به عنوان بردار را محاسبه می کند ایکسمنو ایکسj(نمادگذاری ساده مختصات نقطه x و y). فاصله بین مکان ها با مقیاس بندی یا عادی سازی می شود اسDو با دادن وزن، w1. ضریب مقیاس حداقل فاصله ای است که باید به عنوان مرتبط در نظر گرفته شود و وزن بر یک جزء خاص تأکید می شود. فاصله زمانی بین خوشه ها توسط تابع محاسبه می شود Dتی، و تفاوت خطی بین آنها را فرض نمی کند تیمنو تیj. این فاصله زمانی با مقیاس بندی می شود استی، و با توجه به وزن w2. با فرض پتانسیل یک مجموعه ابعادی بالا از متغیرهای غیر مکانی زمانی، آخرین مؤلفه مجموع فاصله ویژگی برای چندین ویژگی از a تا q است. هر فاصله مشخصه با یک عامل متفاوت مقیاس می شود، اسآبسته به نوع متغیر (اگرچه عددی فرض می شود) و به هر ویژگی وزنی از wآ+2. هنگامی که هر جزء با هم جمع می شود، بر مجموع وزن ها تقسیم می شود.

D(جمن،جj)=1∑من=1nwمن(w1∗Dمتر(ایکسمن،ایکسj)اسD+w2∗Dتی(تیمن،تیj)استی+∑آ=3qwآ∗Dآ(آمن،آj)اسآ)
معادله (2) به طور هدفمند کلی است به طوری که هر یک از توابع فاصله ( Dمتر(·)، Dتی(·)، و Dآ(·)) را می توان به راحتی با انواع مختلف داده سازگار کرد. متریک فاصله مکانی ممکن است فاصله اقلیدسی یا فاصله شبکه را برای رویدادهای محدود یا مختلط شبکه یا سایر معیارها بپذیرد. فاصله زمانی ممکن است با زمان خطی یا چرخه ای تضاد داشته باشد. هر یک از توابع فاصله در بخش های بعدی با عمق بیشتری مورد بررسی قرار خواهند گرفت. زیرشاخص a به شاخص وزن اشاره دارد و برای ویژگی ها وزن ها بعد از 2 شروع می شود و برای هر ویژگی جدید افزایش می یابد.

2.1.1. محاسبات برای فاصله

برای رویدادهای نقطه ای تعریف شده در یک فضای مسطح دو بعدی، فاصله ممکن است با فاصله اقلیدسی بین دو رویداد محاسبه شود. ایکسو yمختصات، همانطور که در رابطه (3) نشان داده شده است. همانطور که در بالا بحث شد، استفاده از فواصل مسطح برای نقاط محدود به شبکه های خطی، خوشه بندی را بیش از حد برآورد می کند [ 11 ، 13 ، 14 ]. متداول است که داده های انسان جسم متحرک، چه مسیرها یا مکان های شناخته شده مجزا، تحت تأثیر شبکه حمل و نقل قرار می گیرند (مثلاً تصادفات وسایل نقلیه موتوری در یک شبکه خیابانی). در این موارد، فاصله شبکه بر اساس طول بخش یک شبکه حمل و نقل فیزیکی است. با این حال، به طور واقع بینانه، حرکت انسان ترکیبی از مکان های محدود شبکه و مکان های مسطح دو بعدی خواهد بود. بنابراین، فاصله باید بتواند با این مخلوط مقابله کند.

DE(ایکسمن،ایکسj)=(ایکسمن-ایکسj)2+(yمن-yj)2
یکی از راه‌های مدیریت این مخلوط از داده‌های محدود شبکه و داده‌های جریان آزاد، توسعه شبکه‌ای در اطراف مکان‌های منحصربه‌فرد در مجموعه‌ای از مشاهدات نقطه‌ای است. برای انجام این کار یک نمودار همسایگی از مجموعه نقاط ( P ) ایجاد می شود. در حالت ایده‌آل، نمودار همسایگی، الگوهای حرکتی عوامل را بین مکان‌های شناخته شده منعکس می‌کند [ 35 ]. این بدان معنی است که اتصال یا لبه بین نقاط نشان دهنده مسیری است که عامل برای رسیدن به آن نقطه طی کرده است. یکی از نمودارهای همسایگی رایج، مثلث سازی دلونی (DT) است که فضا را به یک سری از مثلث های متصل تبدیل می کند [ 36 ]. این کار برای مجموعه P انجام می شود به طوری که هیچ نقطه ای در دایره دایره هیچ یک از مثلث های صفحه نباشد [37 ] انجام می شود. DT نشان دهنده یک ساختار محله سفت و سخت است. شکل 1یک DT را برای مجموعه ای از داده های ردیابی حیوانات ارائه می دهد، که به طور بالقوه مسیرهایی را که حیوان ممکن است دنبال کند با توجه به دنباله ای از نقاط منعکس می کند [ 35 ].

برای محاسبه فاصله برای یک شبکه حمل و نقل فیزیکی، یا یک شبکه مشتق شده از ساختار DT همسایگی، شبکه باید به یک ساختار داده گراف تبدیل شود. جایی که یک نمودار، جی، به عنوان مجموعه ای از گره ها (معادله (4)) و مجموعه ای از یال ها (معادله (5)) تعریف می شود به طوری که جی=(V،E)[ 38 ، 39 ]. لبه ها زیر مجموعه ای از جفت گره ها هستند که گره های شروع و پایان را همانطور که در رابطه (5) نشان داده شده است، تعریف می کنند. به هر یک از این جفت گره ها یک ویژگی یا وزن اختصاص داده می شود، مانند فاصله فیزیکی بین ویژگی هایی که یک گره نشان می دهد.

V={v1،v2،⋯،vn}
E={(vمن،vj)1،⋯،(vمن،vj)متر}={ه1،ه2،⋯،همتر};من≠j;من،j=1،2،3،⋯
پآتیساعت=v1،ه1،v2،ه،⋯،ه،vj
یک مسیر روی یک گراف از گره v1و vjیک دنباله متناوب گره ها و پیوندها است که در معادله (6) نشان داده شده است [ 38 ]. یک مسیر رایج مورد علاقه کوتاه ترین مسیر بین گره ها است و ممکن است با استفاده از الگوریتم هایی مانند Dijkstra یا A* محاسبه شود [ 39 ، 40 ]. با استفاده از این رویکرد مسیر، فاصله بین گره ها v1،v2، کوتاه ترین راه بین آنهاست، Dجی(v1،v2).
ترکیب خطی وزنی نشان داده شده در رابطه (2) فاصله مسطح را می پذیرد، DE(ایکسمن،ایکسj)یا فاصله شبکه، Dجی(v1،v2). هنگامی که فاصله محاسبه می شود، آن را با مقیاس بندی می شود اسD. این دو هدف را دنبال می‌کند: حذف واحدها برای قرار دادن فاصله در مقیاس مشابه با سایر اجزا، و ایجاد محدودیت فضایی به طوری که خوشه‌ها تودرتو باشند و به نقطه Guo [ 24 ] در مورد منطقه‌بندی بپردازند.
چندین گزینه برای انتخاب مقدار مقیاس وجود دارد، اسD، برای مولفه فاصله. به عنوان مثال، مقادیر ثابت مختلفی ممکن است انتخاب شوند مانند حداکثر فاصله بین تمام نقاط مجموعه داده، یا طول کل شبکه در صورت استفاده از فاصله شبکه. اولیویرا و همکاران [ 30 ] پیشنهاد می کند که فواصل را از گوشه سمت چپ پایین مرز منطقه مورد مطالعه گرفته و آن را برای انتخاب تفاوت تجسم کنید.
به طور متناوب، می توان از یک فاصله سازگار استفاده کرد. در این مورد، اسDتغییرات برای هر خوشه، جمن. برای این تحقیق اسDبا استفاده از حداکثر فاصله تنظیم شده است کنزدیکترین همسایگان جمن. این باعث ایجاد خوشه هایی با شکل نامنظم می شود که بسته به میزان فاصله سازگار می شوند جمناز خوشه های دیگر است. اگر فقط از جزء فضایی استفاده شود ( wآ>1=0)، سپس خوشه ها بر اساس خوشه بندی سلسله مراتبی تجمعی در داخل یکدیگر تودرتو می شوند. معادله (7) مجموعه ای از کفواصل برای یک خوشه، جمن، به ترتیب فاصله. سپس حداکثر این مقادیر می شود اسDبرای یک خاص جمن. اگر فاصله بین جمنو جjبزرگتر است از اسD(ضریب مقیاس)، سپس این مؤلفه بزرگتر از 1 خواهد بود. در اصل، ضریب مقیاس را می توان به این صورت تفسیر کرد که دو رویداد باید چقدر از هم فاصله داشته باشند.

انتخاب تعداد همسایگان برای استفاده، ک، سخت است. دانش محلی مجموعه داده ممکن است برای تنظیم این پارامتر استفاده شود. در موارد مشابه، اکتشافی استفاده از لگاریتم طبیعی تعداد مشاهدات می تواند برای تعیین یک مقدار شروع برای k استفاده شود [ 22 ، 41 ]. برای بررسی این گزینه از شبیه سازی های زیر استفاده می شود.

Dک(جمن)=مترآایکس{د1،⋯،دمن،دj،⋯،دک|د1<⋯<دمن<دj<⋯<دک}
2.1.2. محاسبات برای زمان
دومین جزء در معادله (2) مربوط به زمان است که تابع فاصله را تشکیل می دهد. Dتی(تیمن،تیj)و ضریب مقیاس، استی. تابع فاصله زمانی بسته به زمان در نظر گرفته شده می تواند چندین شکل داشته باشد. به عنوان مثال، با نگاه چرخه‌ای به زمان، علاقه به این معنا نیست که رویداد دقیقاً نزدیک یکدیگر در زمان اتفاق افتاده باشد، بلکه الگوی وقوع مشابه است. یعنی دو رویداد در یک قسمت از روز و به طور بالقوه به فاصله چند ماه رخ داده است. این در شناسایی مکان قابل توجهی از الگوهای مکرر استفاده از یک عامل در زمان های خاص روز کاربرد دارد. دیگر دیدگاه‌های زمان ممکن است این باشد که دو رویداد موقتاً نزدیک به هم اتفاق افتاده‌اند (یک سال، ماه، روز و ساعت).
در حالت دوم، مجاورت زمانی این است که آیا رویدادها در یک چارچوب زمانی معین از یکدیگر رخ داده اند یا خیر. این یک تفاوت ساده است تیمنو تیj. رویدادهای نزدیکتر تفاوت کمتری خواهند داشت. معادله (8) یک مورد از تفاوت مطلق در زمان را نشان می دهد که مجموع اختلاف زمانی بین دو رویداد است. به عنوان مثال، نتیجه ممکن است مجموع ثانیه ها یا واحدهای دیگر وابسته به نوع مقادیر زمانی باشد که با یک جسم متحرک مرتبط است.

عامل مقیاس، استی، هنگام در نظر گرفتن فاصله زمانی، مقادیر زمانی را محدود می کند تا در یک چارچوب زمانی بیشتر شبیه باشند. به عنوان مثال، مقیاس دادن همه مقادیر به یک ساعت، تفاوت مطلق کمتر از یک ساعت در یک ساعت، یا بیشتر از یک اگر بیش از یک ساعت باشد، ایجاد می کند. ضریب مقیاس باید در همان واحدها باشد Dتی(تیمن،تیj). ضریب مقیاس همان نقشی را ایفا می کند که با فاصله مکانی. آن را محدود می کند و همچنین زمان را در همان محدوده مقادیر فاصله مکانی و غیر مکانی قرار می دهد.

Dتی(تیمن،تیj)=آبس(تیمن-تیj)

در مورد الگوهای تکراری، مهر زمانی هر رویداد باید در یک جدول زمانی قرار گیرد. این به راحتی با قرار دادن رویداد در همان مقیاس خطی به عنوان تعداد ثانیه از نیمه شب انجام می شود. با این حال، زمان‌ها در نیمه‌شب (0 ساعت) و نزدیک به نیمه‌شب (23 ساعت) با فاصله بیشتر از هم بررسی می‌شود. به طور واقع بینانه، یک رویداد در این زمان ها بیشتر از رویدادهای بین ساعت 0 تا 12 ظهر است. برای جبران این مشکل شباهت، تفاوت بین زمان های رویداد به تناسب a تبدیل می شود cosمنحنی. این باعث می شود که تفاوت بین زمان در نقاط پایانی (0 ساعت و 23 ساعت و 59 دقیقه) از نظر مقدار نزدیکتر شود. این در معادله (9) نشان داده شده است Δتیو T در معادله (10) تعریف شده اند، با فرض اینکه خط زمانی چند ثانیه از نیمه شب باشد در غیر این صورت T مقدار متفاوتی خواهد داشت. ارزش زمانی هر رویداد، تیمنجو تیjج، حول محور (43، 200 ثانیه)، تفاوت مطلق گرفته می شود. نتیجه این تفاوت به رادیان مقیاس می شود. نتایج حاصل از تیمنjبین 0 و 1 هستند. این مقدار را می توان با استفاده از قانون کسینوس ها همانطور که در رابطه (11) نشان داده شده است، به فضای اقلیدسی تبدیل کرد. Dتی(تیمن،تیj).

تیمنj=cos(π∗Δتیتی)
Δتی=آبس(تیمنج-تیjج)، و تی=86400 (ثانیه)
Dتی(تیمن،تیj)=(تیمنج2+تیjج2)-(2∗تیمنج∗تیjج∗تیمنj)
عامل مقیاس، استی، مانند ضریب مقیاس برای فاصله اعمال می شود، اما باید در واحدهای مقدار زمان (مثلاً ثانیه) باشد. برای محدود کردن فاصله زمانی به یک ساعت، از مقدار 3600 ثانیه استفاده کنید. نتیجه این است استیکه مقادیر را در یک ساعت کمتر از یک و بیشتر از یک ساعت اختلاف را بزرگتر از یک قرار می دهد.
شکل 2 دو نمونه از چگونگی فاصله زمانی بین 23 ساعت یا 12 ساعت و هر بار دیگر را در ثانیه از نیمه شب نشان می دهد. به نتیجه فاصله توجه کنید Dتی(تیمن،تیj)در محور y نشان داده شده است. شکل v در پانل بالایی در شکل 2 نشان می دهد که چقدر فاصله از 12 ساعت (ظهر) در حداکثر نزدیکتر به نیمه شب (0 ساعت) است. در مقابل، در ساعت 23، فاصله در ظهر بیشترین فاصله را دارد، اما از ساعت 23 به 0 ثانیه و از نیمه شب به 86400 ثانیه کاهش می یابد. در شکل 2 ، شکل V تیز در پانل پایین، فاصله 0.0 را در 23 ساعت نشان می دهد. اشکال مختلف منحنی بسته به اینکه نقطه مرکزی چه خواهد بود تغییر خواهد کرد (به شکل V در ساعت 12 و منحنی در ساعت 23). این به دلیل تبدیل زمان با استفاده از تابع کسینوس است.
2.1.3. محاسبات برای فضای مشخصه
ممکن است از اطلاعات غیر مکانی یا زمانی بیشتر برای تعریف خوشه استفاده شود. فاصله، Dآ(آمن،آj)، ممکن است یک تفاوت مطلق ساده بین مقادیر باشد. این مقیاس شده است، اسآبرای قرار دادن مقادیر مشخصه در مقیاس اندازه گیری مسافت و زمان. رویدادهای نزدیکتر دارای مقدار کمتر از 1 و رویدادهای دور بزرگتر از 1 خواهند بود. حداکثر مقدار متغیر یا سایر آمارهای مربوطه را می توان برای مقیاس آن استفاده کرد. در مورد یک مقدار باینری، تنها سناریوی تفاوت زمانی است که یکی از ورودی‌ها برابر با 1 و دیگری 0 باشد، وقتی با 1 مقیاس شود برابر با 1 است. هر حالت دیگری به 0 منجر می‌شود. انتخاب تابع به متغیر.
2.1.4. پیاده سازی
معادله (2) در پایتون 2.7 با استفاده از بسته های SciPy و NetworkX [ 42 ، 43 ] پیاده سازی شد. یک تابع فاصله سفارشی یک ماتریس فاصله بین رویدادها برای معادله (2) ایجاد کرد. فاصله شبکه به عنوان کوتاه ترین مسیر بین دو گره با استفاده از الگوریتم Djikstra، همانطور که در NetworkX پیاده سازی شده است، محاسبه شد. مثلث سازی های Delaunay محاسبه شده برای مجموعه داده های نقطه ای با استفاده از کتابخانه SciPy ایجاد شده است. الگوریتم خوشه‌بندی سلسله مراتبی از پیوندهای متوسط ​​برای توسعه خوشه‌ها استفاده کرد.

2.2. ارتباط با مقیاس فضایی

یک دلیل اصلی برای ریشه‌یابی تحلیل فضا-زمان در خوشه‌بندی سلسله مراتبی این است که دیدگاهی از مقیاس را به عنوان یک سلسله مراتب تودرتو در خود دارد. در این نما، مقیاس‌های مکانی و زمانی تو در تو قرار گرفته‌اند و گروه‌های بزرگ‌تری از مشاهدات را در امتداد یک محور عمودی ایجاد می‌کنند. دیدگاه سلسله مراتبی مقیاس، به ویژه در میان جغرافیدانان بیوفیزیکی، جدید نیست [ 44 ]. به عنوان مثال، لوین [ 45 ] نظریه سلسله مراتب خود را به عنوان توضیحی از مقیاس در سیستم های طبیعی و بوم شناسی ارائه کرد. تئوری سلسله مراتب همچنین بر دیدگاهی دلالت دارد که مقیاس های مکانی و زمانی با هم متفاوت هستند. از بسیاری جهات، این تغییرات کمکی در فاصله سلسله مراتبی فضا-زمان که هر دو مؤلفه را ترکیب می کند، منعکس می شود. علاوه بر این، فضای صفت ممکن است با سایر اجزاء متفاوت باشد.
همانند سایر تحلیل‌های فضایی، مسئله واحد منطقه‌ای قابل اصلاح (MAUP) خاطرنشان می‌کند که نتایج یک تحلیل بسته به وضوح داده‌های مکانی متفاوت خواهد بود (به عنوان مثال، بلوک‌های سرشماری در مقابل مسیرهای سرشماری) [ 46 ]. همچنین، با توجه به مشکل بافت جغرافیایی نامشخص (UGCP)، زمینه پدیده های مورد مطالعه در مقیاس های مختلف متفاوت خواهد بود [ 47 ، 48 ]. روش خوشه‌بندی سلسله مراتبی فضا-زمان تحت تأثیر مرزهای مکانی و زمانی کلی منطقه مورد مطالعه قرار می‌گیرد، اما همچنین دارای انعطاف‌پذیری انتخاب و ارزیابی خوشه‌ها در سلسله مراتب یا سطوح مختلف است.
زمانی که تعداد خوشه‌ها از قبل مشخص نباشد، تعیین سطح دشوار است (همانطور که در شبیه‌سازی‌های حقیقت‌یابی زمینی چنین است). با این حال، حداقل سه رویکرد مختلف در دسترس است: تجربی، مناسب و عملیاتی. تجربی ارزیابی دندروگرام را برای تعیین سطح مناسب برای ارزیابی یا شناسایی تعداد خوشه هایی که می تواند برای درک پدیده ها مفید باشد، پیشنهاد می کند. برای تعیین تعداد خوشه‌ها بر اساس تناسب، می‌توان از معیاری مانند امتیاز silhouette برای تعیین اینکه کدام سطح بهترین امتیاز را از همه سطوح ارائه می‌کند، استفاده کرد. در نهایت، مقیاس عملیاتی «به مقیاس منطقی که یک فرآیند جغرافیایی در آن انجام می‌شود» اشاره دارد، و بنابراین سطحی برای خوشه‌ها بر اساس دانش فرآیندهایی که ممکن است آنها را ایجاد کرده باشند ([44 ]، ص. 5).

3. نتایج

3.1. شبیه سازی ها

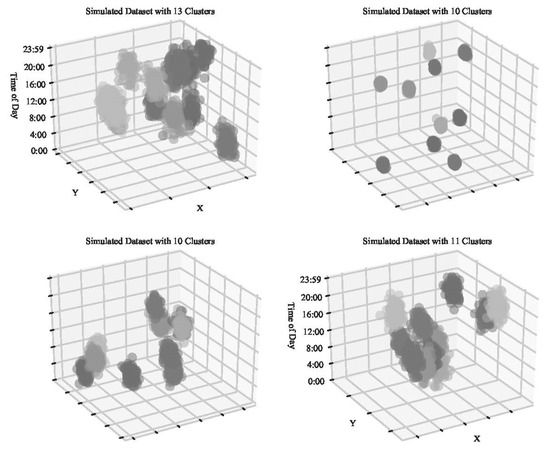
به منظور ارزیابی تأثیر پارامتر نزدیکترین همسایه و انتخاب ضریب مقیاس زمانی، پنجاه مجموعه داده شبیه سازی شده تولید شد. اینها با استفاده از سه متغیر ایجاد شدند: مختصات x، مختصات y و متغیر زمانی که به صورت ثانیه از نیمه شب شبیه سازی شده اند. هر متغیر از یک انحراف استاندارد به طور تصادفی انتخاب شده از توزیع یکنواخت بین 1000 تا 7000 استفاده می کند. تعداد خوشه های تولید شده برای هر شبیه سازی به طور تصادفی بین 5 تا 20 عدد کامل انتخاب شده است. مراکز برای هر خوشه نیز به طور تصادفی از توزیع یکنواخت 500000 تا 780000 برای مختصات x و 370000 تا 500000 برای مختصات y (منعکس کننده سیستم منطقه ای مرکاتور عرضی جهانی) انتخاب شدند. متغیر زمانی به طور تصادفی از توزیع یکنواخت از پایه دو برابر انحراف استاندارد تصادفی انتخاب شده تا 86400 انتخاب شد. این مقدار پایین برای اجتناب از مقادیر زیر 0 انتخاب شد. بخش تابع make_blobs از بسته Sci-Kit Learn برای تولید این خوشه های شبیه سازی شده استفاده شد [49 ]. در مجموع 1000 مشاهده برای هر شبیه سازی ایجاد شد. چهار مورد از شبیه سازی ها در شکل 3 ارائه شده است. تغییر در انحراف معیار را می توان در شکل های مختلف مشاهده کرد، با برخی از خوشه ها که با برخی همپوشانی و برخی به شدت محدود شده اند.
الگوریتم خوشه‌بندی سلسله مراتبی فضا-زمان برای هر شبیه‌سازی برای انتخاب‌های مختلف اعمال شد. اسد(2، 4، 6، 7، 8، 10، 20، و 30) و استی(1000 تا 9000، در 1000). فاصله به عنوان فاصله شبکه با استفاده از DT محاسبه شد. برای ارزیابی بهترین تناسب برای هر یک از متغیرها از دو معیار عملکرد استفاده شد: نمره همگنی و میانگین امتیاز شاخص تصادفی [ 50 ، 51 ]. این معیارهای عملکرد، تخصیص‌های خوشه‌ای را با یک حقیقت اصلی مانند برچسب خوشه اصلی مقایسه می‌کنند. امتیاز همگنی بین 0 تا 1 است که 1 کاملاً همگن است، به این معنی که همه خوشه ها فقط مشاهدات یک گروه را شامل می شوند. امتیاز شاخص تصادفی تنظیم شده از 1- تا 1 متغیر است که 0 تخصیص کاملاً تصادفی است و 1 مطابقت کامل با خوشه های حقیقت زمینی است.
شکل 4 میانگین امتیاز همگنی و میانگین امتیاز شاخص تصادفی تعدیل شده را برای مقادیر مختلف نشان می دهد اسدو استی. در شکل 4 الف، میانگین امتیازات برای مقادیر مختلف نزدیکترین همسایگان است که در مقادیر مختلف به طور میانگین استی. یک خمیدگی جزئی وجود دارد که در آن عملکرد بین 4 تا 10 همسایه نزدیک بهبود یافته است، سپس برای مقادیر کوچکتر، 2 و مقادیر بزرگتر، > 20 کاهش یافته است. در شکل 4 B، میانگین نمرات برای مقادیر مختلف مقیاس زمانی است که در مقادیر مختلف به طور میانگین در نظر گرفته شده است. اسد. عملکرد تا حدود 3000 ثانیه بهبود یافت، اما پس از آن کاهش یافت، و پس از آن مقدار بهبود چندانی حاصل نشد.
همچنین بالاترین امتیاز برای ترکیبی از در نظر گرفته شد استیو اسد. میانگین اینها برای نمره شاخص تصادفی تعدیل شده نزدیکترین همسایه 6.9 (انحراف استاندارد 7.4) و میانگین مقیاس زمانی 3490 (انحراف استاندارد 2968) بود. میانگین از استیو اسدبرای حداکثر امتیاز همگنی 6.8 (انحراف استاندارد 7.2) برای پارامتر نزدیکترین همسایه و 3607 (انحراف استاندارد 3059) بود. همانطور که قبلاً پیشنهاد شد، اکتشافی لگاریتم طبیعی ممکن است برای تعیین پارامتر نزدیکترین همسایه استفاده شود. لاگ طبیعی حجم نمونه، 1000، 6.9 است. در مورد اکثر شبیه سازی ها، مقدار 7 به خوبی کار می کرد. ضریب مقیاس زمانی مقدار تقریباً 3600 را نشان می دهد. این یک ساعت در ثانیه است. این ضریب مقیاس دوم ممکن است با توجه به دانش خارجی (به عنوان مثال، استفاده از سرعت متوسط ​​حرکت جسم برای درک محدوده زمانی جسم) بهتر تنظیم شود.

3.2. مقایسه با رویکردهای خوشه‌بندی جایگزین

برای درک بهتر رویکرد خوشه‌بندی سلسله مراتبی فضا-زمان، نتایج اعمال آن بر روی یک مجموعه داده شبیه‌سازی شده با دو روش دیگر مقایسه شد: خوشه‌بندی سلسله مراتبی مبتنی بر اقلیدسی، و ST-DBSCAN. روش خوشه‌بندی سلسله مراتبی سنتی (به بخش 1.3 مراجعه کنید ) برای مقایسه نحوه عملکرد رویکرد خوشه‌بندی سلسله مراتبی فضا-زمان بر روی داده‌های مکانی-زمانی با یک رویکرد ساده استفاده می‌شود. ST-DBSCAN یک الگوریتم مبتنی بر چگالی برای خوشه بندی داده های مکانی-زمانی بر اساس پارامترهای خاص است [ 22 ، 52 ]. رویکرد ST-DBSCAN حداقل از دو جهت با خوشه‌بندی سلسله مراتبی متفاوت است: نویز در داده‌ها را کاهش می‌دهد و به طور خودکار تعداد خوشه‌ها را در مجموعه داده شناسایی می‌کند.
مجموعه داده مانند بالا، با بیست خوشه و نمونه ای از 1000 و 20 خوشه ایجاد شد. متغیرهای مکانی به طور تصادفی مراکز خوشه ای در امتداد مختصات x و y با انحراف استاندارد انتخاب شده به طور تصادفی بین 1000 و 7000 توزیع شده اند. متغیر زمانی برای منعکس کردن ماهیت داده های چرخه ای شبیه سازی شد. مرکز به‌طور تصادفی انتخاب شد، اما اگر توزیع در نیمه‌شب (86400 ثانیه) کاهش یافت، به +0:00 تغییر یافت. داده ها در شکل 5 ارائه شده است . در برخی موارد، در بالای محور z (زمان)، خوشه بین نیمه شب و 23:59 تقسیم می شود.
ST-DBSCAN به یک آستانه فضایی، که یک نقطه برش برای مولفه فضایی، و آستانه زمانی، یک برش مقدار زمانی است، نیاز دارد. دومی مشابه مقیاس زمانی در خوشه‌بندی سلسله مراتبی فضا-زمان است و برای هر دو از یک مقدار (1 ساعت یا 3600 ثانیه) استفاده شده است. پارامترهای خوشه بندی سلسله مراتبی فضا-زمان بر اساس مطالعات شبیه سازی ارائه شده در شکل 4 انتخاب شدند.(ورود طبیعی حجم نمونه و 3600 برای مقیاس زمانی). ما همان تنظیمات پارامتر را برای خوشه‌بندی سلسله مراتبی فضا-زمان و ST-DBSCAN مقایسه کردیم و سپس به طور مکرر پارامترهای ST-DBSCAN را تغییر دادیم. یکی از مشکلات ST-DBSCAN در مقایسه مستقیم تعداد خوشه های شناسایی شده است. خوشه‌بندی سلسله مراتبی به طور کلی به کاربر امکان می‌دهد تعداد خوشه‌ها را انتخاب کند، در حالی که ST-DBSCAN تعداد خوشه‌ها را از داده‌ها به اضافه نویز شناسایی می‌کند. هنگامی که پارامترهای یکسان برای هر دو رویکرد استفاده شد، ST-DBSCAN تنها توانست 15 خوشه و نویز را در مجموعه داده پیدا کند. برای مقایسه بهتر این دو رویکرد، 15 خوشه برای خوشه بندی سلسله مراتبی فضا-زمان انتخاب شد و یک رویکرد تکراری برای شناسایی پارامترهای بهتر برای ST-DBSCAN استفاده شد. ترکیبات برای مینپت ها (1 تا 30)، آستانه فضایی (1000 تا 100000)، و آستانه زمانی (1800، 3600، 7200 ثانیه) آزمایش شدند. برای مقایسه با رویکردهای غیر مکانی و غیر زمانی، خوشه‌بندی سلسله مراتبی استاندارد و الگوریتم‌های DBSCAN روی مجموعه داده اعمال شد. پارامترهای DBSCAN بر اساس بهترین عملکرد تولید 20 خوشه به صورت تکراری انتخاب شدند.
مانند شبیه‌سازی‌هایی که در بالا توضیح داده شد، نتایج خوشه‌بندی با یک حقیقت پایه با استفاده از امتیاز همگنی (HS) و شاخص تصادفی تنظیم‌شده (ARI) مقایسه شد. جدول 2نتایج روش‌های مختلف، پارامترها، تعداد خوشه‌ها و امتیازات مربوط به معیارهای عملکرد را ارائه می‌دهد. فقط امتیازها و پارامترهای برتر برای نتایج تکراری ST-DBSCAN که 20 خوشه و نویز داشتند نشان داده می شوند. به طور کلی، خوشه بندی سلسله مراتبی فضا-زمان به خوبی ST-DBSCAN انجام شد. امتیاز پایین هنگام استفاده از ST-DBSCAN و پارامترهای مشابه خوشه بندی سلسله مراتبی فضا-زمان می تواند به این دلیل باشد که فقط 15 خوشه به اضافه نویز را شناسایی می کند. با این حال، خوشه‌بندی سلسله مراتبی فضا-زمان حتی با 15 خوشه امتیاز بهتری داشت، که نشان می‌دهد خوشه‌های شکل بهتری تشکیل می‌دهد. به طور کلی، در مقایسه با حقیقت زمینی بیست خوشه ای، خوشه بندی سلسله مراتبی فضا-زمان بهترین عملکرد را داشت و این نشان می دهد که تنظیمات پارامتر برای خوشه بندی سلسله مراتبی فضا-زمان عملکرد خوبی دارد. صرف نظر از انتخاب تعداد خوشه ها. همچنین در برابر رویکردهای سلسله مراتبی استاندارد و DBSCAN عملکرد خوبی داشت.
با استفاده از همان مجموعه داده، انتخاب پیوند خوشه‌بندی سلسله مراتبی مورد بررسی قرار گرفت. مقایسه اولیه از پیوندهای متوسط ​​استفاده کرد، یک تکنیک قوی که تمایل به ایجاد خوشه هایی با واریانس های کوچک دارد [ 2 ]. این ممکن است برای همه داده ها مناسب نباشد. برای مقایسه، پیوندهای بخش و منفرد با استفاده از پارامترهای مشابه با 20 خوشه به یک مجموعه داده اعمال شد: پیوندهای منفرد نسبتاً بدتر (HS = 0.81 و ARI = 0.51) و پیوندهای بخش بسیار بهتر عمل کردند (HS = 0.93 و ARI = 0.87).
شکل خوشه‌های پیش‌بینی‌شده ممکن است بر انتخاب پیوند با خوشه‌بندی سلسله مراتبی تأثیر بگذارد. مجموعه داده های شبیه سازی شده در بالا تمایل به داشتن خوشه های گرد شکل در سراسر بعد فضایی دارند. مجموعه متفاوتی از خوشه های شبیه سازی شده (12 خوشه، 10000 نقطه) با اشکال فضایی کشیده در جهت شمال شرقی به جنوب غربی تولید شد. مجدداً، سه روش مختلف پیوند به طور متوسط ​​(HS = 0.92 و ARI = 0.86)، تک (HS = 0.70 و ARI = 0.48) و بخش (HS = 0.92 و ARI = 0.85) مقایسه شدند. میانگین و بخش نتایج مشابهی داشتند. 3.3. کاربرد خوشه بندی سلسله مراتبی فضا-زمان
برای نشان دادن کاربرد آن در عمل، از خوشه‌بندی سلسله مراتبی فضا-زمان برای شناسایی الگوهای حرکتی در داده‌های ردیابی حیوانات استفاده شد. هدف از تجزیه و تحلیل شناسایی هر گونه خوشه، یا نقطه داغ، از فعالیت در محدوده خانه حیوان، در مکان و زمان بود [ 35 ، 53 ، 54 ]. برای این مثال، مجموعه داده های GPS برای یک اردک مسکووی ( Cairina mocahata ) که توسط داونز و همکاران جمع آوری شده است. [ 53] مورد استفاده قرار گرفت. اردک های مسکووی گونه های مزاحم واقع در فلوریدا و بومی آمریکای مرکزی و جنوبی هستند. آنها معمولاً الگوهای پروازی بسیار نادری دارند. داده های GPS از یک اردک جمع آوری شد. دستگاه جی‌پی‌اس قرار بود هر چهار دقیقه یک‌بار ضبط کند، برای 15 هکتار در روز (شروع ساعت 05:39 صبح) و برای 9 ساعت در شب خاموش شود (1003 مشاهده). شکل 1 توزیع نقاط را با DT نشان می دهد. دوره خاموش شدن دستگاه GPS را می توان در یک شکاف در نماهای سه بعدی نشان داده شده در شکل 6 مشاهده کرد. برای خوشه‌بندی سلسله مراتبی فضا-زمان، از لاگ طبیعی حجم نمونه (تعداد مشاهدات) برای تعیین تعداد نزدیک‌ترین همسایه‌ها (7 همسایه نزدیک)، و 3600 ثانیه به عنوان عامل مقیاس زمانی استفاده شد.
میانگین امتیاز silhouette نشان می دهد که دو یا سه خوشه به خوبی با داده ها مطابقت دارند. این تعجب آور نیست زیرا شواهد بصری در شکل 1 از حداقل دو حوزه مختلف فعالیت در غرب و شرق وجود دارد. شکل 6 زاویه ای از دید از شمال به جنوب را نشان می دهد (برای نشان دادن اطلاعات زمانی به بهترین شکل). دو خوشه در پانل بالا سمت چپ، دو ناحیه را نشان می‌دهند که از شکل 1 قابل مشاهده است. بخش کوچکتر در حوالی ظهر بیشتر فعال بود، در حالی که بخش بزرگتر در طول روز فعال بود. هنگامی که 3 خوشه در پانل بالا سمت راست در نظر گرفته می شود، دوباره بخش کوچکتر جدا است، اما اکنون خوشه هایی وجود دارند که فعالیت را در اواخر شب و ظهر در منطقه بزرگتر نشان می دهند. این جداسازی در شناسایی مراکز فعالیت در ساعات مشخصی از روز مفید است.
دو رویکرد دیگر به خوشه‌بندی سلسله مراتبی فضا-زمان با مجموعه داده اردک مسکووی در نظر گرفته شد. در پانل پایین سمت چپ، به مؤلفه فاصله وزن کم (0.2) و مؤلفه زمانی وزن بالاتر (1.0) داده شد، که بر زمان بر فضا تأکید دارد. در اینجا، تفکیک بین فعالیت در حوالی ظهر تا اواخر بعد از ظهر در مقابل فعالیت در اواخر شب می شود. در نهایت، در گوشه پایین سمت راست، وزنه‌ها معکوس شدند و بر فضا در طول زمان تأکید می‌کردند. در اینجا، خوشه‌ها آن دو منطقه پربازدید را نشان می‌دهند، اما در بخش‌های مختلف روز پراکنده شده‌اند.

4. بحث

این مقاله گسترشی را برای روش خوشه‌بندی سلسله مراتبی سنتی برای ترکیب اطلاعات مکان، زمان و ویژگی پیشنهاد کرد. روش خوشه‌بندی سلسله مراتبی فضا-زمان یک رویکرد انعطاف‌پذیر است که می‌تواند برای مشاهدات دارای مهر زمان گسسته اعمال شود. در حالی که این رویکرد برای هر مشاهده ای با یک جزء زمانی مفید است، تاکید ویژه ای بر مشاهدات مکرر داده شد که امکان خوشه بندی برای داده ها در یک چرخه را فراهم می کند. همچنین، این روش بر مشاهداتی متمرکز بود که محدود به شبکه بودند، یا از ساختار همسایگی مناسب برای داده‌های متوالی سود می‌بردند (مثلاً مثلث‌سازی دلونی). رویکرد خوشه‌بندی سلسله مراتبی فضا-زمان پیشنهادی، بهبودی برای این داده‌های رویدادی گسسته زمانی است. بر اساس مقایسه با روش‌های خوشه‌بندی فضا-زمان موجود و رویکرد خوشه‌بندی سلسله مراتبی پایه. متریک فاصله بهتر می تواند فاصله مکانی و زمانی ترکیبی و ماهیت چرخه ای داده های زمانی را مدیریت کند.
در مقایسه با سایر روش‌های خوشه‌بندی، این روش در برابر یک حقیقت پایه، به‌ویژه در مقایسه با یک رویکرد تجمعی مبتنی بر اقلیدسی ساده، عملکرد خوبی داشت. به طور کلی، خوشه بندی سلسله مراتبی ST-DBSCAN و فضا-زمان مزایای متفاوتی دارند. ST-DBSCAN نویز را کاهش می دهد و همچنان در داده های چرخه ای عملکرد نسبتاً خوبی دارد. خوشه بندی سلسله مراتبی فضا-زمان با داده های چرخه ای کمی بهتر عمل می کند و امکان ارزیابی و مقایسه تعداد مختلف خوشه ها را فراهم می کند، اما نویز در داده ها را حذف نمی کند.
هنگامی که این روش بر روی داده های واقعی اعمال شد، توانست دو محدوده اصلی خانه را برای اردک مسکووی شناسایی کند. همچنین امکان استفاده از ساختار سلسله مراتبی تو در تو را برای تفکیک داده ها به خوشه های بیشتر و بررسی محدوده های خانه در زمان های مختلف فراهم کرد. وزن دهی موجود در معادله (2) این امکان را فراهم می کند که بر اجزای مختلف بسته به نیاز تأکید شود. با این حال، داده ها احتمالاً حاوی برخی از خطاهای احتمالی GPS هستند و این داده های پر سر و صدا توسط خوشه های مختلف ضبط شده است. بنابراین، منطقه فیزیکی محدوده خانه اردک احتمالاً بیش از حد برآورد می شود.
یکی از محدودیت‌های شناخته‌شده رویکرد میانگین‌گیری تجمعی برای خوشه‌بندی سلسله مراتبی، این است که الگوریتم بر اساس یک مدل استاتیک تصمیم ادغام می‌گیرد (به معادله (1) مراجعه کنید). این ممکن است باعث ادغام نادرست شود، به خصوص زمانی که نویز در داده ها وجود دارد [ 55]. بسیاری از الگوریتم‌های خوشه‌بندی مکانی-زمانی که در بالا مورد بحث قرار گرفت (ST-DBSCAN، ST-OPTICS، SNN-4D+) شامل رویکردی برای حذف یا کاهش نویز در رویکرد خوشه‌بندی می‌شوند. برای حذف نویز نیاز به تعریف روشنی از چیستی نویز دارد. نویز می تواند برای هر بعد به طور جداگانه یا به طور کلی در نظر گرفته شود. برای داده های مکانی، نویز ممکن است ناشی از خطا در ضبط اطلاعات GPS باشد، اما این بستگی به نوع و کمیت داده ها دارد. رویکرد خوشه‌بندی سلسله مراتبی فضا-زمان می‌تواند برای فیلتر کردن نویز به عنوان بخشی از یک پیش‌فرایند سازگار شود و سپس به خوشه‌بندی ادامه دهید.
Andrienko و Andrienko [ 29 ] محدودیت بالقوه دیگری را با استفاده از ترکیب خطی وزنی از اجزای مختلف پیشنهاد می کنند. آنها خاطرنشان می کنند که این ترکیب می تواند تفسیر خوشه ها را دشوار کند. حداقل، تفسیر نتایج مسافت ممکن است دشوار باشد زیرا چندین قطعه وجود دارد که نتیجه را تشکیل می دهد. با این حال، استفاده از معیار مرکزیت یا برخی معیارهای عملکرد ممکن است برای شناسایی خوشه‌های مهم استفاده شود و می‌تواند به تفسیر نتایج کمک کند. همچنین دانستن مقادیر اصلی مرتبط با هر مشاهده در یک خوشه می تواند به تفسیر آنها از طریق آمار توصیفی متغیرهای مختلف کمک کند.
در نهایت، عملکرد ممکن است برای کار با مجموعه داده های نقطه ای بزرگ یک نگرانی باشد. روشی که در اینجا اتخاذ شد، تولید یک ماتریس فاصله بود که به الگوریتم‌های خوشه‌بندی سلسله مراتبی تغذیه می‌شد. بسته به زبان برنامه نویسی، این ماتریس ممکن است نیاز به نگه داشتن در حافظه داشته باشد (20000 نقطه یک ماتریس با اندازه 20000 × 20000 تولید می کند). راه حلی که در اینجا برای سرعت بخشیدن به محاسبه و ذخیره حافظه کمتر اتخاذ شد، استفاده از ماتریس های پراکنده بود (مجموعه داده شبیه سازی شده در بالا با 10000 امتیاز دو دقیقه زمان پردازش را روی یک پردازنده 6 هسته ای با 16 گیگابایت رم طول کشید). این رویکرد باید به روش‌های مختلف برای مدیریت مجموعه داده‌هایی که میلیون‌ها یا میلیاردها نقطه را شامل می‌شوند، تطبیق داده شود.
برای درک معیارهای وزن دهی و اینکه چگونه اطلاعات ویژگی با استفاده از داده های واقعی تر بر خوشه بندی تأثیر می گذارد، به کار بیشتری نیاز است. همچنین، تطبیق روش برای حذف احتمالی نویز قبل از توسعه خوشه‌ها ممکن است در صورت لزوم گزینه مفیدی باشد.

منابع

  1. میلر، اچ جی; Han, J. (Eds.) داده کاوی جغرافیایی و کشف دانش ، ویرایش دوم. CRC Press: Boca Raton، FL، USA، 2009; شابک 978-1-4200-7397-3. [ Google Scholar ]
  2. اوریت، BS; لاندو، اس. لیز، ام. استال، دی. خوشه بندی سلسله مراتبی. در تحلیل خوشه ای ; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2011; صص 71-110. شابک 978-0-470-97781-1. [ Google Scholar ]
  3. هان، جی. لی، جی.-جی. کامبر، ام. مروری بر روش های خوشه بندی در تجزیه و تحلیل داده های جغرافیایی. در داده کاوی جغرافیایی و کشف دانش ; Miller, HJ, Han, J., Eds. تیلور و فرانسیس: ابینگدون، انگلستان، 2009; ص 149-187. [ Google Scholar ]
  4. یامادا، آی. راجرسون، PA مقایسه تجربی روش‌های تصحیح اثر لبه به کار رفته در تحلیل تابع K. Geogr. مقعدی 2003 ، 35 ، 97-109. [ Google Scholar ]
  5. منیس، جی. گوو، دی. داده کاوی فضایی و کشف دانش جغرافیایی – مقدمه. محاسبه کنید. محیط زیست سیستم شهری 2009 ، 33 ، 403-408. [ Google Scholar ] [ CrossRef ]
  6. ژانگ، تی. وانگ، جی. کوی، سی. لی، ی. او، دبلیو. لو، ی. Qiao, Q. ادغام تجزیه و تحلیل Geovisual با یادگیری ماشین برای کشف الگوی تحرک انسان. ISPRS Int. J. Geo-Inf. 2019 ، 8 ، 434. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
  7. مدل‌سازی طولانی، JA احتمال حرکت در میدان‌های فضایی ناهمگن. جی. اسپات. Inf. علمی 2018 ، 16 ، 85-116. [ Google Scholar ] [ CrossRef ]
  8. میلر، HJ یک نظریه اندازه گیری برای جغرافیای زمان. Geogr. مقعدی 2005 ، 37 ، 17-45. [ Google Scholar ] [ CrossRef ]
  9. میلر، HJ مدل‌سازی دسترسی با استفاده از مفاهیم منشور فضا-زمان در سیستم‌های اطلاعات جغرافیایی. بین المللی جی. جئوگر. Inf. سیستم 1991 ، 5 ، 287-301. [ Google Scholar ] [ CrossRef ]
  10. ریشتر، K.-F. اشمید، اف. Laube، P. فشرده سازی مسیر معنایی: به طور خلاصه حرکت شهری را نشان می دهد. جی. اسپات. Inf. علمی 2012 ، 3-30. [ Google Scholar ] [ CrossRef ]
  11. اوکابه، ا. یامادا، I. روش تابع K در یک شبکه و اجرای محاسباتی آن. Geogr. مقعدی 2001 ، 33 ، 271-290. [ Google Scholar ] [ CrossRef ]
  12. یامادا، آی. تیل، جی.-سی. مقایسه توابع K مسطح و شبکه در تحلیل حوادث ترافیکی. J. Transp. Geogr. 2004 ، 12 ، 149-158. [ Google Scholar ] [ CrossRef ]
  13. اوکابه، ا. Sugihara, K. تجزیه و تحلیل فضایی در طول شبکه: روش های آماری و محاسباتی . جان وایلی و پسران: هوبوکن، نیوجرسی، ایالات متحده آمریکا، 2012; شابک 978-1-119-96776-7. [ Google Scholar ]
  14. بره، DS; داونز، جی. لی، سی. تابع K شبکه در زمینه: بررسی اثرات ساختار شبکه بر تابع K شبکه. ترانس. GIS. 2015 ، 20 ، 448-460. [ Google Scholar ] [ CrossRef ]
  15. Manson, SM آیا مقیاس وجود دارد؟ یک پیوستار مقیاس معرفت‌شناختی برای سیستم‌های پیچیده انسان-محیط Geoforum 2008 , 39 , 776-788. [ Google Scholar ] [ CrossRef ]
  16. Goodchild، MF Citizens به عنوان حسگر: دنیای جغرافیای داوطلبانه. ژئوژورنال 2007 ، 69 ، 211-221. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  17. ریچاردسون، DB زمان واقعی ادغام فضا-زمان در علم GIS و جغرافیا. ان دانشیار صبح. Geogr. 2013 ، 103 ، 1062-1071. [ Google Scholar ] [ CrossRef ] [ PubMed ]
  18. میلر، اچ جی; Goodchild، جغرافیای داده محور MF. GeoJournal 2015 ، 80 ، 449-461. [ Google Scholar ] [ CrossRef ]
  19. میلر، تجزیه و تحلیل مبتنی بر فعالیت HJ. در کتابچه راهنمای علوم منطقه ای ; Fischer, MM, Nijkamp, ​​P., Eds. Springer: برلین/هایدلبرگ، آلمان، 2014; ص 705-724. شابک 978-3-642-23429-3. [ Google Scholar ]
  20. اشبروک، دی. Starner, T. استفاده از GPS برای یادگیری مکان‌های مهم و پیش‌بینی حرکت در میان کاربران متعدد. پارس Ubiquitous Comput 2003 ، 7 ، 275-286. [ Google Scholar ] [ CrossRef ]
  21. آندرینکو، جی. آندرینکو، ن. باک، پ. کیم، دی. Wrobel, S. Visual Analytics of Movement ; Springer: برلین/هایدلبرگ، آلمان، 2013; شابک 978-3-642-37582-8. [ Google Scholar ]
  22. بیرانت، دی. Kut، A. ST-DBSCAN: الگوریتمی برای خوشه بندی داده های مکانی-زمانی. دانستن داده ها مهندس 2007 ، 60 ، 208-221. [ Google Scholar ] [ CrossRef ]
  23. اوریت، BS; لاندو، اس. لیز، ام. استال، دی. مقدمه ای بر طبقه بندی و خوشه بندی. در تحلیل خوشه ای ; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2011; صص 1-13. شابک 978-0-470-97781-1. [ Google Scholar ]
  24. Guo, D. خوشه بندی فضایی چند متغیره و ژئوویژوالیزاسیون. در داده کاوی جغرافیایی و کشف دانش ; Miller, H., Han, J., Eds. CRC Press: Boca Raton، FL، USA، 2009; صص 325-345. [ Google Scholar ]
  25. کیسیلویچ، اس. منزمن، اف. نانی، م. Rinzivillo، S. خوشه بندی فضایی-زمانی. در کتاب داده کاوی و کشف دانش ; Maimon, O., Rokach, L., Eds. Springer: برلین/هایدلبرگ، آلمان، 2009; صص 855-874. شابک 978-0-387-09822-7. [ Google Scholar ]
  26. وانگ، ام. وانگ، آ. Li، A. خوشه‌های زمانی-مکانی استخراج از پایگاه‌های داده جغرافیایی. در مجموعه مقالات داده کاوی پیشرفته و کاربردها: دومین کنفرانس بین المللی، ADMA 2006، شیان، چین، 14 تا 16 اوت 2006. [ Google Scholar ]
  27. Agrawal، KP; گارگ، اس. شارما، اس. Patel, P. توسعه و اعتبار سنجی تکنیک خوشه بندی فضایی-زمانی مبتنی بر OPTICS. Inf. علمی 2016 ، 369 ، 388-401. [ Google Scholar ] [ CrossRef ]
  28. واردلاو، RL; فرولیچ، سی. دیویس، SD ارزیابی سکون لرزه‌ای پیش‌آزمون در شانزده ناحیه فرورانش با استفاده از تحلیل خوشه‌ای تک پیوندی. Pure Appl. ژئوفیز. 1990 ، 134 ، 57-78. [ Google Scholar ] [ CrossRef ]
  29. آندرینکو، جی. Andrienko، N. تجزیه و تحلیل خوشه ای تعاملی انواع مختلف داده های مکانی-زمانی. SIGKDD Explor Newsl 2010 ، 11 ، 19-28. [ Google Scholar ] [ CrossRef ]
  30. اولیویرا، آر. سانتوس، من؛ Moura Pires، J. 4D+SNN: یک رویکرد خوشه‌بندی مبتنی بر چگالی مکانی-زمانی با شباهت 4 بعدی. در مجموعه مقالات سیزدهمین کنفرانس بین المللی IEEE 2013 در کارگاه های داده کاوی (ICDMW)، دالاس، تگزاس، ایالات متحده آمریکا، 7 تا 10 دسامبر 2013. ص 1045-1052. [ Google Scholar ]
  31. برمینگام، ال. لی، I. چارچوبی از روش‌های ساده‌سازی مسیر مکانی-زمانی. بین المللی جی. جئوگر. Inf. علمی 2017 ، 31 ، 1128-1153. [ Google Scholar ] [ CrossRef ]
  32. لی، جی.-جی. هان، جی. وانگ، K.-Y. خوشه‌بندی مسیر: یک چارچوب پارتیشن و گروهی. در مجموعه مقالات کنفرانس بین المللی ACM SIGMOD 2007 در مورد مدیریت داده ها، پکن، چین، 11-14 ژوئن 2007. صص 593-604. [ Google Scholar ]
  33. گوا، ن. شکر، س. Xiong، W. چن، ال. Jing، N. UTSM: یک معیار تشابه مسیر با در نظر گرفتن عدم قطعیت بر اساس مدل اصلاح شده بیضی. ISPRS Int. J. Geo-Inf. 2019 ، 8 ، 518. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
  34. Sokal, RR; Michener, CD روشی آماری برای ارزیابی روابط سیستماتیک. دانشگاه کانز علمی گاو نر 1958 ، 38 ، 1409-1438. [ Google Scholar ]
  35. داونز، جی. هورنر، MW تجزیه و تحلیل داده‌های ردیابی حیوانات نمونه‌برداری نادر با ترکیب مسیر حرکت تعمیم‌یافته با تخمین چگالی هسته. محاسبه کنید. محیط زیست سیستم شهری 2012 ، 36 ، 302-310. [ Google Scholar ] [ CrossRef ]
  36. مک گوایر، نماینده مجلس؛ جانجا، وی. Gangopadhyay، A. مجموعه داده‌های حسگر معدن با همسایگی‌های مکانی و زمانی. جی. اسپات. Inf. علمی 2013 . [ Google Scholar ] [ CrossRef ]
  37. اوکابه، ا. چکمه، بی. سوگیهارا، ک. Chiu, SN Spatial Tessellations: Concepts and Applications of Voronoi Diagrams ; جان وایلی و پسران: هوبوکن، نیوجرسی، ایالات متحده آمریکا، 2009; شابک 978-0-470-31785-3. [ Google Scholar ]
  38. Gibbons، A. نظریه نمودار الگوریتمی . انتشارات دانشگاه کمبریج: نیویورک، نیویورک، ایالات متحده آمریکا، 1985; ISBN 9780521288811. [ Google Scholar ]
  39. Di Pierro, M. الگوریتم های حاشیه نویسی شده در پایتون با کاربرد در فیزیک، زیست شناسی و امور مالی . EXPERTS4SOLUTIONs: Chicago, IL, USA, 2013; شابک 978-0-9911604-0-2. [ Google Scholar ]
  40. هوانگ، بی. وو، کیو. Zhan، FB یک الگوریتم کوتاه ترین مسیر با اکتشافات جدید برای شبکه های حمل و نقل پویا. بین المللی جی. جئوگر. Inf. علمی 2007 ، 21 ، 625-644. [ Google Scholar ] [ CrossRef ]
  41. ارتوز، ال. اشتاین باخ، ام. Kumar, V. یک الگوریتم جدید خوشه بندی نزدیکترین همسایه مشترک و کاربردهای آن. در مجموعه مقالات کارگاه خوشه بندی داده های با ابعاد بالا و کاربردهای آن در دومین کنفرانس بین المللی SIAM در مورد داده کاوی، آرلینگتون، ویرجینیا، ایالات متحده آمریکا، 11-13 آوریل 2002. صص 105-115. [ Google Scholar ]
  42. Oliphant، TE Python برای محاسبات علمی. محاسبه کنید. علمی & مهندس 2007 ، 9 ، 10-20. [ Google Scholar ]
  43. هاگبرگ، AA; شولت، دی. Swart، PJ کاوش ساختار، دینامیک و عملکرد شبکه با استفاده از NetworkX. در مجموعه مقالات هفتمین کنفرانس پایتون در علم (SciPy2008)، پاسادنا، کالیفرنیا، ایالات متحده آمریکا، 19 تا 24 اوت 2008. صص 11-15. [ Google Scholar ]
  44. مک مستر، آر.بی. شپرد، ای. مقدمه: مقیاس و پرس و جوی جغرافیایی. در مقیاس و جغرافی . Sheppard, E., McMaster, RB, Eds. Blackwell Publishing Ltd.: Malden, MA, USA, 2004; صص 1-22. شابک 978-0-470-99914-1. [ Google Scholar ]
  45. لوین، SA مسئله الگو و مقیاس در اکولوژی: سخنرانی جایزه رابرت اچ مک آرتور. اکولوژی 1992 ، 73 ، 1943-1967. [ Google Scholar ] [ CrossRef ]
  46. Fotheringham، AS; Wong، DWS مسئله واحد مساحتی قابل اصلاح در تحلیل آماری چند متغیره. محیط زیست طرح. A 1991 , 23 , 1025-1044. [ Google Scholar ] [ CrossRef ]
  47. کوان، ام.-پی. مشکل زمینه جغرافیایی نامشخص ان دانشیار صبح. Geogr. 2012 ، 102 ، 958-968. [ Google Scholar ] [ CrossRef ]
  48. کوان، ام.-پی. جغرافیای الگوریتمی: کلان داده، عدم قطعیت الگوریتمی و تولید دانش جغرافیایی. ان صبح. دانشیار Geogr. 2016 ، 106 ، 274-282. [ Google Scholar ]
  49. پدرگوسا، اف. واروکو، جی. گرامفورت، آ. میشل، وی. تیریون، بی. گریزل، او. بلوندل، م. پرتنهوفر، پی. ویس، آر. دوبورگ، وی. و همکاران Scikit-Learn: یادگیری ماشینی در پایتون. جی. ماخ. فرا گرفتن. Res. 2011 ، 12 ، 2825-2830. [ Google Scholar ]
  50. هوبرت، ال. Arabie, P. مقایسه پارتیشن ها. J. Classif. 1985 ، 2 ، 193-218. [ Google Scholar ] [ CrossRef ]
  51. روزنبرگ، ا. Hirschberg، J. V-Measure: یک معیار ارزیابی خارجی خوشه ای مبتنی بر آنتروپی مشروط در مجموعه مقالات EMNLP-CoNLL، پراگ، جمهوری چک، 28 تا 30 ژوئن 2007. جلد 7، ص 410–420. [ Google Scholar ]
  52. پاولیس، م. دولگا، ال. Singleton، A. یک روش خوشه بندی DBSCAN اصلاح شده برای تخمین میزان مرکز خرده فروشی. Geogr. مقعدی 2017 . [ Google Scholar ] [ CrossRef ]
  53. داونز، جی. هورنر، مگاوات؛ هایزر، جی. بره، دی. منشورهای فضا-زمان احتمالی مبتنی بر Loraamm، R. Voxel برای تجزیه و تحلیل حرکات حیوانات و استفاده از زیستگاه. بین المللی جی. جئوگر. Inf. علمی 2014 ، 28 ، 875-890. [ Google Scholar ] [ CrossRef ]
  54. گائو، پی. کوپفر، جی. زو، ایکس. Guo, D. کمی سازی مسیرهای حیوانات با استفاده از تجمع فضایی و تجزیه و تحلیل توالی: مطالعه موردی مسیرهای متمایز کننده گونه های متعدد. Geogr. مقعدی 2016 ، 48 ، 275-291. [ Google Scholar ] [ CrossRef ]
  55. کاریپیس، جی. هان، E.-H. Kumar, V. Chameleon: خوشه بندی سلسله مراتبی با استفاده از مدل سازی پویا. کامپیوتر 1999 ، 32 ، 68-75. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
Ijgi 09 00085 g001 550
شکل 1. مثالی از مثلث سازی Delaunay با استفاده از نقاط ردیابی حیوانات.
Ijgi 09 00085 g002 550
شکل 2. ملاحظات برای مؤلفه زمان. پانل بالا فاصله زمانی را از 12 ساعت (نیمه روز) نشان می دهد، و پانل پایین فاصله از نیمه شب را نشان می دهد.
Ijgi 09 00085 g003 550
شکل 3. نمونه‌ای از مجموعه داده‌های شبیه‌سازی‌شده از گروه‌بندی‌های خوشه‌ای مختلف تصادفی، که برای ارزیابی نزدیک‌ترین همسایه و پارامترهای مقیاس زمانی استفاده می‌شوند.
Ijgi 09 00085 g004 550
شکل 4. میانگین نمرات در مقادیر مختلف برای نزدیکترین همسایگان در تمام مقادیر مقیاس زمانی ( A )، و برای مقادیر مختلف مقیاس زمانی در تمام مقادیر مقیاس نزدیکترین همسایه ( B ).
Ijgi 09 00085 g005 550
شکل 5. مجموعه داده شبیه سازی شده که برای مقایسه روش های مختلف خوشه بندی استفاده می شود.
Ijgi 09 00085 g006 550
شکل 6. کاربرد خوشه بندی سلسله مراتبی فضا-زمان برای خوشه بندی مشاهدات GPS یک اردک مسکووی.

مقالات داخلی و بین المللی

مطالب مرتبط ...

بدون دیدگاه

دیدگاهتان را بنویسید