روششناسی مبتنی بر GIS برای پیشبینی تصادف در بزرگراههای روستایی تک بانده
با توجه به نیاز به به روز رسانی دستورالعمل های فعلی طراحی بزرگراه برای تمرکز بر ایمنی، این مطالعه به دنبال ایجاد یک مدل پیش بینی تصادف با استفاده از یک سیستم اطلاعات جغرافیایی (GIS) برای بزرگراه های روستایی تک خطه، با حداقل متغیرهای آماری معنی دار، کافی است. به واقعیت برزیل، و بهبود پیش بینی تصادف برای مکان هایی با ویژگی های مشابه. یک پایگاه داده برای مرتبط کردن سوابق تصادفات با پارامترهای هندسی بزرگراه و پر کردن شکاف های به جا مانده از عدم وجود طرح های هندسی بزرگراه از طریق بازسازی هندسی یا استخراج نیمه خودکار بزرگراه ها با استفاده از تصاویر ماهواره ای ایجاد شد.
روش معادله تخمین تعمیم یافته (GEE) برای تخمین ضرایب مدل با فرض توزیع منفی خطای دوجمله ای برای شمارش تصادفات مشاهده شده استفاده شد. فرکانس تصادف و میانگین ترافیک روزانه سالانه (AADT) همراه با ویژگیهای مکانی و هندسی 215 کیلومتر بزرگراه روستایی تک خط فدرال بین سالهای 2007 و 2016 مورد تجزیه و تحلیل قرار گرفت. تقسیم بندی، دو بر اساس بخش ها و یکی بر اساس برآوردگر چگالی هسته. برای ارزیابی اثر ترافیک ثابت، دو تغییر دیگر از مدلها با استفاده از AADT به عنوان متغیر افست در نظر گرفته شد. ساختار همبستگی غالب در مدل ها قابل مبادله بود. عوامل اصلی در وقوع برخوردها شعاع منحنی افقی، درجه، طول قطعه و AADT بودند. این مطالعه شاخصهای واضحی را برای پارامترهای طراحی راهها تولید کرد که بر عملکرد ایمنی بزرگراههای روستایی تأثیر میگذارد.
کلید واژه ها
جاده ها ، GEE ، بزرگراه های روستایی تک بانده ، GIS ، پیش بینی تصادف
1. مقدمه
اگرچه بیشتر تصادفات بزرگراهی در مسیرهای مستقیم جاده اتفاق میافتد، اما در پیچهایی است که تصادفات با شدت بیشتری رخ میدهد [ 1 ]. منحنی ها، به ویژه آنهایی که مسطح هستند، 54 درصد از تصادفات مرگبار را که در بزرگراه های روستایی در برزیل رخ می دهد، متمرکز می کنند [ 2 ]. آنها برای رانندگان خطرناک تر هستند زیرا نیروهای متمرکز اضافی بر وسیله نقلیه اعمال می شوند و توجه بیشتری از جانب راننده مورد نیاز است [ 3 ].
به دلیل شدت تصادف، منحنی های صاف مورد توجه بسیاری از محققان بوده است. بیشتر مطالعات بر رابطه بین ویژگیهای منحنی و عملکرد ایمنی آن، از جمله ویژگیهای طراحی [ 4 ]، مانند علائم و نشانهها [ 5 ] [ 6 ] و استراتژیهایی برای بهبود ایمنی [ 7 ] [ 8 ] تمرکز کردهاند. در این سناریو، مدلهای پیشبینی تصادف (APM) به عنوان ابزارهایی ظاهر میشوند که قادر به مدلسازی عوامل مرتبط برای تصادفات رانندگی هستند. آنها مدل های آماری هستند که فراوانی تصادفات رانندگی را به ویژگی های هندسی و عملیاتی جاده مرتبط می کنند. این مدل ها فاقد حجم زیادی از داده ها هستند [ 9 ].
از جمله موانعی که در فرآیند توسعه APM با آن مواجه میشویم، فقدان مستندسازی در مورد شبکههای جادهای و پروژههایی است که تقریباً همیشه فقط امکان مسیر کوتاهتر، جریان بهتر و هزینههای کمتر را بدون در نظر گرفتن دینامیک تصادف و ارتباط آن با ویژگیهای هندسی در نظر میگیرند. جاده ها را در نظر بگیرید [ 10 ]. برنامه ریزی بهتری را می توان از طریق تکنیک های ژئوپردازش و سنجش از دور، استفاده از سیستم های اطلاعات جغرافیایی (GIS) و تفسیر تصاویر ماهواره ای انجام داد. استخراج خودکار یا نیمه خودکار جاده ها از تصاویر ماهواره ای ممکن است راحت ترین راه برای غلبه بر کمبود اسناد پروژه برای ایمنی جاده در برزیل باشد [ 11 ].
محدودیت دیگر در توسعه APM ها در تقسیم بندی مقاطع با مشخصات هندسی مشابه (قطعات همگن) است. این تقسیم همگن برای ایجاد روابط فضایی بین حادثه و محل وقوع حادثه ضروری است. به عنوان مثال، در برزیل، توصیف بین مماس و منحنی بر اساس بازرسی بصری انجام می شود که ممکن است منجر به خطا در شناسایی مقاطع مستقیم و منحنی شود. در این مورد، انتساب تصادف به بخش خاصی از بزرگراه ممکن است نادرست باشد. برای جلوگیری از این امر، لازم است پارامترهایی شناسایی شوند که می توانند بخش را به درستی مشخص کنند.
این مطالعه به دنبال توسعه یک پایگاه داده است که قادر به مرتبط کردن سوابق تصادفات با پارامترهای هندسی بزرگراه است، که با فرآیند بازسازی هندسی زمانی که دادههای برداری در دسترس است یا از طریق استخراج نیمه خودکار بزرگراهها از تصاویر ماهوارهای در حالی که وجود ندارد، به دست میآید. ابزارهای مدلسازی و تحلیل فضایی برای استخراج عناصر فضایی مانند عرض خط، عرض شانه، فوقارتفاع و شعاع منحنی از مدلهای زمین دیجیتال، تصاویر ماهوارهای، و از طراحی هندسی استفاده میشوند و تکمیل کننده هرگونه اطلاعات غیرقابل دسترس در پایگاه دادههای تصادفی سنتی هستند. بخش های همگن با استفاده از روش تحلیلی (HSM) و روش فضایی (تراکم هسته-KDE) تجزیه و تحلیل و طبقه بندی می شوند. هدف، ساخت یک مدل پیشبینی تصادف مناسب برای برزیل با استفاده از GIS برای بزرگراههای روستایی تک خطه است.
2. پس زمینه
2.1. مدل های پیش بینی تصادف
مطالعات متعددی تأثیر ویژگی های جاده را بر فراوانی تصادفات [ 12 ] – [ 21 ] بررسی کرده اند. اکثر مطالعات از مدل های آماری سنتی رگرسیون چندگانه، پواسون و رگرسیون دو جمله ای منفی [ 19 ] [ 22 ] – [ 30 ] استفاده کردند.
مشکل مدلهای سنتی این است که فرض میکنند باقیماندههای بین مشاهدات مستقل هستند. نادیده گرفتن این ساختار سلسله مراتبی، در صورت وجود، ممکن است منجر به مدل هایی با تخمین های مغرضانه پارامترها و خطاهای استاندارد سوگیری شود. هنگام کار با داده های طولی (نمونه ها بیش از یک بار در طول زمان اندازه گیری می شوند) یا گروه بندی می شوند، این فرض استقلال بین متغیرها ممکن است منطقی نباشد. روشهای مختلفی برای حل این مشکل وجود دارد که شاید شناختهشدهترین آنها در زمینه غیر گاوسی، روش معادلات برآورد تعمیمیافته (GEE) باشد. مدل GEE نتایج بهتری را نشان داد، با این حال، برای منحنیهای افقی، کششهایی که در آن علل تصادف به خوبی مورد مطالعه قرار گرفته است [ 31 ]]. یکی از ویژگی های اصلی GEE توانایی آن در یکسان سازی چندین تکنیک آماری است که معمولاً به طور جداگانه مطالعه می شوند. این امکان افزایش تعداد مفروضات پذیرفته شده و بررسی بیش از روابط خطی بین متغیرهای توضیحی و پاسخ را فراهم می کند. این نوع مدل اجازه می دهد تا تعاملات بالقوه بین متغیرها ارزیابی شود و قادر به مدل سازی پایگاه های داده با ساختارهای طولی، فضایی یا چند سطحی است.
2.2. متغیرهای درگیر در مدل سازی
مدلهای مختلف بر اساس متغیرهایی که شامل طول منحنی، درجه انحنا و درجه است، تصادفات را در منحنیهای افقی ترسیم کردهاند. تقریباً همه مدلها از حجم ترافیک برای هر بخش، بر اساس شمارش تخمینی AADT استفاده کردند. این مطالعات نشان میدهد که زاویه مرکزی بیشتر [ 32 ] [ 33 ]، شیب بیشتر [ 21 ] [ 34 ] و فوقارتفاع بیشتر فرکانس تصادف را افزایش میدهد [ 33 ]، در حالی که شعاع بیشتر آن را کاهش میدهد [ 33 ] [ 35 ]. با در نظر گرفتن همین متغیرها و تأثیر پارامترهای هندسی بر شدت تصادف، مطالعات نشان میدهد که شیب بیشتر باعث افزایش شدت میشود [ 36 ] [ 37 ]] در حالی که شعاع بزرگتر [ 36 ] و فوق ارتفاع بیشتر آن را کاهش می دهد [ 38 ].
گنجاندن روابط فضایی در تجزیه و تحلیل ایمنی می تواند یک ملاحظه مهم برای یک رویکرد دقیق تر و جامع تر باشد. رابطه فضایی یک منحنی به منحنیهای مجاور، از جمله فاصله تا منحنیهای مجاور، جهت چرخش منحنیهای مجاور، شعاع منحنیهای مجاور، و طول منحنیهای مجاور و همچنین انحنای عمودی، از ویژگیهای مهمی هستند که میتوانند بر ایمنی تأثیر بگذارند. یک منحنی افقی یا یک سری منحنی [ 3 ].
بر اساس متغیرهای موجود در ادبیات و تأثیر آنها بر فراوانی تصادف، متغیرهای زیر به طور پیشین برای این مطالعه انتخاب شدند: انحنای افقی (شعاع، درجه منحنی، زاویه انحراف، طول منحنی)، عرض خط، عرض شانه و نوع، حجم ترافیک و درجه متغیرهای فضایی کیفی مانند کاربری زمین (روستایی یا شهری)، مشخصات مسیر جاده (مسطح، مواج یا کوهستانی)، طرح (مستقیم یا مسطح)، روز هفته، شرایط آب و هوایی، و نوع تصادف برای کمک استفاده خواهند شد. در انتخاب مقاطع همگن
3. مواد و روشها
3.1. پیش بینی تصادفات مبتنی بر GIS
روش مطالعه با استفاده از سه مرحله اصلی توسعه داده شد: 1) ساخت یک پایگاه داده از جمع آوری داده ها و استخراج نیمه خودکار بزرگراه ها از پایگاه های برداری و/یا تصاویر ماهواره ای، 2) تقسیم بندی همگن بزرگراه ها، و 3) مدل سازی فرکانس تصادف.
3.1.1. جمع آوری داده ها
دادهها و اطلاعات تصادفات ترافیکی برای این مطالعه از طریق صفحات گسترده الکترونیکی بهدستآمده از گزارشهای تصادفات رانندگی اداره پلیس بزرگراه فدرال (DPRF) جمعآوری شد که از 1 ژانویه 2007 تا 31 دسامبر 2016 برای بزرگراه BR-232، بین کیلومتر 141 و کیلومتر 356.
بخش های جاده از برنامه حمل و نقل ملی (PNV) از DNIT (2016) به دست آمد. این بخش از جاده در طول دوره مورد تجزیه و تحلیل هیچ تغییر سازنده ای نداشته است.
حجم ترافیک (AADT) از برنامه ملی کنترل ترافیک (PNCT)، موجود در DNIT (2016) برای سال های 2014، 2015 و 2016 به دست آمد. برای سال های قبل (2007 تا 2013)، مقادیر AADT از گزارش سالانه ANTT (2015).
3.1.2. پردازش دیجیتال شبکه بزرگراه
برای به دست آوردن اطلاعات در مورد امتداد بزرگراه که طراحی هندسی نداشتند، روشی که توسط Macedo و همکاران توسعه داده شد. [ 11 ] استفاده شد که شامل استخراج ویژگی های هندسی جاده ها از تصاویر ماهواره ای بر اساس طبقه بندی کننده های الگو است. مراحل اصلی این رویکرد 1) تشخیص جاده و 2) فیلتر کردن عناصر مورد نظر و به دست آوردن شبکه راه است. در این فرآیند، تلاش شد تا دستورالعمل اصلی جاده ترسیم شود.
برای پایگاه بزرگراههای DNIT، یک فرآیند نیمه خودکار توسعه یافته توسط Macedo و همکاران. [ 11 ] انتخاب شد که شامل ترکیبی از موارد زیر است: 1) تکنیکهای کاهش راس با استفاده از ArcTool Box ArcMap. 2) توسعه یک الگوریتم برای شناسایی منحنی ها در AutoCad Civil 3D. 3) تجسم نتایج با استفاده از تصاویر ماهواره ای به عنوان مرجع. و 4) ایجاد یک تراز در AutoCad Civil 3D.
بر اساس بازسازی تراز، جدولی حاوی تمام اطلاعات منحنی (شعاع، زاویه، انتقال، انحراف، درجه منحنی، مختصات، طول) ایجاد شد و اینها به جدول اکسل صادر شدند.
3.1.3. ساخت پایگاه داده
پایگاه داده اطلاعات مربوط به شبکه جاده ها، محیط زیست و عوامل ایمنی راه، از جمله تصادفات و حجم ترافیک را ذخیره می کند که به منظور ترکیب متغیرها و کمک به تقسیم بندی همگن به هم مرتبط شده اند.
پایگاه بزرگراه با استفاده از تقسیم بندی دینامیک به کیلومتر تقسیم شد و امکان شناسایی هرگونه اطلاعات با استفاده از علائم کیلومتر بزرگراه، مانند داده های تصادف، حجم ترافیک و محیط را فراهم کرد. از این پایگاه جغرافیایی ارجاع داده شده با تمام اطلاعات پیوست شده، یک فایل dBase با استفاده از نرم افزار ArcGis به فایل نقاط تبدیل شد. برای اتصال این داده ها، جداول حاوی اطلاعات دیگر از بزرگراهی که به آن تعلق دارد و علامت های کیلومتر استفاده می کنند. این اطلاعات یا نقطه ای بود یا خطی. حوادث، مکان های دسترسی، علائم و غیره به عنوان اطلاعات نقطه ای ذخیره می شدند، در حالی که طراحی هندسی، ترافیک و غیره اطلاعات جدولی مرتبط با ویژگی های خطی بودند.
برای اطمینان از سازگاری دو مجموعه داده، ترکیبی از دو تکنیک برای ایجاد یک فیلد مشترک برای ادغام مجموعه داده ها استفاده شد. با اولین تکنیک، یک فیلد مرجع کیلومتر (KM_REF) در جدول داده های بزرگراه و همچنین یک جدول تبدیل ایجاد شد که برای ایجاد یک فیلد مشترک ایجاد شد. جدول تبدیل کیلومتر مرجع را تشخیص می دهد و داده های تصادف را به کیلومتر مربوطه آن مرتبط می کند. با تکنیک دوم، یک اتصال فضایی بین جداول انجام شد، یعنی هر حادثه از نظر فضایی به بخشی که به آن تعلق داشت اختصاص داده شد. این دو تکنیک امکان شناسایی و تخصیص بیش از 99.6 درصد از تصادفات را از گزارشهای تصادفات رانندگی DPRF فراهم میکند که دوره از 1 ژانویه 2007 تا 31 دسامبر 2016 را برای بزرگراه BR-232 پوشش میدهد.
3.2. تقسیم بندی همگن
جاده ها و تمام اطلاعات مرتبط به سه روش مختلف به بخش های همگن تقسیم شدند: دو با روش پیشنهادی توسط HSM [ 39 ] و دیگری بر اساس تراکم هسته. آنها در زیر فهرست شده اند:
• روش تقسیم بندی 1: بر اساس HSM، قطعات بین تقاطع ها با حداقل طول 160 متر قرار دارند.
• روش قطعه بندی 2: تغییر روش HSM، با 50 متر قبل و 50 متر بعد از منحنی ها، اجتناب از قطعات کوتاه و به حداقل رساندن مشکل مکان یابی نادرست تصادفات.
• روش تقسیم بندی 3: تقسیم بخش ها بر اساس چگالی هسته و همه متغیرهای مورد استفاده در روش گام به گام در هر بخش با مقادیر اصلی آنها توضیحی است.
3.3. مدل سازی آماری
مدل پیشنهادی به عنوان یک مدل معادلات تخمین تعمیمیافته طبقهبندی میشود، که میتواند به عنوان توسعه مدلهای خطی تعمیمیافته برای دادههای تابلویی تفسیر شود و علاوه بر حجم ترافیک، متغیرهای مختلفی را نیز در بر میگیرد. تابع اولیه توسط لیانگ و زگر [ 40 ] پیشنهاد شد:
μمن=β0∗ (β1ایکس1 i+β2ایکس2 من+ ⋯ +βnایکسn) + εμi=β0∗(β1X1i+β2X2i+⋯+βnXn)+ε(1)
من que: μمنμi= نرخ سالانه پیش بینی شده تصادفات. β0،β1، ⋯ ،βnβ0,β1,⋯,βn= پارامترهای رگرسیون؛ ایکس1 i،ایکس2 من، ⋯ ،ایکسqمنX1i,X2i,⋯,Xqi= متغیرهای مورد علاقه ε = خطای مشخصات
انتخاب روش عمدتاً به دلیل امکان ترکیب متغیرهای کمی و طبقهای، نه تنها به عنوان متغیرهای ساختگی (باینری – 0 یا 1)، بلکه به عنوان متغیرهای چندجملهای (دارای بیش از دو متغیر طبقهای ترتیبی) است. متغیر وابسته از نوع count (تعداد حوادثی که در یک قطعه معین رخ می دهد) و تابع پیوند یک دوجمله ای منفی است.
برای تنظیم یک مدل خطی تعمیم یافته، بردار ( β ) تخمین پارامترها تعیین شد. این ضرایب از روی داده های مشاهده شده برآورد شد.
در این مطالعه، اولین گام بررسی معنی دار بودن ضرایب برآورد شده بود، یعنی اینکه آیا ارتباط آماری معنی داری بین متغیرهای توضیحی و متغیر پاسخ وجود دارد یا خیر. برای ارزیابی پایبندی توزیع تصادف بین داده های واقعی و پیش بینی شده از آزمون آماری کای اسکوئر والد استفاده شد. مقدار calc χ2 از داده های تجربی، با در نظر گرفتن مقادیر مشاهده شده و مورد انتظار، به دست آمد.
از آنجایی که این یک فرضیه جایگزین است، که در آن فرکانسهای تصادف مشاهدهشده با فرکانسهای پیشبینیشده متفاوت است، نیاز به تأیید ارتباط بین گروهها با مقایسه دادههای χ2 محاسبهشده با دادههای χ2 جدولبندی شده وجود داشت . χ 2 جدول بندی شده به تعداد درجات آزادی و سطح اهمیت پذیرفته شده بستگی دارد.
اگر مقدار p مربوط به آماره آزمون کمتر از سطح معنیداری α باشد ، فرضیه مطابقت مدل با دادهها رد میشود . بنابراین، برای سطح اهمیت α ، با مقایسه دو مقدار χ 2 تصمیم گیری می شود :
اگر χ 2 محاسبه شود ≥ χ 2 جدول بندی شده → مدل رد می شود
اگر χ 2 محاسبه شود ≤ χ 2 جدول بندی شده → مدل پذیرفته می شود
هر چه مقدار χ 2 بیشتر باشد، رابطه بین متغیر وابسته و متغیر مستقل معنادارتر است.
نشانههای کیفیت تناسب بر اساس مقادیر آزمون فرضیه والد در مدلهای مختلف است. از آزمون والد برای آزمون فرضیه صفر استفاده می شود که پارامتر β j تخمین زده شده برابر با صفر است.
دو عنصر آماری هنگام تجزیه و تحلیل کیفیت برازش هر مدل تولید شده در نظر گرفته شد: 1) معیار اطلاعات شبه احتمال (QIC) و 2) آزمون باقیمانده انباشته (نقشه CURE).
QIC اصلاحی از معیار اطلاعات Akaike (AIC) در رویه GEE است. مقایسه مدلها با استفاده از لگاریتم حداکثر درستنمایی انجام میشود که بهترین مطابقت را با دادههای مشاهدهشده دارد. QIC با معادله (2) بیان می شود.
QIC = 2 ∗ LIK + 2 KQIC=2∗LIK+2K(2)
که در آن: LIK = ثبت احتمال حداکثر شده، k = تعداد ضرایب رگرسیون، و r = تعداد پارامترهای برآورد شده برای محاسبه E i است.
با توجه به این معیار، بهترین مدل مدلی است که کمترین مقدار QIC را داشته باشد. چندین معیار اطلاعاتی دیگر در ابزارهای آمار فضایی موجود است، که بیشتر آنها تغییراتی از QIC هستند، با تغییراتی در روش جریمه کردن پارامترها یا مشاهدات.
روش CURE برای ارزیابی کیفیت برازش بر اساس مطالعه باقیمانده ها است، یعنی تفاوت بین تعداد تصادفات مشاهده شده در یک مکان و مقدار مورد انتظار برای همان مکان در همان دوره زمانی، با توجه به اینکه باقیمانده ها فرض می کنند توزیع غیر طبیعی نمودار CURE Plot برای بررسی باقیمانده ها پس از تخمین پارامترهای مدل و ارزیابی اینکه آیا تابع انتخاب شده با هر متغیر توضیحی در کل محدوده مقادیر نشان داده شده مطابقت دارد یا خیر، استفاده می شود. روند باقیمانده ها با توجه به AADT (یا سایر متغیرها) را می توان در رابطه با واریانس ارزیابی کرد. انحراف رو به بالا یا پایین نشانه این است که مدل به ترتیب تصادفات کمتر یا بیشتر از شمارش شده را پیش بینی می کند.ρ *) برای باقیمانده های تجمعی.
برای اعتبارسنجی مدل از ریشه میانگین مربعات خطا (RMSE) استفاده شد. RMSE معمولاً برای بیان دقت نتایج عددی با این مزیت استفاده میشود که مقادیر خطا را در ابعادی مشابه با متغیر تحلیل شده ارائه میکند.
4. نتایج
4.1. منطقه مطالعه
محدوده تجزیه و تحلیل بزرگراه BR 232، بین کیلومتر 141 و کیلومتر 356، عرض های جغرافیایی 8˚02’30” S و 8˚39’27” S و طول جغرافیایی 36˚11’56” W و 37˚48’57” W بود. ( شکل 1 ). امتداد 255 کیلومتری بزرگراه فدرال روستایی از میان شهرداریهای سائو کائتانو، پسکوئیرا، آرکوورده، کروزیرو دو نوردسته و کوستودیا در شمال شرقی برزیل میگذرد.
اطلاعات از پایگاه دادههای گشت بزرگراه فدرال برای سالهای بین سالهای 2007 و 2016، که حاوی سوابق حادثه و گزارشهای پلیس است، و همچنین از پایگاه بزرگراه DNIT، پایگاه نقشهبرداری OSM، و مدل زمین دیجیتال ارائهشده توسط Condepe/ به دست آمد. آژانس فیدم.
مقادیر AADT در نظر گرفته شده برای سالهای 2014، 2015 و 2016 از وزارت زیرساخت حملونقل ملی (DNIT)، شامل تعداد ترافیک حجمی و طبقهبندیشده بهدست آمد. برای سال های گذشته (2007 تا 2013)، از آنجایی که هیچ نقطه جمع آوری فعالی در منطقه مورد مطالعه وجود نداشت، AADT از گزارش سالانه ANTT (2015) در نظر گرفته شد، همانطور که در جدول 1 نشان داده شده است.
استاندارد نبودن گزارش های پلیس و عدم دقت در پر کردن آنها باعث کاهش اعتبار و مفید بودن آنها برای مطالعه می شود. بنابراین باید تحلیلی برای شناسایی هرگونه غیبت یا تناقض در اطلاعات ثبت شده در گزارش ها انجام می شد. جداولی که شامل تمام اطلاعات لازم مانند مکان، نوع و تاریخ حادثه نبود، از نمونه حذف شدند.
پایگاه داده ای ایجاد شد که اطلاعات دقیقی را در مورد عرض خطوط، شرایط شانه، انحنای جاده، درجه و AADT در امتداد 215 کیلومتری گروه بندی می کرد.

شکل 1 . بزرگراه BR 232، بین کیلومتر 141 و کیلومتر 356.
بزرگراه روستایی در پرنامبوکو این با استفاده از ابزارهای پردازش جغرافیایی برای استخراج ویژگیهای مرتبط از شبکه جادهها، ویژگیهای فضایی محیط اطراف و جریان ترافیک به دست آمد که سپس با پایگاه داده تصادف ایجاد شده برای مطالعه ترکیب شدند. داده های تصادفات موجود در پایگاه داده شامل تمام تصادفات ثبت شده در یک دوره 10 ساله، از ژانویه 2007 تا دسامبر 2016 است.
4.2. تقسیم بندی همگن
دو گروه از متغیرها، یکی مربوط به متغیرهای مکانی (گروه 1) و دیگری مربوط به هندسه راه (گروه 2) در نظر گرفته شد. متغیرهای مکانی در نظر گرفته شده عبارتند از: علت حادثه، گروه سنی، نوع حادثه، روز هفته، زمان، طرح، وضعیت، علت 1 (با قربانیان مجروح، بدون قربانی، با قربانیان فوتی، نادیده گرفته شده)، نوع جاده، کاربری زمین، دوره روز (تمام روز، تمام شب). متغیرهای گروه دوم عبارتند از: عرض خط، عرض و نوع شانه، طول قطعه، درجه و فوق ارتفاع، شعاع منحنی و طول منحنی، از جمله طول مارپیچ انتقال، در صورت وجود.
برای بخش بندی 1 ( شکل 2 )، نتایج با استفاده از نمونه ای از بخش های جاده همگن، که حداقل طول 160 متر انتخاب شده بودند، تأیید شد. بر اساس این معیار از 253 مقطع مستقیم شناسایی شده، 200 قطعه انتخاب شد. برای کشش های منحنی، 88 مورد از مجموع 226 مورد انتخاب شدند که معیار حداقل شعاع 100 متر را دارند. به دلیل این کاهش قابل توجه در تعداد منحنی ها، آزمایش ها نیز با استفاده از حداقل شعاع 50 متر، در مجموع 115 کشش انجام شد.
برای تقسیم بندی 2، تغییری از تقسیم بندی HSM همگن HSM، کشش های همگن مجاور منحنی ها تا فاصله حداقل 50 متری از نقاط شروع و پایان منحنی حذف شدند ( شکل 3 ). این حذف جزئی از بخشهای مجاور منحنیها برای جداسازی تأثیرات منحنیها هنگام در نظر گرفتن تاریخچه تصادف برای روش کالیبراسیون انجام شد. لازم است تصادفات را به تصادفات روی پیچ ها و مقاطع مستقیم تفکیک کرد، اما این تفکیک به صورت تقریبی بر اساس کیلومتری که تصادف رخ داده انجام می شود. تصادفات رخ داده در این مناطق به مقاطع منحنی مربوطه اضافه شد.
برای تقسیمبندی همگن با در نظر گرفتن معیارهای فضایی، گروهبندی بر اساس بخشهای فرعی بر اساس نوع سطح راه، کاربری زمین، نوع زمین، طرح راه و درجه انجام شد. از طریق ابزار Query Builder، مشاوره

شکل 2 . جدول قطعات HSM همگن.

شکل 3 . جدول بخش های پیوسته به منحنی تائو فاصله 50 متر.
برای شناسایی حوادث مرتبط با هر گروه و محل وقوع آنها، در کل دوره تجزیه و تحلیل ساخته شد.
در ابتدا، برای اطمینان از اینکه تقسیم بندی بر اساس ویژگی های مکانی بدون در نظر گرفتن فراوانی تصادف انجام شده است، یک شاخص ریسک ایجاد شد. با توجه به ویژگیهایی که اغلب در ادبیات ارائه میشوند و محدوده مربوط به آنها، مقادیری از 1 تا 3 ایجاد شد که در آن 1 خطر کم، 2 خطر متوسط و 3 خطر بالا برای حوادث است ( جدول 2 ). جدول 3 مقادیر تخمینی شاخص ریسک را برای متغیرهای دسته بندی روز هفته و گروه سنی نشان می دهد.
شاخص ریسک از 3 تا 8 متغیر است که 3 کمترین ریسک و 8 بیشترین ریسک را دارند. به عنوان مثال، کشش به طول 1880 متر با AADT 4800 vpd در شیب رو به پایین دارای شاخص ریسک 5 است، در حالی که کشش با AADT 4800 vpd در یک شیب رو به پایین با منحنی شعاع 500 متر دارای شاخص ریسک 7 است. با توجه به ترکیب ارائه شده در جدول 4 .
تکنیک تخمین هسته، بر اساس شاخص، به منظور شناسایی مناطق با ویژگی های فضایی مشابه، همانطور که در شکل 4 نشان داده شده است، استفاده شد . چه زمانی

شکل 4 . جدول قطعات همگن با در نظر گرفتن معیارهای مکانی.
با تلاقی متغیرهای مکانی با متغیرهای هندسی، به عنوان مثال، متغیرهای “طرح جاده” و “درجه”، تکنیک تخمین هسته نیز برای شناسایی و تأیید تفاوت در غلظت بین طرح راه و وجود یک صعود یا نزول استفاده شد. شیب. این روش برای ترکیب های مختلف خوشه ها تکرار شد.
پس از تقسیم بندی امتدادهای همگن، تصادفات متناسب با بخش های انتخابی بزرگراه با آنها همراه شد.
با ساختار پایگاه داده به این صورت، امکان مقایسه توزیع شدت تصادف و فراوانی تصادف در کشش های منحنی، با توجه به شیب زمین وجود داشت. نتایج نشان می دهد که تقریباً 68 درصد تصادفات در کشش های مستقیم و 32 درصد در کشش های منحنی رخ می دهد، اما توجه به شدت تصادف جلب می شود. از تصادفات رخ داده در مسیرهای مستقیم (220)، 29٪ (64) شدید و 9٪ (9) فوتی بوده اند، در حالی که به ترتیب 35٪ (37) و 18٪ (19) برای کشش های منحنی که دارای در مجموع 103 تصادف ( شکل 5). تجزیه و تحلیل همچنین نشان می دهد که تقریباً 41٪ از تصادفات در کشش های منحنی در یک شیب نزولی رخ داده است که 40٪ از کل تصادفات جدی و 19٪ مرگبار بوده است، در حالی که این درصد برای همه موارد در امتداد مستقیم کمتر از 1٪ بود ( شکل 6). ).
4.3. کالیبراسیون مدل پیشنهادی
مدلهای توسعهیافته با استفاده از تکنیک GEE، با فرض خطاهایی با توزیع دوجملهای منفی به دلیل وجود تعداد زیادی مشاهدات با مقدار صفر و بنابراین، پراکندگی بالا کالیبره شدند. در نرم افزار SPSS نسخه 23.0.0، این تجزیه و تحلیل را می توان در رویه های تجزیه و تحلیل >> مدل های خطی تعمیم یافته >> معادلات برآورد تعمیم یافته یافت.
داده های کافی برای ساخت مدلی برای مقادیر متغیر عرض شانه و حجم ترافیک وجود نداشت. عرض خط نیز در سراسر بخش مطالعه ثابت بود. اگرچه یک نقطه واحد در کل بخش مورد مطالعه وجود داشت که در آن حجم ترافیک شمارش می شد، AADT به دلیل اهمیت آن در مدل در نظر گرفته شد.

شکل 5 . توزیع تصادفات در مقاطع و منحنی های مستقیم از سال 2007 تا 2016.
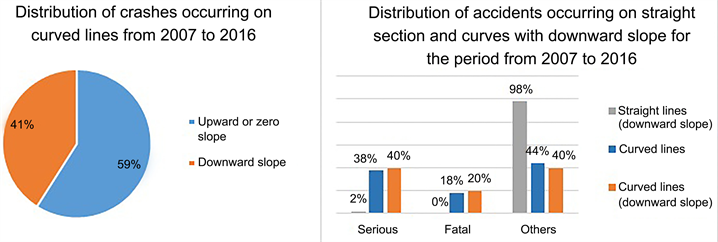
شکل 6 . توزیع تصادفات رخ داده در مقطع مستقیم و منحنی با شیب نزولی برای دوره 1386 تا 1395.
در ادبیات تجمیع شده است. سپس دو مدل تنظیم شده با سه تغییر مربوط به بخشهای همگن تهیه شد. (1، 2، 3) برای هر مدل. آن ها هستند:
مدل 1 – متغیر وابسته (فرکانس). گروه سنی، روز هفته، AADT (متغیرهای طبقه بندی)؛ شعاع، درجه، طول (متغیرهای کمکی)؛ عرض خط و عرض شانه (فقط برای تقسیم بندی نوع 1 و 2).
مدل 2 – متغیر وابسته (فرکانس). درجه (متغیر طبقه بندی)؛ شعاع، طول، AADT (متغیرهای کمکی)؛ عرض خط و عرض شانه (فقط برای تقسیم بندی نوع 1 و 2).
برای ارزیابی اثر ترافیک ثابت، دو تغییر از مدلهای 1 و 2، به نامهای مدل 3 و 4، با استفاده از همان بخشبندیهای 1، 2 و 3 در نظر گرفته شد که AADT به عنوان متغیر افست گنجانده شده است. اصطلاحات مدل به صورت فاکتوری با هم ترکیب شدند تا همه ترکیبات بین متغیرها قابل ارزیابی باشند. خلاصه ای از مدل های برآورد شده در جدول 5 توضیح داده شده است.
معنیداری ضرایب پارامتر و انحراف مشاهده شد تا بررسی شود که آیا متغیرها برای مدل معنیدار هستند یا خیر. با QIC، ساختارهای همبستگی مورد ارزیابی قرار گرفت و بهترین مدل جهانی با طرح CURE انتخاب شد. سطح معنی داری 5 درصد استفاده شد، به این معنی که
متغیرهایی با p-value بیشتر از 5% معنی دار در نظر گرفته نشدند. در تجزیه و تحلیل انحراف از توزیع کای دو با معنی داری 5 درصد استفاده شد. بنابراین، اگر سهم متغیر در انحراف کمتر از 1.96 بود، متغیر نباید در مدل گنجانده شود.
هنگام اضافه کردن متغیرهای عرض خط و عرض شانه، هیچ یک از مدل ها نتایج رضایت بخشی به دست نیاوردند. در هر دو مورد مدل آزمایش شده، پارامتر مرتبط با متغیرهای عرض خط و عرض شانه از نظر آماری برای α = 5٪ معنی دار نبود.
این نتیجه ممکن است به مقادیر ثابت برای همه عناصر نمونه مرتبط باشد. نتایج کالیبراسیون برای مدل های 1، 2، 3 و 4 در جداول 6-9 نشان داده شده است. تفاوت در علائم ضرایب ممکن است بسته به تقسیم بندی، تأثیر متضاد متغیر را بر تعداد مورد انتظار تصادفات برآورد شده توسط مدل نشان دهد.
انتخاب ماتریس همبستگی کاری نشان دهنده وابستگی درون فردی است. بهترین ساختار را باید با استفاده از کمترین QIC به عنوان معیار جستجو کرد. مقادیر QIC که با تنظیم مدل های 1، 2، 3 و 4 با سایر ماتریس های همبستگی یافت می شوند در جداول 10-13 نشان داده شده است.
می توان مشاهده کرد که، با توجه به پارامتر QIC، ساختار همبستگی مبادله ای، ساختاری بود که بهترین تناسب را با داده های طولی برای مدل های تولید شده داشت.
با این ساختار همبستگی می توان گفت که همبستگی بین هر دو مشاهده در یک گروه ثابت است. بخش تنظیم شده 3 بهترین نتیجه را برای همه مدل ها ارائه کرد، با این حال، اکثر پارامترها از نظر آماری معنی دار نبودند (05/0p>).
نمودارهای CURE Plot مدل ها در شکل 7 و شکل 8 ارائه شده است. برای مدلهای 1 و 2، میتوان مشاهده کرد که منحنی باقیماندههای تجمعی حول 0 نوسان میکند و از حد مجاز بالا و پایین نمیگذرد. برای مدل های 3 و 4، منحنی باقیمانده تجمعی حول 0 نوسان می کند اما از حد بالایی فراتر می رود. بنابراین بهترین مدل پیشبینی تصادف مدل 2 است، زیرا کمترین مقدار QIC (600.30) را ارائه میدهد.
نتایج بهدستآمده از اعتبارسنجی نشان میدهد که بهترین مدل برای پیشگیری از تصادف مدل 2 است، زیرا ریشه میانگین مربعات خطای تنظیم مدل (ΔRMSE) با مقدار 0.082- نزدیکترین به صفر است ( جدول 14 ).
شایان ذکر است که پارامترهای بدست آمده برای متغیرهای روز هفته و گروه سنی با مقادیر موجود در شبیه سازی برای انتخاب متغیر مطابقت دارد. با در نظر گرفتن گروه سنی افراد بالای 50 سال به عنوان مرجع، جوانان بین 18 تا 30 سال 22.7 درصد بیشتر در معرض تصادفات مرگبار هستند در حالی که بزرگسالان بین 30 تا 50 سال 34 درصد کمتر در معرض تصادفات هستند. در روزهای آخر هفته، احتمال وقوع تصادفات 67 درصد بیشتر از روزهای هفته است.

شکل 7 . طرح CURE برای مدل های توسعه یافته (1 و 2). (الف) مدل 1؛ (ب) مدل 2.

شکل 8 . طرح CURE برای مدل های توسعه یافته (3 و 4). (الف) مدل 3; (ب) مدل 4.
برای بخش 1، بر اساس HSM، متغیرهای انتخاب شده دارای خطاهای استاندارد بزرگتری نسبت به سایر روش های تقسیم بندی هستند. این احتمالاً به این دلیل است که، در بزرگراهها، بخشهای همگن تنها در تقاطعها تغییر میکنند و بخشهای بسیار طولانی را تولید میکنند، جایی که تعداد زیادی از آنها اسیدیته صفر دارند، و با تغییرات قابلتوجهی در بخشهای جداگانه در سایر متغیرها که نمیتوان به اندازه کافی مدلسازی کرد.
برای مدل تخمین زده شده برای بخش 2، که شامل 50 متر جاده در هر انتهای یک منحنی است، نتایج نیز قابل توجه بود. با این حال، آنها تمایل دارند تعداد تصادفات را برای مقادیر AADT پایین و تصادفات را برای مقادیر بالاتر AADT دست کم برآورد کنند.
در ابتدا، تقسیم بندی که بدترین نتایج را در تعداد متغیرهایی که می تواند در مدل گنجانده شود، بخش 3 بود که در آن همه متغیرها برای هر بخش توضیحی هستند. بنابراین، دستههای متغیر بر اساس محدودههای مقادیر ثابت برای بهبود قدرت آماری مدل ایجاد شدند. این دسته ها با تلاش برای به دست آوردن بهترین برازش مدل و اهمیت آماری برای برآورد پارامترهای اصلی تعریف شدند.
در نهایت، مدل GEE به منظور پیش بینی وقوع حوادث در یک بخش با در نظر گرفتن AADT، شعاع منحنی، طول قطعه و درجه تعریف شد، همانطور که در رابطه (3) نشان داده شده است:
μمن=ه(β0+β1AADT +β2R +β3گرید +β4L + ε )μi=e(β0+β1AADT+β2R+β3Greide+β4L+ε)(3)
جایی که: μمنμi= فراوانی تصادفات مورد انتظار در سال. β0β0= رهگیری β1 ، β2 ، β3 و β4 = پارامترها . _ _ R = شعاع منحنی (m)، L = طول قطعه (m)، درجه = درجه (منفی، مثبت یا صفر)، و ε = عبارت خطا.
جدول 15 اثرات مدل همه متغیرهای مستقل را نشان می دهد. دسته های متغیر مقادیر مطلق ندارند، اما مقدار تخمین پارامتر را تعریف می کنند ( β n در ستون 3). توان پارامتر برآورد شده (و β n در ستون 5) را می توان به عنوان شکلی از ارزش ریسک نسبی برای هر دسته متغیر اعلام شده تفسیر کرد. این بدان معناست که با توجه به ثابت نگه داشتن سایر متغیرهای مدل، می توان بر اساس هر یک از متغیرها، تفاسیر زیر را انجام داد.
این مطالعه نشان داد که منحنیهای با شعاع کمتر یا مساوی 600 متر نسبت به منحنیهای با شعاع بیش از 2200 متر (نسبتاً مستقیم) خطر تصادف 3.2 برابر بیشتر دارند. همچنین نشان داد که بخش هایی با شیب رو به پایین 1.6 برابر بیشتر از سطوح شیب دار یا هموار جاده ها، خطر تصادف دارند. امتداد مستقیم بیش از 1000 متر در یک شیب رو به پایین و به دنبال آن یک منحنی، خطر تصادف 2.2 برابر بیشتر است.
معادله (3) برای همه دسته های متغیر در مدل حل شد. میانگین مقدار نرخ تصادفات با قربانیان در مقاطع منحنی در هر کیلومتر پایین بود: 0.048. این نشان دهنده تعداد کم تصادفات در این مناطق است. با این حال، علل ممکن است مربوط به جریان کم ترافیک در راه های روستایی، وجود یک نقطه واحد که داده های ترافیکی در بخش مورد مطالعه جمع آوری می شود و یا حتی گزارش کم این نوع تصادفات باشد. بنابراین، ارائه نتایج مدل از ترکیب ویژگیهای جاده، از جمله شعاع پیچها، اهمیت بیشتری داشت. برای میانگین نمونه 0.048 تصادف در هر کیلومتر، مقدار 1.0 تعریف شد.
برای تجسم آسانتر داده ها، یک کد رنگی اعمال شد: سبز نشان دهنده مقدار مورد انتظار برای تصادفات با قربانیان زیر میانگین نمونه (کمتر از 1.0) است، زرد نشان دهنده سناریوهایی با خطر بین میانگین و دو برابر میانگین (بین 1 و 2) است. و نارنجی سناریوهایی را نشان می دهد که در آن ریسک دو تا سه برابر مقدار متوسط (بین 2 تا 3) است. رنگ قرمز نشان دهنده یک وضعیت خطر شدید است که در آن مقدار تصادف پیش بینی شده بیش از سه برابر میانگین نمونه بود. جدول 16 تغییرات سطح ریسک مورد انتظار برای حوادث در منحنی ها را بر اساس مقدار پیش بینی شده نشان می دهد.
از این نتایج می توان نتیجه گرفت که شعاع هایی بین 600 تا 1500 متر است
باید در تمام سناریوها برای طراحی جاده های جدید به منظور کاهش فراوانی تصادفات در پیچ ها ترجیح داده شود. نتایج همچنین نشان میدهد که کششهای طولانی با شیب رو به پایین و به دنبال آن منحنیهایی با شعاع کمتر از 600 متر، بیشترین خطر را برای تصادفات دارند. اگر بزرگراه هایی با شعاع کمتر از 600 متر به بزرگراه هایی با شعاع بیشتر از 600 متر تبدیل شوند، تصادفات با قربانیان در پیچ ها حدود 18 درصد کاهش می یابد. جاده هایی با شعاع کمتر از 600 متر در شیب رو به پایین 27 درصد کاهش خواهند داشت. با نتایج مدل و اعداد تصادفات تاریخی برای بخشهای مورد تجزیه و تحلیل، روش کالیبراسیون با تقسیم ارزش کل واقعی بر مقدار تخمینی محاسبهشده انجام شد. مقدار به دست آمده برای بخش 1 2.35 و برای بخش 3 1.75 بود.
5. نتیجه گیری ها
ساختار پایگاه داده با یک GIS بر استفاده از داده های تصادفات، از طریق انواع تصادفات رخ داده، نرخ تصادفات، شاخص های تصادف، وضعیت افراد درگیر، شرایط آب و هوایی، وسایل نقلیه و با توجه به دوره مورد اشاره متمرکز شده است. . ساختار پایگاه داده به دنبال تجسم پارامترهای هندسی، عمدتاً پارامترهای منحنی ها، نه تنها از طریق نقشه هایی است که همیشه واقعیت ساخته شده را منعکس نمی کنند، بلکه از طریق یک فرآیند نیمه خودکار پیشنهاد شده در این مطالعه با ترکیب چندین پایگاه داده فعلی و موجود. تکنیک های ژئوپردازش، مانند کاهش تعداد بیش از حد رئوس، بازسازی عناصر منحنی، و صاف کردن بخش ها، برای بهبود کیفیت هندسی پایه جاده ضروری بودند.
نتایج در هنگام مقایسه تقسیم بندی همگن بین رویکردهای نقشه هسته و روش های آماری سازگار هستند. این نتیجه قابل انتظار بود، زیرا هر دو روش با میانگین شدت هر حادثه کار می کنند. کشف این که تقسیمبندی همگن بر اساس تخمینگر هسته نتایج خوبی ارائه میدهد، نشان میدهد که میتوان سلسله مراتبی ایجاد کرد و ویژگیهای هندسی را ایجاد کرد که بیشترین تأثیر را بر وقوع و شدت تصادفات رانندگی در بزرگراههای تک خطه روستایی برزیل دارد.
این مدل می تواند برای ارائه اطلاعاتی در مورد بازنگری های بعدی دستورالعمل های انتخاب پارامتر منحنی، بر اساس پارامترهای اصلی طراحی جاده موجود در پایگاه داده برزیل، استفاده شود. از نتایج مدلسازی میتوان برای انتخاب منحنی، بر اساس کاهش خطر تصادف استفاده کرد.
این مطالعه شاخصهای روشنی را برای پارامترهای طراحی بزرگراه تولید کرد که بر عملکرد ایمنی بزرگراههای روستایی تأثیر میگذارد. نماهای تخمین پارامترها در p ≤ 0.1 از نظر آماری معنی دار و اکثریت در p ≤ 0.05 معنی دار بود. اگرچه نرخ تصادف در هر کیلومتر در منحنی ها کم بود، اما این مدل شدت تصادفات را در این کشش ها برجسته می کند. به این نتیجه رسیدیم که شعاع های بین 600 تا 1500 متر باید در تمام سناریوها برای طراحی جاده های جدید ترجیح داده شود تا از فراوانی تصادفات کاسته شود.
انجام این مطالعه این امکان را فراهم کرد تا تأیید شود که جاده های روستایی در ایالت پرنامبوکو هنوز 3.3 برابر بیشتر از جاده های شهری در معرض تصادفات با تلفات هستند. طبق بازرسی بصری هنگام پر کردن گزارشهای تصادف، تقریباً 58٪ از تصادفات جادهای منجر به مرگ در پیچهای افقی رخ میدهد، به این معنی که تعداد واقعی ممکن است بیشتر باشد. تجزیه و تحلیل نشان دهنده یک گام مهم به سمت بازنگری دستورالعمل های طراحی منحنی است. یک رویکرد به طراحی منحنی ها بر اساس مدیریت نتایج تصادف ممکن است شامل تعریف افزایش در مقادیر شعاع و در بخش های انتقال برای رسیدن به هدف ایمنی تصادف برای منحنی ها باشد. به عنوان مطالعه آینده، منطقه تجزیه و تحلیل قرار است گسترش یابد و روش به سایر مناطق با ویژگی های مشابه شمال شرقی برزیل اعمال شود.












بدون دیدگاه