برای انجام پرس و جوهای توپولوژیکی بر روی داده های جغرافیایی، لازم است ابتدا یک روش دسترسی توپولوژیکی (TOAM) ایجاد شود. با استفاده از این واقعیت که هر رابطه (تصادفی یا باینری دیگر) توپولوژی تولید می کند که شامل استفاده متداول از توپولوژی برای داده های مکانی یا مکانی-زمانی است، در اینجا، چنین TOAM بر اساس مفهوم قبلاً اعمال شده از Property Graph که به منظور مدیریت اطلاعات توپولوژیکی در داده ها از هر بعد، چه وابسته به زمان باشد یا نباشد. در واقع، داشتن یک TOAM برای پرس و جو در چنین نموداری و همچنین داشتن داده هایی که از نظر توپولوژیکی به معنای خاصی سازگار هستند، ضروری است. در حالی که ارائه سازگاری توپولوژیکی دغدغه کار قبلی بود، در اینجا، هدف توسعه روشی است که بر اساس این مفهوم است. در پایان، یک آزمون تجربی از این رویکرد بر روی یک مدل شهر کوچک انجام شده است. مشخص شد که مشخصه اویلر، یک متغیر توپولوژیکی شناخته شده، می تواند برای اعتبارسنجی داده های اولیه مفید باشد. عملاً، این کار نظری حاضر با توجه به کاربردهای نوآورانه آینده، به عنوان مثال، در زمینه شبیهسازی مدل شهر، از جمله پردازش جغرافیایی توزیع شده، ضروری به نظر میرسد.
کلید واژه ها:
توپولوژی هندسی القا شده ; مجتمع های ساده ; الگوریتم های توپولوژیکی ; مدل حجمی ضد آب ; روش دسترسی توپولوژیکی
1. مقدمه
در [ 1 ]، تمایل به روش دسترسی توپولوژیکی در زمینه داده های CityGML بیان شد. اگر توپولوژی و هندسه یک مدل داده مکانی یا مکانی-زمانی جداگانه مورد بررسی قرار گیرد، آنگاه می توان تنها برای مدل توپولوژیکی زیربنایی به جستارهای توپولوژیکی تکیه کرد. وجود یک روش دسترسی خاص که می تواند برای انجام جستجو در مدل توپولوژیکی استفاده شود، این کار را تسهیل می کند. با این حال، روش های دسترسی موجود تاکنون، مانند Octree یا Rدرخت، مربوط به هندسه است و مستلزم تعبیه مدل در فضای اقلیدسی است. روش دسترسی مورد نظر صرفاً از ساختار مرزی توپولوژیکی مدل به منظور یافتن اشیایی که در این نزدیکی به معنای این رابطه بروز هستند استفاده می کند. اجسام دیگر، حتی اگر از نظر هندسی نزدیک باشند، می توانند بدون هیچ آسیبی نادیده گرفته شوند. این رویکرد از این فرض بهره برداری می کند که مدل توپولوژیکی و هندسی از نظر توپولوژیکی سازگار هستند، به عنوان مثال، هیچ دو جسم اتمی همپوشانی ندارند.
این ایده در تعریف قبلی ما از سازگاری توپولوژیکی که در زیر بررسی شده است، منعکس شده است. برای درک اهمیت مفهوم سازگاری توپولوژیکی، اکنون ابتدا تعریف آن و همچنین ارتباط آن با مفهوم توپولوژی داده های جغرافیایی و به طور کلی را توضیح می دهیم. وضعیتی مانند شکل 1 (سمت چپ) از نظر توپولوژیکی ناسازگار است (به معنای ما)، زیرا مدل توپولوژیکی تنها دو بخش ناهمگون را می بیند. x ←ℓ1→ yایکس←ℓ1→�و یک ←ℓ2→ بآ←ℓ2→ب، در حالی که مدل هندسی تقاطع خط عمودی را نیز می بیند ℓ1ℓ1و خط افقی ℓ2ℓ2. فضای همپوشانی در شکل 1 (سمت راست) از نظر توپولوژیکی از طریق معرفی جسم اضافی ∘ در مرز یکسان است. ℓ1ℓ1و ℓ2ℓ2. نمودار بروز فضای همپوشانی در شکل 2 نشان داده شده است .
این فضا از نظر توپولوژیکی به هم متصل است، و ما میتوانیم به عنوان مثال ببینیم که خطوط ℓ1ℓ1و ℓ2ℓ2با توجه به رابطه بروز نزدیک هستند ، در حالی که در مدل توپولوژیکی اصلی، اینطور نیستند. توجه کنید که در این مثال، فضای همپوشانی یک نمودار فوق العاده است که لبه های بیش از حد آن است ℓ1ℓ1و ℓ2ℓ2دارای رئوس مرزی x ، y، ∘ایکس،�،∘و a ، b ، ∘آ،ب،∘، به ترتیب.
کلی ترین شکل یک مدل توپولوژیک محدود، فضای توپولوژیک محدود X است. توپولوژی این فضاها با بسته شدن بازتابی و انتقالی یک رابطه باینری [ 2 ] ایجاد می شود. یک مورد خاص مهم زمانی که رابطه ضد متقارن باشد، داده می شود. در آن صورت فضای توپولوژیک محدود a نامیده می شود تی0تی0-space، و توپولوژی با نظم جزئی ≤ تولید می شود. یک تفسیر راحت از ≤ یک رابطه بروز است. با این حال، تعابیر دیگری نیز به کار می رود. در هر صورت، a ≤ bآ≤ببه این معنی است که a در بسته شدن b [ 2 ] قرار دارد.
به عنوان مثال، در شکل 3 ، مرز A از مستطیل بیرونی، مثلث داخلی و سوراخ P تشکیل شده است. این می تواند، به عنوان مثال، یک موقعیت نقشه برداری باشد که در آن یک منطقه از یک منطقه شهری بزرگ (مثلث)، یک مرکز کوچکتر ( P ) و بقیه ( A ) تشکیل شده است.
فرض کنید برخی از داده های مکانی-زمانی به صورت متناهی مدل شده اند تی0تی0-فضای X با استفاده از رابطه بروز ≤. نمودار هاس H ( X)�(�)چیزی جز نمودار بروز نیست: مجموعه راس آن X و یک یال است ( x ، y)(�,�)دقیقاً در چه زمانی داده می شود x < y�<�. علاوه بر این، x < z≤ y�<�≤�دلالت دارد z= y�=�. هدف از نمودار Hasse داشتن یک مدل حداقلی برای توپولوژی است، زیرا یک یال نشان دهنده یک رابطه مستقیم است. نتیجه الکساندروف [ 2 ] بیان می کند که هر ترتیب جزئی از یک توپولوژی می آید، حتی اگر همیشه در نگاه اول به طور مستقیم قابل مشاهده نباشد. از آنجایی که روابط مورد استفاده در این مقاله جهت دار و غیر چرخه ای هستند، اغلب می توان آنها را به صورت حاشیه ای تفسیر کرد ، به عنوان مثال، دارای یک معنایی است که توپولوژی زیرین را از دیدگاه کاربر نشان می دهد. بعداً، ما مشاهدات الکساندروف را برای روابطی که معمولاً توسط کاربران توپولوژیکی تلقی نمیشوند، اعمال میکنیم تا بتوانیم رمزگذاری راحت آنها را در نمودارهای Hasse داشته باشیم. توجه داشته باشید که هر گراف جهت دار غیر چرخه ای را می توان به ترتیب جزئی گسترش داد و همین امر را القا کرد تی0�0توپولوژی، و نمودار Hasse نمایش حداقلی منحصر به فرد این توپولوژی است. [ 3 ]. در مورد این مقاله، توپولوژی (یا به عبارت دیگر، نمودار هاس) به نوبه خود روابط معینی را بین ژئواشیاء با هر بعد نشان می دهد.
اگر یک مدل داده به صراحت توپولوژی زیربنایی را مدل کند، باید مراقب بود که هیچ تناقضی با هندسه زیرین وجود نداشته باشد. این بدان معنی است که در واقع دو مدل وجود دارد: مدل توپولوژیکی انتزاعی X با نظم جزئی ≤ و مدل هندسی. حال، مدل هندسی دارای یک مدل توپولوژیکی مشتق شده است، و سازگاری توپولوژیکی در صورتی و تنها در صورتی ارائه میشود که آن دو مدل توپولوژیکی بر هم منطبق باشند. در غیر این صورت، یک ناهماهنگی توپولوژیکی مانند آنچه در شکل 1 در بالا بحث شد، وجود خواهد داشت.
به منظور دستیابی به سازگاری توپولوژیکی، یک پوشش را می توان با محاسبه تمام تقاطعات اجسام اتمی، مانند [ 4 ] به دست آورد.
واضح است که اگر قرار باشد جستجو بر روی یک مدل توپولوژیکی انجام شود، صحت نتیجه تضمین می شود اگر و تنها در صورتی که مدل از نظر توپولوژیکی سازگار باشد (به شرط درست بودن هندسه). از این رو، روش دسترسی توپولوژیکی (TOAM) سازگاری توپولوژیکی یک مدل داده را فرض میکند. در واقعیت، مسائل هندسه محاسباتی محدودیتهایی را بر امکان یافتن و ترمیم صحیح تمام ناسازگاریهای توپولوژیکی قبل از فراخوانی TOAM ایجاد میکند.
دو جامد نه لزوما محدب را فرض کنید، که به صورت چند وجهی به صورت سه بعدی مدلسازی شدهاند و مثلثهای مرزی زیادی بهعنوان نمایشهای مرزی فضایی (BREP) جامدات، که در چند نقطه یکدیگر را لمس میکنند، مدلسازی شدهاند. پرس و جو توپولوژیک برای یافتن این نقاط است. هر روش دسترسی فضایی ( SAM ) مانند Octree [ 5 ]، R -tree [ 6 ] یا R *-tree [ 7 ] می تواند برای حل این پرس و جو استفاده شود.
روش SAM مراحل زیر را طی می کند:
- 1
-
یک SAM برای هر نقطه BREP جامد A ایجاد کنید.
- 2
-
برای هر مثلث مرزی b از جامد B ، از SAM برای بازیابی تمام نقاط BREP C از A که جعبه مرزی b را قطع می کنند، استفاده کنید.
- 3
-
برای هر نقطه BREP c از C ، بررسی کنید که آیا b حاوی c است (درست: به مجموعه نتیجه اضافه کنید).
- 4
-
آخرین مراحل را تکرار کنید تا تمام نقاط BREP جامد B را پیدا کنید .
برای محاسبه پیچیدگی این روش، فرض میکنیم که مرحله اول یک مرحله پیش پردازش است و جزء پیچیدگی محسوب نمیشود. به عنوان مثال، کارایی جستجوی روش R- tree به تقسیم بندی درخت R بستگی دارد که به طور متوسط در O(ورود به سیستممnآ)�(log���)، که در آن M نشان دهنده حداکثر تعداد ورودی در هر گره درخت R وnآ��تعداد نقاط BREP جامد A را نشان می دهد . بدترین حالت به O(nآ)�(��)برای یک جستجو از آنجایی که هر مثلث مرزی جامد B باید بررسی شود، پیچیدگی به آن گسترش می یابد O(nبورود به سیستممnآ)�(��log���)، جایی که nب��تعداد مثلث های مرزی را نشان می دهد.
حال، دو جامد متحرک و شکلگیر نه لزوما محدب را فرض کنید، که بهعنوان چند وجهی توسط یک مدل عکس فوری مدلسازی شدهاند برای چند مرحله زمانی در فضای مکانی-زمانی با مثلثهای زیادی بهعنوان نمایش مرز فضایی جامدات در هر مرحله زمانی، که در چند نقطه BREP یکدیگر را لمس میکنند. مراحل زمانی مشخص ناشناخته پرس و جو توپولوژیکی یافتن این نقاط BREP است.
از نظر تئوری، آخرین شبه الگوریتم باید برای هر مرحله زمانی از بازه همپوشانی زمانی جامدات متحرک و شکلگیری اجرا شود تا هر نقطه تماسی را پیدا کند. بنابراین، این روش یک عامل اضافه می کند nج��به پیچیدگی (هنگام استفاده از درخت R ) به عنوان O(nجnبورود به سیستممnآ)�(����log���)برای تعداد مراحل زمانی که باید بررسی شوند. بدیهی است که دقت نوع داده مورد استفاده برای مختصات زمانی تأثیر قابل توجهی بر پیچیدگی دارد. از سوی دیگر، اگر تغییر فضایی به اندازه کافی کوچک باشد، وضعیت فضایی ممکن است برای چند مرحله زمانی برابر باشد. تحقیقات بیشتری برای مقابله موثرتر با این وضعیت نیاز است تا با تکرار در هر زمان ممکن به دست آید.
روش دیگر شامل چهار وجهیسازی وجههای مرزی متحرک و شکلگیری هر دو جامد است. چهاروجهی ها نمایش مرزهای مکانی – زمانی جامدات در فضای مکانی – زمانی هستند. مراحل توصیف شده قبلی را می توان با بررسی تقاطعات برای هر چهار وجهی مرزی یک جامد با نقاط متحرک نمایش مرزی دیگر اعمال کرد. این روش همان پیچیدگی روش SAM را داردO(nبورود به سیستممnآ)�(��log���)، جایی که nآ��تعداد نقاط متحرک BREP جامد A را نشان می دهد که منحنی های فضایی و زمانی هستند و nب��تعداد چهار وجهی های مرزی جامد B را نشان می دهد . با این حال، SAM به یک روش دسترسی مکانی -زمانی STAM تبدیل میشود و پیچیدگی محاسبه تقاطع منحنیهای مکانی-زمانی و چهار وجهی با پیچیدگی محاسبه تقاطع نقاط و مثلثهای فضایی متفاوت است. با این حال، این مثال تنها دو نوع تقاطع را نشان می دهد، زیرا این دو جامد فقط گاهی اوقات یکدیگر را لمس می کنند. اگر تقاطع یک نقطه باشد، آنگاه جامدات در یک نقطه در یک مرحله زمانی یکدیگر را لمس می کنند. اگر تقاطع منحنی باشد، نقطه تماس در طول زمان و شاید در فضا نیز حرکت می کند. با این حال، تمام تقاطع های احتمالی هر دو نمایش مرز مکانی-زمانی نیازی به محاسبه در این مثال ندارند.
دو مثال آخر نشان می دهد که چگونه توپولوژی هندسی القا شده است. استفاده از روشهای دسترسی فضایی (SAM) یا روشهای دسترسی مکانی-زمانی (STAM) تنها به یک مدل توپولوژی ضمنی دلالت دارد. نقطه ضعف یک مدل توپولوژیکی ضمنی، محاسبه مجدد تقاطع ها و غیره است که در صورت تغییر هندسه های مورد استفاده به روش هایی به دلیل مشکلات هندسه محاسباتی، دقت داده ها و محاسبات (میز شناور یا عدد صحیح) ممکن است به نتایج متفاوتی منجر شود.
راه دیگر تعریف یک مدل توپولوژیکی صریح برای هر نوع هندسه مورد استفاده در علوم جغرافیایی است. توپولوژی هندسی القا شده تنها بخش کوچکی از توپولوژی است، زیرا هر رابطه ای بین برخی موجودیت ها از قبل یک توپولوژی را تعریف می کند [ 2 ]. بنابراین، باید پرسید که چگونه یک مدل توپولوژی عمومی برای اشیاء جغرافیایی ممکن است طراحی شود و چگونه می توان روش های دسترسی توپولوژیکی را برای دسترسی به مدل توپولوژیکی عمومی برای اشیاء جغرافیایی و پاسخگویی کارآمد به پرس و جوهای توپولوژیکی مدل کرد. به سوال اول در [ 4 و 8 ] با کاربرد مناسب نمودارهای خواص پرداخته شده است، در حالی که سوال دوم در این مقاله بررسی شده است.
سهم اصلی این مقاله بر روی نمودارهای ویژگی است که توپولوژی های ممکن را روی اشیاء جغرافیایی مدیریت می کند. این نمودارها با روش های [ 4 و 8 ] به دست می آیند. مشارکت را می توان به شرح زیر خلاصه کرد:
-
استفاده از متغیرهای توپولوژیکی (در اینجا: مشخصه اویلر) در فرآیند اعتبار سنجی (پیش) داده های اولیه.
-
توسعه یک روش دسترسی توپولوژیکی (TOAM) برای پرس و جوی کارآمدتر گره هایی با ویژگی های توپولوژیکی.
-
آزمون تجربی این رویکرد بر روی یک مدل شهر کوچک.
2. کارهای مرتبط
توپولوژی اکنون سابقه طولانی در اطلاعات جغرافیایی و ساختمانی دارد. پس از بررسی برخی از کمک های مهم به موضوع به دست آوردن اطلاعات توپولوژیکی از مدل های داده به طور کلی، ما با جزئیات بیشتر جنبه های توپولوژی مرتبط با کار قبلی و فعلی خود را توضیح خواهیم داد.
از آنجایی که [ 9 ]، توپولوژی مدل های شهر را می توان در یک ساختار داده از نوع xml به نام CityGML ثبت کرد. در حال حاضر یک استاندارد واقعی در اداره پایگاه های داده شهرداری در سراسر جهان است و موضوع مورد توجه بسیاری از تحقیقات است. یک مشکل شناخته شده با CityGML اعتبار توپولوژیکی و هندسی آن است، مهمتر از همه از آنجایی که مدل های واقعی اغلب از ابرهای نقطه ای ارائه می شوند. نویسندگان [ 10 ] یک مدل توپولوژیکی دو سطحی را برای ویژگیهای سه بعدی در CityGML پیشنهاد کردند، که معناشناسی و هندسه را با قوانین سازگاری توپولوژیکی توسعهیافته برای تضمین اعتبار سنجی ابتداییهای CityGML نشان میدهد. قابلیت استفاده کاملا محدود از مکانیسم توپولوژی موجود CityGML به منظور استخراج اطلاعات توپولوژیکی در [ 11].
مدلهای توسعهیافته در [ 12 ، 13 ] اطلاعات هندسی مبتنی بر CityGML را ارائه میکنند و روابط توپولوژیکی فضاهای داخلی- مجاور در این مدل توسط CityGML XLinks نشان داده میشود. این XLinks یک روش صریح برای مدلسازی اتصالات تشکیل میدهند که میتواند با اتصالات احتمالی زیربنایی بین چند ضلعیهای مدل در تضاد باشد. اتصالات اخیر از طریق محاسبات هندسه محاسباتی آشکار می شوند.
در دنیای BIM، تحقیقات اخیر در مورد بازیابی اطلاعات در زمینه شهرهای هوشمند، و همچنین تحقیقاتی که بر مدلهای شبیهسازی توانمند تمرکز دارد، وجود دارد. همه اینها از توپولوژی زیربنایی استفاده می کند، مثلاً [ 14 ، 15 ، 16 ، 17 ] به منظور نام بردن چند مقاله در این حوزه. از آنجایی که دو دنیای BIM و GIS از قبل شروع به تعامل کرده اند، موضوع سازگاری توپولوژیکی در هر دو حوزه بیشتر و بیشتر مرتبط می شود.
طبق مشاهدات ما، پتانسیل رشته ریاضی توپولوژی برای بازیابی اطلاعات کارآمد با استفاده از ساختارهای داده توپولوژیکی موجود هنوز به اندازه کافی مورد بهره برداری قرار نگرفته است و ساختارهای داده موجود نیز این کار را تسهیل نمی کند. به همین دلیل، تحقیقات گروه ما بر یافتن روشهایی متمرکز شده است که توپولوژی (ریاضی) را قادر میسازد تا در وظیفه مدیریت و بازیابی اطلاعات توپولوژیکی به جامعه جغرافیایی خدمت کند. پاراگراف های زیر مفاهیم مختلف مرتبط با این کار را مرور می کنند.
جستجو در میان داده های مکانی یا مکانی-زمانی را می توان با استفاده از یک روش دسترسی مناسب به طور موثر انجام داد. برای فضای n اقلیدسی ، این به عنوان مثال، Octree [ 5 ]، R -tree [ 6 ]، یا R *-tree [ 7 ] است. دلیل ذکر این موارد این است که از روش های دستیابی هندسی خاصی نیز در این مقاله استفاده شده است. بقیه این بخش به روش های توپولوژیکی می پردازد.
توپولوژی یک رشته ریاضی است که مفهوم نزدیکی را رسمیت می دهد. طبیعی است که مدل های توپولوژیکی برای داده های مکانی و مکانی-زمانی در نظر گرفته شود. یک مثال اولیه از یک ساختار داده برای چنین مدل هایی توسط G- maps [ 18 ] ارائه شده است. اینها، به عنوان مثال، در DB4GeO [ 19 ] استفاده می شوند. با این حال، نقشه های G پرمخاطب هستند و دارای پیچیدگی ذخیره سازی نمایی با افزایش ابعاد هستند [ 20 ]. با توجه به 3 D3�به اضافه زمان منجر به الف می شود 4 D4�مدل [ 21 ]. این 3 D3�مقیاس بعلاوه منجر به نوع دیگری از مدل با ابعاد بالاتر [ 22 ] می شود. البته، فضا، زمان، نسخه و مقیاس را می توان برای یکپارچگی ترکیب کرد n D��مدل [ 23 ]. کمپلکس های ساده و پلی توپی برای آن پیشنهاد شد 3 D3�و 4 D4�[ 19 ].
در [ 3 ]، نشان داده شد که فضاهای توپولوژیکی محدود – که برای اولین بار توسط الکساندروف [ 2 ] مورد مطالعه قرار گرفت – امکان مدل سازی کارآمد هر موقعیت توپولوژیکی را که می تواند در رایانه ذخیره شود، می دهد. موارد خاص هستند تی0�0فضاها (همچنین به عنوان poset شناخته می شوند) که باید به اندازه کافی مدل های کلی برای داده های مکانی و زمانی باشند. توپولوژی پوست ها با بسته شدن بازتابی و گذرا یک رابطه دودویی که غیر چرخه ای است، یعنی هیچ چرخه جهت دار ندارد، به دست می آید.
از یک طرف، جداسازی هندسه و توپولوژی منجر به پرس و جوهای توپولوژیکی کارآمد می شود، مثلاً [ 24 ]، که در آن ساختار درختی برای حرکت در اتاق های یک ساختمان استفاده می شود. علاوه بر این، در [ 25 ]، پرس و جوهای فضایی و توپولوژیکی کارآمد در شبکه های چهار وجهی بزرگ با توپولوژی دلخواه و مرزهای پیچیده انجام شده است.
از سوی دیگر، این جدایی نیز منجر به یک موضوع سازگاری می شود [ 26 ]. یعنی یکی دو مدل دارد: یک مدل توپولوژیکی انتزاعی و یک مدل هندسی که با اختصاص مختصات به اشیاء مدل توپولوژیکی انتزاعی به دست میآید. توپولوژی زیربنایی مدل هندسی به طور کلی با مدل توپولوژیکی انتزاعی متفاوت است. اگر اینطور نباشد، می توان مدل ها را از نظر توپولوژیکی سازگار نامید. توجه داشته باشید که ادبیات شامل مفاهیم مختلف سازگاری توپولوژیکی است [ 27 ، 28 ، 29 ، 30 ]. مفهوم فعلی سازگاری توپولوژیکی بر اساس ایده در [ 31] که اولین موردی است که هندسه و نمودار بروز یک مدل توپولوژیکی را حداقل تا آنجا که نویسندگان از آن مطلع هستند، مرتبط می کند.
به منظور توسعه روش های دسترسی توپولوژیکی کارآمد، که منجر به پردازش پرس و جو توپولوژیکی کارآمد می شود، در ادامه فرض می کنیم که مدل از نظر توپولوژیکی سازگار است. این دقیقاً زمانی است که هر پرس و جوی توپولوژیکی در مدل توپولوژیکی پاسخ صحیحی را ارائه دهد. با این حال، از آنجایی که داده های خام از نظر توپولوژیکی سازگار نیستند، ابتدا باید به درستی پیش پردازش شوند، به عنوان مثال، با استفاده از روش های همپوشانی معرفی شده در [ 4 ]. مشخص شد که مشخصه اویلر در این مرحله مفید بوده است.
2.1. مدل نمودار
پیادهسازی روش دسترسی توپولوژیکی در اینجا چارچوب اصلی DB4GeOGraphS را که در [ 8 ، 26 ] معرفی شده بود، برای محاسبه مدلهای حجمی ضد آب از نمایشهای مرزی در [ 4 ، 32 ] گسترش داده و توسط یک p -adic Gray- توسعه داده شد. شاخص منحنی هیلبرت برای ابرهای نقطه در [ 33 ] که همه آنها (از جمله این مقاله) بخشی از پایان نامه هستند [ 34 ].
در این بخش، مدل نمودار استفاده شده توسط چارچوب اصلی DB4GeOGraphS برای هدف خودکنترلی این مقاله را مجدداً معرفی میکنیم. سلف چارچوب اصلی DB4GeOGraphS DB4GeO است که توسط گروه کاری Martin Breunig [ 19 ]، یک پایگاه داده تحقیقاتی شی گرا برای داده های مکانی و مکانی-زمانی توسعه یافته است. چارچوب اصلی DB4GeOGraphS به زبان جاوا نوشته شده است و الگوریتم های اساسی را برای مقایسه اشیاء فضایی و محاسبه تقاطع ها و تفاوت های فضایی پیاده سازی می کند. DB4GeOGraphS _چارچوب اصلی را می توان به عنوان یک چارچوب تحقیقاتی برای آزمایش ساختارهای داده، روش های دسترسی و الگوریتم هایی که قادر به مدیریت و پردازش داده های مکانی و مکانی-زمانی هستند، در نظر گرفت.
انواع داده های مکانی مبتنی بر مجتمع های ساده هستند. سه سطح مختلف تجمع وجود دارد: سطح عنصر، سطح مؤلفه و سطح خالص، که در آن یک عنصر d – بعدی یک سیمپلکس d – بعدی است، یک مؤلفه d – مجموعهای از سادههای d – بعدی است که یک d متصل را تشکیل میدهند. – منیفولد بعدی یا به عبارت دیگر یک مجتمع ساده d -بعدی متصل. شبکه d -dimensional مجموعه ای از مولفه های d- بعدی به شکل مجموع توپولوژیکی است. نام کلاس برای انواع مختلف هندسه از قرارداد پیروی می کند A + “ 3 D�+“3�” + ب+�، جایی که A نشان دهنده بعد شیء ساده ( نقطه ، قطعه ، مثلث و چهار وجهی )، و B نشان دهنده سطح تجمع ( عنصر ، مؤلفه و شبکه ) است.
مدل مکانی-زمانی مبتنی بر مدل پولثیر و رامف [ 35 ] است و چهار سطح مختلف تجمع (عنصر، دنباله، جزء و شبکه) را اضافه میکند. یک عنصر d بعدی a استد+ 1�+1-پلی توپ بعدی در فضای چهار بعدی، که در آن سه مختصات اول مختصات فضایی و مختصات چهارم مرحله زمانی را مشخص می کند. هر عنصر d -بعدی با دو سادگی d -بعدی در یک فضای اقلیدسی 3 بعدی ثابت در دو زمان مختلف برای مدلسازی یک سیمپلکس d – بعدی متحرک و شکلگیری تعریف میشود. یک دنباله d -بعدی با زنجیر کردن آن عناصر d -بعدی در حاشیههای d -بعدی آنها تعریف میشود . مولفه d – بعدی مجموعه ای از دنباله های d – بعدی است که یک متصل را تشکیل می دهد. د+ 1�+1منیفولد بعدی یا. به عبارت دیگر، متصل است د+ 1�+1مجتمع پلی توپ بعدی شبکه d -dimensional به عنوان مجموعه ای از مولفه های d- بعدی در قالب یک مجموع توپولوژیکی تعریف می شود. نام کلاس برای انواع مختلف هندسه از قرارداد پیروی می کند A + “ 4 D�+“4�” + ب+�، جایی که A نشان دهنده بعد شیء ساده ( نقطه ، قطعه ، مثلث و چهار وجهی ) است که در یک بازه زمانی حرکت می کند و شکل می گیرد، و B نشان دهنده سطح تجمع ( عنصر ، مؤلفه ، دنباله و شبکه ) است.
چارچوب اصلی DB4GeOGraphS مدل نمودار ویژگی را با الگوهای طراحی مدل ویژگی OGC برای تعاریف گره ترکیب می کند. مدل نمودار خواصیک پارادایم است که برای مقابله با داده های بدون ساختار مناسب است. این اغلب زمانی اتفاق می افتد که انواع مختلف اطلاعات جغرافیایی باید برای تجزیه و تحلیل ترکیب شوند. مجتمعهای ساده یا مجتمعهای پلیتوپ فضایی-زمانی توصیفشده نیز به کلاس انواع دادههای مکانی یا مکانی-زمانی بدون ساختار تعلق دارند، زیرا توپولوژی منظم نیست که در دادههای وکسل یا شطرنجی دیده شود. این همچنین مدیریت موثر محاسبات و پایداری مجتمعهای ساده را کمی دشوارتر میکند، زیرا توپولوژی باید صریحاً حفظ شود. با این حال، برای مثال، اگر همسایگان برخی از سیمپلکسهای d بعدی با هر سیمپلکسی تعریف شوند که دارای یک د– 1�−1سیمپلکس مرزی بعدی، سپس هر سیمپلکس d- بعدی دارای حداکثر تعداد همسایه های d بعدی است .آm a x����با آm a x= د+ 1آمترآایکس=د+1در یک مجتمع ساده d بعدی. بنابراین ساختار توپولوژیکی “منظم” وجود دارد که می تواند برای پیاده سازی الگوریتم های مکانی یا مکانی-زمانی قوی مورد استفاده قرار گیرد، حتی اگر توپولوژی آنقدر منظم نباشد که در داده های وکسل یا شطرنجی دیده می شود. استفاده از داده های بدون ساختار، دامنه برنامه ها را غنی می کند. از این حیث، توپولوژی منظم (به معنی ثابت بودن تعداد همسایگان مستقیم) یک مورد خاص از فرم غیرساختاری عمومی تر است و به دلیل تحقیق و اجرای پایگاه های داده مکانی یا مکانی مناسب برای طبقه بندی داده های رانده شده است. موارد و به کارگیری کارآمدترین روش برای رسیدگی به آن موارد مختلف. اینها مشکلات فنی هستند و باید از کاربر پنهان شوند.
توپولوژی در چارچوب اصلی DB4GeOGraphS به معنای گسترده تر از تمرکز بر روابط بروز درک می شود . در زمینه ژئو اجسام فضایی یا مکانی-زمانی پیچیده بین و درون مرتبط، انواع روابط مشترک این ژئو اشیاء عبارتند از روابط بروز ( مرز-از ، درون-از )، روابط تجمع ( بخش از ، ترکیب-از ) و روابط انتزاعی ( تعمیم-از ، تخصصی-از ). هر نوع رابطه ممکن است به صورت دو طرفه یا یک طرفه گنجانده شود. انواع رابطه یک طرفه تولید می کنند تی0تی0-فضاها مجموعه ای از تی0تی0-فضاها را می توان با یک نمودار ترکیب کرد که به نوبه خود قابل تجزیه و تحلیل است. مدل Graph Property جایگزین مدل داده شی گرا سابق DB4GeO می شود که نمایش اطلاعات جغرافیایی پیچیده را با تعریف نمودارهای ویژگی با ویژگی ها/ویژگی های مکانی یا زمانی، ویژگی ها/ویژگی های زمانی و ویژگی ها/ویژگی های موضوعی دلخواه در هر گره امکان پذیر می کند. و مطالعات آن نمودارها
با در نظر گرفتن همه اینها، می توان یک نمودار پیچیده را مدل کرد که یک مدل فضایی-زمانی چند مقیاسی با LoD های مختلف را نشان می دهد. به عنوان مثال، میتوانیم کامیونی را در حال رانندگی در یک شهر تصور کنیم. یک سوال رایج این است: “آیا کامیون با شهر تداخل دارد؟” به این معنا که ساختمان ها را لمس می کند یا توسط معابر بسیار باریک مسدود می شود. یک کامیون را می توان دقیقاً به عنوان یک شبکه چهار ضلعی فضایی-زمانی یا فقط به عنوان یک عنصر بخش مکانی-زمانی مدل کرد. این کامیون همچنین می تواند به عنوان یک شبکه چهار وجهی فضایی مدل شود که با تعریف مسیر و جهت های مکانی-زمانی در شهر حرکت می کند. به راحتی می توان دید که این مثال نتایج متفاوتی را برای هر نوع ساده سازی ایجاد می کند. با این حال، مشکل اصلی هنوز هندسه محاسباتی است که با مقیاس های مختلف در یک مدل سروکار داریم. که منجر به نتایج نادرست در محاسبات هندسی مدل های سازگار توپولوژیکی خواهد شد. اگر کامیون با سادهسازیهای نسبتاً کوچک مدلسازی شود و مدل شهری از سادگیهای بسیار بزرگتری استفاده کند، ممکن است تقاطعهای اشتباهی پیدا شود یا تقاطعهای ریاضی واقعی پیدا نشوند. فقط هندسه محاسباتی دقیق و سربار آن ممکن است با این مشکل با دقت بیشتری برخورد کند.
نمونه جالب دیگر درب گردان در ورودی برخی از مراکز خرید است. سپس میپرسیم چگونه به مرکز خرید برویم. مشکل آنقدرها هم که به نظر می رسد بی اهمیت نیست، زیرا یک در گردان همیشه داخل مرکز خرید و بیرون مرکز را مسدود می کند. استفاده از هندسههای مکانی-زمانی سازگار توپولوژیکی برای مدلسازی این مثال، فضای توپولوژیکی را نشان میدهد که بیرونی و درونی مرکز خرید را به هم متصل میکند، حتی با انتخاب تنها یک فضای موضوعی (هوا).
پیچیده ترین راه برای مدل سازی این وضعیت استفاده از مجتمع های چهار ضلعی فضایی و زمانی (مجموعه های چهار وجهی متحرک و شکل گیری)، پنج مجتمع چهار ضلعی برای درب است که شامل تعریف چهار مجتمع متحرک ناپیوسته در کنار درب به عنوان مجموعه شیشه ای و دو چهار وجهی است. مجتمع هایی برای مرکز خرید داخلی و خارجی به عنوان مجتمع های هوایی که توسط دو دیوار طراحی شده به صورت مجتمع های سنگی تقسیم می شوند. ردیف بالای شکل 4 مثالی را نشان می دهد که از نظر هندسی به زمین در یک مرحله زمانی مشخص (سمت چپ) و نمودار خصوصیات مکانی-زمانی صاف شده است.برای نمایش مرزهای مکانی-زمانی مجتمع های هوا، سنگ یا شیشه (راست). مجتمع ها توسط روابط تجمعی به هم متصل می شوند، که به هندسه فضایی-زمانی مشترک آنها (کوچکترین گره ها) متصل می شوند. با استفاده از هندسههای فضایی و حذف گرههای قرمز و سرخابی، یا گرههای سبز و زرد، یا گرههای سرخابی و سبز یا گرههای زرد و قرمز، میتوان چهار نمودار خصوصیات فضایی مختلف را برای چهار مرحله زمانی مختلف تحقق بخشید. مثال فضایی مسطح هندسی از بالای شکل 4هنگام حذف گره های قرمز و سرخابی مورد را نشان می دهد. اما حذف این گره ها تنها با استفاده از مجتمع های هوایی از امکان جابجایی از مجتمع بیرونی به مجتمع داخلی جلوگیری می کند. موضوع هندسه مکانی-زمانی لزوماً نیازی به تغییر زمانی در این مثال ندارد.
یک نوع بسیار رایج سادهسازی، استفاده از مجتمعهای مثلث مکانی-زمانی (مجموعههای مثلث متحرک و شکلگیری) با تبدیل اشکال سه بعدی به نمایش اشکال دو بعدی مورد استفاده در کاداستر یا سایر کاربردهای جغرافیایی دو بعدی سنتی است که جهان را مسطح میکند. این نوع ساده سازی لزوماً توپولوژی را ساده نمی کند و برای حل این مشکل به هندسه های مکانی-زمانی نیز نیاز است. با این حال، این نوع انتزاع، تبدیل اجسام فضایی یا مکانی-زمانی به یک فضای d بعدی دیگر، در اینجا مورد توجه نیست.
یک مدل کمتر پیچیده از اشکال سه بعدی در فضای سه بعدی، کاهش ابعاد آنها است. دیوارها، درها، سقف ها، پنجره ها و کف ها ممکن است به عنوان سطوح و نه به صورت جامد مدل شوند. در این صورت دیوارها، درها، سقف ها، پنجره ها و کف مرکز خرید جزئی از مرز مجموعه داخلی می باشد. ردیف میانی شکل 4 این نوع ساده سازی را نشان می دهد. مدل ممکن است فقط از یک مدل فضایی همراه با یک فاصله زمانی وجود تشکیل شده باشد. برای مدل سازی باز و بسته شدن مرکز خرید، موضوع درب ممکن است به طور موقت تغییر کند (هوا به شیشه و بالعکس).
یکی دیگر از انواع بسیار رایج ساده سازی، کاهش تعداد موجودیت های مورد علاقه است. در مورد LoD های مختلف CityGML ، دیوار، در، سقف، پنجره، کف و مجتمع های هوایی مرکز خرید برای کاهش پیچیدگی مدل تجمیع شده است. مرز مجتمع تجاری سپس نمایانگر دیوار، در، سقف، پنجره و کف مرکز خرید است. ردیف پایین شکل 4 این ساده سازی را نشان می دهد. همانطور که می بینید، این نوع ساده سازی فضای داخلی را از بیرون مسدود می کند. برای مدل سازی باز و بسته شدن مرکز خرید، موضوع دیوار ممکن است به طور موقت تغییر کند (هوا به سنگ و بالعکس).
سه مثال آخر را می توان از طریق روابط انتزاعی به هم مرتبط کرد (ساده سازی به عنوان تعمیم تفسیر می شود). سه مدل فقط از روابط تجمیع درونی و روابط بروز استفاده می کنند. مزیت این است که مدل سازی اضافی (باز و بسته شدن مرکز خرید) لزوماً نیازی به انجام ندارد و یک پرس و جو می تواند به خوشه هایی که دارای LoD کافی هستند تجزیه شود . اگر به دلایل عملکردی مانند کاهش انتقال داده در یک سیستم چند پایگاه داده، مدلسازی اضافی ضروری باشد، در آن صورت تولید خودکار مدلهای سادهشده و/یا بررسی متقابل مدلهای اضافی ممکن است امکانپذیر باشد.
یک راه متداول برای پرس و جو از نمودارهای دارایی ، استفاده از زبان پیمایش گراف (مثلاً Gremlin) است. پرس و جو از یک نمودار ویژگی با اعمال گام به گام گام های اتمی بر روی یک نمودار ویژگی به دست می آید . سه مرحله مختلف وجود دارد: (الف) یک مرحله نقشه (تبدیل اشیاء در جریان)، (ب) یک مرحله فیلتر (حذف اشیاء از جریان)، یا (ج) یک مرحله اثر جانبی (محاسبات آماری در مورد جریان) [ 36 ]. مراحل اتمی توسط پایگاه داده گراف استفاده شده ارائه شده است. چارچوب اصلی DB4GeOGraphS مراحل اتمی را برای رسیدگی به ویژگیهای خاصی اجرا میکند که یک نمودار خصوصیات مکانی یا مکانی زمانی است.پایگاه داده نباید به منظور حفظ توپولوژی بر اساس انواع روابط توصیف شده از دست برود. این شامل عملیات ساخت (الف) گره های مرزی یک گره معین، (ب) گره درونی یک گره BREP (نمایش مرزی) یا حتی درونی یک شبکه d -بعدی است اگر اجزای d -بعدی حاوی مقداری فضا باشند. (ج) گره های تجزیه یک گره تجمع، یا (د) پوشش داخلی یک گره معین با مجموعه ای از گره های دیگر.
توجه داشته باشید که اگرچه ما معمولاً از نمودارهای ویژگی “فضایی” و “مکان زمانی” صحبت می کنیم، ساخت آن در واقع به ابعاد ژئو-اشیاء زیربنایی بستگی ندارد، که به نوبه خود فقط ویژگی های ویژه گره های گراف هستند.
3. روش شناسی
روشی که در بخشهای فرعی زیر توضیح داده میشود شامل توسعه یک روش دسترسی توپولوژیکی (TOAM) با دو بخش است. اول، یک روش دسترسی برای پرس و جوهای توپولوژیکی با استفاده از مختصات ساخته شده است، و دوم، مختصات برای هر توپولوژی به شکل یک تی0تی0-space (از نظر ریاضی) و Property Graph (از لحاظ فنی) تعریف شدهاند و کدگذاری توپولوژی را ارائه میکنند. شکل 5 به صورت شماتیک تجزیه TOAM را به این دو بخش تشکیل دهنده نشان می دهد.
3.1. روش دسترسی
همانطور که در پایان بخش قبل ذکر شد، ما در مورد نمودارهای ویژگی “مکانی” یا “مکان زمانی” صحبت خواهیم کرد، زمانی که آبجکت های جغرافیایی مدیریت شده دارای ویژگی های تغییر زمان هستند یا ندارند. توجه داشته باشید که تعداد ابعاد این اشیا حتی میتواند بدون تغییر روششناسی ارائهشده در زیر، بیشتر از سه یا چهار باشد. علاوه بر تعریف مراحل اتمی برای یک زبان پیمایش نمودار خصوصیات مکانی یا مکانی، ادغام روشهای دسترسی مناسب که ویژگیهای دادههای مکانی یا مکانی-زمانی را به منظور پشتیبانی از تجزیه و تحلیل دادههای جغرافیایی-علمی بزرگ بر اساس این دادههای مکانی یکپارچه میکند، نیز مهم است. یا نمودارهای ویژگی مکانی و زمانی به طور موثر. استفاده از یک روش دسترسی فضایی مانند: مشکلی نیستR*-درخت روی مجموعه ای از گره های فضایی. این شبیه به استفاده از R*-Tree در ستون فضایی یک پایگاه داده شی-رابطه ای مانند PostGreSQL با پسوند PostGIS است. با این حال، روش های دسترسی توپولوژیکی به توپولوژی اشیاء فضایی یا مکانی-زمانی اشاره می کنند تی0تی0-فضاهایی که بخشی از آن هستند یا در امتداد آن قرار می گیرند، نه به فضاهای هندسی که در آن زندگی می کنند. در واقع، فضای هندسی ممکن است از هر بعد باشد، و ژئو اجسام دارای یک توپولوژی کاملاً تعریف شده برای هر نوع رابطه هستند، همانطور که معرفی شد. در بخش های قبلی به طور کلی، و همچنین برای مورد فضایی و زمانی. بنابراین، فضای هندسی توسط فضای متریک مکانی یا مکانی-زمانی و برخی ویژگی های موضوعی متریک دیگر در بر می گیرد. شیهای جغرافیایی با n نوع رابطه پایه برای توصیف n توپولوژی مدیریت شده توسط نمودار خصوصیت مرتبط هستند. در ادامه، مفاهیم با مثالهای فضایی تنها برای سهولت درک توضیح داده شدهاند. نمونه های فضایی و زمانی یا حتی با ابعاد بالاتر (مثلاً مانند شکل 4) را می توان همانطور که توضیح داد به طور مشابه رفتار کرد زیرا انواع روابط تغییر نمی کنند.
بستهبندی هستهای DB4GeOGraphS indizes.api حاوی یک رابط TOAM برای روشهای دسترسی توپولوژیکی (TOAM) است. نمونه اولیه ما، اولین اجرای یک روش دسترسی توپولوژیکی در چارچوب اصلی DB4GeOGraphS ، بر اساس یک R*-Tree گسسته است که نقاط گسسته چند بعدی را مدیریت می کند. هر پیاده سازی دیگری از روش های دسترسی که قادر به مدیریت ابرهای نقاط گسسته چند بعدی باشد برای رویکرد ما قابل تصور است. در واقع، برخی از پیادهسازیهای دیگر (مثلاً یک شاخص منحنی پرکننده فضا) یا حتی ترکیبی از روشهای دسترسی (مثلاً یک روش دسترسی تک بعدی برای هر مختصات) ممکن است کارآمدتر عمل کنند. این کار در حال پیشرفت است.
3.2. رمزگذاری توپولوژی
ما چند روش مختلف را برای تعریف هر مختصات آزمایش کرده ایم. یکی از ساده ترین تعاریف، شمارش تعداد روابط هر گره است. همانطور که قبلاً توضیح داده شد، سه نوع مختلف از انواع رابطه دو طرفه وجود دارد که فقط به عنوان شش نوع مختلف رابطه یک طرفه در چارچوب اصلی DB4GeOGraphS قابل استفاده هستند. بنابراین تعریف را می توان برای تعریف یک کلید چند بعدی با شمارش در هر نوع رابطه گسترش داد. استدلال اصلی برای این تعریف خاص این است که امکان بازیابی ژئواشیاء با ویژگی های توپولوژیکی محلی خاص (به عنوان مثال، بازیابی همه ژئو اشیاء که بخشی از2 تا 4 ژئو شی دیگر). همچنین می توان سایر ویژگی های گره را در نظر گرفت، به عنوان مثال، برخی از ویژگی های موضوعی، بعد فضایی یا سطح تجمع آن یا حتی خود ویژگی مکانی یا مکانی زمانی، که منجر به یک روش دسترسی توپولوژیکی مکانی یا مکانی-زمانی ترکیبی می شود.
اگر روی روشهای دسترسی تمرکز کنیم که ساختار Property Graph را به روشهای خاصی سازماندهی میکنند، تعریف دیگری برای مختصات یک کلید چند بعدی برای شناسایی یک گره با تعداد مراحل برداشتهشده در کوتاهترین مسیر به یک گره محوری در Property ارائه میشود. نمودار با استفاده از الگوریتم Dijkstra. به طور معمول، گره محوری باید قابل دسترسی باشد، که به این معنی است که نمودار ویژگییک جزء منسجم است. یک استدلال برای این تعریف می تواند بر اهمیت عنصر محوری تکیه کند (به عنوان مثال، بازیابی همه ژئو اشیاء که در یک محدوده توپولوژیکی خاص به برخی از شی ژئو شی محوری هستند). این تعریف با تجزیه و تحلیل کوتاه ترین مسیر به گره محوری قابل گسترش است. یک نسخه چند بعدی برای شمارش مراحل کوتاهترین مسیر در هر نوع رابطه به طور جداگانه است. مجموع هر مختصات برابر است با تعداد مراحل کوتاهترین مسیر برای رسیدن به گره محوری. یک کاربرد عملی، امکان پرس و جو برای گره هایی است که در محدوده توپولوژیکی از انواع روابط خاص به گره محوری متصل می شوند (به عنوان مثال، بازیابی همه گره هایی که به گره محوری مورد علاقه حداقل با یک مرحله مرزی ارتباط و 2 به 4 بخشی ازمراحل رابطه). نوع رابطه همچنین ممکن است برای اضافه کردن وزن های مختلف به مراحل الگوریتم Dijkstra استفاده شود. استفاده عملی از ایده آخر، کنترل بیشتر بر الگوریتم Dijkstra است. با این حال، پیچیدگی محاسبه مختصات توسط آن تعاریف به عنوان یک مرحله پیش پردازش به ساختار نمودار بستگی دارد.
تعریف جالب دیگری که منجر به یک مرحله پیش پردازش نسبتاً پیچیده برای محاسبه هر مختصات یک گره در نمودار ویژگی می شود، مجموع کوتاه ترین طول مسیر یک گره به هر گره دیگر است. به عنوان مثال، اگر هر گره بدون انحراف با هر گره دیگری در نمودار خصوصیات متصل باشد، هر گره کوتاهترین طول مسیر را برای هر گره دیگر دارد که برابر با یک است. مختصات برابر خواهد بود با n – 1�-1برای هر n گره اگر یک درخت p -adic را به عنوان مثال دوم تصویر کنیم، گره ریشه در مرکز قرار می گیرد و کمترین مجموع کوتاه ترین طول مسیر را می گیرد و گره های برگ بیشترین مجموع کوتاه ترین طول مسیر را از مسیرهای روی برخی از گره های والد به دست می آورند. گره برگ دیگری به جای رفتن مستقیم به هر یک از گره های برگ از گره والد، همیشه چند مرحله اضافی اضافه می کند. بنابراین این تعریف مختصات معیاری است برای اینکه موقعیت گره در واقع چقدر به مرکز نمودار ویژگی نزدیک است. این تعریف را می توان با استفاده از انواع مختلف روابط نیز گسترش داد.
چند نمونه از تعاریف توصیف شده قبلی در شکل 6 و شکل 7 آورده شده است. تعاریفی که قبلا توضیح داده شد در قالب سه بردار در زیر هر نمودار مثال آورده شده است. هر نمودار نمونه فقط روابط را در کوتاهترین مسیر هنگام شروع از گره با مقدار 0 نشان می دهد. اولین بردار سمت چپ تعداد روابط را در هر نوع رابطه گره با مقدار 0 نشان می دهد. ترتیب ورودی های بردار قسمت- است. از ، مرکب-از ، مرز-از و درون-از. بردار دوم تعداد مراحل انجام شده برای رسیدن به گره محوری (گره محدود قرمز) را نشان می دهد که در آن مختصات اول نوع رابطه را نادیده می گیرد و به دنبال آن تعداد مراحل در هر نوع رابطه به همان ترتیبی که قبلا نشان داده شده است. بردار سوم مجموع طول کوتاه ترین مسیر از گره با مقدار 0 تا هر یک از گره های دیگر را نشان می دهد، جایی که مختصات اول نوع رابطه را نادیده می گیرد و مختصات دیگر گام های برداشته شده توسط انواع رابطه خاص در کوتاه ترین مسیرها را جمع می کند. همان ترتیبی که قبلا نشان داده شد.
4. آزمایشات
در بخش قبل، یک روش دسترسی توپولوژیکی ( TOAM ) را برای دادههای مکانی-زمانی عمومی با ویژگیهای متریک احتمالاً بیشتر همراه با روابط جهتدار کدگذاری شده بین اشیاء جغرافیایی معرفی کردیم. در حال حاضر، روش دسترسی توپولوژیکی پیادهسازی شده DB4GeOGraphS فقط میتواند هندسههای فضایی را مدیریت کند، اما گسترش هندسههای ابعاد بالاتر کار در دست انجام است.
روش دسترسی توپولوژیکی به طور مثال برای یک مدل شهر چهار وجهی از بخش تاریخی سالوادور (برزیل) که توسط گروه کاری Arivaldo Leão de Amorim مدلسازی شده بود، محاسبه میشود. دادهها توسط آزمایشگاه مطالعات پیشرفته در زمینه معماری شهر و فناوریهای دیجیتال (LCAD) در دانشگاه فدرال باهیا (UFBA) در طول پروژه تحقیقاتی «ایجاد الزامات برای مدلسازی اطلاعات شهر» که توسط آژانس دولتی فدرال برزیل پشتیبانی میشود، تولید شد . بهبود پرسنل آموزش عالی (CAPES) و خدمات تبادل علمی آلمان(DAAD). مدل شهری استفاده شده برای این کار نسخه نهایی نیست. در یک کارگاه آموزشی در سالوادور در سال 2019 به عنوان بخشی از برنامه تبادل استفاده شد. داده های کلیدی به شرح زیر خلاصه می شوند:
- 1
-
صفر: 462.851043701172462.851043701172 376.195983886719376.195983886719 71.622505187988371.6225051879883.
- 2
-
گره های درختی CityGML : 22386.
- 3
-
تعداد گروه: 56.
- 4
-
چند ضلعی: 925.
- 5
-
چند ضلعی های متمایز: 924.
- 6
-
مکان های اعشاری: 15.
- 7
-
حداقل فاصله نقطه [m]: 6.216820473225959E-6.
- 8
-
بخش ها: 4446.
- 9
-
حداقل طول [m]: 3.0517578125E-5.
- 10
-
طول متوسط [m]: 5.0552051851945565.
- 11
-
حداکثر طول [m]: 32.06260853268529.
همانطور که مشاهده می شود، مقیاس هندسی به طور قابل توجهی متفاوت است، که برخی از مسائل عددی را در محاسبات تقاطع ایجاد می کند با این اثر که توپولوژی به خوبی تعریف نشده است، زیرا تمرکز بر پیچیدگی های هندسه محاسباتی نیست، بلکه بر فضای همپوشانی محاسبه شده است. . ما در اینجا این موضوع را نادیده می گیریم، حتی اگر نمودار توپولوژی واقعی را منعکس نکند. نکته اصلی در اینجا داشتن داده های توپولوژیکی سازگار (تا جایی که الگوریتم های هندسه محاسباتی اجازه می دهد) برای کار با آنها است.
مدل شهر دقتی را با حداکثر 15 رقم اعشار نشان می دهد. تجزیه و تحلیل حساسیت همانطور که در [ 32 ] یا [ 34 ] توضیح داده شد، نتایج امیدوارکننده ای را با مقدار دقت موقعیتی نشان داد. ϵ =10– 2�=10-2و مقدار دقت زاویه ای ز=10– 14ز=10-14، حتی اگر برخی از نقاط گوشه برخی از چند ضلعی ها در حین واردات نادیده گرفته شوند. این بدان معنی است که فضای پوشش محاسبه شده نیز ممکن است با مدل هندسی سازگاری نداشته باشد. ناسازگاری های توپولوژیکی قابل توجهی ممکن است، همانطور که تجزیه و تحلیل بیشتر ممکن است نشان دهد. با این حال، این موضوع تمرکز این مقاله نیست. در مجموع، 50 ساختمان از 56 ساختمان را می توان با یک مجموعه چهار وجهی در هر ساختمان و حجم کلی 68916 چهار وجهی کرد. متر3متر3(بالای شکل 8 را ببینید ).
در مرحله پیش پردازش، توزیع مشخصه اویلر را که در اینجا باید به شکل ترکیبی آن ارائه شود، تجزیه و تحلیل کردیم، زیرا داده ها در ابتدا از نظر توپولوژیکی ناسازگار هستند. توزیع ویژگی های اویلر ترکیبی نشان می دهد که انتخاب پارامترهای دقیق می تواند با توجه به توپولوژی های مورد انتظار باشد. ویژگی های ترکیبی اویلر راهی سریع برای تجزیه و تحلیل کیفیت توپولوژیکی اجسام جغرافیایی است. بنابراین، اگر ویژگی های ترکیبی اویلر قابل قبول باشد، پوشش های داخلی محاسبه شده و نمودار خواص حاصل(فضای همپوشانی) که در آن هر گره پوشش داخلی به خوبی ادغام شده باشد، احتمالاً تا آنجا که الگوریتمهای هندسه محاسباتی مورد استفاده همه تقاطعهای صحیح را پیدا میکنند، تقریباً درست است. در مورد حاضر، سه مجموعه چهار وجهی ایجاد شده توسط پوشش داخلی با مشخصه اویلر یک وجود دارد. 52 کمپلکس مثلث با پوشش داخلی مرزی یافت می شود که یکی از آنها یک مشخصه ترکیبی اویلر برابر با صفر و بقیه برابر با یک را نشان می دهد ( جدول 1 را در سمت چپ ببینید). به نظر می رسد هیچ کره دو بعدی درگیر نیست، زیرا یک مشخصه ترکیبی اویلر برابر با دو شامل نمی شود. این بدان معنی است که به نظر نمی رسد مجموعه داده حاوی پوسته های بسته باشد. هفت شی Triangle3DNet از حداقل دو مجتمع مثلث و سه تشکیل شده استاشیاء Triangle3DNet از حداقل سه مجتمع مثلثی تشکیل شده اند ( جدول 1 را در سمت راست ببینید). آن اشیاء Triangle3DNet باید برای بررسی های بیشتر مشاهده شوند. پوشش های داخلی مرزی که منجر به تقاطع های یک بعدی و صفر می شود در جدول 2 و جدول 3 ارائه شده است. همانطور که در جدول 3 مشاهده می شود ، یک ابر نقطه ای از 19 نقطه به عنوان محل تقاطع بین دو ساختمان یافت می شود. این بعید است که در واقعیت یافت شود. بنابراین، محاسبات تقاطع که مقادیر مشخصه اویلر بالاتری را نشان میدهند، باید به صورت دستی از نظر منطقی بودن یا خطاهای توپولوژیکی بررسی شوند.
شکل 8 (بالا) فایل چهاروجهی CityGML و پوشش های داخلی آنها را نشان می دهد. شکل 8 (پایین) نمودار مربوطه را نشان میدهد که شامل درخت CityGML با گرههایی است که چند ضلعیهای مسطح را حمل میکنند، تجمعات آنها (گروهبندی شده بر اساس ساختمان)، مثلثبندی و چهار وجهی هر ساختمان، مرز هر ساختمان، و در نهایت تقاطع های داخلی هر ساختمان و حاشیه برای ایجاد فضای پوششی برای ساختمان ها. هر شی Triangle3DNet (ساختمان) توسط buildCores -Algorithm (نگاه کنید به [ 4 ، 32 ] یا [ 34 ]) به طور جداگانه چهار وجهی می شود. این شکل هم مرز را نشان می دهداشیاء Triangle3DComponent از اشیاء Tetrahedron3DComponent . کل نمودار تنها با استفاده از عملیات گره ذکر شده در بخش 2.1 و یک واردکننده CityGML ایجاد شده است که قادر است چند ضلعی های CityGML را با برخی از XML-Tag گروه بندی کند.
ما ترکیبی از 23 ویژگی مختلف را آزمایش کردیم، که نه تنها مختصاتی را که از تنظیمات توپولوژیکی هر گره به دست میآیند، بلکه آنهایی را که از ویژگیهای هندسی (بعد و سطح تجمع) به دست میآیند نیز شامل میشود. این مزیت جستجوی خصوصیات هندسی همراه با تنظیمات توپولوژیکی را دارد (به عنوان مثال، هر سطحی را که بخشی از حداقل دو هندسه است برگردانید). تعاریف مختصات به شرح زیر است:
- 1
-
شناسه TONode.
- 2
-
بعد TONode.
- 3
-
سطح تجمع TONode.
- 4
-
تعداد رابطه
- 5
-
تعداد رابطه SPECIALISATION_OF.
- 6
-
تعداد رابطه GENERALISATION_OF.
- 7
-
تعداد رابطه PART_OF.
- 8
-
تعداد رابطه COMPOSITE_OF.
- 9
-
تعداد رابطه BORDER_OF.
- 10
-
تعداد رابطه INNER_OF.
- 11
-
فاصله تا ریشه
- 12
-
فاصله تا روت توسط SPECIALISATION_OF.
- 13
-
فاصله تا روت توسط GENERALISATION_OF.
- 14
-
فاصله تا ریشه با PART_OF.
- 15
-
فاصله تا ریشه COMPOSITE_OF.
- 16
-
فاصله تا ریشه توسط BORDER_OF.
- 17
-
فاصله تا ریشه توسط INNER_OF.
- 18
-
فاصله های انباشته شده
- 19
-
مسافت انباشته شده توسط SPECIALISATION_OF.
- 20
-
مسافت انباشته شده توسط GENERALISATION_OF.
- 21
-
مسافت انباشته شده توسط PART_OF.
- 22
-
مسافت انباشته شده توسط COMPOSITE_OF.
- 23
-
مسافت انباشته شده توسط BORDER_OF.
- 24
-
مسافت های انباشته شده توسط INNER_OF.
ما از یک R*-Tree مجزا برای ایجاد TOAM استفاده کردیم که این مجموعه 23 بعدی از نقاط را مدیریت می کند (به استثنای شناسه TONode). همانطور که در بخش 3 ذکر شد ، هر روش دسترسی دیگری بر اساس ویژگی های متریک کار می کند. R*-Tree از هفت سطح هایپرمکعبی تشکیل شده است تا بتواند تمام گره های 23570 را مدیریت کند (از درخت CityGML ، مثلث های سطحی، چهار وجهی های جامد و گره های جدید حاصل از پوشش های داخلی). شکل 9 پیش بینی های 3 بعدی R*-Tree را نشان می دهد. ردیف بالا فقط بر مختصات توپولوژیکی تمرکز می کند، جایی که محور X رابطه COMPOSITE_OF، Y را توضیح می دهد.-محور رابطه PART_OF و محور Z نوع رابطه را نادیده می گیرد. ردیف پایین بر دو ویژگی هندسی تمرکز دارد، سطح تجمع در محور X و بعد در محور Y. محور Z در ستون سمت چپ تعداد کل روابط را نشان می دهد، محور Z در ستون میانی فاصله تا گره ریشه را نشان می دهد و محور Z در ستون سمت راست فواصل انباشته شده را نشان می دهد.
5. بحث
وظیفه یافتن ویژگی های توپولوژیکی داده های جغرافیایی نسبتاً پیچیده است. Property Graph قادر به مدیریت هر نوع توپولوژی است. ساختار آن نمودارها را می توان با استفاده از روابط رمزگذاری شده بین اشیاء جغرافیایی تحلیل کرد. کار قبلی ما را قادر ساخت چنین نمودارهایی را از داده های توپولوژیکی ناسازگار (تا عدم قطعیت هندسی) تولید کنیم، و در این کار ما برخی از خواص توپولوژیکی مناسب برای دسترسی کارآمد از طریق TOAM توسعه یافته را استخراج کردیم.
پیچیدگی زمانی برای یافتن، به عنوان مثال، تقاطع ها در رویکرد مبتنی بر هندسی به روش دسترسی مکانی یا مکانی-زمانی استفاده شده و پیچیدگی اشیاء مربوطه درگیر بستگی دارد. اگر برنامه یک شبیه سازی باشد، هر شی فضایی عملیات تقاطع را برای یافتن همسایگان توپولوژیکی تکرار می کند. علاوه بر این، برای یافتن اتصال دو جسم که ممکن است از طریق اشیاء دیگر به هم وصل شوند، مثلاً یک خودکار روی میز با زمین، الگوریتمهای مسیریابی، مانند الگوریتم Dijkstra، باید به طور مکرر مجموعهای از اشیاء را برای تقاطعها بررسی کنند. برای یافتن کوتاه ترین مسیر برای رسیدن به یک شی. این تقاطع ها باید هنگام حل پرس و جوهای توپولوژیکی، مانند یافتن ارتباط بین دو شی، و بازیابی اشیاء متصل کننده، به عنوان مثال، میز، در نظر گرفته شوند. صحبت از مجموعههای تقاطعهایی که به هر شیء متصل است، هر شی ممکن است به یک شیء دیگر متصل شود. این نیز بدترین سناریو است که نتیجه می دهد O(n2)�(�2)به عنوان پیچیدگی زمانی برای هر مرحله از الگوریتم مسیریابی، که اگر هر یک از nاشیاء به هم مرتبط بودند در واقعیت، نمودار توپولوژیکی اشیاء جغرافیایی به این سادگی نیست و مجموعههای تقاطعهای هر شی نسبتاً کوچک هستند (مثلاً قلم روی میز به تعداد محدودی از اشیاء دیگر در پایگاه داده متصل است) که منجر به موارد بیشتر میشود. مراحل الگوریتم های مسیریابی برای یافتن کوتاه ترین مسیر به هر شی دیگری. نگه داشتن آن مجموعه ها در حافظه با نگاشت توپولوژی، پیچیدگی زمانی یافتن تقاطع ها را به پیچیدگی حافظه تبدیل می کند (آنها یک بار به عنوان یک مرحله پیش پردازش پیدا شده اند). مراحل پیش پردازش برای یافتن هر تقاطع و تنظیم نمودار را می توان هر زمان که یک شی فضایی یا مکانی-زمانی تغییر یا اضافه کرد تا نمودار با موقعیت هندسی سازگار باشد، انجام می شود. این می تواند به یک گلوگاه تبدیل شود. با این حال،
ما در اینجا دادههایی را در نظر میگیریم که قبلاً از نظر توپولوژیکی سازگار هستند، و توپولوژیها توسط یک نمودار خصوصیت همانطور که توضیح داده شد، ارائه میشوند. [ 8 ]. این هزینه حافظه اضافی خواهد داشت، اما به ایجاد یک روش دسترسی به گرههای پرسوجو با ویژگیهای توپولوژیکی آنها کمک میکند. ما 23 ویژگی توپولوژیکی را به طور نمونه استخراج کردیم و نتیجه را آزمایش کردیم. پرس و جوهای کارآمد اکنون امکان پذیر است. این نتیجه را می توان به راحتی به تعدادی دلخواه از خواص توپولوژیکی گسترش داد. این به معنای داشتن توانایی جستجوهای توپولوژیکی دلخواه بر روی داده های جغرافیایی است. آنچه برای کار آینده باقی می ماند، گسترش این روش انتزاعی به تولید پرس و جوهای توپولوژیکی خاص مرتبط با کاربر است.
روش دسترسی ارائه شده (TOAM) از ساختار نمودار استفاده می کند. شکل 9 نشان می دهد که در مجموعه داده مثال، تنوع برخی از خواص توپولوژیکی نسبتا کم است، به عنوان مثال، تعداد روابط، که منجر به مشکل زیر در روش های دسترسی منحط می شود که در زیر توضیح داده شده است. این به دلیل این واقعیت است که همانطور که قبلا ذکر شد، تعداد تقاطع های یک شی داده شده با سایر اشیاء در پایگاه داده محدود است. از سوی دیگر، برخی از ویژگی ها (مانند فاصله تا یک گره ریشه، فواصل انباشته شده) توزیع یکنواخت تری را نشان می دهند که به TOAM کمک می کند تا از مسائل انحطاطی که در زیر توضیح داده شده است جلوگیری کند و بنابراین می تواند کارآمدتر عمل کند.
توزیع مختصات (بردار 23 بعدی، در مورد ما) لزوماً برای برخی از روش های دسترسی مناسب نیست، زیرا کدهای هش مساوی ایجاد شده توسط، برای مثال، منحنی پر کردن فضا، منجر به پر شدن بیش از حد بیش از حد مربوطه می شود. مکعب [ 33 ]، یا اگر مختصات روی مقداری میانگین با واریانس نسبتاً کم متمرکز شوند با استفاده از روش دسترسی مانند درخت R میتوانند منجر به همپوشانی ابر مکعبهای آن شود که منجر به رفتار دسترسی بد میشود، زیرا شاخههای بیشتری از R- tree باید جستجو شود تا همه اشیا را پیدا کنید.
مشکلات اصلی عملکرد (نسبتا) هنگام وارد کردن یک گره به روش دسترسی توپولوژیکی هنگام محاسبه فاصله تا برخی از گره های ریشه و فاصله انباشته ظاهر شد. برای محاسبه فاصله تا یک گره ریشه، باید کوتاه ترین مسیر تا آن ریشه پیدا شود. پیچیدگی انجام این کار توسط الگوریتم جستجوی مسیر مورد استفاده داده شده است. محاسبه فاصله های انباشته شده پیچیده تر است، زیرا هر کوتاه ترین مسیر از یک گره پرس و جو به هر گره دیگری باید محاسبه و خلاصه شود. در صورت تغییر نمودار، نگهداری هر دو تعریف نیز آسان نیست.
6. نتیجه گیری
در این مقاله نظری تر، تمرکز بر توسعه یک روش جدید برای فعال کردن پرس و جوهای توپولوژیکی بر روی داده های جغرافیایی از هر بعد است، چه وابسته به زمان باشد یا نه. این مقاله شامل اولین آزمایشها بر روی دادههای مدل شهر است. در مرحله بعد، مطمئناً این امر منجر به تحقیقات بیشتر در مورد اجرای عملی به منظور یافتن راه حل های کارآمد برای مشکلات دنیای واقعی مربوط به داده های جغرافیایی می شود. آزمایشها در اینجا بر روی یک مدل کوچک انجام میشوند، نه بر روی یک مدل شهری تمام عیار در مقیاس بزرگ، زیرا هدف بیشتر نشان دادن روشها است تا یافتن نتایج بهینه.
به منظور اعتبار سنجی نمودار به دست آمده از ساختمانهای چهارتایی و تقاطعهای داخلی، ویژگیهای اویلر به مقایسه ساختار نمودار و بررسیهای قابل قبول کمک کردند. تغییرات توپولوژیکی بیشتر می تواند به اصلاح این تحلیل های کمکی کمک کند. البته، این متغیرها به طور کلی نمیتوانند دادههای توپولوژیکی را تا ایزومورفیسم تشخیص دهند، و علاوه بر این، ثابتهایی که میتوانند این کار را انجام دهند منجر به مشکلات محاسباتی سختی میشوند (مثلاً یک مسئله همشکلی گراف).
موضوع دیگر وجود هندسه در مقیاس های مختلف است. آزمایشها در کار قبلی ما [ 32 ] نشان دادهاند که یافتن تقاطعهای قابل اعتماد زمانی که مقیاسهای هندسهها بیش از حد تغییر میکنند به یک مشکل تبدیل میشود. با این حال، مدل نمودار می تواند داده های هندسی در مقیاس های مختلف را مدیریت کند و ما می توانیم حتی در این مورد بدون مشکل از TOAM خود استفاده کنیم. این “تنها” مرحله پیش پردازش رندر سازگار است که بر حل خوبی از مسائل عددی زمانی که مقیاس ها بسیار متفاوت هستند متکی است.
روش استخراج ویژگی توپولوژیکی کاربرد همه کاره ای را به همراه دارد. نمونه اولیه ارائه شده از روش دسترسی توپولوژیکی (TOAM) از مزایای یافتن گره هایی است که ویژگی های توپولوژیکی خاصی را برآورده می کنند. ما فقط چند تعریف از خواص توپولوژیکی را بررسی کرده ایم. در مورد ما، میتوانیم گرههایی را با ویژگیهای توپولوژیکی محلی خاص، به عنوان مثال، تعداد رابطه کلی و از انواع روابط خاص، و حداقل فاصلههای انباشتهشده با هر گره دیگر به عنوان معیاری برای موقعیت در نمودار، با استفاده از هر رابطهای پیدا کنیم. نوع یا نوع رابطه مشخص شده. ما همچنین میتوانیم گرههایی را با ویژگیهای توپولوژیکی جهانی پیدا کنیم، به عنوان مثال، گرههایی در فاصلهای معین از یک گره ریشه، با استفاده از همه انواع رابطه یا برخی از انواع رابطه مشخص شده. با این حال،
تحقیقات آینده شامل گسترش به n D��توپولوژی، و همچنین تعریف خواص توپولوژیکی مفید که در مدت زمان معقولی قابل محاسبه و در دسترس هستند، و تحقیقات بیشتر در مورد روش های دسترسی ترکیبی برای حل پرس و جوهای هندسی و توپولوژیکی در یک روش دسترسی ترکیبی برای داده های جغرافیایی. ما این ایده را با گنجاندن مختصاتی مانند بعد شی یا سطح تجمع جسم لمس کردیم. ترکیبی از خصوصیات هندسی شی فضایی همراه با تنظیمات توپولوژیکی شی فضایی، پرس و جوهای ممکن را به روشی مفید گسترش می دهد. علاوه بر این، مقایسه روش جدید دسترسی توپولوژیکی ما با روشهای مبتنی بر هندسه برای حل پرس و جوهای توپولوژیکی خاص در یک بازه زمانی قابل قبول، برای کارهای آینده مورد توجه است.
منابع
- جوونلا، ا. بردلی، پی. Wursthorn، S. تشخیص و ارزیابی سازگاری توپولوژیکی در مجموعه داده های CityGML. ISPRS Ann. فتوگرام حسگر از راه دور اسپات. Inf. علمی 2018 ، IV-4 ، 59-66. [ Google Scholar ] [ CrossRef ]
- الکساندروف، P. Diskrete Räume. تشک. Sb. (NS) 1937 ، 2 ، 501-518. [ Google Scholar ]
- بردلی، پی. Paul, N. استفاده از مدل رابطه ای برای گرفتن اطلاعات توپولوژیکی فضاها. محاسبه کنید. J. 2010 ، 53 ، 69-89. [ Google Scholar ] [ CrossRef ]
- جان، م. برادلی، پی. محاسبه مدلهای حجمی ضد آب از نمایشهای مرزی برای اطمینان از عملیات توپولوژیکی سازگار. ISPRS Ann. فتوگرام حسگر از راه دور اسپات. Inf. علمی 2021 ، VIII-4/W2-2021 ، 21-28. [ Google Scholar ] [ CrossRef ]
- Meagher, D. Octree Encoding: A Technique جدید برای نمایش، دستکاری و نمایش اشیاء سه بعدی دلخواه توسط کامپیوتر . گزارش فنی IPL-TR-80-111; موسسه پلی تکنیک Rensselaer: تروی، نیویورک، ایالات متحده آمریکا، 1980. [ Google Scholar ]
- گاتمن، A. R-Trees: یک ساختار شاخص پویا برای جستجوی فضایی. در مجموعه مقالات کنفرانس بین المللی ACM SIGMOD در سال 1984 در مدیریت داده ها–SIGMOD ’84، بوستون، MA، ایالات متحده آمریکا، 18 تا 21 ژوئن 1984. [ Google Scholar ]
- بکمن، ن. کریگل، اچ. اشنایدر، آر. Seeger, B. R *-tree: یک روش دسترسی کارآمد و قوی برای نقاط و مستطیل ها. در مجموعه مقالات کنفرانس بین المللی ACM SIGMOD در سال 1990 درباره مدیریت داده ها-SIGMOD ’90، آتلانتیک سیتی، نیوجرسی، ایالات متحده آمریکا، 23 تا 25 مه 1990. [ Google Scholar ]
- جان، م. کوپر، پی. Breunig، M. مدلسازی مکانی-زمانی کارآمد برای فعال کردن تحلیل توپولوژیکی. ISPRS Ann. فتوگرام حسگر از راه دور اسپات. Inf. علمی 2022; برای انتشار پذیرفته شد . [ Google Scholar ] [ CrossRef ]
- Kolbe, T. ارائه و مبادله مدل های سه بعدی شهر با CityGML. در علوم ژئو اطلاعات سه بعدی ; Lee, J., Zlatanova, S., Eds. یادداشت های سخنرانی در اطلاعات جغرافیایی و نقشه برداری. Springer: برلین/هایدلبرگ، آلمان، 2009. [ Google Scholar ]
- لی، ال. لو، اف. ژوا، اچ. یینگ، اس. Zhao, Z. یک مدل توپولوژیکی دو سطحی برای ویژگی های سه بعدی در CityGML. محاسبه کنید. محیط زیست سیستم شهری 2016 ، 59 ، 11-24. [ Google Scholar ] [ CrossRef ]
- صالح، س. Ujang، U. استخراج اطلاعات توپولوژیکی از ساختمانها در CityGML. IOP Conf. سر. محیط زمین. علمی 2018 , 169 , 012088. [ Google Scholar ] [ CrossRef ]
- صالح، س. اوجانگ، U. آذری، س. Choon، T. تجزیه و تحلیل مجاورت فضایی ساختمان های CityGML از طریق ساختار داده های توپولوژیکی سه بعدی. بین المللی قوس. فتوگرام حسگر از راه دور اسپات. Inf. علمی 2019 ، XLII-4/W16 ، 573–579. [ Google Scholar ] [ CrossRef ]
- سان، س. ژو، ایکس. Hou, D. مدل فضای داخلی سه بعدی ساده شده مبتنی بر CityGML برای کاربردهای داخلی. Appl. علمی 2020 ، 10 ، 7218. [ Google Scholar ] [ CrossRef ]
- دمیان، پ. رویکار، ک. ساهو، تی. موریس، A. بازیابی اطلاعات سه بعدی (3DIR): بهره برداری از هندسه سه بعدی و توپولوژی مدل در بازیابی اطلاعات از محیط های BIM. بین المللی J.-Inf. مدل. (IJ3DIM) 2016 ، 5 ، 67-78. [ Google Scholar ] [ CrossRef ]
- جئونگ، دبلیو. Son, J. An الگوریتمی برای تبدیل توپولوژی ساختمان در مدل سازی اطلاعات ساختمان به مدل سازی فیزیکی مبتنی بر مدل سازی انرژی ساختمان شی گرا. Energies 2016 , 9 , 50. [ Google Scholar ] [ CrossRef ]
- وو، ی. شانگ، جی. هو، ایکس. ژو، زی. مپتری توسعه یافته: نمایشی از توپولوژی ریز دانه و سلسله مراتب فضایی Bim. بین المللی قوس. فتوگرام حسگر از راه دور اسپات. Inf. علمی 2017 ، 42، 2/W7 ، 409–415. [ Google Scholar ] [ CrossRef ]
- پاسکوال، ال. قزی، سی. پاسی، ای. تسیگکانوس، سی. بوبکور، م. فلورنتینو-لیانو، بی. هادزیچ، تی. نصیبه، ب. کنترل دسترسی آگاه به توپولوژی فضاهای هوشمند. کامپیوتر 2017 ، 50 ، 54-63. [ Google Scholar ] [ CrossRef ]
- Lienhardt، P. نقشه های ترکیبی تعمیم یافته N-بعدی و شبه منیفولدهای سلولی. بین المللی جی. کامپیوتر. Geom. Appl. 1994 ، 4 ، 275-324. [ Google Scholar ] [ CrossRef ]
- برونیگ، ام. کوپر، پی. بوتویلوفسکی، ای. تامسن، آ. جان، م. دیتریچ، آ. الدوری، م. گلوفکو، دی. منینگهاوس، ام. داستان DB4GeO – معماری پایگاه داده جغرافیایی مبتنی بر سرویس برای پشتیبانی از تجزیه و تحلیل و تجسم داده های چند بعدی. ISPRS J. Photogramm. Remote Sens. 2016 , 117 , 187–205. [ Google Scholar ] [ CrossRef ]
- بردلی، پی. Paul, N. مقایسه G- maps با دیگر ساختارهای داده توپولوژیکی. GeoInformatica 2014 ، 18 ، 595-620. [ Google Scholar ] [ CrossRef ]
- وربویز، ام. یک مدل واحد برای اطلاعات مکانی و زمانی. محاسبه کنید. J. 1994 , 37 , 26-34. [ Google Scholar ] [ CrossRef ]
- van Oosterom، P. ساختارهای داده توپولوژیکی در مقیاس متغیر مناسب برای انتقال پیشرونده داده: درخت GAP-face و جنگل لبه GAP. Cart.-Graphy Geogr. Inf. علمی 2005 ، 32 ، 331-346. [ Google Scholar ] [ CrossRef ]
- پل، ن. بردلی، پی. ادغام فضا، زمان، نسخه و مقیاس با استفاده از توپولوژی های الکساندروف. بین المللی J.-Inf. مدل. (IJ3DIM) 2015 ، 4 ، 64-85. [ Google Scholar ] [ CrossRef ]
- کرامر، تی. Huhnt, W. اطلاعات توپولوژیکی در مدلهای هندسی ساختمانها . کارگاه بین المللی محاسبات در مهندسی عمران: آستین، تگزاس، ایالات متحده آمریکا، 2009. [ Google Scholar ]
- فلگارا، آر. دی فلوریانی، ال. ماگیلو، پ. Weiss, K. Tetrahedral Trees: A Family of Spatial Indexs Spatial Indexs for Tetrahedral Meshes. ACM Trans. تف کردن سیستم الگوریتم 2020 ، 6 ، 1-34. [ Google Scholar ] [ CrossRef ]
- جان، م. بردلی، پی. الدوری، م. برونیگ، ام. مدلهای سازگار توپولوژیکی برای توزیع دادههای بزرگ جغرافیایی-مکانی-زمانی کارآمد. ISPRS Ann. فتوگرام حسگر از راه دور اسپات. Inf. علمی 2017 ، IV-4/W5 ، 65-72. [ Google Scholar ] [ CrossRef ]
- دوشان، ج. برانیسلاو، ب. عناصر کیفیت داده های مکانی به عنوان پشتیبان فناوری اطلاعات برای برنامه ریزی توسعه پایدار. Spatium 2004 ، 11 ، 77-83. [ Google Scholar ]
- Li، S. در سازگاری و تحقق توپولوژیکی. محدودیتها 2006 ، 11 ، 3151. [ Google Scholar ] [ CrossRef ]
- کانگ، اچ. لی، ک. ارزیابی سازگاری توپولوژیکی برای عملیات فروپاشی در تعمیم پایگاههای داده فضایی. در دیدگاه های مدل سازی مفهومی ; یادداشت های سخنرانی در علوم کامپیوتر; آکوکا، ج.، اد. Springer: برلین/هایدلبرگ، آلمان، 2005; جلد 3770. [ Google Scholar ]
- رودریگز، م. بریسابوآ، ن. مزا، ج. Luaces, M. اندازهگیری سازگاری با توجه به محدودیتهای وابستگی توپولوژیکی. در مجموعه مقالات هجدهمین کنفرانس بین المللی SIGSPATIAL در مورد پیشرفت در سیستم های اطلاعات جغرافیایی، سن خوزه، کالیفرنیا، ایالات متحده آمریکا، 2 تا 5 نوامبر 2010. ص 182-191. [ Google Scholar ]
- برادلی، پی. پشتیبانی از تجزیه و تحلیل داده ها برای شهرهای هوشمند: مروری بر مدل های داده و توپولوژی. در آموزش آماری و علوم داده SLDS 2015 ; Gammerman, A., Vovk, V., Papadopoulos, H., Eds. Springer: برلین/هایدلبرگ، آلمان، 2015; LNCS 9047; ص 406-413. [ Google Scholar ] [ CrossRef ]
- جان، م. برادلی، پی. یک مطالعه استحکام برای استخراج مدلهای حجمی ضد آب از دادههای نمایش مرزی. ISPRS Int. J.-Geo-Inf. 2022 ، 11 ، 224. [ Google Scholar ] [ CrossRef ]
- بردلی، پی. Jahn، M. در مورد رفتار شاخصهای منحنی پرکننده فضای مقیاسشده p -Adic برای دادههای با ابعاد بالا. محاسبه کنید. J. 2020 . [ Google Scholar ] [ CrossRef ]
- Jahn, M. مدیریت داده های توزیع شده و موازی برای پشتیبانی از پیاده سازی های شبیه سازی ژئو-علمی. دکتری پایان نامه، موسسه فناوری کارلسروهه، کارلسروهه، آلمان، 2022. [ Google Scholar ]
- پولثیر، ک. Rumpf, M. مفهومی برای فرآیندهای وابسته به زمان. در تجسم در محاسبات علمی ; Goebel, M., Mueller, H., Urban, B., Eds. Springer: وین، اتریش، 1994; صص 137-153. [ Google Scholar ]
- TinkerPop Gremlin. 2022. در دسترس آنلاین: https://tinkerpop.apache.org/gremlin.html (در 18 اکتبر 2022 قابل دسترسی است).
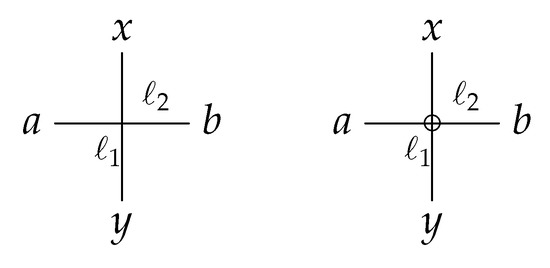
شکل 1. وضعیت توپولوژیکی ناسازگار ( چپ ) و فضای همپوشانی ( راست ).
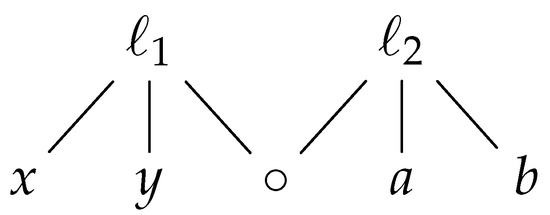
شکل 2. نمودار بروز فضای همپوشانی شکل 1 .
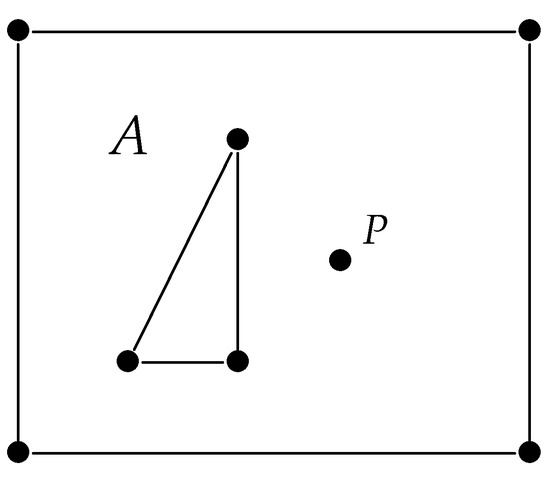
شکل 3. یک مستطیل با یک سوراخ مثلثی و یک سوراخ.
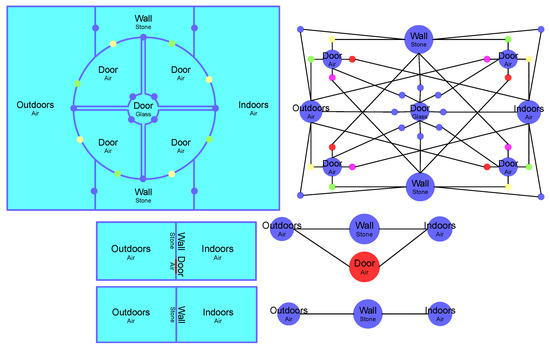
شکل 4. بالا : نمودار ویژگی پیچیده ترین مدل هندسه، که از مجتمع های چهار وجهی مکانی-زمانی برای هر موجودیت انتزاعی مورد علاقه استفاده می کند. گره های کوچک نشان دهنده تقاطع های مکانی و زمانی گره های بزرگ هستند. وسط : نمودار ویژگی مدل هندسی کمتر پیچیده، که ابعاد برخی از هندسه های مرکز خرید را کاهش می دهد. پایین : نمودار ویژگی مدل هندسه کمتر پیچیده، که هندسه مرکز خرید را به یک مجموعه چهار وجهی فضایی و زمانی کاهش می دهد.
شکل 5. روش دسترسی توپولوژیکی از یک روش دسترسی و یک رمزگذاری توپولوژی تشکیل شده است.
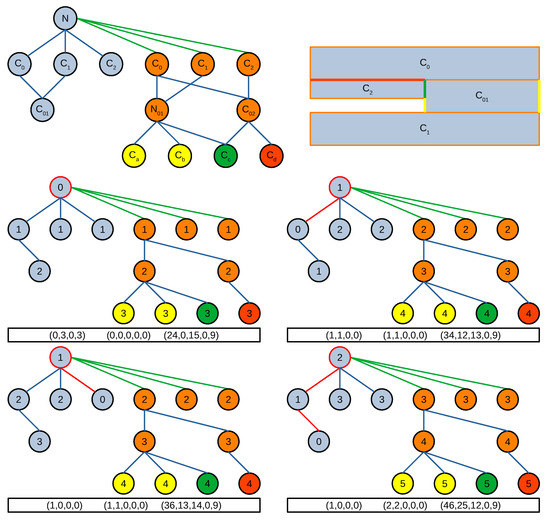
شکل 6. شکل بالا سمت چپ نمودار خواص توپولوژی ها را از شکل های نشان داده شده در شکل بالا سمت راست نشان می دهد. روابط موجود در نمودار ویژگی قسمتی از (قرمز)، ترکیبی از (آبی)، مرزی (نارنجی) و داخلی (سبز) است. شکلهای ردیف دوم و سوم کوتاهترین مسیرهای الگوریتم Dijkstra را هنگام شروع از گره با مقدار 0 نشان میدهند. مقادیر سایر گرهها تعداد گامهای برداشته شده به گره با مقدار 0 را نشان میدهند. بردارهای زیر نشاندهنده توپولوژیک هستند. ویژگی های گره با مقدار 0 (به آخرین پاراگراف بخش 3 مراجعه کنید).
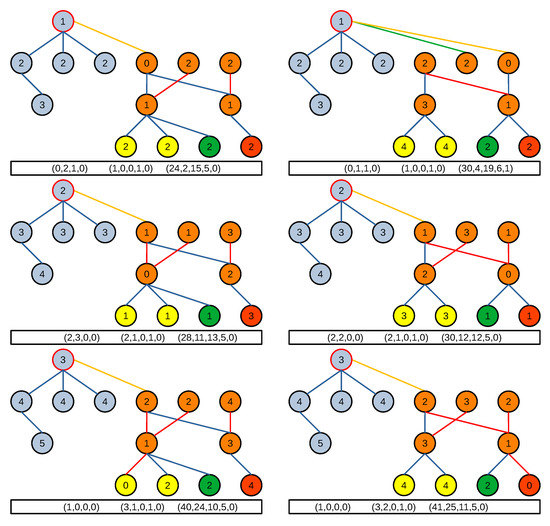
شکل 7. شکل ها انواع رابطه ای را نشان می دهند که الگوریتم Dijkstra هنگام شروع در گره با مقدار 0 از مثال داده شده در شکل 6 (بالا سمت راست) انتخاب کرده است. مقادیر سایر گره ها کوتاه ترین فاصله با گره با مقدار 0 هستند. بردارهای زیر ویژگی های توپولوژیکی گره را با مقدار 0 نشان می دهند (به آخرین پاراگراف بخش 3 مراجعه کنید).
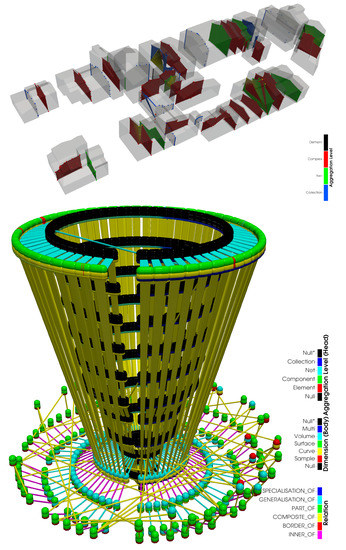
شکل 8. بالا : روکش مجتمع های چهار وجهی مرکز شهر تاریخی سالوادور که بر اساس سطح تجمع رنگ شده اند. پایین: روکشهای داخلی مرکز شهر تاریخی سالوادور (رنگآمیزی بر اساس سطح و ابعاد تجمع) اجسام Tetrahedron3DComponent (سر سبز و بدن فیروزهای) و مرزهای آنها به عنوان اشیاء بسته (بدون مرز) Triangle3DComponent (سر سبز و بدن سبز).
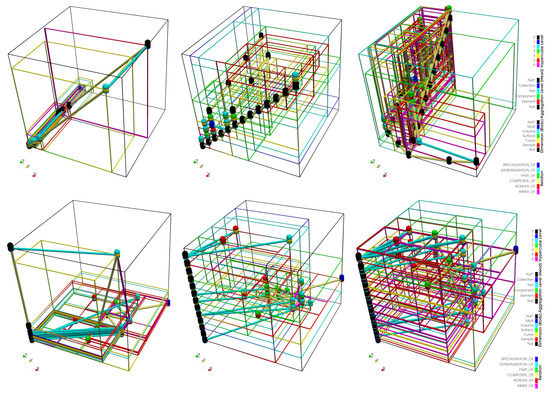
شکل 9. TOP LEFT X: ترکیبی از تعداد. TOP LEFT Y: بخشی از تعداد. TOP MIDDLE X: ترکیبی از فاصله تا ریشه. TOP MIDDLE Y: بخشی از فاصله تا ریشه. بالا سمت راست X: ترکیبی از فواصل انباشته شده. بالا سمت راست Y: بخشی از فواصل انباشته شده. BOTTOM X: سطح تجمع. Y پایین: بعد; LEFT Z: تعداد رابطه. Middle Z: فاصله تا ریشه. RIGHT Z: فواصل انباشته شده.





بدون دیدگاه