روش تطبیق نقشه مسیر فرکانس پایین بر اساس تقسیم بندی سرفصل خودرو

بسیاری از وسایل نقلیه متصل به سیستم موقعیت‌یابی جهانی، داده‌های گسترده‌ای را از راه دور در شهرها جمع‌آوری می‌کنند و برنامه‌ریزی زیرساخت مبتنی بر داده را ممکن می‌سازند. برای بهره‌مندی واقعی از این فناوری نوظهور، ترکیب داده‌های تله‌ماتیک و نقشه برای آسان‌تر کردن استخراج و استخراج اطلاعات مفید از داده‌ها مهم است. با انجام تطبیق نقشه، نقاط داده‌ای که نمی‌توانند به‌طور دقیق در شبکه راه‌ها قرار گیرند، می‌توانند در بخش جاده درست پیش‌بینی شوند. به عنوان یک ابزار مهم برای پردازش داده از راه دور، به یک مرحله مهم پیش پردازش در زمینه داده کاوی تبدیل شده است. با این حال، به دلیل خطاهای مختلف دستگاه های مکان یابی و پیچیدگی شبکه های جاده ای، فناوری تطبیق نقشه نیز با چالش های بزرگی مواجه است. به منظور بهبود کارایی و دقت الگوریتم تطبیق نقشه، این مطالعه یک روش آفلاین را برای تطبیق نقشه داده‌های مسیر فرکانس پایین بر اساس تقسیم‌بندی مسیر خودرو پیشنهاد می‌کند. ابتدا، مسیر بر اساس جهت حرکت وسیله نقلیه تقسیم می شود. سپس، احتمال جامع بخش جاده مربوطه بر اساس احتمال مکانی و احتمال جهت هر بخش جاده در اطراف محل محاسبه می‌شود. سوم،k مسیرهای تطبیق نامزد مورد بررسی بر اساس ارزیابی احتمال جامع انتخاب می شوند. در نهایت، برنامه ریزی کوتاه ترین مسیر و محاسبه احتمال مسیرهای مختلف نامزد برای یافتن مسیر تطبیق بهینه ترکیب می شوند. نتایج تجربی روی مجموعه داده مسیر واقعی در شانگهای و محیط شبکه جاده نشان می‌دهد که الگوریتم پیشنهادی از دقت، کارایی و استحکام بهتری نسبت به سایر الگوریتم‌ها برخوردار است.

کلید واژه ها:

مسیر فرکانس پایین ؛ تطبیق نقشه ; احتمال جامع ; برنامه ریزی کوتاه ترین مسیر

1. مقدمه

در سال های اخیر، سیستم موقعیت یاب جهانی (GPS) به طور گسترده در وسایل نقلیه استفاده شده است، که جمع آوری مقدار زیادی از داده های مسیر توسط مدیریت شهری و خدمات ترافیکی را برای منعکس کردن اطلاعاتی مانند موقعیت، سرعت و جهت وسیله نقلیه تسهیل می کند. در سیستم‌های حمل‌ونقل هوشمند، این داده‌های مسیر GPS معمولاً با سیستم اطلاعات جغرافیایی (GIS) ادغام می‌شوند تا خدمات مختلفی مانند ناوبری وسایل نقلیه، ردیابی و نقشه‌برداری جاده‌های جدید را برای افراد یا مشاغل برای GIS ارائه دهند [ 1 ، 2 ، 3 ، 4 ، 5 ، 6]. در فرآیند نمونه‌برداری مسیر، اشیایی مانند درختان و ساختمان‌ها بر دقت داده‌های مسیر تأثیر می‌گذارند، بنابراین ممکن است نقاط مسیر به‌دست‌آمده به‌طور دقیق روی شبکه راه‌ها قرار نگیرند. بنابراین، یک گام مهم در یکپارچگی با اطلاعات جغرافیایی، تطبیق نقاط مسیر با شبکه راه ها برای تعیین بخش جاده از مسیر حرکت وسیله نقلیه و مکان وسیله نقلیه در شبکه جاده، یعنی تطبیق نقشه است. اگر داده های مسیر GPS و داده های شبکه جاده به اندازه کافی دقیق باشند، تطبیق نقشه موثر آسان است. با این حال، با توجه به ساختار پیچیده شبکه راه، روش‌های تطبیق نقشه دقیق‌تر و کارآمدتر برای غلبه بر مشکلات و چالش‌های تطبیق نقشه مورد نیاز است.

با توجه به فرکانس نمونه برداری متفاوت از نقاط مسیر، می توان بین روش های فرکانس بالا برای تطبیق نقشه مسیر و روش های فرکانس پایین برای تطبیق نقشه مسیر تمایز قائل شد. با استفاده از داده‌های مسیر فرکانس بالا، بخش‌های جاده مطابق با نقاط مکان را می‌توان بهتر پیدا کرد و در نتیجه نتایج تطبیق با دقت بالاتری به دست می‌آید. با این حال، به دلیل محدودیت های سخت باتری، دستگاه دستی تعبیه شده در GPS نمی تواند داده های مسیر فرکانس بالا را برای دوره های طولانی جمع آوری کند. بنابراین، تطبیق نقشه برای داده های مسیر فرکانس پایین به یک موضوع مهم تبدیل می شود. دستیابی به تطبیق نقشه مسیر فرکانس پایین در شبکه راه های شهری پیچیده موضوع این مطالعه است. روش های تطبیق نقشه موجود برای داده های مسیر فرکانس پایین عمدتاً شامل سه دسته زیر است.

(1): روش های مبتنی بر یادگیری ماشین

روش‌های مبتنی بر یادگیری ماشین عمدتاً شامل فیلتر کالمن و تکنیک‌های شبکه عصبی مصنوعی [ 7 ] است. تولدو مورئو و همکاران [ 8 ] یک الگوریتم مبتنی بر فیلتر ذرات پیشنهاد کرد که اندازه‌گیری‌ها را از گیرنده‌های سیستم ماهواره‌ای ناوبری جهانی (GNSS)، ژیروسکوپ‌ها و اورومترها برای حل مشکل تطبیق نقشه برای جاده‌های موازی ترکیب می‌کند. به طور مشابه، Szottka و همکاران. [ 9 ] یک الگوریتم مبتنی بر فیلتر ذرات را با استفاده از داده های تشخیص دوربین با نشانگرهای شبکه جاده و داده های نقشه تجاری پیشنهاد کرد. تائو و همکاران [ 10 ] یک حل‌کننده محلی‌سازی مبتنی بر فیلتر کالمن برای تطبیق نقشه با استفاده از داده‌های GPS، داده‌های خودرو، مشاهدات دوربین و داده‌های نشانگر شبکه جاده‌ای که در نقشه‌های ناوبری دیجیتال جاسازی شده‌اند، توسعه داد. گو و همکاران [11 ] اندازه گیری های چند حسگر و تکنیک های نقشه برداری سه بعدی را برای توسعه یک سیستم محلی سازی قوی در دره های شهری ترکیب کرد. نقشه سه بعدی برای انجام انتقال سیگنال و ردیابی موقعیت ها برای تصحیح موقعیت خودرو استفاده می شود. شونسوکه و همکاران [ 12 ] یک سیستم موقعیت یابی وسیله نقلیه فیلتر شده با ذرات را برای رانندگی خودران پیشنهاد کرد که سیستم ناوبری جهانی، یک سیستم ناوبری اینرسی و داده های مشاهده دوربین را یکپارچه می کند. ژنگ و همکاران [ 13 ] یک الگوریتم تقسیم‌بندی و طبقه‌بندی یادگیری ماشین برای تشخیص تغییر خط با استفاده از زاویه فرمان و داده‌های خودرو در اتوبوس‌های CAN پیشنهاد کرد. این نوع روش از داده‌های حسگر مختلف به‌دست‌آمده از چندین حسگر برای بهبود دقت تطابق استفاده می‌کند [ 14 و 15]. با این حال، این داده‌های حسگر، که نیاز به کسب اضافی دارند، معمولاً نمی‌توانند از دستگاه‌های ناوبری وسایل نقلیه معمولی به دست آیند. علاوه بر این، بیشتر روش‌های تطبیق نقشه مبتنی بر یادگیری ماشین بر فرآیند یادگیری پارامتر تکیه می‌کنند. به طور خلاصه، روش‌های مبتنی بر یادگیری ماشینی بالا همگی نیاز به جمع‌آوری، یادگیری و محاسبه حجم زیادی از داده‌ها دارند. در مقایسه با روش های احتمالی و وزنی، محاسبات پیچیده تری مورد نیاز است.

(2): روش های مبتنی بر محاسبه احتمال

به طور کلی، روش‌های تطبیق نقشه مبتنی بر احتمال از یک مدل مارکوف پنهان برای یافتن محتمل‌ترین مسیر استفاده می‌کنند. در این فرآیند، ترکیب‌های مختلف جاده‌هایی که وسیله نقلیه می‌تواند طی کند، برای یافتن بهترین مسیر منطبق ارزیابی می‌شود. توالی نقاط پیش بینی شده حالت نهفته مدل مارکوف است و نقاط اصلی GPS مشاهدات هستند. الگوریتم‌های مختلف توزیع‌های احتمال انتقال متفاوتی را برای تعیین احتمال عبور از یک بخش جاده کاندید پیشنهاد می‌کنند. اکثر الگوریتم ها از توزیع گاوسی برای توصیف احتمال انتشار استفاده می کنند. نیوزون و همکاران [ 16 ] ابتدا یک مدل مارکوف پنهان برای برازش داده های GPS بر اساس یک چارچوب تطبیق نقشه احتمالی پیشنهاد کرد. زنگ و همکاران [ 17] کاربرد انتگرال انحنای مسیر GPS را در تطبیق نقشه پیشنهاد کرد و از ویژگی انحنا برای یافتن بهترین مسیر تطبیق استفاده کرد. با این حال، هنگامی که نرخ نمونه برداری از نقاط GPS ورودی افزایش می یابد، عملکرد تطبیق نقشه ضعیف است. لو و همکاران [ 18 ] یک روش تطبیق نقشه بر اساس مدل زنجیره مارکوف پنهان، با استفاده از داده‌های هندسی انباشته شبکه راه، ماتریس توپولوژی بخش‌های جاده و ساختار چهاردرختی تصفیه‌شده، ساخت و الگوریتم ویتربی را برای یافتن ترتیب بهینه ترکیب کرد. بخش های جاده چن و همکاران [ 19] یک روش تطبیق نقشه سه مرحله ای بر اساس جهت رانندگی پیشنهاد کرد. در این روش، احتمال جهت و احتمال مکانی بخش های جاده در اطراف نقاط GPS محاسبه می شود تا مسیر تطبیق مربوطه به دست آید. با این حال، هنگام جستجوی مسیر، بهترین مسیر مطابق با محاسبه بیشتر پیدا نمی‌شود.

(3): روش های مبتنی بر تعیین وزن

بر خلاف روش‌های احتمالی، روش‌های تطبیق نقشه وزنی هزینه‌ها را به مسیرهای نامزد مختلف اختصاص می‌دهند و از روش‌های انتخاب متفاوت برای یافتن مسیرهای بالقوه استفاده می‌کنند. لین و همکاران [ 20 ] یک الگوریتم نقشه برداری انتخاب مبتنی بر Dijkstra را برای ارزیابی صحت توالی جاده پیشنهاد کرد. بر اساس داده های نقشه، یک گراف جهت دار مجازی تعریف می شود که گره های آن مجموعه ای از نقاط کاندید هستند و وزن یال ها نشان دهنده احتمال انتقال از یک نقطه کاندید به نقطه دیگر برای یافتن مسیر مناسب است. با این حال، تقریب بین نقطه نامزد و نقطه GPS در نظر گرفته نشده است. پتوشک و همکاران [ 21] یک الگوریتم تطبیق نقشه پیشنهاد کرد که نقشه‌برداری هندسی را با الگوریتم کوتاه‌ترین مسیر Dijkstra ترکیب می‌کند تا مشکلات داده‌های موقعیت خودرو نادرست و بخش‌های بسیار کوتاه جاده را در فرآیند تطبیق حل کند. با این حال، هنگامی که فرکانس نمونه برداری نقطه مسیر به طور مداوم کاهش می یابد، دقت تطبیق نیز به طور مداوم کاهش می یابد.

علاوه بر این، محققان مربوطه نیز تلاش های قابل توجهی برای بهبود کارایی اجرای تطبیق نقشه انجام داده اند. کولر و همکاران [ 22] محاسبه احتمالات و تخصیص وزن ها را با استفاده از روش تطبیق نقشه بر اساس HMM ترکیب کرد، اما الگوریتم ویتربی را با الگوریتم Dijkstra جایگزین کرد. روش اختلاط احتمالات و وزن ها با کاهش سربار در محاسبه احتمالات انتقال، زمان اجرای فرآیند تطبیق نقشه را کاهش می دهد. روش‌های تطبیق نقشه سنتی برای داده‌های مسیر فرکانس پایین اغلب نیاز به یافتن کوتاه‌ترین مسیر بین نقاط نمونه‌گیری مجاور دارند. با ادامه کاهش فرکانس نمونه‌برداری، فاصله بین نقاط نمونه‌برداری مجاور بزرگ‌تر و بزرگ‌تر می‌شود و روش انتخاب کوتاه‌ترین مسیر دیگر نمی‌تواند بهترین مسیر منطبق را برای نقاط مسیر پیدا کند. بنابراین، لازم است نقاط مسیر فرکانس پایین با بخش های جاده مربوطه به روش دقیق تری مطابقت داده شود.

بقیه مطالعه به شرح زیر سازماندهی شده است. بخش 2 مفاهیم اساسی و تشریح مسائل مرتبط را ارائه می دهد و چارچوب و فرآیند الگوریتم پیشنهادی را به تفصیل شرح می دهد. بخش 3 عملکرد الگوریتم پیشنهادی را از طریق آزمایشات تأیید می کند. شرح مشارکت و تحلیل مرتبط روش پیشنهادی در بخش 4 مورد بحث قرار گرفته است. نتیجه گیری و چشم انداز آینده در بخش 5 ارائه شده است.

2. روش ها

2.1. مفاهیم اساسی و شرح مسئله

این بخش مفاهیم مرتبط مورد استفاده در این مقاله را تعریف می کند.

تعریف 1.

(بخش جاده): بخش جاده یک یال جهت دار است که به صورت تعریف می شود

e = (e_{id}, e_{start}^{id}, e_{end}^{id})

، جایی که

e_{id}

نشان دهنده شناسه بخش جاده است،

e_{start}^{id}

نقطه شروع بخش جاده را نشان می دهد

e_{id}

، و

e_{end}^{id}

نقطه پایان بخش جاده را نشان می دهد

e_{id}

. در این مطالعه،

e_{start}^{id} \to e_{end}^{id}

e_{end}^{id} \to e_{start}^{id}

به عنوان جهات مختلف از یک بخش جاده در نظر گرفته می شوند.

تعریف 2.

(گره بخش جاده): گره بخش جاده به نقطه شروع یا پایان بخش جاده اشاره دارد که به صورت بیان می شود.

v = (v_{i d}, v_{l a t}, v_{l o n})

، جایی که

v_{i d}

شناسه منحصر به فرد گره بخش جاده است و

v_{l a t}

v_{l o n}

به ترتیب مختصات طول و عرض جغرافیایی موقعیت مکانی گره قطعه جاده هستند.

تعریف 3.

(شبکه جاده): شبکه جاده با یک گراف جهت دار منفرد G = (V, E) نشان داده می شود، که در آن V مجموعه ای از گره های بخش جاده است که به صورت بیان می شود.

V = {v_{1}, v_{2}, \dots, v_{n}}

، E مجموعه ای از تمام بخش های جاده است که به صورت بیان می شود

E = {e_{1}, e_{2}, \dots, e_{n}}

تعریف 4.

(نقطه مکان): نقطه مکان (که به آن نقطه مسیر نیز گفته می شود) نشان دهنده اطلاعات مکانی است که توسط دستگاه GPS در یک بازه زمانی معین به دست می آید که به صورت تعریف می شود.

p_{i} = {l a t_{i}, l o n_{i}, t_{i}, s_{i}, h_{i}}

، جایی که

l a t_{i}

l o n_{i}

مختصات طول و عرض جغرافیایی نقطه مکان فعلی را به ترتیب نشان می دهد،

t_{i}

نشان دهنده زمان نقطه مکان فعلی است،

s_{i}

سرعت فعلی وسیله نقلیه را نشان می دهد و

h_{i}

جهت رانندگی فعلی وسیله نقلیه را نشان می دهد.

تعریف 5.

(بخش مسیر اصلی): بخش مسیر اصلی شامل مجموعه ای از نقاط مکان است که توسط مهرهای زمانی مرتب شده اند که به صورت تعریف می شوند.

τ = 〈 p_{i}, p_{i + 1}, \dots, p_{i + u - 1} 〉

، جایی که

p_{j} (i \leq j \leq i + u - 1)

نقطه مکان و طول آن است

τ

تعداد نقاط مکان موجود در است

τ

. به این معنا که،

| τ | = u

تعریف 6.

(قطع مسیر منطبق): با توجه به یک قطعه مسیر اصلی، بخش مسیر منطبق آن

τ_{m}

نشان دهنده بخش رانندگی واقعی وسیله نقلیه در شبکه جاده است که به صورت تعریف شده است

τ_{m} = 〈 e_{i}, e_{i + 1}, \dots, e_{n} 〉

، جایی که جاده تقسیم می شود

e_{i}

e_{i + 1}

یک گره بخش جاده مشترک دارند. یعنی به هم متصل هستند.

تعریف 7.

(زاویه جهت سفر): جهت حرکت به جهتی اطلاق می شود که وسیله نقلیه در آن نقطه در حال حرکت است. زاویه ای که با چرخش خلاف جهت عقربه های ساعت جهت جلو به سمت شمال درست می شود، زاویه جهت حرکت نقطه مکان نامیده می شود. زاویه جهت حرکت نقطه مکان

p_{i}

به عنوان ثبت می شود

h_{i}

0 ° \leq h_{i} \leq 360 °

زاویه جهت سمت را می توان از مجموعه داده مسیر بدست آورد.

تعریف 8.

(زاویه جهت بخش جاده): زاویه ای که از چرخش خلاف جهت عقربه های ساعت جهت بخش جاده به سمت شمال تشکیل می شود به عنوان زاویه جهت بخش جاده تعریف می شود. روش محاسبه در رابطه (1) نشان داده شده است.

β = ⎧⎩⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪ (π 2 - arctan (y 2 - y 1 x 2 - x 1)) * 180 π, x 2 > x 1 (3 * π 2 - arctan (y 2 - y 1 x 2 - x 1)) * 180 π, x 2 < x 1 0, x 2 = x 1 \land y 2 \geq y 1 180, x 2 = x 1 \land y 2 < y 1

(1)

اینجا،

(x_{1}, y_{1})

(x_{2}, y_{2})

مختصات طول و عرض جغرافیایی دو نقطه به ترتیب و

0 ° \leq β \leq 360 °

همانطور که در شکل 1 نشان داده شده است ،

E = {e_{1}, e_{2}, e_{3}, \dots, e_{18}}

مجموعه ای از تمام بخش های جاده را نشان می دهد و

V = {v_{1}, v_{2}, v_{3}, \dots, v_{15}}

مجموعه ای از تمام گره های بخش جاده را نشان می دهد. V و E با هم نمونه ای از یک شبکه جاده ای را تشکیل می دهند. توالی نقاط مکان

〈 p_{1}, p_{2}, p_{3}, \dots, p_{7} 〉

بخش مسیر اصلی را تشکیل می دهد

τ

، که در آن هر نقطه مکان حاوی اطلاعات عرض جغرافیایی، طول جغرافیایی، مهر زمانی، سرعت لحظه ای و اطلاعات جهت سفر است. به عنوان مثال، در نظر گرفتن شمال واقعی به عنوان جهت پایه، زاویه جهت حرکت از

p_{1}

به عنوان نشان داده شده است

h_{1}

. بخش مسیر منطبق از

τ

است

τ_{m} = 〈 e_{9}, e_{14}, e_{6}, e_{7}, e_{17} 〉

2.2. الگوریتم تطبیق نقشه مسیر فرکانس پایین

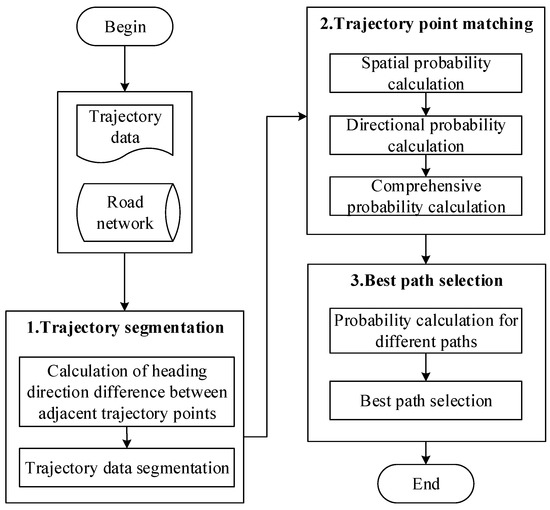
2.2.1. بررسی اجمالی الگوریتم

الگوریتم پیشنهادی ابتدا مسیر کامل را با توجه به جهت حرکت نقطه مکان به چندین مسیر فرعی متوالی تقسیم می کند. دوم، احتمال جهت را برای هر مسیر فرعی پس از تقسیم بندی محاسبه می کند و احتمال مکانی را با توجه به فاصله بین نقطه مکان و بخش جاده به دست می آورد. بر اساس احتمال جهت و احتمال مکانی، احتمال جامع مربوطه به دست می آید. در نهایت، الگوریتم کوتاه ترین مسیر و نتیجه محاسبه احتمال جامع با هم ترکیب می شوند تا مسیرهای تطبیق تحت احتمالات مختلف به دست آید. مسیر بهینه بر اساس ضریب شباهت بین مسیر و بخش های جاده انتخاب می شود، به طوری که نقاط مسیر با شبکه جاده مطابقت دارند.شکل 2 نمودار شماتیک الگوریتم پیشنهادی را نشان می دهد که عمدتا شامل سه مرحله زیر می باشد.

(1): تقسیم بندی مسیر

یک بخش مسیر اصلی را در نظر بگیرید

τ = {p_{1}, p_{2}, p_{3}, \dots, p_{n}}

، که در آن هر نقطه مکان

p_{i}

اطلاعات جهت خود را در طول فرآیند رانندگی دارد. کل مسیر بر اساس جهت حرکت نقطه مکان تقسیم می شود. اولین نقطه در مسیر فرعی قطعه‌بندی‌شده بعدی، آخرین نقطه در مسیر فرعی قطعه‌بندی‌شده قبلی است.

(2): تطبیق نقطه مسیر

برای هر نقطه مسیر

p_{i}

، بخش های جاده کاندید مربوطه در اطراف آن وجود دارد. بر اساس فاصله بین نقطه مسیر و بخش جاده کاندید، احتمال فضایی مربوطه

G_{1}

به دست می آید، و احتمال جهت

G_{2}

از زاویه جهت سفر و زاویه جهت قطعه جاده به دست می آید. در نهایت، با ترکیب احتمال مکانی و احتمال جهت، احتمال جامع G _w بین نقطه مسیر و بخش جاده مورد بررسی به دست می‌آید. بخش‌های جاده‌ای که در نظر گرفته می‌شوند بر اساس مقادیرشان برای احتمال جامع مرتب‌سازی می‌شوند.

(3): انتخاب بهترین مسیر

برای هر مسیر فرعی تقسیم شده

τ_{i}

، ابتدا مسیر اولین نقطه تا آخرین نقطه را پیدا می کنیم

τ_{i}

با استفاده از الگوریتم کوتاه ترین مسیر برای هر نقطه مسیر

p_{i}

چندین بخش جاده کاندید با احتمالات مختلف وجود دارد، بنابراین در جستجوی مسیر، چندین دنباله منطبق شامل بخش‌های جاده با احتمالات مختلف را به دست می‌آوریم. مسیری که به بهترین وجه با بخش مسیر اصلی مطابقت دارد بر اساس فاصله بین بخش مسیر و هر مسیر نامزد انتخاب می شود. پس از تطبیق اولین مسیر فرعی تقسیم‌بندی شده، قسمت جاده کاندید که با آخرین نقطه مسیر فرعی قبلی مطابقت دارد، ثبت می‌شود، سپس مسیر فرعی دوم تطبیق داده می‌شود و به همین ترتیب تا در نهایت بهترین مسیر تطبیق به دست آید.

2.2.2. تقسیم بندی مسیر

در یک بخش مسیر اصلی، هر نقطه مسیر

p_{i}

دارای زاویه جهت حرکت مربوطه است

h_{i} (2 \leq i \leq n)

. زاویه چرخش جهت

θ_{i}

بین نقاط مسیر مجاور است

\min (| h_{i} - h_{i - 1} |, 360 ° - | h_{i} - h_{i - 1} |)

. چه زمانی

θ_{i} \geq θ_{c}

راضی است، ما مسیر را تقسیم بندی می کنیم، جایی که

θ_{c}

آستانه زاویه است. در آزمایش‌ها، دقت تطبیق تحت آستانه‌های زاویه‌ای مختلف آزمایش می‌شود که مقدار

θ_{c}

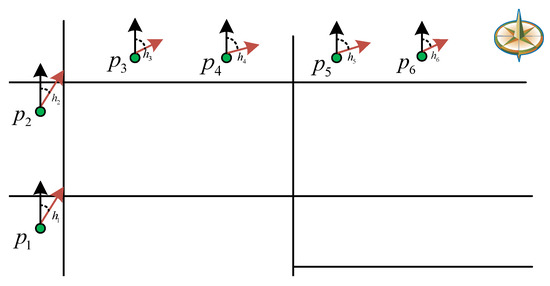
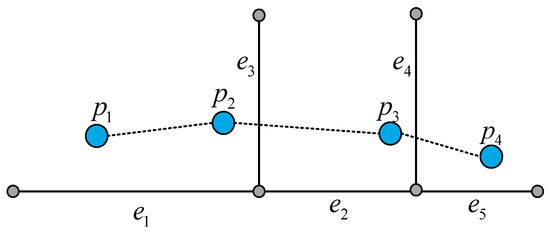
همانطور که در شکل 3 نشان داده شده است، یک قطعه مسیر اولیه وجود دارد $τ = {p_{1}, p_{2}, p_{3}, p_{4}, p_{5}, p_{6}}$ ، $p_{1}$ با زاویه جهت حرکت مطابقت دارد $h_{1}$ ، $p_{2}$ با زاویه جهت حرکت مطابقت دارد $h_{2}$ ، و غیره. در فرآیند تقسیم بندی، تفاوت جهت سفر بین $p_{1}$ و $p_{2}$ ابتدا محاسبه می شود و نتیجه کمتر از $θ_{c}$ . بنابراین، آنها به یک بخش تعلق دارند. سپس، تفاوت جهت سفر را محاسبه می کنیم $p_{2}$ و $p_{3}$ و دریابید که بزرگتر از $θ_{c}$ ، بنابراین آنها به بخش های مختلف تقسیم می شوند. طبق این قانون، مسیر قطعه بندی می شود و مسیرهای فرعی قطعه بندی شده در نهایت به صورت $τ_{1} = {p_{1}, p_{2}}$ و $τ_{2} = {p_{2}, p_{3}, p_{4}, p_{5}, p_{6}}$ . برای اطمینان از اتصال بین مسیرهای فرعی تقسیم شده، آخرین نقطه در $τ_{1}$ اولین نقطه در است $τ_{2}$ . شبه کد برای تقسیم مسیر در الگوریتم 1 نشان داده شده است.

الگوریتم 1: بخش بندی مسیر

ورودی: مسیر T

, θ_{c}

خروجی:

Segmented trajectory set Γ

1 : Initialize Γ = ϕ

, ind = 2, cnt = 1;

2 : Γ_{1}^{1} = p_{1}

;

3 : Γ_{1}^{2} = p_{2}

;
4: برای i = 3 تا | T | انجام
5: اگر

| h (p_{i}) - h (p_{i - 1}) | < θ_{c}

سپس
6: ind = ind + 1;

7 : Γ_{c n t}^{i n d} = p_{i}

;
8: else
9: cnt = cnt + 1;

10 : Γ_{c n t}^{1} = p_{i - 1}

;

11 : Γ_{c n t}^{2} = p_{i}

;
12:        ind = 2;
13:     پایان اگر
14: پایان برای
15: برگردانید

Γ

;

مسیرهای فرعی تقسیم‌بندی شده در آن ذخیره می‌شوند

Γ

، که مبنای تطبیق نقطه مسیر بعدی است.

2.2.3. تطبیق نقطه مسیر

پس از تقسیم‌بندی مسیر، با تجزیه و تحلیل احتمالات بین نقطه مسیر و هر بخش جاده، بخش‌های جاده کاندید با احتمالات متفاوتی یافت می‌شوند. همانطور که در شکل 4 نشان داده شده است ، یک دایره با نقطه مسیر رسم شده است

p_{1}

به عنوان مرکز و r به عنوان شعاع، و بخش های جاده

{e_{1}, e_{2}, e_{3}, e_{4}, e_{5}}

در دایره به عنوان بخش های جاده کاندید انتخاب می شوند. برای یافتن بخش درست جاده که با نقطه مسیر مطابقت دارد، شعاع r را روی مقدار نسبتاً بزرگی (مانند 100 متر) قرار می دهیم. با محاسبه احتمال مکانی و احتمال جهت، m بخش های جاده نامزد مربوط به نقطه مسیر را برای پردازش بیشتر به دست می آوریم.

تعریف 9.

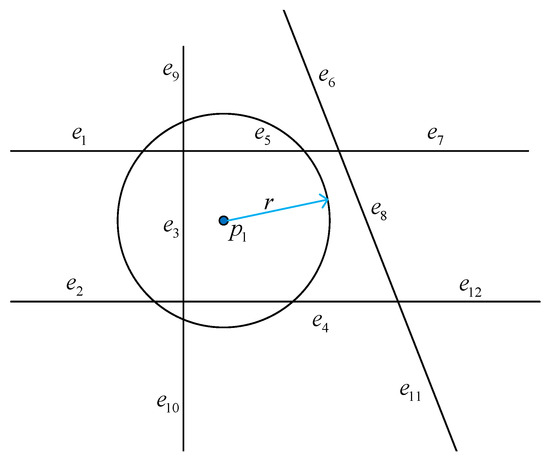
(احتمال مکانی) [ 19 ] : بگذار $H_{p_{i}}^{e_{j}}$ کمترین فاصله از نقطه مسیر باشد $p_{i}$ به بخش جاده $e_{j}$ . ما احتمال فضایی را به عنوان معیاری برای امکان تطبیق فضایی بین $p_{i}$ و $e_{j}$ ، نشان داده شده است $G_{1} (H_{p_{i}}^{e_{j}})$ . روش های محاسبه از $H_{p_{i}}^{e_{j}}$ و $G_{1} (H_{p_{i}}^{e_{j}})$ به ترتیب در معادلات (2) و (3) نشان داده شده است:

H e j p i = min (d i s p (p i, c 1), d i s p (p i, c 2), d i s p (p i, c 3))

(2)

G 1 (H e j p i) = 1 2 π --\sqrt σ 1 e - ( H e j p i ) 2 2 ( σ 1 ) 2

(3)

جایی که $c_{1}$ و $c_{2}$ دو نقطه پایانی بخش جاده هستند $e_{j}$ به ترتیب و $c_{3}$ نقطه طرح عمودی از است $p_{i}$ به $e_{j}$ . اگر $c_{3}$ در واقع نیست $e_{j}$ ، سپس $d i s p (p_{i}, c_{3})$ تنظیم شده است $+ \infty$ ; $σ_{1}$ انحراف استاندارد اندازه گیری مکان است که به طور کلی روی 20 متر تنظیم می شود [ 23 ] . به طور کلی، فاصله بین نقطه مسیر و بخش جاده را می توان به عنوان توزیع نرمال فاصله شبیه سازی کرد $H_{p_{i}}^{e_{j}}$ .

با این حال، بخش‌های جاده منطبق که تنها با احتمال مکانی تعیین می‌شوند، دارای خطاهای مربوطه خواهند بود. همانطور که در شکل 5 ، برای نقطه مسیر نشان داده شده است

p_{2}

(

p_{3}

)

e_{3}

(

e_{4}

) با حداکثر احتمال فضایی یک بخش جاده مطابقت نادرست است. با توجه به جهت حرکت مسیر

p_{1} \to p_{2} \to p_{3} \to p_{4}

، تطبیق صحیح بخش های جاده باید باشد

e_{1} \to e_{2} \to e_{5}

. بنابراین، احتمال جهت گیری برای بهبود دقت تطبیق پیشنهاد شده است.

تعریف 10.

(احتمال جهتی) [ 19 ] : بگذار $A_{h_{i}}^{θ_{j}}$ تفاوت زاویه ای بین زاویه جهت حرکت باشد $p_{i}$ و زاویه جهت بخش جاده. احتمال جهت را به عنوان معیاری برای امکان تطابق جهت بین نقطه مسیر تعریف کنید $p_{i}$ و بخش جاده کاندید $e_{j}$ ، نشان داده شده است $G_{2} (A_{h_{i}}^{θ_{j}})$ . روش های محاسبه از $A_{h_{i}}^{θ_{j}}$ و $G_{2} (A_{h_{i}}^{θ_{j}})$ به ترتیب در معادلات (4) و (5) نشان داده شده است:

A θ j h i = min (| h i - θ 1 j) |, | h i - θ 2 j |)

(4)

G 2 (A θ j h i) = 1 2 π --\sqrt σ 2 e - ( A θ j h i ) 2 2 ( σ 2 ) 2

(5)

جایی که $h_{i}$ زاویه جهت حرکت را نشان می دهد $p_{i}$ ، $θ_{j}^{1}$ و $θ_{j}^{2}$ زاویه ها را در دو جهت مختلف از بخش جاده نشان می دهد. $σ_{2}$ انحراف استاندارد اندازه گیری جهت است و همچنین روی 20 متر تنظیم شده است.

بر اساس رابطه (5)، احتمالات جهتی متفاوتی را بین هر نقطه مسیر و بخش های مختلف جاده کاندید بدست می آوریم. در مورد احتمال فضایی، احتمال جهت نیز می تواند به عنوان توزیع نرمال تفاوت زاویه جهت سفر شبیه سازی شود.

A_{h_{i}}^{θ_{j}}

تعریف 11.

(احتمال جامع) [ 19 ] : این مطالعه با ترکیب احتمال مکانی و احتمال جهتی، احتمال جامع را به صورت تعریف می کند. $G_{w}$ که با رابطه (6) محاسبه می شود.

G w = G 1 \times G 2 -------\sqrt

(6)

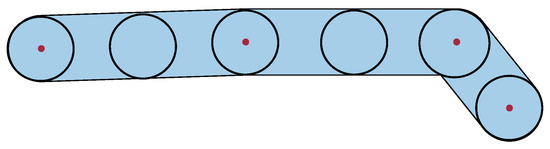
با توجه به محاسبه و بحث فوق، در اطراف هر نقطه مسیر حداقل یک قطعه جاده واجد شرایط وجود دارد، بنابراین حداقل یک احتمال جامع وجود دارد. بر اساس مقدار احتمال جامع، ما بخش‌های جاده کاندید m را با بیشترین احتمال برای انتخاب بهترین مسیر بعدی و ارزیابی الگوریتم تطبیق نقشه انتخاب می‌کنیم. شبه کد تطبیق نقطه مسیر در الگوریتم 2 نشان داده شده است.

الگوریتم 2: تطبیق نقطه مسیر

ورودی:

Segmented trajectory set Γ

, شبکه راه G , آستانه شعاع r , مقدار کاندید k
خروجی: مجموعه قطعه جاده کاندید Cr , مجموعه احتمال جامع G w
1: مقداردهی اولیه Cr

= \emptyset

، ن

= \emptyset

، اچ

= \emptyset

;
2: برای هر کدام

p_{i} \in Γ

انجام
3: یک دایره با C _{i بسازید}

p_{i}

به عنوان مرکز و r به عنوان شعاع.
4: Cr ← Cr

\cup

{بخش های جاده کاندید در اطراف C _i };
5: برای هر کدام

c_{j} \in

Cr do
6: N _ij ← احتمال فضایی

c_{j}

محاسبه شده با معادله (3)؛
7: H _ij ← احتمال عنوان از

c_{j}

محاسبه شده با معادله (5)؛
8: G w _ij ← احتمال جامع

c_{j}

محاسبه شده با معادله (6)؛
9: پایان برای
10: پایان برای
11: بازگشت G w , Cr ;

پس از تطبیق نقاط مسیر با الگوریتم 2، Gw احتمالات جامع برای هر نقطه مسیر را ذخیره می کند و Cr بخش های جاده واجد شرایط را در اطراف هر نقطه مسیر ذخیره می کند. گام بعدی یافتن مسیر بهینه از طریق مسیرهای فرعی تقسیم شده و احتمالات جامع است.

2.2.4. بهترین انتخاب مسیر

در هر زیرمسیر قطعه بندی شده

τ_{i}^{k} = {p_{i}^{a}, p_{i}^{a + 1}, \dots, p_{i}^{b}}

، هر نقطه مسیر دارای بخش های جاده نامزد متناظر با مقادیر احتمال جامع G _w است. از آنجایی که هدف تحقیق این مقاله داده های مسیر فرکانس پایین است، بخش های جاده منطبق با نقاط مسیر مجاور به طور کلی به هم متصل نیستند. بنابراین، ما بهترین بخش جاده را که با نقطه مسیر مطابقت دارد از طریق سه مرحله پیدا می کنیم.

مرحله 1 (ایجاد بافر مسیر): در انتخاب بهترین مسیر، باید با استفاده از الگوریتم کوتاه ترین مسیر، مسیر بین نقاط مسیر را پیدا کنیم. به دلیل وسعت شبکه راه، یافتن مسیر در کل شبکه راه غیرممکن است. بنابراین، قبل از تطبیق، شبکه جاده را بر اساس جهت حرکت نقاط مسیر فیلتر می کنیم. همانطور که در شکل 6 نشان داده شده است ، چهار نقطه مسیر وجود دارد. دایره ای می سازیم با اولین نقطه مسیر به عنوان مرکز و r’به عنوان شعاع، و سپس به طور مداوم در امتداد جهت حرکت مسیر ترجمه کنید. پس از یک تکرار مداوم، بافر جاده مربوطه را بدست می آوریم. در این مطالعه، بافر مسیر با تعیین بخش‌های جاده و گره‌های موجود در بافر جاده ساخته می‌شود.

مرحله 2 (یافتن مسیرهای منطبق): هر مسیر فرعی تقسیم شده

τ_{i}^{k} = {p_{i}^{a}, p_{i}^{a + 1}, \dots, p_{i}^{b}}

مربوط به یک بافر مسیر است. به دلیل فاصله زیاد بین دو نقطه مکان در مسیر فرکانس پایین، دو نقطه پیوسته معمولاً با دو بخش جاده غیر متصل در شبکه جاده مطابقت داده می شوند که ممکن است از هم دور باشند. بنابراین، ما باید مسیرهای ممکن را بین آنها پیدا کنیم. بیایید بگیریم

τ_{i}^{k}

به عنوان مثال، برای

p_{i}^{a}

، m بخش های جاده ای ممکن وجود دارد، و همین امر برای آن صادق است

p_{i}^{b}

. هر نقطه مسیر مربوط به چندین بخش جاده ممکن با احتمالات مختلف است. در این مطالعه، مسیرهای بالقوه با احتمالات مختلف با یافتن مسیرهای بین بخش‌های جاده کاندید با احتمالات مختلف نقطه اول و آخرین نقطه در هر زیرمسیر تقسیم‌بندی شده، یافت می‌شوند. هنگام یافتن مسیرها، بخش جاده کاندید با بیشترین احتمال لزوماً بخش جاده منطبق نیست. بر اساس ملاحظات فوق، عملیات زیر در این تحقیق انجام می شود.

همانطور که در شکل 7 نشان داده شده است، یک مسیر فرعی تقسیم بندی شده وجود دارد

τ' = {p_{1}, p_{2}, p_{3}}

در بافر مسیر. ابتدا نقاط شروع و پایان مسیر را با توجه به جهت حرکت مسیر تعیین می کنیم. بخش های جاده کاندید اولین نقطه مسیر

p_{1}

هستند

{e_{10}, e_{7}, e_{8}}

، بر اساس احتمال جامع مرتب شده و بخش های جاده نامزد آخرین نقطه مسیر مرتب شده است

p_{3}

هستند

{e_{3}, e_{2}, e_{12}}

. شروع از بخش جاده با بیشترین احتمال

p_{1}

(یعنی

e_{10}

، ابتدا نقطه شروع مسیر مربوط به زاویه بین جهت حرکت را پیدا می کنیم

p_{1}

و جهت قطعه جاده که به صورت مشخص شده است

v_{6}

در شکل سپس، تفاوت بین زاویه جهت بخش جاده را در بخش جاده کاندید حداکثر احتمال محاسبه می کنیم

e_{3}

از آخرین نکته

p_{3}

و زاویه جهت حرکت از

p_{3}

، و دریابید که نقطه پایان مسیر است

v_{7}

. بنابراین، ما کوتاه ترین راه را از

v_{6}

به گره

v_{7}

است

e_{10} \to e_{11} \to e_{2}

با این حال، مسیر یافت شده در روش حداکثر احتمال جامع لزوماً مسیر تطبیق نهایی نیست. همانطور که در شکل 8 نشان داده شده است ، مسیرهای فرعی تقسیم شده بر اساس جهت مسیر هستند

τ_{1} = {p_{1}, p_{2}}

τ_{2} = {p_{2}, p_{3}}

. برای آخرین نکته از

τ_{1}

(یعنی

p_{2}

) بخش جاده با بیشترین احتمال جامع است

e_{4}

، اما در شکل 8 می بینیم که

p_{2}

باید مطابقت داشته باشد

e_{5}

. بنابراین، مرحله 3 برای تعیین بهترین مسیر تطبیق استفاده می شود.

مرحله 3 (یافتن بهترین مسیر منطبق): برای هر نقطه مسیر در مسیر فرعی تقسیم‌بندی شده، بخش‌های جاده کاندید با احتمالات جامع مختلف وجود دارد. بنابراین، در این مرحله، همان طور که در جدول 1 نشان داده شده است، k مسیر کاندید از نقطه شروع تا نقطه پایان در مسیرهای فرعی تقسیم شده پیدا می شود . (1) وقتی k = 1، مسیری است از بخش جاده کاندید با بالاترین احتمال جامع نقطه شروع تا بخش جاده کاندید با بالاترین احتمال جامع نقطه پایان. (2) چه زمانی ک= 2، مسیری است از بخش جاده کاندید با بالاترین احتمال جامع نقطه شروع تا بخش جاده کاندید با دومین احتمال بالاتر از نقطه پایان. (3) هنگامی که k = 3، به معنای مسیر از دومین بخش جاده کاندیدای با احتمال زیاد نقطه شروع به بخش جاده با بیشترین احتمال در نقطه پایان است. (4) هنگامی که k = 4، به معنای مسیر از دومین بخش جاده کاندید با احتمال زیاد نقطه شروع به دومین بخش جاده کاندید با احتمال زیاد نقطه پایان است. (5) چه زمانی ک= 5، به معنای مسیر از بخش جاده کاندید با بالاترین احتمال جامع نقطه شروع به بخش جاده کاندید با سومین احتمال بالاتر نقطه پایان است. در آزمایش‌ها، مقادیر k مختلف ( k = 1، 2، 3، 4، 5) برای ارزیابی اثر k مسیرهای مختلف و یافتن بهترین مسیر تنظیم شده‌اند.

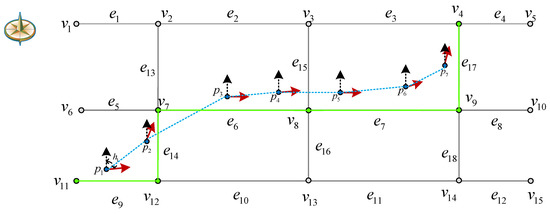
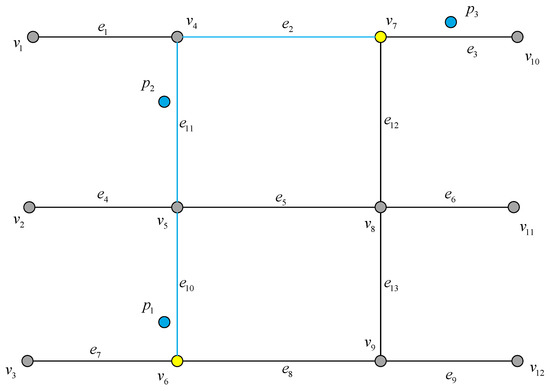
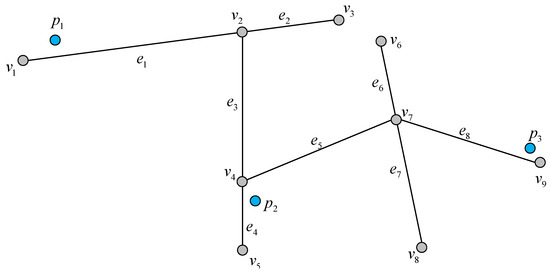
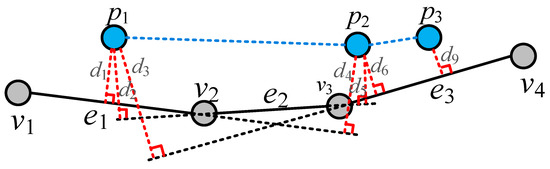
با تجزیه و تحلیل بالا، ما می توانیم k مسیرهای نامزد مربوطه را برای هر زیرمسیر قطعه بندی شده مسیر اصلی پیدا کنیم و مسیرهای نامزد مسیرهای فرعی مختلف را برای بدست آوردن k مسیر نامزد کامل ترکیب کنیم. شکل 9 نقاط مسیر را نشان می دهد $p_{1}, p_{2}, p_{3}$ و بخش‌های جاده منطبق بر آن $e_{1}$ و $e_{3}$ . در فرآیند مسیریابی، $e_{1} \to e_{2} \to e_{3}$ یکی از مسیرهای نامزد است. برای یافتن بهترین مسیر منطبق، فاصله بین مسیر اصلی $p_{1} \to p_{2} \to p_{3}$ و هر مسیر نامزد باید محاسبه شود. ابتدا کمترین فاصله را از هر نقطه مسیر تا هر بخش جاده در مسیر محاسبه کنید. یعنی فاصله پیش بینی شده از نقطه مسیر تا قسمت جاده. اگر نقطه پیش بینی شده در قسمت جاده نیست، فاصله بین نقطه مسیر و نقطه پیش بینی شده در خط توسعه یافته قطعه جاده را محاسبه کنید. همانطور که در شکل 9 نشان داده شده است ، فواصل از $p_{1}$ به بخش های جاده ای $e_{1}$ ، $e_{2}$ ، و $e_{3}$ هستند $d_{1}$ ، $d_{2}$ ، و $d_{3}$ ، به ترتیب؛ فواصل از $p_{2}$ به بخش های جاده ای $e_{1}$ ، $e_{2}$ ، و $e_{3}$ هستند $d_{4}$ ، $d_{5}$ ، و $d_{6}$ ، به ترتیب؛ و فواصل از $p_{3}$ به بخش های جاده ای $e_{1}$ ، $e_{2}$ ، و $e_{3}$ هستند $d_{7}$ ، $d_{8}$ ، و $d_{9}$ به ترتیب. دوم، تمام کوتاه ترین فاصله ها را اضافه کنید تا فاصله بین مسیر و مسیر نامزد فعلی را بدست آورید. از آنجایی که k مسیرهای کاندید وجود دارد که توسط بخش‌های جاده با احتمالات مختلف به هم متصل می‌شوند، فاصله بین هر مسیر و مسیر کاندیدای k- امین آن به صورت نشان داده می‌شود. $D_{k} (k = 1, 2, 3, 4, 5)$ . با استفاده از معادله (7)، مسیر با بیشترین مقدار احتمال $P (D_{k})$ از k مسیرهای کاندید به عنوان بهترین مسیر منطبق انتخاب شده است.

P (D k) = 1 2 π --\sqrt σ 3 e - ( D k ) 2 2 ( σ 3 ) 2,

(7)

جایی که $σ_{3}$ روی 20 متر تنظیم شده است که نشان دهنده همان معنی است $σ_{1}$ و $σ_{2}$ . شبه کد برای انتخاب بهترین مسیر در الگوریتم 3 نشان داده شده است.

الگوریتم 3: انتخاب بهترین مسیر

ورودی: مجموعه بخش مسیر

Γ

, شبکه جاده G , مقدار کاندید k , مجموعه احتمال جامع G w
خروجی: مجموعه مسیر نهایی مسیر 1
: مقداردهی اولیه k ← {1,2,3,4,5}, Path

= \emptyset

;
2: بخش‌های جاده کاندید را بر اساس G w مرتب کنید .
3: dist ← ماتریس مجاورت گره های پیوند در مجموعه مرتب شده از بخش های جاده کاندید.
4: برای هر کدام

τ_{i} \in Γ

انجام
5:

{Path}_{t e m}

← کوتاه ترین مسیرهای مختلف که بر اساس مقادیر k و دور بدست می آیند .
6:

{Path}_{i}

← بهترین مسیر به دست آمده بر اساس رابطه (7)؛
7: پایان برای
8: بازگشت مسیر ;

پس از انتخاب مسیر بهینه با استفاده از الگوریتم 3، مسیر تطبیق نهایی مسیر در Path ذخیره می شود .

2.2.5. تحلیل پیچیدگی الگوریتم

پیچیدگی زمانی الگوریتم 1 عمدتاً به هزینه محاسباتی تفاوت زاویه قطعه بستگی دارد. پیچیدگی زمانی این بخش O ( n ) است، که در آن n تعداد نقاط مکان در مسیر است، بنابراین پیچیدگی زمانی الگوریتم 1 O ( n ) است.

پیچیدگی زمانی الگوریتم 2 عمدتاً به موارد زیر بستگی دارد: (1) هزینه جستجوی بخش های جاده ممکن در اطراف هر نقطه مسیر. (2) هزینه محاسبه احتمال فضایی، احتمال جهت و احتمال جامع. پیچیدگی زمانی اسکن مجموعه نقطه مسیر و اسکن مجموعه قطعه جاده کاندید هر دو O ( n × p ) است، جایی که p تعداد بخش های جاده نامزد، p ≪ n است، بنابراین پیچیدگی زمانی الگوریتم 2 O ( n ) است. ).

پیچیدگی زمانی الگوریتم 3 عمدتاً به موارد زیر بستگی دارد: (1) هزینه یافتن کوتاهترین مسیر هر زیرمسیر قطعه بندی شده، پیچیدگی زمانی این قسمت O ( m ) است، که m تعداد مسیرهای فرعی تقسیم شده است. (2) هزینه یافتن بهترین مسیر منطبق از کوتاهترین مجموعه مسیر، پیچیدگی زمانی این قسمت O ( k ) است، که k تعداد مسیرهای نامزد است. k ≪ m ، بنابراین پیچیدگی زمانی الگوریتم 3 O ( m ) است.

3. نتایج

در این بخش، عملکرد الگوریتم پیشنهادی از جنبه‌های مختلف با داده‌های مسیر واقعی و داده‌های شبکه جاده‌ای ارزیابی می‌شود.

محیط آزمایشی یک پردازنده Corei5 اینتل با CPU 2.4 گیگاهرتز است. پلت فرم عامل ویندوز 10 است و الگوریتم پیشنهادی با استفاده از MATLAB 2018a پیاده سازی شده است. مجموعه داده های مربوطه، شاخص های ارزیابی، تنظیمات پارامتر، نتایج تجربی و تجزیه و تحلیل در زیر ارائه شده است.

3.1. مجموعه داده ها

3.1.1. مجموعه داده شبکه راه

در این مطالعه، شبکه راه های شانگهای از طریق ArcGIS وارد شده است [ 24 ]. داده‌های شبکه راه‌ها شامل جاده‌های اصلی شهری، جاده‌های فرعی شهری، جاده‌های شعب شهری، جاده‌های مسکونی، بزرگراه‌ها، تونل‌ها، بزرگراه‌های مرتفع، مسیرهای حومه‌ای، پیاده‌روها، راهروها و غیره است. داده ها شامل بیش از 100000 بخش جاده و بیش از 70000 گره است.

3.1.2. مجموعه داده مسیر

مجموعه داده مسیر از داده های مسیر بیش از 10000 تاکسی در شانگهای، چین در 20 فوریه 2007 است که توسط گروه تحقیقاتی شهر هوشمند دانشگاه هنگ کنگ جمع آوری شده است. فیلدهای داده مسیر شامل شماره تاکسی، مهر زمانی، طول و عرض جغرافیایی، جهت حرکت وسیله نقلیه، سرعت لحظه ای، و اینکه آیا وسیله نقلیه حامل مسافر است یا خیر. برای نشان دادن ویژگی‌های مربوط به داده‌های مسیر تاکسی، از داده‌های مسیر از ساعت 6 صبح تا 10:00 شب استفاده کردیم. تعداد نقاط نمونه‌برداری و میانگین فاصله بین نقاط مجاور تحت فرکانس‌های نمونه‌گیری مختلف در جدول 2 نشان داده شده است. پیروی از ادبیات [ 25]، از نرم‌افزار ArcGIS برای قرار دادن داده‌های مسیر خودرو و داده‌های شبکه جاده‌ای شانگهای در یک لایه استفاده می‌کنیم و با برچسب‌گذاری دستی، بخش‌های جاده‌ای را که مطابق با نقاط مسیر هستند، پیدا می‌کنیم. در این مطالعه، نرخ نمونه برداری از داده های مسیر برای به دست آوردن داده های مسیر فرکانس پایین کاهش می یابد. بر این اساس، آزمایش هایی برای ارزیابی عملکرد الگوریتم انجام می شود.

3.2. شاخص های ارزیابی

در این تحقیق از سه شاخص ارزیابی برای سنجش برتری الگوریتم استفاده شده است که شامل دو شاخص ارزیابی برای اندازه گیری دقت تطبیق و یکی برای اندازه گیری زمان تطبیق می باشد.

3.2.1. دقت تطبیق نقطه مسیر

دقت تطبیق نقطه مسیر، به عنوان نشان داده شده است $R_{c}$ ، به نسبت بین تعداد نقاط مسیری که به درستی با شبکه جاده تطبیق داده شده اند و تعداد نقاط مسیری که باید مطابقت داده شوند، به شرح زیر محاسبه می شود:

R c = P R \times 100 %,

(8)

که در آن P تعداد نقاط مسیری را نشان می دهد که به درستی با بخش جاده مطابقت دارند، و R نشان دهنده تعداد نقاط مسیر مورد استفاده برای تطبیق است.

3.2.2. دقت تطبیق بخش جاده

دقت تطابق بخش جاده، نشان داده شده به عنوان $R_{m}$ ، به نسبت بین تعداد بخش های جاده ای که به درستی با شبکه جاده مطابقت دارند به تعداد کل بخش های جاده واقعی مسیر اشاره دارد که به شرح زیر محاسبه می شود:

R m = l L \times 100 %,

(9)

که در آن l تعداد بخش های جاده را که به درستی تطبیق داده شده اند، و L نشان دهنده تعداد کل بخش های جاده واقعی مسیر است.

از آنجایی که این الگوریتم برای تطبیق داده‌های مسیر فرکانس پایین استفاده می‌شود، فاصله بین نقاط مسیر نسبتاً زیاد است و بخش‌های جاده بیشتری بین هر دو نقطه مسیر متوالی وجود دارد. بنابراین،

R_{m}

نشانگر برای اندازه گیری دقت تطابق بخش جاده استفاده می شود.

3.2.3. زمان تطبیق نقطه مسیر

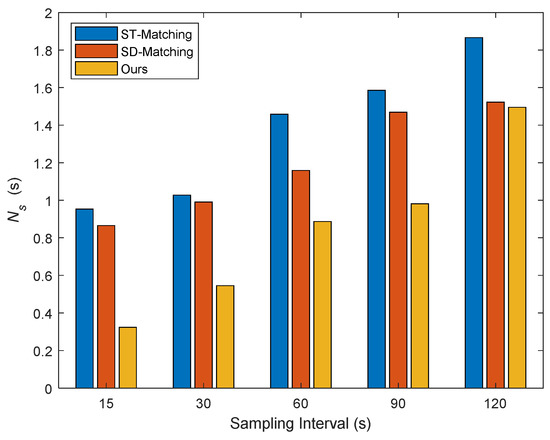
استفاده کنید $N_{s}$ برای نشان دادن میانگین زمان اجرا مورد نیاز برای هر نقطه مسیر برای تکمیل تطابق.

N s = T r t R,

(10)

که در آن Trt کل زمان مورد نیاز برای کل مسیر برای تکمیل فرآیند تطبیق نقشه را نشان می دهد و R نشان دهنده تعداد نقاط مسیر مورد استفاده برای تطبیق است.

با توجه به پیچیدگی شبکه‌های جاده‌ای، دقت تطبیق نقشه مسیر برای شبکه‌های جاده‌ای با توپولوژی‌های مختلف بر این اساس تغییر می‌کند. بنابراین در این تحقیق مقایسه تصویری نتایج تطبیق نقشه الگوریتم های مختلف در شبکه های جاده ای با توپولوژی های مختلف انجام شده است که نشان دهنده برتری الگوریتم پیشنهادی است.

3.3. تنظیم پارامتر

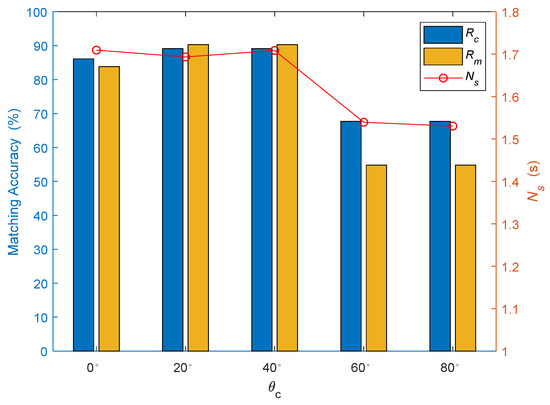
3.3.1. زاویه تقسیم بندی

در مرحله اول الگوریتم، عملیات قطعه بندی مسیر را با توجه به زاویه تقسیم بندی مشخص شده انجام می دهیم.

θ_{c}

) ارزش. بر اساس تجزیه و تحلیل ویژگی مسیر و نتایج تجربی، ما دریافتیم که بهترین زاویه تقسیم‌بندی 20 درجه بود. از آنجایی که مجموعه داده‌های مختلف ویژگی‌های متفاوتی دارند، ما زاویه را روی مقادیر مختلف تنظیم می‌کنیم تا تأثیر آن را بر دقت و زمان بررسی کنیم. به طور خاص، پنج مقدار زاویه مختلف 0 درجه، 20 درجه، 40 درجه، 60 درجه و 80 درجه برای مقایسه دقت تطبیق و زمان تطبیق یک مسیر استفاده می شود.

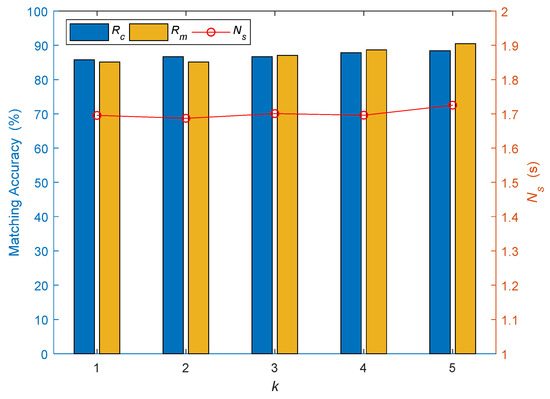
3.3.2. تعداد مسیرهای کاندیدا

در مرحله دوم الگوریتم، بخش‌های جاده‌ای کاندید در اطراف هر نقطه مسیر را با توجه به احتمال جامع به‌دست‌آمده از احتمال مکانی و احتمال جهتی تعیین می‌کنیم و بخش‌های جاده را بر اساس احتمال جامع به ترتیب نزولی مرتب می‌کنیم. در مرحله سوم، متوجه می‌شویم که مسیر تطبیق نهایی لزوماً مسیر بین بخش‌های جاده کاندید با بالاترین احتمالات جامع نیست. بنابراین، با ثابت کردن تعداد مسیرهای کاندید ( k )، می‌توان مسیرهای بالقوه را بین بخش‌های جاده کاندید با احتمالات مختلف پیدا کرد. برای بررسی تأثیر تعداد مسیرهای مختلف k بر دقت تطابق، مقدار k را تعیین می کنیمبه ترتیب به 1، 2، 3، 4 و 5، و از همان مسیر برای تأیید آزمایشی استفاده کنید تا تأثیرات تعداد مسیرها را بر روی دقت تطبیق نقشه و زمان تطبیق بیابید.

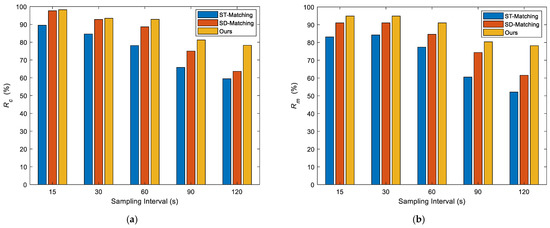
3.3.3. فرکانس نمونه برداری

فرکانس نمونه برداری فاصله زمانی بین دو نقطه مسیر مجاور را منعکس می کند. برای تأیید برتری الگوریتم پیشنهادی، داده‌های مسیر با فواصل نمونه‌گیری مختلف که به ترتیب 15 ثانیه، 30 ثانیه، 60 ثانیه، 90 ثانیه و 120 ثانیه است، جمع‌آوری می‌شوند. دقت تطبیق و زمان تطبیق الگوریتم در فرکانس‌های نمونه‌گیری مختلف با هم مقایسه و تحلیل می‌شود که نشان‌دهنده برتری الگوریتم پیشنهادی است.

3.4. نتایج تجربی

3.4.1. نتایج مقایسه تجربی بر اساس پارامترهای مختلف

(1): نتایج تجربی در زوایای تقسیم بندی مختلف

شکل 10 نتایج مقایسه دقت تطابق را نشان می دهد

R_{c}

R_{m}

و زمان تطبیق

N_{s}

تحت زوایای تقسیم بندی مختلف

θ_{c}

. “(ها)” در نماد ”

N_{s}

(s)” نشان می دهد که واحد زمان از

N_{s}

ثانیه است فاصله نمونه برداری بین نقاط مسیر 60 ثانیه است. مشاهده می شود که وقتی زاویه در محدوده [0°, 40°] باشد، زمان مورد نیاز تقریبا یکسان است و زمانی که زاویه تقسیم بندی در محدوده [60°, 80°] باشد، زمان تطبیق کاهش می یابد. از نظر دقت، متوجه می‌شویم که برای زوایای تقسیم‌بندی 20 درجه و 40 درجه، دقت تطبیق به اوج می‌رسد و دقت تطبیق در دو زاویه تقسیم‌بندی یکسان است. وقتی زاویه 60 درجه و 80 درجه باشد، اتلاف زمان کاهش می یابد، دقت تطبیق نیز به میزان قابل توجهی کاهش می یابد.

از آزمایش ها می توان دریافت که در

θ_{c} = 20 °

، دقت تطبیق به اوج خود می رسد و از دست دادن زمان نسبتاً کم است. این به این دلیل است که در زاویه تقسیم 0 درجه، تمام نقاط مسیر به عنوان قطعه بندی در نظر گرفته می شوند. هنگامی که بخش های جاده در شبکه جاده متراکم هستند، استفاده از زاویه تقسیم 0 درجه در طول فرآیند تطبیق باعث می شود که تعداد مسیرهای فرعی تقسیم شده بیشتر شود و تعداد نقاط مسیر در هر مسیر فرعی کوچکتر شود. نتیجه را نمی توان در فرآیند مسیریابی تصحیح کرد و منجر به خطاهای مربوطه می شود. وقتی زاویه تقسیم بندی باشد

θ_{c} = 40 °

، دقت به همان صورت باقی می ماند

θ_{c} = 20 °

، اما در فرآیند تطبیق به زمان بیشتری نیاز است. برای زوایای 60 درجه و 80 درجه، مسیری که باید قطعه بندی شود، قطعه بندی نمی شود، تعداد قطعات در یک مسیر کاهش می یابد، و تعداد دفعاتی که یک مسیر پیدا می شود به ترتیب کاهش می یابد. با این حال، مسیرها به درستی تقسیم بندی نمی شوند و در نتیجه یک خطای بزرگ ایجاد می شود. یعنی هم دقت تطبیق و هم زمان تطبیق کاهش می یابد. بنابراین، ما تنظیم کردیم

θ_{c}

به

20 °

در آزمایشات زیر

(2): نتایج تجربی تحت مقادیر مختلف مسیر نامزد

همانطور که در شکل 11 مشاهده می شود ، با افزایش تعداد نامزدها، دقت تطابق نیز افزایش می یابد، و زمان در زمانی که k = 5 به اوج می رسد. این به این دلیل است که جستجوی مسیر بهترین مسیر منطبق را با مقایسه بخش های جاده کاندید با احتمالات مختلف انتخاب می کند. . هنگامی که k = 1، مسیر جستجو شده مسیر بین حداکثر احتمال تطبیق بخش های جاده است که با نقاط مسیر مطابقت دارد، بنابراین یک خطای تطبیق بزرگ وجود دارد. با افزایش مقدار k ، دقت تطابق به دلیل اصلاح مداوم مسیر بهبود می یابد. در آزمایش های زیر برای مقایسه با سایر الگوریتم ها، k = 5 را قرار دادیم.

(3): نتایج تجربی در فرکانس های نمونه برداری مختلف

جدول 3 نتایج مربوطه را برای دقت تطبیق نقشه مسیر نشان می دهد

R_{c}

R_{m}

و زمان تطبیق

N_{s}

در فرکانس های نمونه برداری مختلف و مقادیر نامزد مسیرهای مختلف. از جدول مشاهده می کنیم که با افزایش مداوم بازه نمونه برداری، دقت تطبیق نقشه مسیر همچنان کاهش می یابد. زیرا با کاهش مداوم فرکانس نمونه برداری، اطلاعات مربوطه بین نقاط مسیر نیز کمتر می شود و فاصله بین دو نقطه مسیر مجاور همچنان افزایش می یابد که امکان تطابق بخش های جاده را افزایش می دهد. الگوریتم باید در شرایط مختلف محاسباتی را انجام دهد. بنابراین، دقت کاهش خواهد یافت و زمان تطبیق افزایش خواهد یافت.

3.4.2. مقایسه نتایج با سایر الگوریتم ها

شکل 12 a نتایج مقایسه ST-Matching [ 23 ]، SD-Matching [ 19 ]، و الگوریتم پیشنهادی را از نظر دقت تطبیق نقطه مسیر نشان می دهد.

R_{c}

. در این مطالعه، مسیر با تعیین مقدار آستانه برای زاویه تقسیم بندی قطعه بندی می شود

θ_{c}

و نتایج مسیر در مسیریابی تصحیح می شوند تا نقاط مسیر را با شبکه جاده تطبیق دهند. مشاهده می شود که الگوریتم پیشنهادی در مقایسه با الگوریتم SD-Matching حدود 5 درصد دقت تطبیق بالاتری دارد. این به این دلیل است که پس از تقسیم‌بندی مسیر، فقط باید مسیر بین اولین و آخرین نقاط مسیر را در مسیرهای فرعی تقسیم‌بندی شده، تحلیل کنیم. در جستجوی مسیر، مسیرهای بین بخش‌های جاده کاندید با احتمالات مختلف برای تصحیح نتیجه تطابق، برای بهبود دقت تطابق مقایسه می‌شوند. الگوریتم ST-Matching نقاط مکان را به بخش های جاده با فاصله کوتاه اختصاص می دهد و رابطه با نقاط همسایه را در نظر نمی گیرد و در نتیجه یک خطای تطبیق بزرگ ایجاد می کند.

شکل 12 ب نتایج مقایسه ST-Matching، SD-Matching و الگوریتم پیشنهادی را از نظر دقت تطابق بخش جاده نشان می دهد.

R_{m}

. در این مطالعه، بهترین مسیر با مقایسه و غربالگری مسیرهای بین بخش‌های جاده‌ای کاندید با احتمالات مختلف انتخاب می‌شود. مشاهده می‌شود که الگوریتم پیشنهادی بر اساس داده‌های مسیر فرکانس‌های نمونه‌گیری مختلف، در مقایسه با ST-Matching حدود 8 درصد و در مقایسه با SD-Matching حدود 5 درصد بهبود یافته است. از تجزیه و تحلیل فوق، می توان دریافت که پس از محاسبه و تجزیه و تحلیل مسیرهای بین بخش های جاده کاندید با احتمالات مختلف، دقت تطابق بخش جاده بیشتر بهبود می یابد.

شکل 13 نتایج مقایسه ST-Matching، SD-Matching و الگوریتم پیشنهادی را در زمان اجرا نشان می دهد.

N_{s}

. مشاهده می شود که زمان اجرای الگوریتم پیشنهادی در مقایسه با دو الگوریتم دیگر حدود 10 تا 20 درصد کاهش یافته است. هر چه فاصله نمونه برداری بین نقاط مسیر بیشتر باشد، تفاوت زمان اجرا بین این الگوریتم و دو الگوریتم دیگر کمتر می شود. الگوریتم پیشنهادی مسیر را بر اساس آستانه زاویه تقسیم بندی تقسیم می کند. زمان تطبیق داده های مسیر عمدتاً به تعداد مسیرهای فرعی تقسیم شده بستگی دارد. شبکه جاده بر اساس ویژگی جهت حرکت نقطه مسیر کاهش و بهینه سازی شد. در مقایسه با SD-Matching، یک بافر نیم دایره ای ساخته نشده است، اما یک بافر مسیر مطابق با جهت حرکت بین نقاط مسیر ساخته شده است که کارایی تطبیق را بهبود می بخشد.

شکل 14 نتایج تجسم ST-Matching، SD-Matching و الگوریتم پیشنهادی را تحت توپولوژی شبکه جاده ای نوع اتوبوس نشان می دهد. مشاهده می‌شود که سه الگوریتم دارای اثرات تطبیق خوبی در شبکه جاده‌ای بدون عارضه تحت تسلط توپولوژی اتوبوس هستند و همه آنها می‌توانند نقاط مسیر را با شبکه جاده‌ای صحیح مطابقت دهند.شکل 15سه نتیجه تجسم را با چندین توپولوژی جاده موازی نشان می دهد. می‌توانیم ببینیم که ST-Matching عمدتاً نقاط مسیر را با نزدیک‌ترین بخش‌های جاده مطابقت می‌دهد و مسیر بین بخش‌های جاده مربوطه هر نقطه مسیر را پیدا می‌کند. اگرچه الگوریتم SD-Matching تعداد مربوطه نامزدها را در فرآیند تطبیق نیز تعیین می‌کند، اما بخش‌های جاده را بین مسیرهای مختلف کاندید تصحیح نمی‌کند. اگر مسیری بین بخش های جاده کاندید با بیشترین احتمال مربوط به نقاط مسیر وجود داشته باشد، به عنوان مسیر تطبیق نهایی در نظر گرفته می شود که منجر به خطاهای بزرگ می شود. الگوریتم پیشنهادی اصلاحات مناسب را در نتایج تطبیق انجام می دهد و این باعث بهبود دقت تطبیق می شود.

4. بحث

طیف مشخصی از خطاها در داده های جمع آوری شده توسط دستگاه موقعیت یابی وجود دارد. اگر این داده‌ها مستقیماً در تشخیص ترافیک، برنامه‌ریزی شهری و سایر کاربردها استفاده شوند، منجر به خطای زیادی و در نتیجه اتلاف نیروی انسانی و منابع مادی خواهد شد. روش تطبیق نقشه نقش مهمی در مرحله پیش پردازش داده کاوی مسیر دارد. در عمل، وسایل نقلیه معمولا موقعیت‌های GPS خود را با نرخ نمونه‌برداری پایین‌تری به مرکز اعزام گزارش می‌دهند تا در هزینه‌های ارتباطی و انرژی صرفه‌جویی کنند [ 26 ، 27 ، 28 ]. اگر شی پردازشی داده های مسیر فرکانس بالا باشد، جایی که فاصله بین نقاط مکان مجاور کوتاه است، توپولوژی شبکه جاده می تواند برای تجزیه و تحلیل و تطبیق استفاده شود [ 29 ]]. در مقابل، روش تطبیق نقشه مسیر فرکانس پایین به طور کلی نمی تواند یک مسیر تطبیق عملی را تضمین کند، به دلیل فاصله زمانی طولانی بین دو نقطه مسیر مجاور، به عنوان مثال، ممکن است چندین بخش جاده بین بخش ها وجود داشته باشد که با دو نقطه مسیر مجاور همخوانی دارند.

برای داده‌های مسیر فرکانس پایین، محققان مرتبط چندین الگوریتم تطبیق نقشه را پیشنهاد کرده‌اند [ 30 ، 31 ، 32] که معمولاً مدل پنهان مارکوف (HMM) و الگوریتم کوتاه ترین مسیر را برای تعیین کوتاه ترین مسیر بین دو نقطه مسیر متوالی ترکیب می کند. اگرچه این الگوریتم‌ها می‌توانند به دقت تطبیق بالایی دست یابند، اما زمان لازم برای محاسبه کوتاه‌ترین مسیر به‌طور قابل توجهی زیاد است. محاسبات طولانی بار محاسباتی زیادی را بر الگوریتم ها تحمیل می کند و سناریوهای کاربردی الگوریتم ها را محدود می کند. برای غلبه بر این چالش، این مقاله یک الگوریتم تطبیق نقشه کارآمد برای داده‌های مسیر با نرخ نمونه‌برداری پایین پیشنهاد می‌کند. الگوریتم پیشنهادی ابتدا مسیر کامل را با توجه به جهت حرکت نقاط مکان تقسیم می کند. دوما بخش‌های جاده کاندید در اطراف نقاط مسیر تقسیم‌بندی شده با توجه به احتمال جامع به‌دست‌آمده از احتمال فضایی و احتمال جهت‌گیری انتخاب می‌شوند. ثالثاً، بر اساس بخش‌های جاده‌ای کاندید به‌دست‌آمده و الگوریتم کوتاه‌ترین مسیر، هر زیرمسیر تقسیم‌بندی شده با شبکه جاده تطبیق داده می‌شود و مسیرهای کاندید به‌دست می‌آیند. در نهایت، بهترین مسیر مطابق با محاسبه همبستگی پیدا می شود. آزمایش‌ها با مجموعه داده‌های مسیر واقعی و داده‌های شبکه جاده نشان می‌دهد که الگوریتم پیشنهادی دقت تطبیق و کارایی تطبیق بالاتری دارد. بهترین مسیر مطابق با محاسبه همبستگی پیدا می شود. آزمایش‌ها با مجموعه داده‌های مسیر واقعی و داده‌های شبکه جاده نشان می‌دهد که الگوریتم پیشنهادی دقت تطبیق و کارایی تطبیق بالاتری دارد. بهترین مسیر مطابق با محاسبه همبستگی پیدا می شود. آزمایش‌ها با مجموعه داده‌های مسیر واقعی و داده‌های شبکه جاده نشان می‌دهد که الگوریتم پیشنهادی دقت تطبیق و کارایی تطبیق بالاتری دارد.

مشارکت های اصلی این مطالعه به شرح زیر است:

(1): یک الگوریتم تطبیق نقشه مسیر فرکانس پایین جدید پیشنهاد شده است، که با تقسیم بندی داده های مسیر مطابق جهت حرکت نقاط مکان و بهبود دقت تطابق.
(2): روش تطبیق بخش‌بندی، مدل مارکوف پنهان و الگوریتم کوتاه‌ترین مسیر برای بهبود دقت تطبیق و کارایی تطبیق ترکیب شده‌اند.
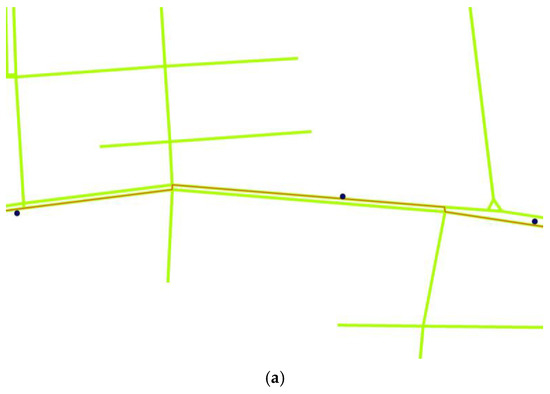
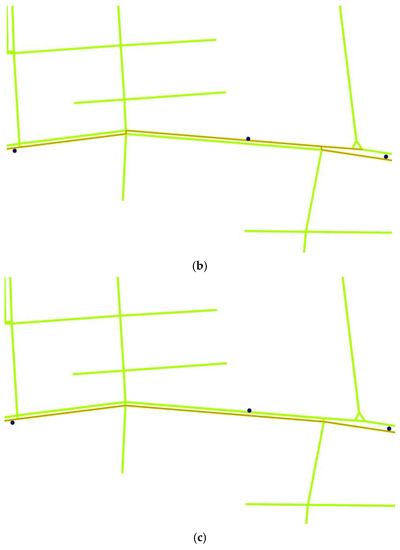
(3): آزمایش‌ها با استفاده از مجموعه داده‌های مسیر واقعی و داده‌های شبکه جاده‌ای شانگهای انجام می‌شوند، و نتایج نشان می‌دهد که الگوریتم تطبیق نقشه مبتنی بر تقسیم‌بندی جهت خودروی پیشنهادی به دقت بالاتری دست می‌یابد و به زمان اجرای کمتری نیاز دارد. به طور خاص، روش پیشنهادی زمان اجرا را تقریباً 10-20٪ کوتاه می کند و دقت تطبیق تقریباً 5٪ بهبود می یابد. به طور همزمان، سازگاری خوبی تحت توپولوژی جاده موازی دارد.

الگوریتم پیشنهادی در این مقاله توانایی تطبیق نقشه داده‌های مسیر را تا حدی بهبود می‌بخشد و دقت تطبیق و کارایی تطبیق داده‌های مسیر را با نرخ نمونه‌برداری پایین بهبود می‌بخشد. نتایج این مطالعه برای ناوبری وسایل نقلیه، ردیابی و نقشه‌برداری جاده‌های جدید مفید است، زیرا برای بهره‌مندی واقعی از فناوری نوظهور برنامه‌ریزی زیرساخت مبتنی بر داده، ترکیب داده‌های تله‌ماتیک و نقشه برای آسان‌تر کردن استخراج و استخراج آن مهم است. استخراج اطلاعات مفید از داده های GPS برای کمک به طراحی سیستم های ترافیکی در مناطق بزرگ شهری برای جلوگیری از ازدحام. ترافیک باعث خسارات اقتصادی زیادی می شود، بنابراین هر چیزی که بتواند به بهبود زمان سفر کمک کند احتمالاً مورد استقبال متخصصان تدارکات و مهندسان عمران قرار خواهد گرفت.

منابع

کیانی، ع. لیو، جی. شی، اچ. خریشا، ع. انصاری، ن. لی، جی. لیو، سی. یک مدل مبتنی بر محاسبات لبه دو لایه برای تشخیص ترافیک پیشرفته. در مجموعه مقالات پنجمین کنفرانس بین المللی اینترنت اشیا: سیستم ها، مدیریت و امنیت، والنسیا، اسپانیا، 15 تا 18 اکتبر 2018؛ ص 208-215. [ Google Scholar ]
ولی، بی. ختک، ای جی; بوزدوگان، اچ. کامرانی، م. نوسانات رانندگی چگونه با ایمنی تقاطع ارتباط دارد؟ تجزیه و تحلیل مبتنی بر ناهمگونی بیزی از داده های وسایل نقلیه ابزار. ترانسپ Res. قسمت C Emerg. تکنولوژی 2018 ، 92 ، 504-524. [ Google Scholar ] [ CrossRef ]
عظیمجونوف، ج. Özmen، A. یک سیستم تشخیص بی‌درنگ خودرو و یک سیستم ردیابی خودرو جدید برای تخمین و نظارت بر جریان ترافیک در بزرگراه‌ها. Adv. مهندس به اطلاع رساندن. 2021 ، 50 ، 101393. [ Google Scholar ] [ CrossRef ]
تانگ، جی. بی، دبلیو. لیو، اف. ژانگ، دبلیو. بررسی الگوهای سفر شهری با استفاده از خوشه‌بندی مبتنی بر تراکم با ویژگی‌های چندگانه از مسیرهای وسایل نقلیه در مقیاس بزرگ. فیزیک یک آمار مکانیک. برنامه آن است. 2021 , 561 , 125301. [ Google Scholar ] [ CrossRef ]
دندالا، تی تی; کریشنامورتی، وی. Alwan, R. اینترنت وسایل نقلیه (IoV) برای مدیریت ترافیک. در مجموعه مقالات کنفرانس بین المللی 2017 کامپیوتر، ارتباطات و پردازش سیگنال، چنای، هند، 10–11 ژانویه 2017؛ صص 1-4. [ Google Scholar ]
لی، های. هو، HW; Zhou، Y. اجتناب از موانع تک چشمی مبتنی بر یادگیری عمیق برای ناوبری وسایل نقلیه هوایی بدون سرنشین در مزارع درختان. جی. اینتل. ربات. سیستم 2021 ، 101 ، 5. [ Google Scholar ] [ CrossRef ]
ولاگا، NR; قدوس، م. Bristow, AL در حال توسعه الگوریتم تطبیق نقشه توپولوژیکی مبتنی بر وزن برای سیستم های حمل و نقل هوشمند. ترانسپ Res. قسمت C Emerg. تکنولوژی 2009 ، 17 ، 672-683. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
تولدو مورئو، آر. Bétaille، D. Peyret، F. ارائه یکپارچگی در سطح خط برای ناوبری و تطبیق نقشه با GNSS، محاسبه مرده، و نقشه های پیشرفته. IEEE Trans. هوشمند ترانسپ سیستم 2009 ، 11 ، 100-112. [ Google Scholar ] [ CrossRef ]
Szottka، I. فیلتر ذرات برای تطبیق نقشه سطح خط در دوشاخه‌های جاده. در مجموعه مقالات شانزدهمین کنفرانس بین المللی IEEE در مورد سیستم های حمل و نقل هوشمند، لاهه، هلند، 6 تا 9 اکتبر 2013. صص 154-159. [ Google Scholar ]
تائو، ز. بونیفیت، پ. فرمونت، وی. Ibanez-Guzman، J. Lane علامت گذاری به محلی سازی وسیله نقلیه کمک کرد. در مجموعه مقالات شانزدهمین کنفرانس بین المللی IEEE در مورد سیستم های حمل و نقل هوشمند، لاهه، هلند، 6 تا 9 اکتبر 2013. صفحات 1509-1515. [ Google Scholar ]
گو، ی. وادا، ی. هسو، ال. Kamijo، S. خود محلی سازی وسیله نقلیه در دره شهری با استفاده از موقعیت یابی GPS و حسگرهای وسیله نقلیه مبتنی بر نقشه سه بعدی. در مجموعه مقالات کنفرانس بین المللی 2014 در مورد وسایل نقلیه متصل و نمایشگاه، وین، اتریش، 3 تا 7 نوامبر 2014. صص 792-798. [ Google Scholar ]
شونسوکه، ک. یانلی، جی. ادغام دوربین Hsu، LT GNSS/INS/بورد برای مکان‌یابی خودکار خودرو در دره شهری. در مجموعه مقالات 2015 IEEE هجدهمین کنفرانس بین المللی سیستم های حمل و نقل هوشمند، گران کاناریا، اسپانیا، 15 تا 18 سپتامبر 2015. صص 2533-2538. [ Google Scholar ]
ژنگ، ی. Hansen، تشخیص تغییر خط JHL از سیگنال فرمان با استفاده از تقسیم بندی طیفی و طبقه بندی مبتنی بر یادگیری. IEEE Trans. هوشمند وه 2017 ، 2 ، 14-24. [ Google Scholar ] [ CrossRef ]
کاساس، ZZM؛ معارف، م. مورالس، جی جی. خلیف، جی جی. Shamei، K. مکان یابی قوی وسیله نقلیه و تطبیق نقشه در محیط های شهری از طریق سیگنال های IMU، GNSS و سلولی. IEEE Intell. ترانسپ سیستم Mag. 2020 ، 12 ، 36-52. [ Google Scholar ] [ CrossRef ]
معارف، م. Kassas، ناوبری وسیله نقلیه زمینی ZM در محیط های به چالش کشیده GNSS با استفاده از سیگنال های فرصت و رویکرد تطبیق نقشه حلقه بسته. IEEE Trans. هوشمند ترانسپ سیستم 2019 ، 21 ، 2723-2738. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
نیوزون، پی. Krumm, J. Hidden Markov نقشه مطابق با نویز و پراکندگی. در مجموعه مقالات هفدهمین کنفرانس بین المللی ACM SIGSPATIAL در مورد پیشرفت در سیستم های اطلاعات جغرافیایی، سیاتل، WA، ایالات متحده آمریکا، 4-6 نوامبر 2009. صص 336-343. [ Google Scholar ]
زنگ، ز. ژانگ، تی. لی، کیو. وو، زی. زو، اچ. Gao, C. ویژگی انحنای تطبیق نقشه محدود برای داده‌های خودروی کاوشگر فرکانس پایین. بین المللی جی. جئوگر. Inf. علمی 2016 ، 30 ، 660-690. [ Google Scholar ] [ CrossRef ]
لو، ا. چن، اس. Xv، B. الگوریتم تطبیق نقشه پیشرفته با مدل مارکوف پنهان برای موقعیت یابی تلفن همراه. ISPRS Int. J. Geo-Inf. 2017 ، 6 ، 327. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
چن، سی. دینگ، ی. Xie، X. ژانگ، اس. یک الگوریتم تطبیق نقشه آنلاین سه مرحله ای با استفاده کامل از جهت حرکت خودرو. J. محیط. هوشمند اومانیز. محاسبه کنید. 2018 ، 9 ، 1623-1633. [ Google Scholar ] [ CrossRef ]
لین، MC-H. هوانگ، F.-M. لیو، پی.-سی. هوانگ، Y.-H. چانگ، Y.-S. انتخاب مبتنی بر Dijkstra برای تطبیق نقشه چند خط موازی و یک سیستم برچسب گذاری مسیر واقعی. در مجموعه مقالات کنفرانس آسیایی اطلاعات هوشمند و سیستم های پایگاه داده، دا نانگ، ویتنام، 14 تا 16 مارس 2016. صص 499-508. [ Google Scholar ]
پتوشک، وی. راپنت، ال. Martinovič, J. تطبیق نقشه داده های خودرو شناور با استفاده از الگوریتم Dijkstra. در مدیریت داده، تجزیه و تحلیل و نوآوری ؛ اسپرینگر: سنگاپور، 2020؛ صص 115-130. [ Google Scholar ]
کولر، اچ. ویدهام، پی. دراگاشنیگ، م. Graser, A. تطبیق سریع مدل مارکوف پنهان برای مسیرهای پراکنده و پر سر و صدا. در مجموعه مقالات 2015 IEEE هجدهمین کنفرانس بین المللی سیستم های حمل و نقل هوشمند، گران کاناریا، اسپانیا، 15 تا 18 سپتامبر 2015. صص 2557–2561. [ Google Scholar ]
لو، ی. ژانگ، سی. ژنگ، ی. Xie، X. وانگ، دبلیو. Huang, Y. تطبیق نقشه برای مسیرهای GPS با نرخ نمونه برداری پایین. در مجموعه مقالات هفدهمین کنفرانس بین المللی ACM SIGSPATIAL در مورد پیشرفت در سیستم های اطلاعات جغرافیایی، سیاتل، WA، ایالات متحده آمریکا، 4-6 نوامبر 2009. صص 352-361. [ Google Scholar ]
کاردونی، ع. کرمانشاه، ع. Derrible، S. پروتکلی برای تبدیل داده های چند خطی فضایی به فرمت های شبکه و برنامه های کاربردی به شبکه های جاده های شهری جهانی. علمی داده 2016 ، 3 ، 160046. [ Google Scholar ] [ CrossRef ]
نیکولیچ، م. Jović, J. پیاده سازی الگوریتم عمومی در مدل تطبیق نقشه. سیستم خبره Appl. 2017 ، 72 ، 283-292. [ Google Scholar ] [ CrossRef ]
یو، جی. یانگ، کیو. لو، جی. هان، جی. پنگ، اچ. الگوریتم‌های تطبیق نقشه پیشرفته: نظرسنجی و روندها. Acta Electron. گناه 2021 ، 49 ، 1818-1829. [ Google Scholar ]
هوانگ، ز. کیائو، اس. هان، ن. یوان، کالیفرنیا؛ آهنگ، X. Xiao, Y. بررسی تکنیک های تطبیق نقشه خودرو. CAAI Trans. هوشمند تکنولوژی 2021 ، 6 ، 55-71. [ Google Scholar ] [ CrossRef ]
چائو، پی. خو، ی. هوآ، دبلیو. ژو، ایکس. نظرسنجی در مورد الگوریتم های تطبیق نقشه. در مجموعه مقالات کنفرانس پایگاه داده استرالیا، ملبورن، VIC، استرالیا، 3 تا 7 فوریه 2020؛ Springer: Cham، سوئیس، 2020؛ صص 121-133. [ Google Scholar ]
یو، کیو. هو، اف. بله، ز. چن، سی. سان، ال. Luo, Y. الگوریتم تطبیق نقشه مسیر فرکانس بالا بر اساس توپولوژی شبکه جاده. IEEE Trans. هوشمند ترانسپ سیستم 2022 ، 3 ، 1-16. [ Google Scholar ] [ CrossRef ]
Hsueh، YL; تطبیق نقشه Chen، HC برای مسیرهای GPS با نرخ نمونه‌برداری پایین با کاوش جهت‌های حرکت در زمان واقعی. Inf. علمی 2018 ، 433 ، 55-69. [ Google Scholar ] [ CrossRef ]
تاناکا، ا. تاتیوا، ن. هاتا، ن. یوشیدا، ا. واکاماتسو، تی. اوزافون، اس. Fujisawa، K. تطبیق نقشه آفلاین با استفاده از نمودار توسعه یافته زمان برای داده های فرکانس پایین. ترانسپ Res. قسمت C Emerg. تکنولوژی 2021 ، 130 ، 103265. [ Google Scholar ] [ CrossRef ]
چن، آر. یوان، اس. مک.؛ ژائو، اچ. فنگ، Z.-Y. THMM: یک مدل مارکوف پنهان طراحی شده که برای تطبیق نقشه مبتنی بر سلولی بهینه شده است. IEEE Trans. الکترون صنعتی 2021 ، 12 ، 1-10. [ Google Scholar ] [ CrossRef ]

شکل 1. نمونه ای از داده های مسیر و مدل شبکه راه.

شکل 2. چارچوب الگوریتمی.

شکل 3. مثال تقسیم مسیر.

شکل 4. انتخاب بخش های جاده ای نامزد.

شکل 5. معایب تطبیق فقط با احتمال مکانی.

شکل 6. ایجاد بافر مسیر.

شکل 7. یافتن مسیرهای منطبق.

شکل 8. مشکلات در جستجوی مسیرهای منطبق.

شکل 9. بهترین مسیر منطبق را پیدا کنید.

شکل 10. تطبیق نتایج تحت زوایای تقسیم بندی مختلف.

شکل 11. نتایج مطابق با مقادیر کاندیدای مختلف برای k .

شکل 12. مقایسه دقت الگوریتم ها در فرکانس های مختلف نمونه برداری. ( الف ) مقایسه

R_{c}

شاخص ها. ( ب ) مقایسه

R_{m}

شاخص ها.

شکل 13. مقایسه زمان اجرای الگوریتم ها در فرکانس های مختلف نمونه برداری.

شکل 14. نتایج مقایسه بصری الگوریتم ها تحت یک توپولوژی جاده. ( الف ) الگوریتم ST-Matching. ( ب ) الگوریتم SD-Matching. ( ج ) الگوریتم پیشنهادی.

شکل 15. نتایج مقایسه بصری الگوریتم ها تحت توپولوژی جاده موازی. ( الف ) الگوریتم ST-Matching. ( ب ) الگوریتم SD-Matching. ( ج ) الگوریتم پیشنهادی.

مقالات داخلی و بین المللی

بدون دیدگاه

دیدگاهتان را بنویسید لغو پاسخ

برای نوشتن دیدگاه باید وارد بشوید.

مشاورین هوش پیروزی

کلید واژه ها:

1. مقدمه

2. روش ها

2.1. مفاهیم اساسی و شرح مسئله

2.2. الگوریتم تطبیق نقشه مسیر فرکانس پایین

2.2.1. بررسی اجمالی الگوریتم

2.2.2. تقسیم بندی مسیر

2.2.3. تطبیق نقطه مسیر

2.2.4. بهترین انتخاب مسیر

2.2.5. تحلیل پیچیدگی الگوریتم

3. نتایج

3.1. مجموعه داده ها

3.1.1. مجموعه داده شبکه راه

3.1.2. مجموعه داده مسیر

3.2. شاخص های ارزیابی

3.2.1. دقت تطبیق نقطه مسیر

3.2.2. دقت تطبیق بخش جاده

3.2.3. زمان تطبیق نقطه مسیر

3.3. تنظیم پارامتر

3.3.1. زاویه تقسیم بندی

3.3.2. تعداد مسیرهای کاندیدا

3.3.3. فرکانس نمونه برداری

3.4. نتایج تجربی

3.4.1. نتایج مقایسه تجربی بر اساس پارامترهای مختلف

3.4.2. مقایسه نتایج با سایر الگوریتم ها

4. بحث

منابع

قبلیتحلیل انجمنی ناکارآمدی ها و سطوح فعالیت ایستگاه در واکنش اضطراری

بعدیLSTM توجه مکانی-زمانی برای پیش‌بینی مسیر خودرو

مطالب مرتبط ...

آموزش مقاله نویسی در رشته ادبیات فارسی

تأثیر همسایگی درونیابی DEM بر عوامل زمین

رگرسیون وزنی جغرافیایی تطبیقی ​​غیر منفی برای تخمین تراکم جمعیت بر اساس نور شب

بدون دیدگاه

دیدگاهتان را بنویسید لغو پاسخ

درباره سرزمین فناوری مکانی GISLAND

دسترسی سریع

اطلاعات

خبرنامه

خبرنامه

درباره سرزمین فناوری مکانی GISLAND

دسترسی سریع

اطلاعات

دسترسی سریع

رگرسیون وزنی جغرافیایی تطبیقی غیر منفی برای تخمین تراکم جمعیت بر اساس نور شب