روش ساخت تطبیقی شاخص مکانی-زمانی سلسله مراتبی برای داده های برداری تحت شبکه های همتا به همتا

خلاصه

نمایه سازی مکانی – زمانی یک تکنیک کلیدی در ذخیره سازی و مدیریت داده های مکانی – زمانی است. روش‌های نمایه‌سازی مبتنی بر منحنی‌های پرکننده فضایی در تحقیقات بر روی نمایه‌سازی مکانی-زمانی داده‌های برداری در پایگاه‌داده غیر رابطه‌ای (NoSQL) محبوب هستند. با این حال، روش‌های موجود بیشتر بر نمایه‌سازی مکانی تمرکز می‌کنند، که تعادل راندمان جستجوهای زمانی و مکانی را دشوار می‌کند. علاوه بر این، برای عناصر غیر نقطه ای (عناصر خط و چند ضلعی)، تعیین سطح شاخص بهینه دشوار است. برای پرداختن به این مسائل، این مقاله یک روش ساخت تطبیقی از شاخص مکانی-زمانی سلسله مراتبی برای داده‌های برداری پیشنهاد می‌کند. در ابتدا، یک کدگذاری اطلاعات مکانی-زمانی مشترک بر اساس ترکیب استراتژی‌های کلیدی پارتیشن و مرتب‌سازی ارائه می‌شود. ثانیاً ساختار بیان چندسطحی عناصر مکانی-زمانی متشکل از عناصر نقطه ای و غیر نقطه ای در کدگذاری مشترک داده شده است. در نهایت، یک درخت شاخص چند سطحی تطبیقی برای تحقق شاخص فضایی-زمانی (Multi-level Sphere 3، MLS3) بر اساس ویژگی‌های مکانی-زمانی موجودیت‌های جغرافیایی پیشنهاد شده‌است. مقایسه با الگوریتم شاخص XZ3 ارائه شده توسط GeoMesa ثابت کرد که روش نمایه سازی MLS3 نه تنها به طور منطقی ویژگی های مکانی-زمانی عناصر غیر نقطه ای را بیان می کند و سطح شاخص بهینه آنها را تعیین می کند، بلکه از کانون های ذخیره سازی در حین دستیابی به بازیابی مکانی-زمانی با کارایی بالا جلوگیری می کند. . یک درخت شاخص چند سطحی تطبیقی برای تحقق شاخص فضایی-زمانی (Sphere چند سطحی 3، MLS3) بر اساس ویژگی‌های مکانی-زمانی موجودیت‌های جغرافیایی پیشنهاد شده‌است. مقایسه با الگوریتم شاخص XZ3 ارائه شده توسط GeoMesa ثابت کرد که روش نمایه سازی MLS3 نه تنها به طور منطقی ویژگی های مکانی-زمانی عناصر غیر نقطه ای را بیان می کند و سطح شاخص بهینه آنها را تعیین می کند، بلکه از کانون های ذخیره سازی در حین دستیابی به بازیابی مکانی-زمانی با کارایی بالا جلوگیری می کند. . یک درخت شاخص چند سطحی تطبیقی برای تحقق شاخص فضایی-زمانی (Sphere چند سطحی 3، MLS3) بر اساس ویژگی‌های مکانی-زمانی موجودیت‌های جغرافیایی پیشنهاد شده‌است. مقایسه با الگوریتم شاخص XZ3 ارائه شده توسط GeoMesa ثابت کرد که روش نمایه سازی MLS3 نه تنها به طور منطقی ویژگی های مکانی-زمانی عناصر غیر نقطه ای را بیان می کند و سطح شاخص بهینه آنها را تعیین می کند، بلکه از کانون های ذخیره سازی در حین دستیابی به بازیابی مکانی-زمانی با کارایی بالا جلوگیری می کند. .

کلید واژه ها:

شاخص مکانی-زمانی سلسله مراتبی ; شبکه های P2P ؛ کدگذاری مشترک اطلاعات مکانی – زمانی ; دانه بندی مکانی-زمانی ; تعیین سطح شاخص بهینه

1. معرفی

با توسعه فناوری‌های اینترنتی، شبکه‌های همتا به همتا (P2P) در حال حاضر مورد توجه قابل توجهی قرار گرفته‌اند، زیرا یک معماری غیرمتمرکز ارائه می‌کنند که در آن منابع مشترک در یک گره می‌توانند مستقیماً توسط سایر همتایان بدون عبور از موجودیت‌های میانی دسترسی داشته باشند [ 1 ] . در سال‌های اخیر، نرم‌افزار ارتباطی P2P به راه‌حل اصلی برای ذخیره‌سازی و مدیریت کلان داده در ساخت‌وساز شهر هوشمند به دلیل ویژگی‌های عالی برای پردازش داده‌های مکانی-زمانی، مانند توزیع کامل، در دسترس بودن بالا، توان عملیاتی بالا و توسعه‌پذیری خطی تبدیل شده است. 3]. در طول این فرآیند، الگوریتم‌های شاخص کارآمد در شبکه‌های P2P با چالش‌های جدی مواجه هستند. برای سیستم معماری استاد برده سنتی، کارایی کل شبکه را می توان با گسترش عملکرد سخت افزار سرور مرکزی بهبود بخشید. با این حال، اعمال این استراتژی برای شبکه‌های P2P دشوار است، زیرا منابع داده در شبکه‌های P2P به طور تصادفی در گره‌های مختلف با وضعیت مساوی توزیع می‌شوند و برخی از آنها عملکرد پایینی دارند. از این رو، یافتن یک ساختار نمایه‌سازی جهانی با کارایی بالا در شبکه‌های P2P ضروری است، که بتواند به سرعت گره‌ای را که داده‌ها در آن ذخیره می‌شود، مکان‌یابی کند و عملکرد پرس و جو جهانی تحت تأثیر به‌روزرسانی داده‌های گره‌های محلی قرار نگیرد.

حجم داده های مکانی-زمانی موجود در چند سال اخیر به شدت افزایش یافته است. چنین داده‌هایی شامل، اما محدود به این نمی‌شود: داده‌های مسیر تاکسی، داده‌های شبکه اجتماعی، داده‌های تصویر سنجش از راه دور، نقشه‌های آب و هوا، و موارد دیگر. در کنار حجم عظیم به دست آمده از داده ها، فضا و زمان دو ویژگی اساسی هستند که تقاضا برای پردازش داده های مکانی-زمانی را افزایش می دهند [ 4 ]. حتی اگر سیستم‌های مدیریت داده‌های مکانی-زمانی بزرگ موجود با ایجاد یک شاخص زمانی یا یک شاخص مکانی برای عملیات زمانی یا مکانی کارآمد هستند، با این وجود، این سیستم‌ها با ساختار تک شاخص یا توالی زمانی که در حال پردازش پرس‌و‌جوهای مکانی-زمانی هستند، آسیب می‌بینند، به عنوان مثال، در دو ماه گذشته در جاده نانجینگ تاکسی پیدا کنید“. اگر صرفاً توالی یک نمایه مکانی و یک شاخص زمانی، مهم نیست که کدام پرس و جو ابتدا انجام شود، همیشه منجر به اسکن بسیاری از داده های نامربوط به پاسخ پرس و جو می شود، زمانی که مجموعه داده ها عالی و پیچیده است. علاوه بر این، این نوع پرس و جو معمولاً از ویژگی های دانه بندی مکانی-زمانی اشیاء، به ویژه زمانی که به طور معمول در مقیاس بزرگ به دست می آیند، بی اطلاع هستند [ 4 ]. ساخت یک شاخص مکانی-زمانی کارآمد برای ذخیره سازی و مدیریت کلان داده ها در سیستم اطلاعات جغرافیایی (GIS) [ 5 و 6 ] در تحقیقات اخیر بسیار مورد توجه بوده است. برای پایگاه های داده توزیع شده غیر رابطه ای (NoSQL)، تحقیقات شاخص مکانی- زمانی را می توان به دو دسته تقسیم کرد:

مطالعات بر بهبود یا گسترش شاخص فضایی سنتی (QuadTree، R-Tree، Grid index، و غیره) برای محیط های توزیع شده متمرکز شده است [ 7 ، 8 ، 9 ، 10 ]. به عنوان مثال، به عنوان یک چارچوب MapReduce توسعه یافته، SpatialHadoop یک الگوریتم نمایه سازی کلی عمومی ارائه می دهد که برای پیاده سازی پارتیشن بندی درختی Grid، R-tree، R+-tree، Quad-tree و k- بعدی (KD) استفاده شد [ 11 ].]. Hadoop فضایی-زمانی (ST) که یک توسعه جامع برای Hadoop و SpatialHadoop است، از مزایای استفاده از تکنیک‌های بارگذاری انبوه فضایی فوق الذکر که قبلاً در SpatialHadoop پیاده‌سازی شده‌اند، بهره می‌برد و داده‌ها را به صورت مکانی-زمانی بارگذاری و بین گره‌های محاسباتی تقسیم می‌کند که منجر به دستیابی به سفارش می‌شود. عملکرد بهتری نسبت به Hadoop و SpatialHadoop [ 4 ] دارد. GeoSpark همچنین شبکه یکنواخت، R-tree، Quad-Tree و KDB-Tree (ترکیبی از KD-tree و B-tree) الگوریتم نمایه سازی داده های فضایی را ارائه می دهد و شاخص های مکانی محلی را روی هر پارتیشن داده Spark ایجاد می کند تا سرعت محلی را افزایش دهد. محاسبه [ 12]. چنین ساختار شاخصی همیشه به زمان ساخت طولانی، هزینه به‌روزرسانی بالا نیاز دارد و حفظ ثبات شاخص دشوار است، بنابراین برای داده‌های مکانی-زمانی که اغلب در محیط‌های توزیع‌شده به‌روزرسانی می‌شوند، مناسب نیست.
مطالعات بر ایجاد یک شاخص بر اساس منحنی های پرکننده فضا (SFCs؛ Z-Order، Hilbert، Google S2 و غیره) متمرکز بود. فاکس و همکاران [ 13 ] یک ساختار شاخص مکانی-زمانی پیشنهاد کرد که از یک رشته GeoHash برای شناسایی اطلاعات مکانی استفاده می‌کند و رشته ویژگی زمان را برای تشکیل مقدار کلید شاخص به هم می‌پیوندد. لی و همکاران [ 14 ] یک روش شاخص فضایی با ترکیب R-Tree و Geohash پیشنهاد کرد. گوگل یک شاخص فضایی به نام S2 را با ترکیب یک چهار درخت و منحنی هیلبرت پیاده‌سازی کرد که امکان بیان عناصر فضایی چند سطحی را فراهم کرد [ 15 ، 16 ]. GeoMesa [ 17 ]، یک پروژه منبع باز محبوب، شامل پیاده‌سازی یک روش نمایه‌سازی مکانی-زمانی با ترتیب Z توسعه یافته (XZ-ordering) بر اساس Z-order [18 ]. در این رویکرد، مرتب‌سازی XZ برای بیان اطلاعات مکانی با وضوح دلخواه مورد استفاده قرار می‌گیرد و عملکرد پرس و جو با افزایش وضوح بدتر نمی‌شود [ 19 ، 20 ]. علاوه بر این، Eldawy و همکاران. [ 21 ] شاخص فضایی سنتی را با معرفی تکنیک‌های تقسیم‌بندی منحنی Z و منحنی هیلبرت در SpatialHadoop گسترش می‌دهد. استراتژی مبتنی بر SFC می‌تواند ویژگی‌های پیوستگی مکانی داده‌های مکانی-زمانی را به دلیل ویژگی‌های تراکم مکانی آن بهتر توصیف کند [ 22 ، 23]. از این رو، این رویکرد در سال‌های اخیر به‌طور گسترده در مطالعات شاخص‌های مکانی-زمانی مورد استفاده قرار گرفته است. با این حال، در تحقیقات مبتنی بر شاخص SFC موجود، ویژگی‌های مکانی و زمانی به طور کلی از هم جدا شده‌اند، که در نظر گرفتن کارایی پرس‌و‌جوهای زمانی و مکانی به طور همزمان دشوار است. علاوه بر این، برای عناصر خط و چند ضلعی با محدوده‌های جغرافیایی مختلف، کارایی و دقت پرس‌و‌جوها ارتباط نزدیکی با سطح شاخص مورد استفاده دارد و ابزاری برای دستیابی به یک بیان مکانی-زمانی منطقی و تعیین سطح شاخص عملی هنوز شناسایی نشده است. .

به عنوان یک پایگاه داده NoSQL در یک شبکه P2P، پایگاه داده Apache Cassandra [ 24 ، 25 ] مزایای زیادی در مدیریت داده های عظیم با رشد پویا در GIS نشان داده است. با این حال، مدیریت مکانی-زمانی پایگاه های داده NoSQL، مانند داده های برداری، به ندرت مورد تحقیق قرار گرفته است [ 26 ، 27 ]]. اگرچه GeoMesa روش شاخص فضایی-زمانی XZ3 را ارائه می‌کند که می‌تواند در شبکه‌های P2P استفاده شود، کارایی آن برای بازیابی داده‌های مکانی به دلیل سطح ثابت و تداوم ضعیف بیان عناصر غیر نقطه‌ای، نیازمند بهبود است. این مقاله بر روی نمایه سازی مشترک مکانی-زمانی جهانی داده های برداری تحت شبکه P2P با پیشنهاد یک ساختار بیان چندسطحی عناصر مکانی-زمانی و یک الگوریتم تعیین سلسله مراتب شاخص بهینه با در نظر گرفتن دانه بندی زمانی و ویژگی توزیع مکانی فایل های ورودی در NoSQL تمرکز می کند. پایگاه داده مبتنی بر شاخص فضایی S2، که می تواند به پرس و جوهای مکانی-زمانی کارآمد و عملکرد پرس و جو پایدار و همچنین هزینه نگهداری شاخص کم دست یابد.

ادامه این مقاله به شرح زیر سازماندهی شده است. بخش 2 دو روش اصلی نمایه سازی مکانی-زمانی و محدودیت های آنها را در مدیریت داده های برداری در شبکه های P2P توضیح می دهد. بخش 3 یک روش ساخت تطبیقی از شاخص مکانی-زمانی سلسله مراتبی را ارائه می دهد. بخش 4 مجموعه ای از آزمایش ها را مورد بحث قرار می دهد که برای تأیید اعتبار و کارایی روش پیشنهادی انجام شد. در نهایت، بخش 5 نتیجه گیری و موضوعاتی را که به کار آینده نیاز دارند، خلاصه می کند.

2. کارهای مرتبط

2.1. شاخص فضایی-زمانی XZ3

شاخص فضایی-زمانی XZ3 بسط سفارش XZ است [ 18 ]. ایده اصلی آن ترکیب چهار درخت با یک منحنی مرتبه Z، درهم آمیختن رشته‌های GeoHash اطلاعات مکانی با رشته‌های اطلاعات زمانی برای دستیابی به رمزگذاری اطلاعات مکانی-زمانی، و توزیع داده‌ها در شبکه‌های P2P با یک عدد باینری تصادفی به عنوان کلید ردیف است. با این حال، این الگوریتم دارای کاستی هایی در مدیریت داده های برداری در شبکه های P2P است که می توان آن ها را به صورت زیر خلاصه کرد:

(1): این الگوریتم از یک منحنی Z-order به عنوان SFC استفاده می کند که هنگام بیان فضای دو بعدی مشکل پرش دارد. در نتیجه، داده‌های بیان‌شده توسط کدگذاری مجاورت از نظر مکانی مجاور نیستند و منجر به تعداد زیادی پرس‌و‌جوی بی‌اثر در هنگام جستجو در مناطق پرش می‌شوند.
(2): هنگام تقسیم سلسله مراتب فضایی، الگوریتم XZ3 با قضاوت در مورد اینکه آیا تعداد سلول های تقسیم شده در یک سلسله مراتب با آستانه خاصی مطابقت دارد یا خیر، تصمیم می گیرد که آیا بیشتر تقسیم شود یا خیر. با این حال، تنظیم آستانه به طور کامل توزیع فضایی و چگالی همه عناصر در یک لایه را در نظر نمی گیرد.

2.2. شاخص فضایی S2

شاخص فضایی-زمانی S2 در سال 2011 توسط گوگل پیشنهاد شد. ایده اصلی ترکیب یک چهار درخت با منحنی هیلبرت برای ژئوکدگذاری یک فضای جهانی است که در آن از چهار درخت برای تحقق تقسیم چند سطحی فضای جغرافیایی و منحنی هیلبرت استفاده می شود. برای کاهش فضای دو بعدی به فضای یک بعدی استفاده می شود. فرآیند ساخت شامل پنج مرحله اصلی است [ 15 ، 16 ].

مرحله 1: مکعبی را با شعاع 1، [-1،1] × [-1،1] × [-1،1] و مرکز زمین به عنوان مبدأ احاطه کرده است. برای یک نقطه یا منطقه معینی از زمین، مختصات طول و عرض جغرافیایی نقطه p در مستطیل حداقل مرزی (MBR) اطراف نقطه یا ناحیه را به مختصات سه بعدی یک مکعب تبدیل کنید، p = ( lat , lng ) => ( x ، y ، z ).
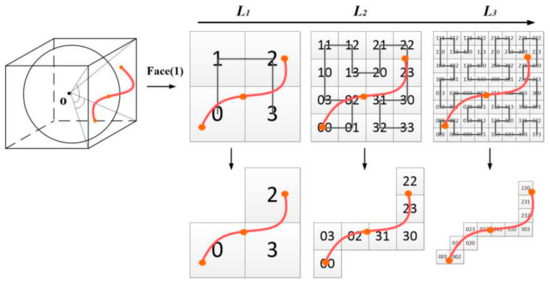
گام 2: نقطه p را بر روی سطح خاصی از مکعب با پیروی از جهت شعاعی، ( x , y , z ) => ( face , u , v ) قرار دهید، جایی که وجه نشان دهنده تعداد سطح مکعب است، وجه = {0، 1، 2، 3، 4، 5}، u و v مختصات طرح ریزی هر سطح را نشان می دهند. سپس مختصات پیش بینی شده u و v را تا بازه [0، 1] نرمال کنید.
مرحله 3: u و v نرمال شده گسسته به ترتیب به i و j ، ( face , u , v ) => ( face , i , j ) که i , j ∈ [0, 2 ⁿ − 1] نشان دهنده حداکثر بیت موثر درخت چهارگانه است. سلول، و n ∈ [0, 30] نشان دهنده عمق چهار درخت است که یک سری سلسله مراتبی است.
مرحله 4: سلول چهاردرختی شناسایی شده با صورت ، i و j را به منحنی هیلبرت با یک سطح معین نگاشت، و شناسه سلول مربوطه را محاسبه کنید، ( face , i , j ) => CellId , جایی که CellId یک عدد صحیح 64 بیتی است و می تواند به طور منحصر به فرد نشان دهنده یک نقطه یا منطقه است.

S2 می تواند ویژگی های پیوستگی فضایی را بهتر از XZ3 به دلیل ویژگی های تراکم فضایی منحنی هیلبرت توصیف کند، بنابراین می تواند به بیان چند سطحی بهتر عناصر جهانی دست یابد. با این حال، محدودیت های زیر باقی می ماند.

(1): با توجه به بیان مشترک اطلاعات مکانی-زمانی، S2 فقط اطلاعات مکانی را بیان می کند. برای عناصر هندسی فضایی با سری های زمانی متعدد، ابزار موثری برای ترکیب اطلاعات زمانی و مکانی هنوز مشخص نشده است.
(2): بیان عناصر غیر نقطه ای. برای عناصر خط و چند ضلعی، مقیاس فضایی بسیار متفاوت است، و برای جستارهای عناصر جغرافیایی، گستره فضایی و حالت پرس و جو فضایی هر دو تصادفی هستند. در نظر گرفتن پرس و جوهای دقیق و سریع در محدوده کوچک و عملیات اسکن در مقیاس بزرگ ضروری است. یک روش معقول از عبارات مکانی-زمانی محدودیت دوم است.
(3): تعیین دانه بندی زمانی و سلسله مراتب بهینه. در تحقیق بر روی شاخص فضایی سنتی شامل شبکه منظم، شبکه مبتنی بر چهاردرخت و شبکه مبتنی بر درخت R، بلوسی و همکاران. [ 28 ] اشاره کرد که کارایی و دقت پرس‌و‌جوها با ویژگی توزیع داده‌های مکانی-زمانی مرتبط است. بنابراین، فقدان ابزار معقول برای دستیابی به بیان مکانی-زمانی و تعیین سطح شاخص عملی با توجه به ویژگی‌های مکانی و زمانی عناصر برای شاخص مبتنی بر SFC سومین محدودیت است.

برای پرداختن به مسائل فوق، این مقاله یک روش ساخت تطبیقی از شاخص مکانی-زمانی سلسله مراتبی برای داده‌های برداری بر اساس شاخص فضایی S2 پیشنهاد می‌کند. در ابتدا، کدگذاری اطلاعات مکانی-زمانی مشترک بر اساس ترکیب استراتژی‌های کلیدی پارتیشن و مرتب‌سازی ارائه می‌شود، که استفاده کامل از ویژگی‌های دانه‌بندی مکانی-زمانی اشیاء را برای پشتیبانی از پرس و جوی مشترک مکان و زمان می‌کند. در مرحله دوم، ساختار بیان چندسطحی عناصر مکانی-زمانی متشکل از عناصر نقطه ای و غیر نقطه ای در کدگذاری مشترک داده شده است و این ساختار ویژگی های سلسله مراتبی عناصر مکانی-زمانی را منعکس می کند. در نهایت، یک درخت شاخص چند سطحی تطبیقی برای تحقق شاخص مکانی-زمانی پیشنهاد شده است.

3. روش شناسی

شاخص فضایی-زمانی توزیع شده در پایگاه داده NoSQL اساساً راهی برای رمزگذاری اطلاعات مکانی-زمانی در کلید ردیف است. بر اساس شاخص فضایی S2، این مقاله یک روش ساخت تطبیقی از شاخص مکانی-زمانی سلسله مراتبی برای داده‌های برداری تحت شبکه‌های P2P را پیشنهاد می‌کند. ما شاخص فضایی S2 را که یک الگوریتم نمایه سازی منحنی چهارگانه + هیلبرت است، با معرفی استراتژی سلسله مراتبی اطلاعات زمان و مکان و الگوریتم تنظیم دینامیکی سلسله مراتبی با توجه به مشخصه توزیع داده های مکانی-زمانی گسترش می دهیم. محتوای دقیق روش ما به شرح زیر است. در مرحله اول، اطلاعات مکانی-زمانی بر اساس دانه بندی زمانی و سلسله مراتب مکانی تقسیم می شوند. ثانیا، رمزگذاری مختلط بر اساس دانه بندی زمانی و سلسله مراتب فضایی انجام می شود. و کدها در Row Key ذخیره می شوند. ثالثاً، یک درخت شاخص چند سطحی تطبیقی برای ساخت شاخص فضایی-زمانی (Multi-level Sphere 3، MLS3) بر اساس ویژگی‌های مکانی-زمانی موجودیت‌های جغرافیایی پیشنهاد شده‌است. در نهایت، طبق یک الگوریتم هش سازگار، کلید ردیف برای دستیابی به ذخیره سازی توزیع شده داده های مکانی-زمانی در شبکه P2P، هش می شود، همانطور که در نشان داده شده است.شکل 1 .

3.1. کدگذاری مشترک اطلاعات مکانی- زمانی

مفهوم جدول در پایگاه داده NoSQL، مانند Cassandra، با مفهوم جدول در پایگاه داده رابطه ای متفاوت است. به طور کلی، هر پارتیشن در یک جدول دارای یک کلید پارتیشن منحصر به فرد است و هر ردیف در یک پارتیشن ممکن است به صورت اختیاری یک کلید مرتب سازی منحصر به فرد (کلید خوشه بندی) داشته باشد. ترکیبی از کلید پارتیشن و مرتب سازی به عنوان کلید ترکیبی تعریف می شود که می تواند به طور منحصر به فرد یک ردیف را در جدول شناسایی کند. مزیت کلیدهای ترکیبی این است که می توانند کارایی بازیابی داده ها را تسریع کنند و اطمینان حاصل کنند که داده هایی که مستقیماً از دیسک خوانده می شوند، داده های مرتب شده ای هستند که شرایط پرس و جو را برآورده می کنند [ 27 ].]. ما یک کدگذاری اطلاعات مکانی-زمانی مشترک بر اساس کلیدهای ترکیبی پیشنهاد کردیم. از کلید پارتیشن برای توصیف فضایی-زمانی با دانه بندی بزرگ استفاده می شود، به طوری که به سرعت گره ذخیره سازی را که در آن داده ها در شبکه های P2P ذخیره می شود، قرار می دهد، و از کلید مرتب سازی برای توصیف زمانی-مکانی با دانه بندی کوچک استفاده می شود، به طوری که بازیابی متوالی داده ها در گره ذخیره سازی را درک کنید.

3.1.1. کدگذاری اطلاعات زمان

اطلاعات زمانی با توجه به دوره به روز رسانی داده ها یا فرکانس نمونه برداری به شش سطح تقسیم می شود. دانه بندی زمانی از ثانیه تا سال متغیر است و همانطور که در جدول 1 نشان داده شده است به صورت g _i ( i = 0, 1, …, 5) مشخص می شود .

با فرض اینکه _پایه T نقطه شروع باشد، _جریان T تعداد میلی ثانیه از زمان جاری تا _پایه T است (تحت دانه بندی زمانی g ₅ )، یعنی T _جریان = T ( g ₅ ) – T _پایه . قسمت صحیح زمان جاری مربوط به دانه بندی زمانی در جدول 1 را به عنوان کلید پارتیشن با نام T _partition ( g _i ) و کلید مرتب سازی T _sort ( g _i ) = در نظر بگیرید._جریان T – _{پارتیشن} T ( g _i ). کدگذاری بخش اطلاعات زمان در کلید ردیف در شکل 2 نشان داده شده است .

3.1.2. کدگذاری اطلاعات مکانی

با توجه به ایده اصلی ساخت S2، هر عنصر فضایی را می توان با یک یا چند سلول حاوی عنصر شناسایی کرد. با در نظر گرفتن عنصر خط به عنوان مثال، همانطور که در شکل 3 نشان داده شده است ، مجموعه سلولی عنصر خط (خط جامد قرمز) که از اولین سطح L ₁ عبور می کند (0، 2، 3) بود، مجموعه سلولی عنصر خطی که از سطح عبور می کند. سطح دوم L ₂ (00, 02, 03, 22, 23, 30, 31) بود و عنصر خطی که از سطح سوم L ₃ عبور می کرد (001, 002, 020, 022, 023, 031, 220, 231، 232، 303، 310، 311).

در این مطالعه، شاخص فضایی S2 برای ایجاد منحنی چهاردرخت + هیلبرت با عمق محدود ( ارتفاع چهارگانه ≤ آستانه عمق، آستانه _ارتفاع ) ، و اطلاعات مکانی با کدگذاری هیلبرت چند سطحی نشان داده شد. برای اشیاء برداری، با فرض اینکه سلسله مراتب آن به Lm – L _n (0 ≤ m < _n ≤ 30) محدود شود، سپس کد اطلاعات مکانی را در سطح m پایین به عنوان کلید پارتیشن بگیرید و کلید مرتب‌سازی کدی است در سطح n بالاتر. کدگذاری قسمت اطلاعات مکانی در Row Key در شکل 4 نشان داده شده است .

3.1.3. کدگذاری اطلاعات شناسایی ویژگی

شناسایی ویژگی (FID) شامل پنج بخش است: شناسایی (ID)، شناسایی مهر زمانی (TI)، شناسایی خوشه (CID)، شناسایی گره (NID)، و شناسایی توالی شمارش (CSI)، همانطور که در شکل 5 نشان داده شده است. FID با استفاده از الگوریتم SnowFlake توسط توییتر [ 29 ] تولید شد که بر اساس مقدار ID به طور کلی مرتب شد و بیشتر توسط CID و NID شناسایی شد تا اطمینان حاصل شود که هیچ FID تکراری نمی تواند در کل شبکه P2P تولید شود.

3.1.4. سازماندهی کدگذاری کلید ردیف

ادغام کدگذاری زمانی، کدگذاری فضایی و FID برای تشکیل ساختار یکپارچه کدگذاری کلید ردیفی، حالت سازماندهی به شرح زیر است. (1) کلید پارتیشن به طور مشترک توسط دانه بندی زمانی بزرگتر و شناسایی سلول فضایی والد تعیین می شود تا اطمینان حاصل شود که ویژگی های دارای روابط مجاور در پارتیشن های منطقی یکسان یا مجاور توزیع شده اند. (2) کلید مرتب سازی در پارتیشن یک ویژگی منحصر به فرد عناصر است و باید هر دو ویژگی مکانی-زمانی را نشان دهد. طراحی کلید مرتب سازی با دانه بندی زمانی کمتر، شناسایی سلول فضایی کودک و شناسایی ویژگی بیان می شود.

برای یک عنصر، فرض کنید که دانه بندی زمانی i و سطح فضایی j باشد، سلول فضایی والد به صورت m -level تعریف می شود و سطح n سلول فضایی فرزند پس از تقسیم بیشتر است، سپس ساختار کامل فضایی-زمانی است. کدگذاری در Row Key همانطور که در شکل 6 نشان داده شده است.

3.2. بیان عناصر مکانی-زمانی

3.2.1. بیان مکانی-زمانی عناصر نقطه ای

در این مطالعه، عناصر نقطه ای تقریباً با استفاده از نقطه مرکزی سطح مشخصی از سلول بیان شدند. هنگامی که سطح تقسیم شبکه بالا باشد، هر نقطه را می توان در یک سلول تضمین کرد. بنابراین اطلاعات مکانی کلید پارتیشن در این تحقیق با توجه به توزیع و شدت عناصر نقطه ای تعیین شد.

با در نظر گرفتن نقطه مورد علاقه (POI) یک ایستگاه عوارضی، فرض کنید که مقیاس زمانی به روز رسانی یک ماه است و سطح تقسیم بهینه منطقه لایه لایه شهر 9-10 است. سپس اطلاعات زمانی «2016-02» و شناسه سلولی «35f0ec» اطلاعات مکانی در سطح نهم به عنوان کلید پارتیشن آن در نظر گرفته شده است. کلید مرتب سازی در پارتیشن ترکیبی از مهر زمانی «01 13:00:00» (روز-ساعت-دقیقه-ثانیه)، شناسه سلولی اطلاعات مکانی در سطح دهم «35f0eb0» و FIDها، همانطور که نشان داده شده است. در شکل 7 .

3.2.2. بیان مکانی-زمانی عناصر غیر نقطه ای

برای عناصر غیر نقطه ای (خط و عناصر چند ضلعی)، رمزگذاری فضایی را می توان با مجموعه ای از سلول های فضایی متعدد نشان داد. بنابراین، یک عنصر غیر نقطه ای می تواند با چندین ترکیب کلید-مقدار مطابقت داشته باشد. کلید پارتیشن با دانه بندی زمانی g ( i ) و کدگذاری فضایی سلول پوشش دهنده عنصر غیر نقطه ای در سطح پایین نشان داده شد. کلید مرتب سازی در پارتیشن با تفاوت زمانی بین زمان فعلی و زمان در کلید پارتیشن، کدگذاری فضایی در سطح بالاتر و FIDها نشان داده شد.

با در نظر گرفتن داده های عنصر جاده به عنوان مثال، فرض کنید که مقیاس زمانی به روز رسانی یک ماه است و سطح شبکه تقسیم بهینه لایه ای که جاده در آن قرار دارد 4-7 است. شناسه سلولی MBR عنصر خط در سطح 4 35b و شناسه سلولی مربوطه در سطوح 5، 6 و 7 35acc، 35ac9b و 35accf بود. بیان جاده در کلید ردیف در شکل 8 نشان داده شده است . در این مقاله، یک هندسه به طور کامل در هر سلول تکرار می شود، که فضای ذخیره سازی بیشتری را اشغال می کند، در حالی که به طور قابل توجهی کارایی پرس و جو را بهبود می بخشد.

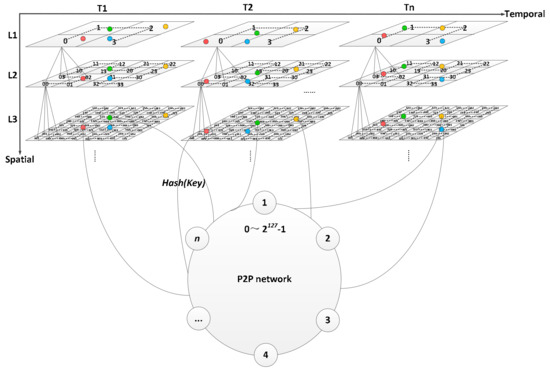
3.3. الگوریتم ساخت شاخص فضایی-زمانی در شبکه همتا به همتا (P2P)

3.3.1. تعیین دانه بندی زمانی

ایده اصلی برای تعیین دانه بندی زمانی برای داده های مکانی-زمانی پویا و پیوسته به شرح زیر است: اگر داده های تولید شده توسط چندین منبع اکتساب داده، اندازه بلوک داده پارتیشن بندی شده بهینه تحت شبکه P2P در بازه نمونه برداری مشخص شده در T (ms) باشد. فاصله زمانی، سپس دانه بندی زمانی در جدول 1 که با T مطابقت دارد ، سطح زمانی بهینه است.

با در نظر گرفتن پایگاه داده Cassandra به عنوان مثال، زمانی که یک پارتیشن از این پایگاه داده بیش از 100 مگابایت باشد، یک پارتیشن بزرگ ایجاد می شود که باعث فشار نسبتاً بزرگ جمع آوری زباله بر روی Cassandra در هنگام فشرده سازی و گسترش خوشه می شود و باعث کاهش عملکرد پایگاه داده می شود. بنابراین، این ویژگی می تواند به عنوان یک محدودیت برای محاسبه دانه بندی زمانی استفاده شود. فاصله نمونه برداری را I (ms)، تعداد حسگرها را N (عدد)، و فضای مورد نیاز برای ذخیره یک رکورد را به صورت S (MB) تعریف کنید. مقدار T (ms) که با معادله زیر محاسبه می شود، می تواند برای تعیین دانه بندی زمان بهینه استفاده شود:

(1)

3.3.2. تعیین سلسله مراتب شبکه فضایی

ایده اصلی برای تعیین سلسله مراتب شبکه فضایی به شرح زیر است: تنظیم آستانه تعداد سلول های اولیه، اگر اشیاء درون لایه توسط سلول هایی که آستانه را در سطح N تقریب می کنند پوشانده شوند، N سلسله مراتب فضای اولیه بهینه است، سپس تقسیم می شود. سلول بیشتر با توجه به تراکم عناصر در هر سلول در سطح N. در محاسبات خاص، تعیین سطح شبکه فضایی مستلزم در نظر گرفتن توزیع المان و هزینه های ذخیره سازی و همچنین زمان پرس و جو است. فرض کنید _سلول E مجموعه ای از عناصر موجود یا قطع شده در یک سلول را نشان می دهد و _{پرس و جو} Eمجموعه ای از عناصر را نشان می دهد که در محدوده پرس و جو قرار گرفته یا قطع شده اند.

تعریف 1.

یک سلول پرس و جو _موثر سلولی است که محدوده پرس و جو را در بر می گیرد یا آن را قطع می کند و برآورده می کند.

تعریف 2.

یک سلول پرس و جو غیر موثر سلول _{ناکارآمد} سلولی است که محدوده پرس و جو را قطع کرده و برآورده می کند

زمان پرس و جو T _k برای k -امین پرس و جو فضایی را می توان به عنوان مجموع زمان مصرف برای i -امین سلول پرس و جو بیان کرد ( ) و j- امین سلول پرس و جو بی اثر ( ). برای پایگاه داده NoSQL، زمان مورد نیاز برای پرس و جو از یک منطقه خاص از داده ها عمدتاً توسط مقدار داده تعیین می شود. بنابراین می توان آن را شبیه سازی کرد و با تعداد عناصر سلول و زمان مورد نیاز برای پرس و جو هر عنصر تعیین می شود، و ، و و زمان مصرف مربوطه را نشان می دهد. سپس، فرض کنید که زمان یکسانی برای پرس و جو از یک عنصر در همان سطح l که به صورت Δ T _l بیان می شود، طول می کشد . بنابراین، زمان پرس و جو را می توان به صورت زیر ساده کرد:

(2)

که در آن m و n تعداد سلول های پرس و جو موثر و سلول های پرس و جو غیر موثر هستند.

کل زمان مورد نیاز برای به حداقل رساندن k- امین پرس و جو را می توان به صورت زیر بیان کرد:

(3)

مجموعه سلسله مراتبی اتخاذ شده L _i ( L _i ∈ L , 1 ≤ l ≤ thresh ) را فرض کنید که تعداد عناصر در هر سلول در L _i برابر است و زمان پرس و جو دارای همبستگی خطی با تعداد عناصر موجود در سلول. سپس معادله (3) را می توان به صورت زیر بیان کرد:

(4)

که در آن N ^l_k تعداد سلول های سطح l را در پرس و جوی k و Δ E _l نشان دهنده تعداد عناصر در هر سلول است. و میانگین تعداد عناصر سلول در مجموعه L و میانگین زمان پرس و جو از یک عنصر را به ترتیب نشان می دهد. این مقادیر به صورت خطی با تعداد سلول های سطح 1، N ₁ مرتبط هستند و λ یک ضریب همبستگی خطی است، که در آن،

(5)

این مشکل را می توان با انتخاب یک مقدار مناسب N _{1 و}thresh چند سطحی (یعنی عمق درخت) برای عبور از حداقل تعداد سلول ها تا حد امکان برای رسیدن به پوشش پرس و جو ساده کرد و در نتیجه کل زمان پرس و جو را به حداقل رساند. برای یک مجموعه داده معین، مقدار N ₁ با میانگین تعداد عناصر در یک سلول منفرد نسبت معکوس دارد. مقدار مناسب N ₁ یک مقدار تجربی است که به محدوده فضایی داده ها، نوع پرس و جو فضایی و محیط سخت افزاری بستگی دارد. در این مقاله، مقدار با تعداد زیادی آزمایش داده های واقعی به دست می آید و محاسبه دقیق در بخش 4.2 نشان داده شده است..

این پارامترهای N ₁ و thresh برای محاسبه درخت شاخص فضایی-زمانی چند سطحی در مقاله ما استفاده می‌شوند. برای یک داده ورودی جدید، اولین سطح شاخص فضایی را می توان با MBR محدوده فضایی آن و N ₁ تعیین کرد و thresh یک محدودیت عملیات تقسیم درخت شاخص است. عملیات تقسیم برای سلول های فرعی تکرار می شود تا زمانی که تعداد عناصر کمتر از آستانه باشد یا عمق درخت فرعی به آستانه عمق برسد. ارتفاع آستانه ( _thresh ). محاسبه دقیق در بخش 3.3.3 نشان داده شده است. درخت شاخص به دست آمده توسط این دو پارامتر تضمین می کند که پرس و جوهای مکانی-زمانی به محدوده خاصی محدود می شوند و از تعداد زیادی پرس و جوهای نامعتبر اجتناب می شود.

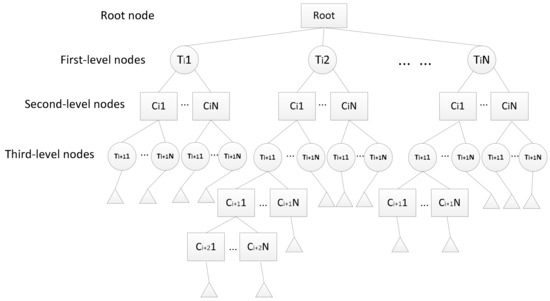
3.3.3. درخت شاخص فضایی-زمانی چند سطحی

بر اساس روش تعیین سلسله مراتب شاخص، این مقاله یک درخت شاخص فضایی-زمانی چند سطحی را پیشنهاد می کند که برای پرس و جوی مکانی-زمانی و تقسیم بندی سلسله مراتبی تطبیقی مناسب است، همانطور که در شکل 9 نشان داده شده است. با توجه به مطلق بودن و تکرارناپذیری زمان، داده ها با گذشت زمان افزایش خواهند یافت. برای ایجاد یک ساختار شاخص یکپارچه برای داده‌های مکانی-زمانی عظیم، بعد زمان برای مبنای تقسیم اولیه مناسب‌تر است تا بعد فضا. از این رو، گره سطح اول یک گره اطلاعات زمانی با دانه بندی بزرگتر است که مربوط به کدگذاری اطلاعات زمانی در کلید پارتیشن کلید ردیف است که به صورت T _{i نشان داده می شود.}; گره سطح دوم، سطح سلولی است که مربوط به کدگذاری اطلاعات مکانی در کلید پارتیشن است که به صورت C _i نمایش داده می شود . و گره سطح سوم نیز یک گره اطلاعات زمانی با دانه بندی کمتر است و مربوط به کدگذاری اطلاعات زمانی کلید مرتب سازی است که به صورت T _i₊₁ نشان داده می شود. این سه سطح سلسله مراتب اولیه هستند و سطوح دیگر را می توان به صورت تطبیقی با توجه به ویژگی های توزیع مکانی و زمانی داده ها، مطابق با کدگذاری اطلاعات مکانی در کلید مرتب سازی، که به صورت C _i_{+1،2،… نمایش} داده می شود، تقسیم کرد.

درخت شاخص را می توان به طور انعطاف پذیر با توجه به زمینه داده تنظیم کرد. برای داده‌هایی که بیشتر به اطلاعات مکانی توجه می‌کنند، می‌توان این درخت شاخص را با تنظیم اطلاعات زمانی در سطح اول به عنوان یک گره، به درختی تبدیل کرد که در آن بعد مکانی به عنوان پارتیشن اصلی در نظر گرفته می‌شود.

مراحل خاص الگوریتم نمایه سازی MLS3 بر اساس درخت شاخص فضایی-زمانی چند سطحی به شرح زیر است.

مرحله 1: دانه بندی زمانی _{پارتیشن} T ( g _i ) مورد استفاده در کلید پارتیشن را تعیین کنید و یک گره سطح اول بسازید، همانطور که با _Ti در شکل 9 نشان داده شده است.
گام 2: با توجه به ایده شاخص S2، MBR یک محدوده مکانی خاص را به صورت Rect تعریف کنید و مختصات چهار گوشه عرض و طول جغرافیایی آن ( Rect _k , k = 0, 1, 2, 3) را به مختصات سه بعدی تبدیل کنید. محدوده فضایی مستطیلی Rect به عنوان گره ریشه درخت شاخص استفاده می شود.
مرحله 3: مختصات چهار گوشه پیش بینی شده را به سطوح مختلف n , n ∈ [0, 30] تقسیم کنید. محدوده مقدار n توسط محدوده فضایی سلول در هر سطح از شاخص S2 تعیین می شود، همانطور که در جدول 2 نشان داده شده است [ 15 ]، حداقل مساحتی که یک شبکه می تواند در سطح 30 توصیف کند 0.43 سانتی متر مربع ^است که به معنای هر سانتی متر است. ² را می توان با استفاده از یک عدد صحیح 64 بیتی نشان داد و این برای سناریوهای رایج مدیریت داده های مکانی به اندازه کافی خوب است [ 30 ، 31 ]. با شروع از سطح n = 0، منطقه فعلی ( صورت ، i _k، j _k ) را می توان با سلول های m پوشش داد ، اگر m > آستانه ( N ₁ )، سطح فعلی سطح مورد نظر است و به عنوان گره سطح دوم C _i استفاده می شود.
مرحله 4: اطلاعات دانه بندی زمانی را در کلید مرتب سازی، به عنوان مثال، _{مرتب سازی} T ( g _i )، به عنوان یک گره سطح سوم، همانطور که توسط T _i₊₁ در شکل 9 نشان داده شده است، بسازید .
مرحله 5: عناصر موجود در کل لایه را نمونه برداری کنید و تعداد عناصر موجود در سلول را بشمارید. اگر عدد بزرگتر از آستانه تقسیم _آستانه باشد ، C _i بیشتر تقسیم می شود. آستانه تقسیم _آستانه یک مقدار تجربی است که ما از طریق تعداد زیادی آزمایش داده های واقعی به دست آوردیم. در این مقاله آن را 30 درصد از کل عناصر قرار می دهیم. متفاوت از تقسیم چهار درختی از چهار سلول، تنها سلول فرعی که تقسیم می شود این است که عنصر را به عنوان گره های درخت فرعی گره سطح سوم T _i+_{1 می پوشاند.}و حداکثر تعداد سلول های فرعی 4 است. سپس مرحله 5 برای سلول های فرعی تکرار می شود تا زمانی که تعداد عناصر از آستانه کمتر شود یا عمق درخت فرعی به آستانه عمق برسد Height _thresh ( thresh ). سطح به عنوان زیرسطح تنظیم می شود و تقسیم متوقف می شود.
مرحله 6: با نگاشت سلول های واحد چهاردرخت m- امین شناسایی شده توسط ( face , i _k , j _k ) به منحنی هیلبرت زیرسطح ، سلول S مجموعه ID سلول مربوطه _محاسبه می شود. _سلول S می تواند به طور منحصر به فرد ناحیه پرس و جو را نشان دهد، جایی که هر شناسه سلولی _سلول S نشان دهنده زیر ناحیه یک پرس و جو است. تمام شناسه های سلولی در _سلول S به عنوان گره های سطح استفاده می شوند و به عنوان رمزگذاری اطلاعات مکانی در کلید مرتب سازی عمل می کنند.
مرحله 7: با توجه به گره های سطح اول و دوم، تابع Murmur Hash برای محاسبه محل پارتیشن مربوطه جایگزین می شود و مکان های گره سطح سوم و گره برگ درخت فرعی آن با توجه به شناسه سلول تعیین می شود.

همانطور که در شکل 9 نشان داده شده است ، MLS3 یک ساختار شاخص جهانی است که برای شبکه P2P مناسب تر است. ایندکس به صورت آرایه ای در ابرداده پایگاه داده NoSQL ذخیره می شود که شامل اطلاعات گره و رابطه بین هر گره است.

3.3.4. به روز رسانی پویا و نگهداری از چند سطح کره 3 (MLS3)

به روز رسانی و نگهداری MLS3 را می توان به سه عملیات اساسی تقسیم کرد: درج، حذف و تقسیم گره ها. الگوریتم های جزئیات به شرح زیر است:

عملیات درج: برای داده های جدید اضافه شده، ابتدا شناسه سلول محاسبه می شود. اگر اطلاعات زمان متعلق به درخت شاخص فعلی نباشد، یک گره سطح اول جدید و یک شاخه درخت شاخص جدید اضافه می شود. در غیر این صورت، گره سطح اول داده های جدید را با توجه به شناسه سلول تعیین کنید و سپس لایه به لایه زیر درخت را از گره سطح اول به گره برگ پیمایش کنید تا پیدا کنید که آیا گره حاوی داده های جدید وجود دارد یا خیر. اگر نه، داده های جدید را به عنوان یک گره برگ جدید وارد کنید. اگر وجود داشته باشد، گره دیگر نیازی به درج [ 4 ، 6 ] ندارد.
عملیات حذف: اگر گره حذف شده یک گره برگ باشد، می توان آن را مستقیماً حذف کرد. در غیر این صورت نمی توان آن را حذف کرد. اگر گره برگ حذف شده دارای همان گره باشد، عملیات حذف خاتمه می یابد و اگر گره دیگری در همان سطح گره برگ وجود نداشته باشد، گره والد حذف می شود. درخت فرعی را به نوبت طی کنید و مرحله بالا را تکرار کنید [ 4 ، 6 ].
عملیات تقسیم: اگر تعداد عناصر یک سلول از آستانه تقسیم _آستانه بزرگتر باشد ، این سلول بیشتر تقسیم می شود. با تقسیم چهار درختی از چهار سلول، تنها سلول فرعی که عنصر را به عنوان گره های درخت فرعی گره سطح سوم T _i₊₁ پوشش می دهد، تقسیم می شود و حداکثر تعداد سلول های فرعی 4 است. عملیات تقسیم برای سلول های فرعی تکرار می شود تا زمانی که تعداد عناصر کمتر از آستانه باشد یا عمق درخت فرعی به آستانه عمق برسد Height _thresh ( thresh ).

علاوه بر این، به روز رسانی و نگهداری الگوریتم شاخص ساخته شده در این مقاله شامل عملیات ادغام نمی شود. MLS3 به عنوان راهی برای رمزگذاری اطلاعات مکانی-زمانی در Row Key وجود دارد، و کلید ردیف برای دستیابی به ذخیره سازی توزیع شده داده های مکانی-زمانی در شبکه P2P، همانطور که در شکل 1 نشان داده شده است، هش می شود. عملیات ادغام مقدار Row Key را که به گره ذخیره سازی اختصاص داده شده است تغییر می دهد که منجر به خطای بازیابی داده می شود. از این رو، اگر تعداد معینی از عملیات حذف انجام شود، و تنها یک گره برگ در یک سطح باقی بماند، برای اطمینان از پایداری شاخص، آن را در گره والد آن ادغام نمی کنیم.

این درخت شاخص پیشنهادی در این مقاله در ابرداده مربوطه به عنوان یک استراتژی شاخص ذخیره می شود و به عنوان پایه ای برای تقسیم محدوده پرس و جو به چندین ناحیه سلولی در طول پرس و جو عمل می کند. پیچیدگی زمان پرس و جو پیمایش O ( n ) است، که در آن n تعداد سلول های محدوده پرس و جو است.

4. نتایج و بحث

4.1. داده های تجربی و محیط

برای تأیید اعتبار و عقلانیت شاخص MLS3 پیشنهاد شده در این مقاله، تجزیه و تحلیل مقایسه ای با شاخص XZ3 با همان مجموعه داده و محیط آزمون اجرا شد. ساختار P2P برای ساخت یک خوشه کاساندرا استفاده شد. با مجموع پنج گره پایگاه داده، و ضریب پشتیبان اضافی 2 بود. عملکرد یک گره بر اساس یک سرور IBM X3850، با 16G حافظه، و یک واحد پردازش مرکزی (CPU) با 16 هسته × 2.294 گیگاهرتز بود.

مجموعه داده آزمایشی (مجموعه داده TDrive) از داده های مسیر (عنصر نقطه ای) سیستم موقعیت یابی جهانی (GPS) 10357 تاکسی در پکن از 2 فوریه تا 8 فوریه 2008، ارائه شده توسط Microsoft Research Asia [ 32 ، 33 ] به دست آمد. مجموعه داده شامل 15 میلیون قطعه داده با مسافت پیموده شده در حدود 9 میلیون کیلومتر بود. داده‌های نوامبر 2017 تا مارس 2018 (5 ماه) در پکن ارائه شده توسط نقشه خیابان باز (OSM) نیز در نظر گرفته شد، از جمله 227258 ساختمان (عناصر چند ضلعی) و 309314 جاده (عناصر خط) (داده‌های OSM) [ 34 ، 35 ].

همانطور که در شکل 10 نشان داده شده است، برای آزمایش اثر پرس و جو در یک محیط دسترسی همزمان، 200 پنجره پرس و جوی مکانی-زمانی برای دو مجموعه داده فوق الذکر به طور تصادفی تولید شد .

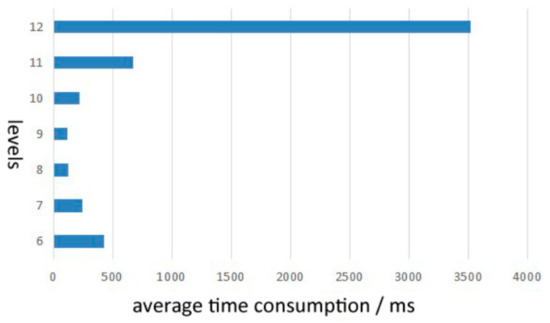
4.2. تایید عقلانیت تعیین سلسله مراتب

برای تأیید منطقی بودن الگوریتم تقسیم پیشنهادی در این مطالعه، مجموعه داده TDrive برای آزمایش انتخاب شد. بیش از 15 میلیون داده GPS به طور تصادفی نمونه برداری شد، نرخ نمونه برداری 20 درصد بود و آستانه تقسیم سلولی آستانه _تقسیم روی 30 درصد نمونه تنظیم شد. با تنظیم آستانه عمق درخت بر روی 2، سطح اولیه بهینه مجموعه داده ها سطح 9 تعیین شد که با استفاده از الگوریتم MLS3 محاسبه شد، محدوده تقسیم چند سطحی شامل سطوح 9-11 بود. زمان مورد استفاده برای تعیین سطح بهینه 1601 میلی ثانیه است.

برای تأیید اینکه سطح 9 سطح بهینه است، ما هفت سطح مختلف، سطوح 6، 7، 8، 9، 10، 11، و 12 را انتخاب کردیم و آنها را به عنوان سطح اولیه در مجموعه داده های مشابه قرار دادیم. سطحی که کمترین میانگین مصرف زمانی 200 پرس و جوی مکانی-زمانی را در بین این سطوح داشت، به عنوان سطح بهینه شناسایی شد. نتایج تجربی در شکل 11 نشان داده شده است. بدیهی است که با افزایش سطح، میانگین زمان مصرف پرس و جو ابتدا کاهش و سپس افزایش می یابد. میانگین زمان مصرف به تدریج از سطح 6 به سطح 9 کاهش می یابد و به حداقل آن در سطح 9 می رسد. این به این دلیل است که با افزایش سطح، دامنه پرس و جو به تدریج اصلاح شد، سلول پرس و جو غیر موثر تقسیم شده به تدریج کاهش یافت و مقدار داده های پرس و جو کاهش یافت. با این حال، از سطح 9 تا سطح 12، میانگین زمان مصرف به تدریج افزایش می‌یابد و در سطح 12 به 3520 میلی‌ثانیه می‌رسد. تعداد زیاد درخواست‌ها منجر به افزایش ورودی و خروجی دیسک (IO) و هزینه‌های ارتباطی شده و در نتیجه افزایش قابل توجهی در زمان پرس و جو از این رو،

مقدار مرجع آستانه تعداد سلول ها در سطح اول به صورت زیر محاسبه می شود: برای محیط آزمایش در این مقاله، ما از یک CPU با 16 هسته استفاده کردیم که می تواند 16 رشته همزمان قابلیت محاسبات موازی را ارائه دهد. به طور کلی، زمان قابل قبول یک پاسخ پرس و جو در پایگاه داده کمتر از 5 ثانیه است [ 36 ، 37 ]. همانطور که در آزمایش در این مقاله می بینیم، برای پرس و جوهای مکانی-زمانی رایج ( جدول 3)، زمان پرس و جو از یک رشته حدود 400-500 میلی ثانیه است. از این رو، حد بالایی و پایینی زمان های پرس و جو در 5 ثانیه 5 ثانیه × 1000/400 میلی ثانیه × 16 ≈ 200 و 5 ثانیه × 1000/500 میلی ثانیه × 16 ≈ 160 است که به عنوان سطح بهینه آستانه شماره سلول در نظر گرفته می شود. کاغذ. علاوه بر این، با توجه به اینکه هر پرس و جوی مکانی-زمانی نیازی به عبور از تمام سلول ها ندارد، بنابراین مقدار آستانه در این مقاله روی 200 تنظیم شده است، و این مقدار نیز در مجموعه داده TDrive فوق الذکر پکن تأیید شده است، نتایج تجربی نشان می دهد که این مقدار موجود است. برای داده‌های ورودی جدید، می‌توانیم به سرعت سطح شاخص بهینه را با توجه به محدوده مکانی داده‌ها و مقدار تجربی 200 تعیین کنیم. با فرض اینکه منطقه فضایی S باشد، ناحیه MBR متناظر S _{MBR است.}، میانگین مساحت سلول در هر سطح AS _level(i) است، سپس حداقل مقدار تفاوت بین و مطابق فرمول زیر (6). سطح مربوط به حداقل مقدار به عنوان مناسب ترین سطح برای داده های جدید در نظر گرفته می شود.

(6)

بر اساس این الگوریتم، ما مطمئن شدیم که مناسب ترین سطح برای لایه ملی (مانند محدوده ملی چین) 4-5، برای لایه استانی (مانند محدوده استان شاندونگ) 7-8 است، و برای لایه شهر (مانند منطقه پکن) 9-10 است. محدوده سطح در پروژه های ساخت پلت فرم ابر اطلاعات مکانی-زمانی در Smart Linyi و Smart Zibo که دو شهر در استان شاندونگ چین هستند تأیید شده است.

4.3. مقایسه عملکرد شاخص

الگوریتم شاخص فضایی-زمانی XZ3 (کد منبع: https://github.com/locationtech/geomesa/releases/tag/geomesa_2.11-2.3.1 )، که در سال 2019 منتشر شد، برای مقایسه با MLS3 پیشنهادی انتخاب شده است. الگوریتم با استفاده از مجموعه داده و محیط یکسان برای آزمایش عملکرد پرس و جو. آخرین آپدیت الگوریتم XZ3 نسخه 2.3.1 است و در این نسخه GeoMesa مقادیر پارامتر پیش فرض را می دهد که عملکرد بهینه الگوریتم را به توسعه دهندگان نشان می دهد. از این رو، این مقادیر پارامتر پیش فرض در این مقاله استفاده خواهد شد. عملکرد شاخص ما از سه جنبه مورد آزمایش قرار می گیرد: کارایی جستجوی شاخص، کارایی ساخت و ساز و نسبت مصرف فضا.

4.3.1. کارایی جستجوی شاخص

از آنجایی که الگوریتم XZ3 به صورت پیش‌فرض یک رشته با اندازه صفحه 1 را ارائه می‌کند که توسط GeoMesa ارائه شده است، ابتدا عملکرد دو الگوریتم را تحت تنظیمات پارامتر پیش‌فرض مقایسه کردیم. از مجموعه داده های TDrive و OSM به عنوان داده های تجربی استفاده شد. به مجموعه‌های متعددی از دسترسی پرس و جوی همزمان، جزئیات 1، 5، 10، 15، 20، 25، 30، 35 و 40 اختصاص داده شد.

همانطور که در جدول 3 نشان داده شده است ، با افزایش وظایف دسترسی به پرس و جو همزمان، میانگین مصرف زمان پرس و جو الگوریتم های نمایه سازی MLS3 و XZ3 هر دو افزایش می یابد، اما الگوریتم MLS3 به زمان کمتری نسبت به الگوریتم XZ3 نیاز دارد. همانطور که در جدول 3 نشان داده شده است، برای پرس و جو از نقاط مسیر GPS مکانی-زمانی در مجموعه داده TDrive، مصرف زمان الگوریتم XZ3 1.7-3.4 برابر بیشتر از الگوریتم MLS3 است. به ویژه برای عناصر لایه غیر نقطه ای مانند خطوط و چند ضلعی ها، الگوریتم MLS3 پیشرفت قابل توجهی را نشان می دهد. الگوریتم MLS3 فشار عملیات پرس و جوی پیچیده مکانی-زمانی را تحت شرایط همزمانی بالا تا حد زیادی کاهش داد و زمان مصرف آن حدود 1/7-1/2 نسبت به الگوریتم XZ3 بود.

علاوه بر این، ما پارامترهای روش خود را بهینه کردیم و آن را با روش XZ3 مقایسه کردیم. رویکرد MLS3 از پنج رشته با اندازه صفحه 1024 استفاده می‌کند، در حالی که الگوریتم XZ3 از پارامترهای پیش‌فرض استفاده می‌کند. نتایج تجربی در شکل 12 ، شکل 13 و شکل 14 نشان داده شده است. مشاهده می شود که برای سه نوع داده (نقاط، خطوط و چند ضلعی)، مصرف زمان پرس و جو با الگوریتم XZ3 به طور قابل توجهی در نوسان است که نه تنها به مقدار داده های مورد استفاده در فرآیند پرس و جو، بلکه به دلیل نوع SFC مورد استفاده در الگوریتم نمایه سازی. الگوریتم XZ3 از منحنی مرتبه Z استفاده می کند که این مشکل را دارد که روابط فضایی داده های مجاور ممکن است جهش کند.

در این مطالعه، منحنی هیلبرت در الگوریتم MLS3 برای اطمینان از کدگذاری عناصر مجاور فضایی در مجاورت استفاده شد. برای سه نوع داده، مصرف زمان الگوریتم MLS3 در 2000 میلی ثانیه ( شکل 12 )، 630 میلی ثانیه ( شکل 13 ) و 500 میلی ثانیه ( شکل 14 ) نوسان می کند. به طور کلی، الگوریتم MLS3 عملکرد بسیار بهبود یافته ای را تحت شرایط چند رشته ای و اندازه صفحه مناسب نشان می دهد، کارایی پرس و جو 4 تا 7 برابر بهبود می یابد، و مصرف زمان پرس و جو پایدار است، که برای سناریوهای عملی مناسب تر است.

4.3.2. راندمان ساخت و ساز و نسبت مصرف فضا

با در نظر گرفتن زمان تولید شاخص داده های تجربی به عنوان راندمان ساخت و نسبت حجم داده های شاخص به حجم داده های برداری متناظر به عنوان نسبت مصرف فضا، نتایج محاسبه دو روش شاخص در هر شاخص در جدول 4 نشان داده شده است.. می توان دریافت که برای عناصر نقطه، خط و چند ضلعی، نسبت مصرف فضایی روش ما کمی بیشتر از شاخص XZ3 است که به ترتیب 7.49٪، 1.54٪ و 3.02٪ افزایش می یابد. با این حال، در مقایسه با کل فضای ذخیره سازی 120G، حجم داده های دو روش نمایه سازی حدود 0.5 درصد است که نشان می دهد میزان مصرف فضا در محیط ذخیره سازی سخت افزار موجود قابل قبول است. علاوه بر این، از نظر کارایی ساخت شاخص، زمان ساخت این روش بالاتر از XZ3 است و زمان افزایش یافته با تعداد عناصر داده همبستگی مثبت دارد. این به این دلیل است که XZ3 فقط مقدار Row Key را محاسبه می کند، در حالی که MLS3 باید یک درخت شاخص چند سطحی بسازد و سطح شاخص بهینه را تعیین کند. با این حال،

5. نتیجه گیری ها

برای پرداختن به مسائل موجود در نمایه سازی مکانی-زمانی سنتی، یک الگوریتم شاخص مکانی-زمانی سلسله مراتبی تطبیقی در این مطالعه توسعه داده شد. این الگوریتم نه تنها می تواند داده های برداری را به طور منطقی توصیف کند، بلکه کارایی بازیابی مکانی-زمانی را نیز بهبود می بخشد و از کانون های ذخیره سازی در شبکه های P2P جلوگیری می کند. در مقایسه با شاخص فضایی-زمانی XZ3، شاخص MLS3 پیشنهاد شده در این مقاله دارای سه مزیت اصلی است: (1) در بعد زمانی، ساختار شاخص سلسله مراتبی با دانه بندی های مختلف برای بهبود کارایی پرس و جو اضافه می شود. (2) در بعد فضا، منحنی مرتبه Z با منحنی هیلبرت جایگزین می شود تا مشکل پرش پرس و جو را حل کند. (3) شاخص زمانی و مکانی در یک شاخص مکانی-زمانی ادغام می شود، که به سادگی یک شاخص مکانی یا یک شاخص زمانی را ترتیب نمی دهد.

بر اساس اعتبارسنجی با تعداد زیادی از داده های واقعی، مشارکت های اصلی این مطالعه را می توان به شرح زیر خلاصه کرد:

(1): برای تعیین سلسله مراتب بهینه، توزیع فضایی و چگالی کل لایه عناصر در نظر گرفته شد. مناسب ترین سطح برای لایه ملی 4-5، برای لایه استانی 7-8 و برای لایه شهرستان 9-10 است.
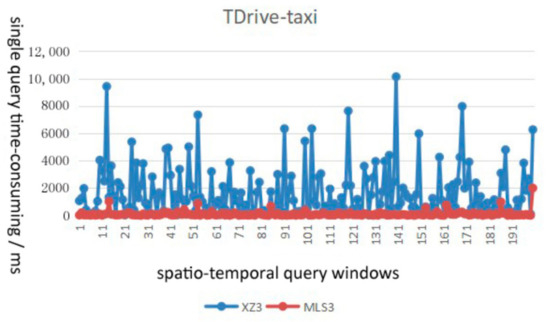
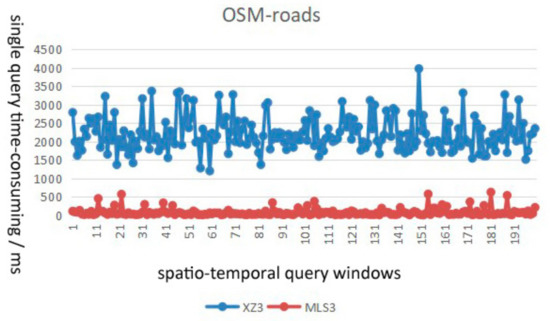
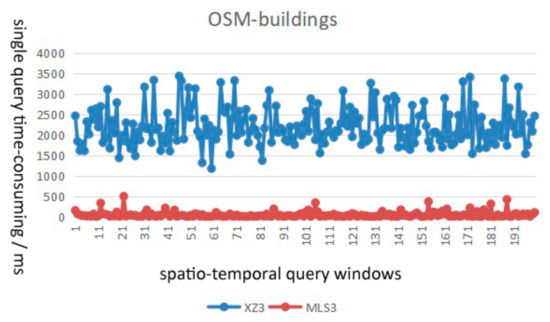
(2): از نظر کارایی پرس و جو، میانگین زمان مصرف الگوریتم MLS3 پیشنهادی حدود 1/7-1/2 از الگوریتم XZ3 با پارامترهای یکسان است، و کارایی پرس و جو شاخص MLS3 را می توان با 4-7 بهبود داد. بارها پس از بهینه سازی پارامتر
(3): از نظر ثبات پرس و جو، شاخص MLS3 با منحنی پرکننده هیلبرت می تواند تداوم داده های مکانی-زمانی را بهتر از شاخص XZ3 با منحنی پرکننده مرتبه Z توصیف کند. شاخص MLS3 عملکرد پرس و جو با ثبات تری را نشان می دهد و برای مدیریت ذخیره سازی توزیع شده داده های عظیم چند مقیاسی مناسب تر است.
(4): از نظر نسبت مصرف فضا، روش ما بخشی از فضای ذخیره سازی را قربانی یک جستجوی کارآمد می کند. با این حال، فضای ذخیره سازی شاخص حدود 0.5٪ از کل فضای ذخیره سازی سخت افزاری را تشکیل می دهد که برای ذخیره سازی و مدیریت داده های بزرگ مکانی-زمانی قابل قبول است.

در کار آینده، کارایی ساخت و نسبت مصرف فضا بهینه خواهد شد و الگوریتم شاخص MLS3 را به پایگاه‌های داده NoSQL توزیع‌شده سرورهای مشتری گسترش خواهیم داد. علاوه بر این، الگوریتم شاخص پیشنهادی در این مقاله عمدتاً برای مکان‌یابی گره‌های ذخیره‌سازی در شبکه‌های P2P برای بازیابی سریع و کارآمد داده‌ها روی گره‌ها استفاده می‌شود، اما توزیع داده‌ها بین هر گره مورد بحث قرار نمی‌گیرد. پرداختن به این موضوع از حوصله این تحقیق خارج است، اما جهتی امیدوارکننده برای کاوش بیشتر است.

منابع

کورنلی، اف. دامیانی، ای. دی ویمرکاتی، SDC; پارابوسچی، اس. سامراتی، ص. انتخاب سرویس های معتبر در یک شبکه P2P. در مجموعه مقالات یازدهمین کنفرانس بین المللی وب جهانی، هونولولو، HI، ایالات متحده آمریکا، 7-11 مه 2002; صص 376-386. [ Google Scholar ]
کوستاکیس، وی. باونز، ام. نیاروس، V. پیکربندی مجدد شهری پس از ظهور زیرساخت های همتا به همتا: چهار سناریوی آینده با تأثیر بر شهرهای هوشمند. در شهرهای هوشمند به عنوان زیست بوم های دموکراتیک ; پالگریو مک میلان: لندن، بریتانیا، 2015; صص 116-124. [ Google Scholar ]
سانتوس، جی. واترز، تی. Volckaert، B. De Turck, F. Fog computing: امکان مدیریت و هماهنگ سازی برنامه های کاربردی شهر هوشمند در شبکه های 5g. Entropy 2018 , 20 , 4. [ Google Scholar ] [ CrossRef ]
اعرابی، ل. موکبل، MF; Musleh, M. St-hadoop: یک چارچوب کاهش نقشه برای داده های مکانی-زمانی. GeoInformatica 2018 ، 22 ، 785-813. [ Google Scholar ] [ CrossRef ]
شن، دی. یو، جی. وانگ، ایکس. نی، تی. Kou, Y. بررسی در NoSQL برای مدیریت داده های بزرگ. جی. سافتو. 2013 ، 24 ، 1786-1803. (به زبان چینی) [ Google Scholar ] [ CrossRef ]
جان، ا. سوگوماران، م. تکنیک های راجش، RS نمایه سازی و پردازش پرس و جو در داده های مکانی-زمانی. ICTACT J. Soft Comput. 2016 ، 6 . [ Google Scholar ] [ CrossRef ]
آگیلرا، MK; گلاب، دبلیو. شاه، MA یک درخت B توزیع شده مقیاس پذیر عملی. در مجموعه مقالات VLDB. مورگان کافمن، اوکلند، نیوزلند، 24 تا 30 اوت 2008. [ Google Scholar ]
کری، ا. سان، ز. هریستیدیس، وی. Rishe, N. تجربیات در پردازش داده های مکانی با MapReduce. در مجموعه مقالات مدیریت پایگاه داده های علمی و آماری، کنفرانس بین المللی (SSDBM 2009)، نیواورلئان، لس آنجلس، ایالات متحده آمریکا، 2-4 ژوئن 2009. صص 302-319. [ Google Scholar ]
موزا، سی. لیتوین، دبلیو. Rigaux، P. نمایه سازی در مقیاس بزرگ داده های مکانی در مخازن توزیع شده: SD-Rtree. VLDB J. 2009 ، 18 ، 933-958. [ Google Scholar ] [ CrossRef ]
وو، اس. جیانگ، DW; Ooi، BC; Wu، KL شاخص‌سازی مبتنی بر درخت B کارآمد برای پردازش داده‌های ابری. Proc. VLDB Enddow. 2010 ، 3 ، 1207-1218. [ Google Scholar ] [ CrossRef ]
الدوی، ا. Mokbel، MF Spatialhadoop: یک چارچوب کاهش نقشه برای داده های مکانی. در مجموعه مقالات سی و یکمین کنفرانس بین المللی IEEE 2015 در زمینه مهندسی داده، سئول، کره، 13 تا 17 آوریل 2015؛ صص 1352–1363. [ Google Scholar ]
یو، جی. ژانگ، ز. Sarwat، M. مدیریت داده های فضایی در اسپارک آپاچی: چشم انداز geospark و فراتر از آن. Geoinformatica 2019 ، 23 ، 37–78. [ Google Scholar ] [ CrossRef ]
فاکس، ا. آیکلبرگر، سی. هیوز، جی. لیون، S. نمایه سازی مکانی-زمانی در پایگاه های داده توزیع شده غیر رابطه ای. در مجموعه مقالات کنفرانس بین المللی IEEE در مورد داده های بزرگ، سیلیکون ولی، CA، ایالات متحده آمریکا، 6-9 اکتبر 2013. ص 291-299. [ Google Scholar ]
Le، HV; آتسوهیرو، تی. یک شاخص توزیع شده کارآمد برای پایگاه‌های اطلاعاتی جغرافیایی. در پایگاه داده و برنامه های کاربردی سیستم های خبره ; Springer: Cham, Switzerland, 2015; ص 28-42. [ Google Scholar ]
شرکت گوگل کتابخانه هندسه S2. 2015. در دسترس آنلاین: https://s2geometry.io/ (در 6 آوریل 2019 قابل دسترسی است).
Procopiuc، O. هندسه در کره: کتابخانه S2 Google. 2011. در دسترس آنلاین: https://docs.google.com/presentation/d/1Hl4KapfAENAOf4gv-pSngKwvS_jwNVHRPZTTDzXXn6Q/view#slide=id.i22 (در 7 آوریل 2019 قابل دسترسی است).
هیوز، JN; پیوست، الف. Eichelberger، CN; فاکس، ا. هالبرت، ا. Ronquest، M. GeoMesa: A Distributed Architecture for Spatio-Temporal Fusion. در انفورماتیک جغرافیایی، فیوژن، و تجزیه و تحلیل ویدئو حرکت V ; انجمن بین المللی اپتیک و فوتونیک: بالتیمور، MD، ایالات متحده آمریکا، 20 آوریل 2015. [ Google Scholar ]
بوکسم، سی. کلمپ، جی. کریگل، HP XZ-Ordering: منحنی پرکننده فضا برای اشیاء با گسترش فضایی. در سمپوزیوم بین المللی پیشرفت در پایگاه داده های فضایی ; Springer: برلین، آلمان، 1999. [ Google Scholar ]
ژانگ، آر. چی، جی. استرادلینگ، ام. Huang, J. به سمت یک شاخص بدون درد برای اشیاء فضایی. ACM Trans. سیستم پایگاه داده 2014 ، 39 ، 19. [ Google Scholar ] [ CrossRef ]
فچر، آر. Whitby، MA بهینه سازی تجزیه و تحلیل مکانی-زمانی با استفاده از نمایه سازی چند بعدی با GeoWave. نرم افزار منبع باز رایگان. ژئوسپات. Conf. Proc. 2017 ، 17 ، 12. [ Google Scholar ]
الدوی، ا. اعرابی، ل. Mokbel، MF تکنیک های پارتیشن بندی فضایی در SpatialHadoop. Proc. VLDB Enddow. 2015 ، 8 ، 1602-1605. [ Google Scholar ] [ CrossRef ]
Eldawy، A. SpatialHadoop: به سمت پردازش فضایی انعطاف پذیر و مقیاس پذیر با استفاده از MapReduce. در مجموعه مقالات سمپوزیوم دکترای Sigmod، Snowbird، UT، ایالات متحده آمریکا، 22 ژوئن 2014; صص 46-50. [ Google Scholar ]
ویتمن، RT; پارک، مگابایت؛ Ambrose، SM; Hoel، EG نمایه سازی فضایی و تجزیه و تحلیل در Hadoop. در مجموعه مقالات بیست و دومین کنفرانس بین المللی ACM SIGSPATIAL در مورد پیشرفت در سیستم های اطلاعات جغرافیایی، دالاس، تگزاس، ایالات متحده آمریکا، 4 تا 7 نوامبر 2014. صص 73-82. [ Google Scholar ]
لاکشمن، ا. Malik, P. Cassandra: یک سیستم ذخیره سازی ساختار یافته در یک شبکه P2P. در مجموعه مقالات سمپوزیوم ACM در مورد موازی سازی در الگوریتم ها و معماری ها، کلگری، AB، کانادا، 10-12 اوت 2009. پ. 47. [ Google Scholar ]
لاکشمن، ا. Malik, P. Cassandra: یک سیستم ذخیره سازی ساختاریافته غیرمتمرکز. ACM SIGOPS Oper. سیستم Rev. 2010 , 44 , 35-40. [ Google Scholar ] [ CrossRef ]
Brahim, MB; دریرا، دبلیو. فیلالی، ف. حمدی، N. پسوند داده های فضایی برای پایگاه داده NoSQL Cassandra. J. Big Data 2016 ، 3 ، 1-16. [ Google Scholar ] [ CrossRef ]
چبوتکو، ا. کشلو، ا. Lu, S. یک روش مدل سازی کلان داده برای آپاچی کاساندرا. در مجموعه مقالات کنگره بین المللی IEEE در مورد داده های بزرگ، نیویورک، نیویورک، ایالات متحده آمریکا، 27 ژوئن تا 2 ژوئیه 2015. صص 238-245. [ Google Scholar ]
بلوسی، ا. میگلیورینی، اس. Eldawy، A. تشخیص چولگی داده های فضایی بزرگ در SpatialHadoop. در مجموعه مقالات بیست و ششمین کنفرانس بین المللی ACM SIGSPATIAL در مورد پیشرفت در سیستم های اطلاعات جغرافیایی، سیاتل، WA، ایالات متحده آمریکا، 6-9 نوامبر 2018؛ صص 432-435. [ Google Scholar ]
گونزالس، آر. مونوز، ا. هرناندز، جی. Cuevas, R. در مورد فرآیند ورود توییت در توییتر: تجزیه و تحلیل و برنامه های کاربردی. ترانس. ظهور. مخابرات تکنولوژی 2014 ، 25 ، 273-282. [ Google Scholar ] [ CrossRef ]
شاو، بی. شی، جی. سینها، س. Hogue, A. یادگیری رتبه بندی برای جستجوی مکانی و زمانی. در مجموعه مقالات ششمین کنفرانس بین المللی ACM در جستجوی وب و داده کاوی، رم، ایتالیا، 4 تا 8 فوریه 2013. صص 717-726. [ Google Scholar ]
ویاند، تی. کوستریکوف، آی. فیلبین، جی. پلانت – موقعیت جغرافیایی عکس با شبکه های عصبی کانولوشن. در کنفرانس اروپایی بینایی کامپیوتر ; Leibe, B., Matas, J., Sebe, N., Welling, M., Eds. Springer: Cham، Switzerland، 2016. [ Google Scholar ]
یوان، جی. ژنگ، ی. ژانگ، سی. زی، دبلیو. Xie، X. سان، جی. Huang, Y. Tdrive: مسیرهای رانندگی بر اساس مسیرهای تاکسی. در مجموعه مقالات هجدهمین کنفرانس بین المللی SIGSPATIAL در زمینه پیشرفت در سیستم های اطلاعات جغرافیایی، GIS’10، سن خوزه، کالیفرنیا، ایالات متحده آمریکا، 2 تا 5 نوامبر 2010. صص 99-108. [ Google Scholar ]
یوان، جی. ژنگ، ی. Xie، X. Sun, G. رانندگی با دانش از دنیای فیزیکی. در مجموعه مقالات هفدهمین کنفرانس بین المللی ACM SIGKDD در مورد کشف دانش و داده کاوی، KDD’11، سن دیگو، کالیفرنیا، ایالات متحده آمریکا، 21 تا 24 اوت 2011. صص 316-324. [ Google Scholar ]
کوران، ک. فیشر، جی. Crumlish، J. OpenStreetMap. بین المللی J. تعامل. اشتراک. سیستم تکنولوژی 2012 ، 2 ، 69-78. [ Google Scholar ] [ CrossRef ]
هاکلی، م. Weber, P. OpenStreetMap: نقشه های خیابانی تولید شده توسط کاربر. محاسبات فراگیر IEEE 2008 ، 7 ، 12-18. [ Google Scholar ] [ CrossRef ]
شائو، جی. لیو، ایکس. لی، ی. Liu, J. بهینه سازی عملکرد پایگاه داده برای SQL Server بر اساس مدل شبکه صف سلسله مراتبی. بین المللی J. Database Theory Appl. 2015 ، 8 ، 187-196. [ Google Scholar ] [ CrossRef ]
کائو، ی. ریتز، سی. رعد، ر. چقدر دیگر باید برود؟ تأثیر زمان انتظار و شاخص‌های پیشرفت بر کیفیت تجربه جستجوی بصری موبایل که در رسانه‌های چاپی اعمال می‌شود. در مجموعه مقالات پنجمین کارگاه بین المللی 2013 در مورد کیفیت تجربه چند رسانه ای (QoMEX)، کلاگنفورت آم وورترزی، اتریش، 3 تا 5 ژوئیه 2013. صص 112-117. [ Google Scholar ]