روش کلی برای گسترش سیستم های شبکه جهانی گسسته به سه بعد

خلاصه

 در حال تولید مقادیر فزاینده ای از داده های سه بعدی (3D) هستند. در حالی که سیستم‌های شبکه جهانی گسسته (DGGS) ابزار مفیدی برای یکپارچه‌سازی داده‌های مکانی هستند، هیچ پشتیبانی بومی برای داده‌های سه بعدی ارائه نمی‌کنند. چندین شبکه جهانی سه بعدی مختلف پیشنهاد شده است. با این حال، این رویکردها با DGGS های پیشرفته سازگار نیستند. در این مقاله، ما یک روش کلی پیشنهاد می کنیم که می تواند هر DGGS را به بعد سوم گسترش دهد تا به عنوان یک DGGS سه بعدی عمل کند.
 این برنامه افزودنی با دقت انجام می شود تا اطمینان حاصل شود که هر DGGS معتبری می تواند پشتیبانی شود، از جمله همه عوامل پالایش و اصلاح ناهمخوان. ما عملیات رمزگذاری، رمزگشایی و نمایه سازی را به گونه ای تعریف می کنیم که مسئولیت را بین DGGS سطحی و جزء 3D تقسیم می کند، که امکان انتقال آسان داده ها را بین نسخه های 2D و 3D DGGS فراهم می کند. به عنوان بخشی از این، ما از توابع نگاشت شعاعی استفاده می کنیم که هدفی مشابه به عنوان طرح ریزی چند وجهی در یک DGGS معمولی دارند. ما روش خود را با ایجاد سه DGGS سه بعدی مختلف که برای سه مورد استفاده خاص طراحی شده اند تأیید می کنیم. این موارد استفاده توانایی ما را در تولید سریع شبکه‌های جهانی سه‌بعدی و در عین حال دستیابی به ویژگی‌های دلخواه مانند پشتیبانی از دامنه‌های بزرگ از ارتفاعات، حفظ حجم بین سلول‌ها و نسبت ابعاد سلولی سفارشی را نشان می‌دهد.

کلید واژه ها:

سیستم شبکه جهانی گسسته ؛ شبکه جهانی سه بعدی ؛ شبکه چند وجهی ; حفظ حجم

1. معرفی

تقریباً فراگیر بودن برخی فناوری‌های هوشمند خاص (گوشی‌های هوشمند، LIDAR، وسایل نقلیه خودران، پهپادها، پهپادها) منجر به افزایش حجم اطلاعات و داده‌های مکانی در حال تولید می‌شود [ 1 ]. به همین دلیل، توسعه فناوری ها و ابزارهای مدیریت این نوع داده ها در کنار سایر اطلاعات جغرافیایی مرسوم، بیش از هر زمان دیگری اهمیت دارد. سیستم‌های اطلاعات جغرافیایی (GIS) به طور سنتی برای این کار استفاده می‌شوند، که در آن مجموعه داده‌های مختلف به عنوان لایه‌های جداگانه در یک سیستم مختصات دوبعدی (2D) – یا اگر ارتفاع نشان داده شود یک سیستم مختصات سه بعدی (3D) نشان داده می‌شوند، که به عنوان عمل می‌کند. یک پروکسی برای زمین [ 2 ، 3]. با این حال، اعوجاج و لبه‌های نقشه که از پرتاب کردن سطح زمین به یک صفحه حاصل می‌شود، می‌تواند بر دقت تحلیل‌های خاص تأثیر بگذارد [ 4 ، 5 ] و همچنین در صورت عدم دقت به تجسم‌های گمراه‌کننده منجر شود [ 6 ]. علاوه بر این، هنگامی که حجم زیادی از داده ها وجود دارد، عملیات همپوشانی مانند تقاطع و استخراج داده ها از نظر محاسباتی گران می شوند [ 7 ].
یک جایگزین برای رویکرد مبتنی بر مختصات GIS برای مدیریت داده‌های مکانی، یک سیستم مبتنی بر ناحیه یا سلول است. تقسیم‌بندی زمین به مجموعه‌ای از سلول‌های غیر همپوشانی به اطلاعات اجازه می‌دهد تا با سلول(های) مرتبط با ناحیه(های) مناسب زمین مرتبط شوند. این پارتیشن بندی ها شبکه های جهانی گسسته نامیده می شوند. برای تطبیق وضوح های مختلف داده ها، می توان از سلسله مراتبی از این شبکه های جهانی گسسته با وضوح های متوالی ظریف تر، که به عنوان سیستم شبکه جهانی گسسته (DGGS) نامیده می شود، استفاده کرد [ 8 ]. DGGS های پیشرفته کنونی از یک چند وجهی تقریبی به عنوان گسسته سازی اولیه سطح زمین استفاده می کنند [ 9 ، 10 ، 11]، و کلاس DGGS هستند که این کار روی آنها تمرکز خواهد کرد.
بسیاری از حسگرهای مکانی که در بالا ذکر شد، همراه با فناوری‌های دیگری مانند پیش‌بینی عددی آب و هوا، داده‌های جغرافیایی سه بعدی، یعنی داده‌هایی با ارتفاع مرتبط علاوه بر مختصات سطح، تولید می‌کنند. در حالی که DGGS ها برای یکپارچه سازی و مدیریت داده های مکانی روی سطح زمین موثر هستند، اما هیچ مکانیزم داخلی برای پشتیبانی از داده های سه بعدی ندارند. به همین دلیل، اخیراً فشارهایی به سمت توسعه فناوری‌ها برای شبکه‌های جهانی سه بعدی و سیستم‌های شبکه وجود داشته است [ 12 ]]. در حالی که بیشتر داده های سه بعدی زمین فضایی در یک منطقه نسبتاً کوچک در بالا و زیر سطح زمین قرار دارند، فرآیندهای حیاتی مانند انتشار امواج لرزه ای و مگنتوسفر بسیار فراتر از این منطقه باریک است. علاوه بر این، ماهواره هایی که در مدار بالای زمین قرار دارند دارای ارتفاع بیش از 35000 کیلومتر هستند. بنابراین، به منظور حمایت از طیف کامل فعالیت‌ها و علاقه‌های انسانی، ممکن است نیاز به شبکه‌های جهانی سه بعدی وجود داشته باشد که بسیار فراتر از جو و به سمت مرکز زمین گسترش یابد.
روش‌هایی برای ایجاد سیستم‌های شبکه جهانی سه‌بعدی وجود دارد [ 13 ، 14 ، 15 ]، با این حال روش‌های فعلی معمولاً بر اساس مختصات طول و عرض جغرافیایی هستند و با DGGS‌های پیشرفته فعلی سازگار نیستند. در حالت ایده آل، یک سیستم شبکه جهانی سه بعدی جدید باید از تحقیق، توسعه و جمع آوری داده های به دست آمده با DGGS معمولی استفاده کند. یکی از راه‌های ایجاد چنین شبکه‌ای، گسترش یک DGGS موجود به بعد سوم است تا به عنوان یک سیستم شبکه جهانی سه‌بعدی عمل کند. با این حال، بسیاری از DGGS های مختلف با ویژگی های مطلوب مختلف وجود دارد [ 16 ، 17 ، 18 ، 19]، و به این ترتیب، DGGS ایده آل برای گسترش به برنامه بستگی دارد. به جای گسترش یک DGGS واحد به سه بعدی، یک رویکرد همه کاره تر ایجاد یک روش کلی است که برای هر DGGS دلخواه کار می کند. این گسترش باید به گونه ای انجام شود که شبکه سه بعدی به دست آمده کاملاً با شبکه معمولی (2 بعدی) سازگار باشد، به این معنی که امکان انتقال کارآمد و ساده داده ها را بین دو شبکه، هم از دو بعدی به سه بعدی و هم از سه بعدی به دو بعدی می دهد. . شبکه های سه بعدی همچنین باید تا حد امکان ویژگی های مطلوب DGGS های معمولی مانند مساحت یا در حجم سه بعدی را حفظ کنند.
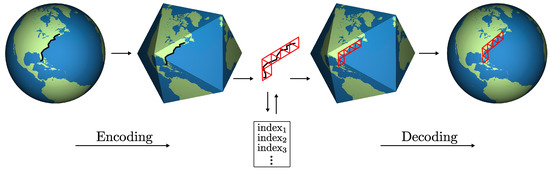
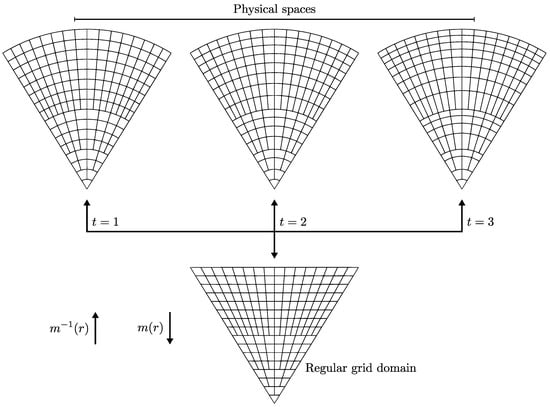
در این مقاله، ما یک روش کلی برای ایجاد سیستم‌های شبکه جهانی سه‌بعدی معرفی می‌کنیم که از DGGS معمولی – که به عنوان ورودی DGGS از آن یاد می‌کنیم – به عنوان نقطه شروع و مشخصات استفاده می‌کنند. ما سیستم شبکه حاصل را DGGS سه بعدی می نامیم. این DGGS های سه بعدی گسترش طبیعی DGGS ورودی را به بعد سوم ارائه می دهند و کاملاً با نمایش های سطح مربوطه خود سازگار هستند. یک نمای کلی از روش ایجاد هندسه شبکه در شکل 1 به تفصیل آمده است. برای ساخت سلول های پایه، ما به سادگی وجه های چند وجهی ورودی DGGS را تا حد عمودی مورد نظر گسترش می دهیم و در نتیجه سلول هایی به شکل منشور می شویم. سپس یک روش پالایش برای ایجاد وضوح بیشتر شبکه از این سلول ها مورد نیاز است. برای سلول های پایه با وسعت شعاعی زیاد، اصلاح سه بعدی منظم، تنوع قابل توجهی در شکل و اندازه سلول ایجاد می کند. این انحطاط یک نتیجه طبیعی از همگرایی سلول های منشوری در مرکز شبکه است. برای پرداختن به این موضوع، ما یک روش پالایش نیمه منظم می سازیم که یکنواختی سلولی را بهبود می بخشد. هر دو اصلاح منظم و نیمه منظم بر اساس پالایش استفاده شده در ورودی DGGS هستند. روش ما برای همه اصلاحات معتبر DGGS، از جمله همه عوامل پالایش و طرح‌های ناهمخوان، کار می‌کند.
با تعریف هندسه شبکه، روشی برای نگاشت داده های مکانی به مجموعه مناسبی از سلول ها مورد نیاز است. به همین ترتیب، فرآیند معکوس نقشه‌برداری داده‌ها که با مجموعه‌ای از سلول‌های شبکه به مناطق مربوطه زمین مرتبط شده‌اند نیز مورد نیاز است. این عملیات، که در شکل 2 نشان داده شده است، به ترتیب به عنوان رمزگذاری شبکه و رمزگشایی نامیده می شوند. به عنوان بخشی از این عملیات، یک DGGS معمولی از یک طرح ریزی چند وجهی استفاده می کند [ 20 ، 21] برای نقشه برداری بین حوزه کروی زمین و حوزه چند وجهی شبکه. برای DGGS سه بعدی ما، مایلیم عملیات رمزگذاری و رمزگشایی تعریف شده در ورودی DGGS را گسترش دهیم تا نقاط و سلول های شبکه با ارتفاع را در خود جای دهند. ما این کار را با تقسیم کدگذاری و رمزگشایی به یک جزء سطحی و شعاعی انجام می‌دهیم که به ترتیب توسط DGGS ورودی و روش‌های ما مدیریت می‌شوند. به عنوان بخشی از این عملیات، ما نگاشت شعاعی معرفی شده در [ 22 ] را گسترش می دهیم] برای استفاده با DGGS های سه بعدی ما. این نگاشتها هدفی مشابه به عنوان طرح ریزی در یک DGGS معمولی دارند و از یک پارامتر واحد برای ترکیب بین حجم و حفظ شکل استفاده می کنند. ما همچنین در مورد چگونگی ترکیب شاخص‌های سطحی و شعاعی جداگانه برای سلول‌ها برای انجام پرس‌وجوهای همسایگی فضایی و ایجاد روابط والد/فرزند برای پیمایش سلسله مراتب سلول بحث می‌کنیم.
ما پتانسیل روش‌شناسی خود را با سه مورد استفاده مثال نشان می‌دهیم، که هر کدام از ترکیبی متفاوت از پارامترهای ورودی DGGS و 3D برای ایجاد DGGS سه‌بعدی مناسب‌ترین برای برنامه استفاده می‌کنند. این موارد استفاده هم تطبیق پذیری و هم پیچیدگی چارچوب را نشان می دهد و می تواند بسیاری از سیستم های شبکه سه بعدی مختلف را ایجاد کند و در عین حال به ویژگی های مطلوبی مانند پشتیبانی از تنوع زیاد در ارتفاع، حفظ حجم، نسبت ابعاد سلولی خاص و دقت برای داده های در مقیاس کوچک دست یابد. .
این مقاله با خلاصه ای از کارهای قبلی برای تجزیه و تحلیل فضایی در کره زمین، DGGS ها و شبکه های جهانی سه بعدی ادامه می دهد، سپس با توضیح مختصری از عناصر تعیین کننده یک DGGS ادامه می دهد. چارچوب ما برای گسترش DGGS ورودی به سه بعدی معرفی می‌شود و با ساخت گسسته‌سازی اولیه منشوری و سپس تعریف طرح‌های اصلاح منظم و نیمه منظم شروع می‌شود. توسعه ای برای تولید سلول هایی با نسبت ابعاد دلخواه نیز شرح داده شده است. سپس نحوه تقسیم بندی شبکه و رمزگشایی به اجزای سطحی و شعاعی را شرح می دهیم و عملیات لازم برای انجام بخش شعاعی هر کدام را ارائه می دهیم. روش‌هایی برای پیمایش سلسله مراتبی و پرس و جوهای همسایگی با استفاده از اجزای سطح تقسیم شده و شاخص شعاعی نیز ارائه شده است. سپس نتایج روش برای سه مورد استفاده بالقوه همراه با یک بحث مختصر ارائه می‌شود. ما با یک خلاصه و جهت گیری های بالقوه برای تحقیقات آینده نتیجه گیری می کنیم.

2. کارهای مرتبط

روش‌های نقشه‌برداری از سطح زمین به یک هواپیما مدت‌هاست که مورد مطالعه قرار گرفته و برای ایجاد نقشه‌های زمین مورد استفاده قرار گرفته است [ 20 ]. این نقشه‌ها یا پیش‌بینی‌ها، تحریف‌های اجتناب‌ناپذیری را ایجاد می‌کنند که در کره‌های مدل زمین وجود ندارند. با وجود این، توانایی نقشه‌های دوبعدی برای ساخت و ذخیره‌سازی آسان، نمایش یک‌باره کل زمین و در نظر گرفتن هر مقیاسی، انگیزه استفاده و مطالعه این پیش‌بینی‌ها را فراهم کرده است. با ظهور نقشه‌های دیجیتال و نمایش‌های زمین، بسیاری از اشکالات نمایش‌های مبتنی بر کره کاهش یا نفی می‌شوند.
در حالی که GIS سنتی هنوز از طرح ریزی برای تجزیه و تحلیل و تجسم داده های جغرافیایی و مکانی استفاده می کند، کارهای زیادی در زمینه توسعه الگوریتم ها و تکنیک هایی برای انجام تحلیل فضایی به طور مستقیم بر روی کره وجود دارد. برخی از نمونه‌های اخیر شامل نمایش بهتر نقاط منطقی [ 23 ]، نمایش چند وضوحی منحنی‌های B-spline [ 24 ] و NURBS [ 25 ]، و روش‌هایی برای جبران منحنی‌ها در هر دو شکل برداری و شطرنجی [ 26 ] است.
با توجه به محدودیت‌های ریاضی پیش‌بینی و افزایش قدرت محاسباتی، فشاری برای دور شدن از نمایش‌های GIS مرسوم و به سمت نمایش‌های مبتنی بر کره وجود دارد [ 27 ]. هسته اصلی این حرکت DGGS است که امکان پشتیبانی بومی از وضوح مکانی و عدم قطعیت موقعیت را از طریق استفاده از سلسله مراتب سلولی فراهم می کند [ 8 ، 28 ]. بسیاری از DGGS های مختلف پیشنهاد و مقایسه شده اند [ 16 ، 17 ، 18 ، 19 ] که هر کدام دارای نقاط قوت و ضعف هستند. به همین ترتیب، کارهای زیادی در مورد الگوریتم‌های DGGS وجود دارد، از جمله نمایه‌سازی کارآمدتر [ 29 ، 30 ]]، شطرنجی سازی برداری سریع تر و دقیق تر [ 31 ]، و تبدیل شاخص ها بین DGGS های مختلف [ 32 ]. یک نمای کلی از DGGS ها در زمینه زمین دیجیتال مبتنی بر کره را می توان در [ 9 ، 11 ] یافت.
علی‌رغم وعده‌های DGGS، اکثر آنها فقط برای سطح زمین پارتیشن بندی می‌کنند. هر داده جغرافیایی با ارتفاع باید برای ادغام با DGGS به سطح هموار شود و ارتفاع اصلی به عنوان میدان داده ذخیره شود. برای بسیاری از کاربردها، این یک راه حل قابل قبول است. با این حال، برای کسانی که داده هایی دارند که دامنه وسیعی از ارتفاعات را اشغال می کنند، مزایای سلسله مراتب DGGS در بعد شعاعی را نفی می کند. همچنین کارایی جستجوی داده‌ها را کاهش می‌دهد، زیرا داده‌ها در تمام ارتفاعات مرتبط با یک سلول باید جستجو شوند تا آن‌هایی که با ارتفاع(های) مورد نظر مطابقت دارند، پیدا شوند. با حجم زیادی از داده‌های سه بعدی جغرافیایی در حال تولید، مانند ابرهای نقطه سه بعدی از LIDAR [ 33 ] و مسیرهای پرواز هواپیما [ 34 ، 35 ]]، نیاز فزاینده ای به شبکه های جهانی سه بعدی و سیستم های شبکه وجود دارد [ 12 ].
یکی از اساسی ترین رویکردها برای ایجاد یک شبکه جهانی سه بعدی، گسترش ساده یک شبکه طول-طول جغرافیایی به سه بعدی یا یک شبکه سه بعدی طول و عرض جغرافیایی (3D LLG) است. این نوع شبکه با تقسیم زمین به پله های مساوی از عرض، طول و شعاع (ارتفاع) ایجاد می شود و به راحتی به یک سیستم سلسله مراتبی از شبکه ها نیز تبدیل می شود. به دلیل سادگی ساخت آن، در مدل‌سازی پوسته جهانی [ 36 ] و کاوش سرعت موج P [ 37 ] در میان دیگر کاربردها استفاده شده است. شبکه GeoSOT3D گونه‌ای از استاندارد سه بعدی LLG است که در آن طول و عرض جغرافیایی به فضاهای مجازی بزرگ‌تر برای بهبود کارایی رمزگذاری و رمزگشایی شبکه گسترش یافته است [ 15 ]] و برای افزایش کارایی تشخیص برخورد هواپیما استفاده شده است [ 34 ، 35 ]. علیرغم سادگی یک LLG سه بعدی، به دلیل ماهیت مختصات کروی، سلول ها در قطب ها و مرکز شبکه تحلیل می روند و بسیار کوچکتر از سلول های دیگر هستند. این انحطاط ها این نوع شبکه را برای بسیاری از کاربردها مشکل ساز می کند، به خصوص اگر سلول های حجمی یکنواخت مورد نیاز باشد.
یک رویکرد برای حل برخی از مسائل با یک LLG سه بعدی ساده، شبکه Yin-Yang [ 38 ] است. این شبکه از دو شبکه اجزای مشابه – شبکه‌های یین و یانگ – تشکیل شده است که LLGهای سه بعدی با طول جغرافیایی 270 درجه و در عرض جغرافیایی 90 درجه در مرکز استوا هستند. سپس این شبکه‌های اجزایی چرخانده شده و روی هم قرار می‌گیرند تا کره را به طور کامل بپوشانند. این شبکه مسئله انحطاط بیش از حد سلول ها به سمت قطب ها را حل می کند و به طور گسترده برای ژئودینامو و شبیه سازی همرفت گوشته استفاده شده است [ 38 , 39 , 40 , 41]، اما موضوع متفاوتی را در سلول هایی که در نزدیکی مرزهای شبکه های یین و یانگ همپوشانی دارند، معرفی می کند. این سلول‌های همپوشانی منجر به مسائلی مانند ابهام یا افزونگی در هنگام مرتبط کردن داده‌های مکانی با سلول‌ها می‌شوند. همچنین، این شبکه به انحطاط سلولی به سمت مرکز کره نمی‌پردازد.
برای از بین بردن انحطاط سلولی هم به سمت قطب ها و هم به سمت مرکز کره – بدون معرفی سلول های همپوشانی – یو و وو شبکه کروی تخریب شده-اکتری (SDOG) را پیشنهاد کردند [ 13 ]. SDOG یک پالایش octree از کره است که در آن سلول های کودکان که منحط هستند (یعنی نه شش وجهی) ترکیب می شوند. نتیجه این است که سلول‌های واقع در مرکز یا یک قطب کره به‌طور متفاوتی – به ترتیب به چهار و شش کودک – نسبت به سلول‌های معمولی دیگر در شبکه پالایش می‌شوند. این روش پالایش حداکثر اختلاف بین حجم سلول‌ها را در شبکه محدود می‌کند و منجر به سلول‌هایی می‌شود که عمدتاً از نظر اندازه و شکل یکنواخت هستند. علاوه بر این، با توجه به نقاط میانی مختصات کروی، این شبکه دارای الگوریتم های کارآمد برای کدگذاری و رمزگشایی شاخص ها است [ 42 ].]. این نوع سیستم شبکه‌ای برای مدل‌سازی اشیاء فضایی در مقیاس بزرگ [ 43 ] و تجسم چند مقیاسی لیتوسفر [ 44 ] استفاده شده است. علاوه بر این، توسعه‌هایی از روش وجود دارد که حفظ حجم شبکه را بدون به خطر انداختن کارایی نمایه‌سازی بهبود می‌بخشد [ 22 ]. رویکرد دیگری شبیه به SDOG، شبکه سه‌بعدی فضای پوسته کره است [ 14 ]، که از پالایش سلول‌ها مبتنی بر octree مشابه استفاده می‌کند، اما بر اساس پوسته‌های کره‌ای چندگانه به جای یک کره واحد است. ما همچنین از این سبک پالایش به عنوان پایه ای برای پالایش منشوری نیمه منظم خود استفاده می کنیم.
یک رویکرد جایگزین برای ایجاد یک شبکه جهانی سه بعدی، ابتدا ایجاد شبکه در یک دامنه ساده تر و سپس نگاشت این شبکه به حوزه کروی است. به عنوان مثال، یک نگاشت حفظ حجم بین مکعب و چهار وجهی [ 45 ] همراه با یک نگاشت حفظ حجم بین چهار وجهی و اکتانت کروی [ 46 ] امکان ایجاد یک شبکه کروی حجم برابر از یکی در مکعب را فراهم می کند. در حالی که این شبکه خاص برای تجزیه و تحلیل چند وضوح و موجک مفید است، شکل سلول های مختلف آن را به یک انتخاب غیر ایده آل برای یکپارچه سازی داده های همه منظوره تبدیل می کند. با این حال، با مجموعه ای متفاوت از نگاشت ها که ویژگی های مورد نیاز را بهتر حفظ می کند، این رویکرد می تواند برای ایجاد یک شبکه جهانی سه بعدی قابل دوام استفاده شود.
علیرغم شیوع روزافزون و استفاده از شبکه های جهانی سه بعدی، زمینه تحقیقات تا کنون عمدتاً از حوزه DGGS جدا بوده است. با وجود ادبیات غنی در مورد این موضوع، طبیعی به نظر می رسد که توسعه شبکه های جهانی سه بعدی باید از دستاوردهایی باشد که قبلاً با DGGS ها انجام شده است. یک راه ساده برای دستیابی به این هدف، گسترش DGGS های معمولی به سه بعدی برای عملکرد به عنوان شبکه های جهانی سه بعدی است. چنین توسعه ای نه تنها به ویژگی های مطلوب DGGS اجازه می دهد تا به سه بعدی گسترش یابد، بلکه انتقال مستقیم داده ها را بین دو نمایش تسهیل می کند.
با توجه به مزایای گسترش یک DGGS به سه بعدی، برخی از کارها از چنین روشی برای ایجاد یک شبکه جهانی سه بعدی استفاده می کنند. رویکردی که در [ 47 ] استفاده می‌شود، تکرارهای یک DGGS را در شعاع‌های افزایش‌یافته برای ایجاد یک شبکه جهانی سه‌بعدی برای ردیابی پرتو حجمی تعاملی داده‌های زمین سه‌بعدی روی هم قرار می‌دهد. در حالی که این برای یک وضوح منفرد مناسب است، جزء شعاعی شبکه جدا از سلسله مراتب سلولی است که مزایای چند وضوح یک DGGS را باطل می کند. به منظور ادغام جزء شعاعی شبکه با سلسله مراتب سلولی، Sirdeshmukh و همکاران. یک DGGS سه بعدی (یا 4 بعدی) با قرار دادن هایپرمکعب های سه بعدی (یا 4 بعدی) روی وجه های چند وجهی DGGS ایجاد کنید [ 33]. سپس این ابر مکعب‌ها تصفیه می‌شوند و با یک منحنی پرکننده فضا عبور می‌کنند تا DGGS سه‌بعدی (یا ۴ بعدی) ایجاد شود که توسط نویسندگان برای رمزگذاری داده‌های ابر نقطه‌ای استفاده می‌شود.
در حالی که روش‌های گسترش شبکه فعلی امیدوارکننده هستند، آنها در رسیدگی به انحطاط شعاعی سلول‌ها به سمت مرکز شبکه شکست می‌خورند. علاوه بر این، روش های به کار گرفته شده جهانی نیستند و فقط برای DGGS های خاص قابل اجرا هستند. هدف ما رسیدگی به این مسائل است. روش ما کاملاً کلی است – برای هر DGGS اعمال می شود – و مشکلاتی را که در روش های دیگر نادیده گرفته شده اند حل می کند. ما تمام اشکال سلولی ممکن و فاکتورهای پالایش را کنترل می‌کنیم، نسبت ابعاد سلول را کنترل می‌کنیم، انحطاط سلول‌ها را به سمت مرکز شبکه مدیریت می‌کنیم، اجازه می‌دهیم حجم بین سلول‌ها حفظ شود، و عملیات رمزگذاری و رمزگشایی را تعریف می‌کنیم که با نمایش‌های سطحی سازگار است.

3. بررسی اجمالی DGGS

سه عنصر کلیدی برای تعریف هر DGGS مورد استفاده قرار می گیرد: گسسته سازی اولیه، روش پالایش سلول، و طرح ریزی و برون ریزی معکوس. علاوه بر این، هر سلول در یک DGGS به یک شناسه منحصر به فرد نیاز دارد که برای فهرست کردن داده های مرتبط با سلول استفاده می شود. قبل از اینکه نحوه گسترش یک DGGS دلخواه به سه بعدی را بررسی کنیم، ابتدا یک پس زمینه مختصر در مورد هر یک از این مؤلفه ها ارائه می دهیم. یک بحث عمیق تر از این عناصر را می توان در [ 9 ، 11 ] یافت.

3.1. گسسته سازی اولیه

گسسته سازی اولیه برای یک DGGS معین به سادگی مجموعه اولیه سلول هایی است که برای گسسته سازی زمین استفاده می شود. این مجموعه سلول‌ها هم تعداد سلول‌ها را در خشن‌ترین نمایش زمین و هم شکل(های) سلول‌های مورد استفاده در سیستم شبکه را تعیین می‌کند. DGGS های ژئودزیک از یک چند وجهی تقریبی استفاده می کنند که به عنوان گسسته سازی اولیه عمل می کند. برخی از رایج ترین انتخاب ها برای این چند وجهی عبارتند از: جامدات افلاطونی و ایکوز وجهی کوتاه. با این حال، می توان از چند وجهی دیگر با چهره های بیشتر نیز استفاده کرد. یک چند وجهی با وجه های بیشتر، تقریب نزدیک تری از زمین را فراهم می کند و بنابراین در هنگام پرتاب کردن سطح زمین به چند وجهی، اعوجاج کمتری را به همراه دارد. برای DGGS های سه بعدی ما،

3.2. اصلاح

روش پالایش یک DGGS فرآیندی را تعریف می کند که طی آن مجموعه ای از سلول های ظریف از مجموعه ای از سلول های درشت تولید می شود. این کار باید به شیوه ای ثابت انجام شود تا بتوان آن را به طور متوالی برای ایجاد گسستگی های بسیار ظریف از زمین به کار برد. طرح‌های پالایش بر اساس شکل(های) سلول ورودی آن‌ها، که با گسسته‌سازی اولیه ارائه می‌شوند، طبقه‌بندی می‌شوند. شکل(های) سلول خروجی، که معمولاً همان ورودی هستند. و ضریب پالایش آنها که نسبت بین تعداد سلولهای درشت و سلولهای ریز است. به عنوان مثال، پالایش مثلث 1-to-4 (1:4) چهار سلول مثلثی برای هر مثلث در مجموعه سلول های درشت تولید می کند. ضریب پالایش تعیین می کند که با هر کاربرد روش پالایش با چه سرعتی وضوح شبکه افزایش می یابد.
پالایش همچنین باید شکل نسبی سلول ها را بین وضوح های مختلف حفظ کند. به عنوان مثال، سلول های مربعی نباید در طول پالایش مستطیل شکل شوند. دو ویژگی مهم دیگر پالایش، همخوانی و همسویی هستند . با پالایش متجانس، هر سلول درشت از اتحادیه ای از سلول های ظریف تشکیل شده است. پالایش تراز مستلزم آن است که هر سلول درشت نقطه مشخصی را با یک سلول ظریف، معمولاً یک راس یا مرکز، به اشتراک بگذارد. روش ما همه فاکتورهای پالایش، پالایش ناهمگون، و هر نوع هم ترازی (از جمله غیر تراز) را در خود جای می دهد.

3.3. پروجکشن و پروجکشن معکوس

به منظور گرفتن داده های تعریف شده بر روی سطح زمین (مثلا مختصات طول و عرض جغرافیایی) و یافتن نقاط مربوطه در یک DGGS، از یک روش طرح ریزی استفاده می شود که حوزه کروی زمین را به حوزه چند وجهی شبکه ترسیم می کند [ 20 ] ، 21 ]. به همین ترتیب، برای نمایش سلول‌ها و داده‌های آن‌ها روی سطح زمین، از معکوس این طرح استفاده می‌شود. این عملیات همیشه با مقداری تحریف همراه است. با این حال، روش های طرح ریزی خاص می تواند انواع خاصی از اعوجاج را حذف کند. پیش بینی های مساوی و منسجم دو کلاس هستند که به ترتیب نواحی و زوایا را حفظ می کنند [ 20 ].

3.4. طرح نمایه سازی

برای اینکه هندسه شبکه و سلول به عنوان یک DGGS مفید باشد، مکانیزمی برای اختصاص یک شاخص منحصر به فرد به هر سلول مورد نیاز است. داده‌های زمین با استفاده از این شاخص‌ها به سلول‌ها اختصاص داده می‌شوند، که امکان بازیابی کارآمد همه داده‌های مرتبط با یک سلول یا منطقه خاصی از زمین را فراهم می‌کند. بنابراین، برای اینکه بتوانیم داده‌های جدید را به طور کارآمد وارد شبکه کنیم، مهم است که بتوانیم سلول (و شاخص مرتبط) را که حاوی نقطه‌ای روی زمین است، پس از پیش‌بینی به سرعت تعیین کنیم. به همین ترتیب، با توجه به یک شاخص سلول، مهم است که بتوانیم هندسه سلول مربوطه را در شبکه تعیین کنیم. سپس این هندسه برای یافتن ناحیه ای از زمین مرتبط با سلول به صورت معکوس پیش بینی می شود. این شاخص ها همچنین امکان تعریف پرس و جوهای روابط فضایی خاصی مانند بازیابی سلول های همسایه را فراهم می کنند.

4. تولید و پالایش شبکه پریسماتوئید

با استفاده از DGGS ورودی به عنوان مشخصات ورودی، هدف ما این است که عناصر کلیدی DGGS سه بعدی مربوطه را به طور منطقی و پیوسته تعریف کنیم. در این بخش، رویکرد ایجاد گسسته سازی اولیه را مورد بحث قرار می دهیم و دو روش پالایش را تعریف می کنیم.

4.1. گسسته سازی اولیه سه بعدی

برای این مقاله، شعاع یک چندوجهی را شعاع کره ی محصور آن تعریف می کنیم. بنابراین، تمام نقاط روی چند وجهی دارای «شعاع» یکسانی هستند ( شکل 3 ). اجازه دهید آردقیقهو آرحداکثرحداقل و حداکثر شعاع هایی باشد که به ترتیب توسط DGGS 3D پشتیبانی می شوند. سپس گسسته سازی سه بعدی اولیه از دو کپی از چند وجهی ورودی در این شعاع ها با لبه های آنها متصل می شود. اگر حداقل شعاع صفر باشد، این سلول های پایه هرم هستند. در غیر این صورت، آنها مشتاق هستند. در هر دو مورد، سلول ها متعلق به یک کلاس والد چند وجهی هستند که به عنوان پریسماتوئید شناخته می شوند. با این گسسته سازی، هر سلول نمایانگر دامنه شعاعی کامل شبکه است – اصلاحات بعدی به این موضوع می پردازد.

4.2. پالایش پریسماتوئید منظم

با گسسته سازی سه بعدی اولیه برای فضای سیستم شبکه، اکنون به روشی برای پالایش سلول ها برای ایجاد گسستگی های دقیق تر نیاز داریم. ما همچنین می‌خواهیم اطمینان حاصل کنیم که DGGS سه بعدی از همان طرح پالایش استفاده شده توسط ورودی DGGS استفاده می‌کند که به آن پالایش سطح می‌گویند. برای سادگی، ابتدا ضریب پالایش سطح را 1:4 فرض می کنیم. تعمیم به سایر عوامل پالایش در بخش 4.4 آورده شده است.
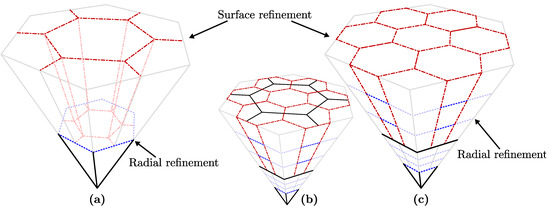
روش منظم برای پالایش سلول های پریسماتوئید در شکل 4 نشان داده شده است . پایه‌های سلول‌ها با استفاده از پالایش سطح تصفیه می‌شوند و لبه‌های حاصل از آن اکسترود می‌شوند تا به هم برسند. در همان زمان، یک شکاف شعاعی در نقطه میانی دو پایه قرار می گیرد. این پالایش منجر به ایجاد یک لایه داخلی و خارجی از سلول ها می شود که هر کدام دارای همان تعداد سلول هستند. لایه بیرونی همیشه از سلول های فروستوم تشکیل شده است، در حالی که لایه داخلی همان شکل سلول هایی است که در حال تصفیه بودند. این اصلاح با برخورد با هر یک از لایه های جدید مانند گسسته سازی اولیه تکرار می شود. تعریف پالایش بر حسب لایه‌های سلولی برخلاف سلول‌های منفرد، اجازه می‌دهد که پالایش‌های سطحی غیرهمخوان به طور ذاتی در نظر گرفته شوند.

4.3. پالایش پریسماتوئید نیمه منظم

در حالی که پالایش منشور معمولی پیشنهاد شده در بالا ساده است، اما اگر نسبت بین آرحداکثرو آردقیقهبزرگ است در این شرایط، لایه هایی که نزدیک به حداقل شعاع هستند، در نهایت بسیار کوچکتر از لایه های نزدیک به حداکثر هستند. برای تولید سلول‌هایی با اندازه یکنواخت‌تر به روش پالایش متفاوتی نیاز است. برای انجام این کار، لایه های شبکه را به دو دسته مرکزی یا عادی طبقه بندی می کنیم. ما استفاده می کنیم rدقیقهو rحداکثربرای اشاره به حداقل و حداکثر شعاع یک لایه. همانند چند وجهی مورد استفاده برای گسسته سازی اولیه، این شعاع ها برابر با شعاع کره های محصور شده هستند. لایه های مرکزی آنهایی هستند که با داخلی ترین قسمت شبکه هم مرز هستند ( rدقیقه=آردقیقه) و تمام لایه های دیگر نرمال در نظر گرفته می شوند. طبق تعریف، در هر وضوح DGGS سه بعدی، تنها یک لایه مرکزی وجود دارد. علاوه بر این، گسسته سازی اولیه به طور کامل از این لایه مرکزی تشکیل شده است. ما فرض خود را در مورد ضریب پالایش سطح 1:4 از قبل ادامه می دهیم.
در این طرح پالایش، پالایش لایه های مرکزی با روش معمولی فوق متفاوت است. ما ادعا می کنیم که آردقیقهبرابر با صفر در نظر گرفته شود و بنابراین لایه های مرکزی از سلول های هرمی تشکیل شده اند. اگر مقدار واقعی از آردقیقهغیر صفر است، سپس هر لایه به دست آمده زیر این شعاع کنار گذاشته می شود یا نادیده گرفته می شود. همانند قبل، پایه های سلول های هرمی با استفاده از طرح سطحی تصفیه شده و یک شکاف شعاعی در وسط لایه ایجاد می شود. با این حال، لبه های جدید به طور کامل به سمت راس هرم امتداد نمی یابند، اما در عوض در شکاف شعاعی متوقف می شوند ( شکل 5 ). این اصلاح منجر به دو لایه جدید می شود: یک لایه مرکزی داخلی که شبیه لایه مرکزی اولیه است و یک لایه عادی بیرونی. همانطور که در شکل 5 نشان داده شده استب، وضوح یا سطح پالایش یک لایه در شبکه سه بعدی ظاهر می‌شود، لزوماً با تعداد دفعاتی که طرح پالایش سطح روی آن اعمال شده است مطابقت ندارد. تعداد دفعاتی که پالایش سطح روی یک لایه معین اعمال شده است را به عنوان وضوح سطحی که توسط آن داده شده است، تعریف می کنیم کس. بنابراین، اگر بگوییم گسسته سازی اولیه دارد کس=0، پس از یک سطح پالایش، لایه مرکزی داخلی نیز دارد کس=0، در حالی که لایه معمولی دارد کس=1. این وضوح سطح برای رمزگذاری/رمزگشایی شبکه و پرس و جوهای مختلف نمایه سازی مورد نیاز است، اما همانطور که بعداً مشاهده خواهد شد می توان آن را محاسبه کرد و نیازی به ذخیره صریح ندارد.
لایه های معمولی در این طرح به سادگی با استفاده از پالایش منشوری معمولی پالایش می شوند. این منجر به دو لایه معمولی می شود که هر دو دارای کسبرابر با یک بزرگتر از لایه شروع. شکل 6 سه کاربرد متوالی پالایش منشوری منظم و نیمه منظم را با یک سلول هرمی منفرد مقایسه می کند.

4.4. سایر عوامل اصلاح سطح

در حالی که می توان از روش های پالایش فوق برای فاکتورهای پالایش سطحی غیر از 1:4 استفاده کرد، انجام این کار منجر به یک مسئله بالقوه مهم می شود که باید مورد توجه قرار گیرد. ابتدا ایده یک ضریب پالایش یک بعدی (1D) را معرفی می کنیم که با گرفتن ریشه مربع سطح (2D) آن را پیدا می کنیم. برای مثال، ضریب پالایش 1 بعدی طرح پالایش سطح 1:4 ( شکل 4 و شکل 5 ) 1:2 است. در حالی که طرح پالایش سطح نیازی به یکنواختی در دو بعد ندارد، ضریب پالایش 1 بعدی تصوری از متوسط ​​پالایش مورد انتظار در هر بعد را ارائه می دهد.
برای ایجاد سلول های یکنواخت، واضح است که ضریب پالایش در امتداد بعد شعاعی برای پالایش منشوری معمولی باید برابر با ضریب پالایش 1 بعدی باشد. اگر اینطور نباشد، عرض سلول ها نسبت به عمق آنها بین سطوح پالایش ثابت نیست، زیرا یک بعد سریعتر پالایش می شود. برای یک ضریب پالایش سطح 1:4، تقسیم شعاعی منفرد استفاده شده دقیقاً با آن مطابقت دارد (یک تقسیم دو لایه جدید ایجاد می کند). برای سایر فاکتورهای پالایش سطح، فاکتورهای پالایش 1 بعدی و شعاعی لزوماً برابر نیستند و شکل سلول با ادامه پالایش دچار انحطاط می‌شود – به طور فزاینده‌ای باریک یا گسترده می‌شود.
برای پرداختن به این موضوع، تعداد شکاف های شعاعی انجام شده را طوری تغییر می دهیم که تعداد لایه های تولید شده برابر با ضریب پالایش 1 بعدی باشد. برای فاکتورهای پالایش سطح که مربع کامل هستند (مثلاً 1:4، 1:9) این امر بی اهمیت است، زیرا ضریب پالایش 1 بعدی یک عدد صحیح است. ضریب پالایش شعاعی مربوطه با ایجاد تعدادی لایه برابر با ضریب 1 بعدی به دست می آید. با این حال، برای سایر عوامل پالایش سطح، این کار دشوارتر می شود. ضریب پالایش 1 بعدی دیگر یک عدد صحیح نیست و از آنجایی که ما فقط می توانیم تعداد زیادی تقسیم شعاعی را انجام دهیم، ضریب پالایش 1 بعدی و شعاعی نمی توانند دقیقاً برابر باشند. بنابراین، ما پیشنهاد می‌کنیم که تعداد متفاوتی از تقسیم‌های شعاعی را در سطوح مختلف پالایش انجام دهیم تا میانگین بدست آید.ضریب پالایش شعاعی برابر با یک بعدی.

چند روش مختلف وجود دارد که می توان برای تعیین تعداد تقسیمات شعاعی برای انجام در یک سطح پالایش معین استفاده کرد. ساده ترین روش این است که بین تولید یک لایه (یعنی بدون شکاف) و تولید تعدادی لایه برابر با ضریب پالایش سطح متناوب شود. هنگامی که ضریب پالایش سطح یک عدد اول نیست، روش بهتر این است که بین دو عضو یک جفت عامل، مانند دو و سه برای یک ضریب سطح 1:6، متناوب شود. به طور کلی، حاصل ضرب تعداد لایه‌ها در هر سطح پالایش باید برابر (یا تا حد امکان نزدیک) به ضریب پالایش 1 بعدی به توان تعداد سطوح پالایش باشد. به طور رسمی،

∏من=1کℓمن=fک،

جایی که ℓمنتعداد لایه های تولید شده در سطح پالایش i ، k سطح پالایش، و f ضریب پالایش 1 بعدی است. این معادله به طور مکرر برای یافتن بهترین تعداد لایه ها برای سطوح متوالی پالایش با فاکتورهای پالایش سطح اولیه استفاده می شود. جدول 1 توالی لایه بندی پیشنهادی ما را برای فاکتورهای پالایش سطح از 1:2 تا 1:9 فهرست می کند.

نمونه ای از پالایش منشوری نیمه منظم با پالایش سطح شش ضلعی 1:3 در شکل 7 نشان داده شده است . سطح اول پالایش مشابه موارد مربوط به ضریب پالایش سطح 1:4 است زیرا هیچ لایه معمولی پالایش نشده است. اما در سطح دوم، دو شکاف شعاعی در لایه‌های معمولی بر خلاف یکی انجام می‌شود. در سطح بعدی پالایش، که نشان داده نشده است، لایه‌های معمولی هیچ گونه اصلاح شعاعی در توالی پیشنهادی در جدول 1 ندارند.

4.5. نسبت ابعاد سلولی

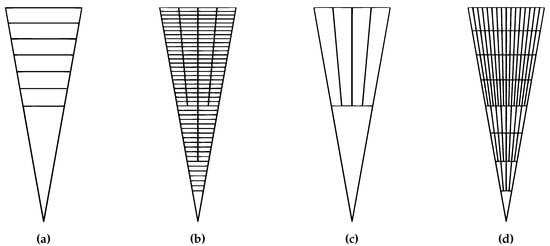
ابعاد سطحی و شعاعی زمین ذاتاً بسیار متفاوت است، و به همین دلیل، اغلب مطلوب است که این دو بعد در وضوح های متفاوت در یک شبکه جهانی سه بعدی باشند. برای DGGS های سه بعدی ما، دستیابی به این مستلزم تغییر عرض سلول ها در شبکه (رزولوشن سطحی) نسبت به عمق آنها (رزولوشن شعاعی) است. ما به نسبت عرض و عمق سلول به عنوان نسبت ابعاد اشاره می کنیماز سلول در حالی که روش‌های اصلاحی که تاکنون توضیح داده شد سلول‌هایی با نسبت ابعادی مشابه تولید می‌کنند – هم بین سلول‌ها با وضوح یکسان و هم متفاوت – هیچ مکانیسم مستقیمی برای کنترل این نسبت تصویر وجود ندارد. برای پرداختن به این موضوع، ما دو اصلاح را معرفی می‌کنیم که می‌توان در پالایش پریسماتوئید برای کاهش و افزایش این نسبت ابعاد ایجاد کرد.
به منظور کاهش نسبت ابعاد سلول ها در شبکه، تعداد دفعاتی که پالایش سطح اعمال می شود نسبت به تعداد شکاف های شعاعی باید افزایش یابد. از آنجایی که کاربردهای بیشتر پالایش منشور، نسبت ابعاد سلولی مورد انتظار را حفظ می کند (نتیجه برابری سطح و فاکتورهای پالایش شعاعی مورد انتظار)، این کار فقط باید در اولین بار انجام شود که یک لایه پایه سلول های خود را با لایه پالایش کند. طرح سطح بنابراین، برای پالایش منشوری نیمه منظم، این کار در حالی انجام می‌شود که لایه نرمال بیرونی که از پالایش لایه‌های مرکزی حاصل می‌شود، تصفیه می‌شود. در مواردی که فقط از پالایش پریسماتوئید معمولی استفاده می شود، این کار تنها در اولین سطح پالایش انجام می شود.
به همین ترتیب، برای افزایش نسبت ابعاد سلول‌ها، باید تعداد دفعاتی که طرح پالایش سطح اعمال می‌شود را نسبت به تعداد شکاف‌های شعاعی کاهش دهیم. این کار به این صورت انجام می‌شود که در اولین بار که معمولاً انجام می‌شود، پالایش سطح روی یک لایه اعمال نمی‌شود ، و در صورت نیاز، همزمان شکاف‌های شعاعی اضافی اعمال می‌شود. این تغییرات همزمان با روش کاهش نسبت تصویر به دلایل مشابه انجام می شود.
بنابراین، با توجه به نسبت ابعاد سلول هدف a ، باید تعیین کنیم که از کدام یک از روش های بالا استفاده کنیم. برای این کار ابتدا باید عرض و عمق یک سلول را کمی کنیم. به طور خاص تر، ما باید میانگین عرض و عمق سلول ها را در یک لایه تعریف کنیم، زیرا پالایش توسط لایه انجام می شود نه توسط سلول. عمق از وسعت شعاعی لایه ناشی می شود ( rحداکثر-rدقیقه). راه های بالقوه زیادی برای اندازه گیری عرض یک سلول وجود دارد. برای اهداف خود، ما از جذر مساحت آن استفاده کردیم. این انتخاب تضمین می‌کند که چارچوب نتایج ثابتی را برای چند وجهی ورودی با تعداد وجه‌های یکسان، صرف نظر از شکل(های) وجه‌های گفته شده تولید می‌کند.

برای ناحیه لایه(های) نرمال بیرونی که با پالایش لایه‌های مرکزی تولید می‌شود، میانگین عمق سلول‌ها، عمق کل منطقه تقسیم بر تعداد لایه‌های منطقه است (با فرض عدم استفاده از طرح پالایش سطح). اجازه دهید υدرصد باشد rحداکثراشغال شده توسط این ناحیه و x تعداد شکاف های شعاعی اضافی باشد، سپس میانگین عمق سلول ها برابر است با

υrحداکثرایکس+1.

به همین ترتیب، میانگین عرض سلول در این ناحیه، مساحت سطح کره تقسیم بر تعداد سلول ها است (با فرض عدم شکاف شعاعی اضافی). فرض کنید n تعداد وجه های روی چند وجهی ورودی و w تعداد دفعاتی باشد که اصلاح سطح اعمال می شود، سپس تعداد سلول ها برابر است. nf2w، و میانگین عرض سلول است

4πrحداکثر2nf2w=2rحداکثرfwπn.

اکنون اینها را با استفاده از نسبت ابعاد مورد نظر برای حل x و w برابر می‌کنیم و به آن می‌دهیم

آυایکس+1=2fwπn.

برای اینکه مفروضات قبلی ما را نقض نکنیم، هنگام حل یک متغیر، متغیر دیگر روی صفر تنظیم می شود. این تضمین می کند که تنها یکی از دو استراتژی برای اصلاح نسبت تصویر به کار گرفته شده است. تنظیمات w=0ما گرفتیم

ایکس=آυ2nπ-1،

و تنظیم ایکس=0ما گرفتیم

w=ورود به سیستمf2آυπn.
مقادیر واقعی x و w که برای استفاده انتخاب شده اند تعیین می شود که کدام یک منفی است. اگر x منفی باشد، روی صفر تنظیم می‌شود و مقدار w استفاده می‌شود – برعکس اگر w منفی باشد. از آنجایی که x یا w ممکن است اعداد صحیح نباشند، به سادگی آنها را به نزدیکترین عدد صحیح گرد می کنیم تا مقدار واقعی مورد استفاده در طی پالایش را بدست آوریم. نتایج پالایش با نسبت ابعاد هدف مختلف در شکل 8 نشان داده شده است.

5. رمزگذاری و رمزگشایی برای DGGS 3D

به یاد بیاورید که به منظور ارتباط داده های مکانی با سلول های مربوطه در یک DGGS سه بعدی، یک عملیات رمزگذاری مورد نیاز است. به همین ترتیب، رمزگشایی نیز برای نقشه‌برداری داده‌های مرتبط با مجموعه‌ای از سلول‌ها به مناطق مربوطه روی زمین مورد نیاز است. این عملیات برای ورودی DGGS تعریف شده‌اند و باید هنگام تعریف نسخه‌های سه‌بعدی این عملیات مورد استفاده قرار گیرند. انجام این کار نه تنها تعریف این عملیات را ساده می کند، بلکه منجر به انتقال ساده داده بین DGGS ورودی و همتای سه بعدی آن می شود.
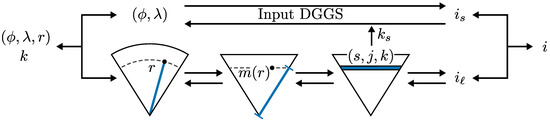
برای انجام این کار، کدگذاری و رمزگشایی را به یک جزء سطحی و شعاعی تقسیم کردیم. با اشاره به شکل 9 ، ما چنین تقسیمی را با ذکر این نکته توجیه می کنیم که دو جزء هر سلول را در یک DGGS سه بعدی تعریف می کنند: سلول در ورودی DGGS که پایه(های) آن را تعریف می کند و لایه شبکه که آن را در بر می گیرد. شناسایی منحصر به فرد هر یک از این اجزا برای شناسایی هر سلول در شبکه به طور منحصر به فرد کافی است. علاوه بر این، هر یک از این مؤلفه ها تقریباً به طور کامل مستقل تعیین می شوند.
تقسیم پیشنهادی ما از این عملیات در شکل 10 نشان داده شده است . جزء سطحی رمزگذاری/رمزگشایی به طور کامل توسط ورودی DGGS مدیریت می شود و بنابراین در اینجا مورد بحث قرار نمی گیرد. برای مولفه شعاعی، ابتدا توابع نگاشت شعاعی را معرفی می کنیم که شعاع فیزیکی r را به شعاع متناظر در شبکه ترسیم می کند.متر(r). این تابع هدفی مشابه با طرح ریزی چند وجهی یک DGGS معمولی دارد و امکان حفظ حجم بهتر بین سلول ها را فراهم می کند. ما همچنین عملیاتی را برای پارامترسازی لایه‌های یک DGGS سه بعدی و به تبع آن یافتن حداقل و حداکثر شعاع شبکه یک لایه از چنین پارامتری ارائه می‌کنیم. ما روش‌هایی را برای تبدیل این پارامترسازی به شاخصی برای لایه یا ترکیب شاخص‌های سطح و لایه در یک شاخص واحد مورد بحث قرار نمی‌دهیم. برای اولی، این به دلیل پیچیدگی های مختلف ساختار لایه در DGGS های سه بعدی مختلف و اهداف رقابتی در یک سیستم نمایه سازی کارآمد است. برای دومی، این عملیات به شدت به ساختار نمایه سازی DGGS ورودی بستگی دارد و بنابراین به راحتی نمی توان آن را به طور کلی تعریف کرد.

5.1. نقشه برداری شعاعی

برای بسیاری از DGGS های معمولی، پیش بینی های حفظ منطقه استفاده می شود تا اطمینان حاصل شود که هر سلول در وضوح مشخصی از شبکه دارای مساحت یکسانی است که به منطقه مربوطه از زمین نگاشت می شود [ 19 ، 21 ، 48 ].]. این ویژگی برای برنامه‌هایی که مساحت سلول‌ها اغلب استفاده می‌شود، مهم است، زیرا محاسبه آن می‌تواند گران باشد. بنابراین، برای یک DGGS سه بعدی، ممکن است خواسته شود که هر سلول دارای حجم مساوی یا تا حد امکان نزدیک به برابر باشد. این را می توان با یک نقشه برداری شعاعی انجام داد که نحوه نگاشت شعاع ها در فضای فیزیکی به شعاع های متناظر در فضای شبکه را کنترل می کند. چنین نقشه برداری شعاعی به شدت مورد نیاز نیست، در این صورت می توان از نقشه هویت استفاده کرد. استفاده از یک هویت، بار محاسباتی رمزگذاری و رمزگشایی را کاهش می دهد، اما کنترلی بر حفظ حجم در شبکه نمی دهد.

برای اینکه یک نقشه برداری M بتواند حجم را حفظ کند، لازم است که

جلد(D)=جلد(م(D))

برای همه زیر دامنه های D در دامنه M. با این حال، اگر حجم سلول ها در حوزه شبکه برابر نباشد (همانطور که در مورد DGGS های سه بعدی ما وجود دارد)، در این صورت یک نگاشت حفظ حجم منجر به سلول هایی با حجم برابر نمی شود. در عوض، تمام سلول ها باید به صورت معکوس به عناصر حجم مساوی در حوزه بدون توجه به حجم آنها در شبکه نگاشت شوند. به طور رسمی،

جلد(م-1(سیمن))=جلد(م-1(سیj))،

برای همه ترکیبات سلولی سیمنو سیj.

در زیر سه نقشه شعاعی مختلف را شرح می دهیم که برای درجات مختلف حفظ حجم بین لایه ها در شبکه استفاده می شود. دو مورد اول – که مشابه موارد ارائه شده در [ 22 ] هستند – موارد خاص سومی عمومی تر هستند. حفظ حجم بین سلول ها نیز به طرح ریزی و اصلاح DGGS ورودی بستگی دارد و بنابراین به طور کلی برای DGGS های سه بعدی ما مورد بحث قرار نمی گیرد. در این نگاشت ها استفاده می کنیم r^برای اشاره به شعاع r نرمال شده به محدوده شبکه ( r/آرحداکثر).
نگاشت حفظ حجم پوسته

با مراجعه به شکل 11 ، می بینیم که شکاف های شعاعی برای لایه های مرکزی، شبکه را به مناطقی که نمایانگر پوسته های کروی هستند، تقسیم می کند. همچنین توجه می کنیم که هر یک از این پوسته ها دارای تعداد متفاوتی سلول هستند. به طور خاص، پوسته n دارای مقدار است کسیکی بزرگتر از پوسته n+1، و بنابراین با ادامه پالایش، انتظار داریم پوسته n حاوی باشد f3چند برابر سلول بنابراین، در حالت ایده آل، پوسته n یک منطقه را با f3برابر حجم نیز. برای انجام این کار، می‌توانیم یک نقشه‌برداری شعاعی تعریف کنیم که شکاف‌های شعاعی در شبکه را به شکاف‌های شعاعی مربوطه که منجر به حجم مناسب می‌شود، ترسیم می‌کند. ما روش زیر را با جزئیات بیشتر در [ 22 ] خلاصه می‌کنیم. پوسته حجمی که n نشان می دهد متناسب است

ج3n-ج3n+1.

جایی که ج∈(0،1)فاصله در امتداد است rحداکثربرای نگاشت شکاف های شعاعی به. بنابراین، نسبت حجم بین پوسته n و n+1است

ج3n-ج3n+1ج3n+1-ج3n+2=ج3n1-ج3ج3ج3n1-ج3=1ج3.

با معادل سازی این نسبت به حجم مورد نظر، به دست می آوریم

1ج3=f3،ج=1f.

از این، نتیجه می گیریم که شعاع در توان های c باید به توان های نگاشت شوند 1/2; شعاع هایی که در بین قرار دارند به صورت خطی درون یابی می شوند. ابتدا پوسته فیزیکی حاوی شعاع را محاسبه می کنیم که به سادگی است س=⌊ورود به سیستمجr^⌋. سپس از پوسته برای یافتن حداقل و حداکثر شعاع پوسته در فضای فیزیکی و شبکه ای (نرمال شده) استفاده می شود. ما به این موارد به ترتیب ℓ و u با زیرنویس‌های g برای فضای شبکه و p برای فیزیکی اشاره می‌کنیم. اینها توسط

ℓپ=جس+1،توپ=جس،ℓg=0.5س+1،وتوg=0.5س.

در صورتی که فقط از پالایش منشور معمولی استفاده شود، آنها به جای آن هستند

ℓپ=ℓg=0،وتوپ=توg=1.

نقشه برداری کامل بدین ترتیب است

متر(r^)=دتوg+(1-د)ℓg،جایی که
د=r^-ℓپتوپ-ℓپ.

برای معکوس، ما داریم

متر-1(r^)=دتوپ+(1-د)ℓپ،جایی که
د=r^-ℓgتوg-ℓg.

برای معکوس، پوسته s از پارامترسازی لایه به جلو منتقل می شود ( بخش 5.2 )، اما همچنین می توان آن را به طور مستقل با استفاده از آن محاسبه کرد. س=⌊ورود به سیستم0.5r^⌋.

نتایج این نقشه برداری در شکل 12 سمت چپ نشان داده شده است. توجه داشته باشید که برای ضریب پالایش سطح 1:4، ج=1/2، یعنی این نقشه برداری معادل هویت است. در موردی که فقط از پالایش منشوری معمولی استفاده می شود، این نقشه برداری نیز معادل هویت است.
این نگاشت – و نقشه های بعدی – دارای اثر جانبی تغییر نسبت ابعاد سلول ها در فضای شبکه در مقایسه با سلول های مربوطه در فضای فیزیکی است. این بدان معنی است که هنگام تعیین پارامترهای پالایش مورد نیاز برای دستیابی به نسبت ابعاد مطلوب، سلول‌های موجود در فضای فیزیکی باید برخلاف فضای شبکه در نظر گرفته شوند، همانطور که در بخش 4.5 انجام شد . این به راحتی با تغییر مقدار برطرف می شود υدر معادلات ( 1 ) و ( 2 ) استفاده می شود (1-ج).
نگاشت حفظ حجم

در حالی که نگاشت فوق حجم را بین پوسته‌های شبکه حفظ می‌کند، سلول‌های درون یک پوسته معین همچنان حجم‌های متفاوتی خواهند داشت. این به دلیل رشد حجم سلول ها به صورت مکعبی نسبت به شعاع است. برای تطبیق با این موضوع، درون یابی خطی نگاشت فوق را با نقشه ای جایگزین می کنیم که تغییرات حجم در فضای فیزیکی را به فاصله خطی در فضای شبکه ترسیم می کند که نتیجه آن

متر(r^)=دتوg+(1-د)ℓg،جایی که
د=r^3-ℓپ3توپ3-ℓپ3.

به همین ترتیب، معکوس با داده می شود

متر-1(r^)=دتوپ3+1-دℓپ33،جایی که
د=r^-ℓgتوg-ℓg.

با این نگاشت، سلول های همان لایه با فرض اینکه DGGS ورودی منطقه را حفظ می کند، حفظ حجم کاملی خواهند داشت. با این حال، بسته به ترتیب لایه‌بندی، لزوماً حجم بین سلول‌ها در پوسته‌های مختلف حفظ نمی‌شود. علاوه بر این، لایه مرکزی هرگز با لایه های دیگر حفظ حجم نخواهد داشت. نتایج این نگاشت در شکل 12 سمت راست نشان داده شده است. همانطور که مشاهده می شود، سلول ها در هر پوسته به منظور اطمینان از حجم برابر، کشیده و له می شوند.

نقشه برداری متوازن
در حالی که حفظ حجم یک ویژگی مهم برای کاربردهای خاص است، ممکن است اجتناب از کشش و له کردن ذکر شده در بالا نیز مطلوب باشد. برای تطبیق تعادل‌های مختلف حفظ حجم و فشردگی سلول، از نقشه‌برداری استفاده می‌کنیم که بین نتایج نگاشت پیشنهادی اول و دوم ترکیب می‌شود. نقشه برداری از درون یابی خطی استفاده می کند و منجر به سلول هایی با وسعت شعاعی برابر می شود. نقشه برداری دو از درون یابی مکعبی استفاده می کند و منجر به سلول هایی با حجم مساوی می شود. استفاده از توان متفاوت، t ، بین یک و سه منجر به ادغام بین این دو ویژگی می شود. یک نتیجه با استفاده از تی=2در شکل 12 مرکز نشان داده شده است.

5.2. پارامترسازی لایه

لایه‌های یک DGGS سه‌بعدی را می‌توان با پوسته‌ای که در آن قرار دارند ( s )، شاخص عدد صحیح لایه نسبت به پوسته ( j ) و سطح پالایش ( k ) پارامتر کرد. پوسته از نگاشت های شعاعی بالا به جلو منتقل می شود یا می تواند به همان روش دوباره محاسبه شود، و سطح پالایش ورودی به فرآیند رمزگذاری است. بنابراین، تنها چیزی که باقی می ماند شاخص عدد صحیح است.

برای محاسبه شاخص عدد صحیح یک لایه، ابتدا به تعداد لایه های پوسته نیاز است. تعداد لایه‌ها در یک پوسته به سطح پالایش، توالی لایه‌بندی و تعداد شکاف‌های شعاعی اضافی بستگی دارد (به بخش 4.5 مراجعه کنید ). یک بار دیگر، سطح پالایش یک ورودی است و سایر متغیرها برای هر DGGS سه بعدی معین ثابت هستند. بنابراین، تعداد لایه ها، nℓ، از رابطه زیر بدست می آید

nℓ=ایکس+1∏من=سک-1ℓمن

در موردی که s بزرگتر یا مساوی باشد ک-1، پوسته در لایه مرکزی قرار دارد. در این صورت تنظیم می کنیم س=-1و توجه داشته باشید که تنها یک لایه در پوسته وجود دارد. شاخص عدد صحیح لایه پس از آن است j=⌊د·nℓ⌋، جایی که d از نگاشت شعاعی به جلو منتقل می شود یا به طور مستقل به همان شیوه محاسبه می شود. در نهایت، به عنوان ورودی به رمزگذاری سطح، مقدار کسبرای پوسته مورد نیاز است. برای لایه های مرکزی، این همیشه صفر است. در غیر این صورت، توسط داده می شود ک-س-1+w.

برای رمزگشایی، محاسبه می کنیم ددقیقهو دحداکثرمانند j/nℓو (j+1)/nℓبه ترتیب، که سپس مستقیماً به عنوان مقادیر d وارد نقشه برداری معکوس می شود .

6. عملیات نمایه سازی

یکی از اجزای مهم یک DGGS معمولی، طرح نمایه سازی سلول ها است. شاخص‌ها در یک DGGS نه تنها برای شناسایی و خطی‌سازی سلول‌ها، بلکه به‌عنوان وسیله‌ای برای پیمایش شبکه برای جستجوهای فضایی مختلف استفاده می‌شوند [ 11 ]. برای این منظور، مهم است که بتوانیم عملیات خاصی را بر روی شاخص های مذکور به طور موثر انجام دهیم. اساسی ترین این عملیات عبارتند از پرس و جوهای والد، که والد (یا با اصلاح ناهمخوان، والدین را برمی گرداند.) یک سلول معین؛ پرسش های فرزند، که فرزندان سلول را برمی گرداند. و پرس و جوهای همسایه، که سلول هایی را که یک لبه (یا به صورت سه بعدی یک چهره) را با سلول به اشتراک می گذارند، برمی گرداند. این عملیات به‌عنوان بلوک‌های ساختمانی برای پرس‌و‌جوهای پیچیده‌تر جغرافیایی که با سیستم شبکه انجام می‌شوند، مانند رشد منطقه، پیچیدگی و همبستگی داده‌ها، شطرنجی‌سازی ویژگی‌ها و بافر کردن عمل می‌کنند. به همین دلیل، ایجاد نمایه سازی مناسب برای یک DGGS سه بعدی یک کار ضروری است.
با روش ما – مشابه رمزگذاری و رمزگشایی – ما این عملیات را بر حسب اجزای سطحی و شعاعی تعریف می کنیم. این تقسیم نه تنها مشکل نمایه سازی را ساده می کند، بلکه تضمین می کند که نمایه سازی سه بعدی با DGGS ورودی مطابقت دارد. با مراجعه به شکل 9 و شکل 10 ، اجازه می دهیم منسشاخص سطح یک سلول باشد و منℓشاخص لایه باشد. برای هر یک از این مؤلفه‌ها، فرض می‌کنیم که یک عملیات والد، فرزند و همسایه مربوطه وجود دارد. برای شاخص سطح، این مستقیماً از نمایه سازی DGGS ورودی می آید، در حالی که برای شاخص لایه، اینها باید تعریف شوند. با استفاده از عملیات کامپوننت، عملیات سه بعدی مربوطه را به صورت زیر تعریف می کنیم.
والدین
والد(های) یک سلول به این بستگی دارد که لایه سلول و لایه والد آن دارای مقادیر یکسان یا متفاوت باشند. کس. اجازه دهید منℓ”=والدین(منℓ); اگر ارزش کسهمان است، پس تک والد به سادگی است (منس،منℓ”). در بیشتر موارد، ارزش کسبرای منℓ”مقداری m (اغلب یک، اما نه همیشه) کمتر از عدد از است منℓ. در این مورد، والدین (های) توسط داده می شوند والدینمتر(منس)×منℓ.
فرزندان
فرزندان یک سلول به این بستگی دارد که سلول به یک لایه مرکزی یا عادی تعلق دارد برای لایه های عادی، مجموعه کودکان به سادگی فرزندان(منس)×فرزندان(منℓ). برای لایه های مرکزی، کودکی که به لایه مرکزی جدید تعلق دارد باید از لایه(های) فرزند دیگر متمایز شود. شاخص لایه مرکزی جدید را فراخوانی کنید جℓ; سپس، این کودک توسط داده می شود (منس،جℓ). اجازه دهید نℓمجموعه ای از شاخص های لایه فرزندان دیگر (لایه های عادی) را ارائه دهید. این لایه‌ها دارای پالایش سطحی هستند که برابر با چند برابر اعمال می‌شود ، بنابراین کودکان به‌دست‌آمده هستند فرزندانw(منس)×نℓ
همسایه ها
همسایه ها را به سه دسته تقسیم می کنیم: همسایگان در لایه های مشابه سلول، همسایگان در لایه بالای سلول و همسایگان در لایه زیر سلول. اگر سلولی به بیرونی ترین یا داخلی ترین لایه (مرکزی) تعلق داشته باشد، به ترتیب در لایه بالا یا پایین همسایه ای نخواهد داشت. همسایگان در همان لایه به سادگی هستند همسایه ها(منس)×منℓ. اجازه دهید منℓ+لایه بالا باشد منℓو منℓ-لایه زیر باشد. اگر منℓ+دارای همان ارزش است کسمانند منℓ، سپس همسایه مجرد بالا است (منس،منℓ+). در مورد دیگر، جایی که ارزش کسبرای منℓ+مقداری m بزرگتر از عدد است منℓ، همسایه ها توسط داده می شود فرزندانمتر(منس)×منℓ+. به همین ترتیب، اگر منℓ-دارای همان ارزش است کسمانند منℓ، یک همسایه در زیر وجود دارد که توسط (منس،منℓ-). در صورتی که ارزش کسبرای منℓ-مقداری m کمتر از عدد است منℓ، همسایه ها توسط داده می شود والدینمتر(منس)×منℓ-.

7. نتایج و ارزیابی

برای ارزیابی رویکرد خود، ما روش کلی را که در بخش‌های قبلی توضیح داده شد، به‌عنوان یک کلاس C++ که با مجموعه ابزار تحقیقاتی ادغام شده برای طراحی و آزمایش DGGS‌های مرسوم مختلف استفاده می‌شود، پیاده‌سازی کرده‌ایم. در این مجموعه ابزار، عملیات ارائه شده توسط یک DGGS توسط یک کلاس انتزاعی که هر پیاده سازی گسترش می یابد، مشخص می شود. کلاس 3D DGGS یک DGGS ورودی و همچنین مقادیری برای نسبت ابعاد هدف ( a )، توان برای نگاشت شعاعی ( t ) و محدوده شعاعی شبکه ( آرحداکثرو آردقیقه) به عنوان ورودی در طول ساخت. DGGS سه بعدی از این مقادیر – همراه با عملیات و اطلاعات ارائه شده توسط DGGS ورودی – برای ارائه عملکرد توصیف شده در مقاله استفاده می کند: رمزگذاری نقطه، رمزگشایی سلول، والدین، فرزندان و همسایگان. ما همچنین توانایی ایجاد تجسم اولیه از شبکه را فراهم می کنیم. این تجسم ها به عنوان مبنایی برای بسیاری از شکل های این مقاله استفاده شد.
ما سیستم خود را با مشاهده سه نمونه استفاده از DGGS های سه بعدی خود ارزیابی می کنیم. این موارد استفاده به معنای اجرای پیشرفته یک سیستم شبکه جهانی سه بعدی نیستند، بلکه به منظور نشان دادن استحکام و تطبیق پذیری رویکرد و توانایی آن در پشتیبانی از برنامه های کاربردی هدف، مجموعه داده ها و ورودی های مختلف هستند. DGGS ها برای هر مورد استفاده، یک DGGS ورودی و پارامترهایی را برای سیستم انتخاب کردیم که منجر به یک DGGS سه بعدی با ویژگی‌های مطلوب برای برنامه مذکور شد. رمزگذاری داده ها در این موارد استفاده همگی با استفاده از عملیات اساسی DGGS سه بعدی ذکر شده در بالا تعریف می شوند.

7.1. مسیرهای هواپیما و ماهواره

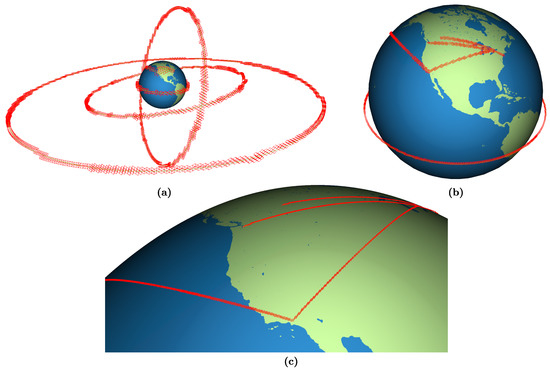
اولین مورد استفاده ای که بررسی می کنیم، ردیابی مسیر هواپیما و فضاپیماها، مانند پروازهای تجاری و خصوصی، هواپیماهای بدون سرنشین، ماهواره ها و موشک ها است. چنین سیستمی می تواند برای افزایش کارایی پرس و جوهای برخورد با استفاده از سلسله مراتب سیستم شبکه، مشابه رویکردهای [ 34 ، 35 ] استفاده شود. مزیت اصلی DGGS سه بعدی ما نسبت به شبکه‌های موجود برای چنین سیستمی این است که سلول‌ها در ارتفاعات کم و بالا در وضوح یکسان قرار دارند و دارای شکل و اندازه تقریباً برابر هستند.
شکل 13 چندین مسیر پروازی تولید شده و مدارهای ماهواره ای را نشان می دهد که در یک DGGS سه بعدی با وضوح فزاینده نشان داده شده اند. DGGS ورودی برای این مثال از یک مثلث ضلعی لوزی به عنوان چند وجهی اولیه، اصلاح چهار ضلعی استاندارد 1:4 و یک طرح عادی سازی ساده استفاده می کند. 3D DGGS دارای نسبت ابعاد هدف یک، توان نقشه برداری شعاعی یک و برد شعاعی 10.66 R (67957 کیلومتر) است. این پارامترها برای اطمینان از اینکه سلول ها تا حد امکان فشرده هستند انتخاب شدند.

7.2. برنامه ریزی شهری

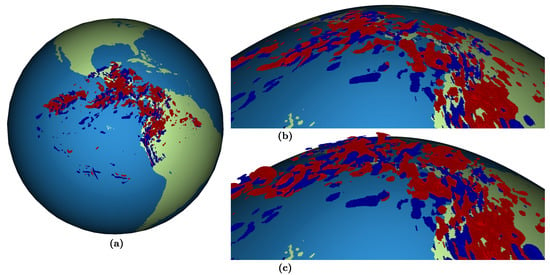
مورد دوم استفاده از شبکه سه بعدی حفظ حجم برای اهداف برنامه ریزی و مدیریت شهری است. یک شبکه حفظ حجم برای تخمین سریع حجم یک ویژگی شطرنجی شده در شبکه با ضرب تعداد سلول ها در حجم آنها مفید است. این مورد استفاده همچنین توانایی DGGS سه بعدی ما را برای رسیدگی به داده های مقیاس کوچک علاوه بر داده های مقیاس بسیار بزرگتر نشان داده شده در بخش 7.1 نشان می دهد.
شکل 14 چندین ساختمان را نشان می دهد که در یک DGGS سه بعدی نشان داده شده اند، با هندسه های ساختمان به دست آمده از نقشه خیابان باز [ 49 ]. DGGS ورودی برای این مثال از یک سه‌ضلعی disdyakis به‌عنوان چند وجهی اولیه، یک اصلاح مثلث غیر استاندارد 1:4 و برش دایره‌ای بزرگ و تاس گرا [ 48 ] برای حفظ منطقه [ 50 ] استفاده می‌کند. DGGS 3D دارای نسبت ابعاد هدف یک، توان نقشه برداری شعاعی 3 برای دستیابی به حفظ حجم کامل (به استثنای لایه مرکزی) و حداکثر شعاع 1.33 R (8495 کیلومتر) است.

7.3. خواص جوی

مورد استفاده نهایی که ما به آن نگاه می کنیم استفاده از یک DGGS سه بعدی برای نمونه برداری مجدد از پیش بینی های جوی است، مانند مواردی که توسط مدل های عددی پیش بینی آب و هوا ایجاد می شود. این مجموعه داده‌ها معمولاً وضوح عمودی بسیار بالاتری نسبت به وضوح سطح دارند، به دلیل اینکه ویژگی‌هایی مانند دما و سرعت باد در این دو بعد چقدر سریع تغییر می‌کنند. برای تطبیق این موضوع با DGGS سه بعدی خود، نسبت ابعاد مناسبی را برای سلول‌ها تعیین می‌کنیم تا اطمینان حاصل کنیم که وضوح عمودی و سطحی تا حد ممکن با داده‌های ورودی مطابقت دارد.
شکل 15 سرعت باد عمودی را از مجموعه داده ERA5 [ 51 ] نمونه برداری شده در یک DGGS سه بعدی نشان می دهد. ورودی DGGS برای این مثال همان است که برای مسیرهای هواپیما و ماهواره استفاده می شود. با این حال، این DGGS سه بعدی دارای نسبت تصویر هدف 31.7، توان نقشه برداری شعاعی یک و حداکثر شعاع 1.33 R (8495 کیلومتر) است.

7.4. بحث

مثال های بالا تنها زیرمجموعه کوچکی از بسیاری از کاربردهای بالقوه DGGS های سه بعدی ما هستند. با وجود این، آنها نه تنها خواص مفید قابل دستیابی با این روش را نشان می دهند (پشتیبانی از دامنه های بزرگ از ارتفاعات، حفظ حجم بین سلول ها، نسبت ابعاد سلولی سفارشی، و پشتیبانی از مقیاس های چندگانه داده) بلکه سه بعدی جهانی جدید را نیز نشان می دهند. شبکه ها را می توان ایجاد کرد. با توجه به یک DGGS معمولی که عملیات مورد نیاز را فراهم می کند، ایجاد یک DGGS سه بعدی به سادگی ارائه شبکه سطح و چهار پارامتر کاملاً تعریف شده برای شبکه سه بعدی است. از آنجایی که ایجاد یک DGGS سه بعدی که برای هر برنامه ای ایده آل است امکان پذیر نیست، این امکان تکرار سریع در ایجاد و مقایسه شبکه های سه بعدی مختلف را برای یافتن شبکه ایده آل برای هر برنامه فراهم می کند.

8. نتیجه گیری و کار آینده

با در دسترس قرار گرفتن مقادیر داده های سه بعدی جغرافیایی، تکنیک های یکپارچه سازی و مدیریت چنین داده هایی اهمیت فزاینده ای پیدا می کنند. برای این منظور، ما یک روش کامل و جامع برای گسترش هر DGGS به 3D برای استفاده به عنوان یک سیستم شبکه جهانی سه بعدی پیشنهاد کرده‌ایم. رویکرد ما کلی است و به درستی هرگونه DGGS بالقوه را بدون در نظر گرفتن چند وجهی اولیه، پالایش یا طرح ریزی به کار گرفته شده در خود جای می دهد. پالایش نیمه منظم استفاده می شود تا بتوان محدوده های شعاعی بزرگ را بدون تخریب قابل توجه در شکل یا اندازه سلول نشان داد. از تکنیک هایی استفاده می شود تا اطمینان حاصل شود که سلول ها نسبت تصویر مورد نظر را دارند و نسبت ابعاد و حجم نسبی سلول ها در طول پالایش حفظ می شوند. ما همچنین یک خط لوله برای مدیریت رمزگذاری و رمزگشایی این شبکه‌ها به روشی ارائه می‌کنیم که انتقال داده‌های ساده بین نمایش‌های دو بعدی و سه بعدی را تسهیل می‌کند. به عنوان بخشی از این، ما یک کلاس از نگاشت شعاعی را استخراج می کنیم که به درجات مختلفی از حفظ حجم در شبکه دست می یابد. اثربخشی این چارچوب در سه مورد استفاده نمونه نشان داده شده است، که هر کدام از یک DGGS سه بعدی متفاوتی استفاده می‌کنند که به صراحت برای نیازهای برنامه طراحی شده است.
هنوز کارهای مهمی در آینده وجود دارد که باید انجام شود. در حالی که ما ابزارهایی را ارائه کرده‌ایم که می‌توانند برای توسعه یک طرح نمایه‌سازی برای DGGS‌های سه‌بعدی مورد استفاده قرار گیرند، کاوش دقیق‌تر درباره موضوع – به‌ویژه روش‌هایی برای درهم‌آمیزی شاخص‌های سطح و لایه برای محل – ضروری است. روش‌های توسعه‌یافته برای ترکیب این شاخص‌ها را می‌توان به بعد زمانی نیز تعمیم داد و ممکن است به عنوان مبنایی برای توسعه تکنیک‌های بهتر برای DGGS با زمان متغیر باشد. همچنین، در حالی که اکثر DGGS ها از یک کره به عنوان مدل مرجع زمین استفاده می کنند، یک کروی مایل به نمایش دقیق تری ارائه می دهد. در حالی که ما گمان می کنیم روش ما به همان اندازه برای یک DGGS بیضی قابل اجرا است، تحقیقات بیشتری برای توجیه این ادعا و رسیدگی به هرگونه تغییر ضروری در روش مورد نیاز است.
سایر مسیرها برای کار آینده شامل تعریف عملیات سطح بالا کارآمدتر برای کار با DGGS سه بعدی است. درج و شطرنجی کردن ویژگی هایی مانند بردارهای سه بعدی، مدل ها و مش ها، عملیات مهمی برای یک شبکه سه بعدی هستند، و الگوریتم هایی که در حال حاضر برای این کار با DGGS سه بعدی ما استفاده می شوند، کاملاً اساسی هستند. همچنین ممکن است راه‌هایی برای ساختار یک DGGS سه بعدی برای کمک به مشکلات انسدادی که در تجسم خاص ظاهر می‌شوند، وجود داشته باشد. نماهای برش و رندر لایه های انتخابی ممکن است ابزار مفیدی در تجسم داده های زیرزمینی و سایر مجموعه های داده با انسداد قابل توجه باشد.

اختصارات

در این نسخه از اختصارات زیر استفاده شده است:

GIS سیستم اطلاعات جغرافیایی
DGGS سیستم شبکه جهانی گسسته
DGGS سه بعدی سیستم شبکه جهانی گسسته سه بعدی

منابع

  1. لی، جی جی; کانگ، ام. داده های بزرگ جغرافیایی: چالش ها و فرصت ها. بیگ دیتا Res. 2015 ، 2 ، 74-81. [ Google Scholar ] [ CrossRef ]
  2. Antenucci، JC; براون، ک. کراسول، PL; کوانی، ام جی؛ آرچر، اچ. سیستم های اطلاعات جغرافیایی: راهنمای فناوری . ون نوستراند راینهولد: نیویورک، نیویورک، ایالات متحده آمریکا، 1991. [ Google Scholar ]
  3. Foresman, TW تاریخچه سیستم‌های اطلاعات جغرافیایی: دیدگاه‌های پیشگامان . جلد 397; Prentice Hall: Upper Saddle River، نیوجرسی، ایالات متحده آمریکا، 1998. [ Google Scholar ]
  4. Hennerdal، P. Beyond the Periphery: درک کودکان و بزرگسالان از تداوم نقشه جهان. ان دانشیار صبح. Geogr. 2015 ، 105 ، 773-790. [ Google Scholar ] [ CrossRef ]
  5. هروبی، اف. Avelino, MC; آیالا، RM Journey to the end of the world map – چگونه لبه های نقشه های جهان ذهن فضایی را شکل می دهند. جی. جئوگر. Inf. علمی 2016 ، 1 ، 314-323. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  6. Flater, D. Understanding Geodesic Buffering. در دسترس آنلاین: https://www.esri.com/news/arcuser/0111/geodesic.html (در 23 ژانویه 2020 قابل دسترسی است).
  7. وانگ، ی. لیو، ز. لیائو، اچ. لی، سی. بهبود عملکرد محاسبه همپوشانی چند ضلعی GIS با MapReduce برای پردازش داده های بزرگ فضایی. محاسبات خوشه ای 2015 ، 18 ، 507-516. [ Google Scholar ] [ CrossRef ]
  8. سحر، ک. White, D. سیستم های شبکه جهانی گسسته. Comp. علمی آمار 1998 ، 269-278. [ Google Scholar ]
  9. مهدوی امیری، ع. آلدرسون، تی. سماواتی، اف. بررسی زمین دیجیتال. محاسبه کنید. نمودار. 2015 ، 53 ، 95-117. [ Google Scholar ] [ CrossRef ]
  10. OGC (2017a). مشخصات چکیده سیستم های شبکه جهانی گسسته. در دسترس آنلاین: https://docs.opengeospatial.org/as/15-104r5/15-104r5.html (در 2 اوت 2018 قابل دسترسی است).
  11. آلدرسون، تی. پرس، م. دو، X. مهدوی امیری، ع. سماواتی، اف. بسترهای دیجیتال زمین. در کتابچه راهنمای زمین دیجیتال ; Springer: برلین/هایدلبرگ، آلمان، 2020؛ صص 25-54. [ Google Scholar ]
  12. یو، جی اس. Min، KJ; Ahn، JW مفهوم و چارچوب سیستم شبکه سه بعدی ژئو فضایی. سمپوزیوم بین المللی وب و سیستم های اطلاعات جغرافیایی بی سیم ; Springer: برلین/هایدلبرگ، آلمان، 2019؛ صص 136-149. [ Google Scholar ]
  13. یو، جی کیو; Wu، LX فضایی فرعی و کدگذاری یک شبکه سه بعدی جهانی: شبکه اکتشافی دژنره شده Spheoid. در مجموعه مقالات سمپوزیوم زمین شناسی و سنجش از دور، کیپ تاون، آفریقای جنوبی، 12 تا 17 ژوئیه 2009. جلد 2، ص 2-361. [ Google Scholar ]
  14. باند، دبلیو. شوفنگ، سی. فنگ، ال. Ke, L. Sphere Shell Space 3D Grid. بین المللی قوس. فتوگرام Remote Sens. Spatial Inf. علمی 2013 ، 40 ، 77-82. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  15. سان، ز. Cheng, C. مدل بازنمایی یکپارچه سه بعدی و تجسم بر اساس وکسل گسسته جهانی-GeoSOT3D. در مجموعه مقالات بیست و سومین کنفرانس بین المللی ژئوانفورماتیک 2015، ووهان، چین، 19 تا 21 ژوئن 2015. صص 1-5. [ Google Scholar ]
  16. فکته، جی. Treinish، LA Sphere Quadtrees: یک ساختار داده جدید برای پشتیبانی از تجسم داده های کروی توزیع شده. در مجموعه مقالات استخراج معنی از داده های پیچیده: پردازش، نمایش، تعامل، سانتا کلارا، کالیفرنیا، ایالات متحده آمریکا، 11-16 فوریه 1990. جلد 1259، ص 242–253. [ Google Scholar ] [ CrossRef ]
  17. داتون، جی. رمزگذاری و مدیریت داده های مکانی با مش های مثلثی سلسله مراتبی. در مجموعه مقالات هفتمین سمپوزیوم مدیریت داده های مکانی ; تیلور و فرانسیس: ابینگدون، بریتانیا، 1996; جلد 43، ص 505–518. [ Google Scholar ]
  18. گورسکی، KM; هیوون، ای. باندی، ای جی; Wandelt، BD; هانسن، FK; راینکه، ام. Bartelmann, M. HEALPix: چارچوبی برای گسسته سازی با وضوح بالا و تجزیه و تحلیل سریع داده های توزیع شده در کره. اخترفیزیک. J. 2005 , 622 , 759. [ Google Scholar ] [ CrossRef ]
  19. هلهوش، ا. Roşca, D. یک تقسیم مساوی هشت وجهی از کره و تنظیمات نزدیک به بهینه نقاط. محاسبه کنید. ریاضی. Appl. 2014 ، 67 ، 1092-1107. [ Google Scholar ] [ CrossRef ]
  20. Snyder، JP Map Projections–A Working Manual ; دفتر چاپ دولت ایالات متحده: واشنگتن، دی سی، ایالات متحده آمریکا، 1987; جلد 1395.
  21. اسنایدر، جی پی پیش بینی نقشه مساحتی برای گلوب های چند وجهی. Cartographica 1992 ، 29 ، 10-21. [ Google Scholar ] [ CrossRef ]
  22. اولمر، بی. سماواتی، F. به سمت شبکه حفظ حجم کروی تولید شده-اکتری. GeoInformatica 2020 ، 1-25. [ Google Scholar ]
  23. بهردت، دی. Seybold، MP نقاط منطقی در حوزه واحد: پیچیدگی تقریبی و ساختارهای عملی. در مجموعه مقالات ACM 2017 در سمپوزیوم بین المللی در محاسبات نمادین و جبری، کایزرسلاترن، آلمان، 25 تا 28 ژوئیه 2017؛ صص 29-36. [ Google Scholar ]
  24. آلدرسون، تی. مهدوی امیری، ع. Samavati، F. چند تفکیک پذیری در منحنی های کروی. نمودار. مدل های 2016 ، 86 ، 13-24. [ Google Scholar ] [ CrossRef ]
  25. آلدرسون، تی. Samavati، F. منحنی های NURBS چند مقیاسی روی کره و بیضی. محاسبه کنید. نمودار. 2019 ، 82 ، 243-249. [ Google Scholar ] [ CrossRef ]
  26. آلدرسون، تی. مهدوی امیری، ع. سماواتی، ف. تعدیل منحنی های کروی به صورت برداری و شطرنجی. کامپیوتر بصری 2018 ، 34 ، 973-984. [ Google Scholar ] [ CrossRef ]
  27. Goodchild، MF بازاندیشی تاریخچه GIS. ان GIS 2018 ، 24 ، 1-8. [ Google Scholar ] [ CrossRef ]
  28. سحر، ک. سفید، دی. کیمرلینگ، سیستم‌های شبکه جهانی گسسته ژئودزیک AJ. کارتوگر. Geogr. Inf. علمی 2003 ، 30 ، 121-134. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  29. Vince، A. نمایه سازی دیافراگم 3 شش ضلعی شبکه گسسته جهانی. J. Vis. اشتراک. تصویر نشان می دهد. 2006 ، 17 ، 1227-1236. [ Google Scholar ] [ CrossRef ]
  30. تانگ، ایکس. بن، جی. وانگ، ی. ژانگ، ی. Pei, T. کدگذاری کارآمد و طرح عملیات فضایی برای سیستم شبکه جهانی گسسته شش ضلعی دیافراگم 4. بین المللی جی. جئوگر. Inf. علمی 2013 ، 27 ، 898-921. [ Google Scholar ] [ CrossRef ]
  31. دو، ال. ما، س. بن، جی. وانگ، آر. Li, J. الگوریتم تولید خط گسسته کاهش دوگانگی و ابعاد برای یک شبکه مثلثی. ISPRS Int. J. Geoinf. 2018 ، 7 ، 391. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
  32. مهدوی امیری، ع. سماواتی، ف. پترسون، P. طبقه بندی و تبدیل برای روش های نمایه سازی سیستم های شبکه جهانی گسسته. ISPRS Int. J. Geoinf. 2015 ، 4 ، 320-336. [ Google Scholar ] [ CrossRef ]
  33. سیردشموک، ن. وربری، ای. Oosterom، PV; پسوماداکی، س. Kodde, M. استفاده از یک سیستم شبکه جهانی گسسته برای مدیریت ابرهای نقطه ای با مکان ها، زمان ها و سطوح مختلف جزئیات. Cartographica 2019 ، 54 ، 4-15. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  34. میائو، اس. چنگ، سی. ژای، دبلیو. رن، اف. ژانگ، بی. لی، اس. ژانگ، جی. ژانگ، اچ. الگوریتم تشخیص تعارض پرواز در ارتفاع پایین بر اساس شاخص فضایی و زمانی شبکه چند سطحی. ISPRS Int. J. Geoinf. 2019 ، 8 ، 289. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
  35. ژای، دبلیو. تانگ، ایکس. میائو، اس. چنگ، سی. Ren, F. تشخیص برخورد برای پهپادها بر اساس شبکه‌های GeoSOT-3D. ISPRS Int. J. Geoinf. 2019 ، 8 ، 299. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
  36. باسین، سی. محدودیت‌های فعلی وضوح برای توموگرافی امواج سطحی در آمریکای شمالی. EOS Trans. AGU. 81: ملاقات پاییزی. تامین چکیده 2000 ، 81 ، F897. [ Google Scholar ]
  37. ژائو، دی. تصاویر توموگرافی جهانی از ستون های گوشته و صفحات فرورانش: بینش دینامیک زمین عمیق. فیزیک سیاره زمین. اینتر 2004 ، 146 ، 3-34. [ Google Scholar ] [ CrossRef ]
  38. کاگیاما، ا. ساتو، تی. “شبکه یین یانگ”: یک شبکه بیش از حد در هندسه کروی. ژئوشیمی. ژئوفیز. Geosyst. 2004 ، 5 . [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  39. یوشیدا، م. کاگیاما، الف. کاربرد شبکه یین یانگ برای انتقال حرارتی سیال بوسینسک با عدد پراندتل بی نهایت در یک پوسته کروی سه بعدی. ژئوفیز. Res. Lett. 2004 ، 31 . [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  40. کاگیاما، ا. شبیه ساز یوشیدا، ام. ژئودینامو و همرفت گوشته روی زمین با استفاده از شبکه یین یانگ. J. Phys. 2005 ، 16 ، 325. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
  41. Tackley، PJ مدل‌سازی همرفت گوشته فشرده با کنتراست‌های ویسکوزیته بزرگ در یک پوسته کروی سه‌بعدی با استفاده از شبکه یین یانگ. فیزیک سیاره زمین. اینتر 2008 ، 171 ، 7-18. [ Google Scholar ] [ CrossRef ]
  42. یو، جی. Wu, L. در مورد کدگذاری و رمزگشایی برای Sphere Degenerated-Octree Grid. Geogr. Geo-Inf. علمی 2009 ، 25 ، 5-9. [ Google Scholar ]
  43. یو، جی. وو، ال. لی، ز. لی، ایکس. یک روش ذاتی مبتنی بر SDOG برای مدلسازی سه بعدی اشیاء فضایی در مقیاس بزرگ. ان GIS 2012 ، 18 ، 267-278. [ Google Scholar ] [ CrossRef ]
  44. یو، جی. وو، ال. زی، جی. Guo, Z. مدلسازی و تجسم سه بعدی چند مقیاسی مبتنی بر SDOG در لیتوسفر جهانی. علمی علوم زمین چین 2012 ، 55 ، 1012. [ Google Scholar ] [ CrossRef ]
  45. هلهوش، ا. Roşca، D. شبکه های سه بعدی قابل پالایش یکنواخت از چندوجهی ها و توپ های محدب منظم. اکتا ریاضی. 2018 ، 156 ، 182-193. [ Google Scholar ] [ CrossRef ]
  46. هلهوش، ا. Roşca، D. منطقه حفاظت از نقشه ها و حجم حفظ نقشه ها بین یک کلاس از چند وجهی و یک کره. Adv. محاسبه کنید. ریاضی. 2017 ، 43 ، 677-697. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  47. زی، جی. یو، اچ. Ma، ریخته گری تعاملی پرتوی شبکه های ژئودزیکی KL. در انجمن گرافیک کامپیوتری ; وایلی: هوبوکن، نیوجرسی، ایالات متحده آمریکا، 2013; جلد 32، ص 481–490. [ Google Scholar ]
  48. ون لیوون، دی. Strebe، D. رویکرد “برش و تاس” به معادل سازی منطقه در پیش بینی های نقشه چند وجهی. کارتوگر. Geogr. Inf. علمی 2006 ، 33 ، 269-286. [ Google Scholar ] [ CrossRef ]
  49. مشارکت کنندگان OpenStreetMap. نقشه خیابان را باز کنید. در دسترس آنلاین: https://www.openstreetmap.org/ (در 27 ژانویه 2020 قابل دسترسی است).
  50. هال، جی. وکر، ال. اولمر، بی. سماواتی، F. Disdyakis Triacontahedron DGGS. نسخه خطی در حال آماده سازی
  51. فروشگاه داده های آب و هوا (CDS) خدمات تغییر اقلیم کوپرنیک. سرویس تغییر اقلیم کوپرنیک (C3S) (2017): ERA5: نسل پنجم ECMWF تجزیه و تحلیل مجدد جوی آب و هوای جهانی. در دسترس آنلاین: https://cds.climate.copernicus.eu/cdsapp (در 4 اکتبر 2019 قابل دسترسی است).
Ijgi 09 00233 g001 550
شکل 1. نمای کلی از نحوه استفاده از سیستم شبکه جهانی گسسته ورودی (DGGS) برای تعریف هندسه DGGS سه بعدی (3D). وجهه های چند وجهی اولیه DGGS ورودی ابتدا برای ایجاد سلول های پایه منشوری DGGS سه بعدی اکسترود می شوند. برای پالایش، پایه‌های این سلول‌های منشوری با استفاده از طرح پالایشی مشابه DGGS ورودی تصفیه می‌شوند و با پالایش شعاعی ترکیب می‌شوند. یک اصلاح نیمه منظم پیشنهاد شده است. با این حال، پالایش منظم نیز امکان پذیر است. شرح مفصل تری از این فرآیندها در بخش 4 ارائه شده است .
Ijgi 09 00233 g002 550
شکل 2. فرآیند رمزگذاری (چپ) و رمزگشایی (راست) با DGGS. رمزگذاری: ویژگی ها از حوزه زمین به حوزه چند وجهی شبکه نمایش داده می شوند. مجموعه ای از سلول های مسطح مرتبط با ویژگی به دست می آیند – که هر یک دارای یک شاخص منحصر به فرد هستند. رمزگشایی: مجموعه ای از شاخص های سلولی مربوط به هندسه سلول در شبکه چند وجهی است. سلول ها در حوزه چند وجهی به صورت معکوس به حوزه زمین بازتاب می شوند. فرآیند یک DGGS سه بعدی مشابه است، به جز اینکه ویژگی ها و سلول ها دارای ارتفاع(های) مرتبط هستند.
Ijgi 09 00233 g003 550
شکل 3. شعاع چند وجهی به عنوان شعاع کره اطراف آن تعریف می شود. در این شکل، تمام نقاط روی یک خط ثابت با یک رنگ مشخص، شعاع یکسانی دارند، زیرا همگی دارای کره‌ی اطراف یکسانی هستند (یعنی روی یک چندوجهی قرار می‌گیرند). کره های مربوطه با همان رنگ ها اما با یک خط چین نشان داده شده اند.
Ijgi 09 00233 g004 550
شکل 4. پالایش منشوری منظم که روی یک سلول هرمی منفرد ( a ) یک بار و ( b ) دو بار اعمال می شود.
Ijgi 09 00233 g005 550
شکل 5. پالایش منشوری نیمه منظم که روی یک سلول هرمی منفرد ( a ) یک بار و ( b ) دو بار اعمال می شود. در ( b )، تعداد دفعاتی که پالایش سطح اعمال شده است ( کس) برای هر لایه نشان داده شده است. ببینید که چگونه اصلاحات شعاعی لایه‌های مرکزی، مناطقی از شبکه را با مقادیر مختلف جدا می‌کند کس.
Ijgi 09 00233 g006 550
شکل 6. سه سطح از کاربردهای متوالی پالایش منشوری معمولی (بالا) و نیمه منظم (پایین). فقط طرف یک سلول شروع هرم نشان داده شده است تا رفتار دو طرح را در شعاع های مختلف برجسته کند. توجه داشته باشید که چگونه سلول ها با پالایش منظم به سمت مرکز منحرف می شوند، در حالی که این موضوع در طرح نیمه منظم وجود ندارد.
Ijgi 09 00233 g007 550
شکل 7. پالایش منشوری نیمه منظم که روی یک سلول پایه شش ضلعی با استفاده از طرح اصلاح سطح 1:3 ( a ) یک بار و ( c ) دو بار اعمال می شود. ( b ) همان تصویر ( c ) است، اما سلول‌های سطحی سطح پالایش قبلی برای مرجع نشان داده شده است. توجه داشته باشید که در سطح دوم پالایش، لایه های معمولی دارای دو پالایش شعاعی در مقابل یک هستند.
Ijgi 09 00233 g008 550
شکل 8. نمایشی از این که چگونه پالایش را می توان تغییر داد تا بر نسبت ابعاد سلول ها تأثیر بگذارد. همه شکل ها یک سلول هرمی شروع را از یک شبکه با 200 سلول در گسسته سازی اولیه نشان می دهند. لایه مرکزی با پنج شکاف شعاعی اضافی ( a = 3 برای به دست آوردن x = 5) در ( a ) یک سطح از پالایش و ( b ) سه سطح. لایه مرکزی با دو کاربرد از طرح پالایش سطح ( a = 1/8 برای بدست آوردن w = 2) در ( c ) یک سطح پالایش و ( d ) سه سطح.
Ijgi 09 00233 g009 550
شکل 9. شاخص های DGGS ورودی سلول ها را در DGGS سه بعدی با پایه های یکسان اما شعاع های متفاوت شناسایی می کنند. به همین ترتیب، هر لایه از یک DGGS سه بعدی شامل تمام سلول هایی با شعاع یکسان اما پایه های متفاوت است. بنابراین، ترکیب این دو بخش از اطلاعات برای شناسایی هر سلول در DGGS سه بعدی به طور منحصر به فرد کافی است. در اینجا ما یک سلول منفرد را نشان می‌دهیم – که با رنگ بنفش مشخص شده است – به همراه تمام سلول‌هایی که دارای یک شاخص سطح (قرمز) و یک شاخص لایه (آبی) هستند.
Ijgi 09 00233 g010 550
شکل 10. خط لوله برای تقسیم کدگذاری و رمزگشایی به اجزای سطحی (بالا) و شعاعی (پایین). این دو جزء کاملاً مستقل هستند به جز وضوح سطح ( کس) از لایه ای که در طول رمزگذاری به جزء سطحی ارائه می شود. نماد استاندارد برای طول و عرض جغرافیایی ( ϕو λ) استفاده می شود.
Ijgi 09 00233 g011 550
شکل 11. شکاف های شعاعی لایه های مرکزی، شبکه را به نواحی منظمی تقسیم می کند که نمایانگر پوسته های کروی است. در سطح پالایش k وجود دارد ک-1پوسته ها و لایه مرکزی این پوسته‌ها شبیه به هم هستند، اما تعداد سلول‌های متفاوتی دارند و بنابراین باید حجم نگاشت متناسب با تعداد سلول‌هایشان داشته باشند.
Ijgi 09 00233 g012 550
شکل 12. سه نگاشت شعاعی ما به همراه یک طرح چند وجهی نرمال سازی روی یک شبکه اعمال شد. سمت چپ: اولین نقشه برداری با درون یابی خطی. سمت راست: نگاشت دوم با درون یابی مکعبی. میانه: نگاشت سوم با درونیابی درجه دوم. توجه داشته باشید که چگونه سلول‌ها در نقشه‌برداری درست کشیده و فشرده می‌شوند تا حجم خود را بهتر حفظ کنند. این اثر در نگاشت میانی نیز وجود دارد اما به میزان کمتر.
Ijgi 09 00233 g013 550
شکل 13. مسیرهای پرواز و مدارهای ماهواره به صورت شطرنجی در یک DGGS سه بعدی. همه مسیرها و مدارها با وضوح شبکه یکسان ( a ) 7، ( b ) 10 و ( c ) 13 شطرنجی می شوند.
Ijgi 09 00233 g014 550
شکل 14. مجموعه ای از ساختمان ها از دانشگاه کلگری که در یک DGGS سه بعدی با وضوح 21 شطرنجی شده اند. در ( a )، هر دو سلول داخلی و مرزی نشان داده شده اند، در حالی که ( b ، c ) به ترتیب فقط سلول های مرزی و داخلی را نشان می دهند.
Ijgi 09 00233 g015 550
شکل 15. سرعت باد عمودی (بار/ثانیه) نمونه برداری شده در یک DGGS سه بعدی با وضوح 9. سرعت منفی که مربوط به باد رو به بالا است، با رنگ قرمز نشان داده شده است. سرعت مثبت، که مربوط به باد رو به پایین است، با رنگ آبی نشان داده شده است. سرعت هایی با قدر کمتر از 0.25 بار در ثانیه برای کاهش درهم و برهمی و برجسته کردن مناطق با بالاترین سرعت نشان داده نمی شود. در ( a , c )، ارتفاع سلول ها با ضریب 15 مقیاس می شود تا تغییرات ارتفاع را بهتر نشان دهد. در ( b )، ارتفاع در مقیاس واقعی نشان داده شده است.

مقالات داخلی و بین المللی

مطالب مرتبط ...

بدون دیدگاه

دیدگاهتان را بنویسید