روش کمی برای عدم قطعیت توزیع نقطه تطبیق در بازسازی سه بعدی

خلاصه

نقاط تطبیق منابع داده مستقیم ماتریس اساسی، پارامترهای دوربین و محاسبه ابر نقطه هستند. بنابراین، عدم قطعیت آنها تأثیر مستقیمی بر کیفیت بازسازی سه بعدی مبتنی بر تصویر دارد و به تعداد، دقت و توزیع نقاط تطبیق بستگی دارد. این مطالعه عمدتاً بر عدم قطعیت توزیع نقطه تطابق تمرکز دارد. اول، رقیق سازی افقی دقت (HDOP) برای تعیین کمیت توزیع نقطه ویژگی در ناحیه همپوشانی چندین عکس استفاده می شود. سپس روش کوانتیزاسیون ساخته می شود.

\bar{H D O P^{*}}

، میانگین از

2 \times \arctan (H D O P \times \sqrt{\frac{n}{5}} - 1) / π

در تمام تصاویر، برای اندازه گیری عدم قطعیت توزیع نقطه تطبیق در بازسازی سه بعدی استفاده می شود. در نهایت، آزمایش‌های صحنه شبیه‌سازی‌شده و واقعی برای توصیف و تأیید منطقی بودن روش پیشنهادی انجام شد. ما دریافتیم که رابطه بین

\bar{H D O P^{*}}

و توزیع نقطه تطبیق در این مطالعه با توزیع نقطه تطبیق و بازسازی سه بعدی سازگار بود. در نتیجه، ممکن است یک روش عملی برای پیش‌بینی کیفیت بازسازی سه بعدی با محاسبه عدم قطعیت توزیع نقطه تطبیق باشد.

کلید واژه ها:

توزیع نقاط تطبیق ; رقت افقی دقت ; روش کمی سازی ; بازسازی سه بعدی ؛ عدم قطعیت

1. معرفی

حجم قابل توجهی از تحقیقات بر روی بازسازی سه بعدی (3D) مبتنی بر تصویر در بازسازی سنتی زمین سه بعدی [ 1 ]، بازسازی شهری (اشیای صلب) [ 2 ]، و بازسازی پوشش گیاهی (اشیاء غیر صلب) [ 3 ] انجام شده است. استخراج و ساخت سریع مدل های سه بعدی از تصاویر، نقش مهمی در جمع آوری داده های مکانی دارد. Carrivick [ 4 ] تحقیقات کمی در مورد خطاها در بازسازی سه بعدی را خلاصه کرد که عمدتاً بر منبع داده ها، نتایج و سایر جنبه های مشابه متمرکز شده است. تحقیق فرآیند یک موضوع تحقیقاتی ضروری در زمینه GIS (سیستم اطلاعات جغرافیایی) برای اطمینان از صحت بازسازی سه بعدی است.

بازسازی سه بعدی مبتنی بر تصویر یک فرآیند پیچیده است که شامل چندین مرحله است: استخراج و تطبیق ویژگی، محاسبه ماتریس اساسی، کالیبراسیون دوربین و بازسازی ابر نقطه. تعداد زیادی از نقاط تطبیق از جفت‌های استریو برای محاسبه ماتریس اصلی، پارامترهای دوربین و ابرهای نقطه استخراج می‌شوند. بنابراین، نقاط تطبیق یک منبع داده مستقیم برای مراحل دیگر بازسازی سه بعدی مبتنی بر تصویر هستند و عدم قطعیت آنها تأثیر مهمی بر کیفیت بازسازی سه بعدی دارد.

عدم قطعیت نقاط تطبیق به عوامل متعددی [ 5 ] از جمله تعداد، دقت و توزیع نقاط تطبیق بستگی دارد. روش های آماری [ 6 ، 7 ، 8 ]، ماتریس کوواریانس [ 9 ، 10 ، 11 ، 12 ، 13 ]، و قانون انتشار کوواریانس [ 14 ، 15 ، 16 ، 17 ، 18 ] برای محاسبه ویژگی های غیر قطعی استفاده شده است. . یک جفت نقطه تطبیق شامل دو نقطه مشخصه است. لیو [ 19] انواع مختلفی از هندسه دوربین و تجزیه و تحلیل خطاهای تطبیق نقاط ویژگی را مورد بحث قرار داد. Gui [ 20 ] یک روش جدید تطبیق نقطه-الگو را بر اساس ویژگی‌های قوی سریع و زمینه شکل برای افزایش دقت تطبیق ارائه کرد. تانگ [ 21 ] الگوریتم تبدیل ویژگی تغییر ناپذیر مقیاس (SIFT) را بهبود بخشید و نقاط ویژگی اطراف مرزهای تصویر را حذف کرد تا دقت تطبیق را افزایش دهد. ژائو [ 22 ] از ضریب همبستگی متقابل نرمال شده و یک استراتژی تطبیق دو طرفه برای بهبود دقت نقطه تطبیق استفاده کرد. هو [ 23] استحکام و دقت نقاط تطبیق را با استفاده از فاصله ساختاری بین مجموعه نقاط مشخصه به عنوان مبنای شباهت تطبیق بهبود بخشید. بیشتر مطالعات قبلی بر دقت و نه توزیع نقاط تطبیق تمرکز کرده اند. بنابراین، کار حاضر بر توزیع نقاط تطبیق تمرکز خواهد کرد. فرض کنید که نقاط تطبیق با دقت یکسان اما توزیع های متفاوت برای بازسازی مدل های سه بعدی استفاده می شود. اینکه آیا نتایج بازسازی شده ثابت خواهند ماند و آیا می توان از نقاط تطبیق توزیع شده برای بازسازی مدل های سه بعدی با کیفیت بالا در این شرایط استفاده کرد یا خیر. علاوه بر این، روش کمی برای تطبیق توزیع نقطه ایجاب می کند که در نظر گرفته شود.

این مطالعه فرض می‌کند که دقت نقاط تطبیق ثابت است و عدم قطعیت توزیع نقاط تطبیق را در بازسازی سه‌بعدی اندازه‌گیری می‌کند. در مرحله اول، رقت افقی دقت (HDOP) برای تعیین کمیت توزیع نقطه ویژگی استفاده شد. سپس روش کوانتیزاسیون ساخته شد.

\bar{H D O P^{*}}

برای اندازه گیری عدم قطعیت توزیع نقطه تطبیق در بازسازی سه بعدی استفاده شد. در نهایت، آزمایش‌های صحنه شبیه‌سازی‌شده و واقعی برای توصیف و تأیید منطقی بودن روش پیشنهادی انجام شد.

2. روش ها

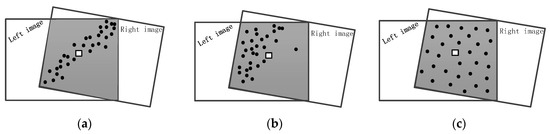
فرض کنید که نقاط تطبیق یک جفت استریو چندین بار با استفاده از یک الگوریتم یکسان استخراج شده است. نتایج ممکن است به دلیل پارامترهای مختلف الگوریتم متفاوت باشد، همانطور که در شکل 1 نشان داده شده است. در اصل، سه گروه از مدل‌های سه‌بعدی بازسازی‌شده بر اساس نقاط تطبیق در شکل 1 دقیقاً یکسان نیستند. تعداد زیادی از آزمایش‌ها در مراحل اولیه نشان داده‌اند که مدل‌های سه‌بعدی هنگامی که بر اساس نقاط تطبیق توزیع شده یکنواخت بازسازی می‌شوند، کیفیت خوبی دارند. در نتیجه، یکنواختی یک شاخص مهم برای اندازه گیری توزیع نقاط تطبیق است.

رقیق‌سازی دقت (DOP) اصطلاحی است که در ناوبری ماهواره‌ای و مهندسی ژئوماتیک برای تعیین اثر ضربی اضافی هندسه ماهواره ناوبری بر دقت اندازه‌گیری موقعیتی استفاده می‌شود، که می‌تواند برای ارزیابی ویژگی‌های چیدمان هندسی فضایی صورت‌های فلکی استفاده شود [ 24 ، 25 ، 26 ] ]. DOP نشان می دهد که توزیع ماهواره در هر صفحه مداری چقدر یکنواخت است [ 27]. HDOP که نوعی DOP است، دقت موقعیت هواپیما را بر اساس مختصات طول و عرض جغرافیایی ماهواره بیان می کند. توزیع نقطه به رابطه موقعیتی مختصات نقطه روی تصویر بستگی دارد. مختصات نقطه ای (x و y) روی تصویر مشابه مختصات طول و عرض جغرافیایی ماهواره است. در این مطالعه، HDOP برای تعیین کمیت یکنواختی توزیع نقطه انتخاب شد.

همانطور که در شکل 1 نشان داده شده است ، نقطه مرکزی (جعبه سفید) با یک گیرنده مقایسه شده است، و نقاط مشخصه (نقاط سیاه) در مناطق همپوشانی با ماهواره ها مقایسه شده است. در اولین مرحله در محاسبات HDOP ، بردار واحد از نقطه مرکزی به یک نقطه دلخواه i $(\frac{(x_{i} - x)}{R_{i}}, \frac{(y_{i} - y)}{R_{i}})$ در نظر گرفته شده اند. اینجا، $R_{i} = \sqrt{{(x_{i} - x)}^{2} + {(y_{i} - y)}^{2}}$ ، که در آن x و y موقعیت نقطه مرکزی را نشان می دهند و $x_{i}$ و $y_{i}$ موقعیت یک نقطه دلخواه i روی تصویر را مشخص کنید. ماتریس A به صورت زیر فرموله شده است:

A = ⎡⎣⎢⎢⎢⎢⎢⎢⎢⎢ ( ایکس 1 - x ) آر 1 ( ایکس 2 - x ) آر 2 ⋮ ( ایکس n - x ) آر n ( y 1 - y ) آر 1 ( y 2 - y ) آر 2 ⋮ ( y n - y ) آر n 11 ⋮ 1 ⎤⎦⎥⎥⎥⎥⎥⎥⎥⎥ .

(1)

سه عنصر هر ردیف A اجزای یک بردار واحد از نقطه مرکزی تا نقطه نشان داده شده هستند. HDOP توسط:

اچ D O P = tr ((آ تی الف) - 1) ———-\sqrt ،

(2)

جایی که:

آ تی A = ⎡⎣⎢⎢⎢⎢⎢⎢ \sum n i = 1 ( ایکس من - x ) 2 آر 2 من \sum n i = 1 ( y من - y ) ( ایکس من - x ) آر 2 من \sum n i = 1 ( ایکس من - x ) آر من \sum n i = 1 ( ایکس من - x ) ( y من - y ) آر 2 من \sum n i = 1 ( y من - y ) 2 آر 2 من \sum n i = 1 ( y من - y ) آر من \sum n i = 1 ( ایکس من - x ) آر من \sum n i = 1 ( y من - y ) آر من n ⎤⎦⎥⎥⎥⎥⎥⎥ .

(3)

در اینجا n تعداد نقاط روی تصویر را نشان می دهد، $t r (A^{T} A) = 2 n$ . فرض کنید که $λ_{1}, λ_{2}$ ، و $λ_{3}$ مقادیر ویژه هستند $A^{T} A$ ، سپس $λ_{1} + λ_{2} + λ_{3} = 2 n$ . قضیه دیسک گرشگورین [ 28 ] در نظریه ماتریس نشان می دهد که محدوده مقادیر ویژه اول و دوم $A^{T} A$ همان هستند. علاوه بر این، ما از ادبیات [ 29 ] می دانیم که $λ_{3} \geq n$ . از این رو:

اچ D O P = tr ((آ تی الف) - 1) ———-\sqrt = tr (حفاری_1 λ 1 ، 1 λ 2 ، 1 λ 3)) —————-\sqrt = 1 λ 1 + 1 λ 2 + 1 λ 3 ———-\sqrt \geq 2 \times (1 λ 1 \times 1 λ 2) 1 2 + 1 λ 3 —————-\sqrt \geq 5 n -\sqrt .

(4)

همانطور که از معادلات (1) تا (4) مشاهده می شود، HDOP به تعداد و موقعیت نقاط مربوط می شود. بنابراین، هدف HDOP تقسیم بر $\sqrt{\frac{5}{n}}$ حذف اثر تعداد امتیاز است. در همین حال، از روش نرمال سازی برای تبدیل استفاده می شود $H D O P \times \sqrt{\frac{n}{5}}$ در محدوده 0-1. به طور مشخص، $H D O P \times \sqrt{\frac{n}{5}} - 1$ می تواند محدوده خود را از (1، + $\infty$ ) تا (0، + $\infty$ ). سپس، تابع ضد تانژانت برای تبدیل، با محدوده بین 0 و π/2 انتخاب می شود. پس از آن، نتیجه تبدیل در 2 ضرب می شود و سپس بر π تقسیم می شود. در نهایت، HDOP را می توان بین 0 و 1 تبدیل کرد:

اچ D O پ * = 2 \times a r c t a n (H D O P \times n 5 -\sqrt - 1) / π .

(5)

نقاط مشخصه ای که موقعیت مکانی یکسان را در دو یا چند تصویر نشان می دهند، یک جفت نقطه تطبیق هستند. همانطور که در شکل 1 نشان داده شده است ، نقاط تطبیق از نقاط مشخصه در تصاویر چپ و راست تشکیل شده است و مختصات پیکسل آنها در تصاویر مختلف متفاوت است. از این رو

H D O P^{*}

محاسبه شده با استفاده از معادلات (1) – (5) در سمت چپ و راست تصاویر متفاوت است. برای سنجش عدم قطعیت توزیع نقاط تطبیق، این مطالعه میانگین را انتخاب کرد

H D O P^{*}

در تمام تصاویر به عنوان نتیجه نهایی.

کمیت برای عدم قطعیت توزیع نقطه تطبیق به صورت زیر طراحی شده است:

مراحل خاص:

1. نقاط تطبیق در چندین تصویر استخراج می شوند.
2. ناحیه همپوشانی یا علاقه مند چندین تصویر تخمین زده می شود و مختصات نقطه مرکزی ناحیه همپوشانی یا علاقه مند محاسبه می شود.
3.

H D O P^{*}

به ترتیب بر اساس نقاط ویژگی در مناطق همپوشانی محاسبه می شود.
4.

\bar{H D O P^{*}}

محاسبه می شود که میانگین آن است

H D O P^{*}

روی همه تصاویر

در این مطالعه،

\bar{H D O P^{*}}

عدم قطعیت توزیع نقطه تطبیق را نشان می دهد و دارای محدوده [0، 1] است. چه زمانی

\bar{H D O P^{*}}

، محاسبه شده توسط نقاط تطبیق یک توزیع خاص، نزدیک به 0 است، کیفیت مدل های سه بعدی بازسازی شده بر اساس این نقاط تطبیق ممکن است عالی باشد. چه زمانی

\bar{H D O P^{*}}

نزدیک به 1 است، ممکن است نیاز به استخراج مجدد نقاط تطبیق برای بازسازی سه بعدی وجود داشته باشد.

3. آزمایش کنید

برای آزمایش اینکه آیا توزیع نقطه تطبیق کوانتیزه شده با روش پیشنهادی می تواند کیفیت بازسازی سه بعدی را منعکس کند، جفت های استریو بر اساس صحنه های شبیه سازی شده و واقعی انتخاب می شوند. در همین حال، داده‌های حقیقت پایه نیز می‌تواند ارائه شود و برای ارزیابی عدم قطعیت مدل‌های سه‌بعدی بازسازی‌شده بر اساس نقاط تطبیق استفاده شود.

3.1. صحنه شبیه سازی

3.1.1. منبع اطلاعات

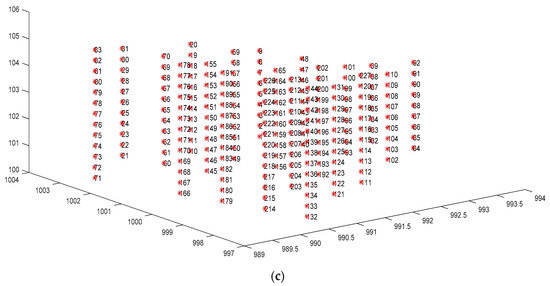
صحنه شبیه سازی این آزمایش، میدان کالیبراسیون داخلی دانشگاه عادی نانجینگ در چین بود. عکس‌ها با OLYMPUS E-20 گرفته شده‌اند و اندازه عکس‌ها ۲۵۶۰×۱۹۲۰ پیکسل، با فاصله کانونی ۹ میلی‌متر بود. جفت استریو از هر دو عکس در شکل 2 a,b تشکیل شده بود و همپوشانی آن 80٪ بود. در مجموع 227 جفت نقطه تطبیق با دست استخراج شد و مختصات مربوط به نقاط سه بعدی آنها (داده های حقیقت زمین) در شکل 2 ج نشان داده شده است. اینها با ساخت سیستم مختصات محلی اندازه گیری شدند و واحد متر بود.

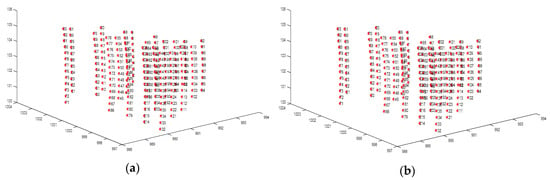
سه گروه از داده های تجربی برای تجزیه و تحلیل طراحی شد. گروه اول شکل 3 (a1-d1) بود. نقاط تطبیقی به طور مساوی با اعداد مختلف توزیع شده است (227 جفت در شکل 3 (a1)، 160 جفت در شکل 3 (b1)، 90 جفت در شکل 3 (c1) و 20 جفت در شکل 3 (d1)). مناطق توزیع شده گروه دوم ( شکل 3 (a2-d2)) و سوم ( شکل 3 (a3-d3)) تعداد مشابهی از نقاط تطبیق را در مناطق مختلف توزیع شده نشان می دهند. پنجاه جفت نقطه تطبیق با نمونه گیری تصادفی و با کنترل مختصات پیکسلی روی تصاویر استخراج شد و مناطق توزیع شده آنها در شکل 3 نشان داده شده است.(a2-d3).

3.1.2. $\bar{H D O P^{*}}$ از امتیازهای تطبیق

روش پیشنهادی در این تحقیق می تواند برای محاسبه استفاده شود

\bar{H D O P^{*}}

نقاط تطبیق با اعداد مختلف و مناطق مختلف توزیع شده است. به طور خاص، ناحیه همپوشانی (مستطیل های قرمز در شکل 3 از جفت استریو باید تخمین زده شود، و نقاط مرکزی آنها (نقاط زرد در شکل 3) قابل محاسبه است.

H D O P_{L}^{*}

در تصویر سمت چپ و

H D O P_{R}^{*}

در تصویر سمت راست با استفاده از معادلات (1) – (5) و سپس محاسبه شد

\bar{H D O P^{*}}

مشخص شد. نتایج محاسبه شده خاص در جدول 1 نشان داده شده است.

را

\bar{H D O P^{*}}

مقدار بین 0-1 توزیع می شود. در جدول 1 ، مقادیر در شکل 3 (a1-d1) مشابه هستند. این نشان می دهد که تعداد نقاط تطبیق تأثیر کمتری بر آن دارد

\bar{H D O P^{*}}

. مقادیر در شکل 3 (a2-d2) نیز مشابه و نزدیک به 0 هستند. این بدان معنی است که مناطق توزیع شده از نقاط تطبیق اطراف نقطه مرکزی مناطق همپوشانی تاثیر کمتری بر روی

\bar{H D O P^{*}}

. مقادیر در شکل 3 (a3-d3) در حال افزایش است. مقدار در شکل 3 (a3) کوچکترین و نزدیک به 0 است و در شکل 3 (d3) بزرگترین و نزدیک به 1 است. این بدان معنی است که یکنواختی توزیع نقاط تطبیق در مناطق همپوشانی تأثیر می گذارد.

\bar{H D O P^{*}}

. هنگامی که نقاط تطبیق به طور مساوی در مناطق همپوشانی توزیع می شوند،

\bar{H D O P^{*}}

مقدار کوچک و نزدیک به 0 است. هنگامی که نقاط تطبیق در مناطق همپوشانی خوشه‌بندی می‌شوند،

\bar{H D O P^{*}}

مقدار بزرگ و نزدیک به 1 است.

3.1.3. ارزیابی نتیجه

منطقی بودن روش پیشنهادی با تعداد و توزیع نقاط تطبیق ارزیابی شد.

با تعداد امتیازهای تطبیق ارزیابی می شود

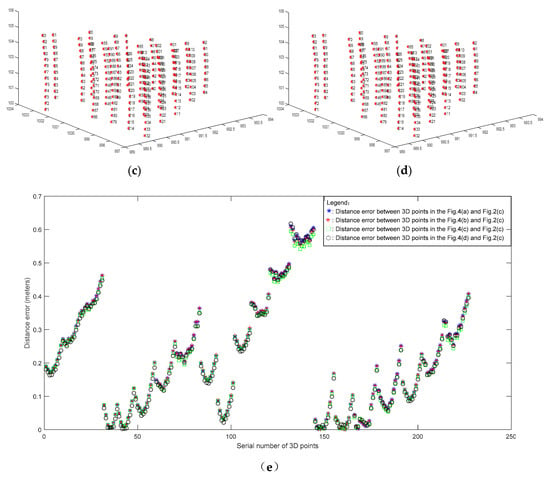
در این آزمایش، پارامترهای داخلی و خارجی جفت استریو در شکل 2 را می توان چهار بار با استفاده از الگوریتم تبدیل خطی مستقیم و نقاط تطبیق در شکل 3 (a1-d1) محاسبه کرد. بنابراین، مختصات نقاط سه بعدی نیز چهار بار محاسبه شد و محاسبات در شکل 4 a-d نشان داده شده است. متعاقباً، محاسبات از مقادیر واقعی در شکل 2 ج کسر شد. خطاهای فاصله پس از تفریق در شکل 4 e نشان داده شده است.

از شکل 4 e می توان دریافت که خطاهای فاصله نقاط سه بعدی محاسبه شده با نقاط تطبیق در شکل 3 (a1–d1) مشابه است و تعداد نقاط تطبیق تأثیر کمتری بر بازسازی سه بعدی دارد. بنابراین، روش پیشنهادی در این مطالعه، اثر تعداد نقاط تطبیق را بر بازسازی سه بعدی حذف می‌کند. همانطور که در شکل 3 (a1-d1) در جدول 1 نشان داده شده است

\bar{H D O P^{*}}

مقادیر محاسبه شده با تطبیق نقاط با اعداد مختلف نیز مشابه هستند و این مقادیر با تعداد نقاط تطبیق تغییر نمی کنند.

توسط توزیع امتیازهای تطبیق ارزیابی شده است

این آزمایش از دو بخش تشکیل شده است. یکی مطالعه قانون تغییر نقاط سه بعدی هنگامی که نقاط تطبیق به سمت نقطه مرکزی مناطق همپوشانی جمع شده اند، و دیگری تجزیه و تحلیل زمانی است که نقاط تطبیق به سمت یک گوشه از مناطق همپوشانی جمع شده اند.

• نقاط تطبیق جمع آوری شده به سمت نقطه مرکزی مناطق همپوشانی

نقاط سه بعدی را نیز می توان چهار بار توسط شکل 3 (a2-d2) محاسبه کرد و مختصات آنها دقیقاً برابر نیست. خطاهای فاصله خاص در شکل 5 نشان داده شده است.

نقاط تطبیق در شکل 3 (a2-d2) به طور مساوی در اطراف نقطه مرکزی نواحی همپوشانی توزیع شده اند و دارای مناطق توزیع شده متفاوتی هستند (مستطیل های زرد). خطاهای فاصله نقاط سه بعدی محاسبه شده توسط این نقاط تطبیق نیز مشابه هستند، همانطور که در شکل 5 نشان داده شده است. مناطق پراکنده نقاط تطبیق اطراف نقطه مرکزی مناطق همپوشانی نیز تأثیر کمتری بر بازسازی سه بعدی دارند. بنابراین، نقطه مرکزی نواحی همپوشانی به عنوان نقطه مهم جفت‌های استریو در نظر گرفته می‌شود و در روش پیشنهادی، به عنوان گیرنده برای اندازه‌گیری عدم قطعیت توزیع نقاط تطبیق انتخاب می‌شود.

• نقاط تطبیق جمع آوری شده به سمت یک گوشه از مناطق همپوشانی

نقاط سه بعدی را نیز می توان چهار بار توسط شکل 3 (a3-d3) محاسبه کرد و مختصات آنها نیز دقیقاً برابر نیست. تفاوت فاصله خاص در شکل 6 نشان داده شده است.

نقاط تطبیق در شکل 3 (a3-d3) دارای تعداد نقاط تطبیقی در مناطق مختلف توزیع شده (مستطیل های زرد) هستند و به تدریج به سمت گوشه سمت راست پایین مناطق همپوشانی جمع می شوند. همانطور که در شکل 6 نشان داده شده است، خطاهای فاصله نقاط سه بعدی محاسبه شده توسط این نقاط تطبیق، تفاوت زیادی دارند . توزیع نقاط منطبق با انحراف از نقطه مرکزی بر دقت نقاط سه بعدی تأثیر می گذارد. هنگامی که نقاط تطبیق بیشتر به صورت خوشه ای و دورتر از نقطه مرکزی هستند، خطاهای نقطه سه بعدی محاسبه شده بزرگتر هستند، همانطور که با نماد ○ در شکل 6 نشان داده شده است.. با این حال، همه خطاهای فاصله نماد ○ بزرگترین نیستند. در میان آنها، شماره های سریال 105-136، 180-195، و 205-220 کوچکترین هستند. این به این دلیل است که نقاط تطبیق متناظر آنها عمدتاً در گوشه سمت راست پایین مناطق همپوشانی توزیع شده است. با تجزیه و تحلیل چهار گروه از خطاهای فاصله در شکل 6 ، می توان گفت که نقاط سه بعدی محاسبه شده در منطقه ای که نقاط تطبیق در آن قرار دارند، دقیق تر هستند و خطاهای فاصله کمتری دارند.

علاوه بر این، جدول 2 میانگین خطاهای فاصله را در شکل 6 نشان می دهد که دقت نقطه سه بعدی را به عنوان یک کل منعکس می کند. در جدول، میانگین خطا در شکل 3 (a3) کوچکترین و به دنبال آن مقدار در شکل 3 (b3) و حداکثر مقدار در شکل 3 (d3) آمده است. این با قانون تغییر سازگار است

\bar{H D O P^{*}}

از شکل 3 (a3-d3) در جدول 1 .

از طریق آزمایش های فوق، رابطه بین نقاط سه بعدی و توزیع نقطه تطبیق به صورت زیر یافت شد:

تعداد نقاط تطبیق تأثیر کمتری بر دقت نقاط سه بعدی داشت.
مناطق توزیع شده از نقاط تطبیق اطراف نقطه مرکزی مناطق همپوشانی تاثیر کمتری بر دقت نقاط سه بعدی داشتند.
توزیع نقطه تطبیق منحرف از نقطه مرکزی مناطق همپوشانی بر دقت نقاط سه بعدی تأثیر می گذارد.

بنابراین، روش پیشنهادی نقطه مرکزی نواحی همپوشانی را به عنوان گیرنده برای اندازه گیری HDOP توزیع نقطه ویژگی انتخاب کرد و تحت تأثیر تعداد نقاط تطبیق حذف شده، از آن استفاده کرد.

\bar{H D O P^{*}}

برای اندازه گیری عدم قطعیت توزیع نقاط تطبیق در بازسازی سه بعدی.

در یک سری از آزمایش های صحنه شبیه سازی شده، ما همچنین دریافتیم که رابطه بین توزیع نقاط تطبیق و

\bar{H D O P^{*}}

با توزیع نقطه تطبیق و دقت نقاط سه بعدی سازگار بود. از این رو،

\bar{H D O P^{*}}

می توان برای اندازه گیری عدم قطعیت توزیع نقطه تطبیق در بازسازی سه بعدی استفاده کرد.

3.2. صحنه واقعی

3.2.1. منبع اطلاعات

در این آزمایش، جفت استریو (دروازه دانشگاه Tsinghua) [ 28 ] منتشر شده توسط موسسه اتوماسیون آکادمی علوم چین برای آزمایش انتخاب شد. نقاط مشخصه در شکل 7 a,b با استفاده از الگوریتم SIFT شناسایی شدند. از این رو، نقاط تطبیق را می توان با استفاده از الگوریتم جستجوی نزدیکترین همسایه درخت K-d استخراج کرد. در مجموع 943 جفت نقطه تطبیق استخراج شد. ابرهای نقطه ای دروازه دانشگاه Tsinghua در شکل 7 c نشان داده شده است که داده های حقیقت زمینی هستند.

برای تأیید منطقی بودن روش پیشنهادی در این مطالعه، داده‌های تجربی زیر برای تجزیه و تحلیل طراحی شدند. 943 جفت نقطه تطبیق در شکل 8 a در سراسر منطقه همپوشانی وجود دارد، و 300 جفت در شکل 8 b اطراف نقطه مرکزی مناطق همپوشانی وجود دارد. در همین حال، 442 جفت در شکل 8 c و 300 جفت در شکل 8 d با نواحی پراکنده متفاوت در اطراف گوشه سمت راست پایین مناطق همپوشانی استخراج شدند.

3.2.2. $\bar{H D O P^{*}}$ از امتیازهای تطبیق

ناحیه همپوشانی (مستطیل های قرمز در شکل 8 ) جفت استریو باید تخمین زده شود و سپس نقاط مرکزی آنها (نقاط زرد در شکل 8 ) قابل محاسبه است.

H D O P_{L}^{*}

در تصویر سمت چپ و

H D O P_{R}^{*}

در تصویر سمت راست با استفاده از معادلات (1) – (5) محاسبه شد و سپس،

\bar{H D O P^{*}}

مشخص شد. نتایج محاسبه شده خاص در جدول 3 نشان داده شده است.

در جدول 3 ،

\bar{H D O P^{*}}

مقادیر در شکل 8 a-d به تدریج در حال افزایش هستند. مقدار در شکل 8 a 0.0284 است. این کوچکترین و نزدیک به 0 است. مقدار در شکل 8 c 0.2530 است. خیلی بزرگ نیست علاوه بر این، مقدار در شکل 8 d 0.9419 است. این بزرگترین و نزدیک به 1 است. ما می توانیم از رابطه بین

\bar{H D O P^{*}}

و نقاط تطبیق که قانون تغییر از

\bar{H D O P^{*}}

مربوط به توزیع است، نه با تعداد نقاط تطبیق. وقتی توزیع نقاط منطبق به صورت خوشه ای و دور از نقطه مرکزی نواحی همپوشانی است، آن است

\bar{H D O P^{*}}

ممکن است یک مقدار بزرگتر و نزدیک به 1 باشد.

3.2.3. ارزیابی نتیجه

در این آزمایش، نرم افزار منبع باز بصری SFM [ 30 ، 31 ] برای بازسازی ابرهای نقطه متراکم انتخاب شد. Visual SFM به شرح زیر عمل می‌کند: جفت‌های استریو (با ویژگی‌ها) در شکل 7 بارگذاری شده‌اند. نقاط تطبیق در شکل 8 وارد شده است. ابرهای نقطه پراکنده محاسبه می شوند. و بازسازی متراکم برای به دست آوردن ابرهای نقطه متراکم اجرا می شود. بازسازی ابرهای نقطه متراکم در شکل 9 نشان داده شده است .

چهار گروه در دسترس هستند که هر یک تصویر نمایشی از ابرهای نقطه متراکم است که بر اساس نقطه تطبیق در شکل 8 بازسازی شده است. می تواند برخی از روابط بین ابرهای نقطه سه بعدی و نقاط تطبیق را منعکس کند.

نقاط تطبیق در شکل 8 b,d دارای تعداد یکسان و توزیع های متفاوت هستند و سه گروه از ابرهای نقطه سه بعدی که بازسازی شده اند از آنها کاملاً متفاوت استفاده می کنند. در اینجا، کیفیت آن با استفاده از نقاط تطبیق اطراف نقطه مرکزی مناطق همپوشانی بالاتر است. بنابراین، می‌توان گفت که تطبیق نقاط اطراف نقطه مرکزی ممکن است تأثیر کمتری بر ابرهای نقطه سه بعدی داشته باشد.
نقاط تطبیق در شکل 8 a,b دارای اعداد مختلفی هستند و عمدتاً در اطراف نقطه مرکزی مناطق همپوشانی توزیع شده اند. با این حال، سه گروه از ابرهای نقطه سه بعدی که بازسازی شدند مشابه هستند. بنابراین، تعداد نقاط تطبیق ممکن است تأثیر کمتری بر ابرهای نقطه سه بعدی داشته باشد.
نقاط تطبیق در شکل 8 a,c,d دارای نواحی توزیع شده متفاوتی هستند و به تدریج به سمت گوشه سمت راست پایین مناطق همپوشانی جمع می شوند. در اینجا، سه گروه از ابرهای نقطه سه بعدی که با استفاده از آنها بازسازی شده اند کاملاً متفاوت هستند. اشکال کلی نشان داده شده در شکل 9 a,c کامل تر هستند و شکل 9 d ناقص است. در همین حال، در مقایسه با شکل 9 a، تعداد کمی در شکل 9 c و تعداد زیادی در شکل 9 d از اشیاء بلوکی وجود دارد که با دروازه بازسازی شده Tsinghua مرتبط نیستند. قانون تغییر فوق با یکنواختی توزیع نقطه تطبیق سازگار است.

روابط فوق بین ابرهای نقطه سه بعدی و نقاط تطبیق در آزمایش صحنه واقعی با آنچه در آزمایش صحنه شبیه سازی شده مطابقت دارد.

علاوه بر این، اندازه گیری کمی شباهت بین مدل های سه بعدی ضروری است. مطالعات زیادی در مورد تخمین وضعیت مدل های سه بعدی یا جستجوی شی در بینایی مبتنی بر مدل انجام شده است [ 32 ، 33 ، 34 ، 35 ]. تطبیق توپولوژی اشکال سه بعدی [ 33 ] با مقایسه نمودارهای Reeb Multiresolutional به سرعت، دقیق و خودکار محاسبه می شود. این مطالعه از آن برای محاسبه شباهت بین مدل‌های سه بعدی بازسازی‌شده و واقعی استفاده کرد. در اینجا، مدل های سه بعدی را می توان از طریق بازسازی سطح پواسون بر اساس ابرهای نقطه متراکم در شکل 7 c و شکل 9 به دست آورد. جدول 4 نشان می دهد که مدل های سه بعدی درشکل 9 a-c بیشتر شبیه هستند و شکل 9 d کمترین شباهت را به شکل 7 c دارد.

تجزیه و تحلیل همبستگی در جدول 4 نشان می دهد که کیفیت مدل 3 بعدی بازسازی شده بر اساس شکل 9 a بهتر است و به دنبال آن بر اساس شکل 9 b است، در حالی که بر اساس شکل 9 d ضعیف است. چنین نتایج تحلیلی با قانون تغییر سازگار است

\bar{H D O P^{*}}

در جدول 3 . بنابراین می توانیم استفاده کنیم

\bar{H D O P^{*}}

برای اندازه گیری عدم قطعیت توزیع نقطه تطبیق در بازسازی سه بعدی. در این مطالعه، یک

\bar{H D O P^{*}}

مقدار نزدیک به 0 ممکن است نشان دهنده بازسازی سه بعدی با کیفیت بالا باشد و مقدار نزدیک به 1 ممکن است نشان دهنده بازسازی سه بعدی با کیفیت پایین باشد.

4. نتیجه گیری

از طریق یک سری آزمایش، ما برخی از نمایش‌های بین بازسازی سه بعدی و نقاط تطبیق را به دست آوردیم.

تعداد نقاط تطبیق در این مطالعه تأثیر کمتری بر دقت بازسازی سه بعدی داشت.
مناطق توزیع شده از نقاط تطبیق اطراف نقطه مرکزی مناطق همپوشانی تاثیر کمتری بر دقت بازسازی سه بعدی داشتند.
توزیع نقطه تطبیق منحرف از نقطه مرکزی مناطق همپوشانی بر دقت بازسازی سه بعدی تأثیر می گذارد.

برای تعیین کمیت عدم قطعیت توزیع نقطه تطبیق در بازسازی سه بعدی، روش پیشنهادی باید بازنمایی های فوق را منعکس کند. بنابراین روش پیشنهادی به صورت زیر طراحی شد:

HDOP از ناوبری ماهواره ای و مهندسی ژئوماتیک به این مطالعه معرفی شد. در اینجا، نقطه مرکزی مناطق همپوشانی به عنوان گیرنده انتخاب شد، که می تواند اثر نقاط تطبیق اطراف نقطه مرکزی را در HDOP کاهش دهد.
$H D O P^{*}$ برای اندازه گیری توزیع نقاط ویژگی ساخته شده است و دارای محدوده [0، 1] است. اینجا، $H D O P^{*} = 2 \times a r c t a n (H D O P \times \sqrt{\frac{n}{5}} - 1) / π$ ، جایی که $H D O P \times \sqrt{\frac{n}{5}}$ اثر تعداد نقاط ویژگی را حذف می کند.
$\bar{H D O P^{*}}$ ، میانگین از $H D O P^{*}$ در تمام تصاویر، برای اندازه گیری عدم قطعیت توزیع نقطه تطبیق در بازسازی سه بعدی استفاده شد.

در این مطالعه آزمایشات صحنه شبیه سازی شده و واقعی انجام شد و مشخص شد که قوانین تغییر از

\bar{H D O P^{*}}

، بازسازی سه بعدی و توزیع نقطه تطبیق سازگار بودند. بنابراین منطقی است برای

\bar{H D O P^{*}}

برای نشان دادن عدم قطعیت توزیع نقطه تطبیق در بازسازی سه بعدی.

در مرحله استخراج ویژگی بازسازی سه بعدی مبتنی بر تصویر، روش پیشنهادی را می توان برای اندازه گیری توزیع نقاط تطبیق استفاده کرد. چه زمانی

\bar{H D O P^{*}}

نزدیک به 0 است، این بدان معناست که کیفیت مدل‌های سه بعدی بازسازی‌شده ممکن است بهتر باشد، و ما می‌توانیم به بازسازی مدل‌های سه بعدی بر اساس این نقاط تطبیق ادامه دهیم. علاوه بر این، وقتی نزدیک به 1 است، ممکن است نیاز به استخراج مجدد نقاط تطبیق برای مدل‌های سه بعدی داشته باشیم.

منابع

رموندینو، اف. الحکیم، اس. مدلسازی سه بعدی مبتنی بر تصویر: یک بررسی. فتوگرام ضبط 2006 ، 21 ، 269-291. [ Google Scholar ] [ CrossRef ]
موسیالسکی، پ. ونکا، پی. Aliaga، DG; ویمر، ام. گول، LV; Purgathofer, W. بررسی بازسازی شهری. محاسبه کنید. نمودار. انجمن 2013 ، 32 ، 1-26. [ Google Scholar ] [ CrossRef ]
Thuy، N. دیوید، اس. نلسون، ام. جولین، ام. Neelima, S. سیستم بازسازی سه بعدی مبتنی بر نور برای گیاهان. Sensors 2015 ، 15 ، 18587-18612. [ Google Scholar ]
کاریویک، جی ال. اسمیت، مگاوات؛ Quincey، DJ Structure from Motion in the Geosciences . John Wiley and Sons Limited: Chichester، UK، 2016. [ Google Scholar ]
هارتلی، آر. زیسرمن، A. هندسه چند نما در بینایی کامپیوتری . انتشارات دانشگاه کمبریج: کمبریج، انگلستان، 2003. [ Google Scholar ]
الحاکیم، SF دقت در اندازه گیری تصویر. بین المللی Soc. انتخاب کنید مهندس 1994 ، 2350 ، 218-228. [ Google Scholar ]
بویر، ک. کراننبورگ، سی. Dougherty، S. ارزیابی آشکارساز لبه با استفاده از منحنی های سنگ تجربی. محاسبه کنید. Vis. تصویر زیر. 2001 ، 84 ، 77-103. [ Google Scholar ] [ CrossRef ]
سانکوفسکی، دبلیو. وکودارچیک، ام. Kacperski, D. برآورد عدم قطعیت اندازه گیری در سیستم دید استریو. تصویر Vis. محاسبه کنید. 2017 ، 60 ، 70-81. [ Google Scholar ] [ CrossRef ]
کانازاوا، ی. کناتانی، ک. آیا واقعاً باید ماتریس های کوواریانس را برای ویژگی های تصویر در نظر بگیریم؟ IEEE Int. Conf. محاسبه کنید. Vis. 2001 ، 2 ، 301-306. [ Google Scholar ]
بروکس، ام جی. Chojnacki، W. گاولی، دی. Hengel, AVD اطلاعات کوواریانس چه ارزشی در تخمین پارامترهای بینایی دارد. IEEE Int. Conf. محاسبه کنید. Vis. 2001 ، 302-308. [ Google Scholar ]
کناتانی، ک. مدل‌سازی عدم قطعیت و انتخاب مدل برای استنتاج هندسی. IEEE Trans. الگوی مقعدی ماخ هوشمند 2004 ، 26 ، 1307-1319. [ Google Scholar ] [ CrossRef ]
ونگ، جی. هوانگ، تی. حرکت و ساختار از دو دیدگاه: الگوریتم‌ها، تحلیل خطا و تخمین خطا. الگوی مقعدی ماخ هوشمند 1989 ، 11 ، 451-476. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
کوی، جی. حداقل، سی. Bai, X. یک روش تخمین وضعیت بهبودیافته بر اساس بردار پروجکشن با عدم قطعیت خطای نویز. IEEE Photonics J. 2019 , 11 . [ Google Scholar ] [ CrossRef ]
استیل، آر. Jaynes, C. عدم قطعیت ناشی از نویز تصویر کوواریانت. محاسبه کنید. Vis. تشخیص الگو 2005 ، 1 ، 1063-1070. [ Google Scholar ]
پارک، اچ. شین، دی. بائه، اچ. Baeg, H. مدل عدم قطعیت فضایی برای ویژگی های بصری با استفاده از کینکت؟ Sensors 2012 , 12 , 8640-8662. [ Google Scholar ] [ CrossRef ] [ PubMed ][ نسخه سبز ]
بلهاوا، ا. کوهلر، اس. Hirsch, E. ارزیابی خطا در یک سیستم بازسازی سه بعدی مبتنی بر استریوویژن. J. فرآیند ویدئو تصویر. 2010 ، 6 ، 1-12. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
هارالیک، آر. انتشار کوواریانس در بینایی کامپیوتر. تشخیص الگو آرتیف. هوشمند 1996 ، 10 ، 561-572. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
دی لئو، جی. لیگوری، سی. Paolillo، A. انتشار کوواریانس برای تخمین عدم قطعیت در Stereo Vision. Ieee Trans. ساز. Meas. 2011 ، 60 ، 1664-1673. [ Google Scholar ] [ CrossRef ]
لیو، بی جی؛ یوان، LX؛ ژنگ، NN; Shu، F. چندین مدل هندسه دوربین و تجزیه و تحلیل خطا برای تطبیق تصویر در ماشین بینایی سه بعدی. Acta Photonica Sin. 1997 ، 26 ، 737-741. [ Google Scholar ] [ CrossRef ]
گی، ی. سو، آ. Du, J. روش تطبیق الگوی نقطه با استفاده از SURF و Shape Context. انتخاب کنید بین المللی J. Light Electron Opt. 2013 ، 124 ، 1869-1873. [ Google Scholar ] [ CrossRef ]
تانگ، جی. وانگ، سی سی; Wang, P. مطالعه بر روی بهبود تشخیص نقاط ویژگی تصویر و دقت تطبیق در سیستم بینایی دوچشمی. در مجموعه مقالات کنفرانس بین المللی انفورماتیک صنعتی و مهندسی کامپیوتر، شیان، چین، 10-11 ژانویه 2015. [ Google Scholar ]
ژائو، ی. الگوریتم تطبیق نقاط مشخصه مبتنی بر توزیع وضوح محلی Su، JB. جی. الکترون. Imaging 2014 , 23 , 013011. [ Google Scholar ] [ CrossRef ]
هو، م. لیو، ی. فن، Y. تطبیق نقطه ویژگی تصویر قوی بر اساس فاصله ساختاری . Springer: برلین/هایدلبرگ، آلمان، 2015. [ Google Scholar ]
کیهارا، م. Okada، T. روش انتخاب ماهواره و دقت برای سیستم موقعیت یابی جهانی. Navigation 1984 , 31 , 8-20. [ Google Scholar ] [ CrossRef ]
وو، CH; هو، YW; چن، LW; Huang, YD کشف عبارات تقریبی رقت هندسی GPS با استفاده از برنامه ریزی ژنتیکی. Adv. مهندس نرم افزار 2012 ، 45 ، 332-340. [ Google Scholar ] [ CrossRef ]
سانتر، آر. گایگر، ا. Banville، S. هندسه رقیق شدن GPS با دقت: بازبینی شده است. حلال جی پی اس. 2017 ، 21 ، 1747-1763. [ Google Scholar ] [ CrossRef ]
لی، جی. لی، ز. Zhou، W. مطالعه بر روی حداقل GDOP در ناوبری ماهواره ای و کاربردهای آن. Acta Geod. Et Cartogr. گناه 2011 ، 40 ، 85-88. [ Google Scholar ]
بو، سی جی; لو، نظریه ماتریس YS . انتشارات دانشگاه مهندس هاربین: هاربین، چین، 2003; صص 164-174. [ Google Scholar ]
شنگ، اچ. یانگ، جی اس. Zeng، FL حداقل مقدار GDOP در موقعیت یابی شبه برد. کنترل فرماندهی کنترل آتش 2009 ، 34 ، 22-24. [ Google Scholar ]
VisualSFM: یک ساختار بصری از سیستم حرکت. در دسترس آنلاین: https://ccwu.me/vsfm/ (در 1 سپتامبر 2018 قابل دسترسی است).
وو، سی. آگاروال، اس. کورلس، بی. تنظیم بسته نرم افزاری چند هسته ای Seitz، SM. محاسبه کنید. Vis. تشخیص الگو 2011.
بسل، پی جی؛ مک کی، ND روشی برای ثبت اشکال سه بعدی. IEEE Trans. پامی 1992 ، 14 ، 239-256. [ Google Scholar ] [ CrossRef ]
چن، ی. مدیونی، جی. مدل‌سازی شی با ثبت تصاویر دامنه‌ای چندگانه. تصویر Vis. محاسبه کنید. 1992 ، 10 ، 145-155. [ Google Scholar ] [ CrossRef ]
ویس، آی. Ray, M. تشخیص شی سه بعدی مبتنی بر مدل از دید منفرد. IEEE Trans. پامی 2001 ، 23 ، 116-128. [ Google Scholar ] [ CrossRef ]
هیلاگا، م. شیناگاوا، ی. کومورا، تی. Kunii, L. تطبیق توپولوژی برای تخمین شباهت کاملاً خودکار اشکال سه بعدی. در مجموعه مقالات بیست و هشتمین کنفرانس سالانه گرافیک کامپیوتری و تکنیک های تعاملی، لس آنجلس، کالیفرنیا، ایالات متحده آمریکا، 12 تا 17 اوت 2001. [ Google Scholar ]

شکل 1. توزیع نقاط تطبیق. ( الف ) نقاط تطبیق خطی توزیع شده. ( ب ) نقاط تطبیق توزیع شده خوشه ای. ( ج ) نقاط تطبیق به طور مساوی توزیع شده است.

شکل 2. منبع داده صحنه شبیه سازی. ( الف ) تصویر سمت چپ و نقاط مشخصه. ( ب ) تصویر سمت راست و نقاط مشخصه. نمادهای + با همان عدد در ( a , b ) یک جفت نقطه مطابق هستند. ( ج ) مختصات واقعی نقاط سه بعدی (نمادهای *) مربوط به نقاط تطبیق.

شکل 3. نقاط تطبیق با اعداد مختلف و مناطق مختلف توزیع شده. 227 جفت در ( a1 )، 160 جفت در ( b1 )، 90 جفت در ( c1 ) و 20 جفت در ( d1 ) در همان مناطق توزیع شده وجود دارد. 50 جفت نقطه تطبیق وجود دارد که به سمت نقطه مرکزی مناطق همپوشانی در ( a2 – d2 ) و به سمت گوشه پایین سمت راست مناطق همپوشانی در ( a3 – d3 ) جمع شده‌اند.). مستطیل قرمز ناحیه همپوشانی جفت‌های استریو را نشان می‌دهد، مستطیل زرد نشان‌دهنده ناحیه‌ای است که نقاط تطبیق در آن قرار دارند، و نقطه زرد نشان‌دهنده موقعیتی است که نقطه مرکزی منطقه همپوشانی قرار دارد.

شکل 4. نقاط سه بعدی و خطاهای فاصله آنها. نقاط سه بعدی محاسبه شده بر اساس نقاط تطبیق در ( a ) شکل 3 (a1)، ( b ) شکل 3 (b1)، ( c ) شکل 3 (c1)، و ( d ) شکل 3 (d1). ( ه ) خطاهای فاصله نقاط سه بعدی بین مقادیر محاسبه شده و واقعی.

شکل 5. خطاهای فاصله نقاط سه بعدی محاسبه شده توسط شکل 3 (a2-d2) بین مقادیر محاسبه شده و واقعی.

شکل 6. خطاهای فاصله نقاط سه بعدی محاسبه شده توسط شکل 3 (a3-d3) بین مقادیر محاسبه شده و واقعی.

شکل 7. منبع داده صحنه واقعی ( https://vision.ia.ac.cn/zh/data/index.html ). ( الف ) تصویر سمت چپ و نقاط مشخصه. ( ب ) تصویر سمت راست و نقاط مشخصه. ( ج ) ابرهای نقطه حقیقت زمینی اسکن شده. نقاط مشخصه با تعداد یکسان در تصاویر چپ و راست نشان دهنده یک جفت نقطه تطبیق هستند.

شکل 8. تطبیق نقاط با الگوهای توزیع مختلف. ( الف ) در سراسر منطقه همپوشانی. ( ب ) اطراف نقطه مرکزی مناطق همپوشانی. با دامنه های مختلف توزیع شده در ( c ، d ) اطراف گوشه سمت راست پایین مناطق همپوشانی.

شکل 9. ابرهای نقطه ای متراکم. بازسازی شده توسط نقاط تطبیق در ( الف ) شکل 8 الف، ( ب ) شکل 8 ب، ( ج ) شکل 8 ج، و ( د ) شکل 8 د. ( ه ) نوار رنگ. رنگ های مختلف فاصله بین دوربین و جسم بازسازی شده را نشان می دهد. واحد فاصله متر است.

مقالات داخلی و بین المللی

بدون دیدگاه

دیدگاهتان را بنویسید لغو پاسخ

برای نوشتن دیدگاه باید وارد بشوید.

مشاورین هوش پیروزی

خلاصه

کلید واژه ها:

1. معرفی

2. روش ها