چکیده

چندین الگوریتم برای ساده سازی ساختمان ها بر اساس ساختار محلی آنها در دهه های گذشته توسعه یافته است. با این حال، ساختارهای محلی مختلف برای اهداف خاصی تعریف شده‌اند و هیچ الگوریتمی نمی‌تواند همه ساختمان‌ها را به‌طور مناسب ساده‌سازی کند. ما یک رویکرد ساده سازی ساختمان ترکیبی را بر اساس طبقه بندی ساختار محلی و استراتژی عقب نشینی پیشنهاد می کنیم. در این رویکرد، سازه‌های محلی طبقه‌بندی شده و با در نظر گرفتن ویژگی‌های متعامد و غیرمتعامد ساختمان‌ها، عملیات مبتنی بر آنها تعریف می‌شود. هر ساختمان برای مقیاس هدف با یک عملیات انتخابی مبتنی بر ساختار محلی به تدریج مقیاس به مقیاس ساده شده است. قوانین برای پشتیبانی از انتخاب عملیات مبتنی بر ساختار محلی با درخت تصمیم دودویی ساخته شده‌اند و زمانی که یک عملیات نامعتبر اعمال می‌شود، از استراتژی عقب‌گردی استفاده می‌شود. وقتی ساختمان خیلی کوچک است یا ارزیابی نشان می‌دهد که نمی‌توان آن را بر اساس ساختارهای محلی ساده کرد، الگوریتم‌های تطبیق یا بزرگ‌نمایی الگو برای ساده‌سازی ساختمان اعمال می‌شوند. یک مجموعه داده (1:10k) جمع آوری شده از Ordnance Survey برای آزمایش و مقیاس ساده شده 1:25k استفاده شد. نتایج، محدودیت‌های خوانایی و تغییر در مساحت، جهت‌گیری و موقعیت ساختمان‌های ساده شده را با مقایسه با نتایج تولید شده بر اساس چهار الگوریتم ساده‌سازی دیگر، در محدوده خاصی کنترل می‌کنند. استفاده احتمالی از رویکرد ما برای تغییر مقیاس مداوم ساختمان ها نیز مورد بحث قرار گرفته است. 10k) جمع آوری شده از Ordnance Survey برای آزمایش و مقیاس ساده 1:25k استفاده شد. نتایج، محدودیت‌های خوانایی و تغییر در مساحت، جهت‌گیری و موقعیت ساختمان‌های ساده شده را با مقایسه با نتایج تولید شده بر اساس چهار الگوریتم ساده‌سازی دیگر، در محدوده خاصی کنترل می‌کنند. استفاده احتمالی از رویکرد ما برای تغییر مقیاس مداوم ساختمان ها نیز مورد بحث قرار گرفته است. 10k) جمع آوری شده از Ordnance Survey برای آزمایش و مقیاس ساده 1:25k استفاده شد. نتایج، محدودیت‌های خوانایی و تغییر در مساحت، جهت‌گیری و موقعیت ساختمان‌های ساده شده را با مقایسه با نتایج تولید شده بر اساس چهار الگوریتم ساده‌سازی دیگر، در محدوده خاصی کنترل می‌کنند. استفاده احتمالی از رویکرد ما برای تغییر مقیاس مداوم ساختمان ها نیز مورد بحث قرار گرفته است.

کلید واژه ها:

تعمیم نقشه ; نمایش مقیاس پیوسته ; ساده سازی ساختمان ; ساختمان ها ; عملیات پیشرونده

1. مقدمه

ساده سازی یک عملیات مهم در تعمیم نقشه برای کاهش پیچیدگی ویژگی های هندسی پس از کاهش مقیاس است [ 1 ، 2 ]. ساختمان‌ها به عنوان ویژگی‌های مهم دست‌ساز در نقشه‌های توپوگرافی، موضوع تحقیقات شدید [ 3 ] شده‌اند. بسیاری از الگوریتم‌های ساده‌سازی ساختمان در چند دهه گذشته پیشنهاد شده‌اند. ساده سازی ساختمان معمولاً روی یک ساختمان واحد انجام می شود که عمدتاً مستقل از اطلاعات زمینه ای است. علاوه بر این، گاهی اوقات می توان آن را به طور جداگانه در فرآیند ساختن تعمیم نقشه انجام داد.
هدف ساده سازی ساختمان، نمایش مختصر ساختمان ها بسته به مقیاس نقشه یا موضوع، با الزامات خوانایی و نمایش خوب واقعیت است [ 4 ]. می توان آن را با جایگزینی ساختمان های اصلی با فرم ساده تر و در عین حال حفظ یا حتی افزایش ویژگی های اصلی آنها اجرا کرد. به عنوان مثال، الگوهای جدید تولید شده (مثلاً اشکال الفبایی مانند E، H و غیره) به عنوان فرم های ساده تر برای نمایش ساختمان های ساده شده در مقیاس کوچکتر استفاده می شوند [ 5 ، 6 ]. اگر یک ساختمان دارای مساحت کوچکی باشد، می توان آن را با یک نماد از پیش تعریف شده (مثلاً یک مستطیل) یا به اصطلاح بزرگ شدن ساختمان ( BE ) جایگزین کرد [ 7 ]]. با این حال، ویژگی‌های ساختمان‌ها می‌تواند در مقیاس‌ها و مناطق متفاوت باشد، که ممکن است برای تعریف الگوهای مناسب برای همه ساختمان‌ها در الگوریتم‌های ساده‌سازی مبتنی بر الگو ( TS ) انعطاف‌ناپذیر باشد. یکی دیگر از ایده‌های رایج برای ساده‌سازی ساختمان، حذف جزئیات بی‌اهمیت ساختمان و در عین حال حفظ جزئیات مهم مرحله به مرحله یا مقیاس به مقیاس است. جزئیات عمدتاً به سازه‌های محلی ساختمان اشاره دارد و بسیاری از الگوریتم‌های ساده‌سازی مبتنی بر ساختار محلی ( LS ) توسعه داده شده‌اند، مانند الگوریتم‌هایی که در آن لبه‌های کوتاه، گوشه‌های کوچک، خم‌های کوچک یا مقعرهای کوچک گام به گام حذف می‌شوند یا مقیاس به مقیاس برای دستیابی به ساده سازی ساختمان [ 8 ، 9 ، 10 ، 11 ،12 ]. با توسعه نقشه وب، خدمات نقشه برای پشتیبانی از بزرگنمایی تعاملی در مقیاس های دلخواه مورد نیاز است. روش های جدیدی مانند تعمیم پیوسته و تعمیم در حین پرواز پدیدار شده اند. آنها را می توان با اعمال عملیات تعمیم برای تولید سطح درشت تری از جزئیات از یک مجموعه داده دقیق به دست آورد، که الگوریتم های LS را نیز می توان روی آن اعمال کرد [ 13 ، 14 ، 15 ].
با این حال، دو مشکل اصلی می تواند در الگوریتم های LS ایجاد شود. اول، ساختارهای محلی مختلف برای اهداف خاصی طراحی شده اند. برای مثال، برخی از الگوریتم‌ها فرض می‌کنند ساختمان‌ها با ویژگی‌های متعامد طراحی شده‌اند، که در آن ساختمان‌ها را می‌توان بر اساس زوایای مربع، ساختارهای مقعر و غیره ساده‌سازی کرد [ 8 ، 9 ، 10 ]. با این حال، ساختمان ها در دنیای واقعی نه تنها دارای ویژگی های متعامد هستند، بلکه برخی از آنها دارای ویژگی های غیر متعامد نیز هستند [ 16 ]. بنابراین، ممکن است برای آنها مناسب نباشد که فقط بر اساس یک نوع ساختار محلی تعریف شده ساده شوند. ساختارهای محلی موجود باید بر اساس ویژگی ساختمان در یک LS تعریف شوندالگوریتم، و ساختاری که باید اعمال شود به الزامات تعمیم و خواسته های کاربر بستگی دارد. دوم، الگوریتم‌های LS برای حذف جزئیات بی‌اهمیت ساختمان طراحی شده‌اند، که گاهی اوقات ممکن است در ساده‌سازی مناسب همه ساختمان‌ها در یک مجموعه داده ناکام باشند. به عنوان مثال، یک ساختمان ممکن است برای ساده سازی بر اساس ساختارهای محلی بسیار کوچک باشد و ممکن است در این شرایط نیاز به استفاده از یک الگوریتم BE باشد [ 7 ]]. بنابراین، در صورتی که ساختمان بر اساس ساختارهای محلی ساده‌سازی نشود، باید سایر الگوریتم‌های ساده‌سازی ترکیب شوند. این ایده که الگوریتم های مختلف را برای دستیابی به کار ساده سازی ساختمان ترکیب می کند، در ابزار Simplify Building Tool ArcGIS نیز پذیرفته شده است. این ترکیبی از مستطیل، مربع کردن، پردازش الگوی منظم، و حذف لبه های کوتاه در اشکال نامنظم [ 17 ] است. اشتاینیگر و همکاران [ 18 ] از یادگیری ماشین برای یادگیری قوانین کنترل در یک مدل عامل برای یک عامل با عملیاتی مانند مستطیل سازی، مربع سازی و مقیاس بندی برای دستیابی به ساده سازی ساختمان استفاده کرد. بسیاری از محققان همچنین ثابت کرده اند که دستیابی به تعمیم نقشه با ترکیب چندین الگوریتم تعمیم موثر است [ 19 , 20 ], 21 , 22 , 23 ].
از این رو، ما یک رویکرد ساده سازی ساختمان مترقی و ترکیبی را با در نظر گرفتن الزامات نقشه برداری بر اساس طبقه بندی ساختار محلی و استراتژی عقب نشینی پیشنهاد می کنیم. سازه های محلی در ساده سازی ساختمان طبقه بندی شده و عملیات مبتنی بر آنها با در نظر گرفتن ویژگی های هر ساختمان تعریف می شود. سپس ساختمان به تدریج بر اساس یک عملیات بر اساس ساختار محلی انتخاب شده ساده می شود، که در آن کاربرد این عملیات توسط قوانین تعریف شده بر اساس الزامات نقشه برداری پشتیبانی می شود. هنگامی که یک نتیجه رضایت بخش با عملیات ساختار محلی انتخاب شده به دست نمی آید، از یک استراتژی عقبگرد استفاده می شود. اگر ارزیابی ساختمان نشان دهد که نمی توان آن را بر اساس ساختارهای محلی ساده کرد، یک TSالگوریتم انجام می شود. اگر ساختمان خیلی کوچک باشد که نمی‌توان آن را ساده کرد، یک الگوریتم BE اعمال می‌شود.

2. آثار مرتبط

2.1. ایجاد محدودیت های ساده سازی

نقشه ها در مقیاس هدف باید الزامات تعمیم ناشی از مشخصات نقشه یا خواسته های کاربر را برآورده کنند. این الزامات را می توان به عنوان محدودیت ها تعریف کرد و محدودیت های زیادی برای اهداف مختلف ایجاد شده است. دو نوع محدودیت اصلی را می توان برای ساده سازی ساختمان خلاصه کرد: خوانایی و حفظ ( شکل 1 ) [ 4 ]. محدودیت‌های خوانایی تضمین می‌کنند که نقشه برای ناظران انسانی قابل خواندن است، در حالی که محدودیت‌های حفظ، نمایش مناسب واقعیت را از نقشه منبع تضمین می‌کند.
محدودیت های خوانایی
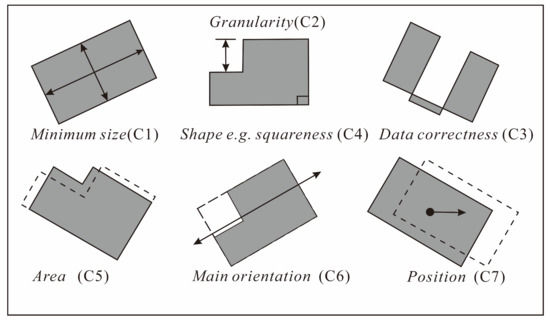
  • حداقل اندازه (C1): اندازه ساختمان باید به اندازه کافی بزرگ باشد تا قابل تفسیر باشد، به عنوان مثال، 0.5 میلی متر × 0.5 میلی متر در مقیاس متوسط ​​[ 24 ]. گاهی اوقات می توان آن را به حداقل طول و عرض مستطیل مرزی ساختمان تبدیل کرد، به عنوان مثال، 0.7 میلی متر و 0.5 میلی متر در مقیاس های 1:25k تا 1:50k [ 7 ].
  • دانه بندی (C2): لبه های ساختمان باید به اندازه کافی بزرگ باشند تا از سردرگمی بصری جلوگیری شود، به عنوان مثال، 0.3 میلی متر [ 25 ].
محدودیت های نگهداری
  • صحت داده ها (C3): هیچ خطای داده مجاز نیست، به عنوان مثال، خود تقاطع [ 26 ].
  • شکل (C4): شکل ساختمان باید حفظ شود، به عنوان مثال، ویژگی های متعامد [ 27 ].
  • اندازه (C5): منطقه ساختمان باید حفظ شود [ 25 ].
  • جهت گیری (C6): جهت گیری اصلی ساختمان باید حفظ شود [ 28 ].
  • موقعیت (C7): ساختمان ساده شده باید نزدیک به موقعیت اصلی خود باشد [ 29 ].
محدودیت های کارتوگرافی در عمل ممکن است الزامات متناقضی داشته باشند و نیاز به بهینه سازی داشته باشند [ 30 ]. ساختمان ها به ناچار محدودیت های خوانایی را با کاهش مقیاس نقض می کنند. تلاش برای رفع محدودیت‌های خوانایی ناقض محدودیت‌های حفظ است. بنابراین، محدودیت‌های خوانایی باید برای ساختمان‌های ساده‌شده رعایت شوند، در حالی که محدودیت‌های حفظ باید تا حد امکان برآورده شوند. این بدان معناست که محدودیت‌های خوانایی اولویت بیشتری نسبت به محدودیت‌های حفظ دارند. علاوه بر این، داده های ساختمان باید قبل و بعد از ساده سازی صحیح باشند. این بدان معناست که صحت داده ها نیز اولویت بیشتری دارد و باید رعایت شود.

2.2. رویکردهای ساده سازی ساختمان

داده های مکانی را می توان به صورت مدل های برداری یا شطرنجی نشان داد و ساده سازی ساختمان نیز بر اساس این دو نوع مدل داده های مکانی انجام می شود.
روش‌های ساده‌سازی ساختمان مبتنی بر برداری را می‌توان به قالب‌محور و مبتنی بر ساختار محلی طبقه‌بندی کرد که به طور جداگانه بر روی خود ساختمان یا ساختارهای محلی آن عمل می‌کنند. در رویکردهای TS ، ساختمان ها با جایگزینی آنها با یک فرم ساده تر، به عنوان مثال، الگوهای از پیش تعریف شده، ساده می شوند. این رویکردها دو دغدغه دارند: تعریف الگوهای مناسب و تطبیق ساختمان با الگوی مناسب. برای تعریف الگوهای مناسب، Rainsford et al. [ 5 ] از اشکال الفبایی مانند E و H برای نشان دادن ساختمان های روستایی استفاده کرد. یان و همکاران [ 6 ] با تجزیه و تحلیل ویژگی های محیط منطقه ای، الگوهای جدیدی تولید کرد. وانگ و همکاران [ 7] از مستطیل ها برای بزرگ کردن ساختمان ها با مساحت کوچک استفاده می کرد. با این حال، از آنجایی که ویژگی‌های ساختمان‌ها در مناطق و مقیاس‌ها متفاوت است، گاهی اوقات استفاده از انواع محدود الگوها برای نمایش همه ساختمان‌ها غیرممکن است. تطبیق ساختمان ها با الگوهای مناسب عمدتاً با تطبیق نامزدهایی با شکل مشابه انجام می شود. به عنوان مثال، Ai et al. [ 3 ] الگوها را با اندازه‌گیری شباهت شکل بر اساس تبدیل فوریه مطابقت داد، در حالی که یان و همکاران. [ 6 ] شباهت شکل را بر اساس زاویه چرخش اندازه گیری کرد. با این حال، شکل تنها یکی از ویژگی های یک ساختمان است و ویژگی های دیگری نیز ممکن است مورد توجه قرار گیرد. علاوه بر این، نمایش ساختمان‌ها با انواع محدود الگوهای ساده‌تر ممکن است منجر به ساده‌سازی بیش از حد برای برخی ساختمان‌های پیچیده شود.
در رویکردهای LS ، ساختمان ها با حذف جزئیات بی اهمیت و در عین حال حفظ موارد مهم ساده می شوند. جزئیات بیشتر به ساختارهای محلی ساختمان ها اشاره دارد. به عنوان مثال، Guo [ 8 ] زاویه مربع را به عنوان یک واحد اساسی برای ساده سازی تدریجی ساختمان ها در نظر گرفت، در حالی که چن و همکاران. [ 10 ] ساختارهای مقعر پر شده بر اساس مثلث بندی محدود شده Delaunay گام به گام شناسایی شدند. خو و همکاران [ 26 ] چهار نقطه مجاور را برای تعریف ساختارهای خمشی به عنوان یک واحد پایه در نظر گرفت و به تدریج لبه های کوتاه را حذف کرد. سستر [ 9] افست، اکستروژن یا نفوذ و گوشه را به عنوان واحدهای اساسی در ساده سازی ساختمان تعریف کرد، سپس برای به دست آوردن نتیجه ساده شده، تنظیم حداقل مربعات را اعمال کرد. روش حداقل مربعات نیز توسط بایر [ 31 ] استفاده شد که رویکردهای بازگشتی را بر اساس الگوریتم داگلاس-پوکر طراحی کرد. در این رویکردهای LS ، ساختارهای محلی مختلف برای اهداف خاصی تعریف شده‌اند که ممکن است برای ساده‌سازی ساختمان‌های متنوع مناسب نباشند. به عنوان مثال، ساختارهای مقعر تعریف شده توسط چن و همکاران. [ 10 ] فرض کنید ساختمان ها با ویژگی های متعامد طراحی شده اند. از این رو، ممکن است ساده سازی ساختمان هایی با ویژگی های غیر متعامد مناسب نباشد.
در رویکردهای مبتنی بر شطرنجی، عمدتاً از استراتژی‌های ریخت‌شناسی استفاده می‌شود. برای مثال، دیمن و همکاران. [ 32 ] ساختمان‌ها را بر اساس عوامل مورفولوژیکی مانند فرسایش و اتساع، جمع‌آوری و ساده‌سازی کرد. Meijers [ 33 ] از همان عملگرهای مورفولوژیکی بر اساس منحنی های افست تولید شده از یک اسکلت مستقیم استفاده کرد، که در آن گوشه های زاویه مربع را بهتر می توان حفظ کرد. کادا [ 34 ] از اتساع و فرسایش برای ساده سازی ساختمان ها بر اساس تجزیه سلولی و مدل سازی نیمه فضا استفاده کرد. با توسعه هوش مصنوعی، چنگ و همکاران. [ 11 ] یک روش جدید برای ساده سازی ساختمان با استفاده از مدل شبکه عصبی پس انتشار (BPNN) ارائه کرد. شن و همکاران [ 16] ساختمان های ساده شده بر اساس تقسیم بندی سوپرپیکسلی، که می تواند برای ساختمان هایی با ویژگی های متعامد یا غیر متعامد اعمال شود. با این حال، از آنجایی که داده های برداری تمرکز این مقاله است، استفاده از این الگوریتم های مبتنی بر شطرنجی شهودی نیست. اگر آنها را روی داده های برداری اعمال کنیم، برخی تبدیل های اضافی ضروری است.

3. روش شناسی

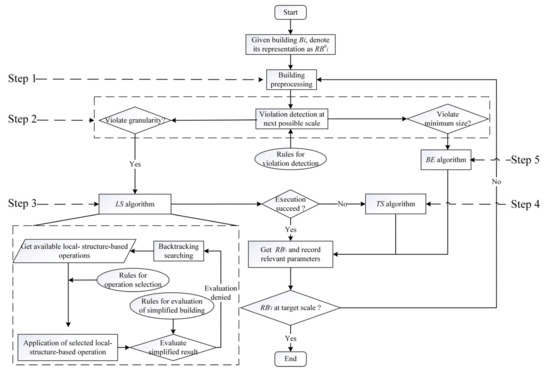
3.1. چارچوب

نمایش ( RB t i ) ساختمان B i در مقیاس هدف (1: Mt ) با ساده کردن نمایش آن ( RB 0 i ) در مقیاس اصلی (1: M 0 ) مقیاس به مقیاس با رویکرد ما به دست می‌آید: RB 0 با کاهش تدریجی مقیاس، محدودیت‌های خوانایی (حداقل اندازه و دانه‌بندی) را در مقیاس ممکن بعدی (1: M 1 ) نقض خواهم کرد. یک عملیات ساده سازی برای به دست آوردن یک نمایش جدید ( RB 1 i ) بر اساس RB 0 i آغاز می شود.; اگر م0>م1�0>�1، RB 1 i را می توان به عنوان نمایشی از B i از مقیاس M 0 تا M 1 در نظر گرفت. عملیات ساده سازی بر روی RB j i مکررا اجرا می شود تا زمانی که RB j+1 i در مقیاس هدف به دست آید. چارچوب برای ساده سازی B i به مقیاس هدف به صورت زیر طراحی شده است ( شکل 2 ).
مرحله 1.
پیش پردازش را برای حذف گره های غیرعادی احتمالی ساختمان ها قبل از اعمال هر گونه عملیات ساده سازی انجام دهید ( بخش 3.2 ).
گام 2.
تشخیص تخلف در مقیاس احتمالی بعدی. نقض بر اساس اینکه آیا محدودیت های خوانایی در مقیاس ممکن بعدی نقض شده است یا خیر ( بخش 3.3 ) تعریف می شوند.
مرحله 3.
اگر RB j i محدودیت های دانه بندی را در مقیاس ممکن بعدی نقض می کند، یک الگوریتم ساده سازی مبتنی بر ساختار محلی ( LS ) را اجرا کنید ( بخش 3.4 ). این الگوریتم ساختارهای محلی را طبقه بندی می کند و عملیات مبتنی بر آنها را تعریف می کند ( بخش 3.4.1 ). قوانینی که محدودیت‌های حفظ را در نظر می‌گیرند که از کاربرد عملیات مبتنی بر ساختار محلی در مرحله فعلی پشتیبانی می‌کنند، ارائه شده‌اند ( بخش 3.4.2 ). یک استراتژی جستجوی عقبگرد نیز در صورت اعمال یک عملیات مبتنی بر ساختار محلی نامعتبر ارائه می شود. اگر بتوان با LS نتیجه رضایت بخشی به دست آوردالگوریتم، بازگشت به مرحله 1. در غیر این صورت، به مرحله 4 بروید. اینکه آیا نتیجه رضایت بخش است یا خیر، بر اساس محدودیت های حفظ تعریف می شود ( بخش 3.4.3 ).
مرحله 4.
اگر الگوریتم LS نمی تواند نتیجه رضایت بخشی به دست آورد، از یک الگوریتم ساده سازی مبتنی بر الگو ( TS ) استفاده کنید. سپس به مرحله 1 ( بخش 3.5 ) برگردید.
مرحله 5.
اگر حداقل محدودیت اندازه در مقیاس ممکن بعدی نقض شود، از الگوریتم بزرگ‌نمایی ساختمان ( BE ) استفاده کنید ( بخش 3.5 ).
در تمام مراحل فوق، فرآیند ساده سازی با به دست آوردن یک ساختمان ساده شده در مقیاس هدف متوقف می شود.

3.2. مرحله 1: پیش پردازش ساختمان

پیش پردازش قبل از اعمال هر عملیات ساده سازی برای خطای احتمالی داده انجام می شود، به عنوان مثال، گره های غیرعادی مانند گره های تکرار شونده، گره های خطی، و گره های تیز [ 8 ]. فرض کنید مجموعه گره از یک چند ضلعی ساختمان به عنوان A P= {پ1،پ2, … ,پn}��=�1,�2,…,��، که در آن پمن≠پn��≠��. زاویه در گره p m به عنوان زاویه Cm در نظر گرفته می شود ، به عنوان زاویه لبه p m −1 p m در خلاف جهت عقربه های ساعت حول گره p m به لبه p m p m +1 می چرخد ، و سیa n gl e∈ [ 0 درجه ، 360 درجه ]������∈[0°,360°]. بنابراین، گره های تکرار شونده، گره های خطی، و گره های تیز به صورت زیر تعریف می شوند.
گره های تکرار شونده: فاصله بین گره های p m و p n در AP را به صورت Dis mn فرض کنید ، اگر دی من _m n< تید�����<��، سپس p m و p n گره های تکرار شونده هستند، به عنوان مثال، گره های G و H در شکل 3 a. Td یک آستانه و تید= 0.01 میلی متر��=0.01mm.
گره های خطی: زاویه در گره p m در AP را به عنوان زاویه C m فرض کنید ، اگر |سیمترa n gl e− 180 درجه | <δ�������−180°<�، سپس p m یک گره خطی است، به عنوان مثال، گره B در شکل 3 a. δ�یک آستانه است و δ= 5 درجه�=5°.
گره های تیز: زاویه در گره p m در AP را به عنوان زاویه C m فرض کنید ، اگر سیمترa n gl e< δ∨ ( 360 −سیمترa n gl e) < δ�������<�∨(360−�������)<�، سپس p m یک گره تیز است، به عنوان مثال، گره E در شکل 3 a. δ�یک آستانه است و δ= 5 درجه�=5°.
پیش پردازش به معنای حذف گره های تکرار شونده، خطی و تیز در مجموعه گره ها است A P= {پ1،پ2, … ,پn}��=�1,�2,…,��به تدریج به عنوان مثال، ساختمان های شکل 3 b-e با حذف گره خطی B ، گره تیز E ، گره خطی D ، تکرار گره G از ساختمان در شکل 3 a به تدریج به دست می آیند.

3.3. مرحله 2: تعاریف نقض محدودیت خوانایی

عملیات ساده سازی برای ساختمان هایی که محدودیت های مختلف خوانایی را با کاهش مقیاس نقض می کنند، آغاز می شود. بنابراین، پارامترهایی که محدودیت‌های خوانایی را توصیف می‌کنند می‌توانند برای تعیین اینکه در چه مقیاسی این محدودیت‌ها نقض می‌شوند استفاده شوند.

دو نوع محدودیت خوانایی در بخش 2.1 تعریف شده است : حداقل اندازه و دانه بندی. محدودیت حداقل اندازه را می توان با حداقل مساحت ساختمان ( ST a ) تعیین کرد و گاهی اوقات می تواند به حداقل طول ( ST L ) و عرض ( ST W ) مستطیل مرزی آن تبدیل شود [ 7 ]. محدودیت دانه بندی بر حداقل طول ( GT L ) لبه های ساختمان حاکم است. ساختمان B i را در مقیاس 1 نمایش دهید: M j به عنوان B j i , مساحت آن به صورت AreaB j iطول و عرض حداقل مستطیل مرزی آن (MBR) به صورت LB j i و WB j i است و طول کوتاه ترین لبه آن به صورت MLe j i است. مقیاس های ممکن بعدی (1: M 1 j + 1 تا 1: M 4 j + 1 ) با در نظر گرفتن AreaB j i , LB j i , WB j i , و MLe j i از B j i به طور جداگانه می توانند به صورت معادلات محاسبه شوند. 1) – (4):

م1j + 1=A r e aبjمن/ استیآ———–√× 1000�1�+1=�������/���×1000
م2j + 1=L Bjمن/ استیL ×1000�2�+1=LB��/���×1000
م3j + 1=W Bjمن/ استیدبلیو× 1000�3�+1=WB��/���×1000
م4j + 1=M L ejمن/ جیتیL× 1000�4�+1=MLe��/���×1000
اگر نقض هر نوع محدودیت خوانایی با کاهش مقیاس تشخیص داده شود، یک ساختمان باید ساده شود. بنابراین، مقیاس ممکن بعدی (1: M j + 1 ) به عنوان نشان داده می شود مj + 1= m i n {م1j + 1،م2j + 1،م3j + 1،م4j + 1، }��+1=min�1�+1,�2�+1,�3�+1,�4�+1,. نقض محدودیت های خوانایی برای نمایش ساختمان ( B ji ) را می توان همانطور که در جدول 1 نشان داده شده است تعریف کرد . علاوه بر این، آنها را می توان به قوانین در شکل اگر – آنگاه در تشخیص نقض برای ساختمان ها در مقیاس ممکن بعدی توسعه داد [ 35 ]. به عنوان مثال، اگر مj + 1= m i n {م1j + 1،م2j + 1،م3j + 1،م4j + 1، }��+1=min�1�+1,�2�+1,�3�+1,�4�+1,، سپس ساختمان به عنوان تخلف در STa شناسایی می شود که مقیاس به بیش از حد کاهش یابد م1j + 1�1�+1.

3.4. مرحله 3: الگوریتم ساده سازی مبتنی بر ساختار محلی

در رویکرد ما، ساختمان‌ها بر اساس ساختار محلی‌شان در صورتی که محدودیت دانه‌بندی را در مقیاس ممکن بعدی نقض کنند، ساده‌سازی می‌شوند. محدودیت دانه بندی بر حداقل طول لبه های ساختمان حاکم است. بنابراین، هدف الگوریتم LS حذف کوتاه ترین لبه ساختمان در مرحله فعلی است. سازه های محلی که ممکن است کوتاه ترین لبه در آنها قرار گیرد ابتدا طبقه بندی می شوند و سپس عملیات مبتنی بر آنها برای حذف کوتاه ترین لبه تعریف می شود ( بخش 3.4.1 ). از آنجایی که ممکن است کوتاه‌ترین لبه در ساختارهای محلی مختلف قرار گیرد، می‌توان از عملیات‌های مبتنی بر ساختار محلی در مرحله فعلی استفاده کرد. یک انتخاب مبتنی بر قانون از عملیات مبتنی بر ساختار محلی کاربردی ارائه شده است ( بخش 3.4.2). اینکه آیا عملیات می تواند نتیجه رضایت بخشی به دست آورد یا خیر، باید ارزیابی شود. در صورت حصول نتیجه نامطلوب، یک استراتژی عقب نشینی اعمال می شود ( بخش 3.4.3 ).

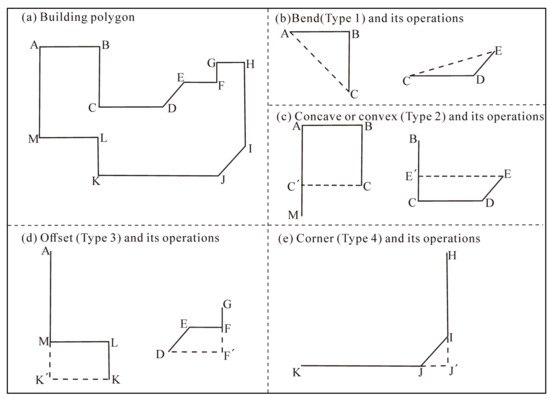
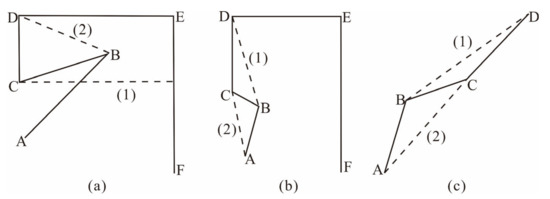
3.4.1. طبقه بندی ساختار محلی و عملیات مبتنی بر آنها

(1) طبقه بندی ساختار محلی
یک چند ضلعی ساختمان را می توان با یک مجموعه گره به عنوان نشان داد A P= {پ1،پ2, … ,پn}��=�1,�2,…,��، که در آن پمن≠پn��≠��; یا یک لبه به عنوان A E= { e (پمن،پj) |پمن،پj∈ A P}��=�(��,��)|��,��∈��. از آنجایی که هر گره دو یال را در چند ضلعی ساختمان به هم متصل می کند، می توان آن را با مجموعه ای از خم های تعریف شده که به عنوان یک مجموعه گره نشان داده می شود، نشان داد. {پm – 1،پمتر،پm + 1}��−1,��,��+1یا یک مجموعه لبه { e (پm – 1،پمتر) ، e (پm – 1،پm + 1) }�(��−1,��),�(��−1,��+1)، پm – 1،پمتر،پm + 1∈ A P��−1,��,��+1∈��[ 36 ]. انواع دیگر خم ها را نیز می توان در چند ضلعی های پیچیده تعریف کرد، به عنوان مثال، مرزهای ناحیه آب [ 37 ]. با این حال، از آنجایی که ساختمان‌ها ساخته دست بشر هستند، ویژگی‌های چند ضلعی آن‌ها تمایل به داشتن اشکال ساده و ویژگی‌های متعامد دارند [ 26 ]. در رویکرد خود، ما تعریف خم را طبق فن و همکاران اتخاذ کردیم. [ 36 ]، که همچنین یک نوع خم اولیه است. زاویه یک خم (Cm ) به عنوان زاویه Cm در گره pm در نظر گرفته می شود، که به عنوان زاویه لبه p m −1 pm در خلاف جهت عقربه های ساعت حول گره p m به لبه چرخانده می شود .p m p m +1 . با توجه به زاویه خم، یک خم را می توان به صورت محدب با تعریف کرد سیمترa n gl e∈ [ 0 درجه ، 180 درجه ]�������∈[0°,180°]یا مقعر با سیمترa n gl e∈ [ 180 درجه ، 360 درجه ]�������∈[180°,360°]. یک ویژگی متعامد در یک ساختمان به این اشاره دارد که دو یال ( e m , e n ) در چند ضلعی ساختمان متعامد هستند، به این معنی که زاویه (زاویه E ) لبه‌های e m و e n مطابق با شرایط است. |Ea n gl e− 90 درجه | <α������−90°<�، جایی که Ea n gl e∈ [ 0 درجه ، 180 درجه )������∈[0°,180°)و α�یک آستانه است. با توجه به اینکه یک ویژگی متعامد برای دو یال در یک خم تعریف شده تشکیل شده است، خم را می توان به صورت متعامد یا غیر متعامد نیز تعریف کرد.
اگر ویژگی های متعامد در ساختمان ها، به عنوان مثال، چند ضلعی های طبیعی مانند مرزهای سطح آب، در نظر گرفته نمی شود. آنها معمولاً از انواع مختلفی از خم ها تشکیل شده اند و بر اساس آن خم ها ساده شده اند [ 37 ]. بنابراین، اگر ویژگی های متعامد در نظر گرفته نشود، ساختمان ها را می توان بر اساس خم های تعریف شده ساده کرد. اگر ویژگی های متعامد در نظر گرفته شود، برخی از الگوریتم های LS پیشنهاد شده است. به عنوان مثال، Sester [ 9 ] ساختمان ها را بر اساس افست، نفوذ (یا اکستروژن) و گوشه ها ساده کرد. چن و همکاران [ 10 ] ساختمان‌های ساده‌سازی شده بر اساس بخش‌های مقعر. خو و همکاران [ 26] چهار گره مجاور را به عنوان واحدهای اصلی گرفت و به تدریج لبه های کوتاه را حذف کرد. در این الگوریتم‌ها، ساختارهای محلی همگی به عنوان ترکیبی از دو خم تعریف‌شده متوالی در نظر گرفته می‌شوند که ممکن است دارای یک ویژگی متعامد باشند. به عنوان مثال، یک قسمت مقعر که توسط Chen و همکاران تعریف شده است. [ 10 ] را می توان به عنوان ترکیبی از دو خم متعامد مقعر در نظر گرفت، در حالی که افست تعریف شده توسط Sester [ 9 ] را می توان به عنوان ترکیبی از خم های متعامد محدب و مقعر در نظر گرفت. بنابراین، اگر ویژگی های متعامد در ساختمان ها در نظر گرفته شود، سازه های محلی را می توان بر اساس دو خم تعریف شده متوالی که حداقل یک ویژگی متعامد در آن وجود دارد، تعریف کرد. بنابراین، در رویکرد ما ساختارهای محلی به صورت زیر تعریف می شوند:
خم (نوع 1): به عنوان یک مجموعه گره نشان داده می شود {پm – 1،پمتر،پm + 1}��−1,��,��+1یا یک مجموعه لبه { e (پm – 1،پمتر) ، e (پm – 1،پm + 1) }�(��−1,��),�(��−1,��+1)، که در آن پm – 1،پمتر،پm – 1∈ A P��−1,��,��−1∈�پبه عنوان مثال، ABC و CDE را در شکل 4 خم می کند.
مقعر یا محدب (نوع 2): شامل دو خم است که به صورت محدب یا مقعر تعریف شده اند و حداقل یکی از آنها خم متعامد است، به عنوان مثال، KABC مقعر و BCDE محدب در شکل 4 ج.
آفست (نوع 3): شامل دو خم تعریف شده، یکی محدب و دیگری مقعر، و حداقل یکی خم متعامد است، به عنوان مثال، AKJI و CDEF را در شکل 4 د.
گوشه (نوع 4): شامل دو خم غیر متعامد تعریف شده است که به عنوان یک مجموعه لبه نشان داده می شود. {هm – 1،همتر،هm + 1}همتر-1،همتر،همتر+1، که در آن em-1 و e m +1 یک ویژگی متعامد را تشکیل می دهند، به عنوان مثال، گوشه FGHI در شکل 4 e.
(2) عملیات مبتنی بر ساختار محلی برای حذف کوتاه ترین لبه
عملیات برای کوتاه ترین لبه ممکن است در ساختارهای محلی تعریف شده متفاوت قرار گیرد. با توجه به کوتاه ترین لبه e (پمن،پj)ه(پمن،پ�)در یک ساختار محلی ( S )، عملیات حذف آن بر اساس نوع S به صورت زیر تعریف می شود:
عملیات 1: اگر S نوع 1 باشد، یعنی e (پمن،پj)ه(پمن،پ�)در یک خم قرار دارد که با مجموعه گره مشخص می شود {پm – 1،پمتر،پm + 1}پمتر-1،پمتر،پمتر+1. عملیات برای از بین بردن e (پمن،پj)ه(پمن،پ�)برای اتصال گره های p m −1 و p m +1 است. به عنوان مثال، همانطور که در شکل 4 ب نشان داده شده است، برای حذف کوتاه ترین لبه AB در خم ABC ، عملیات اتصال گره های A و C است.
عملیات 2: اگر S نوع 2 باشد، یعنی e (پمن،پj)ه(پمن،پ�)در یک خم مقعر یا محدب قرار دارد و به عنوان مجموعه گره نشان داده می شود اسپ= {پ1،پ2،پ3،پ4}اسپ=پ1،پ2،پ3،پ4. عملیات برای از بین بردن e (پمن،پj)ه(پمن،پ�)برای پر کردن مقعر یا محدب است. خطی موازی با لبه رسم کنید e (پ2،پ3)ه(پ2،پ3)از گره p 1 تا لبه e (پ3،پ4)ه(پ3،پ4). اگر یک گره متقاطع p m بدست آید، مجموعه گره S پردازش شده به صورت نمایش داده می شود اسپ= {پ1, p m ,پ4}اسپ=پ1،پمتر،پ4; در غیر این صورت یک خط موازی با لبه رسم کنید e (پ2،پ3)ه(پ2،پ3)از گره p 4 تا لبه e (پ1،پ2)ه(پ1،پ2)برای به دست آوردن یک گره متقاطع ( pn )، سپس مجموعه گره S پردازش شده به صورت اسپ= {پ4،پn،پ1}اسپ=پ4،پ�،پ1. به عنوان مثال، همانطور که در شکل 4c نشان داده شده است ، برای حذف کوتاهترین لبه DE در BCDE مقعر تعریف شده ، عمل به این صورت است که یک خط موازی با لبه CD از گره E رسم می شود و لبه BC را به عنوان یک گره قطع می کند.E“�”، و مجموعه گره S پردازش شده به صورت نمایش داده می شود اسپ= { B _E“، ای}اسپ=ب،�”،�.
عملیات 3: اگر ساختار محلی ( S ) نوع 3 باشد، یعنی e (پمن،پj)ه(پمن،پ�)در یک افست است که با مجموعه گره مشخص می شود اسپ= {پ1،پ2،پ3،پ4}اسپ=پ1،پ2،پ3،پ4با دو خم ب1= {پ1،پ2،پ3}ب1=پ1،پ2،پ3و ب2= {پ2،پ3،پ4}ب2=پ2،پ3،پ4. عملیات برای از بین بردن e (پمن،پj)ه(پمن،پ�)پر کردن قسمت متعامد افست است. اگر B 1 یک خم متعامد است، خطی موازی با لبه رسم کنید e (پ2،پ3)ه(پ2،پ3)از گره p 4 تا تلاقی لبه امتدادی e (پ1،پ2)ه(پ1،پ2)به عنوان گره p m ، و مجموعه گره ساختار محلی پردازش شده ( S ) به صورت نمایش داده می شود اسپ= {پ4،پمتر،پ1}اسپ=پ4،پمتر،پ1. در غیر این صورت، اگر B2 یک خم متعامد است، یک خط موازی با لبه رسم کنید. e (پ2،پ3)ه(پ2،پ3)از گره p 1 تا تلاقی لبه امتدادی e (پ3،پ4)ه(پ3،پ4)به عنوان گره p n ، و مجموعه گره ساختار محلی پردازش شده ( S ) به صورت نمایش داده می شود اسپ= {پ1،پn،پ4}اسپ=پ1،پ�،پ4. B 1 و B 2 ممکن است هر دو خم های متعامد باشند و دو عملیات بر اساس تعاریف فوق در دسترس است. در این حالت خم متعامد مقعر پر می شود. به عنوان مثال، همانطور که در شکل 4 d نشان داده شده است، با فرض اینکه کوتاه ترین لبه در افست DEFG تعریف شده لبه FG باشد، عمل به این صورت است که خطی موازی با لبه EF از گره D رسم می شود و لبه امتدادی FG را به عنوان گره قطع می کند.اف“اف”، و مجموعه گره ساختار محلی پردازش شده ( S ) به صورت نمایش داده می شود اسپ= { D _اف“، جی }اسپ=�،اف”،جی.
عملیات 4: اگر S نوع 4 باشد، یعنی e (پمن،پj)ه(پمن،پ�)در گوشه ای قرار دارد که با مجموعه گره مشخص می شود اسپ= {پ1،پ2،پ3،پ4}اسپ=پ1،پ2،پ3،پ4. عملیات برای از بین بردن e (پمن،پj)ه(پمن،پ�)برای پر کردن گوشه است. توسعه دادن، گسترش e (پ1،پ2)ه(پ1،پ2)و e (پ3،پ4)ه(پ3،پ4)برای به دست آوردن یک گره متقاطع p m ، و مجموعه گره S پردازش شده به صورت نمایش داده می شود اسپ= {پ1،پمتر،پ4}اسپ=پ1،پمتر،پ4. به عنوان مثال، همانطور که در شکل 4 e نشان داده شده است، برای حذف کوتاه ترین لبه IJ در گوشه تعریف شده HIJK ، عملیات به این صورت است که لبه های KJ و HI را گسترش داده و سپس به صورت یک گره قطع می شود.جی“جی”، و مجموعه گره S پردازش شده به صورت نمایش داده می شود اسپ= { K،جی“، اچ}اسپ=ک،جی”،اچ.
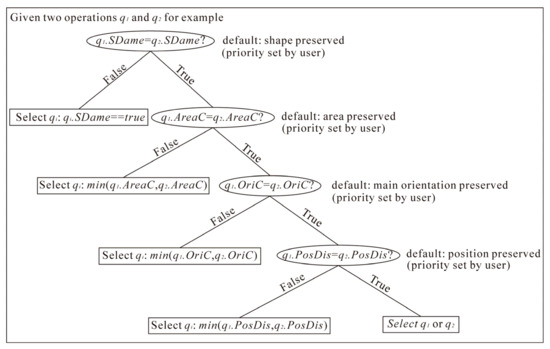
3.4.2. انتخاب عملیات مبتنی بر ساختار محلی کاربردی
برای از بین بردن کوتاه ترین لبه e (پمن،پj)ه(پمن،پ�)در مرحله فعلی، عملیات موجود را می توان بر اساس ساختارهای محلی که در آن واقع شده است، به دست آورد Q = {q1, … ,qn}س={�1،…،��}، که در آن q n عملیاتی را نشان می دهد که می تواند حذف شود e (پمن،پj)ه(پمن،پ�). اعمال یک q n متفاوت در Q می تواند نتایج متفاوتی ایجاد کند. بهترین عملیات برای اعمال را می توان بر اساس ارزیابی نتایج پس از اعمال هر q n در Q انتخاب کرد.
(1) ساختار داده برای هر عملیات مبتنی بر ساختار محلی
استفاده از عملیات q n در Q منجر به نتایج متفاوتی می شود، به ویژه تغییراتی در ویژگی های یک ساختمان، به عنوان مثال، آسیب به ویژگی های متعامد، یا تغییر در ناحیه یا جهت اصلی. این تغییرات را می توان به عنوان ویژگی های هر عملیات q n در Q ثبت کرد. به عنوان مثال، در شکل 5 a، دو عملیات، که با (1) و (2) نشان داده شده اند، برای حذف کوتاه ترین لبه، CD اعمال شده است. اعمال عملیات (1) منجر به تقاطع خود در ساختمان ساده شده می شود، در حالی که اعمال عملیات (2) منجر به این نخواهد شد. به طور مشابه، در شکل 5 ب، دو عملیات برای حذف کوتاه ترین لبه اعمال شده است.قبل از میلاد اعمال عملیات (1) به یک ویژگی متعامد آسیب می رساند، در حالی که اعمال عملیات 2 آسیب نمی رساند. علاوه بر این، پس از اعمال هر عملیاتی می توان یک ساختمان ساده شده جدید به دست آورد. ساختمان ساده شده ممکن است دارای ناحیه، جهت اصلی و موقعیت متفاوتی نسبت به ساختمان قبلی باشد. به عنوان مثال، دو عملیات برای حذف کوتاه ترین لبه، BC ، در شکل 5 ج اعمال شده است. اعمال عملیات (1) منجر به افزایش مساحت خواهد شد، در حالی که اعمال عملیات (2) منجر به کاهش مساحت خواهد شد.
همانطور که در جدول 2 نشان داده شده است، تغییرات در ویژگی های ساختمان ها پس از اعمال عملیات مبتنی بر ساختار محلی q n می تواند به عنوان یک ساختار داده ثبت شود .
(2) انتخاب عملیات مبتنی بر ساختار محلی بر اساس درخت تصمیم باینری
نتیجه به دست آمده پس از اعمال یک عملیات مبتنی بر ساختار محلی برای حذف کوتاه ترین لبه را می توان با توجه به محدودیت های نقشه برداری ارزیابی کرد. از آنجایی که عملیات برای نقض محدودیت های خوانایی راه اندازی می شود، محدودیت های حفظ نگرانی اصلی ارزیابی ما هستند. صحت داده ها محدودیتی است که باید رعایت شود. اگر عملیات اعمالی q n در Q منجر به خودتقاطع ساختمان ساده شده شود، یعنی ویژگی IsInt از q n درست باشد، باید q n از Q حذف شود.. بنابراین، محدودیت های مورد توجه حفظ شکل، اندازه، جهت گیری اصلی و موقعیت است. بهترین عملیات مبتنی بر ساختار محلی با توجه به ارزیابی انتخاب می شود.
محدودیت‌ها ممکن است با یکدیگر تضاد داشته باشند، و دو پارامتر برای محدودیت‌ها را می‌توان هنگام ارزیابی نتایج ساده‌شده تعریف کرد: اهمیت و اولویت (Steiniger et al., 2010). رویکرد ما اولویت محدودیت را اتخاذ می کند. حکم می کند که کدام محدودیت باید ابتدا در نظر گرفته شود و می تواند به عنوان یک درخت تصمیم دودویی نمایش داده شود، شکل 6 [ 38 ]. در این درخت هر گره نشان دهنده نوعی محدودیت است و عبارت منطقی که محدودیت را بیان می کند در گره تعریف می شود. برای مثال، با توجه به دو عملیات q 1 و q 2 ، عبارت منطقی که محدودیت حفظ شکل را بیان می کند، می تواند به صورت تعریف شود. q1. اسD a m e =q2. اسآیا من ؟ _ _�1.اس�آمتره=�2.اس�آمتره?اگر برای عبارت درست باشد، این دو عملیات هر دو محدودیت حفظ شکل را برآورده می کنند یا نقض می کنند. در غیر این صورت، عملیات با SDame نادرست ، بهتر در نظر گرفته می شود. عمق گره نشان دهنده اولویت محدودیت متناظر آن است و عمق بیشتر به معنای اولویت کمتر است. اولویت محدودیت های حفظ پارامترهای اختیاری است که می تواند توسط کاربران در رویکرد ما تنظیم شود. اولویت های پیش فرض نیز در رویکرد ما تعیین شده است. برای ساختمان در رویکرد ما، محدودیت حفظ شکل (حفظ ویژگی‌های متعامد) اولویت بیشتری دارد. علاوه بر این، محدودیت حفظ منطقه در مرحله بعدی و سپس جهت اصلی در نظر گرفته می شود. محدودیت موقعیت آخرین موردی است که باید در نظر گرفته شود.
فرآیند انتخاب در امتداد درخت تصمیم گیری باینری را می توان با اولویت های تعریف شده و عبارات منطقی آنها پیاده سازی کرد ( شکل 6 ).
3.4.3. ارزیابی و استراتژی عقب نشینی
اینکه آیا ساختمان ساده شده نتیجه معقولی پس از اعمال عملیات انتخابی مبتنی بر ساختار محلی است یا خیر، باید ارزیابی شود [ 39 ]. اگر یک نتیجه رضایت بخش به دست آمد، یک استراتژی عقبگرد برای به دست آوردن یک نتیجه رضایت بخش احتمالی دیگر اعمال می شود.
(1) ارزیابی
اگرچه ویژگی های ساختمان به طور اجتناب ناپذیری پس از ساده سازی تغییر می کنند، این تغییرات باید به محدوده خاصی محدود شود [ 8 ]. بنابراین، ارزیابی برای تعیین اینکه آیا تغییرات در منطقه، جهت گیری اصلی، موقعیت، و شکل با توجه به محدودیت های مربوطه حفظ بیش از آستانه انجام می شود. فرض کنید یک عملیات انتخاب شده q n با ویژگی های AreaC ، OriC و PosC (تعریف شده در جدول 2 ) اعمال شده است. قوانین ارزیابی به شرح زیر تعریف شده است.
  • قانون 1: اگر A r e a C>تیآآ�هآسی>تیآ، سپس نتیجه به دست آمده با اعمال q n ​​رضایت بخش ارزیابی می شود.
  • قانون 2: اگر O r i C>تیo��منسی>تی�، سپس نتیجه به دست آمده با اعمال q n ​​رضایت بخش ارزیابی می شود.
  • قانون 3: اگر پo s C>تیپپ�سسی>تیپ، سپس نتیجه به دست آمده با اعمال q n ​​رضایت بخش ارزیابی می شود.
  • قانون 4: اگر ساختمان به دست آمده با اعمال عملیات انتخابی p n کمتر از چهار گره داشته باشد، آن را به عنوان نامطلوب ارزیابی می کنند.
T a , T o , T p در قوانین فوق آستانه هستند و می توانند بر اساس محدودیت های نشان داده شده در بخش 2.1 تنظیم شوند. به عنوان مثال، محدودیت حفظ موقعیت حکم می کند که ساختمان ساده شده باید نزدیک به موقعیت اصلی خود باشد، و فاصله باید محدود شود، به عنوان مثال، 0.5 میلی متر [ 29 ]. علاوه بر این، Tp را می توان به عنوان تنظیم کرد تیپ= 0.5 میلی مترتیپ=0.5میلی متر. بنابراین، نتیجه به‌دست‌آمده با اعمال q n ​​هر یک از قوانین فوق را نقض می‌کند، به عنوان یک نتیجه رضایت‌بخش ارزیابی می‌شود. در غیر این صورت، رضایت بخش است.
(2) استراتژی عقب نشینی
تعریف مسئله: با توجه به ساختمان B i ، نمایش های به دست آمده از B i با عملیات ساده سازی قبلی عبارتند از R B S= {آرب1من،آرب2من, … ,آربk − 1من}آرباس=آرب1من،آرب2من،…،آربک-1من، و عملیات موجود برای RB j i در RBS به صورت نشان داده می شود Q j = {q1j, … ,qnj}س�=�1�،…،�n�. هنگامی که RB k i از RB k-1 i بر اساس عملیات q m k-1 انتخاب شده در مجموعه عملیات موجود Q k-1 به عنوان یک نتیجه رضایت بخش ارزیابی شد، استراتژی عقب نشینی به صورت زیر استفاده می شود: ابتدا به Q k- برگردید. 1 برای انتخاب q m k-1 دیگر . دوم، اگر تمام عملیات های موجود در Q k-1 به عنوان ناتوان برای به دست آوردن یک نتیجه رضایت بخش ارزیابی شوند، برای انتخاب عملیات دیگری به Q k-2 بازگردید و غیره.

با این حال، افزایش عمق ردیابی ممکن است امکان انتخاب ضعیف عملیات برای به دست آوردن نتایج رضایت بخش را افزایش دهد، که همچنین ممکن است به فضای جستجوی بزرگی منجر شود. بنابراین، حداکثر مرحله جستجو ( MaxS ) تنظیم می شود. بعلاوه، جستجوی بازگشتی باید زمانی خاتمه یابد که همه گزینه های موجود انتخاب شده باشند. استراتژی عقب نشینی مطابق شکل زیر انجام می شود.

استراتژی عقب نشینی
ورودی: نمایش های به دست آمده از B i به عنوان R B S= {آرب1من،آرب2من, … ,آربk − 1من} ،k≥1آرباس=آرب1من،آرب2من،…،آربک-1من،ک≥1، عملیات موجود برای RB j i در RBS به عنوان Q j = {q1j, … ,qnj}س�=�1�،…،�n�; حداکثر مرحله جستجو به عنوان خروجی MaxS
: RB k
مرحله جستجو را به صورت p و تنظیم کنیدp = 0پ=0
دریافت Q j : مجموعه عملیات موجود Q j را بر اساس RB j i بدست آورید و با آن شروع کنیدj = k − 1�=ک-1
چه زمانی Q j ≠ n u l lس�≠�توللو p < M a x Sپ<MaxSو j ≥ 2�≥2، سپس
انتخاب: یک عملیات q m j در Q j را بر اساس درخت تصمیم گیری باینری تعریف شده در بخش 3.4.2 برای به دست آوردن انتخاب کنید.R Bکمن، و اینکه آیا  R Bکمن∈ R B SRBکمن، و چهRBکمن∈آرباسباید تعیین شود
اگر R Bکمن∈ R B SRBکمن∈آرباس، q m j را در Q j بردارید ،
اگر دیگر را ادامه دهیدR Bکمن∉ R B SRBکمن∉آرباس، سپس
p = p + 1پ=پ+1
ارزیابی: تعیین اینکه آیا RB k i قوانین تعریف شده برای ساختمان ساده را برآورده می کند یا خیر:
اگر ارزیابی پذیرفته شد، سپس به RB k i ، پایان برگردید.
در غیر این صورت اگر ارزیابی رد شد، q m j را در Q j حذف کنید .
چه زمانی Q j = n u l lس�=�توللو p < M a x Sپ<MaxSو j ≥ 2�≥2، سپس
j = j − 1�=�-1، به Get Q j
Else برگردید.

3.5. مراحل 4 و 5: ساده سازی مبتنی بر الگو و بزرگنمایی ساختمان

استفاده از یک الگوریتم LS ممکن است نتیجه رضایت بخشی را به همراه نداشته باشد، به این معنی که حتی اگر یک استراتژی عقبگرد اعمال شود، باز هم نتیجه رضایت بخشی به دست نخواهد آمد. سپس یک الگوریتم TS اعمال می شود. و اگر یک ساختمان محدودیت حداقل اندازه را نقض کند، یک الگوریتم BE اعمال می شود.
(1) مرحله 4: ساده سازی مبتنی بر الگو
یک الگوریتم TS با توجه به یان و همکاران. [ 6 ] در رویکرد ما اتخاذ شده است. با این حال، الگوها در رویکرد او با تجزیه و تحلیل ویژگی‌های معمولی محیط منطقه‌ای فرموله می‌شوند که ممکن است هنگام تعریف قالب‌های مناسب برای همه ساختمان‌ها انعطاف‌ناپذیر باشد. ما آن تعریف الگو را برای رویکرد خود اصلاح کردیم.
ساختمان‌ها ویژگی‌های ساخته‌شده توسط انسان هستند که با توجه به یک محیط خاص ایجاد می‌شوند و ساختمان‌های مجاور تمایل دارند شکل مشابهی داشته باشند [ 25 ]. بنابراین، سایر ساختمان های ساده شده در مقیاس هدف در همان منطقه نیز می توانند به عنوان الگوهای موجود مورد استفاده قرار گیرند، که به شرح زیر تعریف می شوند: ساختمانی که باید ساده شود به صورت نشان داده می شود. بی اس= { B 1 , … , B m }باس=ب1،…،بمتر، که در آن ساختمان ها با موفقیت ساده شده اند و نمایش آنها در مقیاس هدف به عنوان نشان داده می شود باس“= { B n , … , B n + p }باس”=ب�،…،ب�+پ، سپس ساختمان های داخل باس“باس”همه به عنوان الگوهای موجود در نظر گرفته می شوند. اندازه‌گیری تشابه شکل بر اساس تابع چرخش برای انتخاب بهترین الگو [ 6 ] اتخاذ می‌شود. الگوی انتخاب شده باید برای محدودیت حفظ منطقه بزرگ شود. اگر ساختمان مقیاس‌بندی شده محدودیت‌های خوانایی را در مقیاس هدف نقض کند، الگوی دیگری در این مورد انتخاب می‌شود.
(2) مرحله 5: ساده سازی بزرگ شدن ساختمان
یک الگوریتم BE با اشاره به وانگ و همکاران. [ 7 ] در رویکرد ما پذیرفته شده است. حداقل اندازه توسط مساحت ساختمان ( ST a ) تعیین می شود و گاهی اوقات می توان آن را به حداقل طول ( ST L ) و عرض ( ST W ) مستطیل مرزی ساختمان تبدیل کرد. نقض حداقل محدودیت اندازه برای ساختمانها در مقیاس ممکن بعدی در بخش 3.3 تعریف شده است. با توجه به ساختمان B i ، طول و عرض مستطیل مرزی آن به صورت LB i و WB i نشان داده می شود.. طبق نظر وانگ و همکاران می توان آن را بر اساس نوع تخلف بزرگ کرد. [ 7 ].
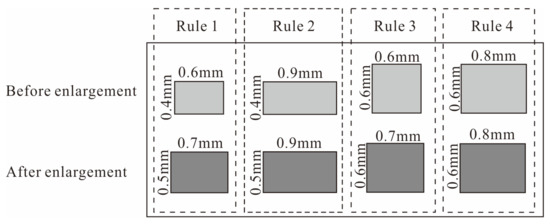
  • قانون 1: اگر B i ST a را در مقیاس ممکن بعدی نقض کند ، با جایگزین کردن آن با یک مستطیل به عنوان ST L × ST W بزرگ می شود.
  • قانون 2: اگر B i ST W را در مقیاس ممکن بعدی نقض کند ، با جایگزین کردن آن با یک مستطیل به عنوان LB i × ST W بزرگ می شود.
  • قانون 3: اگر B i ST L را در مقیاس ممکن بعدی نقض کند ، با جایگزین کردن آن با یک مستطیل به عنوان WB i × ST L بزرگ می شود.
  • قانون 4: اگر در مقیاس احتمالی بعدی تخلفی از محدودیت حداقل اندازه مشاهده نشود، بزرگنمایی ساختمان انجام نخواهد شد.
به عنوان مثال، پارامترهای بزرگنمایی ساختمان در 1:25k را می توان به صورت تنظیم کرد استیa = 0.35 متر متر2استیآ=0.35 مترمتر2، استیL = 0.7 میلی متر استی�=0.7 میلی مترو استیدبلیو= 0.5 میلی متر استیدبلیو=0.5 میلی مترطبق گفته اداره ملی نقشه برداری چین [ 40 ]. ساختمان ها بر اساس قوانین تعریف شده بزرگ می شوند ( شکل 7 ).

4. آزمایش کنید

داده های ساختمان توپوگرافی با 122 ساختمان در اشکال مختلف جمع آوری شده از یک محصول داده باز به نام OS Open Map Local و ارائه شده توسط Ordnance Survey برای آزمایش های ما استفاده شد ( شکل 8 ). اینها داده های نقشه “سطح خیابان” با مقیاس اسمی مشاهده 1:10k هستند [ 41 ]. برخی از ویژگی های اساسی جغرافیایی مانند جاده ها و پوشش گیاهی نیز در این منطقه مورد مطالعه گنجانده شده است. از آنجایی که ما قصد داریم ساختمان ها را ساده کنیم، و آنها در شکل نشان داده نشده اند، رویکرد ما بر روی ArcEngine 10.2 (ESRI، ایالات متحده آمریکا) با استفاده از C# پیاده سازی شد. داده‌ها و کدهای آزمایش‌های ما همه در این آدرس موجود است: https://data.mendeley.com/datasets/tgngv7dkgn/3 (در 21 اکتبر 2020 قابل دسترسی است).

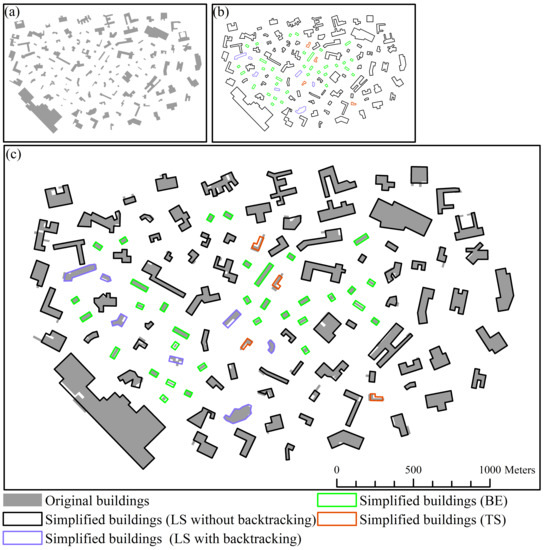
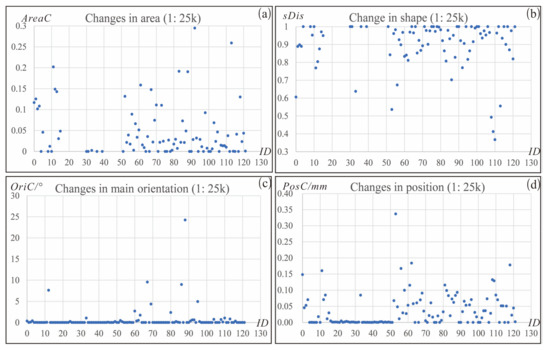
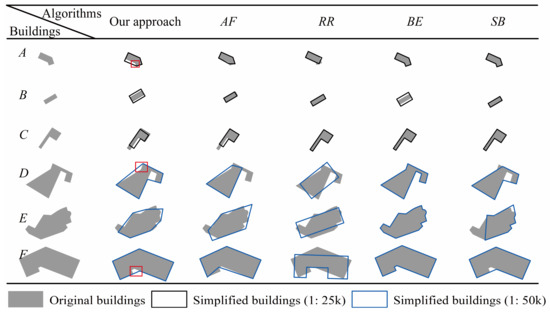
پارامترهای محدودیت خوانایی بر اساس بخش 2.1 و تعریف شده در بخش 3.3 به شرح زیر تنظیم شد: استیa = 0.35 متر متر2، استیL = 0.7 میلی متر ، S تیدبلیو= 0.5 میلی متر ، G T L = 0.3 میلی متر استیآ=0.35 مترمتر2،استی�=0.7 میلی متر،استیدبلیو=0.5 میلی متر،جیتی�=0.3 میلی متر. پارامترهای ارزیابی در الگوریتم LS به صورت زیر تنظیم شدند: A r e a C≤ 0.3 ، O r i C ≤30∘، پo s C≤ 0.5 میلی متر آreaسی≤0.3،OriC≤30درجه،پ�سسی≤0.5 میلی متر. ساختمان های مجموعه داده در مقیاس 1:25k ساده شدند ( شکل 8 ). هیچ انتخاب، تجمیع یا گونه‌سازی در آزمایش‌ها وجود ندارد. تعداد ساختمان های ساده شده بر اساس الگوریتم های مختلف، همانطور که در جدول 3 نشان داده شده است. کیفیت داده های ساختمان های ساده شده در مقیاس های هدف با توجه به محدودیت های تعمیم شرح داده شده در بخش 2.1 ارزیابی شد. تمام ساختمان‌ها در مقیاس‌های هدف، پارامترهای کنترلی مجموعه محدودیت‌های خوانایی را برآورده کردند. محدودیت‌های حفاظتی با مقایسه تغییرات در ناحیه ( AreaC )، جهت‌گیری اصلی ( OriC ) و موقعیت ( PosC ) ساختمان‌ها بین مقیاس اصلی و هدف، که در تعریف شده‌اند، ارزیابی شد.جدول 2 ( شکل 9 ). علاوه بر این، تغییر شکل نیز بر اساس فاصله سطح ( sDis ) با توجه به Yan et al. [ 6 ] همانطور که در رابطه (5) ( شکل 9 ).

s D i s = A r e a ( B o ∩ B s ) / A r e a ( B o ∪ B s )س�منس=آ�هآ(ب�∩بس)/آ�هآ(ب�∪بس)

جایی که A r e a ( B o ∩ B s )آ�هآ(ب�∩بس)منطقه تقاطع ساختمان های Bo و Bs است و A r e a ( B o ∪ B s )آ�هآ(ب�∪بس)منطقه اتحاد ساختمان های Bo و Bs است. از آنجایی که ساختمان هایی که محدودیت حداقل اندازه را نقض می کنند در رویکرد ما بزرگ می شوند، این ممکن است منجر به تغییر بزرگی در مساحت و شکل شود. بنابراین، تغییرات در مساحت و شکل برای ساختمان های بزرگ شده در مقیاس هدف مقایسه نشد. همانطور که در شکل 9 نشان داده شده است ، AreaC تقریباً در 0.10، OriC در 5 درجه، PosC در 0.2 میلی متر و s Dis در 0.8 کنترل می شود. بزرگترین AreaC 0.295، بزرگترین OriC 24.2 درجه و بزرگترین PosC 0.340 میلی متر است. همه این تغییرات در پارامترهای مجموعه کنترل می شوند ( A r e a C≤ 0.3 ، O r i C ≤30∘، پo s C≤ 0.5 میلی متر آreaسی≤0.3،OriC≤30درجه،پ�سسی≤0.5 میلی متر) برای الگوریتم LS . علاوه بر این، sDis برای چندین ساختمان پس از ساده‌سازی کمتر از 0.6 در شکل 9 است، زیرا آنها با الگوریتم TS در رویکرد ما ساده‌سازی شده‌اند.

5. بحث

5.1. مقایسه ها

برای اعتبارسنجی امکان‌سنجی و سازگاری رویکردمان، ساختمان‌های ساده‌شده به‌دست‌آمده در 1:25k را با رویکردمان با الگوریتم چهار نقطه مجاور ( AF ) [ 26 ]، الگوریتم رگرسیون بازگشتی ( RR ) [ 31 ]، بزرگ‌نمایی ساختمان ( BE ) مقایسه کردیم. ) الگوریتم [ 7 ] و ابزار ساده سازی ساختمان ( SB ) در ArcGIS [ 17 ]. همان پارامترهایی که در رویکرد ما وجود داشت (اگر الگوریتم به پارامترهای خاصی نیاز دارد) تنظیم شد. نتایج با توجه به محدودیت‌های تعمیم شرح داده‌شده در بخش 2.1 مقایسه شدند که به شرح زیر اندازه‌گیری شد: تعداد ساختمان‌هایی که حداقل اندازه را نقض می‌کنند ( BNS) یا محدودیت دانه بندی ( BNG )، و میانگین تغییرات در مساحت ( aAreaC )، جهت اصلی ( aOriC )، موقعیت ( aPosC ) و شکل ( asDis ) بین ساختمان ها در مقیاس اصلی و هدف، که در جدول 2 و معادله (5) تعریف شده است. نتایج مقایسه شده به صورت جدول 4 نشان داده شده است.
در مورد محدودیت‌های خوانایی، جدول 4 نشان می‌دهد که همه ساختمان‌های به‌دست‌آمده با رویکرد ما در 1:25 کیلومتر محدودیت خوانایی را برآورده می‌کنند، در حالی که 36 ساختمان به‌دست‌آمده با AF ، 42 ساختمان به‌دست‌آمده با RR ، و 33 ساختمان به‌دست‌آمده با SB در 1:25 کیلومتر، این محدودیت را نقض کردند. حداقل محدودیت اندازه علاوه بر این، یک ساختمان به‌دست‌آمده با AF ، هفت ساختمان به‌دست‌آمده با RR ، 65 ساختمان به‌دست‌آمده با BE ، و 47 ساختمان به‌دست‌آمده با SB در 1:25k محدودیت دانه‌بندی را نقض کردند. در مورد محدودیت حفظ، ساختمان‌های به‌دست‌آمده با رویکرد ما دارای aOriC کوچک‌تری در مقایسه با آن‌ها بودندAF ، RR ، و SB . ساختمان‌های به‌دست‌آمده با الگوریتم‌های ساده‌سازی فهرست‌شده، همگی aPosC کوچک و aPosC کمتر از ۰.۰۴۲ میلی‌متر داشتند. در مورد محدودیت‌های حفظ مساحت و شکل، ساختمان‌ها در رویکرد ما ممکن است بزرگ شوند زیرا بسیار کوچک هستند، که ممکن است منجر به تغییر بزرگ در مساحت و شکل شود. در حالی که ساختمان‌های با مساحت کوچک ۱ در الگوریتم‌های AF ، RR و BE ساده‌سازی نشده‌اند و این ساختمان‌ها محدودیت‌های خوانایی را نقض می‌کنند. با در نظر گرفتن ساختمان های بزرگ شده: aAreaC با رویکرد ما 0.809 و asDis 0.819 بود. و همینطور برای ساختمانهای بدست آمده با BE وaAreaC 0.775 بود. بدون در نظر گرفتن ساختمان های بزرگ شده در رویکرد ما، aAreaC 0.046 بود، که به این معنی است که تغییر در مساحت نیز با رویکرد ما در سطح پایینی کنترل می شود. و asDis 0.899 و مشابه asDis بدست‌آمده توسط AF و SB بود، که به این معنی است که اشکال را نیز می‌توان در ساختمان‌های ساده‌شده با رویکرد ما حفظ کرد، همانطور که سایر رویکردها انجام می‌دهند.
شش ساختمان ساده شده با الگوریتم های ساده سازی مختلف در شکل 10 برای مقایسه دقیق فهرست شده اند. ابتدا، سازه های محلی با در نظر گرفتن ویژگی های متعامد و غیر متعامد ساختمان ها در رویکرد ما طبقه بندی می شوند، بنابراین رویکرد می تواند ویژگی های متعامد و غیر متعامد ساختمان های ساده شده را حفظ کند. همانطور که در شکل 10 نشان داده شده است ، هنگامی که ساختمان های A و F با استفاده از رویکرد ما ساده می شوند، ویژگی های متعامد آنها حفظ می شود. و هنگامی که ساختمان E ساده می شود، ویژگی های غیر متعامد آن حفظ می شود. با این حال، استفاده از AF برای ساده‌سازی ساختمان‌های A و F ممکن است ویژگی‌های متعامد آنها را از بین ببرد. و با استفاده از RRاحتمال مربع شدن گوشه ها بیشتر است، که ممکن است ویژگی های غیر متعامد را از دست بدهند، مانند ساختمان E.
ثانیاً، در صورتی که هنگام اعمال عملیات مبتنی بر ساختار محلی، نتیجه نامطلوب به دست آید، یک استراتژی عقبگرد اعمال می شود. این به این معنی است که احتمال بیشتری برای به دست آوردن یک نتیجه رضایت بخش با استراتژی عقب نشینی در رویکرد ما وجود دارد. به عنوان مثال، عملیات مبتنی بر ساختار محلی برای قطعات قاب شده توسط یک مستطیل قرمز در ساختمان‌های A و D آغاز می‌شود و عملیات با اولویت بالاتر منجر به کاهش زیادی در مساحت ساختمان A، یک خود تقاطع یا یک می‌شود. افزایش زیادی در مساحت ساختمان D. بنابراین، عملیات مناسب با استراتژی عقب نشینی ما برای به دست آوردن یک نتیجه رضایت بخش انتخاب می شوند، همانطور که در شکل 10 نشان داده شده است. با این حال، به دست آوردن ساختمان A با AF همچنان محدودیت دانه بندی را نقض می کند، و به دست آوردن ساختمان D باAF ممکن است باعث تغییر زیادی در ناحیه و موقعیت شود. به نظر می‌رسد ساده‌سازی ساختمان D با RR منجر به ساده‌سازی بیش از حد می‌شود و همین امر برای ساختمان E نیز همین‌طور است.
سوم، ما الگوریتم‌های BE و TS را ترکیب می‌کنیم ، زیرا الگوریتم LS گاهی اوقات برای ساده‌سازی ساختمان‌ها قابل اجرا نیست. به عنوان مثال، ساختمان B برای ساده سازی بر اساس ساختارهای محلی آن بسیار کوچک است و رویکرد ما از الگوریتم BE استفاده می کند. و ساختمان C به‌عنوان غیر قابل ساده‌سازی توسط الگوریتم LS ارزیابی می‌شود و رویکرد ما از الگوریتم TS استفاده می‌کند. با این حال، BE زمانی اعمال می شود که ساختمان محدودیت حداقل اندازه را نقض کند، ساختمان های A، C، D، E و F با این الگوریتم ساده نشده اند. علاوه بر این، هنگام استفاده از ArcGIS، ساختمان‌های با مساحت کوچک، مانند ساختمان‌های A، B و C، ساده‌سازی نمی‌شوند. بنابراین، ترکیبی ازالگوریتم های BE و TS ممکن است به تولید یک نتیجه ساده معقول تر کمک کنند.

5.2. استفاده ممکن برای تغییر مقیاس مداوم ساختمان ها

از آنجایی که ساختمان ها مقیاس به مقیاس در رویکرد ما ساده شده اند، ایجاد یک ساختار داده پیوسته برای ساختمان ها در کاربردهای آینده می تواند مفید باشد. برای یک ساختمان معین ( Bi ) که به مقیاس هدف به تدریج مقیاس به مقیاس ساده شده است، می‌توانیم هر نمایش Bi را که پس از ساده‌سازی با مقیاس‌های مربوطه در دو ردیف منطبق به دست می‌آید ، ثبت کنیم.B R = {بی آر1من،بی آر2من, … ,بی آرnمن}بآر=BR1من،BR2من،…،BR�منو اساس= {S c a l e1من،S c a l e2من, … ,S c a l enمن}اساس=مقیاس1من،مقیاس2من،…،مقیاس�من. اگر مقیاس m i در SS به ترتیب صعودی ثبت شود و هر مقیاس m i در SS شرایط را برآورده کند. S c a l eمترمن<S c a l em + 1من،S c a l eمترمن∈ اساسمقیاسمترمن<مقیاسمتر+1من،مقیاسمترمن∈اساسسپس BR m+1 i را می توان بر اساس BR m i از مقیاس m i تا مقیاس m+1 i به دست آورد. بنابراین، نمایش B i را می توان با جستجو در امتداد SS با هر مقیاس هدف معین به دست آورد. شرایط S c a l eمترمن<S c a l em + 1من،S c a l eمترمن∈ اساسمقیاسمترمن<مقیاسمتر+1من،مقیاسمترمن∈اساسرا می توان با حذف Scale m i در SS برآورده کرد، که ممکن است شرایط را نداشته باشد، و نمایش متناظر آن BR m-1 i نیز باید در BR حذف شود . سپس ردیف های همسان ( BR و SS ) پس از حذف به عنوان ساختار داده Bi در نظر گرفته می شوند تا به نمایش مقیاس پیوسته آن دست یابند.
برای یک ساختمان معین ( B i ) در مقیاس 1:10k در شکل 11 به عنوان مثال، اولین نمایش آن به عنوان BR 1 i نشان داده شده است . یک نمایش جدید ( B m +1 i ) از B i را می توان با ساده کردن BR m i برای نقض محدودیت خوانایی به دست آورد. پارامترهای توصیف کننده محدودیت خوانایی در جدول 5 ثبت شده است. روابط بین B m +1 i و مقیاس های مربوط به آن در بخش 3.3 تعریف شده است. بنابراین، همانطور که در شکل 11 نشان داده شده است، هر نمایش و مقیاس های مربوط به آنها با دو ردیف همسان به دست آمده و ثبت می شود. ترازوهای میانی که شرایط را برآورده نمی کنند S c a l eمترمن<S c a l em + 1من،S c a l eمترمن∈ اساسمقیاسمترمن<مقیاسمتر+1من،مقیاسمترمن∈اساس(مقیاس های مشخص شده با رنگ قرمز در شکل 11 ) حذف می شوند. بنابراین، دو ردیف مطابق پس از حذف، B R = {بی آر1من، بی آر2من، بی آر3من، بی آر5من، بی آر7من، بی آر8من}بآر=BR1من، BR2من، BR3من، BR5من، BR7من، BR8منو اساس= { 10,000 , 11,000 , 15,333 , 19,000 , 42,000 , 56,400     }اساس=10000، 11000، 15,333،19000، 42000، 56400را می توان به عنوان ساختار داده ای برای پشتیبانی از تبدیل مقیاس پیوسته B i در نظر گرفت. با توجه به مقیاس هدف 1:25k، نمایش هدف را می توان به صورت BR 5 i برای 25,000 ∈ [ 19,000 , 42,000 ]25000∈[19000،42000]و با توجه به مقیاس هدف 1:50k، نمایش هدف را می توان به صورت BR 7 i برای 50,000 ∈ [ 42,000 , 56,400 ]50000∈[42000،56400]. اگر مقیاس هدف معین کوچکتر از 1:56400 باشد، نمایش هدف را می توان با مقیاس بندی BR 7 مطابق با مقیاس داده شده به دست آورد.

5.3. محدودیت ها

اگرچه نشان داده شده است که رویکرد ما در ساده‌سازی ساختمان‌ها در یک مجموعه داده مؤثر است، برخی محدودیت‌ها نیز باید مورد بحث قرار گیرند.
اول، الزامات تعمیم ممکن است در مقیاس ها، مناطق و حتی خواسته های کاربر متفاوت باشد. اگرچه الزامات را می توان با پارامترهای تعریف شده در رویکرد ما یا تنظیم شده توسط کاربران کنترل کرد، رویکرد ما هنوز در تخصیص خودکار عملیات مناسب برای ساختمان هایی با الزامات تعمیم متفاوت کمی مشکل دارد. برای مثال، محدودیت‌های حداقل اندازه ممکن است در مقیاس‌ها متفاوت باشد. به عنوان مثال، با توجه به اداره ملی نقشه برداری چین [ 39]، حداقل طول و عرض حداقل مستطیل مرزی ساختمان در مقیاس 1:5k و 1:10k به صورت 1.0 و 0.7 میلی متر و موارد در 1:25k و 1:50k به صورت 0.7 و 0.5 میلی متر نشان داده می شوند. با این حال، در رویکرد ما، هنگامی که حداقل طول و عرض حداقل مستطیل مرزی ساختمان ها توسط کاربر تنظیم شود، در مقیاس ها تغییر نخواهند کرد.
به عنوان مثالی دیگر، ویژگی های ساختمان ها ممکن است در مناطق مختلف متفاوت باشد، به عنوان مثال، ساختمان متعامد A و ساختمان غیر متعامد B نشان داده شده در شکل 12 a. در ساده‌سازی، ویژگی‌های متعامد ممکن است اولین موردی باشد که در ساختمان‌های متعامد حفظ می‌شود و مساحت ممکن است اولین موردی باشد که در ساختمان‌های غیرمتعامد حفظ می‌شود [ 16 ]. شکل 12 a نشان می دهد که ساختمان متعامد A ممکن است نتیجه معقول تری با اولویت بالاتر در محدودیت حفظ شکل داشته باشد، در حالی که ساختمان غیر متعامد B ممکن است نتیجه معقول تری با اولویت بالاتر در محدودیت حفظ منطقه داشته باشد. اگرچه الزامات مختلف برای ساختمان های متعامد و غیر متعامد را می توان با تعیین اولویت محدودیت های حفظ در ما کنترل کرد.الگوریتم LS ، مکانیزمی برای تعیین اولویت‌های مختلف در محدودیت‌های حفاظتی برای ساختمان‌هایی با ویژگی‌های مختلف هنوز مورد نیاز است (توضیح‌شده در بخش 3.4 ). ابزارها و استانداردهای زیادی برای بیان و استدلال دانش یا قوانین با توسعه نمودار دانش معرفی شده است. اگر الزامات تعمیم متفاوت در ساده‌سازی ساختمان به‌عنوان دانش یا قوانین با یک مدل نمایش دانش مؤثر مدل‌سازی شود، ممکن است بتوان رویکرد ما را برای ساختمان‌هایی با الزامات تعمیم متفاوت در مقیاس‌ها، مناطق و حتی درخواست‌های کاربر اعمال کرد.
دوم، ساده‌سازی تنها یک نوع عملیات تعمیم است. گاهی اوقات استفاده از ساده سازی در تعمیم ساختمان مناسب نیست. به عنوان مثال، همانطور که در شکل 12 ب نشان داده شده است، ساختمان های مجاور اصلی پس از ساده سازی ممکن است آنقدر نزدیک شوند که توسط کاربران متمایز شوند. در اینجا، ساختمان های C، D، و E یا ساختمان های F و G. بنابراین، برخی عملیات تعمیم دیگر، مانند انتخاب، تجمیع و نوع بندی نیز ممکن است برای دستیابی به یک نتیجه معقول مورد نیاز باشد. از این رو، برای بهبود رویکرد پیشنهادی ما در آینده، سایر عملیات تعمیم را می توان با اعمال آنها قبل یا بعد از ساده سازی ساختمان ها ترکیب کرد.

6. نتیجه گیری

ما یک رویکرد ساده سازی ساختمان مترقی و ترکیبی را پیشنهاد می کنیم که الزامات نقشه برداری را بر اساس طبقه بندی ساختار محلی و استراتژی عقب نشینی در نظر می گیرد. در رویکرد ما، عملیات ساده‌سازی متفاوتی برای ساختمان‌هایی که محدودیت‌های حداقل اندازه یا دانه‌بندی را نقض می‌کنند، برای تولید نمایش مقیاس بعدی ساختمان‌های ساده‌شده آغاز می‌شود. روابط بین مقیاس‌ها و پارامترهایی که حداقل اندازه یا دانه‌بندی را توصیف می‌کنند محاسبه می‌شوند و ساختمان‌های ساده شده در مقیاس هدف به دست می‌آیند. قوانین حمایت کننده از کاربرد آنها بر اساس محدودیت های حفظ ساختمان ها در حالی که عملیات ساده سازی خاص را اعمال می کنند ساخته می شوند. آزمایش‌ها نشان می‌دهند که ساختمان‌های ساده‌شده به‌دست‌آمده با رویکرد ما محدودیت‌های خوانایی و تغییر مساحت را برآورده می‌کنند. جهت گیری و موقعیت ساختمان های ساده شده با مقایسه با نتایج تولید شده بر اساس چهار الگوریتم ساده سازی در محدوده مشخصی کنترل می شود. نتایج ما همچنین استفاده احتمالی از رویکرد ما در نمایش مقیاس پیوسته ساختمان‌ها را نشان می‌دهد.
کارهای آینده بر موارد زیر تمرکز خواهند کرد: (1) یک مدل دانش برای بیان دانش نقشه‌کشی یا قوانین برای ایجاد ساده‌سازی در مقیاس‌ها و مناطق، که می‌تواند از مناسب شدن رویکرد ما برای الزامات تعمیم مختلف یا خواسته‌های کاربر پشتیبانی کند، و (2) رویکردهایی که ترکیب می‌شوند. عملیات تعمیم معنایی، مانند انتخاب و تجمیع، برای دستیابی به دگرگونی مستمر گروه‌های ساختمانی، نه تنها ساختمان‌های منفرد.

منابع

  1. لی، دی. ابزارهای جدید تعمیم نقشه برداری. در مجموعه مقالات نوزدهمین کنفرانس بین المللی کارتوگرافی ICA، اتاوا، ON، کانادا، 14 تا 21 اوت 1999. ص 1235–1242. [ Google Scholar ]
  2. Sester, M. تعمیم بر اساس تعدیل حداقل مربعات. بین المللی قوس. فتوگرام Remote Sens. 2000 , XXXIII , 931–938. [ Google Scholar ]
  3. آی، تی. چنگ، ایکس. لیو، پی. یانگ، ام. تحلیل شکل و تطبیق الگوی ویژگی‌های ساختمان با روش تبدیل فوریه. محاسبه کنید. محیط زیست سیستم شهری 2013 ، 41 ، 219-233. [ Google Scholar ] [ CrossRef ]
  4. بورگاردت، دی. اشمید، اس. ارزیابی مبتنی بر محدودیت نقشه های توپوگرافی تعمیم یافته خودکار و دستی. در کارتوگرافی در اروپای مرکزی و شرقی ; Springer: برلین، هایدلبرگ، 2009; صص 147-162. [ Google Scholar ]
  5. رینفورد، دی. Mackaness، W. تطبیق الگو در حمایت از تعمیم ساختمان های روستایی. در پیشرفت‌ها در مدیریت داده‌های فضایی، مجموعه مقالات دهمین سمپوزیوم بین‌المللی در مورد مدیریت داده‌های مکانی، اتاوا، ON، کانادا، 9 تا 12 ژوئیه . Richardson, DE, Van O, P., Eds. Springer: برلین/هایدلبرگ، آلمان، 2002; صص 137-151. [ Google Scholar ]
  6. یان، ایکس. آی، تی. Zhang، X. روش تطبیق و ساده‌سازی الگو برای ساخت ویژگی‌ها بر اساس شناخت شکل. بین المللی J. Geo Inf. 2017 ، 6 ، 250. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
  7. وانگ، ال. گوا، کیو. لیو، ی. سان، ی. Wei, Z. انتخاب ساختمان متنی بر اساس الگوریتم ژنتیک در تعمیم نقشه. بین المللی J. Geo Inf. 2017 ، 6 ، 271. [ Google Scholar ] [ CrossRef ]
  8. Guo, Q. روش ساده سازی گرافیکی مرز ویژگی منطقه به عنوان زاویه راست. Geomat. Inf. علمی دانشگاه ووهان 1999 ، 24 ، 255-258. [ Google Scholar ]
  9. Sester, M. رویکردهای بهینه سازی برای تعمیم و انتزاع داده ها. بین المللی جی. جئوگر. Inf. علمی 2005 ، 19 ، 871-897. [ Google Scholar ] [ CrossRef ]
  10. چن، دبلیو. لانگ، ی. شن، جی. لی، دبلیو. شناخت سازه و پیشرونده مقعرهای پس از آن چند ضلعی ساختمان بر اساس D-Tin محدود. Geomat. Inf. علمی دانشگاه ووهان 2011 ، 36 ، 584-587. [ Google Scholar ]
  11. چنگ، بی. لیو، کیو. لی، ایکس. وانگ، ی. ساده سازی ساختمان با استفاده از شبکه های عصبی پس انتشار: ترکیبی از تخصص نقشه نگاران و ادراک محلی مبتنی بر شطرنجی. GISci. Remote Sens. 2013 , 50 , 527–542. [ Google Scholar ] [ CrossRef ]
  12. بوچین، ک. میلمنز، دبلیو. Renssen، AV; Speckmann, B. ساده‌سازی حفظ منطقه و طرح‌واره‌سازی زیربخش‌های چندضلعی. ACM Trans. تف کردن سیستم الگوریتم 2016 ، 2 ، 1-36. [ Google Scholar ] [ CrossRef ]
  13. Oosterom، PV; Meijers, M. ساختارهای داده در مقیاس Vario که از زوم صاف و انتقال پیشرونده داده های دو بعدی و سه بعدی پشتیبانی می کنند. بین المللی جی. جئوگر. Inf. علمی 2014 ، 28 ، 455-478. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  14. هوانگ، ال. آی، تی. Oosterom، PV; یان، ایکس. یانگ، ام. ساختاری مبتنی بر ماتریس برای نمایش برداری در مقیاس متغیر در طیف گسترده ای از مقیاس های نقشه: مورد داده های شبکه رودخانه. ISPRS Int. J. Geo-Inf. 2017 ، 6 ، 218. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
  15. پنگ، دی. Touya, G. تعمیم مستمر ساختمانها به مناطق ساخته شده با تجمیع و رشد. در UrbanGIS’17: 3rd ACM SIGSPATIAL Workshop on Smart Cities and Urban Analytics، 7–10 نوامبر 2017، Redondo Beach، CA، USA . ACM: نیویورک، نیویورک، ایالات متحده آمریکا، 2017؛ 8p. [ Google Scholar ]
  16. شن، ی. آی، تی. لی، سی. ساده سازی ساختمان های شهری برای حفظ ویژگی های هندسی با استفاده از تقسیم بندی سوپرپیکسلی. بین المللی J. Appl. رصد زمین. Geoinf. 2019 ، 79 ، 162-174. [ Google Scholar ] [ CrossRef ]
  17. وانگ، ز. لی، دی. ساده سازی ساختمان بر اساس تشخیص الگو و تجزیه و تحلیل شکل. در مجموعه مقالات نهمین سمپوزیوم بین المللی در مورد مدیریت داده های فضایی، پکن، چین، 10-12 اوت 2000. صص 58-72. [ Google Scholar ]
  18. اشتاینیگر، اس. Taillandier، P. Weibel, R. استفاده از تشخیص بافت شهری و یادگیری ماشین برای بهبود تعمیم ساختمان ها. بین المللی جی. جئوگر. Inf. علمی 2010 ، 24 ، 253-282. [ Google Scholar ] [ CrossRef ]
  19. Ruas، A. Modèle de Généralisation de Données Géographiques à Base de Contraintes et d’autonomie. Ph.D. پایان نامه، Sciences de l’Information G´eographique، Marne La Vallee، فرانسه، 1999. [ Google Scholar ]
  20. دوچن، سی. کریستف، اس. Ruas، A. تعمیم، مشخصات نماد و ارزیابی نقشه: بازخورد از تحقیقات انجام شده در آزمایشگاه COGIT، IGN فرانسه. بین المللی جی دیجیت. Earth 2011 , 4 (Suppl. S1), 25–41. [ Google Scholar ] [ CrossRef ]
  21. دوچن، سی. رواس، ع. کریستف، سی. مدل CartACom: تبدیل ویژگی های نقشه برداری به عوامل ارتباطی برای تعمیم نقشه برداری. کارتوگر. Geogr. Inf. سیستم 2012 ، 26 ، 1533-1562. [ Google Scholar ] [ CrossRef ]
  22. مودت، ا. تویا، جی. دوچن، سی. Picault، S. DIOGEN، یک مدل چند سطحی جهت تعمیم کارتوگرافی. بین المللی جی. کارتوگر. 2017 ، 3 ، 121-133. [ Google Scholar ] [ CrossRef ]
  23. وانگ، ال. گوا، کیو. وی، ز. لیو، ی. حل تعارض فضایی در یک فرآیند چند عاملی با استفاده از مدل مار. دسترسی IEEE 2017 ، 5 ، 24249–24261. [ Google Scholar ] [ CrossRef ]
  24. استوتر، جی. اسمالن، جی. بیکر، ن. هاردی، پی. تعیین الزامات نقشه برای تعمیم خودکار داده های توپوگرافی. کارتوگر. J. 2009 , 46 , 214-227. [ Google Scholar ] [ CrossRef ]
  25. Regnauld، N. نوع سازی ساختمان متنی در تعمیم خودکار نقشه. الگوریتمیکا 2001 ، 30 ، 312-333. [ Google Scholar ] [ CrossRef ]
  26. خو، دبلیو. لانگ، ی. ژو، تی. Chen, L. ساده سازی چند ضلعی ساختمان بر اساس روش چهار نقطه ای مجاور. Acta Geod. کارتوگر. گناه 2013 ، 42 ، 929-936. [ Google Scholar ]
  27. لخت، من. Touya, G. افزایش ردپای ساختمان با عملیات مربع سازی. جی. اسپات. Inf. علمی 2016 ، 13 ، 33-60. [ Google Scholar ] [ CrossRef ]
  28. دوچن، سی. بارد، اس. Barillot, X. توصیف کمی و کیفی جهت گیری ساختمان. در مجموعه مقالات پنجمین کارگاه آموزشی در مورد پیشرفت در تعمیم خودکار نقشه، پاریس، فرانسه، 28 تا 30 آوریل 2003. [ Google Scholar ]
  29. لیو، ی. گوا، کیو. سان، ی. Ma، X. یک رویکرد ترکیبی برای جابجایی نقشه‌برداری برای ساختمان‌ها بر اساس اسکلت و الگوریتم تیر الاستیک بهبودیافته. PLoS ONE 2014 ، 9 ، e113953. [ Google Scholar ] [ CrossRef ] [ PubMed ]
  30. ژانگ، ایکس. استوتر، جی. آی، تی. کراک، ام.-جی. Molenaar, M. ارزیابی خودکار ترازهای ساختمان در نقشه های تعمیم یافته. بین المللی جی. جئوگر. Inf. علمی 2013 ، 27 ، 1550-1571. [ Google Scholar ] [ CrossRef ]
  31. Bayer, T. ساده سازی خودکار ساختمان با استفاده از رویکرد بازگشتی. در کارتوگرافی در اروپای مرکزی و شرقی ; Gartner, G., Ortag, F., Eds. Springer: برلین، هایدلبرگ، 2009; صص 121-146. [ Google Scholar ]
  32. دیمن، جی. ون کرولد، ام. Spaan، B. تعمیم ساختمان با کیفیت بالا با گسترش عملگرهای مورفولوژیکی. در مجموعه مقالات دوازدهمین کارگاه ICA در مورد تعمیم و بازنمایی چندگانه، مونپلیه، فرانسه، 20 تا 21 ژوئن 2008. [ Google Scholar ]
  33. Meijers, M. ساده سازی ساختمان با استفاده از منحنی های افست به دست آمده از اسکلت مستقیم. در مجموعه مقالات نوزدهمین کارگاه ICA در مورد تعمیم و بازنمایی چندگانه، هلسینکی، فنلاند، 14 ژوئن 2016. [ Google Scholar ]
  34. Kada، M. تجمع ساختمانهای سه بعدی با استفاده از رویکرد داده ترکیبی. کارتوگر. Geogr. Inf. سیستم 2011 ، 38 ، 153-160. [ Google Scholar ] [ CrossRef ]
  35. وی، ز. او، جی. وانگ، ال. وانگ، ی. Guo, Q. رویکرد جابجایی مشارکتی برای تعارضات فضایی در تعمیم نقشه ساختمان شهری. IEEE Access 2018 . [ Google Scholar ] [ CrossRef ]
  36. فن، اچ. اسکندر، ز. وو، اچ. تشخیص ساختارهای تکراری بر روی ردپای ساختمان برای اهداف مدل‌سازی و بازسازی سه بعدی. بین المللی جی دیجیت. زمین 2017 ، 10 ، 785–797. [ Google Scholar ] [ CrossRef ]
  37. شن، ی. آی، تی. او، Y. یک رویکرد جدید برای ساده سازی خط بر اساس پردازش تصویر: مطالعه موردی مرزهای منطقه آب. ISPRS Int. J. Geo-Inf. 2018 ، 7 ، 41. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
  38. Taillandier، P. دوچن، سی. Drogoul، A. بازنگری خودکار قوانین مورد استفاده برای هدایت فرآیند تعمیم در سیستم ها بر اساس استراتژی آزمون و خطا. بین المللی جی. جئوگر. Inf. علمی 2011 ، 25 ، 1971-1999. [ Google Scholar ] [ CrossRef ]
  39. یانگ، م. یوان، تی. یان، ایکس. آی، تی. جیانگ، سی. یک رویکرد ترکیبی برای ساده سازی ساختمان با یک ارزیاب از یک شبکه عصبی پس انتشار. بین المللی جی. جئوگر. Inf. علمی 2021 . [ Google Scholar ] [ CrossRef ]
  40. اداره ملی نقشه برداری، نقشه برداری و اطلاعات جغرافیایی چین. مشخصات تلفیقی برای نقشه‌های مقیاس بنیادی ملی-بخش 1: مشخصات تلفیقی برای نقشه‌های توپوگرافی 1:25000، 1:50000 و 1:100000 . انتشارات China Zhijian: پکن، چین، 2008.
  41. بررسی مهمات. OS OPEN MAP-LOCAL: راهنمای محصول و مشخصات فنی. 2016. در دسترس آنلاین: https://www.ordnancesurvey.co.uk/documents/os-open-map-local-product-guide.pdf (در 21 اکتبر 2020 قابل دسترسی است).
Ijgi 10 00302 g001 550
شکل 1. محدودیت برای ساده سازی ساختمان.
Ijgi 10 00302 g002 550
شکل 2. چارچوب رویکرد ما.
Ijgi 10 00302 g003 550
شکل 3. پیش پردازش برای ساختمان ها. ( الف ) چند ضلعی اصلی; ( ب – ث ) پیش پردازش برای ساختمان ها برای حذف گره های غیرعادی.
Ijgi 10 00302 g004 550
شکل 4. طبقه بندی ساختارهای محلی و عملیات اساسی آنها (که با خطوط چین مشخص می شوند). ( الف ) چند ضلعی ساختمان. ( ب ) خم می شود. ( ج ) خمهای مقعر و محدب. ( د ) افست. ( ه ) گوشه
Ijgi 10 00302 g005 550
شکل 5. تغییرات در خصوصیات ساختمان پس از اعمال عملیات مبتنی بر ساختار محلی: ( الف ) ایجاد خود تقاطع. ( ب ) آسیب به ویژگی های متعامد. ( الف – ج ) عملیات ممکن است منجر به تغییر در منطقه، جهت اصلی و موقعیت یک ساختمان شود.
Ijgi 10 00302 g006 550
شکل 6. فرآیند انتخاب عملیات مبتنی بر ساختار محلی در امتداد درخت تصمیم باینری.
Ijgi 10 00302 g007 550
شکل 7. بزرگنمایی ساختمان.
Ijgi 10 00302 g008 550
شکل 8. ساختمان های ساده شده در مقیاس 1:25k: ( الف ) مجموعه داده اصلی. ( ب ) نتیجه ساده شده؛ ج ) مقایسه بین این دو. نتیجه برای نمای واضح بزرگ شده است.
Ijgi 10 00302 g009 550
شکل 9. مقایسه تغییرات در ناحیه ( a )، شکل ( b )، جهت اصلی ( c ) و موقعیت ( d )، شکل بین ساختمان‌ها در مقیاس هدف و مقیاس اصلی.
Ijgi 10 00302 g010 550
شکل 10. مقایسه ساختمان های معمولی با استفاده از الگوریتم های ساده سازی مختلف.
Ijgi 10 00302 g011 550
شکل 11. ساخت ساختار داده: دو ردیف همسان که نمایش B i و مقیاس های مربوط به آن را ثبت می کنند: BR={BR1i,BR2i,…,BRni}بآر=BR1من،BR2من،…،BR�منو SS={Scale1i<Scale2i,Scaleni}اساس=مقیاس1من<مقیاس2من،مقیاس�من. نمایش B i در مقیاس هدف را می توان با جستجو همراه با SS و BR به دست آورد .
Ijgi 10 00302 g012 550
شکل 12. محدودیت ها. ( الف ) ساختمان های A و B با اولویت بالاتر به طور جداگانه در محدودیت های حفظ شکل و حفظ منطقه ساده شده اند. ( ب ) ساختمان‌های C، D، E یا ساختمان‌های F، G ممکن است پس از ساده‌سازی با کاهش زیاد مقیاس، آنقدر نزدیک شوند که قابل تشخیص نباشند.

مقالات داخلی و بین المللی

مطالب مرتبط ...

بدون دیدگاه

دیدگاهتان را بنویسید