شبکه کانولوشن گراف فضایی-زمانی برای پیش بینی ترافیک چند مقیاسی

تحقیقات پیش‌بینی ترافیک کوتاه‌مدت روش‌های زیادی را تولید کرد و به طور کلی می‌توان آنها را به دو دسته روش‌های آماری و روش‌های یادگیری ماشینی تقسیم کرد. بسیاری از روش‌های آماری مدل‌های خطی هستند که بر تفسیرپذیری تمرکز دارند و به فرضیه محکم‌تری نیاز دارند. آثار معرف شامل HA [ 13 ]، ARIMA [ 1 ]، VAR [ 2 ]، حداقل مربعات جزئی (PLS) [ 14 ]] و غیره با این حال، این مدل‌ها در کاربردهای سناریویی عملی عملکرد خوبی ندارند، زیرا ویژگی‌های دینامیکی و غیرخطی داده‌های ترافیک را در نظر نمی‌گیرند و در برآوردن فرضیات خطی ثابت خود مشکل دارند. از سوی دیگر، یادگیری ماشینی می‌تواند همبستگی‌های مکانی-زمانی پیچیده‌تر و مؤثرتری را از خود داده‌ها بیاموزد، بنابراین نتایج پیش‌بینی بهتری ارائه می‌دهد. برخی از کارهای معرف SVR [ 3 ]، KNN [ 4 ] و شبکه های عصبی [ 15 ] هستند. اگرچه ویژگی‌هایی که استخراج می‌کنند حاوی اطلاعات غیرخطی هستند، اما زمان‌برتر و نامطمئن‌تر هستند، زیرا ویژگی‌های آن‌ها عمدتاً به صورت دستی توسط انسان استخراج می‌شوند.

با توسعه یادگیری عمیق، آنها قادر به مدل سازی خودکار وابستگی های پیچیده تر هستند، که توجه زیادی را به مدل سازی داده های مکانی-زمانی پیچیده جلب کرده است [ 5 ]. بسیاری از مدل‌های یادگیری عمیق کلاسیک به دلیل قابلیت‌های پردازش توالی طبیعی‌شان برای پیش‌بینی ترافیک استفاده شده‌اند، به عنوان مثال، RNN [ 7 ]، LSTM [ 8 ] و GRU [ 9 ]. متعاقباً، سایرین برای مدل‌سازی سری‌های زمانی ترافیک توسط CNN، یادگیری اطلاعات زمانی با هسته‌های کانولوشنال و تأیید برتری آنها نسبت به سایر شبکه‌های عصبی تکراری استفاده شده‌اند. 6 ].]. با این حال، این روش ها تمایل دارند فقط بر روی الگوهای زمانی داده های ترافیک تمرکز کنند و الگوهای مکانی را نادیده بگیرند. برای یادگیری کامل الگوهای فضایی، محققان صحنه های ترافیک را به صحنه های مدل تصویری برای یادگیری تقسیم می کنند. CLTFP [ 16 ] سعی می کند ویژگی های مکانی را با استفاده از CNN به تصویر بکشد و یک شبکه پیش بینی مکانی-زمانی با استفاده از LSTM برای حل مشکل پیش بینی زمانی کوتاه مدت بسازد. Convolutional LSTM (Conv-LSTM) [ 17 ] همچنین از شبکه های CNN و LSTM به ترتیب برای گرفتن ویژگی های مکانی و زمانی استفاده می کند. با این حال، تفاوت این است که شبکه Conv-LSTM به جای انباشته کردن یک شبکه CNN و یک شبکه LSTM، CNN را در دروازه شبکه LSTM قرار می دهد و آنها را بطور ذاتی ادغام می کند. ST-ResNet [ 18] از CNN باقیمانده عمیق برای مدیریت شدت در یک شبکه فضایی برای پیش‌بینی جریان‌های جمعیت در سطح شهر در بازه‌های زمانی مختلف استفاده می‌کند. آنها همچنین ویژگی های مکانی-زمانی را برای دوره های زمانی مختلف وارد می کنند و عوامل خارجی را برای بهبود دقت پیش بینی ها اضافه می کنند. همه روش های فوق برای داده های شبکه پردازش می شوند، در حالی که جریان ترافیک اساسا یک داده گرافیکی است. باید به قالبی تبدیل شود که به اندازه کافی راحت نباشد. علاوه بر این، آنها تنها بر روی اطلاعات همسایگی داده‌های شبکه تمرکز می‌کنند و اطلاعات توپولوژیکی خاصی را که توسط بخش‌های جاده‌ای به هم پیوسته ذکر شده است نادیده می‌گیرند.

در مقایسه با شبکه‌های عصبی کانولوشن در فضای اقلیدسی، شبکه‌های عصبی گراف (GNN) می‌توانند در فضاهای نامنظم و نامنظم نمونه‌برداری و جمع شوند و برای پردازش داده‌های ساختار یافته گراف مناسب‌تر هستند. با افزایش محبوبیت GNN، چندین رویکرد برای GNN در سال های اخیر پدیدار شده است، مانند شبکه های کانولوشن گراف (GCN) [ 19 ]، شبکه های Chebyshev (ChebNet) [ 20 ]، شبکه های توجه گراف (GAT) [ 21 ]، کانولوشن انتشاری. شبکه های عصبی (DCNN) [ 22]، و غیره. به خصوص، GCN محبوبیت خاصی دارد. آنها به طور گسترده در طبقه بندی ساختار گراف، سیستم های توصیه و غیره استفاده می شوند. از آنجایی که ویژگی های مکانی داده های ترافیکی به خوبی با ساختار نمودار مطابقت دارد، آنها همچنین کلیدی برای به دست آوردن ویژگی های فضایی ذاتی داده ها شده اند. در سال های اخیر، توسعه مستمر آنها STGNN ها را به مدل اصلی در مدل های پیش بینی ترافیک تبدیل کرده است.

اگرچه انواع زیادی از STGNN وجود دارد، اما به طور کلی، آنها را می توان به دو نوع تقسیم کرد: یکی مدل مبتنی بر RNN و دیگری مدل مبتنی بر CNN.

یکی از مدل‌های STGNN مبتنی بر RNN برای گرفتن ویژگی‌های زمانی با یک شبکه عصبی مکرر و جایگزینی (یا اضافه کردن مستقیم) لایه خطی RNN با پیچیدگی نمودار برای گرفتن ویژگی‌های فضایی استفاده می‌شود. به عنوان مثال، در مورد معرف ترین T-GCN [ 23 ] یا GCRNN [ 24 ]، هر دوی آنها از GRU برای گرفتن ویژگی های زمانی و GCN برای گرفتن ویژگی های مکانی استفاده می کنند، بنابراین به آنها اجازه می دهد تا ویژگی های مکانی-زمانی کامل را ثبت کنند. با توجه به اشکال اشتراک هسته کانولوشن و به اشتراک گذاری GCN، GNN های دیگری برای یادگیری در نظر گرفته می شوند. لی مدل کلاسیک DCRNN را پیشنهاد کرد [ 24]، که ویژگی‌های فضایی را با سرگردانی تصادفی DCNN روی نمودار می‌گیرد و ویژگی‌های زمانی را با استفاده از Seq2Seq ثبت می‌کند و مدل را انعطاف‌پذیرتر و کارآمدتر می‌کند. با این حال، جریان ترافیک داده‌ای پویا و در حال تغییر است و باید در نظر گرفت که پیش‌بینی ممکن است در هر مرحله متفاوت باشد. بنابراین، Cui TGC-LSTM [ 25 ] را پیشنهاد کرد که GCN و LSTM را ادغام می‌کند و با افزودن یک ماتریس دسترس‌پذیری جریان آزاد، گردش کار پیچیدگی نمودار را بهینه می‌کند. Guo OGCRNN را توسعه داد [ 26]، که بر اساس GCRNN بهینه می شود. از تغییرات داده‌ها برای بهینه‌سازی ماتریس لاپلاس در طول پیچیدگی نمودار استفاده می‌کند، بنابراین مدل را قادر می‌سازد تا ویژگی‌های مکانی-زمانی پویا را به دست آورد. هر دوی این کارها همبستگی‌های مکانی-زمانی ثابت را بهبود می‌بخشند، بنابراین تغییرات دینامیکی در همبستگی‌های مکانی-زمانی را ممکن می‌سازند. بای A3T-GCN [ 27 ] را پیشنهاد کرد که توجه را به T-GCN می افزاید و تغییرات دینامیکی داده ها را در مرحله اکتساب ویژگی در نظر می گیرد. با این حال، RNN دارای محدودیت‌هایی است، زیرا پارامترهای یکسانی را در هر مرحله زمانی به اشتراک می‌گذارد، که نشان‌دهنده توانایی ضعیف برای توصیف پویایی پیچیده همبستگی‌های زمانی است.

بسیاری از مدل های STGNN مبتنی بر CNN توسعه یافتند. این روش‌ها اغلب ویژگی‌های زمانی را با CNN و ویژگی‌های مکانی را با GNN دریافت می‌کنند. نماینده ترین آنها STGCN [ 28 ] است که ویژگی های زمانی را با CNN با دروازه GLU و ویژگی های فضایی با GCN ثبت می کند. این همان T-GCN برای به دست آوردن ویژگی های فضایی و زمانی کامل است. با این حال، به دلیل محدوده بسیار کوچک هسته کانولوشن CNN، میدان ادراکی نسبتا کمی دارد که منجر به کاهش توانایی پیش‌بینی بلندمدت آن نیز می‌شود. برای حل این مشکل، Graph WaveNet [ 29]، پیشنهاد شده توسط وو، می خواهد دقت پیش بینی توالی طولانی را با استفاده از پیچش اتساع بهبود بخشد. همچنین یک ماتریس مجاورت یادگیری مستقل ایجاد می کند تا به یادگیری ماتریس مجاورت ناشناخته کمک کند، که بیشتر بر مبنای پویا سازگار است. این اولین مطالعه بر روی ماتریس مجاورت تطبیقی ​​در زمینه پیش‌بینی ترافیک است. علاوه بر این، مدل های دیگری نیز وجود دارند که مکانیسم توجه را برای جبران مشکل یک میدان ادراکی کوچک در نظر می گیرند. Guo ASTGCN را پیشنهاد کرد [ 30] برای ادغام مکانیسم توجه و GCN برای ترسیم همبستگی فضایی و زمانی پویا. نه تنها میدان دریافت را از طریق توجه گسترش می‌دهد، بلکه هوشمندانه از مکانیسم‌های توجه زمانی و مکانی برای دستیابی به توانایی به دست آوردن اطلاعات مکانی-زمانی پویا به طور کامل از خود داده‌ها استفاده می‌کند. آنها همچنین MSTGCN [ 30 ] را بدون توجه دینامیکی برای مقایسه پیشنهاد می‌کنند و نشان می‌دهند که ASTGCN او می‌تواند ویژگی‌های مکانی-زمانی پویا را ثبت کند. ژنگ GMAN را پیشنهاد کرد [ 31]، که همچنین بر تغییرات پویا در فرآیند تمرکز دارد. در مقایسه با ASTGCN، GMAN به طور کامل جایگزین CNN و GCN با توجه می شود و بیشتر به تعامل بین اطلاعات زمانی و مکانی می پردازد. GMAN بر اساس ساختار رمزگذار خودکار و مکانیسم توجه برای محاسبه اثر عوامل مکانی و زمانی بر شرایط ترافیک طراحی شده است. بعدها، برخی از مدل‌های مبتنی بر ASTGCN و GMAN توسعه یافتند و با بهبودهایی مانند DGCN [ 32 ] و MASTGCN [ 33 ] عمل کردند. با توجه به عملکرد قدرتمندشان، چنین مدل هایی برای پیش بینی مسیر [ 11 ] و تعیین داده های ترافیکی [ 11 ، 12 ، 34 ] نیز استفاده می شوند.

همچنین مطالعاتی وجود دارد که می‌خواهند داده‌های دیگری (شرایط آب و هوا، نقاط مورد علاقه (POI) و غیره) را برای کمک به پیش‌بینی‌ها به مطالعات فوق اضافه کنند. Bai یک شبکه عصبی کانولوشنی بازگشتی [ 35 ] را برای مدل‌سازی و پیش‌بینی داده‌های تقاضای خودروی تاریخی در شهر پیشنهاد می‌کند. داده های هواشناسی و عناصر زمانی را به صورت رمزگذاری شده جاسازی می کند و آنها را با استفاده از رمزگذار خودکار مبتنی بر LSTM پیش بینی می کند. زو یک مدل پیش‌بینی به نام AST-GCN [ 36 ] پیشنهاد می‌کند]، که هم POI و هم اثرات آب و هوا را بر جریان ترافیک در نظر می گیرد. این سه نوع داده را ترکیب می کند و آنها را برای آموزش در T-GCN قرار می دهد که ساده و مؤثر است. اگرچه روش های فوق بسیار مؤثر هستند، اما به دلیل محرمانه بودن داده ها و مسائل مربوط به حریم خصوصی، که کار مدل های آنها را محدود می کند، همه داده ها به طور کامل در دسترس نیستند.

همه مدل های فوق اساساً استخراج ویژگی را در مقیاس مکانی-زمانی یکسان انجام می دهند. با این حال، تفاوت‌هایی در الگوهای مکانی-زمانی که به دلیل مقیاس‌های مکانی-زمانی متفاوت یاد می‌شوند، وجود دارد. بنابراین، برخی از محققین به بررسی ویژگی‌های مکانی-زمانی محلی یا ویژگی‌های چند مقیاسی پرداخته‌اند. یو ST-UNet [ 37 ] را پیشنهاد کرد که می تواند اطلاعات فضایی چند مقیاسی را به دست آورد. ST-UNet بر اساس چارچوب مدل ساختار U-Net است و به طور مشترک از ST-pooling و ST-unpooling برای انجام استخراج اطلاعات مکانی در مقیاس های مختلف استفاده می کند. علاوه بر این، از RNN توسعه یافته برای به دست آوردن ویژگی های زمانی طولانی تر استفاده می کند. آهنگ پیشنهادی STSGCN [ 38]، که استخراج ویژگی نمودارهای محلی را در نظر می گیرد و اهمیت ویژگی های نمودار محلی را اثبات می کند. بر اساس GCN، بلوک‌های مکانی-زمانی می‌سازد که می‌توانند هم استخراج اطلاعات زمانی و هم مکانی را انجام دهند، که ناهمگونی پیش‌بینی جریان ترافیک را نیز در نظر می‌گیرد. گوئو HGCN را پیشنهاد کرد [ 39]، که ساختار گراف را به صورت سلسله مراتبی بر اساس خوشه بندی طیفی پردازش می کند تا پیش بینی ترافیک را در ساختارهای گراف خرد و کلان انجام دهد. این برهم نهی از ویژگی های میکروسکوپی و ماکروسکوپی همچنین به ضبط ویژگی های فضایی-زمانی چند مقیاسی دست می یابد. با این حال، اندازه مقیاس مدل های چند مقیاسی پیشنهادی نیاز به تنظیم مصنوعی دارد. به دلیل خطای تنظیم دستی، از یک طرف توانایی بالقوه مدل را محدود می کند. از طرفی نیاز به عملیات دستی بیشتری دارد که بسیار پر زحمت و دردسر است.

با این حال، مطالعات فعلی، مشکلات ساختار گراف را در دانه‌بندی نمودارها یا نمودارهای محلی مورد مطالعه قرار داده‌اند، و فقدان مطالعات ریزدانه خاص گره وجود دارد. بای AGCRN را پیشنهاد کرد [ 40] برای مطالعه جزئیات پیش بینی با دانه بندی گره. از یک GCN با پارامترهای گره برای تولید ماتریس مجاورت تطبیقی ​​استفاده می کند و پارامترها را با GRU جاسازی می کند تا الگوهای ترافیک را به صورت پویا یاد بگیرد. بخشی از مشکلات RNN با GCN را حل می کند و توانایی برخی از مدل ها را برای توصیف پویایی پیچیده همبستگی زمانی و مکانی ریز دانه بهبود می بخشد. با این حال، همچنان دارای کاستی هایی است، نادیده گرفته می شود که تفاوت هایی در الگوهای گره ها در مقیاس های مختلف وجود خواهد داشت. از سوی دیگر، حتی مشکل اشتراک پارامتر RNN با تعبیه گره کاهش می یابد. با این حال، آموزش خاصی متوقف می شود، اطلاعات جاسازی گره ثابت می شود و ویژگی های پارامتر RNN، اگرچه بسیار غنی تر از نسخه اصلی است، هنوز ثابت هستند.

بر اساس مفهوم ساخت گراف، شبکه ترافیک را می توان به صورت تعریف کرد G ( V، ای، الف )، جایی که V∈آرنمجموعه ای از رئوس یا گره ها را نشان می دهد و E∈آرن× Nمجموعه ای از لبه ها را نشان می دهد. شبکه ترافیک G نشان دهنده رابطه بین رئوس در بعد فضایی است و در طول زمان ثابت می ماند. ماتریس مجاورت با نشان داده می شود A∈ _آرن× N. ماتریس سیگنال گراف به صورت مشخص شده است ایکسجیتی∈آرن× F، که در آن F ویژگی های هر گره را در زمان مشخص می کند تی. از نظر پیش بینی جریان ترافیک، هر بار تیماتریس ویژگی دارد ایکستی، داده های تاریخی اچرا می توان به عنوان نشان داد ایکساچ= {ایکسt – i + 1،ایکسt – i + 2, … ,ایکستی}و داده های پیش بینی شده پرا می توان به عنوان نشان داد ایکسپ= {ایکسt + 1،ایکسt + 2, … ,ایکسt + p}.

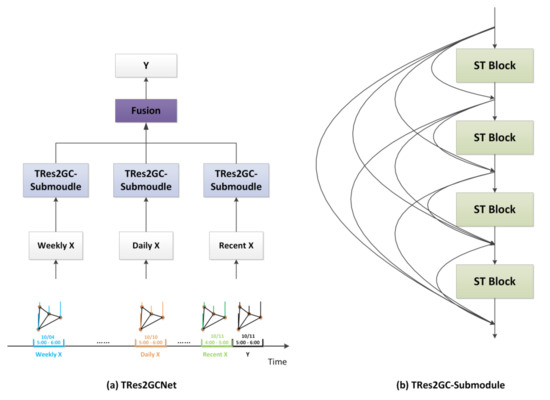
در این بخش، شکل 1 a چارچوب پیشنهادی TRes2GCN را نشان می دهد. این مدل از سه جزء تشکیل شده است که هر یک شامل همان بخش زیرماژول کانولوشنال نمودار باقیمانده زمانی (TRes2GC-Submodule) است ( شکل 1 ب). سه زیر ماژول به ترتیب بر سه دوره زمانی مختلف تمرکز می کنند و ترکیب وزنی هر دوره زمانی توسط مجموعه ای از پارامترهای همجوشی انجام می شود. هر TRes2GC-Submodule شامل چهار بلوک فضایی-زمانی (ST Blocks) است که در اتصال متراکم [ 41 ] به هم متصل شده اند.

به طور خلاصه، مدل ما چندین مفهوم طراحی دارد، به شرح زیر:

• از طریق یک رویکرد چند جزئی، مدل ما ویژگی‌های مکانی-زمانی دوره‌های زمانی مختلف را می‌آموزد و ترکیب می‌کند و الگوهای سفر وسایل نقلیه را بررسی می‌کند.
• TRes2GC-Submodule بلوک‌های فضایی و زمانی را در مسیر DenseNet به هم متصل می‌کند، که عرض ویژگی‌ها را با ترکیب ویژگی‌های مکانی-زمانی سطوح مختلف افزایش می‌دهد و به طور موثر مشکل تخریب و هموارسازی بیش از حد شبکه را کاهش می‌دهد.

اگرچه داده های ترافیک با تغییرات دینامیکی بلادرنگ مشخص می شوند، مطالعات نشان داده اند که داده های ترافیک درجات مختلفی از الگوهای مشابه در مجاورت، دوره های روزانه و هفتگی دارند [ 17 ]. در نظر گرفتن این تغییر دوره ای جریان ترافیک می تواند به طور موثری دقت پیش بینی را بهبود بخشد. در این مطالعه، ما از ASTGCN [ 30 ] برای نمونه برداری از دوره زمانی استفاده کردیم.

فرض کنید زمان فعلی T ₀ است، اندازه پنجره پیش بینی T _p و تعداد نمونه ها در روز است. q. ما سه سری زمانی T h _، Td _و Tw _را به ترتیب در محور زمانی به عنوان ورودی‌های مؤلفه زمانی برای دوره‌های اخیر، دوره‌های روزانه و دوره‌های هفتگی قطع می‌کنیم، که _{در آن Th، Td و Tw} به همان مقدار هستند. تی _پی . ما دوره های زمانی مختلف را برای ورودی نشان داده ایم. جزئیات این سه دوره به شرح زیر است:

(1)

دوره اخیر: دوره اخیر به داده های تاریخی در نزدیکی مقدار پیش بینی اشاره دارد که به صورت نشان داده شده است. ایکسساعت= (ایکستی0–تیک+ 1،ایکستی0–تیک+ 2, … ,ایکستی0) ∈آرن× F×تیکاز آنجایی که تغییرات ناگهانی در جریان ترافیک مقدماتی هستند، قطعه لحظه نزدیک به ویژه برای قطعه پیش‌بینی مهم است. برش خاص در شکل 1 الف نشان داده شده است و رنگ سبز نسبت به رنگ سیاه دوره اخیر آن است.

(2)

دوره روزانه: یک دوره روزانه به داده های تاریخی یک روز قبل همزمان با بخش پیش بینی اشاره دارد که با نشان داده می شود. ایکسد= (ایکستی0– q+ 1،ایکستی0– q+ 2, … ,ایکستی0– q+تیپ) ∈آرن× F×تیدقطعه ای از همان بازه زمانی دوره پیش بینی شده در روز گذشته است. داده‌های ترافیک احتمالاً بخشی از همان الگو را در مدتی نشان می‌دهند، به عنوان مثال، اوج صبح و اوج عصر برای هر روز از یک روز هفته وجود دارد. بنابراین، ما این بخش را به عنوان بخشی از پیش بینی مشترک انتخاب می کنیم، بنابراین ویژگی های مشابه دوره روزانه را به دست می آوریم. برش خاص در شکل 1 الف نشان داده شده است و رنگ نارنجی نسبت به رنگ سیاه دوره روزانه آن است.

(3)

دوره هفتگی: دوره هفتگی به داده های تاریخی یک هفته قبل همزمان با بخش پیش بینی اشاره دارد که با نشان داده شده است. ایکسw= (ایکستی0− 7 ∗ q+ 1،ایکستی0− 7 ∗ q+ 2, … ,ایکستی0− 7 ∗ q+تیپ) ∈آرن× F×تیwقطعه ای از همان بازه زمانی دوره پیش بینی شده در هفته گذشته است. دلیل آن همان دوره روزانه است. به عنوان مثال، تغییر جریان این جمعه بسیار شبیه به جمعه آینده است، اما تفاوت هایی با تغییر جریان آخر هفته وجود دارد. بنابراین، ما از آن برای ثبت ویژگی های مشابه دوره هفتگی استفاده می کنیم. برش خاص در شکل 1 الف نشان داده شده است و رنگ آبی نسبت به رنگ سیاه دوره هفتگی آن است.

هر بلوک مکانی-زمانی ( شکل 2 الف) شامل یک لایه توجه زمانی سلسله مراتبی ( شکل 2 ب) و یک لایه پیچش گراف تطبیقی ​​سلسله مراتبی است ( شکل 2) است.ج). آنها در آرایش عمودی معمول نیستند، اما به صورت افقی مستقر می شوند. آنها تحت تأثیر دروازه ای با یکدیگر تعامل دارند تا ویژگی های مکانی-زمانی را بیشتر به هم مرتبط کنند. در مورد لایه توجه سلسله مراتبی و لایه پیچیدگی گراف تطبیقی ​​سلسله مراتبی، آنها به ترتیب ثبت اطلاعات مکانی چند مقیاسی زمانی و چند مقیاسی را بر اساس لایه به لایه پیاده سازی می کنند. این با جمع‌آوری اطلاعات چند مقیاسی مبتنی بر بلوک که در بالا ذکر شد ترکیب می‌شود، بنابراین چارچوب ما را قادر می‌سازد تا اطلاعات مکانی-زمانی چند مقیاسی را با دانه‌بندی خوب انجام دهد. مشکل تک ویژگی مکانی-زمانی در مسئله پیش‌بینی داده‌های غیراقلیدسی اساساً حل شده است.

لایه توجه زمانی (TAL). برای جریان ترافیک، در بعد زمانی پویا و مرتبط است و چنین ویژگی های پویایی را نمی توان توسط CNN یا RNN معمولی یاد گرفت. بنابراین، این مقاله از مکانیسم توجه در حوزه NLP [ 42 ] استفاده می کند، بنابراین بر اهمیت اطلاعات در گره های زمانی مختلف در یک دوره زمانی کامل تمرکز می کند و وزن های بیشتری را به نقاط زمانی معتبر اختصاص می دهد [ 30 ]. این نه تنها ارتباط زمانی پویا و تطبیقی ​​را به مدل ما اضافه می‌کند، بلکه میدان احساس را برای حل مشکلات پیش‌بینی زمان طولانی‌تر گسترش می‌دهد. فرمول ریاضی آن به صورت زیر نشان داده شده است:

جایی که Vه،به∈آرتی× تی، U1∈آرن، U2∈آراف× N، و U3∈آرافپارامترهای قابل یادگیری هستند، ایکسساعت= (ایکس1،ایکس2, … ,ایکستی) ∈آرن× F× تیخروجی بلوک مکانی-زمانی قبلی را نشان می دهد، Eوزن توجه هر لحظه را نسبت به لحظه های دیگر نشان می دهد و بسته به داده های ورودی و مقدار آن متفاوت خواهد بود. Eمن ، جنشان دهنده همبستگی بین زمان i و زمان j پس از عادی سازی (the اسo fتی امیک xتابع فعال سازی برای عادی سازی استفاده می شود).

لایه توجه زمانی سلسله مراتبی (Res2TAL). Res2Net [ 43 ] توانایی خود را در زمینه بینایی رایانه (پیچیدگی اقلیدسی) برای تقسیم یک پیچیدگی به چند کانولوشن که به هم مرتبط هستند، ثابت کرده است، و به ما امکان می دهد اطلاعات ویژگی های چند مقیاسی را از دیدگاهی دقیق استخراج کنیم. ما با استقرار بخش چارچوب Res2Net با حذف ساختار باقیمانده بر روی لایه توجه زمانی ایجاد کردیم، بنابراین یک لایه توجه زمانی سلسله مراتبی را پیشنهاد کردیم، همانطور که در شکل 2 نشان داده شده است.ب لایه توجه زمانی سلسله مراتبی نه تنها بر اهمیت هر لحظه تمرکز می کند، بلکه شباهت روندهای زمانی را نیز در یک دوره زمانی یاد می گیرد. این به ما امکان می دهد هم تغییرات وزن ارزش زمانی و هم تغییرات روند زمانی را در یک دوره زمانی یاد بگیریم، بنابراین ویژگی های زمانی را در یک چشم انداز دقیق تر یاد بگیریم. از طرف دیگر Res2Net را می توان بدون افزایش تعداد پارامترها با زمان آموزش بیشتر تحت تنظیمات خاص استفاده کرد. بنابراین، Res2TAL می تواند ما را قادر سازد تا اطلاعات ویژگی های زمانی را در مقیاس های مختلف بدون افزایش پارامترها استخراج کنیم. فرمول ریاضی آن به صورت زیر نشان داده شده است:

جایی که سپارامتر مقیاس در Res2Net است و همچنین تعداد مقیاس های زمانی ما را نشان می دهد. هر دو سیh a n ge Co nv1و سیh a n ge Co nv2شبکه های عصبی کانولوشنی با هسته کانولوشنال 1 هستند که برای کاهش تعداد کانال های ویژگی ها استفاده می شوند.

شایان ذکر است که بلوک فشار و برانگیختگی آن (SE-Block) را که در ابتدا وجود داشت [ 44 ] برای جایگزینی ترکیب بین لایه‌های منفرد حذف کردیم و فضایی چند مقیاسی زمانی و چند مقیاسی را به شکل بلوک‌های فضایی-زمانی با هم ترکیب کردیم. . به جای استخراج ویژگی های مشترک، می خواهیم تفاوت بین مقیاس را حفظ کنیم. این امر تعامل بین اطلاعات چند مقیاسی را در دروازه‌بندی بلوک مکانی-زمانی تسهیل می‌کند، در حالی که بهبود جزئی عملکرد آن بعداً تأیید می‌شود.

تولید ماتریس مجاورت تطبیقی در بعد فضایی، در هر گره تفاوت هایی در الگوهای ترافیکی وجود دارد که می تواند تاثیر زیادی در پیش بینی ترافیک داشته باشد. روش کنونی ساخت گراف عمدتاً از ویژگی‌های فردی شروع می‌شود (به عنوان مثال، شبکه جاده، نقطه مورد علاقه (POI)، شباهت ترافیک، و غیره)، که بسیار قابل تفسیر هستند اما حاوی اطلاعات وابستگی مکانی کامل نیستند. علاوه بر این، بیشتر ساختارهای گراف به نمودارهای از پیش تعریف شده نیاز دارند و مدل‌های آن‌ها در صورت از دست دادن نمی‌توانند کار کنند. به منظور حل مشکلات ظاهر شده در بالا، ما یک رویکرد تعبیه گره را برای ساخت ماتریس مجاورت تطبیقی ​​اعمال کردیم [ 29 ، 40 ]. فرمول به صورت زیر نشان داده شده است:

جایی که E∈آرن× Dپارامتر تعبیه گره را نشان می دهد Dبعد، که می تواند به صورت تطبیقی ​​یاد شود و برای یادگیری تغییرپذیری در بین گره ها استفاده شود، منن∈آرن× Nنشان دهنده ماتریس واحد است نابعاد، که برای افزودن حلقه های خود به ساختار گراف استفاده می شود R e L Uتابع فعال سازی برای از بین بردن ارتباطات منفی بین گره ها و گره ها استفاده می شود سافت مکستابع فعال سازی برای عادی سازی ماتریس مجاورت استفاده می شود.

لایه پیچیدگی نمودار تطبیقی ​​(AGCN). از آنجایی که هسته کانولوشن GCN مشترک است، اگرچه می‌تواند مهم‌ترین الگوهای ترافیکی را در کل نمودار ترافیک به تصویر بکشد، در واقع یادگیری تغییرپذیری در بین گره‌ها و یادگیری الگوهای ترافیک گره‌های مختلف به روشی دقیق برای ما دشوار است. . AGCN [ 40] ما را قادر می سازد تا بدون نیاز به داده های مشخصه گره شناخته شده، ویژگی های ریز دانه گره ها را ضبط کنیم. یک پارامتر تعبیه گره دیگر در ماتریس مجاورت فوق به GCN اضافه می کند. این پارامتر می‌تواند به ما کمک کند ماتریس مجاورت تطبیقی ​​را آموزش دهیم و در عین حال بر پارامترهای یادگیری در طول پیچیدگی نمودار تأثیر بگذارد و ویژگی‌های هر گره را کاهش دهد. بنابراین، به ما کمک می‌کند تا تفاوت‌های الگوی گره را در نظر بگیریم تا ویژگی‌های فضایی تطبیقی ​​پویا را در دانه‌ریزی ریز به دست آوریم. معادله آن به صورت زیر نشان داده شده است:

جایی که دبلیو∈آرD × F× F‘و ب ∈آرD × F‘پارامترهای قابل یادگیری هستند متفاوت از GCN، از ایده تجزیه ماتریس برای حل بخشی از مشکلات overfitting و oversmoothing GCN استفاده می کند. با این حال، یک مشکل نیز دارد که دارای محدوده ثابتی از میدان های ادراکی است. این ویژگی‌های فضایی چند مقیاسی گرفته‌شده توسط مدل را محدود می‌کند.

لایه پیچیدگی گراف تطبیقی ​​سلسله مراتبی (Res2GCN). Res2Net [ 43 ] تأیید شده است که توانایی بهتری در استخراج ویژگی ها در مقیاس های چندگانه در فضای اقلیدسی دارد. ما به این ایده اشاره می کنیم و ایده ساخت Res2Net را در AGCN به کار می بریم تا یک لایه پیچیدگی گراف تطبیقی ​​سلسله مراتبی را پیشنهاد کنیم. به طور مشابه، می‌تواند ویژگی‌های فضایی چند مقیاسی را در جریان ترافیک (فضای غیر اقلیدسی) در سطح دانه‌بندی دقیق‌تر به تصویر بکشد، و عملکرد داخلی در شکل نشان داده شده است. شکل 2 نشان داده شده است.ج. ویژگی‌های چند مقیاسی Res2GCN نه تنها میدان ادراکی پیچیدگی را افزایش می‌دهد، بلکه محدودیت‌های عملکرد ناشی از تثبیت هسته GCN و همچنین مشکلات اشتراک‌گذاری را تا حدی کاهش می‌دهد، زیرا AGCN در هر مقیاس پارامترهای مشترکی ندارند. از سوی دیگر، از آنجایی که AGCN از همان بردار تعبیه شده در مقیاس‌های مختلف در فرآیند انتشار برگشت پارامتر استفاده می‌کند، این به ماتریس مجاورت ما اجازه می‌دهد تا برای یادگیری الگوهای گره در مقیاس‌های متعدد ترکیب شوند. در بخش بعدی، ما همچنین تأیید می‌کنیم که ماتریس‌های مجاورت مختلف با رویکردهای پارامتر تعبیه گره، اثرات متفاوتی بر Res2GCN دارند. معادله به شرح زیر است:

جایی که سپارامتر مقیاس در Res2Net است و همچنین تعداد مقیاس های فضایی ما را نشان می دهد و سیh a n ge Co nv1و سیh a n ge Co nv2یک شبکه عصبی کانولوشنال با هسته کانولوشنال 1 هستند که همان نقش را در Res2TAL ایفا می کنند.

این بخش برای توضیح چگونگی ادغام ویژگی های زمانی و مکانی در بلوک ST استفاده می شود. پیش‌بینی جریان ترافیک هر بخش جاده باید بر جریان تاریخی آن بخش جاده و جریان تاریخی سایر بخش‌های جاده مرتبط در گذشته تمرکز کند. بنابراین، ما باید ویژگی های زمانی سلسله مراتبی استخراج شده را به صورت پویا با ویژگی های فضایی سلسله مراتبی در اینجا ترکیب کنیم. در مطالعات گذشته، اکثر مدل‌ها به‌طور متوالی در جهت طولی عمل می‌کنند، که باعث می‌شود همبستگی بین ویژگی‌های زمانی و مکانی به اندازه کافی قوی نباشد. بنابراین، ما از یک تکنیک دروازه‌ای برای ترکیب کردن ویژگی‌های زمانی و مکانی به صورت افقی و پویا استفاده می‌کنیم، بنابراین همبستگی بین ویژگی‌های زمانی و مکانی را افزایش می‌دهیم. فرآیند عملیات ذاتی در نشان داده شده استشکل 2 الف و همچنین معادله ریاضی نشان داده شده در زیر:

جایی که L i n e ar1، L i n e ar2لایه تبدیل خطی است که می تواند به صورت پویا و تطبیقی ​​با خود داده تغییر کند و بر بزرگی عمل تأثیر بگذارد. G a t e، ⊙محصول هادامارد است و σهست سیگموئیدتابع فعال سازی، که می تواند در عادی سازی مقادیر ویژگی ها و در نتیجه جلوگیری از انفجار گرادیان در طول فرآیند همجوشی استفاده شود.

بسیاری از مطالعات گذشته، مانند STGCN [ 28 ]، ASTGCN [ 30 ] و غیره، از اتصالات باقیمانده برای یکپارچه‌سازی ویژگی استفاده کرده‌اند، و استفاده مداوم از همان تابع در اتصالات باقی‌مانده همچنان مانع انتقال ویژگی می‌شود. از آنجایی که TRes2GC-Submodule شامل چندین بلوک ST است، استفاده مداوم از ساختار ResNet [ 45 ] می تواند باعث مشکلاتی مانند ناپدید شدن گرادیان و تخریب شبکه شود. برای حل این مشکلات، از DenseNet [ 41 ] برای اتصال بلوک های ST خود استفاده می کنیم. انتشار ویژگی ها را افزایش می دهد، استفاده مجدد از ویژگی ها را تشویق می کند و تعداد پارامترها را کاهش می دهد. از سوی دیگر، DenseNet می تواند مشکل هموارسازی بیش از حد ناشی از استفاده های متعدد از GCN را کاهش دهد.

خوشبختانه، داده‌های جریان ترافیک به اندازه داده‌های تصویری پیچیده نیستند، که به تعداد زیادی لایه برای عمیق‌تر کردن یادگیری نیاز دارند. برای تکمیل یادگیری ویژگی ها به تعداد معقول و محدود بلوک نیاز دارد، اما نه تعداد بلاک های فوق العاده زیاد. بنابراین، شایان ذکر است که دلیل اصلی ما برای استفاده از DenseNet، گسترش تعداد کانال‌های ویژگی‌های مکانی و زمانی است و دلیل ثانویه، انجام عمق‌سازی شبکه است. در آزمایش‌های فرسایشی بعدی، ما همچنین تفاوت‌های حاصل از روش‌های اتصال مختلف (و تفاوت‌های بین ResNet و DenseNet) و تأثیرات ناشی از گسترش و تعمیق مدل را در پیش‌بینی تأیید می‌کنیم. عملیات ذاتی در شکل 1 ب و همچنین معادله زیر نشان داده شده است:

جایی که استی B l o cکلنشان دهنده بلوک ST از بلوک پشته و [ایکس1،ایکس2, … ,ایکسl – 1]اشاره به اتصال نگاشت ویژگی ایجاد شده پس از عبور از ( 0 , … , l − 1) بلوک ها

این بخش نحوه ادغام چندین زیرماژول TRes2GC را شرح می دهد. از آنجایی که یک قالب چند جزئی برای مدل ما در دوره‌های زمانی مختلف و مکان‌های مختلف استفاده می‌شد، ما به راهی برای ترکیب ویژگی‌ها در اجزای مختلف نیاز داشتیم. به عنوان مثال، مدل یکشنبه تأثیر کمی بر پیش بینی جریان مدل دوشنبه دارد، اما مدل دوشنبه تأثیر زیادی بر مدل سه شنبه دارد. بنابراین، ما سه پارامتر وزن را برای کاهش اهمیت هر جزء تعریف کردیم و آنها را جمع‌بندی کردیم. فرمول آنها در زیر نشان داده شده است:

جایی که ⊙محصول هادامارد است و دبلیوساعت، دبلیود، و دبلیوw∈آرن× تیبه ترتیب پارامترهایی هستند که باید یاد بگیرند و همچنین پارامترهای وزنی برای چرخه های مختلف.

دو مجموعه داده حجم ترافیک دنیای واقعی عمومی انتخاب شدند: PeMS04 و PeMS08، که توسط سیستم اندازه‌گیری عملکرد Caltrans در مناطق اصلی شهری کالیفرنیا [ 46 ] جمع‌آوری شدند. همه داده ها از بیش از 39000 حسگر مستقر در آزادراه های کالیفرنیا در فواصل 30 ثانیه جمع آوری می شوند.

داده های خام قبل از اینکه بتوان آنها را برای آموزش در مدل قرار داد باید از قبل پردازش شوند. ما از همان رویکرد پیش پردازشی مانند STSGCN [ 38 ] و AGCRN [ 40 ] برای برخی از مقادیر گمشده در مجموعه داده استفاده می‌کنیم، این مقادیر گمشده را با درون یابی خطی پر می‌کنیم. علاوه بر این، ما مجموعه داده را با تمام مقادیر داده‌ها بین [0,1] نرمال کردیم و میانگین مقدار مجموعه داده 0 است. مجموعه داده را به صورت زمانی تقسیم کردیم و آن را به مجموعه‌های آموزشی، اعتبارسنجی و آزمایشی به نسبت 6:2 تقسیم کردیم. :2. داده‌ها در نهایت در فواصل 5 دقیقه‌ای تجمیع شدند و در مجموع 288 نقطه داده در روز به دست آمد. اطلاعات فراداده در جدول 1 نشان داده شده است. جایی که میانگین داده ها میانگین هر پنج دقیقه (در هر دوره زمانی) داده را نشان می دهد، و محدوده داده نشان دهنده حدود بالا و پایین تغییرات داده ها در هر پنج دقیقه است.

ما 10 روش پیش‌بینی جریان ترافیک زیر را به عنوان مدل‌های پایه برای مقایسه با مدل خود انتخاب می‌کنیم. علاوه بر این، برای نشان دادن تازگی و اعتبار مدل ما، هفت مورد از خطوط پایه، روش‌های پیش‌بینی جریان ترافیک هستند. جزئیات به شرح زیر است:

• VAR : رگرسیون خودکار برداری یک مدل پیش‌بینی است که ویژگی مکانی-زمانی بین داده‌های ترافیک را ثبت می‌کند.
• SVR : رگرسیون بردار پشتیبان از یک ماشین بردار پشتیبان برای انجام رگرسیون خطی استفاده می کند.
• LSTM : شبکه حافظه کوتاه مدت بلندمدت مدلی از RNN است که می تواند وظایف سری زمانی را بهتر انجام دهد.
• DCRNN : شبکه عصبی بازگشتی پیچیدگی انتشار یک چارچوب رمزگذار خودکار است. از پیچیدگی نقشه انتشار برای به دست آوردن ویژگی های فضایی و Seq2Seq برای رمزگذاری اطلاعات زمانی استفاده می کند.
• STGCN : شبکه کانولوشن گراف فضایی-زمانی از ChebNet برای به دست آوردن همبستگی مکانی و CNN با مکانیزم دروازه برای به دست آوردن همبستگی زمانی استفاده می کند.
• MSTGCN : شبکه پیچیدگی نمودار فضایی-زمانی چند جزئی، اطلاعات مکانی-زمانی را در دوره های زمانی مختلف با مدل سازی الگوهای زمانی مختلف استخراج و ترکیب می کند. ویژگی های زمانی را توسط CNN و ویژگی های مکانی را توسط ChebNet به دست می آورد.
• ASTGCN : شبکه کانولوشن گراف فضایی-زمانی مبتنی بر توجه توجه زمانی و توجه مکانی را به MSTGCN برای استخراج اطلاعات مکانی-زمانی پویا اضافه می کند.
• Graph WaveNet : Graph WaveNet GCN و شبکه کانولوشن گشاد شده را برای به دست آوردن همبستگی مکانی و همبستگی زمانی به طور جداگانه ترکیب می کند. همچنین از تعبیه گره برای یادگیری تطبیقی ​​ماتریس مجاورت از داده ها استفاده می کند.
• STSGCN : شبکه‌های کانولوشن گراف همزمان مکانی-زمانی از GCN برای ساخت بلوک‌های کانولوشن سنکرون مکانی-زمانی استفاده می‌کنند تا به طور همزمان همبستگی‌های زمانی و مکانی را با چیدن ماژول‌های کانولوشن سنکرون مکانی-زمانی به دست آورند.
• AGCRN : شبکه کانولوشن برگشتی گراف تطبیقی ​​یک شبکه کانولوشن گراف تطبیقی ​​جدید پیشنهاد کرد تا ویژگی فضایی ریز دانه را به تصویر بکشد. علاوه بر این، از GRU تقویت شده برای گرفتن ویژگی زمانی استفاده می کند.

TRes2GCN بر اساس چارچوب PyTorch پیاده سازی شده و آموزش آن بر روی کارت گرافیک NVIDIA RTX 2080TI انجام می شود. در مدل ما، 4 مقیاس عرض 26 برای استقرار Res2GCN و 3 مقیاس 26 عرض برای Res2TAL گرفته شده است. علاوه بر این، هر یک از لایه های دیگر دارای 64 ویژگی است. سایز دسته ای این مدل 32 است و بهینه ساز Adam برای 40 دوره آموزش مدل با نرخ یادگیری 0.001 استفاده می شود. در فرآیند آموزش، نرخ یادگیری را با بازپخت کسینوس کاهش می‌دهیم و پایین‌ترین نقطه کاهش نرخ یادگیری را 0.0001 قرار می‌دهیم که ما را برای گرفتن نتایج آموزشی بهتر تسهیل می‌کند. در انتخاب تابع از دست دادن، از SmoothL1Loss استفاده می کنیم (یعنی HuberLoss [ 47]) به جای L2Loss، تا ضد اغتشاش مدل افزایش یابد و خطای ناشی از نویز کاهش یابد. فرمول ریاضی به صورت زیر است:

جایی که Yمقدار واقعی جریان ترافیک را نشان می دهد، Y˜مقدار جریان ترافیک پیش بینی شده توسط مدل را نشان می دهد و σیک پارامتر آستانه است که محدوده تلفات مربع خطا را کنترل می کند.

این آزمایش همچنین از سه معیار ارزیابی پرکاربرد برای اندازه‌گیری عملکرد مدل استفاده می‌کند، یعنی میانگین خطای مطلق (MAE)، ریشه میانگین مربع خطا (RMSE) و میانگین درصد مطلق خطا (MAPE)، مانند AGCRN [ 40 ]. ما از این سه معیار برای اندازه گیری اثربخشی پیش بینی مدل خود در مقایسه با مدل پایه استفاده می کنیم.

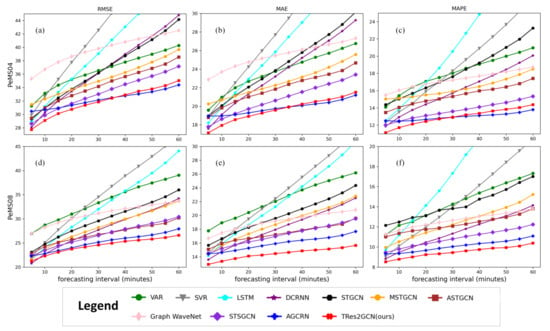
جدول 2 مقایسه ای از میانگین عملکرد چارچوب های مختلف در تمام افق های زمانی را نشان می دهد. به طور کلی، در هر دو مجموعه داده، مدل ما از ده روش پایه دیگر در هر سه معیار عملکرد بهتری دارد. برای توصیف واضح قدرت پیش‌بینی مدل پیشنهادی، آن را از دو جنبه به تفصیل تجزیه و تحلیل می‌کنیم.

(1) توانایی پیش بینی کلی

در جدول 2 می بینیم که روش های SVR و LSTM در مقایسه با سایر شبکه ها دقت کمتری دارند زیرا همبستگی مکانی را در داده های ترافیک در نظر نمی گیرند. VAR در مقایسه با SVR عملکرد بهتری دارد زیرا برخی از اطلاعات مکانی در نظر گرفته شده است. با این حال، این روش‌ها در مقایسه با روش‌های شبکه‌های عصبی نمودار مکانی-زمانی، فضایی برای بهبود در مدیریت اطلاعات مکانی دارند، به همین دلیل است که VAR بیشتر از آنها عملکرد پایین‌تری دارد.

STGCN، DCRNN، MSTGCN، ASTGCN، Graph WaveNet، STSGCN و AGCRN همگی همبستگی فضایی کامل جهانی را در نظر می گیرند و نسبت به مدل های فوق عملکرد بهتری دارند. با این حال، به دلیل طراحی و ساخت متفاوت هر مدل، این مدل‌ها همچنان در نتایج تفاوتی نشان می‌دهند. STGCN، DCRNN و Graph WaveNet همگی ضبط ویژگی های تک دوره ای را از منظر طراحی هدف قرار می دهند، و اهمیت چرخه های زمانی را نادیده می گیرند، و بنابراین، عملکرد کمی پایین تر خواهند داشت. برای MSTGCN و ASTGCN، دوره‌های زمانی متفاوتی را در نظر می‌گیرند و از اطلاعات دوره زمانی بیشتری نسبت به STGCN و DCRNN استفاده می‌کنند. با این حال، مدل های فوق فاقد اطلاعات زمانی چند مقیاسی در مقایسه با TRes2GCN پیشنهادی هستند، بنابراین عملکرد آنها را محدود می کند. برای STSGCN، ویژگی های نمودار محلی نیز در نظر گرفته می شود. بنابراین بهبود جزئی دیگری را در مقایسه با STGCN، DCRNN یا Graph WaveNet ارائه می دهد. با این حال، یک روش استخراج واحد دارد، بنابراین ویژگی‌های مکانی-زمانی استخراج‌شده به اندازه کافی غنی نیستند. در مقابل، مدل ما ویژگی‌های فضایی-زمانی سطوح و مقیاس‌های مختلف را از طریق ساختارهای DenseNet و Res2Net، که از نظر ویژگی‌های مکانی-زمانی غنی‌تر هستند و نتایج پیش‌بینی بهتری دارند، ترکیب می‌کند. برای AGCRN، پارامترهای یادگیری در GCN را به دو پارامتر کوچک برای یادگیری تقسیم می‌کند که از منظری دقیق بهبود می‌یابد. با این حال، تنها ویژگی‌های مکانی و زمانی ریزدانه را در یک مقیاس واحد در نظر می‌گیرد و قادر به در نظر گرفتن الگوهای سفر در دوره‌های زمانی مختلف نیست. مدل پیشنهادی ما، از سوی دیگر، AGCN و TAL را از طریق ایده Res2Net بر اساس برش GCN به کار می‌گیرد. و جمع آوری اطلاعات مکانی-زمانی چند مقیاسی با دانه بندی ریزتر را تکمیل می کند. علاوه بر این، ما همچنین از طریق یک مدل چند جزئی به ضبط ویژگی در دوره‌های زمانی مختلف دست می‌یابیم تا پیش‌بینی با دقت بالاتری را انجام دهیم.

(2) قابلیت پیش بینی چند مرحله ای

برای بررسی عملکرد مدل خود در مقابل مدل پایه در بازه های زمانی مختلف، ما نتایج معیارها را در مراحل زمانی مختلف تجسم می کنیم ( شکل 3). واضح است که برای همه مدل‌ها، با افزایش زمان پیش‌بینی، خطاهای پیش‌بینی روند افزایشی نشان می‌دهند. در این میان، SVR با LSTM پیش‌بینی کوتاه‌مدت بسیار خوبی دارد، اما خطای آن سریع‌ترین روند صعودی را در بین همه مدل‌ها دارد، زیرا تغییر ویژگی‌های فضایی را در نظر نمی‌گیرد. در مقایسه با VAR، توانایی پیش بینی کوتاه مدت آن خیلی خوب نیست. با این حال، به دلیل در نظر گرفتن برخی ویژگی های فضایی، روند صعودی خطای آن با گذشت زمان بیشتر کاهش یافته است. این همچنین ثابت می کند که در نظر گرفتن ویژگی های فضایی می تواند به طور موثری توانایی پیش بینی مدل را در میان مدت و بلند مدت بهبود بخشد. در مورد شبکه‌های عصبی نمودار مکانی-زمانی، در بیشتر موارد، پیش‌بینی‌های میان‌مدت و بلندمدت آنها بهتر از VAR، SVR و LSTM است. این همچنین اثربخشی GCN را در گرفتن ویژگی‌های فضایی در پیش‌بینی ترافیک نشان می‌دهد. شایان ذکر است که AGCRN و TRes2GCN ما، که ویژگی‌های فضایی ریزدانه را در نظر می‌گیرند، به طور قابل توجهی به دلیل سایر مدل‌های پایه در کار پیش‌بینی میان‌مدت و بلندمدت هستند. این همچنین اثربخشی AGCN را در مقایسه با GCN معمولی برجسته می کند. TRes2GCN نسبت به AGCRN پیشرفت زیادی دارد، به ویژه برای پیش بینی کوتاه مدت و میان مدت. این به دلیل مزیت در نظر گرفتن دوره‌های زمانی مختلف است که به مدل ما اجازه می‌دهد تا مشخص شود که ویژگی‌های بیشتری از تغییرات در این دوره زمانی دارد، بنابراین نتایج پیش‌بینی ما را با دقت بیشتری منطبق می‌کند. به طور قابل توجهی به دلیل دیگر مدل های پایه در کار پیش بینی میان مدت و بلند مدت هستند. این همچنین اثربخشی AGCN را در مقایسه با GCN معمولی برجسته می کند. TRes2GCN نسبت به AGCRN پیشرفت زیادی دارد، به ویژه برای پیش بینی کوتاه مدت و میان مدت. این به دلیل مزیت در نظر گرفتن دوره‌های زمانی مختلف است که به مدل ما اجازه می‌دهد تا مشخص شود که ویژگی‌های بیشتری از تغییرات در این دوره زمانی دارد، بنابراین نتایج پیش‌بینی ما را با دقت بیشتری منطبق می‌کند. به طور قابل توجهی به دلیل دیگر مدل های پایه در کار پیش بینی میان مدت و بلند مدت هستند. این همچنین اثربخشی AGCN را در مقایسه با GCN معمولی برجسته می کند. TRes2GCN نسبت به AGCRN پیشرفت زیادی دارد، به ویژه برای پیش بینی کوتاه مدت و میان مدت. این به دلیل مزیت در نظر گرفتن دوره‌های زمانی مختلف است که به مدل ما اجازه می‌دهد تا مشخص شود که ویژگی‌های بیشتری از تغییرات در این دوره زمانی دارد، بنابراین نتایج پیش‌بینی ما را با دقت بیشتری منطبق می‌کند.

در این بخش، برای بررسی بیشتر تأثیر روش اتصال و تغییر چند مقیاسی مدل خود، هفت نوع TRes2GCN را طراحی کردیم و آزمایش‌های فرسایشی را انجام دادیم.

این ها بر اساس تعداد بلوک های مکانی-زمانی روی هم چیده شده، نحوه چیدمان آنها و تأثیر ساختار سلسله مراتبی (ساختار Res2Net) طراحی شده اند. سپس این هفت نوع را با TRes2GCN در مجموعه داده PeMS08 مقایسه کردیم. در طول مقایسه، همه مدل‌های متغیر با فراپارامترهای یکسان آموزش و آزمایش شدند، بنابراین از انصاف و اعتبار علمی اطمینان حاصل شد. تفاوت بین مدل های مختلف در هشت نکته خلاصه شده و در زیر توضیح داده شده است:

(1)

Two Blocks-ResNet: این مدل اساس مطالعه ما است. این شامل دو بلوک فضایی-زمانی است و در ساختار ResNet که در حال حاضر رایج ترین استفاده می شود، انباشته شده است. هر بلوک فضایی-زمانی دارای ساختار سلسله مراتبی نیست، یعنی فقط شامل یک لایه TAL و یک لایه AGCN است.

(2)

Two Blocks-DenseNet: این مدل بر اساس اولین نوع است که ساختار ResNet با ساختار DenseNet جایگزین شده است.

(3)

Three Blocks-ResNet: این مدل بر اساس نوع اول با یک بلوک فضایی-زمانی دیگر روی هم چیده شده و بقیه بدون تغییر است.

(4)

Three Blocks-DenseNet: این مدل بر اساس نوع سوم با جایگزینی ساختار ResNet با ساختار DenseNet است.

(5)

Four Blocks-ResNet: این مدل بر اساس نوع سوم با یک بلوک فضایی-زمانی دیگر انباشته و بقیه بدون تغییر است.

(6)

Four Blocks-DenseNet: این مدل بر اساس نوع پنجم با جایگزینی ساختار ResNet با ساختار DenseNet ساخته شده است.

(7)

Four Blocks-DenseNet + Res2GCN: این مدل بر اساس نوع ششم با افزودن پیچیدگی گراف تطبیقی ​​سلسله مراتبی (Res2GCN) است.

(8)

TRes2GCN: این نسخه کامل TRes2GCN است. این لایه توجه زمانی سلسله مراتبی را در بالای نوع هفتم اضافه می کند.

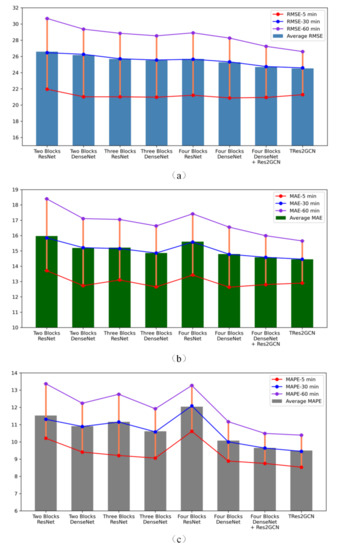
در مقایسه شش نوع اول، بهبود مدل از طریق راه و تعداد بلوک‌های مکانی-زمانی به تفصیل بررسی شده است. همانطور که در شکل 4 نشان داده شده است ، ما انواع 1، 3 و 5 را با هم مقایسه می کنیم و به وضوح می بینیم که اثر نحوه اتصال ResNet رضایت بخش نیست. وقتی پشته سه بلوک باشد، اثر کمی بهتر از دو بلوک خواهد بود. با این حال، هنگامی که تعداد پشته ها بلوک چهارم باشد، یک بازگشت قابل توجه در معیارهای ارزیابی شده توسط مدل وجود دارد، به خصوص بازگشت MAPE بزرگترین است. بنابراین، تعداد موثر بلوک های انباشته شده برای ResNet 3 است و در بلوک چهارم، مدل یک پدیده بسیار جدی تخریب شبکه را نشان می دهد. وقوع این پدیده به احتمال زیاد مربوط به هموار شدن بیش از حد GCN است [ 48]. تأیید شده است که GCN با پشته‌ای از سه یا چهار لایه به دلیل پدیده هموارسازی بیش از حد منجر به روند همگن ویژگی‌ها می‌شود و در نتیجه باعث شکست مدل می‌شود. این نتیجه گیری بسیار شبیه به نتایج تجربی ما است. با مقایسه مدل های 2، 4 و 6 متوجه شدیم که DenseNet از نظر اتصال نتایج بهتری نسبت به ResNet دارد. معیارهای مدل با بزرگتر شدن تعداد بلوک‌های مکانی-زمانی بهبود می‌یابند و هیچ تخریب شبکه وجود ندارد. این به درجه بالای استفاده از ویژگی نسبت داده می شود، که ویژگی ها را غنی می کند و در عین حال مشکل هموارسازی بیش از حد را تا حدی تعدیل می کند. همچنین بسیار موثر است، زیرا حافظه و تعداد پارامترهای فرآیند آموزش را افزایش نمی دهد. با این حال، ما آن را در طول تغییر نوارهای خطا به طور قابل توجهی کوتاهتر نمی یابیم.

شایان ذکر است که ResNet در حال حاضر در اکثر شبکه های عصبی نمودار فضایی-زمانی استفاده می شود. به خصوص نوع 1 (با تعداد انباشته 2) بسیار شبیه به شبکه های فعلی مبتنی بر CNN (STGCN، MSTGCN، ASTGCN، و غیره) است. این همچنین ثابت می‌کند که اکثر مدل‌ها با نادیده گرفتن تأثیر روش‌های تعمیق شبکه و اتصال بر روی مدل‌ها ساخته شده‌اند و جا برای بهبود بیشتر وجود دارد.

از سوی دیگر، میزان بهبود سلسله مراتب خود را بر روی مدل در انواع 6، 7 و 8 بررسی کردیم. پس از اضافه کردن Res2GCN و Res2TAL، به ترتیب، متوجه می‌شویم که مقادیر میانگین هر سه معیار به تدریج بهبود می‌یابند، و به ویژه Res2GCN. بهبود می بخشد. این ثابت می‌کند که گرفتن اطلاعات مکانی-زمانی چند مقیاسی، در واقع می‌تواند مزایای مثبتی برای مدل به همراه داشته باشد. مقیاس‌های فضایی چند مقیاسی، به‌ویژه، در پیش‌بینی ترافیک اهمیت بیشتری دارند. علاوه بر این، ما همچنین دریافتیم که نوارهای خطای انواع 7 و 8 در مقایسه با نوع 6 به طور قابل توجهی باریک تر است. این نشان می دهد که اگر می خواهیم میان مدت و بلندمدت دقیق تری داشته باشیم، باید اطلاعات مکانی و زمانی بیشتری را در مقیاس های مختلف در نظر بگیریم. نتایج پیش بینی

سپس، همانطور که در جدول 3 نشان داده شده است، تأثیر تغییر ساختار Res2Net بر دقت را بیشتر بررسی کردیم.. در همان ابتدا، ما فقط Res2Net بهینه را در ساختار مدل خود اعمال کردیم، یعنی ویژگی های 26 مقیاس 4. با این حال، با مقایسه نتایج بدون استقرار Res2Net، اثر بهبود یافت، اما فقط MAPE بیشتر بهبود یافت. پس از آن، حدس زدیم که آیا مقیاس های زیادی برای TAL وجود دارد یا خیر. بنابراین، ما سعی کردیم تعداد مقیاس‌های Res2TAL را کاهش دهیم و تأثیر آن در واقع بهبود یافت. این به این دلیل است که TAL خود اهمیت هر لحظه را به دست می آورد و میدان ادراکی خود بزرگ است. TAL دوم (یعنی مقیاس برابر با 3) برای یادگیری ارتباط لحظه به لحظه بین سطوح اهمیت انجام شد. از سوی دیگر، انجام TAL بیشتر (یعنی مقیاس برابر با 4)، هیچ معنای عملی ندارد و نتایج در واقع از حالتی که مقیاس 3 است پایین‌تر است. از سوی دیگر، ما همچنین سعی کردیم تعداد مقیاس های Res2GCN را کاهش دهیم و متوجه شدیم که نتایج بهبود نیافته است، بلکه دارای اراده ضعیفی است. بنابراین، ما در نهایت مقیاس 4 را برای Res2GCN و مقیاس 3 را برای Res2TAL، هر دو با عرض 26 انتخاب کردیم. این همچنین نشان می‌دهد که ساختار Res2Net می‌تواند به طور موثر نه تنها در پیچیدگی اقلیدسی، بلکه در مکانیسم توجه و غیر قابل استفاده باشد. -پیچیدگی اقلیدسی که بار دیگر اثربخشی و عمومیت چارچوب آن را ثابت می کند.

علاوه بر این، ما نیز مفید بودن SE-Block را تأیید می کنیم و متوجه می شویم که SE-Block تأثیر بیشتری بر مدل ایجاد می کند. دلیل اصلی این است که SE-Block الگوهای مشترک بین مقیاس ها را استخراج می کند و تفاوت بین مقیاس ها را محو می کند. با مقایسه ردیف دوم با ردیف چهارم، نتایج نشان می‌دهد که Res2Net بدون SE-Block برای پیش‌بینی شبکه‌های عصبی نمودار مکانی-زمانی مناسب‌تر است.

شایان ذکر است که از آنجایی که باید نتایج سه مؤلفه را به صورت تجمعی محاسبه کنیم (در مجموع 12 بلوک مکانی-زمانی)، و افزایش پارامترها در هر لایه باعث افزایش ناگهانی طول و حافظه برای آموزش مدل می شود. بنابراین، در اینجا، ما فقط مورد Res2Net (4 مقیاس 26 عرض) را بدون افزایش در پارامترهای محاسباتی بررسی می کنیم. تنظیمات دیگر، اگرچه نتایج را بهتر می کنند، اما باعث کاهش شدید حافظه آموزشی و زمان تمرین مدل ما می شوند، بنابراین آنها را در نظر نمی گیریم.

بردار تعبیه گره و ماتریس مجاورت تطبیقی ​​مستقیماً بر استخراج ویژگی مکانی-زمانی ریز دانه تأثیر می‌گذارند، بنابراین تأثیر تغییرات بردار تعبیه گره و ماتریس مجاورت تطبیقی ​​را در این بخش بررسی می‌کنیم.

همانطور که ماتریس مجاورت تطبیقی ​​مورد توجه قرار گرفته است، روش های آنها تکثیر شده است [ 29 ، 40 ، 49 ]. با الهام از اینها، ما تأثیر ساختارهای ماتریس مجاورت مختلف با بردارهای جاسازی پیچیدگی نمودارهای مختلف را بر پیش‌بینی بررسی می‌کنیم. با این حال، Graph WaveNet [ 29 ] و MTGNN [ 49 ] تنها ماتریس مجاورت تطبیقی ​​را بدون بردار تعبیه گره در نظر گرفتند. بنابراین، ما بردارهای ترکیب آن دسته از ماتریس‌های مجاورت تطبیقی ​​را که به عنوان بردارهای جاسازی گره در نظر گرفته نشده‌اند، تطبیق می‌دهیم و مناسب بودن آنها را تأیید می‌کنیم، همانطور که در جدول 4 نشان داده شده است.

شایان ذکر است که تمامی این روش‌ها برای شبیه‌سازی بهتر ماتریس مجاورت تایید شده‌اند، اما هیچ تاییدی در مورد مناسب بودن بردار تعبیه وجود ندارد. بنابراین، خوب بودن نتایج این آزمایش تنها می‌تواند نشان‌دهنده مناسب بودن بردارهای آنها برای ساخت ماتریس‌های مجاورت به عنوان بردارهای تعبیه‌کننده برای پیچیدگی نمودار باشد.

با مقایسه دو ردیف اول با سطرهای دیگر، ماتریس مجاورت تطبیقی ​​بدون افزودن جاسازی گره، نتایج مشابهی با ماتریس مجاورت اصلی خواهد داشت، اما باز هم، هیچ کدام نمی توانند تنوع الگوی گره ریز دانه را بدست آورند. علاوه بر این، مهم نیست که از چه روش جاسازی استفاده می شود، عملکرد بهتری نسبت به پیچیدگی نمودار بدون جاسازی خواهد داشت. این همچنین تأیید می کند که ویژگی های فضایی-زمانی ریز دانه با الگوهای گره، در واقع، بهتر از ویژگی های مکانی-زمانی معمولی هستند.

با کمال تعجب، متوجه شدیم که رویکرد تعبیه گره AGCRN (ردیف سوم) ساده تر است، اما نتایج بهتری نسبت به روش های دیگر دارد. در مقابل، دو روش ساخت ماتریس مجاورت تطبیقی ​​ذکر شده در MTGNN پیچیده‌تر هستند (ردیف‌های پنجم و ششم)، اگرچه در مقاله اصلی تأیید شد که نتایج بهتری نسبت به Graph WaveNet (ردیف چهارم بدون جاسازی گراف) بدون افزودن جاسازی گره وجود دارد. . با این حال، هنگامی که تعبیه گره اضافه می شود، نتایج کمتر رضایت بخش هستند. این به احتمال زیاد به دلیل استفاده بیش از حد از لایه‌های کاملاً متصل در بلوک‌های ساختمانی است که منجر به برازش بیش از حد بردارهای پیچیدگی نمودار آموخته شده می‌شود. از سوی دیگر، مقایسه ردیف های سوم و پنجم (گراف های بدون جهت) با ردیف های چهارم و ششم (گراف های جهت دار) نشان می دهد که ماتریس مجاورتی که با استفاده از دو بردار آموخته شده است به طور کلی به خوبی ماتریس مجاورتی که با استفاده از یک بردار یاد می شود نیست. این همچنین ثابت می کند که گراف تطبیقی ​​بدون جهت برای پیش بینی بهتر از گراف جهت دار تطبیقی ​​هنگام در نظر گرفتن تعبیه گره است.

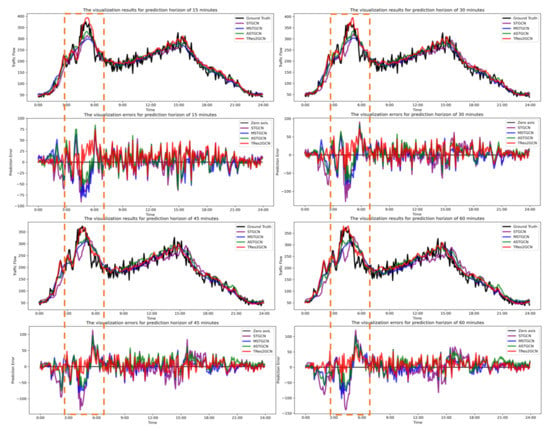
برای تجسم تفاوت‌های پیش‌بینی بین مدل خود و مدل پایه، به طور تصادفی یک حسگر را در مجموعه داده PeMS08 انتخاب کردیم تا تناسب پیش‌بینی و خطای پیش‌بینی را مقایسه کنیم، همانطور که در شکل 5 نشان داده شده است.

برای اینکه مقایسه دقیق‌تر و واضح‌تر باشد، نتایج پیش‌بینی را در بازه‌های زمانی مختلف در یک روز تجسم کردیم. در این حالت تست در چهار نقطه زمانی یعنی ۱۵ دقیقه، ۳۰ دقیقه، ۴۵ دقیقه و ۶۰ دقیقه انجام می‌شود. در هر طرح فرعی، نمودار بالایی حجم پیش‌بینی و حقیقت پایه مدل ما را با برخی از مدل‌های پایه نشان می‌دهد، در حالی که نمودار پایین نشان‌دهنده خطای پیش‌بینی بین مدل‌ها در فاصله‌ای از حقیقت زمین است.

نتایج نشان می‌دهد که منحنی‌های برازش شده هر سه مدل پایه برای یک بازه پیش‌بینی 15 دقیقه بسیار نزدیک هستند. و با افزایش بازه زمانی پیش بینی، خطای STGCN به طور قابل توجهی افزایش می یابد. در مقابل، MSTGCN و ASTGCN به طور قابل توجهی به مقادیر واقعی نزدیکتر از STGCN تحت بازه پیش بینی 45 و 60 دقیقه هستند. این افزایش موثر پیش بینی بلند مدت آنها به دلیل در نظر گرفتن دوره های زمانی متعدد است.

در بین همه مدل‌ها، TRes2GCN در پیش‌بینی تغییرات ترافیک آینده بهتر است و مقادیر پیش‌بینی‌شده آن به Ground Truth نزدیک‌تر است، به خصوص در قسمت اوج، جایی که مزیت مدل ما برجسته‌تر است. ما به وضوح می‌توانیم ببینیم که مدل ما نتایج بهتری برای قسمت در جعبه نارنجی (یعنی قله‌ها برای تمام بازه‌های زمانی) به دست می‌آورد. این به این دلیل است که ساختارهای Res2Net و DenseNet در مدل ما غنی از ویژگی‌های مکانی-زمانی هستند که برخی از مشکلات هموارسازی بیش از حد موجود در GCN را کاهش می‌دهد. بنابراین، در مقایسه با مدل‌های دیگر، مدل ما نه تنها می‌تواند روند آینده ترافیک را پیش‌بینی کند، بلکه اندازه پیک ترافیک را نیز با دقت بیشتری پیش‌بینی می‌کند.

به منظور ارزیابی اثربخشی ترکیب چندین ویژگی ترافیک دوره‌ای، ما تأثیر دوره‌های زمانی مختلف بر پیش‌بینی ترافیک را بررسی کردیم.

با مقایسه ردیف‌های 1، 2 و 3 در جدول 5 ، می‌بینیم که دو مدلی که به ترتیب دوره‌های روزانه و هفتگی را در نظر می‌گیرند، در مقایسه با مدلی که فقط دوره‌های اخیر را در نظر می‌گیرد، افزایش متفاوتی دریافت می‌کنند. این به این دلیل است که رفت و آمد معمولا یک هفته طول می کشد. برای مثال الگوی دوشنبه هفته قبل به الگوی دوشنبه هفته بعد بسیار نزدیک خواهد بود. بنابراین، دوره هفتگی کمی بالاتر خواهد بود.

از سوی دیگر، با مقایسه ردیف سوم با ردیف چهارم در جدول 5 ، متوجه می‌شویم که اگرچه بهبود دوره روز کم است، اما اگر بخواهیم دقت پیش‌بینی را بیشتر کنیم، باید تأثیر آن در نظر گرفته شود. این به این دلیل است که دوره روزانه می تواند تا حدی برای یادگیری الگوی بین روزهای هفته (یا تعطیلات قانونی) در همان هفته مفید باشد. به عنوان مثال، الگوهای ترافیک برای دوشنبه (شنبه) می تواند سهمی در پیش بینی روز سه شنبه (یکشنبه) داشته باشد.

علاوه بر این، ما همچنین تأثیر ساختار Res2Net را بر تناوب بررسی کردیم. تحت شرایط مشابه، متوجه می‌شویم که Res2Net برای مدل‌هایی که فقط مؤلفه‌های اخیر را در نظر می‌گیرند، بهبود بیشتری می‌یابد. در مقابل، افزایش برای تمام دوره های در نظر گرفته شده در مقایسه با آن کمتر است. این به احتمال زیاد به دلیل الگوهای مختلف اشتراک گذاری دوره های مختلف است که باعث تقویت و همچنین تضعیف ویژگی دوره اخیر می شود.

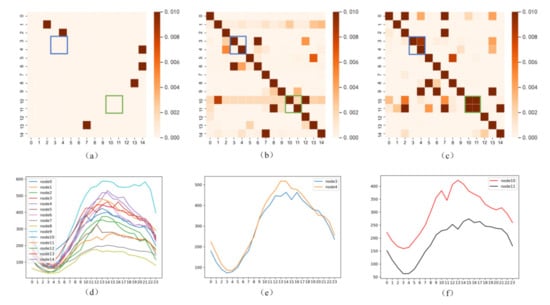
برای نشان دادن اثر عملی ماتریس مجاورت خود تطبیقی ​​چند مقیاسی، ما 15 حسگر از مجموعه داده PeMS08 را برای تجزیه و تحلیل انتخاب کردیم. همانطور که در شکل 6 نشان داده شده است، ماتریس مجاورت از پیش تعریف شده آنها، ماتریس مجاورت خود تطبیقی ​​در یک مقیاس واحد و ماتریس مجاورت خود تطبیقی ​​را در قالب نقشه های حرارتی تجسم کردیم . علاوه بر این، هر ردیف نشان دهنده درجه ارتباط بین سنسورها است، جایی که گره های همبستگی بیشتر، رنگ تیره تر است. مقایسه شکل 6 الف با شکل 6 ب، شکل 6ج، می بینیم که نمودار از پیش تعریف شده بسیار ساده تر از دو نمودار تطبیقی ​​دیگر است. این به این دلیل است که نمودار از پیش تعریف شده فقط بر نحوه اتصال شبکه جاده تمرکز می کند و تغییرات در الگوهای گره را نادیده می گیرد. برای اعتبار بخشیدن به ایده خود، تغییرات ترافیکی این 15 گره را در هر روز مشخص کردیم و آن را به عنوان میانگین ترافیک در ساعت نشان دادیم ( شکل 6 d-f). به عنوان مثال، می بینیم که دو نقطه ای که در نمودار از پیش تعریف شده مرتبط نیستند، اما در الگوی ترافیک (حجم جریان یا روند تغییرات) از کادر آبی و کادر سبز به شدت مرتبط هستند ( شکل 6)e,f). در ماتریس مجاورت تطبیقی ​​تک مقیاسی، به طور جزئی، اما ناقص آموخته می شود. در مقابل، در ماتریس مجاورت تطبیقی ​​چند مقیاسی، رابطه آنها به طور کامل آموخته می شود. این همچنین نیاز به چند مقیاس را در زمینه پیش‌بینی ترافیک، به ویژه یادگیری ماتریس مجاورت تطبیقی ​​نشان می‌دهد.