خلاصه
کلید واژه ها:
همبستگی فضایی ; شاخص های سلامت خاک ; حداقل/حداکثر عوامل خودهمبستگی (MAF) ; تجزیه و تحلیل مؤلفه های مستقل (ICA) ؛ عدم قطعیت فضایی ؛ بهترین شیوه های مدیریت
1. معرفی
2. مواد و روشها
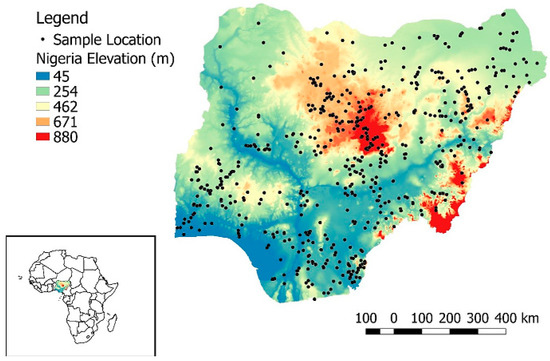
2.1. شرح مجموعه داده ها و منطقه مطالعاتی
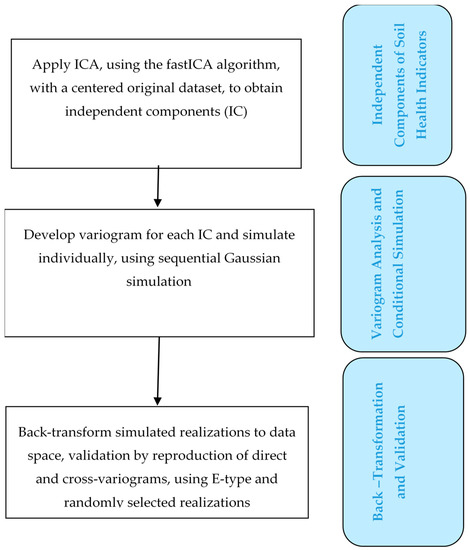
2.2. ICA
ICA تجزیه خطی متغیرهای همبسته به اجزای مستقل (از این پس IC) است که همبستگی ندارند. با توجه به Hyvärinen و همکاران. [ 41 ]، متغیرهای همبسته اصلی مخلوط خطی یا ترکیبی از برخی از متغیرهای پنهان ناشناخته فرض میشوند. مجموعه داده اصلی باید در مرکز قرار گیرد، که می توان با کم کردن میانگین هر ستون از ماتریس داده به دست آورد. ایکس(س)از هر متغیر [ 41 ]. این کار برای ساده سازی الگوریتم ICA [ 41 ] انجام می شود. سپس برای نمایش داده ها به اجزای اصلی آنها، پیش سفیدی لازم است. ز(س)=ایکس(س)∗ک، با K نشان دهنده ماتریس قبل از سفید شدن است. در نهایت، با توجه به Boluwade و Madramootoo [ 22 ]، “بردار میانگین Z(s) برای صفر و همچنین کوواریانس واریانس آن، ماتریس هویت است که دارای واریانس 1 است و همبستگی ندارد”. برای یک بردار تصادفی و سفید شده، Z(s) را می توان به صورت مخلوطی از اجزای مستقل موارد زیر بیان کرد:
جایی که اس(س)ماتریس منبع است که شامل IC مورد نیاز نیز می شود و A یک ماتریس مخلوط است. به گفته ترکان و سهرابیان [ 32 ]، هر دو A و اس(س)ناشناخته هستند و فقط با استفاده از دانش Z ( s ) تخمین زده می شوند. IC از طریق ماتریس unmixing بدست می آید:
بنابراین، W ماتریس دمیکس است و همچنین نشان دهنده ردیف های ماتریس معکوس، A -1 است. بنابراین، ترکیب خطی به صورت زیر محاسبه می شود:
و برابر با آی سی ها [ 41 ] خواهد بود.
2.3. MAF
مفهوم MAF برای اولین بار توسط سوئیس و گرین [ 44 ] معرفی شد و توسط دسباراتس و دیمیتراکپولوس [ 21 ] در زمین آمار پیاده سازی شد. روش MAF را می توان برای تبدیل متغیرهای همبسته به عوامل غیرهمبسته استفاده کرد که سپس می توان آنها را به طور جداگانه شبیه سازی کرد. فرمول ریاضی MAF به خوبی در Desbarats و Dimitrakpoulos [ 21 ]، Rondon [ 45 ]، Boucher و همکارانش مستند شده است. [ 46 ] و بندریان و همکاران. [ 47 ]. به طور کلی، MAF ها را می توان با دو بار انجام PCA به دست آورد [ 48 ، 49 ، 50]. به عبارت دیگر، در تبدیل اول PCA، تجزیه طیفی ماتریس کوواریانس متغیرهای اصلی برای به دست آوردن مولفه های اصلی (PC) انجام می شود، در حالی که در مرحله دوم PCA، تبدیل افزایش واریانس را به حداکثر یا حداقل می رساند. رایانه های شخصی به دست آمده در مرحله اول. به عبارت دیگر، MAF شامل استخراج عوامل آن از یک متغیر تصادفی تبدیل شده با نمره نرمال است. ز(س)، با s نشان دهنده مختصات جغرافیایی، ابتدا با انجام یک PCA با تاخیر، h = 0، و همچنین شامل محاسبه ماتریس کوواریانس [ 48 ، 49 ، 50 ] است:
سپس معادله (4) به صورت طیفی تجزیه می شود تا ماتریس مقادیر ویژه، D 1 و Q 1 ، متعارف بردارهای ویژه به دست آید:
بنابراین، مؤلفههای PCA استاندارد شده (یعنی در این مورد، تبدیل شده با امتیاز نرمال)، PCA 1 ، PCA 2 ، …، PCA p به صورت زیر به دست میآیند:
مرحله دوم شامل انجام یک PCA دیگر در هر فاصله تاخیری بیشتر از صفر است که می تواند به طور دلخواه انتخاب شود، با استفاده از ماتریس واریانس متقاطع عوامل PCA به دست آمده از مرحله 1. به عبارت دیگر، یک ماتریس متقارن متقارن همه جهتی تجربی �¨پسیآ(ساعت)با استفاده از ماتریس PCA [ 21 ، 49 ] ضروری است. بنابراین، تجزیه طیفی ماتریس واریانس متقاطع D 2 (ماتریس دوم مقادیر ویژه) و Q2 (ماتریس دوم متعامد بردارهای ویژه) را از طریق:
بنابراین، MAF، M، را می توان به صورت زیر محاسبه کرد:
ضرایب یا بارگذاری MAF که ” ماتریس A ” نیز نامیده می شود را می توان به صورت زیر بدست آورد:
به عبارت دیگر، عوامل MAF را می توان در نهایت به صورت زیر تعریف کرد:
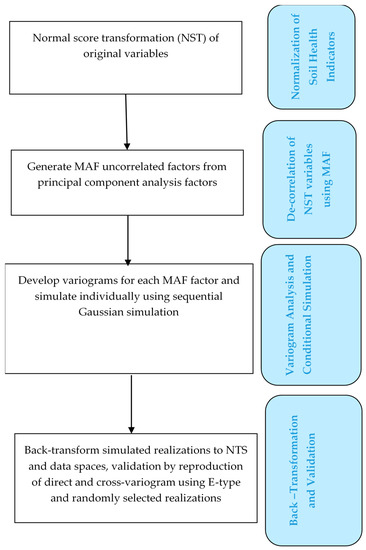
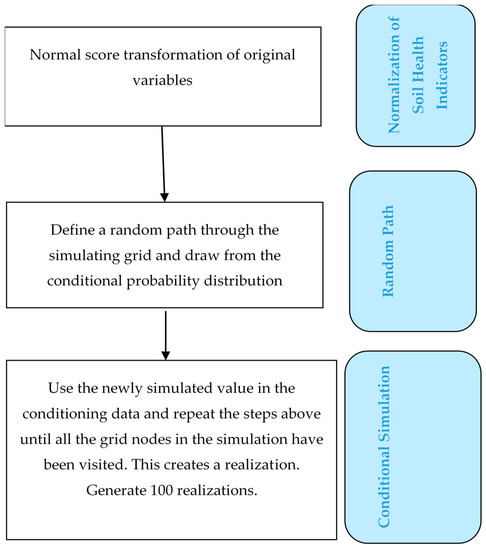
2.4. SGS
2.5. تایید و اعتبار سنجی الگوریتم های MAF و ICA در شبیه سازی مشترک شاخص های سلامت خاک
- (آ)
-
آزمون متعامد فضایی ارزیابی می کند که چگونه روش ها (یعنی MAF و ICA) ماتریس های واریوگرام را در فواصل تاخیری مختلف متعامد می کنند [ 29 ، 52 ]:
-
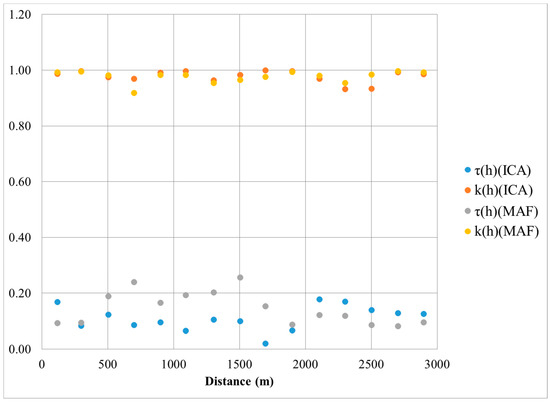
طبق نظر مولر [ 52 ] و ترکان [ 29 ]، τ(h) انحراف نسبی از متعامد است که «مجموع عناصر خارج از مورب را با مجموع مقادیر مطلق عناصر مورب عامل یا مؤلفه واریوگرام تجربی مقایسه میکند. ماتریس �مآاف (ساعت)برای هر تاخیر ساعت”؛
-
بنابراین انحراف نسبی از متعامد بودن را می توان به صورت زیر تعریف کرد:
�(ساعت)=∑ک=1م∑�≠1م|�مآاف(ساعت;ک،�)|∑ک=1م�مآاف(ساعت;ک،ک)،|ساعت|>0که γ MAF ( h : k , j ) واریوگرام متقاطع MAF یا ICA است و γ MAF ( h : k , k ) واریوگرام مستقیم MAF یا IC است. M طول ماتریس های واریوگرام است. برای فضای کامل متعامد، τ ( h ) = 0.
-
کارایی قطری فضایی ک(ساعت)اندازه گیری است که مجموع مربعات عناصر خارج از مورب را در Γ MAF (h) با ویژگی های ماتریس نیمه متغیری Γ Y (h) مقایسه می کند:
ک(ساعت)=1-∑ک=1م∑�≠1م[�مآاف(ساعت;ک،�)]2∑ک=1م∑�≠کم[��(ساعت;�ک،��)]2،|ساعت|>0که γ Y ( h : z k , z j ) متغیرهای متقاطع متغیرهای اصلی را نشان می دهد. برای متعامد بودن کامل، k ( h ) = 1.
-
- (ب)
-
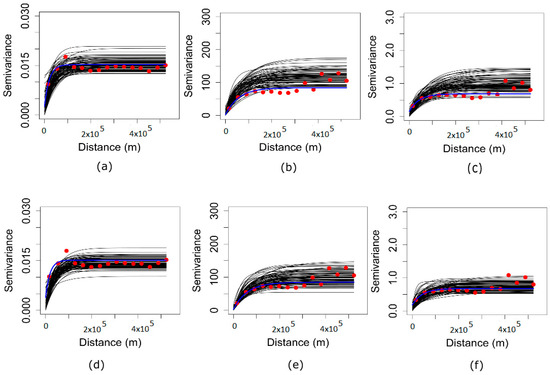
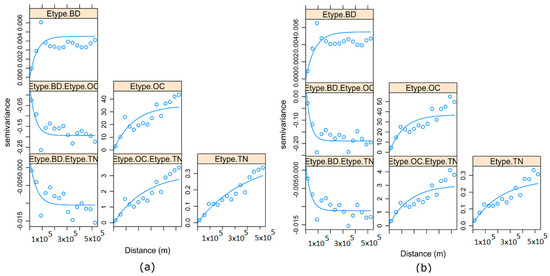
بازتولید واریوگرام های مستقیم و متقاطع با استفاده از میانگین تحقق ها و تحقق های تصادفی انتخاب شده:برای اینکه هر دو الگوریتم معتبر باشند، متغیرهای مستقیم و متقاطع متغیرهای اصلی باید توسط تحقق های شبیه سازی شده با تغییر شکل برگشتی بازتولید شوند. در مجموع 100 تحقق (در فضای داده) به طور میانگین محاسبه می شود. این بهعنوان نوع E تعریف میشود، که در آن E «انتظار مشروط» تحققها (یعنی میانگین برآورد تحققها) است [ 51 ، 53 ]، و متغیرهای مستقیم و متقابل آنها با متغیرهای اصلی برای هر دو مقایسه میشوند. MAF و ICA. علاوه بر این، تحققهای شبیهسازیشده بهطور تصادفی انتخاب شده با هم مقایسه میشوند. هدف این است که اطمینان حاصل شود که این تحقق ها ساختار فضایی و ویژگی های متغیر اصلی را بازتولید می کنند.
- (ج)
-
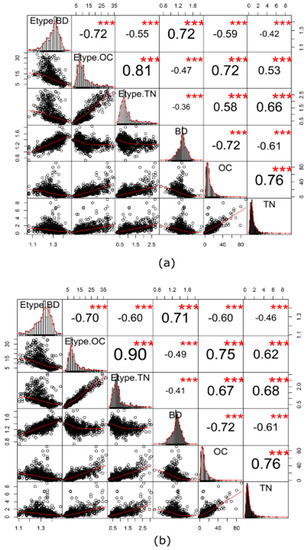
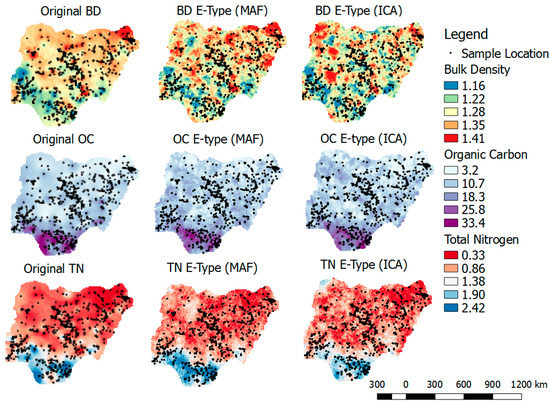
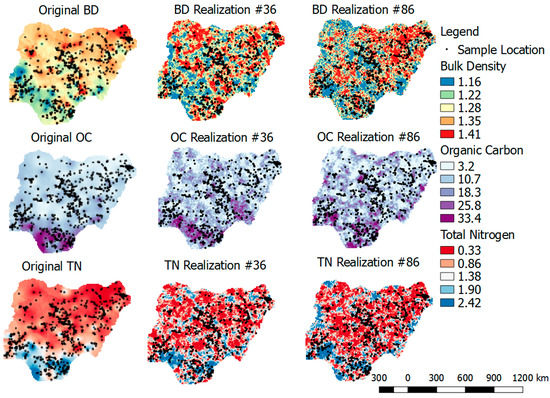
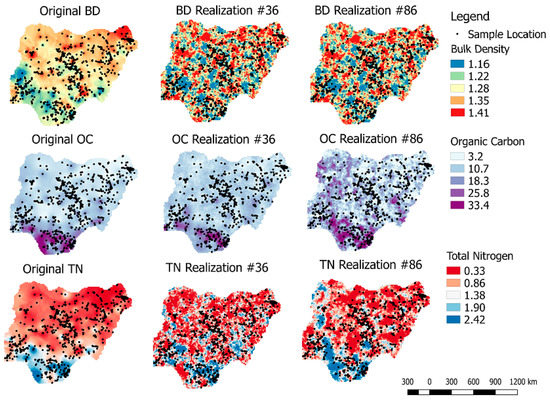
بازتولید توزیع اصلی، همبستگی متقابل و الگوی فضایی:همبستگی متقاطع بین نوع E از تحقق های برگشتی و متغیرهای اصلی مقایسه می شود. بازتولید هیستوگرام متغیرهای اصلی نیز مورد بررسی قرار خواهد گرفت. علاوه بر مقایسه کمی در بالا، بازرسیهای بصری در قالب بازتولید الگوی فضایی متغیر اصلی و تحققهای شبیهسازیشده پسدگرگونشده در نظر گرفته میشوند. این امر برای اطمینان از سازگاری و اعتبار بخشیدن به وابستگی فضایی درون متغیرها و همچنین تضمین رابطه فضایی بین متغیرها است.
3. نتایج و بحث
3.1. نتایج MAF و ICA
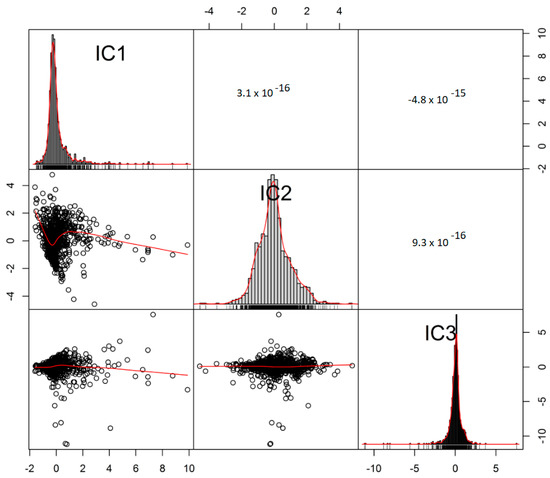
با استفاده از بسته “ica” در آمار R برای تجزیه ICA، ماتریس عدم اختلاط تخمینی W به صورت زیر بدست آمد:
ماتریس پیش سفید کننده، K به صورت زیر بدست آمد:
برای تکنیک MAF، تجزیه طیفی ماتریس متقارن متقارن آزمایشی همه جهته (h = 30 m) برای فاکتورهای PCA با بردارهای ویژه به صورت زیر به دست آمد:
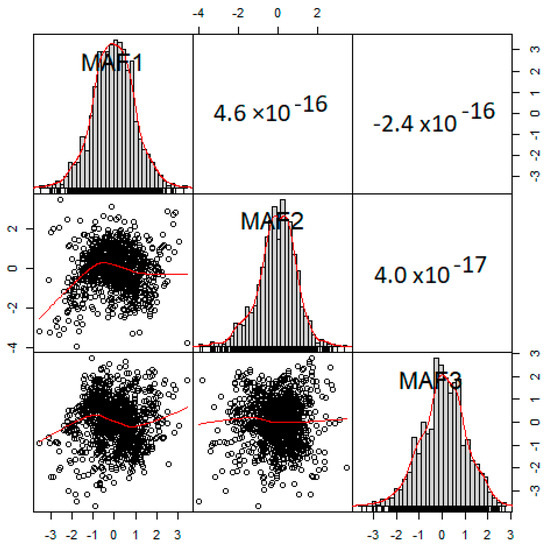
تاخیر تغییر h = 30 متر، به طور دلخواه انتخاب شد زیرا مجموعه داده های اصلی AfSIS از منابع مختلف آمده است، که تعیین فاصله نمونه برداری (برای h) را دشوار می کند. ماتریس PCA با Q2 ضرب شد تا فاکتورهای MAF بدست آید . همانطور که در شکل 8 نشان داده شده است ، نمودار عدم همبستگی بین عوامل را نشان می دهد. فاکتورهای MAF به طور جداگانه شبیه سازی شدند. برای تبدیل مجدد فضای MAF به NST، از ماتریس A -1 ، که در زیر نشان داده شده است، برای ضرب تحقق های شبیه سازی شده استفاده شد:
- (آ)
-
ارزیابی عملکرد اگر فاکتورهای MAF و مؤلفههای ICA برای همه فواصل تأخیر متعامد باشند، با استفاده از اندازهگیری متعامد فضایی.
- (ب)
-
بازتولید واریوگرام های مستقیم و متقاطع SHI های اصلی، با استفاده از میانگین 100 تحقق شبیه سازی شده با تغییر شکل برای هر دو MAF و ICA.
- (ج)
-
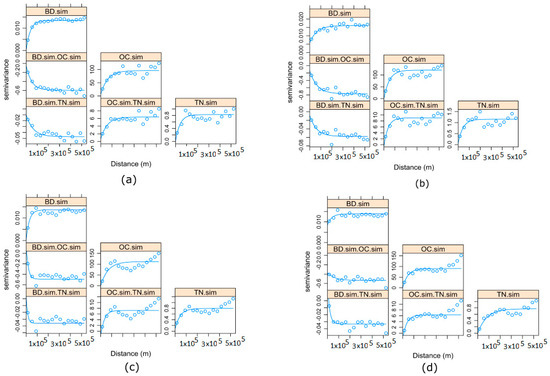
بازتولید واریوگرامهای مستقیم و متقاطع SHIهای اصلی، با استفاده از تحققهای شبیهسازیشده بهطور تصادفی انتخاب شده برای MAF و ICA. و
- (د)
-
کاوش توزیع (هیستوگرام)، همبستگی متقابل، و الگوی فضایی SHIهای اصلی و تحققهای شبیهسازیشده با تغییر شکل برگشتی.
3.2. ارزیابی عملکرد همبستگی MAF و ICA با استفاده از معیارهای متعامد فضایی
3.3. بازتولید واریوگرام های مستقیم اصلی
3.4. بازتولید واریوگرام های مستقیم و متقاطع با استفاده از شبیه سازی های نوع E
3.5. بازتولید واریوگرام های اصلی و واریوگرام های متقاطع، با استفاده از تحقق های انتخابی تصادفی
3.6. بازتولید توزیع ها، همبستگی متقابل و الگوهای فضایی متغیرهای اصلی بر اساس نوع E
3.7. اهمیت عدم قطعیت در شبیه سازی متغیرهای همبسته فضایی و مفاهیم برای بهترین شیوه های مدیریت (BMP) در مدیریت پایدار
4. نتیجه گیری و پیشنهاد
- (آ)
-
تجزیه و تحلیل مقایسه ای بین دو روش هیچ تفاوت مشخصی در عملکرد آنها نشان نداد. با این حال، NST قبل از تبدیل MAF ضروری است. در مورد ICA، انجام NST قبل از تبدیل غیرضروری بود. به عبارت دیگر، NST تنها برای IC مورد استفاده قرار گرفت در حالی که تحققهای احتمالی یکسانی را از طریق SGS ایجاد میکرد. بنابراین، IC را می توان به طور مستقیم در برنامه های کاربردی دیگری که نیازی به شبیه سازی SGS ندارند استفاده کرد.
- (ب)
-
هر دو تکنیک دو معیار برای تعامد فضایی پیشنهاد شده توسط ترکان (1999) را برآورده می کنند. اینها انحراف مطلق از مورب هستند ( �(ساعت)) و انحراف نسبی از قطر ( ک(ساعت)) با مقادیر ایده آل به ترتیب تقریباً 0 و 1. به عبارت دیگر، MAF و ICA باید از نظر فضایی متعامد با یک همبستگی در صفر برای تمام فواصل قبل از استفاده در SGS باشند.
- (ج)
-
اگر MAF و ICA به طور مستقل شبیه سازی شوند، هر دو روش فقط به یک واریوگرام مستقیم برای هر عامل/مولفه نیاز دارند. این در تضاد با سه متغیر مستقیم و سه متغیر متقابل است که در صورت استفاده از یک رویکرد سنتی مانند مدل هممنطقهبندی مورد نیاز است. به عبارت دیگر، هر دو MAF و ICA به درستی واریوگرام های مستقیم و متقاطع متغیرهای اصلی را با وجود واریوگرام های فاکتورهای MAF و ICA که به طور مستقل شبیه سازی شده بودند، بازتولید کردند.
- (د)
-
تحقق واریوگرام شبیه سازی شده با تغییر شکل برگشتی با متغیرهای اصلی هر متغیر قابل مقایسه بود. علاوه بر این، نوع E، که میانگین 100 تحقق است، به خوبی با متغیرهای اصلی مقایسه شده است. همبستگی متقاطع، هیستوگرام، و الگوی فضایی تحقق های برگشتی، با استفاده از انواع E، به درستی بازتولید شدند.
منابع
- گرینر، ال. نوسبام، م. پاپریتز، ا. زیمرمن، اس. گوبلر، ا. گرت-رگامی، ا. کلر، الف. نشانه عدم قطعیت در نقشه های عملکرد خاک – اطلاعات شفاف و با استفاده آسان برای حمایت از استفاده پایدار از منابع خاک. خاک 2018 ، 4 ، 123-139. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
- بوما، جی. کمک های علم خاک به اهداف توسعه پایدار و اجرای آنها: پیوند عملکردهای خاک با خدمات اکوسیستم. J. Plant Nutr. علم خاک 2014 ، 177 ، 111-120. [ Google Scholar ] [ CrossRef ]
- بلوم، WEH نقش خاک برای برآوردن نیازهای جهانی همانطور که توسط اهداف توسعه پایدار سازمان ملل (SDGs) تعریف شده است. در راتن. هورن، راینر ؛ تاکاشی، ک.، ویرایش. Schweizbart’sche Verlagsbuchhandlung: اشتوتگارت، آلمان، 2018. [ Google Scholar ]
- بولواد، ا. Madramootoo، CA مدلسازی اثرات ناهمگونی فضایی در حوضه کرچک بر رواناب، رسوبات و از دست دادن فسفر با استفاده از Swat: I. اثرات تغییرپذیری فضایی خواص خاک. آلودگی خاک هوای آب 2013 ، 224 ، 1692. [ Google Scholar ] [ CrossRef ] [ PubMed ] [ نسخه سبز ]
- ریس، جی. وندروث، او. ماتوچا، سی. زو، جی. تعیین مناطق مدیریتی خاص سایت و ارزیابی دینامیک زمانی آب خاک در مزرعه کشاورز در کنتاکی. Vadose Zone J. 2019 ، 18 ، 180143. [ Google Scholar ] [ CrossRef ]
- شولپ، CJE; بورکهارد، بی. میس، جی. ون ویلیت، جی. وربورگ، عدم قطعیت های PH در نقشه های خدمات اکوسیستم: مقایسه ای در مقیاس اروپایی. PLoS ONE 2014 ، 9 ، e109643. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
- هیولینک، جی. براون، جی. متغیرهای محیطی نامشخص در GIS. در دایره المعارف GIS ; Springer: Boston, MA, USA, 2008. [ Google Scholar ] [ CrossRef ]
- فائو اندازهگیری و مدلسازی ذخایر کربن خاک و تغییرات موجودی در سیستمهای تولید دام: دستورالعملهایی برای ارزیابی (نسخه 1) ; مشارکت ارزیابی و عملکرد زیست محیطی دام (LEAP). فائو: رم، ایتالیا، 2019؛ 170p.
- ژانگ، جی ایکس؛ Goodchild، MF عدم قطعیت در اطلاعات جغرافیایی ; تیلور و فرانسیس: نیویورک، نیویورک، ایالات متحده آمریکا، 2002. [ Google Scholar ]
- Burrough، PA منابع چند مقیاسی تغییرات فضایی در خاک، کاربرد مفاهیم فراکتال در سطوح تو در تو تنوع خاک. J. Soil Sci. 1993 ، 34 ، 577-597. [ Google Scholar ] [ CrossRef ]
- Heuvelink، GBM؛ وبستر، آر. مدل سازی تنوع خاک: گذشته، حال و آینده. Geoderma 2001 ، 100 ، 269-301. [ Google Scholar ] [ CrossRef ]
- Odgers، NP; مک براتنی، AB; میناسنی، ب. نگاشت رقومی ویژگی خاک و تخمین عدم قطعیت با استفاده از رسترهای احتمال کلاس خاک. Geoderma 2015 ، 238 ، 190-198. [ Google Scholar ] [ CrossRef ]
- پوجیو، ال. جیمونا، ا. Brewer، MJ نقشهبرداری در مقیاس منطقهای خواص خاک و عدم قطعیت آنها با تعداد زیادی متغیرهای کمکی مشتق شده از ماهواره. Geoderma 2013 ، 209-210 ، 1-14. [ Google Scholar ] [ CrossRef ]
- Goovaerts، P. متعامد فضایی اجزای اصلی محاسبه شده از متغیرهای coregionalized. ریاضی. جئول 1993 ، 25 ، 281-302. [ Google Scholar ] [ CrossRef ]
- بیوند، RS; Pebesma، EJ; گومز-روبیو، وی. تجزیه و تحلیل داده های مکانی کاربردی با R. Springer: New York, NY, USA, 2008; صص 251-268. [ Google Scholar ]
- بارنت، RM Sphereing و حداقل/حداکثر عوامل خودهمبستگی. در درس زمین آمار ; Deutsch، JL، Ed. 2017; در دسترس آنلاین: https://www.geostatisticslessons.com/pdfs/sphereingmaf.pdf (در 22 اکتبر 2019 قابل دسترسی است).
- بهارم، AST; شیبوساوا، اس. کودایرا، م. Kandac، R. نقشه برداری عمقی چندگانه از ویژگی های خاک با استفاده از حسگر خاک در زمان واقعی مرئی و مادون قرمز نزدیک برای یک شالیزار. مهندس کشاورزی محیط زیست غذا. 2015 ، 8 ، 13-17. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
- یالچین، ای. کوکریجینگ و تأثیر آن بر دقت تخمین. JS Afr. Inst. حداقل فلزی. 2005 ، 105 ، 223-228. [ Google Scholar ]
- آدیکاری، SK; موتیل، ن. Yilmaz، AG Cokriging برای افزایش درون یابی فضایی بارندگی در دو حوضه آبریز استرالیا. هیدرول. روند. 2017 ، 31 ، 2143-2161. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
- Goovaerts, P. Geostatistics for Natural Resources Evaluation ; انتشارات دانشگاه آکسفورد: نیویورک، نیویورک، ایالات متحده آمریکا، 1997. [ Google Scholar ]
- دسباراتس، ای جی; دیمیتراکوپولوس، R. شبیهسازی زمین آماری توزیعهای اندازه منافذ منطقهای با استفاده از عوامل همبستگی حداقل / حداکثر. ریاضی. جئول 2000 ، 32 ، 919-941. [ Google Scholar ] [ CrossRef ]
- بولواد، ا. Madramootoo, CA شبیه سازی مستقل زمین آماری متغیرهای خاک همبسته فضایی. محاسبه کنید. Geosci. 2015 ، 85 ، 3-15. [ Google Scholar ] [ CrossRef ]
- دیمیتراکوپولوس، آر. Makie, S. شبیه سازی مشترک عدم قطعیت خرابی معدن برای تصمیم گیری توانبخشی. در geoENV VI — زمین آمار برای کاربردهای زیست محیطی ; Soares, A., Pereira, MJ, Dimitrakopoulos, R., Eds. Springer: Dordrecht، هلند، 2008; جلد 15، ص 345–355. [ Google Scholar ]
- سهرابیان، بی. Tercan, AE معرفی حداقل کریجینگ همبستگی فضایی به عنوان روشی جدید برای تخمین محتوای فلزات سنگین در خاک. Geoderma 2014 ، 226-227 ، 317-331. [ Google Scholar ] [ CrossRef ]
- سهرابیان، بی. Tercan، E. شبیه سازی زمین آماری چند متغیره با به حداقل رساندن همبستگی متقابل فضایی. CR Geosci. 2014 ، 346 ، 64-74. [ Google Scholar ] [ CrossRef ]
- وارگاس-گوزمان، ج.ا. دیمیتراکوپولوس، R. خواص محاسباتی عوامل همبستگی حداقل/حداکثر. محاسبه کنید. Geosci. 2002 ، 29 ، 715-723. [ Google Scholar ] [ CrossRef ]
- مولر، UA; فریرا، جی. روش تبدیل U-WEDGE برای شبیه سازی زمین آماری چند متغیره. ریاضی. Geosci. 2012 ، 44 ، 427-448. [ Google Scholar ] [ CrossRef ]
- تیچاوسکی، پ. Yeredor، A. دو ضلعی مفصل تقریبی سریع با ماتریس های وزنی. IEEE Trans. فرآیند سیگنال 2009 ، 57 ، 878-891. [ Google Scholar ] [ CrossRef ]
- Tercan، AE اهمیت الگوریتم متعامدسازی در مدلسازی توزیعهای شرطی روشهای شاخص تبدیل شده متعامد. ریاضی. جئول 1999 ، 31 ، 155-173. [ Google Scholar ]
- زی، تی. مایرز، دی. مدلهای واریوگرام با ارزش ماتریس طولانی، AE برازش با قطر همزمان، بخش دوم: کاربرد. ریاضی. جئول 1995 ، 27 ، 877-888. [ Google Scholar ] [ CrossRef ]
- سهرابیان، بی. Ozcelik, Y. تعیین بلوک های قابل بهره برداری در یک معدن آندزیت با استفاده از کریجینگ جزء مستقل. بین المللی جی. راک مکانیک. حداقل علمی 2012 ، 55 ، 71-79. [ Google Scholar ] [ CrossRef ]
- ترکان، ع. سهرابیان، ب. شبیه سازی زمین آماری چند متغیره داده های کیفی زغال سنگ توسط مولفه های مستقل. بین المللی جی. زغال سنگ. 2013 ، 112 ، 53-66. [ Google Scholar ] [ CrossRef ]
- سرویس اطلاعات خاک آفریقا (AfSIS). داده ها. در دسترس آنلاین: https://africasoils.net/services/data/ (در 22 اکتبر 2019 قابل دسترسی است).
- Boluwade، A. منطقهبندی و تقسیمبندی شاخصهای سلامت خاک برای نیجریه با استفاده از خوشهبندی پیوسته فضایی برای توسعههای اقتصادی و اجتماعی-فرهنگی. ISPRS Int. J. Geo-Inf. 2019 ، 8 ، 458. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
- بانک جهانی. جمعیت رو به رشد نیجریه به مشاغل بیشتر و بهتر نیاز دارد. در دسترس آنلاین: https://www.worldbank.org/en/news/press-release/2016/03/15/nigerias-booming-population-requires-more-and-better-jobs (در 22 اکتبر 2019 قابل دسترسی است).
- راکستروم، جی. Falkenmark، M. کشاورزی: افزایش برداشت آب در آفریقا. طبیعت 2015 ، 519 ، 283-285. [ Google Scholar ] [ CrossRef ]
- صدای آمریکا، 2019. پیشبینی میشود که جمعیت نیجریه تا سال 2050 دو برابر شود. در دسترس آنلاین: https://www.voanews.com/a/nigeria-population/4872735.html (در 22 اکتبر 2019 قابل دسترسی است).
- فائو برگه اطلاعات کشور مزارع خانواده کوچک. 2018. در دسترس آنلاین: https://www.fao.org/3/I9930EN/i9930en.pdf (در 22 اکتبر 2019 قابل دسترسی است).
- Leenaars، JGB; ون اوستروم، AJM; Gonzalez، MR Africa Soil Profiles Database، نسخه 1.2. تلفیقی از دادههای مشخصات خاکی ارجاعشده و استانداردشده برای کشورهای جنوب صحرای آفریقا (با مجموعه داده) ؛ گزارش ISRIC 2014/01; پروژه خدمات اطلاعات خاک آفریقا (AfSIS) و ISRIC—World Soil Information: Wageningen، هلند، 2014; 162p. [ Google Scholar ]
- Pebesma، E. زمین آمار چند متغیره در S: بسته GSTAT. محاسبه کنید. Geosci. 2004 ، 30 ، 683-691. [ Google Scholar ] [ CrossRef ]
- هیورینن، آ. کارهونن، ج. Oja, E. تجزیه و تحلیل مؤلفه های مستقل ; جان وایلی و پسران: نیویورک، نیویورک، ایالات متحده آمریکا، 2001. [ Google Scholar ]
- Helwig، NE ica: تجزیه و تحلیل مؤلفه های مستقل. بسته R نسخه 1.0-2. 2018. در دسترس آنلاین: https://CRAN.R-project.org/package=ica (در 22 اکتبر 2019 قابل دسترسی است).
- هیورینن، آ. Oja, E. تجزیه و تحلیل مؤلفه های مستقل: الگوریتم ها و کاربردها. شبکه عصبی 2000 ، 13 ، 411-430. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
- سوئیس، پی. اندرو، جی. حداقل/حداکثر عوامل خودهمبستگی برای تصاویر فضایی چند متغیره: گزارش فنی 6 ; گروه آمار، دانشگاه استنفورد: استانفورد، کالیفرنیا، ایالات متحده آمریکا، 1984. [ Google Scholar ]
- Rondon, O. کمک آموزشی: حداقل/حداکثر عوامل خودهمبستگی برای شبیهسازی مشترک ویژگیها. ریاضی. Geosci. 2012 ، 44 ، 469-504. [ Google Scholar ] [ CrossRef ]
- بوچر، ا. دیمیتراکوپولوس، آر. شبیه سازی های مشترک وارگاس-گوزمان، JA، فاصله سوراخ های بهینه و نقش انبار. در زمین شناسی کمی و زمین آمار، Geostatisitcs Banff 2004 ; Leuangthong, O., Deutsch, CV, Eds.; Springer: Dordrecht، هلند، 2005; جلد 14، ص 35–44. [ Google Scholar ]
- بندریان، EM; بلوم، LM; Mueller، UA مستقیم حداقل/حداکثر عوامل خودهمبستگی برای شبیه سازی چند متغیره. محاسبه کنید. Geosci. 2008 ، 34 ، 190-200. [ Google Scholar ] [ CrossRef ]
- ویلز، ام. ریووارد، جی. Pierre, P. استفاده از حداقل/حداکثر عوامل خودهمبستگی شاخص های مبتنی بر پیمایش برای پیگیری تکامل ذخایر ماهی در زمان. آکوات. منبع زنده. 2009 ، 22 ، 193-200. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
- الون، اس. Leuangthong، O. پیاده سازی حداقل/حداکثر عوامل خودهمبستگی و کاربرد در یک مثال داده واقعی. 2008. در دسترس آنلاین: https://www.ccgalberta.com/ccgresources/report10/2008-406_maf.pdf. (دسترسی در 26 اکتبر 2019).
- Haugen، MA; راجاراتنام، بی. Switzer, P. استخراج روندهای زمانی رایج از سری های زمانی همزمان: حداکثر عوامل همبستگی خودکار با کاربرد در داده های سری زمانی حلقه درختی. arxiv 2015 ، arXiv:1502.01073v3. [ Google Scholar ]
- Goovaerts, P. مدلسازی زمین آماری عدم قطعیت در علوم خاک. ژئودرما 2001 ، 103 ، 3-26. [ Google Scholar ] [ CrossRef ]
- مولر، U. روشهای همبستگی فضایی: فراتر از MAF و PCA. در مجموعه مقالات نهمین کنگره بین المللی زمین آمار، اسلو، نروژ، 11 تا 15 ژوئن 2012. [ Google Scholar ]
- Deutsch، CV; Journel , AG GSLIB: Geostatistical Software Library and User’s Guide , 2nd ed.; انتشارات دانشگاه آکسفورد: آکسفورد، انگلستان، 1998. [ Google Scholar ]
- فولبرث، سی. اسکالسکی، آر. مولچانوا، ای. بالکوویچ، جی. Azevedo، LB; مایکل اوبرشتاینر، م. van der Velde، M. عدم قطعیت در دادههای خاک میتواند بر سیگنالهای تاثیر آب و هوا در شبیهسازیهای عملکرد جهانی محصول برتری داشته باشد. نات. اشتراک. 2016 ، 7 ، 11872. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
- آژانس حفاظت از محیط زیست ایالات متحده (USEPA). بهترین شیوه های مدیریت (BMPs) برای فن آوری های تصفیه خاک. دستورالعملهای عملیاتی پیشنهادی برای جلوگیری از انتقال آلایندهها از طریق رسانهای در طول فعالیتهای پاکسازی. در دسترس آنلاین: https://www.epa.gov/sites/production/files/2016-01/documents/bmpfin.pdf (در 26 اکتبر 2019 قابل دسترسی است).





بدون دیدگاه