خلاصه

تشخیص الگوی ساختمان برای طیف گسترده ای از کاربردهای پایین دستی، مانند ارزیابی منظر شهری، تحلیل های اجتماعی، و تعمیم نقشه، اساسی است. اگرچه مطالعات زیادی انجام شده است، به دلیل عدم دقت مدل جهت نسبی هر دو ساختمان مجاور و روش‌های استخراج ناکارآمد، هنوز نتایج رضایت‌بخشی وجود ندارد. هدف این مطالعه ارائه جایگزینی برای کمی کردن جهت و پیوستگی فضایی هر دو ساختمان بر اساس مثلث دلونی برای شناخت الگوهای ساختمانی خطی است. اول، مثلث‌سازی‌های محدود شده Delaunay (CDTs) برای همه ساختمان‌ها در هر بلوک و هر دو ساختمان مجاور ایجاد می‌شوند. سپس، شاخص پیوستگی فضایی (SCI)، شاخص جهت (DI) و سایر روابط فضایی (مثلاً فاصله) از هر دو ساختمان مجاور با استفاده از CDT مشتق شده است. در نهایت، بلوک ساختمان به عنوان یک نمودار بر اساس ماتریس های مشتق شده مدل می شود و یک رویکرد تقسیم بندی نمودار برای استخراج الگوهای ساختمانی خطی پیشنهاد شده است. در فرآیند تقسیم‌بندی، ابتدا لبه‌های گراف با توجه به آستانه‌های کلی SCI و فاصله حذف می‌شوند و متعاقباً به زیرگراف‌هایی بر اساس قوانین جهت تقسیم می‌شوند. روش پیشنهادی با استفاده از سه مجموعه داده آزمایش شده است. نتایج تجربی نشان می دهد که روش پیشنهادی می تواند الگوهای ساختمانی خطی و منحنی را تشخیص دهد، با توجه به اینکه مقادیر صحت همه بالای 92 درصد برای سه منطقه مورد مطالعه است. نتایج همچنین نشان می دهد که SCI جدید می تواند به طور موثر بسیاری از روابط همسایه ناچیز را در فرآیند تقسیم بندی نمودار فیلتر کند.

کلید واژه ها:

الگوهای خطی ساختمان ; شاخص تداوم فضایی (SCI) ; شاخص جهت (DI) ; الگو شناسی

1. معرفی

ساختمان‌ها به‌عنوان رایج‌ترین موجودات جغرافیایی در مناطق شهری، هنگام استفاده از نقشه‌ها برای ناوبری، اشیاء جهت‌دار مهمی برای کاربران هستند. الگوی خطی تشکیل‌شده توسط ساختمان‌ها به آرایش و فرم نمایش داده شده توسط مجموعه‌ای از ساختمان‌ها در مقیاس معین در فضای نقشه‌برداری اشاره دارد [ 1 ، 2 ]. این الگو مانند یک خط به نظر می رسد و عناصر آن، یعنی ساختمان ها، از نظر ویژگی های فضایی (مانند فاصله، جهت، شکل و تراکم) همگن هستند [ 3 ]. به طور معمول، الگوهای ساختمانی خطی را می توان به ترازهای خطی و ترازهای منحنی طبقه بندی کرد [ 1 ، 3]. به عنوان پیکربندی منظر، الگوهای ساختمان اجزای حیاتی سازه‌های شهری هستند که باید در هنگام کاهش مقیاس‌های فضایی در طول فرآیند تعمیم نقشه حفظ شوند [ 4 ، 5 ، 6 ، 7 ]. علاوه بر این، الگوهای ساختمانی خطی در نقشه های توپوگرافی برای درک فضای جغرافیایی، مانند بررسی طبقه بندی معنایی سازه ها و عملکردهای شهری بر اساس الگوهای خطی ساختمانی استخراج شده، مهم هستند [ 8 ، 9 ، 10 ].
تشخیص الگوهای ساختمانی خطی فرآیندی است که توسط آن عناصر ساختمان در خوشه های خطی مجزا سازماندهی می شوند. شناسایی خودکار الگوهای ساختمانی چالش برانگیز است زیرا آنها اغلب وابسته به مقیاس هستند و با توزیع ساختمان متفاوت هستند (مثلاً فواصل، جهت گیری ها، مساحت و شکل در بین ساختمان ها)، که منجر به تعداد زیادی نامزد می شود [ 11 ]. با این حال، رویکردها و اقدامات مختلفی برای تشخیص الگوهای خطی ساختمان گزارش شده است. روش‌های گروه‌بندی مبتنی بر نمودار رایج‌ترین رویکردها هستند که به طور کلی، ابتدا بلوک ساختمان را به صورت نموداری مدل‌سازی می‌کنند که در آن گره‌ها ساختمان‌ها را نشان می‌دهند و یال‌ها روابط مجاور بین ساختمان‌ها را نشان می‌دهند [ 12 ، 13 ، 14 ].، 15 ]. سپس نمودار برای به دست آوردن گروه های همگن با استفاده از روش های تقسیم بندی قطعه بندی می شود [ 1 ، 16 ، 17 ]. برخی از روش‌های ردیابی را می‌توان در فرآیند تقسیم‌بندی ادغام کرد تا الگوهای ساختمانی خطی به دست آید [ 3 ، 18 ]. روش های مبتنی بر نمودار اغلب از پیمایش های زیادی رنج می برند. این مستلزم بررسی الگوریتم های جایگزین است که می تواند به طور قابل توجهی پیمایش را کاهش دهد. در این زمینه، حداقل درخت پوشا (MST) به پرکاربردترین روش گروه‌بندی مبتنی بر نمودار تبدیل شده است. این الگوریتم به جای همه اشیاء اطراف، هر شی را با نزدیکترین همسایه خود پیوند می دهد [ 19]. با این حال، MST به تغییرات کوچک در وزن لبه ها حساس است. هنگام مدل‌سازی ساختمان‌ها بر اساس نمودار، از مقادیر شاخص به دست آمده از ساختمان‌های مجاور برای وزن دادن به لبه‌های نمودار استفاده می‌شود. این شاخص‌ها عمدتاً از اصول گشتالت مشتق شده‌اند که شامل مجاورت، شباهت، تداوم و سرنوشت مشترک است [ 20 ]. این اصول گشتالت برای شناسایی الگوهای توزیع فضایی برای سال‌ها به کار گرفته شده‌اند. مجاورت با فواصل مختلف ساختمان های مجاور نشان داده می شود، از جمله فاصله نقطه مرکزی، حداقل فاصله مرزهای ساختمان، فاصله متوسط، فاصله مجاور، و شاخص سنتز شده [ 21 ، 22 ، 23 ].]. فاصله متوسط ​​به شناخت انسان نزدیکتر است که با مثلث های بین دو ساختمان مجاور اندازه گیری می شود. تمرین ثابت کرده است که متریک میانگین فاصله پیشنهاد شده توسط [ 22 ] می تواند فاصله بین اشیاء همسایه را با دقت بیشتری نسبت به سایر معیارهای فاصله اندازه گیری کند و به طور گسترده در بسیاری از کاربردها استفاده شده است [ 1 ، 6 ، 12 ]. شباهت، از جمله شباهت شکل و شباهت اندازه، اغلب برای ایجاد قوانین سفت و سخت برای تشخیص الگوهای ساختمان استفاده می شود [ 1 ، 3 ، 24 ]]. با این حال، برخی از اشیاء با تفاوت های بزرگ در مساحت و شکل هنوز به عنوان یک کل شناخته می شوند، مانند الگوهای خطی. جهت مشترک تضمین می کند که انحراف یک زاویه مسیر که توسط هر دو ساختمان در هر دو طرف تشکیل شده است از مقدار تحمل تنظیم شده تجاوز نمی کند. مطالعات زیادی برای تعیین کمیت جهت اجسام انجام شده است. مدل‌های جهت شامل مدل مبتنی بر مخروط [ 25 ]، مدل پیش‌بینی دوبعدی [ 26 ] و مدل نمودار جهت ورونوی (DVD) [ 27 ] است.]. دو مورد قبلی مفید هستند و در استدلال فضایی کیفی کارآمد هستند. مدل DVD یک مدل کمی برای توصیف جهت فضایی دو جسم با استفاده از جهت های متعدد به جای یک جهت واحد است. با این حال، تجربیات ما نشان داد که یک جهت واحد ممکن است برای توصیف کمی زوایای مسیر یک الگوی ساختمانی خطی مناسب‌تر باشد. پیوستگی برای انعکاس درک انسان از مسیرهای منحنی یا موج دار که توسط محرک های بصری مجاور تشکیل شده اند استفاده می شود [ 28 ]. با این حال، این اصل به ندرت در تحقیقات فعلی استفاده می شود.
از آنجایی که تشخیص خودکار بهترین الگوی ساختمان از تعداد زیادی کاندید دشوار است، می‌توانیم ابتدا لبه‌هایی را که شرایط را برآورده نمی‌کنند از نمودار حذف کنیم و سپس بهترین الگو را از بین بقیه انتخاب کنیم. بر اساس ایده فوق، این مقاله ابتدا یک جایگزین برای تعیین کمیت جهت و پیوستگی فضایی هر دو ساختمان بر اساس مثلث دلونی پیشنهاد می‌کند. سپس، ما چارچوبی را برای تشخیص خودکار الگوهای ساختمان خطی از داده‌های توپوگرافی پیشنهاد می‌کنیم.
ادامه این مقاله به شرح زیر سازماندهی شده است. پیش پردازش داده ها، اقدامات برای استخراج مقادیر شاخص، الگوریتم های ردیابی و روش های ارزیابی در بخش 2 توضیح داده شده است. بخش 3 سه مجموعه داده تجربی را ارائه می کند. آزمایش‌های متشکل از بخش‌های نرم‌افزار، پیاده‌سازی، نتایج و بحث در بخش 4 ارائه شده‌اند . در نهایت نتیجه گیری داده می شود.

2. روش شناسی

روش پیشنهادی از یک سری مراحل ارائه شده در جدول 1 پیروی می کند و در زیر توضیح داده شده است.
مرحله 1. مرحله اول، تقسیم نقشه توپوگرافی ساختمان ها به یک سری بلوک های ساختمانی است. یک شبکه جاده برای جدا کردن ساختمان ها به بلوک های مختلف استفاده می شود [ 6 ، 12 ]. هدف اصلی این مرحله بهبود کارایی پردازش است، زیرا چندین بلوک ساختمانی را می توان به صورت موازی پردازش کرد.
مرحله 2. در این مرحله دو نوع مثلث سازی محدود شده Delaunay (CDT) ایجاد شده است ( شکل 1 ). اولین نوع CDT برای تمام ساختمان‌ها در هر بلوک جداگانه محاسبه می‌شود ( شکل 1 a). مثلث های نوع اول برای استخراج رابطه مجاورت (معادله (1))، طول خطوط اسکلت (معادله (2))، فاصله متوسط ​​(معادله (3)) و جهت ساختمان های مجاور استفاده می شوند. نوع دیگری از مثلث بندی محدود دلونی، یعنی مثلث اصلی، فقط برای هر دو ساختمان مجاور محاسبه می شود ( شکل 1).ب). همراه با اولین نوع CDT، از این مثلث ها برای استخراج شاخص تداوم فضایی (SCI) ساختمان های مجاور استفاده می شود. بحث بیشتر در مورد SCI در مرحله بعدی ارائه شده است. قبل از ایجاد CDT، بهتر است برای جلوگیری از تولید مثلث‌های باریک، نقاط اضافی را در بخش‌های خطی چند ضلعی‌ها و جاده‌ها در یک فاصله اضافه کنید [ 29 ].
مرحله 3. شش معیار، شامل رابطه مجاورت (معادله (1))، طول خط اسکلت (معادله (2))، میانگین فاصله ساختمان های مجاور (معادله (3))، SCI، جهت دو ساختمان‌های مجاور و زاویه مسیر در فرآیند ردیابی، بر اساس CDT و مثلث‌های اصلی تعریف می‌شوند. همه این معیارها به جز زوایای مسیر در ماتریس ها ذخیره می شوند.

ماتریس رابطه مجاورت نشان دهنده این است که آیا ساختمان ها از نظر توپولوژیکی مجاور هستند یا خیر و بر اساس اینکه آیا ساختمان ها مثلث های مشترکی در CDT دارند یا خیر به دست می آید:

آر=آرمن،j

جایی که من=1:nو j=1:nساختمان های درون یک بلوک را نشان می دهد و آرمن،jیک متغیر بولی است: آرمن،j=1نشان میدهد که منو jمجاور هستند و آرمن،j=0نشان میدهد که منو jمجاور نیستند

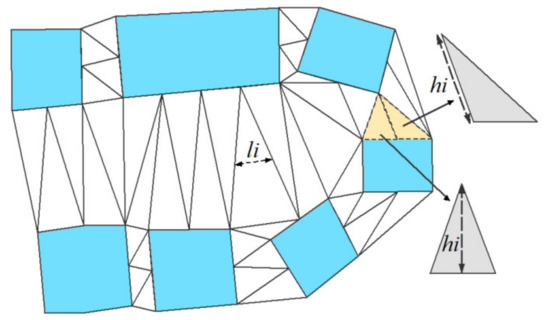
یک خط اسکلت از نقاط میانی اضلاع مثلثی تشکیل می شود که دو ساختمان مجاور را به هم متصل می کند ( شکل 2 )[ 30 ]. طول یک خط اسکلت به صورت زیر بدست می آید:

L=Lمن،j=∑لمن،j،ک

جایی که لمن،j،کنشان دهنده فاصله بین دو نقطه وسط اضلاع مثلث است ککه دو ساختمان مجاور را به هم پیوند می دهد، Lمن،j=∑لمن،j،کنشان دهنده طول مجموع خط اسکلت بین دو ساختمان مجاور است و Lمن،j=0اگر دو ساختمان منو jهمانطور که در رابطه (1) به دست می آید، مجاور نیستند.

میانگین فاصله ساختمان های مجاور بر اساس خط اسکلت به صورت زیر بدست می آید [ 22 ]:

د=دمن،j=∑ساعتمن،j،ک×لمن،j،ک∑لمن،j،ک

جایی که ساعتمن،j،کارتفاع مثلث را نشان می دهد کبا پایه ای که در هر چند ضلعی ساختمان مجاور قرار می گیرد، لمن،j،کنشان دهنده فاصله بین دو نقطه وسط اضلاع مثلث است ککه دو ساختمان مجاور را، همانطور که از رابطه (2) به دست می آید، به هم مرتبط می کند دمن،j=∞اگر دو ساختمان منو jهمانطور که در رابطه (1) به دست می آید، مجاور نیستند. اگر مثلث تیز یا راست باشد، ساعتمن،j،کارتفاع از سمت مشترک با ساختمان است. اگر مثلث منفرد باشد، ساعتمن،j،ککوتاه ترین ضلع مثلثی است که دو ساختمان را به هم پیوند می دهد ( شکل 2 ).

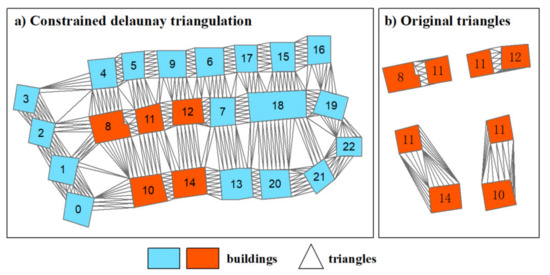
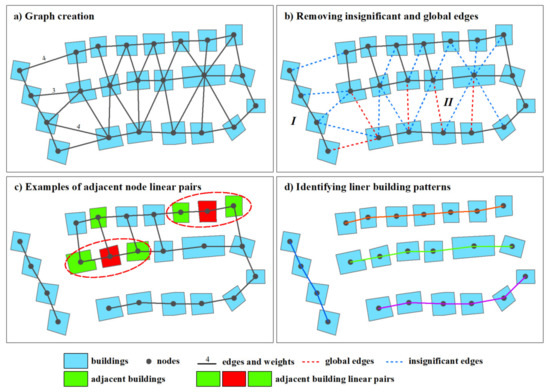
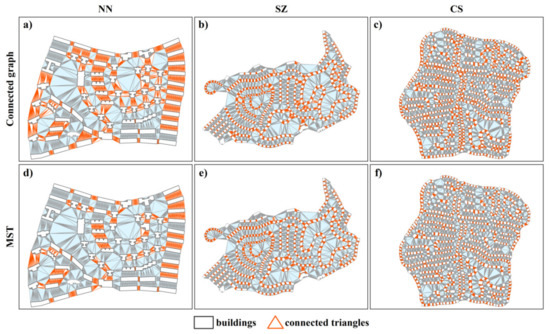
اکنون، در مورد تداوم الگوهای ساختمانی خطی بحث می کنیم. از نظر بصری، مثلث‌های درون نوع اول CDT شبیه پل‌ها هستند که به ساختمان‌های مجاور می‌پیوندند تا الگوهای خطی تشکیل دهند ( شکل 1 a). علاوه بر این، مثلث های بین هر جفت از ساختمان های مجاور یک الگوی خطی از نظر مساحت، جهت و تعداد بسیار مشابه هستند. هنگام مقایسه دو نوع مثلث فوق، متوجه می شویم که مساحت مثلث های اصلی بین دو ساختمان مجاور بزرگتر از مثلث نوع اول است، به ویژه برای ساختمان هایی با آرایش نامنظم یا تفاوت در شکل و اندازه (به عنوان مثال، ساختمان های 10). -11، 11-14 در شکل 1). به طور خاص، در یک الگوی خطی، نسبت مساحت این مثلث ها به مثلث های اصلی بیشتر از بیشتر جفت ساختمان های مجاور از الگوهای غیرخطی است. بر این اساس، ما معتقدیم که رابطه فضایی دو ساختمان مجاور تحت تأثیر ساختمان های اطراف آنها است. در این مقاله، ما از این نسبت به عنوان SCI ساختمان‌های مجاور استفاده می‌کنیم تا درک خود را از تداوم الگوهای ساختمانی خطی منعکس کنیم.

SCI=SCIمن،j=آآرآO

جایی که SCIمن،jتداوم فضایی بین ساختمان ها است منو j، آآرنشان دهنده مساحت مثلث هایی است که به دو ساختمان در CDT تعلق دارند و  آOنشان دهنده مساحت مثلث های اصلی است که دو ساختمان را به هم متصل می کند.

کمتر از سه ساختمان یک الگوی خطی را تشکیل می دهند. از نظر بصری، ساختمان‌ها از یک الگوی خطی یک مسیر خطی را نشان می‌دهند که توسط زوایای مسیر کنترل می‌شود. یک زاویه مسیر توسط آزیموت های دو جسم در دو طرف ساختمان میانی تشکیل می شود. به طور خاص، زاویه مسیر در ساختمان میانی منزاویه ای است که از جهت ساختمان تشکیل می شود ( ساختمانمن-1،ساختمانمن) و جهت ساختمان ( ساختمانمن،ساختمانمن+1) در مسیر ( شکل 3 ). دو روش برای بدست آوردن زوایای مسیر الگوهای خطی بر اساس CDT وجود دارد. تفاوت آنها در این است که مثلث های متصل کننده دو ساختمان در دو طرف دارای تلاقی هستند یا خیر. اولین نوع از زاویه مسیر، که زاویه مسیر مستقیم نامیده می شود، توسط دو مثلث متصل تشکیل می شود (به عنوان مثال، زاویه α در شکل 3 ). هر چه این زاویه به π نزدیکتر باشد، الگوی خطی بهتر است. محاسبه این زاویه با دو مثلث متصل به هم آسان است. ابتدا تقاطع و تمام مثلث هایی که به هر ساختمان متصل می شوند را مشخص کنید. سپس، تمام زوایای شامل این مثلث ها را استخراج کنید. در نهایت کوچکترین زاویه را به عنوان زاویه مسیر مستقیم دو ساختمان مجاور در دو طرف ساختمان میانی انتخاب کنید.

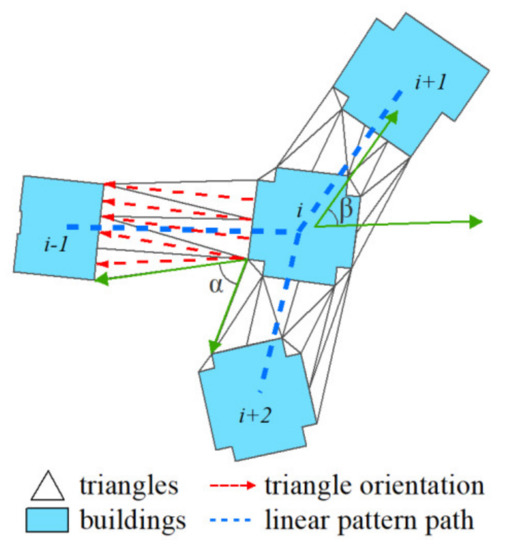
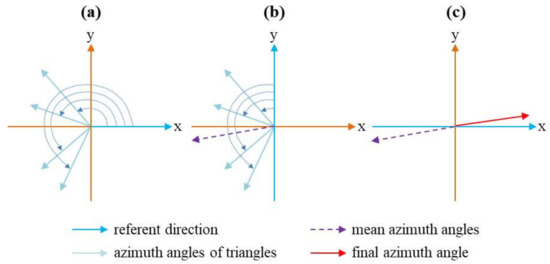
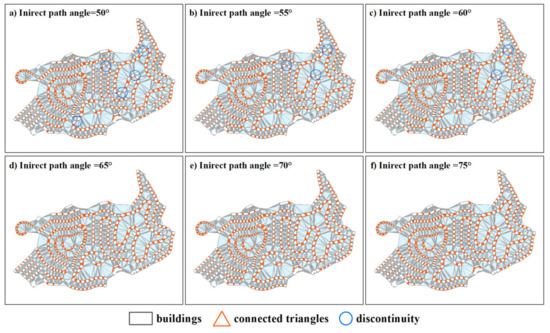
نوع دیگری از زاویه مسیر، یعنی زاویه مسیر غیرمستقیم، توسط زوایای آزیموت ساختمان ها (به عنوان مثال، ساختمان i-1 و ساختمان i+1 در شکل 3 ) در دو طرف ساختمان میانی (به عنوان مثال، ساختمان) تشکیل می شود. i در شکل 3 ). مثلث های متصل به دو ساختمان در دو طرف هیچ تلاقی ندارند. بردارهای میانه این مثلث ها زوایای آزیموت دو ساختمان مجاور را تعیین می کنند (به عنوان مثال، فلش قرمز چین در شکل 3 ). سه مرحله برای محاسبه این نوع زاویه آزیموت وجود دارد ( شکل 4). ابتدا نقطه وسط خط مبنا (یعنی کوتاه ترین ضلع) مثلث و نقطه مربوط به قاعده را تعیین کنید. از دو نقطه برای بدست آوردن زاویه آزیموت مثلث استفاده کنید که در خلاف جهت عقربه های ساعت از جهت مثبت محور X اندازه گیری می شود ( شکل 4 a). واضح است که تمام زوایای آزیموت مثلث ها در محدوده 0 تا 360 درجه هستند. دوم، از آنجایی که تمام جهات بردار خط مرکزی مثلث ها به یک ضلع از محور اشاره می کنند، این زوایای آزیموت نیز می توانند در خلاف جهت عقربه های ساعت از یک جهت از محور اندازه گیری شوند ( شکل 4).ب). بنابراین، همه آنها به محدوده 0 تا 180 درجه تبدیل می شوند و از رابطه (5) برای محاسبه زاویه میانگین با این زوایای آزیموت استفاده می شود. در نهایت، زاویه میانگین به زاویه نهایی تبدیل می شود که در خلاف جهت عقربه های ساعت از جهت مثبت محور X اندازه گیری می شود ( شکل 4 ج). در این مقاله از زاویه نهایی به عنوان DI دو ساختمان مجاور استفاده می کنیم. بنابراین، یک زاویه مسیر غیر مستقیم برابر با مقدار مطلق اختلاف زاویه بین دو زاویه نهایی است (به عنوان مثال، زاویه β در شکل 3 ). هرچه زاویه به 0 نزدیکتر باشد، الگوهای خطی بهتر هستند.

θ=θمن،j=∑αمن،j،ک×لمن،j،ک∑لمن،j،ک

جایی که αمن،j،کزاویه آزیموت یک مثلث را نشان می دهد کبا پایه ای که در هر یک از ساختمان های مجاور می افتد، لمن،j،کنشان دهنده فاصله بین دو نقطه وسط دو ضلع مثلث است کهمانطور که از رابطه (2) به دست می آید، دو ساختمان مجاور را به هم مرتبط می کند.

مرحله 4. این مرحله شامل ایجاد نمودار و وزن دادن به لبه های نمودار با مقادیر شاخص است. ابتدا، یک بلوک ساختمانی به عنوان یک نمودار مدل‌سازی می‌شود، جایی که گره‌ها ساختمان‌ها را نشان می‌دهند، و لبه‌های نمودار روابط مجاور بین ساختمان‌ها را نشان می‌دهند ( شکل 5 a). سپس، هر لبه نمودار را با مقادیر شاخص حاصل از مرحله 3 وزن می کنیم.

مرحله 5. مرحله پنجم ما لبه های ناچیز و سراسری نمودار را حذف می کند، که ممکن است منجر به چندین نمودار قطع شود ( شکل 5 ب). در سطح محلی، لبه های بی اهمیت زیادی روی نمودار وجود دارد (به عنوان مثال، خط چین آبی در شکل 5 ب)، که زمان پیمایش نمودار را افزایش می دهد و ممکن است الگوهای خطا ایجاد کند. این نوع لبه ابتدا حذف می شود. با این حال، در سطح جهانی، فقط اشیاء نزدیک به صورت بصری توسط افراد طبق اصل مجاورت گشتالت، مانند مناطق I و II در شکل 5 ب، به عنوان خوشه درک می شوند. یعنی اگر لبه‌ها با فواصل زیاد طولانی وزن شوند (مثلاً خط چین قرمز در شکل 5)ب) از نمودار حذف می شوند. بنابراین، از دو مقدار برش، از جمله SCI (معادله (4)) و d (معادله (3))، برای شناسایی لبه‌هایی با مقادیر شاخص طولانی استفاده می‌شود. مقدار برش SCI به صورت تجربی تنظیم شده است (به عنوان مثال 0.5) و ابتدا برای حذف لبه ها استفاده می شود. متعاقباً، لبه‌های وزن شده با فواصل بسیار طولانی حذف می‌شوند. برای هر نقطه پمن، مقدار برش d که با نشان داده می شود  برش_ارزشپمنرا می توان به صورت معادله (6) نشان داد.

برش_ارزشپمن=منظور داشتنپمن+n·تغییرپمن

جایی که منظور داشتنپمنمیانگین طول لبه های تشکیل شده توسط نقاط اتصال است پمن. nیک عامل کنترل کننده است که برای تنظیم حساسیت استفاده می شود برش_ارزشپمن.

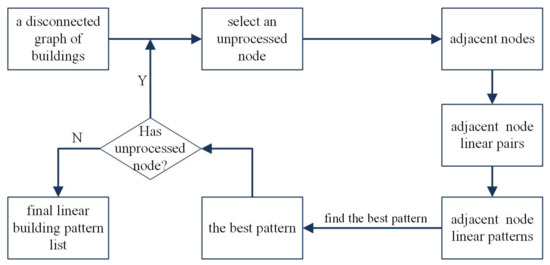
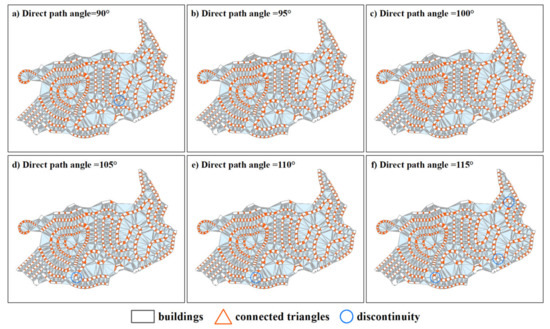
مرحله 6. عمل ششم با هدف تقسیم نمودار قطع شده به زیرگراف های متصل، همانطور که در شکل 5 c,d نشان داده شده است. هر زیرگراف متصل یک الگوی ساختمانی خطی را نشان می دهد ( شکل 5 د). این فرآیند توسط زاویه مسیر تشکیل شده توسط ساختمان های دو طرف کنترل می شود و از چندین مرحله تشکیل شده است ( شکل 6 ). ابتدا یک گره پردازش نشده را انتخاب می کنیم و تمام گره های مجاور آن را تعیین می کنیم. سپس جفت‌های ساختمان خطی آن از ساختمان‌های مجاور بر اساس زوایای مسیرشان شناسایی می‌شوند. یعنی اگر زاویه مسیر دو ساختمان مجاور در دو طرف کمتر از آستانه داده شده باشد، آنها یک جفت خطی ساختمان مجاور در نظر گرفته می شوند ( شکل 5).ج). ثالثاً ساختمان های مجاور ساختمان های مجاور مشخص می شوند. این روند تا زمانی تکرار می شود که هیچ ساختمان مجاوری با شرایط تعیین شده وجود نداشته باشد. بنابراین، ما می توانیم چندین الگوی ساختمان خطی از یک گره را استخراج کنیم. در نهایت الگوی با بهترین ارزش ارزیابی I به عنوان بهترین الگو انتخاب می شود. بهترین ارزش ارزیابی I برای هر الگوی خطی به صورت زیر محاسبه می شود.

من=حداکثرنلمنمنظور داشتنلمن

جایی که لمننشان دهنده الگوی خطی i- امین است، N تعداد یال های الگوی خطی i- امین است، و منظور داشتنلمنمیانگین فاصله الگوی خطی است لمن.

مرحله 7. مرحله نهایی ما شامل ارزیابی دقت و مقایسه روش است. برای تایید کیفیت نتایج شناسایی، یک ارزیابی تخصصی انجام شد. یعنی الگوهای ساختمان خطی مرجع به صورت دستی شناسایی شدند. پنج متخصص نقشه کشی به طور جداگانه در تشخیص الگوی دستی شرکت کردند، در حالی که درگیری بین متخصصان از طریق اکثریت آرا حل شد. در این نظرسنجی، سه مجموعه داده در یک مقیاس مشخص به صورت تصاویر چاپ شدند. کارشناس دعوت شده از مداد برای ترسیم الگوهای خطی تعیین شده استفاده کرد. به عنوان مثال، یک الگوی خطی با یک خط مشخص شد. هنگام ارزیابی نتایج تشخیص الگو، چهار مورد مختلف وجود داشت، از جمله الگوهای صحیح (یعنی الگوهای مدل شده و الگوهای مرجع سازگار بودند)، الگوهای گنجاندن (یعنی، یک الگوی مدل‌سازی‌شده شامل الگوهای مرجع متعدد)، الگوهای درونی (یعنی یک الگوی مرجع حاوی الگوهای مدل‌سازی‌شده متعدد)، و الگوی همپوشانی (یعنی یک الگوی مدل‌شده با الگوی مرجع همپوشانی دارد). در اینجا، از دو معیار، شامل صحت و کامل بودن، برای ارزیابی دقت نتایج تشخیص الگو استفاده شد. درستی به نسبت الگوهای صحیح به کل الگوهای استخراج شده اشاره دارد، در حالی که کامل بودن به نسبت الگوهای صحیح به الگوهای مرجع اشاره دارد. برای ارزیابی دقت نتایج تشخیص الگو استفاده شد. درستی به نسبت الگوهای صحیح به کل الگوهای استخراج شده اشاره دارد، در حالی که کامل بودن به نسبت الگوهای صحیح به الگوهای مرجع اشاره دارد. برای ارزیابی دقت نتایج تشخیص الگو استفاده شد. درستی به نسبت الگوهای صحیح به کل الگوهای استخراج شده اشاره دارد، در حالی که کامل بودن به نسبت الگوهای صحیح به الگوهای مرجع اشاره دارد.
برای درک استحکام روش پیشنهادی بر اساس مطالعات تطبیقی، روش MST نیز برای شناسایی الگوهای ساختمانی خطی در سه مجموعه داده اجرا شد. کد این روش به صورت رایگان به صورت آنلاین در دسترس است، در حالی که بسیاری از روش های موجود دیگر برای استخراج الگوی ساختمان به صورت عمومی در دسترس نیستند.

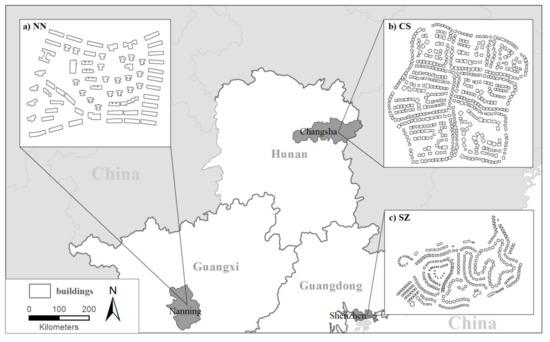
3. داده های تست

سه مجموعه داده توپوگرافی برای مطالعه شناسایی الگوهای ساختمانی خطی استفاده شد ( شکل 7 ). مجموعه داده ها توسط سه مؤسسه تحقیقاتی برنامه ریزی شهری و طراحی استانی در سه استان چین ارائه شده است. این مجموعه داده ها دارای توزیع های مختلف ساختمانی و الگوهای خطی ساختمان هستند که موارد مطالعه ایده آل را در جنوب چین ارائه می دهند. علاوه بر این، توزیع ساختمان‌ها در شنژن (SZ) و چانگ شا (CS) یکنواخت‌تر از توزیع‌های NanNing (NN) است. از نظر بصری، فاصله بین ساختمان‌های متعلق به الگوهای خطی مختلف در مجموعه داده NN کمتر از مجموعه داده‌های SZ و CS بود، که منجر به تأثیر ادراک انسانی الگوهای خطی در مجموعه داده NN نسبت به مجموعه داده‌های SZ و CS شد.

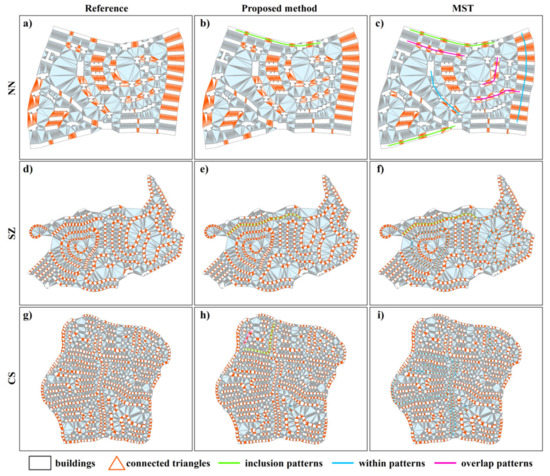
4. نتایج و بحث

تمام آزمایش ها بر روی یک کامپیوتر شخصی با پردازنده مرکزی Intel(R) Core(TM) i7-7700 (واحد پردازش مرکزی) و حافظه 8 گیگابایتی انجام شد. همه الگوریتم‌های پیشنهادی در بخش 2 با استفاده از سی شارپ در ویندوز 10 مایکروسافت (64×) محقق شدند. کتابخانه های مؤلفه و کتابخانه های ابزار ArcGIS Engine 10.1 برای توسعه الگوریتم های مرتبط استفاده شد. روش مرجع مبتنی بر تشخیص بصری انسان است.
شکل 8نتایج تشخیص الگوی خطی استخراج شده با استفاده از روش های مختلف را ارائه می دهد. ساختمان هایی که با مثلث های نارنجی به هم متصل شده اند یک الگوی خطی را تشکیل می دهند. از نظر بصری، روش پیشنهادی در شناخت الگوهای ساختمانی خطی موثر است. برای هر مجموعه داده منفرد، ساختمان ها از نظر الگوهای خطی (به عنوان مثال، الگوی خطی و الگوی منحنی) به طور منطقی شناسایی می شوند. در مقایسه، روش پیشنهادی بهتر از روش MST در سه حوزه مورد مطالعه عمل می‌کند. الگوهای ساختمان خطی استخراج شده توسط الگوریتم MST تا حد زیادی از الگوهای مرجع، به ویژه در منطقه مورد مطالعه NN، منحرف می شوند. این الگوریتم به طور مکرر الگوهای ساختمان را بر اساس فواصل بین اشیاء شناسایی می کند و سایر اصول گشتالت الگوها را نادیده می گیرد.
نتایج ارزیابی دقت تشخیص الگوی ساختمان خطی در جدول 2 خلاصه شده است. به طور کلی، روش پیشنهادی می‌تواند الگوهای ساختمانی خطی را با مقادیر صحت و مقادیر بالای 92 درصد تشخیص دهد که نشان می‌دهد نتایج تشخیص به خوبی با داده‌های مرجع مطابقت دارد. به طور خاص، برای روش پیشنهادی، الگوهای خطی کمتری از مجموعه داده‌های SZ و SC نسبت به الگوهای مرجع استخراج می‌شوند، زیرا پارتیشن بندی پایین ممکن است هنگام انجام پارتیشن بندی نمودار رخ دهد. در مقایسه، عملکرد الگوریتم MST به طور قابل توجهی با روش پیشنهادی در سه مجموعه داده متفاوت است. هر دو مجموعه داده SZ و SC از نظر صحت و کامل بودن مقادیر بالایی دارند، در حالی که مجموعه داده NN دارای مقادیر بسیار پایین تری از کامل بودن و صحت است. علاوه بر این، تعداد الگوهای گروه مدل‌سازی شده شناسایی‌شده توسط این الگوریتم بیشتر از داده‌های مرجع است.
شکل 9 نتایج میانی دو روش را قبل از انجام مرحله 6 نشان می‌دهد. به طور کلی، مرحله 5 در حذف بسیاری از یال‌های بی‌اهمیت و سراسری از نمودار مؤثر است، با توجه به اینکه تعداد کمی از یال‌ها وجود دارند که نیاز به قضاوت برای مرحله بعدی دارند. این عمدتا به دلیل استفاده از SCI در فرآیند تقسیم بندی است. با مقایسه نتایج NN و دو نتیجه دیگر، متوجه می‌شویم که تفاوت‌های آشکاری در نتایج شناسایی استخراج‌شده توسط دو روش در داده‌های NN وجود دارد ( شکل 9 a,d). این ممکن است تفاوت دقت بین دو روش در جدول 1 را توضیح دهد. روش MST از نزدیکترین شی برای ایجاد نمودار استفاده می کند، در نتیجه روابط ساختمان های مجاور که باید به همان الگوهای خطی تعلق داشته باشند، اما کمی دور هستند، به زودی حذف می شوند. با این حال، روابط مجاورتی باقیمانده برخی از نزدیکترین ساختمان‌ها اما به‌طور نامنظم چیده شده‌اند با وزن نابهنجار کم وزن شده‌اند.  SCIs، که منجر به حذف این ساختمان ها ابتدا از الگوها در طی فرآیند فیلتر شد. در نتیجه، نتایج شناسایی پراکنده‌تر بود. این نتیجه با نتایج گزارش شده توسط [ 31 ] سازگار است. در داده های SZ و CS، به دلیل اینکه فاصله بین ساختمان هایی که به الگوهای خطی مختلف تعلق دارند بسیار بیشتر است، تفاوت معنی داری در نتایج میانی به دست آمده توسط دو روش وجود ندارد. با این حال، روش پیشنهادی برخی از روابط نزدیکی اضافی را حفظ می کند.
شکل 10 بیشتر توزیع دقیق الگوهای خطی شناسایی شده توسط روش پیشنهادی برای سه مجموعه داده را نشان می دهد. نمودار نشان می دهد که روش پیشنهادی یک الگوی گنجاندن (یعنی یک الگوی مدل شده حاوی الگوهای مرجع متعدد) را در سه مجموعه داده شناسایی کرد ( شکل 8).ب، ای، ه). این به این دلیل است که مثلث هایی که دو ساختمان متعلق به دو الگوی متفاوت را به هم متصل می کنند، از نظر تعداد و مساحت شبیه به نمونه های یکسان هستند. روش پیشنهادی همچنین یک الگوی درون و یک الگوی همپوشانی را در داده‌های CS شناسایی کرد. اولی به این دلیل است که زاویه مسیر مستقیم که توسط مثلث هایی که دو ساختمان مجاور را به هم متصل می کنند بسیار کوچک است و رابطه آنها حذف شده است. برای الگوی همپوشانی، تشخیص آنها به روشی کاملاً صحیح برای چشمان انسان نیز دشوار است.
در آزمایشات ما، یکی از پارامترهای غالب، زاویه مسیر است. برای نشان دادن بهتر الگوریتم‌ها، مقادیر مختلف زاویه مسیر مورد آزمایش قرار گرفتند تا نشان دهند چگونه بر نتایج تشخیص تأثیر می‌گذارند. ابتدا زاویه مسیر مستقیم ={90°,95°,100°,105°,110°,115°} و زاویه مسیر غیر مستقیم ={50°,55°,60°,65°,70°,75°} برای تشخیص ترازهای خطی در مجموعه داده SZ استفاده می شود ( شکل 11 و شکل 12 ).
شکل 11 نشان می دهد که بهترین محدوده کاری زاویه مسیر مستقیم برای روش پیشنهادی از 95 درجه تا 100 درجه بود. در این محدوده از مقادیر برای آزمون ما، نتایج تشخیص هیچ تفاوتی را نشان نداد. هنگام افزایش مقدار زاویه مسیر مستقیم، الگوهای خطی بیشتری حذف شدند. شکستگی ها معمولاً در ترازهایی با انحنای کم ظاهر می شوند (به عنوان مثال، مثلث هایی که با دایره های آبی در شکل 11 مشخص شده اند ). این به دلیل تقاطع هایی بود که ممکن است از مثلث هایی ایجاد شود که دو ساختمان را در دو طرف به هم متصل می کند.
به طور مشابه، شکل 12 نشان می دهد که بهترین محدوده کاری زاویه مسیر غیر مستقیم برای روش پیشنهادی بیش از 65 درجه بود. هنگام کاهش این آستانه، برخی از هم ترازی ها حذف شدند (دایره های سبز در شکل 12 ). هرچه زاویه مسیر کمتر باشد، ترازهای بیشتری حذف می شوند ( شکل 12 a-c). با این حال، هنگام افزایش مقدار زاویه مسیر، ساختمان‌های بیشتری به عناصر بالقوه ساختمان‌های خطی تبدیل می‌شوند که ممکن است منجر به الگوهای خطا شود. علاوه بر این، این عملیات کارایی تشخیص را کاهش می دهد.

5. نتیجه گیری ها

این مطالعه برای شناسایی الگوهای ساختمانی خطی (به عنوان مثال، الگوهای ساختمانی خطی و منحنی) از طریق یک روش تقسیم بندی نمودار، که به قوانین مجاورت، جهت گیری و تداوم نیاز دارد، تنظیم شده است. برای دستیابی به چنین هدفی، این مطالعه جایگزینی را برای اندازه‌گیری جهت و پیوستگی فضایی هر دو ساختمان بر اساس مثلث دلونی پیشنهاد کرد و یک روش تقسیم‌بندی را برای استخراج الگوهای ساختمانی خطی پیشنهاد کرد.
ما رویکرد خود را بر روی سه مجموعه داده برداری با برخی اندازه‌گیری‌های کمی تأیید کردیم. نتایج تجربی نشان می‌دهد که روش‌های پیشنهادی می‌توانند نتایج رضایت‌بخشی تولید کنند، با توجه به اینکه مقادیر صحت همه بالای 92 درصد برای سه منطقه مورد مطالعه است. مطالعات تطبیقی ​​نشان داد که روش MST یک روش استخراج ناکارآمد برای تشخیص الگوهای خطی ساختمان است، زمانی که فواصل بین ساختمان‌های مجاور که به خوشه‌های مختلف تعلق دارند دور باشد. این به این دلیل است که روش MST از نزدیکترین اشیا برای ایجاد نمودار استفاده می کند. SCI جدید می تواند به طور موثر بر نقص فوق غلبه کند همانطور که به طور تجربی تأیید شده است. این به این دلیل است که SCI شکل، اندازه و جهت ساختمان های اطراف را در نظر می گیرد.
آزمایش‌های بیشتری برای بهبود روش پیشنهادی مورد نیاز است، مانند آزمایش با مجموعه داده‌های فضایی بیشتر از مقیاس‌های مختلف و انواع بیشتری از الگوهای ساختمانی (مانند الگوهای شبکه‌ای). همچنین برای کالیبراسیون خودکار پارامترها (به عنوان مثال، زاویه مسیر) مورد استفاده در استراتژی تقسیم بندی ارائه شده، کار بیشتری لازم است.

منابع

  1. دو، اس. لو، ال. کائو، ک. Shu, M. استخراج الگوهای ساختمان با پارتیشن نمودار چندسطحی و گروه بندی ساختمان. ISPRS J. Photogramm. Remote Sens. 2016 ، 122 ، 81-96. [ Google Scholar ] [ CrossRef ]
  2. دو، اس. شو، م. Feng, C. بازنمایی و کشف الگوهای ساختمانی: یک رویکرد رابطه‌ای سه سطحی. بین المللی جی. جئوگر. آگاه کردن. علمی 2016 ، 30 ، 1161-1186. [ Google Scholar ] [ CrossRef ]
  3. ژانگ، ایکس. آی، تی. استوتر، جی. کراک، ام. Molenaar, M. تشخیص الگوی ساختمان در داده های توپوگرافی: نمونه هایی در ترازهای خطی و منحنی. GeoInformatica 2013 ، 17 ، 1-33. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  4. کریستف، اس. رواس، الف. تشخیص ترازهای ساختمان برای اهداف تعمیم. پیشرفت در مدیریت داده های مکانی ; Springer: برلین، آلمان، 2002; صص 419-432. [ Google Scholar ]
  5. ژانگ، ایکس. استوتر، جی. آی، تی. کراک، ام. Molenaar, M. ارزیابی خودکار ترازهای ساختمان در نقشه های تعمیم یافته. بین المللی جی. جئوگر. آگاه کردن. علمی 2013 ، 27 ، 1550-1571. [ Google Scholar ] [ CrossRef ]
  6. او، X. ژانگ، ایکس. یانگ، جی. ادغام پیشرونده خوشه‌های ساختمانی برای تعمیم نقشه بر اساس زیرگروه‌های مقیاس‌بندی. ISPRS Int. J. Geo-Inf. 2018 ، 7 ، 116. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
  7. وابینسکی، جی. Mościcka، A. تولید نقشه خودکار (لمسی) – مروری بر ادبیات سیستماتیک. ISPRS Int. J. Geo-Inf. 2019 ، 8 ، 293. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
  8. دو، اس. ژانگ، اف. Zhang، X. طبقه بندی معنایی ساختمان های شهری با ترکیب تصویر VHR و داده های GIS: یک رویکرد جنگل تصادفی بهبود یافته. ISPRS J. Photogramm. Remote Sens. 2015 ، 105 ، 107-119. [ Google Scholar ] [ CrossRef ]
  9. نیو، ن. لیو، ایکس. جین، اچ. بله، X. لیو، ی. لی، ایکس. چن، ی. لی، اس. یکپارچه سازی داده های بزرگ چند منبعی برای استنتاج توابع ساختمان. بین المللی جی. جئوگر. آگاه کردن. علمی 2017 ، 31 ، 1871-1890. [ Google Scholar ] [ CrossRef ]
  10. یان، ایکس. آی، تی. یانگ، م. یین، اچ. یک گراف شبکه عصبی کانولوشن برای طبقه بندی الگوهای ساختمان با استفاده از داده های برداری فضایی. ISPRS J. Photogramm. Remote Sens. 2019 ، 150 ، 259–273. [ Google Scholar ] [ CrossRef ]
  11. فروین، وی. فلدمن، جی. گروه بندی سلسله مراتبی سینگ، ام. بیزی: گروه بندی ادراکی به عنوان تخمین مخلوط. روانی Rev. 2015 , 122 , 575-597. [ Google Scholar ] [ CrossRef ]
  12. او، X. ژانگ، ایکس. Xin، Q. شناخت الگوهای گروه ساختمانی در نقشه های توپوگرافی بر اساس تقسیم بندی نمودار و جنگل تصادفی. ISPRS J. Photogramm. Remote Sens. 2018 ، 136 ، 26–40. [ Google Scholar ] [ CrossRef ]
  13. دنگ، م. لیو، کیو. چنگ، تی. Shi, Y. یک الگوریتم خوشه‌بندی فضایی تطبیقی ​​مبتنی بر مثلث‌سازی دلونای. محاسبه کنید. محیط زیست سیستم شهری 2011 ، 35 ، 320-332. [ Google Scholar ] [ CrossRef ]
  14. اندرس، ک. سستر، ام. فریچ، دی. تجزیه و تحلیل ساختارهای نشست با استفاده از خوشه بندی مبتنی بر نمودار. SMATI 1999 ، 99 ، 41-49. [ Google Scholar ]
  15. Anders, KH یک رویکرد گراف-گراف سلسله مراتبی برای یافتن گروه هایی از اشیاء. در مجموعه مقالات پنجمین کارگاه آموزشی در مورد پیشرفت در تعمیم خودکار نقشه، پاریس، فرانسه، 28-30 آوریل 2003. منبع: پرینستون، نیوجرسی، ایالات متحده آمریکا، 2003. [ Google Scholar ]
  16. وانگ، ی. ژانگ، ال. Mathiopoulos، PT; دنگ، اچ. قوانین گشتالت و چارچوب ساده سازی مبتنی بر برش نمودار برای مدل های ساختمان شهری. بین المللی J. Appl. رصد زمین. Geoinf. 2015 ، 35 ، 247-258. [ Google Scholar ] [ CrossRef ]
  17. وانگ، دبلیو. دو، اس. گوا، ز. Luo, L. تجزیه و تحلیل خوشه بندی چند ضلعی با استفاده از پارتیشن نمودار چند سطحی. ترانس. GIS. 2015 ، 19 ، 716-736. [ Google Scholar ] [ CrossRef ]
  18. لی، ز. یان، اچ. آی، تی. چن، جی. تعمیم خودکار ساختمان بر اساس مورفولوژی شهری و نظریه گشتالت. بین المللی جی. جئوگر. آگاه کردن. علمی 2004 ، 18 ، 513-534. [ Google Scholar ] [ CrossRef ]
  19. Zahn، CT گراف – روش های نظری برای تشخیص و توصیف خوشه های گشتالت. IEEE Trans. محاسبه کنید. 1971 ، 100 ، 68-86. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  20. Wertheimer, M. قوانین سازمان در اشکال ادراکی. کتاب منبع روانشناسی گشتالت ; Routledge & Kegan Paul: لندن، انگلستان، 1923; صص 71-88. [ Google Scholar ]
  21. Regnauld، N. نوع سازی ساختمان متنی در تعمیم خودکار نقشه. الگوریتمیکا 2001 ، 30 ، 312-333. [ Google Scholar ] [ CrossRef ]
  22. آی، تی. کاوش الگوی خوشه ای چندضلعی Guo، R. بر اساس اصول گشتالت. Acta Geod. کارتوگر. گناه 2007 ، 36 ، 302-308. [ Google Scholar ]
  23. یانگ، ال. ژانگ، ال. ما، جی. زی، جی. لیو، ال. تجسم تعاملی مدل‌های ساختمان شهری با وضوح چندگانه با در نظر گرفتن شناخت فضایی. بین المللی جی. جئوگر. آگاه کردن. علمی 2011 ، 25 ، 5-24. [ Google Scholar ] [ CrossRef ]
  24. چن، ز. ما، ایکس. وو، ال. Xie, Z. یک رویکرد شباهت فازی شهودی برای تجزیه و تحلیل خوشه‌بندی چندضلعی‌ها. ISPRS Int. J. Geo-Inf. 2019 ، 8 ، 98. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
  25. فرانک، AU استدلال فضایی کیفی: جهت های اصلی به عنوان مثال. بین المللی جی. جئوگر. آگاه کردن. علمی 1996 ، 10 ، 269-290. [ Google Scholar ] [ CrossRef ]
  26. فرانک، AU استدلال فضایی کیفی در مورد فواصل و جهت ها در فضای جغرافیایی. J. ویژوال لنگ. محاسبه کنید. 1992 ، 3 ، 343-371. [ Google Scholar ] [ CrossRef ]
  27. یان، اچ. چو، ی. لی، ز. Guo, R. یک مدل توصیف کمی برای روابط جهت بر اساس گروه های جهت. GeoInformatica 2006 ، 10 ، 177-196. [ Google Scholar ] [ CrossRef ]
  28. فیلد، دی جی; هیز، ا. هس، ادغام RF Contour توسط سیستم بینایی انسان: شواهدی برای یک “میدان انجمن” محلی. Vision Res. 1993 ، 33 ، 173. [ Google Scholar ] [ CrossRef ]
  29. آی، تی. ژانگ، X. تجمع خوشه های ساختمان شهری بر اساس تقسیم بندی اسکلت فضای شکاف. جامعه اطلاعاتی اروپا Springer: برلین، آلمان، 2007; صص 153-170. [ Google Scholar ]
  30. آی، تی. Van Oosterom، P. GAP-tree extensions بر اساس اسکلت. در پیشرفت در مدیریت داده های مکانی ; Springer: برلین، آلمان، 2002; ص 501-513. [ Google Scholar ]
  31. چتینکایا، اس. بسارنر، م. Burghardt، D. گروه‌بندی ساختمان‌ها در بلوک‌های شهری مبتنی بر مجاورت: مقایسه چهار الگوریتم. Geocarto Int. 2015 ، 30 ، 618-632. [ Google Scholar ] [ CrossRef ]
Ijgi 09 00231 g001 550
شکل 1. نمونه هایی برای مثلث سازی محدود شده دلون برای ( الف ) مثلث سازی ساخته شده برای همه ساختمان ها در هر بلوک مجزا و ( ب ) مثلث سازی ساخته شده برای هر جفت ساختمان مجاور نشان داده شده است.
Ijgi 09 00231 g002 550
شکل 2. نمونه ای از ارتفاعات و خطوط اسکلت ساختمان های مجاور.
Ijgi 09 00231 g003 550
شکل 3. تصویر جهت بین دو ساختمان و زاویه مسیر بین ساختمان ها.
Ijgi 09 00231 g004 550
شکل 4. نمونه هایی از محاسبه زوایای آزیموت ساختمان های مجاور برای ( الف ) زوایای آزیموت همه مثلث ها نشان داده شده است. ( ب ) زاویه میانگین دو ساختمان مجاور. ج ) زاویه آزیموت نهایی دو ساختمان مجاور.
Ijgi 09 00231 g005 550
شکل 5. مرحله روش شناختی 4 تا مرحله 6 برای ( الف ) ایجاد نمودار نشان داده شده است. ب ) حذف لبه های ناچیز و سراسری. ج ) جفت های خطی گره مجاور. ( د ) الگوهای خطی نهایی ساختمان.
Ijgi 09 00231 g006 550
شکل 6. نمودار جریان برای شناسایی الگوهای ساختمانی خطی.
Ijgi 09 00231 g007 550
شکل 7. مکان منطقه مورد مطالعه و مجموعه داده های تجربی برای ( الف ) NanNing نشان داده شده است. ( ب ) ChangSha; ( ج ) شنژن.
Ijgi 09 00231 g008 550
شکل 8. نتایج تشخیص الگوی خطی برای ( a )–( c ) سه روش در مجموعه داده NN نشان داده شده است. ( d )–( f ) سه روش در مجموعه داده SZ. ( g )–( i ) سه روش در مجموعه داده CS. ساختمان‌هایی که با مثلث‌های نارنجی به هم متصل می‌شوند به عنوان الگوهای ساختمانی خطی شناخته می‌شوند. الگوهای نادرست با منحنی های رنگی متفاوت مشخص شده اند.
Ijgi 09 00231 g009 550
شکل 9. نتایج میانی قبل از انجام مرحله 6 برای ( a )–( c ) روش پیشنهادی در سه مجموعه داده نشان داده شده است. ( d )–( f ) MST در سه مجموعه داده.
Ijgi 09 00231 g010 550
شکل 10. توزیع الگوهای ساختمانی خطی شناخته شده در سه مجموعه داده.
Ijgi 09 00231 g011 550
شکل 11. نتایج روش پیشنهادی با مقادیر مختلف زاویه مسیر مستقیم و زوایای مسیر غیرمستقیم 65 درجه در مجموعه داده SZ. ساختمان هایی که با مثلث های لبه نارنجی متصل می شوند به عنوان الگوهای ساختمانی خطی شناخته می شوند.
Ijgi 09 00231 g012 550
شکل 12. نتایج تشخیص الگوی خطی روش پیشنهادی با مقادیر مختلف زاویه مسیر غیر مستقیم و زاویه مسیر مستقیم 100 درجه در مجموعه داده SZ. ساختمان هایی که با مثلث های لبه نارنجی متصل می شوند به عنوان الگوهای ساختمانی خطی شناخته می شوند.

مقالات داخلی و بین المللی

مطالب مرتبط ...

بدون دیدگاه

دیدگاهتان را بنویسید