تعمیم خودکار دادههای شبکه جادهای به دلیل اهمیت دادههای جادهای و دشواری موجود، نگرانی زیادی برای جامعه تعمیم نقشه دارد. تقاطع های پیچیده جایی هستند که جاده ها به شکلی پیچیده به هم می رسند و به هم می پیوندند و شناسایی آنها یک موضوع کلیدی در تعمیم شبکه راه ها است. پیوندهای پیچیده علاوه بر پیچیدگی ساختاری، مرز هندسی منظمی ندارند و نمایش آنها در دادههای مکانی وابسته به مقیاس است. همه اینها در کنار هم تشخیص آنها را سخت می کند. روشهای موجود از آمار هندسی و توپولوژیکی برای توصیف و شناسایی آنها استفاده میکنند و بنابراین مستعد خطا، وابسته به مقیاس و فاقد کلیت هستند. مهمتر از آن، آنها نمی توانند یکپارچگی اتصالات پیچیده را تضمین کنند. این مطالعه با روشن کردن مرز توپولوژیکی یک اتصال پیچیده، بر موانع غلبه میکند، که مبنایی برای شناسایی مستقیم آنها فراهم میکند. نتایج آزمایش نشان میدهد که روش پیشنهادی میتواند اتصالات پیچیده در یک شبکه جادهای را با یکپارچگی آنها پیدا و جداسازی کند و قادر به مدیریت نمایشهای جادهای مختلف است. شناسایی یکپارچه بهدستآمده میتواند به تضمین اتصال بین جادهها هنگام سادهسازی اتصالات پیچیده کمک کند و سادهسازی هندسی و معنایی آنها را تا حد زیادی تسهیل کند.
کلید واژه ها:
تعمیم ; مقیاس ; رابطه توپولوژیکی ; شبکه جاده ای ؛ تشخیص الگو
1. مقدمه
تعمیم نقشه یک نوع خاص از مدلسازی فضایی است که شامل استخراج یک نمایش فضایی با جزئیات کمتر از جزئیات است و به طور سنتی توسط نقشهنگاران به صورت دستی انجام میشد [ 1 ]. در محیط دیجیتال، تعمیم دادههای مکانی اساس ساخت نمایشهای چند مقیاسی در پایگاههای اطلاعاتی فضایی است و بسیار مطلوب است که خودکار شود [ 2 ، 3 ].
تعمیم نیاز به پردازش بسیار هوشمندانه داده های مکانی دارد و به طور کلی خودکار کردن آن بسیار دشوار است [ 1 ، 4 ]. تلاش زیادی برای اتوماسیون آن در نیم قرن گذشته انجام شده است [ 5 ]. در سه دهه گذشته، پیشرفت قابل توجهی در تبدیل نمایش داده ها [ 6 ، 7 ]، غنی سازی معناشناسی داده ها [ 5 ، 8 ]، و توسعه الگوریتم های هوشمند [ 9 ، 10 ، 11 ] صورت گرفته است. برخی از دستاوردها در تولید داده اعمال شده است [ 12 ، 13 ].
تعمیم دادههای شبکه جادهای به دلیل اهمیت دادههای جادهای و دشواری موجود، یکی از بزرگترین نگرانیهای محققان و دست اندرکاران تعمیم بوده است [ 6 ، 14 ، 15 ]. تحقیقات زیادی در مورد انتخاب جاده [ 16 ، 17 ، 18 ]، تجزیه و تحلیل الگوها در شبکه های جاده ای [ 19 ، 20 ، 21 ] و تکنیک هایی برای غنی سازی معنایی داده های جاده [ 22 ، 23 ، 24 ] انجام شده است.
این مطالعه به ویژه با شناسایی اتصالات پیچیده در یک شبکه جادهای مرتبط است. تقاطع های پیچیده جایی هستند که جاده ها به روشی پیچیده به هم می رسند و به هم می پیوندند و ساده سازی مناسب آنها یک مسئله کلیدی در تعمیم شبکه جاده ای است [ 25 ، 26 ، 27 ]]. برخلاف تقاطعهای مسطح ساده، مانند تقاطعها و تقاطعهای T که در آنها جادههای اصلی مستقیماً به خودی خود تلاقی میکنند، اتصالات پیچیده میتوانند به صورت مسطح با جادههای لغزنده برای گردش صاف باشند و میتوانند به صورت مبادلهای با درجه جدا شده با سطح شیبدار برای پل زدن شکافهای ارتفاعی باشند. علاوه بر این، آنها می توانند از نظر ساختار بسیار پیچیده و در شکل پیچ خورده باشند. برای ساده سازی نمایش این گونه اتصالات بدون قطع اتصال بین جاده های مربوطه، لازم است ابتدا آنها را دقیقاً در شبکه راه ها شناسایی کنیم [ 25 ، 26 ].
شناسایی اتصالات پیچیده در یک شبکه جاده ای به دلیل مشکلاتی که در مشخص کردن قطعی آنها و تعیین مرز آنها در شبکه وجود دارد، توسط مطالعات قبلی کاملاً چالش برانگیز است [ 21 ، 27 ]. Mackaness و Mackechnie [ 25 ] اتصالات پیچیده را به عنوان جایی که گره های تقاطع جاده متراکم هستند مشخص کردند و یک رویکرد تجزیه و تحلیل تراکم برای تشخیص آنها پیشنهاد کردند. با تنظیم دقیق آستانه تراکم، اتصالات پیچیده به عنوان مجموعه ای از گره های خوشه ای متراکم را می توان شناسایی کرد، اگرچه بلوک های خیابان نیز ممکن است به اشتباه در آن گنجانده شوند. ساوینو و همکاران [ 23 ، 26] متوجه شد که تراکم گره در برخی موارد کار نمی کند. آنها از آمار دایره های اضافی (یا حلقه ها در اصطلاح توپولوژیکی) برای توصیف اشکال مختلف اتصالات پیچیده استفاده کردند و سعی کردند با جستجوی چنین دایره هایی در یک شبکه جاده ای آنها را شناسایی کنند. Touya [ 19 ] از روش Grosso [ 28 ] برای تشخیص تقاطع بزرگراه ها استفاده کرد. روش آنها شبیه به روش Mackaness و Mackechnie است [ 25 ]. اما به جای گره های تقاطع معمولی از دوشاخه و گره y استفاده کردند که بیشتر مشخصه تقاطع بزرگراه ها محسوب می شد. به طور مشابه، ژو و لی [ 27 ] یک اتصال پیچیده را به عنوان مجموعه ای از اتصالات ساده، از جمله اتصالات T-، دوشاخه و عبور و غیره در نظر گرفتند. مانند Savino و همکاران. [ 23 ، 26]، آنها سعی کردند اشکال مختلف اتصالات پیچیده را با آمار ترکیبی خود از اتصالات ساده توصیف و تشخیص دهند.
همانطور که مشاهده می شود، روش های موجود همگی مبتنی بر تحلیل آماری خواص هندسی و توپولوژیکی اتصالات پیچیده هستند. بنابراین آنها از مشکل تعیین آستانه رنج می برند. اتصالات پیچیده دنیای واقعی از نظر چگالی گره، شکل و اندازه محصور و شکل ساختاری بسیار متفاوت است. آستانه آنها ناگزیر از ناحیه ای به منطقه دیگر و شهری به شهر دیگر به دلیل ناهمگونی فضایی متفاوت است. علاوه بر این، هیچ تعریفی از مرز یک اتصال پیچیده در آن روش ها وجود نداشت. بنابراین، آنها نمی توانند اتصالات پیچیده را با یکپارچگی خود شناسایی کنند، زیرا مرز با آستانه های مورد استفاده تغییر می کند. علاوه بر این، نمایش پیوند وابسته به مقیاس است. تغییر از نمایش تک خطی جاده ها به دو خطی می تواند یک اتصال پیچیده را در هندسه و توپولوژی بسیار متفاوت کند. در حال حاضر،
ما یک رویکرد الگوی ساختاری برای شناسایی اتصالات پیچیده اتخاذ کردیم. با توجه به دانش حوزه طراحی اتصالات [ 29 ، 30 ]، اتصالات پیچیده آنهایی هستند که دارای جاده های فرعی هستند، مانند جاده های لغزنده و رمپ ها، تا به جاده های اولیه کمک کنند به هموار بپیوندند. به این معنا، یک اتصال پیچیده را میتوان از نظر ساختاری در شرایط توپولوژیکی تعریف کرد، مهم نیست که چقدر پیچیده باشد. این تعریف دروازه ای را به روی یک راه ساده برای شناسایی اتصالات پیچیده باز می کند.
بقیه این مقاله به شرح زیر سازماندهی شده است. از منظر طراحی جاده و تقاطع، بخش 2 یک الگوی ساختاری از اتصالات پیچیده را رسمیت میدهد که آنها را به روشی مستقل از مقیاس مشخص میکند و مرز توپولوژیکی دقیق آنها را مشخص میکند. سپس یک الگوریتم ساده بر اساس آن الگو برای شناسایی اتصالات پیچیده در بخش 3 پیشنهاد شده است. در بخش 4 ، آزمون تجربی استفاده از روش برای یک مورد چالش برانگیز از شبکه جاده های دنیای واقعی و مقایسه بین این روش و روش معمولی ارائه شده است. تأثیر خطاها در داده های ورودی بر شناسایی در بخش 5 مورد بحث قرار گرفته است. در بخش 6، وابستگی مقیاس در هنگام شناسایی اتصالات پیچیده و ارتباط بین جاده های اولیه – فرعی و تعمیم شبکه جاده مورد بحث قرار می گیرد. در نهایت، نتیجه گیری در بخش 7 آورده شده است.
2. مرز توپولوژیکی یک اتصال پیچیده
همانطور که در بالا تجزیه و تحلیل شد، ویژگی های اساسی تر اتصالات پیچیده باید آشکار شود تا مبنای موثرتری برای شناسایی آنها فراهم شود. ما به دانش حوزه طراحی جاده و تقاطع می پردازیم و یک تعریف توپولوژیکی از اتصال پیچیده را تدوین می کنیم.
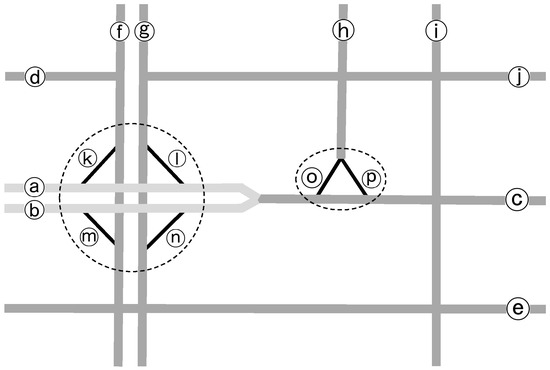
با توجه به اصول طراحی راه و اتصالات [ 29 ، 30 ، 31 ، 32 ]، دو نوع جاده را می توان در یک سیستم شبکه راه متمایز کرد، جاده های اولیه و فرعی. جاده های اولیه (یا جاده های اصلی به معنای رایج) برای پیوند مکان های توزیع شده در فضای جغرافیایی عمل می کنند. در مقابل، جادههای فرعی مانند جادههای لغزنده و رمپها برای اتصال جادههای اولیه به یکدیگر کمک میکنند و به آنها کمک میکنند تا راحتتر از راه تقاطع مستقیم برای افزایش توان در اتصالاتشان به هم بپیوندند. به عبارت دیگر جاده های فرعی وابسته به راه های اولیه هستند. این دو نوع جاده در شکل 1 نشان داده شده استبا یک شبکه جاده ای شماتیک T. جاده ها در T برای ارجاع آسان برچسب گذاری شده اند. آنهایی که خاکستری روشن یا تیره هستند، یعنی a–j، اولیه هستند و آنهایی که سیاه هستند، یعنی k–p، ثانویه هستند. با طبقه بندی جاده ها، ترکیب یک تقاطع پیچیده از نظر مفهومی روشن می شود. دو دایره چین دار در اطراف دو اتصال پیچیده در شکل 1 ترسیم شده است تا ترکیب آنها واضح تر شود. باید واضح باشد که یک تقاطع پیچیده شامل گروهی از راه های فرعی به همراه راه های اولیه مربوطه است که اولی را به بقیه راه ها متصل می کند.
مفهوم فوق از اتصالات پیچیده باید رسمی شود تا دقیق و قابل محاسبه باشد. برای انجام این کار، ما نمایش مبتنی بر بخش معمولی یک شبکه جاده را به یک نمایش مبتنی بر سکته مغزی، و سپس به یک نمایش توپولوژیکی دوگانه (یا شبکه دوگانه برای اختصار) تبدیل میکنیم. مفهوم سکته جاده ای توسط تامسون و ریچاردسون [ 33 ] پیشنهاد شد که به ترکیب بخش های جاده بر اساس اصل تداوم خوب اشاره دارد. به طور شهودی، به جای بخش جاده، سکته مغزی جاده است که به طور طبیعی با مفهوم جاده در استفاده روزمره مطابقت دارد. سکته مغزی از زمان ارائه آن به طور گسترده پذیرفته شده و در تحلیل شبکه راه ها مورد استفاده قرار گرفته است [ 18 ، 19 ، 32 ]. در واقع، برچسب ها درشکل 1 مربوط به سکته های جاده ای به جای بخش های جاده است. بنابراین، شبکه جاده T در شکل 1 از نمایش مبتنی بر سکته مغزی استفاده کرده است.
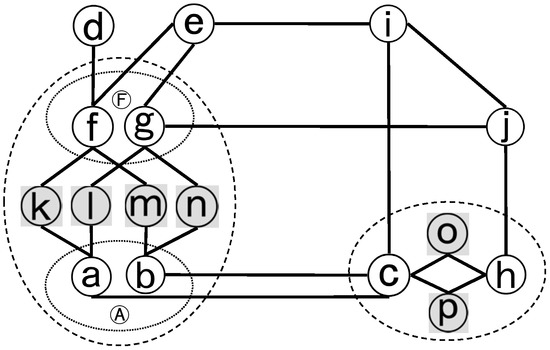
شبکه دوگانه یک شبکه جاده ای مبتنی بر سکته مغزی به طور گسترده در تحلیل توپولوژیکی شبکه های جاده ای استفاده می شود [ 34 ، 35 ، 36 ]. در شبکه دوگانه، یک جاده به یک گره تبدیل می شود و اگر دو جاده ای که آنها نشان می دهند، یک لبه بین دو گره وجود دارد. برای نشان دادن، شبکه دوگانه شبکه جاده T نشان داده شده در شکل 1 در شکل 2 ارائه شده است . همانطور که مشاهده می شود، هر جاده در شکل 1 اکنون یک گره در شکل 2 است. علاوه بر این، بین دو جاده (یعنی گره ها) در صورت تلاقی آنها یک لبه وجود دارد. در شکل 1، رابطه تقاطع بین جاده ها با رنگ های خط نشان داده می شود. به طور کلی، اگر دو خط قطع شوند، دو جاده ای که آنها نشان می دهند، قطع می شوند. استثناء مواردی است که در آن یک خط خاکستری روشن با یک خط خاکستری تیره قطع می شود. به عبارت دیگر، جاده a نه جاده f و نه g را قطع نمی کند و همچنین b نیز قطع نمی کند. بنابراین، شبکه دوگانه T مانند آنچه در شکل 2 نشان داده شده است ، که در آن لبه هایی بین a و f، a و g، b و f، و b و g وجود ندارد.
در شبکه دوگانه نمایش مبتنی بر سکته مغزی یک شبکه جادهای، یک اتصال پیچیده را میتوان به عنوان گروهی از گرههای جاده فرعی که از بقیه شبکه راه توسط گرههای مربوطه جاده اصلی جدا شدهاند، تعریف کرد که اولی در خدمت آن است. متصل شود یا به آن وابسته باشد. که در شکل 2 مشخص است، جایی که گره های جاده فرعی عمداً خاکستری می شوند تا نشان دهند که توسط جاده های اصلی مربوطه “محدود شده اند”. دو بیضی چین دار رسم می شوند تا مرزهای توپولوژیکی دو اتصال پیچیده را مشخص کنند، که در غیر این صورت ممکن است آشکار نباشد. همانطور که مشاهده می شود، گره های جاده فرعی، مثلاً (k, l, m, n) از بقیه شبکه توسط گره های مربوطه جاده اولیه یعنی (a, b, f, g) مسدود می شوند. به عبارت دیگر، از راه های فرعی بدون عبور از راه های اولیه ای که در آنها خدمت می کنند، نمی توان به بقیه شبکه راه ها دسترسی پیدا کرد و این جاده ها مرز توپولوژیکی یک اتصال پیچیده را تشکیل می دهند. برعکس، جاده های فرعی داخلی یک تقاطع پیچیده را نمی توان از جاده های خارجی به تقاطع بدون عبور از جاده های اولیه مرزی آن دسترسی داشت.
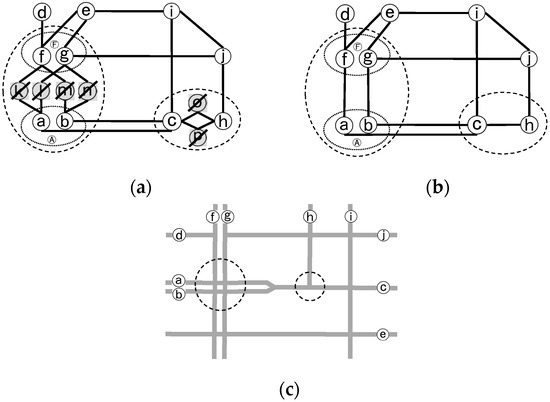
مرز توپولوژیکی یک اتصال پیچیده رویکردی را برای تعمیم اتصال پیچیده با دور انداختن مناسب جادههای فرعی داخلی آن فراهم میکند. شکل 3 نمونه ای را برای نشان دادن این فرآیند تعمیم با ساده کردن اتصالات پیچیده در شبکه جاده ای شماتیک T در شکل 1 نشان می دهد. اتصالات پیچیده با دور انداختن گره های جاده ثانویه، یعنی (k، l، m، n، o، p) تعمیم داده می شوند، اما اتصال بین جاده های اولیه مرزی که توسط آنهایی که دور ریخته می شوند، حفظ می شود.
شایان ذکر است که تعریف فوق یک تعریف کاملاً توپولوژیکی است و بنابراین ذاتاً مستقل از مقیاس است. این بدان معناست که مهم نیست که اتصال پیچیده چقدر پیچیده یا ساده باشد، کار می کند. این بدان معناست که بدون توجه به اینکه یک جاده با یک خط، دو خط یا حتی چندین خط نشان داده می شود، کار می کند. مورد نمایش دو خطی در شکل 2 نشان داده شده است . برای خطوط جفتی a و b یک راهرو دوگانه در شکل 1 ، میتوانیم به طور منطقی آنها را به عنوان یک گره مرکب A در شبکه دوگانه در نظر بگیریم همانطور که در شکل 2 نشان داده شده است.. به طور مشابه، f و g گره مرکب دیگری F را می سازند. علاوه بر این، از آنجایی که این تعریف شامل یک مرز توپولوژیکی دقیق از یک اتصال پیچیده است، بنابراین می توان آن را برای شناسایی اتصالات پیچیده با یکپارچگی آنها، همانطور که در زیر توضیح داده شده است، اعمال کرد.
3. الگوریتم شناسایی اتصالات پیچیده
فرآیند یافتن و جداسازی یک تقاطع پیچیده در شبکه دوگانه با یک گره بذری جاده فرعی (SD) شروع میشود و سپس با گسترش قسمت پیدا شده تا رسیدن به مرز ادامه مییابد. به طور دقیق تر، الگوریتم به صورت زیر پیش می رود:
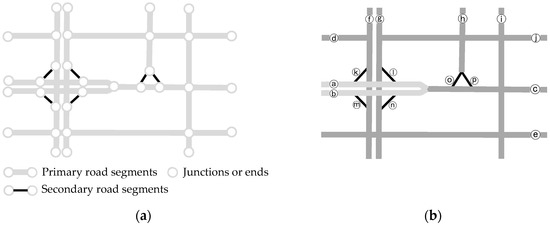
(1) اولیه سازی جهانی: بخش های جاده را به سکته مغزی متصل کنید. نوع اولیه یا ثانویه جاده ها و همتایان جفت را استخراج کنید. با تبدیل به شبکه دوگانه، مجموعه گره های جاده فرعی (SG) را در نظر بگیرید. یک مجموعه خالی (J) برای جمع آوری اتصالات پیچیده آماده کنید. اگر SG خالی است، J را برگردانید و خارج شوید. در غیر این صورت، تمام گرههای SG را بهعنوان پردازشنشده علامتگذاری کنید. مقداردهی اولیه شبکه جاده ای شماتیک T در شکل 4 نشان داده شده است. SG مربوط به مجموعه جاده های فرعی است، یعنی (k، l، m، n، o، p).
(2) بذر: یک جاده ثانویه فرآوری نشده sd را از SG انتخاب کنید. اگر مناسب است (یعنی دو جاده مختلف را به جای همتاهای یک جاده به هم وصل می کند)، به مرحله بعدی بروید. در غیر این صورت، آن را به عنوان پردازش شده در SG علامت گذاری کنید. دیگران را امتحان کنید تا زمانی که مورد مناسب انتخاب شود. یا در غیر این صورت، J را برگردانید و از آن خارج شوید، زیرا هیچ گره پردازش نشده دیگری در SG وجود ندارد.
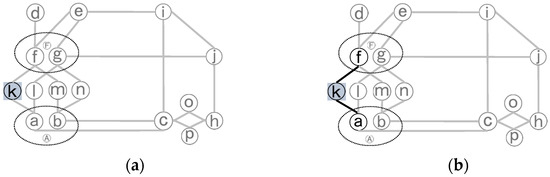
(3) مقدار دهی اولیه محلی: دو مجموعه خالی، یکی برای جاده های اولیه (P) و دیگری برای جاده های ثانویه (S) آماده کنید تا به ترتیب گره های مرزی و گره های داخلی یک اتصال پیچیده را جمع آوری کنید. sd را در S قرار دهید. با انتخاب گره k به عنوان sd همانطور که در شکل 5 a نشان داده شده است، S شامل یک جاده ثانویه در مجموعه خود به عنوان (k) پس از مقداردهی اولیه محلی است.
(4) گسترش S: برای هر گره مناسب توسعه نیافته (x) در S، همه گره های همسایه آن را از شبکه دوگانه واکشی کنید و هر کدام از آنها را با توجه به نوع جاده آن در P یا S قرار دهید و سپس x را به عنوان منبسط شده علامت بزنید. اگر گره های جدیدی به S اضافه شوند، گره های جدید را به صورت بازگشتی گسترش دهید تا به برخی از جاده های اصلی برسید. در فرآیند بسط بازگشتی، آنهایی را که در S قرار دارند بهعنوان منبسط شده علامتگذاری کنید، اما آنهایی را که در P هستند بهعنوان منبسط نشده رها کنید. شکل 5 ب نمونه ای از فرآیند گسترش S با گسترش گره k در شبکه دوگانه را نشان می دهد. گرههای درگیر در فرآیند انبساط S با رنگشان همانطور که در شکل 2 نشان داده شده است نشان داده میشوند و لبههای سیاه با پیوندهای بین گرههای پردازش مطابقت دارند، همانطور که در شکل 6 ، شکل 7 در زیر آمده است.و شکل 8 . با صرف S گره k، P گره a و f را جمع آوری می کند.
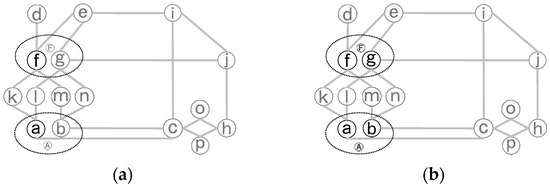
(5) پردازش چند خطی: برای هر گره x در P که همتای یک جاده دوخطی یا چندخطی r است، همتاهای دیگر r را در صورتی که هنوز وارد نشدهاند در P قرار دهید و آنها را بهعنوان گسترش نیافته رها کنید. شکل 6 نمونه ای از پردازش چند خطی را با جمع آوری همتایان g و b گره f و a در شبکه دوگانه نشان می دهد. با پردازش چند خطی، P شامل گره های مرز پیوند پیچیده به صورت (a, b, f, g) است.
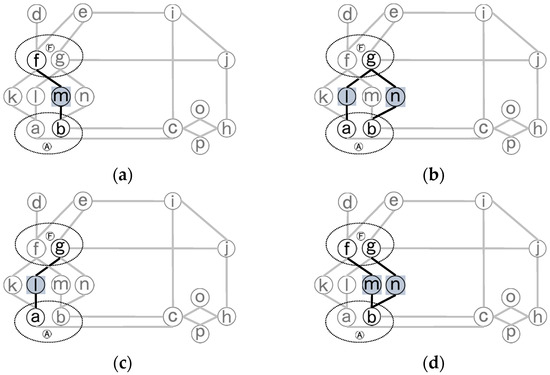
(6) گسترش P:سه مجموعه را برای استفاده موقت آماده کنید: اول برای گره های مناسب توسعه نیافته جاده ثانویه همسایه با یک پردازش (T)، دوم برای جمع آوری جاده های اولیه درگیر در روند گسترش (TP) و سوم برای جمع آوری جاده های فرعی در حین گسترش (TS) . برای هر گره x گسترش نیافته در P، T را پاک کنید، تمام جاده های فرعی مناسب توسعه نیافته همسایه x را واکشی کنید و آنها را در T قرار دهید. رسیده و جاده های به دست آمده را در فرآیند گسترش (از جمله y) به ترتیب در TS یا TP قرار دهید. اگر هر گره ای در TP یکی در P به غیر از x است، اگر هنوز وجود ندارد، تمام گره های موجود در TS و TP را به ترتیب در S و P قرار دهید، و گره هایی را که به S اضافه شده اند به عنوان منبسط شده علامت گذاری کنید و آن هایی را که به P اضافه شده اند به عنوان منبسط نشده رها کنید. اگر x به هر گره ای در S متصل است، آن را به عنوان منبسط شده علامت گذاری کنید. در غیر این صورت، x را از P حذف کنید. گسترش P گره f، g، a، b در شبکه دوگانه در شکل نشان داده شده است.شکل 7 . با گسترش P، S شامل گره های داخلی خود به عنوان (k، l، m، n) است.
(7) بازگشت محلی: مرحله 5-6 را تکرار کنید تا تمام گره ها در هر دو P و S گسترش یابند.
(8) جمع آوری نتایج: اکنون یک اتصال پیچیده j به تازگی شناسایی شده است که P شامل جاده های اولیه مرزی و S شامل جاده های فرعی داخلی آن است. گره ها را در S به عنوان پردازش شده در SG علامت گذاری کنید، j را در J قرار دهید و sd را پاک کنید. شکل 8 نمونه ای از یک اتصال پیچیده با مجموعه گره های آن را نشان می دهد.
(9) بازگشت جهانی: مرحله 2-8 را برای یافتن اتصالات پیچیده تر در شبکه جاده تکرار کنید.
در مورد الگوریتم، توضیحی ممکن است مفید باشد. شایان ذکر است که مرحله 4 از گره بذری یک اتصال پیچیده به سمت بیرون منبسط می شود، در حالی که مرحله 6 ابتدا از گره های مرزی خود در جاده اصلی به سمت داخل گسترش می یابد و سپس به سمت خارج به گره های مرزی دیگر منبسط می شود. علاوه بر این، توجه داشته باشید که پردازش ساده در مرحله 5 باعث می شود که الگوریتم برای نمایش های دو خطی و چند خطی جاده ها علاوه بر یک خطی نیز قابل اجرا باشد. علاوه بر این، نتیجه بهدستآمده در مرحله 8 مبتنی بر سکته مغزی است و به راحتی میتوان آن را به یک نمایش مبتنی بر بخش تبدیل کرد که مرز و داخل یک اتصال پیچیده را از نظر بخش جاده و گره قطعه مشخص میکند. همانطور که مشاهده می شود، فرآیند کلی اساساً یک پیمایش از شبکه دوگانه است و بنابراین بسیار کارآمد است.
4. آزمون های تجربی و تجزیه و تحلیل نتایج
یک شبکه جاده چالش برانگیز دنیای واقعی برای آزمایش روش پیشنهادی استفاده شد. مجموعه داده آزمایشی منطقه ای به ابعاد 6 کیلومتر در 4 کیلومتر از شهر سن دیگو، کالیفرنیا، ایالات متحده را پوشش می دهد که در شکل 3 نشان داده شده است.. همانطور که مشاهده میشود، جادهها بهعنوان بخشهایی در مجموعه داده نشان داده میشوند که با انتهای آنها، نقاط خاکستری روشن روی نقشه نشان داده شده است. مجموعه داده از نمایش دو خطی برای راهروهای دوگانه استفاده کرد. این شامل نوزده اتصال پیچیده بود که برای مرجع آسان از یک تا نوزده برچسب گذاری شده بودند. گسترههای ناهموار اتصالات پیچیده با بیضیهای نقطهدار سیاه روی نقشه دایرهای میشوند. همانطور که نشان داده شده است، اتصالات پیچیده در اندازه و پیچیدگی بسیار متفاوت است و در هزاران جاده تعبیه شده است. بنابراین، اگر روش پیشنهادی بتواند به طور یکپارچه اتصالات پیچیده تعبیه شده در اطراف را شناسایی کند، و همچنین اگر بتواند با نمایش های تک خطی و دو خطی جاده ها مقابله کند، مجموعه داده چالش برانگیز و مناسب برای آزمایش در نظر گرفته می شود.
دادهها با ESRI ArcGIS Desktop 10.2.2 پیش پردازش شدند. مونتاژ سکته مغزی، جفت شدن همتا، و اشتقاق نوع اولیه یا ثانویه جادهها بر اساس ویژگیهای جاده، عمدتاً نام جادهها و درجههای ارتفاع است، که مشخصهای است که نشان میدهد آیا دو بخش جاده متقاطع صفحه دوبعدی در پایگاه داده به هم متصل میشوند یا خیر. با همدیگر. به لطف کیفیت دادههای ویژگی جاده، همه پیشپردازشهای مبتنی بر نرمافزار از نظر درصد استنتاج صحیح از دقت بالایی برخوردار بودند، اما خطاهایی وجود داشت. بررسی دستی و تصحیح خطا پس از هر مرحله اصلی پیش پردازش مبتنی بر نرم افزار برای اطمینان از ورودی تمیز به مرحله بعدی انجام شد.
نتایج هر مرحله اصلی پیش پردازش روی نقشه در شکل 9 نشان داده شده است. حدود 1000 ضربه از نزدیک به 3000 بخش در داده های آزمایش به دست آمد. هر یک از سکتهها بهطور منحصربهفردی روی نقشه رنگبندی میشد تا از محیط اطراف قابل تشخیص باشد، اگرچه خطوط مجاور به دلیل استفاده از یک طرح رنگآمیزی تصادفی ممکن است در رنگهای نزدیک باشند. خطوط دوتایی جفت شده با پس زمینه خاکستری روشن آنها روی نقشه نشان داده شدند. جاده های فرعی با پس زمینه زرد آنها روی نقشه نشان داده شده است.
در نهایت، شبکه دوگانه نمایش مبتنی بر سکته مغزی مجموعه داده تولید و برای شناسایی استفاده شد. ما اتصال پیچیده شماره 9 را همانطور که در شکل 10 نشان داده شده است به عنوان نمونه ای برای نشان دادن فرآیندهای تبدیل و شناسایی در نظر می گیریم. اگرچه ساختار داخلی شماره 9 خیلی پیچیده نیست، تنظیمات اطراف آن پیچیده تر از سایر موارد در منطقه آزمایش است. در کنار شماره 3 و 10 است و پنج راه از راه های اولیه یعنی (الف، ب، ج، د، ه) را به هم متصل می کند که الف و ب دوتایی و سه راه دیگر تک خطی هستند.
برای تظاهرات ساده، ما تقاطع پیچیده شماره 9 و اطراف آن را بریده ایم تا تمرکز کنیم. شبکه جاده ای حاصل N در شکل 10 نشان داده شده است ، جایی که جاده های مورد توجه برای مرجع برچسب گذاری شده اند. شبکه دوگانه آن در شکل 11 نشان داده شده است . همانطور که از شکل 10 می توان تفسیر کرد ، جاده های a-n اولیه و o-v فرعی هستند. علاوه بر این، a و b دوگانه هستند. بنابراین، o–v خاکستری شد و a و b توسط یک بیضی نقطهدار در شکل 11 گروهبندی شدند . بیضی چین دار اطلاعاتی را نشان نمی دهد که تا کنون شناخته شده است و برای کمک به تجسم ترکیب پیوند پیچیده شماره 9، که قرار است شناسایی شود، ترسیم شده است.
با شبکه دوگانه DN، اتصال پیچیده شماره 9 را می توان با الگوریتم پیشنهادی شناسایی کرد . جدول 1 مراحل فرآیند شناسایی را فهرست می کند که در آن حالات هر مرحله آورده شده است.
نتیجه شناسایی در شبکه آزمایشی بر روی نقشه در شکل 12 نشان داده شده است . برای یک تقاطع پیچیده شناسایی شده، جادههای فرعی آن به همان رنگ روشن هستند در حالی که جادههای اصلی شرکتکننده سیاه هستند زیرا یک جاده اصلی میتواند در بیش از یک تقاطع پیچیده شرکت کند. بقیه جاده ها که جزء اتصالات پیچیده نیستند به رنگ خاکستری روشن هستند.
از نتیجه آزمایش، برخی از ویژگی های الگوریتم را می توان مشاهده کرد. ابتدا، الگوریتم تمام نوزده اتصال پیچیده را با یکپارچگی مربوطه شناسایی کرد. به عبارت دیگر، هیچ اتصال پیچیده ای که باید شناسایی شود، از قلم نیفتاد. هیچ بخش غیرپیچیده ای از شبکه راه ها به اشتباه در نتیجه شناسایی گنجانده نشد. هیچ جاده جزئی از هر تقاطع از دست رفت. و هیچ جاده غیر جزئی به اشتباه در هیچ پیوندی گنجانده نشده است. نتایج شناسایی انتگرال از ماهیت قطعی الگوریتم است که بر اساس مرز توپولوژیکی مشخص پیوند پیچیده است. با این اوصاف، ادعا نمی شود که الگوریتم تحمل خطا دارد، بلکه زمانی که ورودی تمیز است، یکپارچگی را حفظ می کند. تأثیر خطاها در داده های ورودی در این مقاله مورد بحث قرار خواهد گرفتبخش 5 .
ثانیاً، الگوریتم مطابق با پیش بینی قابل تطبیق بود. این برای اتصالات پیچیده با ساختار ساده مانند شماره 12-19 و موارد پیچیده مانند شماره 1-11 کار می کند. برای کوچکها مثل شماره 12-19، متوسطها مثل شماره 1، 2، 4، 5، 8، 9، 10، و 11 و بزرگها مانند شماره 3، 6 و 7 کار میکرد. برای خطوط تک خطی مانند شماره 12-19، دو خط مانند شماره 1، 3 و 7، و ترکیبی مانند شماره 2، 4، 5، 6، 8، 9، 10 و 11 کار کرد. .
ثالثاً، الگوریتم تحت تأثیر پیچیدگی هندسی اتصالات قرار نگرفت زیرا بر اساس رابطه توپولوژیکی بین جاده ها است. برای شماره 4 و 11 که به هم متصل نیستند اما به جای دو اتصال بسیار شبیه یک اتصال پیچیده به نظر می رسند، الگوریتم آنها را ترکیب نکرد. برای شماره 5 و 6، که گستره های هندسی تقریباً همپوشانی دارند، الگوریتم آنها را با هم مخلوط نکرد. برای شماره 6، چهار جاده فرعی را که کاملاً از هم دور هستند، اما به طور یکپارچه چهار جاده اصلی (یا شش مسیر اصلی جاده) را به هم متصل میکنند، به درستی جمعآوری کرده است، که از میان آنها دو جاده دوتایی و دو جاده دیگر تک خطی هستند.
مقایسه بین این روش و روش مرسوم، که اتصالات پیچیده را به عنوان مناطق متراکم رئوس تعریف می کند، پیشنهاد شده توسط Mackaness و Mackechnie در سال 1999 در این مطالعه انجام شده است. شکل 13 نتیجه شناسایی پیوندهای پیچیده تولید شده از روش خوشه بندی سلسله مراتبی [ 27 ] را نشان می دهد که برای تشخیص مناطق متراکم رئوس در این مقایسه استفاده شد. با آزمایش دقیق آستانههای درگیر در رویکرد خوشهبندی، نهایتاً Distance را که به معنای حداکثر فاصله بین نقاط یک خوشه است، 130 متر و کمترین تعداد نقاط در یک خوشه را 4 تنظیم میکنیم.
از طریق مقایسه با اتصالات پیچیده مشخص شده در شکل 12 می توان مشاهده کرد که اکثر خوشه ها خارج از اهداف هستند . علاوه بر مناطق شناسایی شده خطا، اتصالات پیچیده با چندین نقص شناسایی شدند. اتصالات پیچیده از دست رفته مانند شماره 8 و 13، اتصالات بیش از حد مانند شماره 4، 12 و 14-19، سایر اتصالات با درجه های مختلف عدم دقت، از جمله تقاطع های از دست رفته، بیش از حد یا هر دو، مانند شماره 1، 2، 3 ، 5، 6، 7، 9، 10 و 11. جزئیات بیشتر در مطالعات قبلی [ 25 ، 26 ، 27 ] مورد بحث قرار گرفت.
5. تأثیر خطاها در داده های ورودی
همانطور که از آزمایش بالا مشاهده میشود، برای غنیسازی معنایی دادههای خام و تبدیل نمایش دادهها قبل از شناسایی، که شامل مونتاژ ضربه، جفتسازی همتا، طبقهبندی جاده و تولید شبکه دوگانه است، به پیش پردازش نیاز است. همانطور که می دانیم، این امر خاص نیست، بلکه در تعمیم نقشه رایج است، زیرا داده های مکانی در شکل معمولی خود معمولاً برای تعمیم مستقیم مناسب نیستند و غنی سازی داده ها و تبدیل نمایش به طور منظم مورد نیاز است [ 2 ].
در حالی که الگوریتم پیشنهادی یکپارچگی را حفظ می کند، ورودی کثیف می تواند بر شناسایی تأثیر بگذارد و حتی آن را خراب کند. برای اینکه تصوری از میزان تأثیرگذاری آن داشته باشیم، با اجازه دادن به فرآیند شناسایی بر روی نتیجه پیش پردازش اصلاح نشده، آزمایشی انجام دادیم. نتیجه پیش پردازش اصلاح نشده و نتیجه شناسایی مربوطه به ترتیب در شکل 14 و شکل 15 نشان داده شده است. در شکل 15، 19 برچسب از اتصالات پیچیده که باید شناسایی شوند در سه سطح خاکستری هستند. رنگ سفید مخفف شناسایی دقیق، خاکستری روشن برای درجات مختلف عدم دقت و خاکستری تیره به معنی اشتباه است. همانطور که مشاهده می شود، ده نفر دقیقاً شناسایی شده اند و هشت مورد به طور غیر دقیق و یک مورد از قلم افتاده است. علاوه بر این، چهار مصنوع به اشتباه شناسایی شدند که با اعداد قرمز رنگ بر روی نقشه مشخص شده بودند. با مقایسه شکل 14 با شکل 9 و شکل 15 با شکل 12، دشوار نیست که بفهمیم همه شناسایی های نادرست به دلیل مونتاژ ناقص سکته مغزی بوده است. علاوه بر این، تمام اتصالات از دست رفته و مجموعه مصنوعات به دلیل طبقه بندی اشتباه جاده ها بود، اگرچه برخی از اشتباهات طبقه بندی مربوط به اشتباهات در مونتاژ سکته مغزی بود. خطاهای جفتسازی دو خطی نیز وجود داشت، اما در نتیجه این آزمایش شناسایی، خود را نشان ندادند.
تأثیری که در بالا نشان داده شد نباید تعجب آور باشد. بدتر از آن، هیچ الگوریتم بدون خطا شناخته شده ای برای سه عملیات پیش پردازش پرکاربرد غنی سازی داده ها، یعنی مونتاژ ضربه، جفت شدن همتا و طبقه بندی جاده وجود ندارد. این بدان معنی است که نتیجه پیش پردازش صرفاً مبتنی بر نرم افزار معمولاً حاوی خطاهایی است که اگر تصحیح نشوند به طور قابل توجهی بر شناسایی تأثیر می گذارد. بنابراین بررسی دستی و اصلاح پس از هر عملیات ضروری است. علاوه بر این، آزمایش فوق نشان می دهد که هنوز هم همینطور است، حتی اگر هر مرحله خروجی با دقت بالایی تولید کند، زیرا خطاها از طریق جریان پیش پردازش منتشر و جمع می شوند. این همچنین به این معنی است که ابزارهای کارآمد کاربر پسند برای بررسی و تصحیح تعاملی در محیط تولید ارزشمند هستند.
6. بحث
در این مقاله، وابستگی مقیاس شناسایی پیوندهای پیچیده را به عنوان دو جنبه در نظر می گیریم: اولی ناهمگونی فضایی در میان پیوندهای پیچیده، و دوم، نمایش های مختلف یک اتصال پیچیده در مقیاس های نسبی آن (نمایش های چندگانه). برای مقابله با وابستگی به مقیاس، این مقاله یک رویکرد جدید برای شناسایی اتصالات پیچیده بر اساس مرزهای توپولوژیکی آنها پیشنهاد می کند. مهم نیست که یک اتصال پیچیده چقدر پیچیده یا ساده باشد، شامل جاده های اولیه مرزی و جاده های فرعی داخلی است. بنابراین، مرز توپولوژیکی یک اتصال پیچیده ذاتاً مستقل از مقیاس است که میتواند از تأثیر ناهمگنی فضایی و نمایشهای متعدد آزاد باشد.
از مقایسه، می توان دریافت که مرز توپولوژیکی یک اتصال پیچیده یک ویژگی عملی برای شناسایی یکپارچه اتصالات پیچیده از اجتناب از مشکلات بیش از حد برازش است. بنابراین، به نظر می رسد که نشان دادن تقاطع پیچیده به عنوان ساختار جاده اولیه-ثانویه تمیزتر و واضح تر از خوشه نقطه محور (یا مبتنی بر تقاطع) در یک شبکه جاده ای است. این رویکرد همچنین می تواند به طور مناسب در فرآیند تعمیم شبکه جاده ها بر اساس نمایش سکته مغزی ادغام شود. با سادهسازی اتصالات پیچیده بدون قطع اتصال بین جادههای نسبی، تعمیم شبکه راهها را میتوان صرفاً با موارد اولیه بررسی کرد. شکل 16مثالی برای توضیح این فرآیند با تبدیل نمایش دو خطی به تک خطی برای شبکه جاده در شکل 3 ج نشان می دهد. خطوط جفتی a و b یک راهرو دوگانه با جاده اصلی c ترکیب می شوند. به طور مشابه، f و g جاده F دیگری را تشکیل می دهند. بنابراین، طبقه بندی جاده ها به دسته های اولیه و ثانویه می تواند به عنوان یک عملیات پیش پردازش غنی سازی داده ها برای تعمیم شبکه راه در نظر گرفته شود.
از این رو معیارهای تمایز بین راه های اولیه و فرعی یک ضرورت است. در این مقاله سکتهها بر اساس ویژگیهای جاده جمعآوری و طبقهبندی میشوند. در دانش حوزه طراحی اتصالات [ 29 ، 30 ، 31 ]، اصل طراحی جاده ثانویه (خطوط کمکی، جاده های لغزنده یا رمپ) به شدت مورد توجه قرار می گیرد، مانند تعداد خطوط، محدودیت سرعت و جهت رانندگی. جاده های اولیه و جاده های فرعی در اصول طراحی خود از قبیل ظرفیت جاده، ایمنی، مکان و فضا تفاوت قابل توجهی دارند [ 29 ]. بنابراین، استاندارد طراحی تبادل ممکن است به عنوان معیاری برای طبقهبندی جادههای نوع اولیه یا ثانویه در آینده اعمال شود.
7. نتیجه گیری
این مقاله یک راه حل ساده برای مشکل شناسایی اتصالات پیچیده ارائه کرده است. روش پیشنهادی علاوه بر حفظ یکپارچگی اتصالات پیچیده، عاری از تعیین آستانه مشکلساز است، قادر به مقابله با نمایشهای مختلف جادهها و کارآمد است. همه اینها با هم آن را برای استفاده عملی مطلوب می کند. با مشخص شدن مرز و فضای داخلی، اتصالات پیچیده در یک شبکه جادهای را میتوان بدون قطع اتصال بین جادهها به درستی سادهسازی کرد، در نتیجه اعتبار توپولوژیکی شبکه جادهای سادهشده حفظ میشود. علاوه بر این، چنین وضوح توپولوژیکی می تواند تا حد زیادی ساده سازی هندسی و معنایی اتصالات پیچیده را تسهیل کند [ 23 ، 25 ، 26 ].
این مطالعه اثربخشی رویکرد هوشمند به تعمیم دادههای مکانی را که با ترکیبی مناسب از غنیسازی دادهها، تبدیل نمایش و تشخیص الگو مشخص میشود، تثبیت میکند [ 8 ، 19 ]]. اگرچه این مطالعه عمدتاً به الگوی ترکیبی پیوند پیچیده می پردازد، اما بر مولفه هایی استوار است که به تدریج از نظر معنایی غنی تر و از نظر ساختار پیچیده تر هستند که به نوبه خود سکته های جاده ها، جاده های طبقه بندی شده و همتایان همراه یک جاده هستند. بنابراین، ما فکر میکنیم که هر سه عملیات غنیسازی دادهها (یعنی مونتاژ ضربه، طبقهبندی جاده و جفتسازی همتایان) بسیار مهم هستند و میخواهیم بهتر مورد توجه قرار گیرند تا دقت الگوریتمها بهبود یابد، تخمین عدم قطعیت قابل اعتماد برای مکانیابی موثر خطاهای احتمالی انجام شود. در نتایج، و ابزارهای تعاملی برای بررسی کارآمد نتایج و تصحیح خطاها فراهم می کند.
در این رابطه نیز، دو مفهوم جدید اتخاذ شده در این مطالعه میتوانند کاربرد وسیعتری نسبت به تعریف ترکیب یک اتصال پیچیده داشته باشند. اولاً، ما معتقدیم که طبقهبندی راهها به دو نوع اصلی، اولیه و ثانویه، نه تنها مناسب است، بلکه در پردازش و تحلیل شبکههای جادهای نیز مفید است. همانطور که در این مطالعه نشان داده شده است، مرز توپولوژیک اتصالات پیچیده بلافاصله پس از طبقه بندی جاده ها به این ترتیب مشخص می شود. در واقع، ما آن را برای جفتسازی بهتر خطوط دوگانه یک جاده دوگانه و تحلیل الگوهای دیگر در شبکههای جادهای در مطالعات مرتبط ما که در حال انجام است، بسیار مفید یافتیم. ثانیاً، مفهوم مرز توپولوژیکی ممکن است برای سایر الگوهای ساختاری در شبکههای جادهای علاوه بر اتصالات پیچیده نیز اعمال شود. برای مثال، بلوک های خیابان ممکن است از نظر توپولوژیکی بهتر از هندسی ترسیم شوند. ما در مطالعات آتی خود چنین امکانی را بررسی خواهیم کرد.
منابع
- براسل، KE; Weibel, R. یک بررسی و چارچوب مفهومی تعمیم خودکار نقشه. بین المللی جی. جئوگر. Inf. سیستم 1988 ، 2 ، 229-244. [ Google Scholar ] [ CrossRef ]
- Weibel, R. تعمیم نقشه در زمینه سیستم های دیجیتال. کارتوگر. Geogr. Inf. سیستم 1995 ، 22 ، 259-263. [ Google Scholar ] [ CrossRef ]
- جونز، CB; مارک ور، جی. تعمیم نقشه در عصر وب. بین المللی جی. جئوگر. Inf. علمی 2005 ، 19 ، 859-870. [ Google Scholar ] [ CrossRef ]
- باتنفیلد، BP; مک مستر، RB تعمیم نقشه: ایجاد قوانین برای بازنمایی دانش . Longman Scientific and Technical: هارلو، انگلستان، 1991; شابک 978-047-021-803-7. [ Google Scholar ]
- لی، زی. تعمیم نقشه دیجیتال در عصر روشنگری: مروری بر چهل سال اول. کارتوگر. J. 2007 , 44 , 80-93. [ Google Scholar ] [ CrossRef ]
- Mackaness، WA; ریش، KM استفاده از نظریه گراف برای پشتیبانی از تعمیم نقشه. کارتوگر. Geogr. Inf. سیستم 1993 ، 20 ، 210-221. [ Google Scholar ] [ CrossRef ]
- جونز، CB; باندی، جی ال. تعمیم ور، MJ Map با ساختار داده مثلثی. کارتوگر. Geogr. Inf. سیستم 1995 ، 22 ، 317-331. [ Google Scholar ] [ CrossRef ]
- نیون، ام. ویبل، آر. Burghardt، D. غنی سازی داده ها برای تعمیم تطبیقی. در مجموعه مقالات هشتمین کارگاه ICA در مورد تعمیم و بازنمایی چندگانه، لستر، بریتانیا، 20 تا 21 اوت 2004. [ Google Scholar ]
- بارو، ام. رگنولد، ن. دوشن، سی. هایر، ک. بایج، سی. دمازو، ی. هاردی، پی. Mackaness، W. رواس، ع. Weibel, R. ادغام تکنیک های چند عاملی، شی گرا و الگوریتمی برای بهبود تعمیم خودکار نقشه. در مجموعه مقالات بیستمین کنفرانس بین المللی کارتوگرافی، پکن، چین، 6 تا 10 اوت 2001. صص 2110–2116. [ Google Scholar ]
- لی، جی. جانگ، اچ. یانگ، جی. Yu, K. طبقه بندی یادگیری ماشینی ساختمان ها برای تعمیم نقشه. Isprs Int. J. Geo-Inf. 2017 ، 6 ، 309. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
- فنگ، ی. تیمن، اف. سستر، ام. یادگیری تعمیم ساختمان نقشه برداری با شبکه های عصبی کانولوشنال عمیق. Isprs Int. J. Geo Inf. 2019 ، 8 ، 258. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
- استوتر، جی. پست، م. ون آلتنا، وی. نیجهویس، آر. Bruns، B. تعمیم کاملاً خودکار نقشه 1: 50k از داده های 1:10k. کارتوگر. Geogr. Inf. علمی 2014 ، 41 ، 1-13. [ Google Scholar ] [ CrossRef ]
- Šuba, R. طراحی و توسعه یک سیستم برای نقشه های در مقیاس مختلف. آرشیت. محیط ساخته شده 2017 ، 13–14. [ Google Scholar ] [ CrossRef ]
- ادواردز، ای جی; Mackaness، WA تعمیم هوشمند شبکه های جاده ای شهری. در مجموعه مقالات کنفرانس GIS Research UK 2000, York, UK, 5-7 آوریل 2000; صص 81-85. [ Google Scholar ]
- تویا، جی. لخت، من. Duchêne, C. CartAGEn: یک بستر تحقیقاتی منبع باز برای تعمیم نقشه. در مجموعه مقالات بیست و نهمین انجمن بین المللی کارتوگرافی (ICC 2019)، توکیو، ژاپن، 15 تا 20 ژوئیه 2019. [ Google Scholar ] [ CrossRef ]
- جیانگ، بی. کلارامونت، سی. یک رویکرد ساختاری به تعمیم مدل یک شبکه خیابان شهری. GeoInformatica 2004 ، 8 ، 157-171. [ Google Scholar ] [ CrossRef ]
- بنز، SA; Weibel, R. انتخاب شبکه جاده برای مقیاس های متوسط با استفاده از الگوریتم ترکیبی مشبک-مش گسترده. کارتوگر. Geogr. Inf. علمی 2014 ، 41 ، 323-339. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
- یو، دبلیو. ژانگ، ی. آی، تی. گوان، کیو. چن، ز. لی، اچ. تعمیم شبکه جاده با در نظر گرفتن الگوهای جریان ترافیک. بین المللی جی. جئوگر. Inf. علمی 2020 ، 34 ، 119-149. [ Google Scholar ] [ CrossRef ]
- Touya, G. فرآیند انتخاب شبکه جاده ای بر اساس غنی سازی داده ها و تشخیص ساختار. ترانس. Gis 2010 , 14 , 595-614. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
- یانگ، بی. لوان، ایکس. لی، کیو. روش تطبیقی برای شناسایی الگوهای فضایی در شبکه های جاده ای. محاسبه کنید. محیط زیست شهری. سیستم 2010 ، 34 ، 40-48. [ Google Scholar ] [ CrossRef ]
- شائو، ال. میتلشتادت، اس. گلدبلات، آر. عمر، آی. باک، پ. Schreck، T. تجزیه و تحلیل و مقایسه الگوهای مبتنی بر ویژگی در شبکه های خیابان شهری. در مجموعه مقالات یازدهمین کنفرانس بین المللی مشترک بینایی کامپیوتری، تصویربرداری و گرافیک کامپیوتری، رم، ایتالیا، 27-29 فوریه 2016. صص 287-309. [ Google Scholar ] [ CrossRef ]
- بالبوآ، JLG؛ لوپز، طبقه بندی خطوط جاده تعمیم گرا FJA با استفاده از یک شبکه عصبی مصنوعی. GeoInformatica 2008 ، 12 ، 289-312. [ Google Scholar ] [ CrossRef ]
- ساوینو، اس. شایعه، م. زانون، م. Lissandron، I. غنی سازی داده ها برای تعمیم جاده از طریق تجزیه و تحلیل مورفولوژی در پروژه CARGEN. در مجموعه مقالات سیزدهمین کارگاه ICA در مورد تعمیم و بازنمایی چندگانه، زوریخ، سوئیس، 12 تا 13 سپتامبر 2010. [ Google Scholar ]
- ونزل، اس. بولاتوف، دی. تشکیل زنجیره همزمان و تعمیم شبکه های جاده ای. فتوگرام مهندس Remote Sens. 2019 ، 85 ، 19–28. [ Google Scholar ] [ CrossRef ]
- Mackaness، WA; Mackechnie، GA خودکارسازی تشخیص و ساده سازی اتصالات در شبکه های جاده ای. GeoInformatica 1999 ، 3 ، 185-200. [ Google Scholar ] [ CrossRef ]
- ساوینو، اس. شایعه، م. Lissandron، I. تعمیم تقاطع جاده در پایگاه های جغرافیایی مقیاس بزرگ . CRC Press/Balkema: لندن، انگلستان، 2009; شابک 978-042-920-671-9. [ Google Scholar ]
- ژو، Q. Li، Z. تجزیه و تحلیل تجربی انواع مختلف تقاطع جاده برای تشخیص تبادل. ترانس. GIS 2015 ، 19 ، 19-41. [ Google Scholar ] [ CrossRef ]
- Grosso, E. Etude des carrefours d’un réseau routier–Première approche: Modélisation et implémentation d’outils de detection des carrefours (Oxygène صفحه ای). پایان نامه کارشناسی ارشد، دانشگاه پاریس 1 پانتئون-سوربون، پاریس، فرانسه، فوریه 2004. [ Google Scholar ]
- لام، آر. پساریانوس، بی. چویری، EM; Mailaender، T. Interchange Planning and Design-An International Perspective. ترانسپ Res. ضبط 1993 ، 1385 ، 69-83. [ Google Scholar ]
- Lunenfeld، H. عوامل انسانی مرتبط با ویژگی های طراحی تبادل. ترانسپ Res. ضبط 1993 ، 1385 ، 84-89. [ Google Scholar ]
- Chlewicki، G. طرح های جدید مبادله و تقاطع: تقاطع فازهای تقسیم شده همزمان و تبادل الماس واگرا. در مجموعه مقالات دومین سمپوزیوم خیابان شهری، آناهیم، کالیفرنیا، ایالات متحده آمریکا، 28 تا 30 ژوئیه 2003. [ Google Scholar ]
- تامسون، RC مفهوم “سکته مغزی” در تعمیم و تحلیل شبکه جغرافیایی. در حال پیشرفت در مدیریت داده های مکانی ; Riedl, A., Kainz, W., Elmes, GA, Eds. Springer: برلین/هایدلبرگ، آلمان، 2006; صص 681-697. [ Google Scholar ] [ CrossRef ]
- تامسون، آرسی ریچاردسون، دی. اصل “ادامه خوب” سازمان ادراکی برای تعمیم شبکه های جاده ای اعمال می شود. در مجموعه مقالات نوزدهمین کنفرانس بین المللی کارتوگرافی، اتاوا، ON، کانادا، 14 تا 21 اوت 1999. [ Google Scholar ]
- لامر، اس. گلسن، بی. Helbing، D. قوانین مقیاس بندی در ساختار فضایی شبکه های جاده ای شهری. فیزیک یک آمار مکانیک. برنامه آن است. 2006 ، 363 ، 89-95. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
- نیومن، شبکه های MEJ: مقدمه ; انتشارات دانشگاه آکسفورد: نیویورک، نیویورک، ایالات متحده آمریکا، 2010; ص 35، 121-124. شابک 978-019-920-665-0. [ Google Scholar ]
- کورکوران، پ. Mooney, P. مشخص کردن تکامل متریک و توپولوژیکی بازنمودهای شبکه OpenStreetMap. یورو فیزیک J. Spec. بالا. 2013 ، 215 ، 109-122. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
شکل 1. یک شبکه جاده ای شماتیک T برای نشان دادن راه های اولیه، جاده های فرعی و اتصالات پیچیده.
شکل 2. شبکه دوگانه شبکه جاده ای شماتیک T و مرز توپولوژیکی اتصالات پیچیده که در شکل 1 نشان داده شده است.
شکل 3. ( الف – ج ) فرآیند تعمیم اتصالات پیچیده با دور ریختن جاده های فرعی داخلی.
شکل 4. ( الف ، ب ) مقداردهی اولیه شبکه شماتیک جاده T.
شکل 5. گره بذر جاده فرعی k ( a ) و S آن در حال گسترش ( b ).
شکل 6. ( الف ، ب ) پردازش چند خطی گره جاده اولیه f و a.
شکل 7. گسترش P گره جاده اولیه f ( a )، g ( b )، a ( c )، b ( d ).
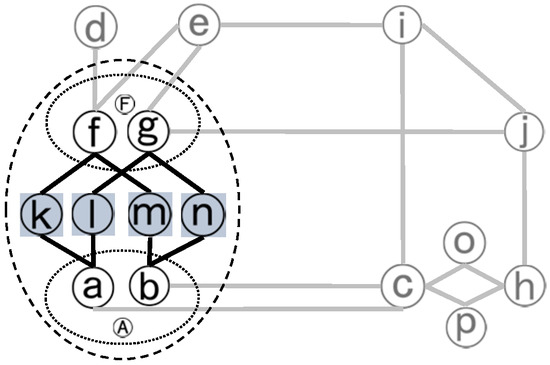
شکل 8. یک اتصال پیچیده در شبکه دوگانه برای نشان دادن مجموعه گره های آن. P شامل گره های مرز اتصال پیچیده به عنوان (a, b, f, g) و S شامل گره های داخلی جاده فرعی به صورت (k, l, m, n) است.
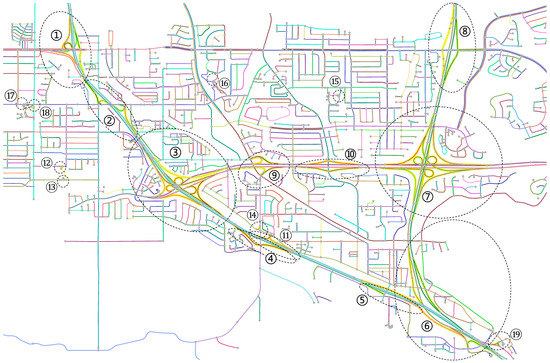
شکل 9. مجموعه داده آزمایشی و نتایج پیش پردازش آن پس از تصحیح دستی. نقاط انتهایی بخشهای جاده در دادههای خام با نقاط خاکستری روشن نشان داده میشوند. نوزده پیوند پیچیده ای که باید شناسایی شوند از یک تا نوزده برچسب گذاری شده اند. گسترههای ناهموار اتصالات پیچیده با بیضیهای نقطهدار سیاه دایره شدهاند. سکته های مونتاژ شده با استفاده از یک طرح رنگ آمیزی تصادفی به طور منحصر به فرد رنگ می شوند. خطوط دوتایی جفت شده با پس زمینه خاکستری روشن آنها مشخص می شوند. جاده های فرعی با پس زمینه زرد آنها مشخص می شود.
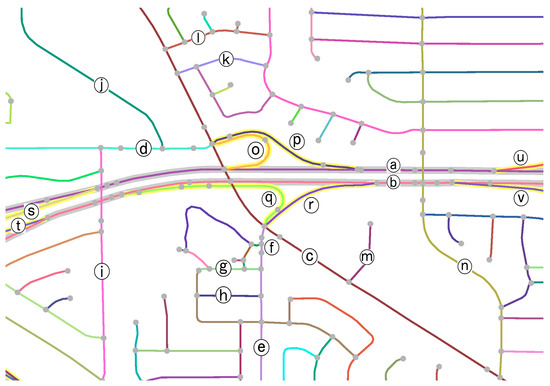
شکل 10. شبکه راه N در اطراف تقاطع پیچیده شماره 9 که از داده های آزمایش بریده شده است.
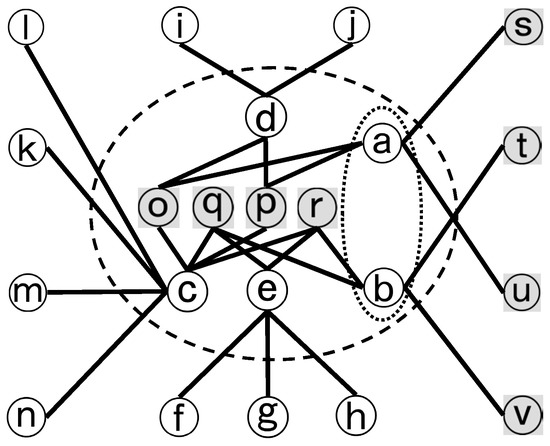
شکل 11. شبکه دوگانه D N شبکه راه N.
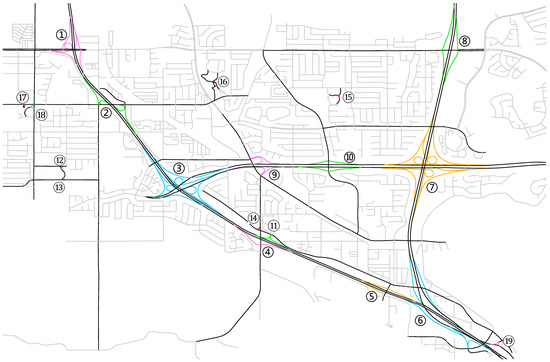
شکل 12. نتیجه اعمال روش پیشنهادی به مجموعه داده آزمایشی. برای یک تقاطع پیچیده شناسایی شده، جادههای فرعی آن به همان رنگ روشن هستند در حالی که جادههای اصلی شرکتکننده سیاه هستند زیرا یک جاده اصلی میتواند در بیش از یک تقاطع پیچیده شرکت کند. بقیه جاده ها که جزء اتصالات پیچیده نیستند به رنگ خاکستری روشن هستند.
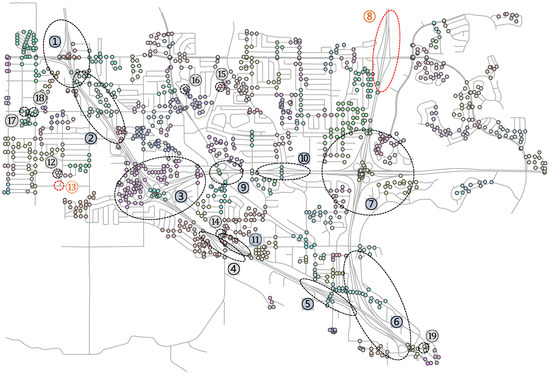
شکل 13. تشخیص اتصالات پیچیده با استفاده از رویکرد ارائه شده توسط Mackaness و Mackechnie (1999). 19 برچسب از اتصالات پیچیده که باید شناسایی شوند در دو سطح خاکستری هستند. خاکستری تیره برای درجات مختلف عدم دقت و خاکستری روشن برای بیش از حد مناسب. برای کسانی که اتصالات پیچیده شناسایی شده را کاملاً از دست داده اند، از بیضی های خط چین قرمز برای دایره کردن دامنه نگرانی استفاده می شود.
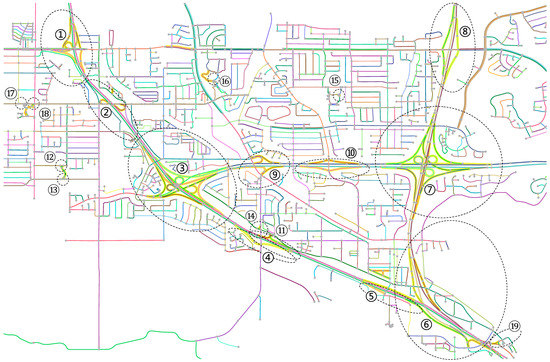
شکل 14. مجموعه داده آزمایشی و نتیجه پیش پردازش آن بدون تصحیح دستی. نقشه از همان نمادسازی شکل 9 به جز رنگ های ضربه ای تصادفی استفاده می کرد. نقاط پایانی بخشهای جاده دادههای خام با نقاط خاکستری روشن نشان داده میشوند. نوزده پیوند پیچیده ای که باید شناسایی شوند از یک تا نوزده برچسب گذاری شده اند. گستره ناهموار اتصالات پیچیده با بیضی های چین دار دایره شده است. سکته های مونتاژ شده با استفاده از یک طرح رنگ آمیزی تصادفی به طور منحصر به فرد رنگ می شوند. خطوط دوتایی جفت شده با پس زمینه خاکستری روشن آنها مشخص می شوند. جاده های فرعی با زمینه زرد آنها نشان داده شده است.
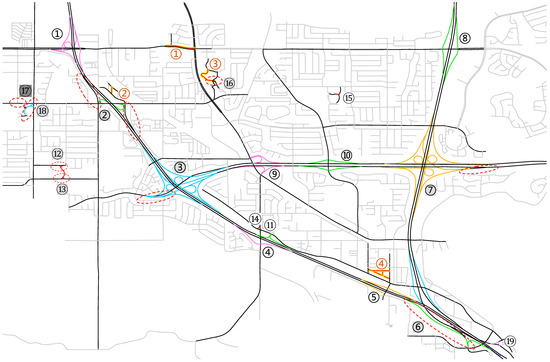
شکل 15. نتیجه شناسایی به دست آمده از ورودی با خطا. 19 برچسب از اتصالات پیچیده که باید شناسایی شوند در سه سطح خاکستری هستند. رنگ سفید مخفف شناسایی دقیق، خاکستری روشن برای درجات مختلف عدم دقت و خاکستری تیره به معنی اشتباه است. برای کسانی که دقیقاً شناسایی نشدهاند یا از قلم افتادهاند، از بیضیهای خطرنگ قرمز برای دور کردن میزان نگرانی استفاده میشود. چهار اتصال پیچیده مصنوع که به اشتباه شناسایی شدهاند، با اعداد قرمز مشخص و مشخص شدهاند.
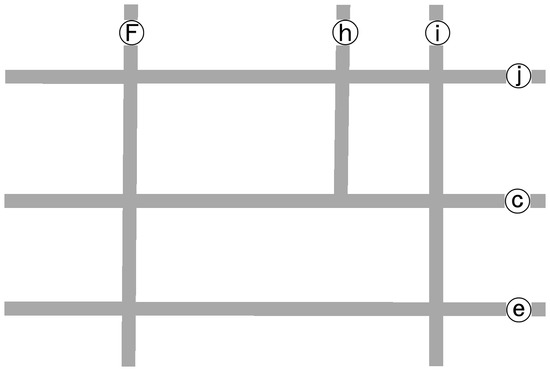
شکل 16. یک نتیجه از تعمیم شبکه جاده با ترکیب جاده های اولیه جفت شده.





بدون دیدگاه