شناسایی خطای تطبیق نقشه در غیاب حقیقت زمین

تطبیق نقشه داده‌های مسیر، کاربردهای گسترده‌ای در ردیابی خودرو، تحلیل جریان ترافیک، برنامه‌ریزی مسیر و سیستم‌های حمل و نقل هوشمند دارد. الگوریتم‌های تطبیق نقشه مجموعه‌ای از نقاط مسیر مشاهده شده توسط یک سیستم ناوبری ماهواره‌ای را به محتمل‌ترین بخش‌های مسیر نقشه می‌چسبانند. با این حال، به دلیل خطاهای اجتناب ناپذیر در نقاط مسیر ثبت شده و داده های نقشه ناقص، الگوریتم های تطبیق نقشه ممکن است نقاط را با بخش های نادرست مطابقت دهند که منجر به خطاهای تطبیق نقشه شود. شناسایی این خطاهای تطبیق نقشه در غیاب حقیقت زمینی تنها با بازرسی بصری و استدلال قابل دستیابی است. بنابراین، شناسایی خطاهای تطبیق نقشه بدون حقیقت زمینی یک کار وقت گیر و پیش پا افتاده است. اگرچه تحقیقات بر بهبود الگوریتم های تطبیق نقشه متمرکز شده است، تا جایی که می دانیم، هیچ تلاشی برای طبقه بندی و شناسایی خودکار خطاهای تطبیق نقشه انجام نشده است. در این کار، ما اولین روش را برای شناسایی خودکار خطاهای تطبیق نقشه در غیاب حقیقت زمین، یعنی تنها با استفاده از نقاط مسیر ثبت شده و مسیر مطابق با نقشه، پیشنهاد می‌کنیم. ما روش خود را بر روی یک مجموعه داده عمومی ارزیابی کرده‌ایم و دقت متوسط 91% را در شناسایی خودکار خطاهای تطبیق نقشه مشاهده کرده‌ایم، بنابراین به تحلیلگران کمک می‌کنیم تا تلاش دستی برای تضمین کیفیت تطبیق نقشه را به میزان قابل توجهی کاهش دهند.

کلید واژه ها:

داده های مسیر ؛ تطبیق نقشه ; شناسایی خطا ؛ طبقه بندی بدون نظارت

1. مقدمه

تطبیق نقشه داده های مسیر برای بسیاری از کاربردهای حمل و نقل هوشمند، مانند ردیابی وسیله نقلیه، تجزیه و تحلیل جریان ترافیک، تشخیص حالت های حمل و نقل و برنامه ریزی مسیر ضروری است [ 1 ، 2 ، 3 ، 4 ، 5 ، 6 ]. داده‌های مسیر شامل نقاط مکان‌یابی است که بر اساس سیستم‌های ماهواره‌ای ناوبری جهانی (GNSS) توسط یک برنامه ردیابی بر روی یک وسیله نقلیه یا هر شی دیگری ثبت شده‌اند، و تطبیق نقشه برای داده‌های مسیر در صورتی که حرکت در امتداد یک شبکه تحرک شناخته شده باشد، اعمال می‌شود [ 7 ] ]. الگوریتم‌های تطبیق نقشه محتمل‌ترین بخش شبکه تحرک را برای هر نقطه GNSS در داده‌های مسیر تعیین می‌کنند [ 5 ،8 ، 9 ].

الگوریتم های تطبیق نقشه موجود، رویکردهای متعددی را برای رسیدگی به خطاهای تطبیق نقشه در نظر می گیرند [ 10 ، 11 ]. با این حال، آنها هنوز هم به دلایل زیادی مستعد خطا هستند، مانند وقوع اجتناب ناپذیر خطاهای سیستماتیک GNSS، از جمله سیگنال های مسدود شده و اثرات چند مسیری (خطای اندازه گیری) [ 4 ، 12 ، 13 ]، مسیرهای GNSS با نرخ نمونه پایین (خطای نمونه گیری) [ 10 ]، محدودیت در کارایی الگوریتم های تطبیق نقشه آنلاین، داده های نقشه ناقص [ 14 ]، خطاهای تطبیق در اتصالات [ 11 ]، و تطبیق با شبکه های تحرک اشتباه [ 8 ، 10 ، 11 ،12 ].

برنامه های کاربردی فوق الذکر به الگوریتم های تطبیق نقشه آنلاین یا آفلاین نیاز دارند [ 6 ]. الگوریتم های تطبیق نقشه آنلاین محتمل ترین بخش شبکه تحرک را به محض ثبت نقطه GNSS تولید می کنند [ 15 ، 16 ]. برعکس، الگوریتم‌های آفلاین از مجموعه‌ای از نقاط GNSS از قبل ثبت‌شده برای شناسایی مسیری که جسم متحرک طی می‌کند در آینده استفاده می‌کنند [ 5 ، 6 ]]. این مقاله به تطبیق نقشه آفلاین می پردازد. در این مورد، شناسایی خطای تطبیق نقشه در حضور داده های مسیر حقیقت زمینی (مثلاً حالت و مسیر سفر) ساده خواهد بود. با این حال، فقدان معمولی داده‌های واقعی، شناسایی و تعیین کمیت خطاهای تطبیق نقشه را دشوارتر می‌کند. در حال حاضر، تطبیق نقشه آفلاین برای بازرسی بصری باز است، که یک فرآیند بصری اعتبار سنجی توسط استدلال انسانی را امکان پذیر می کند. استفاده از این فرآیند برای شناسایی خطاهای تطبیق نقشه زمانی که تعداد زیادی از مسیرها پردازش می شوند، کاری پر زحمت است.

بنابراین، برای این مورد عدم وجود حقیقت زمین، ابتدا یک خطای تطبیق نقشه را تعریف می‌کنیم : وقتی یک بخش منطبق با نقشه، که در یک مسیر مطابق با نقشه گنجانده شده است، یک رفتار سفر غیرواقعی را نشان می‌دهد، آنگاه تطبیق این بخش به عنوان یک خطا. در نتیجه، خطاهای تطبیق نقشه را می‌توان با شمارش تعداد بخش‌های تطبیق نادرست (یا غیرمنطقی) اندازه‌گیری کرد . با در دست داشتن این دو تعریف، سؤال تحقیقاتی زیر را مطرح می‌کنیم: چگونه می‌توانیم به طور خودکار خطاهای تطبیق نقشه را شناسایی و کمیت کنیم، زمانی که حقیقت زمینی در دسترس نیست؟

ما یک تکنیک شناسایی خطای خودکار مقیاس‌پذیر را ارائه می‌کنیم که خطای تطبیق نقشه را با شمارش تعداد بخش‌های منطبق نادرست (یا غیرمنطقی) کمّی می‌کند. شناسایی خودکار خطا بر اساس یک رویکرد یادگیری بدون نظارت مبتنی بر نظریه گراف اجرا می شود، به طوری که نیازی به مداخله انسانی نیست. روش پیشنهادی به عنوان یک مؤلفه در یک ابزار منبع باز مبتنی بر پایتون پیاده‌سازی می‌شود که همچنین به فرد اجازه می‌دهد تا به صورت تعاملی مسیر منطبق بر نقشه مجموعه نقطه مسیر را تجزیه و تحلیل کند ( شکل 1 ). به دلیل فقدان داده‌های حقیقت پایه، تحلیل بصری به فرد اجازه می‌دهد تا این حقیقت پایه را مشخص کند و از این حقیقت پایه برای تحلیل عملکرد تکنیک جدید خود استفاده کند.

ابزار پیاده‌سازی شده در شکل 1 می‌تواند به عنوان یک ابزار کاملا مستقل عمل کند زمانی که هدف صرفه‌جویی در نیروی انسانی باشد. با این حال، یک بازرسی بصری هدایت‌شده برای شناسایی خودکار خطاهای تطبیق نقشه می‌تواند کیفیت فرآیند خودکار را بیشتر بهبود بخشد. سهم عمده این مقاله، با این حال، الگوریتم خودکار برای شناسایی آفلاین خطاها در تطبیق نقشه است. این الگوریتم مقیاس پذیر است زیرا نیازی به دخالت انسان ندارد. فقط برای بررسی کیفیت یا اندازه‌گیری عملکرد، یک جزء تجزیه و تحلیل بصری در دسترس است.

بقیه مقاله به شرح زیر سازماندهی شده است. بخش 2 تکنیک های تطبیق نقشه فعلی را شرح می دهد. بخش 3 نظریه مربوطه را در رابطه با خطاها در تطبیق نقشه توضیح می دهد. بخش 4 روش ما را برای شناسایی نقاط GNSS که به اشتباه نگاشت شده اند ارائه می کند. بخش 5 تکنیک ها و نتایج تجربی را برای اعتبارسنجی روش ما و اندازه گیری عملکرد آن شرح می دهد. نتیجه گیری در بخش 6 ارائه شده است.

2. بررسی ادبیات

دو رویکرد اصلی برای تطبیق نقشه در ادبیات وجود دارد: (1) رویکردهای مبتنی بر هندسه و (2) رویکردهای مبتنی بر آمار.

2.1. تطبیق نقشه مبتنی بر هندسه

رویکردهای مبتنی بر هندسه، تطبیق نقشه را بر اساس ویژگی‌های هندسی خاص (مثلاً نزدیکی) نقاط GNSS و شکل بخش‌های جاده انجام می‌دهند. رویکردهای رایج تطبیق نقشه نقطه به نقطه (تطبیق نقاط GNSS با نزدیکترین گره شبکه جاده ای) [ 17 ]، تطبیق نقشه نقطه به منحنی (تطبیق نزدیکترین نقطه همراه با یک بخش جاده) [ 18 ] انطباق نقشه منحنی به منحنی (تطبیق مجموعه ای از نقاط همراه با یک بخش جاده) [ 19 ]، و تطبیق مبتنی بر فاصله فریشت [ 20 ] (نقاط GNSS ثبت شده بر روی بخش های جاده با نزدیکترین فاصله فرشت مطابقت داده می شود. ) [ 1 ، 21 ، 22 ، 23]. رویکرد مبتنی بر فاصله فرشه نتایج بهتری نسبت به سایر روش‌های تطبیق نقشه هندسی دارد [ 3 ]. با این حال، رویکرد مبتنی بر فاصله Fréchet فرض می‌کند که مسیر کامل قبل از فرآیند تطبیق ثبت می‌شود. از این رو، این رویکرد قادر به ترسیم تطابق در زمان واقعی نیست [ 1 ]. علاوه بر این، تطبیق نقشه مبتنی بر هندسه دارای محدودیت‌هایی در تقاطع‌های جاده‌ای است و اغلب بخش‌هایی را که مطابقت نادرست دارند تولید می‌کند [ 10 ].

2.2. تطبیق نقشه مبتنی بر آمار

در رویکردهای مبتنی بر آمار، دقت تطبیق نقشه با استفاده از مدل‌های آماری مختلف، به عنوان مثال، مدل پنهان مارکوف (HMM) بهبود یافته است [ 5 ، 10 ، 13 ]. هدف HMM تطبیق هر اندازه‌گیری مکان با محتمل‌ترین بخش جاده با یافتن محتمل‌ترین مسیر در شبکه راه است [ 5 ، 13 ]. HMM احتمالات حاکم بر اندازه‌گیری‌های حالت و احتمالات حاکم بر انتقال بین حالت‌ها (بخش‌های جاده) را در هر زمان در نظر می‌گیرد [ 5 ، 13 ]]. HMM احتمال انتشار را با مدل‌سازی نویز اندازه‌گیری و احتمالات انتقال را با مدل‌سازی فاصله بین اندازه‌گیری‌های GNSS و مسیر احتمالی محاسبه می‌کند [ 5 ، 7 ، 9 ، 24 ]. الگوریتم Viterbi برای محاسبه بهترین مسیر از طریق شبکه HMM استفاده می شود [ 5 ، 13 ، 24 ، 25 ]. روش دیگر، استفاده از یک نسخه دو طرفه از الگوریتم دایکسترا منجر به دقت مشابهی می شود [ 9 ]. تطبیق نقشه مبتنی بر HMM نیز در تطبیق نقشه آنلاین استفاده می شود [ 15 ، 16 ، 26]. بهبود در تطبیق نقشه مبتنی بر HMM با استفاده از مدل مارکوف پنهان مبتنی بر بخش در شبکه‌های جاده‌ای متراکم‌تر انجام شده است [ 13 ]. رویکرد دیگر بر روی اتصالات متمرکز است که در آن الگوریتم می تواند بخش جاده اشتباه را ترسیم کند [ 8 ].

یکی دیگر از چالش های اصلی که اغلب به آن پرداخته نمی شود، کشف تطبیق نقشه و تشخیص حالت حمل و نقل است [ 4 ، 12 ]. با توجه به ادبیات فعلی، تشخیص حالت و تطبیق نقشه عمدتاً از دو مرحله تشکیل شده است [ 12 ]: (1) نقاط GNSS بر اساس چندین بخش تک وجهی مرتب می شوند و پس از آن (2) تطبیق نقشه و تشخیص حالت برای هر بخش تک وجهی جداگانه انجام می شود. هنگامی که بخش های تک وجهی به درستی توسط یک الگوریتم تشخیص حالت شناسایی نمی شوند، نقاط GNSS با بخش اشتباهی از شبکه تحرک مطابقت داده می شوند [ 8 ، 12 ]]. علاوه بر این، بخش‌بندی حالت معمولاً منطق سفر را در نظر نمی‌گیرد. به عنوان مثال، انتقال بین دو حالت وسیله نقلیه بدون راه رفتن امکان پذیر نیست [ 4 ]. الگوریتم های تشخیص حالت بسته به قدرت سیگنال GNSS و پراکندگی داده های جمع آوری شده ضعیف عمل می کنند [ 4 ، 12 ]. بنابراین، نقاط GNSS بدون برچسب با حالت های سفر و القا شده با خطای سیستماتیک منجر به تطبیق نقشه اشتباه می شود [ 8 ].

به طور خلاصه، همه الگوریتم‌های موجود ممکن است برخی از نقاط GNSS را به دلیل عوامل زیادی مانند خطاهای اندازه‌گیری در نقاط GNSS، نرخ نمونه‌برداری پایین از نقاط GNSS، محدودیت‌ها در منابع محاسباتی برای تطبیق نقشه آنلاین و توپولوژی پیچیده، به اشتباه برخی از نقاط GNSS را در یک بخش جاده اشتباه نگاشت کنند. در تقاطع های جاده ای [ 10 ]. چالش اجتناب از خطاهای تطبیق نقشه تا به امروز به طور سیستماتیک حل نشده است. روش های اخیر تطبیق نقشه تا به

92 %

دقت برای نرخ نمونه بالا (زیر 1 دقیقه) و تا

82 %

دقت برای نرخ نمونه پایین (یک تا دو دقیقه) از نقاط ثبت شده GNSS، به ترتیب [ 10 ]. بنابراین، احتمال یک خطای تطبیق نقشه باقیمانده به دلیل رویکردهای تصادفی روش‌های موجود وجود دارد [ 11 ]. تا جایی که ما می دانیم، هیچ روشی برای شناسایی این خطاهای تطبیق نقشه باقی مانده پیشنهاد نشده است. برای غلبه بر چالش ذکر شده در بالا در شناسایی خطا در بخش‌های همسان نقشه، ما یک رویکرد مبتنی بر استدلال را برای شناسایی و کمی کردن خطاهای تطبیق نقشه پیشنهاد می‌کنیم.

3. مفاهیم شناسایی خطای تطبیق نقشه

در این بخش، ابتدا در مورد اینکه چگونه خطاهای تطبیق نقشه باقیمانده را می توان مشخص کرد ( بخش 3.1 ) بحث می کنیم. این مشخصه‌سازی اجازه می‌دهد تا خطای کمی را در یک سری نقطه مسیر مطابق با نقشه رسمی‌سازی کنیم ( بخش 3.2 ) و یک فاصله ویرایشی برای این کمی‌سازی معرفی کنیم ( بخش 3.3 ).

3.1. خطای کیفی در تطبیق نقشه

خطای کیفی در تطبیق نقشه نیاز به مشخصه ایستایی دارد. به عنوان مثال، آیا خودرویی که پشت چراغ قرمز توقف می کند، حرکت خود را بین دو فعالیت ثابت قطع می کند؟ این امر مستلزم در نظر گرفتن زمینه حرکت است، یعنی حالت سفر حرکت قبل و بعد از توقف و آستانه‌های خاص مد برای مدت زمان قابل قبول این توقف‌ها. اغلب، این مسیرها در فواصل زمانی منظم نمونه برداری می شوند، اگرچه نمونه برداری در فواصل زمانی منظم و نمونه برداری نامنظم نیز امکان پذیر است. استراتژی‌های نمونه‌گیری منظم همچنین می‌تواند شکاف‌هایی را در ضبط‌های آنها نشان دهد. ما دسته‌بندی‌های زیر از رفتار سفر غیرواقعی را در نظر گرفته‌ایم که با خطاهای کیفی در الگوریتم تطبیق نقشه منعکس می‌شوند:

سرعت بی نهایت
شتاب غیر واقعی
حضور در چندین مکان به طور همزمان

رفتار غیرواقعی سفر در یک بخش منطبق بر نقشه به سه دلیل اصلی رخ می‌دهد: (1) خطای اندازه‌گیری در نقاط جمع‌آوری‌شده GNSS (از آنجایی که نقاط جمع‌آوری‌شده GNSS در معرض خطای اندازه‌گیری قرار می‌گیرند، موقعیت‌های واقعی ناشناخته باقی می‌مانند، و در نتیجه بخش‌های نادرست تطبیق داده می‌شوند. [ 27 ])؛ (2) توپولوژی پیچیده و اطلاعات نقشه ناقص در شبکه جاده [ 11 ]، که منجر به محاسبات احتمال انتقال اشتباه در هر دو روش آماری و مبتنی بر فاصله می شود [ 5 ]]; and (iii) mismatch of travel mode and road network type (e.g., map-matching of a car route on a public transport network) [12]. As a result of map-matching, in a map-matched route, there will be two types of map-matched segments: (i) correctly map-matched segments (reflects realistic travel behavior) and (ii) incorrectly map-matched segments (reflects unrealistic travel behavior).

3.2. خطای کمی در تطبیق نقشه

ما پس از اینکه یک الگوریتم نگاشت مسیر تخمینی و بخش های مطابق با نقشه را تولید کرد، کمی خطاهای نگاشت کیفی را پیشنهاد می کنیم. فرض کنید یک مسیر T حاوی تعداد d از نقاط داده GNSS ثبت شده باشد، $d \geq 2$ ، به طوری که $j th$ نقطه داده ( $d \geq j \geq 1$ ) شامل تاپل است $< x_{j}, y_{j}, t_{j} >$ ، جایی که $x_{j}$ و $y_{j}$ مختصات مکان نقطه j (به عنوان مثال، طول و عرض جغرافیایی، به ترتیب)، و $t_{j}$ مهر زمانی رکورد مکان است. اجازه دهید E مجموعه یال ها و V مجموعه رئوس در نمودار جهت دار (دیگراف) شبکه راه باشد. $G = (V, E)$ . سپس:

E \subseteq {{p, q} ∣ p ، q \in V و p \neq q}

(1)

در اینجا، لبه‌ها بخش‌های جاده را بر روی نقشه نشان می‌دهند، بخش کاندید احتمالی تطبیق نقشه. ما به اصطلاح لبه در زمینه یک نمودار و به یک بخش در زمینه داده های نقشه اشاره خواهیم کرد. مسیر حقیقت زمینی یک داده مسیر T دنباله ای از بخش های جاده متصل مسیر طی شده روی نقشه است. برای این، فرض می کنیم که نقشه کامل است.

فرض کنید R دنباله‌ای از بخش‌های نقشه حقیقت زمین از داده‌های مسیر T باشد. از این رو، R شامل دنباله ای از بخش های جاده متصل است، به عنوان مثال، بخش های نقشه، که انتظار می رود به درستی با نقاط GNSS ثبت شده در همان بخش نقشه تطبیق داده شوند. اجازه دهید R داشته باشد

n \geq 1

لبه ها، و اجازه دهید

V_{R} \subset V

زیر مجموعه ای از رئوس G باشد به طوری که یک زیرگراف متصل القایی وجود داشته باشد

G_{R}

که مجموعه راس آن است

V_{R}

و که لبه مجموعه

E_{R} = {r_{1}, \dots, r_{n}} \subseteq E

به طوری که اتصال راس

κ (G_{R}) = 1

-یعنی

G_{R}

1-راس متصل است. مجموعه برش یا جداکننده راس از

G_{R}

حاوی حداقل یک راس است که حذف آن رندر می شود

G_{R}

قطع شده. بنابراین، مسیر حقیقت زمینی

R = (r_{1} \to r_{2} \to \dots r_{n})

پیاده روی در نمودار است

G_{R}

اجازه دهید مسیر مطابق با نقشه باشد

\hat{R}

برای مسیر T شامل مجموعه ای از

m \geq 1

لبه ها:

{{\hat{r}}_{1}, \dots, {\hat{r}}_{m}} \subseteq E

. بدین ترتیب،

\hat{R} = ({\hat{r}}_{1} \to {\hat{r}}_{2} \to \dots {\hat{r}}_{m})

. تطبیق نقشه تضمین می کند که برای مجموعه ای از نقاط داده GNSS توسط مختصات داده شده است

{(x_{j}, y_{j})}

مجموعه ای منطبق از بخش های جاده وجود دارد

{{\hat{r}}_{i} = {(p, q)}_{i}}

جایی که

(p_{i}, q_{i}) \in V

{(p, q)}_{i} \in E

. مجموعه نقاط موقعیت یک رابطه عملکردی ذهنی با مجموعه بخش‌های منطبق بر نقشه دارد به طوری که چندین نقطه را می‌توان با یک بخش جاده تطبیق داد.

برای یک مسیر درست مطابق با نقشه، $\hat{R} = R$ دارای یک دنباله متناهی از بخش های منطبق بر نقشه است به طوری که هر کدام $i th (i \geq 2)$ بخش منطبق بر نقشه ${\hat{r}}_{i}$ (با رئوس $p_{i}$ و $q_{i}$ ) یک لبه حادثه خواهد داشت ${\hat{r}}_{i - 1}$ جایی که:

q من - 1 = پ من

(2)

یک خطای تطبیق نقشه رخ می دهد اگر:

آر ˆ \neq آر

(3)

معادله ( 3 ) بیانگر این است که با توجه به حقیقت پایه R ، هر تفاوتی از

\hat{R}

می تواند به عنوان یک خطای تطبیق نقشه شناسایی و برچسب گذاری شود. معادله ( 3 ) در ادامه به این واقعیت اشاره دارد که

\hat{R} \neq R

را دنبال می کند

q_{i - 1} \neq p_{i}

در یک خطای تطبیق نقشه

3.3. کمی سازی مبتنی بر فاصله ویرایش

فاصله ویرایش یک متریک رشته ای است که حداقل تعداد عملیات مورد نیاز برای تبدیل یک رشته به رشته دیگر را اندازه می گیرد [ 28 ]. خطاهای تطبیق نقشه شناسایی شده را می توان با محاسبه فاصله ویرایش بین R و

\hat{R}

، به عنوان مثال، با کمی کردن ویرایش های تک بخش (درج، حذف، یا جایگزینی) بین دنباله های R و

\hat{R}

. ما فاصله Levenshtein را در میان فواصل ویرایش های مختلف اعمال می کنیم، زیرا این سه عملیات ویرایش را برآورده می کند [ 28 ].

فاصله لونشتاین بین دو راه R و $\hat{R}$ از طول ها $| R |$ و $| \hat{R} |$ را می توان به ترتیب توسط $lev (R, \hat{R})$ ، جایی که

lev (R, آر ˆ) = ⎧⎩⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪ | R | ∣∣ آر ˆ ∣∣ lev (دم (R), دم (آر ˆ)) 1 + دقیقه ⎧⎩⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪ lev (دم (R), آر ˆ) lev (R ، دم (آر ˆ)) lev (دم (R), دم (آر ˆ)) اگر | آر ˆ | = 0 ، اگر | R | = 0 ، اگر R [0] = آر ˆ [0] در غیر این صورت ،

(4)

جایی که دم راه رفتن همان راه رفتنی است که با لبه اول آن کوتاه شده است. اولین لبه یا عنصر سر یک واک R است $R [0]$ . بنابراین، فاصله Levenshtein تعداد عدم تطابق بین حقیقت زمین و مسیر مطابق نقشه را ارزیابی می کند.

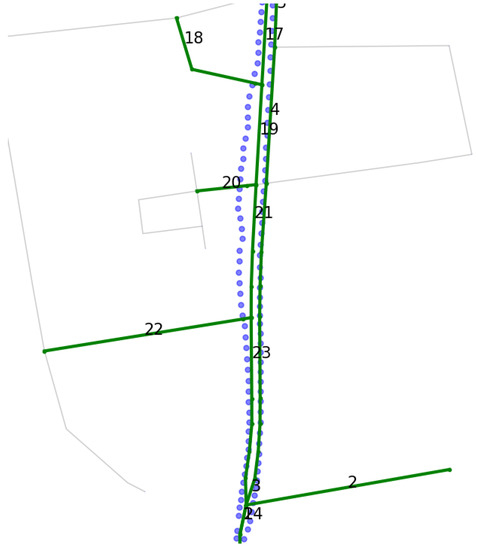
ما چهار نوع خطای رایج در الگوریتم‌های تطبیق نقشه را دسته‌بندی می‌کنیم ( شکل 2 ، شکل 3 ، شکل 4 و شکل 5 )، که همگی رفتار سفر غیرواقعی را در یک بخش مطابق با نقشه نشان می‌دهند. در شکل ها، نقاط ثبت شده GNSS به صورت نقاط آبی و بخش های مطابق نقشه با خطوط سبز نشان داده شده اند. هر بخش منطبق دارای یک شماره شناسایی بخش منحصر به فرد در دنباله سفر است که به رنگ سیاه نشان داده شده است. دسته بندی های رایج شناسایی شده از خطاهای تطبیق نقشه به شرح زیر است:

خطای Cat-I : این نوع خطا زمانی رخ می دهد که بخش های نادرست تطبیق داده شده یک طرفه باشند یا از مسیر واقعی آویزان باشند ( شکل 2 ). با مراجعه به معادله ( 2 )، خطای Cat-I در قسمت منطبق با نقشه من رخ می دهد. ${\hat{r}}_{i} : (p_{i}, q_{i})$ از $\hat{R}$ زمانی که شرایط زیر صادق باشد:

$q من \neq پ من + 1 پ من = پ من + 1 = q من - 1$

(5)

چنین بخش‌های منطبق بر نقشه نشان می‌دهند که مسافر باید از انتهای بخش بپرد ( $q_{i}$ ) بازگشت به آغاز خود ( $p_{i}$ ) به منظور بازگشت به مسیر اصلی. یک مثال گویا از خطای Cat-I در شکل 2 نشان داده شده است .
خطای Cat-II : این نوع خطا زمانی رخ می دهد که خطوط جدا شده با نقاط GNSS مطابقت داده شوند ( شکل 3 ). خطای Cat-II در قسمت منطبق با نقشه I رخ می دهد ${\hat{r}}_{m} : (p_{m}, q_{m})$ از $\hat{R}$ زمانی که شرایط زیر صادق باشد:

$q من \neq پ من + 1 پ من \neq q من - 1 r ˆ من \notin R$

(6)

چنین بخش های تطبیق شده با نقشه نشان می دهد که مسافر باید در آن بخش جدا شده سرعت بی نهایت داشته باشد. یک مثال گویا از خطای Cat-II در شکل 3 نشان داده شده است . توجه داشته باشید که رفتار حرکتی اساسی کاملا قانونی و از نظر فیزیکی امکان پذیر است.
خطای Cat-III : این نوع خطا زمانی رخ می دهد که ناپیوستگی هایی در مسیر منطبق به دلیل پراکندگی نقاط داده ثبت شده وجود داشته باشد ( شکل 4 ). خطای Cat – III در قسمت منطبق شده با نقشه رخ می دهد ${\hat{r}}_{i} : (p_{i}, q_{i})$ از $\hat{R}$ زمانی که شرایط زیر صادق باشد:

$q من \neq پ من + 1 پ من \neq q من - 1 r ˆ من \in ر$

(7)

چنین بخش‌های منطبق بر نقشه نشان می‌دهد که مسافر باید در حین عبور از یک بخش به بخش جدا شده بعدی، سرعت بی‌نهایتی داشته باشد. تصویر خطای Cat-III در شکل 4 نشان داده شده است .
خطای Cat-IV : گاهی اوقات، بخش های منطبق بر نقشه به دلیل خطای اندازه گیری در نقاط ثبت شده، به طور مبهم توسط الگوریتم انتخاب می شوند ( شکل 5 ). این موارد خاص از خطاهای Cat-II و Cat-III هستند :

$q من \neq پ من + 1 پ من \neq q من - 1$

(8)

معادله ( 8 ) مستقل از شرط است ${\hat{r}}_{i} \in R$ یا ${\hat{r}}_{i} \notin R$ . چنین بخش‌های منطبق بر نقشه نشان می‌دهند که مسافر باید همزمان در هر دو بخش باشد، گویی که حضور همزمان در دو خط مختلف وجود دارد. همانطور که در شکل 5 نشان داده شده است، این نوع خطا یک خطای Cat-IV است .

با این حال، در غیاب یک مسیر مطابق با نقشه حقیقت زمینی ( R )، خطاهای تطبیق نقشه (به عنوان مثال، خطاهای Cat-I-IV ) تنها با تجزیه و تحلیل بصری قابل شناسایی هستند.

\hat{R}

بر اساس استدلال عقل سلیم با دانش R و

\hat{R}

، فاصله لونشتاین را می توان با استفاده از رابطه ( 4 ) محاسبه کرد.

4. محاسبه برآورد خطای تطبیق نقشه

ما یک روش دو مرحله‌ای مستقل برای تخمین اینکه آیا یک بخش با نقشه مطابقت دارد پیشنهاد می‌کنیم

{\hat{r}}_{i}

به احتمال زیاد اشتباه است یا خیر ما هر بخش مطابق با نقشه را در آن برچسب گذاری می کنیم

\hat{R}

همانطور که به درستی تطبیق یا نادرست تطبیق داده شده است. مرحله 1 : برآورد اثر نویز اندازه گیری در نقاط ثبت شده GNSS بر روی بخش های مطابق نقشه. مرحله 2 : شناسایی رفتار غیرواقعی سفر به دلیل توالی نامعقول در مسیر مطابق با نقشه. با ترکیب هر دو مرحله 1 و مرحله 2 ، ما هر بخش مطابق با نقشه را به عنوان مطابقت صحیح یا نادرست برچسب گذاری می کنیم. ما از فاصله ویرایش Levenshtein به عنوان اندازه گیری کمی این خطا استفاده می کنیم.

4.1. مرحله 1: شناسایی بخش های منطبق با نقشه تحت تأثیر نقاط GNSS پر سر و صدا

در مرحله 1، هدف ما این است که تشخیص دهیم آیا یک بخش مطابق با نقشه تحت تأثیر خطای اندازه گیری در نقاط GNSS قرار می گیرد یا خیر. تمام نقاط ثبت شده GNSS دارای مقداری خطای اندازه گیری هستند. برای برخی از نقاط، خطای اندازه گیری در کیفیت قابل قبولی برای تطبیق نقشه است. بقیه نقاط در ریزه کاری تطبیق نقشه نیستند. مقدار آستانه برای قابل قبول بودن خطای اندازه گیری القایی برای طبقه بندی نقاط GNSS ناشناخته است. از این رو، ما یک تکنیک طبقه‌بندی بدون نظارت جدید را برای طبقه‌بندی نقاط ثبت‌شده GNSS به دو دسته توسعه دادیم: (i) نقاط اشتباه قابل قبول و (ب) نقاط اشتباه غیرقابل قبول (یا نقاط کاملاً اشتباه). ما یک برچسب‌گذاری باینری برای هر نقطه GNSS و به دنبال آن طبقه‌بندی انجام می‌دهیم. سپس،شکل 6 یک نمودار جریان را برای شناسایی خطاهای تطبیق نقشه و نقاط اشتباه GNSS نشان می دهد.

برای شکل، یک پایگاه داده از نقاط خام GNSS

{(x, y, t)}

و یک نمودار شبکه جاده ایG were used by a map-matching algorithm to generate the sequences of matched segments

\hat{R}

. ما ویژگی های مربوطه را که با استفاده از نقطه داده ثبت شده به دست می آیند تعریف می کنیم

(x_{j}, y_{j}, t_{j})

و بخش مطابق با نقشه مربوطه

{\hat{r}}_{j}

. این مقادیر ویژگی برای طبقه بندی های باینری بدون نظارت نقاط GNSS استفاده می شود

{(x, y, t)}

برای فیلتر کردن نقاط اشتباه غیرقابل قبول از نقاط با خطای کمتر. هر نقطه GNSS دارای یک بخش منطبق با نقشه مربوطه است، و یک نگاشت surjection بین مجموعه نقاط GNSS و مجموعه قطعات مطابق نقشه وجود دارد: چندین نقطه GNSS ممکن است با یک بخش منطبق شود. بسته به حالت آماری نقاط برچسب‌گذاری‌شده GNSS مطابق با آن بخش، یک برچسب‌گذاری باینری برای هر بخش مطابق با نقشه در مسیر انجام دادیم. بنابراین، ما به مرحله 1 شناسایی بخش های نادرست تطبیق می رسیم.

4.1.1. مهندسی ویژگی

در مدل مبتنی بر HMM، انتقال و احتمال انتشار هر بخش مطابق با نقشه به (i) فاصله متعامد یک نقطه GNSS از مجموعه بخش‌های احتمالی و (ب) احتمال خطای اندازه‌گیری در هر نقطه GNSS بستگی دارد. از این رو، طبقه‌بندی هر نقطه GNSS بر اساس دو معیار (یا ویژگی) به دست می‌آید: (1) فاصله یک نقطه GNSS از بخش تطبیق‌شده با نقشه و (ب) چقدر احتمال دارد که نقطه GNSS خراب شود. ویژگی‌ها ویژگی‌های قابل اندازه‌گیری فردی رویدادی هستند که در اینجا در فرآیند تطبیق نقشه مشاهده می‌شوند. هر ویژگی از یک نقطه GNSS (به T ) و بخش نگاشت مربوطه مشتق شده است. بنابراین، هر ویژگی نقطه j تابعی از

(p, q, c_{j})

جایی که

c_{j} = (x_{j}, y_{j})

. ما دو ویژگی را برای طبقه بندی های مورد بحث در بخش های فرعی زیر تعریف کرده ایم: (i) فاصله متعامد و (ii) نویز تخمینی.

فاصله متعامد

می‌توانیم یک خط مستقیم از نقاط بنویسیم $p, q$ مانند: $f_{i} = p + K (p - q)$ ، که در آن bold به معنای بردار و K ثابت است. سپس فاصله متعامد نقطه j امین GNSS از $f_{i}$ را می توان به صورت زیر محاسبه کرد:

o j = f من \cdot ج j ∥ ج j ∥

(9)

نویز تخمینی

ما از یک فیلتر کالمن [ 29 ] برای تخمین نویز نقاط ثبت شده GNSS ناشی از خطای اندازه گیری استفاده می کنیم. اگر بتوانیم موقعیت واقعی یک نقطه GNSS ثبت شده را تخمین بزنیم، نویز را می توان تعیین کرد. یک فیلتر کالمن معمولی موقعیت واقعی بعدی را بر اساس موقعیت واقعی فعلی و موقعیت تخمینی فعلی با استفاده از دو فرآیند، یک فرآیند پیش‌بینی و یک فرآیند تصحیح تخمین می‌زند [ 29 ]. فرآیند پیش‌بینی در مهر زمانی j با معادلات زیر کنترل می‌شود.

ایکس ˆ - j = آ j ایکس ˆ j - 1

(10)

پ - j = آ j پ j - 1 آ ⊤ j + س

(11)

جایی که $X$ بردار حالت است. $\hat{X}$ بردار حالت تخمینی؛ $P_{j}$ ماتریس واریانس-کوواریانس برای حالت j . $P_{0}$ ماتریس واریانس کوواریانس اولیه؛ $Q$ کوواریانس فرآیند، یعنی نویز گاوسی در پیش‌بینی $N (0, q^{2})$ ، که در آن q انحراف استاندارد خطای فرآیند [ 30 ] است. و $A_{j}$ ماتریس انتقال زمانی است. اگر $d t_{j} = t_{j} - t_{j - 1}$ ، سپس:

ایکس j = ⎡⎣⎢⎢⎢⎢ ایکس j y j ایکس j ˙ y j ˙ ⎤⎦⎥⎥⎥⎥

(12)

آ j = ⎡⎣⎢⎢⎢⎢ 10000100 د تی j 0100 د تی j 01 ⎤⎦⎥⎥⎥⎥

(13)

پ j = ⎡⎣⎢⎢⎢⎢⎢ σ ایکس 2 σ y ایکس σ ایکس ˙ ایکس σ y ˙ ایکس σ x y σ y 2 σ ایکس ˙ y σ y ˙ y σ ایکس ایکس ˙ σ y ایکس ˙ σ ایکس ˙ 2 σ y ˙ ایکس ˙ σ ایکس y ˙ σ y y ˙ σ ایکس ˙ y ˙ σ 2 y ˙ ⎤⎦⎥⎥⎥⎥⎥

(14)

فرآیند تصحیح در حالت j با مجموعه معادلات زیر کنترل می شود.

ک j = پ j - اچ ⊤ اچ پ j - اچ ⊤ + م ه

(15)

پ j = (من - ک j ح) پ - j

(16)

ایکس ˆ j = ایکس ˆ - j + ک j [ز j - اچ ایکس ˆ - j]

(17)

جایی که $K_{j}$ ماتریس بهره کالمن در حالت j است، $H$ ماتریس اندازه گیری برای فرآیند مشاهده، $Z_{j}$ مشاهدات در حالت j و $M_{e}$ ماتریس کوواریانس خطای اندازه گیری، یعنی نویز گاوسی در اندازه گیری $N (0, σ^{2})$ ، جایی که $σ$ انحراف استاندارد خطای اندازه گیری است [ 14 ]. ما موقعیت تخمینی را دریافت خواهیم کرد ${\hat{c}}_{j} = {({\hat{x}}_{j}, {\hat{y}}_{j})}^{'}$ از جانب ${\hat{X}}_{j}$ . بنابراین، ما چهارمین ویژگی خود را به عنوان نویز تخمینی در استخراج کردیم $c_{j}$ مانند:

η ˆ j = ∥ ج j - ج ˆ j ∥

(18)

4.1.2. طبقه بندی بدون نظارت-مبتنی بر یادگیری

هنگامی که مقادیر ویژگی هر نقطه GNSS را در داده مسیر T استخراج کردیم، یک مجموعه داده آموزشی آماده کردیم.

U_{T}

برای طبقه بندی نقاط J.

U_{T}

دارای 2 ستون و ردیف J. هر ردیف j از مجموعه داده آموزشی

U_{T}

دارای مقادیر ویژگی است

{o_{j}, {\hat{η}}_{j}}

و بدون برچسب است (یعنی خطای قابل قبول در نقاط GNSS را نمی دانیم). از این رو، ما از یادگیری بدون نظارت برای طبقه بندی نقاط GNSS استفاده کردیم

U_{T}

با استفاده از مدل مخلوط گاوسی [ 31 ]. مدل‌های مخلوط گاوسی (GMMs) مدل‌های احتمالی هستند، که در آن هر خوشه با یک توزیع احتمال چند متغیره طبیعی مطابقت دارد. الگوریتم های خوشه بندی GMM مرزهای نرم را تعریف می کنند. هدف GMM پیشنهادی انجام خوشه‌بندی باینری نقاط GNSS بر اساس برخی ویژگی‌ها برای جداسازی نقاط اشتباه GNSS غیرقابل قبول از نقاط GNSS خطای قابل قبول است. مراکز خوشه برچسب های باینری نقاط ثبت شده GNSS، 1 برای نقاط خطای قابل قبول و 0 برای نقاط خطای قابل قبول را نشان می دهند. ما نقاط GNSS مرتبط با هر بخش مطابق نقشه را شناسایی کردیم. سپس به یک بخش منطبق بر نقشه، برچسبی بر اساس رویکرد مبتنی بر رأی اختصاص داده می‌شود: برچسب‌هایی که بیشترین اکثریت را دارند برنده می‌شوند. هر بخش در

U_{T}

بر اساس برچسب اکثر نقاط GNSS مرتبط با بخش، 0 (به درستی تطبیق داده شده) یا 1 (تطابق نادرست) برچسب گذاری شدند.

4.2. مرحله 2: شناسایی رفتار غیرواقعی سفر به دلیل بی نظمی های توپولوژیکی

هدف این مرحله تخمین حقیقت زمینی R از روی است

\hat{R}

. مسیری که به درستی با نقشه تطبیق داده شده است (زمانی که

R = \hat{R}

) دارای خواص راه رفتن در دیگراف G است. از این رو،

\hat{R}

نمی تواند قطع شود، نمی تواند شامل چندین مؤلفه باشد، و نمی تواند یک قطعه یک طرفه (معادله ( 5 )) یا یک پنجه یک طرفه در G داشته باشد. در نظریه گراف، یک پنجه

S_{3}

ستاره ای با سه لبه است.

S_{3}

درختی است با یک گره داخلی و 2 برگ، یعنی یک گراف دوبخشی کامل

S_{1, 3}

. وجود مولفه های متعدد و/یا پنجه های یک طرفه در یک مسیر مطابق با نقشه

\hat{R}

به عنوان بی نظمی توپولوژیکی در یک مسیر سفر پرداخته می شود. از این رو، در مرحله 2 ، هدف ما تشخیص این است که آیا یک بخش منطبق با نقشه به دلیل بی‌نظمی‌های توپولوژیکی خود تولید شده در مسیر مطابق با نقشه، رفتار سفر غیرواقعی ایجاد می‌کند یا خیر. ما برچسب‌گذاری بخش‌هایی را پیشنهاد می‌کنیم که به اشتباه با روش‌های زیر مطابقت داشته باشند:

4.2.1. تجزیه و تحلیل اجزای متصل

یک مؤلفه متصل، یک زیرگراف با حداکثر اتصال یک گراف است. ما به دنبال تعداد اجزای متصل در مسیر مطابق نقشه گشتیم

\hat{R}

. به این ترتیب، ما می‌توانیم ناپیوستگی‌ها را در مسیر مطابق با نقشه و بخش‌های منطبق با نقشه که مسئول Cat-II هستند تعیین کنیم., Cat-III, and Cat-IV error.

4.2.2. تشخیص پنجه

در تئوری گراف، ستاره ای با سه لبه، پنجه نامیده می شود . از آنجایی که بخش های آویزان یک طرفه مسئول خطاهای Cat-I هستند ، حقیقت زمین R باید بدون پنجه باشد. پس از اتمام مرحله 2 ، هر بخش را وارد کنید

U_{T}

برچسب 0 (به درستی مطابقت داده شده) یا 1 (نادرست تطبیق داده شده) خواهد بود. ما یک پایگاه داده جدید ایجاد می کنیم

L_{T}

برای ذخیره خروجی مرحله 2 پس از برچسب زدن.

5. عملکرد شناسایی خطای تطبیق نقشه خودکار

در این بخش، اعتبار روش و عملکرد آن را با استفاده از داده های مسیر GeoLife [ 32 ] مورد بحث قرار می دهیم. از آنجایی که داده‌های GeoLife اصولاً چندوجهی هستند، اما با حالت حمل و نقل برچسب‌گذاری شده‌اند، ما فقط مجموعه داده‌های برچسب‌گذاری شده درایو/ماشین را انتخاب کردیم تا چالش‌های تطبیق نقشه جداگانه را اشتباه نگیریم. مجموعه داده تجربی ما T از GeoLife شامل 23 مجموعه داده در مجموع است

15, 047

نقاط GNSS علاوه بر این، ما از تطبیق نقشه مبتنی بر HMM پیشرفته [ 5 ] استفاده کردیم که 1296 بخش مطابق با نقشه را تولید کرد.

5.1. ایجاد حقیقت پایه از بازرسی بصری

اعتبارسنجی و ارزیابی عملکرد شناسایی خطای خودکار به داده‌های حقیقت زمینی برای بخش‌های مطابق نقشه نیاز دارد. از آنجایی که حقیقت زمینی داده‌های بخش منطبق بر نقشه با مجموعه داده‌های مسیر بزرگ [ 14 ، 32 ] در دسترس نیست، ما بازرسی بصری بخش‌های تطبیق‌شده با نقشه را اعمال می‌کنیم، و معیارهای توالی معقول توصیف شده در بالا را به کار می‌گیریم.

به عنوان مثال، در شکل 7 ، بخشی از داده های مسیر مجموعه داده 4 ارائه شده است، که در آن ما می توانیم به صورت بصری بخش های نادرست مطابق با نقشه را از استدلال انسانی شناسایی کنیم. ناپیوستگی‌های بین بخش‌های 8 و 9 نشان‌دهنده خطای Cat-III، و ناپیوستگی‌های بین بخش‌های 5 و 6 بر اساس معادلات ( 7 ) و ( 8 ) خطای Cat-IV را نشان می‌دهند. یک فرد برای سفر از بخش 5 به 6 و از بخش 8 به 9 به سرعت بی نهایت نیاز دارد.

هنگامی که یک خطا به صورت بصری شناسایی شد، هر بخش که به اشتباه با نقشه مطابقت دارد را برچسب گذاری می کنیم

{\hat{r}}_{e}

. بنابراین، ما یک مجموعه داده حقیقت پایه ایجاد می کنیم

G_{T}

، که در آن هر بخش تطبیق شده با نقشه T به صورت دستی به عنوان 0 (اگر به درستی مطابقت داشته باشد) یا 1 (اگر مطابقت نادرست باشد) برچسب گذاری می شود.

برای تحقق بازرسی بصری، ما یک ابزار تعاملی مبتنی بر نقشه توسعه داده‌ایم ( شکل 8 ). نقاط ثبت شده GNSS به صورت نقاط قرمز و بخش های مطابق با نقشه به صورت نشانگرهای آبی با اعداد بازشو نشان داده می شوند. این ابزار تعاملات کاربر را ردیابی می کند، مانند شکل، که در آن بخش منطبق بر نقشه 6388 به عنوان یک خطای درستی زمین توسط یک بازرس انسانی کلیک شده است.

5.2. استفاده از حقیقت پایه برای اعتبارسنجی و ارزیابی عملکرد

روش پیشنهادی ما بخش‌های تطبیق‌شده با نقشه را به‌عنوان درست یا نادرست با نقشه تطبیق برچسب‌گذاری می‌کند و ایجاد می‌کند

L_{T}

. مقایسه کردیم

L_{T}

با مجموعه داده حقیقت زمینی

G_{T}

و تحلیل خطای روش ما را انجام داد. برای این تحلیل، ما از معیارهای خطای معمول استفاده کردیم:

مثبت واقعی ( TP ): روش پیشنهادی به درستی یک بخش اشتباه را با توجه به حقیقت زمین شناسایی می کند.
مثبت کاذب ( FP ): روش پیشنهادی زمانی که خطایی در تطبیق نقشه وجود نداشته باشد، خطا را نشان می دهد.
منفی کاذب ( FN ): روش پیشنهادی نشان دهنده خطای مشاهده شده در تطبیق نقشه نیست.
منفی واقعی ( TN ): روش پیشنهادی به درستی یک بخش را به عنوان غیر اشتباه برچسب گذاری کرد.

بگویید مسیر حقیقت زمینی R دارای n بخش و مسیر مطابق با نقشه است $\hat{R}$ دارای m بخش، از آن ها، $m_{C}$ ( $\leq m$ ) بخش ها به درستی مطابقت دارند. اجازه دهید خطای مشاهده شده (صحت زمین) در تطبیق نقشه در رخ دهد $m_{E r r o r}^{o b s}$ از بخش ها سپس:

متر o b s E r o r_= m - متر سی = lev (R, آر ˆ)

(19)

ما دو معیار خطا را برای ارزیابی دقت الگوریتم تطبیق نقشه تعریف کرده‌ایم: (1) درصد خطای الگوریتم تطبیق نقشه. $ε_{M M}$ و (ب) درصد خطای نتیجه مدل $ε_{P M}$ . اجازه دهید ${\hat{m}}_{C}$ تعداد بخش هایی باشد که به درستی برچسب گذاری شده اند. سپس:

متر e s t E r o r_= m - متر ˆ سی

(20)

ε م م = متر o b s E r o r _ متر \cdot 100 %

(21)

ε پ م = ∣∣ متر o b s E r o r _ - متر ˆ سی ∣∣ متر o b s E r o r _\cdot 100 %

(22)

در شکل 7 ، مجموعه داده 4 دارای پنج بخش مطابق با نقشه است. از این رو، $m = 5$ . خطای Cat-III بین بخش های 8 و 9 و خطای Cat-IV بین بخش های 5 و 6 برابر است با $m_{E r r o r}^{o b s} = 2$ . روش خودکار خطای Cat-III را به درستی شناسایی کرد، اما خطای Cat-IV شناسایی نشد. از این رو، ${\hat{m}}_{C} = 1$ ، با یک مثبت واقعی و یک مثبت کاذب. بدین ترتیب،

ε م م = 2 5 \cdot 100 % = 40 %

(23)

ε پ م = 2-1 _ _ 2 \cdot 100 % = 50 %

(24)

ما اعتبار خود را با مقایسه تحلیل حساسیت (نرخ مثبت واقعی) و تحلیل ویژگی (نرخ منفی واقعی) به پایان خواهیم رساند.

5.3. نتایج عملکرد شناسایی خودکار خطا

تصاویر خطاهای شناسایی شده در شکل 9 ، شکل 10 ، شکل 11 و شکل 12 ارائه شده است. تمام نقاط آبی نشان دهنده نقاط ثبت شده GNSS هستند. بخش‌هایی که به‌طور نادرست با نقشه تطبیق داده شده‌اند به‌عنوان نتایج تخمین به‌عنوان خطوط قرمز نشان داده می‌شوند. بخش های مطابق نقشه به درستی تخمین زده شده با خطوط سبز نشان داده می شوند.

در شکل 9 ، یک خطای Cat-I با یک خط قرمز با بخش های 2، 22، 20 و 18 شناسایی و برجسته شده است.
در شکل 10 ، یک خطای Cat-II شناسایی و با یک خط قرمز با بخش 22 مشخص شده است.
در شکل 11 ، یک خطای Cat-III با خطوط قرمز با بخش های 16 و 15 و خط سبز 14 شناسایی و برجسته شده است، زیرا با روش ما شناسایی نشده است.
در شکل 12 ، یک خطای Cat-IV با خط قرمز با بخش های 11 و 10 مشخص و برجسته شده است.

به این ترتیب، ما 23 مسیر منطبق با نقشه فقط درایو از GeoLife را با شمارش کل بخش های حقیقت زمین مقایسه کرده ایم (n), the observed errors in map-matching (

m_{E r r o r}^{o b s}

)، اشتباهات به درستی تخمین زده شده (

{\hat{m}}_{C}

) مثبت کاذب (خطاهای تخمینی نادرست) و منفی کاذب (خطاهای تخمین زده نشده) در روش پیشنهادی. سپس، ما محاسبه کرده ایم

ε_{M M}

ε_{P M}

بر اساس معادلات ( 21 ) و ( 22 ). نتایج در جدول 1 ارائه شده است که بر اساس مقادیر مرتب شده است

ε_{M M}

به ترتیب صعودی

ما یک ماتریس تطبیق دو بعدی ( جدول 1 ) برای تجسم عملکرد روش پیشنهادی استخراج کرده‌ایم. هر ردیف از ماتریس تطبیق نمونه های مشاهده شده را نشان می دهد، یعنی برچسب حقیقت زمینی بخش های مطابق نقشه: (i) بدون خطا و (ii) با خطا. هر ستون از ماتریس تطبیق نمونه‌های تخمینی را نشان می‌دهد، یعنی برچسب‌های تخمینی بخش‌های تطبیق‌شده با نقشه با استفاده از روش پیشنهادی: (i) بخش‌هایی که بدون خطا تخمین زده شده‌اند و (ii) بخش‌هایی که با خطا برآورد شده‌اند. بنابراین، یک ماتریس تطبیق با استفاده از روش پیشنهادی، معیار کمی از بخش‌های برچسب‌گذاری‌شده اشتباه روی نقشه را ارزیابی می‌کند. یک ماتریس تطبیقی تولید شده برای روش پیشنهادی در جدول 2 ارائه شده است که در آن P و N ارائه شده استدر پرانتز به ترتیب موارد مثبت و منفی را نشان می دهد.

روش پیشنهادی ما بر اساس نمرات زیر که پس از ارزیابی ماتریس تطبیق پیشنهادی به دست آمد، ارزیابی شد: AUC (مساحت زیر منحنی) – ROC (ویژگی عملکرد گیرنده)، نرخ مثبت واقعی ( TPR )، نرخ منفی واقعی ( TNR )، پیش بینی مثبت مقدار ( PPV )، میزان حذف نادرست ( FOR )، امتیاز F 1، و دقت کلی ( ACC )، همانطور که در معادلات ( 25 )–( 31 ) تعریف شده است:

یک U سی = 0.87

(25)

تی پ آر = تی پ تی پ + اف ن = 0.93

(26)

تی ن آر = تی ن تی ن + اف پ = 0.82

(27)

پ پ V = تی پ تی پ + اف پ = 0.96

(28)

اف ای آر = اف ن اف ن + تی ن = 0.30

(29)

اف 1 = 2 T پ 2 T پ + اف پ + اف ن = 0.94

(30)

A C سی = تی پ + تی ن تی پ + تی ن + اف ن + اف پ = 0.91

(31)

6. نتیجه گیری

شناسایی خطاها در فرآیندهای تطبیق نقشه آنلاین و آفلاین برای برنامه های حمل و نقل هوشمند مرتبط، از جمله رفتار رانندگی و تحلیل جریان ترافیک، شناسایی تغییرات در شبکه خیابان ها و برنامه ریزی مسیرهای حمل و نقل مهم است. در این مقاله، ما یک روش برای شناسایی آن خطاهای تطبیق نقشه در فرآیندهای آفلاین پیشنهاد کرده‌ایم. ما در مورد تئوری شناسایی خطای تطبیق نقشه بحث کرده ایم. سپس یک نوع شناسی از چهار نوع رایج خطاهای تطبیق نقشه که از خطاهای اندازه گیری و توپولوژی نقشه پیچیده ناشی می شوند، معرفی و رسمیت دادیم. ما به توسعه تئوری برای شناسایی بخش‌های منطبق با نقشه اشتباه در داده‌های مسیر مطابق با نقشه بر اساس طبقه‌بندی بدون نظارت و به دنبال یک رویکرد تئوری گراف برای شناسایی رفتار سفر غیرواقعی ادامه دادیم. بدین ترتیب، به سوال تحقیق ما می توان پاسخ مثبت داد: ما می توانیم به طور خودکار خطاهای تطبیق نقشه را شناسایی و کمیت کنیم زمانی که حقیقت اصلی در دسترس نیست. فراتر از شناسایی، ما همچنین می توانیم این خطاها را با استفاده از طبقه بندی پیشنهادی طبقه بندی کنیم.

ما روش شناسی خود را با استفاده از داده های دنیای واقعی جمع آوری شده در پروژه GeoLife تأیید کرده ایم. نتایج اعتبارسنجی نشان می‌دهد که روش ما در هنگام وجود خطاهای تطبیق نقشه، امتیاز دقت خوبی دارد: این روش به دقت متوسط 91٪ در شناسایی خودکار خطاهای تطبیق نقشه دست می‌یابد. این نتیجه نشان می‌دهد که روش ما می‌تواند به طور موثر به تحلیلگران کمک کند تا تلاش‌های انسانی در کنترل کیفیت تطبیق نقشه را با حاشیه زیادی کاهش دهند. با انتخاب زیرمجموعه مسیر تک‌وجهی GeoLife، داده‌هایی را ارزیابی کردیم که قبلاً باید با الگوریتم‌های تطبیق نقشه (یعنی ارائه یک خط پایه سخت) بهتر کار کنند، و با این حال وجود و توانایی روش خود را برای شناسایی خطاهای مهم نشان دادیم. روش های تطبیق نقشه فعلی مقدار خطاهای بالقوه ای که باید با استفاده از روش پیشنهادی قابل تشخیص باشد، احتمالاً برای مسیرهای چندوجهی، مشاهده شده در شبکه های تحرک چندوجهی، به طور قابل توجهی بیشتر است. روش پیشنهادی و روش طبقه‌بندی خطا برای این مسیرها و خطاها معتبر است.

به عنوان محدودیت روش ما، بخش‌هایی را که به اشتباه با نقشه مطابقت داده شده‌اند، بدون اصلاح شناسایی کردیم. اگرچه روش ما یک گام نظری و عملی به سمت شناسایی خطای تطبیق نقشه کمک می کند، تحقیقات بیشتر در مورد مهندسی ویژگی و الگوریتم های طبقه بندی می تواند بر محدودیت های فعلی غلبه کند. در کار آینده، بررسی معیارهای عملکرد مدل ما در خطاهای Cat-I تا Cat-IV به طور جداگانه جالب خواهد بود. اگرچه روش پیشنهادی با تطبیق نقشه آفلاین استفاده می شود، اما می تواند در تطبیق نقشه آنلاین نیز به کار رود (به عنوان مثال، با استفاده از یک رویکرد مبتنی بر شبیه سازی زمان واقعی با داده های Geolife).

منابع

بنگ، ی. کیم، جی. Yu, K. یک تکنیک تطبیق نقشه بهبود یافته بر اساس رویکرد فاصله Fréchet برای خدمات ناوبری عابر پیاده. Sensors 2016 , 16 , 1768. [ Google Scholar ] [ CrossRef ] [ PubMed ]
دی، س. زمستان، اس. Tomko، M. برآورد جریان مبدأ–مقصد فقط از داده‌های تعداد پیوندها. Sensors 2020 , 20 , 5226. [ Google Scholar ] [ CrossRef ] [ PubMed ]
برکاتسولاس، اس. Pfoser، D.; سالاس، آر. Wenk, C. در مورد داده های ردیابی وسیله نقلیه مطابق با نقشه. در مجموعه مقالات سی و یکمین کنفرانس بین المللی پایگاه های داده بسیار بزرگ، تروندهایم، نروژ، 30 اوت تا 2 سپتامبر 2005. صص 853-864. [ Google Scholar ]
شوسلر، ن. Axhausen، KW پردازش داده های خام از سیستم های موقعیت یابی جهانی بدون اطلاعات اضافی. ترانسپ Res. ضبط 2009 ، 2105 ، 28-36. [ Google Scholar ] [ CrossRef ]
نیوزون، پی. Krumm, J. Hidden Markov نقشه مطابق با نویز و پراکندگی. در مجموعه مقالات هفدهمین کنفرانس بین المللی ACM SIGSPATIAL در مورد پیشرفت در سیستم های اطلاعات جغرافیایی، سیاتل، WC، ایالات متحده، 4-6 نوامبر 2009. صص 336-343. [ Google Scholar ]
راث، جی. مسئله تطبیق نقشه آفلاین و راه حل کارآمد آن. در مجموعه مقالات کنفرانس بین المللی نوآوری برای خدمات اجتماعی، وین، اتریش، 27-29 ژوئن 2016. Springer: برلین/هایدلبرگ، آلمان، 2016; ص 23-38. [ Google Scholar ]
ریموند، آر. موریمورا، تی. اوسوگامی، تی. هیروسو، ن. تطبیق نقشه با مدل مارکوف پنهان در شبکه جاده نمونه. در مجموعه مقالات بیست و یکمین کنفرانس بین المللی شناخت الگو، تسوکوبا، ژاپن، 11 تا 15 نوامبر 2012. IEEE: Piscataway, NJ, USA, 2012; ص 2242-2245. [ Google Scholar ]
چی، اچ. دی، ایکس. Li, J. الگوریتم تطبیق نقشه بر اساس حوزه تصمیم گیری اتصال و مدل پنهان مارکوف. PLoS ONE 2019 , 14 , e0216476. [ Google Scholar ] [ CrossRef ] [ PubMed ]
کولر، اچ. ویدهام، پی. دراگاشنیگ، م. Graser, A. تطبیق سریع مدل مارکوف پنهان برای مسیرهای پراکنده و پر سر و صدا. در مجموعه مقالات 2015 IEEE هجدهمین کنفرانس بین المللی سیستم های حمل و نقل هوشمند، گران کاناریا، اسپانیا، 15 تا 18 سپتامبر 2015. IEEE: Piscataway, NJ, USA, 2015; صص 2557–2561. [ Google Scholar ]
Hsueh، YL; تطبیق نقشه Chen، HC برای مسیرهای GPS با نرخ نمونه‌برداری پایین با کاوش جهت‌های حرکت در زمان واقعی. Inf. علمی 2018 ، 433 ، 55-69. [ Google Scholar ] [ CrossRef ]
خو، ی. لو، سی. کاو، س. Wolf, D. بهبود دقت نقشه برداری Uber با CatchME . گزارش فنی؛ Uber Engineering: سانفرانسیسکو، کالیفرنیا، ایالات متحده آمریکا، 2019. [ Google Scholar ]
چن، جی. Bierlaire، M. تطبیق نقشه چندوجهی احتمالی با داده‌های غنی تلفن هوشمند. جی. اینتل. ترانسپ سیستم 2015 ، 19 ، 134-148. [ Google Scholar ] [ CrossRef ]
کوی، جی. بیان، دبلیو. وانگ، ایکس. تطبیق نقشه مارکوف پنهان بر اساس تقسیم‌بندی مسیر با همگنی عنوان. GeoInformatica 2021 ، 25 ، 179-206. [ Google Scholar ] [ CrossRef ]
دی، س. زمستان، اس. گوئل، اس. Tomko, M. شناسایی فضاهای پارکینگ از داده های مسیر چند وجهی. ترانس. GIS 2021 ، 6 ، 3088-3118. [ Google Scholar ] [ CrossRef ]
گوه، سی. داوولز، جی. میتروویچ، ن. آصف، ام تی; اوران، ا. Jaillet، P. تطبیق نقشه آنلاین بر اساس مدل مارکوف پنهان برای کاربردهای سنجش ترافیک در زمان واقعی. در مجموعه مقالات پانزدهمین کنفرانس بین المللی IEEE در سال 2012 در مورد سیستم های حمل و نقل هوشمند، Anchorage، AK، ایالات متحده، 16-19 سپتامبر 2012. IEEE: Piscataway, NJ, USA, 2012; صص 776-781. [ Google Scholar ]
Jagadeesh, GR; Srikanthan، T. نقشه آنلاین تطبیق داده های مکان پر سر و صدا و پراکنده با مدل های مخفی مارکوف و انتخاب مسیر. IEEE Trans. هوشمند ترانسپ سیستم 2017 ، 18 ، 2423-2434. [ Google Scholar ] [ CrossRef ]
برنشتاین، دی. Kornhauser، A. مقدمه ای بر تطبیق نقشه برای دستیاران ناوبری شخصی . گزارش فنی؛ New Jersey TIDE Center: Newark, NJ, USA, 1996. [ Google Scholar ]
سفید، CE; برنشتاین، دی. Kornhauser، AL برخی از الگوریتم های تطبیق نقشه برای دستیاران ناوبری شخصی. ترانسپ Res. قسمت C Emerg. تکنولوژی 2000 ، 8 ، 91-108. [ Google Scholar ] [ CrossRef ]
روش Phuyal، BP و استفاده از سنسور محاسبه مردگان جمع‌آوری شده و داده‌های GPS برای تطبیق نقشه. در مجموعه مقالات پانزدهمین نشست فنی بین المللی بخش ماهواره ای موسسه ناوبری (ION GPS 2002)، پورتلند، استرالیا، 24-27 سپتامبر 2002. صص 430-437. [ Google Scholar ]
ایتر، تی. Mannila، H. محاسبات گسسته Fréchet Distance ; گزارش فنی؛ آزمایشگاه کریستین داپلر برای سیستم‌های خبره: وین، اتریش، 1994. [ Google Scholar ]
چن، دی. دریمل، ا. Guibas، LJ; نگوین، ا. Wenk, C. تطبیق نقشه تقریبی با توجه به فاصله Fréchet. در مجموعه مقالات سیزدهمین کارگاه مهندسی الگوریتم و آزمایشات، سانفرانسیسکو، کالیفرنیا، ایالات متحده آمریکا، 22 ژانویه 2011; مولر-هانمان، ام.، ورنک، RF، ویراستاران. SIAM: Philadelphia, PA, USA, 2011; صص 75-83. [ Google Scholar ]
Alt، H.; Godau, M. محاسبه فاصله فرچه بین دو منحنی چند ضلعی. بین المللی جی. کامپیوتر. Geom. Appl. 1995 ، 5 ، 75-91. [ Google Scholar ] [ CrossRef ]
Alt، H.; عفرات، ع. روت، جی. Wenk, C. تطبیق نقشه های مسطح. J. Algorithms 2003 ، 49 ، 262-283. [ Google Scholar ] [ CrossRef ]
لو، ا. چن، اس. Xv، B. الگوریتم تطبیق نقشه پیشرفته با مدل مارکوف پنهان برای موقعیت یابی تلفن همراه. ISPRS Int. J. Geo-Inf. 2017 ، 6 ، 327. [ Google Scholar ] [ CrossRef ]
محمد، ر. علی، اچ. یوسف، م. تطبیق نقشه دقیق و کارآمد برای محیط های چالش برانگیز. در مجموعه مقالات بیست و دومین کنفرانس بین المللی ACM SIGSPATIAL در مورد پیشرفت در سیستم های اطلاعات جغرافیایی، دالاس، تگزاس، ایالات متحده آمریکا، 4-7 نوامبر 2014. ص 401-404. [ Google Scholar ]
او، ZC; شی وی، اس. ژوانگ، ال جی؛ Nie, PL چارچوب تطبیق نقشه آنلاین برای داده های شناور خودرو با نرخ نمونه برداری پایین در شبکه های جاده های شهری. IET Intel. ترانسپ سیستم 2013 ، 7 ، 404-414. [ Google Scholar ] [ CrossRef ]
راناچر، پ. بروناور، آر. تروتشنیگ، دبلیو. ون در اسپک، اس. ریچ، اس. چرا GPS مسافت ها را بزرگتر از آنچه که هستند می کند. بین المللی جی. جئوگر. Inf. علمی 2016 ، 30 ، 316-333. [ Google Scholar ] [ CrossRef ] [ PubMed ]
ناوارو، جی. یک تور با راهنما برای تطبیق تقریبی رشته. کامپیوتر ACM. Surv. 2001 ، 33 ، 31-88. [ Google Scholar ] [ CrossRef ]
ولش، جی. Bishop, G. Introduction to the Kalman Filter ; گزارش فنی؛ دانشگاه کارولینای شمالی: چپل هیل، NC، ایالات متحده آمریکا، 1995. [ Google Scholar ]
وان، EA; Van Der Merwe, R. فیلتر کالمن بدون بو برای تخمین غیرخطی. در مجموعه مقالات IEEE 2000 سیستم های تطبیقی برای پردازش سیگنال، ارتباطات و سمپوزیوم کنترل، Lake Louise، AB، کانادا، 4 اکتبر 2000. IEEE: Piscataway, NJ, USA, 2000; صص 153-158. [ Google Scholar ]
Bishop، CM Pattern Recognition and Machine Learning ; Springer: نیویورک، نیویورک، ایالات متحده آمریکا، 2006. [ Google Scholar ]
ژنگ، ی. فو، اچ. Xie، X. ما، وای؛ Li, Q. Geolife GPS Trajectory Dataset—User Guide ; گزارش فنی؛ مایکروسافت تحقیقات آسیا: پکن، چین، 2011. [ Google Scholar ]