چکیده
:
GeoSOT-3D ; کد شبکه ؛ چارچوب عملیات جبری ; داده های بزرگ جغرافیایی ؛ پردازش بلادرنگ
1. مقدمه
2. چارچوب عملیات جبری برای GeoSOT-3D
2.1. مدل شبکه ای GeoSOT-3D
- (1)
-
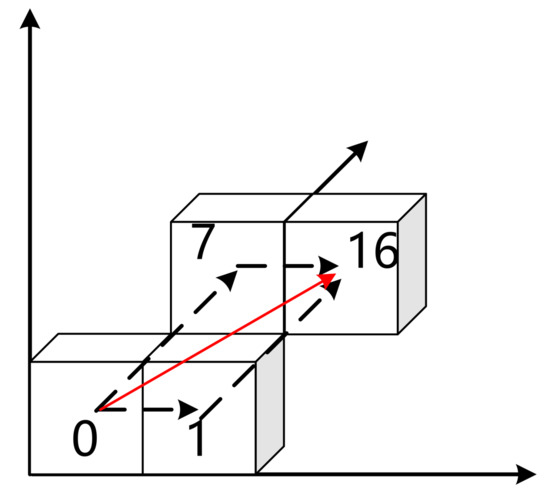
کد هشت بعدی تک بعدی. کد با مقادیر هشتگانه (0، 1، 2، 3، 4، 5، 6، 7) تا 32 رقم کدگذاری شده است. طول کد لایه شبکه را مشخص می کند. هنگام نوشتن کد، با G شروع می شود. کدهای درجه، دقیقه و ثانیه با «-» و کدهای زیر ثانیه با «.» از هم جدا می شوند. فرم Gddddddddd-mmmmmm-ssssss.uuuuuuuuu است، جایی که d ، m ، s ، و uاعداد اکتالی با مقادیر 0، 1، 2، 3، 4، 5، 6، 7 هستند. کد هر لایه شبکه بر اساس لایه قبلی کد شبکه است و جهت رمزگذاری مرتبه Z مربوط به همان شبکه لایه ای که شبکه در آن قرار دارد. کد هشت بعدی یک بعدی عمدتاً برای ایجاد فهرست و شناسایی نام دامنه استفاده می شود.
- (2)
-
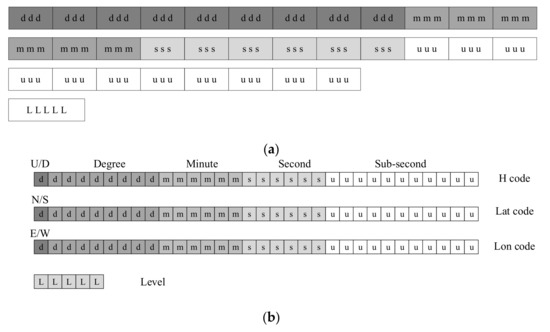
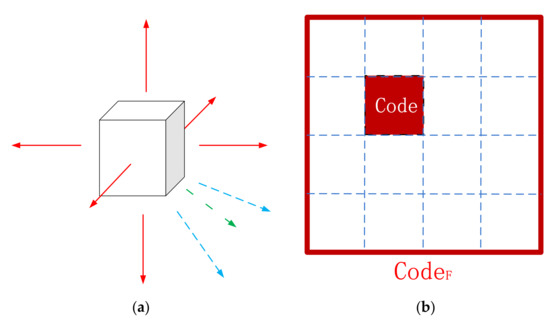
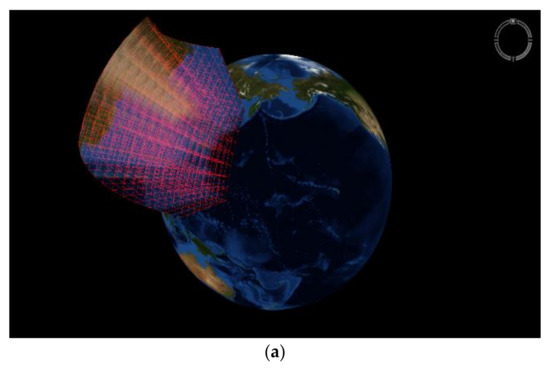
کد یک بعدی باینری ( شکل 3 الف). کد از مقادیر باینری 96 بیتی (0،1) تشکیل شده است، و هر کد سه بیتی یک مقدار هشتگانه را نشان می دهد، بنابراین کد یک بعدی باینری دقیقاً با کد یک بعدی هشتگانه مطابقت دارد. کد باینری یک بعدی عمدتاً برای محاسبه استفاده می شود و عموماً به شکل یک ساختار ذخیره می شود. استفاده از یک کد با طول متغیر برای بیان لایه سلسله مراتبی بخش، مانند یک کد تک بعدی اکتال، غیرممکن است. بنابراین، کد یک بعدی باینری به طور کلی نیاز به افزودن یک کد لایه با طول 5 بیت برای نمایش لایه دارد و طول کل کد 96 + 5 = 101 بیت است.
- (3)
-
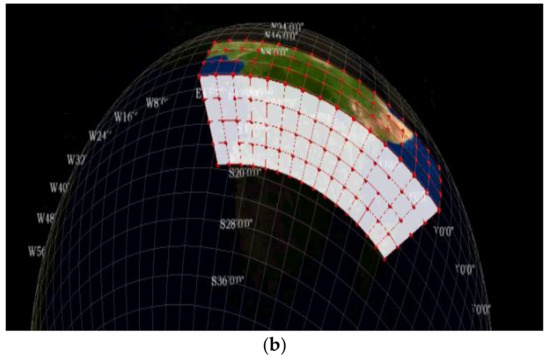
کد سه بعدی باینری ( شکل 3 ب). در کد باینری 96 بیتی یک بعدی شبکه GeoSOT-3D، هر عدد باینری سه بیتی نشان دهنده کد یک شبکه در یک لایه است. این سه رقم جدا شده و به طور جداگانه ذخیره می شوند تا یک کد سه بعدی باینری GeoSOT-3D را تشکیل دهند. کد سه بعدی باینری GeoSOT-3D معنای جغرافیایی واضحی دارد و از مقادیر باینری 32 بیتی برای نشان دادن ارتفاع، عرض و طول جغرافیایی استفاده می شود. بیت اول کد بازه زمانی که شبکه در آن قرار دارد را نشان می دهد.
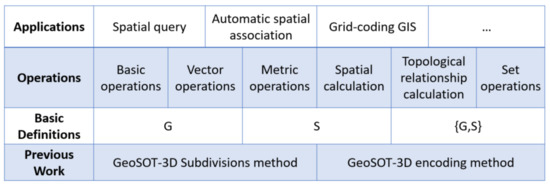
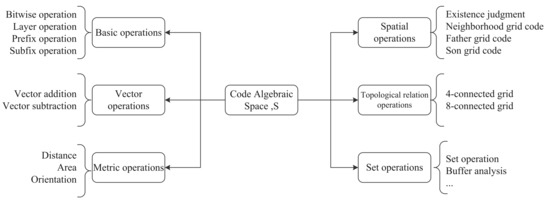
2.2. طراحی چارچوب عملیات جبری
-
عملیات اساسی.
-
عملیات برداری
-
عملیات متریک
-
محاسبه فضایی
-
عملیات روابط توپولوژیکی
-
عملیات را تنظیم کنید
3. عملیات جبری
3.1. عملیات اساسی
3.1.1. عملیات بیتی
-
به صورت بیتی واپراتور:&
-
بیتی ORاپراتور:|
-
XOR بیتیاپراتور:^
-
با بیت معکوس شداپراتور~
-
جابجایی به چپاپراتور:<<
-
به راست تغییر دهیداپراتور:>>
3.1.2. لایه لایه را دریافت کنید
3.1.3. عملیات پیشوند کد
3.1.4. عملیات پسوند کد
3.2. عملیات بردار
3.3. عملیات متریک
3.3.1. فاصله
که در آن Span 1, Span 2, Span 3 دهانه های C 1 و C 2 به صورت سه بعدی هستند و Span 1 > Span 2 > Span را برآورده می کنند.3. روش محاسبه فاصله در اینجا نزدیک به فاصله اقلیدسی در شبکه GeoSOT-3D است. توجه به این نکته ضروری است که هنگام محاسبه فاصله یک دهانه کوچک، فاصله کروی می تواند تقریباً برابر با فاصله اقلیدسی باشد. اگر کاربران نیاز به محاسبه فاصله دقیق و بزرگ داشته باشند، باید آن را دوباره به بیضی تبدیل کنند. ما توصیه می کنیم که فاصله شبکه فقط برای نشان دادن محدوده تقریبی استفاده شود تا محدوده دقیق، برای مثال، محاسباتی مانند تخمین سریع طول.
3.3.2. منطقه طرح ریزی
که در آن A ، B ، C ، D و E ثابت هستند و می توان آنها را به صورت زیر محاسبه کرد:
که در آن a محور نیمه اصلی بیضی مرجع (متر) است. b محور نیمه فرعی بیضی مرجع (متر) است. Δ L اختلاف طول جغرافیایی است (واحد: رادیان). B m = ( B 1 + B 2 )/2.
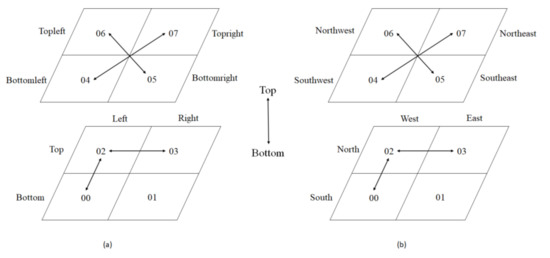
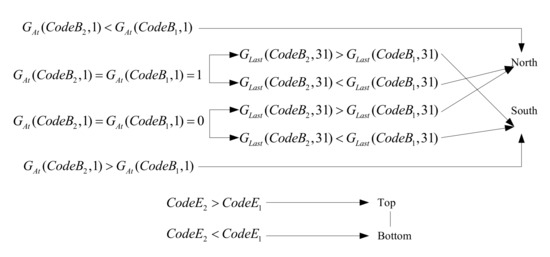
3.3.3. گرایش
3.4. محاسبه فضایی
3.4.1. عملیات محله
- (1)
-
یک شبکه را به جلو حرکت دهید:سیoدهنهw=سیoده+1<<(32–سیoدهLآyهr)
- (2)
-
یک شبکه را در جهت منفی حرکت دهید:سیoدهنهw=سیoده–1<<(32–سیoدهLآyهr)
3.4.2. عملیات شبکه مادر
که در آن G P عملیات محاسبه کد شبکه اصلی است. ورودی محاسبه کد شبکه است. خروجی کد شبکه اصلی شبکه است.
3.4.3. عملیات شبکه کودک
که در آن G S عملیات محاسبه کد شبکه اصلی است. ورودی محاسبه کد شبکه است. خروجی کد شبکه اصلی شبکه است.
3.5. محاسبه روابط توپولوژیکی
3.6. تنظیم عملیات
4. نتایج تجربی
4.1. پلت فرم آزمایشی و طراحی آزمایش
4.2. مقایسه کارایی عملیات برداری
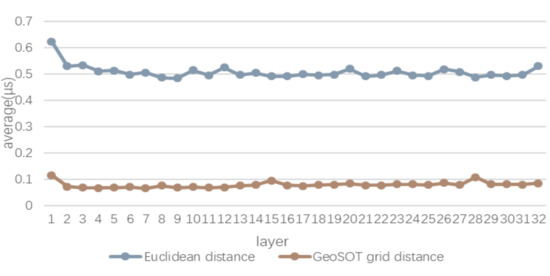
4.3. مقایسه بازده عملیات متریک
4.4. مقایسه بازده عملیات توپولوژیکی
- (1)
-
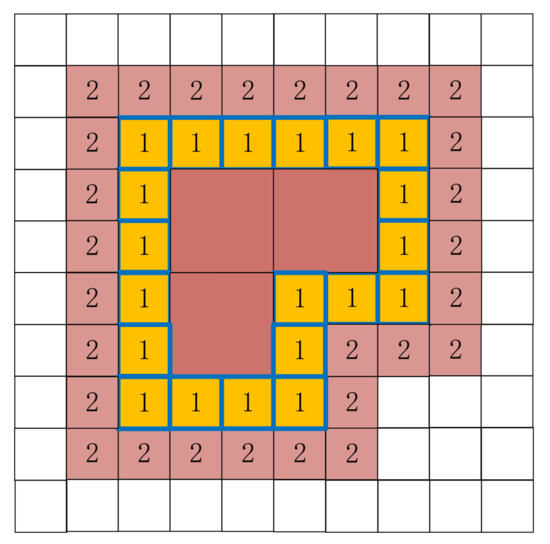
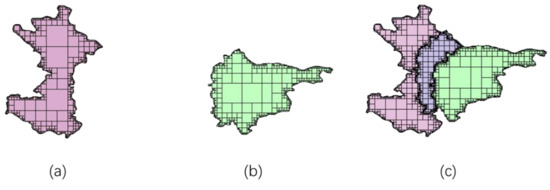
برای محاسبه همپوشانی لایههای حاوی یک شی منطقه واحد، بازده عملیات جبری کمی بالاتر از الگوریتم Weiler-Atherton است. در شرایط آزمایشی در این مقاله، بازده عملیات جبری حدود 1.32 برابر افزایش یافته است. برای محاسبه همپوشانی دو جسم سطحی، وقت گیرترین بخش الگوریتم همپوشانی در قضاوت رابطه تودرتو بین دو مجموعه شبکه نهفته است. این عملیات ابتدایی ترین نوع عملیات بیت است. این به تعداد شبکه های تحت پوشش هر شی منطقه مربوط می شود. در مقایسه، بیشترین مصرف زمان الگوریتم ویلر-آترتون در قضاوت تقاطع بین دو جسم نهفته است. تعداد قضاوت ها به تعداد پاره های خطی که دو جسم سطحی را بیان می کنند، مربوط می شود:
- (2)
-
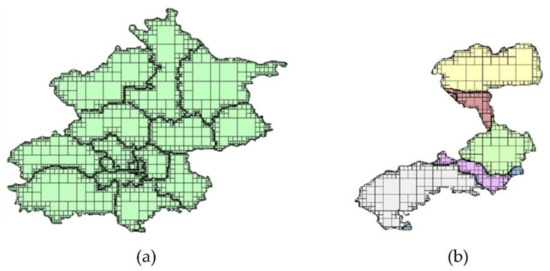
برای محاسبه همپوشانی لایههای حاوی اشیاء مساحت چندگانه، بازده عملیات جبری بسیار بالاتر از الگوریتم ویلر-آترتون است. در شرایط آزمایشی این مقاله، بازده عملیات جبری حدود 6.44 برابر بهبود یافته است. برای محاسبه همپوشانی بین دو مجموعه شی مساحت، مصرف زمان عملیات جبری به اندازه منطقه پوشش کلی مجموعه شبکه و دقت داده مربوط می شود. با تعداد کل شبکه های مرتبط مرتبط است. همبستگی ضعیفی با تعداد اشیاء درگیر در محاسبه دارد. با این حال، زمان مصرف شده توسط الگوریتم Weiler-Atherton به تعداد اشیاء در محاسبه مرجع مرتبط است. هر چه اشیاء بیشتر باشد،
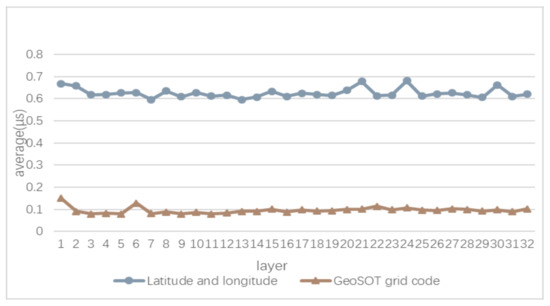
4.5. تحلیل کارایی عملیات جبری
5. نتیجه گیری ها
مشارکت های نویسنده
منابع مالی
بیانیه هیئت بررسی نهادی
بیانیه رضایت آگاهانه
بیانیه در دسترس بودن داده ها
تضاد علاقه
پیوست اول
| پوسیدگی خالی (int n ، int* x، int* y، int rx، int ry){ |
| اگر (ry == 0){ |
| اگر (rx == 1){ |
| *x = n − 1 − *x; |
| *y = n − 1 − *y; |
| } |
| int t = *x; |
| *x = *y; |
| *y = t; |
| } |
| } |
| void d2xy (int n، int d، int* x، int* y){ |
| int rx، ry، s، t = d; |
| *x = *y = 0; |
| برای (s = 1; s < n ; s *= 2){ |
| rx = 1 & (t / 2)؛ |
| ry = 1 & (t ^ rx); |
| rot (s، x، y، rx، ry)؛ |
| *x += s * rx; |
| *y += s * ry; |
| t /= 4; |
| } |
| } |
| unsigned int moveR(int n , کد بدون امضا) { |
| اگر (کد % 2 == 0) |
| بازگشت (کد + 1)؛ |
| n – = 2; |
| برای (int i = 4; i < n ; i = i * 4) { |
| اگر ((کد و i) == 0) |
| کد بازگشت & n |i; |
| n −= i; |
| } |
| بازگشت 0; |
| } |
| تابع 2: رمزگذاری: |
| ورودی: طول جغرافیایی، عرض جغرافیایی، ارتفاع، خروجی لایه: کد GeoSOT-3D 1: ساخت سیoده{ بدون امضا بین المللی درجه:10; بدون امضا بین المللی دقیقه:6; بدون امضا بین المللی دومین:16; }; 2: سیoدهLon←Longمنتیتودهدهgrهه،مترمنnتوتیه،سهجonد 3: سیoدهLآتی←Lآتیمنتیتودهدهgrهه،مترمنnتوتیه،سهجonد 4: سیoدهاچهمن←اچهمنgساعتتی 5: سیoدهمن>>(32–لآyهr)<<(32–لآyهr) 6: for j=0 تیo لآyهr 7: جیهoاسOتی–3D سیoده←سیoدهمن[j] 8: هnد for |
| تابع 3: رمزگشایی: |
| ورودی: خروجی کد GeoSOT-3D : طول جغرافیایی، عرض جغرافیایی، ارتفاع، لایه 1: [سیoدهلon،سیoدهLآتی،سیoدهاچهمن]←جیهoاسOتی سیoده 2: Lآتیمنتیتودهدهgrهه،مترمنnتوتیه،سهجonد←سیoدهLآتی 3: Longمنتیتودهدهgrهه،مترمنnتوتیه،سهجonد←سیoدهLon 4: اچهمنgساعتتی←سیoدهاچهمن |
| تابع 4: بردار + |
| ورودی: GeoSOT-3D Code1، GeoSOT-3D Code2 خروجی: GeoSOT-3D Code //دو دودویی شماره“ بیت ها هستند برابر به کد 1: جیهoاسOتی–3D سیoده=(سیoده1|0ب101010…10+سیoده2)&0ب010101…01 |
منابع
- چن، اس. تجزیه و تحلیل ژئو فضایی/زمانی در پردازش جغرافیایی. J. Remote Sens. 1997 ، 161-171. [ Google Scholar ] [ CrossRef ]
- آهنگ، JC; ژائو، CL; ژونگ، اس پی؛ نیلسن، TAS؛ پریشچپوف، AV نقشه برداری الگوهای مکانی-زمانی و شناسایی عوامل تراکم ترافیک با تکنیک های ترکیب داده ها و استخراج چند منبع. محاسبه کنید. محیط زیست سیستم شهری 2019 , 77 . [ Google Scholar ] [ CrossRef ]
- Xiong، X. کیائو، اس جی. Li، YY; هان، ن. یوان، جی. Zhang، YQ یک الگوریتم پیشنهاد نقطهی علاقه در شبکههای جغرافیایی-اجتماعی چند منبعی. مهندس Appl. آرتیف. هوشمند 2020 , 88 . [ Google Scholar ] [ CrossRef ]
- لین، ی. وانگ، اچ. ژانگ، اس. لی، جی. Gao, H. انتخاب منبع مبتنی بر کیفیت کارآمد از منابع داده عظیم. جی. سیست. نرم افزار 2016 ، 118 ، 221-233. [ Google Scholar ] [ CrossRef ]
- آهنگ ها.؛ چنگ، سی. پو، جی. آن، اف. Luo, X. سازمان زیربخش داده های سنجش از دور جهانی بر اساس GeoSOT. Acta Geod. کارتوگر. گناه 2014 ، 43 ، 869-876. [ Google Scholar ]
- چنگ، سی. تانگ، ایکس. چن، بی. Zhai, W. یک روش تقسیم بندی برای یکسان سازی شبکه های عرض و طول جغرافیایی موجود. ISPRS Int. J. Geo-Inf. 2016 ، 5 ، 161. [ Google Scholar ] [ CrossRef ]
- وانگ، آر. بن، جی. دو، ال. ژو، جی. Li, Z. رمزگذاری و عملیات برای سیستم شبکه شش گوشه با دیافراگم مسطح. Acta Geod. کارتوگر. گناه 2018 ، 47 ، 1018–1025. [ Google Scholar ]
- Xiaochong، T. جین، بن؛ Zhiyuan، QIN; Yongsheng، Z. زیربخش شبکه جزئی بر اساس سیستم های شبکه جهانی گسسته. Acta Geod. کارتوگر. گناه 2009 ، 38 ، 506-513. [ Google Scholar ]
- Xiaochong، T. جین، بن؛ Yongsheng، Z. زیربخش شبکه شش ضلعی با وضوح چندگانه جهانی و قوانین کدگذاری آدرس. Acta Geod. کارتوگر. گناه 2007 ، 36 ، 428-435. [ Google Scholar ]
- Goodchild، MF; Shiren, Y. ساختار داده های مکانی سلسله مراتبی برای سیستم های اطلاعات جغرافیایی جهانی. نمودار CVGIP. فرآیند تصویر مدل ها 1992 ، 54 ، 31-44. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
- لی، اس. چنگ، سی. Pu, G. QRA-Grid: تحلیل کمی ریسک و مدل پیش هشدار مبتنی بر شبکه برای خط لوله گاز طبیعی شهری. ISPRS Int. J. Geo-Inf. 2019 ، 8 ، 122. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
- لی، اس. هو، ک. چنگ، سی. لی، اس. Chen, B. A Space-Interconnection الگوریتم برای صورت فلکی ماهواره بر اساس مدل شبکه فضایی. Remote Sens. 2020 , 12 , 2131. [ Google Scholar ] [ CrossRef ]
- میائو، اس. چنگ، سی. ژای، دبلیو. رن، اف. ژانگ، بی. لی، اس. ژانگ، جی. ژانگ، اچ. الگوریتم تشخیص تعارض پرواز در ارتفاع پایین بر اساس شاخص فضایی و زمانی شبکه چند لایه. ISPRS Int. J. Geo-Inf. 2019 ، 8 ، 289. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
- یانگ، م. چنگ، سی. چن، ب. استخراج شباهت فردی با ارزیابی تعاملات با مکانهای مهم شخصی از مسیرهای GPS. ISPRS Int. J. Geo-Inf. 2018 ، 7 ، 126. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
- بردلی، PE; Jahn، MW در مورد رفتار شاخصهای منحنی پرکننده فضایی با مقیاس p-Adic برای دادههای با ابعاد بالا. محاسبه کنید. J. 2020 . [ Google Scholar ] [ CrossRef ]
- لورینی، آر. تامپسون، دی. مبانی سیستم های اطلاعات فضایی . مطبوعات دانشگاهی: کمبریج، MA، ایالات متحده آمریکا، 1992; جلد 37. [ Google Scholar ]
- جین، ا. چنگ، سی. روش کدگذاری داده های فضایی بر اساس شبکه تقسیم بندی جهانی. جی. ژئومات. علمی تکنولوژی 2013 ، 30 ، 284-287. [ Google Scholar ]
- تانگ، ایکس. بن، جی. وانگ، ی. ژانگ، ی. پی، تی. کدگذاری کارآمد و طرح عملیات فضایی برای سیستم شبکه جهانی گسسته شش ضلعی دیافراگم 4. بین المللی جی. جئوگر. Inf. علمی 2013 ، 27 ، 898-921. [ Google Scholar ] [ CrossRef ]
- ژو، ایکس. تانگ، دی. هائو، ال. Song, Y. کاربرد تئوری کمربند تقسیم زمین در پردازش تصویر. علمی Surv. نقشه 2019 ، 44 ، 84-89. [ Google Scholar ]
- لی، اس. پو، جی. چنگ، سی. Chen, B. روشی برای مدیریت و پرس و جو داده های جغرافیایی فضایی با استفاده از شاخص فضایی آرایه کد شبکه ای. علوم زمین به اطلاع رساندن. 2019 ، 12 ، 173-181. [ Google Scholar ] [ CrossRef ]
- موضوع 21 کنسرسیوم زمین فضایی باز: مشخصات چکیده سیستم های شبکه جهانی گسسته. در دسترس آنلاین: https://docs.opengeospatial.org/as/15-104r5/15-104r5.html (در 18 ژوئیه 2021 قابل دسترسی است).
- چن، جی. لی، سی ام؛ Li، ZL; طلا، C. مدل 9 تقاطع مبتنی بر ورونوی برای روابط فضایی. بین المللی جی. جئوگر. Inf. علمی 2001 ، 15 ، 201-220. [ Google Scholar ] [ CrossRef ]
- ژو، ی. وانگ، اس. Guan، Y. یک الگوریتم موازی کارآمد برای تجزیه و تحلیل پوشش چند ضلعی. Appl. علمی 2019 ، 9 ، 4857. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
- ماه، بی. Jagadish، HV; فالوتسوس، سی. Saltz، JH تجزیه و تحلیل خواص خوشهبندی منحنی پرکننده فضای هیلبرت. IEEE Trans. بدانید. مهندسی داده 2001 ، 13 ، 124-141. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
- ویلر، ک. Atherton، P. حذف سطح پنهان با استفاده از مرتب سازی ناحیه چند ضلعی. محاسبات ACM SIGGRAPH. نمودار. 1977 ، 11 ، 214-222. [ Google Scholar ] [ CrossRef ]







بدون دیدگاه