محاسبه کارآمد تبدیل فاصله بر روی سیستم های شبکه جهانی گسسته

تجزیه و تحلیل داده های مکانی اغلب به محاسبه تبدیل فاصله برای یک ویژگی برداری معین نیاز دارد. به عنوان مثال، در مدیریت آتش سوزی، یافتن فاصله تمام نقاط یک منطقه از مرز آتش سوزی مفید است. محاسبه تبدیل فاصله در سیستم‌های اطلاعات جغرافیایی سنتی (GIS) معمولاً از روش‌های پردازش تصویر اتخاذ می‌شود، اگرچه مستعد اعوجاج ناشی از نقشه‌های مسطح است. سیستم‌های شبکه جهانی گسسته (DGGS) یک سیستم اطلاعات جغرافیایی نسبتاً جدید مبتنی بر کره با اعوجاج کم هستند که زمین را با استفاده از شبکه‌هایی با وضوح چندگانه به سلول‌های بسیار منظم گسسته می‌کنند. در این مقاله، یک الگوریتم تبدیل فاصله کارآمد برای DGGS معرفی می‌کنیم. الگوریتم جدید ما به شدت از سلسله مراتب یک DGGS و ویژگی های ریاضی آن بهره برداری می کند و برای بسیاری از DGGS های مختلف اعمال می شود. ما روش خود را با مقایسه سرعت و اعوجاج آن با روش‌های تبدیل فاصله مورد استفاده در GIS سنتی و مش‌های سه بعدی عمومی ارزیابی می‌کنیم. ما نشان می‌دهیم که روش ما کارآمد است و کمترین اعوجاج را دارد.

کلید واژه ها:

تبدیل فاصله ; سیستم های شبکه جهانی گسسته ; سیستم های اطلاعات جغرافیایی

1. مقدمه

ما در حال جمع آوری حجم عظیمی از داده ها در مورد زمین هستیم که پتانسیل زیادی برای کمک به درک و پیش بینی پدیده های مکانی از طریق تجزیه و تحلیل و شبیه سازی دارد. برای این کار، تعیین فاصله تمام نقاط یک منطقه معین تا یک ویژگی جغرافیایی (مثلاً مرز آتش سوزی) مورد نیاز است. تبدیل فاصله (DT) یک نقشه برداری است که فاصله تمام نقاط یک دامنه را تا یک ویژگی مشخص مشخص می کند و یک عملیات اساسی و مکرر برای انجام تجزیه و تحلیل و شبیه سازی داده های جغرافیایی است. از آن برای تحلیل‌های جغرافیایی مختلف از جمله ترسیم حوضه [ 1 ]، برنامه‌ریزی شهری [ 1 ]، طراحی مسیر خط لوله [ 2 ، 3 ] و تراز راه‌آهن کوهستانی [ 4 ] استفاده شده است.].

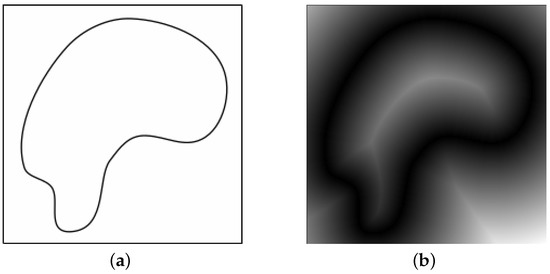
سیستم‌های اطلاعات جغرافیایی سنتی (GIS) معمولاً بر اساس نقشه‌های مسطح هستند و روش‌های تبدیل فاصله را از تکنیک‌های پردازش تصویر اتخاذ کرده‌اند [ 1 ، 5 ]. شکل 1 a تبدیل فاصله اعمال شده به یک ویژگی داخل یک تصویر (یعنی شبکه دو بعدی معمولی) را نشان می دهد. نگاشت زمین منحنی به یک حوزه مسطح باعث ایجاد اعوجاج می شود، در نتیجه، هر تغییر فاصله در فضای تصویر ممکن است حاوی اعوجاج باشد. هنگامی که یک منطقه بزرگ پیش بینی می شود، این اعوجاج طرح ریزی بیشتر است. بنابراین، رویکرد سنتی GIS برای تبدیل فاصله مستقیماً برای کاربردهای مقیاس بزرگ مانند طراحی مسیر خط لوله قابل اجرا نیست [ 2 ]]. جدای از اعوجاج در مقیاس های بزرگ، مشابه بسیاری از عملیات های دیگر برای زمین، DT را می توان به جای نقشه های دوبعدی، در کره زمین بهتر ارائه و تفسیر کرد.

یک رویکرد جدید GIS، سیستم‌های شبکه جهانی گسسته (DGGS)، نمایشی مبتنی بر کره زمین است که با تقریب زمین با یک چندوجهی، اعوجاج را کاهش می‌دهد [ 6 ، 7 ، 8 ]. یک DGGS زمین را با استفاده از سیستم‌های شبکه چند تفکیک‌پذیری به سلول‌های عمدتاً منظم گسسته می‌کند. ویژگی های منظم و چند تفکیک پذیری DGGS نتیجه کاربرد تکراری یک طرح پالایش در وجه های چند وجهی اولیه است [ 6 ]]. به دلیل ماهیت کروی کره، نمی توان گسسته سازی کاملاً منظمی برای آن پیدا کرد. از این رو، هر شبکه DGGS فقط نیمه منظم است که آن را نسبت به یک شبکه کاملاً معمولی چالش برانگیزتر می کند. با این حال، امکان بهره برداری از این نیمه منظمی برای ایجاد الگوریتم کارآمدتر در مقایسه با شبکه های نامنظم وجود دارد ( شکل 1 b,c را ببینید). در زمینه مش های سه بعدی عمومی، الگوریتم های DT بر اساس محاسبات فاصله ژئودزیکی توسعه می یابند [ 9 ، 10 ]]. این الگوریتم های مش کلی را می توان در شبکه DGGS اعمال کرد، اما کندتر هستند، به خصوص با شبکه های بزرگتر. برای شبکه DGGS، می‌توانیم از ویژگی‌های خاص DGGS برای توسعه الگوریتم کارآمدتر استفاده کنیم. الگوریتم‌های تبدیل فاصله سنتی بر روی شبکه‌های کاملاً منظم (یعنی تصاویر) یا مش‌های عمومی کار می‌کنند. این روش‌ها برای مش نیمه منظم یک DGGS مناسب نیستند و از سلسله‌مراتب شبکه چند وضوحی زیرین استفاده نمی‌کنند. بنابراین، یک رویکرد جدید مورد نیاز است. برای رفع این نیاز، در این مقاله، یک الگوریتم جدید و کارآمد تبدیل فاصله برای DGGS معرفی می‌کنیم.

در DGGS، ما تبدیل فاصله را به عنوان فاصله مجموعه ای از سلول ها تا یک یا مجموعه ای از ویژگی ها تعریف می کنیم. ما از ویژگی های یک DGGS، به ویژه سلسله مراتب و هندسه DGGS، برای طراحی یک الگوریتم تبدیل فاصله کارآمد استفاده می کنیم. این الگوریتم هیچ فرضی در مورد شکل سلول‌های DGGS، نوع پالایش و طرح‌ریزی زیربنایی نمی‌کند، که یک مزیت است و باعث می‌شود این الگوریتم برای بسیاری از DGGS‌ها قابل اجرا باشد.

الگوریتم ما بر اساس پیمایش سلسله مراتبی درشت تا ظریف DGGS است. ما با وضوح درشت شروع می کنیم و فاصله هر سلول درشت تا ویژگی را محاسبه می کنیم. این مرحله کارآمد است زیرا تعداد سلول های کمی در این وضوح وجود دارد. در مرحله بعد، بر اساس فواصل محاسبه شده بر روی وضوح درشت فعلی، فضای جستجوی سلول ها را در وضوح بالاتر کاهش می دهیم و تمام لبه های مربوط به ویژگی را در یک ساختار داده ذخیره می کنیم. سپس به طور مکرر شبکه را با وضوح بالاتر اصلاح می کنیم و از فضای جستجوی از پیش محاسبه شده برای یافتن فاصله سلول های فرزند تا ویژگی استفاده می کنیم. ما نشان می‌دهیم که فاصله سلول‌های فرزند تضمین شده است که در مجاورت سلول‌های والد قرار می‌گیرد.

ما یک قضیه ریاضی را اثبات می کنیم که به ما امکان می دهد یک الگوریتم کارآمد طراحی کنیم. ما همچنین عملکرد الگوریتم خود را برای پارامترهای ورودی مختلف تجزیه و تحلیل و گزارش می‌کنیم. این الگوریتم با روش های مبتنی بر تصویر و مبتنی بر مش عمومی مقایسه شده است. این مقایسه نشان می‌دهد که الگوریتم ما اعوجاج فاصله را در مقایسه با روش‌هایی که روی فضای تصویر و فضای مش کار می‌کنند، کاهش می‌دهد. از نظر کارایی، این الگوریتم در مقایسه با الگوریتم های مبتنی بر مش عمومی برای وضوح بالاتر سریعتر است. به طور خلاصه، سهم اصلی این مقاله توسعه یک الگوریتم جدید و کارآمد برای محاسبه تبدیل فاصله برای یک DGGS است.

2. پس زمینه

در این بخش، اطلاعات پیش‌زمینه این مقاله را مورد بحث قرار می‌دهیم. ما آثار و مقالات مرتبط را توضیح می دهیم تا کار خود را در میان دیگران بیان کنیم. این بخش با تعریف DT و کاربردهای آن شروع می شود. سپس اطلاعات لازم در مورد DGGS برای درک این کار توضیح داده شده است. در مرحله بعد، الگوریتم ها و روش های مختلف مورد استفاده برای محاسبه DT در حوزه های مختلف و همچنین مزایا و معایب هر روش را مورد بحث قرار می دهیم.

2.1. تعریف و کاربردهای تبدیل فاصله

در سال 1966، روزنفلد و همکاران. DT را به عنوان یک عملیات متوالی در پردازش تصویر دیجیتال با کاربردهایی در اسکلت سازی شکل معرفی کرد [ 11 ]. در شکل بسیار ابتدایی در Image Space، DT تبدیلی از یک تصویر باینری است که در آن پیکسل‌های سیاه به عنوان شی یا ویژگی و پیکسل‌های سفید پس‌زمینه هستند، به یک تصویر در مقیاس خاکستری. در این تصویر در مقیاس خاکستری، سطح خاکستری فاصله یک پیکسل پس زمینه تا ویژگی را نشان می دهد. شکل 2 تبدیل فاصله اعمال شده به یک تصویر باینری را نشان می دهد. با مشاهده شکل 2 ب مشخص است که اسکلت شکل را می توان با دنبال کردن پیکسل های روشن تصویر استخراج کرد.

پس از آن، ایده DT در بسیاری از مناطق مختلف اعمال شده است و در پردازش تصویر پزشکی [ 12 ، 13 ]، تجزیه و تحلیل شکل [ 14 ، 15 ، 16 ]، گرافیک کامپیوتری [ 17 ]، محاسبات کوتاه ترین مسیر [ 18 ] کاربرد دارد، بخش بندی تصویر [ 19 ] و شبکه های عصبی کانولوشنال [ 20 ]، به نام چند. علاوه بر این، معیارهای مختلف فاصله مانند فاصله منهتن [ 11 ]، فاصله صفحه شطرنج [ 21 ، 22 ]، و فاصله چمفر [ 23 ]] نیز برای یافتن تبدیل فاصله استفاده شده است. با این حال، فاصله اقلیدسی هنوز برای بسیاری از این کاربردها مورد نیاز است [ 24 ].

علاوه بر کاربردهای مختلف ذکر شده از DT، د اسمیت [ 1 ] نشان داد که DT برای بسیاری از کاربردهای مکانی نیز مفید است. به عنوان مثال، DT ممکن است برای محاسبه مناطق بافر چند سطحی برای خطوط حوضه و شیب استفاده شود [ 1 ]. DT همچنین برای ساخت مناطق voronoi مفید است که برای برنامه ریزی شهری مانند ساخت بیمارستان ها و مدارس در یک شهر یا مدیریت یک تیم نجات در یک منطقه مفید است [ 1 ]. علاوه بر این، DT برای برنامه ریزی ساخت و ساز در مقیاس بزرگ مانند طراحی مسیر خط لوله [ 2 ، 3 ] و تراز راه آهن کوهستانی [ 4 ] استفاده شده است.]. کشاورزی هوشمند نمونه دیگری است که از DT استفاده می کند. هنگام نمونه برداری از خاک از یک مزرعه، DT می تواند برای اطمینان از دور بودن نقاط نمونه به اندازه کافی از مناطق نامطلوب مانند مرز مزرعه یا مناطق شناخته شده آلودگی استفاده شود [ 25 ].

2.2. سیستم های شبکه جهانی گسسته

DGGS یک رویکرد جدید به GIS است که زمین را با یک چند وجهی تقریب می‌کند تا یک نمایش جهانی و جهانی از زمین با اعوجاج کمتر در مقایسه با نقشه‌های مسطح ایجاد کند [ 6 ]. DGGS یک نمایش گسسته، سلسله مراتبی و مبتنی بر سلول از زمین است که دسترسی کارآمد همسایگی و پیمایش والد-فرزند را فراهم می کند [ 6 ، 7 ]. هر DGGS از عناصر اصلی زیر ساخته شده است.

2.2.1. عناصر یک DGGS

چند وجهی اولیه: شکل 3 برخی از چند وجهی های اولیه را نشان می دهد که برای ایجاد یک DGGS استفاده شده اند [ 6 ، 7 ]. هرچه این چند وجهی به سطح زمین نزدیکتر باشد، اعوجاج برآمدگی کمتر است. در این کار، ما از یک DGGS Triacontahedron Disdyakis [ 26 ] استفاده می کنیم.

طرح پالایش: سلول های حاصل از وجه های چند وجهی اولیه معمولاً به عنوان اولین وضوح DGGS (یعنی سطح صفر پالایش) در نظر گرفته می شوند. برای ایجاد وضوح بالاتر و مجموعه‌ای از سلول‌های ظریف‌تر، یک طرح پالایش روی وجه‌های چند وجهی اعمال می‌شود. این پالایش می تواند متجانس یا ناهمگون باشد [ 6 ، 7 ]. شکل 4 نمونه هایی از اصلاحات را نشان می دهد. وضوحی که داده ها در آن ارائه می شوند، وضوح هدف DGGS است. شکل 5 DGGS Triacontahedron Disdyakis را در سطوح مختلف پالایش نشان می دهد [ 26 ]. در وضوح 1، مساحت متوسط سلول های DGGS Triacontahedron Disdyakis حدود 4250546.6 کیلومتر مربع است ^.. از آنجایی که این DGGS از اصلاح 1 تا 4 استفاده می کند، هر رزولوشن متوالی مساحت را یک ضریب کاهش می دهد. $1 / 4$ . این منجر به مساحت متوسط 15.4 متر مربع ^در وضوح 20 می شود.

شکل سلولی: شکل سلولی یک DGGS به طور طبیعی از انتخاب چند وجهی اولیه و طرح پالایش ناشی می شود. رایج ترین شکل های سلول چهار گوش، شش ضلعی و مثلث هستند [ 6 ، 7 ].
طرح ریزی: در یک DGGS، طرح ریزی روشی برای انتقال اطلاعات بین حوزه چند وجهی و حوزه کروی زمین است. شکل 6 این طرح را برای Disdyakis Triacontahedron DGGS به عنوان مثال نشان می دهد [ 26 ].

نمایه سازی سلولی: برای تخصیص و بازیابی داده ها به و از سلول ها، باید چند شاخص به سلول ها اختصاص دهیم. هر شاخص به طور منحصر به فرد یک سلول از DGGS را شناسایی می کند و یک پایگاه داده می تواند به جای مختصات برای ذخیره داده ها به این شاخص ها تکیه کند.

2.2.2. فاصله در DGGS

فاصله واقعی بین دو نقطه روی زمین به توپولوژی زمین بین آن دو نقطه بستگی دارد. با این حال، محاسبه این فاصله دشوار است، به همین دلیل است که اغلب از تقریب زمین برای اندازه گیری فواصل بین نقاط استفاده می شود. در این کار، فاصله بین دو نقطه بر روی یک حوزه کروی از طریق محاسبات قوس دایره بزرگ (یعنی ژئودزیک) محاسبه می شود. ما از یک DGGS برای نمایش نقاط به حوزه کروی استفاده می کنیم. سپس از فرمول زیر برای محاسبه فاصله بین دو نقطه p و q استفاده می کنیم ( شکل 7 را ببینید ) با r نشان دهنده شعاع زمین است.

D i s t a n c e (p, q) = یک ثانیه (__پ \to ∣∣ پ \to ∣∣ . q \to ∣∣ q \to ∣∣) * ر

2.3. تبدیل فاصله محاسباتی

در حالی که یک DGGS نسبت به یک GIS سنتی مزایایی دارد، مشکل تبدیل فاصله در DGGS در ادبیات بررسی نشده است. در این بخش می بینیم که چگونه تبدیل فاصله در فضای تصویر و فضای مش محاسبه می شود. فضای تصویر انتهای کاملاً منظم طیف است که در آن الگوریتم‌های تبدیل فاصله کارآمد هستند. در انتهای دیگر طیف مش های عمومی نامنظم هستند که در آنها تبدیل فاصله ناکارآمد است. DGGS در وسط این طیف قرار دارد که در آن سطحی از نظم وجود دارد اما آنها کاملاً منظم نیستند.

2.3.1. محاسبه DT در فضای تصویر

تبدیل فاصله به طور گسترده در پردازش تصویر برای تصاویر دو بعدی از [ 11 ] مورد مطالعه قرار گرفته است (همچنین به [ 24 ] مراجعه کنید). می توان آن را به طور مؤثر در حوزه های دو بعدی کاملاً منظم محاسبه کرد، برای مثال به [ 27 ، 28 ، 29 ] مراجعه کنید. با این حال، این الگوریتم‌ها از نظم کامل دامنه تصویر سوء استفاده می‌کنند و اعمال آن‌ها در یک شبکه DGGS چالش‌هایی را ایجاد می‌کند. یک چالش این است که مفهوم همسایه و فاصله در شبکه DGGS همسو نیستند (یعنی همسایگان از جهات مختلف معمولاً فاصله یکسانی ندارند). چالش دوم این است که شبکه DGGS کاملا منظم نیست بلکه نیمه منظم است.

نقص دیگر استفاده از الگوریتم های مبتنی بر تصویر برای برنامه های GIS در مورد دقت است. کار دی اسمیت [ 1 ] از الگوریتم‌های مبتنی بر تصویر برای انجام یک تبدیل فاصله استفاده می‌کند، بنابراین لازم است که سطح زمین را بر روی صفحه‌ای دوبعدی که اعوجاج ایجاد می‌کند، پخش شود. با استفاده از روش های اخیر طرح ریزی در GIS، اعوجاج فاصله در مقیاس کوچک، مانند یک شهر، ممکن است ناچیز باشد. با این حال، در کاربردهای مقیاس بزرگ، این روش دارای اعوجاج قابل اندازه گیری است که بر دقت تأثیر می گذارد. الگوریتم ما، در مقابل، تبدیل فاصله را بر روی کره زمین محاسبه می کند، به این معنی که الگوریتم برای کاربردهای مقیاس بزرگتر مانند طراحی مسیر خط لوله [ 2 ، 3 ]، تراز راه آهن کوهستانی [ 4 ] قابل اجرا است.] و آنهایی که در مقیاس جهانی عمل می کنند.

2.3.2. محاسبه DT در فضای مش

محاسبه DT روی یک مش عمومی به دلیل تأثیر انحنا بر فاصله و همچنین اتصال نامنظم مش های عمومی دشوارتر از تصاویر دو بعدی است. در سال 1987، میچل و همکاران. الگوریتمی را معرفی کرد که فاصله ژئودزیکی دقیق را روی یک شبکه مثلثی محاسبه می‌کند [ 30 ]. این الگوریتم پس از حروف اول نویسندگان آن، الگوریتم MMP نامیده می شود. با این حال، هیچ الگوریتم MMP به مدت 17 سال اجرا نشد و تا سال 2005 بود که Surazhsky و همکارانش. یکی را معرفی کرد [ 31 ]. چالش این کار این است که فقط برای ویژگی های نقطه ای کار می کند. بومز و همکاران الگوریتم MMP را برای کار با هر ویژگی برداری دلخواه تعمیم داد [ 9]. تقریب فاصله ژئودزیکی نیز در گرافیک کامپیوتری برای مثال با حل معادله گرما روی سطح مش [ 10 ] بررسی شده است. با این حال، در GIS محاسبات دقیق فاصله مهم هستند. در حالی که این الگوریتم ها را می توان در یک DGGS اعمال کرد، آنها از هیچ نظم یا سلسله مراتبی در آن بهره برداری نمی کنند.

2.3.3. محاسبه DT در DGGS

برخلاف الگوریتم‌های فضای تصویر و فضای مش، روش ما از سلسله مراتب و ویژگی‌های هندسی یک شبکه DGGS استفاده می‌کند. این اجازه می دهد تا روش ما کارآمدتر از نسخه های مبتنی بر مش معمولی باشد. علاوه بر این، روش ما از محاسبات فاصله ژئودزیکی (قوس دایره بزرگ) استفاده می کند که فواصل دقیق تری را در مقایسه با الگوریتم های مبتنی بر تصویر و دامنه مش یک DGGS ارائه می دهد.

3. کاهش فضای جستجو برای توسعه یک الگوریتم کارآمد

هدف اصلی ما توسعه یک الگوریتم کارآمد برای محاسبه تبدیل فاصله در یک DGGS است. الگوریتم ما بر کاهش گسترده فضای جستجو با استفاده از سلسله مراتب سلول های DGGS متکی است. ابتدا قضیه ای را مورد بحث و اثبات قرار می دهیم که ما را قادر می سازد از سلسله مراتب برای کاهش فضای جستجو استفاده کنیم.

الگوریتم ما به سه ورودی اصلی نیاز دارد. اول یک ویژگی برداری است، به عنوان مثال، مرز یک کشور. این ورودی شامل فهرستی از لبه‌ها است که در آن هر لبه توسط دو نقطه روی زمین که توسط یک قوس دایره‌ای بزرگ به هم متصل شده‌اند، تعریف می‌شود. ورودی دوم DGGS است که می خواهیم روی آن کار کنیم. DGGS ما را قادر می سازد تا از شبکه سلسله مراتبی برای بهینه سازی الگوریتم استفاده کنیم. علاوه بر این آخرین ورودی وضوح DGGS است که DT باید بر اساس آن محاسبه شود. ما این وضوح را وضوح هدف می نامیم. هدف محاسبه حداقل فاصله از هر سلول یک منطقه در وضوح هدف تا ویژگی است. حداقل فاصله از یک سلول تا ویژگی به عنوان حداقل فاصله از یک نقطه نماینده سلول تا ویژگی تعریف می شود. مانند شکل 8، این نقطه نماینده به طور طبیعی می تواند مرکز سلول باشد، اما هر نقطه داخلی دیگری نیز با الگوریتم ما کار می کند. هدف این است که چنین فاصله ای را برای تمام سلول های منطقه در وضوح هدف محاسبه کنیم تا یک میدان فاصله تشکیل شود.

برای بهره برداری از ماهیت سلسله مراتبی یک DGGS، الگوریتم ما با وضوح درشت شروع می شود که سلول های کمی دارد و به محاسبات فاصله زیادی نیاز ندارد. هنگام پالایش شبکه، از محاسبات روی وضوح درشت استفاده می کنیم تا تعداد محاسبات فاصله در وضوح هدف را کاهش دهیم. ما این کار را با معرفی و اثبات قضیه 1 انجام می دهیم، که به ما امکان می دهد به طور مکرر فضای جستجو را هنگام پیمایش به وضوح بالاتر کاهش دهیم.

قبل از توصیف قضیه، اجازه دهید ابتدا چند نماد و یک تصویر ساده ارائه شده در شکل 9 را مشخص کنیم. فرض کنید p نقطه نماینده سلول C باشد و

r_{p}

فاصله p تا ویژگی F باشد. همانطور که در شکل 9 نشان داده شده است،

r_{p} = | p - f_{p} |

جایی که

f_{p}

نزدیکترین نقطه ویژگی F به نقطه نماینده p است. در طی پیمایش سلسله مراتبی سلول ها، باید ارزیابی کنیم

r_{q}

که در آن q نقطه نماینده یک سلول زاده C است. واضح است که نزدیکترین نقطه است

f_{q}

می تواند متفاوت باشد

f_{p}

. با این حال، زمانی که p و q نزدیک هستند، فضای جستجو از

f_{q}

زیر مجموعه کوچکی از F می شود. قضیه 1 فضای جستجو را کاهش می دهد

f_{q}

با فراهم کردن حدی برای این فضا.

قضیه 1.

با توجه به یک سلول دلخواه C، نقطه نماینده آن p، فاصله آن تا ویژگی

r_{p}

و q، نقطه نماینده یک سلول زاده C، فضای جستجوی

f_{q}

تمام لبه های F در داخل دایره ای است که در مرکز p با شعاع قرار دارد

r_{p} + 2 d

، جایی که d فاصله دورترین q تا p است.

بر اساس قضیه 1، تضمین می شود که نزدیکترین نقطه است

f_{q}

به هر نقطه از مثلث برجسته شده در شکل 9 ، در داخل دایره مرزی (دایره سبز) قرار دارد.

اثبات قضیه 1.

بر اساس تعریف از $r_{q}$ و $f_{q}$ داریم ( شکل 9 را ببینید ):

دقیقه f \in F | f - q | = r q ⩽ | f پ - q |

(1)

در غیر این صورت، $f_{p}$ نزدیکتر به q از $f_{q}$ ، و با این فرض در تضاد است $f_{q}$ نزدیکترین نقطه ویژگی به q است. با استفاده از نابرابری مثلث داریم:

| f پ - q | ⩽ r پ + | p - q |

(2)

بنابراین با استفاده از ( 1 ) و ( 2 ) و تعریف d به دست می‌آییم:

r q ⩽ r پ + | p - q | ⩽ r پ + د

(3)

برای یافتن فضای جستجو از $f_{q}$ در رابطه با p ، با استفاده از نابرابری مثلث، داریم:

| f q - p | ⩽ r q + | p - q |

(4)

و سپس با استفاده از ( 3 ) به دست می آوریم:

| f q - p | ⩽ r پ + د + | p - q | ⩽ r پ + 2 روز

(5)

□

شکل 10 نمونه هایی از d را در شبکه های مثلثی با اصلاحات متجانس با این فرض که p مرکز شکل ها است نشان می دهد. هنگامی که d یک مقدار کوچک است، فضای جستجو کوچکتر می شود و الگوریتم حاصل سریعتر می شود. مقدار d به شکل سلول و پالایش استفاده شده در DGGS بستگی دارد. به طور کلی،

d = max_{q \in c h i l d r e n (C)} | p - q | = | p - q_{m} |

. برای اصلاحات متجانس، d می تواند به سادگی با استفاده از هندسه سلول والد تعیین شود (به عنوان مثال،

q_{m}

نقطه ای در مرز سلول C است). برای اصلاحات ناهمگون، d را می توان با روشی مشابه با استفاده از ردپای سلول C تعیین کرد. به عنوان مثال، کوین سحر [ 32 ] چنین ردپایی را برای سیستم درختی شش ضلعی دیافراگم ناهمگون 3 فراهم می کند. بر اساس [ 32 ]، r نشان داده شده در شکل 11 کل ردپای سلول جد را پوشش می دهد. بنابراین می توان از این شعاع به صورت d استفاده کرد.

4. محاسبه تبدیل فاصله در DGGS

در این بخش دو الگوریتم را معرفی می کنیم که تبدیل فاصله را در شبکه DGGS محاسبه می کند. ایده اصلی در الگوریتم اول ارائه شده است و الگوریتم دوم اصلاح الگوریتم اول است که الگوریتم اول را برای دستیابی به کارایی بیشتر تکرار می کند. ما از قضیه 1 برای توصیف الگوریتم اول به شرح زیر استفاده می کنیم.

4.1. رزولوشن تک پله از پایه تا هدف

برای محاسبه DT روی یک DGGS، از وضوح درشت (یعنی وضوح پایه) شروع می کنیم. هنگامی که در این وضوح، محاسبه فاصله با استفاده از الگوریتم جستجوی جامع بسیار سریع می شود. بنابراین، برای هر سلول فاصله تا تمام لبه های ویژگی را بررسی می کنیم و حداقل را پیدا می کنیم. پس از یافتن DT در وضوح پایه، دایره مرزی را برای هر سلول در آن محاسبه می کنیم. سپس تمام لبه های ویژگی را که در این دایره هستند پیدا کرده و ذخیره می کنیم. ما این لیست یال ها را “لیست نامزد” سلول می نامیم. بر اساس قضیه 1، ما شبکه را به وضوح هدف اصلاح می کنیم و از لیست های نامزد ذخیره شده برای محاسبه DT سلول های فرزند (یا نسل) استفاده می کنیم. بنابراین، در وضوح هدف، ما فقط باید فاصله هر سلول تا لبه های ویژگی را که در لیست نامزدهای والدین (یا اجداد) آنها ذخیره شده است بررسی کنیم. این فرآیند در الگوریتم 1 ارائه شده است. شبه کد نشان می دهد که چگونه این الگوریتم را می توان در سه مرحله پیاده سازی کرد:1 ) محاسبه دایره های مرزی و لیست های نامزد در وضوح پایه (خطوط 1-5)، ( 2 )، پالایش سلول های پایه برای رسیدن سلول های هدف با جهش از وضوح پایه به وضوح هدف (خطوط 6-9). ، و ( 3 ) محاسبه فواصل در وضوح هدف بر اساس لیست های نامزد (خطوط 10-13).

الگوریتم 1 محاسبه تبدیل فاصله.

ورودی:: شبکه، ویژگی، baseRes، targetRes
خروجی:: فاصله فیلد
1:: baseCells ← getCoveringCellsAtResolution (ویژگی، baseRes)
2:: برای هر کدام $c e l l$ که در $b a s e C e l l s$ انجام دادن
3:: فاصله ← محاسبه فاصله (سلول، ویژگی)
4:: cell.candidateList ← computeCandidateList (سلول، فاصله، ویژگی)
5:: پایان برای
6:: targetCells ← new List()
7:: برای هر کدام $c e l l$ که در $b a s e C e l l s$ انجام دادن
8:: targetCells.add(refineToRes(سلول، targetRes))
9:: پایان برای
10:: برای هر کدام $c e l l$ که در $t a r g e t C e l l s$ انجام دادن
11:: kandidatList ← cell.ancestor.candidateList
12:: distanceField.add (سلول، محاسبه فاصله (سلول، فهرست نامزد))
13:: پایان برای
14:: برگشت $d i s t a n c e F i e l d$

بر اساس قضیه 1، لیست نامزد محاسبه شده در وضوح پایه برای همه فرزندان وضوح پایه معتبر است. این ما را قادر می سازد از وضوح پایه به وضوح هدف بپریم. با این حال، در بخش بعدی، ما نشان می‌دهیم که چگونه ترجیح داده می‌شود که رزولوشن مش را در یک زمان اصلاح کنیم تا به طور کامل از سلسله مراتب استفاده کنیم. الگوریتم های 2 و 3 جزئیات را نشان می دهند $c o m p u t e C a n d i d a t e L i s t$ و $c o m p u t e D i s t a n c e$ به ترتیب زیر برنامه ها. اجرای $p o i n t T o G r e a t C i r c l e A r c D i s t a n c e$ زیر برنامه در پیوست A آورده شده است.

الگوریتم 2 محاسبه لیست نامزدها.

ورودی:: سلول، distanceToFeature، edgeList
خروجی:: فهرست نامزدها
1:: نماینده ← getRepresentativePoint(سلول)
2:: d ← getD (سلول)
3:: kandidatList ← فهرست جدید ()
4:: برای هر کدام $e d g e$ که در $e d g e L i s t$ انجام دادن
5:: فاصله ← pointToGreatCircleArcDistance (نماینده، لبه)
6:: اگر فاصله < distanceToFeature + 2d سپس
7:: kandidatList.add(لبه)
8:: پایان اگر
9:: پایان برای
10:: برگشت $c a n d i d a t e L i s t$

الگوریتم 3 محاسبه فاصله.

ورودی:: سلول، edgeList
خروجی:: فاصله
1:: نماینده ← getRepresentativePoint(سلول)
2:: فاصله ← $+ \infty$
3:: برای هر کدام $e d g e$ که در $e d g e L i s t$ انجام دادن
4:: arcDistance ← pointToGreatCircleArcDistance (نماینده، لبه)
5:: فاصله ← دقیقه (فاصله، فاصله کمانی)
6:: پایان برای
7:: برگشت $d i s t a n c e$

4.2. پالایش تکراری

در بخش 4.1، در مورد چگونگی انجام این الگوریتم در یک مرحله از وضوح پایه تا وضوح هدف بحث کردیم. با این حال، این فرآیند را می توان به طور مکرر بین رزولوشن های پایه و هدف تکرار کرد تا گام به گام لیست های نامزد کوچکتر شود (یعنی فضای جستجو کاهش یابد). الگوریتم این اصلاح در الگوریتم 4 ارائه شده است. ایده اصلی این است که از رزولوشن پایه از شبکه عبور کنیم و رزولوشن شبکه را هر بار اصلاح کنیم تا به وضوح هدف برسیم. به این ترتیب، می‌توانیم فهرست‌های کاندیدا را به طور مکرر در هر مرحله اصلاح کنیم. خط 2 الگوریتم 4 حلقه اصلی است که تکرارهای الگوریتم را کنترل می کند. خطوط 3 تا 20 این الگوریتم مشابه الگوریتم 1 با تفاوت کمی در مرحله اول الگوریتم 1 است. برای محاسبه لیست نامزدها، اگر اولین بار است که محاسبه می کنیم، هیچ لیست قبلی و هیچ فیلد فاصله قبلی وجود ندارد (خطوط 4-6). دفعات بعدی، از لیست نامزدهای قبلی استفاده می کنیم و این لیست را فیلتر می کنیم تا لیست های کوچکتری برای وضوح بعدی ایجاد کنیم (خطوط 7-10).

الگوریتم 4 تبدیل فاصله را با پالایش تکراری محاسبه کنید.

ورودی:: شبکه، ویژگی، baseRes، targetRes
خروجی:: فاصله فیلد
1:: coarseCells ← getCoveringCellsAtResolution (ویژگی، BaseRes)
2:: برای $c u r r e n t R e s$ ← $c o a r s e R e s + 1$ به $t a r g e t R e s$ مرحله 1 انجام دهید
3:: برای هر کدام $c e l l$ که در $c o a r s e C e l l s$ انجام دادن
4:: اگر اولین بار است پس
5:: فاصله ← محاسبه فاصله (سلول، ویژگی)
6:: cell.candidateList ← computeCandidateList (سلول، فاصله، ویژگی)
7:: دیگر
8:: فاصله ← distanceField.getDistance(سلول)
9:: cell.candidateList ← computeCandidateList(سلول، فاصله، cell.parent.candidateList)
10:: پایان اگر
11:: پایان برای
12:: fineCells ← فهرست جدید ()
13:: برای هر کدام $c e l l$ که در $c o a r s e C e l l s$ انجام دادن
14:: fineCells.add(refineToRes(cell, currentRes))
15:: پایان برای
16:: () distanceField.clear
17:: برای هر کدام $c e l l$ که در $f i n e C e l l s$ انجام دادن
18:: kandidatList ← cell.parent.candidateList
19:: distanceField.add (سلول، محاسبه فاصله (سلول، فهرست نامزد))
20:: پایان برای
21:: coarseCells ← fineCells
22:: پایان برای
23:: برگشت $d i s t a n c e F i e l d$

5. نتایج و بحث

الگوریتم DT پیشنهادی با هر شبکه DGGS بدون توجه به شکل سلول ها کار می کند. برای آزمایش و محک زدن الگوریتم، آن را روی یک DGGS Triacontahedron Disdyakis [ 26 ] پیاده سازی کرده ایم. سلول‌های این DGGS سلول‌های مثلثی با پالایش یک به چهار هماهنگ هستند که در شکل 5 نشان داده شده است. ابتدا، ما برخی تجسم‌های خروجی DT را نشان می‌دهیم. سپس، چند تست را برای ارزیابی درستی و عملکرد الگوریتم خود شرح می دهیم.

شکل 12 تجسم DT را برای انتاریو در وضوح های هدف مختلف نشان می دهد و شکل 13 تجسم سه استان یا قلمرو دیگر کانادا را نشان می دهد. شکل 14 نتیجه DT را برای دو ویژگی در مقیاس کوچکتر نشان می دهد، مرز شهر کلگری و مزرعه ای در آلبرتا.

5.1. تحلیل درستی

در بخش 4.1 و بخش 4.2، ما درستی الگوریتم های 1 و 4 را مورد بحث قرار دادیم که هر دو به قضیه 1 برای کاهش فضای جستجو با استفاده از ویژگی های سلسله مراتبی یک DGGS متکی هستند. در این بخش، یک آزمون تجربی را معرفی می‌کنیم که شواهد بیشتری برای درستی الگوریتم‌های 1 و 4 ارائه می‌دهد. به عنوان حقیقت پایه، از نتیجه ابزار “تولید جدول نزدیک” از ابزار مجاورت ArcGIS Pro با گزینه فاصله ژئودزیکی استفاده می‌کنیم. . برای استفاده از این ابزار، دو تکه اطلاعات را از نرم افزارمان خروجی می گیریم، (1) نقاط میانی سلول های مورد استفاده برای محاسبات DT ما، و (2) ویژگی (یا مرز) که فاصله از آن اندازه گیری می شود. سیستم ما بخش‌های خطی از ویژگی را به عنوان قوس‌های دایره‌ای بزرگ در نظر می‌گیرد، در حالی که این مورد برای ArcGIS Pro نیست. برای پرداختن به این موضوع، نمونه‌برداری با وضوح بالا از بخش‌های خط ویژگی‌ها (به عنوان مثال، فاصله 10 متری بین نقاط نمونه). در این مقیاس، عملاً هیچ تفاوتی بین یک قوس دایره بزرگ و یک خط مستقیم وجود ندارد. سپس این دو اطلاعات را با سیستم مرجع فضایی EPSG:4047 به ArcGIS Pro وارد می کنیم تا با مدل زمین DGGS ما مطابقت داشته باشد. ما این آزمایش را برای ویژگی ها در سه مقیاس مختلف که در نشان داده شده است، تکرار کردیمشکل 15 .

ابزار “Generate Near Table” فاصله ژئودزیکی از هر نقطه تا مرز را خروجی می دهد. با استفاده از این داده ها، تفاوت فاصله های محاسبه شده برای این نقاط را با استفاده از الگوریتم های 1 و 4 محاسبه می کنیم. جدول 1 میزان تفاوت محاسبه شده را نشان می دهد.

جدول 1 دقت الگوریتم‌های ما را نشان می‌دهد و نشان می‌دهد که الگوریتم‌های اصلی، اجرای همه زیر روال‌ها و نتایج صحیح هستند. همچنین نشان می دهد که وقتی نقاط یکسان داده می شود، هر دو الگوریتم 1 و 4 دقیقاً فاصله یکسانی را ایجاد می کنند. تفاوت کوچک بین ArcGIS Pro و الگوریتم ما ممکن است ناشی از نمونه‌گیری مجدد مرز یا خطاهای ممیز شناور باشد.

5.2. تجزیه و تحلیل عملکرد

برای تجزیه و تحلیل عملکرد، از مرز استان انتاریو کانادا به عنوان ویژگی ورودی استفاده می کنیم که دارای 449 لبه است. در فرآیند این الگوریتم، از عملیات DGGS برای به دست آوردن موقعیت های رأس یک سلول (برای یافتن نقطه نماینده یک سلول و همچنین برای محاسبه d استفاده می شود.) و فرزندان یک سلول. بعلاوه، عملیاتی برای طرح یک نقطه از دامنه چند وجهی یک DGGS به حوزه کروی (در خطوط 1-3 الگوریتم A1 استفاده می شود). هدف از الگوریتم پیشنهادی کارآمد بودن با این فرض است که عملیات DGGS کارآمد هستند. به عبارت دیگر، این الگوریتم سعی می کند با به حداقل رساندن تعداد عملیات محاسبه فاصله مورد نیاز برای محاسبه میدان فاصله، کارآمد باشد. بنابراین، برای ارزیابی الگوریتم مستقل از کارایی عملیات DGGS، تعداد عملیات محاسبه فاصله انجام شده برای هر اجرای الگوریتم را محاسبه و گزارش می کنیم.

عملیات محاسبه فاصله یا الگوریتم A1، حداقل فاصله کروی را از یک نقطه تا یک قوس دایره بزرگ محاسبه می کند. این واحد کار است و الگوریتم ما سعی می کند تعداد وقوع این عملیات را به حداقل برساند. خط مبنا این است که ما از سلسله مراتب DGGS سوء استفاده نمی کنیم و مستقیماً از وضوح هدف برای محاسبه فاصله استفاده می کنیم. برای رسیدن به این هدف، برای هر سلول در وضوح هدف، فاصله سلول تا تمام لبه‌های ویژگی را بررسی می‌کنیم. بنابراین، تعداد کل عملیات، تعداد سلول‌ها در وضوح هدف ضربدر تعداد لبه‌های ویژگی است. در تئوری، سناریوی ایده‌آل این است که برای هر سلول در وضوح هدف، دقیقاً بدانیم کدام لبه نزدیک‌ترین است و فاصله سلول را فقط تا آن لبه محاسبه کنیم. در این مورد،شکل 16 بهبود چشمگیر در عملکرد الگوریتم های ما توضیح داده شده در بخش 4.1 و بخش 4.2 را در مقایسه با خط پایه نشان می دهد که محاسبه DT را برای وضوح بالاتر ممکن می کند.

نمودارهای شکل 16 نمایی هستند زیرا تعداد سلول های هدف به صورت تصاعدی با وضوح هدف افزایش می یابد. برای درک بهتر کارایی الگوریتم خود، می‌توانیم متریک خود را کمی تغییر دهیم. شکل 17 عملکرد الگوریتم ها را در معیار دیگری نشان می دهد که تعداد کل عملیات در هر سلول هدف را گزارش می دهد. دامنه این معیار بین یک (که سناریوی ایده آل ما برای دانستن دقیق نزدیکترین لبه به هر سلول است) و تعداد یال های ویژگی (449 برای مرز انتاریو) است. هر چه این عدد به یک نزدیکتر باشد، عملکرد بهتری دارد.

جالب توجه است، این متریک برای الگوریتم پایه ثابت است، زیرا ما هر لبه ویژگی را برای هر سلول در وضوح هدف بررسی می کنیم. علاوه بر این، با مشاهده وضوح‌های بالاتر، می‌توانیم بهتر از سلسله مراتب استفاده کنیم و به ایده‌آل 1 عملیات در هر سلول هدف نزدیک‌تر شویم.

بر اساس تحلیل ارائه شده در این بخش، الگوریتم تکراری از الگوریتم اول بهتر عمل می کند. برای مرز استان انتاریو و وضوح هدف 12، بهترین تعداد عملیاتی که در هر سلول هدف می‌توانیم با استفاده از الگوریتم اول انجام دهیم، 17.7 است. با این حال، با استفاده از الگوریتم تکرار شونده با ورودی های یکسان، می توانیم به 6.9 عملیات در هر سلول هدف دست یابیم که به میزان قابل توجهی کمتر است.

5.3. بحث

برای وضوح هدف خاص، وضوح پایه ورودی الگوریتم ما است که بر نتیجه تأثیر نمی گذارد اما آزادی انتخاب بیشتری به ما می دهد. ما قبلاً بحث کردیم که این باید یک قطعنامه درشت باشد، اما عدد مشخصی بیان نشده است. شکل 18تعداد عملیات مورد استفاده برای محاسبه DT در وضوح 12 را با استفاده از الگوریتم تکراری از وضوح های پایه مختلف نشان می دهد. مشاهده می کنیم که تعداد عملیات تقریباً با افزایش وضوح پایه افزایش می یابد. با این حال، تفاوت قابل توجهی بین رزولوشن های پایه 3 تا 7 (حداقل 6.9 عملیات و حداکثر 7.5 عملیات) وجود ندارد. واضح است که اگر رزولوشن پایه بسیار نزدیک به رزولوشن هدف باشد، پیشرفت زیادی کسب نمی کنیم. علاوه بر این، الگوریتم ما تا زمانی که وضوح درشت انتخاب شده باشد، به این ورودی حساس نیست.

الگوریتم تک مرحله ای لیست های نامزد را فقط در وضوح پایه محاسبه می کند و سپس به وضوح هدف می پرد. از سوی دیگر، الگوریتم تکرار شونده، پس از محاسبه لیست های نامزدها در قطعنامه های پایه، لیست های نامزدها را در هر قطعنامه در بین آن اصلاح می کند. این دو الگوریتم به صورت افراطی عمل می کنند، به این معنی که گزینه های دیگری نیز امکان پذیر است. ما تمام ترکیبات ممکن برای رسیدن از وضوح پایه به وضوح هدف را بررسی کرده ایم. ما دریافتیم که همیشه بازدید از هر وضوح بین، مانند الگوریتم تکراری، همیشه کارآمدترین است.

6. مقایسه

روش‌های تبدیل فاصله مورد استفاده در GIS سنتی که مبتنی بر فضای تصویر هستند باعث ایجاد اعوجاج می‌شوند. شکل 19 a تبدیل فاصله محاسبه شده در نرم افزار ArcGIS Pro با استفاده از روش های مبتنی بر تصویر را نشان می دهد و اعوجاج ها به وضوح قابل مشاهده هستند. شکل 19 ب و شکل 19 ج تجسمی محاسبه شده بر روی DGGS با روش ما را نشان می دهد.

برای تعیین کمیت میزان اعوجاج ناشی از GIS سنتی (یعنی پیش‌بینی‌های نقشه مسطح)، آزمایشی را انجام دادیم که مشابه بخش 5.1 است. ما از همان ویژگی‌های شکل 15 استفاده می‌کنیم، اما در ابزار «تولید جدول نزدیک» به گزینه فاصله مسطح می‌رویم. برای استفاده از محاسبات مسطح فاصله، ابتدا مرز و نقاط نمونه را با استفاده از سیستم مختصات پیش بینی شده WGS 1984 UTM طرح ریزی می کنیم. جدول 2مقایسه بین محاسبه مسافت مسطح ArcGIS Pro و فواصل تولید شده توسط الگوریتم 4 را نشان می دهد. همانطور که انتظار داریم، اعوجاج فاصله قابل توجهی در تنظیمات مسطح وجود دارد و با کاهش مقیاس به مقادیر کمتری کاهش می یابد. در این آزمایش، اگر ویژگی در یک منطقه UTM واحد وجود نداشته باشد، ما تمام نقاط را به منطقه ای که بیشترین بخش از ویژگی را در بر می گیرد، نمایش می دهیم. به طور خاص، ما از ناحیه UTM 17N برای انتاریو، 11N برای کلگری و 12N برای مزرعه استفاده کردیم.

برای مقایسه الگوریتم MMP [ 30 ] برای مش های عمومی با روش ما، دو جنبه وجود دارد که باید در نظر گرفته شود. ابتدا، الگوریتم MMP فاصله ژئودزیکی دقیق روی مش را نشان می دهد. در مورد DGGS، مش تقریبی از یک کره است و نقاط باید از کره بر روی سطح مش پخش شوند. الگوریتم MMP اثرات طرح ریزی را در نظر نمی گیرد و بنابراین محاسبات ژئودزیکی آن با محاسبات محاسبه شده بر روی کره یکسان نخواهد بود. با این حال، برای وضوح بالاتر از DGGS، که در آن مش به سطح کره نزدیک‌تر است، الگوریتم MMP تقریبی نزدیک‌تر به فواصل ژئودزیکی کروی می‌شود. دوم، الگوریتم MMP کارایی کمتری نسبت به الگوریتم ما برای وضوح بالاتر دارد. برای این مقایسه، از مرز انتاریو برای محک زدن الگوریتم‌ها استفاده کرده‌ایم که فرآیند آن بر روی رایانه‌ای با پردازنده مرکزی Intel Core i7-6700 انجام می‌شود و هر دو الگوریتم در شرایط یکسان با استفاده از ابزار Google Benchmark آزمایش می‌شوند. شکل 20سپس زمان اجرای دو الگوریتم را مقایسه می‌کند و جدول 3 تعداد سلول‌های هدف را در وضوح‌های مختلف در کنار زمان‌های اجرای مربوطه فهرست می‌کند. در وضوح‌های کمتر از 9، الگوریتم MMP سریع‌تر است (اگرچه دقت کمتری دارد)، اما تفاوت آن ناچیز است. همانطور که ما به وضوح بالاتر و تعداد سلول های هدف بیشتر می رویم، الگوریتم MMP زمان بیشتری نسبت به روش ما با یک حاشیه زیاد می گیرد.

7. نتیجه گیری و کار آینده

با در دسترس شدن حجم عظیمی از داده ها، تبدیل فاصله به عنوان ابزاری برای تجزیه و تحلیل چنین داده هایی مهم است. مشکل تبدیل فاصله یک مشکل حل شده در پردازش تصویر است، اما برای داده‌های مکانی، روش‌های مبتنی بر تصویر مناسب نیستند. رویکرد جدید در حال رشد سریع GIS، DGGS، به عنوان ابزاری برای ادغام و تجزیه و تحلیل بهتر چنین داده‌هایی، نیازمند تبدیل فاصله است. برای این منظور، ما یک روش کامل و جامع برای محاسبه موثر تبدیل فاصله در بالای یک شبکه DGGS پیشنهاد کرده‌ایم. رویکرد ما به‌درستی هرگونه DGGS بالقوه را بدون توجه به شکل سلول‌های شبکه و تطابق طرح پالایش، تطبیق می‌دهد. ما در مورد چگونگی تنظیم دقیق پارامترهای الگوریتم خود برای به دست آوردن بهترین نتایج برای مرز انتاریو به عنوان ویژگی ورودی بحث کرده ایم. ما همچنین روش خود را با روش های مبتنی بر تصویر و روش های عمومی مش مقایسه کرده ایم. مقایسه نشان می دهد که روش ما از نظر دقت و کارایی برای مجموعه داده های بزرگ برتر است.

هنوز چند کار مهم در آینده وجود دارد که باید انجام شود. روش ما فاصله را بر اساس یک محاسبه قوس دایره بزرگ کروی محاسبه می کند. با وجود بسیاری از DGGS ها که از یک کره برای مدل مرجع خود از زمین استفاده می کنند، برخی دیگر از DGGS ها از یک کروی مایل استفاده می کنند تا نمایش دقیق تری ارائه دهند. اگر بتوان یک روش محاسبه فاصله کارآمد برای بیضی تعریف کرد، ما گمان می‌کنیم که روش ما برای چنین DGGSهایی قابل اجرا باشد. با این حال، تحقیقات بیشتری برای اثبات این ادعا لازم است.

یکی دیگر از شاخه های فعال جالب تحقیق DGGS، DGGS های سه بعدی است. کارهایی وجود دارد که هدف آنها ساخت یک DGGS سه بعدی یا گسترش DGGS های دو بعدی فعلی به DGGS سه بعدی است [ 34 ، 35 ]. برای این کار، ما یک DGGS دو بعدی را در نظر گرفته ایم، اما همین ایده ممکن است برای یک DGGS سه بعدی دوباره اجرا شود. ایده اولیه این است که قضیه 1 را برای اشکال سه بعدی با استفاده از یک کره پیوندی به جای دایره مرزی اثبات کنیم و از این قضیه جدید برای ساخت الگوریتم استفاده کنیم. اگرچه برای ارزیابی این ایده و ایجاد هرگونه تغییر بالقوه لازم در الگوریتم به تحقیقات بیشتری نیاز است.

اختصارات

در این نسخه از اختصارات زیر استفاده شده است:

GIS	سیستم اطلاعات جغرافیایی
DGGS	سیستم شبکه جهانی گسسته
DT	تبدیل فاصله

پیوست اول

الگوریتم A1 نشان می دهد که چگونه می توان فاصله یک نقطه تا یک کمان دایره بزرگ را محاسبه کرد. این الگوریتم در الگوریتم های 2 و 3 استفاده می شود. در این الگوریتم قوس با دو نقطه انتهایی که با یک قوس دایره ای بزرگ به یکدیگر متصل شده اند نشان داده می شود. فرض بر این است که نقطه و دو نقطه انتهایی در دامنه چند وجهی DGGS قرار دارند، بنابراین اولین قدم این است که آنها را در حوزه کروی قرار دهیم.

شکل A1 زمینه هندسی را نشان می دهد. ما یک کره واحد را فرض می کنیم. بردارها $\vec{v}$ و $\vec{w}$ یک هواپیما تشکیل دهید بردار $\vec{N} = \vec{v} \times \vec{w}$ برای آن هواپیما عادی است. نقطه p را به آن صفحه نمایش می دهیم. سپس با عادی سازی آن بردار پیش بینی شده، آن را به دایره بزرگی که v و w را قطع می کند فشار می دهیم (این $p^{'}$ و خط 6 در الگوریتم A1). بنابراین، $p^{'}$ روی دایره بزرگ قرار دارد، اما نمی دانیم که آیا $p^{'}$ بین v و w (روی قوس) یا خارج از آن است. ما آن را با محاسبه بردارهای متقاطع آزمایش می کنیم $\vec{p^{'}} \times \vec{v}$ و $\vec{p^{'}} \times \vec{w}$ . نتیجه این ضربدرها نیز برای صفحه فوق نرمال است. اگر بردارهای متقاطع در جهات مختلف باشند ( $180^{\circ}$ زاویه بین آنها)، سپس $p^{'}$ بین v و w است، در غیر این صورت ( $0^{\circ}$ زاویه بین آنها) $p^{'}$ خارج از آنهاست

الگوریتم A1 نقطه تا دایره بزرگ فاصله قوس.

ورودی:: نقطه، قوس
خروجی:: فاصله
1:: نقطه ← normalize(dggs.projectToSphericalDomain(نقطه))
2:: v ← normalize(dggs.projectToSphericalDomain(arc.endpoint1))
3:: w ← normalize(dggs.projectToSphericalDomain(arc.endpoint2))
4:: عادی ← normalize(v.cross(w))
5:: pDotNormal ← p.dot(normal)
6:: طرح ریزی ← عادی سازی (نقطه – (pDotNormal * عادی))
7:: cross1 ← projection.cross(v)
8:: cross2 ← projection.cross(w)
9:: dotOfCrosses ← cross1.dot(cross2)
10:: اگر dotOfCrosses < 0 پس
11:: فاصله ← acos(point.dot(projection))
12:: دیگر
13:: d1 ← acos(point.dot(v))
14:: d2 ← acos(point.dot(w))
15:: فاصله ← دقیقه (d1, d2)
16:: پایان اگر
17:: برگشت $d i s t a n c e$ * $r a d i u s O f T h e E a r t h$

شکل A1. خط قرمز قوس دایره بزرگی است که نقاط v و w را به هم متصل می کند و نقطه p نقطه مورد نظر است.

منابع

د اسمیت، MJ Distance به عنوان یک ابزار جدید در تحلیل فضایی، برنامه ریزی شهری و GIS تبدیل می شود. محیط زیست طرح. B طرح. دس 2004 ، 31 ، 85-104. [ Google Scholar ] [ CrossRef ]
Kjaernested، SN; جانسون، ام تی؛ Palsson، H. روش‌شناسی برای انتخاب مسیر خط لوله با استفاده از الگوریتم‌های NSGA II و تبدیل فاصله. در مجموعه مقالات کنفرانس های فنی مهندسی طراحی بین المللی و کنفرانس کامپیوتر و اطلاعات در مهندسی، واشنگتن، دی سی، ایالات متحده آمریکا، 28 تا 31 اوت 2011. جلد 54822، ص 543–552. [ Google Scholar ]
کریستینسون، اچ. جانسون، ام تی؛ Jónsdóttir، F. طراحی مسیر لوله با استفاده از تبدیل فاصله توپوگرافی متغیر. در مجموعه مقالات کنفرانس های فنی مهندسی طراحی بین المللی و کنفرانس کامپیوتر و اطلاعات در مهندسی، لانگ بیچ، کالیفرنیا، ایالات متحده آمریکا، 24-28 سپتامبر 2005. جلد 4739، ص 331–336. [ Google Scholar ]
پو، اچ. ژانگ، اچ. لی، دبلیو. شیونگ، جی. هو، جی. Wang, J. بهینه‌سازی همزمان مسیر راه‌آهن کوهستانی و مکان‌های ایستگاه با استفاده از الگوریتم تبدیل فاصله. محاسبه کنید. مهندسی صنعتی 2019 ، 127 ، 1297-1314. [ Google Scholar ] [ CrossRef ]
ArcGIS. فاصله اقلیدسی. 2021. در دسترس آنلاین: https://desktop.arcgis.com/en/arcmap/latest/tools/spatial-analyst-toolbox/euclidean-distance.htm (دسترسی در 17 ژوئن 2021).
مهدوی امیری، ع. آلدرسون، تی. سماواتی، ف. بررسی زمین دیجیتال. محاسبه کنید. نمودار. 2015 ، 53 ، 95-117. [ Google Scholar ] [ CrossRef ]
آلدرسون، تی. پرس، م. دو، X. مهدوی امیری، ع. سماواتی، اف. سکوهای دیجیتال زمین. در کتابچه راهنمای زمین دیجیتال ; اسپرینگر: سنگاپور، 2020؛ صص 25-54. [ Google Scholar ]
Goodchild، MF بازاندیشی تاریخچه GIS. ان GIS 2018 ، 24 ، 1-8. [ Google Scholar ] [ CrossRef ]
بومز، دی. Kobbelt, L. محاسبه دقیق میدان های فاصله ژئودزیکی برای منحنی های چند ضلعی روی مش های مثلثی . VMV: Saarbrücken، آلمان، 2007; جلد 7، صص 151–160. در دسترس آنلاین: https://www.graphics.rwth-aachen.de/publication/63/bommes_07_VMV_011.pdf (در 17 ژوئن 2021 قابل دسترسی است).
کرین، ک. ویشدل، سی. Wardetzky، M. روش حرارتی برای محاسبه فاصله. اشتراک. ACM 2017 ، 60 ، 90–99. [ Google Scholar ] [ CrossRef ]
روزنفلد، ا. Pfaltz, JL عملیات متوالی در پردازش تصویر دیجیتال. J. ACM 1966 , 13 , 471-494. [ Google Scholar ] [ CrossRef ]
Cuisenaire, O. Distance Transformations: Fast Algorithms and Applications to Medical Processing Image ; گزارش فنی؛ UCL: Louvain-la-Neuve، بلژیک، 1999; در دسترس آنلاین: https://infoscience.epfl.ch/record/61606 (در 17 ژوئن 2021 قابل دسترسی است).
وانگ، ی. وی، ایکس. لیو، اف. چن، جی. ژو، ی. شن، دبلیو. فیشمن، EK; تبدیل فاصله عمیق Yuille، AL برای تقسیم بندی ساختار لوله ای در CT اسکن. در مجموعه مقالات کنفرانس IEEE/CVF در مورد دید رایانه و تشخیص الگو، سیاتل، WA، ایالات متحده آمریکا، 14 تا 19 ژوئن 2020؛ صص 3833-3842. [ Google Scholar ]
لیو، HC; Srinath، MD طبقه بندی شکل جزئی با استفاده از تطبیق کانتور در تبدیل فاصله. IEEE Trans. الگوی مقعدی ماخ هوشمند 1990 ، 12 ، 1072-1079. [ Google Scholar ] [ CrossRef ]
لاوالی، اس. Szeliski، R. بازیابی موقعیت و جهت اشیاء آزاد از خطوط تصویر با استفاده از نقشه های فاصله سه بعدی. IEEE Trans. الگوی مقعدی ماخ هوشمند 1995 ، 17 ، 378-390. [ Google Scholar ] [ CrossRef ]
Teixeira، حرکات انحنای RC، محورهای میانی و تبدیل فاصله . دانشگاه هاروارد: کمبریج، MA، ایالات متحده آمریکا، 1998; در دسترس به صورت آنلاین: https://www.proquest.com/openview/50c844f9001964e3be3073ae12a738ad/1?pq-origsite=gscholar&cbl=18750&diss=y (در 17 ژوئن 2021 قابل دسترسی است).
مستکاس، ک. تزوواراس، دی. Stintzis، MG SQ-Map: تشخیص برخورد لایه ای کارآمد و رندر لمسی. IEEE Trans. Vis. محاسبه کنید. نمودار. 2006 ، 13 ، 80-93. [ Google Scholar ] [ CrossRef ]
چوی، YH; لی، TK; باک، SH; اوه، SY Online برنامه ریزی مسیر پوشش کامل برای ربات های متحرک بر اساس مسیرهای مارپیچی مرتبط با استفاده از تبدیل فاصله معکوس محدود. در مجموعه مقالات کنفرانس بین المللی IEEE/RSJ 2009 در مورد ربات ها و سیستم های هوشمند، سنت لوئیس، MO، ایالات متحده، 10-15 اکتبر 2009. صص 5788-5793. [ Google Scholar ]
آچارجیا، پ. سینها، ا. سرکار، س. دی، س. Ghosh, S. یک رویکرد جدید از الگوریتم حوضه با استفاده از تبدیل فاصله اعمال شده برای تقسیم بندی تصویر. بین المللی J. Innov. Res. محاسبه کنید. اشتراک. مهندس 2013 ، 1 ، 185-189. [ Google Scholar ]
ما، جی. وی، ز. ژانگ، ی. وانگ، ی. Lv، R. زو، سی. گائوکسیانگ، سی. لیو، جی. پنگ، سی. وانگ، ال. و همکاران چگونه نقشه‌های تبدیل فاصله، بخش‌بندی CNN‌ها را تقویت می‌کنند: یک مطالعه تجربی. در تصویربرداری پزشکی با یادگیری عمیق ; مطبوعات PMLR: کمبریج، MA، ایالات متحده آمریکا، 2020؛ صص 479-492. در دسترس آنلاین: https://proceedings.mlr.press/v121/ma20b.html (در 17 ژوئن 2021 قابل دسترسی است).
لی، YH; Horng, SJ الگوریتم های تبدیل فاصله سریع صفحه شطرنج موازی. در مجموعه مقالات کنفرانس بین المللی 1996 در سیستم های موازی و توزیع شده، توکیو، ژاپن، 3-6 ژوئن 1996. ص 488-493. [ Google Scholar ]
لی، YH; Horng، SJ Optimal محاسبه تبدیل فاصله صفحه شطرنج در سیستم های پردازش موازی. محاسبه کنید. Vis. تصویر زیر. 1999 ، 73 ، 374-390. [ Google Scholar ] [ CrossRef ]
Butt, MA; Maragos, P. طراحی بهینه تبدیل فاصله پخ. IEEE Trans. فرآیند تصویر 1998 ، 7 ، 1477-1484. [ Google Scholar ] [ CrossRef ]
فابری، آر. کاستا، LDF؛ تورلی، جی سی. برونو، الگوریتم‌های تبدیل فاصله اقلیدسی OM 2D: یک بررسی مقایسه‌ای. کامپیوتر ACM. Surv. (CSUR) 2008 ، 40 ، 1-44. [ Google Scholar ] [ CrossRef ]
اشمالتز، تی. ملنیچوک، الف. روش تجویز و سیستم‌های مربوط به ورودی‌های خاص محصول منطقه متغیر. ثبت اختراع ایالات متحده CA 2,663,917، دسامبر 2014. [ Google Scholar ]
هال، جی. وکر، ال. اولمر، بی. سماواتی، اف. دیسدیاکیس سه ضلعی DGGS. ISPRS Int. J.-Geo-Inf. 2020 ، 9 ، 315. [ Google Scholar ] [ CrossRef ]
Ciesielski، KC; چن، ایکس. Udupa، JK; گرورا، GJ الگوریتم های زمان خطی برای تبدیل فاصله دقیق. جی. ریاضی. Imaging Vision 2011 ، 39 ، 193-209. [ Google Scholar ] [ CrossRef ]
Shih, FY; Wu، YT تبدیل فاصله اقلیدسی سریع در دو اسکن با استفاده از همسایگی 3×3. محاسبه کنید. Vis. تصویر زیر. 2004 ، 93 ، 195-205. [ Google Scholar ] [ CrossRef ]
Lucet، Y. الگوریتم‌های تبدیل فاصله دقیق اقلیدسی ترتیبی جدید بر اساس تحلیل محدب. تصویر Vis. محاسبه کنید. 2009 ، 27 ، 37-44. [ Google Scholar ] [ CrossRef ]
میچل، جی اس؛ کوه، DM; Papadimitriou، CH مسئله ژئودزیکی گسسته. SIAM J. Comput. 1987 ، 16 ، 647-668. [ Google Scholar ] [ CrossRef ]
سوراژسکی، وی. سوراژسکی، تی. کیرسانوف، دی. گورتلر، اس جی. Hoppe, H. سریع ژئودزیک دقیق و تقریبی روی مش. ACM Trans. نمودار. (TOG) 2005 ، 24 ، 553-560. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
Sahr, K. کدگذاری مکان بر روی شبکه‌های جهانی گسسته با دیافراگم 3 شش ضلعی. شبکه های جهانی گسسته. محاسبه کنید. محیط زیست سیستم شهری 2008 ، 32 ، 174-187. [ Google Scholar ] [ CrossRef ]
بازچاپ شده از Computers, Environment and Urban Systems, 32, Sahr, K., Location Coding on Icosahedral diaperture 3 hexagon gas grids discrete global, 186, Copyright 2022, with مجوز از Elsevier (شماره مجوز 5246110741204).
اولمر، بی. هال، جی. سماواتی، ف. روش عمومی برای گسترش سیستم های شبکه جهانی گسسته به سه بعد. ISPRS Int. J.-Geo-Inf. 2020 ، 9 ، 233. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
اولمر، بی. سماواتی، ف. به سمت شبکه حفظ حجم کروی انحطاط هشت درخت. GeoInformatica 2020 ، 24 ، 505-529. [ Google Scholar ] [ CrossRef ]

شکل 1. DT برای انواع مختلف شبکه ها اعمال می شود ( الف ) شبکه مبتنی بر تصویر معمولی، ( ب ) شبکه نیمه منظم Disdyakis Triacontahedron DGGS، ( ج ) مش عمومی نامنظم. در این تجسم، سلول‌های تیره‌تر به ویژگی نزدیک‌تر و سلول‌های روشن‌تر دورتر از ویژگی هستند.

شکل 2. ( الف ) تصویر باینری قبل از اعمال DT. ( ب ) نتیجه اعمال DT به تصویر باینری.

شکل 3. ( الف ) چهار وجهی ( ب ) هشت وجهی ( ج ) ایکوساهدر ( د ) دوازده وجهی دیسدیاکیس ( ه ) سه ضلعی دیسدیاکیس.

شکل 4. نمونه هایی از چهارگوش متجانس ( الف ) 1 تا 4، ( ب ) مثلث 1 تا 3، و ( ج ) پالایش شش ضلعی ناهمگون. سلول های سیاه سلول های اصلی هستند و خطوط سبز یک سطح از پالایش را نشان می دهند.

شکل 5. Disdyakis Triacontahedron DGGS در وضوح ( a ) 1، ( b ) 2، ( c ) 3.

شکل 6. Disdyakis Triacontahedron DGGS در وضوح سه در حوزه چند وجهی ( سمت چپ ) و حوزه کروی ( راست ).

شکل 7. خط قرمز قوس دایره بزرگی است که نقاط p و q را به هم متصل می کند.

شکل 8. فاصله یک سلول تا یک ویژگی.

شکل 9. نمونه ای از فضای محدود (دایره سبز).

شکل 10. دو نوع مثلث 1 تا 4 اصلاحات با د مناسب. ( الف ) 1:4 دو بخش طولانی ترین لبه، که در [ 26 ] استفاده می شود. ( ب ) پالایش نقطه میانی 1:4 که پالایش رایج تری است.

شکل 11. سلول های خاکستری ردپای شش ضلعی سیاه بزرگ با وضوح 4 بالاتر هستند. تصویر گرفته شده با مجوز Ref. [ 32 ] حق چاپ 2008 Elsevier [ 33 ].

شکل 12. تبدیل فاصله برای مرز انتاریو در وضوح هدف ( a ) 7 (میانگین اندازه سلول: 1037.3 کیلومتر

^{2}

), ( ب ) 9 (میانگین اندازه سلول: 64.8 کیلومتر

^{2}

), ( c ) 12 (میانگین اندازه سلول: 1.0 کیلومتر

^{2}

شکل 13. تبدیل فاصله برای مرز ( a ) سرزمین اصلی بریتیش کلمبیا و ( ب ) نوناووت در وضوح هدف 11 (متوسط اندازه سلول: 4.0 کیلومتر

^{2}

و ( ج ) جزیره ادوارد پرایس با وضوح هدف 15 (میانگین اندازه سلول: 0.016 کیلومتر

^{2}

شکل 14. تبدیل فاصله برای مرز ( a ) شهر کلگری در وضوح هدف 15 (میانگین اندازه سلول: 0.016 کیلومتر

^{2}

) و ( ب ) مزرعه ای در آلبرتا با وضوح هدف 19 (میانگین اندازه سلول: 61.8 متر

^{2}

شکل 15. نقاط نمونه تبدیل فاصله و مرزهای مربوطه وارد شده به ArcGIS Pro برای ( الف ) استان انتاریو، ( ب ) شهر کلگری، و ( ج ) یک مزرعه در آلبرتا.

شکل 16. تعداد عملیات فاصله در وضوح هدف های مختلف برای مرز انتاریو.

شکل 17. تعداد عملیات فاصله در وضوح هدف های مختلف برای مرز انتاریو.

شکل 18. تأثیر رزولوشن پایه بر عملکرد الگوریتم تکراری برای وضوح هدف 12.

شکل 19. تبدیل فاصله از Yellowknife با استفاده از ( a ) ArcGIS و محاسبات مسطح فاصله، ( b ، c ) DGGS و روش ما.

شکل 20. زمان اجرای الگوریتم ما و الگوریتم MMP در وضوح های مختلف برای مرز انتاریو.

مقالات داخلی و بین المللی

10 نظرات

دیدگاهتان را بنویسید لغو پاسخ

برای نوشتن دیدگاه باید وارد بشوید.

مشاورین هوش پیروزی

کلید واژه ها:

1. مقدمه

2. پس زمینه

2.1. تعریف و کاربردهای تبدیل فاصله

2.2. سیستم های شبکه جهانی گسسته

2.2.1. عناصر یک DGGS

2.2.2. فاصله در DGGS

2.3. تبدیل فاصله محاسباتی

2.3.1. محاسبه DT در فضای تصویر

2.3.2. محاسبه DT در فضای مش

2.3.3. محاسبه DT در DGGS

3. کاهش فضای جستجو برای توسعه یک الگوریتم کارآمد

4. محاسبه تبدیل فاصله در DGGS

4.1. رزولوشن تک پله از پایه تا هدف

4.2. پالایش تکراری

5. نتایج و بحث

5.1. تحلیل درستی

5.2. تجزیه و تحلیل عملکرد

5.3. بحث

6. مقایسه

7. نتیجه گیری و کار آینده

اختصارات

پیوست اول

منابع

قبلیمدل‌سازی اولویت بلندمدت و کوتاه‌مدت بر اساس توجه چند سطحی برای توصیه POI بعدی

بعدیتحلیل ویژگی ها و الگوی فضایی صنعت پذیرایی در چهار شهر مرکزی دلتای رودخانه یانگ تسه

مطالب مرتبط ...

آموزش مقاله نویسی در رشته ادبیات فارسی

تأثیر همسایگی درونیابی DEM بر عوامل زمین

رگرسیون وزنی جغرافیایی تطبیقی ​​غیر منفی برای تخمین تراکم جمعیت بر اساس نور شب

10 نظرات

دیدگاهتان را بنویسید لغو پاسخ

درباره سرزمین فناوری مکانی GISLAND

دسترسی سریع

اطلاعات

خبرنامه

خبرنامه

درباره سرزمین فناوری مکانی GISLAND

دسترسی سریع

اطلاعات

دسترسی سریع

رگرسیون وزنی جغرافیایی تطبیقی غیر منفی برای تخمین تراکم جمعیت بر اساس نور شب