چکیده

مدل‌سازی توزیع معیارهای تحرک روزانه و ساعتی انسان برای مطالعه الگوهای سفر انسان مفید است. در مطالعات قبلی، برخی از توابع توزیع احتمال به منظور ایجاد پایگاهی برای تحقیقات تحرک انسانی به کار گرفته شد. با این حال، انتخاب مناسب ترین توزیع هنوز یک کار چالش برانگیز است. در این مقاله، ما بر مدل‌سازی توزیع‌های فاصله سفر، زمان سفر و سرعت سفر تمرکز می‌کنیم. داده‌های سفر روزانه و ساعتی با چندین توزیع نامزد برازش داده می‌شوند و بهترین آنها بر اساس معیار اطلاعات بیزی انتخاب می‌شوند. یک مطالعه موردی با داده‌های آنلاین خودرو در شیان، چین، برای نشان دادن و ارزیابی تناسب مدل ارائه شده است. نتایج نشان می دهد که مسافت سفر و زمان سفر حرکت روزانه و ساعتی انسان از توزیع گاما تبعیت می کند و سرعت سفر را می توان با توزیع Burr تقریب زد. این نتایج می تواند به درک بهتر الگوهای آنلاین سفر با ماشین کمک کند و پایگاهی برای تحقیقات تحرک انسانی ایجاد کند.

کلید واژه ها:

معیارهای تحرک اتصالات توزیع ; توزیع گاما ; توزیع سوراخ ; ماشین سواری آنلاین

1. مقدمه

مدل‌سازی تحرک انسان یک حوزه تحقیقاتی نوظهور است. مطالعه منظم و ویژگی‌های تحرک مکانی-زمانی انسان در بسیاری از زمینه‌ها مانند برنامه‌ریزی شهری [ 1 ، 2 ]، پیش‌بینی ترافیک [ 3 ] و پیشگیری از همه‌گیری [ 4 ، 5 ] اهمیت زیادی دارد.
هنگام مدل‌سازی تحرک انسان، معمولاً تابع توزیع احتمال (PDF) معیارهای آن (مثلاً مسافت سفر، زمان سفر و سرعت سفر) در نظر گرفته می‌شود. به طور کلی پذیرفته شده است که معیارهای تحرک روزانه و ساعتی انسان یک توزیع نماینده دارند [ 6 ]. مدل‌سازی توزیع‌های این معیارها برای مطالعه الگوهای سفر و ایجاد پایگاهی برای تحقیقات تحرک انسانی اساسی، ضروری و مفید است.
اخیراً با توسعه سریع تکنیک‌های اطلاعات و ارتباطات (ICT) و سرویس‌های مبتنی بر مکان (LBS)، حمل‌ونقل آنلاین خودرو مجهز به سیستم موقعیت‌یابی جهانی (GPS) نقش مهمی را در فعالیت‌های سفر روزانه مردم ایفا می‌کند. به عنوان یک منبع داده مهم، پلتفرم های آنلاین حمل خودرو (به عنوان مثال، Uber، Lyft، و Didi Chuxing) حجم زیادی از داده های مکان دقیق را تولید می کنند. برخلاف داده‌های نظرسنجی سنتی، مجموعه داده‌های تلفن همراه، ردیابی شبکه‌های بی‌سیم، و داده‌های مکان تاکسی، داده‌های آنلاین خودرو با کیفیت بالا، وضوح بالا و مقیاس بزرگ مشخص می‌شوند که منعکس‌کننده مسیر دقیق مکانی و زمانی و مبدا و مقصد واقعی هستند. از سفرهای مردم بنابراین، خودرو-هیلینگ آنلاین یک پایه داده غنی و محکم برای مدل‌سازی توزیع ایجاد کرده است.
با توجه به دانش ما، مطالعات قبلی الگوهای بسیار کمی از تحرک انسان را پیشنهاد کرده اند، مانند مدل پرواز لِوی [ 7 ، 8 ]، توزیع قانون توان [ 9 ، 10 ، 11 ، 12 ، 13 ]، توزیع نمایی [ 14 ، 15 ، 16 ] ، 17 ، 18 ]، توزیع لگ نرمال [ 19 ، 20 ، 21 ، 22 ]، توزیع وایبول [ 23 ]، توزیع پارتو [ 24 ]، و توزیع گاما [ 22 ]]. براکمن و همکاران مشاهده کرد که فاصله سفر انسان با تجزیه و تحلیل ویژگی های آماری گردش اسکناس توزیع قانون قدرت را نشان می دهد و مسیرهای سفر انسان ممکن است به صورت پروازهای Lévy (پیاده روی تصادفی دم سنگین) تقریبی شود [ 7 ]. این مشاهدات توسط Rhee و همکاران تایید شد. با استفاده از سیستم موقعیت یاب جهانی (GPS) ردیابی جمع‌آوری‌شده از داوطلبان، احتمال غیر قابل اغماض سفرهای جابه‌جایی بالا و زمان مکث طولانی بین سفرها را نشان می‌دهد [ 8 ]. علیرغم تصادفی بودن نشان داده شده توسط مدل های پرواز Lévy، یک قانون توان با یک قطع نمایی می تواند برای تقریب توزیع جابجایی مسیرهای انسانی به دست آمده از مجموعه داده های تلفن همراه [ 9 ، 11 ]، ردیابی GPS [ 12 ] استفاده شود.] و شبکه های اجتماعی مبتنی بر مکان آنلاین [ 13 ]. با این حال، کانگ و همکاران، جیانگ و همکاران، و لیانگ و همکاران. اشاره کرد که می توان از توزیع نمایی برای تقریب جابجایی و زمان سفر تاکسی ها به جای قانون توان استفاده کرد [ 14 ، 15 ، 16 ، 17 ، 18 ]. علاوه بر این، با تجزیه و تحلیل مجموعه داده تاکسی ردیابی، وانگ و همکاران. دریافتند که جابجایی تمایل به پیروی از توزیع نمایی دارد و زمان سفر با توزیع لگ نرمال تقریبی می شود [ 19 ].
اگرچه یافته‌های ذکر شده در بالا مرجع مفیدی در مورد استخراج تحرک انسان ارائه می‌کنند، اما بیشتر بر روی یک مدل متمرکز هستند که ممکن است به خوبی با همه داده‌ها مطابقت نداشته باشد. ژنگ و همکاران دریافتند که یک تابع همجوشی، بر اساس قانون توان نمایی و توزیع پارتو کوتاه شده، بهترین توزیع زمان سفر را نشان می دهد [ 24 ]. بذانی و همکاران داده‌های GPS اتومبیل‌های شخصی را در فلورانس، ایتالیا مطالعه کرد و دریافت که طول یک سفر از یک رفتار نمایی در مقیاس مسافت کوتاه پیروی می‌کند اما از توزیع قانون قدرت برای سفرهای طولانی‌تر از 30 کیلومتر حمایت می‌کند [ 18 ]. Csáji و همکاران و ژانگ و همکاران دریافتند که توزیع نمایی برای مسافت‌های سفر مناسب نیست و توزیع نرمال لگاریتم برازش‌های معقولی را فراهم می‌کند [ 20 ، 21 ]]. پلوتز و همکاران از توزیع‌های Weibull، Gamma و lognormal برای تناسب با مسافت‌های رانندگی روزانه فردی استفاده کرد و دریافت که Weibull و lognormal اغلب بهتر از گاما عمل می‌کنند و توزیع Weibull با بیشتر داده‌ها مطابقت دارد اما نه با همه [ 23 ]. کو و کای توزیع‌های مسافت سفر و زمان سفر را تجزیه و تحلیل کردند و دریافتند که هر دوی آنها از توزیع لگ نرمال در سیستم‌های اشتراک دوچرخه بزرگ‌تر پیروی می‌کنند، در حالی که توزیع برای سیستم‌های کوچک‌تر در میان Weibull، Gamma و lognormal متفاوت است [ 22 ].
به طور خلاصه، با توجه به مجموعه داده‌های مختلف، بسیاری از مطالعات تجربی نشان داده‌اند که معیارهای تحرک ممکن است با چندین توزیع معنادار، مانند مدل‌های پرواز Lévy، نمایی، قانون قدرت، lognormal، گاما، Weibull و Rayleigh سازگار شوند. با این حال، بر اساس یک مجموعه داده مسیر حرکت خودرو در مقیاس بزرگ، آیا یک مدل منفرد یا ترکیبی می‌تواند به تناسب خوبی برای همه داده‌ها دست یابد؟ باقی مانده است که بیشتر مورد بررسی قرار گیرد. علاوه بر این، مطالعات فوق بر مدل‌سازی توزیع تحرک انسان با داده‌های ساده یا کلی متمرکز شدند، در حالی که تغییرپذیری PDF همراه با روز هفته و زمان روز را نادیده گرفتند. آیا نوع توزیع معیارهای تحرک در دانه بندی زمانی متفاوت با داده های کلی متفاوت است؟ اگر بله، چگونه متفاوت خواهد بود، و آیا می توان آن را با توزیع کلی توصیف کرد؟ این امر توجه بسیاری از علما را برانگیخته است. بنابراین، تحقیقات ما، بر اساس مجموعه داده‌های مسیر حرکت خودرو در مقیاس بزرگ، ضروری است و بینش ارزشمندی در مورد الگوهای تحرک انسان به دست می‌آورد.
برای پر کردن این شکاف، هدف این مقاله مدل‌سازی توزیع معیارهای تحرک انسانی در دانه‌بندی زمانی مختلف است. به طور خاص، سه معیار (مسافت سفر، زمان سفر، و سرعت سفر) برای بررسی داده‌های مسیر عظیم جمع‌آوری‌شده در شیان، چین معرفی شده‌اند. برای هر معیار تحرک، چندین توزیع نامزد بر اساس معیارهای انتخاب مدل مقایسه می‌شوند و بهترین آنها انتخاب می‌شود. توزیع‌های آماری داده‌های سفر روزانه ابتدا تحلیل می‌شوند و ویژگی توزیع کج را نشان می‌دهند. به طور دقیق تر، توزیع های ساعتی بیشتر ارزیابی می شوند و توزیع کلی برای هر متریک تحرک تعیین می شود.
ادامه این مقاله به شرح زیر سازماندهی شده است. بخش 2 به اختصار مجموعه داده آنلاین خودرو-هیلینگ را معرفی می کند و تجزیه و تحلیل اساسی را انجام می دهد. بخش 3 معیارهای سفر، توزیع اتصالات و روش انتخاب مدل را شرح می دهد. بخش 4 نتیجه و تجزیه و تحلیل را ارائه می دهد. بخش 5 یافته ها را مورد بحث قرار می دهد. در نهایت، بخش 6 نتیجه گیری و توصیه هایی را برای تحقیقات بیشتر ارائه می دهد.

2. جمع آوری داده ها و تجزیه و تحلیل پایه

2.1. توضیحات داده ها

داده‌های مسیر اتخاذ شده توسط حدود 18000 سفر آنلاین با خودرو در شیان، چین، از 1 اکتبر 2016 تا 30 نوامبر 2016 تولید شد. مسیرهای خودرو از نقاط GPS با وضوح بالا تشکیل شده بود که هر 2 تا 4 ثانیه ثبت می‌شد. بر این اساس، یک مسیر آنلاین خودرو-هیلینگ دنباله ای از نقاط نمونه برداری GPS با پنج میدان است. شناسه خودرو و شناسه سفارش برای محافظت از حریم خصوصی حساسیت زدایی شدند. «مهر زمان» زمان ثبت داده‌ها را نشان می‌دهد که زمان UTC بود. “Latitude” و “Longitude” اطلاعات موقعیت مکانی حمل و نقل آنلاین خودرو را فراهم می کند.
اجازه دهید تیrمنj=(پ1من،j،پ2من،j،⋯،پنمن،j)نشان دهنده مسیر حرکت jتیساعتسفر وسیله نقلیه من، جایی که پnمن،j=(ایکس،y،تی)nمن،jهست nتیساعتنقطه دنباله ( n=1،2،⋯،ن). (ایکس،y)nمن،jنشان دهنده مکان و تیnمن،jبه ترتیب مهر زمانی با توجه به یک مسیر، تی1من،j<تی2من،j<⋯<تینمن،j. برای یک وسیله نقلیه، مکان مبدا و مقصد (OD) اولین و آخرین نقاط نمونه سفر هستند. منطقی است که تعریف کنیم پOمن،j=پ1من،jو پDمن،j=پنمن،j. از این رو، هر سفر OD را می توان ساده کرد تا بردار از پOمن،jبه پDمن،j.
یک شبکه جاده شامل مجموعه ای از گره ها، پیوندهای هدایت شده و حرکات مجاز است. هر گره یک مکان جغرافیایی است که یک تقاطع شبکه را نشان می دهد که می تواند سیگنال دار یا بدون سیگنال باشد. یک پیوند به عنوان بخش جاده از گره دم تا گره سر تعریف می شود. موقعیت نسبی نشان دهنده نسبت یک نقطه نمونه برداری نسبت به گره شروع پیوند است که محدوده دارد [0، 1]. به عنوان مثال، مقدار 0، 0.5، و 1 از موقعیت نسبی نشان دهنده شروع، وسط و پایان یک پیوند است.

2.2. پردازش داده ها

برای مدل‌سازی توزیع فاصله سفر، تطبیق نقشه (MM) و الگوریتم استنتاج مسیر پیشنهاد شده توسط چن و همکاران. برای اولین بار مورد استفاده قرار گرفتند [ 25 ]. همانطور که در جدول 1 نشان داده شده است ، طول و عرض جغرافیایی اولیه به مختصات ژئودتیکی تبدیل شده است که می تواند مستقیماً برای محاسبه جابجایی سفر مورد استفاده قرار گیرد. در مرحله دوم، موقعیت نسبی نقطه نمونه برداری روی پیوند نیز محاسبه شد و زمان UTC به زمان روز (0-86400 ثانیه) تبدیل شد. ثالثاً، برای محاسبه معیارهای سفر (به عنوان مثال، زمان سفر، جابجایی سفر، مسافت سفر) نقاط تحویل و رها کردن استخراج شد.
در نهایت، تمیز کردن داده ها یک کار ضروری است، زیرا برخی از سوابق سفر برای استفاده در این مطالعه مناسب نبودند. با در نظر گرفتن هزینه‌های سفر، تعداد کمی از مسافران زمانی که زمان و مسافت سفر بسیار کوتاه یا طولانی است، با خودروی آنلاین سفر می‌کنند [ 26 ، 27 ]. علاوه بر این، سرعت سفر باید در محدوده معقولی باشد. بنابراین، شرایط زیر منجر به حذف سوابق سفر از داده‌های مطالعه شد: (1) مسافت سفر و جابجایی بین مبدا و مقصد کمتر از 300 متر. (2) زمان سفر کمتر از 1 دقیقه یا بیشتر از 2 ساعت؛ (3) سرعت متوسط ​​سفر کمتر از 5 کیلومتر در ساعت یا بیش از 80 کیلومتر در ساعت [ 28 ].
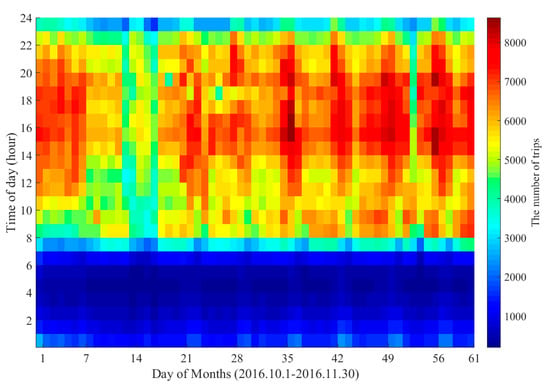
از مجموع سفرهای دو ماهه، 6 میلیون و 203 هزار و 848 سفر از 6 میلیون و 584 هزار و 397 سفر اصلی پس از پاک‌سازی داده‌ها به‌دست آمد که حدود 6 درصد از سفرها فیلتر شدند. از منظر سفرهای روزانه، میانگین در دسترس بودن سفارش 94.22 درصد بوده که بین 93.21 درصد و 94.85 درصد در نوسان بوده است. به طور معمول، دوره مطالعه به 1464 (24 * 61) فواصل 1 ساعته برای تجزیه و تحلیل بیشتر از سفرهای ساعتی ساکنان گسسته شد. مقدار سفر ساعتی از 192 تا 8636 متغیر بود، همانطور که در شکل 1 نشان داده شده است.. در مجموع تعداد سفرها در روز بسیار بیشتر از شب بوده که با تحرک انسان همخوانی دارد. به هر حال، تحرک انسان در طول روز فعال‌تر، مهم‌تر و معنادارتر است. علاوه بر این، تعداد سفرهای ساعتی بین ساعت 00:00 تا 07:00 ممکن است کمتر از 2000 باشد، اما برای اتصال توزیع کافی بود.

3. معیارهای سفر و برازش داده ها

3.1. معیارهای سفر

در مطالعات موجود، به دلیل عدم تطبیق نقشه، معمولاً فاصله سفر با جابجایی یا فاصله منهتن مبدا و مقصد جایگزین می شود. با این حال، فاصله سفر در اینجا به طول مسیر واقعی طی شده توسط سفر OD در شبکه های جاده ای اشاره دارد. یک مسیر از یک سری پیوندهای متوالی تشکیل شده است و طول آن مجموع طول پیوندهای موجود در سفر OD است. شایان ذکر است که پیوندهایی که مبدا و مقصد (OD) در آن قرار دارند، ممکن است از طریق آنها سفر نکنند. بر اساس تطبیق نقشه و نتایج استنتاج مسیر، مسافت سفر دمنj(TD) به صورت زیر محاسبه می شود:

دمنj=(1-rOمن،j)⋅دOمن،j+∑ک=2م-1دکمن،j+rDمن،j⋅دDمن،j

که در آن M تعداد پیوندهای موجود در سفر است. rOمن،jو rDمن،jنسبت OD سفر را نسبت به گره شروع پیوند نشان می دهد که دامنه آن متغیر است [0،1]. دOمن،jو دDمن،jطول پیوندی است که OD سفر در آن قرار دارد.

زمان سفر یکی دیگر از معیارهای مهم است و ارتباط نزدیکی با مسافت سفر دارد. زمان سفر به معنای زمان سپری شده از مبدا تا مقصد است و تحت تأثیر شرایط ترافیکی لحظه ای، شرایط آب و هوایی، عادات رانندگی راننده و غیره است. به عنوان یک شاخص مهم برای تجزیه و تحلیل تحرک انسان، زمان سفر منعکس کننده شرایط دسترسی و ترافیک است. برای یک مسیر سفر jاز وسیله نقلیه من، زمان سفر تیمنj(TT) به صورت زیر تعریف می شود:

تیمنj=تینمن،j-تی1من،j=تیDمن،j-تیOمن،j

برای درک رابطه بین معیارهای توصیف شده در بالا، سرعت سفر یکی دیگر از ویژگی های مهم است. میانگین سرعت سفر vمنj(TS) به صورت زیر تعریف می شود:

vمنj=دمنj/تیمنj

3.2. توزیع مناسب

انتخاب تابع برازش برای شناسایی مناسب ترین توزیع است که توسط داده های سفر واقعی پشتیبانی می شود. در ادبیات موجود، توزیع‌های نمایی، (قطع) قدرت-قانون، لگ نرمال، گاما، وایبول و برر معمولاً توزیع‌هایی برای برازش معیارهای سفر بالا استفاده می‌شوند [ 6 ، 11 ، 15 ، 19 ، 21 ، 29 ، 30 ، 31 ، 32 ]. با این حال، همه توزیع های فوق برای داده های این مطالعه اعمال نمی شود. به منظور محدود کردن دامنه توزیع‌های نامزد، یک روز از داده‌های دو ماهه به‌طور تصادفی انتخاب شد تا ویژگی‌های معیارهای سفر را تجزیه و تحلیل کند. شکل 2هیستوگرام های توزیع فرکانس و توابع توزیع تجمعی (CDF) مسافت سفر، زمان سفر و سرعت سفر را نشان می دهد. بر اساس شکل این هیستوگرام ها، می توان دریافت که این داده ها یک انحراف راست قابل توجه را نشان می دهند که با محاسبه چولگی نیز ثابت می شود (یعنی 1.05، 1.60، 0.95). علاوه بر این، CDF قبل از رسیدن به حداکثر به یک بسیار نزدیک است. به عنوان مثال، احتمال مسافت طی 15 کیلومتر به 99.96 درصد می رسد و 99.93 درصد سفرها زمان سفر کمتر از 1 ساعت دارند. کشیدگی بیش از حد نشان می دهد که داده ها بیش از حد متمرکز هستند، احتمالاً به دلیل وجود مقادیر شدید.
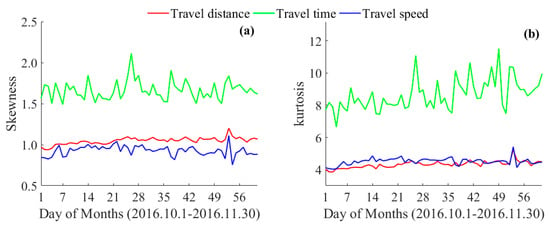
برای درک بیشتر شکل داده ها با جزئیات، چولگی و کشیدگی داده های روزانه در شکل 3 نشان داده شده است. چولگی روزانه بیشتر از 0.6 است که از 0.75 تا 2.1 متغیر است. این نشان می دهد که همه داده ها یک انحراف درست را نشان می دهند، به خصوص داده های زمان سفر. در همین حال، کشیدگی بیشتر از سه نشان‌دهنده شیب پراکندگی توزیع است، که امکان باریک‌تر شدن محدوده گسترش معیارهای سفر را ثابت می‌کند. به طور معمول، چولگی ساعتی و کشیدگی به ترتیب 1.07 و 5.83 هستند، که همچنین نشان می دهد که داده های سفر ساعتی به احتمال زیاد با توزیع اریب مطابقت دارد.

بر اساس تجزیه و تحلیل فوق، پنج توزیع اریب متداول -lognormal، گاما، Weibull، Burr و Rayleigh- به عنوان توزیع‌های کاندید برای تناسب با داده‌های روزانه و ساعتی انتخاب می‌شوند. توابع چگالی احتمال (PDF) این توزیع ها در فرمول های زیر تعریف شده است. با فرض اینکه متغیر ایکساز توزیع لگ نرمال پیروی می کند، PDF آن را می توان به صورت بیان کرد

f(ایکس)=1ایکس⋅σ2π⋅ه(-(لوگاریتمایکس-μ)22⋅σ2)

جایی که μو σمیانگین و انحراف معیار لگاریتم طبیعی متغیر را نشان می دهد ایکس. انتظارات ریاضی و واریانس به ترتیب می باشد E(ایکس)=هμ+σ2/2و Vآr(ایکس)=(هσ2-1)⋅ه2⋅μ+σ2.

توزیع گاما با پارامترهای شکل و مقیاس αو βاست

f(ایکس)=1βα⋅Γ(α)⋅ایکسα-1⋅ه-ایکسβ

جایی که Γ(⋅)تابع گاما را ارائه می دهد و Γ(1)=1. میانگین و واریانس با E(ایکس)=α⋅β،Vآr(ایکس)=α⋅β2. در اینجا لازم به ذکر است که نمایی و χ2توزیع ها موارد خاصی از توزیع گاما هستند. به عنوان مثال، هنگامی که پارامتر شکل α1 است، توزیع گاما یک توزیع نمایی با پارامتر است 1/β.

توزیع Weibull به صورت تعریف شده است

f(ایکس)=کλ⋅(ایکسλ)ک-1⋅ه-(ایکسλ)ک

جایی که ک>0،λ>0به ترتیب پارامترهای شکل و مقیاس هستند. میانگین و واریانس هستند E(ایکس)=λ⋅Γ(1+1ک)و Vآr(ایکس)=λ2⋅[Γ(1+2ک)-Γ(1+1ک)2]. PDF نسخه 3 پارامتری توزیع Burr می باشد

f(ایکس)=ج⋅کα⋅(ایکسα)ج-1⋅(1+(ایکسα)ج)-(ک+1)

جایی که α>0یک پارامتر مقیاس بندی است، ج>0و ک>0پارامترهای شکل هستند. میانگین و واریانس توسط محاسبه می شود E(ایکس)=α⋅ک⋅Γ(ک-1ج)⋅Γ(1+1ج)Γ(1+ک)و Vآr(ایکس)=α2⋅ک⋅Γ(ک-2ج)⋅Γ(1+2ج)Γ(1+ک)-(E(ایکس))2.

PDF Rayleigh فقط یک پارامتر برای تخمین دارد که به دلیل سادگی آن را برای نمایش توزیع معیارهای سفر محبوب می کند. توزیع آن یک مورد خاص از توزیع Weibull است که در آن مقدار پارامتر شکل 2 است. PDF توزیع ریلی با یک پارامتر αاست

f(ایکس)=ایکسα2⋅ه-ایکس22⋅α2
میانگین و واریانس هستند E(ایکس)=π2⋅αو Vآr(ایکس)=4-π2⋅α2، به ترتیب. در ادبیات، پارامترها با تخمین حداکثر درستنمایی (MLE) بهینه می‌شوند و استنتاج دقیق می‌تواند به Clauset و همکارانش مراجعه کند. [ 33 ].

3.3. انتخاب مدل

به منظور ارزیابی مدل برازش بین داده‌های واقعی و توزیع نامزد، دو روش اساساً متفاوت، آزمون‌های فرضیه صفر و معیارهای انتخاب مدل، اغلب برای انتخاب مدل مناسب یا بهترین مدل استفاده می‌شوند [ 34 ]. از نظر تئوری، آنها می توانند به تناسب مدل و پیچیدگی دست یابند. آزمون کولموگروف-اسمیرنوف (K-S) معمولاً برای ارزیابی خوب بودن برازش توزیع‌های کاندید استفاده می‌شود [ 6 ، 22 ، 29 ، 35 .]. با این حال، آزمون K-S برای نمونه های کوچک مناسب است. وقتی داده ها خیلی بزرگ هستند، مقدار بحرانی برای رد بسیار کوچک است و نتیجه اغلب فرضیه صفر را رد می کند. آزمون K-S ممکن است تمام توزیع های نامزد را رد کند. با این حال، ممکن است چندین توزیع را نیز قابل قبول در نظر بگیرد. با توجه به مقدار زیاد سفرهای روزانه و ساعتی نشان داده شده در شکل 1 ، آزمون K-S برای این وضعیت مناسب نیست.

علاوه بر این، معیار اطلاعات آکایک (AIC) می تواند روش تصمیم گیری دیگری را ارائه دهد [ 15 ، 16 ، 19 ]. امتیاز AIC تابعی از حداکثر احتمال log آن است ( Lمن) و تعداد پارامترهای تخمین زده شده ( کمن) برای هر مدل کاندید من، و توسط محاسبه می شود

آمنسیمن=-2⋅لوگاریتمLمن+2⋅کمن

به طور کلی، مدلی با کوچکترین AIC ترجیح داده می شود. در این مطالعه، نمونه کوچک AIC بی طرفانه به دلیل تعداد زیاد سفرهای روزانه یا ساعتی در نظر گرفته نشده است. تعداد سفرهای ساعتی از چند صد تا نزدیک به ده هزار تغییر می کند، بنابراین یافتن توزیع مناسب برای دوره های مختلف مهم است. بنابراین، معیار اطلاعات بیزی (BIC، همچنین به عنوان معیار شوارتز SC شناخته می شود) بیشتر برای انتخاب مدل استفاده می شود. BIC از نظر ساختاری مشابه AIC است، اما شامل یک عبارت جریمه در اندازه نمونه است ( ن) و تمایل به مدل های ساده تر دارد، به ویژه با افزایش حجم نمونه.

بمنسیمن=-2⋅لوگاریتمLمن+کمن⋅لوگاریتمن

BIC در مقیاس نسبی است. تفاوت BIC Δمن=بمنسیمن-بمنسیدقیقه (بمنسیدقیقه=دقیقهمن∈{1،2،⋯،n}{بمنسیمن})اجازه می دهد تا یک رتبه بندی فوری از nمدل های کاندید [ 36 ]. هر چه اختلاف BIC برای یک مدل بیشتر باشد، احتمال اینکه بهترین مدل باشد کمتر است. به طور خاص، وزن Akaike wمن[ 37 ] نشان دهنده عادی سازی احتمال نسبی است (یعنی، ه-Δمن/2) از مدل ها.

wمن=ه-Δمن/2∑j=1nه-Δj/2
وزن آکایک برای ارزیابی عدم قطعیت انتخاب مدل بسیار مفید است. مدلی با بیشترین وزن آکایک باید به عنوان بهترین توزیع انتخاب شود.

3.4. ارزیابی تناسب توزیع

به منظور نشان دادن نزدیکی توزیع‌های فراوانی نظری و تجربی، دقت با استفاده از شاخص‌های آماری زیر ارزیابی می‌شود: ضریب تعیین (R 2 )، میانگین خطای مطلق (MAE)، میانگین درصد مطلق خطا (MAPE)، احتمال خارج از حد پیش‌بینی‌شده. فاصله (POPI)، احتمال خارج از بازه مشاهده شده (POOI)، و معیار مبتنی بر POPI-POOI (PPC).

برای بسیاری از کاربردهای حمل و نقل، ایجاد فاصله در یک سطح اطمینان معین از توزیع برازش معنادار است. دقت فاصله اطمینان نشان دهنده دقت یکپارچه میانگین پیش بینی شده و STD است. علاوه بر این، صدک ها نیز یک روش موثر برای ارزیابی دقت میانگین و STD هستند. در این مطالعه میانگین خطای مطلق (MAE) و میانگین درصد خطای مطلق (MAPE) صدک ها به شرح زیر گسترش یافت:

مآپE=100%n⋅∑من=1n|پتیمنoبس-پتیمنfمنتی|پتیمنoبس
مآE=1n⋅∑من=1n|پتیمنoبس-پتیمنfمنتی|

جایی که nتعداد صدک ها است و پتیمنoبس،پتیمنfمنتیصدک های مشاهده شده به دست آمده از بررسی میدانی و توزیع برازش هستند. کوچکتر مآپEو مآEدقت بالاتر توزیع اتصالات را نشان می دهد.

دو معیار برای ارزیابی دقت توزیع تخمین زده شده یا پیش بینی شده به کار گرفته شد: احتمال خارج از بازه پیش بینی شده (POPI) و احتمال خارج از بازه مشاهده شده (POOI) [ 38 ، 39 ]. POPI درصد داده‌های مشاهده‌شده را خارج از فاصله اطمینان پیش‌بینی‌شده اندازه‌گیری می‌کند، در حالی که POOI درصد توزیع پیش‌بینی‌شده را خارج از فاصله اطمینان مشاهده‌شده اندازه‌گیری می‌کند. اجازه دهید لfمنتی=Φfمنتی-1(α/2)و توfمنتی=Φfمنتی-1(1-α/2)به ترتیب مرزهای پایین و بالایی توزیع برازش در سطح اطمینان باشد 1-α، جایی که Φfمنتی-1(⋅)تابع توزیع تجمعی معکوس (CDF) توزیع برازش است. از نظر ریاضی، POPI به صورت تعریف می شود

پOپمن=(1-∑من=1نجمن/ن)×100%

جایی که جمن=1اگر نمونه ∈[لfمنتی،توfمنتی]، در غیر این صورت جمن=0. مقدار POPI از 0 تا 1 متغیر است. POPI کوچکتر نشان دهنده جذب نسبت بیشتری از داده های مشاهده شده است، به عنوان مثال، دقت بالاتر توزیع برازش. همانطور که شی و همکاران اشاره کردند. [ 38 ، 39 ]، این متریک POPI بسیار مفید است، اما تمایل دارد برای موقعیت هایی با فواصل برازش گسترده به دلیل خطاهای STD بزرگ، سوگیری نشان دهد.

به عنوان یک جایگزین، متریک POOI درصد توزیع پیش‌بینی‌شده در خارج از فاصله زمانی سفر مشاهده‌شده است. اجازه دهید لoبسو توoبسبه ترتیب مرزهای پایین و بالایی بازه مشاهده شده را در سطح اطمینان نشان می دهد 1-α. سپس

پOOمن=(1-(Φfمنتی(توoبس)-Φfمنتی(لoبس)))×100%

Φfمنتی(⋅)نشان دهنده CDF توزیع اتصالات است. POOI همچنین در محدوده [0، 1] قرار دارد و POOI بزرگتر نشان دهنده دقت بازه مناسب کمتر است، زیرا نسبت بزرگتر خارج از بازه مشاهده شده است. بنابراین، ماتریس های POPI و POOI برای ارزیابی دقت توزیع برازش مکمل یکدیگر هستند. هر چه این دو به آن نزدیکتر باشند α، مدل مناسب تر است. هر چه POPI بزرگتر باشد، POOI مربوطه کوچکتر است. بنابراین، معیاری برای متعادل کردن انحراف POPI و POOI مورد نیاز است α. با توجه به این استدلال، معیار مبتنی بر POPI-POOI (PPC) زیر برای ارزیابی جامع POPI و POOI پیشنهاد شده است:

پپسی=12⋅(|پOپمن-α|+|پOOمن-α|)×100%
به طور کلی، کوچک بودن PPC نشانه خوبی از فاصله اطمینان ساخته شده (به طور همزمان دستیابی به تناسب مدل بالا) است.

4. نتایج بهترین توزیع

این بخش نتایج برازش معیارهای سفر را با استفاده از توزیع‌های کج‌شده نامزد گزارش می‌کند. بهترین توزیع معیارهای سفر روزانه ابتدا نشان داده شده است. سپس، بهترین نتایج مربوط به معیارهای سفر ساعتی، مانند مسافت سفر، زمان سفر، و سرعت سفر را بیشتر تحلیل می‌کنیم. در نهایت، ما سعی می کنیم یک توزیع کلی برای هر متریک سفر شناسایی کنیم و پارامترهای آن را تخمین بزنیم.

4.1. بهترین توزیع معیارهای سفر روزانه

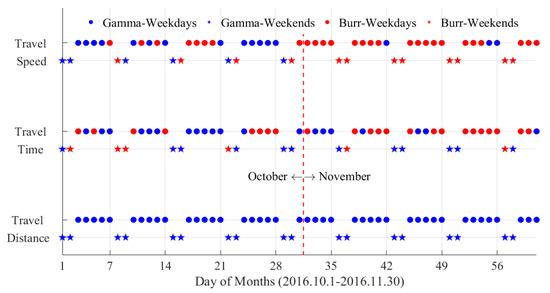
شکل 4 بهترین توزیع معیارهای سفر روزانه را برای 61 روز نشان می دهد. به طور کلی، تنها دو مورد از توزیع‌های کاندید، توزیع‌های گاما و بور (که با آبی و قرمز نشان داده می‌شوند)، برای برازش این معیارهای سفر مناسب هستند. توزیع گاما برای مسافت سفر بهترین عملکرد را دارد و می تواند به طور یکنواخت همه داده های روزانه را مطابق با رنگ آبی در شکل 4 قرار دهد. با این حال، توزیع گاما با تمام داده های زمان سفر یا سرعت به خوبی مطابقت ندارد. در مجموع، 47.54٪ (29 از 61) از داده های زمان سفر و 63.93٪ (39 از 61) از داده های سرعت سفر از توزیع Burr پیروی می کنند (به رنگ قرمز نشان داده شده است).
نتایج برازش برای روزهای هفته و آخر هفته در شکل 4 با دو نشانگر مختلف (نقطه و ستاره) متمایز می شوند. برای مسافت سفر، داده ها در روزهای هفته و آخر هفته را می توان به خوبی با توزیع یکسان تطبیق داد. با این حال، برای داده‌های زمان سفر در آخر هفته‌ها، یک سوم آنها مشمول توزیع گاما، بقیه به توزیع Burr و داده‌های سرعت آخر هفته برعکس هستند. در همین حال، تنها 37.21٪ (16 از 43) از داده های سرعت سفر در روزهای هفته از توزیع گاما تبعیت می کند که در روزهای هفته نوامبر به 13.64٪ (3 از 22) کاهش می یابد.
تجزیه و تحلیل فوق همچنین نشان می دهد که به دلیل توزیع یکنواخت و ساده، مسافت سفر برای تجزیه و تحلیل الگوهای تحرک ساکنان ساده تر است. در مقایسه، زمان سفر و سرعت به دلیل انواع توزیع نامشخص معیارهای نسبتاً پیچیده ای هستند.
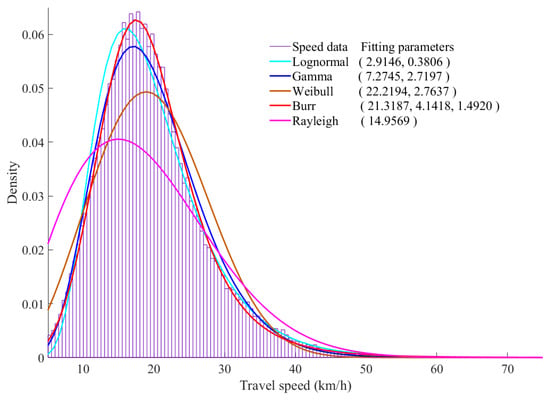
علاوه بر این، میانگین وزن BIC مسافت سفر، زمان سفر و سرعت سفر به ترتیب 1، 0.9996 و 0.9960 است که نشان دهنده عدم قطعیت پایین نتایج برازش است. کوچکترین وزن BIC در داده‌های سرعت سفر در 13 اکتبر رخ می‌دهد و توزیع اتصالات و پارامترهای دقیق در شکل 5 نشان داده شده‌اند . از شکل می توان دریافت که توزیع Burr بیشترین سازگاری را با داده های سرعت دارد و به دنبال آن توزیع گاما قرار دارد. قابل توجه است که توزیع Burr پیچیده تر از توزیع گاما است. احتمال دستیابی به برازش بهتر مدل پیچیده تر به طور قابل توجهی بیشتر از مدل ساده تر است، اما تناسب و پیچیدگی مدل باید به طور جامع در نظر گرفته شود.
جدول 2 پارامترهای بیشتری را در انتخاب مدل نشان می دهد. میانگین مشاهده شده و تغییرات استاندارد (STD) بسیار شبیه به چندین تخمین است. شاخص‌های ارزیابی رایج، مانند میانگین درصد مطلق خطا (MAPE) و ریشه میانگین مربعات خطا (RMSE)، در شناسایی توزیع غالب نیز مشکل هستند. علاوه بر این، احتمال ورود به سیستم توزیع Burr کمی بیشتر از توزیع گاما است، که از نظر کمی ثابت می‌کند که توزیع Burr برازش مدل بهتری دارد. هنگامی که BIC پیچیدگی مدل را در نظر می گیرد، شکاف به 2 کاهش می یابد ( Δ=499,118-499,116=2) به این معنی است که مزایای تناسب مدل بهبود یافته بیشتر از هزینه پیچیدگی مدل اضافه شده است. این مزیت کوچک به وضوح در وزن BIC متمایز است که انتخاب مدل را واضح تر می کند. می توان تعیین کرد که بهترین مدل توزیع Burr است.

4.2. بهترین توزیع فاصله ساعتی سفر

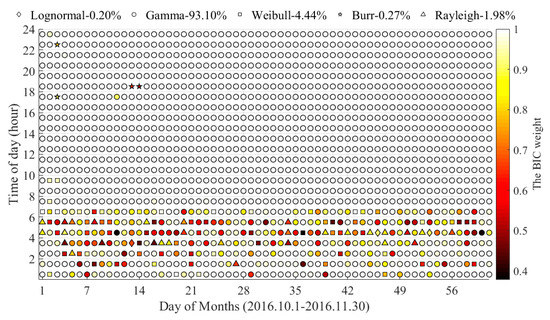
به منظور بررسی بیشتر توزیع‌های ساعتی معیارهای سفر، دوره مطالعه به 1464 (61*24) فواصل 1 ساعتی گسسته‌سازی شده است. شکل 6بهترین توزیع فاصله سفر ساعتی را نشان می دهد. بهترین توزیع‌ها با پنج نشانگر متفاوت متمایز می‌شوند، که توزیع گاما 93.10% را به خود اختصاص می‌دهد – بسیار بالاتر از چهار توزیع دیگر. بین ساعت 07:00 و 24:00، نسبت توزیع گاما به 99.32 درصد افزایش می یابد که مزیت توزیع گاما را در برازش داده های مسافت سفر نشان می دهد. در زمان‌های 00:00 تا 07:00، توزیع بهینه با ساعت‌ها و روزها متفاوت است و به‌طور آشفته در پنج نشانگر مختلف نشان داده می‌شود. تنها 77.99 درصد از داده ها هنوز از توزیع گاما تبعیت می کنند، در حالی که 14.52 درصد برای توزیع Weibull، 6.79 درصد برای توزیع Rayleigh، و کمتر از 1 درصد برای توزیع لگ نرمال. این ممکن است به دلیل حجم نمونه کوچک در شب باشد.
علاوه بر این، وزن‌های BIC در رنگ‌های مختلف از 0.38 تا 1 متغیر است. هر چه رنگ تیره‌تر باشد، وزن BIC کوچک‌تر است. از جدول 3 قابل مشاهده استکه اکثر وزن های BIC بین ساعت 07:00 و 24:00 بسیار نزدیک به 1 هستند. میانگین وزن BIC آنها 0.9986 است که نشان دهنده قابلیت اطمینان بالا در انتخاب مدل است. با این حال، میانگین وزن BIC از ساعت 00:00 تا 7:00 0.8540 است، که نشان می دهد برخی عدم قطعیت در نتایج برازش وجود دارد. به طور دقیق تر، میانگین وزن BIC توزیع های لگ نرمال، ویبول و ریلی به ترتیب 0.8362، 0.7094 و 0.7210 است. عدم قطعیت بالا ممکن است ناشی از حجم نمونه کوچک باشد، زیرا افراد کمتری در شب سفر می کنند. در همین حال، وزن‌های پایین‌تر نیز به این معنی است که بهترین و نابهینه توزیع‌های برازش ممکن است هر دو برای داده‌ها قابل استفاده باشند. در نتیجه، توزیع گاما ممکن است برای تمام داده های مسافت سفر نیز قابل استفاده باشد.

4.3. بهترین توزیع زمان سفر ساعتی

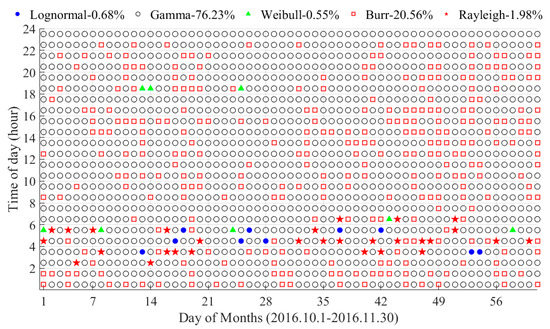
شکل 7 بهترین توزیع زمان سفر ساعتی را نشان می دهد که با نشانگرهای مختلف متمایز می شوند. همانطور که توسط دایره های سیاه و مربع های قرمز نشان داده شده است، توزیع های گاما و برر به ترتیب با نسبت های 76.23٪ و 20.56٪، انواع توزیع غالب هستند. در جدول 4 ، وزن BIC بزرگتر (0.9430 و 0.8982) این دو توزیع مزیت قابل توجهی را نسبت به سه توزیع دیگر در هنگام برازش 96.79 درصد از داده ها نشان می دهد. در همین حال، نتایج برازش قابلیت اطمینان بالاتری دارند.
از سوی دیگر، سه توزیع دیگر که با نقاط آبی، مثلث های سبز و ستاره های قرمز در شکل 7 نشان داده شده اند ، کمتر از 4 درصد را تشکیل می دهند و عمدتاً در شب (02:00-7:00) ظاهر می شوند. در عین حال، میانگین وزن BIC آنها به ترتیب تنها 0.7515، 0.6296 و 0.7853 است. این وزن‌های BIC پایین‌تر نشان‌دهنده عدم قطعیت بیشتر توزیع‌های Lognormal، Weibull و Rayleigh در برازش داده‌ها است که احتمالاً با توزیع گاما یا Burr جایگزین می‌شوند.
در طول تعطیلات روز ملی، 82.74٪ از داده های زمان سفر از توزیع گاما با میانگین وزن BIC 0.9541 پیروی می کند. با این حال، تنها 13.69٪ از توزیع Burr پیروی می کنند، با میانگین وزن BIC 0.9352. این بدان معناست که داده‌های زمان سفر برای تعطیلات روز ملی تمایل بیشتری به توزیع گاما دارد تا توزیع Burr.

4.4. بهترین توزیع سرعت سفر ساعتی

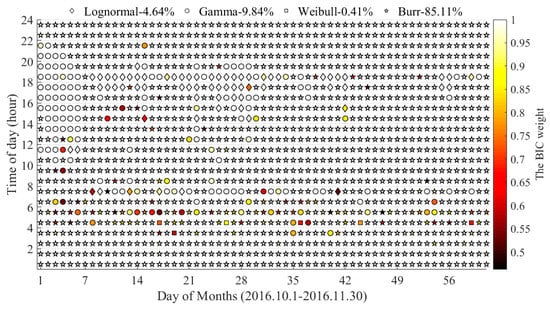
شکل 8 نتایج برازش سرعت سفر ساعتی را نشان می دهد. بهترین توزیع ها با لوزی، دایره، مربع و ستاره متمایز می شوند. به طور کلی، توزیع Burr 85.11٪ (1246 از 1464) از بهترین توزیع ها را با میانگین وزن BIC 0.9830 تشکیل می دهد که مزیت مطلق و قابلیت اطمینان بالا را نشان می دهد. به طور مشابه، توزیع لگ نرمال و گاما وزن BIC بالاتر اما نسبت های پایین تری دارند. در مقابل، نتایج برازش تنها برای 6 بازه 1 ساعته (0.41٪) با توزیع Weibull، با میانگین وزن BIC 0.7007 سازگار است. این بدان معنی است که توزیع Weibull برای داده های سرعت مناسب نیست.
علاوه بر این، برخی از ویژگی‌های خوشه‌بندی را می‌توان در توزیع‌های مناسب و غیر غالب یافت. به عنوان مثال، 77.94٪ (53 از 68) از توزیع های لگ نرمال در طول پیک روزانه عصر رخ می دهد، با میانگین وزن BIC 0.9986. حدود 40٪ از توزیع گاما در تعطیلات روز ملی وجود دارد، با میانگین BIC 0.9246. در نتیجه، توزیع Burr در برازش داده‌های سرعت سفر غالب است.

4.5. انتخاب توزیع عمومی

بر اساس تحلیل فوق، توزیع گاما در برازش مسافت سفر و زمان سفر غالب است، در حالی که توزیع Burr برای سرعت سفر مناسب تر است. سفرهایی که از توزیع های دیگر پیروی می کنند، تنها بخش بسیار کمی از کل سفرها را تشکیل می دهند. حال ممکن است این سوال مطرح شود که آیا می توان همه داده های مربوطه را با توزیع غالب به طور جداگانه برازش داد؟ اگر چنین است، تناسب چقدر بدتر خواهد بود؟ برای پاسخ به این سوال، آزمون K-S، تفاوت BIC، میانگین خطای مطلق (MAE) و میانگین درصد مطلق خطا (MAPE) به طور جداگانه تجزیه و تحلیل می شوند.
همانطور که در جدول 5 نشان داده شده است ، در بین معیارهای سفر، 101، 348، و 218 از 1464 بازه 1 ساعته به ترتیب با توزیع گاما یا Burr جایگزین شده اند. برای مسافت سفر، آزمون K-S هم توزیع جایگزین (گاما) و هم توزیع بهترین تناسب را به ترتیب برای حدود 90 درصد (93 یا 90 از 101) داده ها قابل قبول در نظر می گیرد. در همین حال، توزیع جایگزین برای زمان سفر بهتر عمل می کند زیرا داده های بیشتری (76٪) آزمون K-S را پشت سر می گذارند. با این حال، برای متریک سرعت سفر، برعکس است، که نیاز به توضیح بیشتر توسط شاخص‌های دیگر دارد. علاوه بر این، انتخاب مدل پیچیده‌تر نشان می‌دهد که مزیت برازش مدل بهبود یافته بر هزینه پیچیدگی مدل افزوده می‌شود.
برای دو معیار سفر اول، تفاوت BIC بین توزیع جایگزین و توزیع مناسب نسبتاً کوچک است، هر دو کمتر از 10 هستند. با این حال، تفاوت BIC برای سرعت سفر کمی بزرگ‌تر است، احتمالاً به دلیل بزرگی متفاوت مقادیر BIC بین معیارها. نسبت ( Δ/بمنسیدقیقه) تفاوت BIC با BIC توزیع مناسب کمتر از 0.5٪ است که همچنین نشان می دهد که تفاوت معنی داری بین دو توزیع از انتخاب مدل بر اساس BIC وجود ندارد. علاوه بر این، MAPE و MAE توزیع برازش و توزیع نمونه در صدک‌های 10، 50 و 90 با در نظر گرفتن جامع میانگین و واریانس محاسبه می‌شوند. MAPE کمتر از 4% امکان تطبیق همه داده ها با توزیع غالب را نشان می دهد.

5. بحث

بر اساس تجزیه و تحلیل در بخش قبل، آمار مستقیم (یعنی مسافت سفر و زمان سفر) سفرهای ساعتی همگی از توزیع گاما پیروی می کنند، در حالی که آمار غیر مستقیم (یعنی سرعت سفر) از توزیع Burr تبعیت می کند. جدول 6 میانگین شاخص های معیارهای سفر را فهرست می کند که عملکرد توزیع های گاما و برر را منعکس می کند. هرچه R2 بزرگتر باشد، تناسب بهتری دارد. از طرف دیگر، MAE، MAPE و PPC کوچکتر نیز نشانگر تناسب بهتر است. سه صدک کلیدی، 10، 50، و 90، برای محاسبه MAE و MAPE اتخاذ شد. سطح اطمینان برابر با 80٪ است (یعنی α=0.2، 90%-10%=80%) برای ایجاد فاصله اطمینان اتخاذ شد.
طبق جدول 6 ، میانگین مقادیر R 2 سه معیار سفر از 0.98 بیشتر است و حتی برای زمان سفر به 0.9915 می رسد. این نشان می دهد که توزیع برازش توانایی بالایی در تفسیر داده ها دارد و این مدل در برازش داده ها نیز خوب است. به طور کلی، R2 بالاتر نشان دهنده توانایی تفسیر قوی تر مدل برازش با داده ها است . یعنی اثر مناسب تری. در همین حال، شاخص های MAPE و MAE این را بیشتر ثابت می کنند. MAE مسافت سفر کمتر از 0.1 کیلومتر، کمتر از 0.2 دقیقه برای زمان سفر و حدود 0.21 کیلومتر در ساعت برای سرعت سفر است. کمتر از 3٪ از MAPE ها بیشتر نشان می دهد که توزیع برازش کاملاً با داده های مشاهده شده سازگار است.
میانگین POPI کمی بدتر از هدف (20٪) است، که نشان می دهد کمتر از 80٪ از داده های مشاهده با فاصله اطمینان مناسب پوشش داده شده است. POPI بالاتر به معنای POOI پایین تر است. همانطور که قبلا ذکر شد، زمانی که POPI و POOI هر دو نزدیک به مقدار هدف (20٪) باشند، توزیع های برازش بهترین کار را انجام می دهند. مقادیر PPC، به ترتیب 4.31، 2.54 و 3.11 درصد، درجه انحراف کم POPI و POOI را نشان می‌دهند، که همچنین بیان می‌کند که توزیع برازش سه معیار سفر از دقت خوبی برخوردار است. به طور خلاصه، این نتایج نشان می‌دهد که توزیع گاما با معیارهای سفر مستقیم، مانند مسافت سفر و زمان سفر، به خوبی مطابقت دارد، در حالی که توزیع Burr با سرعت سفر مناسب‌تر است.

6. نتیجه گیری

این مطالعه توزیع معیارهای تحرک انسان را بر اساس مجموعه داده های مسیر واقعی، از جمله حدود 18000 سواری آنلاین با ماشین، که در شیان، چین جمع آوری شده است، مدل می کند. سه معیار سفر – مسافت سفر، زمان سفر، و سرعت سفر – به منظور ایجاد پایگاهی برای تحقیقات تحرک انسانی برجسته شده‌اند. نتایج این مطالعه چندین بینش جدید را در مورد روابط در تحرک انسان ارائه کرد.
اول، معیارهای تحرک به جای توزیع معمولی بر اساس داده‌های مسیر حرکت خودروهای آنلاین، به توزیع انحراف راست تمایل دارند. با تجزیه و تحلیل داده‌های سفر روزانه و ساعتی، پنج مورد از گسترده‌ترین توزیع‌های انحرافی راست (یعنی Lognormal، Gamma، Weibull، Burr و Rayleigh) در ادبیات علمی به عنوان توزیع‌های کاندید انتخاب شدند. با استفاده از معیار اطلاعات بیزی (BIC)، ما به طور جامع خوبی تناسب و پیچیدگی توزیع‌های کاندید را برای هر متریک تجزیه و تحلیل کردیم، بنابراین بهترین توزیع برازش و پارامترهای مناسب را به دست آوردیم. نتایج تجربی مبتنی بر مجموعه داده‌های مسیر حرکت خودروهای آنلاین در شیان، چین، شواهد قوی ارائه کرده‌اند که معیارهای تحرک از توزیع انحراف راست تبعیت می‌کنند.
دوم، انواع توزیع معیارهای تحرک همراه با روز هفته و زمان روز متفاوت است، به این معنی که یک توزیع واحد نمی تواند همه داده های روزانه و ساعتی را به خوبی جا دهد. در ابتدا، توزیع گاما در بین همه توزیع‌های جایگزین برای مسافت سفر بهترین عملکرد را دارد و می‌تواند به طور یکنواخت همه داده‌های روزانه را جابجا کند. سپس، توزیع گاما یا Burr تنها می تواند در بخشی از زمان سفر روزانه یا داده های سرعت به تناسب خوبی دست یابد. برای داده‌های ساعتی، بهترین توزیع‌ها در میان توزیع‌های جایگزین، به ویژه در شب، متفاوت است. توزیع گاما اغلب برای مسافت سفر و زمان سفر بهتر از چهار توزیع دیگر عمل می کند، در حالی که توزیع Burr برای سرعت سفر بهترین عملکرد را دارد.
سوم، اگرچه انواع توزیع نامشخص در داده های روزانه و ساعتی وجود دارد، یک توزیع غالب در هر متریک تحرک وجود دارد. به عنوان مثال، توزیع گاما می‌تواند بیش از 90 درصد داده‌های مسافت سفر ساعتی را جای دهد و توزیع Burr می‌تواند برای 85 درصد داده‌های سرعت سفر ساعتی به تناسب دست یابد. تجزیه و تحلیل بیشتر نشان می دهد که به ترتیب برازش همه داده های ساعتی با توزیع غالب امکان پذیر است.
انتظار می رود که یافته های این مطالعه بتواند درک در مورد تحرک انسانی درون شهری را ارتقا دهد و پایه محکمی برای تحقیقات تحرک انسانی ایجاد کند. با این حال، ما چندین محدودیت را در این تحقیق ذکر می کنیم. اولاً، توزیع‌های کاندید به پنج توزیع اریب که معمولاً مورد استفاده قرار می‌گیرند محدود می‌شوند و ممکن است نیاز به بررسی بیشتر باشد. ثانیا، تنها توزیع داده های سفر روزانه و ساعتی برازش و تحلیل می شود. توزیع ریزدانه تر (به عنوان مثال، 30 دقیقه، 15 دقیقه) نیز مورد توجه است، که هنوز نیاز به مطالعه بیشتر دارد. آخرین اما نه کم اهمیت ترین، توزیع ممکن است با مجموعه داده های مختلف متفاوت باشد. برای تایید نتیجه گیری باید داده های چند منبع را در نظر گرفت.

منابع

  1. پان، جی. Qi، GD; وو، زی. ژانگ، دی کیو؛ Li، SJ طبقه بندی کاربری زمین با استفاده از ردیابی GPS تاکسی. IEEE Trans. هوشمند ترانسپ سیستم 2013 ، 14 ، 113-123. [ Google Scholar ] [ CrossRef ]
  2. سلیمان، ع. سلطانی، ک. یین، جی جی؛ پادمنابان، ع. Wang، SW حس اجتماعی استفاده از زمین شهری بر اساس تجزیه و تحلیل الگوهای تحرک کاربران توییتر. PLoS ONE 2017 , 12 , e0181657. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  3. جیانگ، بی. یین، جی جی؛ ژائو، اس جی مشخص کردن الگوی تحرک انسان در یک شبکه خیابانی بزرگ. فیزیک Rev. E 2009 , 80 , 021136. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
  4. پائولو، بی. کیارا، پی. راماسکو، جی جی. میشل، تی. ویتوریا، سی. الساندرو، V. شبکه های تحرک انسانی، محدودیت های سفر، و گسترش جهانی همه گیری H1N1 در سال 2009. PLoS ONE 2011 ، 6 ، e16591. [ Google Scholar ]
  5. وسولوفسکی، آ. عقاب، ن. تاتم، ای جی; اسمیت، دی.ال. نور، AM; برف، RW; Buckee, CO کمیت کردن تأثیر تحرک انسان بر مالاریا. Science 2012 ، 338 ، 267-304. [ Google Scholar ] [ CrossRef ] [ PubMed ][ نسخه سبز ]
  6. آهنگ، HY; لی، JS یافتن یک توزیع احتمال ساده برای سرعت موبایل انسان. اوباش فراگیر. محاسبه کنید. 2016 ، 25 ، 26-47. [ Google Scholar ] [ CrossRef ]
  7. براکمن، دی. هافناگل، ال. گیزل، تی. قوانین مقیاس پذیری سفرهای انسانی. طبیعت 2006 ، 439 ، 462-465. [ Google Scholar ] [ CrossRef ]
  8. ری، آی. شین، م. هونگ، اس. تره فرنگی.؛ کیم، اس جی. چونگ، اس. در ماهیت لوی-والک تحرک انسان. IEEE ACM Trans. شبکه 2011 ، 19 ، 630-643. [ Google Scholar ] [ CrossRef ]
  9. گونزالس، ام سی؛ هیدالگو، کالیفرنیا؛ Barabási، AL درک الگوهای تحرک فردی انسان. طبیعت 2008 ، 453 ، 779-782. [ Google Scholar ] [ CrossRef ]
  10. ژائو، ک. موصلی، م. هوی، پی. رائو، دبلیو. تارکوما، اس. توضیح توزیع قانون قدرت تحرک انسان از طریق تجزیه روش حمل و نقل. علمی Rep. 2014 , 5 , 9136. [ Google Scholar ] [ CrossRef ] [ PubMed ] [ نسخه سبز ]
  11. کالابرس، اف. دیائو، م. لورنزو، جی دی. فریرا، جی. Ratti, C. درک الگوهای تحرک فردی از داده های سنجش شهری: یک مثال ردیابی تلفن همراه. ترانسپ Res. قسمت C Emerg. تکنولوژی 2013 ، 26 ، 301-313. [ Google Scholar ] [ CrossRef ]
  12. جیا، تی. جیانگ، بی. کارلینگ، ک. بولین، ام. Ban, Y. یک مطالعه تجربی در مورد تحرک انسان و مدل سازی مبتنی بر عامل آن. J. Stat. مکانیک. تئوری Exp. 2012 ، 11 ، P11024. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  13. چو، ای. مایرز، SA; Leskovec, J. دوستی و تحرک: حرکت کاربر در شبکه های اجتماعی مبتنی بر مکان. در مجموعه مقالات هفدهمین کنفرانس بین المللی ACM SIGKDD در مورد کشف دانش و داده کاوی، سن دیگو، کالیفرنیا، ایالات متحده آمریکا، 21 تا 24 اوت 2011. پ. 1082. [ Google Scholar ]
  14. کانگ، سی جی; ما، XJ; تانگ، دی کیو؛ لیو، ی. الگوهای تحرک انسانی درون شهری: دیدگاه مورفولوژی شهری. فیزیک یک آمار مکانیک. Appl. 2012 ، 391 ، 1702-1717. [ Google Scholar ] [ CrossRef ]
  15. جیانگ، اس ایکس; گوان، دبلیو. ژانگ، وای؛ چن، ایکس. یانگ، L. تحرک انسان در فضا از سه حالت حمل و نقل عمومی. فیزیک یک آمار مکانیک. Appl. 2017 ، 483 ، 227-238. [ Google Scholar ] [ CrossRef ]
  16. لیانگ، ایکس. ژنگ، XD; Lv، WF; ژو، TY; Xu، K. مقیاس حرکت انسان توسط تاکسی ها به صورت تصاعدی است. فیزیک یک آمار مکانیک. Appl. 2012 ، 391 ، 2135-2144. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  17. لیانگ، ایکس. ژائو، جی. دونگ، ال. شو، ک. کشف منشأ قانون نمایی در تحرک انسان درون شهری. علمی Rep. 2013 , 3 , 2983. [ Google Scholar ] [ CrossRef ]
  18. بذانی، ع. جورجینی، بی. رامبالدی، س. گالوتی، آر. Giovannini, L. قوانین آماری در تحرک شهری از داده های میکروسکوپی GPS در منطقه فلورانس. J. Stat. مکانیک. تئوری Exp. 2010 ، 2010 ، P05001. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  19. وانگ، WJ; پان، ال. یوان، ن. ژانگ، اس. لیو، دی. تحلیل مقایسه ای تحرک انسان درون شهری با تاکسی. فیزیک یک آمار مکانیک. Appl. 2015 ، 420 ، 134-147. [ Google Scholar ] [ CrossRef ]
  20. Csáji، BC; برویت، ا. تراگ، وی. دلون، جی سی; هوئنس، ای. ون دورن، PM; اسموردا، ز. Blondel, VD بررسی تحرک کاربران تلفن همراه. فیزیک یک آمار مکانیک. Appl. 2013 ، 392 ، 1459-1473. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  21. ژانگ، اس. تانگ، جی جی. وانگ، HX; وانگ، YH; An, S. افشای الگوهای سفر درون شهری و خدمات طیفی از مسیرهای تاکسی. J. Transp. Geogr. 2017 ، 61 ، 72-86. [ Google Scholar ] [ CrossRef ]
  22. Kou، ZY; Cai, H. درک الگوهای سفر به اشتراک گذاری دوچرخه: تجزیه و تحلیل داده های سفر از هشت شهر. فیزیک یک آمار مکانیک. Appl. 2019 ، 515 ، 785–797. [ Google Scholar ] [ CrossRef ]
  23. پلوتز، پی. یاکوبسون، ن. Sprei, F. در مورد توزیع فواصل رانندگی روزانه فردی. ترانسپ Res. روش قسمت B. 2017 ، 101 ، 213-227. [ Google Scholar ] [ CrossRef ]
  24. ژنگ، ز. رسولی، س. Timmermans، H. الگوی دو رژیم در تحرک انسان: شواهد از داده های مسیر تاکسی GPS. Geogr. مقعدی 2016 ، 48 ، 157-175. [ Google Scholar ] [ CrossRef ]
  25. چن، توسط; یوان، اچ. لی، QQ; لام، WHK; Shaw، الگوریتم تطبیق نقشه SL برای داده های ماشین شناور با فرکانس پایین در مقیاس بزرگ. بین المللی جی. جئوگر. Inf. علمی 2014 ، 28 ، 22-38. [ Google Scholar ] [ CrossRef ]
  26. Krause، CM; ژانگ، ال. پیش‌بینی رفتار سفر کوتاه‌مدت با داده‌های GPS، کاربری زمین و نقاط مورد علاقه. ترانسپ Res. روش قسمت B. 2019 ، 123 ، 349-361. [ Google Scholar ] [ CrossRef ]
  27. شیا، اف. وانگ، جی.زی. کنگ، XJ; وانگ، ZB; Li، JX; لیو، سی اف بررسی الگوهای تحرک انسانی در سناریوهای شهری: چشم انداز داده های مسیر. IEEE Commun. Mag. 2018 ، 56 ، 142-149. [ Google Scholar ] [ CrossRef ]
  28. ژانگ، بی. چن، سی. ما، YF; لی، TZ; تانگ، ک. تجزیه و تحلیل تحرک شهری مکانی-زمانی بر اساس داده‌های آنلاین خودرو-تگرگ. J. Transp. Geogr. 2020 , 82 , 102568. [ Google Scholar ] [ CrossRef ]
  29. لین، ام. Hsu، WJ استخراج داده های GPS برای الگوهای تحرک: یک نظرسنجی. اوباش فراگیر. محاسبه کنید. 2014 ، 12 ، 1-16. [ Google Scholar ] [ CrossRef ]
  30. لیو، ی. کانگ، سی جی; گائو، اس. شیائو، ی. Tian, ​​Y. درک الگوهای سفر درون شهری از داده های مسیر تاکسی. جی. جئوگر. سیستم 2012 ، 14 ، 463-483. [ Google Scholar ] [ CrossRef ]
  31. تانگ، جی جی. لیو، اف. وانگ، YH; وانگ، اچ. کشف تحرک انسان شهری از داده های جی پی اس تاکسی در مقیاس بزرگ. فیزیک یک آمار مکانیک. Appl. 2015 ، 438 ، 140-153. [ Google Scholar ] [ CrossRef ]
  32. تیلور، نسبت قابلیت اطمینان زمان سفر MAP Fosgerau و توزیع سوراخ. ترانسپ Res. روش قسمت B. 2017 ، 97 ، 50-63. [ Google Scholar ] [ CrossRef ]
  33. کلاوزت، ا. شالیزی، CR; نیومن، توزیع‌های قانون قدرت MEJ در داده‌های تجربی. SIAM Rev. 2007 , 51 , 661-703. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  34. جانسون، جی. Omland، K. انتخاب مدل در اکولوژی و تکامل. Trends Ecol. تکامل. 2004 ، 19 ، 101-108. [ Google Scholar ] [ CrossRef ]
  35. ژانگ، KP; نینگ، جی. ژنگ، ال. Liu, ZJ یک شبکه متخاصم مولد جدید برای تخمین توزیع زمان سفر با داده های مسیر. ترانسپ Res. قسمت C Emerg. تکنولوژی 2019 ، 108 ، 223-244. [ Google Scholar ] [ CrossRef ]
  36. پوسادا، دی. انتخاب مدل باکلی، TR و میانگین‌گیری مدل در فیلوژنتیک: مزایای معیار اطلاعات آکایک و رویکردهای بیزی نسبت به آزمون‌های نسبت احتمال. سیستم Biol. 2004 ، 53 ، 793-808. [ Google Scholar ] [ CrossRef ] [ PubMed ]
  37. Akaike, H. اندازه گیری اطلاعات و انتخاب مدل. بین المللی آمار Inst. 1983 ، 50 ، 277-291. [ Google Scholar ]
  38. شی، سی. چن، توسط; لام، WHK; روش ترکیب داده‌های ناهمگن لی، QQ برای تخمین توزیع زمان سفر در شبکه‌های جاده‌ای متراکم. Sensors 2017 , 17 , 2822. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  39. شی، سی. چن، توسط; Li، QQ تخمین توزیع زمان سفر در شبکه‌های جاده‌ای شهری با استفاده از داده‌های شناور فرکانس پایین. ISPRS Int. Geo Inf. 2017 ، 6 ، 253. [ Google Scholar ] [ CrossRef ]
Ijgi 10 00268 g001 550
شکل 1. توزیع مقدار سفر ساعتی.
Ijgi 10 00268 g002 550
شکل 2. توزیع معیارهای سفر در روز پنجشنبه، 3 نوامبر 2016: ( الف ) توزیع مسافت سفر. ( ب ) توزیع زمان سفر. و ( ج ) توزیع سرعت سفر.
Ijgi 10 00268 g003 550
شکل 3. تغییرات روزانه چولگی و کشیدگی به مدت 61 روز: ( الف ) چولگی. و ( ب ) کشیدگی
Ijgi 10 00268 g004 550
شکل 4. توزیع مناسب معیارهای سفر روزانه برای 61 روز.
Ijgi 10 00268 g005 550
شکل 5. توزیع های مناسب برای داده های سرعت سفر مشاهده شده در 13 اکتبر.
Ijgi 10 00268 g006 550
شکل 6. توزیع مناسب فاصله سفر ساعتی.
Ijgi 10 00268 g007 550
شکل 7. توزیع برازش زمان سفر ساعتی.
Ijgi 10 00268 g008 550
شکل 8. توزیع برازش سرعت سفر روزانه.

مقالات داخلی و بین المللی

مطالب مرتبط ...

بدون دیدگاه

دیدگاهتان را بنویسید