چکیده

تصادفات وسایل نقلیه در جاده ها ناشی از عوامل زیادی است. با این حال، تأثیر این عوامل لزوماً در سراسر مکان‌ها همگن نیست، که یک چالش برای رویکردهای مدل‌سازی غیر ثابت است. برای پرداختن به این مشکل، این مقاله دو نوع روش را اتخاذ می‌کند که به پارامترها اجازه می‌دهد در بین مشاهدات نوسان کنند، یعنی رویکرد پارامتر تصادفی و رویکرد رگرسیون وزن‌دار جغرافیایی (GWR). با انحنای جاده، طول منحنی، اصطکاک روسازی و حجم ترافیک به عنوان متغیرهای مستقل، فرکانس تصادف خودرو با دو روش غیرمکانی، از جمله مدل دوجمله ای منفی (NB) و دو جمله ای منفی پارامتر تصادفی (RPNB) و همچنین سه روش مدل سازی می شود. روش های فضایی (رویکرد GWR). این مدل‌ها در سطح میکرو با استفاده از مجموعه داده‌ای از 9415 بخش منحنی افقی با طول کل 1545 کیلومتر برای یک دوره سه ساله (2016-2018) در ایالت ایندیانا کالیبره شده‌اند. نتایج نشان داد که رویکرد GWR می‌تواند ناهمگونی فضایی را به تصویر بکشد و بنابراین به طور قابل‌توجهی از رویکرد غیر فضایی مرسوم بهتر عمل می‌کند. بر اساس معیار اطلاعات آکایک (AICc)، رگرسیون دوجمله‌ای منفی وزن‌دار جغرافیایی (GWNBR) یک رویکرد برتر برای تجزیه و تحلیل تصادف در سطح ریز در سطح ایالتی ثابت شد.

کلید واژه ها:

ناهمگونی فضایی ; مدل دوجمله ای منفی پارامتر تصادفی ; رگرسیون وزنی جغرافیایی ; حمل و نقل ; تصادف وسیله نقلیه

1. مقدمه

پیچ های افقی جاده ها به دلیل تعداد نامتناسب تصادفات، عاملی حیاتی برای تصادفات خودرو هستند. تصادفات ترافیکی سالانه جان بیش از 30000 نفر را در آمریکا می گیرد. با توجه به اداره بزرگراه فدرال (FHWA) [ 1 ]، بیش از 25 درصد از تصادفات مرگبار مربوط به منحنی های افقی است که حدود 10 درصد از کل سیستم مسافت پیموده شده را اشغال می کند.
برای آشکار کردن قانون ذاتی این پدیده، چندین مدل پیش‌بینی برای تصادفات منحنی در دهه‌های گذشته توسعه داده شده است. از نظر وضعیت روسازی، بوداواراپو و همکاران. [ 2 ] یک مدل شدت آسیب تصادف در منحنی های افقی دو خطی در تگزاس ایجاد کرد. مشخص شد که بخش‌های منحنی با روسازی صاف‌تر به احتمال زیاد در معرض خطر هستند، در حالی که اندازه‌گیری لغزش طولی همبستگی کمی با شدت آسیب تصادف منحنی نشان می‌دهد. برای بررسی تأثیر ویژگی‌های هندسی بر فرکانس سقوط منحنی، یک مدل دوجمله‌ای منفی توسط اشنایدر و همکاران توسعه داده شد. [ 3] در تصادفات موتورسیکلت تک وسیله نقلیه که در بخش های منحنی بزرگراه های روستایی دو خطه در اوهایو رخ داد. متغیرهای ویژگی هندسی که به طور قابل توجهی بر فرکانس تصادف موتورسیکلت تأثیر می‌گذارند، شعاع منحنی، طول منحنی و عرض شانه منحنی هستند. علاوه بر این، موزی و پارک [ 4 ] مدلی را برای پیش‌بینی شدت تصادف منحنی افقی با اصطکاک روسازی و انحنای جاده ارائه کردند. نتایج نشان داد که آسیب جدی در منحنی‌هایی با درجه انحنای بالاتر رخ می‌دهد و اصطکاک کمتر با تصادفات روسازی مرطوب ارتباط نزدیکی دارد. در همین حال، همبستگی فرکانس تصادف که در همبستگی منحنی های مجاور رخ می دهد توسط گوچ و همکاران معنادار است. [ 5 ].
همه مدل‌های فوق‌الذکر جهانی هستند که فرض می‌کنند تخمین‌های پارامتر در سراسر منطقه جغرافیایی تحلیل ثابت است. با این حال، از آنجایی که اطلاعات مکان به عنوان مرجع داده‌های خرابی جمع‌آوری می‌شود، برخی از متغیرهای پیش‌بینی‌کننده ممکن است ثابت نباشند. برای مثال، ویژگی‌های هندسی (مانند شعاع و طول) منحنی‌های افقی ممکن است باعث ناهمگونی مشاهدات ناشی از عوامل مشاهده‌نشده مانند پاسخ‌های مختلف راننده بر روی منحنی‌ها، ترافیک متغیر با زمان و شرایط آب و هوایی شود [ 6 ].]. اثر اصطکاک روسازی نیز ممکن است در مشاهدات به دلیل تغییرات اصطکاک، پاسخ ناهمگن در رفتار راننده و تأثیر آب و هوا متفاوت باشد. از نظر تأثیر حجم ترافیک بر احتمال تصادف، ممکن است واکنش‌های ناهمگونی راننده به ترافیک و همچنین عوامل محیطی وجود داشته باشد [ 7 ]. از این رو، مدل‌سازی رابطه بین تعداد تصادف و این متغیرهای توضیحی با ضریب کلی ثابت برای کل منطقه مورد مطالعه ممکن است باعث تخمین‌های مغرضانه پارامترهای فردی شود. بنابراین، افزودن واریانس فضایی با مدل‌های غیر ثابت مانند رگرسیون وزن‌دار جغرافیایی (GWR) و رویکردهای پارامتر تصادفی ممکن است دید بهتری برای توسعه وابستگی فضایی به فضا ارائه دهد.
مطالعات فضایی ایمنی ترافیک به دو سطح تجمع فضایی طبقه بندی می شوند: تجزیه و تحلیل سطح کلان و سطح خرد. به طور متعارف، تجزیه و تحلیل سطح خرد بر روی واحدهای جاده ای خاص شبکه جاده ها، مانند تقاطع ها، ریل ها، راهروها و بخش های جاده تمرکز می کند [ 3 ، 8 ، 9 ]. با این حال، تجزیه و تحلیل سطح کلان با تمرکز بر تصادفات سطح منطقه ای با واحدهای فضایی مختلف به عنوان بخشی از فرآیند برنامه ریزی حمل و نقل در مطالعات تحقیقاتی اخیر محبوب شده است. واحدهای فضایی اخیراً به طور جامع توسعه یافته اند، مانند مناطق تجزیه و تحلیل ترافیک (TAZs) [ 10 ، 11 ، 12 ، 13 ]، شهرستان ها [ 14 ، 15 ]]، سرشماری [ 16 ]، بخش [ 17 ، 18 ]، محله های مسکونی [ 19 ] و سطوح منطقه آماری [ 20 ، 21 ]. یکی از مزایای مرتبط با مدل‌سازی خرابی سطح کلان این است که به اندازه مدل‌های خرابی سطح خرد روی داده‌های دقیق حساب نمی‌شود [ 22 ]. با این حال، ثابت شده است که مدل‌های سطح میکرو با داده‌های کم‌تر هنوز دقت قابل قبولی را هنگام اعمال مدل‌های غیر ثابت ارائه می‌کنند [ 23 ]. بنابراین، استفاده از مدل‌های غیر ثابت (به عنوان مثال، رگرسیون وزن‌دار جغرافیایی و پارامتر تصادفی) برای تحلیل ایمنی سطح خرد منطقی و امیدوارکننده است.

2. آثار مرتبط

تعدادی از روش‌های تحلیل تصادف جاده‌ای برای تعیین وابستگی مکانی و ناهمگونی تأثیر پارامترها و یافتن مکان‌های پرخطر توسعه یافته‌اند [ 24 ]. در میان این روش‌ها، رگرسیون وزن‌دار جغرافیایی (GWR) [ 25 ]، مدل‌های بیزی با خودرگرسیون شرطی [ 17 ]، مدل‌های خودرگرسیو با اثرات سرریز فضایی [ 26 ]، مدل فضایی چند عضویت کامل بیز [ 27 ] و مدل‌های پارامتر تصادفی [27] وجود داشت. 28 ].
رویکرد GWR امیدوارکننده‌ترین تکنیک برای آشکار کردن اثر ناهمگن متغیرها بر فضا در بسیاری از زمینه‌ها است (به عنوان مثال، تجزیه و تحلیل بیماری [ 29 ]، مدل‌سازی جرم [ 30 ]). علاوه بر این، برخی از ابزارهای GWR با مقیاس بالا (به عنوان مثال، GWR موازی مبتنی بر CUDA [ 31 ] و FastGWR [ 32 ]) برای پردازش حجم زیادی از داده‌ها در این سال‌ها توسعه یافته‌اند. ما رویکرد GWR را در این مقاله به کار بردیم تا به این موضوع بپردازیم که برخی از متغیرها در مکان‌های مکانی خاص تأثیرات بیشتری دارند اما در برخی دیگر تأثیرات کمتری دارند. علاوه بر این، روش پارامتر تصادفی نیز برای مقایسه مورد استفاده قرار می‌گیرد، زیرا اجازه می‌دهد پارامترهای متفاوت از یکدیگر اما هیچ رابطه فضایی درگیر نباشد. از آنجایی که فاثرینگهام و همکاران. [ 33تئوری GWR به طور سیستماتیک نشان داده شده است، این تکنیک اغلب برای تجزیه و تحلیل ایمنی جاده استفاده شده است [ 34 ]. حدایقی و همکاران. [ 25 ] برنامه GWR را برای شمارش مدل سازی داده ها برای تجزیه و تحلیل ایمنی ترافیک در سطح TAZ بررسی کرد. لی و همکاران [ 35 ] عملکرد یک مدل رگرسیون پواسون وزن‌دار جغرافیایی (GWPR) را در مقایسه با یک مدل خطی تعمیم‌یافته سنتی (GLM) بر روی داده‌های تصادف در سطح شهرستان ارزیابی کرد. بر اساس مطالعه مدل نیمه پارامتریک GWPR ناکایا و همکاران. [ 36 ]، که در آن برخی از متغیرها ممکن است به طور قابل توجهی در فضا تغییر نکنند در حالی که برخی دیگر از نظر فضایی ناهمگن هستند، Xu و Huang [ 28 ]] داده‌های سقوط سطح کلان در فلوریدا را با مدل دوجمله‌ای منفی پارامتر تصادفی (RPNB) و GWPR نیمه پارامتری مورد بررسی قرار داد. سیلوا و رودریگز [ 37 ] GWPR را برای مدل‌سازی داده‌های بیش از حد پراکنده با رگرسیون دو جمله‌ای منفی وزن‌دار جغرافیایی (GWNBR) و رگرسیون دوجمله‌ای منفی وزن‌دار جغرافیایی با پارامترهای overdispersion جهانی (GWNBRg) گسترش دادند. گومز و همکاران [ 12 ] و ثروری و همکاران. [ 13 ] از GWNBR برای مدل‌سازی تصادف‌های بیش از حد پراکنده برای مناطق ترافیکی استفاده کرد که از GWPR و مدل‌های سنتی جهانی بهتر بود. Amoh-Gyimah و همکاران. [ 22] دریافت که در مقایسه با مدل‌های RPNB و مدل‌های GLM، رویکرد GWR عملکرد بهتری را در مدل‌سازی فرکانس تصادف ترافیک بیش از حد پراکنده ماکروسکوپی ارائه می‌کند. با این وجود، تنها تعداد کمی از مطالعات موجود، مدل‌سازی ایمنی منطقه‌ای سطح خرد در سطح کشور را بر روی داده‌های تصادف بیش از حد پراکنده بررسی کرده‌اند. مدل‌سازی فرکانس تصادف غیرایستا در سراسر ایالت شامل واریانس ضریب در تعداد بیشتری از مشاهدات و مناطق وسیع است. بنابراین، مطالعه ناهمگونی فضایی داده‌های تصادف در مقیاس بزرگتر با رویکرد GWR ضروری است.
مدل RPNB، که همچنین به ناهمگونی مشاهده نشده در مدل‌سازی داده‌های پراکنده بیش از حد ایمنی منطقه‌ای می‌پردازد، فرض می‌کند که پارامترها از برخی توزیع‌های تصادفی گرفته می‌شوند و به طور تصادفی از موردی به مورد دیگر متفاوت هستند. برای بررسی ناهمگونی مشاهده نشده در بخش‌های بزرگراه برای پیش‌بینی تعداد تصادف، Shaon و همکارانش. [ 38 ، 39 ] و چن و همکاران. [ 40 ] از پارامترهای تصادفی مدل‌های مبتنی بر پواسون در مطالعات ایمنی خود استفاده کردند. به‌عنوان شاخه‌ای از مدل‌سازی مبتنی بر پارامتر تصادفی پواسون، RPNB به‌طور گسترده‌ای برای محاسبه بیش از حد داده‌ها استفاده شده است و به طور گسترده توسط Venkataraman و همکاران انجام شده است. [ 6 ، 41 ، 42 ]، چن و تارکو [ 43 ] و سعید و همکاران. [44 ]. شین و همکاران [ 45 و 46 ] یک مدل RPNB را برای منحنی های افقی فلوریدا در امتداد تصادفات موتورسیکلت دو خطه، بزرگراه های تقسیم نشده با عوامل طراحی منحنی توسعه داده اند. با این حال، مدل‌سازی ناهمگونی فضایی داده‌های شمارش تصادف بیش از حد پراکنده در مقیاس بزرگ و تجزیه و تحلیل تفاوت‌های محلی آنها همیشه یک چالش است.
با توجه به این واقعیت که مطالعات تحقیقاتی قبلی بیشتر در سطح کلان (سطح منطقه‌ای) انجام شده است، این مقاله به بررسی استراتژی‌های مختلف برای مدل‌سازی تغییرات محلی داده‌های تعداد تصادف بیش از حد پراکنده در منحنی‌های افقی بزرگراه در سراسر ایالت با ارتباط با ویژگی‌های بخش منحنی می‌پردازد. یک سطح خرد (هر مشاهده). این مقاله به شرح زیر سازماندهی شده است: بخش 2 روش های مورد استفاده در این مقاله را معرفی می کند، در حالی که بخش 3 آماده سازی داده ها را شرح می دهد. بخش 4 نتایج تخمین را ارائه می دهد، نتایج حاصل از مدل های مختلف را با هم مقایسه می کند و نتایج را به صورت محلی تفسیر می کند. بخش 5 یافته های کار ما را خلاصه می کند و تلاش های آینده را توصیه می کند.

3. روش شناسی

این بخش اشکال کلی پنج مدل از دو نوع مورد استفاده در این مقاله را ارائه می دهد: دو جمله ای منفی (NB)، RPNB. GWPR، GWNBR و GWNBRg. ما همچنین شرح مختصری از روش های تخمین ارائه می دهیم. این مدل ها در دو گروه مدل های غیر فضایی و مدل های فضایی (رویکرد GWR) مورد بحث قرار می گیرند. این بخش با توصیف دو روش غیر فضایی شروع می شود: رگرسیون سنتی NB و مدل RPNB. سه نوع مدل GWR دیگر، یعنی GWPR، GWNBR و GWNBRg، به عنوان رگرسیون فضایی کالیبره شده‌اند. در پایان، تصویر مختصری از خوبی معیارهای تناسب ارائه شده است.

3.1. مدل های غیر فضایی

برای داده‌های شمارش تصادف اعداد صحیح غیرمنفی، رگرسیون پواسون اساسی‌ترین مورد است [ 47 ]. با این حال، ویژگی توزیع پواسون که واریانس با میانگین یکسان است، اغلب در داده‌های شمارش خرابی نقض می‌شود [ 48 ]. مدل رگرسیون NB به طور کلی برای توضیح مسئله پراکندگی بیش از حد استفاده شده است. مدل رگرسیون NB را می توان با استفاده از تابع log-linear ارائه کرد در حالی که پارامتر پواسون ( λمن) از اصطلاحات سیستماتیک و یک عبارت تصادفی به شرح زیر تشکیل شده است:

لوگاریتمλمن=β0+∑ک=1پβکایکسمنک+θمن

جایی که λمنتعداد مورد انتظار تصادف در مشاهده است من، β0، β1، …، βکپارامترهای مدل هستند، ایکسمنکهست کمتغیر توضیحی برای مشاهده من، پتعداد پارامترهای مدل است، هθمنیک عبارت خطای توزیع شده گاما با میانگین 1 و واریانس است α. اضافه کردن عبارت خطای توزیع شده گاما، واریانس متغیر وابسته را امکان پذیر می کند Yمنبا میانگین آن متفاوت باشد λمنبه طوری که varYمن=λمن+αλمن2. وقتی α به صفر نزدیک می شود، رگرسیون دو جمله ای منفی همان رگرسیون پواسون است. رگرسیون دو جمله ای منفی زمانی مناسب است αبه طور قابل توجهی با صفر تفاوت دارد [ 49 ].

مدل NB می تواند شخصیت بیش از حد پراکندگی داده های تصادف ترافیک را به تصویر بکشد. با این حال، وابستگی فضایی احتمالی در میان بخش‌های منحنی، همانطور که قبلاً گفته شد، ممکن است نادیده گرفته شود. با ترکیب یک عبارت تصادفی در تابع مدل NB، یعنی معادله (2)، یک مدل RPNB می‌تواند در پاسخ به متغیرهای توضیحی غیر ثابت در مدل‌های شمارش استفاده شود:

لوگاریتمλمن=βمن0+∑ک=1پβمنکایکسمنک+θمن
βمنک=βک+φمنک

جایی که βمنکپارامتر از است کمتغیر توضیحی برای مشاهده من، βکپارامتر میانگین در تمام مشاهدات است و φمنکیک عبارت توزیع شده تصادفی با توزیع تعیین شده توسط تحلیلگر است (مانند توزیع نرمال با میانگین 0 و واریانس σک2) که ناهمگونی مشاهده نشده را توصیف می کند. اگر برخی از واریانس‌های توزیع به‌عنوان تفاوت معنی‌داری با صفر برای یک متغیر توضیحی جداگانه آزمایش شوند، پارامتر ثابت مرسوم در همه مشاهدات از نظر آماری مناسب است. اگر عبارت ثابت تنها پارامتر تصادفی باشد، یک مدل پارامتر تصادفی معادل یک مدل اثر تصادفی است.

در بیشتر موارد، مشاهدات به گروه‌هایی ساختار می‌شوند تا ناهمگونی بین گروه‌ها را برای مدل‌های پارامتر تصادفی به دست آورند، و φمنکرا می توان به صورت بازنویسی کرد φgک، جایی که φgکیک اصطلاح تصادفی است که ناهمگنی مشاهده نشده را در بین گروه های مشخص شده توسط تحلیلگر در رابطه با کمتغیر توضیحی ام [ 7 ]. یعنی، یک گروه مشخص شده توسط تحلیلگر، عبارت تصادفی یکسانی را برای متغیرهای توضیحی به اشتراک می‌گذارد.

3.2. مدل های فضایی

برای مقابله با غیر ایستایی فضایی، رویکرد GWR در این مقاله در نظر گرفته شده است. مدل اساسی برای تفسیر مسائل ناهمگونی فضایی، مدل GWPR است که توسط ناکایا و همکاران توسعه یافته است. [ 36 ]، که به پارامترهای رگرسیون تخمینی اجازه می دهد تا در فضا تغییر کنند. چارچوب زیر مدل را تشکیل می دهد:

لوگاریتمλمن=β0تومن+∑ک=1پβکتومنایکسمنک

که در آن ضرایب برآورد شده است βکبر اساس مکان تعیین می شوند تومن= (توایکسمن،  توyمن)نشان دهنده مختصات نقطه میانی بخش منحنی، و دلالت بر این دارد که پارامتر βکدر بین بخش های منحنی متفاوت است.

ماتریس پارامترها برای هر واحد فضایی به صورت زیر برآورد می شود:

β^تومن=(ایکستیدبلیوتومنایکس)-1ایکستیدبلیوتومنY

جایی که β^تومنضرایب رگرسیون محلی برای واحد فضایی است منX ماتریس طراحی متغیرهای توضیحی است ،ایکستیX جابجا شده است ، Y متغیرهای وابسته است و دبلیوتومننشان دهنده یک n×nماتریس وزن دهی فضایی که به صورت زیر تعریف می شود:

دبلیوتومن=دمنآgwمن1،wمن2،⋯،wمنn

جایی که wمنjj=1،2،…، nوزن جغرافیایی است jمشاهده ام در مننقطه رگرسیون در نظریه رویکرد GWR، تخمین پارامترهای هر نقطه رگرسیون بر اساس مشاهدات دیگر در پهنای باند مناسب است. به این مشاهدات نزدیک با توجه به فاصله مشاهدات تا نقطه رگرسیون در فرآیند رگرسیون وزن اختصاص داده می شود. برای هر نقطه رگرسیون، مشاهدات از لبه پهنای باند تا نقطه خروج وزن بیشتری را به همراه خواهد داشت. وزن wمنjمعمولاً توسط دو نوع هسته معمولی محاسبه می شود، یعنی توابع گاوسی و دو مربعی (تطبیقی) که به صورت زیر تعریف می شوند:

گاوسی: wمنj=انقضا-0.5دمنj2ب2
دو مربع تطبیقی: wمنj=1-دمنj2بمنک2             دمنj≤بمنک0                       دمنj>بمنک

جایی که دمنjفاصله بین مشاهدات همسایه است منو j، بپهنای باند ثابت است و بمنکیک اندازه پهنای باند تطبیقی ​​است که با k- امین فاصله نزدیکترین همسایه تعریف شده است [ 50 ]. پهنای باند در تابع گاوسی (هسته ثابت) ثابت است، در حالی که پهنای باند تابع دو مربعی تطبیقی ​​در پاسخ به چگالی مکان نمونه متفاوت است.

معیار اطلاعات Akaike تصحیح شده (AICc)، AIC با اصلاح اندازه نمونه کوچک، برای انتخاب پهنای باند بهینه و مقایسه مدل که در بخش بعدی نشان داده شده است، اعمال می شود. هرچه یک مدل AICc کمتری تولید کند، عملکرد بهتری را ارائه می دهد [ 25 ، 36 ، 50 ].

مشابه مدل‌های شمارش سنتی، نقض توزیع پواسون نیز زمانی اتفاق می‌افتد که واریانس با میانگین متفاوت باشد. شکل دوجمله ای منفی نیز به رویکرد GWR برای توضیح مشکل پراکندگی بیش از حد اعمال می شود. سیلوا و رودریگز [ 37 ] الگوریتمی را برای مدل سازی داده های بیش از حد پراکنده به روشی غیر ثابت توسط GWNBR توسعه دادند. مدل GWNBR پیشنهادی به صورت زیر تعریف می شود:

لوگاریتمλمن=β0تومن+∑ک=1پβکتومنایکسمنک+θمن

که در آن عبارت خطای توزیع شده گاما هθمنبا معادله (1) یکسان است، اما فقط αتومندر واحدهای فضایی متفاوت است. اصطلاحات دیگر همانطور که در رابطه (4) تعریف شده است. برای تخمین پارامترها از روش اصلاح شده حداقل مربعات با وزن مجدد تکراری (IRLS) استفاده می شود. βکو α. با استفاده از الگوریتم نیوتن رافسون (NR)، یک زیربرنامه با روش حداکثر احتمال (ML) می‌تواند در این روش انجام شود. (سیلوا و رودریگز، 2014).

میانگین پیش بینی شده را به عنوان تنظیم کنید μمن، پارامترسازی این مدل بر حسب μمن/تیمن،  تیمنمتغیرهای افست را می دهد. بنابراین، این مدل را می توان به صورت λمن~NBتیمنانقضا∑کβکتومنایکسمنک،αتومنیا λمن~NBμمن،αتومن. بردار پارامتر برای هر واحد فضایی توسط:

β^تومن=(ایکستیدبلیوتومنآتومنمترایکس)-1ایکستیدبلیوتومنآتومنمترzتومن

جایی که آتومنمتریک n است ×n ماتریس وزنی مورب GLM برای تکرار m و مکان من، zتومنمتغیرهای وابسته تعدیل شده اند. اصطلاحات دیگر همانطور که قبلا در مدل GWPR تعریف شده است. تعداد موثر پارامترهای GWNBR کرا می توان با افزودن اعداد موثر پارامتر در پاسخ به محاسبه کرد βو α.

برای ساده کردن محاسبه GWNBR، GWNBRg یک پارامتر پراکندگی جهانی را معرفی می کند. می توان به عنوان اشاره کرد λمن~NBتیمنانقضا∑کβکتومنایکسمنک،αیا λمن~NBμمن،α، که در آن پارامترها مانند GWNBR هستند. تخمین پارامتر overdispersion در GWNBRg همان است که از مدل دوجمله ای منفی غیر فضایی به دست آمده است. به دلیل عدم تغییر فضایی برای α، تعداد موثر پارامترها از آن کمک می‌کند αبرابر 1.

3.3. معیارهای حسن تناسب

برای ارائه میانگین بزرگی متغیر پیش بینی، انحراف مطلق میانه (MAD) استفاده می شود:

مآD=1n∑من=1nλ^من-yمن

جایی که nتعداد مشاهدات است (یعنی تعداد قطعات منحنی در این مقاله)، و λ^منفرکانس تصادف پیش بینی شده است و yمنفرکانس تصادف مشاهده شده است. کوچکترین مقدار MAD بهترین نتیجه در پیش بینی است.

یکی دیگر از خوبی های سنجش تناسب- آمنسیجهمچنین برای در نظر گرفتن پیچیدگی مدل به صورت زیر اتخاذ شده است:

آمنسیج=D+2ک+2کک+1ن-ک-1

جایی که Dنشان دهنده انحراف است، کتعداد پارامترهای تخمین زده شده در مدل است، نتعداد مشاهدات است. انحراف مدل رگرسیون پواسون را می توان به صورت زیر بیان کرد:

D=2∑من=1nyمنلnyمنλ^من+λ^من-yمن

با توجه به تخمین رگرسیون فضایی، تعداد پارامترها به تعداد موثر پارامترها جایگزین می‌شود که می‌توان آن را به این صورت تعریف کرد (Fotheringham et al. 2002):

ک=تیrآجهاس

که در آن ماتریس S توسط [ 36 ] محاسبه می شود:

اس=ایکس(ایکستیدبلیوتومنآتومنایکس)-1ایکستیدبلیوتومنآتومن

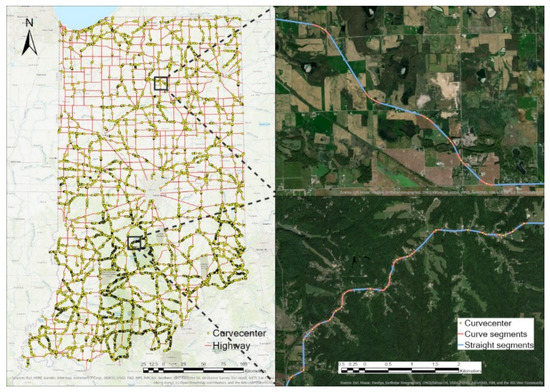
4. شرح داده ها

ما از داده های تصادف در ایالت ایندیانا در ایالات متحده برای ارزیابی عملکرد مدل های مختلف استفاده می کنیم. این داده ها شامل بزرگراه های ایالات متحده و ایالت در ایندیانا از سال 2016 تا 2018 است. آنها از پورتال سیستم تبادل اطلاعات گزارش خودکار (ARIES) ( https://www.ariesportal.com/ ، در 26 آوریل 2021) بازیابی شدند. از آنجا که خطاهایی در مختصات GPS ثبت شده توسط افسران پلیس [ 51 ] وجود دارد، ما از نرم افزار CLIP توسعه یافته توسط مرکز ایمنی جاده [ 52 ] برای تصحیح محل وقوع تصادف با توصیف موقعیت جغرافیایی برای هر رکورد تصادف استفاده کردیم. استفاده از داده‌های تصادف سه ساله کامل نیست، اما داده‌های مورد استفاده در این مقاله شامل حدود 7000 تصادف است که برای یک مطالعه ایمنی ترافیک کافی است.
بخش های منحنی افقی به عنوان داده های اولیه تولید می شوند. برای انجام این کار، پایگاه داده شبکه جاده ارائه شده توسط سیستم نظارت بر عملکرد بزرگراه FHWA ( https://maps.indiana.edu/layerGallery.html?category=Streets ، قابل دسترسی در 26 آوریل 2021) برای شناسایی و استخراج بخش های منحنی افقی توسط ابزار ROCA (تحلیلگر انحنای جاده) [ 53 ] در ESRI ArcGIS. شکل 1توزیع بخش منحنی در سطح ایالت و دو نمونه شناسایی منحنی جاده معمولی را در منطقه دشت و منطقه کوهستانی نشان می دهد. از مجموع 17381 کیلومتر شبکه جاده ای برای مسیر ایالتی ایندیانا و بزرگراه ایالات متحده، 1545 کیلومتر بخش منحنی شناسایی و به عنوان واحدهای پایه اتخاذ شد. چهار متغیر مستقل برای مدل‌سازی تعداد تصادف انتخاب شدند. از این میان، شعاع و طول منحنی ها توسط نرم افزار ROCA به عنوان متغیرهای هندسی محاسبه می شود. اگرچه شعاع منحنی و طول منحنی توسط یک همبستگی خاص در فرآیند برنامه ریزی طراحی می شوند. در این مقاله، بخش‌های منحنی از شکل فایل شبکه جاده‌ها شناسایی می‌شوند، به این معنی که طول یک بخش منحنی با شعاع آن همبستگی ندارد (بازده همبستگی بین آنها 0.337 است).
سومین متغیر مستقل اصطکاک روسازی است. داده‌های اصطکاک روسازی با سرعت 40 مایل در ساعت با لاستیک‌های صاف استاندارد از پایگاه داده اصطکاک روسازی شبکه اداره حمل‌ونقل ایندیانا (INDOT) بازیابی شد. AADT (میانگین ترافیک روزانه سالانه) به عنوان چهارمین پارامتر مستقل انتخاب شد. شکل فایل‌های AADT از سال 2016 تا 2018 از وب‌سایت جریان ترافیک INDOT ( https://www.in.gov/indot/2469.htm ، دسترسی به 26 آوریل 2021)، که در آن بخش‌های جاده‌ای که ویژگی‌های سفر نسبتاً یکنواختی دارند اختصاص داده شده‌اند، دانلود شدند. همان مقدار
تصادفات با یک بخش منحنی افقی 50 متر بافر فیلتر شدند. تعداد تصادفات برای سه سال فرکانس تصادف برای هر بخش منحنی جمع می شود. بخش‌های منحنی با نزدیک‌ترین شکل فایل اصطکاکی روسازی و شکل فایل AADT توسط ArcGIS تجمیع شدند.
متغیرهای مورد استفاده برای مشخصات مدل و آمار توصیفی آنها در جدول 1 خلاصه شده است. به دلیل وجود رابطه خطی نزدیکتر با متغیر وابسته که در مقیاس لگاریتمی مشاهده می شود، تبدیل لگاریتمی به متغیر مستقل در این تحقیق اعمال می شود. عامل تورم واریانس (VIF) برای ارزیابی چند خطی بودن بین متغیرها در این داده ها استفاده می شود. VIFهای همه متغیرها دارای مقادیر کمتر از دو هستند، که نشان می دهد چند خطی قابل توجهی وجود ندارد [ 54 ]

5. نتایج و بحث

فرکانس‌های تصادف منحنی در سطح خرد توسط نمایندگان مدل‌های فضایی (GWPR، GWNBR، و GWNBRg) و غیرمکانی (NB، RPNB) با استفاده از مجموعه داده‌های توصیف‌شده در بخش 4 برآورد شد . برآورد مدل RPNB و رویکرد GWR به ترتیب توسط NLOGIT6 و ماکرو Golden در SAS®9.4 [ 55 ] انجام شد.

5.1. مقایسه مدل

برای رویکرد GWR، یک تابع گاوسی ثابت به‌عنوان بخش‌های منحنی تابع هسته از شبکه جاده‌ها شناسایی شد. با فرض اینکه ناهمگونی مشاهده نشده تصادفات منحنی ناشی از آب و هوا، زمین و رفتار راننده است، ماتریس همبستگی فضایی آنها باید مستقل از تعداد همسایگان باشد. بنابراین، پهنای باند به عنوان توابع هسته ثابت گاوسی همانطور که در رابطه (7) تعریف شده است، و فاصله بین یک جفت قسمت منحنی نقطه میانی به عنوان فاصله اقلیدسی در تابع هسته تنظیم می شود. علاوه بر این، پهنای باند بهینه با کمترین AICc برای رویکرد GWR توسط ماکرو طلایی SAS انتخاب شد.
ما مدل RPNB را با استفاده از توزیع نرمال به عنوان تابع چگالی پارامتر تخمین می زنیم. این توسط 100 نمودار هالتون مبتنی بر حداکثر احتمال انجام شده است. این مدل برای محاسبه ناهمگونی بین بخش‌های منحنی منفرد برای مقایسه با رویکرد GWR استفاده می‌شود که پارامترهای متفاوت را در بین بخش‌های منحنی فرض می‌کند. اگرچه تعیین گروه ها در مدل پارامتر تصادفی رایج است، همانطور که در بخش 3.1 ذکر شد ، در این تحقیق نیازی به تقسیم داده ها به گروه ها نیست.
نتایج تخمین مدل در جدول 2 ارائه شده است. چندین مشاهدات کلی شایان ذکر است. GWNBR با کمترین مقدار AICc و بیشترین مقدار احتمال ورود به سیستم بهترین عملکرد را دارد، که نشان می‌دهد با در نظر گرفتن ناهمگونی فضایی همه متغیرها و پارامترهای پراکندگی، فرکانس سقوط منحنی به بهترین شکل توسط مدل GWNBR نشان داده می‌شود. در مورد متریک MAD، GWPR به طور شگفت انگیزی مقدار MAD کوچکتری را نسبت به مدل های GWNBR مشاهده کرد. یکی از توضیحات این نتیجه این است که مدل GWPR با کوچکترین MAD تمایل به داشتن پهنای باند بسیار کمتر از مدل GWNBR دارد. اندازه پهنای باند کوچکتر به GWPR اجازه می دهد تا پارامترهای متفاوت محلی را به تصویر بکشد و آن را برای مقادیر شدید آسیب پذیرتر می کند. علاوه بر این، RPNB و GWNBRg عملکرد مشابهی برای احتمال ورود و AICc دارند، که در آن هر دو فرض می‌کنند که پارامتر پراکندگی در فضا تغییر نمی‌کند. سرانجام،
برای تعیین کمیت همبستگی فضایی باقیمانده‌های پیش‌بینی‌شده برای این مدل‌ها بر روی بخش‌های منحنی، از شاخص جهانی موران (I) [ 56 ] استفاده می‌شود. مقدار I موران بین -1 تا 1 متغیر است، جایی که 0 یک توزیع فضایی تصادفی کامل را نشان می دهد. مقدار مثبت دلالت بر شباهت بین همسایگان دارد و باقیمانده ها متمرکز هستند، در حالی که مقدار منفی به معنای اختلاف بین همسایگان و باقیمانده ها پراکنده هستند. به طور خلاصه، هر چه قدر مطلق موران I بیشتر باشد، داده های خودهمبستگی مکانی قوی تر است. نتایج در جدول 2 ارائه شده است.
نتیجه موران I نشان می دهد که NB بالاترین مقدار را دارد، که منعکس کننده آن خودهمبستگی فضایی نسبتاً بالا بدون در نظر گرفتن تغییرات فضایی است. GWPR، GWNBR، و GWNBRg مقادیر Moran’s I را کاهش می‌دهند، اما همگی کوچک‌تر از مقادیر NB و RPNB هستند که ممکن است به پهنای باند بهینه متفاوت آنها مرتبط باشد (GWPR <GWNBR <GWBNRg). یعنی، الگوهای محلی که از مدل به تصویر می‌کشند می‌توانند به شدت همبستگی پیش‌بینی باقی‌مانده را کاهش دهند. با این حال، هیچ یک از این مدل‌ها اهمیتی بر عدم همبستگی باقی‌مانده‌های پیش‌بینی نشان نمی‌دهند. از جدول 2 ، کاهش خودهمبستگی باقیمانده از مدل‌های NB به GWNBR 99% اهمیت را نشان می‌دهد، که نشان می‌دهد GWNBR می‌تواند یک تخمین نسبتاً غیر مغرضانه را در مقایسه با مدل جهانی ایجاد کند.

5.2. آمار پارامترهای تخمینی

پارامترهای برآورد شده در جدول 3 خلاصه شده است. پارامترها به صورت LOGR، LOGL، LOGF و LOGA نشان داده می شوند که به ترتیب لگاریتم های شعاع، طول، اصطکاک و AADT را نشان می دهند. پارامترهای محلی در رویکرد RPNB و GWR با مقادیر حداقل، چارک پایین، میانه، چارک بالا و حداکثر توصیف شدند، در حالی که تنها تخمین نقطه ای ضرایب در مدل NB ارائه شده است. پارامترهای NB جهانی علائم مثبتی را برای طول منحنی و حجم ترافیک نشان می‌دهند (LOGL و LOGA)، که نشان‌دهنده افزایش فرکانس تصادف با افزایش طول بخش منحنی و تعداد ترافیک است. تخمین شعاع منحنی و اصطکاک روسازی (LOGR و LOGF) پارامترهای جهانی منفی را نشان داده است، که منطقی است و با یافته های تحقیقات اخیر مطابقت دارد [ 57 ]، 58 ]. همانطور که در جدول 3 و جدول 4 نشان داده شده است ، آمار پارامترها نشان می دهد که: (1) مقادیر میانگین و میانه پارامترهای تخمین زده شده از همه این مدل های غیر ثابت به دست آمده از مدل دو جمله ای منفی جهانی نزدیک است، که نشان می دهد که مدل جهانی به طور کلی میانگین تاثیر این عوامل را در مدل های غیر ثابت منعکس می کند. (2) محدوده پارامترهای متغیر را می توان به صورت GWPR > GWNBR > GWNBRg > RPNB رتبه بندی کرد که با بحث در بخش بعدی مطابقت دارد.
همچنین شایان ذکر است که در GWPR و GWNBR علائم ضد شهودی وجود دارد. مدل GWPR دارای نشانه های ضد شهودی از ضرایب برای برخی مشاهدات برای قطع رگرسیون و LOGR، LOGF، و LOGA بود. مدل GWNBR همچنین دارای برخی از نشانه‌های غیرمستقیم ضرایب برای LOGR بود. از آنجایی که ثابت شده است که چند خطی بودن ضریب فضایی مسئول علائم ضدشهودی [ 59 ] نیست، این نتیجه را می توان با این فرضیه توضیح داد که برخی از متغیرها ممکن است در مناطق خاصی معنی دار نباشند. این نواحی محلی ممکن است برای برخی از متغیرها علائم ضد شهودی ناچیز داشته باشند [ 12 ]. این را می توان با مشاهده ضریب توزیع فضایی GWPR و GWNBR در شکل 2 تأیید کرد.. علائم غیرمنتظره غیرمنتظره غیرمنتظره در بین متغیرها در GWPR ممکن است ناشی از شکست با توجه به پراکندگی بیش از حد داده ها باشد [ 28 ].

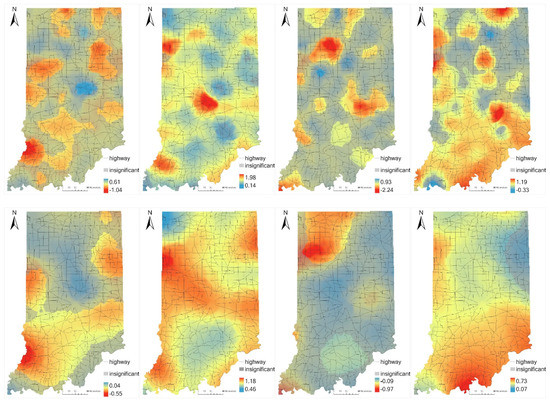
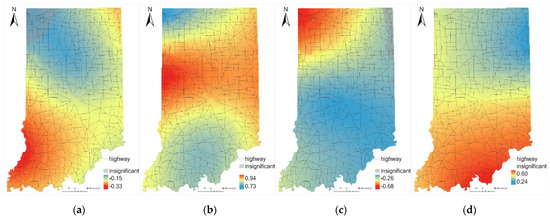
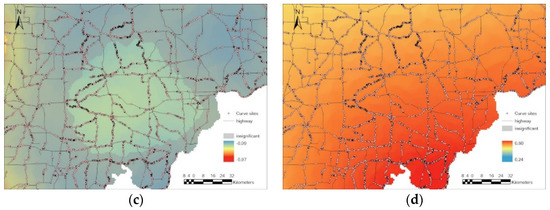
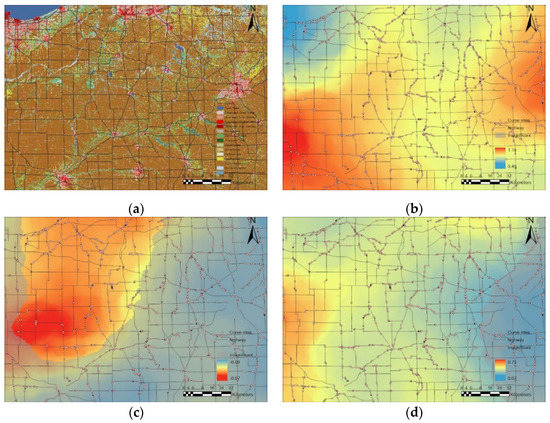
5.3. ناهمگونی مکانی پارامترهای برآورد شده

توزیع تخمین‌های ضرایب محلی و اهمیت آن‌ها با وزن معکوس فاصله (IDW) برای GWPR، GWNBR، GWNBRg در شکل 2 نشان داده شده است. با استفاده از مقادیر پارامتر شناخته شده برای بخش های منحنی 9415، الگوریتم IDW مقادیر مکان های اندازه گیری نشده را با استفاده از مقادیر مکان های اندازه گیری شده اطراف پیش بینی می کند. نواحی با سطح معنی داری کمتر از 90 درصد در تحلیل پارامتر در نظر گرفته نمی شوند و با رنگ خاکستری پوشانده می شوند. به طور کلی، هر یک از توزیع های ضرایب GWPR، GWNBR، یا GWNBRg به دلیل پهنای باند بهینه متفاوتشان همگن تر هستند. هرچه پهنای باند بهینه آنها بیشتر باشد، توزیع ضرایب آنها همگن تر خواهد بود.
از آنجایی که GWNBR با توجه به خوبی تناسب از نظر AICc بهترین عملکرد را دارد، تخمین پارامترها عمدتاً طبق مدل GWNBR نشان داده شده‌اند. مشاهدات با ضرایب قابل توجه به ترتیب برای LOGR، LOGL، LOGF و LOGA، 54.9٪، 100، 22.0٪ و 96.2٪ را تشکیل می دهند. درصد بالایی از اهمیت پارامترهای LOGL و LOGA به دلیل تأثیر غالب عوامل نوردهی در پیش‌بینی فرکانس تصادف، همانطور که انتظار می‌رود ظاهر می‌شود.
با مشاهده توزیع ضریب شعاع منحنی (LOGR) از GWPR در شکل 2 a، ناحیه مرکزی بالاترین ضرایب را نشان می دهد، اما فقط یک ناحیه کوچک علائم مثبت را نشان می دهد. با این حال، مناطق مرکزی و شمال غربی با ضرایب بالا از اهمیت کافی برای در نظر گرفتن در مدل GWNBR برخوردار نیستند. در مدل GWNBR، مقادیر پایین‌تر عمدتاً در بخش جنوبی ایالت ایندیانا توزیع می‌شوند که نشان‌دهنده تأثیر قابل‌توجه شعاع منحنی در این مناطق است. برای مدل GWPR، شکل 2 a چندین منطقه مهم را نشان می دهد که به سختی می توان الگوهای فضایی ضریب شعاع را خلاصه کرد. GWNBRg در شکل 2a کاهش همواری را از شمال غربی به جنوب غربی نشان می دهد که ممکن است ناشی از برخی مقادیر شدید باشد. از این رو، اگرچه 93 درصد مشاهدات ضرایب قابل توجهی را برای مدل GWNBRg LOGR نشان می‌دهند، روند متغیر ضریب ممکن است قابل اعتماد نباشد.
برای طول بخش منحنی (LOGL) در شکل 2 ب، توزیع ضریب GWNBR دو ناحیه با ضریب نسبتاً پایین‌تر را در جنوب ایندیانا و منطقه نزدیک به شیکاگو نشان می‌دهد. مشابه توزیع ضریب LOGR، شکل 2 b GWPR توزیع شکسته ضریب LOGL را بدون الگوی ظاهری نشان می‌دهد و شکل 2 b GWNBRg کاهش ضریب را از مرکز به شمال و جنوب نشان می‌دهد.
هنگام تجزیه و تحلیل توزیع فضایی ضرایب GWNBR برای اصطکاک منحنی (LOGF) در شکل 2 ج، مشاهده می شود که تنها دو ناحیه مجزا وجود دارد که ضرایب قابل توجهی را نشان می دهند. مورد واقع در ناحیه جنوبی که تقریباً با ناحیه ضریب پایین جنوبی LOGL در شکل 2 ب منطبق است GWNBR دارای مقادیر ضریب در حدود -0.25 است، در حالی که دیگری واقع در ناحیه شمالی دارای ضرایب اصطکاک قابل توجهی کمتر است.
در شکل 2 d، توزیع ضریب AADT (LOGA) GWNBR مقادیر بالایی را در جنوب و جنوب شرقی ایندیانا نشان می دهد. همچنین ناحیه کوچکی از ناحیه ضریب غیر معنی دار در شمال شرق وجود دارد. در مورد مدل GWPR در شکل 2 d، یک منطقه ضریب ناچیز عمدتاً در شمال ایندیانا واقع شده است. GWNBRg (ردیف پایین) روند کاهشی ضریب کلی تری را از جنوب به شمال نشان می دهد.
به طور خلاصه، توزیع ضرایب در GWPR و GWNBRg دارای معایب مربوط به توضیح پارامتر است. همه ضرایب یک الگوی بسیار ناهمگن در مدل سازی GWPR نشان می دهند، در حالی که توزیع ضریب GWNBRg بسیار همگن است. حتی بدون در نظر گرفتن بدترین خوبی تناسب آن، توزیع ضریب GWPR برای تجزیه و تحلیل بیش از حد دقیق است. در مقابل، توزیع ضریب GWNBRg یک سطح صاف در سراسر حالت را با تغییرات کوچک نشان می دهد و تقریباً همه مشاهدات دارای ضرایب قابل توجهی برای این چهار پارامتر هستند. با این حال، این مشخصه GWNBRg را به یک مدل جهانی نزدیک‌تر می‌کند که نمی‌تواند ناهمگونی فضایی پارامترها را توضیح دهد.

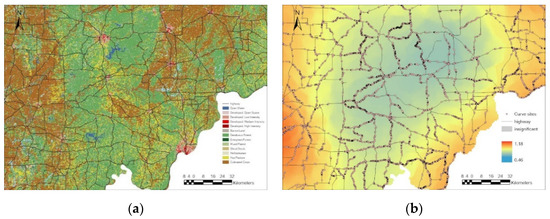
5.4. تجزیه و تحلیل محلی نتایج GWR

با مشاهده تفاوت بین توزیع ضرایب در شمال و جنوب ایندیانا، لازم است مثال‌های محلی برای تحلیل عوامل احتمالی که باعث ناهمگونی شده‌اند، استفاده شود. همانطور که در مقدمه توضیح داده شد، فاکتورهای مشاهده نشده زیادی از جمله واکنش راننده، آب و هوا و پوشش زمین وجود دارد. این مقاله نشان داد که الگوی پوشش زمین با توزیع ضریب اصطکاک روسازی و طول منحنی منطبق است، که می تواند توسط دو منطقه معمولی ایندیانا با پوشش های زمین و توپوگرافی های مختلف نشان داده شود.
با در نظر گرفتن جنوب ایندیانا با مساحت جنگل و شمال ایندیانا با محصولات زراعی برای مقایسه، برخی از الگوهای توزیع ضریب مطابق با پوشش زمین در شکل 3 a و شکل 4 وجود دارد.آ. در منطقه جنگلی جنوب ایندیانا، این منطقه دارای قدر مطلق بالاتر برای ضرایب AADT و مقادیر مطلق پایین برای طول منحنی و ضریب اصطکاک روسازی است، که منعکس کننده تأثیر نسبتاً قوی حجم ترافیک بر فرکانس تصادف منحنی در بخش‌های منحنی جنگل است. در شمال ایندیانا، با پوشش زمین همگن، پارامترها در فضا متفاوت است. در مقایسه با منطقه جنگلی جنوب ایندیانا، ضرایب AADT و ضرایب اصطکاک روسازی در مناطق با ضرایب قابل توجه در سطح اطمینان 95٪ به طور قابل توجهی پایین تر است. مقدار مطلق ضریب اصطکاک روسازی در منطقه جنگلی حدود 75 درصد کمتر از ناحیه دشت شمالی است. با این حال،
در رابطه با چگالی توزیع منحنی، الگوهایی نیز از شکل 4 مشاهده شده است. برای منطقه با ضرایب قابل توجه در شکل 4 ج، مکان های با توزیع قطعه منحنی پراکنده مقادیر مطلق بالاتری از ضریب اصطکاک روسازی را نسبت به منطقه استراحت در سطح اطمینان 95٪ نشان می دهند. با توجه به اینکه زمین زراعی زیر کشت با تراکم جمعیت کم است، قابل توضیح است که اصطکاک روسازی به شدت بر فرکانس تصادف منحنی در مزارع کم جمعیت، جایی که بزرگراه ها عمدتاً مستقیم هستند، تأثیر می گذارد.
بر اساس سه سال سوابق تصادفات منحنی در بزرگراه‌های ایندیانا، می‌توان نتیجه‌گیری کرد که فرکانس تصادف کمتر به اصطکاک و طول منحنی بستگی دارد، اما ارتباط زیادی با AADT در منطقه جنگلی جنوبی دارد. بقیه ایالت ایندیانا با پوشش زمینی عمدتاً کشت شده هنوز دارای برخی عوامل مشاهده نشده دیگر مانند تراکم منحنی است که ممکن است بر فرکانس سقوط منحنی تأثیر بگذارد. این مقاله نشان می‌دهد که عملیات سطح اصطکاک بالاتر (HFST) برای بخش‌های منحنی بزرگراه در مناطق دشت ایندیانا برای بهبود ایمنی بسیار توصیه می‌شود.
به طور کلی، برنامه ریزان می توانند مستقیماً از نتایج به دست آمده از تجزیه و تحلیل توزیع فضایی ضرایب GWNBR برای توسعه استراتژی های افزایش امنیت در طراحی منحنی استفاده کرده و این استراتژی ها را از منظر اثرات امنیتی ارزیابی و اولویت بندی کنند.

6. نتیجه گیری

فرکانس سقوط بیش از حد پراکنده با ناهمگنی فضایی برای بررسی کمی رابطه آن با ویژگی‌های بخش منحنی جمع‌آوری‌شده در سطح خرد (هر مشاهده) مورد استفاده قرار گرفت. دو نوع روش، مدل‌های غیرمکانی و مدل‌های فضایی، برای محاسبه ناهمگونی فضایی ضرایب به دلیل عوامل مشاهده نشده در فضا مورد استفاده قرار گرفتند. برای در نظر گرفتن پراکندگی بیش از حد داده ها، مدل NB سنتی به عنوان یک مدل جهانی پایه مشخص شده است. رویکردهای فضایی RPNB و GWR، از جمله GWPR، GWNBR، و GWNBRg برای یافتن مدل ترجیحی برای توضیح وقوع تصادف جاده‌ای مورد استفاده قرار گرفتند. مدل تخمینی برای تعیین فرکانس تصادف روی منحنی‌ها از متغیرهای توضیحی شعاع منحنی، طول منحنی، اصطکاک روسازی و حجم ترافیک استفاده می‌کند که در بخش‌های منحنی مجزا جمع‌آوری شده‌اند.
GWPR کمترین MAD (0.845) و کوچکترین مقدار مطلق Moran’s I (0.0297) را با برازش بیش از حد به مقادیر شدید با ضریب ناهمگنی خود به دست می‌آورد، در حالی که مدل GWNBR از نظر احتمال ورود به سیستم (-9780.7) و AICc (19،7715) بهتر از سایرین است. ). از آنجایی که هیچ یک از این مدل‌ها عدم همبستگی توزیع فضایی باقی‌مانده را اثبات نمی‌کنند، GWNBR بهترین رویکردی بود که قادر بود ناهمگونی فضایی بین فراوانی تصادف‌های منحنی و متغیرهای توضیحی را به تصویر بکشد. اگرچه مدل RPNB می‌تواند ناهمگنی مشاهده نشده را در فرآیند مدل‌سازی بگنجاند و به‌طور گسترده مورد استفاده قرار گرفته است، اما نمی‌تواند همبستگی فضایی را که در مشاهدات مجاور وجود دارد، در نظر بگیرد، که ممکن است منجر به تخمین‌های پارامتر مغرضانه و استنتاج نادرست شود. فرآیند کالیبراسیون رویکرد GWR بر اساس قانون اول جغرافیا است، که به دلیل همبستگی همه مقادیر ویژگی ها در منطقه مورد نظر اجرا می شود، اما مقادیر نزدیک بیشتر از مقادیر دور مرتبط هستند. مدل GWPR می تواند MAD را با الگوی توزیع ضریب ناهمگن به حداقل برساند، اما با علائم نادرست قابل توجهی برای شعاع و اصطکاک، ممکن است مسائل بیش از حد برازش وجود داشته باشد. مدل GWNBR عملکرد بهتری نسبت به مدل GWNBRg با پارامتر پراکندگی جهانی دارد. این مدل به عنوان بهترین مدل محلی انتخاب شده است که ضرایب فرکانس تصادف منحنی غیر ثابت را در سراسر کشور نشان می دهد. مدل GWPR می تواند MAD را با الگوی توزیع ضریب ناهمگن به حداقل برساند، اما با علائم نادرست قابل توجهی برای شعاع و اصطکاک، ممکن است مسائل بیش از حد برازش وجود داشته باشد. مدل GWNBR عملکرد بهتری نسبت به مدل GWNBRg با پارامتر پراکندگی جهانی دارد. این مدل به عنوان بهترین مدل محلی انتخاب شده است که ضرایب فرکانس تصادف منحنی غیر ثابت را در سراسر کشور نشان می دهد. مدل GWPR می تواند MAD را با الگوی توزیع ضریب ناهمگن به حداقل برساند، اما با علائم نادرست قابل توجهی برای شعاع و اصطکاک، ممکن است مسائل بیش از حد برازش وجود داشته باشد. مدل GWNBR عملکرد بهتری نسبت به مدل GWNBRg با پارامتر پراکندگی جهانی دارد. این مدل به عنوان بهترین مدل محلی انتخاب شده است که ضرایب فرکانس تصادف منحنی غیر ثابت را در سراسر کشور نشان می دهد.
مدل GWNBR نوسان متوسطی از شعاع بخش‌های منحنی و تأثیر اصطکاک روسازی را برای فرکانس تصادف در فضا ارائه می‌کند که ناهمگنی فضایی را در هر دو پارامتر نشان می‌دهد. برای منطقه جنگلی جنوب ایندیانا، اصطکاک روسازی و طول منحنی نقش کمتری در کاهش وقوع تصادف نسبت به سایر مناطق پوشش زمین ایفا می کند، اما AADT در این منطقه بسیار مهم است. در مناطق دشت، پارامترها همچنان در فضا بدون در نظر گرفتن سایر عوامل مشاهده نشده مانند آب و هوا و رفتار راننده تغییر می کنند. مشخص شد که اثر اصطکاک روسازی بر کاهش تصادف در منطقه جنگلی جنوب 75 درصد کمتر از منطقه دشت شمالی است. این یافته ها به متخصصان ایمنی کمک می کند تا ایمنی منحنی های افقی را با دقت بیشتری تخمین بزنند، بودجه را برای کاهش یا جلوگیری از تصادفات احتمالی اختصاص دهند. و بر اساس داده های تصادف منحنی افقی موجود برای به حداقل رساندن خطر تصادف، بخش های جاده بهتری را طراحی کنید. به عنوان مثال، HFST پیشنهاد شده است که در منحنی های بزرگراه در منطقه دشت اجرا شود. در نواحی تپه ای، اگر زمین اجازه نمی دهد شعاع منحنی کاهش یابد، برخی از اقدامات متقابل مانند محدود کردن حجم ترافیک در ساعات اوج بار باید همزمان در اجرای HFST در نظر گرفته شود.
این مقاله محدودیت هایی دارد. از آنجایی که ایندیانا تحت سلطه محصولات زراعی و جنگل ها است، استنباط قابل اعتماد تأثیرات پارامترها در سایر پوشش های زمینی که کمتر نشان داده شده اند دشوار است. علاوه بر این، داده های محدودیت سرعت عامل مهمی برای مطالعه ایمنی منحنی هستند. اگرچه یک مدل غیر ثابت می‌تواند متغیرهای غیرقابل دسترس را جبران کند، افزودن داده‌های محدودیت سرعت احتمالاً منجر به مدل‌سازی واقعی‌تر می‌شود.
چندین زمینه برای کارهای آینده توصیه می شود. همیشه درست نیست که همه پارامترها زمانی که متغیرهای زیادی درگیر هستند، متغیر مکانی هستند. از این رو، می توان یک مدل نیمه پارامتریک برای تنظیم متغیرها بدون تغییرات مکانی قوی در نظر گرفت. برای توضیح اثرات محلی در فضا و زمان، گسترش رویکرد GWR به حوزه زمانی، یعنی مدل GTWR [ 33 ، 60 ]، ممکن است یک مدل معقول برای مطالعات ایمنی ترافیک باشد. در نهایت، از آنجایی که مشاهدات بیش از حد صفر وجود دارد، یک مدل تورم صفر ممکن است با مدل GWR معمولی ترکیب شود، یعنی یک مدل رگرسیون دوجمله‌ای منفی با وزن جغرافیایی با تورم صفر (ZIGWNBR) در نظر گرفته شود.

منابع

  1. درمان های کم هزینه برای ایمنی منحنی افقی 2016–ایمنی|اداره بزرگراه فدرال. در دسترس آنلاین: https://safety.fhwa.dot.gov/roadway_dept/countermeasures/horicurves/fhwasa15084/#toc (در 11 مارس 2021 قابل دسترسی است).
  2. بوداواراپو، پ. بانرجی، ا. تاثیر پروزی، JA از وضعیت روسازی بر ایمنی منحنی افقی. اسید. مقعدی قبلی 2013 ، 52 ، 9-18. [ Google Scholar ] [ CrossRef ]
  3. اشنایدر، WH; Savolainen، PT; مور، DN اثرات انحنای افقی بر تصادفات موتورسیکلت تک وسیله نقلیه در امتداد بزرگراه های دو خطه روستایی. ترانسپ Res. ضبط 2010 ، 2194 ، 91-98. [ Google Scholar ] [ CrossRef ]
  4. موسی، ک. پارک، S. شماره لغزنده روسازی و ایمنی منحنی افقی. Procedia Eng. 2016 ، 145 ، 828-835. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  5. گوچ، جی پی؛ Gayah، VV; دانل، ET اثرات ایمنی منحنی‌های افقی را در جاده‌های روستایی دو طرفه و دو بانده تعیین می‌کند. اسید. مقعدی قبلی 2016 ، 92 ، 71-81. [ Google Scholar ] [ CrossRef ] [ PubMed ]
  6. ونکاتارامان، ن. شانکار، وی. Ulfarsson، GF; Deptuch، D. مدل شمارش ناهمگونی در میانگین برای ارزیابی اثرات نوع تبادل بر تأثیرات ناهمگن هندسه بین ایالتی بر فرکانس های تصادف. مقعدی روش ها اسید. Res. 2014 ، 2 ، 12-20. [ Google Scholar ] [ CrossRef ]
  7. منرینگ، FL; شانکار، وی. Bhat، CR ناهمگونی مشاهده نشده و تجزیه و تحلیل آماری داده های تصادف بزرگراه. مقعدی روش ها اسید. Res. 2016 ، 11 ، 1-16. [ Google Scholar ] [ CrossRef ]
  8. کای، س. عبدالعطی، م. لی، جی. هوانگ، اچ. یکپارچه‌سازی تحلیل‌های ایمنی سطح کلان و میکرو: رویکرد بیزی که تعامل فضایی را در بر می‌گیرد. ترانسپ ترانسپ علمی 2019 ، 15 ، 285–306. [ Google Scholar ] [ CrossRef ]
  9. Wan, D. تجزیه و تحلیل فضایی فرکانس تصادف و شدت آسیب در شهر نیویورک: کاربردهای روش رگرسیون وزن‌دار جغرافیایی. Ph.D. پایان نامه، کالج شهری نیویورک، نیویورک، نیویورک، ایالات متحده آمریکا، 2018. [ Google Scholar ]
  10. دودو، VR؛ Pulugurtha، شبکه های عصبی SS برای برآورد تصادفات در سطح منطقه ای برای برنامه ریزی حمل و نقل. در مجموعه مقالات کنفرانس حمل و نقل اروپا 2012، گلاسکو، اسکاتلند، 8 تا 10 اکتبر 2012. [ Google Scholar ]
  11. لی، جی. عبدالعطی، م. جیانگ، X. توسعه سیستم منطقه برای تجزیه و تحلیل ایمنی ترافیک سطح کلان. J. Transp. Geogr. 2014 ، 38 ، 13-21. [ Google Scholar ] [ CrossRef ]
  12. Gomes، MJTL؛ کانتو، اف. دا سیلوا، رگرسیون دوجمله ای منفی دارای وزن جغرافیایی AR که برای مدل های عملکرد ایمنی سطح منطقه ای اعمال شد. اسید. مقعدی قبلی 2017 ، 106 ، 254-261. [ Google Scholar ] [ CrossRef ] [ PubMed ]
  13. ثروری، ا. مقدم، ع.م. صالحی، محمد. J. Transp. Saf. امن 2020 ، 1-25. [ Google Scholar ] [ CrossRef ]
  14. آگوئرو والورده، جی. Jovanis، PP تجزیه و تحلیل فضایی تصادفات مرگبار و جراحات در پنسیلوانیا. اسید. مقعدی قبلی 2006 ، 38 ، 618-625. [ Google Scholar ] [ CrossRef ] [ PubMed ]
  15. هوانگ، اچ. عبدالعطی، MA; دارویچ، تجزیه و تحلیل ریسک تصادف در سطح شهرستان ایالت AL در فلوریدا: مدلسازی فضایی بیزی. ترانسپ Res. ضبط 2010 ، 2148 ، 27-37. [ Google Scholar ] [ CrossRef ]
  16. عبدالعطی، م. لی، جی. صدیقی، ج. چوی، ک. تجزیه و تحلیل مبتنی بر واحد جغرافیایی در زمینه برنامه ریزی ایمنی حمل و نقل. ترانسپ Res. بخش A سیاست سیاست. 2013 ، 49 ، 62-75. [ Google Scholar ] [ CrossRef ]
  17. Quddus، MA مدل سازی نتایج شمارش گسترده منطقه با همبستگی فضایی و ناهمگونی: تجزیه و تحلیل داده های سقوط لندن. اسید. مقعدی قبلی 2008 ، 40 ، 1486-1497. [ Google Scholar ] [ CrossRef ] [ PubMed ][ نسخه سبز ]
  18. وانگ، سی. قدوس، م. ایسون، اس. اثرات سرعت و انحنای جاده در سطح وسیع بر تلفات ترافیکی در انگلستان. J. Transp. Geogr. 2009 ، 17 ، 385-395. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  19. رحمان، MT; جمال، ع. الاحمدی، HM بررسی نقاط داغ برخوردهای ترافیکی و روابط فضایی آنها با کاربری زمین: یک رویکرد رگرسیون وزن‌دار جغرافیایی مبتنی بر GIS برای دمام، عربستان سعودی. ISPRS Int. J. Geo-Inf. 2020 ، 9 ، 540. [ Google Scholar ] [ CrossRef ]
  20. آموه گیمه، ر. صابری، م. سروی، م. مدلسازی ماکروسکوپی تصادفات عابر پیاده و دوچرخه: مقایسه متقابل روشهای برآورد. اسید. مقعدی قبلی 2016 ، 93 ، 147-159. [ Google Scholar ] [ CrossRef ] [ PubMed ]
  21. آموه گیمه، ر. سروی، م. صابری، م. بررسی اثرات ترافیک، اجتماعی-اقتصادی و ویژگی های کاربری زمین بر تصادفات عابر پیاده و دوچرخه: مطالعه موردی ملبورن، استرالیا. در مجموعه مقالات نود و پنجمین نشست سالانه هیئت تحقیقات حمل و نقل، واشنگتن دی سی، ایالات متحده آمریکا، 10 تا 14 ژانویه 2016. [ Google Scholar ]
  22. آموه گیمه، ر. صابری، م. سروی، م. تأثیر تغییرات در واحدهای فضایی بر ناهمگونی مشاهده نشده در مدل‌های تصادف ماکروسکوپی. مقعدی روش ها اسید. Res. 2017 ، 13 ، 28-51. [ Google Scholar ] [ CrossRef ]
  23. آناستازوپولوس، کامپیوتر؛ Mannering، FL یک ارزیابی تجربی مدل‌های لاجیت پارامترهای ثابت و تصادفی با استفاده از داده‌های آسیب تصادفی و غیر اختصاصی تصادف. اسید. مقعدی قبلی 2011 ، 43 ، 1140-1147. [ Google Scholar ] [ CrossRef ] [ PubMed ]
  24. زیاکوپولوس، ا. یانیس، جی. مروری بر رویکردهای فضایی در ایمنی راه. اسید. مقعدی قبلی 2020 ، 135 ، 105323. [ Google Scholar ] [ CrossRef ] [ PubMed ]
  25. حدایقی، ع. شلبی، ع. Persaud، BN توسعه ابزارهای ایمنی حمل و نقل در سطح برنامه‌ریزی با استفاده از رگرسیون پواسون وزن‌دار جغرافیایی. اسید. مقعدی قبلی 2010 ، 42 ، 676-688. [ Google Scholar ] [ CrossRef ] [ PubMed ]
  26. Sun، Y. مدل‌های خودرگرسیون فضایی تابعی-ضریب با وزن‌های فضایی ناپارامتری. جی. اکونوم. 2016 ، 195 ، 134-153. [ Google Scholar ] [ CrossRef ]
  27. البسیونی، ک. سید، تی. مدل های پیش بینی حوادث شریانی شهری با اثرات فضایی. ترانسپ Res. ضبط 2009 ، 2102 ، 27-33. [ Google Scholar ] [ CrossRef ]
  28. خو، پی. Huang، H. مدل سازی تصادف ناهمگونی فضایی: پارامتر تصادفی در مقابل وزن جغرافیایی. اسید. مقعدی قبلی 2015 ، 75 ، 16-25. [ Google Scholar ] [ CrossRef ] [ PubMed ]
  29. مارک، ال. کمپبل، ام. اپتون، ام. کینگهام، اس. استورر، ام. زمستان در راه است: پایش اجتماعی-محیطی و رویکرد مدل‌سازی مکانی-زمانی برای درک بهتر یک بیماری تنفسی. ISPRS Int. J. Geo-Inf. 2018 ، 7 ، 432. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
  30. چن، جی. لیو، ال. شیائو، ال. خو، سی. Long, D. تحلیل یکپارچه ناهمگونی فضایی و پراکندگی بیش از حد جرم با یک مدل دوجمله ای منفی وزن دار جغرافیایی. ISPRS Int. J. Geo-Inf. 2020 ، 9 ، 60. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
  31. وانگ، دی. یانگ، ی. کیو، ا. کانگ، ایکس. هان، جی. Chai, Z. یک رگرسیون موازی موازی جغرافیایی مبتنی بر CUDA برای داده های جغرافیایی در مقیاس بزرگ. ISPRS Int. J. Geo-Inf. 2020 ، 9 ، 653. [ Google Scholar ] [ CrossRef ]
  32. لی، ز. Fotheringham، AS; لی، دبلیو. اوشان، تی. رگرسیون وزن‌دار جغرافیایی سریع (FastGWR): یک الگوریتم مقیاس‌پذیر برای بررسی ناهمگونی فرآیند فضایی در میلیون‌ها مشاهده. بین المللی جی. جئوگر. Inf. علمی 2019 ، 33 ، 155-175. [ Google Scholar ] [ CrossRef ]
  33. Fotheringham، AS; کرسپو، آر. یائو، جی. رگرسیون وزنی جغرافیایی و زمانی (GTWR). Geogr. مقعدی 2015 ، 47 ، 431-452. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  34. حدایقی، ع. شلبی، ع. Persaud، B. مدل های پیش بینی تصادف در سطح کلان برای ارزیابی ایمنی سیستم های حمل و نقل شهری. ترانسپ Res. ضبط 2003 ، 1840 ، 87-95. [ Google Scholar ] [ CrossRef ]
  35. لی، ز. وانگ، دبلیو. لیو، پی. بیغام، جی.ام. Ragland، DR با استفاده از رگرسیون پواسون وزن‌دار جغرافیایی برای مدل‌سازی تصادف در سطح شهرستان در کالیفرنیا. Saf. علمی 2013 ، 58 ، 89-97. [ Google Scholar ] [ CrossRef ]
  36. ناکایا، تی. Fotheringham، AS; براندون، سی. چارلتون، ام. رگرسیون پواسون دارای وزن جغرافیایی برای نقشه برداری انجمن بیماری. آمار پزشکی 2005 ، 24 ، 2695-2717. [ Google Scholar ] [ CrossRef ] [ PubMed ][ نسخه سبز ]
  37. دا سیلوا، آر. رودریگز، TCV رگرسیون دوجمله‌ای منفی وزن‌دار جغرافیایی – شامل پراکندگی بیش از حد. آمار محاسبه کنید. 2013 . [ Google Scholar ] [ CrossRef ]
  38. Shaon، MRR; Qin، X. شیرازی، م. لرد، دی. Geedipally، SR در حال توسعه یک مدل دوجمله ای-لیندلی منفی با پارامترهای تصادفی برای تجزیه و تحلیل داده های تعداد تصادف بسیار پراکنده. مقعدی روش ها اسید. Res. 2018 ، 18 ، 33-44. [ Google Scholar ] [ CrossRef ]
  39. Shaon، MRR; اشنایدر، RJ; Qin، X. او، ز. صنعتی زاده، ع. Flanagan، MD کاوش قاطعیت عابر پیاده و ارتباط آن با رفتار تسلیم راننده در گذرگاه های کنترل نشده. ترانسپ Res. ضبط 2018 ، 2672 ، 69-78. [ Google Scholar ] [ CrossRef ]
  40. چن، اس. سعید، TU; القاضی، اس.د. Labi، S. اثرات ایمنی ناهمواری سطح روسازی در بزرگراه های دو خطه و چند بانده: حسابداری ناهمگونی و همبستگی ظاهراً نامرتبط بین شدت تصادف. ترانسپ ترانسپ علمی 2019 ، 15 ، 18-33. [ Google Scholar ] [ CrossRef ]
  41. ونکاتارامان، NS; Ulfarsson، GF; شانکار، وی. اوه، جی. پارک، ام. مدل رابطه بین وقوع تصادف بین ایالتی و هندسه: بینش های اکتشافی از رویکرد دو جمله ای منفی پارامتر تصادفی. ترانسپ Res. ضبط 2011 ، 2236 ، 41-48. [ Google Scholar ] [ CrossRef ]
  42. ونکاتارامان، ن. Ulfarsson، GF; Shankar، مدل‌های پارامتر تصادفی VN فرکانس‌های تصادف بین ایالتی بر اساس شدت، تعداد وسایل نقلیه درگیر، برخورد و نوع مکان. اسید. مقعدی قبلی 2013 ، 59 ، 309-318. [ Google Scholar ] [ CrossRef ] [ PubMed ]
  43. چن، ای. Tarko، AP مدلسازی ایمنی مناطق کاری بزرگراه با پارامترهای تصادفی و مدل‌های اثرات تصادفی. مقعدی روش ها اسید. Res. 2014 ، 1 ، 86-95. [ Google Scholar ] [ CrossRef ]
  44. سعید، TU; هال، تی. بارود، ح. Volovski، MJ تحلیل فرکانس‌های تصادف جاده‌ای با مدل‌های تعداد پارامترهای تصادفی ناهمبسته و همبسته: ارزیابی تجربی بزرگراه‌های چند خطی. مقعدی روش ها اسید. Res. 2019 ، 23 ، 100101. [ Google Scholar ] [ CrossRef ]
  45. شین، سی. وانگ، ز. لی، سی. لین، پی.اس. مدلسازی اثرات ایمنی طراحی منحنی افقی بر شدت آسیب تصادفات تک موتورسیکلت با مدل لجستیک اثرات مختلط. ترانسپ Res. ضبط 2017 ، 2637 ، 38-46. [ Google Scholar ] [ CrossRef ]
  46. شین، سی. وانگ، ز. لین، پی اس. لی، سی. Guo, R. اثرات ایمنی طراحی منحنی افقی بر فرکانس تصادف موتور سیکلت در بزرگراه های روستایی، دو خطه، تقسیم نشده در فلوریدا. ترانسپ Res. ضبط 2017 ، 2637 ، 1-8. [ Google Scholar ] [ CrossRef ]
  47. منرینگ، FL; بات، روش‌های تحلیلی CR در تحقیقات حوادث: مرزهای روش‌شناختی و جهت‌گیری‌های آینده. مقعدی روش ها اسید. Res. 2014 ، 1 ، 1-22. [ Google Scholar ] [ CrossRef ]
  48. Agresti, A. مبانی مدل های خطی و تعمیم یافته خطی ; جان وایلی و پسران: هوبوکن، نیوجرسی، ایالات متحده آمریکا، 2015. شابک 978-1-118-73005-8. [ Google Scholar ]
  49. Hilbe، JM رگرسیون دو جمله ای منفی . انتشارات دانشگاه کمبریج: کمبریج، انگلستان، 2011; شابک 978-0-521-19815-8. [ Google Scholar ]
  50. Fotheringham، AS; براندون، سی. چارلتون، ام. رگرسیون وزن‌دار جغرافیایی: تحلیل روابط متغیر فضایی . جان وایلی و پسران: هوبوکن، نیوجرسی، ایالات متحده آمریکا، 2003; شابک 978-0-470-85525-6. [ Google Scholar ]
  51. امپریالو، ام. Quddus, M. کیفیت داده های تصادف برای تحقیقات ایمنی جاده: وضعیت فعلی و جهت گیری های آینده. اسید. مقعدی قبلی 2019 ، 130 ، 84–90. [ Google Scholar ] [ CrossRef ] [ PubMed ][ نسخه سبز ]
  52. رومرو، ام. آتیسو، ای. وانگ، تی. اسلاشر، ال. Tarko، A. استفاده از GIS برای تعیین مکان برای بهبود ایمنی. در دسترس آنلاین: https://docs.lib.purdue.edu/purduegisday/2017/allevents/1/ (در 26 آوریل 2021 قابل دسترسی است).
  53. بیل، ام. آندراشیک، آر. سدونیک، جی. Cícha، V. ROCA – جعبه ابزار ArcGIS برای شناسایی تراز جاده و محاسبه شعاع منحنی افقی. PLoS ONE 2018 , 13 , e0208407. [ Google Scholar ] [ CrossRef ] [ PubMed ][ نسخه سبز ]
  54. هایبرگر، RM; هلند، ب. تجزیه و تحلیل آماری و نمایش داده ها . متون Springer در آمار; Springer: نیویورک، نیویورک، ایالات متحده آمریکا، 2015; شابک 978-1-4939-2121-8. [ Google Scholar ]
  55. الیوت، ای سی؛ Hynan، LS A SAS® ماکرو پیاده‌سازی آزمون تعقیبی مقایسه چندگانه برای تحلیل کروسکال-والیس. محاسبه کنید. روش ها برنامه های Biomed. 2011 ، 102 ، 75-80. [ Google Scholar ] [ CrossRef ] [ PubMed ]
  56. موران، یادداشت های PAP در مورد پدیده های تصادفی پیوسته. Biometrika 1950 ، 37 ، 17-23. [ Google Scholar ] [ CrossRef ] [ PubMed ]
  57. Geedipally، SR; پرت، نماینده مجلس؛ لرد، دی. اثرات هندسه و اصطکاک روسازی بر فرکانس تصادف منحنی افقی. J. Transp. Saf. امن 2019 ، 11 ، 167-188. [ Google Scholar ] [ CrossRef ]
  58. هیمز، اس. پورتر، RJ; همیلتون، آی. دانل، E. ارزیابی ایمنی معیارهای طراحی هندسی: شعاع منحنی افقی و تقاضای اصطکاک جانبی در بزرگراه‌های روستایی، دو خطه. ترانسپ Res. ضبط 2019 ، 2673 ، 516-525. [ Google Scholar ] [ CrossRef ]
  59. Fotheringham، AS; اوشان، TM رگرسیون وزن‌دار جغرافیایی و چند خطی: رد اسطوره. جی. جئوگر. سیستم 2016 ، 18 ، 303-329. [ Google Scholar ] [ CrossRef ]
  60. ژانگ، ایکس. هوانگ، بی. زو، S. تأثیر فضای زمانی محیط شهری بر تاکسی سواری با استفاده از رگرسیون وزنی جغرافیایی و زمانی. ISPRS Int. J. Geo-Inf. 2019 ، 8 ، 23. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
Ijgi 10 00286 g001 550
شکل 1. توزیع قطعات منحنی در ایندیانا (چپ) و نمونه های معمولی در SR-114 (بالا سمت راست) و SR-450 (پایین سمت راست).
Ijgi 10 00286 g002a 550 Ijgi 10 00286 g002b 550
شکل 2. توزیع ( a ) LOGR، ( b ) LOGL، ( c ) LOGF، و ( d ) LOGA در GWPR (بالا)، GWNBR (وسط)، و GWNBRg (پایین).
Ijgi 10 00286 g003a 550 Ijgi 10 00286 g003b 550
شکل 3. پوشش زمین ( a )، توزیع ( b ) LOGL، ( c ) LOGF، و ( d ) LOGA در GWNBR در یک منطقه جنگلی در جنوب ایندیانا.
Ijgi 10 00286 g004 550
شکل 4. پوشش زمین ( a )، توزیع ( b ) LOGL، ( c ) LOGF، و ( d ) LOGA در GWNBR در یک منطقه دشتی در شمال ایندیانا.

مقالات داخلی و بین المللی

مطالب مرتبط ...

بدون دیدگاه

دیدگاهتان را بنویسید