1. مقدمه
خطوط و مناطق، اشیاء فضایی بسیار مهمی در سیستمهای اطلاعات جغرافیایی دو بعدی (2 بعدی) هستند. روابط توپولوژیکی خطوط/مناطق و خطوط/خطوط نیز نقش مهمی در سازماندهی داده های مکانی، پرس و جوها، به روز رسانی ها و کنترل کیفیت دارند. برای نزدیک به سی سال، برخی از مدلهای رسمی که برای نمایش روابط توپولوژیکی در مورد خطوط/مناطق و خطوط/خطوط در فضای دوبعدی مناسب هستند، کاوش یا توسعه یافتهاند. شناخته شده ترین مدل ها مدل چهار تقاطع (4I) [ 1 ] و مدل نه تقاطع (9I) [ 2 ] است.]، که هدف آنها توصیف روابط توپولوژیکی پایه است، مانند جدایی، ملاقات، همپوشانی، پوشش، برابر و داخل. با این حال، هر دو مدل 4I و 9I تنها محتوای تقاطع ها را متمایز می کنند، که منجر به توانایی ضعیف آنها در تشخیص روابط توپولوژیکی خط / منطقه و خط / خط می شود. به عنوان مثال، تنها روابط توپولوژیکی 11، 19 خط/منطقه و 12، 33 خط/خط را می توان به ترتیب با مدل های 4I و 9I تشخیص داد [ 3 ].
متعاقباً، تعدادی مدل توسعهیافته بر اساس مدلهای 4I و 9I برای تشخیص جزئیات توپولوژیکی بیشتر پیشنهاد شدهاند، مانند مدل 9 تقاطع توسعهیافته (DE+9IM) [ 4 ]، مدل 9 تقاطع مبتنی بر Voronoi [4]. 5 ، و مدل 27 تقاطع [ 6 ]. علاوه بر این، برخی از مدلهای بهبود یافته که میتوانند فقط روابط توپولوژیکی خط/منطقه را متمایز کنند، برای شناسایی جزئیات توپولوژیکی بیشتر پیشنهاد شدهاند، مانند مدلسازی همسایگیهای مفهومی روابط خط-منطقه توپولوژیکی [ 7 ]، مدل تقاطع 9+ برای بخشهای خط جهتدار و مناطق [ 8 ]، مدل چند خطی-چند ضلعی جهت دار [ 9 ]، و مدل ناحیه هدایت شده-خط جهت دار [9]10 ]. علاوه بر این مدلهای مبتنی بر تجزیه بالا [ 11 ]، برخی از محققان مدلهای ارتباط توپولوژیکی مختلفی را از منظر شی فضایی به عنوان یک کل توسعه دادهاند، مانند مدل RCC (حساب اتصال منطقه) [ 12 ، 13 ]، ورونوی. مدل جبر فضایی مبتنی بر [ 14 ]، و مدل تقاطع و تفاوت شی کل مبتنی بر عدد اویلر (E-WID) [ 15 ]. در میان آنها بهترین عملکرد مدل E-WID است که دارای تئوری دقیق، عملیات مجموعه کم و توانایی تشخیص قوی است.
با این حال، اگرچه توانایی تمایز برخی از مدل های فوق در مقایسه با توانایی های 4I و 9I بهبود یافته است، این مدل ها نیز درشت هستند، یعنی فقط روابط درشت را نشان می دهند. این مدلها فقط ویژگیهای توپولوژیکی کلی تقاطعها (یا تفاوتها)، مانند محتوا، بعد، عدد اویلر و غیره را توصیف میکنند و بنابراین، برخی از نتایج توصیف آنها مبهم است. به عبارت دیگر، برخی از روابط مختلف، به ویژه روابط پالایش شده که دارای اجزای متقاطع متعدد هستند، نتایج توصیفی یکسانی دارند. در برخی از کاربردهای عملی GIS، نمایش و محاسبه روابط توپولوژیکی تصفیه شده، به ویژه توالی، بعد و نوع توپولوژیکی هر یک از اجزای تقاطع (یا تفاوت) بسیار مهم است. مثلا، در تشخیص و پردازش تضاد توپولوژیکی خط/منطقه و خط/خط برای دادههای OpenStreetMap (OSM)، اشیاء درگیر آنهایی هستند که دارای روابط غیرمتمرکز هستند، به عنوان مثال، متقاطع، ملاقات، داخل، و غیره. این روابط غیر متمایز ممکن است دارای دو یا اجزای تقاطع بیشتر همانطور که در نشان داده شده استشکل 1 الف، مسیر داوطلب (خط) L 1 دارای سه تقاطع یک بعدی ( i 1 ، i 2 و i 3 ) با همان دریاچه (منطقه) R 1 است. به طور مشابه، در شکل 1 b، خط مسیر L 2 دارای سه جزء تقاطع با خط مسیر L 3 است که شامل دو تقاطع یک بعدی ( i 4 و i 6 ) و یک تقاطع صفر بعدی ( i 5 ) است.). این روابط با اجزای تقاطع چندگانه باید یک به یک با توجه به انواع توپولوژیکی تصفیه شده آنها مورد بررسی قرار گیرد. بنابراین، بررسی نمایش و محاسبه روابط توپولوژیکی پالایش شده خط/منطقه و خط/خط، به ویژه طبقه بندی کامل انواع توپولوژیکی هر جزء تقاطع ضروری است.
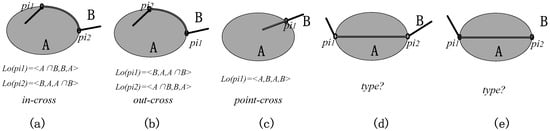
برای خط/منطقه در یک سطح تصفیه شده، روش LRBIS (تقاطعات تنظیم شده بین خط و مرز منطقه) پیشنهاد شده توسط دنگ [ 16 ]] در حال حاضر نماینده است. در این روش، روابط خط-منطقه بر اساس متغیرهای بعد و نظم محلی به 16 نوع رابطه پایه (شامل 1 رابطه منفصل و 15 رابطه غیر منفصل) طبقه بندی می شوند و روابط مرکب به صورت ترکیبی تجزیه و توصیف می شوند. تعداد محدودی از روابط تقاطع پایه. اما تعریف جزء تقاطع در این روش بر اساس تقاطع کل خط و کل منطقه نیست بلکه بر اساس تقاطع بین کل خط و مرز منطقه است. بنابراین، اجزای تقاطع آن به خوبی از عادات شناختی افراد پیروی نمی کند و برخی از انواع واقعی تقاطع های یک بعدی بین خط و منطقه داخلی حذف شده است. به عنوان مثال، این روش تنها سه نوع متقاطع را تعریف می کند (نگاه کنید بهشکل 2 a-c)، در حالی که سایر انواع متقاطع موجود ( شکل 2 d,e) تعریف نشده اند. به عبارت دیگر، روش LRBIS ناقص است.
برای روابط پالایش شده بین خطوط/خطوط، روش نماینده موجود توسط کلمنتینی و فلیس [ 17 ] پیشنهاد شد. در روش، بعد، نوع تقاطع، حس همخطی و جهت پیوند اجزای تقاطع و توالی آنها برای توصیف روابط پالایش شده استفاده می شود. اگرچه نوع مؤلفه تقاطع را نیز توصیف میکند، اما بیشتر بر جزئیات توپولوژیکی کلی خطوط/خطوط تمرکز میکند، که منجر به معرفی متغیرهای توپولوژیکی بیشتر که موازی با نوع مؤلفه تقاطع هستند، میشود و توصیف پیچیده میشود.
در حال حاضر، چند مطالعه دیگر در مورد روابط پالایش شده خط/منطقه و خط/خط وجود دارد، مانند مدل تفصیلی روابط توپولوژیکی و متریک بین خط و منطقه [ 18 ] و مدل رابطه مرکب خط/خط با استفاده از روابط اساسی [ 19 ]. با این حال، این روش ها یا هنوز ناقص هستند یا توصیفات بسیار پیچیده ای دارند. به عنوان مثال، تنها هفت نوع پاره خط تفصیلی برای توصیف روابط توپولوژیکی تصفیه شده بین خطوط/منطقه در مرجع [ 18 ]، و فاکتورهای چند سطحی و چند توصیفی برای توصیف روابط خط/خط تصفیه شده در مرجع [18] استفاده می شود. 19]. علاوه بر این، اگرچه خط/منطقه و خط/خط هر دو دارای و فقط دارای اجزای تقاطع یک بعدی و صفر بعدی هستند، در حال حاضر هیچ روش واحدی برای نمایش روابط پالایش شده آنها وجود ندارد. بنابراین، نمایش معقول (کامل و مختصر) و یکپارچه اجزای خط/منطقه و تقاطع خط/خط هنوز یک موضوع باز در جامعه GIS است. ارائه یک چارچوب مؤثر، مختصر و یکپارچه برای توصیف روابط خط/منطقه و خط/خط پالایش شده ضروری است.
در مرجع [ 2 ]، ژو و همکاران. یک توصیف سلسله مراتبی و روش محاسبه روابط توپولوژیکی بین دو منطقه در فضای دوبعدی ارائه شده است. در این روش، روابط درشت با مدل E-WID، و روابط پالایش شده عمدتاً با مدل مجموعههای تقاطع کل-کلی مبتنی بر عدد اویلر (E-WWIS) نشان داده میشوند. اگرچه برخی از روابط بسیار پیچیده تصفیه شده باید در ترکیب با E-WWIS و مجموعه های تقاطع مرزی (BBIS) متمایز شوند [ 20مدل E-WWIS در کاربردهای عملی به خوبی عمل کرده است. علاوه بر این، مدل E-WWIS بر اساس کل تقاطع شی است و یک چارچوب توصیف معقول دارد. این مدل از توالی، بعد و نوع توپولوژیک مؤلفه تقاطع برای نشان دادن روابط پالایش شده استفاده می کند که مختصر و سازگار با عادات شناختی است. بنابراین، این مقاله همچنین از چارچوب اصلی مدل E-WWIS برای نمایش روابط پالایش شده خط/منطقه استفاده خواهد کرد. با این حال، اگرچه عدد اویلر در تشخیص تقاطعهای دوبعدی به خوبی عمل میکند، اما در تقاطعهای یکبعدی و صفر به خوبی کار نمیکند. از این رو، ثابتهای توپولوژیکی جدید باید به جای اعداد اویلر در مدل E-WWIS برای تمایز انواع اجزای تقاطع یکبعدی و صفر بین خطوط/منطقهها (و خطوط/خطوط) معرفی شوند. پس از تجزیه و تحلیل ویژگی های اجزای تقاطع، متغیرهای توپولوژیکی درجه گره و انواع نقاط مجاور معرفی و تعریف شده و برای شناسایی انواع خطوط تقاطع و نقاط تقاطع استفاده می شود. بنابراین، یک مدل مجموعههای تقاطع کل کل مبتنی بر درجه گره (N-WWIS) برای توپولوژی تصفیهشده بین خطوط/منطقهها (و خطوط/خطوط) تولید میشود. متغیرهای توپولوژیکی درجه گره و انواع نقاط مجاور معرفی و تعریف شده اند و از آنها برای شناسایی انواع خطوط تقاطع و نقاط تقاطع استفاده می شود. بنابراین، یک مدل مجموعههای تقاطع کل کل مبتنی بر درجه گره (N-WWIS) برای توپولوژی تصفیهشده بین خطوط/منطقهها (و خطوط/خطوط) تولید میشود. متغیرهای توپولوژیکی درجه گره و انواع نقاط مجاور معرفی و تعریف شده اند و از آنها برای شناسایی انواع خطوط تقاطع و نقاط تقاطع استفاده می شود. بنابراین، یک مدل مجموعههای تقاطع کل کل مبتنی بر درجه گره (N-WWIS) برای توپولوژی تصفیهشده بین خطوط/منطقهها (و خطوط/خطوط) تولید میشود.
ساختار باقی مانده مقاله به شرح زیر است. در بخش 2 ، اشیاء فضایی ساده در فضای دو بعدی و اجزای تقاطع خط/منطقه (و خط/خط) تعریف شده و درجه گره معرفی شده است. در بخش 3 ، انواع اجزای تقاطع با استفاده از درجه گره و انواع نقاط مجاور طبقه بندی می شوند. نمایش سلسله مراتبی روابط توپولوژیکی خط/منطقه و خط/خط بر اساس مدل های E-WID (سطح درشت) و N-WWIS (سطح تصفیه شده) در بخش 4 مورد بحث قرار گرفته است. آزمایش های کاربردی و تجربی در بررسی خودکار یکپارچگی توپولوژیکی در بخش 5 ارائه شده است. نتیجه گیری و بحث در بخش 6 ارائه شده است.
2. تعریف مولفه تقاطع و معرفی درجه گره
2.1. تعریف یک شی فضایی ساده
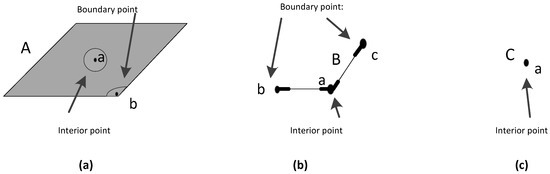
یک تعریف خوب از اشیاء فضایی، مبنای مهمی برای توصیف و تمایز مؤثر روابط توپولوژیکی است. در جامعه GIS، اشیاء فضایی به طور کلی به عنوان زیرمجموعه های فضای اقلیدسی در نظر گرفته می شوند و تعاریف توپولوژیکی آنها از “داخلی” و “مرز” معمولاً بر اساس توپولوژی مجموعه نقطه ای است. با توجه به توپولوژی مجموعه نقطه در فضای اقلیدسی، خطوط و نقاط دارای مرز هستند اما در فضای دوبعدی داخلی ندارند [ 21 ، 22 ]. با این حال، طبق تعریف و شناخت سنتی، هر دو خطوط و نقاط دارای فضای داخلی در فضای دو بعدی هستند [ 4 ، 5 ، 6 ، 7 ، 23 .]. بنابراین، برای جلوگیری از تضاد بین مبانی نظری و تعریف سنتی، اشیاء فضایی بهعنوان منیفولدهای تعبیهشده در فضای دوبعدی در نظر گرفته میشوند و تعاریف توپولوژیکی آنها بر اساس توپولوژی چندگانه است. منیفولدها و مرز و داخلی آنها به صورت زیر تعریف می شوند [ 24 ، 25 ].
«تعریف 2.1» (چندین): فرض کنید R n یک فضای اقلیدسی n بعدی باشد، X یک فضای اقلیدسی محلی با بعد n است، و H n = {( x 1 , x 2 , …, x n ) ∈ R n , n ≥ 0} (نیم فاصله). اگر هر نقطه در X یک همسایگی همومورف با R n داشته باشد ، آنگاه X یک منیفولد n است (بدون مرز). اگر هر نقطه در X یک همسایگی همومورف داشته باشدR n یا همومورف به H n است، پس X یک منیفولد n با مرز است. اگر همسایگی نقطه p در X با R n همومورف باشد ، p را نقطه داخلی X و مجموعه تمام نقاط داخلی X را فضای داخلی ( X °) X می نامند . اگر هر همسایگی نقطه p در X با H n همومورف باشد ، p را نقطه مرزی X می نامند.و مجموعه تمام نقاط مرزی X را مرز (∂A) X می نامند .
قابل ذکر است که منیفولد خود یک فضای توپولوژیک (فضای اقلیدسی محلی) است، بنابراین همسایگی آن تنها به خود مربوط است و مستقل از فضای اقلیدسی است که در آن تعبیه شده است، به این معنی که تعاریف داخلی و نقاط مرزی در یک منیفولد عبارتند از همچنین مستقل از فضایی که منیفولد در آن تعبیه شده است (به تعریف 2.1 مراجعه کنید)، که با تعاریف استفاده از توپولوژی مجموعه نقطه ای در فضای اقلیدسی متفاوت است. همانطور که در شکل 3 نشان داده شده است ، منطقه ( شکل 3 a)، خط ( شکل 3 ب) و نقطه ( شکل 3 ج ) همگی دارای نقاط داخلی در R2 هستند.که با تعاریف سنتی و عادات شناختی همخوانی دارد. علاوه بر این، چون منیفولد یک فضای توپولوژیکی خاص است، برخی از ویژگی های توپولوژیکی خود را نیز دارد، مانند فشرده بودن، متصل بودن، جهت گیری و غیره بودن آن. . با توجه به ویژگی های هندسی اشیاء رایج در پایگاه داده فضایی، اشیاء فضایی (ساده) در فضای دوبعدی در این مقاله به شرح زیر تعریف می شوند.
“تعریف 2.2” (اشیاء فضایی): یک شی فضایی یک منیفولد متصل، فشرده و قابل جهت گیری است (0 ≤ n ≤ 2) که می تواند در فضای دو بعدی جاسازی شود. یک منطقه ساده یک دو منیفولد با یک داخلی متصل و یک مرز متصل است. یک خط ساده یک منیفولد با یک داخلی متصل و دو مرز جداگانه است. یک نقطه ساده یک منیفولد صفر با داخلی متصل اما بدون مرز است.
همانطور که در شکل 3 نشان داده شده است ، هندسه یک منطقه ساده با یک چند ضلعی مطابقت دارد و مرز آن یک منحنی بسته است ( شکل 3 a). هندسه یک خط ساده با چند خط مطابقت دارد و مرزهای آن دو نقطه انتهایی مجزا هستند ( شکل 3 ب). هندسه یک نقطه ساده مربوط به یک نقطه جدا شده است و هیچ مرزی ندارد ( شکل 3 ج).
2.2. تعریف اجزای تقاطع
برای توصیف روابط پالایش شده، مدلهای موجود عمدتاً بر اساس توالی، ابعاد و ویژگیهای توپولوژیکی (نوع توپولوژیکی) اجزای تقاطع هستند. در مدل های تصفیه شده، مانند E-WWIS، اجزا بر اساس تقاطع کل شی به دست می آیند. بنابراین، برای نمایش و محاسبه روابط خط/منطقه و خط/خط پالایش شده، ابتدا اجزای تقاطع آنها باید به خوبی تعریف شوند.
مفهوم اجزا از توپولوژی مشتق شده است. مولفههای توپولوژیکی هر مجموعه X یک زیرمجموعه متصل حداکثری (متصل به مسیر) از X را تشکیل میدهند: این مؤلفهها ناپیوسته و خالی هستند، و اتحاد آنها کل مجموعه X است [ 24 ، 26 ]. در جامعه GIS، ویژگی های اجزای توپولوژیکی معمولاً به طور مستقیم برای تعریف اجزای تقاطع یا تفاوت بین اشیاء فضایی استفاده می شود [ 20 ، 27 ]. با این حال، هنوز تفاوت هایی بین اجزای فضایی و اجزای توپولوژیکی وجود دارد. به عنوان مثال، در پایگاه داده فضایی، یک جزء فضایی باید دارای مرزهای مناسب خود باشد [ 2 ، 28 ]]، در حالی که یک جزء توپولوژیکی ممکن است نباشد (شبیه به یک دیسک باز). علاوه بر این، حتی اگر یک جزء توپولوژیکی به خودی خود مناسب باشد، برخی از آنها باید بیشتر تقسیم شوند تا نیازهای واقعی برنامه ها و عادات شناختی افراد را برآورده کنند.
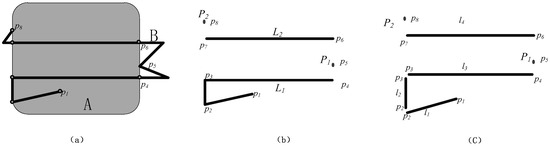
همانطور که در شکل 4 ب نشان داده شده است، مجموعه تقاطع منطقه A و خط B دارای حداکثر چهار زیرمجموعه متصل (مولفه های توپولوژیکی)، یعنی L 1 ( p 1 p 2 p 3 p 4 )، L 2 ( p 6 p 7 ) است. P 1 ( p 5 ) و P 2 ( p 8 ). از جمله P 1 و P 2تقاطع های صفر بعدی هستند زیرا هر دو به سادگی نقاط ایزوله هستند، بنابراین نیازی به تقسیم بندی ندارند. L 1 و L 2 تقاطع های یک بعدی هستند ، جایی که L 2 نیازی به تقسیم بندی ندارد زیرا نقاط داخلی آن همه در داخل منطقه A هستند ، در حالی که L 1 نسبتاً پیچیده است و نقاط داخلی آن توپولوژیکی یکسانی ندارند. ملک در منطقه A. برای مثال، نقاط بین پاره خط l 1 ( p 1 p 2 ) و l 3 ( p 3 p3 ) در داخل A هستند ، در حالی که نقاط بین پاره خط l 2 ( p 2 p 3 ) در مرز ناحیه A قرار دارند. بنابراین، حتی اگر خط تقاطع L 1 متصل است، معقول تر است که در نقاط p 1 و p 2 شکسته شود ، که همچنین با عادات شناختی افراد مطابقت دارد. علاوه بر این، اگر منطقه A را یک دریاچه فرض کنیم ، خط B جاده ای است که توسط مسیر حرکت داوطلب شکل گرفته است. سپس، l 1 ( p 1 p 2) ممکن است مسیری باشد که در دریاچه امتداد می یابد یا یک بخش مسیر اشتباه، l 2 ( p 2 p 3 ) شاید یک جاده در امتداد دریاچه، و l 3 ( p 3 p 3 ) ممکن است پلی بر روی دریاچه باشد. بنابراین، در کاربردهای عملی، خط تقاطع L 1 نیز نیاز به تقسیم بندی دارد.
با توجه به تعریف مولفه های توپولوژیکی و ویژگی های داده های مکانی GIS، مولفه های تقاطع فضایی خط/منطقه و خط/خط به صورت زیر تعریف می شوند:
“تعریف 2.3” (جزء تقاطع فضایی): بگذارید A یک منطقه یا یک خط و B یک خط باشد. اجازه دهید I یک زیر مجموعه متصل حداکثر از A ∩ B باشد. اگر I صفر بعدی باشد، I یک نقطه تقاطع A ∩ B است. اگر I یک بعدی است، فرض کنید که قسمت داخلی قطعه l حداکثر زیر مجموعه متصل A° ∩ I یا ∂A ∩ I است، و l یک خط تقاطع از A ∩ B است ومن = Uمن=1nl i ( i > 1).
بر اساس تعریف 2.3، شش جزء تقاطع فضایی بین منطقه A و خط B در شکل 4 وجود دارد که شامل چهار خط تقاطع ( l 1 ، l 2 ، l 3 و l 4 ) و دو نقطه تقاطع ( P 1 و P است. 2 )، همانطور که در شکل 4 ج نشان داده شده است. در میان آنها، خطوط تقاطع l 1 ، l 2 و l 3 توسط جزء توپولوژیکی یک بعدی L 1 تقسیم می شوند.( شکل 4 ب). علاوه بر این، باید توجه داشت که خط تقاطع در تعریف 2.3 شامل مرزهایی است. یعنی توپولوژی آنها برابر با یک چند خط با دو نقطه پایانی است که در شکل 3 نشان داده شده است. لازم به ذکر است که برای ساده کردن عبارت، عبارت “جزء تقاطع” (به عنوان مثال، “خط تقاطع” و “نقطه تقاطع”) که در این مقاله استفاده شده است به طور خاص به جزء تقاطع فضایی اشاره دارد (مثلاً “خط تقاطع فضایی” “و “نقطه تقاطع فضایی”) اگر اصلاح کننده “توپولوژیکی” وجود نداشته باشد.
2.3. معرفی درجه گره
چارچوب اصلی مدل E-WWIS [ 2 ] همچنین می تواند برای نشان دادن روابط پالایش شده مناطق/مناطق با تقاطع های متعدد (شامل تقاطع های منفرد)، همانطور که در رابطه (1) نشان داده شده است، استفاده شود، که در آن ‘ Ni (1 ≤ i ≤ m )’، ‘ di ‘ و ‘ ti ‘ به ترتیب نشان دهنده دنباله توپولوژیکی ، بعد و نوع مجموعه های تقاطع مربوطه (مؤلفه ها) هستند.
در میان سه متغیر توپولوژیکی توالی، بعد و نوع در مدل E-WWIS، مهم ترین نوع توپولوژیکی است که پیکربندی جامع متغیرهای توپولوژیکی جزء تقاطع را به جز بعد و دنباله نشان می دهد. بنابراین، طبقه بندی انواع اجزای تقاطع (مجموعه) موضوع کلیدی در مدل E-WWIS است. برای تقاطع 2 بعدی، انواع آنها با اعداد اویلر [ 29 ] از تفاوت بین دو منطقه و جزء تقاطع متمایز می شوند، به عنوان مثال، اجازه دهید ” IR ” نشان دهنده جزء تقاطع باشد، و نوع تقاطع دو بعدی با f E ( A \ IR ) و fE ( B \ IR ) [ 2 ].
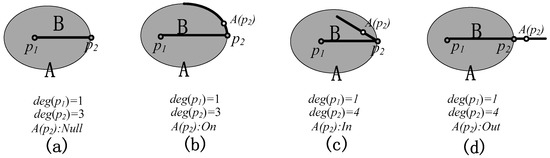
اگرچه چارچوب مدل E-WWIS برای توصیف روابط خط/منطقه و خط/خط پالایش شده با تقاطعهای چندگانه نیز مناسب است، برخی از انواع تقاطع یکبعدی (خط تقاطع) خط/منطقه و خط/خط را نمیتوان انجام داد. تنها با تکیه بر “عدد اویلر” متمایز می شود. برای مثال، اجازه دهید ” IL ” نشان دهنده خط تقاطع l باشد. در شکل 5 ، منطقه (یا خط) A خط B را در قطعه l قطع می کند ( p 1 p 2 ). در شکل 5 a,b مقادیر f E ( A \ I L ) وf E ( B \ I L ) یکسان هستند. با این حال، انواع توپولوژیکی دو خط متقاطع متفاوت است، در شکل 5 a، خط تقاطع l به طور کامل در مرز منطقه A قرار دارد و در شکل 5 b خط تقاطع l داخل منطقه A است. به طور مشابه، انواع خط تقاطع بین دو خط در شکل 5 c,d متفاوت است، اما مقادیر آنها f E ( A \ I L ) و f E ( B \ I L) است.) همان هستند.
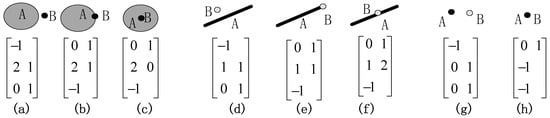
شکل 5 a-d از نظر تعداد یال هایی که به نقاط انتهایی خطوط تقاطع برخورد می کنند متفاوت است. در توپولوژی و نظریه گراف، معیاری که برای حل مسئله پل کونیگزبرگ توسط اویلر در قرن 18 استفاده شد [ 30 ]، به عنوان “درجه نقطه” شناخته می شود [ 31 ، 32 ]. درجه یک نقطه تعداد یال هایی است که به رأس برخورد می کنند. فرض بر این است که درجه یک راس p در یک نمودار d eg ( p ) نشان داده می شود. سپس، نقطه p جدا می شود اگر d eg ( p ) = 0 باشد یا یک نقطه پایانی است اگر d eg ( p) = 1 (فرانک، 1969). از آنجایی که رابطه توپولوژیکی مبتنی بر اشیاء فضایی دوتایی است، درجه گره محاسبه شده در این مقاله، درجه گره نقطه معینی در اتحاد دو شی فضایی است و زمانی که شی یک منطقه باشد، فقط به عنوان مرز آن در نظر گرفته می شود. (به استثنای فضای داخلی آن). به عنوان مثال، هنگامی که دو خط برابر هستند، آنگاه درجه گره ها در نقاط انتهایی آنها یک است ( شکل 6 a). هنگامی که دو خط در نقاط پایانی خود به هم می رسند، درجه نقطه تقاطع آنها دو است ( شکل 6 ب). هنگامی که یکی از نقاط پایانی یک خط در قسمت داخلی خط دیگر قرار می گیرد، درجه نقطه تقاطع آنها سه است ( شکل 6 ج). هنگامی که دو خط در داخل خود قطع می شوند، درجه نقطه تقاطع آنها چهار است ( شکل 6د). برای یک خط و یک منطقه، اگر نقطه پایانی خط در داخل منطقه باشد، درجه آن یک است ( شکل 6 e). اگر نقطه پایانی خط در مرز منطقه باشد، درجه آن دو است ( شکل 6 f). اگر یک قسمت از خط در مرز منطقه باشد و قسمت دیگر نباشد، آنگاه درجه نقطه ای که خواص توپولوژیکی تغییر می کند سه است ( شکل 6 g). اگر نقطه ای نقطه تقاطع خط و مرز منطقه باشد، درجه آن چهار است ( شکل 6 h).
برای خطوط تقاطع خط/منطقه و خط/خط، حتی اگر درجه نقاط داخلی آنها هر دو دو باشد، چهار حالت مختلف از درجه نقاط انتهایی آنها وجود دارد، از جمله چهار مقدار ممکن، یعنی {1،2، 3،4}. در شکل 5 a، درجه p 1 دو و درجه p 2 سه است، در حالی که در شکل 5 b، درجه p 1 یک و درجه p 2 چهار است. در شکل 5 c، درجات p 1 و p 2 هر دو دو هستند، در حالی که در شکل 5 d، درجه p1 یک و درجه p 2 سه است. درجه گره، به عنوان مثال، “درجه نقطه”، می تواند برای تشخیص انواع مختلف خطوط تقاطع در شکل 5 استفاده شود.
واضح است که درجه گره یک متغیر توپولوژیکی است و توانایی آن در تشخیص خطوط متقاطع بهتر از عدد اویلر است. علاوه بر این، از آنجایی که درجه نقطه تقاطع می تواند در تشخیص نقاط تقاطع نیز به خوبی کار کند، درجه گره برای تشخیص هر دو نوع نقاط تقاطع و خطوط تقاطع بین خطوط/منطقه ها و خطوط/خطوط استفاده می شود. بنابراین، یک مدل N-WWIS می تواند برای نشان دادن روابط خط/منطقه و خط/خط تصفیه شده پیشنهاد شود.
3. طبقه بندی خطوط تقاطع و نقاط تقاطع بر اساس درجه گره
3.1. طبقه بندی خط تقاطع بین خط و منطقه
همانطور که در بالا ذکر شد، خط تقاطع خط/منطقه را می توان با استفاده از درجات دو نقطه انتهایی خط تقاطع (یعنی p 1 و p 2 در شکل 7 ) تشخیص داد. از آنجایی که چهار مقدار ممکن برای درجه هر نقطه پایانی وجود دارد، از نظر تئوری 16 (4 × 4) ترکیب ممکن وجود دارد. به استثنای مقادیر غیرممکن و متقارن، میتوانیم 8 نوع از انواع اجزای تقاطع ممکن را به دست آوریم (یعنی انواع در واقع در R2 وجود دارند ) ، که درجه گرههای آنها (1،1)، (1،3)، (1،4) است. ، (2،2)، (2،3)، (3،3)، (3،4)، و (4،4)، همانطور که در شکل 7 نشان داده شده است.
این روش میتواند انواع خطوط تقاطع را که مقادیر درجه نقطههای پایانی آنها یک یا دو است، کاملاً متمایز کند. با این حال، انواع دیگر خطوط تقاطع را نمی توان تنها با مقادیر درجه تشخیص داد. به عنوان مثال، دو جفت از خطوط تقاطع مختلف با مقادیر درجه سه یا چهار در شکل 8 نشان داده شده است. مقادیر درجه نقاط انتهایی خط تقاطع در شکل 8 a,b هر دو برابر (1,3) و درجات در شکل 8 c,d برابر (1,4) هستند.
با تجزیه و تحلیل روابط دو زوج در شکل 8 ، دریافتیم که تفاوت اصلی بین آنها در خواص توپولوژیکی نقطه پایانی p 2 خطوط تقاطع نهفته است. نقطه پایانی p 2 در شکل 8 a نقطه مرزی خط B است، در حالی که در شکل 8 b، خط B دارای یک پاره پس از نقطه پایانی p 2 است و در مرز منطقه B قرار دارد. در شکل 8 c، بخش زیر از نقطه پایانی p 2 در خط B داخل منطقه A است، در حالی که درشکل 8 د، خارج از منطقه A است. خصوصیات توپولوژیکی نقاط انتهایی خط تقاطع فقط درجه گره آنها نیست. آنها همچنین به انواع نقاط مجاور خود مربوط می شوند. تعریف نقاط مجاور به شرح زیر است.
“تعریف 3.1” (نقطه مجاور): فرض کنید L یک جزء تقاطع بین منطقه (یا خط) A و خط B باشد. اگر L یک نقطه تقاطع است، اجازه دهید نقطه p L باشد . اگر L یک خط تقاطع است، بگذارید نقطه p یک نقطه پایانی L باشد. با یک عدد واقعی کوچک دلخواه r ، و اجازه دهید نقطه A ( p) یک نقطه متعلق به خط B باشد اما نه به L. اگر فاصله بین نقطه A ( p) و p r باشد، سپس نقطه A ( p) نقطه مجاور p است. اگر نقطه مجاور p وجود نداشته باشد Null نامیده می شود. اگر نقطه در مرز A باشد، به عنوان On نامیده می شود. اگر نقطه داخل A باشد، به صورت In نامیده می شود. اگر نقطه خارج از A باشد، به عنوان Out نامیده می شود.
تعریف 3.1 نه تنها برای خطوط تقاطع بلکه برای نقاط تقاطع خطوط/منطقه ها و خطوط/خطوط نیز اعمال می شود. نقطه پایانی خط تقاطع حداکثر شامل یک نقطه مجاور است که چهار نوع ممکن وجود دارد: Null، On، In و Out همانطور که در شکل 8 نشان داده شده است. با ترکیب درجات گره و انواع نقاط مجاور نقاط انتهایی، چهار نوع خط تقاطع در شکل 8 قابل تشخیص است.
با ترکیب درجه گره ها (1،2،3،4) و انواع نقاط مجاور (تهی، روشن، داخل و خارج)، مدل ما می تواند 256 (4 × 4 × 4 × 4) نوع تقاطع را تشخیص دهد. – خطوط بین خط / مناطق در تئوری. با این حال، تنها تعداد کمی از آنها (انواع احتمالی) در واقع در R2 وجود دارند . از آنجایی که مقادیر درجه گره در نقاط پایانی خط تقاطع تنها در مجموع 16 مقدار ترکیبی (فقط 10 نامتقارن) وجود دارد، انواع ممکن را می توان یک به یک بر اساس این مقادیر ترکیبی و انواع نقاط احتمالی مجاور مربوطه آنها جستجو کرد. در واقع، همانطور که در شکل 9 نشان داده شده است، 21 نوع از خطوط تقاطع ممکن و نامتقارن با استفاده از این روش طبقه بندی و یافت می شوند.. لازم به ذکر است که درجه گره از اولویت بالاتری نسبت به انواع نقاط مجاور برخوردار است، بنابراین توصیف انواع نقاط مجاور گاهی اوقات در مواقعی که ضروری نیست نادیده گرفته می شود.
اثبات مربوط به 21 نوع خط تقاطع بین خطوط و مناطق به شرح زیر است.
-
مورد جفت درجه (1،1)، (1،2)، (1،3) و (1،4). اگر درجه گره نقطه پایانی خط تقاطع هر دو یک باشد، نقاط انتهایی باید در داخل منطقه قرار داشته باشند و انواع نقاط مجاور آنها باید صفر باشد. در غیر این صورت، حداقل یک نقطه پایانی خط تقاطع با بیش از یک یال متصل خواهد شد. بنابراین، همانطور که در شکل 9 الف نشان داده شده است، تنها یک نوع جفت درجه (1،1) وجود دارد. اگر یک نقطه پایانی در داخل منطقه باشد و نقطه پایانی دیگر خط تقاطع در داخل نباشد، نقطه پایانی دیگر حداقل سه یا بیشتر به آن متصل است، بنابراین جفت درجه وجود ندارد (1،2). اگر درجه گره نقطه پایانی دیگر سه باشد، نوع نقطه مجاور آن باید روشن ( شکل 9 ب) یا تهی ( شکل 9) باشد.ج)، در غیر این صورت این نقطه پایانی دارای 1 یال مجاور یا چهار یال مجاور خواهد بود. بنابراین، تنها دو نوع جفت درجه وجود دارد (1،3). اگر درجه گره نقطه پایانی دیگر چهار باشد، نوع نقطه مجاور آن باید Out ( شکل 9 د) یا داخل ( شکل 9 f) باشد. در غیر این صورت، کمتر از 4 یال در نقطه پایانی ملاقات خواهد کرد.
-
مورد جفت درجه (2،2)، (2،3)، و (2،4). اگر درجه گرههای نقطههای پایانی خط تقاطع هر دو دو باشند، باید در مرز منطقه باشند و انواع نقاط مجاور آنها باید Null باشد. در غیر این صورت، تعداد یال هایی که در نقطه پایانی ملاقات می کنند، برابر با دو نخواهد بود. بنابراین، همانطور که در شکل 9 h نشان داده شده است، تنها یک نوع جفت درجه (2،2) وجود دارد. اگر یک نقطه پایانی در مرز منطقه باشد و درجه گره نقطه پایانی دیگر سه باشد، نوع نقطه مجاور آن باید Out ( شکل 9 f) یا In ( شکل 9 g) باشد. در غیر این صورت، نقطه پایانی آن در دو یال به هم می رسد. بنابراین، تنها دو نوع جفت درجه (2،3) و هیچ نوع جفت درجه (2،4) وجود ندارد.
-
مورد جفت درجه (3،3) و (3،4). اگر درجه گره نقاط پایانی خط تقاطع هر دو سه باشد، انواع نقطه مجاور آنها می تواند Out، In، On یا Null باشد. بنابراین، شش ( سی42) انواع ممکن جفت درجه (3،3)، و به ترتیب در شکل 9 i–n نشان داده شده است. اگر درجه گره یک نقطه پایانی سه و دیگری چهار باشد، نوع نقطه مجاور نقاط انتهایی با درجه گره 3 باید Null یا On باشد و نوع نقطه مجاور نقاط انتهایی با درجه گره 4 باید Out یا In باشد. بنابراین، چهار ( سی21* سی21) انواع جفت درجه (3،4)، همانطور که در شکل 9 o-r نشان داده شده است.
-
مورد درجه-جفت (4،4). اگر درجه گره نقاط پایانی خط تقاطع هر دو 4 باشد، نوع نقطه مجاور آنها باید Out یا In باشد. در غیر این صورت، کمتر از 4 یال در نقاط پایانی ملاقات خواهد کرد. بنابراین، سه نوع نامتقارن جفت درجه (4،4) وجود دارد، همانطور که در شکل 9 s-u نشان داده شده است.
بر خلاف روش های موجود، روش ما کامل است و می تواند انواع بیشتری را طبقه بندی کند. به عنوان مثال، روش LRBIS می تواند تنها 16 نوع پالایش شده (شامل دو نوع نقطه تقاطع و یک نوع رابطه متمایز) را تشخیص دهد. در روش LRBIS، روابط سر-میت و دم-میت، روابط HM-cover-by و TM-cover-by، و روابط درون متقاطع و برون متقارن متقارن زوجی هستند که مربوط به انواع شکل 9 d است. f,j به ترتیب در روش ما. رابطه حاوی، EM-cover-by، point-cross، MT-cover-by، on-boundary، belly meet، BM-cover-by، و رابطه با انواع شکل 9 مطابقت دارد.به ترتیب a,b,d,e,h,i,u. بنابراین، روش LRBIS تنها می تواند 10 نوع از خطوط تقاطع نامتقارن را بین خطوط و مناطق تشخیص دهد. این روش نمی تواند 11 نوع باقی مانده را در شکل 9 شناسایی کند ، مانند آنچه در شکل 9 l,s و غیره نشان داده شده است. نکته دیگری که باید به آن توجه کرد این است که جزء تقاطع توپولوژیکی در روش LRBIS بیشتر تقسیم نمیشود، که آن را در کاربردها، مانند مدیریت خودکار تضادهای توپولوژیکی، ناکافی میکند.
3.2. طبقه بندی خط تقاطع بین خط و خط
در مقایسه با خطوط/مناطق، انواع کمتری از خطوط تقاطع بین خطوط وجود دارد. شکل 10 هشت نوع خط تقاطع ممکن و نامتقارن بین خطوط را نشان می دهد.
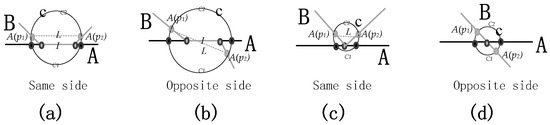
بیشتر خطوط تقاطع در شکل 10 را می توان با درجه گره دو نقطه انتهایی خطوط تقاطع متمایز کرد، به جز انواع (2،2) و (3،3). به طور مشابه، نوع (2،2) در شکل 10 c,d را می توان با انواع نقاط مجاور، به عنوان مثال، “تهی” و “خارج”، همانطور که در تعریف 3.1 تعریف شده است، متمایز کرد. با این حال، همانطور که در شکل 10 g,h نشان داده شده است، نمی توان مستقیماً برای تشخیص نوع (3،3) استفاده کرد . از طریق تجزیه و تحلیل، اگرچه انواع نقاط مجاور این دو خط تقاطع همه بیرون هستند، نقاط مجاور در همان سمت خط A در شکل 10 g و در سمت مخالف خط A در شکل 10 قرار دارند.ساعت بنابراین، انواع توپولوژیکی آنها متفاوت است و تعریف مربوطه به شرح زیر است:
«تعریف 3.2» (اضلاع یکسان و مخالف): فرض کنید I یک جزء تقاطع بین خطوط A و B باشد، نقاط A ( p 1 ) و A ( p 2 ) دو نقطه مجاور L باشند ، و c دایره ای باشد که با آن ساخته شده است. خط مستقیم L ( A ( p 1 ) A ( p 2 )) به عنوان قطر. دایره c را می توان با خط A به دو قوس مختلف c 1 و c 2 تقسیم کرد . اگر نقاط A( p 1 ) و A ( p 2 ) روی یک قوس هستند، سپس با خط A در یک طرف قرار می گیرند و نوع جامع این دو نقطه مجاور یک طرف (SS) نامیده می شود. اگر نقاط A ( p 1 ) و A ( p 2 ) روی کمان های مختلف قرار داشته باشند، در طرف مقابل خط A قرار دارند و نوع جامع این دو نقطه مجاور، طرف مقابل (OS) نامیده می شود.
اثبات مربوط به هشت نوع خط تقاطع بین خط و خط به شرح زیر است. لازم به ذکر است که درجه گره نقاط پایانی خط تقاطع آنها نمی تواند 4 باشد.
-
مورد جفت درجه (1،1)، (1،2)، و (1،3). اگر درجه گرههای نقطههای پایانی خط تقاطع هر دو یک باشند، باید نقاط مرزی خطوط و انواع نقاط مجاور آنها باید تهی باشند ( شکل 10 a). اگر یک نقطه پایانی در مرز یک خط باشد و درجه گره نقطه پایانی دیگر دو باشد، نوع نقطه مجاور آن باید صفر باشد ( شکل 10 ب). اگر درجه گره نقطه پایانی دیگر سه باشد، نوع نقطه مجاور آن باید Out باشد ( شکل 10 e). در غیر این صورت، کمتر از سه یال در نقطه پایانی ملاقات خواهند کرد. بنابراین، تنها یک نوع جفت درجه (1،1)، (1،2)، و (1،3) وجود دارد.
-
مورد جفت درجه (2،2) و (2،3). اگر درجه گره نقطه پایانی خط تقاطع هر دو دو باشد، نوع نقطه مجاور یک نقطه پایانی باید Null باشد و نوع نقطه مجاور دیگری می تواند Null یا Out باشد. بنابراین، دو نوع جفت درجه (2،2) وجود دارد، همانطور که در شکل 10 c,d نشان داده شده است. اگر درجه گره یک نقطه پایانی سه باشد، نوع نقطه مجاور آن باید Out باشد ( شکل 10 f). در غیر این صورت، کمتر از سه یال در نقطه پایانی ملاقات خواهند کرد. بنابراین، تنها یک نوع جفت درجه وجود دارد (2،3).
-
مورد درجه-جفت (3،3). اگر درجه گره نقاط پایانی خط تقاطع هر دو سه باشد، نوع نقطه مجاور آنها باید هر دو Out باشند، و انواع جامع آنها می تواند SS یا OS باشد. بنابراین، دو نوع نامتقارن جفت درجه (3،3) وجود دارد، همانطور که در شکل 10 g,h نشان داده شده است.
شکل 11 a,b تفاوت در انواع جامع نقاط مجاور را برای دو خط تقاطع نشان می دهد. همانطور که در شکل 10 g,h نشان داده شده است، می توان از این تفاوت برای تشخیص دو درجه گره خط تقاطع (3،3) استفاده کرد . اگر نقاط تقاطع بین خط و خط دارای دو نقطه مجاور باشند، انواع جامع نیز اعمال می شوند، همانطور که در شکل 11 c,d نشان داده شده است.
3.3. طبقه بندی نقطه تقاطع
از آنجایی که درجه گره نقطه تقاطع خط/منطقه می تواند تنها سه یا چهار در R2 باشد ، تنها دو نوع ممکن وجود دارد که تنها با استفاده از درجه گره قابل تشخیص هستند. آنها در شکل 12 a,b نشان داده شده اند. درجه گره نقطه تقاطع خط/خط می تواند دو، سه یا چهار در R2 باشد . برای درجه گره دو یا سه، تنها یک نوع ممکن از نقطه تقاطع خط/خط وجود دارد، همانطور که در شکل 12 c,d نشان داده شده است. برای درجه گره چهار، انواع احتمالی آن از نقطه تقاطع خط/خط به انواع جامع نقاط مجاور نیاز دارند تا آنها را متمایز کند. همانطور که در شکل 12 نشان داده شده استe,f، انواع جامع دو نقطه مجاور نقطه تقاطع به ترتیب SS و OS هستند. در نهایت، با ترکیب درجات گره و انواع نقاط مجاور، شش نوع از نقاط تقاطع ممکن و نامتقارن خط/منطقه و خط/خط طبقهبندی میشوند، همانطور که در شکل 12 نشان داده شده است.
4. نمایش سلسله مراتبی روابط توپولوژیکی خط/منطقه و خط/خط
اگرچه روابط پالایش شده می توانند به طور دقیق روابط توپولوژیکی بین دو شی را نشان دهند، اما نیاز به جزئیات توپولوژیکی بیشتری برای توصیف و محاسبه دارند، بنابراین معمولاً در زمینه هایی مانند تشخیص و پردازش تضاد توپولوژیکی استفاده می شوند [ 1 ]. با این حال، زمینه هایی مانند سازماندهی داده های مکانی و پرس و جو فقط به روابط درشت نیاز دارند. بنابراین، برای برآوردن الزامات کاربردی مختلف، مطالعه نمایش سلسله مراتبی روابط توپولوژیکی بین اشیاء فضایی ضروری است [ 1 ، 2 ، 16 ، 20 ]. در این مقاله با اشاره به استراتژی در مرجع [ 2]، مدل E-WID برای نشان دادن روابط خط/منطقه درشت (و خط/خط) استفاده می شود، در حالی که مدل N-WWIS برای نشان دادن روابط خط/منطقه (و خط/خط) تصفیه شده استفاده می شود.
4.1. استفاده از مدل E-WID برای نشان دادن روابط درشت
چارچوب توصیف حالت E-WID در معادله (2) نشان داده شده است. در جایی که مقدار f Di نشان دهنده محتوا و بعد است، f E نشان دهنده عدد اویلر است، تقاطع عملیات مجموعه (∩) و تفاوت (\) بر اساس کل اشیاء A و B است و اجزای فضایی آنها از نظر توپولوژیکی کامل هستند. مقدار f Di می تواند یکی از عناصر {−1، 0، 1، 2، 3، 4، 5، 6} در فضای دوبعدی باشد.
مدل E-WID میتواند روابط توپولوژیکی بین هر دو شی فضایی را در فضای دوبعدی توصیف کند، بنابراین میتوان از آن برای تشخیص روابط توپولوژیکی درشت خط/منطقه و خط/خط استفاده کرد. برای خط/منطقه و خط/خط، فقط پنج مورد (مقدار f Di ) از مولفه های تقاطع یا اختلاف وجود دارد، یعنی خالی (-1)، نقطه صفر خالص (0)، خط یک بعدی خالص ( 1)، منطقه دو بعدی خالص (2) و مخلوطی از نقطه و خط (3). مقدار f E می تواند هر عدد طبیعی باشد و وقتی جزء فضایی خالی باشد، بیان آن نادیده گرفته می شود.
برای روابط خط/منطقه، اگرچه مدل E-WID درشت است، اما میتواند بینهایت روابط درشت را تشخیص دهد، زیرا یک خط و یک منطقه میتوانند تعداد نامتناهی مؤلفههای تقاطع (یا مؤلفههای اختلاف) و مقدار f داشته باشند. E می تواند تفاوت بین آنها را منعکس کند. در این مقاله، تنها روابط با یک تقاطع منفرد (یا رابطه منفصل) که با مدل E-WID قابل تشخیص است، نشان داده شده است، همانطور که در شکل 13 نشان داده شده است. در میان آنها، شکل 13 a ناپیوسته است، و شکل 13 b,c هر دو فقط یک تقاطع صفر بعدی دارند، اما یکی در داخل خط B و دیگری در مرز خط B قرار دارد.شکل 13 d–j همه فقط یک تقاطع تک بعدی دارند. پیکربندی های توپولوژیکی در شکل 13 d-j به شرح زیر است: خط B توسط ناحیه A ( شکل 13 d)، B توسط A پوشانده شده است، اما تنها یک نقطه پایانی در مرز A است ( شکل 13 e)، B با آن همپوشانی دارد. A اما نقطه پایانی در مرز A ندارد ( شکل 13 f)، تقاطع یک بعدی در مرز A است ( شکل 13 g)، B توسط A پوشانده شده است.و نقاط انتهایی آن هر دو روی مرز A هستند ( شکل 13 h)، B با A همپوشانی دارد و یک نقطه پایانی در مرز A دارد ( شکل 13 i) و B از A عبور می کند ( شکل 13 j). شایان ذکر است که برخی از عناصر ماتریس در شکل 13 هنگامی که خالی هستند نادیده گرفته می شوند (هیچ مولفه فضایی متناظری وجود ندارد) و این عبارت از ژو و همکاران پیروی می کند. (2013). دلیل خاص این است که می تواند تفاوت بین آنها و عناصری که محل تقاطع آنها خالی نیست اما عدد اویلر آنها صفر است را نشان دهد.
به طور مشابه، مدل E-WID همچنین می تواند تعداد نامتناهی از روابط درشت خط/خط را متمایز کند. شکل 14 روابط درشت خط/خط را با یک تقاطع منفرد نشان می دهد که با مدل E-WID متمایز شده است. در میان آنها، شکل 14 الف ناپیوسته است، شکل 14 b-d همه فقط یک تقاطع 0 بعدی دارند، و شکل 13 e-j همه فقط یک تقاطع یک بعدی دارند.
4.2. استفاده از مدل N-WWIS برای نشان دادن روابط پالایش شده
همانطور که قبلا ذکر شد، روابط درشت به طور مستقیم ابعاد و انواع توپولوژیکی هر جزء تقاطع را توصیف نمی کند. با این حال، در برخی از کاربردها، مانند تشخیص و پردازش تضاد، باید با هر جزء تقاطع بر اساس نوع توپولوژیکی برخورد کنیم. بنابراین، لازم است روابط با اجزای تقاطع چندگانه در یک سطح تصفیه شده نمایش داده و محاسبه شود. از آنجایی که بخش 3 به طور کامل انواع اجزای تقاطع خط/منطقه و خط/خط را بر اساس درجه گره (و انواع نقاط مجاور) طبقه بندی کرد، مدل N-WWIS به طور موثر ایجاد شده است و می تواند برای نمایش خط/منطقه و خط تصفیه شده استفاده شود. / روابط خط.
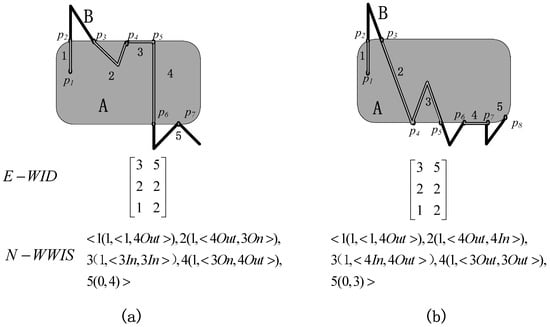
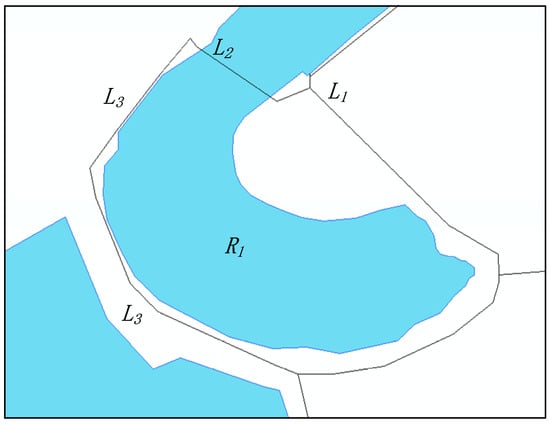
شکل 15 دو رابطه خط/منطقه را با مولفه های تقاطع متعدد نشان می دهد. اگرچه هر دو شامل چهار خط تقاطع و یک نقطه تقاطع در شکل 5 a,b هستند، ابعاد، توالی و انواع توپولوژیکی هر جزء همه یکسان نیستند. این دو رابطه تصفیه شده با پیکربندی های توپولوژیکی مختلف با مدل درشت (E-WID) قابل تشخیص نیستند و باید از مدل تصفیه شده (N-WWIS) استفاده شود. نتیجه توصیف N-WWIS در شکل 15 تفاوت بین آنها را منعکس می کند. به عنوان مثال، نتیجه توصیف مولفه تقاطع با دنباله 2 2 است (1، <4Out، 3On>) در شکل 15آ. در جایی که عدد خارج از براکت نشاندهنده شماره دنباله آن است (یعنی دو)، اولین عدد در براکت نشاندهنده بعد (یعنی 1 بعدی) و عبارت <4Out، 3On> در براکت بقیه نشاندهنده نوع توپولوژیکی آن است. که مطابق با نوع متقارن در شکل 9 ص. نتیجه توصیفی مولفه تقاطع با دنباله 2 2 (1، 4Out، 4In) در شکل 15 ب است، که در آن بعد 1 (خط تقاطع) و نوع توپولوژیک <4Out، 4In> است (یعنی نوع متقارن است. در شکل 9 t).
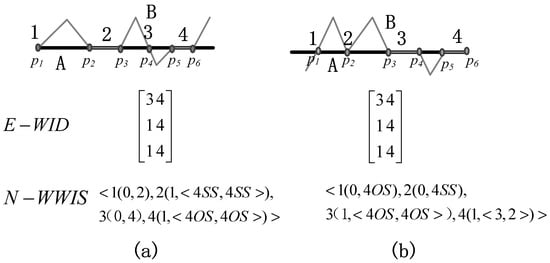
شکل 16 همچنین دو رابطه خط/خط متفاوت را نشان می دهد که با مدل E-WID قابل تشخیص نیستند اما با مدل N-WWIS قابل تشخیص هستند. این دو مدل هر دو دارای دو خط تقاطع و دو نقطه تقاطع هستند، اما انواع اجزای تقاطع با توالی یکسان متفاوت است و مدل N-WWIS می تواند به طور کامل آنها را توصیف و متمایز کند. به عنوان مثال، جزء تقاطع با دنباله شماره 2 یک خط تقاطع در شکل 16 الف است و نوع توپولوژیکی آن <4SS, 4SS> است، یعنی درجه گره دو نقطه پایانی هر دو چهار هستند و نقاط مجاور آنها روی هستند. همان سمت خط A در شکل 16الف، جزء تقاطع با دنباله شماره 2 یک نقطه تقاطع است، نوع توپولوژیکی آن <4SS> است، یعنی درجه گره آن چهار است و نقاط مجاور نیز در همان سمت خط A قرار دارند.
5. کاربرد تجربی
برای ارزیابی مدل تصفیه شده ما (N-WWIS) و کاربرد آن، یک سیستم نمونه اولیه مبتنی بر مدل N-WWIS در محیط Microsoft Visual C# 2010 همراه با پایگاه داده Oracle توسعه داده شده است. رابط کاربری آن در شکل 17 نشان داده شده است .
سیستم نمونه اولیه به طور فشرده با استفاده از داده های OpenStreetMap (OSM) شهر چانگشا، استان هونان، چین، به عنوان داده های آزمایشی (ژوئیه 2019، همانطور که در شکل 17 نشان داده شده است ) آزمایش شد. مساحت منطقه آزمایشی 1938 کیلومتر مربع شامل 8688 خط ترافیک و 277 منطقه آبی است که با لایه TRAFFIC LINE و لایه WATER-AREA در شکل 17 مطابقت دارد.، به ترتیب. از آنجایی که تعداد درگیریهای واقعی در دادههای OSM ناشناخته است، 19 خط ترافیک اضافی، که روابط متناقضی با منطقه آب دارند، برای ارزیابی مدل N-WWIS شبیهسازی شدهاند. علاوه بر این، برای برجسته کردن نتایج تشخیص تضاد توپولوژیکی، اجزای تقاطع مربوطه را روی لایههای کاری موقت قرار میدهیم. به عنوان مثال، خطوط تقاطع و نقاط تقاطع بین خط ترافیک و منطقه آب به ترتیب در لایه TWINSECTLINE و لایه TWINSECTPOINT قرار می گیرند.
در این آزمایش ها از خط ترافیک به عنوان نمونه خط و منطقه آب به عنوان نمونه منطقه استفاده می شود. یک مدل داده مکانی-زمانی شی گرا (یا شی رابطه ای) [ 2 ، 32 ] و یک روش تبدیل مدل مبتنی بر قانون [ 33 ، 34 ] برای تبدیل داده ها به کار گرفته شده اند. علاوه بر این، برای مقابله با تضادهای توپولوژیکی بالقوه، مجموعهای از قوانین (336 برای خط/منطقه و 165 خط/خط) بر اساس روابط پالایش شده N-WWIS و ویژگیهای اشیاء فضایی توسعه مییابد.
با در نظر گرفتن خطوط/منطقهها به عنوان مثال، استراتژیهای بررسی و معامله توپولوژیکی به شرح زیر است:
-
دادههای OSM (فرمت XML) را دانلود کرده و با استفاده از روش تبدیل و مدل دادههای مکانی-زمانی شیگرا به مدل دادههای اطلاعات جغرافیایی بنیادی ملی چین تبدیل کنید.
-
تلورانس (یعنی 1 متر) را بر اساس تجربه برای محاسبه روابط توپولوژیکی خطوط/منطقه های تصفیه شده تنظیم کنید.
-
یک خط Li (1 ≤ i ≤ n ) را از مجموعه داده خط انتخاب کنید و از مستطیل محدود کننده حداقل Li به عنوان مناطق برای فیلتر کردن داده ها استفاده کنید. این می تواند تعداد مناطقی را که هیچ تلاقی با خط Li ندارند کاهش دهد .
-
روابط توپولوژیکی تصفیه شده N-WWIS بین خط Li و مناطق فیلتر شده را به طور خودکار محاسبه کنید، و مناطق غیرمتمرکز و توضیحات اصلاح شده روابط آنها را ذخیره کنید تا مولفه های تقاطع (شامل خط تقاطع و نقطه تقاطع) را تشکیل دهند. A, B,…, W}.
-
به مراحل 3 و 4 برگردید، محاسبه روابط پالایش شده بین خط دیگر و مناطق فیلتر شده را شروع کنید و داده های مربوطه را تا زمانی که تمام اشیاء در مجموعه داده خط محاسبه شوند ذخیره کنید.
-
برای هر جزء تقاطع در مجموعه انواع، آن را با قوانین تنظیم شده برای برخورد خودکار (یا نیمه خودکار) با هر تضاد توپولوژیکی بالقوه مطابقت دهید.
نتایج تشخیص تضاد توپولوژیکی دادههای تست و توضیحات مثال در زیر بسط داده میشود.
5.1. نمونه هایی از اجزای تقاطع بین خطوط و مناطق
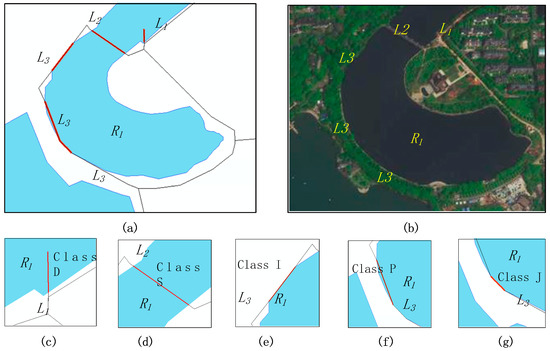
پس از شناسایی تضادهای توپولوژیکی بین خطوط ترافیک و مناطق آبی در دادههای آزمایشی، در مجموع 221 جزء تقاطع شامل 210 خط تقاطع و 11 نقطه تقاطع یافت شد. برای شناسایی آسان، انواع خط تقاطع در شکل 9 و انواع نقطه تقاطع در شکل 12 به عنوان کلاس A (مرتبط با شکل 9 a)، کلاس B ( شکل 9 ب)، کلاس C ( شکل 9 ج) نامگذاری شده اند. …، کلاس V ( شکل 12 الف)، و کلاس W ( شکل 12 ب) در سیستم ما. میز 1نتایج تشخیص انواع اجزای تقاطع بین خطوط ترافیک و مناطق آبی را نشان می دهد. تعداد هر نوع از اجزای تقاطع در نتایج تجربی در ستون های سوم و ششم جدول 1 نشان داده شده است . کلاس های H، K، M، N، Q، R و U که با عدد قرمز نشان داده شده اند از داده های شبیه سازی شده تولید می شوند. مشاهده می شود که تمام انواع اجزای تقاطع بین خطوط ترافیک و مناطق آبی را می توان با مدل ما تشخیص داد.
با توجه به جدول ویژگی های لایه INSECTLINE و لایه INSECTPOINT، انواع هر جزء تقاطع و شیء ترافیک و منطقه آب درگیر قابل استعلام هستند. شکل 18 a یک نقشه تقویت جزئی از منطقه آزمایش را نشان می دهد، که در آن منطقه آبی R1 دارای خطوط متقاطع متعدد با خطوط ترافیک ( L 1 ، L 2 ، و L 3 ) است، و شکل 18 b تصویر ماهواره ای منطقه مربوطه را نشان می دهد. . کلاس (نوع) خط تقاطع بین منطقه R 1 و خط L 1 D است ( شکل 18c) که مربوط به نوع <1, 4Out> در شکل 9 d است. کلاس خط تقاطع بین منطقه R 1 و خط L 2 S است ( شکل 18 d) و نوع آن مطابق با <4Out, 4Out> در شکل 9 s است. طبقات خطوط تقاطع بین منطقه R 1 و خط L 3 I ( شکل 18 e) ، P ( شکل 18 f) و J ( شکل 18 g) هستند و انواع مربوط به آنها <3Out, 3Out> هستند ( شکل 9). k)، <3On، 4Out> ( شکل 9 p)، و <3In، 3Out > ( شکل 9 j)، به ترتیب.
با اشاره به وضعیت واقعی (تصاویر ماهواره ای)، تضادهای توپولوژیکی بالقوه خطوط/منطقه ها در شکل 18 به شرح زیر بیان شده است: در شکل 18 ج، بخشی (خط تقاطع) از خط ترافیک L 1 که به منطقه آبی می افتد. R 1 باید بریده شود. در شکل 18 ب، داده های درگیر نیازی به اصلاح ندارند زیرا خط تقاطع معمولاً یک پل است. در شکل 18 d، موقعیت خط L 3 در تقاطع باید به موقعیت خاصی دور از منطقه R 1 حرکت کند . در شکل 18 e، قسمت خطL 3 در خط تقاطع ممکن است نیاز به اصلاح داشته باشد تا از سقوط به دریاچه جلوگیری شود. در نهایت، در شکل 18 f، جهت خط L 3 در خط تقاطع باید طوری تنظیم شود که بر ناحیه R 1 مماس نباشد . به طور مشابه، انواع دیگری از قوانین برخورد توپولوژیکی بر اساس انواع توپولوژیکی اجزای تقاطع و وضعیت واقعی در سیستم ما ایجاد می شود. با توجه به مجموعه قوانینی که ایجاد کردیم، نتایج آدرس دهی تضاد مربوطه در شکل 18 a در شکل 19 نشان داده شده است.
5.2. نمونه هایی از اجزای تقاطع بین خطوط
در سیستم ما، انواع خط تقاطع در شکل 10 a-h به عنوان کلاس a به کلاس h و انواع نقطه تقاطع بین خطوط/خطوط در شکل 12 c-f به عنوان کلاس i به کلاس l نامگذاری شده اند. با محاسبه مولفه های تقاطع خطوط ترافیک در داده های آزمون، 22 خط تقاطع و 9694 نقطه تقاطع به دست می آید و این اجزا به ترتیب در لایه های موقت TTINSECTLINE و TTINSECTPOINT قرار می گیرند. جدول 2 نتایج تشخیص انواع اجزای تقاطع بین خطوط ترافیک را نشان می دهد. اعداد خاص کلاس های مربوطه در جدول 2 نشان داده شده است. مشاهده می شود که اجزای تقاطع بین خطوط ترافیکی عمدتاً نقاط تقاطع هستند، اما برخی از خطوط تقاطع با انواع (کلاس) متفاوت نیز وجود دارد.
شکل 20 a مولفه تقاطع خط/خط ناحیه محلی را در داده های آزمایشی نشان می دهد و شکل 20 b تصویر ماهواره ای منطقه مربوطه را نشان می دهد. در میان آنها، یک خط تقاطع کلاس c ( شکل 20 ج)، یک خط تقاطع کلاس f ( شکل 20 د)، یک نقطه تلاقی کلاس l ( شکل 20 e)، یک نقطه تقاطع کلاس وجود دارد. i ( شکل 20 f)، و سه نقطه تقاطع کلاس j ( شکل 20 g–i).
در حالت عادی، هنگامی که یک خط تقاطع بین دو خط ترافیک وجود دارد، فقط یک خط ترافیک در قسمت تقاطع رزرو می شود مگر اینکه آنها بالا و پایین باشند. برای خطوط متقاطع کلاس c (<2Null، 2Null>)، معمولاً خط پوشیده شده حذف می شود. با این حال، وضعیت واقعی (تصاویر ماهواره ای) گاهی اوقات پیچیده است. به عنوان مثال، خط L 2 تحت پوشش L 1 در شکل 20 c باید حفظ شود، در حالی که قسمت های همپوشانی خط متقاطع L 2 باید حذف شوند. مورد کلاس f (<2, 3>) مشابه است. معمولاً قسمت همپوشانی L 3 باید حذف شود، اما با توجه به وضعیت واقعی، قسمت همپوشانیL 1 باید حذف شود ( شکل 20 د). برای نقاط متقاطع کلاس l (<4OS>)، دو خط ارتباطی ترافیکی باید در تقاطع قطع شوند، مگر اینکه بالا و پایین باشند، و خطوط شکسته باید حذف شوند اگر خیلی کوتاه باشند ( شکل 20 e) . برای نقاط متقاطع کلاس i (<2>)، معمولاً نیازی به تغییر ( شکل 20 f) یا ادغام دو خط ندارند. برای نقاط متقاطع کلاس j (<3>)، معمولاً نیازی به تغییر ندارند ( شکل 20 g–i) یا باید یکی از دو خط در نقطه تقاطع قطع شود. با توجه به مجموعه قوانین و برخی از کمک های دستی، نتایج مربوط به برخورد با تعارض در شکل 20 a نشان داده شده است.شکل 21 .
6. نتیجه گیری و بحث
در این مقاله، ما یک مدل رابطه توپولوژیکی خط/منطقه و خط/خط تصفیه شده (N-WWIS) ارائه میکنیم. این مدل مکمل و توسعه مدل های سلسله مراتبی E-WID و E-WWIS برای مناطق/منطقه ها است. برای انطباق با عادت شناختی، اشیاء فضایی بر اساس توپولوژی چندگانه به جای توپولوژی مجموعه نقطه، و اجزای تقاطع بر اساس مجموعههای تقاطع شی کل (و نه تجزیه شده) در این مدل تعریف میشوند. متغیر توپولوژیکی درجه گره برای تشخیص نوع توپولوژیکی جزء تقاطع بین خط/منطقه و خط/خط معرفی شده است. با ترکیب درجه گره و انواع نقاط مجاور (“Null”، “On”، “In”، “Out”، “SS” و “OS”)، 29 نوع از خطوط تقاطع ممکن و نامتقارن متمایز می شوند. شامل 21 نوع خط/منطقه و 8 نوع خط/خط). با استفاده از این روش دو نوع خط/منطقه و چهار نوع نقطه تقاطع خط/خط پیدا می کنیم. بنابراین، یک مدل رابطه توپولوژیکی سلسله مراتبی برای خط/منطقه و خط/خط تشکیل شده است، یعنی مدل E-WID در سطح درشت و مدل N-WWIS در سطح تصفیه شده استفاده می شود.
الگوریتمهای مربوطه برای محاسبه نوع جزء تقاطع خط/منطقه و خط/خط پیادهسازی شدهاند و نمونههای کاربردی در بررسی خودکار یکپارچگی توپولوژیکی ارائه شدهاند. سیستم توسعهیافته با استفاده از دادههای OSM شهر چانگشا، استان هونان، چین، بهعنوان دادههای تجربی بهطور فشرده مورد آزمایش قرار گرفت. نتایج این مطالعه نشان دهنده راه جدیدی برای بررسی و مدیریت یکپارچگی توپولوژیکی خودکار است.
روابط توپولوژیکی بین مناطق/نقاط، خطوط/نقاط و نقاط/نقاط را می توان به طور کامل توسط مدل E-WID متمایز کرد ( شکل 22 ). بنابراین، روابط توپولوژیکی بین دو جسم ساده در فضای دو بعدی را می توان با E-WID در سطح درشت نشان داد و متمایز کرد، و E-WWIS و BBIS (در صورت لزوم) برای منطقه/منطقه و N-WWIS برای خط/منطقه و خط/خط در یک سطح تصفیه شده به صورت سلسله مراتبی.
همانطور که توسط مرجع [ 35 ] ذکر شد، کاربردهای GIS سه بعدی (3D) در دامنه و پیچیدگی افزایش یافته است، که به نوبه خود باعث افزایش تقاضا برای ایجاد و نگهداری GIS سه بعدی قابل اعتماد می شود. با این حال، مجموعه داده های سه بعدی موجود حاوی تناقضات توپولوژیکی زیادی است [ 36]، که توسعه پایدار برنامه های کاربردی مرتبط را محدود می کند. از سوی دیگر، نظریه توپولوژی چندگانه، عملوند (یعنی کل شی)، عملیات مجموعه (یعنی تقاطع و تفاوت)، متغیرهای توپولوژیکی (یعنی محتوا، بعد، عدد اویلر و درجه نقطه)، و برخی از انواع نقاط مجاور («تهی»، «روشن»، «در» و «خارج») که در مدلهای سلسله مراتبی ما استفاده میشوند، میتوانند در فضای سه بعدی نیز در تئوری استفاده شوند. بنابراین، گسترش مدلهای ما (شامل E-WID و E/N-WWIS) به اشیاء فضایی سهبعدی بر اساس توپولوژی چندگانه کار آینده ما خواهد بود.





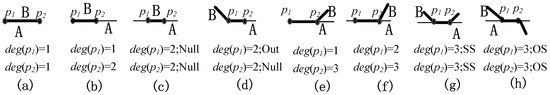











بدون دیدگاه