خلاصه

منحنی‌های ابعاد فراکتالی رشد شهری را می‌توان با توابع سیگموئیدی از جمله تابع لجستیک و تابع لجستیک درجه دوم مدل‌سازی کرد. انواع مختلف توابع لجستیک نشان دهنده پویایی فضایی متفاوت است. منحنی‌های بعد فراکتالی رشد شهری در کشورهای غربی از تابع لجستیک مشترک پیروی می‌کنند، در حالی که منحنی‌های رشد بعد فراکتالی شهرهای شمال چین از تابع لجستیک درجه دوم پیروی می‌کنند. حال می‌خواهیم بررسی کنیم که آیا سایر شهرهای چین، به‌ویژه شهرهای جنوب چین، از قوانین تکامل شهری پیروی می‌کنند یا خیر و سعی می‌کنیم دلایل آن را تحلیل کنیم. این مقاله به بررسی ویژگی‌های فراکتال و ابعاد فراکتال شهر شنژن در جنوب چین اختصاص دارد. منطقه شهری با استفاده از فناوری ArcGIS به چهار زیر منطقه تقسیم می شود. روش شمارش جعبه برای استخراج مجموعه داده های فضایی به کار گرفته شده است و از روش رگرسیون حداقل مربعات برای تخمین پارامترهای فراکتال استفاده می شود. نتایج نشان می‌دهد که (1) شکل شهری شهر شنژن ساختار فراکتالی واضحی دارد، اما مقادیر ابعاد فراکتالی زیرمناطق مختلف متفاوت است. (2) منحنی‌های رشد ابعاد فراکتال هر چهار ناحیه مورد مطالعه را فقط می‌توان با تابع لجستیک مشترک مدل‌سازی کرد و خوبی تناسب در طول زمان افزایش می‌یابد. (3) اوج رشد شهری در شنژن قبل از سال 1986 گذشته بود و رشد بعد فراکتال به حداکثر ظرفیت خود نزدیک می شود. می توان نتیجه گرفت که فرم شهری شنژن دارای ویژگی های چند فرکتال است و ساختار فراکتالی به تدریج از طریق خود سازمان دهی بهتر شده است، اما منابع زمینی آن به مرزهای رشد می رسد. منحنی‌های ابعاد فراکتال رشد شهری شنژن مشابه شهرهای اروپایی و آمریکایی است اما با شهرهای شمال چین متفاوت است. این نشان می‌دهد که مکانیسم‌های پویایی متفاوتی برای توسعه شهر بین شمال و جنوب چین وجود دارد.

کلید واژه ها:

شکل و رشد شهری ; شهرهای فراکتال ; منحنی رشد بعد فراکتال ; شهر شنژن

1. معرفی

مطالعه در مورد شهرها از توصیف شروع می شود و به فهم ختم می شود. برای توصیف یک پدیده شهری، باید مقیاس های مشخصه آن را پیدا کنیم. روش های سنتی ریاضی و تجزیه و تحلیل کمی بر اساس یک مقیاس معمولی است که اغلب به آن طول مشخصه می گویند [ 1 ، 2 ، 3]]. متأسفانه الگوهای فضایی شهرها مقیاس مشخصی ندارند و با معیارهای مرسوم مانند طول و مساحت قابل توصیف نیستند. در این مقیاس، مفهوم مقیاس های مشخصه باید با ایده های مقیاس بندی جایگزین شود. هندسه فراکتال یک ابزار ریاضی قدرتمند برای تجزیه و تحلیل مقیاس شکل و رشد شهری فراهم می کند. از تصاویر سنجش از دور، شکل شهری شبیه به پاشیدن جوهر است که معمولاً یک بی‌نظمی و خود شباهت بسیار زیاد را در مقیاس‌های مختلف نشان می‌دهد [ 4 ، 5 ]. به این معنی است که از قانون گاوس تبعیت نمی کند و معیارهای سنتی و مدل های ریاضی نمی توانند به طور مؤثر آن را توصیف کنند [ 6 ، 7 ]. هندسه فراکتال یک رویکرد کمی مناسب در این جنبه ارائه می دهد [ 8، 9 ]. بعد فراکتال، به ویژه طیف پارامتر چندفراکتالی، می تواند برای مشخص کردن ناهمگنی فضایی و کشف پیچیدگی فضایی مورد استفاده قرار گیرد [ 10 ]. از زمانی که Mandelbrot [ 11 ] هندسه فراکتال را در سال 1983 توسعه داد، این نظریه برای نزدیک به چهل سال در تحقیقات جغرافیایی اعمال شده است. جغرافیای شهری یکی از بزرگترین ذینفعان ایده های فراکتال است [ 12 ].
از دهه 1980، برخی از مطالعات پیشگام در مورد شکل و رشد شهری بر اساس هندسه فراکتال منتشر شده است. آن مطالعات تحقیقاتی اولیه عمدتاً بر دو جنبه از فرم شهری متمرکز است. از یک طرف، آنها ابعاد فراکتالی فرم های شهری را با استفاده از روش شمارش جعبه، مقیاس بندی مساحت-شعاع یا مقیاس بندی محیط-مساحت اندازه گیری می کنند و سپس مقادیر ابعاد فراکتال سری های زمانی مختلف را در یک منطقه یا مناطق مختلف مقایسه می کنند. همزمان برای تحقق تحلیل فرم و رشد شهری (به عنوان مثال، [ 5 ، 13 ، 14 ، 15 ، 16 ، 17 ، 18 ، 19 ، 20]). برخی از این نتایج تحقیقات توسط باتی و لانگلی [ 21 ] و فرانکهاوزر [ 22 ] در سال 1994 خلاصه شد، که به این نتیجه رسیدند که شکل و رشد شهری را می توان به عنوان یک شی فراکتال در نظر گرفت و مقدار متوسط ​​بعد فراکتال حدود 1.7 است. از سوی دیگر، آنها فرآیند رشد شهری را بر اساس مدل‌های تکراری و تئوری‌های آشوب یا خودسازمان‌دهی شبیه‌سازی می‌کنند تا مکانیسم شکل‌گیری یا دلایل ساختار فراکتالی فرم شهری را بیابند (به عنوان مثال، [4، 20 ] ) . 23 ، 24 ، 25 ، 26 ، 27 ، 28 ، 29 ، 30 ،31 ، 32 ، 33 ، 34 ، 35 ، 36 ]). به طور خاص، باتی و همکاران. [ 24 ، 27 ، 28 ] به ترتیب از مدل فراکتال و تجمع محدود با انتشار (DLA) برای شبیه سازی فرآیند ساختار شهری و رشد استفاده کردند. بنگوئی و همکاران [ 4 ، 29 ، 30 ، 31 ] از مدل تجمیع برای شبیه سازی فرم شهری پتاه تیکوا استفاده کرد و مفهوم جهش را به عنوان یکی از فرآیندهای بنیادی که فرکتالیته شهری ایجاد می کند، معرفی کرد. توماس و همکاران [ 34] روابط بین شهرهای فراکتال و خود سازمان دهی را گزارش کرد.
امروزه تحلیل فرم و رشد شهری بر اساس نظریه فراکتال و کاوش در مکانیسم پیدایش ویژگی‌های فراکتالی فرم شهری به موضوعات مهمی در علوم شهری و علم پیچیدگی تبدیل شده است. اخیراً مطالعات بیشتری در مورد شکل و رشد شهری بر اساس بعد فراکتال به عنوان شاخص اعتبار (به عنوان مثال، [ 35 ، 36 ، 37 ، 38 ، 39 ، 40 ، 41 ، 42 ، 43 ]) و مدل های چندفراکتالی (به عنوان مثال، [ 44 ) انجام شده است. , 45 , 46 , 47 , 48 , 49 ,50 ، 51 ]). در مقایسه با مدل فراکتالی ساده، محاسبه مدل‌های چندفرکتالی پیچیده‌تر است اما می‌تواند ناهمگونی و ویژگی‌های محلی توزیع فرم شهری را بهتر منعکس کند [ 45 ]. Encarnação و همکاران [ 52 ] فناوری نقشه برداری فراکتال را با استفاده از روش شمارش جعبه و برنامه نویسی توسعه داد، بنابراین امکان تجسم توزیع ابعاد فراکتالی فرم شهری را فراهم کرد. علاوه بر این، کشفی انجام شد که منحنی‌های ابعاد فراکتالی رشد شهری اثر اسکواش را به خود می‌گیرند و می‌توانند با توابع سیگموئید مدل‌سازی شوند [ 53]]. منحنی‌های رشد ابعاد فراکتال اشکال شهری در اروپا و آمریکا تابع لجستیک مشترک را برآورده می‌کنند، در حالی که شهرهای شمالی چین مانند پکن تابع لجستیک درجه دوم را برآورده می‌کنند [ 6 ، 54 ]. آن مطالعات (به عنوان مثال، [ 6 ، 53 ، 54 ]) عمدتاً بر مدل‌سازی نظری یک سری زمانی مناسب از مقادیر ابعاد فراکتالی یک شهر یا منطقه متمرکز بودند و دریافتند که در انواع توابع لجستیکی بین کشورهای غربی و شمال چین تفاوت وجود دارد. . با این حال، مورد شهرهای جنوبی چین و برخی از دلایل احتمالی خاص برای این پدیده به ندرت مرتبط بودند.
انواع مختلف توابع لجستیک نشان دهنده پویایی فضایی متفاوت است. حال می خواهیم بررسی کنیم که آیا سایر شهرهای چین به ویژه شهرهای جنوب چین از قوانین توسعه یکسانی پیروی می کنند و دلایل احتمالی این پدیده چیست؟ شهر شنژن در جنوب چین یک مورد خاص و قابل توجه است. این شهر نه تنها یک شهر جدید و با رشد سریع است که توسط دولت برنامه ریزی شده است، بلکه یک شهر آزمایشی برای آزمایش های دولتی در مورد عملکرد اقتصاد بازار است. امروزه، این کشور به توسعه اقتصادی و رشد جمعیت شگفت انگیز دست یافته است و از زمان اصلاحات و بازگشایی چین، توسعه اقتصاد چین را رهبری می کند. با در نظر گرفتن شنژن به عنوان نمونه ای از جنوب چین، می توانیم نوع دیگری از شهر فراکتال در سرزمین اصلی چین را مورد بحث قرار دهیم که با بسیاری از شهرهای دیگر مناطق چین متفاوت است. به جز منطقه ساحلی جنوب شرقی چین. بنابراین، این مقاله به بررسی منحنی‌های رشد بعد فراکتالی شهر شنژن و تلاش برای تحلیل بیشتر دلایل اختصاص یافته است. ابتدا شهر شنژن را به چهار منطقه مورد مطالعه تقسیم می کنیم و سپس از روش شمارش جعبه و رگرسیون حداقل مربعات برای استخراج داده های مکانی و تخمین پارامترهای فراکتال استفاده می کنیم. سپس، ما از توابع سیگموئید برای مدل‌سازی منحنی‌های ابعاد فراکتالی رشد شهری در منطقه شنژن استفاده می‌کنیم. از طریق این مطالعه، ما نه تنها می توانیم تفاوت های شمال-جنوب توسعه شهر در چین را آشکار کنیم، بلکه شباهت ها و تفاوت های تکامل شهری بین چین و غرب را نیز منعکس می کنیم. ابتدا شهر شنژن را به چهار منطقه مورد مطالعه تقسیم می کنیم و سپس از روش شمارش جعبه و رگرسیون حداقل مربعات برای استخراج داده های مکانی و تخمین پارامترهای فراکتال استفاده می کنیم. سپس، ما از توابع سیگموئید برای مدل‌سازی منحنی‌های ابعاد فراکتالی رشد شهری در منطقه شنژن استفاده می‌کنیم. از طریق این مطالعه، ما نه تنها می توانیم تفاوت های شمال-جنوب توسعه شهر در چین را آشکار کنیم، بلکه شباهت ها و تفاوت های تکامل شهری بین چین و غرب را نیز منعکس می کنیم. ابتدا شهر شنژن را به چهار منطقه مورد مطالعه تقسیم می کنیم و سپس از روش شمارش جعبه و رگرسیون حداقل مربعات برای استخراج داده های مکانی و تخمین پارامترهای فراکتال استفاده می کنیم. سپس، ما از توابع سیگموئید برای مدل‌سازی منحنی‌های ابعاد فراکتالی رشد شهری در منطقه شنژن استفاده می‌کنیم. از طریق این مطالعه، ما نه تنها می توانیم تفاوت های شمال-جنوب توسعه شهر در چین را آشکار کنیم، بلکه شباهت ها و تفاوت های تکامل شهری بین چین و غرب را نیز منعکس می کنیم.

2. روش ها

2.1. روش شمارش جعبه

با توجه به ویژگی‌های بدون مقیاس فرم شهری، معیارهای مرسوم باید با پارامترهای فراکتالی جایگزین شوند. روش شمارش جعبه در این مقاله برای تخمین بعد فراکتالی فرم شهری چهار منطقه مورد مطالعه در شنزن از سال 1986 تا 2017 استفاده شده است. (به عنوان مثال، [ 18 ، 19 ، 21 ، 52 ، 55]) برای اندازه گیری بعد فراکتال در تصاویر دو بعدی. رویه اصلی آن، به طور کلی، قرار دادن یک سری شبکه های منظم از اندازه های جعبه در حال کاهش به صورت بازگشتی بر روی یک شی هدف و سپس ثبت تعداد اشیاء در هر جعبه متوالی است، جایی که شمارش تعداد کادرها را ثبت می کند که توسط هدف اشغال شده است. هدف – شی. به گفته بنگوئی و همکاران. [ 18 ]، در یک فضای 2 بعدی، جسم توسط شبکه‌ای از مربع‌هایی با اندازه ε پوشیده شده است و عدد N ( ε ) مربع‌هایی که بخشی از جسم در آن ظاهر می‌شود شمارش می‌شود. سپس، تغییر طول ضلع جعبه ε ، منجر به تغییر در شماره جعبه های غیر خالی، N ( ε). اگر معلوم شد که جسم فراکتال است، پس

ن(ε)=ن1(1/ε)D

که در آن N 1 ضریب تناسب، D مقدار ابعاد فراکتال فرم شهری، و فرم لگاریتمی است.

لوگاریتمن(ε)=لوگاریتمن1+Dلوگاریتم(1/ε)

بنابراین، نمودار لگاریتمی ln N ( ε ) در مقابل ln (1/ ε ) یک خط مستقیم با شیب برابر با D به دست می دهد . در این مقاله، اولین مقدار ε نصف اندازه جعبه است. مقدار بعدی برابر با ε /4 است. مقدار i ε /2 i است . بالاترین مقدار شاخص i 9 است. ابزارهای ایجاد شبکه ماهیگیری، تنظیم فضایی و پوشش در ArcMap10.2 برای پیاده سازی جعبه تقسیم بندی و جعبه چرخش و به دست آوردن مقدار I N ( ε ) استفاده شد .

2.2. منحنی رشد ابعاد فراکتال و قانون توان

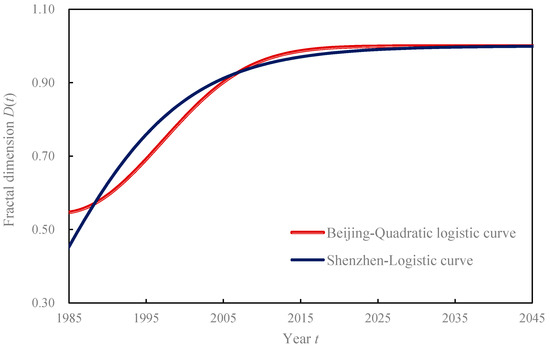
به منظور بررسی قوانین تحول شهری شهر شنژن، مقادیر ابعاد فراکتالی سری‌های زمانی چهار منطقه مورد مطالعه در شنژن را با استفاده از مدل‌سازی تابع لجستیک مدل‌سازی کردیم. با توجه به توضیح چن [ 53 ]، تابع لجستیک تکامل بعد فراکتال را می توان به صورت بیان کرد.

D(تی)=Dحداکثر1+(Dحداکثر/D0)ه-کتی یا D(تی)=Dحداکثر1+آه-ک(n-n0)

جایی که t ترتیب زمانی است (0، 1…)؛ n سال است. n 0 سال اولیه است. D ( t ) یا D ( n ) بعد فراکتال را در زمان t یا سال n نشان می دهد . D 0 بعد فراکتال در سال اول است. D max ≤ 2 حداکثر بعد فراکتال را نشان می دهد. A به یک پارامتر اشاره دارد. k نرخ رشد اصلی بعد فراکتال است. روابط پارامتر و متغیر به شرح زیر است

D(تی)=D(n)،آ=DحداکثرD0-1،تی=n-n0

معادله (3) را می توان به تبدیل لگاریتمی تبدیل کرد و نتیجه این است

لوگاریتم(DحداکثرD0-1)=لوگاریتم(DحداکثرD0)-کتی=لوگاریتمآ-کتی

معادله (5) با یک معادله log-linear هماهنگ شده است و اگر پارامتر مقدار D max شناخته شده باشد، تخمین مقادیر A و K توسط تحلیل رگرسیون خطی ساده است . در اینجا، روش تخمین پارامتر جستجوی مناسب (GOFS) برای تخمین پارامتر انتخاب شد که به ویژه توسط Chen [ 53 ] معرفی شده است.

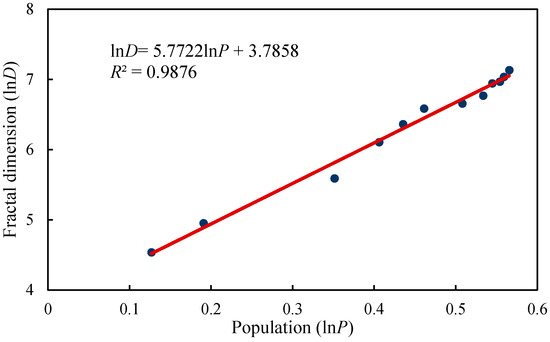
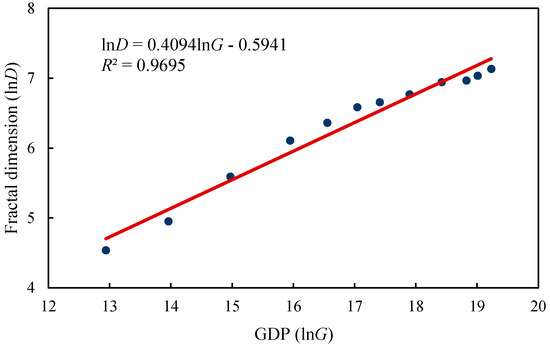
گرفتن عوامل نیروی محرکه از طریق مدل ریاضی نقش مهمی در تلاش برای تبیین دلایل پیدایش ساختار فراکتالی فرم شهری دارد. فرم شهری یک سیستم پیچیده معمولی است [ 56 و 57 ]. شکل و رشد پایدار شهری نتیجه تعامل طولانی مدت عوامل مختلف است. این ارتباط ها را می توان با تابع توان [ 58 و 59 ] دریافت کرد. برای یک سیستم شهری، رابطه بین دو عنصر اندازه‌گیری شده که شهر را نشان می‌دهند، مانند جمعیت، مساحت و تولید ناخالص داخلی، معمولاً قانون قدرت آماری را برآورده می‌کند. بنابراین ما عوامل محرک تکامل و رشد فرم شهری را با استفاده از تابع قانون قدرت، که به صورت

Dتی=کایکستیβ

که در آن X t و D t به ترتیب در یک سال t معین ، مقدار ابعاد فراکتال و تعداد کل عامل محرک را نشان می دهند. k و β برای بعد فراکتال ثابت هستند. مدل خطی شده معادله (6) است

لوگاریتمDتی=لوگاریتمک+βلوگاریتمایکستی

که در آن ln k و β عبارت‌های ثابتی هستند که باید تخمین زده شوند.

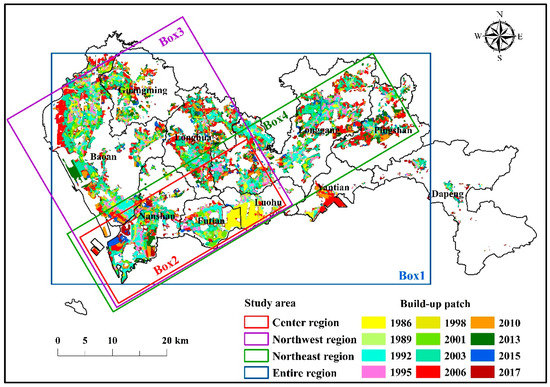
2.3. منطقه مطالعه و مجموعه داده ها

شنژن (22°27′–22°52′ شمالی، 113°46′-114°37′ شرقی)، به عنوان اولین منطقه ویژه اقتصادی چین، در امتداد هزینه دریای چین جنوبی و در مجاورت هنگ کنگ قرار دارد. قبل از اصلاحات و سیاست باز کردن چین در اواخر سال 1978، این شهر فقط یک شهر مرزی خواب‌آلود با حدود 30000 سکنه بود که به عنوان یک توقفگاه سفارشی برای ورود به سرزمین اصلی چین از هنگ کنگ عمل می‌کرد. اکنون، شنژن به یک کلان شهر بین المللی با جمعیت کل 13.0366 میلیون نفر تبدیل شده است [ 60 ]. میانگین دمای سالانه حدود 22.4 درجه سانتی گراد و بارندگی سالانه حدود 1948 میلی متر است [ 61 ]. ویژگی های شکل منطقه اداری شنژن باریک و طولانی است، و دهانه شرقی-غربی بیش از 49 کیلومتر است، در حالی که دهانه شمال-جنوب تنها حدود 7 کیلومتر است [62] .]. در قسمت جنوب شرقی شنژن یک توپوگرافی تپه ای است. در قسمت شمال غربی نسبتاً کم است. در این مقاله، چهار کادر به عنوان مناطق مورد مطالعه ترسیم شد ( شکل 1 ). اولین منطقه جعبه کل منطقه شنژن است که تقریباً کل پچ ساخته شده شنژن را پوشش می دهد. منطقه جعبه دوم یک منطقه مرکزی اصلی است که عمدتاً شامل منطقه Futian، منطقه Luohu، و Nanshan District است. مناطق جعبه سوم و چهارم به ترتیب قسمت شمال غربی و قسمت شمال شرقی هستند. دلیل گنجاندن آنها به این دلیل است که مناطق ساخته شده در این دو منطقه از نظر بصری دارای روند گسترش و توسعه هستند. ارزیابی کامل ویژگی‌های تکامل مکانی-زمانی شکل و رشد شهری کاملاً مفید است.
پردازش چهار جعبه عمدتاً شامل تقسیم بندی جعبه و چرخش جعبه است. در پلتفرم ArcMap10.2، ابتدا از ابزار ایجاد شبکه ماهیگیری برای تولید شبکه های منظم در مقیاس های مختلف بر اساس روش شمارش جعبه استفاده کردیم. ثانیا، ما چهار جعبه را که نمایانگر چهار منطقه مطالعه است با ابزار ویرایشگر چرخاندیم و سپس جعبه‌های دیگر در مقیاس‌های مختلف را با چهار جعبه چرخانده با ابزار تنظیم فضایی تطبیق دادیم. علاوه بر این، داده های مناطق ساخته شده ( شکل 1 ) از تصاویر Landsat TM 4 و 5 و OLI 8 با وضوح 30 متر برای دوازده سال استخراج شد: 1986، 1989، 1992، 1995، 1998، 2001، 2003، 20. ، 2010، 2013، 2015 و 2017. همه آنها از وب سایت کاوشگر زمین ( https://earthexplorer.usgs.gov/ سازمان زمین شناسی ایالات متحده (USGS) جمع آوری شدند.) با پوشش ابری کمتر از 10 درصد. به طور کلی، روش‌های طبقه‌بندی نظارت شده شی گرا و تفسیر بصری پس طبقه‌بندی برای استخراج داده‌های مناطق ساخته شده به کار می‌روند و فرآیند آن را می‌توان به سه بخش تقسیم کرد. ابتدا، ما از جعبه ابزار گردش کار استخراج ویژگی مبتنی بر مثال در نرم افزار ENVI 5.3 برای تولید نقشه های طبقه بندی کاربری زمین و پوشش زمین (LULC) دوازده دوره استفاده کردیم. در اینجا، ما به طور تقریبی انواع زمین را به چهار دسته تقسیم کردیم که عبارتند از بدنه آبی، پوشش گیاهی، مناطق خالی و ساخته شده، و روش طبقه بندی ماشین بردار پشتیبان (SVM) را انتخاب کردیم. در مرحله دوم، کلاس فرم ناحیه شهری را برای هر داده برداری حاصل در نرم افزار ArcMap10.2 انتخاب کردیم. در نهایت، و مهم‌تر از همه، ما یک تفسیر بصری از نقشه‌های منطقه ساخته‌شده 12 دوره انجام دادیم.

3. نتایج و تجزیه و تحلیل

3.1. تجزیه و تحلیل ابعاد فراکتالی فرم شهری

برای تخمین پارامترهای فراکتال می توان از رگرسیون خطی لگاریتمی دوگانه بر اساس روش حداقل مربعات استفاده کرد. مدل سازی فراکتال شامل دو نوع پارامتر است. یکی پارامترهای استنباطی و دیگری پارامترهای توصیفی است. اولی شامل بعد فراکتال و ضریب تناسب است، و دومی شامل خوب بودن برازش و خطای استاندارد [ 63 ، 64 ] است. نتایج برازش بر اساس روش شمارش جعبه نشان داد که از سال 1986 تا 2017، چهار ناحیه مورد مطالعه همگی یک ارتباط خطی قوی بین lnN ( ε ) و ln (1/ ε ) با مقادیر ابعاد فراکتال بین 1 و 2 نشان می‌دهند، و خوب بودن R 2همه مقادیر بالای 0.98 هستند. این مدرک قدرتمندی است که نشان می‌دهد شکل شهری در شنژن، هم مناطق کل و هم قسمتی از آن، واقعاً از نظر آماری در طول سال‌های 1986-2017 فراکتال هستند. نتایج دقیق برآورد ابعاد فراکتالی اشکال شهری چهار منطقه در شنژن از سال 1986 تا 2017 در جدول 1 ارائه شده است . همه آنها در طول زمان به تدریج افزایش یافتند، اما کل منطقه کمی کوچکتر از سه منطقه فرعی دیگر – منطقه مرکزی، منطقه شمال غربی و منطقه شمال شرقی است.
در واقع، بعد فراکتال D اکنون به یک شاخص اعتبار برای ارزیابی میزان پر شدن فضا، پیچیدگی فضایی و همگنی یا فشردگی فضایی زمین شهری تبدیل شده است. یک مقدار بزرگتر نشان دهنده پراکندگی شهری است – ساختار فضایی شهری پیچیده تر و همگن می شود [ 65 ]. در نقشه های دیجیتال دو بعدی، D=2نشان می دهد که یک توزیع فضایی همگن از جسم در صفحه دارد. حد افراطی دیگر این است D=0، که نشان دهنده غلظت محلی بالا است [ 4]. از نتایج بالا، برای 40 سال گذشته، آشکار است که فرم شهری در کل شنژن در وضعیت رشد و گسترش مداوم در فضا بوده است. در همین حال، ساختار فضایی آن به مرور زمان پیچیده‌تر و همگن‌تر شده است. با توجه به توزیع نوع زمین در دنیای واقعی، وجود انواع زمین های دیگر، مانند زمین های اکولوژیکی و آب، در چهار منطقه مورد مطالعه اجتناب ناپذیر است. آنها ممکن است در واقع متعلق به انواع زمین هایی باشند که توسط مقامات محافظت می شوند و اجازه ندارند برای ساخت و ساز شهری در شنژن در دسترس باشند. در سال 2017، به ویژه، مقادیر ابعاد فراکتال چهار منطقه – کل منطقه، بخش مرکزی، قسمت شمال غربی و قسمت شمال شرقی – به بالاترین مقدار خود رسید که به ترتیب 1.7604، 1.8467، 1.8189 و 1.8294 بود.جدول 1 ). نه حداقل به این دلیل که این مقادیر نزدیک به 2 هستند، اما احتمالاً هیچ نوع زمین دیگری برای توسعه شهری در هر منطقه مورد مطالعه مجاز نیست. بنابراین، ما ممکن است حدس بزنیم که شنژن احتمالاً در آینده نزدیک با وضعیت زمین شهری رو به اشباع روبرو خواهد شد.
علاوه بر این، می‌توانیم با محاسبه داده‌های جدول 1 اطلاعات بیشتری را به دست آوریم . میانگین سرعت درجه پر شدن فضای شهری در چهار منطقه مورد مطالعه را می توان با استفاده از آن محاسبه کرد (D2017-D1986)/△تی(2017-1986). مقادیر نتیجه محاسبه به ترتیب 0.0202، 0.0133، 0.0189 و 0.0177 است. از نظر مساحت، کل منطقه بزرگترین منطقه در بین چهار منطقه مورد مطالعه است و مقدار میانگین سرعت درجه پر شدن فضای شهری نیز بزرگترین منطقه است. این نشان می‌دهد که شنژن در این دوره تبدیل تعداد زیادی از انواع زمین‌های دیگر به زمین شهری را تجربه کرد و سریع‌ترین رشد و گسترش زمین شهری در بخش شمال غربی و به دنبال آن قسمت شمال شرقی و بخش مرکزی رخ داد. علاوه بر این، همانطور که در شکل 2 نشان داده شده استواضح است که شهر شنژن طی سال های 1986-2017 دارای دو قله پراکندگی شهری بوده است که در سال های 1992 و 2003 بوده است، اما میزان گسترش شهری در سال 1992 به طور قابل توجهی بیشتر از سال 2003 بوده است. در سال 1992، مناطق شمال غرب و شمال شرق شنژن همان سطح توسعه کاربری زمین شهری را داشت. در مقابل، منطقه مرکزی توسعه آهسته تری داشت، اما در سال 2003، این سه زیرمنطقه اساساً سطح توسعه کاربری اراضی شهری یکسانی داشتند.

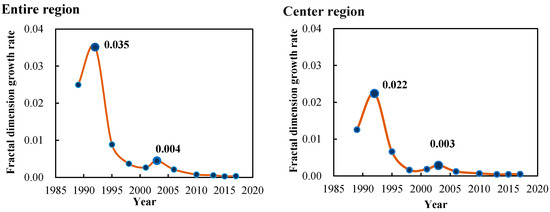
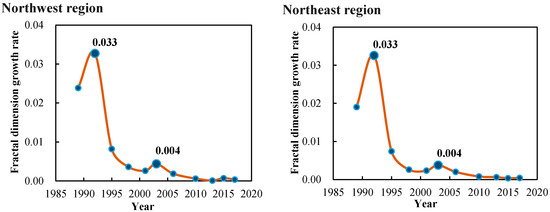
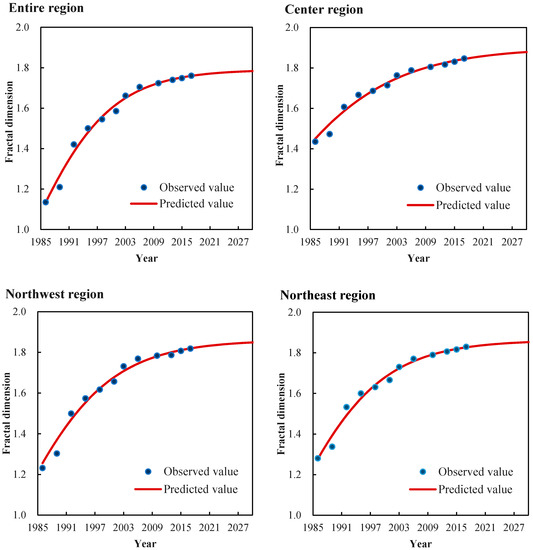
3.2. منحنی های رشد ابعاد فراکتال

نتایج مجموعه‌های ابعاد فراکتالی چهار ناحیه برای برازش مدل لجستیک با تخمین حداقل مربعات معمولی (OLS) و جستجوی برازش مناسب (GOFS) در شکل 3 نشان داده شده است . بدیهی است که منحنی‌های رشد ابعاد فراکتالی چهار منطقه در شنژن می‌توانند به خوبی با تابع لجستیک مرتبه اول برازش شوند. عبارات لجستیک مرتبه اول خاص و پارامترهای مربوطه در جدول 2 نشان داده شده است . مناسب بودن R2 عبارات لجستیکی مرتبه اول برای هر منطقه بسیار زیاد است. در همین حال، ما همچنین می‌توانیم به سادگی بعد فراکتال حداکثر ظرفیت را بدست آوریم و سال رسیدن به حداکثر ظرفیت را با بیان لجستیک هر منطقه پیش‌بینی کنیم. همانطور که در جدول 2 نشان داده شده استحداکثر ظرفیت ابعاد فراکتال فضای چهار منطقه مورد مطالعه – کل، مرکز، شمال غرب و شمال شرق – در شنژن به ترتیب 1.7905، 1.9، 1.86 و 1.8621 است و سال های مربوط به رسیدن به مقادیر بالا 2072، 2197، به ترتیب 2085 و 2082. به سادگی می توان دید که منطقه مرکزی در شنژن هم بیشترین ابعاد فراکتال ظرفیت حداکثر فضا و هم طولانی ترین زمان برای رسیدن به سال رسیدن به بالاتر از مقدار را دارد. اما در ارتباط با وضعیت عملی، آن ارزش ها در واقع بیش از حد ارزش گذاری می شوند، زیرا در محدوده های مورد مطالعه، زمین هایی که برای انسان کاملاً غیرقابل مهمان نوازی هستند، مانند رودخانه ها و کوه های مرتفع را شامل می شود.

3.3. تحلیل قانون قدرت

نتایج اندازه جمعیت، تولید ناخالص داخلی و مقادیر ابعاد فراکتال کل شنژن از سال 1986 تا 2017 در شکل 4 و شکل 5 نشان داده شده است . بین اندازه جمعیت، تولید ناخالص داخلی و بعد فراکتال روابط قانونی قابل توجهی وجود دارد، و مقادیر خوب بودن تناسب R 2 بسیار بالا هستند – همه بالاتر از 0.96. افزایش ابعاد فراکتال با گذشت زمان معمولاً نشان دهنده پراکندگی شهری است. معمولاً به عوامل اندازه جمعیت و سطح توسعه اقتصادی مربوط می شود [ 66]. این نشان می‌دهد که هم اندازه جمعیت و هم تولید ناخالص داخلی عوامل محرک ترویج گسترش شهری در شنزن از سال 1986 تا 2017 هستند. با این حال، نقش شتاب‌دهنده جمعیت در مورد گسترش شهری بسیار بیشتر از تولید ناخالص داخلی بر حسب توان مربوطه است، که نشان می‌دهد که شهر شنژن نیازی به تقویت توسعه اقتصادی خود به قیمت توسعه شهری ندارد. همچنین باید به این مسئله توجه کرد که آیا رفتار فردی و سیاست عمومی هر دو نقش کلیدی در رشد جمعیت و رشد اقتصادی یک شهر دارند یا خیر. در بخش 4 این مقاله مورد بحث قرار خواهد گرفت .

4. بحث

با استفاده از محاسبه و تجزیه و تحلیل پارامترهای فراکتال، می‌توان اطلاعات جدیدی در مورد شهر شنژن به دست آورد. برخی از دانش ها را می توان برای توضیح تحولات مکانی-زمانی شهرهای دیگر تعمیم داد. در مورد فراکتال های شهری، شنژن با بسیاری از شهرهای شمال چین متفاوت است [ 6 ]. تا حدودی مشابه شهرهای اروپا و آمریکا است [ 53 و 54 ]. این برای ما برای درک توسعه شهر آشکار است. نکات اصلی مطالعات فوق را می توان به صورت زیر خلاصه کرد ( جدول 3). اول، شکل شهری شنژن دارای ساختار فراکتالی است. این نشان می دهد که نظم فضایی این شهر با تکامل خود سازمان یافته پدید آمده است. دوم، زیرحوزه های مختلف مطالعه مقادیر ابعاد فراکتالی متفاوتی را به خود می گیرند. این نشان‌دهنده ناهمگونی فضایی شکل شهری شنژن است و ناهمگونی فضایی نشان‌دهنده مقیاس‌بندی چندفراکتالی توسعه شهر است. سوم، به نظر می رسد مقادیر ابعاد فراکتال از مرکز شهر به حومه و حومه نزول می کنند. به خصوص در مراحل اولیه (1986-2001)، مقادیر ابعاد فراکتالی ناحیه مرکز به طور قابل توجهی بالاتر از مقادیر ابعاد فراکتال در ناحیه شمال غربی و منطقه شمال شرقی بود ( شکل 1 ؛ جدول 1).). این نشان دهنده یک ساختار دایره ای پنهان از توسعه شهر است. ساختار دایره ای پشت اشکال شهری نامنظم را می توان با تغییرات ابعاد فراکتال آشکار کرد [ 20 ]. چهارم، خوب بودن تناسب برای تخمین بعد فراکتال در طول زمان افزایش یافت. از سال 1986 تا 2017، مقدار مربع R بالا و بالاتر رفت تا زمانی که نزدیک به 1 شد ( جدول 1). این نشان می دهد که ساختار فراکتالی شنژن، به تدریج، از طریق تکامل خود سازمان یافته، بهتر و بهتر شد. پنجم، منحنی‌های رشد ابعاد فراکتالی فرم شهری را می‌توان با تابع لجستیک معمولی مدل‌سازی کرد. این با منحنی‌های رشد بعد فراکتال شهرهای شمال چین متفاوت است، اما مشابه شهرهای کشورهای توسعه‌یافته غربی است. این احتمالاً ناشی از فرآیند شهرنشینی از پایین به بالا در شهرهای جنوبی چین است که تحت سلطه تکامل خود سازماندهی است که با مکانیسم بازار مرتبط است. ششم، مقادیر ابعاد فراکتال به پارامترهای ظرفیت نزدیک شد. تمام مقادیر ابعاد فراکتال در سال 2017 نزدیک به حداکثر مقدار، D max هستند. این نشان می دهد که فضای شهری شنژن تا حد زیادی پر شده است و فضاهای زیادی برای توسعه آینده باقی نمانده است.
منحنی‌های رشد ابعاد فراکتالی فرم شهری در چهار منطقه مورد مطالعه شنژن را می‌توان به خوبی با تابع لجستیک مرتبه اول مدل‌سازی کرد ( شکل 3 )، که در برخی از شهرهای غربی مانند لندن (بریتانیا)، تل‌آویو (تل آویو) یکسان است. اسرائیل)، و بالتیمور (ایالات متحده آمریکا) [ 53 ، 54 ]، اما متفاوت از شهرهای شمالی چین، مانند پکن. بزرگترین تفاوت بین منحنی لجستیک و منحنی لجستیک درجه دوم، نرخ رشد قبل از رسیدن منحنی به حداکثر ارزش سرمایه است. منحنی لجستیک بسیار کندتر از منحنی لجستیک درجه دوم است ( شکل 6). شکل و رشد شهری با شهرنشینی همراه است و به نظر می رسد روند شهرنشینی یک منطقه بر توسعه مورفولوژی شهری تأثیر می گذارد. شکل شهری یکی از مولفه های مهم شهرنشینی است [ 67 ]. مدل منحنی ابعاد فراکتال رشد شهری همیشه با منحنی شهرنشینی در یک کشور یا یک منطقه مطابقت دارد [ 53 ]. شهرنشینی به دو نوع تقسیم می شود: یکی شهرنشینی از پایین به بالا و دیگری شهرنشینی از بالا به پایین [ 68 ]. شهرنشینی پایین به بالا با اقتصاد بازار مرتبط است و عمدتاً تحت سلطه «دست نامرئی» شناخته شده رقابت آزاد است، در حالی که شهرنشینی از بالا به پایین با اقتصاد دستوری مرتبط است و عمدتاً تحت سلطه دست مرئی مداخله اداری است [69 ]]. مکانیسم های مختلف اقتصادی و انواع شهرنشینی مربوطه مزایا و معایب خاص خود را دارند. شهرنشینی از پایین به بالا با تکامل خود سازمان یافته شهرها مطابقت دارد. همه شهرها را می توان به عنوان شهرهای خودسازمان یافته [ 33 ] در نظر گرفت. با این حال، فرآیندهای خودسازمان دهی شهرها تحت تأثیر سیستم های سیاسی و اقتصادی یک ملت یا یک منطقه است. واقعیت این است که نواحی ساحلی جنوب شرقی چین زودتر باز شده و توسعه اقتصادی آنها به شدت تحت تأثیر جامعه بین المللی قرار گرفته است. این واقعیت ممکن است منحنی های رشد بعد فراکتالی شکل شهری شنژن را توضیح دهد.
اکثر شهرهای شمال چین اغلب برای مدت طولانی تحت تأثیر اقتصاد برنامه ریزی شده قرار داشتند. اقتصاد برنامه‌ریزی‌شده در چین، همچنین به عنوان اقتصاد دستوری شناخته می‌شود، به طور کلی به نوعی سیستم اقتصادی گفته می‌شود که در آن تولید، تخصیص منابع و مصرف توسط دولت از قبل برنامه‌ریزی و تصمیم‌گیری می‌شود. به ویژه در سال های اولیه توسعه چین، قبل از اصلاحات و گشایش، توسعه زمین می توانست به عنوان یک محصول خاص تحت سیستم اقتصاد برنامه ریزی شده تلقی شود و توسعه و بهره برداری از آن همگی تحت تسلط دولت بود. چنین الگوی توسعه شهری منجر به گسترش سریع اشکال شهری چینی در یک دوره زمانی معین شد و سری های زمانی مقادیر ابعاد فراکتال را می توان به خوبی به عنوان ویژگی های رسمی منحنی لجستیک درجه دوم پکن درشکل 6 . تا دهه 1990، چین اصلاحات و گشایش را آغاز کرد، اقتصاد بازار سوسیالیستی ایجاد کرد و برخی از شهرها را به عنوان مناطق ویژه اقتصادی یا به عنوان محل آزمایش برای توسعه اقتصاد بازار راه اندازی کرد. به این ترتیب، توسعه زمین نیز به تدریج از حالت اولیه وام دهی دولت به شیوه مشارکت بنگاه تغییر کرد. شنژن، چین، یکی از این شهرهای نماینده است [ 70 ]. علیرغم اینکه شنژن یک مورد معمولی با ویژگی های اقتصاد بازار و اقتصاد برنامه ریزی شده است، طبق جدول 2، نشان می دهد که اقتصاد بازار در شنژن تأثیر بیشتری نسبت به سیاست عمومی دارد، یا اقتصاد بازار بر توسعه شنژن به جای سیاست عمومی تسلط دارد. با این حال، نقش سیاست عمومی در شنژن بی بدیل است. احتمالاً دقیقاً چنین الگوهای توسعه ای است که به سرعت توسعه اقتصادی و رشد جمعیت شگفت انگیز آن را امکان پذیر کرد و به خط مقدم اصلاحات و گشایش در چین تبدیل شد و توسعه اقتصاد چین را رهبری کرد.
تازگی این اثر در دو جنبه نهفته است. یکی بررسی زیر حوزه های مختلف است. شنژن به سه زیرمنطقه همپوشانی تقسیم شد. سپس ساختار فراکتالی و رشد ابعاد فراکتالی کل منطقه مورد مطالعه و سه زیر ناحیه را بررسی کردیم. اگرچه یک روش مشابه زمانی توسط [ 18]، تقسیم منطقه مورد مطالعه این مقاله دارای ویژگی های آن است. مورد دیگر، مدل‌سازی منحنی‌های ابعاد فراکتالی رشد شهری توسط تابع لجستیک معمولی است. این منجر به کشف جدیدی شد که رشد فراکتالی شهرهای جنوبی با شهرهای شمالی چین متفاوت است. این کشف منجر به درک جدیدی می شود که نحوه رشد شهری با شیوه شهرنشینی مطابقت دارد و پویایی شهرنشینی تحت سلطه ساختار سیستم اقتصادی است. کاستی های اصلی این مطالعات به شرح زیر است. اول، داده های قبل از سال 1986 وجود نداشت. ما فقط تصاویر سنجش از دور را از سال 1986 و پس از آن پیدا کردیم. بنابراین، ما نمی توانیم زمانی را شناسایی کنیم که در آن اوج واقعی رشد شهری ظاهر شد. در واقع، پس از سال 1986، اوج نرخ رشد کاربری اراضی شهری در شنژن سپری شده بود. دومین، تعریف و تقسیم منطقه مورد مطالعه فاقد مبانی عینی کافی است. معیارهای اصلی منطقه و زیرحوزه های مورد مطالعه، تجربی و هدف تحقیق است. سوم، فقط از روش شمارش جعبه استفاده شد. این روش برای اندازه گیری و تخمین بعد فراکتال جهانی مناسب است. بعد فراکتال محلی را می توان با روش رشد خوشه ای محاسبه کرد، یعنی با مقیاس شعاع – ناحیه [9 ، 20 ]. روش رشد خوشه ای می تواند بعد شعاعی [ 71 ] را ایجاد کند. بعد شعاعی می تواند برای انعکاس رشد شهری از زاویه دید دیگری استفاده شود.

5. نتیجه گیری ها

تحلیل فضایی بدون مقیاس فرم شهری ساختار فراکتالی و ویژگی‌های تکاملی شهر شنژن را نشان داد. این تحلیل نه تنها برای درک عمیق شهر شنژن مفید است، بلکه برای درک قوانین و مکانیسم‌های پویای تکامل شهری در مناطق مختلف و حتی در کشورهای مختلف مفید است. نتایج اصلی این مطالعه را می توان به شرح زیر استنباط کرد. اولاً، شکل شهری شهر شنژن دارای ویژگی فراکتالی قابل توجهی است. با این حال، توزیع فضایی زمین شهری دارای ناهمگونی است، زیرا زیرمناطق مختلف منطقه شهری مقادیر ابعاد فراکتالی متفاوتی را در یک زمان نشان می‌دهند، که نشان‌دهنده مقیاس‌پذیری چندفرکتالی است. بعد فراکتال از مرکز به لبه فرو می‌رود که نشان‌دهنده ساختار مدور فرم شهری است. ثانیاً منحنی‌های ابعاد فراکتالی رشد شهری شنژن دارای ویژگی‌های S شکل هستند و می‌توان آن را با تابع لجستیک معمولی مدل‌سازی کرد که با منحنی‌های ابعاد فراکتالی شهرهای شمال چین متفاوت است. عملکردهای مختلف لجستیک انواع مختلفی از پویایی شهرنشینی را نشان می دهد. تابع لجستیک مرسوم شهرنشینی از پایین به بالا را نشان می دهد، در حالی که تابع لجستیک درجه دوم شهرنشینی از بالا به پایین را نشان می دهد. ثالثاً، ساختار فراکتالی فرم شهری شنژن یک روند تکاملی واضح را نشان می دهد. بعد فراکتال یک پارامتر استنتاج است که می تواند برای قضاوت در مورد ساختار فراکتال استفاده شود. در همین حال، ساختار فراکتال را می توان با پارامتر توصیف، یعنی خوب بودن برازش ارزیابی کرد. این که با منحنی های ابعاد فراکتالی شهرهای شمال چین متفاوت است. عملکردهای مختلف لجستیک انواع مختلفی از پویایی شهرنشینی را نشان می دهد. تابع لجستیک مرسوم شهرنشینی از پایین به بالا را نشان می دهد، در حالی که تابع لجستیک درجه دوم شهرنشینی از بالا به پایین را نشان می دهد. ثالثاً، ساختار فراکتالی فرم شهری شنژن یک روند تکاملی واضح را نشان می دهد. بعد فراکتال یک پارامتر استنتاج است که می تواند برای قضاوت در مورد ساختار فراکتال استفاده شود. در همین حال، ساختار فراکتال را می توان با پارامتر توصیف، یعنی خوب بودن برازش ارزیابی کرد. این که با منحنی های ابعاد فراکتالی شهرهای شمال چین متفاوت است. عملکردهای مختلف لجستیک انواع مختلفی از پویایی شهرنشینی را نشان می دهد. تابع لجستیک مرسوم شهرنشینی از پایین به بالا را نشان می دهد، در حالی که تابع لجستیک درجه دوم شهرنشینی از بالا به پایین را نشان می دهد. ثالثاً، ساختار فراکتالی فرم شهری شنژن یک روند تکاملی واضح را نشان می دهد. بعد فراکتال یک پارامتر استنتاج است که می تواند برای قضاوت در مورد ساختار فراکتال استفاده شود. در همین حال، ساختار فراکتال را می توان با پارامتر توصیف، یعنی خوب بودن برازش ارزیابی کرد. این در حالی که تابع لجستیک درجه دوم شهرنشینی از بالا به پایین را پیشنهاد می کند. ثالثاً، ساختار فراکتالی فرم شهری شنژن یک روند تکاملی واضح را نشان می دهد. بعد فراکتال یک پارامتر استنتاج است که می تواند برای قضاوت در مورد ساختار فراکتال استفاده شود. در همین حال، ساختار فراکتال را می توان با پارامتر توصیف، یعنی خوب بودن برازش ارزیابی کرد. این در حالی که تابع لجستیک درجه دوم شهرنشینی از بالا به پایین را پیشنهاد می کند. ثالثاً، ساختار فراکتالی فرم شهری شنژن یک روند تکاملی واضح را نشان می دهد. بعد فراکتال یک پارامتر استنتاج است که می تواند برای قضاوت در مورد ساختار فراکتال استفاده شود. در همین حال، ساختار فراکتال را می توان با پارامتر توصیف، یعنی خوب بودن برازش ارزیابی کرد. اینآرارزش مربع مدل‌سازی فراکتال شنژن در طول زمان بالا رفت و تا زمانی که به عدد 1 نزدیک شد. این نشان می‌دهد که ساختار فراکتال از طریق خود سازمان‌دهی بهینه‌سازی می‌شود. چهارم، بعد فراکتال شکل شهری در شنژن به مرز خود نزدیک می شود و به نظر می رسد الگوهای توسعه شهری گذشته دیگر پایدار نیستند. مقادیر ابعاد فراکتال به سمت حداکثر مقدار تمایل دارند، که نشان می دهد فضای پر شدن شنژن در حال حاضر نزدیک به حد خود است، و منابع زمین کمی در منطقه مورد مطالعه وجود دارد. اگر به گسترش و گسترش خود ادامه دهد، باید منابع گرانبهای زیست محیطی یا منابع آبی را اشغال کند. بنابراین، برای شهر شنژن، یک حالت جدید توسعه در آینده مورد نیاز است. در نهایت بعد فراکتال شاخص پراکندگی شهری است. جمعیت نقش مهمی در رشد شهری شهر شنژن دارد تا تولید ناخالص داخلی. شهر شنژن نیازی به تقویت توسعه اقتصادی خود به قیمت توسعه شهری ندارد.

منابع

  1. Hao, B. فراکتال ها و ابعاد فراکتال. علوم 1986 ، 38 ، 9-17. (به زبان چینی) [ Google Scholar ]
  2. لیو، اس. لیو، اس. موج انفرادی و آشفتگی . انتشارات آموزش علمی و فناوری شانگهای: شانگهای، چین، 1994. (به زبان چینی) [ Google Scholar ]
  3. تاکایاسو، اچ. فراکتال ها در علوم فیزیکی . انتشارات دانشگاه منچستر: منچستر، انگلستان، 1990. [ Google Scholar ]
  4. بنگوئی، ال. Czamanski، D. شبیه سازی تجزیه و تحلیل فراکتالیته شهرها. Geogr. مقعدی 2004 ، 36 ، 69-84. [ Google Scholar ] [ CrossRef ]
  5. فرانکهاوزر، پ. مقایسه مورفولوژی الگوهای شهری در اروپا. در شهرهای اروپایی – بینش در حومه ها، گزارش هزینه اقدام 10 مهندسی عمران شهری، سازه ها . Borsdorf, A., Zembri, P., Eds. Université de Bourgogne Franche-Comté: Dijon، فرانسه، 2004; جلد 2، صص 79-105. [ Google Scholar ]
  6. چن، ی. Huang, L. مدلسازی منحنی رشد بعد فراکتالی فرم شهری پکن. فیزیک یک آمار مکانیک. Appl. 2019 ، 523 ، 1038-1056. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  7. سالات، س. رویکرد سیستمی تاب آوری شهری: قوانین قدرت و الگوهای رشد شهری. بین المللی J. شهری پایدار. توسعه دهنده 2017 ، 9 ، 107-135. [ Google Scholar ] [ CrossRef ]
  8. چن، ی. وانگ، جی. Feng, J. درک ابعاد فراکتالی اشکال شهری از طریق آنتروپی فضایی. Entropy 2017 ، 19 ، 600. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
  9. فرانکهاوزر، پی. رویکرد فراکتالی: ابزاری جدید برای تحلیل فضایی تراکم‌های شهری. جمعیت 1998 ، 10 ، 205-240. [ Google Scholar ]
  10. جوریک، م. رومانوویچ، ام. ابعاد فراکتالی مرز شهری به عنوان معیاری برای مدیریت فضا. Procedia Eng. 2016 ، 165 ، 1478-1482. [ Google Scholar ] [ CrossRef ]
  11. مندلبروت، بی. هندسه فراکتالی طبیعت . WH Freeman and Company: نیویورک، نیویورک، ایالات متحده آمریکا، 1983. [ Google Scholar ]
  12. Dauphiné, A. جغرافیای فراکتال ; Wiley-ISTE: Hoboken، NJ، ایالات متحده، 2013. [ Google Scholar ]
  13. آرلینگهاوس، اس. فراکتال ها در مرکز قرار می گیرند. Geogr. ان سر. B هوم. Geogr. 1985 ، 67 ، 83-88. [ Google Scholar ] [ CrossRef ]
  14. باتی، م. Longley, P. توصیف فرم شهری مبتنی بر فراکتال. محیط زیست طرح. B طرح. دس 1987 ، 14 ، 123-134. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  15. باتی، م. Longley، P. اشکال شهری به صورت فراکتال. Area 1987 , 19 , 215-221. [ Google Scholar ]
  16. باتی، م. Xie, Y. شواهد اولیه برای نظریه شهر فراکتال. محیط زیست طرح. A 1996 ، 28 ، 1745-1762. [ Google Scholar ] [ CrossRef ]
  17. چن، ی. وانگ، ی. مطالعه فراکتالی در مورد تعامل بین شهرها در سیستم های شهری. گاو نر علمی تکنولوژی 1997 ، 13 ، 233-237. (به زبان چینی) [ Google Scholar ]
  18. بنگوئی، ال. چمانسکی، دی. مارینوف، م. پرتغالی، ی. فرکتال شهری کی و کجاست؟ محیط زیست طرح. B طرح. دس 2000 ، 27 ، 507-519. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  19. شن، جی. بعد فراکتالی و رشد فراکتالی مناطق شهری. بین المللی جی. جئوگر. Inf. علمی 2002 ، 16 ، 419-437. [ Google Scholar ] [ CrossRef ]
  20. وایت، آر. Engelen، G. اتوماتای ​​سلولی و فرم شهری فراکتال: یک رویکرد مدلسازی سلولی برای تکامل الگوهای کاربری زمین شهری. محیط زیست طرح. A 1993 , 25 , 1175-1199. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  21. باتی، م. لانگلی، ام. شهرهای فراکتال – هندسه شکل و عملکرد . انتشارات آکادمیک: لندن، بریتانیا، 1994. [ Google Scholar ]
  22. Frankhauser, P. La Fractalité des Structures Urbaines (جنبه های فراکتالی سازه های شهری) ; Economica، Anthropos: پاریس، فرانسه، 1994. [ Google Scholar ]
  23. آلن، پی. شهرها و مناطق به عنوان سیستم های تکاملی و پیچیده. Geogr. سیستم 1997 ، 4 ، 103-130. [ Google Scholar ]
  24. باتی، م. Longley, P. شبیه سازی فراکتالی ساختار شهری. محیط زیست طرح. A 1986 , 18 , 1143-1179. [ Google Scholar ] [ CrossRef ]
  25. باتی، م. Longley, P. مورفولوژی کاربری زمین شهری. محیط زیست طرح. B طرح. دس 1988 ، 15 ، 461-488. [ Google Scholar ] [ CrossRef ]
  26. باتی، م. کیم، ک. مطالعه شهری. 1992 ، 29 ، 1043-1069. [ Google Scholar ] [ CrossRef ]
  27. باتی، م. لانگلی، پی. فاثرینگهام، اس. رشد و شکل شهری: مقیاس بندی، هندسه فراکتال و تجمع محدود با انتشار. محیط زیست طرح. A 1989 ، 21 ، 1447-1472. [ Google Scholar ] [ CrossRef ]
  28. فاثرینگهام، ای. باتی، م. Longley، P. تجمع محدود با انتشار و ماهیت فراکتال رشد شهری. پاپ Reg. علمی دانشیار 1989 ، 67 ، 55-69. [ Google Scholar ] [ CrossRef ]
  29. Benguigui، L. مدل های تجمع برای رشد شهر. فیلوس Mag. قسمت ب 1998 ، 77 ، 1269-1275. [ Google Scholar ] [ CrossRef ]
  30. بنگوئی، ال. چمانسکی، دی. مارینوف، ام. رشد شهر به عنوان یک فرآیند جهشی: برنامه ای برای کلانشهر تل آویو. مطالعه شهری. 2001 ، 38 ، 1819-1839. [ Google Scholar ] [ CrossRef ]
  31. بنگوئی، ال. چمانسکی، دی. مارینوف، ام. پویایی مورفولوژی شهری: مورد پتاه تیکوا. محیط زیست طرح. B طرح. دس 2001 ، 28 ، 447-460. [ Google Scholar ] [ CrossRef ]
  32. چن، ی. مدل جدیدی از تراکم جمعیت شهری که ساختار فراکتالی نهفته را نشان می‌دهد. بین المللی J. شهری پایدار. توسعه دهنده 2009 ، 1 ، 89-110. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  33. پرتغالي، ج. خودسازماني و شهر . Springer: برلین/هایدلبرگ، آلمان، 2000. [ Google Scholar ]
  34. توماس، آی. فرانکهاوزر، پ. Biernacki، C. مورفولوژی مناظر ساخته شده در والونیا (بلژیک): طبقه بندی با استفاده از شاخص های فراکتال. Landsc. طرح شهری. 2008 ، 84 ، 99-115. [ Google Scholar ] [ CrossRef ]
  35. Triantakonstantis، D. مدل‌سازی پیش‌بینی رشد شهری با استفاده از فراکتال‌ها و نظریه آشوب. J. Civ را باز کنید. مهندس 2012 ، 2 ، 81-86. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  36. هاکن، اچ. پرتغالی، ج. رویکرد هم افزایی به خود سازمان دهی شهرها و سکونتگاه ها. محیط زیست طرح. B طرح. دس 1995 ، 22 ، 35-46. [ Google Scholar ] [ CrossRef ]
  37. چن، ی. Feng, J. تجزیه و تحلیل مقیاس بندی آلومتریک سلسله مراتبی شهرهای چین: 1991-2014. گسسته. دین نات Soc. 2017 ، 2017 ، 1-15. [ Google Scholar ] [ CrossRef ]
  38. لاگاریاس، آ. پراستاکوس، ص. مقایسه فرم شهری شهرهای اروپای جنوبی با استفاده از ابعاد فراکتال. محیط زیست طرح. ب مقعد شهری. علوم شهر 2020 ، 47 ، 1149-1166. [ Google Scholar ] [ CrossRef ]
  39. لی، ز. لیو، بی. وانگ، آر. لی، زی. بررسی ویژگی های فراکتالی شهر تپه ای. J. Appl. علمی شبکه آسیایی علمی Inf. 2013 ، 13 ، 1155-1159. [ Google Scholar ]
  40. راستوگی، ک. جین، جی. تجزیه و تحلیل پراکندگی شهری با استفاده از آنتروپی شانون و تجزیه و تحلیل فراکتال: مطالعه موردی در شهر Tiruchirappalli، هند. بین المللی قوس. فتوگرام حسگر از راه دور اسپات. Inf. علمی 2018 ، 42 ، 761-766. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  41. شریواستاوا، ا. رائو، پی. McGrath، G. خصوصیات خود شباهت و مقیاس بندی فراکتال جزایر حرارتی درون شهری برای شهرهای مختلف جهانی. فیزیک Rev. E 2019 , 100 . [ Google Scholar ] [ CrossRef ] [ PubMed ][ نسخه سبز ]
  42. صدقی، ی. توماس، آی. فرانکهاوزر، پ. Retière, N. مقایسه شاخص‌های فراکتال شبکه‌های الکتریکی با جاده‌ها و ساختمان‌ها: مورد گرنوبل (فرانسه). فیزیک یک آمار مکانیک. Appl. 2019 , 531 . [ Google Scholar ] [ CrossRef ]
  43. توچک، پ. بعد فراکتال به عنوان توصیف کننده پویایی رشد شهری. شبکه عصبی جهان 2013 ، 23 ، 93-102. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  44. آریزا-ویلاورده، ا. Jiménez-Hornero، F. Ravé، E. تجزیه و تحلیل چندفراکتالی نقشه های محوری برای مطالعه مورفولوژی شهری. محاسبه کنید. محیط زیست سیستم شهری 2013 ، 38 ، 1-10. [ Google Scholar ] [ CrossRef ]
  45. چن، ی. وانگ، جی. خصوصیات چندفراکتالی شکل و رشد شهری: مورد پکن. محیط زیست طرح. B طرح. دس 2013 ، 40 ، 884-904. [ Google Scholar ] [ CrossRef ]
  46. فرانکهاوزر، پ. تانیر، سی. وویدل، جی. Houot، H. یک مدل سازی چندفراکتالی یکپارچه برای برنامه ریزی شهری و منطقه ای. محاسبه کنید. محیط زیست سیستم شهری 2018 ، 67 ، 132-146. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  47. هوانگ، ال. چن، ی. مقایسه بین دو رویکرد مبتنی بر OLS برای تخمین پارامترهای چندفراکتالی شهری. فراکتال ها 2018 , 26 . [ Google Scholar ] [ CrossRef ]
  48. نی، سی. ژانگ، اس. چن، ز. یان، ی. Li، Y. نقشه‌برداری توزیع فضایی و ویژگی‌های خطواره‌ها با استفاده از مدل‌های فراکتال و چندفرکتال: مطالعه موردی از شمال شرقی استان یوننان، چین. علمی Rep. 2017 , 7 . [ Google Scholar ] [ CrossRef ]
  49. نی، س. خو، جی. لیو، زی. ویژگی فراکتالی و چندفراکتالی الگوی فضایی سطوح غیرقابل نفوذ شهری. علوم زمین آگاه کردن. 2015 ، 8 ، 381-392. [ Google Scholar ] [ CrossRef ]
  50. آهنگ، ز. یو، L. ویژگی های چندفراکتالی تنوع فضایی در زمین ساخت و ساز در پکن (1985-2015). کمون پالگریو 2019 ، 5 ، 1-15. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  51. آهنگ، ز. چن، ی. لی، ی. مطالعات تطبیقی ​​در مورد مکانیسم چندفراکتالی فضایی تکاملی برای زمین های ساخته شده در ژنگژو از سال 1988 تا 2015 با ویژگی های پکن. جی. پاک. تولید 2020 ، 269 . [ Google Scholar ] [ CrossRef ]
  52. انکارناسائو، اس. گائودیانو، م. سانتوس، اف. تندوریو، جی. Pacheco، J. نقشه برداری فراکتال مناطق شهری. علمی Rep. 2012 , 2 , 257. [ Google Scholar ] [ CrossRef ] [ PubMed ] [ نسخه سبز ]
  53. چن، ی. مدل‌های لجستیک رشد ابعاد فراکتالی مورفولوژی شهری. فراکتال ها 2018 , 26 . [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  54. چن، ی. تکامل ابعاد فراکتال و پویایی جایگزینی فضایی رشد شهری. فراکتال های Chaos Solitons 2012 ، 45 ، 115-124. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  55. ماندلبروت، ب. طول ساحل بریتانیا چقدر است؟ خود شباهت آماری و بعد کسری. Science 1967 , 156 , 636-638. [ Google Scholar ] [ CrossRef ] [ PubMed ][ نسخه سبز ]
  56. باتی، ام. اندازه، مقیاس و شکل شهرها. Science 2008 , 319 , 769-771. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  57. باتی، ام. پیچیدگی و ظهور در سیستم های شهر: پیامدهایی برای برنامه ریزی شهری. مالایی ها جی. محیط زیست. مدیریت 2009 ، 10 ، 15-32. [ Google Scholar ]
  58. Bettencourt, L. ریشه‌های مقیاس‌پذیری در شهرها. Science 2013 ، 340 ، 1438-1441. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  59. کوشنیگ، ام. موتگان، اس. هدستروم، ص. مقیاس بندی شهری و شکاف منطقه ای. علمی Adv. 2019 ، 5 ، eaav0042. [ Google Scholar ] [ CrossRef ] [ PubMed ][ نسخه سبز ]
  60. دفتر آمار شنژن (SSB). سالنامه آمار شنژن 2019 ; انتشارات آمار چین: پکن، چین، 2019.
  61. لی، دبلیو. وانگ، ی. پنگ، جی. لی، جی. تغییرات فضایی منظر مرتبط با شهرنشینی سریع در شنژن، چین. بین المللی J. Sustain. توسعه دهنده محیط زیست جهانی 2005 ، 12 ، 314-325. [ Google Scholar ] [ CrossRef ]
  62. نگ، ام. شنژن. شهرها 2003 ، 20 ، 429-441. [ Google Scholar ] [ CrossRef ]
  63. چن، ی. مدلسازی فراکتال و توصیف ابعاد فراکتالی مورفولوژی شهری. Entropy 2020 , 22 , 961. [ Google Scholar ] [ CrossRef ]
  64. شلبرگ، ام. مولرینگ، اچ. Lam, N. اندازه گیری ابعاد فراکتالی منحنی های کارتوگرافی تجربی. Auto Carto 1982 , 5 , 481-490. [ Google Scholar ]
  65. اسلام، ز. مترنیخت، جی. بعد فراکتالی داده های سنجش از دور چندمنبعی و چندمنبعی برای توصیف پیچیدگی فضایی مناظر شهری. بین المللی Geosci. سنسور از راه دور Symp. 2003 ، 3 ، 1715-1717. [ Google Scholar ]
  66. روزنفلد، اچ. ریبسکی، دی. آندراد، جی. باتی، م. استنلی، ای. ماکس، اچ. قوانین رشد جمعیت. Proc. Natl. آکادمی علمی ایالات متحده آمریکا 2008 ، 105 ، 18702-18707. [ Google Scholar ] [ CrossRef ] [ PubMed ][ نسخه سبز ]
  67. ناکس، پی. Marston, S. Places and Regions in Global Context: Human Geography , 5th ed.; Prentice Hall: Upper Saddle River، نیوجرسی، ایالات متحده آمریکا، 2009. [ Google Scholar ]
  68. ژو، ی. کاوش در جغرافیای شهری . The Commercial Press: پکن، چین، 2010. (به زبان چینی) [ Google Scholar ]
  69. Chen, Y. تکامل قانون Zipf نشان دهنده توسعه شهر است. فیزیک یک آمار مکانیک. Appl. 2010 ، 443 ، 555-567. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  70. هائو، پی. گیرتمن، اس. هویمیجر، پ. Sliuzas، R. تجزیه و تحلیل فضایی فرآیند توسعه روستای شهری در شنژن، چین. بین المللی J. Urban Reg. Res. 2013 ، 37 ، 2177-2197. [ Google Scholar ] [ CrossRef ]
  71. فرانکهاوزر، پ. Sadler, R. تجزیه و تحلیل فراکتالی از تجمعات. در ساختارهای طبیعی: اصول، استراتژی ها و مدل ها در معماری و طبیعت ؛ Hilliges، M.، Ed. دانشگاه اشتوتگارت: اشتوتگارت، آلمان، 1991; صص 57-65. [ Google Scholar ]
Ijgi 09 00672 g001 550
شکل 1. نقشه منطقه ساخته شده در شهر شنژن از سال 1986 تا 2017. توجه: مناطق ساخته شده از تصاویر Landsat TM 4 و 5 و OLI 8 با وضوح 30 متر دانلود شده از سازمان زمین شناسی ایالات متحده (USGS) استخراج شده است. وب سایت Earth Explorer ( https://earthexplorer.usgs.gov/ ). چهار کادر، 1-4، مناطق مورد مطالعه هستند که به ترتیب کل منطقه، منطقه مرکز تجاری اصلی، منطقه شمال غربی و منطقه شمال شرقی شنژن را نشان می دهند.
Ijgi 09 00672 g002a 550 Ijgi 09 00672 g002b 550
شکل 2. نمودار نرخ رشد بعد فراکتال چهار منطقه از سال 1986 تا 2017.
Ijgi 09 00672 g003 550
شکل 3. الگوهای لجستیکی رشد ابعاد فراکتال در چهار منطقه مورد مطالعه، 1986-2017.
Ijgi 09 00672 g004 550
شکل 4. نمودار Log-log بین جمعیت (ln P ) و بعد فراکتال (ln D ) در شنژن، 1986-2017. منبع: داده های جمعیت از سالنامه آماری شنژن-2019.
Ijgi 09 00672 g005 550
شکل 5. نمودار تولید ناخالص داخلی Log-log نمودار (ln G ) و بعد فراکتال (ln D ) در شنژن، 1986-2017. منبع: داده های جمعیت از سالنامه آماری شنژن-2019.
Ijgi 09 00672 g006 550
شکل 6. دو نوع بعد فراکتال افزایش منحنی های فرم شهری: منحنی لجستیک و منحنی لجستیک درجه دوم. توجه: منحنی لجستیک بر اساس سری زمانی مقادیر ابعاد جعبه شنژن است، در حالی که منحنی لجستیک درجه دوم بر اساس سری زمانی مقادیر ابعاد جعبه پکن است. مقادیر ابعاد فراکتالی پکن از چن و هوانگ [ 6 ] آمده است. برای مقایسه، مقادیر ابعاد فراکتال با مقادیر حداکثر و حداقل ابعاد فراکتال نرمال می شوند [ 54 ].

مقالات داخلی و بین المللی

مطالب مرتبط ...

بدون دیدگاه

دیدگاهتان را بنویسید