خلاصه

رادار دیافراگم مصنوعی تداخل سنجی (InSAR) یکی از بهترین روش ها برای به دست آوردن مدل های رقومی ارتفاعی (DEMs) است. با این حال، مشکل عدم قطعیت دقت DEM تحت تأثیر خط پایه عمود بر هم همچنان پابرجاست، که باید تا حد امکان طولانی باشد تا از حساسیت فاز به اندازه‌گیری ارتفاع اطمینان حاصل شود، و تا حد امکان کوچک باشد تا از انسجام فضایی بالا اطمینان حاصل شود. علاوه بر این، طراحی پیکربندی پایه سیستم SAR bistatic فاقد یک مدل دقیق تر برای مرجع برای تولید DEM با دقت بالا است. بنابراین، در این مقاله، خط پایه بهینه برای به حداکثر رساندن دقت اندازه‌گیری ارتفاع مدل‌سازی می‌شود. ابتدا، ما تأثیر پارامترهای سیستم را بر دقت اندازه‌گیری ارتفاع تحلیل می‌کنیم و یک مدل انتشار از خطای تخمین پارامتر به خطای ارتفاع مشتق می‌شود. سپس، خطای بازکردن فاز (PUE) که انسجام خط پایه فضایی، شیب زمین و اثربخشی بازکردن فاز را در نظر می‌گیرد، پس از شبیه‌سازی فاز تداخل‌سنجی و باز کردن فاز فیلتر کالمن بدون عطر تطبیقی ​​مدل‌سازی و تحلیل می‌شود. با ترکیب رابطه بین خطای ارتفاع و PUE، مدل پایه بهینه با تجزیه و تحلیل آماری به دست می‌آید. در نهایت، میانگین وزنی برای محاسبه شیب متوسط ​​زمین پیچیده استفاده می‌شود و اعتبار و قابلیت اطمینان مدل پایه بهینه پیشنهادی با دو مثال از زمین‌های پیچیده با زوایای شیب مثبت و منفی توزیع یکنواخت و غیریکنواخت تأیید می‌شود. علاوه بر این، محدوده پایه بهینه انواع مختلف زمین نیز برای مرجع مشتق شده است. شیب زمین و اثر بازکردن فاز پس از شبیه‌سازی فاز تداخل سنجی و باز کردن فاز فیلتر کالمن بدون عطر تطبیقی ​​مدل‌سازی و تحلیل می‌شود. با ترکیب رابطه بین خطای ارتفاع و PUE، مدل پایه بهینه با تجزیه و تحلیل آماری به دست می‌آید. در نهایت، میانگین وزنی برای محاسبه شیب متوسط ​​زمین پیچیده استفاده می‌شود و اعتبار و قابلیت اطمینان مدل پایه بهینه پیشنهادی با دو مثال از زمین‌های پیچیده با زوایای شیب مثبت و منفی توزیع یکنواخت و غیریکنواخت تأیید می‌شود. علاوه بر این، محدوده پایه بهینه انواع مختلف زمین نیز برای مرجع مشتق شده است. شیب زمین و اثر بازکردن فاز پس از شبیه‌سازی فاز تداخل سنجی و باز کردن فاز فیلتر کالمن بدون عطر تطبیقی ​​مدل‌سازی و تحلیل می‌شود. با ترکیب رابطه بین خطای ارتفاع و PUE، مدل پایه بهینه با تجزیه و تحلیل آماری به دست می‌آید. در نهایت، میانگین وزنی برای محاسبه شیب متوسط ​​زمین پیچیده استفاده می‌شود و اعتبار و قابلیت اطمینان مدل پایه بهینه پیشنهادی با دو مثال از زمین‌های پیچیده با زوایای شیب مثبت و منفی توزیع یکنواخت و غیریکنواخت تأیید می‌شود. علاوه بر این، محدوده پایه بهینه انواع مختلف زمین نیز برای مرجع مشتق شده است. در نهایت، میانگین وزنی برای محاسبه شیب متوسط ​​زمین پیچیده استفاده می‌شود و اعتبار و قابلیت اطمینان مدل پایه بهینه پیشنهادی با دو مثال از زمین‌های پیچیده با زوایای شیب مثبت و منفی توزیع یکنواخت و غیریکنواخت تأیید می‌شود. علاوه بر این، محدوده پایه بهینه انواع مختلف زمین نیز برای مرجع مشتق شده است. در نهایت، میانگین وزنی برای محاسبه شیب متوسط ​​زمین پیچیده استفاده می‌شود و اعتبار و قابلیت اطمینان مدل پایه بهینه پیشنهادی با دو مثال از زمین‌های پیچیده با زوایای شیب مثبت و منفی توزیع یکنواخت و غیریکنواخت تأیید می‌شود. علاوه بر این، محدوده پایه بهینه انواع مختلف زمین نیز برای مرجع مشتق شده است.

کلید واژه ها:

سیستم SAR bistatic فضابردی ؛ دقت اندازه گیری ارتفاع ؛ خطای باز کردن فاز ؛ خط پایه بهینه

1. معرفی

رادار دیافراگم مصنوعی تداخل سنجی (InSAR) به یکی از محبوب ترین روش ها در سال های اخیر برای تولید مدل های ارتفاعی دیجیتال (DEMs) تبدیل شده است. InSAR به طور غیرقابل مقایسه ای نسبت به تکنیک های سنتی فتوگرامتری، تراز کردن، و تشخیص و محدوده نور (LiDAR) برتر است زیرا از یک حالت تشخیص سنجش از راه دور مایکروویو فعال استفاده می کند که در طول روز، شب و در هر شرایط آب و هوایی کار می کند. علاوه بر این، ماهواره ها می توانند زمین را به سرعت و به طور گسترده از طریق تغییرات در زاویه نگاه اسکن و مشاهده کنند. بنابراین، سیستم‌های InSAR، مانند مأموریت توپوگرافی رادار شاتل (SRTM) [ 1 ] و افزودنی TerraSAR-X برای اندازه‌گیری دیجیتال ارتفاع (TanDEM-X) [ 2 ]، به موفق‌ترین ابزار اندازه‌گیری DEM جهانی تبدیل شده‌اند.
اگرچه امکان سنجی InSAR به عنوان یک تکنیک نقشه برداری توپوگرافی با موفقیت نشان داده شده است، هنوز مشخص نیست که چگونه دقت اندازه گیری ارتفاع توسط موج های زمین و پردازش داده ها تحت تاثیر قرار می گیرد. دقت اندازه‌گیری ارتفاع InSAR عمدتاً تحت‌تاثیر سیستم موقعیت‌یابی سکوی ماهواره‌ای، محدوده شیب از رادار تا هدف، طول خط پایه، شیب خط پایه و فاز تداخل‌سنجی است. در میان این عوامل، خطاهای ناشی از چهار عامل اول و جبران فاز مطلق [ 3 ] سیستماتیک هستند و خطای فاز تداخل سنجی که توسط فاکتورهای همبستگی مختلف معرفی می شود، تصادفی است [ 3]. 4 ].]. خطاهای سیستماتیک را می توان با نقاط کنترل زمین کاهش داد، در حالی که خطاهای تصادفی اجتناب ناپذیر هستند. بنابراین، عبارت تصادفی خطای فاز تداخل سنجی عمدتاً دقت اندازه گیری ارتفاع را تعیین می کند. برای سادگی، خطای فاز ذکر شده در این مقاله فقط به عبارت تصادفی اشاره دارد. با این حال، خط پایه فضایی یک عامل تأثیرگذار حیاتی است زیرا نه تنها مبنای اندازه‌گیری ارتفاع تداخل سنجی است، بلکه منبع اصلی خطای فاز ناشی از همبستگی هندسی است. بنابراین، روابط بین خط مبنا مکانی، خطای فاز و دقت ارتفاع باید بررسی شود.
در سیستم‌های SAR موجود در فضا، خط مبنا مکانی نشانه‌ای از حساسیت فاز به ارتفاع توپوگرافی، میزان همبستگی ناشی از گرادیان‌های فاز، و اثربخشی روش باز کردن فاز [ 5 ] را نشان می‌دهد. به طور خاص، افزایش در خط مبنا (یعنی فاصله بین مراکز آرایه فاز اصلی و slave) دقت اندازه‌گیری ارتفاع را افزایش می‌دهد اما همبستگی بین سیگنال‌های اصلی و slave را کاهش می‌دهد و چگالی حاشیه و همچنین دشواری باز کردن فاز را افزایش می‌دهد. ، که منجر به خطای فاز بزرگ می شود. بنابراین، باید یک محدوده فضایی بهینه برای به حداقل رساندن خطای ارتفاع وجود داشته باشد. Mrstik V و همکاران. [ 6] به طور سیستماتیک خطای زاویه فرود سیستم‌های InSAR را از درخشش هدف، که مشابه همبستگی پایه است، با دو نما بینش‌های متفاوتی را در مورد دقت اندازه‌گیری تجزیه و تحلیل کرد، و آنها بیان خطای اندازه‌گیری ارتفاع را در حالی که عدم قطعیت محدوده را در نظر گرفتند، استخراج کردند. متعاقباً، محققان [ 7 ، 8 ، 9 ] بر اساس یافته‌های فوق، انتخاب بهینه خط پایه و طراحی را به تفصیل مورد بحث قرار داده‌اند. رودریگز ای و همکاران [ 10 ] و چوی سی و همکاران. [ 11] کران کرامر-رائو انحراف استاندارد فاز را به عنوان خطای فاز تداخل سنجی در نظر گرفت و محدوده بهینه همبستگی و خط پایه را با توجه به تحلیل همبستگی به دست آورد. با این حال، خطای فاز را تنها در صورتی می توان با کران کرامر-رائو تقریب زد که همبستگی بیشتر از 0.9 باشد. در غیر این صورت، آن را دست کم گرفته می شود [ 5 ]. علاوه بر این، اثربخشی بازکردن فاز باید در نظر گرفته شود زیرا همبستگی مجاز با الزام بازکردن موفق فاز محدود شده است. ژانگ [ 12] به طور تجربی پیشنهاد کرد که وقتی تعداد پیکسل ها در هر دوره حاشیه کمتر از پنج باشد، فاز را نمی توان باز کرد. با این حال، او یک تجزیه و تحلیل تجربی دقیق انجام نداد. بنابراین، مدل خطای فاز تداخل سنجی باید از نظر آماری برای داده‌های مختلف شیب زمین شبیه‌سازی شده بر اساس باز کردن فاز تحلیل شود. برای همگام شدن با توسعه الگوریتم بازکردن فاز و تسهیل مطالعات بعدی، روش بازکردن فاز فیلتر کالمن بدون عطر تطبیقی ​​[ 13 ، 14 ]] که یک الگوریتم نسبتاً بهینه است، برای سرکوب خطای بازکردن مربوطه انتخاب خواهد شد. در همین حال، برای جلوگیری از منابع خطای فاز غیرضروری، مانند همبستگی زمانی و همبستگی حجم، ما پلت فرم تداخل سنجی bistatic را برای مدل‌سازی ترجیح می‌دهیم.
در این مقاله، ما تأثیر خطای فاز در اندازه‌گیری ارتفاع را بر اساس یک سیستم SAR bistatic فضایی تحلیل می‌کنیم. خطای بازکردن فاز (PUE) و خطای ارتفاع با در نظر گرفتن خط پایه، شیب زمین، و اثربخشی باز کردن بر اساس داده‌های تداخل سنجی شبیه‌سازی شده و روش باز کردن فاز مدل‌سازی می‌شوند. سپس خط پایه بهینه برای به حداقل رساندن خطای اندازه‌گیری ارتفاع با تحلیل آماری مدل‌سازی می‌شود. علاوه بر این، در ترکیب با مدل PUE، ما روش میانگین وزنی را برای محاسبه شیب متوسط ​​زمین پیچیده پیشنهاد می‌کنیم. در نهایت، اعتبار و قابلیت اطمینان مدل پایه بهینه با شبیه‌سازی یک زمین پیچیده که زمین واقعی را تقریب می‌کند تأیید می‌شود و محدوده‌های پایه بهینه انواع مختلف زمین برای مرجع استخراج می‌شوند.
این مقاله به شرح زیر سازماندهی شده است: در بخش 2 ، عوامل موثر بر اندازه‌گیری ارتفاع بر اساس یک سیستم SAR bistatic فضایی تجزیه و تحلیل شده و فرمول آن استخراج می‌شود. در بخش 3 ، فاز تداخل سنجی را شبیه سازی کرده و آن را با استفاده از روش بازکردن فاز فیلتر کالمن تطبیقی ​​بدون عطر باز می کنیم. سپس رابطه بین PUE و شیب زمین بر اساس نتایج شبیه‌سازی شده برازش می‌شود. و مدل پایه بهینه از طریق تجزیه و تحلیل آماری به دست می آید. در بخش 4 ، مدل پایه بهینه با استفاده از زمین های پیچیده تأیید شده است، و سپس در بخش 5 ، بحث ارائه شده است. در نهایت، در بخش 6 نتیجه گیری مقاله ارائه شده است.

2. دقت اندازه گیری ارتفاع InSAR

هندسه تصویربرداری یک سیستم InSAR در شکل 1 نشان داده شده است . اس1و اس2به ترتیب ماهواره های Master و Slave هستند، آر1و آر2نشان دهنده محدوده شیب از ماهواره اصلی و برده تا هدف پراکنده است، ساعتارتفاع هدف پراکنده است، اچارتفاع آنتن رادار اصلی ماهواره است، آرهشعاع محلی زمین است، θزاویه بروز است، بخط مبنا مکانی است و αمیل پایه است. بیان اندازه گیری ارتفاع هدف به شرح زیر است:

ساعت=(آره+اچ)2+آر12-2آر1(آره+اچ)cos(θ)-آره،

همانطور که در شکل 1 نشان داده شده است ، خط مبنا را می توان به اجزای موازی و عمود بر روی خط دید (LOS) تجزیه کرد که به آنها خط مبنا موازی می گویند. ب||و خط پایه عمود بر ب⊥، به ترتیب. رابطه را می توان به صورت زیر بیان کرد:

ب||=بگناه(θ-α) ب⊥=بcos(θ-α)،

با در نظر گرفتن سیستم SAR bistatic فضایی، فاز تداخل سنجی ϕرا می توان به صورت زیر نشان داد:

ϕ=φ1-φ2=-2πλ(آر1-آر2)=-2πλΔآر،

جایی که λطول موج سیستم رادار است. از آنجا که محدوده شیب بسیار بزرگتر از خط پایه در یک سیستم SAR فضایی است، Δآرمی توان با خط پایه موازی [ 15 ] تقریب زد:

ϕ≈-2πλب||،

با ترکیب معادلات (2) و (4)، معادله (1) را می توان بیشتر به صورت زیر بیان کرد [ 16 ]:

ساعت=(آره+اچ)2+آر12-2آر1(آره+اچ)cos(θ-α+α)-آره=(آره+اچ)2+آر12-2آر1(آره+اچ)[cos(θ-α)cos(α)-گناه(θ-α)گناه(α)]-آره=(آره+اچ)2+آر12-2آر1(آره+اچ)[1-(λϕ2πب)2cos(α)+λϕ2πبگناه(α)]-آره،

عدم قطعیت در هر یک از پارامترها اچ، آر1، ب، ϕ، و αمنجر به عدم قطعیت در اندازه گیری ارتفاع خواهد شد. بنابراین، ما دیفرانسیل را برای هر پارامتر جداگانه محاسبه می کنیم و خطای تخمین ارتفاع با توجه به خطای تخمین هر پارامتر را می توان با رابطه (11) با این فرض که خطاها با یکدیگر همبستگی ندارند بیان کرد.

σساعتاچ=(آراچآرساعت-آر1cos(θ)آرساعت)σاچ،
σساعتآر1=(آر1آرساعت-آراچcos(θ)آرساعت) σآر1،
σساعتب=آراچآرساعت⋅آر1بگناه(θ)برنزه(θ-α)σب،
σساعتα=آراچآرساعت⋅آر1گناه(θ)σα،
σساعتϕ=-آراچآرساعت⋅λآر1گناه(θ)2πبcos(θ-α)σϕ=-آراچآرساعت⋅λآر1گناه(θ)2πب⊥σϕ،
σساعت=(σساعتاچ)2+(σساعتآر1)2+(σساعتب)2+(σساعتα)2+(σساعتϕ)2،

جایی که آراچ=آره+اچو آرساعت=آره+ساعت. معادله (6) سطح دقت مجاز عدم قطعیت های تعیین مدار ماهواره را نشان می دهد. پارامتر σآر1مربوط به خطای محدوده شیب واقعی است که معمولاً ناشی از عدم قطعیت های زمان بندی ساعت سیستم SAR، لرزش ساعت نمونه برداری، تأخیر انتشار به دلیل اثرات جوی و یونوسفر و غیره است. تعیین خط مبنا با مقایسه ضریب انتقال خطا معادلات (8) و (9) نسبت آنها برابر است برنزه(θ-α)ب. با در نظر گرفتن پارامترهای سیستم TanDEM-X به عنوان مثال، نسبت همیشه کوچکتر از 1 است. به عبارت دیگر، خطای برآورد شیب خط پایه در اندازه گیری ارتفاع با مضرب بزرگتر منتشر می شود. در مورد سیستم‌های SAR فضایی، به دلیل خطای زمان‌بندی ساعت ازیموتال، به طور کلی لازم است نقاط کنترل زمین، مانند بازتابنده‌های گوشه‌ای که به صورت دستی قرار داده شده‌اند، برای تصحیح دقیق خطاهای ذکر شده در بالا تنظیم شوند [ 17 ، 18 ، 19 ، 20 ].]. معادله (10) عدم قطعیت اندازه‌گیری ارتفاع مرتبط با خطای فاز تداخل سنجی را نشان می‌دهد که عمدتاً توسط افست فاز مطلق و چندین عامل همبستگی ایجاد می‌شود. اولی را می توان با نقاط کنترل زمینی نیز اصلاح کرد، در حالی که دومی تصادفی است و با روش فوق قابل اصلاح نیست.

با ترکیب ویژگی‌های خطای ذکر شده در بالا، ما بر تجزیه و تحلیل تأثیر خطای تصادفی، یعنی خطای فاز تداخل‌سنجی معرفی‌شده توسط عوامل همبستگی، بر دقت اندازه‌گیری ارتفاع تمرکز خواهیم کرد. پارامترها اچ، آر1، و αیا با استفاده از اطلاعات دقیق مدار یا پس از یک روش تنظیم شامل نقاط کنترل زمینی شناخته می شوند.

3. مدل پایه بهینه

خطاهای فاز تداخل سنجی تصادفی شامل همبستگی فضایی، همبستگی داپلر، همبستگی حجمی، همبستگی زمانی، و همبستگی های ناشی از نسبت سیگنال به نویز حدی، کمی سازی و ابهامات است. در این مقاله، ما فقط همبستگی فضایی را برای بررسی مدل پایه بهینه در نظر می گیریم. هر دو خطای سیستماتیک هندسی و خطای تصادفی همبسته، که بر دقت باز کردن فاز تاثیر می‌گذارند، در این مقاله گنجانده شده‌اند.

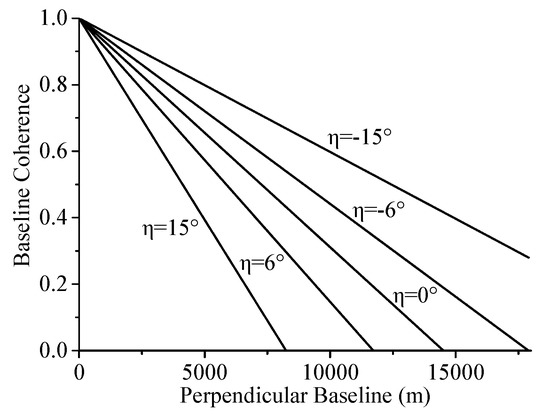
همبستگی فضایی عمدتاً تحت تأثیر خط پایه فضایی است که می تواند با انسجام خط پایه بیان شود. انسجام خط مبنا تابعی از خط مبنا عمود بر و خط پایه بحرانی است [ 21 ]:

γب={1-ب⊥بسیب⊥<بسی0ب⊥≥بسی،

جایی که γبنشان دهنده انسجام پایه و بسینشان دهنده خط پایه بحرانی است. انسجام خط مبنا تنها به خط مبنا عمود بر هم مربوط می شود، که مشابه رابطه بین خطای اندازه گیری ارتفاع و خطای فاز توصیف شده در رابطه (10) است و هیچ یک از آنها تحت تأثیر خط مبنا موازی قرار نمی گیرند. بنابراین، تجزیه و تحلیل خط پایه بهینه ذکر شده در این مقاله به خط مبنا عمود بر هدایت می شود تا از خطاهای ایجاد شده توسط تمایل خط مبنا تا حد امکان جلوگیری شود.

چه زمانی ب⊥بزرگتر است از بسی، تغییر طیفی برابر با پهنای باند در جهت محدوده است و سیگنال را کاملاً با هم مرتبط می کند. خط پایه بحرانی برای سیستم SAR bistatic را می توان به صورت زیر بیان کرد [ 5 ]:

بسی=2λآربرنزه(θ-η)بwج،

جایی که آرمحدوده شیب است، بwپهنای باند فرکانسی سیستم است، جسرعت نور است و ηشیب زمین محلی است. زاویه شیب زمین زمانی مثبت است که زمین رو به سنسور باشد و بالعکس. با گرفتن یک جفت تصویر TanDEM-X که شهر وینان، استان شانشی را در 3 سپتامبر 2013 پوشش می دهد، به عنوان مثال، طول موج 3.2 سانتی متر، محدوده شیب تقریباً 675 کیلومتر، ارتفاع مداری تقریباً 514 کیلومتر، زاویه فرود تقریباً 42.5 است. درجه و پهنای باند فرکانسی 110 مگاهرتز است. روابط بین انسجام خط پایه، خط پایه عمود بر و شیب زمین در شکل 2 نشان داده شده است.

3.1. شبیه سازی اینترفروگرام

برای تعیین یک مدل پایه بهینه دقیق، ما یک تجزیه و تحلیل آماری را بر روی داده های تداخل سنجی شبیه سازی شده بر اساس سیستم Bistatic SAR انجام دادیم. ابتدا، داده های DEM را با استفاده از یک شیب زمین ساده شبیه سازی کردیم. دوم، فاز تداخل سنجی با محاسبه تفاوت در برد شیب بین ماهواره های اصلی و برده در سیستم مختصات رادار بر اساس DEM شبیه سازی شده و پارامترهای تصویربرداری ماهواره ای شبیه سازی می شود. سپس، برای تحلیل مناسب روابط بین خط پایه عمود، شیب زمین و خطای فاز تداخل سنجی، نقشه انسجام تنها با همبستگی فضایی محاسبه شده از پارامترهای تصویربرداری هندسی شبیه‌سازی می‌شود. در این مقاله، شیب زمین بر اساس یک DEM شبیه سازی شده با وضوح 10 متر استخراج شده است. سرانجام،22 ]:

σϕ2(γ،L)=🔻-π+π(φ-E[ϕ])2پدf(ϕ،γ،L،E[ϕ])دϕ،

جایی که σϕ2واریانس فاز را نشان می دهد، γنشان دهنده ضریب همبستگی است، Lتعداد نگاه ها را نشان می دهد، E[⋅]عملگر انتظار را نشان می دهد و پدf(⋅)تابع چگالی احتمال فاز تداخل سنجی است و به صورت زیر قابل محاسبه است:

پدf(ϕ،γ،L،E[ϕ])=1-|γ|22π×11-β2×[β(1-β2)12(π2+آرکسینβ)+1] (L=1)،

جایی که β=|γ|cos(ϕ-E[ϕ]).

بر اساس فرمول فوق، این مقاله نویز فاز را برای L =1 شبیه سازی می کند و با افزودن نویز فاز به فاز واقعی و بسته بندی آن، فاز تداخل سنجی نویز شبیه سازی شده را به دست می آورد. مجموعه داده های شبیه سازی شده بر اساس خطوط پایه و شیب های مختلف عمود بر زمین در شکل 3 نشان داده شده است.

3.2. روش باز کردن فاز

با افزایش خط پایه عمود بر هم، حاشیه های تداخل سنجی تولید شده با تغییر ارتفاع یکسان متراکم تر می شوند و باز کردن فاز دشوارتر می شود. علاوه بر این، انسجام تداخل سنجی و دقت فاز بدون بسته بندی بدتر می شود. بنابراین، اثربخشی بازکردن فاز در طول تحلیل خطای فاز باید بررسی شود.
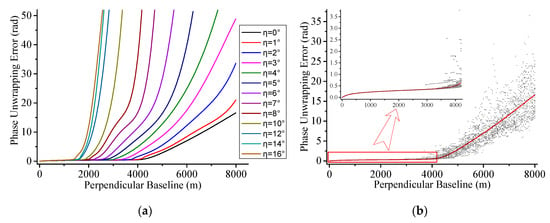
از آنجایی که فیلتر اینترفروگرام فاکتورهای عدم قطعیت بیشتری را معرفی می کند، انجام نمی شود. برای همگام شدن با توسعه الگوریتم بازکردن فاز و اطمینان از میزان موفقیت مشخصی در بازکردن فاز، این مقاله یک روش بازکردن فاز فیلتر کالمن بدون عطر تطبیقی ​​را اتخاذ می‌کند [ 13 ، 14 ] که نسبتاً بهینه است. در مقایسه با روش‌های سنتی بازکردن فاز، این روش که ترکیبی از یک مدل مداد ماتریس اصلاح‌شده، یک فیلتر کالمن بدون عطر تطبیقی، یک استراتژی هدایت‌شده با کیفیت کارآمد بر اساس Heapsort و یک فیلتر میانه است، می‌تواند به نقشه‌های فاز تداخل سنجی دقیق‌تری دست یابد. فاز باز نشده و هیستوگرام خطای تخمین در شکل 3 نشان داده شده است.
هیستوگرام خطای تخمین به سادگی با محاسبه تفاوت بین فاز بدون بسته بندی و فاز تداخل سنجی واقعی به دست می آید، که می تواند به طور شهودی کیفیت نتایج باز کردن را نشان دهد. با این حال، خطای فاز تداخل سنجی به PUE محاسبه شده توسط ریشه میانگین مربع (RMS) بین آنها اشاره دارد. همانطور که در شکل 3 نشان داده شده است، با افزایش خط پایه عمود بر، چگالی حاشیه فاز تداخل سنجی پیچیده افزایش می یابد و تأثیر نویز بر روی فاز افزایش می یابد که باعث تضعیف انسجام خواهد شد. به همین ترتیب، فاز بدون بسته بندی بدتر می شود. به عنوان مثال، در موردی که طول خط پایه 8000 متر است، حاشیه ها بسیار متراکم هستند و فاز تداخل سنجی تقریباً به طور کامل توسط نویز پوشانده شده است. در این حالت میانگین خطای تخمین به 40 رادیان می رسد که نشان می دهد روش بازکردن تا حد زیادی نامعتبر است.

3.3. مدل خطای بازکردن فاز

برای ایجاد یک مدل دقیق برای PUE، خط پایه و شیب زمین، شبیه‌سازی فاز و تحلیل فاز بر اساس طول‌های مختلف خط پایه عمود بر روی زمین ساده با زوایای شیب تقریباً 0 تا 8، 10، 12، 14 انجام می‌شود. ، و 16 درجه. محدوده خط مبنا عمود بین 0 متر و خط پایه بحرانی متغیر است و فاصله گام 50 متر است. با در نظر گرفتن تصادفی بودن نویز، این مقاله همان طول خط پایه عمودی و زاویه شیب زمین را 30 بار شبیه‌سازی می‌کند. میانگین PUE در شرایط یکسان به عنوان تابعی از خط پایه عمود برازش می شود.
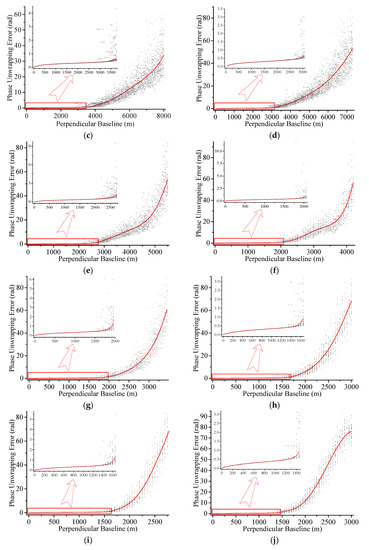
در این مقاله، لونبرگ-مارکوارت (LM) [ 23 ، 24 ، 25 ] با بهینه سازی جهانی جهانی (UGO) [ 26 ] برای بهینه سازی تحلیل برازش توصیف شده در بالا برای مقدار زیادی از داده های شبیه سازی شده استفاده می شود. با توجه به روندهای پیچیده تغییرات PUE، این مقاله برازش تکه‌ای را اتخاذ می‌کند. نقاط ناپیوستگی معمولاً در موقعیت هایی پس از تغییر ناگهانی روند PUE انتخاب می شوند. نتایج جزئی برازش شده در شکل 4 نشان داده شده است.
وقتی طول خط پایه کمتر از 200 متر باشد، PUE به سرعت با افزایش خط پایه عمود بر هم افزایش می‌یابد. هنگامی که خط پایه عمود بین 200 متر و 1200 متر است، PUE به آرامی تغییر می کند، که نشان می دهد روش باز کردن فاز می تواند به طور موثر در برابر همبستگی ناشی از خط پایه در این محدوده مقاومت کند. با این حال، PUE همچنان با افزایش خط پایه عمودی افزایش می‌یابد. متعاقبا، پراکندگی PUE با تغییرات در خط پایه عمودی افزایش می‌یابد، که نشان می‌دهد اثربخشی باز کردن فاز شروع به کاهش تدریجی می‌کند. بر این اساس، منحنی های PUE به سرعت تغییر می کنند. در این مرحله، دلیل اصلی شکست باز کردن فاز، افزایش چگالی حاشیه است. وقتی طول خط پایه عمود بر خط پایه بحرانی می رسد، از نظر تئوری منجر به همبستگی کامل می شود و فاز تداخل سنجی به طور کامل توسط خطای فاز توزیع شده تصادفی پوشانده می شود. بنابراین، فاز باز شده باید کاملاً توسط خطای نویز آلوده شود. در این حالت نویز اضافی حاصل از معادلات (13) و (14) به حداکثر مقدار خود می رسد. علاوه بر این، با نزدیک شدن طول به خط پایه بحرانی، روش باز کردن تقریباً کاملاً نامعتبر است. بنابراین، با نزدیک شدن به خط پایه، PUE به یک حالت اشباع می رسد. یعنی PUE تمایل به تثبیت یا کاهش سرعت رشد دارد. همانطور که در نشان داده شده است نویز اضافی از معادلات (13) و (14) به حداکثر مقدار خود می رسد. علاوه بر این، با نزدیک شدن طول به خط پایه بحرانی، روش باز کردن تقریباً کاملاً نامعتبر است. بنابراین، با نزدیک شدن به خط پایه، PUE به یک حالت اشباع می رسد. یعنی PUE تمایل به تثبیت یا کاهش سرعت رشد دارد. همانطور که در نشان داده شده است نویز اضافی از معادلات (13) و (14) به حداکثر مقدار خود می رسد. علاوه بر این، با نزدیک شدن طول به خط پایه بحرانی، روش باز کردن تقریباً کاملاً نامعتبر است. بنابراین، با نزدیک شدن به خط پایه، PUE به یک حالت اشباع می رسد. یعنی PUE تمایل به تثبیت یا کاهش سرعت رشد دارد. همانطور که در نشان داده شده استشکل 4 j، زمانی که η=16درجه، اگرچه خط پایه به خط پایه بحرانی نمی رسد، باز کردن فاز به دلیل حاشیه های بسیار متراکم تا حد زیادی نامعتبر است. بنابراین، اشباع PUE زود اتفاق می افتد. این پدیده تنها زمانی رخ می دهد که خط پایه حداقل به نصف طول خط پایه بحرانی برسد، که بسیار بیشتر از خط پایه بهینه است و بر تحلیل خط پایه بهینه بعدی تأثیری نخواهد داشت.
علاوه بر این، اگر طول خط پایه عمود بر ثابت نگه داشته شود، PUE با افزایش زاویه شیب زمین افزایش می‌یابد. از یک طرف، خط پایه بحرانی و انسجام در این مورد همانطور که در شکل 2 توضیح داده شده است کاهش می یابد . از سوی دیگر، با افزایش زاویه شیب، تفاوت ارتفاع به تدریج در اندازه تصویر و وضوح DEM یکسان افزایش می‌یابد. یعنی گرادیان فاز به تدریج افزایش می یابد. بنابراین، چگالی حاشیه ای اینترفروگرام به تدریج افزایش می یابد و در نتیجه PUE افزایش می یابد.

3.4. تحلیل پایه بهینه

با توجه به بخش 2 ، با افزایش خط پایه عمود بر، حساسیت فاز تداخل سنجی به تغییرات ارتفاع افزایش می یابد. این حساسیت را می توان با ابهام ارتفاع، یعنی اختلاف ارتفاع مربوط به a توصیف کرد 2πتغییر فاز:

ساعت2π=λآرگناه(θ)ب⊥،

جایی که ساعت2πنشان دهنده ابهام ارتفاع است. با توجه به شیب زمین، می توان آن را به صورت زیر بیان کرد:

ساعت2π=λآرگناه(θ-η)ب⊥.

علاوه بر این، همانطور که در بخش 3.3 توضیح داده شد ، PUE با افزایش خط پایه عمودی افزایش می‌یابد و دقت اندازه‌گیری ارتفاع بدتر می‌شود. بنابراین، یک محدوده پایه بهینه برای اندازه‌گیری ارتفاع وجود دارد. بدون در نظر گرفتن تأثیرات اقلیمی و محیطی، خط پایه بهینه به عنوان خط پایه عمودی تعریف می شود که انحراف استاندارد برآورد ارتفاع هدف را به حداقل می رساند. با در نظر گرفتن تحلیل فوق و نادیده گرفتن برخی از عوامل مؤثر سیستماتیک، انحراف معیار ارتفاع را می توان با رابطه (18) زیر شرح داد. توجه داشته باشید که ک=آراچآرساعت≈1.08; بنابراین، k را می توان به عنوان یک ثابت در نظر گرفت.

σساعت=کλآرگناه(θ-η)2πب⊥σϕ،
بر اساس مدل PUE شرح داده شده در بخش 3.3 ، انحراف استاندارد ارتفاع از زوایای شیب زمین مختلف را می توان با معادله (18) محاسبه کرد. برای مشاهده روابط بین خطای ارتفاع، خط پایه عمود بر و شیب زمین به طور مستقیم، یک خطای ارتفاع کوچک فقط برای نقشه برداری انتخاب می شود همانطور که در شکل 5 نشان داده شده است. نشان داده شده است.
همانطور که در شکل 5 نشان داده شده است نشان داده شده است ، زمانی که طول خط مبنا کمتر از 1000 متر باشد، خطای ارتفاع با خط پایه عمود بر عکس متناسب است. در این حالت PUE بسیار کوچک است و خطای ارتفاع عمدتاً با ابهام ارتفاع تعیین می شود. با این حال، همانطور که طول خط پایه به یک مقدار بحرانی می رسد، خطای ارتفاع به سرعت افزایش می یابد. در این زمان، خطای ارتفاع عمدتاً تحت تأثیر PUE قرار می گیرد زیرا روش باز کردن فاز شروع به شکست می کند. همراه با منحنی های PUE نشان داده شده در شکل 4a، مقدار بحرانی معمولاً در موقعیتی مشابه با نقاط تغییر ناگهانی در منحنی‌های PUE قرار می‌گیرد. بدیهی است که مقدار بحرانی با کاهش زاویه شیب افزایش می یابد، که همچنین به این معنی است که محدوده خط پایه بهینه افزایش می یابد. در واقع، زمانی که طول خط پایه نزدیک به صفر یا خط پایه بحرانی باشد، خطای ارتفاع بسیار بزرگ خواهد بود. با این وجود، از آنجایی که PUE زمانی که خط پایه به خط پایه بحرانی نزدیک می شود، به حالت اشباع می رسد، خطای ارتفاع تحت تأثیر قرار می گیرد و به تدریج تثبیت می شود. برای تحلیل شهودی بیشتر تغییر در خطای ارتفاع حول محدوده خط پایه بهینه، محورهای عرضی و طولی مربوطه در اینجا کوتاه شده‌اند. بنابراین، پدیده اشباع ذکر شده در بالا نشان داده نمی شود. برای دامنه های مختلف زمین،جدول 1 .

همانطور که در جدول 1 توضیح داده شد ، اگرچه خط پایه بهینه با شیب زمین متفاوت است، انسجام خط پایه بهینه مربوطه اساساً در مواردی برابر است. η<2درجهیا η>8درجهدر حدود 0.764 یا 0.853، به ترتیب. در موارد دیگر، تغییر در انسجام خط پایه بهینه تقریباً خطی است. در ترکیب با شکل 5 ، می توانیم محدوده انسجام خط پایه بهینه را به طور مناسب گسترش دهیم و مدل تجربی به صورت زیر بیان می شود:

γب_oپ∈{0.75~0.78η<2درجه(0.756+0.012η-0.01)~(0.756+0.012η+0.01)2درجه≤η≤8درجه0.84~0.87η>8درجه،

بنابراین، محدوده خط پایه بهینه را می توان از رابطه (12) بر اساس مدل انسجام خط پایه بهینه بدست آورد که می توان آن را به صورت زیر بیان کرد:

بoپ=(1-γب_oپ)2λآربرنزه(θ-η)بwج،
به طور مشابه، ما همچنین به طور تجربی تغییرات خط پایه بهینه را برای زوایای شیب منفی تجزیه و تحلیل کردیم. همانطور که در جدول 2 توضیح داده شد ، تغییر در انسجام خط پایه بهینه تا حد زیادی با زاویه شیب مثبت سازگار است. به طور خاص، به عنوان |η|<2درجهو |η|>8درجه، انسجام خط پایه بهینه به آرامی با افزایش در افزایش می یابد |η|; و به عنوان 2درجه≤|η|≤8درجه، به سرعت افزایش می یابد. هنگامی که مقدار مطلق زاویه شیب زمین یکسان است، خط پایه بهینه شیب منفی به دلیل زاویه تابش همیشه بزرگتر از شیب مثبت است. با این حال، زمانی که خط پایه نسبتا بزرگ است، عامل اصلی تاثیرگذار PUE چگالی حاشیه است. بنابراین، افزایش در خط پایه بهینه خیلی زیاد نیست. با این حال، افزایش در خط پایه بحرانی بسیار بزرگتر از خط پایه بهینه است، که منجر به یک انسجام بهینه خط پایه ناسازگار و نرخ رشد بزرگتر از شیب مثبت می شود.
با این حال، در نقشه برداری توپوگرافی واقعی، به دلیل پیچیدگی زمین، پارامتر خط پایه بهینه ثابتی وجود ندارد. بنابراین، انتخاب خط پایه بهینه تنها می تواند با توجه به توزیع گرادیان توپوگرافی انجام شود تا میانگین خطای اندازه گیری ارتفاع در منطقه بررسی شده به حداقل برسد.
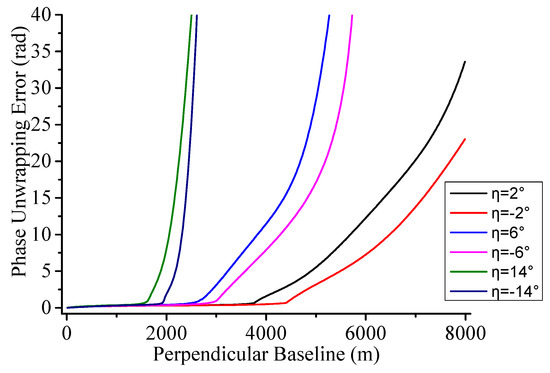
در واقع، زوایای شیب مثبت و منفی زمین واقعی همیشه مطابقت دارند. مطابق با شکل 6، که PUE های شیب های مختلف زمین مثبت و منفی را مقایسه می کند، قبل از تغییر ناگهانی در منحنی های PUE، PUE برای زوایای مثبت اساسا با PUE برای زوایای منفی سازگار است. با این حال، زمانی که شیب های زمین قدر مطلق یکسانی دارند، طول خط مبنا در موقعیت به سرعت در حال تغییر PUE مربوط به زاویه شیب منفی بزرگتر از زاویه شیب مثبت است. بنابراین، تأثیر PUE مربوط به پیکسل‌های شیب مثبت بر کل PUE بیشتر از پیکسل‌های شیب منفی است. علاوه بر این، PUE های مربوط به شیب های منفی ممکن است تأثیر بیشتری نسبت به شیب های زمین کوچک داشته باشند. بنابراین، مقدار مطلق زاویه شیب زمین برای تجزیه و تحلیل توزیع گرادیان توپوگرافی استفاده خواهد شد. سپس،

4. تجزیه و تحلیل تجربی

برای ارزیابی مدل پایه بهینه شرح داده شده در بخش 3.4 ، این مقاله از یک زمین پیچیده برای تجزیه و تحلیل تجربی استفاده می‌کند و پارامترهای سیستم SAR که به کار می‌روند مانند بالا هستند. علاوه بر این، برای افزایش شباهت زمین پیچیده شبیه سازی شده به زمین واقعی، زمین به دو دسته تقسیم شد: زوایای شیب مثبت و منفی با توزیع یکنواخت و غیریکنواخت، که در آن مقادیر میانگین زوایای شیب مثبت و منفی در منطقه مورد مطالعه تعیین شده نزدیک است. به یا انحراف از 0. در نهایت، محدوده پایه بهینه انواع مختلف زمین برای مرجع ارائه شده است.

4.1. توزیع یکنواخت زوایای شیب مثبت و منفی

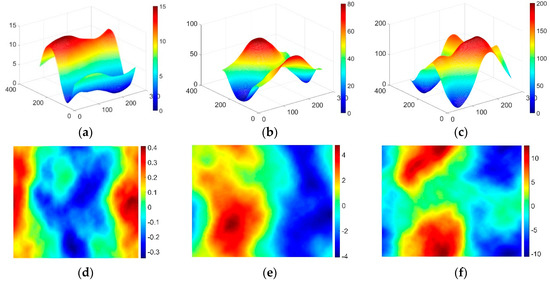
برای توزیع نسبتا یکنواخت زوایای شیب مثبت و منفی، سه نوع زمین پیچیده با زوایای شیب از کوچک تا بزرگ با موفقیت در این مقاله شبیه‌سازی شده‌اند. DEM شبیه سازی شده با اندازه 256 (محدوده) × 256 (زیموت) پیکسل و شیب زمین هر پیکسل محاسبه شده با وضوح DEM در شکل 7 نشان داده شده است.
همانطور که در شکل 7 نشان داده شده است ، زوایای شیب زمین پیچیده شبیه سازی شده تقریبا یکنواخت است و مقادیر متوسط ​​محاسبه شده به ترتیب در شکل 7 d-f به ترتیب 0.005-، 0.018- و 0.262 درجه است. با این حال، دامنه شیب آشکارا متفاوت است، و فواصل به ترتیب تقریباً (0.34-، 0.41)، (4.08-، 4.76) و (-10.64، 12.56) هستند.
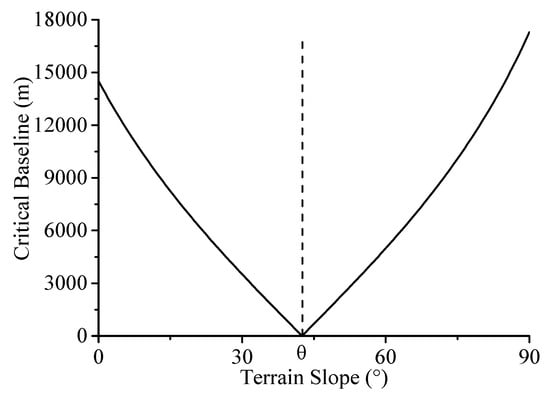
در ترکیب با مدل پایه بهینه، تعیین یک زاویه شیب مناسب برای محاسبه محدوده خط پایه بهینه ضروری است. همانطور که در بخش 3.4 توضیح داده شد ، برای شیب های مثبت و منفی با مقدار مطلق یکسان، تاثیر پیکسل های زاویه شیب منفی بر PUE کلی کمتر از پیکسل های زاویه شیب مثبت است. بنابراین، قدر مطلق زاویه شیب منفی هنگام محاسبه میانگین زاویه شیب یک زمین پیچیده استفاده می شود. با این وجود، محاسبه میانگین حسابی قدر مطلق زاویه شیب هنوز نامناسب است. همانطور که در شکل 4 نشان داده شده استa، تحت همان خط پایه عمود بر هم، تأثیر شیب زمین بر PUE با افزایش زاویه شیب افزایش خواهد یافت. با این حال، تجزیه و تحلیل فوق تنها بر اساس این شرط است که زاویه شیب زمین کوچکتر از زاویه تابش باشد. اگر زاویه شیب زمین بزرگتر از زاویه تابش باشد، عکس آن صادق است. در تئوری، PUE با انسجام خط پایه نسبت معکوس دارد و انسجام خط پایه با خط پایه بحرانی متناسب است. بنابراین، PUE با خط پایه بحرانی نسبت معکوس دارد. رابطه بین خط پایه بحرانی و زاویه شیب زمین در شکل 8 نشان داده شده است .
بنابراین، اگر زاویه شیب کوچکتر از زاویه فرود باشد، PUE با شیب زمین متناسب خواهد بود. در غیر این صورت، نسبت معکوس با شیب زمین خواهد بود.

بر اساس نتیجه‌گیری بالا، ما یک روش میانگین وزنی برای محاسبه میانگین زاویه شیب یک زمین پیچیده پیشنهاد می‌کنیم. ابتدا مقدار مطلق زاویه شیب به چندین بازه با پله های 0.5 درجه تقسیم می شود. سپس میانگین حسابی هر بازه به طور جداگانه محاسبه می شود. در نهایت، مقدار میانگین هر بازه برای به دست آوردن میانگین نهایی زاویه شیب زمین وزن می شود.

η¯=∑من=1متر(ηمن^⋅wمن)∑من=1مترwمن،
ηمن^=∑ηمنن ηمن∈(Δη⋅(من-1)،Δη⋅من]،

جایی که η¯زاویه شیب متوسط ​​نهایی یک زمین پیچیده را نشان می دهد، مترتعداد فواصل تقسیم بر مراحل را نشان می دهد Δη=0.5درجه، ηمن^به میانگین حسابی زاویه شیب در هر بازه اشاره دارد، نتعداد پیکسل ها در هر بازه را نشان می دهد و wمنوزن مربوط به هر بازه را نشان می دهد. وزن به صورت زیر تعریف می شود:

wمن={Δη⋅منθ(Δη⋅من)<θ90درجه-Δη⋅من90درجه-θ(Δη⋅من)>θ،

مطمئناً، اگر تعداد پیکسل‌ها در بازه کم باشد، ممکن است فاصله نادیده گرفته شود. در غیر این صورت، زاویه شیب متوسط ​​نهایی یک زمین پیچیده بیش از حد برآورد می شود.

با توجه به تجزیه و تحلیل فوق، نقشه های شیب زمین از شکل 7 را می توان به هیستوگرام های فاصله ای با مراحل 0.5 درجه که در شکل 9 نشان داده شده است، تقسیم کرد . از آنجایی که حداکثر شیب نشان داده شده در شکل 7 d کمتر از فاصله گام است، تنها می توان آن را به یک بازه تقسیم کرد و میانگین وزنی آن برابر با میانگین حسابی مقادیر مطلق زوایای شیب است. بنابراین، هیستوگرام بازه ای مربوط به شکل 7 d نشان داده نخواهد شد.
در این مقاله، بر اساس اندازه تصویر شبیه سازی شده، تعداد کل پیکسل ها 65536 است. فرض می کنیم فاصله تعداد پیکسل های کمتر از 500 (تقریبا کمتر از 1٪ از تعداد کل) را می توان نادیده گرفت. بنابراین فواصل زوایای شیب بزرگتر از 4.5 درجه و 11.5 درجه در عملیات وزن دهی شرکت نمی کنند. طبق رابطه (21)، شیب متوسط ​​نهایی زمین پیچیده مربوط به شکل 7 a-c به ترتیب 0.15، 2.90 و 7.58 درجه است. با ترکیب مدل پایه بهینه همانطور که در بخش 3.4 توضیح داده شده است، محدوده های پایه بهینه را می توان به صورت زیر محاسبه کرد: بoپ∈(3177 متر، 3610 متر)، بoپ∈(2621 متر، 2883 متر)و بoپ∈(1548 متر، 1769 متر).
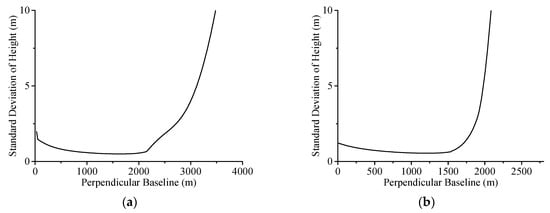
برای ارزیابی اعتبار مدل پایه بهینه، روش برازش داده‌ها که در بخش 3.3 توضیح داده شده است مجدداً برای برازش منحنی PUE زمین پیچیده نشان داده شده در شکل 7 استفاده می‌شود . نقشه های خطای اندازه گیری ارتفاع نهایی مرتبط با خط پایه عمود بر طبق شکل 10 به دست آمده است .
به طور مشابه، برای نشان دادن محدوده بهینه خط پایه به طور واضح تر زمانی که انحراف استاندارد ارتفاع کوچک است، تنها بخشی از انحراف استاندارد ارتفاع در شکل 10 ارائه شده است . از شکل 10 a-c، خطوط پایه بهینه به دست آمده به ترتیب 3308 متر، 2817 متر و 1650 متر است. این مقادیر همگی در محدوده خط پایه بهینه تخمین زده شده توسط مدل پایه بهینه قرار دارند و محدوده بهینه تخمین زده شده با محدوده خط پایه بهینه به دست آمده در شکل 10 مطابقت دارد. بنابراین، اعتبار مدل تایید می شود.

4.2. توزیع غیر یکنواخت زوایای شیب مثبت و منفی

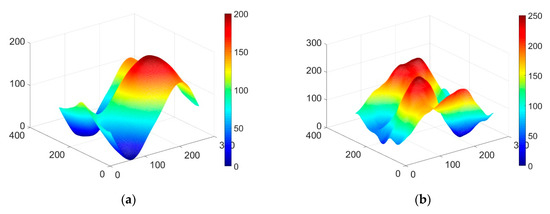
برای در نظر گرفتن جامع تغییرات در زمین پیچیده و ارزیابی بیشتر قابلیت اطمینان مدل پایه بهینه، دو مجموعه از DEM های نامنظم با اندازه های 256 (محدوده) × 256 (زیموت) پیکسل شبیه سازی شده اند. علاوه بر این، شیب های زمین مثبت و منفی به طور غیریکنواخت توزیع می شوند.
شکل 11 a,b دو مجموعه از DEM های شبیه سازی شده برای زمین های پیچیده مختلف است و شکل 11 c,d نقشه های توزیع زاویه شیب زمین مربوطه است که با وضوح DEM و پارامترهای سیستم SAR محاسبه شده است. همانطور که در شکل 11c نشان داده شده است، یک زاویه شیب مثبت بخش بزرگی از منطقه مورد مطالعه اول را به خود اختصاص می دهد ، در حالی که یک زاویه شیب منفی بر منطقه مورد مطالعه دوم غالب است همانطور که در شکل 11 d نشان داده شده است. میانگین حسابی زاویه شیب در زمین های پیچیده تقریباً 1.13 و -3.26 درجه است. با توجه به اینکه تعداد پیکسل ها در هر بازه زاویه شیب باید بزرگتر از 500 باشد، فواصل بیشتر از 12 و 19 درجه مربوط به شکل 11 است.e,f به ترتیب کنار گذاشته خواهد شد. با روش میانگین وزنی پیشنهادی، زوایای شیب متوسط ​​نهایی زمین پیچیده مربوط به شکل 11 a,b به ترتیب تقریباً 7.91 و 12.58 درجه است. انسجام خط پایه بهینه محاسبه شده توسط رابطه (19) می باشد γب_oپ∈(0.84،0.86)و γب_oپ∈(0.84،0.87). سپس، محدوده های پایه بهینه تخمین زده شده است بoپ∈(1530 متر، 1748 متر)و بoپ∈(1185 متر، 1459 متر).
مشابه تجزیه و تحلیل تجربی در بخش 3 ، شبیه سازی فاز تداخل سنجی و تجزیه و تحلیل پردازش داده ها برای زمین های پیچیده فوق انجام شده است. PUE تحت خطوط پایه عمود مختلف برازش و تحلیل می شود و نقشه های خطای ارتفاع نهایی بدست آمده و در شکل 12 a,b نشان داده شده است.
برای زمین های پیچیده فوق الذکر، خطوط پایه بهینه 1632 متر و 1214 متر است. بدیهی است که هر دو در محدوده خط پایه بهینه برآورد شده توسط مدل پایه بهینه پیشنهادی قرار دارند. بنابراین، اعتبار و پایایی مدل پایه بهینه در این مقاله بیشتر تأیید می‌شود. علاوه بر این، امکان‌سنجی روش میانگین وزنی، که مبتنی بر قدر مطلق شیب زمین است، حتی زمانی که زوایای شیب مثبت و منفی نسبتاً غیریکنواخت در منطقه مورد مطالعه هستند، تأیید می‌شود.

4.3. محدوده بهینه خط پایه برای انواع مختلف زمین

همراه با بخش 4.1 و بخش 4.2 ، قابلیت اطمینان مدل پایه بهینه ارائه شده در این مقاله تحت دامنه‌های شیب مختلف، مانند (0.34-، 0.41)، (4.08-، 4.76)، (-10.64، 12.56) تأیید شده است. ، (-11.44، 12.34) و (-21.03، 18.99)، که به ترتیب با میانگین شیب های 0.15، 2.90، 7.58، 7.91 و 12.58 درجه مطابقت دارند. در همین حال، اعتبار روش میانگین وزنی برای محاسبه میانگین زوایای شیب زمین های پیچیده نیز تأیید می شود. با ترکیب تعریف انواع زمین [ 27 ]، محدوده خط پایه بهینه را می توان برای مرجع بر اساس دامنه شیب انواع مختلف زمین نشان داده شده در جدول 3 به دست آورد.. انواع دیگر زمین به جز منطقه آلپ با آزمایش های فوق تجزیه و تحلیل شده است.
علاوه بر این، مطابق شکل 5 ، اگرچه دقت اندازه‌گیری ارتفاع مربوط به شیب زمین‌های مختلف زمانی که خط پایه کمتر از 1500 متر است، بهینه نیست، دقت اندازه‌گیری ارتفاع در این دوره نسبتاً پایدار است. تغییرات دقیق دقت اندازه گیری ارتفاع در شیب زمین های مختلف در طول این دوره در شکل 13 نشان داده شده است.. می توان دریافت که دقت اندازه گیری ارتفاع پایدار است، یعنی دقت اندازه گیری ارتفاع شیب های مختلف زمین اساساً یکسان است و انحراف استاندارد خطاهای اندازه گیری ارتفاع در شیب های مختلف زمین، همه کمتر از 0.1 متر، در محدوده پایه از 100 است. متر تا 1400 متر شاید برای سیستم SAR با تغییرپذیری خط مبنا تغییرناپذیر یا تغییرپذیری خط پایه کوچک، این محدوده پایه برای ارجاع به منظور تطبیق بهتر با مشاهده شیب زمین های مختلف ارزشمندتر باشد.

5. بحث

در این مطالعه، خط پایه بهینه بر اساس یک سیستم SAR bistatic فضابرد مدل‌سازی شد. در مقایسه با مدل قبلی [ 3 ، 7 ]، تأثیر خط مبنا عمود بر، شیب زمین و اثربخشی باز کردن را بر روی PUE در نظر گرفت و یک الگوریتم میانگین وزنی معقول برای محاسبه شیب متوسط ​​یک زمین پیچیده پیشنهاد شد. این مدل برای طراحی سیستم‌های SAR bistatic فضایی بعدی و دستیابی به DEM‌های با دقت بالا برای توپوگرافی‌های خاص اهمیت زیادی دارد.
با این حال، این مقاله فقط همبستگی فضایی را در مدل PUE در نظر گرفت و همبستگی داپلر، همبستگی حجم، همبستگی زمانی و همبستگی‌های ناشی از نسبت سیگنال به نویز حدی، کوانتیزاسیون و ابهامات نادیده گرفته شد. بنابراین، می توان انتظار داشت که انسجام بهینه واقعی کمتر از انسجام خط پایه بهینه برآورد شده باشد، و می توان انتظار داشت که محدوده خط پایه بهینه بزرگتر از محدوده خط پایه بهینه برآورد شده باشد. در کاربردهای عملی، بر اساس برآوردگر، می‌توان تنظیمات جزئی را در محدوده انسجام بهینه انجام داد تا تأثیر انواع دیگر همبستگی کاهش یابد. مطالعات بیشتر در مورد تأثیر سایر مقادیر انسجام برای به دست آوردن یک محدوده خط پایه بهینه دقیق ضروری است. علاوه بر این، برای سرکوب خطای باز کردن مربوطه،13 ، 14 ] که نسبت به روشهای سنتی بازکردن فاز برتری دارد. در تحقیقات آینده، یک روش پردازش بهتر برای به دست آوردن یک DEM با دقت بالاتر انتخاب خواهد شد. بنابراین، انتخاب یک الگوریتم بازگشایی فاز بهتر برای تحلیل تجربی در این مقاله برای تحقیقات بعدی مساعدتر خواهد بود.
علاوه بر این، در تحلیل تجربی شکل 11مجموعه داده b، اگرچه تعداد پیکسل ها در فواصل شیب های بزرگتر از 19 درجه اندک است، حداکثر مقدار زاویه شیب به 21 درجه می رسد، که بر PUE کلی نیز تأثیر می گذارد. بنابراین، زمانی که محدوده قدر مطلق زاویه شیب زیاد باشد، شیب متوسط ​​ممکن است به دلیل رها شدن فواصل بیشتر دست کم گرفته شود. این پدیده همچنین دلیل این است که خط پایه بهینه واقعی بدست آمده توسط آزمایش به حد پایینی محدوده خط پایه بهینه تخمین زده شده نزدیک است. بنابراین، برای جلوگیری از این پدیده، آستانه باید به طور مناسب با توجه به زمین پیچیده واقعی کاهش یابد. برای مثال، می‌توانیم آستانه را روی 400 تنظیم کنیم. به عنوان مثال، فواصل کمتر از 400 پیکسل نادیده گرفته می شود.

6. نتیجه گیری

در این مطالعه، ما تأثیرات پارامترهای سیستم SAR، مانند سیستم موقعیت یابی سکوی ماهواره، محدوده شیب، طول خط پایه، شیب خط پایه، و خطای فاز تداخل سنجی را بر روی دقت اندازه‌گیری ارتفاع از فضاپیما تحلیل کردیم. سیستم Bistatic SAR. از آنجایی که خطای فاز تداخلی معرفی شده توسط چندین عامل عدم همبستگی تصادفی است، نمی توان آن را توسط نقاط کنترل زمین اصلاح کرد. بنابراین، PUE، که عمدتاً تحت‌تاثیر خط پایه عمود، شیب زمین و اثربخشی باز کردن قرار می‌گیرد، بر اساس یک زمین ساده مدل‌سازی می‌شود و انحراف استاندارد ارتفاع محاسبه می‌شود. سپس، مدل پایه بهینه که دقت اندازه گیری ارتفاع را به حداکثر می رساند، به دست می آید. همراه با مدل PUE، یک روش میانگین وزنی نیز برای محاسبه زاویه شیب متوسط ​​زمین پیچیده پیشنهاد شده است. در نهایت، اعتبار و پایایی مدل پایه بهینه با در نظر گرفتن توزیع‌های یکنواخت و غیریکنواخت زوایای شیب مثبت و منفی و تغییر در زاویه شیب در زمین پیچیده تأیید می‌شود. علاوه بر این، محدوده پایه بهینه انواع مختلف زمین برای مرجع ارائه شده است.

منابع

  1. Farr، TG; روزن، PA; کارو، ای. کریپن، آر. دورن، آر. هنسلی، اس. کوبریک، ام. پالر، ام. رودریگز، ای. راث، ال. و همکاران ماموریت توپوگرافی رادار شاتل. کشیش ژئوفیس. 2007 ، 45 . [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  2. کریگر، جی. موریرا، ا. فیدلر، اچ. هاجنسک، آی. ورنر، ام. یونس، م. Zink، M. TanDEM-X: یک سازند ماهواره ای برای تداخل سنجی SAR با وضوح بالا. IEEE Trans. Geosci. Remote Sens. 2007 , 45 , 3317–3341. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  3. روسی، سی. گونزالس، FR; فریتز، تی. یاگو-مارتینز، ن. Eineder، M. TanDEM-X کالیبره شده تولید DEM خام. ISPRS J. Photogramm. Remote Sens. 2012 ، 73 ، 12-20. [ Google Scholar ] [ CrossRef ]
  4. Shi, M. مطالعه فناوری پایه و محدوده آن برای SAR تداخل سنجی متقاطع. کارشناسی ارشد مهندسی ؛ آکادمی علوم چین: پکن، چین، 2006. [ Google Scholar ]
  5. هانسن، تداخل سنجی رادار RF: تفسیر داده ها و تجزیه و تحلیل خطا . Kuwer Academic Publishers: New York, NY, USA, 2001. [ Google Scholar ]
  6. مستیک، وی. ون بلاریکوم، جی. کاردیلو، جی. Fennell, M. دقت اندازه‌گیری ارتفاع زمین رادارهای دهانه مصنوعی تداخل‌سنجی. IEEE Trans. Geosci. Remote Sens. 1996 , 34 , 219-228. [ Google Scholar ] [ CrossRef ]
  7. خو، اچ. ژو، ی. لی، سی. تجزیه و تحلیل خط پایه در SAR تداخل سنجی فضایی. Acta Electron. گناه 2003 ، 31 ، 437-439. [ Google Scholar ] [ CrossRef ]
  8. ژنگ، اف. ما، دی. Pei, H. بحث در مورد نیاز به دقت پایه در InSAR. مد. رادار 2005 ، 27 ، 18-21. [ Google Scholar ] [ CrossRef ]
  9. Wang, W. طراحی بهینه خط پایه و جبران خطا برای Bistatic Spaceborne InSAR. In Proceedings of the Fringe 2005 Workshop, Frascati, Italy, 28 نوامبر–2 دسامبر 2005. [ Google Scholar ]
  10. رودریگز، ای. مارتین، نظریه JM و طراحی رادارهای دهانه مصنوعی تداخل سنجی. پردازش سیگنال رادار IEE Proceeding F ; کتابخانه دیجیتال IET: انگلستان، 1992; جلد 139، صص 147–159. [ Google Scholar ] [ CrossRef ]
  11. چوی، سی. کیم، دی.-جی. خط پایه بهینه یک سیستم تک گذری در SAR برای ایجاد بهترین DEM در Tidal Flats. IEEE J. Sel. بالا. Appl. زمین Obs. Remote Sens. 2018 , 11 , 919–929. [ Google Scholar ] [ CrossRef ]
  12. ژانگ، ی. مطالعه بر روی روش‌های بهبود دقیق تجزیه و تحلیل خطا و روش‌های بهبود فضایی InSAR توزیع‌شده در فضا. دکتری پایان نامه، دانشگاه ملی فناوری دفاع، چانگشا، چین، 2012. [ Google Scholar ]
  13. گائو، ی. ژانگ، اس. لی، تی. چن، کیو. لی، اس. Meng, P. روش بازکردن فاز فیلتر بدون بو کالمن تطبیقی ​​و کاربرد آن در داده‌های تداخل سنجی SAR Gaofen-3. Sensors 2018 , 18 , 1793. [ Google Scholar ] [ CrossRef ] [ PubMed ][ نسخه سبز ]
  14. گائو، ی. ژانگ، اس. لی، تی. چن، کیو. ژانگ، ایکس. لی، اس. روش برنامه‌نویسی دو مرحله‌ای اصلاح‌شده برای باز کردن فاز برای تداخل‌نگارهای SAR چند پایه با استفاده از فیلتر کالمن بدون بو. Remote Sens. 2019 , 11 , 199. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  15. لیو، جی. هائو، ایکس. شو، اچ. Du, Z. مربوط به تجزیه و تحلیل عوامل موثر بر دقت اندازه گیری قد InSAR. Geomat. Inf. علمی دانشگاه ووهان 2007 ، 32 ، 55-58. [ Google Scholar ] [ CrossRef ]
  16. Yu, J. مطالعه تئوری و فناوری تداخل سنجی SAR موجود در فضا. دکتری پایان نامه، دانشگاه تونگجی، شانگهای، چین، 2004. [ Google Scholar ]
  17. چن، جی. زنگ، س. جیائو، جی. بله، اف. Zhu، L. روش تصحیح هندسی تصویر SAR فضایی بدون نقاط کنترل زمینی با استفاده از مدولاسیون پارامترهای مداری. Acta Geod. کارتوگر. گناه 2016 ، 45 ، 1434-1440. [ Google Scholar ] [ CrossRef ]
  18. لو، اچ. سو، ز. لی، ز. زی، جی. ژائو، جی. Zhang، Q. InSAR تخمین پایه برای Gaofen-3 زمان واقعی DEM Generation. Sensors 2018 , 18 , 2152. [ Google Scholar ] [ CrossRef ] [ PubMed ][ نسخه سبز ]
  19. Lv، G. تانگ، ایکس. آی، بی. لی، تی. Chen, Q. روش کالیبراسیون هندسی ترکیبی برای تصویر SAR فضایی چند پلتفرمی با GCPهای پراکنده. Acta Geod. Et Cartogr. گناه 2018 ، 47 ، 986-995. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  20. گونزالس، جی اچ. باخمن، ام. کریگر، جی. Fiedler, H. توسعه مفهوم کالیبراسیون TanDEM-X: تجزیه و تحلیل خطاهای سیستماتیک. IEEE Trans. Geosci. Remote Sens. 2010 , 48 , 716-726. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  21. زبکر، HA; Villasenor, J. Decorrelation در پژواک های رادار تداخل سنجی. IEEE Trans. Geosci. Remote Sens. 1992 , 30 , 950-959. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  22. جیانگ، م. دینگ، ایکس. تیان، ایکس. مالهوترا، آر. کونگ، دبلیو. یک روش ترکیبی برای بهینه‌سازی فیلتر گلدشتاین تطبیقی. ISPRS J. Photogramm. Remote Sens. 2014 ، 98 ، 29-43. [ Google Scholar ] [ CrossRef ]
  23. هاگان، MT; منهاج، MB آموزش شبکه های پیشخور با الگوریتم مارکوارت. IEEE Trans. عصبی. شبکه 1994 ، 5 ، 989-993. [ Google Scholar ] [ CrossRef ] [ PubMed ]
  24. لو، X.-L. لیائو، L.-Z. Wah Tam، H. تجزیه و تحلیل همگرایی روش لونبرگ-مارکوارت. بهینه. Methods Softw. 2007 ، 22 ، 659-678. [ Google Scholar ] [ CrossRef ]
  25. یین، اچ. هوانگ، Z.-H. Qi، L. همگرایی یک روش لونبرگ-مارکوارت برای نابرابری های غیرخطی. عدد. کارکرد. مقعدی بهینه. 2008 ، 29 ، 687-716. [ Google Scholar ] [ CrossRef ]
  26. ردوندو، جی ال. گارسیا، آی. Ortigosa، الگوریتم جهانی بهینه سازی جهانی PM در چند پردازنده حافظه مشترک. در مجموعه مقالات کار کنفرانس بین المللی شبکه های عصبی مصنوعی ; Springer: برلین/هایدلبرگ، آلمان، 2009; ص 219-222. [ Google Scholar ]
  27. GAQSIQ. مشخصات نقشه های توپوگرافی 1:25000 1:50000 1:100000 ایروفوتوگرامتری . چاپ استانداردهای چین: شنژن، چین، 2008; جلد GB/T 12341-2008.
Ijgi 09 00108 g001 550
شکل 1. هندسه تصویربرداری یک سیستم InSAR. آزیموت عمود بر صفحه.
Ijgi 09 00108 g002 550
شکل 2. انسجام خط پایه در مقابل خط مبنا و شیب زمین عمود بر آن.
Ijgi 09 00108 g003 550
شکل 3. نقشه های فاز شبیه سازی شده و بدون پیچ خطوط پایه عمود بر مختلف با η=2درجه. اعداد 1، 2، 3 و 4 به ترتیب با طول های پایه 100 متر، 3000 متر، 6000 متر و 8000 متر مطابقت دارند. ( الف ) فاز تداخل سنجی با نویز. ( ب ) فاز تداخل سنجی پیچیده. ( ج ) فاز بدون بسته بندی؛ و ( د ) هیستوگرام خطای تخمین.
Ijgi 09 00108 g004a 550 Ijgi 09 00108 g004b 550
شکل 4. نتایج متناسب با زوایای شیب زمین مختلف η. ( الف ) مقایسه مدل‌های PUE با زوایای شیب مختلف. ( ب ) η=0درجه; ( ج ) η=2درجه; ( د ) η=4درجه; ( ه ) η=6درجه; ( f ) η=8درجه; ( گرم ) η=10درجه; ( h ) η=12درجه; ( من ) η=14درجه; و ( ج ) η=16درجه.
Ijgi 09 00108 g005 550
شکل 5. انحراف استاندارد ارتفاع در برابر خط پایه عمود بر شیب های مختلف زمین.
Ijgi 09 00108 g006 550
شکل 6. مقایسه منحنی های PUE برازش شده در شیب های مختلف مثبت و منفی، η=±2درجه، η=±6درجه، و η=±14درجهبه عنوان نمونه
Ijgi 09 00108 g007 550
شکل 7. DEM های شبیه سازی شده و نقشه های شیب زمین. ( a – c ) سه DEM نامنظم مختلف (واحد = متر). ( d – f ) نقشه های شیب زمین مربوط به ( a – c )، به ترتیب (واحد = درجه).
Ijgi 09 00108 g008 550
شکل 8. خط پایه بحرانی در مقابل شیب زمین. پارامترهای سیستم SAR مانند موارد ذکر شده در بخش 3 است.
Ijgi 09 00108 g009 550
شکل 9. هیستوگرام های فاصله ای برای یک شیب زمین با پله های 0.5 درجه. ( الف ) هیستوگرام فاصله ای مربوط به شکل 7 e. و ( ب ) هیستوگرام بازه ای مربوط به شکل 7 f.
Ijgi 09 00108 g010 550
شکل 10. انحراف استاندارد ارتفاع در مقابل خط پایه عمود بر. ( الف ) مربوط به شکل 7 a,b; ( ب ) مربوط به شکل 7 b,e; و ( ج ) مربوط به شکل 7 c,f.
Ijgi 09 00108 g011a 550 Ijgi 09 00108 g011b 550
شکل 11. DEM های شبیه سازی شده ( a ، b )، نقشه های شیب زمین ( c ، d ) و هیستوگرام های بازه ای با گام های 0.5 درجه ( e ، f ). ( a , c , e ) مربوط به یک مجموعه داده شبیه سازی شده است. و ( b , d , f ) با مجموعه داده های دیگر مطابقت دارد.
Ijgi 09 00108 g012 550
شکل 12. انحراف استاندارد ارتفاع در برابر خط پایه عمود بر. ( الف ) مربوط به شکل 11 مجموعه داده است. و ( ب ) با مجموعه داده های شکل 11 ب مطابقت دارد.
Ijgi 09 00108 g013 550
شکل 13. میانگین و انحراف معیار خطای اندازه‌گیری ارتفاع در شیب زمین‌های مختلف تحت یک خط پایه عمود بر یکسان.

مقالات داخلی و بین المللی

مطالب مرتبط ...

بدون دیدگاه

دیدگاهتان را بنویسید