مدل چندسطحی فیلتر فضایی بردار ویژه قیمت خانه: مطالعه موردی فروش خانه در شهرستان فیرفکس، ویرجینیا

خلاصه

قیمت خانه‌ها به دلیل ویژگی‌های فیزیکی مشابهی که خانه‌های همسایه به اشتراک می‌گذارند و وجوه مشترکی که به محیط محله آنها نسبت داده می‌شود، تمایل به ارتباط فضایی دارند. یک مدل چند سطحی یکی از روش‌هایی است که به طور مکرر برای پرداختن به اثرات فضایی در مدل‌سازی قیمت مسکن اتخاذ شده است. مطالعات تجربی توانایی آن را در حسابداری خودهمبستگی فضایی خاص محله (SA) و تجزیه و تحلیل عوامل بالقوه مربوط به قیمت خانه در هر دو سطح فردی و محله نشان می دهد. با این حال، یک مدل استاندارد چندسطحی فقط SA درون محله را در نظر می‌گیرد، که به قیمت خانه‌های مشابه در یک محله اشاره می‌کند، اما SA بین محله را نادیده می‌گیرد، که به قیمت خانه‌های مشابه برای محله‌های مجاور اشاره می‌کند که معمولاً می‌توانند در مناطق مسکونی وجود داشته باشند. این نظارت ممکن است منجر به نتایج استنتاج غیرقابل اعتماد برای متغیرهای کمکی و متعاقباً پیش‌بینی دقیق قیمت مسکن شود. این مطالعه پیشنهاد می‌کند یک مدل چندسطحی را با استفاده از روش فیلتر فضایی بردار ویژه موران (MESF) گسترش دهد. این مدل پیشنهادی می‌تواند به طور همزمان SA بین همسایگی با مجموعه‌ای از بردارهای ویژه موران و همچنین SA پتانسیل درون همسایگی با یک عبارت اثرات تصادفی را در نظر بگیرد. تجزیه و تحلیل تجربی قیمت‌های خانه در سال‌های 2016 و 2017 در شهرستان فیرفکس، ویرجینیا، قابلیت یک مدل چندسطحی MESF را در حسابداری SA بین همسایگی موجود در داده‌ها نشان می‌دهد. مقایسه عملکرد مدل و نتایج پیش‌بینی قیمت مسکن با روش‌های مرسوم نیز نشان می‌دهد که مدل MESF چند سطحی از مدل‌های استاندارد چند سطحی و لذت‌جویی بهتر عمل می‌کند.

کلید واژه ها:

خودهمبستگی فضایی ; مدل چند سطحی ; موران بردار ویژه فیلتر فضایی ; قیمت خانه

1. معرفی

مدل قیمت گذاری لذت بخش یکی از پرکاربردترین مشخصات برای پیش بینی قیمت مسکن است. با این حال، قیمت خانه‌های مجاور به دلیل امکانات مشابه محله (مانند دسترسی به امکانات عمومی، وضعیت اجتماعی-اقتصادی) و ویژگی‌های فیزیکی مشابه آنها (مثلاً اندازه زمین، سن خانه) قابل مقایسه است. این همبستگی بالقوه در فضا می‌تواند فرض مشاهدات مستقل در مشخصات مدل لذت‌گرا را نقض کند و ممکن است به تخمین‌های پارامتر ناکارآمد و مغرضانه منجر شود [ 1 ]. برخی از روش‌های معروفی که در ادبیات برای گنجاندن خودهمبستگی فضایی (SA) در یک مدل لذت‌گرایانه استفاده می‌شوند، شامل مشخصات خودبازگشت فضایی [ 2 ، 3 ]، رگرسیون وزن‌دار جغرافیایی [ 4 ] است.، 5 ] و کریجینگ [ 6 ، 7 ، 8 ].

متأسفانه، مشخصات مدل فضایی فعلی یک ساختار سلسله مراتبی ذاتی در قیمت خانه را نادیده می گیرد [ 9 ]. یعنی یک اثر همسایگی، که نشان می‌دهد قیمت خانه‌ها در یک محله خاص مشابه است، هنوز در این مشخصات مدل به درستی در نظر گرفته نشده است. یک مدل چندسطحی، که اثرات ویژگی‌های محله را در تفکیک‌پذیری‌های فضایی مختلف با اجازه دادن به قیمت‌های خانه برای تغییر در فضا [ 10 ] در نظر می‌گیرد، یک روش کارآمد برای پرداختن به همبستگی درون همسایگی (مثلاً قیمت‌های خانه مشابه در یک محله مشخص) ارائه می‌کند [ 11 ]. ]. با این حال، یک مدل استاندارد چند سطحی، SA بین محله‌ها را در نظر نمی‌گیرد [ 12] (به عنوان مثال، قیمت خانه های مشابه برای محله های مجاور)، که می تواند منجر به تخمین پارامترهای مغرضانه شود، زیرا فقط اطلاعات جزئی را برای فرآیند قیمت گذاری فضایی خانه ارائه می دهد.

این مقاله ادغام فیلتر فضایی بردار ویژه موران (MESF) را در مشخصات مدل چند سطحی برای توضیح قیمت خانه پیشنهاد می‌کند. این مشخصات با محاسبه همزمان SA بین همسایگی با مجموعه‌ای از بردارهای ویژه موران و همچنین اثرات بالقوه خاص محله با یک اثر تصادفی، یک مدل لذت‌گرا را بهبود می‌بخشد. این تحقیق بر روی سه موضوع تحقیقاتی زیر متمرکز شده است: (1) ارزیابی اینکه آیا یک مدل MESF چند سطحی داده‌های فروش خانه را بهتر توصیف می‌کند با حسابداری SA بین محله‌ای که توسط یک مدل چند سطحی استاندارد نادیده گرفته می‌شود. (2) مدل سازی قیمت خانه با متغیرهای جمعیتی و اجتماعی-اقتصادی سطح گروه بلوک برای بررسی اثرات محله در قیمت خانه. و (3) بررسی عوامل مرتبط که بر قیمت مسکن تأثیر می‌گذارند، از جمله فصلی بودن بالقوه در داده‌های فروش خانه.

2. پس زمینه

ارزش املاک خانه در فضای جغرافیایی متفاوت است و بستگی به موقعیت جغرافیایی، ویژگی های خانه و محیط محله دارد. به دلیل ماهیت ناهمگون، ارزش‌های خانه به طور سنتی با یک مدل لذت‌گرا توصیف می‌شوند، که به طور کلی از مشخصات رگرسیون خطی استفاده می‌کند که شامل ویژگی‌های خانه‌ها و مکان‌های جغرافیایی به عنوان متغیرهای کمکی برای توصیف ارزش‌های معاملاتی خانه است [ 13 ]. محبوبیت یک ویژگی لذت‌بخش عمدتاً به دلیل محاسبات ساده و قدرت توضیحی نسبتاً قوی آن است. برای مثال، Laurice و Bhattacharya [ 14 ] نشان می‌دهند که مشخصات مدل لذت‌گرا به طور متوسط تقریباً 82.8 درصد از تغییرات قیمت مسکن را در سه منطقه مختلف توضیح می‌دهد. لیمسوبونشای [15 ] گزارش می دهد که یک مدل لذت جو 78.3٪ از تغییرات در مجموعه داده قیمت خانه را توضیح می دهد.

در شکل کلاسیک خود، مشخصات مدل لذت‌گرا که قیمت مسکن را توصیف می‌کند، فرض مشاهدات مستقل آماری را نقض می‌کند، زمانی که قیمت‌های خانه از نظر مکانی وابسته هستند. یکی از عوامل اصلی همبستگی فضایی در قیمت خانه این است که ویژگی‌های خانه‌های مرتبط با قیمت خانه تمایل دارند در فضای جغرافیایی خوشه شوند [ 6 ]. برخی از مطالعات [ 14 ] شامل متغیرهای شاخص مکان در تجزیه و تحلیل رگرسیون برای تطبیق چنین اثرات فضایی هستند، اما لیو [ 16 ] استدلال می کند که این روش نمی تواند به طور کامل SA را در میان ویژگی های خانه توضیح دهد. سایر روش‌های رایج مورد استفاده شامل مدل‌های آماری فضایی است. به عنوان مثال، Can [ 13] یک ویژگی بسط یافته را با ترکیب یک تابع خود رگرسیون در مدل لذت‌گرا پیشنهاد می‌کند. این مدل توسعه یافته عملکرد مدل بهتر و دقت پیش بینی افزایش یافته را با حسابداری SA [ 1 ] به دست می آورد.

یک مدل چند سطحی، که اجازه می‌دهد قیمت‌ها در میان محله‌ها در یک محیط سلسله مراتبی متفاوت باشد، یک جایگزین محبوب برای مدل‌سازی قیمت خانه ارائه می‌کند. به عنوان مثال، اورفورد [ 11 ] بیان می‌کند که یک ویژگی لذت‌گرای چند سطحی با کنترل همزمان تأثیرات فضایی در هر دو سطح فردی و محله، رویکردی جذاب‌تر از نظر مفهومی ارائه می‌دهد. جورجویچ و همکاران [ 9 ] دریافتند که مدل لذت‌طلبی چندسطحی آنها با در نظر گرفتن اثرات درون محله‌ای که به تفاوت‌های شهرداری نسبت داده می‌شوند، بهتر از مدل لذت‌گرای سنتی خود عمل می‌کند. لیشمن و همکاران [ 17] همچنین استدلال می کند که یک مشخصات چند سطحی قادر به دستیابی به قدرت پیش بینی افزایش یافته در حالی که وابستگی فضایی را کاهش می دهد، یک ویژگی فاقد مدل لذت جوی استاندارد است.

در ادبیات، مفهوم یک بازار فرعی خانه برای بررسی ماهیت سلسله مراتبی قیمت مسکن معرفی شده است. بوراسا و همکاران [ 18 ] ادعا می کنند که یک بازار فرعی ارتباط نزدیکی با SA خاص محله در قیمت خانه دارد. قیمت خانه به دلیل ویژگی های فیزیکی مشابه و دسترسی مشابه به امکانات (مانند مراکز کاریابی و مراکز خرید) در یک بازار فرعی مشابه است. بازارهای فرعی ممکن است بر اساس نوع ساختار (به عنوان مثال، خانه شهری) یا با ویژگی های محله (به عنوان مثال، آموزش عمومی) تعریف شوند [ 19 ]. واحدهای منطقه ای سرشماری (به عنوان مثال، مناطق سرشماری و گروه های بلوک سرشماری) می توانند روش تقسیم بندی دیگری را ارائه دهند [ 4 ]]. به دلیل در دسترس بودن عمومی، جغرافیای سرشماری معمولاً برای تعیین بازارهای فرعی برای تجزیه و تحلیل قیمت مسکن استفاده می شود. به عنوان مثال، گودمن و تیبودو [ 19 ] نتایج را با استفاده از تراکت‌های سرشماری با مواردی که از مناطق کد پستی به عنوان بازار فرعی استفاده می‌کنند، مقایسه می‌کنند و نتیجه می‌گیرند که وضوح جغرافیایی کوچکتر نتایج پیش‌بینی بهتری را ایجاد می‌کند. Chasco و Le Gallo [ 10 ] یک مدل فضایی سه سطحی (خانه‌ها، مناطق سرشماری و محله‌ها) را برای ثبت تغییرات در قیمت مسکن مشخص می‌کنند.

اگرچه قابلیت آدرس دهی SA خاص محله با ساختار چند سطحی باعث می شود که یک مدل چند سطحی در بین دانشمندان فضایی ترجیح داده شود، Chasco و Le Gallo [ 10 ] استدلال می کنند که یک مدل چند سطحی قادر به ثبت کامل تمام فرآیندهای فضایی در داده های قیمت خانه نیست. این ضعف همچنین در [ 12 ] مورد بحث قرار گرفته است: یک مدل چند سطحی فقط SA را در واحدهای فضایی نشان می‌دهد، و اطلاعات کاملی در مورد توزیع فضایی نتایج ارائه نمی‌کند. به دلیل غیرقابل توضیح SA بین همسایگی، یک مدل چند سطحی ممکن است تخمین پارامترهای مغرضانه و در نتیجه پیش‌بینی‌های دقیق قیمت مسکن را ارائه دهد. برای غلبه بر این محدودیت، پارک و کیم [ 20] یک مدل چندسطحی فیلتر شده فضایی را پیشنهاد می‌کند که می‌تواند وابستگی‌های فضایی غیرقابل توضیح بالقوه بین محله‌ها را در خود جای دهد. نتایج تجزیه و تحلیل آنها نشان می دهد که رویکرد پیشنهادی با موفقیت قدرت توضیحی مدل چند سطحی استاندارد را بهبود می بخشد.

فراتر از ویژگی های فیزیکی و محیط محله، قیمت خانه نیز تحت تاثیر شرایط کلان اقتصادی و فصل یک سال است. به دلیل نوسانات عرضه و تقاضا، به نظر می رسد بازار مسکن به شدت فصلی باشد. فصلی بودن قیمت مسکن در ادبیات مورد بحث قرار گرفته است. برای مثال، رایچرت [ 21 ] برخی نوسانات فصلی را در داده‌های مسکن مشاهده می‌کند و استدلال می‌کند که روند فصلی ممکن است بسته به زمان سال منجر به یک بازار مسکن فعال یا کساد شود. گودمن و تیبودو [ 19] استدلال می کند که بازار مسکن به شدت فصلی است و یکی از عوامل اصلی این روند فصلی حرکت های جمعیتی است، به طوری که تقاضا در فصل بهار و تابستان به اوج خود می رسد که دلیل آن جابه جایی برای مدارس و مشاغل است که منجر به افزایش جزئی قیمت مسکن می شود. این فرض نیز در [ 22 ، 23 ] مورد بحث قرار گرفته است. Kuo [ 24 ] همچنین دریافت که یک متغیر ساختگی فصلی در مدل بیزی، فصلی بودن قیمت املاک را نشان می‌دهد: قیمت‌ها در سه ماهه دوم بالاتر هستند، اما تمایل دارند در سه ماهه سوم و چهارم پایین‌تر باشند. نگای و تنریرو [ 23] فصل دوم و سوم را به‌عنوان «فصل گرم» تعریف می‌کنند، زیرا بازارهای مسکن در بریتانیا (بریتانیا) و ایالات متحده (ایالات متحده) افزایش‌های سیستماتیک بالاتر از روند را از نظر قیمت مسکن و حجم معاملات و سه ماهه چهارم و اول تجربه می‌کنند. به عنوان یک “فصل سرد” به دلیل اینکه معاملات مسکن و قیمت ها تمایل به کاهش دارند. علاوه بر این، شرایط اقتصاد کلان نیز در ادبیات به خوبی شناخته شده است. برای مثال، بلتراتی و مورانا [ 25 ] دریافتند که شوک های اقتصاد کلان جهانی نقش مهمی در تعیین نوسانات قیمت مسکن دارند. ننجی و همکاران [ 26] همچنین استدلال می کنند که عوامل کلیدی اقتصاد کلان (به عنوان مثال، نرخ بهره، تورم و تولید ناخالص داخلی) به طور قابل توجهی بر پویایی قیمت مسکن تأثیر می گذارد. از آنجا که این مقاله تجزیه و تحلیل ها و مدلی را که با داده های فروش خانه تنها در یک شهرستان در یک سال ساخته شده است، خلاصه می کند، شرایط اقتصاد کلان نسبتاً همگنی در نظر گرفته شده است و چنین عواملی در تجزیه و تحلیل داده های آن گنجانده نشده است.

3. مواد و روشها

این بخش توضیحاتی از داده ها و منطقه مورد مطالعه ارائه می دهد و متغیرهای کمکی موجود در معادلات رگرسیون را خلاصه می کند. همچنین سه مشخصات مدل مختلف و تکنیک MESF را مورد بحث قرار می دهد.

3.1. داده ها و متغیرها

داده های فروش خانه از اداره مالیات شهرستان فیرفکس، ویرجینیا، که در حومه واشنگتن، دی سی است، جمع آوری شد. داده ها شامل تمام معاملات خانه (به عنوان مثال، خانه های تک خانواده، خانه های شهری، و آپارتمان های بلند) در شهرستان فیرفکس در سال 2016 و 2017 است. این تحقیق تمرکز خود را به قیمت خانه های تک خانواده محدود می کند که دارای 8585 و 8525 رکورد فروش در به ترتیب 2016 و 2017. با این حال، 70 و 34 رکورد تکراری برای هر یک از دو سال وجود داشت که تاریخ و قیمت‌های متفاوتی داشتند، اما ویژگی‌های خانه یکسانی داشتند (مثلاً شناسه‌ها و آدرس‌های خانه). برای این موارد تکراری، آخرین رکوردهای فروش برای هر خانه مجزا نگهداری می شد. برای اهداف نقشه برداری و تحلیل فضایی، خانه ها در ArcGIS با آدرس های فیزیکی خود کدگذاری شدند.

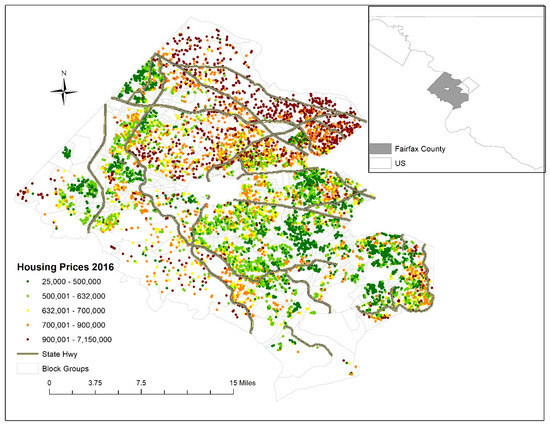
شکل 1 توزیع جغرافیایی قیمت خانه ها را در سراسر شهرستان فیرفکس در سال 2016 نشان می دهد. قیمت خانه نسبتاً بالایی را در شمال، در امتداد رودخانه پوتوماک، و همچنین در مناطقی با دسترسی نسبتاً خوب به بزرگراه هایی که به واشنگتن دی سی متصل می شوند، نشان می دهد. در مقابل، قیمت پایین مسکن در جنوب شرقی و غرب متمرکز است. الگوی نقشه در شکل 1گروه های درون بلوکی و گروه بین بلوکی قیمت مسکن را پیشنهاد می کند. به عنوان مثال، قیمت مسکن مشابه در برخی از گروه‌های بلوک (مثلاً گروه‌هایی از قیمت‌های بالای مسکن در شمال شرق) مشاهده شد، اما قیمت‌های مسکن در برخی گروه‌های بلوک دیگر متفاوت به نظر می‌رسید (به عنوان مثال، قیمت‌های پایین مسکن در مجاورت قیمت‌های بالای مسکن در جنوب است. ). بین گروه‌های بلوکی، قیمت مسکن نیز مشابه است (به عنوان مثال، گروه‌های بلوکی با قیمت مسکن بالا با گروه‌های بلوکی با قیمت‌های مشابه در شمال شرق همسایه بودند). علاوه بر این، شکل 1 نشان می دهد که قیمت مسکن به طور غیریکنواخت در سراسر منطقه مورد مطالعه توزیع شده است، با میانگین فروش 17 خانه در یک گروه بلوکی.

قطعنامه گروه بلوک سرشماری برای مرزهای زیر بازار خانه در این تحقیق عمدتاً به سه دلیل انتخاب شد. اول، یک گروه بلوک سرشماری کوچکترین واحد جغرافیایی است که اداره سرشماری ایالات متحده داده های نمونه را برای متغیرهای اجتماعی-اقتصادی برای آن منتشر می کند. اگرچه گروه‌های بلوک سرشماری شامل بلوک‌های سرشماری هستند، داده‌های نظرسنجی جامعه آمریکا (ACS) که منبع مهمی برای اطلاعات جامعه هستند در سطح بلوک در دسترس نیستند. دوم، یک گروه بلوک سرشماری معمولاً بین 600 تا 3000 نفر را شامل می‌شود، که می‌تواند حجم نمونه خانه معقولی را برای تخمین یک اثر تصادفی در یک مدل چندسطحی فراهم کند. اندازه نمونه خانه برای یک بلوک سرشماری ممکن است برای تخمین کارآمد بسیار کوچک باشد. ثالثاً، یک واحد فضایی بزرگتر (به عنوان مثال، مسیر سرشماری) ممکن است مسائل مربوط به اندازه نمونه خانه و در دسترس بودن داده ها را نداشته باشد.27 ].

داده‌های فروش خانه شامل مشخصات فیزیکی خانه‌ها بود. میز 1آمار توصیفی ویژگی ها را برای مجموعه داده تحلیل شده ارائه می دهد. متغیر فصلی از تاریخ های فروش ساخته شد و به عنوان یک متغیر طبقه بندی برای ارزیابی اثرات بالقوه فصلی در قیمت مسکن گنجانده شد. سه متغیر مرتبط با فاصله، اندازه‌گیری مجاورت خانه‌ها به مناطق مدارس عالی و مراکز تجاری مرکزی، با ArcGIS ساخته شدند. آنها برای بررسی تأثیر مکان های جغرافیایی بر قیمت خانه در تجزیه و تحلیل گنجانده شدند. خانه‌های یک محله مشخص (یعنی گروه بلوک در اینجا) تمایل به اشتراک ویژگی‌های مشابه دارند. علاوه بر این، هشت متغیر جمعیت شناختی و اجتماعی-اقتصادی در سطح گروه بلوکی از اداره سرشماری ایالات متحده برای توضیح پویایی گروه بین بلوک به دست آمد.

3.2. مشخصات مدل

این مقاله مشخصات مدل MESF چند سطحی را برای توصیف قیمت خانه با گسترش مدل لذت‌گرای مرسوم و مدل‌های چند سطحی پیشنهاد می‌کند. اساساً، یک مدل لذت‌گرا یک مشخصات مدل خطی است که قیمت خانه‌ها را با ویژگی‌های خانه و متغیرهای کمکی مرتبط با محیط محله توصیف می‌کند، در حالی که یک مدل چندسطحی یک اصطلاح اثرات تصادفی (RE) را در مشخصات مدل معرفی می‌کند تا به تغییرات در یک محله رسیدگی کند، که معمولاً فقط اجازه می‌دهد عبارت رهگیری در واحدهای فضایی متفاوت است. یک مدل MESF چند سطحی، با گنجاندن مجموعه ای از بردارهای ویژه در مشخصات مدل چند سطحی، برای SA بالقوه بین همسایگی حساب می کند. جدول 2 اشکال عملکردی سه مشخصات مدل را نشان می دهد. اینجا،

y_{i, j}

لگاریتم قیمت فروش را نشان می دهد

i^{t h}

خانه ای که در

j^{t h}

گروه بلوک؛

x_{i}

z_{j}

متغیرهای مستقل را به ترتیب در سطوح خانه و گروه بلوک نشان می دهد.

E_{j}

مجموعه ای از بردارهای ویژه انتخاب شده را نشان می دهد

j^{t h}

سطح گروه بلوک،

π_{j}

عبارت اثر تصادفی را نشان می دهد

j^{t h}

گروه بلوک و

ε_{i, j}

بیانگر عبارت خطا در سطح خانه فردی است.

β

γ

δ

ضرایب ناشناخته ای را نشان می دهد که باید تخمین زده شوند.

مدل چند سطحی داده شده برای بدست آوردن همبستگی در قیمت خانه ها در یک گروه بلوک سرشماری خاص به دلیل ویژگی های مشابهی که آنها به اشتراک می گذارند، مشخص شد. عبارت اثرات تصادفی ( $π_{j}$ تخمین زده شده با قیمت خانه در یک گروه بلوکی، برای رسیدگی به گروه درون بلوکی (یعنی سطح محله) SA معرفی شد. با این حال، گروه بین بلوک SA در مشخصات مدل چند سطحی در نظر گرفته نشد. MESF در مشخصات چند سطحی گنجانده شد تا به درستی به این موضوع رسیدگی شود. MESF یک روش آماری فضایی است که مجموعه ای از بردارهای ویژه ماتریس وزن فضایی را معرفی می کند. $E_{j} δ$ ) را به مشخصات مدل رگرسیون برای گرفتن SA [ 28 ]. بردارهای ویژه را می توان از یک ماتریس وزن های فضایی با مرکز دوگانه استخراج کرد $C$ ، که می تواند به صورت زیر بیان شود:

M C M = (I - 1 1 تی / n) C (I - 1 1 تی / n) ،

(1)

جایی که $I$ هست یک $n$ -توسط- $n$ ماتریس هویت، $1$ هست یک $n$ -بردار یکها، $n$ تعداد واحدهای مساحتی است و $T$ عملگر انتقال ماتریس است. زیرمجموعه ای از این بردارهای ویژه به عنوان متغیرهای مستقل در مشخصات مدل گنجانده شد و SA را به دست می آورد به طوری که یک رگرسیون خطی از نقض فرض استقلال ناشی از SA رنج نمی برد [ 28 ]. این زیر مجموعه را می توان از یک مجموعه بردار ویژه کاندید با روش رگرسیون گام به گام [ 29 ] شناسایی کرد.

از آنجایی که قیمت مسکن به شدت دارای انحراف مثبت بود ( شکل 2 الف)، یک تبدیل لگاریتمی برای عادی سازی داده های فروش اعمال شد ( شکل 2)ب). آمار تست اندرسون-دارلینگ نشان می دهد که فروش خانه های تغییر شکل یافته بسیار نزدیک به توزیع عادی بوده است. متغیر قیمت خانه تغییر یافته به عنوان متغیر پاسخ در هر یک از مشخصات سه مدل استفاده شد. ضرایب متغیر تخمینی، اصطلاحات RE و مؤلفه‌های ESF برای تحلیل پیش‌بینی برای داده‌های خانه سال ۲۰۱۷ اعمال شد. تمامی تجزیه و تحلیل داده ها در استودیو R و ArcGIS انجام شد. به طور خاص، تابع lmer (برازش یک مدل با جلوه های مختلط خطی) در بسته lme4 (شامل مجموعه ای از توابع برای برازش مدل های خطی با اثرات مختلط خطی تعمیم یافته) برای تخمین مولفه های RE مورد استفاده قرار گرفت، در حالی که بسته spdep (شامل یک مجموعه ای از توابع برای تجزیه و تحلیل داده های مکانی) و ArcGIS برای ساخت و تخمین اجزای ESF استفاده شد.

4. نتایج

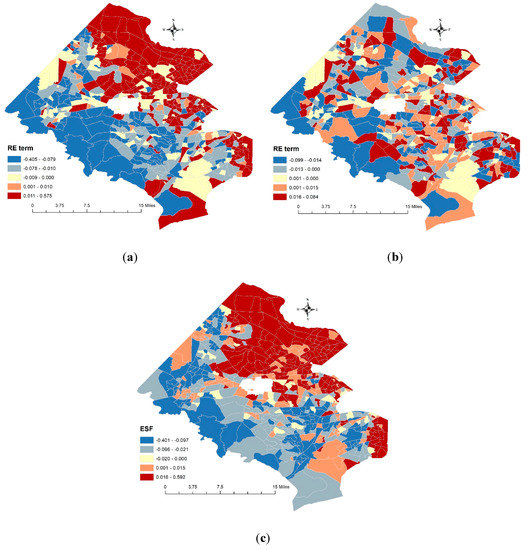
این بخش نتایج رگرسیون را برای سه مشخصات مدل مختلف خلاصه می کند. نقشه ها ( شکل 3 ) اجزای RE و ESF برآورد شده را نشان می دهند. علاوه بر این، نتایج پیش‌بینی خانه مورد تجزیه و تحلیل قرار گرفت و با مقادیر مشاهده‌شده آن‌ها مقایسه شد.

4.1. نتایج رگرسیون

جدول 3 نتایج برآورد را برای سه مشخصات مدل مختلف گزارش می کند. پارامترها (یعنی ضرایب و خطاهای استاندارد) با روش حداکثر احتمال محدود شده (REML) برآورد شدند. R2 مدل ^{لذت‌گرا} نشان داد که متغیرهای کمکی ترکیبی 68.3 درصد از تغییرات در داده‌های فروش خانه را توضیح می‌دهند. معرفی یک عبارت RE در مدل چندسطحی R2 را به 0.752 افزایش ^{داد (}^R2 مشروط ، که به واریانس توضیح داده شده توسط عوامل ثابت و تصادفی اشاره دارد) با حسابداری برای SA (امتیاز z از Moran’s I 24.93 است) که در گروه های بلوکی وجود داشت. عبارت RE به تنهایی 12% را توضیح می دهد (تفاوت بین R2 مشروط و ^R2 حاشیه ^ای، که نشان دهنده واریانس توضیح داده شده توسط عوامل ثابت) تغییرات در داده ها است. در مدل MESF چند سطحی، 82 بردار ویژه (از مجموع 339) از طریق یک روش گام به گام به عنوان متغیرهای کمکی تکمیلی گنجانده شدند. آنها همراه با متغیرهای کمکی، 75.7 درصد از تغییرات جغرافیایی در داده ها را توضیح می دهند. تغییرات توضیح داده شده توسط اصطلاح RE 1.7٪ است، کاهش را از 12٪ در مدل چند سطحی کاهش می دهد. این تغییر نشان می دهد که عبارت RE پس از معرفی بردارهای ویژه به مشخصات مدل، تغییرات زیادی را در بر نمی گیرد. به همین ترتیب، مقدار SA پرداخته شده توسط عبارت RE از 24.93 (امتیاز z موران I ) در مدل چند سطحی به 1.10 (نمره z از Moran’s I ) در مدل MESF چند سطحی کاهش یافت. من مورانz-score (33.21) برای مولفه ESF (ترکیب خطی از بردارهای ویژه انتخاب شده) وجود گروه های مثبت بین بلوک SA را نشان داد. علاوه بر این، مقایسه مقادیر AIC و log-lihood نشان داد که مدل MESF چند سطحی با پرداختن به گروه‌های بین بلوکی SA از دو مشخصات مدل دیگر بهتر عمل می‌کند. نتایج قابل توجه ANOVA ( جدول 4 ) همچنین تأیید کرد که مدل چند سطحی با بردارهای ویژه به عنوان متغیرهای کمکی اضافی با داده‌های فروش خانه تطابق بیشتری دارد. مقادیر p تست تشخیصی اندرسون-دارلینگ نشان می‌دهد که عبارت RE که با مدل MESF چند سطحی تخمین زده می‌شود، بیشتر با توزیع نرمال مطابقت دارد. آزمون اندرسون-دارلینگ صمقادیر نشان می‌دهد که باقی‌مانده‌های سه مدل از منحنی‌های زنگ‌شکل منحرف شده‌اند، اما باقی‌مانده‌های مدل MESF چند سطحی نسبت به مدل چند سطحی نسبتاً به توزیع نرمال نزدیک‌تر بودند. تست اندرسون-دارلینگ به عنوان یک تست نرمال بودن قدرتمند در نظر گرفته می شود و حتی با تعداد زیادی مشاهدات به طور گسترده ای مورد استفاده قرار می گیرد [ 30 ].

شکل 3 مولفه های برآورد شده RE را با دو مشخصات مدل چند سطحی نشان می دهد. شکل 3 a یک الگوی نقشه SA مثبت متوسط را نشان می‌دهد (امتیاز z موران I : 24.93)، که خوشه‌هایی با مقادیر کم در جنوب و خوشه‌هایی با مقادیر بالا در شمال را نشان می‌دهد. مولفه RE یک الگوی تصادفی (نمره z Moran’s I : 1.10) را پس از وارد شدن بردارهای ویژه به مدل نشان می دهد ( شکل 3 ب). شکل 3 c ترکیبی خطی از 82 بردار ویژه انتخاب شده را نشان می دهد که یک الگوی نقشه مشابه با شکل 3 را نشان می دهد.a (مقادیر بالا در شمال شرقی و مقادیر کم در جنوب). معرفی بردارهای ویژه تعدیل شده برای قیمت‌های تخمینی نادرست مسکن – قیمت‌های مسکن دست‌کم‌گرفته در شمال شرق و قیمت‌های بیش از حد برآورد شده خانه در جنوب.

جدول 3نشان می دهد که حسابداری برای اثرات همسایگی منجر به اصلاح برخی از تخمین های ضریب مغرضانه، به ویژه برای متغیرهای کمکی در وضوح گروه بلوک می شود. مقایسه سه مشخصات مدل نشان می‌دهد که تخمین‌های ضریب متغیر برای مدل‌های لذت‌گرا و چند سطحی بسیار مشابه به نظر می‌رسد. با این حال، برآورد ضرایب برای بسیاری از متغیرهای سطح گروه بلوکی برای مدل‌های چندسطحی و چند سطحی MESF، از جمله درصد جمعیت جوان، درصد جمعیت سفیدپوست، درصد جمعیت اسپانیایی تبار، درآمد خانوار، و درصد مهاجران، به‌طور چشمگیری تغییر می‌کند. برآورد ضریب متغیر درصد جمعیت جوان حتی در مدل چندسطحی MESF دارای علامت متفاوتی است. در قطعنامه خانه فردی،

جدول 3همچنین تغییرات سطوح معنی داری را برای برخی از متغیرها با حسابداری SA نشان می دهد. برای مثال، درصد جمعیت جوان، درصد جمعیت سفیدپوست، درصد جمعیت اسپانیایی تبار، درصد مهاجران، و میانگین سن جمعیت در رزولوشن گروه بلوکی در سطح 1 درصد در مدل لذت‌گرا معنی‌دار بود، اما در چند سطح معنی‌دار نشد. مدل MESF. درصد جمعیت سفیدپوست، درصد مهاجران و سن جمعیت متوسط در مدل چندسطحی در سطح 5 درصد معنی‌دار بود، اما در مدل چندسطحی MESF معنی‌دار نبود. همه متغیرها به جز یکی در سطح خانه فردی با قیمت مسکن رابطه معناداری داشتند. استثنا تعداد داستان ها بود. به طور خاص، زمین و مناطق نشیمن، تعداد حمام های کامل، نیم حمام، اتاق خواب، و شومینه ها با قیمت خانه ارتباط مثبت داشتند. سن خانه رابطه معکوس با قیمت مسکن نشان داد. متغیرهای شاخص مکان فاصله تا مناطق مدارس برتر و مراکز تجاری با قیمت خانه رابطه منفی داشتند، به این معنی که قیمت خانه در نزدیکی مناطق تجاری و مناطق خوب مدرسه بالاتر است. این ارتباط قابل توجه با یافته های گزارش شده در ادبیات [1 ، 18 ، 31 ].

ضرایب معنی دار متغیر طبقه بندی فصل نشان دهنده الگوی فصلی قیمت مسکن است ( جدول 3).). یعنی، قیمت مسکن در طول تابستان بیشتر و در طول زمستان پایین تر است، که با یافته های گزارش شده در ادبیات مطابق است، همانطور که در بخش پس زمینه بحث شد. در سطح گروه بلوک، سه متغیر به طور معناداری با قیمت مسکن مرتبط بودند. در میان آنها، درصد جمعیت اسپانیایی تبار رابطه منفی با قیمت خانه دارد، در حالی که میانگین ارزش خانه و درآمد متوسط خانوار به طور مثبت با قیمت خانه مرتبط است. اگرچه اثرات محله بر قیمت خانه به طور گسترده مورد بحث قرار گرفته است، ادبیات نشان می دهد که متغیرهای جمعیت شناختی و اجتماعی-اقتصادی برای جغرافیای سرشماری به ندرت برای توصیف قیمت خانه استفاده شده است. یک استثناء گودمن است [ 27]، که شامل چهار متغیر اجتماعی-اقتصادی در یک مدل لذت‌گرا می‌شود. نتایج تخمینی وی با نتایج ارائه شده در این مقاله سازگار است که بیان می‌کند که قیمت مسکن در محله‌هایی با وضعیت اجتماعی-اقتصادی پایین‌تر (مثلاً درصد کمتری از افراد تحصیل‌کرده) نسبتاً پایین‌تر است.

4.2. تحلیل پیش‌بینی قیمت مسکن

با استفاده از ضرایب کمکی برآورد شده در سال 2016، اصطلاحات RE و مولفه های ESF، قیمت مسکن در سال 2017 پیش بینی شد. نمودارهای پراکنده در شکل 4مقایسه قیمت‌های خانه مشاهده شده و پیش‌بینی‌شده در سال 2017 را نشان می‌دهد. آمار همبستگی پس از انطباق با گروه بلوک SA، 0.061 افزایش یافت، با جفت‌های قیمت خانه از نظر بصری بیشتر در امتداد خط مورب خوشه‌بندی شدند. افزایش جزئی 0.002 برای قیمت مسکن پیش بینی شده با مدل MESF چند سطحی مشاهده شد. به طور کلی، سه مشخصات مدل، پیش‌بینی‌های نسبتاً دقیقی را ارائه کردند. علاوه بر این، مدل لذت‌گرا دارای بالاترین میانگین خطای پیش‌بینی مطلق (16.06%)، در حالی که مدل MESF چند سطحی کمترین میانگین خطای پیش‌بینی مطلق (13.24%) را داشت.

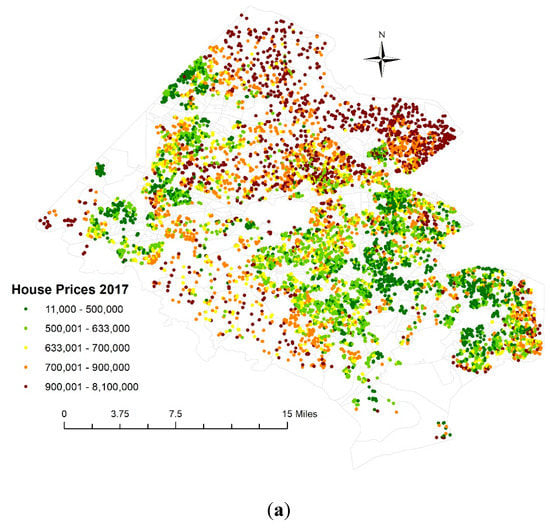
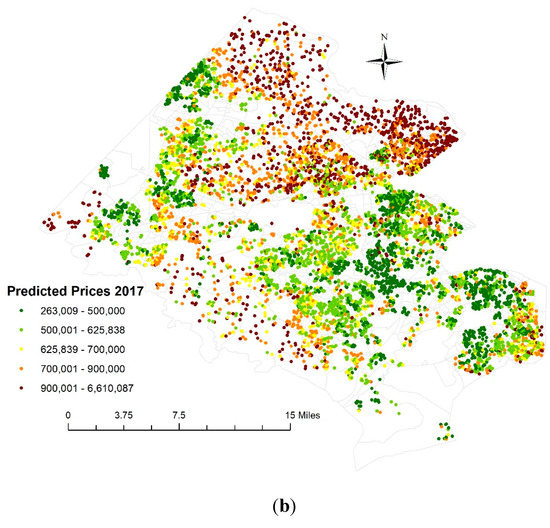
شکل 5 توزیع های جغرافیایی قیمت های مشاهده شده و پیش بینی شده مسکن در سال 2017 را با مشخصات مدل چندسطحی MESF نشان می دهد. آنها الگوهای نقشه تقریباً یکسانی را نشان می دهند، با قیمت خانه های بالا در شمال شرقی و قیمت های پایین در غرب و جنوب شرقی، که با الگوی نقشه مشاهده شده در شکل 1 همسو هستند. یک تفاوت قابل توجه با مقادیر شدید ظاهر شد: کمترین قیمت مشاهده شده 11000 دلار بود، در حالی که پایین ترین قیمت پیش بینی شده مسکن 263009 دلار بود. بالاترین قیمت پیش بینی شده مسکن 6,610,087 دلار و بالاترین قیمت مشاهده شده 8,100,000 دلار بوده است.

5. بحث

مؤلفه مهم ESF ( نمره z Moran: 33.21) و عبارت غیرمعنادار RE (نمره z Moran’s I : 1.10) در مدل MESF چند سطحی نشان می دهد که داده های فروش خانه حاوی مقدار زیادی بین گروه بلوک SA است، اما مقدار کمی از درون گروه بلوک SA. با انطباق با اثرات فضایی زیربنایی، مدل MESF چند سطحی از مشخصات مدل لذت‌گرا و چند سطحی استاندارد با بالاترین R2 بهتر عمل کرد ^.مقادیر (0.774) و log-likelihood (1556.70) و کمترین مقدار AIC (-2911.40). این نتایج نشان می‌دهد که مدل MESF چند سطحی یک مشخصه مؤثر برای توصیف بین محله‌های SA است که در مشخصات مدل چند سطحی استاندارد نادیده گرفته شده است. علاوه بر این، مدل MESF چند سطحی نیز بهترین نتایج پیش‌بینی قیمت مسکن را با کمترین میانگین خطای پیش‌بینی مطلق (13.24 درصد) تولید کرد.

مقایسه نتایج مدل چند سطحی و لذت‌گرا ماهیت سلسله مراتبی قیمت مسکن را تأیید می‌کند، با مدل قبلی که عملکرد مدل بسیار بهتری دارد (به عنوان مثال، R2 بالاتر ^و مقادیر AIC پایین‌تر). گنجاندن یک اصطلاح RE و شش متغیر جمعیت شناختی و اقتصادی-اجتماعی، که در مجموع 6.9٪ از تغییرات در داده های فروش خانه را توضیح می دهند، تا حدی اثرات فضایی در سطح محله را کنترل می کند. شکل 3 سطح گروه بلوک زیرین SA قیمت مسکن را نشان می دهد که به وضوح الگوی فضایی مشاهده شده در شکل 1 را منعکس می کند.. نتایج رگرسیون و نقشه ها نشان می دهد که گروه بلوک سرشماری می تواند به عنوان یک تقسیم بندی جغرافیایی جایگزین مناسبی برای ارزیابی ساختار سلسله مراتبی قیمت مسکن و همچنین برای کاوش الگوهای فضایی قیمت مسکن در سطح محله باشد.

بررسی عوامل مرتبط با قیمت خانه نشان می دهد که خانه های جدیدتر با زمین/مساحت بزرگ و حمام، اتاق خواب و شومینه بیشتر معمولاً با قیمت های بالا فروخته می شوند. علاوه بر این، فاصله از امکانات رفاهی از جمله مناطق مدرسه و مراکز تجاری نیز بر قیمت خانه تاثیر دارد. محله‌هایی با تمرکز بالای اقلیت‌ها با قیمت مسکن پایین‌تر همراه هستند و قیمت خانه‌های بالا در محله‌هایی با درآمد متوسط خانوار مشاهده می‌شود. همچنین، تغییرات فصلی قابل توجهی در قیمت مسکن مشاهده شد. اساساً، قیمت خانه در تابستان، یک فصل قبل از سال تحصیلی جدید بالاتر است، در حالی که قیمت خانه در زمستان نسبتاً پایین تر است. این یافته ها با یافته های گزارش شده در ادبیات مطابقت دارد.

یکی از محدودیت‌های اصلی این تحقیق این است که قیمت مسکن در سال 2016 به‌طور نابرابر در سراسر شهرستان توزیع شده است: 50 گروه بلوک دارای رکورد فروش خانه صفر و 31 گروه بلوک کمتر از 5 رکورد فروش مسکن دارند. تعداد کم مشاهدات در چنین گروه های بلوکی ممکن است منجر به نتایج تخمین ناپایدار، به ویژه برای اجزای RE شود. علاوه بر این، خانه هایی که در سال 2016 فروخته شدند (نه جمعیت خانه در بازار) به عنوان نمونه ای برای تجزیه و تحلیل داده ها استفاده می شدند که ممکن است ساختار فضایی بازار خانه را نشان ندهد. یافته های خلاصه شده در این مقاله دو موضوع تحقیقاتی آتی را پیشنهاد می کند. اول، با یک سری زمانی داده محدود، این تحقیق اثرات زمانی را در نظر نگرفت. در پیش‌بینی قیمت مسکن در سال 2017، از ضرایب تخمینی، مولفه‌های RE و ESF برای قیمت مسکن در سال 2016 استفاده شد. اگر اثرات زمانی نیز در نظر گرفته شود، پیش‌بینی دقیق‌تر قیمت مسکن انتظار می‌رود. دوم، SA را می توان بیشتر در میان خانه های فردی در نظر گرفت. در حالی که SA در سطح گروه بلوک به خوبی در این مقاله در نظر گرفته شده است (به عنوان مثال، گروه درون بلوکی و گروه SA بین بلوک)، SA سطح خانه فردی ممکن است فرآیند فضایی دیگری را نشان دهد. سوم، این تحقیق مدل MESF چند سطحی پیشنهادی را برای یک مجموعه داده تجربی خاص اعمال کرد، و از این رو، قابلیت آن برای گرفتن SA درون همسایگی نیاز به بررسی بیشتر با داده‌ها و مناطق مطالعاتی مختلف دارد. گروه درون بلوکی و گروه بین بلوک SA)، سطح خانه فردی SA ممکن است فرآیند فضایی دیگری را آشکار کند. سوم، این تحقیق مدل MESF چند سطحی پیشنهادی را برای یک مجموعه داده تجربی خاص اعمال کرد، و از این رو، قابلیت آن برای گرفتن SA درون همسایگی نیاز به بررسی بیشتر با داده‌ها و مناطق مطالعاتی مختلف دارد. گروه درون بلوکی و گروه بین بلوک SA)، سطح خانه فردی SA ممکن است فرآیند فضایی دیگری را آشکار کند. سوم، این تحقیق مدل MESF چند سطحی پیشنهادی را برای یک مجموعه داده تجربی خاص اعمال کرد، و از این رو، قابلیت آن برای گرفتن SA درون همسایگی نیاز به بررسی بیشتر با داده‌ها و مناطق مطالعاتی مختلف دارد.

6. نتیجه گیری

مشخصات مدل چند سطحی در ادبیات به مدل‌سازی قیمت خانه ترجیح داده می‌شود، زیرا به دلیل ماهیت سلسله مراتبی داده‌های فروش خانه، اثرات خاص محله را در نظر می‌گیرد. با این حال، مشخصات مدل چند سطحی تنها تا حدی به وابستگی فضایی اساسی (در محله SA) می پردازد. این پتانسیل بین محله‌های SA را نادیده می‌گیرد، که می‌تواند منجر به تخمین پارامترهای مغرضانه، به ویژه برای متغیرهای سطح محله شود. این مقاله مدل استاندارد چند سطحی را با ترکیب یک تکنیک MESF گسترش می‌دهد که می‌تواند روشی انعطاف‌پذیر برای محاسبه گروه بین بلوک SA ارائه دهد که با متغیرهای کمکی و اصطلاح RE توضیح داده شده است. تجزیه و تحلیل تجربی داده های فروش خانه در شهرستان فیرفکس، ویرجینیا، توانایی مدل MESF چند سطحی را برای تطبیق بالقوه بین گروه‌های بلوک SA که در داده‌های فروش خانه وجود دارد، نشان می‌دهد. یکی دیگر از ویژگی های جذاب مشخصات مدل چند سطحی MESF ساختار ساده و انعطاف پذیر آن برای محاسبه SA است. به این معنی که بردارهای ویژه، که به عنوان پراکسی برای متغیرهای کمکی حذف شده عمل می کنند [32 ]، می تواند به سادگی با یک روش استاندارد گام به گام انتخاب شود، تخمین آن را می توان با یک تکنیک استاندارد به جای پرداختن به یک ساختار پیچیده انجام داد (مثلاً یک مشتق احتمال پیچیده ضروری نیست). مشخصات مدل چندسطحی MESF همچنین می تواند به راحتی در نرم افزارهای آماری (مانند R و SAS) پیاده سازی شود.

منابع

باسو، س. Thibodeau، TG تجزیه و تحلیل خودهمبستگی فضایی در قیمت مسکن. جی. امور مالی املاک و مستغلات. اقتصاد 1998 ، 17 ، 61-85. [ Google Scholar ] [ CrossRef ]
کوهن، جی پی. مدل‌های لذت‌جویانه فضایی سر و صدای فرودگاه، نزدیکی، و قیمت مسکن Coughlin، CC. J. Reg. علمی 2008 ، 48 ، 859-878. [ Google Scholar ] [ CrossRef ]
سرعت، RK; بری، آر. Clapp، JM; Rodriquez, M. مدل‌های خودرگرسیون فضایی-زمانی اثرات همسایگی. جی. امور مالی املاک و مستغلات. اقتصاد 1998 ، 17 ، 15-33. [ Google Scholar ] [ CrossRef ]
تلخ، سی. مولیگان، GF; Dall’erba، S. ترکیب تغییرات فضایی در قیمت ویژگی های مسکن: مقایسه رگرسیون وزنی جغرافیایی و روش گسترش فضایی. جی. جئوگر. سیستم 2007 ، 9 ، 7-27. [ Google Scholar ] [ CrossRef ]
هوانگ، بی. وو، بی. Barry, M. رگرسیون وزن‌دار جغرافیایی و زمانی برای مدل‌سازی تغییرات مکانی-زمانی قیمت مسکن. بین المللی جی. جئوگر. Inf. علمی 2010 ، 24 ، 383-401. [ Google Scholar ] [ CrossRef ]
Chica-Olmo, J. پیش بینی قیمت مکان خانه با روش فضایی چند متغیره: Cokriging. J. Real Estate Res. 2007 ، 29 ، 91-114. [ Google Scholar ]
دوبین، RA خودهمبستگی فضایی و کیفیت همسایگی. Reg. علمی اقتصاد شهری 1992 ، 22 ، 433-452. [ Google Scholar ] [ CrossRef ]
گامز ماتینز، م. مونترو لورنزو، جی.ام. گارسیا روبیو، روش N. Kriging برای تجزیه و تحلیل اقتصادی منطقه ای: برآورد قیمت مسکن در آلباسته. بین المللی Adv. اقتصاد Res. 2000 ، 6 ، 438-451. [ Google Scholar ] [ CrossRef ]
جورجویچ، دی. اوگستر، سی. هاس، R. برآورد مدل‌های لذت‌گرا با استفاده از رویکرد چند سطحی: یک برنامه کاربردی برای بازار اجاره سوئیس. سوئیسی جی. اکون. آمار 2008 ، 144 ، 679-701. [ Google Scholar ] [ CrossRef ]
چاسکو، سی. Le Gallo، J. اثرات سلسله مراتبی و خودهمبستگی فضایی در مدل‌های لذت‌گرا. Econ.Bull. 2012 ، 32 ، 1474-1480. [ Google Scholar ]
اورفورد، اس. مدل سازی ساختارهای فضایی در پویایی بازار خانه های محلی: یک دیدگاه چند سطحی. مطالعه شهری. 2000 ، 37 ، 1643-1671. [ Google Scholar ] [ CrossRef ]
چایکس، بی. مرلو، جی. Chauvin، P. مقایسه یک رویکرد فضایی با رویکرد چند سطحی برای بررسی اثرات مکان بر سلامت: مثالی از استفاده از مراقبت های بهداشتی در فرانسه. J. Epidemiol. سلامت جامعه 2005 ، 59 ، 517-526. [ Google Scholar ] [ CrossRef ] [ PubMed ]
Can, A. مشخصات و برآورد مدل‌های قیمت خانه لذت‌بخش. Reg. علمی اقتصاد شهری 1992 ، 22 ، 453-474. [ Google Scholar ] [ CrossRef ]
لوریس، جی. Bhattacharya, R. عملکرد پیش بینی یک مدل قیمت گذاری لذت بخش برای خانه. ارزیابی. J. 2005 , 73 , 198. [ Google Scholar ]
Limsombunchai، V. پیش‌بینی قیمت خانه: مدل قیمت لذت‌گرا در مقابل شبکه عصبی مصنوعی. در مجموعه مقالات کنفرانس انجمن اقتصاد کشاورزی و منابع نیوزیلند، بلنهایم، نیوزلند، 25-26 ژوئن 2004. صص 25-26. [ Google Scholar ]
لیو، X. وابستگی مکانی و زمانی در پیش‌بینی قیمت مسکن. جی. امور مالی املاک و مستغلات. اقتصاد 2013 ، 47 ، 341-369. [ Google Scholar ] [ CrossRef ]
لیشمن، سی. کاستلو، جی. رولی، اس. واتکینز، سی. عملکرد پیش‌بینی مدل‌های چند سطحی بازارهای فرعی خانه: تحلیل مقایسه‌ای. مطالعه شهری. 2013 ، 50 ، 1201-1220. [ Google Scholar ] [ CrossRef ]
Bourassa, SC; هوسلی، م. پنگ، وی سی آیا بازارهای فرعی خانه واقعا اهمیت دارند؟ J. هاوس Econ. 2003 ، 12 ، 12-28. [ Google Scholar ] [ CrossRef ]
گودمن، ای سی؛ Thibodeau، تقسیم‌بندی بازار خانه TG و دقت پیش‌بینی لذت‌گرا. J. هاوس Econ. 2003 ، 12 ، 181-201. [ Google Scholar ] [ CrossRef ]
پارک، YM؛ Kim, Y. یک مدل چندسطحی فیلتر شده فضایی برای توضیح وابستگی فضایی: کاربرد برای وضعیت سلامت خود رتبه‌بندی در کره جنوبی. بین المللی J. Health Geogr. 2014 ، 13 ، 6. [ Google Scholar ] [ CrossRef ]
Reichert، AK تأثیر نرخ بهره، درآمد و اشتغال بر قیمت مسکن منطقه ای. جی. امور مالی املاک و مستغلات. اقتصاد 1990 ، 3 ، 373-391. [ Google Scholar ] [ CrossRef ]
کاجوث، اف. اشمیت، تی. فصلی بودن در قیمت خانه، سری 1: مطالعات اقتصادی، مقاله بحث . Deutsche Bundesbank: فرانکفورت، آلمان، 2011. [ Google Scholar ]
Ngai، LR; Tenreyro, S. فصول گرم و سرد در بازار خانه. صبح. اقتصاد Rev. 2014 , 104 , 3991-4026. [ Google Scholar ] [ CrossRef ]
Kuo، CL سریال همبستگی و فصلی در بازار املاک و مستغلات. جی. امور مالی املاک و مستغلات. اقتصاد 1996 ، 12 ، 139-162. [ Google Scholar ] [ CrossRef ]
بلتراتی، ا. مورانا، سی. قیمت های بین المللی مسکن و نوسانات کلان اقتصادی. جی. بانک. مالی 2010 ، 34 ، 533-545. [ Google Scholar ] [ CrossRef ]
ننجی، او. بروکس، سی. دینامیک قیمت خانه Ward، CW و واکنش آنها به تغییرات کلان اقتصادی. اقتصاد مدل. 2013 ، 32 ، 172-178. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
گودمن، AC مقایسه داده‌های گروه بلوک و دستگاه سرشماری در یک مدل قیمت خانه لذت‌بخش. اقتصاد زمین 1977 ، 53 ، 483-487. [ Google Scholar ] [ CrossRef ]
گریفیث، DA خودهمبستگی فضایی و فیلتر فضایی: به دست آوردن درک از طریق تئوری و تجسم علمی . Springer: برلین، آلمان، 2003. [ Google Scholar ]
چون، ی. گریفیث، دی. لی، ام. Sinha، P. انتخاب بردار ویژه با تکنیک های رگرسیون گام به گام برای ساخت فیلترهای فضایی بردار ویژه. جی. جئوگر. سیستم 2016 ، 18 ، 67-85. [ Google Scholar ] [ CrossRef ]
رزعلی، ن.م. مقایسه قدرت واه، وای بی تست های شاپیرو-ویلک، کولموگروف- اسمیرنوف، لیلیفور و اندرسون-عزیزم. J. Stat. مدل. مقعدی 2011 ، 2 ، 21-33. [ Google Scholar ]
Bin, O. مقایسه پیش‌بینی قیمت فروش مسکن با رگرسیون پارامتری در مقابل نیمه پارامتریک. J. هاوس Econ. 2004 ، 13 ، 68-84. [ Google Scholar ] [ CrossRef ]
گریفیث، دی. Chun, Y. ارزیابی اصلاحات فیلتر فضایی بردار ویژه برای متغیرهای جغرافیایی ارجاع شده حذف شده. اقتصاد سنجی 2016 ، 4 ، 29. [ Google Scholar ] [ CrossRef ]

شکل 1. توزیع های جغرافیایی قیمت خانه های تک خانواری در سال 1395.

شکل 2. توزیع قیمت مسکن در سال 2016. ( الف ) هیستوگرام قیمت مسکن، ( ب ) هیستوگرام قیمت لگاریتمی مسکن.

شکل 3. اثرات تصادفی تخمینی (RE) و مولفه های فیلتر فضایی بردار ویژه (ESF). ( الف ) جزء RE از مدل چند سطحی. ( ب ) مولفه RE از مدل چندسطحی فیلتر فضایی بردار ویژه موران (MESF). ( ج ) جزء ESF از مدل MESF چند سطحی.

شکل 4. نمودارهای پراکنده خانه های مشاهده شده در مقابل قیمت های پیش بینی شده. ( الف ) قیمت‌های خانه مشاهده‌شده در مقابل قیمت‌های پیش‌بینی‌شده با مدل لذت‌بخش. ( ب ) قیمت خانه مشاهده شده در مقابل قیمت های پیش بینی شده با مدل چندسطحی. ( ج ) قیمت‌های خانه مشاهده‌شده در مقابل قیمت‌های پیش‌بینی‌شده با مدل چندسطحی MESF.

شکل 5. توزیع های جغرافیایی قیمت خانه های مشاهده شده ( الف ) و قیمت های پیش بینی شده مسکن ( ب ) در سال 2017.

مقالات داخلی و بین المللی

بدون دیدگاه

دیدگاهتان را بنویسید لغو پاسخ

برای نوشتن دیدگاه باید وارد بشوید.

مشاورین هوش پیروزی

خلاصه

کلید واژه ها:

1. معرفی

2. پس زمینه