هدف تلفیق داده‌های مکانی تطبیق و ادغام اشیاء در دو مجموعه داده در مجموعه‌ای جامع‌تر است. با شروع از “مسئله تخصیص نقشه” در دهه 1980، مدل های ترکیبی بهینه سازی شده تطبیق ویژگی ها را به عنوان یک مشکل بهینه سازی طبیعی برای به حداقل رساندن معیارهای خاص، مانند اختلاف کل، در نظر می گیرند. یکی از پیچیدگی‌های ترکیب بهینه این است که مجموعه داده‌های ناهمگن می‌توانند ویژگی‌های جغرافیایی را متفاوت نشان دهند. ویژگی ها می توانند با ویژگی های هدف در مجموعه داده دیگر مطابقت داشته باشند یا به صورت یک به یک (تشکیل منطبقات کامل) یا به صورت چند به یک (تشکیل منطبقات جزئی). مدل های سنتی به طور انحصاری یا تطابق کامل یا جزئی را در نظر می گیرند. این دوگانگی چند موضوع دارد. اولاً، مدل‌های تطبیق کامل محدود هستند و نمی‌توانند مطابقت جزئی را ثبت کنند. ثانیاً مدل‌های تطبیق جزئی، منطبق‌های کامل را دقیقاً مانند تطابق جزئی تلقی می‌کنند، و بیشتر مستعد پذیرش تطابق‌های نادرست هستند. ثالثاً، مدل‌های ترکیبی موجود ممکن است تطابق‌های جهتی متناقضی را معرفی کنند. این مقاله مدل جدیدی را ارائه می‌کند که هم‌زمان مطابقت کامل و هم جزئی را به طور همزمان ضبط می‌کند. این به ما اجازه می‌دهد تا محدودیت‌های ساختاری را به‌طور متفاوتی روی مسابقات کامل/جزئی اعمال کنیم و سازگاری بین مسابقات جهت‌دار را اعمال کنیم. نتایج تجربی نشان می‌دهد که مدل جدید از نظر دقت (89.2٪) از مدل‌های ادغام بهینه‌سازی شده معمولی بهتر عمل می‌کند، در حالی که به یک فراخوان مشابه (93.2٪) دست می‌یابد. این مقاله مدل جدیدی را ارائه می‌کند که هم‌زمان مطابقت کامل و هم جزئی را به طور همزمان ضبط می‌کند. این به ما اجازه می‌دهد تا محدودیت‌های ساختاری را به‌طور متفاوتی روی مسابقات کامل/جزئی اعمال کنیم و سازگاری بین مسابقات جهت‌دار را اعمال کنیم. نتایج تجربی نشان می‌دهد که مدل جدید از نظر دقت (89.2٪) از مدل‌های ادغام بهینه‌سازی شده معمولی بهتر عمل می‌کند، در حالی که به یک فراخوان مشابه (93.2٪) دست می‌یابد. این مقاله مدل جدیدی را ارائه می‌کند که هم‌زمان مطابقت کامل و هم جزئی را به طور همزمان ضبط می‌کند. این به ما اجازه می‌دهد تا محدودیت‌های ساختاری را به‌طور متفاوتی روی مسابقات کامل/جزئی اعمال کنیم و سازگاری بین مسابقات جهت‌دار را اعمال کنیم. نتایج تجربی نشان می‌دهد که مدل جدید از نظر دقت (89.2٪) از مدل‌های ادغام بهینه‌سازی شده معمولی بهتر عمل می‌کند، در حالی که به یک فراخوان مشابه (93.2٪) دست می‌یابد.

کلید واژه ها:

ادغام داده ها ; تلاطم ; بهینه سازی ; سیستم های اطلاعات جغرافیایی

1. مقدمه

یک نیاز رایج در بسیاری از تحلیل‌های فضایی عملی، ترکیب مؤثر اطلاعات از منابع داده‌های مختلف است. در مطالعات حمل‌ونقل، سازمان‌های دولتی مانند سرشماری ایالات متحده، داده‌های شبکه جاده‌ای را با اطلاعات اقتصادی-اجتماعی غنی ارائه می‌کنند، در حالی که شرکت‌های خصوصی و GIS‌های جمعی، اطلاعات دقیق‌تری درباره زیرساخت‌ها از جمله محدودیت سرعت، تعداد خطوط، نوع سطح و غیره ارائه می‌کنند. با مطالعه مهاجرت و روندهای تاریخی، اغلب لازم است داده های GIS از مقاطع زمانی مختلف که با یکدیگر همسو نیستند ترکیب شوند. در تمام این موارد، تحلیلگر لازم است عناصر داده را از منابع مختلف تطبیق داده و آنها را در یک مجموعه داده بهتر ترکیب کند. این فرآیند به عنوان ادغام شناخته می شود.
از نظر مفهومی، تلفیق را می توان به دو مرحله تقسیم کرد. مرحله اول تطبیق است که در آن ویژگی های GIS مربوط به همان اشیاء در واقعیت به یکدیگر مرتبط می شوند. مرحله دوم ادغام است، که در آن ویژگی ها و/یا هندسه ها از یک مجموعه داده به دیگری منتقل می شوند یا برای تشکیل یک مجموعه داده جدید ادغام می شوند. از بین این دو مرحله، تطبیق اغلب کار دشوارتر است، زیرا اشتباه کردن مطابقت، روند ادغام بعدی را خراب می کند. علاوه بر این، پیچیدگی‌های موجود در داده‌های GIS می‌تواند الگوریتم‌های رایانه‌ای را گیج کند و باعث تطابق اشتباه شود. شکل 1a طرح‌بندی ویژگی‌های جاده مرکز شهر سانتا باربارا، کالیفرنیا را به ترتیب از OpenStreetMap (OSM سبز) و TIGER (قرمز) ارائه می‌کند. برای بقیه مقاله، شبکه جاده OSM را با رنگ سبز و جاده های TIGER را با رنگ قرمز در شکل ها نشان می دهیم. می‌توان مشاهده کرد که فاصله‌های فضایی زیادی بین ویژگی‌های متناظر وجود دارد – به اندازه‌ای بزرگ که اگر از عملیات استاندارد GIS مانند اتصال نزدیک‌ترین همسایه برای تطبیق ویژگی‌ها استفاده کنیم، مشکلاتی ایجاد کند. Bath St. در OSM با خیابان Curley در TIGER مطابقت دارد. به همین ترتیب، خیابان کرلی در OSM با خیابان کاستیلو در TIGER مطابقت دارد. استخراج کبریت های صحیح پیش نیاز تلفیق موفقیت آمیز است.
مفهوم تطبیق ممکن است به آن سادگی که به نظر می رسد نباشد. مفهوم شناسایی ویژگی‌های متناظر در مثال بالا فرض می‌کند که این دو ویژگی یک شی را به طور کامل نشان می‌دهند. مکاتبات در اینجا یک تطابق کامل (یا تطابق یک به یک) است و ساده ترین رابطه مطابقت است. روابط پیچیده تری وجود دارد. شکل 1b همان شبکه جاده را برای بلوک خیابان دیگر نشان می دهد. خیابان Anapamu شرقی به‌عنوان یک چندخط منفرد در مجموعه داده‌های TIGER نشان داده شد، اما توسط یک جاده بدون نام در مجموعه داده OSM به دو چند خط تقسیم شد. مطابقت آنها (فلش های آبی) مسابقات جزئی است (همچنین به عنوان مسابقات چند به یک نیز شناخته می شود). مسابقات جزئی با تعداد احتمالات بیشتر پیچیده تر هستند. یک خیابان را می توان به چند قسمت تقسیم کرد که برخی از قسمت ها به درستی و برخی دیگر نادرست مطابقت داشته باشند. به طور کلی، تطابق جزئی اغلب ناشی از تفاوت در مقیاس یا سطح جزئیات [ 1 ] است. همانطور که در بخش بعدی بحث شد، روابط تطبیق پیچیده تری در سطح زیر ویژگی وجود دارد.
در میان روابط مختلف تطابق، مطابقت کامل را می توان با موفقیت توسط الگوریتم های ترکیبی موجود مانند “مسئله تخصیص نقشه” که در دهه 1980 مفهوم سازی شد، مدیریت کرد. یکی از کاستی های این مدل ها این است که نمی توانند مسابقات جزئی را ضبط کنند و بخشی از تمام مسابقات را از دست بدهند. تطابق جزئی می تواند برای برخی از الگوریتم های ترکیبی فعلی مشکل ساز باشد. الگوریتم‌های تطبیق جزئی فعلی یا به‌صراحت تطابق کامل را در نظر نمی‌گیرند یا آنها را به عنوان یک تطابق جزئی یا دو تطابق جزئی (در جهت مخالف) در نظر می‌گیرند. به دلیل پیچیدگی بیشتر، چنین درمان‌هایی اغلب در مقایسه با الگوریتم‌های تطبیق کامل، تطابق کاذب (مثبت) بالاتر و دقت کمتری دارند.
در این مقاله، ما یک رویکرد بهینه‌سازی برای تلفیق را در نظر می‌گیریم. مشابه “مسئله انتساب نقشه”، ما تلفیقی را به عنوان یک مشکل به حداقل رساندن اختلاف کل یا به حداکثر رساندن شباهت در نظر می گیریم. به طور خاص، ما یک مدل بهینه‌سازی یکپارچه برای ترکیب ارائه می‌کنیم که به طور همزمان مطابقت‌های جزئی کامل و دو طرفه را در نظر می‌گیرد. برخلاف مدل‌های ترکیبی بهینه‌سازی شده سنتی، ما تصمیمات مربوط به ایجاد تطابق کامل و تطابق جزئی را در یک مدل یکسان می‌کنیم. ما به صراحت تطابق کامل و جزئی را با متغیرهای تصمیم جداگانه بیان می کنیم. این درمان امکان اولویت بندی مسابقات کامل (چون قابل اطمینان تر هستند) و در عین حال امکان مسابقات جزئی را فراهم می کند. علاوه بر این، ما محدودیت‌های ساختاری جدیدی را برای جلوگیری از تطابق متناقض در دو جهت مخالف اعمال می‌کنیم. ما همچنین از یک فاصله رشته ساده برای استفاده از اطلاعات نام خیابان استفاده می کنیم. نتایج تجربی با استفاده از مجموعه داده‌های قابل مقایسه نشان می‌دهد که مدل جدید از مدل‌های ترکیبی بهینه‌سازی شده مرسوم از جمله مدل‌های مبتنی بر جریان شبکه و همچنین مشکل انتساب کلاسیک بهتر عمل می‌کند.
بقیه این مقاله به شرح زیر سازماندهی شده است. بخش 2 مروری مختصر از روش های ادغام و ادبیات مربوطه ارائه می دهد. بخش 3 فرمول بندی مدل پیشنهادی و ملاحظات طراحی آن را ارائه می کند. بخش 4 نتایج محاسباتی به‌دست‌آمده با استفاده از دو مجموعه داده شبکه جاده‌ای برای سانتا باربارا، کالیفرنیا را ارائه می‌کند. سپس مقاله را با خلاصه ای از یافته ها به پایان می رسانیم و تحقیقات احتمالی آینده را پیشنهاد می کنیم.

2. پس زمینه

تلفیق در طیف وسیعی از تحلیل‌های فضایی مورد نیاز است زیرا داده‌های مکانی درباره یک پدیده اغلب توسط فروشندگان مختلف و/یا در زمان‌های مختلف تولید می‌شوند. یک مثال از کاربرد تلفیقی، شبکه های جاده ای است. این نه تنها به دلیل پیچیدگی زیاد چنین شبکه هایی است، بلکه به دلیل عملکرد مهم آنها به عنوان دالان حرکت و یک سیستم مرجع مشترک است. بسیاری از منابع داده‌های جاده‌ای را ارائه می‌کنند، از جمله سازمان‌های دولتی، مانند سرشماری ایالات متحده، و شرکت‌های خصوصی مانند Here.com. تحقیقات حمل و نقل اغلب به اطلاعات غنی از همه این منابع نیاز دارد. ترکیب مرزهای اداری تاریخی یکی دیگر از کاربردهای برجسته تلفیق است. استفاده صحیح از داده های تاریخی مستلزم شناسایی تغییرات در طول زمان و پیوند دادن مناطقی است که با یک منطقه در دوره های زمانی مختلف مطابقت دارند. به دلیل کاربرد بالقوه آنها، بسیاری از روش های تلفیقی از دهه 1980 توسعه یافته اند.2 ، 3 ، 4 ]. آنها برای ادغام انواع مختلف ویژگی‌ها، از جمله ویژگی‌های نقطه تطبیق (مثلاً روزنامه‌ها [ 5 ]) و ویژگی‌های خطی (مانند جاده‌ها [ 6 ] و شبکه‌های رودخانه)، و ویژگی‌های منطقه‌ای (مانند ردپاهای ساختمانی و سرشماری [5]) استفاده شده‌اند. 7 ]) به ترتیب.

2.1. اقدامات شباهت

فاصله ها یا معیارهای تشابه مفاهیم رایجی هستند که زیربنای اکثر روش های ترکیبی هستند. آنها میزان متفاوت یا مشابه بودن دو ویژگی را بر اساس هندسه، ویژگی ها و خواص توپولوژیکی آنها اندازه می گیرند. برای بررسی جامع معیارهای تشابه در ترکیب، خواننده به [ 8 ] ارجاع داده می شود. در میان معیارهای مختلف شباهت، شباهت هندسی پرکاربردترین متریک برای همگرایی مکانی است [ 8 ]. می توان آن را مستقیماً از جابجایی فضایی رئوس دو شکل محاسبه کرد. یک فاصله پرکاربرد از این نوع فاصله هاوسدورف است. با توجه به دو ویژگی آAو بB(به عنوان مثال، دو چند خط)، فاصله هاسدورف هدایت شده از آAبه بBاست h ( A , B ) =حداکثرp ∈ Aدقیقهq∈ ب∥ p − q∥hA,B=maxp∈Aminq∈B∥p−q∥. این حداکثر افست از هر نقطه در ویژگی است آAویژگی کردن بB. اگر این فاصله صفر یا نزدیک به صفر باشد، بدیهی است آAیا منطبق بر بخشی از بBیا دروغ نزدیک به بB. به عبارت دیگر، آAاحتمالاً با بخشی از مطابقت دارد بBیا متعلق به بB. فاصله کامل هاسدورف H ( A , B )HA,Bبه عنوان بزرگتر از دو فاصله هاسدورف جهت دار تعریف شده است h ( A , B )hA,Bو h ( B , A )hB,A. اگر (نزدیک) صفر باشد، این دو ویژگی به یکدیگر تعلق دارند یا یکسان هستند. سایر توابع فاصله، مانند فاصله Frechet و تابع چرخش، قابلیت بیشتری برای مشخص کردن تفاوت در شکل دارند، اما از نظر محاسباتی گران‌تر هستند. برخی از محققان با محاسبه معیارهای جایگزین مانند طول، اندازه و فشردگی دو ویژگی را مقایسه کردند و سپس تفاوت‌های آنها را بر اساس چنین معیارهایی مقایسه کردند.
محققان همچنین ویژگی ها را بر اساس تفاوت آنها در ویژگی هایی مانند نام خیابان ها مقایسه کرده اند. نویسندگان [ 9 ] از فاصله هامینگ برای اندازه گیری تفاوت نام خیابان ها علاوه بر متریک فاصله نوع جابجایی (فاصله هاسدورف) استفاده کردند. نویسندگان [ 5 ] از فاصله لونشتاین برای توصیف شباهت نام مکان ها استفاده کردند. معیارهای توپولوژیکی نیز برای مقایسه دو ویژگی بر اساس اطلاعات زمینه‌ای، مانند تعداد یال‌هایی که یک گره به آنها متصل است (یعنی درجه آن) استفاده شده است.

2.2. استخراج روابط مسابقه

اختلاط مؤثر به استفاده از یک معیار شباهت خوب متکی است. علاوه بر این، فرآیندی برای انتخاب جفت ویژگی های متناظر برای مطابقت بر اساس شباهت آنها مورد نیاز است. ساده‌ترین استراتژی انتخاب، اختصاص دادن هر ویژگی به ویژگی‌های نامزد در مجموعه داده دیگر صرفاً بر اساس فواصل آنهاست. این ایده در پس روش های ترکیبی نهفته است که مستقیماً از عملیات استاندارد GIS استفاده می کنند. دو نوع عملیات GIS اغلب در این زمینه استفاده می شود. اولین مورد نزدیکترین پیوستن به همسایه است (برای بحث به [ 10 ] مراجعه کنید). در اینجا، یک ویژگی به نزدیکترین نامزد (نزدیکترین تکلیف) اختصاص داده می شود. یک الگوریتم مرتبط به نام k-Closest Pairs Queries (KCPQ) نیز در تحقیقات پایگاه داده فضایی [ 11 ] وجود دارد که کkجفت ویژگی های منطبق با کمترین فاصله. روش‌های نوع دوم از تحلیل بافر استفاده می‌کنند (به عنوان مثال، [ 12 ] را ببینید). در اینجا، ابتدا بافرهایی برای دو ویژگی ایجاد می شود و قدرت ارتباط بین آنها با میزان همپوشانی بین چند ضلعی های بافر اندازه گیری می شود. به نوعی، روش های بافر نوعی از نزدیک ترین استراتژی تخصیص هستند که در آن به جای مقایسه فاصله ها در مقیاس پیوسته، از آستانه فاصله (یعنی شعاع بافر) استفاده می شود.
اگر دو مجموعه داده درگیر به خوبی همسو باشند، روش‌هایی که صرفاً به فاصله‌های فردی متکی هستند، ممکن است به خوبی کار کنند. با این حال، همانطور که در شکل 1 الف نشان داده شده است، این روش ها می توانند به راحتی در صورت وجود هرگونه جابجایی فضایی قابل توجه، مختل شوند. هنگام استفاده از نزدیکترین استراتژی تخصیص، ممکن است ویژگی ها به نامزدهای نادرست اختصاص داده شود. همپوشانی بافر ممکن است باعث شود چندین نامزد با آستانه مواجه شوند یا اصلاً نامزدی نداشته باشند. به طور کلی، این الگوریتم‌ها ماهیت «طمع‌آمیز» دارند و هنگامی که یک تطابق اشتباه ایجاد شود، تصحیح خطا پس از آن دشوار است.
یک مشکل جدی تر در مورد استراتژی حریصانه بالا این است که می تواند مطابقت های ناسازگار ایجاد کند. همانطور که توسط [ 10 ] اشاره شد، استفاده از اتصالات نزدیکترین همسایه ممکن است تخصیص های انتقالی ایجاد کند. یک ویژگی آAدر مجموعه داده 1 ممکن است ویژگی هایی داشته باشد بBدر سمت راست آن در مجموعه داده 2 به عنوان نزدیکترین ویژگی آن (و بنابراین با انتساب حریصانه مطابقت دارد)، اما ممکن است این ویژگی باشد بBممکن است ویژگی دیگری داشته باشد سیCدر سمت راست در مجموعه داده 1 که حتی نزدیکتر است. بنابراین، الگوریتم تخصیص می دهد آAبه بBو سپس اختصاص دهید بBبه یک ویژگی دیگر سیC. این تکلیف گذرا A → B → CA→B→Cاز نظر منطقی ناسازگار است تحت فرض تطابق کامل، این به این معنی است آAبرابر است با بBدر مجموعه داده 2، اما بBبرابر با چیز دیگری است (ویژگی سیC) در مجموعه داده 1.
برای رسیدگی به تضادهای نزدیکترین اتصالات فضایی، [ 10 ] برای محاسبه مقادیر اطمینان معینی برای جفت ویژگی (بر اساس فواصل در گزینه های رقیب) پیشنهاد شد. چندین قانون مختلف برای انتخاب منطبق‌ها تعریف شد، از جمله استفاده از یک آستانه در مقدار اطمینان، استفاده از یک مقدار “احتمال” پروکسی، و انتخاب جفت با بالاترین مقدار و روش “نزدیک‌ترین همسایه متقابل”. روش‌های پیچیده‌تر انتخاب تطابق عبارتند از [ 13 ]، که در آن نویسندگان از یک روش رگرسیون لجستیک برای تکمیل یک مدل ترکیبی مبتنی بر بهینه‌سازی استفاده کردند. این روش های پیچیده انتخاب بازی اجازه می دهد تا دامنه انتخاب به بسیاری از ویژگی ها در محله گسترش یابد.
برای رسیدگی به مسائل مرتبط با جابجایی فضایی، سرشماری ایالات متحده به اصطلاح روش لایه‌بندی لاستیکی [ 14 ] را در حالی که مجموعه داده‌های آن‌ها را با داده‌های USGS یکپارچه می‌کند، توسعه داد. این شامل انتخاب مجموعه ای از نقاط لنگر است که نشان دهنده نقاط متناظر برجسته (مانند اتصالات جاده) از دو مجموعه داده است. سپس فضا را به مناطق مثلثی بین نقاط لنگر تقسیم می‌کند و نقاط لنگر را از طریق تبدیل‌های پیوسته محلی یکسان می‌کند. ویژگی های بین لنگرها به طور همزمان با آنها جابجا شده و جابجایی های فضایی کاهش می یابد. اگرچه این یک روش پیش پردازش پرکاربرد است [ 6 ، 7 ، 15 ، 16]، روش ورق لاستیکی خود به کار دستی زیادی نیاز دارد و می تواند گران یا زمان بر باشد.

2.3. مدل‌های ادغام بهینه

ترکیب مبتنی بر بهینه سازی یک روش تطبیق شناخته شده است و تمرکز این مطالعه است. از ابتدای تحقیق تلفیق مفهوم سازی شده است. مسئله اختلاط به عنوان یک مسئله بهینه سازی انتخاب تطابق در نظر گرفته می شود که یک مقدار هدف معین مانند فاصله کل را بهینه می کند. نویسندگان [ 14 ] در دهه 1980 ایده فرمول بندی ترکیب را به عنوان “مسئله تخصیص تطبیق نقشه” و استفاده از برنامه ریزی خطی برای حل آن مورد بحث قرار دادند. به طور سنتی، ترکیب بهینه شده با استفاده از مسئله انتساب مورد بررسی قرار می گرفت. این تا قبل از کار لی و گودچایلد [ 17 ] در سال 2010 مورد آزمایش قرار نگرفت. در ابتدا برای اختصاص یک مجموعه اختراع شد منIاز nnکارگران به یک مجموعه جیJاز nnشغل ها. هر تکلیف از منiبه jjبا هزینه همراه است جijcijمنعکس کننده، برای مثال، زمان لازم برای کارگر منiبرای تکمیل کار jj. هدف از مسئله انتساب به حداقل رساندن کل هزینه انتساب است جijcij. واضح است که این تنظیم مشکل را می توان با اجازه دادن به مجموعه ها در ترکیب داده ها استفاده کرد منI، جیJدو مجموعه داده ای باشد که باید با هم ترکیب شوند/تطبیق شوند و یک متریک فاصله یا عدم تشابه (مانند فاصله هاسدورف) هزینه تخصیص باشد. جijcij.
مشکل انتساب یک مدل تطبیق کامل است و به هر ویژگی نیاز دارد منIو جیJبا ویژگی های موجود در مجموعه داده دیگر به صورت یک به یک مطابقت داده شود. اینها تنها محدودیت‌های مشکل انتساب هستند (که گاهی اوقات محدودیت‌های اصلی نامیده می‌شود). این به این معنی است که مجموعه داده ها IIو JJباید به یک اندازه باشد – فرضی که در بیشتر مواقع صادق نیست. در [ 17 ]، نویسندگان یکی از محدودیت‌های اصلی را اصلاح کردند تا دو مجموعه داده با اندازه‌های مختلف با هم تطبیق داده شوند و تنها عناصر مجموعه داده‌های کوچک‌تر برای تخصیص لازم هستند. مشکل تخصیص نقشه می تواند به طور موثر مطابقت کامل را مدیریت کند. نویسندگان [ 17 ] با استفاده از مسئله انتساب به نرخ تطابق بالایی دست یافتند. با این حال، مشکل انتساب نمی تواند مطابقت های جزئی را مدیریت کند. در [ 13 ]، نویسندگان دریافتند که مشکل انتساب هنگام آزمایش در شبکه‌های جاده‌ای پیچیده‌تر، دقت کمتری به میزان 56.5 درصد به دست آورد. آنها مجبور بودند یک مؤلفه رگرسیون لجستیک اضافه کنند تا مسابقات دشوارتر را مدیریت کنند.
نویسندگان [ 9 ] مسئله انتساب را به چندین روش برای رسیدگی به تطابقات جزئی گسترش دادند. اول، آنها یک فاصله هاسدورف جهت دار را به عنوان معیار تشابه (به جای فاصله هاسدورف هدایت نشده) اتخاذ کردند. این به این دلیل است که مسابقات جزئی دارای فواصل هدایت شده کوچکی هستند اما می توانند فواصل کامل زیادی داشته باشند. دوم، از آنجایی که منطبقات جزئی جهت دار هستند، از دو نسخه از یک مدل تخصیص مانند برای انتخاب موارد منطبق استفاده کردند. IIبه JJو از جیJبه منI. آنها سپس فرآیندی را برای ترکیب نتایج دو مدل ایجاد کردند و در صورت لزوم، تناقضات را حذف کردند. آنها با اضافه کردن یک محدودیت ظرفیت که طول کل خیابان هایی را که می توان به یک خیابان هدف اختصاص داد به نسبتی نزدیک به یک محدود کرد، مشکل تخصیص را بیشتر اصلاح کردند. آنها همچنین یک محدودیت ویژه اضافه کردند که به هر ویژگی که دارای یک ویژگی هدف به اندازه کافی نزدیک است نیاز دارد تا اختصاص داده شود.
یکی از محدودیت‌های مشکل انتساب، فرض دقیق آن است که هر ویژگی در (حداقل یکی از) دو مجموعه داده باید اختصاص داده شود. برای پرداختن به چنین مسائلی، [ 18 ] دو مدل مبتنی بر جریان شبکه به نام‌های P-Matching و P-Double-Matching را بر اساس مشکل شبکه حداقل هزینه کلاسیک (که به اختصار مشکلات جریان شبکه نامیده می‌شود) معرفی کرد. مشکل شبکه یکی دیگر از خوشه‌های مدل‌های کلاسیک در تحقیقات عملیات است. بیانگرتر از مسئله انتساب است و چندین مسئله بهینه سازی دیگر از جمله مسئله انتساب و مسئله کوتاه ترین مسیر را به عنوان موارد خاص خود درج می کند. نویسندگان [ 18] نیاز به ایجاد تعادل بین دو هدف را تشخیص داد: ایجاد تعداد زیادی مسابقه و پایین نگه داشتن مثبت کاذب. آنها یک روش تطبیقی ​​برای آزمایش تعداد تطابق فزاینده ایجاد کردند تا زمانی که حداکثر اختلاف/فاصله بین جفت‌های ویژگی به یک مقدار بحرانی از پیش تعریف‌شده برسد. مدل تطبیق p یک گسترش طبیعی از مسئله انتساب بود که نیازی به تخصیص همه ویژگی‌ها ندارد. مسئله تطبیق p-double تخصیص جزئی را در هر دو جهت در یک بهینه سازی فرموله کرد. از آنجایی که شامل دو مدل مجزا نمی شود، زیربهینه بودن را کاهش می دهد و نیازی به پس پردازش ندارد. آنها این مدل را با استفاده از یک حل کننده بهینه سازی منبع باز به نام کتابخانه LEMON حل کردند. این آزمایش در [ 18] نشان داد که مدل تطبیق کامل (یک به یک) (تطابق p) به دقت بالاتری دست یافت (یعنی تطبیق های کاذب کمتری ایجاد می کند)، در حالی که مدل تطبیق جزئی (تطبیق چند به یک) (تطابق p-double) به قیمت نرخ تطابق کاذب بالاتر، مسابقات بیشتری را در حقیقت زمین ثبت می کند.
در [ 19 ]، نویسندگان گونه‌ای از مدل‌های تطبیق p مبتنی بر جریان شبکه به نام مشکلات تطبیق شارژ ثابت را پیشنهاد کردند. این مقاله شامل یک نسخه تطبیق کامل به نام مشکل fc-matching و یک نسخه تطبیق جزئی به نام مشکل fc-bimatching بود. مشکلات تطبیق شارژ ثابت نیازی به فرآیند آزمون و خطا ندارند، مانند مشکلات p-matching، برای جستجوی تعداد صحیح مطابقت. در عوض، تعداد کل موارد منطبق برای انتخاب به صورت پویا بر اساس انگیزه ای تعیین می شود که به عنوان شارژ ثابت (منفی) بر روی یک لینک متعادل کننده جریان ویژه در شبکه جریان اعمال می شود. برای اجازه دادن به ترکیب بهینه در مجموعه داده‌های بزرگ، [ 20 ] استراتژی‌های تقسیم و غلبه را برای مشکلات تطبیق شارژ ثابت [ 19 ] توسعه داد.] با بافر نامتقارن و تعادل حجم کار.
تا این مرحله، مدل‌های ترکیبی بهینه‌سازی شده موجود بر اساس مسئله تخصیص و مشکلات جریان شبکه هستند. محدودیت‌های مدل‌ها به این معنا که عمدتاً محدودیت‌های اصلی هستند، نسبتاً ضعیف هستند. این ممکن است برای مدل‌های تطبیق کامل کافی باشد اما برای مدل‌های تطبیق جزئی ناکافی است، زیرا احتمال خطای بیشتری دارند (به دلیل انتساب‌های گذرا، تقسیم‌بندی‌های جزئی و غیره). هیچ چیز مدل را از ایجاد تطابقات منطقی ناسازگار مانند انتساب های گذرا باز نمی دارد. علاوه بر این، مدل‌های ترکیبی موجود یا فقط تطبیق‌های کامل را در نظر می‌گیرند (مثلاً مسئله انتساب، مدل‌های تطبیق p و fc) یا فقط تطابق‌های جزئی را در نظر می‌گیرند ([ 9 ]] مدل، P-Double-Matching، و fc-bimatching). در مدل‌های تطبیق جزئی، تطابق کامل فقط به عنوان یک تطابق جزئی در برخی مدل‌ها یا به عنوان دو تطابق جزئی مخالف در برخی دیگر در نظر گرفته می‌شود.
هدف این مقاله پرداختن به این مسائل است. همانطور که در بخش بعدی ارائه شده است، ما به صراحت متغیرهای تصمیم گیری را برای مسابقات کامل و جزئی معرفی می کنیم و در طول فرآیند انتخاب بازی بهینه شده با آنها رفتار متفاوتی داریم. ما صراحتاً محدودیت‌های ساختاری را برای منع تخصیص‌های گذرا اعمال می‌کنیم. ما همچنین مطابقت کامل را در اولویت قرار می دهیم، زیرا مطابقت کامل از شواهد تجربی در ادبیات قابل اعتمادتر است.

2.4. کارهای مرتبط

در حالی که ما بر توسعه یک مدل ترکیبی بهینه و بهبود روش انتخاب تطابق تمرکز می‌کنیم، تعداد زیادی کار در ادبیات ترکیب جغرافیایی وجود دارد که با کار ما مرتبط هستند اما لزوماً از بهینه‌سازی استفاده نمی‌کنند. از ابتدا، ما تلاشی برای ارائه یک بررسی جامع از این ادبیات نداریم. خواننده علاقه مند می تواند بررسی های جامعی در مورد روش های ادغام عمومی در مقاله مروری [ 8 ] و همچنین بررسی های خاص تراشیدن شبکه جاده ها در پایان نامه توسط [ 21 ] بیابد.]. خارج از ترکیب هندسی مرسوم، محققان همچنین موضوعات مرتبط با تطبیق ناهمگونی محتوای معنایی مجموعه داده‌های جغرافیایی را مورد مطالعه قرار داده‌اند. این ادبیات ارتباط نزدیکی با مطالعه هستی شناسی در علم GIS دارد. در [ 22 ]، نویسندگان به طور سیستماتیک مسائلی را که هدف آمیختگی معنایی حل آن است و همچنین روش‌ها، معیارها و تکنیک‌های مرتبط را تحلیل کردند.
نزدیک به کار ما، [ 21 ] یک رویکرد تطبیق متنی جدید برای شبکه‌های جاده‌ای بر اساس الگوریتم تعیین‌شده-استروک-گرا (DSO) توسعه و پیاده‌سازی کرده است. الگوریتم DSO قادر به ادغام هر دو شکل (یعنی هندسی) و اطلاعات معنایی است و می تواند با انواع موارد تطبیق مقابله کند. از سوی دیگر، الگوریتم از پیچیدگی کلی بالایی هم از نظر زمان محاسبه و هم از نظر تعداد پارامترهایی که نیاز به تنظیم دارند [ 23 ] دارد. در [ 23 ]، نویسندگان یک روش ترکیبی جدید را پیشنهاد کردند که به طور مکرر بخش های جاده را در امتداد سلسله مراتبی از مقیاس ها در مرحله پایین به بالا و از بالا به پایین جمع و تجزیه می کند.
در [ 24 ]، نویسندگان یک رویکرد تطبیق مبتنی بر سکته مغزی ترکیبی برای شبکه‌های جاده‌ای پیشنهاد کردند که محدودیت‌های تعمیم نقشه‌برداری برای شبکه‌های جاده‌ای را در مقیاس‌های مختلف در نظر می‌گیرد. روش آنها قادر به تطبیق کل سکته مغزی، تطبیق سکته مغزی جزئی و همچنین تطبیق دوربرگردان است.
برای ویژگی های چند ضلعی، [ 25 ] یک چارچوب تطبیقی ​​تکراری طراحی کرد که به طور موثر از مزایای اطلاعات متنی با یک شبکه عصبی مصنوعی (ANN) بهره می برد. ورودی اولیه به ANN شکل ویژگی های جغرافیایی است. در [ 26 ]، نویسندگان یک مشکل ادغام ردپای ساختمان را در چارچوب هستی شناسی فضایی در نظر گرفتند. از آنجایی که این شامل ترکیب چند ضلعی ها می شود، نویسندگان از ناحیه همپوشانی ردپای ساختمان به عنوان معیاری برای تشابه در فرآیند تطبیق مبتنی بر هندسه استفاده کردند.
علیرغم این واقعیت که حجم وسیعی از ادبیات مربوط به کار ما در ترکیب شبکه جاده ای وجود دارد، تفاوت آن با کار پیشنهادی در این است که مبتنی بر یک مدل ترکیبی بهینه نیست. این یک هدف مشترک با ترکیب بهینه به اشتراک می‌گذارد، زیرا تمام روش‌ها با هدف کاهش اختلاف بین مجموعه داده‌ها هستند. مدل‌های ترکیبی بهینه شده به‌صراحت یک تابع هدف را تعریف می‌کنند که این اختلاف را توصیف می‌کند و می‌تواند رابطه تطبیقی ​​را پیدا کند که به حداقل مقدار این متریک اختلاف دست می‌یابد. مدل‌های غیربهینه‌سازی (مانند روش‌های مبتنی بر شبکه عصبی یا بسیاری از روش‌های تکراری) به طور ضمنی اختلاف در تکرارها را به حداقل می‌رسانند. آنها ممکن است به حداقل مقدار برسند یا نشوند و به طور کلی هیچ تضمینی وجود ندارد که به حداقل برسد.
حتی اگر یک مدل ترکیبی بهینه‌سازی‌شده می‌تواند یک جواب بهینه را از نظر الگوریتمی تضمین کند (مثلاً از طریق برنامه‌ریزی ریاضی)، اگر مدل بهینه‌سازی شرایط تطابق را در واقعیت منعکس نکند، راه‌حل ممکن است در دنیای واقعی بهترین نباشد. همانطور که در بخش فرعی قبلی بحث شد، مدل‌های ترکیبی بهینه‌سازی شده موجود بر اساس مسئله تخصیص کلاسیک و اخیراً مشکلات جریان شبکه در تحقیقات عملیاتی است. محدودیت های ساختاری اصلی آنها در درجه اول شرایط اصلی است (به عنوان مثال، یک ویژگی را نمی توان به دو یا چند ویژگی هدف اختصاص داد). این محدودیت ها برای جلوگیری از برخی از تطابقات دوسویه متضاد بالقوه شناسایی شده در ادبیات ناکافی هستند (به عنوان مثال، در [ 10]). در بخش بعدی، یک مدل ترکیبی بهینه‌سازی شده جدید با ساختار اضافی ارائه می‌کنیم که می‌تواند از این تطابقات ثابت جلوگیری کند (و در نتیجه دقت ترکیب را بهبود بخشد).

3. روش ها

این بخش فرمول برنامه ریزی خطی عدد صحیح (ILP) از یک مدل دوتطبیقی ​​متحد (u-bimatching) را ارائه می دهد. همانند مدل‌های ترکیبی بهینه‌سازی شده موجود (یعنی مسئله انتساب و مدل‌های مبتنی بر جریان شبکه)، هدف مدل ما دستیابی به حداکثر شباهت بین ویژگی‌های همسان است. چالش اصلی ما اجتناب از تناقضات احتمالی در تعیین تکالیف برای دو جهت مخالف مسابقه است. برای این منظور، ما تعدادی از اقدامات را برای هماهنگ کردن مسابقات دو طرفه پیشنهاد می کنیم. اولاً، ما با منطبق‌های جزئی و کامل در مدل متفاوت رفتار می‌کنیم زیرا الزامات سازگاری متفاوتی دارند. ثانیاً، ما محدودیت‌های برنامه‌ریزی خطی صحیح را بر اساس این تمایز ایجاد می‌کنیم تا شرایط سازگاری را اعمال کنیم.

3.1. یکپارچه سازی مدل تطبیق دو جهته (U-bimatching)

ما با توصیف داده های مشکل مورد نیاز شروع می کنیم. اول، ما به اندازه گیری شباهت بین دو ویژگی نامزد نیاز داریم. تطابق کامل نشان دهنده رابطه هویتی است و بدون جهت است. در مقابل، مسابقات جزئی نامتقارن و جهت دار هستند. اگر یک ویژگی منiدر مجموعه داده منIمربوط به بخشی از (یا متعلق به) ویژگی است jjدر مجموعه داده جیJ، jjلزوما متعلق به منiدر جهت مخالف. بنابراین، ما از فواصل هدایت شده (مانند فاصله هدایت شده هاسدورف) استفاده می کنیم. دijdijو د“ijd′ijبرای سنجش شباهت جهت ویژگی ها در تطابق جزئی. دij= 0dij=0اگر منiمنطبق با بخشی از jj، و به صورت متقارن د“ijd′ij  د“ij= 0d′ij=0اگر j ∈ Jj∈Jمربوط به بخشی از من ∈ منi∈I. برای مسابقات کامل، از فاصله کلی استفاده می کنیم DijDij(مانند فاصله Hausdorff) برای اندازه گیری شباهت بین ویژگی های نامزد. فاصله کل به عنوان حداکثر دو فاصله جهتی تعریف می شود:

Dij= حداکثر (دij،د“ij)Dij=maxdij,d′ij
فقط زمانی که دو ویژگی صفر است من ∈ منi∈Iو j ∈ Jj∈Jدقیقا یکسان هستند علاوه بر این، نماد زیر مورد نیاز است:
F = { ( i , j ) |دij< c , and i ∈ I , j ∈ J }  F={i,j|dij<c, and i∈I,j∈J}مجموعه ای از تطابق جزئی بالقوه بین ویژگی هایی است که فواصل جهت دار آنهاست دijdijاز جانب من → جیI→Jکمتر از مقدار قطع هستند جc.
G = { ( i , j ) |د“ij< c , and i ∈ I , j ∈ J }  G={i,j|d′ij<c, and i∈I,j∈J}مجموعه ای از تطابق جزئی بالقوه بین ویژگی هایی است که فواصل جهت دار آنهاست د“ijd′ijاز جانب J → IJ→Iکمتر از مقدار قطع هستند جc.
بij= M –دijBij=M−dijیک معیار تشابه جهت دار از من ∈ منi∈Iبه j ∈ Jj∈J، جایی که M = c + 1M=c+1یک مقدار به اندازه کافی بزرگ است که همه معیارهای شباهت را مثبت می کند.
ب“ij= M –د“ijb′ij=M−d′ijیک معیار تشابه جهت دار در جهت مخالف است j ∈ Jj∈Jبه من ∈ منi∈I.
بij= M –DijBij=M−Dijمعیار تشابه برای فاصله بدون جهت است DijDij(مرتبط با مسابقات کامل).
علاوه بر داده های بالا در مورد فاصله ها و مجموعه های نامزد، به دو ثابت زیر نیاز داریم:
نNیک عدد خودسرانه بزرگ مورد نیاز برای فرمول بندی یک محدودیت زیر با استفاده از روش “بزرگ M” در تحقیقات عملیاتی است [ 27 ]. در این مقاله، تنظیم کافی است N = | من | + | J |N=I+J.
α�یک مقدار وزن برای اولویت بندی تکالیف کامل است ایکسijxijبیش از انواع دیگر تکالیف، با α ≥ 2�≥2.
تصمیماتی که باید توسط مدل تلفیق گرفته شود با متغیرهای تصمیم زیر بیان می شود:
ایکسij= 1xij=1اگر منiمطابق با همان شیء است jj.
yij= 1yij=1اگر عناصر من ∈ منi∈Iمتعلق به j ∈ Jj∈Jاما یکسان نیست jj، و 0 در غیر این صورت.
zij= 1zij=1اگر عناصر j ∈ Jj∈Jمتعلق به من ∈ منi∈Iاما یکسان نیست منi، و 0 در غیر این صورت.
همانطور که قبلاً ذکر شد، ما با استفاده از سه متغیر تصمیم گیری فوق، با تطابق کامل و جزئی متفاوت رفتار می کنیم. ایکسijxijاگر تطابق کامل بین وجود داشته باشد یکی است من ، جi,j، و yijyij(یا zijzij) یکی است اگر تطابق جزئی از وجود داشته باشد منiبه jj(یا از به منi، به ترتیب).

الگوریتم ادغام بهینه شده توسط مدل برنامه ریزی خطی عدد صحیح زیر بیان می شود (موسوم به مدل دوتطبیقی ​​متحد (u-bimatching))، که می تواند توسط هر حل کننده استاندارد بهینه سازی ILP مانند IBM ILOG CPLEX یا کیت برنامه نویسی خطی گنو (GLPK) حل شود:

به حداکثر رساندن | Z = α ⋅∑( i , j ) ∈F∩Gبijایکسij+∑( i , j ) ∈Fبijyij+∑( i , j ) ∈Gب“ijzijبه حداکثر رساندن|ز=�⋅∑من،j∈اف∩جیبijایکسij+∑من،j∈افبijyij+∑من،j∈جیب”ijzij

موضوع:

∑( i , j ) ∈F∪Gایکسij≤ 1 ، برای هر i    ∈ I∑من،j∈اف∪جیایکسij≤1، برای هر یک من∈من
∑( i , j ) ∈F∪Gایکسij≤ 1 ، برای هر j    ∈ J∑من،j∈اف∪جیایکسij≤1، برای هر یک j∈جی
∑( i , j ) ∈Fyij≤ 1 ، برای هر i    ∈ I∑من،j∈افyij≤1، برای هر یک من∈من
∑( i , j ) ∈Gzij≤ 1 ، برای هر j    ∈ J∑من،j∈جیzij≤1، برای هر یک j∈جی
ایکسij+yij≤ 1 , برای هر    ( i , j ) ∈ F ∩ Gایکسij+yij≤1، برای هر یک من،j∈اف∩جی
ایکسij+zij≤ 1 , برای هر    ( i , j ) ∈ F ∩ Gایکسij+zij≤1، برای هر یک من،j∈اف∩جی
yij∈ { 0 , 1 } , برای هر    ( i , j ) ∈ Fyij∈0،1، برای هر یک من،j∈اف
zij∈ { 0 , 1 } , برای هر    ( i , j ) ∈ Gzij∈0،1، برای هر یک من،j∈جی
ایکسij∈ { 0 , 1 } , برای هر    ( i , j ) ∈ F ∩ Gایکسij∈0،1، برای هر یک من،j∈اف∩جی
N ⋅yij+∑( k , j ) ∈F∩Gایکسkj+∑( i , l ) ∈F∩Gایکسil+∑( k , j ) ∈Gzkj≤ N , برای هر   ( i , j ) ∈ F ∩ Gن⋅yij+∑ک،j∈اف∩جیایکسkj+∑من،ل∈اف∩جیایکسil+∑ک،j∈جیzkj≤ن، برای هر یکمن،j∈اف∩جی
N ⋅zij+∑( k , j ) ∈F∩Gایکسkj+∑( i , l ) ∈F∩Gایکسil+∑( i , l ) ∈Gyil≤ N , برای هر   ( i , j ) ∈ F ∩ Gن⋅zij+∑ک،j∈اف∩جیایکسkj+∑من،ل∈اف∩جیایکسil+∑من،ل∈جیyil≤ن، برای هر یکمن،j∈اف∩جی
تابع هدف (1) شباهت کل را با تاکید بر مطابقت کامل به حداکثر می رساند. ارزش وزن α�( α ≥ 2�≥2) نشان دهنده اولویت ایجاد منطبقات کامل نسبت به انجام مسابقات جزئی است. محدودیت (4) و محدودیت (5) معتقدند که هر ویژگی را می توان حداکثر به یک ویژگی هدف اختصاص داد، چه به صورت تطبیق کامل یا یک تطابق جزئی. محدودیت‌های (6) و (7) تضمین می‌کنند که یک مسابقه هم به‌عنوان یک مسابقه کامل و هم به‌عنوان یک تطابق جزئی به‌طور هم‌زمان دوبار محاسبه نمی‌شود. محدودیت های (10)، (8) و (9) متغیرهای انتساب را تعریف می کنند ایکسij،yij،zijایکسij،yij،zijبه عنوان متغیرهای تصمیم باینری
محدودیت های (11) و (12) صحت تکالیف جزئی را اعمال می کنند. محدودیت (11) بر این باور است که اگر من ∈ منمن∈منتا حدی به (یعنی متعلق به) اختصاص دارد j ∈ Jj∈جی( yij= 1yij=1) سپس ویژگی هدف jjرا نمی توان به هیچ ویژگی برگرداند k ∈ Iک∈منبه هر طریقی علاوه بر این، نباید تکلیف کاملی از طرف وجود داشته باشد منمنبه هر ویژگی ویژگی هدف jjعملاً از حضور در هر تکلیف دیگری به جز سایر تکالیف جزئی ممنوع است yمن ، جyمن،jبه همان هدف معنای مورد نظر این است که تنها امکانی که در آن یک ویژگی j ∈ Jj∈جیمی تواند با چندین ویژگی در مجموعه داده دیگر مرتبط باشد منمنزمانی است که jjهدف مشترک چندین تکالیف جزئی است y⋅ جy⋅j. اگر ننیک عدد به اندازه کافی بزرگ است، به راحتی می توان تأیید کرد که چه زمانی yij= 1yij=1همه ایکسij،zijایکسij،zijمتغیرها به اجبار صفر می شوند. چه زمانی yij= 0yij=0، محدودیت (11) غیر الزام آور است. به طور متقارن، (12) یک نیاز مشابه را حفظ می کند جیجیبه منمنکه تنها مجاز چند انجمن از یک داده شده است من ∈ منمن∈منهدف تکالیف جزئی است. این شرط ضروری است زیرا از تخصیص نادرست گذرا مانند موارد شناسایی شده توسط [ 10 ] جلوگیری می کند.
شکل 2 نمونه ای از انتساب های انتقالی را ارائه می دهد که توسط یک مدل ترکیبی بدون محدودیت های صحت بالا ایجاد شده اند. در مثال، مدل همسان سازی fc مبتنی بر جریان شبکه برای تطبیق زیر مجموعه ای از داده های شبکه جاده برای مرکز شهر سانتا باربارا CA (در بخش آزمایش) استفاده می شود. این دو شبکه از OpenStreetMap و TIGER/Line هستند. فاصله قطع 500 متر و پیشنهاد شده است β�مقدار 0.4 در طول مسابقه استفاده می شود. از شکل 2 الف، می‌توانیم یک حلقه یا چرخه عجیب و غریب از چهار تخصیص را مشاهده کنیم که شامل دو جفت جاده است (بین خیابان کاستیلو و خیابان کاستیلو و به اشتباه بین خیابان ویکتوریا دبلیو و خیابان آناپاموی غربی). به طور معمول، می توان انتظار داشت که رابطه مسابقه دو مسابقه یک به یک باشد. با این حال، مدل بهینه‌سازی در عوض چهار تطابق جزئی ایجاد کرد. از آنجایی که مقدار برش در اینجا در مقایسه با جابجایی‌های فضایی معمولی (معمولاً 100 متر یا کمتر) بسیار بزرگ است، انگیزه‌های انجام تکالیف (تعریف شده به صورت بij= c + 1 –دijبij=ج+1-دij) بالا هستند. در نتیجه، برای مدل «سودآور» است که تعداد بیشتری تخصیص (چهار در مقابل دو) انجام دهد، در نتیجه یک راه‌حل تحریف شده ایجاد می‌کند. حلقه مشابهی از انتساب های گذرا را می توان در شرق در نزدیکی تقاطع خیابان Bath و خیابان Anapamu غربی مشاهده کرد. تکالیف گذرا در مثال‌های اینجا مشکل‌ساز هستند، زیرا به معنای یک ویژگی هستند من ∈ منمن∈منمتعلق به j ∈ Jj∈جی، ولی jjخودش متعلق به چیز دیگری است منمن. اگر منمنو jjدر واقعیت عین یک شی هستند، پس باید به یکدیگر تعلق داشته باشند. اگر آنها یکسان نیستند، پس این تخصیص متعدی به معنای منمنبخشی از ویژگی دیگر در است منمن، که پوچ است.
محدودیت های (11) و (12) از هر گونه انتساب انتقالی جلوگیری می کند. شکل 2b راه حلی را بر روی همان داده ها با استفاده از مدل u-bimatching ارائه می دهد. مشاهده می شود که رابطه مسابقه بین خیابان کاستیلو (OSM) و خیابان کاستیلو (TIGER) به تطابق کامل بازیابی شده است و خیابان ویکتوریا دبلیو تا حدی به خیابان دیگری (باث) به اشتباه اختصاص داده شده است. با این حال، تخصیص های انتقالی (و حلقه تخصیص بین آنها) دیگر رخ نمی دهد. به همین ترتیب، حلقه نزدیک اطراف باث و غرب آناپامو نیز شکسته شده است.

3.2. کاهش تکالیف جعلی با استفاده از اقدامات کمکی (شباهت نام)

انگیزه های بالا راه حل اختلاط بهینه را مخدوش می کند. این امر به ویژه زمانی صادق است که مدل تلفیقی محدود نباشد (مانند مشکل تخصیص). حتی با وجود محدودیت‌های سازگاری، تطابقات جعلی همچنان می‌تواند رخ دهد. یک راه متداول برای کاهش بیشتر تطابقات ساختگی، استفاده از اقدامات اضافی مانند شباهت نام ها، شکل ها و جهت گیری دو جاده درگیر است. این در ادبیات با استفاده از فواصل رشته ها، مانند فاصله همینگ انجام شده است (به عنوان مثال، [ 9 را ببینید]). با این حال، تطبیق نام خیابان ها آنقدر که به نظر می رسد آسان نیست. در مجموعه داده آزمایشی که استفاده می کنیم، نام همان خیابان را می توان در فایل های OSM و TIGER بسیار متفاوت نوشت. به عنوان مثال، نوع خیابان “avenue” را می توان به صورت “Ave” در OSM و “Avenue” در TIGER نوشت. جهت خیابان در انتهای نام در یک مجموعه داده (به عنوان مثال، “Valerio E St”) و در جلو در مجموعه داده دیگر (به عنوان مثال، “خیابان Valerio شرقی”) نوشته شده است. مقایسه مستقیم رشته ها کاراکتر به کاراکتر، مانند فاصله هامینگ، می تواند نتایج اشتباهی را ارائه دهد. استانداردسازی آدرس یک راه حل بالقوه است، اما هنوز یک موضوع تحقیقاتی است که در این مقاله به دنبال آن نخواهیم بود. در عوض، ما از یک متریک ساده برای مقایسه رشته ها استفاده می کنیم: شمارش تعداد کاراکترهای رایج. ما این متریک را فاصله شمارش می نامیم. برای هر دو رشته، ما آن را به عنوان نسبت بین تعداد کاراکترهای مشترک آنها و طول رشته کوتاهتر تعریف می کنیم. به این معنا که:

د12=1- _متر12دقیقه (n1،n2) +0.1د12=1-متر12دقیقهn1،n2+0.1

جایی که متر12متر12تعداد کاراکترهای مشترک است و n1،n2n1،n2به ترتیب تعداد کاراکترهای دو رشته هستند. وقتی کوتاه‌تر از دو رشته خالی باشد، متریک (14) به بی‌نهایت نزدیک می‌شود. بنابراین یک عدد کوچک (0.1) را در مخرج اضافه می کنیم تا از مقدار بی نهایت جلوگیری کنیم. بعد از ضرب فاصله شمارش در 100 متر، فاصله شمارش را به فاصله هدایت شده هاسدورف اضافه می کنیم. این تضمین می کند که دو معیار مختلف در یک مقیاس هستند. مقدار 100 متر در اینجا به عنوان مقدار تخمینی بزرگترین افست فضایی انتخاب شده است. برای بقیه این مقاله، فرض می‌کنیم که متریک فاصله برای همه مدل‌ها (از جمله مدل همسانی u) متریک فاصله Hausdorff تقویت‌شده (با فاصله تعداد رشته‌ها) است.

نکته قابل توجه این است که معیار تشابه انتخاب خود یک موضوع تحقیقاتی بزرگ در ادبیات تلفیق است. می توان آن را به روش های مختلف در رابطه با افست فضایی (به عنوان مثال، با فاصله هاسدورف و فاصله فریشت)، فاصله رشته، شکل، اندازه، و غیره اندازه گیری کرد. ما فقط دو مورد از ساده ترین معیارها را در میان بسیاری از احتمالات به کار بردیم. در اصل، از آنجایی که معیارهای شباهت، داده های ورودی برای مسئله بهینه سازی هستند، می توان به راحتی از معیارهای پیشرفته تری به جای مواردی که در این مقاله استفاده می کنیم، استفاده کرد.

4. نتایج

4.1. تنظیمات آزمایش

در این بخش، نتایج تجربی را برای ادغام دو شبکه جاده در سانتا باربارا، کالیفرنیا از OpenStreetMap و US Census TIGER/Line به ترتیب گزارش می‌کنیم. مجموعه داده از [ 9 ، 19 ] مشتق شده است و شامل شش مکان آزمایشی است که بخش‌های مختلف شهرستان سانتا باربارا، کالیفرنیا را پوشش می‌دهد ( شکل 3 ). یک داده TIGER/Line در اصل از [ 9 ] بود (و سپس در [ 19 ] استفاده شد). شبکه OpenStreetMap (OSM) از داده های منتشر شده در [ 19 ] است. ما مجموعه داده OSM را با حذف چند خط تکراری (احتمالاً مصنوع فایل‌های تاریخچه OSM) پاکسازی کردیم و حقیقت اصلی را در [ 19 ] پاکسازی کردیم.] با حذف منطبقاتی که نام‌های خیابان متفاوت/اشتباه دارند. تعداد بخش های جاده در شش سایت از 83 (سایت 6) تا 507 (سایت 1) در مجموعه داده OSM و از 77 (سایت 6) تا 423 (سایت 1) در مجموعه داده TIGER متفاوت است. بزرگترین مجموعه داده (سایت 1) اکثریت منطقه مرکز شهر سانتا باربارا را پوشش می دهد. مجموعه داده کوچکتر تنها یک یا دو محله را پوشش می دهد. در حالی که ما از این مجموعه داده خاص استفاده کردیم، باید توجه داشت که سایر مجموعه داده های ترکیبی منتشر شده وجود دارد (به عنوان مثال، [ 28 ] را ببینید).
ما مدل u-bimatching را با استفاده از IBM ILOG CPLEX 20.1 و برنامه‌نویسی خطی عدد صحیح پیاده‌سازی کردیم. رایانه آزمایشی دارای پردازنده Intel i7-11700K با فرکانس 3.60 گیگاهرتز و 8 گیگابایت حافظه است. محاسبات موازی در حل کننده بهینه سازی CPLEX برای سهولت مقایسه غیرفعال شد. برای مقاصد مقایسه، ما از پیاده‌سازی مدل‌های تلفیقی مبتنی بر جریان شبکه در [ 19 ]، از جمله مدل تطبیق کامل fc و مدل تطبیق جزئی fc استفاده کردیم. ما از فواصل هاسدورف افزوده شده (با فاصله شمارش رشته ها تقویت شده) به جای فواصل خام هاسدورف در روش های مبتنی بر جریان شبکه استفاده کردیم. برای مدل fc-bimatching، از a استفاده کردیم β�مقدار 0.4 همانطور که توسط [ 19 ] پیشنهاد شده است. برای مدل U-bimatching پیشنهادی، یک α�مقدار 4 استفاده شده است. ما همچنین مسئله انتساب را در [ 17 ] پیاده سازی کردیم.

4.2. معیارهای ارزیابی

برای ارزیابی دقت مدل‌های ترکیبی، از دو معیار استاندارد پرکاربرد استفاده کردیم: دقت و نرخ فراخوان. اینها همان معیارهای مورد استفاده در [ 9 ، 19 ] هستند. به طور خاص، دقت یک الگوریتم تطبیق با مقایسه مطابقت های ایجاد شده توسط الگوریتم با مواردی که توسط یک متخصص انسانی در حقیقت زمین برچسب گذاری شده بود، محاسبه شد:

دقت = ( TM + TU ) / ( TM + TU + FM + FU )دقت، درستی=TM+TU/TM+TU+FM+FU

جایی که TMTMو FMFMتعداد تطابق های واقعی (ویژگی هایی که به درستی مطابقت دارند) و موارد نادرست (ویژگی هایی که با اهداف اشتباه مطابقت دارند) هستند. TUTUو FUFUبه ترتیب تعداد True Unmatches (ویژگی هایی که به درستی بدون تطابق نگه داشته می شوند) و False Unmatches (ویژگی هایی که باید مطابقت داشته باشند اما به عنوان بی همتا نگه داشته می شوند) هستند. دقت (14) قدرت تمایز یک الگوریتم ترکیبی را اندازه گیری می کند. یک الگوریتم با دقت بالا، پیش‌بینی‌های قابل اعتمادی در مورد منطبقات مثبت ایجاد می‌کند. تعداد کمی از تطابق ایجاد شده توسط چنین الگوریتمی نادرست هستند. از سوی دیگر، ممکن است “بیش از حد محتاط” باشد و مسابقات واقعی را از دست بدهد.

نرخ فراخوان به صورت زیر تعریف می شود:

فراخوان = TM / ( TM + FU )به خاطر آوردن=TM/TM+FU

جایی که ( TM + FU )TM+FUتعداد کل منطبقات در حقیقت زمینی است (که یا به درستی تطبیق داده شده اند یا به طور نادرست مطابقت ندارند). الگوریتمی با یادآوری بالا (15) بیشتر تطابق‌های واقعی را ثبت می‌کند، اما ممکن است این کار را به قیمت ایجاد بسیاری از تطابق‌های نادرست انجام دهد.

از بین دو معیار، نرخ دقت مسلماً مهم‌تر در ترکیب است. اولاً، الگوریتم‌های ادغام معمولاً به نرخ یادآوری نسبتاً بالایی دست می‌یابند. دوم، تعمیر یک تطابق نادرست از یک عدم تطابق کاذب گران‌تر است، زیرا یک متخصص انسانی باید تمام تطابق‌های ایجاد شده توسط الگوریتم را به دقت بررسی کند. در مقایسه، متخصص انسانی به راحتی می‌تواند موارد گوشه‌ای را که الگوریتم نمی‌تواند از عهده آنها برآید، به پایان برساند. اگر یک الگوریتم بتواند به طور قابل اعتماد 90٪ موارد واقعی را ثبت کند، متخصص انسانی می تواند به راحتی 10٪ ویژگی های بی همتا را به پایان برساند. این هنوز در مقایسه با ترکیب دستی صرفه جویی زیادی در زمان و کار دارد.

4.3. نتایج عملکرد

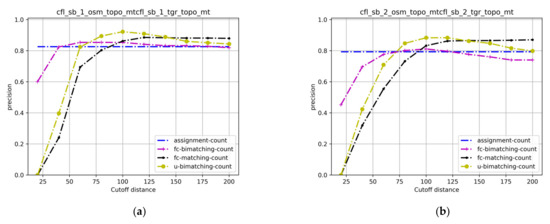
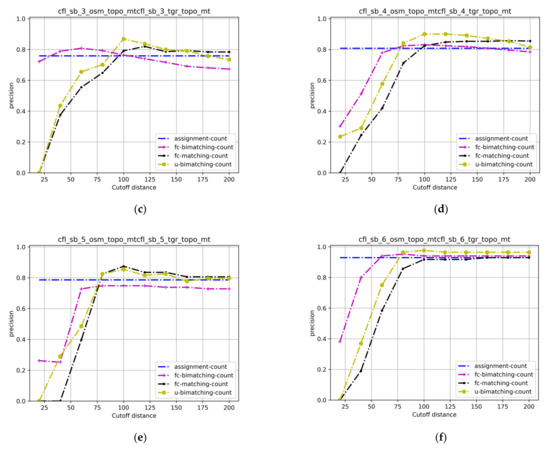
4.3.1. دقت، درستی

شکل 4 نرخ های دقت را برای مدل پیشنهادی با تطبیق u، مدل تطبیق (تطبیق کامل) fc، مدل های تطبیق (تطبیق جزئی) fc، و مدل مسئله انتساب کلاسیک نشان می دهد. را ایکسایکس-axis مقادیر فاصله برش آزمایش شده را نشان می دهد ( جج) از 20 متر تا 200 متر (در فواصل 20 متری). قطع ججنه تنها به این دلیل مهم است که همسایگی ویژگی‌های نامزد مورد بررسی را مشخص می‌کند، بلکه به این دلیل که نشان‌دهنده انگیزه برای ایجاد مسابقات است. هر چه بزرگتر باشد ججارزش، انگیزه بیشتر است.
از این شکل، ما می‌توانیم یک الگوی واضح را در شش مکان آزمایشی برای تغییر عملکرد در همه مدل‌ها به جز مشکل تخصیص مشاهده کنیم. دقت در ابتدا پایین بود c = 20ج=20و به تدریج به حداکثر در حدود افزایش یافت c = 80ج=80یا c = 100ج=100. این به این دلیل است که وقتی مقدار برش کم است، فقط تعداد کمی از مسابقات ضبط می شود (یعنی فراخوان کم است). اینکه کدام ویژگی‌ها گرفته می‌شوند کاملاً تصادفی هستند. نامزدهای خوب ممکن است خارج از محدوده (از نظر جابجایی فضایی و تفاوت نام) باشند. هنگامی که افزایش می یابد، نامزدهای بیشتری در محدوده قرار می گیرند، از جمله ویژگی های واقعی مربوطه. بنابراین دقت افزایش یافت. با این حال، به جز مدل تطبیق کامل fc، دقت پس از رسیدن به حداکثر به درجات متفاوتی کاهش یافت. در سایت 5 ( شکل 4 e)، به عنوان مثال، دقت برای مدل بی تطبیق u و مدل بای تطبیق fc تقریبا پس از رسیدن کاهش یافت. c = 100ج=100. روند کاهشی به ویژه برای مدل fc-bimatching برای سایت 3 (در شکل 4 ج و تا حدودی در سایت 2 در شکل 4 ب) واضح است. این تعجب آور نیست زیرا هر دو مدل fc-bimatching و u-bimatching مطابقت های جزئی پیچیده را امکان پذیر می کنند و انگیزه های بالا باعث ایجاد تعداد بیشتری از تطابق جزئی می شود. مدل fc-bimatching بیشتر آسیب می بیند زیرا نه تنها تطابق جزئی معمولی بلکه تخصیص گذرا را نیز امکان پذیر می کند ( شکل 2 a). مدل u-bimatching همچنان از انگیزه‌های بالایی رنج می‌برد، زیرا همچنان تطابق‌های جزئی را مجاز می‌کند که از نظر منطقی سازگار هستند اما با حقیقت متفاوت هستند ( شکل 2 ب). سایت 3 ( شکل 4ج) افت دقت بیشتری نسبت به سایت‌های دیگر داشت، زیرا این منطقه خاص دارای خیابان‌های زیادی با نام خیابان‌های تک حرفی مانند خیابان O است. بنابراین فاصله شمارش رشته کمک چندانی به تقویت مدل نکرد.
جالب توجه است که شکل 4 نشان می دهد که مدل u-bimatching در واقع به طور متوسط ​​از مدل تطبیق کامل fc در دقت بهتر عمل می کند. میانگین دقت برای مدل‌های انتساب، fc-matching، fc-bimatching و u-bimatching به ترتیب 81.7٪، 85٪، 82.5٪، 89.2٪ است. احتمالاً به این دلیل است که مدل u-bimatching اجازه می‌دهد تا برخی از تطابق‌های جزئی انجام شود، در حالی که مدل تطبیق کامل ممکن است مجبور شود آنها را به‌عنوان تخصیص‌های یک به یک نادرست تطبیق دهد و بنابراین دقت را کاهش می‌دهد.
نرخ های دقت برای مشکل انتساب برای همه فواصل قطع یکسان می ماند. این به این دلیل است که، طبق تعریف، مشکل انتساب باید هر ویژگی در مجموعه داده کوچکتر را به چیزی در مجموعه داده دیگر اختصاص دهد (به عنوان مثال، فرمول بندی در [ 17 ] را ببینید).
4.3.2. به خاطر آوردن
شکل 5 نرخ فراخوان چهار مدل را با فواصل قطع یکسان (از 20 متر تا 200 متر) نشان می دهد. منحنی‌های نرخ فراخوان یک روند افزایشی ثابت و یکنواخت را نشان می‌دهند (به جز مسئله تخصیص، دوباره). این طبیعی است زیرا هر چه فاصله قطع بیشتر باشد، استخر کاندید بزرگتر است. علاوه بر این، مدل‌های بهینه‌سازی شانس بیشتری برای گرفتن تطابق واقعی با به حداقل رساندن اختلاف دارند.
با مقایسه این چهار مدل، مشاهده می‌کنیم که دو مدل تطبیق کامل (تخصیص و تطبیق fc) کمترین یادآوری را دارند. این مورد انتظار است زیرا آنها نمی توانند هیچ تطابق جزئی را با طراحی به تصویر بکشند. مدل تطبیق جزئی fc-bimatching بیشترین یادآوری را دارد. در پنج سایت از شش سایت آزمایشی، مدل u-bimatching به نرخ فراخوانی دست یافت که بسیار نزدیک به مدل fc-bimatching بود. به طور متوسط، مدل fc-bimatching و مدل u-bimatching به ترتیب در فاصله 100 متری به نرخ یادآوری 96.5% و 93.2% دست یافتند.
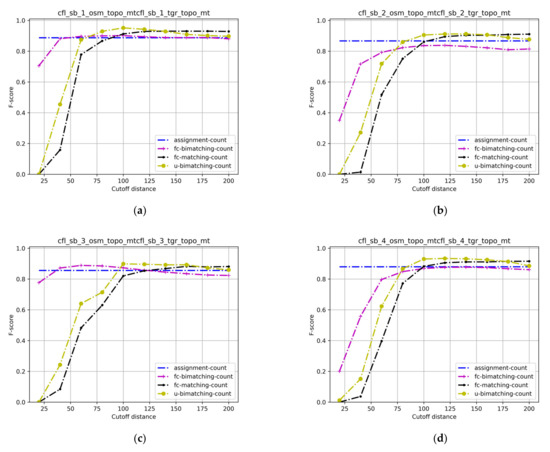
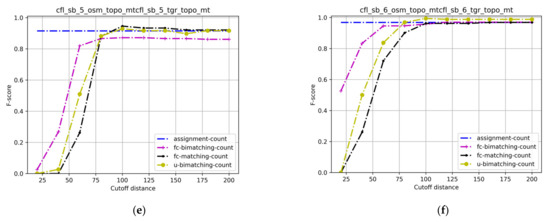
4.3.3. امتیاز اف
نتایج در دو بخش فرعی قبلی یک مبادله معمولی بین دقت و فراخوان را نشان می دهد. یک الگوریتم می تواند با پذیرش تطابق بیشتر (درست و نادرست) به یادآوری بالایی دست یابد و در نتیجه دقت کمتری داشته باشد و بالعکس. امتیاز F یکی دیگر از معیارهای عملکرد رایج است که میانگین (هارمونیک) دقت و یادآوری است. این یک دیدگاه جامع تر (اما تا حدودی کمتر آموزنده) از عملکرد کلی الگوریتم مورد نظر را منعکس می کند.
شکل 6 امتیاز F چهار مدل ترکیبی را نشان می دهد. ما می توانیم مشاهده کنیم که به طور کلی، مدل u-bimatching بالاترین امتیاز F را به دست آورد. به طور متوسط، مدل‌های تخصیص، fc-matching، fc-bimatching و u-bimatching به ترتیب به امتیاز F 89.5٪، 89.7٪، 88.5٪، 92.7٪ در فاصله قطع 100 متر دست یافتند. میانگین امتیازات F نسبتا نزدیک است، با مدل u-bimatching کمی بهتر از سایر مدل ها.
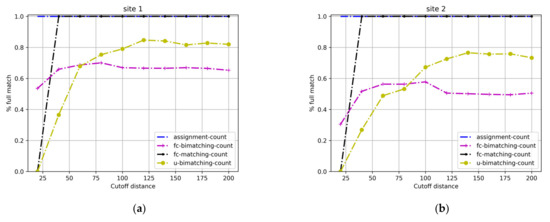
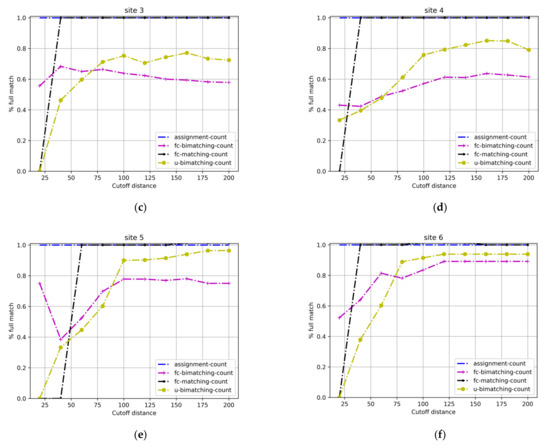
4.3.4. درصد مسابقات کامل
برای درک ترکیب نتایج تطبیق، درصد منطبق‌های کاملی را که توسط مدل‌های تلفیقی آزمایش‌شده در هر فاصله قطعی تولید می‌شوند محاسبه کردیم و آنها را در شکل 7 a-f ارائه کردیم. در موردی که یک مدل به دلیل فواصل برش کوچک (مثلاً 20 متر) هیچ کبریت تولید نمی کند، درصد آن را 0٪ ارائه می کنیم. ما می‌توانیم مشاهده کنیم که برخی ناپایداری‌ها در درصد مسابقات کامل زمانی که فاصله قطع بسیار کم است، وجود دارد (به عنوان مثال، شکل 7)ه) این احتمالاً به دلیل تعداد نامزدهای کوچک‌تر مسابقات در چنین فواصل قطعی است. به غیر از آن، مدل‌های تطبیق کامل (یعنی مسئله تخصیص و مسئله تطبیق fc) با طراحی، 100٪ مطابقت کامل ایجاد می‌کنند. زمانی که فواصل قطع نسبتاً بزرگ باشد (100 متر یا بیشتر)، مدل پیشنهادی u-bimatching عموماً درصد بیشتری از تطابق کامل را نسبت به مدل fc-bimatching ایجاد می‌کند (به عنوان مثال، شکل 7 ب). به نظر می‌رسید که مدل u-bimatching به یکی از اهداف طراحی خود دست یافته است: اولویت‌بندی مسابقات کامل (در حالی که هنوز هم در صورت لزوم امکان تطابق جزئی وجود دارد).
به طور کلی، می‌توانیم ببینیم که مدل جدید بی‌تطبیق u نسبت به مدل مشکل تخصیص و مدل‌های مبتنی بر جریان شبکه، از جمله مدل تطبیق fc یک به یک و مدل دو تطبیق چند به یک fc، بهتر عمل می‌کند. مدل جدید به میانگین فراخوان نسبتاً بالایی 93.2% دست می یابد که نزدیک به مدل چند به یک (fc-bimatching در 96.5%) و به طور قابل توجهی بالاتر از مدل یک به یک (fc-matching) است. با یک استثنا، مدل جدید به دقت بالاتری نسبت به مدل‌های fc-matching و fc-bimatching دست می‌یابد که فاصله قطع نسبتاً بزرگ (بیشتر از 100 متر) باشد. به طور متوسط، دقت مدل جدید 89.2٪ است که 4٪ بیشتر از fc-matching، 6.7٪ بیشتر از مدل fc-bimatching و 7.5٪ بیشتر از مشکل تخصیص است.
مدل u-bimatching (و مدل‌های مبتنی بر جریان شبکه) به حداکثر دقت تقریباً در فاصله قطع 100 متر دست می‌یابند. از نظر تجربی، این منطقی است زیرا بیشتر خیابان ها دارای انحرافات کوچکتر از 100 متر هستند و فایل های TIGER می توانند در موارد شدید تا 150 متر فاصله مکانی داشته باشند [ 19 ]. فراتر از این فاصله، بریدگی باعث تطابق کاذب می شود. از سوی دیگر، مشکل انتساب به فاصله قطع، با طراحی حساس نیست.

5. نتیجه گیری ها

یک کار پیچیده در مدیریت داده‌های GIS، تلفیق است که شامل تطبیق و ادغام مجموعه‌های داده از مبدا یا زمان متفاوت در یک مجموعه داده جدید بهتر است. به دلیل ماهیت ناهمگون داده ها و خطاهای اجتناب ناپذیر در فرآیند نقشه برداری، مجموعه داده های GIS ممکن است در مختصات، سطح جزئیات و نمایش با یکدیگر متفاوت باشند. در نتیجه، الگوریتم های ترکیب خودکار ممکن است توسط این پیچیدگی ها مختل شوند. روش‌های ترکیبی موجود بر اساس نحوه اندازه‌گیری شباهت زوج‌های منفرد از ویژگی‌های کاندید و همچنین نحوه انتخاب زیرمجموعه‌ای از ویژگی‌ها برای مطابقت متفاوت است. دسته ای از روش های ترکیبی، مسئله تطبیق ویژگی ذاتی را به عنوان یک مسئله بهینه سازی برای به حداقل رساندن اختلاف کل یا به حداکثر رساندن شباهت در نظر می گیرند. آنها یک سری مزایای دارند،8 ].
با این حال، مدل های ترکیبی بهینه سازی شده فعلی نیز محدود هستند. همانطور که در بخش 2 بحث شد، آنها اساساً بر اساس فرمول بندی ترکیب به عنوان یک مسئله انتساب یا یک مشکل جریان شبکه هستند – دو مدل کلاسیک از ادبیات تحقیق در عملیات. محدودیت‌های اصلی تا به امروز، محدودیت‌های اصلی هستند، که صرفاً تعداد ویژگی‌های هدفی را که می‌توان با یک ویژگی منبع مشخص مرتبط کرد، مشخص می‌کند. علاوه بر این، هیچ تفاوتی بین مسابقات جزئی و مسابقات کامل وجود ندارد. مدل‌های تطبیق کامل موجود به بهای از دست دادن مسابقات جزئی به دقت بالاتری دست می‌یابند در حالی که مدل‌های تطبیق جزئی به بهای پذیرش تطابق‌های نادرست بیشتر، به یادآوری بالاتری می‌رسند. این مقاله با بیان تطابق کامل و تطابق جزئی در یک مدل، ترکیب بهینه‌شده را گسترش می‌دهد، که ما آن را مدل تطبیق دو جهته متحد (u-bimatching) می‌نامیم. بیان صریح منطبقات کامل و منطبقات جزئی این امکان را فراهم می‌آورد که روابط تطابق کامل‌تر قابل اطمینان‌تر را در اولویت قرار دهیم، در حالی که هنوز مسابقات جزئی را به روشی ارگانیک مجاز می‌دانیم. با استفاده از مسئله انتساب و مدل‌های مبتنی بر جریان شبکه به‌عنوان شبکه‌های جاده‌ای مرجع و قابل مقایسه برای سانتا باربارا، کالیفرنیا، نتایج تجربی ما نشان می‌دهد که به‌طور متوسط، مدل u-bimatching دقت بالاتری را حتی از مدل تطبیق کامل (fc-Matching) به دست آورد. ، در حالی که به یک فراخوان متوسط ​​دست می یابیم که فقط کمی کمتر از مدل تطبیق جزئی است (93.2٪ در مقابل fc-bimatching 96.5٪). بیان صریح تطابقات کامل و جزئی نیز به ما امکان می‌دهد که محدودیت‌های ساختاری بنویسیم تا تخصیص ناسازگار بین دو جهت تطبیق را که از نظر منطقی نادرست هستند، رد کنیم. با استفاده از مسئله انتساب و مدل‌های مبتنی بر جریان شبکه به‌عنوان شبکه‌های جاده‌ای مرجع و قابل مقایسه برای سانتا باربارا، کالیفرنیا، نتایج تجربی ما نشان می‌دهد که به‌طور متوسط، مدل u-bimatching دقت بالاتری را حتی از مدل تطبیق کامل (fc-Matching) به دست آورد. ، در حالی که به یک فراخوان متوسط ​​دست می یابیم که فقط کمی کمتر از مدل تطبیق جزئی است (93.2٪ در مقابل fc-bimatching 96.5٪). بیان صریح تطابقات کامل و جزئی نیز به ما امکان می‌دهد که محدودیت‌های ساختاری بنویسیم تا تخصیص ناسازگار بین دو جهت تطبیق را که از نظر منطقی نادرست هستند، رد کنیم. با استفاده از مسئله انتساب و مدل‌های مبتنی بر جریان شبکه به‌عنوان شبکه‌های جاده‌ای مرجع و قابل مقایسه برای سانتا باربارا، کالیفرنیا، نتایج تجربی ما نشان می‌دهد که به‌طور متوسط، مدل u-bimatching دقت بالاتری را حتی از مدل تطبیق کامل (fc-Matching) به دست آورد. ، در حالی که به یک فراخوان متوسط ​​دست می یابیم که فقط کمی کمتر از مدل تطبیق جزئی است (93.2٪ در مقابل fc-bimatching 96.5٪). بیان صریح تطابقات کامل و جزئی نیز به ما امکان می‌دهد که محدودیت‌های ساختاری بنویسیم تا تخصیص ناسازگار بین دو جهت تطبیق را که از نظر منطقی نادرست هستند، رد کنیم. در حالی که دستیابی به یک فراخوان متوسط ​​که فقط کمی کمتر از مدل تطبیق جزئی است (93.2٪ در مقابل fc-bimatching 96.5٪). بیان صریح تطابقات کامل و جزئی نیز به ما امکان می‌دهد که محدودیت‌های ساختاری بنویسیم تا تخصیص ناسازگار بین دو جهت تطبیق را که از نظر منطقی نادرست هستند، رد کنیم. در حالی که دستیابی به یک فراخوان متوسط ​​که فقط کمی کمتر از مدل تطبیق جزئی است (93.2٪ در مقابل fc-bimatching 96.5٪). بیان صریح تطابقات کامل و جزئی نیز به ما امکان می‌دهد که محدودیت‌های ساختاری بنویسیم تا تخصیص ناسازگار بین دو جهت تطبیق را که از نظر منطقی نادرست هستند، رد کنیم.10 ].
چند حوزه ارزش بررسی بیشتر را دارند. در حالی که ما تطابق نادرست گذرا را رد کردیم، مدل u-bimatching می‌تواند در انجام تکالیف جزئی بیش از حد گمراه شود، اگر انگیزه برای انجام تکالیف بیش از حد بالا باشد. همانطور که در بخش 3 بحث شد، این به این دلیل است که انجام تعداد زیادی تکالیف جزئی از تعداد کمی از منطبقات کامل “سودآورتر” خواهد بود. مدل بهینه‌سازی نمی‌تواند بگوید زیرا راه‌حل با تطابق جزئی بیش از حد همچنان سازگار است. ما این مشکل را با تقویت معیار تشابه با فاصله رشته نسبتاً ضعیف که فقط درصد حروف مشترک بین دو نام را به حساب می‌آورد، کاهش دادیم. همانطور که آزمایش نشان داد، می‌تواند در مواردی که نام‌های خیابان‌های مختلف حروف مشترک زیادی دارند، بی‌اثر باشد (به عنوان مثال، خیابان چاپالا در مقابل خیابان کاریلو). ما از فاصله رشته‌ای قوی‌تر مانند فاصله همینگ استفاده نکردیم، زیرا ممکن است به تفاوت‌های سطحی در املا و ترتیب حساس باشد. یک تحقیق آتی خوب در این راستا، عادی سازی نام خیابان ها بر اساس استانداردهای ملی یا تجاری است. سپس، در عوض می توان از فاصله رشته بسیار حساس تری برای افزایش دقت استفاده کرد. امکان دیگر استفاده از معیارهای تشابه اضافی، مانند درجه گره ها در نظریه گراف، برای تقویت بیشتر مدل است. این جنبه برای تحقیقات آینده باقی مانده است.

منابع

  1. فرانک، AU چرا مقیاس توصیفگر مؤثری برای کیفیت داده است؟ منطق فیزیکی و هستی شناختی برای عدم دقت و سطح جزئیات. در گرایش های پژوهشی در علم اطلاعات جغرافیایی ; Springer: برلین/هایدلبرگ، آلمان، 2009; صص 39-61. [ Google Scholar ]
  2. Saalfeld، A. تبدیل سریع ورق لاستیکی با استفاده از مختصات ساده. صبح. کارتوگر. 1985 ، 12 ، 169-173. [ Google Scholar ] [ CrossRef ]
  3. Saalfeld، A. گردآوری خودکار نقشه Conflation. بین المللی جی. جئوگر. Inf. سیستم 1988 ، 2 ، 217-228. [ Google Scholar ] [ CrossRef ]
  4. والتر، وی. Fritsch، D. تطبیق مجموعه داده های مکانی: یک رویکرد آماری. بین المللی جی. جئوگر. Inf. علمی 1999 ، 13 ، 445-473. [ Google Scholar ] [ CrossRef ]
  5. مک کنزی، جی. یانوویچ، ک. Adams, B. یک روش وزنی چند ویژگی برای تطبیق نقاط مورد علاقه تولید شده توسط کاربر. کارتوگر. Geogr. Inf. علمی 2014 ، 41 ، 125-137. [ Google Scholar ] [ CrossRef ]
  6. Pendyala, RM توسعه ابزارهای ترکیبی مبتنی بر GIS برای یکپارچه سازی و تطبیق داده ها . بخش حمل و نقل فلوریدا: لیک سیتی، فلوریدا، ایالات متحده آمریکا، 2002. [ Google Scholar ]
  7. ماسویاما، الف. روش‌هایی برای تشخیص تفاوت‌های ظاهری بین مجموعه‌های فضایی در مقاطع زمانی مختلف. بین المللی جی. جئوگر. Inf. علمی 2006 ، 20 ، 633-648. [ Google Scholar ] [ CrossRef ]
  8. خاویر، EMA؛ آریزا-لوپز، FJ; Ureña-Cámara, MA بررسی اقدامات و روش‌ها برای تطبیق مجموعه داده‌های برداری جغرافیایی. کامپیوتر ACM. Surv. 2016 ، 49 ، 1-34. [ Google Scholar ] [ CrossRef ]
  9. لی، ال. Goodchild، MF یک مدل بهینه سازی برای تطبیق ویژگی های خطی در ترکیب داده های جغرافیایی. بین المللی J. Image Data Fusion 2011 ، 2 ، 309-328. [ Google Scholar ] [ CrossRef ]
  10. بیری، سی. کانزا، ی. صفرا، ای. Sagiv، Y. همجوشی اشیاء در سیستم های اطلاعات جغرافیایی. در مجموعه مقالات سی امین کنفرانس بین المللی در مورد پایگاه های داده بسیار بزرگ، تورنتو، ON، کانادا، 31 اوت تا 3 سپتامبر 2004. جلد 30، ص 816–827. [ Google Scholar ]
  11. کورال، ا. مانولوپولوس، ی. تئودوریدیس، ی. Vassilakopoulos، M. الگوریتم‌های پردازش پرس‌وجوهای k-closest-pair در پایگاه‌های داده فضایی. دانستن داده ها مهندس 2004 ، 49 ، 67-104. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  12. Goodchild، MF; Hunter، GJ یک اندازه گیری دقت موقعیتی ساده برای ویژگی های خطی. بین المللی جی. جئوگر. Inf. علمی 1997 ، 11 ، 299-306. [ Google Scholar ] [ CrossRef ]
  13. تانگ، ایکس. لیانگ، دی. Jin, Y. روش تطبیق شی جاده خطی برای ادغام بر اساس بهینه سازی و رگرسیون لجستیک. بین المللی جی. جئوگر. Inf. علمی 2014 ، 28 ، 824-846. [ Google Scholar ] [ CrossRef ]
  14. روزن، بی. Saalfeld، A. مطابقت با معیارها برای تراز خودکار. در مجموعه مقالات هفتمین سمپوزیوم بین المللی کارتوگرافی به کمک کامپیوتر (Auto-Carto 7)، واشنگتن، دی سی، ایالات متحده آمریکا، 11–14 مارس 1985; صص 1-20. [ Google Scholar ]
  15. کاب، MA; چانگ، ام جی. III، HF; پتری، FE; شاو، کیلوبایت؛ میلر، HV یک رویکرد مبتنی بر قانون برای ترکیب داده‌های برداری نسبت داده شده. GeoInformatica 1998 ، 2 ، 7-35. [ Google Scholar ] [ CrossRef ]
  16. فیلین، اس. Doytsher, Y. تشخیص اشیاء مربوطه در ترکیب نقشه مبتنی بر خطی. Surv. Land Inf. سیستم 2000 ، 60 ، 117-128. [ Google Scholar ]
  17. لی، ال. Goodchild، MF بهینه شده تطبیق ویژگی در ترکیب. در مجموعه مقالات علم اطلاعات جغرافیایی: ششمین کنفرانس بین المللی، GIScience، زوریخ، سوئیس، 14-17 سپتامبر 2010. ص 14-17. [ Google Scholar ]
  18. لی، تی. لی، زی. تطبیق داده های فضایی بهینه برای ترکیب: یک رویکرد مبتنی بر جریان شبکه. ترانس. GIS 2019 ، 23 ، 1152-1176. [ Google Scholar ] [ CrossRef ]
  19. Lei، TL ترکیب داده های جغرافیایی: یک رویکرد رسمی مبتنی بر بهینه سازی و پایگاه های داده رابطه ای. بین المللی جی. جئوگر. Inf. علمی 2020 ، 34 ، 2296-2334. [ Google Scholar ] [ CrossRef ]
  20. Lei، TL ترکیب داده‌های جغرافیایی در مقیاس بزرگ: چارچوب تطبیق ویژگی مبتنی بر بهینه‌سازی و تقسیم و تسخیر. محاسبه کنید. محیط زیست سیستم شهری 2021 ، 87 ، 101618. [ Google Scholar ] [ CrossRef ]
  21. ژانگ، ام. روش‌ها و پیاده‌سازی تطبیق شبکه جاده‌ای. Ph.D. پایان نامه، Technische Universität München، مونیخ، آلمان، 2009. [ Google Scholar ]
  22. Vilches-Blázquez، LM; راموس، جی. ترکیب معنایی در علم GIS: یک بررسی سیستماتیک کارتوگر. Geogr. Inf. علمی 2021 ، 48 ، 512-529. [ Google Scholar ] [ CrossRef ]
  23. Hackeloeer، A. کلاسینگ، ک. کریسپ، جی.ام. منگ، ال. تلفیق شبکه جاده: یک رویکرد سلسله مراتبی تکراری. در حال پیشرفت در خدمات مبتنی بر مکان 2014 ; Springer: برلین/هایدلبرگ، آلمان، 2015; صص 137-151. [ Google Scholar ]
  24. گوا، کیو. خو، X. وانگ، ی. لیو، جی. رویکرد تطبیق ترکیبی شبکه‌های جاده‌ای تحت مقیاس‌های مختلف با در نظر گرفتن محدودیت‌های تعمیم نقشه‌برداری. دسترسی IEEE 2019 ، 8 ، 944–956. [ Google Scholar ] [ CrossRef ]
  25. لیو، ال. دینگ، ایکس. زو، ایکس. فن، ال. Gong, J. یک رویکرد تکراری مبتنی بر اطلاعات زمینه‌ای برای تطبیق مجموعه داده‌های چند ضلعی چند ضلعی. ترانس. GIS 2020 ، 24 ، 1047-1072. [ Google Scholar ] [ CrossRef ]
  26. ممدو اوغلو، ا. Basaraner، M. رویکردی برای ادغام و غنی سازی داده های ساختمان شهری چند مقیاسی از طریق تطبیق هندسی و وب معنایی. کارتوگر. Geogr. Inf. علمی 2022 ، 49 ، 1-17. [ Google Scholar ] [ CrossRef ]
  27. Hillier، FS; لیبرمن، GJ مقدمه ای بر تحقیق در عملیات ، ویرایش هشتم. McGraw-Hill: نیویورک، نیویورک، ایالات متحده آمریکا، 2005; پ. 1088. [ Google Scholar ]
  28. خاویر، EM; آریزا-لوپز، FJ; Ureña-Cámara، MA MatchingLand، بستر آزمایش داده های مکانی برای ارزیابی روش های تطبیق. علمی داده 2017 ، 4 ، 170180. [ Google Scholar ] [ CrossRef ] [ PubMed ] [ نسخه سبز ]
Ijgi 11 00375 g001 550
شکل 1. مسائل مربوط به شبکه های OpenStreetMap (سبز) و TIGER (قرمز) در مرکز شهر سانتا باربارا، کالیفرنیا. فلش های آبی نشان دهنده مسابقات است. ( الف ) انحرافات فضایی پیوندهای فضایی را شکست می دهند. ( ب ) مسابقات کامل و جزئی در یک بلوک خیابان.
Ijgi 11 00375 g002 550
شکل 2. تخصیص های انتقالی: ( الف ) تخصیص های گذرا در fc-bimatching. ( ب ) حذف تخصیصات متعدی با u-bimatching.
Ijgi 11 00375 g003 550
شکل 3. داده های آزمایشی در شش مکان در شهرستان سانتا باربارا، کالیفرنیا، از OSM (سبز) و TIGER (قرمز)، به ترتیب.
Ijgi 11 00375 g004a 550 Ijgi 11 00375 g004b 550
شکل 4. نرخ های دقیق مدل های ترکیبی بهینه برای مجموعه داده سانتا باربارا (OSM در مقابل TIGER). ( a – f ) نتایج برای سایت های #1 تا #6.
Ijgi 11 00375 g005 550
شکل 5. نرخ های مدل های ترکیبی بهینه را برای مجموعه داده سانتا باربارا به یاد بیاورید (OSM در مقابل TIGER). ( a – f ) نتایج برای سایت های #1 تا #6.
Ijgi 11 00375 g006a 550 Ijgi 11 00375 g006b 550
شکل 6. امتیاز F از مدل های ترکیبی بهینه برای مجموعه داده سانتا باربارا (OSM در مقابل TIGER). ( a – f ) نتایج برای سایت های #1 تا #6.
Ijgi 11 00375 g007a 550 Ijgi 11 00375 g007b 550
شکل 7. درصد منطبقات کامل تولید شده توسط مدل های ترکیبی بهینه آزمایش شده برای مجموعه داده سانتا باربارا (OSM در مقابل TIGER). ( a – f ) نتایج برای سایت های #1 تا #6.

مقالات داخلی و بین المللی

مطالب مرتبط ...

بدون دیدگاه

دیدگاهتان را بنویسید