چکیده

کشف وابستگی‌های مکانی-زمانی در شبکه‌های جاده‌ای شهری که باعث ایجاد الگوهای تراکم مکرر (RC) می‌شوند، برای بسیاری از کاربردهای دنیای واقعی، از جمله برنامه‌ریزی شهری و برنامه‌ریزی خدمات حمل‌ونقل عمومی، حیاتی است. در حالی که اکثر مطالعات موجود الگوهای زمانی پدیده‌های RC را بررسی می‌کنند، تأثیر توپولوژی شبکه جاده‌ای بر روی RC اغلب نادیده گرفته می‌شود. این مقاله الگوریتم ST-Discovery را پیشنهاد می‌کند، یک الگوریتم جدید داده‌کاوی فضایی-زمانی بدون نظارت که کشف مؤثر داده‌محور وابستگی‌های RC ناشی از توپولوژی شبکه جاده‌ای را با استفاده از داده‌های ترافیکی دنیای واقعی تسهیل می‌کند. ما با مدل‌سازی و بهره‌برداری سیستماتیک از نقاط پرت بار ترافیکی، پدیده‌های ترافیکی تکرارشونده منظم، مانند ساعات شلوغی را که عمدتاً ناشی از روز است، بررسی می‌کنیم. ما الگوریتمی را ارائه می‌کنیم که ابتدا زیرگراف‌های متصل شبکه جاده‌ای را بر اساس نقاط پرت سرعت ترافیک می‌سازد. دوم، الگوریتم جفت‌هایی از زیرگراف‌ها را شناسایی می‌کند که نشان‌دهنده همبستگی‌های مکانی-زمانی در رفتار بار ترافیکی آن‌ها برای شناسایی وابستگی‌های توپولوژیکی در شبکه جاده‌ای است. در نهایت، جفت های زیرگراف شناسایی شده را بر اساس امتیاز وابستگی تعیین شده توسط الگوریتم ما رتبه بندی می کنیم. نتایج تجربی ما این را نشان می دهدST-Discovery می تواند به طور موثر وابستگی های توپولوژیکی را در شبکه های جاده های شهری نشان دهد.

کلید واژه ها:

تحلیل شبکه جاده ای ; ازدحام مکرر ؛ داده کاوی مکانی – زمانی

1. مقدمه

شبکه‌های جاده‌ای شهری دارای وابستگی‌های متقابل پیچیده‌ای هستند که می‌توانند در طول رویدادهای ازدحام آشکار شوند [ 1 ]. تحقیقات ترافیکی تثبیت شده بین ازدحام مکرر (RC)، به عنوان مثال، ساعات شلوغی، و رویدادهای ازدحام غیر مکرر، به عنوان مثال، تصادفات [ 2 ] تمایز قائل می شود. هدف این مقاله شناسایی وابستگی‌های توپولوژیکی در شبکه جاده‌ای است که ممکن است باعث ایجاد پدیده‌های RC شوند که از این پس وابستگی‌های ساختاری نامیده می‌شوند.. چنین وابستگی‌هایی اغلب به خوبی درک نمی‌شوند، می‌توانند تنها تحت بار ترافیک واقعی آشکار شوند و می‌توانند باعث ایجاد الگوهای RC همزمان در شبکه جاده‌ها شوند. بنابراین، درک وابستگی‌های توپولوژیکی در شبکه‌های جاده‌ای شهری برای بسیاری از کاربردهای دنیای واقعی، از جمله برنامه‌ریزی شهری، مدیریت ترافیک و خدمات حمل‌ونقل عمومی، حیاتی است.
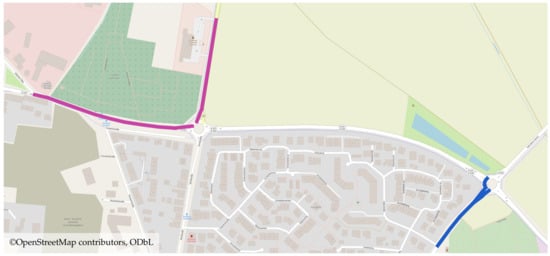
ما وابستگی‌های ساختاری در شبکه‌های جاده‌ای شهری را در مثال ناحیه Gehrden – شهری در ناحیه هانوفر، آلمان – در شکل 1 نشان می‌دهیم . این شکل دو زیرگراف از شبکه جاده ها (با علامت آبی و بنفش) را نشان می دهد. هر دو زیرگراف نشان دهنده جاده های تغذیه کننده به بزرگراه اصلی (B65) است که Gehrden و شهر هانوفر را به هم متصل می کند که مسیر اصلی رفت و آمد ساکنان Gehrden را تشکیل می دهد. در طول یک دوره با بار ترافیکی بالا (به عنوان مثال، در یک ساعت شلوغی)، این زیرگراف ها معمولاً به طور همزمان به دلیل توپولوژی شبکه شلوغ هستند. بنابراین، ما چنین زیرگراف هایی را از نظر ساختاری وابسته می دانیم.
ادبیات موجود در مورد RC عمدتاً الگوهای زمانی را شناسایی می کند [ 3 ، 4 ]. با این حال، ما کمبود روش‌هایی را مشاهده می‌کنیم که تأثیر توپولوژی شبکه جاده‌ای را بر روی RC بررسی می‌کنند. تشخیص چنین وابستگی‌هایی در شبکه‌های جاده‌ای پیچیده بی‌اهمیت نیست، به‌ویژه به دلیل تنوع عوامل تأثیر (به عنوان مثال، رویدادهای ویژه برنامه‌ریزی‌شده، تصادفات، مکان‌های ساخت‌وساز و شرایط آب و هوایی شدید) و تأثیر دینامیکی آن‌ها بر جریان ترافیک مربوط به فضای مکانی و زمانی. ابعاد تا جایی که ما می دانیم، وظیفه کشف وابستگی های ساختاری مبتنی بر داده در شبکه های جاده ای شهری جدید است و در ادبیات به آن پرداخته نشده است.
این مقاله ST-Discovery را ارائه می‌کند – یک الگوریتم داده‌کاوی مکانی-زمانی مبتنی بر داده جدید برای آشکار کردن وابستگی‌های ساختاری در شبکه‌های جاده‌ای شهری. ST-Discoveryمتکی بر این شهود است که وابستگی‌های ساختاری می‌توانند به صورت همبستگی الگوهای تراکم ظاهر شوند. در این مقاله، الگوهای تراکم را به عنوان زیرگراف های شبکه راه ها نشان می دهیم. هدف ما حذف الگوهای RC است که عمدتاً توسط عوامل زمانی ایجاد می‌شوند، مانند الگوهای ساعت شلوغی که عمدتاً به زمان روز بستگی دارد. برای این منظور، ما فقط نقاط پرت بار ترافیکی زمانی را در نظر می گیریم که الگوهای روزانه را برای ساخت زیرگراف ها در نظر می گیرند. ما زیرگراف‌ها را با استفاده از خوشه‌بندی فضایی بخش‌های شبکه متصل شناسایی می‌کنیم که بار ترافیکی بالا را نشان می‌دهند. ما همبستگی‌های زمانی زیرگراف‌های واقع در مجاورت فضایی را به عنوان شاخص‌های وابستگی ساختاری در شبکه جاده‌ای زیربنایی در نظر می‌گیریم.
برای ارزیابی اثربخشی الگوریتم ST-Discovery پیشنهادی ، ما یک مطالعه موردی انجام دادیم. این مطالعه موردی از دو مجموعه داده ترافیکی دنیای واقعی در مناطق هانوفر و برانزویک، آلمان استفاده می‌کند. نتایج مطالعه نشان می‌دهد که روش ما می‌تواند وابستگی‌های ساختاری معنادار در شبکه‌های جاده‌ای شهری را به دقت تشخیص دهد.
به طور خلاصه، مشارکت های ما به شرح زیر است. (1) ما وظیفه جدید کشف وابستگی‌های ساختاری مبتنی بر داده در شبکه‌های جاده‌ای را معرفی می‌کنیم. (2) ما الگوریتم جدید ST-Discovery را برای تشخیص وابستگی‌های ساختاری با استفاده از داده‌های جریان ترافیک پیشنهاد می‌کنیم. (3) ما یک مطالعه موردی برای ارزیابی اثربخشی روش پیشنهادی انجام می‌دهیم.
این مقاله کار قبلی ما [ 5 ] را به این سمت گسترش می دهد. در مقایسه با کارهای [ 5 ]، در این مقاله، توضیح مفصلی از مراحل الگوریتمی فردی ST-Discovery و تحلیل پیچیدگی زمان اجرا ارائه می‌کنیم. علاوه بر این، ما یک ارزیابی گسترده از جمله ارزیابی دستی وابستگی‌های توپولوژیکی شناسایی‌شده و بررسی دقیق تاثیر پارامتر الگوریتم ارائه می‌کنیم. نمایشی که شامل تجسم وابستگی های شناسایی شده توسط ST-Discovery در داشبورد تحلیل ترافیک تعاملی است در [ 6 ] موجود است.

2. کارهای مرتبط

این بخش کار مرتبط در زمینه های تحلیل تراکم و داده کاوی مکانی-زمانی را به همراه منابع داده مرتبط مورد بحث قرار می دهد.

2.1. تحلیل تراکم

ادبیات موجود در مورد الگوهای تراکم بین رویدادهای ازدحام مکرر (RC) و تراکم غیر مکرر (NRC) تمایز قائل شده است [ 2 ]. ازدحام غیر مکرر به عنوان ازدحام تعریف می شود که به دلیل رویدادهای منحصر به فرد مانند تصادفات [ 7 ، 8 ، 9 ]، شرایط آب و هوایی شدید [ 10 ، 11 ، 12 ] یا رویدادهای عمومی در مقیاس بزرگ [ 13 ، 14 ] رخ می دهد. تحقیقات موجود در NRC به مشکلات مختلفی مانند برآورد تاخیر [ 13 ، 14 ]، سازگاری مسیریابی [ 8 ]، پیش‌بینی تراکم [ 10 ، 12 ] پرداخته است.] و تشخیص و ردیابی NRC [ 7 ، 11 ، 15 ]. روش‌های تشخیص NRC شامل خوشه‌بندی مکانی-زمانی [ 15 ]، مدل‌های رگرسیون [ 10 ] و جنگل‌های تصادفی [ 12 ] است.
ازدحام مکرر نشان دهنده رویدادهای ازدحام باقی مانده است. الگوهای ساعت شلوغی برجسته ترین نمونه های رویدادهای RC را تشکیل می دهند [ 16 ]. تعداد زیادی از مطالعات بر تجزیه و تحلیل زمانی RC تمرکز دارند. یک خط از تحقیقات به پیش‌بینی RC می‌پردازد، جایی که مدل‌های یادگیری ماشین مانند شبکه‌های عصبی [ 17 ، 18 ، 19 ] یا ماشین‌های بردار پشتیبان [ 20 ] در حال حاضر پیشرفته‌ترین فناوری‌ها را تشکیل می‌دهند. وظیفه نزدیک پیش بینی ترافیک کوتاه مدت به خوبی در ادبیات موجود مطالعه شده است [ 21]. مدل‌ها هم برای پیش‌بینی RC و هم برای پیش‌بینی کوتاه‌مدت ترافیک معمولاً از الگوهای ترافیکی تکرارشونده دوره‌ای استفاده می‌کنند، به عنوان مثال، ساعات شلوغی و الگوهای روز هفته، برای تسهیل پیش‌بینی‌ها. خط دیگری از تحقیقات به بررسی تکامل الگوهای RC می پردازد. رویکردهای کنونی معمولاً انتشار RC را در یک شبکه فضایی [ 3 ، 4 ، 22 ] یا یک نمودار شبکه جاده ای [ 23 ، 24 ، 25 ] تجزیه و تحلیل می کنند.
در حالی که این مطالعات عمدتاً جنبه‌های زمانی RC را مورد توجه قرار می‌دهند، ما کمبود تحقیقاتی را در مورد بررسی تأثیر توپولوژی شبکه جاده بر روی RC مشاهده می‌کنیم. این مقاله الگوریتمی را پیشنهاد می‌کند که الگوهای ترافیک دوره‌ای را فیلتر می‌کند و وابستگی‌های متقابل زیرگراف‌ها را در شبکه جاده‌ها شناسایی می‌کند.

2.2. داده کاوی مکانی-زمانی

الگوریتم‌های داده‌کاوی مکانی-زمانی چالش استخراج اطلاعات، به عنوان مثال، الگوها یا ناهنجاری‌های مکرر، از مجموعه‌های بزرگ داده‌های مکانی-زمانی را برطرف می‌کنند. آتلوری و همکاران در یک نظرسنجی اخیر، مروری بر رویکردها و مشکلات ارائه دهید [ 26 ].
رویکردهای داده‌کاوی قبلی برای داده‌های شبکه جاده‌ای اغلب با هدف شناسایی جاده‌ها یا تقاطع‌های مهم در داخل شبکه راه‌ها است. نویسندگان [ 1 ] یک رویکرد مبتنی بر داده را برای شناسایی اهمیت جاده های فردی در شبکه جاده با اندازه گیری همبستگی بار ترافیک بین یک جاده خاص و کل شبکه جاده معرفی کردند. به طور مشابه، نویسندگان [ 27 ] تقاطع های مهم فردی را کشف می کنند. نویسندگان سفرهای درون شبکه جاده‌ای را به عنوان یک نمودار سه‌جانبه نشان می‌دهند. آنها اهمیت تقاطع ها را با یک الگوریتم رتبه بندی تکراری محاسبه می کنند. در مقابل، ما مشکل شناسایی وابستگی های زوجی در شبکه جاده را در نظر می گیریم.
چندین مطالعه تشخیص پرت را در داده های ترافیک جاده ای در نظر می گیرند. در [ 28 ]، جریان ترافیک غیرعادی با گروه‌بندی تقاطع‌های جاده‌ای از طریق الگوهای جریان ترافیک و نقشه‌های خودسازمان‌دهی شناسایی می‌شود. نویسندگان [ 29 ] بر تشخیص نقاط پرت در بار ترافیک با تغییرات ناگهانی تمرکز می کنند. ST-Discovery بر اساس روش‌های تشخیص نقاط پرت موجود است و از اتفاقات پرت و اطلاعات متقابل برای تعیین وابستگی‌های مکانی-زمانی استفاده می‌کند.

2.3. منابع اطلاعات

داده‌های ترافیک جاده‌ای اغلب از حسگرهای ثابت، دستگاه‌های GPS یا شبیه‌سازی جمع‌آوری می‌شوند. حسگرهای ثابت، مانند حلقه های القایی که به طور دائم در جاده ها نصب می شوند، منابع داده های ترافیکی سنتی هستند. سنسورهای ثابت معمولا داده‌های ترافیکی با کیفیت و ثابت را اندازه‌گیری می‌کنند، اما فاقد پوشش شبکه جاده‌ای، به‌ویژه در محیط‌های شهری هستند. تحقیقات موجود به طور گسترده ای استفاده از داده های حسگرهای ثابت را پذیرفته اند [ 8 ، 11 ، 15 ، 17]. دیجیتالی شدن روزافزون ترافیک شهری منجر به افزایش در دسترس بودن داده های ترافیکی در دنیای واقعی شده است. به طور خاص، داده‌های شناور خودرو (FCD) معمولاً از دستگاه‌های GPS جمع‌آوری می‌شوند. FCD بینش دقیق و واقعی را در مورد بار ترافیک واقعی مناطق خاص امکان پذیر می کند. ثابت شده است که FCD منبع داده مناسبی برای تجزیه و تحلیل RC [ 4 ، 24 ] و NRC [ 30 ] است. در مقایسه با داده‌های جمع‌آوری‌شده از حسگرهای ثابت، FCD معمولا بخش بزرگ‌تری از شبکه جاده‌ها را پوشش می‌دهد اما سازگاری کمتری دارد. رویکردهای مبتنی بر شبیه سازی (به عنوان مثال، در [ 31 ، 32]) از ویژگی‌های ناشی از توپولوژی و ظرفیت شبکه استفاده می‌کند و می‌تواند بخش‌های حیاتی شبکه‌های جاده‌ای و تأثیر احتمالی حوادث را آشکار کند. با این حال، این روش‌ها با تقریب‌های مدل‌های زیربنایی که می‌توانند تنها تخمین‌های تقریبی از جریان ترافیک واقعی ارائه دهند، محدود شده‌اند. در این مقاله، ما بر FCD تکیه می‌کنیم، که داده‌های جریان ترافیک دنیای واقعی را نشان می‌دهد و می‌توانیم بینشی در مورد وابستگی‌های توپولوژیکی که تنها در شرایط ترافیک واقعی آشکار می‌شوند، ارائه کنیم.

3. بیان مسئله و رسمی سازی

در این مقاله به مشکل شناسایی زیرگراف‌های وابسته به ساختار در یک شبکه جاده‌ای می‌پردازیم. ما زیرگراف ها را از نظر ساختاری وابسته می دانیم if
  • زیرگراف ها در مجاورت مکانی قرار دارند،
  • زیرگراف ها معمولاً به طور همزمان تحت تأثیر ازدحام مکرر یا
  • توپولوژی شبکه جاده باعث ایجاد همبستگی تراکم در این زیرگراف ها می شود.
در ادامه، مفاهیم کلیدی اتخاذ شده در مقاله را رسمیت می دهیم. در این رسمی سازی، ما برخی از مفاهیم تعریف شده در کار قبلی خود را پذیرفته و در صورت لزوم گسترش می دهیم [ 5 ].
نمودار حمل و نقل . ما شبکه جاده را به عنوان یک گراف چندگانه جهت دار نشان می دهیم تیجی:=(V،U)، به عنوان نمودار حمل و نقل شناخته می شود. U مجموعه ای از لبه ها (به عنوان مثال، بخش های جاده) است. V مجموعه ای از گره ها (یعنی اتصالات) است. ما به یک لبه از نمودار حمل و نقل به عنوان یک واحد اشاره می کنیم تو∈U.
بار واحد ما جریان ترافیک مشاهده شده در یک واحد در یک نقطه زمانی خاص را به عنوان بار واحد نشان می دهیم . به طور رسمی، تول(تو،تی)بار ترافیکی واحد u در نقطه زمانی است تی∈تی، جایی که تیمجموعه ای از نقاط زمانی را نشان می دهد.

بار واحد را اندازه گیری می کنیم تول(تو،تی)∈[0،1]به عنوان کاهش سرعت نسبی در واحد u در نقطه زمانی t با توجه به حد سرعت لمنمتر(تو)لبه مربوط به نمودار حمل و نقل:

تول(تو،تی)=لمنمتر(تو)-سپههد(تو،تی)لمنمتر(تو)،

جایی که سپههد(تو،تی)سرعت ترافیک واحد u را در زمان t نشان می دهد.

واحد تحت تأثیر واحدی را که بار ترافیکی غیرعادی بالایی را در یک نقطه زمانی معین t نشان می دهد ، به عنوان یک واحد آسیب دیده در t نشان می دهیم . به طور رسمی، تحت تأثیر ( u , t ) U×تی↦{تیrتوه،افآلسه}نشان می دهد که آیا واحد u در نقطه زمانی t تحت تأثیر قرار می گیرد یا خیر .
زیرگراف ما به یک زیرگراف از نمودار حمل و نقل به عنوان زیرگراف اشاره می کنیم سg:=(V”،U”)با V”⊂V، U”⊂U.
زیرگراف تحت تأثیر یک زیرگراف آسیب‌دیده نشان‌دهنده زیرگرافی است که بار ترافیکی غیرعادی بالایی را در یک نقطه زمانی خاص t نشان می‌دهد (به عنوان مثال، یک بخش بزرگراه متراکم). به طور رسمی، متأثر، تحت تأثیر، دچار، مبتلا(سg،تی):اسجی×تی↦{تیrتوه،افآلسه}نشان می دهد که آیا یک زیرگراف سgدر نقطه زمانی t تحت تاثیر قرار می گیرد ، جایی که اسجی={پ(V)×پ(U)}مجموعه ای از زیرگراف های ممکن را نشان می دهد و پ(·)مجموعه قدرت را نشان می دهد.

یک زیرگراف را در نظر می گیریم سgحاوی واحدها سg.Uاگر حداقل یکی از واحدهای آن در نقطه زمانی t تحت تأثیر قرار گیردتو∈سg.Uدر t تحت تأثیر قرار می گیرد :

آffهجتیهد(سg،تی)=تیrتوه،∃تو∈سg.U:آffهجتیهد(تو،تی)افآلسه،در غیر این صورت.

4. راه حل پیشنهادی

در این مقاله، هدف ما تعیین زیرگراف های وابسته به ساختار در یک شبکه جاده ای است.
رویکرد ST-Discovery ما شامل مراحل اصلی زیر است که در شکل 2 نشان داده شده است : (i) ما واحدهای متاثر از نمودار حمل و نقل را با استفاده از داده های ترافیک شناسایی می کنیم. (ب) ما الگوریتم‌هایی را برای شناسایی زیرگراف‌های آسیب‌دیده از نمودار حمل‌ونقل ایجاد می‌کنیم. (iii) ما یک الگوریتم برای شناسایی وابستگی های مکانی-زمانی ساختاری زیرگراف های شناسایی شده توسعه می دهیم.

4.1. شناسایی واحدهای آسیب دیده

هدف این مرحله شناسایی واحدهای آسیب‌دیده است، یعنی واحدهایی که بار فوق‌العاده بالایی را در هر نقطه زمانی از خود نشان می‌دهند. عوامل مؤثر بر ترافیک جاده‌ای شامل عوامل زمانی تکرارشونده (مانند ساعات شلوغی) و عوامل مکانی مانند توپولوژی شبکه جاده‌ای است. از آنجایی که هدف ما شناسایی تراکم مکرر ناشی از توپولوژی شبکه جاده است، مطلوب است که عوامل زمانی تکرار شونده را از تجزیه و تحلیل خود حذف کنیم. برای اینکه به طور انحصاری الگوهای تراکم زمانی را در نظر بگیریم، واحدهای آسیب‌دیده را به‌عنوان نقاط پرت زمانی با استفاده از قانون محدوده بین‌چارکی (IQR) شناسایی می‌کنیم [ 33 ]]. از آنجایی که آیا روز یک روز هفته است و زمان روز به شدت بر بار ترافیک تأثیر می‌گذارد، واحدهایی را شناسایی می‌کنیم که در مقایسه با میانگین بار ترافیکی این واحدها در همان روز هفته و روز، بار فوق‌العاده بالایی از خود نشان می‌دهند. به طور رسمی تر ، اگر شرایط زیر وجود داشته باشد، شما را در زمان t تحت تأثیر قرار می دهیم:

آffهجتیهد(تو،تی)=تیrتوه،منfتول(تو،تی)>س3(تو،تی)+1.5·منسآرافآلسه،در غیر این صورت،

جایی که سn(تو،تی)نشان دهنده ی چهارمین ربع بار واحد بر روی واحد u در مورد روز هفته و زمان روز است، و منسآر=س3(تو،تی)-س1(تو،تی)محدوده بین چارکی را نشان می دهد.

ما حد بالایی بار واحد را از قبل محاسبه می کنیم س3(تو،تی)+1.5·منسآربرای هر واحد، روزهای هفته و روز. ما هر واحد u را که بار واحد بالاتری از خود نشان می دهد در نظر می گیریمتول(تو،تی)از حد بالایی متناظر که در نقطه زمانی t تحت تأثیر قرار می گیرد .

4.2. شناسایی زیرگراف های تحت تأثیر

هدف این مرحله شناسایی زیرگراف های جداکننده گراف حمل و نقل است. واحدهای یک زیرگراف منفرد باید الگوی بار واحدی را برای یک نقطه زمانی معین نشان دهند. ما با انجام خوشه‌بندی فضایی واحدهای متاثر از نمودار حمل‌ونقل به این هدف نزدیک می‌شویم. در این مرحله، خوشه بندی به طور مستقل در هر نقطه از زمان انجام می شود. برای اطمینان از تداوم فضایی زیرگراف‌های حاصل، خوشه‌بندی واحدهای آسیب‌دیده از اصل رشد منطقه پیروی می‌کند [ 34 ].
خوشه بندی را به صورت زیر انجام می دهیم. ابتدا روی هر واحد آسیب‌دیده یک نقطه بذر قرار می‌دهیم. در طی مراحل بعدی، مناطق با ادغام مناطق همسایه گسترش می یابند تا زمانی که تغییر بیشتری ایجاد نشود. همسایگی دو منطقه با ارزیابی فاصله بین نزدیکترین لبه های آنها در نمودار حمل و نقل تعیین می شود. این فاصله به عنوان شمارش لبه ها اندازه گیری می شود دتودر کوتاه ترین مسیر بین مناطق.
از آنجایی که داده ها به طور بالقوه می توانند ناقص باشند یا حاوی خطاهای اندازه گیری باشند، هنگام تعیین همسایگی، تحمل خاصی را مجاز می کنیم. تا این حد آستانه را معرفی می کنیم دتو،مترآایکسبرای پر کردن شکاف های با اندازه از پیش تعریف شده بین دو منطقه. بنابراین، دو منطقه به عنوان همسایه در نظر گرفته می شوند و در صورت شرط توسط الگوریتم ادغام می شوند دتو≤دتو،مترآایکسدارای. در نتیجه، واحدهای تحت تأثیر در نقطه زمانی t به مجموعه‌ای از n خوشه خوشه‌بندی می‌شوند.سیتی={ج0،…،جn}.
توجه داشته باشید که این رویکرد خوشه‌بندی از ساختار گراف زیربنایی گراف حمل و نقل استفاده می‌کند. بنابراین، یک نگاشت منحصر به فرد بین هر خوشه و زیرگراف مربوطه وجود دارد تیجی. در ادامه، ضمن اشاره به نتایج خوشه بندی، از اصطلاحات خوشه و زیرگراف تحت تأثیر به جای یکدیگر استفاده می کنیم.

4.3. ادغام فضایی زیرگرافهای تحت تأثیر

زیرگراف‌های آسیب‌دیده شناسایی‌شده در بخش 4.2 از نظر مکانی با توجه به زمان‌های خاص از هم جدا هستند. به طور شهودی، هنگام در نظر گرفتن بار ترافیک در نمودار حمل‌ونقل در مدت زمان طولانی‌تر، می‌توانیم تغییرات مکانی زیرگراف‌های آسیب‌دیده را مشاهده کنیم، به عنوان مثال، به دلیل انتشار ازدحام در طول نمودار. علاوه بر این، زیرگراف های تحت تأثیر (و تغییرات آنها) می توانند در مقاطع مختلف زمانی دوباره تکرار شوند. برای ثبت این الگوها، ما ادغام زیرگراف‌های متاثر از همپوشانی مکانی را که در مقاطع زمانی مختلف رخ می‌دهند، انجام می‌دهیم.
الگوریتم 1 یک رویکرد حریصانه فزاینده برای ادغام زیرگراف های متاثر از همپوشانی فضایی ارائه می دهد. الگوریتم شامل یک حلقه اصلی (خط 6-24) است که در آن مراحل جداگانه شامل تولید نامزد (خط 9-11)، محاسبه شباهت (خط 12-14) و ادغام (خط 15-24) است. برای نسل کاندید ، ما همه جفت‌های زیرگراف را که حداقل یک واحد مشترک دارند به عنوان کاندید در نظر می‌گیریم (خط 13). اینجا، [پ(·)]2زیرمجموعه مجموعه توان با عناصر کاردینالیته 2 را نشان می دهد.

محاسبه شباهت برای همه نامزدها (یعنی جفت های زیرگراف) با محاسبه تابع شباهت انجام می شود. شباهت:اسجی×اسجی↦[0،1]به شرح زیر (خط 14):

شباهت(سg1،سg2)=1منfسg1⊂سg2∨سg2⊂سg1،|سg1∩سg2||سg1∪سg2|،در غیر این صورت.
بر اساس تعریف زیرگراف تحت تأثیر، ما جفت‌های زیرگراف را که در آنها یک زیرگراف به طور کامل شامل زیرگراف دیگر می‌شود، به‌عنوان حالت خاصی در نظر می‌گیریم که حداکثر شباهت 1 را دارد. در غیر این صورت، شباهت به عنوان شباهت ژاکارد محاسبه می‌شود ، که اندازه‌گیری می‌کند میزان همپوشانی واحدهای زیرگراف
در نهایت، مرحله ادغام ، جفت‌های زیرگراف را با امتیاز شباهت بالاتر از آستانه جمع می‌کند. تیساعتسمنمتر(خط 19-23). جفت هایی که بیشترین شباهت را دارند ابتدا ادغام می شوند (خط 16). در اینجا تابع ordered() جفت های زیرگراف را به ترتیب تشابه نزولی مرتب می کند. از آنجایی که ادغام بر محاسبه شباهت تأثیر می گذارد، در هر تکرار الگوریتم، هر زیرگراف را می توان تنها یک بار ادغام کرد (خط 17-18).
پیچیدگی زمان اجرا الگوریتم 1 از ترکیب حلقه while اصلی در خط 7 ناشی می شود ( O(|سی|)) و تکرار بر روی مجموعه مرتب شده از جفت های فرعی در خط 16 ( O(|سی|2·ورود به سیستم(|سی|2))=O(|سی|2·ورود به سیستم(|سی|))) منجر به پیچیدگی کلی از O(|سی|3·ورود به سیستم(|سی|)).
برای تسهیل تولید نامزد کارآمد، ما یک نقشه هشم ( commonUnits ) داریم که یک نقشه برداری از یک واحد u به همه زیرگراف هایی که حاوی این واحد u هستند (خطوط 2-5) ارائه می دهد. محاسبه تمام ترکیبات زیرگراف به زمان درجه دوم نیاز دارد ( O(|سی|2)) در هر تکرار. در مقابل، نقشه هاشم یک بار محاسبه می شود ( O(|سی|·|U|)) و سپس در طول الگوریتم با توجه به ادغام انجام شده با استفاده از تابع update() (خط 23) به طور مکرر به روز می شود. حلقه های خطوط 10 و 13 را می توان به صورت موازی برای بهینه سازی بیشتر اجرا کرد.
الگوریتم 1 ادغام زیرگرافها
ورودی:  C : مجموعه ای از زیرگراف ها
خروجی:  SG : مجموعه ای از زیرگراف های ادغام شده
1: اسجی←سی
2: جoمترمترonUnمنتیس←[]
3: برای همه سg∈اسجی انجام دادن
4:   برای همه تو∈سg.U انجام دادن
5:    جoمترمترonUnمنتیس[تو]←جoمترمترonUnمنتیس[تو]∪سg
6: تغییر کرد← درست است
7: در حالی که تغییر انجام دهید
8: تغییر کرد ← نادرست
{تولید نامزدها}
9: نامزدها ←∅
10:   برای همه تو∈جoمترمترonUnمنتیس انجام دادن
11: نامزدها ← نامزدها ∪[پ(جoمترمترonUnمنتیس[تو])]2
{محاسبه شباهت ها}
12:   س[]←∅
13:   برای همه (سg1،سg2)∈نامزدها انجام می دهند
14:    س[(سg1،سg2)]←شباهت (سg1،سg2)
{ادغام زیرگرافها}
15: بازدید شد ←∅
16:   برای همه (سg1،سg2)∈سفارش داده شده (س) انجام دادن
17:    اگر سg1∈ملاقات کرد ∨سg2∈سپس بازدید کرد
18: ادامه دهید
19:    اگر س[(سg1،سg2)]≥تیساعتسمنمتر سپس
20:     سg1←سg1∪سg2
21:     اسجی←اسجی∖سg2
22: بازدید شده ← بازدید شده ∪{سg1،سg2}
23: به روز رسانی (واحدهای مشترک)
24: تغییر کرد ← درست است
25: بازگشت اسجی

4.4. شناسایی وابستگی های مکانی – زمانی

در این مرحله، هدف ما شناسایی زیرگراف‌های وابسته گراف حمل‌ونقل است، یعنی زیرگراف‌هایی که معمولاً به طور همزمان تحت تأثیر قرار می‌گیرند و در مجاورت فضایی قرار دارند. تا این حد، ما زیرگراف های شناسایی شده و ادغام شده در بخش 4.3 را در نظر می گیریم . این زیرگراف‌ها زیرگراف‌های مرتبط توپولوژیکی نمودار حمل‌ونقل را نشان می‌دهند، از جمله تغییرات فضایی آن‌ها، که در نقطه‌ای از زمان تحت تأثیر قرار گرفته‌اند. در این مرحله، بعد زمانی را در نظر می‌گیریم و هدف آن شناسایی جفت‌هایی از این زیرگراف‌ها است که معمولاً به طور همزمان تحت تأثیر قرار می‌گیرند.
الگوریتم 2 روشی را برای شناسایی چنین جفت‌های زیرگرافی ارائه می‌کند که در آن مراحل فردی شامل تولید نامزد (خطوط 8-15)، محاسبه امتیاز (خطوط 16-19) و مرتب‌سازی (خط 20) است.

اول، یک ماتریس رخداد oجج[][]شامل زیرگراف ها و نقاط زمانی محاسبه می شود (خطوط 1-7)، که در آن ستون ها با زیرگراف ها و ردیف ها با نقاط زمانی مطابقت دارند. اگر یک زیرگراف در نقطه زمانی t تحت تأثیر قرار گیرد ، سلول مربوطه روی 1 تنظیم می شود. در غیر این صورت، به 0. از ماتریس وقوع، جفت های فرعی نامزد تولید می شوند (خطوط 8-15). هر جفت زیرگراف که به طور همزمان حداقل در یک نقطه زمانی تحت تأثیر قرار می گیرد به عنوان یک جفت نامزد در نظر گرفته می شود. برای هر جفت نامزد، امتیاز وابستگی زیرگراف را محاسبه می کنیم. شهودی که در پشت این امتیاز وجود دارد، به تصویر کشیدن هم‌وقوع زمانی و هم نزدیکی مکانی زیرگراف‌ها است. بنابراین، امتیاز به عنوان ترکیبی از اطلاعات متقابل و یک متریک فاصله مکانی معکوس محاسبه می‌شود:

وابستگی(سg1،سg2)=0،منfدمنستی(سg1،سg2)≤دمنستیمترمنnمترمن(سg1،سg2)·1دمنستی(سg1،سg2)،oتیساعتهrwمنسه.

اینجا، دمنستی(سg1،سg2)نشان دهنده کوتاه ترین فاصله جغرافیایی بین دو زیرگراف است. آستانه دمنستیمترمنnحداقل فاصله جغرافیایی را برای یک جفت زیرگراف که وابسته در نظر گرفته شود مشخص می کند. دمنستیمترمنnاجازه می دهد تا وابستگی های بی اهمیت، مانند زیرگراف های مجاور را حذف کنید. اطلاعات متقابل مترمن(سg1،سg2)هدف آن ارزیابی همزمانی زمانی دو زیرگراف است که به صورت محاسبه شده است

مترمن(سg1،سg2)=∑تی1∈تی1∑تی2∈تی2پ(تی1،تی2)(تی1،تی2)لogپ(تی1،تی2)(تی1،تی2)پتی1(تی1)پتی2(تی2)،

جایی که تیمن={تی∈تی|آffهجتیهد(سgمن،تی)}مجموعه ای از نقاط زمانی را نشان می دهد که در آن زیرگراف وجود دارد سgمنتحت تاثیر قرار گرفته است. مجاورت فضایی به عنوان فاصله معکوس اندازه گیری می شود دمنستی(سg1،سg2)نشان دهنده کوتاه ترین فاصله جغرافیایی بین دو زیرگراف است. در نهایت، جفت‌های زیرگراف به ترتیب نزولی امتیازات وابستگی آنها مرتب می‌شوند (خط 20، به ترتیب ()).

پیچیدگی زمان اجرای الگوریتم 2 از شناسایی نامزدها ( O(|اسجی|2·تی)) در سطر 9 و 12 و همچنین مرتب سازی جفت های زیرگراف بر اساس امتیاز ( O(|اسجی|2·ورود به سیستم(|اسجی|))) در خط 20. بنابراین، پیچیدگی کلی محدود شده است O(|اسجی|2·(تی+ورود به سیستم(اسجی))). در نهایت، حلقه for در خط 17 را می توان به صورت موازی اجرا کرد.
الگوریتم 2 وابستگی های زیرگراف مکانی-زمانی را تعیین کنید
ورودی:    اسجی: مجموعه ای از زیرگراف ها
تی: مجموعه ای از نقاط زمانی
خروجی:  پدهپهnدهnتی    مجموعه ای از جفت زیرگراف،
مرتب شده بر اساس امتیاز وابستگی
1: oجج[][]←∅
2: برای همه تی∈تی انجام دادن
3:   برای همه سg∈اسجی انجام دادن
4:    اگر ∃تو∈اسجی:منqr(تو،تی) سپس
5:     oجج[تی][سg]←1
6:    دیگری
7:      oجج[تی][سg]←0
{تعیین جفت نامزدها}
8: نامزدها ←∅
9: برای همه (سg1،سg2)∈[پ(اسجی)]2 انجام دادن
10:    اگر (سg1،سg2)∈نامزدها سپس
11: ادامه
12:    برای همه تی∈تی
13:    اگر oجج[تی][سg1]=1∧oجج[تی][سg2]=1 سپس
14: نامزدها ← نامزدها ∪{(سg1،سg2)}
15: شکستن
{محاسبه وابستگی}
16: پدهپهnدهnتی←[]
17: برای همه (سg1،سg2)∈جآnدمندآتیهس انجام دادن
18: امتیاز ←وابستگی (سg1،سg2،تی)
19:    پدهپهnدهnتی[(سg1،سg2)]←سجorه
20: بازگشت سفارش داده شده است (پدهپهnدهnتی)
ما پیاده‌سازی منبع باز الگوریتم‌های ST-Discovery را تحت مجوز MIT ارائه می‌کنیم ( https://github.com/Data4UrbanMobility/st-discovery ، در 19 مارس 2021 قابل دسترسی است).

5. مجموعه داده ها

5.1. OpenStreetMap

OpenStreetMap (OSM) ( https://www.openstreetmap.org ، قابل دسترسی در 19 مارس 2021) ارائه‌دهنده داده‌های نقشه در دسترس عموم است. ما از شبکه جاده ای OSM برای تشکیل نمودار حمل و نقل استفاده می کنیم تیجی. OSM جاده ها را در بخش های کوچکتر جاده که با واحدهای نمودار حمل و نقل مطابقت دارند، تقسیم می کند تیجی. به طور خاص، بخش‌های جاده‌ای واقع در شهرهای هانوفر و برانزویک، آلمان را استخراج می‌کنیم. با در نظر گرفتن طبقه‌بندی OSM برای انواع جاده‌ها، ما نمودار حمل و نقل را به جاده‌های اصلی محدود می‌کنیم، زیرا اطلاعات ترافیکی قابل اعتماد برای جاده‌های کوچک‌تر به ندرت در دسترس است. به طور خاص، ما تمام جاده‌هایی را که به یکی از کلاس‌های زیر تعلق دارند استخراج می‌کنیم: {اولیه، پیوند_اصلی، ثانویه، پیوند_ثانویه، سوم، پیوند_ثالثی، بزرگراه، پیوند_بزرگراه، ترانک، ترانک_پیوند}. نمودارهای حمل و نقل استخراج شده شامل تقریباً 23000 واحد (هانوفر) و 7600 واحد (برونزویک) در کل است. برای هر واحد تو∈تیجی، اطلاعات موجود در مورد محدودیت سرعت لمنمتر(تو)و همچنین نوع جاده از OSM استخراج شده است.

5.2. مجموعه داده های ترافیک

آزمایش‌های انجام‌شده در این مقاله از یک مجموعه داده ترافیکی اختصاصی استفاده می‌کنند که حاوی داده‌های شناور خودرو است. به طور خاص، مجموعه داده رکوردهای سرعت ترافیک را برای هر واحد u از نمودار حمل و نقل فراهم می کندتیجی. مجموعه داده توسط یک شرکت ارائه دهنده نرم افزار مسیریابی جمع آوری شد. مجموعه داده شامل داده‌های به‌دست‌آمده از منابع مختلف، از جمله داده‌های جمع‌آوری‌شده از کاربران نرم‌افزار مسیریابی و داده‌های ترافیکی به‌دست‌آمده از ارائه‌دهندگان داده شخص ثالث است. اگرچه آمار دقیق این مشارکت‌ها، مانند تعداد یا انواع وسایل نقلیه تحت نظارت، به دلیل منابع مختلف در دسترس نویسندگان نیست، ما انتظار هیچ گونه سوگیری خاصی نسبت به انواع خاص خودرو یا کلاس‌های هزینه نداریم.
سوابق داده های ترافیک شامل میانگین سرعت ترافیک بر روی واحدهای نمودار حمل و نقل منفرد در نقاط زمانی گسسته است، به عنوان مثال، سپههد(تو،تی)، هر 15 دقیقه ضبط می شود. رکوردهای سرعت متوسط ​​توسط ارائه‌دهنده داده با محاسبه میانگین سرعت ترافیک از داده‌های خام شناور ماشین محاسبه می‌شود که میانگین آن بر روی تمام وسایل نقلیه‌ای که داده‌ها برای واحد و بازه زمانی داده‌شده در دسترس هستند، محاسبه می‌شوند. در مجموعه داده، فقط اطلاعات سرعت ترافیک جمع آوری شده است سپههد(تو،تی)موجود است. داده های دسته بندی جاده های اصلی ذکر شده در بخش 5.1 به طور منظم در مجموعه داده جمع آوری می شوند. جدول 1 آماری در مورد تعداد سوابق داده های ترافیکی موجود برای هانوفر و برانزویک ارائه می دهد. ما معتقدیم که داده‌های موجود برای ثبت الگوهای تراکم معمولی کافی است.

6. آزمایش ها و بحث

هدف این ارزیابی ارزیابی اثربخشی رویکرد ST-Discovery پیشنهادی و کاربرد آن در مجموعه داده های دنیای واقعی ارائه شده در بخش 5 است. ابتدا، ما یک ارزیابی از وابستگی های شناسایی شده توسط ST-Discovery ارائه می کنیم. دوم، ما نتایج هر مرحله اصلی ST-Discovery را ارزیابی و مورد بحث قرار می‌دهیم ، یعنی شناسایی واحدها و زیرگراف‌های آسیب‌دیده، و زیرگراف‌های ادغام‌شده.

6.1. وابستگی های ساختاری

وظیفه شناسایی وابستگی‌های ساختاری مبتنی بر داده‌ها بین زیرگراف‌های یک شبکه جاده‌ای جدید است، به طوری که نه خط پایه و نه هیچ استاندارد طلایی وجود ندارد. بنابراین، برای ارزیابی کیفیت وابستگی‌های ساختاری شناسایی‌شده، یک ارزیابی دستی انجام می‌دهیم. در این ارزیابی، ما از ST-Discovery برای ایجاد یک لیست رتبه‌بندی شده از جفت‌های زیرگراف top-k با امتیازهای وابستگی بالا استفاده می‌کنیم، در حالی که از مقادیر مختلف استفاده می‌کنیم.تیساعتسمنمتر. برای حذف وابستگی های بی اهمیت، یعنی زیرگراف هایی که مجاور یکدیگر هستند، آستانه را تعیین می کنیم. دمنستیمترمنn=500متر تنظیم کردیم دتو،مترآایکس=1برای هانوفر و دتو،مترآایکس=2برای برانزویک
ما به صورت دستی صحت هر یک از جفت های زیرگراف top-k را با بالاترین امتیاز وابستگی ارزیابی می کنیم. اگر بتوانیم یک وابستگی ساختاری را مشاهده و توضیح دهیم، هر جفت را صحیح می‌دانیم، یا در غیر این صورت نادرست است. نویسندگان مقاله ارزیابی را انجام دادند، در حالی که ما قضاوت های فردی را برای به دست آوردن اجماع مورد بحث قرار دادیم. در نهایت، دقت@k را به عنوان نسبت نتایجی که در جفت‌های زیرگراف top-k درست ارزیابی می‌شوند، محاسبه می‌کنیم.
شکل 3 precision@k را نشان می دهدتیساعتسمنمتر∈{0،0.1،0.2،0.3}برای هانوفر ( شکل 3 الف) و برانزویک ( شکل 3 ب). برای هر دو مجموعه داده، بالاترین دقت@k در k = 10 برای همه مقادیر به دست می آیدتیساعتسمنمترجز تیساعتسمنمتر=0. با افزایش مقدار k (یعنی جفت‌های زیرگراف بیشتری با امتیازات پایین‌تر در نظر می‌گیریم)، ​​دقت در اکثر پیکربندی‌ها کاهش می‌یابد. این رفتار را می‌توان انتظار داشت، زیرا جفت‌هایی که امتیازات پایین‌تری دارند، اطلاعات متقابل کمتری دارند یا در فاصله جغرافیایی بالاتری قرار دارند و بنابراین ارتباط کمتری دارند. نتیجه می‌گیریم که امتیاز پیشنهادی برای تعیین کمیت وابستگی زیرگراف‌های آسیب‌دیده مناسب است.
بهترین دقت در k=10 توسط تیساعتسمنمتر=0.3(هانوفر) و تیساعتسمنمتر=0.1(برانزویک). این نشان می دهد که مقدار بهینه از تیساعتسمنمتروابسته به شبکه جاده هدف است. در هر دو مورد، بدترین عملکرد در آن به دست می آید تیساعتسمنمتر=0. پارتیشن بندی نمودار در تیساعتسمنمتر=0نسبتاً درشت است به طوری که واحدهایی که وابستگی های متفاوتی از خود نشان می دهند می توانند در یک زیرگراف جمع شوند. بنابراین، عملکرد به دست آمده کمتر از مقادیر آستانه بالاتر است.
توجه داشته باشید که روش ارزیابی اتخاذ شده، وابستگی جفت‌های زیرگراف را ارزیابی می‌کند، اما دانه‌بندی زیرگراف‌ها را ارزیابی نمی‌کند. پارتیشن بندی با مقادیر آستانه بالاتر (به عنوان مثال، تیساعتسمنمتر=0.3) منجر به زیرگراف های دانه ای ظریف می شود. در این مورد، پارتیشن‌بندی می‌تواند منجر به تقسیم زیرگراف‌هایی شود که وابستگی‌های ساختاری یکسانی را به زیرگراف‌های مختلف نشان می‌دهند، که ممکن است به طور بالقوه منجر به گنجاندن جفت‌های زیرگراف اضافی در نتایج top-k شود.
بنابراین، در حالی که ترکیب مقادیر کمتر k و مقادیر بالاتر از تیساعتسمنمتر=0.3منجر به بالاترین مقادیر precision@k می‌شود، همچنین می‌تواند منجر به مقداری افزونگی در نتایج top-k شود (یعنی جفت‌های زیرگراف نشان دهنده وابستگی یکسان در سطوح مختلف دانه‌بندی). پس از بازرسی دستی دانه بندی نتیجه در مجموعه داده ما، این مقادیر را مشاهده می کنیم تیساعتسمنمتر∈{0.1،0.2}منجر به نتایج خوب، با دقت 80٪ (هانوفر) و 100٪ (برونزویک) در k = 10، در حالی که از زیرگراف های اضافی در نتایج برتر اجتناب می شود. به طور کلی توصیه می کنیم که تیساعتسمنمترآستانه باید با توجه به مجموعه داده خاص و مورد استفاده مورد بررسی تنظیم شود.
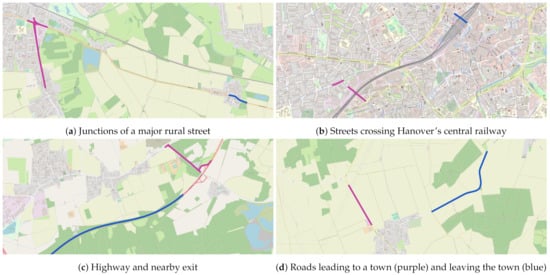
برای تسهیل درک بهتر وابستگی‌های تعیین‌شده، موارد نمونه شناسایی شده توسط ST-Discovery را مورد بحث قرار می‌دهیم . شکل 4 نمونه هایی از جفت های زیرگراف وابسته شناسایی شده در هانوفر را ارائه می دهد که در آن زیرگراف های مربوطه در یک جفت به ترتیب با رنگ آبی و بنفش مشخص شده اند. شکل 4 a دو تقاطع یک خیابان اصلی روستایی را نشان می دهد. زیرگراف آسیب‌دیده در غرب شامل تقاطع و جاده‌های تغذیه‌کننده آن است، در حالی که فقط تقاطع در شرق تحت تأثیر قرار می‌گیرد. این ترکیب می تواند ناشی از رانندگانی باشد که با دسترسی به خیابان در شرق از ازدحام بیشتر در غرب جلوگیری می کنند و منجر به افزایش ترافیک در هر دو تقاطع می شود. شکل 4b دو زیرگراف آسیب دیده را نشان می دهد که از راه آهن مرکزی در شهر هانوفر عبور می کنند. راه آهن دو ناحیه شهری را تقسیم می کند و هنگام تردد بین این مناطق باید از آن عبور کرد. بنابراین، زیرگراف ها مسیرهای جایگزین برای سفرهای شمال به جنوب را نشان می دهند و گلوگاهی را برای چنین سفرهایی تشکیل می دهند. شکل 4 ج یک بزرگراه آسیب دیده (آبی) و آخرین خروجی ممکن قبل از آن بخش (بنفش) را نشان می دهد. اگر بزرگراه تحت تأثیر قرار گیرد، خروجی نزدیک و جاده های متوالی نیز تحت تأثیر قرار می گیرند. این احتمالاً ناشی از تلاش رانندگان برای خروج از بزرگراه قبل از ورود به قسمت شلوغ است که منجر به افزایش بار در آن منطقه می شود. شکل 4d یک جاده منتهی به یک شهر (بنفش) و یک جاده دیگر که از شهر خارج می شود (آبی) را به تصویر می کشد. این نشان دهنده حجم زیادی از ترافیک است که به دلیل فقدان مسیرهای جایگزین از زیرگراف بنفش به آبی عبور می کند. در این صورت، ساخت یک جاده جایگزین جدید می تواند از قرار گرفتن شهر در معرض بار ترافیکی زیاد جلوگیری کند.
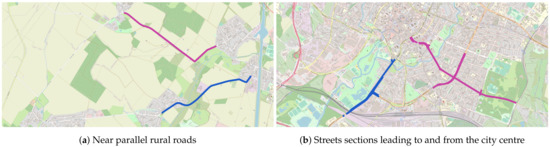
شکل 5 نمونه هایی از جفت های زیرگراف وابسته شناسایی شده در برانزویک را نشان می دهد. شکل 5 a دو بخش جاده نزدیک به موازی را نشان می دهد که مناطق شهری مشابه را به هم متصل می کند. جاده ها مسیرهای جایگزین برای سفر به شرق یا غرب را تشکیل می دهند. اگر یکی از بخش‌های جاده با ازدحام مواجه شود، جاده دیگر احتمالاً با افزایش بار ناشی از رانندگانی که می‌خواهند از ازدحام جلوگیری کنند، مواجه خواهد شد. شکل 5 ب دو زیرگراف وابسته را در نزدیکی مرکز شهر برانزویک نشان می دهد. زیرگراف ها گزینه های برجسته ای برای خروج یا ورود به مرکز شهر هستند. اگر مرکز شهر شلوغ باشد، ازدحام احتمالاً به زیرگراف ها نیز گسترش می یابد. علاوه بر این، اگر یک زیرگراف شلوغ باشد، زیرگراف دیگر یک مسیر جایگزین برای یک سفر مشابه را نشان می دهد.

6.2. تجزیه و تحلیل واحدها و زیرگرافهای تحت تأثیر

در این بخش، توزیع واحدها و زیرگراف های آسیب دیده شناسایی شده توسط ST-Discovery در مجموعه داده های خود و تأثیر پارامتر مربوطه را تجزیه و تحلیل می کنیم.

6.2.1. توزیع واحدهای آسیب دیده

نتایج تجزیه و تحلیل توزیع واحدهای تحت تأثیر شناسایی شده توسط الگوریتم ارائه شده در بخش 4.1 در شکل 6 نشان داده شده است . شکل 6a تعداد واحدهای آسیب دیده را در هر نقطه زمانی بین نوامبر و دسامبر 2017 در هانوفر نشان می دهد. مشاهده می‌کنیم که تعداد واحدهای تحت‌تأثیر به‌طور پیوسته، از 3 تا 7724 در مجموعه داده ما، با مقدار متوسط ​​409 تغییر می‌کند. ما بالاترین قله‌ها را بین 10 دسامبر 2017 و 15 دسامبر 2017 مشاهده می‌کنیم. از طریق یک بررسی دستی (یعنی جستجوی مقالات خبری مربوط به این منطقه و تاریخ‌ها در Google)، متوجه شدیم که بارش برف سنگین باعث تاخیرهای زیاد و غیرعادی در کل شبکه جاده‌ای شده است. در طول این مدت. این در تعداد زیادی از واحدهای تحت تأثیر در سراسر شبکه منعکس می شود. شکل 6b تعداد واحدهای آسیب دیده را در هر نقطه زمانی بین دسامبر 2018 و ژانویه 2019 در برانزویک نشان می دهد. ما یک تغییر مداوم مشابه از تعداد واحدهای آسیب دیده را از 59 تا 770 با مقدار متوسط ​​203 مشاهده می کنیم.
قله‌های کوچک‌تر در چندین زمان رخ می‌دهند، به عنوان مثال، در 3 دسامبر 2017 (هانوفر) و 26 ژانویه 2019 (برونزویک)، که در آن اندازه قله‌ها بسیار متفاوت است. با توجه به این مشاهدات، ما معتقدیم که پیک های موقت در تعداد واحدهای آسیب دیده می تواند نشان دهنده وقوع حوادث فوق العاده باشد. توجه داشته باشید که این مشاهدات صرفاً بر اساس همزمانی‌های زمانی است و هیچ بینشی از ویژگی‌های فضایی حوادث ارائه نمی‌کند.
6.2.2. توزیع زیرگرافهای تحت تأثیر
در این بخش، توزیع زیرگراف های تحت تأثیر شناسایی شده با استفاده از الگوریتم های ارائه شده در بخش 4.2 و تأثیر پارامترهای مربوطه را تجزیه و تحلیل می کنیم.
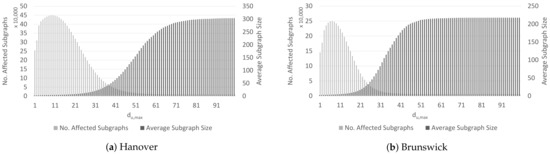
در طی شناسایی زیرگراف های تحت تأثیر با استفاده از خوشه بندی واحدهای تحت تأثیر ارائه شده در بخش 4.2 ، آستانه دتو،مترآایکسمعرفی شد که تحمل فاصله را در تخصیص واحدهای آسیب دیده به یک زیرگراف توصیف می کند. بنابراین، تغییرات در مقدار این آستانه منجر به تعداد و اندازه متفاوتی از خوشه های واحد می شود، همانطور که در شکل 7 a برای هانوفر و در شکل 7 b برای برانزویک نشان داده شده است. ما ارزش های آن را ارزیابی می کنیم دتو،مترآایکس∈[0،100]برای گرفتن الگوهای همگرایی بالقوه در تعداد زیرگراف های تحت تأثیر و اندازه متوسط ​​زیرگراف. با افزایش تحمل (یعنی ارزش دتو،مترآایکس، دو روند را می توان در هر دو شبکه جاده مشاهده کرد. در حالی که اندازه متوسط ​​زیرگراف های حاصل افزایش می یابد، تعداد آنها کاهش می یابد. این به دلیل این واقعیت است که در صورت افزایش تحمل برای تعیین همسایگی بخش، زیرگراف های بیشتری ادغام می شوند.
با مقایسه شبکه‌های جاده‌ای با یکدیگر، مشاهده می‌کنیم که اشباع اندازه زیرگراف در مقادیر کوچک‌تر به دست می‌آید. دتو،مترآایکسبرای برانزویک (در 51) نسبت به هانوفر (در 71)، زیرا شبکه جاده ای برانزویک (7678 واحد) کوچکتر از شبکه جاده هانوفر (23125 واحد) است. در نقطه اشباع، کل شبکه راه توسط یک زیرگراف گرفته شده است. بنابراین، ارزش بیش از حد بالا از دتو،مترآایکسبرای شناسایی وابستگی های معنی دار مناسب نیست.
به طور کلی، انتخاب یک مقدار مناسب برای دتو،مترآایکسبه شدت به سناریوی کاربردی، شبکه جاده و مقیاس تجزیه و تحلیل بستگی دارد. به عنوان مثال، اگر یک منطقه بزرگ، به عنوان مثال، یک شهر کامل، یا یکی از مناطق آن، باید تجزیه و تحلیل شود. زیرگراف های کوچکی که فقط از چند بخش جاده تشکیل شده اند چندان مهم نیستند. برای این مورد، مقدار آستانه بالاتری باید انتخاب شود. در مقابل، برای بازرسی دقیق بخش‌های کوچک‌تر شبکه راه‌ها، به‌عنوان مثال، جاده‌ها یا تقاطع‌های خاص، زیرگراف‌های ظریف‌تر حیاتی‌تر هستند. در این مورد، برای جلوگیری از ادغام زیرگراف های کوچکتر، مقدار کمتری از دتو،مترآایکسباید انتخاب شود. علاوه بر این، دانه بندی تقسیم بندی شبکه جاده ها نقش مهمی در انتخاب دارد دتو،مترآایکس. برای یک تقسیم بندی دانه ریز، مقدار بالاتری از دتو،مترآایکسمی توان برای به دست آوردن زیرگراف های بزرگتر و معنی دارتر استفاده کرد. علاوه بر این، این پارامتر اجازه می دهد تا با پرش از بخش هایی که هیچ داده ای برای آنها در دسترس نیست، به پراکندگی داده ها رسیدگی شود. برای شبکه جاده ای با تقسیم بندی درشت، مقادیر کمتری از دتو،مترآایکسجلوگیری از پوشش زیرگراف ها یک منطقه فضایی بیش از حد بزرگ.
در محیط آزمایشی خود، تنظیم کردیم دتو،مترآایکس=1برای هانوفر و دتو،مترآایکس=2برای برانزویک ما با ارزیابی دستی مشاهده کردیم که مقادیر بالاتری از دتو،مترآایکسدر این مجموعه داده‌ها، زیرگراف‌هایی به‌وجود می‌آیند که برای معنی‌دار بودن بیش از حد بزرگ هستند، در حالی که امکان رد شدن از یک یا دو یال منجر به نتایج پایدار می‌شود.
6.2.3. تداوم موقت زیرگرافهای تحت تأثیر

علاوه بر اندازه زیرگراف‌های آسیب‌دیده شناسایی‌شده، ما ماندگاری زمانی آنها را در مثال هانوفر تحلیل می‌کنیم. این بدان معناست که زیرگراف‌های آسیب‌دیده شناسایی‌شده در نقطه زمانی i (شامل تغییرات معمولی این زیرگراف‌ها، به عنوان مثال، به دلیل انتشار بار ترافیک در طول نمودار حمل‌ونقل) باید در مراحل زمانی بعدی شناسایی شوند. برای این منظور، الگوریتمی بر اساس روش مجارستانی [ 35 ] اعمال می کنیم. هدف این الگوریتم یافتن یک انتساب بهینه از خوشه‌ها (یعنی زیرگراف‌های تحت تأثیر) در دو مرحله زمانی متوالی با به حداقل رساندن هزینه‌های تخصیص است. به منظور محاسبه هزینه های تخصیص، تقاطع واحدهای تحت تأثیر درگیر در هر زیرگراف (خوشه) در دو مرحله زمانی بعدی iو j به صورت محاسبه می شود

جoستیسمن،j=||جمن∩جj||∀جمن∈سیمن،جj∈سیj.
علاوه بر این، هیچ تلورانسی به یک زیرگراف اجازه نمی دهد که مراحل زمانی بعدی را رد کند. این بدان معنی است که اگر این زیرگراف در یک مرحله زمانی ظاهر نشود، زمان وجود زیرگراف طولانی نخواهد شد. بنابراین، اگر برای یک زیرگراف فعلی در مرحله زمانی زیر تخصیصی وجود نداشته باشد، این زیرگراف “می میرد”. اگر در مرحله بعدی اما یک زمان، خوشه‌ای از واحدهای آسیب‌دیده در همان بخش‌های جاده واقع شده باشد، این خوشه به عنوان یک زیرگراف جدید تحت تأثیر قرار می‌گیرد، یعنی یک شناسه جدید به این زیرگراف اختصاص داده می‌شود و یک زمان وجود جدید خواهد بود. آغاز شود.
همانطور که فرض می کنیم زمان وجود یک خوشه به اندازه آن بستگی دارد، زمان وجود زیرگراف را بر حسب اندازه آنها ارزیابی کردیم. همانطور که در بخش 6.2.2 بحث شد ، اندازه زیرگراف ها به این بستگی دارد دتو،مترآایکس. مشابه مطالعه روی اندازه‌های زیرگراف، مقادیر آن را بررسی می‌کنیم دتو،مترآایکس∈[0،100]. شکل 8 میانگین زمان وجود خوشه ها را در رابطه با اندازه متوسط ​​زیرگراف و آستانه انتخاب شده نشان می دهد. دتو،مترآایکس. روند کلی نشان می دهد که زمان وجود زیرگراف های تحت تأثیر با اندازه آنها افزایش می یابد. میانگین زمان وجود برای مقادیر کمتر از دتو،مترآایکس∈[0،40]بین 15 تا 90 دقیقه است. این زمان های وجود با مدت زمان تراکم ترافیک معمولی مطابقت دارد. برای مقادیر بالاتر از دتو،مترآایکس∈[71،100]، یک زیرگراف واحد کل شبکه راه ها را پوشش می دهد. این منجر به زمان وجود شدید تا 105دقیقه به طوری که تداوم زیرگراف تحت تأثیر کل مجموعه داده را پوشش دهد. بنابراین، انتخاب از دتو،مترآایکسنه تنها بر اندازه زیرگراف، بلکه بر زمان وجود آن نیز تأثیر می گذارد.

6.3. ارزیابی ادغام زیرگراف

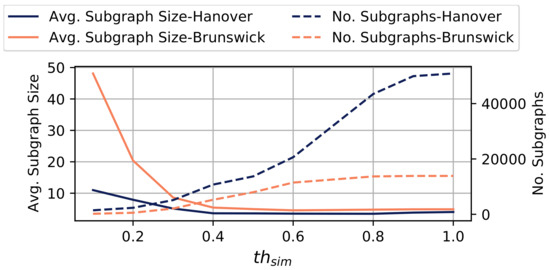
در این بخش، تأثیر آستانه را تحلیل می‌کنیم تیساعتسمنمتردر مورد نتایج ادغام زیرگراف انجام شده با استفاده از الگوریتم 1. شکل 9 با تعداد زیرگراف ها و اندازه متوسط ​​زیرگراف های محاسبه شده توسط الگوریتم 1 با توجه به آستانه تشابه مخالف است. تیساعتسمنمترکه مشخص می کند برای ادغام شدن، دو زیرگراف در کدام کسری باید همپوشانی داشته باشند. مقادیر آستانه بالاتر محدودتر هستند.
به طور کلی، به عنوان تیساعتسمنمترافزایش می یابد، تعداد رو به رشدی از زیرگراف ها را مشاهده می کنیم، در حالی که اندازه متوسط ​​این زیرگراف ها کاهش می یابد. این نشان می دهد که بالاتر است تیساعتسمنمتراین مقادیر منجر به تقسیم ریزتر شبکه جاده به زیرگراف های کوچکتر می شود. بیشترین تغییر اندازه متوسط ​​زیرگراف را می توان برای مشاهده کرد تیساعتسمنمتر∈[0،0.4]. برای تیساعتسمنمتر>0.4، ما فقط تغییرات کوچکی در اندازه متوسط ​​زیرگراف مشاهده می کنیم. نتیجه می گیریم که ارزش های درون [0،0.4]به ویژه برای کالیبره کردن الگوریتم در تنظیمات در نظر گرفته شده مناسب هستند، در حالی که مقادیر آستانه بالاتر منجر به تعداد بیشتری از زیرگراف ها می شود (تا 50 کیلو زیرگراف مستقل در هانوفر) و تنها بر اندازه زیرگراف تأثیر ضعیفی می گذارد.
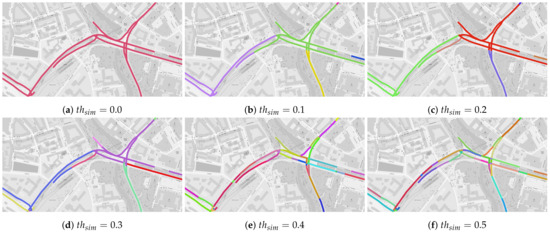
ما تأثیر آن را نشان می دهیم تیساعتسمنمتربه عنوان مثال از یک اتصال اصلی در هانوفر در مجموعه داده ما. شکل 10 شش پارتیشن بندی مختلف شبکه راه ها را در زیر نمودارها با توجه به مقادیر نشان می دهد. تیساعتسمنمتر∈[0،0.5]، که در آن رنگ واحدها نشان دهنده انتساب آنها به زیرگراف های مختلف است. به طور کلی، زیرگراف ها با افزایش مقدار دانه دانه ریزتر می شوند تیساعتسمنمتر. برای تیساعتسمنمتر=0(کمترین مقدار محدود کننده)، مشاهده می کنیم که همه واحدها در ناحیه در نظر گرفته شده به یک زیرگراف اختصاص داده می شوند. توجه داشته باشید که الگوریتم 1 با تیساعتسمنمتر=0به طور خودکار همه زیرگراف ها را ادغام نمی کند، بلکه فقط آنهایی را که حداقل یک واحد مشترک دارند ادغام می کند. برای تیساعتسمنمتر=0.1، محل اتصال به سه زیرگراف اصلی مربوط به بخش شمالی (سبز)، جنوب (زرد) و غرب (بنفش) شبکه تقسیم می شود. افزایش بیشتر از تیساعتسمنمترمنجر به پارتیشن های دانه ای ظریف تر از محل اتصال می شود. به عنوان مثال، برای تیساعتسمنمتر=0.3زیرگراف های جداگانه برای جاده های شمال غربی (صورتی) و شمال شرقی (بنفش) وجود دارد. در نهایت، برای تیساعتسمنمتر∈{0.4،0.5}ما یک پارتیشن بندی دانه ای ظریف از اتصال را در تعداد زیادی زیرگراف مشاهده می کنیم، که در آن زیرگراف های جداگانه ممکن است فقط چند واحد داشته باشند. این مربوط به افزایش تعداد زیرگرافها در شکل 9 برای مقادیر بالای آن است تیساعتسمنمتر.
به طور کلی، تیساعتسمنمترمی توان برای تنظیم دانه بندی ST-Discovery استفاده کرد. در حالی که مقادیر آستانه کمتر منجر به زیرگراف های بزرگ می شود که بخش های بزرگ تری از شبکه جاده را پوشش می دهد ( تیساعتسمنمتر=0، زیرگراف های به دست آمده با استفاده از مقادیر آستانه بالاتر (به عنوان مثال، تیساعتسمنمتر=0.4) گروه های بسیار کوچک تری از واحدهای آسیب دیده را پوشش می دهد.
مشابه سایر پارامترها، انتخاب بتن از تیساعتسمنمتربستگی به مورد استفاده و شبکه جاده دارد. در مثال شکل 10 ، آستانه را می توان روی آن تنظیم کرد تیساعتسمنمتر=0برای بررسی وابستگی های اتصال، به عنوان مثال، سایر اتصالات. مقادیر بالاتر، به عنوان مثال، تیساعتسمنمتر=0.2می تواند بین جهت های اصلی اتصال، یعنی غرب (سبز)، شمال شرقی (قرمز) و جنوب (بنفش) تفاوت قائل شود. افزایش آستانه بیشتر به تیساعتسمنمتر=0.4تمایز بین خطوط جداگانه جاده ها را امکان پذیر می کند.
در محیط آزمایشی خود، مقادیر را ارزیابی کردیم تیساعتسمنمتر∈{0.0،0.1،0.2،0.3}، جایی که معنی دارترین نتایج را با آن به دست آوردیم تیساعتسمنمتر=0.3برای هانوفر و تیساعتسمنمتر=0.1برای برانزویک

7. نتیجه گیری و چشم انداز

در این مقاله، ما به مشکل کشف داده محور وابستگی های توپولوژیکی تراکم مکرر در شبکه های جاده ای شهری پرداختیم. ما رویکرد ST-Discovery را ارائه کردیم – یک روش جدید برای تشخیص چنین وابستگی‌هایی بر اساس تحلیل ترافیک پرت. ST-Discovery واحدها (به عنوان مثال، بخش‌های جاده) را در شبکه جاده شناسایی می‌کند که بار ترافیکی فوق‌العاده بالایی را نشان می‌دهند، الگوریتم‌هایی را برای شناسایی زیرگراف‌های آسیب‌دیده در شبکه جاده‌ای با استفاده از این واحدها پیشنهاد می‌کند و وابستگی‌های مکانی-زمانی را در میان این زیرگراف‌ها شناسایی می‌کند. علاوه بر این، ST-Discovery پارامترهایی را برای تنظیم دانه بندی زیرگراف های شناسایی شده برای موارد استفاده خاص ارائه می دهد. نتایج ارزیابی ما بر روی مجموعه داده های دنیای واقعی این را نشان می دهدST-Discovery می‌تواند وابستگی‌های مکانی-زمانی معنی‌دار را در میان زیرگراف‌ها در شبکه‌های جاده‌ای شهری شناسایی کند. الگوهای RC شناسایی شده شامل وابستگی‌هایی در جاده‌های تغذیه بزرگراه‌ها هستند. مسیرهای جایگزین در صورت اختلال در ترافیک؛ یا مسیرهای معمولی به POI مانند، به عنوان مثال، مکان رویداد.
ما معتقدیم که رویکرد ما در زمینه‌های مختلف، مانند استخراج وابستگی‌های توپولوژیکی در حضور رویدادها و حوادث، و تحت شرایط آب و هوایی مختلف قابل اجرا است. در این مقاله مجموعه داده ای را در نظر گرفتیم که یک فصل واحد یعنی زمستان را پوشش می دهد. اگر الگوهای فصلی مورد توجه هستند، هر فصل را می توان به طور جداگانه با استفاده از روش ما با پارتیشن بندی داده ها با توجه به فصل بررسی کرد. یکی دیگر از موارد جالب توجه به رویکرد ما، استفاده از اطلاعات بیشتر، به عنوان مثال، تعداد وسایل نقلیه یا انواع وسایل نقلیه است. علاوه بر این، ما تصور می کنیم که الگوریتم ما می تواند برای بهینه سازی مسیریابی انحراف در حضور موانع موقت جاده مانند سایت های ساخت و ساز یا حوادث ترافیکی استفاده شود. کاربرد و سودمندی رویکرد در این زمینه ها و موارد استفاده موضوعاتی برای تحقیقات آینده است. در نهایت، ما قصد داریم به جنبه های توضیح پذیری بپردازیمنتایج ST-Discovery برای کاربران نهایی، از جمله، به عنوان مثال، برنامه ریزان شهری و مدیران ترافیک.

منابع

  1. گوا، اس. ژو، دی. فن، جی. تانگ، کیو. زو، تی. Lv، W. لی، دی. هاولین، اس. شناسایی تاثیرگذارترین جاده ها بر اساس شبکه های همبستگی ترافیک. EPJ Data Sci. 2019 ، 8 ، 1-17. [ Google Scholar ] [ CrossRef ]
  2. داولینگ، آر. اسکاباردونیس، ا. کارول، ام. Wang, Z. روش‌شناسی برای اندازه‌گیری تراکم ترافیک مکرر و غیر تکراری. ترانسپ Res. ضبط 2004 ، 1867 ، 60-68. [ Google Scholar ] [ CrossRef ]
  3. آن، اس. یانگ، اچ. وانگ، جی. نشان دادن الگوهای تکامل مکرر تراکم شهری با مسیرهای تاکسی. ISPRS Int. J. Geo-Inf. 2018 ، 7 ، 128. [ Google Scholar ]
  4. آن، اس. یانگ، اچ. وانگ، جی. کوی، ن. کوی، جی. الگوهای تکامل تراکم مکرر شهری استخراج از داده‌های تحرک وسیله نقلیه مجهز به GPS. Inf. علمی 2016 ، 373 ، 515-526. [ Google Scholar ] [ CrossRef ]
  5. تمپلمایر، ن. فوئرهاک، یو. دستمزد، او. Demidova، E. ST-Discovery: کشف وابستگی های ساختاری مبتنی بر داده در شبکه های جاده شهری. در مجموعه مقالات بیست و هفتمین کنفرانس بین‌المللی ACM SIGSPATIAL در مورد پیشرفت‌ها در سیستم‌های اطلاعات جغرافیایی، شیکاگو، IL، ایالات متحده آمریکا، 5 تا 8 نوامبر 2019. [ Google Scholar ]
  6. تمپلمایر، ن. ساندر، ا. فوئرهاک، یو. Löhdefink، M. Demidova، E. TA-Dash: یک داشبورد تعاملی برای تجزیه و تحلیل ترافیک مکانی-زمانی. در مجموعه مقالات بیست و هشتمین کنفرانس بین‌المللی ACM SIGSPATIAL در مورد پیشرفت‌ها در سیستم‌های اطلاعات جغرافیایی، سیاتل، WA، ایالات متحده آمریکا، 3 تا 6 نوامبر 2020. [ Google Scholar ]
  7. وو، اف. وانگ، اچ. Li، Z. تفسیر دینامیک ترافیک با استفاده از داده های شهری همه جا حاضر. در مجموعه مقالات بیست و چهارمین کنفرانس بین المللی ACM SIGSPATIAL در مورد پیشرفت در سیستم های اطلاعات جغرافیایی، سانفرانسیسکو، کالیفرنیا، ایالات متحده آمریکا، 31 اکتبر تا 3 نوامبر 2016. [ Google Scholar ]
  8. پان، بی. Demiryurek، U. گوپتا، سی. شهابی، سی. پیش بینی تأثیر فضایی و زمانی حوادث ترافیکی برای سیستم های ناوبری نسل بعدی. بدانید. Inf. سیستم 2015 ، 81-88. [ Google Scholar ] [ CrossRef ]
  9. Rettore، PHL; سانتوس، BP; ریگولین، اف. لوپس، آر. مایا، جی. ویلا، لس آنجلس; لوریرو، چارچوب غنی‌سازی داده‌های جاده‌ای AAF بر اساس ترکیب داده‌های ناهمگن برای ITS. IEEE Trans. هوشمند ترانسپ سیستم 2020 ، 21 ، 1751-1766. [ Google Scholar ] [ CrossRef ]
  10. لی، جی. هنگ، بی. تره فرنگی.؛ Jang, Y. مدل پیش بینی تراکم ترافیک با استفاده از داده های آب و هوا. در مجموعه مقالات کنفرانس بین المللی IEEE در علم داده و سیستم های فشرده داده، سیدنی، استرالیا، 11 تا 13 دسامبر 2015. [ Google Scholar ]
  11. Chung, Y. ارزیابی ازدحام غیر مکرر ناشی از بارندگی با استفاده از داده های آب و هوا و جریان ترافیک آرشیو شده. ترانسپ سیاست 2012 ، 19 ، 167-173. [ Google Scholar ] [ CrossRef ]
  12. لیو، ی. وو، اچ. پیش‌بینی ازدحام ترافیک جاده‌ای بر اساس جنگل تصادفی. در مجموعه مقالات دهمین سمپوزیوم بین المللی در زمینه هوش محاسباتی و طراحی (ISCID)، هانگژو، چین، 9 تا 10 دسامبر 2017. [ Google Scholar ]
  13. تمپلمایر، ن. دیتزه، اس. دمیدوا، ای. ترافیک کراس‌تاون – پیش‌بینی نظارت شده تأثیر رویدادهای ویژه برنامه‌ریزی‌شده بر ترافیک شهری. GeoInformatica 2020 ، 24 ، 339-370. [ Google Scholar ] [ CrossRef ]
  14. کووچک، اس. مارتینو، اس دی؛ نجدل، دبلیو. در اطراف استادیوم گیر کرده؟ رویکردی برای شناسایی بخش‌های جاده‌ای که تحت تأثیر رویدادهای ویژه برنامه‌ریزی‌شده قرار گرفته‌اند. در مجموعه مقالات هجدهمین کنفرانس بین المللی IEEE در مورد سیستم های حمل و نقل هوشمند، لاس پالماس د گرن کاناریا، اسپانیا، 15 تا 18 سپتامبر 2015. [ Google Scholar ]
  15. انبار اوغلو، بی. هایدکر، بی. چنگ، تی. خوشه بندی فضایی-زمانی برای تشخیص تراکم ترافیک غیرمعمول در شبکه های جاده های شهری. ترانسپ Res. قسمت C Emerg. تکنولوژی 2014 ، 48 ، 47-65. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  16. Laflamme، EM; Ossenbruggen، PJ اثر زمان از روز و روز از هفته بر مدت زمان تراکم و خرابی: مطالعه موردی در یک گلوگاه در Salem، NH. J. Traffic Transp. مهندس (Engl. Ed.) 2017 , 4 , 31-40. [ Google Scholar ] [ CrossRef ]
  17. فولادگر، م. پرچمی، م. الماسری، ر. قادری، ع. شبکه های عصبی جریان ترافیک عمیق مقیاس پذیر برای پیش بینی تراکم ترافیک شهری. در مجموعه مقالات کنفرانس مشترک بین المللی 2017 در مورد شبکه های عصبی (IJCNN)، انکوریج، AK، ایالات متحده آمریکا، 14 تا 19 مه 2017. [ Google Scholar ]
  18. گو، ی. وانگ، ی. دونگ، اس. برآورد تراکم ترافیک عمومی با استفاده از شبکه عصبی مصنوعی. ISPRS Int. J. Geo Inf. 2020 ، 9 ، 152. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
  19. زو، ال. کریشنان، آر. گوا، اف. پولاک، جی دبلیو. Sivakumar، A. شناسایی اولیه ازدحام مکرر در ترافیک شهری ناهمگن. در مجموعه مقالات کنفرانس سیستم های حمل و نقل هوشمند IEEE (ITSC)، اوکلند، NZ، ایالات متحده آمریکا، 27 تا 30 اکتبر 2019. [ Google Scholar ]
  20. Tseng، F. هسوه، ج. تسنگ، سی. یانگ، ی. چائو، اچ. Chou, L. پیش‌بینی ازدحام با داده‌های بزرگ برای ترافیک بلادرنگ بزرگراه. دسترسی IEEE 2018 ، 6 ، 57311–57323. [ Google Scholar ] [ CrossRef ]
  21. ولاهوگیانی، EI; Karlaftis، MG; گلیاس، جی سی پیش بینی ترافیک کوتاه مدت: کجا هستیم و به کجا می رویم. ترانسپ Res. قسمت C Emerg. تکنولوژی 2014 ، 43 ، 3-19. [ Google Scholar ] [ CrossRef ]
  22. زی، دی. وانگ، ام. ژائو، ایکس. رویکرد Apriori فضایی-زمانی برای ثبت انجمن‌های پویا از تراکم ترافیک منطقه‌ای. دسترسی IEEE 2019 ، 8 ، 3695–3709. [ Google Scholar ] [ CrossRef ]
  23. شیونگ، اچ. واحدیان، ع. ژو، ایکس. لی، ی. لو، جی. پیش بینی الگوهای انتشار تراکم ترافیک: رویکرد نمودار انتشار. در مجموعه مقالات یازدهمین کارگاه بین المللی ACM SIGSPATIAL در علوم حمل و نقل محاسباتی، سیاتل، WA، ایالات متحده آمریکا، 6 نوامبر 2018. [ Google Scholar ]
  24. چن، ز. یانگ، ی. هوانگ، ال. وانگ، ای. لی، دی. کشف الگوهای انتشار تراکم ترافیک شهری با داده‌های مسیر تاکسی. دسترسی IEEE 2018 ، 6 ، 69481–69491. [ Google Scholar ] [ CrossRef ]
  25. سعید منش، م. Geroliminis، N. خوشه بندی پویا و انتشار ازدحام در شبکه های ترافیک شهری ناهمگن. ترانسپ Res. Procedia 2017 ، 23 ، 962-979. [ Google Scholar ] [ CrossRef ]
  26. آتلوری، جی. کارپاتنه، ا. کومار، وی. داده کاوی فضایی- زمانی: بررسی مسائل و روش ها. کامپیوتر ACM. Surv. 2018 ، 51 ، 1-41. [ Google Scholar ] [ CrossRef ]
  27. خو، ام. وو، جی. لیو، ام. شیائو، ی. وانگ، اچ. هو، دی. کشف گره های بحرانی در شبکه های جاده ای از طریق استخراج از مسیرهای خودرو. IEEE Trans. هوشمند ترانسپ سیستم 2019 ، 20 ، 583-593. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  28. بروناور، آر. اشمیتزبرگر، ن. Rehrl، K. شناخت الگوهای ترافیک مکانی-زمانی در تقاطع ها با استفاده از نقشه های خودسازماندهی. در مجموعه مقالات یازدهمین ACM SIGSPATIAL Int. کارگاه علوم حمل و نقل محاسباتی، سیاتل، WA، ایالات متحده آمریکا، 6 نوامبر 2018. [ Google Scholar ]
  29. لی، ایکس. لی، ز. هان، جی. Lee, J. تشخیص زمان پرت در داده های ترافیک خودرو. در مجموعه مقالات بیست و پنجمین کنفرانس بین المللی مهندسی داده IEEE 2009، شانگهای، چین، 29 مارس تا 2 آوریل 2009. [ Google Scholar ]
  30. آساکورا، ی. کوزاکابه، تی. نگوین، LX؛ Ushiki، T. روش‌های تشخیص حادثه با استفاده از وسایل نقلیه کاوشگر با تجهیزات GPS داخلی. ترانسپ Res. قسمت ظهور. تکنولوژی 2017 ، 81 ، 330-341. [ Google Scholar ] [ CrossRef ]
  31. تیلور، کارشناسی ارشد زیرساخت های حمل و نقل حیاتی در مناطق شهری: اثرات حوادث ترافیکی با استفاده از تحلیل آسیب پذیری شبکه مبتنی بر دسترسی ارزیابی شده است. رشد چانگ. 2008 ، 39 ، 593-616. [ Google Scholar ] [ CrossRef ]
  32. اسکات، دی.م. نواک، دی سی؛ اولتمن هال، ال. Guo, F. شاخص استحکام شبکه: روشی جدید برای شناسایی پیوندهای حیاتی و ارزیابی عملکرد شبکه های حمل و نقل. J. Transp. Geogr. 2006 ، 14 ، 215-227. [ Google Scholar ] [ CrossRef ]
  33. کوکوسکا، اس. Zwillinger, D. CRC جداول و فرمول های آمار و احتمال استاندارد ; CRC Press: Boca Raton، FL، USA، 2000. [ Google Scholar ]
  34. Fonseca، LMG؛ II، تقسیم‌بندی تصاویر ماهواره‌ای FM: رویکرد رو به رشد منطقه. سوتین SimpóSio. Sensoriamento Remoto 1996 ، 8 ، 677-680. [ Google Scholar ]
  35. کوهن، اچ. روش مجارستانی برای مسئله انتساب. Nav Res. تدارکات. Q. 1955 , 2 , 83-97. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
Ijgi 10 00248 g001 550
شکل 1. نمونه ای از وابستگی های ساختاری در یک شبکه جاده شهری مشاهده شده در نزدیکی Gehrden، آلمان.
Ijgi 10 00248 g002 550
شکل 2. نمای کلی خط لوله ST-Discovery. تصاویر نقشه: ©OpenStreetMap، ODbL.
Ijgi 10 00248 g003 550
شکل 3. Precision@k با توجه به k و تیساعتسمنمتراز وابستگی های زیرگراف ساختاری شناسایی شده.
Ijgi 10 00248 g004 550
شکل 4. نمونه هایی از وابستگی های شناسایی شده بین زیرگراف ها در هانوفر. زیرگراف های وابسته به رنگ آبی و بنفش مشخص شده اند. تصاویر نقشه: ©OpenStreetMap، ODbL.
Ijgi 10 00248 g005 550
شکل 5. نمونه هایی از وابستگی های شناسایی شده بین زیرگراف ها در برانزویک. زیرگراف های وابسته به رنگ آبی و بنفش مشخص شده اند. تصاویر نقشه: ©OpenStreetMap، ODbL.
Ijgi 10 00248 g006 550
شکل 6. تعداد واحدهای تحت تأثیر در هر نقطه زمانی.
Ijgi 10 00248 g007 550
شکل 7. تعداد و اندازه متوسط ​​زیرگرافهای تحت تأثیر شناسایی شده، روندهای متضاد وابسته به آستانه انتخاب شده را نشان می دهد. دتو،مترآایکس. اندازه زیرگراف به عنوان تعداد یال ها اندازه گیری می شود.
Ijgi 10 00248 g008 550
شکل 8. زمان وجود و اندازه زیرگراف های تحت تأثیر به مقدار آن بستگی دارد دتو،مترآایکسآستانه. محورها در مقیاس لگاریتمی هستند.
Ijgi 10 00248 g009 550
شکل 9. تأثیر تیساعتسمنمتردر الگوریتم 1 تعداد زیرگراف ها و اندازه متوسط ​​زیرگراف.
Ijgi 10 00248 g010 550
شکل 10. نمونه ای از زیرگراف های تحت تأثیر محاسبه شده برای یک اتصال اصلی در هانوفر با مقادیر متغیر تیساعتسمنمتر. رنگ بخش های جاده نشان دهنده انتساب زیرگراف بخش ها است. تصاویر نقشه: ©OpenStreetMap، ODbL.

مقالات داخلی و بین المللی

مطالب مرتبط ...

بدون دیدگاه

دیدگاهتان را بنویسید