خلاصه

دریاچه زریبار یکی از بزرگترین دریاچه های آب شیرین ایران است که نقش مهمی در اکوسیستم محیط زیست ایفا می کند و خشک شدن آن تأثیر منفی بر اکوسیستم احاطه شده دارد. با وجود این، این دریاچه یک محیط تفریحی جالب از نظر اکوتوریسم فراهم می کند. پیش‌بینی و پیش‌بینی سطح آب دریاچه با روش‌های ساده اما کاربردی می‌تواند ابزاری قابل اعتماد برای مدیریت منابع آب دریاچه در آینده فراهم کند. در تحقیق حاضر، سطح آب روزانه دریاچه زریبار در ایران را از طریق الگوریتم‌های شناخته شده مبتنی بر درخت تصمیم، از جمله درخت هرس شده M5 (M5P)، جنگل تصادفی (RF)، درخت تصادفی (RT) و درخت هرس کاهش‌یافته پیش‌بینی می‌کنیم. (REPT). ما از پنج ترکیب مختلف ورودی آب برای یافتن موثرترین ترکیب استفاده کردیم. برای مدلسازی ما، ما 70٪ از مجموعه داده را برای آموزش (از 2011 تا 2015) و 30٪ را برای ارزیابی مدل (از 2015 تا 2017) انتخاب کردیم. ما عملکرد مدل ها را با استفاده از مقادیر مختلف کمی (ریشه میانگین مربعات خطا (RMSE)، میانگین خطای مطلق (MAE)، ضریب تعیین (R) ارزیابی کردیم.2 )، درصد سوگیری (PBIAS) و نسبت ریشه میانگین مربعات خطا به انحراف استاندارد داده های اندازه گیری شده (RSR)) و چارچوب های بصری (نمودار تیلور و نمودار جعبه). نتایج ما نشان داد که سطح آب با تأخیر یک روزه بیشترین تأثیر را بر نتیجه داشت و با افزایش زمان تأخیر تأثیر آن بر نتیجه کاهش یافت. این نتیجه نشان داد که همه مدل‌های توسعه‌یافته قابلیت پیش‌بینی خوبی داشتند، اما مدل M5P بهتر از بقیه عمل کرد و پس از آن RF و RT به طور مساوی و سپس REPT قرار گرفتند. نتایج ما نشان داد که این الگوریتم‌ها تنها با تاخیر یک روزه در سطح آب به عنوان ورودی می‌توانند سطح آب را به طور دقیق پیش‌بینی کنند و ابزار مقرون به صرفه‌ای برای پیش‌بینی‌های آینده هستند.

کلید واژه ها:

سطح آب دریاچه ؛ زمان تاخیر ؛ الگوریتم های درخت تصمیم ; دقت پیش بینی ؛ پیش بینی سطح آب

1. معرفی

بسیاری از دریاچه ها علاوه بر اینکه اکوسیستم های آبی مهمی هستند، آب مورد نیاز برای آبیاری مناطق خانگی، کشاورزی و صنعتی را تامین می کنند [ 1 ]. پیش‌بینی نوسانات روزانه سطح آب دریاچه‌ها در برنامه‌ریزی منابع آب و مدیریت حوضه، تاسیسات برق آبی و ناوبری و استخراج آب خانگی، کشاورزی و صنعتی اهمیت دارد [2 ] . سطح آب در دریاچه ها به تبادل آب طبیعی بین دریاچه ها و حوضه های آبریز آنها بستگی دارد و می تواند به تغییرات آب و هوایی و به ویژه بارش و تبخیر حساس باشد [ 3 ، 4 ]. سطح آب نیز تحت تأثیر تغذیه آب زیرزمینی، استخراج آب، سدهای مصنوعی، سیل و غیره است ., 7 , 8 , 9 ]. مطالعات اخیر در مورد نوسانات سطح آب بر کاهش سطح دریاچه ها و همچنین کاهش دبی به جریان های خروجی متمرکز شده است [ 10 ]. هم اندازه‌گیری‌های فیزیکی و هم مدل‌سازی برای نقشه‌برداری نوسانات سطح آب استفاده می‌شوند، که مدل‌سازی یک جایگزین ارزان‌تر است [ 11 ].
مدل‌های یادگیری ماشین (ML) مانند رگرسیون لجستیک (LR)، ماشین‌های بردار پشتیبان (SVM) و شبکه‌های عصبی مصنوعی (ANN)، به دلیل عملکرد، دقت و قابلیت پیش‌بینی بالا، به طور فزاینده‌ای در رشته‌های مدیریت زمین و آب استفاده می‌شوند [12] . ، 13 ، 14 ]. الگوریتم های ML در نگاشت حساسیت به سیل استفاده شده است [ 15 ، 16 ، 17 ، 18 ، 19 ، 20 ، 21 ، 22 ، 23 ، 24 ، 25 ، 26 ، 27 ، 28 ،29 ، 30 ، 31 ]، مدل‌سازی بارش-رواناب [ 32 ، 33 ]، پیش‌بینی جریان ورودی مخزن [ 34 ، 35 ]، پیش‌بینی جریان جریان [ 36 ، 37 ]، برآورد رسوب معلق [ 39 ] و تخمین مرجع روزانه [39 ] [ 40 ، 41]. الگوریتم های مبتنی بر بیز، مانند رگرسیون لجستیک بیزی (BLR) و الگوریتم های درخت تصمیم، مانند جنگل تصادفی (RF)، درخت تصمیم متناوب (ADT)، درختان مدل لجستیک (LMT)، درخت بیز ساده (NBT)، هرس خطا کاهش می یابد. درخت (REPTree) و درختان طبقه‌بندی و رگرسیون (CARTs)، در مسائل مربوط به منابع آب، به ویژه در نقشه‌برداری حساسیت به سیل استفاده شده‌اند [ 18 ، 42 ، 43 ، 44 ، 45 ]. خسروی و همکاران [ 46 ] یک الگوریتم ترکیبی از درخت کیسه‌بندی-تصمیم‌گیری برای پیش‌بینی نرخ انتقال بار بستر ایجاد کرد. خسروی و همکاران [ 47 ] غلظت فلوراید در آب های زیرزمینی را با وجود یادگیرندگان تنبل مختلف پیش بینی کرد. بیو و همکاران [ 48] شاخص کیفیت آب (WQI) را از طریق کیسه‌بندی مختلف (BA)، انتخاب پارامتر CV (CVPS) و طبقه‌بندی فیلتر شده تصادفی (RFC) پیش‌بینی کرد. بیو و همکاران [ 49 ]، در تحقیق دیگری، غلظت فلزات سنگین را در آب‌های زیرزمینی با استفاده از الگوریتم فرآیند گاوسی (GP) پیش‌بینی کرد. صالح و همکاران [ 50 ] مدل‌های طبقه‌بندی‌کننده منتخب (M5P)، M5Rule (M5R) و KStar (KS) را برای پیش‌بینی بار رسوب معلق در ایستگاه هواشناسی ترنتون در رودخانه دلاور، ایالات متحده توسعه داد. با این حال، استفاده از الگوریتم‌های مختلف ML مبتنی بر درخت تصمیم به عنوان الگوریتم‌های قدرتمند و قوی برای پیش‌بینی نوسانات سطح آب روزانه هنوز در ادبیات محدود است و به ندرت در پیش‌بینی سطح آب روزانه در دریاچه‌های کوهستانی استفاده می‌شود.
در این مطالعه، هدف ما ارزیابی الگوریتم‌های مختلف ML مبتنی بر درخت تصمیم برای پیش‌بینی نوسانات سطح آب روزانه در دریاچه زریبار، از جمله هرس M5 (M5P)، جنگل تصادفی (RF)، درخت تصادفی (RT) و هرس با خطای کاهش‌یافته است. الگوریتم های درختی (REPT) اعتبارسنجی و مقایسه این مدل‌ها با استفاده از شاخص‌های کمی متفاوت از جمله ریشه میانگین مربعات خطا (RMSE)، ضریب همبستگی (R 2 )، میانگین خطای مطلق (MAE)، درصد سوگیری (PBIAS)، نسبت ریشه میانگین مربع انجام شد. خطا در انحراف استاندارد داده های اندازه گیری شده (RSR) و ضریب نش- ساتکلیف (NSE). مدلسازی و فرآیند داده با متلب 2018 طراحی و کدگذاری شد.

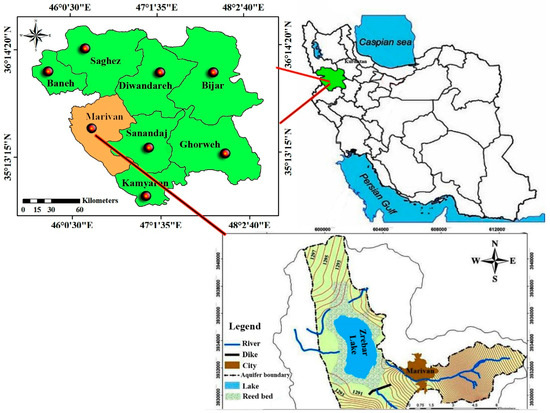
2. منطقه مطالعه

دریاچه زریبار در 3 کیلومتری غرب شهر مریوان در استان کردستان در غرب ایران قرار دارد ( شکل 1 ). این دریاچه 1285 متر ارتفاع دارد، طول آن 5 کیلومتر، حداکثر عرض آن 1.6 کیلومتر، حداکثر عمق آن 6 متر، مساحت آن 8.9 کیلومتر مربع و حجم آن حدود 30 میلیون متر مکعب است [ 51 ]. آب دریاچه زریبار از بارندگی های فصلی (میانگین بارندگی 650 میلی متر در سال) و چشمه های زیر آبی کف دریاچه تامین می شود. دریاچه بلافاصله توسط یک مجموعه تالاب احاطه شده و بیشتر توسط کوه ها، جنگل ها و زمین های زراعی احاطه شده است. مزارع آبی و زمین های زراعی دیم 60 درصد از پوشش زمین، جنگل های بلوط 23 درصد و مراتع 17 درصد را تشکیل می دهند [ 52] .]. دریاچه زریبار تنها دریاچه آب شیرین غرب ایران است و از نظر گردشگری، آبیاری و برداشت ماهی برای اقتصاد محلی اهمیت دارد.

3. مواد و روشها

3.1. جمع آوری و آماده سازی داده ها

یکی از چالش‌های مدل‌سازی فرآیندهای هیدرولوژیکی غیرخطی، انتخاب مهم‌ترین متغیرها از بین همه متغیرهای ورودی ممکن است [ 54 ]. انتخاب ورودی برای سیستم های یادگیری بسیار مهم است، به ویژه در طول فرآیند شناسایی، زمانی که مجموعه داده بزرگ است و تعداد متغیرها زیاد است [ 55 ]. هدف اولیه از جمع آوری و آماده سازی داده ها، انتخاب متغیرهای ورودی مناسب بر اساس داده های موجود است. در مدل، ترکیبی از متغیرهای ورودی مختلف، که به عنوان انتخاب ویژگی (انتخاب زیر مجموعه متغیر) نیز شناخته می‌شود، فرآیندی است برای انتخاب زیرمجموعه بهینه ورودی‌ها با توجه به اصول حاکم [56] .]. بهینه سازی مدل ها از طریق چنین انتخابی برای افزایش دقت و کارایی مدل (برای کاهش زمان کالیبراسیون) انجام می شود.
در مطالعه حاضر، ما از ترکیب‌های متغیر ورودی مختلف برای حل مسائل در حال ظهور در طول فرآیند مدل‌سازی استفاده کردیم. از آنجایی که جریان ورودی به دریاچه زریبار فقط از چشمه های زیرآبی است، سطح آب پیشین را به عنوان متغیر انتخاب کردیم. در این زمینه، ما از ترکیب‌های مختلف سطح آب (WL) در زمان‌های تاخیر مختلف (یعنی WL(t-1 تا t-5)) استفاده کردیم. برای هدف این مطالعه، ما ویژگی‌ها را با استفاده از داده‌های سطح آب مشاهده شده روزانه در طول 6 سال از سپتامبر 2011 تا سپتامبر 2017 کالیبره کردیم. سپس با ترکیب برای 2، 3، 4 و 5 روز قبل ادامه یافت ( جدول 1). همه این سناریوهای ورودی برای توسعه یک مدل (به عنوان مثال، آموزش مدل) برای پیش‌بینی سطح آب دریاچه به عنوان خروجی استفاده شدند. سپس دقت پیش‌بینی را برای هر سناریوی مختلف محاسبه کردیم. به طور کلی، بهترین متغیر ورودی ترکیبی از WL(t-1)، WL(t-2)، WL(t-3)، WL(t-4)، WL(t-5) و متغیر خروجی (WL) بود. (t)) برای آموزش مدل انتخاب شده است. در مرحله بعد، الگوریتم‌هایی را توسعه دادیم که برای پیش‌بینی WL(t) با استفاده از مجموعه داده‌های آزمایشی اعمال شدند.
برای مدل‌سازی، از 70 درصد مجموعه داده برای آموزش (از سال 2011 تا 2015) و 30 درصد برای آزمایش (از سال 2015 تا 2017) استفاده کردیم [57 ] . در حالی که هیچ راهنمای کاربردی جهانی برای تقسیم داده ها وجود ندارد، مجموعه داده های آموزشی و آزمایشی باید دارای ویژگی های آماری مشابهی باشند و 70:30 متداول ترین نسبت مورد استفاده است [ 27 ، 58 ، 59 ، 60 ، 61 ، 62 ].

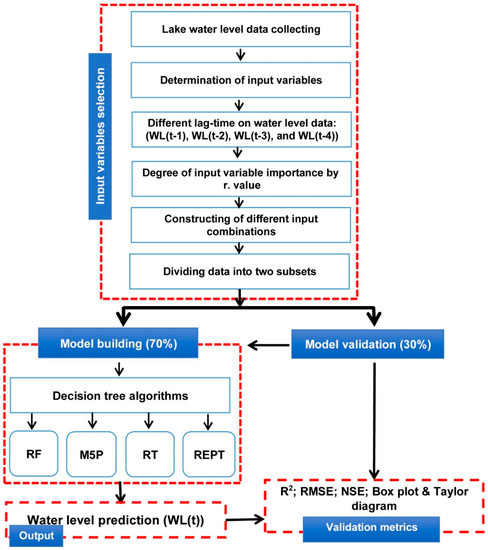
3.2. روش شناسی

3.2.1. M5P

درخت M5 یک مدل پیشرفته بسیار دقیق و از نظر محاسباتی ارزان در میان یادگیرندگان درخت تصمیم است که بر اساس وظایف رگرسیونی که ابعاد بسیار بالایی دارند کار می کند. توسط Quinlan توسعه داده شد [ 63]. M5 به جای تخصیص یک ثابت به گره برگ، یک مدل رگرسیون خطی چند متغیره را در هر برگ برای پیش بینی مقادیر عددی اختصاص می دهد. بنابراین، عملکرد یک مدل درختی M5 به شدت به مدل های خطی انتخاب شده وابسته است. در بین مدل‌های M5، M5P یک درخت رگرسیون باینری است که بر روی آن گره‌های برگ آخر توابع رگرسیون خطی هستند که ویژگی‌های عددی پیوسته را ایجاد می‌کنند. پس از آن، برای انجام هرس درخت، تخلیه و جایگزینی درخت توسط یک تقریب تابع خطی انجام می‌شود، که واریانس در سلول‌ها را کاهش می‌دهد و گره‌های کوچک‌تری با ساختار درختی ایجاد می‌کند.
روش M5P قادر به مدیریت مجموعه داده های بزرگ، همراه با داده های از دست رفته است که با تقسیم فضاهای ورودی به فضاهای فرعی مختلف کوچکتر بازیابی می شوند. به طور کلی، حداقل تعداد نمونه ها، اندازه دسته ای، درختان رگرسیون ساخته شده، تعداد ارقام اعشاری و قابلیت های هرس نشده و بررسی نشده همگی از مزایای مدل های M5P هستند. مطالعه دقیق تری توسط خرسوایی و همکاران بررسی شده است. [ 64 ] در مورد رویکرد مدلسازی M5P.
3.2.2. جنگل تصادفی (RF)
RF، اولین بار توسط Breimen و همکاران تعیین شد. [ 65 ]، یک رویکرد مجموعه ای برای ساخت مدل های پیش بینی برای هر دو وظایف طبقه بندی و رگرسیون است. این روشی برای ترکیب مدل های پایه کمتر پیش بینی کننده برای به دست آوردن مدل های پیش بینی بهتر است. مدل‌های RF به دلیل ماهیت ساده، مفروضات کم و عملکرد بالا، به طور گسترده در یادگیری ماشین (ML) استفاده شده‌اند. اصطلاح “جنگل” به مجموعه ای از درختان تصمیم اطلاق می شود که به خودی خود طبقه بندی کننده های “ضعیف” هستند. یک جنگل رگرسیون قدرت پیش‌بینی مشابهی با درخت رگرسیون منفرد ندارد [ 65 و 66]. جایی که یک درخت تنها به یک معیار تقسیم می شود، آنگاه نسبت به مجموعه داده آموزشی بسیار حساس است. حتی تغییرات کوچک در مجموعه داده ها و معیار تقسیم می تواند ساختارهای درختی مختلف را آغاز کند و توضیحات متفاوتی را ارائه دهد [ 66 ]. بنابراین، مدل‌های RF متغیرها را بر اساس اهمیت آنها برای دستیابی به بهترین مدل RF طبقه‌بندی می‌کنند.
3.2.3. درخت تصادفی (RT)
RT یک مجموعه داده را به فضاهای فرعی تقسیم می کند و برای هر زیرفضا یک ثابت قرار می دهد. یک مدل تک درختی تمایل زیادی به ناپایداری دارد و دقت پیش‌بینی ضعیفی را نشان می‌دهد. با این حال، با کیسه کردن RT به عنوان یک الگوریتم درخت تصمیم، می تواند نتایج بسیار دقیقی را به همراه داشته باشد [ 67 ]. RT دارای انعطاف پذیری بالایی همراه با قابلیت آموزش سریع است [ 68 ].
3.2.4. کاهش خطا در هرس درخت (REPT)
هنگامی که یک درخت تصمیم ساخته می شود، به دلیل نویز یا نقاط پرت، چندین شاخه واریانس را در مجموعه داده آموزشی بازتولید می کنند. این مشکل به عنوان بیش از حد برازش در هرس درختان مطرح شده است که از روش های آماری برای حذف شاخه های کم دقت استفاده می کند و به طور کلی شامل هرس قبل و بعد از هرس می شود. انگیزه اصلی هرس “دقت معامله برای سادگی” است. REPT یک روش یکپارچه از هرس خطای کاهش یافته (REP) و رویکردهای DT است که در آن درختان هرس شده با استفاده از داده های آزمایشی تولید می شوند. از مجموعه داده اعتبارسنجی برای تخمین خطای تعمیم استفاده می کند. این روش برای اولین بار توسط Quinlan [ 63] زمانی که درخت تصمیم را بر اساس اطلاعات موجود و کاهش واریانس اعمال کردند. مزیت REPT در توانایی آن در کاهش پیچیدگی درخت با هرس نهفته است، که باعث کاهش ابعاد درخت تصمیم و تناسب بیش از حد در طول فرآیند یادگیری بدون از دست دادن دقت قابل توجه می شود [69 ] . بنابراین، یک فرآیند هرس برای قطع مجدد درخت مورد نیاز است. REPT قادر به یادگیری سریع با کاهش واریانس برای ایجاد درخت تصمیم است [ 70 ].
3.2.5. ارزیابی و مقایسه مدل
برای اعتبارسنجی و مقایسه مدل ها، پنج آمار کمی شامل: ریشه میانگین مربعات خطا (RMSE)، ضریب همبستگی (R 2)، میانگین خطای مطلق (MAE)، درصد سوگیری (PBIAS)، نسبت ریشه میانگین مربعات خطا به انحراف استاندارد داده های اندازه گیری شده (RSR) و ضریب نش- ساتکلیف (NSE)، برای ارزیابی عملکرد روش های ارزیابی استفاده شد. علاوه بر این، برای مقایسه بصری عملکرد مدل، نمودارهای تیلور و نمودارهای جعبه بررسی شدند [ 71 ]. نمودارهای تیلور توسط تیلور [ 71] معرفی شدند] از نظر تصویری نشان می دهد که یک خروجی تخمینی (یا مجموعه ای از خروجی های تخمینی) چقدر با مشاهدات مطابقت دارد. آنها بر اساس همبستگی و انحراف معیار مجموعه داده های برآورد شده و مشاهده شده ترسیم می شوند. این به ویژه در ارزیابی جنبه های متعدد مدل های پیچیده یا در سنجش مهارت نسبی بسیاری از مدل های مختلف مفید است (به عنوان مثال، [ 72 ]). با این حال، نمودار جعبه اطلاعات بیشتری در مورد توزیع داده ها و همچنین مقادیر حداکثر و حداقل ارائه می دهد که در مدل سازی مهم است.

این شاخص ها با معادلات زیر بیان می شوند:

آر2=∑من=1n(WL(من)-WL¯(من))(WL^(من)-WL¯^(من))∑من=1n[WL(من)-WL¯(من)]2∑من=1n[WL^(من)-yWL˜(من)]2
RMSE=1n ∑من=1n[WL(من)-WL^(من)]2.
MAE=1n ∑من=1n|WL(من)-WL^(من)|.
PBIAS=100∗(∑من=1n(WL(من)-WL^(من))∑من=1nWL(من))
NSE=1-(∑من=1n(WL(من)-WL^(من))∑من=1nWL(من)-WL(من)¯))
PSR=(∑من=1n(WL(من)-WL^(من))2∑من=1n(WL(من)-WL(من)¯)2)

جایی که n تعداد نمونه است، WLمقدار واقعی خروجی است، WL¯میانگین است WLدر کل مجموعه هدف، WL˜میانگین است WL^در کل مجموعه هدف و WL^مقدار خروجی شبیه سازی شده است.

R2 درجه همخطی بین داده های شبیه سازی شده و اندازه گیری شده ما را توصیف می کند . بین 0 تا 1 و بالاتر است آر2مقادیری که دقت پیش‌بینی بهتر را نشان می‌دهند و مقادیر بیشتر از 0.5 قابل قبول در نظر گرفته می‌شوند [ 73 ]. RMSE و MAE خطای مدل ها را اندازه گیری می کنند. مقادیر پایین تر RMSE و MAE نشان دهنده عملکرد پیش بینی مدل بهتر است. NSE یک آمار نرمال شده است که میزان نسبی واریانس باقیمانده را در مقایسه با واریانس داده های اندازه گیری شده کنترل می کند [ 74 ]. محدوده NSE بین -∞ و 1 است. زمانی که NSE = 1 باشد، یک تطابق بی عیب بین مقادیر مشاهده شده و پیش بینی شده را تعیین می کند. عملکرد پیش بینی مدل به عنوان بسیار خوب، خوب، قابل قبول یا غیرقابل قبول با محدوده های 0.75 <NSE ≤ 1.00، 0.65 < طبقه بندی می شود. NSE ≤ 0.75، 0.50 < NSE ≤ 0.65، 0.40 < NSE ≤ 0.50 یا NSE ≤ 0.4، به ترتیب [ 64 ، 75]. PBIAS میانگین تمایل مقادیر شبیه‌سازی‌شده را بزرگ‌تر یا کوچک‌تر از مقادیر مشاهده‌شده تعیین می‌کند [ 76 ] و از این رو، بهترین معیار برای نشان دادن بیش‌ازحد یا دست‌کم گرفتن [ 64 ] است. از -∞ تا 1 متغیر است، با مقادیر منفی بیش برآورد را نشان می دهد، در حالی که مقادیر مثبت نشان دهنده دست کم گرفتن است [ 77 ]. RSR به عنوان نسبت RMSE و انحراف استاندارد داده های اندازه گیری شده در نظر گرفته شده است. RSR از مقدار بهینه 0 تا یک مقدار مثبت بزرگ متفاوت است. RSR کمتر به معنای RMSE کمتر است که عملکرد پیش بینی مدل بهتری را نشان می دهد. محدوده‌های طبقه‌بندی RSR به‌عنوان بسیار خوب، خوب، قابل قبول و غیرقابل قبول با دامنه‌های 0.00 ≤ RSR ≤ 0.50، 0.50 ≤ RSR ≤ 0.60، 0.60 ≤ RSR ≤ 0.70 و RSR ≤ 0.70 > به ترتیب نشان داده شده است .].
علاوه بر این، دو ابزار ارزیابی گرافیکی مناسب، مانند نمودارهای تیلور و نمودارهای جعبه، برای مقایسه بصری عملکرد مدل استفاده شد [ 71 ]. نمودارهای تیلور شباهت بین دو الگو و اینکه یک الگوی مدل به شدت با مشاهده ارتباط دارد را نشان می دهد. از سه آمار عملکرد مدل مربوطه، از جمله انحراف استاندارد (سیگما)، R2 استفاده می کندو RMSE که با قانون کسینوس می توان آن را روی یک نمودار دو بعدی رسم کرد. به طور کلی نمودارهای تیلور ابزار مفیدی برای ارزیابی مهارت مقایسه ای مدل های مختلف است. علاوه بر این، از نمودارهای جعبه برای ارزیابی استفاده شده است، زیرا آنها پنج آمار شامل حداقل، چارک پایین، میانه، چارک بالا و حداکثر را در یک نمایش گرافیکی ارائه می دهند. نمودار شماتیک روش در شکل 2 نشان داده شده است .

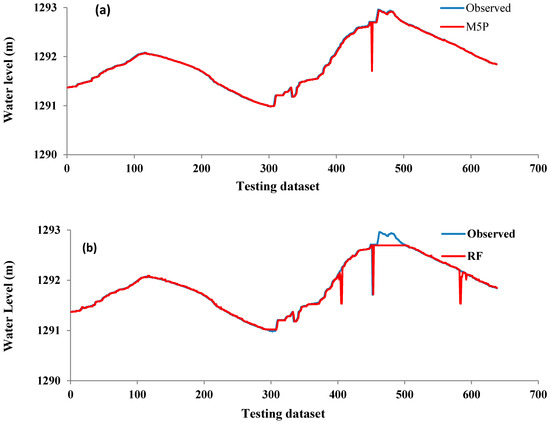
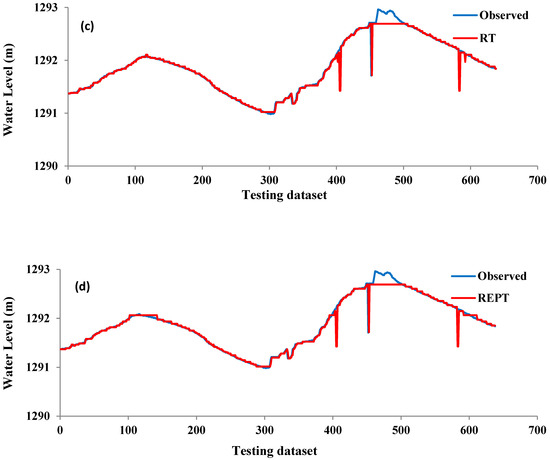
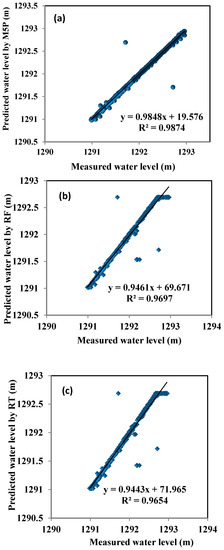
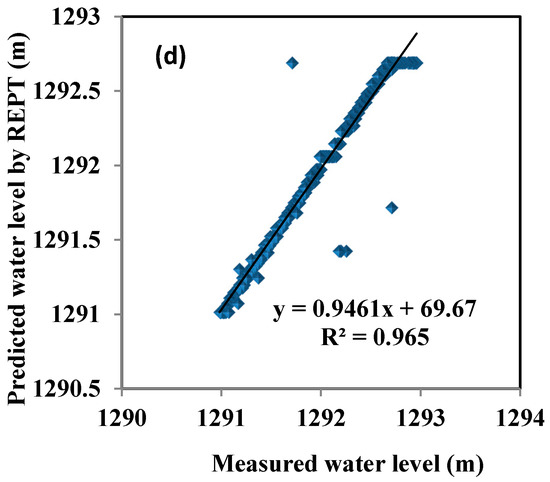
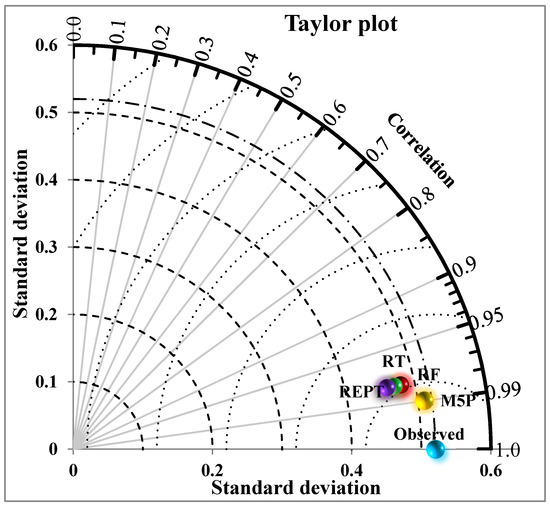
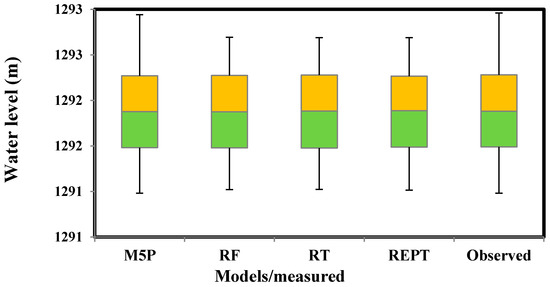
4. نتایج و تجزیه و تحلیل

ما عملکرد چهار مدل را برای پیش‌بینی نوسانات روزانه سطح آب در هر دو مرحله آموزش و آزمایش با استفاده از معیارهای ارزیابی مختلف آزمایش کردیم ( جدول 2 ). با توجه به معیارهای ارزیابی آماری ما، مشاهده کردیم که همه مدل‌ها توانایی پیش‌بینی بسیار خوبی داشتند (R 2 > 0.7). نتیجه ما از ضریب تعیین (R 2 ) نشان داد که این مدل ها همه قابل قبول هستند اما مدل M5P به دلیل داشتن بالاترین R 2 بهترین عملکرد را داشت.مقدار (0.9874) و به دنبال آن مدل های RF (0.9697)، RT (0.9654) و REPT (0.965) قرار دارند. از نظر مقدار RMSE، مدل M5P نیز با داشتن کمترین RMSE (0.05) بالاترین قدرت پیش بینی را داشت و پس از آن مدل های RF و RT (0.09) و REPT (0.1) قرار گرفتند. مدل M5P کمترین معیار MAE (0.01) را به همراه داشت و پس از آن مدل‌های RF (0.02)، RT (0.03) و REPT (0.033) قرار گرفتند. علاوه بر این، متریک NSE از بیشترین قدرت پیش‌بینی به کمترین، به شرح زیر طبقه‌بندی شد: M5P (0.98) > RF و RT (0.96) > REPT (0.95)، که مشابه R2 است .. علاوه بر این، نتایج حاصل از PBIAS نشان می‌دهد که همه مدل‌های اعمال‌شده سطح آب را دست‌کم گرفته‌اند (به دلیل مقدار مثبت PBIAS). مقادیر محاسبه‌شده PBIAS برای همه مدل‌ها بین 0-0.2 بود که نشان‌دهنده عملکرد بسیار خوب در پیش‌بینی نوسانات روزانه سطح آب در منطقه مورد مطالعه است. در نهایت، عملکرد همه مدل‌های اعمال‌شده، بر اساس مقادیر RSR، به چهار کلاس بسیار خوب، خوب، رضایت‌بخش و نامطلوب با دامنه‌های 0.00 ≤ RSR ≤ 0.50، 0.50 ≤ RSR ≤ 0.60 ≤ 0.60، 0.60 ≤ RSR طبقه‌بندی شد. و RSR > 0.70، به ترتیب. بنابراین، RSR عملکرد بسیار خوبی را در تمام مدل های توسعه یافته ما نشان می دهد.
ما از ضریب همبستگی پیرسون (PCC) برای محاسبه اهمیت نسبی متغیرهای ورودی (WL(t-1 تا (t-5)) و سطح آب روزانه برای تاخیرهای زمانی مختلف استفاده کردیم تا مهمترین عامل برای پیش بینی روزانه تعیین شود. سطح آب WL(t-1) (0.981) و به دنبال آن WL(t-2) (0.964)، WL(t-3) (0.946-)، WL(t-4) (0.928) و WL( t-5) (925/0) و نشان می‌دهند که سطح آب با زمان تأخیر یک روزه بیشترین تأثیر را بر نتیجه داشته و این اثربخشی با تأخیر بیشتر کاهش می‌یابد. مقادیر R در جدول 3 نشان داده شده است .، اطلاعات ورودی ها و متغیرهای خروجی/هدف را نشان می دهد. نتایج PCC نشان می دهد که WL(t-1) و WL(t-5) به ترتیب بالاترین و کمترین مقدار سطح آب روزانه را داشتند (PCC = 0.981 و 0.925). پس از تکمیل تحلیل همبستگی، بهترین ترکیب ورودی را با استفاده از مجموعه داده آزمایشی نشان داده شده در جدول 4 اعمال کردیم.. بر اساس مقادیر R، ترکیب‌های ورودی مختلف را در مدل‌ها (M5P، RF، RT و REPT) در هر دو مرحله آموزش و آزمایش ارزیابی کردیم. ما دریافتیم که ترکیب WL(t-1) (ترکیب 1) برای همه مدل‌های توسعه‌یافته، به جز M5P (REPT، RT و RF)، به دلیل بالاترین R در مرحله آزمایش، با مقادیر 0.982، 0.981، بهترین ترکیب ورودی بود. و به ترتیب 0.980. برای M5P، موثرترین ترکیب WL(t-1) و WL(t-2) (ترکیب 2) با مقدار R = 0.933 بود. ما دریافتیم که، به طور کلی، مدل M5P به طور کلی دارای دقت برازش بهتر و بالاترین همبستگی در بین متغیرهای ورودی است و مدل RF ضعیف‌ترین دقت را در تقریب داده‌های آموزشی دارد.
شکل 3 نمودارهای خطی و نمودارهای پراکندگی سطوح آب روزانه مشاهده شده و پیش بینی شده را نشان می دهد. نتایج نشان می‌دهد که تمامی مدل‌ها سطح آب روزانه را با دقت بالایی پیش‌بینی کردند، در حالی که تنها M5P قادر به پیش‌بینی کامل حداکثر مقادیر نوسان سطح آب دریاچه زریبار بود. همچنین M5P نزدیکترین به مقادیر سطح آب مشاهده شده و بهترین خط (خط 45 درجه) با حداقل پراکندگی با معادله خطی بود.  wلپrهد=19.576wلoبس+0.9848. برعکس، مدل REPT بدترین برآوردها را با حداکثر پراکندگی ارائه کرد ( شکل 4 ). این تایید می کند که M5P از ​​سایر مدل ها از جمله RF، RT و REPT بهتر عمل کرده است. این نتیجه مطابق با معیارهای ارزیابی ارائه شده در جدول 2 است .
ما همچنین کارایی مدل را با استفاده از نمودارهای تیلور ( شکل 5 ) و نمودارهای جعبه ( شکل 6 ) تجزیه و تحلیل کردیم. هر چه نقطه هر مدل توسعه‌یافته به محل نقطه مشاهده‌شده نزدیک‌تر باشد، عملکرد بالاتری دارد. در اینجا، نتایج ما همچنین نشان می‌دهد که مدل‌ها قدرت پیش‌بینی خوبی داشتند، اما الگوریتم M5P همبستگی بالاتر و RMSE پایین‌تری داشت. بر اساس مقادیر انحراف استاندارد نرمال شده، SD مدل M5P مشابه SD مشاهده شده بود، در حالی که REPT انحراف استاندارد کمتری داشت و به دنبال آن مدل‌های RT و RF قرار گرفتند.
نتایج باکس پلات در شکل 6 ارائه شده است . نمودار جعبه برای پیش بینی حداکثر مقادیر توسط مدل M5P به مقادیر مشاهده شده نزدیک تر بود، در حالی که REPT، RT و RF سطح آب را دست کم گرفتند. از نظر چارک، مقادیر میانه و حداقل همه مدل‌ها قادر به پیش‌بینی مقادیر WL مشابه مقادیر مشاهده‌شده با درجه دقت قابل‌توجهی بودند، اگرچه مدل M5P از ​​مدل‌های دیگر بهتر عمل کرد.

5. بحث

دریاچه ها می توانند اکوسیستم های پیچیده ای باشند و کاربردهای متعددی را برای جامعه فراهم کنند، از منابع آب آشامیدنی، تفریح، ناوبری، آبیاری، برق آبی و موارد دیگر. ابزارهایی که نوسانات سطح آب را پیش‌بینی می‌کنند برای مدیریت دریاچه‌ها، مصرف آب و حوضه‌های آبریز اطراف آن‌ها مهم هستند. در این مطالعه، ما الگوریتم‌های ML مبتنی بر درخت تصمیم‌گیری محاسباتی نرم پیشرفته، شامل M5P، RF، RT و REPT را برای پیش‌بینی نوسانات روزانه سطح آب دریاچه زریبار، استان کردستان، توسعه و به کار بردیم. طبق اطلاعات ما، این اولین بار است که از این مدل ها برای پیش بینی سطح آب روزانه دریاچه ها استفاده می شود.
ما عملکرد پیش‌بینی مدل‌های یادگیری را برای مجموعه داده‌های آموزشی و اعتبارسنجی با معیارهای RMSE، MAE، NSE، PBIAS، RSR و R2 محاسبه و اندازه‌گیری کردیم، همانطور که توسط دیگران استفاده شد [ 78 ، 79 ، 80 ، 81 ، 82 ، 83 ، 84 ، 85 ]. پس از پیاده‌سازی مدل‌های یادگیری، یک هیستوگرام از مقادیر واقعی و تخمینی، یک نمودار تیلور، نمودار پراکندگی و یک نمودار جعبه ایجاد کردیم. نتایج مراحل اعتبار سنجی اهمیت بیشتری نسبت به عملکرد ارزیابی توسط مجموعه داده آموزشی (مرحله مدل سازی) دارد [ 28 ، 86]. ما مشاهده کردیم که اگرچه مدل‌ها به خوبی آموزش دیده بودند و در همه سناریوها با موفقیت انجام شدند، مدل M5P تحت سناریوی دوم (WL(t-1)، WL(t-2)) عملکرد بهتری داشت و از مدل‌های REPT، RT و RF پیشی گرفت. که فقط در سناریوی اول (فقط WL(t-1)) عملکرد بالایی داشت. دلیل موفقیت مدل M5P نسبت به سایر مدل ها احتمالاً به مزایای این مدل مربوط می شود. اولین مزیت فرآیند یادگیری کارآمدتر آن است که بر مفروضات نوع داده و توزیع تکیه نمی کند، می تواند بسیاری از ویژگی ها و ابعاد بالا را مدیریت کند و در برخورد با داده های از دست رفته قوی است. دومین مزیت M5P توانایی آن در ساخت یک ساختار درختی ساده و معادلات خطی قابل اجرا در چندین برگ است که با آن می تواند رابطه بین پارامترهای ورودی و خروجی متغیر را به صراحت توضیح دهد.64 ، 87 ].
مدل‌های دیگر، مانند مدل‌های RF و RT، به عنوان الگوریتم‌های مبتنی بر درخت تصمیم نیز شناخته می‌شوند که برای مسائل طبقه‌بندی و رگرسیون استفاده می‌شوند، اما این مدل‌ها در توانایی‌های خود برای ساخت تعداد زیادی درخت محدود هستند و الگوریتم‌ها را کند و ناکارآمد می‌کنند. پیش بینی های زمان واقعی به گفته کیسی و همکاران. [ 5 ]، الگوریتم‌های مبتنی بر درخت تصمیم (M5P، RT و RF) قدرت پیش‌بینی بالاتری نسبت به مدل‌هایی با لایه‌های پنهان در ساختار خود دارند (ANN، سیستم استنتاج عصبی-فازی تطبیقی ​​(ANFIS) و منطق فازی (FL)).
سایر محققان آب که از مدل M5P استفاده کرده اند، سطوح مختلف عملکرد را گزارش کرده اند [ 88 ، 89 ، 90 ]. برای مثال بلوچی و همکاران. [ 86 ] دریافتند که عملکرد مدل M5P نسبت به مدل‌های شبکه عصبی ANN-MLP و تابع پایه شعاعی (ANN-RBF) برای پیش‌بینی عمق آبشستگی در تلاقی رودخانه‌ها پایین‌تر است. در مقابل، Onyari و Ilunga [ 90 ] همچنین شبکه‌های عصبی چندلایه (ANN-MLP) را با مدل‌های درختی M5P برای پیش‌بینی جریان جریان در حوضه Luvuvhu، آفریقای جنوبی، با مدل M5P که پیش‌بینی‌های بهتری ارائه می‌دهد، مقایسه کردند.
در مطالعه ما، مدل M5P بهترین پیش‌بینی از نوسانات سطح آب روزانه دریاچه زریبار را ارائه کرد. تفاوت در نتایج حاصل از فرآیند مدل سازی در مقایسه با مدل های دیگر با نتایج کمتر مطلوب، مستلزم بررسی دقیق تر است. در حالی که M5P برای پیش‌بینی سطح دریاچه در دریاچه Zrebar بهینه بود، همانطور که در بالا توضیح داده شد برای سایرین عملکرد ضعیفی داشت و بنابراین نیاز به آزمایش بیشتر در تنظیمات دیگر دارد. محدودیت اصلی تحقیق حاضر فقدان مجموعه داده جامعی از قبیل بارندگی، دبی ورودی، تبخیر و غیره است که تأثیر معناداری بر نتیجه دارد. پیشنهاد می‌شود نتایج مطالعه حاضر با مدل‌های مبتنی بر مجموعه و الگوریتم‌های بهینه‌سازی برای توسعه الگوریتم قوی‌تر مقایسه شود.

6. نتیجه گیری

پیش‌بینی دقیق نوسانات سطح آب دریاچه می‌تواند به توسعه پایدار و مدیریت مصرف آب دریاچه کمک کند. در این مطالعه، تعدادی از پیشرفته‌ترین مدل‌های محاسباتی نرم ML، از جمله M5P، RF، RT و REPT را برای پیش‌بینی فضایی نوسانات سطح آب روزانه دریاچه زریبار، استان کردستان، ایران، آزمایش و توسعه دادیم. ما از سناریوهای مختلفی بر اساس ترکیبی از ورودی داده ها برای انتخاب پارامترهای بهینه استفاده کردیم. ما عملکرد مدل‌های توسعه‌یافته را با استفاده از معیارهای RMSE، MAE، NSE، PBIAS، RSR و R2 به صورت کمی ارزیابی کردیم . نتایج ما به شرح زیر خلاصه می شود:
زمانی که متغیرهای WL(t-1) و WL(t-2)، سناریوی دوم، به عنوان ورودی انتخاب شدند، مدل M5P نسبت به مدل‌های دیگر بهتر عمل کرد، که دلالت بر ترکیبی از زمان‌های تاخیر یک و دو روزه پیش‌بینی سطح آب دارد. بهترین عملکرد توسط سایر مدل‌های ML با تاخیر یک روزه سطح آب اندازه‌گیری شده واقعی به دست آمد.
نتایج ما نشان داد که M5P بالاترین عملکرد و دقت قدرت (کمترین RMSE و بالاترین R2 ) را در مقایسه با سایر مدل‌های یادگیری ماشین دارد. علاوه بر این، مدل M5P با داده های مشاهده شده بر اساس نمودارهای پراکندگی و هیستوگرام مقادیر واقعی و تخمینی تناسب محکم تری داشت، بنابراین نویدبخش کاربردهای گسترده تر در پیش بینی سطح آب بود.
دریاچه ای با تاخیر یک روزه بیشترین تاثیر را بر نتایج دارد، در حالی که با تاخیر بیشتر اثربخشی آن کاهش می یابد.
بهترین سناریو ورودی سناریویی است که در آن همه متغیرهای ورودی در نظر گرفته شوند.
مدل M5P قادر است حداکثر سطح آب دریاچه را در مقایسه با سایر الگوریتم‌های توسعه‌یافته به خوبی پیش‌بینی کند.

منابع

  1. Vuglinskiy, V. سطح آب در دریاچه ها و مخازن, ذخیره آب ; سیستم جهانی رصد زمینی: رم، ایتالیا، 2009. در دسترس آنلاین: https://www.fao.org/gtos/doc/ECVs/T04/T04.pdf (در 21 ژوئیه 2020 قابل دسترسی است).
  2. هوانگ، سی. چنگ، ی.-اس. هان، جی. کائو، آر. هوانگ، سی.-ای. وی، S.-H. وانگ، اچ. نظارت چند دهه ای تغییرات سطح دریاچه در فلات چینگهای-تبت توسط ارتفاع سنج های topex/poseidon-familly: مفهوم آب و هوا. Remote Sens. 2016 ، 8 ، 446. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
  3. کریمی، س. شیری، ج. کیسی، او. پیش بینی نوسانات سطح آب دریاچه ارومیه با استفاده از برنامه ریزی بیان ژن و سیستم استنتاج عصبی فازی تطبیقی. بین المللی J. Ocean Clim. سیستم 2012 ، 3 ، 109-125. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  4. Altunkaynak، A. پیش بینی نوسانات سطح آب سطح دریاچه ون توسط شبکه های عصبی مصنوعی. منبع آب مدیریت 2007 ، 21 ، 399-408. [ Google Scholar ] [ CrossRef ]
  5. کیسی، او. شیری، ج. نیکوفر، ب. پیش بینی تراز روزانه دریاچه با استفاده از رویکردهای هوش مصنوعی. محاسبه کنید. Geosci. 2012 ، 41 ، 169-180. [ Google Scholar ] [ CrossRef ]
  6. رحمتی، ا. چوبین، بی. فتح آبادی، ع. کولون، اف. سلطانی، ا. شهابی، ح. ملایفر، ا. تیفن باخر، جی. سیپولو، اس. احمد، BB پیش‌بینی عدم قطعیت مدل‌های یادگیری ماشین برای مدل‌سازی آلودگی نیتراتی آب‌های زیرزمینی با استفاده از روش‌های رگرسیون کمی و uneec. علمی کل محیط. 2019 ، 688 ، 855–866. [ Google Scholar ] [ CrossRef ]
  7. تین بوی، دی. شیرزادی، ع. چاپی، ک. شهابی، ح. پرادان، بی. فام، بی تی؛ سینگ، معاون; چن، دبلیو. خسروی، ک. بن احمد، ب. رویکرد هوش محاسباتی ترکیبی برای نقشه برداری پتانسیل چشمه آب زیرزمینی. Water 2019 ، 11 ، 2013. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
  8. چن، دبلیو. پرادان، بی. لی، اس. شهابی، ح. ریزه ای، ح.م. هو، ای. وانگ، اس. رویکرد ادغام ترکیبی جدید تابع تفکیک خطی فیشر مبتنی بر کیسه برای تجزیه و تحلیل پتانسیل آب زیرزمینی. نات. منبع. Res. 2019 ، 28 ، 1239-1258. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  9. رحمتی، ا. نقیبی، س. شهابی، ح. Bui، DT; پرادان، بی. آذره، ع. رفیعی سردویی، ا. سامانی، ع. مدل‌سازی پتانسیل چشمه آب زیرزمینی Melesse، AM: شامل قابلیت و استحکام سه رویکرد مدل‌سازی مختلف است. جی هیدرول. 2018 ، 565 ، 248-261. [ Google Scholar ] [ CrossRef ]
  10. لیرا، م. Cantonati، M. اثرات نوسانات سطح آب بر دریاچه ها: کتابشناسی مشروح. در اثرات اکولوژیکی نوسانات سطح آب در دریاچه ها ; Springer: برلین/هایدلبرگ، آلمان، 2008; صص 171-184. [ Google Scholar ]
  11. دای، ایکس. وان، آر. یانگ، جی. نوسانات غیر ثابت سطح آب در دریاچه پویانگ چین و تعاملات آن با رودخانه یانگ تسه. جی. جئوگر. علمی 2015 ، 25 ، 274-288. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  12. احمدلو، م. کریمی، م. علیزاده، س. شیرزادی، ع. پروین نژاد، د. شهابی، ح. پناهی، م. ارزیابی حساسیت سیل با استفاده از ادغام سیستم استنتاج فازی مبتنی بر شبکه تطبیقی ​​(anfis) و بهینه‌سازی مبتنی بر جغرافیای زیستی (bbo) و الگوریتم‌های خفاش (ba). Geocarto Int. 2019 ، 34 ، 1252-1272. [ Google Scholar ] [ CrossRef ]
  13. نقیبی، س. پورقاسمی، HR ارزیابی مقایسه ای بین سه مدل یادگیری ماشین و مقایسه عملکرد آنها با روش های آماری دو متغیره و چند متغیره در نقشه برداری پتانسیل آب های زیرزمینی. منبع آب مدیریت 2015 ، 29 ، 5217-5236. [ Google Scholar ] [ CrossRef ]
  14. باودن، جی جی; مایر، منابع انسانی؛ Dandy، GC تقسیم بهینه داده ها برای مدل های شبکه عصبی در کاربردهای منابع آب. منبع آب Res. 2002 ، 38 ، 2-1-2-11. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  15. پرادهان، ب. نقشه برداری مستعد سیل و ترسیم منطقه خطر با استفاده از رگرسیون لجستیک، gis و سنجش از دور. جی. اسپات. هیدرول. 2010 ، 9 ، 1-18. [ Google Scholar ]
  16. کیا، مگابایت؛ پیراسته، س. پرادان، بی. محمود، ع. سلیمان، WNA; مرادی، ع. یک مدل شبکه عصبی مصنوعی برای شبیه‌سازی سیل با استفاده از gis: حوضه رودخانه جوهور، مالزی. محیط زیست علوم زمین 2012 ، 67 ، 251-264. [ Google Scholar ] [ CrossRef ]
  17. تهرانی، ام اس; پرادان، بی. نقشه‌برداری حساسیت به سیل جبور، MN با استفاده از یک مجموعه جدید وزن‌های شواهد و مدل‌های ماشین بردار پشتیبانی در gis. جی هیدرول. 2014 ، 512 ، 332-343. [ Google Scholar ] [ CrossRef ]
  18. چوبین، بی. مرادی، ا. گلشن، م. آداموفسکی، جی. ساجدی حسینی، ف. موسوی، ع. پیش‌بینی مجموعه‌ای از حساسیت به سیل با استفاده از تجزیه و تحلیل تفکیک چند متغیره، درختان طبقه‌بندی و رگرسیون و ماشین‌های بردار پشتیبان. علمی کل محیط. 2019 ، 651 ، 2087–2096. [ Google Scholar ] [ CrossRef ]
  19. عباس زاده، پ. علیپور، ع. اسدی، س. توسعه تبدیل موجک جفت شده و شبکه های عصبی تکاملی l evenberg-m arquardt برای مدل سازی فرآیند هیدرولوژیکی. محاسبه کنید. هوشمند 2018 ، 34 ، 175-199. [ Google Scholar ] [ CrossRef ]
  20. اسدی، س. فازی سازی تکاملی چاک دهنده برای رگرسیون: مطالعه موردی پیش بینی سهام. محاسبات عصبی 2019 ، 331 ، 121-137. [ Google Scholar ] [ CrossRef ]
  21. اسدی، س. شهرابی، ج. القای قاعده موازی مبتنی بر پیچیدگی برای طبقه‌بندی چند طبقه. Inf. علمی 2017 ، 380 ، 53-73. [ Google Scholar ] [ CrossRef ]
  22. چن، دبلیو. لی، ی. شو، دبلیو. شهابی، ح. لی، اس. هونگ، اچ. وانگ، ایکس. بیان، اچ. ژانگ، اس. پرادان، ب. مدل‌سازی حساسیت به سیل با استفاده از روش‌های مبتنی بر داده‌های درخت بیز ساده، درخت تصمیم متناوب، و روش‌های جنگل تصادفی. علمی کل محیط. 2020 , 701 , 134979. [ Google Scholar ] [ CrossRef ] [ PubMed ]
  23. شهابی، ح. شیرزادی، ع. قادری، ک. امیدوار، ای. الانصاری، ن. کلگ، جی جی. گیرتسما، م. خسروی، ک. امینی، ع. بهرامی، س. تشخیص سیل و نگاشت حساسیت با استفاده از داده‌های سنجش از دور نگهبان-1 و رویکرد یادگیری ماشین: هوش ترکیبی مجموعه کیسه‌ای بر اساس طبقه‌بندی‌کننده k-نزدیک‌ترین همسایه. Remote Sens. 2020 , 12 , 266. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  24. وانگ، ی. هونگ، اچ. چن، دبلیو. لی، اس. پناهی، م. خسروی، ک. شیرزادی، ع. شهابی، ح. پناهی، س. Costache، R. نقشه‌برداری حساسیت سیل در شهرستان dingnan (چین) با استفاده از سیستم استنتاج عصبی فازی تطبیقی ​​با بهینه‌سازی مبتنی بر جغرافیای زیستی و الگوریتم رقابتی امپریالیستی. جی. محیط زیست. مدیریت 2019 ، 247 ، 712-729. [ Google Scholar ] [ CrossRef ]
  25. چن، دبلیو. هونگ، اچ. لی، اس. شهابی، ح. وانگ، ی. وانگ، ایکس. احمد، BB مدل‌سازی حساسیت به سیل با استفاده از رویکرد ترکیبی جدید هرس درختان با خطای کاهش‌یافته با مجموعه‌های کیسه‌ای و زیرفضای تصادفی. جی هیدرول. 2019 ، 575 ، 864-873. [ Google Scholar ] [ CrossRef ]
  26. خسروی، ک. ملسه، AM; شهابی، ح. شیرزادی، ع. چاپی، ک. هنگ، اچ. نقشه‌برداری حساسیت به سیل در حوضه آبریز نینگدو، چین با استفاده از تکنیک‌های دو متغیره و داده‌کاوی. در هیدرولوژی شدید و تغییرپذیری آب و هوا . الزویر: آمستردام، هلند، 2019؛ صص 419-434. [ Google Scholar ]
  27. تین بوی، دی. خسروی، ک. شهابی، ح. داگوپاتی، پ. آداموفسکی، جی اف. Melesse, AM; تای فام، بی. پورقاسمی، HR; محمودی، م. بهرامی، س. مدل‌سازی فضایی سیلاب در شمال ایران با استفاده از سنجش از دور و سیستم اطلاعات جغرافیایی: مقایسه بین توابع باور شواهدی و مجموعه آن با مدل رگرسیون لجستیک چند متغیره. Remote Sens. 2019 ، 11 ، 1589. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
  28. Bui، DT; پناهی، م. شهابی، ح. سینگ، معاون; شیرزادی، ع. چاپی، ک. خسروی، ک. چن، دبلیو. پناهی، س. Li, S. الگوریتم های تکاملی ترکیبی جدید برای پیش بینی فضایی سیل. علمی Rep. 2018 , 8 , 1-14. [ Google Scholar ] [ CrossRef ] [ PubMed ][ نسخه سبز ]
  29. تین بوی، دی. خسروی، ک. لی، اس. شهابی، ح. پناهی، م. سینگ، معاون; چاپی، ک. شیرزادی، ع. پناهی، س. چن، دبلیو هیبریدهای جدید anfis با چندین الگوریتم بهینه‌سازی برای مدل‌سازی حساسیت سیل. Water 2018 , 10 , 1210. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  30. شفیع زاده مقدم، ح. والوی، ر. شهابی، ح. چاپی، ک. شیرزادی، ع. رویکردهای جدید پیش‌بینی با استفاده از ترکیب یادگیری ماشین و مدل‌های آماری برای نقشه‌برداری حساسیت سیل. جی. محیط زیست. مدیریت 2018 ، 217 ، 1-11. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  31. خسروی، ک. فام، بی تی؛ چاپی، ک. شیرزادی، ع. شهابی، ح. Revhaug، I. پراکاش، آی. Bui, DT ارزیابی مقایسه‌ای الگوریتم‌های درخت تصمیم برای مدل‌سازی حساسیت سیلاب ناگهانی در حوزه آبخیز هراز، شمال ایران. علمی کل محیط. 2018 ، 627 ، 744-755. [ Google Scholar ] [ CrossRef ]
  32. نورانی، و. کماسی، م. Mano، A. یک رویکرد موجک چند متغیره برای مدل‌سازی بارش-رواناب. منبع آب مدیریت 2009 ، 23 ، 2877. [ Google Scholar ] [ CrossRef ]
  33. وو، سی. Chau، K. مدل‌سازی بارش-رواناب با استفاده از شبکه عصبی مصنوعی همراه با تجزیه و تحلیل طیف منفرد. جی هیدرول. 2011 ، 399 ، 394-409. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  34. Bae, D.-H.; جئونگ، دی.م. Kim, G. پیش‌بینی ماهانه ورودی سد با استفاده از اطلاعات پیش‌بینی آب و هوا و تکنیک عصبی فازی. هیدرول. علمی J. 2007 ، 52 ، 99-113. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  35. بای، ی. چن، ز. زی، جی. لی، سی. پیش‌بینی جریان ورودی مخزن روزانه با استفاده از یادگیری ویژگی عمیق چند مقیاسی با مدل‌های ترکیبی. جی هیدرول. 2016 ، 532 ، 193-206. [ Google Scholar ] [ CrossRef ]
  36. نوری، ر. کرباسی، ع. مقدم نیا، ع. هان، دی. ذوکایی آشتیانی، م. فرخ نیا، ع. گوشه، MG ارزیابی تعیین متغیرهای ورودی بر روی عملکرد مدل svm با استفاده از تکنیک‌های pca، آزمون گاما و انتخاب رو به جلو برای پیش‌بینی جریان ماهانه. جی هیدرول. 2011 ، 401 ، 177-189. [ Google Scholar ] [ CrossRef ]
  37. یاسین، ز.ام. الشافعی، ع. جعفر، ع. عفان، HA; مدل‌های مبتنی بر هوش مصنوعی Sayl، KN برای پیش‌بینی جریان: 2000-2015. جی هیدرول. 2015 ، 530 ، 829-844. [ Google Scholar ] [ CrossRef ]
  38. Cigizoglu، HK; کیسی، او. روش‌هایی برای بهبود عملکرد شبکه عصبی در تخمین رسوب معلق جی هیدرول. 2006 ، 317 ، 221-238. [ Google Scholar ] [ CrossRef ]
  39. کیسی، او. شیری، جی. تخمین رسوب معلق رودخانه با استفاده از متغیرهای آب و هوایی مفهوم: مطالعه تطبیقی ​​در میان تکنیک های محاسبات نرم. محاسبه کنید. Geosci. 2012 ، 43 ، 73-82. [ Google Scholar ] [ CrossRef ]
  40. اسلامیان، س. عابدی کوپایی، ج. امیری، م. گوهری، س. برآورد تبخیر و تعرق مرجع روزانه با استفاده از بردار پشتیبان. Res. جی. محیط زیست. علمی 2009 ، 3 ، 439-447. [ Google Scholar ]
  41. مهدی زاده، س. برآورد تبخیر و تعرق مرجع روزانه (eto) با استفاده از روش‌های هوش مصنوعی: ارائه رویکردی جدید برای مدل‌سازی مبتنی بر داده‌های eto با تاخیر. جی هیدرول. 2018 ، 559 ، 794-812. [ Google Scholar ] [ CrossRef ]
  42. خسروی، ک. شهابی، ح. فام، بی تی؛ آداموفسکی، جی. شیرزادی، ع. پرادان، بی. دوو، جی. لی، H.-B. گروف، جی. Ho، HL یک ارزیابی مقایسه ای از مدل سازی حساسیت سیل با استفاده از تجزیه و تحلیل تصمیم گیری چند معیاره و روش های یادگیری ماشین. جی هیدرول. 2019 ، 573 ، 311-323. [ Google Scholar ] [ CrossRef ]
  43. هونگ، اچ. سانگاراتوس، پ. ایلیا، آی. لیو، جی. زو، A.-X. چن، دبلیو. کاربرد وزن فازی شواهد و تکنیک های داده کاوی در ساخت نقشه حساسیت به سیل شهرستان پویانگ، چین. علمی کل محیط. 2018 ، 625 ، 575-588. [ Google Scholar ] [ CrossRef ] [ PubMed ]
  44. طحان، MH; اسدی، اس امدید: گسسته سازی چندهدفه تکاملی برای مجموعه داده های نامتعادل. Inf. علمی 2018 ، 432 ، 442-461. [ Google Scholar ] [ CrossRef ]
  45. طحان، MH; اسدی، اس ممود: یک گسسته سازی چند متغیره تکاملی جدید. محاسبات نرم. 2018 ، 22 ، 301-323. [ Google Scholar ] [ CrossRef ]
  46. خسروی، ک. کوپر، جی آر. داگوپاتی، پ. فام، بی تی؛ پیش‌بینی نرخ انتقال بار بستر Bui، DT: کاربرد تکنیک‌های جدید داده کاوی ترکیبی. جی هیدرول. 2020 ، 124774. [ Google Scholar ] [ CrossRef ]
  47. خسروی، ک. برزگر، ر. میراکی، س. آداموفسکی، جی. داگوپاتی، پ. علیزاده، محمدرضا; فام، بی تی؛ عالمی، ام تی مدل‌سازی تصادفی آلودگی فلوراید آب‌های زیرزمینی: معرفی دانش‌آموزان تنبل. آب های زیرزمینی 2019 . [ Google Scholar ] [ CrossRef ]
  48. Bui، DT; خسروی، ک. تیفن باخر، جی. نگوین، اچ. کازاکیس، ن. بهبود پیش‌بینی شاخص‌های کیفیت آب با استفاده از الگوریتم‌های ترکیبی جدید یادگیری ماشین. علمی کل محیط. 2020 , 721 , 137612. [ Google Scholar ] [ CrossRef ]
  49. Bui، DT; خسروی، ک. کریمی، م. بوسیکو، جی. خوزانی، ز.س. نگوین، اچ. ماستروسیکو، ام. تدسکو، دی. کوکو، ای. Kazakis، N. افزایش پیش بینی غلظت نیترات و استرانسیم در آب های زیرزمینی با استفاده از الگوریتم داده کاوی جدید. علمی کل محیط. 2020 , 715 , 136836. [ Google Scholar ] [ CrossRef ]
  50. صالح، SQ; شرافتی، ع. خسروی، ک. فارس، ح. کیسی، او. تائو، اچ. علی، م. یاسین، پیش‌بینی بار رسوب معلق رودخانه ZM بر اساس اطلاعات دبی رودخانه: کاربرد مدل‌های داده کاوی جدید توسعه‌یافته. هیدرول. علمی J. 2019 ، 65 ، 624-637. [ Google Scholar ] [ CrossRef ]
  51. ایمانی، س. نیکسخان، محمدحسن؛ جمشیدی، س. عباسپور، بازار مجوز تخلیه KC و پیوند مدیریت مزرعه: رویکردی برای کنترل اوتروفیکاسیون در حوضه های کوچک با کشاورزان کم درآمد. محیط زیست نظارت کنید. ارزیابی کنید. 2017 ، 189 ، 346. [ Google Scholar ] [ CrossRef ]
  52. ایمانی، س. دلاور، م. نیک‌سخان، MH شناسایی مناطق منبع بحرانی مواد مغذی با مدل سوات تحت شرایط داده‌های محدود. منبع آب 2019 ، 46 ، 128-137. [ Google Scholar ] [ CrossRef ]
  53. گاویلی، س. جوادی، س. بنیحبیب، م. مقایسه مدل‌های هوشمند پیش‌بینی نوسانات سطح آب دریاچه زریوار با توجه به سطح آب زیرزمینی. ایران-منبع آب. Res. 2018 ، 14 ، 339-344. [ Google Scholar ]
  54. بهرامی، س. Wigand، E. پیش بینی جریان روزانه با استفاده از شبکه حالت اکو غیرخطی. بین المللی J. Adv. Res. علمی مهندس تکنولوژی 2018 ، 5 ، 3619–3625. [ Google Scholar ]
  55. هو، سی. Wan, F. انتخاب ورودی در سیستم‌های یادگیری: مروری کوتاه بر برخی مسائل مهم و پیشرفت‌های اخیر. در مجموعه مقالات کنفرانس بین المللی IEEE 2009 در مورد سیستم های فازی، جزیره ججو، کره، 20-24 اوت 2009. صص 530-535. [ Google Scholar ]
  56. شرافتی، ع. خسروی، ک. خسروی نیا، پ. احمد، ک. سلمان، س. یاسین، ز.ام. شهید، س. پتانسیل مدل های داده کاوی جدید برای پیش بینی تابش خورشیدی جهانی. بین المللی جی. محیط زیست. علمی تکنولوژی 2019 ، 16 ، 7147–7164. [ Google Scholar ] [ CrossRef ]
  57. Ayele، GT; Teshale، EZ; یو، بی. رادرفورد، ID; جونگ، جی. جریان و پیش‌بینی عملکرد رسوب برای اولویت‌بندی حوضه آبخیز در حوضه رودخانه نیل آبی بالایی، اتیوپی. Water 2017 , 9 , 782. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  58. طاهری، ک. شهابی، ح. چاپی، ک. شیرزادی، ع. گوتیرز، اف. خسروی، ک. نگاشت حساسیت سینکول: مقایسه ای بین الگوریتم های یادگیری ماشین مبتنی بر بیز. تخریب زمین توسعه دهنده 2019 ، 30 ، 730–745. [ Google Scholar ] [ CrossRef ]
  59. فام، بی تی؛ پراکاش، آی. خسروی، ک. چاپی، ک. Trinh، PT; Ngo، TQ; حسینی، اس.و. Bui, DT مقایسه ماشین‌های بردار پشتیبان و الگوریتم‌های بیزی برای مدل‌سازی حساسیت زمین لغزش. Geocarto Int. 2019 ، 34 ، 1385-1407. [ Google Scholar ] [ CrossRef ]
  60. چن، دبلیو. هونگ، اچ. پناهی، م. شهابی، ح. وانگ، ی. شیرزادی، ع. پیراسته، س. آلشیخ، ع.ا. خسروی، ک. پناهی، س. پیش بینی فضایی حساسیت زمین لغزش با استفاده از تکنیک های داده کاوی مبتنی بر gis از anfis با الگوریتم بهینه سازی نهنگ (woa) و بهینه ساز گرگ خاکستری (gwo). Appl. علمی 2019 ، 9 ، 3755. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
  61. خسروی، ک. داگوپاتی، پ. عالمی، MT; Awadh, SM; غارب، MI; پناهی، م. فام، بی تی؛ رضایی، ف. چی، سی. یاسین، داده‌کاوی هواشناسی ZM و مدل‌های داده-هوش ترکیبی برای شبیه‌سازی تبخیر مرجع: مطالعه موردی در عراق. محاسبه کنید. الکترون. کشاورزی 2019 ، 167 ، 105041. [ Google Scholar ] [ CrossRef ]
  62. خوزانی، ز.س. خسروی، ک. فام، بی تی؛ کلوو، بی. محتر، دبلیو. ملینی، WH; یاسین، ZM تعیین تنش برشی ظاهری کانال مرکب: کاربرد مدل‌های داده کاوی جدید. J. Hydroinform. 2019 ، 21 ، 798–811. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  63. Quinlan، JR ترکیب یادگیری مبتنی بر نمونه و مبتنی بر مدل. در مجموعه مقالات دهمین کنفرانس بین المللی در مورد یادگیری ماشین، Amherst، MA، ایالات متحده آمریکا، 27-29 ژوئن 1993; صص 236-243. [ Google Scholar ]
  64. خسروی، ک. مائو، ال. کیسی، او. یاسین، ز.ام. شهید، س. کمی کردن بار رسوب معلق ساعتی با استفاده از مدل‌های داده کاوی: مطالعه موردی حوضه آبریز آند یخچال‌های طبیعی در شیلی. جی هیدرول. 2018 ، 567 ، 165-179. [ Google Scholar ] [ CrossRef ]
  65. بریمن، L. جنگل های تصادفی. ماخ فرا گرفتن. 2001 ، 45 ، 5-32. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  66. بریمن، ال. پیش بینی کننده های بگینگ. ماخ فرا گرفتن. 1996 ، 24 ، 123-140. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  67. آلدوس، دی. Pitman، J. درختان تصادفی پیوسته ناهمگن و مرز ورودی ترکیب افزودنی. احتمالا. نظریه مربوط. فیلدها 2000 ، 118 ، 455-482. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  68. LaValle, SM Rapidly-Exploring Random Trees: ابزاری جدید برای برنامه ریزی مسیر . Citeseer: University Park, PA, USA, 1998. [ Google Scholar ]
  69. پولو، جی.ام. لیو، اس. فیگوئروآ، من؛ کولالرت، دبلیو. امینلی، س. Tan، KY; آپوستلو، ای. استاتفلد، ام. لی، ی. Shioda، T. نوع منشاء سلول بر خواص مولکولی و عملکردی سلول های بنیادی پرتوان القایی موش تأثیر می گذارد. نات. بیوتکنول. 2010 ، 28 ، 848-855. [ Google Scholar ] [ CrossRef ] [ PubMed ][ نسخه سبز ]
  70. محمد، WNHW; صالح، MNM; Omar, AH مطالعه مقایسه ای روش هرس خطای کاهش یافته در الگوریتم های درخت تصمیم. در مجموعه مقالات کنفرانس بین المللی IEEE 2012 در سیستم کنترل، محاسبات و مهندسی، پنانگ، مالزی، 23 تا 25 نوامبر 2012. صص 392-397. [ Google Scholar ]
  71. تیلور، KE خلاصه کردن چندین جنبه عملکرد مدل در یک نمودار واحد. جی. ژئوفیز. Res. اتمس. 2001 ، 106 ، 7183-7192. [ Google Scholar ] [ CrossRef ]
  72. هاتون، جی تی پایه علمی; مشارکت گروه کاری اول در گزارش ارزیابی سوم هیئت بین دولتی در مورد تغییرات آب و هوایی . انتشارات دانشگاه کمبریج: کمبریج، MA، ایالات متحده آمریکا، 2001. [ Google Scholar ]
  73. سانتی، سی. آرنولد، جی جی؛ ویلیامز، جی آر. دوگاس، WA; سرینیواسان، ر. Hauck، LM اعتبار سنجی مدل swat بر روی یک حوضه rwer بزرگ با منابع نقطه ای و غیر نقطه ای 1. JAWRA J. Am. منبع آب دانشیار 2001 ، 37 ، 1169-1188. [ Google Scholar ] [ CrossRef ]
  74. نش، جی. Sutcliffe، JV پیش‌بینی جریان رودخانه از طریق مدل‌های مفهومی بخش اول – بحثی درباره اصول. جی هیدرول. 1970 ، 10 ، 282-290. [ Google Scholar ] [ CrossRef ]
  75. موریاسی، دی. آرنولد، جی جی؛ ون لیو، مگاوات؛ Bingner, RL; هارمل، RD; دستورالعمل های ارزیابی مدل Veith، TL برای کمی سازی سیستماتیک دقت در شبیه سازی حوزه آبخیز. ترانس. ASABE 2007 ، 50 ، 885-900. [ Google Scholar ] [ CrossRef ]
  76. گوپتا، HV; سروشیان، س. Yapo، PO وضعیت کالیبراسیون خودکار برای مدل های هیدرولوژیکی: مقایسه با کالیبراسیون متخصص چند سطحی. جی هیدرول. مهندس 1999 ، 4 ، 135-143. [ Google Scholar ] [ CrossRef ]
  77. Legates, DR; McCabe، GJ، Jr. ارزیابی استفاده از معیارهای “خوبی تناسب” در اعتبارسنجی مدل هیدرولوژیکی و هیدروکلیماتیک. منبع آب Res. 1999 ، 35 ، 233-241. [ Google Scholar ] [ CrossRef ]
  78. بهزاد، م. اصغری، ک. Coppola, EA, Jr. مطالعه تطبیقی ​​svms و anns در پیش‌بینی سطح آب آبخوان. جی. کامپیوتر. مدنی مهندس 2010 ، 24 ، 408-413. [ Google Scholar ] [ CrossRef ]
  79. یون، اچ. جون، اس.-سی. هیون، ی. Bae, G.-O.; لی، K.-K. مطالعه تطبیقی ​​شبکه‌های عصبی مصنوعی و ماشین‌های بردار پشتیبان برای پیش‌بینی سطح آب زیرزمینی در یک سفره آبی ساحلی. جی هیدرول. 2011 ، 396 ، 128-138. [ Google Scholar ] [ CrossRef ]
  80. کیسی، او. شیری، ج. کریمی، س. شمشیربند، س. معتمدی، س. پتکوویچ، دی. هاشم، ر. بررسی پیش بینی نوسانات سطح آب دریاچه ارومیه با استفاده از ماشین بردار پشتیبان با الگوریتم کرم شب تاب. Appl. ریاضی. محاسبه کنید. 2015 ، 270 ، 731-743. [ Google Scholar ] [ CrossRef ]
  81. شیری، ج. شمشیربند، س. کیسی، او. کریمی، س. باتنی، SM; نژاد، SHH; هاشمی، ع. پیش بینی سطح آب دریاچه ارومیه با رویکرد ماشین یادگیری افراطی. منبع آب مدیریت 2016 ، 30 ، 5217-5229. [ Google Scholar ] [ CrossRef ]
  82. سهو، س. روسو، TA; الیوت، جی. فاستر، I. الگوریتم های یادگیری ماشین برای مدل سازی تغییرات سطح آب زیرزمینی در مناطق کشاورزی ایالات متحده. منبع آب Res. 2017 ، 53 ، 3878-3895. [ Google Scholar ] [ CrossRef ]
  83. Nhu، V.-H. رحمتی، ا. فلاح، ف. شجاعی، س. الانصاری، ن. شهابی، ح. شیرزادی، ع. گورسکی، ک. نگوین، اچ. احمد، BB نقشه‌برداری پتانسیل چشمه آب زیرزمینی در سیستم آبخوان کارستی با استفاده از مدل‌های جدید دو متغیره و چند متغیره. Water 2020 , 12 , 985. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  84. چن، دبلیو. ژائو، ایکس. سانگاراتوس، پ. شهابی، ح. ایلیا، آی. شو، دبلیو. وانگ، ایکس. احمد، BB ارزیابی استفاده از روش‌های مجموعه‌ای مبتنی بر درخت در نقشه‌برداری پتانسیل چشمه‌های آب زیرزمینی. جی هیدرول. 2020 , 583 , 124602. [ Google Scholar ] [ CrossRef ]
  85. چن، دبلیو. لی، ی. سانگاراتوس، پ. شهابی، ح. ایلیا، آی. شو، دبلیو. Bian, H. نقشه‌برداری پتانسیل چشمه آب زیرزمینی با استفاده از رویکرد هوش مصنوعی مبتنی بر رگرسیون لجستیک هسته، جنگل تصادفی و مدل‌های درخت تصمیم متناوب. Appl. علمی 2020 ، 10 ، 425. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
  86. بلوچی، ب. نیکو، آقا؛ Adamowski، J. توسعه سیستم های خبره برای پیش بینی عمق آبشستگی در شرایط بستر زنده در محل تلاقی رودخانه ها: کاربرد انواع مختلف anns و درخت مدل m5p. Appl. محاسبات نرم. 2015 ، 34 ، 51-59. [ Google Scholar ] [ CrossRef ]
  87. الماسی، SN; باقرپور، ر. میکائیل، ر. اوزچلیک، ی. کلهری، ح. پیش‌بینی میزان برش سنگ ساختمانی بر اساس ویژگی‌های سنگ و آمپراژ پس‌کش دستگاه در معادن با استفاده از درخت مدل m5p. ژئوتک. جئول مهندس 2017 ، 35 ، 1311-1326. [ Google Scholar ] [ CrossRef ]
  88. سیهاگ، پ. کریمی، س.م. آنجلکی، ع. جنگل تصادفی، m5p و تحلیل رگرسیون برای تخمین هدایت هیدرولیکی غیراشباع میدان. Appl. علوم آب 2019 ، 9 ، 129. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
  89. یی، H.-S. لی، بی. پارک، اس. کواک، ک.-سی. آن، K.-G. پیش‌بینی کوتاه‌مدت شکوفه جلبکی در سرریز جوکسان با استفاده از درخت مدل m5p و ماشین یادگیری افراطی. محیط زیست مهندس Res. 2018 . [ Google Scholar ] [ CrossRef ]
  90. اونیاری، EK; Ilunga، F. کاربرد شبکه عصبی mlp و درخت مدل m5p در پیش‌بینی جریان جریان: مطالعه موردی حوضه آبریز luvuvhu، آفریقای جنوبی. بین المللی J. Innov. مدیریت تکنولوژی 2013 ، 4 ، 11. [ Google Scholar ]
Ijgi 09 00479 g001 550
شکل 1. موقعیت منطقه مورد مطالعه [ 53 ].
Ijgi 09 00479 g002 550
شکل 2. نمودار جریان روش.
Ijgi 09 00479 g003a 550 Ijgi 09 00479 g003b 550
شکل 3. نمودارهای خطی سطوح آب روزانه مشاهده شده و پیش بینی شده مدل های مختلف در مرحله آزمایش: ( الف ) M5P; ( ب ) RF؛ ( ج ) RT; ( د ) REPT.
Ijgi 09 00479 g004a 550 Ijgi 09 00479 g004b 550
شکل 4. نمودارهای پراکنده سطح آب مشاهده شده در مقابل پیش بینی شده (WL) در مرحله آزمایش: ( الف ) M5P; ( ب ) RF؛ ( ج ) RT; ( د ) REPT.
Ijgi 09 00479 g005 550
شکل 5. نمودار تیلور از مدل ها.
Ijgi 09 00479 g006 550
شکل 6. نمودار جعبه مدل ها.

مقالات داخلی و بین المللی

مطالب مرتبط ...

بدون دیدگاه

دیدگاهتان را بنویسید