پیش بینی تعداد بیماران بستری در بیمارستان در آینده بر اساس نوسانات زمانی و مکانی بیمار با استفاده از مدل ترکیبی ARIMA و تبدیل موجک

نسبت به اطلاعات بیماران بستری در بیمارستان، اطلاعات پذیرش سرپایی نسبتا ساده است. این فقط شامل زمان پذیرش بیمار، محل اقامت و سایر اطلاعات است. به طور سنتی، کاوش این اطلاعات کافی نیست. با این حال، زمانی که تعداد زیادی از بیماران، اطلاعات زمان و محل اقامت را برای در نظر گرفتن، و اضافه کردن برخی فناوری‌های داده کاوی، پذیرش کردند، احتمالاً برخی از اطلاعات معمولی که قبلا نادیده گرفته شده بودند، یافت می‌شوند. با استفاده از 5 سال تحقیق داده کاوی و داده های پذیرش از یک بخش اطفال در یک بیمارستان بزرگ زنان و کودکان در چین، قوانین نوسانات مهمی را در مورد پذیرش با استفاده از تجزیه و تحلیل موجک بر روی داده های پذیرش در بیمارستان در میان مقیاس های مختلف نوسانات چرخه ای پیدا کردیم. روش: توزیع فصلی تعداد بیمار بر اساس تبدیل موجک هار تجزیه و تحلیل شد و سطح 3 و سطح 2 موجک برای برازش داده ها استخراج شد. تابع توزیع بیماران بستری در بیمارستان با تخمین تراکم هسته مشاهده شد. با استفاده از رگرسیون خطی و ARIMA (مدل میانگین متحرک یکپارچه اتورگرسیو) تعداد فصلی بیماران در آینده را پیش‌بینی می‌کند. یافته‌ها: تجزیه و تحلیل داده‌ها نشان می‌دهد که موج کل بیماران بستری به یک موجک مادر و پنج موجک کوچک تجزیه می‌شود که هر کدام فرکانس زمانی متفاوتی را نشان می‌دهند. علاوه بر این، با افزایش فاصله از بیمارستان، تعداد بیماران به طور تصاعدی کاهش یافت. عوامل فصلی بزرگ‌ترین عامل زمانی هستند که بر تغییرات تعداد بیماران تأثیر می‌گذارند. نتیجه‌گیری: با تحلیل موجک و مدل پیش‌بینی بهبودیافته، می‌توانیم روند تعداد بیماران بستری در آینده را پیش‌بینی کنیم و ثابت کنیم که عواملی مانند موقعیت جغرافیایی بر میزان بیماران بستری تأثیرگذار است. علاوه بر این، مفهوم داده کاوی مبتنی بر توزیع فضایی و تجزیه و تحلیل طیفی را می توان در سایر جنبه های مدیریت اجتماعی به کار برد.

 

کلید واژه ها

منابع پزشکی ، داده کاوی ، چند مقیاسی ، ARIMA ، توزیع فضایی تبدیل موجک

1. مقدمه

تظاهر به تغییرات در تعداد بیمار و مشاهده توزیع مکانی-زمانی بیمار از مشکلات اساسی مدیریت بیمارستان بوده است. بسیاری از مطالعات نشان می دهد که توزیع مکانی-زمانی بیمار حاوی اطلاعات مدیریتی مهمی است. تا به حال، بیشتر تحقیقات در مورد پذیرش بیمار بر روی شبیه سازی بلایا و حوادث امنیت عمومی متمرکز شده است [ 1 ]. مطالعات کمی بر توزیع منابع اضطراری متمرکز شده است. گروه هانگ نقاط سیاه تصادف رانندگی در هانوی و ویتنام را با استفاده از رگرسیون خطی برای تعیین رابطه بین نقطه سیاه و توزیع اضطراری گزارش کردند [ 2 ] [ 3 ]] . این مطالعات به ما در درک توزیع و تقاضای منابع پزشکی کمک می کند، اما اغلب، فعالیت بالینی بیشتر با تشخیص و درمان بیمار مرتبط است، بنابراین تخصیص و نوسان بیمار چالش هایی را برای تخصیص منابع پزشکی نشان می دهد.

برای ایجاد یک تجزیه و تحلیل سیستماتیک از روش های معمول پزشکی، دو بعد باید در نظر گرفته شود: زمان و مکان. برای مدتی، بیمارانی که در بیمارستان ها بستری می شوند تحت تأثیر روزها، هفته ها یا فصل ها، بیماری های همه گیر و توسعه اقتصادی قرار می گیرند. احتمال پذیرش بیمار در یک دوره زمانی خاص می تواند دوره بعدی احتمال پذیرش بیمار را تحریک کند، بنابراین ابزارهای تحلیل توالی برای تجزیه و تحلیل پذیرش بیمار مورد نیاز است و یادگیری ماشینی می تواند به این فرآیند کمک کند.

برای ابعاد فضایی، بیماران در مناطق مختلف احتمالاً نیازهای پزشکی متفاوتی دارند. مطالعات Selvin نشان می دهد که بیماران از مناطق نزدیک به احتمال زیاد به بیماری های مشترک و بیماران از مناطق دور افتاده به احتمال زیاد به بیماری های مزمن یا نادر مبتلا هستند [ 4 ]. بیماران مناطق دورافتاده اغلب انتظار تشخیصی را دارند که برای درمان چالش برانگیز است. اگر بتوانیم توزیع بیمار در زمان و مکان را درک کنیم، می‌توانیم منابع پزشکی را بهتر تخصیص دهیم و یک سیستم مدیریت بیمارستان هوشمند بر اساس داده‌های بزرگ ایجاد کنیم.

برای ایجاد یک توزیع معاصر برای پیش‌بینی، رابطه بین عوامل تأثیرگذار و توزیع مکانی-زمانی بیماران بستری در بیمارستان باید درک شود. عواملی که بر بیماران بستری در بیمارستان تأثیر می گذارند از توسعه اقتصادی، تحصیلات، ساختار جمعیت و فاصله تا بیمارستان متفاوت است [ 5 ] [ 6 ]. بنابراین، فناوری برای ارزیابی نیازهای بیمارستانی باید این موارد را برای توزیع دقیق‌تر منابع پزشکی ادغام کند.

اخیراً، تکیه ماشینی برای ابداع مدل‌ها و الگوریتم‌های پیچیده استفاده شده است که امکان تجزیه و تحلیل پیش‌بینی‌کننده را فراهم می‌کند که روابط روند داده‌ها را آشکار می‌کند. داده های خدمات سرپایی کودکان ساده است، اما حاوی اطلاعات پیچیده است. به عنوان یک نتیجه از chorismitization بسیاری از عوامل، هر ورودی از یک رکورد کودکان حاوی اطلاعات عوامل بالقوه است، بنابراین ما می توانیم یک آبشار از لایه های واحد پردازش غیر خطی برای استخراج ویژگی و تبدیل ایجاد کنیم. هر لایه متوالی از خروجی لایه قبلی به عنوان ورودی استفاده می کند. الگوریتم‌ها ممکن است تحت نظارت یا بدون نظارت باشند و برنامه‌های کاربردی شامل تحلیل الگو (بدون نظارت) و طبقه‌بندی (با نظارت) هستند.

تجزیه و تحلیل موجک مبتنی بر یادگیری بدون نظارت سطوح مختلف ویژگی ها یا نمایش داده ها است. ویژگی‌های سطح بالاتر که از ویژگی‌های سطح پایین‌تر مشتق شده‌اند برای تشکیل یک نمایش سلسله مراتبی استفاده شدند. این تعاریف دارای چندین لایه مشترک واحدهای پردازش غیرخطی و یادگیری نظارت شده یا بدون نظارت از نمایش ویژگی ها در هر لایه هستند، با لایه ها که سلسله مراتبی از ویژگی های سطح پایین به سطح بالا را تشکیل می دهند [ 2 ]. ترکیب لایه‌ای از واحدهای پردازش غیرخطی که در الگوریتم یادگیری عمیق استفاده می‌شوند به مسئله‌ای که باید حل شود بستگی دارد. لایه های مورد استفاده در یادگیری عمیق شامل لایه های پنهان یک شبکه عصبی مصنوعی و مجموعه ای از فرمول های گزاره ای پیچیده است [ 3 ]] . آنها همچنین ممکن است شامل متغیرهای پنهان سازمان‌دهی شده به صورت لایه‌ای در مدل‌های مولد عمیق مانند گره‌ها در شبکه‌های باور عمیق و ماشین‌های Deep Boltzmann باشند. به طور کلی، با این روش ها، تجزیه و تحلیل چند متغیره کل سیستم می تواند توسعه آینده را پیش بینی کند و راه حل هایی برای داده های پذیرش ارائه دهد ( شکل 1 ).

2. تجربی (فرمول های ریاضی، جداول و معادلات)

2.1. اکتساب داده ها

داده‌هایی از بیمارستان دوم چین غربی دانشگاه سیچوان از سال 2010 تا 2015 جمع‌آوری شد که شامل زمان پذیرش بیمار، آدرس، نام پزشک معالج، دلیل پذیرش، تشخیص، و چک لیست خدمات سرپایی بود. نام بیماران با حساسیت زدایی رمزگذاری شده md5 شناسایی شد. آدرس ارتباطی بیمار با استفاده از روش رمزگذاری شده با شکل کلیدی ناشناس شد.

2.2. تجزیه و تحلیل توزیع فصلی بر اساس تبدیل موجک

تعداد تقسیم‌بندی شده کودکان بستری در بیمارستان را هر 8 ساعت بشمارید و سایر اطلاعات مربوط به زمان پذیرش، آدرس، دلیل پذیرش، تشخیص را در فایل‌های مقادیر جدا شده با کاما (CSV) ثبت کنید. با استفاده از جعبه ابزار موجک Matlab برای وارد کردن داده ها، موجک Haar را برای تجزیه انتخاب کنید، بهترین مبنای موجک را برای فشرده سازی در سطح تجزیه 5 انتخاب کنید، و آستانه مناسبی را برای حذف نویز انتخاب کنید. صدور یک موج اصلی (a ₁ )، و 5 سطح موجک (d ₁ – d ₅ ). از هیستوگرام برای مشاهده توزیع استفاده کنید. و الگوی کاوی مکرر نیز برای یافتن قانون موجک نزدیک شده است.

2.3. توزیع فضایی

با استفاده از نقشه بزرگترین ارائه دهندگان خدمات چین، یک نقشه (NASDAQ: نقشه)، طول و عرض جغرافیایی بیمار را می توان به دست آورد و تراکم را می توان برای تخمین توزیع داده ها با استفاده از روش Botev محاسبه کرد [ 1 ]. به طور خاص، با استفاده از نتایج تجزیه موجک هار جلو، ما انتخاب هایی را یافتیم که از عملکرد گاوسی بزرگترین سطح تجزیه هار و سطح تعداد بیماران بستری در بیمارستان به عنوان واحد مشاهده سراسری منحرف شده بودند. با استفاده از تراکم هسته، تابع توزیع مقیاس بیماران بستری در بیمارستان با توزیع فضایی مورد تجزیه و تحلیل قرار گرفت و ما تأثیری بر نوسان تعداد بیماران بستری با اطلاعات موقعیت جغرافیایی به دست آوردیم. اصل اساسی الگوریتم تخمین چگالی هسته برای داده های مکانی به شرح زیر است:

تخمین چگالی هسته یک مشکل اساسی هموارسازی داده است که در آن استنباط در مورد جمعیت بر اساس یک نمونه داده محدود انجام می شود. در برخی از زمینه ها مانند پردازش سیگنال و اقتصاد سنجی به آن روش Parzen?Rosenbl at t-window نیز می گویند. این الگوریتم اغلب به صورت [ 1 ] [ 2 ] بیان می شود،

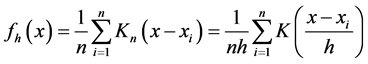
که در آن K(•) هسته است—یک تابع غیرمنفی که با یک ادغام می شود و میانگین آن صفر است—و h > 0 یک پارامتر هموارسازی به نام عرض باند است.

2.4. پیش بینی و یادگیری ماشین

با توجه به تجزیه و تحلیل تبدیل موجک در حوزه زمانی و تخمین چگالی هسته‌ای در تحلیل فضا، داده‌های پذیرش 5 ساله کودکان برای مقیاس‌های مختلف نوسان استخراج شد. از طریق مطالعه تحلیل فضایی داده‌ها، سطح 3 و سطح 2 موجک را برای برازش توزیع داده‌ها انتخاب می‌کنیم که بازه‌های 8 و 15 روزه را نشان می‌دهند که به ترتیب نشان‌دهنده هفته‌ها (7 روز) و نیم ماه (15 روز) هستند. از دوره های زمانی ما از ARIMA و برازش رگرسیون خطی برای پیش‌بینی آینده استفاده کردیم.

3. نتایج و بحث

3.1. تبدیل موجک

در مقیاس زمانی، بیماران بستری شده در بیمارستان پس از شکل موج را می توان به یک موج مادر و پنج موجک تقسیم کرد ( شکل 2 ) و سیگنال ممکن است در هر باند فرکانسی به شکل [f, 2f] برای همه فرکانس های مثبت f> نمایش داده شود. 0. سپس، سیگنال اصلی را می توان با یکپارچگی مناسب روی تمام اجزای فرکانس حاصل بازسازی کرد. باندهای فرکانسی یا زیرفضاها (زیر باندها) نسخه های مقیاس شده یک زیرفضا در مقیاس هستند. بنابراین، نتایج زیر را می توان از تبدیل موجک بالا گرفت:

1) کل موج بیماران بستری شده به یک موجک اصلی (یا مادر) و 5 موجک کوچک تجزیه شد.

2) چون 5 سال 1826 روز است، دوره زمانی موجک هار از 2^n (n = 1، 2، 3، 4، 5) روز مشتق شده است. بزرگترین موجک حدود 32 روز از دوره زمانی است که تقریباً یک ماه است.

3) موجک مادر متناظر باید روند کلی پذیرش در بیمارستان باشد تا با گذشت زمان، پذیرش افزایش یابد.

4) موجک ^پنجم مربوط به پذیرش در روز است که تقریباً یک توزیع نرمال است ( شکل 2 ).

3.2. توزیع زمان و مکان و عوامل مؤثر بر آن

با استفاده از تخمین تراکم هسته، با افزایش تدریجی فاصله بیمار تا بیمارستان، تعداد بیماران به صورت تصاعدی کاهش می‌یابد، با استفاده از جعبه ابزار Matlab®، CF، فاصله بیمار از بیمارستان با تعداد بیماران در این فاصله، متناسب است. فرمول برازش معمولی را به صورت زیر دریافت کنید:

که در آن f(x) تعداد بیماران و x فاصله تا بیمارستان غرب چین است، ضریب همبستگی (R^2) 0.875 است ( شکل 3 ). بنابراین، بیماران بستری شده به تدریج با مسافت کاهش می‌یابند. با استفاده از تبدیل موجک، مقیاس موجک را برای بیماران با برازش توزیع، از موجک هار از 1 – 5 به دست آوردیم. فضای بیمار در این مقیاس و با مقیاس، موجک سوم، موجک دوم، می توان آن را به عنوان توزیع ماهانه و فصلی مشاهده کرد. بنابراین، ماه و فصل را می توان به عنوان یک چرخه توزیع بزرگتر برای آزمایش منبع توزیع فضای بیمار در چنگدو، سیچوان یا چین استفاده کرد ( شکل 2 ).

3.3. پیش بینی شماره بیمار

مدل پیش‌بینی ARIMA 3500 – 4700 بیمار در ماه را پیشنهاد می‌کند که به شرح زیر توضیح داده می‌شود ( شکل 4 و جدول 1 ). و تحت مدولاسیون کوتاه‌مدت تعداد بیمار، موج 3 نشان‌دهنده الگوهای فصلی افزایش‌های بیمار است، بنابراین از مدل‌های ARIMA فصلی (SAM) برای نشان دادن تغییرات روند بیماران استفاده کردیم [ 7 ]. این داده ها در جدول 2 نشان داده شده است.

3.4. تأثیر چرخش فصلی بر بیماری ها و مدل پیش بینی

مدل‌های کلاسیک ARIMA معمولاً برای پیش‌بینی‌های کوتاه‌مدت مناسب هستند، اما نه برای پیش‌بینی‌های بلندمدت به دلیل هم‌گرایی کامرگرسیون خودکار.

مولفه مدل به میانگین سری زمانی. با این حال، همانطور که در بالا ذکر شد، استفاده از یک چرخه زمانی بسیار کوتاه باعث نوسانات تصادفی می شود. بنابراین، انتخاب یک چرخه آماری معقول برای نتیجه گیری های آماری صحیح ضروری است.

با این حال، طبق نظریه چند مقیاسی، یک فرآیند تصادفی تحت یک دیدگاه می‌تواند مشخصه سازمان‌یافته را در مقیاس‌های دیگر تغییر دهد و قوانین مربوطه را نشان دهد. بنابراین ابزارهایی برای مشاهده سری های زمانی در مقیاس های مختلف مورد نیاز است. تجزیه و تحلیل موجک برای کارایی در زمان [ 7 ] [ 8 ] یا فرکانس (به عنوان حوزه هارمونیک، شانون، مایر) [ 9 ] [ 10 ] مناسب است. در توزیع زمانی و نوسانات تصادفی حاضر پذیرش بستری، با استفاده از تجزیه موجک، بیماران با نوسانات در مقیاس های مختلف قوانین متفاوتی دارند. ما همبستگی بین تولید ناخالص داخلی و تعداد بیماران را در یک نقطه خاص از زمان محاسبه می کنیم، فرمول این است:

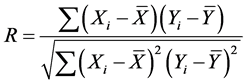
که در آن X _i تعداد بیماران در دوره i را نشان می دهد، Y _i نشان دهنده تولید ناخالص داخلی اعلام شده توسط دولت چین در پایان دوره i است.

از مقیاس موج مادر، رشد پذیرش در طول زمان به شیوه افزایش شاخص شتاب افزایش یافت. این افزایش ارتباط نزدیکی با رشد تولید ناخالص داخلی چین داشت ( شکل 5 ). (R = 0.8826). از مدل ARIMA می توان برای پیش بینی پذیرش های آینده استفاده کرد. از مقیاس 2 ^و 3 ، ^دو مقیاس می تواند تعداد بیماران را در تغییرات ماهانه و سه ماهه منعکس کند، که برای اطفال صادق است. در پاییز، پذیرش بیماران به دلیل فصل مدارس کاهش می یابد. مدل های فصلی ARIMA نشان می دهد که بیماران سرپایی از پایان سال 2014 کاهش یافته است ( شکل 4))، نشان می دهد که سیستم طبقه بندی بیمارستان ممکن است به تعداد بیماران کمک کند. با این حال، این را نمی توان با اتصالات ARIMA خطی کلاسیک مدل کرد. با مدل ARIMA، سیستم طبقه‌بندی موجود کاهش بیماران بیمارستانی به دلیل تفاوت‌های فصلی و ماهانه، نوسانات زیادی نداشت و در سال 2017 پس از اکتبر، بازگشت مجدد بیشتر بود. این بازگشت نیاز به توجه دارد ( شکل 4 ).

3.5. توزیع فضایی بیماران و عوامل مؤثر بر آن

برازش تقسیم بندی نشان می دهد که تعداد بیماران بستری شده در بیمارستان با فاصله از بیمارستان به طور تصاعدی کاهش می یابد و این داده ها با گروه وانگ [ 11 ] مطابقت دارد. مخصوص منطقه شهری چنگدو، پس از اجرای درمان سلسله مراتبی در سال 2015، بیماران در توزیع شهری به طور قابل توجهی تغییر کردند. با افزایش فاصله از بیمارستان، تعداد بیماران کاهش یافت.

سرمایه، و این کاهش به صورت تصاعدی توزیع شد. رابطه با زمان نیز روشن است و نشان می‌دهد که بیماران از حومه‌های بیرونی به بیمارستان عمدتاً به دلیل محدودیت‌های زمانی هستند. بیماران انتخابی به طور کلی از ثبت نام اوج در ماه سپتامبر اجتناب می کنند. تجزیه و تحلیل تراکم فضایی نشان داد که پس از اجرای تشخیص و درمان سلسله مراتبی، الگوهای توزیع بیماران تغییر می کند. در سپتامبر 2015، توزیع بیماران بستری در بیمارستان نسبت به سپتامبر 2014 متمرکزتر است، که نشان می دهد تغییر در توزیع فضایی سیستم تشخیص و درمان توسط الگوریتم KDE (تخمین تراکم هسته) شناسایی شده است ( شکل 6 ).

4. نتیجه گیری

پدیده های چند مقیاسی را می توان در رویدادهای طبیعی متعددی یافت که در دوره های زمانی طولانی و در فضاهای وسیع رخ می دهند. اثرات چند مقیاسی را می توان با استفاده از اثرات چند مقیاسی برای نوسانات پیچیده ناشی از عوامل پیچیده تحلیل کرد. همانطور که از مطالعه ما مشاهده می شود، تعداد بیماران در حال رشد برخی از نوسانات دوره ای فصلی را نشان می دهد و روند افزایش تدریجی را نشان می دهد. این نوسان مکانی و زمانی چالشی مضاعف برای تخصیص منابع پزشکی ایجاد می کند. به منظور مقابله با این چالش دوگانه، توصیه می‌شود در فصل شلوغی که اکثر بیماران با علائم خفیف می‌توانند به دنبال مراقبت‌های پزشکی در نزدیکی باشند، عرضه مراقبت‌های پزشکی در منطقه اطراف افزایش یابد. در تعطیلات زمستانی و تابستانی مدارس، بیمارستان باید عرضه کلینیک های سرپایی انتخابی را افزایش دهد.

پدیده های چند مقیاسی را می توان با تجزیه و تحلیل ولتاژ امواج میکروسکوپ ریاضی متوجه شد. از طریق تجزیه و تحلیل موجک و سایر روش های پیش بینی مانند ARIMA، ما توزیع زمانی و مکانی بیماران در یک بیمارستان چینی را در یک دوره پنج ساله تجزیه و تحلیل می کنیم. داده ها نشان می دهد که حتی یک آدرس بیمار نیز می تواند اطلاعات مفیدی باشد. ایده داده کاوی مبتنی بر تجزیه و تحلیل طیفی و توزیع فضایی را می توان به بسیاری از جنبه های مدیریت اجتماعی مانند ارزیابی منابع آموزشی، ارزیابی توزیع منابع پزشکی و برنامه ریزی منابع اجتماعی آینده تعمیم داد.

منابع

 

[ 1 ]	Bayram, JD, Sauer, L., Catlett, CL, Levin, S., Cole, G., Kirsch, TD, et al. (2013) منابع حیاتی برای ظرفیت جهش بیمارستان: پانل اجماع کارشناسان. PLoS Currents، 5. https://doi.org/10.1371/currents.dis.67c1afe8d78ac2ab0ea52319eb119688
[ 2 ]	Hung, KV and Huyen, LT (2011) تأثیر آموزش در ایمنی ترافیک: مطالعه موردی در ویتنام. تحقیقات IATSS، 34، 87-93. https://doi.org/10.1016/j.iatssr.2011.01.004
[ 3 ]	La، QN، Lee، AH، Meuleners، LB and van Duong، D. (2013) شیوع و عوامل مرتبط با تصادف ترافیک جاده ای در میان رانندگان تاکسی در هانوی، ویتنام. تجزیه و تحلیل تصادف و پیشگیری، 50، 451-455. https://doi.org/10.1016/j.aap.2012.05.022
[ 4 ]	Toor, MR, Singla, A., Devita, MV and Michelis, MF (2014) ویژگی ها، درمان ها و عوامل موثر بر نتایج بیماران سالمندان هیپرناترمیک بستری در بیمارستان. بین المللی اورولوژی و نفرولوژی، 46، 1589-1594. https://doi.org/10.1007/s11255-014-0721-2
[ 5 ]	Koberich, S. and Farin, E. (2016) عوامل مؤثر بر ادراک بیماران بستری در بیمارستان از مراقبت های پرستاری فردی: یک مطالعه مقطعی. BMC Nursing, 15, 1-11. https://doi.org/10.1186/s12912-016-0137-7
[ 6 ]	Livera، AMD، Hyndman، RJ و Snyder، RD (2009) پیش‌بینی سری‌های زمانی با الگوهای فصلی پیچیده با استفاده از هموارسازی نمایی. مقالات اقتصادی موناش و آمار کسب و کار، 106، 1513-1527.
[ 7 ]	Chen, CF and Hsiao, CH (1997) روش موجک هار برای حل سیستم‌های پارامتری توده‌ای و توزیع‌شده. IEE Proceedings-Control Theory and Applications, 144, 87-94. https://doi.org/10.1049/ip-cta:19970702
[ 8 ]	Lewis, AS and Knowles, G. (1991) VLSI Architecture for 2D Daubechies Wavelet Transform without Multipliers. نامه های الکترونیک، 27، 171-173. https://doi.org/10.1049/el:19910110
[ 9 ]	Meyer, Y. (1991) موجک ها: الگوریتم ها و کاربردها. انجمن ریاضیات صنعتی و کاربردی، فیلادلفیا.
[ 10 ]	شانون، سی (1974) یک نظریه ریاضی ارتباطات. مک گراو هیل، نیویورک
[ 11 ]	Wang, F. and Wei, L. (2005) ارزیابی عوامل فضایی و غیر فضایی برای دسترسی به مراقبت های بهداشتی: به سوی یک رویکرد یکپارچه برای تعریف مناطق کمبود حرفه ای سلامت. بهداشت و مکان، 11، 131-146